Electron magnetohydrodynamics Grad–Shafranov reconstruction of the magnetic reconnection electron diffusion region

We present a study of the electron magnetohydrodynamics Grad–Shafranov (GS) reconstruction of the electron diffusion region (EDR) of magnetic reconnection. Two-dimensionality of the magnetoplasma configuration and steady state are the two basic assumptions of the GS reconstruction technique, which represent the method’s fundamental limitations. The present study demonstrates that the GS reconstruction can provide physically meaningful results even when these two assumptions, which are hardly fulfilled in spacecraft observations, are violated. This conclusion is supported by the reconstruction of magnetic configurations of two EDRs, encountered by the Magnetospheric Multiscale (MMS) Mission on July 11, 2017 and September 8, 2018. Here, the former event exhibited a violation of two-dimensionality, and the latter event exhibited a violation of steady state. In both cases, despite the deviations from the ideal model configuration, reasonable reconstruction results are obtained by implementing the herein introduced compressible GS reconstruction model. In addition to the discussed fundamental limitations, all existing versions of the GS reconstruction technique rely on a number of minor simplifying assumptions, which restrict the model scope and efficiency. We study the prospects for further model improvement and generalization analytically. Our analysis reveals that nearly all these minor limitations can be overcome by using a polynomial MMS-tailored reconstruction technique in the space of rotationally invariant variables instead of Cartesian coordinates.

1 Introduction

Magnetic reconnection is an explosive plasma process leading to topological reconfiguration of magnetic fields and plasma heating and acceleration in laboratory and space plasmas (Gonzalez et al., 2016). Since pioneering studies of Giovanelli (1946); Hoyle (1949); and Dungey (1953), analytical studies of the plasma acceleration mechanism resulted in a number of analytical models, such as the Sweet–Parker annihilation (Parker, 1957; Sweet, 1958), the tearing instability model (Furth et al., 1963), the fast reconnection model of Petschek (1964), and other models (Sonnerup, 1970; Priest and Forbes, 1986; Priest and Lee, 1990; Heyn and Semenov, 1996). Particularly, magnetic reconnection has been extensively studied in tokamak and spheromak plasmas (Yamada et al., 2010), solar flares and coronal mass ejections (Parker, 1979; Priest and Schrijver, 2000), planetary magnetospheres (Bagenal, 2013), and in other objects (Hesse and Cassak, 2020). Being, in general, a three-dimensional (3D) time-dependent process (Bhattacharjee, 2004; Xiao et al., 2006; Dorfman et al., 2013; Cozzani et al., 2021), in some cases, magnetic reconnection operates in modes that allow analytical studies in simpler frameworks. Sometimes, it may be treated as a quasi-stationary process, e.g., at Earth’s dayside magnetopause (Gosling et al., 1982; Phan et al., 2004; Retinò et al., 2005; Cassak and Fuselier, 2016) or in Earth’s magnetotail. In the latter case, the reconnection of anti-parallel magnetic fields (i.e., with a shear angle of about 180°) may be often considered (Paschmann et al., 2013). In many cases, a two-dimensional (2D) description seems to be also admissible (Zeiler et al., 2002; Goldman et al., 2016). In the following, we narrow our scope mainly to Earth’s magnetotail reconnection (Øieroset et al., 2001; Egedal et al., 2005; Eastwood et al., 2010; Liu et al., 2015).

In the near-Earth space plasma, allowing, in general, a magnetohydrodynamics (MHD) framework, the particle collisions are rare enough (Cassak and Fuselier, 2016) to bring forth the concept of collisionless reconnection (Birn et al., 2001; Øieroset et al., 2001). Even in the simplest steady-state 2D collisionless reconnection model, the reconnection region occurs as a complex multiscale structure, surrounding the reconnection neutral line, the X-line. In non-resistive plasma, the Hall effect demagnetizes (Sonnerup, 1979) ions at the scale of the ion inertial length, d_i, within the so-called ion diffusion region (IDR), where the plasma obeys Hall MHD (HMHD) and the magnetic field stays frozen in the electron fluid. In some interior of this HMHD domain, the relation between typical values of the ion and electron current densities, j_i ≪ j_e, allows neglecting the ion current, yielding the commonly used electron MHD (EMHD) approximation (Bulanov et al., 1992; Biskamp, 2000; Ji et al., 2014). At last, in the closest vicinity of the X-line, the electron diffusion region (EDR), electrons are also demagnetized due to the electron pressure anisotropy and electron inertia at the scale of the electron inertial length, d_e (Vasyliunas, 1975; Kuznetsova et al., 1998; Hesse et al., 1999; Egedal et al., 2013; 2019; Paschmann et al., 2013). The EDR, in turn, is split in two parts, internal and external (Daughton et al., 2006; Karimabadi et al., 2007; Shay et al., 2007), carrying electron currents in the out-of-plane and longitudinal directions, respectively.

The structure of the entire reconnection region has been explored in numerous numerical simulations and in situ data studies, providing a relatively detailed understanding of particular features of the reconnection picture, such as the spatio-temporal evolution of the reconnection X-line (Wang et al., 2018) reconnection energy budget (Birn and Hesse, 2010; Aunai et al., 2011; Fu et al., 2017; Genestreti et al., 2017; Du et al., 2018; Lu et al., 2018; Wang et al., 2018; Fadanelli et al., 2021; Zaitsev et al., 2021) including the electron acceleration (see Fu et al., 2019b, and references therein); reconnection rate (Sonnerup, 1974; Yokoyama and Shibata, 1994; Birn et al., 2001; Huba and Rudakov, 2004; Fujimoto, 2006; Daughton et al., 2014; Comisso and Bhattacharjee, 2016; Liu et al., 2017; Divin et al., 2019; Tenfjord et al., 2019); the structure of electron pressure and distribution function in the EDR (Cai and Lee, 1997; Hesse and Winske, 1998; Scudder and Daughton, 2008; Divin et al., 2010; 2016; Ng et al., 2011; Le et al., 2013; Egedal et al., 2013; 2016; Cassak et al., 2015; Swisdak, 2016; Wang et al., 2018); the proper reconnection region waves (Khotyaintsev et al., 2019) and instabilities (Roytershteyn et al., 2012), and the ion dynamics (Hoshino et al., 1998; Nakamura et al., 1998; Drake et al., 2009; Nagai et al., 2015; Hietala et al., 2017; Zhou et al., 2019b; Runov et al., 2021).

The investigation of magnetotail reconnection is the main goal of NASA’s Magnetospheric Multiscale (MMS) Mission (Burch et al., 2016). It is the first mission that enabled measuring the full 3D electron distribution function in a time scale of 30 ms by four identical spacecraft separated by about 10–100 km. Together with magnetic and electric field measurements, MMS data make it possible to resolve the electron-scale physics during the crossing of the magnetic reconnection EDRs. A number of proper MMS-tailored techniques, including the first- and second-order Taylor expansions (FOTE and SOTE), to find magnetic nulls and reconstruct the 3D magnetic field topology were developed (Fu et al., 2015, 2019a; Liu et al., 2019). A comparative study of FOTE and other techniques’ efficiency is found in Fu et al. (2016). For reconnection events with the near-2D geometry observed in the magnetotail, the spatial structure of the current sheet (CS) within the EDR, reconnection rate, pressure tensor, and its divergence could be determined from observations (Torbert et al., 2018; Genestreti et al., 2018a; b; Nakamura et al., 2019; Burch et al., 2022). The characteristic pattern of the electron distribution function, scale of the EDR CS, and reconnection rate were well recovered in particle-in-cell (PIC) simulation runs using the observed initial parameters (Nakamura et al., 2018; Bessho et al., 2019; Egedal et al., 2019). MMS also found more complex features of the EDR. These include the EDR in reconnection with the guide field (Zhou et al., 2019a), containing a secondary island (Denton et al., 2021) and wavy CSs associated with lower hybrid waves (Chen et al., 2020; Cozzani et al., 2021). Furthermore, the electron physics in the magnetic separatrix region, where complex wave–particle interactions take place due to the mixing of cold inflow and jetting outflow electrons, was also resolved by MMS (Nakamura et al., 2016; Norgren et al., 2020; Holmes et al., 2021).

Evidently, in situ data analysis, numerical simulations, and their combination represent the most powerful and the most relevant ways for studying the complex magnetic reconnection kernel region. Particularly, utilizing MMS data in hybrid and PIC numerical reconstruction models helps understand MMS observations of the EDR and IDR in a dynamic 2D or 3D context. However, numerical models own a number of drawbacks, which stem from their setup limitations (not fully realistic distribution functions, ion-to-electron mass ratio, and background and boundary conditions), from complexity of computational algorithms and from available high-performance computer resources limiting the size of the simulation box. Moreover, the fundamental constrain is dictated by mathematics, since four-point MMS measurements per se are still not enough for specifying background configurations, even for 2D numerical simulations. An intermediate step, an adequate analytical model, should provide a physically consistent 2D magnetoplasma configuration based on one-dimensional multi-probe MMS data. In Section 2, we discuss a specific family of such models developed for reconstructing magnetoplasma configuration in magnetotail-like (2D, steady-state) EDRs. The results of our study are summarized in Section 3. Section 4 contains the discussion of the obtained results and possibility of their application to studies of some other structures, governed by electron physics.

2 EMHD Grad–Shafranov reconstruction

As we have mentioned previously, from the mathematical perspective, the accurate reconstruction of the 2D spatial magnetic configuration, resting upon the spacecraft measurements, can be performed only by means of a (quasi)-one-dimensional problem solution, since boundary conditions (in situ data) represent a one-dimensional manifold. It turns out that EMHD approximation provides us with the necessary approach.

2.1 The basic approach and the first results

Let us consider the two-fluid problem of steady magnetic reconnection in the collisionless non-resistive non-relativistic compressible plasma in the vicinity of an infinite X-line. The plasma is assumed to consist of two particle species, ions and electrons, obeying the quasi-neutrality condition. The system of coordinates is specified by the z-axis, directed normally to the CS, the y-axis, coinciding with the static X-line and pointing in the current direction, and the x-axis, completing the right-handed Cartesian system. In magnetospheric applications, such a system corresponds to a co-moving LMN coordinate system (Russell et al., 1983; Denton et al., 2018).

Under EMHD approximation, the ions can be left aside (Korovinskiy et al., 2020). Hence, the problem statement includes a time-independent equation of the electron fluid motion (the Ohm’s law), Maxwell’s equations, and the electron mass conservation law and equation of state. For simplicity, these equations are considered in dimensionless forms, where normalization constants are {e, m_e, d_e, B₀, n₀, V_Ae, E_Ae, p₀, T₀, t*}. Here, e is the elementary charge and m_e is the electron mass; electron inertial length d_e = c/ω_e, where c is the speed of light and ${\omega }_e=\sqrt{4\pi n_0{e}^2/m_e}$ is the typical electron plasma frequency; B₀ and n₀ are the typical magnetic field value and number density, respectively; $V_{Ae}=B_0/\sqrt{4\pi n_0{m}_e}$ and E_Ae = (1/c)B₀V_Ae are the typical electron Alfvén velocity and electric field, respectively; $p_0=B_0^2/(4\pi )$ and T₀ = p₀/n₀ are the typical pressure and temperature, respectively; and $t^{*}={\omega }_e^{-1}$ is the time scale. So, without the equation of state, the problem is stated as follows:

$\left({\mathbf{V}}_e\cdot \mathrm{\nabla }\right){\mathbf{V}}_e=-\frac{1}{n}\mathrm{\nabla }\cdot {\widehat{P}}_e-\left(\mathbf{E}+{\mathbf{V}}_e\times \mathbf{B}\right),(1)$

$\mathrm{\nabla }\times \mathbf{B}=-n{\mathbf{V}}_e,(2)$

$\mathrm{\nabla }\times \mathbf{E}=0,(3)$

$\mathrm{\nabla }\cdot \mathbf{B}=0,(4)$

$\mathrm{\nabla }\cdot \left(n{\mathbf{V}}_e\right)=0,(5)$

where subscript e stands for “electron”; E and B are the electric and magnetic fields, respectively; V is the bulk velocity; n is the number density; and $\widehat{P}$ is the pressure tensor. Ampère’s law (2) is written in EMHD approximation, where the ion current is neglected. Since one assumes an infinite X-line, the y-axis becomes an ignorable direction, i.e., ∂/∂y = 0 for all magnetoplasma quantities. In particular, it means that according to Faraday’s law (3), the electric field component E_y = const. Then, the in-plane magnetic field is specified by a scalar magnetic potential (y-component of the vector-potential, the only non-zero one) A(x, z),

$B_x=-\frac{\partial A}{\partial z},B_z=+\frac{\partial A}{\partial x},(6)$

while B_y(x, z) appears to be a stream function of the in-plane electron flow:

$n{V}_{ex}=+\frac{\partial B_y}{\partial z},n{V}_{ez}=-\frac{\partial B_y}{\partial x}.(7)$

The simplest consideration of the problem (1–5), assuming the uniform number density and neglecting electron inertia and pressure anisotropy, was performed by Uzdensky and Kulsrud (2006), who have derived (see Eq. B16 of the cited paper) that under the specified conditions, the magnetic potential satisfies the Grad–Shafranov (GS) equation (Grad and Rubin, 1958; Shafranov, 1966), which, in our notations, takes the form

$\mathrm{\Delta }A=-j_{ey}\left(A\right).(8)$

Here, Δ stands for the Laplace operator (note that ∂/∂y = 0) and j_ey = −nV_ey is the out-of-plane component of the electron current. The same result was obtained independently in the study of Korovinskiy et al. (2006). Thus, the GS equation, well-known in MHD and HMHD reconstruction problems (see Hu, 2017; Chen and Hu, 2022; and references therein) since Sonnerup and Guo (1996) and Hau and Sonnerup (1999) studies, occurred viable in EMHD also.

The EMHD GS reconstruction model, under the same simplifying assumptions, was developed in the studies of Korovinskiy et al. (2006, 2008), where the authors made use of the specific geometry of the reconnection region, exhibiting pronounced stretching in the x-direction due to the small typical value of the reconnection rate E_R ∼ 0.1 (Comisso and Bhattacharjee, 2016; Cassak et al., 2017; Liu et al., 2017). Due to the smallness of this quantity, the ill-posed problem, stated by Eq. 8 with boundary conditions specified at a single line, allows regularization by neglecting the term ∂²A/∂x² ∼ϵ² in comparison with the main term ∂²A/∂z² ∼ 1, where ϵ ∼ E_R is a unit-independent scaling factor. Applying this boundary layer approximation (BLA) (Schlichting, 1979), the authors arrived at a well-posed quasi-one-dimensional reconstruction problem. The study of Korovinskiy et al. (2008) revealed three important features of this simplified problem: a) the equation for B_y is easily solved, when the solution of Eq. 8 is found; b) the Jakobian |∂(A, B_y)/∂(x, z)| = ɛ ≠ 0, where ɛ is the unit-dependent normalized value of E_y; hence, the potentials (A, B_y) can be considered as a pair of independent variables instead of (x, z) and all other quantities can be considered as functions of (A, B_y); and c) as like Cartesian variables (x, z), the variables (A, B_y) are also not peer in terms of the derivative scaling ratio |∂/∂A|≫|∂/∂B_y| [see Eqs 30, 31 of Korovinskiy et al. (2008)]. In spite of the excessive simplicity of this first model, where most part of the electron-scale physics (compressibility, inertia, and anisotropy) was neglected, these results prove useful for the following studies. Notably, the variables (A, B_y) are invariant with respect to the in-plane rotations of the coordinate system.

2.2 Recent advances: Two approaches

The further development of the EMHD GS reconstruction models wended the way for the gradual release of the severe simplifying assumptions. Considerable progress was achieved in the study of Sonnerup et al. (2016), where scalar electron pressure p_e = nT_e was replaced by the more complicated model:

$\mathrm{\nabla }\cdot {\widehat{P}}_e=\mathrm{\nabla }{p}_e+{\left(\mathrm{\nabla }\cdot {\widehat{P}}_e\right)}_y{\mathbf{e}}_y,(9)$

where e_y is the unit vector of the y-axis. Eq. 9 states a minimal model for the reconnection problem, since only the non-zero y-component of the pressure tensor divergence may provide (Vasyliunas, 1975) the non-zero electric field E_y in the X-point (the projection of the X-line onto the reconnection plane) vicinity. It should be noted that the direct usage of Eq. 9 encounters considerable difficulties, since the exact analytical expression for its rightmost term is unknown. In the study of Sonnerup et al. (2016), this problem was coped by using the approximation given in Eq. 14 of Hesse et al. (1999). Meanwhile, the validity of this approximation outside the internal EDR is debatable (Korovinskiy et al., 2020), since it is based on a number of simplifying assumptions.

The model, utilizing Eq. 9, was successfully applied to the reconstruction of EDRs, encountered by MMS, in the studies of Hasegawa et al. (2017, 2019). In the study of Korovinskiy et al. (2021), in addition to Eq. 9, the electron inertia term in Eq. 1 was kept and the assumption of the uniform electron temperature was released. The authors suggested an alternative approach avoiding the direct application of Eq. 9. For the magnetoplasma quantities, specifying the reconstruction model, the following assumptions were adopted: n = const, T_e = T_e(A), V_ey = V_ey(A, B_y). In the following study of Hasegawa et al. (2021), the assumption of the uniform number density was also released, and all three model functions n, T_e, V_ey were treated as functions of magnetic potential A. The equation for the electric potential, introduced in Korovinskiy et al. (2008), was also generalized for this more realistic model setup.

In spite of the seeming similarity, the approach, adopted in the study of Hasegawa et al. (2021), which we, for the shortness, call A1, and the approach, formulated by Model 2 of Korovinskiy et al. (2021), which we call A2, have a number of important distinctions, which we deem are worth discussing. The comparison of A2 and the simplified version of A1 efficiencies can be found in the recent studies of Korovinskiy et al. (2020, 2021).

2.2.1 Regularization

A1 and A2 utilize different methods of problem regularization and, in general, different coordinate systems. The best performance of A2 is gained in a co-moving LMN coordinate system, since problem regularization is achieved by omitting the second derivatives on x as compared with those on z (maximal variance direction); i.e., integration is ever performed in the CS normal direction. Theoretically, the accuracy of this method does not depend on the satellite trajectory inclination angle with respect to EDR (except for vertical crossings, when model fails). A1 utilizes a rotated coordinate system, which one can call the “satellite coordinate system” (SCS), where the longitudinal axis coincides with the satellite trajectory. Integration is performed in the trajectory normal direction, while the longitudinal derivatives are evaluated numerically at each integration step. Problem regularization is achieved by numerical filtering (Sonnerup et al., 2016) to suppress the exponentially growing distortions (Hadamard, 1923). The accuracy of this method should decrease with the increasing trajectory inclination angle, i.e., the rotation angle LMN → SCS. Apparently, the approach of A2 is simpler, while the approach of A1 is more universal, since in contrast with A2, it is appropriate not only for oblique but also for the vertical crossings. For the longitudinal crossings, the accuracies of these two methods seem to be nearly the same (Korovinskiy et al., 2020).

2.2.2 Boundary conditions

In terms of the boundary conditions setup, A1 represents a family of more universal models, since it demands a single spacecraft’s data for initiating reconstruction, while A2 is an MMS-tailored method, requiring data of at least two satellites separated in the xz plane. This discrepancy results in very different techniques of solving the equation for B_y. With equalities (7), the quantity ΔB_y can be written as follows:

$\mathrm{\Delta }{B}_y=Q+V_{ex}\frac{\partial n}{\partial z}-V_{ez}\frac{\partial n}{\partial x},(10)$

where we introduce the notation Q,

$Q=n{\omega }_{ey}=n\left(\frac{\partial V_{ex}}{\partial z}-\frac{\partial V_{ez}}{\partial x}\right),(11)$

and ω_ey stands for the out-of-plane component of the electron vorticity:

${\mathbf{\omega }}_e=\mathrm{\nabla }\times {\mathbf{V}}_e.(12)$

It should be reminded that definition (Eq. 11) is written in dimensionless units. The corresponding normalization constant Q₀ = n₀Ω_0e, where Ω_0e = eB₀/(m_ec) is the typical electron cyclotron frequency. In A2, the assumption Q = Q(A) was adopted, and the functional dependency is obtained from multi-spacecraft data. Since for n = const two rightmost terms of Eq. 10 vanish, the model equation takes the form ΔB_y = Q(A). Apparently, the neglect of the dependence of Q on B_y is a simplifying assumption, i.e., the model limitation.

In A1, the term ΔB_y (in our notations) is calculated from Eq. 21 of Hasegawa et al. (2021). The drawback of this method (stated in their model “Case 1”) stems from the fact that this equation contains a small alternating-sign quantity (the normal electron velocity component) in the denominator. When that equation becomes singular, the authors switch to another model (“Case 2”), which does not contain this singular equation. However, this approach is also not free of obstacles. First, instead of singular equation (21), the authors are forced to use again the modified approximation of Hesse et al. (1999) for the pressure anisotropy term, stated in their Eq. (24). Second, the combination of these two methods (Case 1 and Case 2) in a single reconstruction requires, apparently, some rather non-trivial technique of matching the corresponding solutions.

2.2.3 Compressibility

The uniformity of the number density is a rigid limitation, bounding any model to the internal EDR only, where this assumption seems to be approved and commonly used (Hesse et al., 1999; Sonnerup et al., 2016; Hasegawa et al., 2017; 2019). This limitation of A2 is easily overcome. Indeed, substituting the representation

$\mathrm{\nabla }n=\frac{\partial n}{\partial A}\mathrm{\nabla }A+\frac{\partial n}{\partial B_y}\mathrm{\nabla }{B}_y(13)$

in (10) and assuming n = n(A), Eqs 21, 22 of Korovinskiy et al. (2021) take the following form:

$\mathrm{\Delta }A=n\left(A\right)V_{ey}\left(A\right),(14)$

$\mathrm{\Delta }{B}_y=Q\left(A\right)+\frac{1}{n}\frac{dn}{dA}\left(\mathrm{\nabla }A\cdot \mathrm{\nabla }{B}_y\right).(15)$

Notably, the out-of-plane magnetic field can be presented as a sum of two parts, the uniform part B_g (guide field) and the Hall magnetic field ${\tilde{B}}_y$,

$B_y\left(x,z\right)=B_g+{\tilde{B}}_y\left(x,z\right).(16)$

Since B_y and ${\tilde{B}}_y$ differ from each other for a constant, these quantities are apparently identical with respect to derivative operators.

To introduce and test our incompressible model A2, we have addressed the MMS event of July 11, 2017 (Torbert et al., 2018), when MMS crossed the internal EDR during reconnection in the magnetotail at around 22:34 UT. Considering the same event and using the same setup (Korovinskiy et al., 2021), we applied the compressible model (Eq. 14 and Eq. 15) to perform the reconstruction in the three times extended interval 22:34:01.70—22:34:10.92 UT, during which the number density demonstrated the pronounced non-uniformity. As previously mentioned, we focus not on the event study but at the model benchmarking, since the event itself has been rigorously studied in the previous works (Genestreti K. et al., 2018; Egedal et al., 2019; Nakamura et al., 2019; Denton et al., 2021; Hasegawa et al., 2021). The validity of EMHD approximation within the reconstruction interval is demonstrated in Figure 1A, where the ratios of the electron and full current densities for parallel (black) and perpendicular (red) in-plane current components are plotted at the reconstruction domain boundary (MMS3 trajectory) vs. the spacecraft travel distance x. It is seen that except for some local gaps appearing due to local drops of the parallel current j_e‖, these ratios are close to 1 (the same as the ratio |j_ey|/|j_y| ≈ 1, which is not shown). In panels (B)–(E) of Figure 1, the normalized values of the electron temperature, number density, out-of-plane velocity, and function Q are plotted, respectively, vs. the magnetic potential. The measured (n, T_e, and V_ey) or evaluated (Q) values are plotted by blue curves, while the red curves plot the interpolating functions. The reconstructed configuration of the in-plane magnetic field in SCS is exhibited in Figure 2, where the spacecraft trajectories are plotted by black color for MMS1, red for MMS2, green for MMS3, and blue for MMS4. It is seen that trajectories of MMS2 and MMS4 are extremely close to each other in the xz plane. Figure 3 shows the reconstruction results as compared to the measured values vs. x for the quantities B_x (A), ${\tilde{B}}_y$ (B), B_z (C), V_ex (D), V_ey (E), V_ez (F), and n (G). In Figure 3, green curves plot the MMS3 data (dotted) and their interpolations (boundary conditions, solid), and the red dotted and solid curves plot, respectively, the measured and the reconstructed values at the most remote (from MMS3) probe MMS2. The other reconstruction results are not shown for better visibility. The plots of V_ey and n confirm the accuracy of the chosen approximations for the model functions V_ey(A) and n(A), respectively. Comparing other plots of Figure 3 with Figures 7 and 12 of Korovinskiy et al. (2021), one can see that within the extended reconstruction region, the compressible model (Eqs 14, 15) performs as good as the incompressible one within the internal EDR. In the first half of the reconstruction interval, the reconstruction of V_ez is as bad as it is seen in Figure 12C of Korovinskiy et al. (2021) and Figure 5 of Hasegawa et al. (2019). It demonstrates much better data resemblance in the second half. Curiously, in this second part (x > 37), the vertical magnetic component B_z (Figure 3C) exceeds in magnitude the longitudinal component B_x (Figure 3A). This should not be perceived as a violation of the BLA assumptions, since not the first but the second derivatives of the magnetic potential contribute to the GS equation. As for the latter ones, the calculation of the quantity $\delta =|\partial B_z/\partial x|/\sqrt{{(\partial B_z/\partial x)}^2+{(\partial B_x/\partial z)}^2}$ revealed that at the MMS spacecraft location (between the green and red horizontal lines in Figure 2), the value of δ amounts mainly to 0.01–0.1 or less, except for the very leftmost (x < 0) and the very rightmost (x > 70) intervals. The same estimate of δ is valid for most parts of the entire reconstruction region shown in Figure 2. Thus, neglect of the term ∂²A/∂x² does not cause any remarkable inaccuracy of the presented extended-interval reconstruction [see also Figure 6 of Korovinskiy et al. (2021)].

FIGURE 1

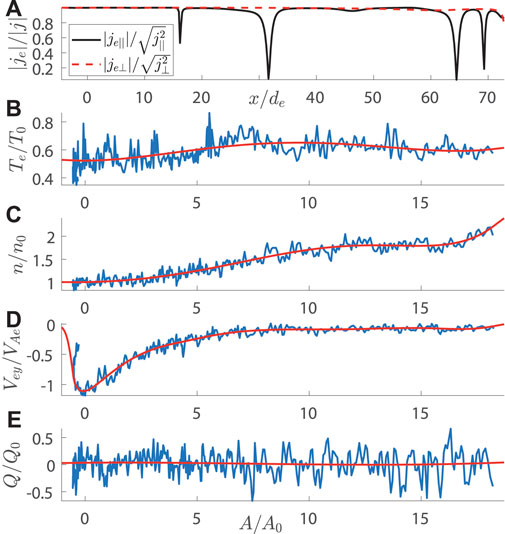
FIGURE 1. Reconstruction of the event of July 11, 2017. The model functions evaluated at the reconstruction region boundary (MMS3 trajectory). Panel (A) represents the ratio of the electron and full currents for parallel (black) and perpendicular (red) in-plane current components vs. the spacecraft travel distance x. Panels (B–E) represent electron temperature, number density, out-of-plane velocity, and the function Q, respectively, vs. magnetic potential, as they were measured (blue) and interpolated (red). The values of the normalization constants, except for Q₀, are provided in Section 3.1 of Korovinskiy et al. (2021), while the corresponding value of Q₀ = 18.5 s⁻¹cm⁻³.

FIGURE 2

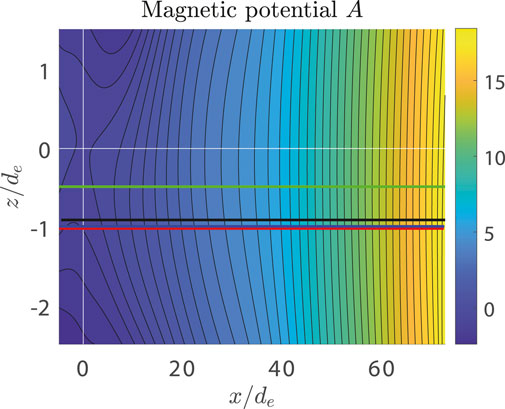
FIGURE 2. Reconstruction of the event of July 11, 2017. The calculations were initiated at the MMS3 trajectory in SCS. The magnetic potential A(x, z) is shown by color, and contour lines plot the in-plane magnetic field lines. The spacecraft trajectories are plotted by black color for MMS1, red for MMS2, green for MMS3, and blue for MMS4. White lines plot the SCS coordinate system. Spacecraft move from the left to the right.

FIGURE 3

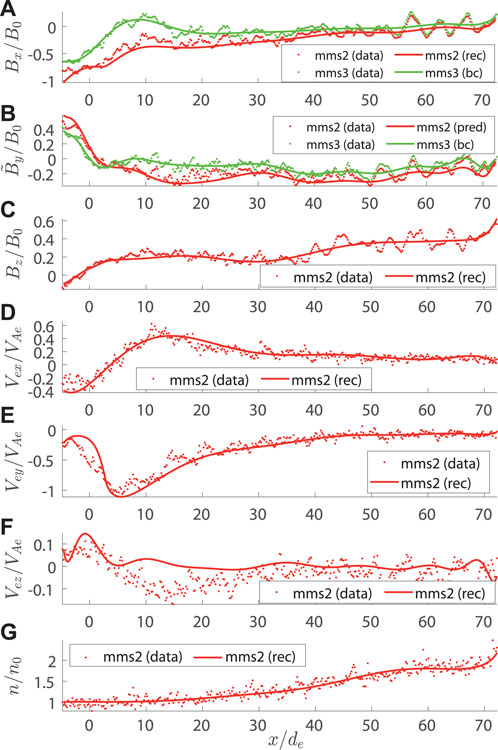
FIGURE 3. Reconstruction of the event of July 11, 2017. The calculations were initiated at the MMS3 trajectory in SCS. The measured values (red and dotted) and the reconstruction results (red and solid) vs. x for B_x (A), ${\tilde{B}}_y$ (B), B_z (C), V_ex (D), V_ey (E), V_ez (F), and n (G) at the MMS2 trajectory, where ${\tilde{B}}_y$ stands for the non-uniform part of B_y. The plots of MMS3 data and corresponding interpolations (boundary conditions) are shown in panels (A,B) by green dotted and solid curves, respectively. The data of MMS1 and MMS4 and corresponding reconstruction results are not shown for better visibility [the same for MMS3 in panels (C–G)].

2.3 The fundamental limitations of the EMHD GS reconstruction technique

2.3.1 Two-dimensionality

All the discussed EMHD GS reconstruction techniques possess the obvious fundamental limitations—they assume the 2D steady-state configuration, which can be hardly found in nature. In particular, the abovementioned failure of reconstruction of the normal component of the electron velocity (V_ez in our notations) within the internal EDR was claimed a signature of the CS two-dimensionality violation at the ground of simple qualitative speculations (Korovinskiy et al., 2021). Indeed, according to Ampère’s law (2), nV_ez = ∂B_x/∂y − ∂B_y/∂x. In the 2D model, the term ∂B_x/∂y is omitted, which can result in considerable error if, in reality, this term is non-zero, because we omit the derivative of B_x – the major magnetic field component (in the LMN coordinate system). This 3D effect should be much less pronounced for the component V_ex = (1/n) (∂B_y/∂z − ∂B_z/∂y) because, here, we neglect the derivative of B_z – the minor magnetic field component. Obviously, the direct evaluation of the derivative ∂B_x/∂y would be the best way to make sure that the failure of V_ez reconstruction is caused by the CS three-dimensionality. Such evaluation is hardly possible; however, the following scaling analysis supports the aforementioned speculations. Fortunately, during this particular event, two coordinate systems, SCS and LMN, were very close, differing from each other for 5.8° only (Korovinskiy et al., 2021). This allows adopting the LMN scaling ratios in SCS.

The spacecraft trajectories represent parallel linear segments in the 3D space. In SCS, each of them represents the inclined line (dy/dx ≈ 0.75) belonging to the plane z_j = const, where subscript j stands for the probe number. Let us assume that CS is two dimensional, ∂/∂y = 0. Then, the equality ∂B_x/∂x + ∂B_z/∂z = 0 is to fulfil, where ∂B_x/∂x = dB_x/dx at any probe trajectory. Since in LMN, ∂/∂z ∼ 1 and ∂/∂x ∼ϵ, we obtain ∂B_x/∂x = −∂²A/∂x∂z ∼ϵ (in the first part of the reconstruction region, within the internal EDR, the magnetic potential A ∼ 1, as seen in Figure 2). With the reconnection rate E_R ≈ 0.15–0.2 (Nakamura et al., 2018; Hasegawa et al., 2019; Korovinskiy et al., 2021), one can estimate the numerical value of ϵ ≈ 0.2. Analogously, for the increment of B_z, we have $d{B}_z=\partial B_z/\partial z\cdot dz+\partial B_z/\partial x\cdot dx+\cancel{\partial B_z/\partial y\cdot dy}$, where ∂B_z/∂z ∼ϵ and ∂B_z/∂x ∼ϵ², and the last summand vanishes in a 2D CS.

Now, let us estimate the terms ΔB_x/Δx and ΔB_z/Δz, where Δ stands for the finite difference. At any probe trajectory, in particular, at the trajectory of MMS2, we have ΔB_x/Δx = dB_x/dx ∼ϵ, where dx is the grid step. To evaluate the term ΔB_z/Δz, we use the data of the two nearest probes, MMS2 and MMS4 (Figure 2), whose trajectories were shifted with respect to each other for Δx = 0.15, Δy = 0.683, and Δz = 0.027. Substituting these values in the formula for dB_z, we obtain ΔB_z/Δz = ∂B_z/∂z + ∂B_z/∂x ⋅Δx/Δz ∼ϵ + ϵ²/ϵ ∼ϵ, where we used the estimate Δx/Δz ≈ 5.6 ∼ 1/ϵ. So, in the 2D configuration, the terms ΔB_x/Δx and ΔB_z/Δz, evaluated this way, are to be the quantities of the same order ϵ, matching the order of the corresponding partial derivatives ∂B_x/∂x and ∂B_z/∂z, respectively.

The plot of ΔB_z/Δz, exhibited in Figure 4, mismatches this conclusion. In Figure 4, we observe the minor term ΔB_y/Δy (evaluated analogously to ΔB_z/Δz) with the peaking value of about 0.07, that is, ∼ϵ² (red), the term ΔB_x/Δx with the peaking value $\approx 0.26$, that is, ∼ϵ (blue), and the term ΔB_z/Δz with the peaking value $\approx 2.4$ (green), which is an order of magnitude higher than ΔB_x/Δx. Apparently, the term ΔB_z/Δz can demonstrate so high values due to the neglected term ∂B_z/∂y ⋅Δy/Δz only. With the evaluated value of max |ΔB_z/Δz|∼ 1 and the given value Δy/Δz ≈ 25 ∼ (1/ϵ²), we obtain the scaling ratio ‖∂B_z/∂y‖ ⋅ (1/ϵ²) ∼ 1, where we use the notation ‖ ⋅‖ to denote the scaling estimate. This yields an estimate ∂B_z/∂y ∼ϵ²; hence, the scaling estimate for the derivative operator ∂/∂y ∼ϵ. Notably, under this estimate, the omitted term of ΔB_x/Δx at the MMS2 trajectory scales as ∂B_x/∂y ⋅ dy/dx ∼ϵ; i.e., it is a quantity of the same order as the accounted term ∂B_x/∂x. The calculated values of ΔB_y/Δy also match the corresponding scaling estimate. Indeed, since the Hall magnetic field itself is a small quantity ${\tilde{B}}_y\sim ϵ$, and Δx/Δy = 0.22 ∼ϵ and Δz/Δy = 0.04 ∼ϵ², we obtain the following scaling estimate: ΔB_y/Δy = ∂B_y/∂y + ∂B_y/∂x ⋅Δx/Δy + ∂B_y/∂z ⋅Δz/Δy ∼ϵ² + ϵ² ⋅ϵ + ϵ ⋅ϵ² ∼ϵ², which is in line with the evaluated value max |ΔB_y/Δy| = 0.07.

FIGURE 4

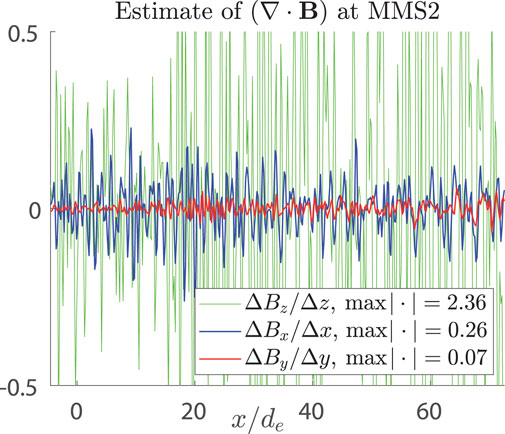
FIGURE 4. Reconstruction of the event of July 11, 2017. The estimate of the terms of (∇ ⋅ B) at the MMS2 trajectory via finite differences ΔB_z/Δz (green), ΔB_x/Δx (blue), and ΔB_y/Δy (red) is plotted vs. the MMS2 path length. The magnitudes are given in the legend.

Thus, we arrive at the following scaling estimates: ∂B_x/∂y ∼ϵ and ∂B_y/∂x ∼ϵ². Clearly, neglect of the first (major) term and keeping the second (minor) one result in the V_ez reconstruction failure in the left part of the reconstruction interval (Figure 3F). In the right part, by contrast with ${\tilde{B}}_y$, the magnetic component B_x reduces for one–two orders of magnitude (Figure 3A); hence, the contribution of the neglected term ∂B_x/∂y becomes the same or smaller than the contribution of the accounted term, hence is the better accuracy of the V_ez reconstruction. Analogously, ∂B_z/∂y ∼ϵ² and ∂B_y/∂z ∼ϵ; hence, neglecting the first term does not ruin the V_ex reconstruction, if V_ex is calculated independently on V_ez. However, when the approximation of Hesse et al. (1999) for the pressure anisotropy term is used, the inaccuracy of the V_ez reconstruction affects the accuracy of V_ex also [see Figure 12B of Korovinskiy et al. (2021) and discussion in Section 5, ibid] because these two quantities are coupled in a single equation. Also, one can note that the representation of the in-plane magnetic field via a scalar magnetic potential is resting upon the neglect of the term ∂B_y/∂y in (∇ ⋅B). As we have seen, during the considered event, the neglected term is scaled as ϵ², while the two kept ones were ∼ϵ. This should result in a reconstruction error of the order of ϵ, which estimate fits the real reconstruction error of about 10–20% (Korovinskiy et al., 2021).

It should be noted that since the scaling analysis operates not with the exact but with the typical values, one can be easily misled. For example, with ϵ = 0.2 and $\text{max}|{\tilde{B}}_y|\approx 0.5$ (Figure 3B), one could estimate ${\tilde{B}}_y\sim \sqrt{ϵ}$, since $\sqrt{ϵ}=2.25ϵ=0.45$. Analogously, with the evaluated value of max |ΔB_z/Δz| ≈ 2.4, one could estimate ∂B_z/∂y ∼ϵ^3/2; hence, $\partial /\partial y\sim \sqrt{ϵ}$. These estimates seem to be appropriate and they do not discard the aforementioned speculations concerning the V_ez and V_ex reconstructions because the ratios between the terms $\partial B_x/\partial y\sim \sqrt{ϵ}$ and ∂B_y/∂x ∼ϵ^3/2 and between the terms ∂B_z/∂y ∼ϵ^3/2 and $\partial B_y/\partial z\sim \sqrt{ϵ}$ do not change (though the estimates of the terms themselves do). Nevertheless, such estimates would be totally wrong, since they would lead to the estimate ∂B_y/∂y ∼ϵ. This, in turn, would mean that the neglected term of (∇ ⋅B) would have the same scale as the kept ones; hence, the reconstruction error would have to reach 100%; i.e., the reconstruction would have to fail totally, which is evidently not the case.

2.3.2 Steady state

The reconstruction of Korovinskiy et al. (2021) has also revealed the signatures of CS time dependence, observed during the first 0.4 s, when the out-of-plane component E_y demonstrated some reduction and the function V_ey(A) was not single-valued (see Figures 2A, 3E of the cited paper), which resulted in a low reconstruction accuracy within this interval (see Figure 6 of Korovinskiy et al. (2021) or Figure 3). To investigate the model failure in an unsteady CS, we addressed the event of September 8, 2018, when at nearly 14:51:30 UT, MMS encountered an EDR near the center of a flux-rope type dipolarization front (Marshall et al., 2020). The reconstruction is performed in the co-moving LMN reference frame. The direction of the M-axis is determined by the maximization of the peaking out-of-plane current density, max (j_eM), and the N-axis is found by the maximization of the B_L variation, where the L-axis completes the right-handed LMN coordinate system. The LMN unit vectors, specified in the Geocentric Solar Ecliptic (GSE) coordinate system, have the following components: e_L = [−0.11648, +0.27887, +0.95324], e_M = [+0.07826, +0.95936, −0.27110], and e_N = [−0.99010, +0.04302, −0.13357]. This LMN coordinate system is nearly the same as the one that was determined by Marshall et al. (2020), differing from the latter mainly by the opposite signs of the M and N orts. The normal component of the structure velocity was determined by the timing method (Russell et al., 1983), and two other components were estimated as the average ion velocity within the 1.5 s reconstruction interval 14.51.30.25–14.51.31.75 UT. This way the value of V₀ = [+117.43, +233.92, −251.34] km/s in LMN (which is [+253.48, +246.35, +082.09] km/s in GSE) was derived. All quantities were cast by Lorentz transform to the LMN coordinate system moving with the velocity V₀ (co-moving reference frame) and normalized for the typical values of t₀ = 0.568 ms, n₀ = 1 cm⁻³, T₀ = 497 keV, p₀ = 79.6 pPa, d_e = 5.31 km, B₀ = 10 nT, V_Ae = 9.35 ⋅ 10³ km/s, E_Ae = 93.5 mV/m, and j₀ = 1.5 μA/m². Since in all previous studies, the simplified model (Eq. 8) performed good enough, while the contribution of the terms accounting the dependence of V_ey on B_y was found rather small (Korovinskiy et al., 2020; 2021), we restricted our study to solving Eq. 8.

The reconstruction setup is exhibited in Figure 5, where MMS1-related curves are plotted by black, MMS2 by red, and MMS3 by green in all panels. Panels (A) and (B), respectively, show the out-of-plane electric field and number density vs. time. These plots reveal that (a) number density was not uniform and (b) the steady-state condition E_y = const was fulfilled up to some moment, then it failed abruptly (E_y peaks at t = 1.17 s at the MMS1 trajectory and at t = 1.08 s at the MMS3 one). Magnetic potential A vs. time and the out-of-plane electron current j_eM vs. A are plotted in panels (C) and (D), respectively. Similar to the event of July 11, 2017, the non-monotonic behavior of A(t) makes our modelling function j_eM(A) double-valued. However, in the study of Korovinskiy et al. (2021), a single-valued analytical continuation of the necessary function could be constructed, since the general appearance of the required curve was evident. In the present case, it is not so. Basically, with the function j_eM(A), shown in Figure 5D, the reconstruction is not possible.

FIGURE 5

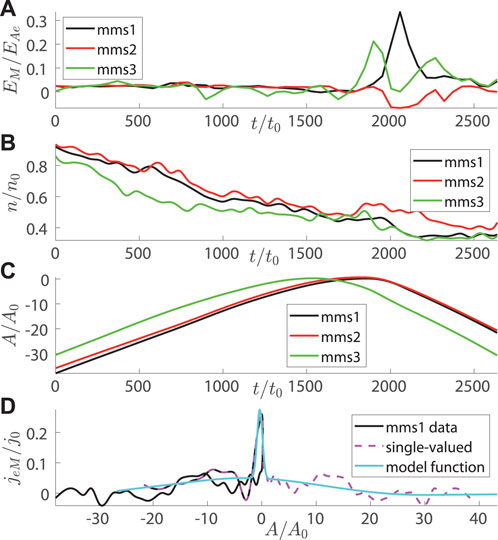
FIGURE 5. Reconstruction of the event of September 8, 2018. The calculations are performed in the co-moving LMN coordinate system. In all panels, the data are plotted by black color for MMS1, by red for MMS2, and by green for MMS3. Panels (A,B), respectively, show the out-of-plane electric field E_M and the number density n vs. time. Magnetic potential A vs. time and the out-of-plane electron current density j_eM vs. A are plotted in panels (C,D), respectively. A single-valued function j′(A) at the MMS1 trajectory, obtained by flipping one of the branches of the double-valued j_eM(A) with respect to the branching point, is plotted in panel (D) by dashed magenta curve, and the interpolating function, used in reconstruction, is shown by the solid cyan curve. The data of MMS4 are not shown for better visibility, the same for data of MMS2 and MMS3 in panel (D).

Nevertheless, BLA allows one trick, resting upon two features and one assumption, which are: (a) magnetic potential is defined with the accuracy of an arbitrary constant; (b) in BLA, the derivatives on x are neglected, hence in any particular vertical cross section, we solve the one-dimensional problem; and (c) since the out-of-plane current is a sharply peaking function, we assume that in some vicinity of the peak, it can be approximated by a symmetrical (Gauss-like) curve. By making use of properties (a) and (b), and adopting assumption (c), we can “unfold” two coalescent branches of j_eM(A). Namely, we make the substitution A − a₀ → A, where a₀ is the point of branching. Then, one branch (in our case, the first one, corresponding to the initial steady period) is flipped with respect to the axis A = 0. This means that for any vertical cross section r_L = r_Lj, where j is the point number, we make the substitution A_j → −A_j (r_L and r_N correspond, respectively, to x and z of the analytical model). This way we obtain a single-valued function j′(A), whose interpolated value is used for solving Eq. 8; then, in each vertical cross section, the reverse substitution A− 2A_j → A is performed. For MMS1-based reconstruction, the function j′(A) and its interpolated values are shown in Figure 5D by dashed magenta and solid cyan curves, respectively. The validity of such approach is obviously predicated upon the validity of assumption (c) and by the accuracy of the LMN coordinate system detection.

The results of reconstruction in the 0.32 s timespan (t = 0.92:1.24 s) are plotted in Figure 6. For reconstruction, initiated at the MMS1 trajectory, a 2D contour plot of magnetic potential and the L-component of the magnetic field is plotted in panels (A) and (B), respectively. For reconstruction, initiated at the MMS3 trajectory, the same quantities are plotted in panels (C) and (D). Since MMS spacecraft (moving from the right to the left) are not aligned in a single vertical line, the plots of panels (A) and (C) demonstrate the time evolution of the CS. Indeed, the colored asterisks in panel (A) mark the spacecraft mutual locations at a single moment. Starting reconstruction, e.g., from the black asterisk, we cross the MMS3 trajectory (green line) at the moment, when MMS3 has already passed farther, and the other way round. Particularly, in panel (C), MMS3 crosses the O-line with two X-lines, one on the right and one on the left. In panel (A), we see the same structure, though shifted to the left and deformed. The magnetic components B_L, shown in panels (B) and (D), demonstrate that the trusted reconstruction area, if it is, spans between the MMS1 and MMS3 trajectories, while at the trajectories of MMS2 and MMS4, the reconstruction error becomes too big, which is reasonable since the latter probes are more remote. Comparing the solid and dashed green curves in Figure 6B, we see that the reconstruction of the magnetic field component B_L at MMS3 exhibits appropriate accuracy in the right part of the reconstruction region, r_L > − 20 (initial period). It means that real existence of the X-line, as shown in Figure 6A at (r_L, r_N) ≈ (−20, 40) may be questionable. The existence of the X-line, crossed by MMS1 in Figure 6C at r_L ≈ − 23, may be claimed more certainly, since the black solid and dashed curves in Figure 6D assure good reconstruction accuracy at MMS1 for r_L < − 22. One can also see that our LMN coordinate system does match the magnetic configuration geometry in the vicinity of the X-point, encountered by MMS1. The existence of the X-line between MMS3 and MMS4 at x_L ≈ − 17, also observed in Figure 6C, requires additional verification by means of some other method, since the comparison of blue solid and dashed curves in Figure 6D does not lead to any unequivocal conclusion.

FIGURE 6

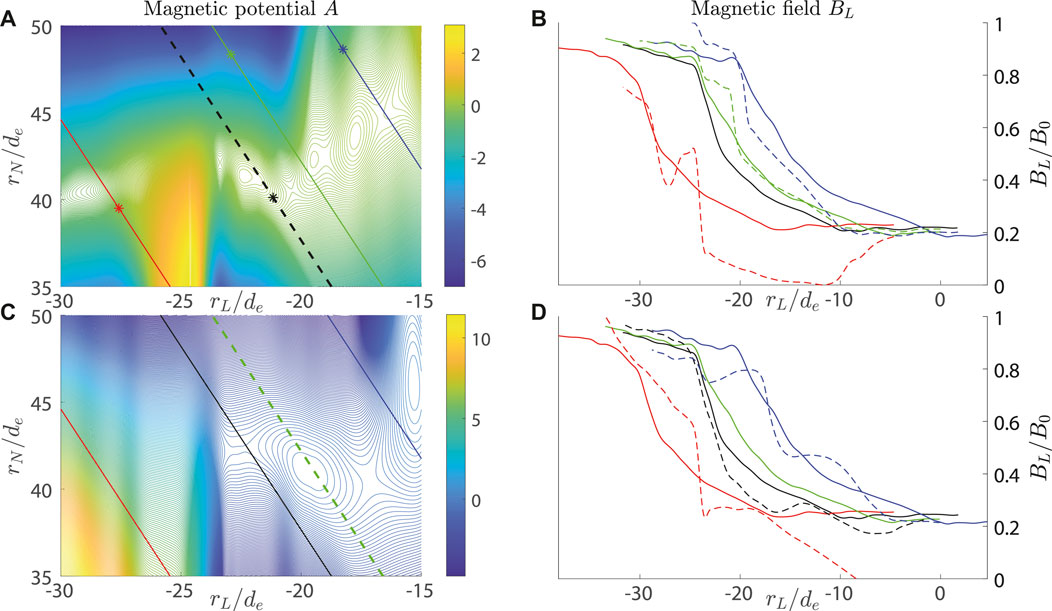
FIGURE 6. Reconstruction of the event of September 8, 2018, in the co-moving LMN coordinate system. Top row: the results of reconstruction initiated at the MMS1 trajectory. The 2D contour plot of the magnetic potential and the L-component of the magnetic field are plotted in panels (A,B), respectively. In the bottom row, the same quantities are plotted in panels (C,D) for the reconstruction initiated at the MMS3 trajectory. The spacecraft trajectories in the left column are plotted by black color for MMS1, red for MMS2, green for MMS3, and blue for MMS4, where dashed lines plot the reconstruction domain boundary. In the right column, the spacecraft data (solid) and the reconstructed values (dashed) at four MMS probes are plotted by the same colors. In panel (A), the colored asterisks demonstrate the spacecraft mutual locations at a single moment (probes move from the right to the left).

The results of Section 2.3 reveal that the 2D steady-state model demonstrates remarkable ability to withstand (to some extent) the violation of the ideal CS conditions, i.e., the violation of both fundamental model limitations. With some gimmickries, the model is capable of providing an overview of the reconnection region even for the time-dependent reconnection event. However, for such events, of course, it would be much better to use some time-depended model, such as those of Denton et al. (2020, 2021).

2.4 Perspectives of the EMHD GS reconstruction technique improvement

Apart from the fundamental limitations discussed previously, the existing EMHD GS techniques also possess some minor limitations which can be coped with (to some extent) in the future studies. Particularly, such limitations are stipulated by the simplifying assumptions adopted for the model functions. Such simplifications ease the calculations but shrink the models’ applicability domain. For example, the assumption of n = const is appropriate within the internal EDR only. The less strict condition n = n(A) allows the considerable expansion of the reconstruction region in the longitudinal direction onto the external EDR; however, the cross size of this region stays rather small, as shown in Figure 10A of Korovinskiy et al. (2020). Also, as for the approximation V_ey = V_ey(A), it seems to be violated nearly everywhere within the internal EDR (see Figure 10B of the cited paper). The correct model would consider all magnetoplasma quantities as functions of two variables (A, B_y). This cannot be applied directly due to the lack of the input data, but this correct treatment may be approached by using a polynomial technique, bearing some similarity to those of Denton et al. (2022), but operating in another variable space. In this section, we present an analytical frame for such extension of A2 [Model 2 of Korovinskiy et al. (2021)] and the recipe to unite A1 and A2 to benefit from the advantages of these two approaches and to master their disadvantages.

To proceed to this goal, one needs to cast the problem (1–5, 9) in another form. Partly, this work was made in the studies of Korovinskiy et al. (2020, 2021), which results we outline here, omitting all intermediate details. The Jakobian of the variables transform (x, z) → (A, B_y) is

$\left|\frac{\partial \left(A,B_y\right)}{\partial \left(x,z\right)}\right|=n{\epsilon }^{*},(17)$

where we introduce the notation ɛ* for the out-of-plane component of the electron convective electric field,

${\epsilon }^{*}=\frac{\epsilon +\left(1/n\right){\left(\mathrm{\nabla }\cdot {\widehat{P}}_e\right)}_y}{1-\left(\partial V_{ey}/\partial A\right)},(18)$

while ɛ is the normalized value of the out-of-plane electric field E_y. The most general form of Eq. 10 takes the form

$\begin{array}{ccc}\hfill \mathrm{\Delta }{B}_y& =\hfill & \hfill Q\left(A,B_y\right)+\frac{1}{n}\left[\frac{\partial n}{\partial A}\left(\mathrm{\nabla }A\cdot \mathrm{\nabla }{B}_y\right)+\frac{\partial n}{\partial B_y}{\left(\mathrm{\nabla }{B}_y\right)}^2\right].\end{array}(19)$

We also introduce the notation φ* for the quantity, which we call the “effective electric potential”,

${\phi }^{*}\left(A,B_y\right)=\phi -T_e-\frac{1}{2n^2}|\mathrm{\nabla }{B}_y{|}^2,(20)$

where φ(A, B_y) is the electric potential of the in-plane electric field: E_x = −∂φ/∂x, E_z = −∂φ/∂z. The problem for φ* is stated in two equations:

$\frac{\partial {\phi }^{*}}{\partial A}=V_{ey}\left(A,B_y\right)+T_e\frac{\partial }{\partial A}\text{ln}\left(n\right),(21)$

$\frac{\partial {\phi }^{*}}{\partial B_y}=\frac{1}{n}{B}_y+T_e\frac{\partial }{\partial B_y}\text{ln}\left(n\right)+R\left(A,B_y\right),(22)$

where the electron inertia and anisotropy are accounted by the term R [see Eqs 14, 15 of Korovinskiy et al. (2021)],

$R\left(A,B_y\right)=\frac{1}{n^2}\left[\left(\mathrm{\nabla }\text{ln}\left(n\right)\cdot \mathrm{\nabla }{B}_y\right)-\mathrm{\Delta }{B}_y\right]=-\frac{Q}{n^2}.(23)$

Multiplying (21) for ∇A and (22) for ∇B_y, we obtain the equation for ∇φ*:

$\mathrm{\nabla }{\phi }^{*}=\left(V_{ey}+\frac{T_e}{n}\frac{\partial n}{\partial A}\right)\mathrm{\nabla }A+\left(\frac{B_y}{n}-\frac{Q}{n^2}+\frac{T_e}{n}\frac{\partial n}{\partial B_y}\right)\mathrm{\nabla }{B}_y.(24)$

Differentiating (21) for B_y and (22) for A and equating the results, we obtain the equation for V_ey. By using (23), it takes the following form:

$\frac{\partial V_{ey}}{\partial B_y}=-\frac{1}{n^2}\left[\frac{\partial Q}{\partial A}+\left(B_y-\frac{2Q}{n}\right)\frac{\partial n}{\partial A}\right]-\frac{1}{n}\left|\frac{\partial \left(n,T_e\right)}{\partial \left(A,B_y\right)}\right|.(25)$

Let us consider Eqs 21, 22, where the terms n, T_e, and V_ey are of the order of 1 due to normalization (Figure 1), the term $R\sim {\partial }^2{B}_y/\partial z^2\sim {\partial }^2{\tilde{B}}_y/\partial z^2\sim ϵ$, and φ* ∼ φ ∼ 1, since ∂φ/∂z = −E_z, and E_z ∼ 1 is the major electric field component. Under these scaling ratios, Eqs 21, 22 reveal two estimates, ∂/∂A ∼ 1 and ∂/∂B_y ∼ B_y, where the second estimate depends on the guide field value. Evidently, the differential operator $\partial /\partial {\tilde{B}}_y$ scales the same as ∂/∂B_y.

2.4.1 Reconstruction in a thin layer

Equation 25 provides us with the condition of the model self-consistency and gives a clue to the first step for model generalization. The rightmost term of this equation vanishes under the following assumptions:

$n=n\left(A\right),T_e=T_e\left(A\right),V_{ey}=V_{ey}\left(A,{\tilde{B}}_y\right),Q=Q\left(A,{\tilde{B}}_y\right),(26)$

while Eq. 25 itself takes the following form:

$\frac{\partial V_{ey}}{\partial {\tilde{B}}_y}=\left(B_g+{\tilde{B}}_y\right)\frac{d}{dA}\left(\frac{1}{n}\right)-\frac{\partial }{\partial A}\left(\frac{Q}{n^2}\right).(27)$

Assumptions (26) are expected to be relevant in a thin current layer spanning both the internal and external EDR, though the cross size of the model applicability domain will highly likely not exceed several d_e [see Figure 10 in Korovinskiy et al. (2020) and the corresponding discussion]. Adopting assumptions (26) and utilizing BLA, i.e., neglecting the second-order terms, Eqs 8, 19, 24 make the following system:

$\frac{{\partial }^{2}A}{\partial z^2}=n\left(A\right)V_{ey}\left(A,{\tilde{B}}_y\right),(28)$

$\frac{{\partial }^2{\tilde{B}}_y}{\partial z^2}=Q\left(A,{\tilde{B}}_y\right)+\frac{1}{n}\frac{dn}{dA}\frac{\partial A}{\partial z}\frac{\partial {\tilde{B}}_y}{\partial z},(29)$

$\frac{\partial {\phi }^{*}}{\partial z}=\left(V_{ey}+\frac{T_e}{n}\frac{dn}{dA}\right)\frac{\partial A}{\partial z}+\frac{1}{n}\left(B_g+{\tilde{B}}_y-\frac{Q}{n}\right)\frac{\partial {\tilde{B}}_y}{\partial z}.(30)$

According to (7), the last term of the definition ${\phi }^{*}=\phi -T_e-0.5(V_{ex}^2+V_{ez}^2)$ is to be neglected (for being the smallest quantity of the second order) to keep the consistency of the adopted approach. The same is valid for the rightmost term of definition (11) for Q. It is seen that initial values of all quantities, contributing Eqs 28–30, and hence the functional dependences of n(A) and T_e(A) are obtained from the boundary conditions (for Q the data of at least two spacecraft are required). However, the exact functional dependences for V_ey and Q cannot be established. Taking in mind that the Hall magnetic field is small as compared to the main magnetic component (which is the reason why zero-order schemes with Q = Q(A) and/or V_ey = V_ey(A) demonstrate good efficiency of the weak guide field reconnection reconstruction), for approximate solution of this problem, we make use of the Taylor series on ${\tilde{B}}_y$:

$V_{ey}\left(A,{\tilde{B}}_y\right)=\sum _{k=0}^{\infty }\frac{1}{k!}{V}_k\left(A\right){\tilde{B}}_y^k,(31)$

$Q\left(A,{\tilde{B}}_y\right)=n\left(A\right)\sum _{l=0}^{\infty }\frac{1}{l!}{\omega }_l\left(A\right){\tilde{B}}_y^l,(32)$

where the sum in the right-hand side of (32) represents the Taylor series for the vorticity component ${\omega }_{ey}(A,{\tilde{B}}_y)$. Substituting (31) and (32) to (27),

$\sum _{k=1}^{k=\infty }\frac{{\tilde{B}}_y^{k-1}}{\left(k-1\right)!}{V}_k\left(A\right)=\left(B_g+{\tilde{B}}_y\right)\frac{d}{dA}\left(\frac{1}{n}\right)-\sum _{l=0}^{l=\infty }\frac{{\tilde{B}}_y^l}{l!}\frac{d}{dA}\left(\frac{{\omega }_l}{n}\right),(33)$

and by equating the terms containing the same powers of ${\tilde{B}}_y$, we derive the relations between the coefficients V_k and ω_l.

$\begin{array}{ll}\hfill V_1& =\frac{d}{dA}\left(\frac{B_g-{\omega }_0}{n}\right),V_2=\frac{d}{dA}\left(\frac{1-{\omega }_1}{n}\right),\hfill \\ \hfill & V_k=-\frac{d}{dA}\left(\frac{{\omega }_{k-1}}{n}\right),\hfill \end{array}(34)$

where k = {3, 4, … }. Assuming that coefficients ω_l(A) for l = {0, 1, … , N − 1} are found, the coefficients {V₁, … , V_N} are evaluated, and V₀(A) is calculated from the boundary conditions as a difference between the data and the truncated Taylor series, $V_0(A)=V_{ey}-{\sum }_{k=1}^{k=N}(1/k!)V_k(A){\tilde{B}}_y^k$. The coefficients ω_l(A) for l > 0 are, in turn, represented by the Taylor series on A.

${\omega }_l\left(A\right)=\sum _{m=0}^{\infty }\frac{1}{m!}{\omega }_{lm}{A}^m,(35)$

where ω_lm are the numerical constants. Thus, the representation for the vorticity takes the following form:

${\omega }_{ey}\left(A,{\tilde{B}}_y\right)={\omega }_0\left(A\right)+\delta \omega \left(A,{\tilde{B}}_y\right),(36)$

$\begin{array}{ll}\hfill \delta \omega \left(A,{\tilde{B}}_y\right)& =\left({\omega }_{10}+{\omega }_{11}A+{\omega }_{12}\frac{A^2}{2!}+\cdots \right){\tilde{B}}_y\hfill \\ \hfill & +\left({\omega }_{20}+{\omega }_{21}A+{\omega }_{22}\frac{A^2}{2!}+\cdots \right)\frac{{\tilde{B}}_y^2}{2!}+\cdots .\hfill \end{array}(37)$

Analogous to V₀(A), the term ω₀(A) is evaluated from the boundary conditions, ω₀(A) = ω_ey − δω, when coefficients ω_lm are known. The coefficients ω_lm are found by solving the boundary value problem (BVP) for the system (28–30). The number of coefficients, which can be found this way, is equal to the number of extra conditions imposed. At the capacity of these conditions, one can use some limiting values of the peaking or average reconstruction error for the calculated quantities. The solution of the system (28–30) provides us with the values of 10 quantities: n, T_e, B, V_e, E_x, and E_z. However, the quantities E_x, B_z, and V_ez cannot provide us with the fiducial markers, since not an exact but the regularized problem is solved, so that only seven quantities are left in the control list. Since both n and T_e are assumed to depend only on A, it is reasonable to eliminate one of these quantities from the list also. Assuming that the data of all four MMS spacecraft are available, we have 24 extra conditions, which are enough for developing the sixth-order reconstruction scheme $(A^p{\tilde{B}}_y^q:p\ge 1,q\ge 0,p+q\le 6)$ with 21 coefficients. To avoid overdetermination, one can control the reconstructed values of T_e(A) or n(A) at a single probe only.

It should be noted that the term ω₀(A) can also be represented in a form of the truncated Taylor series. In this case, the coefficients of this series enlarge the number of unknowns. This reduces the maximal order of the scheme to five, but allows the problem solution when the data on the velocity derivatives are unreliable (too noisy) or unavailable. In this case, it may be convenient to modify the technique by reversing relations (34).

$\begin{array}{ll}\hfill {\omega }_0& =B_g-n\int V_1\left(A\right)dA,{\omega }_1=1-n\int V_2\left(A\right)dA,\hfill \\ \hfill {\omega }_{k-1}& =-n\int V_k\left(A\right)dA.\hfill \end{array}(38)$

Then, V_ey is presented in the form analogous to (35–37), and numerical coefficients V_km and the integration constants of Eq. 38 are found from the solution of the same BVP.

2.4.2 The general case

In the most general case, all quantities are to be considered as functions of two variables, $(A,{\tilde{B}}_y)$, which should allow extending the GS reconstruction region over the entire EMHD domain. This approach causes some modifications of the scheme and complication of the system (28–30), now taking the following form:

$\frac{{\partial }^{2}A}{\partial z^2}=-j_{ey}\left(A,{\tilde{B}}_y\right),(39)$

$\frac{{\partial }^2{\tilde{B}}_y}{\partial z^2}=Q\left(A,{\tilde{B}}_y\right)+\frac{1}{n}\left[\frac{\partial n}{\partial A}\frac{\partial A}{\partial z}\frac{\partial {\tilde{B}}_y}{\partial z}+\frac{\partial n}{\partial {\tilde{B}}_y}{\left(\frac{\partial {\tilde{B}}_y}{\partial z}\right)}^2\right],(40)$

$\frac{\partial {\phi }^{*}}{\partial z}=\frac{1}{n}\left[\left(-j_{ey}+T_e\frac{\partial n}{\partial A}\right)\frac{\partial A}{\partial z}+\left(B_g+{\tilde{B}}_y+T_e\frac{\partial n}{\partial {\tilde{B}}_y}-\frac{Q}{n}\right)\frac{\partial {\tilde{B}}_y}{\partial z}\right].(41)$

Since n depends on ${\tilde{B}}_y$, the representation of Q via ω_ey is out of use and the representation (34) of the V_ey-series’ coefficients via coefficients of ω_ey or Q is not possible due to the term n in the denominator of Eq. 25. So, introducing the notation U = {n, T_e, Q, j_ey}, we state the general scheme as follows:

$U\left(A,{\tilde{B}}_y\right)=U_0\left(A\right)+\delta U\left(A,{\tilde{B}}_y\right),(42)$

$\delta U\left(A,{\tilde{B}}_y\right)=\sum _{l=1}^{l=\infty }\frac{{\tilde{B}}_y^l}{l!}{U}_l\left(A\right)=\sum _{l=1}^{l=\infty }\frac{{\tilde{B}}_y^l}{l!}\sum _{m=0}^{m=\infty }\frac{u_{lm}}{m!}{A}^m,(43)$

$U_0\left(A\right)=U_{bc}-\delta U{|}_{\bar{S}},(44)$

where the subscript bc stands for the boundary conditions and $\bar{S}$ stands for the boundary itself (the trajectory of some particular probe). When data of all the four MMS probes are available, the representation (42–44) allows the third-order approximate solution (24 coefficients) of the system (39–41). The four extra conditions (now, both n and T_e are in the control list) allow the representation of the term Q₀(A) in a form of the truncated Taylor series, when the boundary conditions for Q are not in possession. For these low-order schemes, the piecewise reconstruction in a sliding window may be a good option.

2.4.3 The SCS-tailored technique

As needed, the described technique may be easily tailored for calculations in the SCS x′yz′, presenting the rotated co-moving LMN coordinate system, where the x′-axis coincides with the satellite trajectory and the z′-axis is normal to it. To this end, the neglected terms of the considered equations are to be kept. Particularly, Eqs 39, 40 take the following form:

$\frac{{\partial }^{2}A}{\partial z^2}=-j_{ey}\left(A,{\tilde{B}}_y\right)-\frac{{\partial }^{2}A}{\partial x^2},(45)$

$\begin{array}{ll}\hfill \frac{{\partial }^2{\tilde{B}}_y}{\partial z^2}& =\frac{1}{n}\left[\frac{\partial n}{\partial A}\frac{\partial A}{\partial z}\frac{\partial {\tilde{B}}_y}{\partial z}+\frac{\partial n}{\partial {\tilde{B}}_y}{\left(\frac{\partial {\tilde{B}}_y}{\partial z}\right)}^2\right]+Q\left(A,{\tilde{B}}_y\right)\hfill \\ \hfill & +\frac{1}{n}\left[\frac{\partial n}{\partial A}\frac{\partial A}{\partial x}\frac{\partial {\tilde{B}}_y}{\partial x}+\frac{\partial n}{\partial {\tilde{B}}_y}{\left(\frac{\partial {\tilde{B}}_y}{\partial x}\right)}^2\right]-\frac{{\partial }^2{\tilde{B}}_y}{\partial x^2},\hfill \end{array}(46)$

where we omitted superscript ′ at all entries of x and z for shortening the notations, while the y-components and potentials are invariant with respect to the coordinate system rotating around the y axis. Eq. 41 does not change, but the term $\sim V_{ez}^2$ in the definition of φ* is to be kept, as ∂V_ez/∂x in definition of Q. The modification of Eqs 28, 29 for the thin-layer reconstruction in SCS is similarly straightforward.

Equations 45, 46 do not contain any term requiring the calculation of some extra coefficients as compared to Eqs 39, 40; hence, the same Taylor series technique is applied for solving these equations. However, in SCS, the quantities B_z, E_x, and V_ez augment the control list; hence, we have 12 extra control conditions (if all four MMS probes are in play). With representation (42–44) and 12 additional coefficients, one can build the fourth-order scheme (40 coefficients in total) for the system (41, 45, 46). In contrast with the third-order scheme, in the fourth-order scheme, the quantity Q₀(A) cannot be represented in a form of the Taylor series, since such representation would require five coefficients more, while we can calculate only four by using Eq. 25, which specifies one extra control condition at each spacecraft trajectory. An additional condition q₀₀ = 0, expressing the reasonable assumption of the absence of the constant term, makes such representation available.

3 Results

In the present study, we investigate the technique of EMHD GS reconstruction of the 2D steady-state reconnection kernel region, namely, the EDR. We discuss two families of models, which we call A1 (Sonnerup et al., 2016; Hasegawa et al., 2017; 2019; 2021) and A2 (Korovinskiy et al., 2020; 2021) in terms of comparison of their advantages and disadvantages. A1 represents a more universal technique, appropriate for arbitrary orientation of the spacecraft trajectory with respect to the EDR. It requires single probe data to setup the calculations. A2 is simpler but less universal, it is not appropriate for vertical crossings and it requires at least two probes to evaluate the boundary conditions. Both models, as they are developed for today, adopt some (different) simplifying assumptions, restricting the applicability domain. One of these assumptions, the constancy of number density, adopted in Model 2 of Korovinskiy et al. (2021), is released, and this new compressible model is tested by reconstructing the event of Torbert et al. (2018). This allowed three times expansion of the reconstruction interval as compared to previous studies (Hasegawa et al., 2019; Korovinskiy et al., 2021).

The fundamental limitations of the 2D steady-state treatment are considered in terms of the reconstruction inaccuracy that emerges when this simplified approach is utilized for the reconstruction of real EDRs in Earth’s magnetotail. Particularly, the reconstruction of the event of July 11, 2017, demonstrated the remarkable robustness of the reconstruction technique A2 with respect to the violation of the configuration two-dimensionality. It is found that weak 3D effects (∂/∂y ∼ϵ) do not ruin the reconstruction scheme, crashing the reconstruction of the minor (normal to CS) electron velocity component only, but not the other quantities. The productivity of the EMHD GS technique in the unsteady reconnection region reconstruction is tested by means of Marshall et al.’s (2020) event. The reconstruction results agreed with the conclusion of Marshall et al. (2020) concerning the duration of the reconnection region crossing of about 0.3 s. The X-line between MMS1 and MMS2, reported by Marshall et al. (2020), is also observed in our reconstruction and is found to be close to the MMS1 trajectory. Additionally, the O-line at the MMS3 trajectory and the X-line between MMS3 and MMS4 (Figure 6C), moving toward MMS1 (Figure 6A), are also discovered. However, the abrupt break of the steady state makes the reconstruction-trusted interval too small (of the order of the distance between MMS1 and MMS3 trajectories, i.e., $\sim 2d_e\sim 10km$ in cross section). For this event, the polynomial reconstruction technique of Denton et al. (2020) is more appropriate. In contrast to the herein presented steady-state model, this technique does not rely on a time series of measurement points but can treat each time point independently, contrary to the SOTE method (Liu et al., 2019). It is able to provide information about the magnetic field in 3D space at any given time and is therefore able to resolve temporal evolutions of the field and current structures. With regard to the present results, the existence of both X-lines, as shown in Figure 6C, is confirmed in the studies of Hosner et al. (2022), who utilized the reduced quadratic model of Denton et al. (2020).

The perspectives of improving the existing EMHD GS reconstruction models are studied analytically. The presented study has shown that the self-consistent EDR reconstruction model for the EMHD system (1–5, 9), adoptable for arbitrary-oriented multi-probe mission (MMS or future multi-spacecraft missions capable of resolving the electron-scale physics) crossings, can be developed without using any singular equation and/or simplified model for the electron pressure anisotropy term ${(\mathrm{\nabla }\cdot {\widehat{P}}_e)}_y$. All extra simplifying assumptions, imposed on the model functions, can be released as well. This can be made by implementing the polynomial technique, similar to those of Denton et al. (2022), through operating in variable space $(A,{\tilde{B}}_y)$ instead of in-plane Cartesian coordinates. The coordinates $(A,{\tilde{B}}_y)$ seem to be preferable, since they are rotationally invariant and exhibit the scaling ratio $\partial /\partial {\tilde{B}}_y\ll \partial /\partial A$ (this scaling ratio may violate in configurations with the strong guide field), which is the same as the scaling ratio ∂/∂x ≪ ∂/∂z, resembling the stretched structural geometry in the proper Cartesian coordinates. Apparently, the development of such polynomial reconstruction scheme may come at the price of increased complicity of the technical realization of the suggested method. However, at the analytical level, the insuperable obstacles are not in view.

4 Discussion

In a general sense, EMHD GS reconstruction of any reconnection event represents a complex problem, where reconstruction itself is a final step, which is preceded by the in situ data analysis and event identification, estimate the structure velocity (V₀) and the proper LMN coordinate system. Discussing all these aspects goes beyond the scope of the present study, where we focus on the reconstruction problem in a strict sense. Since two magnetotail reconnection events, addressed in this study, have been introduced previously, for the omitted details, we refer the reader to the corresponding studies of Hasegawa et al. (2019); Marshall et al. (2020); and references therein. In particular, the reconstruction setup in Section 2.2.3 is fully identical to those of Hasegawa et al. (2019); Korovinskiy et al. (2021), which is made to facilitate the results comparison. The setup of Section 2.3.2 differs from the data of Marshall et al. (2020) mainly by the value of V₀, since in the cited study, the latter was estimated too rough. In terms of the event study, the accurate estimate of V₀ is important since it specifies the relative motion of the spacecraft to the structure (spacecraft trajectory). However, in terms of the study of the reconstruction model efficiency, the accuracy of the V₀ estimate is less important since this estimate affects the spacecraft trajectory, hence the model functions and the geometry of the reconstructed magnetic configuration, but neither its topology nor the accuracy of the magnetoplasma quantities reconstruction.

The EMHD GS reconstruction has got its name due to Eq. 8, representing a zero-order scheme for evaluating the magnetic potential A. Meanwhile, the accurate consideration of the problem demands solving the two-dimensional problem, since in steady-state 2D configuration all magnetoplasma quantities stay functions of two variables, whatever variable space is considered. However, in some coordinate systems, these two independent variables are not peer in terms of scaling. Particularly, in the co-moving LMN coordinate system, where the z-axis coincides with the CS normal direction, the scaling ratios ∂/∂z ∼ 1 and ∂/∂x ∼ϵ≪ 1 allow considerable simplification of equations by neglecting the minor terms ∼ϵ² with respect to the major ones $\sim 1$ (BLA). Apart from considerable simplification of the equations, this approach represents the technique of problem regularization (Korovinskiy et al., 2020). If the guide field is small enough, |B_g|≪ 1, similar scaling estimates are valid in the variable space $(A,{\tilde{B}}_y)$, where ∂/∂A ∼ 1 and $\partial /\partial {\tilde{B}}_y\sim ({\tilde{B}}_y+B_g)\sim ϵ$. These scaling estimates result in Eq. 8, where the terms containing ${\tilde{B}}_y$ are neglected as compared to the major term [see, e.g., Eq. 21 of Korovinskiy et al. (2021)]. Nevertheless, both the accuracy and the applicability domain of the zero-order models suffer from excessive simplification. Moreover, the accuracy of such models should decrease with the increasing guide field value. In a strong guide field, the derivative operator $\partial /\partial {\tilde{B}}_y$ may scale the same as ∂/∂A or even higher. For such events, the reconstruction schemes of higher orders are demanded.

Development of such schemes by means of the polynomial technique is considered in Section 2.4. The suggested method benefits from the usage of both BLA and rotationally invariant coordinates $(A,{\tilde{B}}_y)$ and allows the release of all unnecessary simplifying assumptions imposed on the model functions n, T_e, V_ey, and Q of Eq. 11. The practical realization of the polynomial method would presumably allow extending the reconstruction region over the entire EMHD domain, which, in turn, would shed more light at the complex internal structure of EDR and the conditions of the electron physics failure. It should be noted that the applicability of the discussed reconstruction technique is not restricted to the reconnection kernel zone only. The same approach can be adopted for studying any magnetotail (and more general, collisionless plasma) structure in which electron dynamics is paramount and 3D and the temporal evolution effects can be neglected. Particularly, EMHD GS reconstruction seems to be appropriate to studies of the magnetic reconnection separatrix regions (SRs), the regions that are adjacent to magnetic separatrices (topological surfaces that separate reconnected and non-reconnected magnetic field lines), and bear energetic electron and ion beams (Lapenta et al., 2016; Khotyaintsev et al., 2019). These essential features of the SR have been reproduced even by the simplest incompressible model, neglecting both electron pressure anisotropy and inertia, which was utilized for the benchmark reconstruction of the PIC-simulation data (Semenov et al., 2009). The extended model, discussed in this paper, would allow more detailed studies of the SRs, where different motions of magnetized electrons and non-magnetized ions give rise not only to intense Hall electric and magnetic fields (Øieroset et al., 2001; Eastwood et al., 2010) but also to the large density fluctuations, the electron holes (Huang et al., 2014), making the region to exhibit the double layer structure (Paschmann et al., 2013).

The further advantage of EMHD GS reconstruction stems from the fact that the equation of the ion motion splits from the system (1–5, 9). It means that ions move in the applied field, and the ion bulk velocity is evaluated when other magnetoplasma quantities are found. The simplified problem analysis is given in Korovinskiy et al. (2008). Under proper generalization, the analogous approach can be applied in the extended reconstruction models A1 and A2. This, in turn, provides the opportunity of analytical studies of the ion motion in the SR in view of such high-impacting factors as ion mass, temperature, and distance to X-line, affecting both ion heating and acceleration (Zaitsev et al., 2021). For example, the ion mass appears to be a crucial parameter for the kinetic energy gain because of the assumed energization condition |m_i∇E_⊥/(eB²)| > 1 (Cole, 1976). The temperature of the cold ion fraction is also of high importance because these ions may change the reconnection rate (André and Cully, 2012), reduce the Hall current (André et al., 2016; Dargent et al., 2017), and change the energy budget of magnetic reconnection (Toledo-Redondo et al., 2017). At last, the distance to X-line is of high importance because the reconnection electric field, driving cold ions inside the exhaust without thermalization, exists only between the X-line and the pileup front (Alm et al., 2018; Toledo-Redondo et al., 2018), on the contrary to the Hall electric fields that presents in the entire SR.

The less evident, EMHD GS reconstruction can be utilized for studies of the kinetic (Pritchett and Coroniti, 2010) or MHD (Sorathia et al., 2020) ballooning-interchange (BI) instability, explaining the appearance of auroral beads and related ionospheric current disturbances in the late substorm growth phase (Panov et al., 2019; Sorathia et al., 2020). More specifically, this method may be applied for studies of BI heads, which are located in the near-Earth plasma sheet at the distances of 7–14 Earth’s radii downtail, where they can drift in both dusk and dawn directions (Panov et al., 2012; Panov and Pritchett, 2018a). Indeed, the kinetic BI mode is identified as the low-frequency extension in a curved magnetic geometry of the lower-hybrid-drift instability in straight magnetic fields (Pritchett and Coroniti, 2010; 2011; 2013) with |j_i/j_e|∼ 0.2 (Panov and Pritchett, 2018a; b). Thus, BI heads represent slowly varying (as compared to the electron plasma frequency) quasi-2D structures (oriented in the equatorial plane) governed by the electron currents, i.e., they fulfil all the basic assumptions of the EMHD GS reconstruction models. The reconstruction of the proper in situ data would provide an insight to morphology of the BI heads and ion motion driving mechanisms. In particular, the problem of the primary driver of the ion motion in BI heads (the Hall electric field or the ion proper buoyancy) could be addressed.

Apart from providing an intermediate step between satellite data and numerical simulations, EMHD GS reconstruction also allows the analysis of various electron-scale structures in terms of their key parameters, such as plasma β, entropy, magnetic field curvature, and electron kinetic scales. The present study demonstrates the significant potential of this method both in terms of the increase of physical accuracy and in terms of model scope expansion. The furthest improvement of the EMHD GS technique assumes the generalization of the reconstruction model for fully anisotropic electron pressure and temperature, which stays a challenging problem for future studies.

Data availability statement

Publicly available datasets were analyzed in this study. The MMS data used here are available from the MMS Science Data Center: https://lasp.colorado.edu/mms/sdc/public/.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This study has been supported by the Austrian Science Fund (FWF): I 3506-N27 and Austrian FFG project ASAP15/873685.

Acknowledgments

The authors thank the Editor and the Reviewers for their help in improving the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alm, L., Andre, M., Vaivads, A., Khotyaintsev, Y. V., Torbert, R. B., Burch, J. L., et al. (2018). Magnetotail hall physics in the presence of cold ions. Geophys. Res. Lett. 45, 10–941. doi:10.1029/2018GL079857

CrossRef Full Text | Google Scholar

André, M., and Cully, C. M. (2012). Low-energy ions: A previously hidden solar system particle population. Geophys. Res. Lett. 39. doi:10.1029/2011GL050242

CrossRef Full Text | Google Scholar

André, M., Li, W., Toledo-Redondo, S., Khotyaintsev, Y. V., Vaivads, A., Graham, D. B., et al. (2016). Magnetic reconnection and modification of the Hall physics due to cold ions at the magnetopause. Geophys. Res. Lett. 43, 6705–6712. doi:10.1002/2016GL069665

CrossRef Full Text | Google Scholar

Aunai, N., Belmont, G., and Smets, R. (2011). Energy budgets in collisionless magnetic reconnection: Ion heating and bulk acceleration. Phys. Plasmas 18, 122901. doi:10.1063/1.3664320

CrossRef Full Text | Google Scholar

Bagenal, F. (2013). Planetary magnetospheres. Dordrecht, Netherlands: Springer, 251–307. doi:10.1007/978-94-007-5606-9_6

CrossRef Full Text | Google Scholar

Bessho, N., Chen, L.-J., Wang, S., Hesse, M., and Wilson, L. (2019). Magnetic reconnection in a quasi-parallel shock: Two-dimensional local particle-in-cell simulation. Geophys. Res. Lett. 46, 9352–9361. doi:10.1029/2019GL083397

CrossRef Full Text | Google Scholar

Bhattacharjee, A. (2004). Impulsive magnetic reconnection in the Earth’s magnetotail and the Solar corona. Annu. Rev. Astron. Astrophys. 42, 365–384. doi:10.1146/annurev.astro.42.053102.134039

CrossRef Full Text | Google Scholar

Birn, J., Drake, J., Shay, M., Rogers, B., Denton, R., Hesse, M., et al. (2001). Geospace Environmental Modeling (GEM) magnetic reconnection challenge. J. Geophys. Res. Space Phys. 106, 3715–3719. doi:10.1029/1999JA900449

CrossRef Full Text | Google Scholar

Birn, J., and Hesse, M. (2010). Energy release and transfer in guide field reconnection. Phys. Plasmas 17, 012109. doi:10.1063/1.3299388

CrossRef Full Text | Google Scholar

Biskamp, D. (2000). Magnetic reconnection in plasmas. Cambridge University Press.

Google Scholar

Bulanov, S., Pegoraro, F., and Sakharov, A. (1992). Magnetic reconnection in electron magnetohydrodynamics. Phys. Plasmas 4, 2499–2508. doi:10.1063/1.860467

CrossRef Full Text | Google Scholar

Burch, J., Hesse, M., Webster, J., Genestreti, K., Torbert, R., Denton, R., et al. (2022). The EDR inflow region of a reconnecting current sheet in the geomagnetic tail. Phys. Plasmas 29, 052903. doi:10.1063/5.0083169

CrossRef Full Text | Google Scholar

Burch, J., Moore, T., Torbert, R., and Giles, B. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Cai, H.-J., and Lee, L. (1997). The generalized Ohm’s law in collisionless magnetic reconnection. Phys. Plasmas 4, 509–520. doi:10.1063/1.872178

CrossRef Full Text | Google Scholar

Cassak, P., Baylor, R., Fermo, R., Beidler, M., Shay, M., Swisdak, M., et al. (2015). Fast magnetic reconnection due to anisotropic electron pressure. Phys. Plasmas 22, 020705. doi:10.1063/1.4908545

CrossRef Full Text | Google Scholar

Cassak, P., and Fuselier, S. (2016)., 427. Springer, 213–276. of Astrophys. doi:10.1007/978-3-319-26432-5_6Reconnection at Earth’s dayside magnetopauseSpace Sci. Lib.

CrossRef Full Text | Google Scholar

Cassak, P., Liu, Y.-H., and Shay, M. (2017). A review of the 0.1 reconnection rate problem. J. Plasm. Phys. 83, 715830501. doi:10.1017/S0022377817000666

CrossRef Full Text | Google Scholar

Chen, L.-J., Wang, S., Le Contel, O., Rager, A., Hesse, M., Drake, J., et al. (2020). Lower-hybrid drift waves driving electron nongyrotropic heating and vortical flows in a magnetic reconnection layer. Phys. Rev. Lett. 125, 025103. doi:10.1103/PhysRevLett.125.025103

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., and Hu, Q. (2022). Small-scale magnetic flux ropes and their properties based on in situ measurements from the parker solar probe. Astrophys. J. 924, 43. doi:10.3847/1538-4357/ac3487

CrossRef Full Text | Google Scholar

Cole, K. (1976). Effects of crossed magnetic and (spatially dependent) electric fields on charged particle motion. Planet. Space Sci. 24, 515–518. doi:10.1016/0032-0633(76)90096-9

CrossRef Full Text | Google Scholar

Comisso, L., and Bhattacharjee, A. (2016). On the value of the reconnection rate. J. Plasm. Phys. 82, 595820601. doi:10.1017/S002237781600101X

CrossRef Full Text | Google Scholar

Cozzani, G., Khotyaintsev, Y. V., Graham, D. B., Egedal, J., André, M., Vaivads, A., et al. (2021). Structure of a perturbed magnetic reconnection electron diffusion region in the Earth’s magnetotail. Phys. Rev. Lett. 127, 215101. doi:10.1103/PhysRevLett.127.215101

PubMed Abstract | CrossRef Full Text | Google Scholar

Dargent, J., Aunai, N., Lavraud, B., Toledo-Redondo, S., Shay, M., Cassak, P., et al. (2017). Kinetic simulation of asymmetric magnetic reconnection with cold ions. J. Geophys. Res. Space Phys. 122, 5290–5306. doi:10.1002/2016JA023831

CrossRef Full Text | Google Scholar

Daughton, W., Nakamura, T., Karimabadi, H., Roytershteyn, V., and Loring, B. (2014). Computing the reconnection rate in turbulent kinetic layers by using electron mixing to identify topology. Phys. Plasmas 21, 052307. doi:10.1063/1.4875730

CrossRef Full Text | Google Scholar

Daughton, W., Scudder, J., and Karimabadi, H. (2006). Fully kinetic simulations of undriven magnetic reconnection with open boundary conditions. Phys. Plasmas 13, 072101. doi:10.1063/1.2218817

CrossRef Full Text | Google Scholar

Denton, R. E., Liu, Y.-H., Hasegawa, H., Torbert, R. B., Li, W., Fuselier, S., et al. (2022). Polynomial reconstruction of the magnetic field observed by multiple spacecraft with integrated velocity determination. J. Geophys. Res. Space Phys. 127, e2022JA030512. doi:10.1029/2022JA030512

CrossRef Full Text | Google Scholar

Denton, R. E., Torbert, R. B., Hasegawa, H., Genestreti, K. J., Manuzzo, R., Belmont, G., et al. (2021). Two-dimensional velocity of the magnetic structure observed on july 11, 2017 by the magnetospheric multiscale spacecraft. J. Geophys. Res. Space Phys. 126, e2020JA028705. doi:10.1029/2020JA028705

CrossRef Full Text | Google Scholar

Denton, R., Sonnerup, B. Ö., Russell, C., Hasegawa, H., Phan, T.-D., Strangeway, R., et al. (2018). Determining <i>L</i> - <i>M</i> - <i>N</i> current sheet coordinates at the magnetopause from magnetospheric multiscale data. J. Geophys. Res. Space Phys. 123, 2274–2295. doi:10.1002/2017JA024619

CrossRef Full Text | Google Scholar

Denton, R., Torbert, R., Hasegawa, H., Dors, I., Genestreti, K., Argall, M., et al. (2020). Polynomial reconstruction of the reconnection magnetic field observed by multiple spacecraft. J. Geophys. Res. Space Phys. 125, e2019JA027481. doi:10.1029/2019JA027481

CrossRef Full Text | Google Scholar

Divin, A., Markidis, S., Lapenta, G., Semenov, V., Erkaev, N., and Biernat, H. (2010). Model of electron pressure anisotropy in the electron diffusion region of collisionless magnetic reconnection. Phys. Plasmas 17, 122102. doi:10.1063/1.3521576

CrossRef Full Text | Google Scholar

Divin, A., Semenov, V., Korovinskiy, D., Markidis, S., Deca, J., Olshevsky, V., et al. (2016). A new model for the electron pressure nongyrotropy in the outer electron diffusion region. Geophys. Res. Lett. 43, 10,565–10,573. doi:10.1002/2016GL070763

CrossRef Full Text | Google Scholar

Divin, A., Semenov, V., Zaitsev, I., Korovinskiy, D., Deca, J., Lapenta, G., et al. (2019). Inner and outer electron diffusion region of antiparallel collisionless reconnection: Density dependence. Phys. Plasmas 26, 102305. doi:10.1063/1.5109368

CrossRef Full Text | Google Scholar

Dorfman, S., Ji, H., Yamada, M., Yoo, J., Lawrence, E., Myers, C., et al. (2013). Three-dimensional, impulsive magnetic reconnection in a laboratory plasma. Geophys. Res. Lett. 40, 233–238. doi:10.1029/2012GL054574

CrossRef Full Text | Google Scholar

Drake, J., Swisdak, M., Phan, T., Cassak, P., Shay, M., Lepri, S., et al. (2009). Ion heating resulting from pickup in magnetic reconnection exhausts. J. Geophys. Res. Space Phys. 114, A05111. doi:10.1029/2008JA013701

CrossRef Full Text | Google Scholar

Du, S., Guo, F., Zank, G. P., Li, X., and Stanier, A. (2018). Plasma energization in colliding magnetic flux ropes. Astrophys. J. 867, 16. doi:10.3847/1538-4357/aae30e

CrossRef Full Text | Google Scholar

Dungey, J. (1953). LXXVI. Conditions for the occurrence of electrical discharges in astrophysical systems. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 44, 725–738. doi:10.1080/14786440708521050

CrossRef Full Text | Google Scholar

Eastwood, J., Phan, T., Øieroset, M., and Shay, M. (2010). Average properties of the magnetic reconnection ion diffusion region in the Earth’s magnetotail: The 2001–2005 Cluster observations and comparison with simulations. J. Geophys. Res. Space Phys. 115. doi:10.1029/2009JA014962

CrossRef Full Text | Google Scholar

Egedal, J., Le, A., and Daughton, W. (2013). A review of pressure anisotropy caused by electron trapping in collisionless plasma, and its implications for magnetic reconnection. Phys. Plasmas 20, 061201. doi:10.1063/1.4811092

CrossRef Full Text | Google Scholar

Egedal, J., Le, A., Daughton, W., Wetherton, B., Cassak, P., Chen, L., et al. (2016). Spacecraft observations and analytic theory of crescent-shaped electron distributions in asymmetric magnetic reconnection. Phys. Rev. Lett. 117, 185101. doi:10.1103/PhysRevLett.117.185101

PubMed Abstract | CrossRef Full Text | Google Scholar

Egedal, J., Ng, J., Le, A., Daughton, W., Wetherton, B., Dorelli, J., et al. (2019). Pressure tensor elements breaking the frozen-in law during reconnection in Earth’s magnetotail. Phys. Rev. Lett. 123, 225101. doi:10.1103/PhysRevLett.123.225101

PubMed Abstract | CrossRef Full Text | Google Scholar

Egedal, J., Øieroset, M., Fox, W., and Lin, R. (2005). In situ discovery of an electrostatic potential, trapping electrons and mediating fast reconnection in the Earth’s magnetotail. Phys. Rev. Lett. 94, 025006. doi:10.1103/PhysRevLett.94.025006

PubMed Abstract | CrossRef Full Text | Google Scholar

Fadanelli, S., Lavraud, B., Califano, F., Cozzani, G., Finelli, F., and Sisti, M. (2021). Energy conversions associated with magnetic reconnection. J. Geophys. Res. Space Phys. 126, e2020JA028333. doi:10.1029/2020JA028333

CrossRef Full Text | Google Scholar

Fu, H., Cao, J., Cao, D., Wang, Z., Vaivads, A., Khotyaintsev, Y. V., et al. (2019a). Evidence of magnetic nulls in electron diffusion region. Geophys. Res. Lett. 46, 48–54. doi:10.1029/2018GL080449

CrossRef Full Text | Google Scholar

Fu, H., Cao, J., Vaivads, A., Khotyaintsev, Y. V., Andre, M., Dunlop, M., et al. (2016). Identifying magnetic reconnection events using the FOTE method. J. Geophys. Res.: Space Phys. 121, 1263–1272. doi:10.1002/2015JA021701

CrossRef Full Text | Google Scholar

Fu, H., Vaivads, A., Khotyaintsev, Y. V., Andre, M., Cao, J., Olshevsky, V., et al. (2017). Intermittent energy dissipation by turbulent reconnection. Geophys. Res. Lett. 44, 37–43. doi:10.1002/2016GL071787

CrossRef Full Text | Google Scholar

Fu, H., Vaivads, A., Khotyaintsev, Y. V., Olshevsky, V., Andre, M., Cao, J., et al. (2015). How to find magnetic nulls and reconstruct field topology with MMS data?. J. Geophys. Res.: Space Phys. 120, 3758–3782. doi:10.1002/2015JA021082

CrossRef Full Text | Google Scholar

Fu, H., Xu, Y., Vaivads, A., and Khotyaintsev, Y. (2019b). Super-efficient electron acceleration by an isolated magnetic reconnection. Astrophys. J. 870, L22. doi:10.3847/2041-8213/aafa75

CrossRef Full Text | Google Scholar

Fujimoto, K. (2006). Time evolution of the electron diffusion region and the reconnection rate in fully kinetic and large system. Phys. Plasmas 13, 072904. doi:10.1063/1.2220534

CrossRef Full Text | Google Scholar

Furth, H. P., Killeen, J., and Rosenbluth, M. N. (1963). Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6, 459–484. doi:10.1063/1.1706761

CrossRef Full Text | Google Scholar

Genestreti, K., Burch, J., Cassak, P., Torbert, R., Ergun, R., Varsani, A., et al. (2017). The effect of a guide field on local energy conversion during asymmetric magnetic reconnection: MMS observations. J. Geophys. Res. Space Phys. 122, 11–342. doi:10.1002/2017JA024247

CrossRef Full Text | Google Scholar

Genestreti, K. J., Varsani, A., Burch, J. L., Cassak, P. A., Torbert, R. B., Nakamura, R., et al. (2018b). MMS observation of asymmetric reconnection supported by 3-D electron pressure divergence. J. Geophys. Res. Space Phys. 123, 1806–1821. doi:10.1002/2017JA025019

CrossRef Full Text | Google Scholar

Genestreti, K., Nakamura, T., Nakamura, R., Denton, R., Torbert, R., Burch, J., et al. (2018a). How accurately can we measure the reconnection rate e_m for the mms diffusion region event of 11 July 2017? J. Geophys. Res. Space Phys. 123, 9130–9149. doi:10.1029/2018JA025711

PubMed Abstract | CrossRef Full Text | Google Scholar

Giovanelli, R. (1946). A theory of chromospheric flares. Nature 158, 81–82. doi:10.1038/158081a0

CrossRef Full Text | Google Scholar

Goldman, M., Newman, D., and Lapenta, G. (2016). What can we learn about magnetotail reconnection from 2D PIC Harris-sheet simulations? Space Sci. Rev. 199, 651–688. doi:10.1007/s11214-015-0154-y

CrossRef Full Text | Google Scholar

Gonzalez, W., and Parker, E. (2016). Magnetic reconnection, vol. 427 of astrophys. And space sci. Lib. Springer. doi:10.1007/978-3-319-26432-5

CrossRef Full Text | Google Scholar

Gosling, J., Asbridge, J., Bame, S., Feldman, W., Paschmann, G., Sckopke, N., et al. (1982). Evidence for quasi-stationary reconnection at the dayside magnetopause. J. Geophys. Res. Space Phys. 87, 2147–2158. doi:10.1029/JA087iA04p02147

CrossRef Full Text | Google Scholar

Grad, H., and Rubin, H. (1958). Hydromagnetic equilibria and force-free fields. J. Nucl. Energy 7, 284–285. doi:10.1016/0891-3919(58)90139-6

CrossRef Full Text | Google Scholar

Hadamard, J. (1923). Lectures on Cauchy’s problem in linear partial differential equations. New Haven Yale University Press.

Google Scholar

Hasegawa, H., Denton, R. E., Nakamura, R., Genestreti, K. J., Nakamura, T. K. M., Hwang, K.-J., et al. (2019). Reconstruction of the electron diffusion region of magnetotail reconnection seen by the MMS spacecraft on 11 July 2017. J. Geophys. Res. Space Phys. 124, 122–138. doi:10.1029/2018JA026051

CrossRef Full Text | Google Scholar

Hasegawa, H., Nakamura, T. K. M., and Denton, R. E. (2021). Reconstruction of the electron diffusion region with inertia and compressibility effects. J. Geophys. Res. Space Phys. 126, e2021JA029841. doi:10.1029/2021JA029841

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasegawa, H., Sonnerup, B. U., Denton, R. E., Phan, T.-D., Nakamura, T. K. M., Giles, B. L., et al. (2017). Reconstruction of the electron diffusion region observed by the Magnetospheric Multiscale spacecraft: First results. Geophys. Res. Lett. 44, 4566–4574. doi:10.1002/2017GL073163

CrossRef Full Text | Google Scholar

Hau, L., and Sonnerup, B. U. Ö. (1999). Two-dimensional coherent structures in the magnetopause: Recovery of static equilibria from single-spacecraft data. J. Geophys. Res. Space Phys. 104, 6899–6917. doi:10.1029/1999ja900002

CrossRef Full Text | Google Scholar

Hesse, M., and Cassak, P. (2020). Magnetic reconnection in the space sciences: Past, present, and future. J. Geophys. Res. Space Phys. 125, e25935. doi:10.1029/2018JA025935

CrossRef Full Text | Google Scholar

Hesse, M., Schindler, K., Birn, J., and Kuznetsova, M. (1999). The diffusion region in collisionless magnetic reconnection. Phys. Plasmas 6, 1781–1795. doi:10.1063/1.873436

CrossRef Full Text | Google Scholar

Hesse, M., and Winske, D. (1998). Electron dissipation in collisionless magnetic reconnection. J. Geophys. Res. 103, 26479–26486. doi:10.1029/98JA01570

CrossRef Full Text | Google Scholar

Heyn, M. F., and Semenov, V. S. (1996). Rapid reconnection in compressible plasma. Phys. Plasmas 3, 2725–2741. doi:10.1063/1.871723

CrossRef Full Text | Google Scholar

Hietala, H., Artemyev, A., and Angelopoulos, V. (2017). Ion dynamics in magnetotail reconnection in the presence of density asymmetry. J. Geophys. Res. Space Phys. 122, 2010–2023. doi:10.1002/2016JA023651

CrossRef Full Text | Google Scholar

Holmes, J., Nakamura, R., Schmid, D., Nakamura, T., Roberts, O., and Vörös, Z. (2021). Wave activity in a dynamically evolving reconnection separatrix. J. Geophys. Res. Space Phys. 126, e2020JA028520. doi:10.1029/2020JA028520

CrossRef Full Text | Google Scholar

Hoshino, M., Mukai, T., Yamamoto, T., and Kokubun, S. (1998). Ion dynamics in magnetic reconnection: Comparison between numerical simulation and Geotail observations. J. Geophys. Res. Space Phys. 103, 4509–4530. doi:10.1029/97JA01785

CrossRef Full Text | Google Scholar

Hosner, M., Nakamura, R., Schmid, D., Nakamura, T., Panov, E., and Korovinskiy, D. (2022). Investigation of the evolution of energy conversion processes at an EDR-accompanied dipolarization front, using polynomial magnetic field reconstruction techniques. Tech. Rep. Copernic. Meet. doi:10.5194/egusphere-egu22-5853

CrossRef Full Text | Google Scholar

Hoyle, F. (1949). Some recent researches in solar physics. Cambridge University Press.

Google Scholar

Hu, Q. (2017). The grad-shafranov reconstruction in twenty years: 1996–2016. Sci. China Earth Sci. 60, 1466–1494. doi:10.1007/s11430-017-9067-2

CrossRef Full Text | Google Scholar

Huang, C., Lu, Q., Wang, P., Wu, M., and Wang, S. (2014). Characteristics of electron holes generated in the separatrix region during antiparallel magnetic reconnection. J. Geophys. Res. Space Phys. 119, 6445–6454. doi:10.1002/2014JA019991

CrossRef Full Text | Google Scholar

Huba, J., and Rudakov, L. (2004). Hall magnetic reconnection rate. Phys. Rev. Lett. 93, 175003. doi:10.1103/PhysRevLett.93.175003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ji, X.-F., Wang, X.-G., Sun, W.-J., Xiao, C.-J., Shi, Q.-Q., Liu, J., et al. (2014). EMHD theory and observations of electron solitary waves in magnetotail plasmas. J. Geophys. Res. Space Phys. 119, 4281–4289. doi:10.1002/2014JA019924

CrossRef Full Text | Google Scholar

Karimabadi, H., Daughton, W., and Scudder, J. (2007). Multi-scale structure of the electron diffusion region. Geophys. Res. Lett. 34, L13104. doi:10.1029/2007GL030306

CrossRef Full Text | Google Scholar

Khotyaintsev, Y. V., Graham, D. B., Norgren, C., and Vaivads, A. (2019). Collisionless magnetic reconnection and waves: Progress review. Front. Astron. Space Sci. 6, 1–20. doi:10.3389/fspas.2019.00070

CrossRef Full Text | Google Scholar

Korovinskiy, D. B., Divin, A. V., Semenov, V. S., Erkaev, N. V., Kiehas, S. A., and Kubyshkin, I. V. (2020). Grad-Shafranov reconstruction of the magnetic configuration in the reconnection X-point vicinity in compressible plasma. Phys. Plasmas 27, 082905. doi:10.1063/5.0015240

CrossRef Full Text | Google Scholar

Korovinskiy, D. B., Kiehas, S. A., Panov, E. V., Semenov, V. S., Erkaev, N. V., Divin, A. V., et al. (2021). The inertia-based model for reconstruction of the electron diffusion region. J. Geophys. Res. Space Phys. 126, e2020JA029045. doi:10.1029/2020JA029045

CrossRef Full Text | Google Scholar

Korovinskiy, D. B., Semenov, V. S., Erkaev, N. V., Divin, A. V., and Biernat, H. K. (2008). The 2.5-D analytical model of steady-state Hall magnetic reconnection. J. Geophys. Res. Space Phys. 113, A04205. doi:10.1029/2007JA012852

CrossRef Full Text | Google Scholar

Korovinskiy, D. B., Semenov, V. S., and Erkaev, N. V. (2006). “Theoretical model of steady-state magnetic reconnection in electron Hall magnetohydrodynamics approximation,” in Physics of auroral phenomena, proc. XXIX annual seminar, 27 February – 3 March 2006 (Apatity, Russia: Kola Science Centre, RAS), 92–95.

Google Scholar

Kuznetsova, M., Hesse, M., and Winske, D. (1998). Kinetic quasi-viscous and bulk flow inertia effects in collisionless magnetotail reconnection. J. Geophys. Res. 103, 199–213. doi:10.1029/97JA02699

CrossRef Full Text | Google Scholar

Lapenta, G., Wang, R., and Cazzola, E. (2016). Reconnection separatrix: Simulations and spacecraft measurements. Magnetic Reconnect. Concepts Appl. 427, 315–344. doi:10.1007/978-3-319-26432-5_8

CrossRef Full Text | Google Scholar

Le, A., Egedal, J., Ohia, O., Daughton, W., Karimabadi, H., and Lukin, V. (2013). Regimes of the electron diffusion region in magnetic reconnection. Phys. Rev. Lett. 110, 135004. doi:10.1103/PhysRevLett.110.135004

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Fu, H., Olshevsky, V., Pontin, D., Liu, C., Wang, Z., et al. (2019). A nonlinear method for magnetic topology reconstruction in space plasmas. Astrophys. J. Suppl. Ser. 244, 31. doi:10.3847/1538-4365/ab391a

CrossRef Full Text | Google Scholar

Liu, Y.-H., Hesse, M., Guo, F., Daughton, W., Li, H., Cassak, P., et al. (2017). Why does steady-state magnetic reconnection have a maximum local rate of order 0.1? Phys. Rev. Lett. 118, 085101. doi:10.1103/PhysRevLett.118.085101

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Mouikis, C., Kistler, L., Wang, S., Roytershteyn, V., and Karimabadi, H. (2015). The heavy ion diffusion region in magnetic reconnection in the Earth’s magnetotail. J. Geophys. Res. Space Phys. 120, 3535–3551. doi:10.1002/2015JA020982

CrossRef Full Text | Google Scholar

Lu, S., Pritchett, P., Angelopoulos, V., and Artemyev, A. (2018). Magnetic reconnection in Earth’s magnetotail: Energy conversion and its earthward–tailward asymmetry. Phys. Plasmas 25, 012905. doi:10.1063/1.5016435

CrossRef Full Text | Google Scholar

Marshall, A. T., Burch, J. L., Reiff, P. H., Webster, J. M., Torbert, R. B., Ergun, R. E., et al. (2020). Asymmetric reconnection within a flux rope-type dipolarization front. J. Geophys. Res. Space Phys. 125, e2019JA027296. doi:10.1029/2019JA027296

CrossRef Full Text | Google Scholar

Nagai, T., Shinohara, I., and Zenitani, S. (2015). Ion acceleration processes in magnetic reconnection: Geotail observations in the magnetotail. J. Geophys. Res. Space Phys. 120, 1766–1783. doi:10.1002/2014JA020737

CrossRef Full Text | Google Scholar

Nakamura, M., Fujimoto, M., and Maezawa, K. (1998). Ion dynamics and resultant velocity space distributions in the course of magnetotail reconnection. J. Geophys. Res. Space Phys. 103, 4531–4546. doi:10.1029/97JA01843

CrossRef Full Text | Google Scholar

Nakamura, R., Genestreti, K. J., Nakamura, T., Baumjohann, W., Varsani, A., Nagai, T., et al. (2019). Structure of the current sheet in the 11 July 2017 electron diffusion region event. J. Geophys. Res. Space Phys. 124, 1173–1186. doi:10.1029/2018JA026028

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, R., Sergeev, V., Baumjohann, W., Plaschke, F., Magnes, W., Fischer, D., et al. (2016). Transient, small-scale field-aligned currents in the plasma sheet boundary layer during storm time substorms. Geophys. Res. Lett. 43, 4841–4849. doi:10.1002/2016GL068768

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, T. K., Genestreti, K., Liu, Y.-H., Nakamura, R., Teh, W.-L., Hasegawa, H., et al. (2018). Measurement of the magnetic reconnection rate in the Earth’s magnetotail. J. Geophys. Res. Space Phys. 123, 9150–9168. doi:10.1029/2018JA025713

CrossRef Full Text | Google Scholar

Ng, J., Egedal, J., Le, A., Daughton, W., and Chen, L. (2011). Kinetic structure of the electron diffusion region in antiparallel magnetic reconnection. Phys. Rev. Lett. 106, 065002. doi:10.1103/PhysRevLett.106.065002

PubMed Abstract | CrossRef Full Text | Google Scholar

Norgren, C., Hesse, M., Graham, D. B., Khotyaintsev, Y. V., Tenfjord, P., Vaivads, A., et al. (2020). Electron acceleration and thermalization at magnetotail separatrices. J. Geophys. Res. Space Phys. 125, e2019JA027440. doi:10.1029/2019JA027440

CrossRef Full Text | Google Scholar

Øieroset, M., Phan, T., Fujimoto, M., Lin, R., and Lepping, R. (2001). In situ detection of collisionless reconnection in the Earth’s magnetotail. Nature 412, 414–417. doi:10.1038/35086520

PubMed Abstract | CrossRef Full Text | Google Scholar

Panov, E., and Pritchett, P. (2018a). Dawnward drifting interchange heads in the Earth’s magnetotail. Geophys. Res. Lett. 45, 8834–8843. doi:10.1029/2018GL078482

CrossRef Full Text | Google Scholar

Panov, E., and Pritchett, P. (2018b). Ion cyclotron waves rippling ballooning/interchange instability heads. J. Geophys. Res. Space Phys. 123, 8261–8274. doi:10.1029/2018JA025603

CrossRef Full Text | Google Scholar

Panov, E. V., Baumjohann, W., Nakamura, R., Pritchett, P. L., Weygand, J. M., and Kubyshkina, M. V. (2019). Ionospheric footprints of detached magnetotail interchange heads. Geophys. Res. Lett. 46, 7237–7247. doi:10.1029/2019GL083070

CrossRef Full Text | Google Scholar

Panov, E. V., Sergeev, V. A., Pritchett, P. L., Coroniti, F. V., Nakamura, R., Baumjohann, W., et al. (2012). Observations of kinetic ballooning/interchange instability signatures in the magnetotail. Geophys. Res. Lett. 39. doi:10.1029/2012GL051668

CrossRef Full Text | Google Scholar

Parker, E. N. (1979). Cosmical magnetic fields: Their origin and their activity. Oxford University Press.

Google Scholar

Parker, E. N. (1957). Sweet’s mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509–520. doi:10.1029/JZ062i004p00509

CrossRef Full Text | Google Scholar

Paschmann, G., Øieroset, M., and Phan, T. (2013). In-situ observations of reconnection in space. Space Sci. Rev. 178, 385–417. doi:10.1007/s11214-012-9957-2

CrossRef Full Text | Google Scholar

Petschek, H. E. (1964). Magnetic field annihilation. In AAS-NASA symposium on the physics of solar flares: Proceedings of a symposium held at the goddard space flight center, Greenbelt, Maryland 50, 425–439.

Google Scholar

Phan, T., Dunlop, M., Paschmann, G., Klecker, B., Bosqued, J., Reme, H., et al. (2004). Cluster observations of continuous reconnection at the magnetopause under steady interplanetary magnetic field conditions. Ann. Geophys. 22, 2355–2367. doi:10.5194/angeo-22-2355-2004

CrossRef Full Text | Google Scholar

Priest, E., and Forbes, T. (1986). New models for fast steady state magnetic reconnection. J. Geophys. Res. Space Phys. 91, 5579–5588. doi:10.1029/JA091iA05p05579

CrossRef Full Text | Google Scholar

Priest, E., and Lee, L. (1990). Nonlinear magnetic reconnection models with separatrix jets. J. Plasm. Phys. 44, 337–360. doi:10.1017/S0022377800015221

CrossRef Full Text | Google Scholar

Priest, E. R., and Schrijver, C. J. (2000). Aspects of three-dimensional magnetic reconnection. Dordrecht, Netherlands: Springer, 1–24. doi:10.1007/978-94-017-3429-5_1

CrossRef Full Text | Google Scholar

Pritchett, P. L., and Coroniti, F. V. (2010). A kinetic ballooning/interchange instability in the magnetotail. J. Geophys. Res. 115, A06301. doi:10.1029/2009JA014752

CrossRef Full Text | Google Scholar

Pritchett, P. L., and Coroniti, F. V. (2011). Plasma sheet disruption by interchange-generated flow intrusions. Geophys. Res. Lett. 38. doi:10.1029/2011GL047527

CrossRef Full Text | Google Scholar

Pritchett, P. L., and Coroniti, F. V. (2013). Structure and consequences of the kinetic ballooning/interchange instability in the magnetotail. J. Geophys. Res. 118, 146–159. doi:10.1029/2012JA018143

CrossRef Full Text | Google Scholar

Retinò, A., Cattaneo, B., Marcucci, M., Vaivads, A., André, M., Khotyaintsev, Y., et al. (2005). Cluster multispacecraft observations at the high-latitude duskside magnetopause: Implications for continuous and component magnetic reconnection. Ann. Geophys. 23, 461–473. doi:10.5194/angeo-23-461-2005

CrossRef Full Text | Google Scholar

Roytershteyn, V., Daughton, W., Karimabadi, H., and Mozer, F. S. (2012). Influence of the lower-hybrid drift instability on magnetic reconnection in asymmetric configurations. Phys. Rev. Lett. 108, 185001. doi:10.1103/PhysRevLett.108.185001

PubMed Abstract | CrossRef Full Text | Google Scholar

Runov, A., Grandin, M., Palmroth, M., Battarbee, M., Ganse, U., Hietala, H., et al. (2021). Ion distribution functions in magnetotail reconnection: Global hybrid-vlasov simulation results. Ann. Geophys. 39, 599–612. doi:10.5194/angeo-39-599-2021

CrossRef Full Text | Google Scholar

Russell, C., Mellott, M., Smith, E., and King, J. (1983). Multiple spacecraft observations of interplanetary shocks: Four spacecraft determination of shock normals. J. Geophys. Res. 88, 4739–4748. doi:10.1029/JA088iA06p04739

CrossRef Full Text | Google Scholar

Schlichting, H. (1979). Boundary layer theory. McGraw-Hill.

Google Scholar

Scudder, J., and Daughton, W. (2008). Illuminating” electron diffusion regions of collisionless magnetic reconnection using electron agyrotropy. J. Geophys. Res. Space Phys. 113. doi:10.1029/2008JA013035

CrossRef Full Text | Google Scholar

Semenov, V., Korovinskiy, D., Divin, A., Erkaev, N., and Biernat, H. (2009). Collisionless magnetic reconnection: Analytical model and PIC simulation comparison. Ann. Geophys. 27, 905–911. doi:10.5194/angeo-27-905-2009

CrossRef Full Text | Google Scholar

Shafranov, V. (1966). Plasma equilibrium in a magnetic field. Rev. Plasma Phys. 2, 103.

Google Scholar

Shay, M. A., Drake, J. F., and Swisdak, M. (2007). Two-scale structure of the electron dissipation region during collisionless magnetic reconnection. Phys. Rev. Lett. 99, 155002. doi:10.1103/PhysRevLett.99.155002

PubMed Abstract | CrossRef Full Text | Google Scholar

Sonnerup, B. Ö., and Guo, M. (1996). Magnetopause transects. Geophys. Res. Lett. 23, 3679–3682. doi:10.1029/96GL03573

CrossRef Full Text | Google Scholar

Sonnerup, B. Ö., Hasegawa, H., Denton, R. E., and Nakamura, T. K. M. (2016). Reconstruction of the electron diffusion region. J. Geophys. Res. Space Phys. 121, 4279–4290. doi:10.1002/2016JA022430

CrossRef Full Text | Google Scholar

Sonnerup, B. Ö. (1979). Magnetic field reconnection. Sol. Sys. Plasma Phys. 3, 45–108.

Google Scholar

Sonnerup, B. Ö. (1974). Magnetopause reconnection rate. J. Geophys. Res. 79, 1546–1549. doi:10.1029/JA079i010p01546

CrossRef Full Text | Google Scholar

Sonnerup, B. U. (1970). Magnetic-field re-connexion in a highly conducting incompressible fluid. J. Plasm. Phys. 4, 161–174. doi:10.1017/S0022377800004888

CrossRef Full Text | Google Scholar

Sorathia, K., Merkin, V., Panov, E., Zhang, B., Lyon, J., Garretson, J., et al. (2020). Ballooning-interchange instability in the near-Earth plasma sheet and auroral beads: Global magnetospheric modeling at the limit of the MHD approximation. Geophys. Res. Lett. 47, e2020GL088227. doi:10.1029/2020GL088227

PubMed Abstract | CrossRef Full Text | Google Scholar

Sweet, P. (1958). “The neutral point theory of solar flares,” in Symposium-international astronomical union (Cambridge University Press), 6, 123–134. doi:10.1017/S0074180900237704

CrossRef Full Text | Google Scholar

Swisdak, M. (2016). Quantifying gyrotropy in magnetic reconnection. Geophys. Res. Lett. 43, 43–49. doi:10.1002/2015GL066980

CrossRef Full Text | Google Scholar

Tenfjord, P., Hesse, M., Norgren, C., Spinnangr, S. F., and Kolstø, H. (2019). The impact of oxygen on the reconnection rate. Geophys. Res. Lett. 46, 6195–6203. doi:10.1029/2019GL082175

CrossRef Full Text | Google Scholar

Toledo-Redondo, S., André, M., Khotyaintsev, Y. V., Lavraud, B., Vaivads, A., Graham, D. B., et al. (2017). Energy budget and mechanisms of cold ion heating in asymmetric magnetic reconnection. J. Geophys. Res. Space Phys. 122, 9396–9413. doi:10.1002/2017JA024553

CrossRef Full Text | Google Scholar

Toledo-Redondo, S., Dargent, J., Aunai, N., Lavraud, B., André, M., Li, W., et al. (2018). Perpendicular current reduction caused by cold ions of ionospheric origin in magnetic reconnection at the magnetopause: Particle-in-cell simulations and spacecraft observations. Geophys. Res. Lett. 45, 10–033. doi:10.1029/2018GL079051

CrossRef Full Text | Google Scholar

Torbert, R., Burch, J., Phan, T., Hesse, M., Argall, M., Shuster, J., et al. (2018). Electron-scale dynamics of the diffusion region during symmetric magnetic reconnection in space. Science 362, 1391–1395. doi:10.1126/science.aat2998

PubMed Abstract | CrossRef Full Text | Google Scholar

Uzdensky, D. A., and Kulsrud, R. M. (2006). Physical origin of the quadrupole out-of-plane magnetic field in Hall-magnetohydrodynamic reconnection. Phys. Plasmas 13, 062305. doi:10.1063/1.2209627

CrossRef Full Text | Google Scholar

Vasyliunas, V. M. (1975). Theoretical models of magnetic field line merging. Rev. Geophys. 13, 303–336. doi:10.1029/RG013i001p00303

CrossRef Full Text | Google Scholar

Wang, S., Chen, L.-J., Bessho, N., Hesse, M., Yoo, J., Yamada, M., et al. (2018). Energy conversion and partition in the asymmetric reconnection diffusion region. J. Geophys. Res. Space Phys. 123, 8185–8205. doi:10.1029/2018JA025519

CrossRef Full Text | Google Scholar

Xiao, C., Wang, X., Pu, Z., Zhao, H., Wang, J., Ma, Z., et al. (2006). In situ evidence for the structure of the magnetic null in a 3D reconnection event in the Earth’s magnetotail. Nat. Phys. 2, 478–483. doi:10.1038/nphys342

CrossRef Full Text | Google Scholar

Yamada, M., Kulsrud, R., and Ji, H. (2010). Magnetic reconnection. Magn. Reconnect. Rev. Mod. Phys. 82, 603–664. doi:10.1103/RevModPhys.82.603

CrossRef Full Text | Google Scholar

Yokoyama, T., and Shibata, K. (1994). What is the condition for fast magnetic reconnection? Astrophys. J. 436, L197–L200. doi:10.1086/187666

CrossRef Full Text | Google Scholar

Zaitsev, I., Divin, A., Semenov, V., Kubyshkin, I., Korovinskiy, D., Deca, J., et al. (2021). Cold ion energization at separatrices during magnetic reconnection. Phys. Plasmas 28, 032104. doi:10.1063/5.0008118

CrossRef Full Text | Google Scholar

Zeiler, A., Biskamp, D., Drake, J., Rogers, B., Shay, M., and Scholer, M. (2002). Three-dimensional particle simulations of collisionless magnetic reconnection. J. Geophys. Res. Space Phys. 107, 1230. SMP–6. doi:10.1029/2001JA000287

CrossRef Full Text | Google Scholar

Zhou, M., Deng, X., Zhong, Z., Pang, Y., Tang, R., El-Alaoui, M., et al. (2019a). Observations of an electron diffusion region in symmetric reconnection with weak guide field. Astrophys. J. 870, 34. doi:10.3847/1538-4357/aaf16f

CrossRef Full Text | Google Scholar

Zhou, M., Man, H., Zhong, Z., Deng, X., Pang, Y., Huang, S., et al. (2019b). Sub-ion-scale dynamics of the ion diffusion region in the magnetotail: MMS observations. J. Geophys. Res. Space Phys. 124, 7898–7911. doi:10.1029/2019JA026817

CrossRef Full Text | Google Scholar