Statistical investigation on equatorial pitch angle distribution of energetic electrons in Earth’s outer radiation belt during CME- and CIR-driven storms

We present a statistical investigation (September 2012 - September 2017) of pitch angle distribution (PAD) of energetic electrons (∼30 keV - 1 MeV) in the outer radiation belt (L ≥ 3) during CME- and CIR-driven geomagnetic storms using Van Allen Probe measurements. We selected geomagnetic storms based on minimum of SYM-H being less than -50 nT and classified the storms according to their drivers. Thus, we obtained 23 CME- and 24 CIR-driven storms. During the storm intervals, pitch angle resolved electron flux measurements are obtained from the MagEIS instrument on-board Van Allen Probe-A spacecraft. We assume symmetric pitch angle distributions around 90° pitch angle and fit the observed PADs with Legendre polynomials after propagating them to the magnetic equator. Legendre coefficients c₂ and c₄, and the ratio R = |c₂/c₄| are used to categorize the different PAD types. To resolve the spatio-temporal distribution of PADs, these coefficients are binned in 5 L-shell bins, 12 MLT bins for seven energy channels and four storm phases. We found that several hundreds of keV electrons exhibit clear dependence on local time, storm phases and storm drivers, with increased anisotropy for CME-driven storms during main and early recovery phases. On the contrary, we found that tens of keV electrons do not exhibit significant dependence on these parameters. We have discussed the different physical mechanisms responsible for the observed MLT dependent PADs and found drift-shell splitting to be the major contributor.

Introduction

The earth’s radiation belt electron dynamics is highly complex, resulting from a delicate competition between different acceleration, transport and loss mechanisms (e.g., Friedel et al. (2005)). The acceleration mechanism is mostly driven by inward radial diffusion of radiation belt electrons from higher to lower radial distances, or local wave-particle interactions with various magnetospheric waves, or a combination of the two (e.g., Schulz and Lanzerotti (1974); Southwood and Kivelson (1981); Elkington et al. (2003); Horne et al. (2003); Baker and Kanekal (2008); Ukhorskiy et al. (2009); Zong et al. (2009); Thorne (2010); Claudepierre et al. (2013); Reeves et al. (2013); Ma et al. (2015); Boyd et al. (2016); Zong et al. (2017)). Interplanetary (IP) shocks generating strong electric field impulse can also cause rapid energization of radiation belt electrons within a time scale of few minutes (e.g., Foster et al. (2015); Kanekal et al. (2016)). The loss mechanism is driven by pitch-angle scattering of electrons and subsequent atmospheric precipitation led by wave-particle interactions (e.g., Thorne (1977); Rodger et al. (2007); Reidy et al. (2021)), or magnetopause shadowing caused by sudden magnetospheric compression (e.g., Yu et al. (2013); Staples et al. (2020); Cohen et al. (2021)), or a combination of both (e.g., Summers and Thorne (2003); Bortnik et al. (2006); Shprits et al. (2006); Ukhorskiy et al. (2006); Turner et al. (2012); Blum et al. (2015); Shprits et al. (2017)). The relativistic electron dynamics also show strong dependence on several factors, such as, geomagnetic activity, solar wind driving conditions, spatial location, local time, and background magnetospheric conditions (e.g., Li et al. (1997); Reeves et al. (1998, 2003); Meredith et al. (2003); Lee et al. (2013); Ni et al. (2013); Thorne et al. (2013b,a); Baker et al. (2013, 2014b,a)). To comprehensively understand the underlying physical processes responsible for the complex radiation belt electron dynamics, an useful approach is to investigate the evolution of electron pitch angle distribution (PAD). This is because electrons of different energies at different pitch angles respond differently to the external influences (e.g., Chakraborty et al. (2021)) and therefore, PADs can provide important information on the source and loss processes in a specific region.

There are several types of PADs for electrons in the outer radiation belt. The simplest of them is the isotropic distribution, which is usually observed in the midnight MLT sector at geosynchronous (GEO) orbit for substorm-injected electrons having energy in the range of few tens to hundreds of keV (Asnes et al., 2005). Some other commonly observed outer radiation belt electron PADs are the pancake distribution, butterfly distribution and flat top distribution. The pancake distribution is the most prevalent type of PAD for outer radiation belt electrons. This type of PAD is mostly found on the dayside and is identified by electron flux maximum at 90° pitch angle (e.g., West et al. (1973); Gannon et al. (2007)). The mechanisms that have been attributed to the formation of this type of PAD are pitch angle diffusion caused by wave-particle interaction and inward radial diffusion (Schulz and Lanzerotti (1974); Summers et al. (1998); Horne et al. (2003); Xiao et al. (2009b,a, 2012, 2014); Thorne et al. (2013c)). The butterfly PAD is generally observed at nightside at larger L-shells and is characterized by lower electron fluxes at 90° pitch angle compared to field-aligned directions. This type of distribution, at larger L-shells, is mostly attributed to drift-shell splitting of electrons in an asymmetric magnetic field (e.g., Sibeck et al. (1987); Selesnick and Blake (2002)), while at lower L-shells, past studies have shown that wave-particle interactions with chorus and/or magnetosonic waves can generate this type of PAD (e.g., Horne et al. (2005); Li et al. (2016)). The flat top PAD is generally observed at dawn and dusk local times at larger L-shells and has almost similar electron fluxes spread over a wide pitch angle range around 90° pitch angle. Wave-particle interaction is believed to generate this type of PAD and it is considered to be an intermediate distribution between the pancake and butterfly PADs (e.g., Horne et al. (2003); Zhao et al. (2017)).

Past studies have shown that radiation belt electron equatorial pitch angle distributions exhibit an energy dependence. Most of the equatorial PADs of 1–10s of keV electrons in the outer radiation belt are pancake shaped (e.g., Zhao et al. (2020)). On the contrary, for hundreds of keV to few MeV electrons, pancake PADs are prevalent on the dayside of both the outer and inner magnetosphere, while butterfly PADs are prevalent on the nightside magnetosphere over extended radial distances (e.g., West et al. (1973); Gannon et al. (2007); Ni et al. (2015); Pandya et al. (2020)). The electron PADs have also been found to depend on geomagnetic activity, L-shell and magnetic local time (MLT) (e.g., Shi et al. (2016)). During geomagnetic disturbed periods, the anisotropy of electron PADs have been found to increase: pancake PADs become more 90°-peaked. This has mostly been attributed to chorus acceleration for regions outside the plasmasphere and electromagnetic ion cyclotron (EMIC) wave scattering for regions inside the plasmasphere (e.g., Ni et al. (2015)). However, butterfly PADs do not exhibit strong correlation with solar wind parameters, specifically, solar wind dynamic pressure (Ni et al., 2016).

In recent years, several studies have examined the statistical relationship between energetic particle equatorial pitch angle distributions, different phases of geomagnetic storms, and solar wind drivers using Van Allen Probe observations. Ni et al. (2015) used 15 months of electron flux measurements from the Relativistic Electron Proton Telescope (REPT) instrument onboard the Van Allen Probes to study the storm time evolution of PADs of ultra-relativistic ($>$ 2 MeV) electrons. They used sinusoidal functions of the form sinⁿ(α) to fit the observed pitch angle distribution, and used the sine power n to indicate pitch angle anisotropy. The results from Ni et al. (2015) showed that n increases with geomagnetic activity, suggesting increased pitch angle anisotropy during storm main phase. Pandya et al. (2020) used 5 years of Van Allen Probe REPT measurements to study the variation of pitch angle distribution of relativistic electrons (1.8–6.3 MeV) during different phases of 55 geomagnetic storms driven by different solar wind drivers, namely, coronal mass ejections (CMEs) and corotating interacting regions (CIRs). Using the same sinusoidal fitting method, Pandya et al. (2020) found the PADs to exhibit strong dependence on MLT at higher L-shell (L ≈ 5), while at lower L-shells (L ≈ 3), the electron PADs are found to be less affected by geomagnetic activity and storm phase. Although, they couldn’t find any significant dependence of the relativistic electron PADs on the storm drivers (27 CMEs and 28 CIRs). Greeley et al. (2021) studied the energization and isotropization of the same outer radiation belt relativistic and ultra-relativistic electron population (1.8–7.7 MeV) using REPT measurements and sinusoidal fitting methods during storms driven by CMEs and CIRs. They found that electron PADs are, in general, more anisotropic for CME-driven storms compared to CIR-driven storms. Also, the PADs of higher energy electrons are more anisotropic than lower energy electrons, and the anisotropy peaks within a day of DST_min. The isotropization of electron PADs were also found to have faster rates for CME-driven storms than CIR-driven storms. Smirnov et al. (2022) used Van Allen Probe Magnetic Electron Ion Spectrometer (MagEIS) instrument measurements to examine equatorial PADs of electrons in the energy range 30 keV - 1.6 MeV during 129 geomagnetic storms in the entire Van Allen Probe era (2012–2019). They used sinusoidal functions to fit the observed PADs for day and night MLT sectors. Smirnov et al. (2022) found that on the dayside, the distributions are mainly pancake which become more 90° peaked during the storm main phase, and this anisotropy increases with electron energy. They also found butterfly PADs to be more prevalent on the nightside at higher L-shells during geomagnetic quiet conditions, that spread to lower L-shells during enhanced geomagnetic activity.

The previous studies discussed above, although, provide a comprehensive picture of the storm-time evolution of electron PADs in the outer radiation belt, the effect of storm drivers (CMEs/CIRs) on the electron population having energies in the range of few tens to several hundreds of keV has not yet been investigated. Therefore, in this study, using 5 years (September 2012 to September 2017) of energetic electron flux (∼30 keV to ∼1 MeV) measurements from the MagEIS instrument on board the Van Allen Probe-A spacecraft, we have extensively examined the evolution of equatorial PADs in the outer radiation belt (L ≥ 3) as a function of L-shell, MLT and electron kinetic energy during different phases of 23 CME- and 24 CIR-driven geomagnetic storms. The measured electron PADs have been propagated to the magnetic equator and 5-min averages have been calculated. To fit the equatorial PADs, a Legendre polynomial form has been adopted following the method used by Chen et al. (2014); Zhao et al. (2018, 2020), and the coefficients of Legendre polynomials are binned in radial distance (L), local time (MLT) and electron kinetic energy. The coefficients give us information about the electron PAD type and hence, the binned coefficients are plotted on L-MLT polar maps to study the characteristics of equatorial PADs during different phases of geomagnetic storms. The underlying physical mechanisms responsible for the observed PAD types have also been examined.

This paper is organized as follows: in Data and event selection, data used in this study and the event selection criteria are provided; in Methodology, the data analysis methodology is discussed; in Results, the statistical results are presented; in Discussion and conclusion, the possible physical mechanisms are discussed; and finally, in Summary, we provide our concluding remarks.

Data and event selection

The Magnetic Electron Ion Spectrometer (MagEIS) instrument of Energetic Particle, Composition, and Thermal Plasma Suite (ECT; Spence et al. (2013)) on board the Van Allen Probes flying near the equatorial plane (Mauk et al., 2013) provides high resolution electron flux measurements over an energy range of $\sim 30$ keV to 4 MeV (Blake et al., 2013; Spence et al., 2013). In this study, we have used the pitch angle resolved Level 3 MagEIS data from Probe A measurements during the period September 2012 to September 2017 at seven specific energy channels (33 keV, 80 keV, 143 keV, 226 keV, 346 keV, 597 keV, and 909 keV) binned to 11 pitch angles (8.19°, 24.55°, 40.91°, 57.27°, 73.64°, 90°, 106.36°, 122.73°, 139.09°, 155.45°, and 171.82°). Measurements from Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS; Kletzing et al. (2013)) on board the Van Allen Probe - A spacecraft are also used to investigate the chorus and ULF (ultra-low frequency) wave activity during this period. The EMFISIS wave instruments collect survey measurements of the wave electric and magnetic fields during half-second collection periods every 6 s over 65 logarithmically spaced frequency intervals between ∼1 Hz to ∼12 kHz. EMFISIS is also equipped with a fluxgate magnetometer (FGM) that measures the magnetic field with a sampling rate of 64 vectors/sec. In this study, we have used the FGM data that provides magnetic field with 1 s resolution. The key solar wind parameters and geomagnetic indices are procured from the OMNIWEB data service with 1 min resolution.

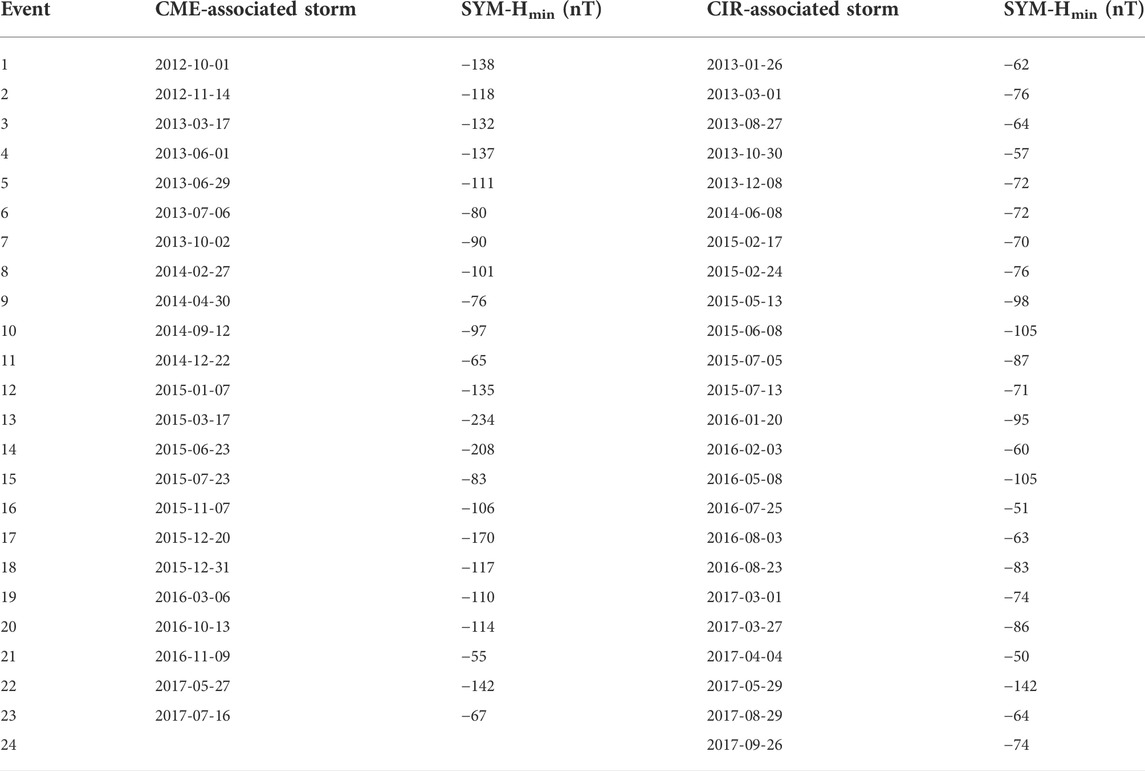
To study the effects of storm drivers on the evolution of radiation belt electron PADs, we created a 5 year period database of geomagnetic storms from September 2012 to September 2017. To create the database, we selected storms such that the minimum SYM-H index was less than -50 nT and classified them according to their drivers, namely coronal mass ejections (CMEs) and corotating interacting regions (CIRs), the details of which are listed in Table 1. The list of storms in Table 1 consists of storms presented in Pandya et al. (2019) and other new storms to complete the 5 year period database. In addition, as our aim is to study the evolution of PADs during different phases of geomagnetic storms driven by different solar wind drivers, we also ensured that the selected storms are isolated events. The new ICME events identified in this work are supported by the event list published by Cane and Richardson (http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm), and the new CIR events are consistent with the list of SIR/HSS events during 1995–2017 published by M. Grandin, A. T. Aikio, and A. Kozlovsky (Grandin et al., 2019). After the storms are selected and classified, they are divided into different storm phases, defined as: main phase - the duration starting from the time when SYM-H index begins to monotonically decrease to when SYM-H reaches its minimum value; pre-storm phase - a period of 10 h prior to the main phase; early recovery phase - a period of 10 h after the main phase; and late recovery phase - a period of 10 h after the early recovery phase.

TABLE 1

TABLE 1. List of CME- and CIR-driven geomagnetic storms.

Methodology

To study the distribution of energetic electron PADs, the PADs need to be quantified. In the past, different models have been used to quantify PADs. Out of them, the most commonly used are PAD models of the form sinⁿ(α), where n is the anisotropy index and α is the pitch angle (e.g., Garcia (1996); Vampola (1997)); and empirical models using the method of Legendre polynomial fitting (e.g., Chen et al. (2014); Zhao et al. (2018, 2020)). The problem with fitting models having the form of sinⁿ(α) is that they can not represent butterfly PADs, whereas a complete set of Legendre polynomials can represent any form of PADs (Chen et al., 2014; Zhao et al., 2018, 2020). This makes Legendre polynomial fitting models better candidates to study electron PADs in the radiation belt. Chen et al. (2014), taking measurements from CRRES, Polar and LANL-GEO satellites and using the method of Legendre polynomial fitting developed an empirical model of relativistic electrons (∼ 150 keV to 1.5 MeV) in the outer radiation belt. Later, Zhao et al. (2018) developed an empirical model of electron PADs in the slot region and inner radiation belt as a function of L-shell, MLT, electron energy and geomagnetic activity using 4 years of Van Allen Probe measurements and Legendre polynomials. Most recently, Zhao et al. (2020) using 7 years of data from Van Allen Probes HOPE instrument and Legendre polynomial fitting of observed PADs examined the equatorial PADs of 1–50 keV electrons in the inner magnetosphere. In this study, we have adapted the same method of Legendre polynomial fitting as described in Chen et al. (2014) and Zhao et al. (2018, 2020) to investigate the effect of storm drivers on the statistical properties of equatorial electron PADs in the outer radiation belt. Although the methodology adapted in this study is the same as mentioned in the previous works, the main focus of this study is to explore any characteristic differences in the PADs of outer radiation belt electrons spanning an energy range from tens of keV to MeV during storms driven by different storm drivers.

Towards that goal, the steps followed in this study can be described as: (1) We selected the electron flux data when Van Allen Probe-A was close to the magnetic equator with the absolute value of magnetic latitude (MLAT) less than 10°. This ensured that we have equatorial PADs with a wide pitch angle coverage. (2) The measured electron PADs are propagated to the magnetic equator using T89D (Tsyganenko, 1989) magnetic field model. The selection of electron flux data when the Van Allen Probe-A was within ±10° MLAT also assured that there is no large data gap near 90° pitch angle after propagating the observed local electron flux data to the magnetic equator. (3) 5-min averages of equatorial PADs are calculated from the ∼ 10.8 s resolution data, assuming symmetric PADs around 90° pitch angle. (4) The measured 5-minute-averaged equatorial PADs are then fitted by Legendre polynomials and represented by a set of normalized Legendre coefficients (c_n). For a more comprehensive description of the Legendre polynomials and coefficients, the readers are encouraged to read the methodology sections of Chen et al. (2014); Zhao et al. (2018, 2020). In this study, we have included only those PADs that are well fitted by Legendre polynomials with a root-mean-square-deviation (RMSD) $<$ 0.1.

Figure 1 shows examples of Legendre polynomial fitting results of the three most prevalent PAD types in the outer radiation belt: (a) pancake, (b) flat top and (c) butterfly. The fitting results are shown by blue curves and the measured equatorial PADs are shown by red filled circles. The sets of first six normalized Legendre coefficients c₁ − c₆ representing the different PAD types are shown at the top of each panel. Although a complete set of Legendre polynomials should be used to represent a PAD, in statistical studies, it is reasonable to retain only a handful of coefficients (Zhao et al., 2018). Chen et al. (2014) demonstrated that electron PADs in the outer radiation belt can be well categorized by Legendre polynomials up to the sixth order and therefore, in this study, we have used normalized Legendre coefficients up to c₆ to represent the measured PADs. Further, as we are considering symmetric PADs around 90° pitch angle, we have taken the odd order Legendre coefficients, i.e., c₁, c₃, and c₅ as zero. Therefore, c₂, c₄ and c₆ become the only three fitting parameters for representing the equatorial PADs. Chen et al. (2014) also showed that as n increases, the value of c_n becomes significantly small and therefore, different pairs of the first two even order Legendre coefficients (c₂, c₄) can be directly read for categorizing PAD types. In this study, our discussions will thus include only c₂ and c₄. Pancake PADs have negative and larger c₂ values and smaller values of |c₄| (Figure 1A), flat top PADs have usually comparable values of c₂ and c₄ (Figure 1B), and butterfly PADs have negative and larger c₄ values and smaller/comparable values of c₂ (Figure 1C). Therefore, if we take ratio of the two coefficients, say R = $|\frac{c_2}{c_4}|$, then for pancake PADs, R will be greater than one; for flattop PADs, R will be comparable to one; and for butterfly PADs, R will be less than 1. Thus, the values of R can be used to directly identify the PAD types. To resolve the spatial and temporal distribution of PADs, the coefficients c₂ and c₄, and the parameter R are binned in L with bin width 0.8 L (5 bins from L = 3 to L = 7), MLT with bin width 2 h (12 bins), electron energy E (7 energy channels) and storm phases (4 storm phases). Then, medians of the coefficients (c₂, c₄) and R in each (L, MLT, E, and storm phase) bin are derived, based on which the characteristics of ∼30 keV to 1 MeV electron equatorial PADs in the outer radiation belt are presented. Further, to ensure that we have enough number of data points in each L-MLT bin for statistical evaluation, we considered only those bins that have at least 40 data points. This is because bins with few number of data points may falsely appear as MLT variation. Supplementary Figure S2 in the supporting document shows the distribution of data points in each L-MLT bin. Supplementary Figure S3 shows the distribution of the parameter R without excluding any bin to highlight the randomness of such distribution if we include bins with few number of data points.

FIGURE 1

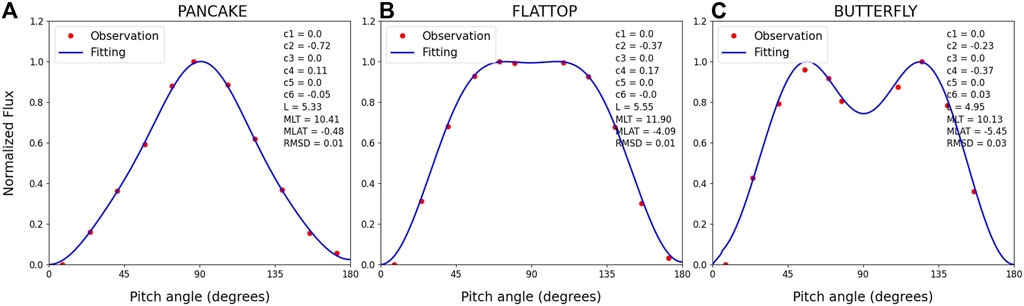
FIGURE 1. Examples of (A) pancake, (B) flattop and (C) butterfly pitch angle distributions. The red filled circles are normalized electron flux of 143 keV electrons measured by MagEIS instrument on-board the Van Allen Probe-A spacecraft (propagated to the magnetic equator and averaged in 5 min assuming symmetric distribution around 90° pitch angle), and blue curves show the Legendre polynomial fitting results. The first six Legendre coefficients (c₁− c₆), RMSD and magnetic ephemeris information (L, MLT, MLAT) are provided in each panel.

To investigate the possible role of wave-particle interactions in driving the different PAD shapes, we examined the statistical properties of whistler mode chorus and Pc5 mode ULF waves during the period of our study. To identify the chorus waves having typical frequencies in the range 0.05–0.8 f_ce, where f_ce is the equatorial electron gyrofrequency, we used the criteria as described in Bingham et al. (2019), such as the Van Allen Probe-A is outside the plasmasphere, and the waves have planarity $>$ 0.6 and ellipticity $>$ 0.7. After identifying the chorus waves, the wave amplitudes are binned in (L, MLT, and storm phase) as defined earlier. To visualize the excitation of the waves, we defined an excitation factor (F) as the ratio of the chorus wave power in each individual (L, MLT, and storm phase) bin to the background chorus wave power. For background chorus wave power, we considered the minimum chorus wave power during the pre-storm phase. Finally, superposed epoch analyses (SEA) is performed to derive the median of the parameter F, based on which the role of chorus waves in outer radiation belt electron dynamics is discussed.

To study the statistical distribution of Pc5 mode ULF waves in the outer radiation belt, 1 s resolution magnetic field data from the fluxgate magnetometer of EMFISIS on board the Van Allen Probe-A spacecraft for the region L ≥ 3 are first projected on a mean-field aligned coordinate system to separate ULF field variations along directions both perpendicular and parallel to the magnetic field Takahashi et al. (1990). In this coordinate system, the mean field is defined as the 400 s running average of the magnetic field vector ⟨B⟩. The individual components are defined as: (1) parallel component $\widehat{e_z}=⟨\mathbf{B}⟩/|⟨\mathbf{B}⟩$; (2) azimuthal component $\widehat{e_y}=⟨\mathbf{B}⟩\times \mathbf{r}$, where r is the position vector of the spacecraft with respect to the earth’s center; and (3) radial component $\widehat{e_x}=\widehat{e_y}\times \widehat{e_z}$. The magnetic field components are defined as: radial (poloidal) component $B_x=\mathbf{B}\cdot \widehat{e_x}$ which is pointing radially outward; azimuthal (toroidal) component $B_y=\mathbf{B}\cdot \widehat{e_y}$ which is positive eastward; and parallel (compressional) component B_z = |B| − |⟨ B⟩|, which is pointing along the magnetic field. Once the observed magnetic field has been resolved into its three directional components, a low-pass Butterworth filter with cut-off frequency of 10 mHz is applied to obtain wavelet power spectra covering the Pc5 frequency range (typically 2–7 mHz) Balasis et al. (2013). For wavelet analysis, we used Morlet mother wavelet function with ω₀ = 6, as Morlet wavelet in the range ω₀ = 5–10 provides high time resolution that is ideal for the study of ULF waves in the Pc4-5 range Balasis et al. (2013). This provided us with ULF wave power in the Pc5 frequency range for the three magnetic field components. We then manually identified and eliminated false wave events for each individual storm. Finally, SEA is performed to derive median Pc5 ULF wave power, based on which, the role of ULF waves in the outer radiation belt PAD is investigated.

Results

Using the methodology as described in Methodology, here we present the statistical results of radiation belt electron PADs as a function of L-shell, MLT and electron energy E during different phases of CME- and CIR-driven geomagnetic storms.

Figure 2 shows the L-MLT distribution of the medians of c₂ (left panel) and c₄ (right panel) at seven specific energy channels (from top to bottom: 33 keV, 80 keV, 143 keV, 226 keV, 346 keV, 597 and 909 keV) during pre-storm, main, early recovery and late recovery phase of CME-driven geomagnetic storms. For each plot, the Earth is at the centre and the Sun is to the left. MLT = 12 is indicated in the leftmost column, and the concentric circles denote L values from L = 1 to 7 with L-width of 2 R_E. The colorbar denotes the c₂ and c₄ values spanning a range from -1 to 1. From Figure 2, we can see that the coefficients c₂ and c₄ exhibit dependence on electron energy, storm phase, L-shell and MLT. We can also see that these coefficients exhibit opposite variations, the combined (c₂, c₄) values being consistent with those defined in Methodology. To understand these features explicitly, first, if we increase the electron energy during a particular storm phase, we can find that the distributions of c₂ and c₄ are different in different energy channels. As an example, during the pre-storm phase, we can see that in the low energy channels, c₂ values are, in general, negative at all L-shell and MLT, while in the higher energy channels, a clear day-night asymmetry can be seen: c₂ values are mostly negative on the dayside and positive on the nightside outside L = 4. The parameter c₄, on the other hand, at lower energy channels, is mostly positive inside L = 4 and near zero to slightly negative outside L = 4. At higher energies, at lower L-shells, c₄ is mostly near-zero, while at higher L-shell and nightside, it exhibits negative values. Second, keeping the energy fixed, if we compare the distribution of c₂ and c₄ during different storm phases, we can find the coefficients to show clear storm phase dependence, particularly in the medium and high energy channels. For example, during the pre-storm phase, c₂ (c₄) values of 597 keV electrons are mostly negative (near-zero) on the dayside and slightly positive (slightly negative) on the nightside outside L = 4. During the main phase, c₂ (c₄) values become mostly negative (positive) on the dayside and positive (negative) on the nightside. During the early recovery phase, the day-night asymmetry further increases. In the late recovery phase, the day-night asymmetry still persists, but the values become less intense, indicating reduced anisotropy. These examples also highlight the L-shell and MLT dependence that itself varies with electron energy and storm phase.

FIGURE 2

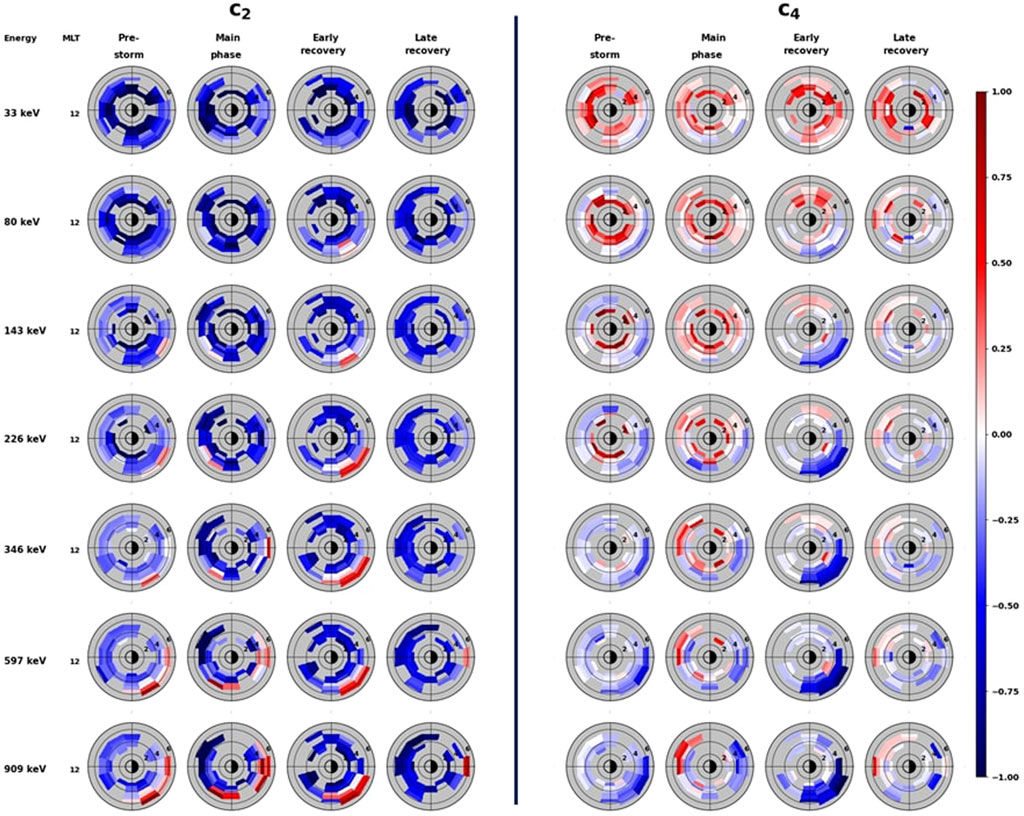
FIGURE 2. The distribution of coefficients c₂ (left panel) and c₄ (right panel) in a respective L-MLT bin during coronal mass ejection (CME) driven geomagnetic storms at seven specific energy channels, from top to bottom: 33 keV, 80 keV, 143 keV, 226 keV, 346 keV, 597 keV, and 909 keV. The columns correspond to different storm phases. MLT = 12 is indicated in the leftmost column and the concentric circles denote L values from L = 1 to 7 with L-width of 2 R_E. For each panel, the Earth is at the centre and the Sun is to the left. The colorbar represents the corresponding c₂ and c₄ values.

Figure 3 shows L-MLT distribution of the medians of c₂ and c₄ values for CIR-driven geomagnetic storms in the same manner as in Figure 2. Similar to CME-driven storms, the coefficients c₂ and c₄ exhibit energy dependence, L-shell dependence, day-night asymmetry and storm phase variations. The overall features of the variations in c₂ and c₄ are found to be common for both the storm drivers (CMEs/CIRs), the only difference being in the values of the coefficients, particularly in the higher energy channels. For CME-driven storms, the c₄ values in the energy range 597–909 keV are close to ∼ -1 for L $>$ 3 and MLT ≈18–4 during early recovery phase, whereas for CIR-driven storms, c₄ values are in the range -0.25 to -0.75 for L $>$ 4 and MLT ≈16–2. This indicates slightly higher anisotropy in c₄ values for CME-driven storms compared to CIR-driven storms. One can also see that for CIR-driven storms, in the energy range 597–909 keV, c₂ values are close to ∼ 1 for L $>$ 5 and MLT ≈16–4 during the main phase, whereas for CME-driven storms, c₂ values are comparably smaller (∼ 0.75).

FIGURE 3

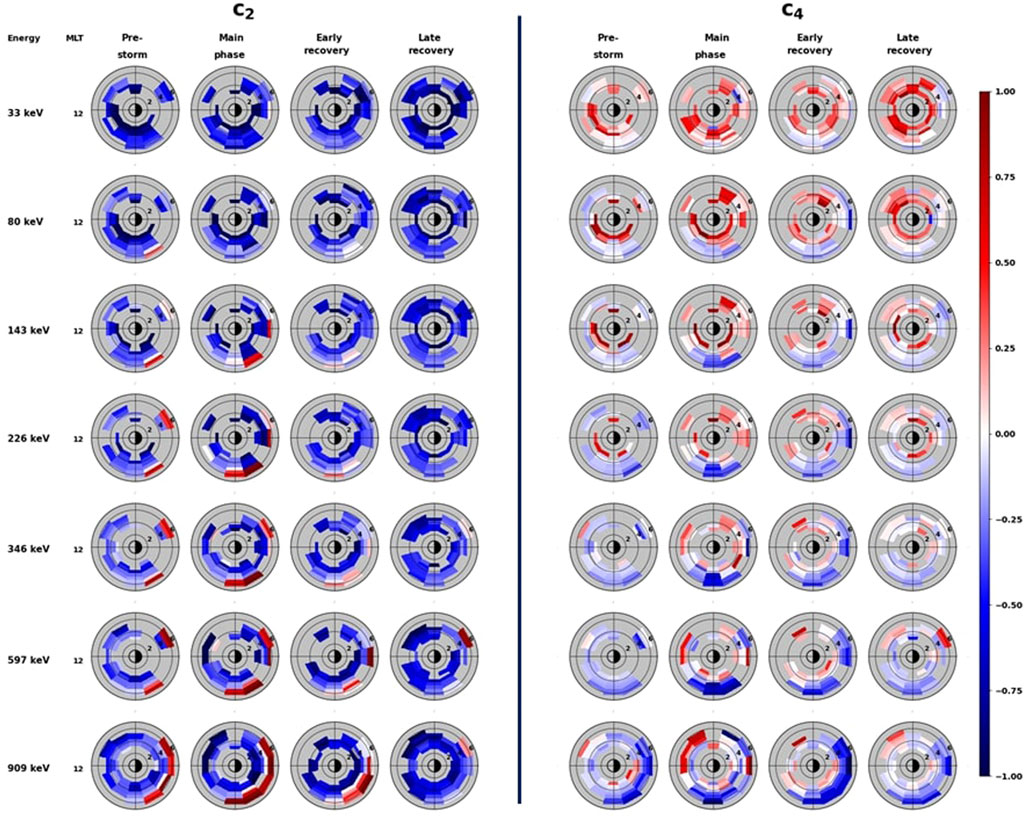
FIGURE 3. Same as in Figure 2 but during corotating interacting region (CIR) driven geomagnetic storms.

Figure 4 shows L-MLT distribution of the medians of the ratio R = |c₂/c₄| for CME-driven (left panel) and CIR-driven (right panel) geomagnetic storms. As defined in Methodology, pancake PADs have R $>$ 1, flattop PADs have R ≈ 1 and butterfly PADs have R $<$ 1. From the colorbar on the right, we can see that R $>$ 1 values are denoted by red to deep red, R ≈ 1 values are denoted by slight red to slight blue, and R $<$ 1 values are denoted by blue to deep blue. These R values are used to identify the different PAD shapes. While identifying the different PAD shapes, we have excluded the single bins that exhibit random values as they might be manifestations of statistical bias and falsely indicate MLT variations. We mostly concentrate on the overall distribution and several intriguing features are revealed from Figure 4:

1. In the low energy channels (33–80 keV), the fitting results suggest that majority of PAD fits have values of R $>$ 1 during all the four storm phases and both the storm drivers (CMEs/CIRs). This indicates that majority of tens of keV electrons in the outer radiation belt exhibit pancake PADs. This is in agreement with the results of Zhao et al. (2020): using observations from the HOPE instrument on board the Van Allen Probes and the same Legendre polynomial fitting technique, they showed that most of the tens of keV electron equatorial PADs in the inner magnetosphere during geomagnetically quiet (Kp ≤ 1+), moderate (1+ $<$ Kp ≤ 3+), and active times (Kp $>$ 3+) are pancake PADs.

2. In the medium energy channels (143–226 keV), for CME-driven storms, during the pre-storm and main phase, R values are $>$ 1; during the early recovery phase, a day-night asymmetry in R values can be seen: R $>$ 1 at the dayside and R ∼ 1 or slightly $<$ 1 at the nightside; and during the late recovery phase, R values again become mostly greater than 1. This indicates that during the pre-storm and main phase, majority of few 100s of keV electrons exhibit pancake PADs; during the early recovery phase, they exhibit pancake PADs at the dayside and flattop PADs at the nightside; and during the late recovery phase, the PADs again become mostly pancake shaped. Just as the combination of c₂ and c₄, and hence R provides information about the PAD shapes, changes in their values give an estimation of the pitch angle anisotropy. Higher values of R suggest higher anisotropy. From Figure 4, it can be seen that during the early and late recovery phases, R values are significantly larger which suggest greater pitch angle anisotropy during these storm phases. For CIR-driven storms, the fitting results suggest that during the pre-storm phase, R values are $>$ 1; during the main phase, R values ∼ 1 or slightly $<$ 1 can be seen at ∼ 18 MLT and ∼ 2 to 5 MLT; and during the early and late recovery phases, R values again become $>$ 1. This indicates that during the pre-storm and recovery phases, the PADs are mostly pancake, while during the main phase, flattop PADs can be seen at around the dusk and dawn MLT sectors. R values are also higher during the early and late recovery phases, suggesting enhanced anisotropy.

3. In the high energy channels (346–909 keV), for CME-driven storms, during the pre-storm phase, fitting results show that most of the dayside PAD fits have values of R $>$ 1 while the nightside PAD fits have values of R ∼ 1 or slightly $<$ 1; during the main phase, R values are mostly greater than 1; during the early recovery phase, R values are largely $>$ 1 at the dayside and $<$ 1 at the nightside; and during the late recovery phase, R values at the dayside are still greater than 1, while a few patches of R values ∼ 1 can be seen at the nightside for regions outside L ≈ 4. This indicates that during the pre-storm phase, several 100s of keV electrons exhibit pancake PADs at the dayside and flattop/butterfly PADs at the nightside; during the main phase, the electron PAD shapes are mostly pancake; during the early recovery phase, the PADs at the dayside are pancake shaped while those at the nightside are butterfly shaped; and in the late recovery phase, electrons at the dayside exhibit pancake PADs while those at the nightside exhibit flattop PADs outside L ≈ 4 and pancake PADs inside L ≈ 4. The ratio R also exhibits larger values during early and late recovery phases indicating increased anisotropy. For CIR-driven storms, the distribution of PADs during the different storm phases follows, in general, the same trend as for CME-driven storms, although the day-night asymmetry is less prominent: during the early recovery phase, R values are $>$ 1 at the dayside and mostly ∼ 1 with few bins of R values slightly less than 1 at the nightside. However, the anisotropy is high during the late recovery phase as evident from larger values of R. Also, during the late recovery phase, R values ∼ 1 or $<$ 1 are confined to regions L $>$ 6 on the nightside, indicating that flattop/butterfly PADs are found outside L = 6 while pancake PADs are found inside L = 6.

FIGURE 4

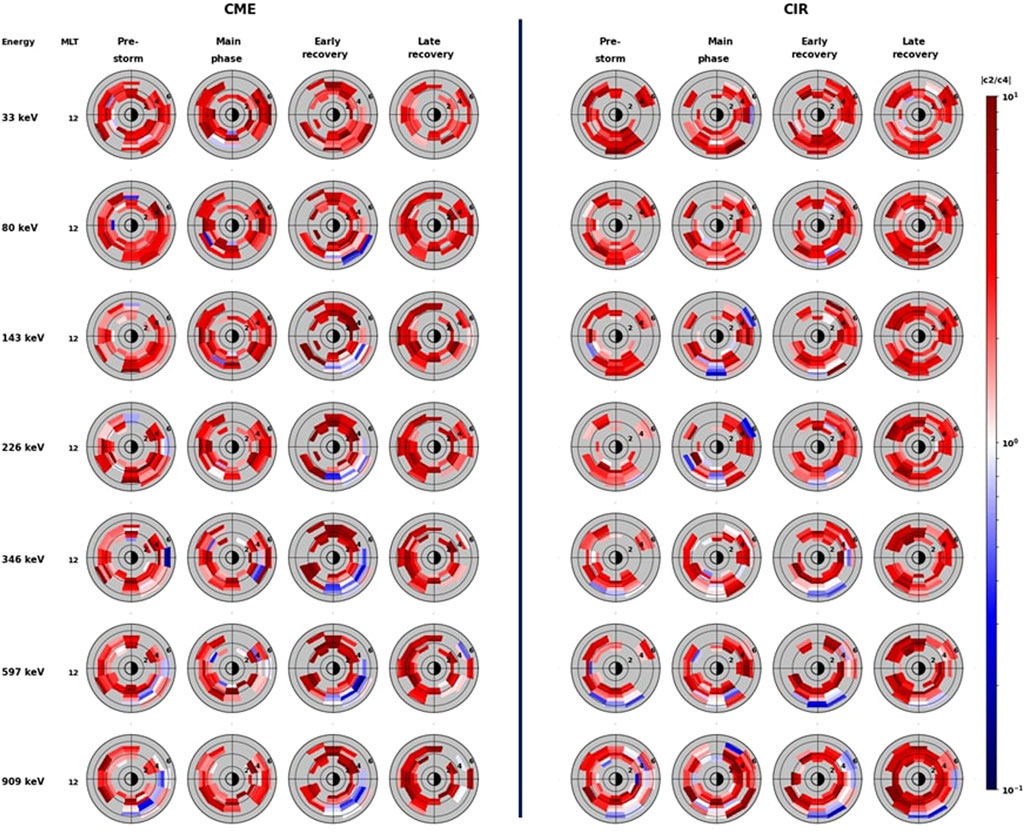
FIGURE 4. Comparison of the ratio R = |c₂/c₄| between CME-driven (left panel) and CIR-driven (right panel) geomagnetic storms. R is plotted in the same manner as in Figure 2, 3.

Discussion and conclusion

The statistical results presented above suggest that there is a dependence of equatorial PADs on electron energy, geomagnetic activity, and spatial location, both radial (L-shell dependence) and azimuthal (MLT dependence). The equatorial PADs of few tens of keV electrons are pancake shaped during all the four phases of geomagnetic storms, although the distributions have higher anisotropy (higher R values) during the main and early recovery phases. For electrons having energy in the range of few to several hundreds of keV, the dayside PADs are mostly pancake shaped while butterfly PADs can be seen at night at higher L-shells. The anisotropy of PADs is also found to increase with geomagnetic activity. All of these results are in good agreement with the previous studies (see e.g., Ni et al. (2015, 2016); Pandya et al. (2020); Zhao et al. (2018, 2020); Greeley et al. (2021); Smirnov et al. (2022)). However, in addition, our results also show prominent influence of storm drivers (CMEs/CIRs) on the PADs of outer radiation belt electrons, especially in the medium (143–226 keV) and high (346–909 keV) energy channels. In general, the pitch angle distributions are found to be more anisotropic for CME-driven storms compared to CIR-driven storms during the storm main and/or early recovery phase.

The dependence of equatorial electron PADs on electron energy and geomagnetic activity has been extensively studied in the past and discussed in details in several papers (e.g., Sibeck et al. (1987); Selesnick and Blake (2002); Korth et al. (1999); Califf et al. (2014, 2017); Zhao et al. (2017, 2018, 2020)). The energy dependence of electron PADs has been attributed to the difference in radial flux gradients of electrons having different energies (see e.g., Zhao et al. (2020) and references therein). The dependence on geomagnetic activity has been explained to happen mostly due to the deformed magnetic field configurations, enhanced wave-particle interactions or/and changes in the electron radial flux gradients during geomagnetic disturbed times (see e.g., Zhao et al. (2018) and references therein). In the discussions that will follow, we will mainly focus on finding a possible explanation for the observed MLT dependence of electron pitch angle distributions.

The MLT dependence of electron PADS are especially found at higher energies and during the storm main phase and/or the early recovery phase. As an example, for CME-driven storms, for 909 keV electrons in the early recovery phase, butterfly PADs can be seen between L ≈ 5 to 6 and MLT ≈18 to 3, while pancake PADs can be seen at all other MLTs and L-shells (Figure 4). One of the possible mechanism for such MLT dependence is enhanced drift-shell splitting caused by stretched geomagnetic fields during active times. Different processes can cause drift shell splitting, the y-component of the interplanetary magnetic field being one of the potential candidates. The IMF By-component exerts a torque on the magnetosphere, and in response, oppositely directed azimuthal flows occur in the dayside cusp. These azimuthal flows imply that open flux tubes are added asymmetrically to the tail lobes. For IMF By $>$ 0, flux tubes are preferentially added to the dawn side and for IMF By $<$ 0, flux tubes are preferentially added to the dusk side (Cowley, 1981). This results in an asymmetrical stretching of the geomagnetic field lines and can result in a day-night asymmetry in the pitch angle distribution of higher energy electrons. For the lower energy electrons, drift shell splitting can not generate butterfly PADs as they have positive radial flux gradients at larger L-shells (Zhao et al., 2018, 2020). This is the reason why tens of keV electrons exhibit pancake PADs at all L-shells and MLTs for different storm phases and both the storm drivers (Figure 4).

Other processes that can contribute to geomagnetic field line stretching and drift-shell splitting are magnetic depressions near the equator driven by injection of hot ions during magnetic disturbances due to the diamagnetic effect (e.g., Lyons (1977); Ebihara et al. (2008)); and changes in magnetic field B_z component near the equator (termed as magnetic dip or bz dip) during substorms (e.g., He et al. (2017); Xiong et al. (2017, 2019)). Past studies have reported that magnetic depressions by 50% or more during the storm main phase can produce nightside butterfly PADs, while 20% decrease in magnetic field B_z component can also contribute to these PADs (He et al. (2017); Xia et al. (2017); Xiong et al. (2017)). Xiong et al. (2019) statistically investigated the global distribution of magnetic dip related butterfly PADs of 466 keV and 2.1 MeV electrons using 6 years of Van Allen Probe measurements from 2012 to 2018. They found that the magnetic dip related butterfly PADs are confined mostly in the duskside to midnight sector within 4.5 $<$ L $<$ 6. In our case, we also found butterfly PADs in the high energy channels (346–909 keV) confined in the nightside MLT sector for regions outside L = 4.5. This is consistent with the findings of Xiong et al. (2019), and thus, suggests that the nightside butterfly PADs may have been formed by substorm induced magnetic dips.

Apart from field line stretching and drift shell splitting, some past studies have reported contribution of local wave-particle interactions in the generation of different pitch angle distributions in different MLT sectors. Interaction with chorus and/or magnetosonic waves are known to generate butterfly PADs (e.g., Xiao et al. (2014); Yue et al. (2016)), while drift-resonance of ULF waves with 90° pitch angle electrons can lead to the formation of characteristic pancake PADs (e.g., Xiao et al. (2009b,a, 2012, 2014); Thorne et al. (2013b)). Therefore, in this study, we statistically investigated any possible role of chorus and ULF waves in the observed MLT-dependence of PADs. In Figure 5A, we have shown the chorus wave excitation factor F (as defined in Methodology) during all the four storm phases and both the storm drivers. We find that during the early recovery phase of CME-driven storms, chorus wave power increases by almost two orders of magnitude above the background level between MLT = 20 and 10. For CIR-driven storms, during the early recovery phase, the increase in chorus wave power is relatively less intense. This region of enhanced chorus wave power coincides with the region of observed butterfly PADs, and therefore, it suggests that enhanced chorus wave activity might have contributed to the formation of butterfly PADs. In Figure 5B, we have shown the ULF wave power in Pc5 frequency range (2–7 mHz) for three magnetic field components, and during the four storm phases for both the storm drivers. We can see that during the main and early recovery phase of geomagnetic storms driven by both the storm drivers, the ULF wave power increases by almost two orders of magnitude above the pre-storm level, with slightly higher intensity for CME-driven storms than CIR-driven storms. We can also see that the enhancement in ULF wave power is mostly in the post-noon to pre-midnight sector. These observations suggest that Pc5 mode ULF waves might have played a role in the formation of pancake PADs. The results also highlight the difference in PADs between the two storm drivers: both chorus and ULF waves are comparably more intense during CME-driven storms, which might have resulted in the higher anisotropy of both pancake and butterfly PADs (higher R values, Figure 4) during CMEs than CIRs.

FIGURE 5

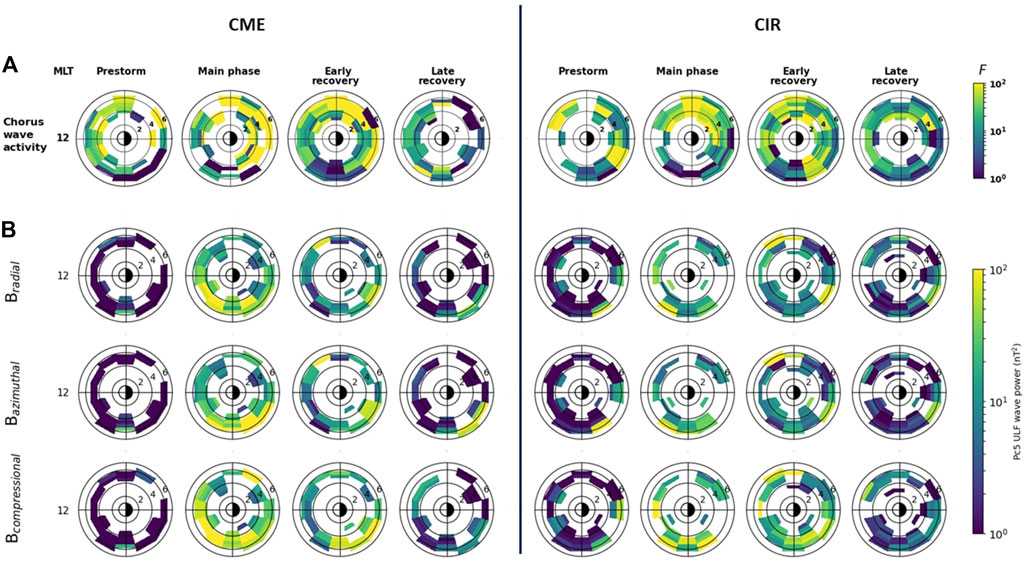
FIGURE 5. (A) L-MLT distribution of average integrated chorus wave excitation factor F during the four storm phases for coronal mass ejection (CME; left panels) and corotating interacting region (CIR; right panels) driven geomagnetic storms in the same manner as in Figures 2–4. The colorbar shows the excitation factor F in logarithmic scale (B) L-MLT distribution of ULF waves covering the Pc5 frequency range (2–7 mHz) for the three magnetic field components (radial, azimuthal and compressional) during the four phases of geomagnetic storms driven by CMEs (left panel) and CIRs (right panel). The colorbar at the right represents Pc5 ULF wave power.

From the statistical results of both the electron pitch angle and magnetospheric wave distribution discussed above, although the regions of wave power enhancements during geomagnetic disturbed periods seem to coincide well with the corresponding PAD types, wave-particle interactions resulting the observed MLT dependent PADs does not seem to be a viable explanation. This is because, the MLT dependence is mostly observed at higher energies. An electron with energy 1 MeV at L = 5 will have a drift period of approximately 15 min. Therefore, to create such MLT-dependence, the local processes have to act faster than this drift period. Also, even if such local wave-particle interactions create a particular PAD type, the same distribution will be observed at all other MLTs. Another possibility is that the local processes have to act simultaneously on the electrons to create different PADs at different MLT sectors. As an example, if the dayside processes make pancake PADs, then the dusk processes will have to change them to butterfly before the electrons drift to the night. Thus, based on these arguments, it seems that the magnetic field line stretching during geomagnetic disturbed times and drift-shell splitting resulted in the observed MLT dependent equatorial electron PADs.

Summary

The major findings from this study can be summarized as follows:

1. Tens of keV (33–80 keV) electrons exhibit mostly pancake PADs at all local times, and do not exhibit significant dependence on storm phases and storm drivers (CMEs/CIRs).

2. Few hundreds of keV (143–226 keV) electrons exhibit clear storm phase and storm driver dependence. For CME-driven storms during the prestorm and main phase, electrons have mostly pancake PADs; during the early recovery phase, the dayside PADs are pancake while nightside PADs are flattop; and during the late recovery phase, PADs again become mostly pancake shaped. For CIR-driven storms, the PADs during pre-storm and recovery phases are mostly pancake, while during the main phase, flattop PADs can be seen at around dusk and dawn, with enhanced anisotropy during the early and late recovery phases.

3. Several hundreds of keV (346–909 keV) electrons exhibit mostly pancake PADs on the dayside and butterfly PADs on the nightside, and show clear dependence on storm phases and storm drivers: for CME-driven storms during the pre-storm phase, these electrons exhibit pancake PADs on the dayside and flattop/butterfly PADs on the nightside; during the main phase, most of the PADs are pancake shaped; during the early recovery phase, they exhibit pancake PADs at the dayside and butterfly PADs at the nightside; and during the late recovery phase, they exhibit pancake PADs at the dayside and flattop PADs at the nightside at higher L-shells. For CIR-driven storms, which are overall less intensive than CME-driven storms, although the overall distribution remains almost similar to those during CME-driven storms, the PADs are less anisotropic (lower R values) compared to CME-driven storms during the main and recovery phases.

4. Magnetic field line stretching and drift-shell splitting during disturbed times resulted in the MLT dependent PAD of 346–909 keV electrons.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://cdaweb.gsfc.nasa.gov/cgi-bin/eval2.cgi, http://emfisis.physics.uiowa.edu/Flight/, http://www.rbsp-ect.lanl.gov/data_pub/, http://www.space.umn.edu/rbspefw-data/.

Author contributions

SC did all the analyses and wrote the paper under the supervision of DC. IJR helped in understanding the role of ULF waves in driving pitch angle anisotropy in the radiation belts. GDR helped in the interpretation and presentation of the results. DNB provided valuable comments on the paper.

Funding

SC is supported in part by STFC Grant ST/V006320/1 and NERC Grants NE/V002554/2 and NE/P017185/2, and in part by the Department of Space, Government of India. DC is supported by the Department of Space, Government of India. IJR is supported in part by STFC Grant ST/V006320/1 and NERC Grants NE/V002554/2 and NE/P017185/2.

Acknowledgments

The interplanetary parameters and geomagnetic indices are obtained from the website (https://cdaweb.gsfc.nasa.gov/cgi-bin/eval2.cgi). The Van Allen Probe data used in this study are available at the websites (http://emfisis.physics.uiowa.edu/Flight/for EMFISIS, http://www.rbsp-ect.lanl.gov/data-pub/for ECT, and http://www.space.umn.edu/rbspefw-data/for EFW). The authors thank all of the MagEIS and EMFISIS teams of the Van Allen Probe for the data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.986061/full#supplementary-material

References

Asnes, A., Friedel, R. W., Stadsnes, J., Thomsen, M., Østgaard, N., and Cayton, T. (2005). Statistical pitch angle properties of substorm-injected electron clouds and their relation to dawnside energetic electron precipitation. J. Geophys. Res. 110, A05207. doi:10.1029/2004JA010838

CrossRef Full Text | Google Scholar

Baker, D., and Kanekal, S. (2008). Solar cycle changes, geomagnetic variations, and energetic particle properties in the inner magnetosphere. J. Atmos. Solar-Terrestrial Phys. 70, 195–206. doi:10.1016/j.jastp.2007.08.031

CrossRef Full Text | Google Scholar

Baker, D. N., Jaynes, A. N., Hoxie, V. C., Thorne, R. M., Foster, J. C., Li, X., et al. (2014a). An impenetrable barrier to ultrarelativistic electrons in the Van Allen radiation belts. Nature 515, 531–534. doi:10.1038/nature13956

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N., Jaynes, A. N., Li, X., Henderson, M. G., Kanekal, S. G., Reeves, G. D., et al. (2014b). Gradual diffusion and punctuated phase space density enhancements of highly relativistic electrons: Van Allen Probes observations. Geophys. Res. Lett. 41, 1351–1358. doi:10.1002/2013GL058942

CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., Hoxie, V. C., Henderson, M. G., Li, X., Spence, H. E., et al. (2013). A long-lived relativistic electron storage ring embedded in Earth’s outer van allen belt. Science 340, 186–190. doi:10.1126/science.1233518

PubMed Abstract | CrossRef Full Text | Google Scholar

Balasis, G., Daglis, I. A., Georgiou, M., Papadimitriou, C., and Haagmans, R. (2013). Magnetospheric ULF wave studies in the frame of swarm mission: A time-frequency analysis tool for automated detection of pulsations in magnetic and electric field observations. Earth Planets Space 65, 1385–1398. doi:10.5047/eps.2013.10.003

CrossRef Full Text | Google Scholar

Bingham, S. T., Mouikis, C. G., Kistler, L. M., Paulson, K. W., Farrugia, C. J., Huang, C. L., et al. (2019). The storm time development of source electrons and chorus wave activity during CME- and CIR-driven storms. JGR. Space Phys. 124, 6438–6452. doi:10.1029/2019JA026689

CrossRef Full Text | Google Scholar

Blake, J. B., Carranza, P. A., Claudepierre, S. G., Clemmons, J. H., Crain, W. R., Dotan, Y., et al. (2013). The magnetic electron ion spectrometer (MagEIS) instruments aboard the radiation belt storm probes (RBSP) spacecraft. Space Sci. Rev. 179, 383–421. doi:10.1007/s11214-013-9991-8

CrossRef Full Text | Google Scholar

Blum, L. W., Halford, A., Millan, R., Bonnell, J. W., Goldstein, J., Usanova, M., et al. (2015). Observations of coincident EMIC wave activity and duskside energetic electron precipitation on 18–19 January 2013. Geophys. Res. Lett. 42, 5727–5735. doi:10.1002/2015GL065245

CrossRef Full Text | Google Scholar

Bortnik, J., Thorne, R. M., O’Brien, T. P., Green, J. C., Strangeway, R. J., Shprits, Y. Y., et al. (2006). Observation of two distinct, rapid loss mechanisms during the 20 November 2003 radiation belt dropout event. J. Geophys. Res. 111, A12216. doi:10.1029/2006JA011802

CrossRef Full Text | Google Scholar

Boyd, A. J., Spence, H. E., Huang, C.-L., Reeves, G. D., Baker, D. N., Turner, D. L., et al. (2016). Statistical properties of the radiation belt seed population. J. Geophys. Res. Space Phys. 121, 7636–7646. doi:10.1002/2016JA022652

CrossRef Full Text | Google Scholar

Califf, S., Li, X., Blum, L., Jaynes, A., Schiller, Q., Zhao, H., et al. (2014). THEMIS measurements of quasi-static electric fields in the inner magnetosphere. JGR. Space Phys. 119, 9939–9951. doi:10.1002/2014JA020360

CrossRef Full Text | Google Scholar

Califf, S., Li, X., Zhao, H., Kellerman, A., Sarris, T. E., Jaynes, A., et al. (2017). The role of the convection electric field in filling the slot region between the inner and outer radiation belts. JGR. Space Phys. 122, 2051–2068. doi:10.1002/2016JA023657

CrossRef Full Text | Google Scholar

Chakraborty, S., Chakrabarty, D., Reeves, G. D., Baker, D. N., Claudepierre, S. G., Breneman, A. W., et al. (2021). Van allen probe observations of disappearance, recovery and patchiness of plasmaspheric hiss following two consecutive interplanetary shocks: First results. JGR. Space Phys. 126. doi:10.1029/2020JA028873

CrossRef Full Text | Google Scholar

Chen, Y., Friedel, R. H. W., Henderson, M. G., Claudepierre, S. G., Morley, S. K., and Spence, H. E. (2014). Repad: An empirical model of pitch angle distributions for energetic electrons in the Earth’s outer radiation belt. J. Geophys. Res. Space Phys. 119, 1693–1708. doi:10.1002/2013JA019431

CrossRef Full Text | Google Scholar

Claudepierre, S. G., Mann, I. R., Takahashi, K., Fennell, J. F., Hudson, M. K., Blake, J. B., et al. (2013). Van Allen Probes observation of localized drift resonance between poloidal mode ultra-low frequency waves and 60 keV electrons. Geophys. Res. Lett. 40, 4491–4497. doi:10.1002/grl.50901

CrossRef Full Text | Google Scholar

Cohen, I. J., Turner, D. L., Michael, A. T., Sorathia, K. A., and Ukhorskiy, A. Y. (2021). Investigating the link between outer radiation belt losses and energetic electron escape at the magnetopause: A case study using multi-mission observations and simulations. JGR. Space Phys. 126. doi:10.1029/2021JA029261

CrossRef Full Text | Google Scholar

Cowley, S. (1981). Magnetospheric asymmetries associated with the y-component of the IMF. Planet. Space Sci. 29, 79–96. doi:10.1016/0032-0633(81)90141-0

CrossRef Full Text | Google Scholar

Ebihara, Y., Fok, M.-C., Blake, J. B., and Fennell, J. F. (2008). Magnetic coupling of the ring current and the radiation belt. J. Geophys. Res. 113. doi:10.1029/2008JA013267

CrossRef Full Text | Google Scholar

Elkington, S. R., Hudson, M. K., and Chan, A. A. (2003). Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. J. Geophys. Res. 108, 1116. doi:10.1029/2001JA009202

CrossRef Full Text | Google Scholar

Foster, J. C., Wygant, J. R., Hudson, M. K., Boyd, A. J., Baker, D. N., Erickson, P. J., et al. (2015). Shock-induced prompt relativistic electron acceleration in the inner magnetosphere. J. Geophys. Res. Space Phys. 120, 1661–1674. doi:10.1002/2014JA020642

CrossRef Full Text | Google Scholar

Friedel, R. H. W., Bourdarie, S., and Cayton, T. E. (2005). Intercalibration of magnetospheric energetic electron data. Space weather. 3. doi:10.1029/2005SW000153

CrossRef Full Text | Google Scholar

Gannon, J. L., Li, X., and Heynderickx, D. (2007). Pitch angle distribution analysis of radiation belt electrons based on Combined Release and Radiation Effects Satellite Medium Electrons A data. J. Geophys. Res. 112. doi:10.1029/2005JA011565

CrossRef Full Text | Google Scholar

Garcia, H. (1996). Energetic electron pitch angle distribution parameters at 6.6Re, as deduced from GOES X-ray observations. Planet. Space Sci. 44, 473–484. doi:10.1016/0032-0633(95)00144-1

CrossRef Full Text | Google Scholar

Grandin, M., Aikio, A. T., and Kozlovsky, A. (2019). Properties and geoeffectiveness of solar wind high-speed streams and stream interaction regions during solar cycles 23 and 24. J. Geophys. Res. Space Phys. 124, 3871–3892. doi:10.1029/2018JA026396

CrossRef Full Text | Google Scholar

Greeley, A. D., Kanekal, S. G., Sibeck, D. G., Schiller, Q., and Baker, D. N. (2021). Evolution of pitch angle distributions of relativistic electrons during geomagnetic storms: Van allen probes observations. J. Geophys. Res. Space Phys. 126. doi:10.1029/2020JA028335

CrossRef Full Text | Google Scholar

He, Z., Chen, L., Zhu, H., Xia, Z., Reeves, G. D., Xiong, Y., et al. (2017). Multiple-satellite observation of magnetic dip event during the substorm on 10 october 2013. Geophys. Res. Lett. 44, 9167–9175. doi:10.1002/2017GL074869

CrossRef Full Text | Google Scholar

Horne, R. B., Meredith, N. P., Thorne, R. M., Heynderickx, D., Iles, R. H. A., and Anderson, R. R. (2003). Evolution of energetic electron pitch angle distributions during storm time electron acceleration to megaelectronvolt energies. J. Geophys. Res. 108, 1016. doi:10.1029/2001JA009165

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Albert, J. M., Meredith, N. P., and Anderson, R. R. (2005). Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. 110, A03225. doi:10.1029/2004JA010811

CrossRef Full Text | Google Scholar

Kanekal, S. G., Baker, D. N., Fennell, J. F., Jones, A., Schiller, Q., Richardson, I. G., et al. (2016). Prompt acceleration of magnetospheric electrons to ultrarelativistic energies by the 17 March 2015 interplanetary shock. J. Geophys. Res. Space Phys. 121, 7622–7635. doi:10.1002/2016JA022596

CrossRef Full Text | Google Scholar

Kletzing, C. A., Kurth, W. S., Acuna, M., MacDowall, R. J., Torbert, R. B., Averkamp, T., et al. (2013). The electric and magnetic field instrument suite and integrated science (EMFISIS) on RBSP. Space Sci. Rev. 179, 127–181. doi:10.1007/s11214-013-9993-6

CrossRef Full Text | Google Scholar

Korth, H., Thomsen, M. F., Borovsky, J. E., and McComas, D. J. (1999). Plasma sheet access to geosynchronous orbit. J. Geophys. Res. 104, 25047–25061. doi:10.1029/1999JA900292

CrossRef Full Text | Google Scholar

Lee, D.-Y., Shin, D.-K., Kim, J.-H., Cho, J.-H., Kim, K.-C., Hwang, J. A., et al. (2013). Long-term loss and re-formation of the outer radiation belt. JGR. Space Phys. 118, 3297–3313. doi:10.1002/jgra.50357

CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., Thorne, R. M., Li, W., Ma, Q., Baker, D. N., et al. (2016). Ultrarelativistic electron butterfly distributions created by parallel acceleration due to magnetosonic waves. JGR. Space Phys. 121, 3212–3222. doi:10.1002/2016JA022370

CrossRef Full Text | Google Scholar

Li, X., Baker, D. N., Temerin, M., Cayton, T. E., Reeves, E. G. D., Christensen, R. A., et al. (1997). Multisatellite observations of the outer zone electron variation during the November 3–4, 1993, magnetic storm. J. Geophys. Res. 102, 14123–14140. doi:10.1029/97JA01101

CrossRef Full Text | Google Scholar

Lyons, L. R. (1977). Adiabatic evolution of trapped particle pitch angle distributions during a storm main phase. J. Geophys. Res. 82, 2428–2432. doi:10.1029/JA082i016p02428

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Thorne, R. M., Ni, B., Kletzing, C. A., Kurth, W. S., et al. (2015). Modeling inward diffusion and slow decay of energetic electrons in the Earth’s outer radiation belt. Geophys. Res. Lett. 42, 987–995. doi:10.1002/2014GL062977

CrossRef Full Text | Google Scholar

Mauk, B. H., Fox, N. J., Kanekal, S. G., Kessel, R. L., Sibeck, D. G., and Ukhorskiy, A. (2013). Science objectives and rationale for the radiation belt storm probes mission. Space Sci. Rev. 179, 3–27. doi:10.1007/s11214-012-9908-y

CrossRef Full Text | Google Scholar

Meredith, N. P., Thorne, R. M., Horne, R. B., Summers, D., Fraser, B. J., and Anderson, R. R. (2003). Statistical analysis of relativistic electron energies for cyclotron resonance with EMIC waves observed on CRRES. J. Geophys. Res. 108, 1250. doi:10.1029/2002JA009700

CrossRef Full Text | Google Scholar

Ni, B., Bortnik, J., Thorne, R. M., Ma, Q., and Chen, L. (2013). Resonant scattering and resultant pitch angle evolution of relativistic electrons by plasmaspheric hiss. JGR. Space Phys. 118, 7740–7751. doi:10.1002/2013JA019260

CrossRef Full Text | Google Scholar

Ni, B., Zou, Z., Gu, X., Zhou, C., Thorne, R. M., Bortnik, J., et al. (2015). Variability of the pitch angle distribution of radiation belt ultrarelativistic electrons during and following intense geomagnetic storms: Van Allen Probes observations. JGR. Space Phys. 120, 4863–4876. doi:10.1002/2015JA021065

CrossRef Full Text | Google Scholar

Ni, B., Zou, Z., Li, X., Bortnik, J., Xie, L., and Gu, X. (2016). Occurrence characteristics of outer zone relativistic electron butterfly distribution: A survey of van allen probes REPT measurements. Geophys. Res. Lett. 43, 5644–5652. doi:10.1002/2016GL069350

CrossRef Full Text | Google Scholar

Pandya, M., Bhaskara, V., Ebihara, Y., Kanekal, S. G., and Baker, D. N. (2020). Evolution of pitch angle-distributed megaelectron volt electrons during each phase of the geomagnetic storm. JGR. Space Phys. 125. doi:10.1029/2019JA027086

CrossRef Full Text | Google Scholar

Reeves, G. D., Baker, D. N., Belian, R. D., Blake, J. B., Cayton, T. E., Fennell, J. F., et al. (1998). The global response of relativistic radiation belt electrons to the January 1997 magnetic cloud. Geophys. Res. Lett. 25, 3265–3268. doi:10.1029/98GL02509

CrossRef Full Text | Google Scholar

Reeves, G. D., McAdams, K. L., Friedel, R. H. W., and O’Brien, T. P. (2003). Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 30. doi:10.1029/2002GL016513

CrossRef Full Text | Google Scholar

Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H. W., Funsten, H. O., et al. (2013). Electron acceleration in the heart of the van allen radiation belts. Science 341, 991–994. doi:10.1126/science.1237743

PubMed Abstract | CrossRef Full Text | Google Scholar

Reidy, J. A., Horne, R. B., Glauert, S. A., Clilverd, M. A., Meredith, N. P., Woodfield, E. E., et al. (2021). Comparing electron precipitation fluxes calculated from pitch angle diffusion coefficients to LEO satellite observations. JGR. Space Phys. 126. doi:10.1029/2020JA028410

CrossRef Full Text | Google Scholar

Rodger, C. J., Clilverd, M. A., Thomson, N. R., Gamble, R. J., Seppälä, A., Turunen, E., et al. (2007). Radiation belt electron precipitation into the atmosphere: Recovery from a geomagnetic storm. J. Geophys. Res. 112. doi:10.1029/2007JA012383

CrossRef Full Text | Google Scholar

Schulz, M., and Lanzerotti, L. (1974). Particle diffusion in the radiation belts. New York: Springer. doi:10.1007/978-3-642-65675-0

CrossRef Full Text | Google Scholar

Selesnick, R. S., and Blake, J. B. (2002). Relativistic electron drift shell splitting. J. Geophys. Res. 107, 1265. doi:10.1029/2001JA009179

CrossRef Full Text | Google Scholar

Shi, R., Summers, D., Ni, B., Fennell, J. F., Blake, J. B., Spence, H. E., et al. (2016). Survey of radiation belt energetic electron pitch angle distributions based on the Van Allen Probes MagEIS measurements. J. Geophys. Res. Space Phys. 121, 1078–1090. doi:10.1002/2015JA021724

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Kellerman, A., Aseev, N., Drozdov, A. Y., and Michaelis, I. (2017). Multi-MeV electron loss in the heart of the radiation belts. Geophys. Res. Lett. 44, 1204–1209. doi:10.1002/2016GL072258

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Thorne, R. M., Friedel, R., Reeves, G. D., Fennell, J., Baker, D. N., et al. (2006). Outward radial diffusion driven by losses at magnetopause. J. Geophys. Res. 111, A11214. doi:10.1029/2006JA011657

CrossRef Full Text | Google Scholar

Sibeck, D. G., McEntire, R. W., Lui, A. T. Y., Lopez, R. E., and Krimigis, S. M. (1987). Magnetic field drift shell splitting: Cause of unusual dayside particle pitch angle distributions during storms and substorms. J. Geophys. Res. 92, 13485–13497. doi:10.1029/JA092iA12p13485

CrossRef Full Text | Google Scholar

Smirnov, A., Shprits, Y., Allison, H., Aseev, N., Drozdov, A., Kollmann, P., et al. (2022). Storm-time evolution of the equatorial electron pitch angle distributions in Earth’s outer radiation belt. Front. Astron. Space Sci. 9. doi:10.3389/fspas.2022.836811

CrossRef Full Text | Google Scholar

Southwood, D. J., and Kivelson, M. G. (1981). Charged particle behavior in low-frequency geomagnetic pulsations 1. transverse waves. J. Geophys. Res. 86, 5643–5655. doi:10.1029/JA086iA07p05643

CrossRef Full Text | Google Scholar

Spence, H. E., Reeves, G. D., Baker, D. N., Blake, J. B., Bolton, M., Bourdarie, S., et al. (2013). Science goals and overview of the radiation belt storm probes (RBSP) energetic particle, composition, and thermal Plasma (ECT) suite on NASA’s van allen probes mission. Space Sci. Rev. 179, 311–336. doi:10.1007/s11214-013-0007-5

CrossRef Full Text | Google Scholar

Staples, F. A., Rae, I. J., Forsyth, C., Smith, A. R. A., Murphy, K. R., Raymer, K. M., et al. (2020). Do statistical models capture the dynamics of the magnetopause during sudden magnetospheric compressions? J. Geophys. Res. Space Phys. 125. doi:10.1029/2019JA027289

CrossRef Full Text | Google Scholar

Summers, D., and Thorne, R. M. (2003). Relativistic electron pitch-angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. J. Geophys. Res. 108, 1143. doi:10.1029/2002JA009489

CrossRef Full Text | Google Scholar

Summers, D., Thorne, R. M., and Xiao, F. (1998). Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. 103, 20487–20500. doi:10.1029/98JA01740

CrossRef Full Text | Google Scholar

Takahashi, K., Mcentire, R. W., Lui, A. T. Y., and Potemra, T. A. (1990). Ion flux oscillations associated with a radially polarized transverse Pc 5 magnetic pulsation. J. Geophys. Res. 95, 3717–3731. doi:10.1029/JA095iA04p03717

CrossRef Full Text | Google Scholar

Thorne, R. M. (1977). Energetic radiation belt electron precipitation: A natural depletion mechanism for stratospheric ozone. Science 195, 287–289. doi:10.1126/science.195.4275.287

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Baker, D. N., et al. (2013a). Evolution and slow decay of an unusual narrow ring of relativistic electrons near L ∼ 3.2 following the September 2012 magnetic storm. Geophys. Res. Lett. 40, 3507–3511. doi:10.1002/grl.50627

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013b). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013c). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt dynamics: The importance of wave-particle interactions. Geophys. Res. Lett. 37. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Tsyganenko, N. (1989). A magnetospheric magnetic field model with a warped tail current sheet. Planet. Space Sci. 37, 5–20. doi:10.1016/0032-0633(89)90066-4

CrossRef Full Text | Google Scholar

Turner, D. L., Sphrits, Y., Hartinger, M., and Angelopoulos, V. (2012). Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nat. Phys. 8, 208–212. doi:10.1038/nphys2185

CrossRef Full Text | Google Scholar

Ukhorskiy, A. Y., Anderson, B. J., Brandt, P. C., and Tsyganenko, N. A. (2006). Storm time evolution of the outer radiation belt: Transport and losses. J. Geophys. Res. 111, A11S03. doi:10.1029/2006JA011690

CrossRef Full Text | Google Scholar

Ukhorskiy, A. Y., Sitnov, M. I., Takahashi, K., and Anderson, B. J. (2009). Radial transport of radiation belt electrons due to stormtime Pc5 waves. Ann. Geophys. 27, 2173–2181. doi:10.5194/angeo-27-2173-2009

CrossRef Full Text | Google Scholar

Vampola, A. (1997). “Outer zone energetic electron environment update,” in Conference on the High Energy Radiation Background in Space. Workshop Record, 128–136. doi:10.1109/CHERBS.1997.660263

CrossRef Full Text | Google Scholar

West, H. I., Buck, R. M., and Walton, J. R. (1973). Electron pitch angle distributions throughout the magnetosphere as observed on Ogo 5. J. Geophys. Res. 78, 1064–1081. doi:10.1029/JA078i007p01064

CrossRef Full Text | Google Scholar

Xia, Z., Chen, L., Zheng, L., and Chan, A. A. (2017). Eigenmode analysis of compressional poloidal modes in a self-consistent magnetic field. JGR. Space Phys. 122 (10369–10), 381. doi:10.1002/2017JA024376

CrossRef Full Text | Google Scholar

Xiao, F., Su, Z., Zheng, H., and Wang, S. (2009a). Modeling of outer radiation belt electrons by multidimensional diffusion process. J. Geophys. Res. 114. doi:10.1029/2008JA013580

CrossRef Full Text | Google Scholar

Xiao, F., Yang, C., He, Z., Su, Z., Zhou, Q., He, Y., et al. (2014). Chorus acceleration of radiation belt relativistic electrons during March 2013 geomagnetic storm. J. Geophys. Res. Space Phys. 119, 3325–3332. doi:10.1002/2014JA019822

CrossRef Full Text | Google Scholar

Xiao, F., Zhang, S., Su, Z., He, Z., and Tang, L. (2012). Rapid acceleration of radiation belt energetic electrons by Z-mode waves. Geophys. Res. Lett. 39. doi:10.1029/2011GL050625

CrossRef Full Text | Google Scholar

Xiao, F., Zong, Q.-G., and Chen, L. (2009b). Pitch-angle distribution evolution of energetic electrons in the inner radiation belt and slot region during the 2003 Halloween storm. J. Geophys. Res. 114. doi:10.1029/2008JA013068

CrossRef Full Text | Google Scholar

Xiong, Y., Chen, L., Xie, L., Fu, S., Xia, Z., and Pu, Z. (2017). Relativistic electron’s butterfly pitch angle distribution modulated by localized background magnetic field perturbation driven by hot ring current ions. Geophys. Res. Lett. 44, 4393–4400. doi:10.1002/2017GL072558

CrossRef Full Text | Google Scholar

Xiong, Y., Xie, L., Fu, S., and Pu, Z. (2019). Statistical study of energetic electron butterfly pitch angle distributions during magnetic dip events. Geophys. Res. Lett. 46, 13621–13629. doi:10.1029/2019GL085091

CrossRef Full Text | Google Scholar

Yu, Y., Koller, J., and Morley, S. K. (2013). Quantifying the effect of magnetopause shadowing on electron radiation belt dropouts. Ann. Geophys. 31, 1929–1939. doi:10.5194/angeo-31-1929-2013

CrossRef Full Text | Google Scholar

Yue, C., An, X., Bortnik, J., Ma, Q., Li, W., Thorne, R. M., et al. (2016). The relationship between the macroscopic state of electrons and the properties of chorus waves observed by the Van Allen Probes. Geophys. Res. Lett. 43, 7804–7812. doi:10.1002/2016GL070084

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Califf, S., Li, X., Jaynes, A. N., Leonard, T., et al. (2017). Van allen probes measurements of energetic particle deep penetration into the low L region (L < 4) during the storm on 8 april 2016. JGR. Space Phys. 122 (12), 140–152. doi:10.1002/2017JA024558

CrossRef Full Text | Google Scholar

Zhao, H., Friedel, R. H. W., Chen, Y., Baker, D. N., Li, X., Malaspina, D. M., et al. (2020). Equatorial pitch angle distributions of 1–50 keV electrons in Earth’s inner magnetosphere: An empirical model based on the van allen probes observations. JGR. Space Phys. 126. doi:10.1029/2020JA028322

CrossRef Full Text | Google Scholar

Zhao, H., Friedel, R. H. W., Chen, Y., Reeves, G. D., Baker, D. N., Li, X., et al. (2018). An empirical model of radiation belt electron pitch angle distributions based on van allen probes measurements. JGR. Space Phys. 123, 3493–3511. doi:10.1029/2018JA025277

CrossRef Full Text | Google Scholar

Zong, Q.-G., Rankin, R., and Zhou, X. (2017). The interaction of ultra-low-frequency pc3-5 waves with charged particles in Earth’s magnetosphere. Rev. Mod. Plasma Phys. 1, 10. doi:10.1007/s41614-017-0011-4

CrossRef Full Text | Google Scholar

Zong, Q.-G., Zhou, X.-Z., Wang, Y. F., Li, X., Song, P., Baker, D. N., et al. (2009). Energetic electron response to ULF waves induced by interplanetary shocks in the outer radiation belt. J. Geophys. Res. 114. doi:10.1029/2009JA014393

CrossRef Full Text | Google Scholar