Interaction of electron acoustic solitons in auroral region for an electron beam plasma system

The propagation of linear and nonlinear electron acoustic waves (EAWs) in an unmagnetized plasma, comprising dynamical inertial electrons, hot (r, q) distributed electrons, warm electron beam, and immobile ions is studied. The linear dispersion relation is investigated for varying beam velocity. The Korteweg-de Vries (KdV) equation for EAWs is derived in the small amplitude limit. Depending on the beam density, temperature and velocity, we get a critical condition for which the quadratic nonlinearity vanishes from the plasma system. For such a condition, the modified Korteweg de Vries (mKdV) equation, with cubic nonlinearity, is derived, which admits both negative and positive potential solitary structures. It is noted that the spectral indices r and q of the generalized (r, q) distribution, the concentration of the cold, hot and the beam electrons, and the temperature ratios, significantly affect the fundamental properties of the propagation and interaction of electron acoustic solitary waves (EASWs). The types of possible overtaking interaction of two mKdV solitons are investigated. The spatial regime for the two soliton interaction is found to vary in accordance with the variation of single soliton for various plasma parameters. The results of present study may be beneficial to comprehend the interaction between two EASWs in laboratory, space and astrophysical plasmas.

1 Introduction

Fried and Gould first predicted the existence of electron acoustic waves (EAWs) while studying the numerical solutions of electrostatic dispersion relation in an unmagnetized, homogeneous plasma (Fried and Gould, 1961). They found the existence of this heavily Landau damped mode besides ion acoustic and Langmuir modes. It was found later on that the presence of cold and hot electrons can make this mode weakly damped (Watanabe and Taniuti, 1977). Tokar and Gary (1984) presented a parametric survey and showed that the existence condition for the electron-acoustic waves is that the hot to cold electron temperature ratio ought to be larger than 10, and that the percentage of the hot electron component ought to be more than 20 percent of the total electron density. The high frequency regime of broad electrostatic noise (BEN) that has been reported in numerous regions of space plasmas like plasma sheet boundary layer (PSBL), inner magnetosphere and geomagnetic tail has been successfully explained in terms of EAWs (Dubouloz et al., 1991; Lakhina et al., 2011; Dillard et al., 2018). Due to its significance with regard to the magnetosphere, the propagation of EAWs has been thoroughly investigated by several researchers in unmagnetized (Dubouloz et al., 1991; Berthomier et al., 2000; Sabry and Omran, 2013) and magnetized plasmas (Mace and Hellberg, 2001; Mamun et al., 2002; Shukla et al., 2004; El-Labany et al., 2012).

There have been observations of drifting electrons along the magnetic field from the solar wind in the upper layer of the Earth’s magnetosphere, generally termed as the electron beam in a two electron temperature population plasma (Lin et al., 1984; Ogilvie et al., 1984; Tokar and Gary, 1984; Pottelette et al., 1990; Dubouloz et al., 1991; Matsumoto et al., 1994; Cattell et al., 1998; Tsurutani et al., 1998; Berthomier et al., 2000; Mace and Hellberg, 2001; Mamun et al., 2002; Shukla et al., 2004; Lakhina et al., 2011; El-Labany et al., 2012; Sabry and Omran, 2013; Dillard et al., 2018), which are surmised to excite EAWs and alter the propagation regimes of the formation of nonlinear structures. The auroral BEN emissions that are frequently encountered in the Earth’s magnetosphere have been shown to correlate strongly with the magnetic field aligned electron beams (Dubouloz et al., 1991). The GEOTAIL observations of the terrestrial auroral zone have revealed that the BEN is composed of nonlinear localized electrostatic solitary waves that are intimately related to the nonlinear dynamics of the electron beam instability (Matsumoto et al., 1994). Electron beams have also been reported to trigger the formation of electrostatic solitary waves in the polar cap boundary layer (PCBL) region (Tsurutani et al., 1998). The Magnetospheric Multiscale (MMS) mission of the terrestrial magnetosphere has indicated that the electrostatic solitary waves in the magnetosheath and magnetopause are most likely be supported by a cold $(\sim 1-20eV)$ field-aligned drifting electron component (Ergun et al., 2016; Holmes et al., 2018). The effects of the electron beam on the propagation of EAWs have been extensively studied in the literature (Lin et al., 1984; Ogilvie et al., 1984; Pottelette et al., 1990; Matsumoto et al., 1994; Cattell et al., 1998; Tsurutani et al., 1998; Berthomier et al., 2000; Mace and Hellberg, 2001; Mamun et al., 2002; Shukla et al., 2004; El-Taibany, 2005; Elwakil et al., 2007; Lakhina et al., 2008; Singh et al., 2011; El-Labany et al., 2012; Ergun et al., 2016; Holmes et al., 2018). The nonlinear dispersive electron acoustic structures in space, in general, can either be compressive or rarefactive and the amplitude of their electric fields are found to have values of a few mV/m in plasma sheet boundary layer to several 100 mV/m in the dayside auroral zone (Pickett et al., 2004).

Many investigations in plasma physics in the past assumed Maxwellian distribution to study the dynamics of constituent charged particles, however, the satellite observations have shown distribution functions that show a significant departure from the Maxwellian distribution especially in space plasmas (Abid et al., 2017). Vasyliunas (1968) was the first scientist to make use of kappa or generalized Lorentzian distribution as an empirical formula to explain various features observed in the satellite data. There is a spectral index κ in this distribution that basically shows the energetic tail of the distribution function from which the Maxwellian distribution is retrieved as κ → ∞. Besides the observations of high energy tails, many satellite missions have observed flat topped electron velocity distributions in the high entropy region behind the terrestrial bow shock and in the magnetotail (Feldman et al., 1983; Masood et al., 2006; Asano et al., 2008; Masood and Schwartz, 2008).

The distribution function comprising flat top and modified tail cannot be described by a single index unlike the Maxwellian, kappa and Cairns distributions. Almost 2 decades ago, Qureshi et al. (2004) devised a double spectral index (r, q) distribution to fit the distribution functions with modified low and high energy behavior. The q-index was used to alter the electron population in the tail of the distribution whereas the r-index was used to give the flat tops at low energies. Since then, the effects of double spectral index (r, q) on the linear and nonlinear propagation of plasma waves have been investigated by a few researchers. Since the successful explanation of terrestrial lion roars employing (r, q) distribution by Qureshi et al. (2014), there has been a substantial literature that highlights importance of using double index (r, q) distribution to explain numerous features observed in space plasmas and also the theoretical exploration of the effects of low and high energy electrons in the distribution function on the linear and nonlinear propagation of waves in plasmas (Shah et al., 2018; Qureshi et al., 2019; Khalid et al., 2020; Naeem et al., 2020; Ullah et al., 2020; Ali et al., 2021; El-Taibany et al., 2021; El-Bedwehy, El-Taibany; Shohaib et al., 2021; Masood et al., 2022; Shohaib et al., 2022).

The standard Korteweg de Vries (KdV) equation involves the quadratic nonlinearity and the balance between nonlinearity and dispersion gives emergence to the solitary wave. The literature is replete with the investigation of KdV equation in a variety of physical situations of interest (Korteweg and Vries, 1895; Kakutani et al., 1968; Jeffrey, 1973; Mamun et al., 1996; Ali et al., 2020). It is well known that in a multi-component plasma, there is a certain critical range of plasma parameters for which the quadratic nonlinearity ceases to exist and one then needs to go to the higher order to obtain physically meaningful solutions. Generally, one obtains the modified Korteweg de Vries (mKdV) equation which contains cubic nonlinearity. Lately, the critical point has also been taken care of and in such a case one obtains Gardner equation which involves both the quadratic and cubic nonlinearities. Many researchers have explored these equations and their versions in the higher dimensions in the recent past (Mannan and Mamun, 2011; Masud et al., 2012; Abdikian et al., 2020; Tamang et al., 2020; Tamang and Saha, 2020; Nawaz et al., 2021; Nawaz et al., 2022).

Multi-soliton solutions are significantly valuable in the context of studying nonlinear wave propagation in real systems and apprehend the properties of interaction of nonlinear waves in physical systems. Solitons maintain their identity after interaction, besides a phase shift, which is important regarding transport of energy and momentum. There are a few methods to comprehend the multi-soliton solutions of nonlinear partial differential equations (nPDEs), such as Bäcklund transform (Miura et al., 1968), Darboux transformation (Matveev and Salle, 1991), inverse scattering transform (Ablowitz et al., 1991), Hirota’s bilinear formalism (Hirota, 1971; Hirota, 2004), etc. Hirota’s method has the advantage that it converts the nPDE to a simple, solvable algebraic equation in terms of the Hirota operators. In Hirota’s formalism, the transformations are used in terms of dependent variable functions for which the perturbation expansions truncate the higher orders to obtain the multi-soliton solutions. Multi-soliton solutions of Korteweg-de Vries (KdV) (Jahangir et al., 2015; Jahangir and Masood, 2020), Kadomtsev Petviashvili (KP) equation (Jahangir et al., 2016), Zakharov Kuznetsov (ZK) equation (Yousaf Khattak et al., 2021) and their variants (Verheest and Hereman, 2019; Nawaz et al., 2021; Nawaz et al., 2022) have been studied in magnetized and unmagnetized plasmas using Hirota’s method.

In this manuscript, we study the single and multi-soliton solutions of EAWs in an unmagnetized, collisionless plasma with cold inertial electrons, (r, q) distributed hot electrons, drifting electron beam and stationary ions. The model is analyzed numerically for the parameters of Viking observations in the auroral region of broadband electrostatic noise (BEN) and compared with the observational data. The layout of the manuscript is given as: Section 2 deals with a physical model for EAWs in a four component plasma. Employing the reductive perturbation technique, we derive the KdV and modified Korteweg-de Vries (mKdV) equations in Section 3, along with the critical condition where quadratic nonlinearity coefficient vanishes. Section 4 presents numerical analysis and discusses the characteristics of electron acoustic solitary waves (EASWs) for parameters of auroral region. Section 5 briefly summarizes main conclusions of the manuscript.

2 Model for electron acoustic waves

We consider an unmagnetized, collisionless plasma comprising cold inertialess electrons (with T_c ≠ 0), (r, q) distributed hot electrons, stationary background ions and warm streaming electron beam. It should be noted at the outset that the words cold and hot electrons are used here to distinguish between the temperatures of the two electron species and cold electrons should not be confused with the standard definition which essentially implies that the thermal velocity of a particular specie is much less than the phase velocity of the wave under consideration. In order to study the propagation of a small but finite amplitude electron acoustic wave (EAW) along x-axis, we use the reductive perturbation technique. The nonlinear properties of EAWs in an unmagnetized plasma are governed by the following continuity and momentum equations, respectively

$\frac{\partial n_j}{\partial t}+\frac{\mathit{\partial }}{\partial x}{n}_j{v}_j=0,(1)$

$\frac{\partial v_j}{\partial t}+v_j\frac{\mathit{\partial }{v}_j}{\partial x}=\frac{e}{m_j}\frac{\mathit{\partial }\varphi }{\partial x}-\frac{1}{m_j{n}_j}\frac{\mathit{\partial }{P}_j}{\partial x},(2)$

for cold and beam electrons, and the Poisson’s equation reads as

$\frac{{\mathit{\partial }}^2\varphi }{\partial x^2}=4\pi e\left(n_h+n_c+n_b-n_{i0}\right),(3)$

Here j = c, b for cold and beam electrons, n_h,c,b are the number densities of hot, cold and beam electrons, v_c,b are the velocities of cold and beam electrons and P_j (≡ n_jT_j) is the adiabatic pressure. We can normalize the above system of equations by scaling the variables in terms of their equilibrium values. Therefore, n_h,c,b are normalized by their corresponding equilibrium densities n_h0, n_c0 and n_b0, respectively, v_c,b are normalized by the acoustic speed $C_e={\left(T_h/\alpha m_e\right)}^{1/2}$, where T_h is the hot electron temperature in energy units and ϕ is the electrostatic potential normalized by T_h/e. The space and time coordinates are scaled by Debye length ${\lambda }_d={\left(T_h/4\pi e^2{n}_{h0}\right)}^{1/2}$and inverse plasma frequency ${\omega }_{pc}={\left(4\pi e^2{n}_{c0}/m_e\right)}^{-1/2}$, respectively. Thus, the set of normalized equations reads as

$\frac{\partial n_j}{\partial t}+\frac{\mathit{\partial }}{\partial x}{n}_j{v}_j=0,(4)$

$\frac{\partial v_j}{\partial t}+v_j\frac{\mathit{\partial }{v}_j}{\partial x}=\alpha \frac{\mathit{\partial }\varphi }{\partial x}-\frac{\alpha {\sigma }_j}{n_j}\frac{\mathit{\partial }{n}_j}{\partial x},(5)$

and

$\frac{{\mathit{\partial }}^2\varphi }{\partial x^2}=\frac{1}{\alpha }{n}_h+n_c+\frac{1}{\beta }{n}_b-\left(1+\frac{1}{\alpha }+\frac{1}{\beta }\right),(6)$

where the ratios are defined as

$\alpha =\frac{n_{h0}}{n_{c0}}\text{,\hspace{0.17em}}\beta =\frac{n_{h0}}{n_{b0}}\text{,\hspace{0.17em}}{\sigma }_c=\frac{T_c}{T_h}\text{\hspace{0.17em}and\hspace{0.17em}}{\sigma }_b=\frac{T_b}{T_h}.(7)$

The inertialess hot electrons, providing the restoring force to EAWs, are governed by the generalized double spectral (r, q) distribution (Qureshi et al., 2004), given as

$f_{\left(r,q\right)}\left(v\right)=A{\left[1+\frac{1}{q-1}{\left(\frac{v^2-2e\varphi /m_e}{B{v}_{th}^2}\right)}^{r+1}\right]}^{-q},(8)$

where

$A=\frac{3\mathrm{\Gamma }\left[q\right]{\left(q-1\right)}^{-3/\left(2+2r\right)}}{4\pi B^{3/2}{v}_{th}^3\mathrm{\Gamma }\left[q-\frac{3}{2+2r}\right]\mathrm{\Gamma }\left[1+\frac{3}{2+2r}\right]},(9)$

and

$B=\frac{3{\left(q-1\right)}^{-1/\left(1+r\right)}\mathrm{\Gamma }\left[q-\frac{3}{2+2r}\right]\mathrm{\Gamma }\left[\frac{3}{2+2r}\right]}{2\mathrm{\Gamma }\left[q-\frac{5}{2+2r}\right]\mathrm{\Gamma }\left[\frac{5}{2+2r}\right]}.(10)$

Here Γ is the gamma function. The normalized number density of generalized (r, q) distributed hot electrons is obtained by integrating over the velocity space

$n_h=1+\sum _{s=1}^{\infty }{\gamma }_s{\varphi }^s,(11)$

where the expansion coefficients γ_s are given as

$\begin{array}{ll}\hfill {\gamma }_1& =\frac{\mathrm{\Gamma }\left[q-\frac{1}{2+2r}\right]\mathrm{\Gamma }\left[\frac{1}{2+2r}\right]{\left(q-1\right)}^{\frac{-1}{1+r}}}{2B\mathrm{\Gamma }\left[\frac{3}{2+2r}\right]\mathrm{\Gamma }\left[q-\frac{3}{2+2r}\right]},\hfill \\ \hfill {\gamma }_2& =\frac{-\mathrm{\Gamma }\left[\frac{-1}{2+2r}\right]\mathrm{\Gamma }\left[q+\frac{1}{2+2r}\right]{\left(q-1\right)}^{\frac{-2}{1+r}}}{8B^2\mathrm{\Gamma }\left[\frac{3}{2+2r}\right]\mathrm{\Gamma }\left[q-\frac{3}{2+2r}\right]},\hfill \\ \hfill {\gamma }_3& =\frac{\mathrm{\Gamma }\left[q+\frac{3}{2+2r}\right]\mathrm{\Gamma }\left[\frac{-3}{2+2r}\right]{\left(q-1\right)}^{\frac{-3}{1+r}}}{16B^3\mathrm{\Gamma }\left[\frac{3}{2+2r}\right]\mathrm{\Gamma }\left[q-\frac{3}{2+2r}\right]},\hfill \end{array}(12)$

and so on. The spectral indices “q” and “r” are the tail and flatness parameters, respectively, that describe the superthermality of high energy particles and flatness of the curve for low energy particles. This is the general distribution such that the Maxwellian distribution is retrieved for r = 0 and q → ∞ and kappa distribution is recovered for r = 0 and q → κ + 1. Moreover, for physically meaningful results, the following conditions must be fulfilled: q > 1 and q (r + 1) > 5/2 (Qureshi et al., 2004).

3 Korteweg de Vries and modified Korteweg de Vries equations with beam electrons

We follow the well-known reductive perturbation technique (RPT) to stretch the space-time coordinates and expand the dependent variables n_j, v_j, and ϕ to study the EAWs in the presence of beam electrons. Thus, the required stretchings and expansions for KdV are given by

$\xi ={ϵ}^{1/2}\left(x-\lambda t\right),\text{\hspace{0.17em}and\hspace{0.17em}}\tau ={ϵ}^{3/2}t,(13)$

where λ represents the phase speed of the wave normalized by C_e, ϵ is the dimensionless parameter (0 < ϵ ≤ 1) determining the small amplitude of nonlinearity, and

$R_j\left(x,t\right)=R_{j0}+\sum _{i=1}^{\infty }{ϵ}^i{R}_{ji}\left(x,t\right).(14)$

Note that R_j (x, t) = [n_j, v_j, ϕ], where j = c, b stands for cold and beam electrons and R_j0 = [1, v_j0, 0] where only beam electrons are considered to stream with a constant speed v_b0 and v_c0 = 0. Now, employing the stretching (13) and expansion (14) into the governing Eqs 1–3 along with Eq 14, we get set of equations for various orders of ϵ. The lowest–order of ϵ (i.e., ϵ^3/2-order) terms can be solved simultaneously to give following expressions of the first order perturbed quantities

$\begin{array}{ll}\hfill & n_{j1}=\frac{-\alpha {\varphi }_1}{\left({\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j\right)},\hfill \\ \hfill & v_{j1}=\frac{-\alpha \left(\lambda -v_{j0}\right){\varphi }_1}{\left({\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j\right)},\hfill \end{array}(15)$

and the linear dispersion relation becomes

${\gamma }_1-\frac{1}{{\lambda }^2-\alpha {\sigma }_c}-\frac{\alpha }{\beta \left({\left(\lambda -v_{b0}\right)}^2-\alpha {\sigma }_b\right)}=0.(16)$

This equation is biquadratic and gives four distinct roots of λ. Here, the dispersion relation depends upon the spectral indices of electron distribution function (r, q) via γ₁, as well as the number densities and temperatures of all three types of electrons and the streaming velocity v_b0. This relation concurs well with the previous result of non-thermal distribution and dynamical ions studied by Singh et al. (2016) provided we assume stationary ions and (r, q) distribution function. In the absence of beam electrons (i.e., v_b0 → 0 and β → ∞), the dispersion relation becomes quadratic and the phase velocity becomes $\lambda =\sqrt{\frac{1}{{\gamma }_1}+\alpha {\sigma }_c}$.

Now collecting the next-order (i.e., ϵ^5/2-order) terms, we obtain the equations in terms of the first and second order perturbed quantities. The algebraic simplifications of higher order equations yield the following nonlinear partial differential equation (nPDE)

${\partial }_{\tau }{\varphi }_1+P{\varphi }_1{\partial }_{\xi }{\varphi }_1+Q{\partial }_{\xi ,\xi ,\xi }{\varphi }_1=0.(17)$

This is the most renowned Korteweg de Vries (KdV) equation having soliton solutions. Here, the coefficients of quadratic nonlinearity P and dispersion Q are defined, respectively, as

$P=\frac{X_2}{X_1},\text{\hspace{0.17em}and\hspace{0.17em}}Q=\frac{1}{X_1},(18)$

with

$X_1=\frac{2\lambda }{{\left({\lambda }^2-\alpha {\sigma }_c\right)}^2}+\frac{2\alpha \left(\lambda -v_{b0}\right)}{\beta {\left({\left(\lambda -v_{b0}\right)}^2-\alpha {\sigma }_b\right)}^2},(19)$

and

$X_2=\frac{\alpha \left(-3{\lambda }^2+\alpha {\sigma }_c\right)}{{\left({\lambda }^2-\alpha {\sigma }_c\right)}^3}+\frac{{\alpha }^2\left(-3{\left(\lambda -v_{b0}\right)}^2+\alpha {\sigma }_b\right)}{\beta {\left({\left(\lambda -v_{b0}\right)}^2-\alpha {\sigma }_b\right)}^3}-2{\gamma }_2.(20)$

It is observed that (r, q) distribution of hot electrons modifies the nonlinearity coefficient P (through γ₂), while the parameters of beam electrons affect all the coefficients. Here, the nonlinearity coefficient may become zero due to the positive and negative competing terms. Then X₂ = 0 and we get a critical condition on β = n_h0/n_b0 as

${\beta }_c=\frac{\alpha \left(-3{\left(\lambda -v_{b0}\right)}^2+\alpha {\sigma }_b\right){\left({\lambda }^2-\alpha {\sigma }_c\right)}^3}{{\left({\left(\lambda -v_{b0}\right)}^2-\alpha {\sigma }_b\right)}^3\left(2{\gamma }_2{\left({\lambda }^2-\alpha {\sigma }_c\right)}^3-\alpha \left(-3{\lambda }^2+\alpha {\sigma }_c\right)\right)}.(21)$

It may be noted that the critical value of density ratio β depends upon all the remaining temperatures and densities of electrons, beam speed v_b0 and the spectral indices q and r. For this critical value, the quadratic nonlinearity vanishes and KdV equation ceases to exist. The solitary structures are no longer formed as the dispersion is not balanced out by nonlinearity. Therefore, we need to change our stretchings of space and time coordinates which gives the nonlinearity other than quadratic to get the modified Korteweg de Vries (mKdV) for this critical value.

For mKdV equation, the stretching becomes (Abdikian et al., 2020; Tamang et al., 2020)

$\xi =ϵ\left(x-\lambda t\right),\text{\hspace{0.17em}and\hspace{0.17em}}\tau ={ϵ}^{3}t.(22)$

Using this stretching for the model equations, we get the same first order perturbed quantities as given by Eqs 15, 16 for the lowest order of ϵ (i.e., ϵ² now). For ϵ³-order, we obtain

$\begin{array}{ll}\hfill n_{j2}& =\left(\frac{-\alpha }{{\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j}\right){\varphi }_2+\frac{{\alpha }^2\left(3{\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j\right)}{2{\left({\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j\right)}^3}{\varphi }_1^2,\hfill \\ \hfill v_{j2}& =\left(\frac{-\alpha \left(\lambda -v_{j0}\right)}{{\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j}\right){\varphi }_2\hfill \\ \hfill & +\frac{{\alpha }^2\left(\lambda -v_{j0}\right)\left({\left(\lambda -v_{j0}\right)}^2+\alpha {\sigma }_j\right)}{2{\left({\left(\lambda -v_{j0}\right)}^2-\alpha {\sigma }_j\right)}^3}{\varphi }_1^2,\hfill \end{array}(23)$

and

${\gamma }_1{\varphi }_2+\frac{1}{\alpha }{n}_{c2}+\frac{1}{\beta }{n}_{b2}+{\gamma }_2{\varphi }_1^2=0,(24)$

which finally gives X₂ϕ₁∂ϕ₁/∂ξ = 0. Therefore, the quadratic nonlinearity coefficient vanishes and we have to go for the higher order of ϵ to obtain the nPDE. For ϵ⁴-order, we arrive at the following equations

$\begin{array}{ll}\hfill \left(\lambda -v_{j0}\right){\partial }_{\xi }{n}_{j3}-{\partial }_{\xi }{v}_{j3}& ={\partial }_{\tau }{n}_{j1}+{\partial }_{\xi }\left(v_{j2}{n}_{j1}\right)+{\partial }_{\xi }\left(v_{j1}{n}_{j2}\right),\hfill \\ \hfill & -\left(\lambda -v_{j0}\right){\partial }_{\xi }{v}_{j3}-\alpha {\partial }_{\xi }{\varphi }_3+\alpha {\sigma }_j{\partial }_{\xi }{n}_{j3}\hfill \\ \hfill & =-{\partial }_{\tau }{v}_{j1}-{\partial }_{\xi }\left(v_{j2}{v}_{j1}\right)+\alpha {\sigma }_j{\partial }_{\xi }\left(n_{j1}{n}_{j2}\right)\hfill \\ \hfill & -\alpha {\sigma }_j{n}_{j1}^2{\partial }_{\xi }{n}_{j1},\hfill \\ \hfill \frac{1}{\alpha }{n}_{c3}+\frac{1}{\alpha }{n}_{b3}+{\gamma }_1{\varphi }_3& ={\partial }_{\xi ,\xi }{\varphi }_1-2{\gamma }_2{\varphi }_1{\varphi }_2-{\gamma }_3{\varphi }_1^3.\hfill \end{array}(25)$

The tedious algebraic manipulation of the above equation along with the values of first and second order perturbed quantities lead to the following modified Korteweg de Vries (mKdV) equation with cubic nonlinearity

${\partial }_{\tau }\mathrm{\Psi }+R{\mathrm{\Psi }}^2{\partial }_{\xi }\mathrm{\Psi }+S{\partial }_{\xi ,\xi ,\xi }\mathrm{\Psi }=0,(26)$

where, Ψ = ϕ₁ and the coefficients of cubic nonlinearity and dispersion are given, respectively, as

$R=\frac{3Y_2}{Y_1},\text{\hspace{0.17em}and\hspace{0.17em}}Q=\frac{1}{Y_1},(27)$

Here,

$Y_1=2\alpha \left[\frac{\alpha \lambda }{{\left({\lambda }^2-\alpha {\sigma }_c\right)}^2}+\frac{\left(\lambda -v_{b0}\right)}{\beta {\left({\left(\lambda -v_{b0}\right)}^2-\alpha {\sigma }_b\right)}^2}\right],(28)$

and

$\begin{array}{ll}\hfill Y_2& =\frac{{\alpha }^2\left(5{\lambda }^4-\frac{4}{3}{\lambda }^2\alpha {\sigma }_c+\frac{1}{3}{\alpha }^2{\sigma }_c^2\right)}{2{\left({\lambda }^2-\alpha {\sigma }_c\right)}^5}\hfill \\ \hfill & +\frac{{\alpha }^3\left(5{\left(\lambda -v_{b0}\right)}^4-\frac{4}{3}{\left(\lambda -v_{b0}\right)}^2\alpha {\sigma }_b+\frac{1}{3}{\alpha }^2{\sigma }_b^2\right)}{2\beta {\left({\left(\lambda -v_{b0}\right)}^2-\alpha {\sigma }_b\right)}^5}-{\gamma }_3.\hfill \end{array}(29)$

4 Multi-soliton solution of modified Korteweg de Vries equation

For mKdV Eq 26, the following dependent variable Hirota transformation (Wazwaz, 2010) is used

$\mathrm{\Psi }=\sqrt{\frac{24S}{R}}{\partial }_{\xi }\left[{\tan }^{-1}\left(\frac{f}{g}\right)\right],(30)$

to find the N-soliton solutions. The transformation generates both compressive and rarefactive solitary solutions for mKdV equation (The details of the solutions are included in Supplementary Appendix A1). Therefore, the single compressive soliton solution becomes

$\mathrm{\Psi }=\sqrt{\frac{24S}{R}}{\partial }_{\xi }\left[{\tan }^{-1}\left(e^{k_1\left(\xi -S{k}_1^2\tau \right)}\right)\right],(31)$

where k₁ is the arbitrary propagation vector. On the other hand, the rarefactive single soliton solution of EAW is given as

$\mathrm{\Psi }=\sqrt{\frac{24S}{R}}{\partial }_{\xi }\left[{\tan }^{-1}\left(\frac{1}{e^{k_1\left(\xi -S{k}_1^2\tau \right)}}\right)\right].(32)$

The two-soliton solution of compressive electron acoustic solitary wave (EASW) with (r, q) distributed electrons is given as

$\mathrm{\Psi }=\sqrt{\frac{24S}{R}}{\partial }_{\xi }\left[{\tan }^{-1}\left(\frac{e^{k_1\left(\xi -S{k}_1^2\tau \right)}+e^{k_2\left(\xi -S{k}_2^2\tau \right)}}{1+a_{12}{e}^{k_1\left(\xi -S{k}_1^2\tau \right)+k_2\left(\xi -S{k}_2^2\tau \right)}}\right)\right].(33)$

Here $a_{12}=-({(k_1-k_2)}^2/{(k_1+k_2)}^2)$ is termed as the interaction parameter. Furthermore, the rarefactive two soliton solution of mKdV equation is of the form

$\mathrm{\Psi }=\sqrt{\frac{24S}{R}}{\partial }_{\xi }\left[{\tan }^{-1}\left(\frac{1+a_{12}{e}^{k_1\left(\xi -S{k}_1^2\tau \right)+k_2\left(\xi -S{k}_2^2\tau \right)}}{e^{k_1\left(\xi -S{k}_1^2\tau \right)}+e^{k_2\left(\xi -S{k}_2^2\tau \right)}}\right)\right].(34)$

5 Numerical results and discussion

In this section, the nonlinear characteristics of electron acoustic solitary waves (EASWs) are numerically analyzed for various plasma parameters and double spectral indices (r, q) of the electron distribution function. The solitary structure varies with the plasma parameters namely, the ratio of densities and temperatures of cold, hot and beam electrons (α, β, σ_c and σ_b), the speed of beam electrons, v_b0, as well as the flattening and superthermality indices, r and q, respectively. The Viking observations in the auroral region of broadband electrostatic noise (BEN) have reported the observations of both upward and downward energetic streaming electrons in Earth’s magnetosphere (Dubouloz et al., 1991; Dubouloz et al., 1993; Singh et al., 2016), which suggests the presence of beam electrons for EAWs in this region. For this region, cold electron density n_c0 = 0.5cm⁻³, hot electron density n_h0 = 1.5–2.0cm⁻³, beam electron density n_b0 = 1.0cm⁻³, cold electron temperature T_c = 2eV, hot electron temperature T_h = 250eV and beam electron temperature T_b = 50eV. The plasma parameters chosen in this section are consistent with the energetic burst of beam electrons in the auroral region (Dubouloz et al., 1991). Moreover, the Viking satellite has observed the Broadband electrostatic noise (BEN) bursts with amplitudes of electric fields as high as 100 mV/m in the dayside auroral zone (Dubouloz et al., 1991).

First, we numerically investigate the linear dispersion relation given by Eq 16. We plot the four roots of the phase velocity λ(= ω/k) in Figures 1A–C for various values of beam streaming velocity v_b0. For small values of beam velocity v_b0 (v_b0 < 0.2), we obtain four distinct roots, out of which two are forward propagating and the remaining two are backward propagating. We term them as cold and beam electron acoustic modes. With the increase in beam velocity v_b0 (i.e., v_b0 ∼ 0.3), only two acoustic modes exist which are the beam electron acoustic modes as shown in Figure 1B. In this case, the other two roots are complex and correspond to the two stream instability, which is not the topic of interest here. For large super-sonic beam velocity (e.g., v_b0 > 3.8), three forward propagating roots and one backward propagating mode exist. Two forward propagating modes correspond to the beam (we can term them as fast and slow with respect to the beam velocity) and the third one is the cold electron mode, whereas the backward propagating mode corresponds to the cold electrons. It is important to mention here that these particular values of v_b0 for the existence of different regions of modes are only valid for a fixed set of remaining plasma parameters and change if the remaining parameters are changed. For the nonlinear analysis presented in next section, we only consider the range of v_b0 for which all the roots are real (to avoid two stream instability).

FIGURE 1

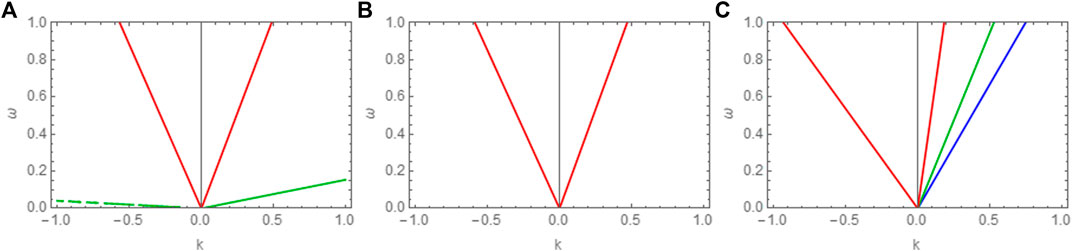
FIGURE 1. Variation of roots of phase velocity λ(= ω/k) for different values of v_b0. (A); v_b0 = 0.2 (B); v_b0 = 0.3 (C); v_b0 = 3.8. Remaining fixed parameters are q = 2.5, r = 0.8, σ_c = 0.001, σ_b = 0.01, n_c0 = 0.5cm⁻³, n_h0 = 2.5cm⁻³, n_b0 = 1cm⁻³.

Berthomier et al. (2000) suggested that the inclusion of beam electrons besides hot and cold population of electrons for nonlinear EAWs gives rise to a critical condition that leads to the formation of both positive and negative potentials for EASWs. These positive and negative potential EASWs have been observed in the auroral region of BEN. In the present case, we have derived an analytical expression of critical condition, which depends upon the parameters of beam electrons, so that the quadratic nonlinearity coefficient vanishes. Thus, we move to the higher order of nonlinearity and obtain mKdV equation with cubic nonlinearity, which generates both compressive and rarefactive EASWs. Therefore, the inclusion of beam electrons for EASWs in our model generates the solitons with both polarities.

In the previous sections, the multi-soliton solutions are given in terms of electric potential. However, to compare our results with the observed data, we convert them in terms of the electric field, where, E (ξ, τ) = −∂_ξΨ. Thus a hump or a dip of solitary structure corresponds to a bipolar electric field structure. Furthermore, an increase in the amplitude of electric potential corresponds to the enhancement of electric field amplitude as well. For mKdV equation, we have obtained both compressive and rarefactive solutions, however, for a single soliton, we study the variation of plasma parameters for compressive solitary structures only given by Eq 31 in the next subsection, since the rarefactive solitons given by Eq 32 exhibit similar behavior.

5.1 Single soliton solution of modified Korteweg de Vries equation

For the nonlinear case of EASWs, we first numerically analyze the impact of spectral parameters r and q of hot electron distribution function on the propagation properties of solitary structures in Figure 2. It may be observed that enhancing the flatness parameter r and the superthermality parameter q increase the amplitude of electric field significantly. However, increasing q is tantamount to decreasing the superthermal electrons, so the amplitude reduces with the increasing superthermality. Here, index r describes the population of electrons in the low energy region, whereas, q describes the population of the high energy particles in the tail of distribution. The corresponding unnormalized values of electric field amplitude enhance from 22.9 mV/m to 33.7 mV/m. The comparison of (r, q) distribution with the limiting case of Maxwellian distributed hot electrons shows that the amplitude of electric field with Maxwellian distributed electrons is greater than the (r, q) distributed electrons for lower values of parameters r and q, whereas, the electric field amplitude with (r, q) distributed electrons exceeds the one with Maxwellian distributed electrons for higher values of q and r.

FIGURE 2

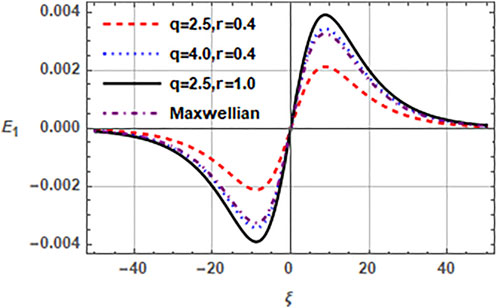
FIGURE 2. Variation of normalized electric field E₁ (ξ, τ) of EASW against the normalized spatial scale ξ by varying the spectral indices r and q and comparison with Maxwellian distribution. Here, n_c0 = 0.5cm⁻³, n_h0 = 2cm⁻³, n_b0 = 1cm⁻³, σ_c = 0.001, σ_b = 0.01, v_b0 = 0.1 and τ = 0.

Next, we observe the impact of beam parameters, i.e., beam speed v_b0, beam temperature through the ratio σ_b (= T_b/T_h) and the beam density through the ratio β(= n_h0/n_b0) on the properties of electron acoustic solitons in Figures 3–5. Figure 3 characterizes the impact of beam speed v_b0 on the EAW in a plasma with (r, q) distributed hot electrons. Note, that the increased beam streaming velocity v_b0 augments the amplitude of electric field. This happens because the beam electrons act as a source of free energy for the EASWs and, therefore, the increasing beam speed enhances the corresponding amplitude of soliton electric field. The related electric field amplitude for v_b0 in (0, − ,0.4) range lies in the range of (21.4–32.6) mV/m. Figure 4 delineates the effect of beam temperature through the ratio β on the electric field of electron acoustic solitary structure. It can be seen from the plots that enhancement of the ratio σ_b leads to the reduction of the electric field amplitude. When the ratio σ_b varies from 0.001 to 1 in Figure 4 for fixed values of remaining parameters, the associated electric field reduces from 12.9 mV/m to 2.7 mV/m. Furthermore, σ_b = 1 refers to the case when T_b= T_h and σ_b = 0 refers to the case of cold electron beam which achieves the maximum amplitude of electric field. The effect of beam number density on the EASW through the ratio β is described in Figure 5. The plots indicate that the amplitude of electric field mitigates with the increasing value of ratio β and the electric field amplitude corresponding to increasing β, reduces from 14.0, −,11.8 mV/m. However, the number density of beam electrons being inversely proportional to β causes an enhancement in the amplitude of electric field for an EASW. Here, beam electrons energize the plasma system, so increasing their concentration tends to increase the amplitude of EASW.

FIGURE 3

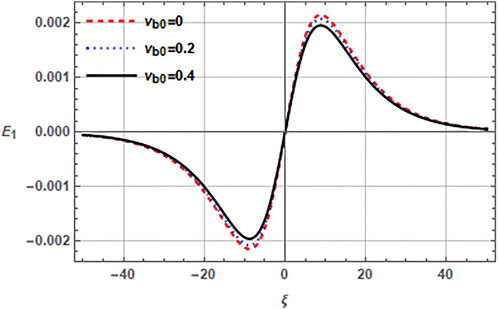
FIGURE 3. Variation of normalized electric field E₁ (ξ, τ) of EASW against normalized ξ by varying the streaming speed of beam electron v_b0 with q = 2.5, r = 0.4, n_c0 = 0.5cm⁻³, n_h0 = 2cm⁻³, n_b0 = 1cm⁻³, σ_c = 0.001, σ_b = 0.01 and τ = 0.

FIGURE 4

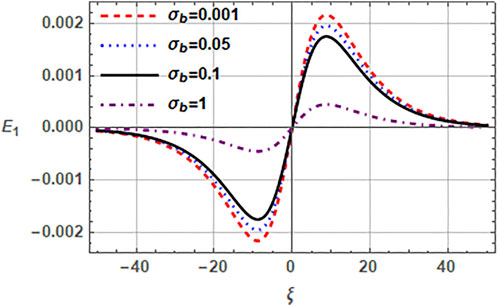
FIGURE 4. Normalized electric field E₁ (ξ, τ) of EASW is plotted against the normalized ξ by varying the beam to hot electron temperature ratio σ_b with q = 2.5, r = 0.4, n_c0 = 0.5cm⁻³, n_h0 = 2cm⁻³, n_b0 = 1cm⁻³, σ_c = 0.001, v_b0 = 0.1 and τ = 0.

FIGURE 5

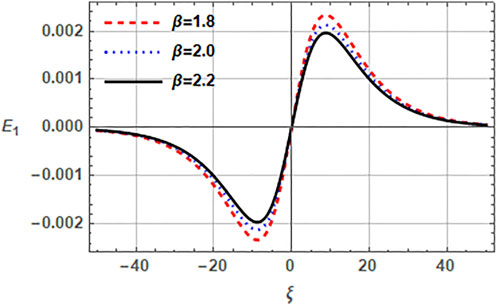
FIGURE 5. Variation of normalized electric field E₁ (ξ, τ) of EASWs against the normalized ξ versus the ratio of densities β(= n_h0/n_b0). Here q = 2.5, r = 0.4, n_h0 = 2cm⁻³, n_c0 = 0.5cm⁻³, σ_c = 0.001, σ_b = 0.01, v_b0 = 0.1 and τ = 0.

Furthermore, we check the effects of concentrations and temperatures of cold and hot electrons on the electric field of EASW in Figures 6, 7. The effect of cold to hot electron temperature ratio σ_c (= T_c/T_h) is depicted in Figure 6, which shows that the amplitude of EASW reduces with the increase of temperature of cold electrons and the related electric field reduces from 12.8 mV/m to 1.5 mV/m. The EAW with hot and cold electron population usually exists when T_h ≥ 10T_c or σ_c ≤ 0.1 (Gary and Tokar, 1985), else the wave gets Landau damped. Thus, increasing the temperature ratio T_c/T_h reduces the amplitude. It is important to mention that the necessary condition for existence of EAWs is the presence of two electron temperatures. Therefore, in the presence of warm beam electrons, when T_c approaches T_h (i.e., σ_c → 1), the beam electrons act as cold electrons and sustain the existence of EAW. Figure 7 specifies the effect of ratio of hot to cold electron concentration α(= n_h0/n_c0) on amplitude of EASW. The amplitude of solitons reduces with the increasing number density of hot to cold electrons and the related electric field exists in range (14.6–11.7)mV/m. It is pertinent to mention here that the range of electric field associated with EASWs in all above cases is in agreement with observational data (Dubouloz et al., 1991), where the electric field varies upto 100 mV/m. Therefore, the present model of EAWs with beam electrons is well suited to explain the electrostatic solitary structures for BEN emissions in auroral region of Earth’s magnetosphere.

FIGURE 6

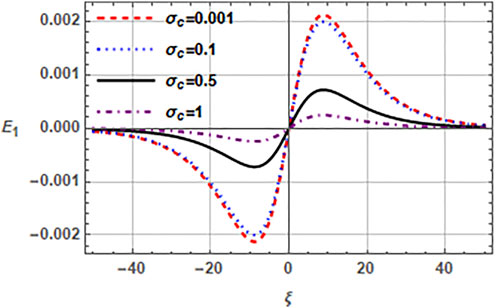
FIGURE 6. Normalized electric field E₁ (ξ, τ) of EASWs is plotted versus the ratio of temperatures σ_c (= T_c/T_h). Here q = 2.5, r = 0.4, n_h0 = 2cm⁻³, n_c0 = 0.5cm⁻³, .n_b0 = 1cm⁻³, σ_b = 0.01, v_b0 = 0.1 and τ = 0.

FIGURE 7

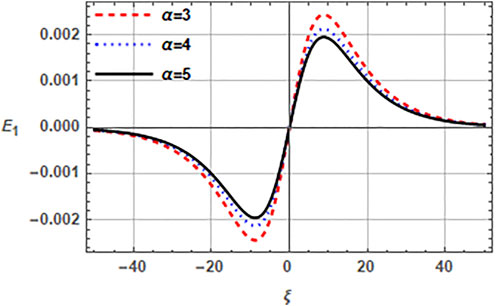
FIGURE 7. Variation of normalized electric field E₁ (ξ, τ) of EASWs is plotted versus the ratio of densities α(= n_h0/n_c0). Here q = 2.5, r = 0.4, n_h0 = 2cm⁻³, .n_b0 = 1cm⁻³, σ_c = 0.001, σ_b = 0.01, v_b0 = 0.1 and τ = 0.

5.2 Interaction of modified Korteweg de Vries electron acoustic waves

For the two soliton solution, we study the interaction of both compressive and rarefactive solitons, as they show peculiar behavior during the interaction. For the variation of plasma parameters belonging to auroral region, Figures 8A–D represent the types of overtaking interactions that may take place for two mKdV soliton solutions in terms of the electric potential Ψ. Figure 8A depicts the two compressive solitons given by Eq 33 before, at and after the interaction times. Before interaction, the taller soliton lags behind the shorter soliton. At the time of interaction, the shape of the composite solitary structure depends upon the ratio of the propagation vectors k₁/k₂, where k₁ (k₂) denote the propagation vector of taller (shorter) soliton. Therefore, we get a single humped composite soliton if the ratio k₁/k₂ is high, else we get a two humped solitary structure at the point of interaction. These two humped solitary waves correspond to the tripolar electric field structures which have been identified in space plasmas (Pickett et al., 2004). Furthermore, the linear superposition principle fails to follow at the point of interaction as the interaction takes place between nonlinear solitary structures. After interaction, the taller soliton overtakes the shorter soliton and leads the shorter soliton. Figure 8B delineates the interaction among two rarefactive solitons obtained by Eq 34, which shows similar behavior for rarefactive soliton interaction to that of compressive soliton interaction in Figure 8A at various times. Figures 8C,D represent the cases when a compressive soliton interacts with the rarefactive soliton. These cases are considered by taking different signs of the propagation vectors k₁ and k₂. We consider the interaction of a taller compressive soliton with a shorter rarefactive soliton in Figure 8C. Now, the composite structure formed at the point of interaction carries a taller compressive (hump) and two shorter rarefactive (dip) structures. However, when a taller rarefactive soliton overtakes a shorter compressive soliton, two shorter humps and a taller dip are produced at interaction time as shown in Figure 8D. This peculiar type of interaction of compressive and rarefactive solitons may only be observed for mKdV type equations (Nawaz et al., 2022) and cannot be seen for KdV type equations (Jahangir et al., 2015; Jahangir et al., 2016; Jahangir and Masood, 2020).

FIGURE 8

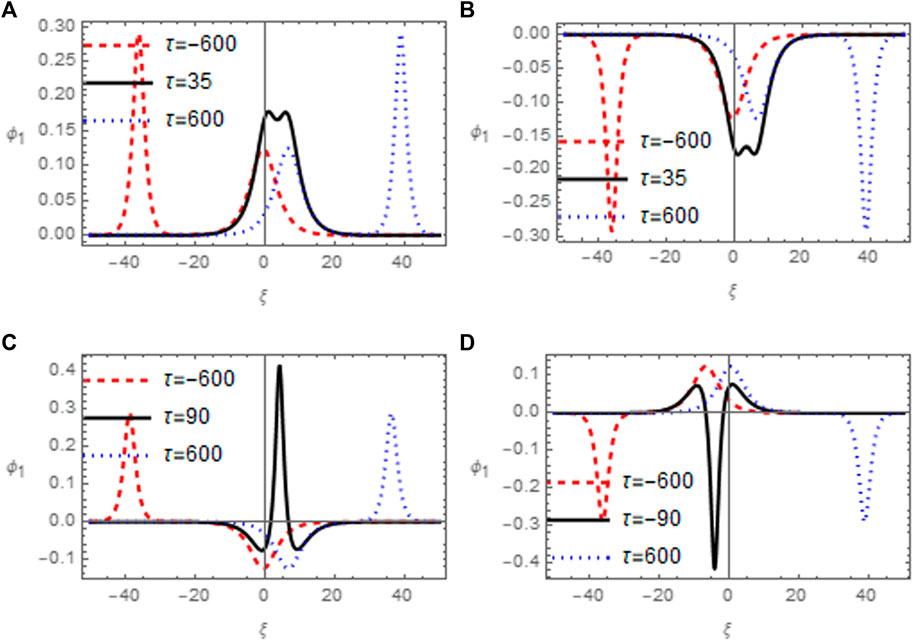
FIGURE 8. Variation of normalized electric potential Ψ(ξ, τ) of two soliton solutions is plotted against the normalized scale ξ. (A); Interaction of two compressive solitons (B); Interaction of two rarefactive solitons (C); Interaction of taller compressive with shorter rarefactive soliton (D); Interaction of shorter compressive with taller rarefactive soliton. Here q = 2.5, r = 0.4, n_h0 = 2cm⁻³, n_c0 = 0.5cm⁻³, .n_b0 = 1cm⁻³, σ_c = 0.001, σ_b = 0.01 and v_b0 = 0.2.

The effect of spectral parameters (r, q) of the distribution function, beam parameters and cold and hot electron parameters may also be analyzed on the interaction of two solitons. Figures 9A–D manifest the impact of indices (r, q) on the two soliton solution given by Eq 33 in terms of the contour plots of electric potential Ψ. The comparison of Figures 9A,B show that when the value of superthermality index q enhances, the interaction regime stretches from 432 to 599 km. This is in accordance with the result of single soliton since the parameter q increases the amplitude of single solitary EAW, thereby, increasing the speed of the soliton. Therefore, the interaction time speeds up or equivalently the spatial regime of interaction stretches. Figures 9A,C show that the interaction regime extends from 432 to 790 km as we enhance the values of the flatness parameter r, since increasing r enhances the amplitude of soliton. Figure 9D shows the broadening of spatial regime of two soliton interaction to 731 km for the case of Maxwellian distributed hot electrons. So, in a nutshell, the spatial regime of Maxwellian distributed electrons is broadened as compared to (r, q) distributed hot electrons with lower values of r and q, but is contracted as compared to (r, q) distributed hot electrons with higher values of r and q. It is discerned that all the remaining effects of plasma parameters of beam, hot and cold electrons for two soliton interaction show a behavior in agreement with their impact on single soliton solutions and, therefore, have not been plotted here due to the paucity of space.

FIGURE 9

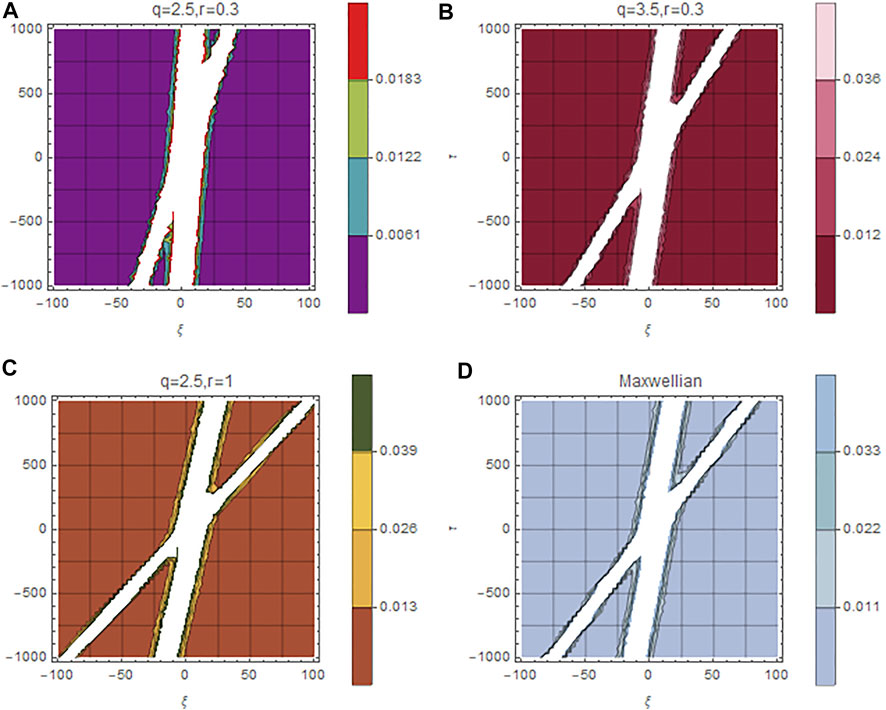
FIGURE 9. Variation of normalized electric potential Ψ(ξ, τ) of compressive two soliton solution is plotted against the normalized scale ξ by varying the spectral indices r and q and comparison with Maxwellian distribution. Here, n_c0 = 0.5cm⁻³, n_h0 = 2cm⁻³, n_b0 = 1cm⁻³, σ_c = 0.001, σ_b = 0.01 and v_b0 = 0.1.

6 Conclusion

Linear and nonlinear electron acoustic waves (EAWs) have been studied in an unmagnetized, collisionless plasma comprising hot (r, q) distributed electrons, cold inertial electrons, warm electron beam and the immobile ions. Introducing an electron beam in such a plasma has led to a Doppler shifted velocity due to the beam velocity. The linear dispersion relation has been investigated for varying beam velocity, which showed that four distinct (two forward propagating and two backward propagating) modes exist for the lower values of beam velocity. For higher beam velocity (v_b0 ∼ 0.3), two of the modes have been found to become imaginary. Moreover, for high super-acoustic beam speeds, three modes have been found to become forward propagating while one has been observed to remain backward propagating. We have derived the Korteweg-de Vries (KdV) equation for EAWs in the small amplitude limit. We have obtained a critical condition for which the coefficient of quadratic nonlinearity vanishes for the given plasma parameters. For this condition, we have derived the modified Korteweg de Vries (mKdV) equation with cubic nonlinearity that has been found to admit both hump and dip solitary structures. We have shown that the spectral indices r and q (that control the shape of the distribution function at low and high energies), the temperature ratio of beam, hot and cold electrons and their relative concentrations considerably affect the propagation features and interaction of electron acoustic solitary waves (EASWs). It has been found that the increased concentration of cold and beam electrons increase the amplitude of electric fields while the enhanced temperatures of cold and beam electrons reduce the amplitude of electric fields. The types of possible overtaking interaction of two mKdV solitons have also been investigated. The interaction regime of two soliton interaction has been found to vary in a manner similar to that of the variation of single soliton for various plasma parameters. Finally, the comparison of (r, q) distribution with the limiting case of Maxwellian distributed hot electrons has shown that the amplitude of soliton with Maxwellian distributed electrons is greater than the (r, q) distributed electrons with lower values of parameters q and r, but smaller than the (r, q) distributed electrons for higher values of q and r. We have shown that the results presented in this paper concur very well with the satellite observations in the auroral region. Finally, we would like to say that the beam of electrons can potentially make the electron acoustic waves unstable which can lead to the local heating of the plasma and charged particle acceleration.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

The idea has come from WM and RJ. Calculations have been done by both of them. Results and discussion and figures have been drawn mutually by all three authors.

Acknowledgments

One of the authors WM acknowledges the support from the Abdus Salam International Centre for Theoretical Physics (AS-ICTP) for his visit under the Regular Associateship Scheme.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.978314/full#supplementary-material

References

Abdikian, A., Tamang, J., and Saha, A. (2020). Supernonlinear wave and multistability in magneto-rotating plasma with (r, q) distributed electrons. Phys. Scr. 96, 095605. doi:10.1088/1402-4896/ac07b7

CrossRef Full Text | Google Scholar

Abid, A. A., Khan, M. Z., Lu, Q., and Yap, S. L. (2017). A generalized AZ-non-Maxwellian velocity distribution function for space plasmas. Phys. Plasmas 24 (3), 033702. doi:10.1063/1.4977447

CrossRef Full Text | Google Scholar

Ablowitz, M. J., Ablowitz, M. A., Clarkson, P. A., and Clarkson, P. A. (1991). Solitons, nonlinear evolution equations and inverse scattering. Cambridge: Cambridge University Press.

Google Scholar

Ali, S., Masood, W., Rizvi, H., Jahangir, R., and Mirza, A. M. (2021). Contribution of the generalized (r, q) distributed electrons in the formation of nonlinear ion acoustic waves in upper ionospheric plasmas. AIP Adv. 11 (12), 125020. doi:10.1063/5.0075007

CrossRef Full Text | Google Scholar

Ali, S., Masood, W., Rizvi, H., and Mirza, A. M. (2020). Nonlinear cnoidal waves and solitary structures in unmagnetized plasmas with generalized (r, q) distributed electrons. Phys. Scr. 95, 075605. doi:10.1088/1402-4896

CrossRef Full Text | Google Scholar

Asano, Y., Nakamura, R., Shinohara, I., Fujimoto, M., Takada, T., Baumjohann, W., et al. (2008). Electron flat-top distributions around the magnetic reconnection region. J. Geophys. Res. 113 (A1). doi:10.1029/2007JA012461

CrossRef Full Text | Google Scholar

Berthomier, M., Pottelette, R., Malingre, M., and Khotyaintsev, Y. (2000). Electron-acoustic solitons in an electron-beam plasma system. Phys. Plasmas 7 (7), 2987–2994. doi:10.1063/1.874150

CrossRef Full Text | Google Scholar

Cattell, C., Wygant, J., Dombeck, J., Mozer, F. S., Temerin, M., and Russell, C. T. (1998). Observations of large amplitude parallel electric field wave packets at the plasma sheet boundary. Geophys. Res. Lett. 25 (6), 857–860. doi:10.1029/98GL00497

CrossRef Full Text | Google Scholar

Dillard, C. S., Vasko, I. Y., Mozer, F. S., Agapitov, O. V., and Bonnell, J. W. (2018). Electron-acoustic solitary waves in the Earth’s inner magnetosphere. Phys. Plasmas 25 (2), 022905. doi:10.1063/1.5007907

CrossRef Full Text | Google Scholar

Dubouloz, N., Pottelette, R., Malingre, M., and Treumann, R. A. (1991). Generation of broadband electrostatic noise by electron acoustic solitons. Geophys. Res. Lett. 18 (2), 155–158. doi:10.1029/90GL02677

CrossRef Full Text | Google Scholar

Dubouloz, N., Treumann, R. A., Pottelette, R., and Malingre, M. (1993). Turbulence generated by a gas of electron acoustic solitons. J. Geophys. Res. 98 (A10), 17415–17422. doi:10.1029/93JA01611

CrossRef Full Text | Google Scholar

El-Bedwehy, N. A., and El-Taibany, W. F. (2020). Modulational instability of dust-ion acoustic waves in the presence of generalized ( r ,   q ) distributed electrons. Phys. Plasmas 27 (1), 012107. doi:10.1063/1.5121540

CrossRef Full Text | Google Scholar

El-Labany, S. K., Shalaby, M., Sabry, R., and El-Sherif, L. S. (2012). Solitons and double-layers of electron-acoustic waves in magnetized plasma; an application to auroral zone plasma. Astrophys. Space Sci. 340 (1), 101–108. doi:10.1007/s10509-012-1045-2

CrossRef Full Text | Google Scholar

El-Taibany, W. F., El-Bedwehy, N. A., El-Shafeay, N. A., and El-Labany, S. K. (2021). Three-dimensional rogue waves in Earth’s ionosphere. Galaxies 9 (3), 48. doi:10.3390/galaxies9030048

CrossRef Full Text | Google Scholar

El-Taibany, W. F. (2005). Electron-acoustic solitary waves and double layers with an electron beam and phase space electron vortices in space plasmas. J. Geophys. Res. A01213 (A1), 1. doi:10.1029/2004JA010525

CrossRef Full Text | Google Scholar

Elwakil, S. A., Zahran, M. A., and El-Shewy, E. K. (2007). Nonlinear electron-acoustic solitary waves in a relativistic electron-beam plasma system with non-thermal electrons. Phys. Scr. 75 (6), 803–808. doi:10.1088/0031-8949/75/6/010

CrossRef Full Text | Google Scholar

Ergun, R. E., Holmes, J. C., Goodrich, K. A., Wilder, F. D., Stawarz, J. E., Eriksson, S., et al. (2016). Magnetospheric Multiscale observations of large-amplitude, parallel, electrostatic waves associated with magnetic reconnection at the magnetopause. Geophys. Res. Lett. 43 (11), 5626–5634. doi:10.1002/2016GL068992

CrossRef Full Text | Google Scholar

Feldman, W. C., Anderson, R. C., Bame, S. J., Gary, S. P., Gosling, J. T., McComas, D. J., et al. (1983). Electron velocity distributions near the Earth’s bow shock. J. Geophys. Res. 88 (A1), 96–110. doi:10.1029/JA088iA01p00096

CrossRef Full Text | Google Scholar

Fried, B. D., and Gould, R. W. (1961). Longitudinal ion oscillations in a hot plasma. Phys. Fluids (1994). 4 (1), 139–147. doi:10.1063/1.1706174

CrossRef Full Text | Google Scholar

Gary, S. P., and Tokar, R. L. (1985). The electron-acoustic mode. Phys. Fluids (1994). 28, 2439. doi:10.1063/1.865250

CrossRef Full Text | Google Scholar

Hirota, R. (1971). Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27 (18), 1192–1194. doi:10.1103/PhysRevLett.27.1192

CrossRef Full Text | Google Scholar

Hirota, R. (2004). The direct method in soliton theory. Cambridge: Cambridge University Press.

Google Scholar

Holmes, J. C., Ergun, R. E., Newman, D. L., Wilder, F. D., Sturner, A. P., Goodrich, K. A., et al. (2018). Negative potential solitary structures in the magnetosheath with large parallel width. JGR. Space Phys. 123 (1), 132–145. doi:10.1002/2017JA024890

CrossRef Full Text | Google Scholar

Jahangir, R., and Masood, W. (2020). Interaction of electron acoustic waves in the presence of superthermal electrons in terrestrial magnetosphere. Phys. Plasmas 27 (4), 042105. doi:10.1063/1.5143400

CrossRef Full Text | Google Scholar

Jahangir, R., Masood, W., Siddiq, M., and Batool, N. (2016). Interaction of solitons for obliquely propagating magnetoacoustic waves in stellar atmosphere. Phys. Plasmas 23 (12), 122301. doi:10.1063/1.4971219

CrossRef Full Text | Google Scholar

Jahangir, R., Masood, W., Siddiq, M., Batool, N., and Saleem, K. (2015). Interaction of fast magnetoacoustic solitons in dense plasmas. Phys. Plasmas 22 (9), 092312. doi:10.1063/1.4930270

CrossRef Full Text | Google Scholar

Jeffrey, A. (1973). The role of Korteweg de Vries equation in plasma physics. Jeffrey, A. Role of the Korteweg-de Vries equation in plasma physics. Q. J. R. Astronomical Soc. 14, 183.

Google Scholar

Kakutani, T., Ono, H., Taniuti, T., and Wei, C. C. (1968). Reductive perturbation method in non-linear wave propagation II: Application to hydromagnetic waves in a cold plasma. J. Phys. Soc. Jpn. 24, 1159–1166. doi:10.1143/JPSJ.24.1159

CrossRef Full Text | Google Scholar

Khalid, S., Qureshi, M. N., and Masood, W. (2020). Alfvenic perturbations with finite Larmor radius effect in non-Maxwellian electron–positron–ion plasmas. AIP Adv. 10 (2), 025002. doi:10.1063/1.5141891

CrossRef Full Text | Google Scholar

Korteweg, D. J., and Vries, G. D. (1895). On the change of form of long waves advancing in a rectangular channel, and on a new type of long stationary waves. Philos. Mag. Ser. 39, 422. doi:10.1080/14786449508620739

CrossRef Full Text | Google Scholar

Lakhina, G. S., Singh, S. V., Kakad, A. P., and Pickett, J. S. (2011). Generation of electrostatic solitary waves in the plasma sheet boundary layer. J. Geophys. Res. 116 (A10), 1. doi:10.1029/2011JA016700

CrossRef Full Text | Google Scholar

Lakhina, G. S., Singh, S. V., Kakad, A. P., Verheest, F., and Bharuthram, R. (2008). Study of nonlinear ion-and electron-acoustic waves in multi-component space plasmas. Nonlinear process. geophys. 15 (6), 903–913. doi:10.5194/npg-15-903-2008

CrossRef Full Text | Google Scholar

Lin, C. S., Burch, J. L., Shawhan, S. D., and Gurnett, D. A. (1984). Correlation of auroral hiss and upward electron beams near the polar cusp. J. Geophys. Res. 89 (A2), 925–935. doi:10.1029/JA089iA02p00925

CrossRef Full Text | Google Scholar

Mace, R. L., and Hellberg, M. A. (2001). The Korteweg–de Vries–Zakharov–Kuznetsov equation for electron-acoustic waves. Phys. Plasmas 8 (6), 2649–2656. doi:10.1063/1.1363665

CrossRef Full Text | Google Scholar

Mamun, A. A., Cairns, R. A., and Shukla, P. K. (1996). Solitary potentials in dusty plasmas. Phys. Plasmas 3, 702–704. doi:10.1063/1.871905

CrossRef Full Text | Google Scholar

Mamun, A. A., Shukla, P. K., and Stenflo, L. (2002). Obliquely propagating electron-acoustic solitary waves. Phys. plasmas 9 (4), 1474–1477. doi:10.1063/1.1462635

CrossRef Full Text | Google Scholar

Mannan, A., and Mamun, A. A. (2011). Nonplanar dust-acoustic Gardner solitons in a four-component dusty plasma. Phys. Rev. E 84, 026408. doi:10.1103/PhysRevE.84.026408

PubMed Abstract | CrossRef Full Text | Google Scholar

Masood, W., Hamid, N., Ullah, S., Rahman, A., Shah, H. A., Alyousef, H. A., et al. (2022). Formation of acoustic nonlinear structures in non-Maxwellian trapping plasmas. Phys. Fluids 34 (5), 053113. doi:10.1063/5.0090923

CrossRef Full Text | Google Scholar

Masood, W., Schwartz, S. J., Maksimovic, M., and Fazakerley, A. N. (2006). Electron velocity distribution and lion roars in the magnetosheath. Ann. Geophys. 24, 1725–1735. doi:10.5194/angeo-24-1725-2006

CrossRef Full Text | Google Scholar

Masood, W., and Schwartz, S. J. (2008). Observations of the development of electron temperature anisotropies in Earth’s magnetosheath. J. Geophys. Res. 113 (A1). doi:10.1029/2007JA012715

CrossRef Full Text | Google Scholar

Masud, M. M., Asaduzzaman, M., and Mamun, A. A. (2012). Dust-ion-acoustic Gardner solitons in a dusty plasma with bi-Maxwellian electrons. Phys. Plasmas 1910, 103706. doi:10.1063/1.4753922

CrossRef Full Text | Google Scholar

Matsumoto, H., Kojima, H., Miyatake, T., Omura, Y., Okada, M., Nagano, I., et al. (1994). Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys. Res. Lett. 21 (25), 2915–2918. doi:10.1029/94GL01284

CrossRef Full Text | Google Scholar

Matveev, V. B., and Salle, M. A. (1991). Darboux transformations and solitons. Springer.

Google Scholar

Miura, R. M., Gardner, C. S., and Kruskal, M. D. (1968). Korteweg-de vries equation and generalizations. II. Existence of conservation laws and constants of motion. J. Math. Phys. 9 (8), 1204–1209. doi:10.1063/1.1664701

CrossRef Full Text | Google Scholar

Naeem, I., Masood, W., and Mirza, A. M. (2020). Dipolar and Kelvin-Stuart’s cat’s eyes vortices in magnetoplasmas with non-Maxwellian electron distribution. Astrophys. Space Sci. 365 (3), 52 (1–11). doi:10.1007/s10509-020-03759-9

CrossRef Full Text | Google Scholar

Nawaz, H., Jahangir, R., Masood, W., and Siddiq, M. (2022). Cubic nonlinearity driven dust ion acoustic solitons with superthermal two-temperature electrons in the Saturn’s magnetosphere. Phys. Scr. 97, 075601. doi:10.1088/1402-4896/ac735e

CrossRef Full Text | Google Scholar

Nawaz, H., Masood, W., Jahangir, R., and Siddiq, M. (2021). Interaction of gardner solitons in plasmas: Applications in the saturn’s magnetosphere. Phys. Scr. 96 (4), 045604. doi:10.1088/1402-4896/abe257

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Fitzenreiter, R. J., and Scudder, J. D. (1984). Observations of electron beams in the low-latitude boundary layer. J. Geophys. Res. 89 (A12), 10723–10732. doi:10.1029/JA089iA12p10723

CrossRef Full Text | Google Scholar

Pickett, J. S., Kahler, S. W., Chen, L. J., Huff, R. L., Santolik, O., Khotyaintsev, Y., et al. (2004). Solitary waves observed in the auroral zone: The cluster multi-spacecraft perspective. Nonlinear process. geophys. 11 (2), 183–196. doi:10.5194/npg-11-183-2004

CrossRef Full Text | Google Scholar

Pottelette, R., Malingre, M., Dubouloz, N., Aparicio, B., Lundin, R., Holmgren, G., et al. (1990). High-frequency waves in the cusp/cleft regions. J. Geophys. Res. 95 (A5), 5957–5971. doi:10.1029/JA095iA05p05957

CrossRef Full Text | Google Scholar

Qureshi, M. N., Nasir, W., Bruno, R., and Masood, W. (2019). Whistler instability based on observed flat-top two-component electron distributions in the Earth’s magnetosphere. Mon. Not. R. Astron. Soc. 488 (1), 954–964. doi:10.1093/mnras/stz1702

CrossRef Full Text | Google Scholar

Qureshi, M. N., Nasir, W., Masood, W., Yoon, P. H., Shah, H. A., and Schwartz, S. J. (2014). Terrestrial lion roars and non-Maxwellian distribution. J. Geophys. Res. Space Phys. 119 (12), 10–059. doi:10.1002/2014JA020476

CrossRef Full Text | Google Scholar

Qureshi, M. N., Shah, H. A., Murtaza, G., Schwartz, S. J., and Mahmood, F. (2004). Parallel propagating electromagnetic modes with the generalized (r, q) distribution function. Phys. Plasmas 11 (8), 3819–3829. doi:10.1063/1.1688329

CrossRef Full Text | Google Scholar

Sabry, R., and Omran, M. A. (2013). Propagation of cylindrical and spherical electron-acoustic solitary wave packets in unmagnetized plasma. Astrophys. Space Sci. 344 (2), 455–461. doi:10.1007/s10509-013-1356-y

CrossRef Full Text | Google Scholar

Shah, K. H., Qureshi, M. N., Masood, W., and Shah, H. A. (2018). Electron acoustic nonlinear structures in planetary magnetospheres. Phys. Plasmas 25 (4), 042303. doi:10.1063/1.5026186

CrossRef Full Text | Google Scholar

Shohaib, M., Masood, W., Jahangir, R., Siddiq, M., Alkhateeb, S. A., and El-Tantawy, S. A. (2021). On the dynamics of nonlinear propagation and interaction of the modified KP solitons in multicomponent complex plasmas. J. Ocean Eng. Sci. doi:10.1016/j.joes.2021.10.005

CrossRef Full Text | Google Scholar

Shohaib, M., Masood, W., Jahangir, R., Siddiq, M., and Rizvi, H. (2022). Interaction of dust ion acoustic solitons with cubic nonlinearity in a magnetized dusty plasma with distributed electrons. Contributions Plasma Phys. 62 (3), e202100134. doi:10.1002/ctpp.202100134

CrossRef Full Text | Google Scholar

Shukla, P. K., Mamun, A. A., and Eliasson, B. (2004). 3D electron-acoustic solitary waves introduced by phase space electron vortices in magnetized space plasmas. Geophys. Res. Lett. 31 (7), 1. doi:10.1029/2004gl019533

CrossRef Full Text | Google Scholar

Singh, S. V., Devanandhan, S., Lakhina, G. S., and Bharuthram, R. (2016). Electron acoustic solitary waves in a magnetized plasma with nonthermal electrons and an electron beam. Phys. Plasmas 23 (8), 082310. doi:10.1063/1.4961961

CrossRef Full Text | Google Scholar

Singh, S. V., Lakhina, G. S., Bharuthram, R., and Pillay, S. R. (2011). Electrostatic solitary structures in presence of non-thermal electrons and a warm electron beam on the auroral field lines. Phys. Plasmas 18 (12), 122306. doi:10.1063/1.3671955

CrossRef Full Text | Google Scholar

Tamang, J., Abdikian, A., and Saha, A. (2020). Phase plane analysis of small amplitude electron-acoustic supernonlinear and nonlinear waves in magnetized plasmas. Phys. Scr. 95, 105604. doi:10.1088/1402-4896/abb05b

CrossRef Full Text | Google Scholar

Tamang, J., and Saha, A. (2020). Bifurcations of small-amplitude supernonlinear waves of the mKdV and modified Gardner equations in a three-component electron-ion plasma. Phys. Plasmas 27, 012105. doi:10.1063/1.5115821

CrossRef Full Text | Google Scholar

Tokar, R. L., and Gary, S. P. (1984). Electrostatic hiss and the beam driven electron acoustic instability in the dayside polar cusp. Geophys. Res. Lett. 11 (12), 1180–1183. doi:10.1029/GL011i012p01180

CrossRef Full Text | Google Scholar

Tsurutani, B. T., Arballo, J. K., Lakhina, G. S., Ho, C. M., Buti, B., Pickett, J. S., et al. (1998). Plasma waves in the dayside polar cap boundary layer: Bipolar and monopolar electric pulses and whistler mode waves. Geophys. Res. Lett. 25 (22), 4117–4120. doi:10.1029/1998GL900114

CrossRef Full Text | Google Scholar

Ullah, S., Masood, W., and Siddiq, M. (2020). Electron acoustic envelope solitons in non-Maxwellian plasmas. Eur. Phys. J. D. 74 (2), 26–29. doi:10.1140/epjd/e2019-100589-1

CrossRef Full Text | Google Scholar

Vasyliunas, V. M. (1968). A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 73 (9), 2839–2884. doi:10.1029/JA073i009p02839

CrossRef Full Text | Google Scholar

Verheest, F., and Hereman, W. A. (2019). Collisions of acoustic solitons and their electric fields in plasmas at critical compositions. J. Plasma Phys. 85 (1), 905850106. doi:10.1017/S0022377818001368

CrossRef Full Text | Google Scholar

Watanabe, K., and Taniuti, T. (1977). Electron-acoustic mode in a plasma of two-temperature electrons. J. Phys. Soc. Jpn. 43 (5), 1819–1820. doi:10.1143/JPSJ.43.1819

CrossRef Full Text | Google Scholar

Wazwaz, A. M. (2010). Partial differential equations and solitary waves theory. Verlag, Berlin, Heidelberg: Springer.

Google Scholar

Yousaf Khattak, M., Masood, W., Jahangir, R., and Siddiq, M. (2021). Interaction of ion acoustic solitons for Zakharov Kuznetsov equation in relativistically degenerate quantum magnetoplasmas. Waves Random Complex Media, 1–17. doi:10.1080/17455030.2021.1968536

CrossRef Full Text | Google Scholar