Dependence of the global dayside reconnection rate on interplanetary magnetic field By and the earth’s dipole tilt

1 Introduction

Understanding the mechanisms that cause the range of different near-Earth space phenomena is often a difficult task. The system is highly coupled, from the thermosphere/ionosphere to the solar wind. It can therefore be challenging to determine the underlying cause of observed phenomena, as multiple processes occurring in different regions, alone or in combination, may produce very similar observational signatures.

This paper addresses why we observe a different behaviour of the magnetosphere-ionosphere system when the B_y component of the Interplanetary Magnetic Field (IMF) is positive vs negative during periods when the Earth’s magnetic axis is tilted towards or away from the Sun. Although first mentioned by Friis-Christensen and Wilhjelm (1975), it was not until recently that this topic has been revisited and further characterized. Friis-Christensen and Wilhjelm noted that during northern hemisphere winter (negative dipole tilt angle, Ψ), the westward electrojet was significantly stronger for positive compared to negative IMF B_y during otherwise similar IMF B_z conditions. Holappa and Mursula (2018) revisited this effect on the westward electrojet and established that these differences were not due to the Russell-McPherron effect (Russell and McPherron, 1973). They called this the explicit B_y effect to differentiate it from the Russell-McPherron effect, which is essentially due to seasonally varying correlation between IMF B_y and the geoeffective B_z component (IMF B_y not directly causing the Russell-McPherron effect). Holappa and Mursula (2018) quantified the difference in electrojet strength to be about 50 percent during winter conditions. During summer conditions, the IMF B_y dependence reverses as the westward electrojet is stronger for negative compared to positive IMF B_y, but the effect on the westward electrojet is minor compared to the difference during winter conditions (Holappa and Mursula, 2018; Holappa et al., 2021b).

The large IMF B_y and seasonal related asymmetries in the westward electrojet sparked the interest for investigating other aspects of the coupled system for similar behavior. Reistad et al. (2020) reported similar asymmetries in the average size of the polar cap. During negative dipole tilt, they found larger polar caps in both hemispheres when IMF B_y is positive compared to negative. The ± B_y asymmetry reversed when the dipole was tilted in the opposite direction. Since the same behaviour was seen in both the winter and summer hemisphere for a specific IMF B_y polarity, ionospheric effects related to season could not alone explain the observations. They suggested that in addition, one or both of the following scenarios must be the case: A) The global dayside reconnection rate depends on IMF B_y polarity when Earth’s dipole is tilted, allowing for a stronger Dungey cycle and more energy input to the system when IMF B_y and Ψ have opposite signs; or B) When Earth’s dipole is tilted, IMF B_y has an influence on the amount of magnetic flux the magentotail lobes typically can support, for a given dayside reconnection rate. While the results reported by Reistad et al. (2020) indicate a global difference in the magnetospheric response, the minor effect on the westward electrojet in the summer hemisphere compared to the winter hemisphere suggests that the influence on the ionospheric currents are more complex than what can be explained by type A and B mechanisms.

Other aspects of the solar wind - magnetosphere coupling has also been investigated in this regard. Holappa et al. (2020) and Holappa and Buzulukova (2022) found that fluxes of precipitating energetic electrons and protons in both hemispheres show a very similar asymmetry, namely that the precipitation is more intense when IMF B_y and Ψ have opposite signs, compared to when they have the same sign, during otherwise similar IMF B_z conditions. Holappa and Buzulukova (2022) showed that the growth rate of the ring current (measured by the Dst index) also exhibits a similar B_y-dependence. Ohma et al. (2021) investigated the occurrence frequency of magnetospheric substorms during periods of either positive or negative IMF B_y. Based on several independent lists of identified substorms, they concluded that substorms are more frequent when the sign of IMF B_y and Ψ are opposite, compared to when IMF B_y has the same sign as the dipole tilt. These findings further indicate that the explicit B_y-effect is a global phenomenon, which is likely related to a type A or B mechanism (or both) as mentioned above. Since dayside and nightside reconnection are the processes that allow for opening and closure of magnetic flux; the steady state, in which we interpret the long-term averages to represent (Laundal et al., 2020), must represent a balance of the two. The observed changes of the steady state open flux content depending on IMF B_y/Ψ polarity must therefore either be due to a type A or B mechanism (or both). These spatially separated processes (A: dayside and B: tail) are nevertheless highly coupled, as the dayside loading affects the conditions in the magnetotail, making the interpretation of the data analysis highly challenging, as will be elaborated on in more detail in the following.

Reistad et al. (2021) studied ionospheric convection on the basis of Doppler-shift from ground based HF radar echoes. They presented climatological patterns of the high latitude convection pattern during IMF B_y dominated periods, for various dipole tilt intervals. By normalizing the observed convection to the present size of the polar cap as inferred from simultaneous observations from the Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE), they were able to distinguish the contribution from lobe reconnection on the global convection pattern, which were found to be more efficient during local summer. This allowed the authors to quantify the part of the convection associated with dayside (and nightside) reconnection. Their results indicated that when IMF B_y and dipole tilt had opposite polarity, the Dungey cycle was slightly enhanced $(\sim 10\%)$.

The results presented above demonstrate that the global magnetospheric response to positive and negative IMF B_y is different when Ψ is nonzero: The westward electrojet is stronger, particle precipitation is more intense, substorms are more frequent, the polar cap is larger, and the ring current increases more rapidly when the signs of IMF B_y and Ψ are opposite. Previous studies have not identified whether this is mainly due to differences in the dayside coupling (type A) or mainly due to differences in how the tail responds to the same flux loading, influencing the amount of magnetic flux the lobes typically sustain (type B). However, there are key differences in how the magnetosphere and ionosphere are expected to respond between the type A and type B mechanisms, enabling new insights to be obtained about their relative importance.

If the observed explicit B_y effects are solely a result of mechanism B, the flux throughput in the (tilted) magnetosphere should be the same for both polarities of IMF B_y, if all other solar wind parameters are equal. Since substorms are more frequent for opposite signs of IMF B_y and Ψ, the substorms must either be stronger (closing more flux) or the flux must be transported by another process when IMF B_y and Ψ have the same sign. In addition to substorms, the magnetosphere can respond to solar wind forcing by entering into steady magnetospheric convection (SMC) periods (e.g., Sergeev et al., 1996; Kissinger et al., 2012). Hence, a type B process would imply weaker substorms and/or less frequent SMC events for opposite signs of IMF B_y and Ψ. On the other hand, mechanism A demands the flux throughput to be greater in the magnetospheric system for positive B_y during Northern Hemisphere (NH) winter and for negative B_y during NH summer. If the occurrence frequency of SMCs and the strength of substorms follow the same dependence as the other observed phenomena (stronger for opposite signs of IMF B_y and Ψ), it would suggest the influence of a type A mechanism in producing the observed explicit B_y effects.

In this paper, we present new analyses to demonstrate how IMF B_y and Ψ in combination affects the response of the magnetosphere-ionosphere system. The goal is to address whether mechanisms A or B are the main contributor to the explicit B_y effects. We will address how the occurrence frequency of SMC events are modulated and use various proxies to assess the global substorm strength. In the following section we will present our new analysis contributing to the investigation of the origin of the explicit B_y effect. The methodology used in the presented analysis is outlined as the results are presented. Our new results are discussed together with the existing knowledge on the topic in section 3. Our main conclusions are explicitly stated in the concluding section.

2 Results

When comparing the magnetosphere responses to intervals of positive and negative IMF B_y and dipole tilt, it is important that we compare instances with similar dayside forcing. This is largely controlled by the IMF B_z component. In all our analyses, we use the dayside coupling function presented by Milan et al. (2012), which is set out to quantify the global dayside reconnection rate, Φ_D [Wb/s], in response to the upstream IMF and solar wind, given by the formula

${\mathrm{\Phi }}_D=\mathrm{\Lambda }{V}_x^{4/3}{B}_{\text{yz}}{\sin }^{9/2}\left(\theta /2\right).(1)$

Here, Λ = 3.3 ⋅ 10⁵ m^2/3s^1/3 is a scaling constant related to the length of the dayside X-line, V_x is the solar wind velocity in the anti-sunward direction, B_yz is the magnitude of the IMF vector perpendicular to the Sun-Earth line, and θ is the IMF clock angle. When SI units are used, Φ_D gets the units of Wb/s = Volt, representing the rate of conversion of magnetic flux from a closed to open topology on the dayside.

As noted by Holappa et al. (2021a), the particular choice of coupling function is typically not crucial for this kind of analyses, yet they provide a convenient way to select periods of similar forcing for comparison. In all plots, the dayside coupling value is normalized to its mean value from the entire analysis period. This normalized coupling parameter we denote Φ_D/⟨Φ_D⟩. We use IMF data time shifted to the bow shock of the Earth from the OMNI database (King and Papitashvili, 2005).

2.1 Occurrence of steady magnetospheric convection intervals: Interplanetary magnetic field B_y and dipole tilt dependence

The magnetosphere can enter different “modes” of response to the energy input from the interplanetary medium. The perhaps most common situation is the so-called loading/un-loading cycle in which the magnetospheric substorm plays a central role. The typical sequence of events is a growth phase (dayside loading dominates) (McPherron, 1970), followed by the onset of a rapid expansion phase coinciding with the initiation of intense tail reconnection. In a typical “isolated” substorm, the magnetosphere transitions into a so-called recovery phase, characterized by the return to a quiet geomagnetic level (Ohtani and Gjerloev, 2020). However, if the IMF remain southward, the system may transition into a situation where the nightside and dayside merging rates are approximately balanced, marking the onset of a Steady Magnetospheric Convection (SMC) period (Sergeev et al., 1996). Milan et al. (2021) did a manual classification of the convection state of the magnetosphere system during the year 2010. He referred to the SMC intervals as a driven phase, and found it to occur during 18% of the time, in contrast to the traditional substorm phases occurring 23% of the time during that year. Hence, it seems likely that a significant amount of the magnetic flux throughput may take place during periods of SMC. Similar to looking at the occurrence rate and strength of substorms, it is thus relevant to look at how the combination of IMF B_y and dipole tilt affect the occurrence of SMC events, as they also represent information about the external forcing and how the magnetosphere responds to the forcing.

To investigate how the occurrence frequency of SMC events are modulated by IMF B_y and dipole tilt conditions, we use two different lists of identified SMC intervals. The Kissinger list contain 3444 SMC intervals with a minimum duration of 90 min, from the time period 1997–2013. The list is described in (Kissinger et al., 2011, 2012) and has been compiled by a combination of selection criteria based on the Auroral Electrojet index and manual inspection, and made publicly available recently (Kissinger et al., 2022). We also make use of the SMC list described by Dejong (2014) that goes from 1997 to 2015. Their list requires steadiness in the AL-index of at least 3 h and uses a seasonal cutoff in activity in AE-index as described in McWilliams et al. (2008). We use an extended version of the list described, where the extended part (2008–2015) only differ from their published list by not having applied the manual inspection of possible particle injection signatures at geosynchronous orbit (such events was removed in the published list). Common for both SMC lists is that steadiness in magnetospheric activity is the core selection criteria, which is quantified by how rapid the AL index is allowed to change in a sliding window [20 min in Dejong (2014) and 30 min in Kissinger et al. (2011)]. We group the SMC events into two groups based on the mean IMF B_y in the hour preceding each event (B_y$<-2$ nT and B_y$>2$ nT). The main reason for considering the hour proceeding the event is that we are interested in whether our selection parameters may influence the initiation of the SMC. We further associate each SMC interval with the rate of dayside reconnection during the hour preceding the SMC onset using the Φ_D parameter normalized to the mean of all the 60 min Φ_D values during the entire time period of each list, referred to as ⟨Φ_D⟩.

In Figure 1, the number of SMC events within the indicated Ψ (different columns) and Φ_D/⟨Φ_D⟩ intervals (x-axis) are normalized to the amount of time the selection conditions was fulfilled in the period of the SMC lists. If one group (shown as a data point in Figure 1) has in total 100 SMC events, and the conditions of that specific group is met for a cumulative total of 100 days during the span of the list, the occurrence frequency will be one per day. This represent our measure of SMC events per day (y-axis), which is computed separately for the positive (orange) and negative (blue) IMF B_y conditions. The number of SMC events in each group is indicated with its respective color in each panel. Similar to Ohma et al. (2021), the uncertainty is estimated by re-sampling with replacement (bootstrapping), leading to a distribution of SMC events per day that is normal, from which its ± 1 standard deviation is interpreted as the uncertainty in Figure 1.

FIGURE 1

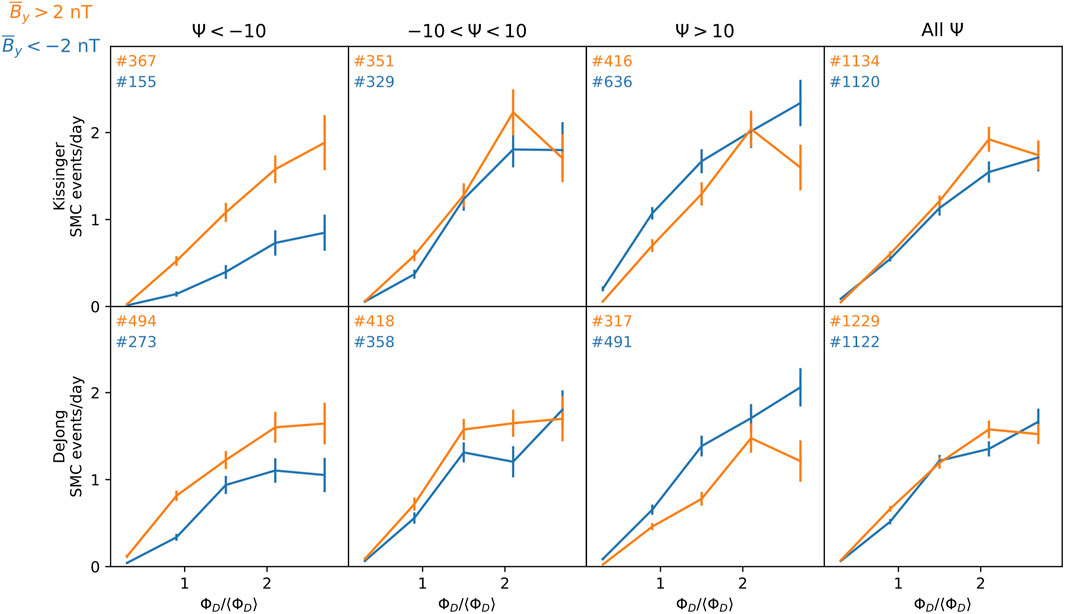
FIGURE 1. Average occurrence rates of SMC intervals (number per day on y-axis) versus increasing levels of dayside reconnection rate. Top row: SMC list described by Kissinger et al. (2012). Bottom row: SMC list described by Dejong (2014). An explicit B_y dependence in the SMC occurence rates are seen in both lists: Opposite B_y/tilt polarity also lead to more frequent SMC intervals.

Similar to the occurrence rates of substorms (Ohma et al., 2021), the SMC occurrences in Figure 1 exhibit a so-called explicit B_y-dependence. Namely, for a given orientation of the dipole tilt, Ψ, SMC intervals take place more frequently when Ψ and IMF B_y have opposite signs compared to when they have the same sign. This is consistently seen for both SMC lists investigated. In the Kissinger list, the explicit B_y effect is more pronounced during negative dipole tilt. The total number of SMC events (irrespective if IMF B_y) in the Kissinger list is also higher for positive than negative dipole tilt. This difference is likely related to the seasonal cut off criteria McWilliams et al. (2008) used only in the DeJong list, that aims to compensate for the elevated AL levels during the more sunlit conditions. This may explain why the IMF B_y polarity difference in DeJong’s list is approximately as strong during positive and negative dipole tilts. Nevertheless, the IMF B_y polarity difference remain in both lists.

2.2 Substorm strength: Mid-latitude positive bay index

The strength of substorms can be routinely quantified from their ground-based magnetic signatures. In NH, substorms produce southward perturbations (negative bays) on the ground in high latitudes and northward perturbations (positive bays) in mid-latitudes. Ohma et al. (2021) showed that substorms identified from high-latitude negative bays have a more pronounced magnetic response (producing stronger AL/SML index in the NH) when the signs of the dipole tilt and IMF B_y are opposite. However, similar to Holappa and Mursula (2018), they found that this explicit B_y-dependence is very weak in the summer hemisphere, indicating that local ionospheric conditions strongly modulate the ground disturbances of substorms at high latitudes. Hence, addressing the strength of a substorm in a global sense (i.e., in terms of magnetic flux closure in the tail) is a very challenging task. As pointed out by Ohma et al. (2021), the local ionospheric conditions are much influenced by the degree of sunlight, and the geometry of the ionospheric current systems depend strongly on IMF B_y, in opposite sense in the two hemispheres. Hence, Ohma et al. (2021) suggested that a metric not associated with such local high latitude phenomenon should be used in assessing the global strength of substorms across various magnitude and polarities of dipole tilt and IMF B_y. Ideally, such a substorm strength metric should be based on observations distributed equally between the two hemispheres. Although Ohma et al. (2021) did not find a statistical significant difference in substorm strength for the different combinations of IMF B_y and dipole tilt, we will show how choices made in the statistical analysis may alter their conclusions.

We here repeat the analysis of substorm strength for different dipole tilt and IMF B_y polarities, as shown in Figure 7 in Ohma et al. (2021). Similar to Ohma et al. (2021), we focus on substorms identified with an algorithm applied to the Mid-latitude Positive Bay (MPB) index developed by Chu et al. (2015) to assess the substorm strength, for the above mentioned reasons. This list includes 57,558 substorms observed in 1982–2012. The list contains the onset times as well as the peak values and area (time-integral of the squared perturbation) of the identified MPB pulses, quantifying the strength of the events. An advantage of the McPherron and Chu list over widely used substorm lists based on the SML index (Newell and Gjerloev, 2011) (using only NH measurements) is that it uses magnetometers observations from both hemispheres, and from mid-latitudes only (20° < |magnetic latitude| < 52°), potentially reducing the hemispheric bias. However, due to inherent geographical limitations, there are sill more stations in NH than SH. The MPB signature is interpreted as a direct signature of the Birkeland currents associated with the substorm (Chu et al., 2015). This is different from magnetic perturbations observed at high latitudes, that are blind to Birkeland and Pedersen currents, i.e., the curl-free component of the 3D ionospheric current system [Fukushima theorem, see e.g., Fukushima (1994)].

Figure 2 shows the median MPB area for negative $(<-10°)$ and positive $(>10°)$ dipole tilts (Ψ) as a function Φ_D/⟨Φ_D⟩ averaged over 6 h prior the substorm onset. The 6 h window is chosen to allow the magnetosphere system to adjust to the upstream forcing. In this way, any potential B_y-dependence in the upstream forcing (from a type A mechanism) is expected to be exaggerated. The choice of averaging window is also discussed more in detail in the next subsection. The error bars indicate ± one-sigma errors of the median derived by bootstrap resampling (with replacement) applied 1,000 times. The MPB area is clearly greater for B_y > 2 nT during negative dipole tilt and for B_y < − 2 nT during positive dipole tilt. Interestingly, the explicit B_y-dependence is about equally strong during negative tilt (NH winter) than during positive tilt (NH summer). We also find very similar results (not shown) for the peak MPB amplitude also given in the McPherron and Chu list. Thus, we interpret the results in Figure 2 as an effect of IMF B_y modulating the global substorm strength during both local summer and winter conditions.

FIGURE 2

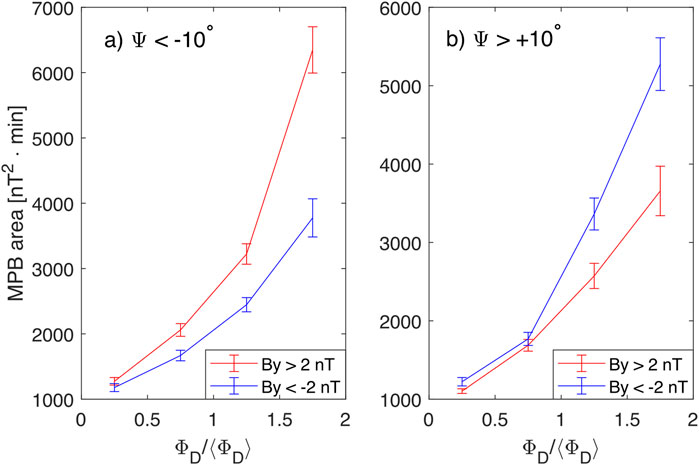
FIGURE 2. The MPB pulse area as a function of the normalized Φ_D parameter separately for B_y$>2$ nT and B_y$<-2$ nT.The error bars indicate ± one standard deviation of the median. Left: Negative dipole tilt. Right: Positive dipole tilt.

The explicit B_y-dependence in Figure 2 is clearer than in the similar analysis of Ohma et al. (2021), which is due to three differences between the analyses. First, the present analysis sorts data by Φ_D instead of the clock angle. Second, instead of the mean we are using the median of the MPB strength, making the analysis less prone to extremes of the distribution. Third, using a long (6-h) averaging window will more efficiently average out noise in the relation between coupling function Φ_D and the response.

2.3 Substorm strength: Onset latitude

The substorm onset latitude is a direct measure of the size of the open magnetosphere at time of onset, which has a dependence on the degree of dayside loading during the time before the substorm [e.g., Milan et al. (2008)]. Figure 3 shows the median substorm onset latitude, as determined from the lists of substorm onsets from global Far Ultraviolet imaging presented by Frey et al. (2004) and Liou (2010). This combined list contain substorms from both hemispheres (71% from NH) from which the onset latitude most often can be placed with confidence within ± 1°. Common for both the Frey et al. (2004) and Liou (2010) substorm lists is that the substorm onset is identified as a sudden localized auroral brightening in the nightside oval, experiencing a poleward and zonal expansion. The binning into positive (orange) and negative (blue) IMF B_y substorms are done similarly as described above. The bins of the normalized dayside coupling parameter Φ_D/⟨Φ_D⟩ is determined such that each of the four bins contain the same number of substorms. These bins are indicated with the vertical dashed lines. The median value of the onset latitude (y-axis) and the normalized loading parameter (x-axis) with its associated ± one-sigma bootstrap error are indicated with crosses. The size of the averaging window used to compute IMF B_y and Φ_D/⟨Φ_D⟩ prior to binning is varied. From left, the columns in Figure 3 represent window sizes of 1 min (no averaging), 1 hr, 2 hr, 4 hr, and 6 hr. To further constrain the IMF B_y polarity within the averaging window used, we require the circular variance of the IMF clock angle (the angle of the IMF vector projected in the GSM YZ plane) to be $<0.1$ based on minute resolution data. In this way, the positive and negative IMF B_y intervals (defined by the mean IMF B_y $>2$ nT or $<-2$ nT during the averaging window) are clearly separated. Due to the constraint on the circular variance of the IMF clock angle, fewer substorms meet the criteria for larger window sizes.

FIGURE 3

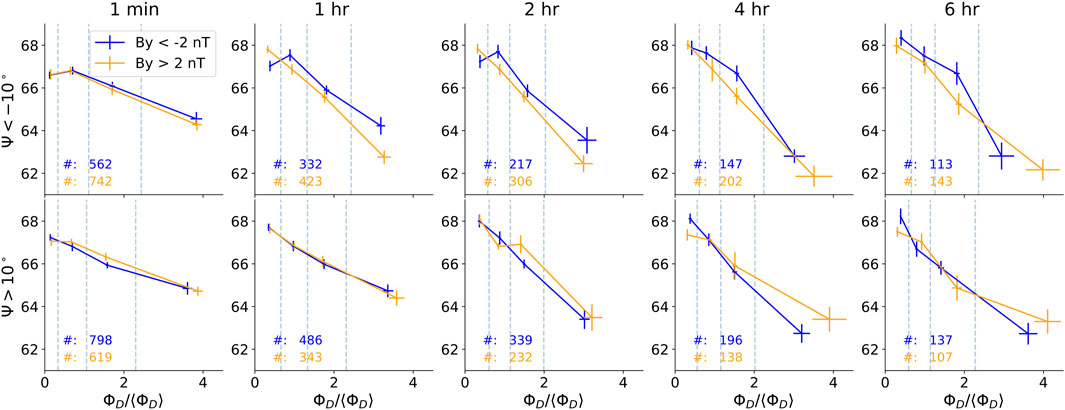
FIGURE 3. Median onset latitude from IMAGE + Polar onset lists. Top row: Negative dipole tilt. Bottom row: Positive dipole tilt. The two lines indicate different IMF B_y regimes. Columns represent size of averaging window applied to IMF B_y and Φ_D parameter. Φ_D bins are indicated with vertical dashed lines. Total number of substorms in each IMF B_y group satisfying the IMF stability criteria is also printed in each panel.

We clearly observe the median onset latitude to have greater dependence on Φ_D for larger window sizes, as expected. On the other hand, we observe no clear explicit B_y dependence on the onset latitude. For window sizes of two or more hrs, Figure 3 may indicate a trend toward lower latitude onsets when IMF B_y and Ψ has opposite signs during the two highest Φ_D intervals, but the difference is not significant. Hence, from the presented evidence, we must conclude that the net effect on onset latitude by the sign of IMF B_y must be small, if any, during times of significant dipole tilt. On the other hand, this means that we also can conclude that there is no evidence suggesting that the more frequent substorms for one IMF B_y polarity are associated with higher latitude onsets, which could be an indication of weaker substorms. These results, together with the MPB analysis of substorm strength, are further discussed in section 3.

2.4 Interplanetary magnetic field B_y dependence of isotropic boundary

The proton isotropic boundary marks the equatorward boundary of proton precipitation. The isotropic boundary (IB) is assumed to be located on a field line on which the radius of curvature is comparable to the proton gyroradius (Sergeev et al., 1993). Poleward of the IB latitude the proton loss cone is efficiently filled by pitch-angle scattering, whereas protons are mainly trapped equatorward of the IB latitude (Newell et al., 1998). The IB latitude can be routinely monitored using the Polar Operational Environmental Satellites (POES) measurements of energetic protons made with the The Medium Energy Proton and Electron Detector (MEPED) instruments. Asikainen et al. (2010) used corrected and calibrated MEPED proton measurements of 80–250 keV energy to determine the isotropic boundary latitude. Instead of 80–250 keV energy we use here proton fluxes between 120 and 250 keV, which have been obtained by interpolating the MEPED measurements at the nominal energy channels. Asikainen and Mursula (2011) showed that as the MEPED proton instruments degrade in time the effective energies they measure increase. They also showed that the lowest proton energy channel could not be reliably corrected if the degradation has been large enough. Asikainen et al. (2012) showed that the lowest energy one can use to get a homogeneous series of proton fluxes from 1979 to present is 120 keV. Therefore, we here use the proton measurements between 120 and 250 keV to determine the isotropic boundary. The IB latitude on each orbit is found by the most equatorward corrected geomagnetic latitude where the fluxes of the two orthogonal MEPED telescopes (I₀ and I₉₀) fulfill the condition

$\frac{|I_0-I_{90}|}{I_0+I_{90}}<0.3(2)$

In addition to this the determined L-value of the IB location must be $>2.5$ and the count rates of the telescopes must exceed 500 cts/(cm² sr s). As shown by Asikainen et al. (2010) the IB latitudes display a systematic MLT dependence. We followed their approach to estimate and subtract the MLT dependence from the IB latitudes. This procedure yields the so called MT index (magnetotail index) separately for both hemispheres. Because the MT indices (IB latitude identifications) are irregularly sampled in time we calculated the hourly averages from all those MT index values, which are located within the hour. In the following, our mentions of IB latitude is in fact referring to this MLT-normalized version, the MT index. We also restrict our analysis to the 18–06 MLT nightside region.

As shown by Meurant et al. (2007), the IB latitude at substorm onset is very similar to the onset latitude. As pointed out by Newell et al. (2007), the IB latitude has its best correlation with solar wind driving when averaging over the previous 6 h. Hence, the IB latitude represents a diagnostic tool of the state of the inner magnetosphere, which depends on the magnitude of dayside loading from at least the previous 6 h. The main advantage of considering the IB latitude for our purposes, in contrast to the onset latitude, is that we do not have to restrict ourselves to the onset of a substorm to get a datapoint indicating the extent of the stretched magnetosphere. The full POES database of high latitude crossings can thus be utilized for this purpose, similar as what was done by Holappa et al. (2021a).

Figure 4 shows the median IB latitude for positive (red) and negative (blue) IMF B_y conditions. Similar to the previous figures, the observations are also binned according to the normalized dayside coupling value (x-axis) over 6 h preceding the measurement. The analysis is shown from both hemispheres (northern hemisphere in top row, south in bottom row) during positive and negative dipole tilt intervals. Note that the same tilt interval represents opposite local season in the two hemispheres. It is evident from Figure 4 that the explicit B_y effect on IB latitude is a pronounced and significant feature. The latitudinal difference between the two IMF B_y polarities are on the order of 1° latitude, similar to what was reported by Reistad et al. (2020) using the field-aligned current estimates of the size of the auroral oval from AMPERE.

FIGURE 4

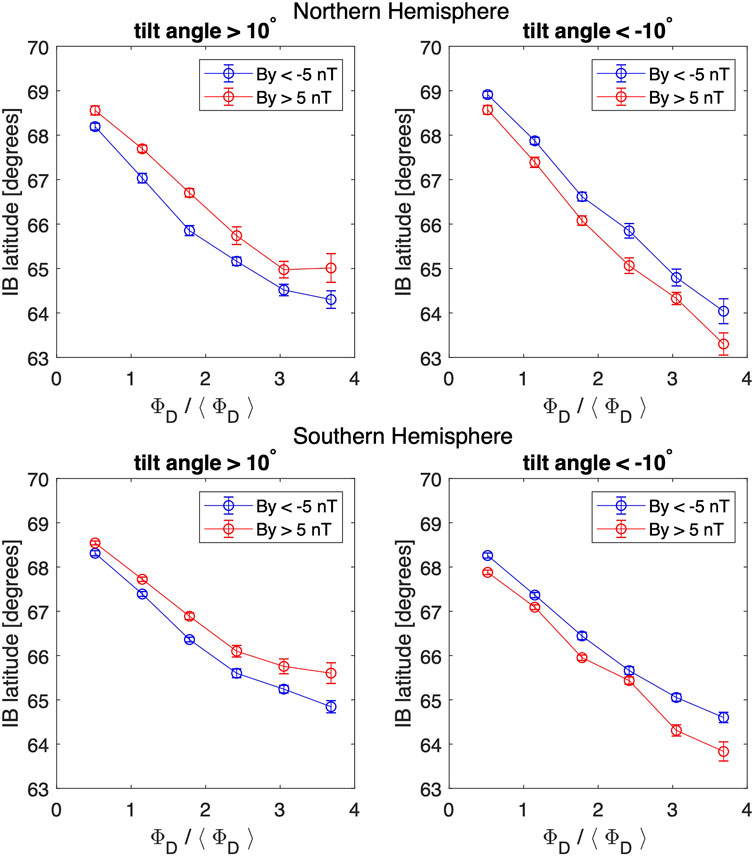
FIGURE 4. Median IB latitude determined from NOAA15-19 satellites in the nightside (18–6 MLT) as a function of the normalized Φ_D parameter separately for B_y$>5$ nT and B_y$<-5$ nT. The error bars indicate ± one standard deviation of the median.

3 Discussion

In recent years, a growing body of evidence (see introduction) has demonstrated how various aspects of the solar wind—magnetosphere—ionosphere interactions depend on the combination of the polarities of IMF B_y and dipole tilt, often referred to as an explicit B_y effect. That is, for a given, nonzero tilt angle Ψ, the system responds differently to positive and negative IMF B_y. In this paper we provide further observational evidence of this effect, aiming to provide observational constraints on the source of the explicit B_y behaviour of the system. Two types of mechanisms have been suggested to explain the explicit B_y effect:

A) The combination of the polarity of IMF B_y and dipole tilt affects the global dayside reconnection rate, with higher flux throughput when the two has opposite polarity compared to equal polarity.

B) The combination of the polarity of IMF B_y and dipole tilt influence the amount of magnetic flux the magnetotail lobes typically support, for a given dayside reconnection rate. The magnetosphere thus responds differently to similar magnetic flux throughput.

Observations consistent with a type B mechanism have been reported on earlier (Holappa et al., 2021a). However, can this type of process, confined to the magnetotail, be the sole explanation for the presented observations? This is the core question we address in this article. Evidence on the existence of a type A mechanism has not been presented to date (to our knowledge). There is an ongoing debate whether the dipole tilt angle modulates the dayside reconnection rate (Cliver et al., 2000; Russell et al., 2003; Lockwood et al., 2020). However, these studies have not addressed the combined action of the dipole tilt and IMF By (which are both included in the type A mechanism). Previous studies focusing on the explicit B_y effect have not been able to make definite conclusions about the relative importance of A versus B type of mechanisms. However, a critical test for the above hypotheses is to determine whether or not the magnetic flux throughput of the system (the strength of the Dungey cycle) is stronger for the opposite signs of Ψ and IMF B_y. This is predicted by mechanism A, but not by mechanism B. By combining the results presented in this study with earlier observations, we can now address how the flux throughput is modulated by IMF B_y and Ψ.

Milan et al. (2008) investigated how the magnetosphere responds to weak and strong solar wind forcing, and showed that enhanced magnetic flux input (Φ_D) lead to both stronger and more frequent substorms. It has also been shown that the substorm occurrence frequency is higher when IMF B_y and Ψ have opposite compared to equal polarity (Ohma et al., 2021). The global substorm strength shown in Figure 2 demonstrates that the strength of substorms is also greater, therefore closing more magnetic flux per substorm (Milan et al., 2009), on average, when signs of IMF B_y and tilt angle are opposite compared to equal. Taken together, these results strongly suggests that the IMF B_y/Ψ polarity combination affect the magnetic flux throughput, hence supporting a type A mechanism.

The IB latitude analysis presented in Figure 4, which can be interpreted as the transition region from dipolar to stretched field lines, is systematically displaced based on IMF B_y and dipole tilt polarity, highlighting the profound influence by these parameters. This region of the magnetotail is known to depend upon the previous magnetospheric activity (and hence solar wind - magnetosphere coupling) with a significant memory. Newell et al. (2007) found the IB latitude to show the best correlation with a 6 h long averaging window of the upstream forcing. It is therefore highly expected that a type A mechanism would lead to the observed differences in Figure 4. The observed shift in IB latitude is remarkably similar to the corresponding shift in polar cap radius during similar conditions, as reported by Reistad et al. (2020). However, as Reistad et al. (2020) pointed out, we can not exclude a type B mechanism influencing these results, when interpreting this analysis alone. However, when interpreting these results in light of our findings regarding the substorm strength as discussed above, the we find that a type A mechanism is the most plausible scenario to explain also the IMF B_y polarity effect on IB latitude.

Interpreting the onset latitude as a metric of the strength of the substorm in terms of flux closure (Milan et al., 2009), the similar onset latitude for ± B_y (Figure 3) combined with their more frequent occurrence (Ohma et al., 2021) suggests a larger flux throughput when IMF B_y and Ψ has opposite polarity, in agreement with a type A mechanism. We find no direct evidence that the substorm onset shifts to higher latitudes for opposite IMF B_y and tilt polarity compared to same polarity, as would be indicative of a type B mechanism (the more frequent substorms closing less flux each, hence taking place at a higher latitude [e.g., Milan et al. (2009)] to accommodate the same flux throughput). This analysis is therefore consistent with the conclusions above, namely that a type A mechanism is likely to exist during these conditions. One may argue that if the global dayside reconnection rate is affected (type A mechanism) as suggested, a lower onset latitude would be expected for opposite B_y and Ψ polarity, contrary to what we see (the weak trend in the suggested direction is below the level of statistical significance). One possibility is that both a type A and B mechanism may be present, since their influence on onset latitude is expected to be opposite. If so, the presence of a type B mechanism indicates inherent limitations of addressing the strength of a substorm only through its onset latitude. Nevertheless, our main conclusion remains, namely, that a type B mechanism alone can not explain the results, and that the global dayside reconnection rate has an explicit B_y dependence during periods of significant dipole tilt.

As mentioned in the introduction, more frequent SMC intervals during the IMF B_y/tilt polarity associated with more frequent substorms would be indicative of a type A mechanism. This is indeed what we see in Figure 1. It is nevertheless relevant to mention the study by Milan et al. (2019) in this regard, showing that the substorm onset latitude is an important parameter in determining whether the magnetotail develop into a period of SMC if the IMF remains southward after a substorm. They found that substorms taking place in an extended oval (below 65° MLAT) was less likely to develop into an SMC interval, and suggested this was due to the atmosphere invoking friction on the ionosphere-magnetosphere system, since lower latitude substorms are typically stronger. From Figure 2 we have seen that the more frequent substorms observed for opposite B_y/tilt polarity (Ohma et al., 2021) are associated with stronger substorms. The fact that we also observe more frequent SMC intervals when IMF B_y and the dipole tilt have opposite signs suggests that the effect reported on by Milan et al. (2019) is less relevant for the more typical substorms considered here. In fact, the quartile binning used in Figure 3 shows that three of four bins (75% of the onsets) have a median onset latitude above 65°, which was the limit for “convection breaking” used by Milan et al. (2019).

For opposite compared to equal polarity of IMF B_y and tilt angle, observations show stronger substorms, more frequent substorms and more frequent SMCs. Furthermore, the average IB latitude and polar cap radius indicate a larger oval, which means that the average flux content is also greater for opposite IMF B_y and Ψ. In addition, Reistad et al. (2021) found 10% stronger flux throughput during the same conditions. Taken together, we conclude that the body of evidence presented is pointing towards mechanism A being the main source of the observed explicit B_y behaviour of the system. However, we can not exclude that a type B mechanism take place at the same time, but taken alone, a type B mechanism is insufficient to explain the observed behavior.

The results from this paper suggests that an explicit B_y effect should be included in future global dayside reconnection rate coupling functions, which is expected to enhance the predictive abilities of geospace activity. When taking this contribution into account, it would likely be easier to make further constraints on the importance of mechanism B type of processes.

Although we suggest that an explicit B_y effect is present on the global dayside reconnection rate, we have at present no good understanding of why. As suggested earlier by Reistad et al. (2020) and Ohma et al. (2021), the many dawn-dusk asymmetries upstream of the magnetopause (Walsh et al., 2014) may introduce dawn-dusk asymmetries in the local dayside reconnection rate. How this combine with a tilted dipole will be a very interesting topic to explore with 3D global kinetic models such as the Vlasiator model (Palmroth et al., 2018).

4 Conclusion

Based on the new analysis presented in section 2, together with recent advances in describing the geospace response during these conditions (Holappa and Mursula, 2018; Holappa et al., 2020; Reistad et al., 2020; Holappa et al., 2021b; Ohma et al., 2021), we conclude that the global dayside reconnection rate is likely to be enhanced when IMF B_y and the dipole tilt have opposite signs (± and −/+), compared to when they have the same signs (−/− and +/+). This is referred to as a type A mechanism. We have also discussed the possible contribution from a type B mechanism, where the magnetotail response may depend on IMF B_y and the dipole tilt, affecting the amount of magnetic flux the magnetotail lobes typically can support. While we can not neglect that a type B mechanism has a significant contribution to the observed response, we find it insufficient to explain our analysis alone, pointing toward the existence of a type A mechanism taking place at the dayside of the magnetosphere. The detailed physical mechanism of such an effect should be further investigated.

Data availability statement

We acknowledge the use of NASA/GSFC Space Physics Data Facility http://omniweb.gsfc.nasa.gov for OMNI data. The Kissinger SMC list is available at https://doi.org/10.5281/zenodo.6147689. The DeJong SMC list is published along with its description in Dejong (2014). The FUV substorm lists can be downloaded from https://supermag.jhuapl.edu/substorms/. The MPB substorm list is available from their publication McPherron and chu (2018). The dipole tilt angle is computed based on the International Geomagnetic Reference Field dipole coefficients using the klaundal/dipole library, available on GitHub. All the original POES/MEPED energetic particle data used here are archived in the NOAA/NGDC dataserver http://www.ngdc.noaa.gov/stp/satellite/poes/index.html.

Author contributions

This paper is a result of a team effort emerging from a breakout group initiated during the initial workshop of the Center for Unified Studies of Interhemispheric Asymmetries (CUSIA). JR did the substorm onset latitude data analysis, organized regular online meetings, and was the lead writer of the manuscript. LH did the MPB and IB latitude data analysis, AO did the SMC data analysis, and both played an active role in shaping the manuscrupt and discussion throughout the entire processs. CG and DS also actively participated in the discussions shaping the paper throughout the entire process, in addition to participating in the writing process. TA has been involved in consulting the IB latitude analysis, as well as writing relevant parts of that section, and providing comments on the manuscript. AD was consulted in the SMC analysis, assisted writing the respective section, and commented on the manuscript.

Funding

JR were funded by the Norwegian Research Council (NRC) through grant 300844/F50. LH was funded by the Academy of Finland postdoctoral project 322459. AO were funded by the Norwegian Research Council (NRC) through grant 223252/F50. DS was supported by NASA LWS 80NSSC17K0718. TA was supported by the Academy of Finland (PROSPECT project 24303278). This work was also supported by the Center for the Unified Study of Interhemispheric Asymmetries (CUSIA), NASA Award 80NSSC20K0606.

Acknowledgments

We thank the Centre for Unified Studies on Interhemispheric Asymmetries for hosting interesting discussions and meeting venues where the collaboration for this work was initiated. We also thank all data vendors across the community contributing to the higher level data products we use, see data availability statement.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Asikainen, T., Maliniemi, V., and Mursula, K. (2010). Modeling the contributions of ring, tail, and magnetopause currents to the corrected Dst index. J. Geophys. Res. 115, A12203. doi:10.1029/2010JA015774

CrossRef Full Text | Google Scholar

Asikainen, T., and Mursula, K. (2011). J. Atmos. Sol. Terr. Phys. 73, 335–347. doi:10.1016/j.jastp.2009.12.011

CrossRef Full Text

Asikainen, T., Mursula, K., and Maliniemi, V. (2012). Correction of detector noise and recalibration of noaa/meped energetic proton fluxes. J. Geophys. Res. 117. doi:10.1029/2012ja017593

CrossRef Full Text | Google Scholar

Chu, X., McPherron, R. L., Hsu, T. S., and Angelopoulos, V. (2015). Solar cycle dependence of substorm occurrence and duration: Implications for onset. JGR. Space Phys. 120, 2808–2818. doi:10.1002/2015JA021104

CrossRef Full Text | Google Scholar

Cliver, E., Kamide, Y., and Ling, A. (2000). Mountains versus valleys: Semiannual variation of geomagnetic activity. J. Geophys. Res. 105, 2413–2424. doi:10.1029/1999ja900439

CrossRef Full Text | Google Scholar

Dejong, A. D. (2014). Steady magnetospheric convection events: How much does steadiness matter? J. Geophys. Res. Space Phys. 119, 4389–4399. doi:10.1002/2013JA019220

CrossRef Full Text | Google Scholar

Frey, H. U., Mende, S. B., Angelopoulos, V., and Donovan, E. F. (2004). Substorm onset observations by image-fuv. J. Geophys. Res. 109, A10304. doi:10.1029/2004JA010607

CrossRef Full Text | Google Scholar

Friis-Christensen, E., and Wilhjelm, J. (1975). Polar cap currents for different directions of the interplanetary magnetic field in the y-z plane. J. Geophys. Res. 80, 1248–1260. doi:10.1029/JA080i010p01248

CrossRef Full Text | Google Scholar

Fukushima, N. (1994). Some topics and historical episodes in geomagnetism and aeronomy. J. Geophys. Res. 99, 19113–19142. doi:10.1029/94ja00102

CrossRef Full Text | Google Scholar

Holappa, L., Asikainen, T., and Mursula, K. (2020). Explicit IMF dependence in geomagnetic activity: Modulation of precipitating electrons. Geophys. Res. Lett. 47, 1–7. doi:10.1029/2019gl086676

CrossRef Full Text | Google Scholar

Holappa, L., and Buzulukova, N. (2022). Explicit IMF By-dependence of energetic protons and the ring current. Geophys. Res. Lett. 49, e2022GL098031. doi:10.1029/2022GL098031

PubMed Abstract | CrossRef Full Text | Google Scholar

Holappa, L., and Mursula, K. (2018). Explicit IMF B_y dependence in high-latitude geomagnetic activity. J. Geophys. Res. Space Phys. 4728, 4728–4740. doi:10.1029/2018JA025517

CrossRef Full Text | Google Scholar

Holappa, L., Reistad, J. P., Ohma, A., Gabrielse, C., and Sur, D. (2021a). The magnitude of IMF b_y-influences the magnetotail response to solar wind forcing. JGR. Space Phys. 126. doi:10.1029/2021JA029752

CrossRef Full Text | Google Scholar

Holappa, L., Robinson, R., Pulkkinen, A., Asikainen, T., and Mursula, K. (2021b). Explicit IMF b_y-dependence in geomagnetic activity: Quantifying ionospheric electrodynamics. JGR. Space Phys. 126, e2021JA029202. doi:10.1029/2021ja029202

CrossRef Full Text | Google Scholar

King, J. H., and Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly wind and ace plasma and magnetic field data. J. Geophys. Res. 110, A02104. doi:10.1029/2004JA010649

CrossRef Full Text | Google Scholar

Kissinger, J., McPherron, R. L., Hsu, T.-S., and Angelopoulos, V. D. (2022). Dataset of steady magnetospheric convection events in earth’s magnetosphere from 1997 to 2013. Zenodo. doi:10.5281/zenodo.6147689

CrossRef Full Text | Google Scholar

Kissinger, J., McPherron, R. L., Hsu, T. S., and Angelopoulos, V. (2012). Diversion of plasma due to high pressure in the inner magnetosphere during steady magnetospheric convection. J. Geophys. Res. 117. doi:10.1029/2012JA017579

CrossRef Full Text | Google Scholar

Kissinger, J., McPherron, R. L., Hsu, T. S., and Angelopoulos, V. (2011). Steady magnetospheric convection and stream interfaces: Relationship over a solar cycle. J. Geophys. Res. 116. doi:10.1029/2010JA015763

CrossRef Full Text | Google Scholar

Laundal, K. M., Reistad, J. P., Hatch, S. M., Moretto, T., Ohma, A., Østgaard, N., et al. (2020). Time-scale dependence of solar wind-based regression models of ionospheric electrodynamics. Sci. Rep. 1, 16406. doi:10.1038/s41598-020-73532-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Liou, K. (2010). Polar ultraviolet imager observation of auroral breakup. J. Geophys. Res. 115, 1–7. doi:10.1029/2010JA015578

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., Barnard, L. A., Watt, C. E., Scott, C. J., Coxon, J. C., et al. (2020). Semi-annual, annual and universal time variations in the magnetosphere and in geomagnetic activity: 3. Modelling. J. Space Weather Space Clim. 10, 61. doi:10.1051/swsc/2020062

CrossRef Full Text | Google Scholar

McPherron, R. L., and Chu, X. (2018). The midlatitude positive bay index and the statistics of substorm occurrence. JGR. Space Phys. 123, 2831–2850. doi:10.1002/2017ja024766

CrossRef Full Text | Google Scholar

McPherron, R. L. (1970). Growth phase of magnetospheric substorms. J. Geophys. Res. 75, 5592–5599. doi:10.1029/ja075i028p05592

CrossRef Full Text | Google Scholar

McWilliams, K. A., Pfeifer, J. B., and McPherron, R. L. (2008). Steady magnetospheric convection selection criteria: Implications of global superdarn convection measurements. Geophys. Res. Lett. 35, L09102. doi:10.1029/2008GL033671

CrossRef Full Text | Google Scholar

Meurant, M., Gérard, J. C., Blockx, C., Spanswick, E., Donovan, E. F., Hubert, B., et al. (2007). El - a possible indicator to monitor the magnetic field stretching at global scale during substorm expansive phase: Statistical study. J. Geophys. Res. 112. doi:10.1029/2006ja012126

CrossRef Full Text | Google Scholar

Milan, S. E., Boakes, P. D., and Hubert, B. (2008). Response of the expanding/contracting polar cap to weak and strong solar wind driving: Implications for substorm onset. J. Geophys. Res. 113, 1–11. doi:10.1029/2008JA013340

CrossRef Full Text | Google Scholar

Milan, S. E., Carter, J. A., Sangha, H., Bower, G. E., and Anderson, B. J. (2021). Magnetospheric flux throughput in the dungey cycle: Identification of convection state during 2010. J. Geophys. Res. Space Phys. 126. doi:10.1029/2020JA028437

CrossRef Full Text | Google Scholar

Milan, S. E., Gosling, J. S., and Hubert, B. (2012). Relationship between interplanetary parameters and the magnetopause reconnection rate quantified from observations of the expanding polar cap. J. Geophys. Res. 117, A03226. doi:10.1029/2011JA017082

CrossRef Full Text | Google Scholar

Milan, S. E., Grocott, A., Forsyth, C., Imber, S. M., Boakes, P. D., and Hubert, B. (2009). A superposed epoch analysis of auroral evolution during substorm growth, onset and recovery: Open magnetic flux control of substorm intensity. Ann. Geophys. 27, 659–668. doi:10.5194/angeo-27-659-2009

CrossRef Full Text | Google Scholar

Milan, S. E., Walach, M. T., Carter, J. A., Sangha, H., and Anderson, B. J. (2019). Substorm onset latitude and the steadiness of magnetospheric convection. J. Geophys. Res. Space Phys. 124, 1738–1752. doi:10.1029/2018JA025969

CrossRef Full Text | Google Scholar

Newell, P. T., and Gjerloev, J. W. (2011). Substorm and magnetosphere characteristic scales inferred from the supermag auroral electrojet indices. J. Geophys. Res. 116, A12232. doi:10.1029/2011JA016936

CrossRef Full Text | Google Scholar

Newell, P. T., Sergeev, V. A., Bikkuzina, G. R., and Wing, S. (1998). Characterizing the state of the magnetosphere: Testing the ion precipitation maxima latitude (b2i) and the ion isotropy boundary. J. Geophys. Res. 103, 4739–4745. doi:10.1029/97JA03622

CrossRef Full Text | Google Scholar

Newell, P. T., Sotirelis, T., Liou, K., Meng, C.-I., and Rich, F. J. (2007). A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables. J. Geophys. Res. 112, 1–16. doi:10.1029/2006JA012015

CrossRef Full Text | Google Scholar

Ohma, A., Reistad, J. P., and Hatch, S. M. (2021). Modulation of magnetospheric substorm frequency: Dipole tilt and IMF B_y effects. JGR. Space Phys. 126. doi:10.1029/2020JA028856

CrossRef Full Text | Google Scholar

Ohtani, S., and Gjerloev, J. W. (2020). Is the substorm current wedge an ensemble of wedgelets?: Revisit to midlatitude positive bays. JGR. Space Phys. 125. doi:10.1029/2020JA027902

CrossRef Full Text | Google Scholar

Palmroth, M., Ganse, U., Pfau-Kempf, Y., Battarbee, M., Turc, L., Brito, T., et al. (2018). Vlasov methods in space physics and astrophysics. Living Rev. comput. Astrophys. 4, 1. doi:10.1007/s41115-018-0003-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Reistad, J. P., Laundal, K. M., Ohma, A., Moretto, T., and Milan, S. E. (2020). An explicit IMF B dependence on solar wind-magnetosphere coupling. Geophys. Res. Lett. 47. doi:10.1029/2019GL086062

CrossRef Full Text | Google Scholar

Reistad, J. P., Laundal, K. M., Østgaard, N., Ohma, A., Burrell, A. G., Hatch, S. M., et al. (2021). Quantifying the lobe reconnection rate during dominant IMF B_y periods and different dipole tilt orientations. JGR. Space Phys. 126. doi:10.1029/2021JA029742

CrossRef Full Text | Google Scholar

Russell, C. T., and McPherron, R. L. (1973). Semiannual variation of geomagnetic activity. J. Geophys. Res. 78, 92–108. doi:10.1029/JA078i001p00092

CrossRef Full Text | Google Scholar

Russell, C., Wang, Y., and Raeder, J. (2003). Possible dipole tilt dependence of dayside magnetopause reconnection. Geophys. Res. Lett. 30. doi:10.1029/2003gl017725

CrossRef Full Text | Google Scholar

Sergeev, V. A., Malkov, M., and Mursula, K. (1993). Testing the isotropic boundary algorithm method to evaluate the magnetic field configuration in the tail. J. Geophys. Res. 98, 7609–7620. doi:10.1029/92JA02587

CrossRef Full Text | Google Scholar

Sergeev, V., Pellinen, R. J., and Pulkkinen, T. (1996). Steady magnetospheric convection: A review of recent results. Space Sci. Rev. 75, 551–604. doi:10.1007/bf00833344

CrossRef Full Text | Google Scholar

Walsh, A. P., Haaland, S., Forsyth, C., Keesee, A. M., Kissinger, J., Li, K., et al. (2014). Dawn-dusk asymmetries in the coupled solar wind-magnetosphere-ionosphere system: A review. Ann. Geophys. 32, 705–737. doi:10.5194/angeo-32-705-2014

CrossRef Full Text | Google Scholar