Production of solar abundances for nuclei beyond Sr: The s- and r-process perspectives

1 Introduction

Based on the first detailed geochemical abundance determinations of Suess and Urey (1956), the neutron shell structure investigations of Coryell (1956; 1961), and the discovery of radioactive Tc in the photospheres of evolved red giants (Merrill, 1952), the seminal works of Burbidge et al. (1957) (B²FH) and Cameron (1957) laid down the fundamental astrophysical conditions for the production of heavy elements. This included, in particular, isotopes beyond Fe, which were found in those works to be synthesized by neutron-capture processes, either slow (the slow or s-process) or fast (the rapid or r-process). Here, the terms slow and rapid consider whether neutron captures proceed at rates slower or faster than those of typical β-decays occurring along the respective nucleosynthesis path.

The slow neutron captures (in particular, their main component, including isotopes across and beyond the neutron magic number N = 50 up to N = 126) were attributed to the final evolutionary stages of red giants (called asymptotic giant branch or AGB stars). This was possible owing to the demonstration by Ulrich (1973) that their repeated ignition of He burning in a thin, unstable shell offered a natural way to produce the exponentially decreasing distribution of neutron exposures, previously invoked by Seeger et al. (1965).

Afterward, several attempts were made in the 70s, adopting intermediate-mass stars (see Iben and Truran, 1978) (IMS) models (4 ≲ M/M_⊙≲ 8) as s-process sites. There, the ${}^{22}\mathrm{N}\mathrm{e}$(α,n)${}^{25}\mathrm{M}\mathrm{g}$ source can be easily activated. However, the excessive neutron densities (n_n ≥ 10¹¹cm⁻³) it generated at the local temperatures (T ≃ 3.510⁸cm⁻³) were shown to be incompatible with observations (Busso et al., 1988) so that lower-mass (M/M_⊙≲ 3) AGB stars were finally considered (Iben and Renzini, 1982; Gallino et al., 1988). This implied assuming that the alternative ${}^{13}\mathrm{C}$(α,n)${}^{16}\mathrm{O}$ neutron source (requiring lower temperatures and producing lower n_n values, around 10⁷ cm⁻³) could be activated, as a consequence of some partial diffusion of protons from the envelope, sufficient to produce ${}^{13}\mathrm{C}$ in the He-rich layers when the H-burning shell reignites.

This ${}^{13}\mathrm{C}$(α,n)${}^{16}\mathrm{O}$ neutron source had been suggested to be at play many years before by Cameron (1957), but even now, the elusive mixing mechanisms necessary to its activation remain a subject of active research. Many attempts were dedicated along the past three decades to this goal, often on parametric grounds (Käppeler et al., 2011; Bisterzo et al., 2012), simulating various deep mixing events (Bisterzo et al., 2014, 2015; Cristallo et al., 2015; Battino et al., 2019). Partial accounts of these efforts can be found in Busso et al. (1999); Busso et al. (2007); Karakas and Lattanzio (2014); and Busso et al. (2021).

In particular, in the present study, we shall concentrate on results obtained in a recent series of models, where the formation of the mentioned neutron source was attributed to the buoyancy of magnetic flux tubes maintained by a dynamo process (Nucci and Busso, 2014).

For what concerns fast neutron captures, the same studies by Burbidge et al. (1957) and Cameron (1957) outlined a reasonable scenario for the first time. In these early studies, a steady-state formation of isotopes by neutron addition and hold-ups for nuclei with shells at N = 50, 82, or 126 neutrons was already postulated. This is presently better known as the r-process waiting-point concept. Since then, r-process research works have been quite diverse in terms of suggested stellar scenarios (for representative historical reviews, see Seeger et al., 1965; Hillebrandt, 1978; Kratz, 1988; Cowan et al., 1991; Kratz et al., 1993).

While for several decades the high-entropy (ν-driven) winds from core collapse supernovae type II (ccSN-II) were proposed as the favored r-process site (see Takahashi et al., 1994; Woosley et al., 1994; Freiburghaus et al., 1999a; Kratz et al., 2008; Farouqi et al., 2010; Kratz et al., 2014), attention was also given to complementary scenarios, in particular to the decompressed ejecta of neutron star mergers (NSM), which were discussed in important articles since the early epochs (Lattimer et al., 1977; Freiburghaus et al., 1999b; Rosswog et al., 1999).

However, still in the early 1990s, none of the suggested r-process scenarios could yield satisfactory results to fit the solar system (S.S.) r-process abundances. Hence, the Mainz −Basel −Los Alamos collaboration started to use improved site-independent calculations (Kratz et al., 1993). Although not (yet) pointed out explicitly in that work, these attempts also implied the possible existence of several r-process sites with different abundance patterns. Therefore, the S.S. abundances generated by fast neutron captures had to be explained by a superposition of r-process components, with varying neutron densities n_n (with n_n ≥ 10²⁰ cm⁻³), and occurring on time scales between 1 and 2 s.

First experimental information on anomalous local abundance yields of an unknown nucleosynthesis origin and corresponding attempts to determine their astrophysical conditions were from cosmochemical isotopic measurements in meteoritic CAI, together with presolar SiC − X grains and nanodiamonds (see Wasserburg et al., 1977; Niederer et al., 1980; Kratz et al., 2001; Pellin et al., 2006; Farouqi et al., 2009). In addition, elemental abundances were determined in metal-poor halo stars (for early articles, see Sneden et al., 1996, 2003; Hill et al., 2002; Honda et al., 2007; Mashonkina et al., 2007).

Initially, the suggested sites were based on a rather indirect way on nucleosynthesis modeling. Early research works suggested that light and intermediate trans-Fe elements could be synthesized due to a “weak r-process” component, while the heavier elements up to the A = 195 peak and the actinides could be synthesized in a “main r-process” variant. Recently, observations of gravitational waves from an NSM event (GW170817 see Abbott et al., 2017), together with the subsequent electromagnetic emission from a kilonova (see Evans et al., 2017), showed the first direct evidence of the ongoing r-process nucleosynthesis (Rosswog et al., 2018). Based on the emission of the red wavelength lanthanide fraction, Ji et al. (2019) suggested however that this NSM event did not actually produce a typical S.S. r pattern: further observations of similar objects are needed to draw firmer conclusions.

In order to accumulate sufficient information on the various r-process contributions from heterogeneous sources, today, systematic and accurate observational constraints from many low-metallicity stars exist (see the HERES survey (Hamburg ESO R-process Enhanced Star) Mashonkina and Christlieb, 2014) and provide adequate databases for comparing model results.

In the present study, after recalling briefly the results of recent work on n-captures, the status of heavy-element production is studied by verifying the compatibility of the scenarios for s- and r-process nucleosynthesis, through a comparison of their respective predictions for the S.S. composition. With this goal in mind, the mentioned research on the classical waiting-point approach (Kratz et al., 2007) turned out to be of special relevance, as it can exclude uncertainties related to the modeling of specific sites.

Reasonably good nuclear inputs for this work are available only below A ≃ 140–142, so this is the mass range on which we focus. Predictions from fast neutron captures are then compared to those for s-processing in AGB stars of low mass (namely, for masses M = 1.3, 1.5, 2.0, and 3.0 M_⊙, computed at metallicities from [Fe/H] = 0.1 down to [Fe/H] = − 0.8), after weighting on the classical Salpeter’s initial mass function (IMF) (Salpeter, 1955) and on the star formation rate (SFR) from Maiorca et al. (2012). Thus, we infer some new hints, including suggestions for future measurements.

A short outline of the adopted s-process models and of their predictions is presented in Section 2, while in Section 3, we discuss the assumptions for the waiting-point scenario of r-processing. The good agreement found between these complementary, independent views and the residual problems emerging are then outlined in Section 4, where improvements expected from future β-decay rate measurements are also underlined. Preliminary conclusions are drawn in Section 5.

2 A model for slow neutron captures and its results

In recent studies, revisions on the status of slow neutron captures, as occurring in evolved stars of low mass (1.3 ≲ M/M_⊙≲ 3) during the AGB stages, were discussed. These works deal with the particular approach that considers the buoyancy of magnetic flux tubes in a stellar dynamo process as responsible for the deep mixing episodes mentioned in Section 1 (see Nordhaus et al., 2008; Denissenkov et al., 2009). This idea led to analytical models of the underlying physical mechanisms in terms of 3D solutions for the magneto-hydrodynamic (MHD) equations involved (Nucci and Busso, 2014), where the previously quoted recent upgrades were obtained with the help of full stellar models (Vescovi et al., 2020; Vescovi, 2021), subsequently integrated by post-process computations, derived with the aim of reproducing the relevant physical parameters without recomputing the energy generation (Busso et al., 2021). In those attempts, comparisons were presented between model predictions and some major available constraints to s-processing (from high-resolution spectroscopy of selected classes of evolved stars to the S.S. abundances as emerging from the chemical evolution of the Galaxy and to isotopic admixtures of heavy elements, as measured in presolar grains recovered in pristine meteorites). In that first analysis, the input data for cross-sections of stable isotopes were mainly obtained from the Kadonis 0.3 repository (Dillmann et al., 2006), partly integrated with more recent measurements. For radioactive nuclei, cross-sections were taken from Shibata et al. (2011) (jend4.0), while rates for β^± decays and electron captures were from Takahashi and Yokoi (1987). The global accord obtained in that work between model predictions and S.S. abundances for s-only nuclei appeared to be fair, with a dispersion of model data roughly at the same level as measurement uncertainties (around σ ≃ 15%). Also, general indications from other constraints suggested a reasonable agreement, although not much could be said on possible further improvements and on discrepancies for individual isotopes.

Recent research on nuclear cross-sections, on the other hand, pointed out that substantial work is still needed in that field, both through real new estimates and through reanalysis of existing datasets (e.g., by Monte Carlo techniques) (Reifarth et al., 2018). Partial results from this work have recently been used (Vescovi and Reifarth, 2021) to study the impact on nuclear upgrades in stellar models. So far, however, a global update of the Kadonis compilation is still waited for. For the aforementioned reasons, it is important that also from the point of view of stellar modeling, a search must be pursued for better constraints on nuclear parameters. Palmerini et al. (2021), in particular, adopted the compilation of cross-sections Kadonis 1.0 (Dillmann, 2014) and made a detailed comparison between stellar predictions from specific masses and metallicities and the record of isotopic anomalies measured in presolar SiC grains (Liu et al., 2015; Stephan et al., 2018), covering the atomic mass interval from Sr to Ba (again, A ≲ 140). The analysis was, in particular, useful to verify the rather detailed agreement that could be reached and, at the same time, to indicate the need for revisions of some weak interactions, e.g., suggesting new measurements for the β-decay rates of Cs isotopes in ionized environments (see also Mascali et al., 2020; Li et al., 2021; Taioli et al., 2021).

As mentioned, the upgrades by Busso et al. (2021) and Palmerini et al. (2021) were based on the idea that, during the so-called third dredge-up or TDU episodes (see Lugaro et al., 2012; Karakas and Lattanzio, 2014), MHD mechanisms maintained by dynamo cycles could induce the downward penetration of protons into the He-rich layers of an evolved star, as required to fuel s-processing. The ensuing models are characterized by the formation of distinctively large reservoirs of protons, up to 5–10 times those initially suggested in more standard articles on the subject (Kaeppeler et al., 1990). In contrast, the local concentration of pollutants, hydrogen primarily, remains very low (see Figure 1 panel i). It is so low, actually, that the subsequent re-ignition of the H-burning shell, allowing proton captures to occur on the abundant ${}^{12}\mathrm{C}$, can produce ${}^{13}\mathrm{C}$, but only minimal traces of ${}^{14}\mathrm{N}$ (see Figure 1, panel ii). Under such conditions, the neutrons that are made available for heavy-element nucleosynthesis by the ${}^{13}\mathrm{C}$(α,n)${}^{16}\mathrm{O}$ source are essentially unfiltered by intermediate-mass nuclei and remain quite abundant.

FIGURE 1

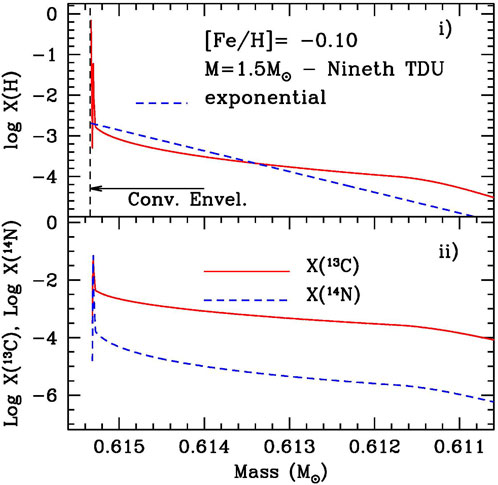
FIGURE 1. Pocket of protons (panel i) and the ensuing distributions of ${}^{13}\mathrm{C}$ and ${}^{14}\mathrm{N}$ (panel ii) in the layers below TDU, in one of the situations modeled by Palmerini et al. (2021). The abundances by mass (X) after the activation of extra-mixing mechanisms due to magnetic buoyancy are shown in the figure. We recall that, for an isotope − i, the abundance by number N_i and that by mass X(i) are related by the formula $N_i=\frac{\rho X_i}{A_i{m}_H}$, where m_H is the atomic mass unit.

Three important differences emerge with respect to previous models.

• First of all, the possibility to synthesize fresh ${}^{19}\mathrm{F}$ from the reactions starting at nitrogen itself is now strongly reduced, and the ensuing fluorine abundance predicted as a function of metallicity is now in close agreement with actual observations (Vescovi et al., 2021).

• A second remarkable implication is the very limited action of the so-called neutron poisons, i.e., the intermediate-mass nuclei with significant cross-sections (${}^{14}\mathrm{N}$ being their progenitor) acting as filters and limiting the number of neutrons captured by iron and its progeny.

• Finally, a reduced ${}^{14}\mathrm{N}$ concentration also implies a reduced formation of ${}^{22}\mathrm{N}\mathrm{e}$.

This last point follows from the activation of the chain:

${}^{14}\mathrm{N}\left(\alpha ,\gamma \right){}^{18}\mathrm{F}\left({\beta }^{+}\nu \right){}^{18}\mathrm{O}\left(\alpha ,\gamma \right){}^{22}\mathrm{N}\mathrm{e}.(1)$

Limiting its efficiency limits the neutron flux that can be released at a higher temperature and with a higher neutron density, when a thermal pulse finally develops, accompanied by the sudden enhancement of the He-burning rate (see Busso et al., 1999; Herwig, 2005, for details).

The aforementioned conditions can, in principle, be met by various mixing mechanisms, beyond the MHD one explored here. Some indications in this sense are contained in Appendix 1, where we present some general comments on the stellar models for neutron captures, which are maintained separate from the main text of this article, dedicated to nuclear issues.

We note that the scenario described here for the s-process is closer to the classical phenomenological approach (Kappeler et al., 1989) than most models discussed in recent years, especially in terms of its generally lower neutron densities, and hence of the operation of reaction branches. As compared to the mentioned models (see e.g., Cristallo et al., 2011), our production of the heavier stable isotopes of neutron-capture elements, like e.g., ${}^{86}\mathrm{K}\mathrm{r}$, ${}^{96}\mathrm{Z}\mathrm{r}$, and ${}^{100}\mathrm{P}\mathrm{d}$ (see Table 1), is now strongly reduced. This is relevant for our estimates of the Mo isotopes discussed later, where the neutron flow now proceeds mainly along the sides requiring low values of n_n (on average below 10⁸ n/cm³). In this respect, while the ${}^{22}\mathrm{N}\mathrm{e}$(α,n)${}^{25}\mathrm{M}\mathrm{g}$ neutron source (yielding higher neutron densities than the ${}^{13}\mathrm{C}$(α,n)${}^{16}\mathrm{O}$ one) remains important for fixing the operation of reaction branchings, its role is, however, reduced and so is that of IMS, where its activation would be very efficient. As far as one can judge now, super-AGB stars, of mass 8–10 M_⊙, currently considered the parents of e-capture supernovae (Leung et al., 186 2020), should be at the best marginal in establishing the galactic average of the s-nuclei, although they might be relevant in rare, individual cases.

TABLE 1

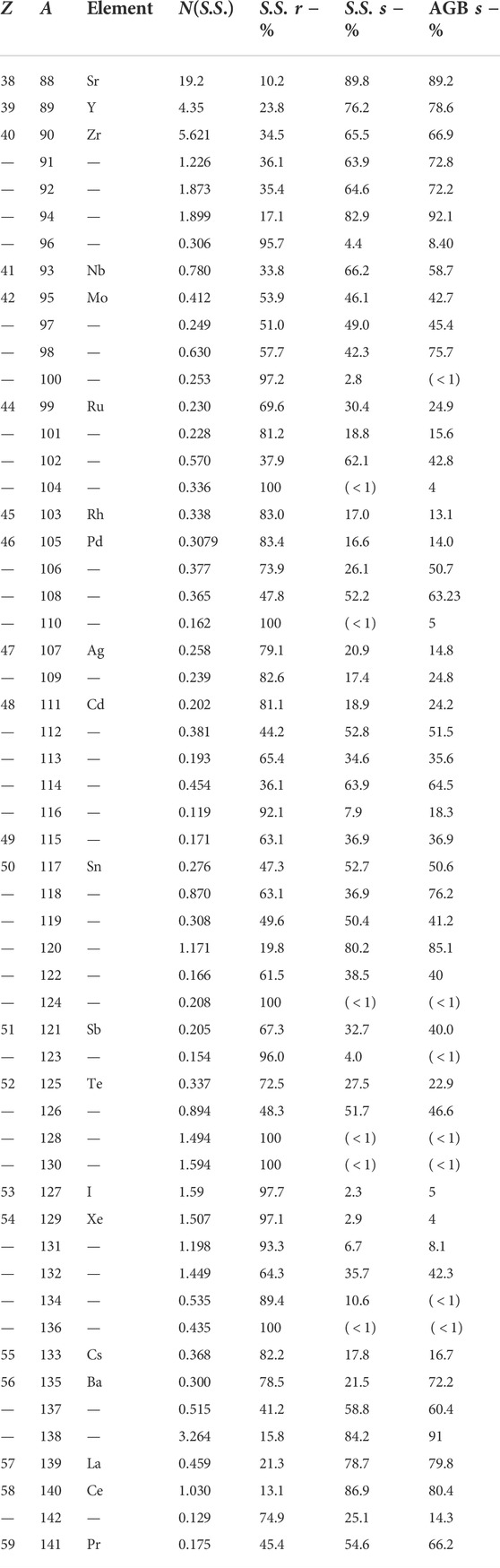
TABLE 1. Predictions of the fractional solar abundances from fast and slow n-captures (88 ≤ A ≤ 142).

In the computations discussed here, AGB models of the type described so far, extended to stellar masses for 1.3–3 M_⊙, with metallicities in the range −0.8 ≲ [Fe/H] ≲ 0.1, have been computed for the purposes described in Section 1, using the Kadonis 1.0 cross-section compilation. They were subsequently averaged on galactic time scales with the mentioned choices for the IMF and SFR. The results, expressed in terms of a distribution of abundances for the isotopes in the adopted atomic mass range, were divided by the solar initial concentrations from Lodders (2021) and normalized to unity so that they express average s-process contributions to the solar composition. This procedure, aimed at reproducing roughly the outcomes of a galactic chemical evolution model up to the solar formation era, is not exempt from serious drawbacks, which must be taken into account in estimating the global uncertainties. Indeed, while the choices for the IMF and SFR are rather standard, the method cannot account for the real complexity of the inter-relations among the many subsystems of the galaxy. In this respect, the accuracy achieved is roughly at the same level as the one for the r-process, described in Section 3; hence, it is adequate for the present purposes. However, in parallel to this, we have, in any case, undertaken a more sophisticated chemo-dynamical simulation of the galaxy and of its enrichment in s- and r-isotopes (Antonuccio-Delogu et al., 2022), based on the GIZMO open-source code (see: http://www.tapir.caltech.edu/).

The resulting fractional S.S. abundances in the chosen mass range (88 ≲ A ≲ 142) are shown in Figure 2, adopting the solar composition from Lodders (2021). As discussed previously in various articles (see Trippella et al., 2016; Busso et al., 2021), the results are largely independent of the specific stellar models and type of mixing adopted, provided these consider some general crucial features. These essentially 1) maintain a moderate temperature in the thermal pulses (low mass Kaeppeler et al., 1990); 2) provide a dominant contribution from the ${}^{13}\mathrm{C}$(α,n)${}^{16}\mathrm{O}$ reaction (Käppeler et al., 2011); and 3) give rise to mixing mechanisms like those in Figure 1, providing extended ${}^{13}\mathrm{C}$ distributions with little ${}^{14}\mathrm{N}$, to account for the effects on the neutron fluxes mentioned earlier (Liu et al., 2014, 2015; Trippella et al., 2016). By respecting these constraints, in general, one obtains predictions close to 100% for the so-called s-only isotopes, where remaining discrepancies can be attributed to nuclear effects. In this respect, given the complexities of stars, it is conceivable that further, non-magnetic, mechanisms suitable to give rise to the same effects might contribute to the picture (see Battino et al., 2016, 2019; Denissenkov and Tout, 2003).

FIGURE 2

FIGURE 2. Distribution of s-process fractional abundances in the mass range 88 ≲ A ≲ 142 considered in the present work, as obtained with the weighting procedure described in Busso et al. (2021) and Palmerini et al. (2021) and (more synthetically) in Section 2. Red symbols refer to the so-called s−only nuclei, which are shielded by stable isotopes against contributions from the r-process.

The specific predictions obtained with our models are shown in Figure 2 (where the s-only nuclei are indicated in red). There, the reproduction of solar abundances is good, with an average dispersion around 11%. This check gives us a general confidence on the method, allowing us to compare our expectations for the other (non-s only) isotopes with the complementary estimates derived from r-processing. We then list our model s-process contributions to S.S. abundances in Table 1, column 7.

3 The waiting-point model for rapid neutron captures and its results

Since none of the presently discussed scenarios for rapid neutron-capture nucleosynthesis seems to produce a complete S.S. r-like pattern, ranging from the light trans-Fe region up to the actinides, for this study (i.e., for comparing the isotopic abundance fractions of the s-process and r-process in the S.S. composition), we decided to choose an updated version of the classical site-independent waiting-point concept (Coryell, 1956; Burbidge et al., 1957; Cameron, 1957; Kratz, 1988; Kratz et al., 1993). It assumes a chemical equilibrium between fast neutron captures (n, γ) and photo-disintegrations (γ, n) within isotopic chains, followed by a β-equilibrium during the freeze-out phase within isobaric chains. In our present approach, we combine the results from our early publications (see Kratz et al., 1993) with the later improvements from experimental data and microscopic models (see Pfeiffer et al., 1997; Kratz et al., 2000; Möller et al., 2003; Farouqi et al., 2010; Kratz et al., 2014, Kratz et al., 2019).

As an example of the r-process abundances we had obtained already two decades ago, in Figure 3, we show the results from three specific waiting-point calculations with different neutron densities and corresponding process duration (solid lines), in comparison to the S.S. r- “residuals” from that time. In these calculations, the global deformed Extended Thomas Fermi Model plus Strutinsky integral and the Bogolyubov-enhanced shell-quenching, (ETFSI-Q) mass model (Pearson et al., 1996) have been used, together with the corresponding Quasi-particle random-phase approximation for Gamow-Teller and first forbidden transitions (QRPA(GT + FF)) (see Pfeiffer et al., 2002; Möller et al., 2003). We show here these exemplary results because, while documenting the importance of the N = 50, 82, and 126 bottlenecks of the r-matter flow, they are completely site-independent and, despite this, they already show the general r-abundance patterns of the different r-process scenarios, more or less as we know them today and as we have published later in Farouqi et al. (2010) and Kratz et al. (2014).

FIGURE 3

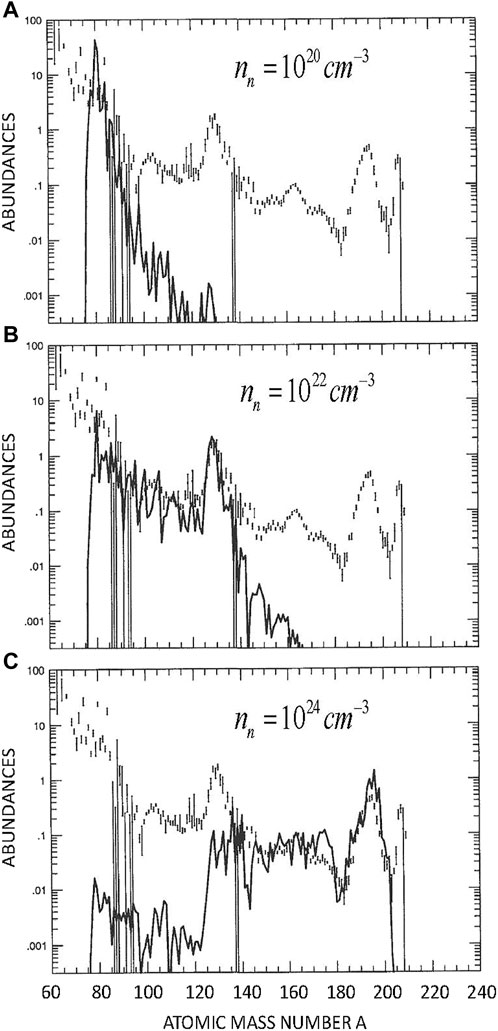
FIGURE 3. Results of time-dependent steady-flow r-process calculations with neutron densities n_n = 10²⁰ cm⁻³ (A), n_n = 10²² cm⁻³ (B), and n_n = 10²⁴ cm⁻³ (C), and corresponding process duration τ_r = 1.2, 1.7, and 2.1 s, respectively. The abundances by number are shown in the figure, in a scale in which N(Si) = 10⁶. This is compared to the S.S. r-“ residuals” in the same scale. In principle, adding up the abundances of those three r-process components will result in the complete S.S. r-process abundance blend (adapted from Kratz et al., 2000).

In the first panel of Figure 3, a low neutron density n_n = 10²⁰ cm⁻³ and a process duration of τ_r = 1.2 s were chosen to obtain a “best fit” of the A ≃ 80 r-process peak from its known N ≃ 50 precursor isotopes between Z = 29 (Cu) and Z = 32 (Ge) (see Kratz et al., 1991). Beyond this peak, a steeply decreasing abundance pattern by about four orders of magnitude is observed for the mass region above, down to the minimum yields at A ≃ 130. Currently, we know that this pattern “mimics” the isotopic distributions of Sr, Zr, Mo, and Ru observed in the presolar SiC grains of type X, measured by the Argonne–Chicago group (see Pellin et al., 2006; Farouqi et al., 2009; Kratz et al., 2019). The nucleosynthesis origin of this abundance pattern up to the rising wing of the second r-process peak at A ≃ 130 has been attributed to classical ccSNe (Kratz et al., 1993; Farouqi et al., 2009, 2022). The second panel of Figure 3 shows an abundance component obtained with a slightly higher neutron density of n_n = 10²² cm⁻³ and a process duration of τ_r = 1.7 s. It covers the S.S. r-region up to the full A ≃ 130 peak and continues with decreasing abundances in the light R.E.E region up to about Eu. This r-process component has been normalized to the r-only isotopes ${}^{128}\mathrm{T}\mathrm{e}$ and ${}^{130}\mathrm{T}\mathrm{e}$, where again a number of experimental data for the progenitor isotopes from Z = 47 (Ag) up to Z = 51 (Sb) exist (see Kratz et al., 2000).

In addition to the A ≃ 130 r-abundance peak, a wide range of (β, γ) and delayed neutron spectroscopic data, as well as accordingly updated microscopic models, are available in the region near Z = 34 (Se) and Z = 40 (Zr), where the shape transition between the magic N = 50 shell via the spherical N = 56 subshell up to the onset of strong (rigid rotor) ground-state deformation plays a decisive role in the determination of various nuclear properties (see Kratz et al., 1983a,b; Lhersonneau et al., 1994; Möller et al., 2003). As an example, the improved understanding of the nuclear structure resulted in changes of theoretical β-decay properties for the N ≃ 56 isotopes by factors from 13 (e.g., for ${}^{89}\mathrm{S}\mathrm{e}$) up to 53 (e.g., for ${}^{93}\mathrm{S}\mathrm{r}$). Fast neutron captures dominant in this regions above A ≃ 90 (our second n_n component) are frequently denoted as the weak r-process. Today, we know that its abundance pattern “mimics” the elemental distribution of metal-poor, r-poor, or incomplete r stars with [Eu/Fe] ≲ 0.2.

A typical example of such a type of star is the so-called “Honda star” (HD122563, see Honda et al., 2007), with its overabundances relative to the S.S. r-pattern of the light trans-Fe elements and its decreasing abundances in the rare earth element (R.E.E.) region between Z = 68 (Er) and Z = 70 (Yb). As one of the signatures to classify the different types of halo stars, astronomers use, for example, the abundance ratio of light-to-heavy mass regions, using Z = 38 (Sr) and Z = 63 (Eu) as representative elements. For the r-poor Honda star, the ratio (Sr/Eu) ≃ 505, which is a factor 24, higher than the S.S. r-ratio of 21. The nucleosynthesis origin of these r-poor stars can very likely be attributed to jet-like or magneto-rotational SNe, with low strengths of magnetic fields and of rotation (see Nishimura et al., 2017; Farouqi et al., 2022).

The third panel in Figure 3 shows a typical abundance pattern for a main r-process component, with consequently higher neutron densities (here, n_n = 10²⁴ cm⁻³) and slightly longer process duration (here, τ_r = 2.1 s), which covers the S.S. r-region of the R.E.E., the full third r-process peak at A ≃ 195 and beyond, up to the actinides. This last n_n component has been normalized to the top of the peak with its r-only isotopes of Os, Ir, and Pt, formed in the back decay of their extremely neutron-rich, experimentally still unknown, N ≃ 126 precursor isotopes of the nuclei from Z = 68 (Er) to Z = 72 (Hf). Presently, we know that this kind of a main or even strong r-process pattern “mimics” the elemental abundances of the so-called r-enriched metal-poor halo stars with [Eu/Fe] $\ge +0.8$. Typical examples for this class of stars are the normal r-II Sneden star (CS22892-052, see Sneden et al., 2003) and the so-called actinide-boost Cayrel-star (CS31082-001, see Hill et al., 2002), attributed to different types of NSM (see Rosswog et al., 2018; Farouqi et al., 2022).

By simply adding up these three abundance patterns, we get a total abundance distribution which comes relatively close to the S.S. r-blend. In particular, our computed estimates for the r-process contributions to S.S. abundances, normalized to N(Si) = 10⁶, and with updated nuclear inputs are presented in Figure 4.

FIGURE 4

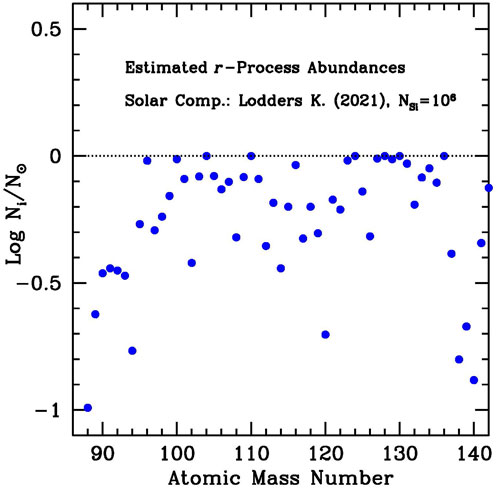
FIGURE 4. Distribution of r-process fractional abundances as estimated by our waiting-point approximation, according to the discussion in the text. Similar to what is shown in Figure 2 for the s-process, nuclei considered to be of essentially pure r-process origin $(\ge 95\%)$ are indicated with red symbols. It should be noted that, following a common habit, the second r-peak was normalized to ${}^{128}\mathrm{T}\mathrm{e}$ and ${}^{130}\mathrm{T}\mathrm{e}$, assumed to be r-only. This has some support in the data of Table 1, column 7, where we show that, even in the estimates from AGB models, their s-fractions are predicted to be ≤1%.

In the simplest possible physical realization of the solar r-process distribution, stellar and NSM models would have to find where exactly the aforementioned “components” are produced by nucleosynthesis models. Quite obviously, this is a very naive view, as no astrophysical source can be imagined to host such simple neutron-capture processes at constant neutron density. The previous indications, and their descending suggestions for nuclear parameters, have instead to be looked at as first-order approximations, good for an assessment of the very complex nuclear problems related to the reaction paths of r-nuclei. As we shall see, even this simple approach already yields useful indications and a remarkable general consistency with Solar System data. Also attributing the aforementioned components to specific stellar sources is a difficult task in the cluster abundance patterns observed in galactic, mainly low-metallicity, stars. With these limits in mind, we comment, however, briefly on this point in Appendix 1.

4 Comparisons and discussion

A comparison of the results from the two neutron-capture approaches outlined so far (Figures 2, 4) is presented in Table 1. As mentioned, for what concerns the r-process model, here the original computations shown in Figure 3 have been updated, considering various different mass models with consistent QRPA(GT + ff) β-decay predictions by Farouqi et al. (2010) and the quoted recent deformed FRDM12/QRPA model combination by Kratz et al. (2014).

In Figure 5, we show the resulting ratios between the two sets of expectations for the s-process fractions of solar abundances. The agreement between these completely independent approaches is quite good. It is actually the best so far published, to our knowledge.

FIGURE 5

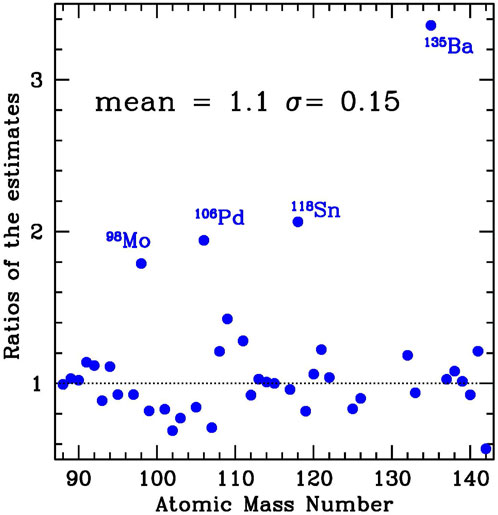
FIGURE 5. Ratios between the two sets of predictions for the s-fractions, as presented in Table 1. Despite the good agreement, with rather randomly distributed differences, a mean value close to unity, and a reasonable variance, a few outliers emerge and are shown here. The plot includes all nuclei predicted to derive from s-processing by a fraction larger than 10%. The mean value and variance are computed excluding nuclei that are off by more than a factor of 3, in this case only ${}^{135}\mathrm{B}\mathrm{a}$.

Despite this satisfactory outcome of our work, some discrepancies remain and require a more detailed analysis, as presented in the following subsections.

4.1 ${}^{98}\mathrm{M}\mathrm{o}$

The element Mo as measured in early S.S. materials provides important tools for understanding the contamination of the presolar nebula in heavy nuclei. On the one hand, its isotopic admixture in the mainstream-type of presolar SiC grains (Stephan et al., 2019) is quite typical of AGB star progenitors (Palmerini et al., 2021). On the other hand, Mo isotopes show very different anomalies in the so-called presolar SiC − X-grains (Pellin et al., 2006), whose origin has been attributed to ccSNe (Farouqi et al., 2009; Kratz et al., 2019).

Stephan and Davis (2021) inferred, from isotopic measurements in presolar SiC grains of AGB origins, estimates for the r- and s-process decoupling of Mo isotopes. In the specific case of ${}^{98}\mathrm{M}\mathrm{o}$, our estimates from the waiting-point approximation would suggest a lower s-process percentage (42.3%) than the one from the aforementioned authors (74.4%, very similar to the expectation from AGB models, 75.7%). In s-process scenarios, the synthesis of lighter Mo isotopes depends on several branching reactions at Nb isotopes, with contributions from isomeric states at ${}^{93}\mathrm{N}\mathrm{b}$, ${}^{94}\mathrm{N}\mathrm{b}$, and ${}^{95}\mathrm{N}\mathrm{b}$ (see Figure 5 in Palmerini et al., 2021). All of them terminate before ${}^{96}\mathrm{M}\mathrm{o}$, which is an s-only nucleus whose abundance is very well reproduced by the models discussed in Section 2 (see Figure 2). We remember, however, that cross-sections in the Zr–Mo region are still very uncertain (for the unstable ${}^{95}\mathrm{Z}\mathrm{r}$, experimental information is essentially missing), and new measurements are crucial here for any conclusion. Cross-sections for Mo isotopes are actually under measurement now by the n_TOF collaboration (Guerrero et al., 2013).

Concerning the r-process predictions, we compare the results from the old mass- and shell model combination ETFSI-Q/QRPA (as used e.g., in Kratz et al., 2000) with our most recent FRDM/QRPA computations (see e.g., Kratz et al., 2014). For both model combinations, the basic nuclear parameters are obtained from the mass model. They are the mass derivatives Q_β and S_n, in addition to the ground-state shape of the β-decay mother isotope, related to the quadrupole deformation parameter, ϵ₂, (for which positive values mean prolate shapes and negative values mean oblate shapes). With these parameters, the so-called β-strength function is calculated within the QRPA shell model, from which spins and parities (J^π), level schemes, β-feedings (log  ft values), and finally the integral quantities, T_1/2 and β-delayed neutron-branchings P_xn, are deduced.

To summarize, for ${}^{98}\mathrm{M}\mathrm{o}$ and the following cases ${}^{118}\mathrm{P}\mathrm{d}$, ${}^{118}\mathrm{S}\mathrm{n}$, and ${}^{135}\mathrm{B}\mathrm{a}$, we compare the respective hold-up points of the isotopic r-matter flow at S_n ≲ 2 MeV for masses A and (A+ 1), which define the r-process progenitor isotopes with their β-decay parameters T_1/2 and P_xn and their resulting initial isotopic waiting-point abundances. After modulation by the β-delayed n-branchings during the freeze-out, the final abundance yields of the stable nuclei of interest are obtained.

For the specific case of ${}^{98}\mathrm{M}\mathrm{o}$ (Z = 42, N = 56), in both mass/shell model combinations, the dominant progenitors at A = 98 are ${}^{98}\mathrm{K}\mathrm{r}$ (Z = 36, N = 62) and ${}^{98}\mathrm{S}\mathrm{e}$ (Z = 34, N = 64). For the ETFSI-Q/QRPA version, they account for ≃ 81% and ≃19%, respectively. The S_n values for the dominant ${}^{98}\mathrm{K}\mathrm{r}$ hold-up point are practically identical for both model combinations, and (to our relief) the β-decay properties T_1/2 and P_n are experimentally known for the whole isobaric decay chain to ${}^{98}\mathrm{M}\mathrm{o}$. Since the relevant nuclear data predictions for ${}^{98}\mathrm{S}\mathrm{e}$ are also quite similar, we can estimate the total effect for A = 98, which is negligible.

More substantially, instead, the effect from the single waiting-point progenitor isotope in the A = 99 mass chain (Z = 35, N = 64), i.e., ${}^{99}\mathrm{B}\mathrm{r}$ will feed the A = 98 mass chain via its predicted high P_n value. Here, relative to ETFSI-Q, in the FRDM12 mass model, the decreasing S_n trend to the hold-up isotopes with S_n ≃ 2 MeV is shifted by two units to higher masses. As a consequence, with the FRDM/QRPA model combination, the calculated waiting-point abundance of ${}^{99}\mathrm{B}\mathrm{r}$ is reduced. In addition, taking into account the slightly different P_n predictions, the final S.S. r-fraction of the stable isotope ${}^{98}\mathrm{M}\mathrm{o}$ would be reduced from 57.7%, as listed in Table 1, to about 45%, which would correspond to an increase of the S.S. s-fraction from 42.3% to about 55%, in better agreement with the AGB s-process model predictions, now being only a factor 1.38 lower than the S.S. s- values.

The aforementioned discussion is only an attempt of clarifying how the present numbers still have an unavoidable local dependence on the choice of nuclear input data. We underline that these difficulties cannot be overcome by referring to specific astrophysical sites, being rooted in the nuclear inputs; they will affect equally any nucleosynthesis model, as all such models require nuclear input parameters. Our estimates represent, therefore, a reasonable approximation to the present state-of-the art. Although a “universal” set of inputs does not exist, we can, nevertheless, receive useful indications from comparisons like the ones discussed here.

4.2 ${}^{106}\mathrm{P}\mathrm{d}$ and ${}^{118}\mathrm{S}\mathrm{n}$

A very complex situation characterizes the region from Pd to Sn, for which the rather intricated s-process branching points are illustrated in Figure 6.

FIGURE 6

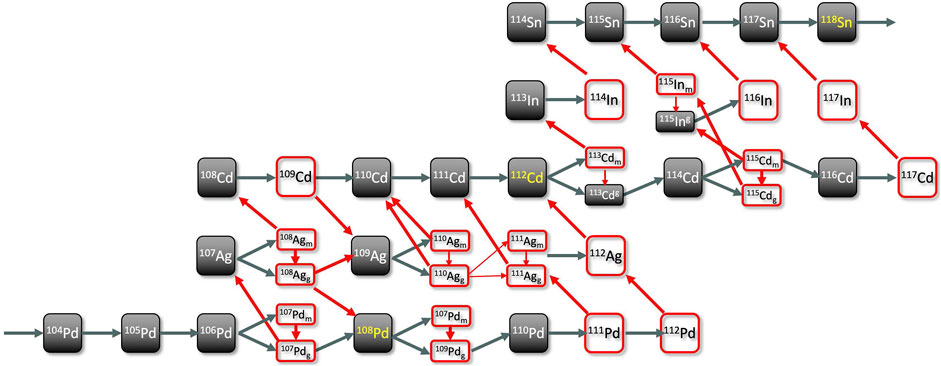
FIGURE 6. Section of the chart of the nuclei from Pd to Sn, including the isotopes ${}^{106}\mathrm{P}\mathrm{d}$ and ${}^{118}\mathrm{S}\mathrm{n}$ for which we have a discrepancy in the predictions from the two models discussed in the text. Crucial isomeric states are shown.

In the past 15 years, this region was the subject of a hot debate on the possible existence of a light element primary production mechanism, or LEPP (Travaglio et al., 2004), just devised to explain abundance deficiencies in this mass region (Montes et al., 2007). Today little remains of that debate, with the understanding that a blend of different r-process components is required (see Figure 3 and Farouqi et al., 2009).

Even now, however, the outliers ${}^{106}\mathrm{P}\mathrm{d}$ and ${}^{118}\mathrm{S}\mathrm{n}$ certify the difficulties in this mass interval. From the s-process point of view, the cross-sections to the various (not always thermalized) isomeric states (Theis et al., 1998) shown in Figure 6 are almost unknown or very uncertain, as is the behavior of the branching β-decays in the stellar plasma. This is, therefore, an atomic mass zone where new experimental studies are needed, both for cross sections and decay rates, before the estimates of Table 1 can be improved significantly. Among the β-decay rates to measure in highly ionized environments, we underline, in particular, the cases of ${}^{\mathrm{113,115}}\mathrm{C}\mathrm{d}$ and ${}^{115}\mathrm{I}\mathrm{n}$, hosting possibly non-thermalized isomeric states (Takahashi and Yokoi, 1987).

From the r-process point of view, for the even–even nucleus ${}^{106}\mathrm{P}\mathrm{d}$ (Z = 46, N = 60), the nuclear data analysis starts to become more difficult than the possible r-process progenitor isotopes of lighter elements. There are two main reasons for this. First, the strongly dominating, single r-process precursor isotope (Z = 38, N = 68) ${}^{106}\mathrm{S}\mathrm{r}$ was not known when the ETFSI-Q/QRPA and FRDM/QRPA calculations were performed. Some β-decay properties were, however, already known from the neighboring Y to Nb isotopes, which could be used to check the reliability of the model predictions for ${}^{106}\mathrm{S}\mathrm{r}$, and second, these progenitor sites already have two neutrons beyond the N = 66 mid-shell, between the magic N = 50 and N = 82 shells, where the transition between strongly deformed and spherical shapes is beginning. As expected for N = 68, both model combinations still predict a strong ground-state deformation of ϵ₂ ≃ 0.3. Hence, the resulting patterns of the β-strength functions should also be quite similar. However, a first difference is already observed for the nuclear mass derivatives Q_β (energy output of the decay) and S_n (binding energy of the last neutron). The old mass formula ETFSI-Q predicts a 1.75-MeV larger Q_β value and a 230 keV lower S_n value relative to the more modern FRDM model. Consequently, the theoretical T_1/2,FRDM is larger (by a factor ≃ 2.3), and the P_n,FRDM is reduced (by a factor ≃ 1.5). By combining the possible effects of these two nuclear quantities, the final result on the S.S. r-fraction will be negligible.

For the predicted trends of the theoretical S_n values, the situation is, however, different. For the FRDM model, the hold-up point of the r-matter flow in the Sr isotopic chain at S_n ≃ 2 MeV will again be slightly shifted to higher masses, as compared to the ETFSI-Q prediction. According to the nuclear Saha equation, this will distribute the initial waiting-point abundances to some extent to the progenitors ${}^{106}\mathrm{S}\mathrm{r}$ and ${}^{108}\mathrm{S}\mathrm{r}$. A rough estimate of the likely effect on the final S.S. r-fraction would result in its reduction from ≃ 74% from the ETFSI-Q/QRPA approach to values between ≃ 67% and ≃ 59%. This would reduce the present “discrepancy” in the latter case from a factor 1.5 to around 1.2.

Again, the (Z = 50, N = 68) even–even isotope ${}^{118}\mathrm{S}\mathrm{n}$ has only a single, strongly dominating (but experimentally completely unknown) r-process progenitor (Z = 42, N = 76), i.e., ${}^{118}\mathrm{M}\mathrm{o}$. Furthermore, this isotope lies in the second part of the shape-transition region, only six neutrons below the spherical N = 82 shell, where practically all global mass models, not only ETFSI-Q and the different FRDM versions, have severe difficulties to predict reliable nuclear structure trends.

According to the aforementioned analysis presented, one can say that, in this mass range, future improvements of the agreement between the r-process and s-process models can possibly come from revisions of the nuclear parameters (cross sections and, probably more important, β-decay rates) for the slow neutron captures. Concerning the r-process, because of its “exponential sensitivity” (Saha equation), we would primarily request new S_n (nuclear mass) revisions and only as a second priority estimates of β-decays far from stability.

4.3 ${}^{135}\mathrm{B}\mathrm{a}$

The s-process production of ${}^{135}\mathrm{B}\mathrm{a}$ remains very uncertain today, as a consequence of the evidence that the decay rates of Cs isotopes adopted for decades (Takahashi and Yokoi, 1987) are not accurate enough. Revisions have been recently presented (Li et al., 2021; Taioli et al., 2021) and thanks to them, it was shown that it is now possible to improve considerably both the reproduction of solar abundances for the s-only nuclei ${}^{\mathrm{134,136}}\mathrm{B}\mathrm{a}$ (see Busso et al., 2021; Taioli et al., 2021) and the isotopic admixture of Ba isotopes in presolar SiC grains (Li et al., 2021; Palmerini et al., 2021). However, our estimate for the s-contribution to ${}^{135}\mathrm{B}\mathrm{a}$ still depends remarkably on other issues. This includes, primarily, the cross sections of the same Ba isotopes and of ${}^{133}\mathrm{C}\mathrm{s}$, then also the details on how the ${}^{134}\mathrm{C}\mathrm{s}$(β⁺ν)${}^{134}\mathrm{B}\mathrm{a}$ and ${}^{135}\mathrm{C}\mathrm{s}$(β⁺ν)${}^{135}\mathrm{B}\mathrm{a}$ operate in stars, which require the precise knowledge of the temperature evolution in the layers where ${}^{135}\mathrm{B}\mathrm{a}$ is produced, i.e., the convective thermal instabilities of the He-shell in AGB stars (Busso et al., 1999). Ultimately, this is linked to how we model convection; hence, here we cannot absolutely mention that the remaining uncertainties are purely nuclear in origin. As shown in Figure 13a of Palmerini et al. (2021), even the most precise constraints available currently (i.e., those from the isotopic Ba admixture in mainstream presolar SiC grains) still offer ample space for a possible lower s-process contribution to this nucleus, which would fit better with the r-process predictions (see Table 1, column 6, and Figure 5. See also the following discussion).

Let us then see whether the origin of the discrepancy in Table 1 and in Figure 5 for ${}^{135}\mathrm{B}\mathrm{a}$ can come from uncertainties in the r-process approach. The potential progenitor isotopes at Z = 49 (In) and up to Z = 51 (Sb) are situated in a shape transition region, in this case between the spherical N = 82 shell closure and the well-known strongly deformed R.E.E. region beyond N ≃ 90.

According to our two model combinations, the three dominating precursor isotopes that may contribute to the abundance of ${}^{135}\mathrm{B}\mathrm{a}$ are ${}^{135}\mathrm{I}\mathrm{n}$ (Z = 49, N = 86), ${}^{136}\mathrm{S}\mathrm{n}$ (Z = 50, N = 86), and ${}^{138}\mathrm{S}\mathrm{n}$ (Z = 50, N = 88). Since these isotopes are predicted to have still spherical ground-state shapes (ϵ₂ ≲ 0.1), they should have quite similar nuclear mass and β-decay rate values. However, since the r-progenitor nuclei lie already quite far from β-stability, their β-delayed neutron-branchings of one to three neutrons play an important role. This is, indeed, confirmed by the available experimental data (Audi et al., 2012), which indicate a clear preference for the FRDM12/QRPA model predictions as compared to the older ETFSI-Q/QRPA approach.

In any case, both model combinations agree on the fact that, in the rather complex β-delayed neutron-branchings during the decay back to stability of both progenitor nuclei ${}^{135}\mathrm{I}\mathrm{n}$ and ${}^{138}\mathrm{S}\mathrm{n}$, only negligible fractions of the initial abundances reach ${}^{135}\mathrm{B}\mathrm{a}$. Hence, only the β-delayed neutron decay of the progenitor ${}^{136}\mathrm{S}\mathrm{n}$ finally populates ${}^{135}\mathrm{B}\mathrm{a}$, with about 40% of its initial abundance. Due to the complex β-delayed neutron decay pattern far from stability, the resulting effect of only a slight reduction in the final S.S. r-fraction of ${}^{135}\mathrm{B}\mathrm{a}$ (maybe by ≃ 10%) can be inferred.

An indication of what should be obtained here for ${}^{135}\mathrm{B}\mathrm{a}$ can be obtained from observations of r-II metal-poor stars, through the Ba − f_odd parameter. In the isotopic composition of Ba of a certain environment, Ba − f_odd expresses the abundance ratio of odd isotopes to the total abundance of the element. Under r-process conditions, this last can be approximated by excluding the even isotopes, except for the dominant ${}^{138}\mathrm{B}\mathrm{a}$ so that

$Ba-f_{odd}\simeq \frac{{}^{135}Ba+{}^{137}Ba}{{}^{135}Ba+{}^{137}Ba+{}^{138}Ba}.(2)$

Ba − f_odd can be measured by high-resolution spectroscopy in a number of metal-poor halo stars (see Mashonkina and Christlieb, 2014; Mashonkina and Belyaev, 2019, and Mashonkina et al., 2017, private communication) by a careful analysis of the hyperfine splitting. From these observations, a mean value of Ba − f_odd = 0.4 ± 0.10 was obtained.

This result can now be compared to that of our model predictions. From the data of ETFSI-Q/QRPA (Kratz et al., 2007), a mean value of 0.49 ± 0.03 could be derived, while from the more recent FRDM12/QRPA version (Kratz et al., 2014), a somewhat lower mean value of 0.43 ± 0.03 was obtained. From Table 1, we would now get ≃ 0.45. These results are all in good agreement with the Ba − f_odd measurements in halo stars. On the contrary, from our AGB s-process estimates shown in Table 1, the resulting value is Ba − f_odd ≲ 0.3, dominated by the estimate for ${}^{135}\mathrm{B}\mathrm{a}$.

These facts suggest that in this case, it is the s-process computation that might be improved by new nuclear data on cross sections and decay rates. For the weak interactions, in particular, experimental measurements in ionized plasmas on the rates for the β⁻ decays of ${}^{\mathrm{134,135}}\mathrm{C}\mathrm{s}$ would be highly needed.

4.4 Nuclei heavier than A = 142

Our estimates for S.S. abundances of heavy nuclei (A ≥ 142) as descending from the AGB models adopted in the present study are shown in Figure 7. As is clear from the plot, over a general trend characterized by a good reproduction of the solar abundances for s-only nuclei (red dots), with a small dispersion, three very remarkable outliers appear, at ${}^{176}\mathrm{L}\mathrm{u}$, ${}^{176}\mathrm{H}\mathrm{f}$, and ${}^{187}\mathrm{O}\mathrm{s}$, which are among the reasons why we did not attempt a complete comparison in this mass range.

FIGURE 7

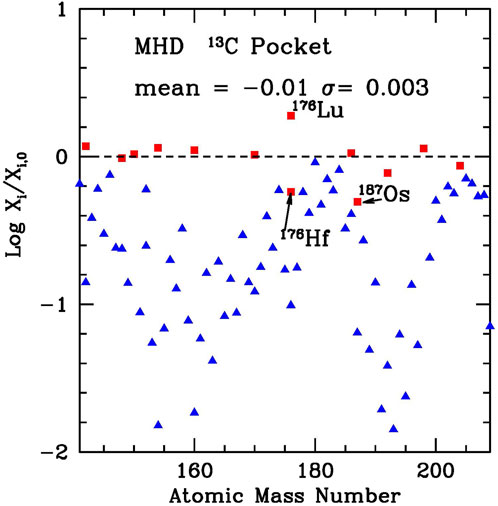
FIGURE 7. Distribution of s-process fractional abundances in the mass range 142 ≲ A ≲ 208, as obtained with the procedure described in Busso et al. (2021) and Palmerini et al. (2021). Red symbols refer to the so-called s − only nuclei, which are shielded by stable isotopes against contributions from the r-process.

The outliers of Figure 7 are related to nuclear problems known since a long time and for which only new measurements of decay rates under partial ionization conditions would help. For the isotopes ${}^{176}\mathrm{L}\mathrm{u}$ and ${}^{176}\mathrm{H}\mathrm{f}$, a thorough analysis was performed by Wisshak et al. (2006a); Wisshak et al. (2006b), to which we address interested readers. Here, isomeric states at ${}^{175}\mathrm{Y}\mathrm{b}$, ${}^{176}\mathrm{L}\mathrm{u}$, and ${}^{177}\mathrm{H}\mathrm{f}$ are involved in the reaction chain. While for ${}^{175}\mathrm{Y}\mathrm{b}$ and ${}^{177}\mathrm{H}\mathrm{f}$, the isomers are depopulated, and the nuclei are in their ground states under s-process conditions, this is not so for ${}^{176}\mathrm{L}\mathrm{u}$. Its ground state is essentially stable (T_1/2 ≃ 3.8 × 10¹⁰ yr) and was considered for a long time as a clock for cosmo-chronology (Audouze et al., 1972). Instead, it is now known that the isomer is partially thermalized at the temperature (T ≃ 23–25 keV) of AGB thermal pulses. This induces a sharp reduction of the half-life due to the high-energy thermal photons. As a consequence, ${}^{176}\mathrm{L}\mathrm{u}$ becomes, in principle, a sensitive thermometer of the environment. For this to occur, however, all the pertinent cross sections and decay rates should be well-known. On the contrary, for the parent ${}^{175}\mathrm{Y}\mathrm{b}$, only theoretical estimates exist, for both parameters, and measurements for ${}^{176}\mathrm{L}\mathrm{u}$ itself were carried out in Karlsruhe (Wisshak et al., 2006a) and are waiting for more modern confirmations. Also, the ${}^{176}\mathrm{H}\mathrm{f}$ destruction, through neutron captures either to ${}^{177}\mathrm{H}\mathrm{f}^g$ or to ${}^{177}\mathrm{H}\mathrm{f}^m$ should in this context be verified. High accuracy is required to settle this problem, as the decay of ${}^{176}\mathrm{L}\mathrm{u}$ was traditionally assumed to control the ${}^{176}\mathrm{H}\mathrm{f}$ abundance (Prantzos, 2019), which is, in general, difficult to achieve, as the solar abundance of Hf is larger than that of Lu.

Another crucial issue concerns ${}^{187}\mathrm{O}\mathrm{s}$. Its parent ${}^{187}\mathrm{R}\mathrm{e}$ is a very long-lived nucleus at low temperatures (T_1/2 ≃ 43.5 Gyr). However, it is known that under stellar conditions, this isotope, like, e.g., ${}^{207}\mathrm{T}\mathrm{l}$ and ${}^{163}\mathrm{D}\mathrm{y}$ (which is stable at laboratory temperatures), can undergo bound state decays, i.e., decays where the electron is not emitted as a free particle but is captured by the daughter nucleus (${}^{187}\mathrm{O}\mathrm{s}$ in this case) to form a hydrogenoid bound state. This significantly increases the decay rate, (by nine orders of magnitudes for completely stripped ${}^{187}\mathrm{R}\mathrm{e}$), as verified, e.g., by works at the ESR storage ring in Darmstadt (Bosch, 2006; Litvinov and Bosch, 2011). Plasma traps like the future PANDORA experiment (Mascali et al., 2020) will soon offer a place where to mimic the partial ionization conditions prevailing in AGB stars, providing new information on several uncertain β-decay rates mentioned in this article for the s-process.

5 Preliminary conclusions and expected improvements

In this study, we present predictions for the contributions to solar abundances of trans-Fe nuclei synthesized by neutron captures. Both the r-process estimates and the complementary s-process ones are shown, in the aim of clarifying the problems that are still affecting their respective nuclear inputs. We limited our analysis to the atomic mass range between Sr and Pr because for heavier nuclei, both models are affected by rather large uncertainties, making such a comparison difficult. In the two independent views, we adopted approaches that are already satisfying basic, universally recognized constraints so that we can trust that the remaining inconsistencies do not come from astrophysical model details but can be traced back to limits in the available nuclear ingredients.

The results are shown in terms of independent predictions for the s-process fraction of solar abundances and demonstrate an unprecedented agreement, where in the majority of cases, the ratios of the two estimates are ≲ 1.20 (a 20% scatter), not far from the uncertainty of the experimental σN curve. For four nuclei (${}^{108}\mathrm{M}\mathrm{o}$, ${}^{106}\mathrm{P}\mathrm{d}$, ${}^{118}\mathrm{S}\mathrm{n}$, and ${}^{135}\mathrm{B}\mathrm{a}$), there is a clear disagreement that requires a critical analysis. From the ensuing discussion, it has been suggested that decay rates crucial for the s-process (in particular at ${}^{\mathrm{113,115}}\mathrm{C}\mathrm{d}$, ${}^{115}\mathrm{I}\mathrm{n}$, and ${}^{\mathrm{134,135}}\mathrm{C}\mathrm{s}$) be verified experimentally, especially in ionized plasma environments. Although, as mentioned, we did not perform a detailed comparison for the R.E.E., from a simple inspection of the existing problems in reproducing s-only nuclei, the same conclusion emerges for some heavy nuclei that are very long-lived in the laboratory but display a different behavior in the high-temperature and high-ionization conditions of a stellar plasma (these are e.g., the cases of ${}^{176}\mathrm{L}\mathrm{u}$ and ${}^{187}\mathrm{R}\mathrm{e}$).

From the r-process point of view, of course, the situation is much more difficult. In the ideal case, one would request experimental data for r-process progenitor isotopes related to nuclear masses (in particular neutron-separation energies, S_n and β-decay properties, T_1/2, and P_xn). Ionic traps like Pandora will have, however, no access to this data region because of significantly short terrestrial half-lives (for the most important neutron magic isotopes, except ${}^{80}\mathrm{Z}\mathrm{n}$, T_1/2 ≲ 200 ms).

For the R.E.E. nuclei and the Pt-peak, actually, progenitor isotopes lie very far from stability and are in most cases out of any experimental reach, even for facilities like RIKEN or CERN/ISOLDE. We should then focus on the nuclear structure development within isobaric chains, from stability toward the progenitor nuclei, in order to derive more reliable, local, and short-range extrapolations.

For lighter nuclei, whenever possible, detailed 1n- to 3n-branchings should be measured, for isotopes involved in the β-decay back to stability. Of particular interest, in this case, are nuclides at magic and semi-magic neutron shells (which act as bottlenecks for the r-process matter flow), as well as isotope sequences in the different shape-transition regions, where practically all global models have large uncertainties.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

MB: conceptualization, computations, and text writing. K-LK: conceptualization, computations, and text writing. VA-D: conceptualization and computations. SP: conceptualization and computations. WA: conceptualization and computations.

Funding

This research was supported by the Italian National Institute for Nuclear Physics (INFN), through the PANDORA and n_TOF projects, inside the National Scientific Commission 3.

Acknowledgments

We are grateful to two unknown referees (expert in nuclear physics and in stellar models), for greatly helping us in improving the clarity and completeness of the manuscript. MB is indebted to the colleagues who helped in building our knowledge of AGB star nucleosynthesis, R. Gallino above the others, for decades of friendship and collaboration. K-LK wants to thank B. Pfeiffer, G. Lhersonneau, P. Möller, and W.B. Walters for many years of pleasant collaboration in experimental and theoretical nuclear physics. We are also indebted to S. Taioli, S. Simonucci, D. Vescovi, and S. Cristallo for useful suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix 1: Some comments on stellar models

A general, synthetic outline of the stellar parents of neutron-rich elements beyond iron can be found in El Eid (2018). We briefly comment on these astrophysical sources below, believing that this brief summary can be sufficient for an article, which is mainly devoted to nuclear, not stellar, effects.

Stellar models for the s-process

Beyond the main s-process component discussed in this study, it is well-known that another, less effective, slow neutron capture process exists, where massive stars (M ≥ 10 M_⊙) contribute to the production of heavy elements between A = 60 and A = 90, in what is called the weak s-process (occurring during core-He and shell-C burning phases, mainly thanks to the activation of the ${}^{22}\mathrm{N}\mathrm{e}$(α,n)${}^{25}\mathrm{M}\mathrm{g}$ reaction). Rotation can also boost this s-process component in massive star models of low metallicity, letting it reach higher atomic masses. While we do not address these issues here, interested readers can find details in Pignatari et al. (2010) and Nishimura et al. (2017).

Rather, some words must be spent on the mixing mechanisms driving the formation of the neutron source ${}^{13}\mathrm{C}$(α,n)${}^{16}\mathrm{O}$ in AGB stars, generating the main component discussed in the previous sections. The general characteristics that these mixing phenomena must have were outlined a few years ago in Busso et al. (2011) and further specified in Nucci and Busso (2014). In the first of these contributions, it was shown that the most common extra-mixing mechanisms explored in stellar evolution (like thermohaline diffusion and various types of rotationally-induced mass transport) would be too slow and ineffective to produce adequate circulation at the H–He interface. It was also argued that a faster process, like magnetic buoyancy, might instead provide the required effects.

While this last mechanism was, indeed, explored by us in recent years and used also in the present study, other physical processes might obtain the same effects. In particular, in Nucci and Busso (2014) it was shown that the geometrical simplifications adopted in our MHD model are equivalent to establish buoyancy with a velocity growing at least quadratically with radius. Any mechanism performing this might then be used, as well. Among promising physical phenomena certainly occurring in stars, but not explored sufficiently so far, we can mention gravity waves (Battino et al., 2016, 2019), and in general any wave-like propagation including some transport of mass. We believe looking for such possible alternatives to MHD mixing would be very important and probably highly rewarding. The first thing to be verified would be the ability of such transport mechanisms to provide the extended pockets with flat ${}^{13}\mathrm{C}$ distributions, which were shown to be necessary by Liu et al. (2015). They would also imply the same reduction in ${}^{14}\mathrm{N}$ and the same low values of the neutron density discussed in the present article.

Stellar models for the r-process

Rather recently (2017), the White paper on Nuclear Astrophysics recognized (Arcones et al., 2017), among the main open problems in our understanding of the origin of the elements, some crucial issues concerning the fast neutron captures. Among other things, there were questions like 1) “where are the 54 elements beyond iron created that are traditionally attributed to a rapid neutron capture process (r-process)?” and 2) “what is the contribution of neutrino-driven winds in core collapse supernovae (ccSNe) to nucleosynthesis and what role do neutrino properties play?” Despite the fact that, in the same year, observations from the kilonova associated to the gravitational wave source GW170817 became available, the same questions remain unanswered now. Indeed, while it seems clear that in the kilonova ejecta there were regions whose high opacities are in line with lanthanide-rich materials (Stratta, 2019) and while also lines of Sr and Y have been observed (Vieira 586 et al., 2022), it appears that the kilonova did not produce a typical solar-like r-process distribution (Ji et al., 2019). Other sources, like collapsars (Siegel et al., 2019) and ccSNe (Suzuki et al., 2019) remain on the stage, in this last case with results remarkably dependent on the nuclear mass model adopted for determining β decays for waiting-point nuclei.

In the present, still uncertain, situation, we remind what has been said in Section 3, commenting Figure 3. The heavier nuclei of the third panel in the figure are today commonly attributed to NSM of various types, while the lighter isotopes of panel 1 can still be safely ascribed to ccSNe (Yamazaki et al., 2022). For the intermediate distribution of panel 2 (corresponding to a weak or incomplete r-process) best candidates remain jet-like magneto-rotational supernovae (Nishimura et al., 2017; Farouqi et al., 2022). Contributions might come also from jet-like emissions in NSM (Yamazaki et al., 2022) and from collapsars (Siegel et al., 2019).

References

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017). GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonuccio-Delogu, V., Busso, M., and Palmerini, S. (2022). Beyond Iron: Numerical models of s- and r-process element distributions. Universe (in press).

Google Scholar

Audi, G., Kondev, F. G., Wang, M., Pfeiffer, B., Sun, X., Blachot, J., et al. (2012). The Nubase2012 evaluation of nuclear properties. Chin. Phys. C 36, 1157–1286. doi:10.1088/1674-1137/36/12/001

CrossRef Full Text | Google Scholar

Audouze, J., Fowler, W. A., and Schramm, D. N. (1972). ¹⁷⁶Lu and s-Process Nucleosynthesis. Nat. Phys. Sci. 238, 8–11. doi:10.1038/physci238008a0

CrossRef Full Text | Google Scholar

Battino, U., Pignatari, M., Ritter, C., Herwig, F., Denisenkov, P., Den Hartogh, J. W., et al. (2016). Application of a theory and simulation-based convective boundary mixing model for AGB star evolution and nucleosynthesis. Astrophys. J. 827, 30. doi:10.3847/0004-637X/827/1/30

CrossRef Full Text | Google Scholar

Battino, U., Tattersall, A., Lederer-Woods, C., Herwig, F., Denissenkov, P., Hirschi, R., et al. (2019). NuGrid stellar data set - III. Updated low-mass AGB models and s-process nucleosynthesis with metallicities Z= 0.01, Z = 0.02, and Z = 0.03. Mon. Not. R. Astron. Soc. 489, 1082–1098. doi:10.1093/mnras/stz2158

CrossRef Full Text | Google Scholar

Bisterzo, S., Gallino, R., Käppeler, F., Wiescher, M., Imbriani, G., Straniero, O., et al. (2015). The branchings of the main s-process: Their sensitivity to α-induced reactions on ¹³C and ²²Ne and to the uncertainties of the nuclear network. Mon. Not. R. Astron. Soc. 449, 506–527. doi:10.1093/mnras/stv271

CrossRef Full Text | Google Scholar

Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., and Käppeler, F. (2012). The s-process in low-metallicity stars - III. Individual analysis of CEMP-s and CEMP-s/r with asymptotic giant branch models. Mon. Not. R. Astron. Soc. 422, 849–884. doi:10.1111/j.1365-2966.2012.20670.x

CrossRef Full Text | Google Scholar

Bisterzo, S., Travaglio, C., Gallino, R., Wiescher, M., and Käppeler, F. (2014). Galactic chemical evolution and solar s-process abundances: Dependence on the¹³c-pocket structure. Astrophys. J. 787, 10. doi:10.1088/0004-637X/787/1/10

CrossRef Full Text | Google Scholar

Bosch, F. (2006). Beta decay of highly charged ions. Hyperfine Interact. 173, 1–11. doi:10.1007/s10751-007-9535-2

CrossRef Full Text | Google Scholar

Burbidge, E. M., Burbidge, G. R., Fowler, W. A., and Hoyle, F. (1957). Synthesis of the elements in stars. Rev. Mod. Phys. 29, 547–650. doi:10.1103/RevModPhys.29.547

CrossRef Full Text | Google Scholar

Busso, M., Picchio, G., Gallino, R., and Chieffi, A. (1988). Are s-elements really produced during thermal pulses in intermediate-mass stars?. Astrophys. J., 196. doi:10.1086/166081

CrossRef Full Text | Google Scholar

Busso, M., Gallino, R., and Wasserburg, G. J. (1999). Nucleosynthesis in asymptotic giant branch stars: Relevance for galactic enrichment and solar system formation. Annu. Rev. Astron. Astrophys. 37, 239–309. doi:10.1146/annurev.astro.37.1.239

CrossRef Full Text | Google Scholar

Busso, M., Vescovi, D., Palmerini, S., Cristallo, S., and Antonuccio-Delogu, V. (2021). s-Processing in AGB stars revisited. III. Neutron captures from MHD mixing at different metallicities and observational constraints. Astrophys. J. 908, 55. doi:10.3847/1538-4357/abca8e

CrossRef Full Text | Google Scholar

Busso, M., Wasserburg, G. J., Nollett, K. M., and Calandra, A. (2007). Can extra mixing in RGB and AGB stars Be attributed to magnetic mechanisms? Astrophys. J. 671, 802–810. doi:10.1086/522616

CrossRef Full Text | Google Scholar

Cameron, A. G. W. (1957). Nuclear reactions in stars and nucleogenesis. Publ. Astron. Soc. Pac. 69, 201. doi:10.1086/127051

CrossRef Full Text | Google Scholar

Coryell, C. D. (1956). MITL.N.S. Prog. Rep. AECU-3423.

Google Scholar

Coryell, C. D. (1961). The chemistry of creation of the heavy elements. J. Chem. Educ. 38, 67. doi:10.1021/ed038p67

CrossRef Full Text | Google Scholar

Cowan, J. J., Thielemann, F.-K., and Truran, J. W. (1991). The R-process and nucleochronology. Phys. Rep. 208, 267–394. doi:10.1016/0370-1573(91)90070-3

CrossRef Full Text | Google Scholar

Cristallo, S., Piersanti, L., Straniero, O., Gallino, R., Domínguez, I., Abia, C., et al. (2011). Evolution, nucleosynthesis, and yields of low-mass asymptotic giant branch stars at different metallicities. II. The FRUITY database. Astrophys. J. Suppl. Ser. 197, 17. doi:10.1088/0067-0049/197/2/17

CrossRef Full Text | Google Scholar

Cristallo, S., Straniero, O., Piersanti, L., and Gobrecht, D. (2015). Evolution, nucleosynthesis, and yields of AGB stars at different metallicities. III. Intermediate-Mass models, revised low-mass models, and the ph-FRUITY interface. Astrophys. J. Suppl. Ser. 219, 40. doi:10.1088/0067-0049/219/2/40

CrossRef Full Text | Google Scholar

Denissenkov, P. A., Pinsonneault, M., and MacGregor, K. B. (2009). Magneto-thermohaline mixing in red giants. Astrophys. J. 696, 1823–1833. doi:10.1088/0004-637X/696/2/1823

CrossRef Full Text | Google Scholar

Denissenkov, P. A., and Tout, C. A. (2003). Partial mixing and formation of the ¹³C pocket by internal gravity waves in asymptotic giant branch stars. Mon. Not. R. Astron. Soc. 340, 722–732. doi:10.1046/j.1365-8711.2003.06284.x

CrossRef Full Text | Google Scholar

Dillmann, I., Heil, M., Käppeler, F., Plag, R., Rauscher, T., and Thielemann, F. K. (2006). “KADoNiS- the Karlsruhe astrophysical database of nucleosynthesis in stars,” in Capture gamma-ray spectroscopy and related topics. Vol. 819 of American Institute of physics conference series. Editors A. Woehr, and A. Aprahamian, 123–127. doi:10.1063/1.2187846

CrossRef Full Text | Google Scholar

Dillmann, I. (2014). “The new KADoNiS v1.0 and its influence on the s-process,” in XIII nuclei in the cosmos (NIC XIII), 57.

Google Scholar

Evans, P. A., Cenko, S. B., Kennea, J. A., Emery, S. W. K., Kuin, N. P. M., Korobkin, O., et al. (2017). Swift and NuSTAR observations of GW170817: Detection of a blue kilonova. Science 358, 1565–1570. doi:10.1126/science.aap9580

PubMed Abstract | CrossRef Full Text | Google Scholar

Farouqi, K., Kratz, K. L., and Pfeiffer, B. (2009). Co-production of light p-s- and r-process isotopes in the high-entropy wind of type II supernovae. Publ. Astron. Soc. Aust. 26, 194–202. doi:10.1071/AS08075

CrossRef Full Text | Google Scholar

Farouqi, K., Kratz, K. L., Pfeiffer, B., Rauscher, T., Thielemann, F. K., and Truran, J. W. (2010). Charged-particle and neutron-capture processes in the high-entropy wind of core-collapse supernovae. Astrophys. J. 712, 1359–1377. doi:10.1088/0004-637X/712/2/1359

CrossRef Full Text | Google Scholar

Farouqi, K., Thielemann, F.-K., Rosswog, S., and Kratz, K.-L. (2022). Correlations of r-process elements in very metal-poor stars as clues to their nucleosynthesis sites. Astron. Astrophys. 663, A70. in press. doi:10.1051/0004-6361/202141038

CrossRef Full Text | Google Scholar

Freiburghaus, C., Rembges, J. F., Rauscher, T., Kolbe, E., Thielemann, F. K., Kratz, K. L., et al. (1999a). The astrophysical r-process: A comparison of calculations following adiabatic expansion with classical calculations based on neutron densities and temperatures. Astrophys. J. 516, 381–398. doi:10.1086/307072

CrossRef Full Text | Google Scholar

Freiburghaus, C., Rosswog, S., and Thielemann, F. K. (1999b). [CLC] [ITAL]r[/ITAL] [/CLC]-Process in neutron star mergers. Astrophys. J. 525, L121–L124. doi:10.1086/312343

PubMed Abstract | CrossRef Full Text | Google Scholar

Gallino, R., Busso, M., Picchio, G., Raiteri, C. M., and Renzini, A. (1988). On the role of low-mass asymptotic giant branch stars in producing a solar system distribution of s-process isotopes. Astrophys. J. 334, L45. doi:10.1086/185309

CrossRef Full Text | Google Scholar

Guerrero, C., Boccone, V., Brugger, M., Calviani, M., Cerutti, F., Chiaveri, E., et al. (2013). “The latest on neutron-induced capture and fission measurements at the CERN n_TOF facility,” in Capture gamma-ray spectroscopy and related topics. Editor P. E. Garrett, 354–364. doi:10.1142/9789814383646_0047

CrossRef Full Text | Google Scholar

Herwig, F. (2005). Evolution of asymptotic giant branch stars. Annu. Rev. Astron. Astrophys. 43, 435–479. doi:10.1146/annurev.astro.43.072103.150600

CrossRef Full Text | Google Scholar

Hill, V., Plez, B., Cayrel, R., Beers, T. C., Nordström, B., Andersen, J., et al. (2002). First stars. I. The extreme r-element rich, iron-poor halo giant CS 31082-001. Implications for the r-process site(s) and radioactive cosmochronology. Astron. Astrophys. 387, 560–579. doi:10.1051/0004-6361:20020434

CrossRef Full Text | Google Scholar

Hillebrandt, W. (1978). The rapid neutron-capture process and the synthesis of heavy and neutron-rich elements. Space Sci. Rev. 21, 639–702. doi:10.1007/BF00186236

CrossRef Full Text | Google Scholar

Honda, S., Aoki, W., Ishimaru, Y., and Wanajo, S. (2007). Neutron-capture elements in the very metal-poor star HD 88609: Another star with excesses of light neutron-capture elements. Astrophys. J. 666, 1189–1197. doi:10.1086/520034

CrossRef Full Text | Google Scholar

Iben, J. I., and Renzini, A. (1982). On the formation of carbon star characteristics and the production of neutron-rich isotopes in asymptotic giant branch stars of small core mass. Astrophys. J. 263, L23–L27. doi:10.1086/183916

CrossRef Full Text | Google Scholar

Iben, J. I., and Truran, J. W. (1978). On the surface composition of thermally pulsing stars of high luminosity and on the contribution of such stars to the element enrichment of the interstellar medium. Astrophys. J. 220, 980–995. doi:10.1086/155986

CrossRef Full Text | Google Scholar

Ji, A. P., Drout, M. R., and Hansen, T. T. (2019). The lanthanide fraction distribution in metal-poor stars: A test of neutron star mergers as the dominant r-process site. Astrophys. J. 882, 40. doi:10.3847/1538-4357/ab3291

CrossRef Full Text | Google Scholar

Kaeppeler, F., Gallino, R., Busso, M., Picchio, G., and Raiteri, C. M. (1990). S-process nucleosynthesis: Classical approach and asymptotic giant branch models for low-mass stars. Astrophys. J. 354, 630. doi:10.1086/168720

CrossRef Full Text | Google Scholar

Käppeler, F., Gallino, R., Bisterzo, S., and Aoki, W. (2011). Thesprocess: Nuclear physics, stellar models, and observations. Rev. Mod. Phys. 83, 157–193. doi:10.1103/RevModPhys.83.157

CrossRef Full Text | Google Scholar

Karakas, A. I., and Lattanzio, J. C. (2014). The dawes review 2: Nucleosynthesis and stellar yields of low- and intermediate-mass single stars. Publ. Astron. Soc. Aust. 31, e030. doi:10.1017/pasa.2014.21

CrossRef Full Text | Google Scholar

Kratz, K.-L., Akram, W., Farouqi, K., and Hallmann, O. (2019). “Production of light trans-Fe elements in core collapse-supernovae: Implications from presolar SiC-X grains,” in Exotic nuclei and nuclear/particle AstroPhysics (VII). Physics with small accelerators. Vol. 2076 of American Institute of physics conference series, 030002. doi:10.1063/1.5091628

CrossRef Full Text | Google Scholar

Kratz, K.-L., Bitouzet, J.-P., Thielemann, F.-K., Moeller, P., and Pfeiffer, B. (1993). Isotopic r-process abundances and nuclear structure far from stability: Implications for the r-process mechanism. Astrophys. J. 403, 216. doi:10.1086/172196

CrossRef Full Text | Google Scholar

Kratz, K.-L., Farouqi, K., and Möller, P. (2014). A high-entropy-wind r-process study based on nuclear-structure quantities from the new finite-range droplet model frdm(2012). Astrophys. J. 792, 6. doi:10.1088/0004-637X/792/1/6

CrossRef Full Text | Google Scholar

Kratz, K.-L., Farouqi, K., Pfeiffer, B., Truran, J. W., Sneden, C., and Cowan, J. J. (2007). Explorations of the r-processes: Comparisons between calculations and observations of low-metallicity stars. Astrophys. J. 662, 39–52. doi:10.1086/517495

CrossRef Full Text | Google Scholar

Kratz, K.-L., Pfeiffer, B., Thielemann, F.-K., and Walters, W. B. (2000). Nuclear structure studies at ISOLDE and their impact on the astrophysical r-process. Hyperfine Interact. 129, 185–221. doi:10.1023/A:1012694723985

CrossRef Full Text | Google Scholar

Kratz, K. L., Böhmer, W., Freiburghaus, C., Möller, P., Pfeiffer, B., Rauscher, T., et al. (2001). On the origin of the Ca-Ti-Cr isotopic anomalies in the inclusion EK-1-4-1 of the Allende-meteorite. Mem. Soc. Astron. It. 72, 453–466.

Google Scholar

Kratz, K. L., Farouqi, K., Mashonkina, L. I., and Pfeiffer, B. (2008). Nucleosynthesis modes in the high-entropy-wind of type II supernovae. New Astron. Rev. 52, 390–395. doi:10.1016/j.newar.2008.06.015

CrossRef Full Text | Google Scholar

Kratz, K. L., Gabelmann, H., Möller, P., Pfeiffer, B., Ravn, H. L., and Wöhr, A. (1991). Neutron-rich isotopes around the r-process “waiting-point” nuclei{$\mmultiscripts{\mathrm{/}}{\postscript{}{79}}{\prescript{29}{}}{}{}$}Cu₅₀ and{$\mmultiscripts{\mathrm{/}}{\postscript{}{80}}{\prescript{30}{}}{}{}$}Zn₅₀. Zeitschrift fur Physik A Hadrons Nucl. 340, 419–420. doi:10.1007/BF01290331

CrossRef Full Text | Google Scholar

Kratz, K. L. (1988). Nuclear physics constraints to bring the astrophysical R-process to the “waiting point”. Rev. Mod. Astronomy 1, 184–209. doi:10.1007/978-3-642-74188-3_9

CrossRef Full Text | Google Scholar

Kratz, K. L., Ziegert, W., Hillebrandt, W., and Thielemann, F. K. (1983a). Determination of stellar neutron-capture rates for radioactive nuclei with the aid of beta-delayed neutron emission. Astron. & Astrophys. 125, 381–387.

Google Scholar

Kratz, K. L., Ziegert, W., Thielemann, F. K., and Hillebrandt, W. (1983b). Beta-delayed neutron emission as the inverse process to neutron-capture on radioactive isotopes. Max Planck Inst. fur Astrophys. Rep. 90, 111–112.

Google Scholar

Lattimer, J. M., Mackie, F., Ravenhall, D. G., and Schramm, D. N. (1977). The decompression of cold neutron star matter. Astrophys. J. 213, 225–233. doi:10.1086/155148

CrossRef Full Text | Google Scholar

Lhersonneau, G., Pfeiffer, B., Kratz, K. L., Enqvist, T., Jauho, P. P., Jokinen, A., et al. (1994). Evolution of deformation in the neutron-rich Zr region from excited intruder state to the ground state. Phys. Rev. C 49, 1379–1390. doi:10.1103/PhysRevC.49.1379

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, K.-A., Qi, C., Lugaro, M., Yagüe López, A., Karakas, A. I., den Hartogh, J., et al. (2021). The stellar β-decay rate of ¹³⁴Cs and its impact on the barium nucleosynthesis in the s-process. Astrophys. J. Lett. 919, L19. doi:10.3847/2041-8213/ac260f

CrossRef Full Text | Google Scholar

Litvinov, Y. A., and Bosch, F. (2011). Beta decay of highly charged ions. Rep. Prog. Phys. 74, 016301. doi:10.1088/0034-4885/74/1/016301

CrossRef Full Text | Google Scholar

Liu, N., Savina, M. R., Davis, A. M., Gallino, R., Straniero, O., Gyngard, F., et al. (2014). Barium isotopic composition of mainstream silicon carbides from murchison: Constraints for s-process nucleosynthesis in asymptotic giant branch stars. Astrophys. J. 786, 66. doi:10.1088/0004-637X/786/1/66

CrossRef Full Text | Google Scholar

Liu, N., Savina, M. R., Gallino, R., Davis, A. M., Bisterzo, S., Gyngard, F., et al. (2015). Correlated strontium and barium isotopic compositions of acid-cleaned single mainstream silicon carbides from murchison. Astrophys. J. 803, 12. doi:10.1088/0004-637X/803/1/12

CrossRef Full Text | Google Scholar

Lodders, K. (2021). Relative atomic solar system Abundances, mass fractions, and atomic masses of the elements and their isotopes, composition of the solar photosphere, and compositions of the major chondritic meteorite groups. Space Sci. Rev. 217, 44. doi:10.1007/s11214-021-00825-8

CrossRef Full Text | Google Scholar

Lugaro, M., Karakas, A. I., Stancliffe, R. J., and Rijs, C. (2012). The s-process in asymptotic giant branch stars of low metallicity and the composition of carbon-enhanced metal-poor stars. Astrophys. J. 747, 2. doi:10.1088/0004-637X/747/1/2

CrossRef Full Text | Google Scholar

Maiorca, E., Magrini, L., Busso, M., Randich, S., Palmerini, S., and Trippella, O. (2012). News on the s process from young open clusters. Astrophys. J. 747, 53. doi:10.1088/0004-637X/747/1/53

CrossRef Full Text | Google Scholar

Mascali, D., Busso, M., Mengoni, A., Amaducci, S., Giuseppe, C., Celona, L., et al. (2020). “The PANDORA project: An experimental setup for measuring in-plasma β-decays of astrophysical interest,” in European physical journal web of conferences. Vol. 227 of European physical journal web of conferences, 01013. doi:10.1051/epjconf/202022701013

CrossRef Full Text | Google Scholar

Mashonkina, L., and Christlieb, N. (2014). The Hamburg/ESO R-process Enhanced Star survey (HERES). IX. Constraining pure r-process Ba/Eu abundance ratio from observations of r-II stars. Astron. Astrophys. 565, A123. doi:10.1051/0004-6361/201423651

CrossRef Full Text | Google Scholar

Mashonkina, L. I., and Belyaev, A. K. (2019). Even-to-Odd barium isotope ratio in selected galactic halo stars. Astron. Lett. 45, 341–352. doi:10.1134/S1063773719060033

CrossRef Full Text | Google Scholar

Mashonkina, L. I., Vinogradova, A. B., Ptitsyn, D. A., Khokhlova, V. S., and Chernetsova, T. A. (2007). Neutron-capture elements in halo, thick-disk, and thin-disk stars. Strontium, yttrium, zirconium, cerium. Astron. Rep. 51, 903–919. doi:10.1134/S1063772907110042

CrossRef Full Text | Google Scholar

Merrill, P. W. (1952). Spectroscopic observations of stars of class. Astrophys. J. 116, 21. doi:10.1086/145589

CrossRef Full Text | Google Scholar

Möller, P., Pfeiffer, B., and Kratz, K.-L. (2003). New calculations of gross β-decay properties for astrophysical applications: Speeding-up the classical r process. Phys. Rev. C 67, 055802. doi:10.1103/PhysRevC.67.055802

CrossRef Full Text | Google Scholar

Montes, F., Beers, T. C., Cowan, J., Elliot, T., Farouqi, K., Gallino, R., et al. (2007). Nucleosynthesis in the early Galaxy. Astrophys. J. 671, 1685–1695. doi:10.1086/523084

CrossRef Full Text | Google Scholar

Niederer, F. R., Papanastassiou, D. A., and Wasserburg, G. J. (1980). Endemic isotopic anomalies in titanium. Astrophys. J. 240, L73–L77. doi:10.1086/183326

CrossRef Full Text | Google Scholar

Nishimura, N., Sawai, H., Takiwaki, T., Yamada, S., and Thielemann, F. K. (2017). The intermediate r-process in core-collapse supernovae driven by the magneto-rotational instability. Astrophys. J. 836, L21. doi:10.3847/2041-8213/aa5dee

CrossRef Full Text | Google Scholar

Nordhaus, J., Busso, M., Wasserburg, G. J., Blackman, E. G., and Palmerini, S. (2008). Magnetic mixing in red giant and asymptotic giant branch stars. Astrophys. J. 684, L29–L32. doi:10.1086/591963

CrossRef Full Text | Google Scholar

Nucci, M. C., and Busso, M. (2014). Magnetohydrodynamics and deep mixing in evolved stars. I. Two- and three-dimensional analytical models for the asymptotic giant branch. Astrophys. J. 787, 141. doi:10.1088/0004-637X/787/2/141

CrossRef Full Text | Google Scholar

Palmerini, S., Busso, M., Vescovi, D., Naselli, E., Pidatella, A., Mucciola, R., et al. (2021). Presolar grain isotopic ratios as constraints to nuclear and stellar parameters of asymptotic giant branch star nucleosynthesis. Astrophys. J. 921, 7. doi:10.3847/1538-4357/ac1786

CrossRef Full Text | Google Scholar

Pearson, C., Krueger, M., and Ganz, E. (1996). Direct tests of microscopic growth models using hot scanning tunneling microscopy movies. Phys. Rev. Lett. 76, 2306–2309. doi:10.1103/PhysRevLett.76.2306

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellin, M. J., Savina, M. R., Calaway, W. F., Tripa, C. E., Barzyk, J. G., Davis, A. M., et al. (2006). “Heavy metal isotopic anomalies in supernovae presolar grains,” in 37th annual lunar and planetary science conference. Lunar and planetary science conference. Editors S. Mackwell, and E. Stansbery, 2041.

Google Scholar

Pfeiffer, B., Kratz, K. L., and Thielemann, F. K. (1997). Analysis of the solar-system r-process abundance pattern with the new ETFSI-Q mass formula. Z. Phys. A -. Part. Fields. 357, 235–238. doi:10.1007/s002180050237

CrossRef Full Text | Google Scholar

Pfeiffer, B., Lhersonneau, G., Gabelmann, H., and Kratz, K. L.the ISOLDE-Collaboration (2002). A tentative 4- isomeric state in Sr-98. arXiv e-prints , nucl-ex/0202025.

Google Scholar

Prantzos, N. (2019). Galactic chemical evolution with rotating massive star yields. Nucl. Cosmos XV 219, 83–89. doi:10.1007/978-3-030-13876-9_1

CrossRef Full Text | Google Scholar

Reifarth, R., Erbacher, P., Fiebiger, S., Göbel, K., Heftrich, T., Heil, M., et al. (2018). Neutron-induced cross sections. From raw data to astrophysical rates. Eur. Phys. J. Plus 133, 424. doi:10.1140/epjp/i2018-12295-3

CrossRef Full Text | Google Scholar

Rosswog, S., Liebendörfer, M., Thielemann, F. K., Davies, M. B., Benz, W., and Piran, T. (1999). Mass ejection in neutron star mergers. Astron. & Astrophys. 341, 499–526.

Google Scholar

Rosswog, S., Sollerman, J., Feindt, U., Goobar, A., Korobkin, O., Wollaeger, R., et al. (2018). The first direct double neutron star merger detection: Implications for cosmic nucleosynthesis. Astron. Astrophys. 615, A132. doi:10.1051/0004-6361/201732117

CrossRef Full Text | Google Scholar

Salpeter, E. E. (1955). The luminosity function and stellar evolution. Astrophys. J. 121, 161. doi:10.1086/145971

CrossRef Full Text | Google Scholar

Seeger, P. A., Fowler, W. A., and Clayton, D. D. (1965). Nucleosynthesis of heavy elements by neutron capture. Astrophys. J. Suppl. Ser. 11, 121. doi:10.1086/190111

CrossRef Full Text | Google Scholar

Shibata, K., Iwamoto, O., Nakagawa, T., Iwamoto, N., Ichihara, A., Kunieda, S., et al. (2011). JENDL-4.0: A new library for innovative nuclear energy systems. J. Korean Phys. Soc. 59, 1046–1051. doi:10.3938/jkps.59.1046

CrossRef Full Text | Google Scholar

Sneden, C., Cowan, J. J., Lawler, J. E., Ivans, I. I., Burles, S., Beers, T. C., et al. (2003). The extremely metal-poor, neutron capture-rich star CS 22892-052: A comprehensive abundance analysis. Astrophys. J. 591, 936–953. doi:10.1086/375491

CrossRef Full Text | Google Scholar

Sneden, C., McWilliam, A., Preston, G. W., Cowan, J. J., Burris, D. L., and Armosky, B. J. (1996). The ultra–metal-poor, neutron-capture–rich giant star CS 22892-052. Astrophys. J. 467, 819. doi:10.1086/177656

CrossRef Full Text | Google Scholar

Stephan, T., and Davis, A. M. (2021). Molybdenum isotope dichotomy in meteorites caused by s-process variability. Astrophys. J. 909, 8. doi:10.3847/1538-4357/abd725

CrossRef Full Text | Google Scholar

Stephan, T., Trappitsch, R., Davis, A. M., Pellin, M. J., Rost, D., Savina, M. R., et al. (2018). Strontium and barium isotopes in presolar silicon carbide grains measured with CHILI-two types of X grains. Geochim. Cosmochim. Acta 221, 109–126. doi:10.1016/j.gca.2017.05.001

CrossRef Full Text | Google Scholar

Stephan, T., Trappitsch, R., Hoppe, P., Davis, A. M., Pellin, M. J., and Pardo, O. S. (2019). Molybdenum isotopes in presolar silicon carbide grains: Details of s-process nucleosynthesis in parent stars and implications for r- and p-processes. Astrophys. J. 877, 101. doi:10.3847/1538-4357/ab1c60

CrossRef Full Text | Google Scholar

Suess, H. E., and Urey, H. C. (1956). Abundances of the elements. Rev. Mod. Phys. 28, 53–74. doi:10.1103/RevModPhys.28.53

CrossRef Full Text | Google Scholar

Taioli, S., Vescovi, D., Busso, M., Palmerini, S., Cristallo, S., Mengoni, A., et al. (2021). Theoretical estimate of the half-life for the radioactive ¹³⁴Cs and ¹³⁵Cs in astrophysical scenarios. arXiv e-prints, Ap.J 2022. in press, arXiv:2109.14230.

Google Scholar

Takahashi, K., Witti, J., and Janka, H. T. (1994). Nucleosynthesis in neutrino-driven winds from protoneutron stars II. The r-process. Astron. & Astrophys. 286, 857–869.

Google Scholar

Takahashi, K., and Yokoi, K. (1987). Beta-decay rates of highly ionized heavy atoms in stellar interiors. Atomic Data Nucl. Data Tables 36, 375–409. doi:10.1016/0092-640X(87)90010-6

CrossRef Full Text | Google Scholar

Theis, C., Käppeler, F., Wisshak, K., and Voss, F. (1998). On the puzzling origin of the rare in and SN isotopes. Astrophys. J. 500, 1039–1048. doi:10.1086/305777

CrossRef Full Text | Google Scholar

Travaglio, C., Gallino, R., Arnone, E., Cowan, J., Jordan, F., and Sneden, C. (2004). Galactic evolution of Sr, Y, and Zr: A multiplicity of nucleosynthetic processes. Astrophys. J. 601, 864–884. doi:10.1086/380507

CrossRef Full Text | Google Scholar

Trippella, O., Busso, M., Palmerini, S., Maiorca, E., and Nucci, M. C. (2016). s-Processing in AGB stars revisited. II. Enhanced 13C production through MHD-induced mixing. Astrophys. J. 818, 125. doi:10.3847/0004-637X/818/2/125

CrossRef Full Text | Google Scholar

Vescovi, D., Cristallo, S., Busso, M., and Liu, N. (2020). Magnetic-buoyancy-induced mixing in AGB stars: Presolar SiC grains. Astrophys. J. 897, L25. doi:10.3847/2041-8213/ab9fa1

CrossRef Full Text | Google Scholar

Vescovi, D., Cristallo, S., Palmerini, S., Abia, C., and Busso, M. (2021). Magnetic-buoyancy-induced mixing in AGB stars: Fluorine nucleosynthesis at different metallicities. Astron. Astrophys. 652, A100. doi:10.1051/0004-6361/202141173

CrossRef Full Text | Google Scholar

Vescovi, D. (2021). Mixing and magnetic fields in asymptotic giant branch stars in the framework of FRUITY models. Universe 8, 16. doi:10.3390/universe8010016

CrossRef Full Text | Google Scholar

Vescovi, D., and Reifarth, R. (2021). s-Processing in asymptotic giant branch stars in the light of revised neutron-capture cross sections. Universe 7, 239. doi:10.3390/universe7070239

CrossRef Full Text | Google Scholar

Wasserburg, G. J., Lee, T., and Papanastassiou, D. A. (1977). Correlated O And Mg isotopic anomalies in Allende Inclusions: II. Magnesium. Geophys. Res. Lett. 4, 299–302. doi:10.1029/GL004i007p00299

CrossRef Full Text | Google Scholar

Wisshak, K., Voss, F., Käppeler, F., Kazakov, L., Bečvář, F., Krtička, M., et al. (2006b). Fast neutron capture on the Hf isotopes: Cross sections, isomer production, and stellar aspects. Phys. Rev. C 73, 045807. doi:10.1103/PhysRevC.73.045807

CrossRef Full Text | Google Scholar

Wisshak, K., Voss, F., Käppeler, F., and Kazakov, L. (2006a). Stellar neutron capture cross sections of the Lu isotopes. Phys. Rev. C 73, 015807. doi:10.1103/PhysRevC.73.015807

CrossRef Full Text | Google Scholar

Woosley, S. E., Wilson, J. R., Mathews, G. J., Hoffman, R. D., and Meyer, B. S. (1994). The r-process and neutrino-heated supernova ejecta. Astrophys. J. 433, 229. doi:10.1086/174638

CrossRef Full Text | Google Scholar