- 1Center for Space Plasma and Aeronomic Research (CSPAR), University of Alabama in Huntsville, Huntsville, AL, United States
- 2Department of Space Science, University of Alabama in Huntsville, Huntsville, AL, United States
We investigate particle acceleration in an MHD-scale system of multiple current sheets by performing 2D and 3D MHD simulations combined with a test particle simulation. The system is unstable for the tearing-mode instability, and magnetic islands are produced by magnetic reconnection. Due to the interaction of magnetic islands, the system relaxes to a turbulent state. The 2D (3D) case both yield −5/3 (− 11/3 and −7/3) power-law spectra for magnetic and velocity fluctuations. Particles are efficiently energized by the generated turbulence, and form a power-law tail with an index of −2.2 and −4.2 in the energy distribution function for the 2D and 3D case, respectively. We find more energetic particles outside magnetic islands than inside. We observe super-diffusion in the 2D (∼ t2.27) and 3D (∼ t1.2) case in the energy space of energetic particles.
1 Introduction
Magnetic reconnection at a current sheet is a fundamental process in plasma physics (Biskamp, 1994; Yamada et al., 2010; Hesse and Cassak, 2020). Magnetic reconnection can be characterized as a topological change of anti-parallel magnetic fields where the frozen-in condition is broken. The reconnected magnetic field drags plasma away due to the magnetic tension force. The outflow speed roughly corresponds to the Alfvén speed. As a result of magnetic reconnection, two separated plasmas are mixed together.
It is thought that magnetic reconnection is capable of generating energetic particles (Blandford et al., 2017). Several mechanisms have been proposed so far: 1) Speiser (meandering) motion across anti-parallel magnetic fields directly accelerates particles by the inductive electric field (Speiser, 1965), 2) particles gain energy due to the conservation of the first adiabatic moment at the pileup region of magnetic field (Hoshino et al., 2001), 3) Fermi-type acceleration occurs due to the compressible and incompressible contraction of the magnetic islands (Drake et al., 2006; Oka et al., 2010; Zank et al., 2014; le Roux et al., 2015; Li et al., 2021). Several kinetic simulations show the existence of non-thermal particles forming a power-law tail in the energy distribution function associated with the evolution of magnetic reconnection (Dahlin et al., 2014; Guo et al., 2014; Sironi and Spitkovsky, 2014; Werner et al., 2016; Li et al., 2017; Arnold et al., 2021; Zhang et al., 2021).
Systems of multiple current sheets have been considered in recent years. The formation of multiple current sheets is common in the heliosphere. For instance, heliospheric current sheets (HCSs) (Smith, 2001) are usually stable in the solar wind, but are compressed at the heliospheric termination shock and can be unstable in the heliosheath. Spacecraft observations across sector boundaries often find multiple thin current sheets inside a HCS, and these can be interpreted as the folding of individual magnetic flux tubes (Crooker et al., 1993; Dahlburg and Karpen, 1995; Maiewski et al., 2020). Besides the heliosphere, pulsar winds also have a similar structure, and it is believed that the interaction of current sheets with the pulsar termination shock produces energetic particles and is responsible for conversion of Poynting dominated outflows to the observed radiation via energetic particles produced by the interaction (Lyubarsky, 2005; Nagata et al., 2008; Sironi and Spitkovsky, 2011; Cerutti and Giacinti, 2020; Lu et al., 2021).
When those current sheets become unstable, it is thought that the system produces several magnetic islands due to magnetic reconnection and then evolves into a turbulent state. Zhang and Ma (Zhang and Ma, 2011), Akramov and Baty (Akramov and Baty, 2017) performed MHD simulations of double current sheets and showed that growing magnetic islands interact with each other and then the system tends to be a turbulent state. Gingell et al. (2015), Burgess et al. (2016) performed 3D hybrid kinetic simulations of multiple current sheets. The system is unstable to the tearing-mode and drift-kink instability, and these instabilities drive the system to a turbulent state with a −7/3 index power-law spectrum for magnetic fluctuations.
Particle acceleration among multiple magnetic islands has been proposed as an efficient acceleration process. Zank et al. (Zank et al., 2014; Zank et al., 2015), le Roux et al. (2015) developed a gyrophase-averaged formulation, while under conditions of near isotropies, which reduces a Parker-like transport equation that includes the effects of the electric field induced by magnetic island reconnection and magnetic island contraction. This has been used to understand the flux of anomalous cosmic rays observed by Voyager spacecraft, which continuously increases in the downstream of the heliospheric termination shock. The model successfully reproduces the observed flux and shows that the energy spectrum becomes harder because of acceleration by magnetic islands in the downstream of a shock wave (Zank et al., 2015; Zhao et al., 2019). This has been also observed at interplanetary shock waves at five au (Zhao et al., 2018; Adhikari et al., 2019).
However, recent kinetic simulations of multiple current sheets for a non-relativistic plasma did not show very efficient particle acceleration as expected by models. Drake et al. (2010) performed 2D full PIC simulations of multiple current sheets and observed particle energization over a few decades in energy, but a power-law energy distribution did not form. 3D hybrid kinetic simulations were done by Burgess et al. (2016), and apparent particle acceleration of ions and pickup ions was not found. Nakanotani et al. (2021) investigated the interaction of current sheets with a shock wave and found an ion flux increase associated with the evolution of the tearing-mode instability of current sheets downstream of the shock wave. However, the power-law index of the energy spectrum was unchanged associated with the generation of multiple islands due to the tearing-mode instability. Note that particle acceleration in multiple current sheets of a relativistic electron-positron plasma has been shown to be efficient (Hoshino, 2012).
An important question that has yet to be fully answered is how efficient is particle acceleration on a larger scale, such as at MHD scales? Recently, Arnold et al. (2021) showed that electrons are efficiently accelerated by Fermi acceleration due to the coalescence of magnetic islands by using MHD simulations combined with a guiding-center approximation for the electrons and including kinetic effects of energetic electrons. They pointed out that standard PIC simulations yield only a short power-law tail which extends a decade in energy because of the limitation of the simulation size. This, therefoer, can be a reason why particle acceleration in previous studies of multiple current sheets is not as efficient as expected. We attempt to answer whether particle acceleration on a larger scale of multiple current sheets is efficient or not.
In this study, we combine MHD simulations and test particle simulations to investigate particle acceleration. This method has been used for several investigations of particle acceleration in magnetic reconnection and turbulence for non-relativistic (Matthaeus et al., 1984; Ambrosiano et al., 1988; Dmitruk et al., 2003; Dmitruk et al., 2004) and relativistic particles (Kowal et al., 2012; Pezzi et al., 2022). Although feedback from energetic particles on the MHD simulation is typically ignored, they provide valuable insight into particle acceleration on the MHD scale, which is not easily obtained from kinetic simulations due to computational limitations. A similar idea has been applied for test-particle electrons in hybrid kinetic simulations (Guo and Giacalone, 2010; Trotta et al., 2020). We perform 2D and 3D MHD simulations of multiple current sheets combined with test particle simulations.
This paper is organized as follows. In Section 2, we describe the scheme of an MHD simulation combined with a test particle simulation and initial conditions. Section 3 shows results of 2D and 3D simulations that present the evolution of multiple current sheets, particle acceleration, and particle diffusion in energy space. The last section provides some discussion and conclusions to show that particle acceleration in MHD-scale multiple current sheets is indeed efficient in both 2D and 3D systems.
2 Method: MHD + test particle simulation
We combine an MHD simulation with a test particle simulation to investigate particle acceleration in a system of multiple current sheets. We solve the following compressible ideal-MHD equations,
where ρ is the plasma density, V plasma velocity, P plasma pressure, B magnetic field, E electric field, η artifitical magnetic resistivity, and J current density. γ is an adiabatic index, and we set γ = 5/3.
We use an MHD scheme proposed by Kawai (Kawai, 2013). The first spatial derivative is calculated by the sixth-order compact scheme, and time integration is done by the third-order total variation diminishing (TVD) Runge–Kutta scheme (Shu and Osher, 1988). The artifitial magnetic resistivity has the following form (Kawai, 2013),
where Cη is an dimensionless and arbitrary parameter, cs the local sound speed, χl referes to the Cartesian coordinates in the l-direction, and Δχl is the lobal grid spacing in the l-direction. Here, we set
We introduce multiple current sheets in a periodic box. We assume the force-free condition for the current sheets (Bobrova et al., 2001; Nishimura et al., 2003; Du et al., 2020).
where B0 is the in-plane magnetic field, d is the distant between two neighboring current sheets, L0 the half thickness of a current sheet, and Bg the background magnetic field. The plasma density and pressure are set to be uniform. We add small fluctuations δAz in the z − componet of the vector potential to initiate magnetic reconnection at current sheets for 2D and 3D simulations,
where δA0 is a constant value, and ϕ2D and ϕ3D are random phases for 2D and 3D simulations, respectively. We use δA0 = 0.05 and 0.02 for the 2D and 3D case, respectively. We confirmed that the overall evolution of the current sheets was similar as uniform random fluctuations were used and, therefore, it does not depend on the choice of initial fluctuations.
The simulation parameters used in the MHD simulations are as follows. We use L0 as the unit length of the simulation and the Alfvén speed vA0 defined by
At the same time, we solve the following equation of motion in a normalized form for non-relativistic particles using the standard Buneman-Boris method,
Here, α = T0Ωc where T0 is the characteristic time scale of the MHD simulation and Ωc is the cyclotron frequency of particles. The parameter α is an arbitrary and user-specified parameter since the system of the ideal MHD is scale-free, and we set α = 500. The same normalization used in the MHD simulation is applied to the equation of motion so that the particle energy is normalized by
3 Results
3.1 2D case
Multiple current sheets evolve into a turbulent state. Figure 1 shows the time evolution of the current density Jz from t = 0 to 300. The black lines show the magnetic field lines There are four current sheets located equidistant at the initial time. The added initial fluctuations initiate the tearing-mode instability, and we can see that magnetic reconnection occurs in the current sheets at t = 50. Since the phase of the fluctuations is random, the location of magnetic reconnection is also random. As the simulation proceeds, magnetic islands produced by magnetic reconnection grow in size and merge with each other in the same current sheet. When the size of magnetic islands is roughly equal to or larger than the initial current sheet distance (10L0), magnetic islands start interacting (t = 150). We observe that regions outside the magnetic islands become turbulent. At the later time (t = 300), the size of merging islands becomes around 20L0, and the system becomes turbulent.
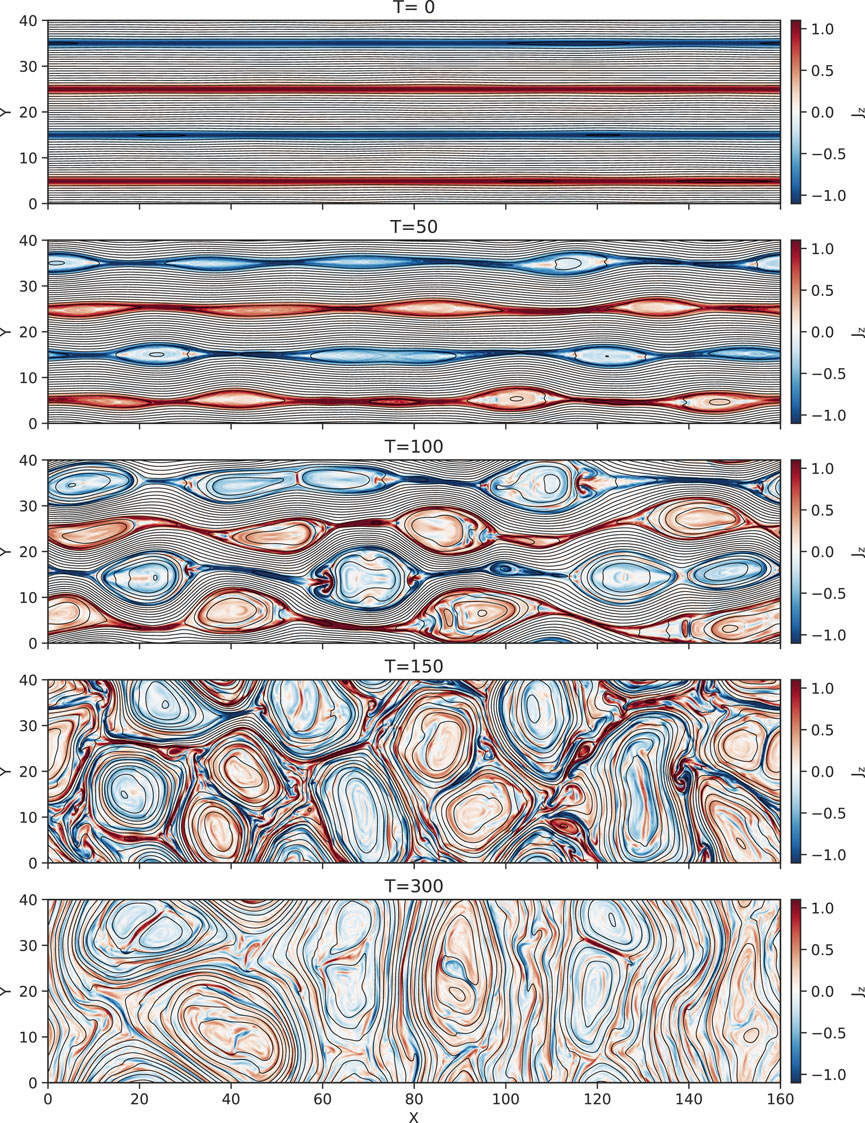
FIGURE 1. Snapshots of the current density Jz in the 2D case at different times, t = 0, 50, 100, 150, 300 from top to bottom. Black lines represent the magnetic field lines (contour lines for the vector potential Az).
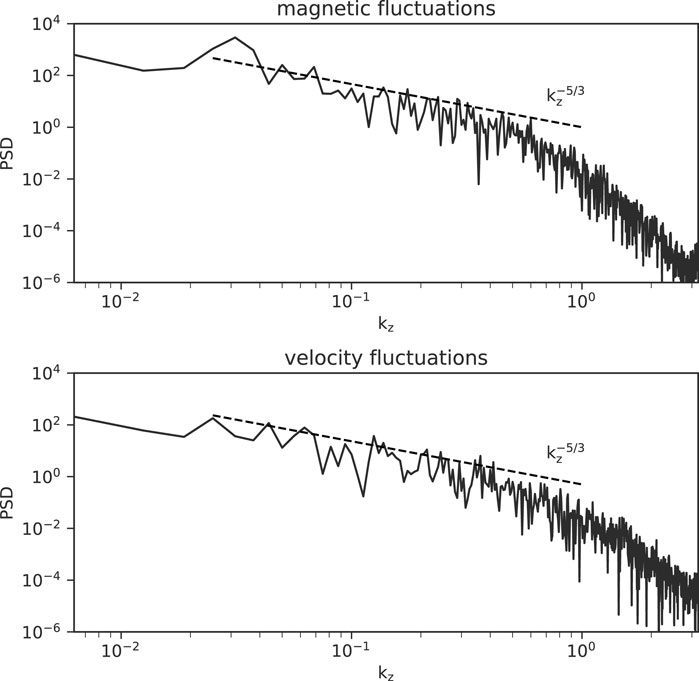
The turbulence exhibits a −5/3 power-law in the magnetic and velocity fluctuations. Figure 2 shows the power spectrum density (PSD) of magnetic
Non-thermal particles are produced during the evolution of the multiple current sheets into turbulence. Figure 3 shows the time evolution of the energy distribution function of particles. We use all particles in the simulation domain to calculate an energy distribution function. At t = 0, the distribution is Maxwellian with a temperature of Tp = 0.25. We can see that a non-thermal tail forms at t = 25 and 50. These times correspond to the onset of magnetic reconnection at current sheets. At later times, non-thermal particles are further produced especially after magnetic islands start interacting (t = 150), and also the distribution is heated. At the end of the simulation time (t = 300), the distribution has a clear non-thermal and power-law tail with an index of −2.2. The final distribution can be fitted by a Kappa distribution (Livadiotis and McComas, 2013),
where Nκ is the number of particles, kB the Boltzmann constant, Tκ the kappa temperature, Γ the Gamma function, κ the Kappa (or power-law) index. The black dashed line is a Kappa distribution with a temperature of Tκ = 1.2 and κ = 2.2. We can clearly see that the power-law tail of the simulated energy distribution at t = 300 is fitted well by the Kappa distribution over the range of E ∈ [1, 100]. The maximum energy of accelerated particles is
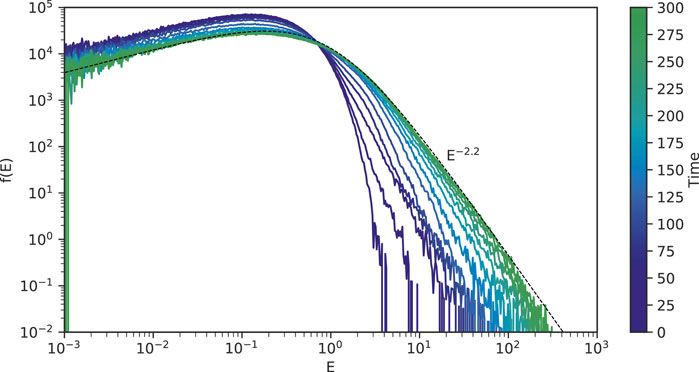
FIGURE 3. Time evolution of the energy distribution of test particles in the 2D case. Black dashed line is a Kappa distribution with a temperature of Tκ = 1.2 and a Kappa index of κ = 2.2.
The location of energetic particles depends on the stage of the evolution of multiple current sheets. Figure 4 shows the time evolution of the energy density defined by,
where Emin is the minimum energy and we set Emin = 4, so that we count only energetic particles. These panels correspond to different times, t = 0, 50, 100, 150, 300 from top to bottom. The white lines are the magnetic fields lines. Note that the color scales are different at each time. It is obvious that there are no energetic particles at the initial time. After the onset of magnetic reconnection (t = 50), some energetic particles are produced along a current sheet. This acceleration is typical for magnetic reconnection (Oka et al., 2010; Arnold et al., 2021). As magnetic islands grow in size, we can see that energetic particles are trapped inside magnetic islands. At t = 150, when magnetic islands interact with each other, it seems that energetic particles are now present among the magnetic islands rather than trapped within them. This is more evident at the end of the simulation (t = 300), and the energy density outside the magnetic islands is much higher than inside. Therefore, we can conclude that energetic particles are initially accelerated inside current sheets and trapped inside magnetic islands, and then are released and further accelerated as magnetic islands start interacting with each other. The transport theory of Zank et al. (2014), le Roux et al. (2015) caputured the transport and acceleration of particles as they interact with multiple magnetic islands. Note that Hoshino (Hoshino, 2012) also observed that energetic particles locate outside of magnetic islands in the full PIC simulation of multiple current sheets.

FIGURE 4. Snapshots of the energy density of particles defined by
Particles are efficiently accelerated by turbulence. In Figure 5, the left-top panel shows the time evolution of the energy of a typically accelerated particle. The shaded regions denoted by (a)-(c) correspond to the other panels in Figure 5 The color scale in the panels (a)-(c) represents the particle energy. There are three major acceleration events, the first one is at t = 130 and the acceleration is a quick energization. As seen in the panel (a), the particle is accelerated by a reconnection outflow of a single current sheet. When the particle enters a current sheet, it is kicked and moves along the outflow. The second (t = 155) and third (t = 270) accelerations are formally similar and accelerated by turbulence. As mentioned early, the turbulence is produced by the interaction of magnetic islands, and it starts from T ∼ 150. The motion of the particle appears stochastic in the panels (b) and (c), and the acceleration time is gradual compared to the first acceleration. The slopes of the two acceleration times are consistent. The particle energy finally reaches E = 60. The particle trajectory indicates that, at first, a particle is energized in a single current sheet and then is further accelerated by turbulence produced by the interaction of magnetic islands.
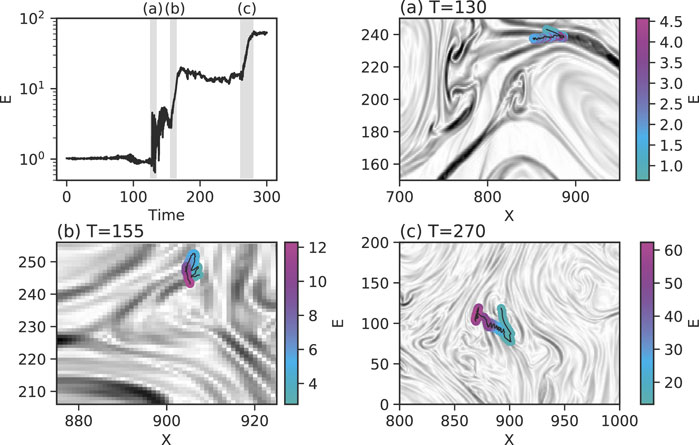
FIGURE 5. A typical tranjectory of an accelerated particle in the 2D case. Top-left panel: time evolution of the particle energy, (A)-(C): particle trajectory (black line) and corresponding energy (color map) in the background of the current density Jz (grey scale). Times (A)-(C) correspond to the shaded region in the top-left panel.
The diffusion of energetic particles in energy space is super-diffusive. Figure 6 shows the mean square displacement (MSD) of the energy
where Np is the number of energetic particles (E > 4). Here, ΔE(t) is the displacement of a particle energy, ΔE(t) = E(t) − E(0) where E(0) is the initial particle energy. However, since the number of energetc particles are few until t = 20 and
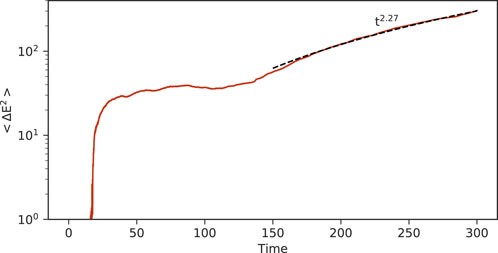
FIGURE 6. Mean square displacement of the energy of energetic particles (E > 4) for the 2D case. The balck dashed line is propotional to t2.27.
3.2 3D case
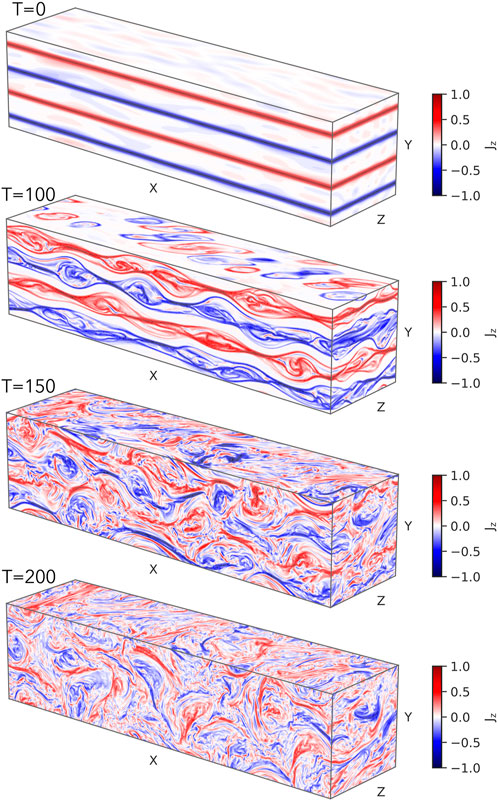
Multiple current sheets in a 3D simulation box become turbulent via the tearing-mode instability. The 3D simulation uses the same conditions as the 2D simulation but the simulation box is extended in the z − direction by 40L0 and we use a smaller value of the CFL number (cCFL = 0.25). Figure 7 shows snapshots of the current density Jz at different times t = 0, 100, 150, 200. As in the 2D simulation, four current sheets are located inside the simulation box parallel to the x − z plane at t = 0. Small fluctuations are seen at t = 0 because of the initial fluctuations defined by Eq. 14. The initial fluctuations initiate the tearing-mode instability, and magnetic reconnection proceeds at the current sheets. The location for magnetic reconnection is also random like the 2D simulation. Although magnetic islands grow in size after the onset of magnetic reconnection, the shape of magnetic islands is not as clear as the magnetic islands in the 2D simulation. This is because magnetic reconnection occurs at random orientations and locations on the current sheets and magnetic islands merge with each other in the 3D simulation. Therefore, the evolution of current sheets is much more complicated in the 3D simulation. Due to the interaction of the destabilized current sheets, the system appears turbulent at t = 150. At the end of the simulation (t = 200), small scale fluctuations are more visible than at t = 150, and the system transits to a highly-turbulent state. The turbulence appears isotropic since there is no background magnetic field.
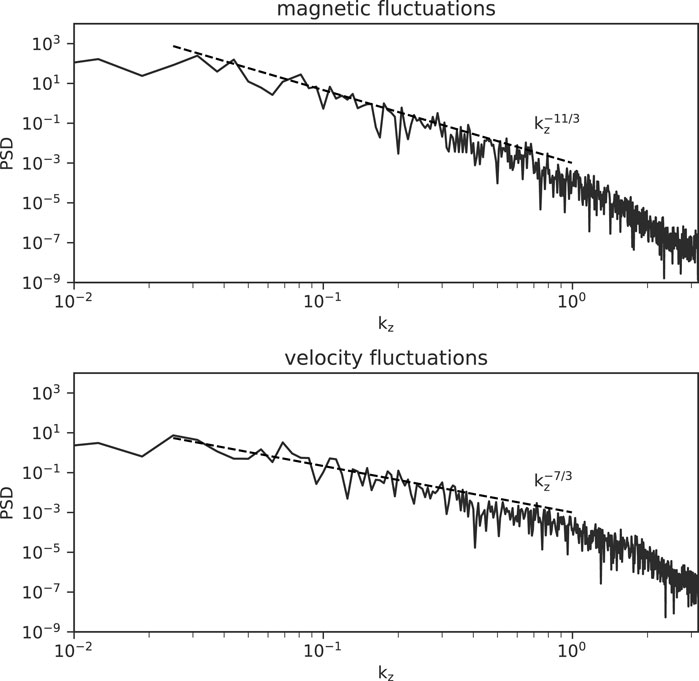
The spectra of the magnetic and velocity fluctuations have the form of a −11/3 and −7/3 power-law, respectively. Figure 8 shows the PSD of magnetic (top panel) and velocity (bottom panel) fluctuations along the x − direction which is averaged over the y − z plane. The magnetic PSD exhibits a −11/3 power-law over the range of kz ∈ [0.03, 0.6], and the larger wavenumber range is dissipated by the artificial dissipation effects (resistivity and bulk viscosity). On the other hand, the velocity PSD can be also fitted by a −5/3 power-law over the range kz ∈ [0.03, 0.7]. The normalized cross helicity and residual energy are 8 × 10–4 and −0.53, respectively. This indicates that the magnetic fluctuations dominate velocity fluctuations.
Non-thermal particles are produced during the evolution of the multiple current sheets and form a power-law tail. Figure 9 shows the energy distribution of test particles at different times corresponding to the color scale. After the onset of the magnetic reconnection, the existence of non-thermal particles is not as obvious as in the 2D simulation. The particles seem to be heated rather than accelerated. However, a power-law tail starts forming after the turbulence begins to be created (t ∼ 125). At the end of the simulation (t = 200), energetic particles are present and form a power-law tail with an index of 4.2. The entire distribution is roughly fitted by a Kappa distribution (Eq. 16) with a temperature of Tκ = 0.8 and a Kappa index of κ = 4.2. The maximum energy of accelerated particles is

FIGURE 9. Time evolution of the energy distribution of test particles in the 3D case. The black dashed line is a Kappa distribution with a temperature of Tκ = 0.8 and a Kappa index of κ = 4.2.
Super-diffusion of energetic particles is observed in energy space. Figure 10 shows the time evolution of the energy MSD of energetic particles. We consider only particles whose energy is larger than 4. The number of particles is few until t = 50, therefore, we focus on later times. After magnetic islands start interacting with each other (t = 125), the MSD is fitted by ∝ t1.2. This indicates that particle acceleration after the deveopment of the turbulence in the 3D system is super-diffusive.
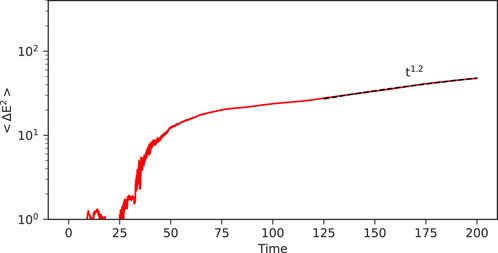
FIGURE 10. Mean square displacement of the energy of energetic particles (E > 4) of the 3D case. The balck dashed line is propotional to t1.2.
4 Discussion and conclusion
Although the evolution of multiple current sheets is different in the 2D and 3D simulations, both cases yield turbulence at the end of the simulation. In the 2D case, current sheets are unstable to the tearing-mode instabiliy, and magnetic islands are produced by magnetic reconnection. In the 3D case, magnetic reconnection occurs at random on current sheets (the x − z plane) and the evolution of magnetic islands differs along the z − direction. This makes the evolution of current sheets more complicated in the 3D case than in the 2D case. However, the system for both cases develops into a highly turbulent state at the end of the simulation.
The efficiency of particle acceleration in the 2D simulation is greater than that in the 3D simulation. While the power-law index of the energy distribution in the 2D case is −2.2, it is −4.2 in the 3D case. This simply implies that particle acceleration in the 2D case is more efficient than in the 3D case. The maximum particle energy in the 2D case (Emax ∼ 300E0) is higher than that of the 3D case (Emax ∼ 100E0). We note that the power-law tails extend to the maximum energies. The index of the observed super-diffusion in the 2D case (2.27) is higher than that in the 3D case (1.2). This also indicates that the 2D acceleration is more efficient than the 3D acceleration. We interpret this because in the 2D case particles can be more easily trapped in the turbulence than in the 3D case.
Compared to previous studies, an MHD scale system of multiple current sheets is an efficient acceleration site. Previous kinetic simulations (Drake et al., 2010; Burgess et al., 2016; Nakanotani et al., 2021) did not show significant particle acceleration, such as, 1) no power-law tail and 2) acceleration by a factor of a few decades only. However, as we have shown, particle acceleration in the both 2D and 3D cases forms a power-law tail and the acceleration is by a factor of more than 100. This corresponds to
Therefore, we conclude that particle acceleration in an MHD-scale system of multiple current sheets is efficient. Although it is possible to directly verify this by extending kinetic simulations to MHD-scale, it may not be realistic due to the current computational power. We comment that NI MHD in the presence of strong guide field predicts quasi-2D leading-order turbulence (Zank and Matthaeus, 1993; Zank et al., 2017), which may contribute to particle acceleration.
The particle acceleration observed in the 2D and 3D cases can be modeled by a fractional Fokker-Planck model, which is a generalization of a classical Fokker-Planck model. It is thought that super-diffusion in energy space is an indication of efficient particle acceleration and can be related to the formation of a power-law tail (Vlahos et al., 2004; Isliker et al., 2017; Isliker et al., 2019; Sioulas et al., 2020). There are several models for anomalous diffusion in energy space as well as real space using a fractional Fokker-Planck model to understand particle acceleration from the perspective of anomalous diffusion as often observed in space plasmas (Milovanov, 2001; Vlahos et al., 2004; Bian and Browning, 2008; Isliker et al., 2017; le Roux and Zank, 2021). In a future study, we will use a fractional Fokker-Planck model and compare it with several simulations by varying the background magnetic field.
We do not expect a plasma beta dependence on particle acceleration. Since the plasma beta does not strongly affect the tearing-mode instability (Landi et al., 2008), we assume that multiple current sheets develop into a turbulent state for various values of the plasma beta. Since the structure of magnetic reconnection appears to be turbulent in a low-beta plasma (Zenitani, 2015; Zenitani and Miyoshi, 2020), we anticipate that particles can be still efficiently accelerated by the turbulence in a way similar to that shown in our simulations.
Altough it is not addressed here, we expect that particle acceleration in turbulence on the strength of the background magnetic field. Several studies of magnetic reconnection show that particle acceleration becomes less efficient as the background magnetic field becomes strong (Fu et al., 2006; Wang et al., 2016; Werner and Uzdensky, 2017; Arnold et al., 2021). This can be because particle motion for Fermi acceleration is limited by the background magnetic field. In a system of multiple current sheets with a strong magnetic field, the initial acceleration by a single magnetic reconnection site becomes less efficient, and therefore the latter acceleration phase due to turbulence can be less efficient as well.
In conclusion, we have performed 2D and 3D MHD simulations of multiple current sheets combined with test particle simulations to investigate particle acceleration. In both cases, multiple current sheets are unstable to the tearing-mode instability and a turbulent state develops with power-law spectra for magnetic and velocity fluctuations. We observe the formation of magnetic islands because of magnetic reconnection during the transition. Non-thermal particles are efficiently produced due to turbulence generated by the interaction of magnetic islands. Their energy distribution can be fitted by a Kappa distribution with a Kappa index (or power-law index) of −2.2 and −4.2 for the 2D and 3D case, respectively. The efficient acceleration is consistent with the observed super-diffusion in the energy space for the both cases, which can be modeled by a fractional Fokker-Planck model.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
MN developed the simulation code, performed the analysis of the simulation results and prepared the first draft. GZ and LZ contributed to the discussion of the method, results, and to the preparation of the article.
Funding
We acknowledge the partial support of an NSF EPSCoR RII Track-1 Cooperative Agreement OIA-1655280, partial support from a NASA Parker Solar Probe contract SV4-84017, partial support from a NASA LWS grant 80NSSC20K1783, and partial support from a NASA IMAP subaward under NASA contract 80GSFC19C0027. The SWEAP Investigation and this study are supported by the PSP mission under NASA contract NNN06AA01C.
Acknowledgments
This work was made possible in part by the provision of high-performance computing resources and technical support from the Alabama Supercomputer Authority.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adhikari, L., Khabarova, O., Zank, G. P., and Zhao, L. L. (2019). The role of magnetic reconnection-associated processes in local particle acceleration in the solar wind. Astrophys. J. 873, 72. doi:10.3847/1538-4357/ab05c6
Akramov, T., and Baty, H. (2017). Non-linear growth of double tearing mode: Explosive reconnection, plasmoid formation, and particle acceleration. Phys. Plasmas 24, 082116. doi:10.1063/1.5000273
Ambrosiano, J., Matthaeus, W. H., Goldstein, M. L., and Plante, D. (1988). Test particle acceleration in turbulent reconnecting magnetic fields. J. Geophys. Res. 93, 14383–14400. doi:10.1029/JA093iA12p14383
Arnold, H., Drake, J. F., Swisdak, M., Guo, F., Dahlin, J. T., Chen, B., et al. (2021). Electron acceleration during macroscale magnetic reconnection. Phys. Rev. Lett. 126, 135101. doi:10.1103/PhysRevLett.126.135101
Bian, N. H., and Browning, P. K. (2008). Particle acceleration in a model of a turbulent reconnecting plasma: A fractional diffusion approach. Astrophys. J. 687, L111–L114. doi:10.1086/593145
Blandford, R., Yuan, Y., Hoshino, M., and Sironi, L. (2017). Space Sci. Rev. 207, 291–317. doi:10.1007/s11214-017-0376-2
Bobrova, N. A., Bulanov, S. V., Sakai, J. I., and Sugiyama, D. (2001). Force-free equilibria and reconnection of the magnetic field lines in collisionless plasma configurations. Phys. Plasmas 8, 759–768. doi:10.1063/1.1344196
Burgess, D., Gingell, P. W., and Matteini, L. (2016). Multiple current sheet systems in the outer heliosphere: Energy release and turbulence. Astrophys. J. 822, 38. doi:10.3847/0004-637X/822/1/38
Cerutti, B., and Giacinti, G. (2020). A global model of particle acceleration at pulsar wind termination shocks. Astron. Astrophys. 642, A123. doi:10.1051/0004-6361/202038883
Cook, A. W., and Cabot, W. H. (2004). A high-wavenumber viscosity for high-resolution numerical methods. J. Comput. Phys. 195, 594–601. doi:10.1016/j.jcp.2003.10.012
Crooker, N. U., Siscoe, G. L., Shodhan, S., Webb, D. F., Gosling, J. T., and Smith, E. J. (1993). Multiple heliospheric current sheets and coronal streamer belt dynamics. J. Geophys. Res. 98, 9371–9382. doi:10.1029/93JA00636
Dahlburg, R. B., and Karpen, J. T. (1995). A triple current sheet model for adjoining coronal helmet streamers. J. Geophys. Res. 100, 23489–23498. doi:10.1029/95JA02496
Dahlin, J. T., Drake, J. F., and Swisdak, M. (2014). The mechanisms of electron heating and acceleration during magnetic reconnection. Phys. Plasmas 21, 092304. doi:10.1063/1.4894484
Dmitruk, P., Matthaeus, W. H., Seenu, N., and Brown, M. R. (2003). Test particle acceleration in three-dimensional magnetohydrodynamic turbulence. Astrophys. J. 597, L81–L84. doi:10.1086/379751
Dmitruk, P., Matthaeus, W. H., and Seenu, N. (2004). Test particle energization by current sheets and nonuniform fields in magnetohydrodynamic turbulence. Astrophys. J. 617, 667–679. doi:10.1086/425301
Drake, J. F., Opher, M., Swisdak, M., and Chamoun, J. N. (2010). A magnetic reconnection mechanism for the generation of anomalous cosmic rays. Astrophys. J. 709, 963–974. doi:10.1088/0004-637X/709/2/963
Drake, J. F., Swisdak, M., Che, H., and Shay, M. A. (2006). Electron acceleration from contracting magnetic islands during reconnection. Nature 443, 553–556. doi:10.1038/nature05116
Du, S., Zank, G. P., Li, X., and Guo, F. (2020). Energy dissipation and entropy in collisionless plasma. Phys. Rev. E 101, 033208. doi:10.1103/PhysRevE.101.033208
Fu, X. R., Lu, Q. M., and Wang, S. (2006). The process of electron acceleration during collisionless magnetic reconnection. Phys. Plasmas 13, 012309. doi:10.1063/1.2164808
Gingell, P. W., Burgess, D., and Matteini, L. (2015). The three-dimensional evolution of ion-scale current sheets: Tearing and drift-kink instabilities in the presence of proton temperature anisotropy. Astrophys. J. 802, 4. doi:10.1088/0004-637X/802/1/4
Guo, F., and Giacalone, J. (2010). The effect of large-scale magnetic turbulence on the acceleration of electrons by perpendicular collisionless shocks. Astrophys. J. 715, 406–411. doi:10.1088/0004-637X/715/1/406
Guo, F., Li, H., Daughton, W., and Liu, Y. H. (2014). formation of hard power laws in the energetic particle spectra resulting from relativistic magnetic reconnection. Phys. Rev. Lett. 113, 155005. doi:10.1103/PhysRevLett.113.155005
Hesse, M., and Cassak, P. A. (2020). Magnetic reconnection in the space Sciences: Past, present, and future. J. Geophys. Res. Space Phys. 125, e25935. doi:10.1029/2018JA025935
Hoshino, M., Mukai, T., Terasawa, T., and Shinohara, I. (2001). Suprathermal electron acceleration in magnetic reconnection. J. Geophys. Res. 106, 25979–25997. doi:10.1029/2001JA900052
Hoshino, M. (2012). Stochastic particle acceleration in multiple magnetic islands during reconnection. Phys. Rev. Lett. 108, 135003. doi:10.1103/PhysRevLett.108.135003
Isliker, H., Archontis, V., and Vlahos, L. (2019). Particle acceleration and heating in regions of magnetic flux emergence. Astrophys. J. 882, 57. doi:10.3847/1538-4357/ab30c6
Isliker, H., Pisokas, T., Vlahos, L., and Anastasiadis, A. (2017). Particle acceleration and fractional transport in turbulent reconnection. Astrophys. J. 849, 35. doi:10.3847/1538-4357/aa8ee8
Kawai, S. (2013). Divergence-free-preserving high-order schemes for magnetohydrodynamics: An artificial magnetic resistivity method. J. Comput. Phys. 251, 292–318. doi:10.1016/j.jcp.2013.05.033
Kawai, S., and Lele, S. K. (2008). Localized artificial diffusivity scheme for discontinuity capturing on curvilinear meshes. J. Comput. Phys. 227, 9498–9526. doi:10.1016/j.jcp.2008.06.034
Kowal, G., de Gouveia Dal Pino, E. M., and Lazarian, A. (2012). Particle acceleration in turbulence and weakly stochastic reconnection. Phys. Rev. Lett. 108, 241102. doi:10.1103/PhysRevLett.108.241102
Landi, S., Londrillo, P., Velli, M., and Bettarini, L. (2008). Three-dimensional simulations of compressible tearing instability. Phys. Plasmas 15, 012302. doi:10.1063/1.2825006
le Roux, J. A., Zank, G. P., Webb, G. M., and Khabarova, O. (2015). A kinetic transport theory for particle acceleration and transport in regions of multiple contracting and reconnecting inertial-scale flux ropes. Astrophys. J. 801, 112. doi:10.1088/0004-637X/801/2/112
le Roux, J. A., and Zank, G. P. (2021). A focused transport-based kinetic fractional diffusion-advection equation for energetic particle trapping and reconnection-related acceleration by small-scale magnetic flux ropes in the solar wind. Astrophys. J. 913, 84. doi:10.3847/1538-4357/abf3c6
Li, X., Guo, F., Li, H., and Li, G. (2017). Particle acceleration during magnetic reconnection in a low-beta plasma. Astrophys. J. 843, 21. doi:10.3847/1538-4357/aa745e
Li, X., Guo, F., and Liu, Y. H. (2021). The acceleration of charged particles and formation of power-law energy spectra in nonrelativistic magnetic reconnection. Phys. Plasmas 28, 052905. doi:10.1063/5.0047644
Livadiotis, G., and McComas, D. J. (2013). Erratum to: Understanding kappa distributions: A toolbox for space science and astrophysics. Space Sci. Rev. 175, 215. doi:10.1007/s11214-013-9996-3
Lu, Y., Guo, F., Kilian, P., Li, H., Huang, C., and Liang, E. (2021). Fermi-type particle acceleration from magnetic reconnection at the termination shock of a relativistic striped wind. Astrophys. J. 908, 147. doi:10.3847/1538-4357/abd406
Lyubarsky, Y. (2005). The termination shock in a striped pulsar wind. Adv. Space Res. 35, 1112–1115. doi:10.1016/j.asr.2005.01.025
Maiewski, E. V., Malova, H. V., Kislov, R. A., Popov, V. Y., Petrukovich, A. A., Khabarova, O. V., et al. (2020). formation of multiple current sheets in the heliospheric plasma sheet. Cosm. Res. 58, 411–425. doi:10.1134/S0010952520060076
Matthaeus, W. H., Ambrosiano, J. J., and Goldstein, M. L. (1984). Particle-acceleration by turbulent magnetohydrodynamic reconnection. Phys. Rev. Lett. 53, 1449–1452. doi:10.1103/PhysRevLett.53.1449
Milovanov, A. V. (2001). Stochastic dynamics from the fractional Fokker-Planck-Kolmogorov equation: Large-scale behavior of the turbulent transport coefficient. Phys. Rev. E 63, 047301. doi:10.1103/PhysRevE.63.047301
Nagata, K., Hoshino, M., Jaroschek, C. H., and Takabe, H. (2008). Interaction between alternating magnetic fields and a relativistic collisionless shock. Astrophys. J. 680, 627–638. doi:10.1086/587640
Nakanotani, M., Zank, G. P., and Zhao, L. L. (2021). Interaction between multiple current sheets and a shock wave: 2D hybrid kinetic simulations. Astrophys. J. 922, 219. doi:10.3847/1538-4357/ac2e06
Nishimura, K., Gary, S. P., Li, H., and Colgate, S. A. (2003). Magnetic reconnection in a force-free plasma: Simulations of micro- and macroinstabilities. Phys. Plasmas 10, 347–356. doi:10.1063/1.1536168
Oka, M., Fujimoto, M., Shinohara, I., and Phan, T. D. (2010). Island surfing” mechanism of electron acceleration during magnetic reconnection. J. Geophys. Res. 115, A08223. doi:10.1029/2010JA015392
Pezzi, O., Blasi, P., and Matthaeus, W. H. (2022). Relativistic particle transport and acceleration in structured plasma turbulence. Astrophys. J. 928, 25. doi:10.3847/1538-4357/ac5332
Shu, C. W., and Osher, S. (1988). Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471. doi:10.1016/0021-9991(88)90177-5
Sioulas, N., Isliker, H., Vlahos, L., Koumtzis, A., and Pisokas, T. (2020). Superdiffusive stochastic Fermi acceleration in space and energy. Mon. Not. R. Astron. Soc. 491, 3860–3869. doi:10.1093/mnras/stz3259
Sironi, L., and Spitkovsky, A. (2011). Acceleration of particles at the termination shock of a relativistic striped wind. Astrophys. J. 741, 39. doi:10.1088/0004-637X/741/1/39
Sironi, L., and Spitkovsky, A. (2014). Relativistic reconnection: An efficient source of non-thermal particles. Astrophys. J. 783, L21. doi:10.1088/2041-8205/783/1/L21
Smith, E. J. (2001). The heliospheric current sheet. J. Geophys. Res. 106, 15819–15831. doi:10.1029/2000JA000120
Speiser, T. W. (1965). Particle trajectories in model current sheets, 1, analytical solutions. J. Geophys. Res. 70, 4219–4226. doi:10.1029/JZ070i017p04219
Tóth, G. (2000). The ∇⋅ B=0 constraint in shock-capturing magnetohydrodynamics codes. J. Comput. Phys. 161, 605–652. doi:10.1006/jcph.2000.6519
Trotta, D., Franci, L., Burgess, D., and Hellinger, P. (2020). Fast acceleration of transrelativistic electrons in astrophysical turbulence. Astrophys. J. 894, 136. doi:10.3847/1538-4357/ab873c
Vlahos, L., Isliker, H., Kominis, Y., and Hizanidis, K. (2008). Normal and anomalous diffusion: A tutorial. arXiv e-printsarXiv:0805.0419.
Vlahos, L., Isliker, H., and Lepreti, F. (2004). Particle acceleration in an evolving network of unstable current sheets. Astrophys. J. 608, 540–553. doi:10.1086/386364
Wang, H., Lu, Q., Huang, C., and Wang, S. (2016). The mechanisms of electron acceleration during multiple X line magnetic reconnection with a guide field. Astrophys. J. 821, 84. doi:10.3847/0004-637X/821/2/84
Werner, G. R., Uzdensky, D. A., Cerutti, B., Nalewajko, K., and Begelman, M. C. (2016). The extent of power-law energy spectra in collisionless relativistic magnetic reconnection in pair plasmas. Astrophys. J. 816, L8. doi:10.3847/2041-8205/816/1/L8
Werner, G. R., and Uzdensky, D. A. (2017). Nonthermal particle acceleration in 3D relativistic magnetic reconnection in pair plasma. Astrophys. J. 843, L27. doi:10.3847/2041-8213/aa7892
Yamada, M., Kulsrud, R., and Ji, H. (2010). Magnetic reconnection. Rev. Mod. Phys. 82, 603–664. doi:10.1103/RevModPhys.82.603
Zank, G. P., Adhikari, L., Hunana, P., Shiota, D., Bruno, R., and Telloni, D. (2017). Theory and transport of nearly incompressible magnetohydrodynamic turbulence. Astrophys. J. 835, 147. doi:10.3847/1538-4357/835/2/147
Zank, G. P., Dosch, A., Hunana, P., Florinski, V., Matthaeus, W. H., and Webb, G. M. (2012). The transport of low-frequency turbulence in astrophysical flows. I. Governing equations. Astrophys. J. 745, 35. doi:10.1088/0004-637X/745/1/35
Zank, G. P., Hunana, P., Mostafavi, P., Le Roux, J. A., Li, G., Webb, G. M., et al. (2015). Diffusive shock acceleration and reconnection acceleration processes. Astrophys. J. 814, 137. doi:10.1088/0004-637X/814/2/137
Zank, G. P., le Roux, J. A., Webb, G. M., Dosch, A., and Khabarova, O. (2014). Particle acceleration via reconnection processes in the supersonic solar wind. Astrophys. J. 797, 28. doi:10.1088/0004-637X/797/1/28
Zank, G. P., and Matthaeus, W. H. (1993). Nearly incompressible fluids. II: Magnetohydrodynamics, turbulence, and waves. Phys. Fluids A Fluid Dyn. 5, 257–273. doi:10.1063/1.858780
Zenitani, S. (2015). Magnetohydrodynamic structure of a plasmoid in fast reconnection in low-beta plasmas: Shock-shock interactions. Phys. Plasmas 22, 032114. doi:10.1063/1.4916104
Zenitani, S., and Miyoshi, T. (2020). Plasmoid-dominated turbulent reconnection in a low-β plasma. Astrophys. J. 894, L7. doi:10.3847/2041-8213/ab8b5d
Zhang, C. L., and Ma, Z. W. (2011). Nonlinear evolution of double tearing mode with guiding magnetic field. Phys. Plasmas 18, 052303. doi:10.1063/1.3581064
Zhang, Q., Guo, F., Daughton, W., Li, H., and Li, X. (2021). Efficient nonthermal ion and electron acceleration enabled by the flux-rope kink instability in 3D nonrelativistic magnetic reconnection. Phys. Rev. Lett. 127, 185101. doi:10.1103/PhysRevLett.127.185101
Zhao, L. L., Zank, G. P., Hu, Q., Chen, Y., Adhikari, L., leRoux, J. A., et al. (2019). ACR proton acceleration associated with reconnection processes beyond the heliospheric termination shock. Astrophys. J. 886, 144. doi:10.3847/1538-4357/ab4db4
Keywords: MHD simulation, multiple current sheets, turbulence, particle acceleration, magnetic reconnection
Citation: Nakanotani M, Zank GP and Zhao L (2022) Particle acceleration in an MHD-scale system of multiple current sheets. Front. Astron. Space Sci. 9:954040. doi: 10.3389/fspas.2022.954040
Received: 26 May 2022; Accepted: 18 July 2022;
Published: 11 August 2022.
Edited by:
Jiansen He, Peking University, ChinaReviewed by:
Zhongwei Yang, National Space Science Center (CAS), ChinaGiovanni Lapenta, KU Leuven, Belgium
Copyright © 2022 Nakanotani, Zank and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Masaru Nakanotani, bW4wMDUyQHVhaC5lZHU=
 Masaru Nakanotani
Masaru Nakanotani Gary P. Zank
Gary P. Zank Lingling Zhao
Lingling Zhao