- Física Teórica y del Cosmos Department, Universidad de Granada, Granada, Spain
Asteroseismology has opened a window on the internal physics of thousands of stars, by relating oscillation spectra properties to the internal physics of stars. Mode identification, namely the process of associating a measured oscillation frequency to the corresponding mode geometry and properties, is the cornerstone of this analysis of seismic spectra. In rapidly rotating stars this identification is a challenging task that remains incomplete, as modes assume complex geometries and regular patterns in frequencies get scrambled under the influence of the Coriolis force and centrifugal flattening. In this article, I will first discuss the various classes of mode geometries that emerge in rapidly rotating stars and the related frequency and period patterns, as predicted by ray dynamics, complete (non-)adiabatic calculations, or using the traditional approximation of rotation. These patterns scale with structural quantities and help us derive crucial constraints on the structure and evolution of these stars. I will summarize the amazing progress accomplished over the last few years for the deciphering of gravity-mode pulsator oscillation spectra, and recent developments based on machine-learning classification techniques to distinguish oscillation modes and pattern analysis strategies that let us access the underlying physics of pressure-mode pulsators. These approaches pave the way to ensemble asteroseismology of classical pulsators. Finally, I will highlight how these recent progress can be combined to improve forward seismic modelling. I will focus on the example of Rasalhague, a well-known rapid rotator, to illustrate the process and the needed advances to obtain à-la-carte modelling of such stars.
1 Introduction
Over the last few decades, helio- and asteroseismology have started a golden age for stellar physics. The advent of space-based photometry missions (such as CoRoT, Baglin et al., 2009, Gilliland et al., 2010, TESS, Ricker 2014, and BRITE, Weiss et al., 2014) has led to the detection of variability in numerous stars, the measurement of oscillation frequencies and their regular spacings, and the identification of the mode geometries. This has triggered a cascade of new theoretical developments for stellar models, oscillation codes and inversion techniques.
However, these developments were long limited to slowly rotating solar-like and red giant stars. Upper main-sequence pulsators present a rapid rotation (Royer, 2009) that affects both their structure and their oscillations. A rotating star is centrifugally distorted (Potter, 2012), which induces a meridional circulation (Zahn, 1992; Rieutord, 2006) and latitudinal surface temperature gradients (von Zeipel, 1924; Espinosa Lara and Rieutord, 2011). Figure 1 presents three examples of interferometric measurements of the surface shape and temperatures for three close pulsating A stars.
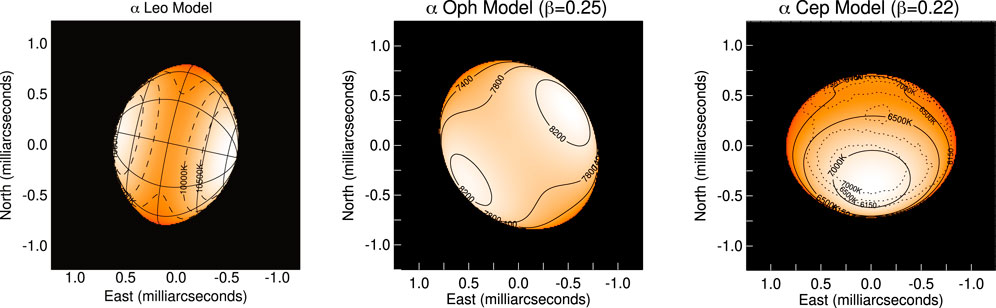
FIGURE 1. Interferometric observations of rapidly rotating stars, showing the centrifugal distortion and gravity darkening phenomena. Left to right: Regulus (α Leo, Che et al., 2011), Rasalhague (α Oph, Zhao et al., 2009), Alderamin (α Cep, Zhao et al., 2009).
Pulsations can be either pressure or gravito-inertial modes. Pressure modes (or acoustic modes) are restored by pressure forces and tend to propagate at high frequencies. Gravity modes are restored by buoyancy and exist at low frequencies. Mixed modes can appear when a pressure and a gravity mode propagating in two separate cavities inside the star at the same frequency couple. In the presence of rotation, the Coriolis force can act as a restoring force to create the so-called inertial modes, or combine with buoyancy to create gravito-inertial modes. At high rotation rates, the Coriolis force is the dominating effect of rotation on gravity modes while pressure modes are mostly affected by the centrifugal distortion, both effects modify the oscillation frequencies and obfuscate regular patterns in the spectra. This creates new complex mode geometries (Reese et al., 2008; Lignières and Georgeot, 2009; Ballot et al., 2013) that render mode identification challenging. Taking these effects fully into account requires dedicated two-dimensional models (Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016) and oscillation calculations (Reese et al., 2009a, 2021; Ouazzani et al., 2012). The mathematical details of these tools are provided in Reese (this volume).
In this review, I consider pulsating stars on the upper main sequence, that can be split into four classes: in increasing order of mass, these are the γ Doradus (F-late A), δ Scuti (A-F), slowly-pulsating B (SPB, B3-B9) and β Cephei (B0-B2) stars (Aerts et al., 2010). γDor stars harbour low-frequency gravito-inertial and inertial modes excited through a combination of convective flux blocking at the base of the surface convection zone (Pesnell, 1987; Guzik et al., 2000; Dupret et al., 2004a; 2005) in colder γDor stars and κ mechanism in their warmer counterparts (Xiong et al., 2016). δSct stars pulsate at higher frequencies because of acoustic modes excited by the κ mechanism (Zhevakin, 1963; Dupret et al., 2004a). These two classes of modes have more massive counterparts: SPBs pulsate with low-frequency (gravito-) inertial modes and βCep stars harbour acoustic and low-order gravity modes, that are explained in both cases by the κ mechanism activated by the metal opacity bump (Cox et al., 1992; Dziembowski et al., 1993).
Due to their overlapping instability ranges, many γDor/δSct hybrids (e.g. Handler et al., 2002; Grigahcène et al., 2010; Balona et al., 2015) and SPB/βCep hybrids (e.g. Handler et al., 2004; De Cat et al., 2007; Handler, 2009; Burssens et al., 2020) have been detected. A series of works by Osaki (1974); Lee and Saio (2020); Lee (2022) also proposes resonant coupling with overstable convection in the core as a possible excitation mechanism for gravity modes in the envelope of early-type stars, with frequencies close to the core rotation rate. This may account for rotational-modulation-like signals observed in SPB stars and hybrid pulsators.
The individual identification of modes in rapidly rotating stars is hampered by a limited knowledge of the mode selection mechanisms, the impact of rotation on both their structure and oscillations, the sheer number of possible oscillation modes theoretically predicted by high-resolution calculations and our impossibility to predict mode amplitudes. Patterns in frequency or period have opened a window on the internal physics of solar-like and red-giant stars, after being described theoretically (e.g. Shibahashi, 1979; Tassoul, 1980; Miglio et al., 2008) and identified in observations (as in Mosser et al., 2013; Vrard et al., 2016). Such patterns, albeit far more elusive, exist in rapidly rotating stars and have been investigated by theoretical works for both p-mode (e.g. Lignières and Georgeot, 2009; Suárez et al., 2014; Mirouh et al., 2019) and g-mode spectra (e.g. Bouabid et al., 2013; Ouazzani et al., 2017, 2020; Dhouib et al., 2021; Tokuno and Takata, 2022). Detections in both p-mode (e.g. García Hernández et al., 2015; Paparó et al., 2016a,b; García Hernández et al., 2017; Bedding et al., 2020) and g-mode pulsators (e.g Van Reeth et al., 2015; Li et al., 2020b; Pedersen et al., 2021; Garcia et al., 2022) yield estimates of the fundamental parameters and the internal physics of an ever-increasing number of stars.
Relating frequency and period spacings to structure quantities thus offers crucial statistical information and precious constraints for forward modelling and paves the way to ensemble seismology for classical pulsators (Michel et al., 2017; Bowman and Kurtz, 2018).
Tools and strategies that are well established for slow rotators have been redeveloped to take into account rotational effects. One such tool is line-profile variations, which can yield oscillation frequencies and a partial identification (see Lee and Saio, 1990; Telting and Schrijvers, 1997; Zima, 2006) for both pressure and gravito-inertial nonradial modes from time series of spectroscopic measurements (e.g. Aerts et al., 1992; Zima et al., 2006; Shutt et al., 2021). Reese et al. (2017a) offers a first adaptation of the technique to complete calculations of pressure modes in rapid rotators.
In this review I will first describe the impact of the Coriolis force and the centrifugal flattening of rotating stars on acoustic, inertial and gravito-inertial mode geometries (Section 2). Comparing with non-rotating stars, I will discuss the intricate frequency and period patterns that rapid-rotator oscillation spectra describe, and the strategies to extract them from space-based photometry data (Section 3). I will then explain how spectroscopic line-profile variations can be evaluated to derive frequencies of rapid rotators (Section 4), and describe the example of the forward modelling of Rasalhague (Section 5).
As I focus on rotation and complete two-dimensional calculations of models and oscillation modes, I will leave out magnetic fields and their impact on oscillations. I refer the reader to the literature regarding detections of magnetic fields in A stars, theoretical study of magneto-acoustic oscillations and extensive results for rapidly-oscillating Ap (roAp) stars (Mathis et al., 2021; Holdsworth, 2021, and references therein). Interactions between magnetic fields and low-frequency oscillations have been the focus of a lot of recent work, regarding internal gravity waves (Rogers and MacGregor, 2010, 2011; Lecoanet et al., 2017, 2022, e.g.), coherent gravito-inertial modes (e.g. Loi, 2020; Prat et al., 2020; Dhouib et al., 2021) and mixed modes (Loi and Papaloizou, 2018; Bugnet et al., 2021) such as depressed dipole modes in red giants (e.g. García et al., 2014; Stello et al., 2016).
2 Mode geometries in rapidly rotating stars
Contrary to the non-rotating case, oscillations in rapidly rotating stars cannot be described using simple spherical harmonics. Perturbative approaches quickly show their limits, and strategies that include rotation from the start (even under some approximations) are necessary to compute models and oscillations. Several approaches have been implemented, with various levels of accuracy and complexity.
2.1 Including rotation to compute oscillations
The simplest way of including the effects of rotation is to treat its effects as corrections to non-rotating solutions of pulsations. These corrections are described, for both the centrifugal flattening and the Coriolis acceleration, as successive powers of the rotation rate Ω, which is supposed to be small (e.g. Ledoux, 1951; Gough and Thompson, 1990; Lee and Baraffe, 1995; Soufi et al., 1998). For high enough rotation rates, even the highest-order perturbative calculations misestimate frequencies and describe the mode geometries poorly: Ballot et al. (2013) and Reese (2006) have evaluated the range of applicability of perturbative treatments for gravito-inertial and pressure modes, respectively.
The traditional approximation (Eckart, 1960; Berthomieu et al., 1978) consists in neglecting the latitudinal component of the rotation vector Ω in the Coriolis acceleration, assuming Ω = Ω cos θer. If the centrifugal distortion of the star and the perturbation to the gravitational potential are neglected as well, the system ruling adiabatic oscillations becomes separable in radius r and colatitude θ, effectively preventing coupling between modes described by different spherical harmonics (Bildsten et al., 1996). This makes the equations much more tractable with the added benefit that the horizontal component of the oscillations can be described mathematically by means of the known Hough functions (Lee and Saio, 1987). Recent developments by Henneco et al. (2021); Dhouib et al. (2021) generalise the traditional approximation to include the effects of the centrifugal distortion and a differential rotation and predict detectable impacts on both low- and high-order gravito-inertial modes. However, and contrary to the other techniques presented here, the traditional approximation is a non-perturbative approach only applicable to high-order g modes (such as those detected in γDor and SPB stars).
Ray theory relies on the short-wavelength approximation (Gough, 1993; Lignières and Georgeot, 2009). In this approximation, it is possible to combine the oscillation equations into only one eikonal equation that relates the wavenumber and the location of a ray in the star (Ott, 1993). This is akin to deriving geometric optics from wave optics. We can thus compute rays, that are the paths waves are expected to follow inside the star. While this calculation does not immediately provide the modes’ energy distribution, it provides insights on mode propagation domains, geometries and identification.
Finally, the most accurate approach consists in the computation of fully two-dimensional models and the linear calculation of their adiabatic and/or non-adiabatic oscillations. This approach provides exact mode geometries and frequencies, allowing us to search for frequency and period patterns, compute visibilities and attempt mode-by-mode identification. However, linear mode calculations cannot yield mode amplitudes, so assumptions (such as the equirepartition of energy, or the same amplitude for all modes) are necessary to discuss mode detectability meaningfully. The tools for these calculations are complex, and were the focus of numerous efforts summarized in Reese (this volume). The analysis of the results they yield is challenging as there is no mathematical function to describe the geometries obtained with this method and that are presented in the rest of this section.
2.2 Complete calculations
The oscillation equations are derived from perturbing the continuity, Euler’s and Poisson’s equations (with additional closure equations such as the equations of state). These equations are presented in detail in the review by Reese (this volume). Choosing the geometrical description and discretization carefully, the perturbed equations form an eigenvalue problem in which each eigenvalue is an oscillation angular frequency ω, which is related to the frequency ν through ω = 2πν, with the associated eigenvector describing the mode geometry. In the non-rotating case, the radial component of the modes is characterised by its radial order n—n being a relative integer, the sum of the numbers of p-mode nodes counted as positive and g-mode nodes counted as negative—and the horizontal component is described using a single spherical harmonic
The equations change when including rotation. In all three of them, the eigenvalue is shifted in the co-rotating frame, so that the inertial angular frequency ω is replaced by the co-rotating value ω + mΩ. The definition of a co-rotating frame here is improper but used for simplicity, as it implies that the rotation is solid: the discussion in this article includes differential rotation. Non-radial modes thus split into multiplets as m values can go from − ℓ to ℓ, m < 0 and m > 0 being prograde and retrograde modes, respectively.
The Euler equation becomes significantly more complex, as to include the Coriolis acceleration, centripetal entrainment and the baroclinicity terms. These rotational terms create a coupling between successive spherical harmonic coordinates, so that each mode can no longer be described as a single spherical harmonic but a (finite) series of them. No simple closure relation limits the number of spherical harmonics to use, and convergence of the solutions requires special care.
Finally, the boundary conditions also change to accomodate the centrifugal distortion of the stellar surface. As the star remains axisymmetric, the solutions do not depend on the azimuth and m remains separable. The detailed derivation of the equations can be found, for instance, in Reese et al. (2008, 2021).
These equations will yield various mode geometries. I present here the various subclasses of modes and their properties, as derived from using the traditional approximation (for g modes), ray dynamics, and/or complete calculations.
2.3 Acoustic modes
Pressure (acoustic) modes propagate at high frequencies and usually probe the outer layers of the stars. They are restored by pressure forces, their propagation properties are impacted not only by the Coriolis force but also by the centrifugal distortion. They are divided into four geometries derived from ray theory, first put forward by Lignières and Georgeot (2009): 2-period island, 6-period island, whispering gallery and chaotic modes. Figure 2 shows examples for the three most-studied classes of acoustic modes.
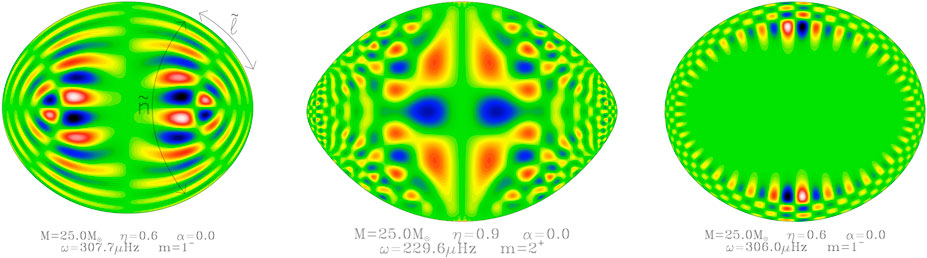
FIGURE 2. Different classes of acoustic modes. Left to right: a 2-period island mode, a chaotic mode, a whispering gallery mode. The shown quantity is the Lagrangian pressure perturbation rescaled by the square root of the stellar density,
2-period island modes are the rapidly rotating counterpart to modes with a low (ℓ − |m|) value—that is, few latitudinal nodal lines. At rotation rates higher than ∼40% of the critical rotation, they propagate in a torus located around the stellar equator, which corresponds to a short, stable trajectory in the ray dynamics. This torus and the associated ray trajectory are smaller and closer to the equator for higher rotation rates. It is possible to define new quantum numbers along the ray trajectory, by defining
This mathematical description of the modes is essential to investigate regular patterns in oscillation spectra, as highlighted in Section 3. Because they have large lengthscales, 2-period island modes induce significant surface signatures, are expected to be the most visible (Reese et al., 2013; 2017b), and have been studied extensively (e.g. Reese et al., 2009a; Pasek et al., 2011; Ouazzani et al., 2015; Mirouh et al., 2019; Reese et al., 2021).
6-period island modes are relatively rare and have low visibility. Their geometry is somewhat similar to that of the more common and visible chaotic modes, described below. Because of this, they are often left out of analyses (so much so that 2-period island modes are often simply dubbed “island modes”). They are the rapidly rotating counterpart of modes with medium (ℓ − |m|) values.
Chaotic modes emerge from the constructive interference of rays that present a chaotic trajectory. They also are related to modes with medium (ℓ − |m|) values. Evano et al. (2019) offers the only extensive study of this class of modes. They characterize their geometry by its complexity and apparent ramdomness. Chaotic modes present irregular nodal lines, except near the stellar surface where nodal lines tend to become radial. They are particularly interesting as they are the only p-mode class to propagate in the entire stellar interior, probing deep layers while reaching the surface.
Finally, whispering gallery modes propagate close to the surface without probing deep layers at any point. While their geometry is somewhat affected by the rotational distortion of the star, they keep lengthscales and a global structure similar to those of their non-rotating counterparts, high-(ℓ − |m|) modes. As such, the geometry of these modes can be described with the number of nodal lines crossed at a given depth d (that is, at a radius r = Rs(θ) − d where Rs(θ) is the surface radius, where d is chosen so that r passes in between the mode’s nodal lines) and perpendicularly to that radius (equivalent to
2.4 Gravito-inertial modes
Gravito-inertial modes, just like non-rotating gravity modes, are in the low-frequency part of the oscillation spectra and propagate in stellar radiative zones. In early-type stars, they are likely to be excited in γDor and SPB stars, in which they can provide insight on the conditions near the stellar core. Their restoring force is buoyancy, that combines with the Coriolis acceleration. As the Coriolis acceleration scales with 2Ω/ω, its effect is more important for low-frequency modes in the co-rotating frame. Gravito-inertial modes are usually divided in three geometries, depending on their frequencies and presented in Figure 3. We distinguish sub-inertial modes which propagate at angular frequencies ω < 2Ω and super-inertial modes at ω > 2Ω.
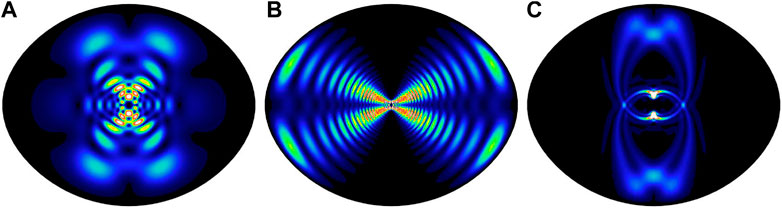
FIGURE 3. Different classes of gravito-inertial modes. (A–C): an unperturbed super-inertial mode, a sub-inertial mode and a rosette super-inertial mode. The shown quantity is the mode kinetic energy. Figure taken from Ballot et al. (2013).
The effect of rotation on sub-inertial modes is the appearance of a forbidden region in which oscillations cannot propagate. Ballot et al. (2010) describes this region in the case where the stratification dominates over rotation (N ≪ Ω) as a cone that extends at an angle θ ∼ arccos(ω/2Ω) from the rotation axis. This confirms the equatorial confinement of the modes in rotating stars predicted by Matsuno (2008); Lee and Saio (1990). The precise shape of the boundary of forbidden regions for the propagation of sub-inertial modes has been refined to include stratification (Dintrans et al., 1999) and differential rotation (Mirouh et al., 2016).
Most super-inertial modes are marginally affected by rotation, as their geometry stays close to their non-rotating equivalent, resembling simple spherical harmonics with radial and horizontal scales of the same order of magnitude at all rotation rates.
The most striking exception is rosette modes, that are super-inertial modes whose geometry is significantly different from any spherical harmonic. They were described for the first time by Ballot et al. (2012). These modes emerge from a close degeneracy between modes whose frequencies would be near-identical in the absence of rotation. Takata and Saio (2013) show that such degeneracies appear for rotation rates as low as 10% of the critical rotation rate and lead to numerous families of rosette modes. This suggests that rosette modes are not a rare occurrence in moderate rotators, even though their distribution in extreme rotators is still unknown. It appears that retrograde non-axisymmetric rosette modes tend to form preferentially over their prograde counterparts (Saio and Takata, 2014). It is also worth noting that because they originate from coupling between different non-rotating modes, rosette modes cannot be found under the traditional approximation.
These modes are spatially concentrated on very thin layers around the stellar core and describe a rosette pattern aligned with the rotation axis. Ray tracing shows that their energy focuses on short closed loops (Ballot et al., 2012; Prat et al., 2016), and that the period and orientation of these closed loops can be related to the original family of modes (whose identification is otherwise lost, Takata, 2014). The surface signature of rosette modes is still to be derived precisely and be identified with observed modes, in which case they could provide useful constraints on a star’s deep layers.
2.5 Other modes
Finally, other classes of modes can exist in rapidly rotating stars. Rossby modes are, among inertial oscillations, the ones that attracted most interest from the astrophysical community. Theoretical studies, notably by Papaloizou and Pringle (1978); Saio (1982); Saio et al. (2018), show they are large-scale toroidal modes that induce significant flows at the stellar surface that are less affected by equatorial confinement at high rotation rates compared to gravito-inertial modes.
Inertial modes can propagate in convective zones, restored by only Coriolis forces. They propagate in the core of intermediate-mass stars in a frequency domain that overlaps with gravito-inertial waves propagating elsewhere in the star (Rieutord et al., 2001; Baruteau and Rieutord, 2013). The signature of such modes in the core of γDor stars can be detected through their coupling with gravito-inertial modes reaching the stellar surface (Ouazzani et al., 2020; Saio et al., 2021). Similarly, so-called overstable convective modes resonances have been suggested as an excitation mechanism in rotating stars from 2M⊙ upwards. These modes are core inertial modes, that couple with gravito-inertial modes in the envelope at frequencies close to core rotation rate multiples (Osaki, 1974; Lee and Saio, 2020; Lee, 2021, 2022).
Mixed modes also exist in rapidly rotating intermediate-mass stars, as rapid rotation extends the gravito-inertial domain to higher frequencies, making coupling with pressure modes more likely (Osaki, 1974). These modes are very interesting as they probe both the deep layers of the star and carry a surface signature, but their geometries and frequencies are affected in a complex way by the coupling. Such modes are detected in δSct stars such as Rasalhague (Monnier et al., 2010) or HD174966 (García Hernández, private comm.), and become more likely with increasing age as the Brunt-Väisälä frequency in the star increases and allows for higher-frequency gravito-inertial modes (Aerts et al., 2010). They have also been computed in two-dimensional models by, e.g., Mirouh et al. (2017).
3 Regular patterns in oscillation spectra
Now that the mode geometries in rapidly rotating stars have been introduced, I will discuss the regular patterns these modes are expected to follow according to theoretical calculations, and how the wealth of space-based measurements and innovative pattern-recognition techniques have permitted their detection.
3.1 Regular patterns in slow rotators
Before delving into the frequency patterns of rapidly rotating star spectra, it is useful to remind the reader here of the regular patterns that can be found in slowly rotating stars with solar-like oscillations. I refer the reader to the review of Jackiewicz (2021) for more details.
Helioseismology has established that solar oscillation frequencies are distributed on a regular comb. Once modes are identified univocally using the quantum numbers (n, ℓ, m), we find that high radial order modes present a regular spacing in frequency ν for acoustic modes and in period Π for gravity modes. We define the p-mode large separation (Tassoul, 1980) as
where cs is the speed of sound. The g-mode period spacing Shibahashi (1979) is defined as
where N is the Brunt-Väisälä frequency that quantifies stratification. In solar-like pulsators, in which mode excitation is due to convection and stochastic, it is possible to define another seismic observable, νmax, the frequency at which the p-mode spectrum envelope reaches its maximum amplitude. The readily-available quantities Δν and νmax can then be linked to the stellar mass and radius via scaling laws (Brown et al., 1991; Kallinger et al., 2010; Mosser et al., 2010). Improving these relations has been a significant part of the recent effort for those stars, to refine the derived masses and radii, include new parameters or automate the process.
When the star rotates, the degeneracy in m is lifted and non-radial modes spawn multiplets as m ranges from − ℓ to ℓ. With the introduction of rotational splittings, the frequencies of non-axisymmetric modes relate to their axisymmetric counterparts through
As mentioned, the exploitation of regular spacings requires univocal mode identification, which presents several challenges in rapidly rotating intermediate-mass pulsators. First, because of Coriolis forces and centrifugal distortion, frequencies are significantly shifted and both gravito-inertial and pressure modes assume complex geometries. Because of the complexity of the excitation mechanisms, there is no reliable way of predicting mode amplitudes theoretically and the mode selection effects are not fully understood.
3.2 Acoustic modes
The ray dynamics analysis of Lignières and Georgeot (2009) identified regular patterns for several subclasses of acoustic modes. There are four geometry classes for p modes: 2- and 6-period island, whispering gallery, and chaotic modes. Modes in each of these classes follow different patterns, as illustrated by the schematic subspectra presented in Figure 4.
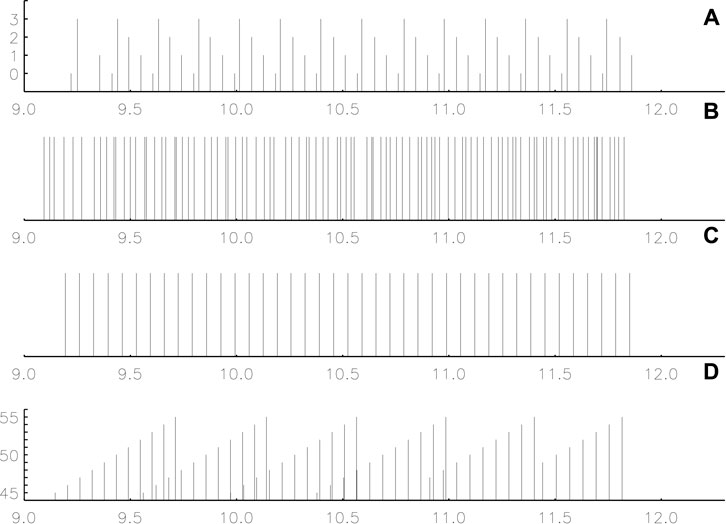
FIGURE 4. Frequency sub-spectra for the four classes of axisymmetric acoustic modes. (A) 2-period island modes, (B) chaotic modes, (C) 6-period island modes, (D) whispering gallery modes. The horizontal axis is the mode frequency in units of ωp—computed from the keplerian velocity computed using the polar radius –, and the vertical axis represents the second quantum number—the rapid rotator equivalent to the degree ℓ—when defined. Figure taken from Lignières and Georgeot (2009).
2-period island modes are the ones for which the most progress has been achieved. They are expected to follow a linear distribution of the kind
where
Owing to the precision of asteroseismic measurements and the development of dedicated techniques, such a regular frequency distribution has been detected in observed spectra. García Hernández et al. (2015) identified regular patterns in acoustic spectra for a sample of eclipsing binaries and extracted a large separation that they attributed to the likely visible 2-period island modes. Using eclipses and the binary orbits, they were able to link the large separation with the mean stellar density through a scaling law. Their scaling relations were later confirmed from fully-2D models and oscillations by Mirouh et al. (2019): in this work, the synthetic 2-period island modes were sorted out by means of a convolutional neural network for a range of models at various rotation rates and ages. It confirmed "the scaling between mean density and large separation, and that this relation does not depend explicitly on the rotation rate. This scaling has also been recovered for low-mass δSct stars using grids of 1D models with enhanced mixing by Rodríguez-Martín et al. (2020) and on the larger samples of Paparó et al. (2016b); García Hernández et al. (2017); Bedding et al. (2020). A further confirmation of the 2-period island nature of the observed modes lies in the detection of half the large separation in the pattern detection (García Hernández et al., 2009; Ramón-Ballesta et al., 2021), which is an exclusive feature of island modes (Evano et al., 2019). It is also worth noting that the modes detected in δSct stars are most often not in the asymptotic regime, so that the measured large separations are about 15% below their asymptotic values (García Hernández et al., 2009; Mirouh et al., 2019).
Rotational splittings have also been found in the 2-period island mode spectra of δSct stars (e.g. Paparó et al., 2016b; Ramón-Ballesta et al., 2021). While rotational splittings in slow rotators are symmetrical (that is, νn,ℓ,−m − νn,ℓ,0 = νn,ℓ,0 − νn,ℓ,m), splittings in rapidly rotating stars lose this property. They also are often so large that asymmetric multiplets blend in the spectrum, making them harder to identify and exploit. Modelling these splittings can rely on perturbative treatments to the first-order (e.g. Schou et al., 1998; Deheuvels et al., 2014), second-order (e.g. Saio, 1981; Suárez, 2009) and third-order (Soufi et al., 1998; Ouazzani and Goupil, 2012) that model the asymmetry of the splittings. A complete calculation that applies to all rotation rates provides the generalised rotational splittings, that is νn,ℓ,−m − νn,ℓ,m, through an integral of the rotation rate over the modes’ propagation domain and the definition of rotational kernels (Reese et al., 2009b, 2021), thus paving the way to inversion methods for rapid rotators. Since the discovery of island-mode regular patterns by García Hernández et al. (2015), several strategies have been developed to extract large separations from observed spectra. Investigating the distribution of frequency differences, computing Fourier transforms of the spectrum itself, spectrum autocorrelation functions have all proved efficient to derive both the large separation and rotational splittings (Mantegazza et al., 2012; Reese et al., 2017b; Ramón-Ballesta et al., 2021). A brand new approach based on the entropy content of observed oscillation spectra offers another promising way of extracting regular separations (Suárez, this volume).
To complement the regular patterns discovered for 2-period island modes and their link with the stellar density, Barceló Forteza et al. (2018, 2020) have investigated the envelope of the oscillation spectra of δSct stars in search of another asteroseismic indicator. They found that the peak frequency of this asymmetric envelope, νmax, can be related to the effective temperature and surface gravity of the star. Assessing these two quantities for stars featuring gravity darkening can yield an estimate of the stellar inclination, and in turn a model-dependent estimate of the stellar mass and radii in a way that is reminiscent of the approach used for solar-like stars.
Recently, Salmon et al. (2022) has developed a forward-modelling framework for β Cep stars, that relies on low-order pressure modes along with gravity and mixed modes, to infer fundamental parameters. Their hare-and-hounds exercise, which relies on 1D Geneva models (Eggenberger et al., 2008), yields accurate parameters starting from only
Frequency subspectra of chaotic modes are dense, and were originally thought not to have structure (Lignières and Georgeot, 2009). Evano et al. (2019) computed the autocorrelation of these subspectra and found evidence of a regular spacing. They show that while chaotic modes do not tend to an exact asymptotic distribution of oscillation frequencies, they exhibit a pseudo-large separation Δcν for all their models at all rotation rates. They relate Δcν with the average acoustic time over the meridional plane T0 through Δcν ∼ 2π/T0. Chaotic modes thus form series of modes that present a very similar geometry. Figure 5 presents an échelle diagram—that is a frequency spectrum folded every Δcν to bring out patterns—for chaotic modes in a polytrope. Well-defined ridges follow the series, but some of them are interrupted at high frequencies, and are replaced in the spectrum by another or by a series of high-frequency island modes. The pseudo-large separation of chaotic modes is very close to that of island modes (within 1%). However, the detected patterns are not expected to come from this spacing, as the half-large separation detection is not expected from chaotic modes.
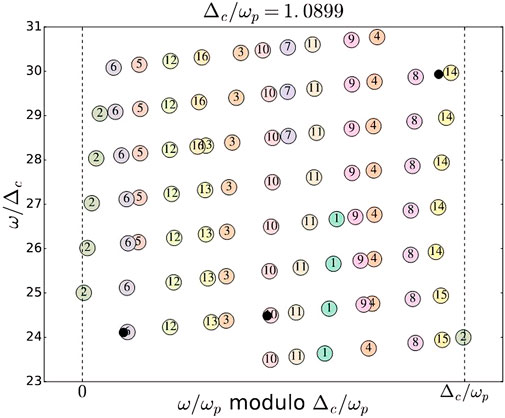
FIGURE 5. Échelle diagram showing all chaotic modes in a polytrope in the high-frequency range—the frequency unit ωp is computed from the keplerian velocity computed using the polar radius –. Series of similar modes are labelled 1 to 16, while black dots are modes that do not belong to any series. Figure taken from Evano et al. (2019).
Island modes of period 6 were identified as one of the four classes of acoustic modes emerging from ray theory by Lignières and Georgeot (2009). They propose a simple asymptotic relation for these modes:
where the various terms match are similar to those of Eq. 5. The details of this asymptotic relation, and the link between the separation
Finally, whispering gallery modes also seem to follow regular patterns. However, while it is straightforward to define suitable quantum numbers from the energy distribution of whispering gallery modes, Lignières and Georgeot (2009) did not find a satisfactory fit of their frequencies to a linear law in the form of Eq. 5 or (6). More studies are required to understand the nature of the patterns these modes follow.
3.3 Gravito-inertial modes
In the absence of rotation, the spectrum of high-order gravity modes is understood as a set of modes regularly spaced in period, which can be represented by a flat line in a P − ΔP diagram. The value of the period separation provides an estimate of the stellar age, as it decreases as a peak in the Brunt-Väisälä builds up at the core-envelope interface. The deviation from this flat distribution, in the form of with regular dips, is an indicator of a chemical gradient at the core-envelope interface whose depth can be related with mixing efficiency (Miglio et al., 2008). The pattern described by these dips informs us about the location of the chemical gradient.
When the star rotates, the general trend in the P − ΔP plane is not necessarily flat but varies monotonically (Bouabid et al., 2013; Van Reeth et al., 2015). Using the traditional approximation, Ouazzani et al. (2017) thus defines the slope of this trend as a new observable that is directly linked to the rotation rate near the stellar core modulated by the azimuthal order m. These ridges were observed in many γDor (e.g. Bedding et al., 2015; Guo and Li, 2019; Li et al., 2020a,b; Garcia et al., 2022) and SPB stars (Pápics et al., 2017; Pedersen et al., 2021; Szewczuk et al., 2021, 2022, e.g), with a variety of behaviors related to mixing and rotation.
Forward modelling has driven a lot of the progress on g-mode asteroseismology of slowly to moderately rotating stars in the recent years. Through the definition of rigorous frameworks (Aerts et al., 2018; Johnston et al., 2019), state-of-the-art 1D models and modes computed assuming the traditional approximation, partial mode identification has been obtained for numerous individual stars (e.g. Szewczuk and Daszyńska-Daszkiewicz, 2018; Zhang et al., 2018). This process yields not only stellar fundamental parameters such as mass and age, but also constraints on core-interface mixing (Wu et al., 2020; Pedersen et al., 2021, e.g.) or binary interactions (Sekaran et al., 2021; Guo et al., 2022).
Recent works relying on the traditional approximation also provide model-independent approaches. For instance, Van Reeth et al. (2016); Li et al. (2020b); Takata et al. (2020a,b) use the rotation frequency and the buoyancy radius as free input parameters. Christophe et al. (2018) suggests a clever rescaling of the period spectra to extract signatures of differential rotation and buoyancy glitches from the gravito-inertial mode spectrum. Christophe et al. (2018) also emphasizes the well-known limits of the traditional approximation of rotation: attempts at extending it to include radially differential rotation (Mathis, 2009) or centrifugal distortion (Dhouib et al., 2021) may provide extra insights on the physics of g-mode pulsators. However, these approaches require a prescription for a differential rotation profile (which is prone to a lot of degeneracy) and are computationally expensive.
While the traditional approximation has led to a significant breakthrough in the analysis of g-mode pulsators, permitting ensemble seismology and forward seismic modelling for this class of stars, performing the full calculation of gravito-inertial modes is the logical next step to include differential rotation and enable the search for rosette modes in observations.
3.4 Rossby modes
Rossby modes have long been theorized, and were first detected in rapid rotators by Van Reeth et al. (2016). They have since been detected in a variety of g-mode pulsators (both γDor and SPB stars, e.g. Saio et al., 2018; Li et al., 2019; Takata et al., 2020b). Their ubiquitous nature suggests an easy excitation mechanism, and stellar activity or tidal forcing have been proposed. Rossby modes present spacings that appear in the P − ΔP plane, like gravito-inertial modes. They present small period spacings, that increase rapidly with the period (leading to a characteristic upward slope, Van Reeth et al., 2016). Saio et al. (2018) suggests that the “hump-and-spike” stars discovered by Balona (2017) are spotted stars in which the “hump” is the Rossby-mode spectrum and the “spike” a harmonic of the stellar rotation rate. The calculations underlying this description are made within the traditional approximation framework, and have no equivalent based on complete two-dimensional calculations.
4 Line-profile variations
Modes that propagate in the outer layers of the star induce a small distortion of the stellar surface along with temperature variations. In rotating stars, these oscillatory motions leave a Doppler signature in the spectral line profile that can be tracked in time through a series of spectroscopic observations. Such line-profile variations (LPVs) are not simple to analyse as they depend on the geometry of each oscillation mode present at the surface, but their analysis can offer a partial mode identification. Once a specific line profile is selected or an averaged one is computed, a spectral analysis of its time variations yields oscillation frequencies and azimuthal orders.
A lot of work has been done on the theoretical description of LPVs induced by both pressure modes and gravito-inertial modes. For instance, the modelling efforts for p-mode LPVs (Balona, 1987; Cugier, 1993; Zima, 2006) permitted the interpretation of spectroscopic measurements in δSct and βCep stars (e.g. Aerts et al., 1992; Zima et al., 2006). Theoretical developments based on the perturbative approach (e.g. Shutt et al., 2021) or the traditional approximation of rotation (such as Lee and Saio, 1990; Townsend, 1997) yielded similar results to interpret γDor pulsators.
Some of these methods have been implemented in widespread software packages. For instance, the BRUCE and KYLIE packages (Townsend, 1997) rely on the traditional approximation for the calculation of theoretical LPVs of gravito-inertial modes in moderate rotators (as demonstrated in Bowman et al., 2022). Another widespread implementation is that of the Fourier Parameter Fitting method (FPF) of Zima (2006). The FAMIAS code (Zima, 2008) does not rely on the traditional approximation but on a first-order perturbative calculation, which enables the analysis of LPVs due to both gravito-inertial and pressure modes, but restricts it to slow rotators.
LPVs have also been detected in several rapidly rotating stars (e.g. Telting and Schrijvers, 1998; Balona and Lawson, 2001; Poretti et al., 2009) and require special care. While the theoretical developments of Lee and Saio (1990); Townsend (1997) are used for gravito-inertial modes in rapid rotators, pressure-mode LPVs have benefitted from two-dimensional codes, starting with Clement (1994). The work of Reese et al. (2017a) is the most up-to-date such effort: it relies on non-adiabatic modes computed with the high-resolution oscillation code TOP (Reese et al., 2009a, 2021) paired with the self-consistent, two-dimensional ESTER models (Rieutord and Espinosa Lara, 2013; Rieutord et al., 2016).
Reese et al. (2017a) shows that p-mode LPV signatures are maximal in the wings of the line profile, contrary to what is expected in slow rotators (Lee and Saio, 1990). This can be explained by the complex geometries of modes in rapidly rotating stars, making LPVs equally more complex to decipher. The centrifugal flattening and gravity darkening make the amplitude of the signatures dependent on the stellar inclination, and different modes affect different spectral lines in various ways, depending on the range of temperature at the stellar surface (see, e.g. Takeda et al., 2008, for the rapid rotator Vega).
Figure 6 presents the result of such calculations for a 2-period island mode 9M⊙ ESTER model at 50% of its breakup velocity, This calculation relies on a few simplifying assumptions such as Gaussian equilibrium line profiles and rather crude limb- and gravity-darkening prescriptions. These assumptions will have to be relaxed to properly interpret time series of high-resolution spectra, and will surely be the topic of upcoming work.
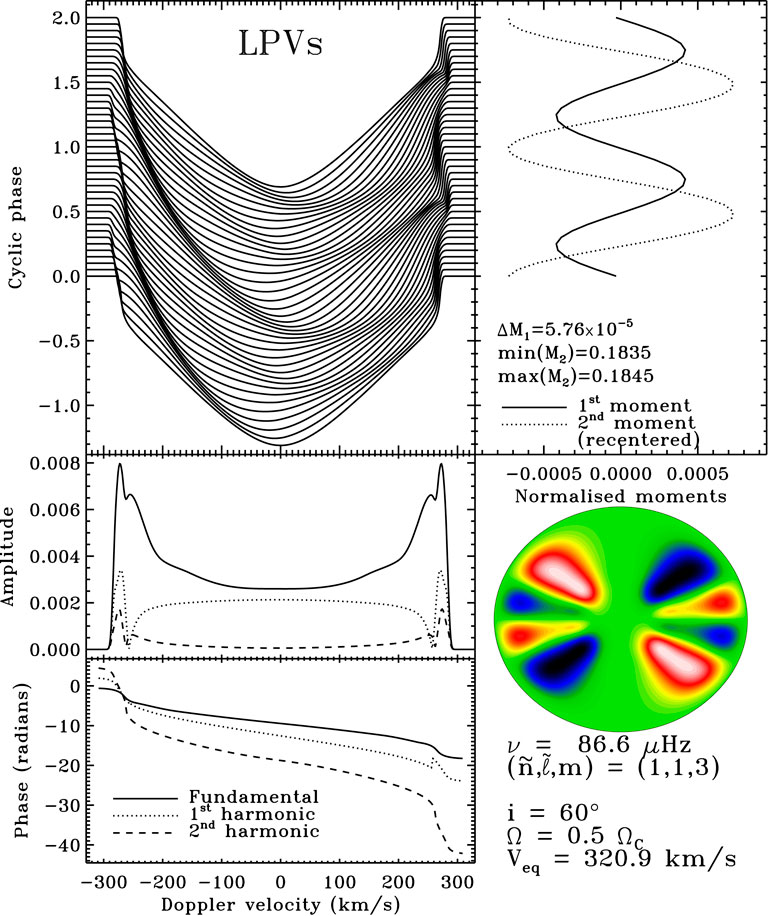
FIGURE 6. Line-profile variations in a 9M⊙ ESTER model at 50% of its breakup velocity. Left, top to bottom: stacked line profiles, amplitudes and phases of the first three harmonics. Right, top to bottom: first and second moments of the LPVs, meridional cut of the oscillation mode, and model properties. Figure taken from Reese et al. (2017b).
Eventually, adapting widespread automated procedures such as the FPF method (Zima, 2006) to two-dimensional models will enable a simpler detection of identified modes that will serve as anchors for both pattern recognition and forward modelling.
5 Forward seismic modelling of fast rotators: The example of Rasalhague
Forward - or direct - modelling is a method of obtaining accurate properties of stars by directly modifying its input parameters and computing associated observables until a satisfactory match with measurements is found. This strategy is adapted for rapidly rotating stars, especially when the number of oscillation modes detected in them is relatively small and the regular patterns in the spectra are difficult to disentangle.
The necessary steps for forward asteroseismic modelling are:
1) Compute an appropriate model for a reasonable set of input parameters, for rotating stars this shall include centrifugal flattening and gravity darkening,
2) Establish criteria—e.g. on mode visibility or excitation—to select the most observable oscillation modes from the synthetic spectrum,
3) Identify the selected modes thus found with the observed ones,
4) Repeat the process by varying the initial model parameters until a good match is obtained.
This strategy was successfully applied to slowly rotating classical pulsators, such as HD 129929 (Aerts et al., 2003) for which 6 gravity-mode frequencies were detected. By means of non-adiabatic oscillations, Aerts et al. (2004); Dupret et al. (2004b) not only obtained a stellar mass and age with uncertainties of a few percent, but also constrained envelope convective penetration and differential rotation. Some other successes of the forward-modelling approach for g-mode pulsators are given in Section 3.3.
I present here an application of the forward modelling approach to the rapidly rotating δ Scuti star Rasalhague (α Ophiuchi A, HD159561). It is a rapidly rotating pressure-mode pulsator, in which the centrifugal distortion is expected to significantly impact oscillation frequencies and geometries.
CHARA interferometry reveals that this A5 star is seen equator-on (v sin i = 239 ± 12 km s−1 and i = 87.5 ± 0.6°, Zhao et al., 2009). It also has a known K6 companion (Cowley et al., 1969; Hinkley et al., 2011), spectroscopic measurements that provide chemical information (Erspamer and North, 2003) and 57 oscillations frequencies measured with MOST (Monnier et al., 2010, including mostly pressure modes and a few gravito-inertial or mixed modes). These numerous observations make Rasalhague an optimal example for forward modelling.
Until recently, the masses derived from fitting the binary orbit of this system (
The first attempt at modelling Rasalhague was by Deupree (2011), using the 2D ROTORC code (Deupree, 1990, 1995). He uses nine solid-body rotating and one slightly differentially-rotating models, and computes adiabatic oscillations with −4 ≤ m ≤ 4, using six or eight spherical harmonics for each mode. He then identifies oscillation modes by matching MOST frequencies to their closest synthetic counterpart within one stardard deviation. Figure 7 presents the match between synthetic frequencies for different azimuthal orders and the observed ones. The échelle diagram is folded with a Δν = 47.6 μHz that emerges from the models, but does not match the estimate of García Hernández et al. (2015).
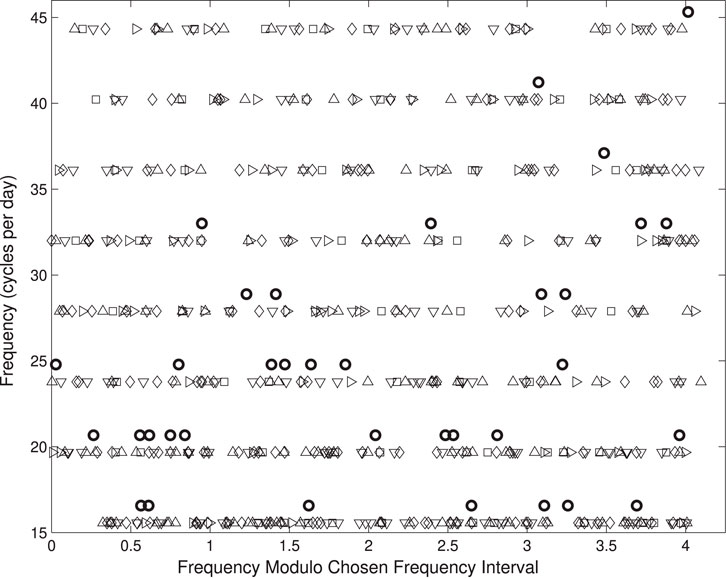
FIGURE 7. Echelle diagram comparing synthetic modes at different azimuthal orders m (squares: |m| = 0, diamonds |m| = 1, inverted triangles |m| = 2, triangles |m| = 3 and right-facing triangles |m| = 4) with observed frequencies (thick circles artifically offset). Figure taken from Deupree (2011).
While an interesting first attempt, this study has clear limitations already mentioned in the original paper. First, the synthetic spectrum computed by Deupree (2011) is so dense that several synthetic frequencies lie within the observational uncertainties for numerous modes, which makes the differentiation between models difficult. More importantly, increasing the number of spherical harmonics to describe each mode from six to eight leads to a drastic change in the mode geometry. This shows that 6- and 8-harmonic calculations are underresolved, which undermines the whole analysis. The MOST dataset has been studied by García Hernández et al. (2015, 2017) who found regular patterns in the oscillation spectrum. For frequencies above 116 μHz they found a large separation of 38 ± 1 μHz that corresponds to a mean density of 0.123 ± 0.021ρ⊙. The 116 μHz frequency is that of the lowest-order radial pressure mode, while the 38 ± 1 μHz pattern is due to 2-period island modes. These seismic parameters and partial mode identification have guided the new modelling effort I describe here.
This new calculation relies on the ESTER and TOP codes and is presented in Mirouh et al. (2013); Mirouh et al. (2017). The ESTER code computes the structure of a rotating star in two dimensions, including centrifugal distortion, gravity darkening and meridional circulation, but treats mixing in a very simplified manner that does not track core recession and cannot include a surface convection zone. It is paired with the TOP code, a high-resolution spectral code to compute the adiabatic and non-adiabatic oscillations of rotating models. For this work, we compute a 2.22M⊙ model whose surface temperature, radii and rotation match the interferometric measurements. We compute adiabatic modes with −4 ≤ m ≤ 4, this time using twenty spherical harmonics for each mode. To select the best candidates for identification, we compute mode visibilities (that is, the induced surface signature Reese et al., 2013; 2017b) and the growth or damping rate (that is, the rate at which the mode is excited or damped in the star). Growth and damping rates are directly obtained through solving the non-adiabatic oscillation equations or from work integrals computed in the adiabatic approximation, that is, assuming that non-adiabatic effects do not impact the mode geometry (Unno et al., 1989; Mirouh et al., 2013).
The aim is to select the most visible excited modes that match the measured frequencies. The top panel of Figure 8 shows the visibility of each mode, and visual inspection brings out two overlapping populations. Pressure modes are the most visible and cover the whole frequency range, while gravito-inertial modes exist at low frequency (
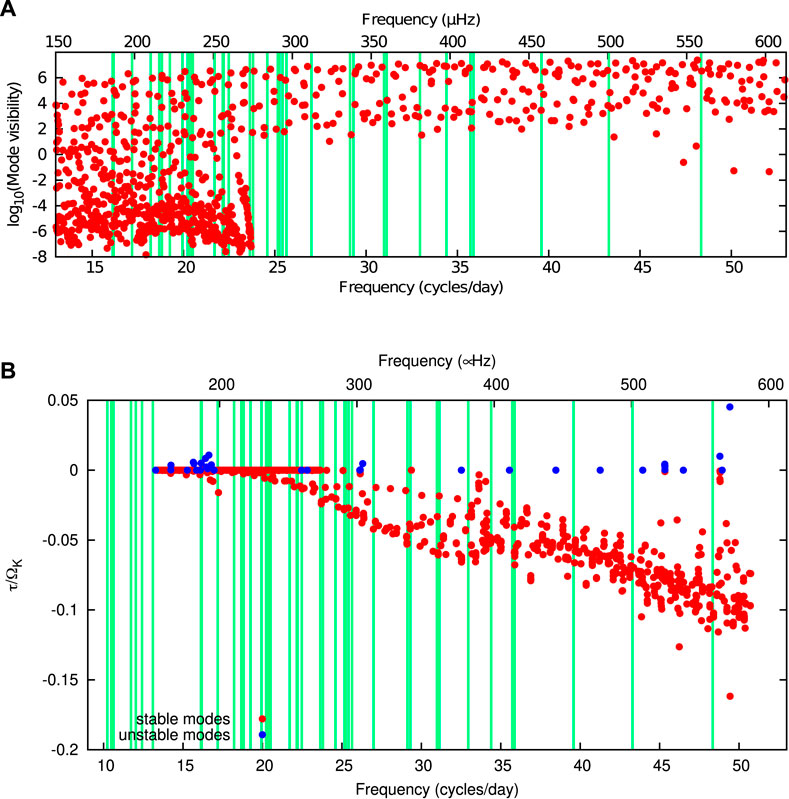
FIGURE 8. Properties of axisymmetric (m = 0) modes. (A): mode visibilities. (B): mode damping (red) or growth (blue) rates obtained from non-adiabatic calculations. Green lines denote frequencies from Monnier et al. (2010). Figure taken from Mirouh et al. (2017).
Computing growth and damping rates using work integrals in the quasi-adiabatic approximation yields only linearly-stable modes, with acoustic modes being more damped than gravito-inertial modes. This can be attributed to a poor description of the modes at the stellar surface and prevents any identification of the observed modes (Mirouh et al., 2013).
Non-adiabatic calculations reveal the presence of linearly-unstable modes (Mirouh et al., 2017), as shown in the bottom plot of Figure 8. However, those modes do not seem to match the expected distribution: most unstable modes are gravito-inertial modes that describe a somewhat regular spacing which does not match the large separation of García Hernández et al. (2015, 2017), while the most visible modes are damped. The origin of unstable (super-inertial) gravito-inertial modes in ESTER models of Rasalhague comes as a surprise: as the models do not feature a convective envelope, they cannot include the convective blocking excitation mechanism. If the computed modes are to explain the gravity modes observed by Monnier et al. (2010), their excitation must be provided by another mechanism. Candidates include the κ mechanism for gravity modes, as proposed by Xiong et al. (2016), the overstable convective modes suggested notably in Lee (2021), or the elusive differential rotation mechanism suggested by Mirouh et al. (2016).
At this point it is thus impossible to identify modes. This may be due to the non-adiabatic calculations whose stability must be ensured, and ESTER models’ inclusion of surface effects. A better understanding of the intertwined regular patterns in the spectra (described in Section 3) can also be obtained by the systematic application of classification algorithms such as that of Mirouh et al. (2019). This algorithm is a supervised machine learning approach, that relies on a bank of well-identified pressure perturbation profiles to separate rapidly a set of computed modes into the various geometries presented in section 2. Mirouh et al. (2019) focused on extracting patterns for island modes, and their algorithm can be extended to study other pressure and gravito-inertial modes. Other machine learning approaches, both supervised and unsupervised, applied to individual modes or entire observed spectra, will undoubtedly be the next step towards mode identification in rapid rotators such as Rasalhague. Rasalhague also seems to be a good candidate for line-profile variation detections (described in Section 4), as it is seen equator-on which would maximize the signature of island modes.
These improvements will be necessary to obtain a satisfactory two-dimensional seismic model of Rasalhague and open the way to the study of other rapidly rotating pulsators observed through interferometry, such as Alderamin, Regulus or Achernar. Another very interesting star is the rapid rotator Altair whose realistic modelling, albeit not seismic, was achieved by Bouchaud et al. (2020) and which features 15 oscillation frequencies (Le Dizès et al., 2021).
6 Summary
Rapid rotation makes early-type main-sequence pulsators a much more complex object of study compared to slowly rotating late-type counterparts. While our understanding of these stars has been lagging behind that of solar-like pulsators for years, the gap is closing at an increasing speed. The application of the traditional approximation for gravito-inertial modes in moderate rotators, and the development of two-dimensional models and oscillation codes for both pressure and gravito-inertial modes at all rotation rates, have unveiled the complex geometries and patterns the modes assume. Pattern analysis in high-quality oscillation spectra reveal an increasing amount of information on rotating stars. I presented the topology of both gravito-inertial and acoustic modes under the combined effect of the Coriolis force and centrifugal distortion.
Kepler and TESS revealed numerous regularities in the low-frequency spectra of γ Doradus and SPB stars, that were matched by gravito-inertial and Rossby modes computed with the traditional approximation. This opened a window on differential rotation and mixing inside those stars, and statistics are now building up to reach a better understanding of the structure and evolution of these stars. Pressure-mode pulsators such as δ Scuti benefitted from recent progress in two-dimensional models and oscillation codes. Theoretical patterns are identified and linked to structure quantities, and an entire toolkit is now available to compute these modes, their visibilities and damping rates. I described in this article two developments that may be the final pieces of the puzzle. One of them is the development of classification algorithms to automate mode identification and derive patterns for each subclass of acoustic modes, and the other is line-profile variations adapted to rapidly rotating stars to provide solid anchor points to forward seismic modelling approaches.
Just like Kepler and TESS have allowed unprecedented progress in the deciphering of classical pulsator oscillation spectra, the future PLATO mission holds the promise of yet another revolution. The sheer amount of stars for which lightcurves will eventually be available will be a stepping stone towards a full understanding of rotation, angular momentum mixing and their impact on intermediate- and high-mass stellar evolution.
Author contributions
GMM has written this entire article and is accountable for its content.
Funding
GMM ackowledges support by “Contribution of the UGR to the PLATO2.0 space mission. Phases C/D-1”, funded by MCNI/AEI/PID 2019-107061GB-C64.
Acknowledgments
The author thanks Daniel R. Reese, Antonio García Hernández and Juan Carlos Suárez for insightful discussions that helped define and improve this review, along with both anonymous referees whose detailed comments led to significant improvements to this article. Special acknowledgements also go to the PIMMS workshop attendees for the interesting discussions that took place there.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aerts, C., de Pauw, M., and Waelkens, C. (1992). Mode identification of pulsating stars from line profile variations with the moment method. An example : The beta Cephei star delta ceti. A&A 266, 294.
Aerts, C., Molenberghs, G., Michielsen, M., Pedersen, M. G., Björklund, R., Johnston, C., et al. (2018). Forward asteroseismic modeling of stars with a convective core from gravity-mode oscillations: Parameter estimation and stellar model selection. Astrophys. J. Suppl. Ser. 237, 15. doi:10.3847/1538-4365/aaccfb
Aerts, C., Thoul, A., Daszyńska, J., Scuflaire, R., Waelkens, C., Dupret, M. A., et al. (2003). Asteroseismology of HD 129929: Core overshooting and nonrigid rotation. Science 300, 1926–1928. doi:10.1126/science.1084993
Aerts, C., Waelkens, C., Daszyńska-Daszkiewicz, J., Dupret, M.-A., Thoul, A., Scuflaire, R., et al. (2004). Asteroseismology of the β Cep star HD 129929. I. Observations, oscillation frequencies and stellar parameters. Astron. Astrophys. 415, 241–249. doi:10.1051/0004-6361:20034142
Ahlborn, F., Bellinger, E. P., Hekker, S., Basu, S., and Angelou, G. C. (2020). Asteroseismic sensitivity to internal rotation along the red-giant branch. Astron. Astrophys. 639, A98. doi:10.1051/0004-6361/201936947
Baglin, A., Auvergne, M., Barge, P., Deleuil, M., Michel, E., and CoRoT Exoplanet Science Team, (2009). “CoRoT: Description of the mission and early results,” in Transiting planets. Editors F. Pont, D. Sasselov, and M. J. Holman, 253, 71.
Ballot, J., Lignières, F., Prat, V., Reese, D. R., and Rieutord, M. (2012). “2D computations of g-modes in fast rotating stars,” in Progress in solar/stellar physics with helio- and asteroseismology. Editors H. Shibahashi, M. Takata, and A. E. Lynas-Gray (Hakone, Japan: Astronomical Society of the Pacific Conference Series), 462, 389.
Ballot, J., Lignières, F., and Reese, D. R. (2013). “Numerical exploration of oscillation modes in rapidly rotating stars,” in Lecture notes in physics, berlin springer verlag. Editors M. Goupil, K. Belkacem, C. Neiner, and F. Lignières (Paris, France: J. J. Green), 865, 91.
Ballot, J., Lignières, F., Reese, D. R., and Rieutord, M. (2010). Gravity modes in rapidly rotating stars. Limits of perturbative methods. Astron. Astrophys. 518, A30. doi:10.1051/0004-6361/201014426
Balona, L. A., Daszyńska-Daszkiewicz, J., and Pamyatnykh, A. A. (2015). Pulsation frequency distribution in δ Scuti stars. Mon. Not. R. Astron. Soc. 452, 3073–3084. doi:10.1093/mnras/stv1513
Balona, L. A., and Lawson, W. A. (2001). Short-period line profile variations in the Be star ϵ Cap. Mon. Not. R. Astron. Soc. 321, 131–142. doi:10.1046/j.1365-8711.2001.03994.x
Balona, L. A. (1987). Mode identification from line profile variations - III. Temperature variation and toroidal modes. Mon. Not. R. Astron. Soc. 224, 41–52. doi:10.1093/mnras/224.1.41
Balona, L. A. (2017). Starspots on A stars. Mon. Not. R. Astron. Soc. 467, 1830–1837. doi:10.1093/mnras/stx265
Barceló Forteza, S., Moya, A., Barrado, D., Solano, E., Martín-Ruiz, S., Suárez, J. C., et al. (2020). Unveiling the power spectra of δ Scuti stars with TESS. The temperature, gravity, and frequency scaling relation. Astron. Astrophys. 638, A59. doi:10.1051/0004-6361/201937262
Barceló Forteza, S., Roca Cortés, T., and García, R. A. (2018). The envelope of the power spectra of over a thousand δ Scuti stars. The Teff - νmax scaling relation. Astron. Astrophys. 614, A46. doi:10.1051/0004-6361/201731803
Baruteau, C., and Rieutord, M. (2013). Inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 719, 47–81. doi:10.1017/jfm.2012.605
Beck, P. G., Montalban, J., Kallinger, T., De Ridder, J., Aerts, C., García, R. A., et al. (2012). Fast core rotation in red-giant stars as revealed by gravity-dominated mixed modes. Nature 481, 55–57. doi:10.1038/nature10612
Bedding, T. R., Murphy, S. J., Colman, I. L., and Kurtz, D. W. (2015). “Échelle diagrams and period spacings of g modes in γ Doradus stars from four years of Kepler observations,” in European physical journal web of conferences, 10, 01005. doi:10.1051/epjconf/201510101005
Bedding, T. R., Murphy, S. J., Hey, D. R., Huber, D., Li, T., Smalley, B., et al. (2020). Very regular high-frequency pulsation modes in young intermediate-mass stars. Nature 581, 147–151. doi:10.1038/s41586-020-2226-8
Berthomieu, G., Gonczi, G., Graff, P., Provost, J., and Rocca, A. (1978). Low-frequency gravity modes of a rotating star. A&A 70, 597.
Bildsten, L., Ushomirsky, G., and Cutler, C. (1996). Ocean g-modes on rotating neutron stars. Astrophys. J. 460, 827. doi:10.1086/177012
Bouabid, M.-P., Dupret, M.-A., Salmon, S., Montalbán, J., Miglio, A., and Noels, A. (2013). Effects of the Coriolis force on high-order g modes in γ Doradus stars. Mon. Not. R. Astron. Soc. 429, 2500–2514. doi:10.1093/mnras/sts517
Bouchaud, K., Domiciano de Souza, A., Rieutord, M., Reese, D. R., and Kervella, P. (2020). A realistic two-dimensional model of Altair. Astron. Astrophys. 633, A78. doi:10.1051/0004-6361/201936830
Bowman, D. M., and Kurtz, D. W. (2018). Characterizing the observational properties of δ Sct stars in the era of space photometry from the Kepler mission. Mon. Not. R. Astron. Soc. 476, 3169–3184. doi:10.1093/mnras/sty449
Bowman, D. M., Vandenbussche, B., Sana, H., Tkachenko, A., Raskin, G., Delabie, T., et al. (2022). The CubeSpec space mission. I. Asteroseismology of massive stars from time-series optical spectroscopy: Science requirements and target list prioritisation. Astron. Astrophys. 658, A96. doi:10.1051/0004-6361/202142375
Brown, T. M., Gilliland, R. L., Noyes, R. W., and Ramsey, L. W. (1991). Detection of possible p-mode oscillations on Procyon. Astrophys. J. 368, 599. doi:10.1086/169725
Bugnet, L., Prat, V., Mathis, S., Astoul, A., Augustson, K., García, R. A., et al. (2021). Magnetic signatures on mixed-mode frequencies. I. An axisymmetric fossil field inside the core of red giants. Astron. Astrophys. 650, A53. doi:10.1051/0004-6361/202039159
Burssens, S., Simón-Díaz, S., Bowman, D. M., Holgado, G., Michielsen, M., de Burgos, A., et al. (2020). Variability of OB stars from TESS southern Sectors 1-13 and high-resolution IACOB and OWN spectroscopy. Astron. Astrophys. 639, A81. doi:10.1051/0004-6361/202037700
Che, X., Monnier, J. D., Zhao, M., Pedretti, E., Thureau, N., Mérand, A., et al. (2011). Colder and hotter: Interferometric imaging of β cassiopeiae and α leonis. Astrophys. J. 732, 68. doi:10.1088/0004-637x/732/2/68
Christensen-Dalsgaard, J., Schou, J., and Thompson, M. J. (1990). A comparison of methods for inverting helioseismic data. Mon. Not. R. Astron. Soc. 242, 353–369. doi:10.1093/mnras/242.3.353
Christophe, S., Ballot, J., Ouazzani, R. M., Antoci, V., and Salmon, S. J. A. J. (2018). Deciphering the oscillation spectrum of γ Doradus and SPB stars. Astron. Astrophys. 618, A47. doi:10.1051/0004-6361/201832782
Clement, M. J. (1994). “Pulsation in rapidly rotating stars,” in Pulsation; rotation; and mass loss in early-type stars. Editors L. A. Balona, H. F. Henrichs, and J. M. Le Contel, 162, 117.
Cowley, A., Cowley, C., Jaschek, M., and Jaschek, C. (1969). A study of the bright stars. I. A catalogue of spectral classifications. Astron. J. 74, 375–406. doi:10.1086/110819
Cox, A. N., Morgan, S. M., Rogers, F. J., and Iglesias, C. A. (1992). An opacity mechanism for the pulsations of OB stars. Astrophys. J. 393, 272. doi:10.1086/171504
Cugier, H. (1993). Modeling line profiles in beta Cephei stars including temperature and pressure effects. Acta Astron. 43, 27.
De Cat, P., Briquet, M., Aerts, C., Goossens, K., Saesen, S., Cuypers, J., et al. (2007). Long term photometric monitoring with the mercator telescope*** - frequencies and mode identification of variable o-b stars. Astron. Astrophys. 463, 243–249. doi:10.1051/0004-6361:20066202
Deheuvels, S., Doğan, G., Goupil, M. J., Appourchaux, T., Benomar, O., Bruntt, H., et al. (2014). Seismic constraints on the radial dependence of the internal rotation profiles of six Kepler subgiants and young red giants. Astron. Astrophys. 564, A27. doi:10.1051/0004-6361/201322779
Deupree, R. G. (1995). Stella evolution with arbitrary rotation laws. 2: Massive star evolution to core hydrogen exhaustion. Astrophys. J. 439, 357–364. doi:10.1086/175179
Deupree, R. G. (1990). Stellar evolution with arbitrary rotation laws. I - mathematical techniques and test cases. Astrophys. J. 357, 175–187. doi:10.1086/168903
Deupree, R. G. (2011). Theoretical p-mode oscillation frequencies for the rapidly rotating δ Scuti star α Ophiuchi. Astrophys. J. 742, 9. doi:10.1088/0004-637x/742/1/9
Dhouib, H., Prat, V., Van Reeth, T., and Mathis, S. (2021). The traditional approximation of rotation for rapidly rotating stars and planets. II. Deformation and differential rotation. Astron. Astrophys. 656, A122. doi:10.1051/0004-6361/202141152
Di Mauro, M. P., Ventura, R., Corsaro, E., and Lustosa De Moura, B. (2018). The rotational shear layer inside the early red-giant star KIC 4448777. Astrophys. J. 862, 9. doi:10.3847/1538-4357/aac7c4
Dintrans, B., Rieutord, M., and Valdettaro, L. (1999). Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 398, 271–297. doi:10.1017/s0022112099006308
Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., and Scuflaire, R. (2005). Convection-pulsation coupling. II. Excitation and stabilization mechanisms in δ Sct and γ Dor stars. Astron. Astrophys. 435, 927–939. doi:10.1051/0004-6361:20041817
Dupret, M.-A., Thoul, A., Scuflaire, R., Daszyńska-Daszkiewicz, J., Aerts, C., Bourge, P.-O., et al. (2004b). Asteroseismology of the β Cep star HD 129929. II. Seismic constraints on core overshooting, internal rotation and stellar parameters. Astron. Astrophys. 415, 251–257. doi:10.1051/0004-6361:20034143
Dupret, M. A., Grigahcène, A., Garrido, R., Gabriel, M., and Scuflaire, R. (2004a). Theoretical instability strips for δ Scuti and γ Doradus stars. Astron. Astrophys. 414, L17–L20. doi:10.1051/0004-6361:20031740
Dziembowski, W. A., Moskalik, P., and Pamyatnykh, A. A. (1993). The opacity mechanism in B-type stars - II. Excitation of high-order g-modes in main-sequence stars. Mon. Not. R. Astron. Soc. 265, 588–600. doi:10.1093/mnras/265.3.588
Eckart, C. (1960). Variation principles of hydrodynamics. Phys. Fluids (1994). 3, 421–427. doi:10.1063/1.1706053
Eggenberger, P., Meynet, G., Maeder, A., Hirschi, R., Charbonnel, C., Talon, S., et al. (2008). The Geneva stellar evolution code. Astrophys. Space Sci. 316, 43–54. doi:10.1007/s10509-007-9511-y
Erspamer, D., and North, P. (2003). Automated spectroscopic abundances of A and F-type stars using echelle spectrographs. Astron. Astrophys. 398, 1121–1135. doi:10.1051/0004-6361:20021711
Espinosa Lara, F., and Rieutord, M. (2011). Gravity darkening in rotating stars. Astron. Astrophys. 533, A43. doi:10.1051/0004-6361/201117252
Espinosa Lara, F., and Rieutord, M. (2013). Self-consistent 2D models of fast rotating early-type stars. Astron. Astrophys. 552, A35. doi:10.1051/0004-6361/201220844
Evano, B., Lignières, F., and Georgeot, B. (2019). Regularities in the spectrum of chaotic p-modes in rapidly rotating stars. Astron. Astrophys. 631, A140. doi:10.1051/0004-6361/201936459
García Hernández, A., Martín-Ruiz, S., Monteiro, M. J. P. F. G., Suárez, J. C., Reese, D. R., Pascual-Granado, J., et al. (2015). Observational Δν- relation for δ Sct stars using eclipsing binaries and space photometry. Astrophys. J. 811, L29. doi:10.1088/2041-8205/811/2/l29
García Hernández, A., Moya, A., Michel, E., Garrido, R., Suárez, J. C., Rodríguez, E., et al. (2009). Asteroseismic analysis of the CoRoT δ Scuti star HD 174936**. Astron. Astrophys. 506, 79–83. doi:10.1051/0004-6361/200911932
García Hernández, A., Suárez, J. C., Moya, A., Monteiro, M. J. P. F. G., Guo, Z., Reese, D. R., et al. (2017). Precise surface gravities of δ Scuti stars from asteroseismology. MNRAS 471, L140–L144. doi:10.1093/mnrasl/slx117
García, R. A., Pérez Hernández, F., Benomar, O., Silva Aguirre, V., Ballot, J., Davies, G. R., et al. (2014). Study of KIC 8561221 observed by kepler: An early red giant showing depressed dipolar modes. Astron. Astrophys. 563, A84. doi:10.1051/0004-6361/201322823
Garcia, S., Van Reeth, T., De Ridder, J., Tkachenko, A., Ijspeert, L., and Aerts, C. (2022). Detection of period-spacing patterns due to the gravity modes of rotating dwarfs in the TESS southern continuous viewing zone. Astron. Astrophys. 662, A82. doi:10.1051/0004-6361/202141926
Gardner, T., Monnier, J. D., Fekel, F. C., Williamson, M., Baron, F., Hinkley, S., et al. (2021). Establishing α oph as a prototype rotator: Precision orbit with new keck, CHARA, and RV observations. Astrophys. J. 921, 41. doi:10.3847/1538-4357/ac1172
Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., Kjeldsen, H., Aerts, C., Appourchaux, T., et al. (2010). Kepler asteroseismology program: Introduction and first results. Pub. Astron. Soc. Pac. 122, 131–143. doi:10.1086/650399
Gough, D. O. (1993). “Linear adiabatic stellar pulsation,” in Astrophysical fluid dynamics, les houches 1987. Editors J.-P. Zahn, and J. Zinn-Justin (Elsevier), 399
Gough, D. O., and Thompson, M. J. (1990). The effect of rotation and a buried magnetic field on stellar oscillations. Mon. Not. R. Astron. Soc. 242, 25–55. doi:10.1093/mnras/242.1.25
Grigahcène, A., Antoci, V., Balona, L., Catanzaro, G., Daszyńska-Daszkiewicz, J., Guzik, J. A., et al. (2010). Hybrid γ doradus-δ Scuti pulsators: New insights into the physics of the oscillations from kepler observations. Astrophys. J. 713, L192–L197. doi:10.1088/2041-8205/713/2/L192
Guo, Z., and Li, G. (2019). A mass-accreting gamma doradus pulsator with a synchronized core in kepler eclipsing binary KIC 7385478. Astrophys. J. 882, L5. doi:10.3847/2041-8213/ab3a53
Guo, Z., Ogilvie, G. I., Li, G., Townsend, R. H. D., and Sun, M. (2022). A new window to tidal asteroseismology: Non-linearly excited stellar eigenmodes and the period spacing pattern in KOI-54. mnras. arXiv e-printsarXiv:2202.06101. doi:10.1093/mnras/stac2611
Guzik, J. A., Kaye, A., Bradley, P., Cox, A., and Neuforge, C. (2000). Driving the gravity mode pulsations in γ doradus variables. Preprint 1, 593.
Handler, G., Balona, L. A., Shobbrook, R. R., Koen, C., Bruch, A., Romero-Colmenero, E., et al. (2002). Discovery and analysis of p-mode and g-mode oscillations in the A-type primary of the eccentric binary HD 209295. Mon. Not. R. Astron. Soc. 333, 262–278. doi:10.1046/j.1365-8711.2002.05295.x
Handler, G. (2009). Confirmation of simultaneous p and g mode excitation in HD 8801 and γ Peg from time-resolved multicolour photometry of six candidate ‘hybrid’ pulsators. Mon. Not. R. Astron. Soc. 398, 1339–1351. doi:10.1111/j.1365-2966.2009.15005.x
Handler, G., Shobbrook, R. R., Jerzykiewicz, M., Krisciunas, K., Tshenye, T., Rodríguez, E., et al. (2004). Asteroseismology of the β Cephei star ν Eridani - I. Photometric observations and pulsational frequency analysis. Mon. Not. R. Astron. Soc. 347, 454–462. doi:10.1111/j.1365-2966.2004.07214.x
Henneco, J., Van Reeth, T., Prat, V., Mathis, S., Mombarg, J. S. G., and Aerts, C. (2021). The effect of the centrifugal acceleration on period spacings of gravito-inertial modes in intermediate-mass stars. Astron. Astrophys. 648, A97. doi:10.1051/0004-6361/202039464
Hinkley, S., Monnier, J. D., Oppenheimer, B. R., Roberts, L. C., Ireland, M., Zimmerman, N., et al. (2011). Establishing α oph as a prototype rotator: Improved astrometric orbit. Astrophys. J. 726, 104. doi:10.1088/0004-637x/726/2/104
Holdsworth, D. L. (2021). The roAp stars observed by the Kepler Space Telescope. Front. Astron. Space Sci. 8, 31. doi:10.3389/fspas.2021.626398
Jackiewicz, J. (2021). Solar-like oscillators in the kepler era: A review. Front. Astron. Space Sci. 7, 595017. doi:10.3389/fspas.2020.595017
Johnston, C., Tkachenko, A., Aerts, C., Molenberghs, G., Bowman, D. M., Pedersen, M. G., et al. (2019). Binary asteroseismic modelling: Isochrone-cloud methodology and application to kepler gravity mode pulsators. Mon. Not. R. Astron. Soc. 482, 1231–1246. doi:10.1093/mnras/sty2671
Kallinger, T., Weiss, W. W., Barban, C., Baudin, F., Cameron, C., Carrier, F., et al. (2010). Oscillating red giants in the CoRoT exofield: Asteroseismic mass and radius determination. Astron. Astrophys. 509, A77. doi:10.1051/0004-6361/200811437
Korzennik, S. G., and Eff-Darwich, A. (2011). The rotation rate and its evolution derived from improved mode fitting and inversion methodology. J. Phys. Conf. Ser. 271, 012067.
Le Dizès, C., Rieutord, M., and Charpinet, S. (2021). Seismology of Altair with MOST. Astronomy and Astrophysics, 653, A26. doi:10.1051/0004-6361/202141291
Lecoanet, D., Bowman, D. M., and Van Reeth, T. (2022). Asteroseismic inference of the near-core magnetic field strength in the main-sequence B star HD 43317. MNRAS 512, L16–L20. doi:10.1093/mnrasl/slac013
Lecoanet, D., Vasil, G. M., Fuller, J., Cantiello, M., and Burns, K. J. (2017). Conversion of internal gravity waves into magnetic waves. Mon. Not. R. Astron. Soc. 466, 2181–2193. doi:10.1093/mnras/stw3273
Ledoux, P. (1951). The nonradial oscillations of gaseous stars and the problem of beta Canis majoris. Astrophys. J. 114, 373. doi:10.1086/145477
Lee, U., and Baraffe, I. (1995). Pulsational stability of rotating main sequence stars: The second order effects of rotation on the nonadiabatic oscillations. Astron. Astrophys. 301, 419.
Lee, U. (2022). Non-linear excitation of low-frequency modes by overstable convective modes in rotating stars. Mon. Not. R. Astron. Soc. 513, 2522–2534. doi:10.1093/mnras/stac1021
Lee, U. (2021). Overstable convective modes in rotating early-type stars. Mon. Not. R. Astron. Soc. 505, 1495–1508. doi:10.1093/mnras/stab1433
Lee, U., and Saio, H. (1990). Line profile variations caused by low-frequency nonradial pulsations of rapidly rotating stars. Astrophys. J. 349, 570. doi:10.1086/168344
Lee, U., and Saio, H. (1987). Low-frequency oscillations of uniformly rotating stars. Mon. Not. R. Astron. Soc. 224, 513–526. doi:10.1093/mnras/224.3.513
Lee, U., and Saio, H. (2020). Rotating convective core excites non-radial pulsations to cause rotational modulations in early-type stars. Mon. Not. R. Astron. Soc. 497, 4117–4127. doi:10.1093/mnras/staa2250
Li, G., Guo, Z., Fuller, J., Bedding, T. R., Murphy, S. J., Colman, I. L., et al. (2020a). The effect of tides on near-core rotation: Analysis of 35 kepler γ doradus stars in eclipsing and spectroscopic binaries. Mon. Not. R. Astron. Soc. 497, 4363–4375. doi:10.1093/mnras/staa2266
Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., Antoci, V., Ouazzani, R.-M., et al. (2020b). Gravity-mode period spacings and near-core rotation rates of 611 γ Doradus stars with Kepler. Mon. Not. R. Astron. Soc. 491, 3586–3605. doi:10.1093/mnras/stz2906
Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., and Antoci, V. (2019). Period spacings of γ Doradus pulsators in the Kepler field: Rossby and gravity modes in 82 stars. Mon. Not. R. Astron. Soc. 487, 782–800. doi:10.1093/mnras/stz1171
Lignières, F., and Georgeot, B. (2009). Asymptotic analysis of high-frequency acoustic modes in rapidly rotating stars. Astron. Astrophys. 500, 1173–1192. doi:10.1051/0004-6361/200811165
Lignières, F., and Georgeot, B. (2008). Wave chaos in rapidly rotating stars. Phys. Rev. E 78, 016215. doi:10.1103/PhysRevE.78.016215
Loi, S. T. (2020). Effect of a strong magnetic field on gravity-mode period spacings in red giant stars. Mon. Not. R. Astron. Soc. 496, 3829–3840. doi:10.1093/mnras/staa1823
Loi, S. T., and Papaloizou, J. C. B. (2018). Effects of a strong magnetic field on internal gravity waves: Trapping, phase mixing, reflection, and dynamical chaos. Mon. Not. R. Astron. Soc. 477, 5338–5357. doi:10.1093/mnras/sty917
Mantegazza, L., Poretti, E., Michel, E., Rainer, M., Baudin, F., García Hernández, A., et al. (2012). Pulsation spectrum of δ Scuti stars: The binary HD 50870 as seen with CoRoT and HARPS. Astron. Astrophys. 542, A24. doi:10.1051/0004-6361/201118682
Mathis, S., Bugnet, L., Prat, V., Augustson, K., Mathur, S., and García, R. (2021). Probing the internal magnetism of stars using asymptotic magneto-asteroseismology. Astron. Astrophys. 647, A122. doi:10.1051/0004-6361/202039180
Mathis, S. (2009). Transport by gravito-inertial waves in differentially rotating stellar radiation zones. I - theoretical formulation. Astron. Astrophys. 506, 811–828. doi:10.1051/0004-6361/200810544
Matsuno, T. (2008). Quasi-geostrophic motions in the equatorial area. J. Meteorological Soc. Jpn. 44, 25–43. doi:10.2151/jmsj1965.44.1_25
Michel, E., Dupret, M.-A., Reese, D., Ouazzani, R.-M., Debosscher, J., Hernández, A. G., et al. (2017). What CoRoT tells us about δ Scuti stars. Existence of a regular pattern and seismic indices to characterize stars. Eur. Phys. J. Web Conf., 160, 03001. doi:10.1051/epjconf/201716003001
Miglio, A., Montalbán, J., Noels, A., and Eggenberger, P. (2008). Probing the properties of convective cores through g modes: High-order g modes in SPB and γ doradus stars. Mon. Not. R. Astron. Soc. 386, 1487–1502. doi:10.1111/j.1365-2966.2008.13112.x
Mirouh, G. M., Angelou, G. C., Reese, D. R., and Costa, G. (2019). Mode classification in fast-rotating stars using a convolutional neural network: Model-based regular patterns in δ Scuti stars. MNRAS 483, L28–L32. doi:10.1093/mnrasl/sly212
Mirouh, G. M., Baruteau, C., Rieutord, M., and Ballot, J. (2016). Gravito-inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 800, 213–247. doi:10.1017/jfm.2016.382
Mirouh, G. M., Reese, D. R., Rieutord, M., and Ballot, J. (2017). “Non-adiabatic oscillations of fast-rotating stars: The example of Rasalhague,” in SF2A-2017: Proceedings of the annual meeting of the French society of Astronomy and Astrophysics, Paris, France. Editors C. Reylé, P. Di Matteo, F. Herpin, E. Lagadec, A. Lançon, Z. Melianiet al. sf2a, Sociét— Française d'Astronomie et d'Astrophysique.
Mirouh, G., Reese, D., Espinosa Lara, F., Ballot, J., and Rieutord, M. (2013). “Asteroseismology of fast-rotating stars: The example of α ophuichi,” in Precision asteroseismology. Editors W. Chaplin, J. Guzik, G. Handler, and A. Pigulski, 865. IAU Symposium 301, 1, astro–ph/.
Monnier, J. D., Townsend, R. H. D., Che, X., Zhao, M., Kallinger, T., Matthews, J., et al. (2010). Rotationally modulated g-modes in the rapidly rotating δ Scuti star Rasalhague (α Ophiuchi). Astrophys. J. 725, 1192–1201. doi:10.1088/0004-637x/725/1/1192
Mosser, B., Belkacem, K., Goupil, M.-J., Miglio, A., Morel, T., Barban, C., et al. (2010). Red-giant seismic properties analyzed with CoRoT. Astron. Astrophys. 517, A22. doi:10.1051/0004-6361/201014036
Mosser, B., Michel, E., Belkacem, K., Goupil, M. J., Baglin, A., Barban, C., et al. (2013). Asymptotic and measured large frequency separations. Astron. Astrophys. 550, A126. doi:10.1051/0004-6361/201220435
Osaki, Y. (1974). An excitation mechanism for pulsations in beta CEP stars. Astrophys. J. 189, 469–477. doi:10.1086/152825
Ouazzani, R.-M., Dupret, M.-A., and Reese, D. R. (2012). Pulsations of rapidly rotating stars. I. The ACOR numerical code. Astron. Astrophys. 547, A75. doi:10.1051/0004-6361/201219548
Ouazzani, R.-M., Roxburgh, I. W., and Dupret, M.-A. (2015). Pulsations of rapidly rotating stars. II. Realistic modelling for intermediate-mass stars. Astron. Astrophys. 579, A116. doi:10.1051/0004-6361/201525734
Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., Bedding, T. R., Murphy, S. J., and Roxburgh, I. W. (2017). A new asteroseismic diagnostic for internal rotation in γ Doradus stars. Mon. Not. R. Astron. Soc. 465, 2294–2309. doi:10.1093/mnras/stw2717
Ouazzani, R. M., and Goupil, M. J. (2012). Rotational splittings for slow to moderate rotators. Astron. Astrophys. 542, A99. doi:10.1051/0004-6361/201117151
Ouazzani, R. M., Lignières, F., Dupret, M. A., Salmon, S. J. A. J., Ballot, J., Christophe, S., et al. (2020). First evidence of inertial modes in γ Doradus stars: The core rotation revealed. Astron. Astrophys. 640, A49. doi:10.1051/0004-6361/201936653
Papaloizou, J., and Pringle, J. E. (1978). Gravitational radiation and the stability of rotating stars. Mon. Not. R. Astron. Soc. 184, 501–508. doi:10.1093/mnras/184.3.501
Paparó, M., Benkő, J. M., Hareter, M., and Guzik, J. A. (2016b). Unexpected series of regular frequency spacing of δ Scuti stars in the non-asymptotic regime. II. Sample-echelle diagrams and rotation. Astrophys. J. Suppl. Ser. 224, 41. doi:10.3847/0067-0049/224/2/41
Paparó, M., Benkő, J. M., Hareter, M., and Guzik, J. A. (2016a). Unexpected series of regular frequency spacing of δ Scuti stars in the non-asymptotic regime. I. The methodology. Astrophys. J. 822, 100. doi:10.3847/0004-637X/822/2/100
Pápics, P. I., Tkachenko, A., Van Reeth, T., Aerts, C., Moravveji, E., Van de Sande, M., et al. (2017). Signatures of internal rotation discovered in the Kepler data of five slowly pulsating B stars. Astron. Astrophys. 598, A74. doi:10.1051/0004-6361/201629814
Pasek, M., Georgeot, B., Lignières, F., and Reese, D. R. (2011). Regular modes in rotating stars. Phys. Rev. Lett. 107, 121101. doi:10.1103/PhysRevLett.107.121101
Pasek, M., Lignières, F., Georgeot, B., and Reese, D. R. (2012). Regular oscillation sub-spectrum of rapidly rotating stars. Astron. Astrophys. 546, A11. doi:10.1051/0004-6361/201219716
Pedersen, M. G., Aerts, C., Pápics, P. I., Michielsen, M., Gebruers, S., Rogers, T. M., et al. (2021). Internal mixing of rotating stars inferred from dipole gravity modes. Nat. Astron. 5, 715–722. doi:10.1038/s41550-021-01351-x
Pesnell, W. D. (1987). A new driving mechanism for stellar pulsations. Astrophys. J. 314, 598–604. doi:10.1086/165089
Pijpers, F. P., and Thompson, M. J. (1994). The SOLA method for helioseismic inversion. Astron. Astrophys. 281, 231.
Poretti, E., Michel, E., Garrido, R., Lefèvre, L., Mantegazza, L., Rainer, M., et al. (2009). HD 50844: A new look at δ Scuti stars from CoRoT space photometry. Astron. Astrophys. 506, 85–93. doi:10.1051/0004-6361/200912039
Potter, A. T. (2012). Rotation and magnetism in massive stars. Ph.D. thesis, University of Cambridge.
Prat, V., Lignières, F., and Ballot, J. (2016). Asymptotic theory of gravity modes in rotating stars. I. Ray dynamics. Astron. Astrophys. 587, A110. doi:10.1051/0004-6361/201527737
Prat, V., Mathis, S., Neiner, C., Van Beeck, J., Bowman, D. M., and Aerts, C. (2020). Period spacings of gravity modes in rapidly rotating magnetic stars. II. The case of an oblique dipolar fossil magnetic field. Astron. Astrophys. 636, A100. doi:10.1051/0004-6361/201937398
Ramón-Ballesta, A., García Hernández, A., Suárez, J. C., Rodón, J. R., Pascual-Granado, J., and Garrido, R. (2021). Study of rotational splittings in δ Scuti stars using pattern finding techniques. Mon. Not. R. Astron. Soc. 505, 6217–6224. doi:10.1093/mnras/stab1719
Reese, D. (2006). La modélisation des oscillations d’étoiles en rotation rapide. Toulouse (France): Université Toulouse III - Paul Sabatier. Ph.D. thesis.
Reese, D., Lignières, F., and Rieutord, M. (2008). Regular patterns in the acoustic spectrum of rapidly rotating stars. Astron. Astrophys. 481, 449–452. doi:10.1051/0004-6361:20078075
Reese, D. R., Dupret, M.-A., and Rieutord, M. (2017a). Non-adiabatic pulsations in ESTER models.” in European Physical Journal Web of Conferences, Angra do Heroismo, Portugal, 160, 02007. doi:10.1051/epjconf/201716002007
Reese, D. R., Lignières, F., Ballot, J., Dupret, M. A., Barban, C., van’t Veer-Menneret, C., et al. (2017b). Frequency regularities of acoustic modes and multi-colour mode identification in rapidly rotating stars. Astron. Astrophys. 601, A130. doi:10.1051/0004-6361/201321264
Reese, D. R., MacGregor, K. B., Jackson, S., Skumanich, A., and Metcalfe, T. S. (2009a). Pulsation modes in rapidly rotating stellar models based on the self-consistent field method. Astron. Astrophys. 506, 189–201. doi:10.1051/0004-6361/200811510
Reese, D. R., Mirouh, G. M., Espinosa Lara, F., Rieutord, M., and Putigny, B. (2021). Oscillations of 2D ESTER models. I. The adiabatic case. Astron. Astrophys. 645, A46. doi:10.1051/0004-6361/201935538
Reese, D. R., Prat, V., Barban, C., van ’t Veer-Menneret, C., and MacGregor, K. B. (2013). Mode visibilities in rapidly rotating stars. Astron. Astrophys. 550, A77. doi:10.1051/0004-6361/201220506
Reese, D. R., Thompson, M. J., MacGregor, K. B., Jackson, S., Skumanich, A., and Metcalfe, T. S. (2009b). Mode identification in rapidly rotating stars. Astron. Astrophys. 506, 183–188. doi:10.1051/0004-6361/200911914
Ricker, G. R. (2014). The transiting exoplanet survey satellite mission. J. Am. Assoc. Var. Star Observers (JAAVSO) 42, 234.
Rieutord, M., and Espinosa Lara, F. (2013). “Ab initio modelling of steady rotating stars,” in Studying stellar rotation and convection. Editors M. Goupil, K. Belkacem, C. Neiner, F. Lignières, and J. J. Green (Roscoff, France: Lecture Notes in Physics, Berlin Springer Verlag).
Rieutord, M., Espinosa Lara, F., and Putigny, B. (2016). An algorithm for computing the 2D structure of fast rotating stars. J. Comput. Phys. 318, 277–304. doi:10.1016/j.jcp.2016.05.011
Rieutord, M., Georgeot, B., and Valdettaro, L. (2001). Inertial waves in a rotating spherical shell: Attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144. doi:10.1017/s0022112001003718
Rieutord, M. (2006). The dynamics of the radiative envelope of rapidly rotating stars. i. a spherical boussinesq model. Astron. Astrophys. 451, 1025–1036. doi:10.1051/0004-6361:20054433
Rodríguez-Martín, J. E., García Hernández, A., Suárez, J. C., and Rodón, J. R. (2020). Study of the low-order Δν-ρ− relation for moderately rotating δ Scuti stars and its impact on their characterization. Mon. Not. R. Astron. Soc. 498, 1700–1709. doi:10.1093/mnras/staa2378
Rogers, T. M., and MacGregor, K. B. (2011). On the interaction of internal gravity waves with a magnetic field - II. Convective forcing. Mon. Not. R. Astron. Soc. 410, 946–962. doi:10.1111/j.1365-2966.2010.17493.x
Rogers, T. M., and MacGregor, K. B. (2010). On the interaction of internal gravity waves with a magnetic field – I. Artificial wave forcing. Mon. Not. R. Astron. Soc. 401, 191–196. doi:10.1111/j.1365-2966.2009.15618.x
Royer, F. (2009). “On the rotation of A-type stars,” in The rotation of Sun and stars. Editors J.-P. Rozelot, and C. Neiner (Lecture Notes in PhysicsBerlin Springer Verlag), 765, 207.
Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., and Lee, U. (2018). Theory and evidence of global Rossby waves in upper main-sequence stars: r-Mode oscillations in many kepler stars. Mon. Not. R. Astron. Soc. 474, 2774–2786. doi:10.1093/mnras/stx2962
Saio, H. (1982). R-mode oscillations in uniformly rotating stars. Astrophys. J. 256, 717–735. doi:10.1086/159945
Saio, H. (1981). Rotational and tidal perturbations of nonradial oscillations in a polytropic star. Astrophys. J. 244, 299–315. doi:10.1086/158708
Saio, H., Takata, M., Lee, U., Li, G., and Van Reeth, T. (2021). Rotation of the convective core in γ Dor stars measured by dips in period spacings of g modes coupled with inertial modes. Mon. Not. R. Astron. Soc. 502, 5856–5874. doi:10.1093/mnras/stab482
Saio, H., and Takata, M. (2014). Rosette modes of oscillations of rotating stars caused by close degeneracies. II. Nonaxisymmetric modes. Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 66, 58. doi:10.1093/pasj/psu027
Salmon, S. J. A. J., Eggenberger, P., Montalbán, J., Miglio, A., Noels, A., Buldgen, G., et al. (2022). Asteroseismology of β Cephei stars: The stellar inferences tested in hare and hound exercises. Astron. Astrophys. 659, A142. doi:10.1051/0004-6361/202142483
Schou, J., Antia, H. M., Basu, S., Bogart, R. S., Bush, R. I., Chitre, S. M., et al. (1998). Helioseismic studies of differential rotation in the solar envelope by the solar oscillations investigation using the michelson Doppler imager. Astrophys. J. 505, 390–417. doi:10.1086/306146
Sekaran, S., Tkachenko, A., Johnston, C., and Aerts, C. (2021). A comparison of the dynamical and model-derived parameters of the pulsating eclipsing binary KIC 9850387. Astron. Astrophys. 648, A91. doi:10.1051/0004-6361/202040154
Shibahashi, H. (1979). Modal analysis of stellar nonradial oscillations by an asymptotic method. Pub. Astron. Soc. Jap. 31, 87.
Shutt, T. R., Brunsden, E., and Pollard, K. R. (2021). Spectroscopic frequency and mode identification of γ Doradus stars HD 109799 and HD 103257. Mon. Not. R. Astron. Soc. 507, 1149–1156. doi:10.1093/mnras/stab1972
Soufi, F., Goupil, M. J., and Dziembowski, W. A. (1998). Effects of moderate rotation on stellar pulsation. I. Third order perturbation formalism. Astron. Astrophys. 334, 911.
Stello, D., Cantiello, M., Fuller, J., Garcia, R. A., and Huber, D. (2016). Suppression of quadrupole and octupole modes in red giants observed by kepler. Publ. Astron. Soc. Aust. 33, e011. doi:10.1017/pasa.2016.9
Suárez, J. C. (2009). “Analysis of the internal rotation profile of stars using rotational mode splitting asymmetries,” in Stellar pulsation: Challenges for theory and observation. Editors J. A. Guzik, and P. A. Bradley (Santa Fe NM, USA: American Institute of Physics Conference Series), 1170, 370–372. doi:10.1063/1.3246515
Suárez, J. C., García Hernández, A., Moya, A., Rodrigo, C., Solano, E., Garrido, R., et al. (2014). Measuring mean densities of δ Scuti stars with asteroseismology. Theoretical properties of large separations using TOUCAN. Astron. Astrophys. 563, A7. doi:10.1051/0004-6361/201322270
Szewczuk, W., and Daszyńska-Daszkiewicz, J. (2018). KIC 3240411 - the hottest known SPB star with the asymptotic g-mode period spacing. Mon. Not. R. Astron. Soc. 478, 2243–2256. doi:10.1093/mnras/sty1126
Szewczuk, W., Walczak, P., Daszyńska-Daszkiewicz, J., and Moździerski, D. (2022). Seismic modelling of a very young SPB star - KIC 8264293. Mon. Not. R. Astron. Soc. 511, 1529–1543. doi:10.1093/mnras/stac168
Szewczuk, W., Walczak, P., and Daszyńska-Daszkiewicz, J. (2021). Variability of newly identified B-type stars observed by Kepler. Mon. Not. R. Astron. Soc. 503, 5894–5928. doi:10.1093/mnras/stab683
Takata, M., Ouazzani, R. M., Saio, H., Christophe, S., Ballot, J., Antoci, V., et al. (2020a). A diagnostic diagram for γ Doradus variables and slowly pulsating B-type stars. Astron. Astrophys. 635, A106. doi:10.1051/0004-6361/201936297
Takata, M., Ouazzani, R. M., Saio, H., Christophe, S., Ballot, J., Antoci, V., et al. (2020b). Inferring the internal structure of γ Doradus variables from Rossby modes. Extension of the ν - diagram. Astron. Astrophys. 644, A138. doi:10.1051/0004-6361/202038098
Takata, M. (2014). Rosette modes of oscillations of rotating stars caused by close degeneracies. III. JWKB analysis. Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 66, 80. doi:10.1093/pasj/psu055
Takata, M., and Saio, H. (2013). Rosette modes of oscillations of rotating stars caused by close degeneracies. I. Axisymmetric modes. Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 65, 68. doi:10.1093/pasj/65.3.68
Takeda, Y., Kawanomoto, S., and Ohishi, N. (2008). Rotational feature of Vega revealed from spectral line profiles. Astrophys. J. 678, 446–462. doi:10.1086/528949
Tassoul, M. (1980). Asymptotic approximations for stellar nonradial pulsations. Astrophys. J. Suppl. Ser. 43, 469–490. doi:10.1086/190678
Telting, J. H., and Schrijvers, C. (1998). A new bright beta Cephei star: Line-profile variability in omega1̂ SCO. Astron. Astrophys. 339, 150.
Telting, J. H., and Schrijvers, C. (1997). Line-profile variations of non-radial adiabatic pulsations of rotating stars. II. The diagnostic value of amplitude and phase diagrams derived from time series of spectra. Astron. Astrophys. 317, 723.
Tokuno, T., and Takata, M. (2022). Asteroseismology of the dip structure in period-spacings of rapidly rotating γ Doradus stars caused by the coupling between core and envelope oscillations. Mon. Not. R. Astron. Soc. 514, 4140–4159. doi:10.1093/mnras/stac1492
Townsend, R. H. D. (1997). Spectroscopic modelling of non-radial pulsation in rotating early-type stars. Mon. Not. R. Astron. Soc. 284, 839–858. doi:10.1093/mnras/284.4.839
Triana, S. A., Corsaro, E., De Ridder, J., Bonanno, A., Pérez Hernández, F., and García, R. A. (2017). Internal rotation of 13 low-mass low-luminosity red giants in the Kepler field. Astron. Astrophys. 602, A62. doi:10.1051/0004-6361/201629186
Unno, W., Osaki, Y., Ando, H., Saio, H., and Shibahashi, H. (1989). Nonradial oscillations of stars. University of Tokyo Press.
Van Reeth, T., Tkachenko, A., and Aerts, C. (2016). Interior rotation of a sample of γ Doradus stars from ensemble modelling of their gravity-mode period spacings. Astron. Astrophys. 593, A120. doi:10.1051/0004-6361/201628616
Van Reeth, T., Tkachenko, A., Aerts, C., Pápics, P. I., Triana, S. A., Zwintz, K., et al. (2015). Gravity-mode period spacings as a seismic diagnostic for a sample of γ doradus stars from kepler space photometry and high-resolution ground-based spectroscopy. Astrophys. J. Suppl. Ser. 218, 27. doi:10.1088/0067-0049/218/2/27
von Zeipel, H. (1924). The radiative equilibrium of a rotating system of gaseous masses. Mon. Not. R. Astron. Soc. 84, 665–684. doi:10.1093/mnras/84.9.665
Vrard, M., Mosser, B., and Samadi, R. (2016). Period spacings in red giants. Astron. Astrophys. 588, A87. doi:10.1051/0004-6361/201527259
Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., Schwarzenberg-Czerny, A., Koudelka, O. F., Grant, C. C., et al. (2014). BRITE-Constellation: Nanosatellites for precision photometry of bright stars. Publ. Astron. Soc. Pac. 126, 573–585. doi:10.1086/677236
Wu, T., Li, Y., Deng, Z.-m., Lin, G.-f., Song, H.-f., and Jiang, C. (2020). Asteroseismic analyses of slowly pulsating B star KIC 8324482: Ultraweak element mixing beyond the central convective core. Astrophys. J. 899, 38. doi:10.3847/1538-4357/aba430
Xiong, D. R., Deng, L., Zhang, C., and Wang, K. (2016). Turbulent convection and pulsation stability of stars - II. Theoretical instability strip for δ Scuti and γ Doradus stars. Mon. Not. R. Astron. Soc. 457, 3163–3177. doi:10.1093/mnras/stw047
Zhang, X. B., Fu, J. N., Luo, C. Q., Ren, A. B., and Yan, Z. Z. (2018). Seismic study of the γ doradus-type pulsations in the eclipsing binary KIC 10486425. Astrophys. J. 865, 115. doi:10.3847/1538-4357/aadd9a
Zhao, M., Monnier, J. D., Pedretti, E., Thureau, N., Mérand, A., ten Brummelaar, T., et al. (2009). Imaging and modeling rapidly rotating stars: α Cephei and α Ophiuchi. Astrophys. J. 701, 209–224. doi:10.1088/0004-637x/701/1/209
Zhevakin, S. A. (1963). Physical basis of the pulsation theory of variable stars. Annu. Rev. Astron. Astrophys. 1, 367–400. doi:10.1146/annurev.aa.01.090163.002055
Zima, W. (2006). A new method for the spectroscopic identification of stellar non-radial pulsation modes I. The method and numerical tests. Astron. Astrophys. 455, 227–234. doi:10.1051/0004-6361:20064876
Zima, W., Wright, D., Bentley, J., Cottrell, P. L., Heiter, U., Mathias, P., et al. (2006). A new method for the spectroscopic identification of stellar non-radial pulsation modes. II. Mode identification of the δ Scuti star FG Virginis. Astron. Astrophys. 455, 235–246. doi:10.1051/0004-6361:20064877
Keywords: stars: oscillations, stars:rotation, stars:interiors, stars:individual α Ophiuchi, stars: evolution
Citation: Mirouh GM (2022) Forward modelling and the quest for mode identification in rapidly rotating stars. Front. Astron. Space Sci. 9:952296. doi: 10.3389/fspas.2022.952296
Received: 24 May 2022; Accepted: 16 September 2022;
Published: 07 October 2022.
Edited by:
Javier Pascual Granado, Spanish National Research Council (CSIC), SpainCopyright © 2022 Mirouh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giovanni M. Mirouh, Z21tQHVnci5lcw==
 Giovanni M. Mirouh
Giovanni M. Mirouh