Recent progress with observations and models to characterize the magnetic fields from star-forming cores to protostellar disks

In this review article, we aim at providing a global outlook on the progresses made in the recent years to characterize the role of magnetic fields during the embedded phases of the star formation process. Thanks to the development of observational capabilities and the parallel progress in numerical models, capturing most of the important physics at work during star formation; it has recently become possible to confront detailed predictions of magnetized models to observational properties of the youngest protostars. We provide an overview of the most important consequences when adding magnetic fields to state-of-the-art models of protostellar formation, emphasizing their role to shape the resulting star(s) and their disk(s). We discuss the importance of magnetic field coupling to set the efficiency of magnetic processes and provide a review of observational works putting constraints on the two main agents responsible for the coupling in star-forming cores: dust grains and ionized gas. We recall the physical processes and observational methods, which allow to trace the magnetic field topology and its intensity in embedded protostars and review the main steps, success, and limitations in comparing real observations to synthetic observations from the non-ideal MHD models. Finally, we discuss the main threads of observational evidence that suggest a key role of magnetic fields for star and disk formation, and propose a scenario solving the angular momentum for star formation, also highlighting the remaining tensions that exist between models and observations.

1 Introduction

The formation of stars takes place in filamentary molecular clouds, when the high-density interstellar medium partly collapses and fragments into bound starless dense cores. Depending on their properties, such cores can undergo further collapse to form a protostar that will accrete its circumstellar material (evolving through the Class 0, I, II, and later stages) until reaching the main sequence. Class 0 protostars are the first (proto)stellar objects, observed only t ≲ 5 × 10⁴ years (André et al., 1993, 2000; Evans et al., 2009; Maury et al., 2011) after their formation, while most of their mass is still in the form of a dense core/envelope collapsing onto the central protostellar embryo. Embedded Class 0 and Class I protostars are also accreting objects, as most of the final stellar mass is assembled during those short phases. During this accretion phase, the circumstellar gas must redistribute most of its initial angular momentum outward or else centrifugal forces will soon balance gravity and prevent inflow, accretion, and the growth of the star. This long-standing “angular momentum problem” was estimated to be quite severe (Bodenheimer, 1995). Comparing observations of the specific angular momentum J/M in star-forming clouds prior to contraction (J/M ∼ 10²¹ cm² s⁻¹, Goodman et al., 1993) to the angular momentum contained in a typical solar-type star (J/M ∼ 10¹⁵ cm² s⁻¹) indicates that during the brief accretion phase, the gas must transfer all but 1 millionth of its initial angular momentum out of the accretion flow (Belloche, 2013). Exactly how the circumstellar mass contained in a star-forming core is transferred to the forming star but not its associated angular momentum has been an active field of research in modern astronomy.

Wherever we have the means of observing them, magnetic fields are detected on nearly all scales and across the full spectrum of astrophysical environments: from our own Earth (Russell, 1991) to stars (Donati and Landstreet, 2009), the Milky Way (Wielebinski, 2005) and cosmological structures (Kunze, 2013). Regarding star formation processes, magnetic fields provide a mechanism for launching and collimating outflow winds and jets (Blandford and Payne, 1982), which are routinely observed around young stellar objects (YSOs), and magnetic fields of typical strengths 10–100 μG are threading nearly all star-forming clouds (Crutcher, 2012). Therefore, it is now widely accepted that most star-forming cores are magnetized to some level. However, it is only recently that the role of these magnetic fields could be investigated in detail.

Indeed, in the past decade, numerical models of star formation have been gradually including most of the physical ingredients for a detailed description of protostellar evolution in the presence of magnetic fields, such as resistive MHD, radiative transfer, and chemical networks, at all the relevant scales. Moreover, observational capabilities resolving the internal environment of star-forming cores, for example, interferometry at (sub)millimeter wavelengths, have started to produce detailed maps of the gas and dust properties at the very small scales of protostellar cores, where material is accreted into a stellar embryo, stored in a disk, and ejected under the form of outflows and jets. The massive development of polarization capabilities on telescopes probing the cold Universe, such as on the submillimeter array (SMA), then on the Atacama Large Millimeter Array (ALMA), and now also developed at the IRAM NOrthern Extended Millimeter Array (NOEMA), have produced sensitive observations of magnetic fields in protostellar cores with a great level of detail. These are used as tools to put unprecedented constraints on magnetic features, which should be able to reproduce the star formation models (Hull and Zhang, 2019).

Hence, the simultaneous major improvements of instrumental and computational facilities have opened an era of detailed confrontation between observed protostellar properties and magnetized model predictions. Testing the detailed interplay of physics at work has allowed a major leap forward in our understanding of the star and disk formation processes and provides a new detailed scenario to describe the early stages of the formation of stars and their planetary systems. In this review, we present a synthetic description of the progresses made in the past decade regarding the properties and roles of magnetic fields in shaping young protostars, their envelopes, disks, and resulting stellar systems.

2 How magnetic field influences gravitational collapse: A theoretical overview

This section is devoted to a review of the fundamental MHD processes relevant in the context of dense core collapse and disk formation.

2.1 The fluid equations

The fluid equations are as follows: ρ, P, v, B, and Φ_g are, respectively, gas density, pressure, velocity, magnetic field, and gravitational potential, while η_O, η_H, and η_AD are the Ohmic, Hall, and ambipolar diffusivities, respectively.

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathbf{v}\right)=0,(1)$

is the continuity equation, which describes matter conservation.

$\begin{array}{ll}\hfill \rho \left(\frac{\partial \mathbf{v}}{\partial t}+\left(\mathbf{v}\cdot \nabla \right)\mathbf{v}\right)& =-\nabla P+\frac{1}{4\pi }\left(\nabla \times \mathbf{B}\right)\times \mathbf{B}-\rho \nabla {\mathrm{\Phi }}_g\hfill \\ \hfill & =-\nabla \left(P+\frac{B^2}{8\pi }\right)+\frac{1}{4\pi }\mathbf{B}.\nabla \mathbf{B}-\rho \nabla {\mathrm{\Phi }}_g,\hfill \end{array}(2)$

represents the momentum conservation. We see in particular that the Lorentz force can be written as a magnetic pressure and a magnetic tension.

$\begin{array}{ll}\hfill \frac{\partial \mathbf{B}}{\partial t}& =\nabla \times \left(\mathbf{v}\times \mathbf{B}\right)-\frac{c^2}{4\pi }\nabla \hfill \\ \hfill & \times \left\{{\eta }_{\text{O}\nabla }\times \mathbf{B}+{\eta }_{\text{H}}\left(\nabla \times \mathbf{B}\right)\times \frac{\mathbf{B}}{B}+{\eta }_{\text{AD}}\frac{\mathbf{B}}{B}\right.\hfill \\ \hfill & \times \left.\left[\left(\nabla \times \mathbf{B}\right)\times \frac{\mathbf{B}}{B}\right]\right\},\hfill \end{array}(3)$

is the Maxwell–Faraday equation. The three non-ideal MHD terms, namely, the Ohm, Hall, and ambipolar diffusion contributions are accounted for.

While this set of equations is complete (after the inclusion of an energy conservation equation, and an equation of state), it is nevertheless enlightening to also discuss the equation describing the conservation of angular momentum. It is obtained by combining the azimuthal component of the momentum equation with the continuity equation (see for instance Joos et al., 2012). The equation of conservation of angular momentum is

$\begin{array}{ll}\hfill & {\partial }_t\left(\rho r{v}_{\varphi }\right)+\nabla \cdot r\hfill \\ \hfill & \times \left[\rho v_{\varphi }\mathbf{v}+\left(P+\frac{B^2}{8\pi }-\frac{g^2}{8\pi G}\right){\mathbf{e}}_{\mathit{\varphi }}-\frac{B_{\varphi }}{4\pi }\mathbf{B}+\frac{g_{\varphi }}{4\pi G}\mathbf{g}\right]=0.\hfill \end{array}(4)$

This equation reveals the existence of two torques, which is able to transport the angular momentum, namely, − rB_ϕB/4π, the magnetic torque and rg_ϕg/(4πG), the gravitational torque. These two torques are playing a fundamental role during the collapse regarding the issue of angular momentum evolution. They have a similar expression, and in particular both require the toroidal and poloidal fields. However, there is an important difference between the two because a toroidal magnetic field, B_ϕ, can be produced in an axisymmetric cloud, once the cloud is in rotation. On the contrary, a toroidal gravitational field requires a non-axisymmetric density distribution such as a spiral wave.

2.2 Magnetic support and magnetic compression: The pseudo-disk

The simplest effect magnetic field on a cloud is through magnetic pressure, which provides a support against gravity. Assuming field freezing within a cloud of radius R, threaded by magnetic field, B, we have that ϕ = πR²B, the magnetic flux, is conserved during collapse. It is easy to calculate the ratio of magnetic over gravitational energy

$\frac{E_{\text{mag}}}{E_{\text{grav}}}\propto \frac{R^3{B}^2}{G{M}^2/R}\propto \frac{1}{G}{\left(\frac{\varphi }{M}\right)}^2.(5)$

Equation 5 shows that the energy ratio stays constant, as long as spherical symmetry is maintained and that it is proportional to ϕ/M, that is, the ratio of the magnetic flux over the cloud mass. Obviously, there is a critical value for (M/ϕ)_cri† above which magnetic field is strong enough to prevent gravitational collapse. The latter is expected to be such as ${(M/\varphi )}_{\mathit{cri†}}\propto 1/\sqrt{G}$. A calibration has been performed by Mouschovias and Spitzer (1976), using exact equilibrium, and it has been inferred that

${\left(\frac{M}{\varphi }\right)}_{\mathit{crit}}=\frac{1}{\sqrt{G}}\frac{c_1\sqrt{5}}{3\pi },(6)$

where c₁ ≃ 0.51. It is then common to define μ, the mass-to-flux over critical mass-to-flux ratio. A value of μ = 1 indicates that the magnetic field and gravity compensate, while a value of μ larger than 1 implies that magnetic field cannot prevent collapse to occur. Another commonly used closely related parameter has traditionally been called λ and uses the column density and magnetic field,

$\lambda =2\pi G^{1/2}\frac{\mathrm{\Sigma }}{B}.(7)$

Due to the anisotropic nature of the magnetic field, and in particular to the fact that the Lorentz force vanishes along the field lines, a magnetized cloud does not collapse spherically but typically get flatten along the field lines. It should be stressed however that as the collapse proceeds, the field lines get strongly pinched by the differential motions, forming an hour glass shape. This has two consequences. First, it creates a magnetic pressure force, $-{\partial }_r(B_z^2)/8\pi$, parallel to the equatorial plane and pointing outward. This typically slows down the collapse when the magnetic field is strong enough. Second, it creates another component of the magnetic force, which is oriented along the z-axis and is equal to $-{\partial }_z(B_r^2)/8\pi$. However, for symmetry reasons, B_r is usually vanishing in the equatorial plane. Therefore, this force is pointing toward the mid-plane and is compressing the gas. Compared to the hydrodynamical collapse, for which the singular isothermal, $\rho =c_s^2/(2\pi G{r}^2)$, is usually an acceptable approximation, particularly for low-mass cores, this creates close to the equatorial plane, a density enhancement which can be as high as a factor of several. Because of its shape, this thin layer is usually called a pseudo-disk. Exact solutions of this equilibrium, called the magnetized isothermal toroids, have been obtained by Li and Shu (1996), while an approximation of the density enhancement and the dense layer thickness is presented in Hennebelle and Fromang (2008). It should be stressed that like for the singular isothermal sphere, the resulting equilibrium is unstable to collapse and thus, unless the core is magnetically dominated, the pseudo-disk collapses. Indeed, the pseudo-disk, unlike a centrifugally supported disk, is not a structure which is at mechanical equilibrium. It is essentially a collapsing envelope that has been flattened by the magnetic field effect.

It is worth stressing that the aligned configuration, that is, magnetic field and rotation being initially parallel, which has generally been assumed in most early calculations, is somehow peculiar because in this configuration only the z-component of the field is not zero in the equatorial plane and therefore the magnetic pressure is squeezing the gas along the z-axis. If magnetic field and rotation are initially misaligned, the magnetic field lines get twisted by rotation and the radial field does not vanish anymore in the equatorial plane. This has as effect to somehow thicken the pseudo-disk (Hennebelle and Ciardi, 2009; Hirano et al., 2020).

2.3 Magnetic braking

The magnetic braking acts through the magnetic torque − rB_ϕB. Since it is a local quantity, it is not straightforward to anticipate its role, and it is enlightening to investigate some of its key properties; thanks to simple cases, as proposed by Mouschovias and Paleologou (1980) and more recently by Joos et al. (2012) and Hirano et al. (2020).

2.3.1 Aligned rotator

Let us first consider a cloud of mass M, density ρ_c, radius R_c, and half-height Z, surrounded by an external medium of density ρ_ext. The cloud is initially in rotation at a speed, Ω, and for simplicity, the magnetic field B is considered uniform and parallel to the rotation axis. The magnetic braking timescale, τ_‖, is estimated as the time needed for a torsional Alfvén wave to transfer the initial angular momentum of the cloud to the external medium (Mouschovias, 1979):

${\rho }_{\text{ext}}{v}_{\text{A,ext}}{\tau }_{\Vert }\sim {\rho }_{c}Z.(8)$

The Alfvén speed in the external medium is given by $v_{\text{A,ext}}=B/\sqrt{4\pi {\rho }_{\text{ext}}}$, the mass of the core is $M\sim 2\pi {\rho }_c{R}_c^{2}Z$, while the magnetic flux is ${\mathrm{\Phi }}_B\sim \pi R_c^{2}B$. This leads to

${\tau }_{\Vert }\sim {\left(\frac{\pi }{{\rho }_{\text{ext}}}\right)}^{1/2}\frac{M}{{\mathrm{\Phi }}_B}.(9)$

Therefore, the magnetic braking timescale depends on the cloud environment through the density of the external medium, ρ_ext. This emphasizes that magnetic braking represents a transfer of angular momentum between a faster rotating cloud and a slowly rotating surrounding medium.

However, as discussed earlier, in a collapsing cloud, the magnetic field lines are strongly bent and therefore in Eq. 8, one should take into account that as the Alfvén waves propagate away from the clouds, the field lines are fanning out. Moreover, at equilibrium the field lines are likely in corotation; otherwise, the field toroidal component will be further growing. This leads to modify Eq. 8 as

$\mathrm{\Omega }{R}_0^2\pi R_0^2{\rho }_{\text{ext}}{v}_{\text{A,ext}}{\tau }_{\Vert ,fo}\sim \mathrm{\Omega }{R}_c^2\pi R_c^2{\rho }_{c}Z,(10)$

where R₀ is the typical distance between the field lines and the rotation axis in the external medium. We thus obtain the magnetic braking time for the case of fan-out, τ_‖,fo, which is given by

${\tau }_{\Vert ,fo}=\frac{{\rho }_c}{{\rho }_{\text{ext}}}\frac{Z}{v_{\text{A,ext}}}{\left(\frac{R_c}{R_0}\right)}^4.(11)$

It is similar to Eq. 8, apart from the term ${(R_c/R_0)}^4$, whose origin is two-fold. First, because the field lines fan-out, the volume of the external medium swept by the Alfvén waves is larger by ${(R_0/R_c)}^2$ than when the field lines are straight. Second, because it is assumed that the field lines are in corotation, the fluid elements which are attached to the field lines have a specific angular momentum that increases like $R_0^2$. This altogether leads to another factor ${(R_0/R_c)}^2$.

Combining Eq. 11 with the expressions of the mass, $M\sim 2\pi {\rho }_c{R}_c^{2}Z$, the magnetic flux of the core ${\mathrm{\Phi }}_B\sim \pi R_0^2{B}_{\text{ext}}=\pi R_c^2{B}_c$, and the expression for v_A,ext, we obtain (Mouschovias and Morton, 1985),

${\tau }_{\Vert ,fo}={\left(\frac{\pi }{{\rho }_{\text{ext}}}\right)}^{1/2}\frac{M}{{\mathrm{\Phi }}_B}{\left(\frac{R_c}{R_0}\right)}^2.(12)$

Compared to the magnetic braking time with straight lines, the magnetic braking timescale is thus significantly reduced since in a collapsing core R_c ≪ R₀, and ${(R_c/R_0)}^2$ is expected to be a small number.

2.3.2 Perpendicular rotator (α = 90°)

In the case of a perpendicular rotator, that is, if magnetic field lines are initially perpendicular to the rotation axis, the braking timescale corresponds to the time it takes for the Alfvén waves to reach R_⊥, the radius at which the angular momentum of the external medium is equal to the initial angular momentum of the cloud. The Alfvén waves propagate in the equatorial plane and sweep a cylinder of half-height Z and radius R_⊥, thus

${\rho }_{\text{ext}}\left(R_{\perp }^4-R_c^4\right)\sim {\rho }_c{R}_c^4.(13)$

Considering that the magnetic field is such that B(r) ∝ r⁻¹, so that v_A(r) = v_A (R_c) × R_c/r, the magnetic braking time is then

${\tau }_{\perp }={\int }_{R_c}^{R_{\perp }}\frac{\mathrm{d}r}{v_{\text{A}}\left(r\right)}=\frac{1}{2}\frac{R_c}{v_{\text{A}}\left(R_c\right)}\left[{\left(1+\frac{{\rho }_c}{{\rho }_{\text{ext}}}\right)}^{1/2}-1\right],(14)$

which leads to

${\tau }_{\perp }\sim 2{\left(\frac{\pi }{{\rho }_c}\right)}^{1/2}\frac{M}{{\mathrm{\Phi }}_B}.(15)$

Comparing the braking timescales between the aligned configuration with straight field lines and the perpendicular rotator, Eqs 9, 15 give

$\frac{{\tau }_{\Vert }}{{\tau }_{\perp }}=\frac{1}{2}{\left(\frac{{\rho }_c}{{\rho }_{\text{ext}}}\right)}^{1/2}.(16)$

Since ρ_c ≫ ρ_ext, magnetic braking is found to be more efficient in the perpendicular case. However, when taking into account the fact that field lines are fanning out, the term ${(R_c/R_0)}^2$ must be taken into account. As an illustrative example, let us assume that the density follows the singular isothermal sphere, that is, ${\rho }_{\text{ext}}(R_0)\propto R_0^{-2}$ and ${\rho }_c(R_c)\propto R_c^{-2}$. With Eqs 12, 15, we obtain

$\frac{{\tau }_{\Vert ,fo}}{{\tau }_{\perp }}=\frac{R_c}{R_0}.(17)$

Since R_c/R₀ ≪ 1, the magnetic braking time is thus shorter in an aligned rotator than in a perpendicular one, provided the field lines are fanning out.

Numerical simulations of misaligned collapsing cores have been performed by Matsumoto and Tomisaka (2004), Joos et al. (2012), Tsukamoto et al. (2018), and Hirano et al. (2020), where analysis of the angular momentum distribution through the core was also performed. The reported results have been in apparent contradiction. While Matsumoto and Tomisaka (2004) and Tsukamoto et al. (2018) concluded that the angular momentum in the core was higher in the aligned configuration than in the perpendicular one, whereas Joos et al. (2012) and Hirano et al. (2020) concluded the opposite. The origin of this apparent contradiction lays on the different timescale that are being probed in these studies. Matsumoto and Tomisaka (2004) and Tsukamoto et al. (2018) analyze their simulations at a relatively early time that is to say before any disk forms. They also analyze the angular momentum within very dense material. However, Joos et al. (2012) and Hirano et al. (2020) investigate later times, that is, after a disk has formed and looked at the angular momentum distribution through the core. The most likely explanation is that at early times and for the densest material, the field lines have not been strongly stretched and thus the braking time is shorter in the perpendicular configuration than in the parallel one. However, as time goes on, the material that falls in the central region, say the star/disk material, was initially located further away and thus the corresponding field lines are more and more bent leading to a stronger braking.

3 The formation of centrifugally supported disks

In recent years, most of the efforts regarding the collapse of dense cores have been devoted to the study of disk formation. This has appeared to be a complex topic, which in particular relies on the assumptions made regarding the microphysics. Here, we follow a progressive approach starting from the basics.

3.1 What is the origin of angular momentum in star formation models?

The very first question to be asked when discussing rotationally supported disks is obviously, what is the value of angular momentum to be considered and where it comes from? Traditionally, the working assumption has been that angular momentum was inherited from large scales and that it was conserved, at least to some degree, during the collapse. While this picture is widely accepted, it should be stressed that, in fact, it partly relies on the underlying assumption that the collapsing cloud is axisymmetric, in which case the distinction between radial and azimuthal velocity fields can be made rigorous. Moreover, observationally, infall and rotational motions can be made easi. However, in the general case, clouds are not axisymmetric and this has important consequences. First, while angular momentum is still conserved with respect to the center of mass, the latter is usually not a relevant point because it is not the collapse center. Moreover, the star that forms is not attached to the center of mass, but its position moves as it evolves, creating small offsets between the global center of mass of the envelope + star system and the star itself. Therefore, angular momentum is not a conserved quantity with respect to the star. From the inertial forces, a torque is actually operating. This implies that angular momentum may not necessarily need to be inherited from the large scales. Indeed, Verliat et al. (2020) investigated the collapse of a non-axisymmetric cloud, which initially had no motion and therefore no angular momentum. They show that in this configuration, disks would form as well.

In the rest of the section, we will not consider this scenario further, but it will be discussed later in this review.

3.2 Disk formation in hydrodynamical models

Let us consider a rotating and axisymmetric cloud without magnetic field. In such circumstance, angular momentum is a conserved quantity. Let M_* be the stellar mass and j be the fluid particle specific angular momentum. The centrifugal radius, r_d, is such that centrifugal and gravitational forces compensate each other, leading to

$r_d=\frac{j^2}{G{M}_{\ast }},(18)$

which clearly shows that disk formation is directly related to angular momentum distribution.

Let us consider a cloud with a density profile initially proportional to 1/r² (Shu, 1977), leading to a mass, M(R₀), within radius R₀, such that M(R₀) ∝ R₀. On the one hand, the specific angular momentum is given by $j(R_0)=R_0^2\mathrm{\Omega }$. Therefore, we get $j(R_0)\propto M{(R_0)}^2$. The centrifugal radius for a fluid particle initially located in R₀ can therefore be expressed as $r_d=j{(R_0)}^2/(GM(R_0))\propto M{(R_0)}^3$ (Terebey et al., 1984). On the other hand, considering a uniform density, $M(R_0)\propto R_0^3$ and $j\propto M{(R_0)}^{2/3}$, which gives $r_d\propto M{(R_0)}^{1/3}$. If for simplicity a constant accretion rate is assumed, the disk is found to grow like t³ when the density is initially in r⁻² and to grow like t^1/3 when it is uniform.

From these two examples, it is seen that the angular momentum distribution sensitively determines the disk radius. To get a quantitative estimate useful for reference, let ρ₀ be the cloud density, and Ω₀ be the angular rotation velocity. For a fluid particle initially located at radius R₀, the centrifugal radius is given by

$\begin{array}{ll}\hfill r_{\text{d,\hspace{0.17em}hydro}}& \simeq \frac{{\mathrm{\Omega }}_0^2{R}_0^4}{4\pi /3{\rho }_0{R}_0^{3}G}=3\beta R_0\hfill \\ \hfill & =106\mathrm{A}\mathrm{U}\frac{\beta }{0.02}{\left(\frac{M}{0.1M_{\odot }}\right)}^{1/3}{\left(\frac{{\rho }_0}{10^{-18}{\text{g\hspace{0.17em}\hspace{0.17em}cm}}^{-3}}\right)}^{-1/3},\hfill \end{array}(19)$

where $\beta =R_0^3{\mathrm{\Omega }}_0^2/3GM$ is the ratio of rotational over gravitational energy. Note that observationally, cores have been initially inferred to have a typical β ≃ 0.02 (Goodman et al., 1993; Belloche, 2013), which is the value used for reference.

3.3 Disk formation in ideal MHD models

The first collapse calculations, which have been performed with a magnetic field, assumed to be parallel to the rotation axis (Allen et al., 2003; Galli et al., 2006; Price and Bate, 2007; Hennebelle and Fromang, 2008; Mellon and Li, 2008). A surprising conclusion has been that even with relatively modest magnetic fields, typically corresponding to μ as high as 5–10, the disk formation was nearly suppressed, a process which has been called catastrophic braking. The reason of this behavior can be understood by using simple orders of magnitude.

The magnetic braking and the rotation time, which are most important, are given by

${\tau }_{\text{br}}\simeq \frac{\rho v_{\varphi }4\pi h}{B_z{B}_{\varphi }},(20)$

${\tau }_{\text{rot}}\simeq \frac{2\pi r}{v_{\varphi }},(21)$

where h is the scale height of the disk. If the rotation time is longer than the braking time, a fluid particle may rotate a few times before it loses a significant amount of angular momentum. Since the magnetic torque is proportional to B_ϕ, we need to estimate it, which can be accomplished using the Maxwell–Faraday equation. Essentially, B_ϕ is produced by the twisting of the poloidal magnetic field by differential rotation. As long as ideal MHD holds, it grows continuously with time, and we have

$B_{\varphi }\simeq {\tau }_{\text{br}}\frac{B_z{v}_{\varphi }}{h}.(22)$

This leads to

$\frac{{\tau }_{\text{br}}}{{\tau }_{\text{rot}}}\simeq {\left(\frac{M_{\ast }}{M_{\text{d}}}\times \frac{h}{r_d}\right)}^{1/2}\frac{G^{1/2}\mathrm{\Sigma }}{2B_z}\simeq {\left(\frac{M_{\ast }}{M_{\text{d}}}\frac{h}{r_d}\right)}^{1/2}\frac{{\lambda }_{\mathit{eff}}}{4\pi },(23)$

where we have assumed $v_{\varphi }\simeq \sqrt{G{M}_{*}/r}$, M_* being the mass of the central star and where $M_{\text{d}}=\pi r_d^2\rho h$ is the disk mass, Σ = 2 hρ is the disk column density, and λ_eff = 2πG^1/2Σ/B is the mass-to-flux ratio. This shows that modest magnetic intensities corresponding to values as high as few times 4π, the magnetic braking timescale is shorter than the rotation time and therefore should prevent or severely limit the formation of centrifugally supported disk in good agreement with what has been inferred from the simulations.

3.4 Disk formation with non-ideal MHD

Since observational estimates of the typical values of μ in dense cores indicate values of a few (Crutcher, 2012), a very efficient magnetic braking capable of suppressing disk formation for most observed cores, are clearly in tension with observations. As mentioned in Section 2.3, misalignment between the magnetic field and rotation (Joos et al., 2012; Li et al., 2013; Gray et al., 2018; Hirano et al., 2020) could help to alleviate the problem by reducing the efficiency of magnetic braking. Indeed, disk formation is reported in all studies, which have considered misalignment for values of μ on the order of several, though the exact value of μ at which disk would form, varies between studies. We stress however that when a disk forms, if ideal MHD applies, the toroidal magnetic field within the disk is continuously amplified and therefore the disk quickly becomes thick and inflated (Hennebelle and Teyssier, 2008). This emphasizes the need to consider non-ideal MHD.

A very important property of ideal MHD is that the magnetic flux through a given fluid particle is conserved. When non-ideal MHD processes are important, significant deviations from flux freezing can be produced, and this may qualitatively change the impact of magnetic braking. Two main classes of process may lead to strong departures from flux freezing. First, if the coupling between the magnetic field and the neutrals is poor, and second, if the flow is strongly turbulent. Let us stress that the latter corresponds to a high magnetic Reynolds number, while the former would correspond to a low magnetic Reynolds number.

3.4.1 The possible role of turbulence

Turbulence violates the frozen-in condition of ideal MHD flows because it drives reconnection, and thus the diffusion of the magnetic field lines. Since the original proposition is made by Lazarian and Vishniac (1999), this has been extensively studied and demonstrated numerically (Kowal et al., 2009; Eyink et al., 2013; Santos-Lima et al., 2021).

The role that turbulence may have on disk formation has been carefully investigated by Santos-Lima et al. (2012), Seifried et al. (2012), and Joos et al. (2013). In all these studies, it has been concluded that the efficiency of magnetic braking is reduced by turbulence, though the proposed explanations were not identical. Santos-Lima et al. (2012) emphasized the role of turbulent reconnection which transports magnetic field outward therefore leading to a reduced magnetic torque, while Joos et al. (2013) stressed that the misalignment induced by turbulence may add up to the reconnection diffusion triggered by turbulence in reducing magnetic braking efficiency. Seifried et al. (2012) proposed that it may be the coherence of the averaged magnetic torque that is reduced by the fluctuating magnetic field, again induced by turbulence. While it is clear that reconnection diffusion is occurring in simulations, which include turbulence (Santos-Lima et al., 2013, for a discussion), it remains difficult to estimate the respective role played by these three effects, which all concur to favor disk formation.

3.4.2 Low ionization and high resistivities

One of the most obvious solutions to the so-called magnetic braking catastrophe is to be searched in high magnetic resistivities. This has been early proposed by Galli et al. (2006), where Ohmic dissipation was envisioned to limit magnetic braking. A long series of increasingly realistic calculations has since been performed by several authors. A comprehensive description of the various calculations performed can be found in Zhao et al. (2020).

For instance, Dapp and Basu (2010) show that when Ohmic dissipation is included in their calculation a small disk forms but not when they assume ideal MHD. This is because at small scale, the magnetic field is efficiently diffused out and therefore the braking time typically becomes longer than the rotation time. Several works have performed simulations that include ambipolar diffusion (Dapp et al., 2012; Tomida et al., 2013, 2015; Masson et al., 2016; Zhao et al., 2016; Hennebelle et al., 2020), finding that centrifugally supported disks of few tens of AU always form. Note that on the contrary, Wurster (2016) and Lam et al. (2019) conclude that ambipolar diffusion is not sufficient to produce a disk.

Analytical arguments to predict the radius of the disks have been developed by Hennebelle et al. (2016). The effect of ambipolar diffusion, τ_diff, is determined by a characteristic timescale, which describes how fast B_ϕ is diffused out of the disk

${\tau }_{\text{diff}}\simeq \frac{4\pi h^2}{c^2{\eta }_{\text{AD}}}\frac{B_z^2+B_{\varphi }^2}{B_z^2}\simeq \frac{4\pi h^2}{c^2{\eta }_{\text{AD}}}.(24)$

To get a stationary B_ϕ within the disk, equilibrium between generation and diffusion must occur. Combining Eqs 22, 24, as well as Eq. 20 with Eq. 21 together with an estimate of the density at the edge of the disk,

$\rho \left(r\right)=\delta \frac{C_{\text{s}}^2}{2\pi G{r}^2}\left(1+\frac{1}{2}{\left(\frac{v_{\varphi }\left(r\right)}{C_{\text{s}}}\right)}^2\right),(25)$

where δ is a coefficient on the order of a few, the following expression is inferred

$\begin{array}{ll}\hfill r_{ad}& \simeq 18\mathrm{A}\mathrm{U}\times {\delta }^{2/9}{\left(\frac{{\eta }_{\text{AD}}}{7.16\times 10^{18}{\text{cm}}^2{s}^{-1}}\right)}^{2/9}{\left(\frac{B_z}{0.1\mathrm{G}}\right)}^{-4/9}\hfill \\ \hfill & \times {\left(\frac{M_{\text{d}}+M_{\ast }}{0.1M_{\odot }}\right)}^{1/3}.\hfill \end{array}(26)$

This expression has been compared with a broad set of MHD simulations (Hennebelle et al., 2016, 2020) and an agreement within a factor of about 2 has been inferred for the simulations, in which the magnetic field is strong enough. It shows in particular that the disk size grows with the magnetic resistivity and also with the stellar mass.

The influence of the Hall effect (see Eq. 3) has been the subject of several studies. Let us first note a peculiarity of the Hall term. Flipping the sign of B in Eq. 3, we see that all terms, but Hall one, change their sign. Physically, this is because the Hall term describes the generation of the magnetic field induced by the motion of the charged particles induced by the Lorentz force. This implies that two configurations, that is, the aligned and anti-aligned cases (Ω.B > 0 and $<$ 0, respectively) have to be distinguished. As a consequence, several teams have found that in the aligned configuration, the magnetic braking is enhanced, and on the contrary, it is reduced. This includes the work of Braiding and Wardle (2012), in which analytical solutions are being used; Tsukamoto et al. (2015), Wurster (2016) perform 3D smooth particle hydrodynamical simulations and Marchand et al. (2019) perform adaptive mesh refinement calculations. Due to these different magnetic braking efficiencies, these authors find that the disks that form in the aligned case are smaller than the disks which form when the Hall effect is not accounted for, which are themselves smaller than the disks which form in the anti-aligned configurations. This has led to the idea of the possible existence of a bimodal population of disks. Lee et al. (2021c) have extended the study of Hennebelle et al. (2016) to include the Hall effect, predicting disks of similar size to that inferred in the simulations. Tsukamoto et al. (2017) present calculations of misaligned configuration and conclude that the impact of anti-alignment persists, even so the differences between 45° and 135° is significantly reduced compared to the differences between 0° and 180°.

Importantly, Zhao et al. (2020) and Zhao et al. (2021) have run 2D simulations for longer period of time and conclude that the external part of the disks formed in the anti-aligned configuration, tend to disappear, leading to a few tens of AU disks. This would suggest that the bimodal distribution could be a transient feature.

Finally, we stress that both the high resistivities and the reconnection diffusion induced by turbulence could contribute simultaneously or in different situations. For instance, if in some dense cores, the ionization fraction is high, the resistivities could be lower, and the reconnection diffusion is possibly dominant. However, so far the studies which areconsidered in isolated dense cores, both high resistivities and turbulence, have concluded that the latter does not substantially modify the formation of disk (Hennebelle et al., 2020; Wurster and Lewis, 2020).

4 Tracing magnetic fields with photons around protostars or at core scales

The current perspective on magnetic fields properties in star-forming cores has been established observationally by the analysis of polarized light, resulting from the interaction of the B-fields with the surrounding gas molecules and dust grains. Several observational techniques have been developed: we detail them concisely here as follows, and then describe how these measurements are used to obtain quantitative constraints from observed objects, and how the physical processes they rely on have been implemented in radiative transfer models to produce synthetic observations.

4.1 Observational signatures of magnetic fields in protostars

Most of the observational signatures of the presence of the magnetic field in the interstellar medium are directly related with polarization. However, there are other mechanisms that can also produce polarization and are not related with the presence of magnetic fields. Here on, we focus on the magnetic field signatures expected in molecular clouds at core’s scales, the possible caveats and other sources of polarization for each case:

4.1.1 Zeeman effect

Molecular rotational lines split in submagnetic levels under the presence of a magnetic field. The frequency separation of these levels is proportional to the magnetic field strength and the magnetic dipole moment. For most molecules, the magnetic dipole moment is very small, making the Zeeman splitting undetectable, except for the maser lines (Alves et al., 2012; Crutcher and Kemball, 2019). However, molecules with an unpaired electron have relatively large magnetic moments, yielding to significant Zeeman splitting. The Zeeman molecules that are abundant in molecular clouds are OH, CN, SO, CCH, and CCS. The splitting can be measured through circular polarization in almost all cases but not in total intensity. This is because the Zeeman splitting in frequency is typically only of the order of Hz μG⁻¹ (Bel and Leroy, 1989, 1998; Shinnaga and Yamamoto, 2000; Uchida et al., 2001; Turner and Heiles, 2006; Cazzoli et al., 2017), which is much smaller than typical linewidths in molecular clouds for the expected magnetic field strength (≲ few mG). The circular polarization is proportional to the magnetic field strength component along the line-of-sight, the intensity derivative, and the specific Zeeman splitting for the observed line. The molecules with hyperfine structure (CCH and CN) are more adequate to observe the Zeeman splitting because different hyperfine levels have different Zeeman splitting values. This allows to separate the possible instrumental polarization, which does not distinguish between hyperfine lines from the Zeeman effect. There have been several attempts to detect Zeeman effect at core scales, mostly through CN rotational transitions, but there are only a handful of detections reported in the literature (Crutcher, 1999; Crutcher et al., 1999; Levin et al., 2001; Falgarone et al., 2008; Maury et al., 2012; Pillai et al., 2016; Nakamura et al., 2019), and none at disk scales (Vlemmings et al., 2019; Harrison et al., 2021).

Caveats: this is the only method that can provide a direct estimation of the field strength along the line-of-sight. Nevertheless, in order to be able to derive the role of the magnetic fields at the core and disk scale, special care has to be made on, where the emission of the Zeeman molecules arise. These are radical molecules, so they are chemically active and their abundances may change significantly depending on the environment conditions. Thus, in prestellar cores, CN appears to behave as other N-bearing molecules and thus survives at high densities (Hily-Blant et al., 2008). On the contrary, CCH, CCS, and SO appear to deplete toward the core’s center (Tafalla et al., 2006; Padovani et al., 2009b; Juárez et al., 2017; Seo et al., 2019). For massive cores, all these molecules but SO appear to be anticorrelated with the dust emission at scales of ≲ 0.05 pc (Dirienzo et al., 2015; Paron et al., 2021). The distribution of these molecules in the planet-forming disk is also complex, and combined with the expected magnetic field configuration, the interpretation of Zeeman observations is made difficult (Mazzei et al., 2020).

4.1.2 Linear polarization of molecular lines

Rotational levels split into magnetic sublevels under the presence of magnetic fields. Transitions where the submagnetic level does not change will be linearly polarized, with the polarization angle parallel to the magnetic field. In the other cases, the polarization will be perpendicular to the magnetic field. In most cases, collisions do not differentiate among magnetic sublevels, so they populate the sublevels equally, which means that the net linear polarization is zero. However, an anisotropic radiation field will generate unbalance of the sublevels, giving a partially linearly polarized emission. This process is known as the Goldreich–Kylafis (G–K) effect because it was initially developed by Goldreich and Kylafis (1981). The level of linear polarization produced by the G–K effect depends on various parameters, such as the ratio of the collisional rate to the radiative decay rate and the optical depth (Goldreich and Kylafis, 1981, 1982; Deguchi and Watson, 1984).

However, the polarization direction can be parallel or perpendicular to the magnetic field. This means that the properties of the emission (optical depth, velocity, and density gradients) should be analyzed to solve this ambiguity. Once this is carried out, then this technique allows obtaining the magnetic field morphology projected in the plane of the sky. Multi-transition observations of the linearly polarized lines can be used to derive the field strength (Cortes et al., 2005). The G–K effect has been detected in a small sample of cores (Lai et al., 2003a; Girart et al., 2004; Cortes et al., 2005, 2008; Cortés et al., 2021), in few disks (Stephens et al., 2020; Teague et al., 2021) and in some molecular outflows (Girart et al., 1999; Ching et al., 2016; Lee et al., 2018a). Differential collisions due to ambipolar diffusion could also produce polarization in the ion molecules Lankhaar and Vlemmings (2020a).

Caveats: the properties of linearly polarized emission from a molecular line produced by the G–K effect can be altered if there is a foreground molecular component at the same velocity (Hezareh et al., 2013). This is the anisotropic resonant scattering (ARS) effect, which not only alters the properties of the linear polarization, but it leaks a fraction of this, generating circular polarization (Houde et al., 2013, 2022). There are some evidence that this may happen (Chamma et al., 2018). Sensitive observations of all Stokes parameters are needed to correct for this effect and obtain the unaltered original signature of the G–K effect. In addition, the detection of this non-Zeeman circular polarization could be used to measure the magnetic field strength (Houde et al., 2013). Molecular ions could also have collisionally driven linear polarization produced by ambipolar drifts (Lankhaar and Vlemmings, 2020a). The resulting polarization has an angle perpendicular to the magnetic field direction. This effect could be distinguished from G–K effect by using optically thin molecular ion lines.

4.1.3 Dust polarization

Since the early 1950s we know that interstellar grains are partially aligned with the magnetic fields (Davis et al., 1951). The major axis of the grains are aligned perpendicular to the magnetic field, yielding to linear polarization in the dust emission with an angle perpendicular to the magnetic field projected in the plane of the sky. There have been some proposed mechanisms that allow the grain angular momentum to align with the magnetic field (see review by Lazarian et al., 2015). Radiative torques (RATs) are thought to be the most efficient way to help grains to align with the magnetic field. Some predictions of this theory have been confirmed observationally (Alves et al., 2014; Jones et al., 2015). However, recent results with ALMA shows that at core scales RATs are not enough to explain the observed dust polarization properties (Le Gouellec et al., 2020). The dust emission appears to be polarized at significant levels (≳ 1%) in a significant high fraction of observed cores, and therefore it is the most used technique in the millimeter through far-IR wavelengths to study the magnetic fields at core and disk scales (Girart et al., 2009; Pattle et al., 2017; Alves et al., 2018; Sanhueza et al., 2021, and for a more complete references see Hull and Zhang, 2019; Pattle et al., 2022).

Caveats: at disks scales, grain growth is so important that self-scattering produced by large grains appears to be the dominant polarization mechanism (Kataoka et al., 2015; Yang et al., 2017; Kirchschlager and Bertrang, 2020), although other mechanisms have also been proposed to generate polarization at disk scales (Tazaki et al., 2017; Brunngräber and Wolf, 2019; Kataoka et al., 2019). Of special interest for environments containing large grains, if feasible, the alignment of these grains with magnetic fields in the Mie regime, when grains start to have a size similar to or larger than the wavelength of the incident light (Guillet et al., 2020a). At the core scales, in the densest part where the dust emission may be optically thick, especially at the shortest wavelengths, the polarization pattern may be altered or even reversed (Liu et al., 2016; Ko et al., 2020).

4.1.4 Ion to neutral velocity drift

The ionization fraction in molecular clouds is tiny, $\sim 10^{-6}$, but the ions and neutrals are well coupled. However, small kinematic differences are expected due to diffuse processes such ambipolar diffusion (Houde et al., 2000; Li and Houde, 2008; Falceta-Gonçalves et al., 2010). This effect can be observed as differences between neutrals and ions, in their linewidth and in the velocity maps. HCO⁺ and HCN lines with the same rotational level from their different isotopologues are ideal to test this because they have similar excitation conditions. The linewidth differences have been observed in several cores (Houde et al., 2000; Lai et al., 2003b). In a magnetized turbulent medium the linewidth difference should change with the length scale, which has been observed at $\sim 0.1$ pc scales, allowing to measure the turbulent dissipation scale and the magnetic field strength (Li and Houde, 2008; Hezareh et al., 2010, 2014). Recent observations of NH₃ and N₂H⁺, at ≲ 0.1 pc scales, show that, contrarily of what is expected in AD, the ion linewidth is systematically broader than the neutral by 20% (Pineda et al., 2021).

Caveats: the expected velocity drift is very difficult to measure at small scales typical of inner envelopes, as the velocity offset is expected to be of the order of the best spectral resolution currently available from typical instruments, and the velocity field is complex (Yen et al., 2018; Cabedo et al., 2022). The main limitation of this method is to ensure that the selected neutral and ion species trace the same gas or are affected by optical depth effects (Pratap et al., 1997; Jørgensen et al., 2004; Girart et al., 2005; Zinchenko et al., 2009).

4.1.5 Observational techniques to infer magnetic field properties

Here, we describe the main techniques that allow to infer the magnetic field properties from observations, independently of the use of the radiative transfer tools that are described in the next subsection. The most popular technique is the Davis–Chandrasekhar–Fermi (CDF) equation (Davis et al., 1951; Chandrasekhar and Fermi, 1953), which allows estimating the magnetic field strength in the scenario of small perturbation due to the anisotropic motions (such as turbulence). The equation relates the magnetic field in the plane of the sky, B_pos with the gas density, ρ, the non-thermal velocity dispersion along the line-of-sight, δv, and the dispersion of the polarization angles of in the plane of the sky, δθ: $B_{\text{pos}}=\sqrt{4\pi \rho }\delta \mathrm{v}/\delta \mathrm{\theta }$ (Chandrasekhar and Fermi, 1953). There have been several works to account for the limitations of this technique, such as line-of-sight smearing or cases with large dispersion, that in general leads to an overestimation of the field strength (Heitsch et al., 2001; Ostriker et al., 2001; Falceta-Gonçalves et al., 2008; Cho and Yoo, 2016; Liu et al., 2021; Skalidis and Tassis, 2021). A more sophisticated method is the use of the structure function, which allows separating the turbulent component from the smooth variations of the polarization angles to the large scale field (Hildebrand et al., 2009; Houde et al., 2009, 2011, 2016). There are other (semi) analytical expressions that allow to evaluate the relevance of magnetic fields for the specific hour glass configuration (Ewertowski and Basu, 2013; Myers et al., 2018).

4.2 Polarized radiative transfer tools for protostellar environments

In this section, we describe how physical processes responsible for producing polarized light as a result of the interaction of magnetic fields with protostellar material are implemented in radiative transfer codes and coupled to the numerical models for star and disk formation. We focus on two codes, which are widely used by the community interested in star formation: POLARIS for dust grain alignment (Reissl et al., 2016) and PORTAL for spectral lines (Lankhaar and Vlemmings, 2020b). While a complete description of the polarization-inducing processes go beyond the scope of this review, we briefly describe them later.

4.2.1 Radiative transfer of emission from magnetically aligned grains

The three-dimensional continuum radiative transfer code POLARIS (Reissl et al., 2016) uses 3D models of astrophysical structures to produce synthetic maps of the polarized dust continuum emission, allowing several flavors of alignment mechanisms for the dust grains. The photon propagation within the 3D model is implemented following a Monte Carlo photon transfer scheme. The interaction of the incoming radiation with dust grains is determined in each cell, and it depends mostly on the cross section of extinction, the dust density. Depending on the local physical conditions such as the dust grain albedo, POLARIS either computes the scattering or the absorption with instantaneous re-emission, then a new wavelength is calculated and the dust thermal energy of the cell is adjusted. In this computation of photon propagation and dust heating mode, POLARIS assumes that dust grains are spherical: this step thus allows to derive the dust temperature in each cell with a limited computational effort. The alignment probability of dust grains in each cell is calculated, accounting for the imperfect internal alignment and the imperfect alignment between the dust grain’s angular momentum and magnetic field. Then, the anisotropy of the radiation field at any given wavelength λ is calculated in each cell, which allows determining the alignment of the different dust grains due to radiative torques (RATs, see previous section). Since a distribution of dust grain sizes is considered (usually following a classical MRN, after Mathis et al. (1977), distribution consisting of power laws of separate populations of bare spherical silicate and graphite grains), the RAT alignment in given irradiation and B-field conditions depends also on the effective grain radius a_align. Dust grains larger than a_align are considered aligned (with a fraction depending on the high-J attractor point f_high−J, which can be manually set to any value between 0 and 1), and contribute to the polarization of the dust thermal emission. Several studies have used the POLARIS code to predict and confront observations of polarized dust emission, from molecular cloud conditions (Liu et al., 2021; Reissl et al., 2021) down to disk conditions (Brunngräber and Wolf, 2021). Note that a few studies have used radiative transfer tools developed in a recent past, such as Dustpol (Padovani et al., 2012; Lee et al., 2017) but here we focus on the most recent results, and hence on POLARIS because it is the most widely used RT code for dust polarization nowadays. An example of synthetic observations of the polarized dust emission, assuming different alignment conditions for the dust from the same numerical model of a collapsing core, is shown in Figure 1. Details and results of the works specifically dedicated to protostars are described in the next Section 4.3 later.

FIGURE 1

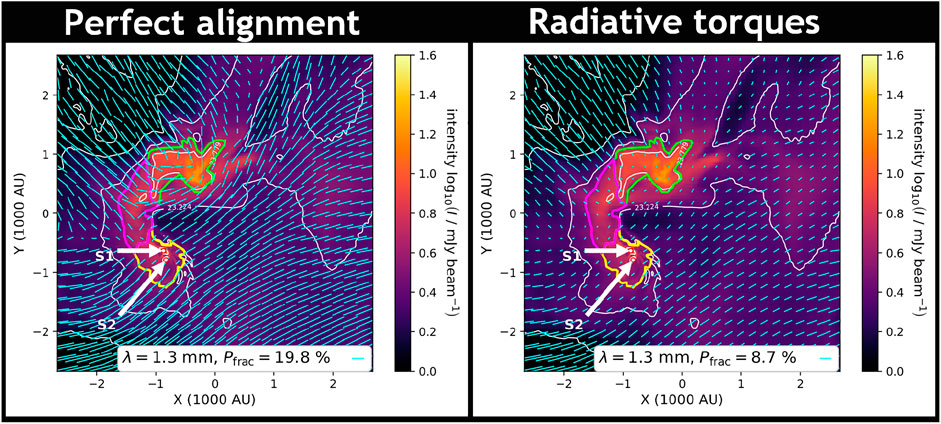
FIGURE 1. Example synthetic maps of the 1.3 mm dust continuum emission from an MHD protostellar formation model, using the POLARIS radiative transfer tool. Overlaid are the polarization vectors rotated by 90°, obtained either considering perfect alignment of the dust grains (right) or RAT grain alignment (left), from Kuffmeier et al. (2020).

4.2.2 Radiative transfer of emission from magnetically sensitive molecular lines

The POLARIS code can also be used to simulate the polarization of spectral lines due to the Zeeman effect, thanks to the ZRAD extension (Brauer et al., 2017). This is based on the line RT algorithm Mol3D (Ober et al., 2015), and makes use of atomic and molecular parameters such as the energy levels and transitions taken from the Leiden Atomic and Molecular Database (LAMDA), the Landé factors of the involved energy levels, the line strengths of the allowed transitions between Zeeman sublevels, and emitting radius of the molecular species. It has been used to test the robustness of Zeeman measurements to infer the magnetic field strengths in molecular clouds, showing that while the gas density affects little uncertainty of the measurements, strong variations in the LOS component of the gas velocity and of the magnetic field strength significantly impact the precision of the method (Brauer et al., 2017).

PORTAL is an adaptive three-dimensional polarized line radiative transfer model that considers the local anisotropy of the radiation field as the only alignment mechanism of molecular or atomic species to calculate the aligned molecular or atomic states. It allows simulating the polarization of photons produced from line emission through a magnetic field of arbitrary morphology. While it can be run in stand-alone mode, PORTAL can also process the outputs of 3D radiative transfer codes on regular grids. It has been used, coupled to the parallelized non-LTE 3D line radiative transfer code line emission modeling engine (LIME, Brinch and Hogerheijde 2010), to predict spectral line polarization of different molecular transitions arising from protoplanetary disks, at the ALMA wavelengths (Lankhaar et al., 2022).

4.3 Synthetic observations of B-fields from protostellar models: Methods

The question of the physical processes causing the polarization of photons from star-forming structures, both from the dust and from molecular species, has been a long-standing one. Some simple analytical models assuming a quasi-perfect alignment of dust grains with magnetic field lines, for example, have been proposed in the past, and sometimes even successfully reproduced some observations (Padovani et al., 2012). The development of more detailed physical models of grain alignment have allowed more predictive studies of the polarized dust emission arising from magnetically aligned grains and quantitative confrontation to observations performed toward protostellar envelopes.

The combination of polarized radiative transfer, as described earlier, to state-of-the-art numerical models of protostellar formation can be used to compare model predictions to actual observations. The general process is quite standard. First, one selects the outputs that correspond the best to the properties of the observed object to be compared to. Usually, a numerical simulation output can be extracted as a data cube containing the gas density, the gas pressure (or equivalently the gas temperature), the three components of the velocity field, and the three components of the magnetic field. These gas properties are extracted and put in a suitable format to be post-processed with a radiative transfer code, such as Polaris. The central radiation source is modeled as a blackbody of chosen luminosity that allows to reproduce the observed bolometric luminosity of the studied object. Note that, to facilitate the propagation of photons and avoid missed photon packages from the central source due to long computational times, many authors choose to artificially empty a small central sphere of radius a few au around the sink particle, as in Valdivia et al. (2019). The radiative transfer can also include an external isotropic radiation field of strength that illuminates the external layers of the core. The dust properties are normally taken from tabulated values and in most studies assumed uniform throughout the model, with a gas-to-dust ratio of 100, and a typical composition and size distribution reproducing observations of dust in the ISM (Mathis et al., 1977; Hildebrand and Dragovan, 1995). The radiative transfer calculation is carried out via Monte Carlo methods or ray tracing methods. For example, the POLARIS code computes the propagation of photons alongside the dust temperature via an MCMC analysis first, and then solves the grain alignment equations, using the density, radiation field, dust grain properties, and temperature, in each cell of the grid. Grain alignment can be assumed to be perfect, or to depend under local conditions, as, for example, when assuming RAT alignment (Hoang and Lazarian, 2014). The outputs are maps of the Stokes I, Q, and U from the dust thermal emission, which can be further convoluted by instrumental effects (e.g., the simobs task in CASA to simulate ALMA datasets) and compared to observations.

5 Observed protostellar properties

Measuring the properties of the gas, the dust, and the magnetic field in embedded protostars is not only a cornerstone to inform the magnetized models of star formation and test their predictions but also understand the role of non-ideal effects in disk formation and evolution. We recall here some key observational results, which relate directly to these questions.

5.1 Dust grains

Because they are the seeds from which planet formation processes are triggered in circumstellar disks, and because they are also key agents in the efficiency of coupling the magnetic field to the gas, characterizing dust grains is a cornerstone in building a comprehensive scenario of star formation.

In the far-IR and longer wavelengths, the opacity of astrophysical dust scales with wavelength as κ_ν ∝ ν^β, where β is the emissivity spectral index of dust emission. β reflects how emissive dust grains are, and is therefore, commonly used to characterize dust grains in astrophysical structures. It is measured by comparing the relative intensity of dust thermal emission when observed at different wavelengths: indeed, if the dust emission is optically thin, the ratio of flux densities at different wavelengths only depends on β. In the diffuse interstellar medium, Planck studies have shown the dust has β ∼ 1.6 (Planck collaboration et al., 2011; Juvela et al., 2015). Observational works show that significant variations in β is found at protostellar core scales, with millimeter wavelength β values much lower than this typical value, however (Martin et al., 2012; Chen et al., 2016; Sadavoy et al., 2016; Bracco et al., 2017; Van De Putte et al., 2020).

While studies dedicated to resolving the dust properties at small radii in embedded protostars (Jørgensen et al., 2007; Kwon et al., 2009; Chiang et al., 2012; Miotello et al., 2014) started before the advent of large millimeter interferometers such as NOEMA and ALMA, the development of these two observatories has allowed a significant leap forward in this area of research. Li et al. (2017), Galametz et al. (2019), Tychoniec et al. (2020), and Bouvier et al. (2021) have measured the dust emissivity spectral index in relatively large samples of embedded protostars, finding β values ranging between 0 and 2, with a majority of the protostellar dust exhibiting β < 1 at envelope radii $\sim 500$ au. Figure 2 shows in its left panel the observations of millimeter dust emissivity indices measured by Galametz et al. (2019) in the CALYPSO survey, finding that most protostars show significantly shallow dust emissivities at envelope radii $\sim 100-500$ au, with β < 1. Galametz et al. (2019) performed an analysis of their interferometric data in the visibility space, allowing to also distinguish a radial evolution of the dust emissivity, with many objects showing a decrease of β with decreasing envelope radius. These observations also confirm that it is the dust pertaining to the innermost envelope, and not to the unresolved disks at smaller scales, which is different from the dust typically observed in the diffuse ISM. In Class I protostars, less observations sensitive to the inner envelope regions are available: despite the poor statistics they also tend to show low dust emissivity in a majority of objects, with sometimes extremely low values (β < 0.5) at disk scales (Harsono et al., 2018; Nakatani et al., 2020; Zhang et al., 2021).

FIGURE 2

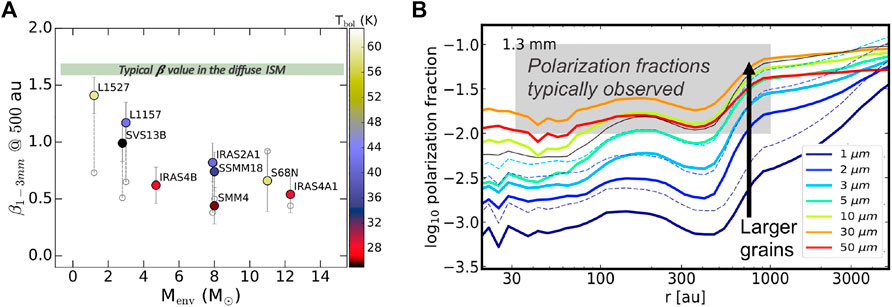
FIGURE 2. (A) Observed millimeter dust emissivity index in a sample of young protostars (Galametz et al., 2019). All protostellar envelopes probed at radii $\sim 500$ au show lower values than the progenitor diffuse ISM. (B) Radial profile of the polarization fraction from the 1.3 mm dust emission predicted from RAT alignment of dust grains in a typical low-mass protostellar envelope (Valdivia et al., 2019). Large ($>10\mu$m) dust grains are required to match the observations of the polarized emission (gray area).

Other effects affecting the millimeter flux could be responsible for the low dust opacities found, such as anomalous emission from spinning dust grains (Planck Collaboration et al., 2011), contamination by non-thermal emission, or the dust self-scattering (Liu et al., 2019). At the typical envelope scales, however, both the effects of optical depth and non-thermal emission are expected to be negligible at millimeter wavelengths (Tychoniec et al., 2020).

Another possible explanation for the observed difference in the dust emissivity β could stem from different dust grain compositions compared to that of the diffuse ISM. For example, it has been suggested that grains with higher ratio of carbonaceous to silicate would exhibit lower β (Jones et al., 2017; Ysard et al., 2019; Zelko and Finkbeiner, 2020). Similarly, grains that are less compact and fluffier could also be associated to low emissivity (Köhler et al., 2008; Brunngräber and Wolf, 2021). These explanations are not favored as the unique cause for the observed low emissivities, however, because of the low values found by observations (around 0), which cannot be matched by current dust models, even with significant changes of composition and compactness. Indeed, laboratory studies probing different interstellar dust analogs suggest that dust emissivities $<$1 at mm wavelengths can only be produced by grains larger than 100 μm (Demyk et al., 2017b,a; Ysard et al., 2019) under the typical physical conditions reigning in protostellar envelopes.

Another independent thread of evidence for the presence of relatively large grains in Class 0 envelopes and disks stems from polarimetric observations (Le Gouellec et al., 2019; Lee C.-F. et al., 2021), and their comparison to synthetic observations (Valdivia et al., 2019; Le Gouellec et al., 2020) is performed as described in 4.3. They show that relatively large grains are required to reproduce the observed level of polarization fractions (see an example in the right panel of Figure 2). Indeed, if dust grains align following the radiative torques (RATs) theory, the radiation field in deeply embedded protostellar environments is not prone to align the small grains where polarization of the dust mm emission is routinely detected. Only synthetic observations performed with dust grain size distributions including grains up to a_max ∼ 20 μm produce polarized dust emission at levels similar to those currently observed in solar-type protostars, at (sub-)millimeter wavelengths.

5.2 Fraction of ionized gas

Characterizing the ionization of the gas in the dense envelope material is critical to set constraints on the coupling of the magnetic field with the infalling-rotating envelope gas, and the role of diffusive processes, such as ambipolar diffusion or reconnection diffusion, to counteract the outward transport of angular momentum from the infalling-rotating envelope due to B-fields is also critical.

Cosmic rays (CRs), mostly relativistic protons, are the dominant source of ionization in relatively dense molecular gas, where ultraviolet radiation cannot penetrate (Grenier et al., 2015). Protostars are deeply embedded sources, where the gas ionization fraction can only be inferred using indirect chemical signatures. A handful of measurements were obtained in Class 0 objects at core scales (typical densities n_{H_{2}} ∼ 10⁴ cm⁻³): they suggest typical cosmic ray ionization rates χ_e ∼ 10^–17 − 10^–15 s⁻¹ with large uncertainties (Ceccarelli et al., 2014; Podio et al., 2014; Favre et al., 2017, 2018). In Class I protostars, only a few studies have been carried out, using the abundance of HCO⁺ to estimate gas ionization from cosmic rays in two young disks around ξ ∼ 10⁻¹⁷s⁻¹ and suggest it is lower in the disk compared to the inner envelope (Harsono et al., 2021; van ’t Hoff et al., 2022). Such low values may suggest it is unlikely that the accretion through the disk to the central star could be driven by magneto-rotational instabilities. In Class 0 protostar B335, Cabedo et al. (2022) used deuteration detected in molecular line emission maps to characterize the ionization of the gas at envelope radii ≲ 500 au (typical densities n_{H_{2}} ∼ 10⁶ cm⁻³) and found a large cosmic ray ionization rate ζ between 10^–16 and 10^–14 s⁻¹. Such high values seem inconsistent with the fiducial value if the interstellar cosmic rays flux is responsible for the gas ionization, as it should be efficiently attenuated while penetrating into the dense cores (Padovani et al., 2018). The observations of Cabedo et al. (2022) also show the CRs ionization rate is increasing at small envelope radii, toward the central protostellar embryo. Several theoretical works have investigated the role of shocks at the protostellar surface and magnetic mirroring within the jets as efficient forges to accelerate locally low-energy cosmic rays, and their role in increasing the ionization rate of the shielded protostellar material (Padovani et al., 2015; Silsbee et al., 2018; Fitz Axen et al., 2021; Padovani et al., 2021). In B335, it seems that local acceleration of CRs, and not the penetration of interstellar CRs, may be responsible for the gas ionization at small envelope radii. This would imply that, in the inner envelope, the collapse transitions from non-ideal to a quasi-ideal MHD occurs once the central protostar starts ionizing its surrounding gas, and very efficient magnetic braking of the rotating-infalling protostellar gas might then take place.

5.3 Gas kinematics: Angular momentum and mass infall rates

The dynamical role of the magnetic field can also be assessed by careful examination of the distribution of angular momentum associated to protostellar gas, and measurement of the mass transported inward, from envelope-to-disk scales (Pineda et al., 2019; Galametz et al., 2020; Yen et al., 2021b). This is not simple from an observational point of view, as the velocity field of the molecular gas is much less organized than expected from the simple monotonous collapse of axisymmetric rotating cores in many protostars. Recent studies have revealed envelopes with complete reversal of the velocity fields, or containing multiple velocity components (Maureira et al., 2017; Gaudel et al., 2020) at radii r < 5,000 au. Figure 3 shows a few recent examples of the detection of well-developed asymmetric features from envelopes to disk scales, which may trace preferred pathways funneling the accretion, such as streamers (Pineda et al., 2020; Chen et al., 2021) or supersonic infall along outflow cavity walls (Cabedo et al., 2021).

FIGURE 3

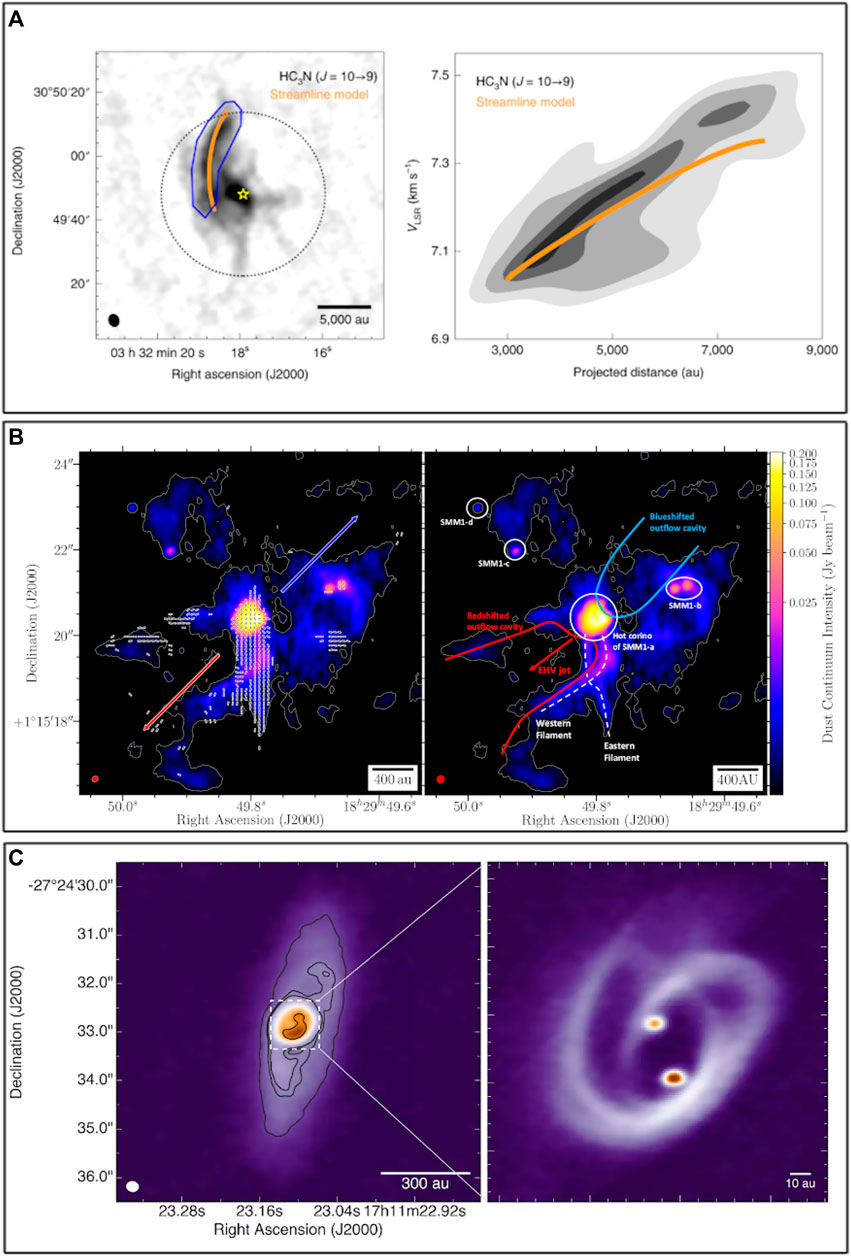
FIGURE 3. Streamer structures seen at different scales and towards different embedded protostars. (A) IRAS 03292+3039 in Perseus (Pineda et al., 2020). (B) Serp-SMM1 in Serpens (Le Gouellec et al., 2019). (C) [BHB2007] 11 in the Pipe (Alves et al., 2019).

Mass infall rates from large to small scales are difficult to estimate, as the complex kinematics of envelopes surrounding embedded protostars produce convoluted signatures, whose degeneracies can only be lifted by a joint analysis of a variety of tracers probing widely varying density conditions and spatial scales. Double-peaked profiles in spectral lines from molecular species (due to self-absorption) with a brighter blue-shifted peak are sometimes used as a signpost of probable infall motions (Choi et al., 1995; Mardones et al., 1997; Evans et al., 2015; He et al., 2015; Yang et al., 2021). These profiles are used to derive infall rates, ${\dot{M}}_{\inf }$, following the expression: ${\dot{M}}_{\inf }=(\mathrm{\Omega }/2)V_{\inf }(R_{\text{c}})\mu m_{\text{H}}⟨n_{\text{H˙}2}⟩R_{\text{c}}^2$, where Ω is the solid angle subtended by the core center over which infall occurs, R_c is the core’s radius, V_inf (R_c) is the infall velocity at this radius, and ⟨n_{H_{2}}⟩ is the core’s average volume density (Beltrán et al., 2022). Surprisingly, few of these line profiles are observed toward embedded protostars at core scales (Mottram et al., 2013, 2017). Interferometric observations resolving the inner envelopes also revealed only a handful of them, for which modeling suggests typical mass infall rates $\sim 10^{-5}{\mathrm{M}}_{\odot }$ per year at $\sim 500$ au scales in Class 0 protostars (Pineda et al., 2012; Evans et al., 2015; Su et al., 2019). Class I protostars in Ophiuchus have been surveyed with ALMA, exhibiting typical mass accretion rates a few 10^–7 M_⊙ per year (Artur de la Villarmois et al., 2019). In the well-characterized Class I protostar TMC1-A, the observed mass infall rate is measured to be larger than the value toward Ophiuchus Class I, estimated around $\sim 10^{-6}{\mathrm{M}}_{\odot }$ per year. This protostar also shows a decelerating infall velocity toward small radii, and an infall velocity $\sim 0.3$ times smaller than the free-fall velocity yielded by the dynamical mass of the protostar (Aso et al., 2015). The accretion rates derived in high mass star-forming cores are significantly larger, typically between $\sim 10^{-4}$ to 10^–2 M_⊙ per year at scales of few hundred to few thousands of au (Beltrán et al., 2006; Qiu et al., 2011; Wyrowski et al., 2012; Liu et al., 2013, 2020). In the case of G31.41 + 0.31, high angular resolution multi-line inverse P-Cygni measurements indicate infall acceleration at decreasing radius (Beltrán et al., 2022).

A key figure to assess the magnitude of rotational energy contained in protostellar cores, and compare these rotational motions to model predictions, is the specific angular momentum of the gas j_spe = r × v_ϕ. High angular resolution observations of molecular line emission in Class 0 protostars have revealed that the gas contained in envelopes has a specific angular momentum j_spe ∼ 10²⁰ cm² s⁻¹ at 1,000 au (Yen et al., 2015a; Tatematsu et al., 2016; Pineda et al., 2019; Gaudel et al., 2020; Hsieh et al., 2021; Heimsoth et al., 2022). In the literature, it is common to find that the conservation of angular momentum in an infalling-rotating envelope should produce a radial profile of rotational velocity v_ϕ ∝ r⁻¹ because j_spe = r × v_ϕ should be constant. If the initial rotation profile at the beginning of collapse follows a v_ϕ ∝ r⁻¹ relationship, this is true, but it is not true in most cases. Indeed, an infalling envelope initially in solid body rotation (v_r ∝ r^−1/2 and v_ϕ ∝ r) should exhibit j_spe ∝ r². If gas particles conserve their specific angular momentum during the collapse, the slope of the radial profile j_spe(r) should be conserved with time as they move inward, and protostellar envelopes should thus be observed with j_spe ∝ r² down to the disk sizes. However, this is not what is observed. At envelope radii between 1,000 and 10,000 au, j_spe scales as a power-law with radius, j_spe ∝ rⁿ with n ∼ 1.6–1.8. Interestingly, as pointed out by Gaudel et al. (2020), this scaling is closer to the trend expected from the dissipation cascade of Kolmogorov-like turbulence than from solid body rotation. This may suggest that large-scale ISM turbulence or turbulence locally driven around/by protostars is actually responsible for the observed angular momentum in outer envelopes. Moreover, resolved observations have identified a break in the specific angular momentum radial profiles, from the steep outer profile j_spe(r) ∝ r^1.6 at envelope radii r > 1,600 au, to a quasi-flat j_spe(r) ∼cte inner profile at radii $<1600$ au (Gaudel et al., 2020). If angular momentum was conserved during the collapse, it suggests that the initial angular momentum profile in these cores was, also, mostly flat and would rule out that cores are built with solid body rotation as initial conditions.

Taken altogether, these observed features suggest that a complex interplay of magnetic fields, turbulence, and gravity are responsible for organizing the collapse along preferential directions, and that the angular momentum contained at small scales does not seem closely related to the gas flows observed at larger envelope radii.

5.4 Magnetic fields at core’s scales

High angular resolution observations at (sub-)millimeter wavelengths show that the thermal dust emission probing the envelope-to-disk scales (∼ 50–10,000 au) is polarized at a few percent level. This has been observed both in low and high mass star-forming regions (Matthews et al., 2009; Zhang et al., 2014; Galametz et al., 2018; Hull and Zhang, 2019; Beltrán et al., 2019; Sanhueza et al., 2021; Eswaraiah et al., 2021). Considering that the polarized flux is a quantity that is prone to cancellation if the polarization angle is highly disorganized along the line-of-sight, observations of rather large polarization fractions suggest the magnetic field lines underlying the alignment of the protostellar dust remain at least partly organized inside star-forming cores (Le Gouellec et al., 2020). Indeed, these observations have already yielded to a large statistical sample to look for morphological trends at core scales. This is even taking into account that in many (mostly pre-ALMA) observations the detected signal was not extended enough to infer a clear, well resolved morphology. In many dense cores, the magnetic lines are often quite organized. Indeed, the expected hourglass configuration expected in the collapse of cores threaded by a uniform magnetic field has been detected (Schleuning, 1998; Girart et al., 2006, 2009; Qiu et al., 2014; Kandori et al., 2017; Maury et al., 2018; Beltrán et al., 2019; Redaelli et al., 2019; Kwon et al., 2019). This configuration implies that either magnetic lines efficiently resist the angular momentum due to rotation or that the latter is weak, otherwise the field lines would show a clear toroidal component. However, there are few cores where a spiral pattern suggests that the kinetic energy associated to angular momentum may dominate (Lee et al., 2019; Beuther et al., 2020; Sanhueza et al., 2021). In some cases (Hull et al., 2017b), the observations reveal quite disorganized B-field topologies, which suggest weak-field conditions, and the possible role of turbulence or anisotropic gas flows in organizing the magnetic field lines.

Moreover, there are two interesting features that ALMA observations have revealed. One is the detection of significant polarization along the outflow cavity walls, as in some cases this is the only place where polarization is indeed detected (Le Gouellec et al., 2019; Hull et al., 2020). The other is the presence of well-organized polarized filaments with the magnetic field along the filament (Le Gouellec et al., 2019; Takahashi et al., 2019; Hull et al., 2020). This may be related with accretion streamers that have been detected recently (Yen et al., 2019; Alves et al., 2020; Pineda et al., 2020), although kinematic information is needed to confirm this scenario.

Koch et al. (2014) compiled the magnetic fields properties of 50 low and high mass protostellar cores. They propose four types of morphology (Koch et al., 2013): 1) magnetic field mostly aligned along the minor axis of the core, 2) magnetic field mostly aligned along the major axis of the core, 3) hourglass and quasi-radial fields, and 4) irregular shapes. This correlation was also confirmed by Zhang et al. (2014), who also found that the magnetic fields in massive dense core scales are either parallel or perpendicular to the parsec-scale magnetic fields. However, there are cases where this correlation at different scales does not hold (Girart et al., 2013; Hull et al., 2017a). Despite the overall trends where magnetic fields appear to be coherent with respect to larger scales and core orientation, there is no correlation with molecular outflow direction (Hull et al., 2013; Zhang et al., 2014). However, there are other works that found some correlation between the outflow direction and the magnetic field, although the alignment is far from being perfect (Galametz et al., 2020; Yen et al., 2021a). These two works show that, on one hand, the misalignment between the outflow and magnetic field direction appears to be correlated with the amount of angular momentum (Galametz et al., 2020), and on the other hand, the observed misalignment is not sufficient to reduce the efficiency of magnetic braking (Yen et al., 2021a).

Most of the observations have relied on indirect methods to derive the magnetic field strength from the (mostly dust) polarization observations (see Section 4.1). In spite of not being very accurate, these methods give a good approximation of the magnetic field strength. Thus, comparison between semi-analytical models or MHD simulations with polarization observations have found good agreement with the values obtained using different Davis–Chandrasekhar–Fermi approximations (Gonçalves et al., 2008; Frau et al., 2011; Juárez et al., 2017; Maury et al., 2018; Beltrán et al., 2019). Overall, the DCF shows that star-forming cores appear to be supercritical by a factor of about 2, and that these cores are gravitationally bound (Myers and Basu, 2021). Measuring directly the (line-of-sight) strength of the magnetic field is very difficult, and there is a small amount of positive detection at core scales (Crutcher et al., 1999; Falgarone et al., 2008; Crutcher et al., 2009; Pillai et al., 2016; Nakamura et al., 2019). DR21(OH) is probably the only core where three different techniques have been used to derive the field strength (Crutcher et al., 1999; Hezareh et al., 2010; Girart et al., 2013). For the few sources with magnetic field strength derived from both (OH) Zeeman and dust polarization, the ratio of the plane of-sky magnetic field component to its line-of-sight component, 4.7 ± 2.8, is larger than the expected average value for random orientations (Myers and Basu, 2021). However, we should note that the OH Zeeman observations probably trace lower densities than (sub)millimeter dust observations. In any case, using both datasets, the magnetic fields appear to increase with volume density as B ∝ n^2/3, indicating that magnetic field strength is significant but not enough to avoid the gravitational collapse (Myers and Basu, 2021). Finally, it is important to be aware that the interpretation of the observational data is sometimes a source of vivid debate (Crutcher et al., 2010; Mouschovias and Tassis, 2010; Tassis et al., 2014), and the application at core scales should be taken with caution (Liu et al., 2021; Reissl et al., 2021).

5.5 Protostellar disks

One of the major predictions of magnetized models regards the properties of rotationally supported disks: embedded young disks are expected to be compact and dust-rich. In this section, we briefly summarize recent constraints brought by observations of the sizes and masses of protostellar disks.

Maury et al. (2010, 2019) used the NOEMA CALYPSO survey at 1.3 and 2.7 mm to characterize the disk properties in 26 Class 0 and Class I protostars. Modeling the millimeter dust continuum emission with a combination of envelope and disk contributions directly in the visibility space, they find an average disk size of $<$ 50 au ± 10 au in the Class 0 objects, and 115 ± 15 au in the Class I objects. The VANDAM survey (Segura-Cox et al., 2018; Tobin et al., 2020) used VLA then ALMA observations of the mm dust continuum emission to characterize the radii of Class 0 and Class I disk sizes in Perseus and Orion. Their most recent results in Orion performing multi-wavelength analysis (25 Class 0 sources and 44 Class I sources) report smaller median dust disk radii than their preliminary analysis, with Class 0 disks having radii $\sim 35$ au in Orion (Sheehan et al., 2022), and no statistically significant difference between the properties of Class 0 and Class I disks were observed. This latter point may be specific to Orion, however, as our census of all embedded disks radii from the literature presented in Figure 4 does show a difference, with Class I disks being statistically more extended. Cox et al. (2017) and Encalada et al. (2021) used 2D Gaussian fits applied to the ALMA dust continuum images of Class I protostars in Ophiuchus and find respectively a median dust disk radius from 12.6 au to $\sim 23.5$ au. These measurements are also included in Figure 4.

FIGURE 4

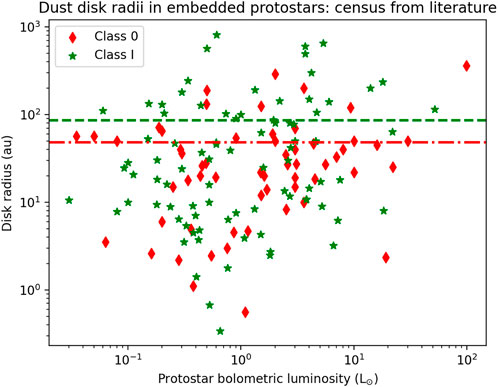
FIGURE 4. Class 0 (in red) and Class I (in green) protostellar disk radii are observed from the dust continuum emission at millimeter wavelengths (λ < 2.7 mm). Most measurements stem from the CALYPSO survey (Maury et al., 2019) and the VANDAM survey (Sheehan et al., 2022). Other sources shown are from the following works: Oya et al. (2014), Lee et al. (2018b), Yen et al. (2015b, 2017), Cox et al. (2017), Aso et al. (2015), Ohashi et al. (2014), Brinch and Jørgensen (2013), Harsono et al. (2014), Miotello et al. (2014), Sheehan and Eisner (2017), Encalada et al. (2021). The mean dust disk radii for each Class are indicated as horizontal lines (48 au for Class 0 and 86 au for Class I).

These aforementioned studies rely mainly on the analysis of the thermal dust emission, but protostellar disks can also be identified, thanks to kinematic signatures. Inside the centrifugal radius, the gas rotates with nearly Keplerian motions as the pressure and centrifugal acceleration balance the radial gravitational acceleration. Measuring the size of rotationally supported disks in embedded protostars needs to distinguish the disk emission from that of the infalling envelope kinematically. Identifying the transition from envelope kinematics dominated by infalling gas (v_r ∝ r^−1/2 and v_r > v_ϕ) to gas contained in a rotationally supported disk, with $v_{\varphi }(\mathrm{r})\propto \sqrt{(G\times M_{\star +disk})/r}$ and v_r ≪ v_ϕ, is thus, in theory, a simple way of measuring disk gaseous sizes. In practice, the simultaneous contribution of gas kinematics from different origins, chemistry effects on molecular gas tracers, and projection effects of asymmetric gas motions make it a hard task to clearly measure the rotation velocity v_ϕ in protostellar envelopes down to the disk outer radius. Only few protostars show clear signatures of Keplerian motions that can be used to characterize their disk: in the few objects that have an estimate of the dusty disk sizes, the gaseous disk size and dusty disk sizes are similar, within the relatively large uncertainties associated (Ohashi et al., 2014; Yen et al., 2017; Bjerkeli et al., 2019; Maret et al., 2020; Harsono et al., 2014; Chou et al., 2014; Yen et al., 2014; Aso et al., 2015). Protostellar disk masses are usually measured from the dust emission, estimating dust masses from a set of hypothesis on the dust properties then correcting by a gas-to-dust ratio to obtain gas masses. The choice of wavelength(s) for the dust observations is crucial: for example, in Perseus, Tychoniec et al. (2020) measure median dust masses of the embedded disks $\sim 5\times 10^{-4}{\mathrm{M}}_{\odot }$ for Class 0 and 2 × 10⁻⁴ M_⊙ for Class I from the VLA dust continuum emission at centimeter wavelengths. In comparison, dust masses from submillimeter dust emission in ALMA bands toward the same population of disks in Perseus are significantly lower, 1.4 × 10⁻⁴ M_⊙ and 4 × 10⁻⁵ M_⊙ for 38 Class 0 and 39 Class I, respectively. These lower dust disk masses are in better agreement with the dust masses found in Orion embedded disks: it suggests that dust masses extrapolated from long wavelengths may be significantly over-estimated, due to the unknown emissivity and size distribution of dust grains in the dense environments that are disks. In Ophiuchus, the mean Class I disk dust mass is found to be significantly lower, 9 × 10⁻⁶ M_⊙ (Williams et al., 2019; Encalada et al., 2021): it is still about five times greater than the mean Class II disk mass in the same region, but the dispersion in each class is so high that there is a large overlap between the two distributions. Sheehan et al. (2022) used multi-wavelength analysis of the SED toward Orion protostars. These estimates are also associated to large error bars, but the multi-wavelength analysis they performed should allow to better discriminate the disk from the envelope contribution, and hence provide more robust results. They find median dust mass 2 × 10⁻⁵ M_⊙ for Class 0 protostars, and 1.5 × 10⁻⁵ M_⊙ for Class I protostars, pointing toward much smaller embedded disk masses and less clear mass differences between the evolutionary stages than suggested by previous simplistic estimates made from single wavelength analysis. Finally, when the temperature of embedded disks can be investigated, observational studies suggest these disks may be warmer than their older counterparts, with typical temperatures around 20–30 K (van’t Hoff et al., 2020; Zamponi et al., 2021).

For the high mass stars, the rapid dynamical evolution and the larger distances make the detection of the rotationally supported disk more difficult, since they are in most cases surrounded by very massive molecular envelopes. This makes the identification of the disks more controversial. Resolving their velocity structures, masses, and sizes have been made possible only recently, thanks to ALMA. Relatively isolated disks are very rare, such as Orion I, which has unique features possibly related to a violent multiple star interaction event (Plambeck and Wright, 2016; Hirota et al., 2017; Ginsburg et al., 2019; Wright et al., 2022). Other clear cases of disks around massive stars, that appear to be a scaled up version of the ones around low-mass stars, are GGD MM1 (Girart et al., 2018; Añez-López et al., 2020b), G11.92–0.61 MM1 (Ilee et al., 2018), and G17.64 + 0.16 (Maud et al., 2019), with very massive (2–5 M_⊙), dense, and hot (≳400 K) disks. However, there are many cases reported in the literature where Keplerian velocity patterns can be fitted toward disk-like structures, which can extend from few hundreds to a thousand au (Sánchez-Monge et al., 2013; Johnston et al., 2015; Beuther et al., 2017; Cesaroni et al., 2017; Girart et al., 2017; Tanaka et al., 2020; Williams et al., 2022). In most cases, a detailed measurement of the gas temperature and surface density is needed to check the stability of such structures. The presence of disks around massive stars has also been found through near/mid-IR interferometry (Kraus et al., 2010; Frost et al., 2019). These two works suggest that the observed massive disks are a scaled up version of low-mass disks, but need to be confirmed with larger samples.

5.6 Fragmentation into multiple systems

Measuring the multiplicity of Class 0 and Class I solar-type protostellar systems and the focus of many observational works have been challenging. Submillimeter/millimeter observations are the only reliable tool for characterizing Class 0 and Class I multiplicity, as near-infrared emission toward embedded protostars suffer from significant extinction due to the envelopes, and contamination by scattered light, while near-infrared observations are usually robust at characterizing multiplicity in more evolved YSOs (Duchêne and Kraus, 2013). The observed faction of binary and multiple systems in low-mass protostars are high, and similar to the multiplicity of main sequence stars in the field. On average, a multiplicity percentage of 64% is found among Class 0 protostars with linear separations in the range of 50–5,000 au (Looney et al., 2000; Maury et al., 2010; Enoch et al., 2011; Tobin et al., 2013; Bouvier et al., 2021), while it is between 18 and 47% for Class I sources with linear separations in the range of 45–5,000 au (Haisch et al., 2004; Duchêne et al., 2004, 2007; Connelley et al., 2008a,b). For example, in the Orion molecular cloud, observations of 300 Class 0, I, or flat spectrum YSOs found a total of 85 multiple systems at separations ≲ 10,000 au, 58 multiples at separations ≲1,000 au, and only 47 multiples with maximum separations less than 500 au (Tobin et al., 2022). No statistically significant difference in the separations with evolutionary stages during the protostellar stages were found in the most complete studies so far, while tentative evidence are found that field stars and non-embedded YSOs may feature a lower number of wide (e.g., a > 1,000 au) multiple systems than their embedded counterparts, in Orion (Tobin et al., 2022). Note that this result may be significantly driven by incompleteness at sampling wide systems around the most evolved YSOs and field stars: this limitation has now been partially lifted, thanks to increasing astrometric precision and led, for example, to the discovery of a new large population of wide systems in Taurus within the range of 1–60 kAU (Joncour et al., 2017). Finally, no statistically significant difference was found regarding the multiplicity fractions observed between regions of high and low YSO density, also in Orion.

Massive stars have a predilection for forming in clustered environments with other protostars, and their young embedded counterparts are thus often studied in cluster star formation modes (Cyganowski et al., 2017). High mass star-forming cores observed at high angular resolution appear to show different level of fragmentation (Beuther and Schilke, 2004; Rodón et al., 2012; Palau et al., 2013; Busquet et al., 2016; Sánchez-Monge et al., 2017; Liu et al., 2019; Sadaghiani et al., 2020). The process of fragmentation is hierarchical (Beuther and Schilke, 2004; Beuther et al., 2015) and appears to proceed down to disk scales (Beuther et al., 2017; Busquet et al., 2019). The first systematic study of the level of fragmentation down to scales of $\sim 1000$ au suggested that this could be set by the initial magnetic field/turbulence balance (Palau et al., 2013). Subsequent studies found that the fragmentation level was only mildly correlated with the density profile, and that it is consistent with thermal or turbulent Jeans fragmentation (Palau et al., 2014, 2015, 2018; Beuther et al., 2018; Liu et al., 2019). However, in a more recent work when the fragmentation level is compared with the magnetic field properties derived from the dust polarization, there is a tentative correlation of the fragmentation level with the mass-to-flux ratio (see Figure 5, and Busquet et al., 2016; Añez-López et al., 2020a; Palau et al., 2021).

FIGURE 5

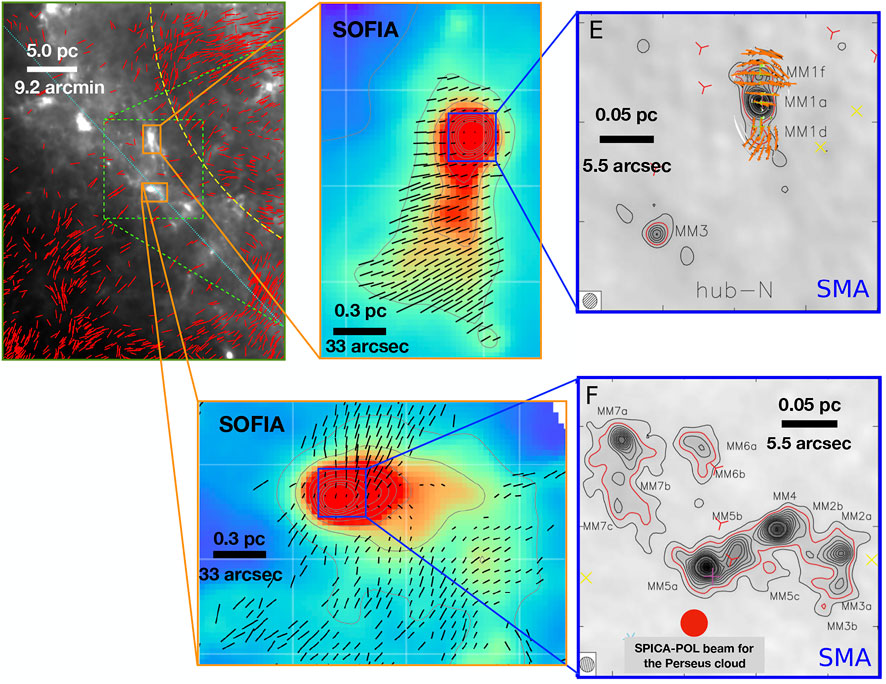
FIGURE 5. Composite images of the G14.225–0.506 massive star-forming region (Busquet et al., 2016; Santos et al., 2016). Top left panel: R band optical polarization vectors (red segments) overlaid on Herschel 250 μm image overlapped (from Santos et al., 2016). Central panels: SOFIA/HAWC +200 μm images (beam 14″) of the northern (top) and southern (bottom) hubs, with black segments showing the magnetic field direction (F. Santos, private communication). Right panels: submillimeter array (SMA) images of the 1.2 mm emission toward the center of the northern (top) and southern (bottom) hubs (Busquet et al., 2016), with orange segments showing the magnetic field direction (Añez et al. in prep.).

6 Discussion: Constraints on magnetized models from the observations

6.1 Magnetic fields

The observations of (sub-)millimeter polarized dust emission show that the magnetic field is detected in all dense environments, producing stellar embryos. Assessing whether the observations can be trusted to infer statistically robust constraints on the magnetic fields threading protostellar cores, and compared to B-fields in models, requires the analysis of synthetic observations from magnetized models. Le Gouellec et al. (2020) and Valdivia et al. (2022) have post-processed outputs from non-ideal MHD models of protostellar evolution with the Ramses code (Fromang et al., 2006) (see also the work of Kuffmeier et al., 2020 in Figure 1). Their work analyses result in synthetic polarized dust emission maps, which are compared to the true B-field properties in the models and to observations. Valdivia et al. (2022) show that measurements of the line-of-sight averaged magnetic field line orientation using the polarized dust emission are precise enough to recover the mean field lines distribution with accuracy $<15\mathrm{deg}$ (typical of the error on polarization angles obtained with observations from large mm polarimetric facilities such as ALMA) in about 95% of the independent lines of sight peering through protostellar envelopes at all radii. When focusing on the smaller envelope radii $<500\mathrm{a}\mathrm{u}$, where the magnetic field lines are more likely perturbed from the initially smooth configuration by infall and outflow and opacity effects kick in, 75% of the lines of sight still give robust results. Finally, Valdivia et al. (2022) and Le Gouellec et al. (2020) find that the polarization fraction is correlated to the degree of organization of the magnetic field along the line-of-sight, confirming that the behavior observed at larger scales, in less dense gas, holds true down to the scales of the envelopes of protostars. Le Gouellec et al. (2020) find that the dust alignment efficiency does not significantly vary with local gas density in their observations, and that the synthetic maps only can reproduce the observed polarimetric data when significant irradiation from the central protostar is included. Lam et al. (2021) have used numerical models compared to ALMA observations of the polarized dust emission by Cox et al. (2018): comparing polarization fractions they also conclude that dust polarization at ALMA wavelengths is most likely due to magnetically aligned grains in inner envelopes and dust scattering in disks.

Observationally, the correlation between the outflow axis and the mean magnetic field direction has received a lot of attention because it is believed that the efficiency of magnetic braking to redistribute angular momentum and prevent the growth of disks to large radii depends on the configuration of the core’s magnetic field with respect to the core’s rotation axis when the collapse starts (Joos et al., 2012; Hirano et al., 2020), as portrayed in Figure 6. Using an SMA survey of 20 low-mass protostars, Galametz et al. (2018, 2020) have found that the protostellar envelopes tend to have a higher angular momentum associated to rotation on 5,000 au scales if the mean envelope magnetic field measured at similar scales is misaligned with the rotational axis of the core, assumed to coincide with the outflow axis. On the other hand, observations analyzed in Yen et al. (2021b) have shown no correlation of the dust continuum protostellar disk radii with the misalignment between the magnetic fields and outflow axes in Orion A cores. Protostellar gas kinematics from the SMA MASSES (sample of 32 protostellar envelopes in Perseus) survey brings further support to the scenario proposed by Galametz et al. (2020), with a significant correlation between the rotational velocity gradients (at 1,000 au, normalized by the infalling velocity gradients) and the misalignment angles between the magnetic fields and outflows (Gupta et al., 2022). At the very small envelope radii, the mean B-field direction is observed to be randomly aligned with respect to the outflow axis (Hull et al., 2013). However, as reported by Hull et al. (2014), there are evidence that cores with lower fractional polarization tend to have their outflows perpendicular to the mean B-field, which may suggest the existence of a non-negligible toroidal field morphology (caused by the core/disk rotation) in addition to the poloidal one caused by the envelope–disk accretion.

FIGURE 6

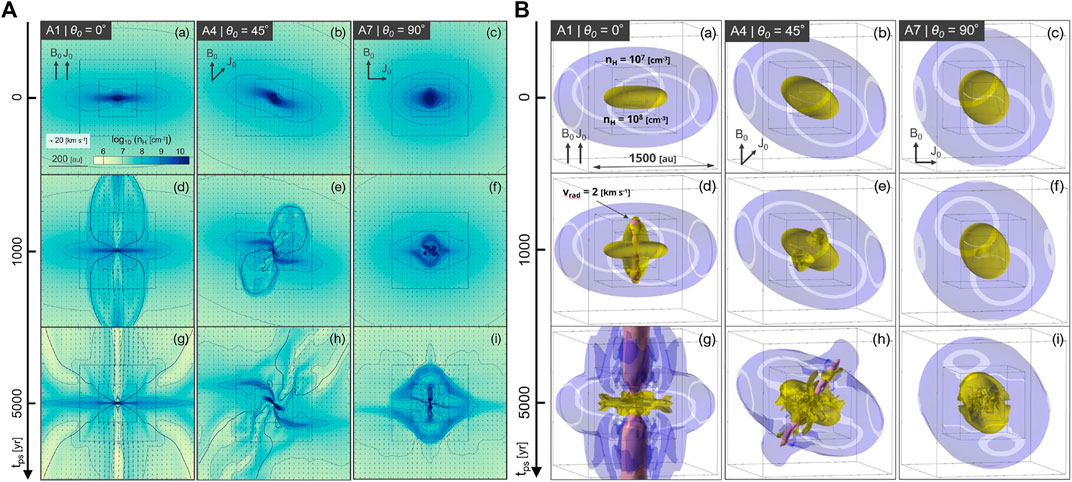
FIGURE 6. (A) Density (color and contours) and velocity (arrows) distributions in models from Hirano et al. (2020), implementing different angles between the magnetic field initial direction and the initial rotation axis of the core, at t_ps = 0, 1,000 and 5,000 years after protostar formation. The box size is 780 au. (B) Three-dimensional structures for the same models, highlighting two isodensity contours in purple and yellow, and one isovelocity contour of radial velocity v_rad = 2 kms (in red). Note the absence of an outflow in the case of orthogonal configuration (third column): this case thus seems unrealistic considering the prevalence of outflows observed around low-mass protostars.

These results may be confronted to models where the magnetic field is efficient at reducing the amount of angular momentum transmitted to the inner envelope scales ($<1000$ au), inhibiting the formation of large hydro-like disks. In some cases, numerical simulations have shown tentative evidence of better alignment of core-scale B fields and outflows in the more magnetized models (Lee et al., 2017). However, these observational results may also support the hypothesis that the angular momentum responsible for the formation and growth in size of protostellar disks has a more local origin, at a few hundreds of au scales, as discussed in recent theoretical studies following the disk evolution and angular momentum evolution in star-forming cores (Verliat et al., 2020; Lee et al., 2021b; Xu and Kunz, 2021). Future observations will undoubtedly bring more constraints on the dynamical role of B-fields to regulate the protostellar collapse and set the pristine disk properties, with the upcoming large surveys, thanks to the development of polarimetric capabilities and tools to model, for example, polarized dust emission. Observations, with example, the large radio interferometers and next generation of mid-infrared facilities, of the small scale structures of these young disks, still largely unresolved spatially, will also shed light on this question.

6.2 Coupling the magnetic field to protostellar material

Observations of the low dust emissivities and high polarization fractions at mm wavelengths in embedded protostars suggest that partial grain growth, may be up to grain sizes $>100\mu \mathrm{m}$, could have already occurred during the first 0.1 Myr of the star formation process. If these low emissivities and high polarization fractions do indeed trace a population of large dust grains in the inner layers of protostellar envelopes less than 0.1 Myrs old, the timescales to grow grains up to sizes $>100\mu \mathrm{m}$ in dense star-forming material may need to be revised. For example, considering porous dust grains may help in growing grains to sub-millimeter sizes in a few dynamical timescales during the protostellar collapse (Ormel et al., 2009). Also, since small grains are not only coupled to the gas but also to the magnetic field, a magnetized collapse may also help segregating the grains with different charges, and ultimately shortening the grain coagulation timescale (Hoang, 2022). Also, the presence of rather large grains at early stages in the protostellar envelopes may increase the ability of protostellar disks to efficiently forge to build up even bigger dust grains that are re-injected in envelopes, thanks to protostellar winds and outflows (Wong et al., 2016; Bate and Lorén-Aguilar, 2017; Lebreuilly et al., 2020; Ohashi et al., 2021; Tsukamoto et al., 2021). Figure 7 shows an artist view of such circulation processes potentially affecting dust grains during the protostellar phase.

FIGURE 7

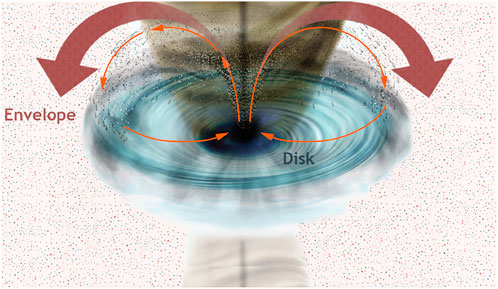
FIGURE 7. Artist impression of the dust growth and recycling from disk to envelope, thanks to outflowing gas during the protostellar stage. Modified from an original illustration in Tsukamoto et al. (2021)

Moreover, observational evidence of grain growth during the embedded stages also bear strong consequences on the efficiency of magnetic fields to regulate the transport of angular momentum. Indeed, whereas in the diffuse interstellar medium, electric charges are carried by electrons and protons, in the dense cores and particularly at high densities, the small dust grains are the main charge carriers (Nishi et al., 1991; Nakano et al., 2002; Zhao et al., 2016). The disappearance of small dust grains while forming bigger grains increases magnetic resistivities (Nishi et al., 1991; Guillet et al., 2020a) and consequently let more B flux leak outward during the collapse of the gas from the envelope onto the star–disk system (Guillet et al., 2020b; Zhao et al., 2021). Hence the disk properties may also depend strongly on the dust properties in the inner envelope.

The influence of the grain distribution on disk formation has been investigated using numerical simulations by Zhao et al. (2016). By removing the population of very small grains, the authors conclude that the ambipolar diffusion is enhanced by 1–2 orders of magnitude, see Figure 8. As expected, the numerical simulations reveal indeed that the centrifugally supported disks, which form, sensitively depend on the presence of the very small grains. For instance, for a particular set of parameters (with a relatively strong field aligned with the rotation axis), no disk would form when a MRN grain distribution is assumed, while disks of several tens of AU radius form when a truncated MRN distribution is employed. Let us stress that the presence of very small grains in dense cores is presently poorly constraint. From a theoretical point of view, Guillet et al. (2020b) have shown that the latter may be efficiently removed by coagulation due to the drift between different dust species induced by ambipolar diffusion (see also Silsbee et al., 2020). To what extent this population could not be replaced, for instance by fragmentation of bigger grains, remains to be investigated. At disk scales, where the large densities are favorable for rapid dust growth, up to a_d ∼ 1 mm, the magnetic resistivity can become many orders of magnitude bigger if small grains are rare, weakening ambipolar diffusion and recoupling the magnetic field and the gas.

FIGURE 8

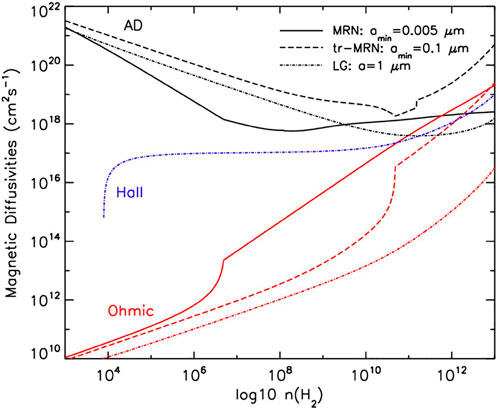
FIGURE 8. Change of MHD resistivities when removing the very small grains, from Zhao et al. (2016).

Resistivities are also strongly dependent on the ionization rate. Whereas most of the calculations assumed a value of a few ζ = 10^–17 s⁻¹ inferred from typical cosmic ray galactic abundances (Padovani et al., 2009a), more extreme ionization rates and their consequences on disk formation have been recently explored. Wurster et al. (2018) performed simulation with ζ varying from 10^–13 to 10^–24 s⁻¹. They concluded that for ζ > 10^–14 s⁻¹, the results are essentially identical to ideal MHD while for ζ < 10^–24 s⁻¹, they are close to hydrodynamics. Kuffmeier et al. (2020) specifically explored the disk radius and mass dependence on the ionization rate, varying it by a factor of 10 from ζ = 10^–17 to ζ = 10^–16 s⁻¹. Performing bidimensional simulations with a mass-to-flux of 2.5, they found that with the highest ζ, no disk forms while a few tens of AU one forms with their smallest ζ. They further propose that cosmic ray abundances may control disk mass and size and explain the differences between disks observed in various regions (Cazzoletti et al., 2019).

6.3 Gas kinematics: Rotation, mass infall, and outflow rates

Observations do not suggest that cloud rotation is transmitted to star-forming cores (Tatematsu et al., 2016; Hsieh et al., 2021). At core scales, both hydrodynamical and magnetized models of core formation and evolution have shown that they do not produce rotating cores with the high angular momentum values measured by Goodman et al. (1998) at 0.1 pc scales. Recent observations and models suggest that the angular momentum measured at core scales ($\sim 5000$ au) could be due to non-axisymmetric motions associated to the turbulent and gravitational processes (Burkert and Bodenheimer, 2000; Offner et al., 2008; Dib et al., 2010; Kuznetsova et al., 2019; Verliat et al., 2020). Hence, large scales velocity gradients in envelopes should not be interpreted automatically as organized rotation: for characterizing the motions responsible for the angular momentum observed, and as illustrated in Figure 9, resolved observations and their comparisons to model predictions are key. Finally, the angular momentum of the gas measured at envelope radii $<1000$ au would predict disk whose sizes are broadly consistent with the observed ones, although observations reveal a tentative decrease of j_spe in inner envelopes, which may trace a decrease of angular momentum at small radii (Gaudel et al., 2020). Observations of complex gas kinematics in protostellar envelopes, from disturbed core scale velocity gradients to localized streamers (see Figure 3) connecting the envelope to the disk scales confirm the wealth of observational evidence that the monolithic vision of collapse, which prevailed in the past decades needs to be revised.

FIGURE 9

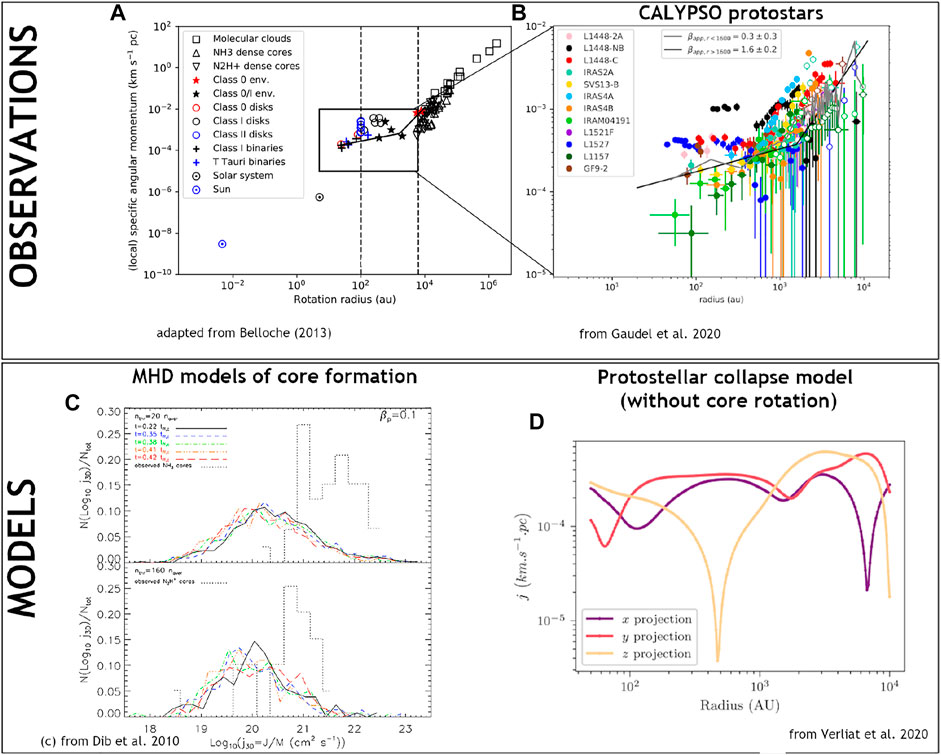
FIGURE 9. Observations and models of the angular momentum at core scales and disk scales. The upper row shows measurements of the gas angular momentum from observations of (A) star forming structures from Belloche (2013) and (B) of Class 0 young protostars from Gaudel et al. (2020). The lower row shows angular momentum from the gas in (C) models of cores from Dib et al. (2010) and (D) models of young protostars from Verliat et al. (2020).

The rather high values of mass infall rates found in Class 0 protostars seem at first sight inconsistent with observed protostellar luminosities. While the bolometric luminosities of Class 0 protostars are typically a few L_⊙ (with large variations from object to object), such accretion rates should produce a accretion luminosities a few tens of L_⊙ Ṫhis is the well-known luminosity problem (Dunham and Vorobyov, 2012), which was proposed to be solved with a scenario of quiet accretion including sporadic large accretion bursts. It remains unclear how such rare events could be captured so efficiently by observations measuring the gas accretion rates, as a recent ALMA survey of protostars in Perseus suggest the frequency of the bursts decrease with protostellar evolution, from a burst every 2,400 years in the Class 0 stage to 8,000 years in the Class I stage (Hsieh et al., 2019). However, this scenario finds support in observations of molecular species: sudden temperature changes due to short but vigorous accretion bursts would explain why CO is observed where the current envelope temperature predicts it should be frozen onto dust grains ($<30$ K) for example (Anderl et al., 2016; Cieza et al., 2016; Frimann et al., 2017). It may also be that our lack of understanding of the physical conditions at the very small scales where most of the radiation is reprocessed to produce the observed luminosity, prevents us from properly model expected luminosities, or that the gas mass infall rates measured at few hundreds of au in the envelopes are not representative of the true accretion rates at much smaller radii, onto the protostellar objects. Supporting this last hypothesis, it is interesting to note that MHD models following the evolution of low-mass cores find typical mass accretion rates $\sim 10^{-6}{\mathrm{M}}_{\odot }$ per year, with large variations (Hennebelle et al., 2020; Kuznetsova et al., 2020). The global mass accretion rate from the disk to the central star is lower when the disk structure is properly modeled, and the short-term variation (bursts) of the mass accretion is also highly attenuated with increased resolution (Kuffmeier et al., 2018; Lee et al., 2021b). It seems therefore that either the protostellar accretion rates obtained from observations are over-estimated, which could be due to sampling the inner envelope and not the disk-star connection, or the models predict slower mass accretion than protostars really do accrete. We stress that the existence of preferential directions along field lines, and the development of highly non-axisymmetric collapse may be responsible, in magnetized models, to regulate the mass accretion rate directly from the inner envelope to the central star, without the need to transit through the disk. In their MHD models of the evolution of massive cores into protostars, Mignon-Risse et al. (2021) find average mass accretion rates on the central object around $\sim 10^{-3}{\mathrm{M}}_{\odot }$ per year, which is also about an order of magnitude lower than estimates from the observations towards similarly massive protostars.

6.4 The formation of disks

Recent observations benefiting from increased spatial resolution and sensitivities have firmly established that most disks around embedded protostars are compact and not as massive as early studies had suggested. The current disk radii estimates from the literature are shown in Figure 4. Such compact disks are difficult to produce in large fractions with purely hydrodynamical analytical models of disk formation conserving angular momentum, but could be a natural outcome of magnetized models of disk formation and models of anisotropic collapse (Hennebelle et al., 2020; Kuznetsova et al., 2022). Obtaining self-consistent disk populations from numerical simulations is quite challenging because it requires being able to treat simultaneously spatial scales sufficiently small to resolve the protostellar disks while in the same time sufficiently advance clump scales allow the formation of a statistically significant number of disks. For this reason, only two studies have been reporting disk population self-consistently formed from numerical simulations. Bate (2018) presents smooth particle hydrodynamical simulations of a 500 M_⊙ clump, including radiative transfer, producing a disk population whose sizes ranges from about 10 to few 100 AU. The author compares the mass distribution inferred from simulations with several observational surveys and concludes that the disk formed in the simulations are up to 10 times more massive. Lebreuilly et al. (2021) present three adaptive mesh refinement simulations of 1000 M_⊙ clump, which treat radiative stellar feedback and both ideal and non-ideal MHD (see a gallery of disks in Figure 10). The spatial resolution is up to 1 AU. Figure 11 shows for the three runs, the mass distribution and the radius distribution, respectively. For comparison, the data of VLA Class 0 disk mass distribution (purple, Tychoniec et al., 2020) have been reported, as well as the disk radius inferred by the CALYPSO (Maury et al., 2019) and VANDAM projects (Segura-Cox et al., 2018; Tobin et al., 2020). Altogether and as already suggested from individual studies that compared HD, MHD, and non-ideal MHD numerical models for single objects, the hydrodynamical disks appear to be bigger than the MHD ones and overall in less good agreement with observations than when the magnetic field is included, particularly regarding the disk radius distribution. Whereas there is some scatter in the distributions, these first population studies, properly taking into account the initial conditions, appear to be promising tools for future comparisons to observations.

FIGURE 10

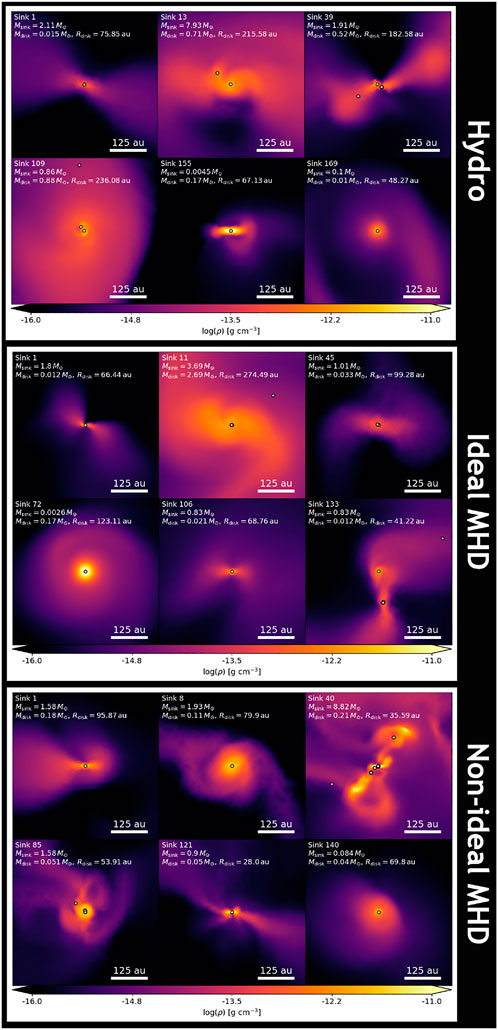
FIGURE 10. A gallery of model disks formed in three massive clump simulations, using either pure hydrodynamics (upper panel), ideal MHD (middle panel) or non-ideal MHD (ambipolar diffusion, lower panel), from Lebreuilly et al. (2021). Hydrodynamical disks tend to be bigger, while ideal MHD ones smaller than when ambipolar diffusion is included.

FIGURE 11

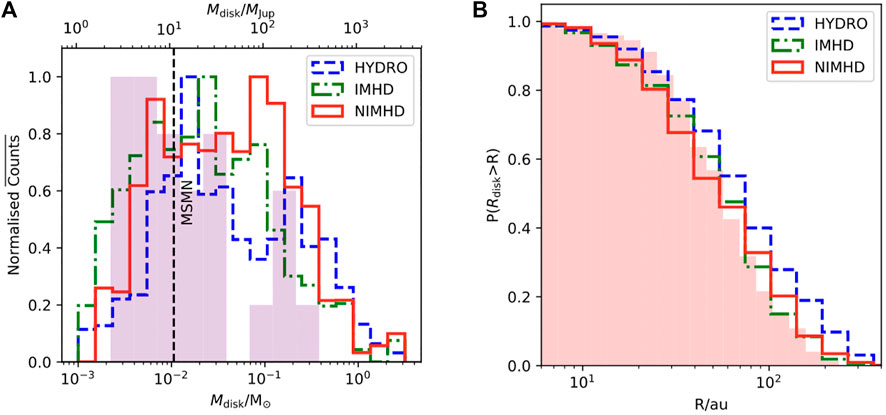
FIGURE 11. (A) Distributions of disk sizes obtained for the three disk population synthesis models presented in Lebreuilly et al. (2021) (note that the sizes are normalized so that their peak in the y-axis is 1). The mass of the minimum mass for the solar nebula (MSMN) is indicated as a dashed line. (B) Cumulative distribution function of disk radius for the three models presented in Lebreuilly et al. (2021).

A local origin of the angular momentum building rotationally supported disks has been proposed by some models: for example, Verliat et al. (2020) have shown that the observations of angular momentum in protostellar envelopes can be satisfactorily reproduced if the disk formation results from anisotropies in the local velocity field, and not a consequence of the transfer of angular momentum from organized large scale core rotation. As shown in Figure 9, some observational evidence may support that scenario, with a good agreement between those models and the observations of the specific angular momentum found in envelopes, or more recently for example the observations of the L1489 protostar suggesting only the inner part of the envelope, at radii $<4000-6000$, may be directly involved in forming the central star (Sai et al., 2022). This would imply that the material participating directly to building the disk and the star contains much less angular momentum than the values measured at core scales, lessening the angular momentum problem for star formation.

Although it was not shown observationally in the most embedded disks, models suggest it may be that the big dust drifts even during the early disk phases, leading to different apparent disk sizes recovered at different wavelengths. The uncertainties regarding dust properties under these specific conditions also affect the dust masses and hence the disk masses that are estimated in these objects. If observations suggesting young embedded disks are confirmed to be warm (20–30 K, van’t Hoff et al., 2020; Zamponi et al., 2021), it could suggest gas kinematics within the disk play a significant role in heating the disk, as the protostellar radiation is expected to be highly extinct at such very high densities. For example, Zamponi et al. (2021) compare observations with synthetic observations of MHD protostellar disk models formed after the collapse of a dense core, and suggest that heating due to gravitational instabilities in the disk is able to generate dust temperatures in agreement with observational constraints in the IRAS 16293 Class 0 disk.

The exact role of magnetic fields in setting the disks sizes and masses during the embedded phases can only be quantitatively addressed, thanks to the comparison of observed properties to the outcomes of models. Maury et al. (2018) have shown that the B-field geometry, small disk size, and the kinematics of the B335 inner envelope can only be explained by a family of MHD models, where the initially poloidal field in B335 is being pulled in the dominant direction of the collapse, but yet is strong enough (μ ∼ 6) to counteract partially the transfer of angular momentum inward. In B335, they show the magnetic field is very likely to regulate the formation processes of the protostellar disk, constraining the size of the protostellar disk to $<20$ au (see Figure 12). The role of the magnetic field in setting the disk size in B335 has also been discussed in subsequent studies (Bjerkeli et al., 2019; Imai et al., 2019; Yen et al., 2019). However, new observations by Cabedo et al. (2022) suggest that the gas at small envelope radii is strongly ionized in B335 and points toward conditions typical of ideal MHD. It may very well be that the star–disk building phase consists in a succession of non-ideal and ideal MHD conditions in the “life of the protostar.” It would be possible to grow a quite large disk if it is formed before the onset of high ionization around the protostar (due to the protostar itself and the production of CR in the B-field lines around the protostar), while if the disks are still compact when the local ionization starts to increase at a fast pace, it may be more difficult to form large disks in the second half of the protostellar phase.

FIGURE 12

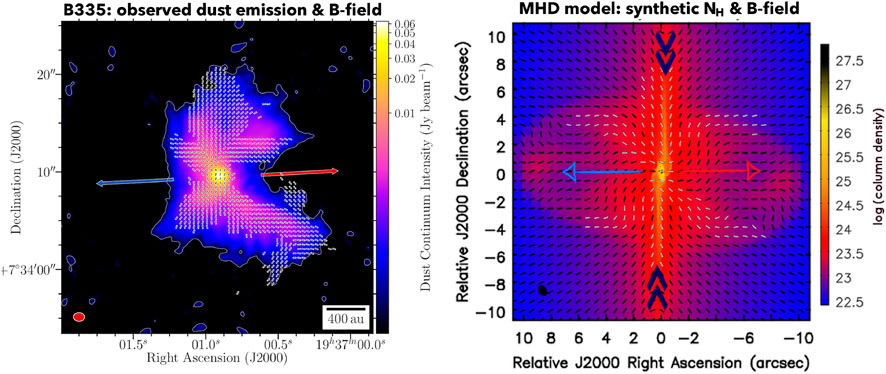
FIGURE 12. Observation and best model to match the properties in the B335 protostar, from Maury et al. (2018). The observed B field geometry is shown in the left panel, the small disk size and the kinematics of the B335 inner envelope can only be explained by a family of MHD models where the initially poloidal field in B335 is being pulled in the dominant direction of the collapse, but yet is strong enough (μ ∼ 6) to counteract partially the transfer of angular momentum inward and set the disk size in this Class 0 protostar: the best model is shown in the right panel.

6.5 Influence of magnetic field on the formation of multiple systems

The fragmentation of low-mass cores has been the subject of several studies (Matsumoto and Hanawa, 2003; Goodwin et al., 2004). Several modes of fragmentation have been identified. Generally speaking, it is induced by the density fluctuations that are generated during the collapse on one hand by gravo-turbulence processes within the envelope and on the other hand through the formation of massive centrifugally supported unstable disks. The outcome of fragmentation therefore not only entirely depends on the initial conditions, particularly rotation and turbulence initial values, but also on the amplitude of the initial density perturbations. It has been generally found that however under typical conditions and in the absence of magnetic field, a solar mass dense core tends to produce few fragments (say 2–10).

Several studies have been dedicated to the influence of magnetic field in this process (Hennebelle and Teyssier, 2008; Machida et al., 2008; Commerçon et al., 2010; Wurster et al., 2017; Wurster and Bate, 2019; Hennebelle et al., 2020), covering a broad range of parameters in terms of magnetic field intensity, rotation, and initial turbulence. From these studies, clear trends can be inferred. First, the higher is the rotational and/or turbulent energy, the more prone to fragmentation is the core. Numerical models of turbulent dense cores suggest that the directions of the specific angular momentum axis tends to vary as a function of envelope scales (Joos et al., 2013; Matsumoto et al., 2017), and that misaligned systems can form under turbulent conditions. Some numerical models also suggest that turbulent velocity fluctuations around protostellar cores may be responsible for setting the rotational motions of these cores (Misugi et al., 2019). However, the magnetic field has a drastic influence and in the case of low-mass cores, mass-to-flux ratios as high as μ > 5–10 may entirely suppress the formation of fragments. This is because in low-mass cores, turbulence is at best trans-sonic and the density fluctuations induced by turbulence remain limited. Therefore, the dominant fragmentation mode is through the formation of massive disks. However, in the presence of the magnetic field the disk sizes and masses are much smaller, and therefore they tend to be stable. Another interesting trend is that the cores in which the magnetic field is initially perpendicular to the rotation axis are less prone to fragmentation than when it is aligned. One important fact to be taken into account is however that the amplitude of the density perturbations is also an important parameter, and the mentioned trends have been inferred for modest density fluctuations (typically below 10%). When the density fluctuations have a large amplitude, say of about 50%, they are sufficiently unstable to collapse individually even in the absence of rotation. In this case, the magnetic field is unable to impede fragmentation (Hennebelle and Teyssier, 2008; Wurster et al., 2017). This would imply that the fragmentation is driven by the larger scales and the assembling process of the dense cores.

The influence of the magnetic field on the fragmentation of massive clumps has also been investigated. Because of the large amplitude of the density fluctuations, the impact of magnetic field on the fragmentation is relatively less important than that found in the case of low-mass cores. For instance, Hennebelle et al. (2011) and Myers et al. (2013) found that in the presence of a significant magnetic field (e.g., a few mG for mass-to-flux ratios around 2), the number of self-gravitating fragments is reduced by a factor of about 2. Fontani et al. (2016) and Fontani et al. (2018) have carried out observations and simulations of massive clumps. They have studied and compared the fragmentation properties of the clumps from observations and simulations using synthetic images that mimic the observations as shown in Figure 13. They concluded that the fragmentation properties within the observations are better reproduced by the significantly magnetized models (typically μ = 2) than by the weakly magnetized ones.

FIGURE 13

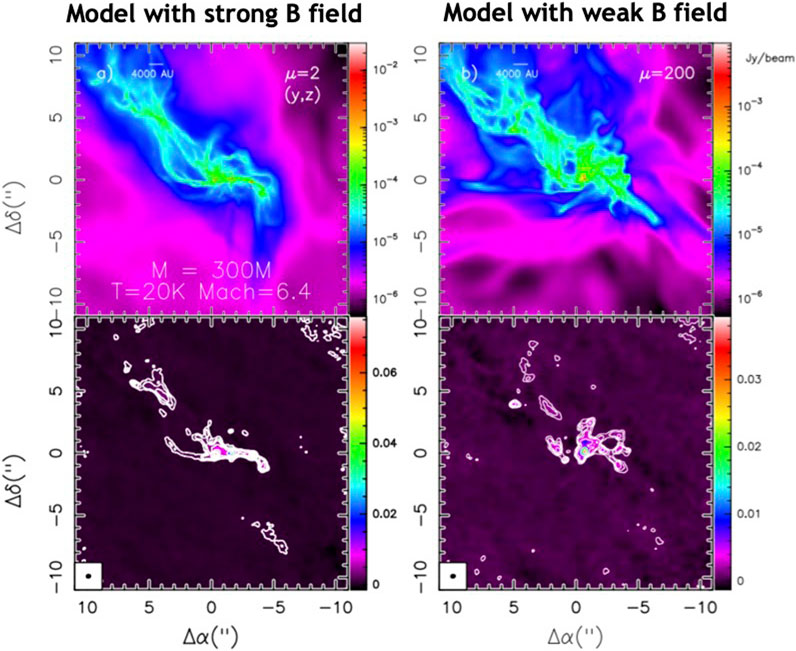
FIGURE 13. Models of the gravitational collapse of a 300 M⊙ clump, with gas temperature T = 20 K, and Mach number 6.4, from Fontani et al., 2018). Column density maps of two models are shown in the upper row, in the presence of a strong (left) magnetic field and a weak one (right). The lower row shows ALMA synthetic observations of the models using the 280 GHz dust continuum emission. Fewer fragments are seen in the more magnetized case.

7 Summary

How protostars and planet-forming disks form are cornerstone questions for us to understand that both the stellar populations setting the evolution of our Universe and the conditions responsible for producing the planetary systems observed around most stars. The recent progresses made through observations and simulations suggest that the magnetic field is modifying in depth the outcome of the collapse and the formation of stars, by adding an extra support to the gas, by reducing the angular momentum available to build the disks, by launching outflows and even possibly favoring the dust grain coagulation into pebbles. Observations suggest that the so-called magnetic braking catastrophe is an issue that is solved, alleviated by implementing realistic physical conditions (turbulence, anisotropies of the density field, non-homogeneous initial B field due to conditions of core assembly and local environment, gas ionization, and dust properties) in MHD models.

If the magnetized scenario we propose is common, recent works suggest that the angular momentum problem for star formation may be actually “solved” not by the formation of large disks but by the combination of 1) lack of organized rotation motions at large envelope radii, 2) the inefficient angular momentum transport due to magnetic braking in the inner envelope (and angular momentum removed through rotating outflows generated by the presence of the magnetic field), and 3) a local origin of the angular momentum incorporated in the star–disk system.

Major questions however remain to be solved for the next generations of astrophysicists. First, our understanding of the origin of the angular momentum that eventually builds the disks is very incomplete. Whereas some of the gas momentum could obviously be inherited from larger scales, inertial processes naturally produce angular momentum in a non-axisymmetric system, opening the possibility to disks weakly related to large scale angular momentum. This possible scenario questions the effective role of magnetic braking at envelope scales to set the disk sizes, as local processes may be more important in shaping the outcome of star and disk formation. That means to better understand the transport of the magnetic field by processes like reconnection diffusion and ambipolar diffusion and their importance on regulating angular momentum transport and disk formation in the different stages. Characterizing the properties of the compact protostellar disks, with very high angular resolution observations, will also be a key to set constraints and refine our models. Second, this scenario deeply relies on the efficiency of magnetic fields to couple to the gas reservoirs. This efficiency is driven by a complex set of physical conditions, which remain largely unconstrained up to this day. Our current knowledge of magnetic resistivities remains thus hampered by very large uncertainties. It is therefore key, in the future, that observations characterize both the gas and dust properties in embedded protostars and are compared to models so we know whether magnetic braking is much more efficient in locations, and epochs, that are critical for setting the disk and stellar properties. Answering these questions will not only be a fascinating challenge that will require us to produce robust measurements of the magnetic intensity and topology in large samples of objects but also find clever ways to access the gas ionization fraction and dust grain properties in young embedded protostars.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

AM acknowledges support from the European Research Council (ERC) under starting grant number 679937—“MagneticYSOs.” This work was also partially supported by the program Unidad de Excelencia María de Maeztu CEX 2020-001058-M. JG also acknowledges support by the grant PID 2020-117710 GB-I00 (MCI-AEI-FEDER,UE). PH acknowledges support from the European Research Council Synergy Grant ECOGAL (Grant: 855130)

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Planck Collaboration Ade, P. A. R., Aghanim, N., Arnaud, M., Ashdown, M., Aumont, J., et al. (2011). Planck early results. XX. New light on anomalous microwave emission from spinning dust grains. Astron. Astrophys. 536, A20. doi:10.1051/0004-6361/201116470

CrossRef Full Text | Google Scholar

Allen, A., Li, Z.-Y., and Shu, F. H. (2003). Collapse of magnetized singular isothermal toroids. II. Rotation and magnetic braking. Astrophys. J. 599, 363–379. doi:10.1086/379243

CrossRef Full Text | Google Scholar

Alves, F. O., Caselli, P., Girart, J. M., Segura-Cox, D., Franco, G. A. P., Schmiedeke, A., et al. (2019). Gas flow and accretion via spiral streamers and circumstellar disks in a young binary protostar. Science 366, 90–93. doi:10.1126/science.aaw3491

PubMed Abstract | CrossRef Full Text | Google Scholar

Alves, F. O., Cleeves, L. I., Girart, J. M., Zhu, Z., Franco, G. A. P., Zurlo, A., et al. (2020). A case of simultaneous star and planet formation. Astrophys. J. 904, L6. doi:10.3847/2041-8213/abc550

CrossRef Full Text | Google Scholar

Alves, F. O., Frau, P., Girart, J. M., Franco, G. A. P., Santos, F. P., and Wiesemeyer, H. (2014). On the radiation driven alignment of dust grains: Detection of the polarization hole in a starless core. Astron. Astrophys. 569, L1. doi:10.1051/0004-6361/201424678

CrossRef Full Text | Google Scholar

Alves, F. O., Girart, J. M., Padovani, M., Galli, D., Franco, G. A. P., Caselli, P., et al. (2018). Magnetic field in a young circumbinary disk. Astron. Astrophys. 616, A56. doi:10.1051/0004-6361/201832935

CrossRef Full Text | Google Scholar

Alves, F. O., Vlemmings, W. H. T., Girart, J. M., and Torrelles, J. M. (2012). The magnetic field of IRAS 16293-2422 as traced by shock-induced H₂O masers. Astron. Astrophys. 542, A14. doi:10.1051/0004-6361/201118710

CrossRef Full Text | Google Scholar

Anderl, S., Maret, S., Cabrit, S., Belloche, A., Maury, A. J., André, P., et al. (2016). Probing the CO and methanol snow lines in young protostars. Astron. Astrophys. 591, A3. doi:10.1051/0004-6361/201527831

CrossRef Full Text | Google Scholar

André, P., Ward-Thompson, D., and Barsony, M. (2000). From prestellar cores to protostars: The initial conditions of star formation. Protostars Planets IV, 59.

Google Scholar

André, P., Ward-Thompson, D., and Barsony, M. (1993). Submillimeter continuum observations of Rho Ophiuchi A - the candidate protostar VLA 1623 and prestellar clumps. Astrophys. J. 406, 122–141. doi:10.1086/172425

CrossRef Full Text | Google Scholar

Añez-López, N., Busquet, G., Koch, P. M., Girart, J. M., Liu, H. B., Santos, F., et al. (2020a). Role of the magnetic field in the fragmentation process: The case of g14.225-0.506. Astron. Astrophys. 644, A52. doi:10.1051/0004-6361/202039152

CrossRef Full Text | Google Scholar

Añez-López, N., Osorio, M., Busquet, G., Girart, J. M., Macías, E., Carrasco-González, C., et al. (2020b). Modeling the accretion disk around the high-mass protostar GGD 27-MM1. Astrophys. J. 888, 41. doi:10.3847/1538-4357/ab5dbc

CrossRef Full Text | Google Scholar

Artur de la Villarmois, E., Jørgensen, J. K., Kristensen, L. E., Bergin, E. A., Harsono, D., Sakai, N., et al. (2019). Physical and chemical fingerprint of protostellar disc formation. Astron. Astrophys. 626, A71. doi:10.1051/0004-6361/201834877

CrossRef Full Text | Google Scholar

Aso, Y., Ohashi, N., Saigo, K., Koyamatsu, S., Aikawa, Y., Hayashi, M., et al. (2015). ALMA observations of the transition from infall motion to keplerian rotation around the late-phase protostar TMC-1A. Astrophys. J. 812, 27. doi:10.1088/0004-637X/812/1/27

CrossRef Full Text | Google Scholar

Bate, M. R., and Lorén-Aguilar, P. (2017). On the dynamics of dust during protostellar collapse. Mon. Not. R. Astron. Soc. 465, 1089–1094. doi:10.1093/mnras/stw2853

CrossRef Full Text | Google Scholar

Bate, M. R. (2018). On the diversity and statistical properties of protostellar discs. Mon. Not. R. Astron. Soc. 475, 5618–5658. doi:10.1093/mnras/sty169

CrossRef Full Text | Google Scholar

Bel, N., and Leroy, B. (1989). Zeeman splitting in interstellar molecules. Astron. Astrophys. 224, 206.

Google Scholar

Bel, N., and Leroy, B. (1998). Zeeman splitting in interstellar molecules. II. The ethynyl radical. Astron. Astrophys. 335, 1025.

Google Scholar

Belloche, A. (2013). “Observation of rotation in star forming regions: Clouds, cores, disks, and jets,” in EAS publications series. Editors P. Hennebelle, and C. Charbonnel (EAS Publications Series), 62. 25–66. doi:10.1051/eas/1362002

CrossRef Full Text | Google Scholar

Beltrán, M. T., Cesaroni, R., Codella, C., Testi, L., Furuya, R. S., and Olmi, L. (2006). Infall of gas as the formation mechanism of stars up to 20 times more massive than the Sun. Nature 443, 427–429. doi:10.1038/nature05074

PubMed Abstract | CrossRef Full Text | Google Scholar

Beltrán, M. T., Padovani, M., Girart, J. M., Galli, D., Cesaroni, R., Paladino, R., et al. (2019). ALMA resolves the hourglass magnetic field in G31.41+0.31. Astron. Astrophys. 630, A54. :doi:10.1051/0004-6361/201935701

CrossRef Full Text | Google Scholar

Beltrán, M. T., Rivilla, V. M., Cesaroni, R., Galli, D., Moscadelli, L., Ahmadi, A., et al. (2022). The sharp ALMA view of infall and outflow in the massive protocluster G31.41+0.31. Astron. Astrophys. 659, A81. doi:10.1051/0004-6361/202142703

CrossRef Full Text | Google Scholar

Beuther, H., Henning, T., Linz, H., Feng, S., Ragan, S. E., Smith, R. J., et al. (2015). Hierarchical fragmentation and collapse signatures in a high-mass starless region. Astron. Astrophys. 581, A119. doi:10.1051/0004-6361/201526759

CrossRef Full Text | Google Scholar

Beuther, H., Linz, H., Henning, T., Feng, S., and Teague, R. (2017). Multiplicity and disks within the high-mass core NGC 7538IRS1. Astron. Astrophys. 605, A61. doi:10.1051/0004-6361/201730575

CrossRef Full Text | Google Scholar

Beuther, H., Mottram, J. C., Ahmadi, A., Bosco, F., Linz, H., Henning, T., et al. (2018). Fragmentation and disk formation during high-mass star formation. IRAM NOEMA (Northern Extended Millimeter Array) large program CORE. Astron. Astrophys. 617, A100. doi:10.1051/0004-6361/201833021

CrossRef Full Text | Google Scholar

Beuther, H., and Schilke, P. (2004). Fragmentation in MassiveStar formation. Science 303, 1167–1169. doi:10.1126/science.1094014

PubMed Abstract | CrossRef Full Text | Google Scholar

Beuther, H., Soler, J. D., Linz, H., Henning, T., Gieser, C., Kuiper, R., et al. (2020). Gravity and rotation drag the magnetic field in high-mass star formation. Astrophys. J. 904, 168. doi:10.3847/1538-4357/abc019

CrossRef Full Text | Google Scholar

Bjerkeli, P., Ramsey, J. P., Harsono, D., Calcutt, H., Kristensen, L. E., van der Wiel, M. H. D., et al. (2019). Kinematics around the B335 protostar down to au scales. Astron. Astrophys. 631, A64. doi:10.1051/0004-6361/201935948

CrossRef Full Text | Google Scholar

Blandford, R., and Payne, D. (1982). Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 199, 883–903. doi:10.1093/mnras/199.4.883

CrossRef Full Text | Google Scholar

Bodenheimer, P. (1995). Angular momentum evolution of young stars and disks. Annu. Rev. Astron. Astrophys. 33, 199–238. doi:10.1146/annurev.aa.33.090195.001215

CrossRef Full Text | Google Scholar

Bouvier, M., López-Sepulcre, A., Ceccarelli, C., Sakai, N., Yamamoto, S., and Yang, Y. L. (2021). ORion Alma New GEneration Survey (ORANGES). I. Dust continuum and free-free emission of OMC-2/3 filament protostars. Astron. Astrophys. 653, A117. doi:10.1051/0004-6361/202141157

CrossRef Full Text | Google Scholar

Bracco, A., Palmeirim, P., André, P., Adam, R., Ade, P., Bacmann, A., et al. (2017). Probing changes of dust properties along a chain of solar-type prestellar and protostellar cores in Taurus with NIKA. Astron. Astrophys. 604, A52. doi:10.1051/0004-6361/201731117

CrossRef Full Text | Google Scholar

Braiding, C. R., and Wardle, M. (2012). The Hall effect in star formation. Mon. Not. R. Astron. Soc. 422, 261–281. doi:10.1111/j.1365-2966.2012.20601.x

CrossRef Full Text | Google Scholar

Brauer, R., Wolf, S., Reissl, S., and Ober, F. (2017). Magnetic fields in molecular clouds: Limitations of the analysis of Zeeman observations. Astron. Astrophys. 601, A90. doi:10.1051/0004-6361/201629001

CrossRef Full Text | Google Scholar

Brinch, C., and Hogerheijde, M. R. (2010). Lime - a flexible, non-LTE line excitation and radiation transfer method for millimeter and far-infrared wavelengths. Astron. Astrophys. 523, A25. doi:10.1051/0004-6361/201015333

CrossRef Full Text | Google Scholar

Brinch, C., and Jørgensen, J. K. (2013). Interplay between chemistry and dynamics in embedded protostellar disks. Astron. Astrophys. 559, A82. doi:10.1051/0004-6361/201322463

CrossRef Full Text | Google Scholar

Brunngräber, R., and Wolf, S. (2019). Polarization reversal of scattered thermal dust emission in protoplanetary disks at submillimetre wavelengths. Astron. Astrophys. 627, L10. doi:10.1051/0004-6361/201935169

CrossRef Full Text | Google Scholar

Brunngräber, R., and Wolf, S. (2021). Self-scattering on large, porous grains in protoplanetary disks with dust settling. Astron. Astrophys. 648, A87. doi:10.1051/0004-6361/202040033

CrossRef Full Text | Google Scholar

Burkert, A., and Bodenheimer, P. (2000). Turbulent molecular cloud cores: Rotational properties. Astrophys. J. 543, 822–830. doi:10.1086/317122

CrossRef Full Text | Google Scholar

Busquet, G., Estalella, R., Palau, A., Liu, H. B., Zhang, Q., Girart, J. M., et al. (2016). What is controlling the fragmentation in the infrared dark cloud g14.225-0.506?: Different levels of fragmentation in twin hubs. Astrophys. J. 819, 139. doi:10.3847/0004-637X/819/2/139

CrossRef Full Text | Google Scholar

Busquet, G., Girart, J. M., Estalella, R., Fernández-López, M., Galván-Madrid, R., Anglada, G., et al. (2019). Unveiling a cluster of protostellar disks around the massive protostar GGD 27 MM1. Astron. Astrophys. 623, L8. doi:10.1051/0004-6361/201833687

CrossRef Full Text | Google Scholar

Cabedo, V., Maury, A., Girart, J. M., Padovani, M., Hennebelle, P., Houde, M., et al. (2022). Magnetically regulated collapse in the B335 protostar?” in Observational constraints on gas ionization and magnetic field coupling. arXiv e-printsarXiv:2204.10043.

Google Scholar

Cabedo, V., Maury, A., Girart, J. M., and Padovani, M. (2021). Structured velocity field in the inner envelope of B335: ALMA observations of rare CO isotopologues. Astron. Astrophys. 653, A166. doi:10.1051/0004-6361/202140754

CrossRef Full Text | Google Scholar

Cazzoletti, P., Manara, C. F., Liu, H. B., van Dishoeck, E. F., Facchini, S., Alcalà, J. M., et al. (2019). ALMA survey of class II protoplanetary disks in corona australis: A young region with low disk masses. Astron. Astrophys. 626, A11. doi:10.1051/0004-6361/201935273

CrossRef Full Text | Google Scholar

Cazzoli, G., Lattanzi, V., Coriani, S., Gauss, J., Codella, C., Ramos, A. A., et al. (2017). Zeeman effect in sulfur monoxide. Astron. Astrophys. 605, A20. doi:10.1051/0004-6361/201730858

PubMed Abstract | CrossRef Full Text | Google Scholar

Ceccarelli, C., Dominik, C., López-Sepulcre, A., Kama, M., Padovani, M., Caux, E., et al. (2014). Herschel finds evidence for stellar wind particles in a protostellar envelope: Is this what happened to the young sun? Astrophys. J. 790, L1. doi:10.1088/2041-8205/790/1/L1

CrossRef Full Text | Google Scholar

Cesaroni, R., Sánchez-Monge, Á., Beltrán, M. T., Johnston, K. G., Maud, L. T., Moscadelli, L., et al. (2017). Chasing discs around O-type (proto)stars: Evidence from ALMA observations. Astron. Astrophys. 602, A59. doi:10.1051/0004-6361/201630184

CrossRef Full Text | Google Scholar

Chamma, M. A., Houde, M., Girart, J. M., and Rao, R. (2018). Non-Zeeman circular polarization of molecular spectral lines in the ISM. Mon. Not. R. Astron. Soc. 480, 3123–3131. doi:10.1093/mnras/sty2068

CrossRef Full Text | Google Scholar

Chandrasekhar, S., and Fermi, E. (1953). Magnetic fields in spiral arms. Astrophys. J. 118, 113. –+. doi:10.1086/145731

CrossRef Full Text | Google Scholar

Chen, M. C.-Y., Di Francesco, J., Johnstone, D., Sadavoy, S., Hatchell, J., Mottram, J. C., et al. (2016). The JCMT gould belt survey: Evidence for dust grain evolution in Perseus star-forming clumps. Astrophys. J. 826, 95. doi:10.3847/0004-637X/826/1/95

CrossRef Full Text | Google Scholar

Chen, X., Ren, Z.-Y., Li, D.-L., Liu, T., Wang, K., Shen, Z.-Q., et al. (2021). Chemically fresh gas inflows detected in a nearby high-mass star-forming region. Astrophys. J. Lett. 923, L20. doi:10.3847/2041-8213/ac3ec8

CrossRef Full Text | Google Scholar

Chiang, H.-F., Looney, L. W., and Tobin, J. J. (2012). The envelope and embedded disk around the class 0 protostar l1157-mm: Dual-wavelength interferometric observations and modeling. Astrophys. J. 756, 168. doi:10.1088/0004-637X/756/2/168

CrossRef Full Text | Google Scholar

Ching, T.-C., Lai, S.-P., Zhang, Q., Yang, L., Girart, J. M., and Rao, R. (2016). Helical magnetic fields in the NGC 1333 IRAS 4A protostellar outflows. Astrophys. J. 819, 159. doi:10.3847/0004-637X/819/2/159

CrossRef Full Text | Google Scholar

Cho, J., and Yoo, H. (2016). A technique for constraining the driving scale of turbulence and a modified chandrasekhar-fermi method. Astrophys. J. 821, 21. doi:10.3847/0004-637X/821/1/21

CrossRef Full Text | Google Scholar

Choi, M., Evans, I., Neal, J., Gregersen, E. M., and Wang, Y. (1995). Modeling line profiles of protostellar collapse in B335 with the Monte Carlo method. Astrophys. J. 448, 742. doi:10.1086/176002

CrossRef Full Text | Google Scholar

Chou, T.-L., Takakuwa, S., Yen, H.-W., Ohashi, N., and Ho, P. T. P. (2014). Transition from the infalling envelope to the keplerian disk around L1551 IRS 5. Astrophys. J. 796, 70. doi:10.1088/0004-637X/796/1/70

CrossRef Full Text | Google Scholar

Cieza, L. A., Casassus, S., Tobin, J., Bos, S. P., Williams, J. P., Perez, S., et al. (2016). Imaging the water snow-line during a protostellar outburst. Nature 535, 258–261. doi:10.1038/nature18612

PubMed Abstract | CrossRef Full Text | Google Scholar

Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., and Teyssier, R. (2010). Protostellar collapse: Radiative and magnetic feedbacks on small-scale fragmentation. Astron. Astrophys. 510, L3. doi:10.1051/0004-6361/200913597

CrossRef Full Text | Google Scholar

Connelley, M. S., Reipurth, B., and Tokunaga, A. T. (2008b). The evolution of the multiplicity of embedded protostars. II. Binary separation distribution and analysis. Astron. J. 135, 2526–2536. doi:10.1088/0004-6256/135/6/2526

CrossRef Full Text | Google Scholar

Connelley, M. S., Reipurth, B., and Tokunaga, A. T. (2008a). The evolution of the multiplicity of embedded protostars. I. Sample properties and binary detections. Astron. J. 135, 2496–2525. doi:10.1088/0004-6256/135/6/2496

CrossRef Full Text | Google Scholar

Cortes, P. C., Crutcher, R. M., Shepherd, D. S., and Bronfman, L. (2008). Interferometric mapping of magnetic fields: The massive star-forming region G34.4+0.23 MM. Astrophys. J. 676, 464–471. doi:10.1086/524355

CrossRef Full Text | Google Scholar

Cortes, P. C., Crutcher, R. M., and Watson, W. D. (2005). Line polarization of molecular lines at radio frequencies: The case of DR 21(OH). Astrophys. J. 628, 780–788. doi:10.1086/430815

CrossRef Full Text | Google Scholar

Cortés, P. C., Sanhueza, P., Houde, M., Martín, S., Hull, C. L. H., Girart, J. M., et al. (2021). Magnetic fields in massive star-forming regions (MagMaR). II. Tomography through dust and molecular line polarization in NGC 6334I(N). Astrophys. J. 923, 204. doi:10.3847/1538-4357/ac28a1

CrossRef Full Text | Google Scholar

Cox, E. G., Harris, R. J., Looney, L. W., Chiang, H.-F., Chandler, C., Kratter, K., et al. (2017). Protoplanetary disks in ρ Ophiuchus as seen from ALMA. Astrophys. J. 851, 83. doi:10.3847/1538-4357/aa97e2

CrossRef Full Text | Google Scholar

Cox, E. G., Harris, R. J., Looney, L. W., Li, Z.-Y., Yang, H., Tobin, J. J., et al. (2018). ALMA’s polarized view of 10 protostars in the Perseus molecular cloud. Astrophys. J. 855, 92. doi:10.3847/1538-4357/aaacd2

CrossRef Full Text | Google Scholar

Crutcher, R. (1999). Magnetic fields in molecular clouds: Observations confront theory. Astrophys. J. 520, 706–713. doi:10.1086/307483

CrossRef Full Text | Google Scholar

Crutcher, R. M., Hakobian, N., and Troland, T. H. (2010). Self-consistent analysis of OH Zeeman observations. MNRAS 402, L64–L66. doi:10.1111/j.1745-3933.2009.00802.x

CrossRef Full Text | Google Scholar

Crutcher, R. M., Hakobian, N., and Troland, T. H. (2009). Testing magnetic star formation theory. Astrophys. J. 692, 844–855. doi:10.1088/0004-637X/692/1/844

CrossRef Full Text | Google Scholar

Crutcher, R. M., and Kemball, A. J. (2019). Review of zeeman effect observations of regions of star formation. Front. Astron. Space Sci. 6, 66. doi:10.3389/fspas.2019.00066

CrossRef Full Text | Google Scholar

Crutcher, R. M. (2012). Magnetic fields in molecular clouds. Annu. Rev. Astron. Astrophys. 50, 29–63. doi:10.1146/annurev-astro-081811-125514

CrossRef Full Text | Google Scholar

Crutcher, R., Troland, T., Lazareff, B., Paubert, G., and Kazès, I. (1999). Detection of the CN zeeman effect in molecular clouds. Astrophys. J. 514, L121–L124. doi:10.1086/311952

CrossRef Full Text | Google Scholar

Cyganowski, C. J., Brogan, C. L., Hunter, T. R., Smith, R., Kruijssen, J. M. D., Bonnell, I. A., et al. (2017). Simultaneous low- and high-mass Star formation in a massive protocluster: ALMA observations of g11.92-0.61. Mon. Not. R. Astron. Soc. 468, 3694–3708. doi:10.1093/mnras/stx043

CrossRef Full Text | Google Scholar

Dapp, W. B., and Basu, S. (2010). Averting the magnetic braking catastrophe on small scales: disk formation due to ohmic dissipation. Astron. Astrophys. 521, L56. doi:10.1051/0004-6361/201015700

CrossRef Full Text | Google Scholar

Dapp, W. B., Basu, S., and Kunz, M. W. (2012). Bridging the gap: disk formation in the class 0 phase with ambipolar diffusion and ohmic dissipation. Astron. Astrophys. 541, A35. doi:10.1051/0004-6361/201117876

CrossRef Full Text | Google Scholar

Davis, J., Leverett, S., and Greenstein, J. L. (1951). The polarization of starlight by aligned dust grains. Astrophys. J. 114, 206. doi:10.1086/145464

CrossRef Full Text | Google Scholar

Deguchi, S., and Watson, W. D. (1984). Linear polarization of molecular lines at radio frequencies. Astrophys. J. 285, 126–133. doi:10.1086/162483

CrossRef Full Text | Google Scholar

Demyk, K., Meny, C., Leroux, H., Depecker, C., Brubach, J. B., Roy, P., et al. (2017a). Low-temperature MIR to submillimeter mass absorption coefficient of interstellar dust analogues. II. Mg and Fe-rich amorphous silicates. Astron. Astrophys. 606, A50. doi:10.1051/0004-6361/201730944

CrossRef Full Text | Google Scholar

Demyk, K., Meny, C., Lu, X. H., Papatheodorou, G., Toplis, M. J., Leroux, H., et al. (2017b). Low temperature MIR to submillimeter mass absorption coefficient of interstellar dust analogues. I. Mg-rich glassy silicates. Astron. Astrophys. 600, A123. doi:10.1051/0004-6361/201629711

CrossRef Full Text | Google Scholar

Dib, S., Hennebelle, P., Pineda, J. E., Csengeri, T., Bontemps, S., Audit, E., et al. (2010). The angular momentum of magnetized molecular cloud cores: A two-dimensional-three-dimensional comparison. Astrophys. J. 723, 425–439. doi:10.1088/0004-637X/723/1/425

CrossRef Full Text | Google Scholar

Dirienzo, W. J., Brogan, C., Indebetouw, R., Chandler, C. J., Friesen, R. K., and Devine, K. E. (2015). Physical conditions of the earliest phases of massive star formation: Single-dish and interferometric observations of ammonia and CCS in infrared dark clouds. Astron. J. 150, 159. doi:10.1088/0004-6256/150/5/159

CrossRef Full Text | Google Scholar

Donati, J.-F., and Landstreet, J. D. (2009). Magnetic fields of nondegenerate stars. Annu. Rev. Astron. Astrophys. 47, 333–370. doi:10.1146/annurev-astro-082708-101833

CrossRef Full Text | Google Scholar

Duchêne, G., Bontemps, S., Bouvier, J., André, P., Djupvik, A., and Ghez, A. (2007). Multiple protostellar systems. II. A high resolution near-infrared imaging survey in nearby star-forming regions. Astron. Astrophys. 476, 229–242. doi:10.1051/0004-6361:20077270

CrossRef Full Text | Google Scholar

Duchêne, G., Bouvier, J., Bontemps, S., André, P., and Motte, F. (2004). Multiple protostellar systems. I. A deep near infrared survey of Taurus and Ophiuchus protostellar objects. Astron. Astrophys. 427, 651–665. doi:10.1051/0004-6361:20041209

CrossRef Full Text | Google Scholar

Duchêne, G., and Kraus, A. (2013). Stellar multiplicity. Annu. Rev. Astron. Astrophys. 51, 269–310. doi:10.1146/annurev-astro-081710-102602

CrossRef Full Text | Google Scholar

Dunham, M. M., and Vorobyov, E. I. (2012). Resolving the luminosity problem in low-mass star formation. Astrophys. J. 747, 52. doi:10.1088/0004-637X/747/1/52

CrossRef Full Text | Google Scholar

Encalada, F. J., Looney, L. W., Tobin, J. J., Sadavoy, S. I., Segura-Cox, D., Cox, E., et al. (2021). 870 μm dust continuum of the youngest protostars in Ophiuchus. Astrophys. J. 913, 149. doi:10.3847/1538-4357/abf4fd

CrossRef Full Text | Google Scholar

Enoch, M. L., Corder, S., Duchêne, G., Bock, D. C., Bolatto, A. D., Culverhouse, T. L., et al. (2011). Disk and envelope structure in class 0 protostars. II. High-Resolution millimeter mapping of the Serpens sample. Astrophys. J. Suppl. Ser. 195, 21. doi:10.1088/0067-0049/195/2/21

CrossRef Full Text | Google Scholar

Eswaraiah, C., Li, D., Furuya, R. S., Hasegawa, T., Ward-Thompson, D., Qiu, K., et al. (2021). The JCMT BISTRO survey: Revealing the diverse magnetic field morphologies in Taurus dense cores with sensitive submillimeter polarimetry. Astrophys. J. Lett. 912, L27. doi:10.3847/2041-8213/abeb1c

CrossRef Full Text | Google Scholar

Evans, I., Neal, J., Di Francesco, J., Lee, J.-E., Jørgensen, J. K., Choi, M., et al. (2015). Detection of infall in the protostar B335 with ALMA. Astrophys. J. 814, 22. doi:10.1088/0004-637X/814/1/22

CrossRef Full Text | Google Scholar

Evans, N. J., Dunham, M. M., Jørgensen, J. K., Enoch, M. L., Merín, B., van Dishoeck, E. F., et al. (2009). The spitzer c2d legacy results: Star-formation rates and efficiencies; evolution and lifetimes. Astrophys. J. Suppl. Ser. 181, 321–350. doi:10.1088/0067-0049/181/2/321

CrossRef Full Text | Google Scholar

Ewertowski, B., and Basu, S. (2013). A mathematical model for an hourglass magnetic field. Astrophys. J. 767, 33. doi:10.1088/0004-637X/767/1/33

CrossRef Full Text | Google Scholar

Eyink, G., Vishniac, E., Lalescu, C., Aluie, H., Kanov, K., Bürger, K., et al. (2013). Flux-freezing breakdown in high-conductivity magnetohydrodynamic turbulence. Nature 497, 466–469. doi:10.1038/nature12128

PubMed Abstract | CrossRef Full Text | Google Scholar

Falceta-Gonçalves, D., Lazarian, A., and Houde, M. (2010). Damping of magnetohydrodynamic turbulence in partially ionized gas and the observed difference of velocities of neutrals and ions. Astrophys. J. 713, 1376–1385. doi:10.1088/0004-637X/713/2/1376

CrossRef Full Text | Google Scholar

Falceta-Gonçalves, D., Lazarian, A., and Kowal, G. (2008). Studies of regular and random magnetic fields in the ISM: Statistics of polarization vectors and the chandrasekhar-fermi technique. Astrophys. J. 679, 537–551. doi:10.1086/587479

CrossRef Full Text | Google Scholar

Falgarone, E., Troland, T., Crutcher, R., and Paubert, G. (2008). CN Zeeman measurements in star formation regions. Astron. Astrophys. 487, 247–252. doi:10.1051/0004-6361:200809577

CrossRef Full Text | Google Scholar

Favre, C., Ceccarelli, C., López-Sepulcre, A., Fontani, F., Neri, R., Manigand, S., et al. (2018). SOLIS IV. Hydrocarbons in the OMC-2 FIR4 region, a probe of energetic particle irradiation of the region. Astrophys. J. 859, 136. doi:10.3847/1538-4357/aabfd4

CrossRef Full Text | Google Scholar

Favre, C., López-Sepulcre, A., Ceccarelli, C., Dominik, C., Caselli, P., Caux, E., et al. (2017). The onset of energetic particle irradiation in Class 0 protostars. Astron. Astrophys. 608, A82. doi:10.1051/0004-6361/201630177

CrossRef Full Text | Google Scholar

Fitz Axen, M., Offner, S. S. S., Gaches, B. A. L., Fryer, C. L., Hungerford, A., and Silsbee, K. (2021). Transport of protostellar cosmic rays in turbulent dense cores. Astrophys. J. 915, 43. doi:10.3847/1538-4357/abfc55

CrossRef Full Text | Google Scholar

Fontani, F., Commerçon, B., Giannetti, A., Beltrán, M. T., Sánchez-Monge, A., Testi, L., et al. (2016). Magnetically regulated fragmentation of a massive, dense, and turbulent clump. Astron. Astrophys. 593, L14. doi:10.1051/0004-6361/201629442

CrossRef Full Text | Google Scholar

Fontani, F., Commerçon, B., Giannetti, A., Beltrán, M. T., Sánchez-Monge, Á., Testi, L., et al. (2018). Fragmentation properties of massive protocluster gas clumps: An ALMA study. Astron. Astrophys. 615, A94. doi:10.1051/0004-6361/201832672

CrossRef Full Text | Google Scholar

Frau, P., Galli, D., and Girart, J. M. (2011). Comparing star formation models with interferometric observations of the protostar NGC 1333 IRAS 4A. Astron. Astrophys. 535, A44. doi:10.1051/0004-6361/201117813

CrossRef Full Text | Google Scholar

Frimann, S., Jørgensen, J. K., Dunham, M. M., Bourke, T. L., Kristensen, L. E., Offner, S. S. R., et al. (2017). Protostellar accretion traced with chemistry. High-resolution C¹⁸O and continuum observations towards deeply embedded protostars in Perseus. Astron. Astrophys. 602, A120. doi:10.1051/0004-6361/201629739

CrossRef Full Text | Google Scholar

Fromang, S., Hennebelle, P., and Teyssier, R. (2006). A high order Godunov scheme with constrained transport and adaptive mesh refinement for astrophysical magnetohydrodynamics. Astron. Astrophys. 457, 371–384. doi:10.1051/0004-6361:20065371

CrossRef Full Text | Google Scholar

Frost, A. J., Oudmaijer, R. D., de Wit, W. J., and Lumsden, S. L. (2019). A multi-scale exploration of a massive young stellar object. A transition disk around G305.20+0.21? Astron. Astrophys. 625, A44. doi:10.1051/0004-6361/201834583

CrossRef Full Text | Google Scholar

Galametz, M., Maury, A., Girart, J. M., Rao, R., Zhang, Q., Gaudel, M., et al. (2020). An observational correlation between magnetic field, angular momentum and fragmentation in the envelopes of Class 0 protostars? Astron. Astrophys. 644, A47. doi:10.1051/0004-6361/202038854

CrossRef Full Text | Google Scholar

Galametz, M., Maury, A., Girart, J. M., Rao, R., Zhang, Q., Gaudel, M., et al. (2018). SMA observations of polarized dust emission in solar-type Class 0 protostars: Magnetic field properties at envelope scales. Astron. Astrophys. 616, A139. doi:10.1051/0004-6361/201833004

CrossRef Full Text | Google Scholar

Galametz, M., Maury, A. J., Valdivia, V., Testi, L., Belloche, A., and André, P. (2019). Low dust emissivities and radial variations in the envelopes of class 0 protostars: Possible signature of early grain growth. Astron. Astrophys. 632, A5. doi:10.1051/0004-6361/201936342

CrossRef Full Text | Google Scholar

Galli, D., Lizano, S., Shu, F. H., and Allen, A. (2006). Gravitational collapse of magnetized clouds. I. Ideal magnetohydrodynamic accretion flow. Astrophys. J. 647, 374–381. doi:10.1086/505257

CrossRef Full Text | Google Scholar

Gaudel, M., Maury, A. J., Belloche, A., Maret, S., André, P., Hennebelle, P., et al. (2020). Angular momentum profiles of Class 0 protostellar envelopes. Astron. Astrophys. 637, A92. doi:10.1051/0004-6361/201936364

CrossRef Full Text | Google Scholar

Ginsburg, A., McGuire, B., Plambeck, R., Bally, J., Goddi, C., and Wright, M. (2019). Orion SrcI’s disk is salty. Astrophys. J. 872, 54. doi:10.3847/1538-4357/aafb71

CrossRef Full Text | Google Scholar

Girart, J. M., Crutcher, R. M., and Rao, R. (1999). Detection of polarized CO emission from the molecular outflow in NGC 1333 IRAS 4A. Astrophys. J. 525, L109–L112. doi:10.1086/312345

PubMed Abstract | CrossRef Full Text | Google Scholar

Girart, J. M., Estalella, R., Fernández-López, M., Curiel, S., Frau, P., Galvan-Madrid, R., et al. (2017). The circumestellar disk of the B0 protostar powering the HH 80-81 radio jet. Astrophys. J. 847, 58. doi:10.3847/1538-4357/aa81c9

CrossRef Full Text | Google Scholar

Girart, J. M., Fernández-López, M., Li, Z. Y., Yang, H., Estalella, R., Anglada, G., et al. (2018). Resolving the polarized dust emission of the disk around the massive star powering the HH 80-81 radio jet. Astrophys. J. 856, L27. doi:10.3847/2041-8213/aab76b

CrossRef Full Text | Google Scholar

Girart, J. M., Frau, P., Zhang, Q., Koch, P. M., Qiu, K., Tang, Y.-W., et al. (2013). DR 21(OH): A highly fragmented, magnetized, turbulent dense core. Astrophys. J. 772, 69. doi:10.1088/0004-637X/772/1/69

CrossRef Full Text | Google Scholar

Girart, J. M., Greaves, J. S., Crutcher, R. M., and Lai, S. P. (2004). BIMA and JCMT spectropolarimetric observations of the CO J = 2 - 1 line towards orion KL/IRc2. Astrophys. Space Sci. 292, 119–125. doi:10.1023/B:ASTR.0000045007.35868.17

CrossRef Full Text | Google Scholar

Girart, J. M., Rao, R., and Estalella, R. (2009). The L723 low-mass star forming protostellar system: Resolving a double core. Astrophys. J. 694, 56–68. doi:10.1088/0004-637X/694/1/56

CrossRef Full Text | Google Scholar

Girart, J. M., Rao, R., and Marrone, D. P. (2006). Magnetic fields in the formation of sun-like stars. Science 313, 812–814. doi:10.1126/science.1129093

PubMed Abstract | CrossRef Full Text | Google Scholar

Girart, J. M., Viti, S., Estalella, R., and Williams, D. A. (2005). The molecular condensations ahead of Herbig-Haro objects. III. Radiative and dynamical perturbations of the HH 2 condensation. Astron. Astrophys. 439, 601–612. doi:10.1051/0004-6361:20041720

CrossRef Full Text | Google Scholar

Goldreich, P., and Kylafis, N. D. (1982). Linear polarization of radio frequency lines in molecular clouds and circumstellar envelopes. Astrophys. J. 253, 606–621. doi:10.1086/159663

CrossRef Full Text | Google Scholar

Goldreich, P., and Kylafis, N. D. (1981). On mapping the magnetic field direction in molecular clouds by polarization measurements. Astrophys. J. 243, L75–L78. doi:10.1086/183446

CrossRef Full Text | Google Scholar

Gonçalves, J., Galli, D., and Girart, J. M. (2008). Modeling the magnetic field in the protostellar source NGC 1333 IRAS 4A. Astron. Astrophys. 490, L39–L42. doi:10.1051/0004-6361:200810861

CrossRef Full Text | Google Scholar

Goodman, A., Barranco, J., Wilner, D., and Heyer, M. (1998). Coherence in dense cores. II. The transition to coherence. Astrophys. J. 504, 223–246. –+. doi:10.1086/306045

CrossRef Full Text | Google Scholar

Goodman, A., Benson, P., Fuller, G., and Myers, P. (1993). Dense cores in dark clouds. VIII - velocity gradients. Astrophys. J. 406, 528–547. doi:10.1086/172465

CrossRef Full Text | Google Scholar

Goodwin, S. P., Whitworth, A. P., and Ward-Thompson, D. (2004). Simulating star formation in molecular cores. II. The effects of different levels of turbulence. Astron. Astrophys. 423, 169–182. doi:10.1051/0004-6361:20040285

CrossRef Full Text | Google Scholar

Gray, W. J., McKee, C. F., and Klein, R. I. (2018). Effect of angular momentum alignment and strong magnetic fields on the formation of protostellar discs. Mon. Not. R. Astron. Soc. 473, 2124–2143. doi:10.1093/mnras/stx2406

CrossRef Full Text | Google Scholar

Grenier, I. A., Black, J. H., and Strong, A. W. (2015). The nine lives of cosmic rays in galaxies. Annu. Rev. Astron. Astrophys. 53, 199–246. doi:10.1146/annurev-astro-082214-122457

CrossRef Full Text | Google Scholar

Guillet, V., Girart, J. M., Maury, A. J., and Alves, F. O. (2020a). Polarized emission by aligned grains in the Mie regime: Application to protoplanetary disks observed by ALMA. Astron. Astrophys. 634, L15. doi:10.1051/0004-6361/201937314

CrossRef Full Text | Google Scholar

Guillet, V., Hennebelle, P., Pineau des Forêts, G., Marcowith, A., Commerçon, B., and Marchand, P. (2020b). Dust coagulation feedback on magnetohydrodynamic resistivities in protostellar collapse. Astron. Astrophys. 643, A17. doi:10.1051/0004-6361/201937387

CrossRef Full Text | Google Scholar

Gupta, A., Yen, H.-W., Koch, P., Bastien, P., Bourke, T. L., Chung, E. J., et al. (2022). Effects of magnetic field orientations in dense cores on gas kinematics in protostellar envelopes. arXiv e-printsarXiv:2204.05636.

Google Scholar

Haisch, J., Karl, E., Greene, T. P., Barsony, M., and Stahler, S. W. (2004). A near-infrared multiplicity survey of class I/Flat-Spectrum systems in six nearby molecular clouds. Astron. J. 127, 1747–1754. doi:10.1086/381952

CrossRef Full Text | Google Scholar

Harrison, R. E., Looney, L. W., Stephens, I. W., Li, Z.-Y., Teague, R., Crutcher, R. M., et al. (2021). ALMA CN zeeman observations of AS 209: Limits on magnetic field strength and magnetically driven accretion rate. Astrophys. J. 908, 141. doi:10.3847/1538-4357/abd94e

CrossRef Full Text | Google Scholar

Harsono, D., Bjerkeli, P., van der Wiel, M. H. D., Ramsey, J. P., Maud, L. T., Kristensen, L. E., et al. (2018). Evidence for the start of planet formation in a young circumstellar disk. Nat. Astron. 2, 646–651. doi:10.1038/s41550-018-0497-x

CrossRef Full Text | Google Scholar

Harsono, D., Jørgensen, J. K., van Dishoeck, E. F., Hogerheijde, M. R., Bruderer, S., Persson, M. V., et al. (2014). Rotationally-supported disks around class I sources in Taurus: disk formation constraints. Astron. Astrophys. 562, A77. doi:10.1051/0004-6361/201322646

CrossRef Full Text | Google Scholar

Harsono, D., van der Wiel, M. H. D., Bjerkeli, P., Ramsey, J. P., Calcutt, H., Kristensen, L. E., et al. (2021). Resolved molecular line observations reveal an inherited molecular layer in the young disk around TMC1A. Astron. Astrophys. 646, A72. doi:10.1051/0004-6361/202038697

CrossRef Full Text | Google Scholar

He, Y.-X., Zhou, J.-J., Esimbek, J., Ji, W.-G., Wu, G., Tang, X.-D., et al. (2015). Infall motions in massive star-forming regions: Results from years 1 and 2 of the MALT90 survey. Mon. Not. R. Astron. Soc. 450, 1926–1936. –1936. doi:10.1093/mnras/stv732

CrossRef Full Text | Google Scholar

Heimsoth, D. J., Stephens, I. W., Arce, H. G., Bourke, T. L., Myers, P. C., and Dunham, M. M. (2022). Evolution and kinematics of protostellar envelopes in the Perseus molecular cloud. ApJ 927, 88. doi:10.3847/1538-4357/ac448e

CrossRef Full Text | Google Scholar

Heitsch, F., Zweibel, E. G., Mac Low, M.-M., Li, P., and Norman, M. L. (2001). Magnetic field diagnostics based on far-infrared polarimetry: Tests using numerical simulations. Astrophys. J. 561, 800–814. doi:10.1086/323489

CrossRef Full Text | Google Scholar

Hennebelle, P., and Ciardi, A. (2009). Disk formation during collapse of magnetized protostellar cores. ArXiv e-prints.

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Chabrier, G., and Marchand, P. (2016). Magnetically self-regulated formation of early protoplanetary disks. Astrophys. J. 830, L8. doi:10.3847/2041-8205/830/1/L8

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Joos, M., Klessen, R. S., Krumholz, M., Tan, J. C., et al. (2011). Collapse, outflows and fragmentation of massive, turbulent and magnetized prestellar barotropic cores. Astron. Astrophys. 528, A72. doi:10.1051/0004-6361/201016052

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Lee, Y.-N., and Charnoz, S. (2020). What determines the formation and characteristics of protoplanetary discs? Astron. Astrophys. 635, A67. doi:10.1051/0004-6361/201936714

CrossRef Full Text | Google Scholar

Hennebelle, P., and Fromang, S. (2008). Magnetic processes in a collapsing dense core. I. Accretion and ejection. Astron. Astrophys. 477, 9–24. doi:10.1051/0004-6361:20078309

CrossRef Full Text | Google Scholar

Hennebelle, P., and Teyssier, R. (2008). Magnetic processes in a collapsing dense core. II. Fragmentation. Is there a fragmentation crisis? Astron. Astrophys. 477, 25–34. doi:10.1051/0004-6361:20078310

CrossRef Full Text | Google Scholar

Hezareh, T., Csengeri, T., Houde, M., Herpin, F., and Bontemps, S. (2014). Probing the turbulent ambipolar diffusion scale in molecular clouds with spectroscopy. Mon. Not. R. Astron. Soc. 438, 663–671. doi:10.1093/mnras/stt2237

CrossRef Full Text | Google Scholar

Hezareh, T., Houde, M., McCoey, C., and Li, H.-b. (2010). Observational determination of the turbulent ambipolar diffusion scale and magnetic field strength in molecular clouds. Astrophys. J. 720, 603–607. doi:10.1088/0004-637X/720/1/603

CrossRef Full Text | Google Scholar

Hezareh, T., Wiesemeyer, H., Houde, M., Gusdorf, A., and Siringo, G. (2013). Non-Zeeman circular polarization of CO rotational lines in SNR IC 443. Astron. Astrophys. 558, A45. doi:10.1051/0004-6361/201321900

CrossRef Full Text | Google Scholar

Hildebrand, R. H., and Dragovan, M. (1995). The shapes and alignment properties of interstellar dust grains. Astrophys. J. 450, 663. doi:10.1086/176173

CrossRef Full Text | Google Scholar

Hildebrand, R. H., Kirby, L., Dotson, J. L., Houde, M., and Vaillancourt, J. E. (2009). Dispersion of magnetic fields in molecular clouds. I. ApJ 696, 567–573. doi:10.1088/0004-637X/696/1/567

CrossRef Full Text | Google Scholar

Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., and Flower, D. (2008). CN in prestellar cores. Astron. Astrophys. 480, L5–L8. doi:10.1051/0004-6361:20079296

CrossRef Full Text | Google Scholar

Hirano, S., Tsukamoto, Y., Basu, S., and Machida, M. N. (2020). The effect of misalignment between the rotation Axis and magnetic field on the circumstellar disk. Astrophys. J. 898, 118. doi:10.3847/1538-4357/ab9f9d

CrossRef Full Text | Google Scholar

Hirota, T., Machida, M. N., Matsushita, Y., Motogi, K., Matsumoto, N., Kim, M. K., et al. (2017). Disk-driven rotating bipolar outflow in Orion Source I. Nat. Astron. 1, 0146. doi:10.1038/s41550-017-0146

CrossRef Full Text | Google Scholar

Hoang, T. (2022). Effects of grain alignment with magnetic fields on grain growth and the structure of dust aggregates. ApJ 928, 102. doi:10.3847/1538-4357/ac5408

CrossRef Full Text | Google Scholar

Hoang, T., and Lazarian, A. (2014). Grain alignment by radiative torques in special conditions and implications. Mon. Not. R. Astron. Soc. 438, 680–703. doi:10.1093/mnras/stt2240

CrossRef Full Text | Google Scholar

Houde, M., Bastien, P., Peng, R., Phillips, T. G., and Yoshida, H. (2000). Probing the magnetic field with molecular ion spectra. Astrophys. J. 536, 857–864. doi:10.1086/308980

CrossRef Full Text | Google Scholar

Houde, M., Hezareh, T., Jones, S., and Rajabi, F. (2013). Non-zeeman circular polarization of molecular rotational spectral lines. Astrophys. J. 764, 24. doi:10.1088/0004-637X/764/1/24

CrossRef Full Text | Google Scholar

Houde, M., Hull, C. L. H., Plambeck, R. L., Vaillancourt, J. E., and Hildebrand, R. H. (2016). Dispersion of magnetic fields in molecular clouds. IV. Analysis of interferometry data. Astrophys. J. 820, 38. doi:10.3847/0004-637X/820/1/38

CrossRef Full Text | Google Scholar

Houde, M., Lankhaar, B., Rajabi, F., and Chamma, M. A. (2022). The generation and transformation of polarization signals in molecular lines through collective anisotropic resonant scattering. Mon. Not. R. Astron. Soc. 511, 295–315. doi:10.1093/mnras/stab3806

CrossRef Full Text | Google Scholar

Houde, M., Rao, R., Vaillancourt, J. E., and Hildebrand, R. H. (2011). Dispersion of magnetic fields in molecular clouds. III. Astrophys. J. 733, 109. doi:10.1088/0004-637X/733/2/109

CrossRef Full Text | Google Scholar

Houde, M., Vaillancourt, J. E., Hildebrand, R. H., Chitsazzadeh, S., and Kirby, L. (2009). Dispersion of magnetic fields in molecular clouds. II. Astrophys. J. 706, 1504–1516. doi:10.1088/0004-637X/706/2/1504

CrossRef Full Text | Google Scholar

Hsieh, C.-H., Arce, H. G., Mardones, D., Kong, S., and Plunkett, A. (2021). Rotating filament in orion B: Do cores inherit their angular momentum from their parent filament? Astrophys. J. 908, 92. doi:10.3847/1538-4357/abd034

CrossRef Full Text | Google Scholar

Hsieh, T.-H., Murillo, N. M., Belloche, A., Hirano, N., Walsh, C., van Dishoeck, E. F., et al. (2019). Chronology of episodic accretion in protostars—an ALMA survey of the CO and H₂O snowlines. Astrophys. J. 884, 149. doi:10.3847/1538-4357/ab425a

CrossRef Full Text | Google Scholar

Hull, C. L. H., Girart, J. M., Tychoniec, Ł., Rao, R., Cortés, P. C., Pokhrel, R., et al. (2017a). ALMA observations of dust polarization and molecular line emission from the class 0 protostellar source Serpens SMM1. Astrophys. J. 847, 92. doi:10.3847/1538-4357/aa7fe9

CrossRef Full Text | Google Scholar

Hull, C. L. H., Le Gouellec, V. J. M., Girart, J. M., Tobin, J. J., and Bourke, T. L. (2020). Understanding the origin of the magnetic field morphology in the wide-binary protostellar system BHR 71. Astrophys. J. 892, 152. doi:10.3847/1538-4357/ab5809

CrossRef Full Text | Google Scholar

Hull, C. L. H., Mocz, P., Burkhart, B., Goodman, A. A., Girart, J. M., Cortés, P. C., et al. (2017b). Unveiling the role of the magnetic field at the smallest scales of star formation. Astrophys. J. 842, L9. doi:10.3847/2041-8213/aa71b7

CrossRef Full Text | Google Scholar

Hull, C. L. H., Plambeck, R. L., Bolatto, A. D., Bower, G. C., Carpenter, J. M., Crutcher, R. M., et al. (2013). Misalignment of magnetic fields and outflows in protostellar cores. Astrophys. J. 768, 159. doi:10.1088/0004-637X/768/2/159

CrossRef Full Text | Google Scholar

Hull, C. L. H., Plambeck, R. L., Kwon, W., Bower, G. C., Carpenter, J. M., Crutcher, R. M., et al. (2014). Tadpol: A 1.3 mm survey of dust polarization in star-forming cores and regions. Astrophys. J. Suppl. Ser. 213, 13. doi:10.1088/0067-0049/213/1/13

CrossRef Full Text | Google Scholar

Hull, C. L. H., and Zhang, Q. (2019). Interferometric observations of magnetic fields in forming stars. Front. Astron. Space Sci. 6, 3. doi:10.3389/fspas.2019.00003

CrossRef Full Text | Google Scholar

Ilee, J. D., Cyganowski, C. J., Brogan, C. L., Hunter, T. R., Forgan, D. H., Haworth, T. J., et al. (2018). G11.92-0.61 MM 1: A fragmented keplerian disk surrounding a proto-O star. Astrophys. J. 869, L24. doi:10.3847/2041-8213/aaeffc

CrossRef Full Text | Google Scholar

Imai, M., Oya, Y., Sakai, N., López-Sepulcre, A., Watanabe, Y., and Yamamoto, S. (2019). Unveiling a few astronomical unit scale rotation structure around the protostar in B335. Astrophys. J. 873, L21. doi:10.3847/2041-8213/ab0c20

CrossRef Full Text | Google Scholar

Johnston, K. G., Robitaille, T. P., Beuther, H., Linz, H., Boley, P., Kuiper, R., et al. (2015). A keplerian-like disk around the forming O-type star AFGL 4176. Astrophys. J. 813, L19. doi:10.1088/2041-8205/813/1/L19

CrossRef Full Text | Google Scholar

Joncour, I., Duchêne, G., and Moraux, E. (2017). Multiplicity and clustering in Taurus star-forming region. I. Unexpected ultra-wide pairs of high-order multiplicity in Taurus. Astron. Astrophys. 599, A14. doi:10.1051/0004-6361/201629398

CrossRef Full Text | Google Scholar

Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., and Verstraete, L. (2017). The global dust modelling framework THEMIS. Astron. Astrophys. 602, A46. doi:10.1051/0004-6361/201630225

CrossRef Full Text | Google Scholar

Jones, T. J., Bagley, M., Krejny, M., Andersson, B. G., and Bastien, P. (2015). Grain alignment in starless cores. Astron. J. 149, 31. doi:10.1088/0004-6256/149/1/31

CrossRef Full Text | Google Scholar

Joos, M., Hennebelle, P., Ciardi, A., and Fromang, S. (2013). The influence of turbulence during magnetized core collapse and its consequences on low-mass star formation. Astron. Astrophys. 554, A17. doi:10.1051/0004-6361/201220649

CrossRef Full Text | Google Scholar

Joos, M., Hennebelle, P., and Ciardi, A. (2012). Protostellar disk formation and transport of angular momentum during magnetized core collapse. Astron. Astrophys. 543, A128. doi:10.1051/0004-6361/201118730

CrossRef Full Text | Google Scholar

Jørgensen, J. K., Johnstone, D., Kirk, H., and Myers, P. C. (2007). Current star formation in the Perseus molecular cloud: Constraints from unbiased submillimeter and mid-infrared surveys. Astrophys. J. 656, 293–305. doi:10.1086/510150

CrossRef Full Text | Google Scholar

Jørgensen, J. K., Schöier, F. L., and van Dishoeck, E. F. (2004). Molecular inventories and chemical evolution of low-mass protostellar envelopes. Astron. Astrophys. 416, 603–622. doi:10.1051/0004-6361:20034440

CrossRef Full Text | Google Scholar

Juárez, C., Girart, J. M., Frau, P., Palau, A., Estalella, R., Morata, O., et al. (2017). A correlation between chemistry, polarization, and dust properties in the Pipe nebula starless core FeSt 1-457. Astron. Astrophys. 597, A74. doi:10.1051/0004-6361/201628608

CrossRef Full Text | Google Scholar

Kandori, R., Tamura, M., Tomisaka, K., Nakajima, Y., Kusakabe, N., Kwon, J., et al. (2017). Distortion of magnetic fields in a starless core II: 3D magnetic field structure of FeSt 1-457. Astrophys. J. 848, 110. doi:10.3847/1538-4357/aa8d18

CrossRef Full Text | Google Scholar

Kataoka, A., Muto, T., Momose, M., Tsukagoshi, T., Fukagawa, M., Shibai, H., et al. (2015). Millimeter-wave polarization of protoplanetary disks due to dust scattering. Astrophys. J. 809, 78. doi:10.1088/0004-637X/809/1/78

CrossRef Full Text | Google Scholar

Kataoka, A., Okuzumi, S., and Tazaki, R. (2019). Millimeter-wave polarization due to grain alignment by the gas flow in protoplanetary disks. Astrophys. J. 874, L6. doi:10.3847/2041-8213/ab0c9a

CrossRef Full Text | Google Scholar

Kirchschlager, F., and Bertrang, G. H. M. (2020). Self-scattering of non-spherical dust grains. The limitations of perfect compact spheres. Astron. Astrophys. 638, A116. doi:10.1051/0004-6361/202037943

CrossRef Full Text | Google Scholar

Ko, C.-L., Liu, H. B., Lai, S.-P., Ching, T.-C., Rao, R., and Girart, J. M. (2020). Resolving linear polarization due to emission and extinction of aligned dust grains on NGC 1333 IRAS4A with JVLA and ALMA. ApJ. 889, 172. doi:10.3847/1538-4357/ab5e79

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., and Ho, P. T. P. (2013). Interpreting the role of the magnetic field from dust polarization maps. Astrophys. J. 775, 77. doi:10.1088/0004-637X/775/1/77

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., Ho, P. T. P., Zhang, Q., Girart, J. M., Chen, H.-R. V., et al. (2014). The importance of the magnetic field from an SMA-CSO-combined sample of star-forming regions. Astrophys. J. 797, 99. doi:10.1088/0004-637X/797/2/99

CrossRef Full Text | Google Scholar

Köhler, R., Neuhäuser, R., Krämer, S., Leinert, C., Ott, T., and Eckart, A. (2008). Multiplicity of young stars in and around R coronae australis. Astron. Astrophys. 488, 997–1006. doi:10.1051/0004-6361:200809897

CrossRef Full Text | Google Scholar

Kowal, G., Lazarian, A., Vishniac, E. T., and Otmianowska-Mazur, K. (2009). Numerical tests of fast reconnection in weakly stochastic magnetic fields. Astrophys. J. 700, 63–85. doi:10.1088/0004-637X/700/1/63

CrossRef Full Text | Google Scholar

Kraus, S., Hofmann, K.-H., Menten, K. M., Schertl, D., Weigelt, G., Wyrowski, F., et al. (2010). A hot compact dust disk around a massive young stellar object. Nature 466, 339–342. doi:10.1038/nature09174

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuffmeier, M., Frimann, S., Jensen, S. S., and Haugbølle, T. (2018). Episodic accretion: The interplay of infall and disc instabilities. Mon. Not. R. Astron. Soc. 475, 2642–2658. doi:10.1093/mnras/sty024

CrossRef Full Text | Google Scholar

Kuffmeier, M., Zhao, B., and Caselli, P. (2020). Ionization: A possible explanation for the difference of mean disk sizes in star-forming regions. Astron. Astrophys. 639, A86. doi:10.1051/0004-6361/201937328

CrossRef Full Text | Google Scholar

Kunze, K. E. (2013). Cosmological magnetic fields. Plasma Phys. control. Fusion 55, 124026. doi:10.1088/0741-3335/55/12/124026

CrossRef Full Text | Google Scholar

Kuznetsova, A., Bae, J., Hartmann, L., and Low, M.-M. M. (2022). Anisotropic infall and substructure formation in embedded disks. Astrophys. J. 928, 92. doi:10.3847/1538-4357/ac54a8

CrossRef Full Text | Google Scholar

Kuznetsova, A., Hartmann, L., and Heitsch, F. (2020). Angular momenta, magnetization, and accretion of protostellar cores. Astrophys. J. 893, 73. doi:10.3847/1538-4357/ab7eac

CrossRef Full Text | Google Scholar

Kuznetsova, A., Hartmann, L., and Heitsch, F. (2019). The origins of protostellar core angular momenta. Astrophys. J. 876, 33. doi:10.3847/1538-4357/ab12ce

CrossRef Full Text | Google Scholar

Kwon, W., Looney, L. W., Mundy, L. G., Chiang, H.-F., and Kemball, A. J. (2009). Grain growth and density distribution of the youngest protostellar systems. Astrophys. J. 696, 841–852. doi:10.1088/0004-637X/696/1/841

CrossRef Full Text | Google Scholar

Kwon, W., Stephens, I. W., Tobin, J. J., Looney, L. W., Li, Z.-Y., van der Tak, F. F. S., et al. (2019). Highly ordered and pinched magnetic fields in the class 0 protobinary system L1448 IRS 2. Astrophys. J. 879, 25. doi:10.3847/1538-4357/ab24c8

CrossRef Full Text | Google Scholar

Lai, S.-P., Girart, J. M., and Crutcher, R. M. (2003a). Interferometric mapping of magnetic fields in star-forming regions. III. Dust and CO polarization in DR 21(OH). Astrophys. J. 598, 392–399. doi:10.1086/378769

CrossRef Full Text | Google Scholar

Lai, S.-P., Velusamy, T., and Langer, W. D. (2003b). The high angular resolution measurement of ion and neutral spectra as a probe of the magnetic field structure in DR 21(OH). Astrophys. J. 596, L239–L242. doi:10.1086/379502

CrossRef Full Text | Google Scholar

Lam, K. H., Chen, C.-Y., Li, Z.-Y., Yang, H., Cox, E. G., Looney, L. W., et al. (2021). The transition of polarized dust thermal emission from the protostellar envelope to the disc scale. Mon. Not. R. Astron. Soc. 507, 608–620. doi:10.1093/mnras/stab2105

CrossRef Full Text | Google Scholar

Lam, K. H., Li, Z.-Y., Chen, C.-Y., Tomida, K., and Zhao, B. (2019). Disc formation in magnetized dense cores with turbulence and ambipolar diffusion. Mon. Not. R. Astron. Soc. 489, 5326–5347. doi:10.1093/mnras/stz2436

CrossRef Full Text | Google Scholar

Lankhaar, B., Vlemmings, W., and Bjerkeli, P. (2022). Tracing the large-scale magnetic field morphology in protoplanetary disks using molecular line polarization. Astron. Astrophys. 657, A106. doi:10.1051/0004-6361/202141285

CrossRef Full Text | Google Scholar

Lankhaar, B., and Vlemmings, W. (2020a). Collisional polarization of molecular ions: A signpost of ambipolar diffusion. Astron. Astrophys. 638, L7. doi:10.1051/0004-6361/202038196

CrossRef Full Text | Google Scholar

Lankhaar, B., and Vlemmings, W. (2020b). Portal: Three-dimensional polarized (sub)millimeter line radiative transfer. Astron. Astrophys. 636, A14. doi:10.1051/0004-6361/202037509

CrossRef Full Text | Google Scholar

Lazarian, A., Andersson, B. G., and Hoang, T. (2015). “Grain alignment: Role of radiative torques and paramagnetic relaxation,” in Polarimetry of stars and planetary systems, 81.

CrossRef Full Text | Google Scholar

Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a weakly stochastic field. Astrophys. J. 517, 700–718. doi:10.1086/307233

CrossRef Full Text | Google Scholar

Le Gouellec, V. J. M., Hull, C. L. H., Maury, A. J., Girart, J. M., Tychoniec, Ł., Kristensen, L. E., et al. (2019). Characterizing magnetic field morphologies in three Serpens protostellar cores with ALMA. Astrophys. J. 885, 106. doi:10.3847/1538-4357/ab43c2

CrossRef Full Text | Google Scholar

Le Gouellec, V. J. M., Maury, A. J., Guillet, V., Hull, C. L. H., Girart, J. M., Verliat, A., et al. (2020). A statistical analysis of dust polarization properties in ALMA observations of Class 0 protostellar cores. Astron. Astrophys. 644, A11. doi:10.1051/0004-6361/202038404

CrossRef Full Text | Google Scholar

Lebreuilly, U., Commerçon, B., and Laibe, G. (2020). Protostellar collapse: The conditions to form dust-rich protoplanetary disks. Astron. Astrophys. 641, A112. doi:10.1051/0004-6361/202038174

CrossRef Full Text | Google Scholar

Lebreuilly, U., Hennebelle, P., Colman, T., Commerçon, B., Klessen, R., Maury, A., et al. (2021). Protoplanetary disk birth in massive star-forming clumps: The essential role of the magnetic field. Astrophys. J. Lett. 917, L10. doi:10.3847/2041-8213/ac158c

CrossRef Full Text | Google Scholar

Lee, C.-F., Hwang, H.-C., Ching, T.-C., Hirano, N., Lai, S.-P., Rao, R., et al. (2018a). Unveiling a magnetized jet from a low-mass protostar. Nat. Commun. 9, 4636. doi:10.1038/s41467-018-07143-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C.-F., Kwon, W., Jhan, K.-S., Hirano, N., Hwang, H.-C., Lai, S.-P., et al. (2019). A pseudodisk threaded with a toroidal and pinched poloidal magnetic field morphology in the HH 211 protostellar system. Astrophys. J. 879, 101. doi:10.3847/1538-4357/ab2458

CrossRef Full Text | Google Scholar

Lee, C.-F., Li, Z.-Y., Hirano, N., Shang, H., Ho, P. T. P., and Zhang, Q. (2018b). ALMA Observations of the Very Young Class 0 Protostellar System HH211-mms: A 30 au Dusty Disk with a Disk Wind Traced by SO? Astrophys. J. 863, 94. doi:10.3847/1538-4357/aad2da

CrossRef Full Text | Google Scholar

Lee, C.-F., Li, Z.-Y., Yang, H., Daniel Lin, Z.-Y., Ching, T.-C., and Lai, S.-P. (2021a). What produces dust polarization in the HH 212 protostellar disk at 878 μm: Dust self-scattering or dichroic extinction? Astrophys. J. 910, 75. doi:10.3847/1538-4357/abe53a

CrossRef Full Text | Google Scholar

Lee, J. W. Y., Hull, C. L. H., and Offner, S. S. R. (2017). Synthetic observations of magnetic fields in protostellar cores. ApJ 834, 201. doi:10.3847/1538-4357/834/2/201

CrossRef Full Text | Google Scholar

Lee, Y.-N., Charnoz, S., and Hennebelle, P. (2021b). Protoplanetary disk formation from the collapse of a prestellar core. Astron. Astrophys. 648, A101. doi:10.1051/0004-6361/202038105

CrossRef Full Text | Google Scholar

Lee, Y.-N., Marchand, P., Liu, Y.-H., and Hennebelle, P. (2021c). Universal protoplanetary disk size under complete nonideal magnetohydrodynamics: The interplay between ion-neutral friction, Hall effect, and ohmic dissipation. Astrophys. J. 922, 36. doi:10.3847/1538-4357/ac235d

CrossRef Full Text | Google Scholar

Levin, S. M., Langer, W. D., Velusamy, T., Kuiper, T. B. H., and Crutcher, R. M. (2001). Measuring the magnetic field strength in L1498 with zeeman-splitting observations of CCS. Astrophys. J. 555, 850–854. doi:10.1086/321518

CrossRef Full Text | Google Scholar

Li, H.-b., and Houde, M. (2008). Probing the turbulence dissipation range and magnetic field strengths in molecular clouds. Astrophys. J. 677, 1151–1156. doi:10.1086/529581

CrossRef Full Text | Google Scholar

Li, J. I.-H., Liu, H. B., Hasegawa, Y., and Hirano, N. (2017). Systematic analysis of spectral energy distributions and the dust opacity indices for class 0 young stellar objects. Astrophys. J. 840, 72. doi:10.3847/1538-4357/aa6f04

CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., and Shang, H. (2013). Does magnetic-field-rotation misalignment solve the magnetic braking catastrophe in protostellar disk formation? Astrophys. J. 774, 82. doi:10.1088/0004-637X/774/1/82

CrossRef Full Text | Google Scholar

Li, Z.-Y., and Shu, F. (1996). Magnetized singular isothermal toroids. Astrophys. J. 472, 211–224. –+. doi:10.1086/178056

CrossRef Full Text | Google Scholar

Liu, H. B., Chen, H.-R. V., Román-Zúñiga, C. G., Galván-Madrid, R., Ginsburg, A., Ho, P. T. P., et al. (2019). Investigating Fragmentation of Gas Structures in OB Cluster-forming Molecular Clump G33.92+0.11 with 1000 au Resolution Observations of ALMA. Astrophys. J. 871, 185. doi:10.3847/1538-4357/aaf6b4

CrossRef Full Text | Google Scholar

Liu, H. B., Lai, S.-P., Hasegawa, Y., Hirano, N., Rao, R., Li, I. H., et al. (2016). Detection of linearly polarized 6.9 mm continuum emission from the class 0 young stellar object NGC 1333 IRAS4A. Astrophys. J. 821, 41. doi:10.3847/0004-637X/821/1/41

CrossRef Full Text | Google Scholar

Liu, J., Zhang, Q., Commerçon, B., Valdivia, V., Maury, A., and Qiu, K. (2021). Calibrating the davis-chandrasekhar-fermi method with numerical simulations: Uncertainties in estimating the magnetic field strength from statistics of field orientations. Astrophys. J. 919, 79. doi:10.3847/1538-4357/ac0cec

CrossRef Full Text | Google Scholar

Liu, S.-Y., Su, Y.-N., Zinchenko, I., Wang, K.-S., Meyer, D. M. A., Wang, Y., et al. (2020). ALMA view of the infalling envelope around a massive protostar in S255IR SMA1. Astrophys. J. 904, 181. doi:10.3847/1538-4357/abc0ec

CrossRef Full Text | Google Scholar

Liu, T., Wu, Y., and Zhang, H. (2013). Uniform infall toward the cometary H II region in the G34.26+0.15 complex? Astrophys. J. 776, 29. doi:10.1088/0004-637X/776/1/29

CrossRef Full Text | Google Scholar

Looney, L., Mundy, L., and Welch, W. (2000). Unveiling the circumstellar envelope and disk: A subarcsecond survey of circumstellar structures. Astrophys. J. 529, 477–498. doi:10.1086/308239

CrossRef Full Text | Google Scholar

Machida, M. N., Tomisaka, K., Matsumoto, T., and Inutsuka, S.-i. (2008). Formation scenario for wide and close binary systems. Astrophys. J. 677, 327–347. doi:10.1086/529133

CrossRef Full Text | Google Scholar

Marchand, P., Tomida, K., Commerçon, B., and Chabrier, G. (2019). Impact of the Hall effect in star formation, improving the angular momentum conservation. Astron. Astrophys. 631, A66. doi:10.1051/0004-6361/201936215

CrossRef Full Text | Google Scholar

Mardones, D., Myers, P. C., Tafalla, M., Wilner, D. J., Bachiller, R., and Garay, G. (1997). A search for infall motions toward nearby young stellar objects. Astrophys. J. 489, 719–733. doi:10.1086/304812

CrossRef Full Text | Google Scholar

Maret, S., Maury, A. J., Belloche, A., Gaudel, M., André, P., Cabrit, S., et al. (2020). Searching for kinematic evidence of Keplerian disks around Class 0 protostars with CALYPSO. Astron. Astrophys. 635, A15. doi:10.1051/0004-6361/201936798

CrossRef Full Text | Google Scholar

Martin, P. G., Roy, A., Bontemps, S., Miville-Deschênes, M.-A., Ade, P. A. R., Bock, J. J., et al. (2012). Evidence for environmental changes in the submillimeter dust opacity. Astrophys. J. 751, 28. doi:10.1088/0004-637X/751/1/28

CrossRef Full Text | Google Scholar

Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., and Commerçon, B. (2016). Ambipolar diffusion in low-mass star formation. I. General comparison with the ideal magnetohydrodynamic case. Astron. Astrophys. 587, A32. doi:10.1051/0004-6361/201526371

CrossRef Full Text | Google Scholar

Mathis, J. S., Rumpl, W., and Nordsieck, K. H. (1977). The size distribution of interstellar grains. Astrophys. J. 217, 425–433. doi:10.1086/155591

CrossRef Full Text | Google Scholar

Matsumoto, T., and Hanawa, T. (2003). Fragmentation of a molecular cloud core versus fragmentation of the massive protoplanetary disk in the main accretion phase. Astrophys. J. 595, 913–934. doi:10.1086/377367

CrossRef Full Text | Google Scholar

Matsumoto, T., Machida, M. N., and Inutsuka, S.-i. (2017). Circumstellar disks and outflows in turbulent molecular cloud cores: Possible formation mechanism for misaligned systems. Astrophys. J. 839, 69. doi:10.3847/1538-4357/aa6a1c

CrossRef Full Text | Google Scholar

Matsumoto, T., and Tomisaka, K. (2004). Directions of outflows, disks, magnetic fields, and rotation of young stellar objects in collapsing molecular cloud cores. Astrophys. J. 616, 266–282. doi:10.1086/424897

CrossRef Full Text | Google Scholar

Matthews, B. C., McPhee, C. A., Fissel, L. M., and Curran, R. L. (2009). The legacy of SCUPOL: 850 μm imaging polarimetry from 1997 to 2005. Astrophys. J. Suppl. Ser. 182, 143–204. doi:10.1088/0067-0049/182/1/143

CrossRef Full Text | Google Scholar

Maud, L. T., Cesaroni, R., Kumar, M. S. N., Rivilla, V. M., Ginsburg, A., Klaassen, P. D., et al. (2019). Substructures in the Keplerian disc around the O-type (proto-)star G17.64+0.16. Astron. Astrophys. 627, L6. doi:10.1051/0004-6361/201935633

CrossRef Full Text | Google Scholar

Maureira, M. J., Arce, H. G., Offner, S. S. R., Dunham, M. M., Pineda, J. E., Fernández-López, M., et al. (2017). A turbulent origin for the complex envelope kinematics in the young low-mass core per-bolo 58. Astrophys. J. 849, 89. doi:10.3847/1538-4357/aa91ce

CrossRef Full Text | Google Scholar

Maury, A. J., André, P., Hennebelle, P., Motte, F., Stamatellos, D., Bate, M., et al. (2010). Toward understanding the formation of multiple systems. Astron. Astrophys. 512, A40. doi:10.1051/0004-6361/200913492

CrossRef Full Text | Google Scholar

Maury, A. J., André, P., Men’shchikov, A., Könyves, V., and Bontemps, S. (2011). the formation of active protoclusters in the aquila rift: A millimeter continuum view. Astron. Astrophys. 535, A77. doi:10.1051/0004-6361/201117132

CrossRef Full Text | Google Scholar

Maury, A. J., André, P., Testi, L., Maret, S., Belloche, A., Hennebelle, P., et al. (2019). Characterizing young protostellar disks with the CALYPSO IRAM-PdBI survey: Large class 0 disks are rare. Astron. Astrophys. 621, A76. doi:10.1051/0004-6361/201833537

CrossRef Full Text | Google Scholar

Maury, A. J., Girart, J. M., Zhang, Q., Hennebelle, P., Keto, E., Rao, R., et al. (2018). Magnetically regulated collapse in the B335 protostar? I. ALMA observations of the polarized dust emission. Mon. Not. R. Astron. Soc. 477, 2760–2765. doi:10.1093/mnras/sty574

CrossRef Full Text | Google Scholar

Maury, A. J., Wiesemeyer, H., and Thum, C. (2012). CN Zeeman observations of the NGC 2264-C protocluster. Astron. Astrophys. 544, A69. doi:10.1051/0004-6361/201219148

CrossRef Full Text | Google Scholar

Mazzei, R., Cleeves, L. I., and Li, Z.-Y. (2020). Untangling magnetic complexity in protoplanetary disks with the zeeman effect. Astrophys. J. 903, 20. doi:10.3847/1538-4357/abb67a

CrossRef Full Text | Google Scholar

Mellon, R. R., and Li, Z.-Y. (2008). Magnetic braking and protostellar disk formation: The ideal mhd limit. Astrophys. J. 681, 1356–1376. doi:10.1086/587542

CrossRef Full Text | Google Scholar

Mignon-Risse, R., González, M., Commerçon, B., and Rosdahl, J. (2021). Collapse of turbulent massive cores with ambipolar diffusion and hybrid radiative transfer. I. Accretion and multiplicity. Astron. Astrophys. 652, A69. doi:10.1051/0004-6361/202140617

CrossRef Full Text | Google Scholar

Miotello, A., Testi, L., Lodato, G., Ricci, L., Rosotti, G., Brooks, K., et al. (2014). Grain growth in the envelopes and disks of Class I protostars. Astron. Astrophys. 567, A32. doi:10.1051/0004-6361/201322945

CrossRef Full Text | Google Scholar

Misugi, Y., Inutsuka, S.-i., and Arzoumanian, D. (2019). An origin for the angular momentum of molecular cloud cores: A prediction from filament fragmentation. Astrophys. J. 881, 11. doi:10.3847/1538-4357/ab2382

CrossRef Full Text | Google Scholar

Mottram, J. C., van Dishoeck, E. F., Kristensen, L. E., Karska, A., San José-García, I., Khanna, S., et al. (2017). Outflows, infall and evolution of a sample of embedded low-mass protostars. Astron. Astrophys. 600, A99. doi:10.1051/0004-6361/201628682

CrossRef Full Text | Google Scholar

Mottram, J. C., van Dishoeck, E. F., Schmalzl, M., Kristensen, L. E., Visser, R., Hogerheijde, M. R., et al. (2013). Waterfalls around protostars. Astron. Astrophys. 558, A126. doi:10.1051/0004-6361/201321828

CrossRef Full Text | Google Scholar

Mouschovias, T. C. (1979). Magnetic braking of self-gravitating, oblate interstellar clouds. Astrophys. J. 228, 159–162. doi:10.1086/156832

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Morton, S. A. (1985). The angular momentum problem during star formation - magnetically linked aligned rotators - Part Two - results. Astrophys. J. 298, 205. doi:10.1086/163599

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Paleologou, E. V. (1980). The angular momentum problem and magnetic braking during star formation - exact solutions for an aligned and a perpendicular rotator. Moon Planets 22, 31–45. doi:10.1007/BF00896865

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Tassis, K. (2010). Self-consistent analysis of OH-zeeman observations: Too much noise about noise. Mon. Not. R. Astron. Soc. 409, 801–807. doi:10.1111/j.1365-2966.2010.17345.x

CrossRef Full Text | Google Scholar

Mouschovias, T., and Spitzer, L. (1976). Note on the collapse of magnetic interstellar clouds. Astrophys. J. 210, 326. –+. doi:10.1086/154835

CrossRef Full Text | Google Scholar

Myers, A. T., McKee, C. F., Cunningham, A. J., Klein, R. I., and Krumholz, M. R. (2013). The fragmentation of magnetized, massive star-forming cores with radiative feedback. Astrophys. J. 766, 97. doi:10.1088/0004-637X/766/2/97

CrossRef Full Text | Google Scholar

Myers, P. C., Basu, S., and Auddy, S. (2018). Magnetic field structure in spheroidal star-forming clouds. Astrophys. J. 868, 51. doi:10.3847/1538-4357/aae695

CrossRef Full Text | Google Scholar

Myers, P. C., and Basu, S. (2021). Magnetic properties of star-forming dense cores. Astrophys. J. 917, 35. doi:10.3847/1538-4357/abf4c8

CrossRef Full Text | Google Scholar

Nakamura, F., Kameno, S., Kusune, T., Mizuno, I., Dobashi, K., Shimoikura, T., et al. (2019). First clear detection of the CCS Zeeman splitting toward the pre-stellar core, Taurus Molecular Cloud 1. Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 71, 117. doi:10.1093/pasj/psz102

CrossRef Full Text | Google Scholar

Nakano, T., Nishi, R., and Umebayashi, T. (2002). Mechanism of magnetic flux loss in molecular clouds. ApJ.

Google Scholar

Nakatani, R., Liu, H. B., Ohashi, S., Zhang, Y., Hanawa, T., Chandler, C., et al. (2020). Substructure formation in a protostellar disk of L1527 IRS. Astrophys. J. 895, L2. doi:10.3847/2041-8213/ab8eaa

CrossRef Full Text | Google Scholar

Nishi, R., Nakano, T., and Umebayashi, T. (1991). Magnetic flux loss from interstellar clouds with various grain-size distributions. Astrophys. J. 368, 181. doi:10.1086/169682

CrossRef Full Text | Google Scholar

Ober, F., Wolf, S., Uribe, A. L., and Klahr, H. H. (2015). Tracing planet-induced structures in circumstellar disks using molecular lines. Astron. Astrophys. 579, A105. doi:10.1051/0004-6361/201526117

CrossRef Full Text | Google Scholar

Offner, S. S. R., Klein, R. I., and McKee, C. F. (2008). Driven and decaying turbulence simulations of low-mass star formation: From clumps to cores to protostars. Astrophys. J. 686, 1174–1194. doi:10.1086/590238

CrossRef Full Text | Google Scholar

Ohashi, N., Saigo, K., Aso, Y., Aikawa, Y., Koyamatsu, S., Machida, M. N., et al. (2014). formation of a keplerian disk in the infalling envelope around L1527 IRS: Transformation from infalling motions to kepler motions. Astrophys. J. 796, 131. doi:10.1088/0004-637X/796/2/131

CrossRef Full Text | Google Scholar

Ohashi, S., Kobayashi, H., Nakatani, R., Okuzumi, S., Tanaka, H., Murakawa, K., et al. (2021). Ring formation by coagulation of dust aggregates in the early phase of disk evolution around a protostar. Astrophys. J. 907, 80. doi:10.3847/1538-4357/abd0fa

CrossRef Full Text | Google Scholar

Ormel, C. W., Paszun, D., Dominik, C., and Tielens, A. G. G. M. (2009). Dust coagulation and fragmentation in molecular clouds. I. How collisions between dust aggregates alter the dust size distribution. Astron. Astrophys. 502, 845–869. doi:10.1051/0004-6361/200811158

CrossRef Full Text | Google Scholar

Ostriker, E. C., Stone, J. M., and Gammie, C. F. (2001). Density, velocity, and magnetic field structure in turbulent molecular cloud models. Astrophys. J. 546, 980–1005. doi:10.1086/318290

CrossRef Full Text | Google Scholar

Oya, Y., Sakai, N., Sakai, T., Watanabe, Y., Hirota, T., Lindberg, J. E., et al. (2014). A substellar-mass protostar and its outflow of IRAS 15398-3359 revealed by subarcsecond-resolution observations of H₂CO and CCH. Astrophys. J. 795, 152. doi:10.1088/0004-637X/795/2/152

CrossRef Full Text | Google Scholar

Padovani, M., Brinch, C., Girart, J. M., Jørgensen, J. K., Frau, P., Hennebelle, P., et al. (2012). Adaptable radiative transfer innovations for submillimetre telescopes (ARTIST). Dust polarisation module (DustPol). Astron. Astrophys. 543, A16. doi:10.1051/0004-6361/201219028

CrossRef Full Text | Google Scholar

Padovani, M., Galli, D., and Glassgold, A. E. (2009a). Cosmic-ray ionization of molecular clouds. Astron. Astrophys. 501, 619–631. doi:10.1051/0004-6361/200911794

CrossRef Full Text | Google Scholar

Padovani, M., Hennebelle, P., Marcowith, A., and Ferrière, K. (2015). Cosmic-ray acceleration in young protostars. Astron. Astrophys. 582, L13. doi:10.1051/0004-6361/201526874

CrossRef Full Text | Google Scholar

Padovani, M., Ivlev, A. V., Galli, D., and Caselli, P. (2018). Cosmic-ray ionisation in circumstellar discs. Astron. Astrophys. 614, A111. doi:10.1051/0004-6361/201732202

CrossRef Full Text | Google Scholar

Padovani, M., Marcowith, A., Galli, D., Hunt, L. K., and Fontani, F. (2021). The double signature of local cosmic-ray acceleration in star-forming regions. Astron. Astrophys. 649, A149. doi:10.1051/0004-6361/202039918

CrossRef Full Text | Google Scholar

Padovani, M., Walmsley, C. M., Tafalla, M., Galli, D., and Müller, H. S. P. (2009b). C₂H in prestellar cores. Astron. Astrophys. 505, 1199–1211. doi:10.1051/0004-6361/200912547

CrossRef Full Text | Google Scholar

Palau, A., Ballesteros-Paredes, J., Vázquez-Semadeni, E., Sánchez-Monge, Á., Estalella, R., Fall, S. M., et al. (2015). Gravity or turbulence? - III. Evidence of pure thermal Jeans fragmentation at ∼0.1 pc scale. Mon. Not. R. Astron. Soc. 453, 3786–3798. doi:10.1093/mnras/stv1834

CrossRef Full Text | Google Scholar

Palau, A., Estalella, R., Girart, J. M., Fuente, A., Fontani, F., Commerçon, B., et al. (2014). Fragmentation of massive dense cores down to <˜1000 AU: Relation between fragmentation and density structure. Astrophys. J. 785, 42. doi:10.1088/0004-637X/785/1/42

CrossRef Full Text | Google Scholar

Palau, A., Fuente, A., Girart, J. M., Estalella, R., Ho, P. T. P., Sánchez-Monge, Á., et al. (2013). Early stages of cluster formation: Fragmentation of massive dense cores down to <˜1000 AU. Astrophys. J. 762, 120. doi:10.1088/0004-637X/762/2/120

CrossRef Full Text | Google Scholar

Palau, A., Zapata, L. A., Román-Zúñiga, C. G., Sánchez-Monge, Á., Estalella, R., Busquet, G., et al. (2018). Thermal Jeans Fragmentation within ∼1000 au in OMC-1S. Astrophys. J. 855, 24. doi:10.3847/1538-4357/aaad03

PubMed Abstract | CrossRef Full Text | Google Scholar

Palau, A., Zhang, Q., Girart, J. M., Liu, J., Rao, R., Koch, P. M., et al. (2021). Does the magnetic field suppress fragmentation in massive dense cores? Astrophys. J. 912, 159. doi:10.3847/1538-4357/abee1e

CrossRef Full Text | Google Scholar

Paron, S., Ortega, M. E., Marinelli, A., Areal, M. B., and Martinez, N. C. (2021). Cyano radical emission at small spatial scales towards massive protostars. Astron. Astrophys. 653, A77. doi:10.1051/0004-6361/202141424

CrossRef Full Text | Google Scholar

Pattle, K., Fissel, L., Tahani, M., Liu, T., and Ntormousi, E. (2022). Magnetic fields in Star formation: From clouds to cores. arXiv e-printsarXiv:2203.11179.

Google Scholar

Pattle, K., Ward-Thompson, D., Berry, D., Hatchell, J., Chen, H.-R., Pon, A., et al. (2017). The jcmt bistro survey: The magnetic field strength in the orion A filament. Astrophys. J. 846, 122. doi:10.3847/1538-4357/aa80e5

CrossRef Full Text | Google Scholar

Pillai, T., Kauffmann, J., Wiesemeyer, H., and Menten, K. M. (2016). CN Zeeman and dust polarization in a high-mass cold clump. Astron. Astrophys. 591, A19. doi:10.1051/0004-6361/201527803

CrossRef Full Text | Google Scholar

Pineda, J. E., Maury, A. J., Fuller, G. A., Testi, L., García-Appadoo, D., Peck, A. B., et al. (2012). The first ALMA view of IRAS 16293-2422. Astron. Astrophys. 544, L7. doi:10.1051/0004-6361/201219589

CrossRef Full Text | Google Scholar

Pineda, J. E., Schmiedeke, A., Caselli, P., Stahler, S. W., Frayer, D. T., Church, S. E., et al. (2021). Neutral versus ion line widths in barnard 5: Evidence for penetration by magnetohydrodynamic waves. Astrophys. J. 912, 7. doi:10.3847/1538-4357/abebdd

CrossRef Full Text | Google Scholar

Pineda, J. E., Segura-Cox, D., Caselli, P., Cunningham, N., Zhao, B., Schmiedeke, A., et al. (2020). A protostellar system fed by a streamer of 10, 500 au length. Nat. Astron. 4, 1158–1163. doi:10.1038/s41550-020-1150-z

CrossRef Full Text | Google Scholar

Pineda, J. E., Zhao, B., Schmiedeke, A., Segura-Cox, D. M., Caselli, P., Myers, P. C., et al. (2019). The specific angular momentum radial profile in dense cores: Improved initial conditions for disk formation. Astrophys. J. 882, 103. doi:10.3847/1538-4357/ab2cd1

CrossRef Full Text | Google Scholar

Plambeck, R. L., and Wright, M. C. H. (2016). ALMA observations of orion source I at 350 and 660 GHz. Astrophys. J. 833, 219. doi:10.3847/1538-4357/833/2/219

CrossRef Full Text | Google Scholar

Podio, L., Lefloch, B., Ceccarelli, C., Codella, C., and Bachiller, R. (2014). Molecular ions in the protostellar shock L1157-B1. Astron. Astrophys. 565, A64. doi:10.1051/0004-6361/201322928

CrossRef Full Text | Google Scholar

Pratap, P., Dickens, J. E., Snell, R. L., Miralles, M. P., Bergin, E. A., Irvine, W. M., et al. (1997). A study of the physics and chemistry of TMC-1. Astrophys. J. 486, 862–885. doi:10.1086/304553

PubMed Abstract | CrossRef Full Text | Google Scholar

Price, D. J., and Bate, M. R. (2007). The impact of magnetic fields on single and binary star formation. Mon. Not. R. Astron. Soc. 377, 77–90. doi:10.1111/j.1365-2966.2007.11621.x

CrossRef Full Text | Google Scholar

Qiu, K., Zhang, Q., Menten, K. M., Liu, H. B., Tang, Y.-W., and Girart, J. M. (2014). Submillimeter Array observations of magnetic fields in G240.31+0.07: An hourglass in a massive cluster-forming core. Astrophys. J. 794, L18. doi:10.1088/2041-8205/794/1/L18

CrossRef Full Text | Google Scholar

Qiu, K., Zhang, Q., and Menten, K. M. (2011). Outflows, accretion, and clustered protostellar cores around a forming O star. Astrophys. J. 728, 6. doi:10.1088/0004-637X/728/1/6

CrossRef Full Text | Google Scholar

Redaelli, E., Alves, F. O., Santos, F. P., and Caselli, P. (2019). Magnetic properties of the protostellar core IRAS 15398-3359. Astron. Astrophys. 631, A154. doi:10.1051/0004-6361/201936271

CrossRef Full Text | Google Scholar

Reissl, S., Stutz, A. M., Klessen, R. S., Seifried, D., and Walch, S. (2021). Magnetic fields in star-forming systems - II: Examining dust polarization, the Zeeman effect, and the Faraday rotation measure as magnetic field tracers. Mon. Not. R. Astron. Soc. 500, 153–176. doi:10.1093/mnras/staa3148

CrossRef Full Text | Google Scholar

Reissl, S., Wolf, S., and Brauer, R. (2016). Radiative transfer with POLARIS. I. Analysis of magnetic fields through synthetic dust continuum polarization measurements. Astron. Astrophys. 593, A87. doi:10.1051/0004-6361/201424930

CrossRef Full Text | Google Scholar

Rodón, J. A., Beuther, H., and Schilke, P. (2012). Fragmentation in the massive star-forming region IRAS 19410+2336. Astron. Astrophys. 545, A51. doi:10.1051/0004-6361/200912994

CrossRef Full Text | Google Scholar

Russell, C. T. (1991). The magnetosphere. Annu. Rev. Earth Planet. Sci. 19, 169–182. doi:10.1146/annurev.ea.19.050191.001125

CrossRef Full Text | Google Scholar

Sadaghiani, M., Sánchez-Monge, Á., Schilke, P., Liu, H. B., Clarke, S. D., Zhang, Q., et al. (2020). Physical properties of the star-forming clusters in NGC 6334. A study of the continuum dust emission with ALMA. Astron. Astrophys. 635, A2. A2. doi:10.1051/0004-6361/201935699

CrossRef Full Text | Google Scholar

Sadavoy, S. I., Stutz, A. M., Schnee, S., Mason, B. S., Di Francesco, J., and Friesen, R. K. (2016). Dust emissivity in the star-forming filament OMC 2/3. Astron. Astrophys. 588, A30. doi:10.1051/0004-6361/201527364

CrossRef Full Text | Google Scholar

Sai, J., Ohashi, N., Maury, A. J., Maret, S., Yen, H.-W., Aso, Y., et al. (2022). Which part of dense cores feeds material to protostars? The case of L1489 IRS. Astrophys. J. 925, 12. doi:10.3847/1538-4357/ac341d

CrossRef Full Text | Google Scholar

Sánchez-Monge, Á., Cesaroni, R., Beltrán, M. T., Kumar, M. S. N., Stanke, T., Zinnecker, H., et al. (2013). A candidate circumbinary Keplerian disk in G35.20-0.74 N: A study with ALMA. Astron. Astrophys. 552, L10. doi:10.1051/0004-6361/201321134

CrossRef Full Text | Google Scholar

Sánchez-Monge, Á., Schilke, P., Schmiedeke, A., Ginsburg, A., Cesaroni, R., Lis, D. C., et al. (2017). The physical and chemical structure of Sagittarius B2. II. Continuum millimeter emission of Sgr B2(M) and Sgr B2(N) with ALMA. Astron. Astrophys. 604, A6. doi:10.1051/0004-6361/201730426

CrossRef Full Text | Google Scholar

Sanhueza, P., Girart, J. M., Padovani, M., Galli, D., Hull, C. L. H., Zhang, Q., et al. (2021). Gravity-driven Magnetic Field at 1000 au Scales in High-mass Star Formation. Astrophys. J. Lett. 915, L10. doi:10.3847/2041-8213/ac081c

CrossRef Full Text | Google Scholar

Santos, F. P., Busquet, G., Franco, G. A. P., Girart, J. M., and Zhang, Q. (2016). Magnetically dominated parallel interstellar filaments in the infrared dark cloud g14.225-0.506. Astrophys. J. 832, 186. doi:10.3847/0004-637X/832/2/186

CrossRef Full Text | Google Scholar

Santos-Lima, R., de Gouveia Dal Pino, E. M., and Lazarian, A. (2013). Disc formation in turbulent cloud cores: Is magnetic flux loss necessary to stop the magnetic braking catastrophe or not? Mon. Not. R. Astron. Soc. 429, 3371–3378. doi:10.1093/mnras/sts597

CrossRef Full Text | Google Scholar

Santos-Lima, R., de Gouveia Dal Pino, E. M., and Lazarian, A. (2012). The role of turbulent magnetic reconnection in the formation of rotationally supported protostellar disks. Astrophys. J. 747, 21. doi:10.1088/0004-637X/747/1/21

CrossRef Full Text | Google Scholar

Santos-Lima, R., Guerrero, G., de Gouveia Dal Pino, E. M., and Lazarian, A. (2021). Diffusion of large-scale magnetic fields by reconnection in MHD turbulence. Mon. Not. R. Astron. Soc. 503, 1290–1309. doi:10.1093/mnras/stab470

CrossRef Full Text | Google Scholar

Schleuning, D. A. (1998). Far-infrared and submillimeter polarization of OMC-1: Evidence for magnetically regulated star formation. Astrophys. J. 493, 811–825. doi:10.1086/305139

CrossRef Full Text | Google Scholar

Segura-Cox, D. M., Looney, L. W., Tobin, J. J., Li, Z.-Y., Harris, R. J., Sadavoy, S., et al. (2018). The VLA nascent disk and multiplicity survey of Perseus protostars (VANDAM). V. 18 candidate disks around class 0 and I protostars in the Perseus molecular cloud. Astrophys. J. 866, 161. doi:10.3847/1538-4357/aaddf3

CrossRef Full Text | Google Scholar

Seifried, D., Banerjee, R., Pudritz, R. E., and Klessen, R. S. (2012). Disc formation in turbulent massive cores: Circumventing the magnetic braking catastrophe. MNRAS 423, L40–L44. –L44. doi:10.1111/j.1745-3933.2012.01253.x

CrossRef Full Text | Google Scholar

Seo, Y. M., Majumdar, L., Goldsmith, P. F., Shirley, Y. L., Willacy, K., Ward-Thompson, D., et al. (2019). An ammonia spectral map of the L1495-B218 filaments in the Taurus molecular cloud. II. CCS and HC₇N chemistry and three modes of star formation in the filaments. Astrophys. J. 871, 134. doi:10.3847/1538-4357/aaf887

CrossRef Full Text | Google Scholar

Sheehan, P. D., and Eisner, J. A. (2017). Disk masses for embedded class I protostars in the Taurus molecular cloud. Astrophys. J. 851, 45. doi:10.3847/1538-4357/aa9990

CrossRef Full Text | Google Scholar

Sheehan, P. D., Tobin, J. J., Looney, L. W., and Megeath, S. T. (2022). The VLA/ALMA nascent disk and multiplicity (VANDAM) survey of orion protostars. VI. Insights from radiative transfer modeling. Astrophys. J. 929, 76. doi:10.3847/1538-4357/ac574d

CrossRef Full Text | Google Scholar

Shinnaga, H., and Yamamoto, S. (2000). Zeeman effect on the rotational levels of CCS and SO in the ³Σ⁻ ground state. Astrophys. J. 544, 330–335. doi:10.1086/317212

CrossRef Full Text | Google Scholar

Shu, F. (1977). Self-similar collapse of isothermal spheres and star formation. Astrophys. J. 214, 488–497. doi:10.1086/155274

CrossRef Full Text | Google Scholar

Silsbee, K., Ivlev, A. V., Padovani, M., and Caselli, P. (2018). Magnetic mirroring and focusing of cosmic rays. Astrophys. J. 863, 188. doi:10.3847/1538-4357/aad3cf

CrossRef Full Text | Google Scholar

Silsbee, K., Ivlev, A. V., Sipilä, O., Caselli, P., and Zhao, B. (2020). Rapid elimination of small dust grains in molecular clouds. Astron. Astrophys. 641, A39. doi:10.1051/0004-6361/202038063

CrossRef Full Text | Google Scholar

Skalidis, R., and Tassis, K. (2021). High-accuracy estimation of magnetic field strength in the interstellar medium from dust polarization. Astron. Astrophys. 647, A186. doi:10.1051/0004-6361/202039779

CrossRef Full Text | Google Scholar

Stephens, I. W., Fernández-López, M., Li, Z.-Y., Looney, L. W., and Teague, R. (2020). Low-level carbon monoxide line polarization in two protoplanetary disks: HD 142527 and IM lup. Astrophys. J. 901, 71. doi:10.3847/1538-4357/abaef7

CrossRef Full Text | Google Scholar

Su, Y.-N., Liu, S.-Y., Li, Z.-Y., Lee, C.-F., Hirano, N., Takakuwa, S., et al. (2019). The infall motion in the low-mass protostellar binary NGC 1333 IRAS 4A1/4A2. Astrophys. J. 885, 98. doi:10.3847/1538-4357/ab4818

CrossRef Full Text | Google Scholar

Tafalla, M., Santiago-García, J., Myers, P., Caselli, P., Walmsley, C., and Crapsi, A. (2006). On the internal structure of starless cores. II. A molecular survey of L1498 and L1517B. Astron. Astrophys. 455, 577–593. doi:10.1051/0004-6361:20065311

CrossRef Full Text | Google Scholar

Takahashi, S., Machida, M. N., Tomisaka, K., Ho, P. T. P., Fomalont, E. B., Nakanishi, K., et al. (2019). ALMA high angular resolution polarization study: An extremely young class 0 source, OMC-3/MMS 6. Astrophys. J. 872, 70. doi:10.3847/1538-4357/aaf6ed

CrossRef Full Text | Google Scholar

Tanaka, K. E. I., Zhang, Y., Hirota, T., Sakai, N., Motogi, K., Tomida, K., et al. (2020). Salt, hot water, and silicon compounds tracing massive twin disks. Astrophys. J. Lett. 900, L2. doi:10.3847/2041-8213/abadfc

CrossRef Full Text | Google Scholar

Tassis, K., Willacy, K., Yorke, H. W., and Turner, N. J. (2014). Effect of OH depletion on measurements of the mass-to-flux ratio in molecular cloud cores. MNRAS 445, L56–L59. doi:10.1093/mnrasl/slu130

CrossRef Full Text | Google Scholar

Tatematsu, K., Ohashi, S., Sanhueza, P., Nguyen Luong, Q., Umemoto, T., and Mizuno, N. (2016). Angular momentum of the N₂H⁺ cores in the Orion A cloud. Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 68, 24. doi:10.1093/pasj/psw002

CrossRef Full Text | Google Scholar

Tazaki, R., Lazarian, A., and Nomura, H. (2017). Radiative grain alignment in protoplanetary disks: Implications for polarimetric observations. Astrophys. J. 839, 56. doi:10.3847/1538-4357/839/1/56

CrossRef Full Text | Google Scholar

Teague, R., Hull, C. L. H., Guilloteau, S., Bergin, E. A., Dutrey, A., Henning, T., et al. (2021). Discovery of molecular-line polarization in the disk of TW hya. Astrophys. J. 922, 139. doi:10.3847/1538-4357/ac2503

CrossRef Full Text | Google Scholar

Terebey, S., Shu, F., and Cassen, P. (1984). The collapse of the cores of slowly rotating isothermal clouds. Astrophys. J. 286, 529–551. doi:10.1086/162628

CrossRef Full Text | Google Scholar

Tobin, J. J., Hartmann, L., Chiang, H.-F., Wilner, D. J., Looney, L. W., Loinard, L., et al. (2013). Modeling the resolved disk around the class 0 protostar L1527. Astrophys. J. 771, 48. doi:10.1088/0004-637X/771/1/48

CrossRef Full Text | Google Scholar

Tobin, J. J., Offner, S. S. R., Kratter, K. M., Megeath, S. T., Sheehan, P. D., Looney, L. W., et al. (2022). The VLA/ALMA nascent disk and multiplicity (VANDAM) survey of orion protostars. V. A characterization of protostellar multiplicity. Astrophys. J. 925, 39. doi:10.3847/1538-4357/ac36d2

CrossRef Full Text | Google Scholar

Tobin, J. J., Sheehan, P. D., Megeath, S. T., Díaz-Rodríguez, A. K., Offner, S. S. R., Murillo, N. M., et al. (2020). The VLA/ALMA nascent disk and multiplicity (VANDAM) survey of orion protostars. II. A statistical characterization of class 0 and class I protostellar disks. Astrophys. J. 890, 130. doi:10.3847/1538-4357/ab6f64

CrossRef Full Text | Google Scholar

Tomida, K., Okuzumi, S., and Machida, M. N. (2015). Radiation magnetohydrodynamic simulations of protostellar collapse: Nonideal magnetohydrodynamic effects and early formation of circumstellar disks. Astrophys. J. 801, 117. doi:10.1088/0004-637X/801/2/117

CrossRef Full Text | Google Scholar

Tomida, K., Tomisaka, K., Matsumoto, T., Hori, Y., Okuzumi, S., Machida, M. N., et al. (2013). Radiation magnetohydrodynamic simulations of protostellar collapse: Protostellar core formation. Astrophys. J. 763, 6. doi:10.1088/0004-637X/763/1/6

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., and Inutsuka, S. (2015). Bimodality of circumstellar disk evolution induced by the Hall current. Astrophys. J. 810, L26. doi:10.1088/2041-8205/810/2/L26

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Machida, M. N., and Inutsuka, S.-i. (2021). Ashfall” induced by molecular outflow in protostar evolution. Astrophys. J. Lett. 920, L35. doi:10.3847/2041-8213/ac2b2f

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Okuzumi, S., Iwasaki, K., Machida, M. N., and Inutsuka, S.-i. (2017). The impact of the Hall effect during cloud core collapse: Implications for circumstellar disk evolution. Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 69, 95. doi:10.1093/pasj/psx113

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Okuzumi, S., Iwasaki, K., Machida, M. N., and Inutsuka, S. (2018). Does misalignment between magnetic field and angular momentum enhance or suppress circumstellar disk formation? Astrophys. J. 868, 22. doi:10.3847/1538-4357/aae4dc

CrossRef Full Text | Google Scholar

Turner, B. E., and Heiles, C. (2006). The C₄H zeeman effect in TMC-1: Understanding low-mass star formation. Astrophys. J. Suppl. Ser. 162, 388–400. doi:10.1086/498431

CrossRef Full Text | Google Scholar

Tychoniec, Ł., Manara, C. F., Rosotti, G. P., van Dishoeck, E. F., Cridland, A. J., Hsieh, T.-H., et al. (2020). Dust masses of young disks: Constraining the initial solid reservoir for planet formation. Astron. Astrophys. 640, A19. doi:10.1051/0004-6361/202037851

CrossRef Full Text | Google Scholar

Uchida, K. I., Fiebig, D., and Güsten, R. (2001). Zeeman line splitting measurements sampling dense gas in dark cloud and star-forming cores. Astron. Astrophys. 371, 274–286. doi:10.1051/0004-6361:20010329

CrossRef Full Text | Google Scholar

Valdivia, V., Maury, A., Brauer, R., Hennebelle, P., Galametz, M., Guillet, V., et al. (2019). Indirect evidence of significant grain growth in young protostellar envelopes from polarized dust emission. Mon. Not. R. Astron. Soc. 488, 4897–4904. doi:10.1093/mnras/stz2056

CrossRef Full Text | Google Scholar

Valdivia, V., Maury, A., and Hennebelle, P. (2022). Is the mm/sub-mm dust polarization a robust tracer of the magnetic field topology in protostellar envelopes ? A model exploration. arXiv e-printsarXiv:2203.14505.

Google Scholar

Van De Putte, D., Gordon, K. D., Roman-Duval, J., Williams, B. F., Baes, M., Tchernyshyov, K., et al. (2020). Evidence of dust grain evolution from extinction mapping in the IC 63 photodissociation region. Astrophys. J. 888, 22. doi:10.3847/1538-4357/ab557f

CrossRef Full Text | Google Scholar

van ’t Hoff, M. L. R., Leemker, M., Tobin, J. J., Harsono, D., Jørgensen, J. K., and Bergin, E. A. (2022). The young embedded disk L1527 IRS: Constraints on the water snowline and cosmic ray ionization rate from HCO+ observations. arXiv e-printsarXiv:2204.08622.

Google Scholar

van’t Hoff, M. L. R., Harsono, D., Tobin, J. J., Bosman, A. D., van Dishoeck, E. F., Jørgensen, J. K., et al. (2020). Temperature structures of embedded disks: Young disks in Taurus are warm. Astrophys. J. 901, 166. doi:10.3847/1538-4357/abb1a2

CrossRef Full Text | Google Scholar

Verliat, A., Hennebelle, P., Maury, A. J., and Gaudel, M. (2020). Protostellar disk formation by a nonrotating, nonaxisymmetric collapsing cloud: Model and comparison with observations. Astron. Astrophys. 635, A130. doi:10.1051/0004-6361/201936394

CrossRef Full Text | Google Scholar

Vlemmings, W. H. T., Lankhaar, B., Cazzoletti, P., Ceccobello, C., Dall’Olio, D., van Dishoeck, E. F., et al. (2019). Stringent limits on the magnetic field strength in the disc of TW Hya. ALMA observations of CN polarisation. Astron. Astrophys. 624, L7. doi:10.1051/0004-6361/201935459

CrossRef Full Text | Google Scholar

Wielebinski, R. (2005). “Magnetic fields in the Milky way, derived from radio continuum observations and faraday rotation studies,” in.Cosmic magnetic fields. Editors R. Wielebinski, and R. Beck (Berlin Springer Verlag), 66489. doi:10.1007/11369875_5

CrossRef Full Text | Google Scholar

Williams, G. M., Cyganowski, C. J., Brogan, C. L., Hunter, T. R., Ilee, J. D., Nazari, P., et al. (2022). ALMA observations of the Extended Green Object G19.01-0.03 - I. A Keplerian disc in a massive protostellar system. Mon. Not. R. Astron. Soc. 509, 748–762. doi:10.1093/mnras/stab2973

CrossRef Full Text | Google Scholar

Williams, J. P., Cieza, L., Hales, A., Ansdell, M., Ruiz-Rodriguez, D., Casassus, S., et al. (2019). The Ophiuchus DIsk survey employing ALMA (ODISEA): Disk dust mass distributions across protostellar evolutionary classes. Astrophys. J. 875, L9. doi:10.3847/2041-8213/ab1338

CrossRef Full Text | Google Scholar

Wong, Y. H. V., Hirashita, H., and Li, Z.-Y. (2016). Millimeter-sized grains in the protostellar envelopes: Where do they come from? Publ. Astron. Soc. Jpn. Nihon. Tenmon. Gakkai. 68, 67. doi:10.1093/pasj/psw066

CrossRef Full Text | Google Scholar

Wright, M., Bally, J., Hirota, T., Miller, K., Harding, T., Colleluori, K., et al. (2022). Structure of the source I disk in orion-KL. Astrophys. J. 924, 107. doi:10.3847/1538-4357/ac391b

CrossRef Full Text | Google Scholar

Wurster, J., and Bate, M. R. (2019). Disc formation and fragmentation using radiative non-ideal magnetohydrodynamics. Mon. Not. R. Astron. Soc. 486, 2587–2603. doi:10.1093/mnras/stz1023

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., and Price, D. J. (2018). The effect of extreme ionization rates during the initial collapse of a molecular cloud core. Mon. Not. R. Astron. Soc. 476, 2063–2074. doi:10.1093/mnras/sty392

CrossRef Full Text | Google Scholar

Wurster, J., and Lewis, B. T. (2020). Non-ideal magnetohydrodynamics versus turbulence - I. Which is the dominant process in protostellar disc formation? Mon. Not. R. Astron. Soc. 495, 3795–3806. doi:10.1093/mnras/staa1339

CrossRef Full Text | Google Scholar

Wurster, J. (2016). Nicil: A stand alone library to self-consistently calculate non-ideal magnetohydrodynamic coefficients in molecular cloud cores. Publ. Astron. Soc. Aust. 33, e041. doi:10.1017/pasa.2016.34

CrossRef Full Text | Google Scholar

Wurster, J., Price, D. J., and Bate, M. R. (2017). The impact of non-ideal magnetohydrodynamics on binary star formation. Mon. Not. R. Astron. Soc. 466, 1788–1804. doi:10.1093/mnras/stw3181

CrossRef Full Text | Google Scholar

Wyrowski, F., Güsten, R., Menten, K. M., Wiesemeyer, H., and Klein, B. (2012). Terahertz ammonia absorption as a probe of infall in high-mass star forming clumps. Astron. Astrophys. 542, L15. doi:10.1051/0004-6361/201218927

CrossRef Full Text | Google Scholar

Xu, W., and Kunz, M. W. (2021). Formation and evolution of protostellar accretion discs - I. Angular-momentum budget, gravitational self-regulation, and numerical convergence. Mon. Not. R. Astron. Soc. 502, 4911–4929. doi:10.1093/mnras/stab314

CrossRef Full Text | Google Scholar

Yang, H., Li, Z.-Y., Looney, L. W., Girart, J. M., and Stephens, I. W. (2017). Scattering-produced (sub)millimetre polarization in inclined discs: Optical depth effects, near-far side asymmetry and dust settling. Mon. Not. R. Astron. Soc. 472, 373–388. doi:10.1093/mnras/stx1951

CrossRef Full Text | Google Scholar

Yang, Y., Jiang, Z., Chen, Z., Ao, Y., and Yu, S. (2021). In search of infall motion in molecular clumps. III. HCO+ (1-0) and H13CO+ (1-0) mapping observations toward confirmed infall sources. Astrophys. J. 922, 144. doi:10.3847/1538-4357/ac22ab

CrossRef Full Text | Google Scholar

Yen, H.-W., Gu, P.-G., Hirano, N., Koch, P. M., Lee, C.-F., Liu, H. B., et al. (2019). HL tau disk in HCO⁺ (3-2) and (1-0) with ALMA: Gas density, temperature, gap, and one-arm spiral. Astrophys. J. 880, 69. doi:10.3847/1538-4357/ab29f8

CrossRef Full Text | Google Scholar

Yen, H.-W., Koch, P. M., Hull, C. L. H., Ward-Thompson, D., Bastien, P., Hasegawa, T., et al. (2021a). The JCMT BISTRO survey: Alignment between outflows and magnetic fields in dense cores/clumps. Astrophys. J. 907, 33. doi:10.3847/1538-4357/abca99

CrossRef Full Text | Google Scholar

Yen, H.-W., Koch, P. M., Takakuwa, S., Ho, P. T. P., Ohashi, N., and Tang, Y.-W. (2015a). Observations of infalling and rotational motions on a 1000 AU scale around 17 class 0 and 0/I protostars: Hints of disk growth and magnetic braking? Astrophys. J. 799, 193. doi:10.1088/0004-637X/799/2/193

CrossRef Full Text | Google Scholar

Yen, H.-W., Koch, P. M., Takakuwa, S., Krasnopolsky, R., Ohashi, N., and Aso, Y. (2017). Signs of early-stage disk growth revealed with ALMA. Astrophys. J. 834, 178. doi:10.3847/1538-4357/834/2/178

CrossRef Full Text | Google Scholar

Yen, H.-W., Takakuwa, S., Koch, P. M., Aso, Y., Koyamatsu, S., Krasnopolsky, R., et al. (2015b). No keplerian disk >10 AU around the protostar B335: Magnetic braking or young age? Astrophys. J. 812, 129. doi:10.1088/0004-637X/812/2/129

CrossRef Full Text | Google Scholar

Yen, H.-W., Takakuwa, S., Ohashi, N., Aikawa, Y., Aso, Y., Koyamatsu, S., et al. (2014). ALMA observations of infalling flows toward the keplerian disk around the class I protostar L1489 IRS. Astrophys. J. 793, 1. doi:10.1088/0004-637X/793/1/1

CrossRef Full Text | Google Scholar

Yen, H.-W., Zhao, B., Koch, P. M., and Gupta, A. (2021b). No impact of core-scale magnetic field, turbulence, or velocity gradient on sizes of protostellar disks in orion A. Astrophys. J. 916, 97. doi:10.3847/1538-4357/ac0723

CrossRef Full Text | Google Scholar

Yen, H.-W., Zhao, B., Koch, P. M., Krasnopolsky, R., Li, Z.-Y., Ohashi, N., et al. (2018). Constraint on ion-neutral drift velocity in the Class 0 protostar B335 from ALMA observations. Astron. Astrophys. 615, A58. doi:10.1051/0004-6361/201732195

CrossRef Full Text | Google Scholar

Ysard, N., Koehler, M., Jimenez-Serra, I., Jones, A. P., and Verstraete, L. (2019). From grains to pebbles: The influence of size distribution and chemical composition on dust emission properties. Astron. Astrophys. 631, A88. doi:10.1051/0004-6361/201936089

CrossRef Full Text | Google Scholar

Zamponi, J., Maureira, M. J., Zhao, B., Liu, H. B., Ilee, J. D., Forgan, D., et al. (2021). The young protostellar disc in IRAS 16293-2422 B is hot and shows signatures of gravitational instability. Mon. Not. R. Astron. Soc. 508, 2583–2599. doi:10.1093/mnras/stab2657

CrossRef Full Text | Google Scholar

Zelko, I. A., and Finkbeiner, D. P. (2020). Implications of grain size distribution and composition for the correlation between dust extinction and emissivity. Astrophys. J. 904, 38. doi:10.3847/1538-4357/abbb8d

CrossRef Full Text | Google Scholar

Zhang, C.-P., Launhardt, R., Liu, Y., Tobin, J. J., and Henning, T. (2021). Pebbles in an embedded protostellar disk: The case of CB 26. Astron. Astrophys. 646, A18. doi:10.1051/0004-6361/202039536

CrossRef Full Text | Google Scholar

Zhang, Q., Qiu, K., Girart, J. M., Liu, H. B., Tang, Y.-W., Koch, P. M., et al. (2014). Magnetic fields and massive star formation. Astrophys. J. 792, 116. doi:10.1088/0004-637X/792/2/116

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., Krasnopolsky, R., Shang, H., and Lam, K. H. (2020). Hall effect in protostellar disc formation and evolution. Mon. Not. R. Astron. Soc. 492, 3375–3395. doi:10.1093/mnras/staa041

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., Krasnopolsky, R., Shang, H., and Lam, K. H. (2021). The interplay between ambipolar diffusion and Hall effect on magnetic field decoupling and protostellar disc formation. Mon. Not. R. Astron. Soc. 505, 5142–5163. doi:10.1093/mnras/stab1295

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., Krasnopolsky, R., Shang, H., and Nakamura, F. (2016). Protostellar disc formation enabled by removal of small dust grains. Mon. Not. R. Astron. Soc. 460, 2050–2076. doi:10.1093/mnras/stw1124

CrossRef Full Text | Google Scholar

Zinchenko, I., Caselli, P., and Pirogov, L. (2009). Chemical differentiation in regions of high-mass star formation - II. Molecular multiline and dust continuum studies of selected objects. Mon. Not. R. Astron. Soc. 395, 2234–2247. doi:10.1111/j.1365-2966.2009.14687.x

CrossRef Full Text | Google Scholar