
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 21 September 2022
Sec. Astrostatistics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.943556
This article is part of the Research Topic Multi-scale Magnetic Field Measurements in the Multi-Phase Interstellar Medium View all 8 articles
Linearly polarized emission from dust grains and molecular spectroscopy is an effective probe of the magnetic field topology in the interstellar medium and molecular clouds. The longstanding Davis-Chandrasekhar-Fermi (DCF) method and the recently developed Histogram of Relative Orientations (HRO) analysis and the polarization-intensity gradient (KTH) method are widely used to assess the dynamic role of magnetic fields in star formation based on the plane-of-sky component of field orientations inferred from the observations. We review the advances and limitations of these methods and summarize their applications to observations. Numerical tests of the DCF method, including its various variants, indicate that its largest uncertainty may come from the assumption of energy equipartition, which should be further calibrated with simulations and observations. We suggest that the ordered and turbulent magnetic fields of particular observations are local properties of the considered region. An analysis of the polarization observations using DCF estimations suggests that magnetically trans-to-super-critical and averagely trans-to-super-Alfvénic clumps/cores form in sub-critical clouds. High-mass star-forming regions may be more gravity-dominant than their low-mass counterparts due to higher column density. The observational HRO studies clearly reveal that the preferential relative orientation between the magnetic field and density structures changes from parallel to perpendicular with increasing column densities, which, in conjunction with simulations, suggests that star formation is ongoing in trans-to-sub-Alfvénic clouds. There is a possible transition back from perpendicular to random alignment at higher column densities. Results from observational studies using the KTH method broadly agree with those of the HRO and DCF studies.
Star formation within molecular clouds, the densest part of the interstellar medium (ISM), is regulated by the complex interplay among gravity, turbulence, magnetic fields, and other factors (e.g, protosteller feedback and feedback from previous generations of stars) at different scales. Magnetic fields interact with the other two major forces (gravity and turbulence) by providing supports against gravitational collapse (Shu et al., 1987) and generating anisotropic turbulence (Goldreich and Sridhar, 1995). Observational studies of magnetic fields are crucial to distinguish between strong-field star formation theories in which magnetically sub-critical clouds slowly form super-critical substructures that subsequently collapse (Mouschovias et al., 2006), and weak-field star formation theories where large-scale supersonic turbulent flows form overdense intersecting regions that dynamically collapse (Mac Low and Klessen, 2004).
Polarized thermal dust emission observations have been the most common way to trace the plane-of-sky (POS) component of magnetic field orientations with the assumption that the shortest axis of irregular dust grains is aligned with magnetic field lines (Davis and Greenstein, 1949; Lazarian, 2007; Lazarian and Hoang, 2007). The Goldreich-Kylafis (GK) effect provides an alternative way to trace the POS field orientation (with a 90° ambiguity) with molecular line polarization observations (Goldreich and Kylafis, 1981). The recently developed Velocity Gradient Technique (VGT) proposed another way to trace the POS field orientation with spectra line observations based on the notion that the gradient of velocity centroids (VCG, González-Casanova and Lazarian, 2017) or thin velocity channels (VChG, Lazarian and Yuen, 2018) is perpendicular to the magnetic field due to the intrinsic properties of magneto-hydrodynamic (MHD) turbulence (Goldreich and Sridhar, 1995).
Several analysis techniques have been developed to infer the properties of magnetic fields based on their orientations: the Davis-Chandrasekhar-Fermi (DCF) method was proposed by Davis (1951) and Chandrasekhar and Fermi (1953) approximately 70 years ago and has been the most widely used method to indirectly derive the magnetic field strength with statistics of field orientations. A new tool, the polarization-intensity gradient method (here after the KTH method, Koch et al., 2012a), was proposed about one decade ago and can also be used to assess the significance of magnetic fields based on ideal MHD equations. The Histogram of Relative Orientations (HRO) analysis (Soler et al., 2013), which was proposed right after the KTH method, measures the relative orientation between the magnetic field and density structures and can be used to link the observed magnetic morphology with the physics of simulations. These methods provide information on the magnetic properties in star-forming molecular clouds and allow us to investigate both qualitatively and quantitatively the dynamical role of magnetic fields in the collapse and fragmentation of dense molecular structures.
In this chapter we review the concept and recent developments of these techniques and discuss their limitations. We also summarize the application of these methods to observations of star formation regions and discuss the role of magnetic fields at different spatial scales. In particular, we focus on the relative importance of the magnetic field as compared to gravity and turbulence at different scales of star-forming clouds. In Section 2, we review the DCF method. In Section 3, we review the HRO analysis. In Section 4, we review the KTH method. In Section 5, we summarize this chapter.
In the middle 20th century, Davis (1951) and Chandrasekhar and Fermi (1953) proposed the DCF method to estimate the mean1 magnetic field strength (Bm) of the interstellar medium (ISM) in the spiral arm based on the first interstellar magnetic field orientation observation made by Hiltner (1949). Since then, the method has been improved and adopted by the community to estimate the field strength in star-forming regions. In this section, we present a review of the original DCF method and its modifications.
The original DCF method assumes an equipartition between the transverse (i.e., perpendicular to the underlying field Bu) turbulent magnetic and kinetic energies (i.e., the Alfvén relation, hereafter the DCF53 equipartition assumption):
in SI units2, where
where “pos” stands for the POS.
Alternatively, Federrath (2016) assumed an equipartition between the coupling-term magnetic field (
where the POS transverse velocity dispersion is neglected.
Conventionally, a sub-Alfvénic state means that the underlying magnetic energy is greater than the turbulent kinetic energy when comparing the magnetic field with the turbulence. It is widely accepted that the DCF53 equipartition assumption is satisfied for pure incompressible sub-Alfvénic turbulence due to the magnetic freezing effect where the perturbed magnetic lines of force oscillate with the same velocity as the turbulent gas in the transverse direction (Alfvén, 1942). However, the star-forming molecular clouds are highly compressible (Hennebelle and Falgarone, 2012). For compressible sub-Alfvénic turbulence, there are still debates on whether the DCF53 or Fed16 equipartition assumptions is more accurate (e.g., Skalidis et al., 2021; Skalidis and Tassis, 2021; Lazarian et al., 2022; Li et al., 2022; Liu et al., 2022).
Observational studies usually adopt the local underlying field within the region of interest instead of the global underlying field at larger scales. In this case, the volume-averaged coupling-term magnetic energy is 0 by definition (Zweibel and McKee, 1995; Liu et al., 2022), which should not be used in analyses. Several numerical studies (Federrath, 2016; Beattie et al., 2020; Skalidis and Tassis, 2021; Beattie et al., 2022) have suggested that the volume-averaged RMS coupling-term magnetic energy fluctuation should be studied instead of the volume-averaged coupling-term magnetic energy. With non-self-gravitating sub-Alfvénic simulations, they found that the coupling-term field energy fluctuation is in equipartition with the turbulent kinetic energy within the whole simulation box. However, it is unclear whether the Fed16 equipartition assumption still holds in sub-regions of their simulations. Investigating the local energetics is very important because the local and global properties of MHD turbulence can be very different (Lazarian and Vishniac, 1999; Brandenburg and Lazarian, 2013). In small-scale sub-regions below the turbulent injection scale and without significant self-gravity, the local underlying magnetic field is actually part of the turbulent magnetic field at larger scales and the local turbulence is the cascaded turbulence (Federrath, 2016). Within self-gravitating molecular clouds, the gravity is comparable to or dominates the magnetic field and turbulence at higher densities (Crutcher, 2012; Kauffmann et al., 2013; Liu et al., 2022), which has a strong effect on both magnetic fields and turbulence. e.g., the gravity can compress magnetic field lines and amplify the field strength; the gravitational inflows can accelerate the gas and enhance turbulent motions. As observations can only probe the magnetic field in part of the diffuse ISM or molecular clouds, it is necessary to test the validity of the Fed16 assumption in sub-regions of simulations with or without self-gravity. Moreover, Li et al. (2022) and Lazarian et al. (2022) pointed out that the physical meaning of the RMS coupling-term energy fluctuation adopted by the Fed16 equipartition assumption is still unclear, which needs to be addressed in the future.
The traditional DCF53 equipartition assumption has been tested by many numerical works (e.g., Haugen and Brandenburg, 2004; Falceta-Gonçalves et al., 2008; Liu et al., 2021; Skalidis et al., 2021; Chen et al., 2022). For non-self-gravitating simulations, Haugen and Brandenburg (2004) found the DCF53 equipartition is violated throughout the inertial range (i.e., between the turbulence injection scale Linj and dissipation scale) in initially very sub-Alfvénic
In summary, the DCF53 equipartition assumption is valid within trans- or slightly sub-Alfvénic self-gravitating molecular clouds, but its validity in very sub-Alfvénic self-gravitating regions still needs more investigations. The Fed16 equipartition assumption can be used as an empirical relation when studying the global underlying and turbulent magnetic field in the diffuse ISM beyond the turbulent injection scale if the ISM is sub-Alfvénic, but its physical interpretation, as well as its applicability in part of the ISM below the turbulent injection scale and within self-gravitating molecular clouds, are still unclear. The equipartition problem has only been investigated theoretically and numerically. We are unaware of any observational attempts to look into this problem within molecular clouds yet. There is also a lack of observational methods to study the energy equipartition.
A super-Alfvénic state of turbulence conventionally means that the underlying magnetic energy is smaller than the turbulent kinetic energy. In super-Alfvénic case, the magnetic field is dominated by the turbulent component. Numerical studies have shown that both the turbulent magnetic energy and the RMS coupling-term magnetic energy fluctuation are smaller than the turbulent kinetic energy in super-Alfvénic simulations (Falceta-Gonçalves et al., 2008; Federrath, 2016; Liu et al., 2021). This energy non-equipartition in super-Alfvénic cases could lead to an overestimation of the magnetic field strength. Lazarian et al. (2022) suggested that the super-Alfvénic turbulence transfers to sub-Alfvénic turbulence at
The original DCF method assumes isotropic turbulent velocity dispersion, thus the unobserved δvpos⊥ in Equation 2 can be replaced by the observable δvlos, which implies
On the other hand, the modified DCF method in Skalidis and Tassis (2021) (hereafter ST21) requires an assumption of isotropic turbulent magnetic field, so that the
However, both incompressible and compressible MHD turbulence are anisotropic in the presence of a strong magnetic field (Shebalin et al., 1983; Higdon, 1984; Goldreich and Sridhar, 1995). In particular, the fluctuations of the Alfvénic and slow modes are anisotropic, while only the fast mode has isotropic fluctuations (Lazarian et al., 2022). The anisotropic velocity field in low-density non-self-gravitating regions has been confirmed by observations (Heyer et al., 2008). Lazarian et al. (2022) suggested that the anisotropy of MHD turbulence is a function of
With non-self-gravitating simulations, Heitsch et al. (2001) and Skalidis et al. (2021) found that the full cube turbulent magnetic field is approximately isotropic within a factor of 2 with their
Studies on the anisotropy of MHD turbulence in the high-density self-gravitating regime are rarer. Spectroscopic observations toward high-density regions did not find obvious evidences for velocity anisotropy (Heyer and Brunt, 2012). A recent numerical work by Liu et al. (2021) found both the turbulent magnetic field and the turbulent velocity dispersion are approximately isotropic within a factor of 2 at 1–0.01 pc scales in their trans-to-super-Alfvénic simulations of clustered star-forming regions. They did not find obvious relation between the anisotropy and levels of initial magnetization in their simulations. This may be due to the local super-Alfvénic turbulence at high densities and/or the complex averaging along the LOS for different local anisotropic turbulent field at various directions. Moreover, Otto et al. (2017) found that the velocity anisotropy due to magnetic fields disappears in high-density and sub-Alfvénic (local
In the POS, the local total field at position i is a vector sum of the underlying field and the local turbulent field:
or
to derive the POS underlying magnetic field strength
to derive the POS underlying magnetic field strength. Both the original DCF method and the ST21 approach have adopted the assumption that the turbulent-to-underlying field strength ratio
The underlying magnetic field reflects the intrinsic property of an unperturbed magnetic field. There are different approaches to relate the dispersion of magnetic field position angles with
All the relations listed in Table 1 have assumed that
The total magnetic field is the sum of the underlying magnetic field and the turbulent magnetic field. There are also different approaches trying to relate the dispersion of magnetic field position angles with
Similarly, all the relations listed in Table 2 have approximated the dispersion on the field angle of the magnetic field with the dispersion of the position angle, which requires
Structure functions and correlation functions have been widely used in astrophysical studies. Falceta-Gonçalves et al. (2008) introduced the structure function in the study of polarization position angles. Later, the ADF method was developed by Hildebrand et al. (2009) to estimate the POS turbulent-to-ordered field strength ratio
where ΔΦ(l) is the POS angular difference of two magnetic field segments separated by a distance l,
Combining Eq. 1 and the ratio between the polarization angle structure function Dϕ and the velocity centroid structure function
where the factor f is a function of γ,
As stated in Section 2.1.3, the turbulent-to-underlying or -total magnetic field strength ratio is assumed to be traced by statistics of magnetic field position angles. Other than the uncertainty on the assumption itself, there are various effects that could introduce uncertainties in the statistics of position angles. Here we describe these effects and summarize on how they are treated in different approaches. Note that the estimation of gas density from dust emission is associated with uncertainties on the dust-to-gas ratio, temperature, dust opacity, and source geometry (e.g., Hildebrand, 1983; Ossenkopf and Henning, 1994), whereas the statistics of turbulent velocity field using spectroscopic data is affected by the chemical processes and excitation conditions of particular line tracers (e.g., van Dishoeck et al., 1993), density fluctuations (e.g., Yuen et al., 2021; Yuen et al., 2022), and ordered velocity fields due to star-forming activities (e.g., infall, rotation, and outflows). We do not discuss the uncertainty on the gas density and turbulent velocity field in this paper as it is beyond the scope of this review.
The original DCF method was derived assuming the large-scale ordered field lines are straight. For a non-linear large-scale field, the contribution from the ordered field structure can overestimate the angular dispersion that should be only attributed to turbulence. For highly ordered magnetic fields, the underlying field structure can be fitted with simple hourglass models (hereafter the HG technique. e.g., Lai et al., 2002; Girart et al., 2006; Rao et al., 2009; Qiu et al., 2014) or even more complex models (e.g., Myers et al., 2018).
Pillai et al. (2015) (the spatial filtering technique. Hereafter the Pil15 technique) and Pattle et al. (2017) (the unsharp masking technique. Hereafter the Pat17 technique) tried to universally derive the ordered field orientation at each position by smoothing the magnetic field position angle among neighboring positions. Pattle et al. (2017) tested the Pat17 technique with a set of Monte Carlo simulations and found that this technique does correctly recover the true angular dispersion if the measurement error is small. By varying the smoothing size, the Pil15 and Pat17 techniques can account for the ordered structure at different scales.
The ADF method analytically takes into account the ordered field structure (see Section 2.1.3.2 for detail) and has been the most widely used method to remove the contribution from the ordered field to the angular dispersion. With a set of Monte Carlo simulations, Liu et al. (2021) found that the ADF method works well on accounting for the ordered field. Figure 1 shows the overestimation factor of the angular dispersion due to the POS ordered field structure, which is quantified by the ratio Ro between the directly estimated angular dispersion δϕobs and the ADF-derived integrated (i.e., without corrections for the LOS signal integration. See Section 2.2.3) turbulent-to-ordered magnetic field strength ratio5
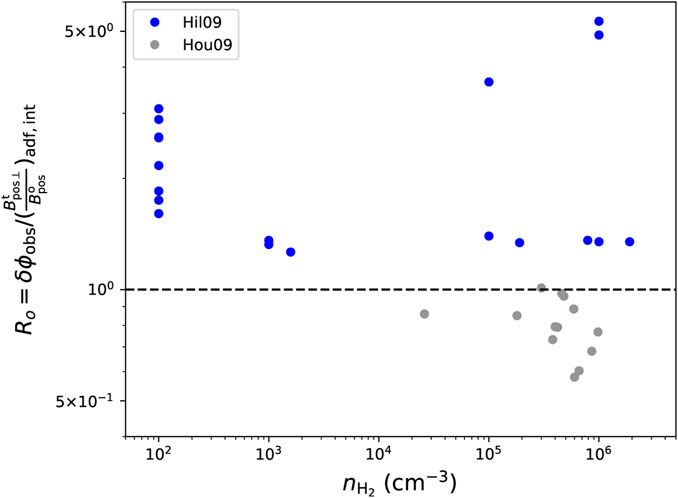
FIGURE 1. Overestimation factor of angular dispersions (Ro) due to contributions from the ordered field structure as a function of gas number density based on the DCF catalogue from Liu et al. (2022) which collected the estimations in the literature. Here δϕobs is the directly estimated angular dispersion for the simplest DCF version as mentioned in Section 2.1.3.1. Different colors indicate different ADF variants used to derive
A deficiency of the original ADF methods (Hil09/Hou09/Hou16) is a lack of a universal way to define the fitting upper limit of l for the
It should be noted that the concept of the “ordered” field is vague and is not well defined. The referred entity of an local ordered field depends on the range of scales (i.e., resolution to maximum size) of the region of interest. An example is that the simple hourglass-like magnetic field in G31.41 at a lower resolution (Girart et al., 2009) show complex poloidal-like structures at a higher resolution (Beltrán et al., 2019). It should also be noted that the non-linearly ordered field structure is not only due to non-turbulent processes such as gravity, shocks, or collisions, but can also result from larger-scale turbulence, where the curvature of the ordered field generated by pure turbulence depends on
It is assumed that the turbulent magnetic field is characterized by a correlation length lδ (Myers and Goodman, 1991; Hildebrand et al., 2009). The turbulent magnetic fields within a turbulent cell of length lδ are mostly correlated with each other, while the turbulent fields separated by scales larger than lδ are mostly independent.
Hou09 and Hou16 assumed a Gaussian form for the turbulent autocorrelation function and included it in the ADF analysis. Figure 2 shows the relation between lδ derived from the ADF method and the resolution lbeam of the observations from the DCF catalogue compiled by Liu et al. (2022). There is an overwhelming trend that the lδ and lbeam are correlated with each other within a factor of 2. At lbeam ∼ 5 mpc, there is a group of data points with lδ > 2lbeam, which mostly correspond to the estimations from Palau et al. (2021).
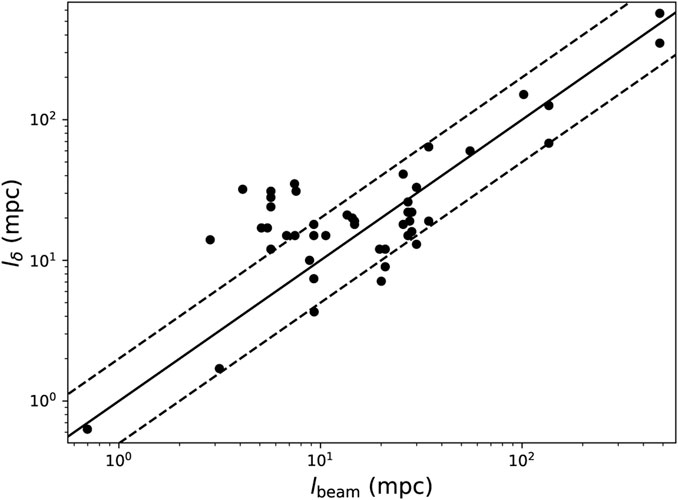
FIGURE 2. The correlation length (lδ) of the turbulent magnetic field derived from the ADF method versus the beam size (lbeam) of observations based on the Liu et al. (2022) catalogue which collected the estimations in the literature. Solid line corresponds to 1:1 relation. Dashed lines correspond to 1:2 and 2:1 relations.
The smallest observed lδ is lδ,min ∼0.6 mpc estimated by Hull et al. (2017a) in Serpens-SMM1. This scale is consistent with the lower limit of the observed ambipolar diffusion scale6 (∼1.8–17 mpc, Li and Houde, 2008; Hezareh et al., 2010; Houde et al., 2011) of ion-neutral decoupling, although recently (Tang et al., 2018) suggested that the previous observational estimates of ambipolar diffusion scales were biased towards small values due to the imperfect method used to analyse the turbulent spectra and the true ambipolar diffusion scale may be much larger (e.g., ∼0.4 pc in NGC 6334). The estimated lδ,min is an order of magnitude smaller than the scale of the observed lower end of the Larson’s law (∼10 mpc, Padoan et al., 2009; Kauffmann et al., 2013; Yuen et al., 2022).
What can we learn from the correlation between lδ and lbeam? One may intuitively think that there is an intrinsic turbulent correlation scale, which is overestimated at insufficient beam resolution. However, in this scenario, the observed angular dispersions at larger scales should be smaller than those at smaller scales due to the signal integration across more turbulent cells along the LOS (see Section 2.2.3), which contradicts observational results (Liu et al., 2022). Thus, it is reasonable to think that the magnetic field and turbulence are correlated at different scales instead of only at the smallest scale (Heitsch et al., 2001).
Alternatively, we propose that the local turbulence confined by the range of scales of the observations (from the size of the considered region, the effective depth along the LOS, or the filtering scale of interferometric observations to the beam resolution) is responsible for generating the local turbulent magnetic field at the particular scales. Note that the local ordered magnetic field partly consists of the turbulent magnetic field at larger scales and the two are not distinguishable in observations of limited scale ranges. i.e., the contribution of low spatial frequency turbulent fields can be removed by the ordered field term in the ADF analysis. In addition, coarser resolutions cannot resolve the high spatial frequency turbulence. Thus, the turbulent correlation scale derived from the ADF method actually corresponds to the local turbulent power spectra with cutoffs at the resolution and the maximum recoverable scale of particular observations. This local turbulence correlation scale in observations of molecular clouds should be much smaller than the driving scale of interstellar supersonic turbulence (∼100 pc, e.g., Heyer and Brunt, 2004; Haverkorn et al., 2008).
Densities may be another factor that affects the local turbulence. The property of the local turbulence relies on the gas component probed by the observations. At smaller scales, the higher densities decrease the mean free path of gas particles and thus the turbulent correlation length, which can also explain the scaling relation seen in Figure 2.
The contribution of the turbulent field responsible for the observed polarization is the mean of the N independent samples of the turbulent field along the LOS (Zweibel, 1990; Myers and Goodman, 1991). The integrated turbulent field seen by observations should be
Lazarian et al. (2022) suggested that the underestimation of angular dispersion is dependent on the mixture of turbulence modes and the inclination of the mean field. With pure Alfvénic simulations and simulations of equal Alfvénic and slow modes, they found that the integrated angular dispersion decreases slower than N−1/2 when the LOS integration depth L is smaller than the turbulence injection scale Linj, but decreases faster than N−1/2 when L ≳ Linj. They also suggested that pure Alfvénic fluctuations decrease as N−1 instead of N−1/2 when the mean field is on the POS, which can quickly vanish if the integration depth is greater than the scale of the studied region. Liu et al. (2021) tested the LOS signal integration effect of angular dispersions with self-gravitating simulations. They found that the angular dispersion is only underestimated by a factor of
The ADF method derives the POS turbulent correlation length by fitting the ADFs and uses this information to derive the number of turbulent cells Nadf along the LOS under the assumption of identical LOS and POS turbulent correlation lengths. Note that this assumption is not satisfied in anisotropic MHD turbulence. Liu et al. (2021) applied the ADF method to simulations and found a significant amount of observed angular dispersions corrected by
Cho and Yoo (2016) proposed an alternative approach (here after the CY16 technique) to estimate the number of turbulent cells along the LOS
where δVc is the standard deviation of centroid velocities. The CY16 technique was developed to account for the LOS signal integration at scales larger than the injection scale in non-self-gravitation media, which does not naturally extend to small-scale and high-density media where self-gravity is important. Liu et al. (2021) tested the CY16 technique with self-gravitating simulations. They found that the observed angular dispersions in synthetic polarization maps corrected by
The non-uniform and complex density and magnetic field structures along the LOS tend to reduce the measured angular dispersion (e.g., Zweibel, 1990). The distribution of the LOS grain alignment efficiency can also affect the derived angular dispersion (e.g., Padoan et al., 2001). The reduction factor of angular dispersions due to these effects is highly dependent on the physical conditions of individual sources and cannot be solved universally.
The observed sky signals are limited by the angular resolution and the sampling of the particular observations. Interferometric observations are further affected by the filtering of large-scale signals.
As discussed in Section 2.2.2, the magnetic field is likely perturbed by the turbulence of different wavenumbers at different scales. In this case, the loss of turbulent power due to beam-smoothing can underestimate the angular dispersion of magnetic field position angles and thus overestimate the magnetic field strength (Heitsch et al., 2001). Falceta-Gonçalves et al. (2008) investigated the resolution effect with numerical simulations and suggested that the ratio between the derived field strength at different spatial resolutions (Rs) and the intrinsic field strength at an infinite resolution follows an empirical relation
The minimal separation of antenna pairs in interferometric observations limits the largest spatial scale that the observations are sensitive to. This filtering effect also introduces uncertainties in the estimation of the turbulent magnetic field. The ADF method attempts to analytically solve this problem by modeling the dirty beam of interferometers with a twin Gaussian profile. With their numerical test, Liu et al. (2021) found the ADF method correctly accounts for this large-scale filtering effect as well.
For observations of polarized starlight extinction or low signal-to-noise-ratio dust polarization emission, the polarization detection is sparsely sampled. Soler et al. (2016) has suggested that this sparse sampling effect can introduce jitter-like features in the ADFs and affect the accuracy of the ADF analysis. Although there are no universal solutions to correct for the effect of sparse sampling, the uncertainties of the ADFs due to the pure statistics can be modeled with Monte Carlo analyses (e.g., Liu et al., 2019). With a simple Monte Carlo test, Liu et al. (2019) found that the ADF of sparsely sampled magnetic field orientations is underestimated at large distance intervals and has larger scatters compared to the ADF of uniformly sampled field orientations. The sparse sampling not only affects the ADF, but can also affect the velocity structure function (VSF). Ha et al. (2021) found similar jitter-like features on the VSF of sparsely sampled stars and estimated the uncertainty of the VSFs with a Monte Carlo random sampling analysis.
The angular relations in Section 2.1.3 are originally derived in 3D spaces where the orientation of the 3D magnetic field is known. Dust polarization observations only traces the POS field orientations, thus the DCF method can only measure the POS magnetic field strength. There are different attempts to reconstruct the 3D magnetic field from the DCF estimations.
The 3D magnetic field can be derived by including the inclination angle of the 3D field in the DCF equations (e.g., Houde, 2004; Lazarian et al., 2022). Note that the inclination angle of the 3D field is only meaningful when the underlying field is prominent (i.e.,
The 3D field strength can also be estimated by combining the POS and LOS components of the magnetic field. This can be done by combining DCF estimations and Zeeman estimations of the same material, where Zeeman observations are the only way to directly derive the LOS magnetic field strength. Recently, Tahani et al. (2018) proposed a new method to estimate the LOS magnetic field strength based on Faraday rotation measurements, which can also be used to reconstruct the 3D magnetic field in combination with the POS magnetic field estimations (e.g., Tahani et al., 2019).
In most cases, the information on the inclination angle and the LOS magnetic field is missing, or the measured POS and LOS magnetic fields do not correspond to the same material. One may still obtain an estimate of the 3D field from the POS field based on statistical relations. Crutcher et al. (2004) suggested that the statistical relation between the 3D and POS underlying magnetic field is
Due to the uncertainties in the assumptions of the DCF method (see Section 2.1) and on the statistics of field orientations (see Section 2.2), a correction factor is required to correct for the magnetic field strength estimated from different modified DCF formulas. Several studies (Heitsch et al., 2001; Ostriker et al., 2001; Padoan et al., 2001; Falceta-Gonçalves et al., 2008; Liu et al., 2021; Skalidis and Tassis, 2021; Chen et al., 2022) have numerically investigated the correction factor Qc at different physical conditions with 3D ideal compressible MHD simulations. Table 3 summarizes these numerically derived correction factors. Recently, Lazarian et al. (2022) made the attempt to analytically derive the correction factor7 f for their proposed DMA formula.
For the most widely used formula
Heitsch et al. (2001) proposed a formula to estimate the geometric mean of
Falceta-Gonçalves et al. (2008) proposed a formula
Liu et al. (2021) also investigated the correction factor for the total magnetic field strength. They found Qc ∼ 0.62 for
Skalidis and Tassis (2021) and Skalidis et al. (2021) proposed a new formula
Other than in situations when the ADF method is improperly applied to observations (e.g., obtaining negative ordered field contribution or only adopting
A recent and important modification of the DCF method is the DMA (Lazarian et al., 2022), which theoretically derives the formula
The original DCF method and its modified forms have been widely applied to observations of magnetic fields in star-forming regions to estimate the magnetic field strength. Statistical studies of DCF estimations are of significant value to extend our understanding of the role of magnetic fields in star formation (e.g., Pattle and Fissel, 2019; Myers and Basu, 2021). Recently, Liu et al. (2022) compiled all the previous DCF estimations published between 2000 and June 2021 from polarized dust emission observations within star-forming molecular clouds. Similarly, Pattle et al. (2022) made a compilation of all types of DCF measurements published between 2001 and May 2021. Here we briefly summarise the previous observational DCF estimations.
During the contraction of molecular clouds, the gravity can compress and amplify the magnetic field. The power-law index of the B − n relation (B ∝ nj) characterise the dynamical importance of magnetic field during the cloud collapse. In the case of extremely weak magnetic fields where gas collapses isotropically due to magnetic freezing, there is relation B ∝ n2/3 for a self-gravitating cloud core during its temporal evolution (Mestel, 1966). In such case, the radial component of the magnetic field also has the 2/3 scaling dependence on the gas density at any time snapshots, whereas the tangential component does not follow this scaling relation. For stronger fields, the density increases faster than the magnetic field due to ambipolar diffusion at higher densities, which results in shallower power-law slopes (e.g., j ≲ 0.5, Mouschovias and Ciolek, 1999).
However, the temporal B − n relation of a single cloud is not obtainable observationally due to the long evolutionary time scale. Studies of the spatial B − n relation for a single cloud (e.g., Li et al., 2015) are also rare. Instead, observational B − n studies usually focus on the spatial B − n relation for an ensemble of star-forming regions at different evolution stages and different scales. Crutcher et al. (2010) made a pioneering study of the spatial B − n relation based on the Bayesian analysis of a collection of Zeeman observations. They found that the magnetic field does not scale with density at nH_{2} < 300 cm−3, but scales with density as B ∝ n0.65 at nH_{2} > 300 cm−3. Myers and Basu (2021) compiled the DCF estimation in 17 dense cores and reported B ∝ n0.66. With compilations of DCF estimations, Liu et al. (2022) and Pattle et al. (2022) found a similar trend to the Zeeman results in that the magnetic field does not scale with density at lower densities, but scales with density at higher densities. Due to the large scatters and the uncertainty in correction factors, they did not report the critical density and magnetic field strength for the transition. Liu et al. (2022) reported B ∝ n0.57 with a simple power-law fit for the high-density regime.
Despite the progress in the observational B − n studies, concerns have been raised on whether the B − n relation from a collection of different sources can be compared with model predictions for individual sources (Li, 2021). For the Zeeman observations, Tritsis et al. (2015) and Jiang et al. (2020) found that adopting different observational uncertainties of n other than the factor of 2 uncertainty adopted by Crutcher et al. (2010) can affect the fitted slope of the B − n relation, which questions the validity of the Bayesian analysis in Crutcher et al. (2010). Tritsis et al. (2015) further found that the samples collected in Crutcher et al. (2010) are preferentially non-spherical, which is inconsistent with the B ∝ n2/3 scaling. The DCF-derived B − n relation is also very uncertain due to the scatters on the DCF estimations and the intrinsic B ∝ n0.5 dependence of the DCF method. We do not aim to present a detailed review of the B − n relation, thus we refer readers to Tritsis et al. (2015), Crutcher and Kemball (2019), Hennebelle and Inutsuka (2019), Li (2021), and Pattle et al. (2022) for additional detailed discussions.
The relative importance between the magnetic field and the gravity of individual sources is usually parameterized by the magnetic critical parameter λ (i.e., mass-to-flux-ratio in units of the critical value). The critical value of the mass-to-flux-ratio is model-dependent (e.g., Strittmatter, 1966; Mouschovias and Spitzer, 1976; Nakano and Nakamura, 1978). The magnetic critical parameter for an isothermal disk-like structure is given by (Nakano and Nakamura, 1978; Crutcher et al., 2004)
where G is the gravitational constant, μH_{2} is the mean molecular weight per hydrogen molecule, and mH is the atomic mass of hydrogen. The magnetic critical parameter for a spherical structure with a density profile of n ∝ r−i is given by (Liu et al., 2022)
where ki = (5 − 2i)/(3 − i). Equation 13 reduces to
Statistical DCF studies have suggested that while molecular clouds are magnetically sub-critical (Planck Collaboration P. A. R. et al., 2016), the molecular dense cores within clouds are super-critical (Myers and Basu, 2021). The recent more complete DCF compilation by Liu et al. (2022) found a clear trend of increasing λ with increasing NH_{2} (see Figure 3), where the average state transits from sub-critical to super-critical at
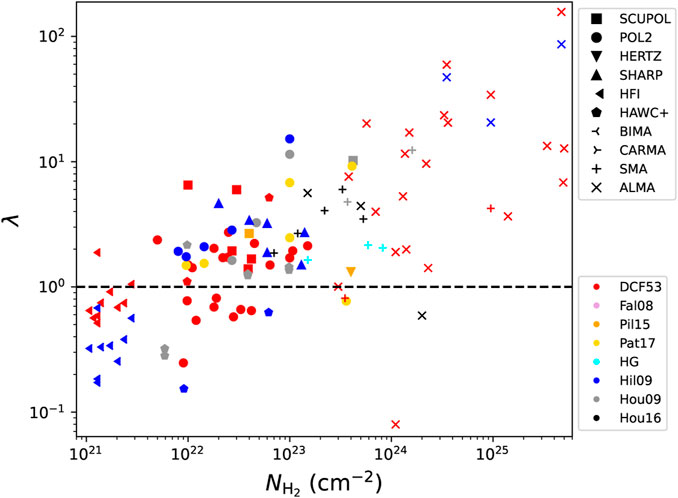
FIGURE 3. The relation between the magnetic critical parameter (Equation 13) and column density from the previous DCF estimations (Liu et al., 2022). Different symbols represent different instruments (see Liu et al. (2022) and references therein). Different colors represent different methods. To avoid an assumption on whether the underlying or turbulent field is more dominant, the magnetic critical parameter is estimated with the 3D total magnetic field strength adopting the statistical relation
The relative importance between the underlying magnetic field and the turbulence of individual sources is usually parameterized by the Alfvénic Mach number
If there is an equipartition between the turbulent magnetic and kinetic energies, Equation 14 reduces to
Liu et al. (2022) has compiled the observed angular dispersion from previous DCF studies (see Figure 4). They suggested that the observed angular dispersion does not provide too much information on the Alfvénic states of molecular clouds due to the maximum angle limit of a random field (δϕobs < 52°) and the lack of an appropriate DCF correction factor at cloud scales. Without knowledge of the inclination angle and turbulence anisotropy for most observations in the compilation, they adopted the statistical correction factor fu ∼ 4/π for a randomly distributed 3D mean field orientation (Crutcher et al., 2004),
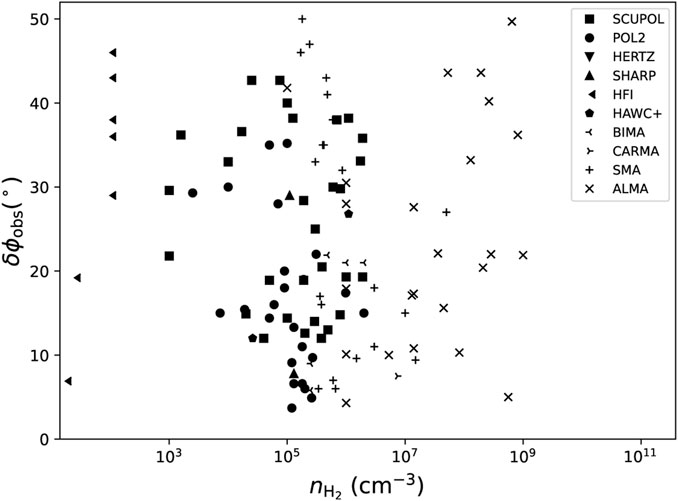
FIGURE 4. The relation between the directly estimated angular dispersion and the number density from the previous DCF estimations (Liu et al., 2022), reproduced with permission. Different symbols represent different instruments. Some data points with δϕobs > 52° are unphysical and are not plotted.
As the ADF method removes the contribution from the ordered field, the turbulent-to-ordered field strength ratio derived by the ADF method should be more suitable for the study of the Alfvénic state than the directly estimated angular dispersions. However, the applicability of the ADF method to determine the
If an alternative assumption of the Fed16 equipartition (see Section 2.1.1) is adopted, the
In summary, the average state of star-forming substructures within molecular clouds may be approximately trans-Alfvénic, but the observed angular dispersions do not yield clues on the Alfvénic state of molecular clouds themselves. Note that the equipartition assumption (either the DCF53 or the Fed16 assumption), which should be independently confirmed, is a prerequisite for using the angular dispersion to determine the Alfvénic Mach number. If the equipartition assumption is not satisfied for some of the sources, the average state should be more super-Alfvénic.
The equilibrium state of a dense structure is usually parameterized by the virial parameter. Neglecting the surface kinetic pressure and the thermal pressure, the total virial parameter for a spherical structure considering the support from both the magnetic field and the turbulence is estimated as the ratio of the total virial mass and the gas mass
The total virial mass is given by (Liu et al., 2020)
where the magnetic virial mass is estimated with
and the turbulent virial mass is estimated with
Alternatively, the equilibrium state can also be studied by comparing 2Eturb + EB with EG, where Eturb is the turbulent kinetic energy, EB is the magnetic energy, and EG is the gravitational energy.
Figure 5 shows the total virial parameter as a function of column density for the dense substructures within molecular clouds based on the DCF compilation by Liu et al. (2022). Due to the lack of mass estimations, we do not show the αturb+B for the molecular clouds observed by the Planck. Since the magnetic field can solely support the clouds (see Section 2.4.1.2), these clouds should have αturb+B > 1 (i.e., super-virial). Low-mass star-forming regions with M ≤ Mcrit = 870M⊙(r/pc)1.33 and high-mass star-forming regions with M > Mcrit (Kauffmann et al., 2010) are indicated with different colors. In Figure 5, the high-mass regions with highest column densities (e.g., NH_{2} > 1024 cm−2) tend to be trans- or sub-virial, but both super- and sub-virial states exist at lower column densities. The median αturb+B in low-mass and high-mass regions are ∼1.1 and ∼0.66, respectively, suggesting that the gravity may be more dominant in high-mass star formation. It may also indicate that high-mass star formation within molecular clouds tends to be more likely in non-equilibrium. It is possible that the magnetic field strength is overestimated for some sources due to the energy non-equipartition, which suggests a even more dynamical massive star formation. In summary, it appears that star-forming regions with higher column densities may have smaller total virial parameters due to more significant roles of gravity, but this trend is highly uncertain due to the large scatters.
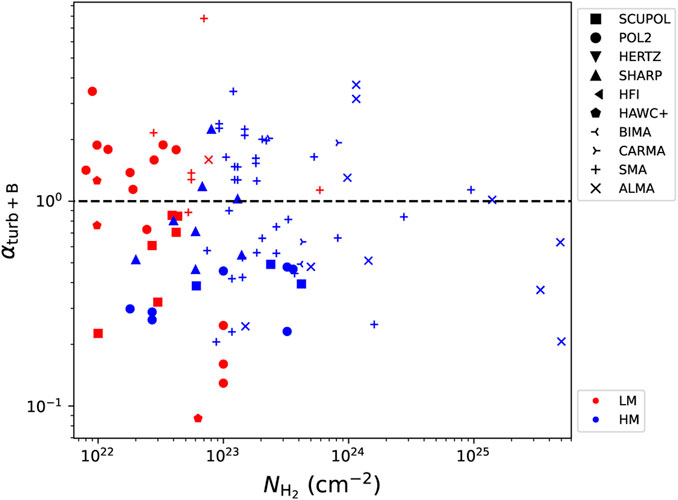
FIGURE 5. The relation between the total virial parameter (Equation 15) and column density for the DCF sample catalogued by Liu et al. (2022). Different symbols represent different instruments. Red and blue colors indicate low-mass (LM) and high-mass (HM) star-forming regions, respectively.
Soler et al. (2013) developed the HRO analysis to characterize the relative orientation of the magnetic field with respect to the density structures, which can be used to establish a link between observational results and the physics in simulations. In 3D, the HRO is the relation between the 3D magnetic field orientation and the number density gradient ∇n. In the POS, the HRO is the relation between the POS magnetic field orientation and the column density gradient ∇N. The calculation of the density gradient is by applying Gaussian derivative kernels to the density structure (Soler et al., 2013). The density gradient at different scales can be studied by varying the size of the derivative kernels. The orientation of the iso-density structure is perpendicular to the direction of the density gradient. For observational data in the POS, the angle ϕB-N between the orientation of the iso-column density structure and the POS magnetic field orientation8 is given by
where E is the POS electric field pseudo-vector (Planck Collaboration P. A. R. et al., 2016). The angle ϕB-N is within ±90°. When ϕB-N = 0°, the magnetic field is parallel to the orientation of the column density structure and is perpendicular to the column density gradient. When |ϕB-N| = 90°, the magnetic field is perpendicular to the orientation of the column density structure and is parallel to the column density gradient. The preferential relative orientation between the magnetic field and the density structure is characterized by the histogram shape parameter (Planck Collaboration P. A. R. et al., 2016; Soler et al., 2017)
where A0 is the percentage of pixels with |ϕB-N| < 22.5° and A90 is the percentage of pixels with 67.5° < |ϕB-N| < 90° in a polarization map. Positive ξ values indicate the column density structure is more likely aligned with the magnetic field, and vice versa. The ξ in 3D can be derived similarly.
Using the parameter ξ to characterize the relative orientation has some drawbacks. For instance, the derivation of the parameter ξ completely ignores angles within 22.5° < |ϕB-N| < 67.5°. It also suffers from intrinsic deficiencies of binning of angles. To overcome these shortcomings, Jow et al. (2018) improved the HRO analysis with the projected Rayleigh statistic (PRS), which uses the PRS parameter Zx instead of ξ to characterize the preferential relative orientation. For a set of n′ angles of relative orientation {ϕB−N,i}, Zx is estimated with
Zx > 0 indicates a preferential parallel alignment between the magnetic field and column density structure, and vice versa. Jow et al. (2018) suggested that the parameter Zx is more statistically powerful than the parameter ξ, especially when the sample size is small or when the angles {ϕB−N,i} are more uniformly distributed. Equation 21 cannot be directly applied to 3D data. The formula for the 3D PRS parameter still needs more theoretical investigations (Barreto-Mota et al., 2021).
The VGT group (e.g., González-Casanova and Lazarian, 2017; Lazarian and Yuen, 2018) introduced an alignment measure (AM) parameter to study the relative orientation between magnetic field orientations and velocity gradients, where the AM can also be used to study the relative orientation between magnetic fields and density structures. The AM for ϕB-N can be expressed as
Similar to Zx, the AM is also based on the Rayleigh statistic. AM is in the range of -1 to 1, which can be regarded as a normalized version of Zx.
The relation between the cloud density structures and magnetic field orientations has been extensively studied observationally. For example, Li et al. (2013) found the orientation of Gould Belt clouds tends to be either parallel or perpendicular to mean orientation of the cloud magnetic field, which they interpreted as strong fields channeling sub-Alfvénic turbulence or guiding gravitational contraction. Toward the same sample, clouds elongated closer to the field orientation were found to have 1) higher star formation rates, which was suggested to be due to their smaller magnetic fluxes as well as weaker magnetic support against gravitational collapse (Li et al., 2017); 2) shallower mass cumulative function slopes (Law et al., 2020), i.e., shallower column density probability distribution functions (N-PDFs), or, in other words, more mass at high densities. In filamentary clouds, there is evidence that the magnetic field is parallel to the low-density striations and is perpendicular to the high-density main filament (e.g., Chapman et al., 2011; Cox et al., 2016), which implies that the main filament accrete gas through the striations along the field lines. Besides the success of those observational studies, the HRO analysis has enabled a way to perform pixel-by-pixel statistics for the local alignment between the column density structure and the magnetic field. Observational studies using the HRO analysis have been focused on studying this alignment at different column densities.
The first HRO analyses were made with observations from the Planck/HFI at large scales. With a smoothed resolution of 15′, Planck Collaboration R. et al. (2016) found that ξ is mostly positive and is anti-correlated with the column density9 NH_{2} over the whole-sky at NH_{2} ≲ 5 × 1021 cm−2. The Planck observations toward 10 nearby (d < 450 pc) clouds (Planck Collaboration P. A. R. et al., 2016) with a smoothed resolution of 10′ (∼0.4–1.3 pc) have revealed a prevailing trend of decreasing ξ with increasing NH_{2}, with ξ being positive at lower NH_{2} and becoming negative at higher NH_{2} in most clouds except for those with low column densities (e.g., CrA). The transition of ξ from positive to negative values was found to be at NH_{2},tr ∼ 2.5 × 1021 cm−2.
Subsequent studies have expanded the HRO analysis to compare the large-scale magnetic field observed with Planck/HFI or the BLASTPol with the smaller-scale column density structures revealed by the Herschel Space Observatory. Malinen et al. (2016) compared the Herschel dust emission structures at a 20′′ (∼0.01 pc) resolution and the large-scale magnetic field orientation revealed by Planck polarization maps at a 10′ (∼0.4 pc) resolution and found a trend of decreasing ξ with increasing NH_{2} in the nearby cloud L1642, which transits at NH_{2},tr ∼ 8 × 1020 cm−2. Soler et al. (2017) found the same decreasing ξ − NH_{2} trend in the Vela C molecular complex by comparing the large-scale magnetic field orientation revealed by BLASTPol at a smoothed resolution of 3′ (∼0.61 pc) with the column density structures revealed by Herschel at a smoothed resolution of 35.2′′ (∼0.12 pc). The transition column density in Vela C is NH_{2},tr ∼ 6 × 1021 cm−2. They also found the slope of the ξ − NH_{2} relation is sharper in sub-regions where the high-column density tails of N-PDFs are flatter. Soler (2019) compared the Herschel column density maps at a resolution of 36′′ (∼0.03–0.08 pc) with the large-scale magnetic field from Planck observations for the ten clouds studied by Planck Collaboration P. A. R. et al. (2016) and found the ξ (or Zx) decreases with increasing NH_{2} in most clouds, which is in agreement with the study by Planck Collaboration P. A. R. et al. (2016). They also found that regions with more negative cloud-averaged ξ (or Zx) tend to have steeper N-PDF tails, but did not find a clear trend between the cloud-averaged ξ (or Zx) and the star formation rate. In addition, Fissel et al. (2019) compared the magnetic field orientation revealed by BLASTPol with the integrated line-intensity structures of different molecular lines observed with Mopra in Vela C. They found that the line emission for low-density tracers are statistically more aligned with the magnetic field, while high-density tracers tend to be perpendicular to the magnetic field. The transition occurs at nH_{2},tr ∼ 103 cm−3.
At smaller scales, the polarization observations from the SOFIA/HAWC + or JCMT/POL2 can be used to study the relative orientation between the magnetic field and column density structures within elongated filamentary structures. Lee et al. (2021) compared magnetic field orientations from the HAWC + observations with the Herschel column density maps in Ophiuchus/L1688 at a smoothed resolution of 36.3′′ (∼0.02 pc). They found smaller ξ values at higher NH_{2}, with ξ being mostly negative except for the first two column density bins. The transition column density in L1688 is NH_{2},tr ∼ 5 × 1021 cm−2. They also found that ξ increases from negative to ∼0 at higher column densities in the dense core Oph A within L1688, which suggests the magnetic alignment behavior is more complex at higher column densities. Li et al. (2022) compared the inferred magnetic field from HAWC+ with the Herschel column density map in Taurus/B211 and found that the magnetic field is more likely perpendicular to the column density structures in B211. Kwon et al. (2022) found negative ξ values in the Serpens Main cloud with JCMT observations at a resolution of 14′′ (∼0.03 pc), where they suggested that the first column density bin at NH_{2} ∼ 9.3 × 1021 cm−2 is approximately the transition column density. In Kwon et al. (2022), the ξ decreases from 0 to negative values from NH_{2} ∼ 9.3 × 1021 cm−2 to
Interferometric polarization observations are capable of revealing the magnetic field orientation within molecular dense cores. With ALMA observations at a resolution of 0.35′′ (∼140 AU), Hull et al. (2017b) found that the magnetic field is slightly more perpendicular than parallel to the column density structure around the class 0 protostellar source Ser-emb 8 in Serpens Main. Using ALMA observations at a resolution of 1.1′′ (∼200 AU), Hull et al. (2020) found that the magnetic field tends to be perpendicular to the column density structure in the class 0 protostellar source BHR 71 IRS1. They also found the magnetic field tends to be perpendicular to the column density structure but is parallel to outflow-cavity walls in another class 0 source BHR 71 IRS2, suggesting that the magnetic field is affected by the outflow activity. With ALMA observations at a resolution of 1.2′′ (∼0.02 pc) toward the high-mass star-forming region G327.3, Beuther et al. (2020) found that the relative orientation between the magnetic field and the dust emission structure changes from perpendicular to a random distribution when it is closer to the dust emission peak (i.e., ξ or Zx increases with increasing NH_{2}). This clearly contradicts the general decreasing ξ − NH_{2} trend at larger scales found by studies of lower resolution data, and might be related to the rotational properties of potential disks.
In summary, there is a general trend that the relative orientation between the magnetic field and the column density structure changes from parallel to perpendicular with increasing gas column densities. The transition from parallel to perpendicular alignment occurs at NH_{2},tr ∼ 1021–1022 cm−2 and may be at nH_{2},tr ∼ 103 cm−3, which are comparable to the transition or critical densities of the B − n and B − N relations measured from DCF estimations (Liu et al., 2022) or Zeeman observations (Crutcher, 2012). Within filaments and molecular dense cores, the relative orientation could return to random alignment in some sub-regions due to the impact of the projection effect (see Section 3.3), accreting gas flows, outflows, and/or the disk rotation. More observations are needed to better understand the returning to random alignment at high densities.
As indicated in Section 3.2, most clouds show a transition from a preferentially parallel alignment between the magnetic field orientation and density structures at low densities to a preferentially perpendicular alignment at higher densities. Numerical HRO studies have been focused on interpreting the contradictory alignment at different densities and understanding the implication of this transition.
Soler et al. (2013), Planck Collaboration P. A. R. et al. (2016), and Soler et al. (2017) have analysed 3 self-gravitating models with different initial magnetization levels (plasma β0 = 100, 1, and 0.1). The 3 models are initially super-Alfvénic (
Chen et al. (2016) analysed 3 self-gravitating models with different initial magnetic levels (
Seifried et al. (2020) performed a set of self-gravitating colliding flow simulations with
Körtgen and Soler (2020) performed a set of initially supersonic (initial Mach number
Girichidis (2021) also found a transition from parallel alignment to perpendicular alignment at higher densities in a 10 pc region of their large-scale simulation. They suggested that the transition happens when the local mass-to-flux ratio exceeds its critical value and the gravitational forces dominates the combination of thermal and magnetic pressures.
Barreto-Mota et al. (2021) studied the relative orientation between the magnetic field and density structure with simulations with a wide range of initial states (sub-Alfvénic and super-Alfvénic; with and without gravity). In non-gravitating simulations, only initially sub-Alfvénic models with the largest initial sonic number
Ibáñez-Mejía et al. (2022) analysed 3 clouds in a galactic-scale simulation with gravity. They found that the gas is trans-Alfvénic at nH_{2} < 102 cm−3. At nH_{2} > 102 cm−3, the gas becomes super-Alfvénic, which they suggested to be due to gravitational collapse. The relative orientation changes from predominantly parallel to much more random or perpendicular at even higher densities. i.e., they also found
Observations can only trace the projected quantities in the POS. The projection effect can make the 2D ξ − NH_{2} relation different from the 3D ξ − nH_{2} relation. Two parallel vectors in 3D are still parallel when projected in 2D, but 2 perpendicular vectors in 3D can have any relative orientations when projected in 2D depending on the viewing angle (e.g., Planck Collaboration R. et al., 2016). Soler et al. (2013) found that the relative orientation preserve well from 3D to 2D in sub-Alfvénic environments, except when the magnetic field orientation is close to the LOS. In contrast, the projected relative orientation does not necessarily reflect the relative orientation in 3D in super-Alfvénic environments. Other numerical studies found similar results for the projection effect (Seifried et al., 2020; Barreto-Mota et al., 2021; Girichidis, 2021).
The transition density at which the relative orientation changes its sign has also been studied by simulations. There is evidence that models with stronger magnetic field tend to have smaller transition densities in individual numerical studies (Soler et al., 2013; Chen et al., 2016), but this transition may not be solely dependent on the Alfvénic Mach number (Pattle et al., 2022). It should be noted that different numerical studies do not have a consistent way for measuring the local
Table 4 summarizes the simulations that show the transition of relative orientation from parallel to perpendicular alignment at higher densities. In most simulations (Soler et al., 2013; Planck Collaboration P. A. R. et al., 2016; Chen et al., 2016; Soler et al., 2017; Körtgen and Soler, 2020; Seifried et al., 2020; Barreto-Mota et al., 2021; Ibáñez-Mejía et al., 2022), the transition of relative orientation only occurs when the large-scale environment is trans- or sub-Alfvénic. For non-self-gravitating simulations, the transition only happens when the initial environment is sub-Alfvénic and supersonic (Körtgen and Soler, 2020; Barreto-Mota et al., 2021). Alternatively, Seifried et al. (2020) proposed that the transition only occurs in an magnetically sub-critical large-scale environment. It is still unclear what triggers the relative orientation to change from parallel to perpendicular. Plausible reasons include local

TABLE 4. Simulations that show transitions of relative orientation from parallel to perpendicular alignment at higher densities.
The analytical explanation for the parallel alignment between the magnetic field and density structure at low densities and the perpendicular alignment at high densities is still unclear. At low densities, the gravity is not dominant, so the alignment is mainly due to the interplay between the magnetic field and turbulence. Soler et al. (2013), Planck Collaboration R. et al. (2016), Planck Collaboration P. A. R. et al. (2016), and Soler et al. (2017) proposed that the initially super-Alfvénic compressive turbulent flows can stretch the magnetic field and density structures in the same direction due to magnetic freezing. However, the parallel alignment is also seen in initially sub-Alfvénic simulations (see Table 4). So an initially super-Alfvénic enviroment might not be a necessary condition for the parallel alignment. Alternatively, Chen et al. (2016) and Fissel et al. (2019) suggested that the anisotropic turbulent eddies in sub-Alfvénic gas naturally create elongated density structures parallel to the magnetic field. The anisotropic nature of sub-Alfvénic turbulence can explain the majority of the low-density gas with local
Koch et al. (2012a) proposed the KTH method to determine the magnetic field strength with the relative orientations between the magnetic field, emission intensity gradient, and local gravity. This method is based on ideal MHD force equations, where the intensity gradient is assumed to trace the resulting direction of motions in the MHD equation (i.e., the inertial term, Koch et al., 2013). This method leads to maps of position-dependent magnetic field strengths and magnetic-to-gravitational force ratios.
Under the assumptions of negligible viscosity, infinite conductivity (ideal MHD), isotropic magnetic field pressure, small turbulent-to-ordered field strength ratio, smoothly and slowly varying field strength, stationarity, and that the intensity gradient indicates the resulting direction of motions, Koch et al. (2012a) considered the force balance among pressure, gravity, and the curvature term of magnetic field to derive the field strength
where ψ is the relative orientation between the gravity and the intensity gradient, α is the relative orientation between the magnetic field and the intensity structure12, P is the hydrostatic dust pressure, ϕG is the local gravitational potential, and RB is the local magnetic field line radius. Koch et al. (2012a) then introduced a parameter ΣB to measure the local field significance. The field significance parameter ΣB is given by the reformulation of Equation 23
which quantifies the relative importance of the magnetic force FB = B2/(4πRB) compared to the combination of the gravitational and pressure forces FG + FP = ∇P + ρ∇ϕG. Koch et al. (2012a) further demonstrated analytically that Eqs 23, 24 do not suffer too much from the geometry and projection effects. If local changes in temperatures and densities are small compared to gravity, the pressure terms (∇P and FP) can be omitted from Eqs 23, 24. Thus, ΣB can be used to quantitatively indicate whether the magnetic field in a region is strong enough to prevent gravitational collapse (ΣB > 1) or not (ΣB < 1). Later, Koch et al. (2012b) suggested that the global mass-to-flux ratio normalized to the critical value within a specific region can be estimated with
where they adopted the magnetic critical mass from Shu et al. (1999) in the derivation of λKTH.
Due the a series of assumptions, the KTH method is subjected to many uncertainties (Koch et al., 2012a). In contrast to the DCF method that requires the information on the turbulent field, the KTH method regards the turbulent field as insignificant and only requires the ordered field structure. The contribution from turbulent field may be removed by averaging several neighboring pixels to derive an averaged local ordered field curvature (e.g., applying the Pil15 or Pat17 technique mentioned in Section 2.2.1), but the KTH method may still fail when the magnetic field is dominated by the turbulent component. The KTH method also is not applicable in the extremely strong field case where the matter can move only along the field lines (i.e., ψ ∼ 0, α ∼ π/2, and RB ∼∞). In some regions with strong rotation, the effect of rotation can lead to a change in the resulting direction of motion, which may be mitigated by adding a centrifugal term in the MHD equation. If the temperature variation is irregular and significant over a map, the intensity gradient should be replaced by the density gradient in the KTH analysis. The biggest uncertainty of the KTH method may come from the basic assumption that the intensity (or density) gradient traces the resulting motion of the MHD force equation. Koch et al. (2013) has investigated this assumption analytically and suggested that its validity relies on the difference between the velocity and density gradient directions. Although the numerical studies of the HRO method can be regarded as a partial test of the KTH method, the KTH method itself has not been fully compared with simulations yet. Further numerical investigations will be of significance to understand the uncertainty of this method in different physical conditions.
Most observational studies using the KTH method only partially applied this method and studied the distribution of the intermediate parameters. Here we summarise the observational studies of each parameter.
The angle δ = 90° − α is the relative orientation between the magnetic field and the intensity (or density) gradient. Basically, studying the distribution of δ is similar to studying the distribution of ϕB-N introduced by the HRO technique.
Similar to ϕB-N, the interpretation of the value and distribution of δ is still not yet well established. Koch et al. (2013) and Koch et al. (2014) suggested that a bimodal distributions of δ can be interpreted as a sign of collapse, where the angle δ measures how efficiently the magnetic field inhibits a collapse. Koch et al. (2013) and Koch et al. (2014) further proposed that the angle δ can used as a tracer of the evolution stage of star-forming regions. They suggested that δ is spatially randomly distributed due to the lack of a gravitational center in the early phase (Type I). In a later stage, elongated dust structures appear in star-forming regions. The magnetic field is parallel to the major axis of elongated dust structures that are created by large-scale flows and/or turbulence (Type IIB) or is perpendicular to the major axis of elongated dust structures when the gravity has just started to shape the field (Type IIA). Types IIB and IIA may further evolve into one and the same system (Type III) where a dominant gravity drags the magnetic field to form a radial, pinched, or hourglass shape. Koch et al. (2014) analysed a sample of 50 star-forming regions with CSO and SMA observations and found that the mean |δ| values for Types IIB, IIA, and III are 51° (CSO and SMA), 30° (CSO) to 34° (SMA), and 30° (SMA only), respectively. The categorization of different δ types is an empirical characterization. The correspondence between the δ types and different evolution stages of low-mass and high-mass star formation at different scales is still unclear and warrants further investigations.
Studies of individual star-forming regions have revealed different values and distributions of δ. Tang et al. (2013) found that the magnetic field is less correlated with the dust intensity gradient at larger scales revealed by JCMT or CSO, while the two angles are more correlated at smaller scales observed by SMA. This trend is consistent with the results from the observational HRO studies (Section 3.2). With SMA polarization observations toward the massive dense cores in the DR21 filament, Ching et al. (2017) found that the magnetic field and the intensity gradient are misaligned in rotation-like cores and are aligned in non-rotation-like cores, which suggests the magnetic field could be distorted by the rotation. Girart et al. (2013) found random distributions of δ with an average value of 40° in the massive dense core DR21(OH) with SMA observations. With ALMA polarization observations toward the massive clumps in the IRDC G28.34, Liu et al. (2020) found random distributions of δ and average δ values of 40° and 46° in the dense cores in two massive clumps MM1 and MM4, respectively. In another IRDC G14.225, Añez-López et al. (2020) found that the δ value in the Hub-N region is mostly small with their CSO observations. More observational studies of δ are still required to better understand its general distributions at different scales and evolution stages of star formation.
The angle ω measures the relative orientation between the magnetic field and the local gravity. The angle ω may be used as a measure for how effectively gravity can shape the magnetic field structure (Koch et al., 2012a), but further explanations of the distribution of ω are still yet to be established.
There are few observational studies of ω. Koch et al. (2012a) found an average ω of 13° in W51 e2, suggesting the magnetic field lines are mainly dragged by gravity in this core. With ALMA polarization observations, Koch et al. (2018) found average sin ω values of 0.4, 0.41, and 0.47 (i.e., ω ∼ 23°, 23°, and 27°) in three massive cores W51 e2, W51 e8, and W51N, respectively. The distributions of ω in three cores vary, but all show some magnetic channels with sin ω ∼ 0. Koch et al. (2018) suggested that the gas collapse can proceed in free-fall in these magnetic channels without magnetic resistance, which may have some interesting implication for the star formation rate. Liu et al. (2020) found average ω values of 34° and 36° in the dense cores in massive clumps G28-MM1 and G28-MM4, respectively, which are lower than the average δ values in the same region. This shows that the magnetic field is more aligned with the gravity direction than the intensity (or density) gradient, which suggests ω may be better than δ (or ϕB-N of the HRO technique) for the study of the correlation between the magnetic field and gravity in high density regions. An interesting future study point of ω may be studying its variation at different densities in a similar way to the studies of the angle ϕB-N.
The angle ψ measures the relative orientation between the intensity (or density) gradient and the local gravity. The angle ψ may indicate how effective gravity can shape the density structure, but further analytical implications of ψ are still yet to be investigated.
There are few observational studies of the angle ψ. Koch et al. (2012a) found an average ψ of 20° in W51 e2. Liu et al. (2020) found average ψ values of 30°, 22°, and 28° in the dense cores in massive clumps G28-MM1, G28-MM4, and G28-MM9, respectively. These observations suggest that the gravity direction is closely aligned with the intensity gradient in high density molecular cores.
The field significance parameter ΣB measures the ratio between the magnetic force and the gravitational force if the gas pressure is negligible. The implication of ΣB is clear, but the accuracy of the estimated force ratio is not tested by simulations yet.
Based on a sample of 50 sources, Koch et al. (2014) found that the different types of star-forming regions categorized by the angle δ (see Section 4.2.1) show clear segregation in ΣB values. Type IIB sources where the magnetic field is aligned with the clump/core major axis have an average ΣB of 1.29 (CSO) to 1.49 (SMA), which suggests that type IIB sources are supported by the magnetic field and do not collapse on average. Type IIA sources where the magnetic field is perpendicular with the clump/core major axis have an average ΣB of 0.69 (CSO) to 0.74 (SMA), which suggests that type IIA sources are collapsing on average. Type III sources at a later stage have a smaller average ΣB value of 0.59 (SMA only), suggesting an even more dynamical collapsing.
Individual studies have mostly found ΣB ≲ 1 in star-forming dense clumps/cores (e.g., W51 e2, W51A, W51N, DR21(OH), clumps in G34.43, cores in G28.34, and clumps in G14.225, Koch et al., 2012a; Koch et al., 2012b; Tang et al., 2013; Girart et al., 2013; Tang et al., 2019; Liu et al., 2020; Añez-López et al., 2020). Specifically, Tang et al. (2013) found that the lower density structures in W51N revealed by the CSO and JCMT have ΣB ∼ 0.71–1.17, while the higher density structures revealed by SMA have ΣB ∼ 0.5. Koch et al. (2012a) and Koch et al. (2012b) found smaller ΣB values in higher column density regions in W51 e2 and W51A. These findings indicate that the gravity plays an more dominant role in higher density regions, which agrees with the observational DCF studies (see Section 2.4.1.2). On the other hand, Liu et al. (2020) found that the ΣB values are higher in more evolved dense cores in the IRDC G28.34, which might suggest a more dynamical star formation at earlier evolution stages.
The KTH method can be used to estimate the magnetic field strength with Equation 23. The accuracy of the estimated field strength is still unclear as it has not been tested by simulations yet.
By far, there are only two observational studies that has applied the KTH method to estimate the field strength. Koch et al. (2012a) found an average field strength of 7.7 mG in W51 e2. Stephens et al. (2013) estimated a field strength of 3.4 mG with the KTH method in L1157-mm, which is ∼2.5 times higher than the DCF estimation of 1.4 mG in the same work.
The mass-to-flux-ratio to critical value λKTH can be estimated from the field significance parameter ΣB through Equation 25. Similarly, the accuracy of λKTH is yet to be investigated by simulations.
Koch et al. (2012b) found larger λKTH values in higher density regions in W51 e2, which agrees with the trend from DCF estimations (see Section 2.4.1.2). Other two observational studies in DR21(OH) and G14.225N have found that the λKTH value estimated with the KTH method approximately agrees with the value of DCF estimations (Girart et al., 2013; Añez-López et al., 2020).
The recent improvement of instrumental sensitivity and development of new techniques (e.g., the VGT) have led to an increasing number of observations that reveal the POS component of magnetic field orientations in star-forming molecular clouds. In this review, we discuss the developments and limitations of the DCF and KTH methods that quantify the dynamic importance of magnetic fields in star-forming molecular clouds based on the field orientations and the HRO analysis that characterize the statistical relation between field orientations and density structures. We also summarize the observational studies using these methods and discuss their implications on star formation.
The original DCF method is based on several assumptions: the total magnetic field is composed of a mean field component and a turbulent field component; the energy equipartition; isotropic turbulence; and the turbulent-to-mean or -total field strength ratio is traced by angular dispersions. The ordered field component is considered instead of the mean field component (e.g., the ADF method) if there are curved ordered magnetic field structures. We suggest that the ordered field and turbulent field of a particular region are local properties and are dependent on the scale range (i.e., the beam resolution to the maximum recoverable scale of interferometric observations or the region size) of the region of interest. There is still a debate on whether there is an equipartition between the turbulent magnetic field and the turbulent kinetic field or between the coupling-term magnetic field and the turbulent kinetic field in the sub-Alfvénic regime, while both equipartitions are not satisfied for super-Alfvénic turbulence. The energy non-equipartition can be the biggest uncertainty in the DCF method, which should be further investigated with simulations and observations. The uncertainty from anisotropic turbulence may be insignificant for the DCF estimations in self-gravitating regions. The turbulent-to-underlying or -total field strength ratio can be expressed as different forms of angular dispersions, but each has its limitations. The ADF method correctly accounts for the beam-smoothing effect, interferometric filtering effect, and the ordered field structure, but its applicability for quantifying the turbulent field and LOS signal integration may need further numerical investigations. The correction factor for the most widely used formula
A compilation of previous DCF estimations suggests a scenario that magnetically sub-critical low-density clouds gradually form super-critical high-density substructures. The critical column density is around 3.4 × 1021 cm−2 on average, which needs to be better constrained and may differ in different clouds. The gravity may be more dominant in high-mass star formation than low-mass star formation. The average state of dense substructures within molecular clouds is approximately trans-Alfvénic if the energy equipartition assumption is satisfied, or super-Alfvénic if the energy equipartition assumption is unsatisfied for some of the sources.
Observational HRO studies mainly focus on the alignment between the magnetic field and density structure. Low-resolution HRO studies have found a general trend of transition from a preferentially parallel alignment at low column densities to a perpendicular alignment at higher column densities. This observational trend agrees with trans-to-sub-Alfvénic simulations, which indicates that the star-forming molecular clouds are trans-to-sub-Alfvénic. This trans-to-sub-Alfvénic state is consistent with the results derived from other techniques (e.g., the VGT, Hu et al., 2019b). The analytical explanation for the transition from parallel to perpendicular alignment is still unclear, but may be related to changes of the local Alfvénic Mach number, A1 + A23 term, mass-to-flux-ratio, and/or ∇v. The transition occurs at 1021–1022 cm−2, which agrees with the critical column density derived from DCF estimations. But it is unclear whether the two transition column densities are related. High-resolution HRO studies have revealed a possible transition from perpendicular alignment back to random alignment at high column density sub-regions. The reason for this reverse transition is also unclear, but may be related to the impact of accretion gas flows, outflows, disk rotation, and/or the projection effect.
The advantage of the KTH method compared to the DCF method is that it does not require the information on the velocity dispersion. However, the uncertainty of the KTH method is still unknown since it has not been fully tested by simulations. Results from observational KTH studies on the relative alignment between the magnetic field and intensity (density) gradient within dense clumps/cores approximately agree with those of the observational HRO studies. The value and density-varying trend of the mass-to-flux-ratio and the magnetic field strength derived from the KTH method approximately agree with those derived from the DCF estimations.
JL, QZ, and KQ contributed to the outline of the review. JL led the writing of the manuscript. QZ and KQ read, commented on, and edited the manuscript.
JL acknowledges the support from the EAO Fellowship Program under the umbrella of the East Asia Core Observatories Association. KQ is supported by National Key R&D Program of China grant No. 2017YFA0402600. KQ acknowledges the support from National Natural Science Foundation of China (NSFC) through grant Nos. U1731237, 11590781, and 11629302.
We thank the referees for constructive comments that improved the clarity of this paper. JL thanks Prof. Martin Houde for insightful discussions about the correlation between turbulent magnetic and kinetic fields. JL thanks Heshou Zhang and Suoqing Ji for helpful discussions on the general concept of MHD turbulence.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1In this paper, the mean field refers to the vector-averaged magnetic field (Bm) and the ordered field refers to the curved large-scale ordered magnetic field (Bo). We also use the term “underlying field” (Bu) to refer to either the mean field or ordered field since many previous studies did not explicitly differ the two. The ordered field and the mean field are equivalent if the large-scale ordered field lines are straight.
2The equations in SI units in this paper can be transformed to Gaussian units by replacing μ0 with 4π.
3The inclination angle γ corresponds to the angle between the 3D mean field and the LOS throughout this paper.
4The field angle considers the direction of the magnetic field and is in the range of -180°–180° (Li et al., 2022), while the position angle ϕ only considers the orientation of the magnetic field and is in the range of -90°–90°. Due to the 180° ambiguity of dust polarization observations, only the magnetic field position angle is observable.
5The Hil09 variant of ADF directly estimates the
6Note that there is a factor of
7Here we use f for the analytically derived correction factor to differ with the numerically derived correction factor Qc.
8Note that there is a 90° difference between the ϕB-N defined in Soler et al. (2013) and in the subsequent HRO papers. In Soler et al. (2013), ϕB-N is defined as the angle between the column density gradient and the POS magnetic field orientation.
9A significant amount of the diffuse ISM is in the atomic phase, while molecular clouds are in the molecular phase. Here we use NH_{2} to describe the column density in diffuse ISM and molecular clouds for uniformity.
10Planck Collaboration et al. (2016b) did not explicitly indicate the time of the snapshot they studied. We consulted their corresponding author to confirm this information.
11It is unclear whether these numerical studies has excluded the non-turbulent motions (e.g., infall, outflow, and/or rotation.) in the calculation of
12The angle α is equivalent to the ϕB-N in Section 3 if the intensity structure perfectly traces the density structure.
Alfvén, H. (1942). Existence of electromagnetic-hydrodynamic waves. Nature 150, 405–406. doi:10.1038/150405d0
Añez-López, N., Busquet, G., Koch, P. M., Girart, J. M., Liu, H. B., Santos, F., et al. (2020). Role of the magnetic field in the fragmentation process: The case of g14.225-0.506. Astron. Astrophys. 644, A52. doi:10.1051/0004-6361/202039152
Barreto-Mota, L., de Gouveia Dal Pino, E. M., Burkhart, B., Melioli, C., Santos-Lima, R., and Kadowaki, L. H. S. (2021). Magnetic field orientation in self-gravitating turbulent molecular clouds. Mon. Not. R. Astron. Soc. 503, 5425–5447. doi:10.1093/mnras/stab798
Beattie, J. R., Federrath, C., and Seta, A. (2020). Magnetic field fluctuations in anisotropic, supersonic turbulence. Mon. Not. R. Astron. Soc. 498, 1593–1608. doi:10.1093/mnras/staa2257
Beattie, J. R., Krumholz, M. R., Skalidis, R., Federrath, C., Seta, A., Crocker, R. M., et al. (2022). Energy balance and Alfvén Mach numbers in compressible magnetohydrodynamic turbulence with a large-scale magnetic field. Mon. Notices R. Astronomical Soc. 515, 5267–5284. doi:10.1093/mnras/stac2099
Beltrán, M. T., Padovani, M., Girart, J. M., Galli, D., Cesaroni, R., Paladino, R., et al. (2019). ALMA resolves the hourglass magnetic field in G31.41+0.31. A&A 630, A54. doi:10.1051/0004-6361/201935701
Beuther, H., Soler, J. D., Linz, H., Henning, T., Gieser, C., Kuiper, R., et al. (2020). Gravity and rotation drag the magnetic field in high-mass star formation. Astrophys. J. 904, 168. doi:10.3847/1538-4357/abc019
Brandenburg, A., and Lazarian, A. (2013). Astrophysical hydromagnetic turbulence. Space Sci. Rev. 178, 163–200. doi:10.1007/s11214-013-0009-3
Chandrasekhar, S., and Fermi, E. (1953). Magnetic fields in spiral arms. Astrophys. J. 118, 113. doi:10.1086/145731
Chapman, N. L., Goldsmith, P. F., Pineda, J. L., Clemens, D. P., Li, D., and Krčo, M. (2011). The magnetic field in Taurus probed by infrared polarization. Astrophys. J. 741, 21. doi:10.1088/0004-637X/741/1/21
Chen, C.-Y., King, P. K., and Li, Z.-Y. (2016). Change of magnetic field-gas alignment at the gravity-driven alfvénic transition in molecular clouds: Implications for dust polarization observations. Astrophys. J. 829, 84. doi:10.3847/0004-637X/829/2/84
Chen, C.-Y., King, P. K., Li, Z.-Y., Fissel, L. M., and Mazzei, R. R. (2019). A new method to trace three-dimensional magnetic field structure within molecular clouds using dust polarization. Mon. Not. R. Astron. Soc. 485, 3499–3513. doi:10.1093/mnras/stz618
Chen, C.-Y., Li, Z.-Y., Mazzei, R. R., Park, J., Fissel, L. M., Chen, M. C. Y., et al. (2022). The Davis-Chandrasekhar-Fermi method revisited. Mon. Not. R. Astron. Soc. 514, 1575–1594. doi:10.1093/mnras/stac1417
Ching, T.-C., Lai, S.-P., Zhang, Q., Girart, J. M., Qiu, K., and Liu, H. B. (2017). Magnetic fields in the massive dense cores of the DR21 filament: Weakly magnetized cores in a strongly magnetized filament. Astrophys. J. 838, 121. doi:10.3847/1538-4357/aa65cc
Cho, J. (2019). A technique for removing large-scale variations in regularly and irregularly spaced data. Astrophys. J. 874, 75. doi:10.3847/1538-4357/ab06f3
Cho, J., and Yoo, H. (2016). A technique for constraining the driving scale of turbulence and a modified chandrasekhar-fermi method. Astrophys. J. 821, 21. doi:10.3847/0004-637X/821/1/21
Cox, N. L. J., Arzoumanian, D., André, P., Rygl, K. L. J., Prusti, T., Men’shchikov, A., et al. (2016). Filamentary structure and magnetic field orientation in Musca. Astron. Astrophys. 590, A110. doi:10.1051/0004-6361/201527068
Crutcher, R. M., and Kemball, A. J. (2019). Review of zeeman effect observations of regions of star formation. Front. Astron. Space Sci. 6, 66. doi:10.3389/fspas.2019.00066
Crutcher, R. M. (2012). Magnetic fields in molecular clouds. Annu. Rev. Astron. Astrophys. 50, 29–63. doi:10.1146/annurev-astro-081811-125514
Crutcher, R. M., Nutter, D. J., Ward-Thompson, D., and Kirk, J. M. (2004). SCUBA polarization measurements of the magnetic field strengths in the L183, L1544, and L43 prestellar cores. Astrophys. J. 600, 279–285. doi:10.1086/379705
Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., and Troland, T. H. (2010). Magnetic fields in interstellar clouds from zeeman observations: Inference of total field strengths by bayesian analysis. Astrophys. J. 725, 466–479. doi:10.1088/0004-637X/725/1/466
Davis, L., and Greenstein, J. L. (1949). The polarization of starlight by interstellar dust particles in a galactic magnetic field. Phys. Rev. 75, 1605. doi:10.1103/PhysRev.75.1605
Davis, L. (1951). The strength of interstellar magnetic fields. Phys. Rev. 81, 890–891. doi:10.1103/PhysRev.81.890.2
Elmegreen, B. G., and Elmegreen, D. M. (1978). Star formation in shock-compressed layers. Astrophys. J. 220, 1051–1062. doi:10.1086/155991
Falceta-Gonçalves, D., Lazarian, A., and Kowal, G. (2008). Studies of regular and random magnetic fields in the ISM: Statistics of polarization vectors and the chandrasekhar-fermi technique. Astrophys. J. 679, 537–551. doi:10.1086/587479
Federrath, C. (2016). Magnetic field amplification in turbulent astrophysical plasmas. J. Plasma Phys. 82, 535820601. doi:10.1017/S0022377816001069
Fissel, L. M., Ade, P. A. R., Angilè, F. E., Ashton, P., Benton, S. J., Chen, C.-Y., et al. (2019). Relative alignment between the magnetic field and molecular gas structure in the Vela C giant molecular cloud using low- and high-density tracers. Astrophys. J. 878, 110. doi:10.3847/1538-4357/ab1eb0
Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., and Estalella, R. (2009). Magnetic fields in the formation of massive stars. Science 324, 1408–1411. doi:10.1126/science.1171807
Girart, J. M., Frau, P., Zhang, Q., Koch, P. M., Qiu, K., Tang, Y. W., et al. (2013). DR 21(OH): A highly fragmented, magnetized, turbulent dense core. Astrophys. J. 772, 69. doi:10.1088/0004-637X/772/1/69
Girart, J. M., Rao, R., and Marrone, D. P. (2006). Magnetic fields in the formation of sun-like stars. Science 313, 812–814. doi:10.1126/science.1129093
Girichidis, P. (2021). Alignment of the magnetic field in star-forming regions and why it might be difficult to observe. Mon. Not. R. Astron. Soc. 507, 5641–5657. doi:10.1093/mnras/stab2157
Goldreich, P., and Kylafis, N. D. (1981). On mapping the magnetic field direction in molecular clouds by polarization measurements. Astrophys. J. 243, L75–L78. doi:10.1086/183446
Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence. Astrophys. J. 438, 763. doi:10.1086/175121
González-Casanova, D. F., and Lazarian, A. (2017). Velocity gradients as a tracer for magnetic fields. Astrophys. J. 835, 41. doi:10.3847/1538-4357/835/1/41
Ha, T., Li, Y., Xu, S., Kounkel, M., and Li, H. (2021). Measuring turbulence with young stars in the orion complex. Astrophys. J. 907, L40. doi:10.3847/2041-8213/abd8c9
Haugen, N. E. L., and Brandenburg, A. (2004). Suppression of small scale dynamo action by an imposed magnetic field. Phys. Rev. E 70, 036408. doi:10.1103/PhysRevE.70.036408
Haverkorn, M., Brown, J. C., Gaensler, B. M., and McClure-Griffiths, N. M. (2008). The outer scale of turbulence in the magnetoionized galactic interstellar medium. Astrophys. J. 680, 362–370. doi:10.1086/587165
Heitsch, F., Zweibel, E. G., Mac Low, M.-M., Li, P., and Norman, M. L. (2001). Magnetic field diagnostics based on far-infrared polarimetry: Tests using numerical simulations. Astrophys. J. 561, 800–814. doi:10.1086/323489
Hennebelle, P., and Falgarone, E. (2012). Turbulent molecular clouds. Astron. Astrophys. Rev. 20, 55. doi:10.1007/s00159-012-0055-y
Hennebelle, P., and Inutsuka, S.-i. (2019). The role of magnetic field in molecular cloud formation and evolution. Front. Astron. Space Sci. 6, 5. doi:10.3389/fspas.2019.00005
Heyer, M., Gong, H., Ostriker, E., and Brunt, C. (2008). Magnetically aligned velocity anisotropy in the Taurus molecular cloud. Astrophys. J. 680, 420–427. doi:10.1086/587510
Heyer, M. H., and Brunt, C. M. (2004). The universality of turbulence in galactic molecular clouds. Astrophys. J. 615, L45–L48. doi:10.1086/425978
Heyer, M. H., and Brunt, C. M. (2012). Trans-Alfvénic motions in the Taurus molecular cloud. Mon. Not. R. Astron. Soc. 420, 1562–1569. doi:10.1111/j.1365-2966.2011.20142.x
Hezareh, T., Houde, M., McCoey, C., and Li, H.-b. (2010). Observational determination of the turbulent ambipolar diffusion scale and magnetic field strength in molecular clouds. Astrophys. J. 720, 603–607. doi:10.1088/0004-637X/720/1/603
Higdon, J. C. (1984). Density fluctuations in the interstellar medium: Evidence for anisotropic magnetogasdynamic turbulence. I - model and astrophysical sites. Astrophys. J. 285, 109–123. doi:10.1086/162481
Hildebrand, R. H., Kirby, L., Dotson, J. L., Houde, M., and Vaillancourt, J. E. (2009). Dispersion of magnetic fields in molecular clouds. I. ApJ 696, 567–573. doi:10.1088/0004-637X/696/1/567
Hildebrand, R. H. (1983). The determination of cloud masses and dust characteristics from submillimetre thermal emission. QJRAS 24, 267–282.
Hiltner, W. A. (1949). Polarization of light from distant stars by interstellar medium. Science 109, 165. doi:10.1126/science.109.2825.165
Houde, M., Bastien, P., Dotson, J. L., Dowell, C. D., Hildebrand, R. H., Peng, R., et al. (2002). On the measurement of the magnitude and orientation of the magnetic field in molecular clouds. Astrophys. J. 569, 803–814. doi:10.1086/339356
Houde, M. (2004). Evaluating the magnetic field strength in molecular clouds. Astrophys. J. 616, L111–L114. doi:10.1086/426684
Houde, M., Hull, C. L. H., Plambeck, R. L., Vaillancourt, J. E., and Hildebrand, R. H. (2016). Dispersion of magnetic fields in molecular clouds. IV. Analysis of interferometry data. Astrophys. J. 820, 38. doi:10.3847/0004-637X/820/1/38
Houde, M. (2011). “Magnetic fields in three dimensions,” in Astronomical polarimetry 2008: Science from small to large telescopes. Editors P. Bastien, N. Manset, D. P. Clemens, and N. St-Louis (San Francisco: Astronomical Society of the Pacific), 213. vol. 449 of Astronomical Society of the Pacific Conference Series.
Houde, M., Rao, R., Vaillancourt, J. E., and Hildebrand, R. H. (2011). Dispersion of magnetic fields in molecular clouds. III. Astrophys. J. 733, 109. doi:10.1088/0004-637X/733/2/109
Houde, M., Vaillancourt, J. E., Hildebrand, R. H., Chitsazzadeh, S., and Kirby, L. (2009). Dispersion of magnetic fields in molecular clouds. II. Astrophys. J. 706, 1504–1516. doi:10.1088/0004-637X/706/2/1504
Hu, Y., Federrath, C., Xu, S., and Mathew, S. S. (2022). The velocity statistics of turbulent clouds in the presence of gravity, magnetic fields, radiation, and outflow feedback. Mon. Not. R. Astron. Soc. 513, 2100–2110. doi:10.1093/mnras/stac972
Hu, Y., Lazarian, A., and Xu, S. (2021). Anisotropic turbulence in position-position-velocity space: Probing three-dimensional magnetic fields. Astrophys. J. 915, 67. doi:10.3847/1538-4357/ac00ab
Hu, Y., Yuen, K. H., and Lazarian, A. (2019a). Intensity gradients technique: Synergy with velocity gradients and polarization studies. Astrophys. J. 886, 17. doi:10.3847/1538-4357/ab4b5e
Hu, Y., Yuen, K. H., Lazarian, V., Ho, K. W., Benjamin, R. A., Hill, A. S., et al. (2019b). Magnetic field morphology in interstellar clouds with the velocity gradient technique. Nat. Astron. 3, 776–782. doi:10.1038/s41550-019-0769-0
Hull, C. L. H., Girart, J. M., Tychoniec, Ł., Rao, R., Cortés, P. C., Pokhrel, R., et al. (2017a). ALMA observations of dust polarization and molecular line emission from the class 0 protostellar source Serpens SMM1. Astrophys. J. 847, 92. doi:10.3847/1538-4357/aa7fe9
Hull, C. L. H., Le Gouellec, V. J. M., Girart, J. M., Tobin, J. J., and Bourke, T. L. (2020). Understanding the origin of the magnetic field morphology in the wide-binary protostellar system BHR 71. Astrophys. J. 892, 152. doi:10.3847/1538-4357/ab5809
Hull, C. L. H., Mocz, P., Burkhart, B., Goodman, A. A., Girart, J. M., Cortés, P. C., et al. (2017b). Unveiling the role of the magnetic field at the smallest scales of star formation. Astrophys. J. 842, L9. doi:10.3847/2041-8213/aa71b7
Hull, C. L. H., and Zhang, Q. (2019). Interferometric observations of magnetic fields in forming stars. Front. Astron. Space Sci. 6, 3. doi:10.3389/fspas.2019.00003
Ibáñez-Mejía, J. C., Mac Low, M.-M., and Klessen, R. S. (2022). Gravity versus magnetic fields in forming molecular clouds. Astrophys. J. 925, 196. doi:10.3847/1538-4357/ac3b58
Jiang, H., Li, H.-b., and Fan, X. (2020). Bayesian revisit of the relationship between the total field strength and the volume density of interstellar clouds. Astrophys. J. 890, 153. doi:10.3847/1538-4357/ab672b
Jow, D. L., Hill, R., Scott, D., Soler, J. D., Martin, P. G., Devlin, M. J., et al. (2018). An application of an optimal statistic for characterizing relative orientations. Mon. Not. R. Astron. Soc. 474, 1018–1027. doi:10.1093/mnras/stx2736
Kauffmann, J., Pillai, T., and Goldsmith, P. F. (2013). Low virial parameters in molecular clouds: Implications for high-mass star formation and magnetic fields. Astrophys. J. 779, 185. doi:10.1088/0004-637X/779/2/185
Kauffmann, J., Pillai, T., Shetty, R., Myers, P. C., and Goodman, A. A. (2010). The mass-size relation from clouds to cores. II. Solar neighborhood clouds. Astrophys. J. 716, 433–445. doi:10.1088/0004-637X/716/1/433
Koch, P. M., Tang, Y.-W., and Ho, P. T. P. (2013). Interpreting the role of the magnetic field from dust polarization maps. Astrophys. J. 775, 77. doi:10.1088/0004-637X/775/1/77
Koch, P. M., Tang, Y.-W., and Ho, P. T. P. (2012a). Magnetic field strength maps for molecular clouds: A new method based on a polarization-intensity gradient relation. Astrophys. J. 747, 79. doi:10.1088/0004-637X/747/1/79
Koch, P. M., Tang, Y.-W., and Ho, P. T. P. (2012b). Quantifying the significance of the magnetic field from large-scale cloud to collapsing core: Self-similarity, mass-to-flux ratio, and star formation efficiency. Astrophys. J. 747, 80. doi:10.1088/0004-637X/747/1/80
Koch, P. M., Tang, Y.-W., Ho, P. T. P., Yen, H.-W., Su, Y.-N., and Takakuwa, S. (2018). Polarization properties and magnetic field structures in the high-mass star-forming region W51 observed with ALMA. Astrophys. J. 855, 39. doi:10.3847/1538-4357/aaa4c1
Koch, P. M., Tang, Y.-W., Ho, P. T. P., Zhang, Q., Girart, J. M., Chen, H.-R. V., et al. (2014). The importance of the magnetic field from an SMA-CSO-combined sample of star-forming regions. Astrophys. J. 797, 99. doi:10.1088/0004-637X/797/2/99
Körtgen, B., and Soler, J. D. (2020). The relative orientation between the magnetic field and gas density structures in non-gravitating turbulent media. Mon. Not. R. Astron. Soc. 499, 4785–4792. doi:10.1093/mnras/staa3078
Kwon, W., Pattle, K., Sadavoy, S., Hull, C. L. H., Johnstone, D., Ward-Thompson, D., et al. (2022). B-Fields in star-forming region observations (BISTRO): Magnetic fields in the filamentary structures of Serpens main. Astrophys. J. 926, 163. doi:10.3847/1538-4357/ac4bbe
Lai, S.-P., Crutcher, R. M., Girart, J. M., and Rao, R. (2002). Interferometric mapping of magnetic fields in star-forming regions. II. NGC 2024 FIR 5. Astrophys. J. 566, 925–930. doi:10.1086/338336
Law, C. Y., Li, H. B., Cao, Z., and Ng, C. Y. (2020). The links between magnetic fields and filamentary clouds - III. Field-regulated mass cumulative functions. Mon. Not. R. Astron. Soc. 498, 850–858. doi:10.1093/mnras/staa2466
Lazarian, A., and Hoang, T. (2007). Radiative torques: Analytical model and basic properties. Mon. Not. R. Astron. Soc. 378, 910–946. doi:10.1111/j.1365-2966.2007.11817.x
Lazarian, A. (2007). Tracing magnetic fields with aligned grains. J. Quant. Spectrosc. Radiat. Transf. 106, 225–256. doi:10.1016/j.jqsrt.2007.01.038
Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a weakly stochastic field. Astrophys. J. 517, 700–718. doi:10.1086/307233
Lazarian, A., Yuen, K. H., and Pogosyan, D. (2022). Magnetic field strength from turbulence theory (I): Using differential measure approach (DMA). arXiv e-prints, arXiv:2204.09731.
Lazarian, A., and Yuen, K. H. (2018). Tracing magnetic fields with spectroscopic channel maps. Astrophys. J. 853, 96. doi:10.3847/1538-4357/aaa241
Lee, D., Berthoud, M., Chen, C.-Y., Cox, E. G., Davidson, J. A., Encalada, F. J., et al. (2021). HAWC+/SOFIA polarimetry in L1688: Relative orientation of magnetic field and elongated cloud structure. Astrophys. J. 918, 39. doi:10.3847/1538-4357/ac0cf2
Li, H.-b., Fang, M., Henning, T., and Kainulainen, J. (2013). The link between magnetic fields and filamentary clouds: Bimodal cloud orientations in the Gould Belt. Mon. Not. R. Astron. Soc. 436, 3707–3719. doi:10.1093/mnras/stt1849
Li, H.-b., and Houde, M. (2008). Probing the turbulence dissipation range and magnetic field strengths in molecular clouds. Astrophys. J. 677, 1151–1156. doi:10.1086/529581
Li, H.-B., Jiang, H., Fan, X., Gu, Q., and Zhang, Y. (2017). The link between magnetic field orientations and star formation rates. Nat. Astron. 1, 0158. doi:10.1038/s41550-017-0158
Li, H.-B. (2021). Magnetic fields in molecular clouds—observation and interpretation. Galaxies 9, 41. doi:10.3390/galaxies9020041
Li, H.-B., Yuen, K. H., Otto, F., Leung, P. K., Sridharan, T. K., Zhang, Q., et al. (2015). Self-similar fragmentation regulated by magnetic fields in a region forming massive stars. Nature 520, 518–521. doi:10.1038/nature14291
Li, P. S., Lopez-Rodriguez, E., Ajeddig, H., André, P., McKee, C. F., Rho, J., et al. (2022). Mapping the magnetic field in the Taurus/B211 filamentary cloud with SOFIA HAWC + and comparing with simulation. Mon. Not. R. Astron. Soc. 510, 6085–6109. doi:10.1093/mnras/stab3448
Liu, J., Qiu, K., Berry, D., Di Francesco, J., Bastien, P., Koch, P. M., et al. (2019). The JCMT BISTRO survey: The magnetic field in the starless core ρ Ophiuchus C. Astrophys. J. 877, 43. doi:10.3847/1538-4357/ab0958
Liu, J., Qiu, K., and Zhang, Q. (2022). Magnetic fields in star formation: A complete compilation of all the DCF estimations. Astrophys. J. 925, 30. doi:10.3847/1538-4357/ac3911
Liu, J., Zhang, Q., Commerçon, B., Valdivia, V., Maury, A., and Qiu, K. (2021). Calibrating the davis-chandrasekhar-fermi method with numerical simulations: Uncertainties in estimating the magnetic field strength from statistics of field orientations. Astrophys. J. 919, 79. doi:10.3847/1538-4357/ac0cec
Liu, J., Zhang, Q., Qiu, K., Liu, H. B., Pillai, T., Girart, J. M., et al. (2020). Magnetic fields in the early stages of massive star formation as revealed by ALMA. Astrophys. J. 895, 142. doi:10.3847/1538-4357/ab9087
Mac Low, M.-M., and Klessen, R. S. (2004). Control of star formation by supersonic turbulence. Rev. Mod. Phys. 76, 125–194. doi:10.1103/RevModPhys.76.125
Malinen, J., Montier, L., Montillaud, J., Juvela, M., Ristorcelli, I., Clark, S. E., et al. (2016). Matching dust emission structures and magnetic field in high-latitude cloud L1642: Comparing Herschel and Planck maps. Mon. Not. R. Astron. Soc. 460, 1934–1945. doi:10.1093/mnras/stw1061
Mestel, L. (1966). The magnetic field of a contracting gas cloud. I, Strict flux-freezing. Mon. Not. R. Astron. Soc. 133, 265–284. doi:10.1093/mnras/133.2.265
Mouschovias, T. C., and Ciolek, G. E. (1999). “Magnetic fields and star formation: A theory reaching adulthood,” in The origin of stars and planetary systems. Editors C. J. Lada, and N. D. Kylafis (Dordrecht: Kluwer), 305. vol. 540 of NATO Advanced Study Institute (ASI) Series C.
Mouschovias, T. C. (1976a). Nonhomologous contraction and equilibria of self-gravitating, magnetic interstellar clouds embedded in an intercloud medium: Star formation. I. Formulation of the problem and method of solution. Astrophys. J. 206, 753–767. doi:10.1086/154436
Mouschovias, T. C. (1976b). Nonhomologous contraction and equilibria of self-gravitating, magnetic interstellar clouds embedded in an intercloud medium: Star formation. II. Results. Astrophys. J. 207, 141–158. doi:10.1086/154478
Mouschovias, T. C., and Spitzer, J., L. (1976). Note on the collapse of magnetic interstellar clouds. Astrophys. J. 210, 326. doi:10.1086/154835
Mouschovias, T. C., Tassis, K., and Kunz, M. W. (2006). Observational constraints on the ages of molecular clouds and the star formation timescale: Ambipolar-Diffusion-controlled or turbulence-induced star formation? Astrophys. J. 646, 1043–1049. doi:10.1086/500125
Myers, P. C., Basu, S., and Auddy, S. (2018). Magnetic field structure in spheroidal star-forming clouds. Astrophys. J. 868, 51. doi:10.3847/1538-4357/aae695
Myers, P. C., and Basu, S. (2021). Magnetic properties of star-forming dense cores. Astrophys. J. 917, 35. doi:10.3847/1538-4357/abf4c8
Myers, P. C., and Goodman, A. A. (1991). On the dispersion in direction of interstellar polarization. Astrophys. J. 373, 509. doi:10.1086/170070
Nakano, T., and Nakamura, T. (1978). Gravitational instability of magnetized gaseous disks 6. PASJ 30, 671–680.
Ostriker, E. C., Stone, J. M., and Gammie, C. F. (2001). Density, velocity, and magnetic field structure in turbulent molecular cloud models. Astrophys. J. 546, 980–1005. doi:10.1086/318290
Otto, F., Ji, W., and Li, H.-b. (2017). Velocity anisotropy in self-gravitating molecular clouds. I. Simulation. Astrophys. J. 836, 95. doi:10.3847/1538-4357/836/1/95
Padoan, P., Goodman, A., Draine, B. T., Juvela, M., Nordlund, Å., and Rögnvaldsson, Ö. E. (2001). Theoretical models of polarized dust emission from protostellar cores. Astrophys. J. 559, 1005–1018. doi:10.1086/322504
Padoan, P., Juvela, M., Kritsuk, A., and Norman, M. L. (2009). The power spectrum of turbulence in NGC 1333: Outflows or large-scale driving? Astrophys. J. 707, L153–L157. doi:10.1088/0004-637X/707/2/L153
Palau, A., Zhang, Q., Girart, J. M., Liu, J., Rao, R., Koch, P. M., et al. (2021). Does the magnetic field suppress fragmentation in massive dense cores? Astrophys. J. 912, 159. doi:10.3847/1538-4357/abee1e
Pattle, K., and Fissel, L. (2019). Submillimeter and far-infrared polarimetric observations of magnetic fields in star-forming regions. Front. Astron. Space Sci. 6, 15. doi:10.3389/fspas.2019.00015
Pattle, K., Fissel, L., Tahani, M., Liu, T., and Ntormousi, E. (2022). Magnetic fields in Star formation: From clouds to cores. arXiv e-prints, arXiv:2203.11179.
Pattle, K., Ward-Thompson, D., Berry, D., Hatchell, J., Chen, H.-R., Pon, A., et al. (2017). The JCMT bistro survey: The magnetic field strength in the orion A filament. Astrophys. J. 846, 122. doi:10.3847/1538-4357/aa80e5
Pillai, T., Kauffmann, J., Tan, J. C., Goldsmith, P. F., Carey, S. J., and Menten, K. M. (2015). Magnetic fields in high-mass infrared dark clouds. Astrophys. J. 799, 74. doi:10.1088/0004-637X/799/1/74
Planck Collaboration, Adam, R., Ade, P. A. R., Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., et al. (2016a). Planck intermediate results. XXXII. The relative orientation between the magnetic field and structures traced by interstellar dust. Astron. Astrophys. 586, A135. doi:10.1051/0004-6361/201425044
Planck Collaboration, Ade, P. A. R., Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., Ashdown, M., et al. (2016b). Planck intermediate results. XXXV. Probing the role of the magnetic field in the formation of structure in molecular clouds. Astron. Astrophys. 586, A138. doi:10.1051/0004-6361/201525896
Qiu, K., Zhang, Q., Menten, K. M., Liu, H. B., Tang, Y.-W., and Girart, J. M. (2014). Submillimeter array observations of magnetic fields in G240.31+0.07: An hourglass in a massive cluster-forming core. Astrophys. J. 794, L18. doi:10.1088/2041-8205/794/1/L18
Rao, R., Girart, J. M., Marrone, D. P., Lai, S.-P., and Schnee, S. (2009). Iras 16293: A “magnetic” tale of two cores. Astrophys. J. 707, 921–935. doi:10.1088/0004-637X/707/2/921
Seifried, D., Walch, S., Weis, M., Reissl, S., Soler, J. D., Klessen, R. S., et al. (2020). From parallel to perpendicular - on the orientation of magnetic fields in molecular clouds. Mon. Not. R. Astron. Soc. 497, 4196–4212. doi:10.1093/mnras/staa2231
Shebalin, J. V., Matthaeus, W. H., and Montgomery, D. (1983). Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 29, 525–547. doi:10.1017/S0022377800000933
Shu, F. H., Adams, F. C., and Lizano, S. (1987). star formation in molecular clouds: Observation and theory. Annu. Rev. Astron. Astrophys. 25, 23–81. doi:10.1146/annurev.aa.25.090187.000323
Shu, F. H., Allen, A., Shang, H., Ostriker, E. C., and Li, Z.-Y. (1999). “Low-mass star formation: Theory,” in The origin of stars and planetary systems. Editors C. J. Lada, and N. D. Kylafis (Dordrecht: Kluwer), 193. vol. 540 of NATO Advanced Study Institute (ASI) Series C.
Skalidis, R., Sternberg, J., Beattie, J. R., Pavlidou, V., and Tassis, K. (2021). Why take the square root? An assessment of interstellar magnetic field strength estimation methods. Astron. Astrophys. 656, A118. doi:10.1051/0004-6361/202142045
Skalidis, R., and Tassis, K. (2021). High-accuracy estimation of magnetic field strength in the interstellar medium from dust polarization. Astron. Astrophys. 647, A186. doi:10.1051/0004-6361/202039779
Soler, J. D., Ade, P. A. R., Angilè, F. E., Ashton, P., Benton, S. J., Devlin, M. J., et al. (2017). The relation between the column density structures and the magnetic field orientation in the Vela C molecular complex. Astron. Astrophys. 603, A64. doi:10.1051/0004-6361/201730608
Soler, J. D., Alves, F., Boulanger, F., Bracco, A., Falgarone, E., Franco, G. A. P., et al. (2016). Magnetic field morphology in nearby molecular clouds as revealed by starlight and submillimetre polarization. Astron. Astrophys. 596, A93. doi:10.1051/0004-6361/201628996
Soler, J. D., Hennebelle, P., Martin, P. G., Miville-Deschênes, M. A., Netterfield, C. B., and Fissel, L. M. (2013). An imprint of molecular cloud magnetization in the morphology of the dust polarized emission. Astrophys. J. 774, 128. doi:10.1088/0004-637X/774/2/128
Soler, J. D. (2019). Using Herschel and Planck observations to delineate the role of magnetic fields in molecular cloud structure. Astron. Astrophys. 629, A96. doi:10.1051/0004-6361/201935779
Stephens, I. W., Looney, L. W., Kwon, W., Hull, C. L. H., Plambeck, R. L., Crutcher, R. M., et al. (2013). The magnetic field morphology of the class 0 protostar L1157-mm. Astrophys. J. 769, L15. doi:10.1088/2041-8205/769/1/L15
Storm, S., Mundy, L. G., Fernández-López, M., Lee, K. I., Looney, L. W., Teuben, P., et al. (2014). CARMA large area star formation survey: Project overview with analysis of dense gas structure and kinematics in barnard 1. Astrophys. J. 794, 165. doi:10.1088/0004-637X/794/2/165
Strittmatter, P. A. (1966). Gravitational collapse in the presence of a magnetic field. Mon. Not. R. Astron. Soc. 132, 359–378. doi:10.1093/mnras/132.2.359
Tahani, M., Plume, R., Brown, J. C., and Kainulainen, J. (2018). Helical magnetic fields in molecular clouds? A new method to determine the line-of-sight magnetic field structure in molecular clouds. Astron. Astrophys. 614, A100. doi:10.1051/0004-6361/201732219
Tahani, M., Plume, R., Brown, J. C., Soler, J. D., and Kainulainen, J. (2019). Could bow-shaped magnetic morphologies surround filamentary molecular clouds? The 3D magnetic field structure of Orion-A. Astron. Astrophys. 632, A68. doi:10.1051/0004-6361/201936280
Tan, J. C., Beltrán, M. T., Caselli, P., Fontani, F., Fuente, A., Krumholz, M. R., et al. (2014). “Massive star formation,” in Protostars and planets VI. Editors H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning. (Tucson, AZ: University Arizona Press), 149. doi:10.2458/azu\_uapress\_9780816531240-ch007
Tang, K. S., Li, H.-B., and Lee, W.-K. (2018). Probing the turbulence dissipation range and magnetic field strengths in molecular clouds. II. Directly probing the ion-neutral decoupling scale. Astrophys. J. 862, 42. doi:10.3847/1538-4357/aacb82
Tang, Y.-W., Ho, P. T. P., Koch, P. M., Guilloteau, S., and Dutrey, A. (2013). Dust continuum and polarization from envelope to cores in star formation: A case study in the W51 north region. Astrophys. J. 763, 135. doi:10.1088/0004-637X/763/2/135
Tang, Y.-W., Koch, P. M., Peretto, N., Novak, G., Duarte-Cabral, A., Chapman, N. L., et al. (2019). Gravity, magnetic field, and turbulence: Relative importance and impact on fragmentation in the infrared dark cloud G34.43+00.24. Astrophys. J. 878, 10. doi:10.3847/1538-4357/ab1484
Tritsis, A., Panopoulou, G. V., Mouschovias, T. C., Tassis, K., and Pavlidou, V. (2015). Magnetic field-gas density relation and observational implications revisited. Mon. Not. R. Astron. Soc. 451, 4384–4396. doi:10.1093/mnras/stv1133
van Dishoeck, E. F., Blake, G. A., Draine, B. T., and Lunine, J. I. (1993). “The chemical evolution of protostellar and protoplanetary matter,” in Protostars and planets III. Editors E. H. Levy, and J. I. Lunine (Tucson, AZ: University Arizona Press), 163.
Yuen, K. H., Ho, K. W., Law, C. Y., Chen, A., and Lazarian, A. (2022). Turbulent universal galactic Kolmogorov velocity cascade over 6 decades. arXiv e-prints, arXiv:2204.13760.
Yuen, K. H., Ho, K. W., and Lazarian, A. (2021). Technique for separating velocity and density contributions in spectroscopic data and its application to studying turbulence and magnetic fields. Astrophys. J. 910, 161. doi:10.3847/1538-4357/abe4d4
Yuen, K. H., and Lazarian, A. (2020). Curvature of magnetic field lines in compressible magnetized turbulence: Statistics, magnetization predictions, gradient curvature, modes, and self-gravitating media. Astrophys. J. 898, 66. doi:10.3847/1538-4357/ab9360
Zweibel, E. G. (1990). Magnetic field line tangling and polarization measurements in clumpy molecular gas. Astrophys. J. 362, 545. doi:10.1086/169291
Keywords: star formation, magnetic fields, polarization, molecular clouds, interstellar medium
Citation: Liu J, Zhang Q and Qiu K (2022) Magnetic field properties in star formation: A review of their analysis methods and interpretation. Front. Astron. Space Sci. 9:943556. doi: 10.3389/fspas.2022.943556
Received: 13 May 2022; Accepted: 12 August 2022;
Published: 21 September 2022.
Edited by:
Martin Houde, Western University, CanadaReviewed by:
Ka Ho Yuen, Los Alamos National Laboratory (DOE), United StatesCopyright © 2022 Liu, Zhang and Qiu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Junhao Liu, ai5saXVAZWFvYnNlcnZhdG9yeS5vcmc=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.