
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Astron. Space Sci. , 06 July 2022
Sec. Stellar and Solar Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.931963
This article is part of the Research Topic Challenges of Asteroseismology in the Era of Space Missions View all 12 articles
Asteroseismology, that is, the use of the frequency content of a time series caused by variations in brightness or radial velocity of a stellar object, is based on the hypothesis that such a series is harmonic and therefore can be described by a sum of sines and cosines. If this were not the case (e.g., the oscillations of an ellipsoid of revolution) it cannot be guaranteed that the Discrete Fourier transform is the least squares approximation to the time series. This report studies the effect of extending the Fourier kernel to a particular quaternion and exploring the impact when it is applied to the best time series that we have (GOLF/SoHO) from the closest star, our Sun. The results are consistent with a notable improvement in the signal-to-noise ratio in the low frequency range. This opens the possibility of detecting the elusive g modes of the Sun in future works.
The solar g modes are still a puzzling problem in Asteroseismology (Christensen-Dalsgaard, 2021). After decades of active search, no definitive direct evidence exists of the detection of the gravity driven solar pulsations although they have been indirectly inferred from their period separation in the Sun (García et al., 2007). Also, in red giant stars some authors (Beck et al., 2011; Mosser et al., 2011) could observe the direct interaction between g-modes and p-modes in the form of mixed modes. Fossat et al. (2017) and Fossat and Schmider (2018) proposed that some hints of the solar g modes appear in the splitting of the pressure oscillations due to the rotation of the solar core. However, the uncertainty about the internal rotational velocity of the Sun, hampers the significance of this indirect findings.
In this report, we propose a modification of the usual Fourier transform analysis that takes advantage of a quaternion formulation. This function is chosen intending to: 1) recovering the usual Fourier kernel at solar frequencies (i.e., the 5-min p-modes); 2) improving the signal-to-noise ratio (SNR) all along the frequency spectrum.
As we discuss in Section 2, the introduction of a quaternion in the kernel of the transform allow us to perform a rotation in the complex plane
If ν, t are the frequency and time parameters of a certain frequency domain transform, we call θ = νt the linear phase of the transform. Complex transforms such as Fourier have just one phase but if we extend to a quaternion domain we can introduce a new phase
Expanding the second exponential in trigonometric form:
This new kernel has two complex components in
Note also that Eq. 5 can be expanded in the quaternion components:
The last equation can be represented in complex matrix representation
defining a operator
which is unitary, since.
therefore,
We observe that Eq. 8 may be interpreted as a rotation in
In previous equations we made co(θ), si(θ) to depend only on θ. Now, the heuristic definition of the new kernel is complete introducing
This definition is motivated by the limitations of the classical analysis of stellar light curves, that is, high frequencies can be detected in the solar power spectrum but low frequencies cannot. If we left θ instead of
We could have also defined co(θ), si(θ) through the mapping:
This equation, which derives from the definition of the inverse hyperbolic sine function, will help us to interpret physically the new proposed formulation.
After some mathematical derivations, we can also express co(θ) and si(θ) as two functions depending on the variable f instead of θ and
therefore.
being these two equations complex numbers instead of quaternions.
We introduce these functions since they allow us to extend the original Fourier transform into quaternions from a sine-cosine decomposition. In this sense, we can recover the tangent function as the ratio si(θ)/co(θ) for every value of θ as can be easily see from Eqs 3,4. Finally, these functions form the basis of a new transform that we can apply to any time series.
This modified kernel allow us to define a new discrete transform
Here νj stands for the discretization of the frequencies ν
where the angular phase Φij is
As usual we take the modulus of the quaternion transform as defined in Eq. 17 to obtain a periodogram that estimates the frequency content of the time series.
In the next section we discuss the goodness of our approach with respect to the classical discrete Fourier transform for the case of the solar radial velocities observed by GOLF/SoHO instrument. We will discuss first the underlying statistics of the new transform.
We devote this sub-section to the study of the underlying statistics that the modified DFT produces. We will follow a similar procedure as Scargle (1982) for the a standard DFT where the author proved that the Lomb-Scargle periodogram has a chi-square distribution with two degrees of freedom.
Taking into account the expansion in quaternion components in Eq. 6 the periodogram corresponding to the modified DFT shown in Eq. 17 is:
Now with the definitions of co(θ) and si(θ) in Eqs 3, 4,
Finally, introducing the heuristic formulation of
In the plots, however, we will use the amplitude which is just the square root of Pmod (ωj). Consider now the case where x (ti) is an independently and normally distributed noise with zero mean and constant variance
which are the content of each parenthesis in Eq. 20. Now our modified periodogram can be expressed with these functions as:
where CC, CS, SC and SS are linear combinations of independent normal random variables since in Eq. 21 the sine and cosine functions act as constant coefficients. Since a linear combination of normally distributed random variables is also normal the mean value will be zero for each of these functions. The corresponding variances are:
where we have used the independence of xi and xk so the cross-terms vanish.
Now, if the 4 variables have equal variances the distribution of Pmod (ωj) is a chi-square with 4 degrees of freedom (Papoulis, 1965). If the variances are different we cannot use a chi-square distribution but we have to use the Bessel function instead.
To summarise, we have included in this research report a brief development of the underlying statistics of our heuristic transform since it will have important implications on the analysis of the power spectrum for the detection of pulsation frequencies. In the application we present in the next section we assume that the distribution of Pmod (ωj) is a chi-square with 4 degrees of freedom. A complete statistical treatment is out of the scope of this note.
We performed our new analysis on a time series of radial velocities, corresponding to 16 days (with 20 s of sampling time) from the GOLF instrument aboard the SoHO satellite (Gabriel et al., 1995). Although there are much longer observations from SoHO/GOLF, we limited the total duration of our dataset to 16 days as a trade-off between avoiding the influence of rotation and preserving frequency resolution. Following the principles of Open Science we have created a repository1 with the code and inputs necessary to reproduce the results.
Figure 1 shows the typical solar 5-min p mode spectrum obtained through GOLF/SoHO radial velocity observations. The region from 2 to 4 mHz is almost identical for both the classical and modified DFT. We have verified that the new transform is as computationally expensive in time as the classical DFT.
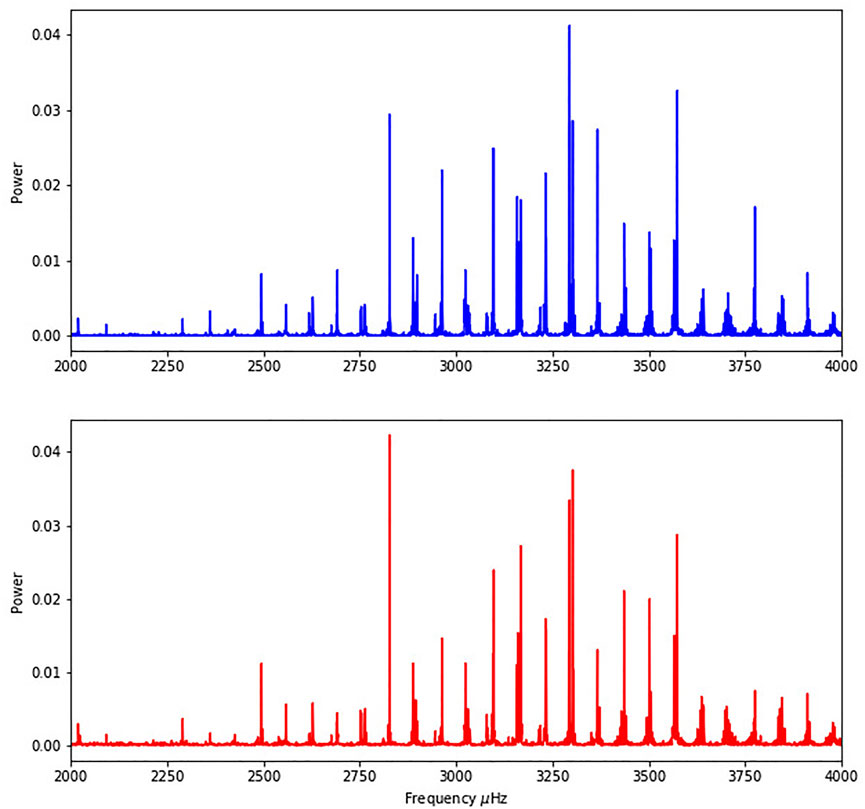
FIGURE 1. Modified (red) and Classical (blue) Fourier Transforms of the SoHO data obtained during 16 days, at the region between 2,000 and 4,000 μHz. Note that the main differences between both transforms in this range is the higher amplitude in the case of the quaternion Fourier transform, compatible with a better signal-to-noise ratio.
Figure 2 shows low degree p-modes with a clear improvement using our heuristic modification of Fourier transform. The identification of solar dipole p-modes could be used to study the rotational splitting and constraint the rotational profile in the core Chaplin et al. (2001). In this work we are interested just in introducing the quaternion transform and showing first results.
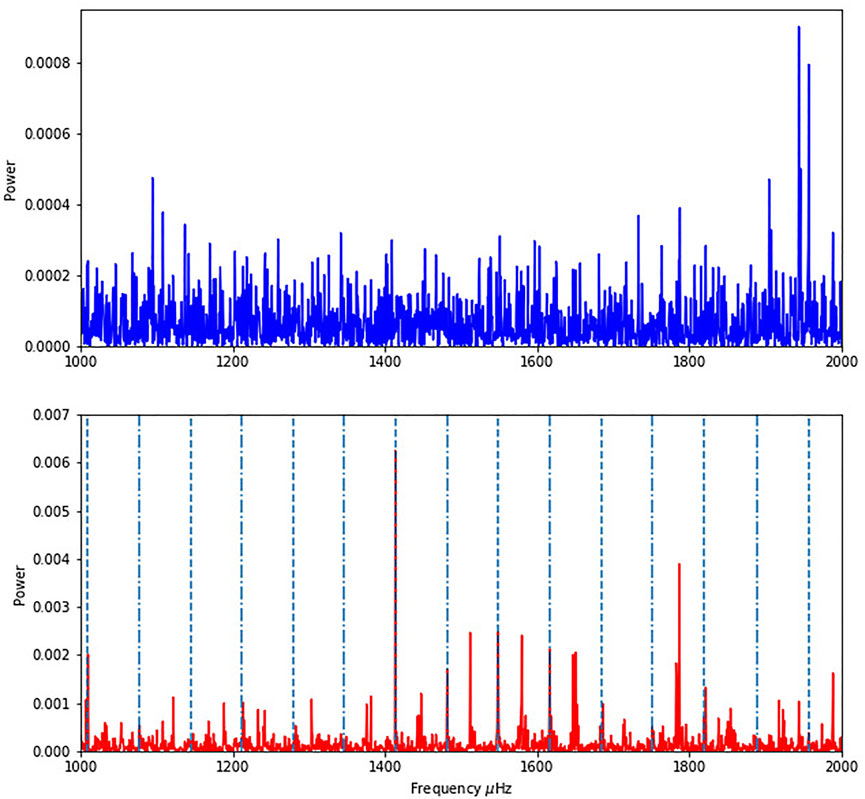
FIGURE 2. Modified (red) and Classical (blue) Fourier Transforms of the SoHO data obtained during 16 days, at the region between 1,000 and 2,000 μHz. In the red plot we include the l = 0 (dashed) and l = 1 (point-dashed) modes we have identified from the analysis of the new quaternion transform. The Gaussian envelope of the structure visible in the red plot could be a hint of the presence of not identified modes in the common Fourier analysis but further analysis is required to confirm this.
In Figure 3 the entire GOLF spectrum is shown in loglog scale to highlight the background. The signature of granulation appears to be similar in both cases.
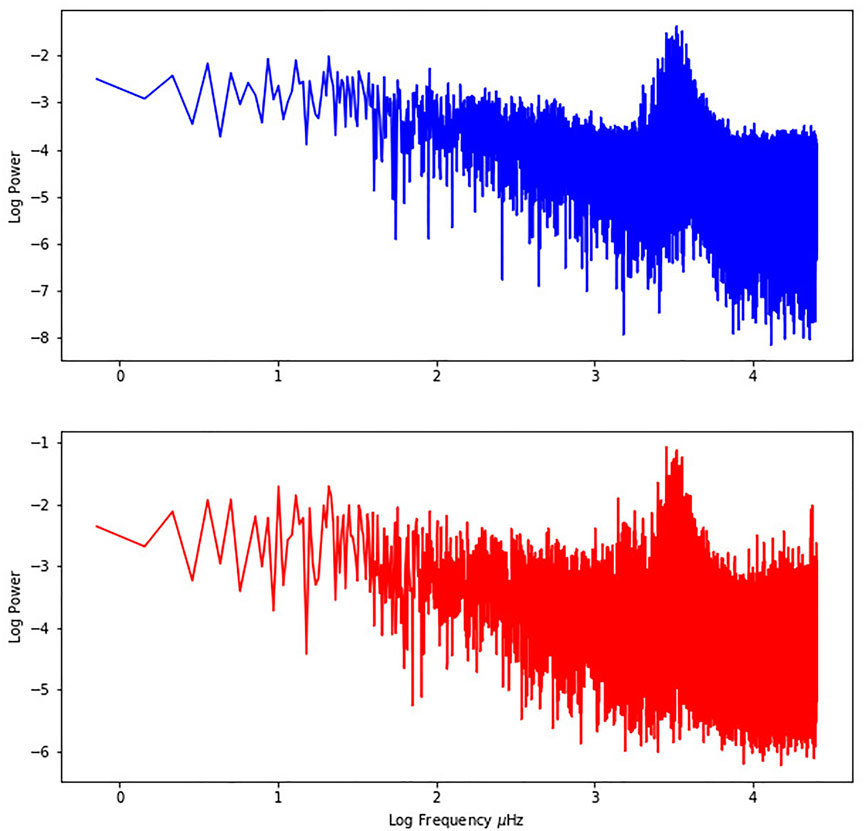
FIGURE 3. Modified (red) and Classical (blue) Fourier Transforms of the SoHO data obtained during 16 days, from 0 to the Nyquist frequency (i.e., 25 mHz) in loglog scale.
The total power in the spectrum obtained through the quaternion transform is higher than in a DFT since the higher frequency harmonics are preserved and the lower frequency harmonics are enhanced. While this might contradict Plancherel’s theorem, it is inherent to the innovative idea of this work since we are assuming that the observed signal is in some way filtered out and that we can invert the filtering with the quaternion transform. The prove for the conservation of energy must obtained through theoretical models that provide proper constraints to the pulsation energy content, but this is out of the scope of this manuscript.
Now we focus on detection and identification of pulsation modes using the frequency separation in the asymptotic regime taking into account the large separation as defined in Tassoul (1980).
We are going to calculate the successive frequencies for l = 0 and l = 1 for asymptotic solar p modes from the estimation of large separation in this way:
assuming D0 = 0, ϵ = 1/2 and a constant large frequency separation Δν0 = 134.699 μHz.
In order to compare with the theoretically calculated frequencies we calculate the modified DFT in a box of ±10 μHz around the expected frequencies from the asymptotic regime. A time span of 44 days is used for this purpose to increase the frequency resolution. Frequencies are estimated in the power spectrum of the modified DFT in a first approximation as the local maxima found in the intervals explored. The formula adopted for the asymptotic regime is given in Tassoul (1980, see Eq.65).
Table 1 shows frequencies calculated from Eq. 23, assuming the aforementioned large separation value, in the asymptotic regime of p modes, and the frequencies extracted with the modified DFT. A good agreement between both frequency lists is clear.
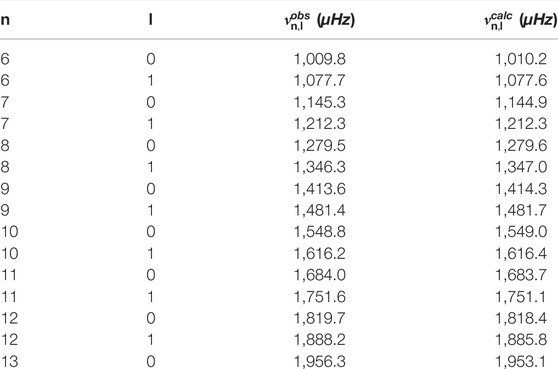
TABLE 1. Asymptotic behaviour of solar p modes detected with the new transform proposed in this paper. n and l stands for the radial order and angular degrees of the mode respectively. We show the frequencies detected with the quaternion Fourier transform,
In summary, we have introduced in this brief research report a modified Fourier transform which is similar to the classical DFT for high frequencies and consistent with the theoretically predicted large separation frequency for low degree and high order p modes. This shows the consistency of the new transform for the case of the Sun. We could identify l = 0 and l = 1 modes in the 1,000–2,000 μHz region and the identification of other modes require further studies. The analysis here performed is an incomplete and rough approximation to the solution but the focus of this brief research report is on the introduction of the new quaternion transform.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://www.ias.u-psud.fr/golf/templates/access.html.
RG proposed the original idea and performed most of the calculations. AA did the plots, contributed to the writing of the manuscript, and mathematical developments. JP-G contributed to mathematical discussion and writing of the manuscript. JG-T introduced the mathematical framework for the second section and contributed to the mathematical rigor to the manuscript. JRR has contributed to the work creating tools for the reproducibility and replicability of the work published in this journal. He has also connected the data and code repository to the Open Science ESCAPE platform. All authors contributed to the revision of the manuscript.
RG, AA, JP-G and JRR acknowledge financial support from the State Agency for Research of the Spanish MCIU through PID2019-107061GB‐C63 from the `Programas Estatales de Generaci\'on de Conocimiento y Fortalecimiento Cient\'ifico y Tecnol\'ogico del Sistema de I+D+i y de I+D+i Orientada a los Retos de la Sociedad', and from the State Agency for Research through the "Center of Excellence Severo Ochoa" award to the Instituto de Astrofísica de Andalucía (SEV‐2017‐0709), all from the Spanish Ministry of Science, Innovation and Universities (MCIU). JG‐T is supported by grant PID2019‐110525GB‐100 from the State Agency for Research and FEDER.\par
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
RG and JP-G acknowledge Jeff Scargle and Lourdes Verdes Montenegro for fruitful discussions.
1https://github.com/AsteroSeismologyIAA/QuaternionTransform
Beck, P. G., Bedding, T. R., Mosser, B., Stello, D., Garcia, R. A., Kallinger, T., et al. (2011). Kepler Detected Gravity-Mode Period Spacings in a Red Giant Star. Science 332, 205. doi:10.1126/science.1201939
Chaplin, W. J., Elsworth, Y., Isaak, G. R., Marchenkov, K. I., Miller, B. A., and New, R. (2001). Rigid Rotation of the Solar Core? on the Reliable Extraction of Low- Rotational P-Mode Splittings from Full-Disc Observations of the Sun. Mon. Notices R. Astronomical Soc. 327, 1127–1136. doi:10.1046/j.1365-8711.2001.04805.x
Christensen-Dalsgaard, J. (2021). Solar Structure and Evolution. Living Rev. Sol. Phys. 18, 2. doi:10.1007/s41116-020-00028-3
Domingo, V., Fleck, B., and Poland, A. I. (1995). The SOHO Mission: an Overview. Sol. Phys. 162, 1–37. doi:10.1007/BF00733425
Fossat, E., Boumier, P., Corbard, T., Provost, J., Salabert, D., Schmider, F. X., et al. (2017). Asymptotic G Modes: Evidence for a Rapid Rotation of the Solar Core. Astronomy Astrophysics 604, A40. doi:10.1051/0004-6361/201730460
Fossat, E., and Schmider, F. X. (2018). More about Solar G Modes. Astronomy Astrophysics 612, L1. doi:10.1051/0004-6361/201832626
Gabriel, A. H., Charra, J., Grec, G., Robillot, J.-M., Cortés, T. R., Turck-Chièze, S., et al. (1997). Performance and Early Results from the GOLF Instrument Flown on the SOHO Mission. Sol. Phys. 175, 207–226. doi:10.1023/A:100491140828510.1007/978-94-011-5236-5_12
Gabriel, A. H., Grec, G., Charra, J., Robillot, J.-M., Roca Cortés, T., Turck-Chièze, S., et al. (1995). Global Oscillations at Low Frequency from the SOHO Mission (GOLF). Adv. Space Res. 162, 61–99. doi:10.1007/978-94-009-0191-9_3
García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., Ballot, J., Pallé, P. L., Eff-Darwich, A., et al. (2007). Tracking Solar Gravity Modes: The Dynamics of the Solar Core. Science 316, 1591–1593. doi:10.1126/science.1140598
Mosser, B., Barban, C., Montalbán, J., Beck, P. G., Miglio, A., Belkacem, K., et al. (2011). Mixed Modes in Red-Giant Stars Observed with CoRoT. Astronomy Astrophysics 532, A86. doi:10.1051/0004-6361/201116825
Papoulis, A. (1965). Probability, Random Variables and Stochastic Processes. Tata McGraw-Hill Education.
Scargle, J. D. (1982). Studies in Astronomical Time Series Analysis. II - Statistical Aspects of Spectral Analysis of Unevenly Spaced Data. Astrophysical J. 263, 835–853. doi:10.1086/160554
Keywords: stellar pulsations, data analysis, solar physics, g-modes, quaternion
Citation: Garrido R, Ayala A, Pascual-Granado J, Gómez-Torrecillas J and Rodón JR (2022) Quaternionic Transform: A new Light on the Solar Power Spectrum. Front. Astron. Space Sci. 9:931963. doi: 10.3389/fspas.2022.931963
Received: 29 April 2022; Accepted: 07 June 2022;
Published: 06 July 2022.
Edited by:
Mario J. P. F. G. Monteiro, University of Porto, PortugalReviewed by:
Enrico Maria Nicola Corsaro, Osservatorio Astrofisico di Catania (INAF), ItalyCopyright © 2022 Garrido, Ayala, Pascual-Granado, Gómez-Torrecillas and Rodón. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rafael Garrido, Z2Fycmlkb0BpYWEuZXM=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.