- 1Space Science Institute, Boulder, CO, United States
- 2Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, Los Angeles, CA, United States
1) Since the outer electron radiation belt is lost on occasion, the radiation belt needs seed electrons to rebuild. 2) The clear candidate for that seed population is energetic substorm-injected electrons in the dipolar magnetosphere. 3) The energetic substorm-injected electrons in the dipole come from the suprathermal electron population in the magnetotail plasma sheet, delivered by substorms. Scenario (1)–3) begs the question: Where do these magnetotail suprathermal electrons come from? We are hypothesizing that one source (perhaps the dominant source) is the energetic field-aligned electron strahl in the solar wind, which are electrons fresh from the solar corona.
Overview
In this Hypothesis paper we will explore the possibility that strahl electrons in the solar wind at Earth follow the pathway into the magnetosphere that is: solar wind → lobe → polar rain → plasma sheet → substorm-injected electrons → electron radiation belt.
It is a reasonable hypothesis that the energetic electron strahl of the solar wind contributes as a source population for the Earth’s outer electron radiation belt. 1) The strahl is seen on lobe field lines and it reaches the polar-cap atmosphere to create the polar-rain aurora (Fairfield and Scudder, 1985). The intensity of the polar-rain aurora is modulated by the intensity of the strahl in the solar wind (Hershbach and Zhang, 2021). 2) Lobe field lines are captured into the magnetotail plasma sheet via the action of the distant reconnection site and these field lines have energetic strahl electrons on them (Zhang and Wing, 2015). 3) The magnetotail plasma sheet is observed to have a suprathermal electron population (Christon et al., 1989; Runov et al., 2018). 4) The suprathermal electron population of the magnetotail plasma sheet becomes the substorm-injected electron population in the dipolar magnetosphere as substorms transport and adiabatically energize this population (Birn et al., 1998, 2014). 5) The substorm-injected electrons are widely considered to be the seed population for the electron radiation belt (Jaynes et al., 2015; Boyd et al., 2016; Borovsky and Valdivia, 2018).
This hypothesis has the potential to uncover another piece of the M-I-T system and how it is driven by the solar wind, and in fact by the solar corona. This hypothesis, if accurate, could have a transformative impact on our system-science understanding of the solar-wind-driven magnetosphere of the Earth (Borovsky and Valdivia, 2018) and could contribute to electron systems science (Vershcaren et al., 2021). This could lead to an increased understanding of the controlling factors for space weather at Earth and an improved ability to predict the evolution of the electron radiation belt.
The Electron Strahl in the Solar Wind
The solar wind has three electron populations (Boldyrev et al., 2019; Bercic et al., 2020): the (cool) core, the hot isotropic halo, and the energetic field-aligned strahl. The strahl is a field-aligned distribution of electrons with a broad range of energies from 100s of eV to a few-keV. The strahl is the hot-electron population of the solar corona escaping along magnetic-field lines out into the heliosphere. The strahl is sometimes referred to as the solar-wind heat flux (e.g., Gary et al., 1975). Strahl electrons move rapidly along the field: a 500-eV strahl electron has a field-aligned velocity of 1.3 × 109 cm/s, which is 2 RE/s. At 1 AU the observed strahl electrons left the Sun about 3 h ago, whereas the solar-wind plasma is about 100 h old. At 1 AU the core represents about 90% of the electron density, the halo about 7%, and the strahl on average about 3% (Stverak et al., 2009), although the strahl fractional density can vary greatly with time. At 1 AU the field-aligned strahl is several degrees wide (Fitzenreiter et al., 1998; de Koning et al., 2007).
The spaghetti magnetic-flux-tube structure of the solar wind (Borovsky, 2008, 2010) forms a ductwork for the outward moving strahl (Borovsky et al., 2021). As the various flux tubes pass the Earth the intensity of the strahl can change from tube to tube (Gosling et al., 2004; Borovsky, 2020a, 2021). This results in intensity changes on 10-min timescales at Earth as the various solar-wind magnetic flux tubes advect past the Earth (Borovsky, 2020b). Additionally, the strahl intensity varies systematically on a few-day timescale as the different types of solar-wind plasma pass the Earth (Borovsky, 2018). An hourly-averaged 272-eV strahl-intensity index I272 at Earth has been created (Borovsky, 2017). I272 is log10 (f (272)) where f (272) is the phase-space density of the strahl at 272 eV: I272 is a proxy for the flux of the strahl, but future studies should use the total integral of the strahl to properly calculate its flux. There is a 27-day periodicity to the intensity of the strahl at Earth; this can be seen in the autocorrelation function of I272 plotted in Figure 1. The intensity of the electron strahl can be used as an indicator of the magnetic connection from the Earth to the Sun (Borovsky, 2021). The strahl is most intense in corotating interaction regions and the beginnings of high-speed streams (Borovsky and Denton, 2016), which at Earth are the times when the electron radiation belt becomes most intense (Borovsky and Denton, 2010).
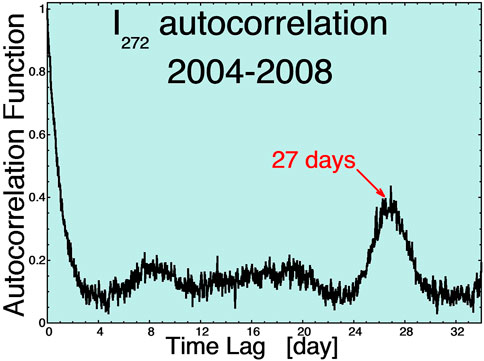
FIGURE 1. The autocorrelation function of the hourly strahl-intensity index I272. Note the autocorrelation time (1/e method) is about 26 h and note the 27-day recurrence of the correlation indicating a 27-day periodicity in the I272 time series.
The Strahl in the Lobes
The electron strahl is seen in the magnetosheath, both in the near-Earth magnetosheath (Terasawa et al., 2000; Kasaba et al., 2000) and in the distant-tail magnetosheath (Aaker et al., 1986). The strahl electrons are commonly seen throughout the lobes at energies of 100s of eV to a few keV (e.g., Fairfield and Scudder, 1985; Aaker et al., 1986).
Figure 2 is a noon-midnight meridional cut from a global MHD simulation of the solar-wind-driven magnetosphere examining the magnetic connection from the solar wind into the magnetosphere. The IMF is purely southward in this simulation and magnetic-field lines are shown in light green. The time labels at the top of the figure indicate the time that has passed since the various solar-wind magnetic-field lines became connected into the magnetosphere via dayside reconnection.
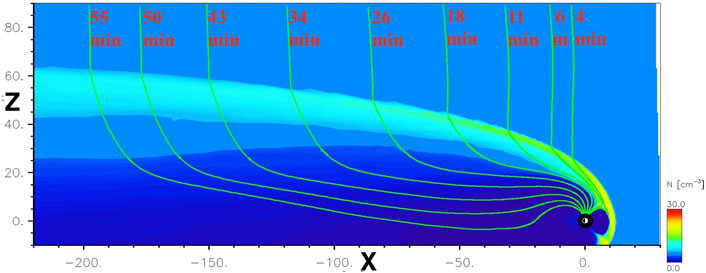
FIGURE 2. A number-density snapshot from an LFM (Lyon et al., 2004) simulation (Joe_Borovsky_081,121_1) at the CCMC with a purely southward IMF: the bow shock is in yellow, the magnetotail is dark blue. Nine open field lines (light green) are traced from the polar cap into the solar wind. The labels (red) are the times since that particular solar-wind flux tube passed a solar-wind monitor at the nose of the bow shock. The solar wind velocity vector is tilted southward (vx = −400 km/s and vz = −66 km/s) to wind-sock move the magnetotail downward (1) to keep the distant magnetotail from flaring out of the simulation domain and (2) to push the northern high-latitude magnetopause onto a higher-resolution region of the simulation grid.
In each flux tube at 1 AU the strahl moves out from the Sun as a steady stream (heat flux) of electrons. When a particular tube passes a solar-wind monitor, the strength of the stream in that tube is gauged by I272. As that tube passes the Earth and its magnetic connection to the magnetosphere changes, the strahl flux in that tube should remain the same. Hence, when comparing lobe observations of the strahl with solar-wind observations of the strahl, a time lag in the solar-wind observations must be accounted for. The time lags are owed to temporal changes in where that tube connects into the magnetosphere. Mirroring strahl electrons are lost to the solar wind on polar-cap flux tubes that are open, and mirroring strahl electrons are captured on closed flux tubes.
Conserving the first adiabatic invariant, the narrow field-aligned strahl in the solar wind has no difficulty going from the solar wind into the lobes. If the field strength in the lobes is ∼30 nT and the field strength in the solar wind is ∼5 nT, then electrons with pitch angles up to ∼23° can enter the stronger field of the lobes. Scatter-free transport of the strahl into the lobes is also expected: unless a strahl-electron gyroradius rge is rge > 0.1 rcurve (Borovsky et al., 2022a,b), where rcurve is the radius of curvature of a field line, there will be no scattering. At 5 nT a 500-eV electron has rge ∼ 1 km and field-line radii of curvatures of 10 km are not expected in the connection of the solar-wind magnetic field into the magnetosphere depending on the spacecraft location in the lobes.
Note in Figure 2 that most of the solar-wind magnetic-field lines connecting into the lobes (and into the polar cap) pass through the distant bow shock, where the shock compression ratio is weak (Greenstadt et al., 1990; Bennett et al., 1997). For these distant field lines, the strahl population should be little effected by passage through the weak bow shock.
Polar Rain Aurora
As solar-wind magnetic-field lines become connected to the Earth, the electron strahl creates the polar-rain aurora in the northern polar ionosphere when the IMF is in an away sector and in the southern polar ionosphere when the IMF is in a toward sector (Fairfield and Scudder, 1985; Newell and Meng, 1990; Wing et al., 1996; 2001; 2005). The intensity of polar-rain aurora is correlated with intensity of the strahl in the solar wind (Hong et al., 2012; Hershbach and Zhang, 2021), hence, polar-rain observations can provide a good estimate of the strahl population in the lobe and in the plasma sheet. The polar rain is structured, similar to the structured strahl population of the solar wind (Borovsky, 2020a).
As seen from the solar wind, the atmospheric loss cone for the Earth’s polar caps is quite small and so not all of the strahl electrons are able to hit the atmosphere and make aurora. For instance, if the field strength in the solar wind is 5 nT = 5 × 10–5 G, then the loss cone for the 0.5-G field of the polar cap is about 0.6°. Strahl electrons outside of the loss cone will mirror above the atmosphere.
As indicated in Figure 2, time lags of 0–2 h are expected between the solar wind and the ionosphere owing to flux-tube advection past the Earth, with the time delays shorter in the sunward portions of the polar cap and longer in the nightside polar cap (cf. Figure 2).
In matching the energy spectra of the polar-rain electrons with the solar wind, evidence of field-aligned potentials has been seen (e.g., Fairfield et al., 2008; Wing et al., 1996; 2001; 2005; 2015). Polar rain intensity or energy flux sometimes shows a negative gradient from the dayside to the nightside, which can be partly attributed to the retarding potential (Newell et al., 1996; Fairfield et al., 2008; Wing et al., 1996; 2001; 2005; 2015). However, this negative gradient is not always seen for the reasons that are not entirely clear (Newell and Meng, 1990);
The Plasma Sheet Suprathermal-Electron Population
The pathway from the electron strahl in the solar wind to the electron strahl in the lobes (where the strahl electrons create the polar-rain aurora) is well established. Then next step in the pathway to the radiation belt is not well established. It is imperative to initiate a research effort 1) to quantify how much of the plasma-sheet suprathermal-electron distribution is owed to the strahl (and halo) electrons of the solar wind and 2) to determine whether there are other candidate sources for the plasma-sheet suprathermal-electron population (Other sources, e.g., recirculation of electrons from the dipolar magnetosphere into the tail, have been documented for much-higher-energy electrons (Borovsky and Denton, 2011; Walsh et al., 2012).).
The suprathermal-electron population of the Earth’s plasma sheet has been well documented (e.g., Christon et al., 1989, 1991; Runov et al., 2018; Stepanov et al., 2021). At 60 RE the suprathermal electron population has energies above about 200 eV (Runov et al., 2018). Measurements of the shapes of velocity distribution functions, phase-space densities, and sudden temporal/spatial changes in the population need to be made. Occurrence distributions of the properties of the suprathermal electrons in the magnetotail plasma sheet need to be compared with occurrence distributions of the electron properties in the lobes and in the solar wind. Occurrence distributions such as the phase-space density at constant μ (μ = v⊥2/B being the first adiabatic invariant) are particularly revealing. Simulations of the field-aligned strahl electron population through the nightside-reconnection process may be informative: the simulations should provide information about the likelihood of pitch-angle scattering at thin current sheets and at the reconnection site and about energy-anisotropy evolution in the collapsing Earthward field lines after reconnection.
Besides entry from the solar wind into the magnetotail plasma sheet from the lobe via nightside reconnection, solar-wind electron populations can also enter into the magnetotail plasma sheet via the low-latitude boundary layer (LLBL).
For the lobe-reconnection pathway, the best estimate of the strahl electrons that enter the nightside closed magnetosphere may be obtained from the polar rain electrons where the polar rain meets the open-closed boundary of the nightside oval (Newell and Meng, 1990; Wing and Zhang, 2015).
Substorm-Injected Electrons
It is well established that the population of energetic substorm-injected electrons in the dipolar magnetosphere is directly related to the suprathermal electron population in the magnetotail plasma sheet, delivered into the dipolar region by the strong electric fields of magnetospheric substorms (Birn et al., 1997, 1998, 2004, 2014).
Using the hourly multispacecraft substorm-injected-electron index Fe130 (Borovsky and Yakymenko, 2017) that is based on SOPA measurements (Belian et al., 1992) from geosynchronous orbit and using the hourly I272 strahl-intensity index (Borovsky, 2017) that is based on ACE measurements in the solar wind, the red curve in Figure 3 plots the time-lagged Pearson linear correlation coefficient between I272 and Fe130. The peak correlation occurs when the Fe130 substorm-injected-electron intensity is lagged by about 1 day from the solar-wind I272 strahl-intensity index.
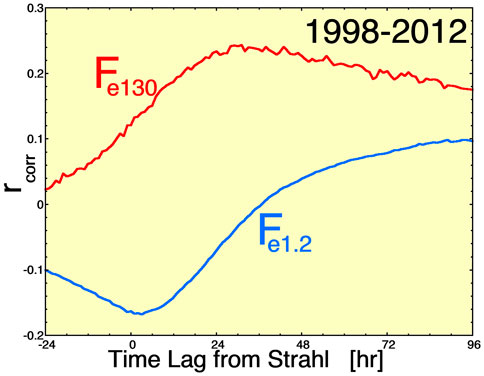
FIGURE 3. The correlation time-lag behavior between the strahl intensity in the solar wind and (red) the peak flux of 130-keV electrons at geosynchronous orbit and (blue) the peak flux of 1.2-MeV radiation-belt electrons at geosynchronous orbit. 11,020 hourly data points were used. The modest, but nonzero, levels of correlation indicate that strahl intensity is not the only controller of these magnetospheric quantities.
Seed Electrons for the Radiation Belt
It is commonly accepted that the energetic substorm-injected electron population in the dipolar magnetosphere is the seed population for the Earth’s electron radiation belt (Jaynes et al., 2015; Boyd et al., 2016; Borovsky and Valdivia, 2018), with the substorm-injected electrons energized primarily by whistler-mode chorus waves, with the chorus waves driven by lower-energy injected electrons. It is well known that the intensity of the electron radiation belt is statistically strongly connected to the time history of the intensity of substorm electron injections (Simms et al., 2016; Borovsky, 2017). Borovsky (2017) found a Pearson correlation coefficient of +74% between the multispacecraft flux Fe1.2 of 1.2-MeV radiation-belt electrons and the 62-h time integral of the Fe130 flux of substorm-injected electrons.
The blue curve of Figure 3 plots the time-lagged Pearson linear correlation coefficient between the strahl electron intensity index I272 in the solar wind and the 1.2-MeV radiation-belt flux index Fe1.2 at geosynchronous orbit: a peak in the correlation coefficient occurs when the radiation-belt index Fe1.2 is lagged by about 4 days.
The Future
A project is needed that will verify and quantify a long chain of events that leads to a seed population of energetic electrons for the Earth’s electron radiation belt: solar wind → lobe → polar rain → plasma sheet → injected electrons → radiation belt. Of particular interest is determining the relative contribution of strahl to the seed population through each stage of the proposed pathway. It will be important distinguished the strahl electron population from other electron populations by comparing phase-space densities for consistency in the various steps of the strahl’s pathway and by correlating the strengths of the various populations.
The project goals would be the following. 1) To determine whether (and by how much) the solar-wind electron strahl (and halo) acts as a seed population for the Earth’s electron radiation belt. 2) To determine the controlling factors for this process. 3) To trace the electron strahl from the solar wind, into the lobe, into the polar-cap ionosphere (polar rain), into the magnetotail plasma sheet. The suprathermal electrons of the plasma sheet have already been traced into substorm injections in the dipole, and evolving into the electron radiation belt has been examined.
A project pursuing this unique hypothesis could have a transformative impact.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
JB initiated this project and JB and AR researched and wrote the manuscript.
Funding
JB was supported by the NSF GEM Program via grant AGS-2027569 and by the NASA HERMES Interdisciplinary Science Program via grant 80NSSC21K1406. AR was supported by the NASA HERMES Interdisciplinary Science Program via grant 80NSSC21K1407.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Joachim Birn, Yuri Shprits, and Simon Wing for helpful conversations.
References
Aaker, D. N., Bame, S. J., Feldman, W. C., Gosling, J. T., Zwickl, R. D., Slavin, J. A., et al. (1986). Strong Electron Bidirectional Anisotropies in the Distant Tail: ISEE 3 Observations of Polar Rain. J. Geophys. Res. 91, 5637–5662. doi:10.1029/JA091iA05p05637
Belian, R. D., Gisler, G. R., Cayton, T., and Christensen, R. (1992). High-Zenergetic Particles at Geosynchronous Orbit during the Great Solar Proton Event Series of October 1989. J. Geophys. Res. 97, 16897. doi:10.1029/92ja01139
Bennett, L., Kivelson, M. G., Khurana, K. K., Frank, L. A., and Paterson, W. R. (1997). A Model of the Earth's Distant Bow Shock. J. Geophys. Res. 102, 26927–26941. doi:10.1029/97ja01906
Bercic, L., Larson, D., Whittlesey, P., Maksimovic, M., Badman, S. T., Landi, S., et al. (2020). Coronal Electron Temperature Inferred from the Strahl Electrons in the Inner Heliosphere: Parker Solar Probe and Helios Observations. Astrophys. J. 892, 88. doi:10.3847/1538-4357/ab7b7a
Birn, J., Runov, A., and Hesse, M. (2014). Energetic Electrons in Dipolarization Events: Spatial Properties and Anisotropy. J. Geophys. Res. Space Phys. 119, 3604–3616. doi:10.1002/2013ja019738
Birn, J., Thomsen, M. F., Borovsky, J. E., Reeves, G. D., McComas, D. J., and Belian, R. D. (1997). Characteristic Plasma Properties during Dispersionless Substorm Injections at Geosynchronous Orbit. J. Geophys. Res. 102, 2309–2324. doi:10.1029/96ja02870
Birn, J., Thomsen, M. F., Borovsky, J. E., Reeves, G. D., McComas, D. J., Belian, R. D., et al. (1998). Substorm Electron Injections: Geosynchronous Observations and Test Particle Simulations. J. Geophys. Res. 103, 9235–9248. doi:10.1029/97ja02635
Birn, J., Thomsen, M. F., and Hesse, M. (2004). Electron Acceleration in the Dynamic Magnetotail: Test Particle Orbits in Three-Dimensional Magnetohydrodynamic Simulation Fields. Phys. of Plasmas 11, 1825–1833. doi:10.1063/1.1704641
Boldyrev, S., and Horaites, K. (2019). Kinetic Theory of the Electron Strahl in the Solar Wind. MNRAS 489, 3412–3419. doi:10.1093/mnras/stz2378
Borovsky, J. E., Delzanno, G. L., and Yakymenko, K. N. (2022a). Pitch-Angle Diffusion in the Earth's Magnetosphere Organized by the Mozer-Transformed Coordinate System. Front. Astron. Space Sci. 9, 810792. doi:10.3389/fspas.2022.810792
Borovsky, J. E., and Denton, M. H. (2011). Evolution of the Magnetotail Energetic-Electron Population during High-Speed-Stream-Driven Storms: Evidence for the Leakage of the Outer Electron Radiation Belt into the Earth’s Magnetotail. J. Geophys. Res. 116, A12228. doi:10.1029/2011ja016713
Borovsky, J. E., and Denton, M. H. (2010). On the Heating of the Outer Radiation Belt to Produce High Fluxes of Relativistic Electrons: Measured Heating Rates for High-Speed-Stream-Driven Storms. J. Geophys. Res. 115, A12206. doi:10.1029/2010ja015342
Borovsky, J. E., and Denton, M. H. (2016). The Trailing Edges of High-Speed Streams at 1 AU. J. Geophys. Res. Space Phys. 121, 6107–6140. doi:10.1002/2016ja022863
Borovsky, J. E. (2021). Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection between the Earth and the Sun. Front. Astron. Space Sci. 8, 646443. doi:10.3389/fspas.2021.646443
Borovsky, J. E., Halekas, J. S., and Whittlesey, P. L. (2021). The Electron Structure of the Solar Wind. Front. Astron. Space Sci. 8, 69005. doi:10.3389/fspas.2021.690005
Borovsky, J. E. (2018). On the Origins of the Intercorrelations Between Solar Wind Variables. JGR Space Phys. 123, 20–29. doi:10.1002/2017ja024650
Borovsky, J. E. (2010). On the Variations of the Solar-Wind Magnetic Field about the Parker-spiral Direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040
Borovsky, J. E. (2008). The Flux-Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU? J. Geophys. Res. 113, A08110. doi:10.1029/2007ja012684
Borovsky, J. E. (2020a). The Magnetic Structure of the Solar Wind: Ionic Composition and the Electron Strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586
Borovsky, J. E. (2017). Time-integral Correlations of Multiple Variables with the Relativistic-Electron Flux at Geosynchronous Orbit: The Strong Roles of the Substorm-Injected Electrons and the Ion Plasma Sheet. J. Geophys. Res. 122, 11961. doi:10.1002/2017ja024476
Borovsky, J. E., and Valdivia, J. A. (2018). The Earth's Magnetosphere: A Systems Science Overview and Assessment. Surv. Geophys 39, 817–859. doi:10.1007/s10712-018-9487-x
Borovsky, J. E. (2020b). What Magnetospheric and Ionospheric Researchers Should Know about the Solar Wind. J. of Atmos. and Solar-Terrestrial Phys. 204, 105271. doi:10.1016/j.jastp.2020.105271
Borovsky, J. E., Yakymenko, K. N., and Delzanno, G. L. (2022b). Modification of the Loss Cone for Energetic Particles in the Earth’s Inner Magnetosphere. J. Geophys. Res. 127:e2021JA030106. in press. doi:10.1029/2021JA030106
Borovsky, J. E., and Yakymenko, K. (2017). Systems Science of the Magnetosphere: Creating Indices of Substorm Activity, of the Substorm-Injected Electron Population, and of the Electron Radiation Belt. J. Geophys. Res. 122, 10012. doi:10.1002/2017ja024250
Boyd, A. J., Spence, H. E., Huang, C. L., Reeves, G. D., Baker, D. N., Turner, D. L., et al. (2016). Statistical Properties of the Radiation Belt Seed Population. J. Geophys. Res. Space Phys. 121, 7636–7646. doi:10.1002/2016ja022652
Christon, S. P., Williams, D. J., Mitchell, D. G., Frank, L. A., and Huang, C. Y. (1989). Spectral Characteristics of Plasma Sheet Ion and Electron Populations during Undisturbed Geomagnetic Conditions. J. Geophys. Res. 94, 13409. doi:10.1029/ja094ia10p13409
Christon, S. P., Williams, D. J., Mitchell, D. G., Huang, C. Y., and Frank, L. A. (1991). Spectral Characteristics of Plasma Sheet Ion and Electron Populations during Disturbed Geomagnetic Conditions. J. Geophys. Res. 96, 1–22. doi:10.1029/90ja01633
de Koning, C. A., Gosling, J. T., Skoug, R. M., and Steinberg, J. T. (2007). Energy Dependence of Electron Pitch Angle Distribution Widths in Solar Bursts. J. Geophys. Res. 112, A04101. doi:10.1029/2006ja011971
Fairfield, D. H., and Scudder, J. D. (1985). Polar Rain: Solar Coronal Electrons in the Earth's Magnetosphere. J. Geophys. Res. 90, 4055. doi:10.1029/ja090ia05p04055
Fairfield, D. H., Wing, S., Newell, P. T., Ruohoniemi, J. M., Gosling, J. T., and Skoug, R. M. (2008). Polar Rain Gradients and Field-Aligned Polar Cap Potentials. J. Geophys. Res. 113, A10203. doi:10.1029/2008JA013437
Fitzenreiter, R. J., Ogilvie, K. W., Chornay, D. J., and Keller, J. (1998). Observations of Electron Velocity Distribution Functions in the Solar Wind by the WIND Spacecraft: High Angular Resolution Strahl Measurements. Geophys. Res. Lett. 25, 249–252. doi:10.1029/97gl03703
Gary, S. P., Feldman, W. C., Forslund, D. W., and Montgomery, M. D. (1975). Electron Heat Flux Instabilities in the Solar Wind. Geophys. Res. Lett. 2, 79–82. doi:10.1029/gl002i003p00079
Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004). Dispersionless Modulations in Low-Energy Solar Electron Bursts and Discontinuous Changes in the Solar Wind Electron Strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338
Greenstadt, E. W., Traver, D. P., Coroniti, F. V., Smith, E. J., and Slavin, J. A. (1990). Observations of the Flank of Earth's Bow Shock to −110 REby ISEE 3/ICE. Geophys. Res. Lett. 17, 753–756. doi:10.1029/gl017i006p00753
Herschback, D. M., and Zhang, Y. (2021). Spatial Structures in Solar Wind Superthermal Electrons and Polar Rain Aurora. J. Atmos. Solar.-Terr. Phys. 218, 105633. doi:10.1016/j.jastp.2021.105633
Hong, J., Lee, J. J., Min, K. W., Kim, V. P., and Hegai, V. V. (2012). Variations in Polar Rain Flux According to IMF Geometries Observed by STSAT-1. Adv. Space Res. 50, 221–227. doi:10.1016/j.asr.2012.03.031
Jaynes, A. N., Baker, D. N., Singer, H. J., Rodriguez, J. V., Lota’aniu, T. M., ali, A. F., et al. (2015). Source and Seed Populations for Relativistic Electrons: Their Roles in Radiation Belt Changes. J. Geophys. Res. Space Phys. 120, 7420–7254. doi:10.1002/2015ja021234
Kasaba, Y., Terasawa, T., Tsubouchi, K., Mukai, T., Saito, Y., Matsumoto, H., et al. (2000). Magnetosheath Electrons in Anomalously Low Density Solar Wind Observed by Geotail. Geophys. Res. Lett. 27, 3253–3256. doi:10.1029/2000gl000086
Lyon, J. G., Fedder, J. A., and Mobarry, C. M. (2004). The Lyon-Fedder-Mobary (LFM) Global MHD Magnetospheric Simulation Code. J. Atmos. Solar Terr. Phys. 66, 1333. doi:10.1016/j.jastp.2004.03.020
Newell, P. T., Feldstein, Y. I., Galperin, Y. I., and Meng, C.-I. (1996). Morphology of Nightside Precipitation. J. Geophys. Res. 101, 10737–10748. doi:10.1029/95JA03516
Newell, P. T., and Meng, C.-I. (1990). Intense keV Energy Polar Rain. J. Geophys. Res. 95, 7869–7879. doi:10.1029/JA095iA06p07869
Runov, A., Angelopoulos, V., Artemyev, A. V., Lu, S., and Zhou, X.-Z. (2018). Near-Earth Reconnection Ejecta at Lunar Distances. J. Geophys. Res. Space Phys. 123, 2736–2744. doi:10.1002/2017JA025079
Simms, L. E., Engebretson, M. J., Pilipenko, V., Reeves, G. D., and Clilverd, M. (2016). Empirical Predictive Models of Daily Relativistic Electron Flux at Geostationary Orbit: Multiple Regression Analysis. J. Geophys. Res. Space Phys. 121, 3181–3197. doi:10.1002/2016ja022414
Stepanov, N. A., Sergeev, V. A., Sormakov, D. A., Andreeva, V. A., Dubyagin, S. V., Ganushkina, N., et al. (2021). Superthemal Proton and Electron Fluxes in the Plasma Sheet Transition Region and Their Dependence on Solar Wind Parameters. J. Geophys. Res. Space Phys. 126, e2020JA028580. doi:10.1029/2020ja028580
Stverak, S., Maksimovic, M., Travnicek, P. M., Marsch, E., Fazakerley, A. N., and Scime, E. E. (2009). Radial Evolution of Nonthermal Electron Populations in the Low-Latitude Solar Wind: Helios, Cluster, and Ulysses Observations. J. Geophys. Res. 114, A04104. doi:10.1029/2008JA013883
Terasawa, T., Kasaba, Y., Tsubouchi, K., Mukai, T., Saito, Y., Frank, L. A., et al. (2000). GEOTAIL Observations of Anomalously Low Density Plasma in the Magnetosheath. Geophys. Res. Lett. 27, 3781–3784. doi:10.1029/2000gl000087
Verscharen, D., Wicks, R. T., Alexandrova, O., Bruno, R., Burgess, D., Chen, C. H. K., et al. (2021). A Case for Electron-Astrophysics. Exp. Astrophys. doi:10.1007/s10686-09761-5
Walsh, b. M., Haaland, S. E., Daly, P. W., Kronberg, E. A., and Fritz, T. A. (2012). Energetic Electrons along the High-Latitude Magnetopause. Ann. Geophys. 30, 1003–1013. doi:10.5194/angeo-30-1003-2012
Wing, S., Fairfield, D. H., Johnson, J. R., and Ohtani, S. I. (2015). On the Field‐aligned Electric Field in the Polar Cap. Geophys. Res. Lett. 42, 5090–5099. doi:10.1002/2015GL064229
Wing, S., Newell, P. T., and Meng, C.-I. (2005). Cusp Modeling and Observations at Low Altitude. Surv. Geophys 26, 341–367. doi:10.1007/s10712-005-1886-0
Wing, S., Newell, P. T., and Onsager, T. G. (1996). Modeling the Entry of Magnetosheath Electrons into the Dayside Ionosphere. J. Geophys. Res. 101, 13155–13167. doi:10.1029/96JA00395
Wing, S., Newell, P. T., and Ruohoniemi, J. M. (2001). Double Cusp: Model Prediction and Observational Verification. J. Geophys. Res. 106, 25571–25593. doi:10.1029/2000ja000402
Wing, S., and Zhang, Y. L. (2015). The Nightside Magnetic Field Line Open-Closed Boundary and Polar Rain Electron Energy-Latitude Dispersion. Ann. Geophys. 33, 39–46. doi:10.5194/angeo-33-39-2015
Keywords: radiation belt, strahl, plasma sheet, polar rain, magnetosphere
Citation: Borovsky JE and Runov A (2022) Is the Solar Wind Electron Strahl a Seed Population for the Earth’s Electron Radiation Belt?. Front. Astron. Space Sci. 9:930162. doi: 10.3389/fspas.2022.930162
Received: 27 April 2022; Accepted: 18 May 2022;
Published: 01 June 2022.
Edited by:
Luca Sorriso-Valvo, Institute for Space Physics, SwedenReviewed by:
David R. Shklyar, Space Research Institute (RAS), RussiaJia Huang, University of Michigan, United States
Copyright © 2022 Borovsky and Runov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
 Joseph E. Borovsky
Joseph E. Borovsky Andrei Runov
Andrei Runov