Compact extra dimensions as the source of primordial black holes

This article discusses a model of primordial black hole (PBH) formation at the reheating stage. These small/massive black holes appear due to the specific properties of the compact extra dimensions. The latter gives rise to the low energy model, containing an effective scalar field potential capable of domain wall production. Formed during inflation, these walls are quite dense, meaning they collapse soon after inflation ends. Discussion of the model is framed by the scope of multidimensional f(R)-gravity. We study the possibility of the pure gravitational formation of primordial black holes (PBHs). Interpreting the scalar curvature of compact extra space R_n as an effective scalar field in an Einstein framework and consider effective scalar-field theory that might potentially be capable of producing domain walls with a certain choice of parameters. Hence, we demonstrate that f(R)-gravity contains a mechanism for PBH formation. The study assumed that cosmological inflation is an external process, which satisfied all the cosmological constraints on our mechanism.

1 Introduction

Extra dimensions are usually studied within the framework of elementary particle physics Feruglio (2004), for example in the context of the unification of interactions Dienes et al. (1999); Hall and Nomura (2001), explaining the nature of Standard Model fields Grobov and Rubin (2013), or searching for their manifestations in collider experiments Hewett and Spiropulu (2002); Deutschmann et al. (2017). This article explores another possible cosmological consequence, indicating that the compact extra dimensions may be the cause of primordial black hole (PBH) formation immediately after the end of the inflation.

One of the central aims of theories with compact extra dimensions is to account for compactification and stabilization Witten (1982) during cosmological evolution. This can be done, for example, by introducing additional scalar fields Carroll et al. (2002) or f(R)-modification of gravity Rador (2007); Bronnikov and Rubin (2006). The latter approach is particularly promising because the Starobinsky quadratic f(R)-gravity Starobinsky (1980); Vilenkin (1985) provides the best fit for the observational constraints of the parameters of inflation Akrami et al. (2020). Moreover, in multidimensional f(R)-gravity, the processes of cosmological inflation and compactification are manifestations of general gravitational dynamics in different subspaces Fabris et al. (2020).

The possibilities of f(R)-gravity are widely studied De Felice and Tsujikawa (2010); Capozziello and De Laurentis (2011); Nojiri and Odintsov (2011); Nojiri et al. (2017). They offer solutions to many cosmological problems Capozziello and Laurentis (2012); Bronnikov et al. (2007, 2017, 2020); Petriakova and Rubin (2022). One of the problems that f(R)-gravity can solve is the existence of primordial black holes. Today, the primordial origin of some discovered black holes (quasars at small z Falomo et al. (2014); Dokuchaev et al. (2007), black holes of intermediate masses detected by gravitational-wave observatories The LIGO Scientific Collaboration (2019)) are widely discussed Carr and Kuhnel (2021); Luca et al. (2020); Sakharov et al. (2021). There are various proposals on the mechanisms that lead to PBH formation, for example, based on hydrodynamic perturbations Escrivà (2022) and scalar field fragmentation Cotner et al. (2019). In this paper we demonstrate how primordial black holes can appear as a result of inflationary dynamics in the framework of the f(R)-gravity model. The proposed mechanism is based on the known possibility of domain wall formation during cosmological inflation followed by their collapse into primordial black holes (Rubin et al. (2000); Belotsky et al. (2019)). The formation of these domain walls requires a scalar field with a nontrivial potential containing several vacuums. This type of scalar field effectively arises in multidimensional f(R)-models in the Einstein frame Lyakhova et al. (2018); Bronnikov and Rubin (2006); Fabris et al. (2020). This field controls the size of the compact extra space, and its different vacuums correspond to different universes. In this paper, we calculate the parameters of the domain walls formed by the field and conclude that, as they appear at the inflationary stage, they will immediately collapse into PBHs during reheating. For a remote observer in the Jordan frame, the appearance of this PBH is interpreted as a manifestation of the non-trivial f(R)-gravitational dynamics of multidimensional space. These PBHs that are formed grow rapidly in the process of further cosmological evolution due to accretion and are capable of turning into observable supermassive quasars at small z Dolgov (2018). In Section 2, we consider multidimensional f(R)-gravity and reduce it to an effective field theory. In Section 3, we explore the potential of the resulting scalar field theory, showing that the theory can contain domain walls. In Section 4, we model domain walls and calculate their characteristic parameters in the considered theory. In Section 5, we discuss how such domain walls can be created in the early Universe and obtain the model parameters for which this mechanism works. In Section 6, we study the collapse of the obtained domain walls and show that it leads to the appearance of primordial black holes of various masses.

2 Model

This study is based on the modified f(R) gravity acting in D = 4 + n dimensions. It is described by the action¹.

$\begin{array}{ll}\hfill S\left[g_{\mu \nu }\right]& =\frac{m_D^{D-2}}{2}\int d^{4+n}x\sqrt{|g_D|}\hfill \\ \hfill & \times \left[f\left(R\right)+c_1{R}_{AB}{R}^{AB}+c_2{R}_{\mathit{ABCD}}{R}^{\mathit{ABCD}}\right],\hfill \end{array}$

$f\left(R\right)=a_2{R}^2+R-2{\mathrm{\Lambda }}_D,(1)$

where m_D is the multidimensional Planck mass. The parameters a₂, c₁, c₂ of the Lagrangian (1) have dimensionality $[m_D^{-2}]$, the cosmological constant Λ has dimensionality $[m_D^2]$. Hereafter we will work everywhere in units m_D ≡ 1, unless it is explicitly specified. In this work we will represent multidimensional space as the direct product of $\mathbb{M}={\mathbb{M}}_4\times {\mathbb{M}}_n$, where ${\mathbb{M}}_4$ is–four-dimensional space, ${\mathbb{M}}_n$—an n-dimensional compact extra space with metric

$d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }-e^{2\beta \left(t,x\right)}d{\mathrm{\Omega }}_n^2.(2)$

Here g_μν is a 4-dimensional metric ${\mathbb{M}}_4$, β is a metric function, and $d{\mathrm{\Omega }}_n^2$ is the linear element square of a maximally symmetric compact extra space ${\mathbb{M}}_n$ with positive curvature.

Cosmological scenarios based on this theory Lyakhova et al. (2018); Fabris et al. (2020); Bronnikov and Rubin (2021). Are finished by an effective 4-dim theory at the low energy. Its properties are defined by the Lagrangian parameters of action (1). The procedure for obtaining such a theory is also described in Bronnikov and Rubin (2006).

Following this procedure, we assume maximal symmetry of the extra space ${\mathbb{M}}_n$. Its radius ρ ≡ e^β does not depend on the extra coordinates. In addition, the useful approximation of this effective theory works in a region where the extra curvature R_n = n (n − 1)/e^2β is large compared to the 4-dimensional curvature and changes slowly:

$R=R_4+R_n+P_k,P_k=2n{\partial }^2\beta +n\left(n+1\right){\left(\partial \beta \right)}^2,$

$R_4,P_k\ll R_n.(3)$

where R₄, R_n are Ricci scalars for ${\mathbb{M}}_4,{\mathbb{M}}_n$.

The approximation (3) applied to action (1) leads to the effective 4-dim model with a non-minimal coupling between the observed 4-dimensional gravity R₄ and the scalar field Bronnikov and Rubin (2006). Let us review briefly this application. Firstly we will reduce (1) to four dimensions, it is done by integrating over extra coordinates:

$\begin{array}{ll}\hfill S& =\frac{m_4^2}{2}\int d^{4}x\sqrt{-g_4}{e}^{n\beta }\hfill \\ \hfill & \times \left[f\left(R\right)+c_1{R}_{AB}{R}^{AB}+c_2{R}_{\mathit{ABCD}}{R}^{\mathit{ABCD}}\right],\hfill \end{array}(4)$

where $m_4=\sqrt{2{\pi }^{\frac{n+1}{2}}/\mathrm{\Gamma }(\frac{n+1}{2})}$ is square root of volume of compact n-dimensional extra space with unit curvature. Using the smallness of R₄ and R_n (3), we can perform a Taylor decomposition like f(R) ≈ f (R_n) + f′(R_n) ⋅ (R₄ + P_k) + ⋯ with f′(R_n) = df/dR, where only linear term would be taken into account. We do the same for R_ABR^AB and R_ABCDR^ABCD (calculations for these terms are omitted due to their tediousness). Therefore (4) is now:

$S^J=\frac{m_4^2}{2}\int d^{4}x\sqrt{-g_4}{e}^{n\beta }\left[f\left(R_n\right)+f^{\prime }\left(R_n\right)\cdot \left(R_4+P_k\right)+\cdots \right].(5)$

We obtained a 4-dimensional theory with a non-minimal coupling between gravity R₄ and the new effective field ϕ ≡ R_n. This is the so-called Jordan frame, and we will use it as a physically observed one Capozziello et al. (2010); Bahamonde et al. (2017). To exclude non-minimum coupling (which greatly simplifies the analysis) it is helpful to perform conformal mapping: $g_{\mu \nu }\Rightarrow {\tilde{g}}_{\mu \nu }=e^{n\beta }{F}^{\prime }(\varphi )g_{\mu \nu }$ that translates the action into Einstein frame Bronnikov and Rubin (2006), Bronnikov and Rubin (2013):

$S^E=\frac{m_4^2}{2}\int d^{4}x\sqrt{-g_4}\text{sign}\left(f^{\prime }\right)\left[R_4+K\left(\varphi \right){\left(\partial \varphi \right)}^2-2V\left(\varphi \right)\right],(6)$

where $g_4^{\mu \nu }$ is a 4-dimensional metric, the Ricci scalar of the extra space is perceived as new effective scalar field ϕ ≡ R_n and f = f(ϕ) = a₂ϕ² + ϕ − 2Λ_D and f′ ≡ df/dϕ.

The action (6) contains a potential term V(ϕ) and a nontrivial kinetic term K(ϕ), which are expressed through the initial parameters of the Lagrangian (1) [see Fabris et al. (2020)]:

$K\left(\varphi \right)=\frac{1}{4{\varphi }^2}\left[6{\varphi }^2{\left(\frac{f^{\prime \prime }}{f^{\prime }}\right)}^2-2n\varphi \left(\frac{f^{\prime \prime }}{f^{\prime }}\right)+\frac{n\left(n+2\right)}{2}\right]+\frac{c_1+c_2}{f^{\prime }\varphi },(7)$

$V\left(\varphi \right)=-\frac{\mathrm{sign}\left(f^{\prime }\right)}{2{\left(f^{\prime }\right)}^2}{\left[\frac{|\varphi |}{n\left(n-1\right)}\right]}^{n/2}\left[f\left(\varphi \right)+\frac{c_1+2c_2/\left(n-1\right)}{n}{\varphi }^2\right].(8)$

The validity of the transition from 1 to 6 dictated by inequalities (3) will be analyzed later.

Thus we have reduced the original f(R)-gravity model to an effective field theory determined by the potential and the kinetic term. Next, we will explore the potential and the kinetic term of this theory.

3 Effective scalar field potential

For a wide range of parameters, the potential term (8) has two minima corresponding to different vacuums of the Universe (Figure 1). The value of the potential at these minima must be almost zero according to the almost zero value of the cosmological constant Λ₄. This leads to a relation of the parameter c = 1/4 (a + c_v/n), where c_v = c₁ + 2c₂/(n − 1).

FIGURE 1

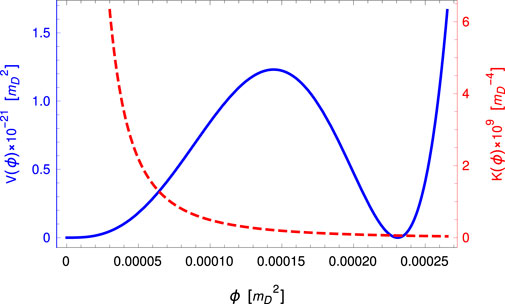
FIGURE 1. Graphs of the potential term and kinetic factor (7), (8) for parameters: n = 6, c₁ = −8,000, c₂ = −5,000, a₂ = −500. The left minimum of the potential is at ϕ = 0, but it is impossible to roll down to it in a finite time because of the increasing friction effect of the kinetic factor, the right minimum is at ϕ_min = 2.3 ⋅ 10^–4.

The rolling of the field ϕ ≡ R_n into the right minimum of the potential (8) corresponds to the stabilization of the compact extra space R_n ≠ 0 (the extra space is compactified and has some radius ρ₀) and leads to the observed cosmology Fabris et al. (2020). The presence of the left minimum R_n ≈ 0 suggests the possibility of another scenario Bronnikov and Rubin (2021), in which the extra space is unstable and expands to the macroscopic scale.

The non-trivial kinetic factor (7) significantly modifies the character of the field evolution ϕ(t) in comparison to the standard scalar-field theory, providing increasing friction when rolling to the left minimum, see Figure 1. One can simplify the Lagrangian by substituting

$\psi =m_4\underset{{\varphi }_0}{\overset{\varphi }{\int }}\sqrt{K\left({\varphi }^{\prime }\right)}d{\varphi }^{\prime },\tilde{V}\left(\psi \right)=m_4^{2}V\left(\varphi \left(\psi \right)\right),K\left({\varphi }^{\prime }\right)>0.(9)$

In this case, ψ(ϕ) is monotonic and invertible (which is required to find the potential in the expression (10)). After simple algebra, the Lagrangian is reduced to the standard form

$S=\frac{m_4^2}{2}\int d^{4}x\sqrt{-g_4}{R}_4+\int d^{4}x\sqrt{-g_4}\left[\frac{1}{2}{\left(\partial \psi \right)}^2-\tilde{V}\left(\psi \right)\right],(10)$

where $m_4^2=16{\pi }^3/15$ for chosen extra space dimensionality n = 6.

It is well known that potentials such as (2), which contain several minima (vacuums), can lead to the formation of non-trivial field configurations Vilenkin and Shellard (1994)—“bubbles” of one vacuum inside another, surrounded by a domain wall. In the next section, we model the domain wall in the potential (2).

4 Domain walls

This configuration was investigated by deriving the field equation for ψ from the effective action (10). For simplicity, we consider it spherically symmetric and static, which gives the equation:

${\psi }_{uu}+\frac{2{\psi }_u}{u}-{\tilde{V}}^{\prime }\left(\psi \right)=0,(11)$

where u is the radial coordinate. When considering a sufficiently large “bubble” (such that its radius is much larger than the characteristic thickness of the domain wall ψ_uu ≫ 2ψ_u/u) it can easily be reduced to a first-order equation

${\partial }_u\psi =\pm \sqrt{2\tilde{V}\left(\psi \right)}.(12)$

The characteristic solution of Eq. 12 connecting the left vacuum of the potential $\tilde{V}(\psi )$ to the right one (Figure 2) is shown in Figure 3 (blue line).

FIGURE 2

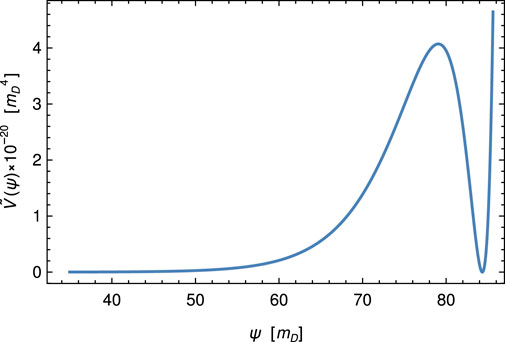
FIGURE 2. Graph of the potential term $\tilde{V}(\psi )$ of the effective theory (10) for the parameters chosen in Figure 1. The right minimum is at ψ_min = 84.3. Strictly speaking, the left minimum is at ψ = −∞, but for this illustration, a very accurate approximation ψ = 0 is sufficient (corresponding to ϕ = ϕ₀), up to which the effective theory (6) still works. The maximum value of the potential in the transition region between vacuums used ${\tilde{V}}_{\max }\approx 4.1\cdot 10^{-20}$ and the steepness of the slope used $\sqrt{{\tilde{V}}^{\prime \prime }({\psi }_{\max })}=2.7\cdot 10^{-11}$.

FIGURE 3

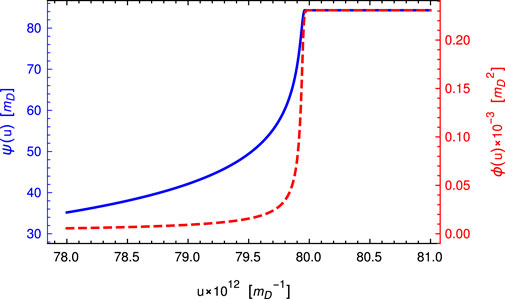
FIGURE 3. Numerical solution of (11) under boundary conditions: the left minimum $\tilde{V}(\psi )$ (Figure 2) is reached inside the bubble ψ(0) = 0, and the right minimum is reached for the remote observer ψ(u → ∞) = ψ_min (and forms our Universe). In the graphs: the blue line is the direct solution of ψ(u) (domain wall) and the red dashed line is its corresponding function ϕ(u). In this example the bubble radius is u₀ ≈ 8 ⋅ 10¹³.

We can calculate the domain wall energy density ɛ_ψ as a component T⁰⁰ of energy-momentum tensor for the scalar field Lagrangian ψ:

$\begin{array}{ll}\hfill {\epsilon }_{\psi }\left(u\right)& =T^{00}\left(u\right)=\frac{\partial {\mathcal{L}}_{\psi }}{\partial \left({\partial }_0\psi \right)}{\partial }^0\psi -{\mathcal{L}}_{\psi }{g}^{00}\hfill \\ \hfill & =\frac{1}{2}{\left({\partial }_u\psi \right)}^2+V\left(\psi \right)=2\tilde{V}\left(\psi \left(u\right)\right).\hfill \end{array}(13)$

Integration over the radial coordinate (13) gives the surface energy density of the domain wall in multidimensional Planck units (m_D = 1):

$\sigma =\underset{0}{\overset{\infty }{\int }}{\epsilon }_{\psi }\left(u\right)du=\underset{0}{\overset{{\psi }_{\mathit{min}}}{\int }}\frac{2\tilde{V}\left(\psi \right)}{{\psi }_u}d\psi =\underset{0}{\overset{{\psi }_{\mathit{min}}}{\int }}\sqrt{2\tilde{V}\left(\psi \right)}d\psi .(14)$

We can also formally estimate the characteristic wall thickness δ as

$\sigma =\underset{0}{\overset{\infty }{\int }}2\tilde{V}\left(\psi \right)du\approx 2\frac{{\tilde{V}}_{\mathit{max}}}{2}\delta \Rightarrow \delta \approx \frac{\sigma }{{\tilde{V}}_{\mathit{max}}}.(15)$

The domain walls considered in this paper appear to be very large (Figure 4). As a result, they could be a source of primordial black holes. The mechanism of formation and collapse of such domain walls is well studied in Liu et al. (2020); Garriga et al. (2016); Rubin et al. (2000) and leads to the formation of primordial black holes in a wide range of masses.

FIGURE 4

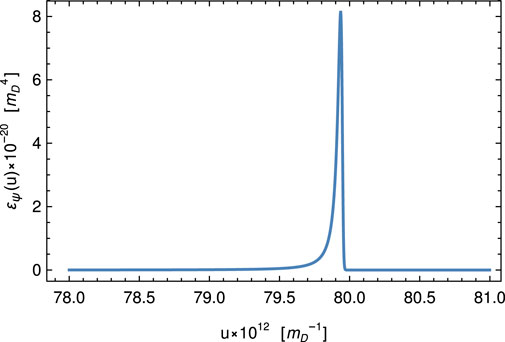
FIGURE 4. Energy density (13) profile along the radial coordinate u for the solution shown in Figure 3. In the case of spherical symmetry, the domain wall forms a bubble with surface energy density σ ≈ 5 ⋅ 10^–9 and wall thickness δ ≈ 1.2 ⋅ 10¹¹, according to (14), (15).

In this section, we calculate the characteristic parameters of the domain wall. However, it is necessary to study how realistic the mechanism of wall formation is, as explored below.

5 Generation of domain walls during inflation

As stated above, the rolling of the ψ field to the right minimum of Figure 2, creates the observable Universe. For its formation, a mechanism of cosmological inflation is required. In order not to complicate our consideration, we will consider inflation as an external process with a characteristic Hubble parameter H.

The mechanism of inflationary production of the bubbles of alternative vacuum is well known Rubin et al. (2000). As a result of repeated quantum fluctuations, the field ψ can be flipped from the region of rolling down to the right minimum to the region of rolling down to the left minimum in some areas of the inflationary Universe. The size of this region is growing during inflation while the ψ field is frozen near the potential maximum. After the end of inflation, the field tends to have one minimum inside the bubble and another minimum outside it. Increasing energy density gradually forms the domain wall (Figure 4) around the bubble.

Several constraints must be imposed on the working model of domain wall production in the considered f(R)-gravity:

1. During cosmological inflation, 4-dimensional space is described by a de Sitter metric with curvature R₄ ≃ 12H², where H is the Hubble parameter. Therefore, the approximation (3) is applicable only for field values ϕ ≡ R_n ≫ R₄ ≃ 12H². From Figure 1 we see that ϕ ∼ 10^–6–10^–4, so to satisfy the constraint we need H ≪ 10^–4.

2. To generate walls via quantum fluctuations of field ψ (near the maximum of potential 2) its slow rolling is required: $\sqrt{{\tilde{V}}^{\prime \prime }({\psi }_{\mathit{max}})}\ll H$. According to Figure 2 we see that $\sqrt{{\tilde{V}}^{\prime \prime }({\psi }_{\mathit{max}})}\sim 10^{-11}$, meaning to satisfy the constraint we need H ≫ 10^–11.

3. Domain walls should not be too dense to avoid dominating the inflaton: ${\epsilon }_{\psi }\ll {\epsilon }_{\inf }\sim H^2{m}_4^2$. From Figure 4 we see that ɛ_ψ ∼ 10^–20, so to satisfy the constraint we need H ≫ 10^–11.

4. The fluctuations of the ψ field during inflation should not be too large to prevent overproduction of the domain walls: δψ = H/2π ≪ ψ. As one can see from Figure 2, ψ ∼ 10, meaning to satisfy the constraint we need H ≪ 10.

All constraints above are satisfied if the inflation has the characteristic scale 10^–11 ≪ H ≪ 10^–4. Here m₄ = 5.75 for n = 6 according to (6). All estimations are given in the Einstein frame and if the dimensionality is not explicitly specified, all calculations are carried out in m_D ≡ 1 units.

As a physically observable example, the Jordan frame is often considered for instances in which it is possible to manipulate the 4-dimensional Planck scale M₄ = Ω(ϕ_min)m₄ by adjusting the size of extra space. Following on from this, we will transform the final physical results into the Jordan frame. Cosmological inflation should be described in a physically observable frame—that is the Jordan frame (denoted by the index J):

$S_{\text{inf}}^J=\int d^{4}x\sqrt{-g_4^J}\left[\frac{1}{2}{\left(\partial {\chi }^J\right)}^2-U^J\left({\chi }^J\right)\right],(16)$

where χ is the inflaton whose potential U(χ) determines the Hubble parameter $H\sim \sqrt{GU(\chi )}$ during the inflation. The constraint above on H has been checked for the inflation in the Einstein frame (denote it by the index E). The transition to it from (16) is known Domènech and Sasaki (2015); Fabris et al. (2020):

$g_{\mu \nu }^J={\mathrm{\Omega }}^{-2}{g}_{\mu \nu }^E,\text{where}{\mathrm{\Omega }}^2=e^{n\beta \left(\varphi \right)}|f^{\prime }\left(\varphi \right)|.(17)$

Substituting (17) into (16), we obtain the action written in Einstein frame:

$\begin{array}{ll}\hfill S_{\text{inf}}^J& =\int d^{4}x\sqrt{-g_4^E}\left[\frac{1}{2}{\mathrm{\Omega }}^{-2}{\left(\partial {\chi }^J\right)}^2-{\mathrm{\Omega }}^{-4}{U}^J\left({\chi }^J\right)\right]\approx \hfill \\ \hfill & \approx \int d^{4}x\sqrt{-g_4^E}\left[\frac{1}{2}{\left(\partial {\chi }^E\right)}^2-U^E\left({\chi }^E\right)\right]=S_{\text{inf}}^E,\hfill \end{array}(18)$

where transformations of the inflaton χ^E = Ω⁻¹χ^J and its potential U^E = Ω⁻⁴U^J to the Einstein frame are made. Here we use the fact that during inflation the field ϕ is practically frozen (constraint 2) and is in the region of maximum of potential, so the factor Ω(ϕ) can be considered constant and equal Ω ≈ Ω(ϕ_max) ∼Ω(ϕ_min) ∼ 10⁸ for the parameters chosen in Figure 1.

The Hubble parameter for the inflaton χ^E observed in the Einstein frame is related to the Hubble parameter for the χ^J inflaton observed in the Jordan frame as follows:

$H^E\sim \sqrt{G{U}^E\left(\chi \right)}=\sqrt{G{\mathrm{\Omega }}^{-4}{U}^J\left(\chi \right)}\sim {\mathrm{\Omega }}^{-2}{H}^J.(19)$

From this, in accordance with the constraint for H obtained above for the Einstein frame, it follows that H^J > 10⁵ ∼ 10^–4 [M₄] ∼ 10¹⁴ [GeV] at the chosen parameters, which is consistent with the observed data Akrami et al. (2020).

We derived constraints on the inflationary production of domain walls formed in effective field theory. Our next step is to discuss the mechanism of their collapse into primordial black holes.

6 Formation of primordial black holes

During the inflationary stage, the classical motion of the scalar field ψ is frozen—this is determined by the constraint two in Section 5). If there is a seed for the future domain wall it appears during quantum fluctuations (the field jumps to the left slope of the potential in Figure 2). Then, in this place the field values ψ should lie near the potential maximum since the fluctuations are small (constraint four in Section 5). At the end of inflation, the inflaton the Hubble parameter vanishes, and the ψ field begins to rapidly roll from the maximum to the potential minima (to the left minimum, for the inner region of the bubble, and to the right minimum for the outer region). During this roll-off, the energy density σ(t) in the transition region gradually grows up to the value σ calculated in the previous sections. In addition, due to postinflationary expansion, the radius of the region is growing u_w(t) = u₀a(t) also, where u₀ is radius at the end of inflation and a(t) is scale factor. Because of this, the mass of the formed domain wall increases m_w(t) = 4πu_w(t)²σ(t) together with its gravitational radius u_g(t) = 2Gm_w(t). At a certain time, the gravitational radius will cross the entire domain wall u_g (t_*) = u_w (t_*) and a primordial black hole with mass m_w (t_*) will form for a remote observer.

The moment t_* of the crossing of the wall by the gravitational radius in our model happens before it reaches the final energy density σ. This can be seen from the fact that the ratio of the gravitational radius to the size of the wall is greater than unity (assuming that the wall has a final energy density σ)

$\frac{u_g}{u_w}=8\pi G\sigma u_w>m_4^{-2}\sigma \delta \approx 16,(20)$

where the fact that the wall radius is always larger than its thickness u_w(t) > δ is used. The ratio (20) is calculated for the wall parameters obtained in Figure 4 and holds for any model parameters (1) satisfying the set of constraints discussed in Section 5. The wall is formed long before the field rolls to the potential minima. The black hole is formed at the time t_* when the horizon radius u_g is approximately equal to the wall radius u_w. Hence, the mass of the PBH can be estimated as

$M_{\mathit{PBH}}\simeq m_w\left(t_{\ast }\right)\simeq u_g\left(t_{\ast }\right)/2G\simeq u_w\left(t_{\ast }\right)/2G\equiv u_{0}a\left(t_{\ast }\right)/2G.(21)$

All processes described above occur in a very short time interval t_*, which is significantly less than the characteristic time of the field ψ roll-off to the minimum of potential, $t_{*}<{\tau }_{\psi }\sim {\sqrt{{\tilde{V}}^{\prime \prime }({\psi }_{\text{max}})}}^{-1}\approx 10^4[M_4^{-1}]$. This time in our model is less than the inflation time ${\tau }_{\text{inf}}\approx 60H^{-1}\sim 10^6[M_4^{-1}]$. Therefore, the roll-off of field ψ process occurs at the reheating stage (as for the inflaton), the scale factor at which we can approximately Lazarides (2002) consider $a(t_{\ast })={\left(({\tau }_{\text{inf}}+t_{\ast })/{\tau }_{\text{inf}}\right)}^{\frac{\nu +2}{3\nu }}<{\left(({\tau }_{\text{inf}}+{\tau }_{\psi })/{\tau }_{\text{inf}}\right)}^{\frac{\nu +2}{3\nu }}\sim {\left(1+10^{-1}\right)}^{\frac{\nu +2}{3\nu }}\sim 1$, where ν is the index of degree in the inflaton potential. It means that the time interval t_* is very short and one can neglect the post-inflationary expansion.

The radius u₀ is determined by the moment of inflationary generation of the fluctuation, leading to the subsequent formation of the wall. If the fluctuation is formed at the e-fold N of total number N_inf, then its size by the end of inflation will be $u_0=H_{\text{inf}}^{-1}{e}^{N_{\text{inf}}-N}$. For example, suppose that the fluctuation of the ψ field leading to the wall formation occurred at N = 25 e-fold of N_inf = 60 and the inflation scale is H ∼ 10¹⁴ GeV (which are characteristic parameters Akrami et al. (2020)) a PBH of mass $M_{\mathit{PBH}}\sim u_w/2G\sim u_0/2G=4\pi M_4^2{H}_{\text{inf}}^{-1}{e}^{35}\sim 10^{41}[GeV]\sim 10^{-16}[M_{\odot }]$ is then formed immediately after the inflation ends. During further cosmological evolution in the reheating stage, the PBH will gain mass as a result of accretion. Since such black holes are formed in the super-dense Universe, immediately after the end of inflation, their masses can reach many solar masses.

The dynamics of the accretion process are rather complicated and depend on the properties of the reheating stage Carr et al. (2018). There are practically no observational data, and properties of that epoch could be calculated via chosen inflation mechanism. The Universe expansion rate at this time is much slower compared to inflation but much faster compared to today. There is still no solution without singularities for accretion problems in expanding universes (Faraoni and Jacques (2007)), especially in high density examples. The properties of the accretion determine the final mass spectrum of PBHs. Therefore, obtaining a final PBH mass spectrum and studying its properties are separate works that should be explored in future research.

Calculation of the initial (post-inflationary) mass spectrum N(M) of the above described PBH is reduced to the calculation of the size spectrum N(u) for the ψ field fluctuations generated at the inflationary stage. It can be done by substituting the connection u ≡ u_w = 2 GM. The spectrum N(u) is calculated in such works as Belotsky et al. (2019); Nikulin et al. (2017, 2019). They investigated the dependence of this spectrum on inflation parameters and the initial field value ψ₀, with which the modern horizon appears. In these works, it was shown that the width of the spectrum, the characteristic masses, and the total number of PBHs strongly depend on the choice of ψ₀. We will not investigate the spectrum in the present paper, since its goal was to demonstrate a new mechanism for PBH formation, arising in f(R)-gravity with the extra dimensions.

7 Conclusion

This article discusses a model of multidimensional f(R)-gravity that gives rise to the formation of primordial black holes at an early stage of cosmological evolution. For a remote observer in the Jordan frame, the formation of such black holes can be interpreted as a manifestation of non-trivial gravitational dynamics of multidimensional space after cosmological inflation.

In this paper, the dynamics of the extra dimensional metric are reduced to the dynamics of the effective scalar field. The domain wall formation occurs just after the completion of cosmological inflation. We show that PBH nucleation is inevitable in our model for that range of parameters of f(R)-gravity, which both satisfies cosmological constraints and leads to a non-trivial effective scalar field potential. The mechanism of collapse into primordial black holes has been studied in Belotsky et al. (2019); Nikulin et al. (2017, 2019).

Primordial black holes arising in the developed mechanism appear at the reheating stage and then actively grow due to accretion. In addition, the formation of several domain walls under one gravitational radius is possible, which modifies our mechanism. These complex processes affect the formation of the final mass spectrum of primordial black holes and will be considered by us in future works.

The cosmological consequences of multidimensional f(R)-gravity are quite rich and lead to a variety of exotic observational manifestations. As our study shows, the widely discussed primordial black holes are such manifestations. Therefore, the confirmation of the primordial origin of some classes of black holes may be evidence in favor of the existence of extra dimensions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The problem of this paper was formulated by SR. VN was responsible for calculating the inflationary constraints on the model and PBH properties. MK calculated the effective potential and domain wall properties.

Funding

The work of VN and MK was supported by the MEPhI Program Priority 2030. The work of SR was supported by the Kazan Federal University Strategic Academic Leadership Program.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In this paper we use the following conventions for the Riemann curvature tensor $R_{\mu \nu \alpha }^{\beta }={\partial }_{\alpha }{\mathrm{\Gamma }}_{\mu \nu }^{\beta }-{\partial }_{\nu }{\mathrm{\Gamma }}_{\mu \alpha }^{\beta }+{\mathrm{\Gamma }}_{\sigma \alpha }^{\beta }{\mathrm{\Gamma }}_{\nu \mu }^{\sigma }-{\mathrm{\Gamma }}_{\sigma \nu }^{\beta }{\mathrm{\Gamma }}_{\mu \alpha }^{\sigma }$, and the Ricci tensor is defined as follows: $R_{\mu \nu }=R_{\mu \alpha \nu }^{\alpha }$.

References

Akrami, Y., Arroja, F., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2020). Planck2018 results. Astron. Astrophys. 641, A10. doi:10.1051/0004-6361/201833887

CrossRef Full Text | Google Scholar

Bahamonde, S., Odintsov, S. D., Oikonomou, V., and Tretyakov, P. V. (2017). Deceleration versus acceleration universe in different frames of F(R) gravity. Phys. Lett. B 766, 225–230. doi:10.1016/j.physletb.2017.01.012

CrossRef Full Text | Google Scholar

Belotsky, K. M., Dokuchaev, V. I., Eroshenko, Y. N., Esipova, E. A., Khlopov, M. Y., Khromykh, L. A., et al. (2019). Clusters of primordial black holes. Eur. Phys. J. C 79, 246. doi:10.1140/epjc/s10052-019-6741-4

CrossRef Full Text | Google Scholar

Bronnikov, K. A., Konoplich, R. V., and Rubin, S. G. (2007). The diversity of universes created by pure gravity. Cl. Quantum Gravity 24, 1261–1277. doi:10.1088/0264-9381/24/5/011

CrossRef Full Text | Google Scholar

Bronnikov, K. A., Popov, A. A., and Rubin, S. G. (2020). Inhomogeneous compact extra dimensions and de sitter cosmology. Eur. Phys. J. C 80, 970. doi:10.1140/epjc/s10052-020-08547-x

CrossRef Full Text | Google Scholar

K. A. Bronnikov, and S. G. Rubin (Editors) (2013). Black holes, cosmology and extra dimensions. doi:10.1142/9789814374217

CrossRef Full Text | Google Scholar

Bronnikov, K. A., and Rubin, S. G. (2021). Local regions with expanding extra dimensions. Physics 3, 781–789. doi:10.3390/physics3030048

CrossRef Full Text | Google Scholar

Bronnikov, K. A., and Rubin, S. G. (2006). Self-stabilization of extra dimensions. Phys. Rev. D. 73, 124019. doi:10.1103/PhysRevD.73.124019

CrossRef Full Text | Google Scholar

Bronnikov, K., Budaev, R., Grobov, A., Dmitriev, A., and Rubin, S. G. (2017). Inhomogeneous compact extra dimensions. J. Cosmol. Astropart. Phys., 001. doi:10.1088/1475-7516/2017/10/001

CrossRef Full Text | Google Scholar

Capozziello, S., and De Laurentis, M. (2011). Extended theories of gravity. Phys. Rep. 509, 167–321. doi:10.1016/j.physrep.2011.09.003

CrossRef Full Text | Google Scholar

Capozziello, S., and Laurentis, M. D. (2012). The dark matter problem from f(R) gravity viewpoint. Ann. Phys. 524, 545–578. doi:10.1002/andp.201200109

CrossRef Full Text | Google Scholar

Capozziello, S., Martin-Moruno, P., and Rubano, C. (2010). Physical non-equivalence of the Jordan and einstein frames. Phys. Lett. B 689, 117–121. doi:10.1016/j.physletb.2010.04.058

CrossRef Full Text | Google Scholar

Carr, B., Dimopoulos, K., Owen, C., and Tenkanen, T. (2018). Primordial black hole formation during slow reheating after inflation. Phys. Rev. D. 97, 123535. doi:10.1103/PhysRevD.97.123535

CrossRef Full Text | Google Scholar

Carr, B., and Kuhnel, F. (2021). Primordial black holes as dark matter candidates. arXiv preprint arXiv:2110.02821. doi:10.48550/arXiv.2110.02821

CrossRef Full Text | Google Scholar

Carroll, S. M., Geddes, J., Hoffman, M. B., and Wald, R. M. (2002). Classical stabilization of homogeneous extra dimensions. Phys. Rev. D. 66, 024036. doi:10.1103/physrevd.66.024036

CrossRef Full Text | Google Scholar

Cotner, E., Kusenko, A., Sasaki, M., and Takhistov, V. (2019). Analytic description of primordial black hole formation from scalar field fragmentation. J. Cosmol. Astropart. Phys. 077, 077. doi:10.1088/1475-7516/2019/10/077

CrossRef Full Text | Google Scholar

De Felice, A., and Tsujikawa, S. (2010). f(R) theories. Living Rev. Relativ. 13, 3. doi:10.12942/lrr-2010-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Deutschmann, N., Flacke, T., and Kim, J. S. (2017). Current LHC constraints on minimal universal extra dimensions. Phys. Lett. B 771, 515–520. doi:10.1016/J.PHYSLETB.2017.06.004

CrossRef Full Text | Google Scholar

Dienes, K. R., Dudas, E., and Gherghetta, T. (1999). Grand unification at intermediate mass scales through extra dimensions. Nucl. Phys. B 537, 47–108. doi:10.1016/S0550-3213(98)00669-5

CrossRef Full Text | Google Scholar

Dokuchaev, V., Eroshenko, Y. N., and Rubin, S. (2007). Origin of supermassive black holes. arXiv preprint arXiv:0709. doi:10.48550/arXiv.0709.00700070)

CrossRef Full Text | Google Scholar

Dolgov, A. D. (2018). Massive and supermassive black holes in the contemporary and early universe and problems in cosmology and astrophysics. Phys. -Usp. 61, 115–132. doi:10.3367/ufne.2017.06.038153

CrossRef Full Text | Google Scholar

Domènech, G., and Sasaki, M. (2015). Conformal frame dependence of inflation. J. Cosmol. Astropart. Phys., 022. doi:10.1088/1475-7516/2015/04/022

CrossRef Full Text | Google Scholar

Escrivà, A. (2022). Pbh formation from spherically symmetric hydrodynamical perturbations: A review. Universe 8, 66. doi:10.3390/universe8020066

CrossRef Full Text | Google Scholar

Fabris, J. C., Popov, A. A., and Rubin, S. G. (2020). Multidimensional gravity with higher derivatives and inflation. Phys. Lett. B 806, 135458. doi:10.1016/j.physletb.2020.135458

CrossRef Full Text | Google Scholar

Falomo, R., Bettoni, D., Karhunen, K., Kotilainen, J. K., and Uslenghi, M. (2014). Low-redshift quasars in the sloan digital sky survey stripe 82. The host galaxies. Mon. Not. R. Astron. Soc. 440, 476–493. doi:10.1093/mnras/stu283

CrossRef Full Text | Google Scholar

Faraoni, V., and Jacques, A. (2007). Cosmological expansion and local physics. Phys. Rev. D. 76, 063510. doi:10.1103/physrevd.76.063510

CrossRef Full Text | Google Scholar

Feruglio, F. (2004). Extra dimensions in particle physics. Eur. Phys. J. C 33, s114–s128. doi:10.1140/epjcd/s2004-03-1699-8

CrossRef Full Text | Google Scholar

Garriga, J., Vilenkin, A., and Zhang, J. (2016). Black holes and the multiverse. J. Cosmol. Astropart. Phys., 064. doi:10.1088/1475-7516/2016/02/064

CrossRef Full Text | Google Scholar

Grobov, A. V., and Rubin, S. G. (2013). Higgs-like field and extra dimensions. Int. J. Theor. Phys. (Dordr). 52, 4283–4292. doi:10.1007/s10773-013-1742-9

CrossRef Full Text | Google Scholar

Hall, L., and Nomura, Y. (2001). Gauge unification in higher dimensions. Phys. Rev. D. 64, 055003. doi:10.1103/PhysRevD.64.055003

CrossRef Full Text | Google Scholar

Hewett, J., and Spiropulu, M. (2002). Particle physics probes of extra spacetime dimensions. Annu. Rev. Nucl. Part. Sci. 52, 397–424. doi:10.1146/annurev.nucl.52.050102.090706

CrossRef Full Text | Google Scholar

Lazarides, G. (2002). “Inflationary cosmology,” in Cosmological crossroads (Springer), 351–391. doi:10.48550/arXiv.hep-ph/0111328

CrossRef Full Text | Google Scholar

Liu, J., Guo, Z.-K., and Cai, R.-G. (2020). Primordial black holes from cosmic domain walls. Phys. Rev. D. 101, 023513. doi:10.1103/physrevd.101.023513

CrossRef Full Text | Google Scholar

Luca, V. D., Franciolini, G., Pani, P., and Riotto, A. (2020). Primordial black holes confront ligo/virgo data: Current situation. J. Cosmol. Astropart. Phys. 2020, 044. doi:10.1088/1475-7516/2020/06/044

CrossRef Full Text | Google Scholar

Lyakhova, Y., Popov, A. A., and Rubin, S. G. (2018). Classical evolution of subspaces. Eur. Phys. J. C 78, 764–777. doi:10.1140/epjc/s10052-018-6251-9

CrossRef Full Text | Google Scholar

Nikulin, V., Grobov, A., and Rubin, S. (2017).A mechanism for protogalaxies nuclei formation from primordial black holes clusters. In Journal of Physics: Conference Series, 934. IOP Publishing. 012040. doi:10.1088/1742-6596/934/1/012040

CrossRef Full Text | Google Scholar

Nikulin, V., Rubin, S., and Khromykh, L. (2019). Formation of primordial black hole clusters from phase transitions in the early universe. Bull. Lebedev Phys. Inst. 46, 97–99. doi:10.3103/S1068335619030060

CrossRef Full Text | Google Scholar

Nojiri, S., and Odintsov, S. D. (2011). Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 505, 59–144. doi:10.1016/j.physrep.2011.04.001

CrossRef Full Text | Google Scholar

Nojiri, S., Odintsov, S., and Oikonomou, V. (2017). Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 692, 1–104. doi:10.1016/j.physrep.2017.06.001

CrossRef Full Text | Google Scholar

Petriakova, P., and Rubin, S. G. (2022). Self-tuning inflation, 04647. arXiv preprint arXiv:2204. doi:10.48550/arXiv.2204.04647

CrossRef Full Text | Google Scholar

Rador, T. (2007). Acceleration of the Universe via f(R) gravities and the stability of extra dimensions. Phys. Rev. D. 75, 064033. doi:10.1103/physrevd.75.064033

CrossRef Full Text | Google Scholar

Rubin, S., Khlopov, M., and Sakharov, A. (2000). Primordial black holes from non-equilibrium second order phase transition. Grav. Cosmol. 6. doi:10.48550/arXiv.hep-ph/0005271

CrossRef Full Text | Google Scholar

Sakharov, A. S., Eroshenko, Y. N., and Rubin, S. G. (2021). Looking at the NANOGrav signal through the anthropic window of axionlike particles. Phys. Rev. D. 104, 043005. doi:10.1103/PhysRevD.104.043005

CrossRef Full Text | Google Scholar

Starobinsky, A. A. (1980). A new type of isotropic cosmological models without singularity. Phys. Lett. B B91, 99–102. doi:10.1016/0370-2693(80)90670-X

CrossRef Full Text | Google Scholar

The Ligo Scientific Collaboration, T. V. C., Abbott, R., Abbott, T., Abraham, S., Acernese, F., Ackley, K., et al. (2019). Search for intermediate mass black hole binaries in the first and second observing runs of the advanced ligo and virgo network. Phys. Rev. D. 100, 064064. doi:10.1103/physrevd.100.064064

CrossRef Full Text | Google Scholar

Vilenkin, A. (1985). Classical and quantum cosmology of the starobinsky inflationary model. Phys. Rev. D. 32, 2511–2521. doi:10.1103/PhysRevD.32.2511

PubMed Abstract | CrossRef Full Text | Google Scholar

Vilenkin, A., and Shellard, E. P. S. (1994). Cosmic strings and other topological defects. Cambridge University Press.

Google Scholar

Witten, E. (1982). Instability of the kaluza-klein vacuum. Nucl. Phys. B 195, 481–492. doi:10.1016/0550-3213(82)90007-4

CrossRef Full Text | Google Scholar