
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci., 12 July 2022
Sec. Space Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.919755
This article is part of the Research TopicNew Challenges in Space Plasma Physics: Open Questions and Future Mission ConceptsView all 13 articles
To obtain measurements that will address some outstanding questions about the properties and origin of the magnetic and plasma structure of the heliosphere a simple single-spacecraft mission at one AU is outlined. By focusing on large-geometric-factor measurements of particles (protons, alphas, heavy ions, and electrons) several longstanding questions can be answered. The key objectives of the large-geometric-factor measurements are lower noise and faster time resolution. Much of the focus is on critical measurements associated with the ubiquitous current sheets (directional discontinuities) of the solar wind that provide information about the origin and evolution of the current sheets and about the origin and evolution of the magnetic and plasma structures that they define.
A simple single-spacecraft mission at one AU that focuses on large-geometric-factor (effective large collecting area) ion and electron measurements could greatly advance the understanding of the heliosphere, specifically on two outstanding questions in heliospheric physics: (A) What is the magnetic and plasma structure of the heliosphere? and (B) Where does that structure come from?
It is critical to unambiguously detect subtle changes in the particle properties (protons, alphas, heavy ions, electrons) across solar-wind directional discontinuities (current sheets). Focusing on obtaining accurate measurements of the changes in the ion and electron properties across solar-wind discontinuities, the mission would determine 1) which discontinuities are fossils from the Sun and which discontinuities could have been created in the solar wind away from the Sun, 2) which discontinuities in the solar wind are rotational discontinuities (propagating Alfvénic field kinks) and which are tangential discontinuities (plasma boundaries), and 3) the fingerprints of discontinuity-evolution processes acting in the solar wind away from the Sun.
Making these determinations about solar-wind discontinuities is important because these determinations 1) provide remote information about processes acting in the solar corona, 2) provide information about the nature and origin of the magnetic ductwork that transports energetic particles and solar heat flux, 3) provide an assessment as to the impact of turbulence on the evolution of the solar wind and the heliospheric structure, 4) provide information about the origin and evolution of the solar wind from an individual-flux-tube point of view, and 5) connect the intermittent driving of the Earth’s magnetosphere-ionosphere system to structure in the corona and to processes occurring in the solar wind.
In this note we will make the case for lower-noise and higher-time-resolution measurements of ions and electrons in the solar wind at one AU. Basically, the push will be to field instruments with larger geometric factors to obtain improved particle count rates resulting in lower statistical noise for ion and electron measurements. Of particular interest will be heavy-ion spectrometers that can measure ion-charge-state ratios with higher time resolution than present spectrometers can.
The measurements of interest are high-time-resolution and low-noise measurements of particle boundaries and their association with current sheets. The particle populations of interest are protons, alphas, heavy-ion charge states, core electrons, and the electron strahl.
Vital information about the structure of the heliosphere and the origin of that structure comes from comparing the plasmas on the two sides of a directional discontinuity (current sheet). Note that there are common thin current sheets and there are rarer thick current sheets in the solar wind, the thick current sheets being for example the heliospheric current sheet that separates magnetic sectors of the heliosphere (Smith, 2001) and current sheets associated with the corotating-interaction-region stream interfaces (Borovsky, 2006). The focus here is not on these thick current-sheet structures, but on the ubiquitous thin current sheets of the solar wind. At 1 AU these current sheets have thicknesses on the order of 1,000 km (Siscoe et al., 1968; Vasquez et al., 2007; Borovsky and Steinberg, 2014) as determined using the Taylor hypothesis with each current sheet passing a spacecraft in 1–4 s. The current sheet thicknesses are much larger than the plasma kinetic scales ion gyroradii and ion inertial lengths (Vasquez et al., 2007) so they tend to be stable against Petschek-type collisionless-plasma reconnection. Additionally, the solar wind plasma is everywhere expanding (except across interplanetary shocks), so the strong current sheets will not thin by compression. (But see Lazarian and Vishniac (1999), Artemyev (2008), Zelenyi et al. (2011), Zelenyi et al. (2021), Lazarian et al. (2020) for other ideas about current-sheet reconnection). Solar-wind current sheets pass a spacecraft at a rate of a few per hour, which is about 30,000 per year. (The current sheet collection of Borovsky (2008) was about 10,000 per year, but that collection only selected very strong current sheets). Each current sheet spatially separates two plasmas. A current sheet is characterized by a sudden large change in the direction of the magnetic field from the one plasma to the other. Examination of the spacings and orientations of the current sheets in the solar wind leads to a “flux-tube spaghetti” picture of the heliospheric magnetic structure with the magnetic flux tubes meandering along the Parker-spiral direction (McCracken and Ness, 1966; Michel, 1967; Bruno et al., 2001; Borovsky, 2008, Borovsky, 2010a; Greco et al., 2008; Pecora et al., 2019). The spacings and orientations of the current sheets in the solar wind are consistent with a flux-tube spaghetti picture of the heliospheric magnetic structure and this will be the picture used in this manuscript. A depiction of the background flux-tube heliosphere appears in Figure 1. In the spaghetti, large temporal changes in the magnetic-field direction are seen when a spacecraft crosses a current sheet and smaller angular wiggles of the magnetic-field direction are seen within the flux tubes (Bruno et al., 2001; Borovsky, 2008).

FIGURE 1. A simple sketch (to scale) of the background heliospheric structure that forms a magnetic ductwork for the transport of energetic particles and that produces the intermittent driving of the Earth’s magnetosphere. In the sketch no fast-versus-slow wind is depicted and no ejecta is depicted.
Besides the flux-tube-spaghetti depiction, there are other depictions of the magnetic structure of the solar wind, e.g., an admixture of flux tubes, plasmoids (flux ropes), magnetic islands, and localized magnetic structures (e.g., Tamano, 1991; Khabarova et al., 2015; Khabarova et al., 2016; Adhikari et al., 2019; Malandraki et al., 2019; Khabarova et al., 2020), depicted in Figure 24c of Khabarova et al. (2021). Flux ropes and plasma blobs are important constituents of the very slow sector-reversal-region plasma originating from coronal streamer stalks (Wang et al., 1999; Sheeley and Rouillard, 2010; Viall et al., 2010; Viall and Vourlidas, 2015; Kepko et al., 2016; Di Matteo et al., 2019). Relatedly, sector-reversal-region plasma at one AU tends to have magnetic fields that are not Parker-spiral oriented (Borovsky, 2020a) and tends to have a weak electron strahl (Borovsky, 2021b), both being indicative of impulsive emission of plasma from the Sun with poor magnetic connections back to the Sun.
The origin of this flux-tube magnetic structure (and the intermittent driving of the Earth) is still an outstanding issue (Neugebauer and Giacalone, 2010, Neugebauer and Giacalone, 2015; Li and Qin, 2011; Owens et al., 2011; Telloni et al., 2016; Tu et al., 2016; Viall and Borovsky, 2020). The origins might involve fossil magnetic flux tubes from the corona (McCracken and Ness, 1966; Borovsky, 2008, Borovsky, 2016), current sheets created by MHD turbulence in the solar wind (Greco et al., 2009; Zhdankin et al., 2012; Vasquez et al., 2013), evolving Alfvén waves propagating out from the Sun (Tsurutani and Ho, 1999; Vasquez and Hollweg, 1999), or advected pressure-balance structures (Riazantseva et al., 2005a; Zhang et al., 2008; Tu et al., 2016).
Current sheets (directional discontinuities) dominate the magnetic structure of the heliosphere, cellularizing the field and plasma into a spaghetti of tubes, as indicated by the common plasma-property jumps seen when crossing current sheets [cf. Figures 3, 5 of Borovsky (2008)]. These tubes form the magnetic ductwork of the heliosphere that enables the long-distance transport of energetic particles and solar heat flux along magnetic-field lines. This transport ductwork is readily seen in the changes of strahl intensity across current sheets (Gosling et al., 2004a,b; Borovsky, 2020b) and the changes in SEP flux from tube to tube (Trenchi et al., 2013). The current sheets that separate the tubes dominate the Fourier power of the solar wind (Siscoe et al., 1968; Borovsky, 2010b) and current-sheet properties (occurrence distribution, thicknesses, and profiles) determine the details of the Fourier magnetic power spectral density that has been analyzed for decades (Borovsky and Podesta, 2015; Borovsky and Burkholder, 2020). As the spaghetti of flux tubes passes the Earth, the Earth sees sudden changes in the orientation of the solar-wind magnetic field from flux tube to flux tube. The driving of the Earth’s magnetosphere by the solar wind is very sensitive to the orientation (“clock angle”) of the solar wind magnetic field (Komar and Cassak, 2016) so flux tube to flux tube the rate of driving changes, resulting in an temporally on-off driving of the Earth (Borovsky, 2020a). The ultimate cause of this intermittent driving of the Earth is unknown: it could be solar-wind turbulence or it could be coronal magnetic structure.
Early analysis of the background heliospheric magnetic structure and its origin focused on the question of whether current sheets (directional discontinuities) are tangential discontinuities (plasma boundaries) versus rotational discontinuities (propagating field kinks) (e.g., Burlaga and Ness, 1969; Turner and Siscoe, 1971; Neugebauer et al., 1984; Lepping and Behannon, 1986; Soding et al., 2001). To discern whether a directional discontinuity is a rotational discontinuity versus a tangential discontinuity, the focus historically has been 1) to determine the orientation of the current sheet, 2) to determine the local magnetic-field direction, and then 3) to discern by the orientation whether or not the magnetic-field lines are crossing the current sheet. Field lines crossing a current sheet indicates that it is a rotational discontinuity. [Another possibility that could be considered for field lines crossing the current sheet is a “contact discontinuity” (e.g., Burlaga, 1971), however indications are that contact discontinuities cannot persist in collisionless plasmas such as the solar wind (cf. Lapenta and Brackbill, 1996)]. When current sheets are highly oblique to the magnetic-field direction [which multispacecraft measurements indicate that they tend to be (Horbury et al., 2001; Knetter et al., 2003,2004; Riazantseva et al., 2005b,c)] this rotational-versus-tangential determination is difficult and tends to yield ambiguous classifications about rotational versus tangential discontinuities (Neugebauer, 2006; Paschmann et al., 2013; Artemyev et al., 2019; Sonnerup, 2022).
When a spacecraft crosses a current sheet from the plasma on one side of the sheet into the plasma on the other side, often changes other than the direction of the magnetic field can be seen. Current-sheet crossings can exhibit “jumps” in the value of the magnetic-field strength |B|, in the value of the proton and electron number densities np and ne, in the proton temperature Tp, in the proton specific entropy Sp = Tp/np2/3, in the proton-beta βp = 8πnpkBTp/B2, in the core electron temperature Te core, in the intensity of the electron strahl, and in the alpha-to-proton number-density ratio α/p (helium abundance).
An example of this appears in Figure 2 where jumps in the α/p time series at one AU are statistically examined from measurements onboard ACE and separately from measurements onboard WIND (cf. Borovsky, 2020b). The measurements utilized for the α/p number-density ratio were 64-s resolution measurements from ACE SWEPAM (McComas et al., 1998) and 97-s resolution measurements from WIND SWE (Ogilvie et al., 1995; Kasper et al., 2006). Times when distinct changes in the α/p value are seen are collected: to be collected, the changes in α/p must be clearly larger than the “shot noise” of the α/p measurements in the time series. Then the temporal changes Δθ in the direction of the solar wind magnetic field at each spacecraft are calculated in the time series. Figure 2 shows superposed-epoch averages of the temporal-field-change angle Δθ for the two collections of α/p jumps with the zero epoch (t = 0) at the time of each α/p jump. The large values of Δθ at the times of the α/p jumps indicate that these α/p jumps are occurring across current sheets in the solar wind. α/p ion-composition boundaries cannot be created in the solar wind away from the Sun. If the plasma has a uniform ion composition, there are no in situ processes that can change that composition. Hence the observed α/p boundary seen at one AU must have been created in the corona and survived intact advected to one AU. It follows that the current sheets observed at one AU that have α/p jumps across them are fossil current sheets from the corona. These particular current sheets are inconsistent with current-sheet formation by MHD turbulence or by other in situ processes in the solar wind. The current sheets being fossils from the Sun implies also that the magnetic-flux tubes adjacent to the current sheets are magnetic fossils from the corona.
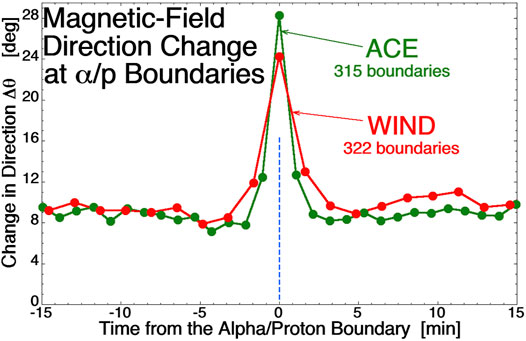
FIGURE 2. Superposed epoch averages of change in the direction of the solar-wind magnetic field with the zero epoch being an ion-composition boundary as identified by a sudden change in the α/p value. The green curve plots the 64-s change in the field direction for 315 α/p boundaries identified with the ACE spacecraft and the red curve plots the 97-s change in the field direction 322 for α/p boundaries identified with the WIND spacecraft.
Note that aside from identifying individual fossil current sheets via α/p boundaries, there are statistical methods that indicate that most of the current sheets of the solar wind are fossils (Borovsky, 2021a): these methods examine the statistical properties of the current-sheet orientations and compare those properties with estimates of the unidirectional compression or rarefaction of the solar-wind plasma (Borovsky and Denton, 2016; Borovsky, 2020e).
The association of jumps in ion and electron parameters at current sheets are in general demonstrated in Figure 3 of Borovsky (2008). The association of proton-specific-entropy jumps with current sheets is shown in Figure 5A of Borovsky (2008). The associations of jumps in the proton number density, the proton specific entropy, and the proton beta with current sheets is shown in Figure 6 of Borovsky (2012). The association of α/p ion-composition boundaries with current sheets is shown in Figure 5B of Borovsky (2008) and examined extensively in Borovsky (2020b). The association of strahl-intensity boundaries with current sheets is discussed in Gosling et al. (2004a,b) and Borovsky (2021b) and studied extensively in Borovsky (2020b). The association of jumps in the electron number density and core-electron temperature with current sheets was studied extensively in Borovsky et al. (2021).
Observing changes in different quantities when crossing a current sheet from one flux tube into another flux tube provides information about the heliospheric magnetic structure and its origins: specifically about the current sheet and about the two adjacent flux tubes. For structure that can be identified as fossil, information about coronal processes might be obtainable. Table 1 summarizes some of the information that is obtained by observing jumps in specific quantities across the solar-wind current sheets.

TABLE 1. Information that is obtained by observing a jump in a specific quantity when crossing a current sheet from flux tube A into flux tube B. (TD = tangential discontinuity and RD = rotational discontinuity).
As noted above, an observable jump in the alpha-to-proton number-density ratio α/p (helium abundance) across a current sheet indicates that current sheet is a fossil (relic) from the solar corona (first row of Table 1). A jump in a heavy-ion charge-state ratio would also indicate a fossil current sheet, however the time resolution of present-day heavy-ion spectrometers is too slow to perform such a measurement across a current sheet. Charge-state-ratio measurements across a current sheet would provide unique insight into the differences in magnetic mapping of the two adjacent flux tubes into the corona and provide information about the magnetic mapping of the corona out into the heliosphere. As noted in Table 1, a change of α/p or the charge-state ratio across a current sheet also indicates that current sheet is a tangential discontinuity, not a rotational discontinuity.
The electron strahl at one AU is a field-aligned population of energetic electrons that are the coronal hot electrons escaping along magnetic field lines out into the heliosphere (Feldman et al., 1976; Pilipp et al., 1987; Maksimovic et al., 2005). This standard picture of the origin of the strahl emanating from the corona is supported by statistical observations of the strahl evolving into the halo-electron population with distance from the Sun (e.g., Stverak et al., 2009), although there are suggestions that strahl-electron populations can be created in situ away from the Sun by whistler waves (Vocks et al., 2005) or by reconnection (Khabarova et al., 2020). Electron-strahl-intensity jumps across current sheets indicate either 1) that the plasma on the two sides of the current sheet magnetically connect to two different regions of the corona (e.g., Gosling et al., 2004a,b; Borovsky, 2021b) or 2) that physical processes in the plasmas on the two sides of the current sheet produce different amounts of scattering of the strahl electrons. Either indication implies that the current sheet is coherent back to the Sun. As noted in the second row of Table 1, a clear conclusion of a current sheet exhibiting a jump in the strahl intensity is that current sheet is not a rotational discontinuity, rather it is a tangential discontinuity (plasma boundary).
Jumps in the core electron temperature Te core from flux tube to flux tube were examined by Borovsky et al. (2021). In exobase models of the solar wind the local value of the core-electron temperature Te core is a direct measure of the local value of the interplanetary electrical potential ϕ with respect to infinity (Feldman et al., 1975; Boldyrev et al., 2020; Moncuquet et al., 2020). As noted in Table 1, differences in Te core across a current sheet imply differences in ϕ in the two flux tubes. Differences in ϕ from tube to tube imply that the exobase model operates independently from one flux tube to another. This leads to a system-science picture of flux tubes (Borovsky, 2021c), each flux tube being an independent system wherein its particle populations (protons, proton beam, alpha particles, heavy ions, core electrons, strahl electrons, and halo electrons) evolve with distance from the Sun independently from the particle populations in adjacent flux tubes. In that picture a spacecraft making measurements from flux tube to flux tube at one AU is seeing independent realizations of system evolution.
General plasma and field variations across current sheets are commonly seen [cf. Figure 3 of Borovsky (2008)]. As noted in the fourth row of Table 1 these jumps are a clear indication that the current sheet is a tangential discontinuity (plasma boundary) and not a rotational discontinuity (propagating Alfvénic kink in the field). These plasma variations often fall into the categorization of “pressure balanced structures” that advect out from the Sun in the solar wind flow (Tu and Marsch, 1993; Riazantseva et al., 2005a; Zhang et al., 2008; Tu et al., 2016). Note that Fourier analysis of variations in the solar-wind magnetic-field strength Bmag and plasma number density n are often interpreted as evidence that there are dynamic fluctuations in the solar wind that have a “compressible” aspect: however, an interpretation that the solar-wind plasma is “inhomogeneous” or “lumpy” is more physically accurate (cf. Borovsky, 2020c).
For understanding the magnetic structure of the heliosphere it is important to discuss the Chandrasekhar dynamical equilibrium (CDE). In the Alfvénic fast wind and in the Alfvénic slow wind the magnetic structure of the heliosphere moves out from the Sun faster than the proton solar wind plasma. The relative speed between the magnetic structure and the proton plasma is about 0.7 vA in the outward-Parker-spiral direction (Borovsky, 2020d; Nemecek et al., 2020). In a temporal block of solar-wind data a single reference frame can be found (the reference frame moving with the magnetic structure) wherein the proton flow has v⊥ ≈ 0 and essentially all flow is parallel to the local magnetic-field direction. [In Borovsky, 2020d this reference frame is found using a genetic algorithm in the data analysis that finds the vector reference frame minimizing arccos (vproton•B)]. Hence, with v⊥ ≈ 0 the magnetic structure moves outward from the Sun without discernable time evolution. This case is discussed in Sect. 7.2 of Parker (1979) with an illustration in Figure 7.1 of Parker (1979) where Parker referred to it as Chandrasekhar’s “dynamical equilibrium solution” (Chandrasekhar, 1961). (See also Birn (1991), Tenerani et al. (2020) for nonlinear V parallel to B equilibrium solutions). Essentially, a nonlinear tangle of magnetic field will propagate through a plasma without evolution. For flux tubes in a CDE spaghetti, a vector jump in the proton flow velocity Δv is seen across each current sheet owing to the sudden rotation of the magnetic-field direction and the proton flow being everywhere parallel to the local field direction. As noted in the last row of Table 1, for those vector velocity jumps Δv and vector magnetic-field jumps ΔB in a CDE it is the case that (Δv•ΔB)/(|Δv||ΔB|) ≈ 1 and (Δv × ΔB)/(|Δv||ΔB|) ≈ 0.
Owing to “shot noise” in the measurement time series, only jumps in the values of measured quantities that are larger than the measurement noise level can be confidently identified. Three examples of the sizes of changes in the solar wind particle properties that can be confidently identified have appeared in the literature.
For the study of α/p number-density-ratio changes in the solar wind at one AU (Borovsky, 2020b) only changes in the ratio that were larger than about 25% of the α/p value could be identified in either the ACE SWEPAM measurements or the WIND SWE measurements (cf. Figure 1 of Borovsky (2020b)). With the faster, multi-head BMSW instrument on the Spektr-R spacecraft jumps in the α/p ratio that are smaller than 25% could probably be identified (e.g., Safrankova et al., 2013; Zastenker et al., 2013), however the Spektr-R spacecraft does not have a magnetometer to correlate the α/p ion-composition jumps with current sheets.
For the study of core-electron-temperature changes in the solar wind, changes of Te core that were larger than about 1 eV could be confidently identified (cf. Figure 5B of Borovsky et al., 2021).
In the study of electron-strahl-intensity changes in the solar wind, changes in the flux of the electron strahl that were greater than about 25% of the flux value could be identified with confidence (cf. Figure 2 of Borovsky, 2020b).
Faster and lower-noise measurements can be obtained with improved particle instrumentation aimed at higher particle count rates via 1) larger geometric factors and 2) multi-head instruments that eliminate energy sweeps. This would enable smaller changes in the ion and electron properties of the solar wind to be confidently identified, enabling the analysis of a much larger fraction of the current sheets of the solar wind to be analyzed and assessed according to Table 1.
The need for larger-geometric-factor heavy-ion spectrometers is particularly acute. Present-day spectrometers with time resolutions of a fraction of an hour have proven very useful for studying the large-scale structure of the solar wind and its origin from the various large-scale regions of the solar corona like coronal holes versus streamer belts versus ejecta (e.g., Geiss et al., 1995; Wimmer-Schweingruber et al., 1997; Zurbuchen et al., 1999; Burton et al., 1999; von Steiger et al., 2001; Zhao et al., 2009) and for studying the heliospheric-plasma-sheet region (Simunac et al., 2012) and large-scale “microstreams” and plumes in coronal-hole-origin plasma (von Steiger et al., 1999; Neugebauer, 2012). Here, with higher time resolution we are calling for heavy-ion spectrometers to be used to study the finer-scale magnetic structure of the heliosphere and the coronal physical processes creating that structure: i.e., flux-tube to flux-tube measurements in the solar wind at one AU that may correspond to loop-to-loop variations in the solar corona. For heavy-ion spectrometers to be useful for this, time resolutions of 1 min or better are critical.
For particle-counting instruments the combination of lower noise and higher time resolution is difficult, with poorer counting statistics being a consequence of shorter measuring intervals. For the solar wind there is an argument that higher-frequency fluctuations have smaller amplitudes than lower-frequency fluctuations, making the higher-time-resolution measurements need even more accuracy and lower noise. That argument is likely false, and it is addressed in the Appendix.
Some specific measurement needs to better evaluate Table 1 are discussed and the resulting improvements to our knowledge are outlined. In all cases lower-noise measurements are needed to be able to locate subtle but distinct changes in the levels of the measurements and measure tube-to-tube variations in particle properties. For this lower-noise measurements with cadences of a fraction of a minute will suffice.
Note that any measurement improvement will lead to progress and lower-noise measurements will enable the exploration of solar wind features that were hidden in the shot noise of the present-day measurements.
Heavy-Ion Charge States: As stated above, time resolutions of about 1 min or better are needed for heavy-ion charge-state ratios. To confidently locate a boundary, several data points are needed on each side of a jump in the charge-state ratio, and of course the jump must be larger than the measurement shot noise. Perhaps designing spectrometers than concentrate their measurement time on specific heavy-ion charge states (e.g., O7+/O6+ or C6+/C5+ or C6+/C4+) would enable the needed faster-yet-low-noise measurements. The proper charge-state measurements would not only identify what is a magnetic fossil at one AU, but perhaps where in the corona it came from and how it was made.
Alpha-to-Proton Number-Density Ratios: α/p ratios (helium abundance) are available at present with fast time resolution at one AU, but in the present data sets the measurement shot noise is very large. Improved geometric factors to lower the shot noise would greatly enhance the ability to identify current sheets that are definitely fossils from the corona. In the count-rate data analysis, sacrificing the time resolution to integrate the count-rates longer to lower the shot noise is also a clear option for the analysis of jumps across current sheets. Reading the changes in α/p from one fossil flux tube to the next might provide information about the coronal origins of the two flux tubes, if the physics driving the solar-wind α/p helium abundance can be sorted out (e.g., Wang, 2008, 2016; Byhring, 2011; McIntosh et al., 2011; Rakowski and Laming, 2012; Fu et al., 2018).
Proton Flow-Velocity Vectors: In analyzing the evolution (or not) of CDEs, it is critical to be able to measure the proton-flow vector relative to the magnetic-field direction. We are looking for cases where v⊥ ≈ 0 in the reference frame of the magnetic structure in the presence of a large value of v|| in that reference frame. The main source of error in v⊥ is the fact that the magnetic-field direction at the spacecraft changes during the time interval when a flow measurement is made. An analysis of a CDE in Figure 3 of Borovsky (2020d) found that the rms change in the field direction during a 3-s proton measurement was 4.8o; if this 4.8o is taken as the uncertainty in the magnetic-field direction then the rms v⊥ value of 5.2 km/s for that CDE is entirely consistent with perpendicular-versus-parallel orientation uncertainty for the observed v|| of 75 km/s. Hence, the v⊥ measurements in the CDE in Borovsky (2020d) were consistent with the noise level in the velocity measurements. To fix this difficulty, either 1) accurate proton measurements that are much faster than 3 s must be made or 2) the moving magnetic-field orientation during the proton measurement interval must be accounted for in the proton-count-rate data analysis. More accurate measurements of the proton flow vector will also yield more-accurate third-order moment calculations of solar-wind heating rates (e.g., Sorriso-Valvo et al., 2007; MacBride et al., 2008; Podesta et al., 2009; Smith et al., 2009). Third-order moments are products of inward- and outward-propagating Elsässer modes: if in the reference frame moving outward with the magnetic structure v⊥ = 0 then the inward-propagating Elsässer mode has an amplitude of zero and the third-order moment vanishes. (See also Wang et al. (2018) for arguments that observed inward Elsässer modes may be measurement noise).
General Plasma Parameters: Lower-noise measurements of general plasma parameters like number density, temperature, and specific entropy would enable the identification of more tangential discontinuities. Higher-time-resolution (and lower-noise) measurements of typical plasma parameters such as number density, temperature, particle pressure, and proton flow velocity would enable current sheets to be well resolved in quantities other than B. Current sheets are typically ∼1,000 km thick, and so resolution considerably better than 1-s is desirable. If current sheets and the co-located plasma boundaries could both be well resolved so that their spatial profiles could be compared, then the door would be opened to the study of evolutionary processes such as particle diffusion, resistivity, and viscosity to learn how and why current-sheet and plasma-boundary thicknesses evolve with distance from the Sun. There are also evolutionary processes for current sheets related to plasma expansion and compression (e.g., Schindler and Birn, 2002; Schindler and Hesse, 2008, Schindler and Hesse, 2010): these result in fine-scale structuring of the current sheet profile. Higher-resolution plasma measurements may open the way to investigating the fine-scale fingerprints of such processes. The higher-resolution plasma measurements would also make possible new studies about the processes that create and evolve magnetic holes in the solar wind (Turner et al., 1977; Winterhalter et al., 2000; Neugebauer et al., 2001).
Total Particle Pressures: Accurate fast measures of ion and electron total particle pressures would enable new studies of the true compressibility in the solar wind and new studies about pressure-balance structures in the solar wind.
Strahl Intensities: Faster and lower-noise measurements of strahl intensities at one AU would enable the identification of more tangential discontinuities and of more current sheets that are coherent back to the Sun. The energetic-electron strahl moving out from the Sun (and the backscattered strahl moving back toward the Sun) both provide very unique information about the structure of the heliosphere. Whereas the proton plasma and the magnetic-field structure seen at one AU left the corona ∼100 h ago, the strahl measured at one AU left the Sun only a few hours ago: in that time difference there could be changes in the magnetic connection of one AU into the corona that the strahl can uncover. Note that strahl measurements suffer from the same magnetic-field-direction changes during a measurement interval of the electron distribution function as do the proton-velocity-vector measurements.
To make progress analyzing the heliospheric, structure measurements of ion and electron properties that are low noise with appropriate time resolutions are needed. For evaluating current sheets (as in Table 1) lower-noise measurements with time resolutions of a fraction of a minute will suffice. If time resolutions of less than 1-s with low noise can be obtained, then the fingerprints of current-sheet evolutionary processes can be obtained.
An overview of the state of the art of particle instruments appears in Table 2. For some desired measurement quantities (e.g., heavy-ion charge-state ratios) the state of the art will need to be exceeded.

TABLE 2. The current state of the art in ion and electron instrumentation. All are ESA based except the faraday cups of BMSW.
To simultaneously satisfy the need for higher time resolution and high signal to noise, instruments must have higher effective collecting areas, typically called geometric factors. In instruments with curved plate electrostatic analyzers (ESAs), the geometric factor includes effects from both the physical size of the instrument and detectors, as well as electrostatic effects, known as ion optics. These include steering, focusing, and transmission through the instrument much in the same way as photons through a telescope, hence the use of the word “optics”. Increasing the geometric factor is as simple as increasing the size of the instrument aperture and ion optical flight path through the instrument. However, there is a key trade off: the energy resolution of the instrument is reduced as the spacing between ESA plates is increased. Energy resolution fundamentally determines the accuracy of the energy spectrum measured by any ion instrument since if effectively determines the uncertainty in the measurement. For ion composition instruments, energy resolution propagates into time of flight (TOF) uncertainty. For charge-resolving composition (TOF-energy) instruments, it also propagates into the uncertainly in the residual energy measurement (ESSD) on the solid-state detectors (SSDs), the intrinsic uncertainty in the SSD energy measurement typically makes the ESA energy resolution negligible. Larger TOF uncertainty affects the ability to identify individual charge states, which is typically done from peaks in TOF-ESSD, as well as suitability for addressing more general problems in plasma physics. As such, general purpose instruments typically need high energy resolutions, ideally 5%–10% for ion instruments and 10%–15% for electron instruments, fundamentally limiting ability to increase geometric factor.
There are several approaches to remove this limitation. The first is to simply add ESA duplicate ESA channels either through multiple copies of full sensor heads or through sensors that incorporate multiple ESAs. The current standard in high time resolution and high signal to noise is the Fast Plasma Investigation (FPI) instrument suite on MMS (Pollock et al., 2016). It employs 8 sensors heads per spacecraft for both ions and electrons, 16 total. There are 4 instruments for each species as each has dual sensor heads. For this primarily magnetospheric instrument, this arrangement allows sampling of many directions simultaneously, at a much higher cadence than would be possible by relying on spacecraft spin alone. While designed primarily for high time resolution, this design also increases the effective geometric factor for each species by a factor of 8. This represents one extreme, applicable only where resources (e.g., mass, power and budget) are abundant. The other extreme is also very straightforward: simply accept lower energy resolutions to increase geometric factor. For example, decreasing the energy resolution by two gives a two-fold increase in geometric factor due to the increase in the energy pass band. For science questions that can be addressed primarily through moments of the particle velocity distribution, i.e., density, velocity and temperature, this might not be a serious limitation. Additional improvements in time resolution can be achieved by limiting the energy range of the instrument. For solar wind heavy ions, limiting the speed range to 1,100 km/s and mass per charge (m/q) to a maximum of Fe6+ (9.33) requires E/q stepping only up to 15 keV/e. The current state of the art Heavy Ion Sensor (HIS) on Solar Orbiter (Owen et al., 2020) goes to much higher E/q, 78 keV/e. The proton instruments in Table 2 go up to 30 keV/e. Limiting the energy range reduces the high voltages that must be applied as well as possibly the number of E/q steps in an energy scan. There are trade offs of a more limited energy range of course. For composition instruments limiting to 15 keV/e greatly limits the usefulness of the instrument for suprathermal or pick-up ion studies, as well as extreme CME analysis.
There are a few other factors can affect time resolution and signal to noise, but they are typically more minor. The analyzer constant, the ratio of the E/q passband peak to the voltage applied to the ESA plates, can affect time resolution. Designs with higher ratios require less voltage which often leads to shorter ramp up times and smaller voltage settling times. For spinning spacecraft, the top hat design, originally described by Carlson et al. (1982) and refined by Young et al. (1988), is an excellent choice at it has a high analyzer constant (∼12–15). For 3-axis stabilized spacecraft, the choice is less clear. A top hat design requires additional deflector plates, causing the uniformity of response across the FOV to suffer. Other designs, such as MESSENGER/FIPS (Andrews et al., 2007), have more uniform response but low analyzer constants (e.g., 1.33 for FIPS) which may limit the maximum speed achievable to 5–10 s scans. In principle, the speed at which the ESA power supplies can be switched through voltages is an important consideration, but in practice very fast designs are available so that these are not limiting factors.
Heliospheric Structure Analyzer (HSA) is envisioned as a single spacecraft that takes low-noise measurements of ions and electrons in the solar wind at one AU. Low-noise particle measurements means instrumentation with large geometric factors. In this report the motivation is given for those measurements, which will help to answer outstanding questions about the magnetic structure of the heliosphere and the origins of that structure. Much of the measurement strategy is collected in Table 1.
The objective of HSA would be to collect low-noise solar-wind measurements, but the data set need not be continuous. Hence a single Earth-orbiting spacecraft that makes excursions into the solar wind (out of the Earth’s foreshock) could suffice.
A pathway forward would be to form a team of scientists 1) to quantify the needed measurement parameters and 2) to explore possible instrument designs to attain those measurement objectives.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
JB initiated this project. JB and JR researched and wrote the manuscript.
JB was supported at the Space Science Institute by the NASA HERMES Interdisciplinary Science Program via grant 80NSSC21K1406 and by the NSF GEM Program via grant AGS-2027569. JR was supported by NASA through the Wind, Advanced Composition Explorer, and Solar Orbiter missions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adhikari, L., Khabarova, O., Zank, G. P., and Zhao, L.-L. (2019). The Role of Magnetic Reconnection-Associated Processes in Local Particle Acceleration in the Solar Wind. ApJ 873, 72. doi:10.3847/1538-4357/ab05c6
Andrews, G. B., Zurbuchen, T. H., Mauk, B. H., Malcom, H., Fisk, L. A., Gloeckler, G., et al. (2007). The Energetic Particle and Plasma Spectrometer Instrument on the MESSENGER Spacecraft. Space Sci. Rev. 131, 523–556. doi:10.1007/s11214-007-9272-5
Artemyev, A. V., Angelopoulos, V., and Vasko, I. Y. (2019). Kinetic Properties of Solar Wind Discontinuities at 1 AU Observed by ARTEMIS. J. Geophys. Res. Space Phys. 124, 3858–3870. doi:10.1029/2019ja026597
Artemyev, A. V. (2008). Evolution of a Harris Current Sheet in an Electric Field. Mosc. Univ. Phys. 63, 193–196. doi:10.3103/s0027134908030089
Birn, J. (1991). Stretched Three‐dimensional Plasma Equilibria with Field‐aligned Flow. Phys. Fluids B Plasma Phys. 3, 479–484. doi:10.1063/1.859891
Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron Temperature of the Solar Wind. Proc. Natl. Acad. Sci. U.S.A. 117, 9232–9240. doi:10.1073/pnas.1917905117
Borovsky, J. E., and Burkholder, B. L. (2020). On the Fourier Contribution of Strong Current Sheets to the High‐Frequency Magnetic Power SpectralDensity of the Solar Wind. J. Geophys. Res. Space Phys. 125, e2019JA027307. doi:10.1029/2019JA027307
Borovsky, J. E. (2020e). Compression of the Heliospheric Magnetic Structure by Interplanetary Shocks: Is the Structure at 1 AU a Manifestation of Solar-Wind Turbulence or Is it Fossil Structure from the Sun? Front. Astron. Space Sci. 7, 582546. doi:10.3389/fspas.2020.582564
Borovsky, J. E. (2010b). Contribution of Strong Discontinuities to the Power Spectrum of the Solar Wind. Phys. Rev. Lett. 105, 111102. doi:10.1103/physrevlett.105.111102
Borovsky, J. E., and Denton, M. H. (2016). The Trailing Edges of High-Speed Streams at 1 AU. J. Geophys. Res. Space Phys. 121, 6107–6140. doi:10.1002/2016ja022863
Borovsky, J. E. (2006). Eddy Viscosity and Flow Properties of the Solar Wind: Co-rotating Interaction Regions, Coronal-Mass-Ejection Sheaths, and Solar-Wind/magnetosphere Coupling. Phys. Plasmas 13, 056505. doi:10.1063/1.2200308
Borovsky, J. E. (2021b). Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection between the Earth and the Sun. Front. Astron. Space Sci. 8, 646443. doi:10.3389/fspas.2021.646443
Borovsky, J. E., Halekas, J. S., and Whittlesey, P. L. (2021). The Electron Structure of the Solar Wind. Front. Astron. Space Sci. 8, 69005. doi:10.3389/fspas.2021.690005
Borovsky, J. E. (2012). Looking for Evidence of Mixing in the Solar Wind from 0.31 to 0.98 AU. J. Geophys. Res. 117, A06107. doi:10.1029/2012ja017525
Borovsky, J. E. (2021c). Magnetospheric Plasma Systems Science and Solar Wind Plasma Systems Science: The Plasma-Wave Interactions of Multiple Particle Populations. Front. Astron. Space Sci. 8, 780321. doi:10.3389/fspas.2021.780321
Borovsky, J. E. (2020d). On the Motion of the Heliospheric Magnetic Structure through the Solar Wind Plasma. J. Geophys. Res. 125, e2019JA027377. doi:10.1029/2019ja027377
Borovsky, J. E. (2010a). On the Variations of the Solar-Wind Magnetic Field about the Parker-spiral Direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040
Borovsky, J. E. (2020c). Plasma and Magnetic-Field Structure of the Solar Wind at Inertial-Range Scale Sizes Discerned from Statistical Examinations of the Time-Series Measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020
Borovsky, J. E., and Podesta, J. J. (2015). Exploring the Effect of Current Sheet Thickness on the High‐frequency Fourier Spectrum Breakpoint of the Solar Wind. J. Geophys. Res. Space Phys. 120, 9256–9268. doi:10.1002/2015ja021622
Borovsky, J. E. (2021a). Solar-Wind Structures that Are Not Destroyed by the Action of Solar-Wind Turbulence. Front. Astron. Space Sci. 8, 721350. doi:10.3389/fspas.2021.721350
Borovsky, J. E., and Steinberg, J. T. (2014). No Evidence for the Localized Heating of Solar Wind Protons at Intense Velocity Shear Zones. J. Geophys. Res. Space Phys. 119, 1455–1462. doi:10.1002/2013ja019746
Borovsky, J. E. (2008). The Flux-Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU? J. Geophys. Res. 113, A08110. doi:10.1029/2007ja012684
Borovsky, J. E. (2020b). The Magnetic Structure of the Solar Wind: Ionic Composition and the Electron Strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019GL084586
Borovsky, J. E. (2016). The Plasma Structure of Coronal Hole Solar Wind: Origins and Evolution. J. Geophys. Res. Space Phys. 121, 5055–5087. doi:10.1002/2016ja022686
Borovsky, J. E. (2020a). What Magnetospheric and Ionospheric Researchers Should Know about the Solar Wind. J. Atmos. Solar-Terrestrial Phys. 204, 105271. doi:10.1016/j.jastp.2020.105271
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying Intermittency Events in the Solar Wind. Planet. Space Sci. 49, 1201–1210. doi:10.1016/s0032-0633(01)00061-7
Burlaga, L. F. (1971). Hydromagnetic Waves and Discontinuities in the Solar Wind. Space Sci. Rev. 12, 600–657. doi:10.1007/bf00173345
Burlaga, L. F., and Ness, N. F. (1969). Tangential Discontinuities in the Solar Wind. Sol. Phys. 9, 467–477. doi:10.1007/bf02391672
Burton, M. E., Neugebauer, M., Crooker, N. U., von Steiger, R., and Smith, E. J. (1999). Identification of Trailing Edge Solar Wind Stream Interfaces: A Comparison of Ulysses Plasma and Composition Measurements. J. Geophys. Res. 104, 9925–9932. doi:10.1029/1999ja900049
Byhring, H. S. (2011). The Helium Abundance in Polar Coronal Holes and the Fast Solar Wind. ApJ 738, 172. doi:10.1088/0004-637x/738/2/172
Carlson, C. W., Curtis, D. W., Paschmann, G., and Michel, W. (1982). An Instrument for Rapidly Measuring Plasma Distribution Functions with High Resolution. Adv. Space Res. 2 (7), 67–70. doi:10.1016/0273-1177/(82)90151-X10.1016/0273-1177(82)90151-x
Chandrasekhar, S. (1961). Hydrodynamic and Hydromagnetic Stability. New York: Oxford University Press. Sect. 113.
Di Matteo, S., Viall, N. M., Kepko, L., Wallace, S., Arge, C. N., and MacNeice, P. (2019). Helios Observations of Quasiperiodic Density Structures in the Slow Solar Wind at 0.3, 0.4, and 0.6 AU. JGR Space Phys. 124, 837–860. doi:10.1029/2018ja026182
Feldman, W. C., Asbridge, J. R., Bame, S. J., Gary, S. P., Montgomery, M. D., and Zink, S. M. (1976). Evidence for the Regulation of Solar Wind Heat Flux at 1 AU. J. Geophys. Res. 81, 5207–5211. doi:10.1029/ja081i028p05207
Feldman, W. C., Asbridge, J. R., Bame, S. J., Montgomery, M. D., and Gary, S. P. (1975). Solar Wind Electrons. J. Geophys. Res. 80, 4181–4196. doi:10.1029/ja080i031p04181
Fu, H., Madjarska, M. S., Li, B., Xia, L., and Huang, Z. (2018). Helium Abundance and Speed Difference between Helium Ions and Protons in the Solar Wind from Coronal Holes, Active Regions, and Quiet Sun. Mon. Not. R. Astron. Soc. 478, 1884–1892. doi:10.1093/mnras/sty1211
Geiss, J., Gloeckler, G., and von Steiger, R. (1995). Origin of the Solar Wind from Composition Data. Space Sci. Rev. 72, 49–60. doi:10.1007/bf00768753
Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004a). Dispersionless Modulations in Low-Energy Solar Electron Bursts and Discontinuous Changes in the Solar Wind Electron Strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338
Gosling, J. T., Skoug, R. M., McComas, D. J., and Mazur, J. E. (2004b). Correlated Dispersionless Structure in Suprathermal Electrons and Solar Energetic Ions in the Solar Wind. ApJ 614, 412–419. doi:10.1086/423368
Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent MHD Structures and Classical Discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008gl035454
Greco, A., Matthaeus, W. H., Servidio, S., Chuychai, P., and Dmitruk, P. (2009). Statistical Analysis of Discontinuities in Solar Wind ACE Data and Comparison with Intermittent MHD Turbulence. Astrophysical J. 691, L111–L114. doi:10.1088/0004-637x/691/2/l111
Horbury, T. S., Burgess, D., Fränz, M., and Owen, C. J. (2001). Three Spacecraft Observations of Solar Wind Discontinuities. Geophys. Res. Lett. 28, 677–680. doi:10.1029/2000gl000121
Kasper, J. C., Lazarus, A. J., Steinberg, J. T., Ogilvie, K. W., and Szabo, A. (2006). Physics-based Tests to Identify the Accuracy of Solar Wind Ion Measurements: A Case Study with the Wind Faraday Cups. J. Geophys. Res. 111, A03105. doi:10.1029/2005ja011442
Kepko, L., Viall, N. M., Antiochos, S. K., Lepri, S. T., Kasper, J. C., and Weberg, M. (2016). Implications of L1 Observations for Slow Solar Wind Formation by Solar Reconnection. Geophys. Res. Lett. 43, 4089–4097. doi:10.1002/2016gl068607
Khabarova, O., Malandraki, O., malova, H., Kislov, R., Greco, A., Bruno, R., et al. (2021). Current Sheets, Plasmoids and Flux Ropes in the Heliosphere. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x
Khabarova, O., Zank, G., Li, G., Le Roux, J. A., Webb, G. M., Dosch, A., et al. (2015). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. I. Dynamics of Magnetic Islands Near the Heliospheric Current Sheet. Astrophys. J. 808, 181. doi:10.1088/0004-637X/808/2/181
Khabarova, O., Zank, G., Li, G., MalandrakiLe Roux, O. E. J. A., and Webb, G. M. (2016). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. II. Particle Energization inside Magnetically Confined Cavities. Astrophys. J. 827, 122. doi:10.3847/0004-637X/827/2/122
Khabarova, O., Zharkova, V., Xia, Q., and Malandraki, O. E. (2020). Counterstreaming Strahls and Heat Flux Dropouts as Possible Signatures of Local Particle Acceleration in the Solar Wind. Astrophysical J. Lett. 894, L12. doi:10.3847/2041-8213/ab8cb8
Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2003). Discontinuity Observations with Cluster. Adv. Space Res. 32 (4), 543–548. doi:10.1016/s0273-1177(03)00335-1
Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2004). Four-point Discontinuity Observations Using Cluster Magnetic Field Data: A Statistical Survey. J. Geophys. Res. 109, A06102. doi:10.1029/2003ja010099
Komar, C. M., and Cassak, P. A. (2016). The Local Dayside Reconnection Rate for Oblique Interplanetary Magnetic Fields. J. Geophys. Res. Space Phys. 121, 5105–5120. doi:10.1002/2016ja022530
Lapenta, G., and Brackbill, J. U. (1996). Contact Discontinuities in Collisionless Plasmas: A Comparison of Hybrid and Kinetic Simulations. Geophys. Res. Lett. 23, 1713–1716. doi:10.1029/96gl01845
Lazarian, A., Eyink, G. L., Jafari, A., Kowal, G., Li, H., Xu, S., et al. (2020). 3D Turbulent Reconnection: Theory, Tests, and Astrophysical Implications. Phys. Plasmas 27, 012305. doi:10.1063/1.5110603
Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a Weakly Stochastic Field. ApJ 517, 700–718. doi:10.1086/307233
Lepping, R. P., and Behannon, K. W. (1986). Magnetic Field Directional Discontinuities: Characteristics between 0.46 and 1.0 AU. J. Geophys. Res. 91, 8725. doi:10.1029/ja091ia08p08725
Livi, R., Larson, D. E., Kasper, J. C., Abiad, R., Case, A. W., Klein, K. G., et al. (2021). The Solar Probe ANalyzer -Ions on Parker Solar Probe. Earth Space Sci. doi:10.1002/essoar.10508651.1
MacBride, B. T., Smith, C. W., and Forman, M. A. (2008). The Turbulent Cascade at 1 AU: Energy Transfer and the Third‐Order Scaling for MHD. Astrophysical J. 679, 1644–1660. doi:10.1086/529575
Maksimovic, M., Zouganelis, I., Chaufray, J. Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial Evolution of the Electron Distribution Functions in the Fast Solar Wind between 0.3 and 1.5 AU. J. Geophys. Res. 110, A09104. doi:10.1029/2005ja011119
Malandraki, O., Khabarova, O., Bruno, R., Zank, G. P., Li, G., Jackson, B., et al. (2019). Current Sheets, Magnetic Islands, and Associated Particle Acceleration in the Solar Wind as Observed by Ulysses Near the Ecliptic Plane. ApJ 881, 116. doi:10.3847/1538-4357/ab289a
McComas, D. J., Bame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Riley, P., et al. (1998). Solar Wind Electron Proton Alpha Monitor (SWEPAM) for the Advanced Composition Explorer. Space Sci. Rev. 86, 563–612. doi:10.1007/978-94-011-4762-0_20
McCracken, K. G., and Ness, N. F. (1966). The Collimation of Cosmic Rays by the Interplanetary Magnetic Field. J. Geophys. Res. 71, 3315–3318. doi:10.1029/jz071i013p03315
McIntosh, S. W., Kiefer, K. K., Leamon, R. J., Kasper, J. C., and Stevens, M. L. (2011). Solar Cycle Variations in the Elemental Abundance of Helium and Fractionation of Iron in the Fast Solar Wind: Indicators of an Evolving Energetic Release of Mass from the Lower Solar Atmosphere. ApJ 740, L23. doi:10.1088/2041-8205/740/1/l23
Michel, F. C. (1967). Model of Solar Wind Structure. J. Geophys. Res. 72, 1917–1932. doi:10.1029/jz072i007p01917
Moncuquet, M., Meyer-Vernet, N., Issautier, K., Pulupa, M., Bonnell, J. W., Bale, S. D., et al. (2020). First In Situ Measurements of Electron Density and Temperature from Quasi-Thermal Noise Spectroscopy with Parker Solar Probe/FIELDS. Astrophysical J. Suppl. Ser. 246, 44. doi:10.3847/1538-4365/ab5a84
Nemecek, Z., Durovcova, T., Safrankova, J., Nemec, F., Matteini, L., Stansvy, D., et al. (2020). What Is the Solar Wind Frame of Reference? Astrophys. J. 889, 163. doi:10.3847/1538-4357/ab65f7
Neugebauer, M., and Giacalone, J. (2010). Progress in the Study of Interplanetary Discontinuities. AIP Conf. Proc. 1216, 194. doi:10.1063/1.3395834
Neugebauer, M., Clay, D. R., Goldstein, B. E., Tsurutani, B. T., and Zwickl, R. D. (1984). A Reexamination of Rotational and Tangential Discontinuities in the Solar Wind. J. Geophys. Res. 89, 5395. doi:10.1029/ja089ia07p05395
Neugebauer, M. (2006). Comment on the Abundances of Rotational and Tangential Discontinuities in the Solar Wind. J. Geophys. Res. 111, A04103. doi:10.1029/2005ja011497
Neugebauer, M. (2012). Evidence for Polar X-Ray Jets as Sources of Microstream Peaks in the Solar Wind. ApJ 750, 50. doi:10.1088/0004-637x/750/1/50
Neugebauer, M., and Giacalone, J. (2015). Energetic Particles, Tangential Discontinuities, and Solar Flux Tubes. J. Geophys. Res. Space Phys. 120, 8281–8287. doi:10.1002/2015ja021632
Neugebauer, M., Goldstein, B. E., Winterhalter, D., Smith, E. J., MacDowall, R. J., and Gary, S. P. (2001). Ion Distributions in Large Magnetic Holes in the Fast Solar Wind. J. Geophys. Res. 106, 5635–5648. doi:10.1029/2000ja000331
Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, a Comprehensive Plasma Instrument for the WIND Spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/bf00751326
Owen, C. J., Bruno, R., Livi, S., Louarn, P., Al Janabi, K., Allrgrini, F., et al. (2020). The Solar Orbiter Solar Wind Analyzer (SWA) Suite. Astron. Astrophys. 642, A16.
Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic Discontinuities in the Near-Earth Solar Wind: Evidence of In-Transit Turbulence or Remnants of Coronal Structure? Sol. Phys. 269, 411–420. doi:10.1007/s11207-010-9695-0
Paschmann, G., Haaland, S., Sonnerup, B., and Knetter, T. (2013). Discontinuities and Alfvénic Fluctuations in the Solar Wind. Ann. Geophys. 31, 871–887. doi:10.5194/angeo-31-871-2013
Pecora, F., Greco, A., Hu, Q., Servidio, S., Chasapis, A. G., and Matthaeus, W. H. (2019). Single-spacecraft Identification of Flux Tubes and Current Sheets in the Solar Wind. ApJ 881, L11. doi:10.3847/2041-8213/ab32d9
Pilipp, W. G., Miggenrieder, H., Montgomery, M. D., Mühlhäuser, K.-H., Rosenbauer, H., and Schwenn, R. (1987). Characteristics of Electron Velocity Distribution Functions in the Solar Wind Derived from the Helios Plasma Experiment. J. Geophys. Res. 92, 1075. doi:10.1029/ja092ia02p01075
Podesta, J. J., and Borovsky, J. E. (2016). Relationship between the Durations of Jumps in Solar Wind Time Series and the Frequency of the Spectral Break. J. Geophys. Res. Space Phys. 121, 1817–1838. doi:10.1002/2015ja021987
Podesta, J. J., Borovsky, J. E., Steinberg, J. T., Skoug, R., Birn, J., Gary, S. P., et al. (2012). “High-resolution, High Accuracy Plasma, Electric, and Magntic Field Measurements for Discovery of Kinetic Plasma Structures and Processes in the Evolving Solar Wind,” in Solar and Space Physics: A Science for a Technological Society (Washington, D. C: National Academies Press). 433. paper 222.
Podesta, J. J., Forman, M. A., Smith, C. W., Elton, D. C., Malécot, Y., and Gagne, Y. (2009). Accurate Estimation of Third-Order Moments from Turbulence Measurements. Nonlin. Process. Geophys. 16, 99–110. doi:10.5194/npg-16-99-2009
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4
Rakowski, C. E., and Laming, J. M. (2012). On the Origin of the Slow Speed Solar Wind: Helium Abundance Variations. ApJ 754, 65. doi:10.1088/0004-637x/754/1/65
Riazantseva, M. O., Khabarova, O. V., Zastenker, G. N., and Richardson, J. D. (2005a). Sharp Boundaries of Solar Wind Plasma Structures and an Analysis of Their Pressure Balance. Cosm. Res. 43 (3), 157–164. doi:10.1007/s10604-005-0030-8
Riazantseva, M. O., Zastenker, G. N., Richardson, J. D., and Eiges, P. E. (2005c). Sharp Boundaries of Small- and Middle-Scale Solar Wind Structures. J. Geophys. Res. 110, A12110. doi:10.1029/2005ja011307
Riazantseva, M. O., Zastenker, G. N., and Richardson, J. D. (2005b). The Characteristics of Sharp (Small-scale) Boundaries of Solar Wind Plasma and Magnetic Field Structures. Adv. Space Res. 35, 2147–2151. doi:10.1016/j.asr.2004.12.011
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The Magnetospheric Multiscale Magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/978-94-024-0861-4_8
Safrankova, J., Memecek, Z., Cagas, P., Pavlu, J., Zastenker, G. N., Riazantseva, M. O., et al. (2013). Short-scale Variations of the Solar Wind Helium Abundance. Astrophys. J. 778, 25. doi:10.1088/0004-637X/778/1/25
Schindler, K., and Birn, J. (2002). Models of Two-Dimensional Embedded Thin Current Sheets from Vlasov Theory. J. Geophys. Res. 107, 1193. doi:10.1029/2001ja000304
Schindler, K., and Hesse, M. (2010). Conditions for the Formation of Nongyrotropic Current Sheets in Slowly Evolving Plasmas. Phys. Plasmas 17, 082103. doi:10.1063/1.3464198
Schindler, K., and Hesse, M. (2008). Formation of Thin Bifurcated Current Sheets by Quasisteady Compression. Phys. Plasmas 15, 042902. doi:10.1063/1.2907359
Sheeley, N. R., and Rouillard, A. P. (2010). Tracking Streamer Blobs into the Heliosphere. ApJ 715, 300–309. doi:10.1088/0004-637x/715/1/300
Simunac, K. D. C., Galvin, A. B., Farrugia, C. J., Kistler, L. M., Kucharek, H., Lavraud, B., et al. (2012). The Heliospheric Plasma Sheet Observed In Situ by Three Spacecraft over Four Solar Rotations. Sol. Phys. 281, 423. doi:10.1007/s11207-012-0156-9
Siscoe, G. L., Davis, L., Coleman, P. J., Smith, E. J., and Jones, D. E. (1968). Power Spectra and Discontinuities of the Interplanetary Magnetic Field: Mariner 4. J. Geophys. Res. 73, 61–82. doi:10.1029/ja073i001p00061
Smith, C. W., Stawarz, J. E., Vasquez, B. J., Forman, M. A., and MacBride, B. T. (2009). Turbulent Cascade at 1 AU in High Cross-Helicity Flows. Phys. Rev. Lett. 103, 201101. doi:10.1103/physrevlett.103.201101
Smith, E. J. (2001). The Heliospheric Current Sheet. J. Geophys. Res. 106, 15819–15831. doi:10.1029/2000ja000120
Söding, A., Neubauer, F. M., Tsurutani, B. T., Ness, N. F., and Lepping, R. P. (2001). Radial and Latitudinal Dependencies of Discontinuities in the Solar Wind between 0.3 and 19 AU and −80° and +10°. Ann. Geophys. 19, 667–680. doi:10.5194/angeo-19-667-2001
Sonnerup, B. U. O. (2022). Reflections by Bengt Ulf Osten Sonnerup. Front. Astron. Space Sci., 943401. submitted to.
Sorriso-Valvo, L., Marino, R., Carbone, V., Noullez, A., Lepreti, F., Veltri, P., et al. (2007). Observation of Inertial Energy Cascade in Interplanetary Space Plasma. Phys. Rev. Lett. 99, 115001. doi:10.1103/physrevlett.99.115001
Stverak, S., Maksimovic, M., Travnicek, P. M., Marsch, E., Fazakerley, A. N., and Scime, E. E. (2009). Radial Evolution of Nonthermal Electron Populations in the Low-Latitude Solar Wind: Helios, Cluster, and Ulysses Observations. J. Geophys. Res. 114, A04104. doi:10.1029/2008JA013883
Tamano, T. (1991). A Plasmoid Model for the Solar Wind. Sol. Phys. 134, 187–201. doi:10.1007/bf00148747
Telloni, D., Perri, S., Carbone, V., and Bruno, R. (2016). Selective Decay and Dynamic Alignment in the MHD Turbulence: the Role of the Rugged Invariants. AIP Conf. Proc. 1720, 040015. doi:10.1063/1.4943826
Tenerani, A., Velli, M., Matteini, L., Reville, V., Shi, C., Bale, S. D., et al. (2020). Magnetic Field Kinks and Folds in the Solar Wind. Astrophys. J. Suppl. Ser. 246, 3. doi:10.3847/1538-4365/ab53e1
Trenchi, L., Bruno, R., Telloni, D., D'amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013). Solar Energetic Particle Modulations Associated with Coherent Magnetic Structures. ApJ 770, 11. doi:10.1088/0004-637x/770/1/11
Tsurutani, B. T., and Ho, C. M. (1999). A Review of Discontinuities and Alfvén Waves in Interplanetary Space: Ulysses Results. Rev. Geophys. 37, 517–541. doi:10.1029/1999rg900010
Tu, C.-Y., and Marsch, E. (1993). A Model of Solar Wind Fluctuations with Two Components: Alfvén Waves and Convective Structures. J. Geophys. Res. 98, 1257–1276. doi:10.1029/92ja01947
Tu, C. Y., Wang, X., He, J., Marsch, E., and Wang, L. (2016). Two Cases of Convecting Structure in the Slow Solar Wind Turbulence. AIP Conf. Proc. 1720, 040017. doi:10.1063/1.4943828
Turner, J. M., Burlaga, L. F., Ness, N. F., and Lemaire, J. F. (1977). Magnetic Holes in the Solar Wind. J. Geophys. Res. 82, 1921–1924. doi:10.1029/ja082i013p01921
Turner, J. M., and Siscoe, G. L. (1971). Orientations of 'rotational' and 'tangential' Discontinuities in the Solar Wind. J. Geophys. Res. 76, 1816–1822. doi:10.1029/ja076i007p01816
Vasquez, B. J., Abramenko, V. I., Haggerty, D. K., and Smith, C. W. (2007). Numerous Small Magnetic Field Discontinuities of Bartels Rotation 2286 and the Potential Role of Alfvénic Turbulence. J. Geophys. Res. 112, A11102. doi:10.1029/2007ja012504
Vasquez, B. J., and Hollweg, J. V. (1999). Formation of Pressure-Balanced Structures and Fast Waves from Nonlinear Alfvén Waves. J. Geophys. Res. 104, 4681–4696. doi:10.1029/1998ja900090
Vasquez, B. J., Markovskii, S. A., and Smith, C. W. (2013). Solar Wind Magnetic Field Discontinuities and Turbulence Generated Current Layers. AIP Conf. Proc. 1539, 291. doi:10.1063/1.4811045
Viall, N. M., and Borovsky, J. E. (2020). Nine Outstanding Questions of Solar Wind Physics. J. Geophys Res. Space Phys. 125, e2018JA026005. doi:10.1029/2018JA026005
Viall, N. M., Spence, H. E., Vourlidas, A., and Howard, R. (2010). Examining Periodic Solar-Wind Density Structures Observed in the SECCHI Heliospheric Imagers. Sol. Phys. 267, 175–202. doi:10.1007/s11207-010-9633-1
Viall, N. M., and Vourlidas, A. (2015). Periodic Density Structures and the Origin of the Slow Solar Wind. ApJ 807, 176. doi:10.1088/0004-637x/807/2/176
Vocks, C., Salem, C., Lin, R. P., and Mann, G. (2005). Electron Halo and Strahl Formation in the Solar Wind by Resonant Interaction with Whistler Waves. Astrophysical J. 627, 540–549. doi:10.1086/430119
von Steiger, R., Fisk, L. A., Gloeckler, G., Schwadron, N. A., and Zurbuchen, T. H. (1999). Composition Variations in Fast Solar Wind Streams. AIP Conf. Proc. 471, 143. doi:10.1063/1.58791
von Steiger, R., Zurbuchen, T. H., Geiss, J., Gloeckler, G., Fisk, L. A., and Schwadron, N. A. (2001). The 3-D Heliosphere from the ULYSSES and ACE Solar Wind Ion Composition Experiments. Space Sci. Rev. 97, 123–127. doi:10.1007/978-94-017-3230-7_20
Wang, X., Tu, C. Y., He, J. S., Wang, L. H., Yao, S., and Zhang, L. (2018). Possible Noise Nature of Elsässer Variable Z − in Highly Alfvénic Solar Wind Fluctuations. JGR Space Phys. 123, 57–67. doi:10.1002/2017ja024743
Wang, Y.-M. (2016). Role of the Coronal Alfvén Speed in Modulating the Solar-Wind Helium Abundance. Astrophysical J. Lett. 833, L21. doi:10.3847/2041-8213/833/2/l21
Wang, Y.-M., Sheeley, N. R., Howard, R. A., Rich, N. B., and Lamy, P. L. (1999). Streamer Disconnection Events Observed with the LASCO Coronagraph. Geophys. Res. Lett. 26, 1349–1352. doi:10.1029/1999gl900177
Wang, Y. M. (2008). Relating the Solar Wind Helium Abundance to the Coronal Magnetic Field. Astrophysical J. 683, 499–509. doi:10.1086/589766
Whittlesey, P. L., Larson, D. E., Kasper, J. C., Halekas, J., Abatcha, M., Abiad, R., et al. (2020). The Solar Probe ANalyzers-Electrons on the Parker Solar Probe. ApJS 246, 74. doi:10.3847/1538-4365/ab7370
Wimmer-Schweingruber, R. F., von Steiger, R., and Paerli, R. (1997). Solar Wind Stream Interfaces in Corotating Interaction Regions: SWICS/Ulysses Results. J. Geophys. Res. 102, 17407–17417. doi:10.1029/97ja00951
Winterhalter, D., Smith, E. J., Neugebauer, M., Goldstein, B. E., and Tsurutani, B. T. (2000). The Latitudinal Distribution of Solar Wind Magnetic Holes. Geophys. Res. Lett. 27, 1615–1618. doi:10.1029/1999gl003717
Young, D. T., Bame, S. J., Thomsen, M. F., Martin, R. H., Burch, J. L., Marshall, J. A., et al. (1988). 2π‐radian Field‐of‐view Toroidal Electrostatic Analyzer. Rev. Sci. Instrum. 59, 743–751. doi:10.1063/1.1139821
Zastenker, G. N., Safrankova, J., Nemecek, Z., Prech, L., Cermak, I., Vaverka, I., et al. (2013). Fast Measurements of Parameters of the Solar Wind Using the BMSW Instrument. Cosm. Res. 51, 78–89. doi:10.1134/s0010952513020081
Zelenyi, L. M., Malova, H. V., Artemyev, A. V., Popov, V. Y., and Petrukovich, A. A. (2011). Thin Current Sheets in Collisionless Plasma: Equilibrium Structure, Plasma Instabilities, and Particle Acceleration. Plasma Phys. Rep. 37, 118–160. doi:10.1134/s1063780x1102005x
Zelenyi, L. M., Malova, K. V., Popov, V. Y., Grigorenko, E. E., and Büchner, J. (2021). Albert Galeev: The Problem of Metastability and Explosive Reconnection. Plasma Phys. Rep. 47, 857–877. doi:10.1134/s1063780x21090075
Zhang, T. L., Russell, C. T., Zambelli, W., Vörös, Z., WangCao, C. J. B., Cao, J. B., et al. (2008). Behavior of Current Sheets at Directional Magnetic Discontinuities in the Solar Wind at 0.72 AU. Geophys. Res. Lett. 35, L24102. doi:10.1029/2008gl036120
Zhao, L., Zurbuchen, T. H., and Fisk, L. A. (2009). Global Distribution of the Solar Wind during Solar Cycle 23: ACE Observations. Geophys. Res. Lett. 36, L14104. doi:10.1029/2009gl039181
Zhdankin, V., Boldyrev, S., Mason, J., and Perez, J. C. (2012). Magnetic Discontinuities in Magnetohydrodynamic Turbulence and in the Solar Wind. Phys. Rev. Lett. 108, 175004. doi:10.1103/physrevlett.108.175004
Zurbuchen, T. H., Hefti, S., Fisk, L. A., Gloeckler, G., and von Steiger, R. (1999). The Transition between Fast and Slow Solar Wind from Composition Data. Space Sci. Rev. 87, 353–356. doi:10.1007/978-94-015-9167-6_62
As stated in Section 3, for particle-counting instruments the combination of lower noise and higher time resolution is difficult, with poorer counting statistics being a consequence of shorter measuring intervals. For the solar wind there is an argument that presents a further difficulty, concluding that higher-frequency fluctuations in the solar wind have smaller amplitudes, making the higher-time-resolution measurements need even more accuracy and lower noise. But that “extra difficulty” argument may be wrong. Looking at a Fourier power spectral density of the solar wind it is very noticeable that the power amplitude decrease with increasing frequency f. A natural interpretation of this is that higher-frequency fluctuations in the solar wind have smaller amplitudes (hence the extra measurement difficulty). In terms of the needed accuracy of high-frequency solar-wind measurements, that argument is made in Podesta et al. (2012). That interpretation of the power spectral density would be correct if the solar-wind time series was comprised of randomly-phased fluctuations: however, the solar-wind time series is highly intermittent and is not comprised of random-phase fluctuations. The counter example to the argument comes from an examination of the high-frequency breakpoint in the solar-wind magnetic power spectral density at a breakpoint frequency of fbreak ∼ 0.5 Hz: analysis shows that the power spectral density break at fbreak is owed to the temporal thicknesses τcs of strong current sheets in the solar-wind time series, thicknesses τcs ∼ 1/fbreak (Borovsky and Podesta, 2015; Podesta and Borovsky, 2016). Instead of the solar-wind time series containing constant low-amplitude random-phased fluctuations with frequency fbreak, a spacecraft occasionally crosses a large-amplitude current-sheet signal with a transition time of 1/fbreak. The measured signals of interest at high frequency need not be of small amplitude, they can be of large amplitude and the “extra difficulty” requiring extra accuracy when measuring signals at high time resolution may not be real.
In conclusion, to study jump properties across current sheets the “even higher accuracy and lower noise” is probably not necessary. However, for survey purposes the exploration of small signals with high time resolution is still desirable, if possible.
Keywords: heliospheric structure, solar wind, current sheets, magnetic flux tubes, directional discontinuities, turbulence
Citation: Borovsky JE and Raines JM (2022) Heliospheric Structure Analyzer (HSA): A Simple 1-AU Mission Concept Focusing on Large-Geometric-Factor Measurements. Front. Astron. Space Sci. 9:919755. doi: 10.3389/fspas.2022.919755
Received: 13 April 2022; Accepted: 07 June 2022;
Published: 12 July 2022.
Edited by:
Alessandro Retino, UMR7648 Laboratoire de physique des plasmas (LPP), FranceReviewed by:
Roman Kislov, Space Research Institute (RAS), RussiaCopyright © 2022 Borovsky and Raines. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.