Low- and Mid-Latitude Ionospheric Response to the 2013 St. Patrick’s Day Geomagnetic Storm in the American Sector: Global Ionosphere Thermosphere Model Simulation

In this study, the low-and mid-latitude ionospheric response to the main phase of the 2013 St. Patrick’s Day geomagnetic storm in the American sector on the dayside has been investigated using the ground-based measurements and the Global Ionosphere Thermosphere Model (GITM). First, it is found that the observed ionospheric response can be well reproduced by GITM when it is driven by the electric potential and electron precipitation patterns derived from the Assimilative Mapping of Ionospheric Electrodynamics (AMIE) technique. The AMIE-driven GITM simulation also significantly improves the data-model comparison as compared with the simulation driven by the high-latitude empirical models. Second, it is found that the transport process associated with the neutral wind is largely responsible for the observed ionospheric response. Specifically, the traveling atmospheric disturbances (TADs) propagating from the opposite hemisphere play an important role in the formation of the negative storm phase at low and middle latitudes. Third, it is found that the asymmetric negative storm phases occurred at the nominal equatorial ionization anomaly (EIA) peak region in the afternoon sector are mainly attributed to the interaction of the TADs launched in different hemispheres with different phase speeds. Specifically, stronger Joule heating deposited in the northern hemisphere (NH) generates TADs with faster phase speeds than those launched in the southern hemisphere (SH). Consequently, the locations where the TADs originated from the different hemispheres interact are asymmetric about the geomagnetic equator, leading to the formation of asymmetric ionospheric negative storm phases. This study highlights the importance of accurately specifying high-latitude electrodynamic forcings in global I-T simulations and provides a new insight into the cause of the interhemispheric asymmetry phenomena during geomagnetic storms.

Introduction

Earth’s ionosphere and thermosphere (I-T) system can be significantly disturbed during geomagnetic storms when the high-latitude electric field and electron precipitation undergo significant modifications. The topology and intensity of the high-latitude electric field are directly influenced by the orientation of the interplanetary magnetic field (IMF) and solar wind conditions. Sudden changes in the IMF and solar wind could cause the high-latitude electric field to penetrate towards to the equatorial region. A sudden southward turning of the IMF could produce an eastward prompt penetration electric field (PPEF) on the dayside (Fejer and Scherliess, 1997) which reinforces the dayside fountain effect and can significantly contribute to the ionospheric positive storm effect (e.g., an increase of the F-region electron density) at low and middle latitudes (e.g., Tsurutani et al., 2004; Mannucci et al., 2005; Huang et al., 2005; Lei et al., 2008a; Lu et al., 2012). Meanwhile, a tremendous amount of electromagnetic energy from the magnetosphere is deposited into the ionosphere-thermosphere (I-T) system during geomagnetic storms, and the majority of this energy input is converted to Joule heating which is an important energy source of the I-T system (e.g., Lu et al., 1995; Thayer et al., 1995; Knipp et al., 2004; Deng et al., 2011; Deng et al., 2018; Knipp et al., 2021). Strong heating at high latitudes could generate equatorward-propagating disturbance neutral winds, which push the plasma upward along the magnetic field line and contribute to a positive ionospheric storm phase at low and middle latitudes (e.g., Lin et al., 2005; Lu et al., 2008). In addition, the storm-time disturbance neutral wind also generates a westward electric field on the dayside (Blanc and Richmond, 1980), which could suppress the dayside fountain effect (Scherliess and Fejer, 1997). Joule heating not only modifies the thermospheric circulation but also alters thermospheric neutral temperature, neutral density and neutral composition, and the changes in thermospheric composition can also change the ion and electron densities through chemical processes (e.g., Fuller-Rowell et al., 1994; Burns et al., 1995; Zhang et al., 2003; Cai et al., 2021). Furthermore, impulsive Joule heating could induce large-scale traveling atmospheric disturbances (TADs) and traveling ionospheric disturbances (TIDs) (Richmond and Matsushita, 1975; Bauske and Prölss, 1997; Balthazor and Moffett, 1999; Lee et al., 2004; Shiokawa et al., 2007; Lei et al., 2008b; Bruinsma and Forbes, 2009; Guo et al., 2014; Lu et al., 2016; Ren and Lei, 2017; Lyons et al., 2019; Zhang et al., 2019; Lu et al., 2020; Sheng et al., 2021; Wang et al., 2021; Pham et al., 2022).

This study focuses on the ionospheric response to the 2013 St. Patrick’s Day geomagnetic storm, which is an intense storm that has drawn substantial community interests and lots of significant processes have been made (e.g., Kalita et al., 2016; Liu et al., 2016; Lyons et al., 2016; Verkhoglyadova et al., 2016; Yue et al., 2016; Dmitriev et al., 2017; Guerrero et al., 2017; Marsal et al., 2017; Xu et al., 2017; Dang et al., 2019; Ferdousi et al., 2019; Kumar and Kumar, 2019; Lin et al., 2019; Zhai et al., 2020; Amaechi et al., 2021). However, it is still challenging for the community to accurately describe and simulate the ionospheric response, including both positive and negative phases, to the geomagnetic storms. For example, the simulation work shown in Yue et al. (2016) utilized the National Center of Atmospheric Research Thermosphere-Ionosphere-Electrodynamics General Circulation model (NCAR-TIEGCM, Qian et al., 2014) to study the ionospheric response to the storm. In their study, high-latitude empirical models were used to specify the high-latitude electrodynamic forcings in the NCAR-TIEGCM. However, the complex coexistence of the ionospheric positive and negative storm phases during the main storm phase in the American sector were not well reproduced in their simulations, preventing us from a better understanding of such interesting ionospheric response at low and middle latitudes. The data-model discrepancies in their study may be attributed to the fact that high-latitude empirical models often fail to capture the dynamic spatial and temporal variations of high-latitude electrodynamic forcings (Heelis and Maute, 2020). In this work, whether and to what extent the more realistic high-latitude electrodynamic forcings could help improve the data-model comparison are assessed. Meanwhile, the physical processes contributing to the ionospheric variations during the 2013 St. Patrick’s Day storm are examined.

In this study, the numerical simulations using the Global Ionosphere Thermosphere Model (GITM, Ridley et al., 2006) are performed, driven by two types of high-latitude electrodynamic forcings: the electric and electron precipitation patterns derived from the Assimilative Mapping Ionospheric Electrodynamics (AMIE) procedure (Richmond and Kamide, 1988; Richmond, 1992) and the patterns provided by a recently developed empirical model, Auroral Spectrum and High-Latitude Electric field variabilitY (ASHLEY, Zhu et al., 2021). The simulation results are compared with the ground-based measurements.

Model and Data Descriptions

Global Ionosphere Thermosphere Model

GITM is a global model for the Earth’s upper atmosphere which self-consistently solves for the density, velocity and temperature of neutrals, ions and electron. Unlike most global models used in the community, GITM relaxes the hydrostatic assumption and allows the propagation of acoustic waves (Deng et al., 2008; Deng and Ridley, 2014; Zhu et al., 2017; Deng et al., 2021). The version of GITM used in this study is the one coupled with the ionospheric electrodynamo solver developed by Maute and Richmond (2017), and the coupling has been described in Zhu et al. (2019). The spatial resolution of GITM is 5° in geographic longitude and 2.5° in geographic latitude and 1/3 scale height in altitude ranging from 100 to 900 km, and the time step is 2 s.

High-Latitude Electrodynamic Forcings in Global Ionosphere Thermosphere Model

In this study, the high-latitude electrodynamic forcings in GITM are specified in two different ways: by an empirical model and by the data assimilative patterns. The empirical model used in this study is the Auroral Spectrum and High-Latitude Electric field variabilitY (ASHLEY) model (Zhu et al., 2021). Specifically, its electric potential (ASHLEY-E) and electron precipitation (ASHLEY-A) components are utilized, which are developed based on the in-situ ion drift and electron precipitation data from the Defense Meteorological Satellite Program (DMSP) satellites, respectively. Both ASHLEY-A and ASHLEY-E use interplanetary magnetic field (IMF) and solar wind data as inputs.

The AMIE ionospheric electric potential and electron precipitation patterns are also used for this study. AMIE provides an optimal estimation of high-latitude electrodynamic fields based on a variety of ground-based and space-based measurements, so it provides more realistic high-latitude electrodynamic forcing than empirical models. A more recent description of AMIE can be found in Lu (2017). The data inputs to AMIE for this event include horizontal magnetic perturbations measured by 217 ground stations (among them 173 stations were in the NH and 44 were in the SH), cross-track ion drift data measured by four DMSP satellites (F15, F16, F17, and F18), electron precipitation inferred from the Special Sensor of Ultraviolet Spectrographic Imager (SSUSI) onboard three DMSP satellites (i.e., F16, F17, and F18), line-of-sight ion drifts measured by Super Dual Auroral Radar Network high frequency radar network, and the horizontal magnetic perturbations measured by the Iridium satellite constellation and provided by the Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE) dataset (Anderson et al., 2014). The temporal resolution of AMIE pattern is 5 min, and the spatial resolution of AMIE pattern is 0.67 h in magnetic local time (MLT) and 1.67° in magnetic latitude (MLAT).

Ionospheric Dataset

In this study, the vertical total electron content (TEC) data estimated from the ground-based dual-frequency global navigation satellite system (GNSS) receivers are used to validate the simulation results. First, the line-of-sight TEC (i.e., line-integrated ionospheric electron density) is estimated by analyzing the processed L1 and L2 pseudorange and phase data (Rideout and Coster, 2006). After removing the ground receiver and satellite biases, the line-of-sight TEC with an elevation angle above 30° is then converted to the vertical TEC using a mapping function (Rideout and Coster, 2006; Vierinen et al., 2016). This study focuses on the vertical TEC data derived from the GNSS receivers distributed in the American Sector are used.

In addition to the TEC data, ionosonde measurements from four stations in the American sector are analyzed. The four stations are: Wallop Island (75.5°W, 37.9°N), Eglin (86.5°W, 30.5°N), Ramey (67.1°W, 18.5°N), and Jicamarca (76.8°W, 12.0°S). In particular, the F2 peak electron density (NmF2) and height (hmF2), which are determined from the measured ionograms using the SAO-Explorer software package (Huang and Reinisch, 1996), are used.

Results and Discussion

Geophysical Conditions

Figure 1 summarizes the geophysical conditions during the 2013 St. Patrick’s Day storm, including the variations of the IMF B_y and B_z components, the Dst and AE indices, along with the cross-polar-cap potential (CPCP) and hemispheric power (HP) in the northern hemisphere (NH). The latter four variables are from the AMIE outputs. The AMIE Dst index is similar to the SYM-H index but using the magnetometer data from 56 stations between −40° and 40° MLAT. The AE index is derived from 98 stations between |55°| and |76°| MLAT in both hemispheres. The northern hemisphere (NH) AMIE outputs are used. The 2013 St. Patrick’s Day storm was triggered by an interplanetary coronal mass ejection (ICME). As illustrated in Verkhoglyadova et al. (2016), the shock of the ICME arrived at the Earth’s bow shock at around 6 UT on 03/17/2013 and was followed by the ICME sheath region. A magnetic cloud arrived at around 15:30 UT and lasted for more than 24 h. During the passage of the sheath region, the IMF B_y and B_z components intensified and exhibited large oscillations. Meanwhile, the Dst index dropped to−120 nT at around 12 UT and gradually recovered until the arrival of the magnetic cloud. During the passage of the magnetic cloud, the IMF B_z turned southward and remained southward for about 6 h. The Dst index decreased again until 20:30 UT when it reached its minimum value of −140 nT. Hence, this storm displayed a two-step growth. During the main phase (6:00–20:30 UT), the auroral electrojet showed two strong (>1,500 nT) intensifications around 7:30 and 16:30 UT as indicated by the AE index, and the maximum AE value reached ∼2,800 nT. The maximum of the NH CPCP was 204 kV. The maximum of the NH HP was 205 GW.

FIGURE 1

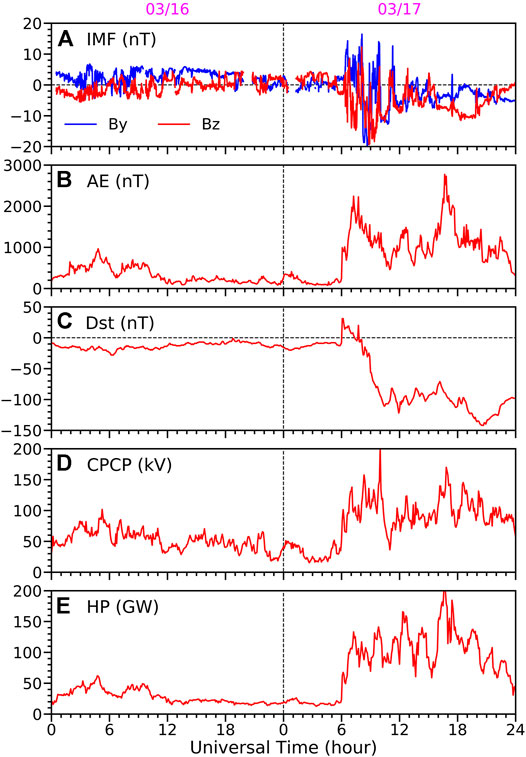
FIGURE 1. Evolutions of (A) IMF (blue: B_y; red: B_z), (B) AE, (C) Dst, (D) CPCP and (E) HP during the 2013 St. Patrick’s day geomagnetic storm. The IMF data is shifted by 30 min. The parameters shown in the bottom four panels are from the Northern Hemisphere AMIE output. IMF, interplanetary magnetic field; AE, auroral electrojet; CPCP, cross-polar cap potential; HP, hemispheric power; AMIE, Assimilative Mapping Ionospheric Electrodynamics.

Data-Model Comparisons in the American Sector

Figure 2 shows the comparisons of the storm-quiet differential TEC in the American sector at different UTs, with the GNSS data shown in the top row and by simulation results shown in the second and third rows. The TEC data on 03/16 is used as the quiet-time reference. We also tried several other quiet-time references, e.g., the 5-day averaged TEC prior to 03/17, and the results do not have significant differences.

FIGURE 2

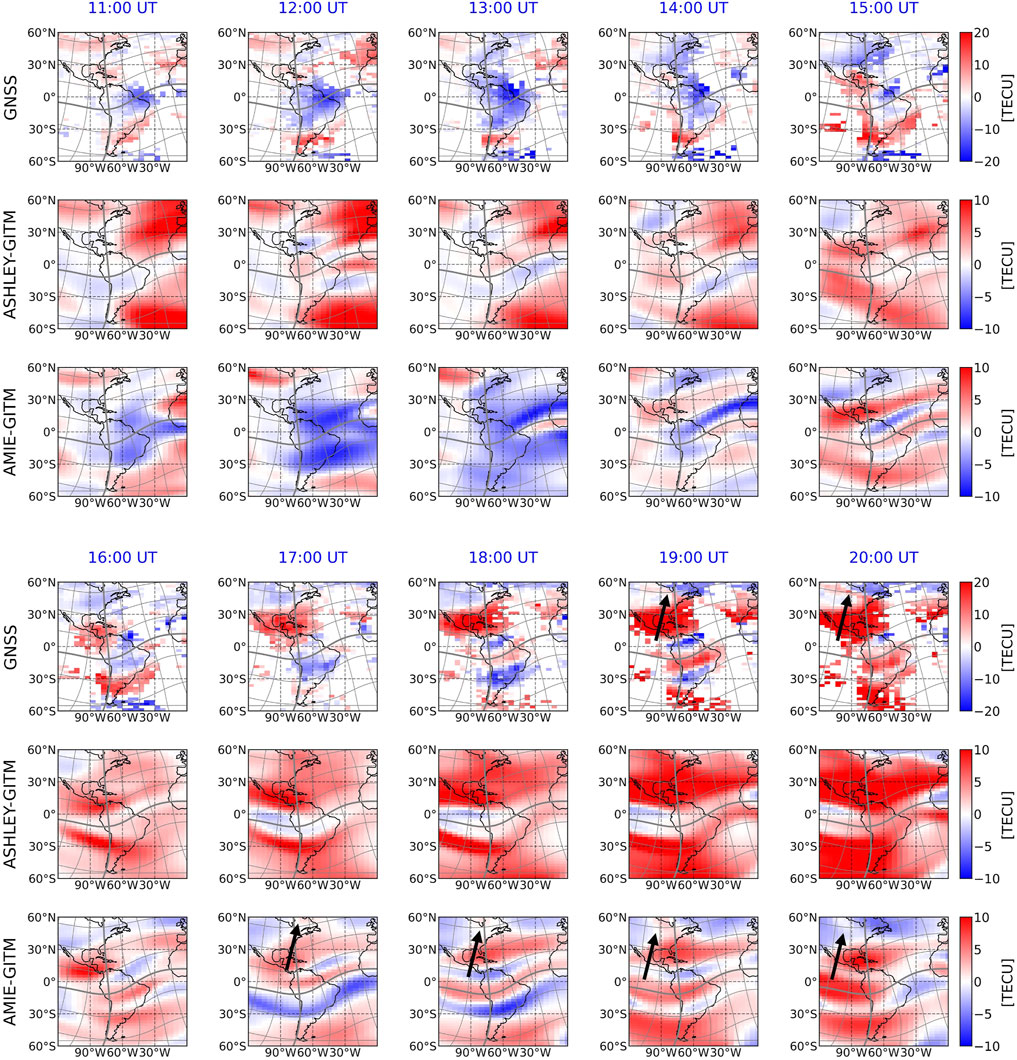
FIGURE 2. Comparisons of the storm-quiet differential TEC in the American sector at different UTs. At each UT, from top to bottom, the results correspond to those calculated from the GNSS data, ASHLEY-driven and AMIE-driven GITM simulation outputs, respectively. Note that the color scale is smaller for the differential TEC calculated from the GITM simulation output. The grey lines indicate the Apex magnetic coordinate, with the MLON and MLAT having a 20° spacing. The 0° MLON and MLAT are marked by the thick grey lines. Black arrows indicate the SED plume. TEC, total electron content; UT, universal time; ASHLEY, Auroral Spectrum and High-Latitude Electric field variabilitY; GITM, Global Ionosphere Thermosphere Model; MLON, magnetic longitude; MLAT, magnetic latitude; GNSS, Global Navigation Satellite System; SED, storm-time enhanced density.

As shown in the GNSS data, a negative storm phase occurs in the equatorial region at 11 UT and extends to higher latitudes afterwards. However, a positive storm phase occurs at around −30° magnetic latitude (MLAT) and lasts for several hours. Around 15 UT, a positive storm phase starts to occur near 30° MLAT and maintains and intensifies throughout the remaining time of the main phase. However, the negative storm phase still remains around the geomagnetic equator until 17 UT when a positive storm phase appears around the geomagnetic equator. Between 17 and 19 UT, negative storm phases occur at the nominal equatorial ionization anomaly (EIA) peak region (±15° MLAT) and are asymmetric about the geomagnetic equator. More specifically, the negative storm phase in the SH is more intense and occurs in a broader region than that in the NH at 17 and 18 UT. At 70°W, the differential TECs at 3°N (∼15° MLAT) are +5 TECU and −9 TECU) at 17and 18 UT, respectively, while the differential TECs at 27°S (∼15° MLAT) are −5 TECU and −17 TECU at 17 and 18 UT, respectively. However, the negative storm in the NH is more intense than its SH counterpart at 19 UT. The differential TECs are −17 TECU and −10 TECU at 15° and −15° MLAT at 70°W, respectively. At 20 UT, positive storm phases cover almost the entire American sector except for the region poleward of 50° MLAT, where a strong storm-enhanced density (SED) plume cuts through a negative storm phase which has been lasted for several hours.

The second row for each UT shows the ASHLEY-driven GITM simulation results. Note that for GITM simulation results, the color scale is half of that used for the GNSS data since the GITM TEC is roughly half of the GNSS TEC during both quiet and storm times. Several reasons may be responsible for the underestimation of TEC such as no plasmasphere contribution and inaccuracy of the top boundary conditions. Improving the quantitative representation of the electron density in GITM, especially during geomagnetic storms, is an important aspect of our future model development plan. It is clear that there are large discrepancies between the observational and ASHLEY-driven simulation results, particularly the negative storm phase shown in the GNSS data is not well captured by the ASHLEY-driven GITM simulation. We have also utilized the Weimer electric potential model (Weimer, 2005) and Fuller-Rowell and Evans electron precipitation model (Fuller-Rowell and Evans, 1987), which are the default high-latitude empirical models in GITM, to specify high-latitude electrodynamic forcings in GITM. However, that GITM simulation cannot well reproduce the observed feature either. In contrast, the major storm-related features shown in the GNSS data are well captured in the AMIE-driven simulation (third row for each UT) although some discrepancies do exist. For example, the AMIE-driven GITM simulation shows that the negative storm phase occurs in a larger area than that shown in the GNSS TEC data before 14 UT (e.g., −40° ∼ −20° MLAT). In addition, the AMIE-driven GITM simulation shows that the positive storm phase occurs in a larger area than that exhibited in the GNSS TEC data between 15 and 17 UT (e.g., around the geomagnetic equator). Interestingly, the SED plume which cuts through the negative storm phase occurred in the region poleward of 50° MLAT (marked by the black arrow) is roughly reproduced in the AMIE-driven simulation at 19 and 20 UT. However, the SED plume in GITM also occurs at 17 and 18 UT which is not seen in the data. Meanwhile, the simulated SED plume at 19 and 20 UT is not as narrow and strong as the observed one, which may be attributed to the fact that the subauroral plasma stream (SAPS) electric field is not well specified in AMIE (Lu et al., 2020) and also to the fact that the GITM grid resolution used in this study is quite coarse. Improving the representation of the SAPS electric field in AMIE would be an interesting future work. The data-model comparisons shown in Figure 2 demonstrate the value of using more realistic high-latitude electrodynamic forcings to investigate the storm-time ionospheric response. In the remaining part of this paper, we will focus on the comparisons of the observations with the AMIE-driven GITM simulation results.

Figure 3 shows detailed data-model comparisons at 70°W (LT∼UT−5 h, LT = local time), with the GNSS differential TEC shown in the top panel and the GITM differential TEC shown in the bottom panel. The latitudinal range we focused on here is 60°S–40°N in terms of the geographic latitude (GLAT), which roughly corresponds to −50°∼50° MLAT. As shown in Figure 3A, before 14 UT (∼9 LT), a negative storm phase occurs at almost all latitudes except for the region around 40°S and 20°N, where a positive storm phase occurs. The negative storm phase is pretty well captured by GITM while the positive storm phase occurred around 20°N before 12 UT (∼7 LT) and around 40°S between 12 and 14 UT (∼7–9 LT) are not well captured in the GITM simulation (Figure 3B). Between 14 and 16 UT (∼9–11 LT), the GNSS data indicates that a positive storm phase occurs from 20°S to 45°S and from 10°N to 20°N, while a weak positive storm phase occurs near the geomagnetic equator. These positive storms are reasonably well captured by GITM except that the positive storm phase at middle latitudes extends to higher latitudes in the NH in GITM simulation than that shown in the GNSS data. After 16 UT (∼11 LT), the GNSS data shows that positive storm phases occur poleward of the 10°N and 40°S, respectively. In addition, a positive storm phase also occurs around the geomagnetic equator (11°S) after 17:30 UT, which is preceded by a negative storm phase between ∼16:00 and 17:30 UT. Moreover, sizable negative storm phases can be seen around 5°N as well as around 30°S after 17 UT following the positive storm phase, with the one occurred around 30°S having larger latitudinal extension and stronger magnitude in general. Again, GITM simulation captures the main TEC variations shown in the observation.

FIGURE 3

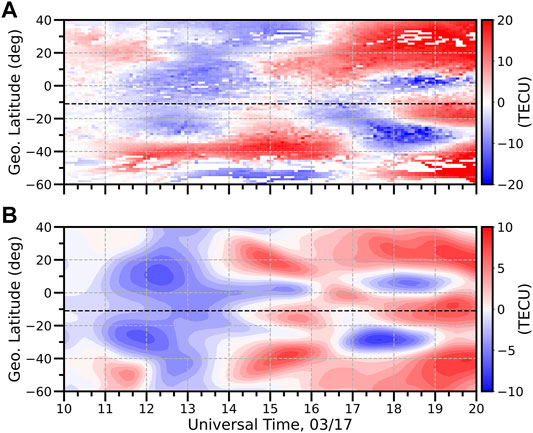
FIGURE 3. Comparison of the storm-quiet differential TEC at 70°W as a function of UT and geographic latitude. The black dashed line in each panel corresponds to the geomagnetic equator at 70°W. (A) GNSS differential TEC. (B) GITM differential TEC.

Figure 4 shows the data-model comparisons of the NmF2 and HmF2 at four stations located around 70°W. The red and blue lines represent the parameters on 03/17 and 03/16, respectively. The solid lines represent the parameters from the GITM simulation and the lines with circles represent the measured parameters. In general, GITM qualitatively captures the variations of NmF2 and HmF2 shown in the observation, but there are some quantitative discrepancies between the observation and simulation, which may result from the inaccurate specifications of the O⁺ flux at the top boundary of the model (Lu et al., 2001). Improving the top boundary condition of GITM is an important aspect of our future model development plan as discussed earlier.

FIGURE 4

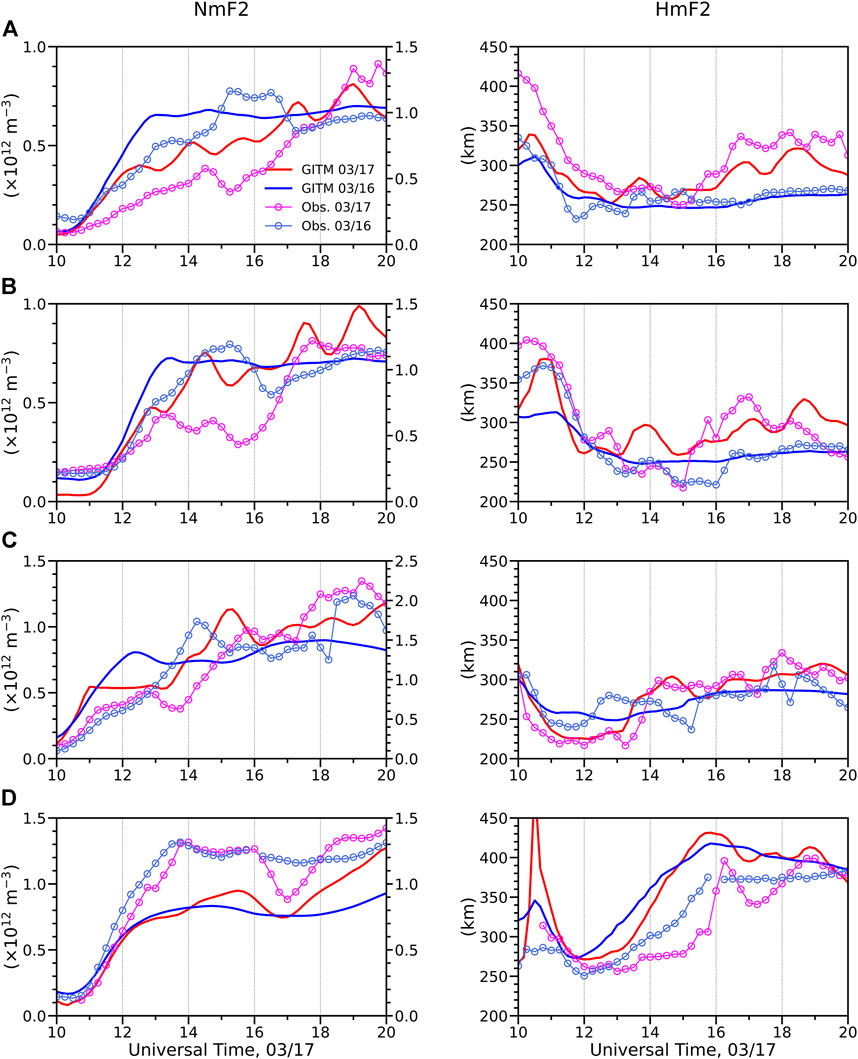
FIGURE 4. Comparisons of the NmF2 and HmF2 between the measurements and AMIE-driven GITM simulation results at four stations at around 70°W. The sky blue and magenta lines with circles represent the parameters measured on 03/16 and 03/17, respectively. The blue and red lines represent the simulation results on 03/16 and 03/17, respectively. (A) Wallop Island (75.5°W, 37.9°N). (B) Eglin (86.5°W, 30.5°N). (C) Ramey (67.1°W, 18.5°N). (D) Jicamarca (76.8°W, 12.0°S).

Physical Processes Responsible for the Electron Density Variations

As illustrated in the above subsection, the AMIE-driven GITM simulation reproduces the observed ionospheric response to the 2013 St. Patrick’s Day geomagnetic storm reasonably well, providing us an opportunity to explore the physical processes responsible for the ionospheric response during this storm.

Figure 5 shows the storm-quiet difference of the electron density, the meridional neutral wind, TEC, NmF2, and HmF2 at five selected latitudes along 70°W. One of them is located at the geomagnetic equator and the other four are located at ±15° MLAT and ±30° MLAT, respectively. The differences of the electron density and meridional neutral wind are shown as a function of UT and altitude while the other three parameters are show as a function of UT. In addition to the storm-time equatorward disturbance neutral winds (negative in NH and positive in SH), there are also poleward disturbance neutral winds at ±15° MLAT and ±30° MLAT, indicating the existence of the TADs. The TEC and ionospheric peak parameters also display quasi-periodic oscillations, which may be associated with the TADs. In particular, the variations of TEC and NmF2 are similar in general, while the correlation between the NmF2 and HmF2 oscillations is quite complicated. The oscillations of NmF2 and HmF2 are generally anti-correlated at ±15° MLAT but they are roughly positively correlated with some phase delay at other latitudes. As discussed in Lu et al. (2001), the correlation between the NmF2 and HmF2 depends on the relative importance of the vertical shear of the meridional neutral wind and the change of recombination near the F2 peak. The negative and positive correlations occur when the former and latter processes dominate, respectively.

FIGURE 5

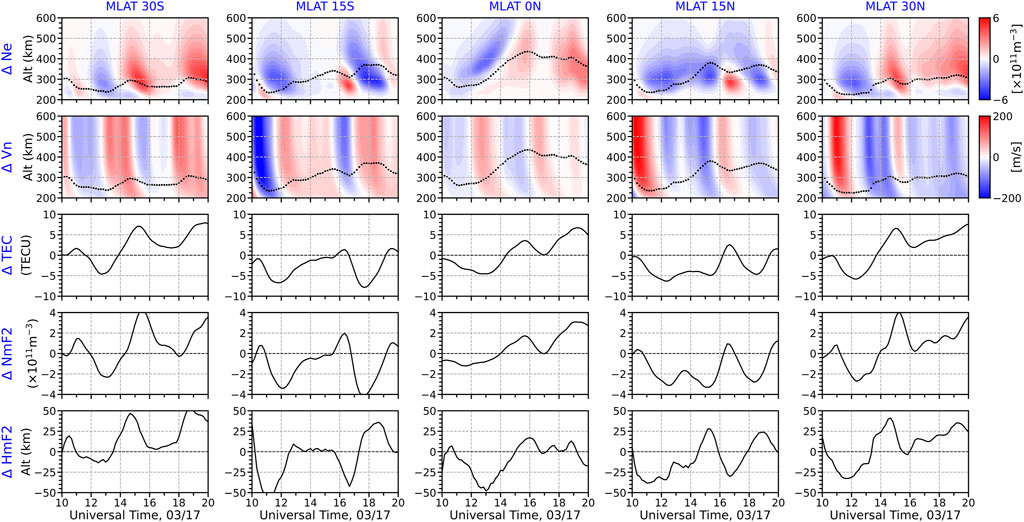
FIGURE 5. (From top to bottom) Storm-quiet differences of the electron density, meridional wind, TEC, NmF2 and HmF2 at five locations at 70°W calculated from the GITM outputs. The electron density and meridional wind are plotted as a function of UT and altitude while other parameters are shown as a function of UT. For the meridional wind, positive values indicate northward winds (poleward in the NH and equatorward in the SH). NH, northern hemisphere; SH, southern hemisphere.

Figure 5 also shows that the reduction of the electron density roughly follows the poleward disturbance wind at low and middle latitudes, indicating a significant contribution of the meridional wind to the formation of the negative storm phase. Then a question arises: how does the neutral wind contribute to the ionospheric response? To address this question, it is necessary to investigate the evolution of the neutral wind at 70°W. Figure 6 shows the storm-quiet differences of height-integrated Joule heating, meridional neutral wind along with the vertical ion drifts associated with the neutral wind and electric field. From the meridional neutral wind and the vertical drift associated with the neutral wind (Figures 6B,C), it is clear that several TADs are launched during this geomagnetic storm. Of particular interest are three pairs of TADs highlighted by the thick black dashed lines. The TADs launched in the NH and SH are labeled by the numbers of 1–3 and 1′–3′, respectively. The first pair of TADs (1 and 1′) launch right after the onset of the geomagnetic storm when there is a significant enhancement of Joule heating, traveling at high phase speeds (∼710 m/s) and having larger magnitudes (in terms of wind perturbations) than the TADs launched afterwards. At around 10 UT, when the 70°W meridian rotates to the dawn side, they encounter each other at the geomagnetic equator. After that, they cross each other and travel to middle and high latitudes in the opposite hemisphere. The poleward disturbance meridional winds associated with the TADs push the plasma downward along the field line (Figure 6C) where the recombination rate becomes large and thus cause a reduction of the electron density between 11and 14 UT at low and middle latitudes (Figure 3). This may also explain why the electron density reduction takes place at low latitudes at first and expands to higher latitudes as shown in Figures 2 and 3. The second pair of TADs (2 and 2′) launch around 12–13 UT, which are also able to travel to the opposite hemisphere before being dissipated. However, they are not as strong as the first pair in terms of wind perturbations so they cannot penetrate to latitudes as high as the first pair of TADs do. Moreover, the phase speed of TAD 2 (710 m/s) is ∼40% higher than that of TAD 2′ (510 m/s). The third pair of TADs (3 and 3′) cause poleward disturbance meridional winds in the hemispheres where they are launched and are associated with the rarefaction of TADs 2 and 2′. The phase speed of TAD 3 (540 m/s) is ∼13% higher than that of TAD 3′ (460 m/s). The phase speeds of those three pairs of TADs fall in the range of large-scale TADs categorized by Hunsucker (1982), and faster TAD launched in the NH has also reported in previous studies (e.g., Valladares et al., 2009; Lu et al., 2014; Pradipta et al., 2016). TAD 2 interferes with TAD 3′ at Location B (∼−20° MLAT) while TAD 2′ interferes with TAD 3 at Location A (∼5° MLAT) between 16 and 17 UT, causing strong poleward disturbance meridional winds at both locations. As noted above, the poleward disturbance meridional wind pushes the plasma downward along the magnetic field line, consequently reducing the plasma density later on.

FIGURE 6

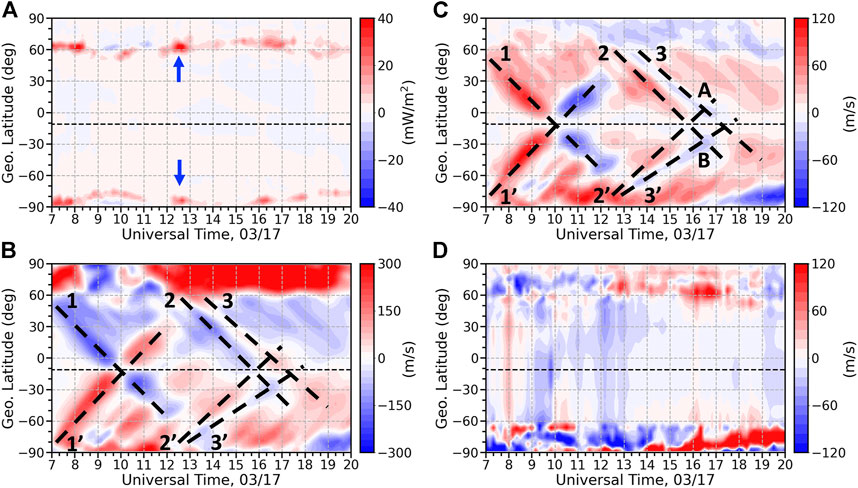
FIGURE 6. Storm-quiet differences of (A) Joule heating, (B) meridional neutral wind, (C) vertical ion drift associated with the neutral wind and (D) vertical ion drift associated with the electric field at 300 km and at 70°W. Positive neutral wind corresponds to northward neutral wind, and positive ion drift correspond to upward ion drift. All parameters are presented as a function of universal time and geographic latitude. The thin black dashed line in each panel denotes the geomagnetic equator. The thick black dashed lines highlight the TADs. TAD, traveling atmospheric disturbance. (A) ΔJoule heating. (B) ΔVn. (C) ΔVi (wind, up). (D) ΔVi (ExB, up).

Although plasma transport by the neutral wind through neutral-ion coupling can explain the observed ionospheric response, its relative importance with respect to other transport and chemical processes remains unclear. For example, Figure 6D shows that the vertical drift associated with the electric field may also be able to contribute to the negative storm phase occurred between 9 and 14 UT at low and middle latitudes shown in Figure 3. To delineate the relative contributions by the different dynamical and chemical process, following the procedures described in Lei et al. (2008a), a term analysis is applied to the ion continuity equation in GITM. Since the O⁺ is the dominant ion species in the F region and is the only species advected in GITM default setup (Ridley et al., 2006), the term analysis is carried out only for the O⁺. The continuity equation of O⁺ is written as:

$\frac{\partial N}{\partial t}=q-\beta N-\nabla \cdot \left(N\mathit{V}\right)(1)$

here, $N$ is the number density of O⁺, q is the production, $\beta$ is the loss coefficient and $\mathit{V}$ is the ion drift vector. On the right-hand side, $\beta N$ and $-\nabla \cdot \left(N\mathit{V}\right)$ represent the loss and transport processes, respectively, and the latter is a combination of transports by the E×B drift, by the neutral wind and by the ambipolar diffusion (Lei et al., 2008a; Liu et al., 2016; Lu et al., 2020). Thus, Eq. 1 can be rewritten as:

$\frac{\partial N}{\partial t}=\left(Production-Loss\right)+Tran{s}_{E\times B}+Tran{s}_{wind}+Tran{s}_{diff}(2)$

Figure 7 shows the storm-time differences of the electron density and all the terms listed in Eq. 2 as a function of UT and altitude at the five locations same as those shown in Figure 5. At the geomagnetic equator (middle column), when compared to the rate of O⁺ density changes shown in the second row, the transport due to the E×B drift plays a more important role before 15 UT and after 19 UT. Transport due to the neutral wind is more dominant between 15 UT and 19 UT. Transport due to the neutral wind increases the electron density at first around 15 UT and reduces the electron density between 16:30 and 17:30 UT and increases the electron density afterward. Although the neutral wind cannot effectively move the plasma upward or downward near the geomagnetic equator (Figure 6C), the convergence and divergence of meridional neutral wind (Figure 6B) are mainly responsible for the enhancement and reduction of the neutral wind transport term at the geomagnetic equator shown in Figure 7. This is consistent with the findings by Ren and Lei (2017) who reported that both the electric field and horizontal neutral wind transport could significantly contribute to the nightside HmF2 enhancement at Sao Luis (near geomagnetic equator) during the October 2013 geomagnetic storm. At ±30° MLAT, the main electron density changes take place in the topside ionosphere, which are mainly associated with the neutral wind transport until 19 UT. At ±15° MLAT, a major electron density reduction takes place in the topside ionosphere for the negative storm phase occurred before 14 UT, which is mainly associated with the neutral wind transport. Between 16 and 19 UT, the changes of electron density occur in both topside and bottomside ionosphere. The neutral wind transport term is still the main contributor to the electron density variation in the topside ionosphere while the combination of the chemical process and neural wind transport dominates in the bottomside ionosphere. However, the variations in the chemical process are also related to the TAD (Prölss, 2011). As shown in Figure 5, while the topside electron density decreases between 16 and 17 UT due to the poleward disturbance neutral wind, the bottomside electron density increases significantly, leading to a net enhancement of TEC. The bottomside electron density enhancement is mainly due to the vertical shear of the meridional wind (Lu et al., 2001). After 17 UT, the bottomside electron density undergoes a reduction while the reduction of the topside electron density subsides and even the topside electron density increases. However, the TEC undergoes a reduction in general since it is a measure of the vertical column electron density. Altogether, the neutral wind transport plays an important role affecting the ionospheric electron density variations during this storm, and TADs play an important role in the formation of the negative storm phase.

FIGURE 7

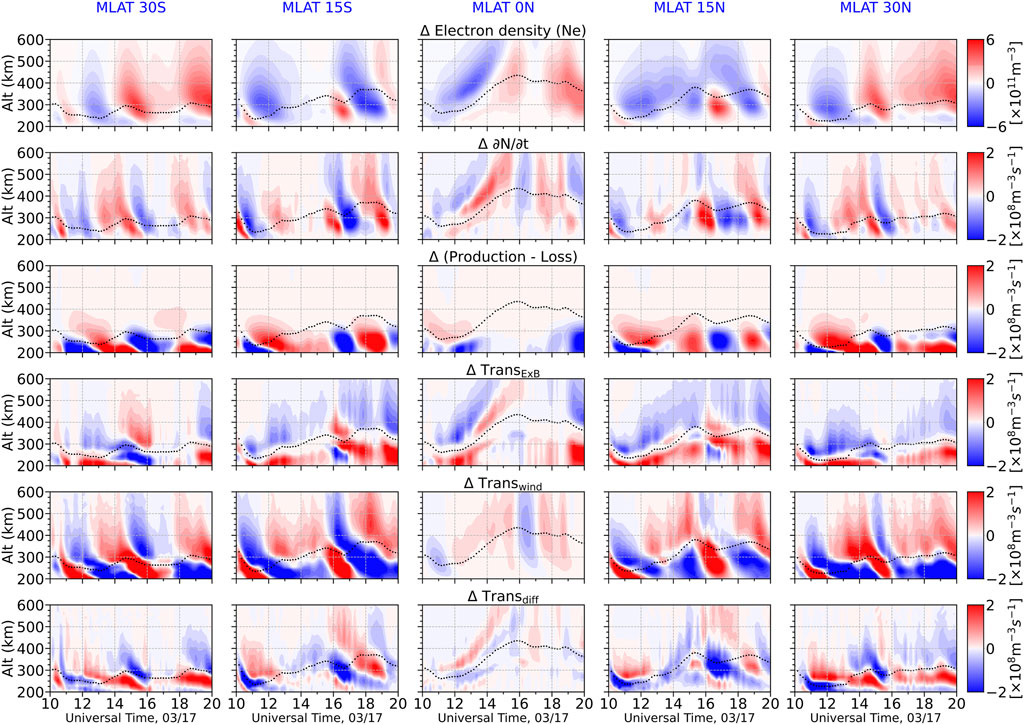
FIGURE 7. The storm-quiet differences of the electron density (top panel) and terms in Eq. 2 (second to last panels) at five locations at 70°W. For each plot, the parameter is shown as a function of universal time and altitude and the dotted line denotes the HmF2 on 03/17.

One noteworthy feature shown in Figure 3 is that the negative storm phase is stronger in the SH than the NH between 17 and 19 UT, which is caused by the stronger downward ion drift associated with the disturbance meridional wind in the SH. As shown in Figure 6B, the disturbance neutral winds that are responsible for the negative storm phase are quite comparable in the NH and SH between 16 and 17 UT, the difference in the vertical ion drift shown in Figure 6C is mainly associated with the location where the different TADs encounter. The location where TADs 3 and 2′ encounter (Location A) is closer to the geomagnetic equator than the location where TADs 2 and 3′ encounter (Location B). Since the inclination angle at the location A is smaller than that at the location B. the effect of vertical ion drift on plasma transport is more pronounced at the location B (Rishbeth and Garriott, 1969). The reason why the location B is further from the geomagnetic equator than the location A is mainly attributed to the fact that TADs 2 and 3 (launched in NH) travel faster than TADs 2′ and 3′ (launched in the SH), and the reason why TADs 2 and 3 travel faster than TADs 2′ and 3′ may lie in the fact that the Joule heating deposited in the NH and SH is asymmetric (Richmond and Matsushita, 1975). As shown in Figure 6A, the Joule heating deposited at 70°W in the NH is generally stronger than that deposited in the SH between 12 and 13 UT (i.e., 7–8 LT). The cause of the interhemispheric asymmetry of Joule heating between 12 and 13 UT will be discussed in detail in the next paragraph. If the phase speeds of TADs 2 and 3 are faster or/and the phase speeds of the TADs 2′ and 3′ are slower, the negative phase occurred between 17 and 19 UT at low latitudes may be located even southward, which is the case shown in the observation (Figure 3). If this is the case, opposite storm phases can take place in the magnetic conjugate locations. Therefore, the northward shift of the negative storm phases in the GITM simulation may be caused by the underestimation of the phase speeds of TADs 2 and 3 or/and the overestimation of the phase speeds of TADs 2′ and 3′.

To investigate the cause of the interhemispheric asymmetry of Joule heating between 12 and 13 UT, especially on the dawn side and morning side that is responsible for the TADs shown in Figure 6, the distributions of high-latitude electric potential, electron precipitation and height-integrated Joule heating in the NH and SH are examined, and Figure 8 shows an example at 12:30 UT for illustrations. Firstly, because the offset between the geomagnetic and geographic poles is different in the different hemispheres, the electric potential and electron precipitation are located more toward the dayside in the NH than in the SH. As a result, the NH receives more solar illuminations than the SH in the region where |MLAT| > 50° at 12:30 UT even this storm occurs very close to the equinox. Secondly, the IMF B_y is not negligible (about −5 nT) and is comparable with the IMF B_z at 12:30 UT (Figure 1), which is responsible for the asymmetric distribution of the electric potential between the two hemispheres. As discussed in Hong et al. (2021), even if the auroral electron precipitation is symmetric and the geomagnetic field is a pure dipole field, the Joule heating displays a significant interhemispheric asymmetry at the equinox if the IMF B_y is not negligible. The stronger Joule heating deposited on the dawn side in the NH also results from the stronger electron precipitation in the NH, which may be associated with the IMF B_y and the substorm effects. Finally, it is worth noting that the ground-based measurements in the SH are less abundant as compared with the NH, which may partly contribute to the asymmetric distributions of high-latitude electrodynamic forcings and Joule heating in the different hemispheres shown in Figure 8. However, the satellite measurements in both hemispheres are comparable and abundant, so that the lack of ground-based measurements in the SH may have a smaller effect compared to the first two points on the inter-hemispheric asymmetry of the Joule heating. Altogether, the interhemispheric asymmetry of Joule heating between 12 and 13 UT may mainly result from the differences of the magnetosphere-ionosphere coupling in the different hemispheres and the geomagnetic field configuration.

FIGURE 8

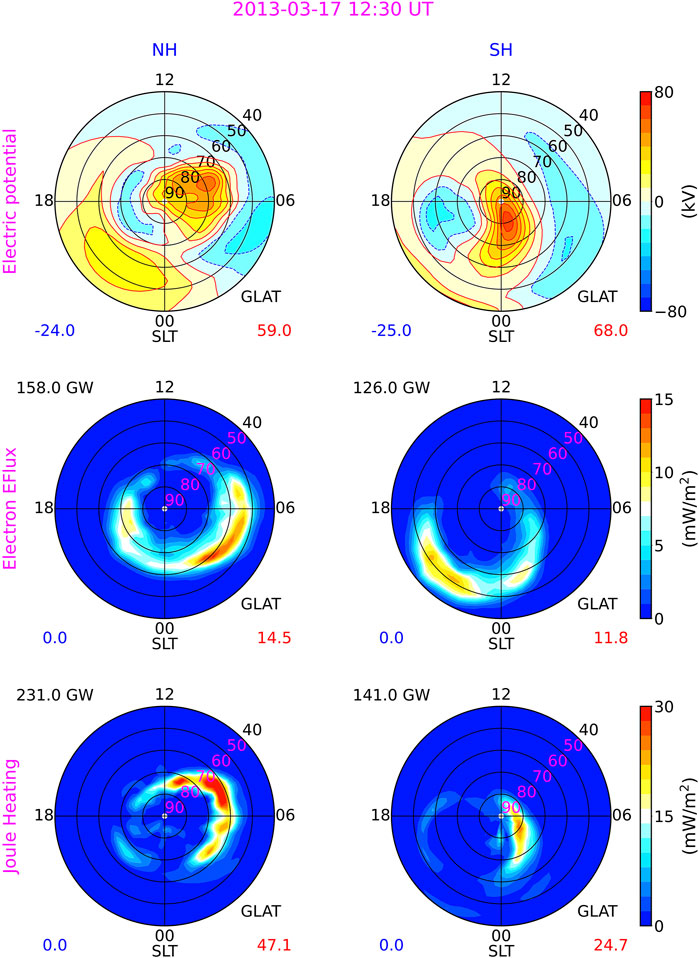
FIGURE 8. Distributions of the (top) electric potential, (middle) total electron energy flux and (bottom) height-integrated Joule heating in the (left) NH and (right) SH at 12:30 UT on 03/17/2013. The minimum and maximum in each plot are labelled at the bottom left and right of each plot, respectively. The value at the top left of each plot in the bottom two rows represents the hemispheric integrated value. All plots are present in geographic coordinates.

Summary

In this study, the dayside ionospheric response to the main phase of the 2013 St. Patrick’s Day geomagnetic storm in the American sector has been studied by a combination of data analysis and numerical simulation. It is found that the GITM simulation driven by the AMIE electric potential and electron precipitation patterns is able to capture the observed ionospheric response reasonably well. In comparison, the GITM simulation driven by the electric potential and electron precipitation patterns from the empirical model ASHLEY does not reproduce the observations very well. Our efforts highlight the significance of properly specifying the high-latitude electrodynamic forcing in GCMs. The physical processes that are responsible for the observed ionospheric response have also been investigated utilizing the GITM simulation. It is found that the most observed storm-related features shown in the GNSS TEC are largely attributed to the transport process associated with the neutral winds. In particular, the negative storm phase is largely associated with the TADs launched in the opposite hemisphere. A noteworthy phenomenon is the interhemispheric asymmetric negative storm phases occurred around the nominal EIA peak latitudes in the local afternoon, with the one occurred in the SH is stronger than that in the NH. The negative storm phase is a consequence of the interference of the TADs launched in both hemispheres and their hemispheric asymmetry is caused by the different phase speeds of TADs due to the asymmetric Joule heating depositions. Particularly, stronger Joule heating deposited in the NH launches TADs with faster phase speeds than those launched in the SH. As a result, the locations where the TADs interfere in the NH is closer to the geomagnetic equator than that in the SH. Consequently, the TAD can more effectively affect the ionosphere in the SH and cause a stronger reduction of electron density in the SH than in the NH. This study also provides a new insight for how the high-latitude electrodynamic forcing can contribute to the interhemispheric asymmetry of the ionospheric response at low and middle latitudes during geomagnetic storms.

Data Availability Statement

The IMF and solar wind data can be found at the NASA/GSFC's Space Physics Data Facility's OMNIWeb (https://omniweb.gsfc.nasa.gov). The GNSS TEC data is available at the CEDAR Madrigal database (http://cedar.openmadrigal.org/). The NmF2 and HmF2 data are available at the Global Ionospheric Radio Observatory (http://giro.uml.edu). The AMIE outputs along with the simulation outputs are stored at the NCAR GDEX repository, which can be accessed via the link: https://doi.org/10.5065/asf8-3d59.

Author Contributions

QZ led the work, carried out the simulation and analyses and wrote the paper. GL created the AMIE electric potential and electron precipitation patterns. GL and YD contributed discussions. All co-authors contributed comments, edits to the manuscript.

Funding

QZ was supported by the National Center for Atmospheric Research Advanced Study Program Postdoctoral Fellowship. GL was supported by in part by NASA under the Living with a Star program under grant 80NSSC17K071, the Heliophysics Supporting Research program under grant NNX17AI39G, and by AFOSR through award FA9559-17-1-0248. QZ and GL were also supported by the NASA GOLD ICON Guest Investigators Program under grant 80NSSC22K0061 through the subaward 2021GC1619. YD was supported by AFOSR through award FA9559-16-1-0364 and NASA grants 80NSSC20K0195, 80NSSC20K0606 and 80NSSC22K0061. This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under Cooperative Agreement No. 1852977.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Astrid Maute for the comments and suggestions for the initial manuscript. We thank the support from the ISSI for the international team on “Multi-Scale Magnetosphere-Ionosphere-Thermosphere Interaction”. We would like to acknowledge high-performance computing support from Cheyenne (doi: 10.5065/D6RX99HX) provided by National Center for Atmospheric Research’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation. We acknowledge use of NASA/GSFC’s Space Physics Data Facility’s OMNIWeb (or CDAWeb or ftp) service, and OMNI data. We acknowledge the CEDAR Madrigal database for the TEC and DMSP SSIES data. We acknowledge the Global Ionospheric Radio Observatory for the NmF2 and HmF2 data. We thank the AMPERE team and the AMPERE Science Center (http://ampere.jhuapl.edu/) for providing the Iridium-derived data products. We thank the APL SSUSI team for providing the electron precipitation data (https://ssusi.jhuapl.edu/). We acknowledge the use of SuperDARN data (http://vt.superdarn.org/tiki-index.php). SuperDARN is a collection of radars funded by national scientific funding agencies of Australia, Canada, China, France, Italy, Japan, Norway, South Africa, United Kingdom, and United States. We also wish to acknowledge the SUPERMAG database (http://supermag.jhuapl.edu) to provide a worldwide network of ground magnetometers: INTERMAGNET, Alan Thomson; CARISMA, PI Ian Mann; CANMOS, Geomagnetism Unit of the Geological Survey of Canada; The S-RAMP Database, PI K. Yumoto and Dr. K. Shiokawa; The SPIDR database; AARI, PI Oleg Troshichev; The MACCS program, PI M. Engebretson; GIMA; MEASURE, UCLA IGPP and Florida Institute of Technology; SAMBA, PI Eftyhia Zesta; 210 Chain, PI K. Yumoto; SAMNET, PI Farideh Honary; IMAGE, PI Liisa Juusola; Finnish Meteorological Institute, PI Liisa Juusola; Sodankylä Geophysical Observatory, PI Tero Raita; UiT the Arctic University of Norway, Tromsø Geophysical Observatory, PI Magnar G. Johnsen; GFZ German Research Centre For Geosciences, PI Jürgen Matzka; Institute of Geophysics, Polish Academy of Sciences, PI Anne Neska and Jan Reda; Polar Geophysical Institute, PI Alexander Yahnin and Yarolav Sakharov; Geological Survey of Sweden, PI Gerhard Schwarz; Swedish Institute of Space Physics, PI Masatoshi Yamauchi; AUTUMN, PI Martin Connors; DTU Space, Thom Edwards and PI Anna Willer; South Pole and McMurdo Magnetometer, PI’s Louis J. Lanzarotti and Alan T. Weatherwax; ICESTAR; RAPIDMAG; British Artarctic Survey; McMac, PI Dr. Peter Chi; BGS, PI Dr. Susan Macmillan; Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radio Wave Propagation (IZMIRAN); MFGI, PI B. Heilig; Institute of Geophysics, Polish Academy of Sciences, PI Anne Neska and Jan Reda; University of L’Aquila, PI M. Vellante; BCMT, V. Lesur and A. Chambodut; Data obtained in cooperation with Geoscience Australia, PI Andrew Lewis; AALPIP, co-PIs Bob Clauer and Michael Hartinger; MagStar, PI Jennifer Gannon; SuperMAG, PI Jesper W. Gjerloev; Data obtained in cooperation with the Australian Bureau of Meteorology, PI Richard Marshall. Additional ground magnetometer data were obtained from the THEMIS database (http://themis.ssl.berkeley.edu/gmag/), and we thank S. Mende and C. T. Russell for use of the GMAG data and NSF for support through Grant AGS-1004814; and I. R. Mann, D. K. Milling, and the rest of the CARISMA team for use of GMAG data. CARISMA is operated by the University of Alberta, funded by the Canadian Space Agency; Martin Connors and C. T. Russell and the rest of the AUTUMN/AUTUMNX team, Erik Steinmetz, Augsburg College, Peter Chi for use of the McMAC data and NSF for support through grant ATM-0245139; United States Air Force Academy (USAFA) and Peter Chi for the Falcon magnetometers; Dr. Kanji Hayashi, University of Tokyo for the STEP polar magnetometers; Tromsø Geophysical Observatory, University of Tromsø, Norway for use of the Greenland and Norway magnetometer data; the Geophysical Institute of University of Alaska for the Alaska magnetometers, Geological Survey of Sweden, and INTERMAGNET for providing the data and promoting high standards of magnetic observatory practice; the USGS Geomagnetism Program (http://geomag.usgs.gov); The Canadian Magnetic Observatory Network (CANMON), maintained and operated by the Geological Survey of Canada, provided the data used in this study (http://www.geomag.nrcan.gc.ca); University of Iceland for the use of Leirvogur data; Arctic and Antarctic Research Institute (AARI) of Department of Geophysics (http://geophys.aari.ru) for the AARI magnetometers; and Polar Experimental Network for Geospace Upper atmosphere Investigations (PENGUIn) Ground Based Observatory led by PI, Dr. C. Robert Clauer of Virginia Tech supported by the National Science Foundation through the following awards: ANT0839858, ATM922979 (Virginia Tech), and ANT0838861 (University of Michigan).

References

Amaechi, P. O., Oyeyemi, E. O., Akala, A. O., Messanga, H. E., Panda, S. K., Seemala, G. K., et al. (2021). Ground‐Based GNSS and C/NOFS Observations of Ionospheric Irregularities over Africa: A Case Study of the 2013 St. Patrick's Day Geomagnetic Storm. Space weather. 19 (2), e2020SW002631. doi:10.1029/2020SW002631

CrossRef Full Text | Google Scholar

Anderson, B. J., Korth, H., Waters, C. L., Green, D. L., Merkin, V. G., Barnes, R. J., et al. (2014). Development of Large-Scale Birkeland Currents Determined from the Active Magnetosphere and Planetary Electrodynamics Response Experiment. Geophys. Res. Lett. 41 (9), 3017–3025. doi:10.1002/2014GL059941

CrossRef Full Text | Google Scholar

Balthazor, R. L., and Moffett, R. J. (1999). Morphology of Large-Scale Traveling Atmospheric Disturbances in the Polar Thermosphere. J. Geophys. Res. 104 (A1), 15–24. doi:10.1029/1998JA900039

CrossRef Full Text | Google Scholar

Bauske, R., and Prölss, G. W. (1997). Modeling the Ionospheric Response to Traveling Atmospheric Disturbances. J. Geophys. Res. 102 (A7), 14555–14562. doi:10.1029/97JA00941

CrossRef Full Text | Google Scholar

Blanc, M., and Richmond, A. D. (1980). The Ionospheric Disturbance Dynamo. J. Geophys. Res. 85 (A4), 1669–1686. doi:10.1029/JA085iA04p01669

CrossRef Full Text | Google Scholar

Bruinsma, S. L., and Forbes, J. M. (2009). Properties of Traveling Atmospheric Disturbances (TADs) Inferred from CHAMP Accelerometer Observations. Adv. Space Res. 43 (3), 369–376. doi:10.1016/j.asr.2008.10.031

CrossRef Full Text | Google Scholar

Burns, A. G., Killeen, T. L., Deng, W., Carignan, G. R., and Roble, R. G. (1995). Geomagnetic Storm Effects in the Low- to Middle-Latitude Upper Thermosphere. J. Geophys. Res. 100 (A8), 14673–14691. doi:10.1029/94JA03232

CrossRef Full Text | Google Scholar

Cai, X., Burns, A. G., Wang, W., Qian, L., Solomon, S. C., Eastes, R. W., et al. (2021). Investigation of a Neutral “Tongue” Observed by GOLD during the Geomagnetic Storm on May 11, 2019. J. Geophys. Res. Space Phys. 126 (6), e2020JA028817. doi:10.1029/2020JA028817

CrossRef Full Text | Google Scholar

Dang, T., Lei, J., Wang, W., Wang, B., Zhang, B., Liu, J., et al. (2019). Formation of Double Tongues of Ionization during the 17 March 2013 Geomagnetic Storm. J. Geophys. Res. Space Phys. 124 (12), 10619–10630. doi:10.1029/2019JA027268

CrossRef Full Text | Google Scholar

Deng, Y., Fuller-Rowell, T. J., Akmaev, R. A., and Ridley, A. J. (2011). Impact of the Altitudinal Joule Heating Distribution on the Thermosphere. J. Geophys. Res. 116 (A5), A05313. doi:10.1029/2010JA016019

CrossRef Full Text | Google Scholar

Deng, Y., Lin, C., Zhu, Q., and Sheng, C. (2021). “Influence of Non-hydrostatic Processes on the Ionosphere-Thermosphere,” in Space Physics and Aeronomy Collection Volume 4: Upper Atmosphere Dynamics and Energetics, Geophys. Monogr. Ser. Editors W. Wang,, and Y. Zhang (Washington, D.C: AGU), 261. doi:10.1002/9781119507512

CrossRef Full Text | Google Scholar

Deng, Y., Richmond, A. D., Ridley, A. J., and Liu, H.-L. (2008). Assessment of the Non-hydrostatic Effect on the Upper Atmosphere Using a General Circulation Model (GCM). Geophys. Res. Lett. 35, L01104. doi:10.1029/2007GL032182

CrossRef Full Text | Google Scholar

Deng, Y., and Ridley, A. J. (2014). Simulation of Non-hydrostatic Gravity Wave Propagation in the Upper Atmosphere. Ann. Geophys. 32, 443–447. doi:10.5194/angeo-32-443-2014

CrossRef Full Text | Google Scholar

Deng, Y., Sheng, C., Tsurutani, B. T., and Mannucci, A. J. (2018). Possible Influence of Extreme Magnetic Storms on the Thermosphere in the High Latitudes. Space weather. 16, 802–813. doi:10.1029/2018SW001847

CrossRef Full Text | Google Scholar

Dmitriev, A. V., Suvorova, A. V., Klimenko, M. V., Klimenko, V. V., Ratovsky, K. G., Rakhmatulin, R. A., et al. (2017). Predictable and Unpredictable Ionospheric Disturbances during St. Patrick's Day Magnetic Storms of 2013 and 2015 and on 8-9 March 2008. J. Geophys. Res. Space Phys. 122 (2), 2398–2423. doi:10.1002/2016JA023260

CrossRef Full Text | Google Scholar

Fejer, B. G., and Scherliess, L. (1997). Empirical Models of Storm Time Equatorial Zonal Electric Fields. J. Geophys. Res. 102 (A11), 24047–24056. doi:10.1029/97JA02164

CrossRef Full Text | Google Scholar

Ferdousi, B., Nishimura, Y., Maruyama, N., and Lyons, L. R. (2019). Subauroral Neutral Wind Driving and its Feedback to SAPS during the 17 March 2013 Geomagnetic Storm. J. Geophys. Res. Space Phys. 124 (3), 2323–2337. doi:10.1029/2018JA026193

CrossRef Full Text | Google Scholar

Fuller-Rowell, T. J., Codrescu, M. V., Moffett, R. J., and Quegan, S. (1994). Response of the Thermosphere and Ionosphere to Geomagnetic Storms. J. Geophys. Res. 99 (A3), 3893–3914. doi:10.1029/93JA02015

CrossRef Full Text | Google Scholar

Fuller-Rowell, T. J., and Evans, D. S. (1987). Height-integrated Pedersen and Hall Conductivity Patterns Inferred from the TIROS-NOAA Satellite Data. J. Geophys. Res. 92 (A7), 7606–7618. doi:10.1029/JA092iA07p07606

CrossRef Full Text | Google Scholar

Guerrero, A., Palacios, J., Rodríguez‐Bouza, M., Rodríguez‐Bilbao, I., Aran, A., Cid, C., et al. (2017). Storm and Substorm Causes and Effects at Midlatitude Location for the St. Patrick's 2013 and 2015 Events. J. Geophys. Res. Space Phys. 122 (10), 9994–10011. doi:10.1002/2017JA024224

CrossRef Full Text | Google Scholar

Guo, J., Liu, H., Feng, X., Wan, W., Deng, Y., and Liu, C. (2014). Constructive Interference of Large-Scale Gravity Waves Excited by Interplanetary Shock on 29 October 2003: CHAMP Observation. J. Geophys. Res. Space Phys. 119 (8), 6846–6851. doi:10.1002/2014JA020255

CrossRef Full Text | Google Scholar

Heelis, R. A., and Maute, A. (2020). Challenges to Understanding the Earth's Ionosphere and Thermosphere. J. Geophys. Res. Space Phys. 125 (7), e2019JA027497. doi:10.1029/2019JA027497

CrossRef Full Text | Google Scholar

Hong, Y., Deng, Y., Zhu, Q., Maute, A., Sheng, C., Welling, D., et al. (2021). Impacts of Different Causes on the Inter‐Hemispheric Asymmetry of Ionosphere‐Thermosphere System at Mid‐ and High‐Latitudes: GITM Simulations. Space weather. 19, e2021SW002856. doi:10.1029/2021SW002856

CrossRef Full Text | Google Scholar

Huang, C.-S., Foster, J. C., and Kelley, M. C. (2005). Long-duration Penetration of the Interplanetary Electric Field to the Low-Latitude Ionosphere during the Main Phase of Magnetic Storms. J. Geophys. Res. 110 (A11). doi:10.1029/2005JA011202

CrossRef Full Text | Google Scholar

Huang, X., and Reinisch, B. W. (1996). Vertical Electron Density Profiles from the Digisonde Network. Adv. Space Res. 18 (6), 121–129. doi:10.1016/0273-1177(95)00912-4

CrossRef Full Text | Google Scholar

Hunsucker, R. D. (1982). Atmospheric Gravity Waves Generated in the High-Latitude Ionosphere: A Review. Rev. Geophys. 20 (2), 293–315. doi:10.1029/RG020i002p00293

CrossRef Full Text | Google Scholar

Kalita, B. R., Hazarika, R., Kakoti, G., Bhuyan, P. K., Chakrabarty, D., Seemala, G. K., et al. (2016). Conjugate Hemisphere Ionospheric Response to the St. Patrick's Day Storms of 2013 and 2015 in the 100°E Longitude Sector. J. Geophys. Res. Space Phys. 121 (11), 11,364–11,390. doi:10.1002/2016JA023119

CrossRef Full Text | Google Scholar

Knipp, D. J., Tobiska, W. K., and Emery, B. A. (2004). Direct and Indirect Thermospheric Heating Sources for Solar Cycles 21-23. Sol. Phys. 224, 495–505. doi:10.1007/s11207-005-6393-4

CrossRef Full Text | Google Scholar

Knipp, D., Kilcommons, L., Hairston, M., and Coley, W. R. (2021). Hemispheric Asymmetries in Poynting Flux Derived from DMSP Spacecraft. Geophys Res. Lett. 48, e2021GL094781. doi:10.1029/2021GL094781

CrossRef Full Text | Google Scholar

Kumar, S., and Kumar, V. V. (2019). Ionospheric Response to the St. Patrick's Day Space Weather Events in March 2012, 2013, and 2015 at Southern Low and Middle Latitudes. J. Geophys. Res. Space Phys. 124 (1), 584–602. doi:10.1029/2018JA025674

CrossRef Full Text | Google Scholar

Lee, C.-C., Liu, J.-Y., Chen, M.-Q., Su, S.-Y., Yeh, H.-C., and Nozaki, K. (2004). Observation and Model Comparisons of the Traveling Atmospheric Disturbances over the Western Pacific Region during the 6-7 April 2000 Magnetic Storm. J. Geophys. Res. 109 (A9), A09309. doi:10.1029/2003JA010267

CrossRef Full Text | Google Scholar

Lei, J., Burns, A. G., Tsugawa, T., Wang, W., Solomon, S. C., and Wiltberger, M. (2008a). Observations and Simulations of Quasiperiodic Ionospheric Oscillations and Large-Scale Traveling Ionospheric Disturbances during the December 2006 Geomagnetic Storm. J. Geophys. Res. 113 (A6), A06310. doi:10.1029/2008JA013090

CrossRef Full Text | Google Scholar

Lei, J., Wang, W., Burns, A. G., Solomon, S. C., Richmond, A. D., Wiltberger, M., et al. (2008b). Observations and Simulations of the Ionospheric and Thermospheric Response to the December 2006 Geomagnetic Storm: Initial Phase. J. Geophys. Res. 113 (A1), A01314. doi:10.1029/2007JA012807

CrossRef Full Text | Google Scholar

Lin, C. H., Richmond, A. D., Heelis, R. A., Bailey, G. J., Lu, G., Liu, J. Y., et al. (2005). Theoretical Study of the Low- and Midlatitude Ionospheric Electron Density Enhancement during the October 2003 Superstorm: Relative Importance of the Neutral Wind and the Electric Field. J. Geophys. Res. 110 (A12), A12312. doi:10.1029/2005JA011304

CrossRef Full Text | Google Scholar

Lin, D., Wang, W., Scales, W. A., Pham, K., Liu, J., Zhang, B., et al. (2019). SAPS in the 17 March 2013 Storm Event: Initial Results from the Coupled Magnetosphere‐Ionosphere‐Thermosphere Model. J. Geophys. Res. Space Phys. 124 (7), 6212–6225. doi:10.1029/2019JA026698

CrossRef Full Text | Google Scholar

Liu, J., Wang, W., Burns, A., Solomon, S. C., Zhang, S., Zhang, Y., et al. (2016). Relative Importance of Horizontal and Vertical Transports to the Formation of Ionospheric Storm‐enhanced Density and Polar Tongue of Ionization. J. Geophys. Res. Space Phys. 121 (8), 8121–8133. doi:10.1002/2016JA022882

CrossRef Full Text | Google Scholar

Lu, G., Goncharenko, L., Nicolls, M. J., Maute, A., Coster, A., and Paxton, L. J. (2012). Ionospheric and Thermospheric Variations Associated with Prompt Penetration Electric Fields. J. Geophys. Res. 117 (A8), A08312. doi:10.1029/2012JA017769

CrossRef Full Text | Google Scholar

Lu, G., Goncharenko, L. P., Richmond, A. D., Roble, R. G., and Aponte, N. (2008). A Dayside Ionospheric Positive Storm Phase Driven by Neutral Winds. J. Geophys. Res. 113 (A8), A08304. doi:10.1029/2007JA012895

CrossRef Full Text | Google Scholar

Lu, G., Hagan, M. E., Häusler, K., Doornbos, E., Bruinsma, S., Anderson, B. J., et al. (2014). Global Ionospheric and Thermospheric Response to the 5 April 2010 Geomagnetic Storm: An Integrated Data‐model Investigation. J. Geophys. Res. Space Phys. 119 (12), 10,358–10,375. doi:10.1002/2014JA020555

CrossRef Full Text | Google Scholar

Lu, G. (2017). Large Scale High-Latitude Ionospheric Electrodynamic Fields and Currents. Space Sci. Rev. 206 (1–4), 431–450. doi:10.1007/s11214-016-0269-9

CrossRef Full Text | Google Scholar

Lu, G., Richmond, A. D., Emery, B. A., and Roble, R. G. (1995). Magnetosphere-ionosphere-thermosphere Coupling: Effect of Neutral Winds on Energy Transfer and Field-Aligned Current. J. Geophys. Res. 100 (A10), 19643–19659. doi:10.1029/95JA00766

CrossRef Full Text | Google Scholar

Lu, G., Richmond, A. D., Lühr, H., and Paxton, L. (2016). High‐latitude Energy Input and its Impact on the Thermosphere. J. Geophys. Res. Space Phys. 121 (7), 7108–7124. doi:10.1002/2015JA022294

CrossRef Full Text | Google Scholar

Lu, G., Richmond, A. D., Roble, R. G., and Emery, B. A. (2001). Coexistence of Ionospheric Positive and Negative Storm Phases under Northern Winter Conditions: A Case Study. J. Geophys. Res. 106 (A11), 24493–24504. doi:10.1029/2001JA000003

CrossRef Full Text | Google Scholar

Lu, G., Zakharenkova, I., Cherniak, I., and Dang, T. (2020). Large‐Scale Ionospheric Disturbances during the 17 March 2015 Storm: A Model‐Data Comparative Study. J. Geophys. Res. Space Phys. 125 (5), e2019JA027726. doi:10.1029/2019JA027726

CrossRef Full Text | Google Scholar

Lyons, L. R., Gallardo‐Lacourt, B., Zou, S., Weygand, J. M., Nishimura, Y., Li, W., et al. (2016). The 17 March 2013 Storm: Synergy of Observations Related to Electric Field Modes and Their Ionospheric and Magnetospheric Effects. J. Geophys. Res. Space Phys. 121 (11), 10,880–10,897. doi:10.1002/2016JA023237

CrossRef Full Text | Google Scholar

Lyons, L. R., Nishimura, Y., Zhang, S. R., Coster, A. J., Bhatt, A., Kendall, E., et al. (2019). Identification of Auroral Zone Activity Driving Large‐Scale Traveling Ionospheric Disturbances. J. Geophys. Res. Space Phys. 124, 700–714. doi:10.1029/2018JA025980

CrossRef Full Text | Google Scholar

Mannucci, A. J., Tsurutani, B. T., Iijima, B. A., Komjathy, A., Saito, A., Gonzalez, W. D., et al. (2005). Dayside Global Ionospheric Response to the Major Interplanetary Events of October 29-30, 2003 "Halloween Storms". Geophys. Res. Lett. 32 (12), L12S02. doi:10.1029/2004GL021467

CrossRef Full Text | Google Scholar

Marsal, S., Torta, J. M., Segarra, A., and Araki, T. (2017). Use of Spherical Elementary Currents to Map the Polar Current Systems Associated with the Geomagnetic Sudden Commencements on 2013 and 2015 St. Patrick's Day Storms. J. Geophys. Res. Space Phys. 122 (1), 194–211. doi:10.1002/2016JA023166

CrossRef Full Text | Google Scholar

Maute, A., and Richmond, A. D. (2017). F-region Dynamo Simulations at Low and Mid-latitude. Space Sci. Rev. 206 (1–4), 471–493. doi:10.1007/s11214-016-0262-3

CrossRef Full Text | Google Scholar

Pham, K. H., Zhang, B., Sorathia, K., Dang, T., Wang, W., Merkin, V., et al. (2022). Thermospheric Density Perturbations Produced by Traveling Atmospheric Disturbances during August 2005 Storm. JGR Space Phys. 127 (2), e2021JA030071. doi:10.1029/2021JA030071

CrossRef Full Text | Google Scholar

Pradipta, R., Valladares, C. E., Carter, B. A., and Doherty, P. H. (2016). Interhemispheric Propagation and Interactions of Auroral Traveling Ionospheric Disturbances Near the Equator. J. Geophys. Res. Space Phys. 121 (3), 2462–2474. doi:10.1002/2015JA022043

CrossRef Full Text | Google Scholar

Prölss, G. W. (2011). Density Perturbations in the Upper Atmosphere Caused by the Dissipation of Solar Wind Energy. Surv. Geophys 32 (2), 101–195. doi:10.1007/s10712-010-9104-0

CrossRef Full Text | Google Scholar

Qian, L., Burns, A. G., Emery, B. A., Foster, B., Lu, G., Maute, A., et al. (2014). “The NCAR TIE-GCM,” in Geophysical Monograph Series. Editors J. Huba, R. Schunk, and G. Khazanov (Chichester: John Wiley & Sons), 73–83. doi:10.1002/9781118704417.ch7

CrossRef Full Text | Google Scholar

Ren, D., and Lei, J. (2017). A Simulation Study of the Equatorial Ionospheric Response to the October 2013 Geomagnetic Storm. J. Geophys. Res. Space Phys. 122 (9), 9696–9704. doi:10.1002/2017JA024286

CrossRef Full Text | Google Scholar

Richmond, A. D. (1992). Assimilative Mapping of Ionospheric Electrodynamics. Adv. Space Res. 12 (6), 59–68. doi:10.1016/0273-1177(92)90040-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Richmond, A. D., and Kamide, Y. (1988). Mapping Electrodynamic Features of the High-Latitude Ionosphere from Localized Observations: Technique. J. Geophys. Res. 93 (A6), 5741–5759. doi:10.1029/JA093iA06p05741

CrossRef Full Text | Google Scholar

Richmond, A. D., and Matsushita, S. (1975). Thermospheric Response to a Magnetic Substorm. J. Geophys. Res. 80 (19), 2839–2850. doi:10.1029/JA080i019p02839

CrossRef Full Text | Google Scholar

Rideout, W., and Coster, A. (2006). Automated GPS Processing for Global Total Electron Content Data. GPS Solut. 10 (3), 219–228. doi:10.1007/s10291-006-0029-5

CrossRef Full Text | Google Scholar

Ridley, A. J., Deng, Y., and Tóth, G. (2006). The Global Ionosphere-Thermosphere Model. J. Atmos. Solar-Terrestrial Phys. 68 (8), 839–864. doi:10.1016/j.jastp.2006.01.008

CrossRef Full Text | Google Scholar

Rishbeth, H., and Garriott, O. K. (1969). Introduction to Ionospheric Physics. New York, London: Academic Press.

Google Scholar

Scherliess, L., and Fejer, B. G. (1997). Storm Time Dependence of Equatorial Disturbance Dynamo Zonal Electric Fields. J. Geophys. Res. 102 (A11), 24037–24046. doi:10.1029/97JA02165

CrossRef Full Text | Google Scholar

Sheng, C., Deng, Y., Gabrielse, C., Lyons, L., Nishimura, Y., Heelis, R., et al. (2021). Sensitivity of Upper Atmosphere to Different Characteristics of Flow Bursts in the Auroral Zone. J. Geophys. Res. Space Phys. 126, e2021JA029253. doi:10.1029/2021ja029253

CrossRef Full Text | Google Scholar

Shiokawa, K., Lu, G., Otsuka, Y., Ogawa, T., Yamamoto, M., Nishitani, N., et al. (2007). Ground Observation and AMIE-TIEGCM Modeling of a Storm-Time Traveling Ionospheric Disturbance. J. Geophys. Res. 112 (A5), A05308. doi:10.1029/2006JA011772

CrossRef Full Text | Google Scholar

Thayer, J. P., Vickrey, J. F., Heelis, R. A., and Gary, J. B. (1995). Interpretation and Modeling of the High-Latitude Electromagnetic Energy Flux. J. Geophys. Res. 100 (A10), 19715–19728. doi:10.1029/95JA01159

CrossRef Full Text | Google Scholar

Tsurutani, B., Mannucci, A., Iijima, B., Abdu, M. A., Sobral, J. H. A., Gonzalez, W., et al. (2004). Global Dayside Ionospheric Uplift and Enhancement Associated with Interplanetary Electric Fields. J. Geophys. Res. 109 (A8), A08302. doi:10.1029/2003JA010342

CrossRef Full Text | Google Scholar

Valladares, C. E., Villalobos, J., Hei, M. A., Sheehan, R., Basu, S., MacKenzie, E., et al. (2009). Simultaneous Observation of Traveling Ionospheric Disturbances in the Northern and Southern Hemispheres. Ann. Geophys. 27 (4), 1501–1508. doi:10.5194/angeo-27-1501-2009

CrossRef Full Text | Google Scholar

Verkhoglyadova, O. P., Tsurutani, B. T., Mannucci, A. J., Mlynczak, M. G., Hunt, L. A., Paxton, L. J., et al. (2016). Solar Wind Driving of Ionosphere‐thermosphere Responses in Three Storms Near St. Patrick's Day in 2012, 2013, and 2015. J. Geophys. Res. Space Phys. 121 (9), 8900–8923. doi:10.1002/2016JA022883

CrossRef Full Text | Google Scholar

Vierinen, J., Coster, A. J., Rideout, W. C., Erickson, P. J., and Norberg, J. (2016). Statistical Framework for Estimating GNSS Bias. Atmos. Meas. Tech. 9 (3), 1303–1312. doi:10.5194/amt-9-1303-2016

CrossRef Full Text | Google Scholar

Wang, Z., Zou, S., Liu, L., Ren, J., and Aa, E. (2021). Hemispheric Asymmetries in the Mid‐latitude Ionosphere during the September 7-8, 2017 Storm: Multi‐instrument Observations. JGR Space Phys. 126 (4), e2020JA028829. doi:10.1029/2020JA028829

CrossRef Full Text | Google Scholar

Weimer, D. R. (2005). Improved Ionospheric Electrodynamic Models and Application to Calculating Joule Heating Rates. J. Geophys. Res. 110 (A5), A05306. doi:10.1029/2004JA010884

CrossRef Full Text | Google Scholar

Xu, Z., Hartinger, M. D., Clauer, C. R., Peek, T., and Behlke, R. (2017). A Comparison of the Ground Magnetic Responses during the 2013 and 2015 St. Patrick's Day Geomagnetic Storms. J. Geophys. Res. Space Phys. 122 (4), 4023–4036. doi:10.1002/2016JA023338

CrossRef Full Text | Google Scholar

Yue, X., Wang, W., Lei, J., Burns, A., Zhang, Y., Wan, W., et al. (2016). Long‐lasting Negative Ionospheric Storm Effects in Low and Middle Latitudes during the Recovery Phase of the 17 March 2013 Geomagnetic Storm. J. Geophys. Res. Space Phys. 121 (9), 9234–9249. doi:10.1002/2016JA022984

CrossRef Full Text | Google Scholar

Zhai, C., Lu, G., Yao, Y., Wang, W., Zhang, S., Liu, J., et al. (2020). 3‐D Tomographic Reconstruction of SED Plume during 17 March 2013 Storm. J. Geophys. Res. Space Phys. 125 (11), e2020JA028257. doi:10.1029/2020JA028257

CrossRef Full Text | Google Scholar

Zhang, S. R., Erickson, P. J., Coster, A. J., Rideout, W., Vierinen, J., Jonah, O., et al. (2019). Subauroral and Polar Traveling Ionospheric Disturbances during the 7-9 September 2017 Storms. Space weather. 17 (12), 1748–1764. doi:10.1029/2019SW002325

CrossRef Full Text | Google Scholar

Zhang, Y., Paxton, L. J., Kil, H., Meng, C.-I., Mende, S. B., Frey, H. U., et al. (2003). Negative Ionospheric Storms Seen by the IMAGE FUV Instrument. J. Geophys. Res. 108 (A9), 1343. doi:10.1029/2002JA009797

CrossRef Full Text | Google Scholar

Zhu, Q., Deng, Y., Maute, A., Kilcommons, L. M., Knipp, D. J., and Hairston, M. (2021). ASHLEY: A New Empirical Model for the High‐Latitude Electron Precipitation and Electric Field. Space weather. 19 (5), e2020SW002671. doi:10.1029/2020SW002671

CrossRef Full Text | Google Scholar

Zhu, Q., Deng, Y., Maute, A., Sheng, C., Lin, C. Y., and Lin, C. (2017). Impact of the Vertical Dynamics on the Thermosphere at Low and Middle Latitudes: GITM Simulations. J. Geophys. Res. Space Phys. 122, 6882–6891. doi:10.1002/2017JA023939

CrossRef Full Text | Google Scholar

Zhu, Q., Deng, Y., Richmond, A., McGranaghan, R. M., and Maute, A. (2019). Impacts of Multiscale FACs on the Ionosphere‐Thermosphere System: GITM Simulation. J. Geophys. Res. Space Phys. 124 (5), 3532–3542. doi:10.1029/2018JA026082

CrossRef Full Text | Google Scholar