Equations of Motion Near Cyclotron Resonance

This work compares several versions of the equations of motion for a test particle encountering cyclotron resonance with a single, field-aligned whistler mode wave. The gyro-averaged Lorentz equation produces both widespread phase trapping (PT) and “positive phase bunching” of low pitch angle electrons by large amplitude waves. Approximations allow a Hamiltonian description to be reduced to a single pair of conjugate variables, which can account for PT as well as phase bunching at moderate pitch angle, and has recently been used to investigate this unexpected bahavior at low pitch angle. Here, numerical simulations using the Lorentz equation and several versions of Hamiltonian-based equations of motion are compared. Similar behavior at low pitch angle is found in each case.

1 Introduction

Cyclotron-resonant wave-particle interactions are a crucial ingredient in magnetospheric dynamics, especially in the radiation belts, and there is a vast tradition of simulating the process as quasi-linear diffusion of phase space density by a broad-band spectrum of small, incoherent waves (Thorne, 2010; Thorne et al., 2013), following the pioneering work of Lyons et al. (1971) and Lyons et al. (1972). A complementary approach is that of test particle simulation, most often in the presence of a single, coherent wave whose amplitude need not be small. Inan et al. (1978) noted both quasi-linear and nonlinear behavior, including the “loss cone reflection effect” whereby low pitch angles increase rather than decrease below zero. In the quasi-linear regime, connections between the two perspectives have been provided by Lemons et al. (2009), Lemons (2012), Allanson et al. (2022), and a unified picture of quasi-linear and nonlinear behavior was obtained by Albert (2001), Albert (2010). These studies all used specified and idealized models of the waves, while Liu et al. (2010), Liu et al. (2012) examined test particles driven by waves from self-consistent particle-in-cell simulations.

This work compares several versions of the equations of motion for a test particle encountering cyclotron resonance with a single, field-aligned whistler mode plane wave. The Lorentz force law, resolved into components parallel and perpendicular to the background magnetic field and gyro-averaged, is commonly used for such simulations. Hamiltonian descriptions are in principle equivalent, and with several approximations they allow the reduction to a one-dimensional (1D) system (one action-angle pair, plus the independent variable playing the role of time). If the time dependence is slow enough, particle motion is nearly along instantaneously drawn contours, with invariant breaking at separatrix crossings. There is a rich literature of work based on these concepts, which has been exploited in this context to some degree. Among others, Shklyar (1986) Albert (1993), Albert (2000), Artemyev et al. (2018) further approximated the Hamiltonian as equivalent to that of a time-dependent pendulum and obtained quantitative estimates of energy and pitch angle changes, which have proved useful and reliable.

Recently, using the gyro-averaged Lorentz equation, Kitahara and Katoh (2019), Gan et al. (2020) found both widespread (or “anomalous”) phase trapping (APT) and “positive phase bunching (PPB)” of low pitch angle electrons by large amplitude waves. Both phenomena lead to pitch angle increase, in contrast to the phase bunching behavior that is the usual alternative to phase trapping, and are associated with low pitch angle, which violates a certain approximation made in obtaining the pendulum Hamiltonian. Albert et al. (2021), Artemyev et al. (2021) presented generalizations of the pendulum Hamiltonian which avoid that specific approximation, but still relied on several others. In particular, differences in the first-order (in wave amplitude) term of the phase evolution equation are present among several versions of the equations of motion. This work shows numerically that, despite these differences, the generalized 1D Hamiltonian reproduces the behavior at low pitch angle, and is therefore an appropriate framework for the future development of refined analytical estimates.

2 Gyro-Averaged Equations of Motion

Starting with the Lorentz equation for a charged particle in a background magnetic field and a single whistler-mode wave,

$\frac{d\mathbf{p}}{dt}=q\left[{\mathbf{E}}_{\mathbf{w}}+\frac{\mathbf{p}}{mc\gamma }\times \left({\mathbf{B}}_0+{\mathbf{B}}_{\mathbf{w}}\right)\right],\frac{d\mathbf{x}}{dt}=\frac{\mathbf{p}}{m\gamma },(1)$

where p = mvγ is the mechanical momentum, γ is the relativistic factor, B₀ is the local geomagnetic field strength with equatorial value B_eq, and E_w and B_w are the electric and magnetic fields of the wave. Gyro-averaged equations of motion valid near a single resonance have been obtained by many authors, including (Chang and Inan, 1983; Bell, 1984; Albert et al., 2012; Li et al., 2015; Kitahara and Katoh, 2019).

For primary resonance (ℓ = −1) between an electron (charge q = −e) and a parallel-propagating whistler wave, equation 3 of Albert et al. (2012) simplifies to

$\begin{array}{ccc}\hfill \frac{d{p}_{\parallel }}{dt}& =\hfill & -\frac{p_{\perp }^2}{2m\gamma }\frac{d\mathrm{\Omega }/dz}{\mathrm{\Omega }}+\frac{e{B}_w}{mc}\frac{p_{\perp }}{\gamma }\cos \xi ,\hfill \\ \hfill \frac{d{p}_{\perp }}{dt}& =\hfill & \frac{p_{\parallel }{p}_{\perp }}{2m\gamma }\frac{d\mathrm{\Omega }/dz}{\mathrm{\Omega }}+\frac{e{B}_w}{mc}\frac{\mathrm{\Omega }}{\omega \eta }\frac{mc}{\gamma }\cos \xi ,\hfill \\ \hfill \frac{d\xi }{dt}& =\hfill & \left[\frac{\mathrm{\Omega }}{\gamma }-\omega +\frac{k{p}_{\parallel }}{m\gamma }\right]-\frac{e{B}_w}{mc}\frac{\mathrm{\Omega }}{\omega \eta }\frac{mc}{p_{\perp }\gamma }\sin \xi ,\hfill \\ \hfill \frac{dz}{dt}& =\hfill & \frac{p_{\parallel }}{m\gamma }.\hfill \end{array}(2)$

The angle ξ is a combination of wave phase and gyrophase, Ω is the local nonrelativistic electron gyrofrequency eB₀/mc, and η is the refractive index kc/ω. The standard resonance condition is just dξ/dt = 0, neglecting the term proportional to B_w.

Equations 3–9 of Kitahara and Katoh (2019) are very similar after shifting ξ by π/2, using ηE_w = B_w (in Gaussian units), and accounting for the opposite sign convention in wave phase:

$\begin{array}{ccc}\hfill \frac{d{p}_{\parallel }}{dt}& =\hfill & -\frac{p_{\perp }^2}{2m\gamma }\frac{d\mathrm{\Omega }/dz}{\mathrm{\Omega }}+\frac{e{B}_w}{mc}\frac{p_{\perp }}{\gamma }\cos \xi ,\hfill \\ \hfill \frac{d{p}_{\perp }}{dt}& =\hfill & \frac{p_{\parallel }{p}_{\perp }}{2m\gamma }\frac{d\mathrm{\Omega }/dz}{\mathrm{\Omega }}+\frac{e{B}_w}{mc}\left(\frac{\gamma }{\eta }-\frac{p_{\parallel }}{mc}\right)\frac{mc}{\gamma }\cos \xi ,\hfill \\ \hfill \frac{d\xi }{dt}& =\hfill & \left[\frac{\mathrm{\Omega }}{\gamma }-\omega +\frac{k{p}_{\parallel }}{m\gamma }\right]-\frac{e{B}_w}{mc}\left(\frac{\gamma }{\eta }-\frac{p_{\parallel }}{mc}\right)\frac{mc}{p_{\perp }\gamma }\sin \xi ,\hfill \\ \hfill \frac{dz}{dt}& =\hfill & \frac{p_{\parallel }}{m\gamma }.\hfill \end{array}(3)$

These two versions are brought into agreement by invoking the lowest-order resonance condition, which consists of setting the bracketed expression in the equation for dξ/dt to zero.

3 Time-dependent Hamiltonian Equations

Ginet and Heinemann (1990), Ginet and Albert (1991) used a Hamiltonian version of the equations of motion near resonance with a constant-frequency wave propagating obliquely to a constant background magnetic field B₀, The Hamiltonan formulation uses canonical momentum P = p + qA/c, where c is the speed of light, and A is the vector potential that describes both B₀ and the wave electromagnetic field. A canonical transformation was made from (x, P_x, y, P_y, z, P_z) to variables (I, ϕ, X, P_X, z, P_z), with z the distance along B₀ in slab geometry. I and ϕ correspond to standard first adiabatic invariant and gyrophase but have modifications proportional to the wave amplitude. After gyro-averaging, and specializing to the case of a parallel-propagating wave, the variables (ϕ, z, t) appeared only in the combination ∫kdz − ωt − ϕ (equation 19 of Ginet and Heinemann (1990) with k_x = 0 and sℓ = 1). Albert (1993) generalized the treatment to include slow dependence of Ω and η on z, obtaining the Hamiltonian

$H\left(I,\varphi ,P_z,z,t\right)=\mathrm{\Upsilon }+\frac{a_{\ell }}{2\mathrm{\Upsilon }}\sin \xi (4)$

where

$\mathrm{\Upsilon }={\left(1+2\frac{\mathrm{\Omega }}{\omega }I+P_z^2\right)}^{1/2},a_{\ell }=-\sqrt{2\frac{\mathrm{\Omega }}{\omega }I}\frac{1}{\eta }\frac{q{B}_w}{mc},(5)$

and

$\xi =\eta z-t+\varphi ,(6)$

using normalized variables (ωz/c, ωt, ωI/mc², P_z/mc) as in Albert (1993). Appropriate partial derivatives of H give equations of motion for (I, ϕ, P_z, z), e.g., dI/dt = −∂H/∂ϕ and dϕ/dt = ∂H/∂I, from which

$\frac{d\xi }{dt}=\eta \frac{P_z}{\mathrm{\Upsilon }}-1+\frac{d\varphi }{dt}.(7)$

It is also found that dH/dt = ∂H/∂t equals dI/dt, so that I − H is a constant, denoted c₂:

$I-H=c_2.(8)$

Following Shklyar (1986), Albert (1993) solved this for P_z after approximating H by ϒ, obtaining

$\mathrm{\Upsilon }\approx {\mathrm{\Upsilon }}_0\equiv I-c_2,P_z^2\approx P_0^2\equiv {\left(I-c_2\right)}^2-1-2\frac{\mathrm{\Omega }}{\omega }I.(9)$

These can be used to eliminate P_z in the equations of motion, giving

$\begin{array}{ccc}\hfill \frac{dI}{dt}& =\hfill & -\frac{a_{\ell }}{2{\mathrm{\Upsilon }}_0}\cos \xi ,\hfill \\ \hfill \frac{d\xi }{dt}& =\hfill & \left[-\eta \frac{P_0}{{\mathrm{\Upsilon }}_0}+\frac{\mathrm{\Omega }}{\omega {\mathrm{\Upsilon }}_0}-1\right]+a_{\ell }\frac{1+P_0^2}{4I{\mathrm{\Upsilon }}_0^3}\sin \xi ,\hfill \\ \hfill \frac{dz}{dt}& =\hfill & -\frac{P_0}{{\mathrm{\Upsilon }}_0},\hfill \end{array}(10)$

as a closed set of equations in (I, ξ, z, t). Since P₀ is defined as always positive, explicit minus signs account for the motion of the particle toward the equator. The bracketed expression in the equation for dξ/dt gives the lowest order resonance condition.

Retaining the wave term in H to first order gives

$\mathrm{\Upsilon }\approx {\mathrm{\Upsilon }}_0-\frac{a_{\ell }}{2{\mathrm{\Upsilon }}_0}\sin \xi ,P_z\approx -P_0+\frac{a_{\ell }}{2P_0}\sin \xi ,(11)$

again allowing P_z to be eliminated. The correction to P_z/ϒ significantly affects Eq. 7, giving

$\begin{array}{ll}\hfill \frac{dI}{dt}& =-\frac{a_{\ell }}{2{\mathrm{\Upsilon }}_0}\cos \xi ,\hfill \\ \hfill \frac{d\xi }{dt}& =\left[-\eta \frac{P_0}{{\mathrm{\Upsilon }}_0}+\frac{\mathrm{\Omega }}{\omega {\mathrm{\Upsilon }}_0}-1\right]+\frac{a_{\ell }}{4I{P}_0{\mathrm{\Upsilon }}_0^3}\left[P_0\left(1+P_0^2\right)\right.\hfill \\ \hfill & \left.+2\eta I\left(1+2\frac{\mathrm{\Omega }}{\omega }I\right)+2I\frac{\mathrm{\Omega }}{\omega }{P}_0\right]\sin \xi ,\hfill \\ \hfill \frac{dz}{dt}& =-\frac{P_0}{{\mathrm{\Upsilon }}_0}+\frac{a_{\ell }}{2P_0{\mathrm{\Upsilon }}_0^3}\left(1+2\frac{\mathrm{\Omega }}{\omega }I\right)\sin \xi ,\hfill \end{array}(12)$

which is also a closed set of equations in (I, ξ, z, t).

4 Position-dependent Hamiltonian Equations

Ginet and Heinemann (1990) and Ginet and Albert (1991) proceeded to transform to variables $(\xi ,P_{\xi },\mu ,P_{\mu },\tilde{\varphi },\tilde{I})$, with P_ξ canonically conjugate to ξ. However, doing so in an inhomogeneous setting reintroduces explicit time dependence in place of z dependence (see equation 68 of Ginet and Albert, 1991).

Instead, following Shklyar (1986), Albert (1993) divided the equations for dI/dt and dξ/dt by the equation for dz/dt and attempted to write the results in Hamiltonian form using z as the independent variable. With a Hamiltonian K of the form

$K\left(I,\xi ,z\right)=K_0\left(I,z\right)+K_1\left(I,z\right)\sin \xi ,(13)$

the choice

$K_1=-\frac{a_{\ell }}{2P_0}(14)$

gives

$\frac{dI}{dz}=-K_1\cos \xi ,(15)$

which agrees with (dI/dt)/(dz/dt) from Eq. 10. Using

$K_0=\eta \left(I-c_2\right)+P_0(16)$

then gives

$\frac{d\xi }{dz}=\frac{\eta P_0+{\mathrm{\Upsilon }}_0-\mathrm{\Omega }/\omega }{P_0}-a_{\ell }\frac{P_0^2-2I\left({\mathrm{\Upsilon }}_0-\mathrm{\Omega }/\omega \right)}{2I{P}_0^3}\sin \xi (17)$

or, once more using the lowest-order resonance condition,

$\frac{d\xi }{dz}=\frac{\eta P_0+{\mathrm{\Upsilon }}_0-\mathrm{\Omega }/\omega }{P_0}-a_{\ell }\frac{P_0+2\eta I}{2I{P}_0^2}\sin \xi .(18)$

It is clear that the first-order term in dξ/dz obtained by this procedure, which enforces the form of Eq. 13, is not the same as that of (dξ/dt)/(dz/dt) from either Eq. 10 or Eq. 12. The analogous disagreement is evident between equations 3.8 and 3.10 of Shklyar (1986), who treated the simpler case of an electrostatic wave and nonrelativistic protons. (Both equations give versions of dξ/ds, the typesetting error in equation 3.8 notwithstanding.)

5 Simulations and Discussion

The consequences of the disagreement in the first-order terms of the various ξ evolution equations is studied here numerically. We choose wave and particle parameters following Kitahara and Katoh (2019); Gan et al. (2020). A Taylor expansion of the geodipole magnetic field about the equator gives the variation along a field line as $B/B_{eq}=1+4.5z^2/{(L{R}_e)}^2$, with L = 4, where R_e is the radius of the Earth and LR_e is the field line equatorial crossing distance. The cold electron density is constant, and chosen to give the ratio of plasma frequency to gyrofrequency as f_pe/f_ce = 4 at the equator. The field-aligned whistler mode wave has frequency such that ω/Ω_e = 0.3 at the equator. We consider ensembles of 24 electrons, with energy 20 keV, uniformly distributed in initial gyrophase. We take equatorial pitch angle α₀ = 5° and B_w/B_eq = 3 × 10^–4 (with B_w fixed), since this case seems particularly complex, exhibiting a mixture of conventional phase trapping and “anomalous” phase trapping (as opposed to the oppositely directed change associated with phase bunching for larger pitch angles). The particles are launched towards the equator (z = 0) from a distance of 1 R_e, and the equations of motion are advanced with a standard Runge-Kutta integrator with variable step size.

Figure 1 shows results using Eq. 2 (in red) and Eq. 3 (in blue). The sets of trajectories are not expected to be identical because of accumulated phase differences far from resonance. Nevertheless the overall behavior is very similar, showing no significant change until reaching resonance around z/R_e = 0.35, after which the equatorial pitch angle increases either over a sustained period (conventional phase trapping, PT) or transiently. The long-time behavior of the phase angle ξ is oscillatory for PT but monotonic otherwise. This corresponds to the NL1 regime of Gan et al. (2020), also referred to as positive phase bunching (PPB). Numerically, PT was identified by a change of sign in dξ/dt from one time step to the next after crossing below z/R_e = 0.1. Of 24 simulated particles, 10 became PT using either Eq. 2 or Eq. 3.

FIGURE 1

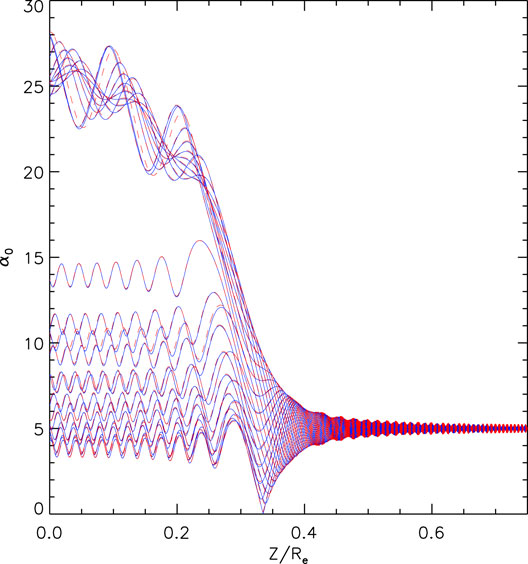
FIGURE 1. Evolution of 24 electrons starting at z/R_e = 1 and interacting with a whistler mode wave, with particle and wave parameters as given in the text. Red curves show results for the equations of motion given in Eq. 2, and blue curves used Eq. 3.

Figure 2 shows results using Eq. 10 (blue) or Eq. 12 (red). The equatorial pitch angle α₀ obtained from the normalized variables (I, z) via

$\frac{B}{B_{eq}}{\sin }^2{\alpha }_0={\sin }^2\alpha =\frac{p_{\perp }^2}{p^2}=\frac{2\left(\mathrm{\Omega }/\omega \right)I}{{\left(I-c_2\right)}^2-1}.(19)$

FIGURE 2

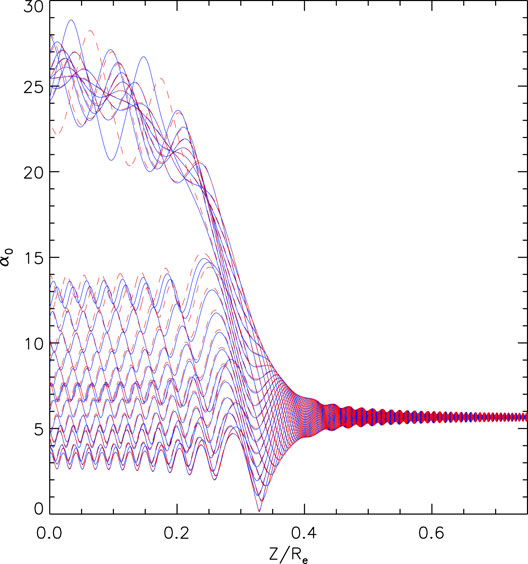
FIGURE 2. Evolution of 24 electrons starting at z/R_e = 1 and interacting with a whistler mode wave, according to equations of motion based on K(I, ξ, z, t). Blue curves show results for the equations of motion given in Eq. 10, and red curves used Eq. 12.

The behavior turns out to be very similar to the previous run, with 9 instances of PT, leading to α₀ ≈ 25° at z = 0, with the rest of the particles ending up with α₀ spread between about 4° and 14°.

Finally, Figure 3 shows results using Eqs. 15, 18. Again the results are very similar in the final α₀ values reached by PT or PPB particles, and in the number of each. The number of PT particles in this run is 8, which does not deviate much from the previous values given the small number (24) of particles in each simulation.

FIGURE 3

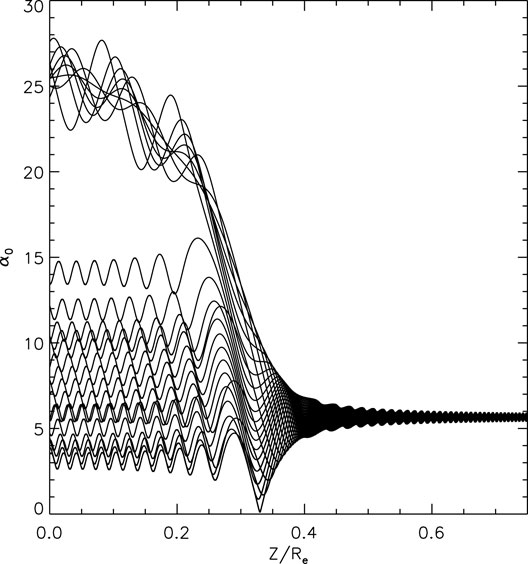
FIGURE 3. Evolution of 24 electrons starting at z/R_e = 1 and interacting with a whistler mode wave, according to equations of motion based on K(I, ξ, z), namely Eqs 15, 18.

We conclude that the reduced Hamiltonian K(I, ξ, z) of Eq. 13 captures the nature of the particle dynamics, including APT and PPB, with fidelity comparable to the other models. This is propitious because it allows access to a rich body of work on invariant breaking at separatrix crossings (e.g., Cary et al., 1986), enabling both qualitative understanding and quantitative analytical estimates.

Some steps have already been taken in that direction. Figure 4 shows the results of Figure 3 in the (I, ξ) plane, with PT trajectories (identified as above) over the interval 0.4 > z > 0 shown in red, and become limited in ξ while reaching large values of I. The remaining paths, shown in blue (over the interval 0.4 > z > 0.22, for clarity), do not reach such large values of I but are less restricted in ξ. Figure 5 shows contours of K(I, ξ, z) at several fixed values of z chosen during the trapping process, based on Figure 3. They indicate that at early times (large values of z) there is only a single, O-type fixed point, while an X-point and separatrix, as well as another O-point, form around the time of the trapping process. Contours circling the O-point at ξ = π/2 correspond to the (red) PT trajectories of Figure 4, and PPB trajectories (in blue) are connected to the development of the O-point at low I and ξ = −π/2. Similar contours, developed from Eq. 13 with further approximation, were obtained and studied by Albert et al. (2021), Artemyev et al. (2021). Quantitative analysis of separatrix formation and crossing, invariant breaking, and energy and pitch angle change will be the subject of future work.

FIGURE 4

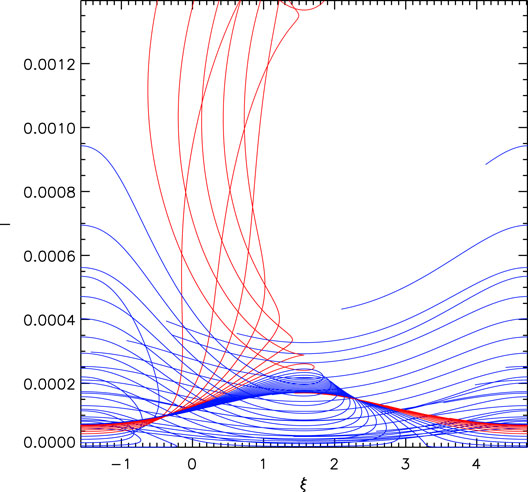
FIGURE 4. Evolution of 24 electrons interacting with a whistler mode wave, according to equations of motion based on K(I, ξ, z), shown in the (I, ξ) plane. Phase-trapped trajectories are shown for 0.4 > z/R_e > 0, in red; other trajectories are shown in blue for 0.4 > z/R_e > 0.22.

FIGURE 5

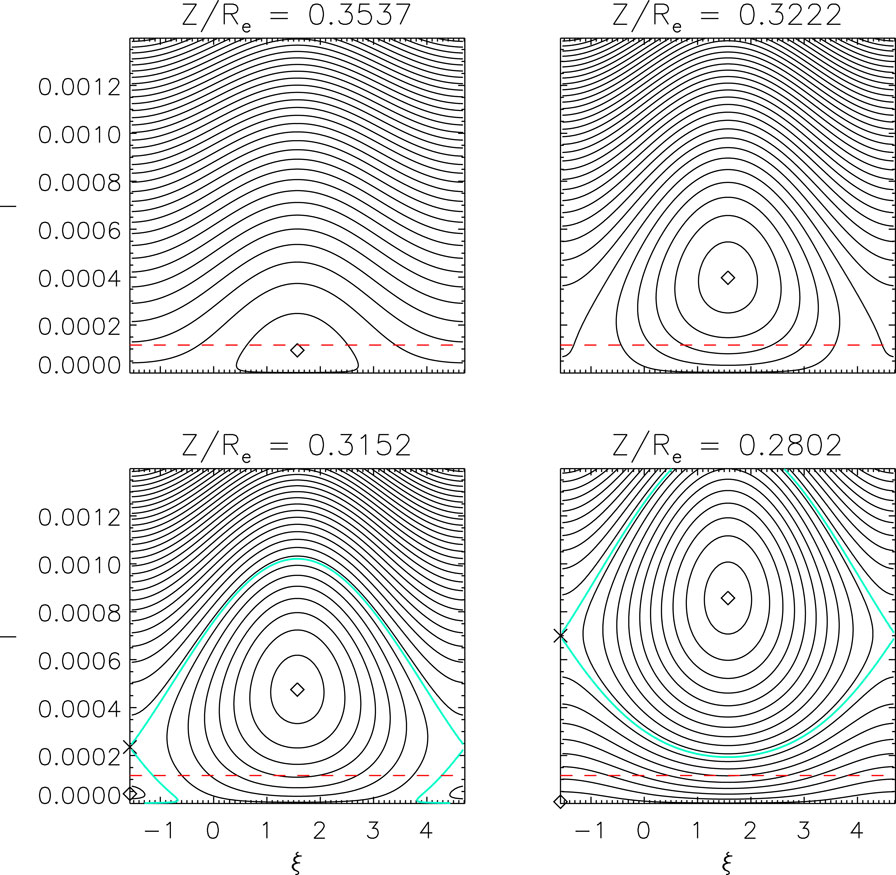
FIGURE 5. Contours of K(I, ξ, z), at several values of z shortly before and after resonance crossing, according to motion based on K(I, ξ, z). O-points are shown as diamonds, and X-points (if present) are shown with an X symbol, with the contour through them is in cyan. The red, dashed curve shows the initial value of I.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

JA conceived this work, and wrote and ran the simulations. AA helped analyze approaches to reducing the dimensionality of the system of equations. WL, QM, and LG consulted on the work and made several useful suggestions on the simulations and presentation.

Funding

JA was supported by NASA grant 80NSSC19K0845 and the Space Vehicles Directorate of the Air Force Research Laboratory. WL, LG, and QM also acknowledge the NASA grants 80NSSC20K1506 and 80NSSC20K0698, NSF grant AGS-1847818, and the Alfred P. Sloan Research Fellowship FG-2018-10936.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The views expressed are those of the author and do not reflect the official guidance or position of the United States Government, the Department of Defense or of the United States Air Force. The appearance of external hyperlinks does not constitute endorsement by the United States Department of Defense (DoD) of the linked websites, or the information, products, or services contained therein. The DoD does not exercise any editorial, security, or other control over the information you may find at these locations.

References

Albert, J. M., Artemyev, A. V., Li, W., Gan, L., and Ma, Q. (2021). Models of Resonant Wave‐Particle Interactions. J. Geophys. Res. Space Phys. 126, e2021JA029216. doi:10.1029/2021JA029216

CrossRef Full Text | Google Scholar

Albert, J. M. (2001). Comparison of Pitch Angle Diffusion by Turbulent and Monochromatic Whistler Waves. J. Geophys. Res. 106, 8477–8482. doi:10.1029/2000JA000304

CrossRef Full Text | Google Scholar

Albert, J. M. (1993). Cyclotron Resonance in an Inhomogeneous Magnetic Field. Phys. Fluids B Plasma Phys. 5, 2744–2750. doi:10.1063/1.860715

CrossRef Full Text | Google Scholar

Albert, J. M. (2010). Diffusion by One Wave and by Many Waves. J. Geophys. Res. 115, A00F05. doi:10.1029/2009JA014732

CrossRef Full Text | Google Scholar

Albert, J. M. (2000). Gyroresonant Interactions of Radiation Belt Particles with a Monochromatic Electromagnetic Wave. J. Geophys. Res. 105, 21191–21209. doi:10.1029/2000JA000008

CrossRef Full Text | Google Scholar

Albert, J. M., Tao, X., and Bortnik, J. (2012). “Aspects of Nonlinear Wave-Particle Interactions,” in Dynamics of the Earth’s Radiation Belts and Inner Magnetosphere. Editor D. Summers (Washington, DC: American Geophysical Union), 255–264. doi:10.1029/2012GM001324

CrossRef Full Text | Google Scholar

Allanson, O., Elsden, T., Watt, C., and Neukirch, T. (2022). Weak Turbulence and Quasilinear Diffusion for Relativistic Wave-Particle Interactions via a Markov Approach. Front. Astron. Space Sci. 8, 805699. doi:10.3389/fspas.2021.805699

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Albert, J. M., Gan, L., Li, W., and Ma, Q. (2021). Theoretical Model of the Nonlinear Resonant Interaction of Whistler-Mode Waves and Field-Aligned Electrons. Phys. Plasmas 28, 052902. doi:10.1063/5.0046635

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Vainchtein, D. L., Vasiliev, A. A., Vasko, I. Y., and Zelenyi, L. M. (2018). Trapping (Capture) into Resonance and Scattering on Resonance: Summary of Results for Space Plasma Systems. Commun. Nonlinear Sci. Numer. Simul. 65, 111–160. doi:10.1016/j.cnsns.2018.05.004

CrossRef Full Text | Google Scholar

Bell, T. F. (1984). The Nonlinear Gyroresonance Interaction between Energetic Electrons and Coherent VLF Waves Propagating at an Arbitrary Angle with Respect to the Earth's Magnetic Field. J. Geophys. Res. 89, 905–918. doi:10.1029/JA089iA02p00905

CrossRef Full Text | Google Scholar

Cary, J. R., Escande, D. F., and Tennyson, J. L. (1986). Adiabatic-Invariant Change Due to Separatrix Crossing. Phys. Rev. A 34, 4256–4275. doi:10.1103/PhysRevA.34.4256

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, H. C., and Inan, U. S. (1983). Quasi-Relativistic Electron Precipitation Due to Interactions with Coherent VLF Waves in the Magnetosphere. J. Geophys. Res. 88, 318–328. doi:10.1029/ja083iA01p00318

CrossRef Full Text | Google Scholar

Gan, L., Li, W., Ma, Q., Albert, J. M., Artemyev, A. V., and Bortnik, J. (2020). Nonlinear Interactions between Radiation Belt Electrons and Chorus Waves: Dependence on Wave Amplitude Modulation. Geophys. Res. Lett. 47, e2019GL085987. doi:10.1029/2019GL085987

CrossRef Full Text | Google Scholar

Ginet, G. P., and Albert, J. M. (1991). Test Particle Motion in the Cyclotron Resonance Regime. Phys. Fluids B 3, 2994–3012. doi:10.1063/1.859778

CrossRef Full Text | Google Scholar

Ginet, G. P., and Heinemann, M. A. (1990). Test Particle Acceleration by Small Amplitude Electromagnetic Waves in a Uniform Magnetic Field. Phys. Fluids B 2, 700–714. doi:10.1063/1.859307

CrossRef Full Text | Google Scholar

Inan, U. S., Bell, T. F., and Helliwell, R. A. (1978). Nonlinear Pitch Angle Scattering of Energetic Electrons by Coherent VLF Waves in the Magnetosphere. J. Geophys. Res. 83, 3235–3253. doi:10.1029/ja083iA07p03235

CrossRef Full Text | Google Scholar

Kitahara, M., and Katoh, Y. (2019). Anomalous Trapping of Low Pitch Angle Electrons by Coherent Whistler Mode Waves. J. Geophys. Res. Space Phys. 124, 5568–5583. doi:10.1029/2019JA026493

CrossRef Full Text | Google Scholar

Lemons, D. S., Liu, K., Winske, D., and Gary, S. P. (2009). Stochastic Analysis of Pitch Angle Scattering of Charged Particles by Transverse Magnetic Waves. Phys. Plasmas 16, 112306. doi:10.1063/1.3264738

CrossRef Full Text | Google Scholar

Lemons, D. S. (2012). Pitch Angle Scattering of Relativistic Electrons from Stationary Magnetic Waves: Continuous Markov Process and Quasilinear Theory. Phys. Plasmas 19, 012306. doi:10.1063/1.3676156

CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., Xie, L., Pu, Z., Chen, L., Ni, B., et al. (2015). Comparison of Formulas for Resonant Interactions between Energetic Electrons and Oblique Whistler-Mode Waves. Phys. Plasmas 22, 052902. doi:10.1063/1.4914852

CrossRef Full Text | Google Scholar

Liu, K., Lemons, D. S., Winske, D., and Gary, S. P. (2010). Relativistic Electron Scattering by Electromagnetic Ion Cyclotron Fluctuations: Test Particle Simulations. J. Geophys. Res. 115, A04204. doi:10.1029/2009JA014807

CrossRef Full Text | Google Scholar

Liu, K., Winske, D., Gary, S. P., and Reeves, G. D. (2012). Relativistic Electron Scattering by Large Amplitude Electromagnetic Ion Cyclotron Waves: The Role of Phase Bunching and Trapping. J. Geophys. Res. 117, A06218. doi:10.1029/2011JA017476

CrossRef Full Text | Google Scholar

Lyons, L. R., Thorne, R. M., and Kennel, C. F. (1971). Electron Pitch-Angle Diffusion Driven by Oblique Whistler-Mode Turbulence. J. Plasma Phys. 6, 589–606. doi:10.1017/S0022377800006310

CrossRef Full Text | Google Scholar

Lyons, L. R., Thorne, R. M., and Kennel, C. F. (1972). Pitch-Angle Diffusion of Radiation Belt Electrons within the Plasmasphere. J. Geophys. Res. 77, 3455–3474. doi:10.1029/JA077i019p03455

CrossRef Full Text | Google Scholar

Shklyar, D. R. (1986). Particle Interaction with an Electrostatic vlf Wave in the Magnetosphere with an Application to Proton Precipitation. Planet. Space Sci. 34, 1091–1099. doi:10.1016/0032-0633(86)90021-8

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid Local Acceleration of Relativistic Radiation-Belt Electrons by Magnetospheric Chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation Belt Dynamics: The Importance of Wave-Particle Interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar