- 1Department of Earth and Planetary Science, School of Science, The University of Tokyo, Tokyo, Japan
- 2Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, Kanagawa, Japan
- 3National Astronomical Observatory of Japan, Tokyo, Japan
- 4Department of Astronomical Science, SOKENDAI (The Graduate University for Advanced Studies), Tokyo, Japan
Nanoflares and the shock formation of magnetohydrodynamic waves in the solar chromosphere have been considered as key physical mechanisms of the heating of the chromosphere and corona. To investigate candidates of their signature in the mm-wavelength, a tiny active region located on the solar disk was observed with the Atacama Large millimeter and sub-millimeter Array (ALMA) at 3 mm, coordinated with observatories on orbit including Hinode SOT spectro-polarimeter in the Cycle 4 solar campaign (19 March 2017). ALMA’s spatial resolution was moderate, far from the best performance, but it provided stable conditions that are suitable to investigate temporal variations in the mm-wavelength. We determined that the noise level is less than 20 K (σ) over 1 hour in the 20-s cadence time series of synthesized ALMA images. The time variations with amplitudes above the noise level were observed throughout the field of view, but variations exceeding 200 K, corresponding to energy input to the chromosphere on the order of 1020-22 erg, were localized in two locations. One location was on the polarity inversion line, where tiny concentrated magnetic patches exist in weak field and a tiny magnetic flux may be emergent. The other location was at the outer edge of a bipolar magnetic region, which was under development with a successive series of magnetic flux emergence. This observation suggests that nanoflare-class energy inputs in the chromosphere can occur associated with emerging flux activities.
1 Introduction
The solar chromosphere is the interface layer connecting the solar surface (photosphere) to the corona. The corona is permeated with bundles of both open and closed magnetic fields that are rooted in the photosphere. The corona is heated to over 1 MK, whereas the temperature of the photosphere is 6,000 K. The chromosphere has a temperature of approximately 10,000 K; however, because of its high density, it requires heat input that is one order of magnitude higher than that of the corona. The energy is believed to transfer through chromospheric structures towards the corona. Thus, much attention has been given recently to the dynamical behaviors of chromospheric structures. Observationally, high spatial and temporal resolution observations, provided by space-borne observatories, such as the Hinode Solar Optical Telescope (Kosugi et al., 2007; Ichimoto et al., 2008; Shimizu et al., 2008; Suematsu et al., 2008; Tsuneta et al., 2008; Lites et al., 2013) and Interface Region Imaging Spectrograph (IRIS) (De Pontieu et al., 2014), and recent 1-m class ground-based telescopes, such as Swedish Solar Telescope (Scharmer et al., 2003) and Goode Solar Telescope (Cao et al., 2010), have revealed propagating magnetohydrodynamics (MHD) waves (e.g., De Pontieu et al., 2007; Okamoto et al., 2007; Okamoto and De Pontieu, 2011; Stangalini et al., 2011; Martínez-Sykora et al., 2017; Abbasvand et al., 2020) and the ubiquitous occurrence of small-scale magnetic reconnection events in the chromosphere (Katsukawa et al., 2007; Shibata et al., 2007; Shimizu et al., 2009). Meanwhile, significant progress has been made recently in modeling the three-dimensional chromospheric structures and their dynamics with sophisticated radiative MHD models, helping to capture a physical picture of the chromospheric fine structures and their dynamics (e.g., Martínez-Sykora et al., 2017). It has been considered that MHD waves excited by the convective gas motions at the photosphere propagate through the chromosphere toward the corona and are also dissipated in the chromosphere by the formation of shocks (e.g., Carlsson and Stein, 1997). As an alternate model, the convective gas motions generate tangential discontinuity and braiding in magnetic field lines in the corona, leading to numerous numbers of tiny magnetic reconnection events, so-called nanoflares (Parker, 1988). It is noted that the terminology nanoflare in Parker (1988) represents a swarm of tiny energy releases in order of 1024 erg produced in coronal loops, but hereafter we will use the terminology nanoflare for a transient release in nanoflare energy range, i.e., 1022 − 1024 erg.
Most of the solar radiation at millimeter (mm) wavelengths comes from the chromosphere, providing a unique diagnostic for the chromosphere (Vernazza et al., 1981). The mm-wavelength emission is free-free emission (thermal bremsstrahlung), produced by free electrons scattering off ions without being captured. Assuming the free electrons to be in local thermodynamic equilibrium (LTE), the source function is equivalent to the Planck function. In the mm wavelengths, the Rayleigh–Jeans law is an approximation to the Plank function, giving a linear relation from the emission intensity to the brightness temperature (Kraus, 1986). However, the electrons are mostly regulated by the ionization degree of hydrogen atoms that significantly departs from LTE in the chromosphere. 3D non-LTE radiative MHD simulations show that the formation height range of the radiation at millimeter wavelengths depends on the location in the simulation domain and is related to the underlying magnetic structure (Loukitcheva et al., 2015; Martínez-Sykora et al., 2020). Nonetheless, millimeter emission can image the chromospheric thermal structure at the height at which the radiation is formed. This suggests that the radiation at mm wavelengths can be used as a thermometer to probe the chromospheric temperature. The thermometer provides a useful tool to detect changes in chromospheric temperature. Variations in brightness temperature could be due to variations in formation height depending on the chromospheric structure. For large class of variations to be examined in this paper, however, it would be plausible that brightness variations are caused dominantly by changes in chromospheric temperature. Therefore, transient energy inputs in the chromosphere either by nanoflare and microflare (da Silva Santos et al., 2020; Shimizu et al., 2021) or by shock formation (Eklund et al., 2020; Nindos et al., 2021a; Chintzoglou et al., 2021) may be identified by monitoring transient increases in the thermometer.
The Atacama Large millimeter and sub-millimeter Array (ALMA) (ALMA Partnership et al., 2016) is capable of performing interferometric observations of the Sun at mm wavelengths, allowing both high spatial and temporal resolution imaging observations of a few arcsec or higher spatial resolution (Shimojo et al., 2017a). Using ALMA observations in early phase, transient time variability was studied primarily in the quiet Sun (Nindos et al., 2021a; Nindos et al., 2021b). The number of studies addressing temporal variations of brightness temperature associated with strong magnetic flux concentrations is increasing; for example, a solar plasmoid ejection from an X-ray bright point (Shimojo et al., 2017b), tiny brightenings in a group of pores (da Silva Santos et al., 2020), oscillations in chromospheric plage regions (Chintzoglou et al., 2021; Narang et al., 2022), and the ALMA counterpart at the footpoints of a soft X-ray loop-type microflare observed in a tiny active region (Shimizu et al., 2021). The objective of this article is to present the temporal variations in mm-wavelength data recorded with an ALMA observation for a small active region. Section 2 describes observations and data analysis. Section 3 presents the results of the data analysis, followed by discussions in Section 4 and a summary in Section 5.
2 Observations and Data Analysis
The ALMA observation was coordinated with Hinode from 13:36-19:41 UT on 19 March 2017, as an execution of the ALMA Project code 2016.1.00030.S (PI: Shimizu). The Hinode program was numbered as IHOP 327. The target region was a tiny active region located on the solar disk at (-495, -40) arcsec on the heliocentric coordinate seen as a compact bright region in soft X-rays with a magnetic bipolar distribution on photospheric SDO/HMI magnetograms. It is noted that no any NOAA number was designated to this region. The ALMA performed its observations at 100 GHz (3 mm, Band 3) with the C40-1 antenna configuration, which is the most compact layout in the solar observing mode, giving a spatial resolution of 5”.0, ×, 3”.9. See Shimizu et al. (2021) for further details of the observations and data processing. It should be noted that no single-dish (total power) data were acquired to calibrate the absolute brightness temperature in this observation. Thus, the temporal profiles presented in this article show the deviation from the averaged brightness temperature in the observation field of view. Time variations in temperature brightness can be derived even without absolute temperature information. The co-alignment of the data from the different instruments was carefully investigated to identify a better method among alignment methods examined, and we finally appear to achieve a precision better than 2”. Details of the co-alignment procedure are also described in Shimizu et al. (2021).
3 Results
3.1 Noise Level in ALMA Time Series
We use the method described in Shimojo et al. (2017a) to evaluate the noise level in the ALMA time series. ALMA Band 3 has two receivers sensitive to orthogonal components of the linear polarization (ALMA Partnership et al., 2016). The interferometric measurements in each component can be used independently to synthesize an image and the two synthesized images should be identical to each other if no noise is included in the data. Thus, the noise level was estimated from the difference between the two polarizations for a 20 s integration. The difference should be zero for thermal emission from optically-thick chromospheric plasma in the absence of flare emission. Furthermore, circularly polarized light due to the presence of strong magnetic fields (Miyawaki et al., 2016) may produce net linear polarization due to differential Faraday rotation; however, it is negligibly small at 100 GHz (Iwai et al., 2017; Loukitcheva et al., 2017). The difference in two synthesized images, which were generated independently with interferometric measurements by the two receivers sensitive to orthogonal components of the linear polarization, gives the standard deviation smaller than 20 K for the entire period. Weak spatial dependence may be visible when it is compared to the brightness temperature derived from the ALMA data, although the dependence is small in magnitude and may be roughly regarded as random distribution. Therefore, we set 20 K as the noise level in σ in the subsequent results, although this would represent the most conservative evaluation.
3.2 Spatial Distribution of Large Time Variability
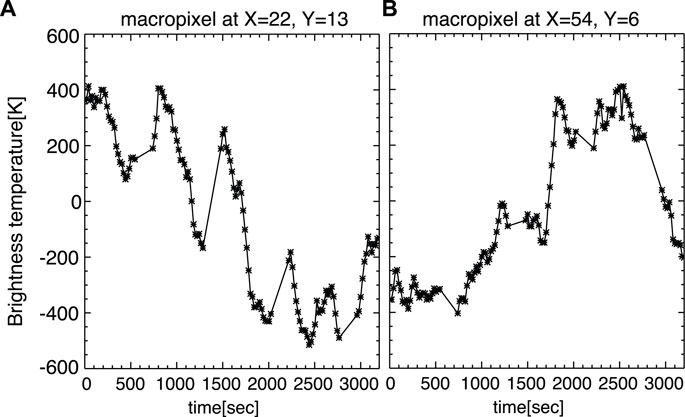
Figure 1B is the spatial distribution of time variations detected in the ALMA brightness temperature map in panel (a). For each location, the standard deviation was derived from the time series of brightness temperature. The map is shown at 4 arcsec/pixel. The contours in Figure 1B represent the spatial distribution of magnetic flux density: positive 300 gauss in red and negative 300 gauss in black, from Figure 1C. Time variations with amplitudes much larger than the noise level (20 K in σ) are observed in most of the binned pixels. The variations exceeding 200 K are observed in the lower middle (around X = 22, Y = 13; area A1 hereafter) and the lower right (around X = 54, Y = 6; area A2 hereafter), both of which are located at or close to polarity inversion lines. Figure 2 shows the time profile of ALMA brightness temperature at these locations. At area A1, the brightness temperature is gradually decreased with some enhancements during the observation. The largest enhancement is about 400 K increase from the base brightness just before the enhancement. The appearance of the observed enhancement looks periodic, but the interval exceeds 10 min, which is different from 3 to 5 min expected from p-mode oscillations. The temporal profile of enhancements shows an increase in relatively short timescale (100–200 s) and gradual decrease after the peak. At area A2, a large enhancement is observed at the latter half of the observation and its duration is about 1,000 s.
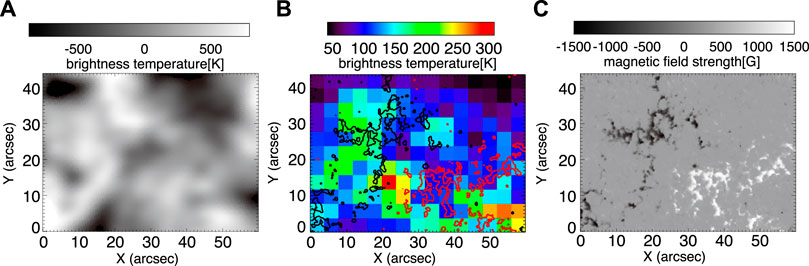
FIGURE 1. The spatial distribution of (A) the mean brightness temperature and (B) the standard deviation in the time series of ALMA data. The contours represent the spatial distribution of (C) magnetic flux density: positive 300 gauss in red and negative 300 gauss in black.
The magnitude of the time variations is compared to the time-averaged brightness temperature in Figure 3A. The figure shows a fairly dispersive distribution between them. The binned pixels with large variation over 200 K are widely distributed from -300 to 500 K. The correlation coefficient is 0.34, suggesting poor correspondence. In Figure 3B, the magnitude of time variations is compared with the magnetic flux density at the photosphere. Large variations over 200 K are observed in the regions where the magnetic flux density is less than 200 gauss. At the magnetic flux concentrations (higher than 300 gauss) in the photosphere, large variations over 200 K are not observed and dominant variations have a standard deviation of 90-170 K.
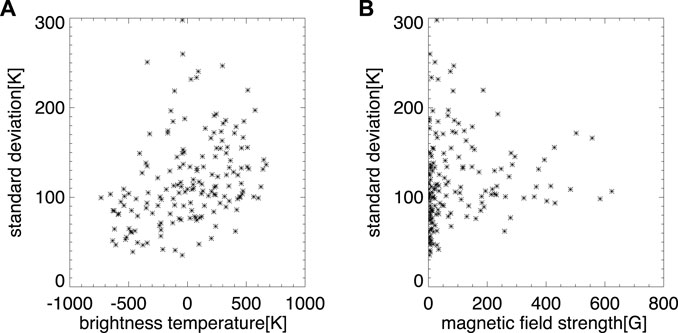
FIGURE 3. The magnitude of time variations measured as the standard deviation in the time series of ALMA data is compared (A) to the time-averaged brightness temperature and (B) to the magnetic flux density in the photosphere. The value of magnetic flux density (magnetic strength) is derived from the magnetic flux density map binned to 4 arcsec/pixel.
3.3 Magnetic Flux Evaluation at the Photosphere
According to the previous subsection, two areas showed large temperature variations exceeding 200 K. Figure 4 is the magnetic flux distribution at the photospheric level, measured with the Hinode/SOT Spectro-Polarimeter (SP) during the first and last half of the ALMA observing period. The two areas are marked by yellow squares in Figure 4.
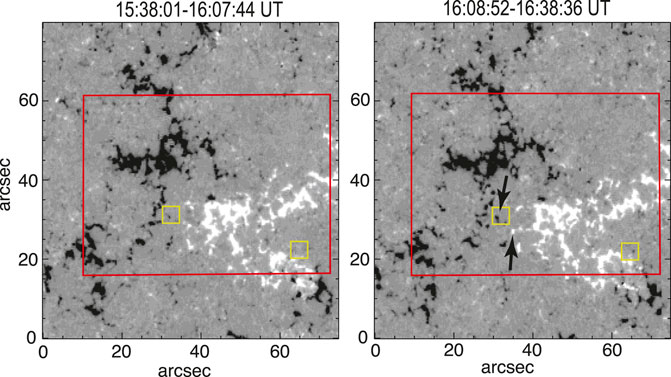
FIGURE 4. Stokes V amplitude maps from two Hinode/SOT Spectro-Polarimeter’s scans during the ALMA observing period. The field of view is 75 × 80 arcsec, where the slit is moved from the left to the right. The left map was recorded from 15:38:01-16:07:44 UT and the right from 16:08:52-16:38:36 UT. The red rectangle gives the field of view used in Figure 1. The yellow squares are the location of two macro-pixels where large variations exceeding 200 K are observed. The arrows specify newly appeared magnetic flux patches.
The large variations observed in area A1 (around X = 30, Y = 30 arcsec in Figure 4) are located in a weak-field area at the polarity inversion. Positive polarity patches are dominant at the right of this area, whereas negative polarity patches are distributed at the left. In the square, a tiny negative polarity patch exists and shows an increase in the magnetic flux. Positive and negative magnetic patches located around the square also show changes their locations and shapes, as well as strength within about 30 min. As given by arrows in the second map, a small negative polarity patch and a small positive polarity patch appeared, indicating emergence of tiny magnetic flux around the polarity inversion line. Note that it is difficult to look into the temporal evolution of such a tiny magnetic patch in the time series of HMI magnetograms (Scherrer et al., 2012; Schou et al., 2012).
The large variations at area A2 are located at the outer edge of a small bipolar magnetic region that is under development with successive series of magnetic flux emergence from below the photosphere. A group of positive polarity fluxes moves toward the upper left direction. The ALMA pixels showing large variations are located near the front side of this moving positive polarity flux. Weak signals for negative polarity flux can be recognized there in the SP maps, suggesting that a mixed polarity or polarity inversion configuration is formed. It should also be noted that the brightness temperature is high in this emerging flux region, as shown in Figure 1A.
4 Discussions
In this study, we synthesized time series of ALMA maps by integrating the data acquired over each 20 s and investigated the temporal variations in the brightness temperature for a tiny active region with a magnetic bipolar distribution at the photosphere (Figure 1). Following the method described in Shimojo et al. (2017a), we derived the noise level of the examined data less than 20 K, which is similar to that derived by Shimojo et al. (2017a) for verification data acquired in December 2015. Moreover, the level of noise is quite stable for about 1 h, indicating that the examined ALMA data are valuable for investigating temporal variations in brightness temperature.
Time variations above the noise level can be recognized in most of regions, even when the spatial resolution of the synthesized images (4 arcsec/pixel) is lower than the best resolution ALMA can achieve (ALMA Partnership et al., 2016). The chromosphere is dynamic; there is consistently dynamic behavior of fine scale structures such as spicules and fibrils, and the height of the chromospheric structure is always changing (Pereira et al., 2012). Time variations in ALMA time series would reflect the dynamic nature of the chromosphere, and thus, it is not surprising to observe time variations above the noise level. In this study, we focused on significant variations, namely variations exceeding 200 K, which are ten times larger than the noise level. The emission of the chromosphere is closely related to magnetic field concentrations at the solar surface. It is well established that the relation between chromospheric emission and magnetic field is nonlinear (Barczynski et al., 2018). Figure 3 shows that the magnitude of time variations is weakly correlated with the brightness temperature with a fairly board distribution. The brightness temperature is not enhanced in the locations where large time variations above 200 K are observed. This indicates that large time variations have no clear relationship with the heating level of the chromosphere. In terms of the relationship with the magnetic field strength, large time variations above 200 K are not observed in magnetic flux concentrations above 200 G, but occur above regions with weak magnetic fields below 100 G. This is not the case in magnetic flux concentrations, but in the geometry of the magnetic field expanding from the concentrations in the photosphere into the chromosphere, i.e., magnetic canopy structure. When a magnetic flux emerges from below the photosphere to the canopy structure, the sudden change in geometry, such as a sudden expansion or change in shape of the magnetic field lines that have emerged above the photosphere, may lead to magnetic reconnection with the pre-existing field, resulting in large time variations.
Pervasive presence of brightness temperature variations due to p-mode oscillations are expected in the examined time series. We applied an FFT analysis on the time series and found that the power of variations in 3–5 mHz is not significant and p-mode oscillations may contribute to time variations much smaller than the significant variations discussed. The time profiles shown in Figure 2 do not show strong signals for oscillations in 3–5 mHz. In contrast, in a past observation, intensity oscillations with significant power in the frequency range 3–5 mHz were found in the quiet-Sun and active region (White et al., 2006). Recently, Jafarzadeh et al. (2021) have obtained the power spectra for 10 ALMA datasets (of which, 6 datasets for Band 3) and found a lack of dominant chromospheric oscillations within the frequency range of 3–7 mHz for most of the datasets. These datasets are largely influenced by the strong magnetic fields originating within the observed field of view, while clear power enhancements at around 4 mHz were observed for the magnetically quiescent datasets. The result from our FFT analysis for the data examined in this study seems to be in line with the Jafarzadeh et al. (2021)’s findings.
Time variations exceeding 200 K were dominantly observed at two locations; one is at the outer edge of a small emerging flux region, and the other is at the polarity inversion line where tiny concentrated magnetic flux patches exist in weak field. In the series of chromospheric images, such as AIA 1600 Å, SOT Ca II H, and IRIS 1400 Å slit jaw, many point-like transient brightenings are observed in emerging flux regions in general (e.g., Toriumi & Wang, 2019). They may correspond to Ellerman bombs, burst intensity enhancements in Hα line wings (Ellerman, 1917), which may be caused by magnetic reconnection occurring at the magnetic flux dips (Bernasconi et al., 2002; Georgoulis et al., 2002; Pariat et al., 2004; Matsumoto et al., 2008). They may be formed by horizontal motions of magnetic flux driven either by the flux emergence or by gas convection. Small-scale transient brightenings are observed in common when opposite magnetic polarities come into contact with or cancel each other at the photospheric level (Shimizu, 2015). In particular, magnetic reconnection may occur when an emerging flux interacts with the pre-existing, overlying magnetic field, creating high-temperature plasma in localized volume with hot and cold ejections (e.g., Yokoyama and Shibata, 1995; Cheung and Isobe, 2014). In IRIS observations, high-temperature plasma in localized volume may appear as UV bursts (Peter et al., 2014). Many such bursts appear to be associated with the cancellation of magnetic fluxes. Tian et al. (2018) investigated the 3D magnetic field topology through a magnetohydrostatic model and found that a small fraction of the bursts are associated with bald patches (magnetic dips), which are similar to the magnetic configuration for Ellerman bombs. In active regions, newly emerging magnetic flux interacts with the pre-existing magnetic field, leading to magnetic reconnection events. Indeed, this scenario has been reported with high spatial resolution observations of granular-sized emerging fluxes and of their chromospheric response carried out in recent years (e.g., Guglielmino et al., 2008, 2010; Vargas Domínguez et al., 2012; Ortiz et al., 2014; de la Cruz Rodríguez et al., 2015; Centeno et al., 2017; Guglielmino et al., 2018; Díaz Baso et al., 2021). A complex fan-spine magnetic topology may be responsible for triggering UV bursts (Chitta et al., 2017; Smitha et al., 2018). The same scenario has also been considered as one of major magnetic configuration for producing coronal transient brightenings or microflares in active regions (Shimizu et al., 2002; Kano et al., 2010). Thus, it is natural that the time variations with relatively large amplitude in ALMA data can occur associated with small evolving magnetic flux driven by the flux emergence and may be a counterpart of magnetic reconnection events, such as Ellerman bombs, UV bursts and transient brightenings in active regions.
The ALMA data can be used as a thermometer to probe changes in the temperature of chromospheric plasma, at least in the range 6,500–12,000 K (Molnar et al., 2019). The 200 K increase may be interpreted as the thermal energy increase (3nkBδTV) of approximately 1021−22 erg for a brightening at one pixel (4 arcsec), if we assume that the density (n) is 1010−11 cm−3 according to the standard solar atmospheric model in Fontenla et al. (1993). Here, kB is the Boltzmann constant and δT is the temperature increase. The increased brightness temperature was used for the δT. This is valid when the optical thickness is unity or larger at 3 mm. If the optical thickness is much smaller than unity, the increased brightness temperature divided by the optical thickness should be used for the δT. As discussed in Shimizu et al. (2021), however, we have concluded that the optical thickness for the layer where the ALMA observes at 3 mm is about unity or higher. The volume V is simply given by multiplying the pixel size (4 × 4 arcsec2) by the line-of-sight depth. We used 500 km for the line-of-sight depth, coming from the width of the contribution function, which describes how much of the emergent radiation is contributed over height, by Loukitcheva et al. (2015), who studied the formation height of the millimeter radiation with a snapshot of a 3D radiative MHD simulation performed with the Bifrost code (Gudiksen et al., 2011). It is noted that even the Bifrost simulation resembles quiet-Sun conditions despite the stronger magnetic fields, and that 500 km is only an average value. The width of the contribution function depends largely on the atmospheric structure; it ranges from 100 to 1,000 km. The contribution function can be quite localized (100 km in width) for Band 3 in active region conditions or shows multiple peaks (100 km in width each) from distinct layers with different electron densities and temperatures spanning several megameters, particularly during flux emergence (da Silva Santos et al., 2022), which may be relevant for the science case in this study. The actual width of the contribution function for the observed targets is unknown and thus when we used 100−1000 km for the line-of-sight depth, the thermal energy would be in a range between 4 × 1020 and 4 × 1022 ergs. This rough estimate indicates that transient variations with a temperature change of 200 K can be considered as nanoflare-class energy inputs to the chromosphere.
The amount of energy was estimated with the ALMA 3 mm data, which are sensitive to temperature changes in a limited line-of-sight depth at the chromosphere. Depending on the structure of an energy release event in the solar atmosphere, the energy of the time variation observed with ALMA may be only a small fraction of the energy release event. If it is a counterpart such as UV burst or Ellerman bomb, the overall energy content will be larger than the energy evaluated with ALMA. For example, if the energy is released deeper than the chromosphere, the energy will be larger; The total energy of the Ellerman bombs are estimated to be 1026 to 5 × 1027 ergs (Fang et al., 2006). More interestingly, semiempirical atmospheric models for Ellerman bombs indicate that the inclusion of nonthermal particles can reduce the temperature enhancement compared to the thermal only model (Fang et al., 2006). This situation is also the same even if an energy release occurs in the transition region above the chromosphere, as in the case of a UV burst. When the energy is released in the coronal loops, a counterpart can be observed at the loop footpoints as the transient response of the chromosphere with ALMA; Shimizu et al. (2021) have found that this transient response is caused by the non-thermal particles impinging to the footpoints and that its energy is much smaller than what is released in the corona. This tells that the overall energy content may be larger compared to the energy estimated with ALMA.
Energy evaluations are important for understanding the role of observed time variations in coronal and chromospheric heating. Nindos et al. (2020) performed a systematic survey for transient brightenings with ALMA data at 3 mm and found a significant number of weak brightenings everywhere (not only at network boundaries and in cell interiors) in the quiet solar chromosphere. Their brightness temperatures are from 70 K to more than 500 K, and they derived the energies between 1.5 × 1024 and 9.9 × 1025 ergs. As briefly discussed above, the energy estimate contains a significant uncertainty due to uncertainties in the input parameters, such as the electron density and line-of-sight depth for volume. To reduce the uncertainties, we need to have additional modeling for the height of formation, especially on transient energy releases in the regions where successive series of magnetic flux bundles emerge from below the solar surface and develop the complex of magnetic structures in the chromosphere.
5 Summary
We investigated time variations, especially those with relatively large amplitude, in series of ALMA synthesized maps, acquired for a small active region on 19 March 2017. We found several time variations exceeding 200 K, which is ten times larger than the noise level, in a 1-h observation. The 200 K variations correspond to energy input on the order of 1020-22 erg. Such large variations were observed at two locations; one is at the outer edge of a small emerging flux region, and the other is at the polarity inversion line where tiny concentrated magnetic patches exist in weak field and a tiny magnetic flux may be emergent. This observation suggests that nanoflare-class energy inputs in the chromosphere can occur associated with emerging flux activities.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
Most of the results presented in this article were obtained by MA as a part of his master thesis with supervision of TS for science and Hinode data analysis and MS for ALMA data analysis. TS proposed this joint-observation project to ALMA and Hinode and led the observations for this study and wrote this article with help of MS.
Funding
This work was partially supported by JSPS KAKENHI Grant Number 15H05750, 15H05814, and 18H05234.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
ALMA is a partnership of ESO (representing its member states), NSF (United States) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (United Kingdom) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway).
References
Abbasvand, V., Sobotka, M., Švanda, M., Heinzel, P., García-Rivas, M., Denker, C., et al. (2020). Observational Study of Chromospheric Heating by Acoustic Waves. Astronomy Astrophysics 642, A52. doi:10.1051/0004-6361/202038559
ALMA Partnership Asayama, S., Biggs, A., de Gregorio, I., Dent, B., Di Francesco, J., Fomalont, E., et al. (2016). ALMA Cycle 4 Technical Handbook. Available at: http://almascience.org/documents-and-tools/cycle4/alma-technical-handbook.978-3-923524-66-2.
Barczynski, K., Peter, H., Chitta, L. P., and Solanki, S. K. (2018). Emission of Solar Chromospheric and Transition Region Features Related to the Underlying Magnetic Field. Astronomy Astrophysics 619, A5. doi:10.1051/0004-6361/201731650
Bernasconi, P. N., Rust, D. M., Georgoulis, M. K., and Labonte, B. J. (2002). Sol. Phys. 209, 119–139. doi:10.1023/a:1020943816174
Cao, W., Gorceix, N., Coulter, R., Ahn, K., Rimmele, T. R., and Goode, P. R. (2010). Scientific Instrumentation for the 1.6 M New Solar Telescope in Big Bear. Astron. Nachr. 331, 636–639. doi:10.1002/asna.201011390
Carlsson, M., and Stein, R. F. (1997). Formation of Solar Calcium H and K Bright Grains. Astrophysical J. 481, 500–514. doi:10.1086/304043
Centeno, R., Rodríguez, J. B., Del Toro Iniesta, J. C., Solanki, S. K., Barthol, P., Gandorfer, A., et al. (2017). A Tale of Two Emergences: Sunrise II Observations of Emergence Sites in a Solar Active Region. Astrophysical J. Suppl. Ser. 229, 3. doi:10.3847/1538-4365/229/1/3
Chintzoglou, G., De Pontieu, B., Martínez-Sykora, J., Hansteen, V., Cruz Rodríguez, J. d. l., Szydlarski, M., et al. (2021). ALMA and IRIS Observations of the Solar Chromosphere. II. Structure and Dynamics of Chromospheric Plages. Astrophysical J. 906, 83. doi:10.3847/1538-4357/abc9b0
Chitta, L. P., Peter, H., Young, P. R., and Huang, Y.-M. (2017). Compact Solar UV Burst Triggered in a Magnetic Field with a Fan-Spine Topology. Astronomy Astrophysics 605, A49. doi:10.1051/0004-6361/201730830
da Silva Santos, J. M., Danilovic, S., Leenaarts, J., de la Cruz Rodríguez, J., Zhu, X., White, S. M., et al. (2022). arXiv:2202.03955.
da Silva Santos, J. M., de la Cruz Rodríguez, J., White, S. M., Leenaarts, J., Vissers, G. J. M., and Hansteen, V. H. (2020). ALMA Observations of Transient Heating in a Solar Active Region. Astronomy Astrophysics 643, A41. doi:10.1051/0004-6361/202038755
de la Cruz Rodríguez, J., Hansteen, V., Bellot-Rubio, L., and Ortiz, A. (2015). Astrophysical J. 810, 145.
De Pontieu, B., McIntosh, S. W., Carlsson, M., Hansteen, V. H., Tarbell, T. D., Schrijver, C. J., et al. (2007). Chromospheric Alfvénic Waves Strong Enough to Power the Solar Wind. Science 318, 1574–1577. doi:10.1126/science.1151747
De Pontieu, B., Title, A. M., Lemen, J. R., Kushner, G. D., Akin, D. J., Allard, B., et al. (2014). The Interface Region Imaging Spectrograph (IRIS). Sol. Phys. 289, 2733. doi:10.1007/s11207-014-0485-y
Díaz Baso, C. J., de la Cruz Rodríguez, J., and Leenaarts, J. (2021). An Observationally Constrained Model of Strong Magnetic Reconnection in the Solar Chromosphere. Atmospheric Stratification and Estimates of Heating Rates. Astronomy Astrophysics 647, 188. doi:10.1051/0004-6361/202040111
Eklund, H., Wedemeyer, S., Szydlarski, M., Jafarzadeh, S., and Guevara Gómez, J. C. (2020). The Sun at Millimeter Wavelengths. Astronomy Astrophysics 644, A152. doi:10.1051/0004-6361/202038250
Fang, C., Tang, Y. H., Xu, Z., Ding, M. D., and Chen, P. F. (2006). Spectral Analysis of Ellerman Bombs. Astrophysical J. 643, 1325–1336. doi:10.1086/501342
Fontenla, J. M., Avrett, E. H., and Loeser, R. (1993). Energy Balance in the Solar Transition Region. III - Helium Emission in Hydrostatic, Constant-Abundance Models with Diffusion. Astrophysical J. 406, 319. doi:10.1086/172443
Georgoulis, M. K., Rust, D. M., Bernasconi, P. N., and Schmieder, B. (2002). Statistics, Morphology, and Energetics of Ellerman Bombs. Astrophysical J. 575, 506–528. doi:10.1086/341195
Gudiksen, B. V., Carlsson, M., Hansteen, V. H., Hayek, W., Leenaarts, J., and Martínez-Sykora, J. (2011). The Stellar Atmosphere Simulation codeBifrost. Astronomy Astrophysics 531, A154. doi:10.1051/0004-6361/201116520
Guglielmino, S. L., Bellot Rubio, L. R., Zuccarello, F., Aulanier, G., Vargas Domínguez, S., and Kamio, S. (2010). Astrophysical J. 724, 1098. doi:10.1088/0004-637x/724/2/1083
Guglielmino, S. L., Zuccarello, F., Romano, P., and Bellot Rubio, L. R. (2008). Hinode Observations of Chromospheric Brightenings in the Ca Ii H Line during Small-Scale Flux Emergence Events. Astrophysical J. 688, L111–L114. doi:10.1086/595657
Guglielmino, S. L., Zuccarello, F., Young, P. R., Murabito, M., and Romano, P. (2018). IRISObservations of Magnetic Interactions in the Solar Atmosphere between Preexisting and Emerging Magnetic Fields. I. Overall Evolution. Astrophysical J. 856, 127. doi:10.3847/1538-4357/aab2a8
Ichimoto, K., Lites, B., Elmore, D., Suematsu, Y., Tsuneta, S., Katsukawa, Y., et al. (2008). Polarization Calibration of the Solar Optical Telescope Onboard Hinode. Sol. Phys. 249, 233–261. doi:10.1007/s11207-008-9169-9
Iwai, K., Loukitcheva, M., Shimojo, M., Solanki, S. K., and White, S. M. (2017). ALMA Discovery of Solar Umbral Brightness Enhancement at λ = 3 Mm. Astrophysical J. 841, L20. doi:10.3847/2041-8213/aa71b5
Jafarzadeh, S., Wedemeyer, S., Fleck, B., Stangalini, M., Jess, D. B., Morton, R. J., et al. (2021). Philosophical Trans. R. Soc. A 379, 20200174.
Kano, R., Shimizu, T., and Tarbell, T. D. (2010). Hinode Observation of Photospheric Magnetic Activities Triggering X-Ray Microflares Around a Well-Developed Sunspot. Astrophysical J. 720, 1136–1145. doi:10.1088/0004-637x/720/2/1136
Katsukawa, Y., Berger, T. E., Ichimoto, K., Lites, B. W., Nagata, S., Shimizu, T., et al. (2007). Small-Scale Jetlike Features in Penumbral Chromospheres. Sci 318, 1594. doi:10.1126/science.1146046
Kosugi, T., Matsuzaki, K., Sakao, T., Shimizu, T., Sone, Y., Tachikawa, S., et al. (2007). The Hinode (Solar-B) Mission: An Overview. Sol. Phys. 243, 3–17. doi:10.1007/s11207-007-9014-6
Lites, B. W., Akin, D. L., Card, G., Cruz, T., Duncan, D. W., Edwards, C. G., et al. (2013). The Hinode Spectro-Polarimeter. Sol. Phys. 283, 579–599. doi:10.1007/s11207-012-0206-3
Loukitcheva, M. A., Iwai, K., Solanki, S. K., White, S. M., and Shimojo, M. (2017). Solar ALMA Observations: Constraining the Chromosphere above Sunspots. Astrophysical J. 850, 35. doi:10.3847/1538-4357/aa91cc
Loukitcheva, M., Solanki, S. K., Carlsson, M., and White, S. M. (2015). Millimeter Radiation from a 3D Model of the Solar Atmosphere. Astronomy Astrophysics 575, A15. doi:10.1051/0004-6361/201425238
Martínez-Sykora, J., De Pontieu, B., de la Cruz Rodriguez, J., and Chintzoglou, G. (2020). Astrophysical J. 891, L8.
Martínez-Sykora, J., De Pontieu, B., Hansteen, V. H., Rouppe van der Voort, L., Carlsson, M., and Pereira, T. M. D. (2017). On the Generation of Solar Spicules and Alfvénic Waves. Sci 356, 1269. doi:10.1126/science.aah5412
Matsumoto, T., Kitai, R., Shibata, K., Shin’ichi, N., Kenichi, O., Tahe i, N., et al. (2008). Cooperative Observation of Ellerman Bombs between the Solar Optical Telescope Aboard Hinode and Hida/Domeless Solar Telescope. PASJ 60, 577. doi:10.1093/pasj/60.3.577
Miyawaki, S., Iwai, K., Shibasaki, K., Shiota, D., and Nozawa, S. (2016). Coronal Magnetic Fields Derived from Simultaneous Microwave and Euv Observations and Comparison with the Potential Field Model. Astrophysical J. 818, 8. doi:10.3847/0004-637x/818/1/8
Molnar, M. E., Reardon, K. P., Chai, Y., Gary, D., Uitenbroek, H., Cauzzi, G., et al. (2019). Astrophys. J. 881, 99. doi:10.3847/1538-4357/ab2ba3
Narang, N., Chandrashekhar, K., Jafarzadeh, S., Fleck, B., Szydlarski, M., and Wedemeyer, S. (2022). arXiv:2202.11547.
Nindos, A., Alissandrakis, C. E., Patsourakos, S., and Bastian, T. S. (2021a). Astronomy Astrophysics 638, A62.
Nindos, A., Patsourakos, S., Alissandrakis, C. E., and Bastian, T. S. (2021b). ALMA Observations of the Variability of the Quiet Sun at Millimeter Wavelengths. Astronomy Astrophysics 652, A92. doi:10.1051/0004-6361/202141241
Okamoto, T. J., and De Pontieu, B. (2011). Propagating Waves along Spicules. Astrophysical J. 736, L24. doi:10.1088/2041-8205/736/2/l24
Okamoto, T. J., Tsuneta, S., Berger, T. E., Ichimoto, K., Katsukawa, Y., Lites, B. W., et al. (2007). Coronal Transverse Magnetohydrodynamic Waves in a Solar Prominence. Science 318, 1577–1580. doi:10.1126/science.1145447
Ortiz, A., Bellot Rubio, L. R., Hansteen, V. H., de la Cruz Rodríguez, J., and van der Voort, L. R. (2014). Emergence of Granular-Sized Magnetic Bubbles through the Solar Atmosphere. I. Spectropolarimetric Observations and Simulations. Astrophysical J. 781, 126. doi:10.1088/0004-637x/781/2/126
Pariat, E., Aulanier, G., Schmieder, B., Georgoulis, M. K., Rust, D. M., and Bernasconi, P. N. (2004). Resistive Emergence of Undulatory Flux Tubes. Astrophysical J. 614, 1099–1112. doi:10.1086/423891
Parker, E. N. (1988). Nanoflares and the Solar X-Ray Corona. Astrophysical J. 330, 474. doi:10.1086/166485
Pereira, T. M. D., De Pontieu, B., and Carlsson, M. (2012). Quantifying Spicules. Astrophysical J. 759, 18. doi:10.1088/0004-637x/759/1/18
Peter, H., Tian, H., Curdt, W., Schmit, D., Innes, D., De Pontieu, B., et al. (2014). Hot Explosions in the Cool Atmosphere of the Sun. Science 346 (6207), 1255726. doi:10.1126/science.1255726
Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., and Petterson, B. (2003). Proc. SPIE Conf. Ser. 4853, 341.
Scherrer, P. H., Schou, J., Bush, R. I., Kosovichev, A. G., Bogart, R. S., Hoeksema, J. T., et al. (2012). The Helioseismic and Magnetic Imager (HMI) Investigation for the Solar Dynamics Observatory (SDO). Sol. Phys. 275, 207–227. doi:10.1007/s11207-011-9834-2
Schou, J., Scherrer, P. H., Bush, R. I., Wachter, R., Couvidat, S., Rabello-Soares, M. C., et al. (2012). Design and Ground Calibration of the Helioseismic and Magnetic Imager (HMI) Instrument on the Solar Dynamics Observatory (SDO). Sol. Phys. 275, 229. doi:10.1007/s11207-011-9842-2
Shibata, K., Nakamura, T., Matsumoto, T., Otsuji, K., Okamoto, T. J., Nishizuka, N., et al. (2007). Chromospheric Anemone Jets as Evidence of Ubiquitous Reconnection. Sci 318, 1591. doi:10.1126/science.1146708
Shimizu, T. (2015). 3D Magnetic Field Configuration of Small-Scale Reconnection Events in the Solar Plasma Atmosphere. Phys. Plasmas 22, 101207. doi:10.1063/1.4933056
Shimizu, T., Katsukawa, Y., Kubo, M., Lites, B. W., Ichimoto, K., Suematsu, Y., et al. (2009). Hinode Observation of the Magnetic Fields in a Sunspot Light Bridge Accompanied by Long-Lasting Chromospheric Plasma Ejections. Astrophysical J. 696, L66–L69. doi:10.1088/0004-637x/696/1/l66
Shimizu, T., Nagata, S., Tsuneta, S., Tarbell, T., Edwards, C., Shine, R., et al. (2008). Image Stabilization System for Hinode (Solar-B) Solar Optical Telescope. Sol. Phys. 249, 221–232. doi:10.1007/s11207-007-9053-z
Shimizu, T., Shimojo, M., and Abe, M. (2021). Simultaneous ALMA-Hinode-IRIS Observations on Footpoint Signatures of a Soft X-Ray Loop-like Microflare. Astrophysical J. 922, 113. doi:10.3847/1538-4357/ac27a4
Shimizu, T., Shine, R. A., Title, A. M., Tarbell, T. D., and Frank, Z. (2002). Photospheric Magnetic Activities Responsible for Soft X‐Ray Pointlike Microflares. I. Identifications of Associated Photospheric/Chromospheric Activities. Astrophysical J. 574, 1074–1088. doi:10.1086/340998
Shimojo, M., Bastian, T. S., Hales, A. S., White, S. M., Iwai, K., Hills, R. E., et al. (2017a). Sol. Phys. 292, 87. doi:10.1007/s11207-017-1095-2
Shimojo, M., Hudson, H. S., White, S. M., Bastian, T. S., and Iwai, K. (2017b). The First ALMA Observation of a Solar Plasmoid Ejection from an X-Ray Bright Point. Astrophysical J. 841, L5. doi:10.3847/2041-8213/aa70e3
Smitha, H. N., Chitta, L. P., Wiegelmann, T., and Solanki, S. K. (2018). Observations of Solar Chromospheric Heating at Sub-arcsec Spatial Resolution. Astronomy Astrophysics 617, A128. doi:10.1051/0004-6361/201833276
Stangalini, M., Del Moro, D., Berrilli, F., and Jefferies, S. M. (2011). MHD Wave Transmission in the Sun's Atmosphere. Astronomy Astrophysics 534, A65. doi:10.1051/0004-6361/201117356
Suematsu, Y., Tsuneta, S., Ichimoto, K., Shimizu, T., Otsubo, M., Katsukawa, Y., et al. (2008). The Solar Optical Telescope of Solar-B (Hinode): The Optical Telescope Assembly. Sol. Phys. 249, 197–220. doi:10.1007/s11207-008-9129-4
Tian, H., Zhu, X., Peter, H., Zhao, J., Samanta, T., and Chen, Y. (2018). Magnetic Reconnection at the Earliest Stage of Solar Flux Emergence. Astrophysical J. 854, 174. doi:10.3847/1538-4357/aaaae6
Toriumi, S., and Wang, H. (2019). Flare-productive Active Regions. Living Rev. Sol. Phys. 16, 3. doi:10.1007/s41116-019-0019-7
Tsuneta, S., Ichimoto, K., Katsukawa, Y., Nagata, S., Otsubo, M., Shimizu, T., et al. (2008). The Solar Optical Telescope for the Hinode Mission: An Overview. Sol. Phys. 249, 167–196. doi:10.1007/s11207-008-9174-z
Vernazza, J. E., Avrett, E. H., and Loeser, R. (1981). Structure of the Solar Chromosphere. III - Models of the EUV Brightness Components of the Quiet-Sun. Astrophysical J. Suppl. Ser. 45, 635. doi:10.1086/190731
White, S. M., Loukitcheva, M., and Solanki, S. K. (2006). High-resolution Millimeter-Interferometer Observations of the Solar Chromosphere. Astronomy Astrophysics 456, 697–711. doi:10.1051/0004-6361:20052854
Keywords: the sun, radio radiation, alma, chromosphere, magnetic field, nanoflare
Citation: Abe M, Shimizu T and Shimojo M (2022) An ALMA Observation of Time Variations in Chromospheric Temperature of a Solar Plage Region. Front. Astron. Space Sci. 9:908249. doi: 10.3389/fspas.2022.908249
Received: 30 March 2022; Accepted: 09 May 2022;
Published: 13 June 2022.
Edited by:
Mario J. P. F. G. Monteiro, University of Porto, PortugalReviewed by:
João M. da Silva Santos, National Solar Observatory, United StatesPeng-Fei Chen, Nanjing University, China
Copyright © 2022 Abe, Shimizu and Shimojo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Toshifumi Shimizu, c2hpbWl6dUBzb2xhci5pc2FzLmpheGEuanA=
 Masashi Abe1,2
Masashi Abe1,2 Toshifumi Shimizu
Toshifumi Shimizu Masumi Shimojo
Masumi Shimojo