Nuclear Symmetry Energy and Hyperonic Stars in the QMC Model

The nuclear symmetry energy, together with the other saturation properties of symmetric nuclear matter, plays an important role in low energy nuclear structure of terrestrial systems, as well as astrophysical objects. In particular, its density dependence, both in sub- and supra-saturation regions in high density matter in neutron stars, is of utmost significance and has been a subject of active research for decades, usually within a mean-field framework. We report results obtained using the latest version of Quark-Meson-Coupling Model (QMC-A) with just three variable parameters, the baryon-meson coupling constants in free space. It is shown that these parameters can be determined directly using nuclear matter (NM) properties at saturation; two parameters of symmetric nuclear matter (SNM), the baryon number density and the energy per particle, and the symmetry energy coefficient of asymmetric nuclear matter (ANM). The effects of uncertainties in the these parameters and propagation of these uncertainties through the calculation of properties of dense hyperonic matter and cold neutron stars are demonstrated. This approach leads to new limits on both the NM parameters and the QMC coupling constants. The results, which exploit the unique features of the QMC model, are discussed and future prospects are outlined.

1 Introduction

The role of the nuclear symmetry energy in nuclear binding was identified in the 1930s (Gamow, 1930; Weizsäcker, 1935; Bethe and Bacher, 1936) in the effort to understand the binding energy of atomic nuclei, modeled as a spherical drop of incompressible liquid, introducing the well-known semi-empirical mass formula (SMF).

$\begin{array}{ll}\hfill B\left(A,Z\right)& =a_{\text{vol}}A+a_{\text{surf}}{A}^{2/3}\hfill \\ \hfill & +a_{\mathrm{C}}{Z}^2{A}^{-1/3}+a_{\text{sym}}{\left(N-Z\right)}^2{A}^{-1}\hfill \end{array}(1)$

$\begin{array}{ll}\hfill E\left(A,Z\right)/A& \equiv B\left(A,Z\right)/A=a_{\text{vol}}+a_{\text{surf}}{A}^{-1/3}+a_{\mathrm{C}}{Z}^2{A}^{-4/3}\hfill \\ \hfill & +a_{\text{sym}}{\left(N-Z\right)}^2{A}^{-2}\hfill \end{array}(2)$

While the volume, surface and Coulomb terms were fully phenomenological, the symmetry effect required basic quantum mechanics. It arises in systems made of non-interacting distinguishable Fermi gases which obey the Pauli principle and as such are treated separately. In nuclear matter there will be a difference between the energy levels occupied by protons and neutrons which will contribute to the total energy of the nucleus and decrease its binding energy. For terrestrial finite nuclei with A = N + Z particles the coefficients in Equation 1 are fitted to experimental nuclear masses. As demonstrated in Figure 1 the symmetry term plays the least important role, except for light nuclei (A ≤ 50) and the symmetry energy decreases with increasing A. However, in highly asymmetric nuclear matter, such as in cold neutron stars, it is important.

FIGURE 1

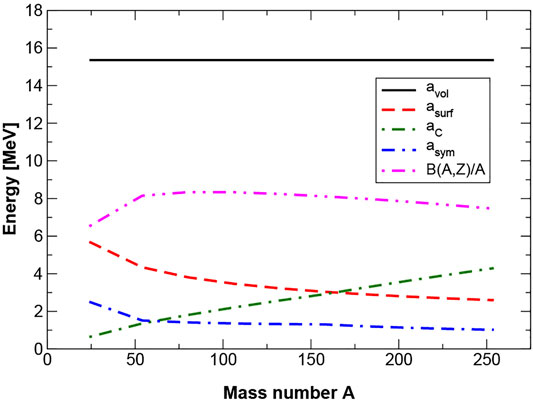
FIGURE 1. Binding energy per particle as calculated in Equation 2. The magnitude of the volume, surface, Coulomb and symmetry contribution to the total nuclear binding are displayed vs mass number A. Individual terms in the top Equation 1 were calculated as a function of A = N + Z of selected nuclei between ¹⁶O and ²⁵⁴Fm. The coefficients a_vol, a_surf, a_C and a_sym are taken as 15.36, 16.42, 0.691 and 22.53 MeV, respectively. These values were determined by (Kirson, 2008) from a fit of the basic Equation 1 to the 2003 mass table (Audi et al., 2003). The figure has been taken from Ref. (Stone, 2021) under Creative Commons Attribution License.

Equation 1 has been constructed assuming that the nucleus is a sphere with radius R, containing closely packed spherical nucleons. The mass number independence of the volume term in the expression for the energy per particle E(A, Z)/A leads to the concept of infinite nuclear matter (INM) ((Bethe and Bacher, 1936; Bethe, 1971) and refs. therein), a hypothetical medium consisting of an infinite number of uniformly distributed protons and neutrons, with a given proton/neutron ratio, and no Coulomb field. There are only two quantities characterizing INM, the binding energy per particle and the particle number density. As discussed in detail in Ref. (Stone, 2021), in the special case of INM with N = Z, symmetric nuclear matter (SNM), the binding energy per particle, E₀/A, is given by the coefficient a_vol in Equation 2 as all the other terms tend to zero for A → ∞ and N = Z. To determine the particle number density, ρ₀, of SNM, nuclear and nucleon radii have to be determined from experiment. The constant values E₀/A and ρ₀ of SNM are a consequence of saturation of nuclear forces and have become fundamental constraints on nuclear models. To study other bulk nuclear properties, in particular the symmetry energy in nuclei and nuclear matter, the physics included in the SMF has been extensively refined by inclusion of shell effects, variable proton and neutron density distributions throughout the nuclear volume of arbitrary shape, decreasing smoothly to zero in the surface region, and the nuclear surface diffuseness and thickness (Myers and Swiatecki, 1966; Myers and Swiatecki, 1969; Myers and Swiatecki, 1974; Moller et al., 1995; Möller et al., 2012; Möller et al., 2016). Different strategies for parameterizations of the energy per particle were used, based on Taylor expansion around the SNM values, in terms of two variables, the proton-neutron asymmetry, δ=(ρ_n − ρ_p)/ρ (ρ = ρ_n + ρ_p), and the deviation of the density ρ from its SNM value ρ₀, ϵ = (ρ₀ − ρ)/(3ρ₀). Taking Equation 2 to the limit of A → ∞ and neglecting the long-range Coulomb force in (Myers and Swiatecki, 1969) we get for the bulk energy per particle,

$E\left(\rho ,\delta ,ϵ\right)/A=-a_{\text{vol}}+J{\delta }^{\mathrm{2}}+\frac{1}{2}K{ϵ}^{\mathrm{2}}-Lϵ{\delta }^{\mathrm{2}}+\cdots (3)$

with J being the symmetry energy coefficient a_sym, L giving the density dependence of the symmetry energy and K being the volume nuclear compressibility coefficient at saturation density. For SNM with equal number of protons and neutrons δ = 0 and the minimum value of the binding energy per particle E(δ = 0, ϵ = 0)/A equals E₀/A and occurs at ρ = ρ₀. In asymmetric nuclear matter (ANM), at ρ = ρ₀ the energy per particle is dependent on the proton-neutron asymmetry as − a_vol + Jδ², always higher than −E₀/A. At densities around the saturation density, the energy per particle can be expanded to the second order in a form

$E\left(\rho ,\delta \right)/A=E\left(\rho ,\delta =0\right)/A+S\left(\rho \right){\delta }^2+\cdots (4)$

where E(ρ, δ = 0)/A is the energy per particle of SNM and S(ρ) is the symmetry energy

$S\left(\rho \right)\equiv \frac{1}{2}\left(\frac{{\partial }^{2}E\left(\rho ,\delta \right)/A}{\partial {\delta }^2}\right)|{|}_{\delta =0}\approx E\left(\rho ,\delta =1\right)/A-E\left(\rho ,\delta =0\right)/A(5)$

which is approximately equal to the difference between the energy per particle of the pure neutron and symmetric matter.

To study the departure of the symmetry energy from its value at saturation density, a Taylor expansion is again used

$S\left(\rho \right)=J+Lϵ+\frac{1}{2}{K}_{\mathit{sym}}{ϵ}^2+\cdots (6)$

with

$L\equiv 3{\rho }_0\left(\frac{\partial S}{\partial \rho }\right)|{|}_{{\rho }_0}(7)$

and K_sym being the curvature of the symmetry energy, sometimes called the symmetry incompressibility.

There has been a consolidated effort to find experimental and theoretical constraints for the S, L and K parameters and their density dependence in Equation 3, without a consensus being reached. Values obtained from different relevant experiments are dependent on models used for their analysis, and the data themselves often suffer from large uncertainties. (see e.g., (Tsang et al., 2012; Dutra et al., 2012; Horowitz et al., 2014)). The value of the symmetry energy coefficient J in Equation 3 at the saturation density of the symmetric nuclear matter ρ₀ is reasonably well constrained between about 28–34 MeV, but its slope at saturation, the parameter L, is still unclear. Stone et al. (Rikovska Stone et al., 2003) investigated the relation between the slope of the symmetry energy and the maximum mass of cold neutron stars using the Equation of State (EoS) based on the Skyrme model (Rikovska Stone et al., 2003). Bao-An Li et al. (Li et al., 2014) comprehensively reviewed papers up to 2014, including open theoretical issues, constraints from terrestrial laboratory experiments and astrophysical observations but no tighter limits, especially on the density dependence of the symmetry energy were obtained. Recent progress reports on the subject were published by Bao-An Li and collaborators (Li et al., 2019; Li et al., 2021), including current data and data from gravitational wave (GW) observations but, again, leaving space for further improvement in better understanding of the symmetry energy and its attributes. One of the problems is that some data lead to contradictory allowed values. For example, L < 45 from NS cooling and between 100 and 130 MeV from X-ray tails of giant flares from SGRs (Li et al., 2021). An exhaustive review of the symmetry energy and hyperonic stars (Providência et al., 2019) considered 11 non-linear and 2 density dependent relativistic mean-field (RMF) models and presented a comprehensive list of references. In particular, they searched for a correlation between the cooling processes and hyperonic content in neutron stars. However, the current (model dependent) limit on the range of L at ρ₀ remains between about 30–100 MeV, its density dependence is not constrained and the incompressibility K ranges between low values, around 220–240 MeV in non-relativistic models, mainly based on experiments with giant resonances and Skyrme-type models), and above ∼260 MeV in relativistic models of high density matter (Stone et al., 2014; Providência et al., 2019).

In this work we employ the QMC-A version of the QMC model of high density matter to explore the effect of uncertainties in the NM parameters and of the propagation of these uncertainties through the calculation of cold neutron star properties. The QMC model offers a unique opportunity to perform such study. In contrast with more traditional models, QMC depends on only three variable parameters, the nucleon-meson coupling constants in free space. The properties of NM at saturation are also determined by three principle quantities with a fundamental physical significance, the saturation density ρ₀, and energy per particle E₀/A and the symmetry energy coefficient J. These quantities form a basic calibration set for all models providing other properties of high density matter, such as S(ρ), L, and K. Noting the QMC and NM parameter space are of the same dimension, their mapping offers the best chance to find their relationship and consequences for experiments and observations. Although in both systems the parameters are correlated, we show that a comparison with observation offers a unique chance to establish these constraints. To do that, we use only observational data with minimal model dependence, leaving to the reader a comparison with other model calculations (Fortin et al., 2017; Providência et al., 2019; Fortin et al., 2020).

2 The Quark-Meson-Coupling Model

The Quark-Meson-Coupling (QMC) model was developed by Guichon, Thomas and collaborators (Guichon, 1988; Saito and Thomas, 1994; Guichon et al., 1996; Guichon and Thomas, 2004; Saito et al., 2007; Guichon et al., 2018). This effective relativistic mean-field model assumes that forces between individual baryons are self-consistently mediated by exchange of virtual mesons between the valence quarks in the baryons. The effect of the medium the baryons are embedded in, such as NS cores and nuclei, alters the dynamics of the valence quarks in the individual baryons. As a consequence, the self-consistently calculated scalar meson-baryon couplings acquire an effective density dependence. This dependence stems from the response of the quark structure of the baryons to the meson fields.

In the QMC model, the baryons are represented by non-overlapping MIT bags (but other models of confinement can be used without a loss of generality (Bentz and Thomas, 2001). Coupling the mesons to the quarks throughout the bag volume would be unnatural in a literal interpretation of the model, where only quarks and gluons can live inside the cavity. However, in a more realistic picture, the quarks are attached to a string (see Figure 2) but otherwise move in the non-perturbative QCD vacuum. There, they feel vacuum fluctuations, which are represented by meson fields. This feature allows the QMC model to be used well above ρ₀ without concerns about the bag overlap.

FIGURE 2

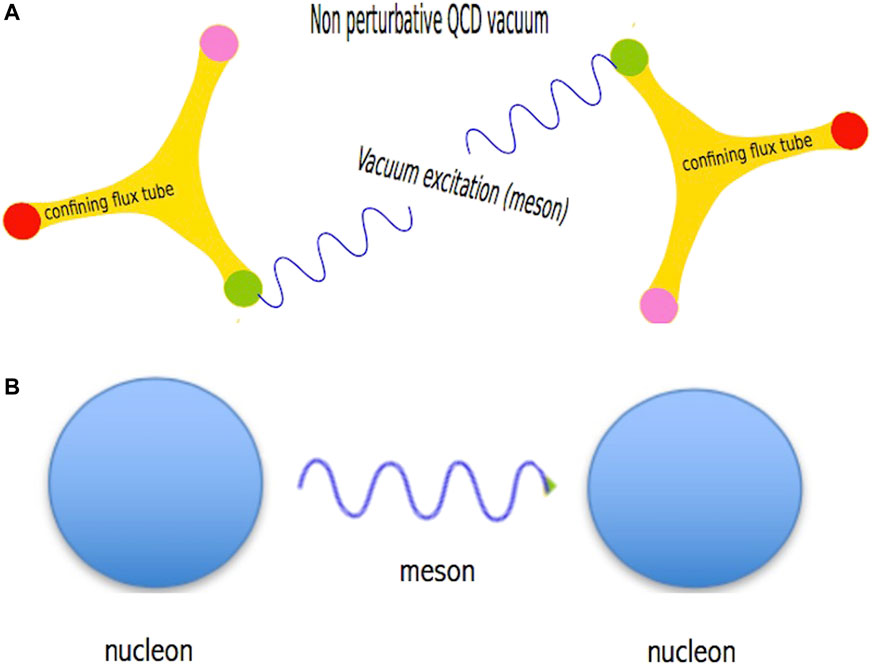
FIGURE 2. (A): Cartoon of the mechanism of interaction in the QMC model. Shown is the distribution of valence quarks and gluon tubes as predicted by lattice QCD (see http://www.physics.adelaide.edu.au/theory/staff/leinweber/VisualQCD/Nobel/index.html). The figure was adapted from Ref. (Guichon et al., 2018). (B): Traditional image of interaction between baryons without considering their internal structure.

We assume that the total energy of a classical system of baryons at zero temperature, modeled as non-overlapping bags coupled to meson fields σ, ω and ρ is expressed as (Guichon et al., 2018)

$\begin{array}{ll}\hfill E_{\mathit{QMC}}& =\sum _{i=1,\dots }\sqrt{P_i^2+M_i^2\left(\sigma \left({\vec{R}}_i\right)\right)}+g_{\omega }^i\omega \left({\vec{R}}_i\right)\hfill \\ \hfill & +g_{\rho }{\vec{I}}_i.\vec{B}\left({\vec{R}}_i\right)+E_{\sigma }+E_{\omega ,\rho },\hfill \end{array}(8)$

where ${\vec{R}}_i$ and ${\vec{P}}_i$ are the position and momentum of a baryon i and $\vec{I}$ is the isospin matrix. Following the notation of Ref. (Guichon et al., 2018), $\vec{B}$ stands here for the isovector ρ field to avoid a confusion with the baryon number density ρ (Guichon et al., 2018). E_σ and E_ω,ρ are the static meson fields energies.

The dynamical mass of a bag, representing a baryon i (short for b(i)) immersed in a constant scalar field is obtained by solving the bag equations to be

$M_i\left(\sigma \right)=M_i-w_{\sigma i}{g}_{\sigma N}\sigma +\frac{d}{2}{w}_{\sigma i}̃{\left(g_{\sigma N}\sigma \right)}^2,(9)$

The quark-meson couplings are related to the nucleon couplings to σ, ω and ρ mesons in free space as

$g_{\sigma N}=3g_{\sigma }^q{\int }_{\mathit{Bag}}d\vec{r}\bar{q}q\left(\vec{r}\right)g_{\omega N}=3g_{\omega }^q{g}_{\rho N}=g_{\rho }^q(10)$

where q is the valence quark wave function for a free bag.

It is convenient to use effective coupling constants G_σ, G_ω, and G_ρ

$G_{\sigma }=\frac{g_{\sigma N}^2}{m_{\sigma }^2}{G}_{\omega }=\frac{g_{\omega N}^2}{m_{\omega }^2}{G}_{\rho }=\frac{g_{\rho N}^2}{m_{\rho }^2},(11)$

using the free σ, ω and ρ meson masses.

The coefficient d in the third term in Equation 9, is known as the “scalar polarizability”. This term is a natural consequence of the quark structure of the nucleon and is sufficient to lead to nuclear saturation. The scalar polarizability is related to the radius of the bag R_B as (Guichon et al., 2018)

$d=0.0044+0.211R_B-0.0357R_B^2.(12)$

The weights w_σi and $w_{\sigma i}̃$ control the flavor dependence of the effective mass and in a naive first approximation they are equal to 1 + s(i)/3 (s being strangeness), since the σ meson is taken to couple only to the non-strange light quarks. This simple relation is however broken by the difference in bag radii of the hyperons as well as the hyperfine color interaction and the exact values are also dependent on the bag radii and the experimental masses of the nucleon, Δ, and Λ, Σ and Ξ hyperons. In the present work, we take R_B = 1 fm (for the nucleon in free space) and the weights summarized in Table 2 in Guichon et al. (2018) (see also the Appendix in the Ref. (Rikovska Stone et al., 2007).

The meson fields in Equation 8 are time independent and are solved through the equations of motion

$\frac{\delta E_{\mathit{QMC}}}{\delta \sigma \left(\vec{r}\right)}=\frac{\delta E_{\mathit{QMC}}}{\delta \omega \left(\vec{r}\right)}=\frac{\delta E_{\mathit{QMC}}}{\delta B_{\alpha }\left(\vec{r}\right)}=0.(13)$

and substituted into Equation 8. The model is then quantized by replacement

${\vec{P}}_i\to -i{\vec{\nabla }}_i.(14)$

The heavy σ, ω and ρ mesons, which account for the exchange of correlated pions with the corresponding t-channel quantum numbers, are represented by their mean fields. Parity conservation means that there can be no pion mean field, so that single pion exchange enters only through the exchange or Fock terms. Thus, single pion exchange must be added separately, however this does not involve any additional parameters.

The full Hamiltonian reads (for details see (Guichon et al., 2018))

$H_{\mathit{QMC}}=H_{\sigma }+H_{\omega }+H_{\rho }+H_{so}+H_{\pi },(15)$

where individual terms describe contributions of different mesons and H_so is the spin-orbit term. For practical use, we use expansion of the mean field σ assuming that the field operator σ can be written as

$\sigma =⟨\sigma ⟩+\delta \sigma (16)$

where the C-number $⟨\sigma ⟩\equiv \bar{\sigma }$ denotes the ground state expectation value and the fluctuation δσ is considered as a small quantity. Using this expansion, the σ part of the Hamiltonian becomes ⟨H_σ⟩ and the full Hamiltonian reads (Guichon et al., 2018)

$\langle H_{\mathit{QMC}}\rangle =\langle H_{\sigma }\rangle +\langle H_{\omega }\rangle +\langle H_{\rho }\rangle +\langle H_{so}\rangle +\langle H_{\pi }\rangle .(17)$

This Hamiltonian significantly simplifies in infinite nuclear matter, a medium with uniform density ρ without surface and spin-orbit effects. All gradient terms vanish and ⟨H_QMC⟩ reduces to ⟨H_NM⟩. The ground state of the system is specified by a set of Fermi levels and the σ exchange part of the expression for the total energy density is calculated in the Hartree-Fock approximation (Rikovska Stone et al., 2007). The spin-orbit term vanishes in nuclear matter as being dependent on derivatives of density and the ω and ρ exchange can be calculated exactly as they are purely 2-body. Finally we add the long-range pion exchange and write

$\epsilon =\frac{\langle H_{\sigma }\rangle }{V}+\frac{\langle V_{\omega }\rangle }{V}+\frac{\langle V_{\rho }\rangle }{V}+\frac{\langle V_{\pi }\rangle }{V}(18)$

where ⟨V_ω⟩, ⟨V_ρ⟩ and ⟨V_π⟩ denote the infinite nuclear matter form of ⟨H_ω⟩, ⟨H_ρ⟩ and ⟨H_π⟩. For more detail see (Guichon et al., 2018). The energy per particle

$E\left(\rho ,\delta \right)/A=\frac{\epsilon }{\rho }\left(\rho ,\delta \right).(19)$

is used to calculate the asymmetry coefficient J, the symmetry energy S, slope L and the volume incompressibility K, both at the saturation point of the SNM and their density dependence, in the usual way (Guichon et al., 2018). The isovector scalar meson has also been considered in relation to the properties of neutron stars(Motta et al., 2019; Motta et al., 2020; Motta et al., 2021) but here focus on the dominant components of the NN force.

There are some other parameters in the QMC model which are not varied in this work. The bag radius R_B is fixed to be 1 fm, while the σ meson mass, m_σ, which is not well determined as a parameter of the NN force, is fixed to be 700 MeV. We also set the σ self-interaction parameter, λ₃, which appears to be needed in finite nuclei(Martinez et al., 2019), to zero. The bag radius and the σ meson mass effect were examined in our previous work in Section 2.5 in Ref. (Rikovska Stone et al., 2007). and in Sections 2.1.1 and 4.1.2 in Ref. (Guichon et al., 2018). The bag radius is tightly constrained by lattice QCD calculations of the proton radius and should be close to 1 fm. The QMC model of nuclear matter is rather insensitive to m_σ once the G_σ is fixed. In the version of the model for finite nuclei, the sensitivity to m_σ mainly comes from the fact that it controls the shape of nuclear surface, irrelevant in nuclear matter. The role of the parameter λ₃ has been explored in detail only in finite nuclei (Martinez et al., 2019; Martinez et al., 2020). In the current nuclear matter studies, it is constrained to a close-to-zero value by the rich experimental data on the single particle potential of the Λ hyperon. This is the value we use here and further research is be carried out in future work.

The ω and ρ meson masses and the isoscalar and isovector nucleon magnetic moments, which appear in the spin-orbit interaction in finite nuclei (Guichon et al., 1996; Guichon et al., 2018) are taken at their physical values. Once fixed, the adjustable parameters form a set which is so constrained that any variation would disturb the internal integrity of the model. If a serious discrepancy between the model prediction and some new observational and experimental data would occur, physics missing in the model would have to be sought. We stress that, as explained above, the number of variable parameters in the QMC model is not a matter of choice, but is a consequence of physics of the model.

The concept of the QMC model has several fundamental consequences. As shown in Ref. (Guichon, 1988). the model offers a natural explanation for the saturation of the nuclear force. Even more importantly, the model automatically includes many-body forces and there is no need to change the number of parameters when the baryonic composition of the matter changes, i.e., when hyperons appear in dense matter. In other words, matter consisting only of nucleons and matter containing the full baryon octet (nucleons and hyperons) is described by the same set of three parameters. All the hyperon-nucleon and hyperon-hyperon couplings are fixed by the quark structure calculated within the model. We emphasize that exchange terms are always included in Hartree-Fock calculations and single-particle potentials are calculated within the model, in contrast with most relativistic mean field models of high density nuclear matter.

Having outlined the QMC model, we turn to consider its application to neutron stars (NSs). Although the nucleonic content in the lower density outer is reasonably well modelled, the inner crust (Fortin et al., 2016; Newton et al., 2022) and the properties and composition of the core are still a subject of intensive research.

In this work, the DD2 model with light and heavy clusters (Pais and Typel, 2017) was used for inhomogeneous matter at sub-saturation densities. The DD2 calculation gives a fully thermodynamically consistent result, with the crust including phase transitions between different forms of nuclear and particle species, and the transition from inhomogeneous to homogeneous matter at higher densities. The transition was treated individually in each case, searching for the baryon number density region where there is a simultaneous smooth connection between the energy density, pressure and particle number density and their derivatives, and interpolating over this region if necessary (for more details see (Stone et al., 2021).

In the core, following the Pauli principle, hyperons appear naturally at T = 0 in nucleonic matter, when their chemical potentials, which increase with the density of the degenerate matter, become large enough. Strangeness non-conserving weak processes become possible, and create a hyperon population in the core of the star [(Glendenning, 1985; Balberg et al., 1999; Glendenning, 2012)]. The variation in the threshold densities is related to the differences in hyperon couplings and the consequent hyperon binding energies, defining their chemical potentials, in different models (see e.g., (Fortin et al., 2020)). These quantities require additional variables in traditional models but, as already discussed, are fixed by the quark structure within the QMC model and cannot be varied without violating the internal consistency of the model. It is the consequence of the more fundamental nature of the QMC model that, besides already mentioned natural explanation for the saturation of the nuclear force, and automatic inclusion of many-body forces (Guichon and Thomas, 2004), there is no need to change the number of parameters when the baryonic composition of the matter changes.

Some variants of the QMC model of dense matter in compact objects, using simplified expressions for the bag representing the nucleon, the effective mass of the nucleon and the treatment of meson fields have been reported in Refs. (Guichon et al., 2018; Lourenço et al., 2021; Motta and Thomas, 2022). and references therein. The authors of these QMC versions allow some flexibility in their parameters not permitted in the fully self-consistent Saclay-Adelaide formulation (the latest version is labeled as QMC-A), which is used throughout this work.

The first application of the QMC model to NSs (Rikovska Stone et al., 2007) was reported in 2007 and predicted the existence of a cold NS, with Λ and Ξ⁰ hyperons in their cores and a maximum mass of 1.97 M_⊙, 3 years before such a star was observed by (Demorest et al., 2010). Very recently the QMC-A model was extended to finite temperature (Stone et al., 2021) and yielded EoS tables suitable for use in modeling proto-neutron stars (PNSs), core-collapse supernovae (CCSN), and, potentially, remnants of binary neutron star mergers (BNSM) (https://compose.obspm.fr/eos/205, https://compose.obspm.fr/eos/206). The full derivation of the finite temperature formalism for the QMC model will appear in a separate publication. We note that calculation of quantities in this work include the full Fock (exchange) term in the solution of the Hartree-Fock equations. This is in contrast with most of the models used until now.

Application of a non-relativistic energy density functional derived within the QMC model to finite nuclei has yielded predictions of ground state properties of finite nuclei in excellent agreement with experimental data across the entire periodic table, including superheavy nuclei far beyond the parameter fitting range (Stone, 2016; Martinez et al., 2019; Stone et al., 2019; Martinez et al., 2020). Interestingly, the non-relativistic reduction of the QMC model shows clearly that the spin-orbit coupling appears naturally and has the correct magnitude. Crucial tests of the predicted change in the structure of a bound nucleon, which is intrinsic to the QMC model (Thomas, 2021), are being pursued actively. Such changes include a large reduction in the axial charge, which is potentially very important in the search for double beta-decay; a dramatic reduction in the Coulomb sum rule(Cloët et al., 2016) and of course the EMC effect (Thomas et al., 1989; Cloët et al., 2005; Cloët et al., 2006; Wang et al., 2022).

3 Computational Method

The QMC-A model of nuclear matter has in principle six parameters as detailed in Section 2. In the version of the model used in this work, we have chosen to fix R_B to 1 fm, M_σ to 700 MeV and λ₃ to zero, leaving variable only the three coupling constants, which are however correlated. As already mentioned in the introduction, these couplings are adjusted in the model based on accepted saturation properties of the SNM, ρ₀, the energy per particle E₀/A and the symmetry energy coefficient J of ANM at ρ₀. These quantities form a three-dimensional NM parameter space. They are also correlated and not exactly known. Their range is a subject of active research, e.g., (Horowitz et al., 2014). However, the fact that there are three major nuclear matter quantities which determine principal coupling constants of the QMC-A model offers a interesting opportunity to study their relation and sensitivity to their variation. QMC-A offers this simple mapping of the variable parameter spaces of the same dimension with a direct relation between them. There has been another attempt to relate gross properties of cold neutron stars with higher order coefficients in the expansion of the EoS of isospin asymmetric nuclear matter calculated in a relativistic mean field model with the DD-ME2 parameterization (Li and Sedrakian, 2019). This mapping is however rather involved due to more complicated framework of the multiparameter models used.

Because of this unique feature, it is possible to explore in detail the consequences of varying each of the NM parameters to establish ranges giving rise to best agreement coupling constants in a manner which includes correlations. These in turn give better model predictions of the related quantities. In this work we have developed a mesh (cuboid) of points with ‘coordinates’ ρ₀ = 0.14, 0.15, 0.16 and 0.17 fm⁻³, ${\mathrm{E}}_0/\text{A}$ = -15, -16, -17 and -18 MeV and J between 27–36 MeV with a step of 1 MeV. These coordinates were chosen to cover a wide enough area around the frequently used ρ₀ = 0.16 fm⁻³, ${\mathrm{E}}_0/\text{A}$ = -16 MeV and J around 30 MeV [but higher values were recently suggested, up to 36 MeV, in Ref. (Reed et al., 2021)]. At each mesh point a number of quantities at saturation density were calculated: the slope of the symmetry energy L, the volume incompressibility K, the coupling constants G_σ, G_ω, G_ρ, and the single-particle potentials U_Y for Y = Λ, Σ and Ξ hyperons. In addition, we have computed the gravitational mass, radius and central density of a maximum mass cold neutron star and the radius, central density and tidal deformability of a 1.4 M_⊙ neutron star, threshold densities for appearance of hyperons and for the onset of direct nucleonic URCA process (DUrca).

4 Results and Discussion

4.1 Nuclear Matter Parameters

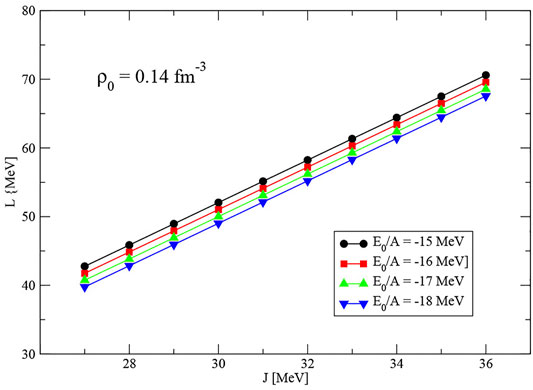
We start with the examination of the correlation between ρ₀, J, L and K. As shown in Figure 3, top left panel, there is a clear, almost perfect, linear correlation between the symmetry energy coefficient J and its slope L for ρ₀ = 0.14 fm⁻³ for four values the energy per particle E_0/A. The correlation curves calculated for each E₀/A are parallel, shifted by about 3 MeV downwords towards lower L. As given in detail in Supplementary Table S1, the total uncertainty in the NM parameters, represented by the cuboid, limits the predicted range of L to between 40 and 70 MeV. This range is within other predictions of the L − J correlation see e.g., (Drischler et al., 2020; Reed et al., 2021) but does not offer any constraints on the symmetry energy coefficient.

FIGURE 3

FIGURE 3. Correlation between L and J for ρ₀ = 0.14 fm⁻³ and E₀/A = -15, -16, -17, -18 MeV.

A more interesting correlation is found between the volume incompressibility K and the energy per particle E₀/A. As illustrated in Figure 4, the incompressibility is almost independent of J, but is different by as much as 40 MeV for a difference in E₀/A of 3 MeV. We show only lower and upper values of ρ₀ in the figure, the results for the other two values, being between these limits. The overall uncertainty in the NM parameters allows for values of K between 275 and 320 MeV. The general consensus is that high values of K, above about 300 MeV, are unlikely [but see (Stone et al., 2014)]. If this is the case, the highest value of E₀/A (-18 MeV), will be disfavored, thus offering the first constraint on the NM parameters.

FIGURE 4

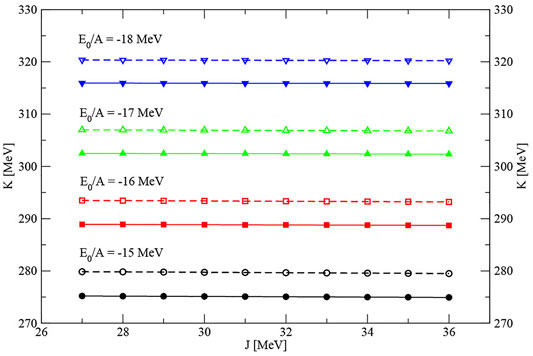
FIGURE 4. Correlation between the volume incompressibility K and the energy per particle E₀/A. as a function of the symmetry energy coefficient J. The results are shown for two values ρ₀, 0.14 fm⁻³ (solid curves and full symbols) and 0.17 fm⁻³ (dashed curves and empty symbols).

4.2 The Quark-Meson Coupling Constants

As discussed in Section 2, the coupling constants G_σ, G_ω and G_ρ are the only variable parameters of the QMC model of cold dense matter and are adjusted to reproduce the chosen NM parameters ρ₀, E₀/A and J. We illustrate in Figure 5 the effects of the choice of NM parameters on the coupling values. Increasing the saturation density ρ₀ decreases all three couplings by about 20%. The effect of E₀/A is maximal in G_σ (about 10%) but reduces to around 2% in G_ρ (bottom panel in Figure 5). G_σ is almost independent of J which has the maximum affect on G_ρ, increasing it by more that a factor of 1.5 between J = 27 and 36 MeV. G_ω, the coupling constant of the isoscalar ω meson would be expected to have no or very small sensitivity to J, similarly to G_σ. We speculate that the about 6% rise between J = 27 and 36 MeV is due to the contribution of the isovector ρ meson through the Fock term. The total ranges of G_σ, G_ω and G_ρ throughout the cuboid space are (9.1–12.2), (5.3–7.6) and (2.1–5.7), respectively (see Supplementary Table S2 for details). Since the coupling constants are parameters of the model, these calculations do not offer constraints within these ranges. The constraints established below on the NM parameters are further discussed in the conclusions.

FIGURE 5

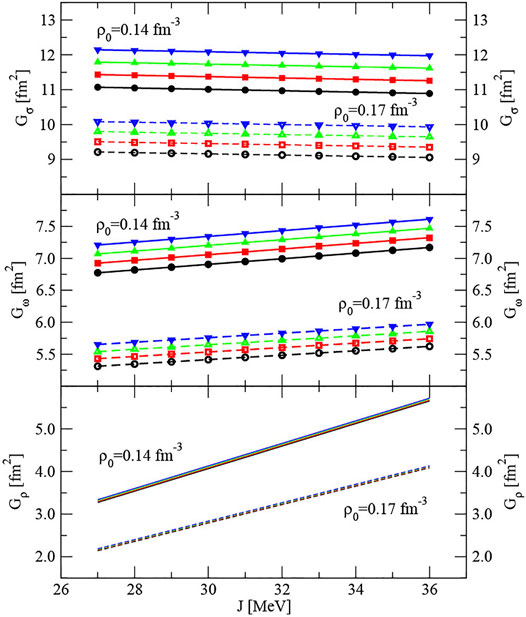
FIGURE 5. G_σ, G_ω and G_ρ as a function of the symmetry energy coefficient J for ρ₀ = 0.14 fm⁻³ (full symbols and solid lines) and ρ₀ = 0.17 fm⁻³ (empty symbols and dashed lines) and E₀/A = -15, -16, -17 and -18 MeV depicted by black, red, green and blue symbols, respectively. Symbols have not been added to the bottom panel because the lines are closer then their width.

4.3 Hyperonic Single-Particle Potentials

The single-particle potentials of hyperons in high density nucleonic matter determine their appearance in neutron stars. These potentials are dependent on the nucleon-hyperon and hyperon-hyperon interactions, which are treated as variable parameters in traditional RMF models and have to be fitted to experiment and observation. Specifically, the appearance of Σ hyperons which has been an issue for many years (Providência et al., 2019). Both positive and negative U_Σ values have been considered in these models (Providência et al., 2019). By constrast in the QMC model, the interactions and potentials are not a subject of choice, but emerge naturally from the formalism (Tsushima et al., 1998). In particular, as explained earlier, they are calculated under the assumption that the mesons couple only to non-strange light quarks, following the Zweig rule, using the self-consistenly calculated quark wave functions.

In this model, Σ hyperons do not appear in the cores of cold neutron stars at baryon number densities below ρ = 1.2 fm^-3. This effect was recognized already in our early work (Rikovska Stone et al., 2007; Guichon et al., 2018)) and understood as a consequence of the fact that the hyperfine interaction that splits the Λ and Σ masses in free space is significantly enhanced in-medium [(Guichon et al., 2008)], leading to what is effectively a repulsive three-body force for the Σ hyperons (Tsushima et al., 2010). The absence of Σ hyperons in cold matter is supported by the fact that despite great efforts, no bound Σ⁻ hypernuclei at medium or high mass have been found (Harada and Hirabayashi, 2006; Harada and Hirabayashi, 2015). We therefore adopt the experimental finding (Harada and Hirabayashi, 2006; Harada and Hirabayashi, 2015) that there is no bound Σ hypernucleus in nature. It follows that the Σ⁻ nucleon potential has to be repulsive, that is U_Σ is positive, at least in the medium and heavy nuclear region. This provides a very strong constraint on the NM parameters range as shown in Figure 6. Note that the non-existence of a Σ hypernucleus does not necessarily mean that the hyperonic potential should be repulsive. It could be also attractive, but too shallow to allow a bound state. However, there are many experimental studies of Σ hyperon production to show a repulsive potential, see for example (Saha, 2004). If a strong experimental evidence is found in the contrary, our analysis would have to be revised.

FIGURE 6

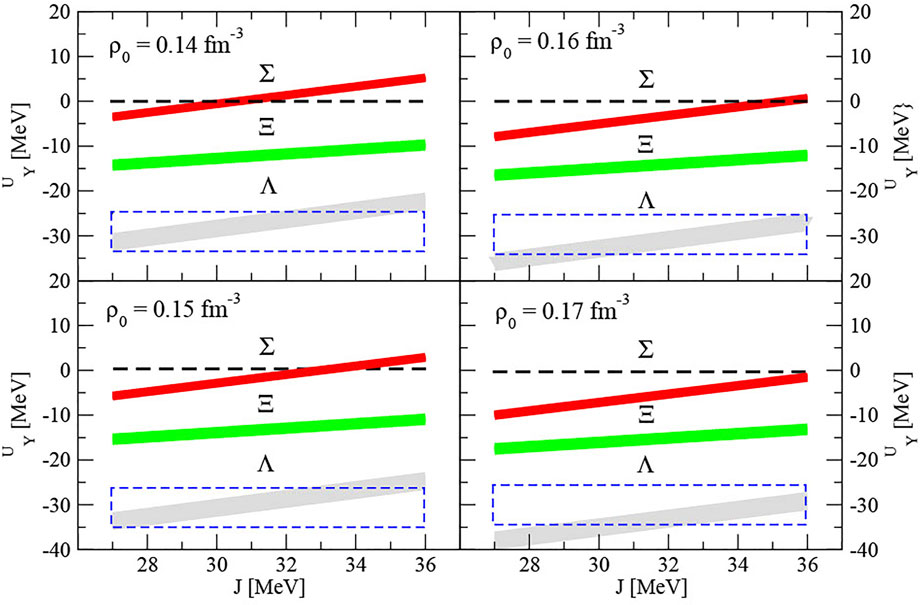
FIGURE 6. Single-particle potentials U_Λ (grey), U_Σ (red) and U_Ξ (green) as a function of J for ρ₀ = 0.14, 0.15, 0.16 and 0.17 fm⁻³. The filled width of the rectangles depicting the potentials represents the uncertainty due to the spread of E₀/A between -15.0 and -18 MeV. The dashed blue rectangle around U_Λ illustrates the region of experimental values reported in the literature. The horizontal black dashed line guides the eye to zero, dividing positive and negative values of U_Σ. No established experimental constraint on U_Ξ is available.

The constraint on U_Λ has been relatively well established from experiments with hypernuclei (Gal et al., 2016). We note that what is actually measured in experiments with hypernuclei are binding energies of the hyperon in the s and p shells of a single Λ hypernucleus in a range of the mass number A. The value of the single Λ baryonic potential in the symmetric baryonic matter at saturation is obtained by extrapolation to infinite A (as a function of A^−2/3) in a model dependent way (Fortin et al., 2017). The generally accepted value of U_Λ is around -30 MeV. We adopted the range of values from -25 to -35 MeV in our analysis.

Up to now, two single events involving Ξ ${\mathrm{h}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{i},}_{{\mathrm{\Xi }}^{-}}^{12}$Be [(Kchaustov, 2000)] ${\mathrm{a}\mathrm{n}\mathrm{d}}_{{\mathrm{\Xi }}^{-}}^{15}$C (Nakazawa et al., 2015), have been reported [(Yoshida et al., 2019)]. (Yoshimoto, 2021). reported the first observation of a nuclear s-state of a Ξ hypernucleus ${\mathrm{h}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{u}\mathrm{s}}_{\mathrm{\Xi }}^{15}$C but the single particle U_Ξ potential has not yet been derived from these observations with any certainty.

Examination of Figure 6 shows a dramatic narrowing down of acceptable parameter ranges. Requiring simultaneous satisfaction of the constraints on U_Σ (being positive) and U_Λ (being within the blue dashed rectangle) and taking into account the spread due to the uncertainty in E₀/A, we find that all cases calculated with ρ₀ = 0.17 fm⁻³ can be eliminated and cases with ρ₀ = 0.16, 0.15 and 0.14 fm⁻³ are allowed only for J = 36, 33–34 and 31–32 MeV respectively (for details see Supplementary Table S3).

Additional data on U_Ξ would be extremely valuable as they should provide selection of rather narrow ranges for ρ₀, E₀/A and J, fully based on experimental data and the QMC-A model.

4.4 The Equation of State of Cold Hyperonic Matter

Moving on to the density dependence of the symmetry energy, tested in modeling cold neutron stars, we first calculate the EoS of cold dense matter containing the full baryon octet, that is the dependence of E/A on baryon number density ρ₀. To maximize demonstration of the effects we wish to discuss, a combination of the minimum and maximum values of J = 27 and 36 MeV and of ρ₀ = 0.14 and 0.17 fm⁻³ were chosen (see Figure 7). The calculation was performed for the saturation energy per particle E₀/A = -15 to -18 MeV in all cases which resulted in the spread depicted by the grey and green shaded areas in the figure. In the left panels, we observe a significant decrease in E/A, softening of the EoS, with increasing saturation density from 0.14 to 0.17 fm⁻³, however the calculation shows that the EoS is virtually independent of J.

FIGURE 7

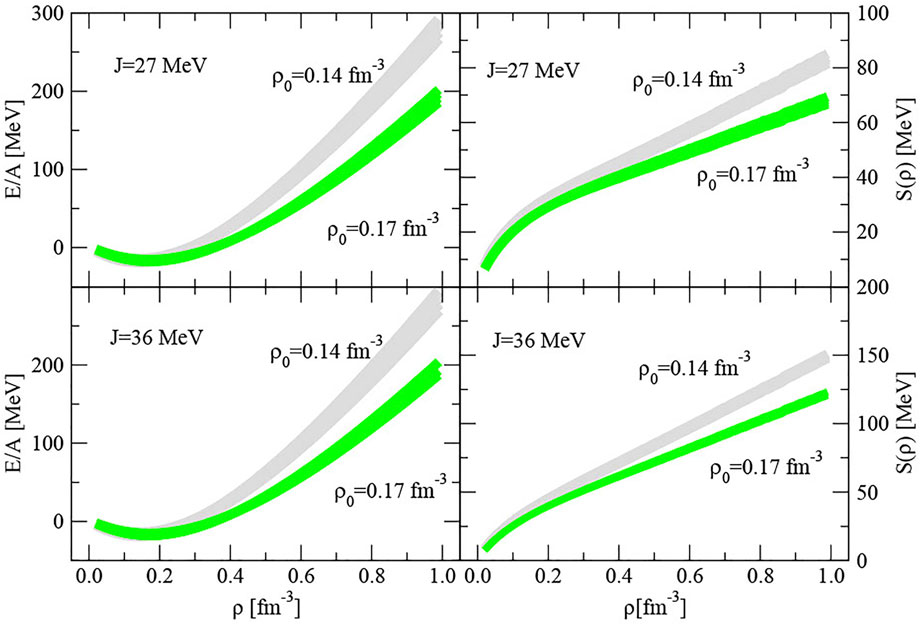
FIGURE 7. Energy per particle (E/A) (left panels) and the density dependence of the symmetry energy S(ρ) (right panels) vs baryon number density ρ. A combination of minimum and maximum values of J = 27 and 36 MeV and of ρ₀ = 0.14 and 0.17 fm⁻³ were selected to demonstrate the effects. The grey and green shadowed areas represent the uncertainties due to the spread of E₀/A in the range of -15 to -18 MeV. Note that the y-scale of the top-right panel is a half of that in the bottom-right panel.

There are three effects to observe in the right panels of Figure 7 showing the density dependence of the symmetry energy S(ρ). First, it increases with ρ in all cases. Second, the rate of the increase is strongly dependent on J. The change of J from 27 MeV (top-right panel) to 36 MeV (bottom-right panel) causes an increase in S(ρ) by almost a factor of 2 at about 6 times ρ₀ (note the change in y-scale in the two panels). Third, similarly to the EoS, the increase in S(ρ) with density is less for higher ρ₀. Should there be a well founded experimental constraint on these effects, this would provide a valuable constraint on the value of J.

4.5 Hyperonic Stars

Correct modelling of high-mass neutron stars has been of prime interest to the community since the first announcement of observation of a heavy pulsar J1614-2230 by (Demorest et al., 2010) with a gravitational mass 1.97±0.04 M_⊙. We take its current mass, obtained after 11 years of refined observation (Arzoumanian et al., 2018), 1.908±0.016 M_⊙, as a lower limit on a maximum gravitational mass neutron star to be compared with calculations. The current upper limit is the pulsar J0740 + 6620 with 2.08±0.07 M_⊙ (Fonseca et al., 2021). The radius of a NS with the know mass is a more difficult observable to obtain. We adopt the very recent result (Miller et al., 2021) for the equatorial circumferential radius of PSR J0740 + 6620 to be ${13.7}_{1.5}^{2.6}$ km with 68% credibility, and the Bayesian inference by the same group for the full radius range of the PSR J0740 + 6620 to be 12.35 ± 0.75 km.

We compare QMC-A predictions of the maximum mass of a NS containing the full hyperon octet in the core (the hyperonic star) with the above data in the left panels of Figure 8. The calculation has been made for 27 ≤ J ≤ 36 MeV, four values of ρ₀ between 0.14–0.17 fm⁻³ and -15 ≤ E₀/A ≤ -18 MeV. It can been seen that maximum mass excludes ρ₀ = 0.16 fm⁻³ and higher. The radii of the stars are shown in the right panels of Figure 8, corroborating the outcome obtained from the masses. We find that both maximum masses and radii of hyperonic stars show only a weak dependence on J. The observational constraints would have to be much tighter to make a conclusion about the role of the symmetry energy in mass and radii of hyperonic stars.

FIGURE 8

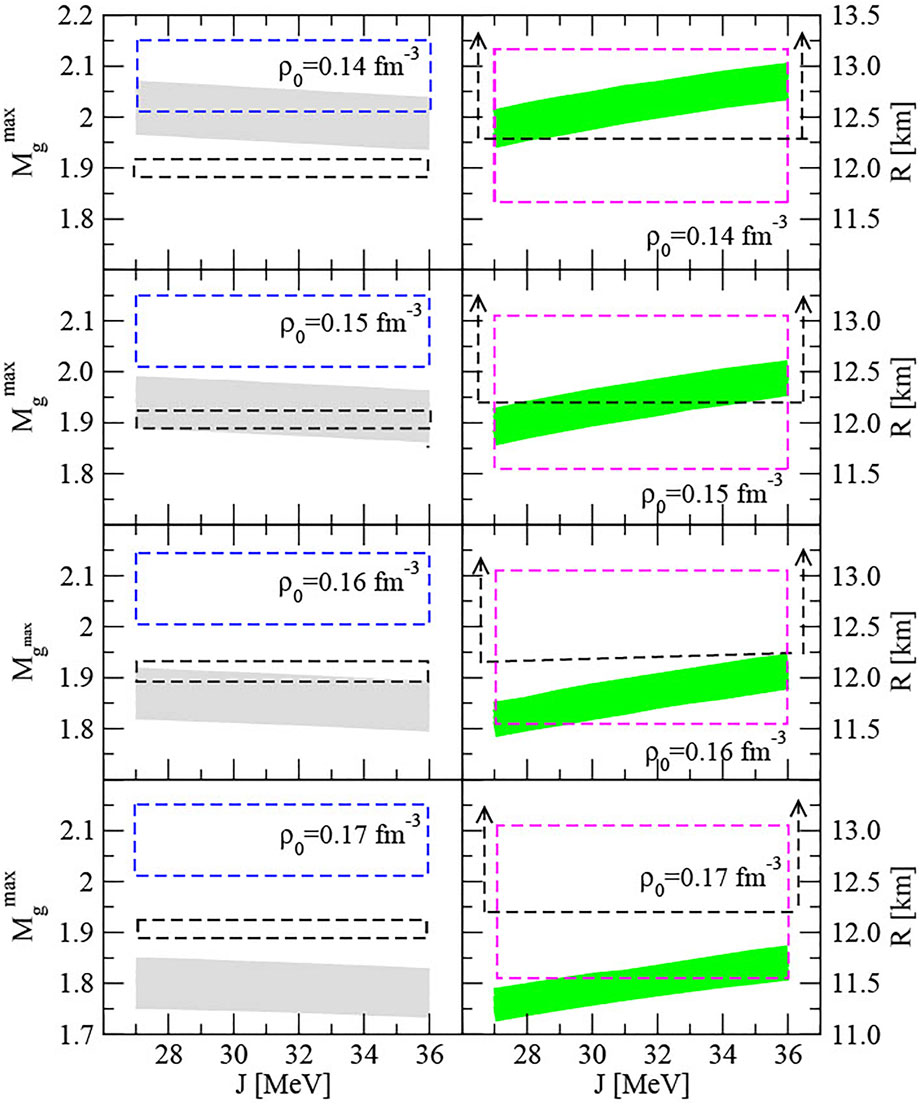
FIGURE 8. Shown are the maximum mass in units of M_⊙ (left panels) and radius (right panels) of a cold neutron star as a function of the symmetry energy coefficient J for four values of the saturation density 0.14–0.17 fm⁻³ and the saturation energy per particle -15 ≤ E₀/A ≤ -18 MeV. The spread of masses (radii) due to the uncertainty in the saturation energy is shown by the grey (green) shaded areas. The blue (black) dashed boxes in the left panels show the latest observational constraints on the gravitational mass of PSR J0740 + 6620 (Fonseca et al., 2021) [PSR J1614-2230 (Arzoumanian et al., 2018)]. The open black dashed boxes in the right panels depict the radius of the PSR J0740 + 6620 reported by (Miller et al., 2021) reaching upper limit of 16.3 km which is outside the dimensions of the figure. The magenta dashed box shows results of statistical analysis by (Miller et al., 2021). For more discussion see text.

Inspection of Figures 4, 7 and 8 suggests that smaller volume incompressibility K leads to larger NS radius. Recent metamodeling of the sensitivity of the nucleonic EoS and properties of cold NS to an extended set of empirical parameters of high density nuclear matter (Margueron et al., 2018) led to an opposite result, i.e., higher K implies higher radius. We do not have a definitive answer to this tension at present, except that there are significant differences between the QMC model of hyperonic matter and the models of nucleonic matter employed in (Margueron et al., 2018). Also, our analysis is limited only to quantities up to second order in the Taylor expansions outlined in Section 1 because we need only three NM quantities to be compared with the three variable parameters of the QMC model. Higher order terms in the expansions could be calculated but are not included in the fit. If they would make a difference, it would be an interesting feature to explore. With the advent of binary neutron star mergers, radii and tidal deformability of neutron stars with gravitational mass 1.4 M⊙ became a subject of interest. There observables are extracted from observations in a model dependent way. The most frequently used analysis is based on statistical methods. The approach used for determination of the radius of PSR J0740 + 6620 (Miller et al., 2021) also yielded the radius of a 1.4 M⊙ star to be 12.45 ± 0.65 km with the 68% credibility. We compare this result with the QMC-A predictions in the left panels of Figure 9 which seems to exclude ρ₀ = 0.14 fm⁻³ but allow higher values. However, we note that the constraints on radii of a 1.4 M⊙ star (which is not hyperonic but nucleon-only) are a developing field. We demonstrate the situation in Figure 10 illustrating one of the most recent attempts to construct Bayesian inference using a combination of GW data and electromagnetic signals from NICER observation to constrain the radii of 1.4 M_⊙ stars. The results are broadly compatible with those of (Miller et al., 2021) although exhibiting a wider spread towards lower radii.

FIGURE 9

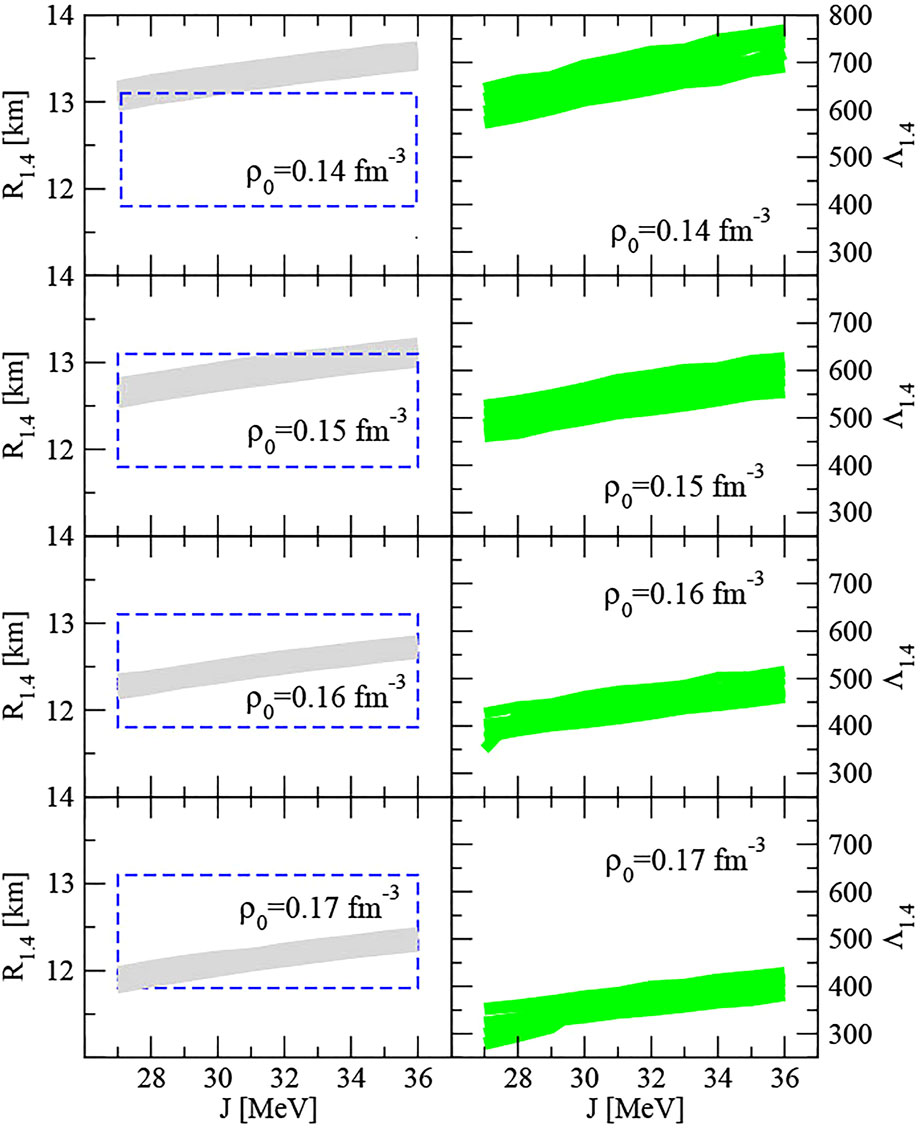
FIGURE 9. Left panels:Radius of a 1.4 M_⊙ star as a function of the symmetry energy coefficient J at four values of the saturation density 0.14–0.17 fm⁻³ and the saturation energy per particle -15 ≤ E₀/A ≤ -18 MeV. The spread due to the uncertainty in E₀/A is shown by grey shaded areas. The dashed blue box shows the constraint on the radius reported by (Miller et al., 2021). Right panels: Tidal deformation Λ_1.4, computed with the same NM parameters. The effect of the spread in E₀/A is shown in green.

FIGURE 10

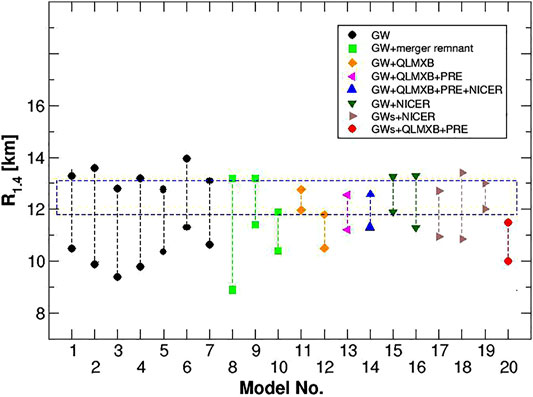
FIGURE 10. Radius of a NS with a fixed gravitational mass 1.4 M_⊙ as extracted from data on GW170817 (GW) alone, combined GW170817 and GW190425 (GWs) events, and GW data in combination with electromagnetic data from NICER, quiescent low mass x-ray binaries (QLMXB), and photo-spheric radius expansion x-ray burst source (PRE) observations. The figure has been adopted from Ref. (Stone, 2021) (under the Creative Commons Attribution License) where the references to individual models and other details can be found. The dashed blue box again shows the constraint on the radius reported by (Miller et al., 2021).

For completeness, we show the QMC-A model predictions for the tidal deformability Λ_1.4 as defined in (Yagi and Yunes, 2017) (right panels on Figure 9). This quantity shows high sensitivity to ρ₀ and should be a valuable tool to constrain the NM parameters. Unfortunately, there are still only model-dependent data on its value which cover the full range between about 200–800 and detailed conclusions cannot presently be drawn (see Supplementary Tables S4 and S5 for details).

4.6 Hyperonic Thresholds

Threshold densities for appearance of hyperons provide an important physics based constraint. It is unlikely that Ξ hyperons can be created by weak processes directly from nucleon decay (ΔS = 2) rather than by ΔS = 1 decays from Λ hyperons, already existing in the matter. That is, the Λ hyperon threshold density should not be higher than that of the Ξ⁻ and Ξ⁰. The threshold for appearance of Ξ⁻ hyperons is determined by the delicate balance between their chemical potential and the sum of chemical potentials of the neutron and electron. The onset of the Λ hyperons depends only on the balance between their chemical potential and that of the neutron. The threshold for Ξ⁰ is always above that for Λ as only the mass difference (and the interactions) play a role. Our findings are summarized in Table 1. The data eliminate ρ₀ = 0.14 fm⁻³ and place narrow limits on the other parameters for ρ₀ = 0.15 fm⁻³.

TABLE 1

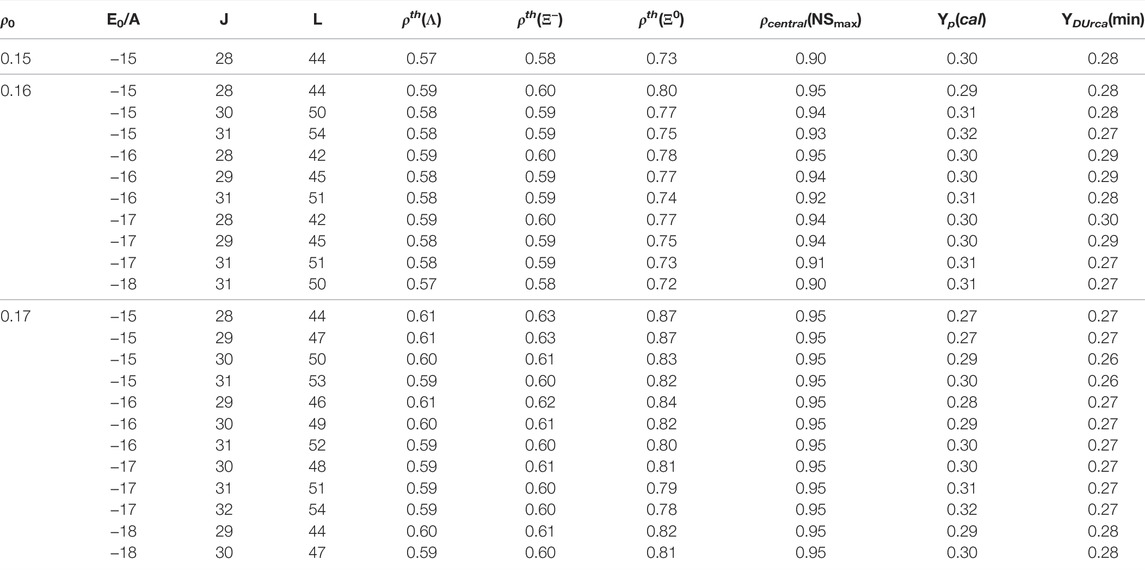
TABLE 1. Hyperon threshold densities in the maximum mass NS as a function of the NM parameters ρ₀, E₀/A and J (first three columns). The slope of the symmetry energy L at ρ₀ is given in the fourth column for completeness. The last three columns give the NS central density of the star and the calculated Y_p(cal) and minimal proton fractions Y_DUrca(min), as defined in Equation 22, for the same NM parameters. Only sets of the NM parameters which satisfy both, the constraint ρ^th(Λ) is less than ρ^th(Ξ⁻) and ρ^th(Ξ⁰) and the conditions for the hyperon threshold for DUrca to proceed, Y_DUrca(min) ≤ Y_p(cal), are satified are shown. E₀/A, J and L are in MeV and all densities are in units [fm⁻³].

4.7 Cooling Mechanism

In nucleon-only NS the most efficient cooling mechanism of is neutrino emission via electron DUrca (Lattimer et al., 1991)

$n\to p+e^{-}+\overline{{\nu }_e}andp+e^{-}\to n+{\nu }_e.(20)$

These processes can occur only if momentum is conserved which leads to the requirement that the proton fraction must above the minimum value (Klähn et al., 2006),

$Y_p^{\mathit{min}}=\frac{1}{1+{\left(1+x_e^{1/3}\right)}^3}.(21)$

where x_e = ρ_e/(ρ_e + ρ_μ) with ρ_e and ρ_μ are electron and muon densities. In the presence of hyperons, other channels are opened for neutrino emission (Prakash et al., 1992). As discussed in (Raduta et al., 2017; Providência et al., 2019; Raduta et al., 2019; Anzuini et al., 2021) the occurrence of hyperons will affect the neutron, proton and electron fractions. The momentum conservation requirement in these processes leads to a modified condition for the minimum proton fraction for nucleonic DUrca

$\frac{{\rho }_p}{{\rho }_p+{\rho }_n}=\frac{1}{1+{\left(1+x_e^{Y1/3}\right)}^3}(22)$

where $x_e^Y={\rho }_e/({\rho }_e+{\rho }_{\mu }+{\rho }_{{\mathrm{\Sigma }}^{-}}-{\rho }_{{\mathrm{\Sigma }}^{+}}+{\rho }_{{\mathrm{\Xi }}^{-}})$.

The density dependence of the proton fraction in the core of a maximum mass hyperonic star is calculated in the QMC-A model. Shown in Figure 11 is an example of a scenario yielded by a selected set of NM parameters ρ₀ = 0.16 fm⁻³, J = 31 MeV and -15 ≤ E₀/A ≤ -18 MeV. We observe a dramatic increase in the proton fraction (by almost a factor of three at ρ close to 1 fm⁻³) at densities above the hyperon threshold, as compared to the nucleon-only matter at lower densities. At the central density of the NS, the proton fraction (green) is well above the minimum fraction required for the onset of the nucleonic DUrca proces (grey), i.e., the star will be cooling. Summary of all the results, satisfying the conditions for the nucleonic DUrca process, is given the last three columns of in Table 1. They appear to put even more stringent constraints in the NM parameter sets than the hyperonic thresholds densities, not only eliminating ρ₀ = 0.14 fm⁻³ but also J = 27 MeV in all cases. Sets with J = 28 and 29 MeV are progressively excluded with increasing ρ₀.

FIGURE 11

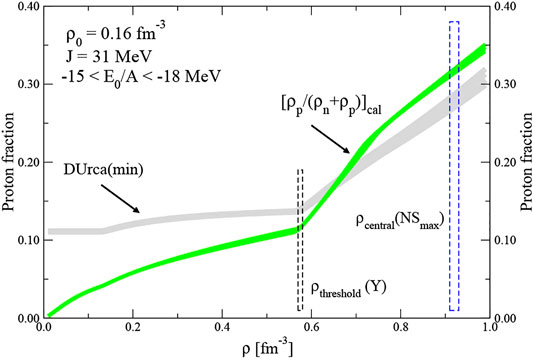
FIGURE 11. Density dependence of the minimal proton fraction (grey), required for the onset of the nucleonic DUrca cooling process (see Equation 22) and the computed proton fraction in the NS core (green) for a selected set of NM parameters. The shadowed areas show the spread due to uncertainty -15 ≤ E₀/A ≤ -18 MeV. The black dashed rectangle shows the threshold density for onset of the Λ and Ξ hyperons. The blue one indicates the central density of the NS. For details see Table 1 and the text.

5 Summary and Outlook

The QMC model has been developed over a number of years and achieved an impressive description of a wide range of experimental phenomena in the fields of low energy nuclear physics and stellar properties. In its simplest form the model has only three adjustable parameters, the nucleon-meson coupling constants in free space G_σ, G_ω and G_ρ which, once fixed, are held constant in calculation of all quantities accessible to the model. Similarly, theoretical decriptions of NM have evolved with basic dependence upon three properties ρ₀, E₀/A and J whose values are used as calibration points for many nuclear models.

This work was undertaken in a wide-ranging attempt to explore correlations between the elements of these trios and to examine whether narrower limits on their acceptable ranges could be established on the basis of current theory and experimental data.

Using these coupling constants the properties L, J, K and ρ of NM were calculated. In addition, properties of hyperonic matter and hyperonic stars, including hyperonic single-particle potentials and onset densities, the EoS, maximum gravitation mass of NS, central density and radius, as well as radius and tidal deformation of a 1.4 M⊙ star and cooling conditions were examined. These properties and their allowed values based on experimental analysis, proved essential in leading the conclusions below.

The main results lead to the following observations:

• The requirement that U_Σ be positive restricts ρ₀ to the range 0.14–0.16 fm⁻³ and J ≥ 31 MeV.

• The same restriction on ρ₀ is found in ${\mathrm{M}}_g^{\max }$.

• R_1.4 allows ρ₀ between 0.14–0.17 fm⁻³.

• The hyperonic threshold densities, satisfying the condition that Λ hyperon appears at lower baryon number density than that heavier hyperons, are predicted for ρ₀ between 0.15 and 0.17 fm⁻³ with J between 27 and 31 MeV.

• The conditions for the onset of DUrca process are satisfied for ρ₀ between 0.15 and 0.17 fm⁻³ with J between 28 and 32 MeV.

• The condition for K being less than 300 MeV restricts E₀/A to between -15 and -16 MeV.

In conclusion, only two sets, ρ₀ = 0.16 fm⁻³, E₀/A = -15 or -16 MeV and J = 31 MeV, were found to comply with all constraints. Considering the mesh size used, these results considerably narrow the ranges of the QMC-A coupling constants to 9.5 ≤ G_σ ≤ 10.0 fm², 5.8 ≤ G_ω ≤ 6.1 fm² and 3.35 ≤ G_ρ ≤ 3.45 fm². We find a weak dependence on J in most scenarios, in particular in NS. The variation in E₀/A has less that 15% influence on most calculated quantities. These results based on existing evidence and with no fine tuning of the QMC-A model are remarkably close to the general consensus on the NM parameters, supporting the model and broadening its predictive power. The results further emphasize correlations between the NM parameters and the dangers of choosing one without considering the consequences for the other two.

Future progress in this research would be much advanced by new, precise data on Σ and Ξ hypernuclei, yielding the hyperonic single-particle potential. Improved limits on the maximum gravitational mass and radius of cold NS and the radius of low mass stars is also called for. Further development of the QMC model, for example including the effect of overlapping quark bags at high density, is underway potentially leading to further narrowing down of the parameter space of NM.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was funded by Australian Research Council Discovery Project, DP180100497.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The softwere we used to model neutron stars was partially developed by John Miller. JRS and PAMG acknowledge hospitality during their stay at the University of Adelaide. Fruitful discussions with Nick Stone are gratefully acknowledged.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.903007/full#supplementary-material

References

Anzuini, F., Melatos, A., Dehman, C., Viganò, D., and Pons, J. A. (2021). Fast Cooling and Internal Heating in Hyperon Stars. Mon. Notices R. Astronomical Soc. 509, 2609. doi:10.1093/mnras/stab3126

CrossRef Full Text | Google Scholar

Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., Chamberlin, S., Chatterjee, S., Christy, B., et al. (2018). The NANOGrav 11-year Data Set: High-Precision Timing of 45 Millisecond Pulsars. ApJS 235, 37. doi:10.3847/1538-4365/aab5b0

CrossRef Full Text | Google Scholar

Audi, G., Wapstra, A. H., and Thibault, C. (2003). The Ame2003 Atomic Mass Evaluation. Nucl. Phys. A 729, 337–676. doi:10.1016/j.nuclphysa.2003.11.003

CrossRef Full Text | Google Scholar

Balberg, S., Lichtenstadt, I., and Cook, G. B. (1999). Roles of Hyperons in Neutron Stars. Astrophys. J. Suppl. S 121, 515–531. doi:10.1086/313196

CrossRef Full Text | Google Scholar

Bentz, W., and Thomas, A. W. (2001). The Stability of Nuclear Matter in the Nambu-Jona-Lasinio Model. Nucl. Phys. A 696, 138–172. doi:10.1016/s0375-9474(01)01119-8

CrossRef Full Text | Google Scholar

Bethe, H. A., and Bacher, R. F. (1936). Nuclear Physics A. Stationary States of Nuclei. Rev. Mod. Phys. 8, 82–229. doi:10.1103/revmodphys.8.82

CrossRef Full Text | Google Scholar

Bethe, H. A. (1971). Theory of Nuclear Matter. Annu. Rev. Nucl. Sci. 21, 93–244. doi:10.1146/annurev.ns.21.120171.000521

CrossRef Full Text | Google Scholar

Cloët, I. C., Bentz, W., and Thomas, A. W. (2006). EMC and Polarized EMC Effects in Nuclei. Phys. Lett. B 642, 210–217. doi:10.1016/j.physletb.2006.08.076

CrossRef Full Text | Google Scholar

Cloët, I. C., Bentz, W., and Thomas, A. W. (2016). Relativistic and Nuclear Medium Effects on the Coulomb Sum Rule. Phys. Rev. Lett. 116, 032701. doi:10.1103/PhysRevLett.116.032701

PubMed Abstract | CrossRef Full Text | Google Scholar

Cloët, I. C., Bentz, W., and Thomas, A. W. (2005). Spin-dependent Structure Functions in Nuclear Matter and the Polarized EMC Effect. Phys. Rev. Lett. 95, 052302. doi:10.1103/PhysRevLett.95.052302

PubMed Abstract | CrossRef Full Text | Google Scholar

Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., and Hessels, J. W. T. (2010). A Two-Solar-Mass Neutron Star Measured Using Shapiro Delay. Nature 467, 1081–1083. doi:10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

Drischler, C., Furnstahl, R. J., Melendez, J. A., and Phillips, D. R. (2020). How Well Do We Know the Neutron-Matter Equation of State at the Densities inside Neutron Stars? a Bayesian Approach with Correlated Uncertainties. Phys. Rev. Lett. 125. doi:10.1103/physrevlett.125.202702

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutra, M., Lourenço, O., Sá Martins, J. S., Delfino, A., Stone, J. R., and Stevenson, P. D. (2012). Skyrme Interaction and Nuclear Matter Constraints. Phys. Rev. C 85. doi:10.1103/physrevc.85.035201

CrossRef Full Text | Google Scholar

Fonseca, E., Cromartie, H. T., Pennucci, T. T., Ray, P. S., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. ApJL 915, L12. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

Fortin, M., Avancini, S. S., Providência, C., and Vidaña, I. (2017). Hypernuclei and Massive Neutron Stars. Phys. Rev. C 95. doi:10.1103/physrevc.95.065803

CrossRef Full Text | Google Scholar

Fortin, M., Providência, C., Raduta, A. R., Gulminelli, F., Zdunik, J. L., Haensel, P., et al. (2016). Neutron Star Radii and Crusts: Uncertainties and Unified Equations of State. Phys. Rev. C 94. doi:10.1103/physrevc.94.035804

CrossRef Full Text | Google Scholar

Fortin, M., Raduta, A. R., Avancini, S., and Providência, C. (2020). Relativistic Hypernuclear Compact Stars with Calibrated Equations of State. Phys. Rev. D. 101, 034017. doi:10.1103/physrevd.101.034017

CrossRef Full Text | Google Scholar

Gal, A., Hungerford, E. V., and Millener, D. J. (2016). Strangeness in Nuclear Physics. Rev. Mod. Phys. 88. doi:10.1103/revmodphys.88.035004

CrossRef Full Text | Google Scholar

Gamow, G. (1930). Mass Defect Curve and Nuclear Constitution. Proc. R. Soc. Lond. A 126, 632–644. doi:10.1098/rspa.1930.0032

CrossRef Full Text | Google Scholar

Glendenning, N. K. (2012). Compact Stars: Nuclear Physics, Particle Physics and General Relativity. Berlin, Germany: Springer Science & Business Media.

Google Scholar

Glendenning, N. K. (1985). Neutron Stars Are Giant Hypernuclei? ApJ 293, 470–493. doi:10.1086/163253

CrossRef Full Text | Google Scholar

Guichon, P. A. M. (1988). A Possible Quark Mechanism for the Saturation of Nuclear Matter. Phys. Lett. B 200, 235–240. doi:10.1016/0370-2693(88)90762-9

CrossRef Full Text | Google Scholar

Guichon, P. A. M., Saito, K., Rodionov, E., and Thomas, A. W. (1996). The Role of Nucleon Structure in Finite Nuclei. Nucl. Phys. A 601, 349–379. doi:10.1016/0375-9474(96)00033-4

CrossRef Full Text | Google Scholar

Guichon, P. A. M., Stone, J. R., and Thomas, A. W. (2018). Quark-Meson-Coupling (QMC) Model for Finite Nuclei, Nuclear Matter and beyond. Prog. Part. Nucl. Phys. 100, 262–297. doi:10.1016/j.ppnp.2018.01.008

CrossRef Full Text | Google Scholar

Guichon, P. A. M., and Thomas, A. W. (2004). Quark Structure and Nuclear Effective Forces. Phys. Rev. Lett. 93, 132502. doi:10.1103/PhysRevLett.93.132502

PubMed Abstract | CrossRef Full Text | Google Scholar

Guichon, P. A. M., Thomas, A. W., and Tsushima, K. (2008). Binding of Hypernuclei in the Latest Quark-Meson Coupling Model. Nucl. Phys. A 814, 66–73. doi:10.1016/j.nuclphysa.2008.10.001

CrossRef Full Text | Google Scholar

Harada, T., and Hirabayashi, Y. (2015). P-Wave Resonant State of the ⁴He Σ-Hypernucleus in the ⁴He (K^-,π^-) Reaction. Phys. Lett. B 740, 312–316. doi:10.1016/j.physletb.2014.11.057

CrossRef Full Text | Google Scholar

Harada, T., and Hirabayashi, Y. (2006). Production Spectrum in the Inclusive () Reaction on 209Bi and the Σ-nucleus Potential. Nucl. Phys. A 767, 206–217. doi:10.1016/j.nuclphysa.2005.12.018

CrossRef Full Text | Google Scholar

Horowitz, C. J., Brown, E. F., Kim, Y., Lynch, W. G., Michaels, R., Ono, A., et al. (2014). A Way Forward in the Study of the Symmetry Energy: Experiment, Theory, and Observation. J. Phys. G. Nucl. Part. Phys. 41, 093001. doi:10.1088/0954-3899/41/9/093001

CrossRef Full Text | Google Scholar

Kchaustov, P. (2000). Evidence of Hypernuclear Production. Phys. Rev. C 61, 054603. doi:10.1103/PhysRevC.61.054603

CrossRef Full Text | Google Scholar

Kirson, M. W. (2008). Mutual Influence of Terms in a Semi-empirical Mass Formula. Nucl. Phys. A 798, 29–60. doi:10.1016/j.nuclphysa.2007.10.011

CrossRef Full Text | Google Scholar

Klähn, T., Blaschke, D., Typel, S., van Dalen, E. N. E., Faessler, A., Fuchs, C., et al. (2006). Constraints on the High-Density Nuclear Equation of State from the Phenomenology of Compact Stars and Heavy-Ion Collisions. Phys. Rev. C 74. doi:10.1103/physrevc.74.035802

CrossRef Full Text | Google Scholar

Lattimer, J. M., Pethick, C. J., Prakash, M., and Haensel, P. (1991). Direct URCA Process in Neutron Stars. Phys. Rev. Lett. 66, 2701–2704. doi:10.1103/physrevlett.66.2701

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B.-A., Cai, B.-J., Xie, W.-J., and Zhang, N.-B. (2021). Progress in Constraining Nuclear Symmetry Energy Using Neutron Star Observables since GW170817. Universe 7, 182. doi:10.3390/universe7060182

CrossRef Full Text | Google Scholar

Li, B.-A., Krastev, P. G., Wen, D.-H., and Zhang, N.-B. (2019). Towards Understanding Astrophysical Effects of Nuclear Symmetry Energy. Eur. Phys. J. A 55. doi:10.1140/epja/i2019-12780-8

CrossRef Full Text | Google Scholar

Li, B.-A., Ramos, À., Verde, G., and Vidaña, I. (2014). Topical Issue on Nuclear Symmetry Energy. Eur. Phys. J. A 50. doi:10.1140/epja/i2014-14009-x

CrossRef Full Text | Google Scholar

Li, J. J., and Sedrakian, A. (2019). Constraining Compact Star Properties with Nuclear Saturation Parameters. Phys. Rev. C 100. doi:10.1103/physrevc.100.015809

CrossRef Full Text | Google Scholar

Lourenço, O., Lenzi, C. H., Dutra, M., Frederico, T., Bhuyan, M., Negreiros, R., et al. (2021). Neutron Star Cooling and GW170817 Constraint within Quark-Meson Coupling Models *. Chin. Phys. C 45, 025101. doi:10.1088/1674-1137/abca1c

CrossRef Full Text | Google Scholar

Margueron, J., Hoffmann Casali, R., and Gulminelli, F. (2018). Equation of State for Dense Nucleonic Matter from Metamodeling. II. Predictions for Neutron Star Properties. Phys. Rev. C 97. doi:10.1103/physrevc.97.025806

CrossRef Full Text | Google Scholar

Martinez, K. L., Thomas, A. W., Guichon, P. A. M., and Stone, J. R. (2020). Tensor and Pairing Interactions within the Quark-Meson Coupling Energy-Density Functional. Phys. Rev. C 102, 034304. doi:10.1103/physrevc.102.034304

CrossRef Full Text | Google Scholar

Martinez, K. L., Thomas, A. W., Stone, J. R., and Guichon, P. A. M. (2019). Parameter Optimization for the Latest Quark-Meson Coupling Energy-Density Functional. Phys. Rev. C 100, 024333. doi:10.1103/physrevc.100.024333

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. ApJL 918, L28. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

Möller, P., Myers, W. D., Sagawa, H., and Yoshida, S. (2012). New Finite-Range Droplet Mass Model and Equation-Of-State Parameters. Phys. Rev. Lett. 108. doi:10.1103/physrevlett.108.052501

CrossRef Full Text | Google Scholar

Moller, P., Nix, J. R., Myers, W. D., and Swiatecki, W. J. (1995). Nuclear Ground-State Masses and Deformations. Atomic Data Nucl. Data Tables 59, 185–381. doi:10.1006/adnd.1995.1002

CrossRef Full Text | Google Scholar

Möller, P., Sierk, A. J., Ichikawa, T., and Sagawa, H. (2016). Nuclear Ground-State Masses and Deformations: FRDM(2012). Atomic Data Nucl. Data Tables 109-110, 1–204. doi:10.1016/j.adt.2015.10.002

CrossRef Full Text | Google Scholar

Motta, T. F., Guichon, P. A. M., and Thomas, A. W. (2021). On the Sound Speed in Hyperonic Stars. Nucl. Phys. A 1009, 122157. doi:10.1016/j.nuclphysa.2021.122157

CrossRef Full Text | Google Scholar

Motta, T. F., Kalaitzis, A. M., Antić, S., Guichon, P. A. M., Stone, J. R., and Thomas, A. W. (2019). Isovector Effects in Neutron Stars, Radii, and the GW170817 Constraint. ApJ 878, 159. doi:10.3847/1538-4357/ab218e

CrossRef Full Text | Google Scholar

Motta, T. F., Thomas, A. W., and Guichon, P. A. M. (2020). Do Delta Baryons Play a Role in Neutron Stars? Phys. Lett. B 802, 135266. doi:10.1016/j.physletb.2020.135266

CrossRef Full Text | Google Scholar

Motta, T. F., and Thomas, A. W. (2022). The Role of Baryon Structure in Neutron Stars. Mod. Phys. Lett. A 37, 2230001. doi:10.1142/S0217732322300014

CrossRef Full Text | Google Scholar

Myers, W. D., and Swiatecki, W. J. (1969). Average Nuclear Properties. Ann. Phys. 55, 395–505. doi:10.1016/0003-4916(69)90202-4

CrossRef Full Text | Google Scholar

Myers, W. D., and Swiatecki, W. J. (1966). Nuclear Masses and Deformations. Nucl. Phys. 81, 1–60. doi:10.1016/0029-5582(66)90639-0

CrossRef Full Text | Google Scholar

Myers, W. D., and Swiatecki, W. J. (1974). The Nuclear Droplet Model for Arbitrary Shapes. Ann. Phys. 84, 186–210. doi:10.1016/0003-4916(74)90299-1

CrossRef Full Text | Google Scholar

Nakazawa, K., Endo, Y., Fukunaga, S., Hoshino, K., Hwang, S. H., Imai, K., et al. (2015). The First Evidence of a Deeply Bound State of Xi--14N System. Prog. Theor. Exp. Phys. 2015, 33D02. doi:10.1093/ptep/ptv008

CrossRef Full Text | Google Scholar

Newton, W. G., Cantu, S., Wang, S., Stinson, A., Kaltenborn, M. A., and Stone, J. R. (2022). Glassy Quantum Nuclear Pasta in Neutron Star Crusts. Phys. Rev. C 105. doi:10.1103/physrevc.105.025806

CrossRef Full Text | Google Scholar

Pais, H., and Typel, S. (2017). Comparison of Equation of State Models with Different Cluster Dissolution Mechanisms. Nucl. Part. Correl. Clust. Phys. (World Sciemtific) 2017, 95–132. doi:10.1142/9789813209350_0004

CrossRef Full Text | Google Scholar

Prakash, M., Prakash, M., Lattimer, J. M., and Pethick, C. J. (1992). Rapid Cooling of Neutron Stars by Hyperons and Delta Isobars. ApJ 390, L77. doi:10.1086/186376

CrossRef Full Text | Google Scholar

Providência, C., Fortin, M., Pais, H., and Rabhi, A. (2019). Hyperonic Stars and the Nuclear Symmetry Energy. Front. Astron. Space Sci. 6. doi:10.3389/fspas.2019.00013

CrossRef Full Text | Google Scholar

Raduta, A. R., Li, J. J., Sedrakian, A., and Weber, F. (2019). Cooling of Hypernuclear Compact Stars: Hartree-Fock Models and High-Density Pairing. Mon. Notices R. Astronomical Soc. 487, 2639–2652. doi:10.1093/mnras/stz1459

CrossRef Full Text | Google Scholar

Raduta, A. R., Sedrakian, A., and Weber, F. (2017). Cooling of Hypernuclear Compact Stars. Mon. Notices R. Astronomical Soc. 475, 4347–4356. doi:10.1093/mnras/stx3318

CrossRef Full Text | Google Scholar

Reed, B. T., Fattoyev, F. J., Horowitz, C. J., and Piekarewicz, J. (2021). Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 126. doi:10.1103/physrevlett.126.172503

CrossRef Full Text | Google Scholar

Rikovska Stone, J., Guichon, P. A. M., Matevosyan, H. H., and Thomas, A. W. (2007). Cold Uniform Matter and Neutron Stars in the Quark-Meson-Coupling Model. Nucl. Phys. A 792, 341–369. doi:10.1016/j.nuclphysa.2007.05.011

CrossRef Full Text | Google Scholar

Rikovska Stone, J., Miller, J. C., Koncewicz, R., Stevenson, P. D., and Strayer, M. R. (2003). Nuclear Matter and Neutron-Star Properties Calculated with the Skyrme Interaction. Phys. Rev. C 68, 034324. doi:10.1103/physrevc.68.034324

CrossRef Full Text | Google Scholar

Saha, P. K. (2004). Study of the Σ-nucleus Potential by the (π⁻,K⁺) Reaction on Medium-To-Heavy Nuclear Targets. Phys. Rev. C 70, 044613.

Google Scholar

Saito, K., and Thomas, A. W. (1994). A Quark-Meson Coupling Model for Nuclear and Neutron Matter. Phys. Lett. B 327, 9–16. doi:10.1016/0370-2693(94)91520-2

CrossRef Full Text | Google Scholar

Saito, K., Tsushima, K., and Thomas, A. W. (2007). Nucleon and Hadron Structure Changes in the Nuclear Medium and the Impact on Observables. Prog. Part. Nucl. Phys. 58, 1–167. doi:10.1016/j.ppnp.2005.07.003

CrossRef Full Text | Google Scholar

Stone, J. R., Dexheimer, V., Guichon, P. A. M., Thomas, A. W., and Typel, S. (2021). Equation of State of Hot Dense Hyperonic Matter in the Quark-Meson-Coupling (QMC-A) Model. Mon. Notices R. Astronomical Soc. 502, 3476–3490. doi:10.1093/mnras/staa4006

CrossRef Full Text | Google Scholar

Stone, J. R., Morita, K., Guichon, P. A. M., and Thomas, A. W. (2019). Physics of Even-Even Superheavy Nuclei with 96 < Z < 110 in the Quark-Meson-Coupling Model. Phys. Rev. C 100. doi:10.1103/physrevc.100.044302

CrossRef Full Text | Google Scholar

Stone, J. R. (2016). Neutron Stars Interiors: Theory and Reality. Eur. Phys. J. A 52, 66. doi:10.1140/epja/i2016-16066-5

CrossRef Full Text | Google Scholar

Stone, J. R. (2021). Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State. Universe 7, 257. doi:10.3390/universe7080257

CrossRef Full Text | Google Scholar

Stone, J. R., Stone, N. J., and Moszkowski, S. A. (2014). Incompressibility in Finite Nuclei and Nuclear Matter. Phys. Rev. C 89. doi:10.1103/physrevc.89.044316

CrossRef Full Text | Google Scholar

Thomas, A. W., Michels, A., Schreiber, A. W., and Guichon, P. A. M. (1989). A New Approach to Nuclear Structure Functions. Phys. Lett. B 233, 43–47. doi:10.1016/0370-2693(89)90612-6

CrossRef Full Text | Google Scholar

Thomas, A. W. (2021). Role of Quarks in Nuclear Structure. doi:10.1093/acrefore/9780190871994.013.1Role of Quarks in Nuclear Structure

CrossRef Full Text | Google Scholar

Tsang, M. B., Stone, J. R., Camera, F., Danielewicz, P., Gandolfi, S., Hebeler, K., et al. (2012). Constraints on the Symmetry Energy and Neutron Skins from Experiments and Theory. Phys. Rev. C 86. doi:10.1103/physrevc.86.015803

CrossRef Full Text | Google Scholar

Tsushima, K., Guichon, P. A. M., Shyam, R., and Thomas, A. W. (2010). Binding of Hypernuclei, and Photoproduction of Λ-hypernuclei in the Latest Quark-Meson Coupling Model. Int. J. Mod. Phys. E 19, 2546–2551. doi:10.1142/S021830131001706X

CrossRef Full Text | Google Scholar

Tsushima, K., Saito, K., Haidenbauer, J., and Thomas, A. W. (1998). The Quark-Meson Coupling Model for Λ, Σ and Ξ Hypernuclei. Nucl. Phys. A 630, 691–718. doi:10.1016/S0375-9474(98)00806-9

CrossRef Full Text | Google Scholar

Wang, X. G., Bentz, W., Cloët, I. C., and Thomas, A. W. (2022). Gluon EMC Effects in Nuclear Matter. J. Phys. G. Nucl. Part. Phys. 49, 03LT01. doi:10.1088/1361-6471/ac4c90

CrossRef Full Text | Google Scholar

Weizsäcker, C. F. v. (1935). Zur theorie der kernmassen. Z. Phys. 96, 431–458. doi:10.1007/bf01337700

CrossRef Full Text | Google Scholar

Yagi, K., and Yunes, N. (2017). Approximate Universal Relations for Neutron Stars and Quark Stars. Phys. Rep. 681, 1–72. doi:10.1016/j.physrep.2017.03.002

CrossRef Full Text | Google Scholar

Yoshida, J., Agari, K., Ahn, J. K., Akaishi, T., Akazawa, Y., Ashikaga, S., et al. (2019). Status of the j-PARC e07, systematic study of double strangeness nuclei with the hybrid emulsion method. JPS Conf. Proc. 26, 023006. doi:10.7566/jpscp.26.023006

CrossRef Full Text | Google Scholar

Yoshimoto, M. (2021). First Observation of a Nuclear S − State of a Hypernucleus, ${\mathrm{Hypernucleus}\ }^{15}_{\upXi}$C. Prog. Theor. Exp. Phys. doi:10.1093/ptep/ptab073

CrossRef Full Text | Google Scholar