From Coronal Holes to Pulsars and Back Again: Learning the Importance of Data

Although wanting to become an astronomer from an early age, I ended up in solar physics purely by chance, after first working in high-energy astrophysics. I’ve never regretted switching from the pulsar to the solar magnetosphere, because solar physics has a great advantage over other areas of astrophysics—in the enormous amount of high-quality data available, much of it underutilized. I’ve often wondered why theoreticians and modelers don’t spent more time looking at these data (perhaps they feel that it is cheating, like taking a peek at the answers to a difficult homework assignment?). Conversely, I wonder why observers and data analysts aren’t more skeptical of the theoretical models—especially the fashionable ones.

1 Introduction

I decided to become an astronomer after I read Fred Hoyle’s “Frontiers of Astronomy” at the age of fourteen. Written in 1955, just before the start of the space age, the book covers everything from the Earth’s rotation to the steady-state theory of the Universe, even touching on coronal heating along the way. I’ve always regarded Hoyle’s writing as a model of clarity, in which he focused on the essence of each problem and discussed it in simple physical terms. This seems to be a rare ability, judging from most science writing, which often relies on jargon to disguise a lack of real understanding, or is devoid of meaningful content, like a typical NASA news release (“SDO Peers Into Huge Hole on Sun!”).

Deciding which area of astronomy/astrophysics to specialize in was much more difficult than deciding to become an astronomer. I ended up in solar physics as a result of a long series of fortuitous events:

1) My first experience with solar physics was as an astronomy major at Harvard College, when Gene Avrett, the head of the tutorial section, suggested that I work with him and George Withbroe. As a result, as part of my senior thesis, I helped analyze OSO-4 spectroheliograms showing an area of greatly reduced EUV emission (which we referred to as a “hole”) near the Sun’s south pole. Unfortunately, in our model for the polar transition region and corona in November 1967 (Withbroe and Wang 1972), we completely missed the big thing: that the reason for the low densities and temperatures was that solar wind was escaping from our “hole.” Just a year later, Skylab showed conclusively that such “holes” were sources of high-speed solar wind. I think that George afterwards greatly regretted not making the connection, which might seem obvious in hindsight.

I must admit that I did not find the solar physics done at Harvard at that time, with its emphasis on spectroscopy and plane-parallel models of the solar atmosphere, terribly exciting. However, it was probably because of my undergraduate connections that I was eventually able to return to solar physics.

2) Perhaps the most important thing I learned as an astronomy major is that doing astronomy requires a solid knowledge of physics. After resolving to switch from solar physics to “real” astrophysics, I enrolled in MIT’s physics department, where I was (fortunately) required to take the same courses as the other physics graduate students, in order to pass the general exam by the end of the second year. For my research advisor, I chose the plasma physicist Bruno Coppi, who seemed to believe that all magnetized objects in the Universe were tokamaks. With almost no supervision, I wrote a very skimpy, 60-page thesis on pulsar magnetospheres, which I paid an MIT secretary to type. As she handed me the typewritten manuscript, she said: “If I had known it was so easy to write a Ph.D. thesis, I would have done one myself!” Although this lack of supervision and less-than-stellar thesis work meant that I was off to a very slow start careerwise, it at least forced me to learn to work and think independently. Many of the postdocs I encounter today seem to just parrot the ideas of their thesis supervisors rather than trying to think for themselves. This might be for funding reasons, but I sometimes wonder if it is because they’re not really that interested in what they’re doing.

3) After MIT, I spent almost a decade in Europe, doing mainly theoretical work on pulsar magnetospheres and accretion onto neutron stars. The only data that I was able to use were timing measurements for a handful of binary X-ray pulsars, and I eventually felt that I was running out of ideas. In 1985, while at Bonn University, I applied for another research grant from the Deutsche Forschungsgemeinschaft. The evaluation began with the words: “Herr Wang is now approaching his mid-thirties, and it is time for him to look for a long-term position. Therefore, we will be extending his funding for only two more years.” I shall be forever grateful to the reviewer(s) for this warning.

4) For the third time in my career, I was able to survive only by networking. As it happened, two senior scientists from NRL, Maurice Shapiro and Ken Johnston, were visiting the adjoining Max Planck Institute for Radio Astronomy as Humboldt Fellows. Maury (a pioneer cosmic ray physicist) attended our seminars and was friendly to the younger scientists, so I asked him about the possibility of a job at NRL. Maury told me to talk to Ken, who offered me a job in radio astronomy as we had lunch at the pizza restaurant next door.

5) I then made the luckiest “mistake” of my career: I waited almost half a year before showing up at Ken Johnston’s office at NRL. When I reminded him of who I was, he said: “I thought you weren’t coming, and I’ve run out of money. But don’t worry, I’ll send you to Anand.” Anand was the owner of a Beltway Bandit company called Applied Research Corporation. Just by chance, in the spring of 1986, Neil Sheeley obtained funding from NRL’s Research Advisory Committee to hire two scientists to work on magnetic flux transport models. As Neil later told me, he chose me not because of my work in high-energy astrophysics, but because he was familar with my undergraduate paper with George Withbroe (which was actually written by George). His other hire was Ana Nash, who had just obtained her doctorate in astronomy from the University of Wisconsin, doing her thesis on molecular clouds.

Switching from pulsar magnetospheres and accretion disks to the solar magnetic field was easy; the big difference was that an enormous amount of data was now available to test models and suggest new ideas. I was also extremely fortunate to have a boss who could explain solar concepts in a clear and simple way (like Fred Hoyle) and who was also an excellent mathematician. Neil’s ability to explain things well may have been due to the influence of Richard Feynman, his freshman physics honors section instructor at Caltech, who would urge his students to try to think through questions themselves rather than just reading the textbook. Another great piece of luck was that I “returned” to solar physics in time for the launches of Ulysses and SOHO.

In the remainder of this Perspective article, I describe what I would consider to be my most significant contributions to research in solar physics. These contributions all relied heavily on the type of detailed observational data that are not available in most other areas of astrophysics.

2 The Quasi-Rigid Rotation of Coronal Holes

One of the exciting discoveries made by Skylab was that coronal holes often rotate much more rigidly than the underlying photosphere. This mysterious property was even a topic of discussion in my plasma physics courses in the 1970s. During my first few years at NRL, the rotation of solar magnetic fields was the main focus of our small group.

We first tried to understand the quasi-rigid rotation shown by large-scale photospheric field patterns. According to Stenflo (1989), these unipolar patterns consisted of magnetic flux that emerged in situ from a rigidly rotating source at the bottom of the convection zone. Our flux transport simulations showed instead that they consisted of flux migrating poleward and equatorward from decaying active regions (Sheeley, Nash, and Wang 1987; Wang and Sheeley 1994). To understand why the patterns maintain their shape, consider a long line of ducks crossing a stream, with the current faster on one side than the other. If the ducks just drifted with the current, the line would become increasingly sheared with time. However, if each duck (flux element) continually swims toward the far bank (Sun’s pole) and the line is continually replenished by new ducks entering from the near bank (active region latitudes), a stationary pattern will be set up.

Although this mechanism might at first seem applicable to coronal holes, the physical basis for their quasi-rigid rotation turns out to be different from that of the large-scale unipolar patterns. Coronal holes consist of open magnetic flux, whose sources are the lowest-order multipoles of the photospheric field (the high-order multipoles fall off rapidly with height and are associated with smaller closed loops). By its very nature, a structure consisting of low-order multipoles, such as the outer coronal field or its footpoint areas (coronal holes), must rotate more rigidly than one consisting of high-order multipoles. To offset the effect of rotational shearing (which converts lower-order multipoles into higher-order ones), continual reconnection is required. When I presented these ideas during a discussion session at the 1992 G. S. Vaiana Memorial Symposium, I heard skeptical noises from the luminaries sitting in the front row, whose consensus opinion was that the rotation of coronal holes reflected that of its deep-seated sources.

The mixed reaction at the Vaiana Symposium motivated us to revisit the topic of coronal hole rotation and to look more closely at the Skylab observations. Comparing an image of the boot-shaped “Coronal Hole 1” with a Kitt Peak magnetogram taken one rotation earlier, I noticed that CH1 was connected to a decaying active region complex just below the equator. I then used the potential-field source-surface (PFSS) model to simulate the evolution of CH1, representing the photospheric field by an axisymmetric dipole and an east–west oriented bipole centered at the equator (In the PFSS model, the coronal field is assumed to be current-free and is constrained to be radial at a heliocentric distance of 2.5 R_⊙; all field lines that cross this “source surface” are considered to be “open.”) To further simplify things, the only transport process that I included was differential rotation. As shown in Figure 1, the equatorial bipole distorts the open field areas at the poles, creating a pair of equatorward extensions that connect to the bipole. The extensions retain their vertical orientation from rotation to rotation, despite the underlying differential rotation. This result is easily understood: in a frame corotating with the equatorial bipole, the photospheric flux distribution remains almost unchanged from rotation to rotation; therefore the coronal field and distribution of open flux must also remain unchanged, at least in the current-free approximation (Wang and Sheeley 1993).

FIGURE 1

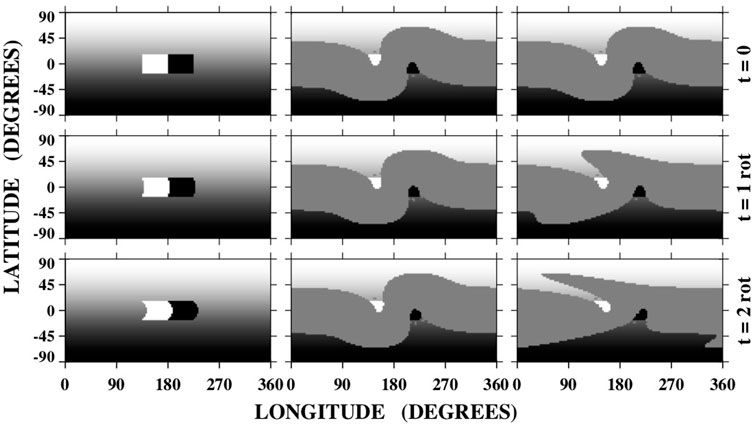
FIGURE 1. The quasi-rigid rotation of a coronal hole, as illustrated by a configuration consisting of a bipole at the equator and an axisymmetric dipole field. The underlying photosphere rotates at the Snodgrass rate ω(L)=13.38−2.30 sin²L −1.62 sin⁴L deg day⁻¹, where L is latitude. Left column: Photospheric flux distribution after the lapse of 0, 1, and 2 rotations. Middle column: Corresponding open field regions, determined by applying a PFSS extrapolation to the photospheric field. Right column: Open field regions as they would appear if they rotated at the photospheric plasma rate. In a frame corotating with the equatorial bipole, the photospheric flux distribution and thus the distribution of open flux remain practically unchanged with time.

The reaction to our new explanation from Herb Gursky, then the superintendent of NRL’s Space Science Division, was that we had made an interesting problem “boring.” Spiro Antiochos dismissed the explanation with a wave of the hand, saying that it was “so obvious.” The most insightful comment came from Eugene Parker, who said to Neil at a Chapman Conference dinner: “So you’re saying it’s just a property of potential fields.”

A prediction of the model is that reconnection between open and closed field lines (“interchange reconnection”) must be occurring continually at the boundaries of coronal holes. The reconnection site is high in the corona at the streamer cusps (and thus relatively difficult to observe), not near the photosphere as sometimes assumed. A possible observational signature of the reconnection is the heliospheric plasma sheet itself, which (as seen in white-light coronagraph images) consists of narrow raylike structures; these rays may represent newly reconnected, open field lines along which streamer material escapes into the heliosphere (Wang et al., 1998).

Judging from the fact that most studies of coronal and coronal hole rotation continue to invoke subsurface phenomena, it would appear that our explanation is still not widely accepted, perhaps because it is so “boring.”

3 The Flux Transport Dynamo

Shortly before we started our flux transport simulations, helioseismologists had detected the presence of a ∼10–20 m s⁻¹ poleward flow at the solar surface, and also shown that the radial gradient in the subsurface differential rotation was relatively small and opposite in sign to that assumed in earlier dynamo models, such as that of Leighton (1969). This led us to modify Leighton’s model by adding meridional circulation and including only the latitudinal gradient in the differential rotation. We also required that the toroidal flux emerging at the surface be eventually resubmerged and annihilated by merging with its opposite-hemisphere counterpart at the equator, rather than being expelled from the Sun as assumed by Babcock (1961) and Leighton (1969). In our two-level model, the poleward-migrating flux at the photosphere was linked to the equatorward-migrating subsurface flux through flux conservation, with the implicit assumption that continual reconnection acts to reduce any magnetic stresses that build up (as in the corona). Our main result was that a ∼1 m s⁻¹ equatorward flow at the bottom of the convection zone would give rise to an equatorward progression of flux emergence and a reversal of the polar fields with an 11 year period (Wang, Sheeley, and Nash 1991). The ∼10 m s⁻¹ poleward surface flow resulted in highly concentrated “topknot” polar fields, consistent with magnetograph observations.

The only reaction to our model came from Arnab Choudhuri, who wrote: “We do not know what to make of this paper. The authors seem to be unaware of any of the dynamo research that has been done in the last 2 decades.” Four years later, Choudhuri et al. (1995) published a paper entitled “The solar dynamo with meridional circulation” without mentioning our earlier work. Their model differed in that it was based on classical mean-field dynamo theory rather than the Babcock–Leighton picture, which takes proper account of magnetograph observations showing that the polar fields are formed from the surface transport of active region fields. It was only much later that Charbonneau (2010) called attention to our work as the “first post-helioseismic dynamo model based on the Babcock–Leighton mechanism.”

4 “Unipolar” Plages, Looplike Fine Structure, and Coronal Heating

The coronal heating problem has been “solved” many times, with the current paradigm being the nanoflare model of Parker (1988), according to which footpoint motions generate tangential discontinuities in the corona (see, e.g., Dahlburg et al., 2016; Pontin and Hornig 2020). But if “nanoflares” and energy dissipation are occurring well above the loop footpoints, it is surprising that the upper parts of the loops appear so smooth and featureless. In contrast, the footpoint areas show a great deal of topologically complex fine structure (Aschwanden et al., 2007). Until now, however, a strong argument against heating via reconnection with small bipoles is that active region plages generally show almost no minority-polarity flux, even in high-resolution magnetograms.

However, by comparing SDO/AIA images of plages with HMI magnetograms, we have found numerous cases where the EUV images show small, looplike structures with horizontal dimensions of 3″–6′′ (2-4 Mm), but the magnetograms (with 0.5″ pixels) show no minority-polarity flux at all (Wang 2016; Wang, Ugarte-Urra, and Reep 2019). The same holds for the “unipolar” network inside coronal holes, where the cores of Fe IX 17.1 nm plumes contain clusters of small loops which often do not have corresponding minority-polarity signatures in the magnetograms (Wang, Warren, and Muglach 2016). Because the loops have horizontal extents greatly exceeding the HMI pixel size, the failure to detect the minority-polarity flux is probably not simply the result of inadequate spatial resolution, but suggests a problem with instrument sensitivity in the presence of a strongly dominant polarity.

In 17.1 nm images, plage areas have a spongy or reticulated appearance. This so-called moss is generally interpreted as the transition region of the overlying hot loops (e.g., Berger et al., 1999). However, De Pontieu et al. (2003) found that the moss emission is only weakly correlated with the distribution of Ca II K emission, a proxy for the photospheric field strength. In my view, the 17.1 nm moss consists mainly of small, barely resolved loops that are continually being churned by the underlying granular motions and continually reconnect with the overlying loops. Figure 2 shows some examples of loops with horizontal dimensions of ∼3-4 Mm that are embedded inside “unipolar” plage areas. The inverted-Y structures are jets formed when the moss loops reconnect with the overlying active region loops.

FIGURE 2

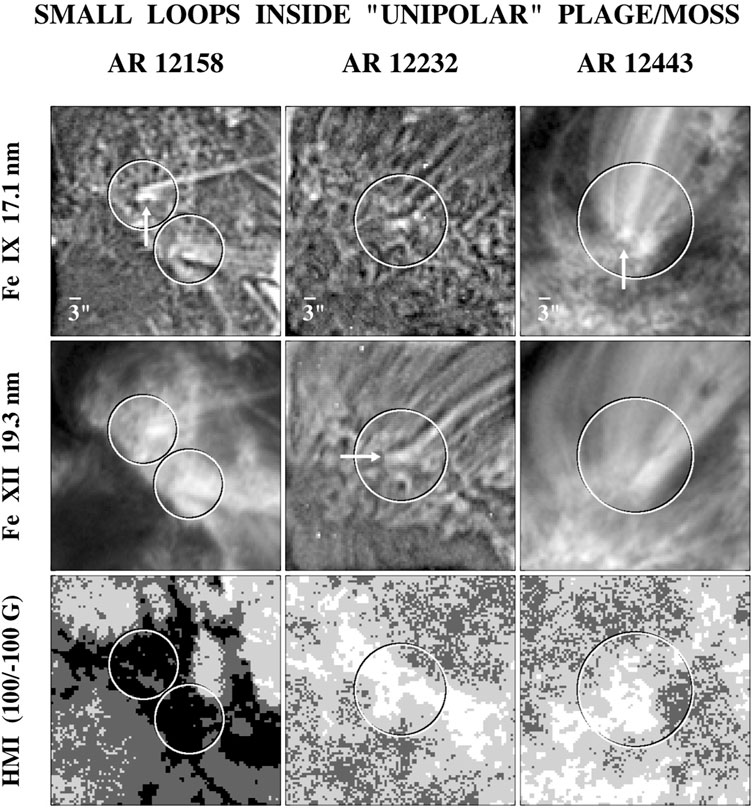
FIGURE 2. Examples of small loops embedded in active region plages that are purely unipolar according to simultaneous magnetograms. The EUV images and magnetograms are from SDO. Gray scale for the magnetograms is as follows: white (B_los >100 G); light gray (0 G $<B_{\text{los}}<100$ G); dark gray (−100 G $<B_{\text{los}}<0$ G); black (B_los <−100 G). The inverted-Y structures represent jet-like outflows along long coronal loops that are reconnecting with the underlying small-scale loops. Our hypothesis is that the reticulated EUV “moss” covering the plage areas consists mainly of small loops that continually reconnect with the active region loops and are the main source of the coronal heating in active regions.

Using SOHO/MDI magnetograms, Hagenaar et al. (2008) found that the emergence rate of ephemeral regions, defined as having fluxes ≲ 10²⁰ Mx, was at least 3 times lower inside unipolar areas than in the quiet Sun. If we instead take the emergence or churning rate of small-scale loops to be the same everywhere on the Sun and assume that the energy released by reconnection with the large-scale field scales as the local field strength B (Wang 2020), we find that the energy flux density is of order 10⁷ erg cm⁻² s⁻¹ when B ∼ 300 G. This would be sufficient to heat the active region corona (Withbroe and Noyes 1977). Similarly, reconnection between small loops and the open flux inside coronal holes would give an energy flux of $\sim 3\times 10^5$ erg cm⁻² s⁻¹ (for B ∼ 10 G), enough to drive the solar wind. In both cases, the energy input would be in the form of Ohmic heating, jets, and MHD waves. Heat would be conducted downward from the reconnection site into the transition region, leading to chromospheric evaporation, which would fill the overlying active region loops with hot, dense material (as in solar flares) and drive the solar wind mass flux along open field lines. In closed loops, the Alfvén waves generated by reconnection events near the coronal base would be reflected by the steep gradients in the transition region at the opposite end, and the trapped waves would interact with each other and undergo turbulent decay. In models where the Alfvén waves are excited by photospheric footpoint motions (e.g., van Ballegooijen et al., 2011), only a small fraction of the available energy leaks into the corona.

5 Concluding Remarks

Perhaps the most important thing I’ve learned from my astrophysical career is that it pays to look closely at the available observations, and theoretical models that are not based on a close examination of observations are likely to be wrong. An example of this precept is provided by mean field dynamo models, which have long ignored magnetograph observations showing the essential role of surface flux transport in the formation and evolution of the polar fields. I’m also puzzled as to why specialists in coronal heating and coronal loops continue to ignore the fact (or even possibility) that magnetograms do not show most of the minority-polarity flux present inside plages. As in the case of the mean field dynamo theorists, perhaps it’s due to inertia (“the inherent property of a body that makes it oppose any force that would cause a change in its motion”).

Conversely, I think that those who are mainly focused on observations should be familiar enough with basic physical concepts to properly (critically) relate their data to theoretical models. Physical interpretation of data doesn’t necessarily require elaborate 3D MHD simulations. For example, when studying the formation and evolution of filaments/prominences, it is important to recognize that flux cancellation at a polarity inversion line acts to decrease the transverse component of the field but not the parallel component. This may lead one to be more skeptical of models where filaments are formed by strong footpoint shearing (which may be easier to include in numerical simulations than flux cancellation/submergence). In any case, observations should be used to evaluate the relative importance of flux cancellation and shearing motions around the polarity inversion line.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by the Office of Naval Research.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aschwanden, M. J., Winebarger, A., Tsiklauri, D., and Peter, H. (2007). The Coronal Heating Paradox. ApJ 659, 1673–1681. doi:10.1086/513070

CrossRef Full Text | Google Scholar

Babcock, H. W. (1961). The Topology of the Sun's Magnetic Field and the 22-YEAR Cycle. ApJ 133, 572–589. doi:10.1086/147060

CrossRef Full Text | Google Scholar

Berger, T. E., De Pontieu, B., Schrijver, C. J., and Title, A. M. (1999). High-resolution Imaging of the Solar Chromosphere/Corona Transition Region. ApJL 519, L97–L100. doi:10.1086/312088

CrossRef Full Text | Google Scholar

Charbonneau, P. (2010). Dynamo Models of the Solar Cycle. Living Rev. Sol. Phys. 7, 3. doi:10.12942/lrsp-2010-3

CrossRef Full Text | Google Scholar

Choudhuri, A. R., Schüssler, M., and Dikpati, M. (1995). The Solar Dynamo with Meridional Circulation. A&A 303, L29–L32.

Google Scholar

Dahlburg, R. B., Einaudi, G., and Taylor, B. D. (2016). Observational Signatures of Coronal Loop Heating and Cooling Driven by Footpoint Shuffling. ApJ 817, 47. doi:10.3847/0004-637X/817/1/47

CrossRef Full Text | Google Scholar

De Pontieu, B., Tarbell, T., and Erdélyi, R. (2003). Correlations on Arcsecond Scales between Chromospheric and Transition Region Emission in Active Regions. ApJ 590, 502–518. doi:10.1086/374928

CrossRef Full Text | Google Scholar

Hagenaar, H. J., DeRosa, M. L., and Schrijver, C. J. (2008). The Dependence of Ephemeral Region Emergence on Local Flux Imbalance. ApJ 678, 541–548. doi:10.1086/533497

CrossRef Full Text | Google Scholar

Leighton, R. B. (1969). A Magneto-Kinematic Model of the Solar Cycle. ApJ 156, 1–26. doi:10.1086/149943

CrossRef Full Text | Google Scholar

Parker, E. N. (1988). Nanoflares and the Solar X-Ray Corona. ApJ 330, 474–479. doi:10.1086/166485

CrossRef Full Text | Google Scholar

Pontin, D. I., and Hornig, G. (2020). The Parker Problem: Existence of Smooth Force-free Fields and Coronal Heating. LRSP 17, 5. doi:10.1007/s41116-020-00026-5

CrossRef Full Text | Google Scholar

Sheeley, N. R., Nash, A. G., and Wang, Y.-M. (1987). The Origin of Rigidly Rotating Magnetic Field Patterns on the Sun. ApJ 319, 481–502. doi:10.1086/165472

CrossRef Full Text | Google Scholar

Stenflo, J. O. (1989). Differential Rotation of the Sun’s Magnetic Field Pattern. A&A 210, 403–409.

Google Scholar

van Ballegooijen, A. A., Asgari-Targhi, M., Cranmer, S. R., and DeLuca, E. E. (2011). Heating of the Solar Chromosphere and Corona by Alfvén Wave Turbulence. ApJ 736, 3. doi:10.1088/0004-637X/736/1/3

CrossRef Full Text | Google Scholar

Wang, Y.-M., Sheeley, N. R., and Nash, A. G. (1991). A New Solar Cycle Model Including Meridional Circulation. ApJ 383, 431–442. doi:10.1086/170800

CrossRef Full Text | Google Scholar

Wang, Y.-M., and Sheeley, N. R. (1994). The Rotation of Photospheric Magnetic Fields: A Random Walk Transport Model. ApJ 430, 399–412. doi:10.1086/174415

CrossRef Full Text | Google Scholar

Wang, Y.-M., and Sheeley, N. R. (1993). Understanding the Rotation of Coronal Holes. ApJ 414, 916–927. doi:10.1086/173135

CrossRef Full Text | Google Scholar

Wang, Y.-M., Sheeley, N. R., Walters, J. H., Brueckner, G. E., Howard, R. A., Michels, D. J., et al. (1998). Origin of Streamer Material in the Outer Corona. ApJL 498, L165–L168. doi:10.1086/311321

CrossRef Full Text | Google Scholar

Wang, Y.-M. (2020). Small-scale Flux Emergence, Coronal Hole Heating, and Flux-Tube Expansion: A Hybrid Solar Wind Model. ApJ 904, 199. doi:10.3847/1538-4357/abbda6

CrossRef Full Text | Google Scholar

Wang, Y.-M. (2016). The Ubiquitous Presence of Looplike Fine Structure inside Solar Active Regions. ApJL 820, L13. doi:10.3847/2041-8205/820/1/L13

CrossRef Full Text | Google Scholar

Wang, Y.-M., Ugarte-Urra, I., and Reep, J. W. (2019). Further Evidence for Looplike Fine Structure inside “Unipolar” Active Region Plages. ApJ 885, 34. doi:10.3847/1538-4357/ab45f6

CrossRef Full Text | Google Scholar

Wang, Y.-M., Warren, H. P., and Muglach, K. (2016). Converging Supergranular Flows and the Formation of Coronal Plumes. ApJ 818, 203. doi:10.3847:0004-637X/818/2/20310.3847/0004-637x/818/2/203

CrossRef Full Text | Google Scholar

Withbroe, G. L., and Noyes, R. W. (1977). Mass and Energy Flow in the Solar Chromosphere and Corona. ARA&A 15, 363–387. doi:10.1146/annurev.aa.15.090177.002051

CrossRef Full Text | Google Scholar

Withbroe, G. L., and Wang, Y.-M. (1972). A Model for the Polar Transition Layer and Corona for November 1967. SoPh 27, 394–401. doi:10.1007/BF00153110

CrossRef Full Text | Google Scholar