
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 14 June 2022
Sec. Space Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.892236
The electron velocity distributions measured in-situ in space plasmas reveal two central populations, a low-energy and highly dense (quasi-)thermal core, and a more diffuse but hotter suprathermal halo. Even if the core contributes much more to the total number density than the suprathermal particles, the energetic electrons play an important role in the higher moments. Using a dataset of more than 120,000 solar wind observations of electron distributions, measured in the ecliptic between 0.35 and 3.3 AU, we investigate here the main characteristics of the halo population and its potential influence on the core, and macroscopic properties of electrons, i.e., number density (n), bulk velocity (u), temperature (T) and temperature anisotropy (T⊥/Τ//). The analysis indicates that the parameters exhibit interdependence trends characterized by correlations between certain of these parameters and the kappa exponent (κ) corresponding to the power law of the halo population tail. The links between low kappa and low number densities (of both the core and halo populations) confirm that Coulomb collisions can be quite ineffective even at low radial distances if the density of the plasma is sufficiently low. Moreover, halo populations with lower values of κ are also associated to higher temperature anisotropies, and to higher bulk velocity. An interdependence between core and halo populations is also suggested by an apparent (inverse) correlation between their density and temperature ratios. We further show relations between the parameters fitting the sum of a Maxwellian core and a Kappa halo, and those of a global (single) Kappa fit that incorporates both the core and halo components. Such a global Kappa is used in an exospheric model of the solar wind, to predict the influence of suprathermal electrons on the characteristics of the solar wind. These results should stimulate future detailed analysis of these relationships and correlations, which may contribute to a realistic modeling of the solar wind and the formation and evolution of suprathermal populations.
Early measurements of solar wind electron distributions have revealed thermal cores well fitted by bi-Maxwellians, but non-Maxwellian high-velocity tails (Montgomery et al., 1968). Vasyliunas (1968) and Olbert (1968) showed that such distributions with enhanced tails are well described by Kappa power-law distribution functions. Since then, these suprathermal electrons have been observed not only in the solar wind (see Pierrard and Meyer-Vernet, 2017 for a review), but also in the entire heliospheric plasmas suggesting various mechanisms for their formation (see Pierrard and Lazar, 2010 for a review). Major steps in this field were reached with the first in-ecliptic observations of solar wind distributions close to the Sun by HELIOS (Rosenbauer et al., 1977), and the first measurements outside the ecliptic plane by ULYSSES (McComas et al., 1998). Two solar wind types were identified by ULYSSES when flying at different latitudes: the high speed solar wind, e.g., with bulk speed u > 600 km/s (Stverak et al., 2008), associated to low plasma density n (high u, low n) at high latitudes during minimum solar activity, and the slow speed solar wind much more variable and associated to high density (low u, higher n) and low latitudes, also during minimum solar activity (McComas et al., 1998). The understanding of the solar wind has made considerable progress based on in situ and remote sensing observations, as well as kinetic and fluid modeling [see Marsch (2018) and Rouillard et al. (2021) for reviews]. Still, the origin of suprathermal populations in the Kappa tails of velocity distributions remains a topic of high interest, and the physical mechanisms that may explain their formation and evolution remain debated [see for instance Yoon (2020); Livadiotis (2017); Lazar and Fichtner (2021) and references therein].
In the present analysis, we investigate the Kappa-distributed halo electrons by using the fits of solar wind electron velocity distributions established by Stverak et al. (2008), which describe core and halo parameters from more than 120,000 distributions measured by HELIOS 1 and 2, CLUSTER and ULYSSES missions in the ecliptic, within an extended range of heliocentric distances from 0.29 to 4 AU. Stverak et al. (2008) subtracted the field-aligned strahl component and fitted the observed velocity distribution functions with a dual model, summing up a Bi-Maxwellian core (subscript c) characterized by three fitting parameters, respectively the core number density nc, the core temperature parallel Tc// and perpendicular Tc⊥ to the magnetic field, and a bi-Kappa halo (subscript h) with four parameters, the halo density nh, the halo parallel temperature Th//, the halo perpendicular temperature Th⊥, and the power law index κ. A low exponent κ indicates a high suprathermalization, while a high κ means more thermalized halo electrons. The low-energy core of the velocity distributions is almost Maxwellian, with a core/halo breakpoint around 7 kBTc (where kB = 1.38 10–23 J/K is the Boltzmann parameter) or about 2 times the thermal velocity (Scudder and Olbert, 1979; Stverak et al., 2009). The halo and the magnetic field-aligned strahl fall in the energy range of about 102–103 eV (Pierrard et al., 2001a). The strahl is in general reduced with increasing the heliocentric distance and in the absence of energetic solar outflows (Maksimovic et al., 2005; Stverak et al., 2009). Here, we analyze the main macroscopic parameters characterizing the core and halo populations (with energies up to 1 keV), aiming to show how these properties are influenced by the presence of suprathermal halo electrons. From the solar wind data set mentioned above, we select three different heliocentric distances in the ecliptic plane: data from about 0.4 AU collected by HELIOS between 1975 and 1978, from 1 AU by HELIOS and CLUSTER between 2002 and 2003, and from large distance, about 3 AU, by ULYSSES in 1990 and 1991. In order to increase the degree of confidence in the present analysis, we consider a large enough number of events, explicitly given for each mission in Table 1, noting that the number of samples is much smaller at 3 AU due to limited data set.
Our present study is structured as follows. In the next section, we start by analyzing the relationships between the kappa (κ) parameter that characterizes the power law of the suprathermal electrons, and the other properties of the halo and core populations, motivated by the fact that core and halo populations are not isolated, but can interact, interchanging particles and energy. The links between the suprathermal population and the characteristics of the global population of electrons are analyzed in Influence of Suprathermals on the Global Electron Properties (up to 1 keV). Influence of the Halo Density shows the influence of the halo density on the other parameters. Maxwellian + Kappa Versus Global Kappa shows the links between a fit with a single Kappa and a sum of a Maxwellian and a Kappa distribution. The effects of suprathermal tails in electron distributions if present in the low corona are illustrated in Consequences of Suprathermal Tails at Low Distances on the Solar Wind. Finally, we discuss and summarize the results in the last Discussion and Conclusion.
By the dual model itself, the electron velocity distribution is divided into two parts: the core is fitted by a bi-Maxwellian and the halo by a bi-Kappa (Stverak et al., 2008), leading to seven fitting parameters: nc, Tc//, Tc⊥, nh, Th//, Th⊥, κ. Due to the importance of the suprathermal electrons in the velocity distribution function (VDF) characteristics, we first start by determining the links that exist between κ and other parameters specific to the halo population.
Figure 1 illustrates the density of the halo as a function of the kappa exponent. As also in the following figures, the diamonds correspond to the averaged values obtained for the observed data in the intervals [κ-1/2, κ+1/2] associated with each integer value of κ. Error bars corresponding to standard deviations are illustrated by the vertical lines. The linear Pearson’s correlation coefficients are given in the figure: they are very high if we use the average values (cm), and lower if we use all the data (cc). We have verified that the correlation coefficients are statistically significant. Note that a low linear Pearson correlation coefficient does not mean that no relationship exists between the variables: they may have a nonlinear relationship. Here, the best linear correlation is obtained at 3 AU.
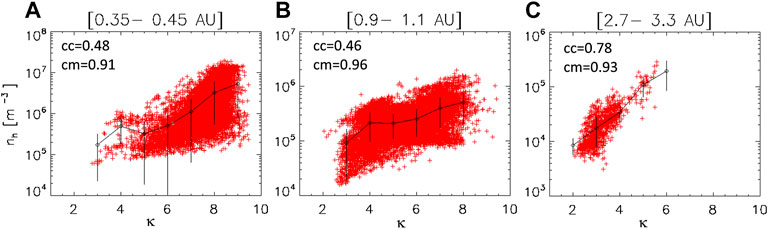
FIGURE 1. Density of the halo electrons versus the kappa exponent κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). The red crosses correspond to the observed data. Black diamonds correspond to the averaged values obtained for integer values of κ. Black vertical lines represent the error bars corresponding to the standard deviations. Linear Pearson’s correlation coefficients are given for all the observations (cc) and for the averaged values (cm).
It is clear from Figure 1 that the kappa parameter decreases with the distance, since the average value of κ is 7.5 at 0.4 AU, 5.4 at 1 AU and 3.2 at 3 AU, with no values κ > 6 at this large distance. Previous studies have confirmed that from 0.29 to 4 AU in the solar wind, the power exponent κ characterizing suprathermal electrons decreases with increasing radial distance (Pierrard et al., 2016). The halo seems to be enhanced with increasing the distance from the Sun, on the expense of electron strahl population (Maksimovic et al., 2005; Stverak et al., 2009; Bercic et al., 2019), but these effects, more specific to fast winds, are not analyzed here.
The results in Figure 1 show for the first time that a smaller (in average) parameter kappa is linked to lower halo densities at a given radial distance, and not only when the density decreases with the radial distance as shown in previous studies (e.g. Maksimovic et al., 2005). These results also suggest that suprathermalization is a fast process and may also act (more or less locally) at low heliospheric distances.
A direct correlation between nh and κ is clearly visible on Figure 1, at all radial distances, including the one close to the Sun (left panel). It is very strong at 3 AU, even if less data is available, suggesting that the link increases with the distance due to the density decrease. The kappa parameter κ is low for low density of the high-energy halo nh, in agreement with the fact that lower densities means less important effects of collisions for the energetic electrons and thus stronger high-energy tails, more departed from a Maxwellian shape. Kappa distributions tend to standard Maxwellians when κ is very large (tending to infinity), as reviewed in Pierrard and Lazar (2010) with the other properties of Kappa distributions in space plasmas.
Figure 2 illustrates the temperature of the halo as a function of halo κ parameter at 0.35–0.45 AU (upper panel), 0.9–1.1 AU (middle panel) and 2.7–3.3 AU (bottom panel). One can observe that a low κ is associated to a high halo temperature. The anti-correlation trend is clear and not linear: the halo temperature decreases asymptotically, becoming (almost) constant for high values of κ > 7. The slope seems to remain the same at all radial distances. It is logical since lower κ gives much enhanced tails at high energies, thus it increases the corresponding VDF moment giving the temperature. Plots show the same decreasing tendency as in Maksimovic et al. (2005) using another solar wind dataset outside the ecliptic plane. This may be due to the kappa dependence of the temperature for Kappa distributions: Tκ = κ TM/(κ-3/2) where TM is the temperature of the Maxwellian distribution reproducing the core of a global Kappa function incorporating both the core and halo (Lazar et al., 2017). Physically, this means that the kinetic temperature of the halo is naturally enhanced by the presence of suprathermals in the high energy tails of Kappa distributions (Lazar et al., 2017). Note that higher temperatures can also mean lower collisionality, and thus higher κ. A positive correlation of kappa to local collisional frequency can also be obtained combining Figure 1 (positive kappa/n correlation) and Figure 2 (negative kappa/T correlation) since the frequency is proportional to ∼ n/T^3/2 (Salem et al., 2003).
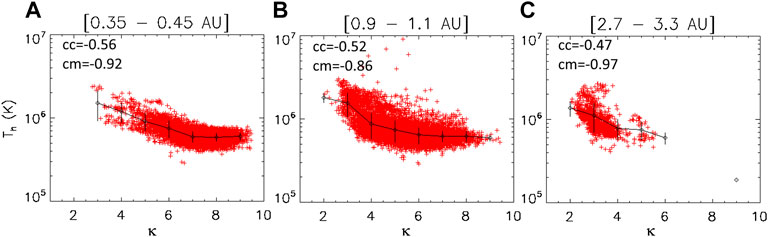
FIGURE 2. Temperature of halo electrons versus κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
Figure 3 shows the temperature anisotropy (Th⊥/Th//) of halo electrons as a function of the kappa parameter at 0.35–0.45 AU (left panel), 0.9–1.1 AU (middle panel) and 2.7–3.3 AU (right panel). The temperature anisotropy Th⊥/Th// of the halo is generally lower than 1, especially for κ < 5 at 0.4 AU and becomes closer to 1 with increasing κ. Indeed, the anisotropy is expected to approach 1 (i.e. isotropy) when collisions are abundant and thus when the distributions are closer to isotropic Maxwellians associated to large κ values. This is thus conform with more intense Coulomb collision effects associated to larger κ, especially at low radial distances (Scudder and Olbert, 1979; Pierrard et al., 2001b). At larger heliocentric distances, the seemingly flat data distribution indicates that the collisionless conditions could also bring the solar wind electrons to near-isotropic condition, potentially due to wave-particle interactions.
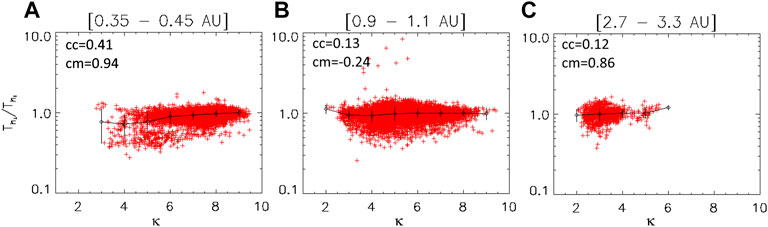
FIGURE 3. Temperature anisotropy of halo electrons versus κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
Figure 4 illustrates the density of the core electrons as a function of κ at 0.4 AU (left panel), 1 AU (middle panel) and 3 AU (right panel). A direct correlation is again well visible between the density of the core and the parameter κ at all radial distances, like for the halo but with less sharp slopes. A positive slope is visible at low distances, and as the solar wind expands, the correlation remains visible at distances as large as 3 AU, where the slope is even higher.
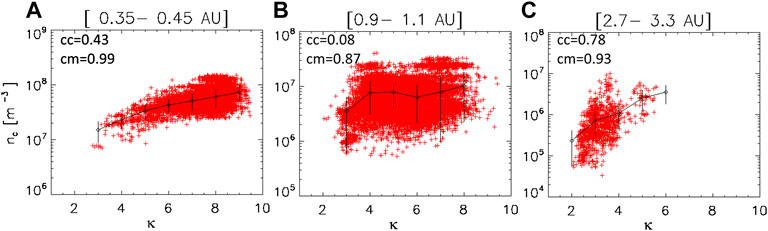
FIGURE 4. Density of the core electrons versus the exponent κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
Thus, low densities of the core corresponds to low values of κ: this indicates that high suprathermal tails for the halo are more present in low-density plasmas, when interactions between the particles, i.e., Coulomb collisions, are less frequent. The same conclusion is valid for the total number density, since it is close to the core density, as the ratio between halo and core density is always lower than 20% (Pierrard et al., 2020). This is quite logical since higher densities lead to VDF closer to Maxwellians, due to higher effects of Coulomb collisions, as shown in solar wind simulations based on the Fokker-Planck equation including Coulomb collisions (Pierrard et al., 2001b).
Note that the trend is inversed for the ratio of the core on halo density nc/nh as a function of κ: it is then anti-correlated so that κ is slightly lower for high ratios of number densities nc/nh (and on the contrary κ is directly correlated with the inverted ratio nh/nc that is always <1). Since the slope of the halo density versus κ is higher than that of the core, the ratio nc/nh (that ranges between 5 and 300) is anti-correlated with κ: the density ratio decreases with the value of κ. This is related to the fact that the number density of the halo is always lower when the density of the core is lower [as it will be shown in Total Temperature (T) Versus Halo Density (nh)]. This indicates also that the physical process that generates the Kappa tails is much more efficient at low densities and for high energies, as suggested by theoretical models explaining these processes (e.g., Yoon (2020) and references therein).
Figure 5 shows the temperature of core electrons as a function of κ at 0.35–0.45 AU, 0.9–1.1 AU and 2.7–3.3 AU. Contrary to the halo temperature that was clearly anti-correlated to κ, the core temperature is only slightly increasing with κ at low radial distances, with a high κ value corresponding to a high core average temperature. This is also observed at 3 AU. The correlation is not very clear at 1 AU, maybe due to the mix of Helios and Cluster observations at this distance. Correlations are generally better visible at low distance (thus here between 0.35 and 0.45 AU) because the shocks and interactions between fast wind and slow wind have not yet corrupted the clear link.
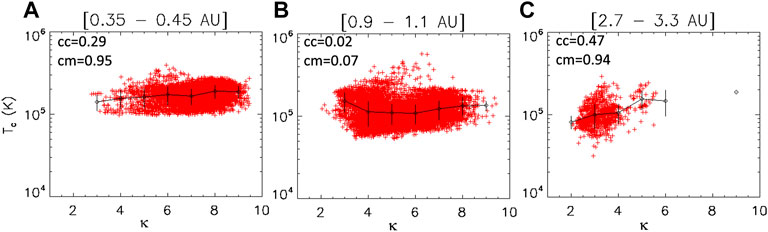
FIGURE 5. Temperature of core electrons versus κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
Figure 6 shows the temperature anisotropy (Tc⊥/Tc//) of core electrons as a function of κ at 0.35–0.45 AU (left), 0.9–1.1 AU (middle) and 2.7–3.3 AU (right). The temperature anisotropy Tc⊥/Tc// of the core is generally <1 and becomes closer to 1 for large κ at all radial distances, like for the halo. This is well visible at 0.4 AU, and also at 3 AU. This relation is again less visible at 1 AU, may be due to the large amount of data mixing Helios and Cluster taken during different periods of time. The anisotropy is expected to approach 1 when collision frequency is high and thus when κ is large, because the distributions are then closer to isotropic Maxwellians. This is thus conform with more intense Coulomb collision effects associated to larger κ, like for the halo anisotropy. Note that the low anisotropy is not due to the high κ, but because both are affected by the Coulomb collisions in the same way.
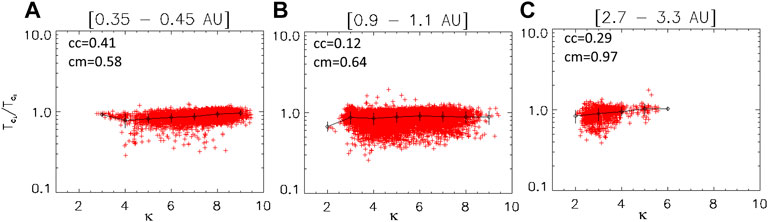
FIGURE 6. Temperature anisotropy of core electrons versus κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
The figures obtained for the total number density are not shown here because they are exactly similar to Figure 4 that showed only the core density. This is because the halo density is very small in comparison to the core density. The same conclusions from Total Density (n) Versus Kappa Exponent (κ) can thus be generalized to the total number density.
The bulk velocity is not clearly related to κ, as shown in Figure 7. At low distance (Helios observations), the spread of data is very large for high values of κ, while the low values of κ are more rare and associated to values around 500 km/s. At higher distances, the variation of velocity as a function of κ is not anymore significant (Pierrard et al., 2020). The link between the bulk velocity and the suprathermal population was already briefly studied in Lazar et al. (2020a).
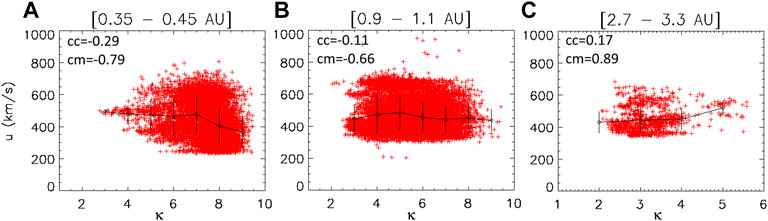
FIGURE 7. Bulk velocity of electrons versus κ of the halo at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
Note that on the contrary, a clear link between κ and the bulk velocity was obtained by fitting ULYSSES observeddistributions, averaged over all pitch-angles (thus including halo and strahl components), with a single Kappa function (Maksimovic et al., 1997b). Note that the strahl and its associated κs have a more important influence than the halo on the velocity to accelerate the wind in exospheric models (Pierrard and Pieters, 2014).
Figure 8 shows the total temperature T= (ncTc + nhTh)/(nc + nh) of the electrons as a function of κ at 0.35–0.45 AU, 0.9–1.1 AU and 2.7–3.3 AU. All panels show profiles similar to Figure 5 that illustrated only the core temperature, but values in Figure 8 are higher, by the influence/contribution of the halo temperature to the total temperature. Note that the standard deviation is also affected, due to the combination of the different measured data (i.e., Tc, Th, nc and nh) to calculate the total temperature. Contrary to the halo temperature that was clearly anti-correlated to κ, the total electron temperature (likewise Tc) does not show a clear correlation with κ, regardless of distance.
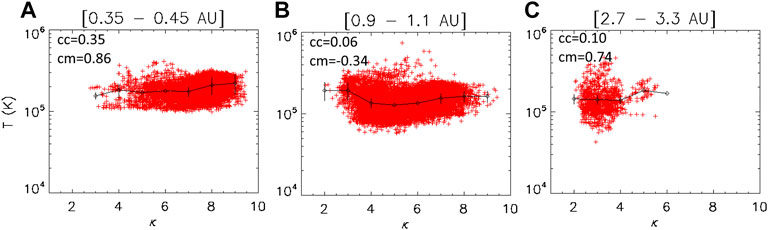
FIGURE 8. Total temperature of the electrons versus κ at 0.35–0.45 AU (A), 0.9–1.1 AU (B) and 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
The κ parameter is not the only one that controls the importance of the suprathermal tail, also conditioned by the halo/core density. The presence of suprathermal electrons at low distance is also attested by a high halo/core density ratio (nh/nc), even if κ is high, e.g. at 0.4 AU (Pierrard et al., 2016). Pierrard et al. (2020) had already shown that low halo density was associated to a higher bulk velocity. In the following, we study the interlinks between nh and other electron characteristics, first considering the core density nc.
Figure 9 shows the core density as a function of the halo density for electrons observed by ULYSSES at 3 AU. Notice a direct link between density of the core and the halo, confirming that the correlation found in Pierrard et al. (2020) between 0.4 and 1 AU persists also at large distance. High halo densities are always related to high density core populations.
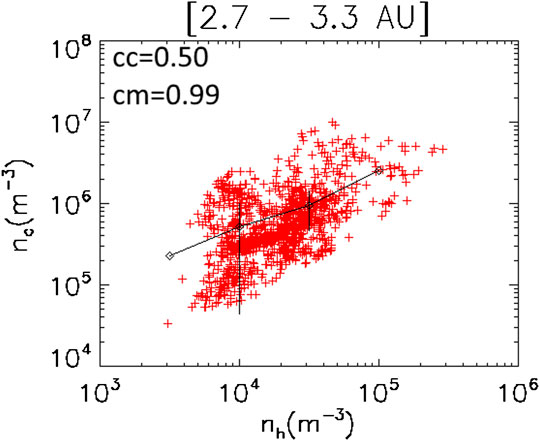
FIGURE 9. Core density versus halo density for electrons observed by ULYSSES at 3 AU. Error-bars, average values and correlation coefficients as in Figure 1.
The total temperature illustrated in Figure 10 as a function of nh shows a modest increase with the density of the halo at low distances (0.4 AU, left). At larger distances, variation is less monotonic, i.e., high total temperatures are obtained for extremely low or extremely high halo densities. There is no clear correlation between the total temperature and the density of the halo. Plots are always very similar for parallel and perpendicular temperatures, and thus not shown because these details do not bring any new information.
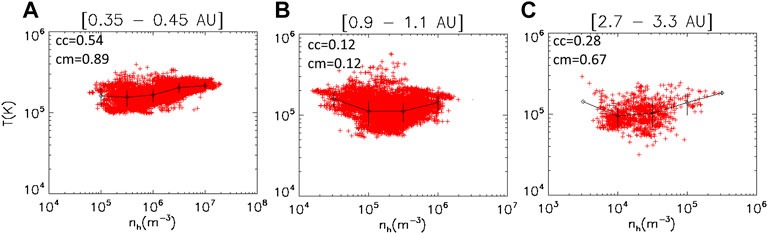
FIGURE 10. Total temperature versus density of the halo at 0.35–0.45 AU (A), at 0.9–1.1 AU (B) and at 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
Figure 11 shows the halo/core temperature ratio as a function of the core/halo density ratio, such that these ratios are always supra-unitary (>1). The halo/core temperature ratio is clearly related to the core/halo density ratio at all distances, and especially at 0.4 AU: a higher temperature ratio is obtained for higher density ratio. The ratio Th/Tc typically ranges from 2 to 10 and seems to slightly increase with the distance. The density ratio nc/nh ranges from 5 to 300 (which corresponds to nh/nc from 20% to less than 1%). Note that the temperature of the halo is directly related to the temperature of the core, with Th larger when Tc is larger. The same is true for the density, as shown in Figure 9.
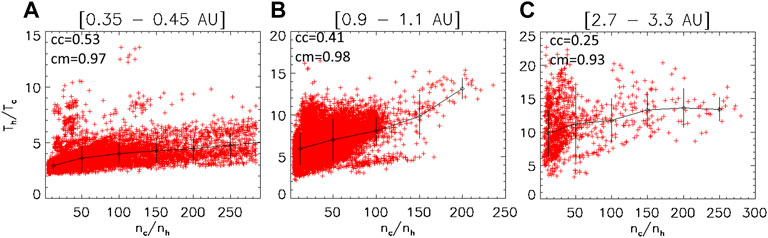
FIGURE 11. Ratio of the halo on core temperatures versus density ratio of the core on halo at 0.35–0.45 AU (A), at 0.9–1.1 AU (B) and at 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
In general, the temperature ratio is larger when the density ratio is larger, but the profiles of this dependency change much with heliospheric distance, as also found before for, e.g., κ that decreases with distance from the Sun (Maksimovic et al., 2005; Pierrard et al., 2016). We should also remind that halo temperature Th decreases with increasing κ, while core temperature Tc slightly increases with κ (Lazar et al., 2017), which means that lower temperature ratios Th/Tc should correspond to lower heliospheric distances, as confirmed by our plots in Figure 11. This inverse correlation between Th and Tc reveals a natural correlation between a hotter core and a more thermalized and cooler halo. With the results in Figure 11, these conditions also correspond to a less dense core and a more dense halo, as expected.
It has been suggested that the electron halo observed in the solar wind may originate from nanoflare-accelerated electron beams below the solar surface (i.e., less than 1.1 Rs) through the nonlinear electron two-stream instability (ETSI) (Che et al., 2019). One of the important predictions of this model is that the halo-core temperature ratio is anti-correlated with the density ratio, and the minimum temperature ratio is ∼4. The present solar wind observations show temperature ratio that can be as low as 2, but with average values around 4 and slightly increasing with the density ratio nc/nh>1.
Figure 12 shows the total temperature as a function of the core/halo density ratio (>1). One can see a clear link, with a higher temperature associated to lower nc/nh (or a high nh/nc), which is expected because the halo temperature can contribute more to the total temperature. When the ratio nh/nc is small (thus nc/nh is high), this influence is minimal, and the temperature remains almost constant with the density ratio.
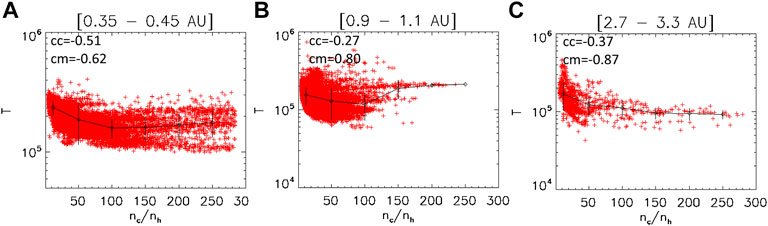
FIGURE 12. Total temperature versus density ratio of the core on halo at 0.35–0.45 AU (A), at 0.9–1.1 AU (B) and at 2.7–3.3 AU (C). Error-bars, average values and correlation coefficients as in Figure 1.
In the dataset used in the present paper, the entire electron velocity distribution is divided into two parts: f = fM + fh, i.e., the low-energy core fitted by a bi-Maxwellian distribution fM, and the halo by a bi-kappa distribution fκ (Stverak et al., 2008, 2009). This fitting model contains 7 parameters (nM, TM//, TM⊥, nh, Th//, Th⊥, κh) so that the characteristics of the suprathermal electrons depend not only on κh, but also on the number density and temperature ratio between the core and halo populations.
The fitting method of Stverak et al. (2008) has to be distinguished from another fitting model used in other studies like Maksimovic et al. (1997b), using for instance a single (global) Kappa, which incorporates both the core and suprathermal halo. The early descriptions of the observed VDFs were made using such single Kappa distribution fs, isotropic or integrated over all pitch angles, thus using only 3 parameters to fit the VDF: ns, Ts and κs. In Maksimovic et al. (1997b) for instance, Ulysses observations at a distance larger than 1 AU give a low kappa index around κs = 2.7 in average for v < 550 km/s and κs = 2 in average for v > 550 km/s. A low κs in such a global Kappa distribution indicates then high suprathermal tails while κs tending to infinity corresponds to the Maxwellian case (Pierrard and Lazar, 2010), approximating the core (Lazar et al., 2015, 2016). The global power exponent κs is then the only parameter to give distinct information about the importance of the suprathermal electrons.
Figure 13A illustrates a single Kappa distribution (dashed green line) and how it would be fitted by a sum of a Maxwellian core (black line) and a Kappa halo with a higher temperature (blue line). The parameter v represents the electron velocity normalized by the thermal velocity (2kBT/m)1/2 where m = 9.11 10–31 kg is the mass of the electrons and T their temperature in Kelvin. If the distribution is fitted on a sufficiently large energy range, the kappa index is the same for the single Kappa and for the sum of Maxwellian + Kappa, i.e., κh = κs. Indeed, the index kappa controls the slope of the high-energy tails. Note that halo electrons can be thermalized if κh tends to infinity, i.e., if the halo population is well described by a second Maxwellian with higher temperature. In a sum of two VDFs, the ratio of halo density on the core density indicates also the presence of the suprathermal particles and their importance, as illustrated in Figure 13B.
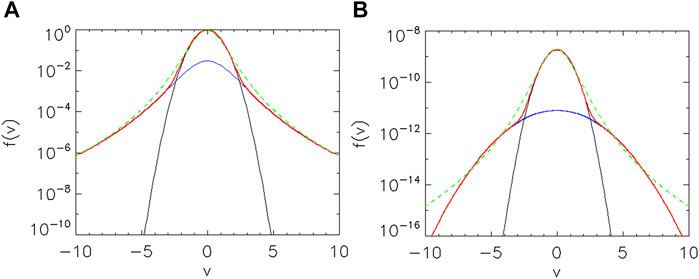
FIGURE 13. (A): Example of a single Kappa distribution (here fkappa= (1 + v2/κ))(−κ−1) in green with κ = 3) and sum of Maxwellian +0.03 Kappa (total in red): exp (-v2) (in black) +0.03∗(1 + v2/(2.5κ))(−κ−1) (in blue). (B): Example of the sum of 2 Maxwellians (red) with n1 = 1010, n2 = 109, T1 = 105 K, T2 = 8 105 K, and a single Kappa using here κs = 3, ns = n1+n2κs3/2 Γ(κs+1/2)/Γ(κs+1), Ts = T1.
Links between a single Kappa and dual Maxwellian + Kappa can be established as follow:
1) κs = κh for isotropic distributions, so that the tails decrease with the same power law at high velocities. This is true only if the fit is made on a sufficiently large range of the velocity, so that the tails are the same at large values (i.e., for normalized velocity v > 6 in Figure 13A).
For a sum of two Maxwellians as illustrated in Figure 13B for typical solar wind values, a Kappa distribution can represent the suprathermal tails due to the second Maxwellian with a higher temperature Th, but at very large velocities (here v > 8), the asymptotic behaviors differ. This shows that the quality of the fit and the values of the fit parameters will depend very much on the energy range that is taken into account. Note that the observations show in general tails decreasing more as power laws than exponentially. Anyway, in such an extreme case of a Maxwellian to represent the suprathermal tails, κs is not equal to κh (that would be very large for a Maxwellian) but should depend on nh and Th.
2) ns depends on nM and nh but it is not simply their sum. To have the VDFs normalized at the same value at v = 0: Ns = NM + Nh ∼ NM where Ni = ni (m/(κi 2 π k Ti))3/2 Γ(κi+1)/Γ(κi-1/2) for Kappa functions as defined by Olbert (1968), where i = s for single Kappa and i = h for halo Kappa, and NM = nM (m/(2πkTM))3/2 for Maxwellians. This gives a relation between the densities n of the different fit functions, but note that the kappa index κs of the single Kappa is necessary to determine the exact value of ns. This relation is valid for the Olbertian form of the Kappa VDFs (Olbert, 1968), and can easily be adapted for cases of modified Kappa with κ-independent temperatures (Lazar and Fichtner, 2021).
3) Ts depends in a non-trivial way on nM, TM, nh, Th and κh where Ts can be anisotropic, with different components in the parallel and perpendicular directions. Ts ∼ TM gives generally good fits at low velocities, when the ratio nM/nh is large enough, as illustrated in Figure 13.
Suprathermal electrons are observed in the solar wind from 0.3 to 4 AU with a κ decreasing with the radial distance (Maksimovic et al., 2005; Pierrard et al., 2016). The presence of suprathermal electrons already at low distance is also attested by a high ratio of suprathermal electron density nh/nc, (Pierrard et al., 2016, 2020; Lazar et al., 2020a). The observations of Parker Solar Probe at lower distances indicate also that suprathermal electrons are already present (Maksimovic et al., 2021). Parker Solar Probe provides new observations at radial distances as low as 0.17 AU showing an anticorrelation between the bulk speed and the electron temperature in the pristine solar wind (Halekas et al., 2020; Maksimovic et al., 2020), as already observed with HELIOS in the seventies. At high radial distances, the observations show that the number density of the strahl electrons slightly decreases while the halo electron population slightly increases, suggesting scattering isotropizing the strahl and enhancing the halo (Maksimovic et al., 2005; Stverak et al., 2009; Bercic et al., 2019). Observations down to less than 10 Rs in 2024 will allow to determine the origin and evolution of the halo and strahl suprathermal halo and strahl electrons in the acceleration region, and compare with the results of different solar wind models including these energetic populations (Lemaire and Pierrard, 2001).
The presence of suprathermal electrons at low altitude in the solar corona has important consequences for the characteristics of the solar wind. In exospheric models, the kappa parameter of the strahl suprathermal population has a direct influence on the acceleration of the wind (Pierrard et al., 2021). Figure 14 illustrates the profiles of the solar wind moments obtained with an exospheric model using a Kappa distribution for the electrons (Pierrard and Lemaire, 1996; Pierrard and Pieters, 2014; Moschou et al., 2017). In the model, the kappa of the strahl is the same as the kappa of the halo at the exobase. The black and red lines illustrate respectively the cases of κ = 3 and κ = 7, for an exobase at 1.5 Rs. The wind is more accelerated when the index κ is low. A low exobase also accelerates the wind (Lamy et al., 2003). The κ parameter has to be > 2 so that the heat flux can be calculated, except when the Kappa distributions are regularized to take into account the cut-off of the distributions at velocities larger than the light speed (Lazar et al., 2020b).
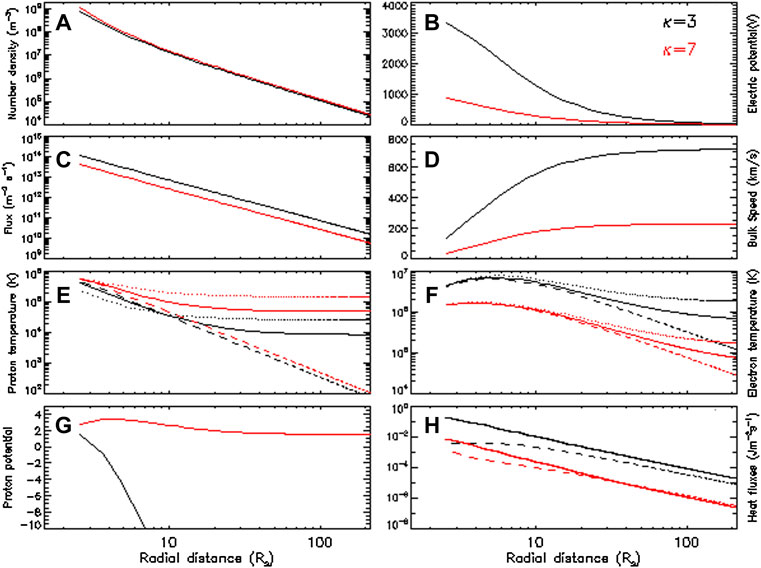
FIGURE 14. Moments of Kappa VDFs obtained with the exospheric model from Pierrard and Pieters (2014) with κ = 3 (black) and κ = 7 (red). (A). Number density, (B). Electric potential, (C). Escape flux, (D). Bulk velocity, (E). Proton temperatures (solid: total, dotted: T//, dashed: T⊥), (F). Electron temperatures (same symbols), (G). Proton potential energy, (H). Heat flux (solid: electrons, dashed: protons).
Figure 14 illustrates the profiles of the moments for two Kappa VDFs: low κ = 3 in black and higher κ = 7 in red in a purely exospheric model of the solar wind using Kappa Olbertian distributions for the electrons (Pierrard and Lemaire, 1996; Pierrard and Pieters, 2014). One can see that the flux is higher for low κ (panel C), while the density has almost similar slope when starting with the same value at the exobase (panel A), leading thus to higher bulk velocity at all distances for low κ (panel D). This relation between high velocity and low κ is indeed confirmed by observations (Maksimovic et al., 1997a; Pierrard et al., 2020). The velocity increases with the radial distance for any value of κ, leading to a supersonic velocity already at a few solar radii, including for κ tending to infinity corresponding to the Maxwellian case (Lemaire and Pierrard, 2001). This acceleration is due to the high electric potential (panel B) associated to the high asymmetry of the distribution for high suprathermal tails (thus low κ).
The proton temperature perpendicular to the direction of the magnetic field (dashed line) is higher than the parallel temperature (dotted line) at low distance, but this trend is inverted at large distance (see panel E), as indeed observed. For the electrons, the parallel temperature is larger than the perpendicular one, and the anisotropy increases with the radial distance (panel F). It becomes too large as compared to the observations at large distances (Bercic et al., 2019). This is due to the fact that exospheric models completely neglect any interactions between the different particles, while solar wind models including Coulomb collisions (Pierrard and Lemaire, 1996) or whistler waves (Pierrard et al., 2011) show that such effects influence the anisotropy of the velocity distribution function, without modifying significantly the average values of the moments. Recent studies of the heat flux instabilities have also shown their effects on the shape of the VDF and especially their anisotropies (Shaaban et al., 2021; Sun et al., 2021; Zhao et al., 2022).
Panel G shows that κ has a high influence on the proton potential. Panel H illustrates the heat flux that is higher for low κ (black), and generally higher for electrons (solid lines) than for protons (dashed lines).
The relations found in the previous sections are especially useful to determine links between the parameters that can be used to estimate boundary conditions in such solar wind models and provide predictions of solar wind characteristics at all radial distances in the Solar System.
To our knowledge, the present work provides the first study where the kappa exponent κ characterizing the halo is exhaustively opposed to all the other parameters (nc, nh, Tc, Th, Tc⊥/Tc//, Th⊥/Th//, n, T, u) allowing us to explore the potential correlations, but also the influence of suprathermal halo electrons on the other properties of the solar wind plasma. We unveil correlations, more than apparent, between the observed kappa exponent, and the core, halo and total density of the electrons at all radial distances. We find strong links between κ and the density, even at low distances (0.4 AU), confirming the anti-correlation between the formation of the power law tails and the collision frequency, which is known as a factor that contributes to the relaxation of the power law tails (Pierrard et al., 2001b and references therein). The implication of the Coulomb collisions is counter-balanced by energization mechanisms, given by the interaction with plasma waves.
The population of energetic (suprathermal) electrons is already present at low distances. Even if κ is higher at low distance, the ratio of halo on core electrons remains high. This is important since the presence of suprathermal electrons tends to accelerate the wind, whatever the VDF is represented by a Kappa distribution or a sum of two Maxwellians, due to the higher escaping flux in exospheric models (Pierrard, 2012). A similar study of the strahl κ index would be useful since Stverak et al. (2009) have shown that the average ratio of suprathermal electrons (halo + strahl) to core density remains constant with the distance, as the strahl is scattered into halo.
Low κ for the halo (indicating strong suprathermal tails) is markedly related to low number density of the core and even more to low density of the halo. Low κ is also associated to T// slightly larger than T⊥. This can be explained by the lower effects of Coulomb collisions when the density is low, as simulated with solar wind models based on the solution of the Fokker-Planck equation (Pierrard et al., 1999, 2001b). No clear link between κ of the halo and the solar wind speed is observed. This seems to indicate that the physical process creating the power law tails of the halo population (for which κ decreases with the radial distance) is more efficient when the density is low (thus in absence of collisions), but does not influence the bulk velocity of the wind.
It was shown recently that non-equilibrium systems described by linear Fokker-Planck equations for the VDFs yield steady state Kappa distributions for particular choices of the system parameters (Shizgal, 2018). Solutions of Fokker-Planck equation for the distribution function of a test particle subject to wave-particle interactions mediated by Coulomb collisions with heat bath particles are Kappa distributions in the lowest limit for ratio of the test particle mass m to the heat bath particle mass M: m/M → 0. The time evolution and the steady-state distributions are dependent on the particle mass ratio and on the strength of the wave-particle interaction perturbing the system from equilibrium. Solutions of Fokker-Planck equations taking into account Coulomb collisions and wave turbulence are the most appropriate to model the evolution of all the characteristics of the VDFs. Whistler waves were shown to be able to produce power law tails and temperature anisotropies for solar wind electrons (Vocks et al.,. 2005; Pierrard et al., 2011). Nevertheless, the lack of whistlers observed by Parker Solar Probe for low heliospheric distances <30 Rs suggests that the modification of the electron VDF associated with the ambipolar electric field or changes in other plasma properties must result in lower instability limits for the other modes (including the observed solitary waves and ion acoustic waves) that are observed close to the Sun (Cattell et al., 2022). Resonant and non-resonant wave-particle interactions can induce energy transfer at different timescales in collisionless plasmas, which leads to the reshaping of the particle VDF, as recently quantified by Zhao et al. (2022) for typical Alfvén mode waves. Proton VDFs can also be modified by waves, as shown by Voitenko and Pierrard (2015) revealing the influence of kinetic Alfvén waves in the formation of the proton tails and beams. The characteristics of all these mechanisms differ depending on the systems. The comparison with observations as provided in the present study, provides a series of agreements able to confirm these models of kappa tails formation.
By fitting WIND electron measurements at energies up to 1.5 keV at 1 AU, Tao et al. (2021) reported many interesting links between different parameters associated to the halo and the strahl. They especially found a positive correlation between the halo temperature and halo kappa index and a positive correlation between the electron temperature and the integrated halo density, different from the results shown in the present manuscript. These differences can be due to the energy range used to make the fit, as well as to the different fitting method that can induce artificial mathematical relations. Some parameters, like the halo temperature for instance, are less precise than others because good fits can be obtained with different sets of values. There exist observational and fitting constraints that can lead to errors, making sometimes difficult to identify when the links are fully due to physical effects or affected by the fitting procedure or the energy range of measurements.
Nevertheless, the present results may contribute to understanding the source of the suprathermal electrons and determine their evolution with the radial distance. The low parameter κ in low-density plasma suggests the existence of a suprathermalization or energization of electrons by interaction with kinetic plasma waves and turbulent fluctuations, counteracting collisions that become less efficient with decreasing density. Moreover, detailed parametrization, including the interlinks between quasi-thermal core and suprathermal populations, is particularly useful for modeling and understanding plasma processes like, for instance, the energy and heat transport, or the wave instabilities self-generated by the kinetic anisotropies of plasma particles.
Publicly available datasets were analyzed in this study. This data can be found here: https://omniweb.gsfc.nasa.gov/.
VP has written this article and made the analyses of the data. SS made the fits of the velocity distribution functions to determine the parameters used in the study. ML contributed to the writing of the article.
This research was supported by the Solar-Terrestrial Center of Excellence. The SafeSpace project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 870437.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
VP thanks the editors for their invitation to contribute to this special issue about Solar Wind Evolution: Interplay of Large and Small Scale Physics. The authors thank the International Space Sciences Institute (ISSI) and the participants in a 2021 ISSI workshop for the project “Heliospheric energy budget: from kinetic scales to global solar wind dynamics”. ML acknowledges support in the framework of the project SIDC Data Exploitation (ESA Prodex-12).
Bercic, L., Maksimovic, M., Landi, S., and Matteini, L. (2019). Scattering of Strahl Electrons in the Solar Wind between 0.3 and 1 AU: Helios Observations, MNRAS486. United Kingdom: Monthly Notices of the Royal Astron. Soc., 3404
Cattell, C., Breneman, A., Dombeck, J., Hanson, E., Johnson, M., Halekas, J., et al. (2022). Parker Solar Probe Evidence for the Absence of Whistlers Close to the Sun to Scatter Strahl and to Regulate Heat Flux. ApJL 924 (10pp), L33. doi:10.3847/2041-8213/ac4015
Che, H., Goldstein, M. L., Salem, C. S., and Vinas, A. F. (2019). The Solar Wind Electron Halo as Produced by Electron Beams Originating in the Lower Corona: Beam Density Dependence. Astrophys. J. 883 (11pp), 151. doi:10.3847/1538-4357/ab3b5a
Halekas, J. S., Whittlesey, P., Larson, D. E., McGinnis, D., Maksimovic, M., Berthomier, M., et al. (2020). Electrons in the Young Solar Wind: First Results from the Parker Solar Probe. ApJS 246 (2), 22. doi:10.3847/1538-4365/ab4cec
Lamy, H., Pierrard, V., Maksimovic, M., and Lemaire, J. (2003). A Kinetic Exospheric Model of the Solar Wind with a Nonmonotonic Potential Energy for the Protons. J. Geophys. Res. 108, 1047–1057. doi:10.1029/2002ja009487
Lazar, M., and Fichtner, H. (2021). “Introduction and Motivation,” in Chapter in Book Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas. Editors M. Lazar, and H. Fichtner (Germany: Springer/Nature -Astrophysics and Space Science Library)eBook ISBN 978-3-030-82623-9
Lazar, M., Fichtner, H., and Yoon, P. H. (2016). On the Interpretation and Applicability Ofκ-Distributions. A&A 589, A39. doi:10.1051/0004-6361/201527593
Lazar, M., Pierrard, V., Poedts, S., and Fichtner, H. (2020a). Characteristics of Solar Wind Suprathermal Halo Electrons. A&A 642, A13. doi:10.1051/0004-6361/202038830
Lazar, M., Pierrard, V., Shaaban, S. M., Fichtner, H., Poedts, S., and Stverak, S. (2017). Dual Maxwellian-Kappa Modeling of the Solar Wind Electrons: New Clues on the Temperature of Kappa Populations. Astronom. Astrophys. 602, 602. doi:10.1051/0004-6361/201630194
Lazar, M., Poedts, S., and Fichtner, H. (2015). Destabilizing Effects of the Suprathermal Populations in the Solar Wind. A&A 582, A124. doi:10.1051/0004-6361/201526509
Lazar, M., Scherer, K., Fichtner, H., and Pierrard, V. (2020b). Toward a Realistic Macroscopic Parametrization of Space Plasmas with Regularized κ-distributions. A&A 634, A20. doi:10.1051/0004-6361/201936861
Lemaire, J., and Pierrard, V. (2001). Kinetic Models of Solar and Polar Winds. Astrophys. Space Sci. 277 (2), 169–180. doi:10.1007/978-94-010-0904-1_22
Livadiotis, G. (2017). Kappa Distributions: Theory and Applications in Plasmas. Netherlands: Elsevier.
Maksimovic, M., Bale, S. D., Bercic, L., Bonnell, J. W., Case, A. W., Dudok de Wit, T., et al. (2020). Anticorrelation between the Bulk Speed and the Electron Temperature in the Pristine Solar Wind: First Results from the Parker Solar Probe and Comparison with Helios. Astrophys. J. Suppl. Ser. 246, 2. doi:10.3847/1538-4365/ab61fc
Maksimovic, M., Pierrard, V., and Lemaire, J. (1997a). A Kinetic Model of the Solar Wind with Kappa Distributions in the Corona. Astron. Astrophys. 324, 725
Maksimovic, M., Pierrard, V., and Riley, P. (1997b). Ulysses Electron Distributions Fitted with Kappa Functions. Geophys. Res. Lett. 24 (9), 1151–1154. doi:10.1029/97GL00992
Maksimovic, M., Walsh, A. P., Pierrard, V., Štverák, Š., and Zouganelis, I. (2021). “Electron Kappa Distributions in the Solar Wind: Cause of the Acceleration or Consequence of the Expansion?,” in Chapter in Book Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas. Editors M. Lazar, and H. Fichtner (Germany: Springer/Nature -Astrophysics and Space Science Library), 39–51. doi:10.1007/978-3-030-82623-9_3
Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial Evolution of the Electron Distribution Functions in the Fast Solar Wind between 0.3 and 1.5 AU. J. Geophys. Res. Space Phys. 110, A9. doi:10.1029/2005ja011119
Marsch, E. (2018). Solar Wind and Kinetic Heliophysics. Ann. Geophys. 36, 1607–1630. doi:10.5194/angeo-36-1607-2018
McComas, D. J., Bame, S. J., Barraclough, B. L., Feldman, W. C., Funsten, H. O., Gosling, J. T., et al. (1998). Ulysses' Return to the Slow Solar Wind. Geophys. Res. Lett. 25, 1–4. doi:10.1029/97gl03444
Montgomery, M. D., Bame, S. J., and Hundhausen, A. J. (1968). Solar Wind Electrons: Vela 4 Measurements. J. Geophys. Res. 73 (15), 4999–5003. doi:10.1029/ja073i015p04999
Moschou, S.-P., Pierrard, V., Keppens, R., and Pomoell, J. (2017). Interfacing MHD Single Fluid and Kinetic Exospheric Solar Wind Models and Comparing Their Energetics. Sol. Phys. 292 (139), 1–25. doi:10.1007/s11207-017-1164-6
Olbert, S. (1968), Summary of Experimental Results from M.I.T. Detector on IMP-1, in Physics of the Magnetosphere, Astrophysics and Space Science Library, Editiors R. D. L. Carovillano, J. F. McClay, and Astrophysics and (Euston Square: Space Science Library), 10. 641, 659.doi:10.1007/978-94-010-3467-8_23
Pierrard, V., and Lazar, M. (2010). Kappa Distributions: Theory and Applications in Space Plasmas. Sol. Phys. 267 (1), 153–174. doi:10.1007/s11207-010-9640-2
Pierrard, V., Lazar, M., and Maksimovic, M. (2021). “Suprathermal Populations and Their Effects in Space Plasmas: Kappa vs. Maxwellian,” in Suprathermal Populations and Their Effects in Space Plasmas: Kappa vs. Maxwellian, Chapter in Book Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas. Editors M. Lazar, and H. Fichtner (Germany:Springer/Nature -Astrophysics and Space Science Library), 15–38. eBook ISBN 978-3-030-82623-9, Print ISBN 978-3-030-82622-2. doi:10.1007/978-3-030-82623-9_2
Pierrard, V., Lazar, M., Poedts, S., Štverák, Š., Maksimovic, M., and Trávníček, P. M. (2016). The Electron Temperature and Anisotropy in the Solar Wind. Comparison of the Core and Halo Populations. Sol. Phys. 291 (7), 2165–2179. doi:10.1007/s11207-016-0961-7
Pierrard, V., Lazar, M., and Schlickeiser, R. (2011). Evolution of the Electron Distribution Function in the Whistler Wave Turbulence of the Solar Wind. Sol. Phys. 269 (2), 421–438. doi:10.1007/s11207-010-9700-7
Pierrard, V., Lazar, M., and Štverák, S. (2020). Solar Wind Plasma Particles Organized by the Flow Speed. Sol. Phys. 295 (151), 1–14. doi:10.1007/s11207-020-01730-z
Pierrard, V., and Lemaire, J. (1996). Lorentzian Ion Exosphere Model. J. Geophys. Res. 101, 7923–7934. doi:10.1029/95ja03802
Pierrard, V., Maksimovic, M., and Lemaire, J. (2001a). Core, Halo and Strahl Electrons in the Solar Wind. Astrophys. Space Sci. 277 (2), 195–200. doi:10.1007/978-94-010-0904-1_25
Pierrard, V., Maksimovic, M., and Lemaire, J. (1999). Electron Velocity Distribution Functions from the Solar Wind to the Corona. J. Geophys. Res. 104, 17021–17032. doi:10.1029/1999JA900169
Pierrard, V., Maksimovic, M., and Lemaire, J. (2001b). Self-consistent Kinetic Model of Solar Wind Electrons. J. Geophys. Res. 107 (A12), 29305–29312.
Pierrard, V., and Meyer-Vernet, N. (2017). “Electron Distributions in Space Plasmas,” in Kappa Distributions: Theory and Applications in Plasmas. Editor L. George(Netherlands:Elsevier), 465–479. doi:10.5772/207910.1016/b978-0-12-804638-8.00011-5
Pierrard, V., and Pieters, M. (2014). Coronal Heating and Solar Wind Acceleration for Electrons, Protons, and Minor Ions Obtained from Kinetic Models Based on Kappa Distributions. J. Geophys. Res. Space Phys. 119, 9441–9455. doi:10.1002/2014JA020678
Pierrard, V. (2012). Solar Wind Electron Transport: Interplanetary Electric Field and Heat Conduction. Space Sci. Rev. 172 (172), 315–324. doi:10.1007/s11214-011-9743-6
Rosenbauer, H., Schwenn, R., Marsch, E., Meyer, B., Miggenrieder, H., Montgomery, M., et al. (1977). A Survey on Initial Results of the HELIOS Plasma Experiment. J. Geophys. Res. 42, 561
Rouillard, A. P., Viall, N., Vocks, C., Wu, Y., Pinto, R., Lavarra, M., et al. (2021). “The Solar Wind,” in AGU Book Solar Physics and Solar Wind coordinated by Nour-Eddine Raouafi and Angelos Vourlidas, 320doi:10.1002/9781119815600.ch1
Salem, C., Hubert, D., Lacombe, C., Bale, S. D., Mangeney, A., Larson, D. E., et al. (2003). Electron Properties and Coulomb Collisions in the Solar Wind at 1 AU:WindObservations. Astrophys. J. 585, 1147–1157. doi:10.1086/346185
Scudder, J. D., and Olbert, S. (1979). A Theory of Local and Global Processes Which Affect Solar Wind Electrons, 1. The Origin of Typical 1 AU Velocity Distribution Functions-Steady State Theory. J. Geophys. Res. 84, 2755–2772. doi:10.1029/JA084iA06p02755
Shaaban, S. M., Lazar, M., Lopez, R. A., Yoon, P. H., and Poedts, S. (2021). Advanced Interpretation of Waves and Instabilities in Space Plasmas, Chapter in Book Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas. Editors M. Lazar, and H. Fichtner (Germany: Springer/Nature -Astrophysics and Space Science Library), 15–38. eBook ISBN 978-3-030-82623-9, Print ISBN 978-3-030-82622-2.
Shizgal, B. D. (2018). Kappa and Other Nonequilibrium Distributions from the Fokker-Planck Equation and the Relationship to Tsallis Entropy. Phys. Rev. E 97, 052144. doi:10.1103/PhysRevE.97.052144
Štverák, Š., Maksimovic, M., Trávníček, P. M., Marsch, E., Fazakerley, A. N., and Scime, E. E. (2009). Radial Evolution of Nonthermal Electron Populations in the Low-Latitude Solar Wind: Helios, Cluster, and Ulysses Observations. J. Geophys. Res. 114, a–n. doi:10.1029/2008JA013883
Štverák, Š., Trávníček, P., Maksimovic, M., Marsch, E., Fazakerley, A. N., and Scime, E. E. (2008). Electron Temperature Anisotropy Constraints in the Solar Wind. J. Geophys. Res. 113, a–n. doi:10.1029/2007JA012733
Sun, H., Zhao, J., Liu, W., Voitenko, Y., Pierrard, V., Shi, C., et al. (2021). Electron Heat Flux Instabilities in the Inner Heliosphere: Radial Distribution and Implication on the Evolution of the Electron Velocity Distribution Function. ApJL 916 (9pp), L4. doi:10.3847/2041-8213/ac0f02
Tao, J., Wang, L., Li, G., Wimmer-Schweingruber, R. F., Salem, C., Jian, L. K., et al. (2021). Solar Wind ∼0.15-1.5 keV Electrons around Corotating Interaction Regions at 1 au. ApJ 922, 198–216. doi:10.3847/1538-4357/ac2505
Vasyliunas, V. M. (1968). A Survey of Low-Energy Electrons in the Evening Sector of the Magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 73 (9), 2839–2884. doi:10.1029/JA073i009p02839
Vocks, C., Salem, C., Lin, R. P., and Mann, G. (2005). Electron Halo and Strahl Formation in the Solar Wind by Resonant Interaction with Whistler Waves. Astrophys. J. 627, 540–549. doi:10.1086/430119
Voitenko, Y., and Pierrard, V. (2015). Generation of Proton Beams by Non-uniform Solar Wind Turbulence. Sol. Phys. 290, 1231–1241. doi:10.1007/s11207-006-0262-7
Yoon, P. H. (2020). Non-equilibrium Statistical Mechanical Approach to the Formation of Non-maxwellian Electron Distribution in Space. Eur. Phys. J. Spec. Top. 229, 819–840. doi:10.1140/epjst/e2020-900215-4
Keywords: solar wind, halo, kappa distributions, suprathermal tails, electrons
Citation: Pierrard V, Lazar M and Stverak S (2022) Implications of Kappa Suprathermal Halo of the Solar Wind Electrons. Front. Astron. Space Sci. 9:892236. doi: 10.3389/fspas.2022.892236
Received: 08 March 2022; Accepted: 23 May 2022;
Published: 14 June 2022.
Edited by:
Peter Haesung Yoon, University of Maryland, United StatesReviewed by:
Muhammad Fraz Bashir, University of California, Los Angeles, United StatesCopyright © 2022 Pierrard, Lazar and Stverak. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Viviane Pierrard, dml2aWFuZS5waWVycmFyZEBhZXJvbm9taWUuYmU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.