Diagnosing Turbulent Magnetic Field in Supernova Remnants

We review recent investigations of the statistical nature of turbulent magnetic fields in supernova remnants. After a brief presentation of the role of the magnetic field in the cosmic-ray acceleration and synchrotron emissions from the accelerated electrons, we introduce previous investigations about the turbulent magnetic field in the supernova remnants. Then we describe the new method to analyze the statistical nature of the fields and introduce observational results reported on. Finally, we also discuss about the origin of the turbulent magnetic field and future prospects of observational studies of cosmic-ray acceleration in the supernova remnants.

1 Introduction

Supernova remnants (SNRs) are main energy sources of the dynamical evolutions of the interstellar medium (ISM, McKee and Ostriker, 1977). The dynamics of the ISM is driven by the pressures of the thermal particles, turbulence, magnetic field, and cosmic-rays (CRs), which are comparable with each other in our galaxy (Boulares and Cox, 1990; Ferrière, 2001). The CRs are energetic, charged particles that move through the ISM at nearly the speed of light. The supernovae can provide the CRs and ISM turbulence though the origin of the CRs is still under debate (Gabici et al., 2019). There is another suggestion in which the ISM turbulence is driven by gravitational instabilities (Krumholz and Burkhart, 2016; Krumholz et al., 2018). As a consequence of the ISM dynamics driven by the supernovae, the molecular clouds formation and subsequent star formation occur (Inutsuka et al., 2015; Hennebelle and Inutsuka, 2019). Burkhart (2021) recently reviews diagnostics of turbulence in the neutral and molecular ISM. The formed stars with a mass larger than $\sim 10M_{\odot }$ finally explode as supernovae and the ISM dynamics continues. Krumholz et al. (2019) recently provided reviews on the star clusters, suggesting a picture of their life cycle. It is also pointed out that the gaseous matter can be blown away from the galactic disk by the supernovae, and the star formation can be self-regulated (e.g., Kim and Ostriker, 2018; Armillotta et al., 2020, and see also Diesing and Caprioli (2018)). The CR pressure also affects the dynamics of the thermal gas and can drive the galactic wind (e.g., Girichidis et al., 2018; Hopkins et al., 2018; Mao and Ostriker, 2018; Holguin et al., 2019). Shimoda and Inutsuka (2021) recently showed that the ISM conditions observed in our galaxy are sufficient to drive the galactic wind over a long time and the mass loss rate of the galactic disk due to the wind is comparable to the star formation rate. Although the processes of the CR production in the SNRs, the CR transport in the ISM, and interactions between the CRs and the ISM have been widely investigated, they remain to be resolved. Thus, our understandings of the interplay between the CRs and the ISM (background plasma), and the galaxy evolution, are far from sufficient.

The interplay between the CRs and background plasma is also important for the CR production in the SNR shocks. The SNR shocks are formed by the interaction between the particles and electromagnetic fields. Such shock is called as “collisionless shock” in which the particle-particle collision is inefficient. The electric current of the CRs affects the magnetic field via plasma instabilities and the field is amplified (e.g., Bell, 2004). Since the CRs are scattered by disturbances in the magnetic field, the amplified field also affects the behavior of the CRs. Thus, the CR production in the SNR shocks are closely related to the magnetic-field disturbances. From the energy spectrum of the CR proton measured around the Earth, the SNR shocks are expected to produce the CR protons with energies up to 10^15.5 eV, which is the so-called the knee energy. To realize the knee energy CR protons in the SNR shocks, the strength of the amplified field should be $>100\mu \text{G}$ (e.g., Lagage and Cesarsky, 1983a; Lagage and Cesarsky, 1983b; Bell, 2004). Although many kinetic simulations studying the collisionless shock and the production of the nonthermal particles are reported on (e.g., Ohira, 2016a; Ohira, 2016b; Matsumoto et al., 2017; Caprioli et al., 2018; Caprioli et al., 2020; Marcowith et al., 2020; Haggerty and Caprioli, 2020, see also Crumley et al. (2019); Haggerty and Caprioli (2019) for the case of relativistic shocks), the CR-production process is still unsettled issue due to the limitation of too short simulation time compared to the actual SNR shocks. Related to the CR-production issues, the electron heating at the collisionless shocks is also widely studied (e.g., Ohira and Takahara, 2007; Ohira and Takahara, 2008; Rakowski et al., 2008; Laming et al., 2014; Guo et al., 2017; Guo et al., 2018) The actual nature of the magnetic-field disturbances is important clue to understand the CR production in the SNRs.

The plan of the paper is as follows. In Section 2, we briefly review a standard scenario of the CR production in the SNR shocks. The role of magnetic field is also described. In Section 3, the magnetic-field structure in the SNRs obtained by the radio synchrotron polarimetry is introduced. The field in the SNRs shows a radial orientation which is non-trivial. We review a possible origin suggested in previous studies. In Section 4, diagnostics of disturbances in the magnetic-filed by spatial two-point correlation analysis of the synchrotron intensity are reviewed. We also introduce the results reported on. Finally, we summarize the review and discuss prospects of the magnetic-filed diagnostics and the CR production in the SNRs.

2 The Diffusive Shock Acceleration

Here we review the diffusive shock acceleration (DSA, Bell, 1978; Blandford and Ostriker, 1978) which is the most generally accepted mechanism of the CR production in the SNR shocks. We mainly discuss on the maximum energy of the CRs feasible in the SNR shocks. Then, the diffusion coefficient of the CR is briefly introduced by following Kulsrud (2005). It is convenient to consider the problem in the inertial frame of reference moving at the speed of the propagation of the shock front. We consider a one-dimensional shock along with the z-axis for simplicity (see Figure 1). The velocity of the fluid (background plasma) incoming from the far upstream region is defined as u (−∞) = u₀ and the velocity of the downstream region is defined as u (+∞) = u₂. We set the position of the shock front at z = 0.

FIGURE 1

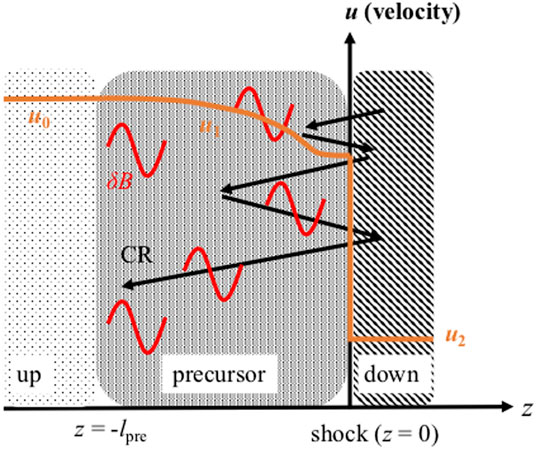
FIGURE 1. Schematic illustration of the CR accelerating shock. The plane-parallel shock is located at z = 0. The velocity of fluid u(z) is represented by orange line. The black allows indicate the trajectory of the accelerating CR which is bouncing back and force between the upstream and downstream region. The red curves show magnetic disturbances δB which are generated by the CRs or pre-existing in the ISM. The CR well confined region is referred to the precursor and the thickness of the precursor is l_pre. The structure of the fluid velocity is modified by the CR pressure before entering the shock front. Reproduced from Shimoda and Laming (2019).

In the DSA mechanism, the injection of energetic particles at the shock front is assumed. The energetic particles (CRs) are assumed to be bouncing back and forth between the upstream and downstream region by scattering particles. The scattering is supposed to result from the interaction between the particles and disturbances in the magnetic field (e.g., Jokipii, 1966, we analyze this later). Then, the CRs can diffuse ahead the shock upstream via the scattering. The CRs gain an energy by the upstream scattering because the interaction between the CRs and the upstream disturbances convected toward the downstream region can be regarded as a head-on collision. On the other hand, the CRs loose their energy by the downstream scattering because the collision can be regarded as a rear-end collision. The convection speed of the upstream disturbances u₀ is always larger than that of the downstream disturbances u₂. Therefore, the CRs accelerate per one cycle of going the upstream and downstream regions. When the mean free path of the accelerated particles becomes much larger than the size of the SNR, they escape from the system and the acceleration is finished. The mean free path depends on the intensity of the magnetic-field disturbances (e.g., Jokipii, 1966). Thus, the nature of the magnetic field is important to predict the maximum energy of the accelerated particles.

Since the pressure of the CRs is usually expected to be comparably large with the upstream ram pressure, the fluid incoming from the upstream region decelerates before crossing the shock front (e.g., Drury and Voelk, 1981). Moreover, the electric current of the CRs can induce and amplify magnetic-field disturbances especially in the upstream region (e.g., Wentzel, 1968; Kulsrud and Pearce, 1969; Bell, 2004). The strength of the induced field can reach up to $\sim 100\mu \text{G}$ for the SNR shocks (Bell, 2004). These back reaction effects prevent us from quantifying the behavior of the CRs by the diffusion coefficient for example. Detail investigations of the back reaction effects, nature of the magnetic field, and resultant diffusion coefficient are one of the most important issues in the modern scenario of the CR production. The CR accelerating region (i.e., confined region) is often referred to the CR precursor region like the radiative shock. We define the fluid velocity at the CR precursor region as u = u₁(z) and suppose the velocity field satisfies the conditions of u₁ (−l_pre) = u₀ and u₁ (0) = u₂, where l_pre > 0 indicates the length of the precursor region (e.g., Ohira et al., 2010). The value of l_pre may depend on the CR energy density (ultimately the injection rate at the shock front) which is one of the most uncertain parameters in the DSA mechanism. At the region x < − l_pre, the intensity of the magnetic-field disturbances weakens. We also notice that the length of the CR accelerating region depends more directly on the intensity of disturbances in the magnetic field via the scattering particles. Therefore, the value of l_pre may also depend on the intensity of the turbulence pre-existing in the upstream medium.

Here we evaluate the maximum energy of the CRs feasible in the SNR shocks (cf., Ohira et al., 2010). The CRs diffusing toward the far upstream region are simultaneously convected toward the downstream region at the speed of u. This means that if the particles have a large spatial diffusion coefficient compared with the convection speed, they escape from the system. From a dimensional argument, the diffusion length-scale of the CRs with a momentum of p is estimated as

$l_d\left(p,x\right)\sim \frac{D\left(p,x\right)}{u},(1)$

where D (p, x) is the spatial diffusion coefficient of the particle with a momentum of p. As we pointed out above, a precise expression of the diffusion coefficient is currently not available. If the intensity of electromagnetic disturbances is weak, the diffusion coefficient can be calculated with the test particle approximation (e.g., Schlickeiser, 2002, we analyze a simple case later). In the modern scenario of the CR acceleration at the shock, generations or amplifications of the electromagnetic disturbances are important. Since the injection process of the CRs is not fully understood, the resultant electromagnetic disturbances and diffusion coefficient are unsettled (see e.g., Caprioli and Spitkovsky, 2014, for numerical studies of the diffusion coefficient). The smallest diffusion coefficient is given by D (p, x) = r_L (p, x)c/3 ≡ D_B, where the r_L is the Larmor radius of the particle with a momentum of p, and c is the speed of light, respectively. The spatial dependence of r_L arises from the strength of the magnetic field. This smallest diffusion coefficient can be valid in very turbulent media and is called as the Bohm diffusion. Note that r_L = γmcv/qB, where γ is the Lorentz factor, m is the particle rest mass, v is the speed of particle, q is the electric charge, and B is the strength of the magnetic field. For a relativistic particle, the energy is given by E ≃ cp ≃ γmc² and thus r_L ≃ E/qB. Since the coefficient in the Bohm diffusion shows a dependence of D_B ∝ E/B, the particles with a higher energy have a longer diffusion length. The CR precursor length l_pre should be equal to or smaller than the diffusion length of the maximum energy CRs, l_d,max. The situation of l_d,max < l_pre represents that the CRs are well confined around the shock. This can be achieved if the shock inject a large amount of the energetic particles, or if the intensity of turbulence pre-existing in the upstream media is quite large. In this review, we suppose this limit (see Ohira et al., 2010, for the case of l_d,max ∼ l_pre). Then, the diffusion length of the maximum energy CRs should be comparable with the shock propagation length scale u₀t_age, where the t_age is the time elapsed from the supernova explosion to the present. This is the so-called age-limited acceleration (Lagage and Cesarsky, 1983a; Lagage and Cesarsky, 1983b). The maximum energy of accelerated protons is obtained from l_d (E_max, − l_pre) ∼ u₀t_age as

$E_{\text{max}}\sim 8.4\times 10^{15}\mathrm{e}\mathrm{V}\left(\frac{B}{100\mu \text{G}}\right){\left(\frac{u_0}{3000{\text{kms}}^{-1}}\right)}^2\left(\frac{t_{\text{age}}}{1\mathrm{k}\mathrm{y}\mathrm{r}}\right).(2)$

Thus, to accelerate the knee-energy CRs in the SNR shocks, the strength of the magnetic field around the shock should be $\sim 100\mu \text{G}$ though typical strength of the magnetic field in the ISM is only $\sim 1\mu \text{G}$ (Beck, 2001). It should be emphasised that this estimate is based on the Bohm-diffusion limit which results in the smallest diffusion-length and is valid only in highly turbulent media. Bell (2004) pointed out that the field strength of $\sim 100\mu \text{G}$ can be achieved by the back reaction effects of the accelerated CRs with assuming the injection rate of the CRs at the shock front. However, the nature of disturbances in the magnetic field and the resultant diffusion coefficient are yet unclear in actual SNR shocks.

Finally, we briefly introduce the diffusion coefficient with a test particle approximation in which the CRs do not affect the background media. In addition, the intensity of the disturbances in the magnetic-field δB is assumed to be small compared with the strength of the mean magnetic-field $\bar{B}$. We analyze the diffusion coefficient for the direction along the mean field (the z-axis) following Kulsrud (2005). Let us suppose a single Alfvén-wave packet of length l and consider the inertial frame of reference such that the wave packet is at rest. In such frame, the electric field vanishes. The Alfvén wave is assumed to be linearly polarized in the x-direction (perpendicular to the mean field) and its perturbed magnetic-field is sinusoidal as $\delta B_x=\widehat{x}\delta B\sin (kz-\omega t)$, where k = 2π/l, ω = kV_A, and V_A is the Alfvén speed. The CR moving along the z-axis at the speed of v_z enters the wave packet from the minus z-direction (v_z > 0). Then, the Lorentz force at the CR is written as

${\mathit{F}}_{\text{L}}=\frac{q}{c}\left(\mathit{v}\times \mathit{B}\right)=\frac{q}{c}\left(\begin{array}{c}\hfill v_y\bar{B}\hfill \\ \hfill -v_x\bar{B}\hfill \\ \hfill 0\hfill \end{array}\right)+\frac{q}{c}\left(\begin{array}{c}\hfill 0\hfill \\ \hfill v_z\delta B_x\hfill \\ \hfill -v_y\delta B_x\hfill \end{array}\right).(3)$

The first term of the right-hand side of the equation represents the rotation about $\bar{B}$. The second term represents the perturbation in the gyration due to the existence of the Alfvén wave. The z component of the Lorentz force gives the simplest analysis. Let Ω be the cyclotron frequency of the CR, so $v_y=v_{\perp }\sin \left(\mathrm{\Omega }t+\varphi \right)$, where the ϕ takes into account the random phase between the CR and the Alfvén wave. Substituting the z position of the CR, z = z₀ + v_zt, we rewrite the z component of the Lorentz force as

$\begin{array}{ll}\hfill F_{\text{L},z}& =\frac{1}{2}q{v}_{\perp }\delta B\left\{\cos \left[\left(k{v}_z-\omega +\mathrm{\Omega }\right)t+\left(k{z}_0+\varphi \right)\right]\right.\hfill \\ \hfill & -\left.\cos \left[\left(k{v}_z-\omega -\mathrm{\Omega }\right)t+\left(k{z}_0-\varphi \right)\right]\right\}.\hfill \end{array}(4)$

For v_z > 0, the first term has a higher frequency of kv_z − ω + Ω and vanishes in a long time average. The second term has a lower frequency of kv_z − ω − Ω and does not average out in a long time average if

$k{v}_z-\omega -\mathrm{\Omega }\approx 0,(5)$

which is the so-called resonance condition. For the CRs accelerating around the SNR shocks, we can regard as v_z ≫ u₀ ≫ V_A. Then, the resonance condition is reduced to be kv_z ≈ Ω, or l ≈ 2πΩ/v_z. Thus, the CRs are scattered strongly when they interact with magnetic-field disturbances whose scale-length l = 2π/k is comparable to the Larmor radius of the CRs, r_L = v_z/Ω. If the resonance condition is satisfied and v_z ≫ V_A, the change in the z-component of the momentum can be estimated by averaging the wave period $\tau =2\pi /\omega =2\pi /\left(k{v}_z-k{V}_{\text{A}}\right)\approx 2\pi /k{v}_z$ as

$\begin{array}{ccc}\hfill \delta p_z& =\hfill & \int dt{F}_{\text{L},z}\hfill \\ \hfill & =\hfill & \frac{1}{2}\frac{q{v}_{\perp }\delta B}{c}\tau \cos \left(k{z}_0-\varphi \right)\hfill \\ \hfill & \approx \hfill & \frac{1}{2}\frac{q{v}_{\perp }\delta B}{c}\frac{2\pi }{k{v}_z}\cos \left({\varphi }^{\prime }\right),\hfill \\ \hfill & =\hfill & \pi p\sin \theta \left(\frac{\delta B}{\bar{B}}\right)\cos {\varphi }^{\prime }\hfill \end{array}(6)$

where ϕ′ = kz₀ − ϕ, θ is the pitch angle of the CR, and p is the magnitude of momentum. In the inertial frame of reference moving with the Alfvén wave packet, the electric field is zero. Therefore, the energy of the CR dose not vary during the interaction. Note that in the shock rest frame, a change of the energy due to the scattering should be measured because the electric field dose not vanish in this frame. Thus, in the rest frame of the wave packet, the interaction only results in a change of the pitch angle θ. Let p_z = p cos θ be the momentum component parallel to the mean field. Then, the change of p_z due to the scattering can be written as δp_z = − sin θδθ and we obtain the change of the pitch angle as

$\delta \theta =-\pi \frac{\delta B}{\bar{B}}\cos {\varphi }^{\prime }.(7)$

The pitch angle increases or decreases according to the relative phase between the CR gyration and the perturbation behavior of the Alfvén wave, ϕ′. Now, let us consider the diffusion of the CR due to a multiple interaction in the random phase approximation on ϕ′. Suppose the CR enters the wave packets one after another. Each wave packet is tightly packed and each interaction occurs individually with the time of τ ≈ 2π/kv_z ≈ 2π/Ω. The CR can be regarded as in a random walk and the number of interaction occurring within a time of t is t/τ. In a random walk process, the square of the total change $⟨{\left(\mathrm{\Delta }\theta \right)}^2⟩$ is equal to the sum of the average of squares of each interaction $\sum ⟨{\left(\delta \theta \right)}^2⟩$. Thus, we obtain

$⟨{\left(\mathrm{\Delta }\theta \right)}^2⟩=\sum ⟨{\left(\delta \theta \right)}^2⟩=\frac{t}{\tau }\frac{{\pi }^2}{2}⟨{\left(\frac{\delta B}{\bar{B}}\right)}^2⟩,(8)$

where ⟨ cos ϕ′⟩ = 1/2 is used. The diffusion rate of the pitch angle becomes

$D_{\theta \theta }=\frac{\langle {\left(\mathrm{\Delta }\theta \right)}^2\rangle }{2t}=\frac{\pi }{8}\mathrm{\Omega }⟨{\left(\frac{\delta B}{\bar{B}}\right)}^2⟩.(9)$

Thus, the scattering particles becomes strong when the disturbances in the magnetic field are intense on the length scale comparable with the Larmor radius of the CRs. In the following, we omit the bracket ⟨…⟩. The large angle scattering (Δθ = π/2) takes a time of τ_sc = (π/2)²/D_θθ. Thus, the spatial diffusion coefficient becomes

$D_{zz}=\frac{1}{3}{\tau }_{\text{sc}}{v}^2\approx \frac{c}{3}{r}_{\text{L}}{\left(\frac{\delta B}{\bar{B}}\right)}^{-2},(10)$

where we regard v ≃ c for the CRs. A larger intensity of the disturbances δB results in a smaller spatial diffusion coefficient, indicating that the CRs are well confined by the pitch angle scattering. If the disturbances have a smooth energy spectrum P_B(k) = A_kk^−a, where A_k is a normalization factor, we obtain ${\left(\delta B/\bar{B}\right)}^2\approx k{P}_B(k)\approx A_k{r}_{\text{L}}^{a-1}$. Here the resonance condition k ≈ 1/r_L is used by omitting a numerical factor. Then, the diffusion coefficient becomes

$D_{zz}\approx \frac{c{A}_k}{3}{r}_{\text{L}}^{-a+2}\propto {\left(\frac{E}{\bar{B}}\right)}^{-a+2}.(11)$

The spectral slope of the magnetic energy spectrum is related to the energy dependence of the diffusion coefficient via the resonance condition. It should be noted that our analysis is restricted to the small amplitude Alfvén waves and the CRs are assumed to be the test particles. In magnetohydrodynamics (MHD), there is also fast and slow magnetosonic modes which are compressible modes unlike the Alfvén mode. Yan and Lazarian (2002) pointed out that in turbulent ISM (turbulence described by MHD), the resonant scattering by the fast mode can be more important for the diffusion coefficient than the Alfvén and slow modes. This conclusion is derived from the anisotropy of MHD turbulence: the Alfvén and slow modes propagating perpendicularly to the local magnetic-field cannot have a large amplitude while the fast mode can propagate isotropically. Note that even if the slow and Alfvén modes are likely dominated at a large astrophysical scale, the disturbances at a small gyro motion scale (say, $r_{\text{L}}\simeq 0.2\mathrm{A}\mathrm{U}(E/1\mathrm{G}\mathrm{e}\mathrm{V}){(\bar{B}/1\mu \text{G})}^{-1}$) is important. Therefore, the anisotropic cascading nature of the MHD turbulence becomes significant to estimate the diffusion coefficient. These arguments are employed to explain some features in CR data by Evoli and Yan (2014), and used for a systematic investigation with global CR transport simulations in Fornieri et al. (2021). Moreover, in turbulent media, the mean magnetic-field would vary spatially and temporally, also affecting the diffusion (e.g., Lazarian and Xu, 2021). When the energy density of the CR is large, the test particle approximation becomes not applicable. The electric current of the CR can induce magnetic-field disturbances and the CR would be scattered by the self-generated disturbances. Caprioli and Spitkovsky (2014) studied the diffusion coefficient in the CR accelerating shocks by using results of hybrid simulations though the hybrid simulations are generally limited to too short a timescale compared to actual SNR shocks. The injection process of the CRs in a well-developed shock is still unclear (i.e., the degree of the back reaction effects is not quantified yet). Diagnosing the nature of the turbulent magnetic-field in the SNR is a necessary step to quantify the diffusion coefficient and to study the CR acceleration.

3 Magnetic-Filed Structure in the Supernova Remnants

Global structures of the magnetic field in SNRs are measured by the radio synchrotron polarimetry (e.g., Dickel and Milne, 1976; Dickel et al., 1991; Reynolds and Gilmore, 1993; DeLaney et al., 2002; Reynoso et al., 2013; Dubner and Giacani, 2015). The synchrotron emission is radiated by relativistic electrons rotating around the magnetic field. The Lorentz force at the electron is always perpendicular to the direction of its motion and the emitted radiation fields is concentrated in the direction about the electron’s velocity due to the relativistic beaming effect. As a consequence, the observed photon is linearly polarized in the direction perpendicular to the direction of the magnetic field projected onto the sky (Westfold, 1959; Rybicki and Lightman, 1979). Hence, the magnetic field orientation is estimated by rotating the observed polarization orientation by 90°. Let N (γ_e) be the number density of electrons with the Lorentz factors between γ_e and γ_e + dγ_e. For a power-law distribution of electrons,

$N\left({\gamma }_{\text{e}}\right)d{\gamma }_{\text{e}}\propto {\gamma }_{\text{e}}^{-p}d{\gamma }_{\text{e}},(12)$

the total intensity per frequency ν (the Stokes I) can be written as

$i_{\nu }=K{\nu }^{-\alpha }{B_{\perp }}^{1+\alpha },(13)$

where K is a function linearly depending on the total density of the relativistic electrons, α = (p − 1)/2 is the spectral index of the radiated photons, and B_⊥ is the strength of the magnetic-field component perpendicular to the line of sight. The degree of polarization can be derived as (see, Westfold, 1959; Rybicki and Lightman, 1979),

$\mathrm{\Pi }=\frac{\alpha +1}{\alpha +5/3}\mathrm{o}\mathrm{r}\mathrm{\Pi }=\frac{p+1}{p+7/3}.(14)$

The photon spectra at the radio wavelength band show typically α ≈ 0.6 in the Galactic SNRs (e.g., Green, 2009). Thus, the polarization degree can be up to Π ≈ 0.7 if the magnetic field is completely aligned.

Figure 2 shows the magnetic-field orientation on SNR SN 1006 (Reynoso et al., 2013). The polarization degree is shown in Figure 3. The magnetic fields show the radial orientation with the polarization degree of p ∼ 20–30%. Interestingly, such radial orientation with p ∼ 20–30% is ubiquitously observed at “young” SNRs [Dickel et al. (1991) for SN 1572, DeLaney et al. (2002) for SN 1604, Dubner and Giacani (2015) for SNR Cas A, Zanardo et al. (2018) for SN 1987A, and see also Dickel and Milne (1976)]. In the case of SN 1006, we can find that some regions show transitions of the field orientation: the fields at the shock front are along to the tangential direction of the shell and rotate by 90° at far downstream regions (the southern west region is representative).

FIGURE 2

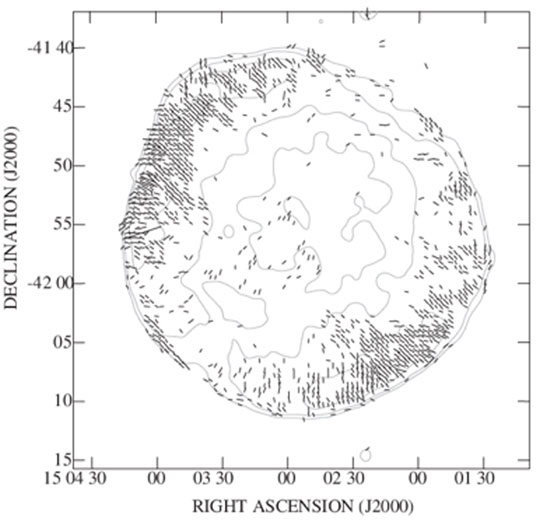
FIGURE 2. Magnetic-field orientation on SNR SN 1006 derived from the radio polarimetry at 10 arcsec resolution (1.4 GHz). The polarization angle is corrected for Faraday rotation (assuming uniform rotation measure as 12 rad m⁻²). Total intensity contours at 10, 20, and 50 mJy beam⁻¹ are superposed. For the bars, a length of 30 arcsec represents 0.25 mJy beam⁻¹ of polarized flux. This figure is taken from Reynoso et al. (2013, The Astronomical Journal, 145,4,104).

FIGURE 3

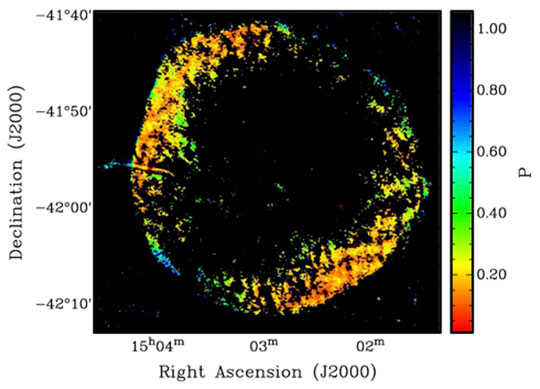
FIGURE 3. Fractional polarization of SN 1006 at 1.4 GHz. The resolution is 10 arcsec. Only pixels where p was at least twice its error were kept. This figure is taken from Reynoso et al. (2013, The Astronomical Journal,145,4,104).

Inoue et al. (2013) studied this field orientation by using three-dimensional MHD simulations and showed that the global, radial field-orientation can be explained by the downstream turbulence driven by the effect of rippled shock, namely Richtmyer-Meshkov instability (RMI). The RMI is induced by the interaction between the shock and upstream density fluctuations (see Sano et al., 2012, for details). Figure 4A shows two-dimensional slice of the magnetic-field strength (upper half) and the number density (lower half). The upstream magnetic-field is assumed to be uniformly aligned along the y-direction. The upstream density has fluctuations which follow the observed power spectra in the ISM (the so-called big power-law in the sky Armstrong et al., 1995). The initial density fluctuation is characterized by the mean density $\bar{\rho }$ and dispersion $\mathrm{\Delta }\rho \equiv \sqrt{⟨{\rho }^2⟩-{\bar{\rho }}^2}$. The power spectrum of the density fluctuation is assumed to be kP_ρ(k) ∝ k^−2/3 by following the observed spectra (Armstrong et al., 1995) and the fluctuations are given as a superposition of sinusoidal functions with various wave numbers ranging in 2π/L_box ≤ |k| ≤ 256π/L_box, where L_box = 2 pc is the box size. Note that the density fluctuations are assumed to be isotropic.

FIGURE 4

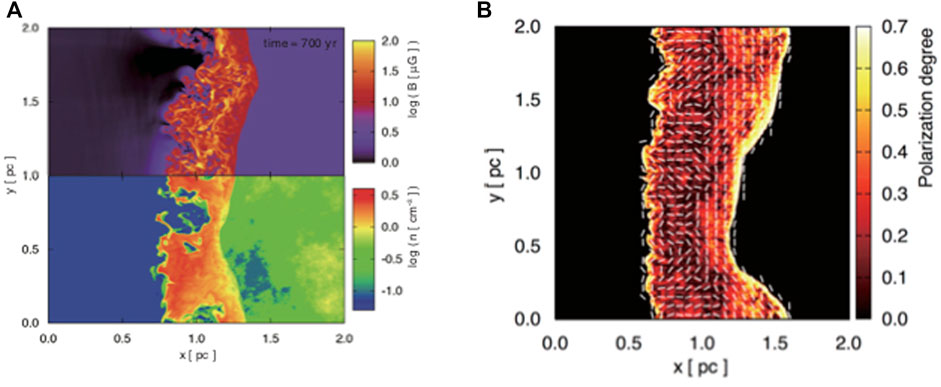
FIGURE 4. The simulation results of Inoue et al. (2013). The left panel (A) shows the two-dimensional slice of the magnetic-field strength (upper half) and the number density (lower half). The right panel (B) shows the results of synthetic observations of the synchrotron polarimetry. The white bars indicate the magnetic-field orientation and the color indicates the fractional polarization. Reproduced from Inoue et al. (2013, The Astrophysical Journal Letters,772,2,L204).

Figures 4A,B show the case of Δρ/⟨ρ⟩₀ = 0.3. The Alfvén Mach number estimated from the mean density is about 60 (the mean shock velocity is ${\bar{v}}_{\text{sh}}\simeq 1800{\mathrm{k}\mathrm{m}\mathrm{s}}^{-1}$). The shock front is rippled by reacting the upstream density fluctuations. Then, considering at the shock rest frame, the velocity component tangential to the shock front is transmitted to the downstream region without the shock dissipation. As a consequence, shear flows are generated at the downstream region. The sound waves are also generated at the downstream region due to the transmission of the density fluctuations (McKenzie and Westphal, 1968) and the waves modify the local circulation of the shear flow (vorticity mode), leading to a growth of the vorticity (Nishihara et al., 2010). Note that if there is only vorticity modes or sound modes, the vorticity would not grow (it may be understood by Crocco’s theorem in hydrodynamics). Hence, turbulence develops at the downstream region. The growth time of the RMI is estimated as t_RMI ∼ l_Δρ/v_RMI, where l_Δρ is a typical length scale of the density fluctuation, and $v_{\text{RMI}}\sim (\mathrm{\Delta }\rho /\bar{\rho })/(1+\mathrm{\Delta }\rho /\bar{\rho }){\bar{v}}_{\text{sh}}$, respectively (Sano et al., 2012; Inoue et al., 2013). The magnetic fields are amplified by the developed turbulence, i.e., by turbulent dynamo processes. From the upper part of Figure 4A, we can find that the fields can be amplified up to $\sim 100\mu \text{G}$ (see also Giacalone and Jokipii, 2007; Sano et al., 2012). Inoue et al. (2013) showed that the RMI-driven turbulence is anisotropic toward the direction of the shock travel. Figure 4B shows results of synthetic observations of the synchrotron polarimetry with assuming a uniform, spatial distribution of the CR electrons in the downstream region. The white bars indicate the magnetic-field directions estimated from the polarization angles and the color indicates the polarization degree. The results show very good agreements with the observations in particular the polarization degree and the transition of the polarization direction. The mean polarization degree is 20–30%. The transition of the magnetic-field directions may result from the turbulent modification of the magnetic field in the RMI-driven turbulence. The characteristic length-scale of the modification can be written as (Sano et al., 2012)

$l_{\text{RMI}}\sim \frac{{\bar{v}}_{\text{sh}}}{r_c}{t}_{\text{RMI}}\sim \frac{l_{\mathrm{\Delta }\rho }}{r_{c}A},(15)$

where r_c is the shock compression ratio and $A\equiv (\mathrm{\Delta }\rho /\bar{\rho })/(1+\mathrm{\Delta }\rho /\bar{\rho })$ is the Atwood number. Since the compression ratio converges quickly to a value of four in the monoatomic gas, the characteristic length and the transition length are insensitive on the Mach number. Inoue et al. (2013) confirmed the insensitivity of the transition length on the Mach number by comparing the cases of ${\bar{v}}_{\text{sh}}\sim 1800{\mathrm{k}\mathrm{m}\mathrm{s}}^{-1}$ and ${\bar{v}}_{\text{sh}}\simeq 3600{\mathrm{k}\mathrm{m}\mathrm{s}}^{-1}$ (the other parameters are the same as each case). Thus, the radial orientation of the magnetic fields in the young SNRs can be explained by the RMI-driven turbulence. It should be notice that in this scenario, the downstream turbulence is super Alfvénic and the CR back reaction effects are implicitly assumed to be small. If there is significant amplification of the magnetic fields due to the CR back reactions, trans- or sub-Alfvénic turbulence can be driven. If the case that, the “bending” of the magnetic field by turbulent motions is modest, so the RMI scenario should be improved. Further investigations on the nature of the turbulent magnetic-fields are required.

It is known that the Alfvénic, incompressible turbulence is anisotropic with respect to a local magnetic-field direction (Goldreich and Sridhar, 1995; Lazarian and Vishniac, 1999; Cho and Vishniac, 2000; Maron and Goldreich, 2001) though Inoue et al. (2013) assumed an isotropic density fluctuations in the ISM.¹ The density fluctuations of MHD turbulence are likely associated with the presence of compressive modes (slow and fast magnetosonic modes). The slow modes follow the anisotropy seen in the Alfvénic turbulence with a scaling relation of kP(k) ∝ k^−2/3 while the fast modes are likely developing a more isotropic cascades with a scaling relation of kP(k) ∝ k^−1/2. Zhang et al. (2020) recently reported that the large scale turbulence in the multi-phase ISM can be associated to the magnetosonic modes. From the results reported by Armstrong et al. (1995) and Zhang et al. (2020), the slow modes dominated turbulence may be driven in the ISM. The influence of the anisotropy in the pre-existing upstream turbulence on the downstream RMI turbulence may also be interesting subject.

The difference on the associated cascades not only has consequences on the CR diffusion (Yan and Lazarian, 2002; Evoli and Yan, 2014; Fornieri et al., 2021; Lazarian and Xu, 2021; Hu et al., 2022), but potentially also on the differential heating/energization of the ions or electrons (i.e., depending on the main mechanism at play, e.g., Chandran et al., 2010; Howes, 2010; Cranmer, 2014; Comisso and Sironi, 2019; Rowan et al., 2019; Zhdankin et al., 2019; Kawazura et al., 2020; Cerri et al., 2021; Zhdankin, 2021). How much energies left to heat/energize the electrons at smaller scales (e.g., the electron cyclotron scales), after part of it has been dissipated by ion heating/energization at larger scales (e.g., the ion cyclotron scales), is crucial to determine the CR electron population (the density and spectral slope) which is related to the synchrotron emissivity and is assumed to be spatially uniform in the analysis by Inoue et al. (2013) and the synchrotron correlation introduced later. The observational results of the kinetic scale turbulence in the solar wind are summarized by Goldstein et al. (2015).

West et al. (2017) argued another explanation on the radial magnetic-field orientation assuming the injection and diffusion of the CR electrons. In their scenario, the electrons are selectively accelerated at “locally” quasi-parallel shocks. They assumed that the CR-electron density is concentrated at the region adjacent to the shock front and the density is scaled by cos²2ϕ_B, where ϕ_B is the angle between the shock normal and the post-shock magnetic field. Then, the observed orientation is biased toward the radial direction even if the intrinsic distribution of the magnetic-field directions is isotropic. They also argued the case of quasi-perpendicular shock (the density of the CR electrons is scaled by sin²2ϕ_B) and pointed out that the polarization properties can be similar to the case of SN 1006 if there is radially aligned magnetic fields. Recent investigations on the injection of CR electrons suggest that the quasi-perpendicular shock is favored to accelerate the electrons efficiently (Katou and Amano, 2019; Amano et al., 2020; Amano and Hoshino, 2022). Thus, the combination of the efficient acceleration at quasi-perpendicular shocks and the existence of the radially aligned magnetic fields may be favored though the assumption about the CR diffusion remains to be resolved.

4 Diagnostics of the Turbulent Magnetic-Field in the Supernova Remnants

The spectral slopes of the magnetic energy in SNRs are recently examined by spatial two-point correlation functions of synchrotron intensities (Roy et al., 2009; Shimoda et al., 2018a; Saha et al., 2019; Vishwakarma and Kumar, 2020; Saha et al., 2021). Lazarian and Pogosyan (2012, 2016) provided mathematical formalisms describing how the correlation functions of synchrotron intensities are related to the energy spectrum of magnetic disturbances. Here we review simplify analysis (see also appendix of Shimoda et al., 2018a).

Defining position vectors of the two-point r and r′, the second-order correlation function of the local synchrotron intensity is written as

$C_{i_{\nu },\alpha }^{\left(2\right)}={⟨i_{\nu }\left(\mathit{r}\right)i_{\nu }\left(\mathit{r}+\mathit{l}\right)⟩}_{\mathit{r}},(16)$

where i_ν is the local synchrotron intensity given by Eq. 13 and l ≡r′ − r. The bracket ⟨…⟩_r means the statistical average which is given by a volume average. The local intensity of the synchrotron radiation depends on ${B_{\perp }}^{1+\alpha }$. Thus, with assuming spatially uniform distribution of CR electrons, the second-order correlation function of the synchrotron intensity is related to the correlation of the magnetic-field strength as

$C_{i_{\nu },\alpha }^{\left(2\right)}\propto {⟨B_{\perp }{\left(\mathit{r}\right)}^{1+\alpha }{B}_{\perp }{\left(\mathit{r}+\mathit{l}\right)}^{1+\alpha }⟩}_{\mathit{r}}.(17)$

When α = 0 (i.e. p = 0), the function reproduces the correlation of the magnetic-field strength. The case of α = 1 (p = 3) is also simple and can be representative for the case of arbitrary α. In the following, we omit the notations as B_⊥(r) → B_⊥ and $B_{\perp }(\mathit{r}+\mathit{l})\to B_{\perp }^{\prime }$. Then, the correlation function can be written as

$\begin{array}{ll}\hfill C_{i_{\nu },\alpha =2}^{\left(2\right)}\propto {⟨{B_{\perp }}^2{B_{\perp }^{\prime }}^2⟩}_{\mathit{r}}& =\frac{{⟨{B_{\perp }}^4+{B_{\perp }^{\prime }}^4⟩}_{\mathit{r}}}{2}-\frac{1}{2}\hfill \\ \hfill & {⟨{\left(B_{\perp }+B_{\perp }^{\prime }\right)}^2{\left(B_{\perp }-B_{\perp }^{\prime }\right)}^2⟩}_{\mathit{r}}.\hfill \end{array}(18)$

Decomposing the magnetic-field strength into the mean strength ${\bar{B}}_{\perp }={⟨B_{\perp }⟩}_{\mathit{r}}$ and the fluctuating component $\mathrm{\Delta }{B}_{\perp }=B_{\perp }-{\bar{B}}_{\perp }$, we can rewrite the above equation as

$\begin{array}{ll}\hfill C_{i_{\nu },\alpha =2}^{\left(2\right)}\propto {⟨{B_{\perp }}^2{B_{\perp }^{\prime }}^2⟩}_{\mathit{r}}& =\frac{{⟨{B_{\perp }}^4+{B_{\perp }^{\prime }}^4⟩}_{\mathit{r}}}{2}-2{\bar{B}}_{\perp }\hfill \\ \hfill & ⟨{\left(1+\frac{\mathrm{\Delta }{B}_{\perp }+\mathrm{\Delta }{B}_{\perp }^{\prime }}{{\bar{B}}_{\perp }}\right)}^2\hfill \\ \hfill & {{\left(\frac{\mathrm{\Delta }{B}_{\perp }-\mathrm{\Delta }{B}_{\perp }^{\prime }}{{\bar{B}}_{\perp }}\right)}^2⟩}_{\mathit{r}}.\hfill \end{array}(19)$

For small standard deviations of the fluctuating strength $|\left(\mathrm{\Delta }{B}_{\perp }+\mathrm{\Delta }{B}_{\perp }^{\prime }\right)/{\bar{B}}_{\perp }|<1$, we obtain

$\begin{array}{ll}\hfill C_{i_{\nu },\alpha =2}^{\left(2\right)}\propto \langle {B_{\perp }}^2{B_{\perp }^{\prime }}^2{\rangle }_{\mathit{r}}& \approx \frac{\langle {B_{\perp }}^4+{B_{\perp }^{\prime }}^4{\rangle }_{\mathit{r}}}{2}-2{\bar{B}}_{\perp }\hfill \\ \hfill & {⟨{\left(\frac{\mathrm{\Delta }{B}_{\perp }-\mathrm{\Delta }{B}_{\perp }^{\prime }}{{\bar{B}}_{\perp }}\right)}^2⟩}_{\mathit{r}}\hfill \\ \hfill & =4{{\bar{B}}_{\perp }}^2\langle \mathrm{\Delta }{B}_{\perp }\mathrm{\Delta }{B}_{\perp }^{\prime }{\rangle }_{\mathit{r}}+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.,\hfill \end{array}(20)$

where we have assumed statistically homogenous turbulent fields as ${⟨{B_{\perp }}^4⟩}_{\mathit{r}}={⟨{B_{\perp }^{\prime }}^4⟩}_{\mathit{r}}$ and ${⟨{B_{\perp }}^2⟩}_{\mathit{r}}={⟨{B_{\perp }^{\prime }}^2⟩}_{\mathit{r}}$. Hence, the correlation function $C_{i_{\nu },\alpha =2}^{(2)}$ reproduces the second-order correlation of the magnetic-field strength. Note that even if the turbulent fields are completely random without the mean component, the approximation of the small standard deviation is valid for small scales. This is because the disturbances on the larger scales act as a guide field for the field disturbances on the smaller scales (Lazarian and Vishniac, 1999; Cho and Vishniac, 2000; Cho and Lazarian, 2003). Lazarian and Pogosyan (2012) showed relations of

$\frac{\langle {B_{\perp }}^2{B_{\perp }^{\prime }}^2{\rangle }_{\mathit{r}}}{\langle {B_{\perp }}^4{\rangle }_{\mathit{r}}-\langle {B_{\perp }}^2{\rangle }_{\mathit{r}}^2}\approx \frac{\langle {B_{\perp }}^{1+\alpha }{B_{\perp }^{\prime }}^{1+\alpha }{\rangle }_{\mathit{r}}}{\langle {B_{\perp }}^{2\left(1+\alpha \right)}{\rangle }_{\mathit{r}}-\langle {B_{\perp }}^{1+\alpha }{\rangle }_{\mathit{r}}^2}(21)$

for several α for a power-law correlation function of B_⊥. In the range of 0.2 ≤ α ≤ 2, they reported that the maximum difference of ${⟨{B_{\perp }}^{1+\alpha }{B_{\perp }^{\prime }}^{1+\alpha }⟩}_{\mathit{r}}$ from ${⟨{B_{\perp }}^2{B_{\perp }^{\prime }}^2⟩}_{\mathit{r}}$ is only three per cent. Thus, the correlation functions with 0.2 ≤ α ≤ 2 can be written as

$C_{i_{\nu },\alpha }^{\left(2\right)}\propto \langle {B_{\perp }}^{1+\alpha }{B_{\perp }^{\prime }}^{1+\alpha }{\rangle }_{\mathit{r}}\approx D\left(\alpha \right)\langle {B_{\perp }}^2{B_{\perp }^{\prime }}^2{\rangle }_{\mathit{r}}.(22)$

where D(α) is a function of α. This argument is numerically confirmed by Lee et al. (2016). They performed synthetic observations of synchrotron radiations from simulated magnetic fields and derived the Fourier power spectrum from the correlation of the observed synchrotron polarization intensity for the parameter range of 0.5 ≤ α ≤ 3. They found that the power spectrum successfully reproduced the spectral index of the given magnetic fields. In the case of SNRs, the index of photon spectrum is typically α ≈ 0.6 (e.g., Green, 2009). Thus, the correlation function $C_{i_{\nu },\alpha }^{(2)}$ can reproduce the second-order correlation of the magnetic-field strength in the SNRs.

The correlation functions derived from the “observed” synchrotron emissions suffer from the uncertainty of the geometry of the emission regions via the projection effects. We define the observed intensity of the synchrotron emission per frequency at the two-dimensional sky position X = (x, y) as

$I_{\nu }\left(\mathit{X}\right)={\int }_0^{L\left(\mathit{X}\right)}K{\nu }^{-\alpha }{B}_{\perp }{\left(\mathit{X},z\right)}^{1+\alpha }dz,(23)$

where the z represents the coordinate along the line of sight and L(X) is the extent of the emission region. The correlation function for I_ν is written as

$C_{I_{\nu }}^{\left(2\right)}\left(\mathit{\lambda }\right)=\frac{\int I_{\nu }\left(\mathit{X}\right)I_{\nu }\left({\mathit{X}}^{\prime }\right)}{\int d^2\mathit{X}}\equiv {⟨I_{\nu }\left(\mathit{X}\right)I_{\nu }\left(\mathit{X}+\mathit{\lambda }\right)⟩}_{\mathit{X}},(24)$

where λ = X′ −X is the position vector of two separated positions in the sky X and X′. Then, the correlation function can be represented as

$\begin{array}{ll}\hfill C_{I_{\nu }}^{\left(2\right)}\left(\mathit{\lambda }\right)& =K{\nu }^{-\alpha }{\int }_0^{L\left(\mathit{X}\right)}dz{\int }_0^{L\left({\mathit{X}}^{\prime }\right)}d{z}^{\prime }⟨B_{\perp }{\left(\mathit{X},z\right)}^{1+\alpha }\hfill \\ \hfill & {B_{\perp }{\left(\mathit{X}+\mathit{\lambda },z^{\prime }\right)}^{1+\alpha }⟩}_{\mathit{X}}.\hfill \end{array}(25)$

For the constant L(X) = L₀, Lazarian and Pogosyan (2012) and Lee et al. (2016) demonstrated that $C_{I_{\nu }}^{(2)}$ reproduces the scaling relation of a given magnetic-field correlation. If L varies spatially, $C_{I_{\nu }}^{(2)}$ is affected by the geometrical structure of the emission region which is usually unknown. However, the emission regions of some young SNRs are known to be spherical. If we select the two points X and X′ on the concentric circle of the SNR image, the condition of L(X) = constant is satisfied (Shimoda et al., 2018a). Figure 5 shows a schematic of the SNR shell and projected image. Hence, the correlation can be analyzed in SNRs with shell like geometry.Shimoda et al. (2018a) demonstrated the spatial two-point correlation analysis of the synchrotron intensity for SN 1572. Figure 6 shows regions where they analyze the two-point correlations. The original image data are published in Williams et al. (2016). The analyzed correlation functions are shown in Figure 7. The intensity correlation functions follow a power-law and the spectral slopes are close to the Kolmogorov scaling λ^2/3. When the Aflvén Mach number of turbulence is approximately unity, i.e., M_A,turb ≡ u_inj/V_A, where u_inj is the turbulent velocity at the injection scale, the magnetic energy can have such single power-law spectrum (Goldreich and Sridhar, 1995, and see also Brandenburg and Lazarian, 2013 for reviews). The shock velocity of the SN 1572 is estiamted as V_sh ∼ 5000 km s⁻¹ (Williams et al., 2016). If we consider the typical magnetic-field strength in the ISM (∼ 3 μG Beck, 2001) and number density of $\sim 1{\text{cm}}^{-3}$, we obtain M_A,turb ∼ 500 with assuming u_inj ∼ V_sh. Thus, the correlations at the outer circles (R ≳ 0.9R_SNR) imply smaller turbulent velocity as u_inj ≪ V_sh and/or larger magnetic-field strength at R ≳ 0.9R_SNR. As we dicussed in Section 3, turbulence can be driven in the downstream region due to the existence of upstream density flucuations with the significant field amplification. Williams et al. (2013) examined the ambient density structure of SN 1572 from infrared dust emissions and found ourder-of-magnitude variations in the density at the length scale of l_Δρ ∼ R_SNR (along the azimuthal angle direction of the shell). Therefore, u_inj ∼ V_sh may be satisfied. Then, the characteristic length of the field amplification due to the RMI-driven turbulence is estimated as $l_{\text{RMI}}\sim 0.2R_{\text{SNR}}(l_{\mathrm{\Delta }\rho }){(r_c/4)}^{-1}$, where the Atwood number $A\equiv (\mathrm{\Delta }\rho /\bar{\rho })/(1+\mathrm{\Delta }\rho /\bar{\rho })$ is approxmated as unity. Thus, the condition of M_A,turb ≃ 1 can be satisfied at the outer region R ≳ 0.9R_SNR due to the field-amplification by the RMI-driven turbulence. In this scneario, in the dowsntream region just behind the shock front, the magnetic-field strength is not large yet and thus the turbulence should be super-Alfvénic (M_A,turb > 1). In the super-Alfvénic turbulence, the Kolmogorov-like scaling λ^2/3 is seen on a length scale smaller than l_A, at which turbulent velcoity is equal to the Alfvén velocity. With progress of the turbulent dynamo, the l_A evoleves toward a larger length-scale with increasing the distance from the shock front. On the other hand, if the fields are significantly amplified by the CR back reaction effects, which occur at upstream, such evolution would not be observed. Therefore, we are able to examine the real field-amplification scenario once the most outer circle (R = 1.00R_SNR) is resolved. For such observation, we need a higher sensitivity with sub-arcsecond resolution at GHz band. Future interferometric observations (e.g., by the Squre Kilometer Array; SKA) will provide such data and may distinguish these scenario. The inner circes (R ≲ 0.9R_SNR) show flatter spectra than the outer ones (R ≳ 0.9R_SNR) at larger scalse λ/R ≳ 0.2. In SN 1572, the contact discontinuity, at which Rayleigh-Taylor instability (RTI) works, is located at R ≈ 0.9R_SNR (Warren et al., 2005). The correlation function of the synchrotron intensity can reflect the correlation of the magnetic-field only if the fluctuating components of the field are weak as $|(\mathrm{\Delta }{B}_{\perp }+\mathrm{\Delta }{B}_{\perp }^{\prime })/{\bar{B}}_{\perp }|<1$. Lee et al. (2016) analyzed synthetically the intensity correlations for magnetic disturbances, which have the Kolmogrov-like power spectrum, without the mean field. They obtained such intensity correlation flattend at nearby the injection scale of turbulence. Note that in such case, fluctuating componets at a larger scale act as a guide field for fluctuations at a smaller scale, so the intensity correlation functions can reporoduce given the magnetic energy spectrum at the smaller scales. Thus, if the RTI behaves as an additional, large energy injection mechanism of turbulence at R ≈ 0.9R_SNR, the intensity correlations could be flattened. This arugumet may require relatively large growth rate of the RTI. The rate depends on the ambitent density sturucture, the initial ejecta profile including the anisotropies, and the effective addiabatic index for instance. These effects on the groeth rate can be studied via the relative distance between the shock front and fronts of the “fingers” of the RTI (e.g., Warren et al., 2005; Orlando et al., 2012; Bao et al., 2021; Orlando et al., 2022). The investigations of the RTI and RMI are on-going (Zhou et al., 2021, for recent reviews).

FIGURE 5

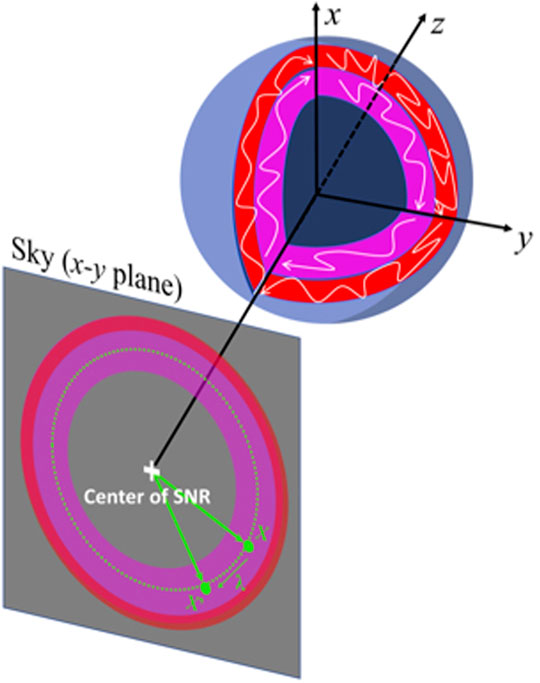
FIGURE 5. Schematic of SNR shell and projected image. The blue spherical shell with partial cross-sections shows the SNR shell. The line of sight is along the z-axis, and the x–y plane corresponds to the projected sky. The white lines schematically indicate turbulent magnetic-fields. The synchrotron radiations from turbulent media are projected onto the sky (red and magenta toruses). The white cross indicates the center of the SNR image. If we analyze the intensity correlation between the two positions X and X′ = X + λ on the concentric circle (the green dots), the line of sight extent L(X) becomes constant and the correlation functions is not affected by the structure of the SNR shell. Reproduced form Shimoda et al. (2018a, Monthly Notices of the Royal Astronomical Society,480,2200).

FIGURE 6

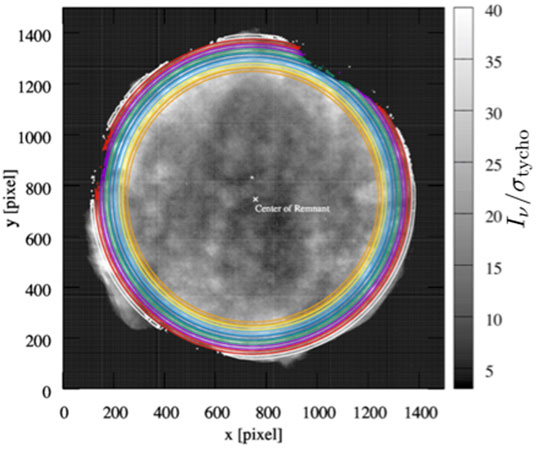
FIGURE 6. Radio synchrotron intensity image of SN 1572. The image noise level is σ_tycho = 5.3 × 10^–5 Jy beam⁻¹. x and y are in units of the number of pixels (one pixcel size is 0.4 arcsec). The origin of the coordinates (J2000) is (R.A, Dec.)=(0^h25^m19^s.1, +64°08′23.0″). The region enclosed by colored lines (white, red, purple, green, blue, light blue, yellow, and orange) indicate I_ν ≥ 3σ_tycho at each concentric circle (R = 1.00R_SNR, 0.97R_SNR, 0.94R_SNR, 0.91R_SNR, 0.88R_SNR, 0.85R_SNR, 0.82R_SNR, and 0.79R_SNR), where R_SNR = 632 pixcels ≈253 arcsec ≈5 pc is the radius of the SNR. The width of each circle is set to be 0.0091 R_SNR. Reproduced form Shimoda et al. (2018a, Monthly Notices of the Royal Astronomical Society, 480,2200).

FIGURE 7

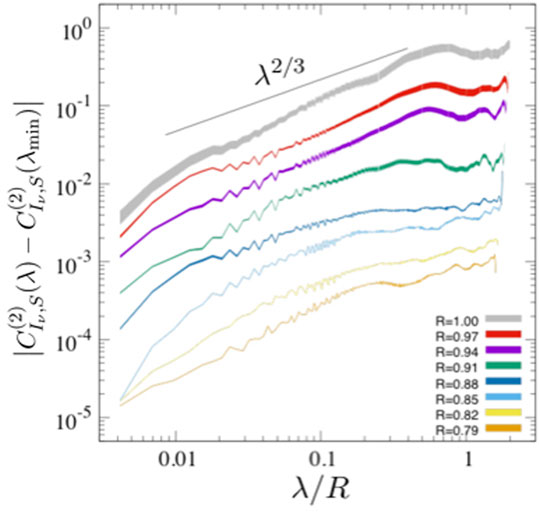
FIGURE 7. Second-order correlation functions of the observed synchrotron intensities per frequency I_ν, which imply the spectra of magnetic energy in SN 1572. To clarify the fluctuating component of the correlation, the subtraction of $|C^{{(2)}_{I_{\nu }}}(\lambda )-C^{{(2)}_{I_{\nu }}}({\lambda }_{\text{min}})|$, where λ = |λ| and λ_min ≈ 1.4 arcsec is the minimum separation distance between X′ and X. The results are normalized to be ordered according to the radius of the concentric circles as R = 1.00R_SNR (gray), 0.97R_SNR (red), 0.94R_SNR (purple), 0.91R_SNR (green), 0.88R_SNR (blue), 0.85R_SNR (light blue), 0.82R_SNR (yellow), and 0.79R_SNR (orange), from top to bottom. Reproduced form Shimoda et al. (2018a, Monthly Notices of the Royal Astronomical Society,480,2200).

Vishwakarma and Kumar (2020) reported similar results of the intensity correlations in SNR Cas A by using the same method as Shimoda et al. (2018a).² The correlation functions in Cas A show also the Kolmogrov-like scaling and are flattened at inner regoins. These results imply that the magnetic energy spectra in young SNRs can be understood in similar ways to the case of SN 1572. Systematic investigations of the synchrotron intensity in young SNRs with shell-like geometries would bring useful insights about the nature of turbulence in future.

5 Discussion

This review introduce recent investigations of the magnetic field structures in young SNRs. The correlation analysis of the synchrotron intensities are significant progress for studying the magnetic energy spectra which are closely related to the diffusion coefficient of the CRs. Future observations with high sensitivity and angular resolution at GHz band could examine whether the CR back reaction effects are significant in the SNR shocks or not; this would be a science case of the SKA.

The relations between the nature of magnetic disturbances and the CR injection at the shock front are also interesting subject, however, the CR injection processes are one of the most uncertain issues in the SNR shocks. Helder et al. (2009) pointed out that if the shock produce the CRs with consuming a significant fraction of its kinetic energy, the downstream temperature becomes lower than the case of adiabatic shocks without the CRs (see also Morlino et al., 2013; Shimoda et al., 2015; Hovey et al., 2018; Shimoda et al., 2018b; Shimoda et al., 2022). Thus, once the shock velocity and downstream temperature are independently measured, we can estimate the CR injection efficiency. The shock velocity is measured from the expansion rate of the SNR shell. The downstream ion temperature is measured from widths of the atomic line emissions. The line width is also affected by the turbulent Doppler broadening. Shimoda et al. (2022) constructed a novel CR injection model in SNR shocks and performed synthetic observations of the X-ray line emissions in SNR RCW 86 considering the turbulent Doppler broadening in the downstream region. They found that the observed line width in the CR accelerating shock becomes sufficiently smaller than the case without the CRs even if the turbulence exists. They also found that future X-ray spectroscopic observations by XRISM (Tashiro et al., 2020) and Athena (Barret et al., 2018) can resolve the line width to distinguish whether the shock accelerates the CRs or not. Thus, by a combination of the future observations of the X-ray atomic line observations and correlation analysis of the radio synchrotron intensities, the interplays between the CRs and background plasma can be observationally studied.

In this review, we introduce studies at relatively “young” SNRs at which the shock speed are large. A larger shock speed is preferred for the confinement of the diffusing CRs around the shock front by the advection. For the study of SNRs as energy sources of the ISM turbulence, investigating an ‘old’ SNR is also important. The blast wave of an SNR expands with accumulating the ISM. When the accumulated mass is comparable to the ejecta mass of the supernova, the blast wave begins to decelerate (Sedov, 1959), then the radiative cooling of the shocked ISM and ejecta becomes important, and finally merges into the ISM. Raymond et al. (2020a,b) recently reported observational results at radiative shocks of the SNR Cygnus Loop, provided various shock parameters in the cooling layer (shock speed, ram pressure, density, compression ratio, dust destruction efficiency, magnetic field strength, and vorticity), and discussed the radio synchrotron emissivity by CR electrons, pion decay emission by CR nuclei, and thermal/thin-shell instabilities of thermal gas. The future (soft) X-ray observations by XRISM and Athena may also contribute or improve such study by providing more accurate plasma diagnostics.

Author Contributions

JS was responsible for writing and editing the manuscript.

Funding

This work is supported by JSPS Grant-in-Aid for Scientific Research No. 20J01086.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

JS thanks the reviewers for their useful comments and various contributions from Shu-ichiro Inutsuka, Estela Reynoso, and Tsuyoshi Inoue.

Footnotes

¹The anisotropy was originally defined along a mean field which is fixed along an axis of the global system of reference (Goldreich and Sridhar, 1995). Later investigations (Lazarian and Vishniac, 1999; Cho and Vishniac, 2000; Maron and Goldreich, 2001; Cho and Lazarian, 2003) showed that the anisotropy discussed by Goldreich and Sridhar (1995) appears along the local field whose direction can vary from point-to-point.

²Saha et al. (2019) and Saha et al. (2021) analyzed the correlations in the SN 1604 and SNR Cas A, respectively, using the interferometric data directly (i.e., the data are represented in the Fourier space), a different approach to that of Shimoda et al. (2018a). In this way, the geometrical effects are not concerned and only over all spectrum is obtained unlike the cases of Shimoda et al. (2018a) and Vishwakarma and Kumar (2020).

References

Amano, T., and Hoshino, M. (2022). Theory of Electron Injection at Oblique Shock of Finite Thickness. The Astrophy. J. 927 (1), 22. doi:10.3847/1538-4357/ac4f49

CrossRef Full Text | Google Scholar

Amano, T., Katou, T., Kitamura, N., Oka, M., Matsumoto, Y., Hoshino, M., et al. (2020). Observational Evidence for Stochastic Shock Drift Acceleration of Electrons at the Earth's Bow Shock. Phys. Rev. Lett. 124, 065101. doi:10.1103/PhysRevLett.124.065101

PubMed Abstract | CrossRef Full Text | Google Scholar

Armillotta, L., Krumholz, M. R., and Di Teodoro, E. M. (2020). The Life Cycle of the Central Molecular Zone - II. Distribution of Atomic and Molecular Gas Tracers. Mon. Notices R. Astronomical Soc. 493, 5273–5289. doi:10.1093/mnras/staa469

PubMed Abstract | CrossRef Full Text | Google Scholar

Armstrong, J. W., Rickett, B. J., and Spangler, S. R. (1995). Electron Density Power Spectrum in the Local Interstellar Medium. Astronomical J. 443, 209. doi:10.1086/175515

CrossRef Full Text | Google Scholar

Bao, B., Peng, Q., Yang, C., and Zhang, L. (2021). Evolutions of Young Type Ia Supernova Remnants with Two Initial Density Profiles in a Turbulent Medium. Astronomical J. 909, 173. doi:10.3847/1538-4357/abe124

CrossRef Full Text | Google Scholar

Barret, D., Lam Trong, T., den Herder, J.-W., Piro, L., Cappi, M., Houvelin, J., et al. (2018). “The ATHENA X-Ray Integral Field Unit (X-IFU),” in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray. Editors J.-W. A. den Herder, S. Nikzad, and K. Nakazawa (Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series), 10699, 106991G. doi:10.1117/12.2312409

CrossRef Full Text | Google Scholar

Beck, R. (2001). Galactic and Extragalactic Magnetic Fields. Space Sci. Revies 99, 243–260. doi:10.1007/978-94-017-3239-0_21

CrossRef Full Text | Google Scholar

Bell, A. R. (1978). The Acceleration of Cosmic Rays in Shock Fronts - I. Mon. Notices R. Astronomical Soc. 182, 147–156. doi:10.1093/mnras/182.2.147

CrossRef Full Text | Google Scholar

Bell, A. R. (2004). Turbulent Amplification of Magnetic Field and Diffusive Shock Acceleration of Cosmic Rays. Mon. Notices R. Astronomical Soc. 353, 550–558. doi:10.1111/j.1365-2966.2004.08097.x

CrossRef Full Text | Google Scholar

Blandford, R. D., and Ostriker, J. P. (1978). Particle Acceleration by Astrophysical Shocks. Astronomical J. 221, L29–L32. doi:10.1086/182658

CrossRef Full Text | Google Scholar

Boulares, A., and Cox, D. P. (1990). Galactic Hydrostatic Equilibrium with Magnetic Tension and Cosmic-Ray Diffusion. Astronomical J. 365, 544. doi:10.1086/169509

CrossRef Full Text | Google Scholar

Brandenburg, A., and Lazarian, A. (2013). Astrophysical Hydromagnetic Turbulence. Space Sci. Rev. 178, 163–200. doi:10.1007/s11214-013-0009-3

CrossRef Full Text | Google Scholar

Burkhart, B. (2021). Diagnosing Turbulence in the Neutral and Molecular Interstellar Medium of Galaxies. PASP 133, 102001. doi:10.1088/1538-3873/ac25cf

CrossRef Full Text | Google Scholar

Caprioli, D., Haggerty, C. C., and Blasi, P. (2020). Kinetic Simulations of Cosmic-Ray-modified Shocks. II. Particle Spectra. Astronomical J. 905, 2. doi:10.3847/1538-4357/abbe05

CrossRef Full Text | Google Scholar

Caprioli, D., and Spitkovsky, A. (2014). Simulations of Ion Acceleration at Non-relativistic Shocks. III. Particle Diffusion. Astronomical J. 794, 47. doi:10.1088/0004-637X/794/1/47

CrossRef Full Text | Google Scholar

Caprioli, D., Zhang, H., and Spitkovsky, A. (2018). Diffusive Shock Re-acceleration. J. Plasma Phys. 84, 715840301. doi:10.1017/S0022377818000478

CrossRef Full Text | Google Scholar

Cerri, S. S., Arzamasskiy, L., and Kunz, M. W. (2021). On Stochastic Heating and its Phase-Space Signatures in Low-Beta Kinetic Turbulence. Astronomical J. 916, 120. doi:10.3847/1538-4357/abfbde

CrossRef Full Text | Google Scholar

Chandran, B. D. G., Li, B., Rogers, B. N., Quataert, E., and Germaschewski, K. (2010). Perpendicular Ion Heating by Low-Frequency Alfvén-Wave Turbulence in the Solar Wind. Astronomical J. 720, 503–515. doi:10.1088/0004-637X/720/1/503

CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2003). Compressible Magnetohydrodynamic Turbulence: Mode Coupling, Scaling Relations, Anisotropy, Viscosity-Damped Regime and Astrophysical Implications. Mon. Notices R. Astronomical Soc. 345, 325–339. doi:10.1046/j.1365-8711.2003.06941.x

CrossRef Full Text | Google Scholar

Cho, J., and Vishniac, E. T. (2000). The Anisotropy of Magnetohydrodynamic Alfvenic Turbulence. Astronomical J. 539, 273–282. doi:10.1086/309213

CrossRef Full Text | Google Scholar

Comisso, L., and Sironi, L. (2019). The Interplay of Magnetically Dominated Turbulence and Magnetic Reconnection in Producing Nonthermal Particles. Astronomical J. 886, 122. doi:10.3847/1538-4357/ab4c33

CrossRef Full Text | Google Scholar

Cranmer, S. R. (2014). Ensemble Simulations of Proton Heating in the Solar Wind via Turbulence and Ion Cyclotron Resonance. Astronomical J. 213, 16. doi:10.1088/0067-0049/213/1/16

CrossRef Full Text | Google Scholar

Crumley, P., Caprioli, D., Markoff, S., and Spitkovsky, A. (2019). Kinetic Simulations of Mildly Relativistic Shocks - I. Particle Acceleration in High Mach Number Shocks. Mon. Notices R. Astronomical Soc. 485, 5105–5119. doi:10.1093/mnras/stz232

CrossRef Full Text | Google Scholar

DeLaney, T., Koralesky, B., Rudnick, L., and Dickel, J. R. (2002). Radio Spectral Index Variations and Physical Conditions in Kepler's Supernova Remnant. ApJ 580, 914–927. doi:10.1086/343787

CrossRef Full Text | Google Scholar

Dickel, J. R., van Breugel, W. J. M., and Strom, R. G. (1991). Radio Structure of the Remnant of Tycho's Supernova (SN 1572). Astronomical J. 101, 2151. doi:10.1086/115837

CrossRef Full Text | Google Scholar

Diesing, R., and Caprioli, D. (2018). Effect of Cosmic Rays on the Evolution and Momentum Deposition of Supernova Remnants. Phys. Rev. Lett. 121, 091101. doi:10.1103/PhysRevLett.121.091101

PubMed Abstract | CrossRef Full Text | Google Scholar

Drury, L. O. C., and Voelk, J. H. (1981). Hydromagnetic Shock Structure in the Presence of Cosmic Rays. Astrophysical J. 248, 344–351. doi:10.1086/159159

CrossRef Full Text | Google Scholar

Dubner, G., and Giacani, E. (2015). Radio Emission from Supernova Remnants. Astron Astrophys. Rev. 23, 3. doi:10.1007/s00159-015-0083-5

CrossRef Full Text | Google Scholar

Evoli, C., and Yan, H. (2014). Cosmic Ray Propagation in Galactic Turbulence. Astrophysical J. 782, 36. doi:10.1088/0004-637X/782/1/36

CrossRef Full Text | Google Scholar

Ferrière, K. M. (2001). The Interstellar Environment of Our Galaxy. Rev. Mod. Phys. 73, 1031–1066. doi:10.1103/revmodphys.73.1031

CrossRef Full Text | Google Scholar

Fornieri, O., Gaggero, D., Cerri, S. S., De La Torre Luque, P., and Gabici, S. (2021). The Theory of Cosmic Ray Scattering on Pre-existing MHD Modes Meets Data. Mon. Notices R. Astronomical Soc. 502, 5821–5838. doi:10.1093/mnras/stab355

CrossRef Full Text | Google Scholar

Gabici, S., Evoli, C., Gaggero, D., Lipari, P., Mertsch, P., Orlando, E., et al. (2019). The Origin of Galactic Cosmic Rays: Challenges to the Standard Paradigm. Int. J. Mod. Phys. D. 28, 1930022–1930339. doi:10.1142/s0218271819300222

CrossRef Full Text | Google Scholar

Giacalone, J., and Jokipii, J. R. (2007). Magnetic Field Amplification by Shocks in Turbulent Fluids. Astrophysical J. 663, L41–L44. doi:10.1086/519994

CrossRef Full Text | Google Scholar

Girichidis, P., Naab, T., Hanasz, M., and Walch, S. (2018). Cooler and Smoother - the Impact of Cosmic Rays on the Phase Structure of Galactic Outflows. Mon. Notices R. Astronomical Soc. 479, 3042–3067. doi:10.1093/mnras/sty1653

CrossRef Full Text | Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a Theory of Interstellar Turbulence. 2: Strong Alfvenic Turbulence. Astrophysical J. 438, 763. doi:10.1086/175121

CrossRef Full Text | Google Scholar

Goldstein, M. L., Wicks, R. T., Perri, S., and Sahraoui, F. (2015). Kinetic Scale Turbulence and Dissipation in the Solar Wind: Key Observational Results and Future Outlook. Phil. Trans. R. Soc. A 373, 20140147. doi:10.1098/rsta.2014.0147

PubMed Abstract | CrossRef Full Text | Google Scholar

Green, D. A. (2009). A Revised Galactic Supernova Remnant Catalogue. Bull. Astronomical Soc. India 37, 45

Google Scholar

Guo, X., Sironi, L., and Narayan, R. (2018). Electron Heating in Low Mach Number Perpendicular Shocks. II. Dependence on the Pre-shock Conditions. Astrophysical J. 858, 95. doi:10.3847/1538-4357/aab6ad

CrossRef Full Text | Google Scholar

Guo, X., Sironi, L., and Narayan, R. (2017). Electron Heating in Low-Mach-Number Perpendicular Shocks. I. Heating Mechanism. Astrophysical J. 851, 134. doi:10.3847/1538-4357/aa9b82

CrossRef Full Text | Google Scholar

Haggerty, C. C., and Caprioli, D. (2019). dHybridR: A Hybrid Particle-In-Cell Code Including Relativistic Ion Dynamics. Astrophysical J. 887, 165. doi:10.3847/1538-4357/ab58c8

CrossRef Full Text | Google Scholar

Haggerty, C. C., and Caprioli, D. (2020). Kinetic Simulations of Cosmic-Ray-modified Shocks. I. Hydrodynamics. Astrophysical J. 905, 1. doi:10.3847/1538-4357/abbe06

CrossRef Full Text | Google Scholar

Helder, E. A., Vink, J., Bassa, C. G., Bamba, A., Bleeker, J. A. M., Funk, S., et al. (2009). Measuring the Cosmic-Ray Acceleration Efficiency of a Supernova Remnant. Science 325, 719–722. doi:10.1126/science.1173383

PubMed Abstract | CrossRef Full Text | Google Scholar

Hennebelle, P., and Inutsuka, S.-i. (2019). The Role of Magnetic Field in Molecular Cloud Formation and Evolution. Front. Astron. Space Sci. 6, 5. doi:10.3389/fspas.2019.00005

CrossRef Full Text | Google Scholar

Holguin, F., Ruszkowski, M., Lazarian, A., Farber, R., and Yang, H.-Y. K. (2019). Role of Cosmic-Ray Streaming and Turbulent Damping in Driving Galactic Winds. Mon. Notices R. Astronomical Soc. 490, 1271–1282. doi:10.1093/mnras/stz2568

CrossRef Full Text | Google Scholar

Hopkins, P. F., Wetzel, A., Kereš, D., Faucher-Giguère, C.-A., Quataert, E., Boylan-Kolchin, M., et al. (2018). FIRE-2 Simulations: Physics versus Numerics in Galaxy Formation. Mon. Notices R. Astronomical Soc. 480, 800–863. doi:10.1093/mnras/sty1690

CrossRef Full Text | Google Scholar

Hovey, L., Hughes, J. P., McCully, C., Pandya, V., and Eriksen, K. (2018). Constraints on Cosmic-Ray Acceleration Efficiency in Balmer Shocks of Two Young Type Ia Supernova Remnants in the Large Magellanic Cloud. Astrophysical J. 862, 148. doi:10.3847/1538-4357/aac94b

CrossRef Full Text | Google Scholar

Howes, G. G. (2010). A Prescription for the Turbulent Heating of Astrophysical Plasmas. Mon. Notices R. Astronomical Soc. 409, L104–L108. doi:10.1111/j.1745-3933.2010.00958.x

CrossRef Full Text | Google Scholar

Hu, Y., Lazarian, A., and Xu, S. (2022). Superdiffusion of Cosmic Rays in Compressible Magnetized Turbulence. Mon. Notices R. Astronomical Soc. 512, 2111–2124. doi:10.1093/mnras/stac319

CrossRef Full Text | Google Scholar

Inoue, T., Shimoda, J., Ohira, Y., and Yamazaki, R. (2013). The Origin of Radially Aligned Magnetic Fields in Young Supernova Remnants. ApJ 772, L20. doi:10.1088/2041-8205/772/2/L20

CrossRef Full Text | Google Scholar

Inutsuka, S. i., Inoue, T., Iwasaki, K., Stone, J. M., Suzuki, T. K., Tsukamoto, Y., et al. (2015). “Phase Transition Dynamics of the Interstellar Medium: Theory, Methodology, and Implications,” in Numerical Modeling of Space Plasma Flows ASTRONUM-2014. Editors N. V. Pogorelov, E. Audit, and G. P. Zank (Astronomical Society of the Pacific Conference Series), 75.

Google Scholar

Jokipii, J. R. (1966). Cosmic-Ray Propagation. I. Charged Particles in a Random Magnetic Field. Astrophysical J. 146, 480. doi:10.1086/148912

CrossRef Full Text | Google Scholar

Katou, T., and Amano, T. (2019). Theory of Stochastic Shock Drift Acceleration for Electrons in the Shock Transition Region. Astrophysical J. 874, 119. doi:10.3847/1538-4357/ab0d8a

CrossRef Full Text | Google Scholar

Kawazura, Y., Schekochihin, A. A., Barnes, M., TenBarge, J. M., Tong, Y., Klein, K. G., et al. (2020). Ion versus Electron Heating in Compressively Driven Astrophysical Gyrokinetic Turbulence. Phys. Rev. X 10, 041050. doi:10.1103/PhysRevX.10.041050

CrossRef Full Text | Google Scholar

Kim, C.-G., and Ostriker, E. C. (2018). Numerical Simulations of Multiphase Winds and Fountains from Star-forming Galactic Disks. I. Solar Neighborhood TIGRESS Model. Astrophysical J. 853, 173. doi:10.3847/1538-4357/aaa5ff

CrossRef Full Text | Google Scholar

Krumholz, M. R., Burkhart, B., Forbes, J. C., and Crocker, R. M. (2018). A Unified Model for Galactic Discs: Star Formation, Turbulence Driving, and Mass Transport. Mon. Notices R. Astronomical Soc. 477, 2716–2740. doi:10.1093/mnras/sty852

CrossRef Full Text | Google Scholar

Krumholz, M. R., and Burkhart, B. (2016). Is Turbulence in the Interstellar Medium Driven by Feedback or Gravity? an Observational Test. Mon. Not. R. Astron. Soc. 458, 1671–1677. doi:10.1093/mnras/stw434

CrossRef Full Text | Google Scholar

Krumholz, M. R., McKee, C. F., and Bland-Hawthorn, J. (2019). Star Clusters across Cosmic Time. Annu. Rev. Astron. Astrophys. 57, 227–303. doi:10.1146/annurev-astro-091918-104430

CrossRef Full Text | Google Scholar

Kulsrud, R. M. (2005). Plasma Physics for Astrophysics. Princeton series in astrophysics. Princeton, NJ: Princeton University Press.

Google Scholar

Kulsrud, R., and Pearce, W. P. (1969). The Effect of Wave-Particle Interactions on the Propagation of Cosmic Rays. Astrophysical J. 156, 445. doi:10.1086/149981

CrossRef Full Text | Google Scholar

Lagage, P. O., and Cesarsky, C. J. (1983a). Cosmic-ray Shock Acceleration in the Presence of Self-Excited Waves. Astronomy Astrophysics 118, 223

Google Scholar

Lagage, P. O., and Cesarsky, C. J. (1983b). The Maximum Energy of Cosmic Rays Accelerated by Supernova Shocks. Astronomy Astrophysics 125, 249

Google Scholar

Laming, J. M., Hwang, U., Ghavamian, P., and Rakowski, C. (2014). Electron Heating, Magnetic Field Amplification, and Cosmic-Ray Precursor Length at Supernova Remnant Shocks. Astrophysical J. 790, 11. doi:10.1088/0004-637X/790/1/11

CrossRef Full Text | Google Scholar

Lazarian, A., and Pogosyan, D. (2016). Spectrum and Anisotropy of Turbulence from Multi-Frequency Measurement of Synchrotron Polarization. Astrophysical J. 818, 178. doi:10.3847/0004-637X/818/2/178

CrossRef Full Text | Google Scholar

Lazarian, A., and Pogosyan, D. (2012). Statistical Description of Synchrotron Intensity Fluctuations: Studies of Astrophysical Magnetic Turbulence. Astrophysical J. 747, 5. doi:10.1088/0004-637x/747/1/5

CrossRef Full Text | Google Scholar

Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a Weakly Stochastic Field. Astrophysical J. 517, 700–718. doi:10.1086/307233

CrossRef Full Text | Google Scholar

Lazarian, A., and Xu, S. (2021). Diffusion of Cosmic Rays in MHD Turbulence with Magnetic Mirrors. Astrophysical J.J 923, 53. doi:10.3847/1538-4357/ac2de9

CrossRef Full Text | Google Scholar

Lee, H., Lazarian, A., and Cho, J. (2016). Polarimetric Studies of Magnetic Turbulence with an Interferometer. Astrophysical J.J 831, 77. doi:10.3847/0004-637x/831/1/77

CrossRef Full Text | Google Scholar

Mao, S. A., and Ostriker, E. C. (2018). Galactic Disk Winds Driven by Cosmic Ray Pressure. Astrophysical J. 854, 89. doi:10.3847/1538-4357/aaa88e

CrossRef Full Text | Google Scholar

Marcowith, A., Ferrand, G., Grech, M., Meliani, Z., Plotnikov, I., and Walder, R. (2020). Multi-scale Simulations of Particle Acceleration in Astrophysical Systems. Living Rev. Comput. Astrophys. 6, 1. doi:10.1007/s41115-020-0007-6

CrossRef Full Text | Google Scholar

Maron, J., and Goldreich, P. (2001). Simulations of Incompressible Magnetohydrodynamic Turbulence. Astrophysical J. 554, 1175–1196. doi:10.1086/321413

CrossRef Full Text | Google Scholar

Matsumoto, Y., Amano, T., Kato, T. N., and Hoshino, M. (2017). Electron Surfing and Drift Accelerations in a Weibel-Dominated High-Mach-Number Shock. Phys. Rev. Lett. 119, 105101. doi:10.1103/PhysRevLett.119.105101

PubMed Abstract | CrossRef Full Text | Google Scholar

McKee, C. F., and Ostriker, J. P. (1977). A Theory of the Interstellar Medium: Three Components Regulated by Supernova Explosions in an Inhomogeneous Substrate. Astrophysical J. 218, 148. doi:10.1086/155667

CrossRef Full Text | Google Scholar

McKenzie, J. F., and Westphal, K. O. (1968). Interaction of Linear Waves with Oblique Shock Waves. Phys. Fluids 11, 2350–2362. doi:10.1063/1.1691825

CrossRef Full Text | Google Scholar

Morlino, G., Blasi, P., Bandiera, R., and Amato, E. (2013). Broad Balmer Line Emission and Cosmic Ray Acceleration Efficiency in Supernova Remnant Shocks. Astronomi. Astrophysics 558, A25. doi:10.1051/0004-6361/201322006

CrossRef Full Text | Google Scholar

Nishihara, K., Wouchuk, J. G., Matsuoka, C., Ishizaki, R., and Zhakhovsky, V. V. (2010). Richtmyer-Meshkov Instability: Theory of Linear and Nonlinear Evolution. Phil. Trans. R. Soc. A 368, 1769–1807. doi:10.1098/rsta.2009.0252

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohira, Y. (2016a). Injection to Rapid Diffusive Shock Acceleration at Perpendicular Shocks in Partially Ionized Plasmas. Astrophysical J. 827, 36. doi:10.3847/0004-637X/827/1/36

CrossRef Full Text | Google Scholar

Ohira, Y. (2016b). Magnetic Field Amplification by Collisionless Shocks in Partially Ionized Plasmas. Astrophysical J. 817, 137. doi:10.3847/0004-637X/817/2/137

CrossRef Full Text | Google Scholar

Ohira, Y., Murase, K., and Yamazaki, R. (2010). Escape-limited Model of Cosmic-Ray Acceleration Revisited. Astronomi. Astrophysics 513, A17. doi:10.1051/0004-6361/200913495

CrossRef Full Text | Google Scholar

Ohira, Y., and Takahara, F. (2007). Absence of Electron Surfing Acceleration in a Two-Dimensional Simulation. Astrophysical J. 661, L171–L174. doi:10.1086/518888

CrossRef Full Text | Google Scholar

Ohira, Y., and Takahara, F. (2008). Oblique Ion Two‐Stream Instability in the Foot Region of a Collisionless Shock. Astrophysical J. 688, 320–326. doi:10.1086/592182

CrossRef Full Text | Google Scholar

Orlando, S., Bocchino, F., Miceli, M., Petruk, O., and Pumo, M. L. (2012). Role of Ejecta Clumping and Back-Reaction of Accelerated Cosmic Rays in the Evolution of Type Ia Supernova Remnants. Astrophysical J. 749, 156. doi:10.1088/0004-637X/749/2/156

CrossRef Full Text | Google Scholar

Orlando, S., Wongwathanarat, A., Janka, H. T., Miceli, M., Nagataki, S., Ono, M., et al. (2022). Cassiopeia A Reveals Past Interaction with Circumstellar Shell. arXiv e-printsarXiv:2202.01643.

Google Scholar

R Dickel, J., and Milne, D. (1976). Magnetic Fields in Supernova Remnants. Aust. J. Phys. 29, 435–460. doi:10.1071/PH760435

CrossRef Full Text | Google Scholar

Rakowski, C. E., Laming, J. M., and Ghavamian, P. (2008). The Heating of Thermal Electrons in Fast Collisionless Shocks: The Integral Role of Cosmic Rays. Astrophysical J. 684, 348–357. doi:10.1086/590245

CrossRef Full Text | Google Scholar

Raymond, J. C., Chilingarian, I. V., Blair, W. P., Sankrit, R., Slavin, J. D., and Burkhart, B. (2020a). Turbulence and Energetic Particles in Radiative Shock Waves in the Cygnus Loop. I. Shock Properties. Astrophysical J. 894, 108. doi:10.3847/1538-4357/ab886d

CrossRef Full Text | Google Scholar

Raymond, J. C., Slavin, J. D., Blair, W. P., Chilingarian, I. V., Burkhart, B., and Sankrit, R. (2020b). Turbulence and Energetic Particles in Radiative Shock Waves in the Cygnus Loop. II. Development of Postshock Turbulence. Astrophysical J.J 903, 2. doi:10.3847/1538-4357/abb821

CrossRef Full Text | Google Scholar

Reynolds, S. P., and Gilmore, D. M. (1993). Radio Observations of the Remnant of the Supernova of AD 1006. II - Polarization Observations. Astronomical J. 106, 272. doi:10.1086/116635

CrossRef Full Text | Google Scholar

Reynoso, E. M., Hughes, J. P., and Moffett, D. A. (2013). On the Radio Polarization Signature of Efficient and Inefficient Particle Acceleration in Supernova Remnant SN 1006. Astronomic. J 145, 104. doi:10.1088/0004-6256/145/4/104

CrossRef Full Text | Google Scholar

Rowan, M. E., Sironi, L., and Narayan, R. (2019). Electron and Proton Heating in Transrelativistic Guide Field Reconnection. Astrophysical J. 873, 2. doi:10.3847/1538-4357/ab03d7

CrossRef Full Text | Google Scholar

Roy, N., Bharadwaj, S., Dutta, P., and Chengalur, J. N. (2009). Magnetohydrodynamic Turbulence in Supernova Remnants. Mon. Notices R. Astronomical Soc. 393, L26–L30. doi:10.1111/j.1745-3933.2008.00591.x

CrossRef Full Text | Google Scholar

Rybicki, G. B., and Lightman, A. P. (1979). Radiative Processes in Astrophysics. New York: A Wiley-Interscience Publication; Wiley.

Google Scholar

Saha, P., Bharadwaj, S., Chakravorty, S., Roy, N., Choudhuri, S., Günther, H. M., et al. (2021). The Auto- and Cross-Angular Power Spectrum of the Cas A Supernova Remnant in Radio and X-Ray. Mon. Notices R. Astronomical Soc. 502, 5313–5324. doi:10.1093/mnras/stab446

CrossRef Full Text | Google Scholar

Saha, P., Bharadwaj, S., Roy, N., Choudhuri, S., and Chattopadhyay, D. (2019). A Study of Kepler Supernova Remnant: Angular Power Spectrum Estimation from Radio Frequency Data. Mon. Notices R. Astronomical Soc. 489, 5866–5875. doi:10.1093/mnras/stz2528

CrossRef Full Text | Google Scholar

Sano, T., Nishihara, K., Matsuoka, C., and Inoue, T. (2012). Magnetic Field Amplification Associated with the Richtmyer-Meshkov Instability. Astrophysical J. 758, 126. doi:10.1088/0004-637x/758/2/126

CrossRef Full Text | Google Scholar

Schlickeiser, R. (2002). Cosmic Ray Astrophysics/Reinhard Schlickeiser, Astronomy and Astrophysics Library; Physics and Astronomy Online Library. Berlin: Springer.

Google Scholar

Sedov, L. I. (1959). Similarity and Dimensional Methods in Mechanics. New York: Academic Press.

Google Scholar

Shimoda, J., Akahori, T., Lazarian, A., Inoue, T., and Fujita, Y. (2018a). Discovery of Kolmogorov-like Magnetic Energy Spectrum in Tycho's Supernova Remnant by Two-point Correlations of Synchrotron Intensity. Mon. Notices R. Astronomical Soc. 480, 2200–2205. doi:10.1093/mnras/sty2034

CrossRef Full Text | Google Scholar

Shimoda, J., Inoue, T., Ohira, Y., Yamazaki, R., Bamba, A., and Vink, J. (2015). On Cosmic-Ray Production Efficiency at Su0Pernova Remnant Shocks Propagating into Realistic Diffuse Interstellar Medium. Astrophysical J. 803, 98. doi:10.1088/0004-637X/803/2/98

CrossRef Full Text | Google Scholar

Shimoda, J., and Inutsuka, S.-i. (2021). The Effects of Cosmic-Ray Diffusion and Radiative Cooling on the Galactic Wind from the Milky Way. The Astrophy. J. 926 (1), 14. doi:10.3847/1538-4357/ac4110

CrossRef Full Text | Google Scholar

Shimoda, J., and Laming, J. M. (2019). Diagnosing cosmic ray modified shocks with Hα polarimetry. Mon. Not. R. Astron. Soc. 489 (2), 2723–2731.

CrossRef Full Text | Google Scholar

Shimoda, J., Ohira, Y., Bamba, A., Terada, Y., Yamazaki, R., Inoue, T., et al. (2022). X-ray Line Diagnostics of Ion Temperature at Cosmic-Ray Accelerating Collisionless Shocks. arXiv e-printsarXiv:2201.07607.

Google Scholar

Shimoda, J., Ohira, Y., Yamazaki, R., Laming, J. M., and Katsuda, S. (2018b). Polarized Balmer Line Emission from Supernova Remnant Shock Waves Efficiently Accelerating Cosmic Rays. Mon. Notices R. Astronomical Soc. 473, 1394–1406. doi:10.1093/mnras/stx2339

CrossRef Full Text | Google Scholar

Tashiro, M., Maejima, H., Toda, K., Kelley, R., Reichenthal, L., Hartz, L., et al. (2020). Status of X-Ray Imaging and Spectroscopy Mission (XRISM).” in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. vol. 11444 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series (SPIE Astronomical Telescopes + Instrumentation), 1144422. doi:10.1117/12.2565812

CrossRef Full Text | Google Scholar

Vishwakarma, P. K., and Kumar, J. (2020). Trans-Alfvénic Magnetohydrodynamic Turbulence in the Vicinity of Supernova Remnant Cassiopeia-A Shocks. Mon. Notices R. Astronomical Soc. 498, 1093–1100. doi:10.1093/mnras/staa2293

CrossRef Full Text | Google Scholar

Warren, J. S., Hughes, J. P., Badenes, C., Ghavamian, P., McKee, C. F., Moffett, D., et al. (2005). Cosmic‐Ray Acceleration at the Forward Shock in Tycho's Supernova Remnant: Evidence from Chandra X‐Ray Observations. Astrophysical J. 634, 376–389. doi:10.1086/496941

CrossRef Full Text | Google Scholar

Wentzel, D. G. (1968). Hydromagnetic Waves Excited by Slowly Streaming Cosmic Rays. Astrophysical J. 152, 987. doi:10.1086/149611

CrossRef Full Text | Google Scholar

West, J. L., Jaffe, T., Ferrand, G., Safi-Harb, S., and Gaensler, B. M. (2017). When Disorder Looks like Order: A New Model to Explain Radial Magnetic Fields in Young Supernova Remnants. Astrophysical J. 849, L22. doi:10.3847/2041-8213/aa94c4

CrossRef Full Text | Google Scholar

Westfold, K. C. (1959). The Polarization of Synchrotron Radiation. Astrophysical J. 130, 241. doi:10.1086/146713

CrossRef Full Text | Google Scholar

Williams, B. J., Borkowski, K. J., Ghavamian, P., Hewitt, J. W., Alwin Mao, S., Petre, R., et al. (2013). Azimuthal Density Variations Around the Rim of Tycho’s Supernova Remnant. Astrophysical J. 770, 129. doi:10.1088/0004-637X/770/2/129

CrossRef Full Text | Google Scholar

Williams, B. J., Chomiuk, L., Hewitt, J. W., Blondin, J. M., Borkowski, K. J., Ghavamian, P., et al. (2016). An X-Ray and Radio Study of the Varying Expansion Velocities in Tycho's Supernova Remnant. Astrophysical J. 823, L32. doi:10.3847/2041-8205/823/2/l32

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, H., and Lazarian, A. (2002). Scattering of Cosmic Rays by Magnetohydrodynamic Interstellar Turbulence. Phys. Rev. Lett. 89, 281102. doi:10.1103/physrevlett.89.281102

PubMed Abstract | CrossRef Full Text | Google Scholar

Zanardo, G., Staveley-Smith, L., Gaensler, B. M., Indebetouw, R., Ng, C.-Y., Matsuura, M., et al. (2018). Detection of Linear Polarization in the Radio Remnant of Supernova 1987A. Astrophysical J. 861, L9. doi:10.3847/2041-8213/aacc2a,

CrossRef Full Text | Google Scholar

Zhang, H., Chepurnov, A., Yan, H., Makwana, K., Santos-Lima, R., and Appleby, S. (2020). Identification of Plasma Modes in Galactic Turbulence with Synchrotron Polarization. Nat. Astron 4, 1001–1008. doi:10.1038/s41550-020-1093-4

CrossRef Full Text | Google Scholar

Zhdankin, V. (2021). Particle Energization in Relativistic Plasma Turbulence: Solenoidal versus Compressive Driving. Astrophysical J. 922, 172. doi:10.3847/1538-4357/ac222e

CrossRef Full Text | Google Scholar

Zhdankin, V., Uzdensky, D. A., Werner, G. R., and Begelman, M. C. (2019). Electron and Ion Energization in Relativistic Plasma Turbulence. Phys. Rev. Lett. 122, 055101. doi:10.1103/PhysRevLett.122.055101

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Y., Williams, R. J. R., Ramaprabhu, P., Groom, M., Thornber, B., Hillier, A., et al. (2021). Rayleigh-Taylor and Richtmyer-Meshkov Instabilities: A Journey through Scales. Phys. D. Nonlinear Phenom. 423, 132838. doi:10.1016/j.physd.2020.132838

CrossRef Full Text | Google Scholar