
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci., 14 June 2022
Sec. Stellar and Solar Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.879045
This article is part of the Research TopicWhite Dwarfs in the Age of the Great CollaborationsView all 6 articles
Probing internal properties of white-dwarf stars has been amongst the earliest objectives of asteroseismology, following the first discovery in the late 1960s of non-radial pulsations in these evolved compact stars. It was swiftly recognized that white-dwarf pulsators could offer new opportunities to unravel their inner structure and dynamics from the observed low-degree, low-order gravity (g-)modes. From these early days on, many approaches have been attempted to fully exploit this potential, with various levels of success. Here, we review the most recent efforts from our group to perform a complete seismic cartography of white-dwarf interiors. Our approach involves new models incorporating flexible internal profiles for the main chemical constituents (H, He, C, and O) that are optimized, along with other fundamental parameters (Teff and log g), to determine the stellar structure that best reproduces the observed period spectrum of a given star. The method is meant to reduce as much as possible solution dependency relative to stellar evolution uncertainties. The outcome is a full seismic model of the pulsating white-dwarf star under consideration, including its internal core and envelope chemical stratification. Searching for seismic solutions that do not depend on stellar evolution calculations is a key requirement of this strategy. Late stages of evolution that ultimately shape the inner structure of white dwarf stars are known to rely on still uncertain processes. One of our hopes is to be able to test these processes, therefore requiring that seismic models do not incorporate strong preconceived expectations from evolutionary models. We present and discuss results obtained so far from the application of this method to a handful of DB and DA pulsators. In all cases, significant qualitative improvements of the seismic solutions is obtained, providing as an outcome strong quantitative constraints on the core chemical structure of these stars. In particular, we consistently find that the homogeneous C/O mixed core, inherited from the core helium-burning phase, is
Low-to intermediate-mass stars (up to
Inferring the properties of white dwarf stars from their pulsations was one of the very first application of asteroseismology to stars other than the Sun, driven at that time by the discoveries of a growing number of pulsators of the kind (see Fontaine and Brassard 2008 for a complete overview of the historical developments in this field). Pulsators in this evolutionary stage are found in three main flavors as white dwarf stars cross the GW Vir (DOV), V777 Her (DBV), or ZZ Cet (DAV) instability strips when they cool down. Other groups of white-dwarf variables have also recently been identified, suspected, or predicted, adding further potential to an already promising situation. The oscillation modes detected in these stars are low degree (typically ℓ = 1 and 2), low-to-mid radial order g-modes with periods of a few minutes to about half an hour. Their periods are sensitive to the global stellar structure (and stellar fundamental parameters), internal chemical stratification, and rotation, as demonstrated by thorough explorations of the pulsation properties of DA (Brassard et al., 1991, Brassard et al., 1992a, Brassard et al., 1992b, Brassard et al., 1992c), DB (Bradley et al., 1993), and GW Vir (Kawaler and Bradley 1994) stars. This led to the first quantitative asteroseismic1 inferences of white-dwarf properties, starting with the analysis of the hot GW Vir star PG 1159–035 (Winget et al., 1991), followed by numerous attempts. However, it is mostly from the year 2000 and beyond that the technique improved, triggered in part by the increasing power of computers allowing for more systematic forward modeling approaches (e.g., Metcalfe et al., 2000; Metcalfe 2001). Fontaine and Brassard (2008) and Giammichele et al. (2017a) provide very complete reviews and critical discussions–which we do not repeat here–of the various quantitative asteroseismic determinations that have been claimed for pulsating white dwarfs in the past 20 years. Most analyses were (and still very often are) focused on deriving global parameters and envelope thickness of the white dwarf, but one must acknowledge early efforts to probe the core, in particular to measure the 12C(α,γ)16O nuclear reaction rate from asteroseismology (Metcalfe et al., 2001), a result that we however considered as premature due to issues with the models used for the analysis (Fontaine and Brassard 2002).
In a nutshell, not all seismic analyses of white-dwarf pulsators rest on the same solid grounds, due to significant differences in the quality of the equilibrium models used for the task and due to how the optimal model is ultimately found. Readers new to the field should always keep a critical mind to this respect. Various methods have been used, ranging from basic trial-and-errors modeling to systematic searches in more-or-less constrained parameter spaces involving up to hundreds of thousands of model computations through grids or optimization algorithms (e.g., Pech et al., 2006; Castanheira and Kepler 2008; Giammichele et al., 2016). In the past 15 years, the field has been strongly influenced by the rising belief that using full evolutionary models (or internal C/O profiles predicted by such models) for white dwarf asteroseismology was the way to go (e.g., Córsico et al., 2013; Romero et al., 2013). This strategy has however significant drawbacks because it implicitly assumes that evolution structures are accurate enough for that purpose, a questionable assumption considering the already mentioned uncertainties in the physics involved. Recently, De Gerónimo et al. (2017) explored the effects on core chemical stratification of various known uncertainties that plague central and shell helium-burning phases preceding the white-dwarf stage, and indeed the impact on pulsation periods can be quite large (up to 20–30 s period shifts according to the authors). The magnitude of such variations naturally raises concerns about the reliability of any approach that considers fixed (i.e., assumed perfectly known) composition profiles in the white-dwarf core. More generally, evolution-based approaches for seismic modeling do not allow, by construction, possibilities to provide independent measurements of several aspects of the internal structure, contrary to more flexible models. An additional caveat of this method is that it imposes the use of relatively coarse grids to explore rather limited (low dimension) model parameter spaces, due to large computation times. Grid-based approaches also have inherent drawbacks due to grid-resolution limitations as discussed by Charpinet et al. (2015).
In the meantime, efforts carried out by our group to exploit white-dwarf asteroseismology have taken a different route, based mainly on static white-dwarf models (as opposed to structures derived from evolution). Model grids and, later on, grid-free optimization tools were developed to achieve optimal seismic fits of the observed period spectra. Early applications of these methods include a derivation of the envelope structure of the DBV star GD358 (Fontaine and Brassard 2002), probes of the internal rotation of white dwarfs (Charpinet et al., 2009; Fontaine et al., 2013), and estimations of their bulk core composition (Giammichele et al., 2013a; Giammichele et al., 2013b, Giammichele et al., 2014, Giammichele et al., 2015, Giammichele et al., 2016). More recently, after establishing the period sensitivity of some deeply confined g-modes to the inner core chemical stratification that provide a chance to infer independent constraints on it from asteroseismology, we engaged into a significant extension of our seismic analyses in order to incorporate the detailed core structure in the fitting process. These developments were reported in detail in Giammichele et al. (2017a, 2017b, and 2018), Charpinet et al. (2019a), Charpinet et al. (2021). In the present paper, we review these latest developments (Section 2), discuss available and new results of the method applied to a handful of white dwarf pulsators (Section 3), and discuss some implications for our understanding of stellar modeling in the late stages of evolution (Section 4).
The foundations of our method are by themselves not new, as they rely on the widely-used forward-modeling approach, which in asteroseismology consists of searching for the best possible match between a set of pulsations periods detected in the star under consideration and periods computed from stellar models. Our implementation of this strategy originated from the pioneering work of Brassard et al. (2001), carried out in the context of pulsating hot subdwarf stars, and has been considerably improved since then, as detailed in Charpinet et al. (2005); Van Grootel et al. (2013a). Its adaptation to white dwarf asteroseismology, following the initial work by Fontaine et al. (2001), led to notable results (e.g., Charpinet et al., 2009), but mostly boomed over the last decade with developments carried out by Giammichele et al. (2014, 2015, 2016, 2017a, 2017b, 2018) that we summarize in subsequent subsections.
The technique relies on a double-optimization scheme that incorporates, along with the search in model parameter space, a nested minimization step that simultaneously matches observed and modeled periods (see Figure 1). This first, combinatorial optimization is performed each time a model of given parameters is evaluated, ensuring that the best possible fit for that model–which may not be a good fit in absolute terms, if the model is not a good representation of the star–is found. This step is necessary because in most cases observed periods are not univocally identified to a single mode of given degree ℓ and radial order k. With this first optimization, a mode identification is therefore achieved based on its ability to globally best-match the period spectrum, and an often-lacking pre-identification of the modes is no longer a requirement. Note that in cases where a mode identification is available a priori (from the observation of rotational splittings, through the analysis of period spacings, or from other independent methods such as multicolour photometry), these constraints can easily be incorporated in the combinatorial optimization process. The quality of the period match is evaluated quantitatively through a so-called merit function. This function could take many different forms (as long as it can be minimized or maximized), but using a formulation that is conveniently related to χ2-statistics (for error estimates) has been our preferred choice, to date. The merit function, S2, that we use in the white-dwarf context is defined in its most general form by the relation
where N is the number of detected modes, Pth,i is the model period matched to the observed period Pobs,i, and σi is the error associated to the measured period. In practice, model uncertainties dominate by orders of magnitude over the usually tiny observational errors associated to period measurements (in particular with current long-baseline data from space) and in most cases we simply disregard σi (i.e., we set σi = 1) in the definition of the merit function. Again, we stress that the first optimisation step is a combinatorial minimization of S2 amongst all possible (Pobs,i, Pth,i)-pairs given a set of observed periods and a seismic model. The obtained minimized value,
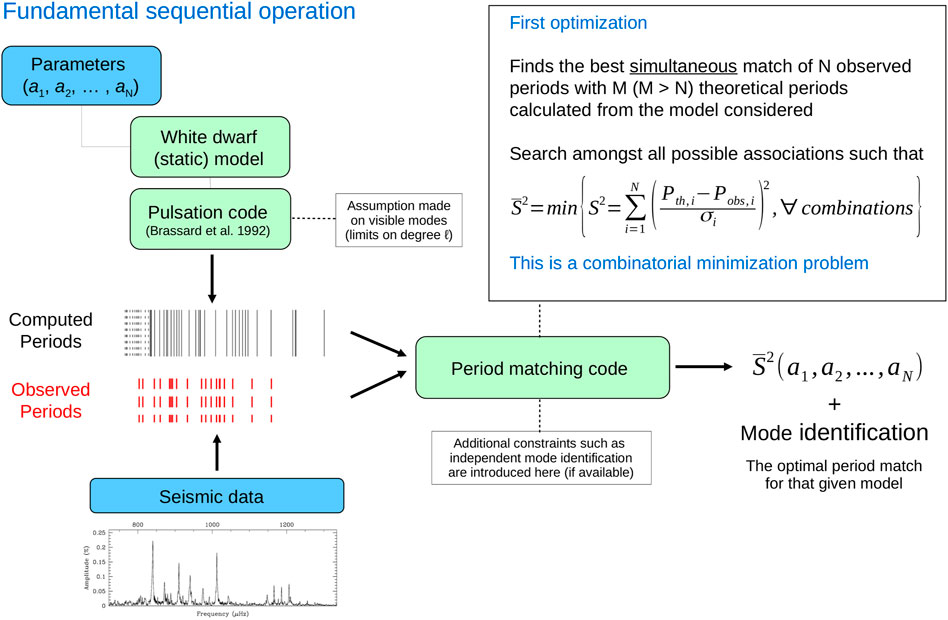
FIGURE 1. Schematic representation of the fundamental operation (a sequential chain of calculations) that enters our double optimization scheme. The observed pulsation periods are optimally matched (through a first combinatorial optimization), taking external constraints into account (if any), with periods computed for a model of given parameters. The quality of fit is quantified using a χ2-type merit function. This quantity,
An essential component of our approach to quantitative asteroseismology is the estimation of errors associated to the inferred properties. This requires that not only the optimal model shall be found, but also that its surroundings in parameter space be thoroughly explored in order to assess its statistical significance. Brassard et al. (2001) originally made these assessments from approximating the region localized around the
The density of probability for each parameter is then obtained through marginalization
Both the search for an optimal model and the sampling of the Likelihood function to estimate errors are very computationally intensive tasks that require the evaluation of many seismic models. Efficient strategies to solve this generally difficult optimization problem are therefore needed. There are two factors on which we can act to mitigate this difficulty. The first one is by using stellar models that are fast to calculate and which permits a wide exploration of the model parameter space. The second is by adopting clever optimization techniques to reduce the total number of model evaluations. Disregarding these technical constraints usually leads to oversimplifying artificially the problem, e.g., by limiting the number of free parameters only to keep computation times acceptable and therefore implicitly disregarding entire sets of potentially valid solutions.
An important aspect of our strategy is to rely on full (but static, as opposed to evolutionary) white dwarf models. This approach has two main advantages: First, various parametrization of the internal structure can more easily be introduced, thus permitting more systematic explorations of a wide variety of stellar configurations. Second, computation of such models is fast (of the order of seconds on modern hardware, typically). These are key assets when pursuing the forward modeling optimization route described previously. Beyond these technical justifications, it is also worth recalling that timescales for oscillation waves to travel across the star (roughly the pulsation periods, which are of the order of minutes in white dwarfs) are much shorter than any timescale related to evolution (cooling) or mixing processes (e.g., microscopic diffusion; but with the notable exception of convective mixing that can have turnover timescales similar to the oscillation periods; Montgomery 2005). This fact implies that for the propagating waves, the background in which they travel is effectively static to a very high level of accuracy. The pulsations mode properties reflect this static configuration, but are not directly sensitive to the mechanisms that produce the structures during evolution. For instance, they can “see” a chemical transition of some shape at, e.g., the envelope or core boundary, since they are sensitive to μ-gradients, whatever the process that caused this chemical stratification. Pulsation modes are “agnostic” instruments allowing us to measure the structure of a star at a given time of its evolution, considering that by themselves they are fully independent of the evolution processes taking place on much longer timescales. The use of static models for asteroseismology (of white-dwarfs in particular, but this applies to many other types of stars), is therefore well justified in this context.
Realistic static models of white dwarfs can be computed from the fact that in these cooling objects the approximate relationship between the local luminosity and integrated mass, L(r) ∝ M(r), is quite accurate and, consequently, may be used to obtain an excellent estimate of the luminosity profile. This is true in particular for the lowest temperature white dwarfs including the pulsating ZZ Ceti stars. Note that Timmes et al. (2018) pointed out that this relation is no longer satisfied for the hottest white dwarfs (in particular the hot DBVs) which still have significant cooling occurring from neutrino emission. However, ways exist to overcome such complications by adapting the models and optimization strategy (see Charpinet et al., 2019a for further details concerning this specific case).
In order to define a full static white dwarf model, one must specify two fundamental parameters, the surface gravity log g (or equivalently the mass, via the mass-radius relation) and the effective temperature Teff, as well as a set of structural parameters that controls the envelope layering and the core stratification. Thus far, we have restricted ourselves to the main chemical constituents forming typical white dwarfs, namely oxygen, carbon, helium, and hydrogen. Massive oxygen-neon white dwarfs are not currently covered by our different flavors of static models, but there is no hard point, in principle, preventing us to do so in the future. Additional parameters associated to components of the constitutive physics could also be considered too, such as the convective efficiency via one or another mixing-length theory prescription. However, Fontaine and Brassard (2008) showed that the periods of low-order g-modes in pulsating white-dwarf models practically do not depend on the assumed convective efficiency. This parameter can therefore be fixed (to the so-called ML2/α = 1 version calibrated by Van Grootel et al., 2013b, in our case).
The envelope layering is generally dealt with a set of parameters–D(H), D(He), PfH, and PfHe–that indicates the position (D-parameters) and shape (Pf-parameters) of the H and He composition profiles at the transitions. These parameters fully define a sigmoïd function inspired by analytical expressions derived when diffusive equilibrium is reached. A more detailed description of this method is provided by Giammichele et al. (2017a). For the specific case of DB pulsators, which are thought to have experienced C/He mixing during a late thermal pulse before the pre-white dwarf stage, which gravitational settling does not have time to erase, a double-layered envelope structure that can account for this possibility is more appropriate. This case is described in the Supplementary Informations of Giammichele et al. (2018).
Our treatment of the core is the part that has seen the most significant improvements recently. The most recent developments are described in the next subsection. We recall here that various assumptions can been considered when specifying the core structure in our static models. The simplest approach is to assume an homogeneous C/O core requiring only the mass fraction of C (or O) to be specified. These simple models were used in all of our asteroseismic studies of white dwarf pulsators up to (and including) the analyses of Giammichele et al. (2016) that helped determine the bulk composition in some white dwarf stars. This approach is however crude and does not fully exploit the asteroseismic potential of white dwarf pulsators. Another implemented option is to incorporate a pre-calculated C/O profile that mimic the features of an evolutionary-based chemical profile. This more sophisticated treatment originally proposed by Metcalfe (2005) only employs two free parameters, the constant central abundance of oxygen and the fractional mass at which the constant oxygen mass fraction starts dropping. Everything else is predetermined by scaling the shape of the drop from an evolutionary track at the specific white dwarf mass of 0.61M⊙ computed by Salaris et al. (1997). Over the years, these “physically motivated” C/O profiles were used for the study of numerous DAV and DBV by Bischoff-Kim and Metcalfe (2011) and Bischoff-Kim et al. (2014, 2019). While this may sound as an attractive alternative (in line with other studies based on evolution models), the lack of flexibility in defining the core configuration becomes a major limitation. Quite notably, this parametrization fails at reproducing the core composition profiles from evolutionary models at other masses and is unable to reproduce the triple chemical transition at the edge of the core, where oxygen, carbon, and helium are expected to coexist, according to current evolutionary sequences (see, e.g., Althaus et al., 2010).
Finally, once all components (parameters) defining the white dwarf structure have been specified, stellar structure equations are solved to determine the corresponding equilibrium state. This is done with the Montreal stellar structure and evolution code STELUM (Bédard et al., 2021; see also Section 4.2), which is the most recent evolution of our white-dwarf and hot-subdwarf modeling tool. The code is based on a Galerkin finite element solver and implements current state-of-the-art physics (EOS, opacities) to describe the star interior. Importantly, special care is taken by the code to produce models with smooth profiles for all physical quantities. Profile smoothness, which may not be as important in a stellar evolution context, is absolutely key for calculating pulsation periods accurately (see Brassard et al., 1991, Brassard et al., 1992a, Brassard et al., 1992b, Brassard et al., 1992c).
The novelty introduced by Giammichele et al. (2017a) in our static modeling capabilities has been to consider more realistic depth dependent core compositions, as obtained from detailed evolution calculations, without sacrificing flexibility. Determining the best (optimal) composition stratification given a set of observed pulsations periods sensitive to the core structure can be defined as an optimal design (or shape optimization) problem. These are encountered in many domains, such as aerodynamics, hydrodynamics, acoustics, electromagnetism, just to name a few. The typical problem is to find the shape that is optimal in that it minimizes some merit function, while satisfying given constraints. For example, in airfoil shape design, the problem is entirely defined by a set of parameters controlling the shape that are adjusted to minimize a merit function, typically the inverse of the lift-to-drag ratio. Our situation, the “design” of the chemical profile optimally matching the pulsation period spectrum through minimization of the
If the chosen parametrization is not flexible enough, meaning it cannot represent all possible shapes, then the solution will generally be sub-optimal, i.e., the true optimal shape can never be reached. Conversely, if the number of design parameters is too large, the underlying optimization problem becomes impractical due to prohibitive computation times. Various strategies, with their advantages and drawbacks, exists for the shape parametrization, involving either analytical, discrete, polynomial or spline representations (Gallart 2004). The most commonly used methods are based on spline representations which provide excellent compromises between flexibility and sparsity of the shape parameters. With this approach, a set of well-positioned weighting parameters, called control points, is used as the design variables and spline interpolation is applied to produce the profiles in between points. The great advantages of using splines are: it allows for a reduction of the number of control points (fewer parameters to optimize) while retaining a high level of flexibility (large variety of attainable shapes); the perturbation of one control point only has local effects on the overall shape (increased independence of the shape parameters), and it produces curves with C2-continuity (guarantying a smooth shape without high frequency oscillations). The latter property, in particular, is key for our problem of asteroseismology because smoothness in the composition profiles is essential to avoid artificial perturbations of the pulsation period spectrum, which is very sensitive to steep gradients.
In our context, amongst the many possibilities, we adopt spline representations to reproduce the oxygen chemical profile in a white-dwarf core based either on Akima (Akima 1970) or Fritsch-Carlson (Fritsch and Carlson 1980) splines. Both are continuously differentiable sub-spline interpolations using piece-wise third-order polynomials. Only the data from the next neighbor points are used to determine the coefficients of the interpolation polynomial, improving locality. Fritsch-Carlson assumes in addition a monotonic (either always decreasing or increasing) behavior of the function, which is generally relevant in our case. Both schemes are roughly equivalent, but the Fritsch-Carlson splines tend to be smoother near sharp chemical transitions. Compared to other more classical splines, such as cubic splines, both Akima and Fritsch-Carlson splines are immune to oscillations (also called “Gibbs noise”) in the vicinity of outliers or when gradients change abruptly. Their key advantage is to provide a stable and robust way to construct a wide variety of chemical stratification in the core.
When adopting this prescription, eight parameters are necessary to fully define a chemical stratification in the core that can resemble that of a white dwarf, as evolution models predict. It is expected from such calculations that the oxygen profile decreases outward following a double-ramp structure (see, e.g., Salaris et al., 2010). From our perspective, this double-ramp profile is obtained (see Figure 1 of Giammichele et al., 2017a) by specifying the position t1 and t2 (in fractional mass depth log q) of the two transitions, their respective half-width Δt1 and Δt2 (in log q), and the amount of oxygen (in mass fraction) at key locations, that is core(O) at the center, t1(O) and t2(O) at the bottom of the t1 transition and top of the t2 transition, respectively, and envl(O) at the bottom of the t2 transition. This last parameter accounts for specific cases involving DB white dwarfs for which it is believed that the mass fraction of oxygen may not drop to zero at the edge of the C/O core because of some dredge-up that occurred in the pre-white dwarf stage. In the context of DA white dwarfs, the envl(O) parameter is simply set to zero and the problem reduces to a seven-parameter shape optimization.
Figure 2 illustrates the flexibility of this approach by closely reproducing a set of configurations obtained from detailed evolution calculations. The C, O, He profiles are those derived by De Gerónimo et al. (2017) from a series of evolutionary models assuming different input physics for the helium-burning core (i.e., changing nuclear rates, overshoot at the boundary of the convective core) and the subsequent helium-shell burning phase (modifying the number of thermal pulses). As mentioned previously, these illustrate the significant changes occurring in the white dwarf interior just by taking into account typical uncertainties associated with these processes. Such considerations apart, the goal of the present exercise was to mimic each of these configurations with our static models incorporating the new parametrized core structure. This is achieved with no difficulty in all cases. In a context of detailed asteroseismic studies, it means that all of these configurations would belong to the searched parameter space and one of them could therefore be isolated if it happens to be the optimal representation of the real star. However, the power of the method extends well beyond choosing amongst predicted evolution profiles. A wide variety of configurations, including many that are unreachable with current evolution models, can be generated through this technique and tested for their ability to match the observed pulsation properties. Hence, this flexibility provides the opportunity to let the pulsation modes themselves determine the internal composition profiles in a way that is mostly independent of stellar evolution.
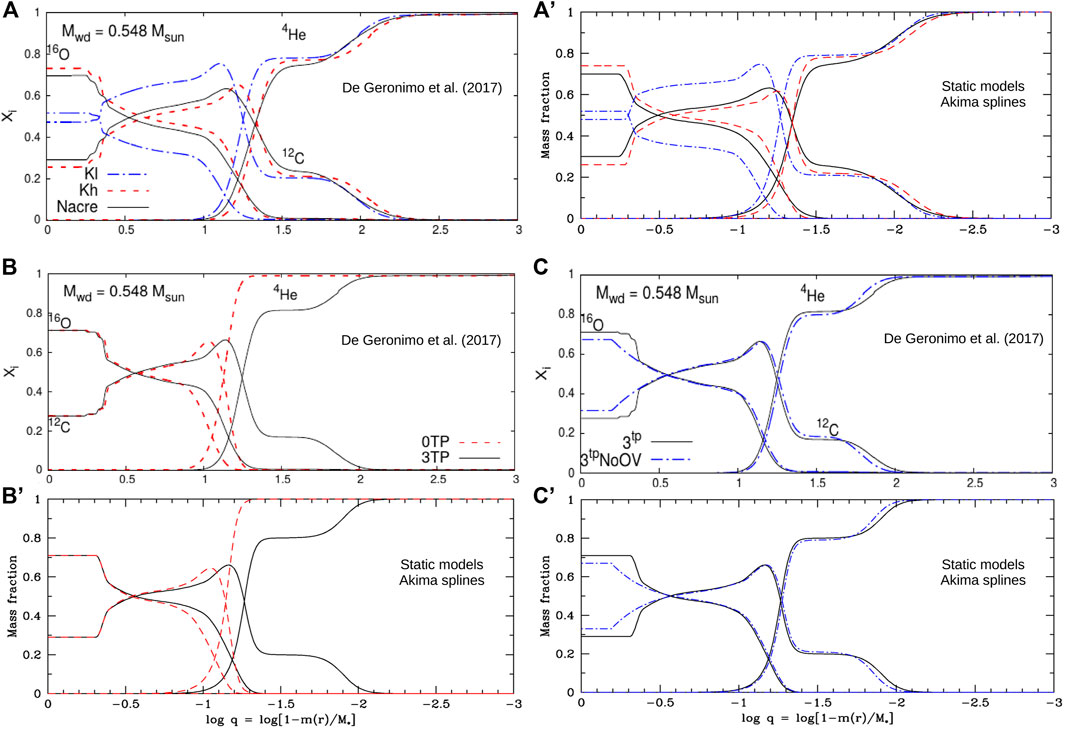
FIGURE 2. Panel (A) and (A′): Composition profiles of helium, carbon, and oxygen as functions of the fractional mass depth in a typical DA white dwarf produced by assuming different nuclear reaction rates in evolution calculations. Panel (A) is from De Gerónimo et al. (2017), while panel (A′) is a reproduction of these profiles with our parametrized static models. Panel (B) and (B′): Same as above, but for models when no thermal pulse or 3 thermal pulses occur during the post-AGB phase. Panel (C) and (C′): Same as above but for models with and without convective overshoot in evolution calculations.
The approach described previously, in particular the inclusion of parametrized shapes to construct the chemical profiles in the core, defines a multi-dimensional global optimization problem where the quantity
In order to address this complex global optimization problem, we developed a specific package that, amongst other tools, includes an hybrid real-coded genetic algorithm (RCGA; e.g., Eshelman and Schaffer 1993) multi-modal optimizer (a code named LUCY) whose role is to locate efficiently, in a single pass, the global optimum of the function to optimize, as well as eventual secondary optima. The basic principle of genetic algorithms (GA; Holland 1975; Goldberg 1989), which otherwise exist in many different flavors (see the recent review of Lambora et al., 2019), is to evolve a population of solutions, with each individual solution defined by a set of genes (coded from the parameters) and a merit value (evaluated from the function to optimize), through a set of selection, mating (crossover), and mutation (random sampling) operators. A selection pressure in favor of more fitted solutions, along with the mixing of their properties (mating) ensures the overall migration of the population toward best-fit regions of the parameter space, while randomness (through mutation) preserves diversity and the ability to explore all regions of the search domain. GA have proven to be highly effective to address hard optimization problems, while keeping the number of function evaluations relatively low. They are less effective in converging rapidly to the solution with precision, however, which is why hybridation (in our case by using the simplex method; Nelder and Mead 1965) is often considered in the final stage of the optimization run. The implementation in LUCY has several critical properties for the purposes of asteroseismology. First, the code uses real-coded genes (as opposed to more traditional binary-coded GAs) that allow to search parameter space continuously, i.e., there is no such thing as a resolution since the code generates solutions (models) with any value for their parameters in the specified range. Second, the code is multi-modal, by allowing subsets of its generated population to exist and evolve independently, and can therefore locate local optima at the same time as it robustly converges toward the global optimum. This capacity is fundamental to assess unicity of the solution, an aspect that is often overlooked in asteroseismic studies. Finally, the code is massively parallel and can perform hundreds-to-thousands of model evaluations simultaneously (when run on high-performance computing facilities), which is also a key property for the success of our approach. Just to give an idea of the computing power needed when white-dwarf asteroseismology is the objective, a typical optimization run with LUCY requires from several hundred thousand to nearly a million of seismic model evaluations (i.e., sequential operations as illustrated in Figure 1). This is many orders of magnitude less than an equivalent (and unfeasible) grid computation, but still a heavy calculation task that typically requires several hours using a few hundred CPU cores working in parallel on modern hardware. An application of the LUCY optimizer to a “noisy” 2D test function that would be challenging for traditional methods is presented in Figure 3, demonstrating how the code can locate multiple optima (including of course the global optimum) and perform some sampling in relevant regions of parameter space (near most significant optima) to estimate the local shape of the merit function. We see that the 3 lowest minima of interest are easily recovered, while other secondary deeps (up to the maximum number of subgroups of independent solutions that the code can sustain given the initial population size) are also spotted. If this function was a χ2-type distribution, such as in a real asteroseismic optimization exercise, parameter marginalization would lead to the probability distribution of each parameter (and therefore the error estimate), as illustrated in the lower left panel (and see Giammichele et al., 2016).
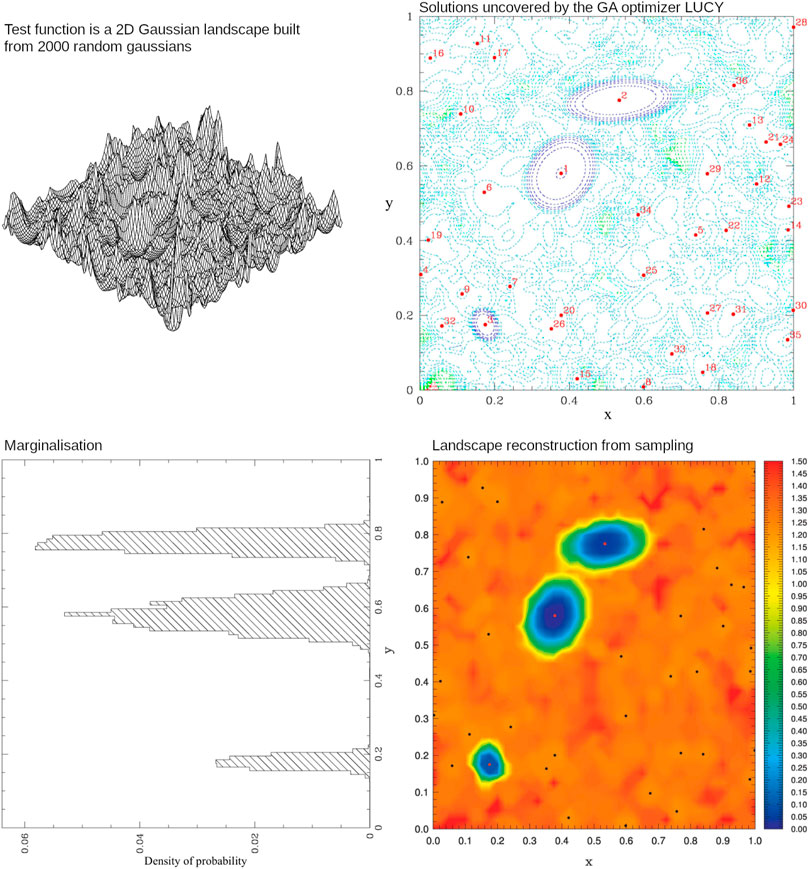
FIGURE 3. Illustration of the RCGA optimizer (LUCY) capabilities in finding the global minimum and most significant local minima of a complex test function with many local deeps. The upper left panel shows the function considered. It has 3 well defined minima, more visible in the contour map in the upper right panel. All solutions found by LUCY after convergence are indicated by numbered dots (each number giving the rank, by decreasing depth, of the identified minimum). The lower right panel shows the reconstruction of the test function shape based on the sampling done by the code during the search.
Our approach to tackle quantitative asteroseismology (of white-dwarf stars, in particular) has therefore a number of key methodological advantages that we summarize once more here. Among these, objectivity is an essential requirement that we always seek to achieve. To be objective, the search for the optimal seismic model has to derive from a wide and thorough exploration of model parameter space (criterion 1), using a robust method for finding the best-fit solution(s) (criterion 2). Uniqueness of the optimal solution should be stated in light of the quality of fit achieved for the best solution and its significance when compared to secondary optima (criterion 3). Finally, consistency with other independent constraints (e.g., from spectroscopy or parallax measurements) must be checked as well (criterion 4). Several of these requirements, in particular criteria 1 and 3, are often overlooked in the literature. Romero et al. (2012) and Castanheira and Kepler (2008), for instance, due to the use of grids of evolutionary models, generally impose a highly constrained search often limited to 3 parameters only. Uniqueness of the solution, often related to the achieved quality of fit (in an absolute sense) are rarely evaluated in this context. Most methods also use rather coarse grids (with the inherent problems associated to grids mentioned previously) using a relatively small number of model evaluations. If a high number of model calculations is not by itself a guarantee to find the global minimum and assess its unicity, it is necessary to ensure this last criterion is met. It should be obvious that a global search for best-fit models in a wide parameter space, owing to also assess errors and uniqueness, cannot be achieved with only a few hundred of seismic model calculations. Hundred of thousands of such models are actually needed to effectively sample the function that is optimized. The numerical tools that we developed are designed to give us the means to reach all of these criteria of objectivity. They do not rely on model grids and are computationally efficient to allow for a detailed exploration of parameter space.
This approach still has some limitations which one should also keep in mind. In particular it is not fully model independent. Whilst dependency on stellar evolution has been highly mitigated through the introduction of flexible static models, the latter still depend on constitutive ingredients, such as radiative and conductive opacities, equation of state, convection, just to name a few, which all have their underlying uncertainties. It should be clear, however, that the same limitations apply to all methods found in the literature, in particular those based on full evolutionary models which make use of the same ingredients for the input physics. Because of this, a seismic solution can still be biased, in the sense that whatever the precision achieved for the period fit and parameter determination, the solution may not be accurate, i.e., prone to systematics. Quality of fit (in an absolute sense) and consistency with independent constraints (criterion 4) become particularly important in this context, as they offer the only way to evaluate solution accuracy. There exist other sources of systematics linked to the numerical schemes themselves, such as how composition profiles are approximated with splines for instance, or to various assumptions entering the definition of the static models. Neglecting or not neutrino cooling or the presence of minor species is one of them, but other sources of (not necessarily known) uncertainties in the constitutive ingredients of the models could also influence the solution. These can, to some extent, be treated when evaluating realistic errors (as opposed to formal errors of the fit that can be very small) to the derived stellar parameters. This issue will be discussed further in Section 3 (see also the various discussions provided in Giammichele et al., 2018; Charpinet et al., 2019a).
Using the new seismic DA white dwarf models, we applied our optimization technique to 4 ZZ Ceti stars that we estimated were promising candidates: KIC 11911480 (Greiss et al., 2014), L19-2 (Sullivan and Sullivan 2000), SDSS J1136 + 0409 (Pyrzas et al., 2015), and EPIC 220347759. These stars were selected on the basis of the simplicity of their pulsation properties, a general characteristic of stars located near the blue edge of the ZZ Ceti instability strip, and exhibit as such pulsation periods in the range 100–500 s. These stars have high quality photometric lightcurves obtained from space with the Kepler spacecraft, except for L19-2 whose analysis relies on data from a former ground based multi-site campaign (Sullivan and Sullivan 2000). We present in this work, a selection of the results obtained from the seismic fits performed for these 4 DAV stars, while the details (fit analysis, errors assessments, comparison with other works, comparison with independent observational constraints, and analysis of rotation) will be disclosed elsewhere (Giammichele et al., 2022; in preparation).
Five independent periods were isolated for the seismic inferences of KIC 11911480 and L19-2, while SDSS J1136 + 0409, and EPIC 220347759 were analyzed based on eight and seven independent modes, respectively. These stars being close to the blue edge of the DAV instability strip, show few, but sufficient, low-degree and low-order g-modes, to obtain non-ambiguous seismic solutions in all cases.
We find that the seismic fits uncovered reproduce very closely the measured frequencies for all 4 stars, although less so for SDSS J1136 + 0409, as illustrated in Figure 4. While still reaching the precision of observations, the quality of fit for SDSS J1136 + 0409 is significantly lower than those obtained for the other stars. This case shows that our approach is not by nature an under-constrained problem that could match perfectly any period spectra. Another important point to highlight is that matching the periods at this precision with a model just reflects the fact that internal errors of the fit are very small, and that we are not limited, for example, by the flexibility of the parametrization or by insufficient grid resolution. Of course it should be clear that an almost perfect fit does not necessarily imply that the parameters inferred from it are perfectly constrained, for the reason that additional sources of uncertainty or systematics must also be taken into account (see below).
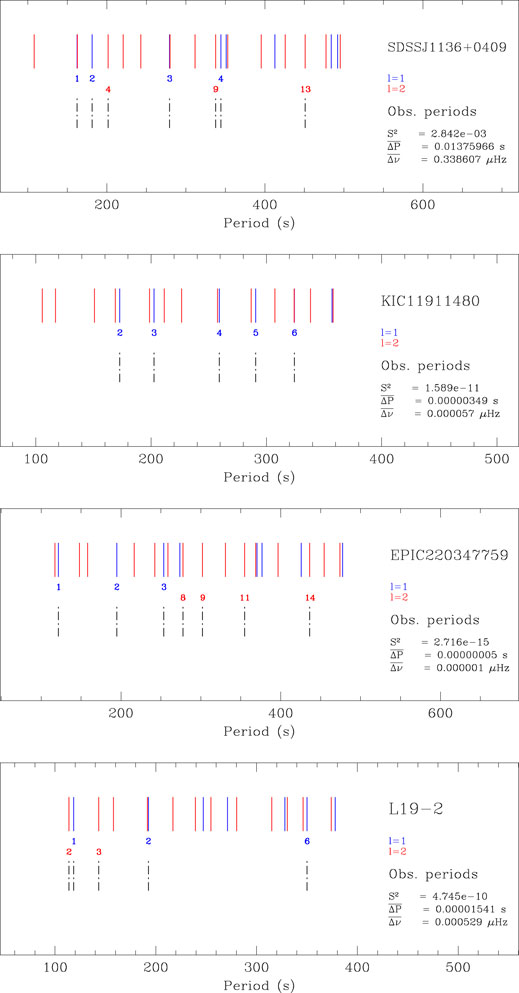
FIGURE 4. Periods of the ℓ = 1 and ℓ = 2 g-modes from the optimal seismic models superimposed with the fitted observed periods for the 4 ZZ Ceti stars analysed: SDSS J1136 + 0409, KIC 11911480, EPIC 220347759 and L19-2 (from top to bottom). Colors and numbers provide the corresponding mode identification (degree and radial order, respectively). Values obtained for the merit function, as well as the mean period and frequency dispersion of the fit are also given as indicators of the achieved quality of fit.
Our seismic estimates of the most relevant parameters derived for the 4 stars considered are provided in Table 1. In all cases but L19-2, we find seismic solutions that show a very good consistency with independent measurements of Teff and log g from spectroscopy. The latter were obtained from the most recent grids of DA model atmospheres (Bergeron et al., 1995; Gianninas et al., 2011) and by applying the 1D/3D correction from Tremblay et al. (2013). The apparent discrepancy for L19-2 is due to the fact that the optimal seismic model rather belongs to a family of solutions defining a long valley mainly oriented along the effective temperature axis, meaning that the observed pulsation modes in L19-2 do not constrain very tightly that parameter. It is important to note that, as was mentioned earlier, an almost perfect fit as obtained for L19-2 does not prevent possible degeneracies in some parameters of the solution.
The seismic solutions uncovered lead to a complete mapping of the chemical stratification inside these stars. Some of the values defining these composition profiles are given in Table 1, including the estimated masses for the hydrogen-rich envelope (log q(H) = log[1 − M(H)/M*]), the helium mantle, log q(He), and the central homogeneous C/O core, log q(core). We also indicate the oxygen mass fraction in that central region, O(core). In addition, we show in Figures 5–8 the derived composition profiles (with estimated uncertainties) for these objects. As a general rule of thumb, we typically find that the best determined profile parameters are the positions of the main chemical transitions–which is not surprising as they have a direct and usually strong impact on the period spectrum through mode trapping effects –, followed by central oxygen mass fraction in the core, which is also rather tightly estimated. In contrast, the inter-shell mixed C-O-He regions are usually the least constrained ones (larger uncertainties), with some variations from one target to the other (see also Charpinet et al., 2019a).
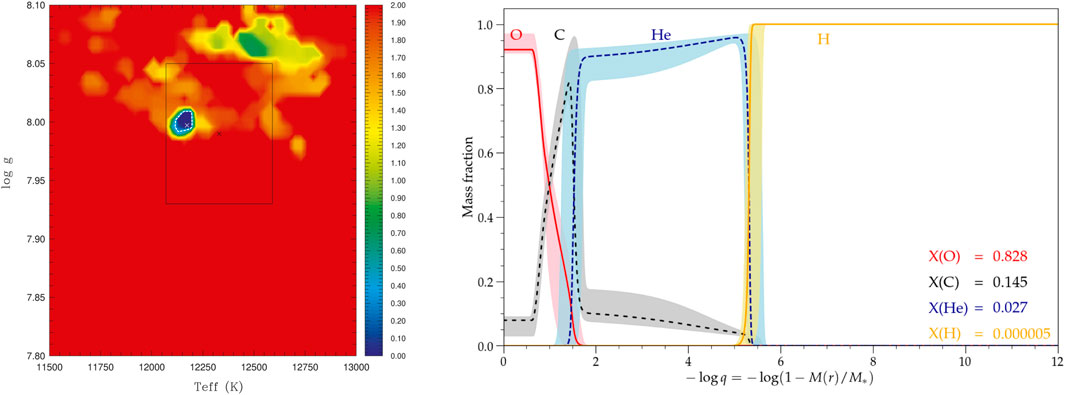
FIGURE 5. Left panel: Map of the merit function
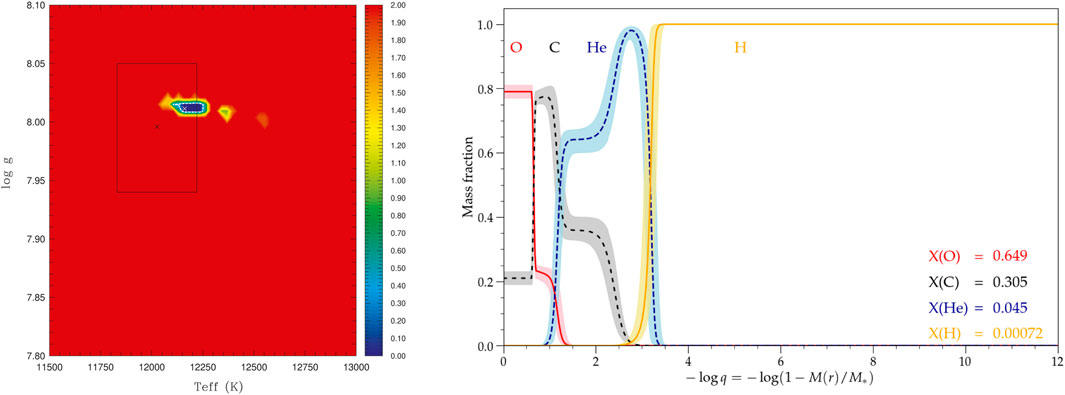
FIGURE 6. Same as Figure 5, but for the star KIC 11911480.
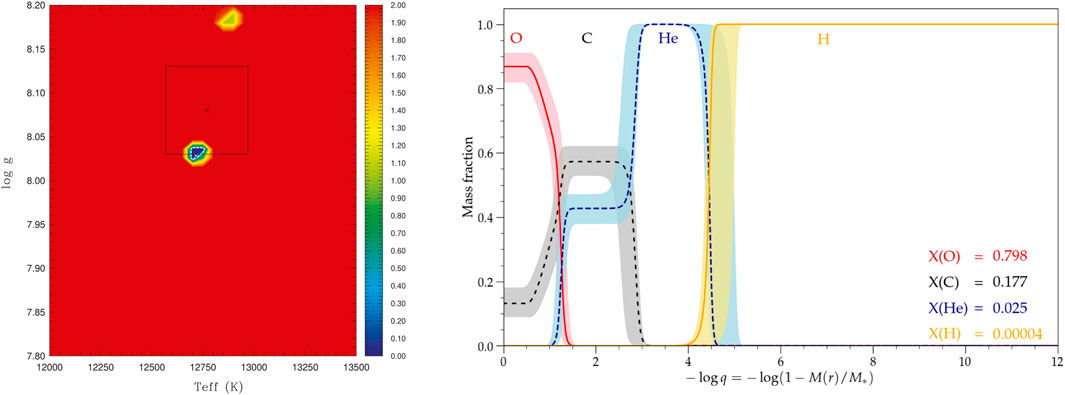
FIGURE 7. Same as Figure 5, but for the star EPIC 220347759.
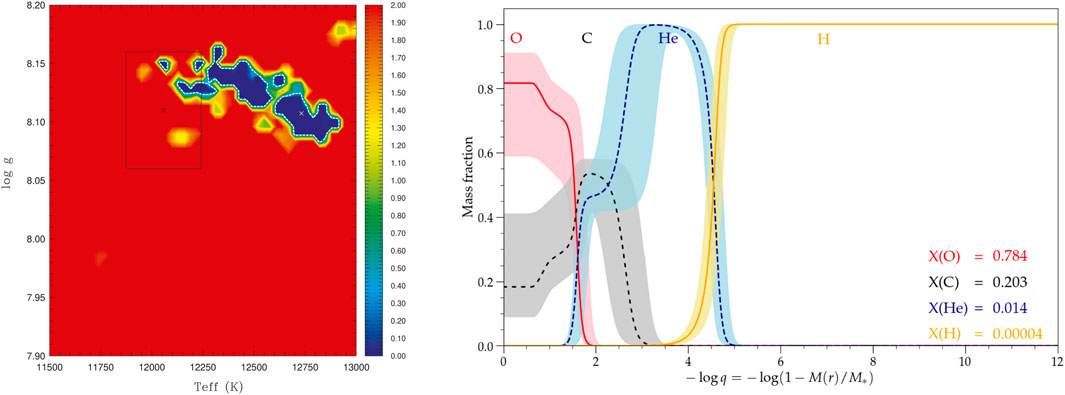
FIGURE 8. Same as Figure 5, but for the star L19-2. The core structure is less tightly constrained in this case which correlates to the degeneracy of the solution seen in the log g − Teff map, while the thickness of the H-rich envelope is still well determined.
Overall, our results point towards rather thick hydrogen envelops and helium mantles, by mass. Remarkably, the derived central core extent is found to be quite similar for the four stars, ranging from log q(core) ∼ − 0.63 to ∼ − 0.82. We emphasize that a similar core size has also been obtained from the seismic analysis of the DB white dwarf pulsator KIC 08626021 for which log q(core) = −0.72 ± 0.03 (Giammichele et al., 2018). These values lead to a mass for the central homogeneous C/O core–mainly produced by the former helium burning core–that is
Quantifying proper uncertainties is a mandatory exercise in evaluating what information can be extracted from the seismic solutions. Giammichele et al. (2018), and later on Charpinet et al. (2019a), attempted to evaluate additional sources of uncertainty (systematics or external errors), that could overcome the (often very small) internal errors estimated from the period fit propagated to the derived parameters. Internal chemical profiles and global parameters inferred do, to some extent, depend specifically on the particular components of the constitutive physics that went into building any model. That is, the results must be sensitive to, for example, our choice of radiative opacity, conductive opacity, or equation of state for the fully ionized interior as well as the partially ionized non-ideal envelope.
Beside those basic physics constituents, many other choices come down in the building of one single model. In the evolutionary approach, each WD chemical structure is the result of stacking numerous physical processes through the evolution of progenitor stars from the ZAMS to the thermally pulsing and mass-loss phases on the AGB, and from time-dependent element diffusion in the WD stage. Accepted standard prescriptions are routinely used without proper evaluation of systematics associated to them, and how those uncertainties can propagate to the final stages of evolution. Uncertain convective boundary mixing during the He-core burning and the thermally pulsating AGB phase (e.g., Constantino et al., 2015), coupled with the occurrence of possible extra-mixing episodes generate major variations on the extent of the convective boundary, and therefore on the resulting WD chemical transitions. Efforts to secure an Initial-Final Mass Relationship (IFMR) for stellar evolution models are weakened by the lack of proper prescription for convective boundary mixing, uncertainties on mass loss rates and effects of metallicity or He content dependence (Salaris et al., 2009).
Efforts have been made in the past few years to quantifying some uncertainties inherent to WD progenitor evolution and assess their impact on parameters of the resulting model (De Gerónimo et al., 2017, De Gerónimo et al., 2019; Pepper et al., 2022). These authors have tested the impact of the occurrence of thermal pulses (TPs) in WD progenitors, the uncertainty in the 12C(α,γ)16O cross section, and the occurrence of extra mixing during core He burning. For example, they found that the 12C(α,γ)16O reaction rate, as one of the main sources of uncertainties, is alone, responsible for varying the central oxygen abundance from 26% up to 45%. They also estimated that comparing models derived from having experienced 0 or 10 TPs leads to average variations in the period spectrum of the order of 10–20 s, with absolute difference going up to 30 s. This is by no mean a small effect on the pulsation periods of white dwarf stars.
Such large period variations are obviously important uncertainties propagating to parameters obtained from optimal fits based on evolution models. In addition, we recall that other sources of systematic errors are still left unaccounted for. The He content of the final WD model, for instance, can vary by a factor up to 3–4 (Romero et al., 2012), but is usually assumed fixed in model grids used for asteroseismology. The thickness of the H layer (the principal inference that comes out from seismic analyses built upon evolution models) is based on an artificial procedure, which does not reconcile with a consistent standard WD formation. The suppression of breathing pulses, occurring at the end of the core He burning, which we will go into more details in the next section, is also an overlooked model prescription that could be source of uncertainties. Numerical smoothness of the models is yet another critical point for accurate pulsation period calculations. Worth noting in this context, Salaris et al. (2013) evaluated that the sole effect of different numerical implementations of the stellar evolution equations, while having rigorously the same physics modules input, can lead to a difference of 2–8% in WD cooling times, hence without even taking into account different physics prescriptions, nor the probable accumulation of numerical noise over the complete stellar evolution.
Figure 9 illustrates the impact of various global (non-adiabatic effects, presence of 22Ne traces, impact of neutrino cooling) and localized (in that they affect the core stratification; e.g., a varying number of TPs, uncertain rate for the 12C(α,γ)16O reaction, extra mixing) sources of uncertainties on low radial-order g-mode pulsation spectra representative of a pulsating white dwarf near the blue edge (i.e., showing low radial-order g-modes). We emphasize that in this comparison, static models were used to provide a strictly identical structure (and parameters), except for the part of the model that is modified to reproduce the effect being investigated. For instance, the model corresponding to an evolution that experienced no TP is exactly the same as the model corresponding to 10 TPs, except for the internal chemical profiles which were reconstructed from the evolution models shown in Figure 2. This ensures that only the signature coming from the effect under consideration is measured, a disentanglement that is usually difficult to achieve when comparing evolution models. From Figure 9, we clearly see how the global effects considered tend to be minor in magnitude compared to other sources of uncertainties coming from the core structure generated by past evolution. It is also important to note that the periods are almost uniformly shifted in those cases, meaning that trapping/confinement properties of the modes are essentially preserved (we point out that this was explicitly verified by Timmes et al. (2018), in the context of the impact of neutrino cooling). A consequence is that these global sources of uncertainties are unlikely to significantly bias model quantities that can be derived from asteroseismology thanks to their sensitivity to mode trapping, namely the positions of steep chemical gradients inside the white-dwarf star (Charpinet et al., 2019a showed that these are indeed robust determinations). In contrast, processes affecting locally the core chemical profiles can greatly modify periods on an individual basis. It is clear from just a glimpse at Figure 9 that the period distribution itself is strongly affected, meaning that the trapping/confinement status of the modes are changed. Therefore, we warn that adopting a fixed, potentially inaccurate chemical stratification for the core structure could be disruptive regarding the reliability of the seismic solution uncovered.

FIGURE 9. Impact of various identified global and localized sources of uncertainties on a selection of 10 low-order (k = 1 − 10), low-degree (ℓ = 1) g-mode periods, representative of modes typical seen in the spectrum of a blue-edge pulsating DB white dwarf. The illustrated models are parametrized static structures in which everything is kept identical except the varied chemical profiles as reconstructed from Figure 2 models. The references for the chemical profiles with varying TPs (0: DB-0TP, and 10:DB-10TP), with different 12C(α,γ)16O reaction rates (DB-Kh,DB-Kl), and with extra-mixing (DB-3TP-noov) are from De Gerónimo et al. (2017). Global effects, including trace amount of 22Ne (DB-3TP-Ne22), non-adiabatic effects (DB-3TP-nad), and the resolved neutrino cooling problem (DB-3TP-neut) are also calculated. Mean and maximum values on the period and frequency differences relative to a reference model (DB-3TP-ad) are shown on the before last column. Largest seen period variation is indicated at the bottom.
Table 2 is an effort to gather and sum-up all possible contributions that could contribute to the external error budget when using our static seismic models with the parameterized cores or when using approaches based on evolutionary models. The two approaches are not equivalent in that respect, as the use of static models can in many occasions mitigate the uncertainties associated to a given process by an increased flexibility on how the model is designed. An example of this comes from the parametrization of the core chemical stratification which, in our static models, can handle any profile generated by the processes shaping the core of a white dwarf, including those deriving from the uncertainties associated to such processes. Deviations from the expected profiles (i.e., the uncertainties in the processes that produce them) are already part of the search space for a best-fit seismic solution in that case. From the table, we clearly see that the more physical processes we add to the making of a pulsating WD model, the more uncertainties pile up. What is especially important to realize is that many of the processes involved in the making of a WD model through an entire evolutionary loop are not thoroughly asserted yet. And for those already evaluated, the impact on the error budget is already an order of magnitude greater than the remaining external uncertainties estimated for the static seismic models.
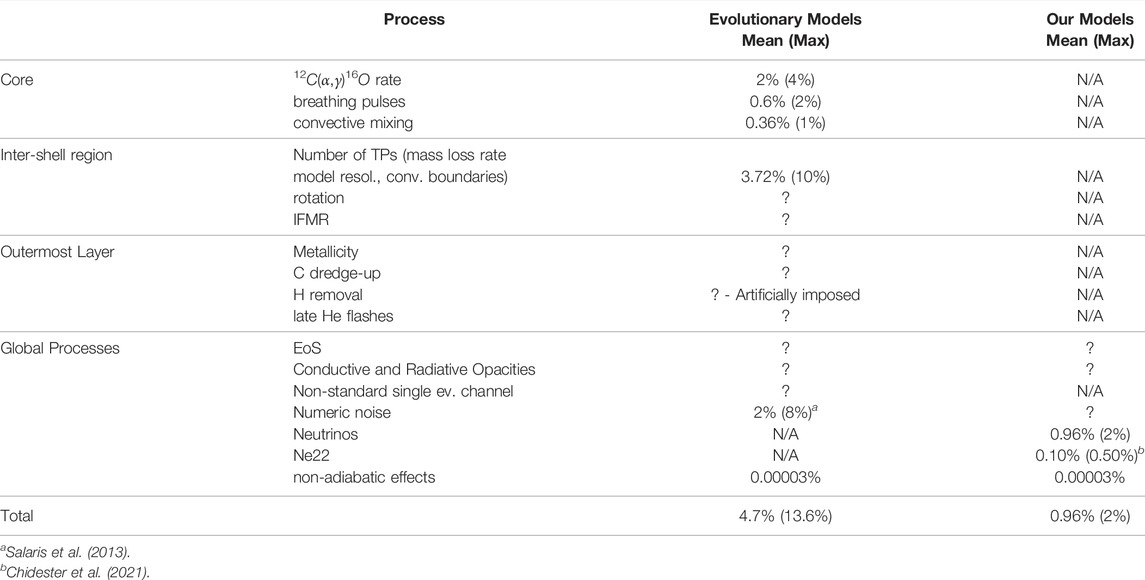
TABLE 2. List of potential contributions to the error budget that result from global processes and from specific prescriptions affecting the various layers of a white dwarf. These are estimated for evolutionary models (before last column) and for our static models (last column). We note that various potential sources of uncertainties that can affect the models have never been evaluated and their magnitude is unknown (those are indicated by question marks). We estimate the overall effect of TPs, overshooting prescriptions, and different12C(α,γ)16O reaction rates with the chemical profiles retrieved from De Gerónimo et al. (2017). The last line sums-up all effects of the listed external uncertainties in both cases, when known.
Beside a proper assessment of uncertainties, another essential aspect when performing a seismic analysis, is the criterion used to quantify the goodness of the fit. Recently, we have seen number of studies that rely on the Bayes Information Criterion (BIC) to evaluate and compare quality of different fits, which has the advantage of taking into account different numbers of data points and free parameters. As we mentioned before, finding an optimal fit does not guarantee that it is a good or even an acceptable fit. The same reasoning goes into comparing different fits with a BIC value. There is absolutely no guarantee that a better BIC value will yield a better fit (i.e., if the comparison model is a bad fit to the periods to start with, having a better BIC value does not guarantee that the new model indeed provides a good fit, merely that the fit is better). We therefore advocate here for the use of more robust criteria and more thorough analyses to ensure the conclusiveness of the optimal solution and quality of the parameters extracted.
As an example of why this is a critical point, we illustrate in Figure 10 the different orders of magnitude achieved in terms of quality of fit (here quantitatively evaluated as the mean and maximal differences achieved between the matched observed and computed periods) for typical DAV pulsators at the blue-edge using both methods. We show in the process some relevant precision limits that those fits should be compared with. First of all, we argue that caution should be used when the quality of fit reaches close to half the mean period spacing of the ℓ = 1 and 2 g-mode series, as it is the case for many DAV analyses performed with evolutionary models. This is an indication that the fit might be inconclusive to properly identify modes and derive reliable structural parameters, because the “best” seismic solution then becomes dangerously close to the worst cases that might be achieved when matching the periods. In addition to that, the impact on pulsation periods of the uncertainties associated with the core stratification (see again Figure 9), which would normally add up to the quality of fit, is also approaching the limit of half the value of the mean period spacing. To this account, we find Figure 10 to be particularly suggestive that what currently limits evolutionary models to achieve seismic solutions with a better quality of fit is the adoption of a core chemical structure that derives from evolution without considering its associated uncertainties. On average, the quality of fit obtained from evolutionary models remain close to two or three orders of magnitude larger than the actual precision of the measured periods, while static models provide a significant improvement in terms of quality of fit to that respect.
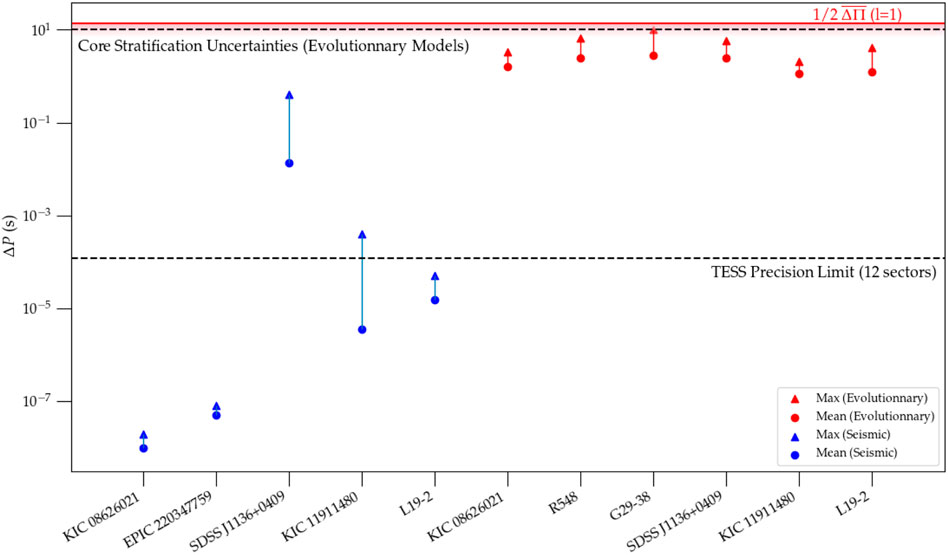
FIGURE 10. Mean and maximum period differences, on a logarithmic scale, between the observed and computed periods for the DAV pulsators presented in this work and the DBV KIC08626021 (Giammichele et al., 2018) using our new parametrized seismic models (in blue), compared to results obtained with full evolutionary models (in red) for the same stars, when available (KIC08626021:Córsico et al. (2012), R548, G29-38, and L19-2:Romero et al. (2012), SDSSJ1136 + 0409, KIC11911480:Romero et al. (2017)). We also indicate with a red horizontal line, half the value of the mean period spacing calculated for a typical DAV star of
Our most constant and robust finding from the analyses of KIC08626021 by Giammichele et al. (2018) and of the 4 DA pulsators reported in Section 3, is that the central homogeneous core in white-dwarf stars is significantly more massive (by
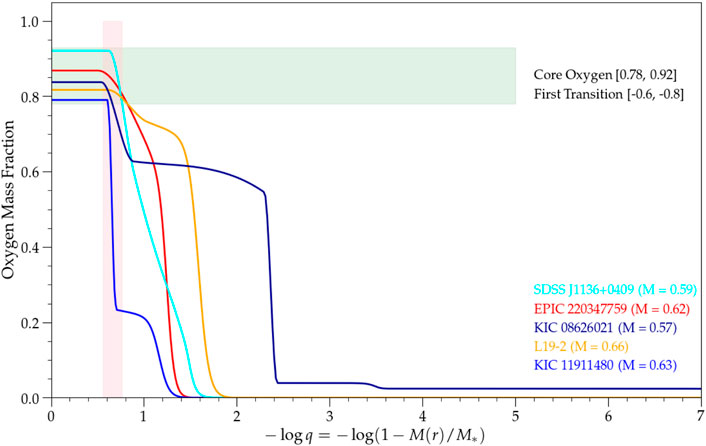
FIGURE 11. Inferred core oxygen profiles for the 4 DAV stars presented in this work, namely: SDSSJ1136 + 0409, EPIC 220347759, KIC11911480, and L19-2, and for the DBV star KIC08626021 (Giammichele et al., 2018).
This has implications at various levels, starting with our basic understanding of the core helium burning phase that shape these layers. We discuss specifically this aspect in the next Section 4.2. It also has impact on the estimation of white-dwarf cooling ages which depend on the internal C/O composition ratio. To this respect, our seismic estimates provide a powerful calibration of the internal composition profiles that is of direct benefit for white-dwarf cosmochronology (Fontaine et al., 2001). The total C/O ratio–that we find lower than expected–also has an impact for the study of type Ia supernovae (Domínguez et al., 2001). Less 56Ni is produced during the supernova explosion when this ratio is lower, with a direct influence on the light curve of type Ia supernovae which is governed by the decay of 56Ni. These supernovae are often used as standard candles in Cosmology, notably for testing the cosmological equation of state which might then benefit from a more accurate seismic calibration of white-dwarf core composition. Finally, we point out that our findings should also impact the field of white-dwarf asteroseismology itself, when methods based on full evolutionary models or models incorporating profiles from evolution calculations are used to estimate fundamental and structural parameters of white dwarf pulsators. The core composition and structure has a significant impact–in fact much larger than other effects of lesser importance, such as neutrino cooling (Charpinet et al., 2019a) or the presence of minor species like 22Ne–on the g-mode period spectrum. Therefore, assuming a canonical core structure derived by evolution calculations is likely to introduce a significant bias in the obtained seismic solutions.
The internal chemical stratification inferred from our white dwarf seismic models naturally raise the question of how such profiles can be produced by stellar evolution processes. Significant differences exist between these profiles and those predicted by standard evolutionary models and reconciling the two may indeed be challenging, possibly requiring deep introspection into our current understanding and modelling of stellar interiors and evolution. De Gerónimo et al. (2019) has been among the first to explore this issue by attempting to reproduce the seismic model uncovered by Giammichele et al. (2018) for the DBV pulsator KIC08626021. Exploring with some of the constitutive physics making up their evolution models (mostly varying parameters and values of already well identified and implemented processes), they could not easily reach a structure similar to the one found by Giammichele et al. (2018) unless–they find–unrealistic adjustments are imposed to the constitutive physics. Their underlying conclusion was therefore that it is not possible to reproduce the seismic model of KIC08626021, thus casting doubts about its validity. We have, however, to point out that De Gerónimo et al. (2019) did not consider all possible reasons, even amongst already known phenomena, that might have led to the differences suggested by asteroseismology.
As an illustration of this, we hereafter focus specifically on the problem of producing more oxygen at the white dwarf centre and overall larger cores than predicted by evolution. On that matter, De Gerónimo et al. (2019) reported that the rate of the 12C(α,γ)16O reaction would have to be increased by at least a factor 100 to reach the mass fraction of oxygen found by Giammichele et al. (2018), which by far sounds unrealistic. However, raising the rate of nuclear reactions is not the only lever that can affect the amount of oxygen ultimately produced in the helium-burning core. In order to illustrate this point, we present a full evolutionary sequence computed with our most recent version of the STELUM package3, our specialized stellar structure code used for asteroseismology (among other applications) and evolution of evolved compact stars. STELUM cannot, in its current state, evolve stars through the Asymptotic Giant Branch (AGB; i.e., the usual path followed by low-to-intermediate mass stars prior the white dwarf stage), but it can produce Extreme Horizontal Branch (EHB) models and evolve them through the helium-core and helium-shell burning phases, and then let them contract and cool on the white-dwarf sequence. Therefore, if STELUM cannot currently account for all the processes that ultimately shape the white-dwarf internal chemical stratification (those occurring during the AGB), it is useful to explore the evolution of helium burning cores that determine white dwarf most central layers, considering that these cores are expected to be similar, in structure and evolution, for all horizontal branch stars.
A full description of STELUM is beyond the scope of the present paper. We refer the interested reader to Bédard et al. (2021; see also Brassard and Fontaine 2015) for a detailed presentation of this numerical instrument and the historical background behind it. Yet, it is worth mentioning that one of the most important and defining particularity of STELUM is that it uses the so-called Galerkin finite-element scheme to solve the stellar structure equations, unlike most other stellar evolution codes that rely on finite-difference methods. Brassard et al. (1992b) showed, in the context of solving stellar pulsation equations, that Galerkin finite elements outperform finite-difference schemes in terms of stability, accuracy, and effectiveness. Another particularity of STELUM, which is most relevant in our present discussion, is that it treats element transport, including ordinary convection, convective overshoot, semi-convection, chemical and thermal diffusion, gravitational settling, thermohaline convection, stellar winds and external accretion as time-dependent diffusive processes that are all considered simultaneously. Special care is taken to resolve these processes over their highly varying timescales during evolution, meaning that substantial computational effort (and time) is invested by the code into computing many (often thousands of) intermediate models between each evolution time step. This implementation turns out to be important for following the evolution of convective helium burning cores. In this specific context, the mixing processes that we find to be essential are convection, convective overshoot, and gravitational settling. Convection is treated in the framework of the mixing length theory using our so-called ML1/α = 1 flavor (Tassoul et al., 1990) for the sequence described below. Convective overshoot at the edge of the convective core is modeled as suggested by Freytag et al. (1996), using an exponentially decaying diffusion coefficient. In the calculated evolution sequence, the overshoot parameter was set to its “standard”, 3D simulation-calibrated value fov = 0.02 (Herwig et al., 1997). Gravitational settling and diffusion in general (including thermal and chemical diffusion) are treated with the formalism of Burgers (1969) using diffusion coefficients evaluated from the results of Fontaine et al. (2015) based on an improved version of the method described in Paquette et al. (1986). Finally, the nuclear reaction rates adopted for these calculations are those of Angulo et al. (1999).
Figure 12 shows, in the log g − Teff plane, our reference STELUM evolutionary track computed from an initial structure of 0.48 M⊙ on the Zero Age Extreme Horizontal Branch (ZAEHB) to a Teff ∼ 8500 K white dwarf. The model evolves through the typical core helium-burning phase (EHB)–the main focus of the present discussion –, followed by the shell helium-burning (post-EHB), pre-white dwarf and white dwarf stages. Figure 13 shows the evolution of the central composition and core size from ZAEHB until full exhaustion of helium at the center of the star. Figure 14 illustrates how the core helium, carbon, and oxygen mass fraction profiles evolve during core helium burning (left and middle panels), and during the post-EHB and white dwarf stages (right panel).
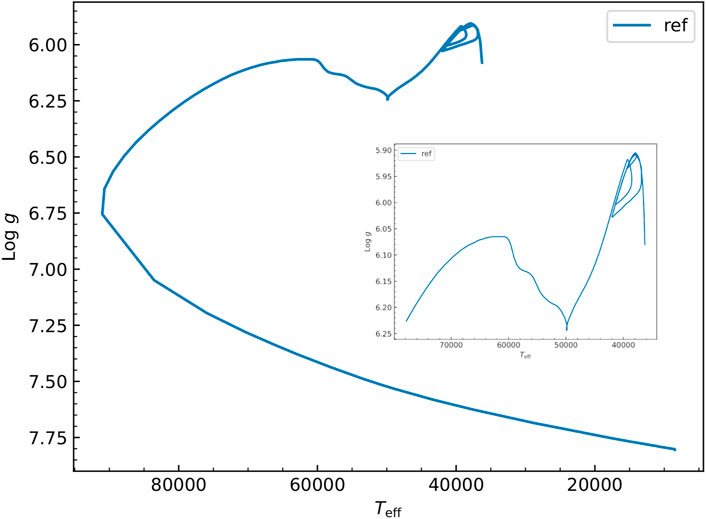
FIGURE 12. log g − Teff diagram showing a representative evolutionary track computed with STELUM for a typical, Mtot = 0.48 M⊙, EHB star having a thin hydrogen-rich envelope of logarithmic mass fraction log q(H) ≡ log(Menv/Mtot) = −5.0. The sequence starts at helium ignition (ZAEHB; upper right end of the curve) and proceeds through core helium burning (until the dip near 50,000 K), helium shell burning, and ultimately the white dwarf cooling stage down to Teff ∼ 8500 K. The insert shows a closer view of the track during the helium-core and helium-shell burning phases.
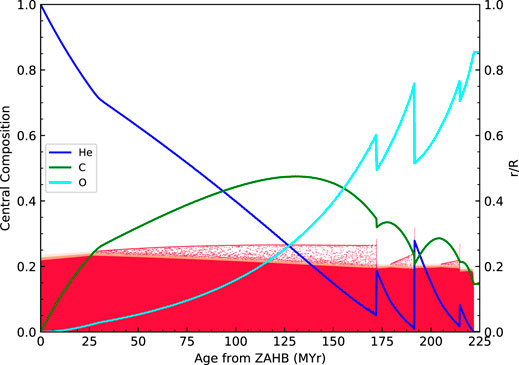
FIGURE 13. Evolution of the convective core (red-shaded area) and central C, O, and He mass fractions throughout the core helium-burning phase in the representative EHB evolutionary sequences computed with STELUM. The core evolution experience three main phases : 1) a steady core growth until X(He) ∼ 0.7, 2) the development of a partially mixed (semi-convective) region above the fully convective core whose size increases over time, and 3) the onset of breathing pulses when X(He) reaches
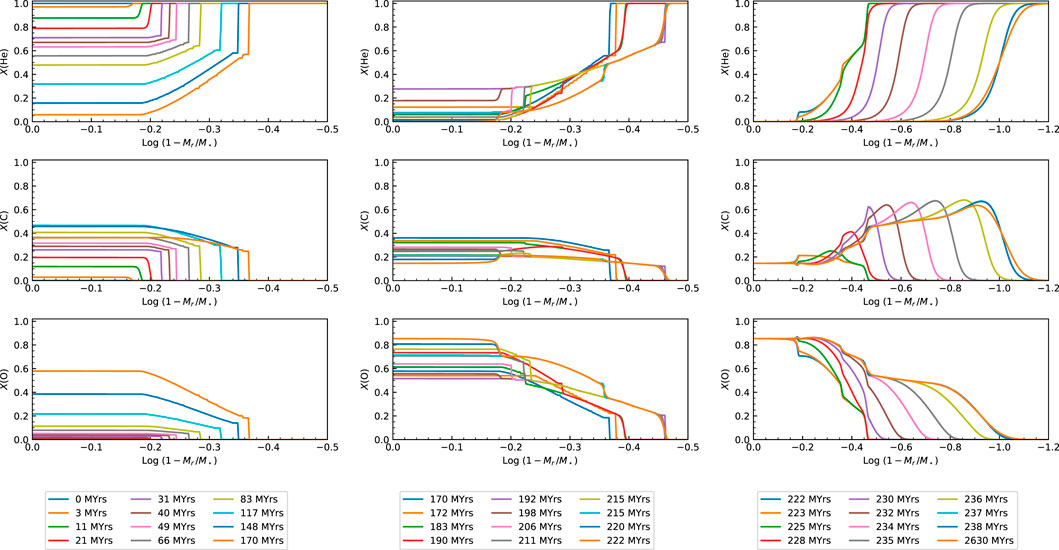
FIGURE 14. Evolution of the helium, carbon, and oxygen mass fraction profiles, from the onset of helium burning in the core to the white-dwarf cooling stage, in our reference evolutionary model. Left panel shows the growth of the helium burning core until the first breathing pulse. Middle panel shows the profiles evolving during third stage of the helium-burning core that experiences three breathing pulses before complete exhaustion of helium at the center. For completeness, right panel shows the chemical distribution that builds up during the shell helium-burning and white dwarf cooling phases. The last model represented in this panel corresponds to a white dwarf that has cooled down to
During central helium burning, the core experience three main phases. In a first early stage that last for
The second stage of the core evolution is therefore characterized in our model by the development of a partial mixing region that further extend the overall core size over time. During that period, occurring from
When Yc reaches
In summary, it is not necessary to modify the 12C(α,γ)16O reaction rate to obtain more oxygen in white-dwarf cores at levels comparable to the seismically determined ones. Breathing pulses during the late stage of core helium-burning evolution lead to such oxygen enrichment and appear to be the key process that is generally missing (or dismissed) in current stellar evolution models used to predict white-dwarf interior structures. More specifically, the breathing pulses were suppressed in the models discussed by De Gerónimo et al. (2019) and they were not considered as an alternative to solve some of the discrepancies these authors find between their evolution calculations and the seismic model obtained by Giammichele et al. (2018). We also find that the breathing pulses, along with the careful numerical treatment of mixing in the STELUM evolution code, contribute to produce cores that are larger than those obtained from canonical evolution calculations, thus closing or narrowing the gap between seismic and evolutionary models on that respect too. Overall, this demonstrates that reconciling our white-dwarf seismic models with evolution is not an impossible task, as claimed by De Gerónimo et al. (2019), but requires to review more critically how star interiors and evolution are modeled during the ultimate stages, keeping open the possibility that key events or processes may have been overlooked.
Stellar structures derived solely from observed oscillation frequencies using direct modeling or inversion techniques (that we commonly refer to as seismic models) have also been obtained for other types of stars. In particular, helioseismology has led to the construction of a seismic model of the Sun which shows puzzling differences with evolution calculations (see, e.g., Gough et al., 1996). An example of this is the sound speed profile at the base of the Sun’s convective envelope that appears to be shallower than expected from standard evolutionary models. While the seismic Sun still cannot be fully reproduced by evolution models, it is not an argument that is used to invalidate the seismic model itself, but rather to question the treatment of physics in the evolution calculations. White-dwarf seismic models, as the ones we presented in this paper and in Giammichele et al. (2018), have a vocation in all accounts similar to the establishment of the referential seismic Sun, with the added observation that uncertainties in the evolutionary path leading to white dwarfs are certainly far greater than the uncertainties in evolution that led to the Sun structure. We are therefore convinced that building seismic models of white dwarfs, and more generally of evolved compact stars (including hot-subdwarf pulsators; see Charpinet et al., 2019b and references therein), will be amongst the most prolific ways to shed light on the grey zones that still plague our understanding of the late stages of stellar evolution. For that purpose, the context is particularly favorable on the observation side, as large amounts of high-quality seismic data collected from space with instruments such as Kepler and the still operating TESS are available. We are committed to fully exploit these data in the upcoming years and refine our tools to do so.
NG and SC contributed equally on the analysis, interpretation of the data and redaction of the manuscript. PB contributed to sections of data analysis and programing. All authors contributed to manuscript revision, read, and approved the submitted version.
NG and Stephane Charpinet acknowledge financial support from the Centre National d'Etudes Spatiales (CNES, France) and from the Agence Nationale de la Recherche (ANR, France) under grant ANR-17-CE31-0018, funding the INSIDE project. This work was granted access to the high-performance computing resources of the CALMIP computing center under allocation numbers 2021-p0205.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1Here and after we employ the term “quantitative asteroseismology” to specifically refer to work that leads to quantitative estimates of fundamental parameters and inner structure of a given star. This is to make a distinction with the more generic use of the term “asteroseismology” that often refers, in the literature, to various types of analyses involving stellar pulsations in general (frequency extraction, mode identification, pulsation properties, etc).
2For instance, Córsico et al., 2012 used 2 free parameters in their analyses of DBVs: stellar mass (9 grid points ranging from 0.515 to 0.870 M⊙) and effective temperature Teff (between 300 and 900 grid points from 30,000 to 21,000 K). Córsico et al., 2013; Romero et al., 2017 used 3 free parameters for their analyses of DAVs: stellar mass (19 grid points from 0.525 to 1.050 M⊙), the hydrogen layer log q(H) (between 5 and 8 grid points from -3.5 and -9.5), and effective temperature Teff (200 grid points from 14,000 to 9,000 K). For extremely low-mass variables stars, Calcaferro et al., 2018 used 3 free parameters: stellar mass (14 grid points from 0.1554 to 0.4352 M⊙), hydrogen layer log q(H) (between 5 and 7 grid points from -1.69 and -5.79), and effective temperature Teff (200 grid points from 13,000 to 6,000 K). In other parts of the HR diagram, for β-Cephei stars Salmon et al., 2022 used 4 free parameters: stellar mass (110 grid points from 7.6 to 18.6 M⊙), envelope hydrogen mass fraction (3 grid points from 0.68 to 0.74), metallicity (4 grid points from 0.010 to 0.018), overshoot parameter (10 grid points from 0 to 0.5). For Slowly Pulsating B stars, Moravveji et al., 2015 used grids of mostly 4 free parameters (see their Table 2 for details on the grid-point distributions). For solar-like pulsators, among other methods based on scaling relations, model grids with typically 2 to 4 free parameters are used (see Silva Aguirre et al., 2017 and references therein).
3STELUM is for STELar modeling from Université de Montréal and is actively maintained and developed by one of us (P.B.).
4We emphasize that resolving accurately the abundance variations in this partial mixing zone, as done by STELUM, comes at a high cost in terms of computation time. The computation of our reference model sequence took several weeks using a contemporary fast multi-core CPU. Most of the computation time was spent on the mid/late stages of the core helium-burning phase.
Akima, H. (1970). A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures. J. ACM 17, 589–602. doi:10.1145/321607.321609
Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., Romero, A. D., Renedo, I., García-Berro, E., et al. (2010). New Chemical Profiles for the Asteroseismology of ZZ Ceti Stars. Astrophysical J. 717, 897–907. doi:10.1088/0004-637X/717/2/897
Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A Compilation of Charged-Particle Induced Thermonuclear Reaction Rates. Nucl. Phys. A 656, 3–183. doi:10.1016/S0375-9474(99)00030-5
Bédard, A., Brassard, P., Bergeron, P., and Blouin, S. (2021). On the Spectral Evolution of Hot White Dwarf Stars. II. Time-dependent Simulations of Element Transport in Evolving White Dwarfs with STELUM. Astrophysical J. in press. arXiv:2112.09989.
Bergeron, P., Wesemael, F., Lamontagne, R., Fontaine, G., Saffer, R. A., and Allard, N. F. (1995). Optical and Ultraviolet Analyses of ZZ Ceti Stars and Study of the Atmospheric Convective Efficiency in DA White Dwarfs. Astrophysical J. 449, 258. doi:10.1086/176053
Bischoff-Kim, A., and Metcalfe, T. S. (2011). Asteroseismic Constraints on Diffusion in White Dwarf Envelopes. MNRAS 414, 404–409. doi:10.1111/j.1365-2966.2011.18396.x
Bischoff-Kim, A., Østensen, R. H., Hermes, J. J., and Provencal, J. L. (2014). Seven-period Asteroseismic Fit of the Kepler DBV. Astrophysical J. 794, 39. doi:10.1088/0004-637X/794/1/39
Bischoff-Kim, A., Provencal, J. L., Bradley, P. A., Montgomery, M. H., Shipman, H. L., Harrold, S. T., et al. (2019). GD358: Three Decades of Observations for the In-Depth Asteroseismology of a DBV Star. Astrophysical J. 871, 13. doi:10.3847/1538-4357/aae2b1
Bradley, P. A., Winget, D. E., and Wood, M. A. (1993). The Potential for Asteroseismology of DB White Dwarf Stars. Astrophysical J. 406, 661. doi:10.1086/172477
Brassard, P., and Fontaine, G. (2015). “Improvements in the Montréal Evolutionary Code and Application to White Dwarfs,” in 19th European Workshop on White Dwarfs. Astronomical Society of the Pacific Conference Series. Editors P. Dufour, P. Bergeron, and G. Fontaine, Vol. 493, 125.
Brassard, P., Fontaine, G., Billères, M., Charpinet, S., Liebert, J., and Saffer, R. A. (2001). Discovery and Asteroseismological Analysis of the Pulsating sdB Star PG 0014+067. Astrophysical J. 563, 1013–1030. doi:10.1086/323959
Brassard, P., Fontaine, G., Wesemael, F., and Hansen, C. J. (1992a). Adiabatic Properties of Pulsating DA White Dwarfs. II - Mode Trapping in Compositionally Stratified Models. ApJS 80, 369. doi:10.1086/191668
Brassard, P., Fontaine, G., Wesemael, F., Kawaler, S. D., and Tassoul, M. (1991). Adiabatic Properties of Pulsating DA White Dwarfs. I - the Treatment of the Brunt-Vaisala Frequency and the Region of Period Formation. Astrophysical J. 367, 601. doi:10.1086/169655
Brassard, P., Fontaine, G., Wesemael, F., and Tassoul, M. (1992c). Adiabatic Properties of Pulsating DA White Dwarfs. IV - an Extensive Survey of the Period Structure of Evolutionary Models. ApJS 81, 747. doi:10.1086/191704
Brassard, P., Pelletier, C., Fontaine, G., and Wesemael, F. (1992b). Adiabatic Properties of Pulsating DA White Dwarfs. III - A Finite-Element Code for Solving Nonradial Pulsation Equations. ApJS 80, 725. doi:10.1086/191679
Calcaferro, L. M., Córsico, A. H., Althaus, L. G., Romero, A. D., and Kepler, S. O. (2018). Pulsating Low-Mass White Dwarfs in the Frame of New Evolutionary Sequences. VI. Thin H-Envelope Sequences and Asteroseismology of ELMV Stars Revisited. Astronomy Astrophysics 620, A196. doi:10.1051/0004-6361/201833781
Caputo, F., Chieffi, A., Tornambe, A., Castellani, V., and Pulone, L. (1989). The 'Red Giant Clock' as an Indicator for the Efficiency of Central Mixing in Horizontal-Branch Stars. Astrophysical J. 340, 241. doi:10.1086/167387
Cassisi, S., Castellani, V., Degl'Innocenti, S., Piotto, G., and Salaris, M. (2001). Asymptotic Giant Branch Predictions: Theoretical Uncertainties. Astronomy Astrophysics 366, 578–584. doi:10.1051/0004-6361:20000293
Castanheira, B. G., and Kepler, S. O. (2008). Seismological Studies of ZZ Ceti Stars - I. The Model Grid and the Application to Individual Stars. MNRAS 385, 430–444. doi:10.1111/j.1365-2966.2008.12851.x
Castellani, V., Chieffi, A., Tornambe, A., and Pulone, L. (1985). Helium-burning Evolutionary Phases in Population II Stars. I Breathing Pulses in Horizontal Branch Stars. Astrophysical J. 296, 204–212. doi:10.1086/163437
Charpinet, S., Giammichele, N., Brassard, P., Fontaine, G., Bergeron, P., Zong, W., et al. (2021). Toward a Systematic Cartography of the Chemical Stratification inside White Dwarfs from Deep Asteroseismic Probing of ZZ Ceti Stars. arXiv e-prints. arXiv:2107.03797.
Charpinet, S., Giammichele, N., Brassard, P., Van Grootel, V., and Fontaine, G. (2015). “Method and Tools for an Objective Approach of White Dwarf Asteroseismology,” in 19th European Workshop on White Dwarfs. Astronomical Society of the Pacific Conference Series. Editors P. Dufour, P. Bergeron, and G. Fontaine, Vol. 493, 151.
Charpinet, S., Brassard, P., Fontaine, G., Van Grootel, V., Zong, W., Giammichele, N., et al. (2019b). TESS First Look at Evolved Compact Pulsators. Astronomy Astrophysics 632, A90. doi:10.1051/0004-6361/201935395
Charpinet, S., Brassard, P., Giammichele, N., and Fontaine, G. (2019a). Improved Seismic Model of the Pulsating DB White Dwarf KIC 08626021 Corrected from the Effects of Neutrino Cooling. Astronomy Astrophysics 628, L2. doi:10.1051/0004-6361/201935823
Charpinet, S., Fontaine, G., Brassard, P., Green, E. M., and Chayer, P. (2005). Structural Parameters of the Hot Pulsating B Subdwarf PG 1219+534 from Asteroseismology. Astronomy Astrophysics 437, 575–597. doi:10.1051/0004-6361:20052709
Charpinet, S., Fontaine, G., and Brassard, P. (2009). Seismic Evidence for the Loss of Stellar Angular Momentum before the White-Dwarf Stage. Nature 461, 501–503. doi:10.1038/nature08307
Chidester, M. T., Timmes, F. X., Schwab, J., Townsend, R. H. D., Farag, E., Thoul, A., et al. (2021). On the Impact of 22Ne on the Pulsation Periods of Carbon-Oxygen White Dwarfs with Helium-Dominated Atmospheres. Astrophysical J. 910, 24. doi:10.3847/1538-4357/abdec4
Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., and Stello, D. (2015). The Treatment of Mixing in Core Helium Burning Models - I. Implications for Asteroseismology. Mon. Not. R. Astron. Soc. 452, 123–145. doi:10.1093/mnras/stv1264
Constantino, T., Campbell, S. W., and Lattanzio, J. C. (2017). The Treatment of Mixing in Core Helium-Burning Models - III. Suppressing Core Breathing Pulses with a New Constraint on Overshoot. MNRAS 472, 4900–4909. doi:10.1093/mnras/stx2321
Constantino, T., Campbell, S. W., Lattanzio, J. C., and van Duijneveldt, A. (2016). The Treatment of Mixing in Core Helium Burning Models - II. Constraints from Cluster Star Counts. Mon. Not. R. Astron. Soc. 456, 3866–3885. doi:10.1093/mnras/stv2939
Córsico, A. H., Romero, A. D., Althaus, L. G., and Miller Bertolami, M. M. (2013). “Asteroseismology of White Dwarfs with Fully Evolutionary Models,” in 18th European White Dwarf Workshop. Astronomical Society of the Pacific Conference Series. Editors J. Krzesiński, G. Stachowski, P. Moskalik, and K. Bajan, Vol. 469, 41.
Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., and Bischoff-Kim, A. (2012). Asteroseismology of theKeplerV777 Herculis Variable White Dwarf with Fully Evolutionary Models. Astronomy Astrophysics 541, A42. doi:10.1051/0004-6361/201118736
De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., and Kepler, S. O. (2017). Asteroseismology of ZZ Ceti Stars with Fully Evolutionary White Dwarf Models. Astronomy Astrophysics 599, A21. doi:10.1051/0004-6361/201629806
De Gerónimo, F. C., Battich, T., Miller Bertolami, M. M., Althaus, L. G., and Córsico, A. H. (2019). On the Recent Parametric Determination of an Asteroseismological Model for the DBV Star KIC 08626021. Astronomy Astrophysics 630, A100. doi:10.1051/0004-6361/201834988
Domínguez, I., Höflich, P., and Straniero, O. (2001). Constraints on the Progenitors of Type Ia Supernovae and Implications for the Cosmological Equation of State. Astrophysical J. 557, 279–291. doi:10.1086/321661
Dorman, B., and Rood, R. T. (1993). On Partial Mixing Zones in Horizontal-Branch Stellar Cores. Astrophysical J. 409, 387. doi:10.1086/172671
Eshelman, L. J., and Schaffer, J. D. (1993). Real-coded Genetic Algorithms and Interval-Schemata. Found. Genet. algorithms 2, 187–202. doi:10.1016/b978-0-08-094832-4.50018-0
Fields, C. E., Farmer, R., Petermann, I., Iliadis, C., and Timmes, F. X. (2016). Properties of Carbon-Oxygen White Dwarfs from Monte Carlo Stellar Models. Astrophysical J. 823, 46. doi:10.3847/0004-637X/823/1/46
Fontaine, G., Brassard, P., Dufour, P., and Tremblay, P. E. (2015). “Metal Accretion onto White Dwarfs. I. The Approximate Approach Based on Estimates of Diffusion Timescales,” in 19th European Workshop on White Dwarfs. Astronomical Society of the Pacific Conference Series. Editors P. Dufour, P. Bergeron, and G. Fontaine, 493, 113.
Fontaine, G., Brassard, P., and Bergeron, P. (2001). The Potential of White Dwarf Cosmochronology. Publ. Astron Soc. Pac 113, 409–435. doi:10.1086/319535
Fontaine, G., and Brassard, P. (2002). Can White Dwarf Asteroseismology Really Constrain the [TSUP]12[/TSUP]C(α, γ)[TSUP]16[/TSUP]O Reaction Rate? Astrophysical J. 581, L33–L37. doi:10.1086/345787
Fontaine, G., Brassard, P., and Charpinet, S. (2013). The Angular Momentum of Isolated White Dwarfs. EPJ Web Conf. 43, 05011. doi:10.1051/epjconf/20134305011
Fontaine, G., and Brassard, P. (2008). The Pulsating White Dwarf Stars. Publ. Astron Soc. Pac 120, 1043–1096. doi:10.1086/592788
Fontaine, G., and Wesemael, F. o. (2000). “Encyclopedia of Astronomy and Astrophysics,” in White Dwarfs (Bristol: Institute of Physics Publishing). doi:10.1888/0333750888/1894
Freytag, B., Ludwig, H. G., and Steffen, M. (1996). Hydrodynamical Models of Stellar Convection. The Role of Overshoot in DA White Dwarfs, A-type Stars, and the Sun. Astronomy Astrophysics 313, 497–516.
Fritsch, F. N., and Carlson, R. E. (1980). Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 17 (2), 238. doi:10.1137/0717021
Gallart, M. S. (2004). Development of a Design Tool for Aerodynamic Shape Optimization of Airfoils. Ph.D. thesis. Victoria, Canada: University of Victoria.
Giammichele, N., Fontaine, G., and Brassard, P. (2013b). “Quantitative Asteroseismology: Determination of the Core Composition and Layering of the ZZ Ceti Star R 548. Part II,” in 18th European White Dwarf Workshop. Astronomical Society of the Pacific Conference Series. Editors J. Krzesiński, G. Stachowski, P. Moskalik, and K. Bajan, Vol. 469, 49.
Giammichele, N., Fontaine, G., and Brassard, P. (2014). “Updates on the Asteroseismological Study of the ZZ Ceti Star R548: Determination of the Bulk Core Composition,” in 6th Meeting on Hot Subdwarf Stars and Related Objects. Astronomical Society of the Pacific Conference Series. Editors V. van Grootel, E. Green, G. Fontaine, and S. Charpinet, Vol. 481, 187.
Giammichele, N., Charpinet, S., Brassard, P., and Fontaine, G. (2017b). The Potential of Asteroseismology for Probing the Core Chemical Stratification in White Dwarf Stars. Astronomy Astrophysics 598, A109. doi:10.1051/0004-6361/201629935
Giammichele, N., Charpinet, S., Fontaine, G., Brassard, P., Green, E. M., Van Grootel, V., et al. (2018). A Large Oxygen-Dominated Core from the Seismic Cartography of a Pulsating White Dwarf. Nature 554, 73–76. doi:10.1038/nature25136
Giammichele, N., Charpinet, S., Fontaine, G., and Brassard, P. (2017a). Toward High-Precision Seismic Studies of White Dwarf Stars: Parametrization of the Core and Tests of Accuracy. Astrophysical J. 834, 136. doi:10.3847/1538-4357/834/2/136
Giammichele, N., Fontaine, G., Bergeron, P., Brassard, P., Charpinet, S., Pfeiffer, B., et al. (2015). A New Analysis of the Two Classical ZZ Ceti White Dwarfs GD 165 and Ross 548. I. Photometry and Spectroscopy. Astrophysical J. 815, 56. doi:10.1088/0004-637X/815/1/56
Giammichele, N., Fontaine, G., Brassard, P., and Charpinet, S. (2016). A New Analysis of the Two Classical ZZ Ceti White Dwarfs GD 165 and Ross 548. II. Seismic Modeling. ApJS 223, 10. doi:10.3847/0067-0049/223/1/10
Giammichele, N., Fontaine, G., and Brassard, P. (2013a). Quantitative Asteroseismology: Determination of the Core Composition and Layering of the ZZ Ceti Star R548. Part I. EPJ Web Conf. 43, 05007. doi:10.1051/epjconf/20134305007
Gianninas, A., Bergeron, P., and Ruiz, M. T. (2011). A Spectroscopic Survey and Analysis of Bright, Hydrogen-Rich White Dwarfs. Astrophysical J. 743, 138. doi:10.1088/0004-637X/743/2/138
Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Boston, MA, United States: Addison-Wesley Longman Publishing.
Gough, D. O., Kosovichev, A. G., Toomre, J., Anderson, E., Antia, H. M., Basu, S., et al. (1996). The Seismic Structure of the Sun. Science 272, 1296–1300. doi:10.1126/science.272.5266.1296
Greiss, S., Gänsicke, B. T., Hermes, J. J., Steeghs, D., Koester, D., Ramsay, G., et al. (2014). KIC 11911480: the Second ZZ Ceti in the Kepler Field. MNRAS 438, 3086–3092. doi:10.1093/mnras/stt2420
Herwig, F., Bloecker, T., Schoenberner, D., and El Eid, M. (1997). Stellar Evolution of Low and Intermediate-Mass Stars. IV. Hydrodynamically-Based Overshoot and Nucleosynthesis in AGB Stars. Astronomy Astrophysics 324, L81–L84.
Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. Cambridge, MA, USA: MIT Press.
Kawaler, S. D., and Bradley, P. A. (1994). Precision Asteroseismology of Pulsating PG 1159 Stars. Astrophysical J. 427, 415. doi:10.1086/174152
Lambora, A., Gupta, K., and Chopra, K. (2019). “Genetic Algorithm- A Literature Review,” in International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), 380–384. doi:10.1109/COMITCon.2019.8862255
Li, Y., Chen, X.-h., Xiong, H.-r., Guo, J.-j., Chen, X.-f., and Han, Z.-w. (2018). Convective Overshooting in sdB Stars Using the K-ω Model. Astrophysical J. 863, 12. doi:10.3847/1538-4357/aacdf9
Li, Z., and Li, Y. (2021). Convective Overshooting in Extreme Horizontal-Branch Stars Using MESA with the K-Omega Model*. Astrophysical J. 923, 166. doi:10.3847/1538-4357/ac2d8e
Metcalfe, T. S. (2005). A Deeper Understanding of White Dwarf Interiors. Mon. Notices R. Astronomical Soc. Lett. 363, L86–L90. doi:10.1111/j.1745-3933.2005.00091.x
Metcalfe, T. S. (2001). Computational Asteroseismology. Publ. Astron Soc. Pac 113, 1308. doi:10.1086/323287
Metcalfe, T. S., Nather, R. E., and Winget, D. E. (2000). Genetic‐Algorithm-based Asteroseismological Analysis of the DBV White Dwarf GD 358. Astrophysical J. 545, 974–981. doi:10.1086/317862
Metcalfe, T. S., Winget, D. E., and Charbonneau, P. (2001). Preliminary Constraints on12C (α,γ)16O from White Dwarf Seismology. Astrophysical J. 557, 1021–1027. doi:10.1086/321643
Montgomery, M. H. (2005). A New Technique for Probing Convection in Pulsating White Dwarf Stars. Astrophysical J. 633, 1142–1149. doi:10.1086/466511
Moravveji, E., Aerts, C., Pápics, P. I., Triana, S. A., and Vandoren, B. (2015). Tight Asteroseismic Constraints on Core Overshooting and Diffusive Mixing in the Slowly Rotating Pulsating B8.3V Star KIC 10526294. Astronomy Astrophysics 580, A27. doi:10.1051/0004-6361/201425290
Nelder, J. A., and Mead, R. (1965). A Simplex Method for Function Minimization. Comput. J. 7, 308–313. doi:10.1093/comjnl/7.4.308
Ostrowski, J., Baran, A. S., Sanjayan, S., and Sahoo, S. K. (2021). Evolutionary Modelling of Subdwarf B Stars Using MESA with the Predictive Mixing and Convective Pre-mixing Schemes. MNRAS 503, 4646–4661. doi:10.1093/mnras/staa3751
Paquette, C., Pelletier, C., Fontaine, G., and Michaud, G. (1986). Diffusion Coefficients for Stellar Plasmas. ApJS 61, 177. doi:10.1086/191111
Paxton, B., Cantiello, M., Arras, P., Bildsten, L., Brown, E. F., Dotter, A., et al. (2013). Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. ApJS 208, 4. doi:10.1088/0067-0049/208/1/4
Paxton, B., Schwab, J., Bauer, E. B., Bildsten, L., Blinnikov, S., Duffell, P., et al. (2018). Modules for Experiments in Stellar Astrophysics (${\Mathtt{M}}{\Mathtt{E}}{\Mathtt{S}}{\Mathtt{A}}$): Convective Boundaries, Element Diffusion, and Massive Star Explosions. ApJS 234, 34. doi:10.3847/1538-4365/aaa5a8
Paxton, B., Smolec, R., Schwab, J., Gautschy, A., Bildsten, L., Cantiello, M., et al. (2019). Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. ApJS 243, 10. doi:10.3847/1538-4365/ab2241
Pech, D., Vauclair, G., and Dolez, N. (2006). Asteroseismological Constraints on the Structure of the ZZ Ceti Star HL Tau 76. Astronomy Astrophysics 446, 223–235. doi:10.1051/0004-6361:20053150
Pepper, B. T., Istrate, A. G., Romero, A. D., and Kepler, S. O. (2022). The Impact of the Uncertainties in the 12C(α, γ)16O Reaction Rate on the Evolution of Low- to Intermediate-Mass Stars. MNRAS 513, 1499–1512. doi:10.1093/mnras/stac1016
Pyrzas, S., Gänsicke, B. T., Hermes, J. J., Copperwheat, C. M., Rebassa-Mansergas, A., Dhillon, V. S., et al. (2015). Discovery of ZZ Cetis in Detached White Dwarf Plus Main-Sequence Binaries. MNRAS 447, 691–697. doi:10.1093/mnras/stu2412
Romero, A. D., Córsico, A. H., Althaus, L. G., Kepler, S. O., Castanheira, B. G., and Miller Bertolami, M. M. (2012). Toward Ensemble Asteroseismology of ZZ Ceti Stars with Fully Evolutionary Models. MNRAS 420, 1462–1480. doi:10.1111/j.1365-2966.2011.20134.x
Romero, A. D., Córsico, A. H., Castanheira, B. G., Gerónimo, F. C. D., Kepler, S. O., Koester, D., et al. (2017). Probing the Structure ofKeplerZZ Ceti Stars with Full Evolutionary Models-Based Asteroseismology. Astrophysical J. 851, 60. doi:10.3847/1538-4357/aa9899
Romero, A. D., Kepler, S. O., Córsico, A. H., Althaus, L. G., and Fraga, L. (2013). Asteroseismological Study of Massive ZZ Ceti Stars with Fully Evolutionary Models. Astrophysical J. 779, 58. doi:10.1088/0004-637X/779/1/58
Salaris, M., Althaus, L. G., and García-Berro, E. (2013). Comparison of Theoretical White Dwarf Cooling Timescales. Astronomy Astrophysics 555, A96. doi:10.1051/0004-6361/201220622
Salaris, M., and Cassisi, S. (2017). Chemical Element Transport in Stellar Evolution Models. R. Soc. open Sci. 4, 170192. doi:10.1098/rsos.170192
Salaris, M., Cassisi, S., Pietrinferni, A., Kowalski, P. M., and Isern, J. (2010). A Large Stellar Evolution Database for Population Synthesis Studies. VI. White Dwarf Cooling Sequences. Astrophysical J. 716, 1241–1251. doi:10.1088/0004-637X/716/2/1241
Salaris, M., Domínguez, I., Garcia‐Berro, E., Hernanz, M., Isern, J., and Mochkovitch, R. (1997). The Cooling of CO White Dwarfs: Influence of the Internal Chemical Distribution. Astrophysical J. 486, 413–419. doi:10.1086/304483
Salaris, M., Serenelli, A., Weiss, A., and Bertolami, M. M. (2009). Semi-empirical White Dwarf Initial-Final Mass Relationships: A Thorough Analysis of Systematic Uncertainties Due to Stellar Evolution Models. Astrophysical J. 692, 1013–1032. doi:10.1088/0004-637X/692/2/1013
Salaris, M. (2008). “White Dwarf Cosmochronology: Techniques and Uncertainties,” in Proc. IAU. The Ages of Stars. Editors E. E. Mamajek, D. R. Soderblom, and R. F. G. Wyse, Vol. 4, 287–298. doi:10.1017/S1743921309031937
Salmon, S. J. A. J., Eggenberger, P., Montalbán, J., Miglio, A., Noels, A., Buldgen, G., et al. (2022). Asteroseismology of β Cephei Stars: The Stellar Inferences Tested in Hare and Hound Exercises. Astronomy Astrophysics 659, A142. doi:10.1051/0004-6361/202142483
Silva Aguirre, V., Lund, M. N., Antia, H. M., Ball, W. H., Basu, S., Christensen-Dalsgaard, J., et al. (2017). Standing on the Shoulders of Dwarfs: the Kepler Asteroseismic LEGACY Sample. II.Radii, Masses, and Ages. Astrophysical J. 835, 173. doi:10.3847/1538-4357/835/2/173
Sullivan, D. J., and Sullivan, T. (2000). Frequency Stabilities of Two Pulsating White Dwarfs. Balt. Astron. 9, 81–86. doi:10.1515/astro-2000-0114
Sweigart, A. V., and Demarque, P. (1973). “Semiconvection and the RR Lyrae Variables,” in IAU Colloq. 21: Variable Stars in Globular Clusters and in Related Systems. Astrophysics and Space Science Library. Editor J. D. Fernie, Vol. 36, 221–228. doi:10.1007/978-94-010-2590-4_32
Tassoul, M., Fontaine, G., and Winget, D. E. (1990). Evolutionary Models for Pulsation Studies of White Dwarfs. ApJS 72, 335. doi:10.1086/191420
Timmes, F. X., Townsend, R. H. D., Bauer, E. B., Thoul, A., Fields, C. E., and Wolf, W. M. (2018). The Impact of White Dwarf Luminosity Profiles on Oscillation Frequencies. Astrophysical J. 867, L30. doi:10.3847/2041-8213/aae70f
Tremblay, P.-E., Ludwig, H.-G., Steffen, M., and Freytag, B. (2013). Spectroscopic Analysis of DA White Dwarfs with 3D Model Atmospheres. Astronomy Astrophysics 559, A104. doi:10.1051/0004-6361/201322318
Van Grootel, V., Charpinet, S., Brassard, P., Fontaine, G., and Green, E. M. (2013a). Third Generation Stellar Models for Asteroseismology of Hot B Subdwarf Stars. Astronomy Astrophysics 553, A97. doi:10.1051/0004-6361/201220896
Van Grootel, V., Fontaine, G., Brassard, P., and Dupret, M.-A. (2013b). The Newly Discovered Pulsating Low-Mass White Dwarfs: An Extension of the ZZ Ceti Instability Strip. Astrophysical J. 762, 57. doi:10.1088/0004-637X/762/1/57
Keywords: stars, white-dwarfs, structure, evolution, asteroseismology
Citation: Giammichele N, Charpinet S and Brassard P (2022) Seismic Cartography of White-Dwarf Interiors From the Toulouse-Montréal Optimal-Design Approach. Front. Astron. Space Sci. 9:879045. doi: 10.3389/fspas.2022.879045
Received: 18 February 2022; Accepted: 28 April 2022;
Published: 14 June 2022.
Edited by:
Santiago Torres, Universitat Politecnica de Catalunya, SpainReviewed by:
Giovanni Catanzaro, Osservatorio Astrofisico di Catania (INAF), ItalyCopyright © 2022 Giammichele, Charpinet and Brassard. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Noemi Giammichele, bm9lbWkuZ2lhbW1pY2hlbGVAaXJhcC5vbXAuZXU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.