Multi-Physics Constraints at Different Densities to Probe Nuclear Symmetry Energy in Hyperonic Neutron Stars

The appearance of strangeness in the form of hyperons within the inner core of neutron stars is expected to affect its detectable properties, such as its global structure or gravitational wave emission. This work explores the parameter space of hyperonic stars within the framework of the Relativistic Mean Field model allowed by the present uncertainties in the state-of-the-art nuclear and hypernuclear experimental data. We impose multi-physics constraints at different density regimes to restrict the parameter space: Chiral effective field theory, heavy-ion collision data, and multi-messenger astrophysical observations of neutron stars. We investigate possible correlations between empirical nuclear and hypernuclear parameters, particularly the symmetry energy and its slope, with observable properties of neutron stars. We do not find a correlation for the hyperon parameters and the astrophysical data. However, the inclusion of hyperons generates a tension between the astrophysical and heavy-ion data constraining considerably the available parameter space.

1 Introduction

Understanding strong interaction among hadrons is one of the most intriguing topics in nuclear physics. Despite the recent progress in understanding the phase diagram of Quantum Chromodynamics (QCD), the theory of strong interactions (Baym et al., 2018; David et al., 2020), we are still far from achieving a unified description of nuclear matter under extreme conditions of density and temperature. While terrestrial nuclear experiments probe densities close to nuclear saturation density (n₀ ∼ 0.16 fm⁻³) (Gandolfi et al., 2015; Lattimer, 2015), heavy-ion collision (HIC) experiments (Le Fèvre et al., 2016; Russotto et al., 2016) provides information about the hot and dense matter at several times n₀. Recent progress in Lattice QCD (Inoue, 2016; Inoue, 2019; Fabbietti et al., 2021) also provides new constraints on the properties of matter at high temperature and low densities. Neutron stars, on the contrary, are astrophysical laboratories that provide us an opportunity to investigate ultra-high density (up to 10 times n₀) and low-temperature regime of the QCD phase diagram, given the conditions that exist only in its interior (Lattimer and Prakash, 2004; Glendenning, 2012).

Strangeness adds a new dimension to the description of nuclear matter. The presence of strangeness has already been established in heavy-ion collisions (appearance of hyperons and kaons) or in finite nuclear systems (hypernuclei). It is also conjectured that strangeness-containing matter, in the form of hyperons, kaons, or even deconfined quark matter, can appear at the ultra-high densities that exist in the core of a neutron star (NS). The appearance of strangeness can have a significant impact on NS composition, structure, and observable astrophysical properties, such as its mass, radius, cooling, or gravitational wave (GW) emission (Oertel et al., 2017).

In order to connect the NS internal composition with its global properties, one requires an equation of state (EoS) (Lattimer, 2012; Lattimer, 2015; Baym et al., 2018). The theoretical description of NS matter, therefore, requires the construction of models of hadron–hadron interaction, using non-relativistic (such as Skyrme or Gogny interactions) (Vautherin and Brink, 1972; Stone and Reinhard, 2007; Dutra et al., 2012) or relativistic (Relativistic Mean Field or Dirac-Brueckner-Hartree-Fock methods) (Serot and Walecka, 1992; Serot and Walecka, 1997) techniques. In the case of microscopic models (such as the Brueckner-Hartree-Fock method), the interactions are rigorously calculated from lowest order term to increasing order. Nevertheless, the poor knowledge of three-nucleon forces limits their applicability to reproduce real astrophysical data. Phenomenological models are more successful, with the model parameters usually constrained at densities close to n₀ and low isospin values (neutron-proton ratio), but the uncertainty increases at larger densities and asymmetries. The nuclear symmetry energy (the difference between the binding energies of symmetric nuclear matter and neutron matter) is a key quantity that governs the difference in the behavior of infinite symmetric nuclear matter and neutron star matter.

Neutron stars are particularly interesting, as they can be observed via electromagnetic (X-ray, γ-ray, radio waves) and gravitational waves, opening up a new era of multi-messenger astronomy. Electromagnetic multi-wavelength observations of NSs reveal a wealth of details about its global structure (Demorest et al., 2010; Antoniadis et al., 2013). NS masses can be determined to high precision using post-Keplerian effects in NSs in binary (Thorsett and Chakrabarty, 1999). Traditionally radius measurements from thermal emission suffered from large uncertainties (Özel et al., 2010; Guillot et al., 2013; Steiner et al., 2013), but the recently launched NICER (Neutron Star Interior Composition Explorer) (Arzoumanian et al., 2014; Miller et al., 2019a; Riley et al., 2019; Miller et al., 2021; Riley et al., 2021) mission has improved NS estimates by exploiting a novel scheme of modulation profiles of pulses. Finally, with the recent detection of GWs for the first time from NS-NS (GW170817) (Abbott et al., 2017), NS-BH (GW200105 and GW200115) (Abbott et al., 2021), and GW190425 (Abbott et al., 2020) systems by LIGO (Aasi et al., 2015) and Virgo (Acernese et al., 2014), GW astronomy is allowing us to probe the interior of NSs directly. The tidal deformation of NSs in the strong gravitational field of its binary companion measured during the inspiral phase of the merger depends on the EoS and, therefore, reveals information about its radius and interior composition (Abbott et al., 2018; Annala et al., 2018; Most et al., 2018; Abbott et al., 2019).

In the recent past, there have been several attempts to impose constraints on the NS EoS using data from NS multi-messenger astrophysical observations within a statistical Bayesian scheme (Coughlin et al., 2019; Dietrich et al., 2020; O’Boyle et al., 2020; Biswas, 2021a; Biswas, 2021b; Biswas et al., 2021; Pang et al., 2021). In such a scheme, the low-density EOS constrained by theoretical and experimental nuclear physics is matched with parametrized high-density EOSs satisfying gravitational wave and electromagnetic data (Tews et al., 2018; Tews et al., 2019a; Tews et al., 2019b; Gandolfi et al., 2019; Capano et al., 2020). Usually, the EoSs are based on different parametrization schemes such as piecewise polytropes (Read et al., 2009; Hebeler et al., 2013; Annala et al., 2018; Gamba et al., 2019), spectral representation (Lindblom, 2018; Fasano et al., 2019), speed-of-sound parametrization (Tews et al., 2018; Greif et al., 2019; Landry et al., 2020), or nuclear meta-modeling technique (Güven et al., 2020). Only a few recent works used the RMF model (Traversi et al., 2020) or hybrid (nuclear + piecewise polytope) parametrizations (Biswas et al., 2021) to obtain posterior distributions of empirical parameters. Correlations among empirical nuclear parameters and some chosen NS observables have only recently been explored (Carson et al., 2019; Xie and Li, 2019; Zhang and Li, 2019; Zimmerman et al., 2020). Although several of these works suggested probing the effect of the presence of hyperons, none of them consistently included hyperons within such a scheme. It, therefore, remains to be investigated whether one can restrict the parameter space of uncertainties associated with hyperons (hypernuclear potentials or hyperon couplings) or if they show any physical correlations with measurable properties such as nuclear saturation parameters or NS astrophysical observables.

In recent work (Ghosh et al., 2022), multi-physics constraints were imposed at different density regimes on the nuclear EoS using a “cut-off scheme,” and correlations of nuclear saturation parameters with astrophysical observables were investigated. Motivated by the Bayesian approach, the parameters of the realistic nuclear model were varied within their allowed uncertainties, compatible with the state-of-the-art nuclear experimental data and the parameter space, constrained using a combination of current best-known physical constraints at different density regimes: theoretical (chiral effective field theory) at low densities, multi-messenger (multi-wavelength electromagnetic as well as GW) astrophysical data at high densities, and experimental (nuclear and heavy-ion collision) at intermediate densities (Tsang et al., 2018; Dexheimer et al., 2021) to restrict the parameter space of the nuclear model. Furthermore, nuclear and heavy-ion collision experiments are isospin symmetric (same number of neutrons and protons), so studying NS matter provides information about the unknown nuclear symmetry energy.

This article extends the above investigation to neutron star matter including strangeness, particularly hyperons. Within the framework of the RMF model and allowing for a parameter space spanning current uncertainties in nuclear and hypernuclear physics, we impose multi-physics constraints in different density regimes from terrestrial nuclear/hypernuclear and multi-messenger astrophysical data. This study aims to investigate possible correlations between empirical nuclear and hypernuclear parameters (particularly the symmetry energy and its slope) with NS astrophysical observables.

The structure of the article is as follows: in Section 2, we describe the methods used to determine the composition of NS matter including hyperons in the framework of the RMF model. In Section 3, we impose constraints at different densities on the hyperonic EoS. In Section 4, we discuss the results of this investigation, and in Section 5 we discuss the implications of these findings.

2 Methods

As discussed in Section 1, we calculate the beta equilibrated, charge-neutral NS EoS within the RMF framework. For our investigation, we consider the standard baryon octet, as well as electrons and muons. The interaction Lagrangian density $(\mathcal{L})$ considered in this work is given in Eq. 1 (Weissenborn et al., 2012; Pradhan and Chatterjee, 2021). In this model, the baryon–baryon interaction is mediated by the exchange of scalar (σ), vector (ω), isovector (ρ) mesons, and the strange baryon. In other words, hyperon–hyperon interactions are carried out by additional strange scalar (σ*) and strange vector (ϕ) mesons:

$\begin{array}{ccc}\hfill \mathcal{L}& =\hfill & \sum _B{\bar{\psi }}_B\left(i{\gamma }^{\mu }{\partial }_{\mu }-m_B+g_{\sigma B}\sigma -g_{\omega B}{\gamma }_{\mu }{\omega }^{\mu }-g_{\rho B}{\gamma }_{\mu }\overrightarrow{I_B}.{\vec{\rho }}^{\mu }\right){\psi }_B+\frac{1}{2}\left({\partial }_{\mu }\sigma {\partial }^{\mu }\sigma -m_{\sigma }^2{\sigma }^2\right)-U_{\sigma }\hfill \\ \hfill & \hfill & +\frac{1}{2}{m}_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }-\frac{1}{4}{\omega }_{\mu \nu }{\omega }^{\mu \nu }-\frac{1}{4}\left({\vec{\rho }}_{\mu \nu }.{\vec{\rho }}^{\mu \nu }-2m_{\rho }^2{\vec{\rho }}_{\mu }.{\vec{\rho }}^{\mu }\right)+{\mathrm{\Lambda }}_{\omega }\left(g_{\rho N}^2{\vec{\rho }}_{\mu }.{\vec{\rho }}^{\mu }\right)\left(g_{\omega N}^2{\omega }_{\mu }{\omega }^{\mu }\right)\hfill \\ \hfill & \hfill & +\sum _Y{\bar{\psi }}_Y\left(g_{{\sigma }^{*}Y}{\sigma }^{*}-g_{\varphi Y}{\gamma }_{\mu }{\varphi }^{\mu }\right){\psi }_Y+\frac{1}{2}{m}_{\varphi }^2{\varphi }_{\mu }{\varphi }^{\mu }-\frac{1}{4}{\varphi }_{\mu \nu }{\varphi }^{\mu \nu }+\frac{1}{2}\left({\partial }_{\mu }{\sigma }^{*}{\partial }^{\mu }{\sigma }^{*}-m_{{\sigma }^{*}}^2{{\sigma }^{*}}^2\right)\hfill \\ \hfill & \hfill & +\sum _{\ell =\left\{e^{-},{\mu }^{-}\right\}}{\bar{\psi }}_{\ell }\left(i{\gamma }^{\mu }{\partial }_{\mu }-m_{\ell }\right){\psi }_{\ell }\hfill \end{array}(1)$

where

$U_{\sigma }=\frac{1}{3}b{m}_N{\left(g_{\sigma N}\sigma \right)}^3+\frac{1}{4}c{\left(g_{\sigma N}\sigma \right)}^4$

In Eq. 1, B stands for the baryon octet (p, n, Λ, Σ⁻, Σ⁰, Σ⁺, Ξ⁻, Ξ⁰) whereas Y stands for hyperons (Λ, Σ⁻, Σ⁰, Σ⁺, Ξ⁻, Ξ⁰). One can solve the equation of motion governing constituent particle fields (Ψ) as well as those of the following mesons (Hornick et al., 2018; Pradhan and Chatterjee, 2021). Replacing the meson fields with their mean values in RMF framework, the energy density (ϵ) corresponding to the Lagrangian given in Eq. 1 can be expressed as

$\begin{array}{ccc}\hfill ϵ& =\hfill & \frac{1}{2}{m}_{\sigma }^2{\bar{\sigma }}^2+\frac{1}{2}{m}_{\omega }^2{\bar{\omega }}^2+\frac{1}{2}{m}_{\rho }^2{\bar{\rho }}^2+\frac{1}{2}{m}_{{\sigma }^{*}}^2{\overline{{\sigma }^{*}}}^2+\frac{1}{2}{m}_{\varphi }^2{\bar{\varphi }}^2+\frac{1}{3}b{m}_N{\left(g_{\sigma N}\bar{\sigma }\right)}^3+\frac{1}{4}c{\left(g_{\sigma N}\bar{\sigma }\right)}^4\hfill \\ \hfill & +\hfill & 3{\mathrm{\Lambda }}_{\omega }{\left(g_{\rho }N{g}_{\omega }N\bar{\rho }\bar{\omega }\right)}^2+\sum _B\frac{g_{sB}}{2{\pi }^2}{\int }_0^{k_{FB}}\sqrt{k^2+{m_B^{*}}^2}dk+\sum _{\ell }\frac{g_{s\ell }}{2{\pi }^2}{\int }_0^{k_{F\ell }}\sqrt{k^2+{m_{\ell }}^2}dk\hfill \end{array}(2)$

where g_si and k_Fi represent the spin degeneracy and Fermi momentum of the ith species, respectively. The baryon effective mass $(m_B^{*})$ is then defined as $m_B^{*}=m_B-g_{\sigma B}\bar{\sigma }-g_{{\sigma }^{*}B}\overline{{\sigma }^{*}}$. The pressure can be expressed using Gibbs–Duhem relation:

$p=\sum _{i=B,\ell }{\mu }_i{n}_i-ϵ(3)$

with n_i being the number density of ith constituent. The chemical potentials for baryon (μ_B) and lepton (μ_ℓ) are given by

$\begin{array}{ccc}\hfill {\mu }_B& =\hfill & \sqrt{k_{FB}^2+{m_B^{*}}^2}+g_{{\omega }_B}\bar{\omega }+g_{{\varphi }_B}\bar{\varphi }+I_{3_B}{g}_{{\rho }_B}\bar{\rho }\hfill \\ \hfill {\mu }_{\ell }& =\hfill & \sqrt{k_{F\ell }^2+{m_{\ell }}^2}\hfill \end{array}(4)$

2.1 Nucleonic Matter

The isoscalar nucleon-meson coupling parameters (g_σN, g_ωN, b, and c) are determined by fixing the nuclear saturation parameters: nuclear saturation density (n₀), binding energy per nucleon at saturation (E_sat), incompressibility (K_sat), and the effective nucleon mass (m*) at saturation. On the other contrary, the isovector couplings g_ρN and Λ_ω are fixed to the symmetry energy (E_sym) and slope of symmetry energy (L_sym) at saturation (Chen and Piekarewicz, 2014; Hornick et al., 2018; Ghosh et al., 2022). The range of empirical parameters considered in this work are consistent with the state-of-the-art nuclear experimental data (Ghosh et al., 2022) and are summarized in Table 1.

TABLE 1

TABLE 1. Range (minimum and maximum values) of nuclear and hypernuclear parameters at saturation density used in this work. Masses of mesons and the nucleon are fixed as m_σ = 550 MeV, m_ω = 783 MeV, m_ρ = 770 MeV, m_ϕ = 1020 MeV and m_N = 939 MeV.

2.2 Hyperonic Matter

In the Lagrangian Eq. 1, the attractive interaction among hyperons is mediated by the exchange of strange scalar (σ*) meson, and the repulsive interaction is mediated by the exchange of strange vector (ϕ) meson. However, it has been concluded that models with attractive hyperon–hyperon interaction show incompatibility with observations of the maximum NS mass (Weissenborn et al., 2012). Hence, we set the strange scalar couplings to 0, i.e., g_σY = 0, and the remaining non-strange hyperon meson coupling constants (g_σY) are fitted to the hyperon-nucleon potential (U_Y) at saturation using Eq. 5 (Weissenborn et al., 2012). Among the nucleon-hyperon potentials, the best-known potential is that of the hyperon Λ, having a value of U_Λ = −30 MeV (Millener et al., 1988; Schaffner et al., 1992). Although the potential depths for hyperons Σ and Ξ are not known precisely, it has been concluded that the Σ-nucleon potential is repulsive (Mareš et al., 1995; Schaffner-Bielich and Gal, 2000; Friedman and Gal, 2007) whereas U_Ξ is attractive in nature (Fukuda et al., 1998; Khaustov et al., 2000; Schaffner-Bielich and Gal, 2000). Hence, for this investigation, we vary U_Σ in the range of 0 to +30 MeV and U_Ξ from −30MeV to 0. The vector hyperon couplings (g_ωY, g_ϕY) are fixed to their SU(6) values (see Eq. 6) (Schaffner et al., 1993; Weissenborn et al., 2012):

$U_Y\left(n_0\right)=-g_{\sigma Y}\bar{\sigma }+g_{\omega Y}\bar{\omega },(5)$

$\begin{array}{ccc}\hfill g_{\omega \mathrm{\Lambda }}=g_{\omega \mathrm{\Sigma }}=2g_{\omega \mathrm{\Xi }}& =\hfill & \frac{2}{3}{g}_{\omega N}\hfill \\ \hfill 2g_{\varphi \mathrm{\Lambda }}=2g_{\varphi \mathrm{\Sigma }}=g_{\varphi \mathrm{\Xi }}& =\hfill & \frac{-2\sqrt{2}}{3}{g}_{\omega N}\hfill \end{array}(6)$

Recent lattice QCD calculations by the HALQCD group extracted hyperon potentials at almost physical quark masses and used it to estimate the hyperon potentials in pure neutron matter and the nuclear matter using the Brueckner-Hartree-Fock approximation (Inoue, 2016; Inoue, 2019). They find that the hyperon potentials in nuclear matter are U_Λ = −28 MeV, U_Σ = +15MeVand U_Ξ = −4 MeV. From Figure 4 in Inoue (2019), one can read off the hyperon potentials for Σ⁻ and Σ⁺, as well as for Ξ⁰ and Ξ⁻ in pure neutron matter. The relevant potentials for neutron star matter are the ones for the Σ⁻ and the Ξ⁻ with the potentials of +25 MeV and +6 MeV, respectively. However, these results suggest that the isovector hyperon coupling (g_ρY) differs from its SU(6) quark model values, where the isospin potential for the Ξ would be as large as the one for nucleons, and the one for the Σ is even twice as large. For a typical nucleon isospin potential of about 32 MeV, one arrives at hyperon isospin potentials, which are more than a factor two larger than those from the HALQCD analysis. We, therefore, introduce a scaling parameter y, which ranges from 0 to 1 (0 to SU(6) coupling strength) to span the uncertainty in the hyperon-isovector coupling. In that case, g_ρY can be expressed as

$\begin{array}{ccc}\hfill g_{\rho \mathrm{\Lambda }}& =\hfill & 0\hfill \\ \hfill \frac{g_{\rho \mathrm{\Xi }}}{g_{\rho N}}& =\hfill & \frac{1}{2}\frac{g_{\rho \mathrm{\Sigma }}}{g_{\rho N}}=y,y\in \left[\mathrm{0,1}\right]\hfill \end{array}(7)$

The effect of the variation in the y-parameter (isovector hyperon coupling) on the particle fractions can be understood from Figure 1. For a chosen parameter set from Table 1, Ξ⁻ starts to appear at 2.27, 2.34, and 2.45 n₀ for y values 0, 0.5, and 1, respectively. However, Ξ⁰ starts to appear at 6.977, 6.943, and 6.850 n₀ for y changing from 0 to 1 in steps of 0.5. One must note that the threshold of appearance of the hyperons will depend upon the hyperon potentials and the nuclear saturation parameters chosen for the EoS.

FIGURE 1

FIGURE 1. Particle fractions for varying y parameter (isovector hyperon coupling). The nuclear and hyper nuclear parameters are fixed to m* = 0.65 m_N, E_sat = −16 MeV, K_sat = 240 MeV, J_sym = 32 MeV, L_sym = 60 MeV, U_Λ = −30 MeV, U_Σ = +30 MeV, U_Ξ = −28 MeV. (A) Particle fractions with y = 0. (B) Particle fractions with y = 0.5. (C) Particle fractions with y given by SU(6) symmetry.

2.3 Global Structure

The equilibrium structure of a non-rotating, relativistic NS is obtained by solving the coupled equations of hydrostatic equilibrium known as the Tolman-Oppenheimer-Volkof (TOV) equations (Glendenning, 2012; Schaffner-Bielich, 2020):

$\begin{array}{ccc}\hfill \frac{dm\left(r\right)}{dr}& =\hfill & 4\pi \epsilon \left(r\right)r^2,\hfill \\ \hfill \frac{dp\left(r\right)}{dr}& =\hfill & -\frac{\left[p\left(r\right)+\epsilon \left(r\right)\right]\left[m\left(r\right)+4\pi r^{3}p\left(r\right)\right]}{r\left(r-2m\left(r\right)\right)}\hfill \\ \hfill & \hfill & \hfill \end{array}(8)$

with the given equation of state, which gives a relation between the energy density (ɛ) and pressure (p). These TOV in Eq. 8 are integrated from the center of the star to the surface with the boundary conditions of vanishing mass, m|_r=0 = 0, at the center of the star, and a vanishing pressure, p|_r=R = 0, at the surface. By varying the central density for a given EoS, we can get a sequence of NSs with different mass and radii, thus giving the M-R curves.

The tidal deformability parameter quantifies the degree of the tidal deformation effects due to the companion in coalescing binary NS systems during the early stages of an inspiral. It is defined as

$\lambda =-\frac{Q_{ij}}{{\epsilon }_{ij}}(9)$

where Q_ij is the induced mass quadrupole moment of the NS and ɛ_ij is the gravitational tidal field of the companion. The tidal deformability λ is related to the dimensionless l = 2 tidal Love number k₂ as follows (Flanagan and Hinderer, 2008; Hinderer, 2008):

$\mathrm{\Lambda }=\frac{2}{3}{k}_2{\left(\frac{R}{M}\right)}^5(10)$

The tidal Love number (k₂) can be obtained by solving a set of differential equations coupled with the TOV equations (Yagi and Yunes, 2013). The total tidal effect of two neutron stars in an inspiraling binary system is given by the mass-weighted (dimensionless) tidal deformability $\tilde{\mathrm{\Lambda }}$ defined as (Hinderer et al., 2010)

$\tilde{\mathrm{\Lambda }}=\frac{16}{13}\frac{\left(M_1+12M_2\right)M_1^4{\mathrm{\Lambda }}_1+\left(M_2+12M_1\right)M_2^4{\mathrm{\Lambda }}_2}{{\left(M_1+M_2\right)}^5}(11)$

where Λ₁ = Λ₁(M₁) and Λ₂ = Λ₂(M₂) are the (dimensionless) tidal deformabilities and M₁, M₂ are the masses of the individual binary components, respectively.

3 Multi-Density Constraints

In this work, we constrain the parameter space of the nucleonic and hyperonic matter as described in Section 2 using a “cut-off filter” scheme where we impose strict limits from nuclear and astrophysical observation to obtain the posteriors. In the language of Bayesian analysis, the priors are obtained by varying the nuclear empirical parameters, hyperon potentials, and isovector couplings uniformly within their uncertainty range in Table 1, and the likelihood functions are appropriately chosen physical conditions as the Filter functions described in Section 3.1.

Miller et al. (2019b) pointed out the statistical uncertainties in constraining EoS by putting strict limits from multi-messenger observations of neutron stars like we have used here. With many priors, this cut-off scheme gives a correct estimate of the nuclear parameter ranges consistent with the observations. Recent works (Annala et al., 2018; Most et al., 2018; Annala et al., 2020; Wei et al., 2020; Annala et al., 2021) also used similar cut-off schemes for constraining the EoS of ultra-dense matter. In the recent work by Ghosh et al. (2022), it was explicitly shown that including the statistical re-weighting using χ-squared statistics might change the posterior probability distribution slightly, but it does not significantly alter the physical correlation between nuclear empirical parameters and astrophysical observables. So, we adopt this “cut-off filter” scheme for this work.

3.1 Filter Functions

The following physical constraints at different densities from multi-disciplinary physics are applied in this work:

• At Low Densities: χEFT

Chiral EFT is an effective theory of QCD that describes strong many-body interactions among nucleons using order by order expansions in terms of contact interactions and long-range pion exchange interactions. In particular, the χ EFT expansion gives estimates of theoretical uncertainties depending on local chiral two and three-nucleon interactions using quantum Monte Carlo methods, which are one of the most precise many-body methods for nuclear physics (Drischler et al., 2016; Drischler et al., 2020). The EoS of pure neutron matter (PNM) can be well constrained at low baryon densities n_b in the range of ∼ 0.5–1.4 n₀ (Drischler et al., 2019).

• At High Densities: NS Astrophysical Data

The constraints on the EoS at high density come from multi-messenger astrophysical observations, such as high mass NS observations, GW measurement of tidal deformability from binary neutron star mergers as follows:

(1) From the recent observations of the heaviest known pulsar PSR J0740+6620, the maximum mass of the neutron stars should be equal to or exceed $2.08_{-0.07}^{+0.07}{M}_{\odot }$ (Fonseca et al., 2021). This sets an upper bound on the maximum NS masses corresponding to the EoSs considered.

(2) The recent analyses of the GW170817 event (Abbott et al., 2019) apply a constraint on the upper bound of the effective tidal deformability $\tilde{\mathrm{\Lambda }}<$ 720 (Tong et al., 2020) using the low-spin highest posterior density interval for tidal deformability. We do not consider the lower limit on tidal deformability in this study. As explained in Section 2.3, the tidal deformability depends on the mass and radius (see Eq. (10)), and therefore this result also leads to a constraint on the mass-radius relation (Annala et al., 2018; Most et al., 2018).

• At Intermediate Densities: Heavy-Ion Collision Experiments

Heavy-ion collision experiments can provide additional information about the behavior of hot dense matter at intermediate densities $\sim 1-3n_0$. As in our previous investigation (Ghosh et al., 2022), we impose constraints from three different heavy-ion collision experiments:

(1) KaoS experiment: subthreshold K⁺ meson production in Au+Au & C+C nuclear collisions at the Kaon Spectrometer (KaoS) experiment at GSI, Darmstadt (Hartnack et al., 2006) yield kaon multiplicity, which is an indicator of the compressibility of dense matter at densities $\sim 2-3n_0$. The analysis of the experimental data using Isospin Quantum Molecular Dynamics (IQMD) transport models points toward a soft EoS (Fuchs et al., 2001; Hartnack et al., 2006) and can be described by a simple Skyrme ansatz with an incompressibility ≲ 200 MeV. The constraint given by the KaoS data implies that only those nucleon potentials, which are more attractive than the Skyrme parametrization within the considered density regime, will be allowed.

(2) FOPI experiment: elliptic flow data in Au+Au collisions between 0.4 and 1.5A GeV by the FOPI collaboration (Le Fèvre et al., 2016) provide constraints for the EoS of compressed symmetric nuclear matter (SNM). By analyzing the FOPI data using IQMD transport codes, one can obtain a constraint for the binding energy of SNM in the density region of n_b/n₀ ∼ 1.4–2.0 (Le Fèvre et al., 2016). In order to impose this constraint, the binding energy for SNM is calculated for the input parameters and only permitted if they lie inside the band allowed by the FOPI data in this density range.

(3) ASY-EOS experiment: information about the symmetry energy for ANM at supra-saturation densities can be obtained from directed and elliptic flows of neutrons and light charged particles measured for the reaction ¹⁹⁷Au+¹⁹⁷Au at 400 MeV/nucleon incident energy within the ASY-EOS experimental campaign at the GSI, Germany (Russotto et al., 2016). In order to impose the ASY-EOS filter, the symmetry energy of ANM EoS is calculated for the input parameters and allowed only if the symmetry energy lies inside the band allowed by the data in the range of $\sim 1.1-2.0n_0$.

3.2 Correlations

Using the posterior obtained from the analysis, we look for any physical correlation of the nuclear parameters, hyperon potentials, and isovector coupling among themselves and also with the astrophysical observables such as the mass and radius of the canonical 1.4M_⊙ and the massive 2M_⊙ NS. For this study, we use Pearson’s linear correlation coefficient defined as (Kirch, 2008)

$R_{XY}=\frac{\mathit{Cov}\left(X,Y\right)}{\sqrt{\mathit{Cov}\left(X,X\right)}\sqrt{\mathit{Cov}\left(Y,Y\right)}}(12)$

where Cov(X, Y) is the co-variance between two variables X and Y defined as

$\mathit{Cov}\left(X,Y\right)=\frac{1}{N}\sum _i\left(X_i-M\left(X\right)\right)\left(Y_i-M\left(Y\right)\right)(13)$

where N is the number of sample points and M(X) is the mean of the variable X defined as $M(X)=\frac{1}{N}{\sum }_i{X}_i$.

4 Results

4.1 Effect of χEFT + Astro Filters

By randomly varying the parameter space of the nuclear parameters and hyperon potentials from Table 1, we generate the uniformly distributed prior set. After generating the random EoSs, we use the χEFT and astrophysical filters described in Section 3.1 to obtain filtered sets for the parameters and NS observables. For χEFT, we evaluate the binding energies in the density range of n_b/n₀ ∼ 0.5–1.4 corresponding to the χEFT data and allow only those parameter sets that lie within the band allowed by χEFT calculations (Figure 2).

FIGURE 2

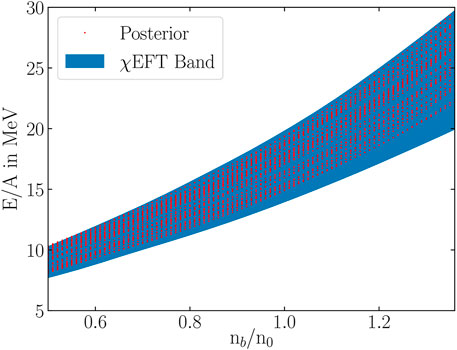
FIGURE 2. Binding energy E/A of posterior pure neutron matter EoSs as a function of normalized density n_b/n₀ allowed by chiral effective field theory (χEFT) data (Drischler et al., 2019).

After obtaining the posterior χEFT, we use the same parameter set to obtain the hyperonic EoS using hyperon potentials and couplings given in Section 2.2. We then solve the coupled TOV Equations 8 and 10 to obtain the mass, radius, and tidal deformability of the NSs. Using the multi-messenger astrophysical and GW observation of NSs given in Section 3.1, we rule out further combinations of parameter sets and allow only the combinations that simultaneously satisfy all constraints on NS observables. In Figure 3, we plot the mass-radius relations and the dimensionless tidal deformability as a function of NS mass corresponding to the filtered hyperonic EoSs. We can see that NS radii span a wide range from 11 to 14 km.

FIGURE 3

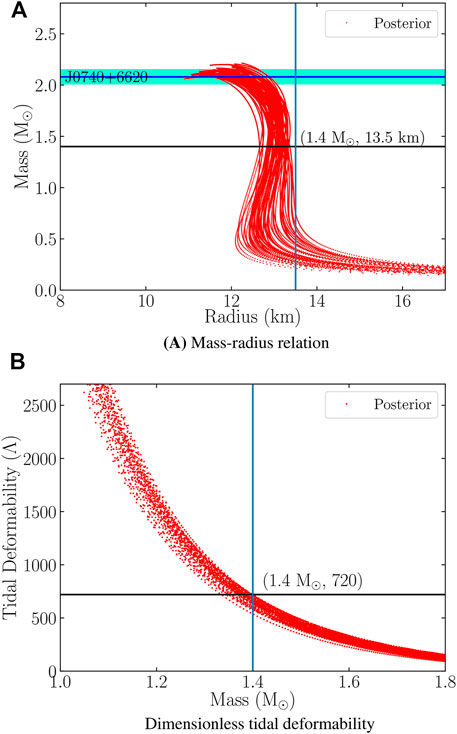
FIGURE 3. NS observables for the posterior hyperon EoSs after passing through χEFT and NS observations filters. The light green band indicates the uncertainty in the measurement of the maximum mass of PSR J0740 + 6620 (Fonseca et al., 2021) (A) Mass-radius relation. (B) Dimensionless tidal deformability.

4.2 Correlations

After obtaining the posterior parameter space, we look for any physical correlation among the parameters and the NS observables as well as within themselves. In Figure 4, we display the correlation matrix of the following quantities: nuclear empirical parameters (n₀, E_sat, K_sat, E_sym, L_sym), the effective mass m*/m, hyperon potentials (U_Σ, U_Ξ), hyperon-isovector coupling parameter y, and the NS observables ($R_{1.4M_{\odot }}$, ${\mathrm{\Lambda }}_{1.4M_{\odot }}$, $R_{2M_{\odot }}$, ${\mathrm{\Lambda }}_{2M_{\odot }}$) after applying both χEFT and astrophysical observations filter. Some of the main observations from the correlation matrix are listed below:

• n₀ and m*/m show a high correlation (0.71).

• n₀ has a moderate correlation with the NS observables. The correlation is noticeable (0.54) for the constraints for 1.4M_⊙ NS but is negligible for the constraints for 2 M_⊙.

• Symmetry energy E_sym and its slope L_sym display a strong correlation (0.79) which only appears when we apply the χEFT filter. This correlation only comes from the χEFT filter around saturation density, which is in agreement with previous literature (Hornick et al., 2018; Ghosh et al., 2022).

• We see a moderate correlation (0.44) between L_sym and effective mass m*/m after applying the χEFT filter.

• The correlation of m*/m with the NS observables is pretty low ($\sim 0.1$ for 1.4M_⊙ and $\sim 0.3$ for 2.0M_⊙ stars) which is quite the opposite to the purely nucleonic case (Ghosh et al., 2022).

• The correlation between slope of symmetry energy L_sym and radius of 1.4M_⊙ NS is also lower (around 0.4). A correlation between L_sym and $R_{1.4M_{\odot }}$ has been reported in several articles in the literature (Fattoyev et al., 2013; Alam et al., 2016; Lim and Holt, 2018; Zhu et al., 2018), although recent articles find $R_{1.4M_{\odot }}$ to be nearly independent of L_sym (Hornick et al., 2018; Ghosh et al., 2022).

• All the NS observables (radius and dimensionless tidal deformability for 1.4 M_⊙ and 2 M_⊙ NS), as expected, show a strong correlation with each other (according to Eq. 9), although we find a moderate correlation with the observables between 1.4 M_⊙ and 2 M_⊙ NSs.

• We did not find any correlation between the hyperon potentials and the isovector coupling parameter y with other nuclear parameters and the astrophysical observables.

FIGURE 4

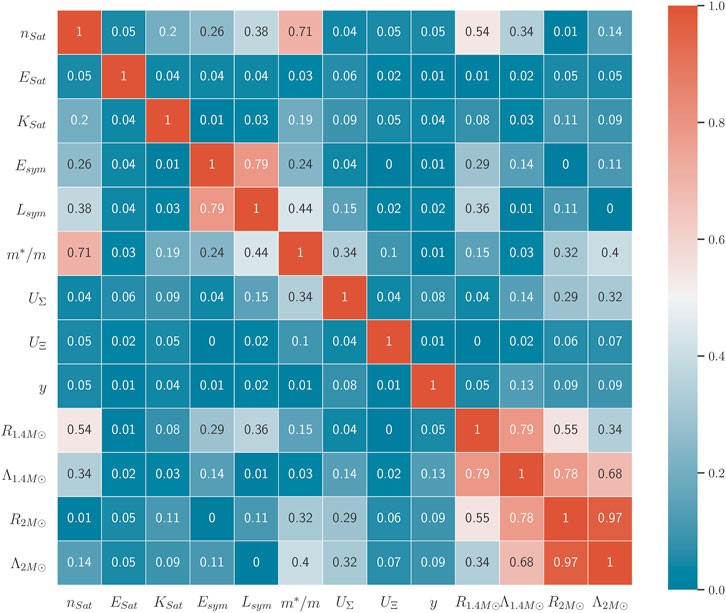
FIGURE 4. Posterior correlation matrix for variation of nuclear empirical parameters and NS observables, after application of the χEFT and NS observations filter.

To understand the correlations better, in Figure 5, we plot the posterior distribution of the nuclear parameters (n₀, E_sym, L_sym, and m*/m), which show significant correlations and the astrophysical observables ($R_{1.4M_{\odot }}$, $R_{2M_{\odot }}$, and ${\mathrm{\Lambda }}_{2M_{\odot }}$) after applying both the χEFT and the astrophysical constraints.

FIGURE 5

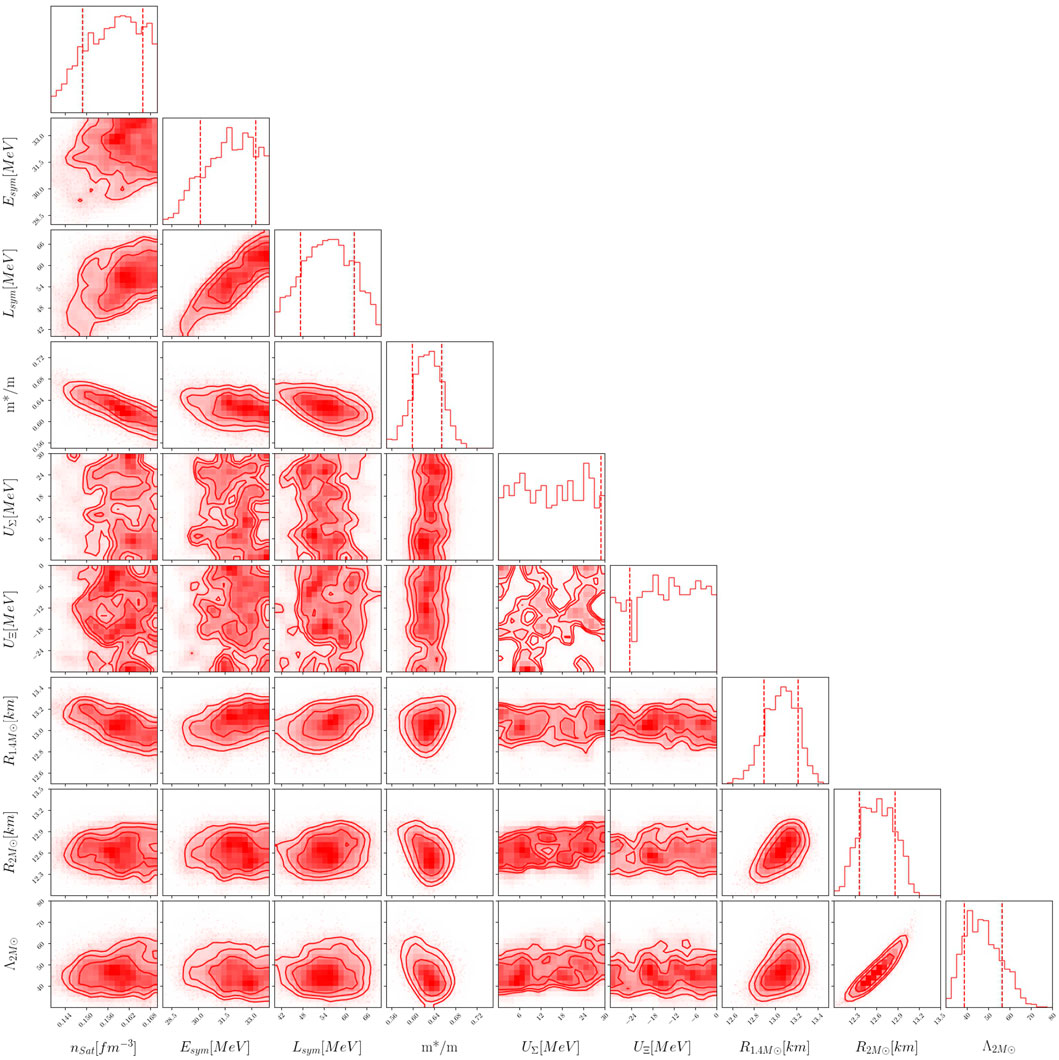
FIGURE 5. Posterior distributions of nuclear parameters and astrophysical observables after applying the χEFT and the astrophysical constraints.

From the corner plots, we see that after applying the χEFT filter, both the median values of symmetry energy and its slope L_sym shift toward a higher value compared to their prior range in Table 1, which leads to their strong correlation. For the effective mass, we see that the peak is around 0.63, which is lower than what we observed for purely nucleonic matter (Hornick et al., 2018; Ghosh et al., 2022) because when we include hyperon, the EoSs become softer (Pradhan and Chatterjee, 2021). Therefore, in order to satisfy the astrophysical constraint of maximum mass above 2M_⊙ and tidal deformability, the posterior of m*/m shifts toward a lower value. Also, from Figure 5 in Ghosh et al. (2022), we know that the χEFT filter removes parameter sets with low effective mass and slope of symmetry energy, which gives rise to a moderate correlation between L_sym and m*/m observed here. For this reason, for the hyperonic case along with the χEFT filter, the range of effective mass becomes narrow and peaks toward a lower value (around 0.63), which indeed restricts the radius of 1.4M_⊙ star to 12.6–13.4 km. That is why we observe a very low correlation between m*/m and the astrophysical observables. We also conclude that there is no correlation between the hyperon potentials (U_Σ, U_Ξ) and the NS astrophysical observables.

4.3 Effect of all Filters: χEFT + Astro + HIC (KaoS + FOPI + ASY-EOS)

We first generated 50,000 prior sets, and applying all filters (χEFT, astrophysical data, HIC) obtained almost no posterior sets. In order to understand the effect of the HIC filters, we then passed the prior sets only through the KaOS, FOPI, and ASY-EOS filters and plotted the posterior of each nuclear parameter (see Figure 6). From the figures, we observe that, in the K_sat distribution, the values are restricted below 240 MeV after HIC filters, which is the effect of the KaoS filter. In the L_sym distribution, the values are restricted to $>$ 55 MeV after HIC filters, resulting in a decreased correlation between L_sym and E_sym. Both these effects were observed in the nucleonic case also and discussed in our previous paper (Ghosh et al., 2022). The most interesting is the distribution of m*/m. In Section 4.2, we noted that including hyperons shifts m*/m to lower value for astrophysical filters. When we apply HIC filters, we see m*/m values peak at a higher value around 0.70. The distributions intersect at the two tail ends of the Gaussian curves, giving a very narrow range with low probabilities. This explains why there are so few posterior points due to the combined filters.

FIGURE 6

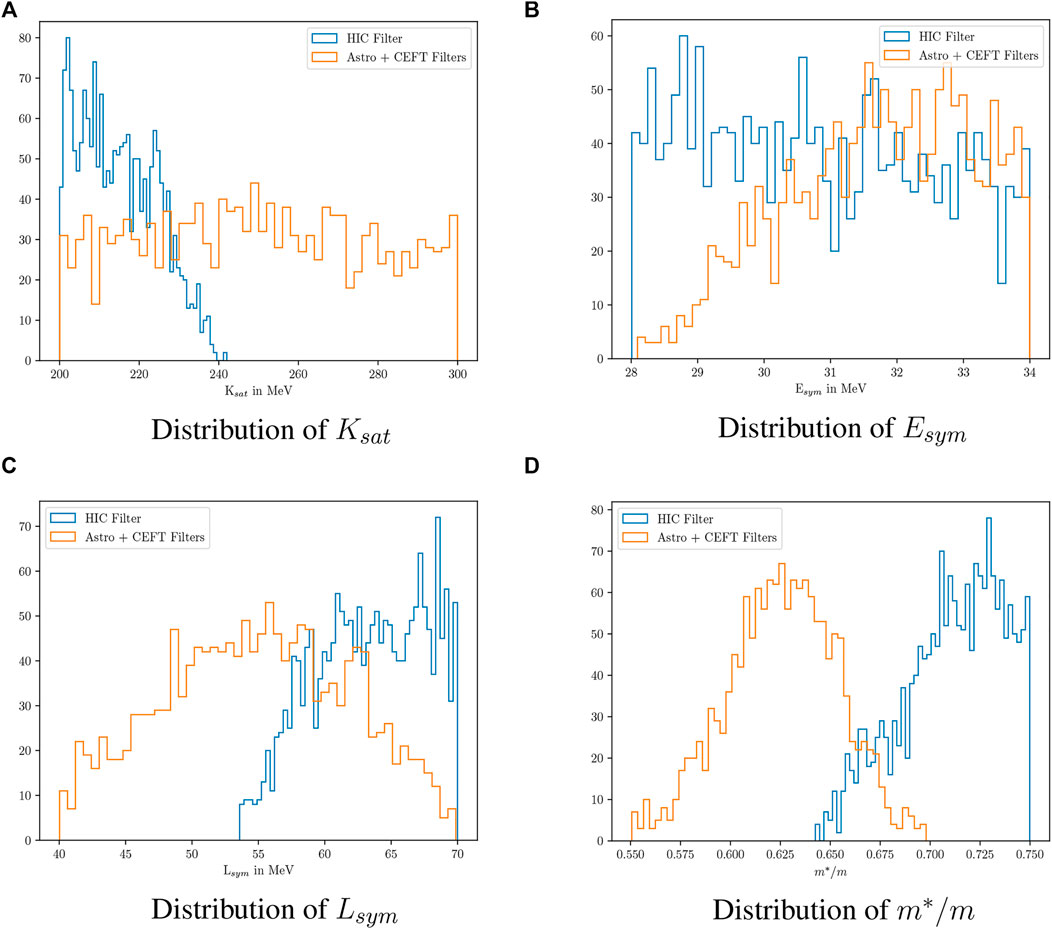
FIGURE 6. Distribution of some nuclear saturation parameters after application of the HIC filters (KaoS, FOPI, ASY-EOS). (A) Distribution of K_sat. (B) Distribution of E_sym. (C) Distribution of L_sym. (C) Distribution of m*/m

In order to obtain a correlation plot after applying all filters, we generated a very large number (2 million) of priors after restricting the prior range to m*/m to 0.64–0.7 and managed to obtain 200 posterior sets. The resulting correlation plot with this set is given in Figure 7. We see that the effects of the HIC filters on correlations are the same as in the nucleonic case (Ghosh et al., 2022): decrease in L_sym − E_sym correlation, increase in n₀ correlation with NS astrophysical observables, and increase in K_sat − m*/m correlation. We checked that allowing for hyperons means that hyperons appear in all the cases investigated; Λ hyperons always appear close to 2n₀, while the threshold for the appearance of Σ and Ξ hyperons depends on the value of the corresponding hyperon potentials. One may also note that, for 1.4M_⊙ stars, the fraction of hyperons in the core is lower than in more massive 2M_⊙ stars.

FIGURE 7

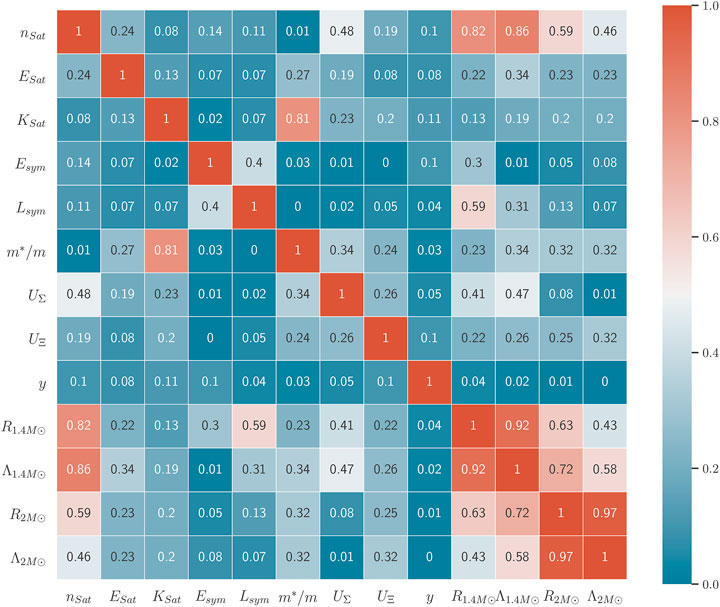
FIGURE 7. Posterior correlation matrix for variation of nuclear empirical parameters and NS observables, after application of the χEFT, HIC, and NS observations filters.

5 Discussion

5.1 Summary of Present Results

The motivation of this study is to investigate any existing correlations between empirical nuclear and hypernuclear parameters (particularly the symmetry energy and its slope) and with NS multi-messenger astrophysical observables such as its mass, radius, and tidal deformability. To this aim, we extended our previous investigation (Ghosh et al., 2022) from nucleonic to hyperonic matter in NSs. In other words, within the framework of the RMF model, we constrained the parameter space allowed by current uncertainties in nuclear and hypernuclear physics by imposing multi-physics constraints at different density regimes: chiral effective field theory at low densities, astrophysical constraints at high densities, and heavy-ion collision data at intermediate energies.

First, using the filtered EoSs satisfying constraints from both χEFT and astrophysical data, we searched for any physical correlation among the parameters and the NS observables, as well as among themselves. We found that the effective nucleon mass m*/m and saturation nuclear density n₀ show a strong correlation. We found n₀ to be moderately correlated with radius and tidal deformability of 1.4M_⊙ NSs, but weakly correlated with those of 2M_⊙ stars. The correlation of m*/m with the NS observables was low, contrary to the purely nucleonic case. Interestingly, the symmetry energy E_sym and its slope L_sym showed a significant correlation after imposing the χEFT filter. There is a non-negligible correlation of m*/m with L_sym.

On applying all filters from χEFT, astrophysical and heavy-ion data, we found that very few nuclear parameter sets can satisfy all constraints simultaneously. By monitoring the individual posterior distributions of the nuclear saturation parameters, we confirmed the existence of a “tension” between the constraints from the first two filters with those of heavy-ion data. The values of K_sat are restricted to below 240 MeV due to the KaoS constraint and L_sym to values larger than 55 MeV, drastically reducing the available parameter space. Further, low values of m*/m are allowed by astrophysical filters, while heavy-ion data allow large values. The overall effect of applying the heavy-ion filters was the same as in the nucleonic case (Ghosh et al., 2022): a decreased L_sym − E_sym correlation, increased n₀ correlation with NS astrophysical observables, and enhanced K_sat − m*/m correlation.

5.2 Comparison With Prior Research

There are several contrasting results in the hyperonic case compared with the nucleonic case (Ghosh et al., 2022). Mainly, we found a decreased correlation of m*/m with the NS observables and an increased correlation of n₀ with m*/m and NS observables for 1.4M_⊙ NS. Radii and dimensionless tidal deformability (for 1.4M_⊙ and 2M_⊙) show a strong correlation with each other, as expected. However, we find a moderate correlation with observables of 1.4M_⊙ with 2M_⊙ stars because of the reduced range of radii for hyperonic stars. We checked that the distribution of m*/m shifts to lower values (peak around 0.63) in posteriors for hyperons compared to nucleons, which peak around 0.7, restricting values of $R_{1.4M_{\odot }}$ to a reduced range ⪆ 13 km. The correlation between the slope of symmetry energy L_sym and radius of 1.4M_⊙ NS is also lower than that in the nucleonic case. A correlation between L_sym and $R_{1.4M_{\odot }}$ was reported in several articles in the literature (Fattoyev et al., 2013; Alam et al., 2016; Lim and Holt, 2018; Zhu et al., 2018), although recent articles find $R_{1.4M_{\odot }}$ to be nearly independent of L_sym (Hornick et al., 2018; Ghosh et al., 2022). Finally, the astrophysical observables studied in this work (mass, radius, tidal deformability) do not seem to provide correlations with hyperon potentials or the isovector coupling parameter y. However, one must note that this is not generic for all astrophysical observables. One has to look for other observables, which are sensitive to the hyperon content in the NS interior, such as r-modes, cooling, and thermal evolution (Chatterjee and Vidaña, 2016).

In another recent work (Traversi et al., 2020), Bayesian inference of the NS EoS was performed within the RMF model using astrophysical and nuclear saturation data. Using a selected class of nucleonic models with five empirical parameters and exploring different types of priors, they reported that the EoSs with the largest evidence were the ones featuring a strong reduction of the nucleon effective mass. However, the major drawback of this model was the omission of interaction terms (Λ_ω in our work) in the Lagrangian, due to which other saturation parameters, such as symmetry energy or its slope, were not included. A preliminary investigation of the effect of hyperons was also performed by switching on only the Λ hyperon, with a fixed potential depth and coupling constants. However, the effect of the other baryons of the octet and variation of the couplings and their correlations with other nuclear saturation parameters or NS observables were unexplored.

Another recent study (Güven et al., 2020) used Bayesian statistics to combine low-density nuclear physics data, such as the ab initio χEFT predictions and the isoscalar giant monopole resonance, with astrophysical NS data, within the “meta-model” approach for the dense matter EoS. The posterior probability distribution functions were marginalized over several higher-order nuclear empirical parameters (L_sym, K_sym, Q_sat, Q_sym) and observational quantities such as a radius of 1.4M_⊙ NS. This study also explored correlations among L_sym − K_sym and K_sat − Q_sym parameters and reported marked tension between astrophysical and nuclear physics constraints. Biswas (2021b) combined laboratory experiments and NS astrophysical observation using Bayesian statistics along with the LIGO/Virgo and NICER observations within a hybrid nuclear + piecewise polytrope (PP) EoS parameterization. This work reported a very weak correlation between L_sym and $R_{1.4M_{\odot }}$. Recently, Huth et al. (2021) used a Bayesian inference technique to analyze the nuclear EoS and NS properties, combining data from heavy-ion collisions (FOPI (Le Fèvre et al., 2016) and ASY-EOS (Russotto et al., 2016) experiments, EoS constraint for symmetric nuclear matter (Danielewicz et al., 2002)), microscopic χEFT calculations, and multi-messenger information from NICER and XMM Newton missions, as well as GW data and the associated kilonova AT2017gfo9. The study concluded that HIC constraints are in excellent agreement with NICER observations. However, hyperons were not considered in the above investigations.

5.3 Limitations and Future Directions

In this work, the correlations between nuclear and hypernuclear parameters and NS astrophysical observables have been explored within the framework of the Relativistic Mean Field model. Although the advantage of this realistic phenomenological model is that, unlike polytropic or parametrized EoSs, the results provide important understanding of the underlying nuclear physics, it, however, remains to be established whether such physical correlations are also found in other realistic EoS models in order to generalize the results of this investigation. It would be interesting, for example, to see whether the conclusions would still hold for a Lagrangian with density-dependent couplings. Such possibilities will be addressed in a forthcoming publication. We recall here that the constraints from heavy-ion data are model-dependent and should therefore be treated on a different footing from astrophysical constraints and their implications on the results discussed with a word of caution.

In the future, improved measurements of hyperon potentials in hypernuclear experiments, such as GSI in Germany, JLAB in the United States, and J-PARC in Japan (Chatterjee and Vidaña, 2016), will reduce the uncertainties in the hyperon-nucleon and hyperon-hyperon coupling strengths. With the advent of multi-messenger astronomy, new upcoming observations of NS properties will also help provide more stringent constraints on the dense matter EoS in NSs.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SG and BP contributed equally to this work and shared first authorship. DC and JS-B shared senior authorship and contributed to the conception of the study. DC was the corresponding author of this article. Both SG and BP performed the theoretical, numerical, and statistical analysis. DC wrote the first draft. SG and BP wrote sections of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the CRC-TR 211 “Strong-Interaction Matter Under Extreme Conditions”– project number 315477589—TRR 211.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

DC is grateful to the hospitality of the Institut für Theoretische Physik, J. W. Goethe Universität Frankfurt, Germany, where this work was carried out within the collaborative project “Astrophysical Constraints for Hyperons in Neutron Stars.” SG, BP, and DC acknowledge the usage of the IUCAA HPC computing facility for numerical calculations.

References

Aasi, J., Abbott, B. P., Abbott, R., Abbott, T., Abernathy, M. R., Ackley, K., et al. (2015). Advanced LIGO. Classical Quan. Gravity 32, 074001. doi:10.1088/0264-9381/32/7/074001

CrossRef Full Text | Google Scholar

Abbott, B. P., et al. (2017). Gw170817: Observation of Gravitational Waves from a Binary Neutron star Inspiral. Phys. Rev. Lett. 119, 161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2018). Gw170817: Measurements of Neutron star Radii and Equation of State. Phys. Rev. Lett. 121, 161101. doi:10.1103/PhysRevLett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2019). Properties of the Binary Neutron star Merger Gw170817. Phys. Rev. X 9, 011001. doi:10.1103/PhysRevX.9.011001

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2020). GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M. Astrophys. J. Lett. 892, L3. doi:10.3847/2041-8213/ab75f5

CrossRef Full Text | Google Scholar

Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., Adams, A., et al. (2021). Observation of Gravitational Waves from Two Neutron star–black Hole Coalescences. Astrophys. J. Lett. 915, L5. doi:10.3847/2041-8213/ac082e

CrossRef Full Text | Google Scholar

Acernese, F., Agathos, M., Agatsuma, K., Aisa, D., Allemandou, N., Allocca, A., et al. (2014). Advanced Virgo: a Second-Generation Interferometric Gravitational Wave Detector. Classical Quan. Gravity 32, 024001. doi:10.1088/0264-9381/32/2/024001

CrossRef Full Text | Google Scholar

Alam, N., Agrawal, B. K., Fortin, M., Pais, H., Providência, C., Raduta, A. R., et al. (2016). Strong Correlations of Neutron star Radii with the Slopes of Nuclear Matter Incompressibility and Symmetry Energy at Saturation. Phys. Rev. C 94, 052801. doi:10.1103/PhysRevC.94.052801

CrossRef Full Text | Google Scholar

Annala, E., Gorda, T., Kurkela, A., and Vuorinen, A. (2018). Gravitational-wave Constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 120, 172703. doi:10.1103/PhysRevLett.120.172703

PubMed Abstract | CrossRef Full Text | Google Scholar

Annala, E., Gorda, T., Kurkela, A., Nättilä, J., and Vuorinen, A. (2020). Evidence for Quark-Matter Cores in Massive Neutron Stars. Nat. Phys. 16, 907–910. doi:10.1038/s41567-020-0914-9

CrossRef Full Text | Google Scholar

Annala, E., Gorda, T., Katerini, E., Kurkela, A., Nättilä, J., Paschalidis, V., et al. (2021). Multimessenger Constraints for Ultra-dense Matter. arXiv e-prints. arXiv:2105.05132.

Google Scholar

Antoniadis, J., Freire, P. C. C., Wex, N., Tauris, T. M., Lynch, R. S., van Kerkwijk, M. H., et al. (2013). A Massive Pulsar in a Compact Relativistic Binary. Science 340, 1233232. doi:10.1126/science.1233232

PubMed Abstract | CrossRef Full Text | Google Scholar

Arzoumanian, Z., Gendreau, K. C., Baker, C. L., Cazeau, T., Hestnes, P., Kellogg, J. W., et al. (2014). “The Neutron star interior Composition Explorer (NICER): mission Definition,” in Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray. Editors T. Takahashi, J. W. A. den Herder, and M. Bautz (Montréal, QC, Canada: SPIE), 9144, 914420. doi:10.1117/12.2056811

CrossRef Full Text | Google Scholar

Baym, G., Hatsuda, T., Kojo, T., Powell, P. D., Song, Y., and Takatsuka, T. (2018). From Hadrons to Quarks in Neutron Stars: a Review. Rep. Prog. Phys. 81, 056902. doi:10.1088/1361-6633/aaae14

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, B., Char, P., Nandi, R., and Bose, S. (2021). Towards Mitigation of Apparent Tension between Nuclear Physics and Astrophysical Observations by Improved Modeling of Neutron star Matter. Phys. Rev. D 103, 103015. doi:10.1103/physrevd.103.103015

CrossRef Full Text | Google Scholar

Biswas, B. (2021). Impact of PREX-II and Combined Radio/NICER/XMM-Newton’s Mass–Radius Measurement of PSR J0740+6620 on the Dense-Matter Equation of State. Astrophys. J. 921, 63. doi:10.3847/1538-4357/ac1c72

CrossRef Full Text | Google Scholar

Biswas, B. (2021). Bayesian Model-Selection of Neutron star Equation of State Using Multi-Messenger Observations. arXiv e-prints. arXiv:2106.02644.

Google Scholar

Capano, C. D., Tews, I., Brown, S. M., Margalit, B., De, S., Kumar, S., et al. (2020). Stringent Constraints on Neutron-star Radii from Multimessenger Observations and Nuclear Theory. Nat. Astron. 4, 625–632. doi:10.1038/s41550-020-1014-6

CrossRef Full Text | Google Scholar

Carson, Z., Steiner, A. W., and Yagi, K. (2019). Constraining Nuclear Matter Parameters with Gw170817. Phys. Rev. D 99, 043010. doi:10.1103/PhysRevD.99.043010

CrossRef Full Text | Google Scholar

Chatterjee, D., and Vidaña, I. (2016). Do hyperons Exist in the interior of Neutron Stars? Eur. Phys. J. A52, 29. doi:10.1140/epja/i2016-16029-x

CrossRef Full Text | Google Scholar

Chen, W. C., and Piekarewicz, J. (2014). Building Relativistic Mean Field Models for Finite Nuclei and Neutron Stars. Phys. Rev. C 90, 044305. doi:10.1103/PhysRevC.90.044305

CrossRef Full Text | Google Scholar

Coughlin, M. W., Dietrich, T., Margalit, B., and Metzger, B. D. (2019). Multimessenger Bayesian Parameter Inference of a Binary Neutron star Merger. Monthly Notices R. Astronom. Soc. Lett. 489, L91–L96. doi:10.1093/mnrasl/slz133

CrossRef Full Text | Google Scholar

Danielewicz, P., Lacey, R., and Lynch, W. G. (2002). Determination of the Equation of State of Dense Matter. Science 298, 1592–1596. doi:10.1126/science.1078070

PubMed Abstract | CrossRef Full Text | Google Scholar

David, B., Alexander, A., Alexandra, F., and Hovik, G. (2020). Compact Stars in the QCD Phase Diagram. Basel, Switzerland: Universe. doi:10.3390/books978-3-03921-959-9

CrossRef Full Text | Google Scholar

Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., and Hessels, J. W. T. (2010). A Two-Solar-Mass Neutron star Measured Using Shapiro Delay. Nature 467, 1081–1083. doi:10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

Dexheimer, V., Noronha, J., Noronha-Hostler, J., Yunes, N., and Ratti, C. (2021). Future Physics Perspectives on the Equation of State from Heavy Ion Collisions to Neutron Stars. J. Phys. G: Nucl. Part. Phys. 48, 073001. doi:10.1088/1361-6471/abe104

CrossRef Full Text | Google Scholar

Dietrich, T., Coughlin, M. W., Pang, P. T. H., Bulla, M., Heinzel, J., Issa, L., et al. (2020). Multimessenger Constraints on the Neutron-star Equation of State and the Hubble Constant. Science 370, 1450–1453. doi:10.1126/science.abb4317

PubMed Abstract | CrossRef Full Text | Google Scholar

Drischler, C., Carbone, A., Hebeler, K., and Schwenk, A. (2016). Neutron Matter from Chiral Two- and Three-Nucleon Calculations up to N³LO. Phys. Rev. C 94, 054307. doi:10.1103/PhysRevC.94.054307

CrossRef Full Text | Google Scholar

Drischler, C., Hebeler, K., and Schwenk, A. (2019). Chiral Interactions up to Next-To-Next-To-Next-To-Leading Order and Nuclear Saturation. Phys. Rev. Lett. 122, 042501. doi:10.1103/PhysRevLett.122.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

Drischler, C., Furnstahl, R. J., Melendez, J. A., and Phillips, D. R. (2020). How Well Do We Know the Neutron-Matter Equation of State at the Densities inside Neutron Stars? a Bayesian Approach with Correlated Uncertainties. Phys. Rev. Lett. 125, 202702. doi:10.1103/PhysRevLett.125.202702

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutra, M., Lourenço, O., Sá Martins, J. S., Delfino, A., Stone, J. R., and Stevenson, P. D. (2012). Skyrme Interaction and Nuclear Matter Constraints. Phys. Rev. C 85, 035201. doi:10.1103/PhysRevC.85.035201

CrossRef Full Text | Google Scholar

Fabbietti, L., Sarti, V. M., and Doce, O. V. (2021). Study of the strong Interaction Among Hadrons with Correlations at the LHC. Ann. Rev. Nucl. Part. Sci. 71, 377–402. doi:10.1146/annurev-nucl-102419-034438

CrossRef Full Text | Google Scholar

Fasano, M., Abdelsalhin, T., Maselli, A., and Ferrari, V. (2019). Constraining the Neutron star Equation of State Using Multiband Independent Measurements of Radii and Tidal Deformabilities. Phys. Rev. Lett. 123, 141101. doi:10.1103/physrevlett.123.141101

PubMed Abstract | CrossRef Full Text | Google Scholar

Fattoyev, F. J., Carvajal, J., Newton, W. G., and Li, B. A. (2013). Constraining the High-Density Behavior of the Nuclear Symmetry Energy with the Tidal Polarizability of Neutron Stars. Phys. Rev. C 87, 015806. doi:10.1103/PhysRevC.87.015806

CrossRef Full Text | Google Scholar

Flanagan, E. E., and Hinderer, T. (2008). Constraining Neutron-star Tidal Love Numbers with Gravitational-Wave Detectors. Phys. Rev. D 77, 021502. doi:10.1103/PhysRevD.77.021502

CrossRef Full Text | Google Scholar

Fonseca, E., Cromartie, H. T., Pennucci, T. T., Ray, P. S., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. Astrophys. J. Lett. 915, L12. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

Friedman, E., and Gal, A. (2007). In-medium Nuclear Interactions of Low-Energy Hadrons. Phys. Rep. 452, 89–153. doi:10.1016/j.physrep.2007.08.002

CrossRef Full Text | Google Scholar

Fuchs, C., Faessler, A., Zabrodin, E., and Zheng, Y. M. (2001). Probing the Nuclear Equation of State by K⁺ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 86, 1974–1977. doi:10.1103/PhysRevLett.86.1974

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukuda, T., Higashi, A., Matsuyama, Y., Nagoshi, C., Nakano, J., Sekimoto, M., et al. (1998). Cascade Hypernuclei in the (K⁻,K⁺) Reaction on ¹²C. Phy. Rev. C 58, 1306–1309. doi:10.1103/physrevc.58.1306

CrossRef Full Text | Google Scholar

Gamba, R., Read, J. S., and Wade, L. E. (2019). The Impact of the Crust Equation of State on the Analysis of GW170817. Classical Quan. Gravity 37, 025008. doi:10.1088/1361-6382/ab5ba4

CrossRef Full Text | Google Scholar

Gandolfi, S., Gezerlis, A., and Carlson, J. (2015). Neutron Matter from Low to High Density. Annu. Rev. Nucl. Part. Sci. 65, 303–328. doi:10.1146/annurev-nucl-102014-021957

CrossRef Full Text | Google Scholar

Gandolfi, S., Lippuner, J., Steiner, A. W., Tews, I., Du, X., and Al-Mamun, M. (2019). From the Microscopic to the Macroscopic World: from Nucleons to Neutron Stars. J. Phys. G: Nucl. Part. Phys. 46, 103001. doi:10.1088/1361-6471/ab29b3

CrossRef Full Text | Google Scholar

Ghosh, S., Chatterjee, D., and Schaffner-Bielich, J. (2022). Imposing Multi-Physics Constraints at Different Densities on the Neutron Star Equation of State. Eur. Phys. J. A 58, 37.

CrossRef Full Text | Google Scholar

Glendenning, N. (2012). Compact Stars: Nuclear Physics, Particle Physics and General Relativity. Astronomy and Astrophysics Library. New York: Springer.

Google Scholar

Greif, S. K., Raaijmakers, G., Hebeler, K., Schwenk, A., and Watts, A. L. (2019). Equation of State Sensitivities when Inferring Neutron star and Dense Matter Properties. Monthly Notices R. Astronom. Soc. 485, 5363–5376. doi:10.1093/mnras/stz654

CrossRef Full Text | Google Scholar

Guillot, S., Servillat, M., Webb, N. A., and Rutledge, R. E. (2013). Measurement of the Radius of Neutron Stars with High Signal-To-Noise Quiescent Low-Mass X-ray Binaries in Globular Clusters. Astrophys. J. 772, 7. doi:10.1088/0004-637x/772/1/7

CrossRef Full Text | Google Scholar

Güven, H., Bozkurt, K., Khan, E., and Margueron, J. (2020). Multimessenger and Multiphysics Bayesian Inference for the Gw170817 Binary Neutron star Merger. Phys. Rev. C 102, 015805. doi:10.1103/PhysRevC.102.015805

CrossRef Full Text | Google Scholar

Hartnack, C., Oeschler, H., and Aichelin, J. (2006). Hadronic Matter Is Soft. Phys. Rev. Lett. 96, 012302. doi:10.1103/PhysRevLett.96.012302

PubMed Abstract | CrossRef Full Text | Google Scholar

Hebeler, K., Lattimer, J. M., Pethick, C. J., and Schwenk, A. (2013). Equation of State and Neutron star Properties Constrained by Nuclear Physics and Observation. Astrophys. J. 773, 11. doi:10.1088/0004-637x/773/1/11

CrossRef Full Text | Google Scholar

Hinderer, T., Lackey, B. D., Lang, R. N., and Read, J. S. (2010). Tidal Deformability of Neutron Stars with Realistic Equations of State and Their Gravitational Wave Signatures in Binary Inspiral. Phys. Rev. D 81, 123016. doi:10.1103/PhysRevD.81.123016

CrossRef Full Text | Google Scholar

Hinderer, T. (2008). Tidal Love Numbers of Neutron Stars. Astrophys. J. 677, 1216–1220. doi:10.1086/533487

CrossRef Full Text | Google Scholar

Hornick, N., Tolos, L., Zacchi, A., Christian, J. E., and Schaffner-Bielich, J. (2018). Relativistic Parameterizations of Neutron Matter and Implications for Neutron Stars. Phys. Rev. C 98, 065804. doi:10.1103/PhysRevC.98.065804

CrossRef Full Text | Google Scholar

Huth, S., Pang, P. T. H., Tews, I., Dietrich, T., Le Fèvre, A., Schwenk, A., et al. (2021). Constraining Neutron-Star Matter with Microscopic and Macroscopic Collisions. arXiv e-prints. arXiv:2107.06229.

Google Scholar

Inoue, T. (2016). “Hyperon Single-Particle Potentials from QCD on Lattice,” in PoS INPC, 2016, Adelaide, SA, Australia, September 11–16, 2016, 277. doi:10.22323/1.281.0277

CrossRef Full Text | Google Scholar

Inoue, T. (2019). Hyperon Forces from QCD and Their Applications. JPS Conf. Proc. 26, 023018. doi:10.7566/jpscp.26.023018

CrossRef Full Text | Google Scholar

Khaustov, P., Alburger, D. E., Barnes, P. D., Bassalleck, B., Berdoz, A. R., Biglan, A., et al. (2000). Evidence of Ξ Hypernuclear Production in the 12C(K-,K+)12Ξ Be Reaction. Phys. Rev. C 61, 054603. doi:10.1103/physrevc.61.027601

CrossRef Full Text | Google Scholar

Kirch, W. (2008). Pearson’s Correlation Coefficient. Dordrecht: Springer Netherlands, 1090–1091. doi:10.1007/978-1-4020-5614-7_2569

CrossRef Full Text | Google Scholar

Landry, P., Essick, R., and Chatziioannou, K. (2020). Nonparametric Constraints on Neutron star Matter with Existing and Upcoming Gravitational Wave and Pulsar Observations. Phys. Rev. D 101, 123007. doi:10.1103/PhysRevD.101.123007

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2004). The Physics of Neutron Stars. Science 304, 536–542. doi:10.1126/science.1090720

PubMed Abstract | CrossRef Full Text | Google Scholar

Lattimer, J. M. (2012). The Nuclear Equation of State and Neutron star Masses. Annu. Rev. Nucl. Part. Sci. 62, 485–515. doi:10.1146/annurev-nucl-102711-095018

CrossRef Full Text | Google Scholar

Lattimer, J. M. (2015). Introduction to Neutron Stars. AIP Conf. Proc. 1645, 61–78. doi:10.1063/1.4909560

CrossRef Full Text | Google Scholar

Le Fèvre, A., Leifels, Y., Reisdorf, W., Aichelin, J., and Hartnack, C. (2016). Constraining the Nuclear Matter Equation of State Around Twice Saturation Density. Nucl. Phys. A 945, 112–133. doi:10.1016/j.nuclphysa.2015.09.015

CrossRef Full Text | Google Scholar

Lim, Y., and Holt, J. W. (2018). Neutron star Tidal Deformabilities Constrained by Nuclear Theory and experiment. Phys. Rev. Lett. 121, 062701. doi:10.1103/PhysRevLett.121.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindblom, L. (2018). Causal Representations of Neutron-star Equations of State. Phys. Rev. D 97, 123019. doi:10.1103/physrevd.97.123019

CrossRef Full Text | Google Scholar

Mareš, J., Friedman, E., Gal, A., and Jenning, B. (1995). Constraints on σ-nucleus Dynamics from Dirac Phenomenology of σ⁻ Atoms. Nucl. Phys. A 594, 311–324. doi:10.1016/0375-9474(95)00358-8

CrossRef Full Text | Google Scholar

Millener, D. J., Dover, C. B., and Gal, A. (1988). Λ-Nucleus Single-Particle Potentials. Phys. Rev. C 38, 2700–2708. doi:10.1103/PhysRevC.38.2700

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). Psr J0030+0451 Mass and Radius from Nicer Data and Implications for the Properties of Neutron star Matter. Astrophys. J. 887, L24. doi:10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

Miller, M. C., Chirenti, C., and Lamb, F. K. (2019). Constraining the Equation of State of High-Density Cold Matter Using Nuclear and Astronomical Measurements. Astrophys. J. 888, 12. doi:10.3847/1538-4357/ab4ef9

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The Radius of Psr J0740+6620 from Nicer and Xmm-newton Data. Astrophys. J. Lett. 918, L28. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

Most, E. R., Weih, L. R., Rezzolla, L., and Schaffner-Bielich, J. (2018). New Constraints on Radii and Tidal Deformabilities of Neutron Stars from Gw170817. Phys. Rev. Lett. 120, 261103. doi:10.1103/PhysRevLett.120.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Boyle, M. F., Markakis, C., Stergioulas, N., and Read, J. S. (2020). Parametrized Equation of State for Neutron star Matter with Continuous Sound Speed. Phys. Rev. D 102, 083027. doi:10.1103/PhysRevD.102.083027

CrossRef Full Text | Google Scholar

Oertel, M., Hempel, M., Klähn, T., and Typel, S. (2017). Equations of State for Supernovae and Compact Stars. Rev. Mod. Phys. 89, 015007. doi:10.1103/RevModPhys.89.015007

CrossRef Full Text | Google Scholar

Özel, F., Baym, G., and Güver, T. (2010). Astrophysical Measurement of the Equation of State of Neutron star Matter. Phys. Rev. D 82, 101301. doi:10.1103/PhysRevD.82.101301

CrossRef Full Text | Google Scholar

Pang, P. T. H., Tews, I., Coughlin, M. W., Bulla, M., Van Den Broeck, C., and Dietrich, T. (2021). Nuclear Physics Multimessenger Astrophysics Constraints on the Neutron Star Equation of State: Adding NICER’s PSR J0740+6620 Measurement. Astro. Phys. J. 922, 14. doi:10.3847/1538-4357/ac19ab

CrossRef Full Text | Google Scholar

Pradhan, B. K., and Chatterjee, D. (2021). Effect of Hyperons on F-Mode Oscillations in Neutron Stars. Phys. Rev. C 103, 035810. doi:10.1103/PhysRevC.103.035810

CrossRef Full Text | Google Scholar

Read, J. S., Lackey, B. D., Owen, B. J., and Friedman, J. L. (2009). Constraints on a Phenomenologically Parametrized Neutron-star Equation of State. Phys. Rev. D 79, 124032. doi:10.1103/physrevd.79.124032

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A Nicer View of Psr J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. 887, L21. doi:10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Ray, P. S., Bogdanov, S., Guillot, S., Morsink, S. M., et al. (2021). A Nicer View of the Massive Pulsar Psr J0740+6620 Informed by Radio Timing and Xmm-newton Spectroscopy. Astrophys. J. Lett. 918, L27. doi:10.3847/2041-8213/ac0a81

CrossRef Full Text | Google Scholar

Russotto, P., Gannon, S., Kupny, S., Lasko, P., Acosta, L., Adamczyk, M., et al. (2016). Results of the Asy-Eos experiment at Gsi: The Symmetry Energy at Suprasaturation Density. Phys. Rev. C 94. doi:10.1103/physrevc.94.034608

CrossRef Full Text | Google Scholar

Schaffner, J., Greiner, C., and Stöcker, H. (1992). Metastable Exotic Multihypernuclear Objects. Phys. Rev. C 46, 322–329. doi:10.1103/PhysRevC.46.322

CrossRef Full Text | Google Scholar

Schaffner, J., Dover, C. B., Gal, A., Greiner, C., and Stöcker, H. (1993). Strange Hadronic Matter. Phys. Rev. Lett. 71, 1328–1331. doi:10.1103/PhysRevLett.71.1328

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaffner-Bielich, J., and Gal, A. (2000). Properties of Strange Hadronic Matter in Bulk and in Finite Systems. Phys. Rev. C 62, 034311. doi:10.1103/PhysRevC.62.034311

CrossRef Full Text | Google Scholar

Schaffner-Bielich, J. (2020). Compact Star Physics. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/9781316848357

CrossRef Full Text | Google Scholar

Serot, B. D., and Walecka, J. D. (1992). Relativistic Nuclear many Body Theory. Rec. Prog. Many Body Theor. 3, 49–92. doi:10.1007/978-1-4615-3466-2_5

CrossRef Full Text | Google Scholar

Serot, B. D., and Walecka, J. D. (1997). Recent Progress in Quantum Hadrodynamics. Int. J. Mod. Phys. E 06, 515–631. doi:10.1142/s0218301397000299

CrossRef Full Text | Google Scholar

Steiner, A. W., Lattimer, J. M., and Brown, E. F. (2013). The Neutron star Mass-Radius Relation and the Equation of State of Dense Matter. Astrophys. J. 765, L5. doi:10.1088/2041-8205/765/1/l5

CrossRef Full Text | Google Scholar

Stone, J., and Reinhard, P. G. (2007). The Skyrme Interaction in Finite Nuclei and Nuclear Matter. Prog. Part. Nucl. Phys. 58, 587–657. doi:10.1016/j.ppnp.2006.07.001

CrossRef Full Text | Google Scholar

Tews, I., Margueron, J., and Reddy, S. (2018). Critical Examination of Constraints on the Equation of State of Dense Matter Obtained from Gw170817. Phys. Rev. C 98, 045804. doi:10.1103/PhysRevC.98.045804

CrossRef Full Text | Google Scholar

Tews, I., Margueron, J., and Reddy, S. (2019). Constraining the Properties of Dense Matter and Neutron Stars by Combining Nuclear Physics and Gravitational Waves from Gw170817. AIP Conf. Proc. 2127, 020009. doi:10.1063/1.5117799

CrossRef Full Text | Google Scholar

Tews, I., Margueron, J., and Reddy, S. (2019). Confronting Gravitational-Wave Observations with Modern Nuclear Physics Constraints. Eur. Phys. J. A 55, 97. doi:10.1140/epja/i2019-12774-6

CrossRef Full Text | Google Scholar

Thorsett, S. E., and Chakrabarty, D. (1999). Neutron star Mass Measurements. I. Radio Pulsars. Astrophys. J. 512, 288–299. doi:10.1086/306742

CrossRef Full Text | Google Scholar

Tong, H., Zhao, P., and Meng, J. (2020). Symmetry Energy at Supra-saturation Densities via the Gravitational Waves from Gw170817. Phys. Rev. C 101, 035802. doi:10.1103/PhysRevC.101.035802

CrossRef Full Text | Google Scholar

Traversi, S., Char, P., and Pagliara, G. (2020). Bayesian Inference of Dense Matter Equation of State within Relativistic Mean Field Models Using Astrophysical Measurements. Astrophys. J. 897, 165. doi:10.3847/1538-4357/ab99c1

CrossRef Full Text | Google Scholar

Tsang, C. Y., Tsang, M. B., Danielewicz, P., Lynch, W. G., and Fattoyev, F. J. (2018). Constraining Neutron-star Equation of State Using Heavy-Ion Collisions. arXiv e-prints. arXiv:1807.06571.

Google Scholar

Vautherin, D., and Brink, D. M. (1972). Hartree-fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 5, 626–647. doi:10.1103/PhysRevC.5.626

CrossRef Full Text | Google Scholar

Wei, J. B., Lu, J. J., Burgio, G. F., Li, Z. H., and Schulze, H. J. (2020). Are Nuclear Matter Properties Correlated to Neutron star Observables? Eur. Phys. J. A. 56, 63. doi:10.1140/epja/s10050-020-00058-3

CrossRef Full Text | Google Scholar

Weissenborn, S., Chatterjee, D., and Schaffner-Bielich, J. (2012). Hyperons and Massive Neutron Stars: The Role of Hyperon Potentials. Nucl. Phys. A 881, 62–77. doi:10.1016/j.nuclphysa.2012.02.012

CrossRef Full Text | Google Scholar

Xie, W. J., and Li, B. A. (2019). Bayesian Inference of High-Density Nuclear Symmetry Energy from Radii of Canonical Neutron Stars. Astrophys. J. 883, 174. doi:10.3847/1538-4357/ab3f37

CrossRef Full Text | Google Scholar

Yagi, K., and Yunes, N. (2013). I-love-q Relations in Neutron Stars and Their Applications to Astrophysics, Gravitational Waves, and Fundamental Physics. Phys. Rev. D 88, 023009. doi:10.1103/PhysRevD.88.023009

CrossRef Full Text | Google Scholar

Zhang, N. B., and Li, B. A. (2019). Implications of the Mass M = 2.17 +0.11 −0.10 M ⊙ of Psr J0740+6620 on the Equation of State of Super-dense Neutron-Rich Nuclear Matter. Astrophys. J. 879, 99. doi:10.3847/1538-4357/ab24cb

CrossRef Full Text | Google Scholar

Zhu, Z. Y., Zhou, E. P., and Li, A. (2018). Neutron star Equation of State from the Quark Level in Light of Gw170817. Astrophys. J. 862, 98. doi:10.3847/1538-4357/aacc28

CrossRef Full Text | Google Scholar

Zimmerman, J., Carson, Z., Schumacher, K., Steiner, A. W., and Yagi, K. (2020). Measuring Nuclear Matter Parameters with NICER and LIGO/Virgo. arXiv e-prints. arXiv:2002.03210.

Google Scholar