The Joined-up Magnetosphere

Systems science is a relatively new way of studying the magnetosphere. This perspective outlines the need for it and how it can contribute to our understanding and so give more reliable forecasts, predictions, and space weather climatologies.

Description, Understanding and Prediction

In 1970 Hannes Alfvén won the Nobel Prize for his formulation of magnetohydrodynamics (MHD), the fluid theory of a magnetoplasma. With some assumptions, MHD gives us a self-consistent and predictive description of magnetospheric behavior by quantifying the 3-dimensional structure of the electric and magnetic fields, E and B, but with particles only represented by the moments of their (assumed Maxwellian) distributions. However, we should not lose sight of the fact that the magnetosphere is a massive, highly complex multibody system of interacting charged particles.

In lectures to new students, I often compare and contrast magnetospheric behavior with the murmuration of a flock of starlings (see Figure 1). Numerical modelling and systems analysis has revealed that each bird in the flock is following the simple interaction law of copying the flight of its seven nearest neighbors, the number that gives the optimum trade-off between group cohesion and individual effort (Young et al., 2013). Any changes in flight by one bird, induced either through error in replicating the flight direction of adjacent birds or by variability in atmospheric conditions (e.g., a gust of wind), will propagate through the flock because of the birds’ reaction time and hence the flocks behave as critical systems, poised to respond maximally to environmental perturbations (Cavagna et al., 2010). In the magnetosphere, there are far too many charged particles to numerically model all the mutual interactions but the smaller number of birds in a flock mean it can be modelled that way, as well as by using an analytic theory such as the Vicsek model (Ginellia, 2016), which is the equivalent of MHD for the magnetosphere. These models readily reproduce the types of evolving forms that are seen in bird murmuration¹, which are so varied that they can, by chance, take on ironically coincidental forms². This means that we have a description of the objects (the birds) and how they interact. From this we can predict the types of collective behavior of the flock that are seen—but we cannot define the perturbations well enough to allow us to predict exactly what a given bird flock will do. Hence for complex interacting systems the collective behaviors may not be predictable, even though we have a good description of the objects and good understanding of how they interact.

FIGURE 1

FIGURE 1. Starling murmuration photographed at the village of Rigg, near Gretna in the Scottish borders, on 25 November 2013. The text discusses similarities and differences between the dynamics of such bird flocks and of the magnetosphere. One coincidental similarity of these two non-equilibrium, multi-body, interacting systems is the potential to cause disruption to power grids. Magnetosphere-ionosphere current systems cause Geomagnetically Induced Currents (GICs) that can give disruption and damage to power supply networks and the weight of the very large number of starlings roosting on the power grid cables in this picture also caused local power disruptions (See The Guardian newspaper (UK), Tuesday 21 January 2014 https://www.theguardian.com/environment/gallery/2014/jan/21/starling-mumuration-season-in-pictures). Photo: Owen Humphreys/PA.

A flock of birds has some parallels to the magnetosphere, but is the magnetosphere as unpredictable? The answer, fortunately, is no because it does not have the equivalent of the error that individual starlings make in assessing the flight of their nearest neighbors. It does, however, have the equivalent of highly variable atmospheric conditions, because it is constantly buffeted by the solar wind and subject to variations in solar wind-magnetosphere coupling by the variability of the north-south component of the interplanetary magnetic field (IMF). This means that systems analysis, of the kind used to study a flock of birds and swarming phenomena in general, does have applications in understanding the magnetosphere.

If we start from the equations of special relativity and the Coulomb force law, we can readily derive the Lorentz equation, which gives us mathematical expressions for E and B, defining what they are. The electric field E is a net effect of all the charged particles in the cosmos on the point in question, dependent only on their charge and position, whereas the magnetic field B is the net effect of all the moving charged particles and dependent on their charge, position and motion. As the effects of both decrease rapidly with increased distance between the charged particle and the point (the inverse square laws), the effect of local charges is much greater than distant ones. Hence the (limited) parallel to the flock of birds. We see this distance-dependent connectivity directly in the magnetosphere where, for example, the Dst, Sym-H and SMR indices are computed from perturbations to the ground-level geomagnetic field at low-latitudes. They are influenced most by the relatively nearby ring current, but also by the more-distant magnetopause currents (Siscoe et al., 1968) and by the tail currents Turner et al., 2000; Asikainen et al., 2010).

Every charged particle in a magnetoplasma influences every other through its contribution to E and B, giving a collective behavior which means changes spread through the magnetosphere at propagation speeds set by the speeds of the variety of wave phenomena that are possible. The typical speeds of the information propagation, the spatial scales of the magnetosphere and the temporal variability of the driving interplanetary conditions mean that the magnetosphere, like the bird flock, is often not an equilibrium system and some part, if not all of it, will always still be responding to a prior influence.

Jim Dungey often used to complain about “overly mechanistic and insufficiently holistic thinking” about the magnetosphere. His point was that scientists would often argue that “the change in A generates B which changes C, etc.” when A, B, and C were so coupled that the chain of causality running through them was not necessarily the one that people thought. To make matters worse, these chains often contained element pairs that were actually two different descriptions of the same thing, arising from the way people think about Maxwell’s equations. JD’s “socio-educational” theory was that we are first taught electromagnetism through the dynamo and the motor, where the mechanical construction causes there to be a direction of causality in the equals symbol of Faraday’s law. But that is not the meaning of the equals sign in Faraday’s law in general which, in Oliver Heaviside’s brilliant formulation of Maxwell’s equations, tells us that the curl of the electric field and the rate of change of the magnetic field are two different descriptions of exactly the same thing—not that one generates the other. Another example is Ampère’s law (the relevant form of another of Maxwell’s equation in a plasma because the displacement current can be neglected compared to the free currents for all but exceptionally high frequency phenomena).

$\left(\nabla \times \underset{¯}{\mathbf{B}}\right)=\mathrm{\mu }\mathrm{o}\underset{¯}{\mathbf{J}}(1)$

JD’s point was that Equation 1 doesn’t tell us that a magnetic shear generates a current, nor that a current generates a magnetic shear—it tells us that they are two different descriptions of exactly the same thing: you cannot have one without the other. It means that, for example, the cross-tail current disruption during a substorm onset and the dipolarisation in the near-Earth geomagnetic field (and the associated Earthward convection surge of the frozen-in plasma) are just different ways of describing precisely the same phenomenon: one does not cause the other (see Figure 2E). One reason why this matters is that a causal link would involve a lag and a growth time, neither of which exist when they are really two different descriptions of the same thing.

FIGURE 2

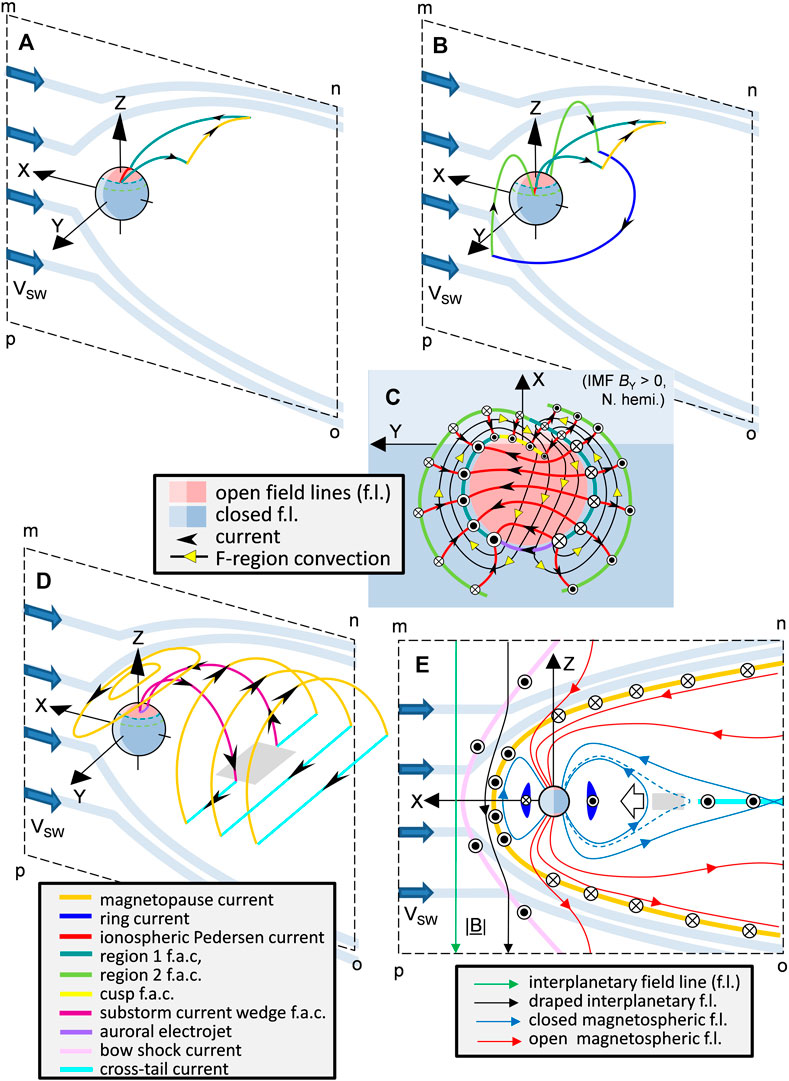
FIGURE 2. Five different views of the magnetosphere-ionosphere system. Parts (A),(B) and (D) show the main current loops (in the northern hemisphere only for clarity), viewed from mid-latitudes in the northern hemisphere in the pre-midnight sector. The X, Y, and Z axes of the Geocentric Solar Ecliptic (GSE) reference frame are shown and the blue block arrows show the undisturbed solar wind flow, upstream of the bow shock. Pink areas in the ionosphere are where geomagnetic field lines are open (i.e., they thread the magnetopause) and light blue areas are where field lines are closed (i.e., they do not thread the magnetopause). Solar wind coupling occurs because closed field lines are opened by magnetic reconnection in the dayside magnetopause and closed again some time later by reconnection in the cross-tail current sheet. The key gives the color codes of the types of current in each segment of each loop. Note that the currents are shown as single filaments for clarity but in reality form extended sheets. Part (A) shows the “polar cap circuit” in which the field aligned currents (f.a.c.) that bring momentum and energy from the shocked solar wind (magnetosheath) to the ionosphere (the “Region 1” currents) enable a current loop completed by dissipative ionospheric Pedersen currents and magnetopause currents. The return sunward convection in the auroral ionosphere requires dusk-to-dawn Pedersen currents across the auroral oval and (B) shows the “polar cap/ring current circuit” that makes this possible: this circuit enhances the nightside ring current via the “Region 2” f. a.c.s at lower latitudes and is completed by a Region 1 f. a.c. and magnetopause current loop. The pattern of ionospheric currents and flows is shown in (C) which is a view from above the north pole for the case of IMF B_Y > 0. Part (D) shows the magnetopause and cross-tail current loops, the inner part of the latter being deflected into the ionosphere in the “current wedge” during substorm expansion phases when the central, near-Earth edge of the cross-tail current (in the grey area) is disrupted. This means there is a dipolarisation within the wedge and a sunward convection surge of frozen-in plasma. Part (E) is a cross-section view of the magnetosphere from its dusk flank and shows the currents and the corresponding magnetic field lines in the meridian (XZ) plane. The white arrow shows a convection surge and the dashed and solid blue lines the position of nightside closed field lines before and after dipolarisation.

Another reason why everything in the magnetosphere is connected to the other parts of the magnetosphere is quasi-neutrality of the plasma which means currents are very close to divergence-free, i.e., sources and sinks of current are very small and so they must flow in closed loops, as shown in Figure 2. It is remarkable to think that the flux circulation of magnetospheric convection could not happen without not only ion-neutral and electron-neutral collisions in the upper atmosphere that generate Pedersen conductivity, but also a completely different phenomenon in the gradient and curvature drift of trapped particles, that give the ring current. This is because both the ionospheric Pedersen current and the ring current are involved in closing the global field-aligned currents that transfer energy and momentum from the sources in the magnetopause and cross-tail current sheet to the upper atmosphere (see Figure 2).

Its behavior may not be as unpredictable as a flock of birds, but the magnetosphere is a joined-up, complex, interacting, many-bodied system and the concepts of Self-Organized Criticality (SOC) have been applied to it in some areas (see review by Watkins et al., 2016).

The Phases of Exploration of Near-Earth Space

I am lucky enough to sit between two generations of magnetospheric scientists. Nowadays I meet a generation of young scientists armed with the latest computational, modelling and visualization techniques that are fed by multi-point and multi-instrument data of unprecedented resolution, accuracy and scope. But I also met a generation before mine that thought its way through to some basic understanding of the terrestrial space environment with unbelievably limited resources and the crudest of observations.

Understanding this joined-up, time-dependent magnetosphere has come in (overlapping) stages. The first stage was to follow the seminal paper of Chapman and Ferraro (1931) and consider temporal changes as a series of equilibrium steady-states. This established some mechanisms, connections and behaviors but kept others well concealed. This approach can, of course, be valid if the changes are slower than the response time constants (Milan et al., 2021) but, as one of my big heroes outside science, Peter Gabriel, sang: “We’ve tried making movies from a handful of stills”³.

As more data from near-Earth interplanetary space and the magnetosphere was obtained, statistical studies grew in importance. To reduce noise and to help spot trends, data from long intervals were averaged together. This inherently puts time derivates to zero and so gives an average, but steady-state view of the magnetosphere.

It was realized that steady state hides a great many mechanisms at work in the magnetosphere because one has no chance of identifying the chain of causality in a coupled system. Case studies were used to study the temporal evolutions of the magnetosphere. Examples included geomagnetic storms, sudden compressions by the solar wind, the substorm cycle and, on temporal scales down to a few minutes, studies of ULF wave phenomena and of flux transfer events (bursts in magnetic reconnection in the dayside magnetopause). Much was done from studying transient responses in the magnetosphere - but there is a serendipitous element to such studies. Not all behaviors were revealed because some events are very rare and even if they did happen we did not always have the instrumentation that we needed in the right places at the right time. These studies revealed mechanisms but could not give understanding of their overall importance and occurrence. There are classes of statistical studies that can help in this, such as superposed epoch analysis (a.k.a. “Chree analysis”, and in meteorology termed “compositing”) and statistical studies that divide the data by the phase of a sequence (e.g., by the phase of the substorm cycle) but these can only inform about a pre-determined sequence (which defines over which intervals to average data).

The next phase of studying the joined-up, time-dependent magnetosphere was the development of numerical modelling. Global MHD models and targeted kinetic models allow us to generate unusual, even unrealistic, scenarios that can reveal facets of the response of the magnetosphere that we had not seen, or maybe seen but not recognized, in the observations. The difficulty here is understanding what is an artefact of the modelling (due to numerical errors) and what is a realistic magnetospheric behavior. To make it even more confusing, a key mechanism, magnetic reconnection, is both! This makes it vital that modelling is constantly referenced back to observational case and statistical studies.

Many studies implicitly used the idea that the magnetosphere would return towards a steady state after perturbation. It was realized that, particularly at sunspot maximum, the temporal variability of the solar wind and IMF was great enough to mean that the magnetosphere would always be returning towards a steady state, in which case the magnetosphere became a non-equilibrium system. It is often assumed that northward-IMF conditions, that persist for exactly half the time, give the steady-state towards which the magnetosphere relaxes. However, we know steady state is never achieved because, although the magnetic flux in the geomagnetic tail weakens during northward IMF, we have never seen the tail completely disappear. Quiet times are when the IMF points northward, so the solar wind flow gives a dusk-to-dawn electric field that is applied across the magnetosphere. However, the persistence of the tail means that the magnetic shear between the tail lobes across the cross-tail current sheet remains and magnetic reconnection can only give a dawn-to-dusk electric field (it may be weak or even be zero but it cannot match the dusk-to-dawn electric field applied by the solar wind). This means that there is a curl of E within the magnetosphere which, by Faraday’s law, means that there is a rate of change in the magnetic field, i.e., non-steady-state conditions (Lockwood, 2004; Lockwood, 2019). Hence, rather than northward IMF being a steady-state, it is an interval a slow decline of the open flux caused by continued low-level reconnection in the cross tail current sheet and by open flux closure by lobe reconnections taking place simultaneously or sequentially in both hemispheres (Lockwood and Moen, 1999). Northward IMF conditions can persist for long enough for the magnetosphere to become very close to becoming fully closed (Wang et al., 2022) but has never yet been seen to last so long that the tail completely disappears. This argues that, rather than the magnetosphere sometimes not being an equilibrium system, that is never an equilibrium system.

This brings us to what I see as a new phase of study that we are just embarking upon, systems analysis of the magnetosphere, the analysis of the joined-up magnetosphere (Borovsky & Valdivia, 2018). This will often aided by new machine learning techniques (Camporeale, 2019).

The Joined-up Magnetosphere

This idea is inspired by the development of Earth Systems Science, ESS, in environmental sciences (Steffen et al., 2020). Driven by anthropogenic changes to the natural world, such as ozone depletion, greenhouse trapping of heat by increased carbon dioxide, deforestation and pollution, there was a greater realization in the 1980s that the various aspects of terrestrial environmental science, such as the oceans, the atmospheric layers, the biomass and its many ecosystems, the soil, the ice sheets, were all interconnected—and that the mechanisms and feedbacks of those interconnections were important but not understood. It was also realized that the interactions were perturbed by both human activities and natural events such as volcanoes, large meteorite impacts and solar change and there were a variety of timescales on which the subsequent interactions took place. The early development of numerical climate models highlighted limitations in our understanding of behavior of the holistic system.

That is not dissimilar to the state of magnetospheric science until quite recently—we knew of the various regions, we knew their main behaviors, we knew a lot of mechanisms—but we had only a limited holistic view of the whole system. Hence it was almost the complete opposite of the study of bird murmuration, where we can visually see the holistic behavior but needed research to understand the mechanisms that were at work. We do have numerical models of the various regions of geospace and we had learned how to couple them together to some extent, although very often the links have been rather crude parameterizations rather using fully self-consistent numerical modelling and changes in scale lengths and times are a problem.

ESS studies the relationships between various global parameters that quantify the state of all or key parts of the system such as the Global Mean Air Surface Temperature (GMAST), the global warming index or the global radiative forcing, the volume of ice in the polar cap ice sheets, the global mean sea level, the carbon dioxide mixing ratio, ocean acidity, total ocean heat content, the drought severity index and potentially other global or region aggregates of factors such as mean soil water content, tundra extent, vegetation growth rates, stratospheric aerosol content and biomass dryness.

We have a number of analogous indices and indicators that tell us about the state of aspects of the magnetosphere. These include: the transpolar voltage Φ_PC (physically more meaningful when split into the magnetopause and tail reconnection voltages, Φ_D and Φ_N but these are not so routinely measured) which tell us about magnetic flux transfer through the system; the total open solar flux F_PC, given by the area of the ionospheric polar caps A_PC = F_PC/B_i, which tells us about the amount of energy stored in the geomagnetic tail; the dayside auroral AU (or SMU) geomagnetic indices that tell us about reconnection in the dayside magnetopause, and the nightside auroral AL (or SML) geomagnetic indices, that tell us about reconnection in the tail (Lockwood and McWilliams, 2021a); the Dst, Sym-H or SMR indices (or their time derivatives) that are mainly dominated by the ring current and so tell us the fluxes of energetic particles in that region; the Polar Cap Indices PCN and PCS that quantify of the current and electric field in the polar caps; the mid-latitude range indices kp (ap) and am and mid-latitude hourly indices such as IDV and IHV that tell us about the disturbance level of the geomagnetic field on a global basis; and the TIROS or mPe and mPi precipitation power indices (for electrons and ions respectively). There are also a great many near-continuous measurement series of specific variables that monitor a specific aspect of the magnetosphere.

In the past, these have been used in correlative studies with combinations of interplanetary parameters (“coupling functions”, designed to quantify solar wind control of the magnetosphere; see reviews by Lockwood and McWilliams (2021b) and Lockwood (2022)) and one index or indicator which was tacitly taken to quantify the state of the whole magnetosphere. The corollary that one index can do this is that the coupling function should predict all magnetospheric indices and indicators equally well. Newell et al. (2007) proposed is that there is a “universal coupling function” that best predicts all terrestrial space weather indices and indicator. However, this idea runs counter to the method now routinely used to reconstruct interplanetary parameters from historic observations of geomagnetic activity which exploit the finding that different geomagnetic indices have different responses to interplanetary parameters and so combinations of historic index observations can be used to infer the separate interplanetary parameters (e.g., Lockwood et al., 2014) and this led to the reconstruction of a space weather climatology over the last 400 years from geomagnetic, sunspot and cosmogenic isotopes data (Lockwood et al., 2018). That different, seemingly-global terrestrial indices correlate best with different coupling functions has been demonstrated directly using simultaneous datasets by Lockwood and McWilliams (2021b). The limitation of coupling functions is that they cannot account for factors such as variable feedback loops between different aspects and parts of the magnetosphere or the effects of preconditioning space weather conditions on the prior state of the magnetosphere (Borovsky, 2021).

Borovsky and Osmane (2019) present a composite correlation system analysis scheme that points to the way forward, being aimed at exploiting all the best correlations with interplanetary parameters and various state indices of the magnetosphere. The challenge now is to make use of all best knowledge of the interconnections between different parts and aspects of the magnetosphere to generate optimum prediction schemes. These would include allowance for different lags - both the lags between the interplanetary parameters and the magnetospheric state indicators and the lags associated with the interaction chains within the magnetosphere. This development should go hand-in-hand with the findings from machine learning techniques about the correlations and interaction chains (Camporeale, 2019). There are a number of technical developments to explore. For example, correlations might need weighting according to significance, and the difference between correlations evaluated allowing for the fact that the different parameters are inter-correlated. Alternatively, or additionally, time-integral correlations may appropriate in some or all cases (Lockwood et al., 2016; Borovsky, 2017). These steps should mean that the prediction schemes can allow for one of the biggest limitations of coupling functions, namely pre-conditioning by the existing state of the magnetosphere (Lockwood and McWilliams, 2021b; Lockwood, 2022). This should allow us to make more reliable and accurate forecasts of space weather systems, with better defined uncertainties. In turn, this will aid the operators of the various operational systems perturbed or damaged by space weather effects.

Like the previous overlapping “phases” of magnetospheric discovery, the development of what one could term GSS (“Geospace System Science”) will both contribute to and learn from new theory, case studies, statistical studies, and numerical modelling. One important benefit of better understanding of magnetospheric dynamics is in the development of a space climatology and, in particular, predictions of extreme event occurrence probabilities, which is information urgently needed to allow more cost-effective design of robust systems such as power grids, spacecraft, and communications and navigation systems.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

The work of the author is supported by the UK Science and Technology Facilities Council consolidated grant number ST/R000921/1.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹A real-time movie of a starling murmuration recorded by Paula McCracken in County Galway, Ireland on 21 January 2022 can be seen at https://www.personal.reading.ac.uk/∼ym901336/movies/murmuration.mp4.

²For example, “Very Impressive Starling Murmurations” by Daniel Biber—a series of images captured in a 10-s window on the 31 December 2016 near Sant Pere Pescador in Catalonia, Spain. https://www.worldphoto.org/zh/sony-world-photography-awards/winners-galleries/2018/professional/shortlisted/natural-world/very).

³Peter Gabriel, “Slowburn” first solo album 1977 (a.k.a. “Car”).

References

Asikainen, T., Maliniemi, V., and Mursula, K. (2010). Modeling the Contributions of Ring, Tail, and Magnetopause Currents to the correctedDstindex. J. Geophys. Res. 115, a–n. doi:10.1029/2010JA015774

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2021). Is Our Understanding of Solar-Wind/Magnetosphere Coupling Satisfactory? Front. Astron. Space Sci. 8, 634073. doi:10.3389/fspas.2021.634073

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Osmane, A. (2019). Compacting the Description of a Time-dependent Multivariable System and its Multivariable Driver by Reducing the State Vectors to Aggregate Scalars: the Earth's Solar-Wind-Driven Magnetosphere. Nonlin. Process. Geophys. 26, 429–443. doi:10.5194/npg-26-429-2019

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2017). Time-integral Correlations of Multiple Variables with the Relativistic-Electron Flux at Geosynchronous Orbit: The strong Roles of the Substorm-Injected Electrons and the Ion Plasma Sheet. J. Geophys. Res. 122, 11961–11990. doi:10.1002/2017ja024476

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Valdivia, J. A. (2018). The Earth's Magnetosphere: A Systems Science Overview and Assessment. Surv. Geophys. 39, 817–859. doi:10.1007/s10712-018-9487-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Camporeale, E. (2019). The challenge of Machine Learning in Space Weather: Nowcasting and Forecasting. Space Weather 17, 1166–1207. doi:10.1029/2018SW002061

CrossRef Full Text | Google Scholar

Cavagna, A., Cimarelli, A., Giardina, I., Parisi, G., Santagati, R., Stefanini, F., et al. (2010). Scale-free Correlations in Starling Flocks. Proc. Natl. Acad. Sci. 107 (26), 11865–11870. doi:10.1073/pnas.1005766107

PubMed Abstract | CrossRef Full Text | Google Scholar

Chapman, S., and Ferraro, V. C. A. (1931). A New Theory of Magnetic Storms. J. Geophys. Res. 36 (3), 171–186. doi:10.1029/TE036i003p00171

CrossRef Full Text | Google Scholar

Ginelli, F. (2016). The Physics of the Vicsek Model. Eur. Phys. J. Spec. Top. 225, 2099–2117. doi:10.1140/epjst/e2016-60066-8

CrossRef Full Text | Google Scholar

Lockwood, M. (2004). Solar Outputs, their variations and their effects of Earth. The Sun, Solar Analogs and the Climate. Proc. Saas-Fee Advanced Course 34. Handel, Switzerland: Nature, 107–304.

Google Scholar

Lockwood, M. (2019). Does adding solar wind Poynting flux improve the optimum solar wind-magnetosphere coupling function? J. Geophys. Res. Space Phys. 124, 5498–5515. doi:10.1029/2019JA026639

CrossRef Full Text | Google Scholar

Lockwood, M., and McWilliams, K. A. (2021a). A survey of 25 years’ transpolar voltage data from the SuperDARN radar network and the Expanding–Contracting Polar Cap model. J. Geophys. Res. Space Phys. 126, e2021JA029554. doi:10.1029/2021JA029554

CrossRef Full Text | Google Scholar

Lockwood, M., and McWilliams, K. A. (2021b). On Optimum Solar Wind‐Magnetosphere Coupling Functions for Transpolar Voltage and Planetary Geomagnetic Activity. JGR Space Phys. 126, e2021JA029946. doi:10.1029/2021JA029946

CrossRef Full Text | Google Scholar

Lockwood, M., and Moen, J. (1999). Reconfiguration and Closure of Lobe Flux by Reconnection during Northward IMF: Possible Evidence for Signatures in Cusp/cleft Auroral Emissions. Ann. Geophys. 17, 996–1011. doi:10.1007/s00585-999-0996-2

CrossRef Full Text | Google Scholar

Lockwood, M., Nevanlinna, H., Barnard, L., Owens, M. J., Harrison, R. G., and Scott, A. P. C. J. (2014). Reconstruction of Geomagnetic Activity and Near-Earth Interplanetary Conditions over the Past 167 Yr - Part 4: Near-Earth Solar Wind Speed, IMF, and Open Solar Flux. Ann. Geophys. 32, 383–399. doi:10.5194/angeo-32-383-2014

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., Barnard, L. A., Bentley, S., Scott, C. J., and Watt, C. E. (2016). On the Origins and Timescales of Geoeffective IMF. Space Weather 14, 406–432. doi:10.1002/2016SW001375

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., Barnard, L. A., Scott, C. J., Watt, C. E., and Bentley, S. (2018). Space Climate and Space Weather over the Past 400 years: 2. Proxy Indicators of Geomagnetic Storm and Substorm Occurrence. J. Space Weather Space Clim. 8, A12. doi:10.1051/swsc/2017048

CrossRef Full Text | Google Scholar

Lockwood, M. (2022). Solar Wind – Magnetosphere Coupling Functions: Pitfalls, Limitations and Applications. Space Wea. 20, e2021SW002989. doi:10.1029/2021SW002989

CrossRef Full Text | Google Scholar

Milan, S. E., Carter, J. A., Sangha, H., Bower, G. E., and Anderson, B. J. (2021). Magnetospheric Flux Throughput in the Dungey Cycle: Identification of Convection State during 2010. J. Geophys. Res. Space Phys. 126, e2020JA028437. doi:10.1029/2020JA028437

CrossRef Full Text | Google Scholar

Newell, P. T., Sotirelis, T., Liou, K., Meng, C.-I., and Rich, F. J. (2007). A Nearly Universal Solar Wind-Magnetosphere Coupling Function Inferred from 10 Magnetospheric State Variables. J. Geophys. Res. 112, a–n. doi:10.1029/2006JA012015

CrossRef Full Text | Google Scholar

Siscoe, G. L., Formisano, V., and Lazarus, A. J. (1968). Relation between Geomagnetic Sudden Impulses and Solar Wind Pressure Changes-An Experimental Investigation. J. Geophys. Res. 73 (15), 4869–4874. doi:10.1029/JA073i015p04869

CrossRef Full Text | Google Scholar

Steffen, W., Richardson, K., Rockström, J., Schellnhuber, H. J., Dube, O. P., Dutreuil, S., et al. (2020). The Emergence and Evolution of Earth System Science. Nat. Rev. Earth Environ. 1, 54–63. doi:10.1038/s43017-019-0005-6

CrossRef Full Text | Google Scholar

Turner, N. E., Baker, D. N., Pulkkinen, T. I., and McPherron, R. L. (2000). Evaluation of the Tail Current Contribution toDst. J. Geophys. Res. 105 (A3), 5431–5439. doi:10.1029/1999JA000248

CrossRef Full Text | Google Scholar

Wang, X.–Y., Zhang, Q.–H., Wang, C., Zhang, Y.–L., Tang, B.–B., Xing, Z.–Y., et al. (2022). A Small and Nearly Fully Closed Earth’s Magnetosphere for Strongly Northward Interplanetary Magnetic Field. PNAS, US National Academy of Sciences submitted.

Google Scholar

Watkins, N. W., Pruessner, G., Chapman, S. C., Crosby, N. B., and Jensen, H. J. (2016). 25 Years of Self-Organized Criticality: Concepts and Controversies. Space Sci. Rev. 198, 3–44. doi:10.1007/s11214-015-0155-x

CrossRef Full Text | Google Scholar

Young, G. F., Scardovi, L., Cavagna, A., Giardina, I., and Leonard, N. E. (2013). Starling Flock Networks Manage Uncertainty in Consensus at Low Cost. Plos Comput. Biol. 9 (1), e1002894. doi:10.1371/journal.pcbi.1002894

PubMed Abstract | CrossRef Full Text | Google Scholar