Understanding Large-Scale Structure in Global Ionospheric Maps With Visual and Statistical Analyses

We applied two different techniques to identify high-density structures in global maps of height-integrated electron density of the Earth’s ionosphere. We discuss benefits and limitations of these approaches to structure identification. We suggest that they are complementary and can aid our understanding of the properties of the global ionosphere. We stress out importance of a consistent definition of large-scale ionospheric structures.

Introduction

Global ionospheric state of the Earth’s upper atmosphere is frequently characterized by the total electron content (TEC) that is vertically integrated electron density. TEC distribution over the globe features prominent daytime equatorial ionization anomalies (EIAs), see for instance (Schunk and Nagy, 2009). Observations and follow-up modeling provide evidence of multiple regions with elevated TEC (Maruayama et al., 2016; Astafyeva et al., 2016; Astafyeva et al., 2017) that also include EIAs, i.e., high density regions (HDRs). Physical mechanisms responsible for HDR formations are not well understood. However, knowledge of HDRs, their occurrence, morphology, and evolution are important for space weather forecasting. We suggest that a robust methodology needs to be developed to identify TEC structures, i.e., HDRs, and create an extensive database of the structure occurrences. Such a database should contain information on locations of HDRs, TEC magnitude, time and local time of occurrences, and ancillary information on geomagnetic and solar activity. The data will be crucial for identifying physical mechanisms, testing physical hypotheses and validating modeling results.

To illustrate two different approaches to HDR identification, we use a timeseries of global ionospheric maps (GIMs), a gridded 2D data product for TEC that is commonly used to visualize global ionospheric state. We used two techniques, a mixture method approach and a computer vision approach, that can be utilized to address the following questions. How many anomalies and how many HDRs are present in a GIM? How does the number of the HDRs and their intensities depend on solar and geomagnetic activity? We used the GIM dataset (binned 1° by 1° for every 15 min, https://sideshow.jpl.nasa.gov/pub/iono_daily/gim_for_research/jpli/) produced by Jet Propulsion Laboratory, California Institute of Technology for over 20 years to demonstrate these two approaches. We would like to note that there are several GIM data products available (see the reviews by Hernandez-Pajares et al. (2017); Roma-Dollase et al. (2018)). We chose JPL GIM in this study as a representative GIM dataset with 15-min temporal resolution. Figure 1 shows an example of JPL GIM with two EIAs over the South America and several other HDRs. Below we will briefly discuss our approaches. We focus on large-scale (thousands of km) structuring of the ionosphere.

FIGURE 1

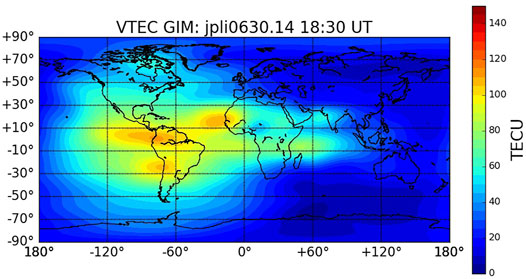
FIGURE 1. Example of GIM on 4 March, 2014. TEC is shown in TEC units (TECU), where 1 TECU = 10¹⁶ electrons/m². Horizontal and vertical axes correspond to geographic longitude and latitude, correspondingly.

Mixture Method

An unsupervised Gaussian Mixture (GM) method, as implemented by scikit-learn (Pedregosa et al., 2011) is utilized to identify unique TEC sub-populations or HDRs (https://scikit-learn.org/stable/modules/mixture.html#mixture). This approach is informative and can be used to understand hierarchical layering of Gaussian clusters. We assume TEC data points arise from a mixture of a finite number of Gaussian distributions whose parameters are unknown. Due to the topology of GIMs, we had to extend scikit’s GM implementation to account for periodic boundaries, i.e., a high-density region that “wraps around” the zero meridian will not be counted as two regions. For each possible number of expected clusters (one to ten, but no higher, to reduce computational requirements and match the order of magnitude of the Computer Vision Method), we compute GM parameters and identify the associated Bayesian Information Criteria (BIC) of each fit. The optimal cluster count was then selected by choosing the knee of the emerging plot of cluster count vs. BIC. This method is sometimes called the Elbow method in statistical clustering. Figures 2A,B show examples of identifications of 2 and 5 clusters, correspondingly. Here, horizontal axes correspond to geographic latitude and longitude. The vertical axis shows the cluster number. This approach is based on statistical properties of the TEC distribution and is sensitive to visually small changes in background density. Note that the GM method designates the background as one of the clusters. Thus, upon visual inspection there is one HDR on Figure 2A. However, it is difficult to determine visually which cluster or clusters correspond to the background density in Figure 2B. For our purpose of understanding large-scale structure, we appreciate that this method accounts for information contained in the data which has physical significance, whether or not that information is visually discernible. For this reason, we believe the following method based on image processing to be complementary.

FIGURE 2

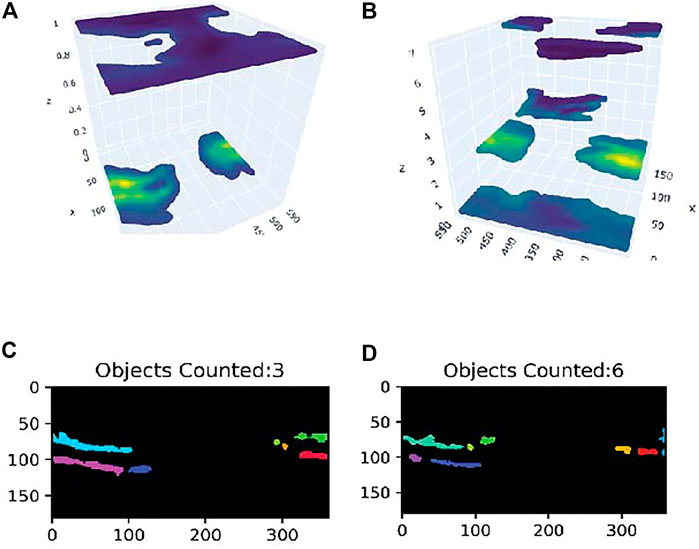
FIGURE 2. Results of GM method application to HDR identification for a GIM on 27 October, 2002 (A) and on 19 July, 2001 (B). Corresponding results for the image processing approach are shown in (C,D). For 27 October, 2002, the GM method identifies 3 HDRs (A), while the image processing approach identifies 3 HDRs (C). For 19 July, 2001, the GM method identifies 5 HDRs (B), while the image processing approach identifies 6 HDRs (D).

Computer Vision Method

Large scale TEC dynamics was analyzed by Dmitriev (2018) by applying visual analysis to individual GIMs. This technique allowed to consider detailed dynamics and provided insight into corresponding physical processes. We advocate building upon such visual approaches and develop ways for automated classification of large-scale TEC features that will be applicable for large datasets. Alternatively, the image processing library OpenCV for Python together with edge-enhancing technique was applied to identify HDRs in a selected GIM dataset with visual inspection. This is an improvement upon our image classification approach (Verkhoglyadova et al., 2021). First, for each TEC map, represented by gridded TEC values, we round the float TEC values to integer numbers and linearly scale the TEC values to numbers between 0 and 255. The TEC map is thus converted to a gray-scale image. Second, we apply the Laplacian operator often used to detect edges in an image, to the gray-scale TEC image brightness over the 2D map. Third, going back to the original TEC map, we neglect regions with TEC values smaller than the half of the TEC global maximum and regions with the Laplacian values greater than a threshold chosen after visual testing of a variety of values for the limited number of TEC maps, and then apply the Dilate, Erode, and medianBlur methods from OpenCV. Finally, HDRs on the TEC map are identified and counted by OpenCV’s connectedComponents operator. A minimum absolute-value threshold for an “edge sharpness” in an image can be applied in order to focus on regions with significantly higher TEC than the surrounding area. Wide range of thresholds were tested and classification results were qualitatively compared to find an optimal value. We found out that our approach works successfully when there are visually identified sharp edges to a TEC brightening. We are fairly confident in selection of an HDR as relatively bright TEC region (by the TEC magnitude) compared to neighboring regions. Since success of the automated classification relies partially on sharpness of the main features of a TEC map, visual inspection is necessary to correctly identify HDRs. Figures 2C,D show examples of identifications of 3 and 6 HDRs on a latitude by longitude map, correspondingly. Introducing an additional procedure of image sharpening allowed to separate two EIAs and identify faint HDRs even if they are not well separated. However, there is a bias in adapting this algorithm to accommodate for visual perception. The identification results are not evident for everyone but for an expert in ionospheric physics and GIMs. Additional complication is encountered when neighboring bright regions are not well separated. We suggest that development of a quantitative criterion of a degree of separation based on statistical properties of TEC distribution is necessary to determine efficiency and applicability of the method.

Discussion

The unexpected result of the study is a realization that different approaches to GIM classification and TEC feature extraction result in different HDR counts and provide different information, each with their own utility for identifying large-scale structure. The GM method is an advanced mixture method that identifies TEC clusters as sub-populations in a GIM by assuming Gaussian distribution of TEC within the clusters. Background TEC is also selected as a separate cluster. GM is a robust method that utilizes optimization tools to select the most common clustering result and account for periodic boundaries. However, it does not always identify visually bright structures inside an extended but less bright structure as separate clusters. Instead, the image classification approach allows for a threshold on TEC value to select the most intense HDRs and ignore the background. The results were validated by visual inspection. However, the latter approach is biased towards sharpening edges of bright features in a map and does not have a selection criterion based on strict statistical properties of TEC distribution. Inter-comparison between these two methods showed different clustering results for several GIMs. Thus, the algorithm based on visual perception of bright regions and the algorithm based on statistical properties of TEC sub-populations in a GIM can produce different outcomes. These results raise an important question of how to robustly define HDRs in GIMs and calls for further investigation. How physical is the definition of distinct HDRs and EIAs? Shall we rely on strict statistics-based approaches or the ones tailored to human eye? How to determine if bright TEC regions are well separated? It is likely that a realistic view of global ionosphere includes HDRs of varying density embedded into backgrounds of varying density that change with solar cycle phases in long term and eruptive solar events in short-term. Depending on the purpose of specific studies, HDRs could be identified using a universal criterion to allow for cross comparison among different background TECs, or using different criteria to make the HDRs outstanding in individual TEC maps. Sharp gradients between different large-scale ionospheric features may not typically occur. Addressing these questions and further research will provide important insights into large -scale ionospheric structure and are crucial for space weather forecast.

Data Availability Statement

The datasets used in this study can be found in https://sideshow.jpl.nasa.gov/pub/iono_daily/gim_for_research/jpli/.

Author Contributions

The authors equally contributed to the ideas presented in the manuscript. XM developed software for the image processing approach. JK developed software for mixture method approach. OV took a lead on writing the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Portions of work were performed at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA. Sponsorship of the Heliophysics Division of the NASA Science Mission Directorate is gratefully acknowledged.

References

Astafyeva, E., Zakharenkova, I., and Huba, J. D. (2017). “Three-Peak Ionospheric Equatorial Ionization Anomaly: Development, Drivers, Statistics,” in Proceedings of the 15th ionospheric effects symposium, Alexandria, VA, May 9–11, 2017.

Google Scholar

Astafyeva, E., Zakharenkova, I., and Pineau, Y. (2016). Occurrence of the Dayside Three-Peak Density Structure in the F2 and the Topside Ionosphere. J. Geophys. Res. 121 (6936), 6936–6949. doi:10.1002/2016ja022641

CrossRef Full Text | Google Scholar

Dmitriev, A. (2018). Spatial Characteristics of Recurrent Ionospheric Storms at Low Latitudes during Solar Minimum. J. Atmos. Solar-Terrestrial Phys. 179, 553–561. doi:10.1016/j.jastp.2018.09.013

CrossRef Full Text | Google Scholar

Hernández-Pajares, M., Roma-Dollase, D., Krankowski, A., García-Rigo, A., and Orús-Pérez, R. (2017). Methodology and Consistency of Slant and Vertical Assessments for Ionospheric Electron Content Models. J. Geod 91, 1405–1414. doi:10.1007/s00190-017-1032-z

CrossRef Full Text | Google Scholar

Maruayama, N., Sun, Y.-Y., Richards, P. G., Middlecoff, J., Fang, T.-W., Fuller-Rowell, T. J., et al. (2016). A New Source of the Midlatitude Ionospheric Peak Density Structure Revealed by a New Ionosphere-Plasmasphere Model. Geophys. Res. Lett. 43 (2429), 2429–2435. doi:10.1002/2015GL067312

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-Learn: Machine Learning in Python. J. Machine Learn. Res. 12 (85), 2825–2830. Available at: https://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html.

Google Scholar

Roma-Dollase, D., Hernández-Pajares, M., Krankowski, A., Kotulak, K., Ghoddousi-Fard, R., Yuan, Y., et al. (2018). Consistency of Seven Different GNSS Global Ionospheric Mapping Techniques during One Solar Cycle. J. Geod 92, 691–706. doi:10.1007/s00190-017-1088-9

CrossRef Full Text | Google Scholar

Schunk, R. W., and Nagy, A. (2009). Ionospheres: Physics, Plasma Physics, and Chemistry. Cambridge: Cambridge University Press.

Google Scholar

Verkhoglyadova, O., Maus, N., and Meng, X. (2021). Classification of High Density Regions in Global Ionospheric Maps with Neural Networks. Earth Space Sci. 8, e2021EA001639. doi:10.1029/2021ea001639

CrossRef Full Text | Google Scholar