Parameterizing the AGN Radius–Luminosity Relation from the Eigenvector 1 Viewpoint

The study of the broad-line region (BLR) using reverberation mapping has allowed us to establish an empirical relation between the size of this line-emitting region and the continuum luminosity that drives the line emission (i.e., the R_Hβ − L₅₁₀₀ relation). To realize its full potential, the intrinsic scatter in the R_Hβ − L₅₁₀₀ relation needs to be understood better. The mass accretion rate (or equivalently the Eddington ratio) plays a key role in addressing this problem. On the other hand, the Eigenvector 1 schema has helped to reveal an almost clear connection between the Eddington ratio and the strength of the optical Fe II emission that originates from the BLR. This article aims to reveal the connection between theoretical entities, such as the ionization parameter (U) and cloud mean density (n_H) of the BLR, with physical observables obtained directly from the spectra, such as optical Fe II strength (R_FeII) that has shown immense potential to trace the accretion rate. We utilize the photoionization code CLOUDY and perform a suite of models to reveal the physical conditions in the low-ionization, dust-free, line-emitting BLR. The key here is the focus on the recovery of the equivalent widths (EWs) for the two low-ionization emission lines—Hβ and the optical Fe II—in addition to the ratio of their EWs, i.e., R_FeII. We compare the spectral energy distributions, I Zw 1 and NGC 5548, of prototypical Population A and Population B sources, respectively, in this study. The results from the photoionization modeling are then combined with the existing reverberation-mapped sources with observed R_FeII estimates taken from the literature, thus allowing us to assess our analytical formulation to tie together the aforementioned quantities. The recovery of the correct physical conditions in the BLR then suggests that—the BLR “sees” only a very small fraction (∼1–10%) of the original ionizing continuum.

1 Introduction

The study of the broad-line regions in active galaxies has a long and inspiring history. The first signs of the detection of such emitting regions were noticed by Seyfert (1943) using a sample of nearby, low-luminosity active galaxies, which became popular as Seyfert galaxies. Then came the seminal work by Schmidt (1963) in which he discovered quasars to be of extragalactic origin. He studied the optical spectrum of a bright radio Galaxy–3C 273 and noted that the source had a redshift, z ∼ 0.158, using the strong, broad Balmer lines that were found to be shifted redward to the reference lab-frame spectrum. Another, equally important discovery was the discovery of the variation in the intensities of these emission lines over some time, especially in the timescales of weeks to months. This implied very small emitting regions, of the order of a few 10³ Schwarzschild radii (Greenstein and Schmidt, 1964). This emitting region is now well known as the broad-line region (BLR). This crucial discovery opened up a new subfield in the form of reverberation mapping and led to the estimation of the black hole masses of over hundreds of low-to high-luminosity Seyferts and quasars (Blandford and McKee, 1982; Peterson, 1988, 1993; Peterson et al., 2004) supplemented by single-/multi-epoch spectroscopy (Kaspi et al., 2000; Bentz et al., 2013; Du et al., 2014). As we can already notice, the location of the BLR (R_BLR) is closely related to the continuum properties, one that is linked to the underlying accretion disk. The primary observable quantity among these properties is the luminosity of the source which was realized already in Kaspi et al. (2005) and references. Later studies (e.g., Bentz et al., 2013) improved on the Hβ-based R_Hβ − L₅₁₀₀ by the inclusion of more sources and removing the contribution of the host Galaxy from the total luminosity. There has been a significant increase in the monitoring of archival sources and inclusion of newer ones which has begun to show a significant scatter from the empirical R_Hβ − L₅₁₀₀ relation (Grier et al., 2017; Panda et al., 2019b; Du and Wang, 2019; Martínez-Aldama et al., 2019). This scatter informs us that there is a subset of sources that are observed at relatively high luminosities (log L₅₁₀₀ ≳ 43.0, in erg s⁻¹) for which the reverberation mapping yields shorter time-lags, thus shorter R_BLR than expected from the empirically derived estimates. Studies have pointed out the link to the accretion rate that could factor into explaining this scatter and provided corrections to the empirical relation in terms of observables that trace the accretion rate, for e.g., strength of the optical Fe II emission (Du and Wang, 2019).

The spectral diversity of Type-1 AGNs was brought together under a single framework by the study of Boroson and Green (1992). The work of Boroson and Green (1992) is fundamental for two reasons: (A) it provided one of the first templates for fitting the Fe II pseudo-continuum¹ extracted from the spectrum of a prototypical narrow line Seyfert type-1 (NLS1) source, I Zw 1 and (B) for introducing the main sequence of quasars to unify the diverse group of AGNs. They were among the first to use dimensionality reduction on observed properties of quasars to obtain this main sequence, specifically the Eigenvector 1 which eventually led to the connection between the FWHM of the broad Hβ and the strength of the Fe II blend between 4,434–4,684 Å (i.e., the ratio of the EW(Fe II) to the EW(Hβ_broad), or more commonly known as R_FeII). This is now the well-established “quasar main sequence” in the optical plane (see, for e.g., the right panel in Figure 1) which is found to be primarily driven by the Eddington ratio among other physical properties² (Sulentic et al., 2000; Shen and Ho, 2014; Marziani et al., 2018; Panda et al., 2018, 2019a,c).

FIGURE 1

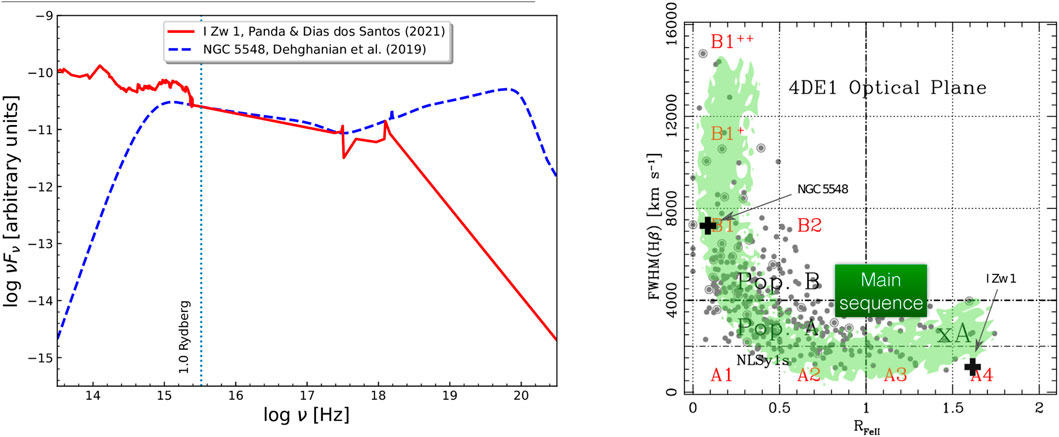
FIGURE 1. (Left) Comparison of the spectral energy distributions (SEDs) for I Zw 1 (in red) and NGC 5548 (in dashed blue). The I Zw 1 SED is taken from Panda and Dias dos Santos (2021), and for NGC 5548 we use the Dehghanian et al. (2019) version of the Mehdipour et al. (2015) SED. The SEDs are normalized at 1 Rydberg (right) optical plane of the quasar main sequence (or 4DE1). Abridged version of Marziani et al. (2018). The locations of I Zw 1 (Marziani et al., 2021, submitted) and NGC 5548 Du and Wang (2019) are marked with plus symbols.

In addition to these developments, a classification based on the narrowness or broadness of the Hβ emission line profile in an AGN spectrum was introduced, i.e., Population A and Population B. Population A sources can be understood as the class that includes local NLS1s as well as more massive high accretors which are mostly classified as radio-quiet (e.g., Marziani and Sulentic, 2014) and that have FWHM(Hβ) ≲ 4,000 km s⁻¹. Previous studies have found that the Population A sources have typical Lorentzian-like Hβ profile shape (Sulentic et al., 2002; Zamfir et al., 2010) in contrast to Population B sources, whereas the latter are shown to have broader Hβ (≳ 4,000 km s⁻¹), are predominantly “jetted” sources (Padovani et al., 2017), and have been shown to have Hβ profiles that are a better fit with Gaussian (for sources with still higher FWHMs, we observe disk-like double Gaussian profiles in Balmer lines). The cutoff in the FWHM of Hβ at 4,000 km s⁻¹ was suggested by Sulentic et al. (2000), Marziani et al. (2018) who found that AGN properties appear to change more significantly at this broader line-width cutoff. Later studies revealed that the two populations rather form a smooth link and are related (Fraix-Burnet et al., 2017; Berton et al., 2020). The shape of the emission line profiles and continuum strength and shape is directly connected to the central engine, especially to the black hole mass and the accretion rate in addition to the black hole spin and the angle at which the central engine is viewed by a distant observer (Czerny et al., 2017; Marziani et al., 2018; Panda et al., 2018, 2019c; Panda, 2021a).

Another important factor in the context of line formation in the BLR is the ionizing continuum that is incident on the BLR and as a result produces those emission lines that we see in an AGN spectrum. The study of the spectral energy distribution (SED) is a key element in understanding how the BLR responds to the continuum, and especially through the study of the emission lines, as a whole, be able to answer how much of this incoming radiation is intercepted by the BLR and how much of this intercepted radiation leads to the line-formation and emission (Korista and Goad, 2004; Czerny and Hryniewicz, 2011; Czerny, 2019; Marziani et al., 2019). The characterization of the ionizing SED, the part of it that comes from regions closer than the BLR, is important for our study of the emission lines, especially that carry photon energy at or above 1 Rydberg. This threshold marks the minimum energy required to ionize neutral hydrogen. From the photoionization point of view, this fraction of the broad-band SED is closely related to the number of ionizing photons that eventually lead to the line production. Wandel et al. (1999); Negrete et al. (2014); Martínez-Aldama et al. (2015) have used this method to estimate the photoionization radius of the line-emitting region of the BLR.

Negrete et al. (2014); Martínez-Aldama et al. (2015) have used line diagnostic ratios in the UV to infer the densities and ionization parameters, especially for the high-ionization line-emitting regions in the BLR³, but we lack such direct diagnostics for the density and ionization parameters in the optical regime. The optical part of the AGN spectrum contains emission lines, for e.g., Hβ and Fe II, that belong to the class of the low-ionization lines, i.e., with ionization potential (IP$<$20 eV, Collin-Souffrin et al., 1988; Marziani et al., 2019) that is theorized to be produced at scales that are larger than the regions that emit the high-ionization lines, for e.g., C ivλ1549 or He iiλ1640 (Joly, 1987; Martínez-Aldama et al., 2015; Marinello et al., 2016). In Panda (2021b) (see also Panda and Dias dos Santos 2021), we outlined a method to account for the line EWs of Hβ and optical Fe II in addition to their ratio (i.e., R_FeII). This allows us to evaluate the appropriate physical conditions, primarily in terms of density, ionization parameter, and metal content. This method also brings into agreement the radius estimated using the photoionization method to that of the reverberation mapping for sources that are accreting at or below the Eddington limit, such that they agree with the empirical R_Hβ − L₅₁₀₀ relation. In this article, we reiterate on the formalism but incorporate the standard R_Hβ − L₅₁₀₀ (Bentz et al., 2013) as well as the R_FeII-dependent R_Hβ − L₅₁₀₀ relation (Du and Wang, 2019) to study the effect of the accretion rate-dependent R_FeII on our existing inferences. We test our model by incorporating the spectral properties of a prototypical Population A source–I Zw 1 and a prototypical Population B source–NGC 5548 and assess how much fraction of the ionizing continuum actually leads to the low-ionization line formation and emission in the dust-free BLR. The location of the two sources on the main sequence diagram is shown in the right panel of Figure 1.

The article is organized as follows: We describe the analytical prescription in Section 2 to combine the information from the R_Hβ − L₅₁₀₀ relations into the photoionization theory accounting for different bolometric corrections. We outline our photoionization modeling setup in Section 3. We analyze the results obtained from our analyses highlighting the strengths and weaknesses of our current model in Section 4 and discuss open issues in the context of our work in Section 5. We summarize our findings from this study in Section 6. Throughout this work, we assume a standard cosmological model with Ω_Λ = 0.7, Ω_m = 0.3, and H₀ = 70 km s⁻¹ Mpc⁻¹.

2 Analytical Description

In order to realize the parameter space for the BLR and to link the physical quantities (U, n_H) and the observables—the AGN continuum luminosity at 5100 Å (L₅₁₀₀ = 5100 Å*L₅₁₀₀, where L₅₁₀₀ is directly estimated from the observed spectrum) and later also with the strength of the optical Fe II emission (i.e., R_FeII)—we present the analytical relationships as described in the following sub-sections. We separately show the relations based on (A) the R_Hβ − L₅₁₀₀ relation used and (B) the format of the bolometric correction used to scale the L₅₁₀₀ to the bolometric luminosity (L_bol). We use two instances of the R_Hβ − L₅₁₀₀ relation—1) the classical Bentz et al. (2013) R_Hβ − L₅₁₀₀ relation in which the separation between the continuum source and the onset of the BLR (R_BLR) is dependent only on the continuum luminosity of the source; and 2) a new R_Hβ − L₅₁₀₀ relation that incorporates the dependence of R_FeII in addition to L₅₁₀₀ on R_BLR (Du and Wang, 2019).

In order to scale L₅₁₀₀ to obtain the corresponding bolometric luminosity (L_bol), we incorporate two formats of the bolometric correction (hereafter k_bol) factor—1) a fixed value derived from the mean SED from Richards et al. (2006) and 2) a variable factor that is dependent on the luminosity of the source (Netzer, 2019). The value for the Richards et al. (2006) k_bol = 9.26⁴ has been used widely in statistical studies for large quasar catalogs (Shen et al., 2011; Rakshit et al., 2020). Here, k_bol scales with the monochromatic luminosity (L₅₁₀₀) to give a rough estimation of L_bol = k_bol ⋅L₅₁₀₀. Usually, k_bol is taken as a constant for a monochromatic luminosity; however, results such as the well-known nonlinear relationship between the UV and X-ray luminosities (Lusso and Risaliti, 2016 and references therein) indicate that k_bol should be a function of luminosity (Marconi et al., 2004; Krawczyk et al., 2013). Along the same line, Netzer (2019) proposed new bolometric correction factors as a function of the luminosity assuming an optically thick and geometrically thin accretion disk, over a large range of black hole mass (10⁷–10¹⁰ M_⊙), Eddington ratios (0.007–0.5), spin (−1 to 0.998), and a fixed disk inclination angle of 56°. For the optical range (at 5100 Å), the bolometric correction factor is given by:

$k_{\mathrm{b}\mathrm{o}\mathrm{l}}=40{\left(\frac{L_{\mathrm{o}\mathrm{p}\mathrm{t}}}{10^{42}}\right)}^{-0.2},(1)$

which is taken from Table 1 in Netzer 2019. Here, L_opt = L₅₁₀₀. The wide option of parameters considered for the model process provides a better approximation corroborating previous results (Nemmen and Brotherton, 2010; Runnoe et al., 2012a,b). In addition, it provides a better accuracy than the fixed bolometric factor correction which led to errors as large as 50% for individual measurements. Therefore, we also explore the use of the two different k_bol—fixed and the luminosity-dependent versions, in our analyses.

TABLE 1

TABLE 1. Estimates for log(Un_H) for the various relations considered in this article.

We start with the conventional description of the ionization parameter,

$U=\frac{\mathrm{\Phi }\left(H\right)}{n_{H}c}=\frac{Q\left(H\right)}{4\pi R_{BLR}^2{n}_{H}c},(2)$

where Φ(H) is the surface flux of ionizing photons (in cm⁻² s⁻¹), and n_H is the total hydrogen density (in cm⁻³). Q(H) is the number of hydrogen-ionizing photons emitted by the central object (in s⁻¹), and R_BLR is the separation between the central source of ionizing radiation and the inner face of the cloud (in cm).

The Q(H) term in the aforementioned equation can then be replaced with the equivalent instantaneous bolometric luminosity (L_bol),

$Q\left(H\right)=\chi \frac{L_{bol}}{h\nu }.(3)$

Here, we consider the average photon energy, hν = 1 Rydberg⁵ (Wandel et al., 1999; Marziani et al., 2015). Not all of the bolometric luminosity is used to ionize the BLR. Based on the average photon energy, we consider a fraction of the total luminosity, i.e., the ionizing luminosity (L_ion). The coefficient χ accounts for this fraction. The exact value of this coefficient is dependent on the shape of the input SED. In this work, we assume χ = 0.5, which is estimated for the default AGN SED in CLOUDY (Mathews and Ferland, 1987; Ferland et al., 2017).

Combining Eqs 2, 3, we have

$\log \left(U{n}_H\right)=\log \left(L_{bol}\right)-\log \left(\mathbf{2}h\nu 4\pi c\right)-2\log \left(R_{BLR}\right).(4)$

Next, we look into the classical R_Hβ − L₅₁₀₀, i.e., from the Clean sample of Bentz et al. (2013), we have,

$\log \left(\frac{R_{BLR}}{1light-day}\right)=\kappa +\alpha \log \left(\frac{{\mathrm{L}}_{5100}}{10^{44}}\right),(5)$

where L₅₁₀₀ is the monochromatic luminosity at 5,100 Å (in units of 10⁴⁴ erg s⁻¹). κ and α take the values 1.555 ± 0.024 and ${0.542}_{-0.026}^{+0.027}$, respectively, for the Clean sample (see Table 14 in Bentz et al., 2013). Here, R_BLR is normalized to 1 light day⁶.

Substituting the Richards et al. (2006) value for the k_bol (=9.26) and the form of R_BLR (from Eq. 5) in Eq. 4, we have for the fixed k_bol case:

$\log \left(U{n}_H\right)=9.815-0.084\log \left(\frac{{\mathrm{L}}_{5100}}{10^{44}}\right).(6)$

Substituting the Netzer (2019) relation (Eq. 1) for the k_bol and the form of R_BLR (from Eq. 5) in Eq. 4, we have for the luminosity-dependent k_bol case:

$\log \left(U{n}_H\right)=10.050-0.284\log \left(\frac{{\mathrm{L}}_{5100}}{10^{44}}\right).(7)$

Now, alternatively, a new R_Hβ − L₅₁₀₀ relation has been proposed by Du and Wang (2019) in which the authors have incorporated the dispersion noticed in the classical R_Hβ − L₅₁₀₀, especially due to some sources that deviated from the standard relation because shorter time-lags from reverberation mapping were obtained for them (Figure 1 in Panda et al., 2020b, for a recent compilation of reverberation-mapped sources). This aspect has been studied for quite some time, and certain correction factors were suggested to alleviate the dispersion in order to keep the classical R_Hβ − L₅₁₀₀ relation intact., for e.g., in Martínez-Aldama et al. (2019), we found that this dispersion can be accounted for the standard R_Hβ − L₅₁₀₀ with an added dependence on the Eddington ratio (L_bol/L_Edd) or the dimensionless accretion rate parameter ($\dot{\mathcal{M}}$). In their article, Du and Wang (2019) propose a dependence on the R_FeII parameter which can be viewed as a proxy of the accretion rate effect. Inclusion of the R_FeII parameter in the R_Hβ − L₅₁₀₀ relation has substantially reduced the scatter in the existing relation, from 0.299 dex (see Martínez-Aldama et al., 2021a) to ∼ 0.19 dex. We refer the readers to Figures 5, 6 in their article (Du and Wang, 2019) for a comparison between the classical R_Hβ − L₅₁₀₀ relation and the new R_FeII-dependent R_Hβ − L₅₁₀₀ relation. The formalism of Du and Wang (2019) has the following form,

$\log \left(\frac{R_{BLR}}{1light-day}\right)={\kappa }^{\prime }+{\alpha }^{″}\log \left(\frac{{\mathrm{L}}_{5100}}{10^{44}}\right)+{\gamma }^{\prime }{R}_{\mathsf{\text{FeII}}}.(8)$

Here, κ′ = 1.65 ± 0.06, α^″ = 0.45 ± 0.03, and γ′ = −0.35 ± 0.08. Substituting the Richards et al. (2006) value for the k_bol (=9.26) and the form of R_BLR (from Eq. 8) in Eq. 4, we have for the fixed k_bol case:

$\log \left(U{n}_H\right)=9.625+0.1\log \left(\frac{{\mathrm{L}}_{5100}}{10^{44}}\right)+0.7R_{\mathrm{F}\mathrm{e}\mathrm{I}\mathrm{I}}.(9)$

In the same manner as before, substituting the Netzer (2019) relation (Eq. 1) for k_bol and the form of R_BLR (from Eq. 8) in Eq. 4, we have for the luminosity-dependent k_bol case:

$\log \left(U{n}_H\right)=9.860-0.1\log \left(\frac{{\mathrm{L}}_{5100}}{10^{44}}\right)+0.7R_{\mathrm{F}\mathrm{e}\mathrm{I}\mathrm{I}}.(10)$

These aforementioned analytical forms (Eqs 6, 7, 9, 10) are tabulated in Table 1. We highlight the resulting values for the product of ionization parameter (U) and local BLR density (n_H) for the two sources considered in this work, i.e., NGC 5548 and I Zw 1. Since, we later used the SEDs for these two sources, we have the exact value for χ reported by CLOUDY for them: 0.82 (NGC 5548) and 0.12 (I Zw 1). We report the estimates for all the cases accounting for these appropriate χ values for the two sources in the last two columns in Table 1. We will come back to these estimates in Section 4.3.

3 Photoionization Computations With CLOUDY

We apply the photoionization setup prescription similar to that was demonstrated in Panda (2021b). We describe briefly the setup here—we perform a suite of CLOUDY (version 17.02, Ferland et al., 2017) models⁷ by varying the mean cloud density over a broad range, 10⁵ ≤ n_H ≤ 10¹³ (in cm⁻³), as well as the ionization parameter, − 7 ≤ log  U ≤ 0. We consider the gas cloud at a cloud column density, N_H = 10²⁴ cm⁻². We consider two spectral energy distributions (SEDs—one for NGC 5548 and the other for I Zw 1. We show the SEDs covering the optical-to-X-ray energy range in Figure 1. For NGC 5548, we incorporate the SED from Dehghanian et al. (2019) that is an extension of the SED shown in Mehdipour et al. (2015). The SED was prepared using quasi-simultaneous observations taken in 2013–2014 with XMM-Newton, Swift, NuSTAR, INTEGRAL, Chandra, HST, and two ground-based observatories—Wise Observatory and Observatorio Cerro Armazones. We refer the readers to Mehdipour et al. (2015) for more details on the spectral modeling and continuum extraction over the broad-band energies. On the other hand, the SED for I Zw 1 is directly derived from the continuum extraction over the near-infrared to ultraviolet range (between $\sim 1000\mathring{\mathrm{A}}$-1 μm) supplemented with the photometric data points in the X-ray region and wavelengths above 2.5 μm from the previously used SED (Panda et al., 2020a; Panda, 2021b). We combine almost all concomitant spectra for this source observed with the HST-Faint Object Spectrograph (FOS, Bechtold et al., 2002) in the UV that is complemented with data in the optical (obtained using the 2.15-m Complejo Astronomico El Leoncito–CASLEO, Rodríguez-Ardila et al., 2002) and in the NIR (obtained using the 3.2-m NASA Infrared Telescope Facility–IRTF, Riffel et al., 2006). For the continuum point extraction, we automatically identify the emission lines and select regions in the spectrum free of them to extract these points. A full description of the procedure can be found in an upcoming work (Dias dos Santos et al. in prep.). We consider three cases for the metallicity—at solar composition (Z_⊙), at 3 times solar (3Z_⊙), and at 10 times solar (10Z_⊙) values to model the emission from the low-ionization line-emitting region for I Zw 1, while we limit ourselves to only solar metallicity case for modeling NGC 5548. This assumption for the metal content for the case of NGC 5548 is made on the basis of our prior results in modeling this source (Panda et al., 2021) in which Hβ and optical Fe II emission were successfully modeled using CLOUDY.

3.1 Dust Sublimation Radius Prescription

Similar to Panda (2021b), we incorporate the prescription from Nenkova et al. (2008) to separate the dusty and non-dusty regime in the BLR, which has a form:

${\mathrm{R}}_{\mathrm{s}\mathrm{u}\mathrm{b}}=0.4{\left(\frac{{\mathrm{L}}_{\mathrm{U}\mathrm{V}}}{10^{45}}\right)}^{0.5},(11)$

where R_sub is the sublimation radius (in parsecs) computed from the source luminosity (L_UV) that is consistent for a characteristic dust temperature.

This is a simplified version of the actual relation which, in addition to the source luminosity term, contains the dependence on the dust sublimation temperature and the dust grain size. We assume a dust temperature T_sub = 1500 K, which has been found consistent with the adopted mixture of the silicate and graphite dust grains, and a typical dust grain size, a = 0.05 microns. The dependence of R_sub on the temperature is quite small—the exponent on the temperature term is −2.8. On the other hand, the dust grain size is a more complex problem, yet the value adopted is fair in reproducing the characteristic dust sublimation radius in our case (see Nenkova et al., 2008; Hönig, 2019, for more details). The sublimation radius, hence, is estimated using only the integrated optical–UV luminosity for the two representative sources—NGC 5548 and I Zw 1. This optical–UV luminosity is the manifestation for an accretion disk emission and can be used as an approximate for the source’s bolometric luminosity. We note that in this case, the ionizing luminosity that leads to the sublimation is almost close to the bolometric luminosity for both the sources considered in this work. The assumed sublimation temperature, 1500 K, corresponds to an average photon energy of 0.0095 Rydberg, or a frequency ∼ 14 (in log-scale). This is the lower limit of the SEDs shown in Figure 1 and used in our computations. Hence, the value for χ (ratio of the L_ion to the L_bol) is set to unity to retrieve the corresponding pairs of the ionization parameter (U) and local density (n_H). Table 2 provides the estimates for R_sub considering the fixed and variable k_bol factors. Using these estimates for L_bol and the sublimation radius (R_sub) and substituting in Eq. 2, we get the values for the product of U and n_H. This is not to be confused with the BLR density as this product (Un_H) relates to the dust sublimation radius and not the BLR photoionization radius, i.e., R_BLR. For the four pairs of (L_bol, R_sub) tabulated in Table 2, we get values for Un_H: 1) for NGC 5548, 7.9016 (for the fixed k_bol) and 7.9030 (for the luminosity-dependent k_bol); 2) for I Zw 1, 7.9027 (for the fixed k_bol) and 7.9040 (for the luminosity-dependent k_bol).

TABLE 2

TABLE 2. Estimates for dust sublimation radius for NGC 5548 and I Zw 1.

3.2 Estimating the EWs for the Low-Ionization Emission Lines in the BLR

To estimate the EWs for Hβ and optical Fe II, we use the continuum luminosity given by CLOUDY for each model as a reference. By default, the EWs extracted with this approach assume the 100% covering factor. We then rescale this value to 20% of its original value. The assumption of 20% has been shown to be a reliable ad hoc estimate for the covering factor (Korista and Goad, 2000; Baldwin et al., 2004; Panda, 2021b; Sarkar et al., 2021). In Figure 2, we illustrate the result for the two cases of SEDs (I Zw 1 and NGC 5548) with the base setup, i.e., at solar metallicity (Z_⊙) and cloud column density, N_H = 10²⁴ cm⁻². The upper and lower panels show the   log  U − log  n_H parameter space with the auxiliary axis (colormap) depicting the EW(Fe II) and the corresponding EW(Hβ), respectively. The threshold for the dusty (shaded in orange) and dustless (in blue) line-emitting region is set using the prescription described in the previous section (Section 3.1). We use the luminosity-dependent k_bol versions of the Un_H (in log-scale), i.e., 7.9040 for the I Zw 1 and 7.9030 for the NGC 5548. Henceforth, we will only discuss the results in the context of emission from the dustless BLR.

FIGURE 2

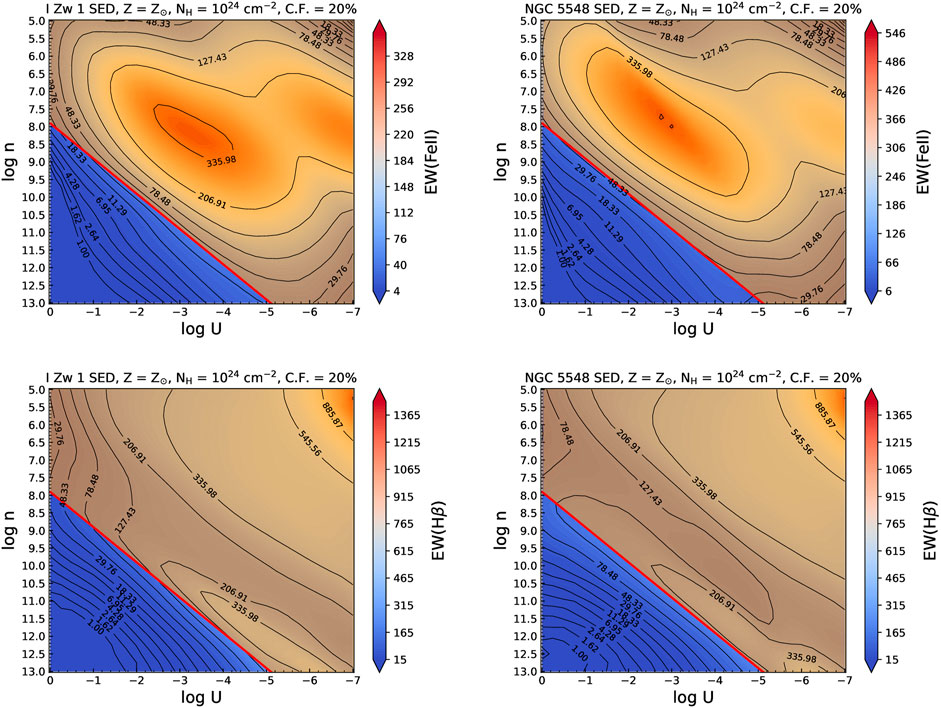
FIGURE 2.  log  U −  log  n_H 2D histograms color-weighted by (top panels) equivalent widths (EWs) Fe II and (bottom panels) EW(Hβ). The EWs are computed assuming the continuum luminosity at 5,100 Å and at 20% covering fraction. Two different spectral energy distributions (SEDs), as previously shown in Figure 1, are used representing (left panels) I Zw 1—a prototypical Population A object with high R_FeII and (right panels) NGC 5548—a prototypical Population B object with relatively low R_FeII. Models are shown for a characteristic BLR cloud with solar composition (Z = Z_⊙) and column density, N_H = 10²⁴ cm⁻². The solid red lines in each panel mark the boundary between the non-dusty (in blue) and the dusty (in orange). This is set uniquely for each case of SED using the luminosity-dependent k_bol (Netzer, 2019) values for L_bol and R_sub as shown in Table 2.

In Figure 3, we show the   log  U − log  n_H parameter space with the auxiliary axis depicting the ratio R_FeII, i.e., the EW(Fe II) to the EW(Hβ) for the two SEDs. We have assumed that the two emission lines are produced from a similar region in the BLR (Barth et al., 2013; Hu et al., 2015; Panda et al., 2018; Gaskell et al., 2021b) and hence the covering factor is set to be equal for both the emission lines.

FIGURE 3

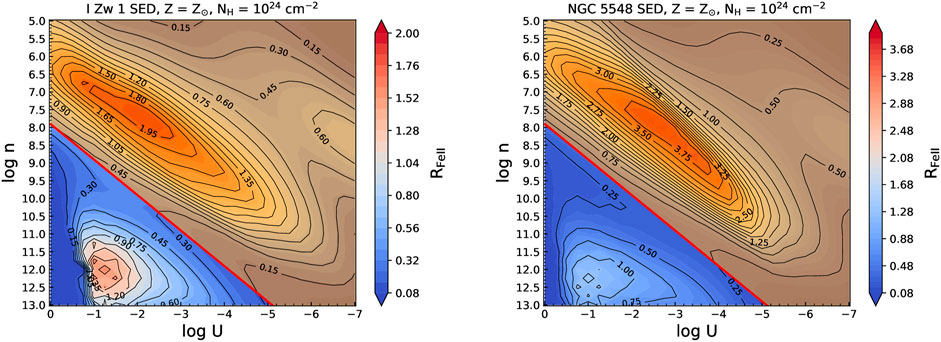
FIGURE 3.  log  U − log  n_H 2D histograms color-weighted by R_FeII. Remaining labels and parameters shown here are identical to Figure 2.

We also consider a case with a higher covering factor (i.e., 60%) to highlight the effect due to non-radial motions (Kollatschny and Zetzl, 2013) or changes in the accretion disk structure (Abramowicz et al., 1988; Wang et al., 2014). This higher value for the covering factor is an upper threshold as modeled in the locally optimized cloud models by Korista and Goad (2000) for NGC 5548. This is shown in Supplementary Figure S12 under the same conditions as for the case with the 20% covering factor.

3.3 Comparison With Reverberation-Mapped Estimates

To make a quantitative comparison with the results from the CLOUDY simulations, we utilize the sample of reverberation-mapped AGNs from Du and Wang (2019). The sample consists of 75 AGNs for which an independent and homogenous spectral fitting in the optical region (including the 4430–5550 Å window in the rest frame) was performed in their article. The spectral window includes the Hβ and optical Fe II emission blend (between 4,434–4,684 Å) that is necessary to estimate the ratio, R_FeII, the bolometric luminosity using the AGN luminosity at 5100 Å, and the black hole mass using the FWHM(Hβ) in association with the distance of the BLR from the central continuum source which is obtained from various reverberation-mapping campaigns (see Section 2.1 in Du and Wang, 2019, where they list the various campaigns), and thus the Eddington ratio or its equivalent—the dimensionless accretion rate $(\dot{\mathcal{M}})$. We present the spectral and derived properties of this sample in Supplementary Table S4 that includes the AGN luminosity at 5100 Å (L₅₁₀₀), the black hole mass (M_BH), the $\dot{\mathcal{M}}$, R_FeII, and the ${\mathcal{D}}_{\mathrm{H}\beta }$, where the latter is the ratio of FWHM(Hβ) to the dispersion of Hβ. To estimate the $\dot{\mathcal{M}}$, the authors (Wang et al., 2013; Du et al., 2015, 2016; Du and Wang, 2019) use the following form:

$\dot{\mathcal{M}}=20.1{\left(\frac{l_{44}}{\cos \mathrm{i}}\right)}^{\frac{3}{2}}{m}_7^{-2},(12)$

where l₄₄ is the AGN luminosity at 5100 Å in the units of 10⁴⁴ erg s⁻¹, m₇ is the black hole mass in the units of 10⁷ M_⊙, and i is the inclination angle of the accretion disk. The estimates for the $\dot{\mathcal{M}}$ tabulated in their article (Du and Wang, 2019) and in Supplementary Table S4 assume an average value of cos i = 0.75. Since the $\dot{\mathcal{M}}$ and Eddington ratio are equivalent, we can express the Eddington ratio (L_bol/L_Edd) as follows:

$\frac{L_{\mathrm{b}\mathrm{o}\mathrm{l}}}{L_{\mathrm{E}\mathrm{d}\mathrm{d}}}=7.455\times 10^{-18}\left(k_{\mathrm{b}\mathrm{o}\mathrm{l}}{M}_{\mathrm{B}\mathrm{H}}^{\frac{1}{3}}{\dot{\mathcal{M}}}^{\frac{2}{3}}\right).(13)$

Thus, any inferences that will be drawn based on $\dot{\mathcal{M}}$ can be extended directly to the corresponding estimates of the Eddington ratios. We decided to use this particular sample to ensure that the sources are treated in the same manner. This removes the bias from fitting techniques employed by different groups. An independent spectral fitting incorporating newer measurements and newer sources is needed which is outside the scope of this article.

Next, we show the distribution of the estimates for R_FeII and for ${\mathcal{D}}_{\mathrm{H}\beta }$ for this sample in the left panel of Figure 4. The range of R_FeII values lies between [0.04, 2.17], while for ${\mathcal{D}}_{\mathrm{H}\beta }$ this range is between [0.89, 3.12]. Thus, according to the definition of the spectral subtypes in the optical plane of the main sequence (see Figure 1, also in Marziani et al., 2018; Panda et al., 2019c, 2020b), this sample is dominated by Population A sources (51/75) and covers the spectral types from A1–A4. Here, A1 is the more typical, low-R_FeII (≤0.5) AGNs, and the A4 is the more rare, strong-Fe II emitters (≥2.0). In addition, we have a considerable number of Population B sources in this sample (24/75) including NGC 5548. We refer the readers to Table 1 in Du and Wang (2019) for the estimates for the FWHMs for the sources in the sample. In the right panel of 4, we show the strong anticorrelation between R_FeII and ${\mathcal{D}}_{\mathrm{H}\beta }$ (see also Figure 2 in Du and Wang 2019). This figure reiterates an already known fact, i.e., the sources with high R_FeII (especially ≳ 1) also are found to have higher accretion rates, and this then affects the emission line profiles—making them more Lorentzian, as opposed to the generally well-fitted Gaussian profiles that is suited for the sources with low R_FeII estimates (e.g., typical Population B sources). This change in the line profiles affects directly the value of ${\mathcal{D}}_{\mathrm{H}\beta }$—for a pure Lorentzian, this value tends to zero, while for a single Gaussian this value is 2$\sqrt{2\ln (2)}$ = 2.35. For a rectangular function, ${\mathcal{D}}_{\mathrm{H}\beta }$ = 2$\sqrt{3}$ = 3.46 (Collin et al., 2006). We describe the analytical formulations including ${\mathcal{D}}_{\mathrm{H}\beta }$ in our prescription in Supplementary Appendix 1.

FIGURE 4

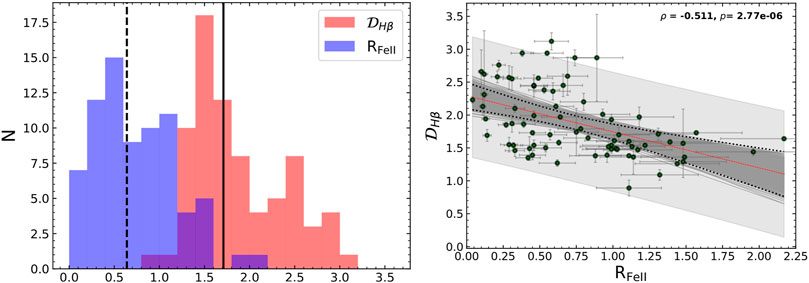
FIGURE 4. (Left) Distribution of ${\mathcal{D}}_{\mathrm{H}\beta }$ (in red) and R_FeII (in blue) for the sample from Du and Wang (2019) and as shown in Supplementary Table S4. The median values for the two parameters are shown using the vertical lines–solid $({\mathcal{D}}_{\mathrm{H}\beta })$ and dashed (R_FeII) (right) Correlation between ${\mathcal{D}}_{\mathrm{H}\beta }$ and R_FeII for this sample [see also Figure 2 in Du and Wang (2019)]. Spearman’s rank correlation coefficients (ρ) and the p − values are also reported. The ordinary least-square (OLS) fit for each panel is shown using red solid line. Black dotted lines mark the confidence intervals at 95% for the 1,000 realizations (dark gray lines) of the bootstrap analysis. The corresponding prediction intervals are shown in the background using light gray color.

4 Results

4.1 Understanding the   log  U − log  n_H Parameter Space for I Zw 1 and NGC 5548

In the following sections, we describe the results from the various CLOUDY photoionization models that were made to constrain the physical parameter space in terms of the   log  U − log  n_H diagrams. The key here is the focus on the recovery of the EWs for the two low ionization emission lines—Hβ and Fe II, in addition to the ratio of their EWs, i.e., R_FeII. In Figure 2, we depict the EW(Fe II) and the EW(Hβ) for the two sources (I Zw 1 and NGC 5548) under the assumption that the BLR in the two cases has solar composition and the covering factor is identical, i.e., 20%. Another important highlight is the separation of the dustless region from the region where dust can survive. Species such as Fe II get strongly depleted in the presence of dust and can be used as a tracer for the dust in the extended, intermediate-line regions that are located further away from the BLR (Adhikari et al., 2016). As described in Section 3.1, we have made a simple assumption on the location of the dust sublimation radius that is effectively dependent only on the AGN luminosity. This uniquely sets the dust sublimation radius for each source (see Table 2). In Figure 2 (and henceforth), we have used the dust sublimation radius case assuming the luminosity-dependent k_bol correction that gives a slightly larger value for this radius. In the figure, the radius (R) is shown using a red solid line which corresponds not to the R_BLR but to a radius that is much larger than R_BLR. The values for this larger R in terms of Un_H are very similar for the two sources as the differences in their luminosities and radial extensions almost balance out–1) for NGC 5548, 7.9030 (for the luminosity-dependent k_bol) and 2) for I Zw 1, 7.9040 (for the luminosity-dependent k_bol). The corresponding R_FeII estimates for the two cases (see Figure 3) also have similar demarcations.

4.2 Comparing the Reverberation-Mapped Sources With the CLOUDY Models

Another way of looking at this scenario is by comparing the product of U and n_H directly versus the R_FeII. This is already shown from the estimates tabulated in our Table 1 for the two sources. But, as there are various considerations for the k_bol and the R_Hβ − L₅₁₀₀ relations, the values obtained for the photoionization radius estimator, i.e., the product Un_H varies albeit slightly. In this section, we organize the  log  U − log  n_H parameter space from each model and compare the relevance of these results to the reverberation-mapped sources with spectral coverage that includes the R_FeII measurements. We intend to assess the changes in the SED of the two prototypical sources considered in the work to see if they account for the R_FeII estimates reported from spectral fitting. We highlight the salient differences between the two cases, and how our analytical prescriptions reported in Section 2 perform against the numerical estimates from CLOUDY.

In Figure 5, we show the grid from one of our CLOUDY simulations (I Zw 1 SED, N_H = 10²⁴ cm⁻², and at solar composition). The grid is composed of the family of distributions for Un_H (in log-scale) as a function of R_FeII. These are identical to what we show in the left panel of Figure 3 just represented differently. The shaded region in orange depicts the region within the dust, and the solid red line marks the location of the dust sublimation radius as per Table 2. The location of the dust sublimation radius is neatly poised at one of the minima for R_FeII.

FIGURE 5

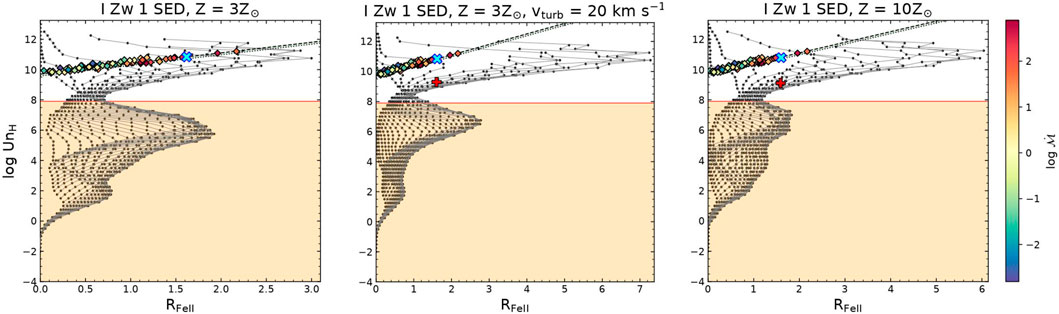
FIGURE 5. Grid composed of the family of distributions for Un_H (in log-scale) as a function of R_FeII (gray lines with black dots) from one of our CLOUDY simulations—I Zw 1 SED, N_H = 10²⁴ cm⁻² and at solar composition. The shaded region in orange depicts the region within the dust, and the solid red line marks the location of the dust sublimation radius as per Table 2. The sample of 75 reverberation-mapped sources (see Supplementary Table S4) is shown for the corresponding cases of Un_H as per the four analytical forms shown in Table 1. These sources are color-coded with their corresponding $\dot{\mathcal{M}}$ estimates. The location of the source I Zw 1 is shown using a blue cross for the lower panels in which there is an explicit dependence on the R_FeII.

Preparing broadband SEDs for the diverse population of AGNs is not easy, especially to get contemporaneous spectral or photometric data over a wide range of energies. Having SEDs that can be representative of the subpopulations, e.g., Population A and Population B, is quite useful. This was our intention from this work. To test the validity of our models on the observational estimates for sources with spectral coverage and reverberation mapping, we overlay the 75 sources from Supplementary Table S4 on these maps. These sources are color-coded as a function of the dimensionless accretion rate ($\dot{\mathcal{M}}$). For each of the four panels, we evaluate Un_H for each source using the four relations as shown in Table 1, i.e., accounting for 1) the standard R_Hβ − L₅₁₀₀ relation from Bentz et al. (2013) with fixed k_bol (Case 1) and with luminosity-dependent k_bol (Case 2); and 2) the R_FeII-dependent R_Hβ − L₅₁₀₀ relation from Du and Wang (2019) with fixed k_bol (Case 3) and with luminosity-dependent k_bol (Case 4). For the first two cases (upper panels), we show Un_H for I Zw 1 using L₅₁₀₀ as also reported in Table 1. These are shown using the two solid blue lines on the upper panels. As we can notice, the location of the sources on this plane is affected due to the change of k_bol—a larger scatter in ]Un_H is seen, especially for sources that have relatively low R_FeII and low to mid $\dot{\mathcal{M}}$. For the latter cases (lower panels), we show Un_H for I Zw 1 which is now dependent on L₅₁₀₀ and R_FeII, and hence, changes with the change in R_FeII. These are shown using the dashed (fixed k_bol case) and dotted (luminosity-dependent k_bol) black lines on the panels. The location of I Zw 1 is shown using the blue plus and a blue cross symbol in these two panels. The scatter in these panels is lower than that in Case 2 (upper right panel). The I Zw 1 SED under the solar composition can incorporate a large fraction of the sources in the sample, although as expected the observed R_FeII estimates for I Zw 1 and two other sources (SDSS J101000 and IRAS 04416 + 1,215) are higher than predicted from these base models.

For completeness, we also show a comparison between the two SED cases at solar composition with the observed sample side-by-side in Figure 6. The left panel is identical to Case 4 already shown in Figure 5. The right panel shows the case with the Un_H grid extracted from our CLOUDY simulations but for the NGC 5548 SED. Like in the bottom panels of Figure 5, we show Un_H from the analytical relations for the two panels dependent on L₅₁₀₀ and R_FeII (shown using the dashed (fixed k_bol case) and dotted (luminosity-dependent k_bol) black lines on the panels). We also locate the sources in the corresponding panels using a blue cross symbol. We can notice that the NGC 5548 sits among the lowest R_FeII sources. It agrees well in all of the four cases shown earlier in Figure 5 and hence is rather unaffected by the inclusion/exclusion of the fixed/variable k_bol or the change in the R_Hβ − L₅₁₀₀ relation used to infer Un_H. Right away, we notice that the NGC 5548 case predictions encompass a lower fraction of the sources than the I Zw 1 case, especially those with reportedly high R_FeII values. The strip showing Un_H from Case 3 and Case 4 is thicker in the NGC 5548 that is due to the effect of luminosity (see Table 1 with the R_Hβ − L₅₁₀₀ relation cases with R_FeII-dependence). The location of the observed sources is the same in these two panels, but the extent of the overall R_FeII predicted with the NGC 5548 case from the models is higher—the dominant peak is located well within the dusty region. Thus, the I Zw 1 case predicts higher R_FeII in the dustless region, as expected from the observed values. We also mark a red plus symbol on the right panel of this figure which marks the position of the value obtained for Un_H after careful filtering of the possible pairs of solutions by comparing the EWs of both Fe II and Hβ belonging to the non-dusty part of the BLR. We expand more on this issue in the next section (see Section 4.3). We also make a comparative analysis between the two cases including the ${\mathcal{D}}_{\mathrm{H}\beta }$ parameterization within our analytical formalism (see Supplementary Figure S11).

FIGURE 6

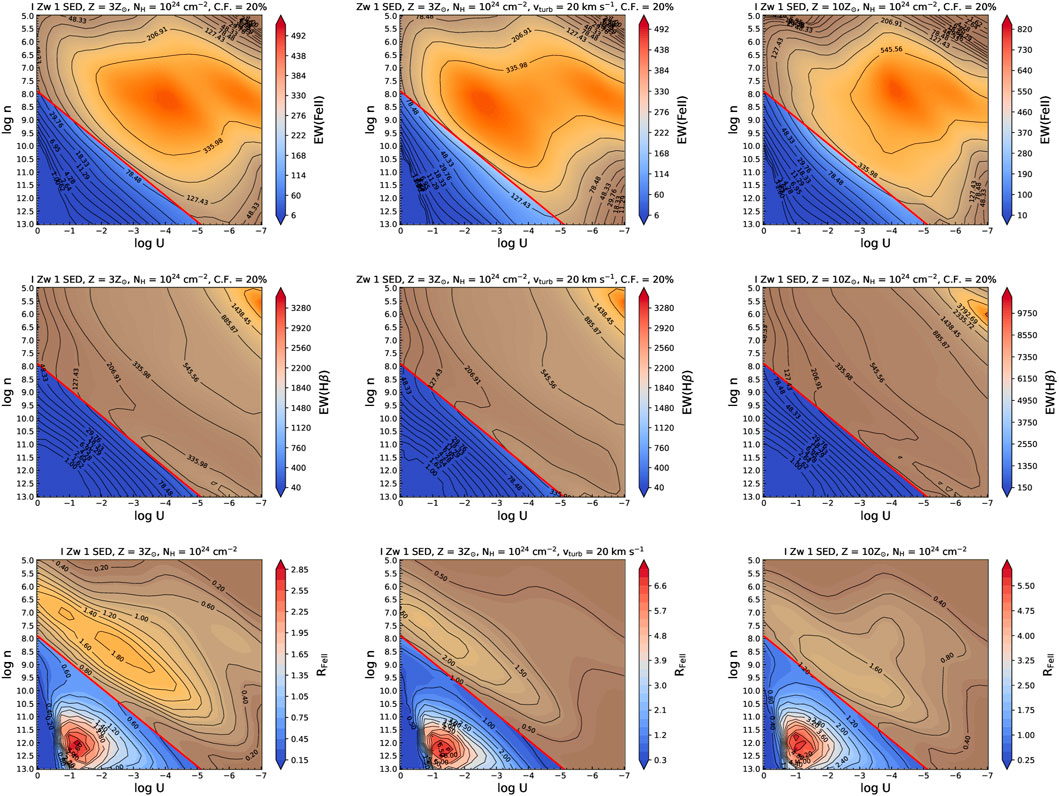
FIGURE 6. Similar to the last panel (Case 4) in Figure 6. Here, we compare the solar composition model for the two sources—I Zw 1 and NGC 5548. The location of the respective sources is marked using a blue cross in the corresponding panels. The red plus symbol on the right panel marks the position of the value obtained for Un_H using the filtering of EWs (see Section 4.3).

Subsequently, following the results that were obtained earlier with I Zw 1 necessitating an increased metal content (and turbulent motions) within the BLR (see Section 4.1), we show the grids of Un_H for each of the three cases—at 3Z_⊙, at 3Z_⊙ with 20 km s⁻¹ microturbulence, and finally, the case with the 10Z_⊙. Figure 7 shows these three cases. The dominant peak in these cases shifts to the region that corresponds to the dustless BLR (i.e., with Un_H ≳ 8.0). Already in just the 3Z_⊙ case (left panel in Figure 7), all the observed estimates are well within the grid lines extracted from the models. But, as we have emphasized before, this needs to be supplemented with the EWs recovered for the sources using the models. With these plots, we wanted to show that the effect of the SED with the added contribution of the metal content and microturbulence can significantly affect the recovery of R_FeII and that SEDs for prototypical sources (such as NGC 5548 and I Zw 1) can be used to infer properties of sources alike. Similar to the previous figure (the right panel with NGC 5548), we show the value obtained for Un_H after the EW filtering using a red plus symbol.

FIGURE 7

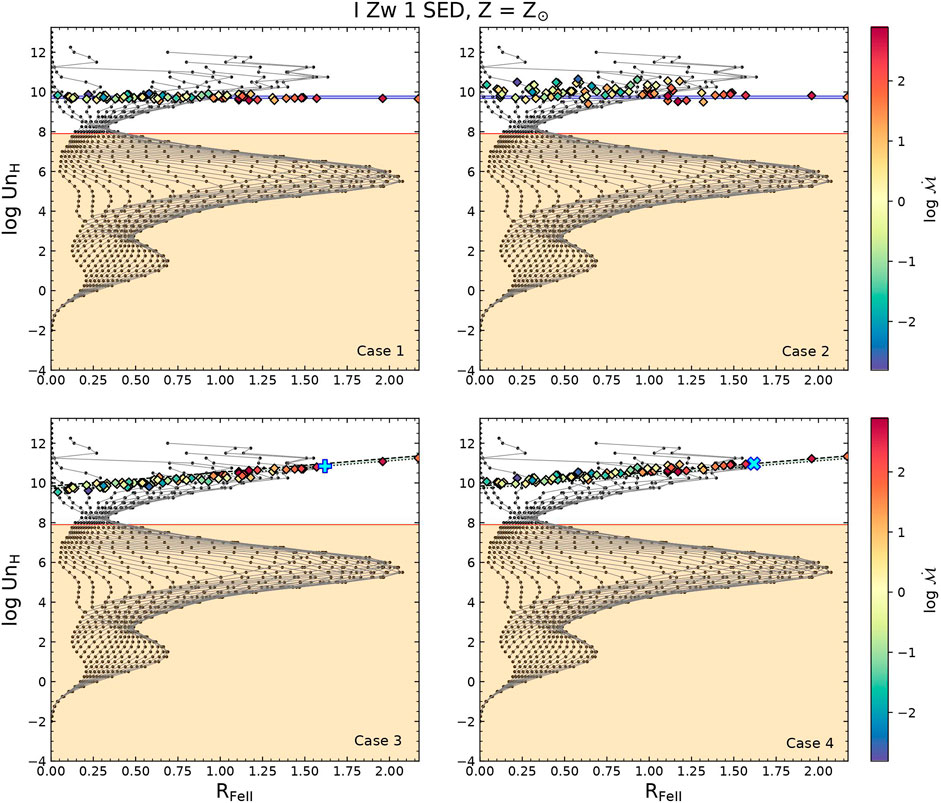
FIGURE 7. Similar to the last panel (Case 4) in Figure 6. Here, we compare I Zw 1 models at 3Z_⊙, at 3Z_⊙ with an additional microturbulent velocity 20 km s⁻¹, and at 10Z_⊙. The location of the respective sources ismarked using a blue cross in the corresponding panels. The red plus symbol on the right panel marks the position of the value obtained for Un_H using the filtering of EWs (see Section 4.3).

4.3 Bringing it All Together—Filtering the Optimal (U,n_H), and EWs

Now focusing our attention to the non-dusty part of the BLR, we would like to compare the estimates for the EWs for these two lines obtained from the observations and extract the optimal pairs of solution(s) for U and n_H. We use the estimates that were quoted by Du and Wang (2019) for 1) NGC 5548: EW(Fe II) = 11.8 ± 1.4 and EW(Hβ) = 117.8 ± 27.3 (this gives R_FeII = 0.1 ± 0.02); and from Marziani et al. (2021, submitted) for 2) I Zw 1: EW(Fe II) = 72.86 ± 15.04 and EW(Hβ) = 45.0 ± 9.42 (this gives R_FeII = 1.619 ± 0.06).

We can see from the right panels in Figure 2, which is depicting the case of NGC 5548, that we are successful in recovering these estimates for the EWs for the two species. Although, for the case of I Zw 1, while we are almost able to get the match for the EW(Hβ), the EW(Fe II) is considerably underestimated. The higher values for the EWs are seen for the regions which are shrouded in the dust where both the ionization parameter and BLR densities are quite low from the viewpoint of the BLR emission (Negrete et al., 2012; Marziani et al., 2018; Panda et al., 2018; Śniegowska et al., 2021). There is a slight increase when we consider a higher covering factor (60%, see Supplementary Figure S12) but still a deficit of ∼10–20 Å is found for this case. Next, we proceed on to testing with the higher metal content in the BLR. In Figure 8, we show the results for the consideration of two cases of super-solar metallicity—3Z_⊙ (left panels) and 10Z_⊙ (right panels). We have again assumed the 20% covering factor to estimate the EWs. As we can notice, the case with 3Z_⊙ is still unable to recover the EW(Fe II) as suggested from the observations. But, when we go to an even higher metal content (10Z_⊙), we are eventually successful. On the other hand, the BLR cloud can be locally turbulent (Baldwin et al., 2004; Bruhweiler and Verner, 2008; Shields et al., 2010; Kollatschny and Zetzl, 2013), and it has been shown to substantially affect the Fe II spectrum by facilitating continuum and line–line fluorescence (Shields et al., 2010; Panda et al., 2018, 2019a; Sarkar et al., 2021). We consider a microturbulence value of 20 km s⁻¹ suggested by our previous works (Panda et al., 2018; 2019a) and complement it with the case at 3Z_⊙. The middle panels in Figure 8 show the results from this model. We notice that this case can reproduce the EW(Fe II) as well, in addition to the successful recovery of the EW(Hβ) and hence, R_FeII. We would like to emphasize that the suggested solutions in terms of U and n_H are not the ones that show the maximum R_FeII, rather the ones in which both the EWs and the R_FeII are in agreement with the observations. Thus, a small microturbulence can affect the recovery of Fe II and hence R_FeII and the model thus do not necessitate the exceptionally high metal content. For I Zw 1, we find that the best agreement is obtained with a metal content that is slightly super-solar (Z ≳3Z_⊙) with the inclusion of turbulent motions within the BLR cloud (see also Panda, 2021b, for an overview on the effect of microturbulence in I Zw 1).

FIGURE 8

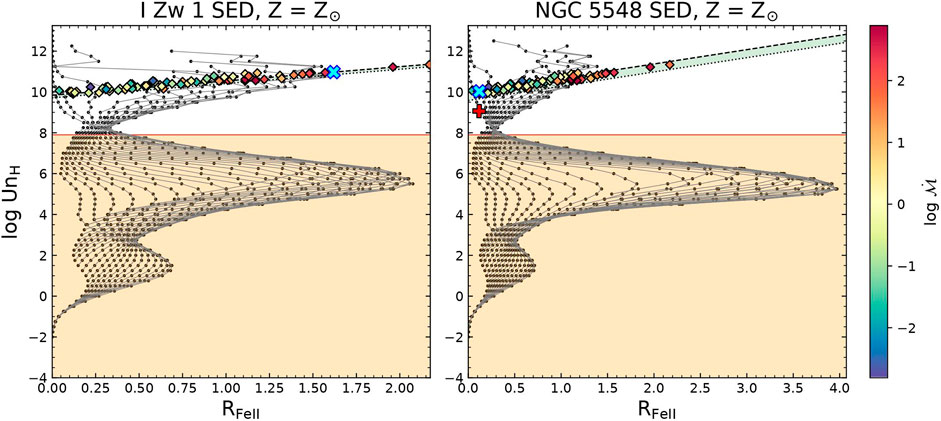
FIGURE 8.  log  U − log  n_H 2D histograms color-weighted by (top panels) equivalent widths (EWs) Fe II (middle panels) EW(Hβ) and (bottom panels) R_FeII. The labels and parameters shown here are identical to Figure 2. The panels depict the models considered for a BLR metallicity of 3Z_⊙ (left panels), then for a metallicity of 3Z_⊙ with additional microturbulence of 20 km s⁻¹ (middle panels), and for a metallicity of 10Z_⊙ (right panels).

In order to finalize the pairs of (U,n_H), we illustrate our filtering process in Figure 9. This outlines how we arrive at the solutions for these physical parameters in the non-dusty part of the BLR that the best represents the conditions in the Hβ and Fe II line-emitting region. We start with making a first filtering by accounting for the subset of log  U − log  n_H in which their product is at or larger than Un_H estimated using the dust sublimation radius for the corresponding cases, for e.g., for I Zw 1, considering the luminosity-dependent k_bol, we have the Un_H (in log-scale) = 7.9040. Next, we filter from the remaining set of those that agree in their EWs (simultaneously for Fe II and Hβ) predicted by CLOUDY to their observed values within 1-σ dispersion (of the observed value). The final remaining solutions are plotted in Figure 10 for the cases in which the agreement is found on all counts. We see that as we expected, for I Zw 1, the cases with 3Z_⊙ with a small microturbulent velocity (v_turb = 20 km s⁻¹) and the case with 10Z_⊙, are well suited. While for NGC 5548, the BLR cloud with solar abundance is sufficient. Although in this case, we recover only one pair of solution (see the triangle marked in Figure 10) in which the predicted density is quite low and the ionization parameter is significantly higher. The single cloud assumption that we make here to perform the CLOUDY modeling needs to be revisited and compared against its counterpart, for e.g., the locally optimized cloud model (LOC, Baldwin et al., 1995; Korista and Goad, 2000), in which the setup assumes a system of clouds with distribution in density and location from the central source. The LOC model has been shown to agree better particularly in the case of NGC 5548. A subsequent work is under progress that deals with this exact issue. While, in the case of I Zw 1, as also discussed in Panda (2021b), the increase in the accretion rate may puff up the very inner regions of the accretion disk leading to the BLR receiving a filtered SED, one that is significantly different from the SED that is observed by a distant observer, and with much less ionizing photons. This may further lead to the inward shift in the location of the clouds due to reduced radiation pressure in the BLR region. This may lead to cloud coagulation, one that is well described by a single cloud model.

FIGURE 9

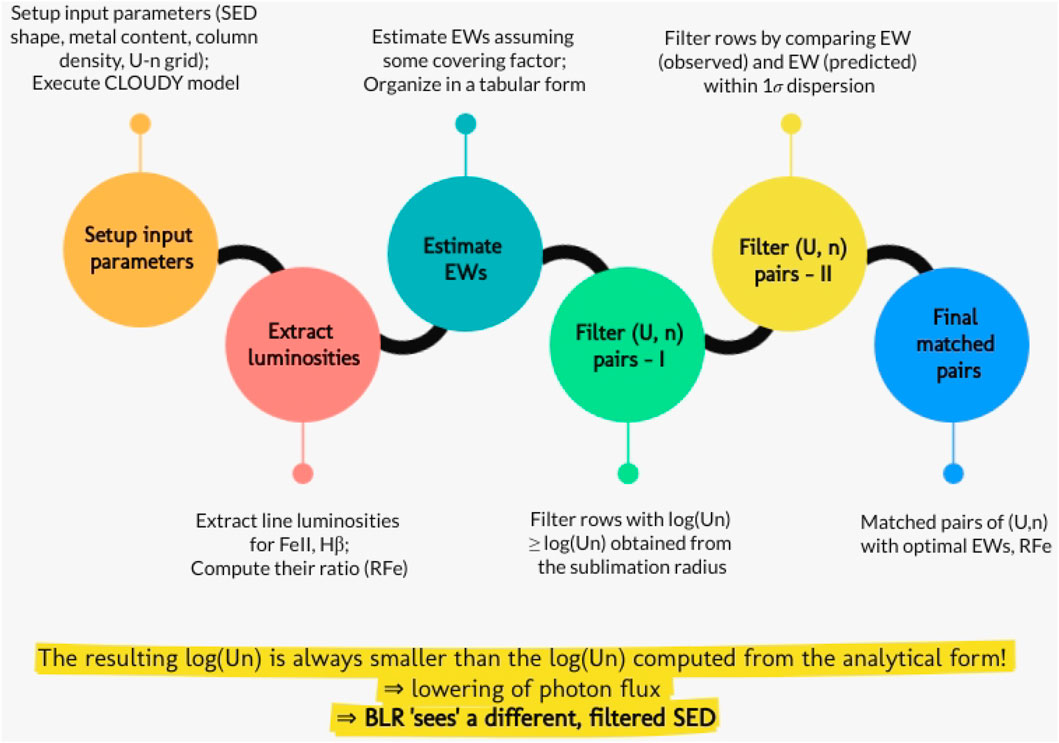
FIGURE 9. Flowchart depicting the steps taken in the filtering process—starting from the preparation of the input setup till procuring the matched pairs of (U,n_H) for each model described in this article.

FIGURE 10

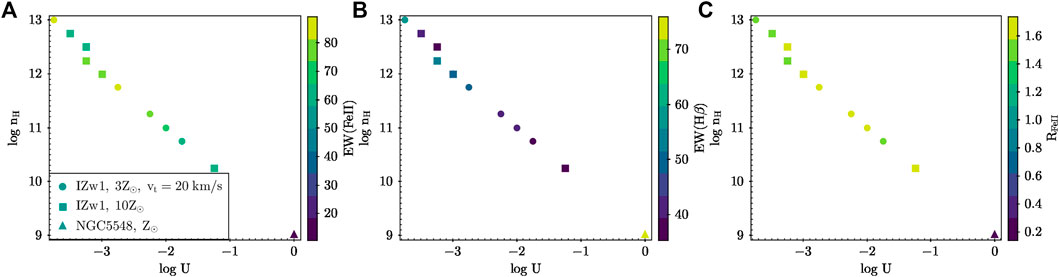
FIGURE 10. log  U − log  n_H parameter space as a function of: (A) EW(Fe II), (B) EW(Hβ), and (C) R_FeII. These mark the final filtered solutions adopting the steps shown in Figure 9. The three successful cases (two for I Zw 1 and one for NGC 5548) are shown using respective symbols.

In Figure 10, we can get the exact values of the product of Un_H which is in the range of 9–9.25 for I Zw 1 and 9 for NGC 5548. Now coming back to the red plus symbol that was marked in the panels of Figures 6, 7, we see that the solution obtained from our analytical formulation (see Table 1) and the solution obtained from this filtering process differ by almost 2 dex, i.e., for the luminosity-dependent k_bol case with the R_FeII-based R_Hβ − L₅₁₀₀ relation, we get Un_H = 10.939. Taking a ratio of the two Un_H values from these different formalisms, we get a value between 1 and 2%. This is the fraction of the actual number of ionizing photon flux that is received at the BLR that leads to the line-formation and emission of Hβ and Fe II in I Zw 1. This is exactly what we realized in our previous work (Panda, 2021b)—that the BLR “sees” a different, filtered SED with only a very small fraction (∼1%) that leads to the line emission in the low-ionization emitting region of the BLR. With a rigorous filtering approach, we have confirmed this hypothesis in this work. Similarly for NGC 5548, for the luminosity-dependent k_bol case with the R_FeII-based R_Hβ − L₅₁₀₀ relation, we get Un_H = 10.008. The fraction of the photon flux recovered is ∼10%. We note that these estimates for the fraction of ionizing continuum received by the BLR are obtained for a pre-assumed value of χ = 0.5 (where χ is the ratio of L_ion to L_bol predicted by CLOUDY for each input SED). Changing χ to a value consistent for the I Zw 1 SED, i.e., 0.12, we get the actual ionizing continuum received by the BLR to be between ∼5–10%. For NGC 5548, this fraction is much higher (χ = 0.82). Thus, the actual ionizing continuum in this case received by the BLR is still ∼10%.

Hence, through this analysis, we realize the importance of the actual ionizing luminosity, in addition to L₅₁₀₀ and R_FeII estimated from their respective spectra that recovers the pairs of the ionization parameter and local BLR density, one that is representative of the properties of the low-ionization line-emitting BLR. This ionizing luminosity is estimated with the knowledge of the exact shape of the SED for the corresponding source. In view of a series of work (Negrete et al., 2013; Marziani and Sulentic, 2014; Panda et al., 2019c; Ferland et al., 2020; Marziani et al., 2021) that have highlighted the importance of having the SED shape properly modeled, subsequent studies accounting for the proper SED fitting of other sources will strengthen the framework presented in this article.

5 Discussions

As briefly mentioned in the earlier sections, the assumption of the covering factor is perhaps the only weakness in the current model. This value is important to estimate the EW for the respective emission lines. Broadband SED modeling that includes the torus properties can allow constraining this parameter, either through the study of individual sources (Mor et al., 2009) or from large surveys utilizing the optical and infrared fluxes as a proxy for the covering factors (Roseboom et al., 2013). Another effective way would be to estimate this parameter using dynamical modeling of the BLR (Pancoast et al., 2014; Li et al., 2016).

Next, is the issue of constraining the SED through robust modeling and high-quality contemporaneous spectroscopic measurements across the optical, ultraviolet, and X-ray energies as has been carried out for NGC 5548 and a few other sources (Kubota and Done, 2019; Ferland et al., 2020). We need to test the viewing of angle-dependent SEDs (Wang et al., 2014) and compare the modeled predictions to infer physical conditions of the BLR more appropriately.

The location of the dust sublimation radius affects the results obtained in this work. Our assumptions are also supported by Suganuma et al. (2006) which found lags of hot dust emission in AGNs to be ∼3.5 times the lag of Hβ (see their Figure 32a). They thus confirm that the region with species such as O°, Mg⁺, Ca⁺, and Fe⁺ lies just inside the hot dust and in the very outermost part of the BLR. This inference is also validated from our results obtained in this work and earlier in Panda et al. (2020a), Panda (2021b).

Another important aspect of the work is the reliability of the spectral fitting techniques and the inference of the R_FeII. The tests with refined templates (Park et al., 2021; Marziani et al., 2021) need to be made to constrain the R_FeII better for the available sources with high S/N spectroscopy. These then need to be compared with better photoionization models that include Fe II databases including higher number of transitions (Sarkar et al., 2021). Our results have shown that whatever is causing Hβ to vary is also similarly causing Fe II to vary as well. One can also see in Figure 8 of Gaskell et al., 2021b that both Hβ and Fe II track the broad features of the continuum variability suggesting similar origins with subtle differences. Better Fe II-based reverberation mapping estimates are needed to constrain the location of the Fe II-emitting region in the BLR. This is located further away from the central engine compared to Hβ—by a factor ∼2 (Gaskell et al., 2021b, 2007) that is confirmed by the high-cadence reverberation mapping results from Barth et al. (2013); Hu et al. (2015). Another interesting aspect is the “breathing” mode that has been seen, especially in the Balmer lines (Korista and Goad, 2004; Barth et al., 2015; Runco et al., 2016; Gaskell et al., 2021a). The variability pattern in the Balmer lines, also studied in MgII (Guo et al., 2020), indicates that the location of the onset of the BLR (R_BLR) can change due to the increase/decrease in the intrinsic luminosity of the source. In order to study this effect and incorporate into our formalism, we need to systematically prepare broadband SEDs that are representative of such varied epochs in a source. This requires a wide coverage in wavelength, spanning from the optical to X-rays, in addition to AGN continuum light curves. A combination of the two can allow us to test the implication of the breathing mode in terms of the systematic shift in the location of the source in terms of   log  U −  log  n_H.

On the other hand, the R_Hβ − L₅₁₀₀ relation needs to be tested with the inclusion of more reverberation-mapped sources spanning the extent of the continuum luminosity. Better proxies of the accretion rate (or L_bol/L_Edd) are now available, for e.g., the near-infrared Ca ii triplet emitting at λ8498 Å, λ8542 Å,  and λ8662 Å (Panda et al., 2020a; Martínez-Aldama et al., 2021a; Martínez-Aldama et al., 2021b). The prospects for this channel will only get better with the upcoming James Webb Space Telescope and other ground-based observatories, for e.g., the Maunakea Spectroscopic Explorer (Marshall et al., 2019) and the European Extremely Large Telescope (Evans et al., 2015).

Finally, GRAVITY is just starting to resolve the outer BLR for nearby sources, for e.g., 3C 273 (GRAVITY Collaboration et al., 2018) and IRAS 09149-6206 (Gravity Collaboration et al., 2018) using fantastic interferometric capabilities. Also with the upcoming upgrade leading to GRAVITY+, this will only get better providing us with a spectacular angular resolution that will enable us to pinpoint the location of the BLR in nearby AGNs. Yet, currently, the combination of reverberation mapping and photoionization-based results remains the only credible way to infer the location and physical conditions of these media.

6 Conclusion

Through this study, we have performed the following:

• Tested the variation in the low-ionization emitting regions of the BLR, by accounting for the changes in the shape of the ionizing continuum (the SED) and the location of the BLR from the central ionizing source (or R_BLR) from the reverberation mapping, in the Eigenvector-1 context. We compare the SEDs for a prototypical Population A and Population B sources, I Zw 1, and NGC 5548 in our photoionization modeling using CLOUDY.

• Brought together our knowledge of the BLR R_Hβ − L₅₁₀₀ relations (Bentz et al., 2013; Du and Wang, 2019) and the photoionization theory into a unified picture. We highlight the importance of the estimation of the bolometric luminosity that is either (a) scaled-up using the monochromatic luminosity at, for e.g., 5,100 Å, with a fixed factor derived using composite SEDs for Type-1 quasars by combining mid-infrared and optical colors (Richards et al., 2006); or (b) uses a luminosity-dependent factor derived using theoretical calculations of optically thick, geometrically thin accretion disks, and observed X-ray properties of AGNs (Netzer, 2019). We incorporated the two widely used R_Hβ − L₅₁₀₀ relations—the classical Bentz et al. (2013) relation and the R_FeII-dependent R_Hβ − L₅₁₀₀ from Du and Wang (2019) in this approach and compared their behavior with the photoionization models. Additionally, we tested the effect of the inclusion of ${\mathcal{D}}_{\mathrm{H}\beta }$ in our prescription.

• Tested the dependence of the location of the optical Fe II and Hβ emitting region within the dustless BLR for various cloud parameters, namely, the metal content and turbulence within the BLR cloud. We found that for the case of NGC 5548, the solar composition is optimal in recovering the flux ratios. While, for the I Zw 1 case, the successful models require a BLR composition of at least 3Z_⊙ with an added effect from turbulence within the cloud. This leads to the enhanced Fe II emission that then matches the observed estimates.

• Estimated the EWs for Hβ and Fe II from our photoionization models accounting for covering factors that are verified from previous studies (Korista and Goad, 2000; Baldwin et al., 2004; Panda, 2021b). We identified pair(s) of solutions for the ionization parameter (U) and local BLR density (n_H) that agree with the observed line EWs for the low-ionization emitting regions of the dustless BLR. This result highlights the shift in the overall Un_H recovered from our analysis toward lower values (by up to 2 dex) than the Un_H value estimates from the photoionization theory. This confirms our hypothesis that the BLR “sees” a different, filtered SED with only a very small fraction (∼1–10%) that leads to the line emission in the dustless, low-ionization emitting region of the BLR.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

The idea, analysis, and writing of the manuscript have been carried out by SP.

Funding

The project was partially supported by the Polish Funding Agency National Science Centre, project 2017/26/A/ST9/00756 (MAESTRO 9) and by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) Fellowship (164753/2020-6).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

SP thanks the reviewers ABK and SB for their useful suggestions that led to improving the content of the paper. SP would like to thank Prof. Bożena Czerny, Prof. Paola Marziani, and Dr Mary Loli Martínez-Aldama for fruitful discussions and Ms Denimara Dias dos Santos, Dr Murilo Marinello and Prof. Alberto Rodríguez-Ardila for assisting with the continuum extraction of the I Zw 1 continuum. The numerical computations have been performed and analyzed using the supercomputing facility at the Nicolaus Copernicus Astronomical Center.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.850409/full#supplementary-material

Footnotes

¹The Fe II emission manifests as a pseudo-continuum owing to many, blended multiplets over a wide wavelength range (Verner et al., 1999; Kovačević et al., 2010 and references therein).

²Modelling the Fe II pseudo-continuum requires the knowledge of 8-dimensional parameter space, one that encompasses the full diversity of Type-1 AGNs as has been concluded from prior works (Panda et al., 2018, 2019a,c, 2020b). These eight parameters consist of the fundamental black hole (BH) and BLR properties, namely (1) the Eddington ratio (L_bol/L_Edd); (2) the BH mass (M_BH), (3) the shape of the ionizing continuum or the spectral energy distribution (SED), (4) the BLR local density (n_H), (5) the metal content in the BLR, (6) the velocity distribution of the BLR including turbulent motion within the BLR cloud, (7) the orientation of the source (as well as the BLR) to the distant observer, and (8) the sizes of the BLR clouds (see Panda, 2021a, for a comprehensive review).

³Ionization parameter (U) is a dimensionless parameter that informs about the total number of ionizing photons available for photoionization of a medium at a given density (n_H).

⁴This value is estimated at 5100 Å for the mean SED from Richards et al. (2006).

⁵≈ 2.18 × 10^–11 erg.

⁶= 2.59 × 10¹⁵ cm

⁷N(U) × N(n_H) × N(Z) = 29 × 33 × 3 = 2871 models

References

Abramowicz, M. A., Czerny, B., Lasota, J. P., and Szuszkiewicz, E. (1988). Slim Accretion Disks. ApJ 332, 646–658. doi:10.1086/166683

CrossRef Full Text | Google Scholar

Adhikari, T. P., Różańska, A., Czerny, B., Hryniewicz, K., and Ferland, G. J. (2016). The Intermediate-Line Region in Active Galactic Nuclei. ApJ 831, 68. doi:10.3847/0004-637X/831/1/68

CrossRef Full Text | Google Scholar

Baldwin, J., Ferland, G., Korista, K., and Verner, D. (1995). Locally Optimally Emitting Clouds and the Origin of Quasar Emission Lines. Astrophys. J. 455, L119. doi:10.1086/309827

CrossRef Full Text | Google Scholar

Baldwin, J. A., Ferland, G. J., Korista, K. T., Hamann, F., and LaCluyzé, A. (2004). The Origin of FeiiEmission in Active Galactic Nuclei. ApJ 615, 610–624. doi:10.1086/424683

CrossRef Full Text | Google Scholar

Barth, A. J., Pancoast, A., Bennert, V. N., Brewer, B. J., Canalizo, G., Filippenko, A. V., et al. (2013). The Lick AGN Monitoring Project 2011: Fe II Reverberation from the Outer Broad-Line Region. Astrophys. J. 769, 128. doi:10.1088/0004-637X/769/2/128

CrossRef Full Text | Google Scholar

Barth, A. J., Bennert, V. N., Canalizo, G., Filippenko, A. V., Gates, E. L., Greene, J. E., et al. (2015). The Lick AGN Monitoring Project 2011: Spectroscopic Campaign and Emission-Line Light Curves. Astrophys. J. Suppl. Ser. 217, 26. doi:10.1088/0067-0049/217/2/26

CrossRef Full Text | Google Scholar

Bechtold, J., Dobrzycki, A., Wilden, B., Morita, M., Scott, J., Dobrzycka, D., et al. (2002). A Uniform Analysis of the Lyα Forest at Z = 0-5. III. Hubble Space Telescope Faint Object Spectrograph Spectral Atlas. Astrophys. J. Suppl. Ser. 140, 143–238. doi:10.1086/342489

CrossRef Full Text | Google Scholar

Bentz, M. C., Denney, K. D., Grier, C. J., Barth, A. J., Peterson, B. M., Vestergaard, M., et al. (2013). The Low-Luminosity End of the Radius-Luminosity Relationship for Active Galactic Nuclei. ApJ 767, 149. doi:10.1088/0004-637X/767/2/149

CrossRef Full Text | Google Scholar

Berton, M., Björklund, I., Lähteenmäki, A., Congiu, E., Järvelä, E., Terreran, G., et al. (2020). Line Shapes in Narrow-Line Seyfert 1 Galaxies: a Tracer of Physical Properties? Contrib. Astronom. Observ. Skalnate Pleso 50, 270–292. doi:10.31577/caosp.2020.50.1.270

CrossRef Full Text | Google Scholar

Blandford, R. D., and McKee, C. F. (1982). Reverberation Mapping of the Emission Line Regions of Seyfert Galaxies and Quasars. Astrophys. J. 255, 419–439. doi:10.1086/159843

CrossRef Full Text | Google Scholar

Boroson, T. A., and Green, R. F. (1992). The Emission-Line Properties of Low-Redshift Quasi-Stellar Objects. Astrophys. J. 80, 109. doi:10.1086/191661

CrossRef Full Text | Google Scholar

Bruhweiler, F., and Verner, E. (2008). Modeling Fe II Emission and Revised Fe II (UV) Empirical Templates for the Seyfert 1 Galaxy I Zw 1. Astrophys. J. 675, 83–95. doi:10.1086/525557

CrossRef Full Text | Google Scholar

Collin, S., Kawaguchi, T., Peterson, B. M., and Vestergaard, M. (2006). Systematic Effects in Measurement of Black Hole Masses by Emission-Line Reverberation of Active Galactic Nuclei: Eddington Ratio and Inclination. Astron. Astrophys. 456, 75–90. doi:10.1051/0004-6361:20064878

CrossRef Full Text | Google Scholar

Collin-Souffrin, S., Dyson, J. E., McDowell, J. C., and Perry, J. J. (1988). The Environment of Active Galactic Nuclei. I - A Two-Component Broad Emission Line Model. Monthly Notices R. Astron. Soc. 232, 539–550. doi:10.1093/mnras/232.3.539

CrossRef Full Text | Google Scholar

Czerny, B., and Hryniewicz, K. (2011). The Origin of the Broad Line Region in Active Galactic Nuclei. A&A 525, L8. doi:10.1051/0004-6361/201016025

CrossRef Full Text | Google Scholar

Czerny, B., Li, Y.-R., Hryniewicz, K., Panda, S., Wildy, C., Sniegowska, M., et al. (2017). Failed Radiatively Accelerated Dusty Outflow Model of the Broad Line Region in Active Galactic Nuclei. I. Analytical Solution. Astrophys. J. 846, 154. doi:10.3847/1538-4357/aa8810

CrossRef Full Text | Google Scholar

Czerny, B. (2019). “Modelling Broad Emission Lines in Active Galactic Nuclei,” in Proceedings of the conference 12th Serbian Conference on Spectral Line Shapes in Astrophysics, Vrdnik, Serbia, June 3–7, 2019.

CrossRef Full Text | Google Scholar

Dehghanian, M., Ferland, G. J., Kriss, G. A., Peterson, B. M., Mathur, S., Mehdipour, M., et al. (2019). Space Telescope and Optical Reverberation Mapping Project. X. Understanding the Absorption-Line Holiday in NGC 5548. Astrophys. J. 877, 119. doi:10.3847/1538-4357/ab1b48

CrossRef Full Text | Google Scholar

Du, P., and Wang, J.-M. (2019). The Radius-Luminosity Relationship Depends on Optical Spectra in Active Galactic Nuclei. Astrophys. J. 886, 42. doi:10.3847/1538-4357/ab4908

CrossRef Full Text | Google Scholar

Du, P., Hu, C., Lu, K.-X., Wang, F., Qiu, J., Li, Y.-R., et al. (2014). Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. I. First Results from a New Reverberation Mapping Campaign. Astrophys. J. 782, 45. doi:10.1088/0004-637X/782/1/45

CrossRef Full Text | Google Scholar

Du, P., Hu, C., Lu, K.-X., Huang, Y.-K., Cheng, C., Qiu, J., et al. (2015). Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. IV. Hβ Time Lags and Implications for Super-Eddington Accretion. Astrophys. J. 806, 22. doi:10.1088/0004-637X/806/1/22

CrossRef Full Text | Google Scholar

Du, P., Wang, J.-M., Hu, C., Ho, L. C., Li, Y.-R., and Bai, J.-M. (2016). The Fundamental Plane of the Broad-Line Region in Active Galactic Nuclei. Astrophys. J. 818, L14. doi:10.3847/2041-8205/818/1/L14

CrossRef Full Text | Google Scholar

Evans, C., Puech, M., Afonso, J., Almaini, O., Amram, P., Aussel, H., et al. (2015). The Science Case for Multi-Object Spectroscopy on the European ELT, ELT-MOS White Paper presented at the “Shaping E-ELT Science & Instrumentation” workshop, February 2013 (Garching: ESO). arXiv e-prints. arXiv:1501.04726.

Fausnaugh, M. M., Denney, K. D., Barth, A. J., Bentz, M. C., Bottorff, M. C., Carini, M. T., et al. (2016). Space Telescope and Optical Reverberation Mapping Project. III. Optical Continuum Emission and Broadband Time Delays in NGC 5548. Astrophys. J. 821, 56. doi:10.3847/0004-637X/821/1/56

CrossRef Full Text | Google Scholar

Ferland, G. J., Chatzikos, M., Guzmán, F., Lykins, M. L., van Hoof, P. A. M., Williams, R. J. R., et al. (2017). The 2017 Release Cloudy. Revista Mexicana de Astron. y Astrofísica 53, 385–438.

Google Scholar

Ferland, G. J., Done, C., Jin, C., Landt, H., and Ward, M. J. (2020). State-of-the-art AGN SEDs for Photoionization Models: BLR Predictions Confront the Observations. Monthly Notices R. Astron. Soc. 494, 5917–5922. doi:10.1093/mnras/staa1207

CrossRef Full Text | Google Scholar

Fraix-Burnet, D., Marziani, P., D’Onofrio, M., and Dultzin, D. (2017). The Phylogeny of Quasars and the Ontogeny of Their central Black Holes. Front. Astron. Space Sci. 4, 1. doi:10.3389/fspas.2017.00001

CrossRef Full Text | Google Scholar

Gaskell, C. M., Klimek, E. S., and Nazarova, L. S. (2007). NGC 5548: The AGN Energy Budget Problem and the Geometry of the Broad-Line Region and Torus. arXiv e-prints. arXiv:0711.1025.

Google Scholar

Gaskell, C. M., Bartel, K., Deffner, J. N., and Xia, I. (2021a). Anomalous Broad-Line Region Responses to Continuum Variability in Active Galactic Nuclei - I. Hβ Variability. Monthly Notices R. Astron. Soc. 508, 6077–6091. doi:10.1093/mnras/stab2443

CrossRef Full Text | Google Scholar

Gaskell, C. M., Thakur, N., Tian, B., and Saravana, A. (2021b). Fe II Emission in Active Galactic Nuclei. arXiv e-prints. arXiv:2112.06559.

Google Scholar

GRAVITY Collaboration Sturm, E., Dexter, J., Pfuhl, O., Stock, M. R., Davies, R. I., et al. (2018). Spatially Resolved Rotation of the Broad-Line Region of a Quasar at Sub-parsec Scale. Nature 563, 657–660. doi:10.1038/s41586-018-0731-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gravity Collaboration Amorim, A., Bauböck, M., Brandner, W., Clénet, Y., Davies, R., et al. (2018). Spatially Resolved Rotation of the Broad-Line Region of a Quasar at Sub-parsec Scale. Nature 563, 657–660. doi:10.1038/s41586-018-0731-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Greenstein, J. L., and Schmidt, M. (1964). The Quasi-Stellar Radio Sources 3C 48 and 3C 273. Astrophysical J. 140, 1. doi:10.1086/147889

CrossRef Full Text | Google Scholar

Grier, C. J., Trump, J. R., Shen, Y., Horne, K., Kinemuchi, K., McGreer, I. D., et al. (2017). The Sloan Digital Sky Survey Reverberation Mapping Project: Hα and Hβ Reverberation Measurements from First-Year Spectroscopy and Photometry. Astrophys. J. 851, 21. doi:10.3847/1538-4357/aa98dc

CrossRef Full Text | Google Scholar

Guo, H., Shen, Y., He, Z., Wang, T., Liu, X., Wang, S., et al. (2020). Understanding Broad Mg II Variability in Quasars with Photoionization: Implications for Reverberation Mapping and Changing-Look Quasars. Astrophysical J. 888, 58. doi:10.3847/1538-4357/ab5db0

CrossRef Full Text | Google Scholar

Hönig, S. F. (2019). Redefining the Torus: A Unifying View of AGNs in the Infrared and Submillimeter. Astrophys. J. 884, 171. doi:10.3847/1538-4357/ab4591

CrossRef Full Text | Google Scholar

Hu, C., Du, P., Lu, K.-X., Li, Y.-R., Wang, F., Qiu, J., et al. (2015). Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. III. Detection of Fe II Reverberation in Nine Narrow-Line Seyfert 1 Galaxies. Astrophys. J. 804, 138. doi:10.1088/0004-637X/804/2/138

CrossRef Full Text | Google Scholar

Joly, M. (1987). Formation of Low Ionization Lines in Active Galactic Nuclei. Astron. Astrophys. 184, 33–42.

Google Scholar

Kaspi, S., Smith, P. S., Netzer, H., Maoz, D., Jannuzi, B. T., and Giveon, U. (2000). Reverberation Measurements for 17 Quasars and the Size-Mass-Luminosity Relations in Active Galactic Nuclei. Astrophys. J. 533, 631–649. doi:10.1086/308704

CrossRef Full Text | Google Scholar

Kaspi, S., Maoz, D., Netzer, H., Peterson, B. M., Vestergaard, M., and Jannuzi, B. T. (2005). The Relationship between Luminosity and Broad-Line Region Size in Active Galactic Nuclei. Astrophys. J. 629, 61–71. doi:10.1086/431275

CrossRef Full Text | Google Scholar

Kollatschny, W., and Zetzl, M. (2013). The Shape of Broad-Line Profiles in Active Galactic Nuclei. Astron. Astrophys. 549, A100. doi:10.1051/0004-6361/201219411

CrossRef Full Text | Google Scholar

Korista, K. T., and Goad, M. R. (2000). Locally Optimally Emitting Clouds and the Variable Broad Emission Line Spectrum of NGC 5548. Astrophys. J. 536, 284–298. doi:10.1086/308930

CrossRef Full Text | Google Scholar

Korista, K. T., and Goad, M. R. (2004). What the Optical Recombination Lines Can Tell Us about the Broad-Line Regions of Active Galactic Nuclei. Astrophys. J. 606, 749–762. doi:10.1086/383193

CrossRef Full Text | Google Scholar

Kovačević, J., Popović, L. Č., and Dimitrijević, M. S. (2010). Analysis of Optical Fe II Emission in a Sample of Active Galactic Nucleus Spectra. Astrophys. J. 189, 15–36. doi:10.1088/0067-0049/189/1/15

CrossRef Full Text | Google Scholar

Krawczyk, C. M., Richards, G. T., Mehta, S. S., Vogeley, M. S., Gallagher, S. C., Leighly, K. M., et al. (2013). Mean Spectral Energy Distributions and Bolometric Corrections for Luminous Quasars. Astrophys. J. 206, 4. doi:10.1088/0067-0049/206/1/4

CrossRef Full Text | Google Scholar

Kubota, A., and Done, C. (2019). Modelling the Spectral Energy Distribution of Super-Eddington Quasars. Monthly Notices R. Astron. Soc. 489, 524–533. doi:10.1093/mnras/stz2140

CrossRef Full Text | Google Scholar

Li, Y.-R., Wang, J.-M., and Bai, J.-M. (2016). A Non-parametric Approach to Constrain the Transfer Function in Reverberation Mapping. Astrophys. J. 831, 206. doi:10.3847/0004-637X/831/2/206

CrossRef Full Text | Google Scholar

Lusso, E., and Risaliti, G. (2016). The Tight Relation between X-Ray and Ultraviolet Luminosity of Quasars. Astrophys. J. 819, 154. doi:10.3847/0004-637X/819/2/154

CrossRef Full Text | Google Scholar

Marconi, A., Risaliti, G., Gilli, R., Hunt, L. K., Maiolino, R., and Salvati, M. (2004). Local Supermassive Black Holes, Relics of Active Galactic Nuclei and the X-ray Background. Monthly Notices R. Astron. Soc. 351, 169–185. doi:10.1111/j.1365-2966.2004.07765.x

CrossRef Full Text | Google Scholar

Marinello, M., Rodríguez-Ardila, A., Garcia-Rissmann, A., Sigut, T. A. A., and Pradhan, A. K. (2016). The Fe II Emission in Active Galactic Nuclei: Excitation Mechanisms and Location of the Emitting Region. Astrophys. J. 820, 116. doi:10.3847/0004-637X/820/2/116

CrossRef Full Text | Google Scholar

Marshall, J., Bolton, A., Bullock, J., Burgasser, A., Chambers, K., DePoy, D., et al. (2019). The Maunakea Spectroscopic Explorer. Bull. Am. Astron. Soc. 51, 126. doi:10.2172/1568876

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Czerny, B., Kawka, D., Karas, V., Panda, S., Zajaček, M., et al. (2019). Can Reverberation-Measured Quasars Be Used for Cosmology? Astrophys. J. 883, 170. doi:10.3847/1538-4357/ab3728

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Panda, S., and Czerny, B. (2021a). A New Radius-Luminosity Relation: Using the Near-Infrared CaII Triplet. XIX Serbian Astronomical Conf. 100, 287–293.

Google Scholar

Martínez-Aldama, M. L., Panda, S., Czerny, B., Marinello, M., Marziani, P., and Dultzin, D. (2021b). The CaFe Project: Optical Fe II and Near-Infrared Ca II Triplet Emission in Active Galaxies. II. The Driver(s) of the Ca II and Fe II and its Potential Use as a Chemical Clock. Astrophys. J. 918, 29. doi:10.3847/1538-4357/ac03b6

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Dultzin, D., Marziani, P., Sulentic, J. W., Bressan, A., Chen, Y., et al. (2015a). O I and Ca II Observations in Intermediate Redshift Quasars. ApJS 217, 3. doi:10.1088/0067-0049/217/1/3

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Marziani, P., Dultzin, D., Sulentic, J. W., Bressan, A., Chen, Y., et al. (2015b). Observations of the Ca Ii IR Triplet in High Luminosity Quasars: Exploring the Sample. J. Astrophysics Astron. 36, 457–465. doi:10.1007/s12036-015-9354-9

CrossRef Full Text | Google Scholar

Marziani, P., and Sulentic, J. W. (2014). Highly Accreting Quasars: Sample Definition and Possible Cosmological Implications. MNRAS 442, 1211–1229. doi:10.1093/mnras/stu951

CrossRef Full Text | Google Scholar

Marziani, P., Sulentic, J. W., Negrete, C. A., Dultzin, D., Del Olmo, A., Martínez Carballo, M. A., et al. (2015). UV Spectral Diagnostics for Low Redshift Quasars: Estimating Physical Conditions and Radius of the Broad Line Region. ApSS 356, 339–346. doi:10.1007/s10509-014-2136-z

CrossRef Full Text | Google Scholar

Marziani, P., Dultzin, D., Sulentic, J. W., Del Olmo, A., Negrete, C. A., Martínez-Aldama, M. L., et al. (2018). A Main Sequence for Quasars. Front. Astron. Space Sci. 5, 6. doi:10.3389/fspas.2018.00006

CrossRef Full Text | Google Scholar

Marziani, P., Bon, E., Bon, N., del Olmo, A., Martínez-Aldama, M., D’Onofrio, M., et al. (2019). Quasars: From the Physics of Line Formation to Cosmology. Atoms 7, 18. doi:10.3390/atoms7010018

CrossRef Full Text | Google Scholar

Marziani, P., Berton, M., Panda, S., and Bon, E. (2021). Optical Singly-Ionized Iron Emission in Radio-Quiet and Relativistically Jetted Active Galactic Nuclei. Universe 7, 484. doi:10.3390/universe7120484

CrossRef Full Text | Google Scholar

Mathews, W. G., and Ferland, G. J. (1987). What Heats the Hot Phase in Active Nuclei? ApJ 323, 456–467. doi:10.1086/165843

CrossRef Full Text | Google Scholar

Mehdipour, M., Kaastra, J. S., Kriss, G. A., Cappi, M., Petrucci, P. O., Steenbrugge, K. C., et al. (2015). Anatomy of the AGN in NGC 5548. I. A Global Model for the Broadband Spectral Energy Distribution. Astron. Astrophys. 575, A22. doi:10.1051/0004-6361/201425373

CrossRef Full Text | Google Scholar

Mor, R., Netzer, H., and Elitzur, M. (2009). Dusty Structure Around Type-I Active Galactic Nuclei: Clumpy Torus Narrow-Line Region and Near-Nucleus Hot Dust. Astrophys. J. 705, 298–313. doi:10.1088/0004-637X/705/1/298

CrossRef Full Text | Google Scholar

Negrete, A., Dultzin, D., Marziani, P., and Sulentic, J. (2012). BLR Physical Conditions in Extreme Population A Quasars: a Method to Estimate Central Black Hole Mass at High Redshift. ApJ 757, 62. doi:10.1088/0004-637x/757/1/62

CrossRef Full Text | Google Scholar

Negrete, C. A., Dultzin, D., Marziani, P., and Sulentic, J. W. (2013). Reverberation and Photoionization Estimates of the Broad-Line Region Radius in Low-Z Quasars. Astrophys. J. 771, 31. doi:10.1088/0004-637X/771/1/31

CrossRef Full Text | Google Scholar

Negrete, C. A., Dultzin, D., Marziani, P., and Sulentic, J. W. (2014). A Photoionization Method for Estimating BLR “Size” in Quasars. Adv. Space Res. 54, 1355–1361. doi:10.1016/j.asr.2013.11.037

CrossRef Full Text | Google Scholar

Nemmen, R. S., and Brotherton, M. S. (2010). Quasar Bolometric Corrections: Theoretical Considerations. Monthly Notices R. Astron. Soc. 408, 1598–1605. doi:10.1111/j.1365-2966.2010.17224.x

CrossRef Full Text | Google Scholar

Nenkova, M., Sirocky, M. M., Ivezić, Ž., and Elitzur, M. (2008). AGN Dusty Tori. I. Handling of Clumpy Media. Astrophys. J. 685, 147–159. doi:10.1086/590482

CrossRef Full Text | Google Scholar

Netzer, H. (2019). Bolometric Correction Factors for Active Galactic Nuclei. Monthly Notices R. Astronomical Soc. 488, 5185–5191. doi:10.1093/mnras/stz2016

CrossRef Full Text | Google Scholar

Padovani, P., Alexander, D. M., Assef, R. J., De Marco, B., Giommi, P., Hickox, R. C., et al. (2017). Active Galactic Nuclei: What’s in a Name? Astron. Astrophys. 25, 2. doi:10.1007/s00159-017-0102-9

CrossRef Full Text | Google Scholar

Pancoast, A., Brewer, B. J., and Treu, T. (2014). Modelling Reverberation Mapping Data - I. Improved Geometric and Dynamical Models and Comparison with Cross-Correlation Results. Monthly Notices R. Astron. Soc. 445, 3055–3072. doi:10.1093/mnras/stu1809

CrossRef Full Text | Google Scholar

Panda, S., and Dias dos Santos, D. (2021). Revisiting the Spectral Energy Distribution of I Zw 1 under the CaFe Project, Acta Astrophysica Taurica (Nauchny, Bakhchisarai Dist., CrAO) Proceedings for Crimean-2021 AGN Conference “Galaxies with Active Nuclei on Scales From Black Hole to Host Galaxy” Dedicated to the E.A. Dibai’s 90th Anniversary, September 13–17, 2021.

Google Scholar

Panda, S., Czerny, B., Adhikari, T. P., Hryniewicz, K., Wildy, C., Kuraszkiewicz, J., et al. (2018). Modeling of the Quasar Main Sequence in the Optical Plane. Astrophys. J. 866, 115. doi:10.3847/1538-4357/aae209

CrossRef Full Text | Google Scholar

Panda, S., Czerny, B., Done, C., and Kubota, A. (2019a). CLOUDY View of the Warm Corona. Astrophysical J. 875, 133. doi:10.3847/1538-4357/ab11cb

CrossRef Full Text | Google Scholar

Panda, S., Martínez-Aldama, M. L., and Zajaček, M. (2019b). Current and Future Applications of Reverberation-Mapped Quasars in Cosmology. Front. Astron. Space Sci. 6, 75. doi:10.3389/fspas.2019.00075

CrossRef Full Text | Google Scholar

Panda, S., Marziani, P., and Czerny, B. (2019c). The Quasar Main Sequence Explained by the Combination of Eddington Ratio, Metallicity, and Orientation. Astrophys. J. 882, 79. doi:10.3847/1538-4357/ab3292

CrossRef Full Text | Google Scholar

Panda, S., Martínez-Aldama, M. L., Marinello, M., Czerny, B., Marziani, P., and Dultzin, D. (2020a). The CaFe Project: Optical Fe II and Near-Infrared Ca II Triplet Emission in Active Galaxies. I. Photoionization Modeling. Astrophys. J. 902, 76. doi:10.3847/1538-4357/abb5b8

CrossRef Full Text | Google Scholar

Panda, S., Marziani, P., and Czerny, B. (2020b). Main Trends of the Quasar Main Sequence - Effect of Viewing Angle. Contrib. Astron. Observ. Skalnate Pleso 50, 293–308. doi:10.31577/caosp.2020.50.1.293

CrossRef Full Text | Google Scholar

Panda, S., Bon, E., Marziani, P., and Bon, N. (2021). Taming the Derivative: Diagnostics of the Continuum and Hβ Emission in a Prototypical Population B Active Galaxy. Astron. Nachr. 343, e210091. doi:10.1002/asna.20210091

CrossRef Full Text | Google Scholar

Panda, S. (2021a). Physical Conditions In the Broad-Line Regions of Active Galaxies. Centrum Fizyki Teoretycznej, Polskiej Akademii Nauk. Phd Thesis

Google Scholar

Panda, S. (2021b). The CaFe Project: Optical Fe II and Near-Infrared Ca II Triplet Emission in Active Galaxies: Simulated EWs and the Co-dependence of Cloud Size and Metal Content. Astron. Astrophys. 650, A154. doi:10.1051/0004-6361/202140393

CrossRef Full Text | Google Scholar

Park, D., Barth, A. J., Ho, L. C., and Laor, A. (2022). A New Iron Emission Template for Active Galactic Nuclei. I. Optical Template for the Hβ Region. Astrophys. J. 258, 38. doi:10.3847/1538-4365/ac3f3e

CrossRef Full Text | Google Scholar

Persson, S. E. (1988). Calcium Infrared Triplet Emission in Active Galactic Nuclei. Astrophys. J. 330, 751. doi:10.1086/166509

CrossRef Full Text | Google Scholar

Peterson, B. M., Ferrarese, L., Gilbert, K. M., Kaspi, S., Malkan, M. A., Maoz, D., et al. (2004). Central Masses and Broad-Line Region Sizes of Active Galactic Nuclei. II. A Homogeneous Analysis of a Large Reverberation-Mapping Database. Astrophysical J. 613, 682–699. doi:10.1086/423269

CrossRef Full Text | Google Scholar

Peterson, B. M. (1988). Emission-Line Variability in Seyfert Galaxies. Publ. Astron. Soc. Pac. 100, 18. doi:10.1086/132130

CrossRef Full Text | Google Scholar

Peterson, B. M. (1993). Reverberation Mapping of Active Galactic Nuclei. Publ. Astron. Soc. Pac. 105, 247. doi:10.1086/133140

CrossRef Full Text | Google Scholar

Rakshit, S., Stalin, C. S., and Kotilainen, J. (2020). Spectral Properties of Quasars from Sloan Digital Sky Survey Data Release 14: The Catalog. Astrophys. J 249, 17. doi:10.3847/1538-4365/ab99c5

CrossRef Full Text | Google Scholar

Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., Hall, P. B., Gallagher, S. C., Hines, D. C., et al. (2006). Spectral Energy Distributions and Multiwavelength Selection of Type 1 Quasars. Astrophys. J. 166, 470–497. doi:10.1086/506525

CrossRef Full Text | Google Scholar

Riffel, R., Rodríguez-Ardila, A., and Pastoriza, M. G. (2006). A 0.8-2.4 μm Spectral Atlas of Active Galactic Nuclei. Astron. Astrophys. 457, 61–70. doi:10.1051/0004-6361:20065291

CrossRef Full Text | Google Scholar

Rodríguez-Ardila, A., Viegas, S. M., Pastoriza, M. G., and Prato, L. (2002). Infrared Fe II Emission in Narrow-Line Seyfert 1 Galaxies. Astrophys. J. 565, 140–154. doi:10.1086/324598

CrossRef Full Text | Google Scholar

Roseboom, I. G., Lawrence, A., Elvis, M., Petty, S., Shen, Y., and Hao, H. (2013). IR-derived Covering Factors for a Large Sample of Quasars from WISE-UKIDSS-SDSS. Monthly Notices R. Astronomical Soc. 429, 1494–1501. doi:10.1093/mnras/sts441

CrossRef Full Text | Google Scholar

Runco, J. N., Cosens, M., Bennert, V. N., Scott, B., Komossa, S., Malkan, M. A., et al. (2016). Broad Hβ Emission-Line Variability in a Sample of 102 Local Active Galaxies. Astrophys. J. 821, 33. doi:10.3847/0004-637X/821/1/33

CrossRef Full Text | Google Scholar

Runnoe, J. C., Brotherton, M. S., and Shang, Z. (2012a). Updating Quasar Bolometric Luminosity Corrections. Monthly Notices R. Astronomical Soc. 422, 478–493. doi:10.1111/j.1365-2966.2012.20620.x

CrossRef Full Text | Google Scholar

Runnoe, J. C., Brotherton, M. S., and Shang, Z. (2012b). Updating Quasar Bolometric Luminosity Corrections - II. Infrared Bolometric Corrections. Monthly Notices R. Astron. Soc. 426, 2677–2688. doi:10.1111/j.1365-2966.2012.21644.x

CrossRef Full Text | Google Scholar

Sarkar, A., Ferland, G. J., Chatzikos, M., Guzmán, F., van Hoof, P. A. M., Smyth, R. T., et al. (2021). Improved Fe II Emission-Line Models for AGNs Using New Atomic Data Sets. Astrophysical J. 907, 12. doi:10.3847/1538-4357/abcaa6

CrossRef Full Text | Google Scholar

Schmidt, M. (1963). 3C 273 : A Star-Like Object with Large Red-Shift. Nature 197, 1040. doi:10.1038/1971040a0

CrossRef Full Text | Google Scholar

Seyfert, C. K. (1943). Nuclear Emission in Spiral Nebulae. Astrophys. J. 97, 28. doi:10.1086/144488

CrossRef Full Text | Google Scholar

Shen, Y., and Ho, L. C. (2014). The Diversity of Quasars Unified by Accretion and Orientation. Nature 513, 210–213. doi:10.1038/nature13712

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Y., Richards, G. T., Strauss, M. A., Hall, P. B., Schneider, D. P., Snedden, S., et al. (2011). A Catalog of Quasar Properties from Sloan Digital Sky Survey Data Release 7. Astrophys. J. 194, 45. doi:10.1088/0067-0049/194/2/45

CrossRef Full Text | Google Scholar

Shields, G. A., Ludwig, R. R., and Salviander, S. (2010). Fe II Emission in Active Galactic Nuclei: The Role of Total and Gas-phase Iron Abundance. Astrophys. J. 721, 1835–1842. doi:10.1088/0004-637X/721/2/1835

CrossRef Full Text | Google Scholar

Śniegowska, M., Marziani, P., Czerny, B., Panda, S., Martínez-Aldama, M. L., del Olmo, A., et al. (2021). High Metal Content of Highly Accreting Quasars. Astrophys. J. 910, 115. doi:10.3847/1538-4357/abe1c8

CrossRef Full Text | Google Scholar

Suganuma, M., Yoshii, Y., Kobayashi, Y., Minezaki, T., Enya, K., Tomita, H., et al. (2006). Reverberation Measurements of the Inner Radius of the Dust Torus in Nearby Seyfert 1 Galaxies. Astrophys. J. 639, 46–63. doi:10.1086/499326

CrossRef Full Text | Google Scholar

Sulentic, J. W., Zwitter, T., Marziani, P., and Dultzin-Hacyan, D. (2000). Eigenvector 1: An Optimal Correlation Space for Active Galactic Nuclei. ApJl 536, L5–L9. doi:10.1086/312717

PubMed Abstract | CrossRef Full Text | Google Scholar

Sulentic, J. W., Marziani, P., Zamanov, R., Bachev, R., Calvani, M., and Dultzin-Hacyan, D. (2002). Average Quasar Spectra in the Context of Eigenvector 1. ApJl 566, L71–L75. doi:10.1086/339594

CrossRef Full Text | Google Scholar

Verner, E. M., Verner, D. A., Korista, K. T., Ferguson, J. W., Hamann, F., and Ferland, G. J. (1999). Numerical Simulations of Fe II Emission Spectra. Astrophys. J. 120, 101–112. doi:10.1086/313171

CrossRef Full Text | Google Scholar

Wandel, A., Peterson, B. M., and Malkan, M. A. (1999). Central Masses and Broad-Line Region Sizes of Active Galactic Nuclei. I. Comparing the Photoionization and Reverberation Techniques. Astrophys. J. 526, 579–591. doi:10.1086/308017

CrossRef Full Text | Google Scholar

Wang, J.-M., Du, P., Valls-Gabaud, D., Hu, C., and Netzer, H. (2013). Super-Eddington Accreting Massive Black Holes as Long-Lived Cosmological Standards. Phys. Rev. Lett. 110, 081301. doi:10.1103/PhysRevLett.110.081301

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J.-M., Qiu, J., Du, P., and Ho, L. C. (2014). Self-shadowing Effects of Slim Accretion Disks in Active Galactic Nuclei: The Diverse Appearance of the Broad-Line Region. ApJ 797, 65. doi:10.1088/0004-637X/797/1/65

CrossRef Full Text | Google Scholar

Zamfir, S., Sulentic, J. W., Marziani, P., and Dultzin, D. (2010). Detailed Characterization of Hβ Emission Line Profile in Low-Z SDSS Quasars. Monthly Notices R. Astron. Soc. 403, 1759. doi:10.1111/j.1365-2966.2009.16236.x

CrossRef Full Text | Google Scholar