The Need for a System Science Approach to Global Magnetospheric Models

This perspective advocates for the need of a combined system science approach to global magnetospheric models and to spacecraft magnetospheric data to answer the question “Do simulations behave in the same manner as the magnetosphere does?” (instead of the standard validation question “How well do simulations reproduce spacecraft data?”). This approach will 1) validate global magnetospheric models statistically, without the need for a direct comparison against spacecraft data, 2) expose the deficiencies of the models, and 3) provide physics support to the system analysis performed on the magnetospheric system.

Introduction

The Helio2050 workshop was organized in May 2021 to develop a vision for Heliophysics (the Sun, the solar wind, and planetary magnetospheres and ionospheres) for the next 30 years. Acknowledging the tremendous progress made in understanding the various parts of the heliospheric system over many decades, one of the themes for the future that had strong support from diverse areas of the community is the need to understand the heliospheric system as a whole. The same considerations also apply to the Earth’s magnetosphere. In fact, the idea of the magnetosphere as a “system of systems” is not new. For decades researchers have applied the tools of system science to data from solar wind, from magnetospheric spacecraft, and from geomagnetic indices and analyzed the correlations between causes (i.e., solar wind drivers) and effects (magnetospheric response). Reviews of magnetospheric system science are in Valdivia et al. (2005), Valdivia et al. (2013), and Borovsky and Valdivia (2018).

Here we are suggesting that system-science techniques be applied in parallel to 1) global magnetospheric simulations and 2) the actual magnetosphere. This methodology will result in a better assessment of the validity of the simulations and it will enable the identification of deficiencies in the simulation models. To validate the models, we will ask the question “Does the simulation behave in the same manner as the magnetosphere behaves?” rather than the standard validation question “How well does the simulation describe the data?”. This methodology can also clarify the utility of system-science techniques for the magnetosphere, and help refining those techniques. A final motivation for this methodology is to open an avenue of communication between two diverse magnetospheric research communities: 1) the systems analysis community and 2) the more-mainstream reductionist community of data analysis, instrument designers, plasma and space physicists, and numerical simulators.

Magnetospheric System Science

The magnetosphere-ionosphere system exhibits many forms of activity when driven by the solar wind (cf. Borovsky and Valdivia, 2018): magnetospheric convection, morphology changes, substorms, aurora, ionospheric outflows, plasma-wave activity, radiation-belt intensification, and radio emission. Magnetospheric system science examines correlations and information flow between the solar wind and the magnetosphere and looks at statistical properties of the multiple behaviors of the solar-wind-driven magnetosphere. Much of the motivation for these methods comes from the science of systems. The earliest form of magnetospheric system analysis was correlation studies between the spacecraft measurements of the solar wind and geomagnetic indices (Snyder et al., 1963; Bargatze et al., 1985), a method that is still heavily used today, (e.g., McPherron et al., 2015): this methodology yields information about how the solar wind drives the magnetosphere and about various system reaction times. For the driving of the magnetosphere, cause-and-effect among the solar-wind variables can be better established using similar methods based on information transfer (cf. Wing and Johnson, 2019). State vector analysis has built on these simpler solar-wind/magnetosphere correlative studies (Fung and Shao, 2008; Borovsky and Osmane, 2019). Using the proper tools, analysis of magnetospheric time series (typically geomagnetic indices) can yield information about the statistics of magnetospheric dynamics through measurements of fractality, dimensionality, criticality, chaotic output: these time-series studies are discussed in multiple reviews [Voros, 1994; Lakhina, 1994; Klimas et al., 1996; Vassiliadis, 2000; Vassiliadis, 2006; Chapman et al., 2004; Valdivia et al., 2005; Valdivia et al., 2013; Dendy and Chapman, 2006; Sharma, 2010, 2014; Pavlos et al., 2011; and Stepanova and Valdivia, 2016. See also Watkins et al., 2001; Watkins et al., 2012; and Watkins, 2002]. A different type of time-series analysis identifies events in the time series and examines the statistics of event occurrences and amplitudes (Liou et al., 2018). Finally, there is a long history of building and analyzing mathematical (analog) models of the magnetosphere (Smith et al., 1986; Goertz et al., 1991; Goertz et al., 1993; Vassiliadis et al., 1993; Klimas et al., 1997; Klimas et al., 2004; Freeman and Morley 2004; Valdivia et al., 2006; Spencer et al., 2018). These models provide information 1) that can be used to test our physical understanding about how the solar-wind-driven system works, 2) that can inform us about which parameters in the solar wind are key to controlling the reaction of the magnetosphere-ionosphere system, 3) about the global modes of reaction of the magnetosphere to the solar wind, 4) about the flow of information into and through the system, and 5) about where in the system chaotic behaviors emerges. These system methods can improve our scientific knowledge of the magnetosphere (e.g., the uncovering of secondary modes of reaction of the Earth system to the solar wind (Borovsky and Osmane, 2019) and can uncover improved ways to predict space weather (e.g., the expectation of accurately predicting the reaction of the Earth-system to as-yet-unseen severe levels of solar-wind driving (Borovsky and Denton, 2018)). Note that, at present, system science methods do not appear to be used yet in their most general form for space weather prediction outside academia.

Global Magnetospheric Models

In what at first might appear as an unrelated topic of magnetospheric research, global magnetospheric models have long been used to describe and understand the behavior of the Earth’s magnetosphere. Initial efforts focused on a fluid magnetohydrodynamics (MHD) description of the solar wind and magnetospheric plasmas, owing to the limitations in available computer power (Gombosi et al., 2000; Raeder et al., 2001a; White et al., 2001; Lyon et al., 2004). More recently global magnetospheric models are evolving towards a description of the underlying kinetic plasma beyond MHD, acknowledging the importance of non-MHD physics for several key processes operating in the magnetosphere, such as solar-wind/magnetosphere coupling (day-side reconnection, plasma entry, Kelvin-Helmholz coupling), the ion foreshock, tail reconnection, and for wave-particle interactions [see the discussion in Palmroth et al., 2018]. This is in part because MHD becomes problematic for thin boundary layers such as those at the bow shock and the magnetopause. Examples of beyond-MHD approaches at various stages of development include more-sophisticated fluid models (Wang et al., 2018), hybrid approaches that treat ions kinetically and electrons as a massless fluid (Karimabadi et al., 2014; Lin et al., 2017; Palmroth et al., 2018; Omelchenko et al., 2021), spectral methods (Koshkarov et al., 2021) and MHD models locally coupled with kinetic solvers (Daldorff et al., 2014; Chen et al., 2017). Global magnetospheric models are also becoming more complex in terms of the number of sub-systems that they include. For instance, global MHD models have evolved to include ionospheric models (Fedder and Lyon, 1987; White et al., 2001; Raeder et al., 2001b; Wang et al., 2004; Ridley et al., 2004), ion outflow (Winglee, 2000; Glocer et al., 2009; Brambles et al., 2010), plasmaspheric models (Ouellette et al., 2016; Glocer et al., 2020), inner magnetospheric models to capture drift physics (Toffoletto et al., 2004; Welling and Ridley, 2010; Jordanova et al., 2018), and, as mentioned above, some embed kinetic solvers locally (Chen et al., 2017).

One critical aspect of global magnetospheric models is validation against spacecraft observations. Earlier works focused on applying global MHD codes to specific event challenges (Raeder et al., 1997; Ridley et al., 2002), which led to community-wide event challenges to assess the performance of different codes against observational data (see for instance Pulkkinen et al., 2013). This type of study is very useful in identifying the general trends of different models, in providing physics support and understanding magnetospheric reactions, and in providing comparisons with other codes. However, it is limited in its ability to achieve true validation in light of uncertainties in initial conditions, in particular the lack of knowledge of the actual solar wind hitting the magnetosphere (e.g., Borovsky, 2018; Walsh et al., 2019), boundary conditions, and lack of adequate physics that make it hard to really capture the local spatial and temporal variability of the magnetosphere. Indeed, the magnetosphere is a high-Reynolds number system that can exhibit unpredictable and chaotic behavior.¹. Attempts to reproduce all details of its spatial and temporal variability should be taken with a “grain of salt”.

Recognizing the limitations just described, other efforts have taken a statistical approach to model validation. Some of these approaches still involve a direct comparison with data. For instance, Ridley et al. (2016) analyzed 662 global MHD simulations at the Community Coordinated Modeling Center to make statistical comparisons of different MHD codes against spacecraft magnetic field measurements. They concluded that models perform worse for higher geomagnetic activity and that coupling global MHD codes with inner magnetospheric models produced statistically better results (the latter conclusion agrees with Rastatter et al. (2013)). Other approaches do not involve a direct comparison with data but rather a ‘behavioral’ comparison against expressions derived from data. White et al. (2001) used the ISM code to study turbulent transport in the magnetotail under various IMF conditions and computed autocorrelation functions that were in reasonable agreement with autocorrelation functions calculated from ISEE-2 spacecraft measurements in the magnetotail. Specifically, the simulations could recover the general ordering of the decorrelation times for magnetic field component B_x, density n and magnetic field components B_y and B_z and the fact that the velocity components decorrelated more rapidly than the magnetic field components and density (Fig. 4 of White et al. (2001)) but could not recover the long tails seen in the data. El-Alaoui et al. (2013) studied plasma-sheet turbulence with MHD simulations and compared simulation power spectral densities against power spectral densities calculated from THEMIS spacecraft data, finding good agreement in the inertial range but not in the dissipative range. Gordeev et al. (2015) used different MHD models to evaluate several quantities representative of magnetospheric activity (examples include the subsolar magnetopause distance or the cross polar cap potential) against empirical relations obtained from spacecraft data. They found that no code provided satisfactory scores for all the magnetospheric variables considered. Haiducek et al. (2020) performed a month-long MHD simulation wherein over 100 substorms occurred: to validate the model for substorm occurrence, a distribution of substorm-to-substorm waiting times from the code was compiled and compared to equivalent distributions created from geomagnetic indices. The comparison showed a magnetospheric response in the code that was qualitatively similar to that observed for the real magnetosphere. The MHD simulation was also shown to have a small but statistically significant skill in predicting substorm occurrence times.

Discussion: System Science of Global Magnetospheric Models

In this perspective, we point out the need to apply system science tools to global magnetospheric models to understand if the system behavior of the global models is the same as the system behavior of the real magnetosphere and to overcome the limitations described above. There are clear advantages to this strategy. First, this approach offers the opportunity to validate the global models statistically, without attempting a direct comparison with spacecraft measurements in a high-Reynolds-number magnetosphere. Second, insight could be gained from a side-by-side statistical comparison of system science techniques applied to the outputs of global models and to spacecraft data. One could look at classic quantities of non-linear time series analysis (such as fractality, dimensionality, Lyapunov exponents, …) and check whether these quantities are the same in the models and in the real data. For those quantities that do not behave in the same manner, one can investigate why the behavior is different. From a correlation-analysis or information-analysis point of view, several natural questions immediately arise:

1) Are the same solar-wind variables important in the simulation as in the real system?

2) Is the derived driver function for the simulation similar to the derived driver function of the real system?

3) Are the time lags the same in the simulation and the real system?

4) Does the simulation show the same degrees of correlation as does the real system?

5) Does the simulation show the same modes of reaction to the solar wind as does the real system?

6) Does the code exhibit the same patterns of information flow as does the magnetosphere?

Third, as a corollary to the previous point, the system science of global models will facilitate exposing the deficiencies of the models. By turning on and off certain couplings in the simulations, one could ascertain how well the simulations reproduce the statistical correlations of the real system and what is the sensitivity to the various coupling elements. This will also provide guidance on what parts of the global models need more improvement. Fourth, from the perspective of system science of the real data, it could provide the physics basis to understand the meaning of the driver functions and state vectors identified by system science tools.

To enable the application of system science tools to global models and its comparison against data, the first step is to determine a set of measurements from the global simulations and match them with an equivalent set of measurements in the magnetospheric system. Table 1 shows examples of such equivalent quantities. Initially one could look at a single quantity in the simulations and the equivalent quantity in the magnetosphere to 1) compare the statistical behaviors of the pair of quantities, and 2) discern if the correlations with the solar wind are similar. Next, time-dependent state vectors comprised of multiple quantities could be created with the goal of 1) discerning whether the simulations exhibit the same collective modes of reaction to the solar wind as does the magnetosphere, 2) discerning whether the simulations have similar composite scalars as does the magnetosphere, and 3) discerning whether the simulations have the same high vector-vector correlations with the solar wind as the magnetosphere does.

TABLE 1

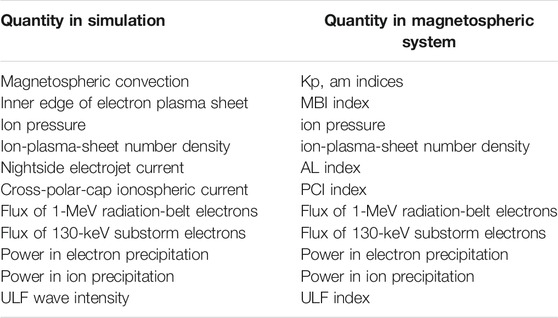
TABLE 1. Examples of equivalent quantities that could be compared between simulations and the magnetospheric systems.

An important question to consider is how much data would actually be needed to perform a meaningful system science analysis of global models. There are two distinct aspects to this point. The first is how much data from the solar wind input is necessary to obtain a magnetospheric response that is sufficiently representative of the variability of the environment. The second is the computational cost to obtain the necessary data through the simulations. To answer the first point, we turn to the analysis performed by Borovsky and Denton (2018) (hereafter “BD2018”). They used canonical correlation analysis (CCA) to correlate 8 solar wind state variables and 11 magnetospheric state variables for the years 1991–2007, a total of 102,672 hourly points for each state variable, i.e., 102,672*19 = 1,950,768 total points. They found a high prediction efficiency (PE) of 84% and a correlation coefficient (CC) of 0.92. We have performed the same canonical correlation analysis on a subset of the data to understand the minimum dataset that would give us a similar PE and CC. To do this, we select samples with N_sample = 19*N points randomly from the whole dataset; perform CCA on those N_sample points; construct S₁ⁱⁿ (S₁^out) and E₁ⁱⁿ (E₁^out) from the CCA coefficients for points inside (outside) the sample; compute CC_in (CC_out) between the solar wind state vector S₁ⁱⁿ (S₁^out) and the magnetospheric state vector E₁ⁱⁿ (E₁^out); compute the linear regression relating S₁ⁱⁿ to E₁ⁱⁿ and S₁^out to E₁^out; use the linear regression formula to predict values of E₁ from S₁, for the data points within and outside the sample; compute PE_in and PE_out as in BD2018. We also compute the error of the coefficients of each state variable relative to those found in BD2018. For a generic coefficient C_i, we define the relative error as $\mathit{\epsilon }=ma{x}_i\frac{\left|C_i-C_i^{BD2018}\right|}{{\displaystyle {\sum }_i\left|C_i^{BD2018}\right|}}$. Note that we repeat this procedure 100 times and average the results, to reduce the noise associated with random sampling. The results are plotted in Figure 1A, where we show the relative error for the solar wind state vector (red line) and magnetospheric state vector (blue line) versus the number of points per variable N. One can see that in general there is a decreasing trend of the error and that with only 3 points per variable (i.e., 57 points) the error is fairly small, ∼10%. Figure 1B show CC and PE versus N. CC_in and PE_in are monotonically decreasing functions of N (note that for N = 1, CC_in = PE_in = 1 because CCA can fit the data points exactly) while CC_out and PE_out are monotonically increasing functions of N. Asymptotically, all quantities converge to the values of BD2018 computed from the whole dataset. N∼3-4 (7) is sufficient for CC_out (PE_out) to be within 3% of the results of BD2018, i.e., to be within the shaded area of Figure 1B. These results are consistent with those of Hair et al. (2010) who indicate that CCA can be applied effectively with only 10 data points per independent variable, showing that CCA is extremely robust and does not need a lot of data. Finally, we also note that applying CCA on the data for January 2005 (i.e., the same time interval used by Haiducek et al. (2020) to study substorm onset with global MHD) yields CC_in = 0.93, CC_out = 0.97, PE_in = 0.87, and PE_out = 0.79, with ${\mathit{ϵ}}_{SW}=0.09$ and ${\mathit{ϵ}}_{MS}=0.13$. Although preliminary, these results are very encouraging as they show that fairly little data is sufficient to enable effective multi-variable correlation analysis. In terms of computational performance, we note that currently global MHD codes are sufficiently fast to enable system-science studies. For instance, the data from January 2005 is sufficient for meaningful CCA and so the simulation output from Haiducek et al. (2020) could already be used for this purpose. As another example, the GAMERA-REMIX code (Zhang et al., 2019; Sorathia et al., 2020), which combines the GAMERA global MHD solver and the REMIX ionospheric potential solver, runs at ∼3,000 core-hours per hour of real time [K. Sorathia, private communication], implying that a simulation study that requires ∼200 hourly points could be completed with ∼600,000 core-hours. These performance numbers correspond to the high-resolution simulations, e.g., resolving plasma sheet mesoscale dynamics (Sorathia et al., 2021). This is a fairly small allocation on modern high-performance computing architectures. On the other hand, the cost of a single computational run of the more sophisticated global models under development is still very high. For instance, a representative simulation cost of the hybrid global code HYPERS is ∼1-million core-hrs for a 1-hour-long simulation of the Earth’s magnetosphere [Y. Omelchenko, private communication], extrapolated from the simulations presented in Omelchenko et al. (2021) for that specific resolution. As another example, the recent first 6D run of the hybrid global code Vlasiator cost ∼15-million core-hrs for a 30-minutes-long simulation of the coupled solar wind—magnetosphere system using the Earth’s dipole magnetic field [M. Palmroth, private communication]. Further computational optimization of the beyond-MHD global codes will be necessary to take full advantage of the upcoming exascale computing facilities and render statistical studies accessible with these codes. Note also that approaches targeting information theory have already been applied effectively without requiring as many simulation runs, e.g., Johnson et al. (2019) who are using transfer entropy to study causal relationships in a single global hybrid simulation run. We therefore conclude that a system science approach to global magnetospheric models is feasible with present-day tools and should be pursued. In general, it will be important to test a variety of system-science methods to obtain complementary information and understanding of the system.

FIGURE 1

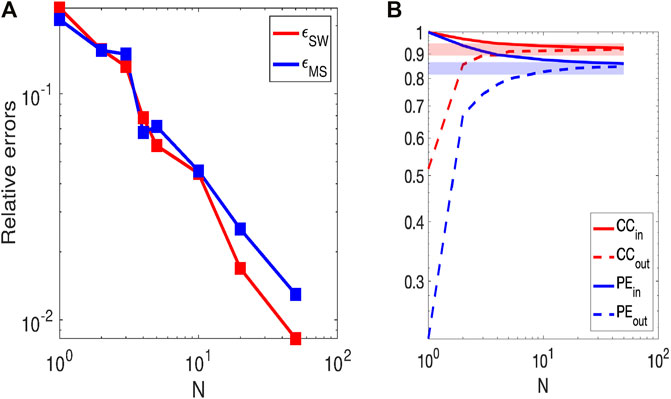
FIGURE 1. (A) Relative errors for the mean solar wind state (red line, maximum over 8 state variables) and magnetospheric (blue line, maximum over 11 state variables) coefficients as a function of the number of data points per independent variable N used in the canonical correlation analysis. The errors are relative to the results of Borovsky and Denton (2018). (B) Prediction efficiency and correlation coefficient as a function of N, obtained for points inside (solid line, labelled as “in”) and outside (dashed line, “out”) of a given sample. The shaded areas are within ±3% of CC (red) and PE (blue) evaluated in BD2018 over the whole dataset. See the text for more details.

As a final remark, we have focused this perspective on global magnetospheric models because of the general interest of the magnetospheric community to develop a holistic view of the magnetosphere. However, many of the same considerations are still applicable to the individual sub-systems and much could be learned from a side-by-side system science comparison of models and spacecraft data at the sub-system level.

Data Availability Statement

The data set used to perform the analysis shown in Figure 1 can be found in the Supplementary Material information of Borovsky and Denton (2018). The data of Figure 1 is provided as Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

GLD and JB both equally contributed to the ideas presented in the manuscript and to its writing.

Funding

GLD was supported by the Laboratory Directed Research and Development program at Los Alamos National Laboratory (LANL) under project 20220104DR. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (DOE) (Contract No. 89233218CNA000001). JB was supported at the Space Science Institute by the NSF GEM Program via grant AGS-2027569, by the NASA Heliophysics LWS program via award NNX16AB75G, by the NASA HERMES Interdisciplinary Science Program via grant 80NSSC21K1406, and by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer AO declared a past co-authorship with one of the authors JB to the handling Editor.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors wish to thank Humberto Godinez, Oleksandr Koshkarov, Slava Merkin, Yuri Omelchenko, Minna Palmroth, Vadim Roytershteyn, Kareem Sorathia and Simon Wing for useful conversations.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.808629/full#supplementary-material

Footnotes

¹Note, also, that collisionless or weakly-collisional plasmas can develop an effective viscosity due to kinetic physics that can be significantly larger than that induced by collisions (see, for instance, Squire et al. (2017)) and that, even if this might effectively lower the Reynolds number of the system, an MHD description would still be inadequate (see also the discussion in Borovsky and Gary (2009)).

References

Bargatze, L. F., Baker, D. N., McPherron, R. L., and Hones, E. W. (1985). Magnetospheric Impulse Response for many Levels of Geomagnetic Activity. J. Geophys. Res. 90, 6387–6394. doi:10.1029/ja090ia07p06387

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Denton, M. H. (2018). Exploration of a Composite index to Describe Magnetospheric Activity: Reduction of the Magnetospheric State Vector to a Single Scalar. J. Geophys. Res. Space Phys. 123, 7384–7412. doi:10.1029/2018ja025430

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Gary, S. P. (2009). On Shear Viscosity and the Reynolds Number of Magnetohydrodynamic Turbulence in Collisionless Magnetized Plasmas: Coulomb Collisions, Landau Damping, and Bohm Diffusion. Phys. Plasmas 16, 082307. doi:10.1063/1.3155134

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Osmane, A. (2019). Compacting the Description of a Time-dependent Multivariable System and its Multivariable Driver by Reducing the State Vectors to Aggregate Scalars: the Earth's Solar-Wind-Driven Magnetosphere. Nonlin. Process. Geophys. 26, 429–443. doi:10.5194/npg-26-429-2019

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2018). The Spatial Structure of the Oncoming Solar Wind at Earth and the Shortcomings of a Solar-Wind Monitor at L1. J. Atmos. Solar-Terrestrial Phys. 177, 2–11. doi:10.1016/j.jastp.2017.03.014

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Valdivia, J. A. (2018). The Earth's Magnetosphere: A Systems Science Overview and Assessment. Surv. Geophys. 39, 817–859. doi:10.1007/s10712-018-9487-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Brambles, O. J., Lotko, W., Damiano, P. A., Zhang, B., Wiltberger, M., and Lyon, J. (2010). Effects of Causally Driven Cusp O+ Outflow on the Storm Time Magnetosphere-Ionosphere System Using a Multifluid Global Simulation. J. Geophys. Res.:Space Phys. 115 (A9), A00J04. doi:10.1029/2010ja015469

CrossRef Full Text | Google Scholar

Chapman, S. C., Dendy, R. O., and Watkins, N. W. (2004). Robustness and Scaling: Key Observables in the Complex Dynamic Magnetosphere. Plasma Phys. Control Fusion 46, B157–B166. doi:10.1088/0741-3335/46/12b/014

CrossRef Full Text | Google Scholar

Chen, Y., Toth, G., Cassak, P., Jia, X., Gombosi, T. I., Slavin, J. A., et al. (2017). Global Three-Dimensional Simulation of Earth’s Dayside Reconnection Using a Two-Way Coupled Magnetohydrodynamics with Embedded Particle-In-Cell Model: Initial Results. J. Geophys. Res. Space Phys. 122 (1010318–10), 335. doi:10.1002/2017ja024186

CrossRef Full Text | Google Scholar

Daldorff, L. K. S., Tóth, G., Gombosi, T. I., Lapenta, G., Amaya, J., Markidis, S., et al. (2014). Two-way Coupling of a Global Hall Magnetohydrodynamics Model with a Local Implicit Particle-In-Cell Model. J. Comput. Phys. 268, 236–254. doi:10.1016/j.jcp.2014.03.009

CrossRef Full Text | Google Scholar

Dendy, R. O., and Chapman, S. C. (2006). Characterization and Interpretation of Strongly Nonlinear Phenomena in Fusion, Space and Astrophysical Plasmas. Plasma Phys. Control Fusion 48, B313–B328. doi:10.1088/0741-3335/48/12b/s30

CrossRef Full Text | Google Scholar

El-Alaoui, M., Richard, R. L., Ashour-Abdalla, M., Goldstein, M. L., and Walker, R. J. (2013). Dipolarization and Turbulence in the Plasma Sheet during a Substorm: THEMIS Observations and Global MHD Simulations. J. Geophys. Res. Space Phys. 118, 7752–7761. doi:10.1002/2013JA019322

CrossRef Full Text | Google Scholar

Fedder, J. A., and Lyon, J. G. (1987). The Solar Wind-Magnetosphere-Ionosphere Current-Voltage Relationship. Geophys. Res. Lett. 14, 880–883. doi:10.1029/gl014i008p00880

CrossRef Full Text | Google Scholar

Freeman, M. P., and Morley, S. K. (2004). A Minimal Substorm Model that Explains the Observed Statistical Distribution of Times between Substorms. Geophys. Res. Lett. 31, L128071–L128074. doi:10.1029/2004gl019989

CrossRef Full Text | Google Scholar

Fung, S. F., and Shao, X. (2008). Specification of Multiple Geomagnetic Responses to Variable Solar Wind and IMF Input. Ann. Geophys. 26, 639–652. doi:10.5194/angeo-26-639-2008

CrossRef Full Text | Google Scholar

Glocer, A., Toth, G., Gombosi, T., and Welling, D. (2009). Modeling Ionospheric Outflows and Their Impact on the Magnetosphere, Initial Results. J. Geophys. Res. 114, A05216. doi:10.1029/2009ja014053

CrossRef Full Text | Google Scholar

Glocer, A., Welling, D., Chappell, C. R., Toth, G., Fok, M.-C., Komar, C., et al. (2020). A Case Study on the Origin of Near-Earth Plasma. J. Geophys. Res. Space Phys. 125, e2020JA028205. doi:10.1029/2020ja028205

CrossRef Full Text | Google Scholar

Goertz, C. K., Shan, L.-H., and Smith, R. A. (1993). Prediction of Geomagnetic Activity. J. Geophys. Res. 98, 7673–7684. doi:10.1029/92ja01193

CrossRef Full Text | Google Scholar

Goertz, C. K., Smith, R. A., and Shan, L.-H. (1991). Chaos in the Plasma Sheet. Geophys. Res. Lett. 18, 1639–1642. doi:10.1029/91gl01782

CrossRef Full Text | Google Scholar

Gombosi, T. I., DeZeeuw, D. L., Groth, C. P. T., and Powell, K. G. (2000). Magnetospheric Configuration for Parker-spiral IMF Conditions: Results of a 3D AMR MHD Simulation. Adv. Space Res. 26, 139–149. doi:10.1016/s0273-1177(99)01040-6

CrossRef Full Text | Google Scholar

Gordeev, E., Sergeev, V., Honkonen, I., Kuznetsova, M., Rastätter, L., Palmroth, M., et al. (2015). Assessing the Performance of Community-Available Global MHD Models Using Key System Parameters and Empirical Relationships. Space Weather 13, 868–884. doi:10.1002/2015SW001307

CrossRef Full Text | Google Scholar

Haiducek, J. D., Welling, D. T., Morley, S. K., Ganushkina, N. Y., and Chu, X. (2020). Using Multiple Signatures to Improve Accuracy of Substorm Identification. J. Geophys. Res. Space Phys. 125, e2019JA027559. doi:10.1029/2019ja027559

CrossRef Full Text | Google Scholar

Hair, J. F., Black, W. C., Babin, B. J., and Anderson, R. E. (2010). Canonical Correlation: A Supplement to Multivariate Data Analysis. Upper Saddle River, New Jersey: Pearson Prentice Hall Publishing.

Google Scholar

Johnson, J., Cheng, L., Lin, Y., Wing, S., Wang, X., Perez, J. D., et al. (2019). A System Science Approach to Understanding the Coupling between Tail Flows and Alfvenic Poynting Flux in a Global Hybrid Simulation. American Geophysical Union, Fall meeting. Abstract #SM13F-3365.

Google Scholar

Jordanova, V. K., Delzanno, G. L., Henderson, M. G., Godinez, H. C., Jeffery, C. A., Lawrence, E. C., et al. (2018). Specification of the Near-Earth Space Environment with SHIELDS. J. Atmos. Solar-Terrestrial Phys. 177, 148–159. doi:10.1016/j.jastp.2017.11.006

CrossRef Full Text | Google Scholar

Karimabadi, H., Roytershteyn, V., Vu, H. X., Omelchenko, Y. A., Scudder, J., Daughton, W., et al. (2014). The Link between Shocks, Turbulence, and Magnetic Reconnection in Collisionless Plasmas. Phys. Plasmas 21 (6), 062308. doi:10.1063/1.4882875

CrossRef Full Text | Google Scholar

Klimas, A. J., Uritsky, V. M., Vassiliadis, D., and Baker, D. N. (2004). Reconnection and Scale-free Avalanching in a Driven Current-Sheet Model. J. Geophys. Res. 109, A02218 1–14. doi:10.1029/2003ja010036

CrossRef Full Text | Google Scholar

Klimas, A. J., Vassiliadis, D., and Baker, D. N. (1997). Data-derived Analogues of the Magnetospheric Dynamics. J. Geophys. Res. 102, 26993–27009. doi:10.1029/97ja02414

CrossRef Full Text | Google Scholar

Klimas, A. J., Vassiliadis, D., Baker, D. N., and Roberts, D. A. (1996). The Organized Nonlinear Dynamics of the Magnetosphere. J. Geophys. Res. 101, 13089–13113. doi:10.1029/96ja00563

CrossRef Full Text | Google Scholar

Koshkarov, O., Manzini, G., Delzanno, G. L., Pagliantini, C., and Roytershteyn, V. (2021). The Multi-Dimensional Hermite-Discontinuous Galerkin Method for the Vlasov-Maxwell Equations. Comp. Phys. Commun. 264, 107866. doi:10.1016/j.cpc.2021.107866

CrossRef Full Text | Google Scholar

Lakhina, G. S. (1994). Solar Wind-Magnetosphere-Ionosphere Coupling and Chaotic Dynamics. Surv. Geophys. 15, 703–754. doi:10.1007/bf00666091

CrossRef Full Text | Google Scholar

Lin, Y., Wing, S., Johnson, J. R., Wang, X. Y., Perez, J. D., and Cheng, L. (2017). Formation and Transport of Entropy Structures in the Magnetotail Simulated with a 3‐D Global Hybrid Code. Geophys. Res. Lett. 44 (12), 5892–5899. doi:10.1002/2017gl073957

CrossRef Full Text | Google Scholar

Liou, K., Sotirelis, T., and Richardson, I. (2018). Substorm Occurrence and Intensity Associated with Three Types of Solar Wind Structure. J. Geophys. Res. Space Phys. 123, 485–496. doi:10.1002/2017ja024451

CrossRef Full Text | Google Scholar

Lyon, J. G., Fedder, J. A., and Mobarry, C. M. (2004). The Lyon-Fedder-Mobarry (LFM) Global MHD Magnetospheric Simulation Code. J. Atmos. Solar-Terrestrial Phys. 66, 1333–1350. doi:10.1016/j.jastp.2004.03.020

CrossRef Full Text | Google Scholar

McPherron, R. L., Hsu, T.-S., and Chu, X. (2015). An Optimum Solar Wind Coupling Function for theALindex. J. Geophys. Res. Space Phys. 120, 2494–2515. doi:10.1002/2014ja020619

CrossRef Full Text | Google Scholar

Omelchenko, Y. A., Chen, L.-J., and Ng, J. (2021). 3D Space-Time Adaptive Hybrid Simulations of Magnetosheath High-Speed Jets. J. Geophys. Res. Space Phys. 126, e2020JA029035. doi:10.1029/2020ja029035

CrossRef Full Text | Google Scholar

Ouellette, J. E., Lyon, J. G., Brambles, O. J., Zhang, B., and Lotko, W. (2016). The Effects of Plasmaspheric Plumes on Dayside Reconnection. J. Geophys. Res. Space Phys. 121, 4111–4118. doi:10.1002/2016ja022597

CrossRef Full Text | Google Scholar

Palmroth, M., Ganse, U., Pfau-Kempf, Y., Battarbee, M., Turc, L., Brito, T., et al. (2018). Vlasov Methods in Space Physics and Astrophysics. Living Rev. Comput. Astrophys 4 (1), 1. doi:10.1007/s41115-018-0003-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavlos, G. P., Iliopoulos, A. C., Athanasiou, M. A., Karakatsanis, L. P., Tsoutsouras, V. G., Sarris, E. T., et al. (2011). Complexity in Space Plasmas: Universality of Non-equilibrium Physical Processes. AIP Conf. Proc. 1320, 77–81. doi:10.1063/1.3544341

CrossRef Full Text | Google Scholar

Pulkkinen, A. (2013). Community-wide Validation of Geospace Model Ground Magnetic Field Perturbation Predictions to Support Model Transition to Operations. SpaceWeather 11, 369–385. doi:10.1002/swe.20056

CrossRef Full Text | Google Scholar

Raeder, J., Berchem, J., Ashour-Abdalla, M., Frank, L. A., Paterson, W. R., Ackerson, K. L., et al. (1997). Boundary Layer Formation in the Magnetotail: Geotail Observations and Comparisons with a Global MHD Simulation. Geophys. Res. Lett. 24, 951. doi:10.1029/97gl00218

CrossRef Full Text | Google Scholar

Raeder, J., Wang, Y., and Fuller-Rowell, T. J. (2001b). “Geomagnetic Storm Simulation with a Coupled Magnetosphere-Ionosphere-Thermosphere Model,” in Space Weather. Editors P. Song, H. J. Singer, and G. L. Siscoe.

Google Scholar

Raeder, J., Wang, Y. L., Fuller-Rowell, T. J., and Singer, H. J. (2001a). Global Simulation of Magnetospheric Space Weather Effects of the Bastille Day Storm. Solar Phys. 204, 325–338. doi:10.1023/a:1014228230714

CrossRef Full Text | Google Scholar

Rastatter, L. (2013). Geospace Environment Modeling 2008–2009 challenge: Dst index. Space Weather 11, 187–205. doi:10.1002/swe.20036

CrossRef Full Text | Google Scholar

Ridley, A. J., De Zeeuw, D. L., and Rastatter, L. (2016). Rating Global Magnetosphere Model Simulations through Statistical Data-Model Comparisons. Space Weather 14, 819–834. doi:10.1002/2016sw001465

CrossRef Full Text | Google Scholar

Ridley, A. J., Gombosi, T., and De Zeeuw, D. L. (2004). Ionospheric Control of the Magnetospheric Configuration: Conductance. Ann. Geophys. 22, 567–584. doi:10.5194/angeo-22-567-2004

CrossRef Full Text | Google Scholar

Ridley, A. J., Hansen, K. C., Toth, G., De Zeeuw, D. L., Gombosi, T. I., and Powell, K. G. (2002). University of Michigan MHD Results of the Geospace Global Circulation Model Metrics challenge. J. Geophys. Res. 107 (A10), 1290. doi:10.1029/2001ja000253

CrossRef Full Text | Google Scholar

Sharma, A. S. (2014). Complexity in Nature and Data-Enabled Science: The Earth’s Magnetosphere. AIP Conf. Proc. 1582, 35–45.

Google Scholar

Sharma, A. S. (2010). The Magnetosphere: A Complex Driven System. AIP Conf. Proc. 1308, 120–131. doi:10.1063/1.3526148

CrossRef Full Text | Google Scholar

Smith, R. A., Goertz, C. K., and Grossman, W. (1986). Thermal Catastrophe in the Plasma Sheet Boundary Layer. Geophys. Res. Lett. 13, 1380–1383. doi:10.1029/gl013i013p01380

CrossRef Full Text | Google Scholar

Snyder, C. W., Neugebauer, M., and Rao, U. R. (1963). The Solar Wind Velocity and its Correlation with Cosmic-ray Variations and with Solar and Geomagnetic Activity. J. Geophys. Res. 68, 6361. doi:10.1029/jz068i024p06361

CrossRef Full Text | Google Scholar

Sorathia, K. A., Merkin, V. G., Panov, E. V., Zhang, B., Lyon, J. G., Garretson, J., et al. (2020). Ballooning‐Interchange Instability in the Near‐Earth Plasma Sheet and Auroral Beads: Global Magnetospheric Modeling at the Limit of the MHD Approximation. Geophys. Res. Lett. 47, 18. doi:10.1029/2020GL088227

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorathia, K. A., Michael, A., Merkin, V. G., Ukhorskiy, A. Y., Turner, D. L., Lyon, J. G., et al. (2021). The Role of Mesoscale Plasma Sheet Dynamics in Ring Current Formation. Front. Astron. Space Sci. 8, 761875. doi:10.3389/fspas.2021.761875

CrossRef Full Text | Google Scholar

Spencer, E., Vadepu, S. K., Srinivas, P., Patra, S., and Horton, W. (2018). The Dynamics of Geomagnetic Substorms with the WINDMI Model. Earth PlanetSpace 70, 118. doi:10.1186/s40623-018-0882-9

CrossRef Full Text | Google Scholar

Squire, J., Kunz, M. W., Quataert, E., and Schekochihin, A. A. (2017). Kinetic Simulations of the Interruption of Large-Amplitude Shear-Alfvén Waves in a High-β Plasma. Phys. Rev. Lett. 119, 155101. doi:10.1103/physrevlett.119.155101

PubMed Abstract | CrossRef Full Text | Google Scholar

Stepanova, M., and Valdivia, J. A. (2016). Contribution of Latin-American Scientists to the Study of the Magnetosphere of Earth. A Review. Adv. Space Res. 58, 1968–1985. doi:10.1016/j.asr.2016.03.023

CrossRef Full Text | Google Scholar

Toffoletto, F. R., Sazykin, S., Spiro, R. W., Wolf, R. A., and Lyon, J. G. (2004). RCM Meets LFM: Initial Results of One-Way Coupling. J. Atmos. Solar-terr. Phys. 66, 1361–1370. doi:10.1016/j.jastp.2004.03.022

CrossRef Full Text | Google Scholar

Valdivia, J. A., Rogan, J., Muñoz, V., Gomberoff, L., Klimas, A., Vassiliadis, D., et al. (2005). The Magnetosphere as a Complex System. Adv. Space Res. 35, 961. doi:10.1016/j.asr.2005.03.144

CrossRef Full Text | Google Scholar

Valdivia, J. A., Rogan, J., Muñoz, V., Toledo, B. A., and Stepanova, M. (2013). The Magnetosphere as a Complex System. Adv. Space Res. 51, 1934. doi:10.1016/j.asr.2012.04.004

CrossRef Full Text | Google Scholar

Valdivia, J. A., Rogan, J., Munoz, V., and Toledo, B. (2006). Hysteresis Provides Self-Organization in a Plasma Model. Space Sci. Rev. 122, 313–320. doi:10.1007/s11214-006-7846-2

CrossRef Full Text | Google Scholar

Vassiliadis, D., Sharma, A. S., and Papadopoulos, K. (1993). An Empirical Model Relating the Auroral Geomagnetic Activity to the Interplanetary Magnetic Field. Geophys. Res. Lett. 20, 1731–1734. doi:10.1029/93gl01351

CrossRef Full Text | Google Scholar

Vassiliadis, D. (2000). System Identification, Modeling, and Prediction for Space Weather Environments. IEEE Trans. Plasma Sci. 28, 1944–1955. doi:10.1109/27.902223

CrossRef Full Text | Google Scholar

Vassiliadis, D. (2006). Systems Theory for Geospace Plasma Dynamics. Rev. Geophys. 44, RG2002 1–39. doi:10.1029/2004rg000161

CrossRef Full Text | Google Scholar

Voros, Z. (1994). The Magnetosphere as a Nonlinear System. Studia Geophysica et Geodaetica 38, 168–186. doi:10.1007/bf02295912

CrossRef Full Text | Google Scholar

Walsh, B. M., Bhakyapaibul, T., and Zou, Y. (2019). Quantifying the Uncertainty of Using Solar Wind Measurements for Geospace Inputs. J. Geophys. Res. 124, 3291–3302. doi:10.1029/2019ja026507

CrossRef Full Text | Google Scholar

Wang, L., Germaschewski, K., Hakim, A., Dong, C., Raeder, J., and Bhattacharjee, A. (2018). Electron Physics in 3-D Two-Fluid 10-moment Modeling of Ganymede’s Magnetosphere. J. Geophys. Res. Space Phys. 123, 2815–2830. doi:10.1002/2017ja024761

CrossRef Full Text | Google Scholar

Wang, W., Wiltberger, M., Burns, A., Solomon, S., Killeen, T., Maruyama, N., et al. (2004). Initial Results from the Coupled Magnetosphere - Ionosphere - Thermosphere Model: Thermosphere - Ionosphere Responses. J. Atm. Solar-terr. Phys. 66, 1425–1441. doi:10.1016/j.jastp.2004.04.008

CrossRef Full Text | Google Scholar

Watkins, N. W., Freeman, M. P., Chapman, S. C., and Dendy, R. O. (2001). Testing the SOC Hypothesis for the Magnetosphere. J. Atmos. Solar-Terrestrial Phys. 63 (13), 1435–1445. doi:10.1016/s1364-6826(00)00245-5

CrossRef Full Text | Google Scholar

Watkins, N. W., Hnat, B., and Chapman, S. C. (2012). “On Self-Similar and Multifractal Models for the Scaling of Extreme Bursty Fluctuations in Space Plasmas,” in Extreme Events and Natural Hazards: The Complexity Perspective. Editors A. S. Sharma, A. Bunde, V. P. Dimri, and D. N. Baker. doi:10.1029/2011gm001084

CrossRef Full Text | Google Scholar

Watkins, N. W. (2002). Scaling in the Space Climatology of the Auroral Indices: Is SOC the Only Possible Description. Nonlin. Process. Geophys. 9, 389–397. doi:10.5194/npg-9-389-2002

CrossRef Full Text | Google Scholar

Welling, D. T., and Ridley, A. J. (2010). Validation of SWMF Magnetic Field and Plasma. Space Weather 8 (S03002), 1–11. doi:10.1029/2009sw000494

CrossRef Full Text | Google Scholar

White, W. W., Schoendorf, J. A., Siebert, K. D., Maynard, N. C., Weimer, D. R., Wilson, G. L., et al. (2001). “MHD Simulation of Magnetospheric Transport at the Mesoscale,” in Space Weather. Editors P. Song, H. J. Singer, and G. L. Siscoe.

Google Scholar

Wing, S., and Johnson, J. R. (2019). Applications of Information Theory in Solar and Space Physics. Entropy 21, 140. doi:10.3390/e21020140

PubMed Abstract | CrossRef Full Text | Google Scholar

Winglee, R. M. (2000). Mapping of Ionospheric Outflows into the Magnetosphere for Varying IMF Conditions. J. Atmos. Sol.-Terr. Phys. 62 (6), 527–540. doi:10.1016/s1364-6826(00)00015-8

CrossRef Full Text | Google Scholar

Zhang, B., Sorathia, K. A., Lyon, J. G., Merkin, V. G., Garretson, J. S., and Wiltberger, M. (2019). Gamera: A Three-Dimensional Finite-Volume Mhd Solver for Non-orthogonal Curvilinear Geometries. ApJS 244, 20. doi:10.3847/1538-4365/ab3a4c

CrossRef Full Text | Google Scholar