Modeling Long-Term Photometric Data of Trans-Neptunian Objects and Centaurs

1 Introduction

Trans-Neptunian objects (TNOs) are small Solar System bodies that orbit the Sun with orbital semi-major axes larger than that of Neptune but smaller than where the Oort Cloud begins (Oort, 1950; Gladman et al., 2008). They were formed outside of the frost line, namely, far enough from the Sun so that chemical compounds with low sublimation points (i.e., ices such as N₂, CO, and CH₄) were able to survive and condensate to form these objects. TNOs are therefore composed of a mixture of ices and silicates incorporated as grains during accretion from the solar nebula. Because of their large distances that separate them from the Sun, TNOs have undergone few thermo-chemical processes when compared with other small bodies in the Solar System. Hence, in some sense, these objects are time capsules containing almost pristine material from when the Solar System was formed. Thus, the study of TNOs provides important information about the primitive solar nebula.

When studying TNOs, it is also common to include the so-called Centaurs because these objects originally formed and have spent most of their life-time in the trans-Neptunian region (Horner et al., 2004) but have been injected into inner parts of the Solar System due to planetary encounters, mostly with Neptune (Fernandez, 1980). Therefore, Centaurs present an excellent opportunity to study smaller TNOs much closer to the Earth, providing a better characterization of their physical properties.

1.1 Synopsis on Trans-Neptunian Objects Formation

Current theoretical models suggest that the formation of planetesimals in the trans-Neptunian region was driven through the streaming instability, achieving up to ∼ 100 km in size (Johansen et al., 2015; Simon et al., 2016). These planetesimals would initially have a phase of collisional coagulation, with the largest objects acquiring a size of 300–400 km in radius (Lambrechts and Morbidelli, 2016), and then, those bodies would accrete individual pebbles (Lambrechts and Johansen, 2014; Lambrechts and Morbidelli, 2016). These physical processes are able to reproduce the primordial size distribution in the trans-Neptunian disk (Morbidelli and Nesvorný, 2020). Then, the massive disk phase took place, during which collisional activity was very intense (Morbidelli and Rickman, 2015), and TNOs suffered strong impacts that, without complete disruption, would convert them into gravitational aggregates. This implies that TNOs $>100$ km can be treated as a fluid in a first approximation.

1.2 Equilibrium Shapes for Homogeneous Bodies

A fluid, under the assumption of hydrostatic equilibrium with null angular momentum, L, would adopt a spherical shape with semi-axes a, b, and c (where a = b = c, see left panel in Figure 1). If the fluid rotates, i.e., L ≠ 0, then the fluid would adopt a MacLaurin spheroid shape (with a = b > c). This happens until $L=0.302\times {(G{M}^3\bar{a})}^{1/2}$, where G is the gravitational constant, M is the mass of the fluid, and $\bar{a}$ is the radius of a sphere of the same mass as the spheroid or ellipsoid that is given by ${(a^{2}c)}^{1/3}$, or (abc)^1/3, respectively. Beyond this point, the fluid can adopt a Jacobi ellipsoid shape (with a > b > c), as described with the mathematical formalism of Chandrasekhar (1969).

FIGURE 1

FIGURE 1. Equilibrium shapes for homogeneous bodies.

2 Short-Term Variability of Trans-Neptunian Objects and Centaurs

To understand the long-term photometric evolution of TNOs and Centaurs, first, we need to understand short-term variability and the reasons behind the different behaviors. The short-term variability of TNOs and Centaurs (and small bodies in general) is generally produced by the body’s rotational modulation, and it is commonly recognized as its rotational light-curve. It is also possible that the short-term variability might be caused by a binary system when one of the components is being occulted by the other; however, this would not be a rotational light-curve, because the variability would not be due to the rotational modulation of the object. Note that these light curves have specific shapes that differ from those explained below and should be carefully analyzed as explained by Harris and Warner (2020). The rotational light-curve of a small body is generally due to albedo variability on the surface, a non-spherical body shape, or a combination of both. Specifically, for TNOs and Centaurs, because of their large sizes, tumbling effects are not expected.

For MacLaurin spheroids, the rotational light-curve is expected to be featureless or flat, i.e., with no variability, unless the object presents an albedo spot (or several) that produces a variation in the amount of reflected light by the surface. This is the case of the dwarf planet Pluto, with a MacLaurin spheroid shape that presents a single-peaked rotational light-curve induced by the large N₂ albedo spot on its surface, although this case is somewhat atypical because the variability produced by the albedo spot is of 0.26 mag in V-band (Buratti et al., 2003). We do not expect a variability larger than 0.2 mag to be due to an albedo spot in asteroids (Degewij et al., 1979; Magnusson, 1991). This value is even smaller for TNOs, which usually do not produce variabilities larger than 0.1 mag due to albedo spots (Thirouin et al., 2010). However, this is for objects much smaller than Pluto that are not able to retain volatile material during large periods of time (i.e., over the age of the Solar System). Therefore, when the rotational light-curve presents a large peak-to-valley amplitude (above 0.2 mag), it is common to think that the variability is due to the body shape, with the rotational light-curve presenting a double-peaked shape.

An inspection of the rotational light-curve is important to determine whether the shape is double-peaked or single-peaked. For instance, a double-peaked rotational light-curve presenting different depths among the minima and maxima might indicate that a tri-axial shape is more likely than an oblate spheroid with an albedo spot. This is the case of (20000) Varuna (e.g., Jewitt et al., 2001; Fernández-Valenzuela et al., 2019), (84922) 2003 VS₂ (Vara-Lubiano et al., 2020), and (470599) 2008 OG₁₉ (Fernández-Valenzuela et al., 2019), among others. Note that detecting the difference between the brightness minima and/or the brightness maxima of the rotational light-curve requires high quality data, as is the case in the mentioned examples. In an opposite scenario, we found Pluto. If we plot Pluto’s rotational light-curve doubling its rotation period, then the resulting rotational light-curve will present a double-peaked shape with two identical minima and maxima. It is very unlikely that a Solar System object with a tri-axial shape would be identical along with its rotational modulation, being this an indication of an object with a single-peaked rotational light-curve due to an albedo spot.

For objects whose rotational light-curve is due to an albedo spot, i.e., a single-peaked rotational light-curve, the amplitude will indicate the difference in brightness produced by the different materials on their surfaces. On the other hand, for objects whose rotational light-curve is due to body shape, i.e., the amplitude of their rotational light-curve depends on the axial ratios and the aspect angle of the body¹ as follows:

$\mathrm{\Delta }m=-2.5\log \left[\frac{b}{a}{\left(\frac{a^2{\cos }^2\left(\delta \right)+c^2{\sin }^2\left(\delta \right)}{b^2{\cos }^2\left(\delta \right)+c^2{\sin }^2\left(\delta \right)}\right)}^{1/2}\right](1)$

(e.g., Surdej and Surdej, 1978; Pospieszalska-Surdej and Surdej, 1985) where Δm is the peak-to-valley amplitude of the rotational light-curve; δ is the aspect angle; and a, b, and c are the semi-axes of the tri-axial body (Figure 1). If we consider that the object has an aspect angle of 90°, the equation will be simplified as follows:

$\mathrm{\Delta }m=-2.5\log \left(\frac{b}{a}\right).(2)$

However, a Solar System object might present any aspect angle from 0° to 180°, and therefore, from a single rotational light-curve, it is only possible to obtain an upper limit of the axes ratio b/a.

3 Long-Term Variability of Trans-Neptunian Objects and Centaurs

The long-term variability of a TNO or Centaur is generally due to a change in the aspect angle of the body, δ, which is given by the following equation:

$\delta =\frac{\pi }{2}-\sin \left[\sin \left({\beta }_{\text{e}}\right)\sin \left({\beta }_{\text{p}}\right)+\cos \left({\beta }_{\text{e}}\right)\cos \left({\beta }_{\text{p}}\right)\cos \left({\lambda }_{\text{e}}-{\lambda }_{\text{p}}\right)\right],(3)$

where β_e and λ_e are the ecliptic latitude and longitude of the object reference frame and β_p and λ_p are the ecliptic latitude and longitude of the pole orientation of the body, i.e., the coordinates indicating the orientation (not direction²) of the rotational axis. Therefore, observing rotational light-curves at different orbit’s locations will result in different values of Δm, allowing the obtainment of the pole orientation of the body, by fitting Equations 1 and 3 to the observational data. This method has been extensively use for asteroids (Magnusson et al., 1989). However, for outer Solar System objects, this method was applied for the first time by Tegler et al. (2005) to the Centaur (5145) Pholus. They used observations of Pholus in three different epochs that produced three different values of Pholus’ rotational light-curve amplitude (0.15, 0.39, and 0.60 mag published in the works of Buie and Bus, 1992; Farnham, 2001; Tegler et al., 2005, respectively), obtaining two different pole orientations (with their supplementary direction also possible) and the axial ratios of Pholus tri-axial shape.

The change in the aspect angle affects not only Δm but also the absolute magnitude, H³, because the amount of area that is reflecting light from the Sun of a tri-axial body varies with δ. For a given epoch (i.e., a specific δ), the area of the body will be the average value from the rotational modulation of the object, i.e.,

$A\left(\delta \right)=\frac{{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\delta \right)+{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\delta \right)}{2},(4)$

where the maximum and minimum area exposed are given by the following equations:

${\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\text{max}}=\pi a{\left[b^2{\cos }^2\left(\delta \right)+c^2{\sin }^2\left(\delta \right)\right]}^{1/2},(5)$

and

${\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\text{min}}=\pi b{\left[a^2{\cos }^2\left(\delta \right)+c^2{\sin }^2\left(\delta \right)\right]}^{1/2}.(6)$

Thus, the absolute magnitude is given by the equation:

$H=-M_{\odot }+2.5\log \left(\frac{\pi C^2}{pA\left(\delta \right)}\right),(7)$

where M_⊙ is the absolute magnitude of the Sun, C = 1,330 ± 18 km is a constant (Masiero et al., 2021), and p is the geometric albedo of the object.

The long-term variability of the absolute magnitude, in which a change of the aspect angle is considered⁴, was first modeled for the centaur (10199) Chariklo in the work of Duffard et al. (2014), where a compilation of H values from the literature was done. Duffard et al. (2014) found variability of 0.6 mag in a time span of 10 years. One might think that this H magnitude variability could be due to the rotational modulation of the object, if those measurements were not corrected from it; however, this variability is much larger than any of Chariklo’s rotational light-curve amplitudes found in the literature (e.g., Peixinho et al., 2001; Fornasier et al., 2014). Therefore, this change in magnitude could not be due to rotational variability but due to a change in the aspect angle. From the stellar occultation produced by this object in 2013, Braga-Ribas et al. (2014) obtained the tri-axial shape of the object (i.e., values for a, b, and c) and two possible solutions for the pole orientation (with their supplementary directions also possible). Using those results, Duffard et al. (2014) found that only one of the solutions of the pole orientation is compatible with the observational data. The case of Chariklo is somewhat special because it possesses a ring system, which contributes enormously to this variation in absolute magnitude. This is because the variation of the exposed area of a ring is much larger than for a tri-axial body (see Figure 2C and section 4). In this case, Equation (7) needs to be modified as follows:

$H=-M_{\odot }+2.5\log \left(\frac{\pi C^2}{pA\left(\delta \right)+p_{\text{R}}{A}_{\text{R}}\left(\delta \right)}\right),(8)$

where p_R is the ring’s albedo and A_R = πR²| cos(δ)| is the area of the ring as a function of the aspect angle. Currently, there are four Centaurs and one TNO for which their long-term photometric behavior has been modeled: Pholus (Tegler et al., 2005), Chariklo (Duffard et al., 2014), (2060) Chiron (Ortiz et al., 2015), (54598) Bienor (Fernández-Valenzuela et al., 2017), and Varuna (Fernández-Valenzuela et al., 2019). For those objects, shape, pole orientation, and, more importantly, density have been obtained, with the exception of Chiron, for which its past comae behavior prevented from obtaining a good constrain of its shape, and, therefore, only allowing an estimation of the density).

FIGURE 2

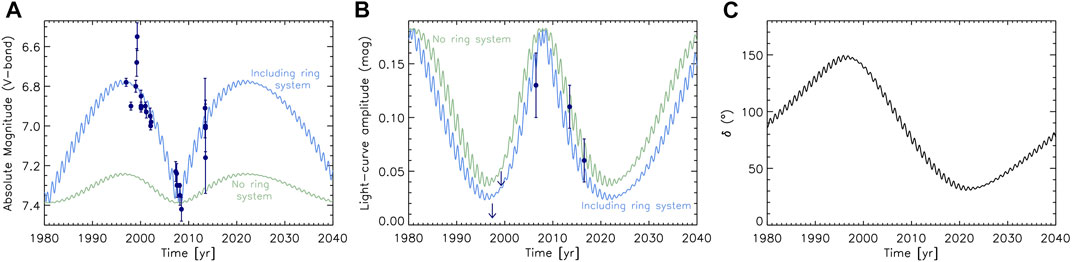
FIGURE 2. Comparison of Chariklo’s models with (blue lines) and without (green lines) the ring system for the absolute magnitude (A), addapted from Duffard et al. (2014), and the amplitude of the rotational light-curve (B). Dark blue circles and arrows (upper limits) represent observational data from the literature, Duffard et al. (2014), and references therein for panel (A); and Davies et al. (1998); Peixinho et al. (2001); Galiazzo et al. (2016); Fornasier et al. (2014); Leiva et al. (2017) for panel (B). Panel (C) provides the aspect angle of Chariklo over one orbital period.

Density is one of the most important properties to understand the interiors of the small bodies in the Solar System, and obtaining statistically meaningful results is pivotal for comprehending the Solar System formation and evolution. However, measuring density in small objects on the outer system is challenging. Density is usually obtained by studying binary systems or objects hosting satellites, but at the distances at which TNOs are found, the separation is generally too small to resolve the system and obtain its orbital properties. The Hubble Space Telescope (HST) was very successful when the High Resolution Camera was available. Currently, the Wide Field Camera on board HST can resolve objects separated over 0.04”, which is very limited for distances over 30 au. The James Webb Space Telescope (JWST) might provide a better resolution with NIRCam thanks to the exquisite Point Spread Function, but this needs still to be evaluated once the JWST is working. In any case, this technique is biased toward finding satellites or binary systems separated by at least the resolution of the instrument from which they are observed.

For single objects, studying the shape and rotation state is the only way to measure their density from ground-based observations. Good estimations can be obtained through the study of rotational light-curves (see, for instances, Tancredi and Favre, 2008; and Rambaux et al., 2017). However, the combination of multi-chord stellar occultations with rotational light-curves would provide the most accurate results. Rotational light-curves are needed not only to measure the rotation period but also to obtain the rotational phase at which the stellar occultation occurs, thus providing the three-dimensional shape of the object. Unfortunately, the statistic suggests that to observe a multi-chord stellar occultation, it is required to have at least 15 different observing sites distributed along the shadow path, which is not always possible (Ortiz et al., 2020).

An alternative technique would be the study of the long-term photometric behavior, fitting observational data and obtaining not only the pole orientation but also the shape (i.e., axial ratios). Because of the distances at which TNOs and Centaurs orbit the Sun, this technique has the inconvenience of requiring measurements taken with a time span in the order of decades. This is, the arc of the orbit traveled by the object needs to be large enough to produce a significant change in its aspect angle. Currently, it has been almost 30 years since the first TNO, 1992 QB₁ (without considering Pluto), was discovered (Jewitt and Luu, 1993) and the community has accumulated enough data of some objects that this might be a solution to obtain statistically meaningful results for the outer Solar System. This technique would also require us to assume hydrostatic equilibrium to obtain the density of these objects; however, as we discuss in Section 1.1, this seems to be a reasonable solution.

4 Extracting Peculiarities From Long-Term Variability

The long-term photometric data can serve as indications of different peculiarities, such as rings, in small bodies. Rings are located in the equator of the body, presenting very similar pole orientations (i.e., errors related to assuming the same pole orientation for the host body and the rings are negligible for our purpose). Both absolute magnitude and amplitude of the rotational light-curve will be affected if the body presents a ring (or rings). In the case of the absolute magnitude, when the system is found in an edge-on orientation, i.e., the aspect angle is close to 90°, the area reflecting light from the ring is negligible, with almost all the light being reflected by the host body. As the aspect angle changes to smaller values, the ring’s area that is reflecting light increases and starts to play an important role. When the system is found in a pole-on orientation, i.e., the aspect angle is close to 0°, the rings’ area is maximized contributing to a large percentage of the total brightness. Figure 2A shows a comparison between the expected evolution of Chariklo’s absolute magnitude when no ring system is included (in green) and with the ring system (in blue). It can be seen how, where the system is close to 90° or an edge-on orientation, both models agree in the expected absolute magnitude (around the years 1980 and 2008, see panel c for the evolution of the aspect angle); whereas for the rest of the epochs, the rings affect increasing enormously the brightness of the system. In the case of Δm (Figure 2B), the rings produce a shield effect when measuring Δm, resulting in a slightly smaller amplitude of what it is expected for a Jacobi ellipsoid shape.

Chiron presents a similar long-term photometric behavior as Chariklo but with a more complex scenario due to its cometary activity back in the 1970s (e.g., Kowal, 1979; Tholen et al., 1988; Meech and Belton, 1990). Chiron’s absolute magnitude was affected not only by the rings but also by the reflected light from the comae at that time. This was modeled in the work of Ortiz et al. (2015) that included an exponential brightness decay for the comae behavior (see figure 7 in Ortiz et al., 2015). The later work analyzed several stellar occultations produced by Chiron in different years and once again the long-term photometric models helped to distinguish between the two pole orientations offered by the analysis of the stellar occultations. Later, Cikota et al. (2018) obtained new data for both H and Δm compatible with the prediction of the models in Ortiz et al. (2015).

In the cases of Chiron and Chariklo, rings and cometary active were found prior to the fit of the long-term models, but it is clear that the absolute magnitude is highly affected by different characteristics that the body can host and long-term photometric data can show deviations from a simple hydrostatic equilibrium. This is the case for the centaur Bienor, for which its photometric behavior clearly deviates from that of a simple Jacobi ellipsoid shape (Fernández-Valenzuela et al., 2017). Different scenarios were studied by Fernández-Valenzuela et al. (2017), including rings, albedo variability, and shapes out the hydrostatic equilibrium. Although the different models cannot be statistically ruled out (see Tables 12 and 13 in Fernández-Valenzuela et al., 2017), it is clear that Bienor possesses some peculiarity yet to be discovered.

To date, only three small Solar System bodies have been discovered to possess rings: Chariklo (Braga-Ribas et al., 2014), Chiron (Ortiz et al., 2015; Ruprecht et al., 2015), and Haumea (Ortiz et al., 2017). The discovery of rings has opened a new brand of research in planetary science. Although some theories have been proposed for their formation, with collisions and rotational disruptions being the most plausible scenarios (see Braga-Ribas et al., 2014; Ortiz et al., 2015; Melita et al., 2017; Sicardy et al., 2019, and references therein), it is still not clear how they form and survive, especially for Centaurs that have suffered “recent” planetary encounters, or how common these features are in the outer solar region. To answer these open questions, more ring systems need to be discovered; however, their detection is extremely difficult, with the only known ground-based method to date being stellar occultations (which would require instrumental deployment in anywhere on the Earth, depending on where the shadow of the object is produced). A careful study of existing databases and analysis of long-term photometric data can point out what targets might be the most interesting in order to put our effort in specific campaigns for stellar occultation events, or to have a selection of targets to be observed with the future James Webb Space Telescope, or even visited by future spacecraft missions.

5 Conclusion

Long-term photometric measurements can be used to obtain different physical properties of TNOs and Centaurs, when the variability is driven by the change of the aspect angle of the object. Currently, this modelization has only been performed for four Centaurs and one TNO for which pole orientation, shape, and density have been obtained (with the exception of Chiron for which density was only estimated due to its comae behavior). Density is one of the most important properties about Solar System objects yet is one of the most difficult. To date, no more than 20 objects have density values with relative small uncertainties (e.g., Kiss et al., 2019). A larger number of objects with accurate density values is crucial to understand the evolution of the trans-Neptunian region and the material from the primitive solar nebula that was incorporated into TNOs at the time of their formation and would help interpreting the collisional history in the outer Solar System (Barr and Schwamb, 2016; Bierson and Nimmo, 2019).

Other peculiarities, such as shape out of the hydrostatic equilibrium, rings, or satellites can be inferred by analyzing the long-term variability of TNOs and Centaurs. In particular, rings extremely influence the absolute magnitude of the system, and therefore, exploring existing data of different objects whether in databases (as the Small Body Node within the Planetary Data System) or current and future surveys (e.g., the Vera Rubing Survey Telescope) might result in a source of targets in which to hunt these features; for instance, for dedicated campaigns to predict stellar occultations or even spacecraft visits. Specific campaigns to find more rings around small bodies are pivotal to statistically analyze how common these features are and, therefore, to understand their formation and survival around small bodies.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

EF-V acknowledges financial support from the Florida Space Institute and the Space Research Initiative. EF-V acknowledges Alvaro Alvarez-Candal and Yan Fernandez for their useful comments that help to improve this manuscript.

Footnotes

¹The aspect angle of a Solar System body is defined as the angle between the line of sight and its rotational axis.

²Because TNOs and Centaurs are far from the Earth, it is only possible to observe them at small phase angles (with a maximum of around 2° and 5° for TNOs and Centaurs, respectively), and therefore, the techniques used to obtain the direction of the rotational axis in asteroids cannot be carried out for objects beyond Jupiter.

³The absolute magnitude of a Solar System body is the apparent magnitude of the object when located at 1 au from the Sun, 1 au from the Earth, and 0° aspect angle.

⁴We should not confuse this long-term variability that is driven by the change in the aspect angle, with changes of brightness due to outburst or sudden cometary activity. Although some things can be done in this regard, as we describe for the case of Chiron, this kind of activity involves increase and decrease of brightness that behave completely different from the ones we are describing here.

References

Barr, A. C., and Schwamb, M. E. (2016). Interpreting the Densities of the Kuiper belt's dwarf Planets. Mon. Not. R. Astron. Soc. 460, 1542–1548. doi:10.1093/mnras/stw1052

CrossRef Full Text | Google Scholar

Bierson, C. J., and Nimmo, F. (2019). Using the Density of Kuiper Belt Objects to Constrain Their Composition and Formation History. Icarus 326, 10–17. doi:10.1016/j.icarus.2019.01.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Braga-Ribas, F., Sicardy, B., Ortiz, J. L., Snodgrass, C., Roques, F., Vieira-Martins, R., et al. (2014). A Ring System Detected Around the Centaur (10199) Chariklo. Nature 508, 72–75. doi:10.1038/nature13155

PubMed Abstract | CrossRef Full Text | Google Scholar

Buie, M. W., and Bus, S. J. (1992). Physical Observations of (5145) Pholus. Icarus 100, 288–294. doi:10.1016/0019-1035(92)90101-C

CrossRef Full Text | Google Scholar

Buratti, B., Hillier, J. K., Heinze, A., Hicks, M. D., Tryka, K. A., Mosher, J. A., et al. (2003). Photometry of Pluto in the Last Decade and before: Evidence for Volatile Transport. Icarus 162, 171–182. doi:10.1016/S0019-1035(02)00068-4

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1969). Ellipsoidal Figures of Equilibrium. Yale University Press.

Google Scholar

Cikota, S., Fernández-Valenzuela, E., Ortiz, J. L., Morales, N., Duffard, R., Aceituno, J., et al. (2018). Activity of (2060) Chiron Possibly Caused by Impacts. MNRAS 475, 2512–2518. doi:10.1093/mnras/stx3352

CrossRef Full Text | Google Scholar

Davies, J. K., McBride, N., Ellison, S. L., Green, S. F., and Ballantyne, D. R. (1998). Visible and Infrared Photometry of Six Centaurs. Icarus 134, 213–227. doi:10.1006/icar.1998.5931

CrossRef Full Text | Google Scholar

Degewij, J., Tedesco, E. F., and Zellner, B. (1979). Albedo and Color Contrasts on Asteroid Surfaces. Icarus 40, 364–374. doi:10.1016/0019-1035(79)90029-0

CrossRef Full Text | Google Scholar

Duffard, R., Pinilla-Alonso, N., Ortiz, J. L., Alvarez-Candal, A., Sicardy, B., Santos-Sanz, P., et al. (2014). Photometric and Spectroscopic Evidence for a Dense Ring System Around Centaur Chariklo. A&A 568, A79. doi:10.1051/0004-6361/201424208

CrossRef Full Text | Google Scholar

Farnham, T. (2001). The Rotation Axis of the Centaur 5145 Pholus. Icarus 152, 238–245. doi:10.1006/icar.2001.6656

CrossRef Full Text | Google Scholar

Fernández, J. A. (1980). On the Existence of a Comet belt beyond Neptune. MNRAS 192, 481–491. doi:10.1093/mnras/192.3.481

CrossRef Full Text | Google Scholar

Fernández-Valenzuela, E., Ortiz, J. L., Duffard, R., Morales, N., and Santos-Sanz, P. (2017). Physical Properties of Centaur (54598) Bienor from Photometry. Mon. Not. R. Astron. Soc. 466, stw3264–4158. doi:10.1093/mnras/stw3264

CrossRef Full Text | Google Scholar

Fernández-Valenzuela, E., Ortiz, J. L., Morales, N., Santos-Sanz, P., Duffard, R., Aznar, A., et al. (2019). The Changing Rotational Light-Curve Amplitude of Varuna and Evidence for a Close-In Satellite. ApJL 883, L21. doi:10.3847/2041-8213/ab40c2

CrossRef Full Text | Google Scholar

Fornasier, S., Lazzaro, D., Alvarez-Candal, A., Snodgrass, C., Tozzi, G. P., Carvano, J. M., et al. (2014). The Centaur 10199 Chariklo: Investigation into Rotational Period, Absolute Magnitude, and Cometary Activity. A&A 568, L11. doi:10.1051/0004-6361/201424439

CrossRef Full Text | Google Scholar

Galiazzo, M., de la Fuente Marcos, C., de la Fuente Marcos, R., Carraro, G., Maris, M., and Montalto, M. (2016). Photometry of Centaurs and Trans-neptunian Objects: 2060 Chiron (1977 UB), 10199 Chariklo (1997 CU26), 38628 Huya (2000 EB173), 28978 Ixion (2001 KX76), and 90482 Orcus (2004 DW). Astrophys Space Sci. 361, 212. doi:10.1007/s10509-016-2801-5

CrossRef Full Text | Google Scholar

Gladman, B., Marsden, B. G., and Vanlaerhoven, C. (2008). “Nomenclature in the Outer Solar System,” in The Solar System Beyond Neptune. Editors M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, and A. Morbidelli (Tucson, AZ: University of Arizona Press), Vol. 592, 43–57.

Google Scholar

Harris, A., and Warner, B. D. (2020). Asteroid Lightcurves: Can't Tell a Contact Binary from a brick. Icarus 339, 113602. doi:10.1016/j.icarus.2019.113602

CrossRef Full Text | Google Scholar

Horner, J., Evans, N. W., and Bailey, M. E. (2004). Simulations of the Population of Centaurs - I. The Bulk Statistics. MNRAS 354, 798–810. doi:10.1111/j.1365-2966.2004.08240.x

CrossRef Full Text | Google Scholar

Jewitt, D., Aussel, H., and Evans, A. (2001). The Size and Albedo of the Kuiper-belt Object (20000) Varuna. Nature 411, 446–447. doi:10.1038/35078008

PubMed Abstract | CrossRef Full Text | Google Scholar

Jewitt, D., and Luu, J. (1993). Discovery of the Candidate Kuiper belt Object 1992 QB1. Nature 362, 730–732. doi:10.1038/362730a0

CrossRef Full Text | Google Scholar

Johansen, A., Low, M.-M. M., Lacerda, P., and Bizzarro, M. (2015). Growth of Asteroids, Planetary Embryos, and Kuiper belt Objects by Chondrule Accretion. Sci. Adv. 1, 1500109. doi:10.1126/sciadv.1500109

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiss, C., Marton, G., Parker, A. H., Grundy, W. M., Farkas-Takács, A., Stansberry, J., et al. (2019). The Mass and Density of the dwarf Planet (225088) 2007 OR10. Icarus 334, 3–10. doi:10.1016/j.icarus.2019.03.013

CrossRef Full Text | Google Scholar

Kowal, C. T. (1979). “Chiron,” in Asteroids. Editors T. Gehrels, and M. Mildred Shapley (Tucson, AZ: University of Arizona Press), 436–439.

Google Scholar

Lambrechts, M., and Johansen, A. (2014). Forming the Cores of Giant Planets from the Radial Pebble Flux in Protoplanetary Discs. A&A 572, A107. doi:10.1051/0004-6361/201424343

CrossRef Full Text | Google Scholar

Lambrechts, M., and Morbidelli, A. (2016). “Reconstructing the Size Distribution of the Small Body Population in the Solar System,” in AAS/Division for Planetary Sciences Meeting Abstracts #48. vol. 48 of AAS/Division for Planetary Sciences Meeting Abstracts, 105.08.

Google Scholar

Leiva, R., Sicardy, B., Camargo, J. I. B., Ortiz, J.-L., Desmars, J., Bérard, D., et al. (2017). Size and Shape of Chariklo from Multi-Epoch Stellar Occultations. AJ 154, 159. doi:10.3847/1538-3881/aa8956

CrossRef Full Text | Google Scholar

Magnusson, P. (1991). Analysis of Asteroid Lightcurves. III. Albedo Variegation. A&A 243, 512–520.

Google Scholar

Magnusson, P., Barucci, M. A., Drummond, J. D., Lumme, K., Ostro, S. J., Surdej, J., et al. (1989). “Determination of Pole Orientations and Shapes of Asteroids,” in Asteroids II. Editors R. P. Binzel, T. Gehrels, and M. S. Matthews, 66–97.

Google Scholar

Masiero, J. R., Wright, E. L., and Mainzer, A. K. (2021). Uncertainties on Asteroid Albedos Determined by Thermal Modeling. Planet. Sci. J. 2, 32. doi:10.3847/PSJ/abda4d

CrossRef Full Text | Google Scholar

Meech, K. J., and Belton, M. J. S. (1990). The Atmosphere of 2060 Chiron. AJ 100, 1323. doi:10.1086/115600

CrossRef Full Text | Google Scholar

Melita, M. D., Duffard, R., Ortiz, J. L., and Campo-Bagatin, A. (2017). Assessment of Different Formation Scenarios for the Ring System of (10199) Chariklo. A&A 602, A27. doi:10.1051/0004-6361/201629858

CrossRef Full Text | Google Scholar

Morbidelli, A., and Nesvorný, D. (2020). “Kuiper belt: Formation and Evolution,” in The Trans-Neptunian Solar System. Editors D. Prialnik, M. Antoinetta Barucci, and L. Young (Elsevier), 25–59. doi:10.1016/B978-0-12-816490-7.00002-3

CrossRef Full Text | Google Scholar

Morbidelli, A., and Rickman, H. (2015). Comets as Collisional Fragments of a Primordial Planetesimal Disk. A&A 583, A43. doi:10.1051/0004-6361/201526116

CrossRef Full Text | Google Scholar

Oort, J. H. (1950). The Structure of the Cloud of Comets Surrounding the Solar System and a Hypothesis Concerning its Origin. Bain 11, 91–110.

Google Scholar

Ortiz, J. L., Santos-Sanz, P., Sicardy, B., Benedetti-Rossi, G., Bérard, D., Morales, N., et al. (2017). The Size, Shape, Density and Ring of the dwarf Planet Haumea from a Stellar Occultation. Nature 550, 219–223. doi:10.1038/nature24051

PubMed Abstract | CrossRef Full Text | Google Scholar

Ortiz, J. L., Duffard, R., Pinilla-Alonso, N., Alvarez-Candal, A., Santos-Sanz, P., Morales, N., et al. (2015). Possible Ring Material Around Centaur (2060) Chiron. A&A 576, A18. doi:10.1051/0004-6361/201424461

CrossRef Full Text | Google Scholar

Ortiz, J. L., Sicardy, B., Camargo, J. I. B., Santos-Sanz, P., and Braga-Ribas, F. (2020). “Stellar Occultations by Trans-Neptunian Objects: From Predictions to Observations and Prospects for the Future,” in The Trans-Neptunian Solar System. Editors D. Prialnik, M. Antoinetta Barucci, and L. Young (Elsevier), 413–437. doi:10.1016/B978-0-12-816490-7.00019-9

CrossRef Full Text | Google Scholar

Peixinho, N., Lacerda, P., Ortiz, J. L., Doressoundiram, A., RoosSerote, M., and Gutiérrez, P. J. (2001). Photometric Study of Centaurs 10199 Chariklo (1997 CU$_\mathsf{26}$) and 1999 UG$_\mathsf{5}$. A&A 371, 753–759. doi:10.1051/0004-6361:20010382

CrossRef Full Text | Google Scholar

Pospieszalska-Surdej, A., and Surdej, J. (1985). Determination of the Pole Orientation of an Asteroid - the Amplitude-Aspect Relation Revisited. A&A 149, 186–194.

Google Scholar

Rambaux, N., Baguet, D., Chambat, F., and Castillo-Rogez, J. C. (2017). Equilibrium Shapes of Large Trans-neptunian Objects. ApJ 850, L9. doi:10.3847/2041-8213/aa95bd

CrossRef Full Text | Google Scholar

Ruprecht, J. D., Bosh, A. S., Person, M. J., Bianco, F. B., Fulton, B. J., Gulbis, A. A. S., et al. (2015). 29 November 2011 Stellar Occultation by 2060 Chiron: Symmetric Jet-like Features. Icarus 252, 271–276. doi:10.1016/j.icarus.2015.01.015

CrossRef Full Text | Google Scholar

Sicardy, B., Leiva, R., Renner, S., Roques, F., El Moutamid, M., Santos-Sanz, P., et al. (2019). Ring Dynamics Around Non-axisymmetric Bodies with Application to Chariklo and Haumea. Nat. Astron. 3, 146–153. doi:10.1038/s41550-018-0616-8

CrossRef Full Text | Google Scholar

Simon, J. B., Armitage, P. J., Li, R., and Youdin, A. N. (2016). The Mass and Size Distribution of Planetesimals Formed by the Streaming Instability. I. The Role of Self-Gravity. ApJ 822, 55. doi:10.3847/0004-637X/822/1/55

CrossRef Full Text | Google Scholar

Surdej, A., and Surdej, J. (1978). Asteroid Lightcurves Simulated by the Rotation of a Three-Axes Ellipsoid Model. A&A 66, 31–36.

Google Scholar

Tancredi, G., and Favre, S. (2008). Which Are the Dwarfs in the Solar System. Icarus 195, 851–862. doi:10.1016/j.icarus.2007.12.020

CrossRef Full Text | Google Scholar

Tegler, S. C., Romanishin, W., Consolmagno, G. J., Rall, J., Worhatch, R., Nelson, M., et al. (2005). The Period of Rotation, Shape, Density, and Homogeneous Surface Color of the Centaur 5145 Pholus. Icarus 175, 390–396. doi:10.1016/j.icarus.2004.12.011

CrossRef Full Text | Google Scholar

Thirouin, A., Ortiz, J. L., Duffard, R., Santos-Sanz, P., Aceituno, F. J., and Morales, N. (2010). Short-term Variability of a Sample of 29 Trans-neptunian Objects and Centaurs. A&A 522, A93. doi:10.1051/0004-6361/200912340

CrossRef Full Text | Google Scholar

Tholen, D. J., Hartmann, W. K., Cruikshank, D. P., Lilly, S., Bowell, E., and Hewitt, A. (1988). Chiron. IAUC 4554 (2060), 2.

Google Scholar

Vara-Lubiano, M., Benedetti-Rossi, G., Santos-Sanz, P., Ortiz, J. L., Sicardy, B., Popescu, M., et al. (2020). “The 2019 October 22nd Multi-Chord Stellar Occultation by (84922) 2003 VS2,” in 14th Europlanet Science Congress 2020, September 21–October 9, 2020. EPSC2020–1041. Available at: https://www.epsc2020.eu/

Google Scholar