The spectral features and detectability of small, cyclic silicon carbide clusters

Rovibrational spectral data for several tetra-atomic silicon carbide clusters (TASCCs) are computed in this work using a CCSD(T)-F12b/cc-pCVTZ-F12 quartic force field. Accurate theoretical spectroscopic data may facilitate the observation of TASCCs in the interstellar medium which may lead to a more complete understanding of how the smallest silicon carbide (SiC) solids are formed. Such processes are essential for understanding SiC dust grain formation. Due to SiC dust prevalence in the interstellar medium, this may also shed light on subsequent planetary formation. Rhomboidal Si₂C₂ is shown here to have a notably intense (247 km mol⁻¹) anharmonic vibrational frequency at 988.1 cm⁻¹ (10.1 μm) for ν₂, falling into one of the spectral emission features typically associated with unknown infrared bands of various astronomical regions. Notable intensities are also present for several of the computed anharmonic vibrational frequencies including the cyclic forms of C₄, SiC₃, Si₃C, and Si₄. These features in the 6–10 μm range are natural targets for infrared observation with the James Webb Space Telescope (JWST)’s MIRI instrument. Additionally, t-Si₂C₂, d-Si₃C, and r-SiC₃ each possess dipole moments of greater than 2.0 D making them interesting targets for radioastronomical searches especially since d-SiC₃ is already known in astrophysical media.

Introduction

Small silicon carbide (SiC) clusters are hypothesized to be an integral step in the process that begins with the nucleosynthesis of carbon and silicon in small, carbonaceous asymptotic giant branch (AGB) stars and leads to the formation of SiC dust grains found in the interstellar medium (ISM) (Mélinon et al., 2007). Several steps along the process of formation from the atomic level to fractal aggregate dust grain structures are not entirely known (Matthews et al., 2007), but their aggregation is thought to have a direct impact on protoplanetary disk formation. Understanding the composition of stellar atmospheres and nebulae may lead to newfound insight into these processes of dust formation.

The only direct way to study interstellar dust grains is through chemical inspection of primitive chondrite meteorites which accreted before the formation of our Solar System. A chemical isolation technique for SiC dust grains found on primitive chondrite meteorites has long been established (Bernatowicz and Fraundorf., 1987; Nittler and Alexander, 2003) and has shown that SiC dust grains are prevalent in proto-planetary dust clouds. The prevalence of these grains on chondrite meteorites may indicate that SiC species should be targeted for observation in the unidentified infrared/microwave spectra of the interstellar medium.

In addition to terrestrial identification from meteorites containing proto-solar SiC dust grains, some SiC clusters have been accurately identified in stellar environments of carbonaceous AGB stars. The diatomic radical, SiC (Cernicharo and Gottlieb., 1989) along with the triatomic radical (Thaddeus et al., 1984) and closed-shell (Prieto et al., 2015) species of SiC₂ and Si₂C (Cernicharo et al., 2015), have all been identified in the circumstellar envelope of IRC+10216 (CW Leo). The only cyclic tetra-atomic species identified to date in the ISM is SiC₃ (Apponi and McCarthy., 1999a), which was also detected in the aforementioned star IRC+10216. These species have all been detected with rotational spectroscopy. Such observations suggest that the SiC chemistry of these astronomical regions may be richer than has been observed to date. However, the observations so far have been limited to molecules with permanent dipole moments allowing for their detection via rotational spectroscopy. With the new JWST, similar molecules without dipole moments, such as some tetra-atomic silicon carbide clusters (TASCCs), may now be observable by infrared spectroscopy, but the data needed to elucidate such spectra first need to be generated here on Earth.

To that end, the spectral data for the pure carbon cluster, rhomboidal (r-)C₄, has been extensively studied both experimentally (Algranati et al., 1989; Blanksby et al., 2000) as well as theoretically (Martin et al., 1996; Martin and Taylor, 1996; Varandas and Rocha, 2018; Wang and Whithey, 2018) at many different levels of theory including at the CCSD(T)/cc-pCV5Z level of theory by Wang and Bowman in 2013 (Wang and Bowman, 2013). In stepping into the silicon analogues of this molecule, cyclic SiC₃ includes two C_2v isomers, one exhibiting a transannular C-C bond and the other a transannular Si-C bond. The former will be referred to as diamond SiC₃, or d-SiC₃ hereafter. The d-SiC₃ isomer, in particular has been a focus of previous theoretical and experimental work as it is currently the only cyclic tetra-atomic species identified in the ISM (Apponi and McCarthy., 1999a). Thus, previous theoretical (Linguerri et al., 2006), experimental microwave spectroscopy (Apponi and McCarthy., 1999b; McCarthy et al., 2019), and astronomically-observed (Apponi and McCarthy., 1999a; McCarthy et al., 2019) spectral data are available. The isomer of SiC₃ with a transannular Si-C bond, which will be referred to as r-SiC₃ hereafter, has been previously studied theoretically (Linguerri et al., 2006) and experimentally (McCarthy et al., 1999). While some spectral data do exist, the complete set of spectral data have yet to be produced especially for vibrational spectra of these SiC₃ isomers. As such, the existing experimental data for these molecules will serve to benchmark the computations performed herein, but new data will also be provided beyond these benchmarks.

Two isomers of Si₂C₂, a rhomboidal D_2h structure with a transannular C-C bond and a C_s trapezoidal isomer with a transannular Si-C bond, have been studied experimentally (Presilla-Márquez et al., 1995) using vibrational spectroscopy. The r-Si₂C₂ species with a C-C transannular bond has also been theoretically studied using density functional theory (DFT) at the B3LYP/6-311G(3df) level of theory (Yadav et al., 2006). Trapezoidal (t-)Si₂C₂ and r-Si₂C₂ isomers with transannular Si-Si bonds have only been studied theoretically at the MP2/6-31G* level (Lammertsma and Güner, 1988). A higher level of theory could be useful in corroborating these early computations making more modern computations on these structures necessary.

Two isomers of Si₃C are studied in this work. Like with the SiC₃ isomers, r-Si₃C exhibits a transannular Si-C bond, while d-Si₃C possesses a transannular Si-Si bond. The r-Si₃C isomer has been studied in the laboratory via vibrational spectroscopy (Presilla-Márquez and Graham, 1992; Stanton et al., 2005; Truong et al., 2015). Both isomers have only been theoretically studied in regards to their spectroscopic constants (Rittby, 1992) more than 30 years ago at the Hartree-Fock level of theory. Lastly, only the r-Si₄ cation has been both theoretically and experimentally studied (Savoca et al., 2012). Conversely, theoretical spectral data are currently unavailable for the neutral species of r-Si₄ leaving the door open for a more complete theoretical analysis and spectroscopic characterization of these structures.

Despite all the previous work discussed previously, high level theoretical methods have only been applied to three of the nine TASCCs with various levels of spectral completeness reported. Additionally, one experimental study has investigated the spectral data of heteroatomic TASCCs (Babin et al., 2021), while another study has undertaken DFT analysis with the 6-311G* basis set for various TASCC cations (Lavendy et al., 1997). The current work applies recent advancements in modern approaches to all nine TASCCs herein including the first high-level computations for the remaining six species. By covering every combination of Si and C in a tetra-atomic molecule, this work will examine the effect of silicon doping on the IR emission bands for carbide clusters, which previously has only been briefly studied (Inostroza et al., 2008; Savoca et al., 2013), and no work has studied this effect on TASCCs.

In light of a need for modern approaches, this work utilizes quartic force field (QFF) methods to produce highly-accurate, explicit anharmonic vibrational frequencies, rotational constants, and other spectroscopic constants for each of the molecules studied herein. A QFF is a fourth-order Taylor series expansion of the potential portion of the internuclear Watson Hamiltonian (Fortenberry and Lee, 2019). Previous work has shown that QFF techniques produce fundamental anharmonic frequencies that are accurate to within 5–7 cm⁻¹ of gas-phase vibrational frequencies and within about 20 MHz of experimental rotational constants (Huang and Lee, 2008, 2009; Huang et al., 2011; Fortenberry et al., 2012; Huang et al., 2013; Fortenberry et al., 2014a, 2015; Zhao et al., 2014; Kitchens and Fortenberry, 2016; Bizzocchi et al., 2017; Fortenberry et al., 2018a; Valiev et al., 2020; Gardner et al., 2021). These constants may be used to aid in determination of the molecules responsible for unidentified peaks in the infrared and microwave spectra in nebulae, gas clouds, circumstellar envelopes, or other astronomical environments. Accurate characterization of these environments may lead to a more complete understanding of the processes that lead to their evolution possibly including dust nucleation and planet formation. Vibrational observation may be promising for the novel molecules studied herein as JWST’s MIRI instrument can resolve spectra at frequencies down to roughly 350 cm⁻¹ (28 μm).

Computational methods

The present QFFs are computed at two different levels of theory for each TASCC. Both methods use coupled cluster theory at the singles, doubles, and perturbative triples level (Raghavachari et al., 1989) within the explicitly correlated F12b formalism, or CCSD(T)-F12b (Adler et al., 2007; Peterson et al., 2008; Knizia et al., 2009; Huang et al., 2010). The first QFF method utilizes the cc-pVTZ-F12 basis set alone, and this combination will henceforth be abbreviated as “F12-TZ”. F12-TZ has been shown to yield accurate results for vibrational frequencies, within 5–7 cm⁻¹ compared to gas-phase experiment, and it still exhibits far greater time savings than previously used composite, coupled cluster methods (Agbaglo et al., 2019; Agbaglo and Fortenberry, 2019a,b; Gardner et al., 2021). The second QFF method employs the cc-pCVTZ-F12 (Hill and Peterson, 2010) basis set to include the effects from core electron correlation (cC) with additional corrections for scalar relativity (R). This composite method is hereafter abbreviated “F12-TZ-cCR” (Watrous et al., 2021). In addition to including core correlation in the computation, the F12-TZ-cCR method utilizes Douglas-Kroll scalar relativistic corrections (Douglas and Kroll, 1974) in its single-point energy computations at the CCSD(T)/cc-pVTZ-DK level of theory to produce a more accurate description of the potential energy surface for an increased computational cost relative to F12-TZ that is still far less than the composite methods used previously.

All of the QFFs reported in this work are computed in the same, general manner beginning with the optimization of the molecular geometry with the CCSD(T)-F12b method whether excluding (F12-TZ) or including (F12-TZ-cCR) core electron correlation in the computation. All also utilize the MOLPRO 2020.1 quantum chemical program (Werner et al., 2020). The resulting optimized geometry serves as a reference point from which the INTDER program (Allen., 2005) displaces bond lengths and angles/torsions by 0.005 Å and radians, respectively (Huang and Lee, 2008). For the tetra-atomic D_4h and D_2h molecules, such as rhomboidal C₄ and Si₄ and the rhomboidal and diamond isomers of Si₂C₂, 233 displacement points are required utilizing the following symmetry-internal coordinates (SICs) with atomic labels, as shown in Figure 1. QFFs of this connectivity have previously employed such a coordinate system (Westbrook and Fortenberry, 2020).

$S_1\left(a_g\right)=\frac{1}{\sqrt{2}}\left[r\left({\text{Si}}_1-{\text{Si}}_4\right)+r\left({\text{C}}_2-{\text{C}}_3\right)\right](1)$

$S_2\left(a_g\right)=\frac{1}{\sqrt{2}}\left[r\left({\text{Si}}_1-{\text{Si}}_4\right)-r\left({\text{C}}_2-{\text{C}}_3\right)\right](2)$

$\begin{array}{cc}\hfill S_3\left(b_{3g}\right)=& \frac{1}{2}\left[r\left({\text{Si}}_1-{\text{C}}_2\right)-r\left({\text{Si}}_1-{\text{C}}_3\right)-r\left({\text{C}}_2-{\text{Si}}_4\right)\right.\hfill \\ \hfill & +\left.r\left({\text{C}}_3-{\text{Si}}_4\right)\right]\hfill \end{array}(3)$

$S_4\left(b_{3u}\right)=\tau \left({\text{Si}}_4-{\text{C}}_3-{\text{C}}_2-{\text{Si}}_1\right)(4)$

$\begin{array}{cc}\hfill S_5\left(b_{1u}\right)=& \frac{1}{2}\left[r\left({\text{Si}}_1-{\text{C}}_2\right)+r\left({\text{Si}}_1-{\text{C}}_3\right)-r\left({\text{C}}_2-{\text{Si}}_4\right)\right.\hfill \\ \hfill & -\left.r\left({\text{C}}_3-{\text{Si}}_4\right)\right]\hfill \end{array}(5)$

$\begin{array}{cc}\hfill S_6\left(b_{2u}\right)=& \frac{1}{2}\left[r\left({\text{Si}}_1-{\text{C}}_2\right)-r\left({\text{Si}}_1-{\text{C}}_3\right)+r\left({\text{C}}_2-{\text{Si}}_4\right)\right.\hfill \\ \hfill & -\left.r\left({\text{C}}_3-{\text{Si}}_4\right)\right]\hfill \end{array}(6)$

FIGURE 1

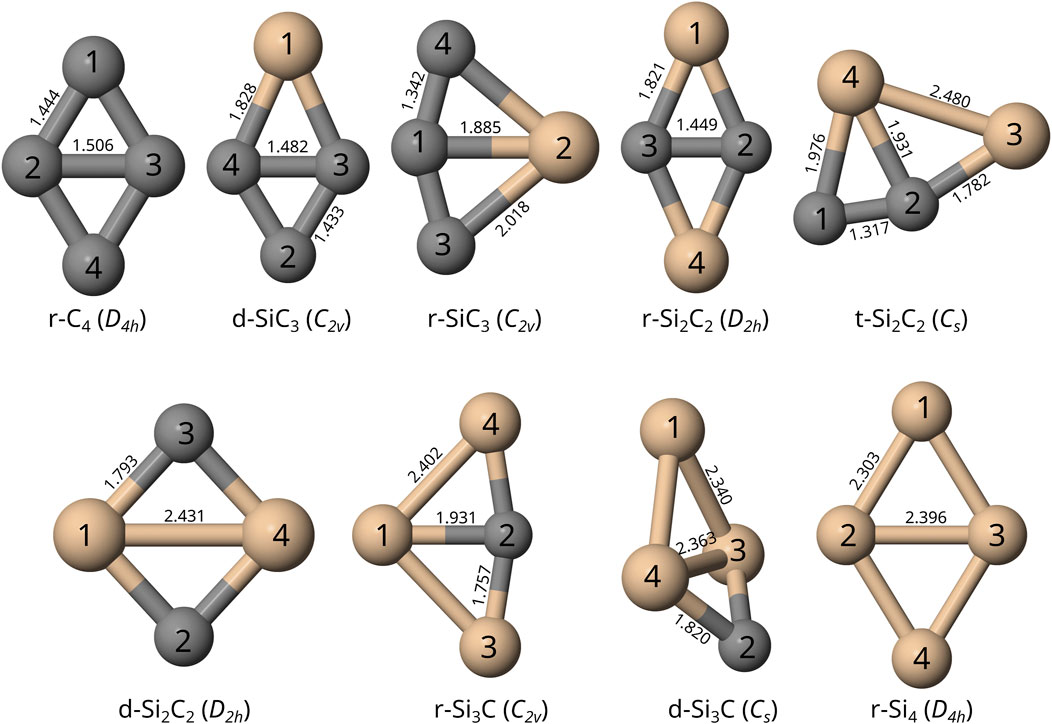
FIGURE 1. Visual depiction of the optimized structures for each TASCC with atomic labels, including molecular bond lengths reported in Å, computed at the F12-TZ-cCR level of theory. Silicon is shown in tan and carbon is shown in gray. These are ordered as (top row, from left) r-C₄, d-SiC₃, r-SiC₃, r-Si₂C₂, t-Si₂C₂ (bottom row) d-Si₂C₂, r-Si₃C, d-Si₃C, r-Si₄.

Differently, 413 displacement points, as employed previously (Fortenberry et al., 2013; Bassett and Fortenberry, 2018), are computed for the cyclic C_2v molecules (r-Si₃C and d-SiC₃) incorporating the following SICs with atom labels given in Figure 1.

$S_1\left(a_1\right)=r\left({\text{Si}}_1-{\text{C}}_2\right)(7)$

$S_2\left(a_1\right)=\frac{1}{\sqrt{2}}\left[r\left({\text{C}}_2-{\text{C}}_3\right)+r\left({\text{C}}_2-{\text{C}}_4\right)\right](8)$

$S_3\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{C}}_3\right)+\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{C}}_4\right)\right](9)$

$S_4\left(b_2\right)=\frac{1}{\sqrt{2}}\left[r\left({\text{C}}_2-{\text{C}}_3\right)-r\left({\text{C}}_2-{\text{C}}_4\right)\right](10)$

$S_5\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{C}}_3\right)-\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{C}}_4\right)\right](11)$

$S_6\left(b_1\right)=\tau \left({\text{Si}}_1-{\text{C}}_2-{\text{C}}_3-{\text{C}}_4\right)(12)$

Furthermore, 665 points are used for the C_s molecule in this study (d-Si₃C) with the following SICs from earlier work (Fortenberry et al., 2018b, 2019; Fortenberry, 2019) with atomic labels, shown in Figure 1.

$S_1\left(a_1\right)=r\left({\text{Si}}_1-{\text{C}}_2\right)(13)$

$S_2\left(a_1\right)=\frac{1}{\sqrt{2}}\left[r\left({\text{C}}_2-{\text{Si}}_3\right)+r\left({\text{C}}_2-{\text{Si}}_4\right)\right](14)$

$S_3\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{Si}}_3\right)+\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{Si}}_4\right)\right](15)$

$S_4\left(b_2\right)=\angle \left({\text{Si}}_3-{\text{C}}_2-{\text{Si}}_4\right)(16)$

$S_5\left(a_1\right)=\frac{1}{\sqrt{2}}\left[r\left({\text{C}}_2-{\text{Si}}_3\right)-r\left({\text{C}}_2-{\text{Si}}_4\right)\right](17)$

$S_6\left(b_1\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{Si}}_3\right)-\angle \left({\text{Si}}_1-{\text{C}}_2-{\text{Si}}_4\right)\right](18)$

Finally, 743 symmetry-unique (for a total of 805) points, as incorporated in previous work (Fortenberry et al., 2011, 2012, 2020), are used for the planar C_s molecule in this study (t-Si₂C₂). The SICs for such a connectivity are labeled as shown in Figure 1.

$S_1\left(a^{\prime }\right)=r\left({\text{C}}_1-{\text{C}}_2\right)(19)$

$S_2\left(a^{\prime }\right)=r\left({\text{C}}_2-{\text{Si}}_3\right)(20)$

$S_3\left(a^{\prime }\right)=r\left({\text{Si}}_3-{\text{Si}}_4\right)(21)$

$S_4\left(a^{\prime }\right)=\angle \left({\text{C}}_1-{\text{C}}_2-{\text{Si}}_3\right)(22)$

$S_5\left(a^{\prime }\right)=\angle \left({\text{C}}_2-{\text{Si}}_3-{\text{Si}}_4\right)(23)$

$S_6\left(a^{″}\right)=\tau \left({\text{Si}}_4-{\text{Si}}_3-{\text{C}}_2-{\text{C}}_1\right)(24)$

Regardless of the number of displacements, single-point energy computations are conducted at both levels of theory for each of the molecules analyzed in this work. Once the single-point energy computations finish, their relative energies are fit to a potential function by a least squares procedure with sums of squared residual values of better than 10^–16 a. u.², excluding d-Si₃C, r-SiC₃, and t-Si₂C₂/d-SiC₃ which have slightly higher residuals of 10^–13, 10^–14, and 10^–15 a. u.², respectively. The QFF is then refit including corrections from the initial fitting to produce the final equilibrium geometry and zero-gradient force constants. The INTDER program (Allen., 2005) then converts the force constants from SICs into Cartesian coordinates. The Cartesian force constants provide greater flexibility for use in the SPECTRO program (Gaw et al., 1991), which utilizes second-order rotational and vibrational perturbation theory (Mills, 1972; Watson, 1977; Papousek and Aliev, 1982) (VPT2) to produce highly-accurate rovibrational constants and fundamental vibrational frequencies. SPECTRO also incorporates Fermi resonances as well as resonance polyads (Martin and Taylor, 1997), of the Supplementary Material, to increase the accuracy of the computed fundamental anharmonic vibrational frequencies and rotational constants. Coriolis resonances are included in the rotational constant computations, as well.

Additionally, the Gaussian16 (Frisch et al., 2016) program is used to compute transition intensities for each anharmonic vibrational frequency at the MP2/cc-pVDZ level of theory. This method has been shown to produce semi-quantitative accuracy for anharmonic infrared intensities at a low computational cost (Fortenberry et al., 2014b). Finally, dipole moments for each molecule are computed using the Molpro 2020.1 quantum chemical program (Werner et al.,2020).

Results and discussion

The fundamental anharmonic frequencies for r-C₄ from a CCSD(T)/cc-pCV5Z semi-global potential energy surface within a variational approach (Wang and Bowman, 2013) compare well with the QFF VPT2 current data provided in Table 1. In each of these tables, ω represents the harmonic values of the vibrational frequencies, ν represents the anharmonic values, and the description of the modes (Desc.) is given in terms of the SICs from the previous section. These values all fall within 3.6 cm⁻¹ (ν₂) and 1.00% (ν₆) of the F12-TZ-cCR data in this work while averaging a 1.8 cm⁻¹ (0.32%) difference. Such correlation suggests that the F12-TZ-cCR QFF VPT2 treatment is handling the system well. In contrast, the F12-TZ values do not compare as well as the F12-TZ-cCR data to the previously determined CCSD(T)/cc-pCV5Z data. The ν₂ frequency has the largest absolute difference of 10.7 cm⁻¹ (0.85%), and the difference for the total set averages 4.6 cm⁻¹ (0.46%). Thus, the F12-TZ-cCR method may come at the optimal ratio of accuracy and computational efficiency for chemical systems of the current nature. Equilibrium (_e), vibrationally-averaged (₀), and singly-vibrationally excited (_n>0) rotational constants for r-C₄ can be found in Table 2, along with the quartic (Δ and δ) and sextic (Φ and ϕ) distortion coefficients in the Watson A-reduced Hamiltonian and the dipole moment (μ), which by symmetry is zero in this case. The vibrational frequency at 1315.1 cm⁻¹ (ν₁) is the best candidate for potential vibrational observation as the frequency is above the $\sim 350$ cm⁻¹ cutoff for JWST’s MIRI, and the intensity is notable with a value of 159 km mol⁻¹. The antisymmetric stretch of water, used here as a familiar basis for comparison, has an intensity of 70 km mol⁻¹ implying that this frequency in r-C₄ has a higher oscillator strength by more than a factor of two.

TABLE 1

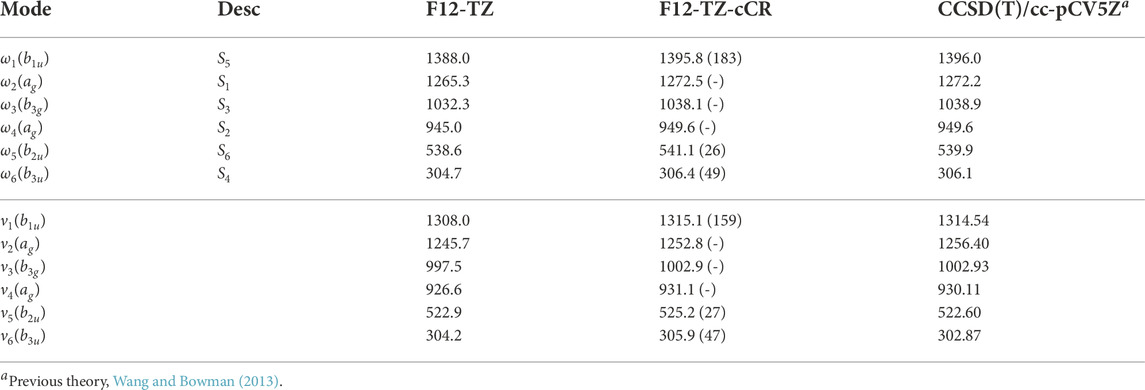
TABLE 1. Harmonic (ω) and Fundamental (ν) Vibrational Frequencies (in cm⁻¹) with Intensities (in km mol⁻¹, in Parentheses) for r-C₄. Mode descriptions (Desc.) refer to the SICs in Eqns. 1-24.

TABLE 2

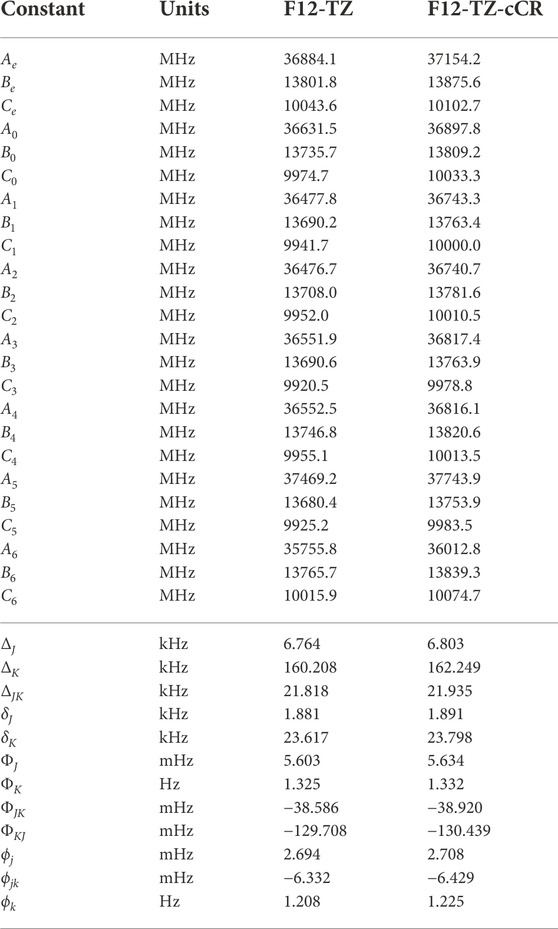
TABLE 2. Equilibrium (_e), vibrationally-averaged (₀), and singly-vibrationally excited (_n>0) principal rotational constants, quartic (Δ/δ) and sextic (Φ/ϕ) distortion constants, principal rotational constants, and quartic for r-C₄.

The d-SiC₃ structure is found to be the lowest energy cyclic isomer for the first silicon replacement analogue. It lies approximately 6.1 kcal mol⁻¹ below r-SiC₃. The d-SiC₃ F12-TZ-cCR rotational constants compare well with previously determined experimental values by McCarthy et al. (McCarthy et al., 2019). The experimental and present theoretical F12-TZ-cCR spectroscopic constants found in Table 3 differ by just 0.20% for A₀, 0.04% for B₀, and 0.02% for C₀, suggesting high-accuracy for the current method. The dipole moment of d-SiC₃ is computed to be 4.03 D, comparing well with previous work (Alberts et al., 1990) which determined the dipole moment to be 4.2 D. This large dipole moment is likely the cause of d-SiC₃’s previous detection in the ISM. F12-TZ-cCR rotational constants for r-SiC₃ compare well with experimental values determined by McCarthy et al. (McCarthy et al., 1999), with the A₀, B₀, and C₀ constants displaying differences of 0.08%, 0.02%, and 0.02%, respectively. The r-SiC₃ isomer is shown to have a dipole moment of 2.07 D, also comparing well with a previous 2.2 D value (Alberts et al., 1990). The strength of the dipole moment for r-SiC₃ may also lead to its radioastronomical detection. However, the slightly higher relative energy of this isomer and roughly half dipolar strength of the d isomer imply that the r isomer will likely have a notably smaller emission profile.

TABLE 3

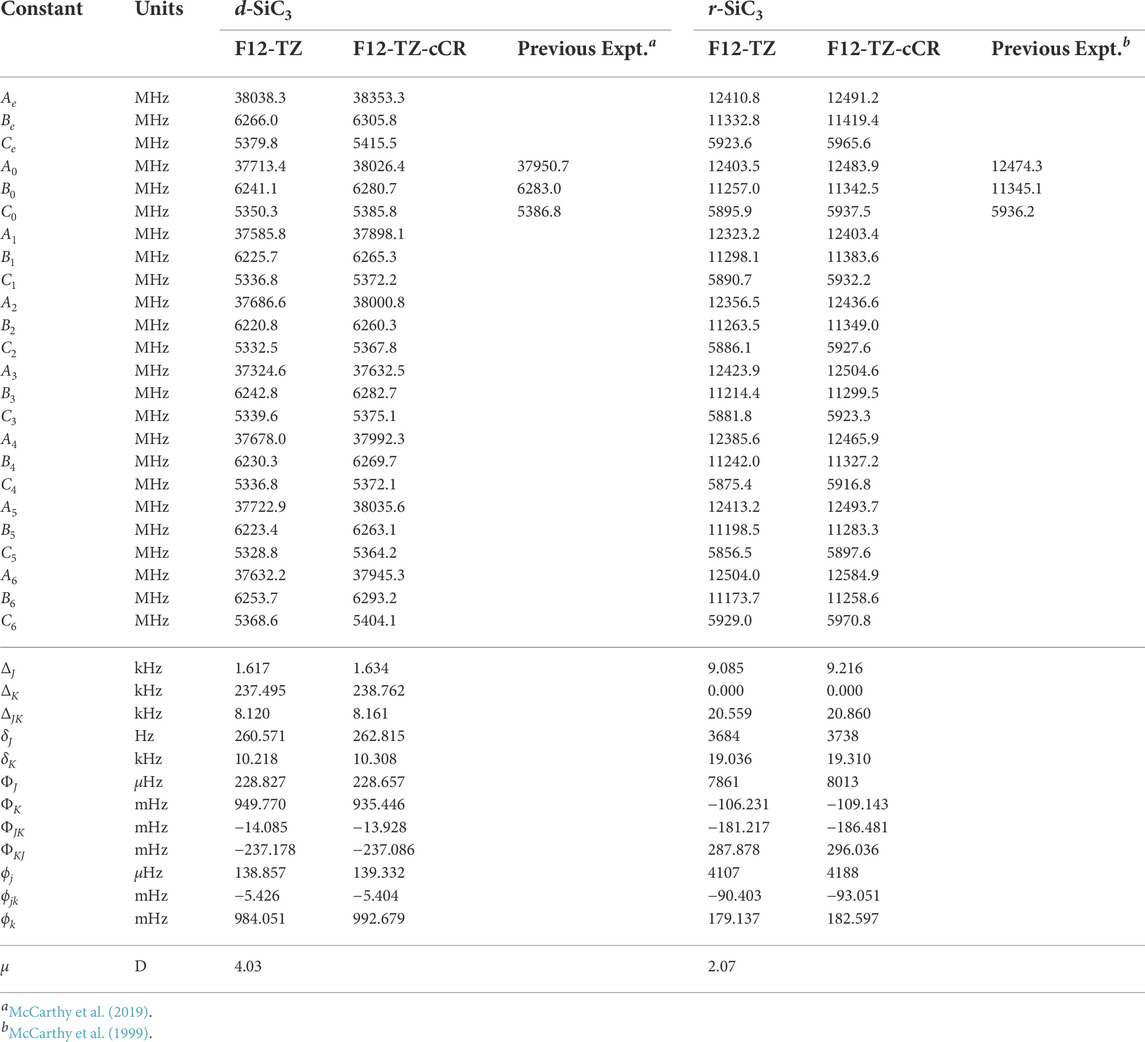
TABLE 3. Equilibrium (_e), vibrationally-averaged (₀), and singly-vibrationally excited (_n>0) principal rotational constants, quartic (Δ/δ) and sextic (Φ/ϕ) distortion constants, and dipole moments (μ) for SiC₃ Isomers.

Differently, all harmonic frequencies reported for d-SiC₃ and r-SiC₃, found in Table 4, at the F12-TZ-cCR level provided herein exhibit notable deviations from previous theoretical work done by Linguerri et al. (2006) at the CCSD(T)/cc-pVQZ level of theory. The largest differences are 16.2 cm⁻¹ (ω₃ from d-SiC₃; 1.64%) and 11.4 cm⁻¹ (ω₂ from r-SiC₃; 1.01%). Linguerri et al. (2006) also report fundamental anharmonic frequencies using VSCF for both cyclic isomers of SiC₃. These values compare poorly for both isomers with fundamental frequencies differing by up to 16.3 cm⁻¹ (ν₅; 3.98%) and 27.2 cm⁻¹ (ν₃; 3.31%) for the presently analyzed d-SiC₃ and r-SiC₃ isomers’ F12-TZ-cCR data, respectively. Such poor comparison of the anharmonic frequencies is to be expected for the relatively poor agreement in the harmonic frequencies. The most obvious difference between the present and previous studies is the inclusion of core electron correlation (or lack thereof). As a result, the present F12-TZ-cCR results should be producing more accurate data for subsequent experimental or observational comparison. Additionally, potentially observable fundamental frequencies for r-SiC₃ include ν₁ at 1525.5 cm⁻¹ and ν₃ at 793.8 cm⁻¹ with intensities of 77 and 54 km mol⁻¹, respectively, given favorable ISM conditions.

TABLE 4

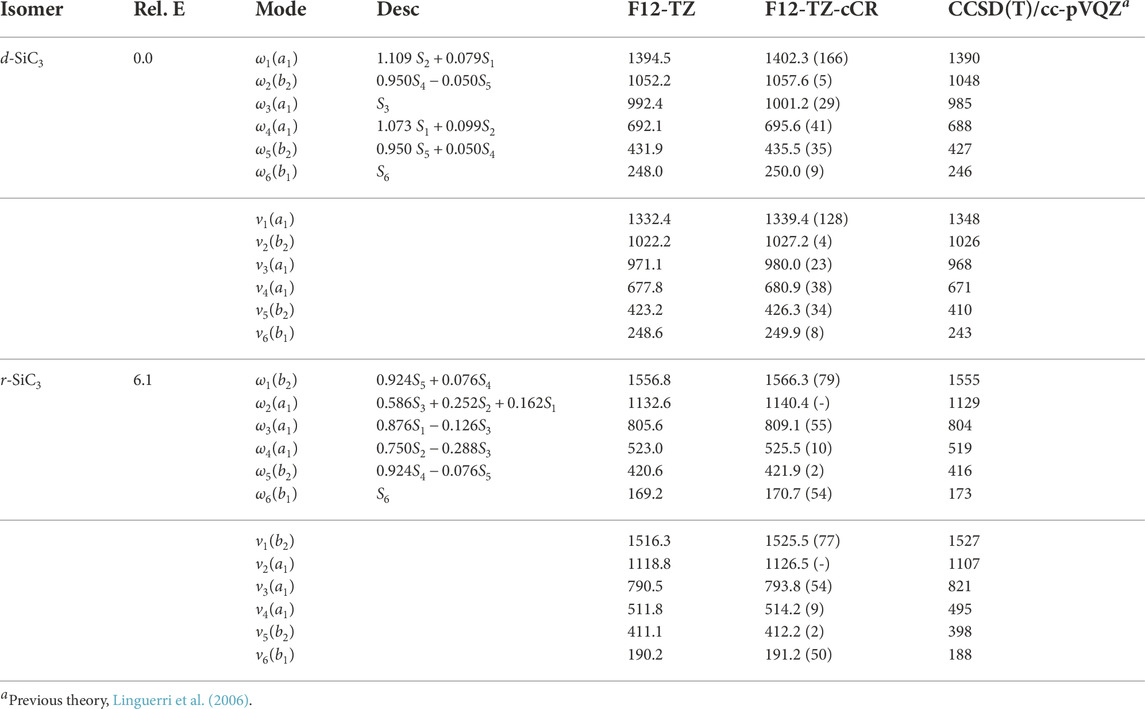
TABLE 4. Harmonic (ω) and Fundamental (ν) Vibrational Frequencies (in cm⁻¹) with Intensities (in km mol⁻¹, in Parentheses) and Relative Energies (in kcal mol⁻¹) for SiC₃ Isomers. Mode descriptions (Desc.) refer to the SICs in Eqns. 1-24.

With the accuracy of the current methods benchmarked on the aforementioned species, this work presents the first high level theoretical data for the remaining isomers herein. Relative energies computed at the F12-TZ-cCR level for the three cyclic Si₂C₂ isomers determine that r-Si₂C₂ with the transannular C-C bond is the lowest energy isomer, followed by t-Si₂C₂, which is 7.5 kcal mol⁻¹ higher in energy, and, lastly, the other d-Si₂C₂ isomer with the transannular Si-Si bond resides 83.8 kcal mol⁻¹ higher in energy. Experimental matrix studies are available for ν₂, shown to be 988.1 cm⁻¹ in this work, and ν₅, 383.0 cm⁻¹ here, for r-Si₂C₂ with a transannular C-C bond (Presilla-Márquez et al., 1995). These values are determined to be about 5.2 (0.53%) and 0.8 cm⁻¹ (0.21%) lower than the F12-TZ-cCR data found in Table 5, respectively. This agreement is relatively good, especially for ν₅ which suggests the accuracy of both the experiment and computations. Matrix studies performed by Presilla-Márquez et al. (Presilla-Márquez et al., 1995) considered ν₁ and ν₃ as potential candidates for accurately observed vibrational frequencies of t-Si₂C₂, and the current work shows values for these modes differing by only 0.4 cm⁻¹ (0.03%) for ν₁ at 1537.6 cm⁻¹ and 4.9 cm⁻¹ (0.78%) for ν₃ at 636.9 cm⁻¹ for the F12-TZ-cCR computations found in Table 5. This may be promising for the vibrational observation of ν₃ for t-Si₂C₂ in the ISM as the intensity is determined to be 63 km mol⁻¹. The lowest energy isomer of cyclic Si₂C₂ is found to have an anharmonic vibrational intensity of 247 km mol⁻¹ for ν₂ at 988.1 cm⁻¹, which is over three times more intense than that of the aforementioned antisymmetric stretch of water. Also, t-Si₂C₂ is found to have a strong dipole moment of 2.90 D given in Table 6, which suggests the molecule may be rotationally observable if present in high concentrations. This may be likely given the prevalence of SiC dust on chondrite meteorites and in the observed ISM.

TABLE 5

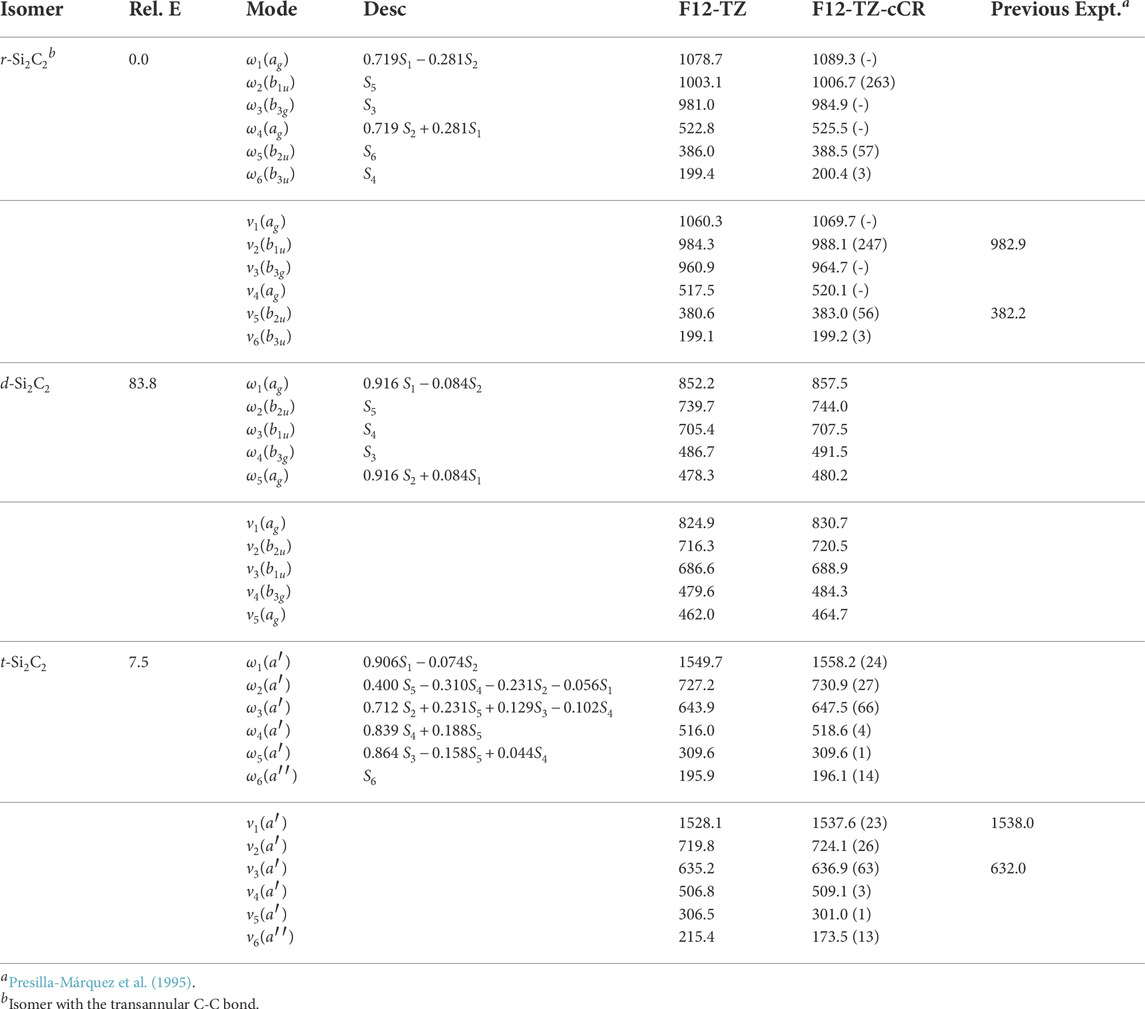
TABLE 5. Harmonic (ω) and Fundamental (ν) Vibrational Frequencies (in cm⁻¹) with Intensities (in km mol⁻¹, in Parentheses) and Relative Energies (in kcal mol⁻¹) for Si₂C₂ Isomers. Mode descriptions (Desc.) refer to the SICs in Eqns. 1-24.

TABLE 6

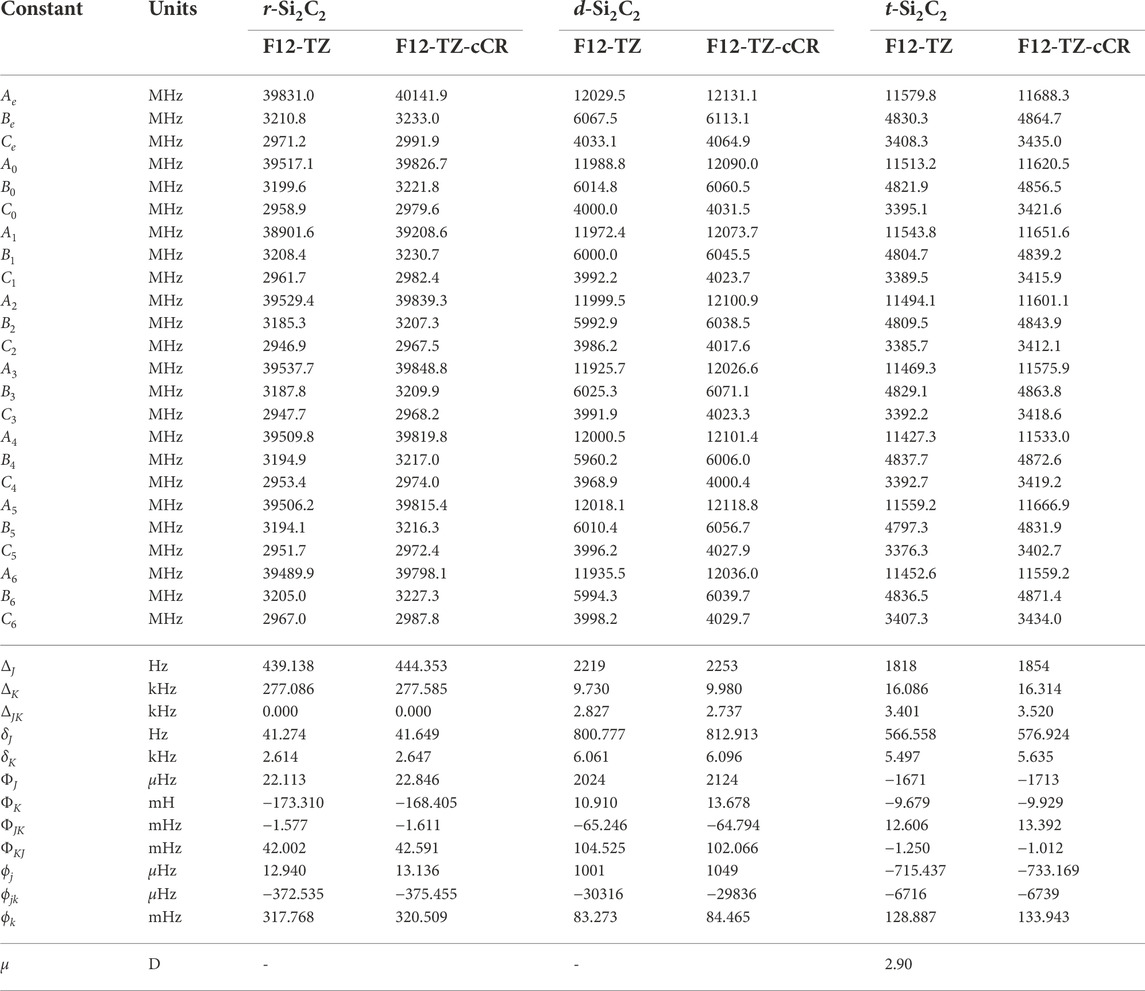
TABLE 6. Equilibrium (_e), vibrationally-averaged (₀), and singly-vibrationally excited (_n>0) principal rotational constants, quartic (Δ/δ) and sextic (Φ/ϕ) distortion constants, and dipole moments (μ) for Si₂C₂ Isomers.

The d-Si₂C₂ isomer with the transannular Si-Si bond displays a strong pseudo-Jahn Teller type-2 distortion effect in the potential energy surface of the molecule (Mintz and Crawford, 2010; Bersuker, 2021). Such behavior causes overlap in the surfaces between this isomer and r-Si₂C₂. This negates the computation for all of the fundamental vibrational frequencies, but the five that can be determined are reported in Table 5. The one that is missing involves the out-of-plane bend. The coordinates for this motion cause the orbital occupations to collapse to that of the r-Si₂C₂ isomer where the C_s symmetry is too low to distinguish the wavefunctions in the reference. Even so, the fundamentals reported herein should serve as estimates for any subsequent analysis. Intensities for d-Si₂C₂ are not computed due to the complexity of the type 2 pseudo-Jahn Teller distortion.

The current work presents the only spectroscopic constants computed at a high level of theory for cyclic Si₃C isomers. The r-Si₃C species is found to be the lowest energy isomer residing 49.6 kcal mol⁻¹ below d-Si₃C. Anharmonic vibrational modes of r-Si₃C, found in Table 7, computed at the F12-TZ-cCR level compare well with previous experimental matrix studies performed by Presilla-Márquez and Graham (1992) differing by 5.8 cm⁻¹ (1.62%) for ν₄ and 5.4 cm⁻¹ (1.06%) for ν₃. Similarly, ν₂ shows a maximum difference of 3.2 cm⁻¹ (0.49%). Table 8 displays the rotational constants for both isomers. The d-Si₃C species may be rotationally observable as the dipole moment for this molecule is determined to be 2.64 D. The d-Si₃C isomer has no observable vibrational modes, meaning no modes above JWST’s high resolution cutoff of 350 cm⁻¹ have an intensity near the anti-symmetric stretch of water, or 70 km mol⁻¹. However, ν₁ of r-Si₃C has a higher intensity at 80 km mol⁻¹. This may lead to the vibrational observation of this species in the ISM if found in sufficient quantities relative to adjacent molecular species.

TABLE 7

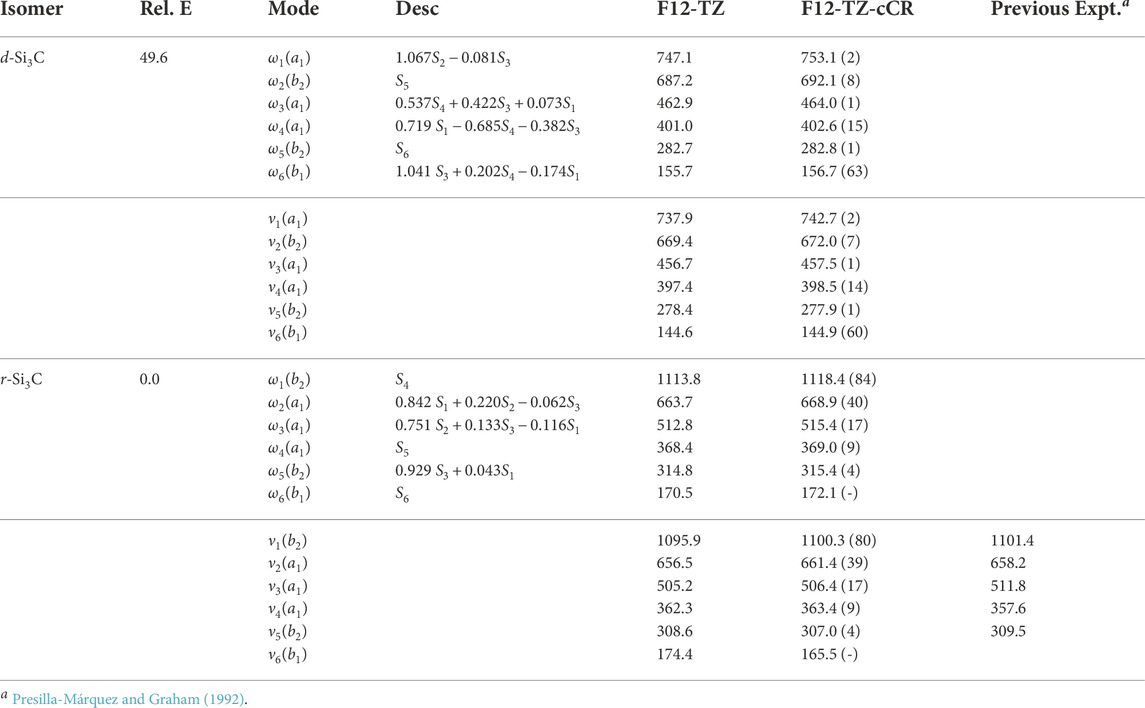
TABLE 7. Harmonic (ω) and Fundamental (ν) Vibrational Frequencies (in cm⁻¹) with Intensities (in km mol⁻¹, in Parentheses) and Relative Energies (in kcal mol⁻¹) for Si₃C Isomers. Mode descriptions (Desc.) refer to the SICs in Eqns. 1-24.

TABLE 8

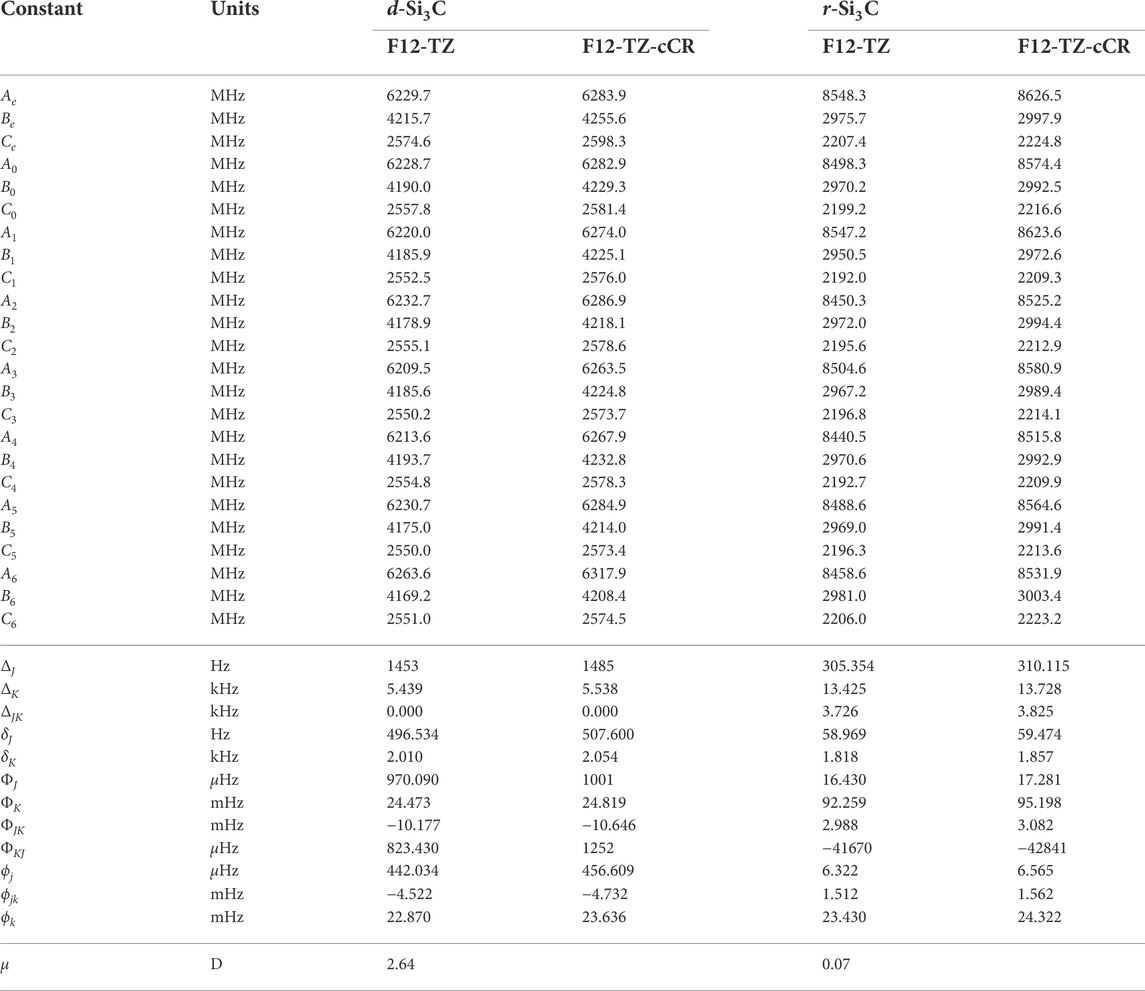
TABLE 8. Equilibrium (_e), vibrationally-averaged (₀), and singly-vibrationally excited (_n>0) principal rotational constants, quartic (Δ/δ) and sextic (Φ/ϕ) distortion constants, and dipole moments (μ) for Si₃C Isomers.

Similarly to the previous isomers, this work provides the first high level theoretical spectral data for neutral r-Si₄. Computed spectral data for r-Si₄ are presented in Tables 9 and 10. The anharmonic frequency ν₁ may be observable experimentally, as it is shown to have a reasonable intensity of 41 km mol⁻¹.

TABLE 9

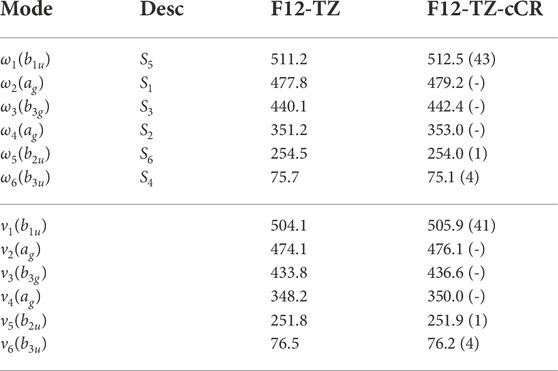
TABLE 9. Harmonic (ω) and Fundamental (ν) Vibrational Frequencies (in cm⁻¹) with Intensities (in km mol⁻¹, in Parentheses) for r-Si₄. Mode descriptions (Desc.) refer to the SICs in Eqns. 1-24.

TABLE 10

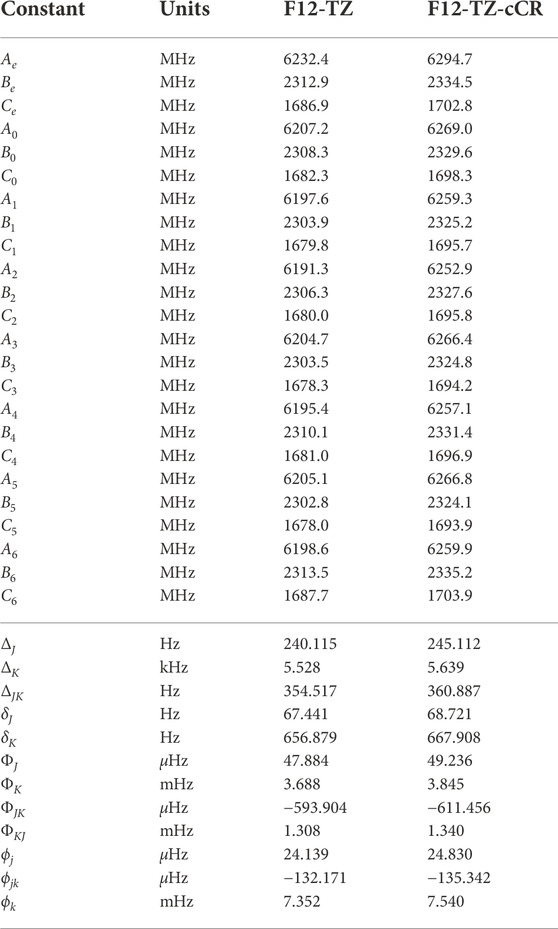
TABLE 10. Equilibrium (_e), vibrationally-averaged (₀), and singly-vibrationally excited (_n>0) principal rotational constants, quartic (Δ/δ) and sextic (Φ/ϕ) distortion constants, principal rotational constants, and quartic for r-Si₄.

As silicon composition increases with each TASCC, the current data sheds some light on the effects of silicon doping on the spectral frequencies of tetra-atomic carbon clusters. This is possible due to a similar connectivity between r-C₄, r-Si₂C₂ with a transannular C-C bond, and r-Si₄. Tables 1, 5, and 9 and Figure 2 demonstrate that the addition of silicon to carbon clusters causes a redshift in each of the vibrational frequencies, agreeing with the work done on larger silicon clusters by Savoca et al. (2013). This can be seen with ν₁ for each species with r-C₄ coming at 1315.1 cm⁻¹, C-C r-Si₂C₂ falling to 1069.7 cm⁻¹, and r-Si₄ coming down to 505.9 cm⁻¹. While such a relationship is expected for heavier atoms, quantification of this relationship may aid in accurately identifying the silicon composition in stellar atmospheres of large carbonaceous stars, or subsequent novae and nebulae. Identifying the molecular framework and elemental ratios in these environments may lead to a more holistic understanding of their processes of formation, i.e. novae processes and the formation of the first interstellar dust grains. With SiC dust making up a large portion of the available cosmic dust for research on chondrite meteorites, characterization of carbon to silicon ratios in various astronomical environments may lead to a better understanding of the ISM and the processes that lead to its formation but only if data such as those provided herein can be utilized to detect more SiC molecules and clusters.

FIGURE 2

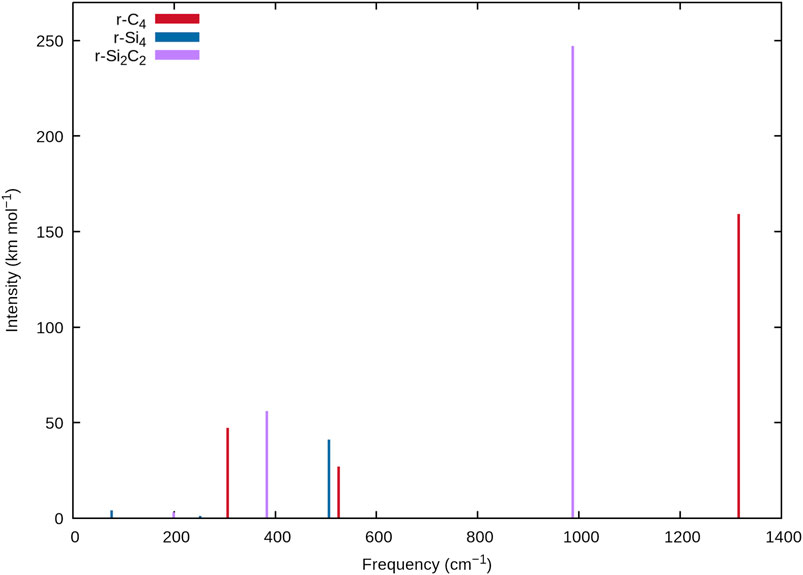
FIGURE 2. Stick spectra of r-C₄, r-Si₄, and r-Si₂C₂ at the F12-TZ-cCR level of theory showing the decreasing frequencies with Si concentration.

Conclusion

The most promising anharmonic fundamental frequency for astronomical vibrational detection for these silicon carbide clusters is the ν₂ frequency at 988.1 cm⁻¹ (10.1 μm) of r-Si₂C₂ with a transannular C-C bond displaying a very large intensity of 247 km mol⁻¹. This frequency may be a distinct feature in the unidentified IR spectrum and would be a likely candidate for observation if found in sufficient concentrations. Other notable IR features for possible observation include ν₁ of r-C₄ (1315.1 cm⁻¹; 7.6 μm) with an intensity of 159 km mol⁻¹, ν₁ of d-SiC₃ (1339.4 cm⁻¹; 7.5 μm) with an intensity of 128 km mol⁻¹, ν₁ of r-Si₃C (1100.3 cm⁻¹; 9.1 μm) with an intensity of 80 km mol⁻¹, and ν₁ of r-SiC₃ (1525.5 cm⁻¹; 6.6 μm) with an intensity of 77 km mol⁻¹. Each of these anharmonic frequencies are good candidates for observation with the recently operational MIRI instrument aboard the JWST between 9.09 μm and 6.56 μm. Finally, rotational observation may be possible for t-Si₂C₂, d-Si₃C, and r-SiC₃ due to dipole moments of 2.90, 2.63, and 2.07 D, respectively. Because of this, the prevalence of SiC dust in the ISM, and the known observation of the related d-SiC₃, these molecules are strong candidates for radioastronomical observation.

Data availability statement

The original contributions presented in the study are included in the article and Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CS performed the computational work with guidance from CP and BW. RF conceived of the idea, managed the project, and secured the funding. All authors were involved in analyzing the results as well as writing and editing the manuscript.

Funding

This work was supported by NASA Grant NNX17AH15G, NSF Grant CHE-1757888, and startup funds provided by the College of Liberal Arts at the University of Mississippi.

Acknowledgments

The authors would also like to thank the Mississippi Center for Supercomputing Research (MCSR) for the provision of the computational resources used in this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.1074879/full#supplementary-material

References

Adler, T. B., Knizia, G., and Werner, H.-J. (2007). A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 127, 221106. doi:10.1063/1.2817618

PubMed Abstract | CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019a). The performance of explicitly correlated methods for the computation of anharmonic vibrational frequencies. Int. J. Quantum Chem. 119, e25899. doi:10.1002/qua.25899

CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019b). The performance of explicitly correlated wavefunctions [CCSD(T)-F12b] in the computation of anharmonic vibrational frequencies. Chem. Phys. Lett. 734, 136720. doi:10.1016/j.cplett.2019.136720

CrossRef Full Text | Google Scholar

Agbaglo, D., Lee, T. J., Thackston, R., and Fortenberry, R. C. (2019). A small molecule with PAH vibrational properties and a detectable rotational spectrum: c-(C)C₃H₂, cyclopropenylidenyl carbene. Astrophys. J. 871, 236. doi:10.3847/1538-4357/aaf85a

CrossRef Full Text | Google Scholar

Alberts, I., Grev, R., and Schaefer, H. (1990). Geometrical structures and vibrational frequencies of the energetically low-lying isomers of SiC₃. J. Chem. Phys. 93, 5046–5052. doi:10.1063/1.458642

CrossRef Full Text | Google Scholar

Algranati, M., Feldman, H., Kella, D., Malkin, E., Miklazky, E., Naaman, R., et al. (1989). The structure of C₄ as studied by the Coulomb explosion method. J. Chem. Phys. 90, 4617–4618. doi:10.1063/1.456597

CrossRef Full Text | Google Scholar

Allen, W. (2005). INTDER 2005 is a general program written by W. D. Allen and coworkers, which performs vibrational analysis and higher-order non-linear transformations. Athens: University of Georgia.

Google Scholar

Apponi, A., McCarthy, M., Gottlieb, C. A., and Thaddeus, P. (1999a). Astronomical detection of rhomboidal SiC₃. Astrophys. J. 516, L103–L106. doi:10.1086/311998

CrossRef Full Text | Google Scholar

Apponi, A., McCarthy, M., Gottlieb, C. A., and Thaddeus, P. (1999b). The rotational spectrum of rhomboidal SiC₃. J. Chem. Phys. 111, 3911–3918. doi:10.1063/1.479694

CrossRef Full Text | Google Scholar

Babin, M., DeWitt, M., Weichman, J., DeVine, M., and Neumark, D. (2021). High-resolution anion photoelectron spectroscopy of cryogenically cooled 4-atom silicon carbides. Mol. Phys. 119, e1817596. doi:10.1080/00268976.2020.1817596

CrossRef Full Text | Google Scholar

Bassett, M. K., and Fortenberry, R. C. (2018). Magnesium in the formaldehyde: The theoretical rovibrational analysis of ˜X3B1 MgCH₂. J. Mol. Spectrosc. 344, 61–64. doi:10.1016/j.jms.2017.10.012

CrossRef Full Text | Google Scholar

Bernatowicz, T., Fraundorf, G., Ming, T., Anders, E., Wopenka, B., Zinner, E., et al. (1987). Evidence for interstellar SiC in the Murray carbonaceous meteorite. Nature 330, 728–730. doi:10.1038/330728a0

CrossRef Full Text | Google Scholar

Bersuker, I. (2021). Jahn-Teller and pseudo-Jahn-Teller effects: From particular features to general tools in exploring molecular and solid state properties. Chem. Rev. 121, 1463–1512. doi:10.1021/acs.chemrev.0c00718

PubMed Abstract | CrossRef Full Text | Google Scholar

Bizzocchi, L., Lattanzi, V., Laas, J., Spezzano, S., Giuliano, B. M., Prudenzano, D., et al. (2017). Accurate sub-millimetre rest frequencies for HOCO⁺ and DOCO⁺ ions. Astron. Astrophys. 602, A34. doi:10.1051/0004-6361/201730638

CrossRef Full Text | Google Scholar

Blanksby, S., Schröder, D., Dua, S., Bowie, J., and Schwarz, H. (2000). Conversion of linear to rhombic C₄ in the gas phase: A joint experimental and theoretical study. J. Am. Chem. Soc. 122, 7105–7113. doi:10.1021/ja000951c

CrossRef Full Text | Google Scholar

Cernicharo, J., Gottlieb, C., Guelin, M., Thaddeus, P., and Vrtilek, J. M. (1989). Astonomical and laboratory detection of the SiC radical. Astrophys. J. 341, L25–L28. doi:10.1086/185449

CrossRef Full Text | Google Scholar

Cernicharo, J., McCarthy, M. C., Gottlieb, C. A., Agúndez, M., Prieto, L. V., Baraban, J. H., et al. (2015). Discovery of SiCSi in IRC+10216: A missing link between gas and dust carriers of Si-C bonds. Astrophys. J. 806, L3. doi:10.1088/2041-8205/806/1/l3

PubMed Abstract | CrossRef Full Text | Google Scholar

Douglas, M., and Kroll, N. (1974). Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. (N. Y). 82, 89–155. doi:10.1016/0003-4916(74)90333-9

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Crawford, T. D., and Lee, T. J. (2013). High-accuracy quartic force field calculations for the spectroscopic constants and vibrational frequencies of 1¹A′ l-C₃H⁻: A possible link to lines observed in the horsehead nebula PDR. Astrophys. J. 772, 39. doi:10.1088/0004-637x/772/1/39

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Crawford, T. D., and Lee, T. J. (2014a). Quartic force field rovibrational analysis of protonated acetylene, C₂H₃⁺, and its isotopologues. J. Phys. Chem. A 118, 7034–7043. doi:10.1021/jp506441g

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2012). Quartic force field predictions of the fundamental vibrational frequencies and spectroscopic constants of the cations HOCO⁺ and DOCO⁺. J. Chem. Phys. 136, 234309. doi:10.1063/1.4729309

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2011). The trans-HOCO radical: Fundamental vibrational frequencies, quartic force fields, and spectroscopic constants. J. Chem. Phys. 135, 134301. doi:10.1063/1.3643336

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Schwenke, D. W., and Lee, T. J. (2014b). Limited rotational and rovibrational line lists computed with highly accurate quartic force fields and ab initio dipole surfaces. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 119, 76–83. doi:10.1016/j.saa.2013.03.092

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., and Lee, T. J. (2019). Computational vibrational spectroscopy for the detection of molecules in space. Ann. Rep. Comput. Chem. 15, 173–202.

Google Scholar

Fortenberry, R. C., Lee, T. J., and Müller, H. S. P. (2015). Excited vibrational level rotational constants for SiC₂: A sensitive molecular diagnostic for astrophysical conditions. Mol. Astrophys. 1, 13–19. doi:10.1016/j.molap.2015.07.001

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Novak, C. M., Layfield, J. P., Matito, E., and Lee, T. J. (2018a). Overcoming the failure of correlation for out-of-plane motions in a simple aromatic: Rovibrational quantum chemical analysis of c-C₃H₂. J. Chem. Theory Comput. 14, 2155–2164. doi:10.1021/acs.jctc.8b00164

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C. (2019). The ArNH₂⁺ noble gas molecule: Stability, vibrational frequencies, and spectroscopic constants. J. Mol. Spectrosc. 357, 4–8. doi:10.1016/j.jms.2019.02.001

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Trabelsi, T., and Francisco, J. S. (2020). Anharmonic frequencies and spectroscopic constants of OAlOH and AlOH: Strong bonding but unhindered motion. J. Phys. Chem. A 124, 8834–8841. doi:10.1021/acs.jpca.0c07945

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Trabelsi, T., and Francisco, J. S. (2018b). Hydrogen sulfide as a scavenger of sulfur atomic cation. J. Phys. Chem. A 122, 4983–4987. doi:10.1021/acs.jpca.8b02923

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Trabelsi, T., Westbrook, B. R., Del Rio, W. A., and Francisco, J. S. (2019). Molecular oxygen generation from the reaction of water cations with oxygen atoms. J. Chem. Phys. 150, 201103. doi:10.1063/1.5102073

PubMed Abstract | CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 revision C.01. Wallingford CT: Gaussian Inc.

Google Scholar

Gardner, M. B., Westbrook, B. R., Fortenberry, R. C., and Lee, T. J. (2021). Highly-accurate quartic force fields for the prediction of anharmonic rotational constants and fundamental vibrational frequencies. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 248, 119184. doi:10.1016/j.saa.2020.119184

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaw, J. F., Willets, A., Green, W. H., and Handy, N. C. (1991). “Spectro: A program for the derivation of spectrscopic constants from provided quartic force fields and cubic dipole fields,” in Advances in molecular vibrations and collision dynamics. Editors J. M. Bowman, and M. A. Ratner (Greenwich, Connecticut: JAI Press, Inc.), 170.

Google Scholar

Hill, J. G., and Peterson, K. A. (2010). Correlation consistent basis sets for explicitly correlated wavefunctions: Valence and core-valence basis sets for Li, Be, Na, and Mg. Phys. Chem. Chem. Phys. 12, 10460–10468. doi:10.1039/c0cp00020e

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., Fortenberry, R. C., and Lee, T. J. (2013). Protonated nitrous oxide, NNOH⁺: Fundamental vibrational frequencies and spectroscopic constants from quartic force fields. J. Chem. Phys. 139, 084313. doi:10.1063/1.4819069

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., and Lee, T. J. (2008). A procedure for computing accurate ab initio quartic force fields: Application to HO₂⁺ and H₂O. J. Chem. Phys. 129, 044312. doi:10.1063/1.2957488

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., and Lee, T. J. (2009). Accurate ab initio quartic force fields for NH₂⁻ and CCH⁻ and rovibrational spectroscopic constants for their isotopologs. J. Chem. Phys. 131, 104301. doi:10.1063/1.3212560

CrossRef Full Text | Google Scholar

Huang, X., Taylor, P. R., and Lee, T. J. (2011). Highly accurate quartic force field, vibrational frequencies, and spectroscopic constants for cyclic and linear C₃H₃⁺. J. Phys. Chem. A 115, 5005–5016. doi:10.1021/jp2019704

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., Valeev, E. F., and Lee, T. J. (2010). Comparison of one-particle basis set extrapolation to explicitly correlated methods for the calculation of accurate quartic force fields, vibrational frequencies, and spectroscopic constants: Application to H₂O, N₂H⁺, NO₂⁺, and C₂H₂. J. Chem. Phys. 133, 244108. doi:10.1063/1.3506341

PubMed Abstract | CrossRef Full Text | Google Scholar

Inostroza, N., Hochlaf, M., Senent, M., and Letelier, J. (2008). Ab initio characterization of linear C₃Si Isomers. Astron. Astrophys. 486, 1047–1052. doi:10.1051/0004-6361:200809556

CrossRef Full Text | Google Scholar

Kitchens, M. J. R., and Fortenberry, R. C. (2016). The rovibrational nature of closed-shell third-row triatomics: HOX and HXO, X = Si⁺, P, S⁺, and Cl. Chem. Phys. 472, 119–127. doi:10.1016/j.chemphys.2016.03.018

CrossRef Full Text | Google Scholar

Knizia, G., Adler, T. B., and Werner, H.-J. (2009). Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300

PubMed Abstract | CrossRef Full Text | Google Scholar

Lammertsma, K., and Güner, O. F. (1988). Structures and energies of disilicon dicarbide, C2Si2. C₂Si₂. J. Am. Chem. Soc. 110, 5239–5245. doi:10.1021/ja00224a001

CrossRef Full Text | Google Scholar

Lavendy, H., Robbe, J., Flament, J., and Pascoli, G. (1997). Density functional study of small silicon carbide cluster cations C₄⁺, C₃Si⁺, C₂Si₂⁺, CSi₃⁺, and Si₄⁺. J. Chim. Phys. 94, 1779–1793. doi:10.1051/jcp/1997941779

CrossRef Full Text | Google Scholar

Linguerri, R., Rosmus, P., and Carter, S. (2006). Anharmonic vibrational levels of the two cyclic isomers of SiC₃. J. Chem. Phys. 125, 034305. doi:10.1063/1.2209693

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1997). Accurate ab initio quartic force field for trans-HNNH and treatment of resonance polyads. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 53, 1039–1050. doi:10.1016/s1386-1425(96)01869-0

CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1996). Structure and vibrations of small carbon clusters from coupled-cluster calculations. J. Phys. Chem. 100, 6047–6056. doi:10.1021/jp952471r

CrossRef Full Text | Google Scholar

Martin, J., Schwenke, D., Lee, T., and Taylor, P. R. (1996). Is there evidence for detection of cyclic C₄ in IR spectra? An accurate ab initio computed quartic force field. J. Chem. Phys. 104, 4657–4663. doi:10.1063/1.471212

CrossRef Full Text | Google Scholar

Matthews, L., Hayes, R., Michael, S., Freed, T., and Hyde, W. (2007). Formation of cosmic dust bunnies. IEEE Trans. Plasma Sci. IEEE Nucl. Plasma Sci. Soc. 35, 260–265. doi:10.1109/tps.2007.892718

CrossRef Full Text | Google Scholar

McCarthy, M., Apponi, A., and Thaddeus, P. (1999). A second rhomboidal isomer of SiC₃. J. Chem. Phys. 111, 7175–7178. doi:10.1063/1.480044

CrossRef Full Text | Google Scholar

McCarthy, M. C., Gottlieb, C. A., and Cernicharo, J. (2019). Building blocks of dust: A coordinated laboratory and astronomical study of the archtype Agb carbon star IRC+10216. J. Mol. Spectrosc. 356, 7–20. doi:10.1016/j.jms.2018.11.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Mélinon, P., Masenelli, B., Tournus, F., and Perez, A. (2007). Playing with carbon and silicon at the nanoscale. Nat. Mat. 6, 479–490. doi:10.1038/nmat1914

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, I. M. (1972). “Vibration-rotation structure in asymmetric- and symmetric-top molecules,” in Molecular spectroscopy - modern research. Editors K. N. Rao, and C. W. Mathews (New York: Academic Press), 115–140.

CrossRef Full Text | Google Scholar

Mintz, B., and Crawford, T. D. (2010). Symmetry breaking in the cyclic C₃C₂H radical. Phys. Chem. Chem. Phys. 12, 15459–15467. doi:10.1039/c0cp00864h

PubMed Abstract | CrossRef Full Text | Google Scholar

Nittler, L., and Alexander, C. (2003). Automated isotopic measurements of micron-sized dust: Application to meteoritic presolar silicon carbide. Geochimica Cosmochimica Acta 67, 4961–4980. doi:10.1016/s0016-7037(03)00485-x

CrossRef Full Text | Google Scholar

Papousek, D., and Aliev, M. R. (1982). Molecular vibration-rotation spectra. Amsterdam: Elsevier.

Google Scholar

Peterson, K. A., Adler, T. B., and Werner, H.-J. (2008). Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 128, 084102. doi:10.1063/1.2831537

PubMed Abstract | CrossRef Full Text | Google Scholar

Presilla-Márquez, J., Gay, S., Rittby, C., and Graham, W. R. M. (1995). Vibrational spectra of tetra-atomic silicon– carbon clusters. II. Si₂C₂ in Ar at 10 K. J. Chem. Phys. 102, 6354–6361. doi:10.1063/1.469352

CrossRef Full Text | Google Scholar

Presilla-Márquez, J., and Graham, W. (1992). Vibrational spectra of tetra-atomic silicon– carbon clusters. I. rhomboidal Si₃C in Ar at 10 K. J. Chem. Phys. 96, 6509–6514. doi:10.1063/1.462588

CrossRef Full Text | Google Scholar

Prieto, L. V., Cernicharo, J., Quintana-Lacaci, G., Agúndez, M., Castro-Carrizo, A., Fonfría, J. P., et al. (2015). Si-Bearing molecules toward IRC+10216: ALMA unveils the molecular envelope of CWLeo. Astrophys. J. 805, L13. doi:10.1088/2041-8205/805/2/l13

PubMed Abstract | CrossRef Full Text | Google Scholar

Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6

CrossRef Full Text | Google Scholar

Rittby, C. M. L. (1992). An ab initio study of the structure and infrared spectrum of Si₃C. J. Chem. Phys. 96, 6768–6772. doi:10.1063/1.462564

CrossRef Full Text | Google Scholar

Savoca, M., Lagutschenkov, A., Langer, J., Harding, D., Fielicke, A., and Dopfer, O. (2013). Vibrational spectra and structures of neutral Si_mC_n clusters (m + n = 6): Sequential doping of silicon clusters with carbon atoms. J. Phys. Chem. A 117, 1158–1163. doi:10.1021/jp305107f

PubMed Abstract | CrossRef Full Text | Google Scholar

Savoca, M., Langer, J., Harding, D., Dopfer, O., and Fielicke, A. (2012). Incipient chemical bond formation of Xe to a cationic silicon cluster: Vibrational spectroscopy and structure of the Si₄Xe+ complex. Chem. Phys. Lett. 557, 49–52. doi:10.1016/j.cplett.2012.12.020

CrossRef Full Text | Google Scholar

Stanton, J., Dudek, J., Theulé, P., Gupta, H., McCarthy, M. C., and Thaddeus, P. (2005). Laser spectroscopy of Si₃C. J. Chem. Phys. 122, 124314. doi:10.1063/1.1869981

PubMed Abstract | CrossRef Full Text | Google Scholar

Thaddeus, P., Cummins, S. E., and Linke, R. A. (1984). Identification of the SiCC radical toward IRC +10216: The first molecular ring in an astronomical source. Astrophys. J. 283, L45–L48. doi:10.1086/184330

CrossRef Full Text | Google Scholar

Truong, N., Savoca, M., Harding, D., Fielicke, A., and Dopfer, O. (2015). Vibrational spectra and structures of Si_nC clusters (n = 3–8). Phys. Chem. Chem. Phys. 17, 18961–18970. doi:10.1039/c5cp02588e

PubMed Abstract | CrossRef Full Text | Google Scholar

Valiev, R. R., Nasibullin, R. T., Cherepanov, V. N., Baryshnikov, G. V., Sundholm, D., Ågren, H., et al. (2020). First-principles calculations of anharmonic and deuteration effects on the photophysical properties of polyacenes and porphyrinoids. Phys. Chem. Chem. Phys. 22, 22314–22323. doi:10.1039/d0cp03231j

PubMed Abstract | CrossRef Full Text | Google Scholar

Varandas, A., and Rocha, C. (2018). C_n(n = 2 − 4): Current status. Phil. Trans. R. Soc. A 376, 20170145. doi:10.1098/rsta.2017.0145

CrossRef Full Text | Google Scholar

Wang, X., Bowman, J. M., and Lee, T. J. (2013). Anharmonic rovibrational calculations of singlet cyclic C₄ using a new ab initio potential and a quartic force field. J. Chem. Phys. 139, 224302. doi:10.1063/1.4837177

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z. D., and Whithey, P. A. (2018). Comprehensive survey of the structures of C₄, C₄⁻ and C₄⁺ Clusters. ChemistrySelect 3, 13355–13364. doi:10.1002/slct.201801831

CrossRef Full Text | Google Scholar

Watrous, A. G., Westbrook, B. R., and Fortenberry, R. C. (2021). F12-TZ-cCR: A methodology for faster and still highly-accurate quartic force fields. J. Phys. Chem. A 125, 10532–10540. doi:10.1021/acs.jpca.1c08355

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. K. G. (1977). “Aspects of quartic and sextic centrifugal effects on rotational energy levels,” in Vibrational spectra and structure. Editor J. R. During (Amsterdam: Elsevier), 1–89.

Google Scholar

Werner, H.-J., Knowles, P. J., Manby, F. R., Black, J. A., Doll, K., Heßelmann, A., et al. (2020). Molpro, version 2020.1, a package of ab initio programs. WIREs Comput. Mol. Sci. 2012, 242. doi:10.1002/wcms.82

CrossRef Full Text | Google Scholar

Westbrook, B. R., and Fortenberry, R. C. (2020). Anharmonic frequencies of (MO)₂ & related hydrides for M = Mg, Al, Si, P, S, Ca, & Ti and heuristics for predicting anharmonic corrections of inorganic oxides. J. Phys. Chem. A 124, 3191–3204. doi:10.1021/acs.jpca.0c01609

PubMed Abstract | CrossRef Full Text | Google Scholar

Yadav, P., Yadav, R., Agrawal, S., and Agrawal, B. (2006). Theoretical study of the physical properties of binary Si_mC_n (m+n>5) clusters: An ab initio study. Phys. E Low-dimensional Syst. Nanostructures 33, 249–262. doi:10.1016/j.physe.2006.03.132

CrossRef Full Text | Google Scholar

Zhao, D., Doney, K. D., and Linnartz, H. (2014). Laboratory gas-phase detection of the cyclopropenyl cation (c-C₃H₃⁺). Astrophys. J. 791, L28. doi:10.1088/2041-8205/791/2/l28

CrossRef Full Text | Google Scholar