
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 18 November 2022
Sec. Space Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.1064098
This article is part of the Research Topic The Future of Space Physics 2022 View all 66 articles
 Federico Fraternale1*
Federico Fraternale1* Lingling Zhao1
Lingling Zhao1 Nikolai V. Pogorelov1,2
Nikolai V. Pogorelov1,2 Luca Sorriso-Valvo3,4
Luca Sorriso-Valvo3,4 Seth Redfield5
Seth Redfield5 Ming Zhang6
Ming Zhang6 Keyvan Ghanbari1
Keyvan Ghanbari1 Vladimir Florinski1,2
Vladimir Florinski1,2 Thomas Y. Chen7
Thomas Y. Chen7Turbulence is ubiquitous in space plasmas. It is one of the most important subjects in heliospheric physics, as it plays a fundamental role in the solar wind—local interstellar medium interaction and in controlling energetic particle transport and acceleration processes. Understanding the properties of turbulence in various regions of the heliosphere with vastly different conditions can lead to answers to many unsolved questions opened up by observations of the magnetic field, plasma, pickup ions, energetic particles, radio and UV emissions, and so on. Several space missions have helped us gain preliminary knowledge on turbulence in the outer heliosphere and the very local interstellar medium. Among the past few missions, the Voyagers have paved the way for such investigations. This paper summarizes the open challenges and voices our support for the development of future missions dedicated to the study of turbulence throughout the heliosphere and beyond.
Turbulence is one of the most important processes in the heliospheric and astrophysical plasmas, routing energy from the largest to the smallest scales and mediating the transport of energetic particles (Bruno and Carbone, 2013). It plays a critical role in the interaction of the solar wind (SW) with the local interstellar medium (LISM). However, its properties in the outermost regions of the heliosphere and beyond are poorly understood. Figure 1 shows the plasma mixture’s temperature and the neutral hydrogen density distributions along the BLISM−VLISM plane, obtained from the most recent MHD-plasma/kinetic-neutrals model employed in MS-FLUKSS, the Huntsville global heliosphere numerical code. It highlights the distinct regions that can be explored in situ by future missions: the supersonic solar wind (SW), the inner heliosheath (IHS), and the interstellar regions, including an outer heliosheath (OHS). The portion of the LISM affected by the presence of the heliosphere is called the very local interstellar medium (VLISM) (Zank, 2015; Zhang et al., 2020; Fraternale and Pogorelov, 2021). It can extend to hundreds of AU along the upwind direction and thousands of AU into the heliotail (Zhang et al., 2020). At the heliospheric termination shock (HTS) the SW violently transitions to a subsonic flow. The heliopause (HP) separates the SW from the VLISM. A heliospheric boundary layer (HBL) with decreased plasma density and draped magnetic field is adjacent to the HP on the VLISM side (Pogorelov et al., 2017b).
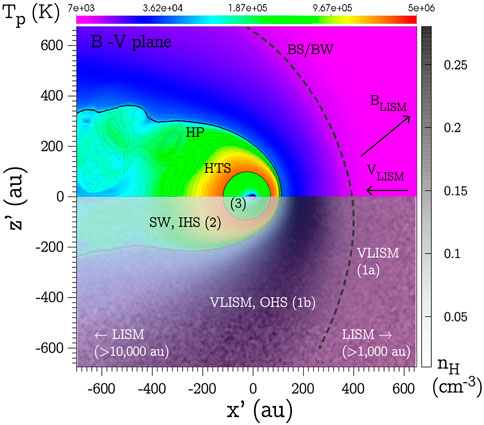
FIGURE 1. Heliospheric regions illustrated using a global heliosphere simulation with kinetic neutral H and He atome, and steady-state boundary conditions (Fraternale and Pogorelov, 2021; Fraternale et al., 2022b). Region (1a) includes the VLISM beyond the bow shock (BS) or bow wave (BW). Region (1b) represents the OHS (filled with the disturbed VLISM). Region (2) represents the IHS (subsonic SW). Region (3) represents the supersonic SW. The color plot shows the proton temperature distribution in the BLISM-VLISM plane, overlayed, in the bottom half, to the neutral hydrogen density distribution.
The global and fine-scale properties of these regions are significantly affected by the presence of pickup ions (PUIs), i.e., interstellar neutrals that were ionized as they flowed into the heliosphere, or neutrals of heliospheric origin that were deposited in the LISM (Möbius et al., 1985; Williams et al., 1995; Zank, 1999). Their thermal energy becomes dominant beyond ∼10 AU from the Sun (Zank et al., 2018; Zhao et al., 2018; Zhao et al., 2019a).
Much of our current understanding of the outer heliosphere and VLISM relies on a few missions, namely Voyager (V1, V2), Ulysses, IBEX, and New Horizons (NH). Ulysses has provided the first latitude scan of the heliosphere, sampling SW plasma and neutral atoms from the solar equator to the poles as far as 5 AU from the Sun. IBEX has been providing us with more than one solar cycle of remote observations of neutral atom fluxes, including Energetic Neutral Atoms (ENAs). The upcoming Interstellar Mapping and Acceleration Probe (IMAP) will further shed light into the global properties of the heliosphere and its interaction with the LISM through high resolution neutral atoms measurements (McComas et al., 2018). The Voyagers, launched in 1977, have paved the way to in-situ investigations of the distant SW and VLISM. To date, they are the only spacecraft that made in-situ measurements from the IHS, and they are both currently in the OHS. They have revealed the very dynamic nature of the SW and VLISM in these regions of space. The more recent NH mission has been measuring PUIs beyond 20 AU for the first time and is now at ∼50 AU from the Sun.
However, such missions have been limited in their ability to collect data because instruments doing the in-situ measurements were not specifically designed for turbulence analysis. Major limitations to turbulence measurements are related to the 1D sampling by a single-spacecraft; the cadence of measurements; and instrumental issues such as noise, limited telemetry coverage, failure or shutdown of subsystems, and partial availability of measurements (e.g., lack of PUI measurements at Voyager and of magnetic field measurements at New Horizons, low plasma cadence and reduced aphelion distance at Ulysses). Besides, it is still unfeasible to resolve turbulence directly over the whole range of scales in global models.
Our understanding of turbulence in space plasmas would greatly benefit from new missions to the outer heliosphere, such as the Interstellar Probe (ISP) mission (Brandt et al., 2022; McNutt et al., 2022). It is desirable to have a variety of plasma conditions observed in the different regions of the heliosphere, covering particle composition, distribution functions, collisionality, ionization ratio, and their correlation with turbulence properties. In Table 1, we indicate the typical plasma parameters and relevant scales in different regions of the heliosphere and in the LISM. For turbulence studies, future missions should be equipped with both a high–cadence magnetometer and a plasma instrument with the capability to distinguish PUIs from thermal ions. Here in the following, we summarize some specific science objectives focused on the study of turbulence.
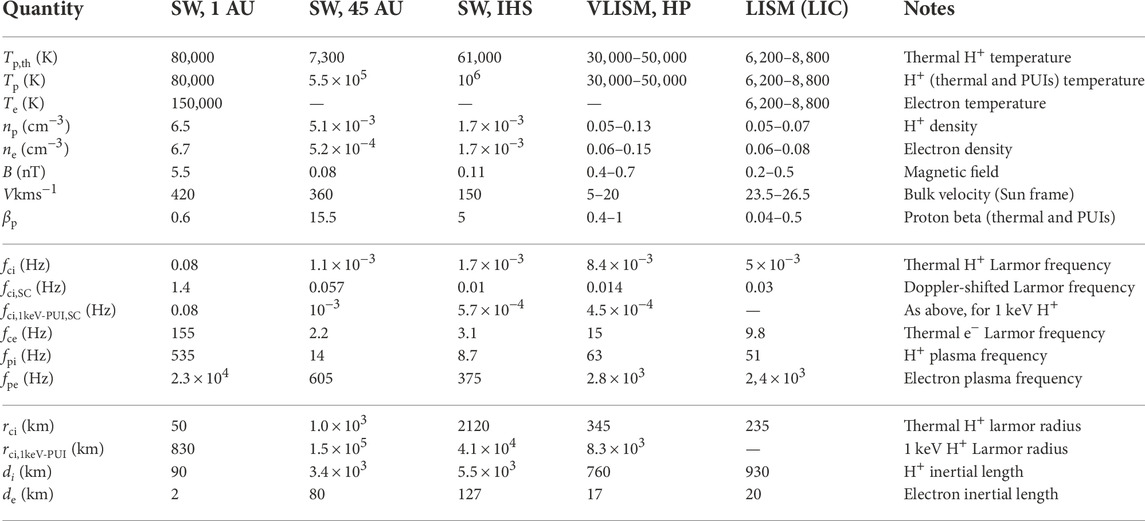
TABLE 1. Typical plasma parameters in various regions of space. The values at 1 AU are average SW conditions in the Ecliptic from 2012 to 2022 (OMNI and Wind data https://omniweb.gsfc.nasa.gov/). At 45 AU, we report the SW and PUI observations made by New Horizons (McComas et al., 2021), and the magnetic field at V2. In the IHS, we use average V2 observations form 2008 to 2018 (e.g., Richardson et al., 2022). Since PUI were not measured by Voyager, we assumed the density fraction of 25% and TPUI = 5 × 106. There are no electron measurements in the distant SW. In the VLISM in proximity of the HP, we show the range of values observed by V1 and V2 (within 150 AU from the Sun). In particular, we present V1 and V1 magnetic field observations (e.g., Burlaga et al., 2022), temperature measured by V2 (Richardson et al., 2019), electron density from V1/PWS observations (Gurnett et al., 2021), flow speed from simulations (Pogorelov et al., 2017a; Kim et al., 2018). Lastly, about the LISM properties in the LIC, we indicate the range of values based on the extensive literature, see (e.g., see Slavin, 2009; Frisch et al., 2011; McComas et al., 2015; Zirnstein et al., 2016; Wood et al., 2019; Linsky et al., 2022, and references therein). Some of the LISM properties are subject to large uncertainties and still the subject of current research. Frequencies and scales are obtained using the above quantities (for the electron inertial length, we have assumed Te = Tp,th). For more details, see the Tables published by Fraternale et al. (2019a); Fraternale et al. (2019b); Fraternale and Pogorelov (2021).
This paper is also published as a white paper for the Heliophysics 2,024 Decadal Survey (Fraternale et al., 2022d), in support of future missions aimed at investigated turbulence from the Sun to the LISM.
Turbulence observed in the SW can be divided into the pre-existing turbulence coming from the Sun and that generated locally by the complex small- and large-scale structures in the SW. Its radial evolution and the mechanisms that control it during the expansion are not fully understood. Our knowledge of turbulence mostly relies on observations within 1 AU form the Sun, where a wealth of available spacecraft including multi-spacecraft missions such as MMS, CLUSTER, and the upcoming HelioSwarm, have helped resolve the distribution of wave vectors and underlying dynamics. The SW has a complex magnetic structure from large to small scales that includes dynamically interacting spaghetti-like magnetic flux tubes separated by current sheets (CSs) (Borovsky, 2008; Greco et al., 2009; Borovsky, 2020), magnetic islands or plasmoids near the heliospheric current sheet (HCS) (Khabarova et al., 2015; Khabarova et al., 2016; Khabarova et al., 2021; Eriksson et al., 2022), compressive and Alfvénic coherent structures (Perrone et al., 2016; Perrone et al., 2017), plasma waves, and shocks (see Sections 2.3, 2.7). These structures show random, intermittent features with power-law spectral distributions (Sorriso-Valvo et al., 2005; Sorriso-Valvo et al., 2017; Bruno, 2019). The statistical nature has led to an apparent dichotomy between “random” turbulence and more “ordered” features possibly not manifestations of turbulence, thus posing challenging questions about their origin, interplay and roles in the SW heating and energetic particle transport and acceleration. Between ∼15 and ∼35 AU, corotating interaction regions (CIRs) coalesce, producing merged interaction regions (MIRs) where the plasma features broad pressure jumps and shock-like structures. Tangential discontinuities (TDs) within CIRs between the forgoing slow and following fast SW can contribute to the in-situ generation of turbulence (Ghanbari et al., 2019; Sorriso-Valvo et al., 2021). Plasma instabilities such as Rayleigh-Taylor (RT) and Kelvin-Helmholtz (KH) can set in due to shear layers in CIRs (Neugebauer et al., 1986; Odstrcil and Pizzo, 1999; Kieokaew et al., 2021). Beyond ∼10 AU, PUI thermal energy becomes dominant. As PUI are isotropized, they generate turbulence.
High-resolution plasma and magnetic field measurements obtained by new missions in the distant SW could be used to understand turbulence and SW structures in an environment where PUIs are energetically dominant. Since a spacecraft directed to the outer heliosphere will likely use gravity assistance (e.g., at Jupiter or Saturn), the mission can also provide an opportunity to study planetary magnetospheric turbulence.
Solar wind turbulence is anisotropic with respect to the background mean magnetic field (B0). As a result, observed features of turbulence depend on the sampling angle between the SW velocity and the direction of the large-scale field. This is a consequence of Taylor’s hypothesis (Taylor, 1938), where the observed timescales are translated to length scales based on the flow velocity. The anisotropy shows several aspects. For example, the turbulence correlation function has a “Maltese cross” shape (Matthaeus et al., 1990), suggesting a superposition or alternation of the different modes with wavevectors perpendicular (k⊥) and parallel (k‖) to B0. The 2D + slab is a popular model of anisotropic turbulence, where the 2D component contains fluctuations with k⊥ and the slab component contains fluctuations with k‖. However, the presence of different plasma populations in mixed fast and slow SW conditions complicates the Maltese cross analysis and interpretation (Dasso et al., 2005).
The anisotropy also shows significant differences in the turbulence power density when they are measured parallel and perpendicular to B0. In the SW at 1 AU, fluctuation in modes with k ⊥B0 typically dominates over the parallel propagating modes, consistent with the dominance of 2D component as shown by Bieber’s “ratio test” (Bieber et al., 1996). Efforts to employ such method beyond 10 AU, however, have not been satisfactory (Pine et al., 2020b), which leaves an open question about the evolution of anisotropy with radial distance.
Another still active area of research focuses on the anisotropy of the spectral index. The spectral index clearly depends on the angle between the magnetic field and the radial direction. This makes it ambiguous in interpreting observations because any perceived change in turbulence properties can be interpreted as either due to intrinsic modification of the turbulence itself or simply due to the change in the sampling angle. Observations from the Sun to the VLISM can help us better understand how turbulence anisotropy evolves with external parameters by modeling the observed power spectrum to disentangle the effects of sampling angles. External parameters can include radial distance, SW speed, proton beta (βp), and solar activity.
Waves in the SW are characterized by fluctuations that follow a certain dispersion relation (e.g., Gary, 1993). Waves with clear frequency and polarization signatures can sometimes be observed in SW in-situ measurements, including both magnetohydrodynamic- (MHD-) and kinetic-scale waves. Kinetic-scale waves are especially important for SW heating via wave-particle interaction and stochastic heating. These waves usually exist in imbalanced Alfvénic turbulence.
Different waves can be distinguished by the range of frequency or wavelength, wavevector direction, and polarization properties. For low-frequency MHD waves, Alfvén modes typically dominate in the supersonic SW, with a small fraction of fast or slow magnetosonic waves. However, this might not be true in the IHS (Borovikov et al., 2012; Fraternale et al., 2019a; Zieger et al., 2020). In the kinetic range, ion cyclotron waves (ICWs) propagate nearly ‖ B0 and possess a left-handed polarization in the SW frame; kinetic Alfvén waves (KAWs) propagate nearly ⊥ B0 and are right-handed polarized, and whistler waves are right-hand polarized and propagate quasi-parallel or obliquely to B0. They tend to have large magnetic compressibility with strong parallel fluctuations. In contrast, KAWs are mostly dominated by perpendicular fluctuations. In the distant SW, PUIs generate Alfvénic cyclotron, right-hand polarized waves during the process of isotropization (Lee and Ip, 1987). The exact mechanisms underlying this process and the role of either background or self-generated turbulence and eventually the heating of the SW due to PUIs are still the subject of current investigations. PUI waves have been detected in specific intervals as far as 45 AU from the Sun (e.g., Hollick et al., 2018) at frequencies near the ion cyclotron frequency. Why these waves are not always seen, if they exist in the IHS and VLISM, and what is their contribution to SW heating energetic and particle scattering (Engelbrecht, 2017) are open points.
In the VLISM, low-frequency, quasi-periodic oscillations in B have been identified out to 150 AU form the Sun (Burlaga and Ness, 2016; Fraternale and Pogorelov, 2021; Burlaga et al., 2022). The wavelength is ∼0.2–3 AU and they contribute significantly to the power spectrum on frequencies fsc ≲ 10−6 Hz, at in the relatively narrow heliospheric boundary layer adjacent to the HP, whose thickness along the heliospheric nose direction may be of the order of
Future missions should enable us to identify both low-frequency and kinetic-scale waves form the near-Sun to the VLISM environments. A study of growth/damping rate of various kinetic wave modes under different plasma conditions would also be beneficial. The connection between different wave modes and particle scattering also ought to be the subject of detailed investigations.
The transport of energetic cosmic ray (CR) particles throughout the heliosphere relies on the large-scale SW flow and on the magnetized turbulence embedded in it (Schlickeiser, 2002; Zhang, 2006; Shalchi, 2009; Oughton and Engelbrecht, 2021). Two important processes responsible for the modulation of GCRs are drift along the HCS and diffusion caused by SW turbulence. The role of stochastic acceleration by plasma turbulence in the production and transport of energetic particles has been reviewed in Zhang and Lee (2013).
The most successful models of CRs propagation are based on Parker (1965), which essentially includes all important modulation mechanisms such as outward convection by the SW, diffusion through the turbulent interplanetary magnetic field (IMF), gradient and curvature drifts, and adiabatic deceleration from the divergence of the expanding SW. The diffusive shock acceleration (DSA) at supernova remnant shocks produces GCRs. The same mechanism operates at interplanetary shocks producing relatively low-energy particles and at the HTS, producing some fraction of the anomalous CRs (ACRs). The key to the DSA mechanism for generating energetic particles is plasma turbulence that can scatter particles across the shock repeatedly.
The diffusion coefficient κ quantifies the scattering of energetic particles by fluctuations in the irregular IMF. A well-known approach for evaluating the diffusion of charged particles is quasi-linear theory (QLT; Jokipii, 1966) based on a resonant wave-particle interaction. QLT requires that waves have a finite propagation speed along the magnetic field but they do not need to be parallel. Ensembles of both Alfvén waves and magnetosonic waves with different levels of anisotropy have been considered (Shalchi and Schlickeiser, 2004). The diffusion coefficient is usually expressed in terms of the turbulence power spectrum, often assumed to be in the Kolmogorov’s form at inertial scales, with a flatter energy-containing range. Such approximation is insufficient when the low-energy particles’ speed is comparable to the wave propagating speed, such as PUIs, as they may resonate with fluctuations in the dissipation range. QLT is inaccurate for parallel diffusion if turbulence is not Alfvénic, and the effects of gyro-resonance and transit time damping need to be clarified. Moreover, compressible turbulence is very effective in scattering and accelerating energetic particles, in particular the fast-modes waves provide the dominant contribution to CR scattering (e.g., Yan and Lazarian, 2002; Lazarian and Beresnyak, 2006; Zhang, 2006). Compressive modes may be an important component of turbulence in the IHS and VLISM.
Using observations from the outer heliosphere, it will be possible to determine in which regimes and regions turbulence is dominated by Alfvén waves or by compressible fluctuations, and improve the derivation of CR diffusion coefficients. There are still open questions on particle scattering due to turbulence. For instance, it remains unclear under which conditions compressible fluctuations needs to be taken into account, and how much they affect the CR transport; how the efficiency of scattering depends on the fluctuation properties at different radial distances; what is the role of SW structures such as CIRs and shocks in the CRs cross field scattering; and how VLISM fluctuations affect the small-scale variations of CR fluxes.
Understanding the pathways of energy dissipation into ion and electron heating is one of the most fundamental and long-standing challenges of space plasma physics. The ion “dissipation range” is described as fsc > f (di) and at 1 AU it is generally characterized as a steepening of the power spectrum (Figure 2). This terminology refers to the onset of dissipation effects, besides the cross scale transfer, at sub-ion scales in weakly collisional plasmas (Howes et al., 2011; Matthaeus and Velli, 2011; Matthaeus, 2021).

FIGURE 2. Scheme of the magnetic power spectrum of SW turbulence at 1 AU. The correlation scale (LC), proton gyrofrequency (fci), proton Larmor radius (rci) and the proton and electron inertial lengths (di and de, respectively) derived from the Doppler-shift relation are also shown. Reproduced from Fraternale et al. (2022a).
Smith et al. (2006) found that the steepness of the ion dissipation spectrum depends on the strength of the inertial range energy transport and can be absent beyond ∼2 AU (Pine et al., 2020a). At higher frequencies there is an electron inertial range where the dynamics are supported by the thermal electrons until dissipation occurs. Many aspects of how the cascade operates in the kinetic regime are unknown, especially in the outer heliosphere. Debated topics include the preferential ion heating vs. the electron heating and temperature anisotropy (Breech et al., 2009; Boldyrev et al., 2020; Phillips et al., 2022; Sioulas et al., 2022; Squire et al., 2022); specific phenomenology dominating in the kinetic regimes; role of turbulence in driving ion beams (Sorriso-Valvo et al., 2019a, Sorriso-Valvo et al., 2019b) and kinetic microinstabilities (Bowen et al., 2020); role of ICWs (Bale et al., 2019), and PUI-driven instabilities (Florinski et al., 2016; Roytershteyn et al., 2019).
Understanding turbulent dissipation may also shed light into some global features of the heliosphere. It was argued, based on 3D, time-dependent simulations, that small magnetic fields in the IHS may be a signature of the presence of dissipation due to turbulence, reconnection, or both (Pogorelov et al., 2017b). High-cadence measurements of ions and electrons are needed together with magnetic field measurements to reveal the dissipation mechanisms at far distances.
Compressible turbulence in space plasmas has long been investigated (e.g., Marsch and Mangeney, 1987; Zank and Matthaeus, 1993; Matthaeus et al., 1996; Cho and Lazarian, 2002; Kowal and Lazarian, 2010; Oughton et al., 2016; Ferrand et al., 2020; Yang et al., 2021). Despite supersonic SW turbulence being mostly incompressible, low-frequency compressive fluctuations have been found in the slow wind (Perrone et al., 2016) and near ion scales (Alexandrova et al., 2013). Compressible turbulence is more efficient in accelerating energetic particles than incompressible turbulence (e.g., Bykov and Toptygin, 1982, 1993; Fisk and Gloeckler, 2006; Fisk and Gloeckler, 2008; Fisk et al., 2010; Zhang, 2010; Zhang and Schlickeiser, 2012). In regions where strong compressible turbulence is generated, particle acceleration can occur so efficiently that energetic particles can automatically establish a ∝ p−5 distribution function (p particle momentum), a spectral shape containing critical amount of energy. Compressible turbulence is still an open problem. Relevant questions regard the existence of universal scaling laws; role and formation of shocklets; channels of energy dissipation and existence of exact laws; role of the forcing; nature of intermittency and locality of the energy cascades; and role in star formation (e.g., Carbone et al., 2009; Aluie et al., 2012; Banerjee and Galtier, 2013; Falgarone et al., 2015; Banerjee et al., 2016; Yang et al., 2016; Andrés et al., 2018; Andrés et al., 2021; Simon and Sahraoui, 2022). It is important to stress that turbulence transport models applicable beyond the HTS have not been developed yet (Oughton and Engelbrecht, 2021), even though the first steps have been taken (Fichtner et al., 2020). The outer heliosphere is an ideal laboratory for addressing these questions, as discussed in details in a recent review paper by Fraternale et al. (2022a).
In the IHS, the nature of “turbulence” appears to be fundamentally different than that in the supersonic SW (Burlaga and Ness, 2009). Here turbulence still coexists with coherent structures and certainly there is no single physical mechanism that describes all observed characteristics. Our current understanding of IHS turbulence includes: Differences in sector and unipolar IHS regions (Burlaga et al., 2009); multifractal, intermittent, and compressible fluctuations (e.g., Burlaga and Ness, 2009; Burlaga and Ness, 2010); different power-law spectral regimes and anisotropy (Fraternale et al., 2019a; Fraternale et al., 2019b); coherent structures and current sheets (Burlaga and Ness, 2011; Zhao et al., 2019a); and possible PUI-mediated regimes including mirror mode or soliton waves (e.g., Avinash and Zank, 2007; Fahr and Siewert, 2007; Liu et al., 2007; Burlaga and Ness, 2009; Tsurutani et al., 2011; Fichtner et al., 2020). Open questions remain regarding the nature of the observed turbulence spectra; the sub-ion regime of turbulence, still entirely unexplored; role of magnetic reconnection at the HCS in generating turbulence in the outer heliosphere (e.g., Eyink, 2015; Pogorelov et al., 2017b; Drake et al., 2017); and the role of PUIs in both energy release and mediation of turbulence and waves, existence, and formation of flux ropes and CSs in sector and unipolar regions (Burlaga and Ness, 2010; Richardson et al., 2016); the generation of shocks, their reflection at the HP (Washimi et al., 2011; Pogorelov et al., 2021), still not detected in observations but predicted by global models.
We suggest that future missions should be capable of resolving power spectral densities of ∼10−8 nT2Hz−1 to fully describe the turbulence magnetic spectrum in the IHS and VLISM. The noise level for B at Voyager reaches Pnoise [B] ∼ 10−2−10−1 nT2Hz−1. For density fluctuations, the spectral noise level at V2 is Pnoise [np] ∼ 5 × 10−4−10−3 cm−6Hz−1. For velocity fluctuations,
The distant SW offers an opportunity to investigate turbulence and waves at interplanetary collisionless shocks, including PUI-mediated shocks recently observed at New Horizons (McComas et al., 2022), and at collisional VLISM shocks and compression waves, whose dissipative structure is still the subject of current investigations (Mostafavi and Zank, 2018; Fraternale et al., 2020; Burlaga et al., 2022; Mostafavi et al., 2022). The presence of turbulence responsible for scattering energetic particles is central to understanding particle acceleration at shocks and energy partition of ions and electrons (e.g., Wilson et al., 2019; Guo et al., 2021). The HTS is perhaps most complicated multi-ion shock in the distant heliosphere. Compressible turbulence in the IHS is critically controlled by processes occurring at the HTS. The question of if and how the HTS might accelerate ACRs (Pesses and Eichler, 1981; Zank et al., 2015; Zhao et al., 2019b) and electrons remains open. The structure of the HTS is mediated by both PUIs (Mostafavi and Zank, 2018; Zank et al., 2018) and energetic particles accelerated near the shock (Decker et al., 2008; Florinski et al., 2009). To date, the HTS has only been observed by the Voyagers. Enhanced compressible fluctuations were detected inside the HTS structure (Burlaga et al., 2008), which still lack an explanation and may be critical to explain observed ENA fluxes, as suggested by Zirnstein et al. (2021). However, the possible effects of turbulence within the structure of collisionless shocks, in addition to the contribution of pre-existing upstream turbulence, is still unclear and should be the subject of future studies.
Data-driven modelling of the SW has been conducted for many years. In recent years, turbulence in the SW has been studied using data-driven modelling, including machine learning (ML) and artificial intelligence (AI) approaches (Feng et al., 2015). Roberts et al. (2020) harness unsupervised k-means clustering to output unbiased states of the SW, providing a novel framework for automated classification of solar structures and events. Further, neural network-based techniques (multilayered ML, see Ishikawa et al., 2022) have enabled accurate prediction of multi-scale turbulent convection in the photosphere. In the next decade, it will be important to address interpretability in deep learning (Zhang et al., 2021) to ensure sustainable and trustworthy science advances at the intersection of ML, high performance computing, and turbulence anisotropy. MHD models studying the corona and inner heliosphere have been a focus of recent research. Next-generation supercomputing capabilities will enable modeling from the chromosphere through the heliosphere, yielding novel insight into the generation of coronal turbulence in the SW and its evolution (Mostafavi et al., 2021).
Being about 150 AU away from the Sun, the Voyagers are still in the OHS, in particular within the dynamical HBL. This region is filled with the VLISM, but its properties are significantly different from those of the VLISM at much farther distances. The medium is collisional with respect to Coulomb collisions. Charge-exchange collisions are fundamental, especially in the OHS where they effectively slowdown the interstellar flow, creating a region with compressed plasma, draped magnetic field, and the hydrogen and helium walls. Since the VLISM is partially ionized, elastic collisions associated with the presence of neutral atoms are also expected to play a role. These processes, solar activity and geometric effects can affect the properties of fluctuations and turbulence in the VLISM in vicinity of the heliosphere. The possible presence of a bow shock at about 350–450 AU along the upstream direction (Figure 1) is another factor, as suggested by studies of other stellar bow shocks using remote observations (Ocker et al., 2021).
Observations indicate the presence of low-intensity, compressible turbulence of the VLISM (Burlaga et al., 2015). The observed spacecraft-frame frequency range is 10−8 < fsc < 10−2 Hz, as shown in the power spectrum of Figure 3A. This figure also shows the limits of magnetic field measurements, and some of the typical scales associated with the thermal plasma, energetic particles and Coulomb collisions. The properties of turbulence evolve with distance and are reviewed in Fraternale et al. (2022a). The current consensus, built on observational evidence and theoretical analyses, is that the observed turbulence is forced by the SW-driven motion of the HP and superimposed on the pristine LISM turbulence (Zank et al., 2017; Matsukiyo et al., 2019). Perhaps, the outer scale of the locally injected turbulence is ∼100 AU (Zank et al., 2019). This scenario is supported by electron density spectra (Lee and Lee, 2019; Lee and Lee, 2020; Ocker et al., 2021) derived recently from V1/PWS data, showing that the local spectrum is enhanced by a factor ∼100 with respect to the ISM spectrum, “The Big Power Law” first derived by Armstrong et al. (1995) and recently updated by Ocker et al. (2021) with new data. At low frequencies, fsc ≲ 10−6 Hz, magnetic spectral indices range from −3/2 to −2. The latter index may be associated with the presence of steepened waves and a coherent-cascade, Burgers-like, phenomenology as argued by Fraternale and Pogorelov (2021), instead of a classic Kolmogorov-like cascade. However, the possibility for a wave-turbulence phenomenology for the local, forced turbulence should also be investigated, which requires a careful evaluation of the forcing and the strength of nonlinear interactions.
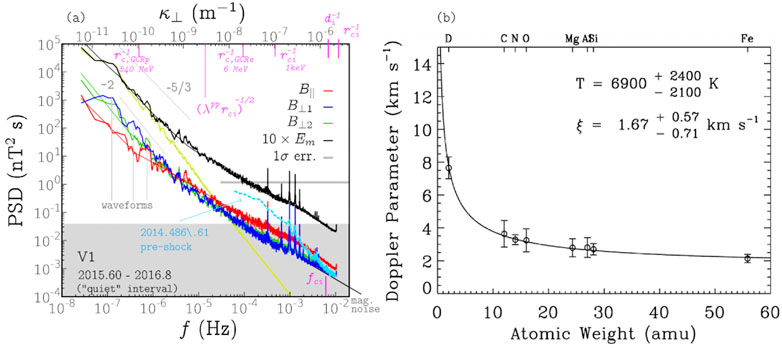
FIGURE 3. VLISM turbulence. (A) Power spectra of magnetic field fluctuations observed in situ by V1 at ∼135 AU from the Sun (reproduced from Fraternale et al., 2022a).(B) Turbulence properties inferred from absorption line observations (reproduced from Redfield and Linsky, 2004a).
The magnetic compressibility, as defined by the ratio of the power spectrum of |B| and the trace power spectrum, decays with distance (Burlaga et al., 2018; Zank et al., 2019; Burlaga et al., 2020b; Zhao et al., 2020; Fraternale and Pogorelov, 2021), but surprisingly remains large at fine scales, at V1 (Fraternale and Pogorelov, 2021). Intermittency of VLISM fluctuations and fine-scale features (0.01 ≲ k⊥di ≲ 1) have been observed only recently by Fraternale et al. (2019a); Fraternale et al. (2020b); Burlaga et al. (2020a). This results suggest that local processes may operate at scales below the proton-proton Coulomb-collisional mean free path (∼0.3–5 AU, for temperature values between ∼7,500 and ∼40,000 K). Two hypothesis that have been advanced include the presence of instabilities associated with PUIs created from charge-exchange collisions between fast neutrals of SW origin and OHS protons, and shock-related kinetic processes. Is still unclear, however, if broad and weak interstellar shocks can effectively accelerate ions and electrons (a discussion can be found in the recent review paper by Mostafavi et al., 2022).
Future missions will shed light into the nature of compressible and Alfvénic turbulence of the VLISM; collisionality of plasma in the partially ionized medium and the possibility that the VLISM is collisional on larger scales and collisionless on smaller scales (Mostafavi and Zank, 2018; Fraternale et al., 2020); self-generated turbulence due to the instability of PUI distributions (Florinski et al., 2016; Roytershteyn et al., 2019); and the contribution to VLISM turbulence by shocks due to major solar eruptive events or solar cycle effects.
Interstellar absorption in the spectra of nearby stars offers opportunities to measure the turbulence in the absorbing medium. Frisch et al. (2011) provided a recent review of the physical properties of the VLISM. Spectral observations represent a valuable comparison to the in-situ observations. Absorption line observations can probe a wider range of environments along many different sight lines, but the measurements are line-of-sight-averaged, providing only a smeared combined picture of various regions. Therefore, it is valuable to obtain and compare both kinds of measurements to get a complete picture of the nature of turbulence in nearby plasmas. In simulations of the ISM, turbulence drives a wide range of values for local temperature, density, magnetic field strength and kinematics (de Avillez and Breitschwerdt, 2005).
High spectral resolution observations of nearby stars at ultraviolet (UV), optical, and infrared (IR) wavelengths all show interstellar absorption. The absorption lines are broadened by thermal motions and turbulence. These two broadening mechanisms can be decoupled if absorption is measured for ions of different masses. The broadening due to thermal motion will anticorrelate with the mass of the ion, whereas broadening due to turbulent motion will typically be constant for all ions. Figure 3B, from Redfield and Linsky (2004a) shows the measured width of several observed ions for all observations of the VLISM, which results in an average T = 6,900 K and a turbulent velocity (ξ) of 1.67 km s−1. The decreasing impact of the thermal broadening is evident, as is the plateau of constant broadening, independent of mass, for the heavier ions. The turbulent measurements of 50 VLISM absorbers were presented in Redfield and Linsky (2004b), showing the turbulence was subsonic. The RMS velocity estimated using magnetic field fluctuations measured by V1 near the HP is 1.2–1.7 km s−1 (Fraternale and Pogorelov, 2021), but it includes only scales smaller than ∼ 10 AU. This speaks in favour of the scenario of enhanced VLISM turbulence in the OHS described in the previous Section. Spangler et al. (2011) found that VLISM does not have turbulent properties similar to the solar corona, namely temperature anisotropy, mass-proportional temperatures, and velocities aligned with the magnetic field direction. This is likely due to the prevalence of ion-neutral collisions in the partially ionized plasmas of the VLISM.
There are exciting new opportunities to couple small scale, in-situ spacecraft observations with the line-of-sight-averaged measurements of nearby stars. One example was explored by Zachary et al. (2018), where UV observations of nearby stars by the Hubble Space Telescope were taken along the same sight lines in which Voyagers are traveling. Electron density measurements were obtained by Voyager using electron plasma oscillations by Gurnett et al. (2013), and compared to electron density measurements along the same sight line using interstellar absorption line widths of the excited and resonance transitions of ionized carbon. Similar comparative studies could be made regarding the turbulence measurements. Linsky et al. (2022) look for correlations of turbulent measurements with a variety of parameters, including temperature, direction of strong photoionization, cloud boundaries, and interstellar flow directions.
The solar wind and the very local interstellar medium surrounding our heliosphere are turbulent plasmas featuring a vast range of parameters in terms of thermodynamic quantities, composition, degree of ionization, bulk properties, particle distribution function and magnetic fields. Only a tiny portion of space and time has been explored so far by in-situ spacecraft, and a substantial imbalance exists between the number of missions orbiting at heliocentric distances within 1 AU and those directed to the outer heliosphere. The former include several spacecraft that are suitable to investigate turbulence, including multi-spacecraft missions and near-Sun missions (e.g., PSP, SolO). They have been providing us with critical insights into the nature of turbulence in the inner heliosphere. The latter include in-situ missions such as Voyager, New Horizons, and remote ones such as IBEX and HST, that continue to provide evidences of the complex physical processes governing the far regions at the interface between the heliosphere and interstellar space. Such missions were not specifically designed for investigating turbulence, nonetheless they have demonstrated the existence of a turbulent energy cascade, the presence of waves, coherent dynamic structures, and opened a number of science questions about their relative roles and nature. We do not know exactly for how long V1 and V2 will remain operational. Perhaps, they will be able to send data until 2027 or 2028 (Richardson et al., 2022). In the extended mission, NH will make distant observations of Uranus and Neptune. It is also expected that NH will be able to reach the TS in the next decade. In this case, it will be able to provide unique measurements of the TS crossing by PUIs, which is a topic of great scientific interest in the heliospheric community, and further sample the IHS plasma. Therefore, data of these missions, together with IMAP scheduled to launch in 2025, still state the nearest future.
In this brief review paper, we have illustrated the major compelling challenges associated with the study of turbulence and fluctuations of various nature in the heliosphere and beyond, and present our perspective about which investigations future missions should carry out. The range of scales in which turbulence is observed from both in situ and remote measurements is staggering. Understanding turbulence in the closest astrophysical plasmas is a challenging and rewarding task. This topic also touches a wide range of phenomena of interest for both the Space Science and Astrophysics communities. In fact, future missions expected to reach ∼500 AU will reveal the properties of a less perturbed state of LISM turbulence. Traversing such immense distances will thus offer critical insights into one of the dominant phases of the interstellar medium. Pursuing the investigation of turbulence in the distant SW and VLISM may lead our community to a better understanding of plasma turbulence itself as a universal and ubiquitous process, and of its influence on the macro- and micro-scale features of the heliosphere and nearby interstellar medium.
FF lead the effort in the review. FF and LZ designed the section structure of the article. All authors have made a substantial intellectual contribution and participated in writing the article.
FF and NP acknowledge support by NASA grants 80NSSC19K0260, 80NSSC18K1212, 80NSSC22K0524, 80NSSC18K1649, AFOSR grant FA9550-19-1-0027, NSF-BSF grant PHY-2010450, and Hubble Space Telescope GO-15380.002-A. Our work was also partially supported by the IBEX mission as a part of NASA’s Explorer program. LZ acknowledges the partial support from NASA grant 80NSSC20K1783. LS-V was supported by SNSA grants 86/20 and 145/18.
We acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources on Frontera supported by NSF LRAC award 2031611. Supercomputing time allocations were also provided on SGI Pleiades by NASA High-End Computing Program award SMD-17-1537 and Stampede2 by NSF XSEDE project MCA07S033.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar wind turbulence and the role of ion instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8
Aluie, H., Li, S., and Li, H. (2012). Conservative cascade of kinetic energy in compressible turbulence. Astrophys. J. 751, L29. doi:10.1088/2041-8205/751/2/l29
Andrés, N., Galtier, S., and Sahraoui, F. (2018). Exact law for homogeneous compressible hall magnetohydrodynamics turbulence. Phys. Rev. E 97, 013204. doi:10.1103/PhysRevE.97.013204
Andrés, N., Sahraoui, F., Hadid, L. Z., Huang, S. Y., Romanelli, N., Galtier, S., et al. (2021). The evolution of compressible solar wind turbulence in the inner heliosphere: PSP, THEMIS, and MAVEN observations. Astrophys. J. 919, 19. doi:10.3847/1538-4357/ac0af5
Armstrong, J. W., Rickett, B. J., and Spangler, S. R. (1995). Electron density power spectrum in the local interstellar medium. Astrophys. J. 443, 209–221. doi:10.1086/175515
Avinash, K., and Zank, G. P. (2007). Magnetic structures in the heliosheath. Geophys. Res. Lett. 34, L05106. doi:10.1029/2006GL028582
Bale, S., Badman, S., Bonnell, J. e. a., Bowen, T. A., Burgess, D., Case, A. W., et al. (2019). Highly structured slow solar wind emerging from an equatorial coronal hole. Nature 576, 237–242. doi:10.1038/s41586-019-1818-7
Banerjee, S., and Galtier, S. (2013). Exact relation with two-point correlation functions and phenomenological approach for compressible magnetohydrodynamic turbulence. Phys. Rev. E 87, 013019. doi:10.1103/PhysRevE.87.013019
Banerjee, S., Hadid, L. Z., Sahraoui, F., and Galtier, S. (2016). Scalings of compressible magnetohydrodynamic turbulence in the fast solar wind. Astrophys. J. 829, L27. doi:10.3847/2041-8205/829/2/l27
Bieber, J. W., Wanner, W., and Matthaeus, W. H. (1996). Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport. J. Geophys. Res. 101, 2511–2522. doi:10.1029/95JA02588
Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron temperature of the solar wind. Proc. Natl. Acad. Sci. U. S. A. 117, 9232–9240. doi:10.1073/pnas.1917905117
Borovikov, S. N., Pogorelov, N. V., and Ebert, R. W. (2012). Solar rotation effects on the heliosheath flow near solar minima. Astrophys. J. 750, 42. doi:10.1088/0004-637X/750/1/42
Borovsky, J. E. (2008). Flux tube texture of the solar wind: Strands of the magnetic carpet at 1 AU? J. Geophys. Res. 113, A08110. doi:10.1029/2007JA012684
Borovsky, J. (2020). On the motion of the heliospheric magnetic structure through the solar wind plasma. J. Geophys. Res. Space Phys. 125. doi:10.1029/2019JA027377
Bowen, T. A., Mallet, A., Huang, J., Klein, K. G., Malaspina, D. M., Stevens, M., et al. (2020). Ion-scale electromagnetic waves in the inner heliosphere. Astrophys. J. Suppl. Ser. 246, 66. doi:10.3847/1538-4365/ab6c65
Brandt, P. C., Provornikova, E. A., Cocoros, A., Turner, D., DeMajistre, R., Runyon, K., et al. (2022). Interstellar probe: Humanity’s exploration of the galaxy begins. Acta Astronaut. 199, 364–373. doi:10.1016/j.actaastro.2022.07.011
Breech, B., Matthaeus, W. H., Cranmer, S. R., Kasper, J. C., and Oughton, S. (2009). Electron and proton heating by solar wind turbulence. J. Geophys. Res. 114. doi:10.1029/2009JA014354
Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10, 1–208. doi:10.12942/lrsp-2013-2
Bruno, R. (2019). Intermittency in solar wind turbulence from fluid to kinetic scales. Earth Space Sci. 6, 656–672. doi:10.1029/2018EA000535
Burlaga, L. F., and Ness, N. F. (2009). Compressible “turbulence” observed in the heliosheath by Voyager 2. Astrophys. J. 703, 311–324. doi:10.1088/0004-637X/703/1/311
Burlaga, L. F., and Ness, N. F. (2010). Sectors and large-scale magnetic field strength fluctuations in the heliosheath near 110 AU: Voyager 1, 2009. Astrophys. J. 725, 1306–1316. doi:10.1088/0004-637X/725/1/1306
Burlaga, L. F., and Ness, N. F. (2011). Current sheets in the heliosheath: Voyager 1, 2009. J. Geophys. Res. 116. doi:10.1029/2010JA016309
Burlaga, L. F., and Ness, N. F. (2016). Observations of the interstellar magnetic field in the outer heliosheath: Voyager 1. Astrophys. J. 829, 1–10. doi:10.3847/0004-637X/829/2/134
Burlaga, L. F., Ness, N., Acuña, M., Lepping, R. P., Connerney, J. E. P., and Richardson, J. D. (2008). Magnetic fields at the solar wind termination shock. Nature 454, 75–77. doi:10.1038/nature07029
Burlaga, L. F., Ness, N. F., Acuna, M. H., Wang, Y. M., and Sheeley, N. R. (2009). Radial and solar cycle variations of the magnetic fields in the heliosheath: Voyager 1 observations from 2005 to 2008. J. Geophys. Res. 114. doi:10.1029/2009JA014071
Burlaga, L. F., Florinski, V., and Ness, N. F. (2015). In situ observations of magnetic turbulence in the local interstellar medium. Astrophys. J. 804, L31. doi:10.1088/2041-8205/804/2/L31
Burlaga, L. F., Florinski, V., and Ness, N. F. (2018). Turbulence in the outer heliosheath. Astrophys. J. 854, 20. doi:10.3847/1538-4357/aaa45a
Burlaga, L. F., Ness, N. F., Berdichevsky, D. B., Jian, L. K., Park, J., and Szabo, A. (2020a). Intermittency and q-Gaussian distributions in the magnetic field of the very local interstellar medium (vlism) observed by Voyager 1 and Voyager 2. Astrophys. J. Lett. 901, L2. doi:10.3847/2041-8213/abb199
Burlaga, L. F., Ness, N. F., Berdichevsky, D. B., Jian, L. K., Park, J., and Szabo, A. (2020b). Voyager 1 and 2 observations of a change in the nature of magnetic fluctuations in the VLISM with increasing distance from the heliopause. Astron. J. 160, 40. doi:10.3847/1538-3881/ab94a7
Burlaga, L. F., Ness, N. F., Berdichevsky, D. B., Jian, L. K., Kurth, W., Park, J., et al. (2022). Magnetic field observations in the very local interstellar medium by Voyagers 1 and 2. Astrophys. J. 932, 59. doi:10.3847/1538-4357/ac658e
Bykov, A. M., and Toptygin, I. N. (1982). The theory of particle acceleration in astrophysical objects containing shock waves and turbulent plasma motions. J. Geophys. Zeitschrift Geophys. 50, 221–226.
Bykov, A. M., and Toptygin, I. (1993). Particle kinetics in highly turbulent plasmas (renormalization and self-consistent field methods). Phys. -Usp. 36, 1020–1052. doi:10.1070/PU1993v036n11ABEH002179
Cairns, I. H., and Zank, G. P. (2002). Turn-on of 2–3 kHz radiation beyond the heliopause. Geophys. Res. Lett. 29, 47–1–47–4. doi:10.1029/2001GL014112
Carbone, V., Marino, R., Sorriso-Valvo, L., Noullez, A., and Bruno, R. (2009). Scaling laws of turbulence and heating of fast solar wind: the role of density fluctuations. Phys. Rev. Lett. 103, 061102. doi:10.1103/PhysRevLett.103.061102
Cho, J., and Lazarian, A. (2002). Compressible sub-Alfvénic mhd turbulence in low- β plasmas. Phys. Rev. Lett. 88, 245001. doi:10.1103/PhysRevLett.88.245001
Dasso, S., Milano, L. J., Matthaeus, W. H., and Smith, C. W. (2005). Anisotropy in fast and slow solar wind fluctuations. Astrophys. J. 635, L181–L184. doi:10.1086/499559
de Avillez, M. A., and Breitschwerdt, D. (2005). Global dynamical evolution of the ism in star forming galaxies - i. high resolution 3D simulations: Effect of the magnetic field. Astron. Astrophys. 436, 585–600. doi:10.1051/0004-6361:20042146
Decker, R. B., Krimigis, S. M., Roelof, E. C., Hill, M. E., Armstrong, T. P., Gloeckler, G., et al. (2008). Mediation of the solar wind termination shock by non-thermal ions. Nature 454, 67–70. doi:10.1038/nature07030
Drake, J. F., Swisdak, M., Opher, M., and Richardson, J. D. (2017). The formation of magnetic depletions and flux annihilation due to reconnection in the heliosheath. Astrophys. J. 837, 159. doi:10.3847/1538-4357/aa6304
Engelbrecht, N. E. (2017). On the effects of pickup ion-driven waves on the diffusion tensor of low-energy electrons in the heliosphere. Astrophys. J. 849, L15. doi:10.3847/2041-8213/aa9372
Eriksson, S., Swisdak, M., Weygand, J. M., Mallet, A., Newman, D. L., Lapenta, G., et al. (2022). Characteristics of multi-scale current sheets in the solar wind at 1 AU associated with magnetic reconnection and the case for a heliospheric current sheet avalanche. Astrophys. J. 933, 181. doi:10.3847/1538-4357/ac73f6
Eyink, G. L. (2015). Turbulent general magnetic reconnection. Astrophys. J. 807, 137. doi:10.1088/0004-637x/807/2/137
Fahr, H. J., and Siewert, M. (2007). Anisotropic unstable ion distribution functions downstream of the solar wind termination shock. Astrophys. Space Sci. Trans. 3, 21–27. doi:10.5194/astra-3-21-2007
Falgarone, E., Momferratos, G., and Lesaffre, P. (2015). “The intermittency of ism turbulence: What do the observations tell us?,” in Magnetic fields in diffuse media (Springer), 227–252. doi:10.1007/978-3-662-44625-6_9
Feng, X., Ma, X., and Xiang, C. (2015). Data-driven modeling of the solar wind from 1 Rsto 1 AU. J. Geophys. Res. Space Phys. 120, 10, 159–210, 174. doi:10.1002/2015JA021911
Ferrand, R., Galtier, S., Sahraoui, F., and Federrath, C. (2020). Compressible turbulence in the interstellar medium: New insights from a high-resolution supersonic turbulence simulation. Astrophys. J. 904, 160. doi:10.3847/1538-4357/abb76e
Fichtner, H., Kleimann, J., Yoon, P. H., Scherer, K., Oughton, S., and Engelbrecht, N. E. (2020). On the generation of compressible mirror-mode fluctuations in the inner heliosheath. Astrophys. J. 901, 76. doi:10.3847/1538-4357/abaf52
Fisk, L. A., and Gloeckler, G. (2006). The common spectrum for accelerated ions in the quiet-time solar wind. Astrophys. J. 640, L79–L82. doi:10.1086/503293
Fisk, L. A., and Gloeckler, G. (2008). Acceleration of suprathermal tails in the solar wind. Astrophys. J. 686, 1466–1473. doi:10.1086/591543
Fisk, L. A., Gloeckler, G., and Schwadron, N. A. (2010). On theories for stochastic acceleration in the solar wind. Astrophys. J. 720, 533–540. doi:10.1088/0004-637X/720/1/533
Florinski, V., Decker, R. B., le Roux, J. A., and Zank, G. P. (2009). An energetic-particle-mediated termination shock observed by voyager 2. Geophys. Res. Lett. 36, L12101. doi:10.1029/2009GL038423
Florinski, V., Heerikhuisen, J., Niemiec, J., and Ernst, A. (2016). The ibex ribbon and the pickup ion ring stability in the outer heliosheath. I. theory and hybrid simulations. Astrophys. J. 826, 197. doi:10.3847/0004-637x/826/2/197
Fraternale, F., and Pogorelov, N. V. (2021). Waves and turbulence in the very local interstellar medium: from macroscales to microscales. Astrophys. J. 906, 75. doi:10.3847/1538-4357/abc88a
Fraternale, F., Pogorelov, N. V., Richardson, J. D., and Tordella, D. (2019a). Magnetic turbulence spectra and intermittency in the heliosheath and in the local interstellar medium. Astrophys. J. 872, 40. doi:10.3847/1538-4357/aafd30
Fraternale, F., Pogorelov, N. V., Richardson, J. D., and Tordella, D. (2019b). The structure of magnetic turbulence in the heliosheath region observed by Voyager 2 at 106 AU. J. Phys. Conf. Ser. 1225, 012006. doi:10.1088/1742-6596/1225/1/012006
Fraternale, F., Pogorelov, N. V., and Burlaga, L. F. (2020). Signatures of intermittency and fine-scale turbulence in the very local interstellar medium. Astrophys. J. 897, L28. doi:10.3847/2041-8213/ab9df5
Fraternale, F., Adhikari, L., Fichtner, H., Kim, T. K., Kleimann, J., Oughton, S., et al. (2022a). Turbulence in the outer heliosphere. Space Sci. Rev. 218, 50. doi:10.1007/s11214-022-00914-2
Fraternale, F., Bera, R. K., and Pogorelov, N. V. (2022b). The role of electrons and helium atoms in global models of the heliosphere. submitted.
Fraternale, F., Cummings, A. C., Pogorelov, N. V., and Heikkala, B. (2022c). Quasi periodic oscillations of cosmic ray eletrons and protons in the VLISM. in preparation.
Fraternale, F., Zhao, L.-L., Pogorelov, N. V., Sorriso-Valvo, L., Redfield, S., Zhang, M., et al. (2022d). Exploring turbulence from the Sun to the local interstellar medium. White paper, Heliophysics 2024 Decadal Survey.
Frisch, P. C., Redfield, S., and Slavin, J. D. (2011). The interstellar medium surrounding the sun. Annu. Rev. Astron. Astrophys. 49, 237–279. doi:10.1146/annurev-astro-081710-102613
Gary, P. S. (1993). Theory of plasma microinstabilities. Cambridge, United Kingdom: Cambridge University Press.
Ghanbari, K., Florinski, V., Guo, X., Hu, Q., and Leske, R. (2019). Galactic cosmic rays modulation in the vicinity of corotating interaction regions: Observations during the last two solar minima. Astrophys. J. 882, 54. doi:10.3847/1538-4357/ab31a5
Greco, A., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2009). Waiting-time distributions of magnetic discontinuities: Clustering or Poisson process? Phys. Rev. E 80, 046401. doi:10.1103/PhysRevE.80.046401
Guo, F., Giacalone, J., and Zhao, L. (2021). Shock propagation and associated particle acceleration in the presence of ambient solar-wind turbulence. Front. Astron. Space Sci. 8, 27. doi:10.3389/fspas.2021.644354
Gurnett, D. A., Kurth, W. S., Allendorf, S. C., and Poynter, R. L. (1993). Radio emission from the heliopause triggered by an interplanetary shock. Science 262, 199–203. doi:10.1126/science.262.5131.199
Gurnett, D. A., Kurth, W. S., Burlaga, L. F., and Ness, N. F. (2013). In situ observations of interstellar plasma with Voyager 1. Science 341, 1489–1492. doi:10.1126/science.1241681
Gurnett, D. A., Kurth, W. S., Stone, E. C., Cummings, A. C., Krimigis, S. M., Decker, R. B., et al. (2015). Precursors of interstellar shocks of solar origin. Astrophys. J. 809, 121. doi:10.1088/0004-637X/809/2/121
Gurnett, D. A., Kurth, W. S., Stone, E. C., Cummings, A. C., Heikkila, B., Lal, N., et al. (2020). A foreshock model for interstellar shocks of solar origin: Voyager 1 and 2 observations. Astron. J. 161, 11. doi:10.3847/1538-3881/abc337
Gurnett, D. A., Kurth, W. S., Burlaga, L. F., Berdichevsky, D. B., Pogorelov, N. V., Pulupa, M., et al. (2021). Origin of the weak plasma emission line detected by Voyager 1 in the interstellar medium: Evidence for suprathermal electrons. Astrophys. J. 921, 62. doi:10.3847/1538-4357/ac1c7a
Hollick, S. J., Smith, C. W., Pine, Z. B., Argall, M. R., Joyce, C. J., Isenberg, P. A., et al. (2018). Magnetic waves excited by newborn interstellar pickup ions measured by the voyager spacecraft from 1 to 45 AU. I. Wave properties. Astrophys. J. 863, 75. doi:10.3847/1538-4357/aac83b
Howes, G. G., TenBarge, J. M., Dorland, W., Quataert, E., Schekochihin, A. A., Numata, R., et al. (2011). Gyrokinetic simulations of solar wind turbulence from ion to electron scales. Phys. Rev. Lett. 107, 035004. doi:10.1103/PhysRevLett.107.035004
Ishikawa, R. T., Nakata, M., Katsukawa, Y., Masada, Y., and Riethmüller, T. L. (2022). Multi-scale deep learning for estimating horizontal velocity fields on the solar surface. Astron. Astrophys. 658, A142. doi:10.1051/0004-6361/202141743
Jokipii, J. R. (1966). Cosmic-ray propagation. I. Charged particles in a random magnetic field. Astrophys. J. 146, 480. doi:10.1086/148912
Khabarova, O., Zank, G. P., Li, G., le Roux, J. A., Webb, G. M., Dosch, A., et al. (2015). Small-scale magnetic islands in the solaw wind and their role in particle acceleration. I. Dynamics of magnetic islands near the heliospheric current sheet. Astrophys. J. 808, 181. doi:10.1088/0004-637x/808/2/181
Khabarova, O. V., Zank, G. P., Li, G., Malandraki, O. E., le Roux, J. A., and Webb, G. M. (2016). Small-scale magnetic islands in the solar wind and their role in particle acceleration. II. Particle energization inside magnetically confined cavities. Astrophys. J. 827, 122. doi:10.3847/0004-637x/827/2/122
Khabarova, O., Malandraki, O., Malova, H., Kislov, R., Greco, A., Bruno, R., et al. (2021). Current sheets, plasmoids and flux ropes in the heliosphere. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x
Kieokaew, R., Lavraud, B., Yang, Y., Matthaeus, W. H., Ruffolo, D., Stawarz, J. E., et al. (2021). Solar orbiter observations of the Kelvin-Helmholtz instability in the solar wind. arXiv e-prints.
Kim, T., Kryukov, I., Pogorelov, N., Elliott, H., and Zank, G. P. (2018). A data-driven model of the solar wind, interstellar pickup ions, and turbulence throughout interplanetary space. Earth Space Sci. Open Arch. 1. doi:10.1002/essoar.b60497724eca58de.7c985d5380f54d2b.1
Kowal, G., and Lazarian, A. (2010). Velocity field of compressible magnetohydrodynamic turbulence: Wavelet decomposition and mode scalings. Astrophys. J. 720, 742–756. doi:10.1088/0004-637X/720/1/742
Lazarian, A., and Beresnyak, A. (2006). Cosmic ray scattering in compressible turbulence. Mon. Not. R. Astron. Soc. 373, 1195–1202. doi:10.1111/j.1365-2966.2006.11093.x
Lee, M. A., and Ip, W. H. (1987). Hydromagnetic wave excitation by ionized interstellar hydrogen and helium in the solar wind. J. Geophys. Res. 92, 11041–11052. doi:10.1029/JA092iA10p11041
Lee, K. H., and Lee, L. C. (2019). Interstellar turbulence spectrum from in situ observations of Voyager 1. Nat. Astron. 3, 154–159. doi:10.1038/s41550-018-0650-6
Lee, K. H., and Lee, L. C. (2020). Turbulence spectra of electron density and magnetic field fluctuations in the local interstellar medium. Astrophys. J. 904, 66. doi:10.3847/1538-4357/abba20
Linsky, J., Redfield, S., Ryder, D., and Möbius, E. (2022). Inhomogeneity in the local ISM and its relation to the heliosphere. Space Sci. Rev. 218, 16. doi:10.1007/s11214-022-00884-5
Liu, Y., Richardson, J. D., Belcher, J. W., and Kasper, J. C. (2007). Temperature anisotropy in a shocked plasma: Mirror-mode instabilities in the heliosheath. Astrophys. J. 659, L65–L68. doi:10.1086/516568
Marsch, E., and Mangeney, A. (1987). Ideal MHD equations in terms of compressive Elsässer variables. J. Geophys. Res. 92, 7363–7367. doi:10.1029/JA092iA07p07363
Matsukiyo, S., Noumi, T., Zank, G. P., Washimi, H., and Hada, T. (2019). PIC simulation of a shock tube: Implications for wave transmission in the heliospheric boundary region. Astrophys. J. 888, 11. doi:10.3847/1538-4357/ab54c9
Matthaeus, W. H., and Velli, M. (2011). Who needs turbulence? A review of turbulence effects in the heliosphere and on the fundamental process of reconnection. Space Sci. Rev. 160, 145–168. doi:10.1007/s11214-011-9793-9
Matthaeus, W. H., Goldstein, M. L., and Roberts, D. A. (1990). Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J. Geophys. Res. 95, 20673–20683. doi:10.1029/JA095iA12p20673
Matthaeus, W. H., Zank, G. P., and Oughton, S. (1996). Phenomenology of hydromagnetic turbulence in a uniformly expanding medium. J. Plasma Phys. 56, 659–675. doi:10.1017/S0022377800019516
Matthaeus, W. H. (2021). Turbulence in space plasmas: Who needs it? Phys. Plasmas 28, 032306. doi:10.1063/5.0041540
McComas, D. J., Bzowski, M., Fuselier, S. A., Frisch, P. C., Galli, A., Izmodenov, V. V., et al. (2015). Local interstellar medium: Six years of direct sampling by IBEX. Astrophys. J. Suppl. Ser. 220, 22. doi:10.1088/0067-0049/220/2/22
McComas, D. J., Christian, E. R., Schwadron, N. A., Fox, N., Westlake, J., Allegrini, F., et al. (2018). Interstellar mapping and acceleration probe (IMAP): A new NASA mission. Space Sci. Rev. 214, 116. doi:10.1007/s11214-018-0550-1
McComas, D. J., Swaczyna, P., Szalay, J. R., Zirnstein, E. J., Rankin, J. S., Elliott, H. A., et al. (2021). Interstellar pickup ion observations halfway to the termination shock. Astrophys. J. Suppl. Ser. 254, 19. doi:10.3847/1538-4365/abee76
McComas, D. J., Shrestha, B. L., Swaczyna, P., Rankin, J. S., Weidner, S. E., Zirnstein, E. J., et al. (2022). First high-resolution observations of interstellar pickup ion mediated shocks in the outer heliosphere. Astrophys. J. 934, 147. doi:10.3847/1538-4357/ac7956
McNutt, R. L., Wimmer-Schweingruber, R. F., Gruntman, M., Krimigis, S. M., Roelof, E. C., Brandt, P. C., et al. (2022). Interstellar probe - destination: Universe. Acta Astronaut. 196, 13–28. doi:10.1016/j.actaastro.2022.04.001
Möbius, E., Hovestadt, D., Klecker, B., Scholer, M., Gloeckler, G., and Ipavich, F. M. (1985). Direct observation of He+ pick-up ions of interstellar origin in the solar wind. Nature 318, 426–429. doi:10.1038/318426a0
Mostafavi, P., and Zank, G. (2018). The structure of shocks in the very local interstellar medium. Astrophys. J. 854, L15. doi:10.3847/2041-8213/aaab54
Mostafavi, P., Merkin, V. G., Provornikova, E., Raouafi, N. E., Velli, M., Zank, G. P., et al. (2021). High-resolution modeling of the solar wind turbulence: from global to micro-scales. Heliophysics 2050 White Papers.
Mostafavi, P., Burlaga, L. F., Cairns, I. H., Fuselier, S. A., Fraternale, F., Gurnett, D. A., et al. (2022). Shocks in the very local interstellar medium. Space Sci. Rev. 218, 27. doi:10.1007/s11214-022-00893-4
Mousavi, A., Liu, K., and Min, K. (2020). Mirror instability driven by pickup ions in the outer heliosheath. Astrophys. J. 901, 167. doi:10.3847/1538-4357/abb1a1
Neugebauer, M., Alexander, C. J., Schwenn, R., and Richter, A. K. (1986). Tangential discontinuities in the solar wind: Correlated field and velocity changes and the Kelvin-Helmholtz instability. J. Geophys. Res. 91, 13694–13698. doi:10.1029/JA091iA12p13694
Ocker, S. K., Cordes, J. M., Chatterjee, S., and Dolch, T. (2021). An in situ study of turbulence near stellar bow shocks. Astrophys. J. 922, 233. doi:10.3847/1538-4357/ac2b28
Odstrcil, D., and Pizzo, V. J. (1999). Distortion of the interplanetary magnetic field by three-dimensional propagation of coronal mass ejections in a structured solar wind. J. Geophys. Res. 104, 28225–28239. doi:10.1029/1999JA900319
Oughton, S., and Engelbrecht, N. E. (2021). Solar wind turbulence: Connections with energetic particles. New Astron. 83, 101507. doi:10.1016/j.newast.2020.101507
Oughton, S., Matthaeus, W. H., Wan, M., and Parashar, T. N. (2016). Variance anisotropy in compressible 3-D MHD. JGR. Space Phys. 121, 5041–5054. doi:10.1002/2016JA022496
Parker, E. (1965). The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 13, 9–49. doi:10.1016/0032-0633(65)90131-5
Perrone, D., Alexandrova, O., Mangeney, A., Maksimovic, M., Lacombe, C., Rakoto, V., et al. (2016). Compressive coherent structures at ion scales in the slow solar wind. Astrophys. J. 826, 196. doi:10.3847/0004-637x/826/2/196
Perrone, D., Alexandrova, O., Roberts, O. W., Lion, S., Lacombe, C., Walsh, A., et al. (2017). Coherent structures at ion scales in fast solar wind: Cluster observations. Astrophys. J. 849, 49. doi:10.3847/1538-4357/aa9022
Pesses, M. E., Eichler, J. R. J. D., and Jokippi, J. R. (1981). Cosmic ray drift, shock wave acceleration, and the anomalous component of cosmic rays. Astrophys. J. 246, L85. doi:10.1086/183559
Phillips, C., Bandyopadhyay, R., McComas, D. J., and Bale, S. D. (2022). Association of intermittency with electron heating in the near-Sun solar wind. arXiv, 1–8. Available at: https://arxiv.org/abs/2206.10084.
Pine, Z. B., Smith, C. W., Hollick, S. J., Argall, M. R., Vasquez, B. J., Isenberg, P. A., et al. (2020a). Solar wind turbulence from 1 to 45 AU. I. evidence for dissipation of magnetic fluctuations using voyager and ACE observations. Astrophys. J. 900, 91. doi:10.3847/1538-4357/abab10
Pine, Z. B., Smith, C. W., Hollick, S. J., Argall, M. R., Vasquez, B. J., Isenberg, P. A., et al. (2020b). Solar wind turbulence from 1 to 45 AU. III. Anisotropy of magnetic fluctuations in the inertial range using Voyager and ACE observations. Astrophys. J. 900, 93. doi:10.3847/1538-4357/abab11
Pogorelov, N. V., Fichtner, H., Czechowski, A., Lazarian, A., Lembege, B., Roux, J. A. I., et al. (2017a). Heliosheath processes and the structure of the heliopause: Modeling energetic particles, cosmic rays, and magnetic fields. Space Sci. Rev. 212, 193–248. doi:10.1007/s11214-017-0354-8
Pogorelov, N. V., Heerikhuisen, J., Roytershteyn, V., Burlaga, L. F., Gurnett, D. A., and Kurth, W. S. (2017b). Three-dimensional features of the outer heliosphere due to coupling between the interstellar and heliospheric magnetic field. V. The bow wave, heliospheric boundary layer, instabilities, and magnetic reconnection. Astrophys. J. 845, 9. doi:10.3847/1538-4357/aa7d4f
Pogorelov, N. V., Fraternale, F., Kim, T. K., Burlaga, L. F., and Gurnett, D. A. (2021). Magnetic field draping of the heliopause and its consequences for radio emission in the very local interstellar medium. Astrophys. J. Lett. 917, L20. doi:10.3847/2041-8213/ac14bd
Redfield, S., and Linsky, J. L. (2004a). The structure of the local interstellar medium. II. Observations of D I, C II, N I, O I, Al II, and Si II toward stars within 100 parsecs. Astrophys. J. 602, 776–802. doi:10.1086/381083
Redfield, S., and Linsky, J. L. (2004b). The structure of the local interstellar medium. III. Temperature and turbulence. Astrophys. J. 613, 1004–1022. doi:10.1086/423311
Richardson, J. D., Burlaga, L. F., Drake, J. F., Hill, M. E., and Opher, M. (2016). Voyager observations of magnetic sectors and heliospheric current sheet crossings in the outer heliosphere. Astrophys. J. 831, 115. doi:10.3847/0004-637X/831/2/115/
Richardson, J. D., Belcher, J. W., Garcia-Galindo, P., and Burlaga, L. F. (2019). Voyager 2 plasma observations of the heliopause and interstellar medium. Nat. Astron. 3, 1019–1023. doi:10.1038/s41550-019-0929-2
Richardson, J. D., Burlaga, L. F., Elliott, H., Kurth, W. S., Liu, Y., and von Steiger, R. (2022). Observations of the outer heliosphere, heliosheath, and interstellar medium. Space Sci. Rev. 218, 35. doi:10.1007/s11214-022-00899-y
Roberts, D. A., Karimabadi, H., Sipes, T., Ko, Y.-K., and Lepri, S. (2020). Objectively determining states of the solar wind using machine learning. Astrophys. J. 889, 153. doi:10.3847/1538-4357/ab5a7a
Roytershteyn, V., Pogorelov, N. V., and Heerikhuisen, J. (2019). Pickup ions beyond the heliopause. Astrophys. J. 881, 65. doi:10.3847/1538-4357/ab2ad4
Schlickeiser, R. (2002). Cosmic ray astrophysics. Heidelberg, DE: Springer Berlin. doi:10.1007/978-3-662-04814-6
Shalchi, A., and Schlickeiser, R. (2004). Cosmic ray transport in anisotropic magnetohydrodynamic turbulence - III. Mixed magnetosonic and Alfvénic turbulence. Astron. Astrophys. 420, 799–808. doi:10.1051/0004-6361:20034304
Shalchi, A. (2009). Nonlinear cosmic ray diffusion theories, 362. Heidelberg, DE: Springer Berlin. doi:10.1007/978-3-642-00309-7
Simon, P., and Sahraoui, F. (2022). Exact law for compressible pressure-anisotropic magnetohydrodynamic turbulence: Toward linking energy cascade and instabilities. Phys. Rev. E 105, 055111. doi:10.1103/PhysRevE.105.055111
Sioulas, N., Shi, C., Huang, Z., and Velli, M. (2022). Preferential heating of protons over electrons from coherent structures during the first perihelion of the Parker Solar Probe. Astrophys. J. Lett. 935, L29. doi:10.3847/2041-8213/ac85de
Slavin, J. (2009). The origins and physical properties of the complex of local interstellar clouds. Space Sci. Rev. 143, 311–322. doi:10.1007/s11214-008-9342-3
Smith, C. W., Hamilton, K., Vasquez, B. J., and Leamon, R. J. (2006). Dependence of the dissipation range spectrum of interplanetary magnetic fluctuationson the rate of energy cascade. Astrophys. J. 645, L85–L88. doi:10.1086/506151
Sorriso-Valvo, L., Carbone, V., and Bruno, R. (2005). On the origin of the strong intermittent nature of interplanetary magnetic field. Space Sci. Rev. 121, 49–53. doi:10.1007/s11214-006-5559-1
Sorriso-Valvo, L., Carbone, F., Leonardis, E., Chen, C. H. K., Safrankova, J., and Nemecek, Z. (2017). Multifractal analysis of high resolution solar wind proton density measurements. Adv. Space Res. 59, 1642–1651. doi:10.1016/j.asr.2016.12.024
Sorriso-Valvo, L., Catapano, F., Retinò, A., Le Contel, O., Perrone, D., Roberts, O. W., et al. (2019a). Turbulence-driven ion beams in the magnetospheric Kelvin-Helmholtz instability. Phys. Rev. Lett. 122, 035102. doi:10.1103/PhysRevLett.122.035102
Sorriso-Valvo, L., De Vita, G., Fraternale, F., Gurchumelia, A., Perri, S., Nigro, G., et al. (2019b). Sign singularity of the local energy transfer in space plasma turbulence. Front. Phys. 7, 1–11. doi:10.3389/fphy.2019.00108
Sorriso-Valvo, L., Yordanova, E., Dimmock, A. P., and Telloni, D. (2021). Turbulent cascade and energy transfer rate in a solar coronal mass ejection. Astrophys. J. Lett. 919, L30. doi:10.3847/2041-8213/ac26c5
Spangler, S. R., Savage, A. H., and Redfield, S. (2011). Properties of turbulence in the very local interstellar clouds. Astrophys. J. 742, 30. doi:10.1088/0004-637x/742/1/30
Squire, J., Meyrand, R., Kunz, M. W., Arzamasskiy, L., Schekochihin, A. A., and Quataert, E. (2022). High-frequency heating of the solar wind triggered by low-frequency turbulence. Nat. Astron. 935, 715–723. doi:10.1038/s41550-022-01624-z
Taylor, G. I. (1938). The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490. doi:10.1098/rspa.1938.0032
Tsurutani, B. T., Lakhina, G. S., Verkhoglyadova, O. P., Echer, E., Guarnieri, F. L., Narita, Y., et al. (2011). Magnetosheath and heliosheath mirror mode structures, interplanetary magnetic decreases, and linear magnetic decreases: Differences and distinguishing features. J. Geophys. Res. 116, A02103. doi:10.1029/2010JA015913
Washimi, H., Zank, G. P., Hu, Q., Tanaka, T., Munakata, K., and Shinagawa, H. (2011). Realistic and time-varying outer heliospheric modelling. Mon. Not. R. Astron. Soc. 416, 1475–1485. doi:10.1111/j.1365-2966.2011.19144.x
Williams, L. L., Zank, G. P., and Matthaeus, W. H. (1995). Dissipation of pickup-induced waves: A solar wind temperature increase in the outer heliosphere? J. Geophys. Res. 100, 17059–17067. doi:10.1029/95JA01261
Wilson, L. B., Chen, L.-J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2019). Electron energy partition across interplanetary shocks. I. Methodology and data product. Astrophys. J. Suppl. Ser. 243, 8. doi:10.3847/1538-4365/ab22bd
Wood, B. E., Müller, H.-R., and Möbius, E. (2019). Evidence for asymmetry in the velocity distribution of the interstellar neutral helium flow observed by IBEX and ulysses. Astrophys. J. 881, 55. doi:10.3847/1538-4357/ab2e74
Yan, H., and Lazarian, A. (2002). Scattering of cosmic rays by magnetohydrodynamic interstellar turbulence. Phys. Rev. Lett. 89, 281102. doi:10.1103/PhysRevLett.89.281102
Yang, Y., Shi, Y., Wan, M., Matthaeus, W. H., and Chen, S. (2016). Energy cascade and its locality in compressible magnetohydrodynamic turbulence. Phys. Rev. E 93, 061102. doi:10.1103/PhysRevE.93.061102
Yang, Y., Wan, M., Matthaeus, W. H., and Chen, S. (2021). Energy budget in decaying compressible MHD turbulence. J. Fluid Mech. 916, A4. doi:10.1017/jfm.2021.199
Zachary, J., Redfield, S., Linsky, J. L., and Wood, B. E. (2018). Measuring the local ISM along the sight lines of the two voyager spacecraft with hst/stis. Astrophys. J. 859, 42. doi:10.3847/1538-4357/aac017
Zank, G. P., and Matthaeus, W. H. (1993). Nearly incompressible fluids. II: Magnetohydrodynamics, turbulence, and waves. Phys. Fluids A Fluid Dyn. 5, 257–273. doi:10.1063/1.858780
Zank, G. P., Hunana, P., Mostafavi, P., le Roux, J. A., Li, G., Webb, G. M., et al. (2015). Diffusive shock acceleration and reconnection acceleration processes. Astrophys. J. 814, 137. doi:10.1088/0004-637X/814/2/137
Zank, G. P., Du, S., and Hunana, P. (2017). The origin of compressible magnetic turbulence in the very local interstellar medium. Astrophys. J. 842, 114. doi:10.3847/1538-4357/aa7685
Zank, G. P., Adhikari, L., Zhao, L.-L., Mostafavi, P., Zirnstein, E. J., and McComas, D. J. (2018). The pickup ion-mediated solar wind. Astrophys. J. 869, 23. doi:10.3847/1538-4357/aaebfe
Zank, G. P., Nakanotani, M., and Webb, G. M. (2019). Compressible and incompressible magnetic turbulence observed in the very local interstellar medium by Voyager 1. Astrophys. J. 887, 116. doi:10.3847/1538-4357/ab528c
Zank, G. P. (1999). Interaction of the solar wind with the local interstellar medium: A theoretical perspective. Space Sci. Rev. 89, 413–688. doi:10.1023/A:1005155601277
Zank, G. P. (2015). Faltering steps into the galaxy: The boundary regions of the heliosphere. Annu. Rev. Astron. Astrophys. 53, 449–500. doi:10.1146/annurev-astro-082214-122254
Zhang, M., and Lee, M. A. (2013). Stochastic acceleration of energetic particles in the heliosphere. Space Sci. Rev. 176, 133–146. doi:10.1007/s11214-011-9754-3
Zhang, M., and Schlickeiser, R. (2012). A theory of bimodal acceleration of pickup ions by compressive solar wind turbulence under pressure balance. Astrophys. J. 756, 129. doi:10.1088/0004-637X/756/2/129
Zhang, M., Pogorelov, N. V., Zhang, Y., Hu, H. B., and Schlickeiser, R. (2020). The original anisotropy of TeV cosmic rays in the local interstellar medium. Astrophys. J. 889, 97. doi:10.3847/1538-4357/ab643c
Zhang, Y., Tiňo, P., Leonardis, A., and Tang, K. (2021). A survey on neural network interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 5, 726–742. doi:10.1109/TETCI.2021.3100641
Zhang, M. (2006). Theory of energetic particle transport in the magnetosphere: A noncanonical approach. J. Geophys. Res. 111, A04208. doi:10.1029/2005JA011323
Zhang, M. (2010). Acceleration of suprathermal particles by compressional plasma wave trains in the solar wind. J. Geophys. Res. 115, A12102. doi:10.1029/2010JA015723
Zhao, L.-L., Zank, G. P., Khabarova, O., Du, S., Chen, Y., Adhikari, L., et al. (2018). An unusual energetic particle flux enhancement associated with solar wind magnetic island dynamics. Astrophys. J. 864, L34. doi:10.3847/2041-8213/aaddf6
Zhao, L.-L., Zank, G. P., Chen, Y., Hu, Q., le Roux, J. A., Du, S., et al. (2019a). Particle acceleration at 5 AU associated with turbulence and small-scale magnetic flux ropes. Astrophys. J. 872, 4. doi:10.3847/1538-4357/aafcb2
Zhao, L.-L., Zank, G. P., Hu, Q., Chen, Y., Adhikari, L., Cummings, A., et al. (2019b). ACR proton acceleration associated with reconnection processes beyond the heliospheric termination shock. Astrophys. J. 886, 144. doi:10.3847/1538-4357/ab4db4
Zhao, L.-L., Zank, G. P., and Burlaga, L. F. (2020). Turbulence in the very local interstellar medium (VLISM). Astrophys. J. 900, 166. doi:10.3847/1538-4357/ababa2
Zieger, B., Opher, M., Tóth, G., and Florinski, V. (2020). Dispersive fast magnetosonic waves and shock-driven compressible turbulence in the inner heliosheath. JGR. Space Phys. 125. doi:10.1029/2020JA028393
Zirnstein, E. J., Heerikhuisen, J., Funsten, H. O., Livadiotis, G., McComas, D. J., and Pogorelov, N. V. (2016). Local interstellar magnetic field determined from the Interstellar Boundary Explorer ribbon. Astrophys. J. 818, L18. doi:10.3847/2041-8205/818/1/L18
Keywords: turbulence, solar wind, heliosphere, local interstellar medium (LISM), waves and instabilities, magnetic fields
Citation: Fraternale F, Zhao L, Pogorelov NV, Sorriso-Valvo L, Redfield S, Zhang M, Ghanbari K, Florinski V and Chen TY (2022) Exploring turbulence from the Sun to the local interstellar medium: Current challenges and perspectives for future space missions. Front. Astron. Space Sci. 9:1064098. doi: 10.3389/fspas.2022.1064098
Received: 07 October 2022; Accepted: 31 October 2022;
Published: 18 November 2022.
Edited by:
Joseph E. Borovsky, Space Science Institute, United StatesReviewed by:
Anna Wawrzaszek, Space Research Center, Polish Academy of Sciences, PolandCopyright © 2022 Fraternale, Zhao, Pogorelov, Sorriso-Valvo, Redfield, Zhang, Ghanbari, Florinski and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Federico Fraternale, ZmVkZXJpY28uZnJhdGVybmFsZUB1YWguZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.