Solar-wind/magnetosphere coupling: Understand uncertainties in upstream conditions

1 Introduction

Space physicists conduct many investigations of the Earth’s magnetosphere response to solar wind forcing. They use single satellite measurements of solar wind conditions∼230 R_E upstream of the Earth at the L1 Lagrange point. However, magnetic reconnection closer to Earth at the magnetopause mainly drives the solar wind magnetosphere coupling. Since local plasma parameters determine the magnetic reconnection rates, the strength of the coupling depends on these localized plasma and field parameters. As a result, we are forced to estimate the plasma parameters at the magnetopause, and this is mostly done [e. g., in OMNI database (King and Papitashvili, 2005; Weimer and King, 2008)] by time-shifting the measurements at the first Lagrange point (L1) to the bow-shock nose. Sources of time delay inaccuracy comes from assumptions of planarity and non-propagation of solar wind parcel (Collier et al., 1998, 2000; Weimer et al., 2002; Mailyan et al., 2008) and the consequent need of multiple methodologies to address deviation from these conditions (e. g., Horbury et al., 2001; Weimer et al., 2003; Weimer and King, 2008). Though inadequate (Borovsky, 2016), such approximations have been reasonably successful in demonstrating correlations of solar wind parameters with magnetosphere-ionosphere responses. Such assumptions are considered justified as average scale sizes of solar wind magnetic field and plasma are about 45 R_E which is larger than the magnetosphere (Chang and Nishida, 1973; Crooker et al., 1982; Richardson and Paularena, 2001; Matsui et al., 2002; Weimer et al., 2002; Mailyan et al., 2008). However, recent studies have shown substantial variations in the magnetosphere-ionosphere response for the same solar wind driving, with the variation becoming significant during extreme space weather. For example, sometimes, contrary to our expectations, observations of strong solar wind driving do not lead to a corresponding strong response in the magnetosphere, and weak solar wind driving leads to extreme magnetosphere responses. As a matter of fact, successful association of solar wind features with magnetosphere processes decreases with upstream condition derived from observations at many tens of R_E from the Earth-Sun line (e. g., Borodkova et al., 1995; Sibeck and Korotova, 1996; Lyons et al., 1997). In addition, properties of the incoming solar wind can lead to delayed response to the same transient in different part of the magnetosphere (e. g., Maynard et al., 2001). There are many explanations for such discrepancies, which include:

i) gradients in the transverse direction of the solar wind flow leading to a structural variation of magnetospheric scale sizes (Chang and Nishida, 1973; Borovsky, 2018; Burkholder et al., 2020; Kepko et al., 2020),

ii) bow shock and magnetosheath plasma substantially altering the solar wind parameters (Walsh et al., 2019),

iii) inaccurate propagation time estimates (Ridley, 2000; Case and Wild, 2012; Cameron and Jackel, 2016),

iv) systematic errors, introduced for example by Earth’s orbital characteristics (Lockwood et al., 2020; Borovsky, 2022c; Lockwood, 2022),

v) pre-conditioning of the magnetosphere-ionosphere system (Lavraud et al., 2006),

vi) instrument errors altering solar wind parameters (King and Papitashvili, 2005),

vii) location of the L1 monitors (Milan et al., 2022).

Therefore, the solar wind parcel observed at L1 by a single monitor may not be what actually impacts the magnetopause, especially at the reconnection site. Not accounting for the phenomena in (i)-(vii) leads to uncertainties in our estimate of the solar wind that impact the magnetosphere (Lockwood, 2022). We believe that quantifying these uncertainties is extremely crucial to understanding solar-wind/magnetosphere coupling, especially during extreme space weather events, and hence a major challenge for the next decade of Heliophysics.

2 Uncertainties in solar wind upstream conditions

2.1 Inherent variability and transverse gradients in solar wind properties

Recent studies reiterate the importance of transverse gradients in the solar wind properties on the same order of or greater than the size of the Earth’s day-side magnetosphere (Borovsky, 2018; Burkholder et al., 2020; Kepko et al., 2020). In such conditions, the solar wind upstream conditions based on a single spacecraft might not be enough to correctly interpret the magnetosphere response missing the inherent variability of the solar wind, either due to en route processes or its formations at the Sun (Viall et al., 2021). For example, different physical processes can occur on different sides of the Earth’s magnetosphere (Kessel et al., 1999; Nykyri et al., 2019) or observations from a single L1 monitor may not represent the actual upstream conditions [e.g., dusk-dawn aberrations of the solar wind plasma and magnetic structure approaching Earth (Borovsky, 2022c)], leading to misinterpretation of the magnetosphere response (Piersanti et al., 2022; Villante et al., 2022).

An example of the inherent variability of the solar wind is the observation of Periodic Density Structures (PDSs)—solar wind density fluctuations on time scales ranging from a few minutes to a few hours (Figure 1). When accounting for the solar wind velocity, PDSs correspond to advected “meso-scale” structures (Viall et al., 2021; Gershkovich et al., 2022) at preferential length-scales ranging from a few Earth radii (R_E) up to 1000 R_E (Kepko et al., 2020) The size-scales of the periodic density structures are such that they can play a fundamental role in regulating the dynamics of the Earth’s magnetosphere. In fact, these transients produce sudden changes in solar wind dynamic pressure that, in turn, can determine periodic compressional fluctuations of the Earth’s magnetic field (Borovsky and Denton, 2016) at similar frequencies (Kepko and Spence, 2003) which overlap with Ultra Low Frequency (ULF) waves in the Pc5 range (=1.7–6.7 mHz). Magnetic field compressional fluctuations at these time scale have important consequences on the Earth’s magnetosphere system coupling with Field Line Resonances and affecting the dynamics and loss of radiation belt electrons (Zong et al., 2017). Recently, Di Matteo et al(2022) provided a comprehensive study of the Earth’s magnetosphere response to the impact of PDSs. On 9 November 2002, solar wind proton density observations at the Wind spacecraft (Figure 1A) showed quasi periodic 90-min fluctuations. The combination of spacecraft and ground magnetometer observations showed that the magnetospheric response was characterized by forced breathing by periodic solar wind dynamic pressure variations (Figure 1A), field line resonances and local changes in radiation belt particle flux (Figure 1B). While these conclusions seem quite straightforward when looking at the observations in Figure 1, our interpretation of the magnetosphere response is different when using Geotail or ACE to monitor the upstream condition. Using these data, the force breathing process would have been excluded.

FIGURE 1

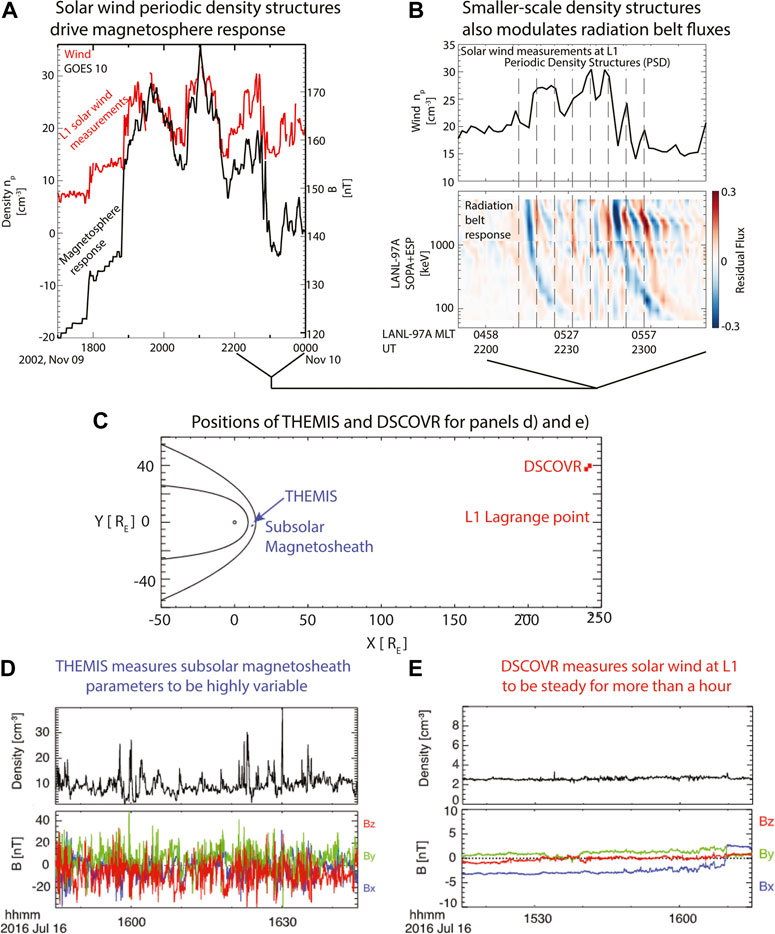
FIGURE 1. Solar wind periodic density structures (PSD) affects magnetosphere response. (A) comparison of solar wind proton density (red) and north-south magnetic field component at GOES 10; (B) detail of solar wind density measured by Wind at L1, and electron residual flux in the radiation belts by LANL-97A. Adapted from Di Matteo et al. (2022). Steady solar wind measurements at L1 does not guarantee steady local parameters in the subsolar magnetosheath. (C) Location of DSCOVR and THEMIS spacecraft, (D) THEMIS measures substantial variation in local plasma parameters, (E) DSCOVR measures very steady solar wind parameters at L1 during the corresponding period. Adapted from Walsh et al. (2019).

An example of transverse gradient in solar wind properties is in Figure 2A. In this case, we observed discrepancies in the B_z component of the interplanetary magnetic field measured by the Wind and ACE spacecraft (Figure 2B). In particular, on 11 November 2002, between 8:00 and 9:00 UT the two spacecraft measured magnetic field of similar intensity, about 10 nT, but of opposite sign. In summary, the use of single interplanetary monitor could lead to misinterpretation of the magnetospheric response.

FIGURE 2

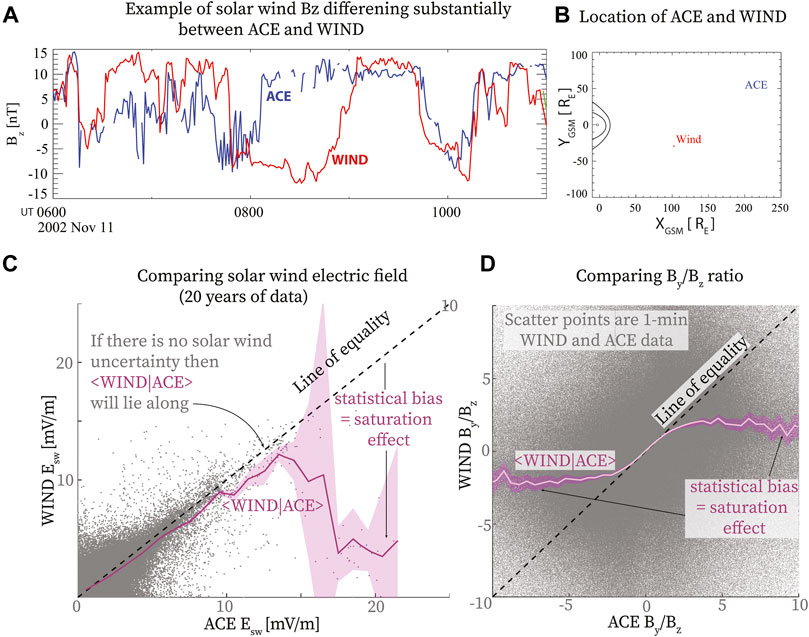
FIGURE 2. Solar wind measurements at L1 are an uncertain measure of the solar wind that affects the magnetosphere. (A) Northward component of solar wind magnetic field time-shifted to the nose of the bow shock based on measurements from ACE and Wind, (B) spacecraft positions in the ecliptic plane. (C) Comparing solar wind electric field measured by Wind and ACE. Solar wind uncertainty statistically biases the average Wind measurements to lower values than the corresponding ACE measurements. Without measurement uncertainty, the result would lie along the “Line of equality.” The bias creates an appearance of Wind measurements saturating with increasing ACE measurement on average. (D) Comparing the ratio of IMF By and Bz estimated from Wind and ACE measurements. Adapted from Sivadas and Sibeck (2022).

These examples highlights the importance of studies directed to the understanding of solar wind uncertainties and the need for satellite constellations to improve: 1) our understanding of solar-wind/magnetosphere coupling; 2) global magnetospheric simulations; 3) space weather operational capabilities.

2.2 Effect of bow shock and magnetosheath on solar wind parameters

Even if the solar wind plasma measured at L1 is the same as that which impacts the Earth, it can be significantly altered by the foreshock, structured bow shock, and magnetosheath processes. In fact, there are a variety of processes that can affect solar wind plasma upstream of the magnetopause interaction region. They include foreshock bubbles, hot flow anomalies, mirror mode waves, cavitons, and high-speed jets (Zhang et al., 2022). Even when an L1 monitor measures very steady solar wind values, the plasma that impacts the Earth’s magnetosphere can be highly variable. Figures 1D,E presents an example where very steady solar wind measured at L1 still leads to substantial fluctuations in magnetic field and density within the magnetosheath. Figure 1E shows steady solar wind measurements made using DSCOVR spacecraft at L1, while Figure 1D shows that during the same time simultaneous measurements made by THEMIS spacecraft within the magnetosheath observed substantial fluctuations in its measurements. These fluctuations are due to unknown physics happening in this region. Figure 1C shows the configuration of the two satellites.

A statistical analysis of the variability of local plasma parameters near the magnetopause interaction region suggests that the uncertainty in the clock angle of the interplanetary magnetic field (IMF) can reach a standard deviation of $\sim 50°$. The IMF clock angle substantially influences the day-side reconnection rate. When the clock angle is 0° IMF Bz is northwards, solar wind magnetosphere coupling is low. When the clock angle is 180°, the IMF Bz is southward, leading to maximum coupling. Hence a $\sim 50°$ uncertainty in the clock angle is a significant error in our estimates generated by plasma processes in the magnetosheath.

3 Uncertainty leads to a bias in the inferred geomagnetic response

A common perception within the community is that uncertainties in the solar wind estimates do not affect studies of average magnetospheric response to solar wind forcing since the uncertainties are random and “underestimates will cancel overestimates”. However, this is not true when using solar wind parameters as input or independent variable in correlation studies (Borovsky, 2022a; Borovsky, 2022b; Sivadas and Sibeck, 2022). These uncertainties can create an appearance that magnetosphere or ionosphere response saturates with increasing solar wind driving even when it does not. The effect results from a statistical bias because the observed response is more likely the result of a lower and more common solar wind driver value than the measured extreme driver value. In fact, the statistical bias is more severe for extreme and rare solar wind driver values.

Figures 2C,D shows an example of this effect by comparing available time-shifted 1-min ACE and Wind measurements from the OMNI database. If ACE and Wind measure the same solar wind plasma, the average Wind measurement given an ACE measurement will lie along the line of equality. ACE and Wind, however, do not measure the same plasma ∼70% of the time during which the Impact Parameter (King and Papitashvili, 2005) between the spacecraft is greater than 60 RE (Sivadas and Sibeck, 2022). Hence, a statistical bias creeps in, leading to Wind measuring a lower value than ACE on average (Sivadas and Sibeck, 2022). At extreme values, the average Wind measurements for increasing ACE measurements appear to be saturating. Clearly, this is a statistical effect and can be corrected if we have a quantitative estimate for the solar wind uncertainty, its statistics, and how it correlates with the measured parameter.

The implication of quantifying the uncertainty becomes apparent in the context of an important open question in magnetospheric physics: what is the geomagnetic response to solar wind forcing? A well-established inference from observations is that certain geomagnetic indices like the polar cap index, a measure of the cross-polar cap potential, and the auroral electrojet index, a measure of the auroral electrojet strength, increase linearly for low solar wind driving but saturate at high values (Borovsky, 2021). However, a literature survey shows vast disagreements in the extent of saturation and at least ten models proposing to explain the effect (Borovsky et al., 2009; Lopez et al., 2010), with no theory emerging as the dominant explanation. Preliminary analysis suggests that uncertainties in the solar wind driver estimates might be the source of this saturation effect. And correcting for this uncertainty reveals that geomagnetic response may be linear for the range of our measurements (Sivadas et al., 2022).

Statistical bias caused by uncertainties in solar wind that affects the magnetosphere can lead to 1) underestimating the response of the magnetosphere-ionosphere system to extreme space weather, 2) misinterpreting the bias as a physical process or instrumental bias, 3) incorrect model validation due to incorrectly biased data, and 4) biased predictions from coupled global models. Quantifying and removing this bias is important for the accuracy of many previous, current, and future studies within Heliophysics, as a large number of Heliophysics studies rely on uncertain estimates of solar wind parameters and their association with planetary responses.

Uncertainty analysis impacts a broad set of studies that might focus on extreme space weather, solar wind magnetosphere-ionosphere coupling, OMNI database, global geospace model validation, machine learning, and data science models. It can change our understanding of how the Earth system responds to solar wind forcing. In addition, there is currently a proliferation of machine learning and data science projects that use large amounts of solar wind data as input, so it becomes even more important to quantify the uncertainties and understand their effects on them. Being misled by unidentified uncertainties and statistical biases can be very costly in terms of research time and expense, and we must dedicate resources to avoid such errors.

4 Discussion

The improved knowledge of the properties of solar wind structures will advance our understanding of solar wind coupling with the Earth’s magnetosphere. The advancement of our understanding of the connections between solar variability and the Earth’s environment requires synergy between different research fields e.g., solar physics, solar wind physics, magnetosphere physics, planetary science, ionospheric physics, astrostatistics, data science, machine learning, and other.

The next decades will provide an unprecedented view of the interplanetary environment thanks to the combination of in situ and remote sensing observations from recent missions, e.g. Parker Solar Probe (Fox et al., 2016), Solar Orbiter (Müller et al., 2013), BepiColombo (Benkhoff et al., 2010), and (possible) future ones, e.g., Polarimeter to UNify the Corona and Heliosphere (PUNCH; DeForest et al., 2022), Seven Sister (Nykyri et al., 2022), HelioSwarm (Klein et al., 2019; Matthaeus et al., 2019), Magnetic Topology Reconstruction Explorer (MagneToRE; Maruca et al., 2021), Interplanetary Mesoscale Observatory (InterMeso; Allen et al., 2022), Solar-Terrestrial Observer for the Response of the Magnetosphere (STORM; Sibeck et al., 2018). These missions have the capability to resolve transverse gradients, spatial scales, and temporal dynamics of the solar wind as well as provide new wealth of data for the characterization of “uncertainties” in combination with spacecrafts such as Time History of Events and Macroscale Interactions during Substorm (THEMIS Burch and Angelopoulos, 2009), Magnetospheric Multiscale (MMS; Burch et al., 2016; Fuselier et al., 2016), Cluster (Escoubet et al., 2001) and possibly Magnetospheric Constellation (MagCon; Kepko et al., 2022) that orbit closer to the magnetopause.

Over the next decade we will have the capability to address these overarching questions:

• What creates the meso-scale structures and dynamics of the solar wind, and how do they affect the magnetosphere?

• What are the uncertainties in upstream solar wind conditions that affect planetary magnetospheres?

• How does solar wind uncertainty affect our interpretation of the magnetosphere response and dynamics, and accuracy of space weather forecasting?

To answer these open questions its pertinent that we plan for the following in the next decade:

1. Promote Heliophysics community projects which include the quantification and correction for uncertainties in studies of solar-wind/magnetosphere/ionosphere coupling for Earth and other planets.

2. Plan for innovative multi-spacecraft missions that help quantify the scale-size and structure of the solar wind, the 3D structure of the solar-wind/magnetosphere interaction region, as well as the uncertainties from using L1 monitors (Collier et al., 1998; Weimer et al., 2002; Weimer and King, 2008).

Though multi-spacecraft missions will help us improve the spatial and temporal resolution and scales of our measurements, uncertainties resulting from our assumptions are unavoidable in solar-wind/magnetosphere/ionosphere coupling studies. Therefore, we stress the need for more research in the area of solar wind uncertainties and innovative techniques to correct them, as a large number of projects in Heliophysics depends on these measurements. Nevertheless, to fully resolve the scale-sizes of solar wind transients and distinguish between their spatial advection and/or time dynamics, simultaneous multi-point measurements that span 3D spatial directions on meso-scales are also essential.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://cdaweb.gsfc.nasa.gov/istp_public/ http://themis.ssl.berkeley.edu/ https://zenodo.org/record/5758163 https://www.ngdc.noaa.gov/dscovr/portal/index.html#/.

Author contributions

SDM and NS conceptualized, wrote, and revised the manuscript.

Funding

The work of SDM was supported under the NASA Grant 80NSSC21K0459, and NS was supported through NASA Cooperative Agreement 80NSSC21M0180G: Partnership for Heliophysics and Space Environment Research.

Acknowledgments

The authors thank the National Space Science Data Center of the Goddard Space Flight Center for the Wind and ACE data (plasma and magnetic field) and the NASA CDAWeb team for making these data available. The GOES magnetic field data were provided by H. Singer (National Oceanic and Atmospheric Administration Space Environment Center, Asheville, N.C.) through the NASA’s National Space Science Data Center and Space Physics Data Facility. DSCOVR data were obtained from the NOAA’s National Centers for Environmental Information (NCEI) data centre. We acknowledge NASA contract NAS5-02099 and V. Angelopoulos for use of data from the THEMIS Mission. Authors also acknowledge productive discussions with Dr. Joe Borovsky and Dr. Maria-Theresia Walach. Finally, the authors would like to thank the supporter of this work listed in the white paper for the Decadal Survey for Solar and Space Physics (Heliophysics) 2024–2033.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, R. C., Smith, E. J., Anderson, B. J., Borovsky, J., Ho, G. C., Lan, J., et al. (2022). Interplanetary mesoscale observatory (InterMeso): A mission to untangle dynamic mesoscale structures throughout the heliosphere. Front. Astron. Space Sci. 9, 1002273. doi:10.3389/fspas.2022.1002273

CrossRef Full Text | Google Scholar

Benkhoff, J., van Casteren, J., Hayakawa, H., Fujimoto, M., Laakso, H., Novara, M., et al. (2010). BepiColombo–Comprehensive exploration of Mercury: Mission overview and science goals. Planet. Space Sci. 58, 2–20. doi:10.1016/j.pss.2009.09.020

CrossRef Full Text | Google Scholar

Borodkova, N. L., Zastenker, G. N., and Sibeck, D. G. (1995). A case and statistical study of transient magnetic field events at geosynchronous orbit and their solar wind origin. J. Geophys. Res. 100, 5643–5656. doi:10.1029/94JA03144

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Denton, M. H. (2016). Compressional perturbations of the dayside magnetosphere during high-speed-stream-driven geomagnetic storms. J. Geophys. Res. Space Phys. 121, 4569–4589. doi:10.1002/2015JA022136

CrossRef Full Text | Google Scholar

Borovsky, J. E., Lavraud, B., and Kuznetsova, M. M. (2009). Polar cap potential saturation, dayside reconnection, and changes to the magnetosphere. J. Geophys. Res. 114, A03224. doi:10.1029/2009JA014058

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2022a). Noise and solar-wind/magnetosphere coupling studies: Data. Front. Astron. Space Sci. 9, 990789. doi:10.3389/FSPAS.2022.990789

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2022b). Noise, regression dilution bias, and solar-wind/magnetosphere coupling studies. Front. Astron. Space Sci. 9, 867282. doi:10.3389/FSPAS.2022.867282

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2021). On the saturation (or not) of geomagnetic indices. Front. Astron. Space Sci. 8, 175. doi:10.3389/fspas.2021.740811

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2016). “Solar wind–magnetosphere interaction,” in Space weather fundamentals. Editor G. V. Khazanov (Boca Raton, Florida, United States: CRC Press). doi:10.1201/9781315368474

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2018). The spatial structure of the oncoming solar wind at Earth and the shortcomings of a solar-wind monitor at L1. J. Atmos. Solar-Terrestrial Phys. 177, 2–11. doi:10.1016/j.jastp.2017.03.014

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2022c). The triple dusk-dawn aberration of the solar wind at Earth. Front. Astron. Space Sci. 9, 917163. doi:10.3389/fspas.2022.917163

CrossRef Full Text | Google Scholar

Burch, J. L., and Angelopoulos, V. (2009). The THEMIS mission. New York, NY: Springer. doi:10.1007/978-0-387-89820-9

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Burkholder, B. L., Nykyri, K., and Ma, X. (2020). Use of the L1 constellation as a multispacecraft solar wind monitor. JGR. Space Phys. 125, e27978. doi:10.1029/2020JA027978

CrossRef Full Text | Google Scholar

Cameron, T., and Jackel, B. (2016). Quantitative evaluation of solar wind time-shifting methods. Space weather. 14, 973–981. doi:10.1002/2016SW001451

CrossRef Full Text | Google Scholar

Case, N. A., and Wild, J. A. (2012). A statistical comparison of solar wind propagation delays derived from multispacecraft techniques. J. Geophys. Res. 117, 2101. doi:10.1029/2011JA016946

CrossRef Full Text | Google Scholar

Chang, S. C., and Nishida, A. (1973). Spatial structure of transverse oscillations in the interplanetary magnetic field. Astrophys. Space Sci. 23, 301–314. doi:10.1007/BF00645159

CrossRef Full Text | Google Scholar

Collier, M. R., Slavin, J. A., Lepping, R. P., Szabo, A., and Ogilvie, K. (1998). Timing accuracy for the simple planar propagation of magnetic field structures in the solar wind. Geophys. Res. Lett. 25, 2509–2512. doi:10.1029/98GL00735

CrossRef Full Text | Google Scholar

Collier, M. R., Szabo, A., Slavin, J. A., Lepping, R. P., and Kokubun, S. (2000). IMF length scales and predictability: The two length scale medium. Int. J. Geomagnetism Aeronomy 2, 3–16.

Google Scholar

Crooker, N. U., Siscoe, G. L., Russell, C. T., and Smith, E. J. (1982). Factors controlling degree of correlation between ISEE 1 and ISEE 3 interplanetary magnetic field measurements. J. Geophys. Res. 87, 2224–2230. doi:10.1029/JA087iA04p02224

CrossRef Full Text | Google Scholar

DeForest, C., Killough, R., Gibson, S., Henry, A., Case, T., Beasley, M., et al. (2022). “Polarimeter to unify the corona and heliosphere (punch): Science, status, and path to flight,” in Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 05-12 March 2022, 1–11. doi:10.1109/AERO53065.2022.9843340

CrossRef Full Text | Google Scholar

Di Matteo, S., Villante, U., Viall, N., Kepko, L., and Wallace, S. (2022). On differentiating multiple types of ULF magnetospheric waves in response to solar wind periodic density structures. J. Geophys. Res. Space Phys. 127, e2021JA030144. doi:10.1029/2021JA030144

PubMed Abstract | CrossRef Full Text | Google Scholar

Escoubet, C. P., Fehringer, M., and Goldstein, M. (2001). IntroductionThe cluster mission. Ann. Geophys. 19, 1197–1200. doi:10.5194/angeo-19-1197-2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar Probe plus mission: Humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuselier, S. A., Lewis, W. S., Schiff, C., Ergun, R., Burch, J. L., Petrinec, S. M., et al. (2016). Magnetospheric Multiscale science mission profile and operations. Space Sci. Rev. 199, 77–103. doi:10.1007/s11214-014-0087-x

CrossRef Full Text | Google Scholar

Gershkovich, I., Lepri, S. T., Viall, N. M., Di Matteo, S., and Kepko, L. (2022). Periodic solar wind structures observed in measurements of elemental and ionic composition in situ at L1. Astrophys. J. 933, 198. doi:10.3847/1538-4357/ac73ee

CrossRef Full Text | Google Scholar

Horbury, T. S., Burgess, D., Fränz, M., and Owen, C. J. (2001). Prediction of Earth arrival times of interplanetary southward magnetic field turnings. J. Geophys. Res. 106, 30001–30009. doi:10.1029/2000JA002232

CrossRef Full Text | Google Scholar

Kepko, L., Sibeck, D., Nakamura, R., Wiltberger, M., Merkin, V., Walsh, B., et al. (2022). “Magnetospheric constellation: A key to unlocking the cross-scale coupling in the magnetosphere,” in Proceedings of the 44th COSPAR Scientific Assembly, Athens, Greece, 16-24 July 2022, 1605.

Google Scholar

Kepko, L., and Spence, H. E. (2003). Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. 108, 1257. doi:10.1029/2002JA009676

CrossRef Full Text | Google Scholar

Kepko, L., Viall, N. M., and Wolfinger, K. (2020). Inherent length scales of periodic mesoscale density structures in the solar wind over two solar cycles. JGR. Space Phys. 125, e28037. doi:10.1029/2020JA028037

CrossRef Full Text | Google Scholar

Kessel, R. L., Quintana, E., and Peredo, M. (1999). Local variations of interplanetary magnetic field at Earth’s bow shock. J. Geophys. Res. 104, 24869–24878. doi:10.1029/1999JA900230

CrossRef Full Text | Google Scholar

King, J. H., and Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. 110, A02104. doi:10.1029/2004JA010649

CrossRef Full Text | Google Scholar

Klein, K. G., Alexandrova, O., Bookbinder, J., Caprioli, D., Case, A. W., Chandran, B. D. G., et al. (2019). [Plasma 2020 decadal] multipoint measurements of the solar wind: A proposed advance for studying magnetized turbulence. Priprint arXiv e-prints, arXiv:1903.05740

Google Scholar

Lavraud, B., Thomsen, M. F., Borovsky, J. E., Denton, M. H., and Pulkkinen, T. I. (2006). Magnetosphere preconditioning under northward IMF: Evidence from the study of coronal mass ejection and corotating interaction region geoeffectiveness. J. Geophys. Res. 111, A09208. doi:10.1029/2005JA011566

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., Barnard, L. A., Haines, C., Scott, C. J., McWilliams, K. A., et al. (2020). Semi-annual, annual and universal time variations in the magnetosphere and in geomagnetic activity: 1. Geomagnetic data. J. Space Weather Space Clim. 10, 23. doi:10.1051/SWSC/2020023

CrossRef Full Text | Google Scholar

Lockwood, M. (2022). Solar wind–magnetosphere coupling functions: Pitfalls, limitations, and applications. Space weather. 20, e2021SW002989. doi:10.1029/2021SW002989

CrossRef Full Text | Google Scholar

Lopez, R. E., Bruntz, R., Mitchell, E. J., Wiltberger, M., Lyon, J. G., and Merkin, V. G. (2010). Role of magnetosheath force balance in regulating the dayside reconnection potential. J. Geophys. Res. 115, 12216. doi:10.1029/2009JA014597

CrossRef Full Text | Google Scholar

Lyons, L. R., Blanchard, G. T., Samson, J. C., Lepping, R. P., Yamamoto, T., and Moretto, T. (1997). Coordinated observations demonstrating external substorm triggering. J. Geophys. Res. 102, 27039–27051. doi:10.1029/97JA02639

CrossRef Full Text | Google Scholar

Mailyan, B., Munteanu, C., and Haaland, S. (2008). What is the best method to calculate the solar wind propagation delay? Ann. Geophys. 26, 2383–2394. doi:10.5194/angeo-26-2383-2008

CrossRef Full Text | Google Scholar

Maruca, B. A., Agudelo Rueda, J. A., Bandyopadhyay, R., Bianco, F. B., Chasapis, A., Chhiber, R., et al. (2021). MagneToRE: Mapping the 3-D magnetic structure of the solar wind using a large constellation of nanosatellites. Front. Astron. Space Sci. 8, 108. doi:10.3389/fspas.2021.665885

CrossRef Full Text | Google Scholar

Matsui, H., Farrugia, C. J., and Torbert, R. B. (2002). Wind-ACE solar wind correlations, 1999: An approach through spectral analysis. J. Geophys. Res. 107, 1355. doi:10.1029/2002JA009251

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Bandyopadhyay, R., Brown, M. R., Borovsky, J., Carbone, V., Caprioli, D., et al. (2019). [Plasma 2020 decadal] the essential role of multi-point measurements in turbulence investigations: The solar wind beyond single scale and beyond the taylor hypothesis. arXiv e-prints, arXiv:1903.06890

Google Scholar

Maynard, N. C., Burke, W. J., Sandholt, P. E., Moen, J., Ober, D. M., Lester, M., et al. (2001). Observations of simultaneous effects of merging in both hemispheres. J. Geophys. Res. 106, 24551–24577. doi:10.1029/2000JA000315

CrossRef Full Text | Google Scholar

Milan, S. E., Carter, J. A., Bower, G. E., Fleetham, A. L., and Anderson, B. J. (2022). Influence of off-sun-earth line distance on the accuracy of L1 solar wind monitoring. JGR. Space Phys. 127, e2021JA030212. doi:10.1029/2021JA030212

CrossRef Full Text | Google Scholar

Müller, D., Marsden, R. G., StCyr, O. C., and Gilbert, H. R.Solar Orbiter Team (2013). Solar orbiter. Sol. Phys. 285, 25–70. doi:10.1007/s11207-012-0085-7

CrossRef Full Text | Google Scholar

NOAA Space Weather Prediction Center (2016). Deep space climate observatory (DSCOVR). Boulder, Colorado, United States: Space Weather Prediction Center. doi:10.7289/V51Z42F7

CrossRef Full Text | Google Scholar

Nykyri, K., Balikhin, M. A., Wing, S., Opher, M., Sibeck, D., Hesse, M., et al. (2022). Societal and science case for inner heliospheric solar wind constellation. In Proceedings of the 44th COSPAR Scientific Assembly, Athens, Greece, 16-24 July 2022, 1607.

Google Scholar

Nykyri, K., Bengtson, M., Angelopoulos, V., Nishimura, Y., and Wing, S. (2019). Can enhanced flux loading by high-speed jets lead to a substorm? Multipoint detection of the christmas day substorm onset at 08:17 UT, 2015. JGR. Space Phys. 124, 4314–4340. doi:10.1029/2018JA026357

CrossRef Full Text | Google Scholar

Piersanti, M., Di Matteo, S., Zhima, Z., Yang, Y., Zhang, Z., Marcucci, M. F., et al. (2022). On the source of the anomalous ULF waves detected at both ground and space-borne data on 23 june 2020. JGR. Space Phys. 127, e30044. doi:10.1029/2021JA030044

CrossRef Full Text | Google Scholar

Reeves, G. (2021). Los Alamos National Laboratory (LANL) Geosynchronous Particle Data for Di Matteo, S., et al., (2022). Meyrin, Switzerland: Zenodo, an open repository operated by CERN. doi:10.5281/zenodo.5758163

CrossRef Full Text | Google Scholar

Richardson, J. D., and Paularena, K. I. (2001). Plasma and magnetic field correlations in the solar wind. J. Geophys. Res. 106, 239–251. doi:10.1029/2000JA000071

CrossRef Full Text | Google Scholar

Ridley, A. J. (2000). Estimations of the uncertainty in timing the relationship between magnetospheric and solar wind processes. J. Atmos. Solar-Terrestrial Phys. 62, 757–771. doi:10.1016/S1364-6826(00)00057-2

CrossRef Full Text | Google Scholar

Sibeck, D. G., Allen, R., Aryan, H., Bodewits, D., Brandt, P., Branduardi-Raymont, G., et al. (2018). Imaging plasma density structures in the soft X-rays generated by solar wind charge exchange with neutrals. Space Sci. Rev. 214, 79. doi:10.1007/s11214-018-0504-7

CrossRef Full Text | Google Scholar

Sibeck, D. G., and Korotova, G. I. (1996). Occurrence patterns for transient magnetic field signatures at high latitudes. J. Geophys. Res. 101, 13413–13428. doi:10.1029/96JA00187

CrossRef Full Text | Google Scholar

Sivadas, N., and Sibeck, D. G. (2022). Regression bias in using solar wind measurements. Front. Astron. Space Sci. 9, 924976. doi:10.3389/FSPAS.2022.924976

CrossRef Full Text | Google Scholar

Sivadas, N., Sibeck, D., Subramanyan, V., Walach, M.-T., Murphy, K., and Halford, A. (2022). Uncertainty in solar wind forcing explains polar cap potential saturation, Priprint, doi:10.48550/arxiv.2201.02137

CrossRef Full Text | Google Scholar

Viall, N. M., DeForest, C. E., and Kepko, L. (2021). Mesoscale structure in the solar wind. Front. Astron. Space Sci. 8, 139. doi:10.3389/fspas.2021.735034

CrossRef Full Text | Google Scholar

Villante, U., Recchiuti, D., and Di Matteo, S. (2022). The transmission of ULF waves from the solar wind to the magnetosphere: An analysis of some critical aspects. Front. Astron. Space Sci. 9, 835539. doi:10.3389/fspas.2022.835539

CrossRef Full Text | Google Scholar

Walsh, B. M., Bhakyapaibul, T., and Zou, Y. (2019). Quantifying the uncertainty of using solar wind measurements for geospace inputs. JGR. Space Phys. 124, 3291–3302. doi:10.1029/2019JA026507

CrossRef Full Text | Google Scholar

Weimer, D. R., and King, J. H. (2008). Improved calculations of interplanetary magnetic field phase front angles and propagation time delays. J. Geophys. Res. 113, A01105. doi:10.1029/2007JA012452

CrossRef Full Text | Google Scholar

Weimer, D. R., Ober, D. M., Maynard, N. C., Burke, W. J., Collier, M. R., McComas, D. J., et al. (2002). Variable time delays in the propagation of the interplanetary magnetic field. J. Geophys. Res. 107 (A8), SMP 29-1–SMP 29-15. doi:10.1029/2001JA009102

CrossRef Full Text | Google Scholar

Weimer, D. R., Ober, D. M., Maynard, N. C., Collier, M. R., McComas, D. J., Ness, N. F., et al. (2003). Predicting interplanetary magnetic field (IMF) propagation delay times using the minimum variance technique. J. Geophys. Res. 108, 1026. doi:10.1029/2002JA009405

CrossRef Full Text | Google Scholar

Zhang, H., Zong, Q., Connor, H., Delamere, P., Facskó, G., Han, D., et al. (2022). Dayside transient phenomena and their impact on the magnetosphere and ionosphere. Space Sci. Rev. 218, 40. doi:10.1007/s11214-021-00865-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zong, Q., Rankin, R., and Zhou, X. (2017). The interaction of ultra-low-frequency Pc3-5 waves with charged particles in Earth’s magnetosphere. Rev. Mod. Plasma Phys. 1, 10. doi:10.1007/s41614-017-0011-4

CrossRef Full Text | Google Scholar