Theoretical spectra and energetics for c-C3HC2H, l-C5H2, and bipyramidal D3h C5H2

1 Introduction

The unidentified infrared bands (UIRs) are unattributed spectral features observed in virtually all types of astronomical objects whose provenance is not firmly established (Peeters et al., 2002). The UIRs were first recognized in 1973 in the 8–13 μm region and have since been detected in nebulae and in the diffuse interstellar medium (ISM) among other astronomical environments (Peeters et al., 2002). The UIRs were first believed to originate from mostly grain mantle molecules (Allamandola et al., 1979). However, since 1984 most of the UIR spectral features have been hypothesized to be caused by polycyclic aromatic hydrocarbons (PAHs) (Leger and Puget, 1984; Sellgren, 1984; Molster et al., 2001). One difficulty with supporting this so-called PAH hypothesis is that most PAHs are not rotationally active at worst or weakly dipolar at best. This leads many PAHs to be poor candidates for rotational astronomical detection, which has been the primary vehicle for most astrochemical molecular observation including the recent detection of PAH-like molecules (Cabezas et al., 2021; Cernicharo et al., 2021). However, some small PAH-like molecules, like isomers of C₅H₂, have a lower symmetry which can allow for a nonzero dipole moment and possible rotational activity. Recently, two isomers of C₅H₂, l-C₅H₂ and ethynyl cyclopropenylidene (c-C₃HC₂H), have been independently detected in Taurus Molecular Cloud-1 and pathways of formation have been determined experimentally and supported theoretically (He et al., 2020; Cabezas et al., 2021; Cernicharo et al., 2021; Karton and Thimmakondu, 2022). The detection of C₅H₂ isomers could allude to other rotationally dark PAHs lurking in the interstellar medium. Insight into the presence, and identity, of PAHs in various astronomical environments can shed light on the chemical and physical aspects of these environments and how they contribute to the UIRs (Tielens, 2008). Additionally the recently launched James Webb Space Telescope (JWST) will allow for more detections through vibrational/infrared spectroscopy which can be used for the detection of PAHs that previously could not be detected through rotational spectroscopy.

In addition to the astronomical interest, previous theoretical works have disagreed about the relative energy of C₅H₂ isomers. These have been quantum chemically computed using coupled cluster theory at the CCSD/DZP, CCSD/TZ2P, and CCSD(T)/cc-pVTZ levels, but there are still discrepancies in the relative energies (Balaji and Michl, 1988; Seburg et al., 1997; Veis et al., 2008). Specifically, the bipyramidyl C₅H₂ isomer, shown in Figure 1, has an inconsistent magnitude of relative energy when compared to other C₅H₂ isomers depending on the level of theory utilized (Balaji and Michl, 1988; Seburg et al., 1997; Veis et al., 2008). A previous study at the HF/6-31G* level (Pople et al., 1993) places bipyramidal C₅H₂ 100 kcal mol⁻¹ higher than other C₅H₂ isomers while another study utilizing MBPT(2)/6-31G* puts the bipyramidal C₅H₂ isomer only 30 kcal mol⁻¹ higher (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997). Furthermore, previous density functional and coupled cluster theory computations also place the bipyramidyl C₅H₂ isomer 47–70 kcal mol⁻¹ higher than other isomers (Seburg et al., 1997; Karton and Thimmakondu, 2022). Despite the different levels of theory agreeing that the bipyramidyl C₅H₂ isomer is not the lowest energy isomer, there is a clear disagreement on the magnitude of energy difference for the isomer (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997; Karton and Thimmakondu, 2022). Determining more accurate relative energies is necessary because the ambient energy in the ISM allows for the formation of non-global-minimum structures. However, the energy can not be too much higher; a higher energy difference closer to 100 kcal mol ⁻¹ is much more unreasonable for formation in the ISM (Seburg et al., 1997). Newer, higher-level computations could help to settle the disagreements as to the relative energy of the bipyramidal C₅H₂ structure compared to the other isomers of C₅H₂. A further look into the l-C₅H₂ isomer, shown in Figure 2, and the c-C₃HC₂H isomer, shown in Figure 3, can provide a common reference to determine the relative energy of the bipyramidal C₅H₂ isomer. Additionally the c-C₃HC₂H isomer and the l-C₅H₂ isomer have been detected in the laboratory by Fourier transform spectrometry which provides a benchmark to the theoretical methods utilized herein (McCarthy et al., 1997; Travers et al., 1997).

FIGURE 1

FIGURE 1. Bipyramidal C₅H₂.

FIGURE 2

FIGURE 2. l-C₅H₂.

FIGURE 3

FIGURE 3. c-C₃HC₂H.

The present work utilizes high level quantum chemical computations to compute molecular structures, energies, and spectroscopic data for the bipyramidal C₅H₂ isomer shown in Figure 1, the l-C₅H₂ isomer shown in Figure 2, and the c-C₃HC₂H isomer shown in Figure 3. The spectroscopic data is computed using quartic force fields (QFFs) which are fourth-order Taylor series expansions of the internuclear potential energy portion of the Watson Hamiltonian (Fortenberry and Lee, 2019). QFFs based on coupled cluster theory at the singles, doubles, and perturbative triples level within the explicitly correlated F12b construction [CCSD(T)-F12b] (Adler et al., 2007; Knizia et al., 2009) and a triple-ζ basis set can frequently achieve agreement to within 5–7 cm⁻¹ of gas-phase experimental vibrational frequencies (Gardner et al., 2021). However a shortcoming of this method is that the rotational constants are only accurate to about 60 MHz (Agbaglo et al., 2019; Agbaglo and Fortenberry, 2019a,b; Watrous et al., 2021). An improvement would be to utilize a composite method combining core-correlated CCSD(T)-F12b with the cc-pCVTZ-F12 basis set and a correction for scalar relativity (Watrous et al., 2021). This method is referred to as F12-TZ-cCR and offers closer agreement, compared to previous methods, to experimental rotational constants on the order of 7.5 MHz which is necessary for accurate detection (Westbrook et al., 2021b; Watrous et al., 2021). Thus the fundamental vibrational frequencies and rotational constants at this level of theory provided here will lend theoretical support to experiments that will help NASA missions such as the Stratospheric Observatory for Infrared Astronomy (SOFIA) and JWST to facilitate the detection of these isomers in space.

2 Computational details

All four levels of theory in the present work utilize CCSD(T)-F12b (Raghavachari et al., 1989; Adler et al., 2007; Knizia et al., 2009; Shavitt and Bartlett, 2009). The first two QFFs use the cc-pVXZ-F12 basis sets (Peterson et al., 2008; Yousaf and Peterson, 2008; Knizia et al., 2009) where X is D or T. This combination is abbreviated as F12-XZ in the following. F12-DZ and F12-TZ QFFs are utilized for all three isomers. The other two levels of theory are based on core-correlated CCSD(T)-F12b with the cc-pCVXZ-F12 basis sets, (Watrous et al., 2021), where X is again D or T. Additionally this method includes a correction for scalar relativity computed with canonical CCSD(T) with a cc-pVTZ-DK basis set (Douglas and Kroll, 1974; Jansen and Hess, 1989). This combination is hereafter referred to as F12-XZ-cCR. F12-DZ-cCR and F12-TZ-cCR QFFs are only utilized for the c-C₃HC₂H isomer due to the substantial increase in computational cost. The QFF for the c-C₃HC₂H isomer is composed of 20,641 displacements from the equilibrium geometry along the symmetry-internal coordinates (SICs) shown below with atom labels corresponding to Figure 3.

$S_1\left(a\prime \right)=r\left({\text{H}}_1-{\text{C}}_2\right)(1)$

$S_2\left(a\prime \right)=r\left({\text{C}}_2-{\text{C}}_3\right)(2)$

$S_3\left(a\prime \right)=r\left({\text{C}}_3-{\text{C}}_4\right)(3)$

$S_4\left(a\prime \right)=r\left({\text{C}}_4-{\text{C}}_5\right)(4)$

$S_5\left(a\prime \right)=r\left({\text{C}}_4-{\text{C}}_6\right)(5)$

$S_6\left(a\prime \right)=r\left({\text{C}}_4-{\text{H}}_7\right)(6)$

$S_7\left(a\prime \right)=\angle \left({\text{H}}_1-{\text{C}}_2-{\text{C}}_3\right)(7)$

$S_8\left(a^{″}\right)=\angle \left({\text{C}}_2-{\text{C}}_3-{\text{C}}_4\right)(8)$

$S_9\left(a^{″}\right)=\angle \left({\text{C}}_3-{\text{C}}_4-{\text{C}}_5\right)(9)$

$S_{10}\left(a^{″}\right)=\angle \left({\text{C}}_3-{\text{C}}_4-{\text{C}}_6\right)(10)$

$S_{11}\left(a^{″}\right)=\angle \left({\text{C}}_3-{\text{C}}_4-{\text{H}}_7\right)(11)$

$S_{12}\left(a^{″}\right)=\tau \left({\text{H}}_1-{\text{C}}_2-{\text{C}}_3-{\text{C}}_4\right)(12)$

$S_{13}\left(a\prime \right)=\tau \left({\text{C}}_2-{\text{C}}_3-{\text{C}}_4-{\text{C}}_5\right)(13)$

$S_{14}\left(a^{″}\right)=\tau \left({\text{C}}_2-{\text{C}}_3-{\text{C}}_4-{\text{C}}_6\right)(14)$

$S_{15}\left(a\prime \right)=\tau \left({\text{C}}_2-{\text{C}}_3-{\text{C}}_4-{\text{H}}_7\right)(15)$

The QFFs for the l-C₅H₂ and bipyramidal C₅H₂ isomers are run directly in Cartesian coordinates composed of 46,064 points and 38,968 points respectively. This increase in the number of points for Cartesians instead of SICs exacerbates the increase in computational cost that would be needed for the F12-DZ-cCR and F12-TZ-cCR methods. For the SIC-based QFFs, the geometry is first optimized at each of the four levels of theory, then each geometry is displaced by 0.005 Å or 0.005 radians along the SICs to form the QFF. For the c-C₃HC₂H isomer, in addition to the previous displacements, the out-of-plane bends (OPB) are instead displaced by 0.010 Å or 0.010 radians to help combat the well-known OPB problem (Westbrook et al., 2020; Lee and Fortenberry, 2021). At each of the displaced geometries, single-point energies are calculated. The resulting energies are then fit by a least-squares procedure to yield the optimized geometry. A refit to the function minimum zeroes the gradients and yields the new equilibrium geometry as well as the corresponding force constants. The force constants are then converted from SICs to Cartesian coordinates by using the INTDER program (Allen and coworkers, 2005). For the Cartesian QFFs, each geometry is first optimized at the F12-DZ and F12-TZ levels of theory. Then, each geometry is displaced by 0.005 Å along the Cartesian x, y, and z axes. For l-C₅H₂ at the F12-DZ level of theory, each geometry was displaced by 0.010 Å in the out-of-plane coordinates. The force constants are computed numerically by central finite differences (Westbrook et al., 2021b).

For all of the QFFs, the rovibrational spectral data is computed using the SPECTRO software package (Gaw et al., 1991) which uses the Cartesian force constants in vibrational perturbation theory at second order (Watson, 1977; Papousek and Aliev, 1982; Franke et al., 2021) and second-order rotational perturbation theory (Mills, 1972). Type-1 and -2 Fermi resonances, Fermi polyads (Martin and Taylor, 1997) and Coriolis resonances are taken into account to further increase the accuracy of the rovibrational data (Martin et al., 1995; Martin and Taylor, 1997). These are shown in Supplementary Tables S1–S3 of the Supplemental Information (SI) along with the optimized geometrical parameters and T₁ diagnostics shown in Supplementary Tables S4–S6. The anharmonic zero point vibrational energy (ZPVE) from the refit geometry, refit energy (only for the SIC QFF), and energy from the optimized minima are added together to calculate the relative energy.

The geometry optimizations, harmonic frequencies, single point energies, and dipole moments are computed using the Molpro 2020.1 software package (Werner et al., 2020). The dipole moments are computed at the F12-TZ level of theory. Double-harmonic and anharmonic infrared intensities are computed using Gaussian16 (Frisch et al., 2016) with the MP2/aug-cc-pVTZ (Møller and Plesset, 1934; Kendall et al., 1992), B3LYP/aug-cc-pVTZ (Yang et al., 1986; Lee et al., 1988; Becke, 1993), and B3LYP/N07D (Barone et al., 2008) levels of theory. Previous work has shown semi-quantitative accuracy for harmonic infrared intensities for the MP2 level of theory for a substantial decrease in cost relative to higher-level computations (Yu et al., 2015; Finney et al., 2016; Westbrook et al.,2021a).

3 Results and discussion

The relative energies of l-C₅H₂, c-C₃HC₂H, and bipyramidal C₅H₂ are compared at the F12-DZ and the F12-TZ levels of theory as shown in Table 1. The relative energies of the c-C₃HC₂H and l-C₅H₂ isomers are similar to previous (Seburg et al., 1997) relative energy computations with the l-C₅H₂ isomer being 13.79 kcal mol⁻¹ higher in energy than the c-C₃HC₂H isomer. However, the bipyramidal C₅H₂ isomer is lower in relative energy than some previous computations (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997). The relative energy of the bipyramidal C₅H₂ isomer at the F12-TZ level of theory is 44.98 kcal mol⁻¹ compared to the c-C₃HC₂H isomer. This relative energy is much closer to the previous MBPT(2)/6-31G* calculations, at about 30 kcal mol⁻¹, as opposed to previous calculations at the HF/6-31G* level of theory where the relative energy was roughly 100 kcal mol⁻¹ higher than other C₅H₂ isomers (Balaji and Michl, 1988; Pople et al., 1993; Seburg et al., 1997). While this highly-symmetric isomer gives indication of possessing multi-reference effects due to its large T₁ diagnostic (0.059), the extent to which this will affect the relative energies is left for future work.

TABLE 1

TABLE 1. Relative energy of C₅H₂ Isomers in kcal mol⁻¹ compared to previous experiment.

3.1 Rotational constants

Out of the three isomers, the l-C₅H₂ isomer has the largest dipole moment of 5.94 D and its equilibrium (_e) and vibrationally-averaged (₀) rotational constants, shown in Table 2, demonstrate near prolate character (κ = − 0.99987 for the F12-TZ level of theory, where κ is defined as (2B₀ − A₀ − C₀)/(A₀ − C₀)). This large dipole moment has helped with detection of the molecule through rotational spectroscopy. The F12-DZ and F12-TZ rotational constants agree well with a maximum relative difference of 0.57% in the B₀ rotational constant. Compared to experimental Fourier transform microwave spectroscopy (McCarthy et al., 1997), the F12-TZ B₀ and C₀ rotational constants differ from experiment by only 3.0 MHz (0.13%) and 1.1 MHz (0.05%) respectively. This benchmarking constrains the expected accuracy for other, unknown spectral observables provided in this work. The A₀ rotational constant differs from experiment by 10,200 MHz (3.67%), but the error for the A₀ rotational constant is known to have a higher error for near prolate molecules (Gardner et al., 2021). The complete set of the vibrationally excited rotational constants are reported in Supplementary Table S7 of the SI. The quartic and sextic distortion constants in the S-reduced Hamiltonian are reported in Table 2. The D_J constant is about 13 Hz lower than experiment while the D_JK constant differs from experiment by around 24 kHz at the F12-DZ level of theory, but has a much higher difference at the F12-TZ level of theory at around 2,596 kHz. While D_JK often exhibits minor effects on the rotational spectrum of near-prolate molecules (Stein et al., 2015), this erroneous l-C₅H₂D_JK value for F12-TZ (and, in fact, all of its sextic distortion constants, as well) presently stems from a compounding error brought about by the step size and the resulting QFF improperly representing these data. The F12-DZ data are consistent within step size and experimental comparison implying that these data are reliable as are the F12-TZ data behaving in similar ways.

TABLE 2

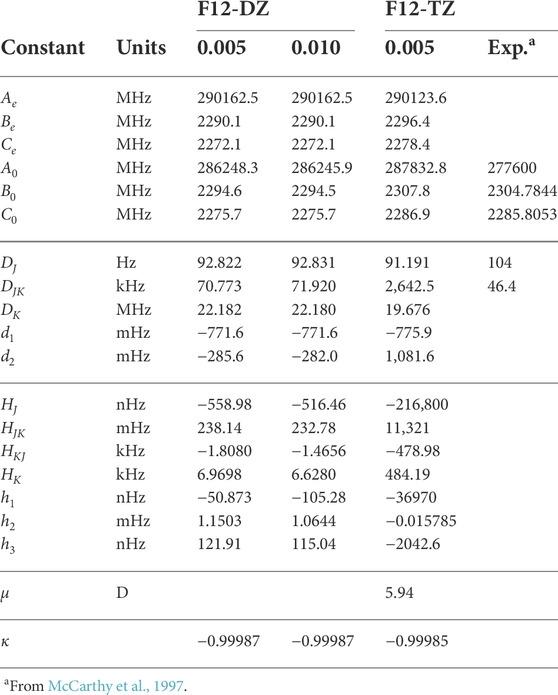
TABLE 2. Rotational constants of l-C₅H₂ compared to previous experiment^a.

The c-C₃HC₂H isomer has a smaller dipole moment than the l-C₅H₂ isomer at 3.59 D. The c-C₃HC₂H isomer also shows near prolate character (κ = − 0.98026 at the F12-TZ-cCR level of theory) as exhibited by the rotational constants B₀ and C₀ being almost the same as shown in Table 3. The F12-TZ-cCR data agrees extremely well with previous Fourier transform spectrometry results (Travers et al., 1997), differing by only 1.1 MHz (0.03%) for the B₀ rotational constant, 0.96 MHz (0.03%) for the C₀ rotational constant, and even 15 MHz (0.04%) for the A₀ rotational constant. Both the F12-DZ-cCR and F12-TZ-cCR methods produce rotational constants closer to experiment than F12-DZ and F12-TZ which in line with previous work (Watrous et al., 2021). Doubling the step size for the OBPs has little-to-no effect in the rotational constants as expected. The S-reduced Hamiltonian quartic and sextic distortion constants are reported in Table 3, and the D_K constant compares well with experiment, only differing by 0.2 kHz at the F12-TZ-cCR level of theory. The experimental D_J rotational constant is 288 Hz while the computed D_J rotational constant is 246.14 Hz. However, the computed A-reduced Hamiltonian Δ_J, determined in this work, has a value of 285.28 Hz which aligns closely with the reported experimental value, suggesting a potential misattribution in the experimental work.

TABLE 3

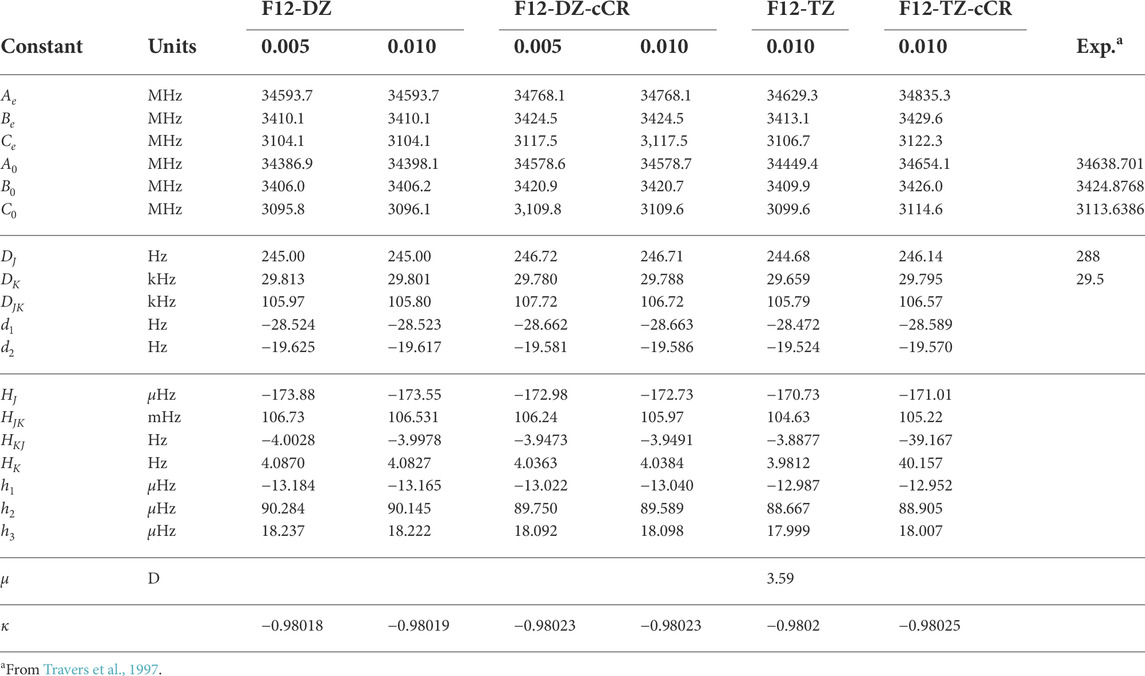
TABLE 3. Rotational constants of c-C₃HC₂H compared to previous experiment^a.

Unlike the other two isomers, the bipyramidal C₅H₂ isomer does not have a dipole due to its D_3h symmetry. Even so, the rotational constants for the bipyramidal C₅H₂ isomer are given in Table 4 for completeness. Additionally, the molecule is oblate and has only B₀ and C₀ rotational constants. The bipyramidal C₅H₂ molecule has not been detected in astrophysical observations or even observed experimentally. The F12-DZ and the F12-TZ methods have good agreement differing by only 9.2 MHz for the C₀ rotational constant. Hence, the results presented here provide the most accurate predictions of its rotational constants which may be helpful for the accurate kinetic rate determination or the thermochemical analysis that requires the full rotational partition function.

TABLE 4

TABLE 4. Rotational constants of bipyramidal C₅H₂.

3.2 Vibrational frequencies

The l-C₅H₂ isomer has the largest anharmonic intensities out of the three C₅H₂ isomers, as shown in Table 5. The two most intense modes are ν₃ with an intensity of 738 km mol⁻¹ at 2076.3 cm⁻¹ (4.81 μm) and ν₄ with an intensity of 182 km mol⁻¹ at 1887.5 cm⁻¹ (5.30 μm). These intensities represent the movements in the linear carbon chain and are up to ten times larger than the anti-symmetric stretch in water, which has an intensity of about 70 km mol⁻¹ at the same level of theory. The large intensities of these two frequencies imply that l-C₅H₂ should be observable right at the edge of the NIRspec instrument onboard JWST in a region often bereft of known transitions for organic molecules. Out of the three levels of theory in this work used to compute intensities, only the B3LYP/N07D results are reported for the l-C₅H₂ isomer as it is the only method with all real frequencies in line with the present high-level computations. The previous theory used to compute the intensities agrees qualitatively with the order of intensities computed with B3LYP/N07D. Additionally, the N07D basis set is designed to handle hydrocarbon systems like this and has been used to produce anharmonic frequencies in reasonable agreement with experiment (Barone et al., 2008; Barone et al., 2013). However in this case, the anharmonic frequencies produced by B3LYP/N07D fall short in comparison with the fundamental frequencies produced by the F12-TZ level of theory. In contrast, the F12-DZ and F12-TZ anharmonic frequencies have relatively close agreement. The exceptions to this are the modes involving an in-plane bend (IPB) or OPB of the carbon chain, ν₁₀-ν₁₅. The portions of the QFF involving these modes have problems with the cubic and quartic force constants. Those modes are reported as the harmonic values, and most anharmonic corrections are within the margin of error for the levels of theory. A larger step size is also used at the F12-DZ level of theory to combat the OPB problem (Fortenberry et al., 2018; Westbrook et al., 2020; Lee and Fortenberry, 2021; Lee and Fortenberry, 2021). However there is no significant improvement of the issue. As a result, the larger step size is not repeated for the F12-TZ level of theory. This will not affect possible detection via JWST because the NIRSpec and MIRI instruments on the JWST only capture spectra to about 333 cm⁻¹, but the resolution drops for the lower frequencies below 2000 cm⁻¹ since the larger range MIRI instrument does not have the same capabilities as NIRspec. The harmonic frequencies for both the F12-DZ and F12-TZ levels of theory agree well with previous theoretical harmonic frequencies for most modes (Karton and Thimmakondu, 2022), but vary more for the OPB and IPB which is likely due to the aforementioned OPB problem (Westbrook et al., 2020; Lee and Fortenberry, 2021).

TABLE 5

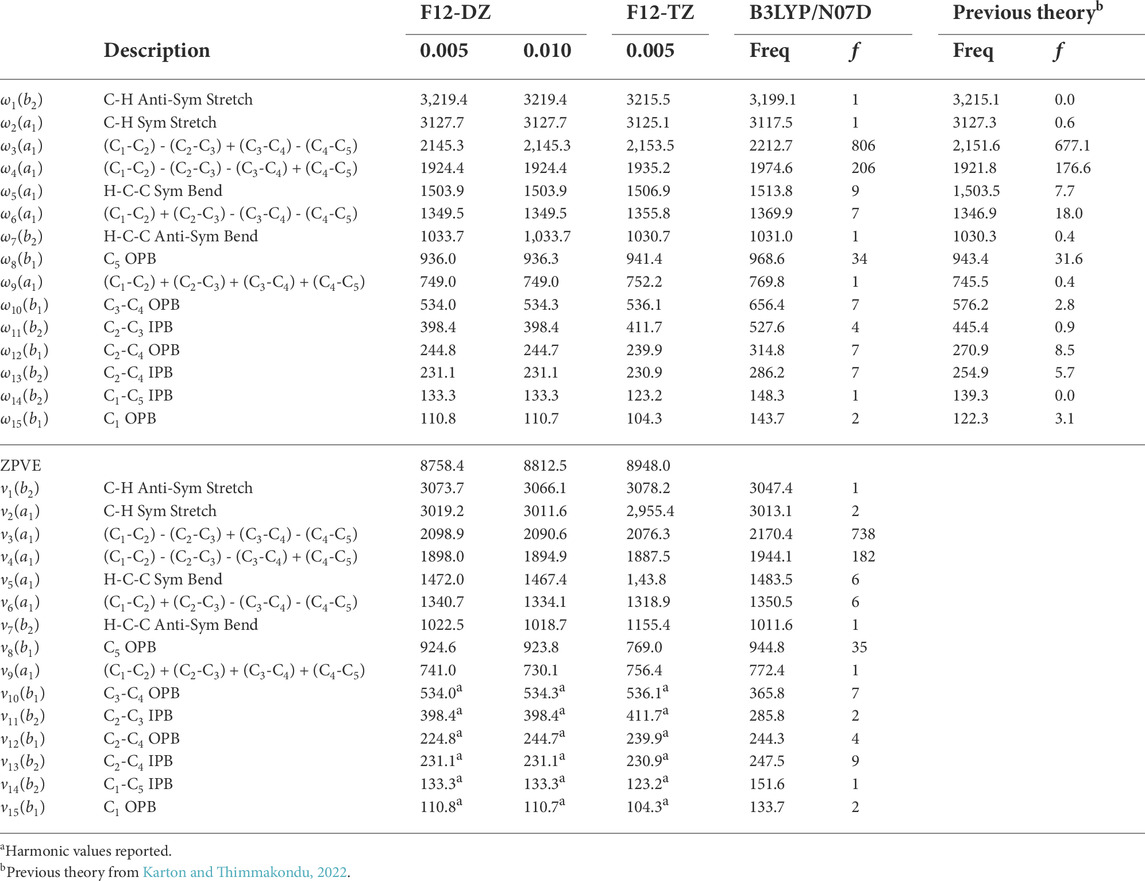
TABLE 5. F12-DZ and F12-TZ harmonic and fundamental vibrational frequencies and B3LYP/N07D intensities (in km mol⁻¹) of l-C₅H₂ compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theory^b.

For the c-C₃HC₂H isomer, the vibrational frequencies are in Table 6, and the double-harmonic intensities are in Table 7. The c-C₃HC₂H isomer has two intense peaks with the most intense peak being the acetylene C-H stretch, ν₁, at 3,347.8 cm⁻¹ (2.99 μm) with an anharmonic intensity of 84 km mol⁻¹ at the B3LYP/N07D level of theory. The second most intense peak is the C₅-C₆-H₇ in-plane bend (IPB), ν₁₁, at 577.9 cm ⁻¹ (17.3 μm) with an intensity of 52 km mol⁻¹. The intensity changes depending on which level of theory is used to calculate the double-harmonic intensities, but all three methods computed for the intensities agree on the qualitative order of intensities for the modes, as does the previous theory (Karton and Thimmakondu, 2022). The intensities for c-C₃HC₂H are not as strong as the intensities for l-C₅H₂, but are still strong enough for detection.

TABLE 6

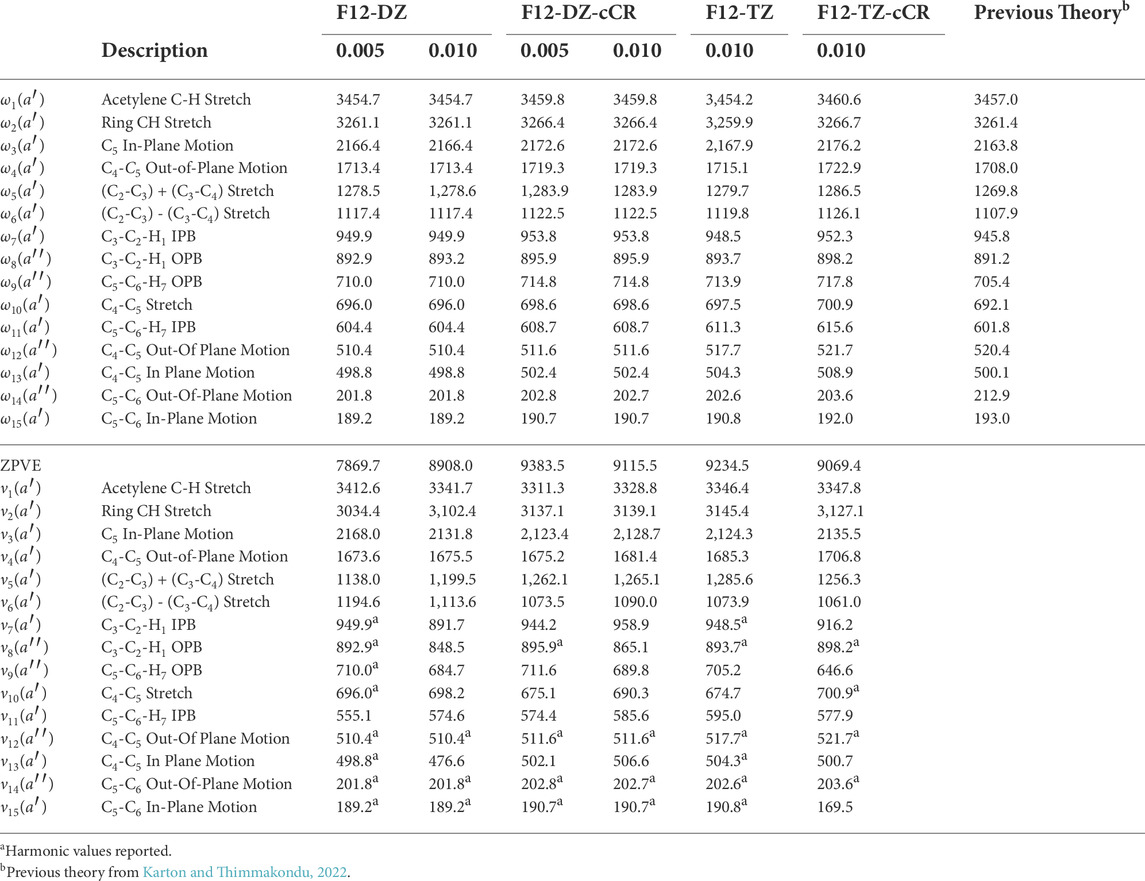
TABLE 6. Harmonic and fundamental vibrational frequencies of c-C₃HC₂H compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theory^b.

TABLE 7

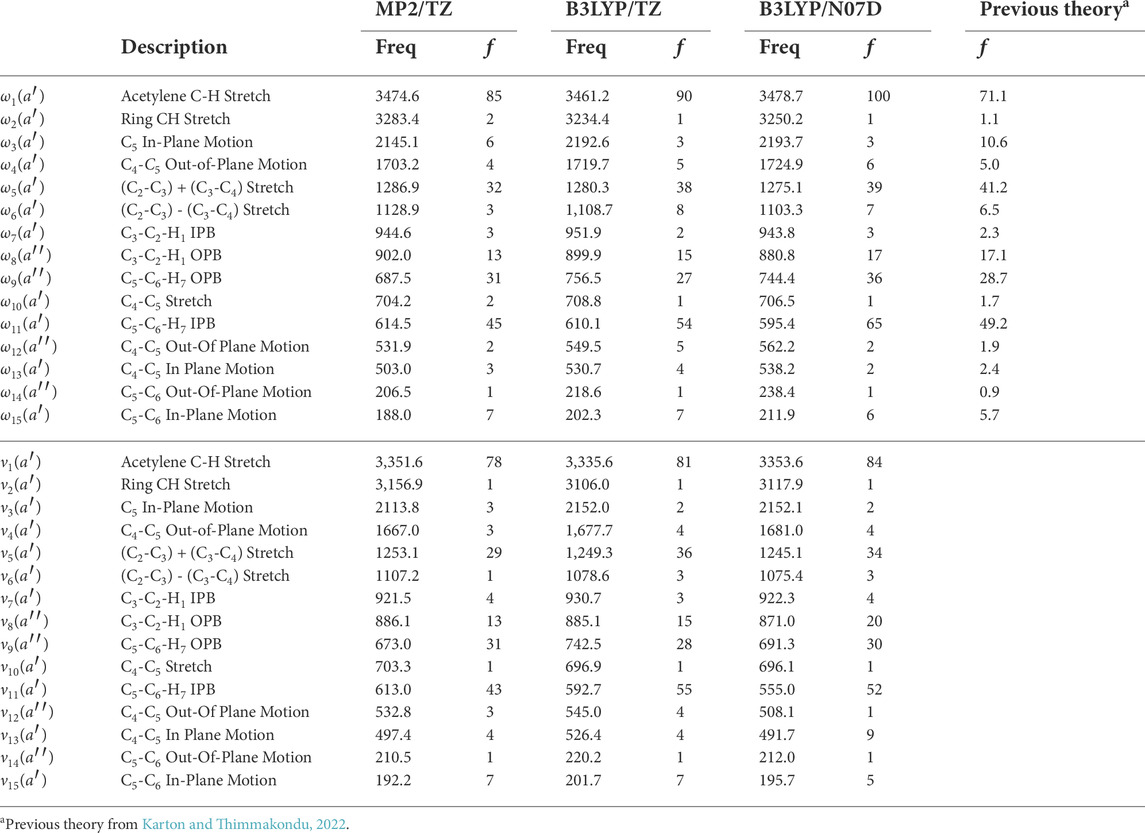
TABLE 7. Intensities in km mol⁻¹ of c-C₃HC₂H compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theory^a.

For the c-C₃HC₂H, there are differences in the anharmonic frequencies between the levels of theory and step sizes as shown in Table 6. Fundamental frequencies ν₁₂, ν₁₄, and ν₁₅ produce questionable positive anharmonicities, although they are below or on the lower edge of the range to be detected through the aforementioned instruments on JWST. Additionally, these three modes have a maximum intensity of 5 km mol⁻¹. Both considerations make these frequencies unlikely to be detected. Increasing the level of theory to F12-DZ-cCR improves the anharmonic correction for the ν₉, ν₁₀, and ν₁₃ fundamentals. The doubled step size in the OPB coordinates further improves the anharmonic correction for F12-DZ and F12-DZ-cCR. As a result only the doubled step size is calculated at the higher levels of theory due to the increased computational cost. Similarly, this doubled step size helps the anharmonic correction for ν₇ and ν₈ with F12-DZ and F12-DZ-cCR. There is much less variation in the harmonic frequencies between the levels of theory. Additionally, the harmonic frequencies compare well to previous theory (Karton and Thimmakondu, 2022). Figure 4 shows a simulated spectrum of the F12-TZ-cCR anharmonic frequencies and the B3LYP/N07D intensities with all bands incorporated; only those with notable intensities are present.

FIGURE 4

FIGURE 4. Simulated spectrum of c-C₃HC₂H.

For the bipyramidal C₅H₂ isomer, the vibrational frequencies for the F12-DZ and F12-TZ QFFs, shown in Table 8, have close agreement for most of the frequencies. The bipyramidal C₅H₂ isomer has one intense frequency in which is ν₁₀, the symmetric C₂-C₃ + C₂-C₄ stretch, with an intensity of 78 km mol⁻¹ at 426.1 cm ⁻¹ (23.5 μm) which is slightly smaller than the c-C₃H₂H isomer and much smaller than the most intense peaks for the l-C₅H₂ isomer. Unlike the other isomers, the bipyramidal C₅H₂ isomer only has three other fundamentals that have intensities over 10 km mol⁻¹ at the B3LYP/N07D level of theory. These are ν₄ at 1,273.6 cm⁻¹ (7.85 μm), ν₅ at 1,108.7 cm⁻¹ (9.02 μm), and ν₈ at 829.5 cm⁻¹ (12.0 μm). While the different methods differ in the quantitative value of the intensities, they again agree qualitatively with each other and with previous theory on what will be the most and least intense peaks (Karton and Thimmakondu, 2022). However only having one fundamental with a large intensity could increase the difficulty for the detection of the bipyramidal C₅H₂ isomer compared to the other two isomers. The F12-DZ and the F12-TZ QFFs show good agreement for the harmonic and anharmonic fundamental frequencies and the harmonic frequencies further show good agreement to previous theory (Karton and Thimmakondu, 2022). The largest discrepancy arises in ν₁₀, with a difference of 26.5 cm⁻¹, but a majority of the frequencies agree to within 3 cm⁻¹. However, given the greater computational rigor of F12-TZ, its data should be considered the more reliable of the two.

TABLE 8

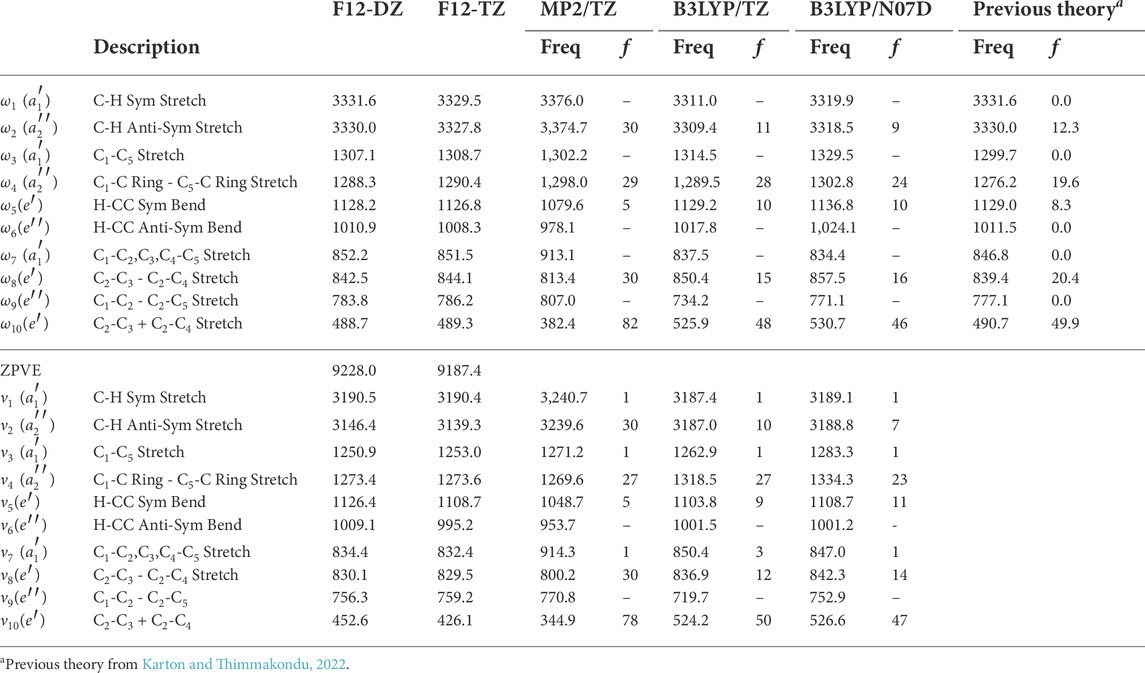
TABLE 8. F12-DZ and F12-TZ harmonic and fundamental frequencies of bipyramidal C₅H₂ with intensities in km mol⁻¹ compared to previous theory computed at the fc-CCSD(T)/cc-pVTZ level of theory^a.

4 Conclusion

The large intensities for some of the fundamental frequencies in all of the isomers may facilitate the detection of these C₅H₂ structures via JWST. Such spectral data could lead to the identification for some UIRs as well as unknown transitions of known interstellar molecules such as l-C₅H₂ and c-C₃HC₂H. The bipyramidal C₅H₂ isomer has some of the lowest intensities of the three isomers but still has one peak at 426.1 cm⁻¹ (23.5 μm) with an intensity of 78 km mol⁻¹. The c-C₃HC₂H isomer has one intense fundamental frequency at 3,347.8 cm⁻¹ with an intensity of 84 km mol⁻¹. The l-C₅H₂ isomer has the two highest intensities out of the three isomers for its ν₄ at 1887.5 cm⁻¹ with a large intensity of 182 km mol⁻¹ and ν₃ at 2076.3 cm⁻¹ with a very large intensity of 738 km mol⁻¹ making this fundamental the most likely of the group especially since, again, l-C₅H₂ has been previously detected via radioastronomy. The F12-TZ methodology produces rotational constants for l-C₅H₂ within 3 MHz (0.13%) for the B₀ and C₀ rotational constants. Improving upon this high level of accuracy, the F12-TZ-cCR methodology for c-C₃HC₂H produces B₀ and C₀ rotational constants within 1.1 MHz (0.03%) of experiment. This close agreement to experiment lends supports to the accuracy of the other theoretical values, notably the fundamental vibrational frequencies, reported herein. Out of the three C₅H₂ isomers presented in this work, the c-C₃HC₂H isomer has the lowest relative energy, with l-C₅H₂ 13.79 kcal mol⁻¹ higher in line with previous work (Seburg et al., 1997). The bipyramidal C₅H₂ isomer is 44.98 kcal mol⁻¹ higher in energy compared previous computations which places this D_3h isomer 100 kcal mol⁻¹ or more higher than other C₅H₂ isomers (Seburg et al., 1997). The dipole moments for the c-C₃HC₂H and l-C₅H₂ isomers are large at 3.59 D and 5.94 D, respectively, which has facilitated the previous detections of the isomers in space through rotational spectroscopy. Overall, the anharmonic vibrational frequencies and rotational constants presented herein may help to facilitate the laboratory or astronomical detection of unknown transitions of known molecules. In particular, the high-intensity fundamental frequencies of each molecule that fall within the high-resolution range of JWST may also help to disentangle some of the heretofore unidentified features in the UIRs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

AW, BW, and RF contributed to conception and design of the study. AW performed the computations. AW and BW analyzed the data. AW wrote the first draft of the manuscript, and BW and RF edited the manuscript. RF secured funding for the research and provided administration for the project. All authors contributed to manuscript revision, read, and approved the submitted version.

Acknowledgments

The authors wish to acknowledge funding from NASA grant NNX17AH15G, NSF grant CHE-1757888, NSF grant OIA-1757220, and the University of Mississippi’s College of Liberal Arts as well as computational resources from the Mississippi Center for Supercomputing Research (MCSR).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.1051535/full#supplementary-material

References

Adler, T. B., Knizia, G., and Werner, H.-J. (2007). A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 127, 221106. doi:10.1063/1.2817618

PubMed Abstract | CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019b). The performance of explicitly correlated wavefunctions [CCSD(T)-F12b] in the computation of anharmonic vibrational frequencies. Chem. Phys. Lett. 734, 136720. doi:10.1016/j.cplett.2019.136720

CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019a). The performance of explicitly correlated methods for the computation of anharmonic vibrational frequencies. Int. J. Quantum Chem. 119, e25899. doi:10.1002/qua.25899

CrossRef Full Text | Google Scholar

Agbaglo, D., Lee, T. J., Thackston, R., and Fortenberry, R. C. (2019). A small molecule with PAH vibrational properties and a detectable rotational spectrum: c-(C)C₃H₂, cyclopropenylidenyl carbene. Astrophys. J. 871, 236. doi:10.3847/1538-4357/aaf85a

CrossRef Full Text | Google Scholar

Allamandola, L. J., Greenberg, J. M., and Norman, C. A. (1979). On the middle infra-red fluorescence and absorption of molecules in grain mantles. Astron. Astrophys. 77, 66–74.

Google Scholar

Allen, W. D.coworkers (2005). INTDER 2005 is a general program written by W. D. Allen and coworkers, which performs vibrational analysis and higher-order non-linear transformations, Athens, GA: University of Georgia.

Google Scholar

Balaji, V., and Michl, J. (1988). New strained organic molecules: Theory guides experiment. Pure Appl. Chem. 60, 189–194. doi:10.1351/pac198860020189

CrossRef Full Text | Google Scholar

Barone, V., Biczysko, M., Bloino, J., Egidi, F., and Puzzarini, C. (2013). Accurate structure, thermodynamics, and spectroscopy of medium-sized radicals by hybrid coupled cluster/density functional theory approaches: The case of phenyl radical. J. Chem. Phys. 138 (23), 234303.

PubMed Abstract | CrossRef Full Text | Google Scholar

Barone, V., Cimino, P., and Stendardo, E. (2008). Development and validation of the B3LYP/N07D computational model for structural parameter and magnetic tensors of large free radicals. J. Chem. Theory Comput. 4, 751–764. doi:10.1021/ct800034c

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (1993). Density-functional thermochemistry. III. the role of exact exchange. J. Chem. Phys. 98, 5648–5652. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

Cabezas, C., Tercero, B., Agúndez, M., Marcelino, N., Pardo, J. R., de Vicente, P., et al. (2021). Cumulene carbenes in TMC-1: Astronomical discovery of l-H₂C₅. Astron. Astrophys. 650, L9. doi:10.1051/0004-6361/202141274

PubMed Abstract | CrossRef Full Text | Google Scholar

Cernicharo, J., Agúndez, M., Cabezas, C., Tercero, B., Marcelino, N., Pardo, J. R., et al. (2021). Pure hydrocarbon cycles in TMC-1: Discovery of ethynyl cyclopropenylidene, cyclopentadiene, and indene. Astron. Astrophys. 649, L15. doi:10.1051/0004-6361/202141156

PubMed Abstract | CrossRef Full Text | Google Scholar

Douglas, M., and Kroll, N. (1974). Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. (N. Y). 82, 89–155. doi:10.1016/0003-4916(74)90333-9

CrossRef Full Text | Google Scholar

Finney, B., Fortenberry, R. C., Francisco, J. S., and Peterson, K. A. (2016). A spectroscopic case for SPSi detection: The third-row in a single molecule. J. Chem. Phys. 145, 124311. doi:10.1063/1.4963337

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., and Lee, T. J. (2019). Computational vibrational spectroscopy for the detection of molecules in space. Ann. Rep. Comput. Chem. 15, 173–202. doi:10.1016/bs.arcc.2019.08.006

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Novak, C. M., and Lee, T. J. (2018). Rovibrational analysis of c-SiC₂H₂: Further evidence for out-of-plane bending issues in correlated methods. J. Chem. Phys. 149, 024303. doi:10.1063/1.5043166

PubMed Abstract | CrossRef Full Text | Google Scholar

Franke, P. R., Stanton, J. F., and Douberly, G. E. (2021). How to VPT2: Accurate and intuitive simulations of CH stretching infrared spectra using VPT2+K with large effective Hamiltonian resonance treatments. J. Phys. Chem. A 125, 1301–1324. doi:10.1021/acs.jpca.0c09526

PubMed Abstract | CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 revision C.01. Wallingford CT: Gaussian Inc.

Google Scholar

Gardner, M. B., Westbrook, B. R., Fortenberry, R. C., and Lee, T. J. (2021). Highly-accurate quartic force fields for the prediction of anharmonic rotational constants and fundamental vibrational frequencies. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 248, 119184. doi:10.1016/j.saa.2020.119184

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaw, J. F., Willets, A., Green, W. H., and Handy, N. C. (1991). SPECTRO: A program for the derivation of spectrscopic constants from provided quartic force fields and cubic dipole fields. Advances in Molecular Vibrations and Collision Dynamics. Editor Bowman Joel M., and Ratner Mark A. (Greenwich, Connecticut: JAI Press, Inc.), 170–185.

Google Scholar

He, C., Galimova, G. R., Luo, Y., Kaiser, R. I., Eckhardt, A. K., Sun, R., et al. (2020). A chemical dynamics study on the gas-phase formation of triplet and singlet C₅H₂ carbenes. Proc. Natl. Acad. Sci. U. S. A. 117, 30142–30150. doi:10.1073/pnas.2019257117

PubMed Abstract | CrossRef Full Text | Google Scholar

Jansen, G., and Hess, B. A. (1989). Revision of the douglas-kroll transformation. Phys. Rev. A 39, 6016–6017. doi:10.1103/physreva.39.6016

PubMed Abstract | CrossRef Full Text | Google Scholar

Karton, A., and Thimmakondu, V. S. (2022). From molecules with a planar tetracoordinate carbon to an astronomically known C₅H₂ carbene. J. Phys. Chem. A 126, 2561–2568. doi:10.1021/acs.jpca.2c01261

PubMed Abstract | CrossRef Full Text | Google Scholar

Kendall, R. A., Dunning, T. H., and Harrison, R. J. (1992). Electron affinities of the first-row atoms revisited. systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

Knizia, G., Adler, T. B., and Werner, H.-J. (2009). Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C., Yang, W. T., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789. doi:10.1103/physrevb.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. J., and Fortenberry, R. C. (2021). The unsolved issue with out-of-plane bending frequencies for C C multiply bonded systems. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 248, 119148. doi:10.1016/j.saa.2020.119148

PubMed Abstract | CrossRef Full Text | Google Scholar

Leger, A., and Puget, J. L. (1984). Identification of the “unidentified IR emission features” of interstellar dust? Astron. Astrophys. 137, L5–L8.

Google Scholar

Martin, J. M. L., Lee, T. J., Taylor, P. R., and François, J.-P. (1995). The anharmonic force field of ethylene, C₂H₄, by means of accurate ab initio calculations. J. Chem. Phys. 103, 2589–2602. doi:10.1063/1.469681

CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1997). Accurate ab initio quartic force field for trans-HNNH and treatment of resonance polyads. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 53, 1039–1050. doi:10.1016/s1386-1425(96)01869-0

CrossRef Full Text | Google Scholar

McCarthy, M. C., Travers, M. J., Kovács, A., Gottlieb, C. A., and Thaddeus, P. (1997). Eight new carbon chain molecules. Astrophys. J. Suppl. Ser. 113, 105–120. doi:10.1086/313050

CrossRef Full Text | Google Scholar

Mills, I. M. (1972). “Vibration-rotation structure in asymmetric- and symmetric-top molecules,” in Molecular spectroscopy - modern research. Editors K. N. Rao, and C. W. Mathews (New York: Academic Press), 115–140.

CrossRef Full Text | Google Scholar

Møller, C., and Plesset, M. S. (1934). Note on an approximation treatment for many-electron systems. Phys. Rev. 46, 618–622. doi:10.1103/physrev.46.618

CrossRef Full Text | Google Scholar

Molster, F. J., Lim, T. L., Sylvester, R. J., Waters, L. B. F. M., Barlow, M. J., Beintema, D. A., et al. (2001). The complete ISO spectrum of NGC 6302. Astron. Astrophys. 372, 165–172. doi:10.1051/0004-6361:20010465

CrossRef Full Text | Google Scholar

Papousek, D., and Aliev, M. R. (1982). Molecular vibration-rotation spectra. Amsterdam: Elsevier.

Google Scholar

Peeters, E., Hony, S., Van Kerckhoven, C., Tielens, A. G. G. M., Allamandola, L. J., Hudgins, D. M., et al. (2002). The rich 6 to 9 μm spectrum of interstellar PAHs. Astron. Astrophys. 390, 1089–1113. doi:10.1051/0004-6361:20020773

CrossRef Full Text | Google Scholar

Peterson, K. A., Adler, T. B., and Werner, H.-J. (2008). Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 128, 084102. doi:10.1063/1.2831537

PubMed Abstract | CrossRef Full Text | Google Scholar

Pople, J. A., Scott, A. P., Wong, M. W., and Radom, L. (1993). Scaling factors for obtaining fundamental vibrational frequencies and zero-point energies from HF/6-31G* and MP2/6-31G* harmonic frequencies. Isr. J. Chem. 33, 345–350. doi:10.1002/ijch.199300041

CrossRef Full Text | Google Scholar

Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6

CrossRef Full Text | Google Scholar

Seburg, R. A., McMahon, R. J., Stanton, J. F., and Gauss, J. (1997). Structures and stabilities of C₅H₂ isomers: Quantum chemical studies. J. Am. Chem. Soc. 119, 10838–10845. doi:10.1021/ja971412j

CrossRef Full Text | Google Scholar

Sellgren, K. (1984). The near-infrared continuum emission of visual reflection nebulae. Astrophys. J. 277, 623–633. doi:10.1086/161733

CrossRef Full Text | Google Scholar

Shavitt, I., and Bartlett, R. J. (2009). Many-body methods in Chemistry and physics: MBPT and coupled-cluster theory. Cambridge: Cambridge University Press.

Google Scholar

Stein, C., Weser, O., Schroder, B., and Botschwina, P. (2015). High-level theoretical spectroscopic parameters for three ions of astrochemical interest. Mol. Phys. 113, 2169–2178. doi:10.1080/00268976.2015.1017019

CrossRef Full Text | Google Scholar

Tielens, A. G. G. M. (2008). Interstellar polycyclic aromatic hydrocarbon molecules. Annu. Rev. Astron. Astrophys. 46, 289–337. doi:10.1146/annurev.astro.46.060407.145211

CrossRef Full Text | Google Scholar

Travers, M. J., McCarthy, M. C., Gottlieb, C. A., and Thaddeus, P. (1997). Laboratory detection of the ring-chain molecule C₅H₂. Astrophys. J. 483, L135–L138. doi:10.1086/310744

CrossRef Full Text | Google Scholar

Veis, L., Čàrsky, P., Pittner, J., and Michl, J. (2008). Coupled cluster study of polycyclopentanes: Structure and properties of C₅H_2n, n = 0-4. Collect. Czechoslov. Chem. Commun. 73, 1525–1551. doi:10.1135/cccc20081525

CrossRef Full Text | Google Scholar

Watrous, A. G., Westbrook, B. R., and Fortenberry, R. C. (2021). F12-TZ-cCR: A methodology for faster and still highly-accurate quartic force fields. J. Phys. Chem. A 125, 10532–10540. doi:10.1021/acs.jpca.1c08355

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. K. G. (1977). “Aspects of quartic and sextic centrifugal effects on rotational energy levels,” in Vibrational spectra and structure. Editor J. R. During (Amsterdam: Elsevier), 1–89.

Google Scholar

Werner, H.-J., Knowles, P. J., Manby, F. R., Black, J. A., Doll, K., Heßelmann, A., et al. (2020). Molpro, version 2020.1, a package of ab initio programs. WIREs Comput. Mol. Sci. 2, 242–253. See http://www.molpro.net. doi:10.1002/wcms.82

CrossRef Full Text | Google Scholar

Westbrook, B. R., Del Rio, W. A., Lee, T. J., and Fortenberry, R. C. (2020). Overcoming the out-of-plane bending issue in an aromatic hydrocarbon: The anharmonic vibrational frequencies of c-(CH)C₃H₂⁺. Phys. Chem. Chem. Phys. 22, 12951–12958. doi:10.1039/d0cp01889a

PubMed Abstract | CrossRef Full Text | Google Scholar

Westbrook, B. R., Patel, D. J., Dallas, J. D., Swartzfager, G. C., Lee, T. J., and Fortenberry, R. C. (2021a). Fundamental vibrational frequencies and spectroscopic constants of substituted cyclopropenylidene (c-C₃HX, x=F, Cl, CN). J. Phys. Chem. A 125, 8860–8868. doi:10.1021/acs.jpca.1c06576

PubMed Abstract | CrossRef Full Text | Google Scholar

Westbrook, B. R., Valencia, E. M., Rushing, S. C., Tschumper, G. S., and Fortenberry, R. C. (2021b). Anharmonic vibrational frequencies of ammonia borane (BH₃NH₃). J. Chem. Phys. 154, 041104. doi:10.1063/5.0040050

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, W. T., Parr, R. G., and Lee, C. T. (1986). Various functionals for the kinetic energy density of an atom or molecule. Phys. Rev. A 34, 4586–4590. doi:10.1103/physreva.34.4586

PubMed Abstract | CrossRef Full Text | Google Scholar

Yousaf, K. E., and Peterson, K. A. (2008). Optimized auxiliary basis sets for explicitly correlated methods. J. Chem. Phys. 129, 184108. doi:10.1063/1.3009271

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Q., Bowman, J. M., Fortenberry, R. C., Mancini, J. S., Lee, T. J., Crawford, T. D., et al. (2015). The structure, anharmonic vibrational frequencies, and intensities of NNHNN⁺. J. Phys. Chem. A 119, 11623–11631. doi:10.1021/acs.jpca.5b09682

PubMed Abstract | CrossRef Full Text | Google Scholar