Slow solar wind acceleration through the middle corona: Spacecraft radio studies

The “Middle Corona”, defined by recent consensus as the region spanning 1.5–6 solar radii (R_⊙, heliocentric), is an important zone through which several structural and dynamic changes occur in coronal streamer regions. Among these is a regime change from high density, closed magnetic field structures to open field structures of much lower electron concentration. Along with this complex restructuring, the forming slow solar wind is channeled and accelerated through the middle corona. Solar wind (SW) outflow speeds can be estimated from trans-coronal radio observations. The method of radio frequency fluctuation (FF) analysis considers the frequency variations arising from density inhomogeneities crossing the sensing line-of-sight (LOS). Below 2 R_⊙, where the SW is beginning to form and outflow speed is expected to be below the acoustic wave speed, the radio FF can be attributed to the density oscillations of acoustic waves crossing the radio sensing path. With increasing helioaltitudes through the middle corona, the FF are dominated by density disturbances advected across the sensing LOS. This property enables estimation of solar wind outflow speed at various heliodistances. The coronal plasma is believed to enter the middle corona in a subsonic state, then accelerate to exit the zone generally with supersonic, but sub-Alfvénic flows. Trans-coronal radio sensing complements imaging and other remote coronal observations, and helps bridge the observational gap across the full distance range of the middle corona. Radio techniques enrich the study of solar wind, and should be utilized in next-generation, multiwavelength campaigns that tackle the challenging physics of coronal plasma acceleration.

1 Introduction

Historically, the term “middle corona” was applied variably to regions ranging roughly from the upper limits of EUV images at about 1.4 solar radii (R_⊙, heliocentric), to the inner margins from white-light coronagraphic imagers, e.g. LASCO C2 on SOHO. Some reports used middle corona terminology for the heliocentric range generally within the bounds 1.4–2.5 R_⊙ (Badalyan, 1996; Koutchmy, 2004; Mancuso and Garzelli, 2013). Wexler (2020) set the upper limit of the middle corona at 2.5 R_⊙ to coincide with the standard “source surface” height often used in 3-D global coronal models. More recent studies have also alluded to the middle corona in terms of a restricted range with an upper limit no greater than 3.0 R_⊙. Seaton et al. (2021) gave a 1.5–3.0 R_⊙ range in extended EUV studies. Meyer et al. (2020) discussed SWAP data over range 1.7–2.5 R_⊙ under a title referencing the middle corona. All these approaches for defining the middle corona were anchored primarily in technical limitations, emphasizing the need to better characterize the “observational gap” over about 1.5–2.2 R_⊙.

Recent discussions of the multidisciplinary middle corona working group have highlighted the need to study large-scale transformations in coronal structure and dynamics occurring in zone spanning 1.5–6.0 R_⊙ as an integrated system (West et al., 2022a; West et al., 2022b). This modern conception of the middle corona has particular suitability for study of solar wind formation and acceleration associated with the streamer formations. While compositional features and exact source regions are still being elucidated, the streamer-related wind is generally considered the main source of “slow solar wind”, typically defined as that reaching outflow speeds $<450$ km/s by one AU (see e.g. Strachan et al., 2002; Ofman, 2004; Abbo et al., 2016). The range of the modern definition middle corona encompasses the main complex magnetic field reconfiguration from closed-to open structures, with related change from relative plasma confinement to a solar wind outflow regime. The transition between these two disparate regimes remains poorly understood, due in part to the paucity of measurements available in the mid-coronal gap, and the lack of uniform measurement techniques across the middle corona into adjacent regions. Suggested nomenclature for coronal levels is given in Table 1.

TABLE 1

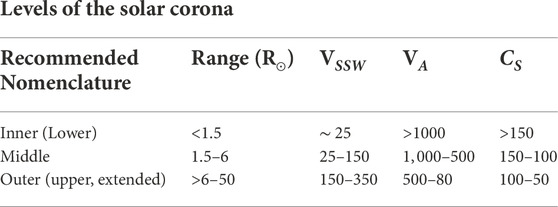
TABLE 1. Levels of the Solar Corona, with heliocentric ranges and representative speeds (km/s); slow solar wind (SSW), Alfvén wave (A), acoustic waves (S).

Radio methods can play a role in bridging the middle corona “observational gap”. Acceleration of the solar wind, a key process occurring in the middle corona, is amenable to study using radio techniques. Radio propagation disturbances produced by time-varying plasma density inhomogeneities allow probing of solar wind speeds in regions inaccessible to direct measurements (Bastian, 2001; Yakovlev and Pisanko, 2018). Woo (1978) for example, estimated a sub-sonic solar wind speed of 24 km/s at 1.7 R_⊙ using spectral broadening and Doppler scintillation analysis of solar occultation spacecraft radio observations. Imamura et al. (2014) studied modern trans-coronal spacecraft radio observations over 1.5–20.5 R_⊙, producing a solar wind speed profile from analysis of intensity scintillations in the strong scattering regime. The frequency fluctuation (FF) methods are closely linked to electron density variations on the sensing line-of-sight (LOS). Observationally, coronal radio FF are well studied with spectral analysis (e.g. Efimov et al., 2017; Yakovlev and Pisanko, 2018) and applicable to the evaluation of solar wind acceleration. Wexler et al. (2019) studied composite FF data from relatively modern, MESSENGER spacecraft radio observations together with historical radio data from HELIOS spacecraft. They found that the radial dependence of FF data demonstrated a break-point within the middle corona zone, requiring a dual-component model to handle the two different FF-producing regimes. This cross-over is the radio FF correlate of the relatively confined inner corona transforming to the streamer/slow solar wind outflow corona.

In this Perspectives article, we will illustrate the method of trans-coronal spacecraft radio frequency fluctuation (FF) analysis as developed by Wexler et al. (2019) from MESSENGER and HELIOS radio observations, and subsequently extended with additional radio observations from the Akatsuki spacecraft (Wexler et al., 2020). The methods explore coronal electron density fluctuations, leading to a model giving solar wind speeds through the middle corona and beyond. The successes, limitations and areas for further investigation are discussed.

2 Trans-coronal radio frequency fluctuations

2.1 Stacked slab model

Here we present the method for evaluating time-varying plasma density disturbances along a trans-coronal sensing path (e.g. Yakovlev and Pisanko, 2018), by analysis of the observed radio signal frequency fluctuations. A stacked plasma slab model with relatively simple features is implemented, as developed in Wexler et al. (2019), Wexler et al. (2020).

The instantaneous difference Δf between transmitted and observed radio frequencies for a signal propagating through a plasma is (see, e.g. Vierinen et al., 2014):

$\mathrm{\Delta }f=-\frac{V_{\mathit{rel}}}{c}+\frac{1}{2\pi }{r}_e\lambda \frac{d}{dt}{\int }_0^S{n}_e\left(s,t\right)dS(1)$

where the first term on the right is the fractional Doppler shift resulting from spacecraft relative velocity V_rel, and the second term incorporates the refractive index shift due to time-rate of change in the electron density, n_e, on the line-of-sight (LOS), over distance S. λ is the radio wavelength c is the speed of light and r_e is the classical electron radius, equal to 2.82 × 10^–15 m. The point of closest solar approach along the LOS is called the proximate point, and the heliocentric distance to this point is termed the solar offset (SO). The frequency shift effects are generally strongest near the proximate point, where the electron density is usually highest. It is customary to associate each radio LOS observation, and pertinent proximate point parameters, with the corresponding SO.

When the Doppler shift and other slow baseline shifts are removed through a suitable detrend procedure (see e.g. Kolosov et al., 1982; Efimov et al., 2005), the FF due to changing electron density in a single plasma slab having width L_LOS¹ is

$\delta f\left(t\right)=\frac{1}{2\pi }{r}_e\lambda L_{\mathit{LOS}}\frac{d}{dt}{n}_e\left(t\right).(2)$

For a density oscillation of form δn_e(t) = δn_e exp^−iωt the time derivative has magnitude ωδn_e. This relation is captured in the Fourier transform, and the associated power spectral density, |FF(ω)|²:

$|FF\left(\omega \right){|}^2=\frac{1}{4{\pi }^2}{r}_e^2{\lambda }^2{\omega }^2{L}_{\mathit{LOS}}^2|\delta n_e\left(\omega \right){|}^2(3)$

where |δn_e(ω)|² is the corresponding power spectral density of electron concentration fluctuations. Re-expressing as radio-wavelength normalized frequency fluctuation measure², FM, now with oscillation frequency ν, in Hz, we obtain

$|FM\left(\nu \right){|}^2=r_e^2{\nu }^2{L}_{\mathit{LOS}}^2|\delta n_e\left(\nu \right){|}^2(4)$

If we consider the case of an effective LOS integration length equal to the solar offset, R, then the number of consecutive slabs is R/L_LOS and the power spectrum of the frequency fluctuation for the set of slabs becomes

$|FM\left(\nu \right){|}^2=r_e^2{\nu }^2{L}_{\mathit{LOS}}R|\delta n_e\left(\nu \right){|}^2.(5)$

Thus the observed fluctuation measure spectrum implies an underlying electron density fluctuation spectrum, even without yet specifying the physical nature of the fluctuations along the LOS.

Fluctuation variances ${\sigma }_{FM}^2$ and ${\sigma }_{n_e}^2$ are defined for power spectral frequency integration range [a,b] by

${\sigma }_{FM}^2\equiv {\int }_a^b|FM\left(\nu \right){|}^{2}d\nu (6)$

${\sigma }_{n_e}^2\equiv {\int }_a^b|\delta n_e\left(\nu \right){|}^{2}d\nu (7)$

The electron density fluctuation variances can then be related to the FM spectrum as:

${\sigma }_{n_e}^2=\frac{1}{r_e^2{L}_{\mathit{LOS}}R}{\int }_a^b\frac{|FM\left(\nu \right){|}^2}{{\nu }^2}d\nu (8)$

Further development leads to a relation between variances of FM and density fluctuation:

${\sigma }_{FM}^2=r_e^2{\nu }_c^2{L}_{\mathit{LOS}}R{\sigma }_{n_e}^2(9)$

provided a scaling frequency ν_c is found observationally from the frequency fluctuation measure power spectra

${\nu }_c^2=\frac{{\int }_a^b|FM\left(\nu \right){|}^{2}d\nu }{{\int }_a^b|FM\left(\nu \right){|}^2{\nu }^{-2}d\nu }(10)$

as shown in Wexler et al. (2020), or more roughly, by using the power spectral index, α:

${\nu }_c^2=\frac{\alpha +1}{\alpha -1}\frac{{\nu }^{1-\alpha }{|}_a^b}{{\nu }^{-\alpha -1}{|}_a^b}(11)$

described in Wexler et al. (2019). Therefore, ${\sigma }_{n_e}^2$ can be estimated from known ${\sigma }_{FM}^2$ if spectral index α is known or well-approximated.

It should be noted that values for electron density variance are specific to the integration frequency range. Integration over the inertial range of the spectrum is desired, but in practice the range is subject to technical limitations. The lower frequency limit is set by the analysis frame temporal length and effects of detrend procedures on low-frequency power, while the upper frequency limit is set where the negative power spectral density curve drops into the noise floor, or by the cadence of data sampling. Wexler et al. (2019) implemented an integration range 1–28 mHz for 2000-s MESSENGER data segments, with second-order polynomial detrend procedure applied. The archival HELIOS data had a 1.11–8.33 mHz band based on the data interval length and sampling rate, but was scaled to an equivalent 1–28 mHz integration band. However, other frequency bands can be considered. The Akatsuki data in Wexler et al. (2020) were analyzed in sequential 4000-s segments, with ${\sigma }_{FF}^2$ calculated from the mean of 1–28 mHz and 0.5–100 mHz integration results. This dual-band approach allowed for an estimate of uncertainly, and still produced FF results concordant with the MESSENGER-HELIOS findings. Care should be taken to avoid including excessively low frequencies from long data frames, as these may suffer from distorted spectral power from suboptimal detrending, and inclusion of changing bulk coronal density structure rather than plasma density inhomogeneities in the computed FF.

2.2 Density fluctuations in the subsonic regime

It is useful to define a fractional density fluctuation ϵ

$ϵ=\frac{{\sigma }_{n_e}}{n_e}(12)$

where the mean local electron number density n_e(r) may be estimated from an existing parameter model or from LOS measurements, either by inversion of polarized brightness white light observations, or from radio ranging calculations (Kooi et al., 2022). The observational model to calculate the fractional density fluctuation based on randomized density fluctuations across stacked slab coronal plasma is

$ϵ=\frac{{\sigma }_{FM}}{r_e{\nu }_c{n}_e\sqrt{L_{\mathit{LOS}}R}}.(13)$

The ϵ values must be interpreted in the context of the specific spectral integration frequency limits, accuracy of ν_c and suitability of the electron number density model. All factors which influence σ_FM, such as of shifting frequencies on the sounding LOS from acceleration of the solar wind, influence the observational determination of ϵ.

Accounting for shifting of the fluctuation power spectrum by solar wind advection of the density inhomogeneities, Wexler et al. (2019) modeled the density fluctuation fraction as

${ϵ}_{\mathit{model}}={ϵ}_{BL}\frac{\sqrt{V_{SW}^2+C_s^2}}{C_s^2}(14)$

where V_SW is the solar wind outflow speed, C_s is the speed of sound, and ϵ_BL is the baseline fractional fluctuation in the low-outflow regime. Below SO about 2.5R_⊙, the acoustic wave speed is expected to exceed the solar wind outflow speed. Thus in the initial, subsonic part of the middle corona, ϵ_BL can be determined from Eq. (13). Wexler et al. (2019) reported ϵ_BL = 0.017 ± 0.002, averaged over SO 1.4–1.7 R_⊙.

The baseline value for ϵ, determined over SO 1.5–1.57R_⊙ using Akatsuki spacecraft radio frequency fluctuation data was 0.019 ± 0.002 (Wexler et al., 2020). The value compares favorably with ϵ = 0.013–0.016 ± 0.001 determined independently in radio burst methods (Mohan et al., 2019). Mugundhan et al. (2017) found ϵ = 0.006 ± 0.0002 over 1.6–2.2R_⊙ in studies of type III solar radio bursts. Hollweg et al. (2010) determined ϵ ∼ 0.023–0.031 at SO 2R_⊙, and larger at higher SO, based on HELIOS data. While acknowledging these variable and uncertain estimates, here we use ϵ = 0.019.

From the stacked slab variances model of the prior section, the RMS FF measure is now written as

${\sigma }_{FM}=r_e{\nu }_cϵn_e\sqrt{L_{\mathit{LOS}}R}.(15)$

The quantity ${\sigma }_{FM}/\sqrt{r}$ (r = R/R_⊙, R_⊙ = 696,000 km) should scale with density to the extent that other parameters are constant. The top panel of Figure 1 shows the radial dependence of ${\sigma }_{FM}/\sqrt{r}$, taken from the multi-spacecraft data provided in (Wexler et al., 2020). A steep profile with near-straight line fit on semi-log plot is found at low mid-coronal heights, indicating negative exponential density stratification. This finding is consistent with a low-flow, quasi-static scheme of relative plasma confinement. In contrast, the remaining data trend with r⁻² consistent with a mass-flux expanding outflow regime (see next section). The cross-over occurs around SO 2.5_⊙, similar to radio spectral broadening and Doppler scintillation results reported long ago by (Woo, 1978). Comparing with imaging shown in the middle panel of Figure 1, the break-point around 2.5 Rs corresponds to the region where the closed magnetic field structures are giving way to nascent near-radial streamer open-field structures.

FIGURE 1

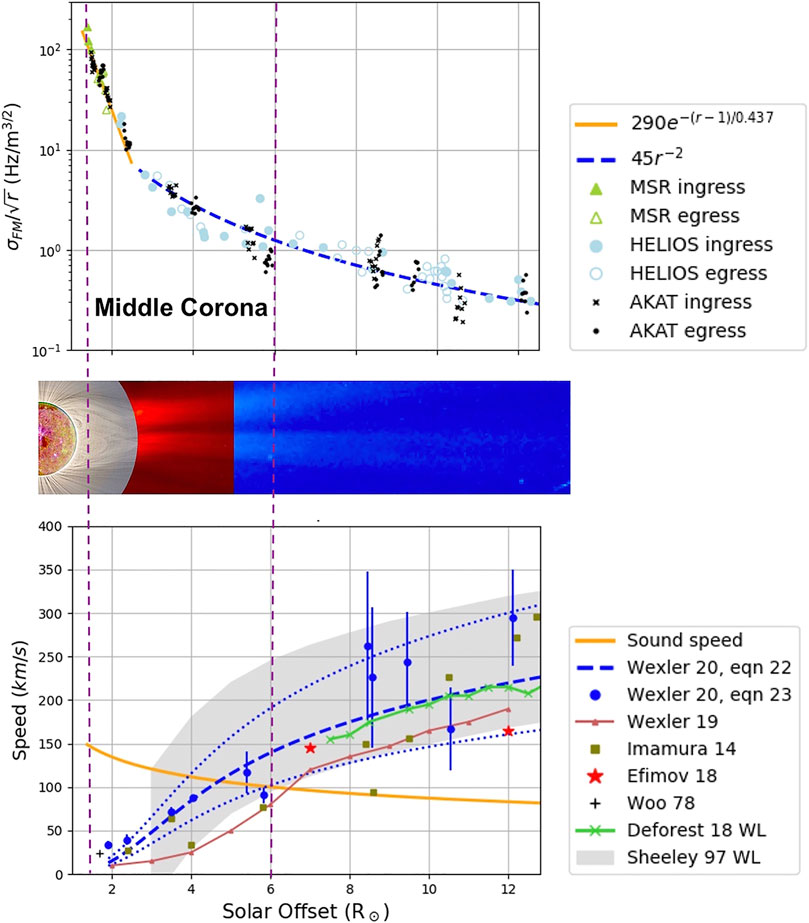
FIGURE 1. Transcoronal radio frequency fluctuation results, based on Wexler et al. (2020). Upper Panel. ${\sigma }_{FM}/\sqrt{r}$ with dual regimes of subsonic fit (orange line) and acceleration zone fit (blue dashed line). Middle Panel. Composite imaging through the corona. From left to right Composite EUV of solar surface (NOAA SUVI, courtesy of Daniel B. Seaton.), Eclipse image of low-to-middle corona (courtesy of Jay M. Pasachoff, Williams College Eclipse Expedition/NSF), middle corona in white light (SOHO/LASCO C2), outer corona in white light (SOHO/LASCO C3 imager). Lower Panel. Solar wind speed profile, composite of several studies (references in text). The solar wind approaches or exceeds supersonic speeds as reaching the middle corona upper boundary at 6 RR_⊙.

Eq. (15) is interpreted in two sub-models corresponding to the segments below and above the break. Following through with ϵ_model in Eq. (14), for the inner part of the middle corona, below $\sim 2.5{\mathrm{R}}_{\odot }$, the density fluctuations are attributed primarily to acoustic waves, with $\frac{d}{dt}$ of Equation (2) corresponding to density oscillations propagating across the LOS. In the acoustic wave regime, ${\nu }_cϵ\sqrt{L_{\mathit{LOS}}}$ was assumed constant over the observation interval. The acoustic wave contribution to the observed FF in the inner mid-coronal region should scale as

${\sigma }_{FM}=K{n}_e\sqrt{r}(16)$

where K represents the consolidation of constants. The Mercier-Hollweg electron density model (Wexler et al., 2019) was used in these studies

$n_e\left(r\right)=\left[\frac{65}{r^{5.94}}+\frac{0.768}{{\left(r-1\right)}^{2.25}}\right]\times 10^{12}\left[{\mathrm{m}}^{-\mathrm{3}}\right].(17)$

In Wexler et al. (2020), the final version of the modeled acoustic wave σ_FM profile is

${\sigma }_{FM}=9.69\times 10^{-12}{n}_e\sqrt{r}(18)$

In summary, the radio FF data demonstrate a steep radial profile segment that scales with $n_e\sqrt{r}$ in the inner part of the middle corona, with an unmistakable paradigm shift in the remainder.

2.3 Acceleration of the solar wind

Beyond about 2.5 R_⊙ in the middle corona, and continuing into the extended corona, Eq. (9) must be reframed to account for solar wind outflow. The effect of solar wind outflow dominates the FF by advecting spatial fluctuations of electron density across the sensing LOS. Higher wind speed advects density variations of given length scale more quickly across the sensing radio LOS, resulting in higher observational σ_FM.

Allowing that the radial configuration of the system near the point of closest solar approach on the LOS is approximated by horizontal flow, with density variations of characteristic length scale L_RAD crossing perpendicularly, the time-derivative in Eq. (2) expressed as the equivalent frequency is simply V_SW/L_RAD. In the solar wind acceleration region, the RMS frequency measure fluctuation becomes

${\sigma }_{FM}=r_e\frac{V_{SW}}{L_{\mathit{RAD}}}ϵn_e\sqrt{L_{\mathit{LOS}}R}.(19)$

Considering the simple mass flux relation for outflow in a radially expanding system,

$n_e{V}_{SW}=\frac{K_1}{r^2},(20)$

with flux constant K₁, substitution into Eq. (19) yields

${\sigma }_{FM}=K_2{r}^{-3/2}(21)$

where $K_2=K_1{r}_eϵ\sqrt{L_{\mathit{LOS}}{R}_{\odot }}$. The σ_FM data beyond SO 2.5R_⊙ were fitted to find K₂ = 49.7. The final two-term fit is

${\sigma }_{FM}=9.69\times 10^{-12}{n}_e\sqrt{r}+49.7r^{-3/2}.(22)$

The first term dominates in the inner mid-corona, and potentially gives information to estimate the fractional fluctuation of electron density. The second term incorporates information on solar wind outflow speed. From Eq. (19), and using the above specification for K₂, solar wind speed calculates to

$V_{SW}\left(r\right)=\frac{49.7L_{\mathit{RAD}}}{r_eϵn_e{r}^2\sqrt{L_{\mathit{LOS}}{R}_{\odot }}}.(23)$

Values for L_LOS and L_RAD are needed to implement the speed equation. L_LOS = 10,000 km is assigned as a fixed value, suggested by enhanced white-light solar eclipse images (Rušin et al., 2010) showing grouped streamer density structures of about that width at about 2R_⊙ and maintaining a reasonably constant dimension at least over the next solar radius or two as viewed on the sky plane. Hollweg’s model for the correlation scale (Hollweg et al., 2010), based on spacing between magnetic flux tubes, is L_LOS =3.35×10⁶r^0.918 in meters, and yields about 10,000 km at SO 3.5R_⊙. The simple case of fixed values ϵ = 0.019, L_LOS = 10,000 km, and L_RAD = 10,000 km was applied. Of course, radially elongated density oscillations, L_RAD > L_LOS, are possible. In the case of density structures with an aspect ratio of, say 10:1, only a 10th of the slab elements would be contributing FF at any given time. The observed σ_FM would then imply increased density fluctuation RMS amplitude on the remaining slabs by a factor of $\sqrt{10}$, yielding ϵ = 0.06. This value is consistent with recent results from studies of solar radio bursts using STEREO (Krupar et al., 2018) and Parker Solar Probe spacecraft (Krupar et al., 2020) observations.

The solar wind speed profile based on this model (Wexler et al., 2020) is shown together with estimates from other studies in panel three of the Figure. The dashed line represents the model implementation using the fitted σ_FM data (Eq. (22)), and the blue stippling indicates the estimates net error in deduced V_SW. This error band estimate is roughly similar to the spread in speeds from Sheeley et al. (1997), shown as the broad gray band. Radio scintillation analysis of this same Akatsuki 2011 data set (Imamura et al., 2014) and MESSENGER-HELIOS radio FF analysis (Wexler et al., 2019) determined comparable speeds in the extended corona, but comparatively lower speeds at low SO, probably due to breakdown in the isotropic turbulence modeling assumption used in those studies. The two-station radio FF study of Efimov et al. (2018) also shows generally comparable results. The mass-flux r^−3/2 model shows reasonable concordance to speeds obtained in white-light imaging (Sheeley et al., 1997; DeForest et al., 2018). Other radio FF data sets show radial dependencies differing from the -3/2 power law (Efimov et al., 2008; Efimov et al., 2013). Such differing results suggest departure from strict r² scaling of the coronal expansion regionally, and warrant further study. A representative sound speed curve from Wexler et al. (2019) is coplotted, indicating the sonic point to be at ∼ 5R_⊙.

All FF models include scaling parameters requiring independent determination or else estimation, e.g. the radial dependence of electron number density and a density disturbance length scale. Here we have used a simple model with the width scale of spatial density variation, L_LOS, set equal to the radial density variation scale, L_RAD, but that issue needs further study with combined techniques.

3 Expanding the role of transcoronal radio probes

Trans-coronal spacecraft radio sensing methods are well-suited to probe the middle corona properties, with relatively strong monochromatic signals passing through otherwise inaccessibly deep helioaltitudes. Here we have addressed the FF radio methods in particular to highlight the slow solar wind speed profile, but additional radio techniques provide further insights into aspects of coronal structure, solar wind features and outburst phenomena. For example, Faraday rotation (FR) analysis of linearly polarized radio signals provides important information on the integrated product of electron density with the LOS-aligned magnetic field. FR methods can provide valuable information on the coronal magnetic field (e.g,. Patzold et al., 1987; Bird, 2007; Wexler D. B. et al., 2021) and on FR fluctuations that may signify energy transport via MHD waves (Hollweg et al., 1982; Jensen et al., 2013b; Efimov et al., 2015; Wexler et al., 2017; Kooi et al., 2022). The FR effect scales with the inverse square of radio frequency; at low frequencies, incremental rotation beyond the ± π measurement limit can cause FR ambiguity. Thus the early HELIOS FR studies in S-band (2.2 GHz) radio provided useful data down to about 3 R_⊙. More recent work by Jensen et al. (2013a), Jensen et al. (2013b); Wexler et al. (2017), Wexler D. B. et al. (2021) yielded FR results down to 1.6 R_⊙ in X-band (8.4 GHz) radio observations. In general, the higher frequency radio transmissions are used to probe the deeper coronal regions, including the middle corona.

Dual- or multi-frequency radio measurements are highly desirable in trans-coronal radio studies. Differential arrival times for simultaneously transmitted radio signals of different frequency can be used to determine the electron column density (Bird et al., 1994). This helps constrain electron density near the point of closest solar approach on the LOS via models of density, especially if more than one LOS is available through the region of interest. The density information is most helpful in unlocking the Faraday rotation integral in applicable cases, separating the density and magnetic field contributions in order to isolate the LOS-aligned magnetic field strength. In addition, multi-frequency measurements improve reliability of FR analysis and help resolve uncertainties in angular “turnover” beyond ± π rotation.

Looking forward, the value of continuous radio trans-coronal observations from multiple vantage points is emphasized. The T-CRAF concept presented by Kooi et al. in this special collection gives one example of multi-point radio sensing in multiple frequencies as needed for proper sensitivity at different helioaltitudes through the middle corona. T-CRAF transmissions would include linearly polarized signals, such that transcoronal Faraday rotation (FR) could be measured. Also, multi-frequency sensing would allow for concurrent study of electron density.

Another recent mission concept is the MOST (Multiview Observatory for Solar and Terrestrial science) mission (Gopalswamy et al., 2021) with the radio science FETCH (Faraday Effect Tracker of Corona and Heliospheric phenomena) instrument (Jensen et al., 2021; Wexler D. et al., 2021). FETCH will couple radio FR and differential propagation time delay measurements with the full complement of heliospheric instrument packages on the two main MOST spacecraft that are situated to observe on views approximately perpendicular to the motion of Earth-bound large-scale heliospheric disturbances. While these two outer MOST spacecraft will be situated at Sun-Earth Lagrange points L4 and L5, the two inner spacecraft have potential for variable placement, potentially probing down into the middle coronal heights. In all cases, the mission designs and operations should strive for multiple probe points/LOS, multiple frequencies, satisfactory signal-to-noise ratios that allow high cadence and continuous or extended observation intervals. For the middle corona, the goal is development of coordinated campaigns in which the radio observations are concurrent with white-light and EUV imaging, to fully track structures and flows across the region.

Spacecraft radio techniques complement imaging and other remote coronal observations, with the advantages of being applicable across the full distance range of the middle corona, and for varying states of solar activity. The radio data provide an avenue to cross-check on parameters derived by other methods. Radio confirmations also help validate specific models and SO ranges over which they are operative. More work will be needed on constraining scaling parameters like the characteristic transverse density length, L_LOS, at various SO. The availability of PSP in-situ data provides opportunities to explore the in-situ manifestation of radio correlation scales and flux tube domains (e.g. Borovsky et al., 2021; Ruffolo et al., 2021), at least down to $\sim 10$R_⊙.

Trans-coronal radio FF observations support the study of a 1.5–6 R_⊙ middle corona in which the slow solar wind reaches supersonic speeds. The expanded set of radio techniques to enable magnetic field and density measurements will be extremely valuable in creating improved models of middle corona MHD physics. These established radio methods enrich solar wind investigation generally, and should be utilized in next-generation, multiwavelength campaigns that tackle the challenging problem of coronal plasma acceleration.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DW conceived the work, prepared with main text and illustrations and assumes overall responsibility for the work. JK and EJ performed scientific review of the work and contributed to the final text. PS provided senior scientific review and recommendations for the final text.

Funding

Basic research at the U.S. Naval Research Laboratory (NRL) is supported by 6.1 Base funding.

Acknowledgments

The authors appreciate earlier contributions of Takeshi Imamura and Anatoli Efimov in providing spacecraft radio data and insight reflected in the published works on which this paper is based. Panel three of the Figure comes from Wexler et al. (2020) and was reproduced in part here by permission of the publisher (Springer). We thank the reviewer for helpful comments that improved the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹This could also be called the electron density fluctuation correlation scale.

²The wavelength-normalized frequency fluctuation measure is analogous to the rotation measure, which normalizes Faraday rotation by squared wavelength.

References

Abbo, L., Ofman, L., Antiochos, S. K., Hansteen, V. H., Harra, L., Ko, Y.-K., et al. (2016). Slow solar wind: Observations and modeling. Space Sci. Rev. 201, 55–108. doi:10.1007/s11214-016-0264-1

CrossRef Full Text | Google Scholar

Badalyan, O. G. (1996). Temperature and density in the middle corona through the activity cycle determined from white light observations. Astronomical Astrophysical Trans. 9, 205–223. doi:10.1080/10556799608208224

CrossRef Full Text | Google Scholar

Bastian, T. S. (2001). Radio wave propagation in the corona and the interplanetary medium. Astrophys. Space Sci. 277, 107–116. doi:10.1023/A:1012232111843

CrossRef Full Text | Google Scholar

Bird, M. K. (2007). Coronal Faraday rotation of occulted radio signals. Astronomical Astrophysical Trans. 26, 441–453. doi:10.1080/10556790701595236

CrossRef Full Text | Google Scholar

Bird, M. K., Volland, H., Paetzold, M., Edenhofer, P., Asmar, S. W., and Brenkle, J. P. (1994). The coronal electron density distribution determined from dual-frequency ranging measurements during the 1991 solar conjunction of the ULYSSES spacecraft. Astrophys. J. 426, 373. doi:10.1086/174073

CrossRef Full Text | Google Scholar

Borovsky, J. E., Halekas, J. S., and Whittlesey, P. L. (2021). The electron structure of the solar wind. Front. Astron. Space Sci. 8, 93. doi:10.3389/fspas.2021.690005

CrossRef Full Text | Google Scholar

DeForest, C. E., Howard, R. A., Velli, M., Viall, N., and Vourlidas, A. (2018). The highly structured outer solar corona. Astrophys. J. 862, 18. doi:10.3847/1538-4357/aac8e3

CrossRef Full Text | Google Scholar

Efimov, A. I., Chashei, I. V., Bird, M. K., Samoznaev, L. N., and Plettemeier, D. (2005). Turbulence in the inner solar wind determined from frequency fluctuations of the downlink signals from the ULYSSES and GALILEO spacecraft. Astron. Rep. 49, 485–494. doi:10.1134/1.1941491

CrossRef Full Text | Google Scholar

Efimov, A. I., Lukanina, L. A., Chashei, I. V., Bird, M. K., Pätzold, M., and Wexler, D. (2018). Velocity of the inner solar wind from coronal sounding experiments with spacecraft. Cosm. Res. 56, 405–410. doi:10.1134/S0010952518060023

CrossRef Full Text | Google Scholar

Efimov, A. I., Lukanina, L. A., Rogashkova, A. I., Samoznaev, L. N., Chashei, I. V., Bird, M., et al. (2015). Faraday-rotation fluctuations from radio-sounding measurements of the circumsolar plasma using polarized signals from the HELIOS-1 and HELIOS-2 space probes. Astron. Rep. 59, 313–326. doi:10.1134/S1063772915040022

CrossRef Full Text | Google Scholar

Efimov, A. I., Lukanina, L. A., Rudash, V. K., Samoznaev, L. N., Chashei, I. V., Bird, M. K., et al. (2013). Frequency fluctuations of coherent signals from spacecraft observed during dual-frequency radio sounding of the circumsolar plasma in 2004-2008. Cosm. Res. 51, 13–22. doi:10.1134/S0010952513010036

CrossRef Full Text | Google Scholar

Efimov, A. I., Lukanina, L. A., Samoznaev, L. N., Chashei, I. V., Bird, M. K., and Pätzold, M. (2017). Frequency fluctuations in the solar corona investigated with radio sounding experiments on the spacecraft ROSETTA and MARS EXPRESS in 2010/2011. Adv. Space Res. 59, 1652–1662. doi:10.1016/j.asr.2017.01.001

CrossRef Full Text | Google Scholar

Efimov, A. I., Samoznaev, L. N., Bird, M. K., Chashei, I. V., and Plettemeier, D. (2008). Solar wind turbulence during the solar cycle deduced from Galileo coronal radio-sounding experiments. Adv. Space Res. 42, 117–123. doi:10.1016/j.asr.2008.03.025

CrossRef Full Text | Google Scholar

Gopalswamy, N., Kucera, T., Leake, J., MacDowall, R., Wilson, L., Kanekal, S., et al. (2021). The multiview observatory for solar terrestrial science (MOST). AGU Fall Meeting, New Orleans, LA, December 13–17, 2021, American Geophysical Union, 2021. SH12A–07.

Google Scholar

Hollweg, J. V., Bird, M. K., Volland, H., Edenhofer, P., Stelzried, C. T., and Seidel, B. L. (1982). Possible evidence for coronal Alfven waves. J. Geophys. Res. 87, 1–8. doi:10.1029/JA087iA01p00001

CrossRef Full Text | Google Scholar

Hollweg, J. V., Cranmer, S. R., and Chandran, B. D. G. (2010). Coronal Faraday rotation fluctuations and a wave/turbulence-driven model of the solar wind. Astrophys. J. 722, 1495–1503. doi:10.1088/0004-637X/722/2/1495

CrossRef Full Text | Google Scholar

Imamura, T., Tokumaru, M., Isobe, H., Shiota, D., Ando, H., Miyamoto, M., et al. (2014). Outflow structure of the quiet sun corona probed by spacecraft radio scintillations in strong scattering. Astrophys. J. 788, 117. doi:10.1088/0004-637X/788/2/117

CrossRef Full Text | Google Scholar

Jensen, E. A., Bisi, M. M., Breen, A. R., Heiles, C., Minter, T., and Vilas, F. (2013a). Measurements of Faraday rotation through the solar corona during the 2009 solar minimum with the MESSENGER spacecraft. Sol. Phys. 285, 83–95. doi:10.1007/s11207-012-0213-4

CrossRef Full Text | Google Scholar

Jensen, E. A., Nolan, M., Bisi, M. M., Chashei, I., and Vilas, F. (2013b). MESSENGER observations of magnetohydrodynamic waves in the solar corona from Faraday rotation. Sol. Phys. 285, 71–82. doi:10.1007/s11207-012-0162-y

CrossRef Full Text | Google Scholar

Jensen, P. E., Elizabeth, C. S. P., Manchester, W., Fung, S., Gopalswamy, N., Jian, L., et al. (2021). Novel magnetic field and electron density measurements of CMEs (within AU) with the proposed multiview observatory for solar terrestrial science (MOST) mission. AGU Fall Meeting, New Orleans, LA, December 13–17, 2021, American Geophysical Union, 2021. SH33A–08.

Google Scholar

Kolosov, M. A., Iakovlev, O. I., Efimov, A. I., Rogalskii, V. I., Razmanov, V. M., and Shtrykov, V. K. (1982). Decimeter radio wave propagation in the turbulent plasma near the sun, using Venera 10 spacecraft. Radio Sci. 17, 664–674. doi:10.1029/RS017i003p00664

CrossRef Full Text | Google Scholar

Kooi, J. E., Wexler, D. B., Jensen, E. A., Kenny, M. N., Nieves-Chinchilla, T., Wilson, I., et al. (2022). Modern Faraday rotation studies to probe the solar wind. Front. Astron. Space Sci. 9, 841866. doi:10.3389/fspas.2022.841866

CrossRef Full Text | Google Scholar

Koutchmy (2004). Multi-Wavelength Investigations of Solar Activity, IAU Symposium, eds. V. S. Alexander, E. S. Elena, and G. K. Alexander, Cambridge, UK: Cambridge University Press 223, 509–516. doi:10.1017/S1743921304006702

CrossRef Full Text | Google Scholar

Krupar, V., Maksimovic, M., Kontar, E. P., Zaslavsky, A., Santolik, O., Soucek, J., et al. (2018). Interplanetary type III bursts and electron density fluctuations in the solar wind. Astrophys. J. 857, 82. doi:10.3847/1538-4357/aab60f

CrossRef Full Text | Google Scholar

Krupar, V., Szabo, A., Maksimovic, M., Kruparova, O., Kontar, E. P., Balmaceda, L. A., et al. (2020). Density fluctuations in the solar wind based on type III radio bursts observed by parker solar probe. Astrophys. J. Suppl. Ser. 246, 57. doi:10.3847/1538-4365/ab65bd

CrossRef Full Text | Google Scholar

Mancuso, S., and Garzelli, M. V. (2013). Coronal magnetic field strength from type II radio emission: Complementarity with Faraday rotation measurements. Astron. Astrophys. 560, L1. doi:10.1051/0004-6361/201322645

CrossRef Full Text | Google Scholar

Meyer, K. A., Mackay, D. H., Talpeanu, D.-C., Upton, L. A., and West, M. J. (2020). Investigation of the middle corona with SWAP and a data-driven non-potential coronal magnetic field model. Sol. Phys. 295, 101. doi:10.1007/s11207-020-01668-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohan, A., Mondal, S., Oberoi, D., and Lonsdale, C. J. (2019). Evidence for super-alfvénic oscillations in solar type III radio burst sources. Astrophys. J. 875, 98. doi:10.3847/1538-4357/ab0ae5

CrossRef Full Text | Google Scholar

Mugundhan, V., Hariharan, K., and Ramesh, R. (2017). Solar type IIIb radio bursts as tracers for electron density fluctuations in the corona. Sol. Phys. 292, 155. doi:10.1007/s11207-017-1181-5

CrossRef Full Text | Google Scholar

Ofman, L. (2004). The origin of the slow solar wind in coronal streamers. Adv. Space Res. 33, 681–688. doi:10.1016/S0273-1177(03)00235-7

CrossRef Full Text | Google Scholar

Patzold, M., Bird, M. K., Volland, H., Levy, G. S., Seidel, B. L., and Stelzried, C. T. (1987). The mean coronal magnetic field determined from HELIOS Faraday rotation measurements. Sol. Phys. 109, 91–105. doi:10.1007/BF00167401

CrossRef Full Text | Google Scholar

Ruffolo, D., Ngampoopun, N., Bhora, Y. R., Thepthong, P., Pongkitiwanichakul, P., Matthaeus, W. H., et al. (2021). Domains of magnetic pressure balance in parker solar probe observations of the solar wind. Astrophys. J. 923, 158. doi:10.3847/1538-4357/ac2ee3

CrossRef Full Text | Google Scholar

Rušin, V., Druckmüller, M., Aniol, P., Minarovjech, M., Saniga, M., Mikić, Z., et al. (2010). Comparing eclipse observations of the 2008 August 1 solar corona with an MHD model prediction. Astron. Astrophys. 513, A45. doi:10.1051/0004-6361/200912778

CrossRef Full Text | Google Scholar

Seaton, D. B., Hughes, J. M., Tadikonda, S. K., Caspi, A., DeForest, C. E., Krimchansky, A., et al. (2021). The Sun’s dynamic extended corona observed in extreme ultraviolet. Nat. Astron. 5, 1029–1035. doi:10.1038/s41550-021-01427-8

CrossRef Full Text | Google Scholar

Sheeley, N. R., Wang, Y.-M., Hawley, S. H., Brueckner, G. E., Dere, K. P., Howard, R. A., et al. (1997). Measurements of flow speeds in the corona between 2 and 30 R. Astrophys. J. 484, 472–478. doi:10.1086/304338

CrossRef Full Text | Google Scholar

Strachan, L., Suleiman, R., Panasyuk, A. V., Biesecker, D. A., and Kohl, J. L. (2002). Empirical densities, kinetic temperatures, and outflow velocities in the equatorial streamer belt at solar minimum. Astrophys. J. 571, 1008–1014. doi:10.1086/339984

CrossRef Full Text | Google Scholar

Vierinen, J., Norberg, J., Lehtinen, M. S., Amm, O., Roininen, L., Väänänen, A., et al. (2014). Beacon satellite receiver for ionospheric tomography. Radio Sci. 49, 1141–1152. doi:10.1002/2014RS005434

CrossRef Full Text | Google Scholar

West, M. J., Seaton, D. B., Alzate, N., Caspi, A., DeForest, C. E., Gilly, C. R., et al. (2022a). “A strategy for a coherent and comprehensive basis for understanding the middle corona,” in Heliophysics 2050: Measurements and Technologies Workshop, February 23–25, 2022, 4060.

Google Scholar

West, M. J., Seaton, D. B., Wexler, D. B., Raymond, J. C., Del Zanna, G., Rivera, Y. J., et al. (2022b). Defining the middle corona. eprint arXiv:2208.04485, arXiv:2208.04485.

Google Scholar

Wexler, D. B., Hollweg, J. V., Efimov, A. I., Lukanina, L. A., Coster, A. J., Vierinen, J., et al. (2019). Spacecraft radio frequency fluctuations in the solar corona: A MESSENGER-HELIOS composite study. Astrophys. J. 871, 202. doi:10.3847/1538-4357/aaf6a8

CrossRef Full Text | Google Scholar

Wexler, D. B., Jensen, E. A., and Heiles, C. (2021). Middle corona magnetic field strength determined by spacecraft radio Faraday rotation. Res. Notes AAS 5, 165. doi:10.3847/2515-5172/ac1521

CrossRef Full Text | Google Scholar

Wexler, D. B., Jensen, E. A., Hollweg, J. V., Heiles, C., Efimov, A. I., Vierinen, J., et al. (2017). Faraday rotation fluctuations of MESSENGER radio signals through the equatorial lower corona near solar minimum. Space 15, 310–324. doi:10.1002/2016SW001558

CrossRef Full Text | Google Scholar

Wexler, D., Imamura, T., Efimov, A., Song, P., Lukanina, L., Ando, H., et al. (2020). Coronal electron density fluctuations inferred from Akatsuki spacecraft radio observations. Sol. Phys. 295, 111. doi:10.1007/s11207-020-01677-1

CrossRef Full Text | Google Scholar

Wexler, D., Jensen, E., Gopalswamy, N., Wilson, L., Fung, S., Nieves-Chinchilla, T., et al. (2021). FETCH concept: Investigating quiescent and transient magnetic structures in the inner heliosphere using Faraday rotation of spacecraft radio signals. AGU Fall Meeting, New Orleans, LA, December 13–17, 2021, American Geophysical Union, 2021. SH31A–05.

Google Scholar

Wexler, D. (2020). On the fluctuations of electron density and magnetic field in the solar mid-corona: Space radio observations. Toowoomba, AU: University of Southern Queensland. Ph.D. thesis, Available at: http://eprints.usq.edu.au/id/eprint/43957.

Google Scholar

Woo, R. (1978). Radial dependence of solar wind properties deduced from Helios 1/2 and Pioneer 10/11 radio scattering observations. Astrophys. J. 219, 727–739. doi:10.1086/155831

CrossRef Full Text | Google Scholar

Yakovlev, O. I., and Pisanko, Y. V. (2018). Radio sounding of the solar wind acceleration region with spacecraft signals. Adv. Space Res. 61, 552–566. doi:10.1016/j.asr.2017.10.052

CrossRef Full Text | Google Scholar