- 1Max Planck Institute for Solar System Research, Göttingen, Germany
- 2INAF Osservatorio Astronomico di Roma, Rome, Italy
Full-disc observations of the Sun in the Ca ii K line provide one of the longest collections of solar data. First such observations were made in 1892 and since then various sites around the world have carried out regular observations, with Kodaikanal, Meudon, Mt Wilson, and Coimbra being some of the most prominent ones. By now, Ca ii K observations from over 40 different sites allow an almost complete daily coverage of the last century. Ca ii K images provide direct information on plage and network regions on the Sun and, through their connection to solar surface magnetic field, offer an excellent opportunity to study solar magnetism over more than a century. This makes them also extremely important, among others, for solar irradiance reconstructions and studies of the solar influence on Earth’s climate. However, these data also suffer from numerous issues, which for a long time have hampered their analysis. Without properly addressing these issues, Ca ii K data cannot be used to their full potential. Here, we first provide an overview of the currently known Ca ii K data archives and sources of the inhomogeneities in the data, before discussing existing processing techniques, followed by a recap of the main results derived with such data so far.
1 Introduction
The Sun is the closest star to Earth and its all-dominant energy source (Kren et al., 2017). The last couple of decades have seen immense advancement in solar monitoring. Observations made with satellites, such as the Solar and Heliospheric Observatory (SoHO; Domingo et al., 1995), Hinode (Kosugi et al., 2007), or Solar Dynamics Observatory (SDO; Pesnell et al., 2012), allowed us to study the Sun close-up and provided time series of many solar parameters with high quality and high cadence, such as with the Geostationary Operational Environmental Satellites (GOES; Donnelly et al., 1977), Variability of solar IRradiance and Gravity Oscillations (VIRGO; Fröhlich et al., 1995), PRoject for On-Board Autonomy (PROBA; Teston and Creasey, 1997; Hochedez et al., 2006), Solar Radiation and Climate Experiment (SORCE; Rottman, 2005), or Solar TErrestrial RElations Observatory (STEREO; Kaiser et al., 2005) among others. Observations from space have the advantage of being unaffected by Earth’s atmosphere, allowing measurement of quantities sensible to the atmospheric absorption, one example being the Total Solar Irradiance (TSI, the total, spectrally-integrated solar radiative energy flux measured at the top of Earth’s atmosphere). Current and future missions, such as the Solar Orbiter (Müller et al., 2020), Parker Solar Probe (Fox et al., 2016), Aditya-L1 (Seetha and Megala, 2017; Tripathi et al., 2017), Solar-C (Watanabe, 2014; Shimizu et al., 2020), and balloon-borne Sunrise (Solanki et al., 2010; Solanki et al., 2017; Feller et al., 2020) will keep pushing our understanding of the physics of the Sun (Kusano et al., 2021).
As marvellous and beneficial as they are, satellite observations of the Sun exist for only a few decades, which is a rather short time interval to assess potential long term changes in various characteristics of the Sun. Among others, this is particularly critical for assessing the long-term variability in TSI and its effect on Earth’s climate (Gray et al., 2010; Solanki et al., 2013; Krivova, 2018; Intergovernmental Panel on Climate Change, 2021).
Luckily, a wealth of ground-based solar observations exist that can be used to study solar behaviour over longer periods in the past. The invention of the telescope in 1600s marked the start of systematic observations of the Sun (Vaquero and Vázquez, 2009), which however became regular only in the 1800s. These early solar observations were limited to the white-light (or visible) part of the solar spectrum, which samples the photosphere bringing out mostly dark regions, called sunspots. They revealed the variable nature of solar activity, represented by increases and subsequent decreases in the number of sunspots, the famous 11-year sunspot cycle (Wolf, 1850).
The use of a prism to disperse the solar spectrum, e.g. by Herschel (Herschel, 1800) or Secchi (Chinnici and Consolmagno, 2021; Ermolli and Ferrucci, 2021), in the 1800s allowed sampling different heights in the solar atmosphere. However, systematic photographic observations of different heights of the solar atmosphere only started after the invention of the spectroheliograph by (Hale, 1890; Hale, 1891; Hale, 1893). The first line that was systematically observed with a spectroheliograph was the singly ionized Calcium line (Ca ii K), at 3933.67 Å. The earliest recorded observation goes back to 1892 and since then a plethora of such observations from many places around the globe has been collected (Chatzistergos et al., 2020c).
Observations in the Ca ii K line sample the lower chromosphere and provide direct information on plage and network regions, which are the chromospheric counterpart of faculae and network in the photosphere. These regions are manifestations of the solar surface magnetic field and one of the keys to studies of its evolution. They are also indispensable to reconstructions of past irradiance variations (see, e.g., Solanki et al., 2013). There are various other chromospheric data (Ermolli et al., 2015) that can provide information on plage regions, such as the series of the 10.7 cm radio flux (available since 1947; Tapping and Morton, 2013), Lyman α emission (available since 1969; Woods et al., 2000), Mg II index (available since 1978; Heath and Schlesinger, 1986; Snow et al., 2014), He i (10830Å) equivalent width (since 1977); Ca ii (8542Å) central depth (since 1978), Hα central depth (since 1984), CN (3883 Å) bandhead index (since 1979; Livingston et al., 2007), and Ca ii K 0.5 or 1 Å disc-integrated emission index (since 1974; White et al., 1998). However, all these measurements cover significantly shorter periods of time and are disc-integrated quantities, carrying less information than the full-disc Ca ii K observations. This renders Ca ii K observations a unique dataset for studying past solar magnetism and activity, solar irradiance reconstructions and studies of the solar influence on Earth’s climate.
Despite the invaluable information encrypted in Ca ii K data, they are known for suffering from numerous issues which are challenging to be accounted for and eventually lead to their disuse. Over the last couple of decades there has been a renewed interest in these data. In view of this, considerable efforts have been put into the digitisation of historical archives, which allows a more systematic exploitation of these data.
Here we provide an overview of recent efforts aimed at a systematic exploitation of the potential of full-disc Ca ii K data. We first review the currently known Ca ii K archives and describe instruments used for such observations (Section 2). We then discuss the main techniques that have been developed for processing Ca ii K images (Section 3). This is followed by an overview of the main results derived with Ca ii K data so far, specifically focusing on studies regarding Carrington maps (Section 4), Ca ii K plage areas (Section 5), network regions (Section 6), the relationship between magnetic field strength and Ca ii K brightness (Section 7), as well as reconstructions of irradiance variations (Section 8). Finally, we summarise the current status of studies employing Ca ii K data in Section 9.
2 Ca ii K data
Ca ii K line was the first line to be systematically monitored, with full-disc observations starting in 1892 and continuing up to the present day. Since then, observations have been performed in Ca ii K by over 40 observatories, covering different periods in time (see Tables 1, 2), with (to the best of our knowledge) 16 sites performing observations in the Ca ii K line at present. Figure 1 maps the approximate locations of the ground-based Ca ii K observatories known to us, complemented by the SOlar Diameter Imager and Surface Mapper (SODISM) instrument onboard the PICARD (Meftah et al., 2012) satellite. All observatories are situated in the Northern hemisphere, with the exception of some observations performed at the South Pole (not shown on the map). The majority of sites are in Europe, with 11 currently active observatories (see underlined observatories in Figure 1). Three other active stations are located in Asia (Kodaikanal, Mitaka, Baikal), one in north America (San Fernando), and one on Canary islands (Teide). All together, Ca ii K archives provide an excellent temporal coverage of the entire 20th century, with at least one Ca ii K observation per day for 88% of all days from 1892 onwards and 98% from 1907 onwards among the data analysed by Chatzistergos et al. (2020c).
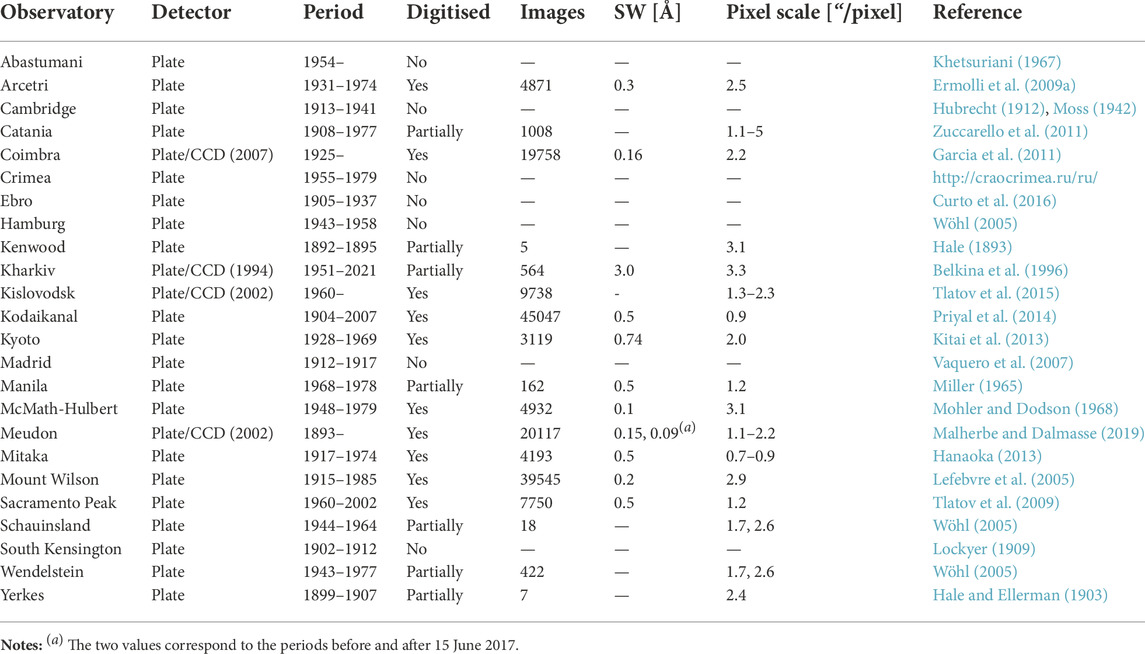
TABLE 1. List of spectroheliograph Ca ii K datasets. Columns are: name of the observatory, type of detector (if both plate and CCD were used then the date in parenthesis refers to the year the transition occurred), estimated period of observations, whether the data have been digitised, total number of digital images (including multiple images on a single day when available), spectral width of the spectrograph, average pixel scale of the images, and the bibliography entry.
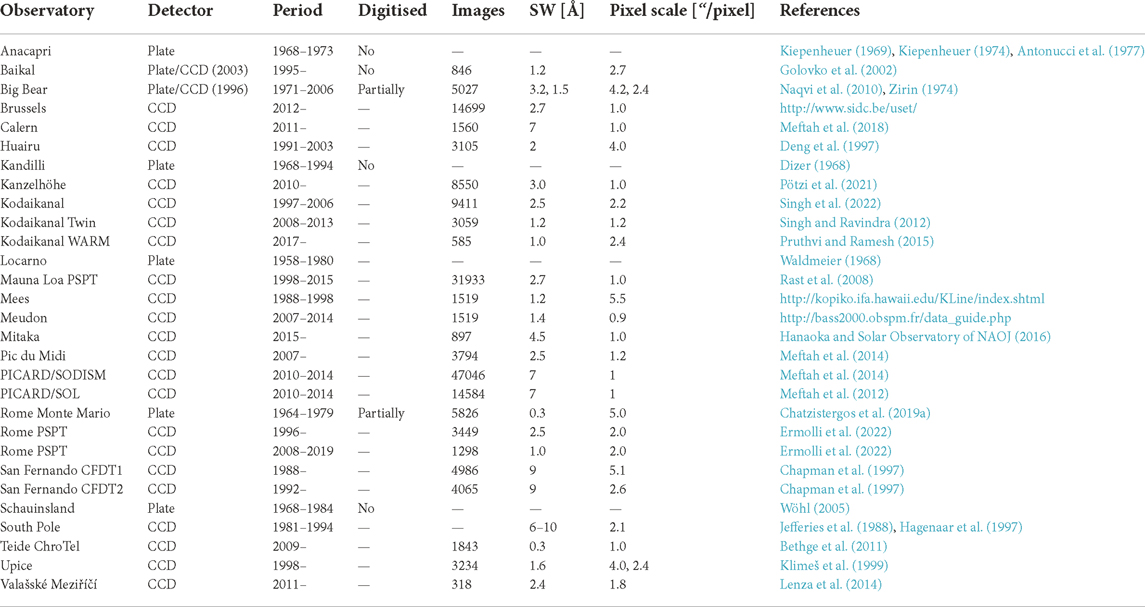
TABLE 2. List of filtergram Ca ii K datasets. Columns are: name of the observatory, type of detector (if both plate and CCD were used then the date in parenthesis refers to the year the transition occurred), estimated period of observations, whether the data have been digitised, total number of digital images (including multiple images on a single day when available, except for Baikal, Calern, Kanzelhöhe, and Teide ChroTel. The values are approximate for the currently running observatories), spectral width of the interference filter, average pixel scale of the images, and the bibliography entry.
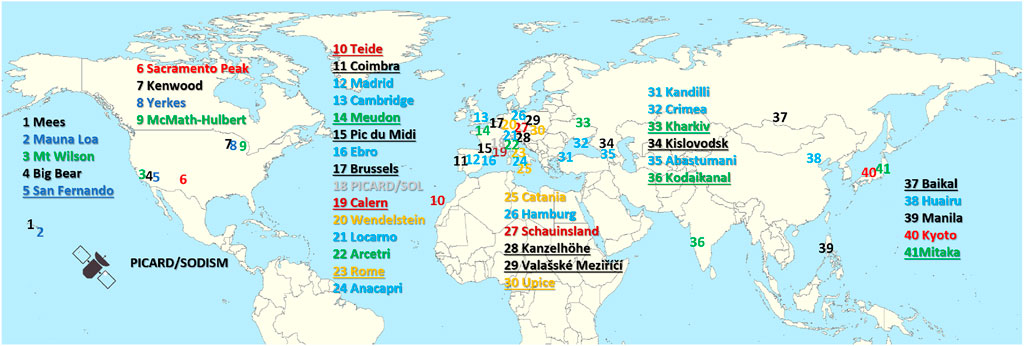
FIGURE 1. Map showing approximate locations of the Ca ii K observatories. Observatories marked in ciel either do not yet have data in digital form or there have been no published results from the digital images. All other archives are shown in various random colours. The locations are marked by numbers, while the names of the sites are listed with the corresponding numbers and colours to help associating the name with the observatory. The underlined names refer to sites performing Ca ii K observations at present.
Tables 1, 2 list the main characteristics of all Ca ii K archives known to us. There are unfortunately only a few long-running archives, with the series from Meudon and Kodaikanal being the only ones extending for more than a century, although, at the time of writing this, Coimbra falls marginally short of a century. Most archives perform only a few observations per day (typically between one and five), but some more recent ones (such as Rome Monte Mario, Kanzelhöhe, and Brussels) also have high-cadence observations. For most applications of Ca ii K data one observation per day is typically sufficient, however having multiple observations per day from various sources is extremely important. On the one hand, there are applications for which the exact time of observation might be needed, for instance for comparing Ca ii K images to magnetograms to select data pairs as close in time as possible (Chatzistergos et al., 2019d), or to recover TSI variations within a day (Chatzistergos et al., 2021a). On the other hand, complementary observations from different sites over the same days allow assessment of the quality of the available datasets and identification of potential inconsistencies within the archives. Furthermore, multiple overlapping days from many archives allow a better cross-calibration of parameters extracted from these data, such as plage and network areas, discussed in Section 5 and Section 6. Examples of historical Ca ii K observations of good quality are given in the first row of Figure 2. Tables 1, 2 reveal how different the observational characteristics of the various archives are. Some sites used spectroheliographs, while others filters. More recent set-ups used a charge-coupled device (CCD; Janesick, 2001) camera to directly produce digital files, while the historical data were stored on photographic plates some of which are now available also in digital form. To understand the underlying differences between the archives, we first introduce the instruments used to obtain Ca ii K observations.

FIGURE 2. Exemplary raw full-disc images of the Sun in the Ca ii K line. The first row shows images of good quality from four historical photographic archives, indicated at the top of each image together with the date of observation. The next three rows aim at highlighting some characteristics of such data. In particular, the second row shows image distortions due to spectroheliograph problems, while the third row showcases visual differences due to variations in central wavelength or bandpass used for observations. The last row shows Ca ii K drawings from Kenwood and Rome observatories as compared to a filtergram and spectroheliogram from Rome and Kodaikanal taken on the same day as the Rome drawing.
2.1 Instrumentation used for observations
2.1.1 Spectroheliograph and optical filters
We first discuss instruments used to isolate a selected limited range of wavelengths around the Ca ii K line, which are the spectroheliograph and optical filters. Spectroheliographs are in general big and bulky instruments. A spectroheliograph employs a prism or a diffraction grating to disperse the incident solar light. A slit, with a controllable width, is then placed such as to allow only the radiation within the desired wavelength band to pass. In this way, spectroheliographs allow isolating a spectral window around the Ca ii K line. Ca ii K was the first line observed with a spectroheliograph, with the Hα line following shortly after (Chatterjee et al., 2017a). It is important to note that a spectroheliograph does not allow observing the entire solar disc instantaneously, rather only a narrow strip imposed by another narrow slit at the entrance of the telescope. Various mechanical components are used to smoothly move the entrance slit and/or the photographic plate to scan and image the entire solar disc. As a result, a full scan of the solar disc requires a few minutes. Figure 3 shows photographs from some of the most prominent spectroheliographs, including Meudon, Kodaikanal, Kyoto, and Mitaka.

FIGURE 3. Spectroheliographs used at the observatories of Meudon ((A); https://www.observatoiredeparis.psl.eu/the-meudon-spectroheliograph.html?lang=en, Kodaikanal ((B); https://kso.iiap.res.in/new/instruments, Mitaka ((C); https://solarwww.mtk.nao.ac.jp/en/topics/topics_0001.html, and Kyoto ((D); photo taken by T. Chatzistergos).
Unfortunately, neither the motion of the mechanical parts of the spectroheliograph nor the width and position of the slits are consistently precise. The uneven motion of the instrument leads to geometrical distortions of the recorded image, leading to certain strips being sometimes more stretched than others or even overlapping. Thus brightness of the images might vary over different strips. Four such examples are shown in the second row of Figure 2. In certain archives, such as Kyoto (see the first image of the second row in Figure 2), these strips are curved (Chatzistergos et al., 2020b), most likely due to the arrangement of the optical parts of the telescopes. We note that such brightness variations across strips can also be introduced by changes of the atmospheric transmission during scanning of the entire disc. Problems with maintaining the position and width of the spectral slit constant affect the altitude of the solar atmosphere that is sampled. The third row of Figure 2 shows three images from Kodaikanal observatory and one from Mt Wilson, demonstrating the effects of different setups of the spectral slit on the observations. The first two of them, from Kodaikanal, were taken on the same day but clearly sample different heights in the atmosphere (as can be seen by the absence of sunspots in the first image and their clear appearance in the second one). The third (Kodaikanal) and the fourth (Mt Wilson) images show the cases, where either the width or the centering of the slit changed over the course of scanning the solar disc. This produced images that look more photospheric (with large sunspots regions) on the left, while more chromospheric on the right sides of the images. Instrumental changes also affect the bandwidth of observations and thus the consistency of the long-running archives. For instance, the grating system in Mt Wilson series was changed on the 21 of August 1923 (Chatzistergos et al., 2019b), while Meudon changed from a 1-prism to a 3-prism system in 1908 (D’Azambuja, 1930), both leading to a better dispersed solar spectrum and thus narrower bandwidth observations. Chatzistergos et al. (2019b) and Chatzistergos et al. (2019c) also discussed potentially degrading quality of Kodaikanal data with time.
Optical filters allow instantaneous observations of the whole solar disc. These are wavelength-selective filters placed at the optical path of the telescope, which means they are employed with a much simpler instrumental configuration than spectroheliographs. Due to that, filtergrams do not exhibit severe image distortions like the ones mentioned for the spectroheliograms, e.g. brightness variations across linear segments. However, the way the filter is placed (for example if there is a potential tilt; Löfdahl et al., 2011) can still affect the bandpass, while there can also be deterioration with time, thus changing the filter transmission profile.
One very important aspect to keep in mind is that various observatories use non-identical observational settings, that is either filters with different transmission profiles or spectroheliographs with different slit widths, and thus sample different heights in the solar atmosphere (See Figure 3 in Ermolli et al., 2010). Spectroheliographs were used since 1892, and thus most long-running archives were produced with spectroheliographs. Filters started being used for Ca ii K observations in the late 1950s (e.g. Ohman, 1956), and are employed at most of the currently running observatories. Currently, only four sites use a spectroheliograph, namely those at Coimbra, Kharkiv, Kislovodsk, and Meudon. In general, filtergrams, have broader bandwidths than spectroheliographs. Chatzistergos et al. (2020c) showed that the average nominal bandwidth of 43 available datasets remained about 0.3 Å between 1904 and 1987 when mainly spectroheliographs were used, while it increased to about 2.5 Å on average for the later periods when filtergrams became more common. Figure 4 shows the average quiet Sun Ca ii K line profile from the high-resolution disk-integrated atlas from the Hamburg Observatory1 (Neckel, 1999; Doerr et al., 2016) highlighting various features of this line: the core denoted as K3, the emission peaks K2v and K2r, as well as the secondary minima K1v and K1r, where “v” and “r” stand for the violet and red parts of the wing, respectively. Coloured vertical bars mark wavelength bands of some prominent Ca ii K series, for comparison. In particular, we show the passbands of spectroheliograph observations at Meudon (green), which since 2017 employs the narrowest known to us nominal bandwidth of 0.09 Å (prior to 2017, it was 0.15 Å) and thus includes only part of the K3 minimum. However, Meudon also took observations with offsets to the central wavelength (shown in light blue, purple, blue, orange, and brown). An average over modern CCD-based data is represented by the Rome/PSPT (precision solar photometric telescope; shown in dark grey) which has a considerably broader bandwidth than Meudon, including all K1, K2, and K3 features of the Ca ii K line, but also extending more to the wing of the line, thus having more photospheric contribution. We also show the bandwidth of the San Fernando archive (light grey), which is, to our knowledge, the broadest one and extends even further into the wing than Rome/PSPT. We note that San Fernando observatory uses two telescopes called Cartesian full disk telescope, CFDT, 1 and 2. To highlight the effects of the passband on the observations, in the lower half of Figure 4 we show examples of observations taken on the same day at different sites having different characteristics. We emphasise that the previous discussion refers to the nominal bandwidth of the various observatories, while the actual ones might differ.
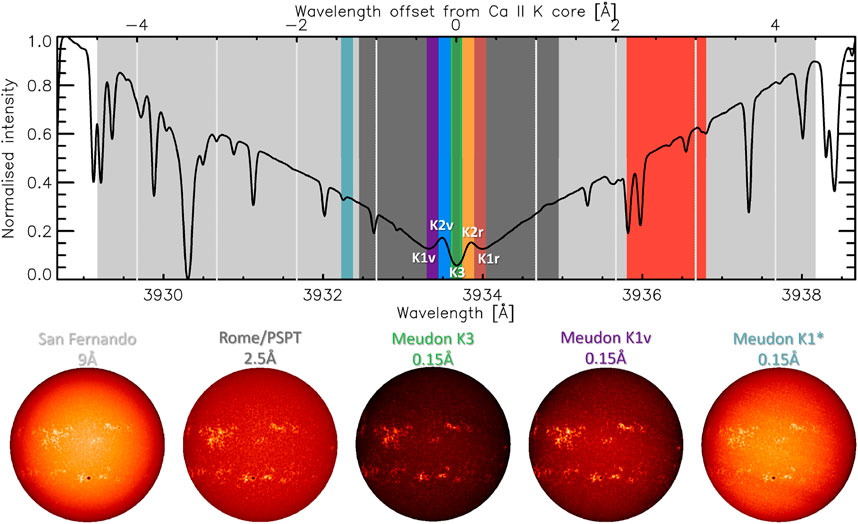
FIGURE 4. The normalised high-resolution disc-integrated solar spectrum over a 10 Å interval centred at the core of the Ca ii K line from the atlas of the Hamburg Observatory. Also shown are the nominal pass-bands of selected Ca ii K archives, including the two extreme cases from San Fernando (light grey) and Meudon K3 (light green up to 2017, darker green since 2017), an average case for CCD-based archives from the Rome/PSPT (dark grey), along with six off-band archives: MLSO/PSPT (red), Meudon K2r (orange), K1r (brown), K2v (blue), K1v (purple), and Meudon K1* (light blue, this is referred to as K1 in the Meudon database even though it is not at the K1 minimum, but centred further away at the wing of the line at 3932.3Å). The vertical light grey lines mark wavelength intervals of 1 Å from the core of the Ca ii K line. The bottom part of the figure presents five exemplary observations taken on the same day (2013/09/23) at San Fernando, Rome/PSPT, Meudon K3, Meudon K1v, and Meudon K1*.
2.1.2 Image capturing devices
The more recent observations use a CCD (Janesick, 2001) or a complementary metal-oxide semiconductor (CMOS; Fossum, 1993) sensor to store the images directly in digital formats (to simplify the discussion, in the following we will refer to CCD and CMOS collectively as CCD). These are essentially linear detectors, meaning that the recorded image value is directly proportional to the incident radiation. However, there can still be saturated or dark regions below the noise level. CCD-based data are subject to the standard dark, bias, and flat-field calibration of CCD detectors (Meurs, 1987). This is an important step to reduce intensity biases and artefacts due to issues with the detector or dust in the telescope components. To our knowledge, the earliest employment of such devices for Ca ii K observations might have been at the South Pole in 1981 and then at the Mees and San Fernando observatories in 1988. All sites that started observations after 1995 use a CCD sensor.
Earlier data were stored on photographic plates, which comprise a photosensitive emulsion coated on a glass plate or celluloid film (we will collectively refer to them as plates in the following). The photographic process involves the exposure of the emulsion to create a latent image, which is revealed after the application of developing agents (Mees, 1942; James and Higgins, 1968; Dainty and Shaw, 1974). Thus, exposed regions turn darker depending on the incident radiation. In contrast to CCD sensors, photographic plates are not linear detectors. This means the recorded darkening on the plates is not directly proportional to the incident radiation. The response of the plates, typically referred to as the characteristic curve or Hurter–Driffield curve (Hurter and Driffield, 1890), is defined as d = f (log E), where E is the exposure (defined as intensity multiplied by time) and d is the density (defined as d = log10 (1/T), where T is the transparency of the emulsion, a term describing how darkened the emulsion got). The characteristic curve has in general a sigmoid shape (Figure 5) and is linear only in its central part (part c in Figure 5A), which is the region of proper exposure. Regions with low intensity of incident radiation usually end up on the underexposure level or even below the fog level (thus escaping being registered), while under excessive exposure, darkening turns weaker than what is expected from the linear relation. Knowledge of the characteristic curve is crucial for photometric calibration of photographic observations. Unfortunately, this curve depends on multiple additional factors (emulsion composition, developing agents, temperature and humidity levels at the time of the observation, storage conditions of the plates etc; Chatzistergos, 2017), with the consequence that each observation has its own unique characteristic curve, which needs to be determined to allow the photometric calibration.
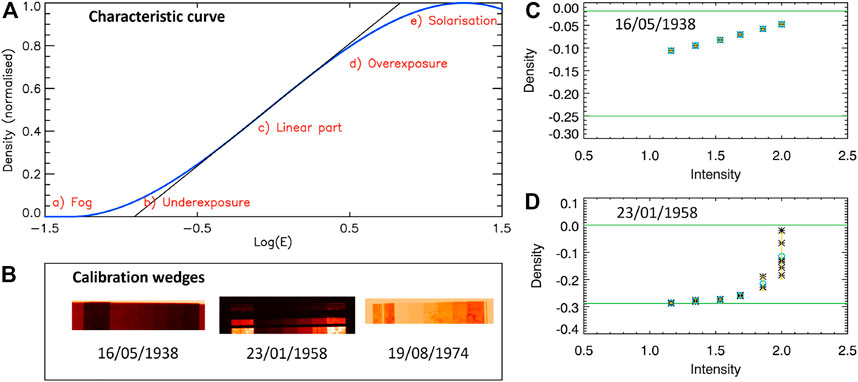
FIGURE 5. (A) Schematic of a characteristic curve of photographic observations (blue) and a linear fit (black) to the central part of the curve. (B) Examples of calibration wedges from the Arcetri observatory. (C–D) Characteristic curves determined from the first two Arcetri calibration wedges shown in (B). Black asterisks show individual measurements from the wedges, blue circles the mean density value for each intensity value, while yellow marks the symmetric 1σ interval. The green horizontal lines denote the minimum and maximum values found within the solar disc for each day.
The bulk of the historical Ca ii K data are stored on photographic plates. However, there are also some plage drawings in Ca ii K, such as the ones from the Rome observatory (see Figure 2 fourth row). Rome observatory has a collection of 1564 drawings covering 14 July 1965 to 14 July 1981, and thus ending 2 years after the last photographic observation from the same site. Such drawings are of much more limited use than the photographic data, since they do not include information on the brightness of plage regions and carry additional uncertainty due to the manual aspect of the recorded observation (including some subjectivity in the definition and selection of the plage boundaries and the accuracy of drawing). It is unclear how many observatories maintained drawings in the Ca ii K line. We are not aware of any other Ca ii K plage area drawings other than the ones from Rome and Kenwood observatories. However, considering that many photographic data have been displaced due to shift of scientific interests at various observatories, it would not be surprising if similar fate found datasets of drawings as well. Furthermore, digitising such collections is time consuming, while priorities would obviously be given to photographic Ca ii K data due to their greater potential yield. Notwithstanding these limitations, any such drawing collection would also be very important for recovering plage areas in the past, potentially even before the photographic data or to fill temporal gaps in the plage area series from photographic data.
2.2 Digitisation
An important step to allow drawings and observations stored on photographic plates to be used for quantitative analyses is to convert them into digital format. Most early studies with Ca ii K data in digital form were restricted to the authors digitising themselves a small subset of the data they needed for their specific purposes (e.g. Antonucci et al., 1977; Münzer et al., 1989; Mein and Ribes, 1990; Kariyappa and Sivaraman, 1994; Nesme-Ribes et al., 1996; Caccin et al., 1998b). It is unclear how many of those data are still available. Unfortunately, most of these data do not seem to have survived or, at least, are not publicly available.
A more systematic work on Ca ii K data started only after the first digitisations of large samples or even entire data collections. This process started in the mid 1990s with the data from Mt Wilson. In particular, Foukal (1996) digitised the Mt Wilson data covering 1915–1984 with an 8-bit CCD camera, which were then re-digitised by Lefebvre et al. (2005) with a 12-bit camera a few years later. The next long series of Ca ii K data to be digitised were the ones from Kodaikanal and Arcetri. Makarov et al. (2004) digitised Kodaikanal data covering 1907–1999 with an 8-bit CCD camera. Also in this case, it was recognised that this digitisation was not perfect and also missing a big part of the data, which led to a new digitisation of the Kodaikanal data (now covering 1904–2007) by Priyal et al. (2014) with a 16-bit CCD camera. Chatzistergos et al. (2019c) compared the 8 and 16 bit digitisations of Kodaikanal data. They showed that the quality of data in terms of spatial resolution was better in the 16 bit version, which allowed a more accurate extraction of plage areas from these images. The series from Arcetri was digitised in 2004 with a 1200 dpi and 16 bit scanner (Centrone et al., 2005; Giorgi et al., 2005; Marchei et al., 2006; Ermolli et al., 2009a).
The following years saw increased interest in digitisation of Ca ii K archives, with Wöhl (2005) having digitised a small sample of the Wendelstein and Schauinsland Ca ii K data, Tlatov et al. (2009) the Sacramento Peak data with an 8-bit CCD camera, Garcia et al. (2011) the Coimbra data, National oceanic and atmopheric administration (NOAA) National Centers for Environmental Information (NCEI) the McMath-Hulbert data (over 2012–2014), Kitai et al. (2013) the Kwasan observatory (in Kyoto) data, and Tlatov et al. (2015) the Kislovodsk data. Meudon has the longest collection among all Ca ii K archives, however initially only the data since 1980 were digitised. More recently, the digitisation of the data prior to 1980 was completed with a commercial scanner (EPSON perfection 4990 photo), while the data since 1980 are currently being redigitised with the same scanner (Malherbe et al., 2022). The Mitaka data have been digitised three times (see also Chatzistergos et al., 2019b). The first time the entire data collection was digitised with 8-bit depth (Hanaoka, 2013). The next two digitisations were done with 16-bit depth, but included only subsets of the data. In particular, the second digitisation included only the data before 02 March 1960, while the third one includes the data after 02 March 1960, but with a different set-up, and the first 10 observations of each year for the periods before 1961. Chatzistergos et al. (2019a) presented the digitised Rome Ca ii K observations which were stored in 35 mm celluloid films. These were patrol high-cadence observations with approximately 100 images recorded per day, and only a small sub-sample of the data could be digitised so far, typically two observations for each day when data exist.
The observations from Catania, Kenwood, Kharkiv, Manila, and Yerkes are largely not digitised yet. Only four Kenwood images were found as lantern slides and digitised by the Division of History of Science and Technology at Yale University’s Peabody Museum of Natural History. Similarly, a small subset of Yerkes observations were found and digitised by the University of Chicago Photographic Archive, Special Collections Research Center, University of Chicago Library. Only a small sample of Kharkiv Ca ii K data (Chatzistergos et al., 2020c), and 92 observations (between 1970 and 1971) from Catania (Chatzistergos et al., 2019a) have been digitised so far.
Chatzistergos et al. (2020c) digitised additional samples of Catania, Manila, Wendelstein, Rome, and Kodaikanal observations with the reflecta RPS 10M commercial film scanner. These observations were part of the Photographic journal of the Sun, which was published between 1967 and 1978 by the observatory of Rome. The Photographic journal of the Sun included one Ca ii K observation for each day in the form of 35 mm celluloid films. Rome observatory was the main provider of the data, but days without observations from Rome were filled with data from Catania, Wendelstein, Kodaikanal, or Manila observatories. These digitised data from Kodaikanal, Rome, Wendelstein, and Catania complement the already available datasets (but only in cases when previously digitised archives did not include the data from the Photographic journal of the Sun). For Manila, this is to our knowledge the only available digital record of Ca ii K data. We emphasise, however, that a recovery and digitisation of the originals would be beneficial.
Unfortunately, there are still numerous archives that have either not or only partially been digitised. For example, the data from Kenwood, Kandilli, and Ebro have not yet been digitised. Furthermore, since finding information about old Ca ii K observations is not straightforward, there is a high chance that the list of archives in Tables 1, 2 is not complete. For instance, Bates and McDowell (1972) had presented a spectroheliograph for operation on a rocket or balloon and showed example observations in the Ca ii K line. However, besides one observation included in their paper, it is unclear how many observations were performed or whether they have survived to this day. Further, it cannot be excluded that many of the historical Ca ii K observations have been lost. This seems to most likely have been the fate of the data from Madrid and Hamburg sites. Also, the fate of Kharkiv data is up in the air at the time of writing this review. This highlights the importance of recovering such historical photographic archives and digitising them for preservation reasons (see also Pevtsov et al.,2019).
2.3 Amateur observations
All datasets listed so far come from professional observatories. However, in more recent years optical filters and telescopes became also accessible to the public, which led to many observations in the Ca ii K line by amateur astronomers. There are even dedicated online archives where amateur astronomers host their solar observations, such as the international online solar database (IOSD; http://solardatabase.free.fr/tableau_cak.php). The IOSD website hosts a large number of solar observations from all over the world with observations going back to 2005.
To our knowledge, such amateur observations have not been used for scientific purposes yet, for various reasons, including the following. Different observers have different setups and therefore should be treated as different series (see, e.g., the discussion on the bandwidth effect in Section 2.1.1). Observations from a single observer might be very sporadic or too few to allow a proper inter-comparison with data from other sources. The intended purpose of such observations is not, in principle, to maintain an archive of scientific data, rather to create a collection of visually appealing images. This means there might be image editing, varying between images, aiming at improving the attractiveness of the image at the potential cost of information. It is unclear if the standard CCD calibration has always been applied, or if it is applied consistently. The recording or observing equipment might be constantly changing thus making it almost impossible to produce a coherent series of data for scientific use, while the location of observation might be varying too. Lastly, the images are typically stored in reduced size compressed file formats such as JPG, which are optimised for internet storage of the files, but induce some loss of information.
All these factors considerably reduce the applicability of such data for scientific studies, especially for studies such as reconstructions of past irradiance variations (see Section 8). However, that is not to say that such data might not be usable at all. In Figure 6 we present raw images from five observers from IOSD along with a co-temporal image from a professional observatory showing that the data can be of comparable quality. Thus, potentially, such data from amateur observers might be used for studies of plage areas to fill temporal gaps in professional archives. Should amateur observers account for the issues mentioned above, they would potentially complement the professional archives and provide valuable information for solar and stellar physics studies. For instance, some of the issues mentioned above can be alleviated if the observer preserved the original raw observation in a lossless file format.

FIGURE 6. Examples of amateur Ca ii K observations (bottom row) along with co-temporal images from professional observatories (top row). From left to right, the images were taken on 24/12/2015, 21/04/2022, 19/10/2014, 28/10/2014, and 13/02/2010 by the amateur observers (top): Michael Borman, Didier Favre, André Gabriël, Lastrofieffe, Stefano Sello, and at professional observatories (bottom): Kanzelhöhe, Meudon, Valašské Meziříčí, Calern, and Pic du Midi.
3 Processing methods
In this section, we briefly describe and discuss the processing methods that are applied on Ca ii K data. The typical order of the processing steps is to apply the CCD calibration (including the data digitised with a CCD camera from photographic archives), then the photometric calibration for the photographic plates, followed by a number of pre-processing steps aiming at the compensation of the limb-darkening. To make the description of the methods easier to understand, here we will, however, deviate from this order. After an introduction into the various pre-processing steps, we will first describe the limb-darkening compensation process and finally the photometric calibration process.
3.1 Pre-processing
As pre-processing we consider all steps that need to be applied to the data before the compensation for the limb darkening. As a first step, all images that are not yet stored as Flexible Image Transport System (FITS; Wells et al., 1981) files, are converted into this format. CCD-based data (again, including those digitised with a CCD camera) require the standard dark, bias, and flat-field calibration.
The most important step is to identify the solar disc on the images. This is usually done in an automatic way with edge detection techniques, such as Sobel filter, a Canny edge detector, or Hough transform (Veronig et al., 2000; Zharkova et al., 2003; Curto et al., 2008; Ermolli et al., 2009a; Chatterjee et al., 2016; Suo, 2020; Zhu et al., 2020; Pötzi et al., 2021), while in some cases this was done manually by clicking with the computer mouse at three to five points at the limb (e.g. Priyal et al., 2014). The assumed shape of the recorded solar disc is usually either circular or elliptical. Assuming the recorded disc as an ellipse is more accurate in view of the fact that due to instrumental issues the recorded disc typically has an elliptical shape. The ellipticity is usually relatively weak for filtergrams but can be quite high for spectroheliograms (ellipticities up to 0.82 have been found among the data analysed by Chatzistergos et al., 2020c). The coordinates of the centre of the disc along with the radius or the semi-major and semi-minor axes are typically added in the header of the FITS files. An exception to that was by Priyal et al. (2014) who determined a circular disc and then resized and cropped the images. If the disc is identified as an ellipse it has to be re-sampled so to be circularised (Tlatov et al., 2009; Chatzistergos et al., 2020b). This is not always straightforward either. Sometimes stretching is inhomogeneous over individual parts of the disc. In such cases circularisation introduces new distortions. Also other processing artefacts sometimes occur (see Chatzistergos et al., 2020b, for more details).
Another pre-processing step is the determination of the orientation of the solar disc. During this step, the images are typically (re-)oriented such as to have the north pole at the top and East at the left side. The optical components of the telescope (e.g. existence and number of mirrors) determine whether the image needs to be inverted. Typically, compensation for ephemeris is sufficient to orient the images. If the plates were placed appropriately and consistently during their digitisation, this would be the case for the historical photographic data as well. However, since this is not always the case, pole markings were placed on the photographic plates of some archives, either during the observation or right before their digitisation, which should allow the determination of the orientation of the solar disc after the digitisation. Such pole markings exist at least for samples of the Meudon, Kodaikanal, Mt Wilson, and Sacramento Peak data. The pole markings were used by Priyal et al. (2014) and Tlatov and Tlatova (2019) to orient the Kodaikanal and Kodaikanal, Mt Wilson, Sacramento Peak, and Meudon images, respectively. Sheeley et al. (2011) and Bertello et al. (2020) used a cross-correlation approach applied on subsequent images in order to determine the orientation of the images.
Finally, the photographic data are typically given in negatives (values of transparency). These need to be converted into densities (see Section 2.1.2).
Additional processing steps, often individual for specific archives, might be implemented at this point. For instance, this can include assessment of the quality of images or simply excluding very problematic observations. As an example, Jarolim et al. (2020) used generative adversarial networks to assess the quality of the images within the Kanzelhöhe data (they used Hα but in principle it is applicable to Ca ii K too) and categorise them. They also used their approach to correct for various observational artefacts, such as large scale intensity variations or patterns introduced by the passage of clouds in the sky.
3.2 Limb-darkening and artefact compensation
Limb darkening refers to the gradual decrease of the intensity of the disc from centre to its edge, when observed at near ultraviolet, visual, and near infrared bands, due to the decrease of the temperature of the solar plasma with height from the solar surface to the bottom of the chromosphere. It is important to compensate for the limb darkening in order to render the intensity values across the solar disc consistent and directly comparable with each other. Furthermore, the recorded images suffer from numerous artefacts (see Section 2.1.1), which need to be accounted for too. In the following we describe processing techniques employed to compensate the limb darkening and correct various image artefacts. Some of them have been applied on different lines, such as Hα or 1600 Å, but in principle they are applicable on Ca ii K data too. All methods described below are typically used up to 0.98R, in a few cases up to 0.99R (Chatzistergos et al., 2018b). The available processing techniques can be put in the following five categories:
• 1D polynomial fit to the average radial intensity profile;
• 2D polynomial fit to the entire image;
• 1D polynomial fits along columns and rows of the image;
• 2D running window median filter;
• combination of the above approaches.
The first group of methods determine a radially symmetric limb darkening background (Brandt and Steinegger, 1998; Johannesson et al., 1998; Walton et al., 1998; Denker et al., 1999; Zharkova et al., 2003; Diercke and Denker, 2019; Pötzi et al., 2021). This is done by fitting polynomial functions (typically fourth order) along the average radial profile of the solar disc in terms of μ (cosine of the heliocentric angle). A caveat is that the recorded solar disc is rarely radially symmetric due to various observational circumstances (see Section 2.1.1), including essentially all photographic data and spectroheliograms. Obviously, this will not be accounted for with such methods. Sometimes, this approach is used as a first approximation followed by another approach, such as Zernike polynomials, removing the residual patterns (e.g. Diercke et al., 2022; Dineva et al., 2022).
Several studies applied a 2D (fourth order) polynomial fitting to the entire image (Caccin et al., 1997; Caccin et al., 1998b; Worden et al., 1998b). This approach returned a background that was not radially symmetric, but it could not properly handle artefacts in the images.
More suitable for processing of spectroheliograms proved to be 1D polynomial fittings along columns and rows of the images (Worden et al., 1998a). Worden et al. (1998a) and Priyal et al. (2014) used fifth and third degree polynomials, respectively. The downside is that different linear cuts through the solar disc cover quite different μ-ranges, while they are all fitted with polynomials of a fixed degree. This reduces the accuracy of the fits, especially closer to the limb. To account for this, Worden et al. (1998a) repeated the fits after rotating the image by 45°.
A more commonly used approach to determine the limb darkening employs a 2D running window median filter (Lefebvre et al., 2005; Bertello et al., 2010, Bertello et al., 2020; Chatterjee et al., 2016; Bose and Nagaraju, 2018; Tähtinen et al., 2022). This means that for each pixel, the median of the values within a square box with a predefined width is assigned. This approach makes no assumption on the shape of the limb darkening, thus it can easily be used for data with very different observational characteristics (for instance, data taken in different spectral lines), while it also accounts for artefacts in the images, which are typically larger than the window width. The width of the window is thus an important factor determining the performance of this approach. Bose and Nagaraju (2018) used ∼ R/2, while Chatterjee et al. (2016) used ∼ R/6. Chatzistergos et al. (2018b) studied how the window width affects the results and found that the optimum value for Ca ii K data is within the range R/8 − R/6, while Tähtinen et al. (2022) found the same optimum values for 1600 Å AIA data. Using a median filter to compensate for the limb darkening has three major caveats: 1) how to treat regions closer than half-width of the median filter to the limb, 2) how to avoid biasing the background by the presence of bright regions, and 3) how to account for artefacts that are not smooth (such as the intensity variations across linear segments caused by the changed exposure of different rasters with a spectroheliograph; see Section 2.1.2). The performance of the method declines near the limb, because the median filter typically considers pixels outside of the solar disc and thus artificially underestimates the background. Active regions make parts of the disc in Ca ii K line appear brighter, which means that the median filter might overestimate the limb darkening over active regions. Depending on the window width this might spill over to the surrounding pixels. Thus when correcting the image with the determined background, besides lowering the intensity of the bright regions, it might also create a dark ring with width depending on the window of the median filter, around the active regions (see last column in Figure 7).
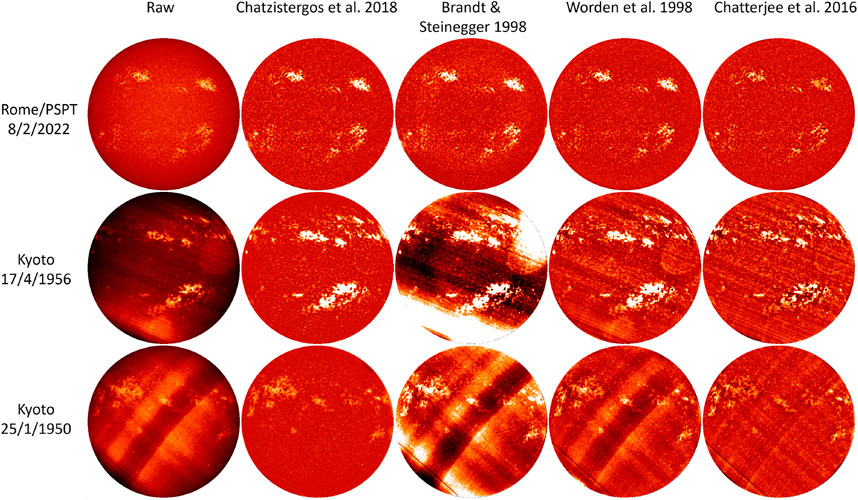
FIGURE 7. Examples of the performance of selected methods to compensate for the limb darkening on observations from Rome/PSPT (8 February 2022; top row) and Kyoto observatory (17 April 1956 in the middle row and 25 January 1950 in the bottom row). Raw images (i.e. including the limb darkening and image artefacts) are shown in the left column. Columns 2–5 show images compensated for the limb-darkening with the methods by Chatzistergos et al. (2020c), Brandt and Steinegger (1998), Worden et al. (1998a), and Chatterjee et al. (2016), respectively. Raw images are shown to their full intensity range, while the limb darkening-compensated images are shown in the range (−0.5–0.5) in contrast.
As already mentioned, all of the proposed techniques have caveats and cannot account for all issues affecting the images. For this reason, a number of studies have employed diverse combinations of the above approaches (Centrone et al., 2005; Ermolli et al., 2009b; Singh et al., 2012; Singh et al., 2022; Priyal et al., 2014; Priyal et al., 2017, Priyal et al., 2019; Chatzistergos et al., 2016; Chatzistergos et al., 2018b; Chatzistergos et al., 2020c; Tähtinen et al., 2022).
Here we will briefly discuss the method used by Chatzistergos et al. (2018b), Chatzistergos et al. (2019b); Chatzistergos et al. (2019a); Chatzistergos et al. (2019c), Chatzistergos et al. (2020b); Chatzistergos et al. (2020c) because it is the only method whose performance was tested, and it was shown to fare better than other techniques. The method combines some of the methods mentioned above, partly modified and extended. The processing starts with a first quick and rough estimate of the background using 1D 5th order polynomial fit on radial profiles (which is a variation of the method by Brandt and Steinegger, 1998), but applied to azimuthal slices of 30° in steps of 5° rather than the whole disc at once. This first background is used to preliminary exclude bright and dark regions. Then a map is constructed by applying the method by Worden et al. (1998a), that is 1D polynomial fittings along columns and rows of the images, here without the 45° rotation (because the latter raises the noise in the result). An important aspect of this process is that it allows the fits on curved segments so to account for such artefacts present in some historical archives, such as Kyoto (Chatzistergos et al., 2020b). This first map is merely used to replace active regions in the original image, and then the 2D running window median filter is applied to the result. The final background is the sum of a map resulting from the application of a 2D running-window median filter and a map produced by stitching together 1D 5th order polynomial fits across columns and rows applied to the residual image between the original observation and the result of the 2D running-window median filter. This process is repeated iteratively until the active region exclusion converges. In this way, the method by Chatzistergos et al. (2018b) overcomes all three caveats mentioned above.
Figure 7 shows examples of application of four limb-darkening compensation methods on Ca ii K observations. In particular, we show results obtained with the methods by Chatzistergos et al. (2018b), Brandt and Steinegger (1998), Worden et al. (1998a), and Chatterjee et al. (2016). The figure illustrates the limitations of the various approaches. All methods perform rather well with artefact-free CCD-based images, although there are still some mild artefacts evident on the image processed with the method by Brandt and Steinegger (1998). However, all methods, except the one by Chatzistergos et al. (2018b), perform poorly on the historical data suffering from severe artefacts. Furthermore, the figure highlights the effect of inaccurate active region exclusion on processing, which manifests as a decrease of plage contrast as can be seen in the last column of Figure 7.
3.3 Photometric calibration
As already mentioned in Section 2.1.2, due to non-linear response to the incident radiation, data stored on photographic plates need to be photometrically calibrated. Some observatories complemented the images with so-called calibration wedges. These were typically obtained by exposing part of the same plate outside the solar disc (although not necessarily at an unexposed part of the plate which would be ideal) with a narrow-field view of the Sun or a controlled light box, using different known exposures. Three examples from Arcetri observations are shown in Figure 5. Unfortunately, utilisation of the calibration wedges has serious limitations (see also Foukal et al., 2009). Firstly, the exposure range covered by the wedges often does not cover the entire range needed to accurately determine the characteristic curve (see Figure 5C). Wedges taken with the same exposure sometimes exhibit big differences, thus not allowing accurate assessment of the sigmoid curve. Finally and most importantly, the need for photometric calibration was not recognised at those times, and the majority of available data do not include calibration wedges. For instance, wedges exist for Arcetri data after 22 February 1938 (Ermolli et al., 2009a), for Mt Wilson data after 9 October 1961, and Kodaikanal data between 1958 and 2006 (Priyal et al., 2014).
Despite these shortcomings, various studies employed the calibration wedges to perform the photometric calibration (Fredga, 1971; Kariyappa and Sivaraman, 1994; Worden et al., 1998a; Giorgi et al., 2005; Ermolli et al., 2009a), but they were limited by the availability of the wedges.
For photometric calibration of data lacking calibration wedges (that is the bulk of the data), four main approaches have been proposed:
1) Steinegger et al. (1996a) and Priyal et al. (2014) applied an average characteristic curve, computed from all wedges of Sacramento Peak and Kodaikanal data, respectively. However, as mentioned in Section 2.1.2 there are significant deviations between characteristic curves of different observations, rendering this approach not recommendable.
2) Ermolli et al. (2009b) applied the method by Mickaelian et al. (2007), originally used to photometrically calibrate star survey plates, on Ca ii K data. Mickaelian et al. (2007) proposed the following formula to recover the characteristic curve:
where Ii is the intensity of the ith pixel, V the average value in an unexposed section of the photographic plate, B is the mean value of the darkest exposed regions, and Ti the transparency value of the ith pixel.
3) Tlatov et al. (2009) calibrated Ca ii K data with linear scaling. The scaling law was determined by relating the measured plate density at two μ positions (0 and 0.9) to that of standard centre-to-limb variation (CLV, hereafter) profiles measured by Pierce and Slaughter (1977).
4) Chatzistergos et al. (2018b) proposed a novel approach to perform the photometric calibration. This approach relates the centre-to-limb variation (CLV, hereafter) of the quiet Sun regions measured in the photographic data to a reference CLV of quiet-Sun regions determined from high-quality modern CCD-based data. The method is based on the assumption that the darker parts of quiet Sun regions do not vary significantly with time, which is in agreement with the results by White and Livingston (1978), White and Livingston (1981), Livingston and Wallace (2003), Livingston et al. (2007), Bühler et al. (2013), Lites et al. (2014). Kakuwa and Ueno (2021) used a rather similar method to that by Chatzistergos et al. (2018b). Importantly, Chatzistergos et al. (2018b) and Chatzistergos et al. (2019b) tested the accuracy of their approach with synthetic data created to imitate most issues affecting historical data (e.g. large scale inhomegeneities, non-linear and varying characteristic curves). They found that their approach allowed to recover the intensity with a mean error of
One common drawback of all the previously described methods is that they derive one characteristic curve for each plate. This is reasonable for filtergrams stored on photographic plates, but not very accurate for spectroheliograms. That is because spectroheliograms are slowly scanned, 1 strip after the other (see Section 2.1.1). In practice, it can happen that different image strips have different exposures, which introduces uncertainties in recovering the characteristic curve. Also, the observational conditions sometimes changed over the course of the scan leading to variations of the characteristic curve over the image. We note, however, that these uncertainties are still lower than when using photometrically uncalibrated data, while severe cases of variable exposure over an image are very likely to be excluded by the researchers from further analyses during data processing.
4 Carrington maps
For most purposes, no further processing of the Ca ii K images after the photometric calibration and limb-darkening compensation is required. However, there are applications for which information on the entire surface of the Sun is needed, for example coronal field extrapolations with potential field source-surface models (Wang and Sheeley, 1992; Wiegelmann et al., 2014; Asvestari et al., 2021). In such cases, Carrington maps are produced (Sheeley et al., 2011; Chatterjee et al., 2016; Bertello et al., 2020).
Carrington maps are Mercator projections of the Sun, showing the entire solar surface in one map. Due to the fact that we essentially have Ca ii K observations (as in fact most other solar observations) from only one vantage point, that of the Earth, Carrington maps are not instantaneous snapshots, but a collage of observations taken over the course of one solar rotation (27.2753 days). That means that values in Carrington maps at certain longitudes result from averaging observations taken a few days apart, which can smear and smooth out features. To reduce this effect, usually only a window in longitudes for each observation is used instead of the entire solar disc, for example Chatterjee et al. (2016) used 60° longitudinal bands. Maps are produced by summing up all the slabs and dividing this map by a streak map, which is essentially a map counting how many images have been used for each pixel.
Figure 8 shows Carrington maps produced by Chatzistergos et al. (2020c), Bertello et al. (2020), and Chatterjee et al. (2016) from Mt Wilson and Kodaikanal data. The figure reveals differences between the various Carrington maps even when derived from the same data. The majority of the differences arise from differences in processing applied to compensate for the limb darkening. Quite evident are darkened rings around plage areas due to inaccurate exclusion of plage areas when computing the background as well as residual artefacts which were not properly accounted for by the respective processing method (see Section 3.2). However, there are also differences caused by the procedures through which the Carrington maps were created. For instance, maps from Chatzistergos et al. (2020c) and Chatterjee et al. (2016) have clear gaps over the areas not covered by observations, while the maps from Bertello et al. (2020) do not show gaps, but stretched parts, which actually belong to regions outside of the disc, instead.
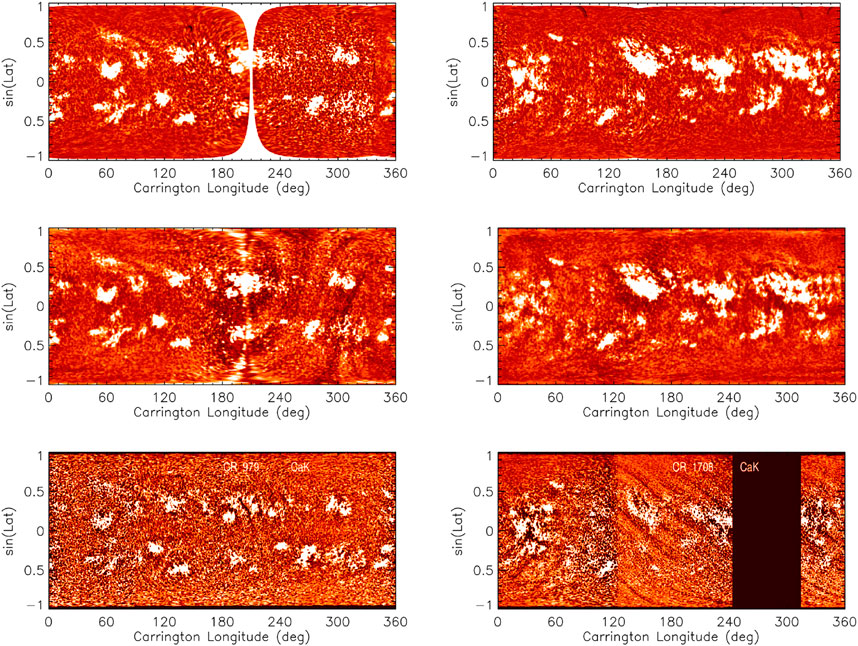
FIGURE 8. Examples of Carrington maps constructed from Ca ii K data over rotations 979 (23 November–19 December 1926, left) and 1708 (2 May–29 May 1981, right). Shown are Mt Wilson data processed by Chatzistergos et al. (2020c, top panel) and by Bertello et al. (2020, middle panel) as well as Kodaikanal data processed by Chatterjee et al. (2016, bottom panel). Due to differences in the image processing the images are saturated at different levels in order to show plage at roughly similar levels. In particular, the contrast ranges are (−0.2–0.2) and (−0.5–0.5) for the first and second rows, respectively, while the third row shows images to their entire range. The data by Chatterjee et al. (2016) are provided in PNG file format so the exact contrast values are not known to us.
5 Plage areas
One of the most commonly studied quantities derived from Ca ii K data is the total plage area on the visible solar hemisphere and its evolution with time. Determining plage areas, in principle, does not require any image processing and can be done on images without photometric calibration or limb-darkening compensation. This allowed various studies to determine plage areas without following the processing steps described in Section 3 (e.g. Kuriyan et al., 1983; Seguí et al., 2019; de Paula and Curto, 2020; de Paula et al., 2021, de Paula et al., 2022; Carrasco and Vaquero, 2022). Plage areas in these studies were counted manually from the physical photographs, typically by overlaying transparencies with circles of known areas. The early plage area timeseries were thus produced in a more qualitative way, applying classification schemes based on characteristics of plage regions. One of the earliest such series is from the Ebro observatory, which kept records of plage areas between 1910 and 1937 (Seguí et al., 2019; de Paula et al., 2021, shown in Figure 9). They used a classification scheme, where they presented areas for four classes (one class had three further subdivisions) of plage regions identified based on their appearance (whether they were compact, scattered, a combination of both, or plage they could not associate with any of these groups). Similarly, the Quarterly Bulletin on Solar Activity (QBSA)2 series included a plage index from Mitaka Ca ii K data where plage regions were manually sorted depending on their size and brightness. NOAA Solar geophysical data, (SGD)3 also maintained a series of plage areas derived from physical photographs from McMath-Hulbert (06/1942–09/1979), Mt Wilson (10/1979–09/1981), and Big Bear (10/1981–11/1987) observatories.
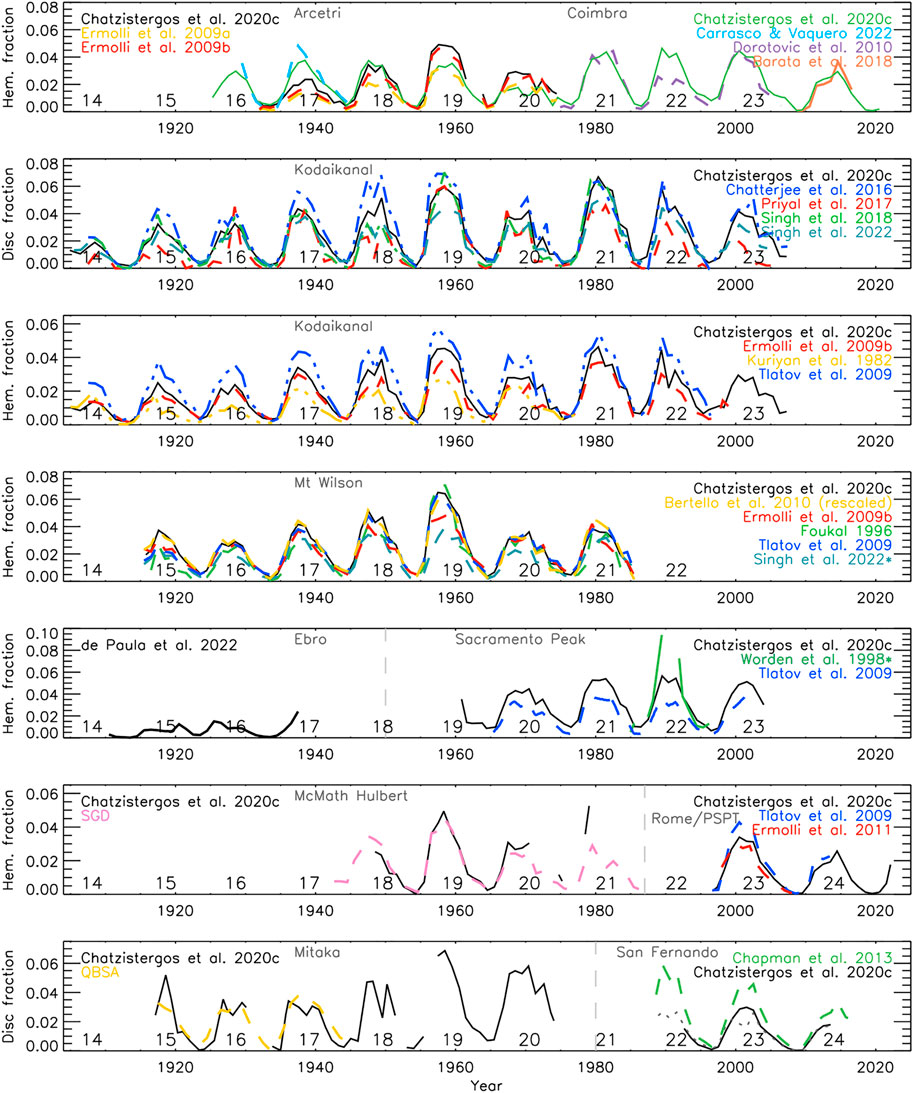
FIGURE 9. Plage areas derived from various Ca ii K archives (as indicated in grey) and different studies. For the San Fernando series by Chatzistergos et al. (2020c) we show separately the results for CFDT1 (dotted grey) and CFDT2 (black) data. Shown are annual median values in hemispheric fraction, except for the series in second and seventh rows as well as the one by Singh et al. (2022) in the fourth row and Worden et al. (1998a) in the fifth row which are given in disc fraction. The numbers in the lower part of each panel denote the conventional solar cycle numbering. The vertical lines roughly mark the separation of archives in panels including timeseries from more than one archive.
Digitisation of the data over the last decades (see Section 2.2) allowed more quantitative analyses of Ca ii K data. Limb-darkening compensation and automatic approaches to identify plage regions have been developed and applied. Various series were produced in this way both from historical photographic and modern CCD-based data (e.g. Chapman et al., 1997; Chapman et al., 2001; Ermolli et al., 2009a; Ermolli et al., 2009b; Tlatov et al., 2009; Bertello et al., 2010, Bertello et al., 2020; Dorotovič et al., 2010; Priyal et al., 2014; Priyal et al., 2017, Priyal et al., 2019; Chatterjee et al., 2016; Singh et al., 2018; Singh et al., 2022). The segmentation of plage regions was typically done with a contrast threshold, which was either set to a constant value for all images, or was allowed to vary depending on the standard deviation of contrast values over the disc or the quiet Sun regions (see Ermolli et al., 2007; Ermolli et al., 2009b; Chatzistergos, 2017). We note, however, that one of the earliest series based on digitised data from Mt Wilson by Foukal (1996) still selected plage regions manually. Further, Barata et al. (2018) used morphological operators to single out plage areas from CCD-based Coimbra data, without the need to compensate the images for the limb-darkening.
Even though plage areas can be derived from uncalibrated data, there are nevertheless disadvantages of using photometrically uncalibrated historical data (see Section 2.1.2). Photometric calibration returns data with homogeneous intensity in plage regions, which in turn allows more accurate identification of plage areas. Also the accuracy of the limb-darkening compensation affects the resulting plage areas (see Section 3.2), for instance through unaccounted or introduced artefacts, or due to potentially varying accuracy of the processing, especially if it depends on activity.
Figure 9 shows some of the available plage area series, focusing on those from historical long-term datasets. It is immediately evident that the various published series show (sometimes significant) differences. This is not only the case for plage areas derived from different Ca ii K archives, but also for those derived from the same archive but with different processing techniques (see also Ermolli et al., 2018). Most of the discrepancies come from the applied processing, including the limb darkening compensation, photometric calibration, the segmentation, and even divergence in the definition of plage. Furthermore, the samples of the data used for the analysis are typically not identical either. However, part of the differences is also due to the intrinsic differences between the archives, in particular in the employed bandwidth (see Section 2.1.1). This was shown by Chatzistergos et al. (2020c) who analysed 43 Ca ii K datasets (38 centred at the core of the line and five centred at different wavelengths across the wings) processed with exactly the same methods.
In addition to purely plage area series, some authors constructed various composite records of facular indices or proxies, which also included plage areas. For instance, Fligge and Solanki (1998) combined the series of the international sunspot number, sunspot areas, F10.7 flux, white-light facular areas, and Mt Wilson plage areas by Foukal (1996). Bertello et al. (2016) and Bertello et al. (2017) produced a composite emission index by combining disc-integrated 1 Å Ca ii K indices from Sacramento Peak and Synoptic Optical Long-term Investigations of the Sun (SOLIS) Integrated sunlight Spectrometer (ISS) with the plage areas from Kodaikanal by Tlatov et al. (2009). The first composite of plage areas based solely on Ca ii K data was presented by Chatzistergos et al. (2019b), who combined the data from nine Ca ii K datasets (Arcetri, Kodaikanal, McMath-Hulbert, Meudon, Mitaka, Mt Wilson, Rome/PSPT, Schauinsland, and Wendelstein). Later, the composite was updated to include data from 38 Ca ii K datasets (Chatzistergos et al., 2020c). It provides daily values between 1892 and 2019 and is shown in Figure 10 along with the sunspot area series by Mandal et al. (2020).
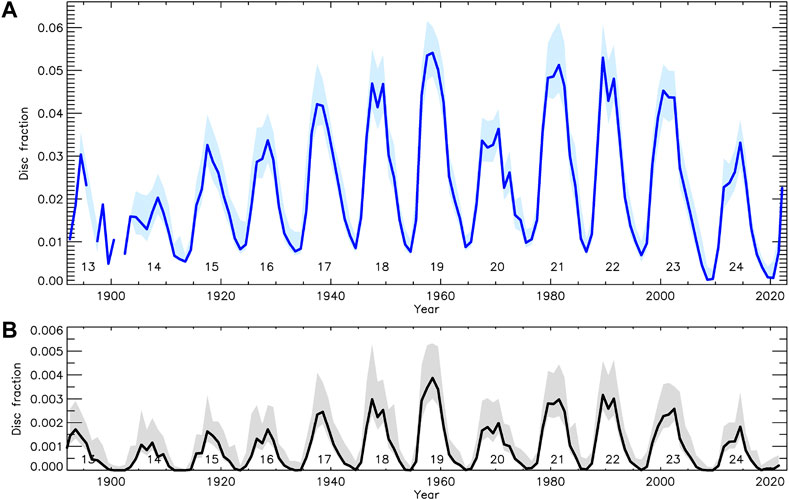
FIGURE 10. (A) Plage area composite series by Chatzistergos et al. (2020c) extended to 10 March 2022 with Rome/PSPT data processed in the same way as the rest of the data used for the composite series. (B) Sunspot area series by Mandal et al. (2020). Shaded areas mark the asymmetric 1σ intervals, while the numbers at the lower part of each panel denote the conventional solar cycle numbering.
Chatterjee et al. (2016); Priyal et al. (2017) and Tlatov and Tlatova (2019) have also analysed the distribution of plage areas over latitudes and time, the so-called butterfly diagrams, analogous to the well-known sunspot butterfly diagram. At the beginning of a cycle, active regions typically emerge at mid latitudes, while as the cycle progresses they move towards lower latitudes, such that the shape of these graphs resembles wings of a butterfly.
The North–South asymmetry of solar cycles has usually been studied with sunspot data (e.g. Ravindra et al., 2021; Veronig et al., 2021), but Dorotovič et al. (2007), Dorotovič et al. (2010), Segu et al. (2019), El-Borie et al. (2020), de Paula and Curto (2020), de Paula et al. (2022) and Chowdhury et al. (2022) used Ca ii K data for this purpose. Most of these studies covered relatively short intervals up to two solar cycles, with the exception of El-Borie et al. (2020) and Chowdhury et al. (2022). The result of the study by El-Borie et al. (2020) is, however, simply mirroring that from sunspot data, as these authors used the composite of full-disc plage areas by Chatzistergos et al. (2019b), which they separated into the north and south components by imposing the same asymmetry level as found in Royal Greenwich observatory sunspot area data. Using Kodaikanal plage areas from Chatterjee et al. (2016) over cycles 14–21 derived for each hemisphere separately Chowdhury et al. (2022) found only three cycles (14, 15, and 21), for which the activity peak roughly coincided in both hemispheres, while higher activity was found in the northern hemisphere for all cycles except 14, 17, and 21. This differs from the results based on sunspot data (Veronig et al., 2021) which imply that cycles 16, 18, 22, 23, and 24 had higher activity in the southern hemisphere. The North–South asymmetry was found to be highest over cycle 19, in agreement with Veronig et al. (2021).
The relation between plage areas and sunspot areas or numbers has also been studied (see Foukal and Vernazza, 1979; Schatten et al., 1985; Lawrence, 1987; Steinegger et al., 1996b; Chapman et al., 1997, Chapman et al., 2011; Fligge and Solanki, 1998; Bertello et al., 2016; Mandal et al., 2017a; Chatzistergos et al., 2018a; Chatzistergos et al., 2022; Yeo et al., 2020a). Past studies, in general, suggest a quadratic relation between plage and sunspot areas for daily values. A linear relationship is typically favored for annual sunspot values, however Chatzistergos et al. (2022) reported a, in general, non linear relationship even for annual values. For sunspot numbers the reported relation is typically linear when annual values are considered, but non-linearities have been reported for daily values (Chatzistergos et al., 2022). No qualitative difference has been reported when alternative sunspot number series, such as those by Svalgaard and Schatten (2016); Usoskin et al. (2016); Chatzistergos et al. (2017); Willamo et al. (2017), were used for the analysis. Chatzistergos et al. (2022) also reported that the bandwidth of the Ca ii K observations affects the relationship between plage areas and sunspot data.
Finally, Penza et al. (2021) used the composite by Chatzistergos et al. (2019b) going up to the end of 2018 to make, to our knowledge, the first prediction of the amplitude of solar cycle 25 in terms of plage areas (Figure 11) They used an empirical parametrisation of the solar cycle in plage and sunspot areas as suggested by Volobuev (2009). This model has one free parameter varying from cycle to cycle. By determining an empirical relation between the free parameter of the model for subsequent odd and even cycles, Penza et al. (2021) estimated the amplitude of cycle 25 using the value of the parameter for cycle 24. Their prediction suggests the amplitude of cycle 25 to be rather similar to or slightly higher than that of cycle 24. Extending the composite by Chatzistergos et al. (2019b) with more recent data from Rome/PSPT (up to 10 March 2022), agrees with the prediction until then within the uncertainty level. However, data covering the next few years will be required to assess the performance of the prediction more meaningfully.
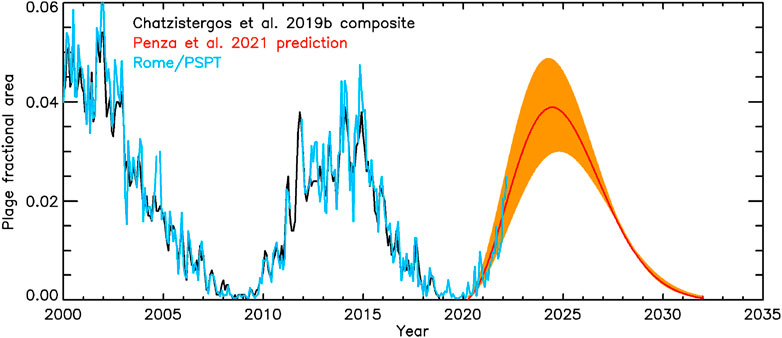
FIGURE 11. Prediction of solar cycle 25 amplitude in plage fractional areas by Penza et al. (2021, red, with confidence intervals in shaded orange surface). Shown also is the Chatzistergos et al. (2019b) plage area composite (black), on which the prediction was based, as well as more recent data from Rome/PSPT (light blue), which was the reference observatory in the Chatzistergos et al. (2019b) plage area composite since 1996.
6 Network
6.1 Network area evolution
Network regions are small magnetic flux concentrations appearing as bright web-like structures outlining dark cells, which are the chromospheric counterparts of the supergranulation pattern. Studying the network evolution is particularly important, because they are thought to be responsible for the secular variation of solar irradiance (e.g. Solanki et al., 2002).
Network regions are usually subdivided into active, enhanced, and quiet network in order to distinguish between products of decaying active regions and the “quiet-Sun” network outside of active regions. However, often this distinction is rather arbitrary and is based merely on the contrast of network regions. In the following we will refer to all of them collectively as network unless specified otherwise.
The mean level of network fractional areas varies significantly among the various studies, lying on average between 0.02 (Foukal, 1998, using Mt Wilson data) and 0.35 (Ermolli et al., 2003a, using Rome/PSPT data). The total network area varies in-phase with the solar cycle (Caccin et al., 1997; Caccin et al., 1998a; Foukal, 1998; Worden et al., 1998a,b; Ermolli et al., 2003a; Priyal et al., 2014; Priyal et al., 2017; Ermolli et al., 2022). A latitudinal dependence of network areas on the solar cycle has also been reported (Devi et al., 2021, using Kodaikanal data), with the amplitude of variations decreasing from the equator towards ±50° latitude and increasing again towards the poles. Foukal and Milano (2001) argued that there is no evidence for a long-term trend in network areas by analysing Mt Wilson and Sacramento Peak data around cycle minima periods between 1914 and 1996. However, the scatter of their derived fractional areas is rather large (roughly between 0.1 and 0.19) with too few data points (Three images per cycle minimum) to accurately assess this. Furthermore, they used photometrically uncalibrated data, which is an additional important limiting factor.
The controversies described above are largely due to different definitions of network regions, but also due to the employed data and the processing. In particular, the accuracy of the processing becomes more important for determining network regions than for plage ones, because of the lower contrast of network regions, which is frequently lower than that of artefacts found in historical data. Furthermore, the segmentation approach can also significantly affect the determined network regions. Analysing modern high-quality Rome/PSPT observations Chatzistergos (2017) showed that segmentation with a constant threshold resulted in an in-phase relation between network areas and the solar cycle. Thresholding with a multiplicative factor to the standard deviation of the solar disc contrast resulted in anti-phase variability, instead. They also noticed that the latter effect was more pronounced when the contrast of the entire disc (that is including also active regions) was used to compute the standard deviation (thus being affected by activity variations), which is in fact the more commonly used method. This effect is marginal when active regions are excluded for the computation of the standard deviation (as used by Chatzistergos et al., 2020c), suggesting a very small to no variation of network areas over the solar cycle. This is in good agreement with the conclusion of Harvey (1993) and Harvey (1994), who found that the amplitude of the solar cycle variation decreased markedly with size of magnetic regions, being several times stronger for active regions than for smaller ephemeral regions.
Due to the absence of information on network regions before the beginning of Ca ii K observations, there have been studies aiming to establish a relationship between network areas and other solar indices which go further back in time than Ca ii K observations. For instance, Singh et al. (2021) compared the network areas from Kodaikanal to the international sunspot number series (Clette and Lefèvre, 2016) and reported linear correlation factors of 0.87 and 0.77 for the active and enhanced network, respectively. Berrilli et al. (2020) reconstructed monthly network areas back to 1749 with a power law relation applied to the international sunspot number series.
Finally, Chatterjee et al. (2019) produced time-latitude maps of network areas (Figure 12). They used Carringtom maps from Kodaikanal produced by Chatterjee et al. (2016) and Mt Wilson by Sheeley et al. (2011). For each Carrington map they counted the network areas within latitudinal strips of 5°. They also applied a smoothing to each latitudinal strip with a kernel of 200 Carrington rotations (roughly 15 years). Their results show branches of equatorward migration of network areas that start at approximately ±55° latitude and take approximately 15 ± 1 year to reach the equator.
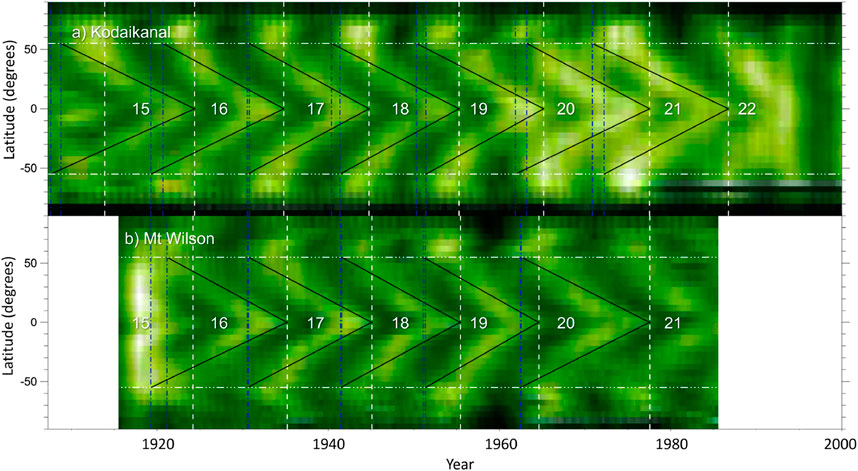
FIGURE 12. Time-latitude maps of network areas from Kodaikanal (A) and Mt Wilson (B) observatories. The black lines are fits to the extended equatorward branches. The vertical dashed blue lines denote the onset of the extended equatorward branches, while the white vertical dashed lines denote the time when those branches reach the equator. The horizontal white dashed lines mark latitudes at ±55°. The numbers at the centre of each panel denote the conventional solar cycle numbering. The figure is adapted from Chatterjee et al. (2019) © AAS. Reproduced with permission.
6.2 Network cell characteristics
Simon and Leighton (1964) noticed a spatial correspondence between the chromospheric network in Ca ii K observations and boundaries of supergranular cells seen in the photosphere. This triggered a series of studies of supergranular parameters by using Ca ii K observations (Sotnikova, 1978; Singh and Bappu, 1981; Raghavan, 1983; Münzer et al., 1989; Kariyappa and Sivaraman, 1994; Hagenaar et al., 1997; Berrilli et al., 1998; Berrilli et al., 1999; Ermolli et al., 1998a; Ermolli et al., 1998b; Pietropaolo and Ermolli, 1998; Raju et al., 1998; Goldbaum et al., 2009; Raju and Singh, 2014; Raju, 2020; McIntosh et al., 2011; Chatterjee et al., 2017b; Mandal et al., 2017b; Rajani et al., 2022). The cell sizes determined from Ca ii K data were in general smaller than the diameter of the supergranular cells in the photosphere reported by Simon and Leighton (1964, about 32 Mm). For instance, Hagenaar et al. (1997), McIntosh et al. (2011), and Singh and Bappu (1981) with South Pole, Mauna Loa Solar observatory (MLSO) PSPT, and Kodaikanal Ca ii K data found the mean cell diameter of 13–18 Mm, 22–32 Mm, and 22 Mm, respectively. However, the estimate by Singh and Bappu (1981) was obtained by selecting network regions manually, whereas if an auto-correlation technique was applied, the cell diameter increased to about 32 Mm, in accordance with Simon and Leighton (1964). We note that procedures employed to determine the network cells as well as the data used differ considerably among different studies, causing discrepancies in the reported values (Rincon and Rieutord, 2018).
In general, results from the literature suggest that cell sizes decrease with increasing activity level. This was reported by Singh and Bappu (1981), Raghavan (1983), Kariyappa and Sivaraman (1994), and Rajani et al. (2022) using Kodaikanal data, and by McIntosh et al. (2011) using Mt Wilson data covering 1944–1976. In contrast, Chatterjee et al. (2017b) used Kodaikanal, Rome/PSPT, and MLSO/PSPT data and found an increase of cell sizes with increasing solar activity when considering the entire solar disc without distinguishing between active and quiet regions. However, they also found an anti-correlation between cell sizes and activity when only quiet regions were considered. Furthermore, based on Arcetri spectroheliograms covering 1950–1970, Caccin et al. (1998a) found that the histogram of contrast values of non-plage regions exhibited an asymmetry depending on the activity level.
7 Connection between Ca ii K brightness and magnetic field strength
Ca ii K data have been recognised very early as good tracers of solar surface magnetic fields (Babcock and Babcock, 1955; Howard, 1959; Leighton, 1959). Various studies assessed the relationship between Ca, ii brightness and magnetic field strength (Frazier, 1971; Skumanich et al., 1975; Schrijver et al., 1989; Nindos and Zirin, 1998; Harvey and White, 1999; Rast, 2003; Ortiz and Rast, 2005; Rezaei et al., 2007; Loukitcheva et al., 2009; Kahil et al., 2017; Kahil et al., 2019; Chatzistergos et al., 2019d). Most of them favoured a power law relationship between the Ca, ii brightness and the magnetic field strength, while Kahil et al. (2017) and Kahil et al. (2019) found a logarithmic function to fit the data best. These previous studies used very diverse data, in terms of the periods covered, the bandwidth of observations, and types of considered regions. Most of them considered only small parts of the disc in either the quiet Sun or active regions separately. All of these factors led to a rather high spread in the derived power-law exponents, typically between 0.3 and 0.6. The analysis by Chatzistergos et al. (2019d) is the most comprehensive to date, considering high-quality full-disc data covering half a solar cycle. They saw no dependence (within the uncertainty of the fits) of the relation on the μ position or activity level.
The connection between the Ca ii K brightness and the magnetic field strength suggests that Ca ii K data can be used to reconstruct magnetograms. This is very important considering that high-quality magnetograms of the Sun exist since the 1970s (Livingston et al., 1976) and Ca ii K data can be used to extend the magnetic field data back to 1892. To our knowledge, there have been only four such reconstructions until now.
Shin et al. (2020) employed a machine learning image-to-image translation approach to convert CCD-based Rome/PSPT Ca ii K images to SDO/HMI-like magnetograms. They based their work on the “pix2pixHD” model by Wang et al. (2018). They reported a linear correlation factor between the total unsigned magnetic flux measured in the generated magnetograms to the actual one of 0.99. They reported that pixel-by-pixel correlation is on average 0.74, but it depends on the selected regions, being higher for active regions (0.81) and considerably lower for quiet Sun regions (0.24). However, it should be noted that they employed data without compensation for limb-darkening, which might be a factor affecting the performance of the training.
Pevtsov et al. (2016) was, to our knowledge, the first to reconstruct magnetograms from historical photographic Ca ii K data. They used low resolution Carrington maps produced from photometrically uncalibrated Mt Wilson Ca ii K data processed by Bertello et al. (2020) (see Section 4). Their magnetogram reconstruction is based on the empirical relation between the magnetic flux and the integrated intensity of a plage region. They singled out plage regions with a contrast threshold of 2σ from each synoptic map and assigned to each region a single value of magnetic field strength. They also used the Mt Wilson sunspot dataset, which includes information on the polarity of sunspots, to recover the polarity of plage regions in the vicinity of sunspots. The processing applied by these authors has, unfortunately, introduced clear artefacts affecting the brightness of plage regions and thus the recovered magnetic field strength (see Carrington maps in Figure 8 and Section 3.2). Other limitations of this study are the low resolution of the Carrington maps, the single value of the magnetic field strength assigned to plage regions, and the absence of magnetic field and polarity information outside of bright plage regions.
Similarly, Mordvinov et al. (2020) reconstructed magnetograms over 1907–1965 from Kodaikanal Ca ii K Carrington maps produced by Chatterjee et al. (2016). They used a polynomial relationship between the magnetic flux density and Ca ii K contrast. The degree of the polynomial was chosen to vary depending on the activity level. In particular, a third degree polynomial was used for low activity levels and fourth degree for high activity levels. This cycle-dependent variation of the relation might be an artefact introduced by the processing of the images (see Section 3.2).
Another approach for reconstructing unsigned magnetograms was proposed by Chatzistergos et al. (2019d). The pixel-by-pixel relation between Ca ii K brightness and magnetic field strength was directly used to reconstruct solar magnetograms. This approach produces unsigned magnetograms and does not recover the magnetic field strength in sunspot regions. Chatzistergos et al. (2021a) used this approach to reconstruct unsigned magnetograms from 13 Ca ii K archives, including the historical photographic datasets from Mt Wilson and Meudon. We note that the spatial resolution is an important factor when recovering magnetograms, since low spatial resolution results in high probability of “missing” part of the magnetic flux due to sub-pixel cancellation of opposite-polarity elements (Krivova and Solanki, 2004).
8 Irradiance reconstruction
One of the most important applications of Ca ii K data is reconstruction of past irradiance variations. Measurements of TSI variations from space exist only since 1978, while longer records are required for example for climate studies. The driver of the irradiance variations on timescales of days and longer is the evolution of the solar surface magnetic field (Shapiro et al., 2017; Yeo et al., 2017), as a result of a competition between plage and sunspot regions enhancing and suppressing TSI, respectively. Thus, appropriate facular and sunspot data are needed by models to reconstruct past irradiance variations. While sunspot data are readily available back to early 1600s (Vaquero et al., 2016), facular data are significantly more scarce. In fact, most of the available facular data cover roughly the same period as direct TSI measurements, while Ca ii K data are the only direct facular dataset extending back to 1892 (potentially also white-light faculae; Foukal, 1993; Carrasco et al., 2021). Most of the existing irradiance reconstructions extending back to 1600s use sunspot data to infer the characteristics of faculae. This results in a roughly an order of magnitude difference among the various estimates of the long-term evolution of TSI since 1700s (Solanki et al., 2013), although more recently Yeo et al. (2020b) set an upper limit of 2.0 ± 0.7 W/m2 on the possible difference between the TSI at modern activity minima and grand minima.
Until now, most studies used CCD-based Ca ii K data for irradiance reconstructions, covering shorter periods than the direct TSI measurements (Chapman et al., 1996; Chapman et al., 2013; Ermolli et al., 2003b; Ermolli et al., 2011; Penza et al., 2003; Walton et al., 2003; Fontenla and Landi, 2018; Puiu, 2019; Chatzistergos et al., 2020a; Choudhary et al., 2020). Notwithstanding the short interval, such data allowed an assessment of the accuracy of the irradiance reconstructions. Furthermore, they provided an independent estimate on the TSI variations between activity minima over the last three cycles. For instance, by reconstructing TSI variations with an empirical model using Rome/PSPT Ca ii K and continuum observations, Chatzistergos et al. (2020a) found that TSI in general declined over the minima of the last three cycles.
Use of historical photographic data for irradiance reconstructions has so far been rather limited, with only five TSI reconstructions from historical Ca ii K observations known to us, namely, by Ambelu et al. (2011), Foukal (2012), Penza et al. (2022), Xu et al. (2021), and Chatzistergos et al. (2021a). Ambelu et al. (2011), Foukal (2012), and Xu et al. (2021) used the photometrically uncalibrated Mt Wilson, Mt Wilson, and Kodaikanal Ca ii K data, respectively to reconstruct TSI variations with a linear regression model. These studies also did not account for the various instrumental changes affecting the data, thus rendering their results highly uncertain. Penza et al. (2022) used the plage area composite seriequiet Sun or active regions separately. All of these factors lets by Chatzistergos et al. (2019b) to reconstruct TSI over the last five centuries with an empirical model. Chatzistergos et al. (2021a) and Chatzistergos et al. (2021b) used 13 Ca ii K archives, including historical photographic archives from Meudon and Mt Wilson, to reconstruct past irradiance variations with the Spectral and Total Iiradiance REconstruction (SATIRE Krivova et al., 2003) model. Figure 13 shows the reconstructed TSI series from four Ca ii K archives by Chatzistergos et al. (2021a), in particular those from Rome/PSPT, San Fernando CFDT2, Meudon K3, and Meudon K1v (see Figure 4 for the correspondence of the K3 and K1v parts of the Ca ii K line). The reconstructions done by Chatzistergos et al. (2021a) were limited to the periods with overlap to the direct TSI measurements, since their aim was to assess the quality of the reconstruction. Their results showed that Ca ii K data can be used to recover past irradiance variations almost as accurately as with SATIRE-S (Yeo et al., 2014) which employs actual magnetograms. This was a very important step, which demonstrated the ability of Ca ii K data to produce highly accurate irradiance reconstructions, provided the data have been consistently and accurately processed, while also accounting for the various inhomogeneities within the datasets.
FIGURE 13. Reconstructed TSI series by Chatzistergos et al. (2021a) with Ca ii K data from Rome/PSPT, San Fernando CFDT2, Meudon K3, and Meudon K1v. The reconstructions are shown in green dots for daily values and dashed yellow for 81-day running means. Also shown is the PMOD TSI composite (black dots for daily values and black line for 81-day running mean values). The numbers at the lower part of the figures denote the conventional solar cycle numbering. Also listed within the figures are the bandwidth used for the observations as well as the pixel scale (for Meudon K1v we also list the central wavelength).
9 Conclusion
Full-disc Ca ii K observations of the Sun have a long legacy, which is unrivaled by most direct solar data. Such observations have been performed routinely since 1892 at numerous sites around the world and continue to this day.
In this review, we have highlighted the fact that Ca ii K archives are far from a coherent and consistent dataset, rather they are collections made with quite diverse instruments and observational settings. Deriving accurate and reliable results from Ca ii K data requires robust processing as well as knowledge of and accounting for the various differences and inconsistencies of the available archives. A very important aspect, usually neglected, is the need for the photometric calibration to account for the non-linear response of the photographic plates to the incident radiation.
The increased interest of the recent decades and digitisation of historical photographic Ca ii K datasets have opened up the possibility for precise quantitative studies. This led to the development of various modern processing techniques allowing one to overcome many of the issues affecting the images, including the photometric calibration of the images (e.g. Chatzistergos et al., 2018b; Chatzistergos et al., 2019b). Comprehensive analyses of plage and network regions have been performed on diverse Ca ii K data, while plage areas determined from 43 archives have been combined into a composite series covering 1892–2019 (Chatzistergos et al., 2020c) with an almost full temporal coverage since 1907.
Ca ii K observations are also invaluable for recovering information on the solar surface magnetic field, especially in the past. Due to the tight relation between the magnetic field strength and Ca ii K brightness they can be used to reconstruct magnetograms back to 1892. One of the most important applications of Ca ii K observations is their potential to help us improve our understanding of the long-term variations in solar irradiance. Chatzistergos et al. (2021a) showed that, if accurately processed and after accounting for the problems and artefacts, Ca ii K data can be used to reconstruct past irradiance variations almost as accurately as with actual high-quality magnetograms. This highlights the significance of Ca ii K data for irradiance studies as well as for studies of the solar influence on Earth’s climate.
We stress, however, that there are still a lot of unexplored Ca ii K observations around, either because they have not been digitised yet (such as the data from Kenwood and Kandilli) or because their whereabouts are unknown (like the data from Hamburg). Recovering and digitising the remaining Ca ii K observations would be highly beneficial.
Author contributions
TC drafted the manuscript, while all co-authors provided parts of the text and proofread it.
Funding
This work was supported by the Italian MIUR-PRIN grant 2017 “Circumterrestrial Environment: Impact of Sun–Earth Interaction”, by the German Federal Ministry of Education and Research (Project No. 01LG 1909C), and by the European Union’s Horizon 2020 research and Innovation program under grant agreement No 824135 (SOLARNET) and No 739500 (PRE-EST).
Acknowledgments
The authors thank the observers at the Arcetri, Calern, Coimbra, Ebro, Kanzelhöhe, Kharkiv, Kodaikanal, Kyoto, Meudon, Mitaka, Mt Wilson, Pic du Midi, Rome, Sac Peak, San Fernando, and Valašské Meziříčí sites as well all other Ca ii K observatories helping to create such an important archive of solar data. We thank Isabelle Buale for her continued efforts at digitising the archive of Meudon observatory. We also thank NOAA NCEI and Karen Horan for digitising the McMath-Hulbert data. We thank Teresa Barata, Luca Bertello, Victor M. S. Carrasco, Subhamoy Chatterjee, Angie Cookson, Juan José Curto, Ivan Dorotovič, Muthu Priyal, Jagdev Singh, and Andrey Tlatov for providing us with their produced timeseries. This publication uses data from the solar section of the solar observatory in Roquetes, Spain, owned and operated by the Fundació Observatori de l’Ebre. We thank Michael Borman, Didier Favre, André Gabriël, Lastrofieffe, Stefano Sello, and the other amateur observers at the international online solar database for their efforts at observing the Sun and allowing us to use their observations in this publication. We thank the referees who helped to improve this paper. This research has made use of NASA’s Astrophysics Data System.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1ftp://ftp.hs.uni-hamburg.de/pub/outgoing/FTS-Atlas/.
2https://solarwww.mtk.nao.ac.jp/en/wdc/qbsa.html.
3https://www.ngdc.noaa.gov/stp/solar/calciumplages.html.
References
Ambelu, T., Falayi, E. O., Elemo, E. O., and Oladosu, O. (2011). Estimation of total solar irradiance from sunspot number. Latin-American J. Phys. Educ. 5.
Antonucci, E., Azzarelli, L., Casalini, P., and Cerri, S. (1977). Chromospheric rotation during 1972-73, years of declining activity. Sol. Phys. 53, 519–529. doi:10.1007/BF00160294
Asvestari, E., Pomoell, J., Kilpua, E., Good, S., Chatzistergos, T., Temmer, M., et al. (2021). Modelling a multi-spacecraft coronal mass ejection encounter with EUHFORIA. Astron. Astrophys. 652, A27. doi:10.1051/0004-6361/202140315
Babcock, H. W., and Babcock, H. D. (1955). The sun’s magnetic field, 1952-1954. Astrophys. J. 121, 349. doi:10.1086/145994
Barata, T., Carvalho, S., Dorotovič, I., Pinheiro, F. J. G., Garcia, A., Fernandes, J., et al. (2018). Software tool for automatic detection of solar plages in the Coimbra Observatory spectroheliograms. Astronomy Comput. 24, 70–83. doi:10.1016/j.ascom.2018.06.003
Bates, B., and McDowell, M. W. (1972). A compact grating spectroheliograph for the Mg ii resonance lines. Sol. Phys. 23, 26–29. doi:10.1007/bf001538892326B
Belkina, I. L., Beletskij, S. A., Gretskij, A. M., and Marchenko, G. P. (1996). CCD observations of the Sun in the lines He I 1083 nm, Hα, and K Ca II. Kinemat. Phys. Celest. Bodies 12, 55.
Berrilli, F., Criscuoli, S., Penza, V., and Lovric, M. (2020). Long-term (1749–2015) variations of solar UV spectral indices. Sol. Phys. 295, 38. doi:10.1007/s11207-020-01603-5
Berrilli, F., Ermolli, I., Florio, A., and Pietropaolo, E. (1999). Average properties and temporal variations of the geometry of solar network cells. Astronomy Astrophysics 344, 965–972. doi:10.3389/fspas.2022.1042740
Berrilli, F., Ermolli, I., Florio, A., and Pietropaolo, E. (1998). Geometrical properties of the chromospheric network cells from OAR/PSPT images. Mem. della Soc. Astron. Ital. 69, 635.
Bertello, L., Marble, A. R., and Pevtsov, A. A. (2017). Ca II K 1-A emission index composites. ArXiv e-prints 1702, arXiv:1702.00838.
Bertello, L., Pevtsov, A. A., and Ulrich, R. K. (2020). 70 Years of chromospheric solar activity and Dynamics. Astrophys. J. 897, 181. doi:10.3847/1538-4357/ab9746
Bertello, L., Pevtsov, A., Tlatov, A., and Singh, J. (2016). Correlation between sunspot number and Ca II K emission index. Sol. Phys. 291, 2967–2979. doi:10.1007/s11207-016-0927-9
Bertello, L., Ulrich, R. K., and Boyden, J. E. (2010). The mount Wilson Ca ii K plage index time series. Sol. Phys. 264, 31–44. doi:10.1007/s11207-010-9570-z
Bethge, C., Peter, H., Kentischer, T. J., Halbgewachs, C., Elmore, D. F., and Beck, C. (2011). The chromospheric telescope. Astron. Astrophys. 534, A105. doi:10.1051/0004-6361/201117456
Bose, S., and Nagaraju, K. (2018). On the variability of the solar mean magnetic field: Contributions from various magnetic features on the surface of the sun. Astrophys. J. 862, 35. doi:10.3847/1538-4357/aaccf1
Brandt, P. N., and Steinegger, M. (1998). On the determination of the quiet-sun center-to-limb variation in Ca II K spectroheliograms. Sol. Phys. 177, 287–294. doi:10.1023/a:1004953032251
Bühler, D., Lagg, A., and Solanki, S. K. (2013). Quiet Sun magnetic fields observed by Hinode: Support for a local dynamo. Astron. Astrophys. 555, A33. doi:10.1051/0004-6361/201321152
Caccin, B., Ermolli, I., Fofi, M., and Sambuco, A. M. (1998a). Variations of the chromospheric network with the solar cycle. Sol. Phys. 177, 295–303. doi:10.1023/A:1004938412420
Caccin, B., Ermolli, I., Fofi, M., and Sambuco, A. M. (1997). Variations of the network contribution to the solar irradiance. Mem. della Soc. Astron. Ital. 68, 459.
Caccin, B., Staro, F., and Gomez, M. T. (1998b). Variation of the effective temperature with the solar cycle. Mem. della Soc. Astron. Ital. 69, 595.
Carrasco, V. M. S., Nogales, J. M., Vaquero, J. M., Chatzistergos, T., and Ermolli, I. (2021). A note on the sunspot and prominence records made by Angelo Secchi during the period 1871–1875. J. Space Weather Space Clim. 11, 51. doi:10.1051/swsc/2021033
Carrasco, V. M. S., and Vaquero, J. M. (2022). A catalog of faculae, prominences, and filaments for the period 1929–1944 from the astronomical observatory of the university of Coimbra. Astrophys. J. Suppl. Ser. 262, 44. doi:10.3847/1538-4365/ac85dd
Centrone, M., Ermolli, I., and Giorgi, F. (2005). Image processing for the Arcetri solar archive. Mem. della Soc. Astron. Ital. 76, 941.
Chapman, G. A., Cookson, A. M., and Dobias, J. J. (1997). Solar variability and the relation of facular to sunspot areas during solar cycle 22. Astrophys. J. 482, 541–545. doi:10.1086/304138
Chapman, G. A., Cookson, A. M., and Dobias, J. J. (1996). Variations in total solar irradiance during solar cycle 22. J. Geophys. Res. 101, 13541–13548. doi:10.1029/96JA00683
Chapman, G. A., Cookson, A. M., Dobias, J. J., and Walton, S. R. (2001). An improved determination of the area ratio of faculae to sunspots. Astrophys. J. 555, 462–465. doi:10.1086/321466
Chapman, G. A., Cookson, A. M., and Preminger, D. G. (2013). Modeling total solar irradiance with san Fernando observatory ground-based photometry: Comparison with ACRIM, PMOD, and RMIB composites. Sol. Phys. 283, 295–305. doi:10.1007/s11207-013-0233-8
Chapman, G. A., Dobias, J. J., and Arias, T. (2011). Facular and sunspot areas during solar cycles 22 and 23. Astrophys. J. 728, 150. doi:10.1088/0004-637X/728/2/150
Chatterjee, S., Banerjee, D., McIntosh, S. W., Leamon, R. J., Dikpati, M., Srivastava, A. K., et al. (2019). Signature of extended solar cycles as detected from Ca ii K synoptic maps of kodaikanal and mount Wilson observatory. Astrophys. J. 874, L4. doi:10.3847/2041-8213/ab0e0e
Chatterjee, S., Banerjee, D., and Ravindra, B. (2016). A butterfly diagram and Carrington maps for century-long Ca II K spectroheliograms from the Kodaikanal observatory. Astrophys. J. 827, 87. doi:10.3847/0004-637X/827/1/87
Chatterjee, S., Hegde, M., Banerjee, D., and Ravindra, B. (2017a). Long-term study of the solar filaments from the synoptic maps as derived from Hα spectroheliograms of the kodaikanal observatory. Astrophys. J. 849, 44. doi:10.3847/1538-4357/aa8ad9
Chatterjee, S., Mandal, S., and Banerjee, D. (2017b). Variation of supergranule parameters with solar cycles: Results from century-long kodaikanal digitized Ca II K data. Astrophys. J. 841, 70. doi:10.3847/1538-4357/aa709d
Chatzistergos, T. (2017). Analysis of historical solar observations and long-term changes in solar irradiance. PhD thesis. Uni-edition.
Chatzistergos, T., Ermolli, I., Falco, M., Giorgi, F., Guglielmino, S. L., Krivova, N. A., et al. (2019a). Historical solar Ca II K observations at the Rome and Catania observatories. Il Nuovo Cimento 42C, 5. doi:10.1393/ncc/i2019-19005-2
Chatzistergos, T., Ermolli, I., Giorgi, F., Krivova, N. A., and Puiu, C. C. (2020a). Modelling solar irradiance from ground-based photometric observations. J. Space Weather Space Clim. 10, 45. doi:10.1051/swsc/2020047
Chatzistergos, T., Ermolli, I., Krivova, N. A., Barata, T., Carvalho, S., and Malherbe, J. M. (2022). Scrutinising the relationship between plage areas and sunspot areas and numbers. Astron. Astrophys. doi:10.1051/0004-6361/202244913
Chatzistergos, T., Ermolli, I., Krivova, N. A., and Solanki, S. K. (2019b). Analysis of full disc Ca II K spectroheliograms - II. Towards an accurate assessment of long-term variations in plage areas. Astron. Astrophys. 625, A69. doi:10.1051/0004-6361/201834402
Chatzistergos, T., Ermolli, I., Krivova, N. A., Solanki, S. K., Banerjee, D., Barata, T., et al. (2020c). Analysis of full-disc Ca II K spectroheliograms. Astron. Astrophys. 639, A88. doi:10.1051/0004-6361/202037746
Chatzistergos, T., Ermolli, I., Krivova, N. A., and Solanki, S. K. (2018a). “Ca II K spectroheliograms for studies of long-term changes in solar irradiance,” in Long-term datasets for the understanding of solar and stellar magnetic cycles. vol. 340 of IAU Symposium. Editors D. Banerjee, J. Jiang, K. Kusano, and S. Solanki (Cambridge, UK: Cambridge University Press), 125–128. doi:10.1017/S1743921318001825
Chatzistergos, T., Ermolli, I., Krivova, N. A., and Solanki, S. K. (2020b). Historical solar Ca II K observations at the Kyoto and Sacramento peak observatories. J. Phys. Conf. Ser. 1548, 012007. doi:10.1088/1742-6596/1548/1/012007
Chatzistergos, T., Ermolli, I., Solanki, S. K., Krivova, N. A., Giorgi, F., and Yeo, K. L. (2019d). Recovering the unsigned photospheric magnetic field from Ca II K observations. Astron. Astrophys. 626, A114. doi:10.1051/0004-6361/201935131
Chatzistergos, T., Ermolli, I., Solanki, S. K., and Krivova, N. A. (2018b). Analysis of full disc Ca II K spectroheliograms - I. Photometric calibration and centre-to-limb variation compensation. Astron. Astrophys. 609, A92. doi:10.1051/0004-6361/201731511
Chatzistergos, T., Ermolli, I., Solanki, S. K., Krivova, N. A., Banerjee, D., Jha, B. K., et al. (2019c). Delving into the historical Ca ii K archive from the kodaikanal observatory: The potential of the most recent digitized series. Sol. Phys. 294, 145. doi:10.1007/s11207-019-1532-5
Chatzistergos, T., Ermolli, I., Solanki, S. K., and Krivova, N. A. (2016). “Exploiting four historical Ca II K spectroheliogram archives,” in Coimbra solar physics meeting: Ground-based solar observations in the space instrumentation era. Vol. 504 of astronomical society of the pacific conference series. Editors I. Dorotovic, C. E. Fischer, and M. Temmer (San Francisco: Astronomical Society of the Pacific), 227–231.
Chatzistergos, T., Krivova, N. A., Ermolli, I., Yeo, K. L., Mandal, S., Solanki, S. K., et al. (2021a). Reconstructing solar irradiance from historical Ca II K observations - I. Method and its validation. Astron. Astrophys. 656, A104. doi:10.1051/0004-6361/202141516
Chatzistergos, T., Krivova, N. A., Ermolli, I., Yeo, K. L., Solanki, S. K., Puiu, C. C., et al. (2021b). Reconstructing solar irradiance from Ca II K observations. San Francisco: ESSOAr, 3. doi:10.1002/essoar.10505862.1
Chatzistergos, T., Usoskin, I. G., Kovaltsov, G. A., Krivova, N. A., and Solanki, S. K. (2017). New reconstruction of the sunspot group numbers since 1739 using direct calibration and ”backbone” methods. Astron. Astrophys. 602, A69. doi:10.1051/0004-6361/201630045
I. Chinnici, and G. Consolmagno (Editors) (2021). “Angelo Secchi and nineteenth century science: The multidisciplinary contributions of a pioneer and innovator,” Historical & cultural Astronomy (Cham: Springer International Publishing).
Choudhary, D. P., Cadavid, A. C., Cookson, A., and Chapman, G. A. (2020). Variability in irradiance and photometric indices during the last two solar cycles. Sol. Phys. 295, 15. doi:10.1007/s11207-019-1559-7
Chowdhury, P., Belur, R., Bertello, L., and Pevtsov, A. A. (2022). Analysis of solar hemispheric chromosphere properties using the kodaikanal observatory Ca–K index. Astrophys. J. 925, 81. doi:10.3847/1538-4357/ac3983
Clette, F., and Lefèvre, L. (2016). The new sunspot number: Assembling all corrections. Sol. Phys. 291, 2629–2651. doi:10.1007/s11207-016-1014-y
Curto, J. J., Blanca, M., and Martínez, E. (2008). Automatic sunspots detection on full-disk solar images using mathematical morphology. Sol. Phys. 250, 411–429. doi:10.1007/s11207-008-9224-6
Curto, J. J., Solé, J. G., Genescà, M., Blanca, M. J., and Vaquero, J. M. (2016). Historical heliophysical series of the Ebro observatory. Sol. Phys. 291, 2587–2607. doi:10.1007/s11207-016-0896-z
Dainty, J. C., and Shaw, R. (1974). Image science. Principles, analysis and evaluation of photographic-type imaging processes. London: Academic Press.
D’Azambuja, L. (1930). Annales de l’Observatoire de Paris, Section de Meudon (Gauthier-Villars Gauthier-Villars (Paris)).
de Paula, V., Curto, J. J., and Oliver, R. (2022). The cyclic behaviour in the N-S asymmetry of sunspots and solar plages for the period 1910 to 1937 using data from Ebro catalogues. Mon. Notices R. Astronomical Soc. 512, 5726–5742. doi:10.1093/mnras/stac424
de Paula, V., Curto, J. J., and Sole, T. (2021). Application of the Markov chain model to sunspots and solar plages for the period 1910 to 1937 using data from Ebro catalogues. Sol. Phys. 296, 92. doi:10.1007/s11207-021-01838-w
de Paula, V., and Curto, J. J. (2020). The evolution over time and North–South asymmetry of sunspots and solar plages for the period 1910 to 1937 using data from Ebro catalogues. Sol. Phys. 295, 99. doi:10.1007/s11207-020-01648-6
Deng, Y., Ai, G., Wang, J., Song, G., Zhang, B., and Ye, X. (1997). Reports on test observations with the multi-channel solar telescope. Sol. Phys. 173, 207–221. doi:10.1023/a:1004960617982
Denker, C., Johannesson, A., Marquette, W., Goode, P. R., Wang, H., and Zirin, H. (1999). Synoptic Hα full-disk observations of the sun from BigBear solar observatory - I. Instrumentation, image processing, data products, and first results. Sol. Phys. 184, 87–102. doi:10.1023/A:1005047906097
Devi, P., Singh, J., Chandra, R., Priyal, M., and Joshi, R. (2021). Variation of chromospheric features as a function of latitude and time using Ca-K spectroheliograms for solar cycles 15–23: Implications for meridional flow. Sol. Phys. 296, 49. doi:10.1007/s11207-021-01798-1
Diercke, A., and Denker, C. (2019). Chromospheric synoptic maps of polar crown filaments. Sol. Phys. 294, 152. doi:10.1007/s11207-019-1538-z
Diercke, A., Kuckein, C., Cauley, P. W., Poppenhäger, K., Alvarado-Gómez, J. D., Dineva, E., et al. (2022). Solar Hα excess during solar cycle 24 from full-disk filtergrams of the chromospheric telescope. Astron. Astrophys. 661, A107. doi:10.1051/0004-6361/202040091
Dineva, E., Pearson, J., Ilyin, I., Verma, M., Diercke, A., Strassmeier, K. G., et al. (2022). Characterization of chromospheric activity based on Sun-as-a-star spectral and disk-resolved activity indices. Astron. Nachr. 343, e223996. doi:10.1002/asna.20223996
Doerr, H. P., Vitas, N., and Fabbian, D. (2016). How different are the Liège and Hamburg atlases of the solar spectrum? Astron. Astrophys. 590, A118. doi:10.1051/0004-6361/201628570
Domingo, V., Fleck, B., and Poland, A. I. (1995). The SOHO mission: An overview. Sol. Phys. 162, 1–37. doi:10.1007/BF00733425
Donnelly, R. F., Grubb, R. N., and Cowley, F. C. (1977). Solar X-ray measurements from SMS-1, SMS-2, and GOES-1, information for data users. NASA STI/Recon Tech. Rep. N. 78, 13992.
Dorotovič, I., Journoud, P., Rybák, J., and Sýkora, J. (2007). North-South asymmetry of Ca II K plages. Phys. Chromospheric Plasmas 368, 527.
Dorotovič, I., Rybák, J., Garcia, A., and Journoud, P. (2010). “North-South asymmetry of Ca II K regions determined from OAUC spectroheliograms: 1996 - 2006.” in Proceedings of the 20th National Solar Physics Meeting, 58.
El-Borie, M. A., El-Taher, A. M., Thabet, A. A., Ibrahim, S. F., Aly, N. S., and Bishara, A. A. (2020). The influence of asymmetrical distribution of hemispheric sunspot areas on some solar parameters’ periodicities during the period 1945–2017: Wavelet analysis. Astrophys. J. 898, 73. doi:10.3847/1538-4357/ab9d21
Ermolli, I., Berrilli, F., and Florio, A. (2003a). A measure of the network radiative properties over the solar activity cycle. Astron. Astrophys. 412, 857–864. doi:10.1051/0004-6361:20031479
Ermolli, I., Berrilli, F., Florio, A., and Pietropaolo, E. (1998a). “Chromospheric network properties derived from one year of PSPT images,” in Synoptic solar physics. Vol. 140 of astronomical society of the pacific conference series (San Francisco: Astronomical Society of the Pacific), 223.
Ermolli, I., Caccin, B., Centrone, M., and Penza, V. (2003b). Modeling solar irradiance variations through full-disk images and semi-empirical atmospheric models. Mem. della Soc. Astron. Ital. 74, 603.
Ermolli, I., Chatzistergos, T., Krivova, N. A., and Solanki, S. K. (2018). “The potential of Ca II K observations for solar activity and variability studies,” in Long-term datasets for the understanding of solar and stellar magnetic cycles. vol. 340 of IAU Symposium. Editors D. Banerjee, J. Jiang, K. Kusano, and S. Solanki (Cambridge, UK: Cambridge University Press), 115–120. doi:10.1017/S1743921318001849
Ermolli, I., Criscuoli, S., Centrone, M., Giorgi, F., and Penza, V. (2007). Photometric properties of facular features over the activity cycle. Astron. Astrophys. 465, 305–314. doi:10.1051/0004-6361:20065995
Ermolli, I., Criscuoli, S., and Giorgi, F. (2011). Recent results from optical synoptic observations of the solar atmosphere with ground-based instruments. Contributions Astronomical Observatory Skalnate Pleso 41, 73–84.
Ermolli, I., Criscuoli, S., Uitenbroek, H., Giorgi, F., Rast, M. P., and Solanki, S. K. (2010). Radiative emission of solar features in the Ca II K line: Comparison of measurements and models. Astron. Astrophys. 523, 55. doi:10.1051/0004-6361/201014762
Ermolli, I., and Ferrucci, M. (2021). “The legacy of angelo Secchi at the forefront of solar physics research,” in Angelo Secchi and nineteenth century science: The multidisciplinary contributions of a pioneer and innovator. Historical & cultural Astronomy. Editors I. Chinnici, and G. Consolmagno (Cham: Springer International Publishing), 123–136.
Ermolli, I., Giorgi, F., and Chatzistergos, T. (2022). Rome/PSPT: Precision solar full-disk photometry during solar cycles 23-25. Front. Astronomy Space Sci.
Ermolli, I., Marchei, E., Centrone, M., Criscuoli, S., Giorgi, F., and Perna, C. (2009a). The digitized archive of the Arcetri spectroheliograms. Preliminary results from the analysis of Ca II K images. Astron. Astrophys. 499, 627–632. doi:10.1051/0004-6361/200811406
Ermolli, I., Pietropaolo, E., Florio, A., and Berrilli, F. (1998b). “Chromospheric network properties on short time scales from PSPT images,” in Synoptic solar physics. Vol. 140 of astronomical society of the pacific conference series (San Francisco: Astronomical Society of the Pacific), 231.
Ermolli, I., Shibasaki, K., Tlatov, A., and van Driel-Gesztelyi, L. (2015). “Solar cycle indices from the photosphere to the corona: Measurements and underlying physics,” in The solar activity cycle: Physical causes and consequences. Space Sciences series of ISSI. Editors A. Balogh, H. Hudson, K. Petrovay, and R. von Steiger (New York, NY: Springer), 105–135. doi:10.1007/978-1-4939-2584-1_4
Ermolli, I., Solanki, S. K., Tlatov, A. G., Krivova, N. A., Ulrich, R. K., and Singh, J. (2009b). Comparison among Ca II K spectroheliogram time series with an application to solar activity studies. Astrophys. J. 698, 1000–1009. doi:10.1088/0004-637X/698/2/1000
Feller, A., Gandorfer, A., Iglesias, F. A., Lagg, A., Riethmüller, T. L., Solanki, S. K., et al. (2020). The SUNRISE UV Spectropolarimeter and imager for SUNRISE III. Proc. SPIE 1447, 11447AK. Conference Name: Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series ISBN: 9781510636811. doi:10.1117/12.2562666
Fligge, M., and Solanki, S. K. (1998). Long-term behavior of emission from solar faculae: Steps towards a robust index. Astronomy Astrophysics 332, 1082–1086.
Fontenla, J. M., and Landi, E. (2018). Bright network, UVA, and the physical modeling of solar spectral and total irradiance in recent solar cycles. Astrophys. J. 861, 120. doi:10.3847/1538-4357/aac388
Fossum, E. R. (1993). Active pixel sensors: Are CCDs dinosaurs? Proc. SPIE 1900, 2–14. doi:10.1117/12.148585
Foukal, P. (2012). A new look at solar irradiance variation. Sol. Phys. 279, 365–381. doi:10.1007/s11207-012-0017-6
Foukal, P., Bertello, L., Livingston, W. C., Pevtsov, A. A., Singh, J., Tlatov, A. G., et al. (2009). A century of solar Ca ii measurements and their implication for solar UV driving of climate. Sol. Phys. 255, 229–238. doi:10.1007/s11207-009-9330-0
Foukal, P. (1998). Extension of the F10.7 index to 1905 using Mt. Wilson Ca K spectroheliograms. Geophys. Res. Lett. 25, 2909–2912. doi:10.1029/98GL02057
Foukal, P., and Milano, L. (2001). A measurement of the quiet network contribution to solar irradiance variation. Geophys. Res. Lett. 28, 883–886. doi:10.1029/2000GL012072
Foukal, P. (1996). The Behavior of solar magnetic plages measured from Mt. Wilson observations between 1915-1984. Geophys. Res. Lett. 23, 2169–2172. doi:10.1029/96GL01356
Foukal, P. (1993). The curious case of the Greenwich faculae. Sol. Phys. 148, 219–232. doi:10.1007/BF00645087
Foukal, P., and Vernazza, J. (1979). The effect of magnetic fields on solar luminosity. Astrophys. J. 234, 707–715. doi:10.1086/157547
Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar Probe plus mission: Humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6
Frazier, E. N. (1971). Multi-Channel magnetograph observations. III: Faculae. Sol. Phys. 21, 42–53. doi:10.1007/BF00155772
Fredga, K. (1971). A comparison between Mg II and Ca II spectroheliograms. Sol. Phys. 21, 60–81. doi:10.1007/BF00155775
Fröhlich, C., Romero, J., Roth, H., Wehrli, C., Andersen, B. N., Appourchaux, T., et al. (1995). Virgo: Experiment for helioseismology and solar irradiance monitoring. Sol. Phys. 162, 101–128. doi:10.1007/BF00733428
Garcia, A., Sobotka, M., Klvana, M., and Bumba, V. (2011). Synoptic observations with the Coimbra spectroheliograph. Contributions Astronomical Observatory Skalnate Pleso 41, 69–72.
Giorgi, F., Ermolli, I., Centrone, M., and Marchei, E. (2005). Calibration of the Arcetri solar archive images. Mem. della Soc. Astron. Ital. 76, 977.
Goldbaum, N., Rast, M. P., Ermolli, I., Summer Sands, J., and Berrilli, F. (2009). The intensity profile of the solar supergranulation. Astrophys. J. 707, 67–73. doi:10.1088/0004-637X/707/1/67
Golovko, A. A., Golubeva, E. M., Grechnev, V. V., Myachin, D. Y., Trifonov, V. D., and Khlystova, A. I. (2002). “Data base of full solar dilk H-alpha images from the Baikal Observatory,” in Solar variability: From core to outer Frontiers (Noordwijk: ESA Publications Division), Vol. 506, 929–932.
Gray, L. J., Beer, J., Geller, M., Haigh, J. D., Lockwood, M., Matthes, K., et al. (2010). Solar influences on climate. Rev. Geophys. 48, 4001. doi:10.1029/2009RG000282
Hagenaar, H. J., Schrijver, C. J., and Title, A. M. (1997). The distribution of cell sizes of the solar chromospheric network. Astrophys. J. 481, 988–995. doi:10.1086/304066
Hale, G. E., and Ellerman, F. (1903). The rumford spectroheliograph of the Yerkes observatory. Publ. Yerkes Observatory 3, I.1–XV.2.
Hale, G. E. (1890). Note on solar prominence photography. Astr. Nachr. ;.126, 81–82. doi:10.1002/asna.18911260602
Hale, G. E. (1893). Solar photography at the Kenwood astro-physical observatory. Mem. della Soc. Degli Spettrosc. Ital. 21, 68–74.
Hale, G. E. (1891). The Kenwood physical observatory. Publ. Astron. Soc. Pac. 3, 30–34. doi:10.1086/120231
Hanaoka, Y. (2013). Long-term synoptic observations of the sun at the national astronomical observatory of Japan. J. Phys. Conf. Ser. 440, 012041. doi:10.1088/1742-6596/440/1/012041
Hanaoka, Y.Solar Observatory of NAOJ (2016). “Past and present of the synoptic observations of the sun at the national astronomical observatory of Japan,” in Coimbra solar physics meeting: Ground-based solar observations in the space instrumentation era. Vol. 504 of astronomical society of the pacific conference series. Editors I. Dorotovic, C. E. Fischer, and M. Temmer (San Francisco: Solar Observatory of NAOJ), 313.
Harvey, K. L. (1993). Magnetic bipoles on the Sun. Ph.D. thesis (Utrecht, Netherlands: Utrecht University).
Harvey, K. L. (1994). “The solar magnetic cycle,” in Solar surface magnetism. Editors R. J. Rutten, and C. J. Schrijver (London, UK: Kluwer academic publishers), Vol. 433, 347.
Harvey, K. L., and White, O. R. (1999). Magnetic and radiative variability of solar surface structures. I. Image decomposition and magnetic-intensity mapping. Astrophys. J. 515, 812–831. doi:10.1086/307035
Heath, D. F., and Schlesinger, B. M. (1986). The Mg 280-nm doublet as a monitor of changes in solar ultraviolet irradiance. J. Geophys. Res. 91, 8672–8682. doi:10.1029/JD091iD08p08672
Herschel, W. (1800). “Investigation of the powers of the prismatic colours to heat and illuminate objects; with remarks, that prove the different refrangibility of radiant heat. To which is added, an inquiry into the method of viewing the sun advantageously, with telescopes of large apertures and high magnifying powers,” in Philosophical transactions of the royal society of london series I 90. Editor L. L. William Herschel, 255–283. ADS Bibcode: 1800RSPT…90..255H.
Hochedez, J. F., Schmutz, W., Stockman, Y., Schühle, U., BenMoussa, A., Koller, S., et al. (2006). LYRA, a solar UV radiometer on Proba2. Adv. Space Res. 37, 303–312. doi:10.1016/j.asr.2005.10.041
Howard, R. (1959). Observations of solar magnitic fields. Astrophys. J. 130, 193. doi:10.1086/146708
Hubrecht, J. B. (1912). Spectrographic observations of the sun's rotation at cambridge observatory. Mon. Notices R. Astronomical Soc. 73, 5–28. doi:10.1093/mnras/73.1.5
Hurter, F., and Driffield, V. C. (1890). Photochemical investigations and a new method of determination of the sensitiveness of photographic plates. J. Soc. Chem. Industry 9, 455–469.
Intergovernmental Panel on Climate Change (2021). Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Geneva, Switzerland: Intergovernmental Panel on Climate Change. in press.
James, T. H., and Higgins, G. C. (1968). Fundamentals of photographic theory. 2nd edn. Orlando, FL, USA: Morgan and Morgan.
Janesick, J. R. (2001). Scientific charge-coupled devices. Bellingham, WA, USA: SPIE Press. Google-Books-ID: 3GyE4SWytn4C.
Jarolim, R., Veronig, A. M., Pötzi, W., and Podladchikova, T. (2020). Image-quality assessment for full-disk solar observations with generative adversarial networks. Astron. Astrophys. 643, A72. doi:10.1051/0004-6361/202038691
Jefferies, S. M., Pomerantz, M. A., Duvall, T. L., Harvey, J. W., and Jaksha, D. B. (1988). Helioseismology from the south Pole: Comparison of 1987 and 1981 results. Seismol. Sun Sun-Like Stars 286, 279–284.
Johannesson, A., Marquette, W. H., and Zirin, H. (1998). A 10-year set of CA II K-line filtergrams. Sol. Phys. 177, 265–278. doi:10.1023/A:1004940227692
Kahil, F., Riethmüller, T. L., and Solanki, S. K. (2017). Brightness of solar magnetic elements as a function of magnetic flux at high spatial resolution. Astrophys. J. Suppl. Ser. 229, 12. doi:10.3847/1538-4365/229/1/12
Kahil, F., Riethmüller, T. L., and Solanki, S. K. (2019). Intensity contrast of solar plage as a function of magnetic flux at high spatial resolution. Astron. Astrophys. 621, A78. doi:10.1051/0004-6361/201833722
Kaiser, C., Hempel, M., Schmitt, J. H. M. M., and Reiners, A. (2005). “Analysis of Ca II emission lines in active stars.” in Proceedings of the 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, 693.
Kakuwa, J., and Ueno, S. (2021). Investigation of the long-term variation of solar Ca ii K intensity. I. Density-to-intensity calibration formula for historical photographic plates. Astrophys. J. Suppl. Ser. 254, 44. doi:10.3847/1538-4365/abfbe3
Kariyappa, R., and Sivaraman, K. R. (1994). Variability of the solar chromospheric network over the solar cycle. Sol. Phys. 152, 139–144. doi:10.1007/BF01473196
Khetsuriani, T. S. (1967). Abastumani astrophysical observatory of the academy of Sciences of the Georgian SSR. Sol. Phys. 2, 237–239. doi:10.1007/BF00155927
Kiepenheuer, K. O. (1969). Fraunhofer Institut mit den Observatorien Schauinsland und Anacapri. Report 1968. Mittl. Astron. Ges. Hambg. 26, 42–47.
Kiepenheuer, K. O. (1974). Fraunhofer-Institut mit den Observatorien Schauinsland und Anacapri. Report 1973. Mittl. Astron. Ges. Hambg. 35, 60–66.
Kitai, R., Ueno, S., Maehara, H., Shirakawa, S., Katoda, M., Hada, Y., et al. (2013). The digital database of long-term solar chromospheric variation. Data Sci. J. 12, WDS213–WDS215. doi:10.2481/dsj.WDS-037
Klimeš, J., J., Bělik, M., Klimeš, S., J., and Marková, E. (1999). “Simultaneous observation of the sun in white-light, H-alpha, Ca and radio waves on observatory upice,” in 8th SOHO workshop: Plasma Dynamics and diagnostics in the solar transition region and corona. Vol. 446 of ESA special publication. Editors J. C. Vial, and B. Kaldeich-Schü, 375.
Koechlin, L., Dettwiller, L., Audejean, M., Valais, M., and Ariste, A. L. (2019). Solar survey at Pic du Midi: Calibrated data and improved images. Astron. Astrophys. 631, A55. doi:10.1051/0004-6361/201732504
Kosugi, T., Matsuzaki, K., Sakao, T., Shimizu, T., Sone, Y., Tachikawa, S., et al. (2007). The Hinode (solar-B) mission: An overview. Sol. Phys. 243, 3–17. doi:10.1007/s11207-007-9014-6
Kren, A. C., Pilewskie, P., and Coddington, O. (2017). Where does Earth’s atmosphere get its energy? J. Space Weather Space Clim. 7, A10. doi:10.1051/swsc/2017007
Krivova, N. A., and Solanki, S. K. (2004). Effect of spatial resolution on estimating the Sun’s magnetic flux. Astron. Astrophys. 417, 1125–1132. doi:10.1051/0004-6361:20040022
Krivova, N. A., Solanki, S. K., Fligge, M., and Unruh, Y. C. (2003). Reconstruction of solar irradiance variations in cycle 23: Is solar surface magnetism the cause? Astron. Astrophys. 399, L1–L4. doi:10.1051/0004-6361:20030029
Krivova, N. A. (2018). “Solar irradiance variability and Earth’s climate,” in Climate changes in the holocene (Boca Raton, FL, USA: CRC Press), 107–120. doi:10.1201/9781351260244-4
Kuriyan, P. P., Muralidharan, V., and Sampath, S. (1983). Long-term relationships between sunspots, Ca-plages and the ionosphere. J. Atmos. Terr. Phys. 45, 285–287. doi:10.1016/S0021-9169(83)80034-8
Kusano, K., Ichimoto, K., Ishii, M., Miyoshi, Y., Yoden, S., Akiyoshi, H., et al. (2021). PSTEP: Project for solar–terrestrial environment prediction. Earth Planets Space 73, 159. doi:10.1186/s40623-021-01486-1
Lawrence, J. K. (1987). Ratio of calcium plage to sunspot areas of solar active regions. J. Geophys. Res. 92, 813–817. doi:10.1029/JD092iD01p00813
Lefebvre, S., Ulrich, R. K., Webster, L. S., Varadi, F., Javaraiah, J., Bertello, L., et al. (2005). The solar photograph archive of the Mount Wilson Observatory. A resource for a century of digital data. Mem. della Soc. Astron. Ital. 76, 862.
Leighton, R. B. (1959). Observations of solar magnetic fields in plage regions. Astrophys. J. 130, 366. doi:10.1086/146727
Lenza, L., Srba, J., Gregorova, B., Exnerova, M., and Lenzova, N. (2014). System for simultaneous observation of solar flares in spectral lines of H-alpha and CaII K. Presenters: _:n17573.
Lites, B. W., Centeno, R., and McIntosh, S. W. (2014). The solar cycle dependence of the weak internetwork flux. Publ. Astronomical Soc. Jpn. 66, S4. doi:10.1093/pasj/psu082
Livingston, W. C., Harvey, J., Pierce, A. K., Schrage, D., Gillespie, B., Simmons, J., et al. (1976). Kitt Peak 60-cm vacuum telescope. Appl. Opt. 15, 33–39. doi:10.1364/AO.15.000033
Livingston, W., and Wallace, L. (2003). The Sun’s immutable basal quiet atmosphere. Sol. Phys. 212, 227–237. doi:10.1023/A:1022994002653
Livingston, W., Wallace, L., White, O. R., and Giampapa, M. S. (2007). Sun-as-a-Star spectrum variations 1974-2006. Astrophys. J. 657, 1137–1149. doi:10.1086/511127
Lockyer, W. J. S. (1909). The magnetic storm of september 25, 1909, and the associated solar disturbance : (Plates 1, 2.). Mon. Notices R. Astronomical Soc. 70, 12–19. doi:10.1093/mnras/70.1.12
Löfdahl, M. G., Henriques, V. M. J., and Kiselman, D. (2011). A tilted interference filter in a converging beam. Astron. Astrophys. 533, A82. doi:10.1051/0004-6361/201117305
Loukitcheva, M., Solanki, S. K., and White, S. M. (2009). The relationship between chromospheric emissions and magnetic field strength. Astron. Astrophys. 497, 273–285. doi:10.1051/0004-6361/200811133
Makarov, V. I., Tlatov, A. G., Singh, J., and Gupta, S. S. (2004). “22-years magnetic cycle in polar activity of the Sun,” in Multi-wavelength Investigations of solar activity. Vol. 223 of proceedings of the international astronomical union. Editors A. V. Stepanov, E. Benevolenskaya, and A. G. Kosovichev (Cambridge, UK: Cambridge University Press), 125–126. doi:10.1017/S1743921304005368
Malherbe, J. M., Corbard, T., Barbary, G., Morand, F., Collin, C., Crussaire, D., et al. (2022). Monitoring fast solar chromospheric activity: The MeteoSpace project. Exp. Astron. (Dordr). 53, 1127–1148. doi:10.1007/s10686-022-09848-7
Malherbe, J. M., and Dalmasse, K. (2019). The new 2018 version of the Meudon spectroheliograph. Sol. Phys. 294, 52. doi:10.1007/s11207-019-1441-7
Mandal, S., Chatterjee, S., and Banerjee, D. (2017a). Association of plages with sunspots: A multi-wavelength study using kodaikanal Ca ii K and Greenwich sunspot area data. Astrophys. J. 835, 158. doi:10.3847/1538-4357/835/2/158
Mandal, S., Chatterjee, S., and Banerjee, D. (2017b). Association of supergranule mean scales with solar cycle strengths and total solar irradiance. Astrophys. J. 844, 24. doi:10.3847/1538-4357/aa76e3
Mandal, S., Krivova, N. A., Solanki, S. K., Sinha, N., and Banerjee, D. (2020). Sunspot area catalog revisited: Daily cross-calibrated areas since 1874. Astron. Astrophys. 640, A78. doi:10.1051/0004-6361/202037547
Marchei, E., Ermolli, I., Centrone, M., Giorgi, F., and Perna, C. (2006). Digitization of the Arcetri solar photographic archive. Mem. della Soc. Astron. Ital. Suppl. 9, 51.
McIntosh, S. W., Leamon, R. J., Hock, R. A., Rast, M. P., and Ulrich, R. K. (2011). Observing evolution in the supergranular network length scale during periods of low solar activity. Astrophys. J. 730, L3. doi:10.1088/2041-8205/730/1/L3
Meftah, M., Corbard, T., Hauchecorne, A., Morand, F., Ikhlef, R., Chauvineau, B., et al. (2018). Solar radius determined from PICARD/SODISM observations and extremely weak wavelength dependence in the visible and the near-infrared. Astron. Astrophys. 616, A64. doi:10.1051/0004-6361/201732159
Meftah, M., Hochedez, J. F., Irbah, A., Hauchecorne, A., Boumier, P., Corbard, T., et al. (2014). Picard SODISM, a space telescope to study the sun from the middle ultraviolet to the near infrared. Sol. Phys. 289, 1043–1076. doi:10.1007/s11207-013-0373-x
Meftah, M., Irbah, A., Corbard, T., Morand, F., Thuillier, G., Hauchecorne, A., et al. (2012). PICARD SOL mission, a ground-based facility for long-term solar radius measurement. Ground-based Airborne Instrum. Astronomy IV 8446, 844676. doi:10.1117/12.925712
Mein, P., and Ribes, E. (1990). Spectroheliograms and motions of magnetic tracers. Astronomy Astrophysics 227, 577–582.
Meurs, E. J. A. (1987). Flattening the field - a user’s view. Eur. South. Observatory Conf. Workshop Proc. 25, 105–110.
Mickaelian, A. M., Nesci, R., Rossi, C., Weedman, D., Cirimele, G., Sargsyan, L. A., et al. (2007). The digitized first Byurakan survey - DFBS. Astron. Astrophys. 464, 1177–1180. doi:10.1051/0004-6361:20066241
Miller, R. A. (1965). New spectroheliograph at Manila observatory. Appl. Opt. 4, 1085–1089. doi:10.1364/ao.4.001085
Mohler, O. C., and Dodson, H. W. (1968). McMath-hulbert observatory of the university of Michigan. Sol. Phys. 5, 417–422. doi:10.1007/BF00147154
Mordvinov, A. V., Karak, B. B., Banerjee, D., Chatterjee, S., Golubeva, E. M., and Khlystova, A. I. (2020). Long-term evolution of the sun’s magnetic field during cycles 15–19 based on their proxies from kodaikanal solar observatory. Astrophys. J. 902, L15. doi:10.3847/2041-8213/abba80
Moss, W. (1942). Report of the proceedings of the (1940 and 1941), cambridge university, solar physics observatory. Mon. Notices R. Astronomical Soc. 102, 86.
Müller, D., Cyr, St.O. C., Zouganelis, I., Gilbert, H. R., Marsden, R., Nieves-Chinchilla, T., et al. (2020). The solar orbiter mission: Science overview. Astron. Astrophys. 642, A1. doi:10.1051/0004-6361/202038467
Münzer, H., Hanslmeier, A., Schröter, E. H., and Wöhl, H. (1989). “Pole-Equator-Difference of the size of the chromospheric Ca II ’ K ’ network in quiet and active solar regions,” in Solar and stellar granulation. no. 263 in NATO ASI Series. Editors R. J. Rutten, and G. Severino (Dordrecht, Netherlands: Springer Netherlands), 217–218. doi:10.1007/978-94-009-0911-3_25
Naqvi, M. F., Marquette, W. H., Tritschler, A., and Denker, C. (2010). The big bear solar observatory Ca II K-line index for solar cycle 23. Astron. Nachr. 331, 696–703. doi:10.1002/asna.201011399
Neckel, H. (1999). Spectral atlas of solar absolute disk-averaged and disk-center intensity from 3290 to 12510 Å (Brault and Neckel, 1987) now available from Hamburg observatory FTP site. Sol. Phys. 184, 421–422. doi:10.1023/A:1017165208013
Nesme-Ribes, E., Meunier, N., and Collin, B. (1996). Fractal analysis of magnetic patterns from Meudon spectroheliograms. Astronomy Astrophysics 308, 213–218.
Nindos, A., and Zirin, H. (1998). The relation of CA II K features to magnetic field. Sol. Phys. 179, 253–268. doi:10.1023/A:1005046114362
Ortiz, A., and Rast, M. (2005). How good is the Ca II K as a proxy for the magnetic flux? Mem. della Soc. Astron. Ital. 76, 1018.
Penza, V., Berrilli, F., Bertello, L., Cantoresi, M., Criscuoli, S., and Giobbi, P. (2022). Total solar irradiance during the last five centuries. Astrophys. J. 937, 84. doi:10.3847/1538-4357/ac8a4b
Penza, V., Berrilli, F., Bertello, L., Cantoresi, M., and Criscuoli, S. (2021). Prediction of sunspot and plage coverage for solar cycle 25. Astrophys. J. Lett. 922, L12. doi:10.3847/2041-8213/ac3663
Penza, V., Caccin, B., Ermolli, I., Centrone, M., and Gomez, M. T. (2003). “Modeling solar irradiance variations through PSPT images and semiempirical models,” in Solar variability as an input to the Earth’s environment. Vol. 535 of ESA special publication. Editor A. Wilson (Noordwijk: ESA Publications Division), 299–302.
Pesnell, W. D., Thompson, B. J., and Chamberlin, P. C. (2012). The solar Dynamics observatory (SDO). Sol. Phys. 275, 3–15. doi:10.1007/s11207-011-9841-3
Pevtsov, A. A., Virtanen, I., Mursula, K., Tlatov, A., and Bertello, L. (2016). Reconstructing solar magnetic fields from historical observations. I. Renormalized Ca K spectroheliograms and pseudo-magnetograms. Astron. Astrophys. 585, A40. doi:10.1051/0004-6361/201526620
Pevtsov, A., Griffin, E., Grindlay, J., Kafka, S., Bartlett, J., Usoskin, I., et al. (2019). Historical astronomical data: Urgent need for preservation, digitization enabling scientific exploration. Bull. Am. Astronomical Soc. 51, 190. ADS Bibcode: 2019BAAS…51c.190P.
Pierce, A. K., and Slaughter, C. D. (1977). Solar limb darkening. Sol. Phys. 51, 25–41. doi:10.1007/BF00240442
Pietropaolo, E., and Ermolli, I. (1998). Chromospheric intensity oscillations from Ca II K OAR/PSPT images. Mem. della Soc. Astron. Ital. 69, 583.
Pötzi, W., Veronig, A., Jarolim, R., Rodríguez Gómez, J. M., Podlachikova, T., Baumgartner, D., et al. (2021). Kanzelhöhe observatory: Instruments, data processing and data products. Sol. Phys. 296, 164. doi:10.1007/s11207-021-01903-4
Priyal, M., Singh, J., Belur, R., and Rathina, S. K. (2017). Long-term variations in the intensity of plages and networks as observed in kodaikanal Ca-K digitized data. Sol. Phys. 292, 85. doi:10.1007/s11207-017-1106-3
Priyal, M., Singh, J., Ravindra, B., Priya, T. G., and Amareswari, K. (2014). Long term variations in chromospheric features from Ca-K images at kodaikanal. Sol. Phys. 289, 137–152. doi:10.1007/s11207-013-0315-7
Priyal, M., Singh, J., Ravindra, B., and Shekar B, C. (2019). Periodic and quasi-periodic variations in the Ca K index during the 20th century using kodaikanal data. Sol. Phys. 294, 131. doi:10.1007/s11207-019-1522-7
Pruthvi, H., and Ramesh, K. B. (2015). Two-channel imaging system for the white light active region monitor (WARM) telescope at kodaikanal observatory: Design, development, and first images. Int. Conf. Opt. Photonics 9654, 96540I. doi:10.1117/12.2182889
Puiu, C. C. (2019). Modeling solar irradiance variations on timescales from day to solar cycle with ground-based observations. Master’s thesis (Rome: Sapienza – University of Rome).
Raghavan, N. (1983). A quantitative study of CA II network geometry. Sol. Phys. 89, 35–42. doi:10.1007/BF00211950
Rajani, G., Sowmya, G. M., Paniveni, U., and Srikanth, R. (2022). Solar supergranular fractal dimension dependence on the solar cycle phase. Res. Astronomy Astrophysics 22, 045006. doi:10.1088/1674-4527/ac5020
Raju, K. P. (2020). Asymmetry in the length scales of the solar supergranulation network. Astrophys. J. 899, L35. doi:10.3847/2041-8213/abacb7
Raju, K. P., and Singh, J. (2014). Network and plage indices from Kodaikanal Ca-K data. Res. Astron. Astrophys. 14, 229–232. doi:10.1088/1674-4527/14/2/010
Raju, K. P., Srikanth, R., and Singh, J. (1998). The dependence of chromospheric CA II K network cell sizes on solar latitude. Sol. Phys. 180, 47–51. doi:10.1023/a:1005072907000
Rast, M. P., Ortiz, A., and Meisner, R. W. (2008). Latitudinal variation of the solar photospheric intensity. Astrophys. J. 673, 1209–1217. doi:10.1086/524655
Rast, M. P. (2003). The scales of granulation, mesogranulation, and supergranulation. Astrophys. J. 597, 1200–1210. doi:10.1086/381221
Ravindra, B., Chowdhury, P., and Javaraiah, J. (2021). Solar-cycle characteristics in kodaikanal sunspot area: North–South asymmetry, phase distribution and gnevyshev gap. Sol. Phys. 296, 2. doi:10.1007/s11207-020-01744-7
Rezaei, R., Schlichenmaier, R., Beck, C. A. R., Bruls, J. H. M. J., and Schmidt, W. (2007). Relation between photospheric magnetic field and chromospheric emission. Astron. Astrophys. 466, 1131–1144. doi:10.1051/0004-6361:20067017
Rincon, F., and Rieutord, M. (2018). The Sun’s supergranulation. Living Rev. Sol. Phys. 15, 6. doi:10.1007/s41116-018-0013-5
Schatten, K. H., Miller, N., Sofia, S., Endal, A. S., and Chapman, G. (1985). The importance of improved facular observations in understanding solar constant variations. Astrophys. J. 294, 689. doi:10.1086/163339
Schrijver, C. J., Cote, J., Zwaan, C., and Saar, S. H. (1989). Relations between the photospheric magnetic field and the emission from the outer atmospheres of cool stars. I - the solar CA II K line core emission. Astrophys. J. 337, 964–976. doi:10.1086/167168
Seetha, S., and Megala, S. (2017). Aditya-L1 mission. Curr. Sci. 113, 610. doi:10.18520/cs/v113/i04/610-612
Seguí, A., Curto, J. J., Paula, V. d., Rodríguez-Gasén, R., and Vaquero, J. M. (2019). Temporal variation and asymmetry of sunspot and solar plage types from 1930 to 1936. Adv. Space Res. 63, 3738–3748. doi:10.1016/j.asr.2019.02.018
Shapiro, A. I., Solanki, S. K., Krivova, N. A., Cameron, R. H., Yeo, K. L., and Schmutz, W. K. (2017). The nature of solar brightness variations. Nat. Astron. 1, 612–616. doi:10.1038/s41550-017-0217-y
Sheeley, N. R., Cooper, T. J., and Anderson, J. R. L. (2011). Carrington maps of Ca II K-line emission for the years 1915-1985. Astrophys. J. 730, 51. doi:10.1088/0004-637X/730/1/51
Shimizu, T., Imada, S., Kawate, T., Suematsu, Y., Hara, H., Tsuzuki, T., et al. (2020). “The solar-C (EUVST) mission: The latest status,” in Space telescopes and instrumentation 2020: Ultraviolet to gamma ray (proc. SPIE), Vol. 11444, 114440N. doi:10.1117/12.2560887
Shin, G., Moon, Y. J., Park, E., Jeong, H., Lee, H., and Bae, S. H. (2020). Generation of high-resolution solar pseudo-magnetograms from Ca II K images by deep learning. Astrophys. J. 895, L16. doi:10.3847/2041-8213/ab9085
Simon, G. W., and Leighton, R. B. (1964). Velocity fields in the solar atmosphere. III. Large-scale motions, the chromospheric network, and magnetic fields. Astrophys. J. 140, 1120. doi:10.1086/148010
Singh, J., and Bappu, M. K. V. (1981). A dependence on solar cycle of the size of the Ca/+/network. Sol. Phys. 71, 161–168. doi:10.1007/BF00153615
Singh, J., Belur, R., Raju, S., Pichaimani, K., Priyal, M., Gopalan Priya, T., et al. (2012). “Determination of the chromospheric quiet network element area index and its variation between 2008 and 2011” (RAA, Vol. 12, p.201 [2012]). Res. Astronomy Astrophysics 12, 472. doi:10.1088/1674-4527/12/4/011
Singh, J., Priyal, M., Ravindra, B., Bertello, L., and Pevtsov, A. A. (2022). On the application of the equal-contrast technique to Ca-K data from kodaikanal and other observatories. Astrophys. J. 927, 154. doi:10.3847/1538-4357/ac4e82
Singh, J., Priyal, M., and Ravindra, B. (2021). Determining the variations of Ca–K index and features using century-long equal-contrast images from kodaikanal observatory. Astrophys. J. 908, 210. doi:10.3847/1538-4357/abd021
Singh, J., Priyal, M., Sindhuja, G., and Ravindra, B. (2018). Variations in Ca-K line profiles and Ca-K line features as a function of latitude and solar cycle during the 20th century. Proc. Int. Astron. Union 13, 23–26. doi:10.1017/S1743921318001540
Singh, J., and Ravindra, B. (2012). Twin telescope observations of the sun at kodaikanal observatory. Bull. Astronomical Soc. India 40.
Skumanich, A., Smythe, C., and Frazier, E. N. (1975). On the statistical description of inhomogeneities in the quiet solar atmosphere. I - linear regression analysis and absolute calibration of multichannel observations of the Ca/+/emission network. Astrophys. J. 200, 747–764. doi:10.1086/153846
Snow, M., Weber, M., Machol, J., Viereck, R., and Richard, E. (2014). Comparison of Magnesium II core-to-wing ratio observations during solar minimum 23/24. J. Space Weather Space Clim. 4, A04. doi:10.1051/swsc/2014001
Solanki, S. K., Barthol, P., Danilovic, S., Feller, A., Gandorfer, A., Hirzberger, J., et al. (2010). SUNRISE: Instrument, mission, data, and first results. Astrophys. J. 723, L127–L133. doi:10.1088/2041-8205/723/2/L127
Solanki, S. K., Krivova, N. A., and Haigh, J. D. (2013). Solar irradiance variability and climate. Annu. Rev. Astron. Astrophys. 51, 311–351. doi:10.1146/annurev-astro-082812-141007
Solanki, S. K., Riethmüller, T. L., Barthol, P., Danilovic, S., Deutsch, W., Doerr, H. P., et al. (2017). The second flight of the Sunrise balloon-borne solar observatory: Overview of instrument updates, the flight, the data, and first results. Astrophys. J. Suppl. Ser. 229, 2. doi:10.3847/1538-4365/229/1/2
Solanki, S. K., Schüssler, M., and Fligge, M. (2002). Secular variation of the Sun’s magnetic flux. Astron. Astrophys. 383, 706–712. doi:10.1051/0004-6361:20011790
Sotnikova, R. T. (1978). Statistical analysis of the intensity fluctuations of the undisturbed chromosphere in the H-alpha and CA II K lines. Sov. Astron. Lett. 4, 246–249. ADS Bibcode: 1978SvAL….4..246S.
Steinegger, M., Brandt, P. N., and Haupt, H. F. (1996a). Sunspot irradiance deficit, facular excess, and the energy balance of solar active regions. Astronomy Astrophysics 310, 635–645.
Steinegger, M., Vazquez, M., Bonet, J. A., and Brandt, P. N. (1996b). On the energy balance of solar active regions. Astrophys. J. 461, 478. doi:10.1086/177075
Suo, L. (2020). A full-disk image standardization of the chromosphere observation at Huairou Solar Observing Station. Adv. Space Res. 65, 1054–1061. doi:10.1016/j.asr.2019.10.035
Svalgaard, L., and Schatten, K. H. (2016). Reconstruction of the sunspot group number: The backbone method. Sol. Phys. 291, 2653–2684. doi:10.1007/s11207-015-0815-8
Tähtinen, I., Virtanen, I., Pevtsov, A., and Mursula, K. (2022). Reconstructing solar magnetic fields from historical observations. VIII. AIA 1600 Å contrast as a proxy of solar magnetic fields. Astron. Astrophys. 664, A2. doi:10.1051/0004-6361/202141164
Tapping, K. F., and Morton, D. C. (2013). The next generation of Canadian solar flux monitoring. J. Phys. Conf. Ser. 440, 012039. doi:10.1088/1742-6596/440/1/012039
Teston, F., and Creasey, R. (1997). “PROBA - project for onboard Autonomy,” in Data systems in aerospace - DASIA 97. Editor T. D. Guyenne (Paris, France: European Space Agency), Vol. 409, 109.
Tlatov, A. G., Dormidontov, D. V., Kirpichev, R. V., Pashchenko, M. P., and Shramko, A. D. (2015). Synoptic and fast events on the sun according to observations at the center and wings of the Ca II K line at the Kislovodsk Mountain station patrol telescope. Geomagn. Aeron. 55, 961–968. doi:10.1134/s0016793215070245
Tlatov, A. G., Pevtsov, A. A., and Singh, J. (2009). A new method of calibration of photographic plates from three historic data sets. Sol. Phys. 255, 239–251. doi:10.1007/s11207-009-9326-9
Tlatov, A. G., and Tlatova, K. A. (2019). Polar activity of the sun and latitudinal activity drifts in cycles 15–24. Geomagn. Aeron. 59, 1016–1021. doi:10.1134/S0016793219080218
Tripathi, D., Ramaprakash, A. N., Khan, A., Ghosh, A., Chatterjee, S., Banerjee, D., et al. (2017). The solar ultraviolet imaging telescope on-board aditya-L1. Curr. Sci. 113, 616. doi:10.18520/cs/v113/i04/616-619
Usoskin, I. G., Kovaltsov, G. A., Lockwood, M., Mursula, K., Owens, M., and Solanki, S. K. (2016). A new calibrated sunspot group series since 1749: Statistics of active day fractions. Sol. Phys. 291, 2685–2708. doi:10.1007/s11207-015-0838-1
Vaquero, J. M., Gallego, M. C., Acero, F. J., and García, J. A. (2007). “Spectroheliographic observations in Madrid (1912 – 1917),” in The physics of chromospheric plasmas. Vol. 368 of astronomical society of the pacific conference series. Editors P. Heinzel, I. Dorotovic, and R. J. Rutten, 17–20.
Vaquero, J. M., Svalgaard, L., Carrasco, V. M. S., Clette, F., Lefèvre, L., Gallego, M. C., et al. (2016). A revised collection of sunspot group numbers. Sol. Phys. 291, 3061–3074. doi:10.1007/s11207-016-0982-2
Vaquero, J. M., and Vázquez, M. (2009). The Sun recorded through history: Scientific data extracted from historical documents, vol. 361 of Astrophysics and space science library. New York, NY: Springer New York.
Veronig, A. M., Jain, S., Podladchikova, T., Pötzi, W., and Clette, F. (2021). Hemispheric sunspot numbers 1874–2020. Astron. Astrophys. 652, A56. doi:10.1051/0004-6361/202141195
Veronig, A., Steinegger, M., Otruba, W., Hanslmeier, A., Messerotti, M., Temmer, M., et al. (2000). Automatic image processing in the frame of a solar flare alerting system. Hvar. Obs. Bull. 24, 195–205. ISSN: 0351-2657.
Volobuev, D. M. (2009). The shape of the sunspot cycle: A one-parameter fit. Sol. Phys. 258, 319–330. doi:10.1007/s11207-009-9429-3
Waldmeier, M. (1968). The Swiss federal observatory, Zürich. Sol. Phys. 5, 423–426. doi:10.1007/BF00147155
Walton, S. R., Chapman, G. A., Cookson, A. M., Dobias, J. J., and Preminger, D. G. (1998). Processing photometric full-disk solar images. Sol. Phys. 179, 31–42. doi:10.1023/A:1005070932205
Walton, S. R., Preminger, D. G., and Chapman, G. A. (2003). The contribution of faculae and network to long-term changes in the total solar irradiance. Astrophys. J. 590, 1088–1094. doi:10.1086/375022
Wang, T. C., Liu, M. Y., Zhu, J. Y., Tao, A., Kautz, J., and Catanzaro, B. (2018). High-resolution image synthesis and semantic manipulation with conditional GANs. arXiv:1711.11585 [cs] ArXiv: 1711.11585.
Wang, Y. M., and Sheeley, N. R. (1992). On potential field models of the solar corona. Astrophys. J. 392, 310–319. doi:10.1086/171430
Watanabe, T. (2014). “The solar-C mission,” in Space telescopes and instrumentation 2014: Optical, infrared, and millimeter wave (proc. Of SPIE), Vol. 9143, 91431O. doi:10.1117/12.2055366
Wells, D. C., Greisen, E. W., and Harten, R. H. (1981). FITS - a flexible image Transport system. Astronomy Astrophysics Suppl. Ser. 44, 363.
White, O. R., Livingston, W. C., Keil, S. L., and Henry, T. W. (1998). “Variability of the solar call K line over the 22 Year Hale cycle,” in ASP conference series (San Francisco: Astronomical Society of the Pacific), Vol. 140, 293.
White, O. R., and Livingston, W. C. (1981). Solar luminosity variation. III - calcium K variation from solar minimum to maximum in cycle 21. Astrophys. J. 249, 798–816. doi:10.1086/159338
White, O. R., and Livingston, W. (1978). Solar luminosity variation. II - behavior of calcium H and K at solar minimum and the onset of cycle 21. Astrophys. J. 226, 679–686. doi:10.1086/156650
Wiegelmann, T., Thalmann, J. K., and Solanki, S. K. (2014). The magnetic field in the solar atmosphere. Astron. Astrophys. Rev. 22, 78. doi:10.1007/s00159-014-0078-7
Willamo, T., Usoskin, I. G., and Kovaltsov, G. A. (2017). Updated sunspot group number reconstruction for 1749–1996 using the active day fraction method. Astron. Astrophys. 601, A109. doi:10.1051/0004-6361/201629839
Wöhl, H. (2005). The Old Archives of Solar Images of the Former Frauenhofer Institut (now: Kiepenheuer-Institut für Sonnenphysik, KIS). Hvar. Obs. Bull. 29, 319–328.
Wolf, R. (1850). Mittheilungen über die Sonnenflecken I. Astron. Mittl. Eidgenössischen Sternwarte Zurich 1, 3–13.
Woods, T. N., Tobiska, W. K., Rottman, G. J., and Worden, J. R. (2000). Improved solar Lyman α irradiance modeling from 1947 through 1999 based on UARS observations. J. Geophys. Res. 105, 27195–27215. doi:10.1029/2000JA000051
Worden, J. R., White, O. R., and Woods, T. N. (1998a). Evolution of chromospheric structures derived from Ca II K spectroheliograms: Implications for solar ultraviolet irradiance variability. Astrophys. J. 496, 998–1014. doi:10.1086/305392
Worden, J. R., White, O. R., and Woods, T. N. (1998b). Plage and enhanced network indices derived from Ca II K spectroheliograms. Sol. Phys. 177, 255–264. doi:10.1023/a:1004921707249
Xu, H., Lei, B., and Li, Z. (2021). A reconstruction of total solar irradiance based on wavelet analysis. Earth Space Sci. 8, e2021EA001819. doi:10.1029/2021EA001819
Yeo, K. L., Krivova, N. A., Solanki, S. K., and Glassmeier, K. H. (2014). Reconstruction of total and spectral solar irradiance from 1974 to 2013 based on KPVT, SoHO/MDI, and SDO/HMI observations. Astron. Astrophys. 570, A85. doi:10.1051/0004-6361/201423628
Yeo, K. L., Solanki, S. K., and Krivova, N. A. (2020a). How faculae and network relate to sunspots, and the implications for solar and stellar brightness variations. Astron. Astrophys. 639, A139. doi:10.1051/0004-6361/202037739
Yeo, K. L., Solanki, S. K., Krivova, N. A., Rempel, M., Anusha, L. S., Shapiro, A. I., et al. (2020b). The dimmest state of the sun. Geophys. Res. Lett. 47, e2020GL090243. doi:10.1029/2020GL090243
Yeo, K. L., Solanki, S. K., Norris, C. M., Beeck, B., Unruh, Y. C., and Krivova, N. A. (2017). Solar irradiance variability is caused by the magnetic activity on the solar surface. Phys. Rev. Lett. 119, 091102. doi:10.1103/PhysRevLett.119.091102
Zharkova, V. V., Ipson, S. S., Zharkov, S. I., Benkhalil, A., Aboudarham, J., and Bentley, R. D. (2003). A full-disk image standardisation of the synoptic solar observations at the Meudon Observatory. Sol. Phys. 214, 89–105. doi:10.1023/A:1024081931946
Zhu, G., Lin, G., Wang, D., and Yang, X. (2020). A new approach for the regression of the center coordinates and radius of the solar disk using a deep convolutional neural network. Astrophys. J. 902, 72. doi:10.3847/1538-4357/abb2a0
Keywords: solar observation, solar chromosphere, solar activity, plages sun: sunspots, solar irradiance, solar magnetism
Citation: Chatzistergos T, Krivova NA and Ermolli I (2022) Full-disc Ca ii K observations—A window to past solar magnetism. Front. Astron. Space Sci. 9:1038949. doi: 10.3389/fspas.2022.1038949
Received: 07 September 2022; Accepted: 24 October 2022;
Published: 17 November 2022.
Edited by:
Mausumi Dikpati, High Altitude Observatory (UCAR), United StatesReviewed by:
João Manuel Fernandes, University of Coimbra, PortugalClementina Sasso, Astronomical Observatory of Capodimonte (INAF), Italy
Copyright © 2022 Chatzistergos, Krivova and Ermolli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Theodosios Chatzistergos, Y2hhdHppc3Rlcmdvc0BtcHMubXBnLmRl
 Theodosios Chatzistergos
Theodosios Chatzistergos Natalie A. Krivova1
Natalie A. Krivova1 Ilaria Ermolli
Ilaria Ermolli