S. C. Chapman1,2*- 1Centre for Fusion, Space and Astrophysics, University of Warwick, Coventry, United Kingdom
- 2Department of Mathematics and Statistics, University of Tromso, Tromso, Norway
Sunspot records reveal that whilst the Sun has an approximately 11 year cycle of activity, no two cycles are of the same duration. Since this activity is a direct driver of space weather at Earth, this presents an operational challenge to quantifying space weather risk. We recently showed that the Hilbert transform of the sunspot record can be used to map the variable cycle length onto a regular “clock” where each cycle has the same duration in Hilbert analytic phase. Extreme geomagnetic storms rarely occur within the quiet part of the cycle which is a fixed interval of analytic phase on the clock; there is a clear active-quiet switch-off and quiet-active switch-on of activity. Here we show how the times of the switch-on/off can be determined directly from the sunspot time-series, without requiring a Hilbert transform. We propose a method-charting-that can be used to combine observations, and reports of societal impacts, to improve our understanding of space weather risk.
1 Introduction
Extreme space weather storms can disrupt power distribution, communication, aviation and satellites. They are directly driven by solar activity, but the severity of the technological and societal impact of a geomagnetic storm depends on many factors, from the amplitude of structure emitted from the corona, to how it propagates from Sun to Earth, how it interacts with the magnetosphere of the Earth (Yermolaev et al., 2013; Hathaway, 2015; Baker and Lanzerotti, 2016), and where geographically the maximum ground induced currents occur (Thomson et al., 2010). The largest events can result in significant societal impact and financial loss (Oughton et al., 2016; Oughton et al., 2017; Hapgood, 2019).
Decision making for mitigating the effects of space weather is supported by 1) forecasts of individual events that use modelling to map forwards in time a prediction of how a given space weather event will evolve in time and 2) risk estimates, that is, probabilistic estimates of the likelihood of occurrence of events of a given severity. The first of these supports real-time operational decisions, whereas the latter provides guidance on planning and preparedness which necessarily must balance resilience against cost. It is the latter that is the topic of this paper.
Risk estimates for extreme space weather events are usually aggregated over multiple solar cycles, (Siscoe, 1976; Silbergleit, 1996; Silbergleit, 1999; Thomson et al., 2011; Riley, 2012; Riley and Love, 2016; Chapman et al., 2020a), which improves the statistical sample size at the expense of averaging over different levels of solar activity. Risk estimates suggest that geomagnetic storms are more likely in the active phase of the cycle (Tsubouchi and Omura, 2007) and this solar cycle modulation appears to be stronger for the more extreme events (Tsurutani et al., 2006; Chapman et al., 2020b). However, extreme events are rare, so that statistical quantification of the solar cycle variation of their occurrence probability is challenging (Riley and Love, 2016).
Each solar cycle differs in its duration and amplitude [see e.g., (Hathaway, 2015; Russell et al., 2019)] and overall geomagnetic activity tracks this variation both within and between solar cycles (Chapman et al., 2018b; Lockwood et al., 2018; Bergin et al., 2022). Quantifying the solar cycle dependence of the risk of extreme space weather events therefore requires timing the start and end of each 11 year cycle. Sunspot data can be used to time solar cycles [e.g., Owens et al. (2011)] to facilitate comparison of long-term observations across multiple cycles. Cycle terminators (McIntosh et al., 2014; McIntosh and Leamon, 2014; McIntosh et al., 2019) have been identified based on multiple observations of coronal magnetic activity, they coincide with a rapid “switch-on” of activity. Recently Chapman et al. (2020b) used the Hilbert transform of smoothed sunspot number (SSN) to map the non-uniform duration solar cycle onto a uniform interval 2π of analytic phase. This provides a regular clock for the solar cycle which can be used to organise long-term observations of solar and geomagnetic activity. From the solar clock, a clear quiet interval in the solar cycle can be identified, with a switch-on of activity at the terminators, and a switch-off that occurs at an analytic phase
In this paper we will map back from the phase of the solar cycle clock to the time domain. This provides a cycle-by-cycle chart which can be used to integrate heterogeneous information. On the one hand, long-term observations, such as the time-series of geomagnetic indices, can form the basis of statistical quantification of risk (i.e., event return times). On the other hand, information that is partially qualitative, such as reports of technological impacts, historical auroral sightings, and lists of the most severe storms based on a variety of indicators [e.g., Knipp et al. (2021); Cliver and Svalgaard (2004)], contain valuable information about the potential hazard [e.g., Mitchell-Wallace et al. (2017)], of extreme space weather events. Charting provides a method to combine this information.
Extreme events have occurred in quiet conditions so that their risk is never zero (Thomson et al., 2010). There have been several instances where extreme storms have occurred under relatively quiet conditions, that is, not at solar maximum. The most notable of these are the 1903 event (Hayakawa et al., 2020) and the 2012 Carrington class storm that missed the Earth (Baker et al., 2013). We will see that these are examples of events that did not occur during the quiet interval, but that can occur just before/after the switch-off/on of activity.
Quantifying, and potentially predicting, the switch-off and switch-on of activity is thus of key importance to space weather resilience planning. It has the potential to translate an overall awareness of a solar cycle modulation of risk, into a quantitative estimate of the specific time intervals when the risk is high or low. Whilst it is possible to directly extrapolate the analytic phase forwards to make a prediction (Leamon et al., 2020), the well known edge effects of the Hilbert transform [e.g., Boashash (1992)] can introduce subtle systematic errors (Booth, 2021; Leamon et al., 2021). In this paper we show how the switch-on and switch-off can be directly estimated from the SSN time-series, without recourse to a Hilbert transform.
The organization of the paper is as follows. Section 2 introduces the data and provides a brief summary of how the Sun clock is constructed using Hilbert transform of the sunspot number (SSN) record. Section 3.1 details how the solar cycle switch-on and switch-off times can be directly read-off the SSN time-series. Section 3.2 discusses charting as a method to integrate heterogeneous data. This is followed by a summary.
2 Methods
2.1 Data
We will determine the activity switch-on and switch-off times direct from the SILSO SSN version 2.0 record. Monthly sunspot observations are available since 1749 and daily sunspot number are available since 1818; data downloaded to 28 August 2022. To identify active times we will use geomagnetic indices definitive and preliminary data. The aa index is available since 1868, downloaded to 28 August 2022 and the Dst index is available since 1957, downloaded to 31 December 2021. The aa index (units, nT) (Mayaud, 1980) is discretized in amplitude (Bubenik and Fraser-Smith, 1977; Chapman et al., 2020a) so that throughout this paper we will consider days within which the aa exceeds a given threshold as an activity indicator, rather than the peak aa value. Other data and lists of events will be introduced as they are used.
2.2 Solar clock via Hilbert transform
A time-series S(t) can be expressed in terms of a time-varying amplitude A(t) and phase ϕ(t) by obtaining its analytic signal (Gabor, 1946; Boashash, 1992) A(t) exp [iϕ(t)] = S(t) + iH(t) where H(t) is the Hilbert transform of S(t). It is routinely used to test for synchronisation [e.g., Chapman et al. (2018a)] and for amplitude-frequency (Palŭs and Notovna, 1999) and mode-mode (Vecchio et al., 2017) relationships. Here it maps the variable duration of each solar cycle into a corresponding uniform 0 to 2π phase interval.
In this paper we will use both daily and monthly sunspot number for S(t). After 1818, we construct the solar cycle clock using daily sunspot number as described in Chapman et al. (2020b), again working with the 180 days smoothed daily sunspot number. Post 1749, we work with the 13 month smoothed monthly sunspot number. For both these time-series we obtain the slow trend by performing a robust local linear regression which down-weights outliers (“rlowess”) using a 40 year span (or window). The procedure is shown in Figure 1 for the monthly sunspot number record. Panel (a) plots the monthly sunspot number (black dots), its 13 month running mean (red line) and the 40 year slow trend (blue). We found previously [Figure 13 of (Chapman et al., 2021)] that this slow trend simply tracks the Gleissberg cycle (Gleissberg, 1967). The results are robust for a reasonable range of the spans over which the running mean and slow trend are obtained, the times of occurrence of the terminators obtained from the monthly sunspot number vary within ±2 months for running mean span in the range 6–25 months and for slow trend span in the range 30–60 years.
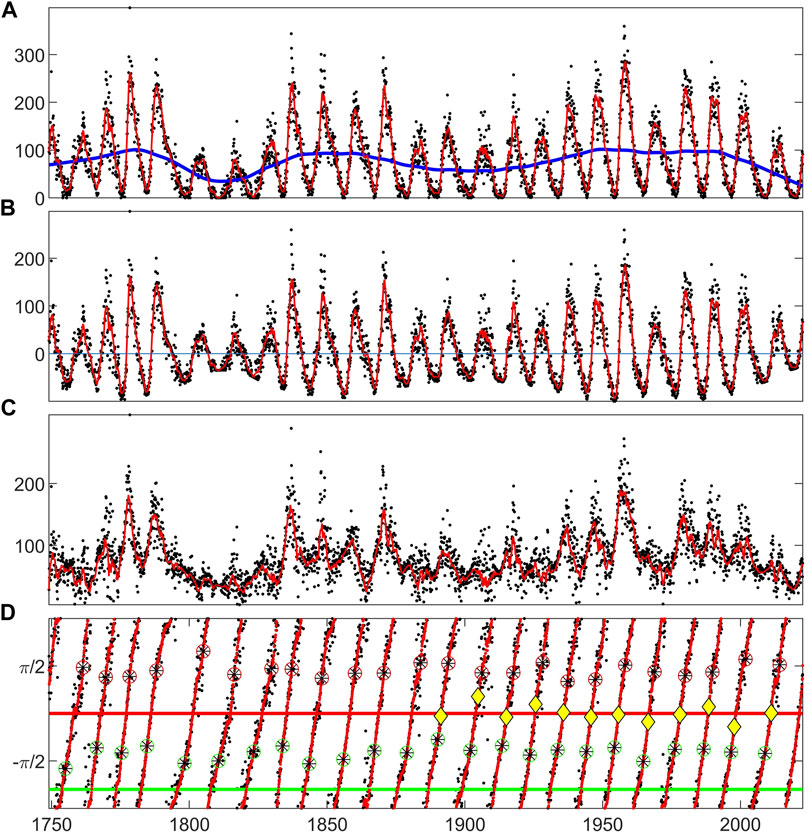
FIGURE 1. Analytic signal of the monthly sunspot record time-series. Monthly sunspot number (black dots) and its 13 month running mean (red) are plotted: (A) with the slow trend (blue), the 40 year window local linear regression of monthly sunspot number. (B) with the slow trend subtracted. This is Hilbert transformed to obtain the analytic signal with amplitude (C) and phase (D). In (D), solar maxima and minima are indicated by the red and green circled asterisks respectively, terminators by yellow diamonds. Zero phase is set at the average of the terminator times from McIntosh et al. (2019). Horizontal lines are at phases zero (terminator, red) and −4π/5 (pre-terminator, green).
For the analytic signal to be meaningful we require an oscillatory, albeit irregular, signal that crosses zero every half cycle as input. We therefore work with the SSN smoothed sufficiently to remove fast fluctuations from which a slow trend is then subtracted [see e.g., Chapman et al. (2018a); Boashash (1992); Chapman et al. (2020b)]. Panel (b) plots the slow trend subtracted 13 month running average smoothed SSN. This is Hilbert transformed and panel (c) and (d) plot the analytic signal amplitude A(t) and phase ϕ(t) respectively. We can plot any other quantity on these plots for which we have an occurrence time, here, we plot the solar maxima and minima (red/green circles around black asterisks). The yellow diamonds indicate cycle terminators identified in (McIntosh et al., 2019); we set zero phase at the average of these.
The switch-off (pre-terminators) and switch-on (terminators) [see Chapman et al. (2020b)] are at analytic phases −4π/5 and zero, indicated by horizontal green and red and lines respectively on Panel (d) of Figure 1. These bracket the quiet intervals of each solar cycle. They are identified by inspection of the solar cycle clock as shown here in Figure 2 [see Chapman et al. (2020b) for a statistical analysis]. The Figure 2 solar cycle clock summarizes the rationale for these particular values of analytic phase; it is a composite of results presented in (Chapman et al., 2020b) which has also been updated with current data. The clock plots as its angular coordinate the analytic phase with time increasing clockwise. It has been constructed from the daily SSN since 1818 and can overplot observations from the last 18 Schwabe cycles. The maxima and minima of these 18 cycles are shown in red and green circles respectively, along with their average phases (black lines). The terminators, identified for the last 12 cycles by McIntosh et al. (2019) are plotted (blue circles) with their average (red line). The terminator average phase estimates the switch-on of activity.
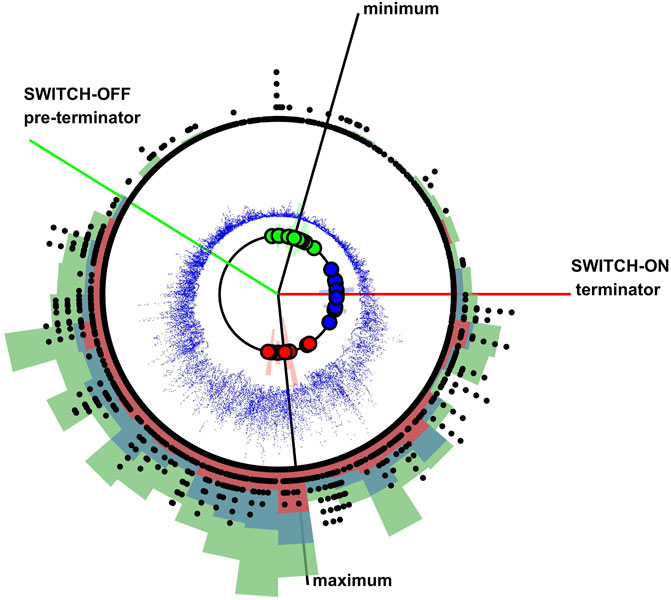
FIGURE 2. Solar cycle clock. Increasing time (analytic phase) is read clockwise. The clock shown is obtained from the daily sunspot number record since 1818. Analytic phases of the maxima and minima of the last 18 solar cycles are indicated by red and green circles respectively and the blue circles indicate terminators for the last 12 solar cycles (McIntosh et al., 2019). Black lines indicate the average analytic phase for the maxima and minima. A red line indicates the average analytic phase of the terminators. The pre-terminator (green line) is at a phase −4π/5 w.r.t. the terminator. Black dots arranged on concentric circles where increasing radius indicates aa values which in any given day exceeded 100, 200, 300, 400, 500, 600 nT. Blue dots overplot daily F10.7 and overplotted red, blue and green histograms show counts in non-overlapping (normalized) 3-month long bins for X-class, M-Class and C-class flare occurrence (scaled relative to each other in ratio 75:500:2000).
We plot long-term observations on the clock; binned occurrences of solar flares (6 month binned GOES X-ray flux catalog, four cycles), the F10.7 index time-series [daily solar radio flux at 10.7 cm, six cycles (Tapping, 2013)] (blue dots). Activity in the aa index (14 cycles) is indicated by plotting black dots arranged on concentric circles at any day when aa > 100, 200, 300, 400, 500, 600 nT so that extreme events appear as outward radiating “spokes”. We can then see that there is an increase (switch-on) in activity just following the terminator. By inspection, activity declines (switch-off) around the pre-terminator (green line) which we simply identified as being −4π/5 in phase w.r.t the terminator, this locates the switch-off and switch-on at approximately ± 2π/5 either side of the average phase of the minimum [see (Chapman et al., 2020b)]. Both the switch-on and switch-off provide approximate markers that bracket the quiet interval of the cycle which we now map back into the time domain.
3 Results
3.1 Activity switch-off/on direct from the sunspot record
The occurrence times of the pre-terminators (switch-off) and terminators (switch-on) are essentially read off Panel (d) of Figure 1 across the entire monthly sunspot record from 1750. To improve accuracy, the 13 month smoothed SSN was up-sampled by a factor of 10 in time resolution by linear interpolation in determining these occurrence times. The times of the pre-terminators (switch-off) are when the analytic phase crosses −4π/5 and all the terminators (switch-on) are at phase zero.
In Figure 3 the pre-terminators (switch-off) and terminators (switch-on) are mapped back onto the SSN time-series. Panel (a) and (b) of Figure 3 show that the terminators (red lines/circles) occur just before the 13 month smoothed monthly SSN up-crosses its slow trend. The pre-terminators (green lines/circles) occur after the corresponding down-crossing. This immediately suggests a straightforward method to roughly estimate these occurrence times direct from the SSN record, without first performing a Hilbert transform to obtain the analytic phase. In Panel (c) of Figure 3, the black crosses provide a rough estimate of the switch-on as occurring when the smoothed SSN up-crosses the slow trend, and the switch-off as occurring 12 months after the SSN down-crosses the slow trend. We can see that these rough estimates correspond quite closely to the actual terminator and pre-terminator occurrence times found from the analytic phase via Hilbert transform. For example, the terminator that ends cycle 24 and starts cycle 25 is found from the Hilbert transform to be at decimal year 2021.3, whereas the up-crossing is at 2021.5 We emphasise that the analytic phase determined by Hilbert transform is relative, to plot a phase value we have chosen a reference, here we set the phase to zero at the average phase of the terminators found by (McIntosh et al., 2019). The times at which the terminators and pre-terminators occur are independent of how the reference phase is chosen.
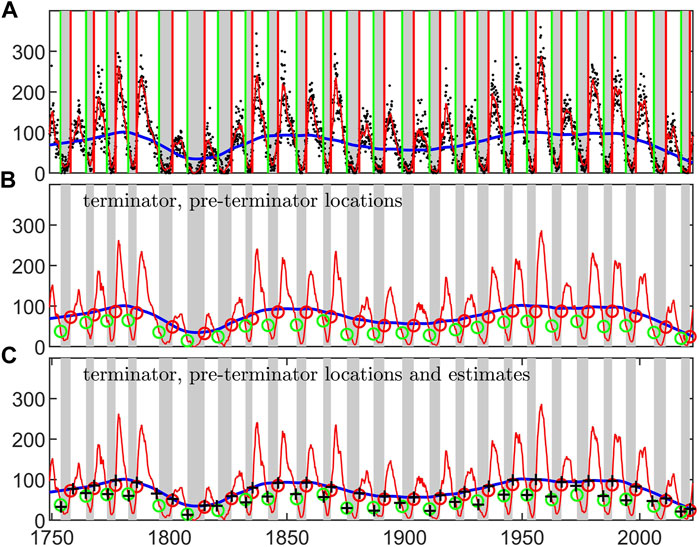
FIGURE 3. Switch-on and switch-off times overplotted on the monthly sunspot record. The 13 month running mean of the monthly sunspot number (red) and its 40 year (lowess) slow trend (blue) are overplotted on the quiet intervals (grey shading) between each pre-terminator and terminator. (A) also plots the monthly sunspot number (black dots) and vertical lines indicating the pre-terminators (green) and terminators (red) at the start and end of each quiet interval. (B) overplots circles on the 13 month running mean of the monthly SSN when the pre-terminators (green circles) and terminators (red circles) occur, that is, when the analytic phase is at −4π/5 and zero respectively. (C) is the same as (B) except that it also overplots (black crosses) estimates of the pre-terminators and terminators based solely on the monthly sunspot record; these are at the value of the 13 month smoothed SSN 12 month after the SSN down-crosses the slow trend (for the pre-terminators) and at the time when the SSN up-crosses the slow trend (for the terminators).
In identifying the pre-terminators (switch-off) and terminators (switch-on) times directly from the SSN time-series we exploited the fact that they occur close to the down-and up-crossings respectively of the slow trend by the smoothed SSN. We would expect a linear relationship between smoothed SSN and SSN slow trend to hold if we are sufficiently close to the times where they cross each other and share the same value. In Figure 4 we test to what extent the pre-terminators and terminators are within this linear regime. We performed a linear regression of the 13 month smoothed sunspot number on the slow trend for values determined at the pre-terminators (left panel) and terminators (right panel). The coefficients with 95% confidence bounds for the line y = a (x − b) are for the terminators: a = 0.89 (0.85, 0.93); b = −0.60 (−3.75, 2.56) and the pre-terminators a = 0.70 (0.56, 0.84); b = 12.13 (−1.07, 25.34). The values of the coefficient of determination, R2 of 0.83 and 0.99 for the pre-terminators and terminators respectively, suggest that they are indeed both within this linear regime. The linear relationship is stronger for the terminators as they are closer to the up-crossings than the pre-terminators are to the down-crossings. These linear relationships between smoothed and slow trend SSN then could form the basis of a method to translate forward predictions of the SSN into a prediction of when the next switch-off or switch-on of activity will occur. A forward prediction of the SSN would provide a prediction of both the slow trend and the 13 month smoothed SSN, when these two values satisfy the linear relationships in Figure 4, they predict the next switch-on or switch-off (where the 13 month smoothed SSN up-crosses or down-crosses the slow trend respectively). The uncertainties of this prediction are given by the 95% confidence bounds on the linear fit coefficients stated above, and can be read off the 95% confidence bounds plotted in Figure 4. These uncertainties would need to be combined with that of the underlying prediction of the SSN.
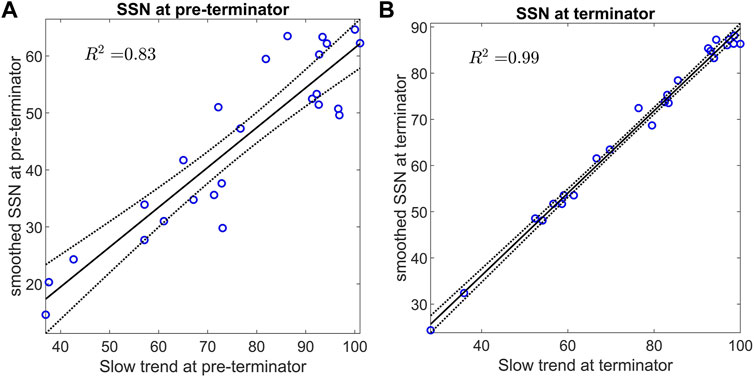
FIGURE 4. The slow trend predicts the smoothed sunspot number at the switch-off and switch-on of activity. Linear regression of 13 month smoothed sunspot number on its slow (40 year rlowess) trend (left) at the pre-terminators and (right) at the terminators. Best fit line (solid black line) and 95% confidence bounds (dashed black lines) are overplotted on the data (blue circles). The R2 of each fit is indicated.
3.2 Charting
Both quantitative observations of geomagnetic activity, and qualitative indicators of space weather impacts, contain useful information in assessing risk, and relating it to hazard. Charting offers a method to combine this information on a cycle-by-cycle basis. Figure 5 charts the last 24 Schwabe cycles. Each of the panels plots analytic phase versus time for the monthly, and overplotted, the daily SSN. Solar cycle maxima and minima are plotted in Panel (a) for reference. The analytic phases zero and −4π/5, that is, the switch-on and switch off obtained via Hilbert transform of the SSN as described above, are indicated with horizontal red and green lines respectively. Estimates of the switch-on and switch-off times, obtained directly from the SSN timeseries as detailed in Figure 3, are indicated by black crosses. These bracket the quiet interval of activity.
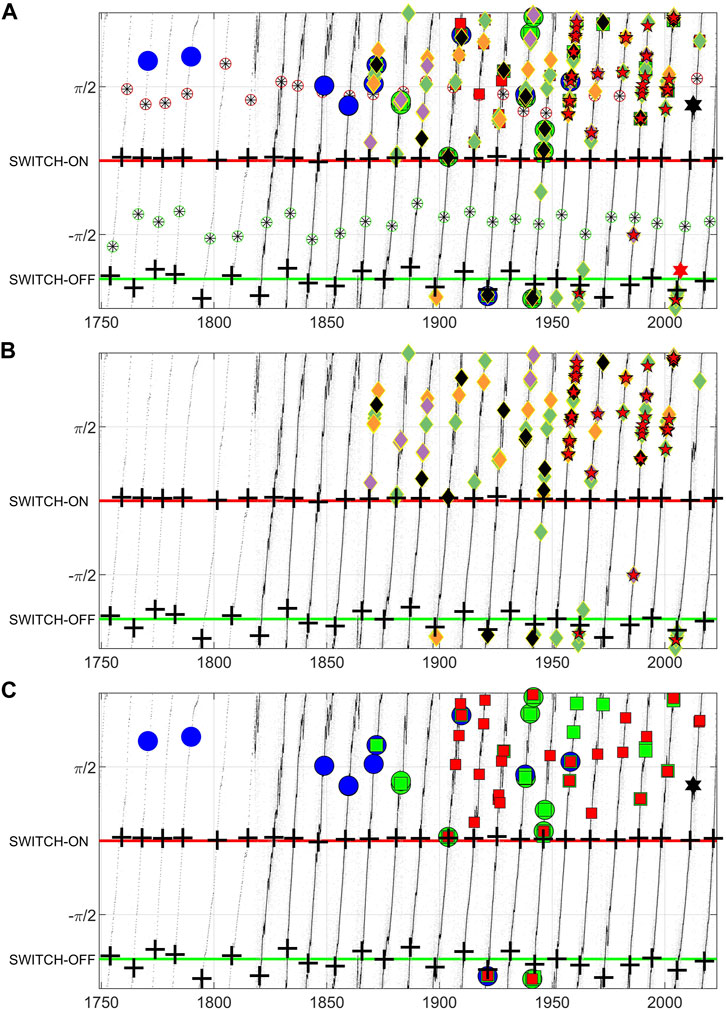
FIGURE 5. Charting solar cycle dependence of space weather impacts. The analytic phase of the monthly, and after 1818, daily SSN is plotted versus time. In all panels horizontal lines for phase −4π/5 (green) and zero (red) indicate the switch-off (pre-terminators) and switch-on (terminators) of activity. The black crosses are estimates of the switch-on/off times obtained directly from the monthly SSN as in Figure 3. (A): Solar maxima and minima are plotted as red and green circled black asterisks respectively. Extreme space weather events are plotted on the chart. These are as follows. (A, B): Red 5-pointed stars plot days when Dst <−250 nT. Diamonds plot days when the aa index has exceeded 300, 400, 500, and 600 nT (green, orange, cyan, and black). (A, C): Blue and green circles from Table 1 and Table 2 of Knipp et al. (2021). Red 6-pointed star: a moderate December 2006 event discussed by Knipp et al. (2021). Green squares: Tables I, III, IV, and VII of Cliver and Svalgaard (2004). Red squares: Table 1 of Love (2021). Black 6-pointed star: July 2012 Carrington class event that missed the Earth Baker et al. (2013).
In Panel (b) we plot indicators of extreme space weather activity obtained directly from geomagnetic index time-series. Red 5-pointed stars plot days when Dst < − 250 nT. This may plot more than one star for an intense storm that lasts several days. Days when the aa index has exceeded 300, 400, 500, 600 nT are plotted as diamonds, coloured green, orange, cyan, and black respectively. There is one extreme event during the quiet interval in 1986 [the event noted by Thomson et al. (2010)] and two more moderate events in 1944 and 1963.
We can instead plot notable storms that have been identified using a variety of different criteria. In Panel (c) we plot the following notable storms. The green squares plot events from Tables I, III, IV, and VII of Cliver and Svalgaard (2004). These range from storms seen in a single ground based magnetometer station that correlate with preceeding solar flares, to low latitude aurorae. The red squares plot the most intense storms in each solar cycle from cycle 14 on, identified from ground magnetograms and the Dst index in Table 1 of Love (2021). Blue and green circles are Table 1 (low latitude aurorae) and Table 2 (CSAGI list, storms which were associated with disruptive technology effects) respectively of Knipp et al. (2021). None of these events occur in the quiet interval.
We overplot all of the events in Panels (b) and (c) on Panel (a). These are heterogeneous data which could not be readily combined in a statistical study to quantify risk. Importantly, the effective “coverage” is not uniform in time, it depends on availability of observations, and in assessing impact, the nature and prevalence of technology which has evolved significantly over the last two centuries. Nevertheless, the chart provides a useful method to bring together and summarize these distinct classes of information. We can see that extreme events within the quiet interval are quite rare, but importantly, some of the most intense events can occur right at the boundaries of the quiet interval. For example, the “quiet time” 1903 event Hayakawa et al. (2020) which is an aa > 600 nT event (black diamond) and which features in multiple Tables of notable events is just at the switch-on. The black 6-pointed star plots the July 2012 Carrington class event that missed the earth Baker et al. (2013) in Panel (a) and although it is not at solar maximum, it is within the active interval.
The chart shown in Figure 5 focuses on the most extreme events. These are more clearly organised by the Schwabe cycle than more moderate events (Tsurutani et al., 2006; Chapman et al., 2020b). The 27-days recurrence (solar rotation) seen in the aa index has a Hale cycle dependence (Sargent, 1985; 2021). This can be clearly resolved as a Hale cycle modulated declining phase in the approximately 22 year Hale cycle clock (Chapman et al., 2021). The occurrence of extreme events, as identified in geomagnetic index time-series, show the same solar cycle ordering as solar flare occurrence as can be seen in Figure 3 [see also (Chapman et al., 2020b)], albeit over four cycles of X-ray flux observations. This is consistent with the idea that more moderate events are more likely to be associated with Hale cycle modulated high speed streams. Further work is needed to develop a chart appropriate for more moderate events; important since these can be disruptive to technology. An example is indicated in Panel (a) of Figure 5 by the red 6-pointed star which is a December 2006 event discussed by Knipp et al. (2021) which, whilst having moderate Dst = - 147 nT had technological impact.
4 Summary and discussion
This paper is focused on how rare, extreme space weather storms are ordered by the Schwabe solar cycle. No two Schwabe cycles are of the same duration, but the Hilbert transform of the sunspot number (SSN) record can be used to map the non-uniform cycle duration onto a uniform 0 to 2π interval of analytic phase. The quiet interval of the solar cycle is located at a fixed phase interval of this solar cycle clock (Chapman et al., 2020b). In this paper the switch-off and switch-on of activity that bracket the quiet interval of the cycle are mapped from the clock (their analytic phases) back into the time-domain, to create a cycle-by-cycle chart of activity.
Once the chart is constructed from the SSN record, any event which has a known time of occurrence can be plotted on the chart. It thus provides a method to combine heterogeneous information. Space weather risk is routinely estimated from the statistics of events identified in long-term geomagnetic indices (Siscoe, 1976; Silbergleit, 1996; Silbergleit, 1999; Thomson et al., 2011; Riley, 2012; Riley and Love, 2016; Chapman et al., 2020a). Information on space weather hazard on the other hand is embodied in narratives around impacts on technological systems, economic, and societal impacts (Knipp et al., 2016; Knipp et al., 2021; Hapgood, 2019; Oughton et al., 2016; Oughton et al., 2017). It is well understood that the relationship between these is non-trivial, and solar cycle charting has the potential to yield new insights by combining this information.
When lists of the most notable storms are charted, none are found to occur in the quiet interval. Extreme events identified in geomagnetic indices only rarely occur in the quiet interval but the chance is not zero. There are examples of extreme events previously noted as occurring away from solar maximum, which when charted are found to be outside the quiet interval. One example is the Carrington class 2012 event that missed the Earth (Baker et al., 2013). Another is the 1903 event (Hayakawa et al., 2020) which occurred just at the switch-on. The fact that some of the most extreme events are found just at the boundary of the switch-off/on of activity underlines the need to quantify, and ideally predict, the switch-off and switch on times.
This paper shows how the switch-off and switch-on times can be extracted direct from the SSN time-series, without recourse to a Hilbert transform. They can be located with reference to the times at which the smoothed SSN crosses its (40 year smoothed, Gleissberg cycle tracking) slow trend. A rough approximation is that the switch-on is when the smoothed SSN up-crosses its slow trend, and that the switch-off occurs 12 months after the down-crossing. There is no unique method for predicting the next activity switch-off/on from the SSN. The appropriate method will depend on the time horizon required for the prediction. If this time horizon is several years in advance of the times where the smoothed SSN up- or down-crosses its slow trend, then a full prediction of the non-linearly varying SSN is required. However, for a prediction horizon of perhaps less than a year, a simple linear extrapolation of the smoothed SSN and the slow trend may suffice. The linear relationships found here between smoothed SSN and slow trend at the switch-off/on would form part of this prediction. As extreme events have occurred close to the switch-off and switch-on times, these linear relationships could also be used to add a safety margin to any prediction based on forwards extrapolation. Determining the optimal methodology for such a prediction, and quantifying its accuracy and skilfulness is the topic of future work.
Finally, the locations of the switch-on and switch-off are estimated to be at particular fixed values of the analytic phase of the smoothed SSN, based on an 11 year Schwabe cycle (Chapman et al., 2020b). Whilst this orders the most extreme events, more moderate events have a Hale cycle dependence in their occurrence likelihood (Chapman et al., 2021). A variety of indicators of solar output are found to exhibit sharp changes at the switch-off (pre-terminator) and switch-on (terminator) of activity (Chapman et al., 2020b; Leamon et al., 2022), offering new insights into the physics of the solar cycle of activity. The estimated switch-on and switch-off times may change when our physical understanding is more complete.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: ISGI http://isgi.unistra.fr/. SILSO http://www.sidc.be/silso/datafiles F10.7 index https://www.spaceweather.gc.ca/solarflux/sx-en.php The GOES X-ray Flare dataset (NGDC) https://www.ngdc.noaa.gov/stp/space-weather/solar-data/solar-features/solar-flares/x-rays/.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
AFOSR grant FA8655-22-1-7056 and STFC grant ST/T000252/1.
Acknowledgments
The results presented in this paper rely in part on geomagnetic indices calculated and made available by ISGI Collaborating Institutes from data collected at magnetic observatories. We acknowledge the involved national institutes, the INTERMAGNET network (www.intermagnet.org) and ISGI (isgi.unistra.fr). We thank the World Data Center for Geomagnetism, Kyoto. We thank the World Data Center SILSO, Royal Observatory of Belgium, Brussels for provision of sunspot data. SC acknowledges AFOSR grant FA8655-22-1-7056 and STFC grant ST/T000252/1. SC thanks N. W. Watkins for useful discussions.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Baker, D. N., and Lanzerotti, L. J. (2016). Resource letter SW1: Space weather. Am. J. Phys. 84, 166–180. doi:10.1119/1.4938403
Baker, D. N., Li, X., Pulkkinen, A., Ngwira, C. M., Mays, M. L., Galvin, A. B., et al. (2013). A major solar eruptive event in July 2012: Defining extreme space weather scenarios. Space weather. 11, 585–591. doi:10.1002/swe.20097
Bergin, A., Chapman, S. C., Moloney, N., and Watkins, N. W. (2022). Variation of geomagnetic index empirical distribution and burst statistics across successive solar cycles. J. Geophys. Res. 127. doi:10.1029/2021JA029986
Boashash, B. (1992). Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals. Proc. IEEE®. 80 (4), 520–538. doi:10.1109/5.135376
Booth, R. J. (2021). Limitations in the Hilbert transform approach to locating solar cycle terminators. Sol. Phys. 296, 108. doi:10.1007/s11207-021-01833-1
Bubenik, D. M., and Fraser-Smith, A. C. (1977). Evidence for strong artificial components in the equivalent linear amplitude geomagnetic indices. J. Geophys. Res. 82, 2875–2878. doi:10.1029/ja082i019p02875
Chapman, S. C., Horne, R. B., and Watkins, N. W. (2020a). Using the aa index over the last 14 solar cycles to characterize extreme geomagnetic activity. Geophys. Res. Lett. 47. doi:10.1029/2019GL086524
Chapman, S. C., Lang, P. T., Dendy, R. O., Giannone, L., and Watkins, N. W. (2018a). Control system-plasma synchronization and naturally occurring edge localized modes in a tokamak. Phys. Plasmas 25, 062511. doi:10.1063/1.5025333
Chapman, S. C., McIntosh, S. W., Leamon, R. J., and Watkins, N. W. (2020b). Quantifying the solar cycle modulation of extreme space weather. Geophys. Res. Lett. 47. doi:10.1029/2020GL087795
Chapman, S. C., McIntosh, S. W., Leamon, R. J., and Watkins, N. W. (2021). The Sun’s magnetic (Hale) cycle and 27 day recurrences in the aa geomagnetic index. Ap. J. 917, 54. doi:10.3847/1538-4357/ac069e
Chapman, S. C., Watkins, N. W., and Tindale, E. (2018b). Reproducible aspects of the climate of space weather over the last five solar cycles. Space weather. 16, 1128. doi:10.1029/2018SW001884
Cliver, E. W., and Svalgaard, L. (2004). The 1859 Solar-terrestrial disturbance and the current limits of extreme space weather activity. Sol. Phys. 224, 407–422. doi:10.1007/s11207-005-4980-z
Gabor, D. (1946). Theory of communication. Part 1: The analysis of information. J. IEE Lond. 93 (3), 429–441. doi:10.1049/ji-3-2.1946.0074
Gleissberg, W. (1967). Secularly smoothed data on the minima and maxima of sunspot frequency. Sol. Phys. 2, 231–233. doi:10.1007/bf00155925
Hapgood, M. (2019). The great storm of May 1921: An exemplar of a dangerous space weather event. Space weather. 17, 950–975. doi:10.1029/2019sw002195
Hayakawa, H., Ribeiro, P., Vaquero, J. M., Gallego, M. C., Knipp, D. J., Mekhaldi, F., et al. (2020). The extreme space weather event in 1903 october/november:an outburst from the quiet sun. Astrophysical J. Lett. 897, L10. doi:10.3847/2041-8213/ab6a18
Knipp, D. J., Bernstein, V., Wahl, K., and Hayakawa, H. (2021). Timelines as a tool for learning about space weather storms. J. Space Weather Space Clim. 11, 29. doi:10.1051/swsc/2021011
Knipp, D. J., Ramsay, A. C., Beard, E. D., Boright, A. L., Cade, W. B., Hewins, I. M., et al. (2016). The May 1967 great storm and radio disruption event: Extreme space weather ande xtraordinary responses. Space weather. 14, 614–633. doi:10.1002/2016SW001423
Leamon, R. J., McIntosh, S. W., Chapman, S. C., and Watkins, N. W. (2021). Response to “limitations in the Hilbert transform approach to locating solar cycle terminators” by R. Booth. Sol. Phys. 296, 151. doi:10.1007/s11207-021-01897-z
Leamon, R. J., McIntosh, S. W., Chapman, S. C., and Watkins, N. W. (2020). Timing terminators: Forecasting sunspot cycle 25 onset. Sol. Phys. 295, 36. doi:10.1007/s11207-020-1595-3
Leamon, R. J., McIntosh, S. W., and Title, A. M. (2022). Deciphering solar magnetic activity, the solar cycle clock. Front. Astron. Space Sci. 9, 886670. doi:10.3389/fspas.2022.886670
Lockwood, M., Owens, M. J., Barnard, L. A., Scott, C. J., Watt, C. E., and Bentley, S. (2018). Space climate and space weather over the past 400years: 2. Proxy indicators of geomagnetic storm and substorm occurrence. J. Space Weather Space Clim. 8, A12. doi:10.1051/swsc/2017048
Love, J. J. (2021). Extreme-event magnetic storm probabilities derived from rank statistics of historical Dst intensities for solar cycles 14–24. Space weather. 19, e2020SW002579. doi:10.1029/2020SW002579
Marple, S. L. (1999). Computing the discrete-time analytic signal via FFT. IEEE® Trans. Signal Process. 47, 2600–2603. doi:10.1109/78.782222
Mayaud, P. N. (1980). “Derivation, meaning, and use of geomagnetic indices,” in Geophys. Monogr. Ser. (Washington, D.C: AGU), Vol. 22. doi:10.1029/GM022
McIntosh, S. W., Leamon, R. J., Egeland, R., Dikpati, M., Fan, Y., and Rempel, M. (2019). What the sudden death of solar cycles can tell us about the nature of the solar interior. Sol. Phys. 294 (7), 88. doi:10.1007/s11207-019-1474-y
McIntosh, S. W., and Leamon, R. J. (2014). On magnetic activity band overlap, interaction, and the formation of complex solar active regions. Astrophys. J. Lett. 796, L19. doi:10.1088/2041-8205/796/1/l19
McIntosh, S. W., Wang, X., Leamon, R. J., and Scherrer, P. H. (2014). Identifying potential markers of the sun’s giant convective scale. Astrophys. J. Lett. 784, L32. doi:10.1088/2041-8205/784/2/l32
Mitchell–Wallace, K., Jones, M., Hillier, J., and Foote, M. (2017). Natural catastrophe risk management and modelling: A practitioner’s guide. New York, NY, USA: Wiley-Blackwell.
Oughton, E., Copic, J., Skelton, A., Kesaite, V., Yeo, Z. Y., Ruffle, S. J., et al. (2016). Solar storm scenario, cambridge risk framework series, centre for risk studies. Cambridge, England: University of Cambridge.
Oughton, E. J., Skelton, A., Horne, R. B., Thomson, A. W. P., and Gaunt, C. T. (2017). Quantifying the daily economic impact of extreme space weather due to failure in electricity transmission infrastructure. Space weather. 15, 65–83. doi:10.1002/2016SW001491
Owens, M. J., Lockwood, M., Barnard, L., and Davis, C. J. (2011). Solar cycle 24: Implications for energetic particles and long-term space climate change. Geophys. Res. Lett. 38, L19106. doi:10.1029/2011GL049328
Palŭs, M., and Notovná, D. (1999). Sunspot cycle: A driven nonlinear oscillator? PRL 83, 3406–3409. doi:10.1103/physrevlett.83.3406
Riley, P., and Love, J. J. (2016). Extreme geomagnetic storms: Probabilistic forecasts and their uncertainties. Space weather. 15, 53–64. doi:10.1002/2016SW001470
Riley, P. (2012). On the probability of occurrence of extreme space weather events. Space weather. 10, S02012. doi:10.1029/2011sw000734
Russell, C. T., Jian, L. K., and Luhmann, J. G. (2019). The solar clock. Rev. Geophys. 57, 1129–1145.
Sargent, H. H. (1985). Recurrent geomagnetic activity evidence for long-lived stability in solar wind structure. J. Geophys. Res. 90 (A2), 1425–1428. doi:10.1029/ja090ia02p01425
Silbergleit, V. M. (1999). Forecast of the most geomagnetically disturbed days. Earth Planets Space 51, 19–22. doi:10.1186/bf03352205
Silbergleit, V. M. (1996). On the occurrence of geomagnetic storms with sudden commencements. J. Geomagn. Geoelectr. 48, 1011–1016. doi:10.5636/jgg.48.1011
Siscoe, G. L. (1976). On the statistics of the largest geomagnetic storms per solar cycle. J. Geophys. Res. 81, 4782–4784. doi:10.1029/ja081i025p04782
Tapping, K. F. (2013). The 10.7 cm solar radio flux (F10.7). Space weather. 11, 394–406. doi:10.1002/swe.20064
Thomson, A. W. P., Dawson, E. B., and Reay, S. J. (2011). Quantifying extreme behavior in geomagnetic activity. Space weather. 9, S10001. doi:10.1029/2011SW000696
Thomson, A. W. P., Gaunt, C. T., Cilliers, P., Wild, J. A., Opperman, B., McKinnell, L.-A., et al. (2010). Present day challenges in understanding the geomagnetic hazard to national power grids. Adv. Space Res. 45, 1182–1190. doi:10.1016/j.asr.2009.11.023
Tsubouchi, K., and Omura, Y. (2007). Long-term occurrence probabilities of intense geomagnetic storm events. Space weather. 5, S12003. doi:10.1029/2007SW000329
Tsurutani, B. T., Gonzalez, W. D., Gonzalez, A. L. C., Guarnieri, F. L., Gopalswamy, N., Grande, M., et al. (2006). Corotating solar wind streams and recurrent geomagnetic activity: A review. J. Geophys. Res. 111, A07S01. doi:10.1029/2005JA011273
Vecchio, A. A., Lepreti, F., Laurenza, M., Alberti, T., and Carbone, V. (2017). Connection between solar activity cycles and grand minima generation. Astron. Astrophys. 599, A58. doi:10.1051/0004-6361/201629758
Keywords: solar cycle, space weather, geomagnetic storms, Hilbert transform, sunspot record, Gleissberg cycle
Citation: Chapman SC (2023) Charting the solar cycle. Front. Astron. Space Sci. 9:1037096. doi: 10.3389/fspas.2022.1037096
Received: 05 September 2022; Accepted: 12 December 2022;
Published: 09 February 2023.
Edited by:
Simon Wing, Johns Hopkins University, United StatesReviewed by:
Scott William McIntosh, National Center for Atmospheric Research (UCAR), United StatesAntonio Vecchio, Radboud University, Netherlands
Copyright © 2023 Chapman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. C. Chapman, Uy5DLkNoYXBtYW5Ad2Fyd2ljay5hYy51aw==