Near-ultraviolet continuum modeling of the 1985 April 12 great flare of AD Leo

White-light stellar flares are now reported by the thousands in long-baseline, high-precision, broad-band photometry from missions like Kepler, K2, and TESS. These observations are crucial inputs for assessments of biosignatures in exoplanetary atmospheres and surface ultraviolet radiation dosages for habitable-zone planets around low-mass stars. A limitation of these assessments, however, is the lack of near-ultraviolet spectral observations of stellar flares. To motivate further empirical investigation, we use a grid of radiative-hydrodynamic simulations with an updated treatment of the pressure broadening of hydrogen lines to predict the λ ≈ 1800 − 3300 Å continuum flux during the rise and peak phases of a well-studied superflare from the dM3e star AD Leo. These predictions are based on semi-empirical superpositions of radiative flux spectra consisting of a high-flux electron beam simulation with a large, low-energy cutoff (≳ 85 keV) and a lower-flux electron beam simulation with a smaller, low-energy cutoff (≲ 40 keV). The two-component models comprehensively explain the hydrogen Balmer line broadening, the optical continuum color temperature, the Balmer jump strength, and the far-ultraviolet continuum strength and shape in the rise/peak phase of this flare. We use spatially resolved analyses of solar flare data from the Interface Region Imaging Spectrograph, combined with the results of previous radiative-hydrodynamic modeling of the 2014 March 29 X1 solar flare (SOL20140329T17:48), to interpret the two-component electron beam model as representing the spatial superposition of bright kernels and fainter ribbons over a larger area.

1 Introduction

Rapidly rotating, magnetically active M dwarf (dMe) stars occasionally flare with energies that are factors of 100–10,000 greater than the most energetic solar flares that have been observed in the modern era. These so-called “superflares” provide insight into the physics of extreme plasma conditions attained in stars (Osten et al., 2007; Testa et al., 2008; Osten et al., 2010, 2016; Karmakar et al., 2017) and possibly also the young Sun (Ayres, 2015; Maehara et al., 2015; Namekata et al., 2021). Further afield, observations of these superflares are widely used in the characterization of the high-energy radiation environments in the habitable zones of low-mass stars (Smith et al., 2004; Segura et al., 2010), which are a primary target for exoplanet transit spectroscopy (e.g., Scalo et al., 2007; Belu et al., 2011; Barstow et al., 2016; Barstow and Irwin, 2016; de Wit et al., 2018; Fauchez et al., 2019) with the James Webb Space Telescope (JWST). The JWST and future extremely large telescope facilities provide a means to determine whether exoplanets in or around the habitable zone of low-mass stars retain atmospheres in the presence of high fluxes of stellar energetic particles and X-ray and extreme ultraviolet (XEUV) flare radiation. The evolution of the atmosphere of Mars is thought to have undergone significant mass loss due to coronal mass ejections and XEUV heating from the Sun (Jakosky et al., 2018), which motivates investigations into the evolution of exoplanetary atmospheres that are much closer to stars that are highly magnetically active for billions of years (West et al., 2008).

Segura et al. (2010) simulated the impact of a superflare event on a non-magnetic, but otherwise Earth-like, exoplanet atmosphere in the habitable zone of the dM3e flare star AD Leo. They found that planetary ozone is largely depleted due to chemical reactions (e.g., Scalo et al., 2007) that follow from incident scaled-up fluxes (Belov et al., 2005) of solar energetic protons. More recent simulations have considered the effects of repeated flaring and particle events after such a superflare has occurred (Howard et al., 2018; Tilley et al., 2019). Howard et al. (2018) and Tilley et al. (2019) discuss the role of UV-C¹ (λ = 2000 − 2800Å), and in particular the wavelengths λ = 2400 − 2800 Å, from repeated flaring in germicidal radiation surface fluxes following an ozone-depletion event. Recently, Abrevaya et al. (2020) conducted laboratory measurements of survival curves of microorganisms through exposure to a UV-C radiation flux inferred from optical observations of a superflare from the dM5.5e star Proxima Centauri (Howard et al., 2018).

The transient (Loyd et al., 2018a) and secular (Venot et al., 2016) effects on ozone biosignature photochemistry caused by ultraviolet flares is an ongoing subject of research, especially in light of the lack of direct observations of stellar energetic proton fluences and exoplanetary magnetic field properties (see discussion in Tilley et al., 2019). Loyd et al. (2018a) demonstrate that assumptions of the ultraviolet continuum shape during flares can affect ozone photolysis rates (see also Howard et al., 2020), while effects spanning several orders of magnitude on other important atmospheric constituents (CH₄, H₂O, O₂) are expected. Significant effort has been invested into the empirical characterization of the quiescent and flaring spectra of low-mass stars in the far-ultraviolet wavelength region of λ = 1100 − 1800 Å through the MUSCLES, Mega-MUSCLES, and HAZMAT treasury programs with the Hubble Space Telescope (Shkolnik and Barman, 2014; Loyd and France, 2014; Froning et al., 2019; Loyd et al., 2018b; France et al., 2020; Wilson et al., 2021, and see also Feinstein et al., 2022). However, much still remains unknown about the spectral characteristics of transient, impulsive-phase, near-ultraviolet (NUV) enhancements in flare radiation from λ ≈ 2000 − 3300 Å (e.g., Robinson et al., 2005; Hawley et al., 2007; Brasseur et al., 2019; Fleming et al., 2022), which is thought to account for a large percentage (≈25%) of the λ = 1200 − 8000 Å radiated energy (Hawley and Pettersen, 1991). The largest X-ray solar flare of Sunspot Cycle 24 was recently studied in spatially integrated light at continuum wavelengths through a Δλ ≈ 300 Å bandpass around λ ≈ 2000 Å (Dominique et al., 2018).

Many studies of stellar flares have utilized photometry from high-precision missions of Kepler, K2, and TESS, which observe through broad white-light bandpasses in the optical and near-infrared. Photochemistry and habitability calculations often use extrapolations to shorter ultraviolet wavelengths by assuming a T ≈ 9000 − 10, 000 K blackbody spectrum (e.g., Günther et al., 2020); this assumption has also been widely employed for calculations of bolometric energies in statistical analyses (e.g., Shibayama et al., 2013; Yang et al., 2017). We refer the reader to Howard et al. (2020) and Brasseur et al., 2022, submitted to ApJ) for discussions about several unprecedented problems raised by recent studies of multi-wavelength broadband photometry of stellar superflares.

Very few stellar flare spectral observations exist with near-ultraviolet coverage and contemporaneous optical spectra (Hawley and Pettersen, 1991; Robinson et al., 1993; Wargelin et al., 2017; Kowalski et al., 2019b) that would facilitate detailed tests of and improvements upon blackbody modeling of flares. However, ground-based spectra suggest that the NUV flare continuum has non-negligible contributions from Balmer continuum radiation (Kowalski et al., 2010, 2013, 2016). Most recently, Kowalski et al. (2019b) analyze λ ≈ 2500 − 7400 Å flare spectra and photometry over two events from the dM4e star GJ 1243. Detailed modeling demonstrates that a T = 9000 K blackbody fit to the blue-optical continuum at λ ≈ 4000 − 4800 Å underpredicts the NUV flare flux by factors of 2 − 3 during these two events; the discrepency was tied to a moderately-sized jump in the continuum flux around the Balmer limit, a confluence of Fe II emission lines through the NUV, and the bright Mg II h and k resonance lines (see also Hawley et al., 2007). These “hybrid flare” (HF) or “gradual flare” (GF) (see Kowalski et al., 2013) events exhibit the largest Balmer jumps that have been detected spectroscopically in dMe flares, and Kowalski et al. (2019b) argue that other dMe events that are categorized as “impulsive flare” (IF) events according to their broadband time evolution, smaller Balmer jumps, and hotter blackbody fits to the optical (Kowalski et al., 2013) and U-band (λ = 3260 − 3940 Å) continua (Fuhrmeister et al., 2008) yet require spectroscopic investigation at shorter wavelengths. The optical spectral properties of impulsive-type M dwarf flares are crucial in our understanding of fundamental flare physics because they are not reproduced in simulations with typical, solar-type electron beam (Allred et al., 2006) or intense XEUV radiation fields (Hawley and Fisher, 1992); large continuum optical depths are required in the flare chromosphere (e.g., Livshits et al., 1981; Kowalski et al., 2015) or photosphere.

In this paper, we present radiative-hydrodynamic model predictions of the NUV flare continuum during the Great Flare of AD Leo (Hawley and Pettersen, 1991), a particularly well-studied, impulsive-type superflare. The optical emission line data have previously been modeled in detail in Hawley and Fisher (1992) using NLTE, X-ray backwarming calculations and in Allred et al. (2006) with electron beam heating with the RADYN code. However, comprehensive models of the powerful optical continuum radiation and the broadening of the hydrogen Balmer line series have not yet been addressed. The multi-wavelength spectra of this event have been widely utilized for empirically-driven models of exoplanet photochemistry and surface UV dosages (Segura et al., 2010; Venot et al., 2016; Ranjan et al., 2017; Tilley et al., 2019; Estrela et al., 2020).

This paper is organized as follows. In Section 2, the AD Leo Great Flare spectrum and photometry data that are used for model fitting are briefly reviewed. Section 3 describes the radiative-hydrodynamic flare models, which are fit to the Hγ emission line in the spectrum corresponding to the rise and peak phases of the Great Flare (Section 4). We calculate the Balmer line merging in the spectral region around the Balmer limit (Section 4.3) to further justify our two-component model fitting approach. We consider the FUV spectrum during the early impulsive phase and independently fit to the observed continuum distribution of the Great Flare in order to make a new continuum model prediction for the NUV wavelength range that was not observed during this time (Section 4.4). The interpretation of the results is discussed in Section 5 in terms of the spatial distribution of intensity in an image of a well-studied solar flare; we present new calculations for habitable zone UV-C fluxes in Section 5.2. We conclude in Section 6.

2 Observations

2.1 The 1985 April 12 great flare of AD Leo

The Great Flare of AD Leo was a large-amplitude, superflare event with an energy of nearly 10³⁴ erg emitted in the U band. The available data are the broadband UBVR photometry and the optical spectra covering λ = 3560 − 4400 Å at a resolving power of R ≈ 1240. The exposure times of the spectra varied between one and 3 minutes (see Hawley and Pettersen, 1991, for details). Here, we model the spectrum that integrated over most of the rise and first peak, labeled as the “542s” spectrum in Hawley and Pettersen (1991) and “S# 36” in the analysis of Kowalski et al. (2013)². The light curve of the U band is shown in Figure 1 with the integration time of the rise/peak spectrum indicated.

FIGURE 1

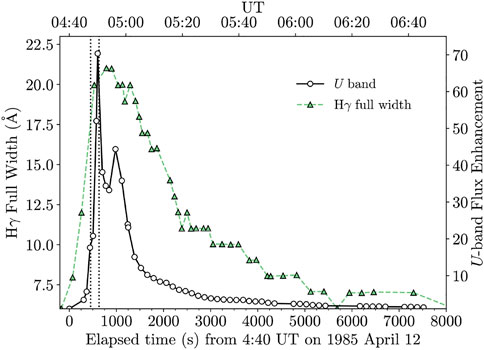
FIGURE 1. The U-band light curve (right axis) of the Great Flare of AD Leo and the full-width (left axis) of the Hγ emission line from Hawley and Pettersen (1991). The U-band flux is normalized to quiescence. The start and stop times of the exposure corresponding to the rise/peak phase spectrum is indicated with two vertical dotted lines.

The Great Flare exhibits all of the spectral and light curve characteristics of a highly “impulsive-type” stellar flare, according to the “IF” classification in Kowalski et al. (2013). Specifically, the blue-optical spectra were fit with a color temperature of T ≈ 11, 600 K, and the small Balmer jump in the U band suggests that Balmer recombination radiation is important at shorter wavelengths (Figure 9 of Kowalski et al., 2013). During the early impulsive phase, a FUV spectrum (described below) constrains the peak of the continuum to the U band with a turnover toward shorter wavelengths that was found to be most consistent with a T = 8500 − 9500 K blackbody among the models that were available at the time (Hawley and Fisher, 1992). Hawley and Pettersen (1991) analyzed the highly broadened, symmetric wings of the Balmer series, which were attributed to the Stark effect. The full-width evolution of the hydrogen Balmer Hγ emission line from Hawley and Pettersen (1991) is reproduced in Figure 1. The rise/peak spectrum corresponds to the first observation that exhibits very broad Hγ wings.

The AD Leo Great Flare was observed with ultraviolet spectroscopy with the International Ultraviolet Explorer (IUE). A FUV spectrum was observed in the short-wavelength channel (SWP; λ = 1150 − 2000 Å), which integrated over the first 900 s of the flare (up until 4:55 UT) and included 41 min of quiescence. The fluxes in the major emission lines and in the continuum longward of 1780 Å saturated the detector. NUV spectral observations in the long wavelength band (LWP; λ = 1900 − 3100 Å) of IUE started at 5:00 UT, which is about midway during the second, fast decay phase in the U-band light curve in Figure 1. The LWP observation from 5:00–5:20 UT was split into five sub exposures, each 3 − 8 min in duration (see Figure 1 of Hawley and Pettersen (1991) for the λ = 2000 Å and 2800 Å continuum flux evolution over the first set of five sub-exposures). In the flare, some emission lines in the NUV were saturated as well (see Segura et al., 2010, for details about how these data have been utilized by interpolation and binning). Since there were no NUV spectra covering the rise and peak phases, we do not consider the IUE/LWP spectra further in this study. For detailed descriptions of the reduction and analyses of the IUE spectra, we refer the reader to Hawley and Pettersen (1991).

2.2 The 2014 March 29 X1 solar flare

The 2014 March 29 GOES class X1 flare (SOL20140329T17:48) is one of the best-observed and most-widely studied solar flares from Sunspot Cycle 24 (e.g., Heinzel and Kleint, 2014; Aschwanden, 2015; Battaglia et al., 2015; Young et al., 2015; Rubio da Costa et al., 2016; Rubio da Costa and Kleint, 2017; Woods et al., 2017; Kleint et al., 2018; Polito et al., 2018; Zhu et al., 2019). The flare was observed by the Interface Region Imaging Spectrograph (IRIS; De Pontieu et al., 2014) with FUV and NUV longslit spectroscopy (see, e.g., Kleint et al., 2016; Kowalski et al., 2017a, for detailed descriptions of these spectra). Narrow-band (Δλ ∼ 4 Å), slit jaw images (SJI) in the NUV at Mg II 2796 (SJI 2796) and at 2830 Å (SJI 2832) are available for contextual information about the flare brightenings that cross the IRIS slit. For this study, a level-2, SJI 2832 image at 17:46 UTC is retrieved from the IRIS data archive hosted at the Lockheed Martin Solar and Astrophysical Laboratory³. The SJI 2832 image corresponds to the early impulsive phase of the hard X-rays at E ≥ 25 keV and has been analyzed in Kowalski et al. (2017a). The IRIS slit location stepped through the ribbons in this flare, resulting in a cadence of 75 s for the raster and SJI 2832 images. Following previous analyses (e.g., Kowalski et al., 2017a), we convert the level-2 data in units of DN s⁻¹ pix⁻¹ to an equivalent, constant intensity value, ${⟨I_{\lambda }⟩}_{\text{SJI}}$, over the SJI bandpass using the time-dependent effective area curves (Wülser et al., 2018) provided by the IRIS mission.

X-ray imaging data from the Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI; Lin et al., 2002) were retrieved from the new RHESSI data archive⁴. We use the 6–12 keV and 50–100 keV imaging over the time-interval of 17:45:58.7 to 17:46:32.0. We refer the reader to Battaglia et al. (2015) and Kleint et al. (2016) for higher temporal and spatial resolution analyses of the RHESSI data for the 2014 March 29 flare.

3 Radiative-hydrodynamic flare models

To model the rise/peak phase spectrum of the AD Leo flare, we use results from a grid of radiative-hydrodynamic (RHD) models calculated with the RADYN code (Carlsson and Stein, 1992, 1995, 1997, 2002; Allred et al., 2015). All of the details about the simulation setup will be described in a separate paper (Kowalski et al. in preparation), but a brief summary is presented here. To simulate flare heating, we model the energy deposition from a power-law distribution (hereafter, “beam”) of electrons, which is calculated in a 1D magnetic loop of half-length 10⁹ cm, a constant surface gravity of log₁₀ g/[cm s⁻²] = 4.75, and a uniform cross-sectional area. The effective temperature of the starting atmosphere is T_eff ≈ 3600 K (see the Appendix of Kowalski et al., 2017b, for details regarding the starting atmosphere). The equations of mass, momentum, internal energy, and charge are solved on an adaptive grid with the equations of radiative transfer and level populations for hydrogen, helium, and Ca II. The electron beam is injected at the loop apex with a ramping flux to a maximum value at t = 1 s, followed by a decrease until t = 10 s according to the pulsed injection profile prescription in Aschwanden (2004). The heating rate as a function of depth is determined by the steady-state solution to the Fokker-Planck equation for energy loss and pitch angle scattering due to Coulomb collisions using the module that was further developed into the FP code (Allred et al., 2020). The heating rate is recalculated at every time-step in the radiative-hydrodynamic simulation (see Allred et al., 2015). In this first generation of models, return current electric fields and magnetic mirroring forces (Allred et al., 2020) are not considered. However, hydrogen Balmer line spectra (Hα, Hβ, Hγ) are properly modeled using the Doppler-convolved, TB09 + HM88 line profile functions (Smith et al., 1969; Vidal et al., 1970, 1971, 1973; Hummer and Mihalas, 1988; Tremblay and Bergeron, 2009), which accurately capture the pressure broadening from ambient, thermal electrons and ions in the density regimes of flare chromospheres (Kowalski et al., 2017b, 2022).

Stellar flare hard X-ray emission is below current detection limits, except in the most energetic events (e.g., Osten et al., 2007, 2016), and millimeter/radio observations at optically thin frequencies have been reported only recently (MacGregor et al., 2020). The paucity of direct constraints on accelerated electrons in stellar flares thus necessitates a grid of models covering a large parameter space of electron beam heating. Our grid of M dwarf flare models includes a large range of low-energy cutoff (E_c) values: 17, 25, 37, 85, 150, 200, 350, and 500 keV. All of the selected models from the grid are calculated for injected electron beam number fluxes with hard power-law indices of δ = 2.5 − 4, which are consistent with available stellar flare constraints (Osten et al., 2007; MacGregor et al., 2018, 2020, 2021). The peak injected beam energy flux densities (hereafter, “flux”) span four orders of magnitude: 10¹⁰ (F10), 10¹¹ (F11), 10¹² (F12), and 10¹³ (F13) erg cm⁻² s⁻¹. For this study, we select five models with maximum (“m”) injected beam fluxes of 10¹³ erg cm⁻² s⁻¹ (“mF13”), low-energy cutoffs of E_c = 37, 85, 150, 200, and 500 keV, and a power-law index of δ = 3; these are referred to as the mF13-37-3, mF13-85-3, mF13-150-3, mF13-200-3, and mF13-500-3 models, respectively⁵. These models are especially notable because they reproduce T ≈ 10, 000 K color temperatures in the blue-optical wavelength range and small Balmer jump ratios, as reported in many M dwarf flare spectral observations (e.g., Mochnacki and Zirin, 1980; Fuhrmeister et al., 2008; Kowalski et al., 2013, 2016). The justification for selecting these high-flux models will be discussed further in Section 4.2.

The mF13-37-3 model is a recalculation of the RADYN simulation from Kowalski et al. (2016) (see also Kowalski et al. (2015)) with a pulsed beam flux injection. The atmosphere in the new model follows a similar evolution with the development of a dense (n_e = 5 × 10¹⁵ cm⁻³), cool chromospheric condensation at t ≈ 2.2 s. The mF13-85-3 and mF13-150-3 models produce relatively small amounts of coronal heating and relatively fast upflows ($\approx 5-20$ km s⁻¹) in the flare chromosphere because most of the beam energy is deposited into the deep chromosphere. Without magnetic mirroring and return current electric field forces, long-lasting chromospheric condensations do not develop as in the mF13-37-3 model. However, large ambient electron densities (n_e ≈ 1 − 7 × 10¹⁵ cm⁻³) are attained due to thermal ionization of hydrogen by the beam heating in low-lying chromospheric layers (see the Appendices of Kowalski et al., 2017b, for a description of several, similar large, low-energy-cutoff models). These charge densities refer to the atmospheric (ambient/thermal) proton and electron densities that pressure broaden the hydrogen lines that we model in Section 4.2 and Section 4.3. The nonthermal electron densities are many orders of magnitude smaller in the chromosphere. The large, low-energy-cutoff models represent a semi-empirical approach in the spirit of the static flare atmospheres of Cram and Woods (1982), but the RADYN models include time-dependent atmospheric thermodynamics that are calculated self-consistently with beam heating.

In addition to the F13 models, a lower beam flux that has been used to model IRIS NUV spectra of a solar flare (Kowalski et al., 2017a) and the broadening of the hydrogen Balmer series (Kowalski et al., 2022) has been injected into our M dwarf atmosphere for a duration of 15 s. The electron beam parameters (E_c = 25 keV, δ = 4, flux of 5 × 10¹¹ erg cm⁻² s⁻¹) for this model (“c15s-5F11-25-4”) were selected to be consistent with those that were inferred through the collisional thick target modeling of RHESSI hard X-ray data of the 2014 March 29 solar flare (Kleint et al., 2016). Similar to the analogous simulation in the solar atmosphere, a dense chromospheric condensation develops by t ≈ 4 s with densities of n_e ≈ 5 × 10¹⁴ cm⁻³. We also calculate a model (m5F11-25-4) with a shorter, pulsed injection profile in the same form as for the pulsed F13 beams. Several other models that are considered in this work are two intermediate flux models (mF12-37-3 and m2F12-37-2.5) with hard power-law distributions (δ = 2.5 and 3) and intermediate low-energy cutoff values (E_c = 37 keV). A similar model to the mF12-37-3 beam was analyzed in Namekata et al. (2020), who found satisfactory agreement between the broadening of the hydrogen Balmer α emission line in the model and in the observation of a superflare event from AD Leo.

The parameters of the RHD models that are used in the remainder of this work are summarized in Table 1.

TABLE 1

TABLE 1. RADYN electron beam heating models.

4 Model spectrum analysis

We leverage the new hydrogen pressure broadening profiles that have been incorporated into RADYN to examine the models that reproduce the Balmer jump strength and blue-optical continuum color temperature. The Balmer Hγ emission line broadening and nearby blue-optical continuum fluxes of the Great Flare are the focus of our modeling analyses (Section 4.1 and Section 4.2). In Section 4.3, we extend the detailed calculations to spectra of the entire Balmer line series.

4.1 Average model line-to-continuum ratios

We first describe a simple method that allows comparisons of 1D loop models to the Great Flare spectra, which are not spatially resolved. Over an exposure time of 180 s, we reasonably expect that many sequentially ignited, spatially distinct, Δt = 10 s pulses accumulate flare radiation in the spatially unresolved, observed flare spectrum. For each RHD model, we thus calculate a coadded spectrum from the radiative surface flux spectra at every Δt = 0.2 s by temporal averaging over the duration given by t_end in Table 1. These coadded spectra are used in all analyses, unless otherwise indicated.

Several coadded F13 model spectra around the Hγ emission line are normalized to the observed continuum flare-only flux averaged over λ = 4155 − 4185 Å in the Great Flare (Figure 2). With an older, less accurate prescription of hydrogen line pressure broadening, Kowalski et al. (2015) found that a coadded F13 model with a double power-law beam distribution and E_c = 37 keV was an adequate model of the early/mid rise phase of a giant flare from the dM4.5e star YZ CMi. As Figure 2 clearly demonstrates, the mF13-37-3 model profile with the updated hydrogen broadening is far too broad even though times when the chromospheric condensation is not extremely dense and the emission lines are relatively narrow are included in the coadd. The coadded mF13 spectra from the models with large, low-energy-cutoffs (E_c = 85 − 150 keV) adequately account for some or all of the flux in the Hγ wings, but these models of deep flare heating vastly under-predict the relative Hγ line-peak flux.

FIGURE 2

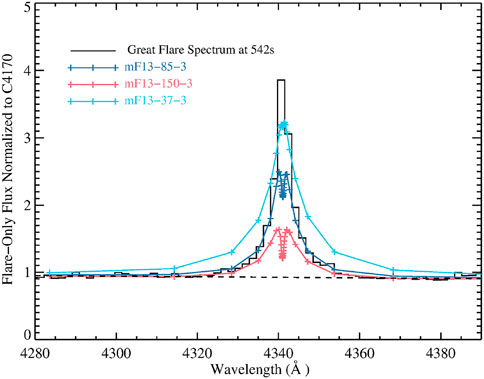
FIGURE 2. Comparisons of several F13 model spectra of Hγ directly from RADYN (and thus have relatively coarse wavelength sampling in the far wings) to the Great Flare rise/peak phase spectrum. Each model has been scaled to the observed continuum flux, C4170’. The mF13-37-3 model prediction is far too broad, while the mF13-85-3 and mF13-150-3 models do not exhibit an amount of broadening that exceeds the observation in the line wings. The dashed line shows a detailed continuum spectrum that is interpolated to the wavelengths over the Hγ line.

To quantitatively assess the models, we calculate several quantities from the detailed Hγ line profiles and the continuum spectra. Specifically, we calculate the continuum-subtracted, preflare-subtracted, line-integrated flux over the Hγ emission line (hereafter, $F_{\mathrm{H}\gamma }^{\prime }$), the preflare-subtracted flux⁶ at λ = 4170 Å (hereafter, C4170’), and the ratio of these quantities (Table 1). The 5F11 and F12 models produce ratios that are far too large compared to $F_{\mathrm{H}\gamma }^{\prime }$/C4170’ ≈ 20 that is calculated from the Great Flare observation (Kowalski et al., 2013), while the ratios from the F13 models with large low-energy cutoffs are too small. This motivates linear superpositions of two RHD model components–one high-flux (F13) component and one lower-flux (5F11 or F12) component–to comprehensively reproduce the observed line-to-continuum ratios, the shape of the Hγ wing broadening, and the Hγ emission line peak flux.

4.2 Two-component model fits to the Hγ line in the AD Leo great flare

A linear superposition of a high flux (F13), large low-energy cutoff beam component and a lower flux (5F11, F12, or 2F12), smaller low-energy cutoff beam component is represented by the equation (Eq. 1),

$f_{\lambda ,\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}^{\prime }=\left(X_{\mathrm{F}\mathrm{13}}{S}_{\lambda ,\mathrm{F}\mathrm{13}}^{\prime }+X_{\mathrm{5}\mathrm{F}\mathrm{11}}{S}_{\lambda ,\mathrm{5}\mathrm{F}\mathrm{11}}^{\prime }\right)\frac{R_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}}^2}{d^2}(1)$

where $f_{\lambda ,\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}^{\prime }$ is the model flux at Earth. The filling factor, X, is the exposure-time-averaged fraction of the visible hemisphere of the star that is flaring with the temporal coadd of the radiative surface flux spectrum, S_λ, calculated from each RHD model component. R_star = 3 × 10¹⁰ cm is the radius of AD Leo, and d = 1.5 × 10¹⁹ cm is the distance to the star. The preflare model surface flux spectrum is subtracted to give the flare-only, model surface flux spectra, $S_{\lambda }^{\prime }=S_{\lambda }-S_{\lambda ,o}$, in Equation 1. To mitigate systematic errors in the far wings of the Hγ line (Figure 2), which are coarsely sampled at 31 wavelength points in the RADYN calculation, we recalculate⁷ the emergent surface flux spectra using a Feautrier solver on a 327 point wavelength grid with the frequency-independent, non-LTE source function from RADYN and a four-point, third-order interpolation of the line profile opacity from the Appendix of Vidal et al. (1973). The emergent radiative flux spectra of Hγ are time-averaged over the duration of each simluation, convolved with a Gaussian with a full-width-at-half maximum that corresponds to the instrumental resolution of 3.5 Å, and binned to the wavelengths of the Great Flare spectra.

We perform an inverse-variance-weighted, linear least-squares fit of the two parameters X_F13 and X_5F11 to the observed spectrum around the Hγ line. The model surface flux spectra are the basis functions in the nλ × 2 design matrix, Λ. The maximum likelihood (ML) estimates of the parameters are given by the standard matrix equation (Eq. 2),

${\widehat{\vec{X}}}_{\mathrm{M}\mathrm{L}}=\left(\begin{array}{c}\hfill {\widehat{X}}_{\text{F}13,\text{ML}}\hfill \\ \hfill {\widehat{X}}_{5\text{F}11,\text{ML}}\hfill \end{array}\right)={\left({\mathrm{\Lambda }}^{\mathrm{T}}{C}_{{\overrightarrow{f }}_{\lambda }\prime }^{-1}\mathrm{\Lambda }\right)}^{-1}\left({\mathrm{\Lambda }}^{\mathrm{T}}{C}_{{\overrightarrow{f }}_{\lambda }\prime }^{-1}{\overrightarrow{f }}_{\lambda }\prime \right)(2)$

where ${\vec{f}}_{\lambda }^{\prime }$ is the observed nλ × 1 flare-only flux at Earth (hereafter dropping the vector notation) as a function of wavelength and the nλ × nλ covariance matrix C is populated with independent, Gaussian uncertainties, which are estimated from the data, $f_{\lambda }^{\prime }$. The wavelength range from λ = 4320 − 4361 Å is used in the fits, which are performed for all combinations of two models from the grid. The models in Table 1 are among the combinations with the lowest values of χ² and were thus chosen as the focus of this study. Figure 3 shows the result of one of the best fits with ${\chi }_{\mathrm{d}\mathrm{o}\mathrm{f}}^2=1.2$ for 21 degrees of freedom (dof). The quality of this fit is representative of many such results with two RHD component spectra consisting of a high-flux, large low-energy cutoff beam and a lower-flux, smaller low-energy cutoff beam. In the right panel of Figure 3B, we show likelihood contours for this fit to visualize typical uncertainties on the maximum-likelihood estimates of the parameters. The comparisons of the inferred filling factors of the high-flux (e.g., F13) and lower-flux (e.g., 5F11) models in each fit will be more useful in comparison to solar flare data (Section 5.3), and therefore we report values of $X_{\mathrm{r}\mathrm{e}\mathrm{l}}=\frac{X_{\mathrm{5}\mathrm{F}\mathrm{11}}}{X_{\mathrm{F}\mathrm{13}}}$. For the model combination in Figure 3, the best-fit parameters and standard error propagation give X_rel = 2.28 ± 0.08. The value of $F_{\mathrm{H}\gamma }^{\prime }/$C4170’ = 19.9 is remarkably consistent with this measured quantity from the observed flare spectrum.

FIGURE 3

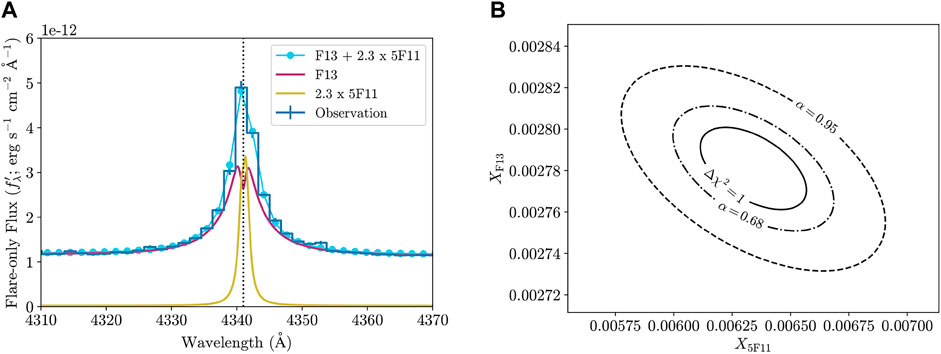
FIGURE 3. (A) A representative example of a satisfactory, two-component (mF13-85-3, m5F11-25-4) RHD model fit to the observed Hγ line profile and nearby continuum flux in the Great Flare of AD Leo. (B) Constant joint-likelihood contours for the model fit in the left panel. The maximum-likelihood estimates of the parameters and 1σ, Gaussian marginal uncertainties are ${\widehat{X}}_{\mathrm{F}\mathrm{13},\mathrm{M}\mathrm{L}}=2.78\times 10^{-3}\pm 2\times 10^{-5}$ and ${\widehat{X}}_{\mathrm{5}\mathrm{F}\mathrm{11},\mathrm{M}\mathrm{L}}=6.34\times 10^{-3}\pm 2.3\times 10^{-4}$ with a correlation coefficient of ρ = −0.53.

The results for several representative combinations of models in Table 1 with small values of χ² are presented in Table 2, indicating a range of values of X_rel ≈ 1.5 − 10. Since these fits include only the Hγ line data for this flare, the relatively small differences in the various χ² values in Table 2 are not strictly indicative of a global minimum. The vast majority of all model combinations from the entire grid, however, result in χ² values far in excess of those shown in Table 2. We think that an exploratory approach to the model grid predictions is more productive than an effort to find one model that best satisfies all constraints from the data, given the many assumptions in the RHD modeling (e.g., specific choice of low-energy cutoff values in the grid, assumptions of constant-area loop geometry and a constant power-law index value over each pulse). The small values of χ² are thus most informative for limiting the vast parameter space for further comparisons of our general modeling paradigm to the multi-wavelength data of the Great Flare.

TABLE 2

TABLE 2. Least-squares fitting results for Hγ.

4.3 Models of the balmer limit

In order to robustly extrapolate the models of this flare to the NUV wavelength range that was not observed during most of the impulsive phase, the Balmer jump strength in the observation should be satisfactorily reproduced. However, many linear combinations of two models in the RADYN flare grid produce small Balmer jump ratios that are consistent with the measured range (χ_flare ≈ 1.7 − 1.9; Kowalski et al., 2013) from the spectrum of the Great Flare. For supplementary constraints, we compare the details of the merging of the Balmer series at λ = 3646 − 4000 Å. The last visible Balmer emission line is often used as an indication of the electron density, and Hawley and Pettersen (1991) discusses that the Balmer lines up to and including H15 or H16 are resolved in the Great Flare spectra. Thus, our RHD model combinations should reproduce this salient property.

We use the RH code (Uitenbroek, 2001) with a 20-level hydrogen atom and the occupational probability modifications to the bound-bound and bound-free opacities that account for level dissolution at the Balmer limit (Dappen et al., 1987; Hummer and Mihalas, 1988; Nayfonov et al., 1999; Tremblay and Bergeron, 2009). The RH calculation setup is the same as described in Kowalski et al. (2017b). These calculations are intensive because they involve a large numerical convolution at each atmospheric depth, and not every time-step in all models readily converges to a solution. To demonstrate a representative solution with the two-component modeling approach from the previous section, we use atmospheric snapshots from the mF13-150-3 simulation at t = 0.0, 0.4, 1.0, 2.0, 4.0, 6.0, 8.0, 9.8 s and a snapshot from the m5F11-25-4 simulation at t = 0.8 s. The F13 model spectra are coadded, and the preflare spectrum is subtracted from the two model components. We then use the equation (Eq. 3),

${\left(F_{\mathrm{H}\gamma }^{\prime }/{\mathrm{C}\mathrm{4170}}^{\prime }\right)}_{\mathrm{o}\mathrm{b}\mathrm{s}}=\frac{X_{\mathrm{r}\mathrm{e}\mathrm{l}}\times F_{\mathrm{H}\gamma \text{,\hspace{0.17em}}5\text{F}11}^{\prime }+F_{\mathrm{H}\gamma \text{,\hspace{0.17em}F}13}^{\prime }}{X_{\mathrm{r}\mathrm{e}\mathrm{l}}\times {\mathrm{C}\mathrm{4170}}_{\mathrm{5}\mathrm{F}\mathrm{11}}^{\prime }+{\mathrm{C}\mathrm{4170}}_{\mathrm{F}\mathrm{13}}^{\prime }}(3)$

to solve for X_rel given ${(F_{\mathrm{H}\gamma }^{\prime }/{\mathrm{C}\mathrm{4170}}^{\prime })}_{\mathrm{o}\mathrm{b}\mathrm{s}}=20$. The total two-component model flux spectrum is scaled to the continuum flare flux, C4170′, in the observed spectrum. For the two-component model combination above, a value of X_rel ≈ 3.9 is obtained, which is close to 4.5 that is obtained from fitting the Hγ line profile (Table 2). We convolve the flare model with the spectral resolution of the data and show the result against the observations in Figure 4, which demonstrates consistency with the observed Balmer jump flux ratio, the detailed merging of the line series wings, and in the bluest visible Balmer line. Without the additional narrow-line flux from the 5F11, the highest balmer line in emission is H13, which is inconsistent with the observations. Without the continuum and Balmer wing flux from the F13 model, the Balmer jump ratio and the $F_{\mathrm{H}\gamma }^{\prime }/{\mathrm{C}\mathrm{4170}}^{\prime }$ value from the 5F11 model are far larger (Table 2) than measured from the observed spectrum.

FIGURE 4

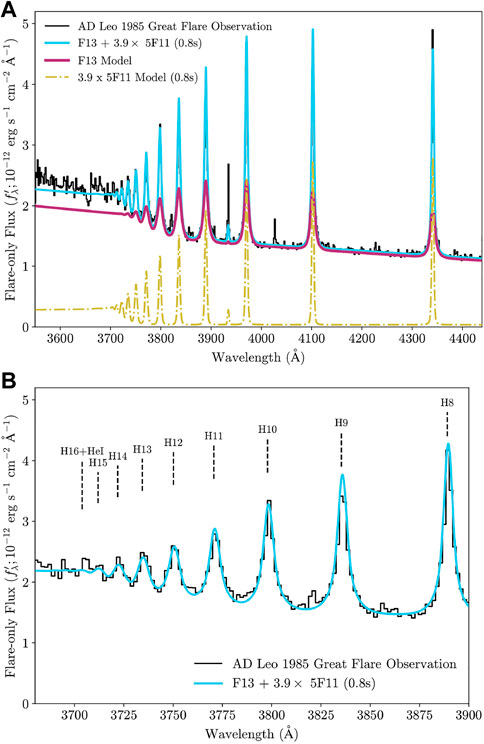
FIGURE 4. (A) RH calculations with non-ideal opacity effects at the Balmer limit. A linear superposition of the mF13-150-3 model, averaged over its duration, and the m5F11-25-4 model at t = 0.8 s is shown for the combination that is constrained by a value of $F_{\mathrm{H}\gamma }^{\prime }/{\mathrm{C}\mathrm{4170}}^{\prime }$ that is measured from the observed spectrum. The individual component model calculations are shown: the m5F11 contributes to the narrow hydrogen line flux, the highest order Balmer lines, and optically thin Balmer continuum flux in addition with the optically thick Balmer continuum flux from the F13. The mF13 model accounts for nearly all of the optical continuum flux and far wing radiation. (B) The pseudo-continuum from the merging of the Balmer H8—H15 line wings, the dissolved level continuum between the lines, the fading of the emission line fluxes into the dissolved-level continuum at λ < 3700 Å, and the bluest Balmer line (H15) are adequately reproduced in the RHD model superposition. The wavelengths of the hydrogen series and a helium I line noted by Hawley and Pettersen (1991) are indicated.

4.4 Broadband continuum fitting

In this section, we fit the observed continuum fluxes from the FUV to the red-optical during the early impulsive phase of the AD Leo Great Flare to compare to the results from fitting to the Hγ spectrum (Table 2) and high-order series merging (Section 4.3).

Figure 5 shows a comparison of the detailed continuum fluxes for several combinations of the models that satisfactorily explain the early-impulsive phase, blue-optical spectrum of the Great Flare of AD Leo. A representative RHD model combination (mF13-150-3, m5F11-25-4 (t = 0.8s)) from Section 4.3 exhibits a peak at λ ≈ 2350 − 2400 Å followed by a turnover toward shorter wavelengths. Qualitatively, these properties are consistent with FUV constraints of this superflare and other, smaller flares from AD Leo (Hawley et al., 2003), but the IUE/SWP observation allows a more detailed comparison. To adjust the flux calibration of the data for the different exposure times between the early-impulsive phase, IUE/SWP spectrum (t < 900 s in Figure 1) and the λ > 3560 Å ground-based spectrum (t = 542 ± 90 s in Figure 1; see Section 2), we apply the relative scaling between the U-band and the FUV continuum flux at λ ≈ 1600 Å within the first 900 s of the flare that is presented in the upper left panel of Figure 11 of Hawley and Fisher (1992). The relative scale factor (1.3) is used to adjust the lower envelope of the SWP continuum flux relative to a synthetic U-band flux that we calculate from the blue-optical spectrum. The scaled and original IUE/SWP spectra are shown in Figure 5. We also include the V- and R-band photometry from the same figure in Hawley and Fisher (1992) and apply the scaling in the same way as for the FUV continuum. We calculate two-parameter, linear least-squares fits to the seven flare-only flux measurements of the continuum in the Great Flare⁸. Minimizing χ² (Section 4.2) gives several combinations of models with very large low-energy cutoffs (E_c = 350 − 500) as the X_F13 model component superimposed with the m2F12-37-2.5 model spectrum. Note, the m2F12-37-2.5 model is the only simulation in our RADYN grid with such a hard, δ < 3, electron beam power-law index.

FIGURE 5

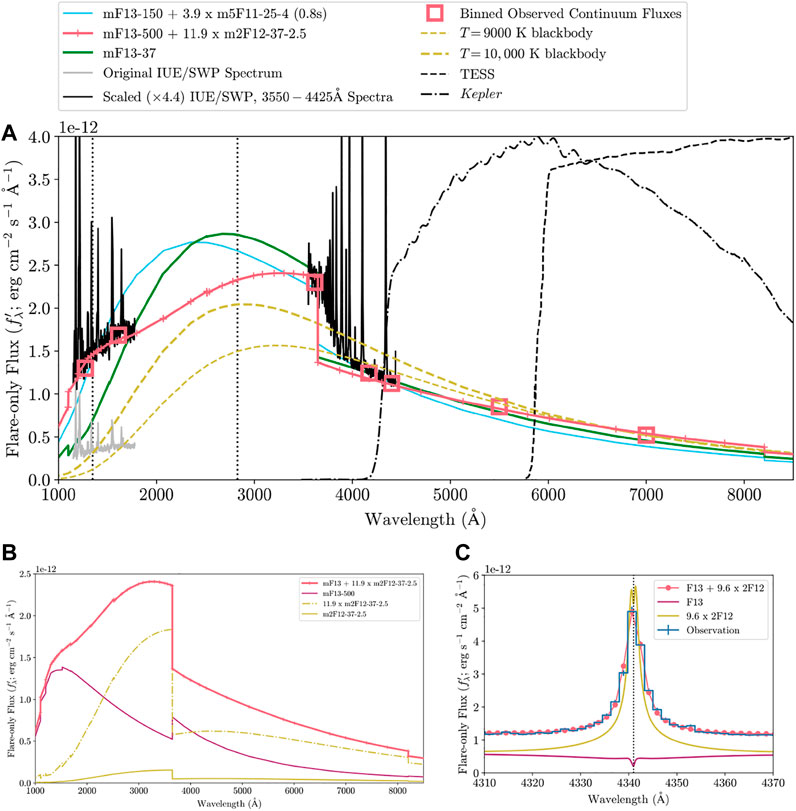
FIGURE 5. (A) Models of the early-impulsive phase broadband continuum flux distribution of the Great Flare of AD Leo compared to the IUE/SWP spectrum, optical ground-based spectrum, and broadband V and R photometry. All observed fluxes have been adjusted to the synthetic U-band flux according to the broadband distribution at t = 0 − 900 s in Figure 11 of Hawley and Fisher (1992). The wavelength-binned, flare-only fluxes that are used to fit the models are indicated by square symbols with a best-fit, two-component RHD model continuum spectrum shown as the solid red line. Other model predictions are scaled to the observations as follows: the blackbody functions are scaled to the R band flux observation, and the other two RHD models are scaled to the average continuum flux at λ = 4155 − 4185Å. (B) Individual model components in the best-fit mF13-500-3 + 11.9× m2F12-37-2.5 combination, which compares the relative contributions to the spectral luminosity of the continuum radiation in the Great Flare. The m2F12-37-2.5 model component is also shown without scaling by the best-fit filling factor to facilitate direct comparison to the radiative surface flux of the mF13-500-3. (C) Best-fit Hγ line profile model using the mF13-500-3 and m2F12-37-2.5 flux spectra gives a similar value of X_rel as for the fits to the broadband continuum fluxes.

The best-fit superposition of the mF13-500-3 and m2F12-37-2.5 radiative flux spectra is shown in Figure 5A (top panel) with X_rel ≈ 11.9. Notably, this fit comprehensively accounts for the slope of the lower-envelope of the FUV flare spectrum, the Balmer jump strength, and the optical continuum constraints. The middle, left panel of Figure 5B shows the contributions of the individual model components to the spectral luminosity of the flare continuum from the 'panel (A). The mF13-500-3 accounts for most of the FUV continuum luminosity, whereas the Balmer jump in the m2F12-37-2.5 contributes a larger fraction in the NUV and in the U band. At optical wavelengths, relative contributions to the blue continuum spectral luminosity are about equal, but the lower beam-flux model is larger toward near-infrared wavelengths. The comparisons of the surface flux spectra without adjustments by the best-fit filling factors emphasize that the F13 model is the much brighter source at all wavelengths. A fit using these two model component to the observed Hγ line profile (Section 4.2) is shown in Figure 5C (bottom, right panel); the fit is excellent and, moreover, returns a similar, independent estimate for the parameter X_rel = 9.6 (Table 2).

The fully-relativistic electron beam parameters of the mF13-500-3 beam are rather extreme, but they are not without precedent and sufficient semi-empirical necessity. Kowalski et al. (2017b) used a superposition of three RADYN simulations to model the decay phase spectra of a superflare from the dM4.5e star YZ CMi. A RADYN model with a constant electron beam energy flux injection of 2 × 10¹² erg cm⁻² s⁻¹, a low-energy cutoff of E_c = 500 keV, and a power-law index of δ = 7 was used to explain the spectra of a secondary flare event, which exhibit features that are similar to an A-type star photospheric spectrum: namely, broad Balmer lines and a Balmer jump “in absorption” (see also Kowalski et al., 2012, 2013). Secondary flare events in the decay phase of a large flare from the young G-dwarf, EK Dra, were reported in Ayres (2015) to exhibit a response in only the FUV continuum. Finally, we note that increasing the value of X_rel after the peak flare phase may be able to explain the relatively rapid nature of the FUV continuum radiation that has been reported in other M dwarf flares (Hawley et al., 2003; MacGregor et al., 2020).

5 Discussion

5.1 Summary of fitting results

We fit the Great Flare impulsive phase (rise/peak) spectrum using simulations of electron beam heating from a new grid of RADYN flare models. The data require two, independent RHD model components, resulting in relative filling factors (X_rel) of the components between $\approx 1-10$, with the lower beam flux model component exhibiting the larger filling factor. The time-evolution of the simulated atmosphere and emergent radiative flux spectra over each heating pulse is included in these comparisons to the data. Several examples of fits were presented and discussed. The shape of the Hγ line profile far into the wings and nearby continuum flux constrains combinations of a high-flux model (F13) with large low-energy cutoff values (E_c = 85 − 500 keV) and a lower-flux model (5F11–2F12) with smaller low-energy cutoff values (E_c = 25 − 37 keV). In the (mF13-85-3, m5F11-25-4) spectral luminosity, most of the Hγ wing broadening and blue-optical continuum radiation is attributed to the F13 model component. In the (mF13-200-3, mF12) model fits, most of the blue-optical continuum luminosity is due to the F13 spectrum, but much of the wing broadening can be attributed to the lower beam flux, F12, component. This is qualitatively consistent with the modeling results from Namekata et al. (2020), who found that similar F12 electron beam models produce satisfactory agreement in the broadening of the Hα line in a superflare. In their work, however, detailed comparisons to the spectra of the blue-optical continuum radiation were not possible.

We examined the prediction of one of the fits to the Great Flare Hγ line against the spectrum of the hydrogen series at the Balmer limit; there is remarkable agreement with the highest-order Balmer line in emission and with other features in the rise/peak spectrum (Figure 4). Models are also independently fit to the broadband photometry and spectral distribution during the first 900s of the Great Flare, and the superposition of spectra from the mF13-500-3 (or mF13-350-3) and the m2F12-37-2.5 RHD model components gives an excellent fit; moreover, this fit results in about the same relative filling factor as inferred from the Hγ line profile fitting. For this combination of models, the relative contributions to the optical continuum luminosity are comparable, but the E_c = 500 keV model dominates the FUV flare luminosity. In all model combinations, the F13 model component produces the brightest continuum surface flux.

In this section, we use the results from the fits to discuss the implications for models of the NUV radiation environment of the habitable zones of low-mass flare stars (Section 5.2). Then, we examine a high-spatial resolution image of a widely-studied X-class solar flare to speculate on the origin of these two spectral components in terms of solar flare phenomenology (Section 5.3). We show how the relative filling factors of the two model components are consistent with the relative areas of solar flare kernels and ribbon intensities, respectively, in the impulsive phase of this solar flare. In Section 5.4, we discuss further empirical investigation to anchor the two-component continuum and Hγ broadening models of stellar flares in reality.

5.2 The NUV radiation field in habitable zones of low-mass, flare stars

The detailed RHD models provide insight into the magnitude of the possible systematic errors for the inferred NUV radiation field in the habitable zones of low-mass flare stars. The RHD spectra in the NUV reveal that simple extrapolations from flare photometry in the red-optical and near-infrared (e.g., from the Kepler or TESS bands) that do not account for the Balmer jump strength, may result in rather large systematic modeling errors. We scale a T = 9000 K and T = 10, 000 K blackbody to the observed R-band flux of the Great Flare in Figure 5A (top panel). Compared to the RHD models, the blackbody models under-predict the λ = 1800 − 3646 Å flare-only flux by factors ranging from 1.2 to 2.0. The peaks and slopes of the UV and U-band continuum spectra are largely in disagreement as well. Scaling all models to a common RHD continuum flux at a redder continuum wavelength, λ = 7810 Å, that is closer to the central wavelength of the TESS white-light band (Figure 5) generally results in larger underestimates of the NUV continuum flare-only flux by factors up to 2.6. The inadequacies of single-temperature, blackbody models are even more evident at λ = 1100 − 1800 Å and in the expected amount of Lyman continuum fluxes at λ ≲ 911 Å (not shown) that are present in the RHD model spectra.

The recent laboratory experiments of Abrevaya et al. (2020) measured survival curves of microorganisms that were irradiated by sustained fluxes of monochromatic NUV light at λ = 2540 Å. In the worst-case scenario of direct irradiation, they found that a large UV-C flux from a superflare in the habitable zone (d = 0.0485 au; Anglada-Escudé et al., 2016) of the dM5.5e star Proxima Centauri fails to terminate biological function in a small but non-negligible fraction of the initial sample. The UV-C flux⁹ of 92 W m⁻² was calculated by scaling a T = 9000 K blackbody curve to the peak magnitude change in the Evryscope g′ bandpass as described in Howard et al. (2018); we refer the reader to Law et al. (2015) and Howard et al. (2019) for details about the Evryscope survey. We estimate that the peak B-band (λ = 3910 − 4890 Å) luminosity of the Great Flare of AD Leo was at least a factor of three larger than the g′-band (λ ≈ 4050 − 5500 Å) peak luminosity of the Proxima Centauri superflare. If a flare as luminous as the Great Flare (and the same in all other regards) were to occur on Proxima Centauri, the RHD models in Figure 5 predict UV-C, impulsive-phase, habitable-zone fluxes of 800 − 1000 W m⁻². This range is rather similar to the habitable-zone, UV-C fluxes inferred in Howard et al. (2020) using extrapolations from much higher temperature blackbody fits to broadband optical and near-IR photometry. As Howard et al. (2020) discuss, it would be interesting for laboratory experiments to determine whether there is an upper limit to the UV-C flux at which a microbial population achieves a steady-state survival fraction.

The pioneering study of Segura et al. (2010) combined the multi-wavelength AD Leo flare spectra for empirically-driven photochemistry and surface UV dosage modeling of an Earth-like planet in the habitable zone at d = 0.16 au from a dM3 star. In their approach, Segura et al. (2010) used the first IUE/LWP (NUV) spectrum available (starting at 5:00 UT in Figure 1) to bridge the blue-optical and IUE/SWP spectra during the early impulsive phase in the first 900 s of Figure 1. This approach assumes that the peak impulsive-phase NUV flare spectrum is the same as that at the end of the fast decay and start of the gradual decay phase in this event. At longer wavelengths, this assumption is not consistent with analyses of more recent, time-resolved spectra (Kowalski et al., 2013). However, we think that this approach is reasonably justified given the vagaries inherent in such spectral observations with relatively long exposure times that are not contemporaneous within the Great Flare.

Our scaling of the IUE/SWP spectrum (Figure 5) follows a different approach and is consistent with the relative surface fluxes at λ ≈ 1600 Å and the U band that are shown in the upper left panel of Figure 11 of Hawley and Fisher (1992) and in Table 5 of Hawley and Pettersen (1991). In the IUE/LWP decay phase spectra of the Great Flare, the ratio of the λ = 2800 Å to λ = 2000 Å continuum fluxes is $\approx 5$ (Hawley and Pettersen, 1991, see also Segura et al. (2010)), which effectively force the FUV continuum flux to a lower value relative to the fluxes at longer wavelengths in the NUV and U band. In our best-fit (mF13-500-3, m2F12-37-2.5) continuum flux model of the early impulsive phase (Figure 5), the λ = 2800 Å to 2000 Å continuum flux ratio is only 1.3. Thus, one expects the wavelength-integrated, UV-C flux of this model combination to be a factor of $\approx 1.5$ larger than the empirical model of Segura et al. (2010), assuming equal top-of-the-atmosphere fluxes at λ ≈ 2800 Å. However, further comparison reveals that the Segura et al. (2010) composite flare spectrum is similarly flat at λ ≳ 2400 Å. This effect is apparently due to the large number of blended (and saturated) Fe II and Mg II emission lines, which are generally much more prominent relative to the flare continuum radiation in the decay phase (Kowalski et al., 2019b). This coincidence is fortuitous for many follow-up studies (e.g., Venot et al., 2016; Tilley et al., 2019) that have adopted the composite NUV flare spectra from Segura et al. (2010) for photochemistry modeling: the pseudo-continuum of blended, saturated lines in the decay phase of the Great Flare mimics the shape of our RHD model continuum distribution that best reproduces the available observations in the rise and peak phases.

5.3 A solar flare “kernel + ribbon” interpretation of the great flare rise/peak phase

In this section, we argue that the results from the two-component model RHD fits are ostensibly consistent with the relative areas of high-intensity and medium-intensity sources in the impulsive phase of well-studied solar flare. The IRIS SJI 2832 image during the impulsive phase of the 2014 March 29 X1 solar flare is shown in Figure 6. We calculate the areas corresponding to several intensity ranges in the SJI 2832 image: ${⟨I_{\lambda }⟩}_{\mathrm{S}\mathrm{J}\mathrm{I}}=2-4\times 10^6$ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹ (faint threshold), 4 − 8 × 10⁶ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹ (medium threshold), and $\ge 8\times 10^6$ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹ (bright threshold). The bright threshold selects the pixels corresponding to the bright kernel (which is referred to as BK#1 in Kowalski et al., 2017a), and the medium threshold corresponds to the elongated ribbons on both sides of the brightest kernel¹⁰. In Figure 6, the dashed contour outlines the faint threshold area, the green-colored pixels correspond to the medium threshold pixels, and the purple and white pixels isolate the bright threshold kernel. We sum the exclusive areas within these three intensity ranges, and the equivalent circular areas that correspond to the assumed stellar footpoint geometry (Eq. 1) are illustrated in the bottom left of the figure. The ratios of these areas are ≈ 25:5:1 for the faint:medium:bright areas, respectively. Coincidentally, the ratio of medium:bright areas is 5:1, and the ratio of faint:medium brightness areas is also 5:1. These ratios are very similar to the areal ratios (X_rel; Table 2) that we inferred between the higher flux and lower flux models through our spectral fitting to the AD Leo Great Flare. Thus, we attribute the two model components as representing a bright kernel–or several bright kernels–and fainter ribbons over a larger area.

FIGURE 6

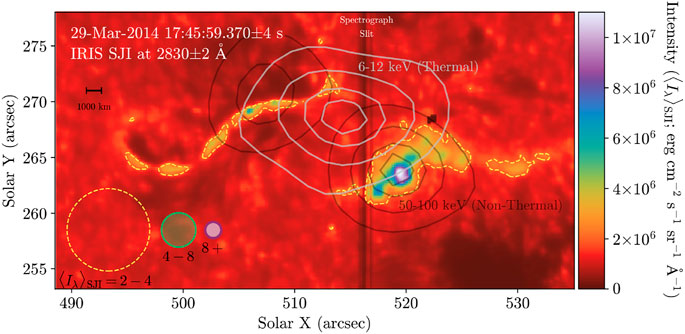
FIGURE 6. IRIS SJI 2832 image during the hard X-ray impulsive phase of the 2014 March 29 solar flare. The spatial resolution of the IRIS image is 0.′′4 (0.′′167 pix⁻¹; 724 km arcsec⁻¹). The projected, exclusive areas of 2.3 × 10¹⁷, 3.9 × 10¹⁶, and 8.6 × 10¹⁵ cm² correspond to the intensity ranges indicated in the figure below the equivalent circular areas. Note, an excess image formed by subtracting the image from 150 s earlier reveals much fainter emission; in this case, an excess threshold value of 6 × 10⁵ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹ (Kowalski et al., 2017a) show that the faintest parts of the ribbons extend over an area of $\approx 5\times 10^{17}$ cm². The RHESSI X-ray contours are plotted at 25, 50, 75, and 90% of the maxima.

The two RHD model components could also represent the faint-intensity and medium-intensity areas, respectively, which exhibit an areal ratio of 5:1. To justify this interpretation as the less plausible analogy for stellar flares, we bring in analyses of a solar, RADYN flare model (“c15s-5F11-25-4.2”) from Kowalski et al. (2017a) and Kowalski et al. (2022). Kowalski et al. (2017a) synthesized the SJI 2832 intensity from this model, accounting for the emission lines and continuum response in this bandpass. At the brightest times of the 5F11 model (t ≈ 4 s), they calculate a synthetic SJI 2832 intensity of ${⟨I_{\lambda }⟩}_{\mathrm{S}\mathrm{J}\mathrm{I}}\approx 10^7$ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹, which is consistent with the brightest pixels in Figure 6. Since this study, a detailed identification of the emission lines that contribute to the SJI 2832 data in solar flares has been presented (Kowalski et al., 2019a, see also Kleint et al., 2017), and several updates to the atomic physics of Fe II have been implemented (which are to be described elsewhere in detail). The new calculations result in fainter emission line flux but similar redshift evolution of the Fe II lines. Averaging the solar c15s-5F11-25-4.2 model from Kowalski et al. (2022) over a simulated SJI 2832 exposure time of 8 s, so as to be directly comparable to the brightest pixels in the data in Figure 6, results in a synthetic model intensity of only ${⟨I_{\lambda }⟩}_{\mathrm{S}\mathrm{J}\mathrm{I}}\approx 5\times 10^6$ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹. This intensity is above the medium-intensity threshold area corresponding to the green-colored ribbon pixels in Figure 6, but it is not nearly as bright as the most intense pixels. The IRIS raster clearly “steps over” the brightest kernel¹¹ in Figure 6 (see Figure 1 in Kowalski et al. (2017a) and the discussion in Kleint et al., 2016). Thus, the 5F11 electron-beam, solar flare modeling with a small, low-energy cutoff is apparently most appropriate for the medium-intensity ribbons instead of the fainter ribbons that extend beyond the hard X-ray contours or the brightest pixels at the centroid of the hard X-ray contours. The faintest ribbon intensity in the impulsive phase¹² may correspond to locations of impulsive energy deposition by thermal conduction (Battaglia et al., 2015; Ashfield et al., 2022) and/or XEUV backheating over a large area (Fisher et al., 2012). The latter has been investigated in detail with 1D non-LTE models for the Great Flare data (Hawley and Fisher, 1992); we speculate that radiative backheating from an arcade of hot loops (e.g., Kerr et al., 2020) may account for additional Ca II K line flux in the model spectra in Figure 4A (top panel).

Is there evidence that a much stronger source of heating than a 5F11 beam contributes to the brightest SJI 2832 kernel pixels in this solar flare? Using an even brighter intensity threshold of ${⟨I_{\lambda }⟩}_{\mathrm{S}\mathrm{J}\mathrm{I}}=10^7$ erg cm⁻² s⁻¹ sr⁻¹ Å⁻¹ to mask the solar flare kernel in Figure 6 gives an area of 3.3 × 10¹⁵ cm⁻², or four IRIS pixels. Dividing this area into the nonthermal electron power (8 × 10²⁷ erg s⁻¹) above 20 keV that is inferred through standard collisional thick target modeling in Kleint et al. (2016) gives an injected electron beam flux of 2 × 10¹² erg cm⁻² s⁻¹ (2F12). This is not as high as the maximum injected beam fluxes in the F13 models, but it is much larger than typically considered in solar flare RHD modeling. This line of reasoning implies that a much higher beam flux model is a more appropriate collisional thick target inference for the brightest SJI 2832 kernel in this solar flare. For these large beam fluxes, however, the standard assumptions in collisional thick target modeling of the hard X-ray footpoints are not applicable when the ambient coronal densities are small (Krucker et al., 2011). Although the RHESSI sources are largely unresolved (with a spatial resolution of 3.′′6, or 5.4 × 10¹⁶ cm² at the Sun; Battaglia et al., 2015), the spatially integrated hard X-ray and IRIS SJI 2832 powers provide upper limits on necessitated modifications to the thick-target physics (e.g., Kontar et al., 2008; Brown et al., 2009; Kontar et al., 2012; Hannah et al., 2013; Alaoui and Holman, 2017; Allred et al., 2020) that are implemented in future modeling of the heterogeneous atmospheric response within the hard X-ray source contours. Graham et al. (2020) investigated the deficiencies in chromospheric condensation model predictions of the red-wing asymmetry evolution of Fe II flare lines in IRIS spectra. Resolving the disagreements, and drawing on implications for the standard collisional thick target inferences of beam parameters, would greatly enhance the realism of the analogous stellar flare RHD component with small low-energy cutoff values.

5.4 Future observational constraints

Graham et al. (2020) used two intensity thresholds in faster-cadence SJI 2796 imaging of a different X1 solar flare to quantify newly brightened areas as a function of time. The ratios of these areas are $\approx 10:1$, and the areal evolution is rather similar to the timing of the spatially integrated, hard X-ray emission peaks from Fermi/GBM. Further verification of the heterogeneity between kernel and the medium-brightness ribbon pixels are clearly needed from solar flare spectral observations. One such unexplored constraint is the NUV and FUV continuum evolution from IRIS flare spectra. In Figure 5A (top), we show the locations of two continuum windows in the IRIS spectra around λ ≈ 2826 Å and λ ≈ 1349 Å. The two spectral components obtained from our fits exhibit distinct, time-dependent C2826′/C1349′ emergent intensity ratios. A detailed investigation of the relative continuum intensities for a large sample of solar flares would help to determine the heterogeneity of the atmospheric response between the brightest kernels and nearby bright ribbons.

Reality checks could also be attained through spatially resolved characterization of the hydrogen Balmer line broadening along the slit length of observations of solar flares with the Visible Spectropolarimeter (ViSP; de Wijn et al., 2022) on the Daniel K. Inouye Solar Telescope (DKIST; Rimmele et al., 2020). Our stellar flare phenomenological modeling paradigm (Section 5.3) implies that the continuum-subtracted effective widths of the Hγ emission line (Kowalski et al., 2022) from the emergent intensity spectra of the brightest kernels should exhibit much larger effective widths (Table 1, rightmost column) than the medium-brightness ribbon component. In solar observations, the pixels with the largest Hγ effective widths should also show the brightest blue-optical continuum intensity. A statistical classification of hydrogen line spectra should reveal distinct components that correlate with timing and position along the solar flare ribbons, similar to the groupings that were reported for a large sample of Mg II flare lines in IRIS spectra (Panos et al., 2018).

On the stellar side, high-cadence spectral observations of low-mass stellar flares at λ = 1800 − 3200 Å during the impulsive phase would clarify how the NUV continuum flux peaks and turns over into the FUV in events like the Great Flare, which exhibits a small Balmer jump and a highly-impulsive, broadband temporal evolution. The Cosmic Origins Spectrograph on the Hubble Space Telescope provides such an opportunity: the G230L grating with a central wavelength at λ = 3000 Å gives simultaneous spectral coverage at λ = 1700 − 2100 Å and λ = 2800 − 3200 Å, which would provide the necessary observations to test the RHD models. Recently, Kowalski et al. (2019b) reported on flare spectra from the Cosmic Origins Spectrograph (using a different central wavelength) and constrained the peak continuum flux to the U band. It was argued that these events are gradual-flare (GF) events with large Balmer jumps and large line-to-continuum ratios, which are in stark contrast to the measured quantities from the Great Flare optical spectra. We briefly comment that our two-component modeling can readily reproduce the properties of these gradual-type flare events as well. For example, a two-component model consisting of the mF13-150-3 and the m5F11-25-4 spectra with X_rel ≈ 90 results in a Balmer jump ratio of 3.9 and a value of $F_{\mathrm{H}\gamma }^{\prime }/{\mathrm{C}\mathrm{4170}}^{\prime }\approx 150$, which are consistent with the quantities from HST-1 in Kowalski et al. (2019b). A parameter study of the detailed hydrogen line broadening and NUV spectra are planned as the subject of Paper II in that series.

6 Summary and conclusion

We have comprehensively modeled the multi-wavelength spectra during the rise and peak phase of the Great Flare of AD Leo (Hawley and Pettersen, 1991). We have shown that fitting two RHD spectral components to the detailed properties of the hydrogen series using an updated treatment of the pressure broadening, combined with a mechanism that heats deep chromospheric heights to T ≳ 10⁴ K, is readily feasible with satisfactory statistical significance. This semi-empirical modeling approach accounts for the evolution of height- and wavelength-dependent emission line and continuum opacities in the flare atmosphere, which is self-consistently calculated in response to high-flux electron beam heating. A simulation (Kowalski et al., 2015, 2016) with a large electron beam flux and the largest low-energy cutoff value range (≲ 40 keV) that is inferred from solar flare data (Holman et al., 2003; Ireland et al., 2013) produces a dense chromospheric condensation and hydrogen Balmer wings that are far too broad compared to the observation. Models that exhibit a large (≳ 85 keV), low-energy cutoff and high electron beam flux ($\approx 10^{13}$ erg cm⁻² s⁻¹) are able to explain the observed continuum distribution and highly broadened Balmer line wings that are within the constraints of the Balmer Hγ–H16 emission line series. Large, low-energy cutoffs are sometimes inferred in the so-called “late impulsive peaks” in solar flares (Holman et al., 2003; Warmuth et al., 2009), and significant progress has been made to improve the hard X-ray modeling of these events beyond the physics in the standard collisional thick target model (Alaoui and Holman, 2017).

A second, lower electron beam flux model exhibiting more similarities to nonthermal electron parameters that are typically inferred in collisional thick target modeling of hard X-ray data of solar flares (e.g., fluxes of 5 × 10¹¹ erg cm⁻² s⁻¹, low-energy cutoffs of E_c ≈ 25 keV) is necessary to fit the narrower hydrogen Balmer emission peak fluxes and account for the bluest Balmer line in the AD Leo Great Flare spectrum. We suggest that this second component represents heterogeneity of nonthermal beam injection and the differences between bright, larger area ribbons and brightest kernel morphologies that are readily seen in the impulsive phase of solar flare imagery. However, further verification is needed from solar observations: specifically, comparisons of hydrogen spectra at different locations in early flare development are critical. The implementation of this two-component, semi-empirical RHD modeling approach to Balmer line profiles of other M dwarf flares with higher resolving-power, echelle observations is underway (Kowalski et al., 2022, ApJ that is currently in the bibliography; Notsu et al., 2022; in preparation) and will further constrain plausible linear combinations of RHD model spectra.

The effects of transient UV radiation during flares is a relatively new topic in the study of exoplanet habitability (e.g., surface dosages) and atmospheric photochemistry (e.g., ozone photodissociation). These studies would benefit from new NUV spectral observations of stellar flares. The semi-empirical combination of RHD model spectra that are fit to the Great Flare observations predict unexpected properties of the NUV continuum spectra of impulsive-type M dwarf flares with small Balmer jumps, highly broadened Balmer lines, and small line-to-continuum ratios. We conclude that small Balmer jumps, which appear as relatively small deviations from a T = 9000 K or T = 10, 000 K blackbody fit to optical data in some flares, actually are consistent with much more energetic sources of ultraviolet radiation than previously thought were possible from solar and stellar chromospheres.

Data availability statement

The data and models supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AK contributed by analyzing the AD Leo flare data, running the RHD models, and performing the least squares fitting analysis. AK lead the analysis of the solar flare imaging, and he wrote the manuscript and produced the figures.

Funding

AK acknowledges funding support from, NASA ADAP 80NSSC21K0632, and NASA grant 20-ECIP20_2-0033. AK acknowledges publication cost support from the University of Colorado Library’s Open Access Fund established through an institutional membership agreement with Frontiers.

Acknowledgments

We thank two anonymous referees for their detailed comments that helped improve this work. AK thanks Suzanne L. Hawley for many stimulating conversations about flare spectra, flare modeling, and the AD Leo Great Flare data. AK thanks Joel C. Allred and Mats Carlsson for access to and assistance with the RADYN code, and Han Uitenbroek for access to and assistance with the RH code. AK thanks Pier-Emmanuel Tremblay for access to the TB09 + HM88 hydrogen broadening profiles. Many discussions with Rachel A. Osten, Clara Brasseur, Isaiah Tristan, Ward Howard, and John P. Wisniewski about NUV and optical flare continuum radiation were important for the motivation and development of the ideas in this work. AK thanks Eduard Kontar for helpful discussions about the collisional thick target model of solar flare hard X-ray emission. AK thanks Eric Agol for suggesting ten years ago to explore large, low-energy cutoffs in flare heating models. Many discussions about Balmer jump solar flare spectra and instrumentation with Gianna Cauzzi, Hoasheng Lin, and Tetsu Anan led to refining the ideas about the solar-stellar connection presented in this work. IRIS is a NASA small explorer mission developed and operated by LMSAL with mission operations executed at NASA Ames Research Center and major contributions to downlink communications funded by ESA and the Norwegian Space Centre.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹According to the World Health Organization, the ultraviolet is comprised of three bands: UV-C (λ = 1000 − 2800 Å), UV-B (λ = 2800 − 3150 Å), and UV-A (λ = 3150 − 4000 Å). We follow Abrevaya et al. (2020) and other recent studies of the biological impact of UV flares and denote the continuum radiation at λ = 2000 − 2800 Å as UV-C; the ultraviolet radiation at λ = 1000 − 2000 Å is also known as the very ultraviolet (VUV).

²Segura et al. (2010) refers to the spectrum at 915 s as the peak spectrum; this is S# 39 in the labeling scheme of Kowalski et al. (2013) and corresponds to the second, lower-amplitude peak in the impulsive phase.

³https://iris.lmsal.com/search/.

⁴https://hesperia.gsfc.nasa.gov/rhessi_extras/flare_images/image_archive_guide.html.

⁵A corresponding grid of models is calculated using a constant beam flux injection; these models are indicated with a “c”-prefix, such as cF13-85-3.

⁶Following traditional use, we denote flare-only quantities with a prime-symbol, and we refer to an observed spectral/monochromatic/specific flux density at Earth as the “flux”; we use “spectral luminosity” to refer to the luminosity per unit wavelength.

⁷All analyses have been performed on both the original 31-wavelength array and the 327-wavelength array.

⁸Instead of U and B-band photometry used for model fitting in Hawley and Fisher (1992), we use C3615’, C4170’, and C4400’ calculated from averages of the continuum fluxes at Δλ ≈ 30 Å around λ = 3615, 4170, 4400Å, respectively.

⁹For continuity with these studies, we momentarily express quantities in S.I. units.

¹⁰The medium threshold approximately corresponds to the “high thresh” area calculated from the excess intensity images in Kowalski et al. (2017a).

¹¹We further confirm this by inspecting the Mg II slit jaw images: though large regions of the ribbon are saturated, most of the saturation occurs away from the slit.

¹²The next SJI 2832 image corresponds to the beginning of the fast decay phase of the hard X-rays, and the faint intensity threshold clearly selects a large area in the “wakes” of the bright ribbons. In these wakes, the emission lines may exhibit broad, nearly symmetric profiles as the red-wing asymmetries have coalesced with the line component near the rest wavelength (Graham et al., 2020) while the flare continuum intensity is still at a detectable level in the IRIS NUV spectra (Kowalski et al., 2017a; Panos et al., 2018; Zhu et al., 2019).

References

Abrevaya, X. C., Leitzinger, M., Oppezzo, O. J., Odert, P., Patel, M. R., Luna, G. J. M., et al. (2020). The UV surface habitability of Proxima b: First experiments revealing probable life survival to stellar flares. Mon. Notices R. Astronomical Soc. 494, L69–L74. doi:10.1093/mnrasl/slaa037

CrossRef Full Text | Google Scholar

Alaoui, M., and Holman, G. D. (2017). Understanding breaks in flare X-ray spectra: Evaluation of a cospatial collisional return-current model. Astrophysical J. 851, 78. doi:10.3847/1538-4357/aa98de

CrossRef Full Text | Google Scholar

Allred, J. C., Kowalski, A. F., and Carlsson, M. (2015). A unified computational model for solar and stellar flares. Astrophys. J. 809, 104. doi:10.1088/0004-637X/809/1/104

CrossRef Full Text | Google Scholar

Allred, J. C., Alaoui, M., Kowalski, A. F., and Kerr, G. S. (2020). Modeling the transport of nonthermal particles in flares using fokker-planck kinetic theory. Astrophys. J. 902, 16. doi:10.3847/1538-4357/abb239

CrossRef Full Text | Google Scholar

Allred, J. C., Hawley, S. L., Abbett, W. P., and Carlsson, M. (2006). Radiative hydrodynamic models of optical and ultraviolet emission from M dwarf flares. Astrophys. J. 644, 484–496. doi:10.1086/503314

CrossRef Full Text | Google Scholar

Anglada-Escudé, G., Amado, P. J., Barnes, J., Berdiñas, Z. M., Butler, R. P., Coleman, G. A. L., et al. (2016). A terrestrial planet candidate in a temperate orbit around Proxima Centauri. Nature 536, 437–440. doi:10.1038/nature19106

PubMed Abstract | CrossRef Full Text | Google Scholar

Aschwanden, M. J. (2015). Magnetic energy dissipation during the 2014 March 29 solar flare. Astrophys. J. 804, L20. doi:10.1088/2041-8205/804/1/L20

CrossRef Full Text | Google Scholar

Aschwanden, M. J. (2004). Pulsed particle injection in a reconnection-driven dynamic trap model in solar flares. Astrophys. J. 608, 554–561. doi:10.1086/392494

CrossRef Full Text | Google Scholar

Ashfield, I., William, H., Longcope, D. W., Zhu, C., and Qiu, J. (2022). Connecting chromospheric condensation signatures to reconnection-driven heating rates in an observed flare. Astrophys. J. 926, 164. doi:10.3847/1538-4357/ac402d

CrossRef Full Text | Google Scholar

Ayres, T. R. (2015). The flare-ona of EK draconis. Astron. J. 150, 7. doi:10.1088/0004-6256/150/1/7

CrossRef Full Text | Google Scholar

Barstow, J. K., Aigrain, S., Irwin, P. G. J., Kendrew, S., and Fletcher, L. N. (2016). Telling twins apart: exo-Earths and venuses with transit spectroscopy. Mon. Not. R. Astron. Soc. 458, 2657–2666. doi:10.1093/mnras/stw489

CrossRef Full Text | Google Scholar

Barstow, J. K., and Irwin, P. G. J. (2016). Habitable worlds with JWST: Transit spectroscopy of the TRAPPIST-1 system? Mon. Not. R. Astron. Soc. Lett. 461, L92–L96. doi:10.1093/mnrasl/slw109

CrossRef Full Text | Google Scholar

Battaglia, M., Kleint, L., Krucker, S., and Graham, D. (2015). How important are electron beams in driving chromospheric evaporation in the 2014 March 29 flare? Astrophys. J. 813, 113. doi:10.1088/0004-637X/813/2/113

CrossRef Full Text | Google Scholar

Belov, A., Garcia, H., Kurt, V., Mavromichalaki, H., and Gerontidou, M. (2005). Proton enhancements and their relation to the X-ray flares during the three last solar cycles. Sol. Phys. 229, 135–159. doi:10.1007/s11207-005-4721-3

CrossRef Full Text | Google Scholar

Belu, A. R., Selsis, F., Morales, J.-C., Ribas, I., Cossou, C., and Rauer, H. (2011). Primary and secondary eclipse spectroscopy with JWST: Exploring the exoplanet parameter space. Astron. Astrophys. 525, A83. doi:10.1051/0004-6361/201014995

CrossRef Full Text | Google Scholar

Brasseur, C. E., Osten, R. A., and Fleming, S. W. (2022). Short-duration stellar flares in GALEX data. Astrophys. J. 883, 88. doi:10.3847/1538-4357/ab3df8

CrossRef Full Text | Google Scholar

Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., and Vlahos, L. (2009). Local re-acceleration and a modified thick target model of solar flare electrons. Astron. Astrophys. 508, 993–1000. doi:10.1051/0004-6361/200913145

CrossRef Full Text | Google Scholar

Carlsson, M., and Stein, R. F. (1995). Does a nonmagnetic solar chromosphere exist? Astrophys. J. 440, L29. doi:10.1086/187753

CrossRef Full Text | Google Scholar

Carlsson, M., and Stein, R. F. (2002). Dynamic hydrogen ionization. Astrophys. J. 572, 626–635. doi:10.1086/340293

CrossRef Full Text | Google Scholar

Carlsson, M., and Stein, R. F. (1997). Formation of solar calcium H and K bright grains. Astrophys. J. 481, 500–514. doi:10.1086/304043

CrossRef Full Text | Google Scholar

Carlsson, M., and Stein, R. F. (1992). Non-LTE radiating acoustic shocks and CA II K2V bright points. Astrophys. J. 397, L59. doi:10.1086/186544

CrossRef Full Text | Google Scholar

Cram, L. E., and Woods, D. T. (1982). Models for stellar flares. Astrophys. J. 257, 269–275. doi:10.1086/159985

CrossRef Full Text | Google Scholar

Dappen, W., Anderson, L., and Mihalas, D. (1987). Statistical mechanics of partially ionized stellar plasma - the Planck-Larkin partition function, polarization shifts, and simulations of optical spectra. Astrophys. J. 319, 195–206. doi:10.1086/165446

CrossRef Full Text | Google Scholar

De Pontieu, B., Title, A. M., Lemen, J. R., Kushner, G. D., Akin, D. J., Allard, B., et al. (2014). The Interface region imaging Spectrograph (IRIS). Sol. Phys. 289, 2733–2779. doi:10.1007/s11207-014-0485-y

CrossRef Full Text | Google Scholar

de Wijn, A. G., Casini, R., Carlile, A., Lecinski, A. R., Sewell, S., Zmarzly, P., et al. (2022). The visible spectro-polarimeter of the Daniel K. Inouye solar telescope. Sol. Phys. 297, 22. doi:10.1007/s11207-022-01954-1

CrossRef Full Text | Google Scholar

de Wit, J., Wakeford, H. R., Lewis, N. K., Delrez, L., Gillon, M., Selsis, F., et al. (2018). Atmospheric reconnaissance of the habitable-zone Earth-sized planets orbiting TRAPPIST-1. Nat. Astron. 2, 214–219. doi:10.1038/s41550-017-0374-z

CrossRef Full Text | Google Scholar

Dominique, M., Zhukov, A. N., Heinzel, P., Dammasch, I. E., Wauters, L., Dolla, L., et al. (2018). First detection of solar flare emission in mid-ultraviolet balmer continuum. Astrophys. J. 867, L24. doi:10.3847/2041-8213/aaeace

CrossRef Full Text | Google Scholar

Estrela, R., Palit, S., and Valio, A. (2020). Surface and oceanic habitability of trappist-1 planets under the impact of flares. Astrobiology 20, 1465–1475. doi:10.1089/ast.2019.2126

PubMed Abstract | CrossRef Full Text | Google Scholar

Fauchez, T. J., Turbet, M., Villanueva, G. L., Wolf, E. T., Arney, G., Kopparapu, R. K., et al. (2019). Impact of clouds and hazes on the simulated JWST transmission spectra of habitable zone planets in the TRAPPIST-1 system. Astrophys. J. 887, 194. doi:10.3847/1538-4357/ab5862

CrossRef Full Text | Google Scholar

Feinstein, A. D., France, K., Youngblood, A., Duvvuri, G. M., Teal, D. J., Cauley, P. W., et al. (2022). AU microscopii in the far-UV: Observations in quiescence, during flares, and implications for AU mic b and c. Astron. J. 164, 110. doi:10.3847/1538-3881/ac8107

CrossRef Full Text | Google Scholar

Fisher, G. H., Bercik, D. J., Welsch, B. T., and Hudson, H. S. (2012). Global forces in eruptive solar flares: The lorentz force acting on the solar atmosphere and the solar interior. Sol. Phys. 277, 59–76. doi:10.1007/s11207-011-9907-2

CrossRef Full Text | Google Scholar

Fleming, S. W., Million, C., Osten, R. A., Kolotkov, D. Y., and Brasseur, C. E. (2022). New time-resolved, multi-band flares in the GJ 65 system with gPhoton. Astrophys. J. 928, 8. doi:10.3847/1538-4357/ac5037

CrossRef Full Text | Google Scholar

France, K., Duvvuri, G., Egan, H., Koskinen, T., Wilson, D. J., Youngblood, A., et al. (2020). The high-energy radiation environment around a 10 Gyr M dwarf: Habitable at last? Astron. J. 160, 237. doi:10.3847/1538-3881/abb465

CrossRef Full Text | Google Scholar

Froning, C. S., Kowalski, A., France, K., Loyd, R. O. P., Schneider, P. C., Youngblood, A., et al. (2019). A hot ultraviolet flare on the M dwarf star GJ 674. Astrophys. J. 871, L26. doi:10.3847/2041-8213/aaffcd

CrossRef Full Text | Google Scholar

Fuhrmeister, B., Liefke, C., Schmitt, J. H. M. M., and Reiners, A. (2008). Multiwavelength observations of a giant flare on CN Leonis. I. The chromosphere as seen in the optical spectra. Astron. Astrophys. 487, 293–306. doi:10.1051/0004-6361:200809379

CrossRef Full Text | Google Scholar

Graham, D. R., Cauzzi, G., Zangrilli, L., Kowalski, A., Simões, P., and Allred, J. (2020). Spectral signatures of chromospheric condensation in a major solar flare. Astrophys. J. 895, 6. doi:10.3847/1538-4357/ab88ad

CrossRef Full Text | Google Scholar

Günther, M. N., Zhan, Z., Seager, S., Rimmer, P. B., Ranjan, S., Stassun, K. G., et al. (2020). Stellar flares from the first TESS data release: Exploring a new sample of M dwarfs. Astron. J. 159, 60. doi:10.3847/1538-3881/ab5d3a

CrossRef Full Text | Google Scholar

Hannah, I. G., Kontar, E. P., and Reid, H. A. S. (2013). Effect of turbulent density-fluctuations on wave-particle interactions and solar flare X-ray spectra. Astron. Astrophys. 550, A51. doi:10.1051/0004-6361/201220462

CrossRef Full Text | Google Scholar

Hawley, S. L., Allred, J. C., Johns-Krull, C. M., Fisher, G. H., Abbett, W. P., Alekseev, I., et al. (2003). Multiwavelength observations of flares on AD Leonis. Astrophys. J. 597, 535–554. doi:10.1086/378351

CrossRef Full Text | Google Scholar

Hawley, S. L., and Fisher, G. H. (1992). X-ray-heated models of stellar flare atmospheres - theory and comparison with observations. Astrophys. J. Suppl. Ser. 78, 565–598. doi:10.1086/191640

CrossRef Full Text | Google Scholar

Hawley, S. L., and Pettersen, B. R. (1991). The great flare of 1985 April 12 on AD Leonis. Astrophys. J. 378, 725–741. doi:10.1086/170474

CrossRef Full Text | Google Scholar

Hawley, S. L., Walkowicz, L. M., Allred, J. C., and Valenti, J. A. (2007). Near-ultraviolet spectra of flares on YZ CMi. Publ. Astronomical Soc. Pac. 119, 67–81. doi:10.1086/510561

CrossRef Full Text | Google Scholar

Heinzel, P., and Kleint, L. (2014). Hydrogen balmer continuum in solar flares detected by the Interface region imaging Spectrograph (IRIS). Astrophys. J. 794, L23. doi:10.1088/2041-8205/794/2/L23

CrossRef Full Text | Google Scholar

Holman, G. D., Sui, L., Schwartz, R. A., and Emslie, A. G. (2003). Electron bremsstrahlung hard X-ray spectra, electron distributions, and energetics in the 2002 july 23 solar flare. Astrophys. J. 595, L97–L101. doi:10.1086/378488

CrossRef Full Text | Google Scholar

Howard, W. S., Corbett, H., Law, N. M., Ratzloff, J. K., Galliher, N., Glazier, A. L., et al. (2020). EvryFlare. III. Temperature evolution and habitability impacts of dozens of superflares observed simultaneously by evryscope and TESS. Astrophys. J. 902, 115. doi:10.3847/1538-4357/abb5b4

CrossRef Full Text | Google Scholar

Howard, W. S., Corbett, H., Law, N. M., Ratzloff, J. K., Glazier, A., Fors, O., et al. (2019). EvryFlare. I. Long-Term evryscope monitoring of flares from the cool stars across half the southern sky. Astrophys. J. 881, 9. doi:10.3847/1538-4357/ab2767

CrossRef Full Text | Google Scholar

Howard, W. S., Tilley, M. A., Corbett, H., Youngblood, A., Loyd, R. O. P., Ratzloff, J. K., et al. (2018). The first naked-eye superflare detected from Proxima Centauri. Astrophys. J. 860, L30. doi:10.3847/2041-8213/aacaf3

CrossRef Full Text | Google Scholar

Hummer, D. G., and Mihalas, D. (1988). The equation of state for stellar envelopes. I - an occupation probability formalism for the truncation of internal partition functions. Astrophys. J. 331, 794–814. doi:10.1086/166600

CrossRef Full Text | Google Scholar

Ireland, J., Tolbert, A. K., Schwartz, R. A., Holman, G. D., and Dennis, B. R. (2013). Estimating the properties of hard X-ray solar flares by constraining model parameters. Astrophys. J. 769, 89. doi:10.1088/0004-637X/769/2/89

CrossRef Full Text | Google Scholar

Jakosky, B. M., Brain, D., Chaffin, M., Curry, S., Deighan, J., Grebowsky, J., et al. (2018). Loss of the Martian atmosphere to space: Present-day loss rates determined from MAVEN observations and integrated loss through time. Icarus 315, 146–157. doi:10.1016/j.icarus.2018.05.030

CrossRef Full Text | Google Scholar

Karmakar, S., Pandey, J. C., Airapetian, V. S., and Misra, K. (2017). X-ray superflares on CC eri. Astrophys. J. 840, 102. doi:10.3847/1538-4357/aa6cb0

CrossRef Full Text | Google Scholar

Kerr, G. S., Allred, J. C., and Polito, V. (2020). Solar flare arcade modeling: Bridging the gap from 1D to 3D simulations of optically thin radiation. Astrophys. J. 900, 18. doi:10.3847/1538-4357/abaa46

CrossRef Full Text | Google Scholar

Kleint, L., Heinzel, P., Judge, P., and Krucker, S. (2016). Continuum enhancements in the ultraviolet, the visible and the infrared during the X1 flare on 2014 March 29. Astrophys. J. 816, 88. doi:10.3847/0004-637X/816/2/88

CrossRef Full Text | Google Scholar

Kleint, L., Heinzel, P., and Krucker, S. (2017). On the origin of the flare emission in IRIS’ SJI 2832 filter:balmer continuum or spectral lines? Astrophys. J. 837, 160. doi:10.3847/1538-4357/aa62fe

CrossRef Full Text | Google Scholar

Kleint, L., Wheatland, M. S., Mastrano, A., and McCauley, P. I. (2018). Nonlinear force-free modeling of flare-related magnetic field changes at the photosphere and chromosphere. Astrophys. J. 865, 146. doi:10.3847/1538-4357/aadc5c

CrossRef Full Text | Google Scholar

Kontar, E. P., Hannah, I. G., and MacKinnon, A. L. (2008). Chromospheric magnetic field and density structure measurements using hard X-rays in a flaring coronal loop. Astron. Astrophys. 489, L57–L60. doi:10.1051/0004-6361:200810719

CrossRef Full Text | Google Scholar

Kontar, E. P., Ratcliffe, H., and Bian, N. H. (2012). Wave-particle interactions in non-uniform plasma and the interpretation of hard X-ray spectra in solar flares. Astron. Astrophys. 539, A43. doi:10.1051/0004-6361/201118216

CrossRef Full Text | Google Scholar

Kowalski, A. F., Wisniewski, J. P., Hawley, S. L., Osten, R. A., Brown, A., Fariña, C., et al. (2019b). The near-ultraviolet continuum radiation in the impulsive phase of HF/GF-type dMe flares. I. Data. Astrophys. J. 871, 167. doi:10.3847/1538-4357/aaf058

CrossRef Full Text | Google Scholar

Kowalski, A. F., Allred, J. C., Carlsson, M., Kerr, G. S., Tremblay, P.-E., Namekata, K., et al. (2022). The atmospheric response to high nonthermal electron-beam fluxes in solar flares. II. Hydrogen-Broadening predictions for solar flare observations with the Daniel K. Inouye solar telescope. Astrophys. J. 928, 190. doi:10.3847/1538-4357/ac5174

CrossRef Full Text | Google Scholar

Kowalski, A. F., Allred, J. C., Daw, A., Cauzzi, G., and Carlsson, M. (2017a). The atmospheric response to high nonthermal electron beam fluxes in solar flares. I. Modeling the brightest NUV footpoints in the X1 solar flare of 2014 March 29. Astrophys. J. 836, 12. doi:10.3847/1538-4357/836/1/12

CrossRef Full Text | Google Scholar

Kowalski, A. F., Allred, J. C., Uitenbroek, H., Tremblay, P.-E., Brown, S., Carlsson, M., et al. (2017b). Hydrogen balmer line broadening in solar and stellar flares. Astrophys. J. 837, 125. doi:10.3847/1538-4357/aa603e

CrossRef Full Text | Google Scholar

Kowalski, A. F., Butler, E., Daw, A. N., Fletcher, L., Allred, J. C., De Pontieu, B., et al. (2019a). Spectral evidence for heating at large column mass in umbral solar flare kernels. I. IRIS near-UV spectra of the X1 solar flare of 2014 october 25. Astrophys. J. 878, 135. doi:10.3847/1538-4357/ab1f8b

CrossRef Full Text | Google Scholar

Kowalski, A. F., Hawley, S. L., Carlsson, M., Allred, J. C., Uitenbroek, H., Osten, R. A., et al. (2015). New insights into white-light flare emission from radiative-hydrodynamic modeling of a chromospheric condensation. Sol. Phys. 290, 3487–3523. doi:10.1007/s11207-015-0708-x

CrossRef Full Text | Google Scholar

Kowalski, A. F., Hawley, S. L., Holtzman, J. A., Wisniewski, J. P., and Hilton, E. J. (2010). A White Light Megaflare on the dM4.5e Star YZ CMi. Astrophys. J. 714, L98–L102. doi:10.1088/2041-8205/714/1/L98

CrossRef Full Text | Google Scholar

Kowalski, A. F., Hawley, S. L., Holtzman, J. A., Wisniewski, J. P., and Hilton, E. J. (2012). The Multiple Continuum Components in the White-Light Flare of 16 January 2009 on the dM4.5e Star YZ CMi. Sol. Phys. 277, 21–29. doi:10.1007/s11207-011-9839-x

CrossRef Full Text | Google Scholar

Kowalski, A. F., Hawley, S. L., Wisniewski, J. P., Osten, R. A., Hilton, E. J., Holtzman, J. A., et al. (2013). Time-resolved properties and global trends in dMe flares from simultaneous photometry and spectra. Astrophys. J. Suppl. Ser. 207, 15. doi:10.1088/0067-0049/207/1/15

CrossRef Full Text | Google Scholar

Kowalski, A. F., Mathioudakis, M., Hawley, S. L., Wisniewski, J. P., Dhillon, V. S., Marsh, T. R., et al. (2016). M dwarf flare continuum variations on one-second timescales: Calibrating and modeling of ULTRACAM flare color indices. Astrophys. J. 820, 95. doi:10.3847/0004-637X/820/2/95

CrossRef Full Text | Google Scholar

Krucker, S., Hudson, H. S., Jeffrey, N. L. S., Battaglia, M., Kontar, E. P., Benz, A. O., et al. (2011). High-resolution imaging of solar flare ribbons and its implication on the thick-target beam model. Astrophys. J. 739, 96. doi:10.1088/0004-637X/739/2/96

CrossRef Full Text | Google Scholar

Law, N. M., Fors, O., Ratzloff, J., Wulfken, P., Kavanaugh, D., Sitar, D. J., et al. (2015). Evryscope science: Exploring the potential of all-sky gigapixel-scale telescopes. Publ. Astronomical Soc. Pac. 127, 234. doi:10.1086/680521

CrossRef Full Text | Google Scholar

Lin, R. P., Dennis, B. R., Hurford, G. J., Smith, D. M., Zehnder, A., Harvey, P. R., et al. (2002). The reuven ramaty high-energy solar spectroscopic imager (RHESSI). Sol. Phys. 210, 3–32. doi:10.1023/A:1022428818870

CrossRef Full Text | Google Scholar

Livshits, M. A., Badalian, O. G., Kosovichev, A. G., and Katsova, M. M. (1981). The optical continuum of solar and stellar flares. Sol. Phys. 73, 269–288. doi:10.1007/BF00151682

CrossRef Full Text | Google Scholar

Loyd, R. O. P., and France, K. (2014). Fluctuations and flares in the ultraviolet line emission of cool stars: Implications for exoplanet transit observations. Astrophys. J. Suppl. Ser. 211, 9. doi:10.1088/0067-0049/211/1/9

CrossRef Full Text | Google Scholar

Loyd, R. O. P., France, K., Youngblood, A., Schneider, C., Brown, A., Hu, R., et al. (2018a). The MUSCLES treasury survey. V. FUV flares on active and inactive M dwarfs. Astrophys. J. 867, 71. doi:10.3847/1538-4357/aae2bd

CrossRef Full Text | Google Scholar

Loyd, R. O. P., Shkolnik, E. L., Schneider, A. C., Barman, T. S., Meadows, V. S., Pagano, I., et al. (2018b). HAZMAT. IV. Flares and superflares on young M stars in the far ultraviolet. Astrophys. J. 867, 70. doi:10.3847/1538-4357/aae2ae

CrossRef Full Text | Google Scholar

MacGregor, A. M., Osten, R. A., and Hughes, A. M. (2020). Properties of M Dwarf flares at millimeter wavelengths. Astrophys. J. 891, 80. doi:10.3847/1538-4357/ab711d

CrossRef Full Text | Google Scholar

MacGregor, M. A., Weinberger, A. J., Loyd, R. O. P., Shkolnik, E., Barclay, T., Howard, W. S., et al. (2021). Discovery of an extremely short duration flare from Proxima Centauri using millimeter through far-ultraviolet observations. Astrophys. J. Lett. 911, L25. doi:10.3847/2041-8213/abf14c

CrossRef Full Text | Google Scholar

MacGregor, M. A., Weinberger, A. J., Wilner, D. J., Kowalski, A. F., and Cranmer, S. R. (2018). Detection of a millimeter flare from Proxima Centauri. Astrophys. J. 855, L2. doi:10.3847/2041-8213/aaad6b

CrossRef Full Text | Google Scholar

Maehara, H., Shibayama, T., Notsu, Y., Notsu, S., Honda, S., Nogami, D., et al. (2015). Statistical properties of superflares on solar-type stars based on 1-min cadence data. Earth Planets Space 67, 59. doi:10.1186/s40623-015-0217-z

CrossRef Full Text | Google Scholar

Mochnacki, S. W., and Zirin, H. (1980). Multichannel spectrophotometry of stellar flares. Astrophys. J. 239, L27–L31. doi:10.1086/183285

CrossRef Full Text | Google Scholar

Namekata, K., Maehara, H., Sasaki, R., Kawai, H., Notsu, Y., Kowalski, A. F., et al. (2020). Optical and X-ray observations of stellar flares on an active M dwarf AD Leonis with the Seimei Telescope, SCAT, NICER, and OISTER. Publications of the Astronomical Society of Japan 72, 68. doi:10.1093/pasj/psaa051

CrossRef Full Text | Google Scholar

Namekata, K., Maehara, H., Honda, S., Notsu, Y., Okamoto, S., Takahashi, J., et al. (2021). Probable detection of an eruptive filament from a superflare on a solar-type star. Nat. Astron. 6, 241–248. doi:10.1038/s41550-021-01532-8

CrossRef Full Text | Google Scholar

Nayfonov, A., Däppen, W., Hummer, D. G., and Mihalas, D. (1999). The MHD equation of state with post-holtsmark microfield distributions. Astrophys. J. 526, 451–464. doi:10.1086/307972

CrossRef Full Text | Google Scholar

Osten, R. A., Drake, S., Tueller, J., Cummings, J., Perri, M., Moretti, A., et al. (2007). Nonthermal hard X-ray emission and iron kα emission from a superflare on II pegasi. Astrophys. J. 654, 1052–1067. doi:10.1086/509252

CrossRef Full Text | Google Scholar

Osten, R. A., Godet, O., Drake, S., Tueller, J., Cummings, J., Krimm, H., et al. (2010). The mouse that roared: A superflare from the dMe flare star ev lac detected by swift and konus-wind. Astrophys. J. 721, 785–801. doi:10.1088/0004-637X/721/1/785

CrossRef Full Text | Google Scholar

Osten, R. A., Kowalski, A., Drake, S. A., Krimm, H., Page, K., Gazeas, K., et al. (2016). A very bright, very hot, and very long flaring event from the M dwarf binary system DG CVn. Astrophys. J. 832, 174. doi:10.3847/0004-637X/832/2/174

CrossRef Full Text | Google Scholar

Panos, B., Kleint, L., Huwyler, C., Krucker, S., Melchior, M., Ullmann, D., et al. (2018). Identifying typical Mg II flare spectra using machine learning. Astrophys. J. 861, 62. doi:10.3847/1538-4357/aac779

CrossRef Full Text | Google Scholar

Polito, V., Galan, G., Reeves, K. K., and Musset, S. (2018). Possible signatures of a termination shock in the 2014 March 29 X-class flare observed by IRIS. Astrophys. J. 865, 161. doi:10.3847/1538-4357/aadada

CrossRef Full Text | Google Scholar

Ranjan, S., Wordsworth, R., and Sasselov, D. D. (2017). The surface UV environment on planets orbiting M dwarfs: Implications for prebiotic chemistry and the need for experimental follow-up. Astrophys. J. 843, 110. doi:10.3847/1538-4357/aa773e

CrossRef Full Text | Google Scholar

Rimmele, T. R., Warner, M., Keil, S. L., Goode, P. R., Knölker, M., Kuhn, J. R., et al. (2020). The Daniel K. Inouye solar telescope - observatory overview. Sol. Phys. 295, 172. doi:10.1007/s11207-020-01736-7

CrossRef Full Text | Google Scholar

Robinson, R. D., Carpenter, K. G., Woodgate, B. E., and Maran, S. P. (1993). A search for proton beams during flares on AU Microscopii. Astrophys. J. 414, 872–876. doi:10.1086/173129

CrossRef Full Text | Google Scholar

Robinson, R. D., Wheatley, J. M., Welsh, B. Y., Forster, K., Morrissey, P., Seibert, M., et al. (2005). GALEX Observations of an Energetic Ultraviolet Flare on the dM4e Star GJ 3685A. Astrophys. J. 633, 447–451. doi:10.1086/444608

CrossRef Full Text | Google Scholar

Rubio da Costa, F., and Kleint, L. (2017). A parameter study for modeling Mg II h and k emission during solar flares. Astrophys. J. 842, 82. doi:10.3847/1538-4357/aa6eaf

CrossRef Full Text | Google Scholar

Rubio da Costa, F., Kleint, L., Petrosian, V., Liu, W., and Allred, J. C. (2016). Data-driven radiative hydrodynamic modeling of the 2014 March 29 X1.0 solar flare. Astrophys. J. 827, 38. doi:10.3847/0004-637X/827/1/38

CrossRef Full Text | Google Scholar

Scalo, J., Kaltenegger, L., Segura, A. G., Fridlund, M., Ribas, I., Kulikov, Y. N., et al. (2007). M stars as targets for terrestrial exoplanet searches and biosignature detection. Astrobiology 7, 85–166. doi:10.1089/ast.2006.0125

PubMed Abstract | CrossRef Full Text | Google Scholar

Segura, A., Walkowicz, L. M., Meadows, V., Kasting, J., and Hawley, S. (2010). The effect of a strong stellar flare on the atmospheric chemistry of an earth-like planet orbiting an M dwarf. Astrobiology 10, 751–771. doi:10.1089/ast.2009.0376

PubMed Abstract | CrossRef Full Text | Google Scholar

Shibayama, T., Maehara, H., Notsu, S., Notsu, Y., Nagao, T., Honda, S., et al. (2013). Superflares on solar-type stars observed with kepler. I. Statistical properties of superflares. Astrophys. J. Suppl. Ser. 209, 5. doi:10.1088/0067-0049/209/1/5

CrossRef Full Text | Google Scholar

Shkolnik, E. L., and Barman, T. S. (2014). HAZMAT. I. The evolution of far-UV and near-UV emission from early M stars. Astron. J. 148, 64. doi:10.1088/0004-6256/148/4/64

CrossRef Full Text | Google Scholar

Smith, D. S., Scalo, J., and Wheeler, J. C. (2004). Transport of ionizing radiation in terrestrial-like exoplanet atmospheres. Icarus 171, 229–253. doi:10.1016/j.icarus.2004.04.009

CrossRef Full Text | Google Scholar

Smith, E. W., Vidal, C. R., and Cooper, J. (1969). Classical path methods in line broadening. I. The classical path approximation. J. Res. Natl. Bur. Stand A Phys. Chem. 73A, 389–404. doi:10.6028/jres.073A.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Testa, P., Drake, J. J., Ercolano, B., Reale, F., Huenemoerder, D. P., Affer, L., et al. (2008). Geometry diagnostics of a stellar flare from fluorescent X-rays. Astrophys. J. 675, L97–L100. doi:10.1086/533461

CrossRef Full Text | Google Scholar

Tilley, M. A., Segura, A., Meadows, V., Hawley, S., and Davenport, J. (2019). Modeling repeated M dwarf flaring at an earth-like planet in the habitable zone: Atmospheric effects for an unmagnetized planet. Astrobiology 19, 64–86. doi:10.1089/ast.2017.1794

PubMed Abstract | CrossRef Full Text | Google Scholar

Tremblay, P.-E., and Bergeron, P. (2009). Spectroscopic analysis of DA white dwarfs: Stark broadening of hydrogen lines including nonideal effects. Astrophys. J. 696, 1755–1770. doi:10.1088/0004-637X/696/2/1755

CrossRef Full Text | Google Scholar

Uitenbroek, H. (2001). Multilevel radiative transfer with partial frequency redistribution. Astrophys. J. 557, 389–398. doi:10.1086/321659

CrossRef Full Text | Google Scholar

Venot, O., Rocchetto, M., Carl, S., Roshni Hashim, A., and Decin, L. (2016). Influence of stellar flares on the chemical composition of exoplanets and spectra. Astrophys. J. 830, 77. doi:10.3847/0004-637X/830/2/77

CrossRef Full Text | Google Scholar

Vidal, C. R., Cooper, J., and Smith, E. W. (1970). Hydrogen Stark broadening calculations with the unified classical path theory. J. Quantitative Spectrosc. Radiat. Transf. 10, 1011–1063. doi:10.1016/0022-4073(70)90121-4

CrossRef Full Text | Google Scholar

Vidal, C. R., Cooper, J., and Smith, E. W. (1973). Hydrogen Stark-broadening tables. Astrophys. J. Suppl. Ser. 25, 37. doi:10.1086/190264

CrossRef Full Text | Google Scholar

Vidal, C. R., Cooper, J., and Smith, E. W. (1971). Unified theory calculations of Stark broadened hydrogen lines including lower state interactions. J. Quantitative Spectrosc. Radiat. Transf. 11, 263–281. doi:10.1016/0022-4073(71)90013-6

CrossRef Full Text | Google Scholar

Wargelin, B. J., Saar, S. H., Pojmański, G., Drake, J. J., and Kashyap, V. L. (2017). Optical, UV, and X-ray evidence for a 7-yr stellar cycle in Proxima Centauri. Mon. Not. R. Astron. Soc. 464, 3281–3296. doi:10.1093/mnras/stw2570

CrossRef Full Text | Google Scholar

Warmuth, A., Holman, G. D., Dennis, B. R., Mann, G., Aurass, H., and Milligan, R. O. (2009). Rapid changes of electron acceleration characteristics at the end of the impulsive phase of an X-class solar flare. Astrophys. J. 699, 917–922. doi:10.1088/0004-637X/699/1/917

CrossRef Full Text | Google Scholar

West, A. A., Hawley, S. L., Bochanski, J. J., Covey, K. R., Reid, I. N., Dhital, S., et al. (2008). Constraining the age-activity relation for cool stars: The sloan digital sky survey data release 5 low-mass star spectroscopic sample. Astronomical J. 135, 785–795. doi:10.1088/0004-6256/135/3/785

CrossRef Full Text | Google Scholar

Wilson, D. J., Froning, C. S., Duvvuri, G. M., France, K., Youngblood, A., Schneider, P. C., et al. (2021). The mega-MUSCLES spectral energy distribution of TRAPPIST-1. Astrophys. J. 911, 18. doi:10.3847/1538-4357/abe771

CrossRef Full Text | Google Scholar

Woods, M. M., Harra, L. K., Matthews, S. A., Mackay, D. H., Dacie, S., and Long, D. M. (2017). Observations and modelling of the pre-flare period of the 29 March 2014 X1 flare. Sol. Phys. 292, 38. doi:10.1007/s11207-017-1064-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wülser, J. P., Jaeggli, S., De Pontieu, B., Tarbell, T., Boerner, P., Freeland, S., et al. (2018). Instrument calibration of the Interface region imaging Spectrograph (IRIS) mission. Sol. Phys. 293, 149. doi:10.1007/s11207-018-1364-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, H., Liu, J., Gao, Q., Fang, X., Guo, J., Zhang, Y., et al. (2017). The flaring activity of M dwarfs in the kepler field. Astrophys. J. 849, 36. doi:10.3847/1538-4357/aa8ea2

CrossRef Full Text | Google Scholar

Young, P. R., Tian, H., and Jaeggli, S. (2015). The 2014 March 29 X-flare: Subarcsecond resolution observations of Fe XXI λ1354.1. Astrophys. J. 799, 218. doi:10.1088/0004-637X/799/2/218

CrossRef Full Text | Google Scholar

Zhu, Y., Kowalski, A. F., Tian, H., Uitenbroek, H., Carlsson, M., and Allred, J. C. (2019). Modeling Mg II h, k and triplet lines at solar flare ribbons. Astrophys. J. 879, 19. doi:10.3847/1538-4357/ab2238

CrossRef Full Text | Google Scholar