Superposed epoch analysis using time-normalization: A Python tool for statistical event analysis

A superposed epoch analysis (SEA) is a simple, yet powerful statistical analysis technique, used to identify patterns in the temporal evolution of observed quantities relative to defined epochs. In some cases, the event duration and time between epochs (epoch length) can be highly variable. If the measured response scales with the event duration or epoch length, then the underlying temporal patterns can be suppressed when analyzed in absolute time. In this article, we describe an adaptation of the traditional SEA, where we apply time-normalization to each event and present a Python package sea_norm which implements the time-normalized SEA. Rather than defining a singular epoch time, a start, epoch, and end time are defined for each event, separating each event into two intervals. For every event, the duration of both intervals is normalized to a common time axis, essentially stretching or compressing each interval, such that each respective epoch interval is the same length for all events. This technique has the advantage of identifying temporal patterns not observed in a traditional SEA. Given a time series, a list of event start, epoch, and end times, and specified binning dimensions the Python package sea_norm returns a time-normalized SEA analysis of the time-series. This technique is widely applicable across the Space Physics field, where events have defined start and end times, and where the response to those events may scale proportionally with event length. We provide examples demonstrating how the SEA code works with one-dimensional and two-dimensional time series, and how users can specify their own statistics to use in the superposed analysis (e.g., percentiles).

1 Introduction

Many sciences and scientific fields of research use measurements of observed quantities in response to a specific event, usually with the aim of understanding the mechanics of the physical system which have led to that response, not least, within the various fields of space science. Repeated events such as geomagnetic storms and substorms, can drive activity throughout Earth’s magnetosphere, prompting the response of many measurable processes, including magnetic field dipolarizations, substorms injections, wave-particle interactions, and local or global precipitation of electrons and ions (e.g. O’Brien et al., 2003; Summers and Thorne, 2003; Meredith et al., 2011; Katsavrias et al., 2019; Wang et al., 2019). While these processes can typically be analyzed as individual events, sparse measurements and limited data availability may not provide sufficient temporal or spatial coverage required to develop a comprehensive understanding of the processes (e.g. Wang et al., 2019). For common and repeatable events, a statistical analysis, utilizing data obtained from many events can provide improved spatial and temporal coverage of the region of interest (e.g., the outer radiation belt), allowing researchers to gain additional insight into the events and more importantly, the underlying physical processes (e.g. Yokoyama, 1997; Halford et al., 2010; Hutchinson et al., 2011; Murphy et al., 2018; Murphy et al., 2020; Olifer et al., 2021; Walton et al., 2022).

A superposed epoch analysis (SEA) is one of the most powerful and widely used statistical analysis techniques for studying the temporal evolution of observed quantities in response to a specific type of event, and relative to a defined epoch. Studies have utilized a conventional SEA for a range of physical phenomena and Python packages have previously been released which perform this conventional SEA analysis (Larsen et al., 2010; Morley et al., 2011). For example, Turner et al. (2019) used near-equatorial measurements of energetic electrons in Earth’s outer radiation belt during geomagnetic storm events. In their analysis, the point of minimum Sym-H in each event was used as the singular epoch time and a range of statistics (including median, mean, etc.) were calculated. In particular, Turner et al. (2019) demonstrated the existence of both an energy and storm driver dependence in the storm-time response of electrons in the outer radiation belt. In space physics, this conventional SEA has been extensively used in relation to geomagnetic storm activity. For example, authors have studied both the response of energetic particles during storms (e.g. Meredith et al., 2011; Whittaker et al., 2014; Olifer et al., 2021; Smirnov et al., 2022), as well as the storm-time response of various plasma waves (e.g. O’Brien et al., 2003). SEA studies are not limited to storms, rather any event which can be studied in large numbers is ideal for SEA studies. This includes, for example, substorms (e.g. Boakes et al., 2011; Liu et al., 2011; Katsavrias et al., 2019), the response of the radiation belt to varying solar wind drivers (e.g. Hietala et al., 2014) and nightside particle injections (e.g. Gabrielse et al., 2014).

In some cases, such as that of geomagnetic storms, event duration can be highly variable. If the measured response of an event scales with the event duration, or the event can be separated into phases which scale with phase duration (e.g. geomagnetic storm phases), then the underlying temporal patterns can be suppressed when analyzed in absolute time, as with a traditional SEA. A solution to this is an adaptation of the traditional SEA, where time-normalization is applied to each event. Such an analysis helps to identify temporal patterns not observed in a traditional SEA. In a time-normalized SEA, rather than defining a singular epoch time, a start, epoch and end time are defined for each event, separating each event into two intervals (or phases). For every event, the duration of the two intervals is normalized to a common time axis, essentially stretching or compressing each interval, such that each respective epoch interval is the same length for all events. The SEA statistics (e.g., mean) are then calculated along the time-normalized axis of each phase using a binning algorithm.

Studies in space physics have utilized the time-normalized SEA technique for geomagnetic storms in a number of ways. Halford et al. (2010) used a time-normalized SEA to examine electromagnetic ion cyclotron (EMIC) wave occurrence in the outer radiation belt during geomagnetic storms, clearly showing heightened EMIC wave occurrence during the main phase of storms. Time-normalized SEA has also revealed further characteristics of geomagnetic storms and shock events, including the response of energetic electrons (e.g. Murphy et al., 2018, 2020; Walton et al., 2022), geomagnetic indices (e.g. Yokoyama, 1997) and various solar wind parameters (e.g. Hutchinson et al., 2011; Kilpua et al., 2015). To our knowledge, there is no widely available Python code which performs a time-normalized SEA.

In this article, we present a new Python package, sea_norm (GitHub link: https://github.com/samwalton7645/SEA_Code), capable of performing the adapted time-normalized SEA, given a time series, specified binning dimensions and list of events with defined start, epoch and end times. In the following sections, we describe the Python code and it is functionality, before providing examples demonstrating both a one-dimensional and a two-dimensional time-normalized SEA. This technique is widely applicable across the Space Physics field, where events have defined start and end times, and where the response to those events may scale proportionally with event length.

2 The sea_norm module

In this section, we detail the methodology behind the time-normalized SEA implemented in the sean() function, within the sea_norm module. We further describe the prerequisites for the sea_norm module, the input parameters and return values of the sean() function.

The time-normalized SEA is executed as follows:

1) Each event in the superposed epoch analysis is split into two phases defined by three times, the start, epoch, and end of each event. The first phase is defined as the start of the event to the epoch time (phase 1). The second phase is defined from the epoch time until the end of the event (phase 2). The phase 1 and 2 arrays are produced and input by the user.

2) For every event, phase 1 and 2 are then normalized between 0 and 1.

3) The normalized phases are then binned into a set of equally spaced bins, the number of bins being defined by the user. For example, if phase 1 was divided into four bins, the time axis would be divided into bins with edges [0, 0.25, 0.50, 0.75, 1.00].

4) For each phase, a set of statistics is then determined for the data residing in each bin (e.g. the mean and median).

5) If a 2D superposed epoch analysis is performed the data is binned in a second dimension before calculating the statistics of each bin.

The process described above is illustrated in Figure 1. The top panel shows the setup of a conventional SEA with Dst data for three storms of differing lengths, aligned at their respective epoch times. The bottom panel shows the time-normalized SEA setup. Each event is separated into phase 1 (st to the epoch time) and phase 2 (epoch time to et). For each event, phase 1 and 2 are normalized, and the time-normalized axes are binned into equally spaced bins. In the example here, phase 1 is binned into three bins and phase 2 into 16 bins (identified by the colored blocks), plotted with the time axis labeled relative to the epoch time and in terms of the number of normalized time bins. As Figure 1(bottom) illustrates, this process effectively stretches (e.g., the red event) or compresses (e.g., the orange event) events about the epoch time such that they are all the same length. Finally, a set of statistics is calculated for each bin, completing the time-normalized superposed epoch analysis.

FIGURE 1

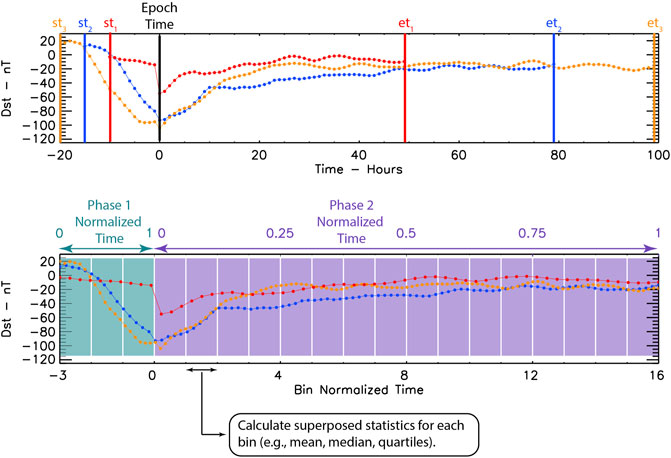
FIGURE 1. Illustration of how the time-normalized superposed epoch analysis is performed on the Dst index. The top panel shows the conventional SEA alignment, where st_1,2,3 and et_1,2,3 represent the start times and end times, respectively, of three different geomagnetic storms, aligned at their epoch times. The bottom panel shows the time-normalized SEA for the same storms. Phase 1 and phase 2 are highlighted as labeled, where each colored block represents a single normalized time bin.

The time-normalized SEA analysis described above is implemented in the sea_norm module (Walton and Murphy, 2022), which can be downloaded via the GitHub link: https://github.com/samwalton7645/SEA_Code. The user can download a .zip file of the repository to a local repository, extract the files, and then installed via the terminal using the command ‘pip install’, within the ‘SEA_Code’ directory. The prerequisite packages are Pandas v1.1.5 or later, Numpy v1.21.6 or later, Scipy v1.2.1 or later, and tqdm v4.36.1 or later, used within Python 3.6. sea_norm may work on earlier versions of Python and the respective packages, but is untested. Pandas and Numpy are used for data handling and manipulation; Scipy is used for the .stats.binned_statistic() and .stats.binned_statistic_2d() functions, which bin the time-normalized data and calculate the SEA statistics for each bin; tqdm is used to add progress bars to the display when using the sea_norm package, since statistical analysis can be somewhat time intensive.

The sean() function is the bulk of the time-normalized SEA code and implements the analysis described above and illustrated in Figure 1. sean() requires input data in the form of a Pandas DataFrame with a datetime index, as the index is used to normalize the data within phases. The list of events is specified using the events argument as a list of three arrays [st, ep, et], containing start times in st, epoch times in ep and end times in et, in a datetime format. Unless otherwise specified using the cols argument, a 1D SEA is performed on every column in the DataFrame. x_dimensions must also be specified as a list [x1, x2], containing the number of bins in phase 1 and phase 2 of the superposed epoch analysis. If sean() is being used for a 2D SEA, the y_col argument must be used to specify the column which should be used for the y-axis, and a 2D SEA will be performed on the remaining columns. For a 2D SEA, y_dimensions must also be specified as a list [y_min, y_max, y_spacing], containing the minimum and maximum y boundaries, as well as the desired bin spacing for the second dimension.

The sean() function returns a Pandas DataFrame containing the time-normalized SEA time-series, as well as a dictionary of metadata for the performed analysis (e.g., which statistics were returned and which columns the analysis was run on). The returned DataFrame contains a column with the SEA for each data column and statistic calculated in the analysis. By default, sean() returns the mean, median, lower and upper quartiles, and counts for each data column. If a 2D SEA was performed, the returned DataFrame further contains a column for each bin of the second dimension and the metadata dictionary contains a dictionary of y-axis metadata (e.g., y-axis min, max and bin size). As an example, Table 1 shows the columns of a returned DataFrame when the input DataFrame contains a single time-series AE (see also the examples below). In a 2D analysis the same columns are returned but each column is further binned by the second dimension and the column names are appended with the second dimensions bin number. For example, in a 2D analysis the AE median column in Table 1 would become AE_median_n where n is the second dimension bin number. Finally, in both the 1D and 2D cases, the index of the returned DataFrame is the bin normalized time. For example if phase 1 was binned into 20 bins and phase 2 120 bins then the index goes from -20 to 119 in steps of 1.

TABLE 1

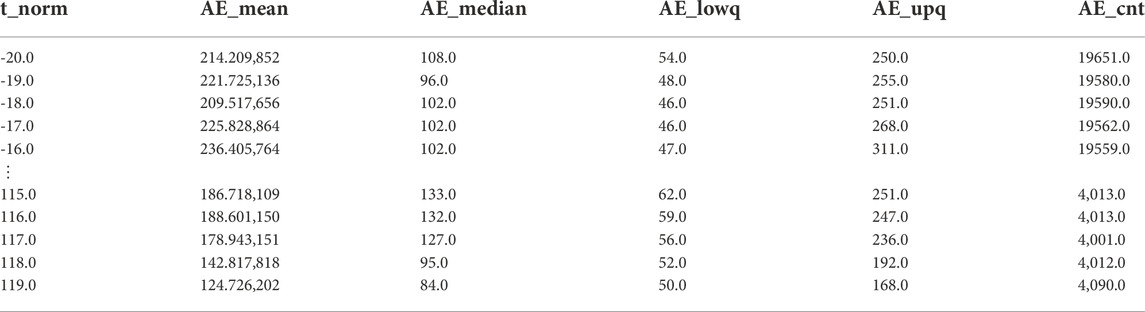
TABLE 1. An example array for when sean() is used to perform a 1D superposed epoch analysis on AE data only, using the default statistics.

For additional functionality, sean also allows users to define their own statistics via the seastats argument. This can simplify or speed up the SEA analysis by calculating only a subset of the default statistics. This can also be used for a more in-depth analysis by allowing users to define a more complex set of statistics to be calculated. The seastats argument is passed as a dictionary of the form: {“stat_name”:stat_function}. stat_function can be a string e.g. as defined in scipy.stats.binned_statistic(), a callable, e.g., np.nanmean, or a lambda defined callable e.g., the 90th percentile: p90 = lambda stat:np.nanpercentile(stat, 90). The ‘stat_name’ key is used to label of the columns of the returned DataFrame (see Table 1).

3 Examples of use

In this section, we demonstrate how the sea_norm package can be used to analyze both 1D and 2D data for 168 geomagnetic storm events within a 12-year time period (1992–2004). For the purposes of the examples presented, we import the Pandas and Numpy packages as below, as well as the Matplotlib package, which is used for plotting the examples. Finally, we import the sean() function from the sea_norm package:

We then load all data required for the examples in this section:

For the 1D examples, we use OMNIWeb parameters solar wind speed (V), dynamic pressure (P), Southward interplanetary magnetic field (B_z), Sym-H and the Auroral Electrojet (AE) index. For the 2D example, we use SAMPEX PET flux measurements from the low energy (ELO, 1.5–6.0 MeV) electron channel and the high energy (EHI, 2.5–14.0 MeV) electron channel, and L-shell (L) for the y-axis data. The list of events, ‘StormList_short.txt’, is a list of geomagnetic storms identified by the algorithm described in Walach and Grocott (2019). All data is during the 1992–2004 time period.

The number of bins is defined for phase 1 and phase 2 as below, which remain the same for all examples:

We use 20 bins for the pre-epoch phase and 120 bins for the post-epoch phase to loosely reflect the relative proportions of a geomagnetic storm.

3.1 One-dimensional SEA

The below Python code shows a simple example use of the sean() function to produce a 1D, time-normalized SEA for all of the OMNI parameters in our DataFrame (V, P, B_z, Sym-H and AE). A subset of columns can be specified by passing the column names via the cols argument. For example, to perform the analysis on only AE, use sea_cols = [‘AE’].

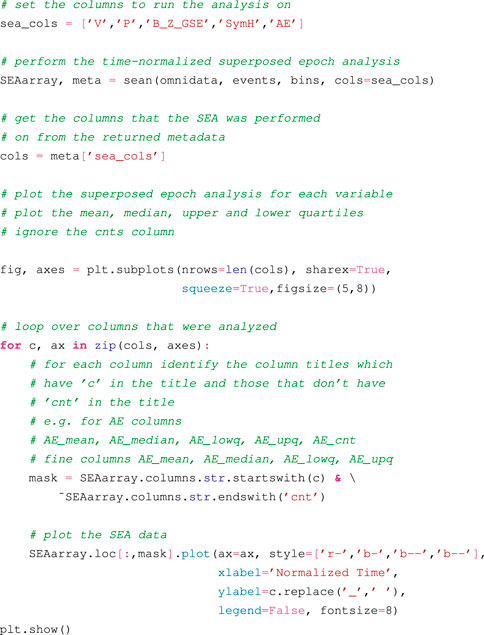
Figure 2 shows the plot resulting from the above code, presenting the mean, median and quartiles of, from top to bottom, V, P, B_z, Sym-H and AE. It is clear that a successful execution of the sean() function has produced the characteristic geomagnetic storm profile for the OMNI parameters. V, P and AE show characteristic increases before the storm epoch, while B_z shows a characteristic negative turn. Sym-H shows the typical storm shape, sharply turning negative pre-epoch, before gradually recovering post-epoch.

FIGURE 2

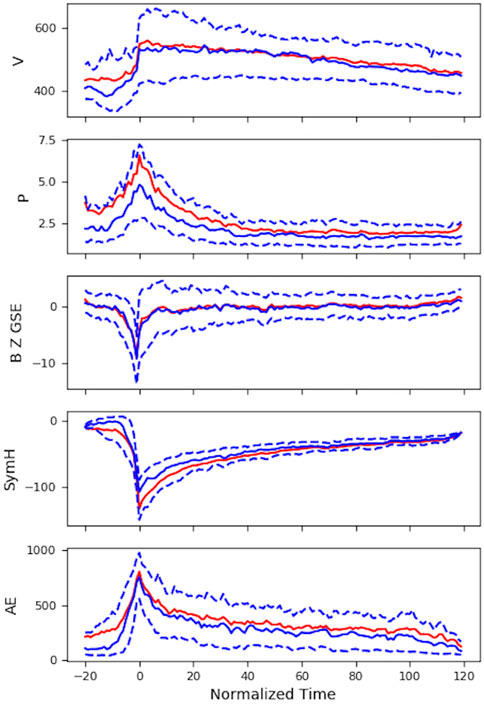
FIGURE 2. Result of the one-dimensional, time-normalised superposed epoch analysis for OMNIWeb parameters solar wind speed (V), dynamic pressure (P), southward interplanetary magnetic field (B_z), Sym-H and the Auroral Electrojet (AE) index. The statistics plotted are the mean (red), median (blue solid), upper and lower quartiles (blue dashed) for data within 168 geomagnetic storms from 1992–2004.

3.1.1 User-defined statistics

As mentioned in Section 2, the default for sean() is to return the mean, median, lower and upper quartiles and counts. However, sean() is capable of accepting user-defined statistics. In the below Python code, we define a set of lambda functions to be input into sean() as the user-defined statistic. In this case, the np.percentile() function is used to define the deciles using the makepercentile() function and a simple for loop. The seastats variable is assigned to a dictionary containing ten lambda functions, which are input into sean() via the seastat parameter. To speed up the analysis, the deciles are only calculated for solar wind velocity.

The resulting plot is shown in Figure 3. All ten deciles are plotted with a color assigned as displayed to the right of the plot. The temporal storm profile is similar to the V panel in Figure 3 median (50th percentile) and the upper and lower (25th and 75th percentiles, respectively), showing the characteristic rapid increase in solar wind speed V pre-epoch, followed by a gradual decrease post-epoch.

FIGURE 3

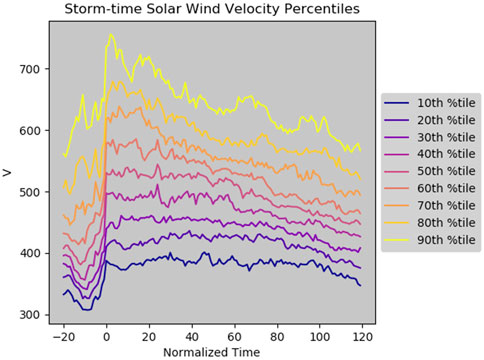
FIGURE 3. Result of the one-dimensional, time-normalised superposed epoch analysis for solar wind speed (V), for data within 168 geomagnetic storms. Deciles are calculated for data between 1992 and 2004. The color indicates the exact decile, referring to the legend plotted on the right.

3.2 Two-dimensional SEA

To also demonstrate the sean() function’s 2D capability, we present the below Python code, which produces the plot in Figure 4 for SAMPEX PET flux data. For the y-dimensions (L-shell dimension), we set boundaries of L = 2.5 and L = 5.5, with a bin-spacing of L = 0.2. L-shell dimensions are chosen to reflect data availability in this particular data set.

FIGURE 4

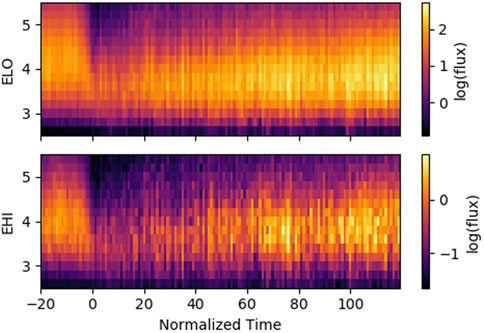
FIGURE 4. Result of the two-dimensional (L-shell vs. time), time-normalised superposed epoch analysis for SAMPEX PET fluxes between 1992 and 2004, for 168 geomagnetic storms. The colors are on a logarithmic scale, and show flux from the low energy (ELO, 1.5–6.0 MeV) electron channel on the top panel and from the high energy (EHI, 2.5–14.0 MeV) electron channel on the bottom panel.

Figure 4 shows the result of the above Python code. Once again, the time-normalized SEA has produced the characteristic temporal storm profile for the ELO and EHI (relativistic) energies. Pre-epoch, electron flux shows rapid decreases at outside L ≈ 3.5, before recovering post-epoch.

4 Conclusion and future possibilities

In this article, we have presented sea_norm, a new python package which is able to perform a time-normalized SEA on both 1D and 2D data. The bulk of sea_norm is contained within the sean() function, where the only required inputs are a time series, a list of events and specified binning dimensions for the normalized time-axis (and for the y-dimensions if performing a 2D analysis). sean() returns a Pandas DataFrame with the completed SEA, along with the relevant metadata.

We have demonstrated three potential uses of sean(): a 1D SEA, performed on multiple time series parameters; a 1D SEA with user-defined statistics; and a 2D SEA for two time series binned by L-shell.

While the 1D and 2D functionality of the sea_norm package covers the vast majority of common SEA uses, future developments of sea_norm could incorporate a 3D version. This would provide sea_norm the capability of producing more in-depth analysis of events where more than one spatial dimension is of interest. For example, a 3D SEA could be used with SAMPEX flux data in both the L-shell and magnetic local time (MLT) dimensions throughout a geomagnetic storm. An animated L vs. MLT plot could then be produced, depicting the 2D spatiotemproal evolution of electrons in the radiation belts during a storm.

The superposed epoch analysis (SEA) has been used as an effective tool in time-series data analysis for over 100 years (Chree, 1913) and extensively used in Space Physics. The simple nature of the SEA makes it a powerful tool for statistical analysis whose results are easy to interpret and analyze. The time-normalized SEA discussed here provides a solution to a potential short-coming of the conventional SEA, whereby events of differing length can smear the underlying dynamics researchers wish to study. sea_norm provides a convenient method to perform a time-normalized SEA, allowing researchers to circumvent potential pitfalls in a traditional SEA analysis. Overall, sea_norm provides any researcher in any field who utilizes time series in their work to rapidly perform a time-normalized superposed epoch analysis and identify the underlying statistical patterns in their data.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

SW and KM equally contributed to development of the code, writing of the manuscript and production of figures.

Funding

SW was supported by Science and Technology Facilities Council (STFC) studentship ST/S50578X/1 and by the UKRI/NERC and Mitacs Canada grant NE/T014164/1 as part of the UK-Canada Globalink doctoral exchange scheme. KM is partially supported by NERC grant NE/V002554/2.

Acknowledgments

The authors would like to thank all of the individuals involved in the upkeep of the OMNIWeb and SAMPEX data websites.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boakes, P. D., Milan, S. E., Abel, G. A., Freeman, M. P., Chisham, G., and Hubert, B. (2011). A superposed epoch investigation of the relation between magnetospheric solar wind driving and substorm dynamics with geosynchronous particle injection signatures. J. Geophys. Res. 116. doi:10.1029/2010JA016007

CrossRef Full Text | Google Scholar

Chree, C. (1913). Some phenomena of sunspots and of terrestrial magnetism at kew observatory. Philosophical Trans. R. Soc. Lond. Ser. A 212, 75–116. doi:10.1098/rsta.1913.0003

CrossRef Full Text | Google Scholar

Gabrielse, C., Angelopoulos, V., Runov, A., and Turner, D. L. (2014). Statistical characteristics of particle injections throughout the equatorial magnetotail. JGR. Space Phys. 119, 2512–2535. doi:10.1002/2013JA019638

CrossRef Full Text | Google Scholar

Halford, A. J., Fraser, B. J., and Morley, S. K. (2010). EMIC wave activity during geomagnetic storm and nonstorm periods: CRRES results. J. Geophys. Res. 115. doi:10.1029/2010JA015716

CrossRef Full Text | Google Scholar

Hietala, H., Kilpua, E. K., Turner, D. L., and Angelopoulos, V. (2014). Depleting effects of ICME-driven sheath regions on the outer electron radiation belt. Geophys. Res. Lett. 41, 2258–2265. doi:10.1002/2014GL059551

CrossRef Full Text | Google Scholar

Hutchinson, J. A., Wright, D. M., and Milan, S. E. (2011). Geomagnetic storms over the last solar cycle: A superposed epoch analysis. J. Geophys. Res. 116. doi:10.1029/2011JA016463

CrossRef Full Text | Google Scholar

Katsavrias, C., Daglis, I. A., and Li, W. (2019). On the statistics of acceleration and loss of relativistic electrons in the outer radiation belt: A superposed epoch analysis. J. Geophys. Res. Space Phys. 124, 2019JA026569–2768. doi:10.1029/2019JA026569

CrossRef Full Text | Google Scholar

Kilpua, E. K., Hietala, H., Turner, D. L., Koskinen, H. E., Pulkkinen, T. I., Rodriguez, J. V., et al. (2015). Unraveling the drivers of the storm time radiation belt response. Geophys. Res. Lett. 42, 3076–3084. doi:10.1002/2015GL063542

CrossRef Full Text | Google Scholar

Larsen, B. A., Morley, S. K., Niehof, J. T., and Welling, D. T. (2010). Spacepy. doi:10.5281/zenodo.3252523

CrossRef Full Text | Google Scholar

Liu, J., Gabrielse, C., Angelopoulos, V., Frissell, N. A., Lyons, L. R., McFadden, J. P., et al. (2011). Superposed epoch analysis of magnetotail flux transport during substorms observed by THEMIS. J. Geophys. Res. 116. doi:10.1029/2010JA015886

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., Lam, M. M., Denton, M. H., Borovsky, J. E., and Green, J. C. (2011). Energetic electron precipitation during high-speed solar wind stream driven storms. J. Geophys. Res. 116. doi:10.1029/2010JA016293

CrossRef Full Text | Google Scholar

Morley, S. K., Koller, J., Welling, D. T., Larsen, B. A., Henderson, M. G., and Niehof, J. T. (2011). “Spacepy - a Python-based library of tools for the space sciences,” in Proceedings of the 9th Python in Science conference, Austin, TX, June 28–July 3, 2011.

Google Scholar

Murphy, K. R., Mann, I. R., Sibeck, D. G., Rae, I. J., Watt, C., Ozeke, L. G., et al. (2020). A framework for understanding and quantifying the loss and acceleration of relativistic electrons in the outer radiation belt during geomagnetic storms. Space weather. 18, e2020SW002477. doi:10.1029/2020SW002477

CrossRef Full Text | Google Scholar

Murphy, K. R., Watt, C. E. J., Mann, I. R., Jonathan Rae, I., Sibeck, D. G., Boyd, A. J., et al. (2018). The global statistical response of the outer radiation belt during geomagnetic storms. Geophys. Res. Lett. 45, 3783–3792. doi:10.1002/2017GL076674

CrossRef Full Text | Google Scholar

O’Brien, T. P., Lorentzen, K. R., Mann, I. R., Meredith, N. P., Blake, J. B., Fennell, J. F., et al. (2003). Energization of relativistic electrons in the presence of ULF power and MeV microbursts: Evidence for dual ULF and VLF acceleration. J. Geophys. Res. 108, 1329. doi:10.1029/2002JA009784

CrossRef Full Text | Google Scholar

Olifer, L., Mann, I. R., Kale, A., Mauk, B. H., Claudepierre, S. G., Baker, D. N., et al. (2021). A tale of two radiation belts: The energy-dependence of self-limiting electron space radiation. Geophys. Res. Lett. 48, e2021GL095779. doi:10.1029/2021GL095779

CrossRef Full Text | Google Scholar

Smirnov, A., Shprits, Y., Allison, H., Aseev, N., Drozdov, A., Kollmann, P., et al. (2022). Storm-time evolution of the equatorial electron pitch angle distributions in Earth’s outer radiation belt. Front. Astron. Space Sci. 9, 62. doi:10.3389/fspas.2022.836811

CrossRef Full Text | Google Scholar

Summers, D., and Thorne, R. M. (2003). Relativistic electron pitch-angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. J. Geophys. Res. 108, 1143. doi:10.1029/2002JA009489

CrossRef Full Text | Google Scholar

Turner, D. L., Kilpua, E. K. J., Hietala, H., Claudepierre, S. G., O’Brien, T. P., Fennell, J. F., et al. (2019). The response of Earth’s electron radiation belts to geomagnetic storms: Statistics from the van allen probes era including effects from different storm drivers. JGR. Space Phys. 124, 1013–1034. doi:10.1029/2018JA026066

CrossRef Full Text | Google Scholar

Walach, M., and Grocott, A. (2019). SuperDARN observations during geomagnetic storms, geomagnetically active times, and enhanced solar wind driving. JGR. Space Phys. 124, 5828–5847. doi:10.1029/2019JA026816

CrossRef Full Text | Google Scholar

Walton, S. D., Forsyth, C., Rae, I. J., Meredith, N. P., Sandhu, J. K., Walach, M.-T., et al. (2022). Statistical comparison of electron loss and enhancement in the outer radiation belt during storms. JGR. Space Phys. 127, e2021JA030069. doi:10.1029/2021JA030069

CrossRef Full Text | Google Scholar

Walton, S. D., and Murphy, K. R. (2022). samwalton7645/SEA_Code: sea_norm Frontiers initial release. doi:10.5281/zenodo.6867860

CrossRef Full Text | Google Scholar

Wang, H., He, Y., Lühr, H., Kistler, L., Saikin, A., Lund, E., et al. (2019). Storm time EMIC waves observed by swarm and van allen probe satellites. J. Geophys. Res. Space Phys. 124, 293–312. doi:10.1029/2018JA026299

CrossRef Full Text | Google Scholar

Whittaker, I. C., Clilverd, M. A., and Rodger, C. J. (2014). Characteristics of precipitating energetic electron fluxes relative to the plasmapause during geomagnetic storms. J. Geophys. Res. Space Phys. 119, 8784–8800. doi:10.1002/2014JA020446

CrossRef Full Text | Google Scholar

Yokoyama, N., and Kamide, Y. (1997). Statistical nature of geomagnetic storms. J. Geophys. Res. 102, 14215–14222. doi:10.1029/97JA00903

CrossRef Full Text | Google Scholar