Joseph E. Borovsky- Center for Space Plasma Physics, Space Science Institute, Boulder, CO, United States
Building upon the research legacies of Peter Gary and Richard Thorne, this perspective discusses a plasma-system picture wherein multiple ion and electron populations interact with each other via multiple types of plasma waves. The two cases discussed are 1) the Earth’s magnetosphere with ion and electron populations trapped in the closed flux tubes of the magnetic dipole and 2) the solar wind with ion and electron populations expanding away from the Sun in open magnetic flux tubes. For the magnetosphere, internal convection drives particle populations into stronger magnetic fields, leading to particle anisotropies; for the solar wind the expansion of the plasma away from the Sun results in the particle populations moving into weaker magnetic fields, leading also to particle anisotropies. In both cases, the anisotropies of the diverse ion and electron populations produce kinetic instabilities resulting in the production of diverse types of plasma waves and wave-particle interactions. Following the extensive research of Richard Thorne, web diagrams of plasma-wave interactions are laid out for the multiple ion and electron populations of the magnetosphere and following the extensive research of Peter Gary web diagrams of plasma-wave interactions are laid out for the multiple ion and electron populations of the solar wind. The advantages of a systems-analysis approach to these two plasma systems is discussed.
Introduction
The Earth’s magnetosphere and the solar wind provide two valuable opportunities to bring systems science into the field of plasma physics. Both the magnetospheric system and the solar-wind system are comprised of multiple electron and ion populations with interactions between the populations occurring largely via plasma waves. Many of the plasma-wave interactions of the magnetosphere were uncovered and quantified by Richard Thorne in over 4 decades of research (e.g. Thorne, 1968; Thorne et al., 2017) and many of the plasma-wave interactions of the solar wind were uncovered and quantified by Peter Gary in over 4 decades of research (e.g. Gary, 1974; Gary et al., 2020). Without theses two visionary researchers, these two coherent plasma-systems pictures could not be created.
Both the magnetosphere and the solar wind exhibit multiple populations of ions and electrons that are co-located (i.e. that reside on the same magnetic-field lines) so that the multiple populations easily interact with each other. The evolution of magnetized plasmas often leads to anisotropies giving rise to instabilities and wave-particle interactions: for the magnetosphere the particle anisotropies arise from solar-wind-driven magnetospheric internal convection pushing particle populations into the strong magnetic field of the dipolar regions and for the solar wind the particle anisotropies arise from the solar-wind expansion into weaker magnetic fields away from the Sun. For every plasma-wave instability, wave-particle interactions act in two fashions: in driving the waves and in dissipating the waves. In this manner two diverse particle populations can interact with each other.
In this perspective article the plasma system science of the magnetosphere and the plasma system science of the solar wind will be briefly outlined. The magnetosphere is a driven closed system (more or less), with the multiple particle populations trapped in dipolar (or stretched) magnetic flux tubes. The solar wind is an open system with multiple particle populations born in the solar corona and moving outward at different speeds from the Sun in open magnetic flux tubes.
This paper is organized as follows. In The Magnetospheric System Section the magnetospheric plasma system is described. In The Solar-Wind System Section the solar-wind plasma system is described. Discussion Section contains discussions of 1) previous system-science analysis that has been done for the magnetosphere and the solar wind, 1) the availability of data for future studies, and 3) some advantages that systems analysis may provide.
The Magnetospheric System
The Earth’s magnetosphere is a system of multiple trapped particle populations with free energy added from the solar wind, which drives internal convection. Convection of particle populations into the stronger field of Earth’s dipole drives particle anisotropies and free energy for plasma waves. The resulting multiple plasma instabilities gives rise to multiple couplings between the diverse particle populations, resulting in a complex evolution of those diverse particle populations. A thorough review of the Earth’s magnetosphere as a system wherein the multiple ion and electron populations interact via plasma waves appears in Borovsky and Valdivia (2018).
The key to the interaction of the different particle populations is the fact that they are co-located on the same magnetic field lines. There are three major regions in the Earth’s magnetosphere and the three regions contain differing particle populations. The first region is the stretched-field “magnetotail” on the nightside of the Earth. The major particle populations of the magnetotail are the ion plasma sheet, the electron plasma sheet, the cusp-mantle (ions and electrons), and the polar wind (ions and electrons). The second region is the “outer dipole”: this region contains the ion plasma sheet (ions), the electron plasma sheet (electrons), substorm-injected ions, substorm-injected electrons, the electron radiation belt, the ion radiation belt, cloak ions, cloak electrons, and polar-wind ions and electrons. The third region is the “inner dipole” closest to the Earth: this region contains the plasmasphere (ions and electrons), the ion plasma sheet, substorm-injected ions, the electron radiation belt, and the ion radiation belt. The boundary between the inner and outer dipole regions is the plasmapause, which is the outer boundary of the dense, cold plasmasphere.
As an example of the co-location of multiple particle populations, Figure 1 provides a sketch of the distribution functions of the ions and electrons in the inner dipolar region at local midnight. The plot is a log-log plot, sketching each particle distribution as a Maxwellian, which in general they are not. (The hotter populations often have anisotropies and biteouts). The populations range in energy from the ionosphere (Ti ≈ Te ∼ 0.1 eV) and plasmasphere (Ti ≈ Te ∼ 0.5 eV) to the ion radiation belt (which has a tail of particles in the 1-MeV range of energies) and the electron radiation belt (which has a tail of particles in the 10-MeV range).
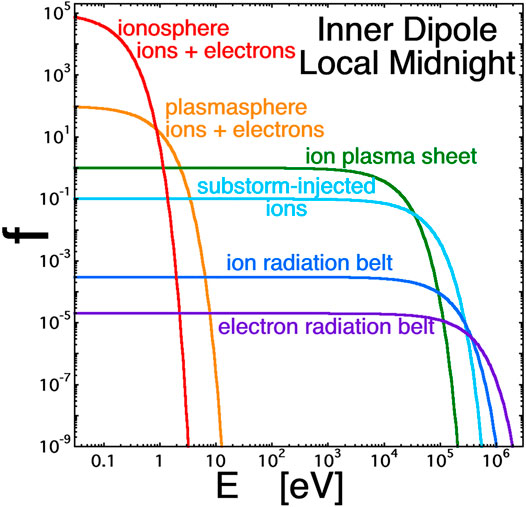
FIGURE 1. A sketch of the distribution functions of 5 ion populations and 3 electron populations on the same magnetic field line in the inner-dipole region of the nightside magnetosphere.
The plasma populations of the magnetosphere interact via plasma waves. The typical types of plasma waves observed depend on the region of the magnetosphere and the ion and electron populations in that region that can drive the waves. Figure 2 is a classic sketch from Thorne (2010) that has been reproduced in numerous scientific publications: the sketch depicts the equatorial plane of the Earth’s magnetosphere and the major types of plasma waves that impact the electron radiation belt observed in the various regions. The types of plasma waves seen inside the plasmapause (inner dipole) differ from the types seen outside the plasmapause (outer dipole), with drastically different consequences for the particle populations in those two regions. Critical to the evolution of the electron radiation belt, Figure 2 depicts that whistler-mode chorus waves exist outside of the plasmasphere (outer dipole), whistler-mode hiss waves exist inside of the plasmasphere (inner dipole), and electromagnetic ion-cyclotron (EMIC) waves tend to exist inside the plasmasphere (inner dipole).
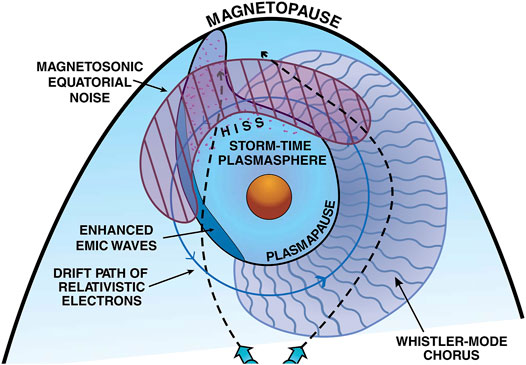
FIGURE 2. A reproduction of the classic Figure 1 of Thorne (2010) that sketches in the equatorial plane of the Earth’s magnetosphere the major types of plasma waves observed in the different regions of the magnetosphere. The viewing is from above the north pole of the Earth: the Sun is at the top of the sketch, dawn is to the right, and dusk is to the left.
In the interactions of co-located particle populations via plasma waves in the Earth’s magnetosphere, typically a warm (keV) population of particles with medium density is the driver for the waves and typically a very-energetic populations (100’s of keV) with a very-low-density is the absorber of the wave energy. And often there is a high-density cold population of ions or electrons that regulates the plasma-wave dispersion relation, determining what waves can be driven and determining the resonance conditions for those waves (cf. Delzanno et al., 2021).
In Figure 3 a map is displayed of the basic web of interactions between the multiple electron and ion populations of the Earth’s magnetosphere and the type of plasma wave that mediates each interaction. (The various plasma waves in Figure 3 are elaborated upon in Section 6 of Borovsky and Valdivia (2018).). In the map of Figure 3 the direction of each arrow indicates the transfer of wave action: from the driving population to the receiving population. For the receiving population, the waves can lead to energization and/or to pitch-angle scattering, with pitch-angle scattering often leading to scattering into the atmospheric loss cone where the scattered ions or electrons are lost from the magnetospheric system into the atmosphere. Note in Figure 3 that a number of “circular” wave interactions are indicated: here one portion of a single population will drive waves that affect another portion of the same population. This often produces pitch-angle scattering into the atmospheric loss cone, resulting in a loss from the magnetospheric system and perhaps producing aurora in the upper atmosphere.
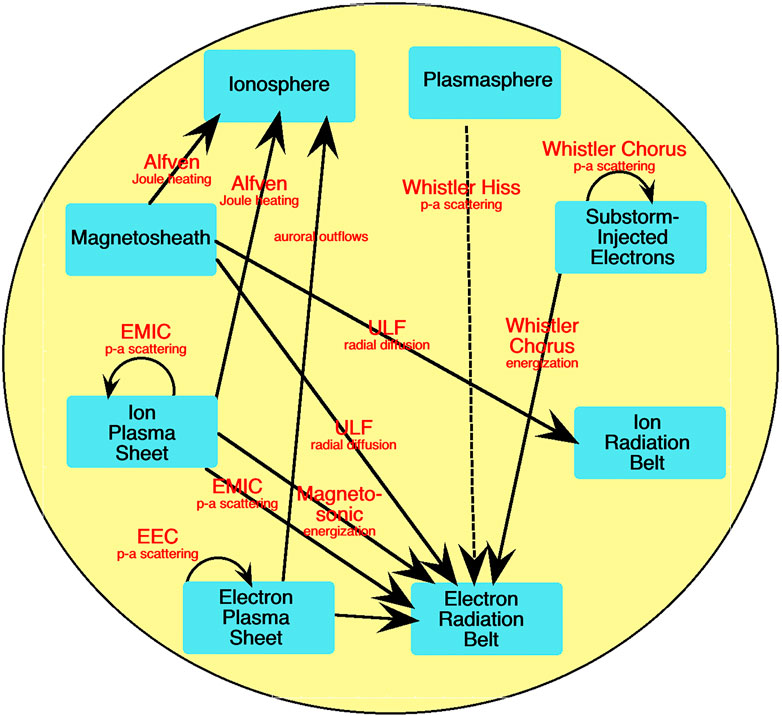
FIGURE 3. A sketch of the web of plasma-wave interactions between the major ion and electron populations of the Earth’s magnetosphere.
The complicated system of instability-driven wave-particle interactions that drive the evolution of the multiple ion and electron populations of the Earth’s magnetosphere were largely worked out by Richard Thorne. Focused review articles on these various interactions can be found in Thorne and Kennel (1971), Thorne et al., (1973, 1979, 2010, 2013, 2017), Thorne (1974, 2010), Thorne and Summers (1991), and Thorne and Horne (1992, 1994).
One hallmark of a “complex system” is that the system exhibits “emergence”, new things “emerge”, i.e. the system creates something from nothing. Examples of emergence are given in Borovsky and Valdivia (2018). On example of emergence in the Earths magnetospheric system is the electron radiation belt: here the system takes medium-energy short-lifetime substorm-injected electrons and, via a complex web of interactions, creates a population of high-energy long-lifetime relativistic electrons.
The Solar-Wind System
The magnetic structure of the solar-wind plasma resembles a spaghetti of magnetic flux tubes with strong current sheets forming the boundaries between adjacent flux tubes (Michel, 1967; Bruno et al., 2001; Borovsky, 2008; Greco et al., 2008; Pecora et al., 2019). The field of most of the solar wind is “open”, with field lines magnetically connecting the Sun to the distant heliosphere. The multiple solar-wind particle populations are born in the solar corona and move outward (at different speeds) along the magnetic field in the open flux tubes. Note, however, that many of the details of the physical processes in the corona that are acting in the birth of the solar wind are not known (cf. Cranmer et al., 2017).
The solar-wind plasma in the inner heliosphere has 7 major particle populations: protons, alpha particles, highly charged heavy ions, an antisunward proton beam, core electrons, halo electrons, and a field-aligned energetic electron strahl. Minor populations can include a sunward streaming proton beam.
As the fast energetic strahl electrons move outward from the Sun they produce an ambipolar electric field that pulls ions outward from the Sun against the Sun’s gravity (Jockers, 1970; Lemaire, 2010). This magnetic-field-aligned electrostatic “interplanetary electric field”, in part, accelerates the solar wind to high velocities. (A similar process occurs on the sunlit ionosphere of Earth where multi-eV photoelectrons from the atmosphere produce an ambipolar electric field that pulls sub-eV ions out against the Earth’s gravity: this is the “polar wind” (Schunk, 2007).) The field-aligned potential drop from the Sun to infinity is on the order of 1 kV, with most of that drop occurring between the Sun and the orbit of Mercury. As the ion and electron populations of the solar wind move outward from the Sun (at different speeds), they interact and evolve. Some of the plasma-wave interactions between the major particle populations are mapped out in Figure 4.
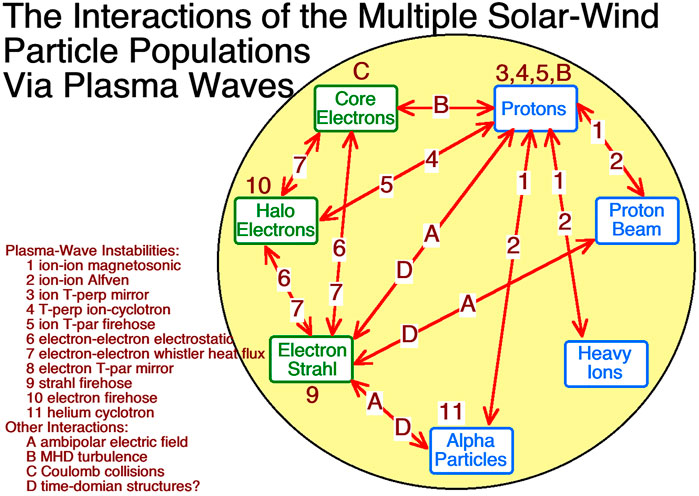
FIGURE 4. A sketch of the web of plasma-wave interactions between the major ion and electron populations of the solar wind. (This interaction map is an update of Figure 8 of Viall and Borovsky (2020), which was assembled by the author with critical guidance from Peter Gary).
Free energy sources for the system evolution are (cf. Borovsky and Gary, 2014; Smith and Vasquez, 2021) 1) electron heat flux, 2) large-amplitude Alfvén waves, 3) the relative drift between alpha particles and protons, and 4) anisotropies driven by the changing magnetic-field strength. Well beyond 1 AU other sources are interplanetary shocks (Smith et al., 1985) and interstellar pickup ions (Lee, 2018).
It is thought that whistle-mode scattering of the field-aligned strahl electrons gives rise to the quasi-isotropic energetic electron halo population (Gary and Saito, 2007): as evidence, with distance from the Sun the strahl population becomes fractionally less dense and the halo population becomes fractionally more dense (Stverak et al., 2009).
A key source of energy in the solar wind resides in outward propagating Alfvénic fluctuations from the corona. About half of the solar wind at 1 AU is Alfvénic, with strong correlations between the vector changes in the magnetic field and the vector changes in the proton flow velocity. In the Alfvénic solar wind, it is observed that the magnetic structure moves en masse relative to the proton plasma at a speed of about 0.7 vA (Borovsky, 2020a; Nemecek et al., 2020), where vA is the measured Alfvén speed. In the reference frame of the magnetic structure, to within measurement error all proton flows v are parallel to the local magnetic-field direction B; with v⊥ = 0 there is (to within measurement error) no time evolution of the magnetic structure as it moves outward through the inner heliosphere. This is an example of the Chadrasekhar dynamic equilibrium (“CDE”) (cf. Fig. 7.1 of Parker (1979)) where a nonlinear tangle (spaghetti) of magnetic field will propagate en masse without evolution provided that the flow is everywhere parallel to the local field. The alpha particles of the solar wind (and perhaps also the heavy ions) reside nearly at rest in the reference frame of the magnetic structure (Nemecek et al., 2020): it is not known why. The outward-propagating Alfvénic structure interacts with the particle populations 1) via parametric instabilities (e.g. Malara et al., 2001; Vasquez and Hollweg, 1996) and 2) via an MHD-turbulence cascade where the Alfvén waves transfer energy into electrons and ions via mode conversion (Gary and Smith, 2009; Gary et al., 2020) followed by kinetic (cyclotron or Landau) damping (Leamon et al., 1998; Gary and Borovsky, 2004, 2008).
Because of the relative motion of the alpha particles with respect to the proton population, ion-ion streaming instabilities can couple the two populations (Gary, 1991; Gary et al., 2000a). In particular, the alpha-proton magnetosonic instability acts to heat both populations in a fashion such that the protons and alpha particles both have the same thermal speed (Gary et al., 2000b), which is observed in the solar wind (Feynman, 1975).
As the particle populations move outward from the Sun into weaker magnetic fields, conservation of the particle first adiabatic invariants v2perp/B decreases the perpendicular temperatures of the populations and leads to anisotropy. For the protons the firehose instability driven by Tparallel > Tperp acts to return the proton population toward isotropy (Gary et al., 1998, 2001). Similar instabilities act on the alpha-particle anisotropy (Gary et al., 2003) and on the electron anisotropy (Gary and Nishimura, 2003).
Core electrons originate from the low-energy portion of the strahl population (e.g. Boldyrev et al., 2020). The core electrons are locally trapped along the magnetic field (Marsch, 2006): 1) moving toward the Sun the core electrons mirror as the interplanetary magnetic field gets stronger nearer to the Sun and 2) moving away from the Sun the interplanetary electric field pulls them back. The core-electron temperature reflects the local potential of the plasma with respect to infinity (away from the Sun) (Feldman et al., 1975).
Review articles on the diverse types of solar-wind plasma waves and their impact on the solar-wind particle populations can be found in Gary (1991, 1992, 1999), Gary et al. (1975a,b, 1976, 1984, 1994, 1999, 2000a), and Gary and Karimabadi (2006) and in the monograph Gary (1993).
Here we see the system, with the strahl driving the interplanetary potential that drives the solar wind outward. As the populations move through each other at different speeds (all moving outward), they interact via plasma waves (cf. Figure FF03).
The magnetic-field structure of the solar wind resembles a spaghetti of magnetic flux tubes separated by current sheets. The diameters of the flux tubes vary, but a typical flux tube at 1 AU has a diameter of about 4 × 105 km, and a spacecraft crosses from one flux tube to the next every 10 or 20 min. From tube to tube there can be differences in the plasma properties: proton specific entropy, ion composition, magnetic-field strength, plasma beta, etc. Important for this system-science picture, the strahl intensity (Borovsky, 2020b) and the electron temperature (Borovsky et al., 2021) can vary from tube to tube with sudden jumps in the values as the current-sheet wall between flux tubes is crossed. The electron-temperature jumps indicate that the interplanetary electric potential differs from flux tube to flux tube. This implies that each flux tube is an independent evolving system, and that as a solar-wind spacecraft crosses from tube to tube it is measuring different realizations of system evolution. This opens the possibility of statistical plasma system science.
Discussion
This section discusses previous system-science analysis that has been done for the magnetosphere and the solar wind, the availability of quality data for future studies, and the advantages that systems analysis may provide.
Plasma Systems Science and Data Availability
Reviews of magnetospheric system-science work can be found in Valdivia et al., [2005, 2013], Vassiliadis (2006), Stepanova and Valdivia, 2016, and Borovsky and Valdivia (2018). Early magnetospheric system science began with two-variable correlation studies between near-Earth solar-wind measurements and measures of the strength of magnetospheric activity (Snyder et al., 1963; Clauer et al., 1981; McPherron et al., 2015): those studies yielded critical information about the processes by which the solar wind drives magnetospheric activity and important information about the multiple reaction times of the magnetospheric system to changes in the solar wind. Later, vector-vector correlation studies (Borovsky and Osmane, 2019) yielded information about multiple modes of reaction of the magnetospheric system to the solar wind. Information-transfer studies (Wing and Johnson, 2019) have further refined our knowledge about solar-wind driving and in future can be used to examine the causality pathways through the multiple ion and electron populations of the magnetosphere as they undergo the web of interactions (cf. Figure 3). Toy mathematical models (Smith et al., 1986; Goertz et al., 1993; Vassiliadis et al., 1993; Klimas et al., 1997; Freeman and Morley 2004; Spencer et al., 2018) have also been constructed and used to gain understandings of the dynamical behaviors of the solar-wind-driven magnetospheric system. In contrast, for the solar-wind plasma system very little system analysis has been performed. Most of the data analytics applied to the solar wind has focused on investigating the nature of the MHD fluctuations in the wind (e.g. Burlaga and Klein, 1986; Marsch and Tu, 1997; Wawrzaszek et al., 2019), not on the particle-population evolution. Here again, information-transfer analysis may be helpful for uncovering and gauging the importance of the various intercouplings of the particle populations with distance from the Sun.
For magnetospheric systems science diverse measurements of the magnetosphere-ionosphere system have been available for over 5 decades, as are measurements of the solar wind at Earth that drives the system. For solar wind system science quality spacecraft data throughout the inner heliosphere from about 15 solar radii to 1 AU (215 solar radii) and beyond are available from multiple spacecraft. For the most part this spacecraft data is centralized and publically available, but with effort more plasma data from the spacecraft of diverse government agencies could be made publically available for scientific purposes.
Advances That Could be Made With a Systems Science Approach
For the Earth’s magnetosphere, global simulations codes cannot build in all of the diverse ion and electron populations, all of the kinetic wave processes, and the huge span of important spatial scales. Ring-current-subsystem codes (Jordanova et al., 2001, 2012; Gamayunov et al., 2009) and radiation-belt-subsystem codes (Varotsou et al., 2005; Shprits et al., 2008a,b; Jordanova et al., 2018) resort to using diffusion coefficients or particle lifetimes to represent the action of waves (energization, pitch-angle scattering, and radial diffusion) acting upon the particle populations, typically with diffusion coefficients based on statistical pictures of plasma-wave observations parameterized by magnetospheric-activity levels. Systems analysis examines the behavior of the actual measured system that includes all of these attributes, extracting information about the behavior of the true, fully realized system. This perspective article encourages the development of systems science methodologies specifically for the critical science challenge of understanding the time-evolving solar-wind-driven magnetosphere-ionosphere system, where physics-based simulations are a long way from containing the physics necessary to simulate the coupled system. The situation is similarly difficult for the evolving solar wind: in the near future simulation codes will not be able to capture all of the diverse ion and electron populations and kinetic wave-particle processes that act as the solar wind evolves from the solar corona outward into the heliosphere. System science analysis of the actual system will be needed.
A systems science analysis can yield unique information about the behavior of a system, including the uncovering of hidden or unnoticed modes of behavior. Systems science analysis works even before all of the physics is identified or understood. It can find couplings and feedback loops in the operation of a system. This information has the potential to guide reductionist data analysis, to guide the development of simulation techniques, and to guide the design of new instruments and new measurement techniques. Systems analysis can be used to test the veracity of simulation codes: performing the same systems analysis on simulation data as on the actual system can compare the statistical behavior of the simulations and the actual system.
Systems science tools that may be developed specifically for the multiple interacting plasmas of the magnetospheric system or the solar-wind system may be generalizable to other problems: laboratory plasma experiments, fusion machines, solar physics, and plasma astrophysics. The tools developed for the solar-wind-driven magnetospheric system may also be useful for other driven systems, such as biological organisms and economic systems.
An integration of magnetospheric systems science into the broader research field of “Earth systems science” could enhance the scientific and societal impact of plasma physics (Thorne, 1977, 1980; Tinsley 2000; Georgieva et al., 2005; Rycroft et al., 2012; Sinnhuber et al., 2012; Clilverd et al., 2016; Lam and Tinsley 2016).
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.
Author Contributions
JB initiated this project, performed the analysis, and wrote the manuscript.
Funding
This work was supported at the Space Science Institute by the NSF GEM Program via grant AGS-2027569, by the NSF SHINE program via grant AGS-1723416, by the NASA Heliophysics LWS program via award NNX16AB75G, and by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
This paper is dedicated to the memory of my friend, collaborator, and mentor Peter Gary and to the memory of my friend and colleague Richard Thorne. The author thanks Gian Luca Delzanno, Mick Denton, Adnane Osmane, and Juan Valdivia for helpful conversations.
References
Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron temperature of the solar wind. Proc. Natl. Acad. Sci. USA 117, 9232–9240. doi:10.1073/pnas.1917905117
Borovsky, J. E., and Gary, S. P. (2014). How important are the alpha-proton relative drift and the electron heat flux for the proton heating of the solar wind in the inner heliosphere. J. Geophys. Res. Space Phys. 119, 5210–5219. doi:10.1002/2014ja019758
Borovsky, J. E., Halekas, J. S., and Whittlesey, P. L. (2021). The electron structure of the solar wind. Front. Astron. Space Sci. 8, 69005. doi:10.3389/fspas.2021.690005
Borovsky, J. E. (2020a). On the motion of the heliospheric magnetic structure through the solar wind plasma. J. Geophys. Res. 125, e2019JA027377. doi:10.1029/2019ja027377
Borovsky, J. E., and Osmane, A. (2019). Compacting the description of a time-dependent multivariable system and its multivariable driver by reducing the state vectors to aggregate scalars: the Earth's solar-wind-driven magnetosphere. Nonlin. Process. Geophys. 26, 429–443. doi:10.5194/npg-26-429-2019
Borovsky, J. E. (2008). The flux-tube texture of the solar wind: Strands of the magnetic carpet at 1 AU. J. Geophys. Res. 113, A08110. doi:10.1029/2007ja012684
Borovsky, J. E. (2020b). The magnetic structure of the solar wind: Ionic composition and the electron strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586
Borovsky, J. E., and Valdivia, J. A. (2018). The Earth's Magnetosphere: A Systems Science Overview and Assessment. Surv. Geophys. 39, 817–859. doi:10.1007/s10712-018-9487-x
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying intermittency events in the solar wind. Planet. Space Sci. 49, 1201–1210. doi:10.1016/s0032-0633(01)00061-7
Burlaga, L. F., and Klein, L. W. (1986). Fractal structure of the interplanetary magnetic field. J. Geophys. Res. 91, 347–350. doi:10.1029/ja091ia01p00347
Clauer, C. R., McPherron, R. L., Searls, C., and Kivelson, M. G. (1981). Solar wind control of auroral zone geomagnetic activity. Geophys. Res. Lett. 8, 915–918. doi:10.1029/gl008i008p00915
Clilverd, M. A., Rodger, C. J., Andersson, M. E., Seppälä, A., and Verronen, P. T. (2016). Linkages between the radiation belts, polar atmosphere and climate: electron precipitation through wave particle interactions. in Waves, Particles, and Storms in Geospace, G. Balasis, I. A. Daglis, and I. R. Mann (eds.), pg. 354–376. Oxford University Press, Oxford.doi:10.1093/acprof:oso/9780198705246.003.0015
Cranmer, S. R., Gibson, S. E., and Riley, P. (2017). Origins of the ambient solar wind: Implications for space weather. Space Sci. Rev. 212, 1345–1384. doi:10.1007/s11214-017-0416-y
Delzanno, G. L., Borovsky, J. E., Henderson, M. G., Resendiz Lira, P. A., Roytershteyn, V., and Welling, D. T. (2021). The impact of cold electrons and cold ions in magnetospheric physics. J. Atmos. Solar-Terrestrial Phys. 220, 105599. doi:10.1016/j.jastp.2021.105599
Feldman, W. C., Asbridge, J. R., Bame, S. J., Montgomery, M. D., and Gary, S. P. (1975). Solar wind electrons. J. Geophys. Res. 80, 4181–4196. doi:10.1029/ja080i031p04181
Feynman, J. (1975). On solar wind helium and heavy ion temperatures. Sol. Phys. 43, 249–252. doi:10.1007/bf00155156
Freeman, M. P., and Morley, S. K. (2004). A minimal substorm model that explains the observed statistical distribution of times between substorms. Geophys. Res. Lett. 31, L12807 1–4. doi:10.1029/2004gl019989
Gamayunov, K. V., Khazanov, G. V., Liemohn, M. W., Fok, M.-C., and Ridley, A. J. (2009). Self-consistent model of magnetospheric electric field, ring current, plasmasphere, and electromagnetic ion cyclotron waves: Initial results. J. Geophys. Res. 114, A03221. doi:10.1029/2008ja013597
Gary, S. P., Bandyopadhyay, R., Qudsi, R. A., Matthaeus, W. H., Maruca, B. A., Parashar, T. N., et al. (2020). Particle-in-cell Simulations of Decaying Plasma Turbulence: Linear Instabilities versus Nonlinear Processes in 3D and 2.5D Approximations. ApJ 901, 160. doi:10.3847/1538-4357/abb2ac
Gary, S. P., and Borovsky, J. E. (2004). Alfvén-cyclotron fluctuations: Linear Vlasov theory. J. Geophys. Res. 109, A06105. doi:10.1029/2004ja010399
Gary, S. P., and Borovsky, J. E. (2008). Damping of long-wavelength kinetic Alfvén fluctuations: Linear theory. J. Geophys. Res. 113, A12104. doi:10.1029/2008ja013565
Gary, S. P. (1999). Collisionless dissipation wavenumber: Linear theory. J. Geophys. Res. 104, 6759–6762. doi:10.1029/1998ja900161
Gary, S. P. (1991). Electromagnetic ion/ion instabilities and their consequences in space plasmas: A review. Space Sci. Rev. 56, 373–415. doi:10.1007/bf00196632
Gary, S. P., Feldman, W. C., Forslund, D. W., and Montgomery, M. D. (1975a). Electron heat flux instabilities in the solar wind. Geophys. Res. Lett. 2, 79–82. doi:10.1029/gl002i003p00079
Gary, S. P., Feldman, W. C., Forslund, D. W., and Montgomery, M. D. (1975b). Heat flux instabilities in the solar wind. J. Geophys. Res. 80, 4197–4203. doi:10.1029/ja080i031p04197
Gary, S. P., and Karimabadi, H. (2006). Linear theory of electron temperature anisotropy instabilities: Whistler, mirror, and Weibel. J. Geophys. Res. 111, A11224. doi:10.1029/2006ja011764
Gary, S. P., Li, H., O'Rourke, S., and Winske, D. (1998). Proton resonant firehose instability: Temperature anisotropy and fluctuating field constraints. J. Geophys. Res. 103, 14567–14574. doi:10.1029/98ja01174
Gary, S. P., Montgomery, M. D., Feldman, W. C., and Forslund, D. W. (1976). Proton temperature anisotropy instabilities in the solar wind. J. Geophys. Res. 81, 1241–1246. doi:10.1029/ja081i007p01241
Gary, S. P., and Nishimura, K. (2003). Resonant electron firehose instability: Particle-in-cell simulations. Phys. Plasmas 10, 3571–3576. doi:10.1063/1.1590982
Gary, S. P., and Saito, S. (2007). Broadening of solar wind strahl pitch-angles by the electron/electron instability: Particle-in-cell simulations. Geophys. Res. Lett. 34, L14111. doi:10.1029/2007gl030039
Gary, S. P., Scime, E. E., Phillips, J. L., and Feldman, W. C. (1994). The whistler heat flux instability: Threshold conditions in the solar wind. J. Geophys. Res. 99, 23391–23399. doi:10.1029/94ja02067
Gary, S. P., Skoug, R. M., and Daughton, W. (1999). Electron heat flux constraints in the solar wind. Phys. Plasmas 6, 2607–2612. doi:10.1063/1.873532
Gary, S. P., Skoug, R. M., Steinberg, J. T., and Smith, C. W. (2001). Proton temperature anisotropy constraint in the solar wind: ACE observations. Geophys. Res. Lett. 28, 2759–2762. doi:10.1029/2001gl013165
Gary, S. P., Smith, C. W., Lee, M. A., Goldstein, M. L., and Forslund, D. W. (1984). Electromagnetic ion beam instabilities. Phys. Fluids 27, 1852. doi:10.1063/1.864797
Gary, S. P., and Smith, C. W. (2009). Short-wavelength turbulence in the solar wind: Linear theory of whistler and kinetic Alfvén fluctuations. J. Geophys. Res. 114, A12105. doi:10.1029/2009ja014525
Gary, S. P. (1974). Solar cosmic-ray acceleration by a plasma instability. ApJ 187, 195–196. doi:10.1086/152611
Gary, S. P. (1992). The mirror and ion cyclotron anisotropy instabilities. J. Geophys. Res. 97, 8519–8529. doi:10.1029/92ja00299
Gary, S. P. (1993). Theory of Space Plasma Microinstabilities. Cambridge: Cambridge University Press.
Gary, S. P., Yin, L., Winske, D., and Ofman, L. (2003). Consequences of proton and alpha anisotropies in the solar wind: Hybrid simulations. J. Geophys. Res. 198, 1068. doi:10.1029/2002ja009654
Gary, S. P., Yin, L., Winske, D., and Reisenfeld, D. B. (2000b). Alpha/proton magnetosonic instability in the solar wind. J. Geophys. Res. 105, 20989–20996. doi:10.1029/2000ja000049
Gary, S. P., Yin, L., Winske, D., and Reisenfeld, D. B. (2000a). Electromagnetic alpha/proton instabilities in the solar wind. Geophys. Res. Lett. 27, 1355–1358. doi:10.1029/2000gl000019
Georgieva, K., Kirov, B., Atanassov, D., and Boneva, A. (2005). Impact of magnetic clouds on the middle atmosphere and geomagnetic disturbances. J. Atmos. Solar-Terrestrial Phys. 67, 163–176. doi:10.1016/j.jastp.2004.07.025
Goertz, C. K., Shan, L.-H., and Smith, R. A. (1993). Prediction of geomagnetic activity. J. Geophys. Res. 98, 7673–7684. doi:10.1029/92ja01193
Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent MHD structures and classical discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008gl035454
Jordanova, V. K., Delzanno, G. L., Henderson, M. G., Godinez, H. C., Jeffery, C. A., Lawrence, E. C., et al. (2018). Specification of the near-Earth space environment with SHIELDS. J. Atmos. Solar-Terrestrial Phys. 177, 148–159. doi:10.1016/j.jastp.2017.11.006
Jordanova, V. K., Farrugia, C. J., Thorne, R. M., Khazanov, G. V., Reeves, G. D., and Thomsen, M. F. (2001). Modeling ring current proton precipitation by electromagnetic ion cyclotron waves during the May 14-16, 1997, storm. J. Geophys. Res. 106, 7–22. doi:10.1029/2000ja002008
Jordanova, V. K., Welling, D. T., Zaharia, S. G., Chen, L., and Thorne, R. M. (2012). Modeling ring current ion and electron dynamics and plasma instabilities during a high-speed stream driven storm. J. Geophys. Res. 117, A00L18. doi:10.1029/2011ja017433
Klimas, A. J., Vassiliadis, D., and Baker, D. N. (1997). Data-derived analogues of the magnetospheric dynamics. J. Geophys. Res. 102, 26993–27009. doi:10.1029/97ja02414
Lam, M. M., and Tinsley, B. A. (2016). Solar wind-atmospheric electricity-cloud microphysics connections to weather and climate. J. Atmos. Solar-Terrestrial Phys. 149, 277–290. doi:10.1016/j.jastp.2015.10.019
Leamon, R. J., Smith, C. W., Ness, N. F., Matthaeus, W. H., and Wong, H. K. (1998). Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J. Geophys. Res. 103, 4775–4787. doi:10.1029/97ja03394
Lee, M. A. (2018). The story of interstellar pickup ions and their excitation of hydromagnetic waves in the solar wind. ASP Conf. Ser. 513, 205–214.
Lemaire, J. (2010). Half a century of kinetic solar wind models. AIP Conf. Proc. 1216, 8. doi:10.1063/1.3395971
Malara, F., Primavera, L., and Veltri, P. (2001). Nonlinear evolution of the parametric instability: numerical predictions versus observations in the heliosphere. Nonlin. Process. Geophys. 8, 159–166. doi:10.5194/npg-8-159-2001
Marsch, E. (2006). Kinetic physics of the solar corona and solar wind. Living Rev. Solar Phys. 3, 1. doi:10.12942/lrsp-2006-1
Marsch, E., and Tu, C.-Y. (1997). Intermittency, non-gaussian statistics and fractal scaling of MHD fluctuations in the solar wind. Nonlin. Process. Geophys. 4, 101–124. doi:10.5194/npg-4-101-1997
McPherron, R. L., Hsu, T.-S., and Chu, X. (2015). An optimum solar wind coupling function for theALindex. J. Geophys. Res. Space Phys. 120, 2494–2515. doi:10.1002/2014ja020619
Michel, F. C. (1967). Model of solar wind structure. J. Geophys. Res. 72, 1917–1932. doi:10.1029/jz072i007p01917
Nemecek, Z., Durovcova, T., Safrankova, J., Nemec, F., Matteini, L., StansbyJantizek, D. N., et al. (2020). What is the solar wind frame of reference. Astrophys. J. 889, 163.
Pecora, F., Greco, A., Hu, Q., Servidio, S., Chasapis, A. G., and Matthaeus, W. H. (2019). Single-spacecraft identification of flux tubes and current sheets in the solar wind. ApJ 881, L11. doi:10.3847/2041-8213/ab32d9
Rycroft, M. J., Nicoll, K. A., Aplin, K. L., and Giles Harrison, R. (2012). Recent advances in global electric circuit coupling between the space environment and the troposphere. J. Atmos. Solar-Terrestrial Phys. 90-91, 198–211. doi:10.1016/j.jastp.2012.03.015
Schunk, R. W. (2007). Time-dependent simulations of the global polar wind. J. Atmos. Solar-Terrestrial Phys. 69, 2028–2047. doi:10.1016/j.jastp.2007.08.009
Shprits, Y. Y., Elkington, S. R., Meredith, N. P., and Subbotin, D. A. (2008a). Review of modeling of losses and sources of relativistic electrons in the outer radiation belt I: Radial transport. J. Atmos. Solar-Terrestrial Phys. 70, 1679–1693. doi:10.1016/j.jastp.2008.06.008
Shprits, Y. Y., Subbotin, D. A., Meredith, N. P., and Elkington, S. R. (2008b). Review of modeling of losses and sources of relativistic electrons in the outer radiation belt II: Local acceleration and loss. J. Atmos. Solar-Terrestrial Phys. 70, 1694–1713. doi:10.1016/j.jastp.2008.06.014
Sinnhuber, M., Nieder, H., and Wieters, N. (2012). Energetic particle precipitation and the chemistry of the mesosphere/lower thermosphere. Surv. Geophys. 33, 1281–1334. doi:10.1007/s10712-012-9201-3
Smith, C. W., and Vasquez, B. J. (2021). Driving and dissipation of solar-wind turbulence: What is the evidence. Front. Astron. Space Sci. 7, 611909. doi:10.3389/fspas.2020.611909
Smith, R. A., Goertz, C. K., and Grossman, W. (1986). Thermal catastrophe in the plasma sheet boundary layer. Geophys. Res. Lett. 13, 1380–1383. doi:10.1029/gl013i013p01380
Smith, Z. K., Dryer, M., and Steinolfson, R. S. (1985). A study of the formation, evolution, and decay of shocks in the heliosphere between 0.5 and 30.0 AU. J. Geophys. Res. 90, 217–220. doi:10.1029/ja090ia01p00217
Snyder, C. W., Neugebauer, M., and Rao, U. R. (1963). The solar wind velocity and its correlation with cosmic-ray variations and with solar and geomagnetic activity. J. Geophys. Res. 68, 6361–6370. doi:10.1029/jz068i024p06361
Spencer, E., Vadepu, S. K., Srinivas, P., Patra, S., and Horton, W. (2018). The dynamics of geomagnetic substorms with the WINDMI model. Earth Planets Space 70, 118. doi:10.1186/s40623-018-0882-9
Stepanova, M., and Valdivia, J. A. (2016). Contribution of Latin-American scientists to the study of the magnetosphere of the Earth. A review. Adv. Space Res. 58, 1968–1985. doi:10.1016/j.asr.2016.03.023
Stverak, S., Maksimovic, M., Travnicwk, P. M., Marsch, E., Fazakerley, A. N., and Scime, E. E. (2009). J. Geophys. Res. 114, A05104.
Thorne, R. M. (1974). A possible cause of dayside relativistic electron precipitation events. J. Atmos. Terrestrial Phys. 36, 635–645. doi:10.1016/0021-9169(74)90087-7
Thorne, R. M., Bortnik, J., Li, W., Chen, L. J., Ni, B. B., and Ma, Q. L. (2017). How whistler-mode waves and thermal plasma density control the global distribution of the diffuse aurora and the dynamical evolution of radiation belt electrons. Geophys. Monog. Ser. 222, 117–125. doi:10.15142/T38G6X
Thorne, R. M., Church, S. R., and Gorney, D. J. (1979). On the origin of plasmaspheric hiss: The importance of wave propagation and the plasmapause. J. Geophys. Res. 84, 5241–5247. doi:10.1029/ja084ia09p05241
Thorne, R. M. (1977). Energetic radiation belt electron precipitation: A natural depletion mechanism for stratospheric ozone. Science 195, 287–289. doi:10.1126/science.195.4275.287
Thorne, R. M., and Horne, R. B. (1994). Energy transfer between energetic ring current H+and O+by electromagnetic ion cyclotron waves. J. Geophys. Res. 99, 17275–17282. doi:10.1029/94ja01007
Thorne, R. M., and Horne, R. B. (1992). The contribution of ion-cyclotron waves to electron heating and SAR-arc excitation near the storm-time plasmapause. Geophys. Res. Lett. 19, 417–420. doi:10.1029/92gl00089
Thorne, R. M., and Kennel, C. F. (1971). Relativistic electron precipitation during magnetic storm main phase. J. Geophys. Res. 76, 4446–4453. doi:10.1029/ja076i019p04446
Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889
Thorne, R. M., Ni, B., Tao, X., Horne, R. B., and Meredith, N. P. (2010). Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 467, 943–946. doi:10.1038/nature09467
Thorne, R. M. (2010). Radiation belt dynamics: The importance of wave-particle interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010gl044990
Thorne, R. M., Smith, E. J., Burton, R. K., and Holzer, R. E. (1973). Plasmaspheric hiss. J. Geophys. Res. 78, 1581–1596. doi:10.1029/ja078i010p01581
Thorne, R. M., and Summers, D. (1991). Landau damping in space plasmas. Phys. Fluids B: Plasma Phys. 3, 2117–2123. doi:10.1063/1.859624
Thorne, R. M. (1980). The importance of energetic particle precipitation on the chemical composition of the middle atmosphere. Pageoph 118, 128–151. doi:10.1007/bf01586448
Thorne, R. M. (1968). Unducted whistler evidence for a secondary peak in the electron energy spectrum near 10 keV. J. Geophys. Res. 73, 4895–4904. doi:10.1029/ja073i015p04895
Tinsley, B. A. (2000). Influence of solar wind on the global electric circuit, and inferred effects on cloud microphysics, temperature, and dynamics in the troposphere. Space Sci. Rev. 94, 231–258. doi:10.1007/978-94-010-0888-4_22
Valdivia, J. A., Rogan, J., Muñoz, V., Gomberoff, L., Klimas, A., Vassiliadis, D., et al. (2005). The magnetosphere as a complex system. Adv. Space Res. 35, 961–971. doi:10.1016/j.asr.2005.03.144
Valdivia, J. A., Rogan, J., Muñoz, V., Toledo, B. A., and Stepanova, M. (2013). The magnetosphere as a complex system. Adv. Space Res. 51, 1934–1941. doi:10.1016/j.asr.2012.04.004
Varotsou, A., Boscher, D., Bourdarie, S., Horne, R. B., Glauert, S. A., and Meredith, N. P. (2005). Simulation of the outer radiation belt electrons near geosynchronous orbit including both radial diffusion and resonant interaction with whistler-mode chorus waves. Geophys. Res. Lett. 32, L19106. doi:10.1029/2005gl023282
Vasquez, B. J., and Hollweg, J. V. (1996). Formation of arc-shaped Alfvén waves and rotational discontinuities from oblique linearly polarized wave trains. J. Geophys. Res. 101, 13527–13540. doi:10.1029/96ja00612
Vassiliadis, D., Sharma, A. S., and Papadopoulos, K. (1993). An empirical model relating the auroral geomagnetic activity to the interplanetary magnetic field. Geophys. Res. Lett. 20, 1731–1734. doi:10.1029/93gl01351
Vassiliadis, D. (2006). Systems theory for geospace plasma dynamics. Rev. Geophys. 44, RG2002 1–39. doi:10.1029/2004rg000161
Viall, N. M., and Borovsky, J. E. (2020). Nine outstanding questions of solar wind physics. J. Geophys. Res. Space Phys. 125, e2018JA026005. doi:10.1029/2018JA026005
Wawrzaszek, A., Echim, M., and Bruno, R. (2019). Multifractal analysis of heliospheric magnetic field fluctuations observed by Ulysses. ApJ 876, 153. doi:10.3847/1538-4357/ab1750
Keywords: magnetosphere, solar wind, system science, plasma waves, plasma instabilities
Citation: Borovsky JE (2021) Magnetospheric Plasma Systems Science and Solar Wind Plasma Systems Science: The Plasma-Wave Interactions of Multiple Particle Populations. Front. Astron. Space Sci. 8:780321. doi: 10.3389/fspas.2021.780321
Received: 20 September 2021; Accepted: 19 October 2021;
Published: 03 November 2021.
Edited by:
Xochitl Blanco-Cano, National Autonomous University of Mexico, MexicoReviewed by:
Alexei V. Dmitriev, Lomonosov Moscow State University, RussiaArnaud Masson, European Space Astronomy Centre (ESAC), Spain
Copyright © 2021 Borovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=