Unusual Chemical Processes in Interstellar Chemistry: Past and Present

Introduction

The Interstellar Medium

The interstellar medium is exceedingly diverse (Tielens, 2005). Much of it is composed of so-called interstellar clouds of gas and dust, which range from rather wispy diffuse clouds to dense clouds that are impervious to background light and so can appear black against the sky. Temperatures range from 50—100 K in diffuse clouds down to 10 K or below in cold dense clouds. Cold regions in clouds with warmer regions are often called “cold cores.” Gas densities can be as low as 10 cm⁻³ in diffuse clouds to upwards of 10⁵ cm⁻³ in dense regions. The larger clouds can be very heterogeneous in both temperature and density.

Portions of dense interstellar clouds are also the sites of star and exoplanet formation, which occur via a long sequence of individual stages of differing physical conditions, mainly higher temperatures and densities, which depend strongly on whether low-mass stars such as our sun or high-mass stars are the final product (Draine, 2011). The production of low-mass stars arises from the collapse and warm-up of cold cores through regions known as “prestellar cores” followed by “protostellar cores,” a term for stars in the act of formation, during which gas and dust collapse inwards to form so-called “hot corinos” with temperatures exceeding 100 K. During this stage, early-stage disks are formed surrounding the protostar. As the disks form, the collapsing dust particles eventually collide with each other to form larger objects, such as comets, meteors, and terminating in exo-planets, while the disks become so-called planetary disks. So-called giant clouds can have thousands of stars already formed from protostars and probably equally many in the act of formation. The evolutionary stages of high-mass stars are somewhat different than the stages for low-mass stars. Here, the term “hot core” for example refers to hot objects that occur post-massive star formation and can be linked to ultra-compact HII regions.

In most interstellar sources, molecules can be found in the gas-phase; altogether more than 250 molecules have been detected in interstellar and circumstellar clouds (see Woon, 2021 for a detailed listing). The collection of molecules in sources of differing physical conditions are different; indeed the chemical composition can help to understand these physical conditions. The dominant molecule in virtually all sources is molecular hydrogen, which is not surprising because it is the most abundant element. Rather than listing all of the interstellar molecules observed to date, we have preferred to give the reader a sense of the different types of molecules detected in the interstellar medium. Groups of selected gaseous molecules such as “carbon-chains” and “complex organic molecules” are listed in rows in Table 1. The chosen molecules are well-known species. Also listed in this table are some molecules detected on and in ice mantles that surround dust particles in cold regions of clouds. The dust particles themselves consist either of carbonaceous or silicate materials and range in size from several Angstroms to over a micro-meter. Most gas-phase molecules in dense clouds are detected via their rotational spectra (Townes and Schawlow, 1955); most of these molecules are organic in nature. Some are very much like terrestrial organic species whereas others are very unusual by the standards of our planet. The larger terrestrial-like molecules are semi-saturated and are known as “Complex Organic Molecules”, or COMs for short, even though the criterion of complexity is applied at the rather low value of a minimum of six atoms (Herbst and van Dishoeck, 2009). The more unusual species are often referred to as “carbon chains” and are highly unsaturated linear or near-linear species. These carbon chains include radicals and ions, both positively and negatively charged. The most abundant species in granular ices is water, with other abundant species either carbonaceous in nature, such as carbon monoxide and dioxide, and other small species such as ammonia. Molecules found in granular icy mantles are detected via vibrational spectroscopy and range in size up to methanol, which is also found in the gas (Wilson et al., 1980). Vibrational spectroscopy can in general not be done easily from the ground, and space observatories such as the JWST, now planned for launch in December 2021, are needed.

TABLE 1

TABLE 1. Classes of gaseous and icy interstellar molecules.

Interstellar molecules are synthesized via a diverse collection of chemical processes that consist of well-known reactions and very unusual processes, an improved understanding of which has occurred because of their likely interstellar importance. These reactions are collected together in networks, such as KIDA (Kinetic Database for Astrochemistry; Wakelam et al., 2015; http://kida.astrophy.u-bordeaux.fr/) and UDFA (UMIST Database For Astrochemistry; Markwick, 2012; McElroy et al., 2013, http://udfa.ajmarkwick.net/) and used in large simulations with up to a hundred thousand chemical reactions to determine molecular abundances or synthetic spectra via solutions of kinetic equations and radiative transfer. Reactions on grain surfaces have been added to KIDA and the combined gas-grain network is known as Nautilus (Ruaud et al., 2016). Another gas-grain network, named MAGICKAL, has been built by Garrod (2013a) and, albeit complete, particularly emphasizes surface chemistry. In this review, some of the unusual gas-phase and granular processes will be discussed within a historical background. These reactions include those that can occur efficiently only in low density regions.

Gas Phase Processes

Radiative Association

Radiative association is a process in which two atoms or molecules collide to form a short-lived intermediate, which can be stabilized by emission of radiation. The process has rarely been seen in the laboratory (Gerlich and Horning, 1992; Luca et al., 2002), but is thought to be of importance in both diffuse and dense interstellar clouds. In the early days of astrochemistry, the gas-phase chemistry in diffuse clouds was of paramount importance, because some of these clouds, with gas densities of 10² cm⁻³ and temperatures of 50–100 K (Black and Dalgarno, 1977) are relatively close to the earth and could be studied by absorption in the visible and ultraviolet (Federman et al., 1980; Carruthers, 1970).

Radiative association of two atoms in diffuse clouds has been investigated theoretically. If we consider two atoms colliding, the most common mechanism allows the atoms to travel along an excited electronic state, while radiating to bound levels of the ground state. This process can be treated semiclassically or fully quantum mechanically (Giusti-Suzor et al., 1976). The formation of the diatomic molecule CH⁺ was originally thought to occur via the radiative association (Solomon and Klemperer, 1972; Giusti-Suzor et al., 1976).

${\text{C}}^{+}+\text{H}\to {\text{CH}}^{+}+h\nu (1)$

with a rate coefficient of approximately 10⁻¹⁷ cm³ s⁻¹, which corresponds to 1 in 10⁸ collisions. This process is not sufficiently rapid to produce the observed abundance of CH⁺. Once it was known that much of the hydrogen in diffuse clouds could be molecular in nature, however, the production of both CH and CH⁺ was predicted to occur via the precursor CH₂⁺ produced in the radiative association (Black and Dalgarno, 1973; Herbst et al., 1977):

${\text{C}}^{+}+{\text{H}}_2\to {\text{CH}}_2^{+}+h\nu ,(2)$

which occurs via several excited electronic states, and was calculated to be more rapid than reaction (1) by two to three orders of magnitude. The production of CH₂⁺ then leads to CH via dissociative recombination:

${\text{CH}}_2^{+}+e^{-}\to \text{CH}+\text{H}(3)$

although there is a competitive channel in which ${\text{CH}}_2^{+}$ reacts with H₂ to form CH₃⁺ + H. The formation of CH⁺ was thought to occur via photodissociation of the species CH₂⁺ and CH₃⁺. Although this mechanism produces a sufficient abundance of CH in diffuse clouds, the production of CH⁺ was once again insufficient to account for its abundance. A shock-wave mechanism which powers the endothermic reaction to form CH⁺ (Elitzur and Watson, 1978):

${\text{C}}^{+}+{\text{H}}_2\to {\text{CH}}^{+}+\text{H,}(4)$

is still under consideration. Calculated state-to-state rate constants involving the lowest two vibrational states of H₂ under the conditions of the Orion Bar photon-dominated region indicate a role for vibrational excitation to power Equation 4 (Zanchet et al., 2013). A more recent candidate is intermittent turbulence (Falgarone and Puget, 1995; Moseley et al., 2021).

By the mid 1970s, the chemistry of so-called dense interstellar clouds began to overtake the study of diffuse clouds due to the development of radio astronomical techniques and to the abundance of organic molecules starting with H₂CO (Snyder et al., 1969), which are abundant in these regions. With gas densities of at least 10⁴ cm⁻³, and temperatures as low as 10 K, these clouds provide a better environment for chemistry than diffuse clouds (Watson, 1972a; Watson, 1972b; Herbst and Klemperer, 1973). The original thinking was that the gas-phase chemistry is dominated by barrierless ion-neutral reactions with ions produced by cosmic ray bombardment. Among the ion-neutral processes, radiative association was considered in early models of dense cloud chemistry (Herbst and Klemperer, 1973). Unlike the simple approach to radiative association of diatomic species, the basic idea is that the multidimensional potential surface from reactants to products has an intermediate deep well, known as a complex, rather than the more common transition state barrier. The complex, in its ground electronic state, can relax via emission of excited vibrational states to stable levels of the ground state. Although complexes involving neutral species are less studied theoretically, they can be important for systems with two neutral radicals (Vuitton et al., 2012). Whether we are considering an ion-molecule or a neutral-neutral system, we can write the overall radiative association as

$\text{A}+\text{B}\rightleftarrows {\text{AB}}^{\ast }\to \text{AB};\text{C}+\text{D},(5)$

where A and B designate reactants, AB^* the intermediate complex, AB, the relaxed stable association product formed via emission from the complex, and C and D competitive reaction products. These products can form from the complex and so compete directly with complex emission or they can be formed from reactants and compete indirectly by division of the total rate coefficient.

Theoretical Methods

If the complex can be stabilized by emission of radiation with some degree of efficiency, radiative association can be an important process for the growth of molecules in the cold interstellar medium at densities far too low for collisional stabilization. In most instances, however, the stabilization by radiation is less efficient than the re-dissociation of the complex into reactants. The competition between dissociation into products and radiative stabilization of the complex depends strongly on whether the C + D products are endothermic. In the simplest treatment, which assumes the complex to be at steady-state, the rate coefficient for radiative association k_ra (cm³ s⁻¹) is given by the equation (Herbst, 1980a):

$k_{ra}=k_1{k}_r/\left\{k_{-1}+k_2+k_r\right\}(6)$

where k₁ (cm³ s⁻¹) is the rate coefficient for complex formation, k_-1 (s⁻¹) is the complex re-dissociation rate, k_r (s⁻¹) is the radiative stabilization rate, normally assumed to consist of single photon emission in the infrared, and k₂ (s⁻¹) is the rate at which the complex dissociates into new products, a process which often possesses a barrier. Indeed, if there is no barrier in the exit channel and the process is exothermic, the complex normally produces products rapidly, perhaps even more rapidly than re-dissociation, vitiating the radiative channel, and radiative association becomes too inefficient to be of importance. In a common case, there is no rapid process for complex destruction so that only redissociation and radiative stabilization compete, although the re-dissociation rate normally exceeds the radiative stabilization rate, k_r. With the assumption that polyatomic molecular vibrations can be treated as coupled harmonic oscillators, the rate of emission of an infra-red photon can be obtained as a linear function of overall vibrational energy in excess of the zero-point energy (Herbst, 1982) with values ranging from 10—10³ s⁻¹.

Under the condition that $k_{-1}>k_r$, the radiative association rate coefficient reduces to the much simpler equation:

$k_{ra}=\left(k_1/k_{-1}\right)k_r.(7)$

With the assumption that the ratio k₁/k_-1 can be treated via the principle of detailed balancing (Herbst, 1980a,b), the rate coefficient can be written in terms of canonical partition functions q, which are normalized sums over the populations of individual levels at a temperature T for the reactants and the complex (Herbst, 1980a,b):

$k_{ra}= \frac{q_{AB\ast }}{q_A{q}_B} k_r.(8)$

Solution of Equation 8 shows that a larger radiative association rate coefficient is associated with 1) a lower temperature, 2) a larger number of atoms in the complex, and 3) a deeper complex well. Looked at another way, the inverse temperature dependence stems from the longer period of time necessary for the complex vibrational motion to transfer sufficient energy to a mode, so that it leads to re-dissociation. In a temperature range when the rotational partition functions can be treated continuously and the vibrational partition functions discretely, the temperature dependence of the radiative association rate coefficient is given by the expression $k_{ra}\propto T^{-\left(ra+rb+1\right)/2}$ where r_a and r_b are the number of rotational degrees of freedom of the two reactants A and B. Thus, for two asymmetric tops, the inverse temperature dependence goes as T^–3.5. Equations 7 and 8 fail if the re-dissociation rate falls below the radiative stabilization rate of the complex $\left(k_{-1}<k_r\right)$, at which the radiative association rate is predicted to exceed the collisional rate of the two reactants, an unphysical result. If $k_{-1}$ is only slightly larger than $k_r$, use of Equation 6 in the absence of a competitive exothermic channel (k₂ = 0) leads to a much lower temperature dependence, especially at low temperatures.

The canonical expression in Equation 8 does not deal directly with the long-range attractive potential nor with detailed angular momentum considerations. Following Bates (1979a) and (1979b), Herbst (1980b) modified the canonical expression to include the orbital angular momentum L in a quasi-diatomic centrifugal barrier term built upon the long-range Langevin potential for ion-neutral collisions. The result is a modification of the canonical approach leading to a weaker temperature dependence.

A far more complex treatment, including all assorted angular momenta, was introduced by Klots (1976), and Chesnavich and Bowers (1977), and was later utilized by Herbst (1985a) and Tennis et al. (2021). This approach, known as the phase space approach, allows the use of different long-range potentials, including those applicable to neutral-neutral systems, and is microcanonical in nature. Moreover, it is able to treat non-equilibrium systems such as shocks, as well as systems in which radiative association competes with barriers in the exit channel of non-associative channels. An example occurs for the association of CH₃⁺ + NH₃ to form CH₃NH₃⁺ in competition with the barriered exit channel leading to H₄CN⁺ + H₂ (Herbst, 1985b).

With the phase space theory, the overall microcanonical rate coefficient k_ra for radiative association is given by the equation (Herbst, 1985a)

$k_{ra}\left(J_A,J_B,E_{coll}\to J,E\right)=\frac{k_1\left(J_A,J_B,E_{coll}\to J,E\right)k_r}{k_{-1}\left(J,E\right)+k_r+k_2},(9)$

where E is the total energy of the system, E_coll is the collision energy, J is the total angular momentum, and J_A and J_B are the angular momenta of the reactants. The rate coefficients k_i in Equation 9 designate the rates of the same processes as those in Equation 6. The value of k₁ is determined by the product of the relative velocity of the reactants and the phase space capture cross section, determined by either the long-range attractive potential relevant to ion-neutral or neutral-neutral collisions. The complex re-dissociation rate k_-1 is obtained from k₁ by microscopic reversibility (Klots, 1976). Roaming, a term designating motion between two different potentials, can also be included in the k₂ term in Equation 8 (Sivaramakrishnan et al., 2011; Tennis et al., 2021). Thermal or non-thermal rate coefficients of k_ra can be obtained by suitable integrations (Chesnavich and Bowers, 1977). A recent example of a calculated radiative association rate coefficient between the radicals CH₃ + CH₃O to form dimethyl ether using the phase space approach has been done by Tennis et al. (2021). With the inclusion of a competitive roaming channel in the calculations to form the exothermic products CH₄ + H₂CO, the radiative association rate coefficient at 10 K is approximately 3 × 10⁻¹¹ cm³ s⁻¹, or 0.1 of the collisional value. The rate coefficient is possibly large enough to account for the abundance of dimethyl ether in the low temperature source TMC-1 (Balucani et al., 2015).

Although phase space theories (and simpler approaches) can be used to study neutral-neutral radiative association, this is not as common as theories based on the re-dissociation of the complex. In a major paper, Ryzhov et al. (1996) showed that both the RRKM approach and the Variational transition state theoretical approach (VTST) can be utilized to obtain radiative association rate coefficients. Although this paper discussed these approaches with regard to an ion-neutral system, later papers have reported studies of neutral-neutral association, both radiative and collisional. An important paper in this field involves the atmosphere of Titan, the moon of Saturn with a large number of organic species (Vuitton et al., 2012). The theoretical method used in this paper involves transition state approaches in which the barrier is defined from the bottom of the complex well. Detailed balance converts complex dissociation into complex stabilization. The potential can be defined in much more detail than in the phase space approaches, which utilize long-range capture potentials only. Since there is no experimental information to the best of our knowledge for any neutral-neutral radiative association, comparison can only be made with other theoretical treatments. Let us compare the phase space/canonical and transition state theories for similar reactions. The radical-radical reaction

${\text{CH}}_3+{\text{CH}}_3\to {\text{C}}_2{\text{H}}_6+h\upsilon (10)$

has been studied from 50 to 300 K by Vuitton et al. (2012) whereas Tennis et al. (2021) have studied the similar reaction

${\text{CH}}_3+{\text{CH}}_3\text{O}\to {\text{C}}_2{\text{H}}_6\text{O}+h\upsilon (11)$

using the phase space and canonical theories in the range 10—100 K. At 100 K, the methyl-methyl reaction is calculated to have a rate coefficient of 1.3 × 10⁻¹² cm³ s⁻¹, whereas the methyl-methoxy reaction has a calculated rate coefficient of 3.2 × 10⁻¹² cm³ s⁻¹ with the phase space theory and, for completeness, a value of 3.3 × 10⁻¹¹ cm³ s⁻¹ with the canonical theory. The binding energies of the complex in the two reactions are similar. Note that reaction (11) has one more heavy atom so, according to Vuitton et al. should have roughly the larger rate coefficient by 1-2 orders of magnitude if the complex species have similar binding energies. The temperature dependence of CH₃ + CH₃ goes as T^−3.23 where that of CH₃ + CH₃O goes as roughly T⁻³, at temperatures well above 100 K, but shows a lesser temperature dependence as the association approaches the limiting collisional value.

Radiative Association and Laboratory Experiments

Radiative association has not been studied extensively in the laboratory because it only occurs at low densities; at higher densities collisional stabilization of the complex dominates, a process often known as three-body or ternary association. At even higher densities, saturation sets in. Ion-molecule collisions leading to one type of association or another have been studied in the laboratory by a variety of techniques. As listed roughly in order of decreasing gas density, the techniques include the SIFT (Selected Ion flow drift-tube; Smith et al., 1990) and CRESU (reaction kinetics in uniform supersonic flow; Marquette et al., 1985) techniques, which operate at higher densities, and the ion-cyclotron resonance technique (Huntress and Beauchamp, 1969) as well as a variety of ion traps such as the Penning trap which can operate at low enough densities to reach a region where radiative association can be studied (Barlow et al., 1984). The CRESU technique can be used for both ion-neutral and neutral-neutral collisions and operates down to temperatures of near 10 K (Cooke and Sims, 2019).

For a wide range of densities of the bath gas M, the rate law for collisional stabilization of the complex is third-order (ternary) and increases linearly with the bath gas density:

$\frac{d\left[AB\right]}{dt}=k_{3b}\left[A\right]\left[B\right]\left[M\right],(12)$

where

$k_{3b}= k_1{k}_2/k_{-1}.(13)$

Here k₂ is the collisional stabilization rate coefficient, which is estimated to be 10⁻¹⁰ cm³ s⁻¹ for neutral complexes and 10⁻⁹ cm³ s⁻¹ for ionic complexes. At still higher densities, the rate law reaches saturation, where all collisions produce stable complexes. The radiative stabilization of the complex is independent of [M] at low densities and the rate of radiative association can be written as

$\frac{d\left[AB\right]}{dt}=k_{ra}\left[A\right]\left[B\right](14)$

where

$k_{ra}= k_1{k}_r/k_{-1},(15)$

as already discussed in Section 2.2. The two derivatives are equal when $k_2\left[M\right]= k_r$. Assuming the emission rate to be ≈ 10² s⁻¹ (Herbst, 1982), this occurs when the bath gas [M] = 10¹² cm⁻³ for neutral reactants and an order of magnitude less for ionic-neutral reactants if the collision rate coefficient k₂ is assumed to be 10⁻¹⁰ cm³ s⁻¹ for neutral-neutral collisions and 10⁻⁹ cm³ for ion-neutral collisions.

Although ternary processes are not expected to occur in the interstellar medium, they can be used indirectly in experiments to measure radiative association. If an experiment starts at higher densities and the density is gradually lowered until the two association mechanisms are equal, one should expect to see a region in which extrapolation to zero density shows a feature that gradually becomes horizontal when radiative association is dominant. Figure 1 illustrates the experimental dependence of the rate of association between CH₃⁺ + H₂O in a bath gas of Helium with a 22-pole ion trap at an effective temperature of 50 ± 30 K (Luca et al., 2002). The figure shows that by a density of 10¹² cm⁻³, the dependence loses its linear relationship with He and tends to flatten out, eventually reaching an extrapolated value for the radiative association rate coefficient at a density of 10¹¹ cm⁻³ of approximately 5 × 10⁻¹³ cm³ s⁻¹, or (more accurately) an upper limit of 2 × 10⁻¹² cm³ s⁻¹. This value at 50 K is lower than the calculated canonical value of 9 × 10⁻¹² cm³ s⁻¹ and is closer to the centrifugal barrier value of 2 × 10⁻¹² cm³ s⁻¹ (Herbst, 1980a; Herbst, 1980b). It should be noted that the extrapolation to low densities is dependent to some extent on the bath gas used, so that a more detailed experiment would involve the use of different bath gases. Another ion trap measurement was undertaken by Barlow et al. (1984), who used a Penning trap to study radiative association directly at low density. For the system CH₃⁺ + H₂ at a temperature of 13 K, the rate coefficient was measured to be 1.1 × 10⁻¹³ cm³ s⁻¹. It is likely that the Penning trap is the more reliable result, but the value at 13 K is well below the canonical theoretical value at 10 K of 6 × 10⁻¹⁰ cm³ s⁻¹ and the centrifugal barrier result at the same temperature of 7 × 10⁻¹¹ cm³ s⁻¹. (Herbst, 1980a,b).

FIGURE 1

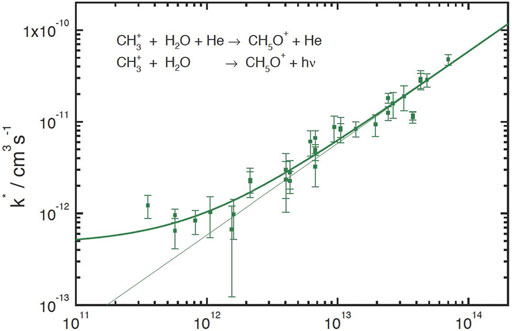
FIGURE 1. Dependence of the effective rate coefficient for CH₃⁺ + H₂O association as a function of the He number density. The ion trap was operated at 20 K. The average H₂O density was 8 × 10⁷ cm⁻³. The measured values have been approximated by the function k* = k_3b [He] + k_ra which shows curvature above the ternary regime and leads to an approximate value for the radiative association rate coefficient of k_ra = 5 × 10⁻¹³ cm³ s⁻¹. The thin linear line simulates the pure ternary regime. Permission requested to reproduce Figure 3 of Luca et al. (2002) as printed originally by MATFYZPRESS (Sokolovská 49/83, 186 00 Praha 8-Karlín, Czechia) in the WDS’02 Proceedings of Contributed Papers, PART II, 294–300, 2002.

A more approximate use of ternary (three-body) association in the determination of radiative association rates is to convert the measured ternary rate into the unmeasured radiative association. From Eqs 13 and 15, one can see that the removal of k₂ and its replacement by k_r converts a ternary rate coefficient into a radiative rate coefficient. This approach is most accurate if the ternary association is not in or near the collisionally saturated regime where complex formation occurs on every collision and Equation 9 no longer holds. Although the SIFT apparatus is often used for the conversion, its operating density at roughly 10¹⁶ cm⁻³ (Adams and Smith, 1978; Smith and Adams, 1978) can put it close to the saturation limit at very low temperatures (Schiff and Bohme 1979). A detailed study of this approach with an emphasis on the CRESU apparatus has been reported by Herbst (2022).

A number of additional complications can confuse the issue when there is more than one product possibly undergoing radiative association. For example, McEwan et al. (1980), with an ion-cyclotron apparatus, studied the association reactions

${\text{CH}}_3^{+}+\text{HCN}\to {\text{CH}}_3{\text{NCH}}^{+};{\text{CH}}_3{\text{CNH}}^{+}(16)$

at room temperature and found, over a large density range of 3.5 × 10¹⁰ cm⁻³—7.0 × 10¹² cm⁻³, an observed rate coefficient of 2 × 10⁻¹⁰ cm⁻³, independent of density, but less than an experimental result of 2 × 10⁻⁹ cm⁻³ at the much higher density of 10¹⁶ cm⁻³, which can be assumed to be the saturated collisional rate. A subsequent experimental paper by Anicich et al. (1995) confirms that radiative association does indeed occur. But theoretical calculations by Defrees et al. (1985) indicate that the radiative association can produce both CH₃CNH⁺ and CH₃NCH⁺ and that the use of a master equation calculation leads to an approximate abundance ratio for CH₃NC/CH₃CN between 0.1 and 0.4.

Role in Molecular Synthesis in Cold Dense Clouds

In addition to the well-studied association reaction between CH₃⁺ and H₂ (Gerlich and Horning, 1992), Smith (1992), reviewing the approach of Smith and Adams (1978) which used conversion from ternary association rates, concluded that association reactions between CH₃⁺ and a variety of neutral molecules (e.g. CO, CH₃OH, H₂CO, NH₃, H₂O, HCN, CH₃CN, and HC₃N) can occur as radiative association in the low densities of interstellar clouds. The product molecular ions produced react subsequently via dissociative recombination with electrons to form neutral species including some now regarded as COMs, such as CH₂CO, CH₃OH, C₂H₅OH, CH₃OCH₃, CH₃CHO, CH₃NH₂, CH₃CN, CH₃NC, C₂H₅CN, and CH₃C₃N. (See Figure 2 as shown in Smith, 1992). In addition to these processes, Huntress and Mitchell (1979) proposed analogous association reactions involving the ions CH₃O⁺, CH₃CO⁺, CH₅⁺, HCO⁺, NO⁺, and H₂CN⁺ leading to the synthesis of a large number of species up to eight atoms in size.

FIGURE 2

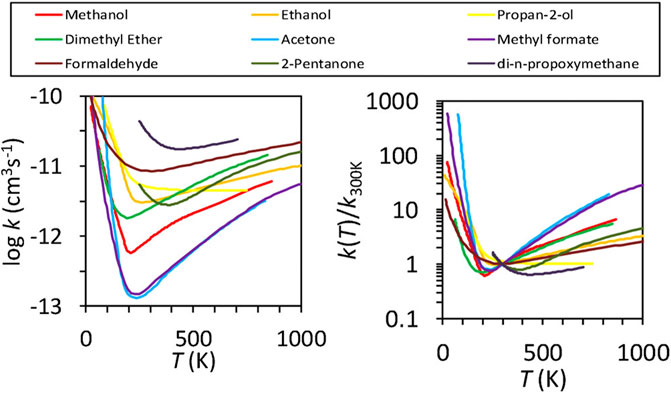
FIGURE 2. Rate coefficients, k (left panel), and the ratio, k(T)/k (300 K) (right panel), as functions of temperature for reactions of OH with assorted organic molecules. The lines, which show the “U-shaped” dependence of rate on temperature, are interpolated fits to literature data. Permission requested to reproduce this figure, which originally appeared as Figure 3 in Heard (2018).

In retrospect, although some of these suggestions for COM formation have some merit pending more detailed theory or experiment, others may be optimistic because of a number of problems. First, much of the existing information on radiative association rates has been obtained by conversion of ternary collisional processes measured in the laboratory. As discussed above, this conversion ideally requires a collisional association process far removed from saturation, or extrapolation of ternary systems to low densities to reach the radiative limit (Gerlich and Horning, 1992; Luca et al., 2002). In the absence of evidence to the contrary, the radiative association reaction coefficients can be obtained from ternary measurements at higher temperatures where it its more likely that the three-body region is reached. The proper temperature dependence is then needed to obtain radiative association rates at lower temperatures. A large number of reported radiative association rate coefficients were tabulated by Smith and Adams (1978), using this approach. The value obtained for CH₃⁺ + H₂O at 20 and 50 K is considerably higher than the value obtained by Luca et al. (2002). Conversion using an ion-cyclotron apparatus, which can operate at low densities, is likely to avoid the high-density problem, although reaching low temperatures is also a problem. The complex case of CRESU studies has been discussed by Herbst (2022).

The second problem concerns the products of dissociative recombination reactions. Some of the rate coefficients for these processes had been known during the early years of astrochemistry and typically range from 10⁻⁶—10⁻⁷ cm³ s⁻¹ at room temperature with a temperature dependence of T^−1/2. The neutral products and their branching fractions, however, were almost completely undetermined, to the best of our knowledge. Much of the early literature on chemical simulations of dense clouds contained the guess that the branching fractions were dominated by a product channel with one hydrogen atom and a heavy species, or by a heavy molecule with two hydrogen atoms removed. The situation regarding product branching fractions gradually improved with experiments using both bench top experiments (Herd et al., 1990) and large-scale experiments with magnetic storage rings (Zajfman et al., 2003; Mitchell et al., 2005; Geppert and Larsson, 2013). The net result is that branching fractions in which atomic H and a larger species are formed most often constitute a minor fraction of the products; e.g., 5–10%, not the 50–100% as assumed earlier. The case of NH₄⁺ is an exception. Here the NH₃ + H channel has a measured branching fraction of 0.8—0.9, which can be partially explained by dynamic studies, which indicate that the dissociation occurs via the ground neutral potential (Öjekull et al., 2004). This process coupled with the efficient production of NH₄⁺ (see below) allows the gas-phase production of ammonia to proceed efficiently at low temperatures.

If we consider the formation of methanol via the radiation association between CH₃⁺ and H₂O to form CH₃OH₂⁺ followed by the dissociative recombination to form methanol:

${\text{CH}}_3{\text{OH}}_2^{+}+\text{e}\to {\text{CH}}_3\text{OH}+\text{H,}(17)$

and compare optimistic rates (Adams and Smith, 1978; Smith and Adams, 1978) with the best current estimates (Luca et al., 2002; Geppert et al., 2006), the overall rate using current estimates is the lower by 3-4 orders of magnitude. The net result is that the current explanation to explain the abundance of methanol probably does not involve the radiative association and dissociative recombination steps, but involves a totally different and much more rapid process: successive addition of atomic H to CO on grains followed by desorption into the gas:

$\text{CO}-\text{s}\to \text{HCO}-\text{s}\to {\text{H}}_2\text{CO}-\text{s}\to {\text{H}}_3\text{CO}\left({\text{H}}_2\text{COH}\right)-\text{s}\to {\text{CH}}_3\text{OH}\uparrow (18)$

where the s refers to surface species (Watanabe and Kouchi, 2002). Moreover, even if the radiative associative processes proposed by Smith and Adams (1978) and Huntress and Mitchell (1979) and reviewed by Smith (1992) are accurate, there is no guarantee that they are more important than other gas-phase and grain-surface mechanisms.

In addition to radiative association by ion-molecule systems, radiative association via two neutral species, typically radicals, has been suggested as a possible source of complex organic molecules. In particular, the radiative association between the radicals CH₃ and CH₃O to form CH₃OCH₃ (dimethyl ether) has been suggested as an important synthetic process in cold cores (Balucani et al., 2015). A phase space calculation at 10 K leads to a rate coefficient of 3 × 10⁻¹¹ cm³ s⁻¹, which is close to the collisional limit (Tennis et al., 2021). A number of other radical-radical association reactions are probably important in the upper atmosphere of Titan (Vuitton et al., 2012).

Reactions With a U-Shaped Rate Dependence on Temperature

As in radiative association, there are other bimolecular reactions in which both a collision complex and a barrier along a potential exist. The most interesting of these reactions are those in which the rate coefficient has a U-shaped temperature dependence in which the rate coefficient has a minimum at intermediate temperatures and then increases as the temperature increases and decreases from the minimum. One of the earliest studies of such a reaction concerns NH₃⁺ and H₂ (Herbst et al., 1991):

${\text{NH}}_3^{+}+{\text{H}}_2\to {\text{NH}}_4^{+}+\text{H,}(19)$

which has been studied both experimentally and theoretically. It was thought initially that this reaction could lead to the formation of ammonia in cold interstellar clouds (10 K) with the ammonia formed by dissociative recombination of NH₄⁺. Early experimental studies, however, showed the reaction to be slow at room temperature with a rate coefficient of 5 × 10⁻¹³ cm³ s⁻¹, and to increase in rate at higher temperatures with a fitted barrier of 2.1 kcal mol⁻¹ (Smith and Adams, 1981). Such an activation energy would imply an exceedingly slow rate at low temperatures such as 10 K, leading to the need for another mechanism to produce ammonia in the cold interstellar medium. Smith and Adams (1981) then found surprisingly that although the rate coefficient decreased at temperatures down to about 100 K, it then leveled off at 80—100 K. An ion-trap study by Luine and Dunn (1985) and a drift-tube study by Böhringer (1985) found that the rate coefficient actually begins to increase at still lower temperatures, reaching approx.10⁻¹² cm³ s⁻¹ at 10 K, a rate coefficient large enough to reinstate reaction (19) followed by dissociative recombination as a prime candidate to produce ammonia in the cold ISM. The initial suggestion for a mechanism to explain the overall temperature dependence of NH₃⁺ + H₂ was a complex in the entrance channel followed by tunneling under a subsequent transition state barrier. (See Figures 1, 2 of Herbst et al., 1991). Quantum chemical and phase space calculations including tunneling led to satisfactory agreement with the experimental results (Herbst et al., 1991). An experimental study of an analogous reaction between C₂H₂⁺ and H₂ at temperatures near 2 K also invoked a tunneling mechanism to explain the inverse temperature dependence (Hawley and Smith, 1989).

More recently, CRESU experiments have been employed to study a number of neutral-neutral reactions with the same U-shaped temperature dependence. The initial investigation was done by Shannon et al. (2013) on the system OH + CH₃OH:

$\text{OH}+{\text{CH}}_3\text{OH}\to {\text{CH}}_3\text{O}+{\text{H}}_2\text{O}(20)$

and showed a strong inverse temperature dependence at temperatures below 70 K, with the result at 63 K two orders of magnitude higher than at 200 K. See also the subsequent measurements of Ocaña et al. (2019) at temperatures from 177.5 K down to 11.7 K. Note that at lower temperatures, the dominant product is methoxy (CH₃O) rather than the lower energy form hydroxymethane (H₂COH), although transition states for both processes exist. Shannon et al. (2013) suggested the same mechanism mentioned above by Herbst et al. (1991) in which the formation of a hydrogen-bonded complex is followed by tunneling under a barrier. To support this mechanism, they utilized the MESMER code (Glowacki et al., 2012), which handles multiple potential wells, to reproduce their experimental results. A specific theoretical approach is discussed by Cooke and Sims (2019) for reactions involving CN. Here the system first enters a so-called loose transition followed by a tight transition state, which can be still lower in energy than the reactants. The results of a two-transition state model are shown in their Figure 3. The dominant transition state switches from loose at low temperatures to tight at higher temperatures.

FIGURE 3

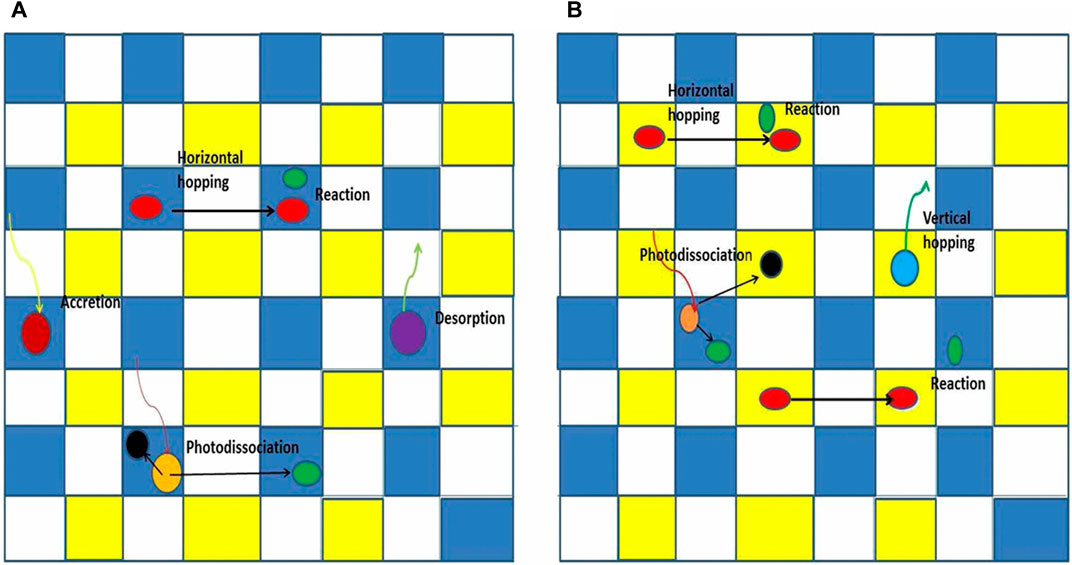
FIGURE 3. Drawings of stochastic motions in a rectangular grid of sites in two situations. Major stochastic processes on grain surfaces in the form of a rectangular grid of sites. Blue sites are normal sites, occupied by normal species, while yellow sites are interstitial sites, normally unoccupied or occupied by weakly bound interstitial species, and white sites cannot be occupied. (Panel A) shows the topmost layer, while (Panel B) shows an inner (bulk) layer. Figure reproduced from Figure 1 of Chang and Herbst. (2014).

Much experimental and theoretical work followed the initial work of Shannon et al. (2013). Heard (2018) plotted a large number of reactions studied with the CRESU technique involving the radical OH and a variety of organic species that have a U-shaped rate dependence on temperature. Figure 2 reproduces the plot: one panel shows the rate coefficient vs temperature, the other the rate coefficient divided by the 300 K value vs temperature. Both show the characteristic U-shape with an increase in rate down to temperatures near 10 K. One point of contention is whether or not the process is binary or tertiary, given the high density of the CRESU experiments. Low temperature results on OH + CH₃OH show the results to be independent of total density, hence binary, but there are theoretical (Gao et al., 2018) and experimental results to the contrary. For example, Ocaña et al. (2019) showed the process to show some pressure dependence at 120–150 K, whereas no pressure dependence was found at temperatures below 100 K. A number of other theoretical treatments, including the quasi-classical trajectory approach and the ring polymer approach have been discussed by Canosa (2019). From the point of view of astrochemistry, if the OH + CH₃OH reaction is indeed rapid and binary at 10 K, it is clearly important in the formation of CH₃O (Acharyya et al., 2015; Balucani et al., 2015). The methoxy radical can then undergo radiative association with the methyl radical (CH₃) to form dimethyl ether (Balucani et al., 2015).

Granular Processes

Reactions on interstellar grains play an important role in interstellar chemistry, especially for low temperature regions, where dust particles are covered by a thick layer of ices dominated by water, CO, and CO₂. Perhaps the most important process, however, is the formation of molecular hydrogen from two hydrogen atoms, which can even occur in diffuse clouds. A detailed review of this process has recently appeared (Wakelam et al., 2017). Hydrogen atoms are also important in the formation of surface methanol from carbon monoxide, where four reactions are needed, as shown in Equation 18. Methanol remains the most complex molecule detected on grain surfaces, although theoretical calculations show that molecules as complex as glycine can also be formed on granular surfaces (Garrod, 2013a).

Direct experiments on surface reactions (Minissale et al., 2013; He et al., 2015), and on related processes such as non-thermal reactive desorption (Minissale et al., 2016), photodesorption (Fayolle et al., 2011), radiolysis (Tomosada et al., 2012), and photodissociation followed by reaction (Dupuy et al., 2021) have also been undertaken. Experimental tests of reaction mechanisms—diffusive (Langmuir-Hinshelwood; Katz et al., 1999) and Eley-Rideal (Yuan et al., 2014)—have also been performed, although the latter occurs rarely. Measurements on diffusive surface reactions can often be fit by models of diffusion with important parameters being two types of barriers—those due to diffusion and those due to chemical activation (Herbst and Millar, 2008). Simple models for diffusion are often used in place of more complex analyses of reactions when inserted into chemical simulations. Unlike the case of gas-phase reactions though, the connection between laboratory experiments and processes in the low-density interstellar medium is a complex one, and necessitates a larger amount of theoretical discussion.

For many years, the chemistry occurring on ice mantles surrounding interstellar grains of carbon or silicates has been treated by coupled rate equations which treat reactions via random diffusive motion of weakly bound adsorbates, a process known as the Langmuir-Hinshelwood mechanism (Hasegawa, 1993). There are two main problems with this approach, although both can be ameliorated if not totally cured. The first problem, historically, has to do with the small number of reactive species that can be available for reactions on a single grain, which leads to the need for discrete treatments with uncertainties (Biham et al., 2001; Green et al., 2001). This need can be treated by a variety of stochastic methods, or, less rigorously, by a modification of the diffusive rate equations. The second, which is much less historical, has to do with the rate of diffusion at low temperatures, which can in some instances be too slow to explain the synthesis of large molecules. The solution here is to find more rapid processes, which typically involve three bodies and are at least partially non-diffusive in nature (Jin and Garrod, 2020).

Rate Equations vs Stochastic Treatments

Before we discuss stochastic treatments of the chemistry occurring on interstellar dust particles, we need to review the more standard rate equations. Rate equations in standard chemical treatments normally contain the assumption that large numbers of species are involved so that chemical concentrations can be treated as averages. This assumption is normally so common that chemists don’t even have to worry about the possibility that the assumption need not hold in all instances. Although the rate equations for gas-phase processes in the interstellar medium can use this standard form, the equations for chemistry on dust particles are more complex (Hasegawa, 1993). Here the simplest approach is to compute the probability that a moving particle A, normally assumed to be weakly bound or “physisorbed” to the grain or to a lower monolayer of the ice mantle, will hop over a potential or tunnel through it and react according to the probability that a second particle B is available for reaction at the adjacent site. The probability that this adjacent site contains a reactive molecule is simply the fraction of granular minimum energy sites occupied by B. The first-order (s⁻¹) hopping rate for a species A is given by the equation:

$k_{hop}=\nu \exp \left(-\frac{E_b}{T}\right)(21)$

where ν is the “attempt” frequency and E_b is the diffusive energy barrier, which is normally assumed to be a fraction of the desorption energy. The term “attempt frequency” stands for the pre-exponential term when it is in frequency units. For physisorbed species, it is typically 1-3 x 10¹² s⁻¹. The tunneling rate, typically through a rectangular barrier with a width of a = 0.1–0.2 nm, is given by the expression

$k_{tun}=\nu \exp \left[-2\left(\frac{a}{\hslash }\right)\sqrt{2\mu E_b}\right],(22)$

where μ is the reduced mass of A and B, although more realistic potentials such as the Eckart potential have been utilized. The overall rate of diffusive reaction occurring via hopping to an adjacent site in which A and B react to form AB is given by the equation

$\frac{d\left[AB\right]}{dt}=-\left(\frac{d\left[A\right]}{dt}+\frac{d\left[B\right]}{dt}\right)=-\left(k_{\text{hop},\text{A}}+k_{\text{hop},\text{B}}\right)\left[\text{A}\right]\left[\text{B}\right]/N,(23)$

where [A] and [B] are defined by the number of sites they occupy while N is the number of sites on the monolayer on which A and B diffuse, which is typically 10⁶ for a grain of 0.1 μ. The formula can be extended to inner monolayers of the mantle. This approach does not account for long-range motion in between collisions (Willis and Garrod, 2017).

If species A and B react without a chemical activation barrier, the probability of a reaction between the two species is 100% if located in the same site. If, on the other hand, there is a chemical activation energy barrier E_A, the rate of reaction is reduced. While tunneling is often assumed to occur for chemical reactions, it is often ignored for diffusive barriers. There are two ways to account for activation energy. In the simpler of the two, one multiplies the right-hand side of Equation 23 with a Boltzmann term of the type κ = exp (−E_A/T) or an equivalent form for tunneling with E_A replacing E_b in Equation 22. The second and more accurate method, known as the competitive approach, defines κ in terms of the competition between the diffusive barrier and the activation energy barrier. Assume that the activation energy is much smaller than the diffusive barrier. Then the species A and B will have many chances to react before they move off to other sites. On the other hand, if the activation energy is much larger than the diffusive barrier, the A and B species will be much more likely to move on rather than react. If we assume that tunneling under the activation energy barrier dominates diffusive hopping, the formula for κ is given by (Herbst and Millar, 2008):

$\kappa =\frac{k_{tun}}{k_{tun}+ k_{hop,A }+k_{hop,B}}.(24)$

If the activation tunneling exceeds the diffusive hopping, κ approaches unity, so that the activation energy is essentially zero.

Although the earliest gas-grain models of interstellar chemistry assumed that diffusion occurred throughout the ice mantle, an approach known as a two-phase model, it is now more common to utilize a three-phase model, where the three phases refer to the gas, the surface of the ice mantle, and the bulk mantle ice. It is typically assumed that diffusion is slower in the bulk (Garrod, 2013a; Ruaud et al., 2015, Ruaud et al., 2016). Three-phase gas-grain models (e.g., Nautilus and Magickal) have been reasonably successful in simulating the chemistry of cold dense cores, hot cores, protoplanetary disks, and photon-dominated regions.

Stochastic Approaches

But suppose that we deal with small closed systems, such as the surfaces of tiny dust particles, in which there may be small numbers of reactive species, and suppose there are many such dust particles. One could take the standard volume average used in rate equations and get a totally wrong answer. As an extreme example, assume that on each dust grain there exists one hydrogen atom and we are interested in the rate of the formation of molecular hydrogen. The rate approach would ignore on which grains the hydrogen atoms exist, and come up with a non-zero rate of formation of H₂. But it is obvious that in reality the answer would be that zero hydrogen molecules are formed. Of course, a more common situation might be that only a few hydrogen atoms exist per grain, so that the rate of formation of H₂ over a large number of grains would be non-zero, but the uncertainties in these small numbers per grain would be quite large. So, a more accurate treatment under these conditions would include discrete numbers of species per grain with large fluctuations. Such techniques include the master equation approach, in which differential equations involving probabilities are used instead of normal rate equations. Each differential equation consists of the relationship between the time derivative of the probability that a specific discrete number of each species, say three atoms of species A, and terms involving the incoming flux of species from the gas, the desorption rate of molecules from the surface, and the recombination on the surface, all involving the probability of gain or loss of three atoms of species A.

Let us take the simple system of atomic and molecular hydrogen, as done by Biham et al. (2001), and consider the time dependence of the probability of zero hydrogen atoms P_H(0) on a grain. The appropriate differential equation is given by:

$\frac{d{P}_H\left(0\right)}{dt}=-F_H{P}_H\left(0\right)+W_H{P}_H\left(1\right)+2\times 1\times A_H{P}_H\left(2\right).(25)$

Here the first term on the right concerns incoming flux (which does not occur), the second term consists of desorption, in which one atom on a grain desorbs and increases the probability that no atoms remain, while the third term increases the probability that no atoms remain by the recombination of two hydrogen atoms on a grain. The master equation consists of all of the differential equations involving the time-dependent probability of discrete numbers of H atoms and H₂ molecules. In principle, there is no limit to the number of equations, but if only one monolayer is considered the limit can be obtained from the number of adsorption sites. Assuming that the number of species of H or H₂ eventually decreases, cut-off can occur when the probability of a given number becomes arbitrarily small. From the individual probabilities, an expectation value can be obtained as well as the average of the squared probabilities, leading to a standard deviation of the concentrations of H and H₂. The results are normally tabulated in terms of a recombination efficiency, which is equal to the flux of desorbing H₂ per adsorbed H atoms. For large grains, the standard rate treatment and the master equation treatment get the same efficiency. For smaller grains, however, the standard rate approach and the master equation approach differ; the smaller the grain, the larger the difference. In particular, recombination efficiency of the standard rate approach stays constant at a given value while the master equation efficiency decreases beyond a certain size grain. The drop occurs because the average number of H atoms approaches a number smaller than 2, confirming that for small grains, there is insufficient atomic hydrogen to produce H₂.

Biham et al. (2001) also developed a somewhat more complex system, which involves both oxygen and hydrogen atoms and the molecules formed from them—H₂, OH, O₂, and H₂O− as had been studied by Caselli et al. (1998) in a study of how to improve rate equations. They also showed that to a good approximation one can use rate equations for some species and the master equation for the others. This hybrid approach is useful when extending the simulations to larger gas-grain systems (Stantcheva et al., 2002).

In addition to Biham et al. (2001), early master equation stochastic treatments include those of Charnley (2001), and Green et al. (2001). Green et al. (2001) used a similar master equation technique to study the simple system of H and H₂, as had Biham et al. (2001), but solved the system exactly rather than numerically. They also studied the hydrogen-oxygen system of Caselli et al. (1998) as well as a more complex system of these authors involving the atoms H, N, and O forming the additional molecules NH, NH₂, NH₃, N₂, and NO.

Charnley (2001) used a system of reactions involving the adsorption of H, O, CO and exothermic reactions. He calculated the surface abundances of CO, CO₂, O₂, and H₂O as a function of time. Stantcheva et al. (2002) used a somewhat larger system, which followed the reactions and products starting with H, O, and CO species in the gas, including ten reactions to produce H₂, OH, H₂O, HCO, H₂CO, H₃CO, CH₃OH, O₂ and CO₂. These surface species were divided into major and minor ones. The purpose of the division is to restrict the master equation to minor species on the surface, so simpler and fast normal rate equations can be used for major species on the surface and all species in the gas. The master equation of Stantcheva et al. (2002) included a five-fold joint probability $\frac{dP}{dt}\left(i_1,i_2,i_3,i_4,i_5\right)$ for minor species (H, O, OH HCO, H₃CO) on the surface. In a subsequent paper, Stantcheva and Herbst. (2004) reported the results of a gas-grain model, in which rate equations were used for the gas chemistry and a master equation for the surface chemistry.

Master equation solutions can be mimicked by an assortment of Monte Carlo techniques, in which random numbers are utilized to follow the motions of species. Depending upon the degree of detail, Monte Carlo calculations can be divided into macroscopic and microscopic approaches, the latter determining the position of all atoms in an ensemble such as a dust particle, whether on lattices or off them. Although interstellar clouds are composed of both gas and dust particles, the problems discussed up to now clearly involve mainly the dust chemistry.

The advantage of the master equation approach over the Monte Carlo approach is that the differential equations for the surface species—master equation or rate equation—and the gas-phase species can be solved simultaneously. When a Monte Carlo approach is utilized for the surface, rate equations cannot be used for the gas-phase species because the clocks for rate equations and for random number generation are different. One can use a macroscopic Monte Carlo approach for the gas-phase chemistry, in which the coordinates of individual molecules are not followed, while a microscopic Monte Carlo approach can be used for the more detailed trajectories of the atoms and molecules on and in the ice mantle. Although this hybrid Monte Carlo approach may be slower than the master equation approach, it is less difficult to set up, especially when dealing with large numbers of equations. The Monte Carlo procedure has two advantages over the master equation approach: it can be used for inhomogeneous surfaces, and it treats random walk correctly.

There are a number of different Monte Carlo techniques depending upon the problem to be solved.

An early approach was used by Tielens and Hagen (1982). Another approach—a purely microscopic system - has been used to study molecular hydrogen formation on various regular and irregular surfaces (Chang et al., 2005; Iqbal et al., 2012). Here we report studies that use a technique known sometimes as the continuous-time random walk approach (CTRW), formulated originally by Montroll and Weiss (1965). The CTRW technique can follow the motion of atoms between discrete surface sites, which cannot be done with other MC techniques (Figure 3). The basic idea is to call random numbers to determine where on a surface a given type of atom is, what process it is undergoing, and at what time it occurs (Chang et al., 2005). The physics occurs on a 2D or 3D grid of boxes, with the boxes representing sites for atoms or molecules, ranging from atop the mantle to deep within the granular structure. The output consists of the molecules in specific binding sites on the surface or a number of monolayers atop the ice mantle as a function of time. although barriers between sites can slow the process, as mentioned above. The time between successive events is known as a waiting time, and the waiting time between successive events for a given process is given by a Poisson distribution with a random number in the range (0,1). The system moves forward by choosing the process with the time in the future nearest the current time.

For a simulation in which both gaseous and granular chemistry occur, two variants of the CTRW process are needed. In macroscopic approaches, used for the gas, one starts with an initial volume V containing initial abundances of gaseous atoms and molecules (Charnley, 1998; Vasyunin et al., 2009; Chang and Herbst, 2012). The following discussion comes from Chang et al. (2005). Here, the volume is not divided into sites. The unimolecular rate (s⁻¹) for each reaction considered, designated r_i, is calculated according to the type of process: a one-body process such as photodissociation, a two-body process such as any two-body reaction, and accretion onto a grain. The time for each reaction i to occur—the so-called waiting time −is given by the expression ${\tau }_i=-\text{ln}\left(Z\right)/r_i$, where Z is a random number in the range (0,1). For example, if Z = ½, the waiting time is equal to 0.693/r_i, and if Z = 0.9, the waiting time is 0.105/r_i. We then consider the absolute time for each reaction by adding the waiting time to either the time when the reaction last occurred or when the chemistry started. If the ith reaction occurs first, we recalculate the concentrations of reactants and species involved in this reaction. The rates of other reactions are also recalculated if the numbers of their reactants change.

The microscopic approach, used for the grain chemistry, must be coupled to the macroscopic model for the gas. The details of the coupling are discussed by Chang and Herbst (2012). Comparison between microscopic-macroscopic Monte Carlo and master equation calculations for small gas-grain systems can show reasonable agreement. For large gas-grain systems the macroscopic-microscopic system is by far the easier to use even though treatment of the gas-phase chemistry does require the macroscopic CTRW approach. The microscopic Monte Carlo approach for three-dimensional dust mantles is very time-consuming, however, and, in addition, there are problems caused by the random number generation for systems in which concentrations vary greatly. For example, the concentration of molecular hydrogen is so much larger than all other species that specific fixes are needed to avoid choosing H₂ each time a random species is picked. A few large-scale simulations have been done with the microscopic-macroscopic technique (see Figure 4), and the chemical simulations show that stochastic methods can be used to produce complex organic molecules at low temperatures (Chang and Herbst, 2014, Chang and Herbst, 2016). A third stochastic approach, known as the hybrid moment approach, has also been formulated (Du and Parise, 2011) and found to be faster than the Monte Carlo method.

FIGURE 4

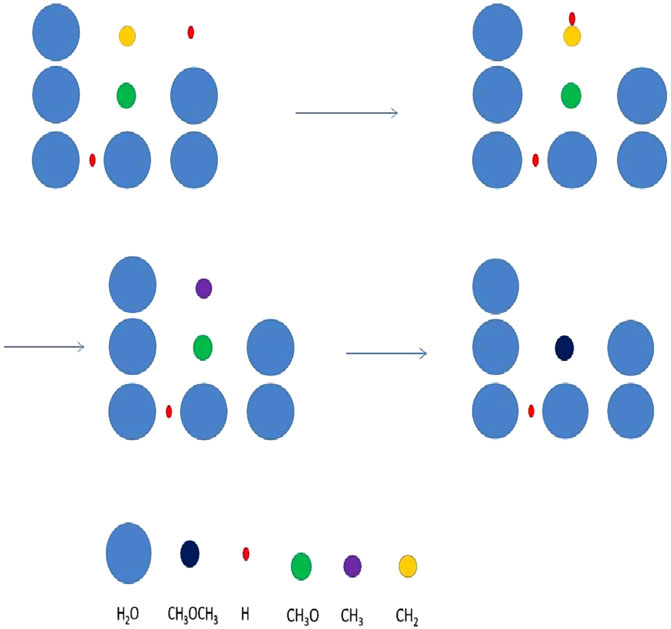
FIGURE 4. A mechanism of stochastic surface motions leading to the formation of dimethyl ether. The mechanism is labelled three-body motion or a chain reaction, and here consists of a diffusive and a short distance nondiffusive motion. The process commences when H and CH₂ produce CH₃, mainly by diffusive motion by atomic hydrogen. The methyl radical (purple) quickly reacts with a methoxy radical (CH₃O) lying immediately beneath it in a diffusionless manner to form dimethyl ether. Figure reproduced from Figure 1 of Chang and Herbst (2016).

The simulations of surface, mantle, and bulk chemistry of grains can be divided into two types of methods, known as on-lattice and off-lattice approaches. The on-lattice approach equates a grid of boxes with sites in which molecules can be found, but can still mimic irregular systems. The off-lattice uses an actual potential, typically composed of sums of Lennard-Jones potentials. Motion of atoms and molecules then leads to a change in the overall potential. Off-lattice calculations are often used for the joint build-up of dust particles, determination of porosity, and the chemistry that occurs during the build-up (Garrod, 2013b; Christianson and Garrod, 2021).

Modifications of Rate Equations

Given the difficulties of carrying out chemical simulations using stochastic approaches, several investigators have attempted to modify the rate equations to bring the results closer to those of stochastic calculations. The first attempt was reported by Caselli et al. (1998), who used several simple systems at 10 K. In the first, a gas of O and H atoms accretes onto grain surfaces to form H₂, OH, and O₂, while in the second, N atoms are also added to the gas to form the additional surface molecules NH₃ and H₂O. In the third system the gas also contains H₂. Monte Carlo simulations similar to those of Tielens and Hagen (1982) were used to calculate chemical abundances, and a number of modifications to the rate equations were tested to see how well the modifications allow the rate equation approach to reproduce the results of the Monte Carlo approach. Suitable modifications involving the O, H system were found for the following diffusive rate coefficients: k_HH, k_HO, and k_OO, by converting them to sums of rates of evaporation and sweeping, or accretion and sweeping, depending upon whether x > 1 or x < 1 where x is defined by the division of the evaporation rate of H by the accretion rate of H (t_evap⁻¹/t_acc⁻¹). With these corrections and some others, it was possible to reproduce some Monte Carlo results for the simple system. The authors noted that the use of modifications for complex gas-grain systems will lead to smaller effects given the large number of alternative pathways. This outcome was tested by Shalabiea et al. (1998) using the time-dependent gas-grain model for dark interstellar clouds of Hasegawa and Herbst (1993); it was also found that the modifications were needed at only the earliest times.

An improved set of modifications was introduced by Garrod, (2008), and utilized and compared successfully with a large gas-grain simulation treated by the unified Monte Carlo method of Vasyunin et al. (2009). One important rate coefficient concerns the switch-over between deterministic and stochastic contributions. It is based on two equations, the first of which governs the rate of the probabilistic surface reaction between species A and B, R_mod (AB):

$R_{mod}\left(AB\right)=R_{arr}\left(B\right)\cdot P\left(A\right)\cdot {\eta }_{AB}\left(A\right)+R_{arr}\left(A\right)\cdot P\left(B\right)\cdot {\eta }_{AB}\left(B\right)(26)$

where R_arr stands for arrival/formation rate of a species, P for the probability of a species being present when the other arrives, and $\eta$ for the efficiency of the reaction between A and B. The efficiency takes into account competition with selected other reactions. The probability P(i = A or B) is given by the Poisson probability distribution {N(i)}, which can be obtained by use of a random number. The other major equation yields the total production rate, which includes the deterministic and modified rates for reaction A+ B:

$R_{tot}\left(AB\right)=f_{AB}\cdot R_{mod}\left(AB\right)+\left(1-f_{AB}\right)\cdot k_{AB}\cdot <N\left(A\right)><N\left(B\right)>(27)$

Here f is a switching function, equal to 1 when both expectation values < N(A)> and <N(B)> are less than or equal to unity, but which is much lower when either of these quantities is greater than unity. The second term is written in terms of a rate coefficient, with expectation values of A and B, as shown in Equation 15 of Garrod (2008).

These improved modified rate equations do an excellent job of reproducing the Monte Carlo calculations of Vasyunin et al. (2009). The modified rate approach of Garrod (2008) has also been used successfully to study the effect of surface inhomogeneity on surface reaction rates (Cuppen and Garrod, 2011), where it agrees well with CTRW Monte Carlo results for a study of the surface formation of molecular hydrogen.

Diffusionless Processes

The idea of diffusionless processes on a surface was first discussed by Theulé et al. (2013) and reviewed in Theulé (2020). If we consider two species in adjacent sites, they need not undergo a long-range barriered diffusive motion, although chemical activation energy can still play a role. In this situation, the rate coefficient can be given by the simple Arrhenius Law (Theulé, 2020):

$k\left(T\right)=A \text{exp}\left(-\frac{E_a}{T}\right)(28)$

where A is the pre-exponential factor and E_a is the activation energy in K. In the absence of such chemical activation energy, one can imagine a process that is essentially “instantaneous,”or, more realistically, on the order of a vibrational frequency. This two-body process can be considered part of a more complex process, one example of which is a three-body surface process. As an example, consider the formation of CO₂ on an ice mantle. The CO + O reaction has a significant activation barrier and also a diffusion barrier on the surface or inner ice monolayers. As a result, this process is rather slow at low temperatures. Imagine, on the other hand, two surface atoms H and O, which can diffuse rapidly even at 10 K (Katz et al., 1999; Minissale et al., 2014). If they form an OH radical, and the radical lies above a CO molecule in an inner monolayer, the OH and CO can undergo a well-known reaction to form CO₂ and H with a small activation energy in a rapid diffusionless process. So, this three-body process contains both diffusive and nondiffusive aspects (see Figure 5).

FIGURE 5

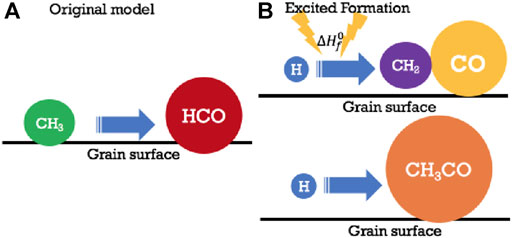
FIGURE 5. Several other mechanisms involving diffusive and nondiffusive formation mechanisms on grains. In (A), a simple diffusive reaction involving radicals CH₃ and HCO leads to acetaldehyde, albeit slowly at low temperatures. In (B) once again H and CH₂ produce CH₃, which in this case has sufficient energy from the exothermic process to react with a neighboring CO molecule to form CH₃CO, which can easily be hydrogenated with H atoms via diffusive reaction to form CH₃CHO. Permission given to reproduce this figure, originally appearing as Figure 1 in Jin and Garrod. (2020), by IOP Publishing.

How does one treat the mathematics of combined diffusive and non-diffusive processes? If a CTRW stochastic treatment is used, the process occurs naturally since one follows the motion of all particles, using an on-lattice or off-lattice potential. For ordinary rate equations, a useful equation for the rate R_AB of either of these processes has been written by Jin and Garrod (2020):

$R_{AB}=f_{act}\left(AB\right)R_{comp}\left(A\right)\left(\frac{N\left(B\right)}{N_S}\right)+f_{act}\left(AB\right)R_{comp}\left(B\right)\left(\frac{N\left(A\right)}{N_S}\right),(29)$

in which individual reactants can be treated separately. Here R_AB is an overall rate coefficient, f_act is the efficiency related to activation energy barriers (and κ; see Eq. (24)) if they exist, R_comp is a so-called “completion rate” for species A or B, and is defined by the specific process, N(A) and N(B) are the numbers of A and B species on the grain mantle, and N_S is the number of surface (or bulk) mantle sites. For an ordinary diffusive process with both A and B diffusing, the completion rate is related to the hopping or tunneling over a diffusive barrier, which is similar to Equations 21 and 23.

For a process between two species that do not undergo diffusive motion (e.g. CO + OH above), the completion rate involves the probability that A and B lie in adjacent sites and can undergo an “instantaneous” nondiffusive motion to lead to a product. For a diffusive process followed by a nondiffusive one (as is the case for CO₂ above), one can compute the diffusive rate via Equation 29 to obtain the result for H + O forming OH, and multiply the result by the probability that OH lies above or adjacent to a CO molecule. Here use of Equation 29 has a single R_comp for OH that does not include a Boltzmann term because the completion rate only involves the probability that a CO molecule lies in an adjacent site to OH, which is N(CO)/N_S. More complex approaches exist if there is activation energy for one process.

Particular values of R_comp are mentioned in Jin and Garrod (2020) for the following diffusionless processes: the Eley-Rideal mechanism, a number of types of three-body processes involving collisions, and photodissociation-induced reactions, in which photons produce a reactant. The Eley-Rideal mechanism involves no diffusion or horizontal motion; a species lands vertically atop an adsorbate and undergoes reaction. For example, suppose we consider the reaction between O and CO to form CO₂, a process that has an activation energy of about 1000 K. If the O atom lands upon CO at a constant rate, the value of R_comp(O) is equal to its rapid accretion rate if there is no activation energy.

Now consider an unusual photodissociation process in which oxygen-containing species on a grain surface (e.g. O_2, H₂O) undergo photodissociation to produce a metastable state of an oxygen atom–O (¹D)—which lives for a long enough period to react nondiffusively with almost any other species on the grain mantle that lies in an adjacent site. There are two values of R_comp = R_photo N(i) for each molecule i undergoing photodissociation to form O (¹D): one for external radiation and the other for cosmic-ray-induced radiation (Carder et al., 2021). The particular reaction with methane (CH₄) has been studied in the laboratory, and produces methanol and formaldehyde (Bergner et al., 2017). The results can be reproduced assuming that after photodissociation, the newly formed metastable oxygen instantaneously reacts with methane lying adjacent to or under the O (¹D) to form methanol and formaldehyde (Carder et al., 2021). Analogous reactions with larger hydrocarbons than methane can lead to larger complex organic molecules.

According to Jin and Garrod (2020), large organic molecules can be formed efficiently in cold regions with the inclusion of diffusionless processes of various types. An extension to higher temperatures can be found in Garrod et al. (2021). In addition to providing an explanation for the formation of complex organic molecules in cold interstellar clouds, the nondiffusive surface chemistry explains a number of experiments in the laboratory at low temperatures in which species such as glycolaldehyde, ethylene glycol, and methyl formate are produced starting from HCO and H₂CO (Fedoseev et al., 2015; Chuang et al., 2016). Although these experiments do not mimic interstellar conditions, they do provide additional evidence that nondiffusive chemistry does exist in interstellar clouds. Moreover, non-diffusive chemistry can often be much more efficient than diffusive chemistry at these low temperatures. In more recent work, an extension of the research of Jin and Garrod (2020) to determine the rate of formation of complex organic molecules in regions of active star formation as temperatures rise shows a rather complex time and temperature dependence (Garrod et al., 2021).

Radiolysis

One approach in which both chemists and astronomers played a significant role is known as radiolysis. In this process, cosmic rays bombard an icy grain mantle to initiate a complex series of reactions starting with secondary electrons and neutrals and finishing up with neutral radicals, which can combine to form complex organic molecules as long as carbonaceous material, even as simple as CO or CO₂, is present in the ice. Cosmic rays are mainly highly ionized ions ranging in mass from protons to heavy nuclei. The laboratory study of radiolysis using high-energy protons or electrons but occasionally high-energy nuclei (Wakelam et al., 2021) is well advanced with many experiments in many laboratories (Bennett et al., 2005; Hudson and Moore, 2018; Christoffersen et al., 2020; Ioppolo et al., 2021) and some corresponding theory (see Figure 6). It was not until a few years ago that a theoretical approach to the chemistry was developed by astrochemists (Shingledecker et al., 2018), tested successfully against simple cold interstellar ices in the laboratory such as O₂ and amorphous water, and applied to interstellar icy mantles (Shingledecker and Herbst, 2018; Shingledecker et al., 2020). At the present stage, the theoretical approach has been used to study how radiolysis can form complex organic molecules such as methyl formate (HCOOCH₃) at low temperatures (Paulive et al., 2021).

FIGURE 6

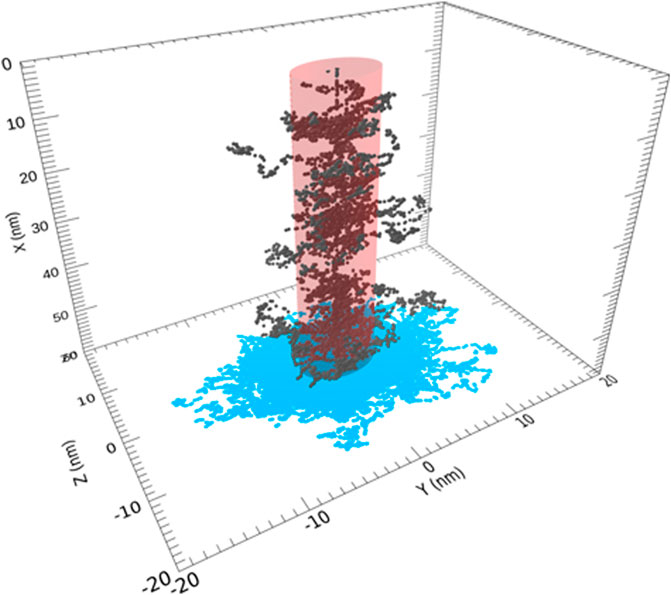
FIGURE 6. Portion of the track for a 0.1 MeV proton and secondary electrons within the cylindrical region of amorphous ices is shown. The incident ion enters through the center of the top surface. Permission requested to reproduce this figure, originally appearing as Figure 2 of Shingledecker et al. (2020).

Summary

In this review, a number of unusual chemical processes thought to occur in the interstellar medium have been described. These processes include reactions in the gas phase and reactions on the surface and in the bulk of icy grain mantles. The understanding or partial understanding of these processes has aided both the fields of chemistry and astronomy. Although astrochemists can be first to suggest unusual processes that might help to solve astrochemical problems, more detailed studies—both theoretical and experimental—by chemists and chemical physicists can lead to a much greater knowledge of these unusual processes. The knowledge in turn can be used to improve chemical simulations and lead to an increase in what they can tell us about physical conditions and dynamics in the interstellar medium. Most of the unusual processes reviewed here have a history in which astrochemists played an important role, if not as exact an order as mentioned.

In the future, processes mentioned here such as radiative association, metastable reactions on icy surfaces, stochastic kinetics, and diffusionless surface reactions as well as other processes such as sputtering, negative ion formation, reactive desorption, reactive excitation, and nuclear spin astrochemistry will take a larger place in large chemical simulations and aid our understanding of the interstellar medium in general and star and planetary formation in particular.

Author Contributions

EH has totally written this review manuscript.

Funding

This work was funded by the National Science Foundation (US) Division of Astronomical Sciences through Grant AST-19-06489.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acharyya, K., Herbst, E., Caravan, R. L., Shannon, R. J., Blitz, M. A., and Heard, D. E. (2015). The Importance of OH Radical-Neutral Low Temperature Tunnelling Reactions in Interstellar Clouds Using a New Model. Mol. Phys. 113, 2243–2254. doi:10.1080/00268976.2015.1021729

CrossRef Full Text | Google Scholar

Adams, N. G., and Smith, D. (1978). Reactions of CH₃⁺ Ions With Molecules at 300 K. Chem. Phys. Lett. 54, 530–534. doi:10.1016/0009-2614(78)85278-6

CrossRef Full Text | Google Scholar

Anicich, V. G., Sen, A. D., Huntress, W. T., and McEwan, M. J. (1995). Association Reactions at Low Pressure. V. The CH₃⁺/HCN System. A Final Word? J. Chem. Phys. 102, 3256–3261. doi:10.1063/1.468636

CrossRef Full Text | Google Scholar

Balucani, N., Ceccarelli, C., and Taquet, V. (2015). Formation of Complex Organic Molecules in Cold Objects: the Role of Gas-phase Reactions. MNRAS 449, L16–L20. doi:10.1093/mnrasl/slv009

CrossRef Full Text | Google Scholar

Barlow, S. E., Dunn, G. H., and Schauer, M. (1984). Radiative Association of CH₃⁺ and H₂ at 13 K. Phys. Rev. Lett. 52, 902–905. doi:10.1103/PhysRevLett.52.902

CrossRef Full Text | Google Scholar

Bates, D. R. (1979a). Ion-molecule Association. J. Phys. B: Mol. Phys. 12, 4135–4146. doi:10.1088/0022-3700/12/24/018

CrossRef Full Text | Google Scholar

Bates, D. R. (1979b). Temperature Dependence of Ion-Molecule Association. J. Chem. Phys. 71, 2318–2319. doi:10.1063/1.438568

CrossRef Full Text | Google Scholar

Bennett, C., Jamieson, C. S., Lebar, M. T., Osamura, Y., Mebel, A. M., and Kaiser, R. I. (2005). “A Combined Experimental and Theoretical Study on the Charged Particle Processing of Low Temperature Ices, Astrochemistry: Recent Successes And Current Challenges,” in Proceedings of the 231st Symposium of the International Astronomical Union held in Pacific Grove, California, USA, August 29-September 2, 2005. Poster sessions., p.113.

Google Scholar

Bergner, J. B., Öberg, K. I., and Rajappan, M. (2017). Methanol Formation via Oxygen Insertion Chemistry in Ices. Astrophys. J. 845, 29. doi:10.3847/1538-4357/aa7d09

CrossRef Full Text | Google Scholar

Biham, O., Furman, I., Pirronello, V., and Vidali, G. (2001). Master Equation for Hydrogen Recombination on Grain Surfaces. Astrophys. J. 553, 595–603. doi:10.1086/320975

CrossRef Full Text | Google Scholar

Black, J. H., and Dalgarno, A. (1973). The Formation of CH in Interstellar Clouds. Astrophys. Lett. 15, 79–82.

Google Scholar

Black, J. H., and Dalgarno, A. (1977). Models of Interstellar Clouds. I - the Zeta Ophiuchi Cloud. Astrophys. J. Suppl. Ser. 34, 405–423. doi:10.1086/190455

CrossRef Full Text | Google Scholar

Böhringer, H. (1985). Third-body-assisted, Binary Ion-Molecule Reactions. The Reaction NH₃⁺ + H₂ → NH₄⁺ + H. Chem. Phys. Lett. 122, 185–189. doi:10.1016/0009-2614(85)80560-1

CrossRef Full Text | Google Scholar

Canosa, A. (2019). Gas Phase Reaction Kinetics of Complex Organic Molecules at Temperatures of the Interstellar Medium: The OH + CH₃OH Case. Proc. IAU 15, 35–40. doi:10.1017/S1743921319006446

CrossRef Full Text | Google Scholar

Carder, J. T., Ochs, W., and Herbst, E. (2021). Modelling the Insertion of O(¹D) into Methane on the Surface of Interstellar Ice Mantles. MNRAS 508, 1526–1532. doi:10.1093/mnras/stab2619

CrossRef Full Text | Google Scholar

Carruthers, G. R. (1970). Rocket Observation of Interstellar Molecular Hydrogen. Astrophys. J. 161, L81. doi:10.1086/180575

CrossRef Full Text | Google Scholar

Caselli, P., Hasegawa, T. I., and Herbst, E. (1998). A Proposed Modification of the Rate Equations for Reactions on Grain Surfaces. Astrophys. J. 495, 309–316. doi:10.1086/305253

CrossRef Full Text | Google Scholar

Chang, Q., Cuppen, H. M., and Herbst, E. (2005). Continuous-time Random-Walk Simulation of H₂ Formation on Interstellar Grains. Astron. Astrophys. 434, 599–611. doi:10.1051/0004-6361:20041842

CrossRef Full Text | Google Scholar

Chang, Q., and Herbst, E. (2012). A Unified Microscopic-Macroscopic Monte Carlo Simulation of Gas-Grain Chemistry in Cold Dense Interstellar Clouds. Astrophys. J. 759, 147. doi:10.1088/0004-637X/759/2/147

CrossRef Full Text | Google Scholar

Chang, Q., and Herbst, E. (2014). Interstellar Simulations Using a Unified Microscopic-Macroscopic Monte Carlo Model with a Full Gas-Grain Network Including Bulk Diffusion in Ice Mantles. Astrophys. J. 787, 135. doi:10.1088/0004-637X/787/2/135

CrossRef Full Text | Google Scholar

Chang, Q., and Herbst, E. (2016). Unified Microscopic-Macroscopic Monte Carlo Simulations of Complex Organic Molecule Chemistry in Cold Cores. Astrophys. J. 819, 145. doi:10.3847/0004-637X/819/2/145

CrossRef Full Text | Google Scholar

Charnley, S. B. (1998). Stochastic Astrochemical Kinetics. Astrophys. J. 509, L121–L124. doi:10.1086/311764

CrossRef Full Text | Google Scholar

Charnley, S. B. (2001). Stochastic Theory of Molecule Formation on Dust. Astrophys. J. 562, L99–L102. doi:10.1086/324753

CrossRef Full Text | Google Scholar

Chesnavich, W. J., and Bowers, M. T. (1977). Statistical Phase Space Theory of Polyatomic Systems: Rigorous Energy and Angular Momentum Conservation in Reactions Involving Symmetric Polyatomic Species. J. Chem. Phys. 66, 2306–2315. doi:10.1063/1.434292

CrossRef Full Text | Google Scholar

Christianson, D. A., and Garrod, R. T. (2021). Chemical Kinetics Simulations of Ice Chemistry on Porous versus Non-porous Dust Grains. Front. Astron. Space Sci. 8, 21. doi:10.3389/fspas.2021.643297

CrossRef Full Text | Google Scholar

Christoffersen, R., Keller, L. P., and Dukes, C. (2020). “The Role of Solar Wind Ion Processing in Space Weathering of Olivine: Unraveling the Paradox of Laboratory Irradiation Results Compared to Observations of Natural Samples,” in 51st Lunar and Planetary Science Conference, The Woodlands, TX, March 16–20, 2020. LPI Contribution No. 2326, id.2147.

Google Scholar

Chuang, K.-J., Fedoseev, G., Ioppolo, S., van Dishoeck, E. F., and Linnartz, H. (2016). H-atom Addition and Abstraction Reactions in Mixed CO, H₂CO and CH₃OH Ices - an Extended View on Complex Organic Molecule Formation. MNRAS 455, 1702–1712. doi:10.1093/mnras/stv2288

CrossRef Full Text | Google Scholar

Cooke, I. R., and Sims, I. R. (2019). Experimental Studies of Gas-phase Reactivity in Relation to Complex Organic Molecules in Star-Forming Regions. ACS Earth Space Chem. 3, 1109–1134. doi:10.1021/acsearthspacechem.9b00064

CrossRef Full Text | Google Scholar

Cuppen, H. M., and Garrod, R. T. (2011). Modelling of Surface Chemistry on an Inhomogeneous Interstellar Grain. Astron. Astrophys. 529, A151. doi:10.1051/0004-6361/201016013

CrossRef Full Text | Google Scholar

Defrees, D. J., McLean, A. D., and Herbst, E. (1985). Theoretical Investigation of the Interstellar CH₃CN CH₃NC Ratio. Astrophys. J. 293, 236–242. doi:10.1086/163229

PubMed Abstract | CrossRef Full Text | Google Scholar

Draine, B. T. (2011). Physics of the Interstellar and Intergalactic Medium. Princeton, New Jersey: Princeton University Press.

Google Scholar

Du, F., and Parise, B. (2011). A Hybrid Moment Equation Approach to Gas-Grain Chemical Modeling. Astron. Astrophys. 530, A131. doi:10.1051/0004-6361/201016262

CrossRef Full Text | Google Scholar

Dupuy, R., Bertin, M., Féraud, G., Michaut, X., Marie-Jeanne, P., Jeseck, P., et al. (2021). Mechanism of Indirect Photon-Induced Desorption at the Water Ice Surface. Phys. Rev. Lett. 126, 15600. doi:10.1103/PhysRevLett.126.156001

CrossRef Full Text | Google Scholar

Elitzur, M., and Watson, W. D. (1978). Formation of Molecular CH⁺ in Interstellar Shocks. Astrophys. J. 222, L141–L144. doi:10.1086/182711

CrossRef Full Text | Google Scholar

Falgarone, E., and Puget, J.-L. (1995). The Intermittency of Turbulence in Interstellar Clouds: Implications for the Gas Kinetic Temperature and Decoupling of Heavy Particles from the Gas Motions. Astron. Astrophys. 293, 840–852.

Google Scholar

Fayolle, E. C., Bertin, M., Romanzin, C., Michaut, X., Öberg, K. I., Linnartz, H., et al. (2011). CO Ice Photodesorption: A Wavelength-dependent Study. Astrophys. J. 739, L36. doi:10.1088/2041-8205/739/2/L36

CrossRef Full Text | Google Scholar

Federman, S. R., Glassgold, A. E., Jenkins, E. B., and Shaya, E. J. (1980). The Abundance of CO in Diffuse Interstellar Clouds - an Ultraviolet Survey. Astrophys. J. 242, 545–559. doi:10.1086/158489

CrossRef Full Text | Google Scholar

Fedoseev, G., Cuppen, H. M., Ioppolo, S., Lamberts, T., and Linnartz, H. (2015). Experimental Evidence for Glycolaldehyde and Ethylene Glycol Formation by Surface Hydrogenation of CO Molecules under Dense Molecular Cloud Conditions. MNRAS 448, 1288–1297. doi:10.1093/mnras/stu2603

CrossRef Full Text | Google Scholar

Gao, L. G., Zheng, J., Fernández-Ramos, A., Truhlar, D. G., and Xu, X. (2018). Kinetics of the Methanol Reaction with OH at Interstellar, Atmospheric, and Combustion Temperatures. J. Am. Chem. Soc. 140, 2906–2918. doi:10.1021/jacs.7b12773

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrod, R. T. (2008). A New Modified-Rate Approach for Gas-Grain Chemical Simulations. Astron. Astrophys. 491, 239–251. doi:10.1051/0004-6361:200810518

CrossRef Full Text | Google Scholar

Garrod, R. T. (2013a). A Three-phase Chemical Model of Hot Cores: The Formation of Glycine. Astrophys. J. 765, 60. doi:10.1088/0004-637X/765/1/60

CrossRef Full Text | Google Scholar

Garrod, R. T., Jin, M., Matis, K. A., Jones, D., Willis, E. R., and Herbst, E. (2021). Astrophys J. Supp. Ser.. In press.

Garrod, R. T. (2013b). Three-dimensional, Off-Lattice Monte Carlo Kinetics Simulations of Interstellar Grain Chemistry and Ice Structure. Astrophys. J. 778, 158. doi:10.1088/0004-637X/778/2/158

CrossRef Full Text | Google Scholar

Geppert, W. D., Hamberg, M., Thomas, R. D., Österdahl, F., Hellberg, F., Zhaunerchyk, V., et al. (2006). Dissociative Recombination of Protonated Methanol. Faraday Discuss. 133, 177–190. doi:10.1039/B516010C

PubMed Abstract | CrossRef Full Text | Google Scholar

Geppert, W. D., and Larsson, M. (2013). Experimental Investigations into Astrophysically Relevant Ionic Reactions. Chem. Rev. 113 (12), 8872–8905. doi:10.1021/cr400258m

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerlich, D., and Horning, S. (1992). Experimental Investigation of Radiative Association Processes as Related to Interstellar Chemistry. Chem. Rev. 92, 1509–1539. doi:10.1021/cr00015a003

CrossRef Full Text | Google Scholar

Giusti-Suzor, A., Roueff, E., and Regemorter, H. v. (1976). A New Calculation of the Radiative Association Rate of the CH⁺ radical: Comparison between Semiclassical and Quantal Results (Interstellar Abundance). J. Phys. B: Mol. Phys. 9, 1021–1033. doi:10.1088/0022-3700/9/6/024

CrossRef Full Text | Google Scholar

Glowacki, D. R., Liang, C.-H., Morley, C., Pilling, M. J., and Robertson, S. H. (2012). MESMER: an Open-Source Master Equation Solver for Multi-Energy Well Reactions. J. Phys. Chem. A. 116, 9545–9560. doi:10.1021/jp3051033

CrossRef Full Text | Google Scholar

Green, N. J. B., Toniazzo, T., Pilling, M. J., Ruffle, D. P., Bell, N., and Hartquist, T. W. (2001). A Stochastic Approach to Grain Surface Chemical Kinetics. Astron. Astrophys. 375, 1111–1119. doi:10.1051/0004-6361:20010961

CrossRef Full Text | Google Scholar

Hasegawa, T. I., Herbst, E., and Leung, C. M. (1992). Models of Gas-Grain Chemistry in Dense Interstellar Clouds with Complex Organic Molecules. Astrophys. J. Suppl. Ser. 82, 167–195. doi:10.1086/191713

CrossRef Full Text | Google Scholar

Hasegawa, T. I., and Herbst, E. (1993). New Gas-Grain Chemical Models of Quiescent Dense Interstellar Clouds: the Effects of H₂ Tunnelling Reactions and Cosmic ray Induced Desorption. MNRAS 261, 83–102. doi:10.1093/mnras/261.1.83

CrossRef Full Text | Google Scholar

Hawley, M., and Smith, M. A. (1992). The Gas Phase Reaction of C₂H₂⁺ with H₂ below 3 K the Reopening of the Bimolecular C₂H₂⁺ + H₂ Channel at Low Energy. J. Chem. Phys. 96, 1121–1127. doi:10.1063/1.462198

CrossRef Full Text | Google Scholar

He, J., Vidali, G., Lemaire, J.-L., and Garrod, R. T. (2015). Formation of Hydroxylamine on Dust Grains via Ammonia Oxidation. Astrophys. J. 799, 49. doi:10.1088/0004-637X/799/1/49

CrossRef Full Text | Google Scholar

Heard, D. E. (2018). Rapid Acceleration of Hydrogen Atom Abstraction Reactions of OH at Very Low Temperatures through Weakly Bound Complexes and Tunneling. Acc. Chem. Res. 51, 2620–2627. doi:10.1021/acs.accounts.8b00304

PubMed Abstract | CrossRef Full Text | Google Scholar

Herbst, E. (2022). “Cold Chemistry and beyond, Chapter 10,” in Uniform Supersonic Flows in Chemical Physics: Chemistry Close to Absolute Zero Studied Using the CRESU Method. Editors B. R. Rowe, A. Canosa, and D. E. Heard (Singapore: World Scientific).

Google Scholar

Herbst, E. (1985a). Radiative Association Rate Coefficients under Shocked Conditions in Interstellar Clouds - the Case of CH₃⁺ + H₂. Astron. Astrophys. 153, 151–156.

Google Scholar

Herbst, E. (1980a). A New Look at Radiative Association in Dense Interstellar Clouds. Astrophys. J. 237, 462–470. doi:10.1086/157889

CrossRef Full Text | Google Scholar

Herbst, E. (1980b). An Additional Uncertainty in Calculated Radiative Association Rates of Molecular Formation at Low Temperatures. Astrophys. J. 241, 197–199. doi:10.1086/158331

CrossRef Full Text | Google Scholar

Herbst, E. (1982). An Approach to the Estimation of Polyatomic Vibrational Radiative Relaxation Rates. Chem. Phys. 65, 185–195. doi:10.1016/0301-0104(82)85067-2

CrossRef Full Text | Google Scholar

Herbst, E., DeFrees, D. J., Talbi, D., Pauzat, F., Koch, W., and McLean, A. D. (1991). Calculations on the Rate of the Ion-Molecule Reaction between NH₃⁺ and H₂. J. Chem. Phys. 94, 7842–7849. doi:10.1063/1.460119

CrossRef Full Text | Google Scholar

Herbst, E., and Klemperer, W. (1973). The Formation and Depletion of Molecules in Dense Interstellar Clouds. Astrophys. J. 185, 505–534. doi:10.1086/152436

CrossRef Full Text | Google Scholar

Herbst, E., and Millar, T. J. (2008). “The Chemistry of Cold Interstellar Cloud Cores,” in Low Temperatures and Cold Molecules. Editor I. W. M. Smith (London, UK: Imperial College Press), 1–54. doi:10.1142/9781848162105_0001

CrossRef Full Text | Google Scholar

Herbst, E., Schubert, J. G., and Certain, P. R. (1977). The Radiative Association of CH₂⁺. Astrophys. J. 213, 696–704. doi:10.1086/155199

CrossRef Full Text | Google Scholar

Herbst, E. (1985b). The Rate of the Radiative Association Reaction between CH₃⁺ and NH₃ and its Implications for Interstellar Chemistry. Astrophys. J. 292, 484–486. doi:10.1086/163179

CrossRef Full Text | Google Scholar

Herbst, E., and van Dishoeck, E. F. (2009). Complex Organic Interstellar Molecules. Annu. Rev. Astron. Astrophys. 47, 427–480. doi:10.1146/annurev-astro-082708-101654

CrossRef Full Text | Google Scholar

Herd, C. R., Adams, N. G., and Smith, D. (1990). OH Production in the Dissociative Recombination of H₃O⁺, HCO₂⁺, and N₂OH⁺- Comparison with Theory and Interstellar Implications. Astrophys. J. 349, 388–392. doi:10.1086/168322

CrossRef Full Text | Google Scholar

Hudson, R. L., and Moore, M. H. (2018). Interstellar Ices and Radiation-Induced Oxidations of Alcohols. Astrophys. J. 857, 89. doi:10.3847/1538-4357/aab708

CrossRef Full Text | Google Scholar

Huntress, W. T., and Mitchell, G. F. (1979). The Synthesis of Complex Molecules in Interstellar Clouds. Astrophys. J. 231, 456–467. doi:10.1086/157207

CrossRef Full Text | Google Scholar

Huntress, W. T., and Beauchamp, J. L. (1969). Application of Ion Cyclotron Resonance to the Study of Ionizing Reactions of Metastable Molecules. Int. J. Mass Spectrom. Ion Phys. 3, 149–152. doi:10.1016/0020-7381(69)80068-9

CrossRef Full Text | Google Scholar

Ioppolo, S., Kaňuchová, Z., James, R. L., Dawes, A., Ryabov, A., Dezalay, J., et al. (2021). Vacuum Ultraviolet Photoabsorption Spectroscopy of Space-Related Ices: Formation and Destruction of Solid Carbonic Acid upon 1 keV Electron Irradiation. Astron. Astrophys. 646, A172. doi:10.1051/0004-6361/202039184

CrossRef Full Text | Google Scholar

Iqbal, W., Acharyya, K., and Herbst, E. (2012). Kinetic Monte Carlo Studies of H₂ Formation on Grain Surfaces over a Wide Temperature Range. Astrophys. J. 751, 58. doi:10.1088/0004-637X/751/1/58

CrossRef Full Text | Google Scholar

Jin, M., and Garrod, R. T. (2020). Formation of Complex Organic Molecules in Cold Interstellar Environments through Nondiffusive Grain-Surface and Ice-Mantle Chemistry. Astrophys. J. Suppl. Ser. 249, 26. doi:10.3847/1538-4365/ab9ec8

CrossRef Full Text | Google Scholar

Katz, N., Furman, I., Biham, O., Pirronello, V., and Vidali, G. (1999). Molecular Hydrogen Formation on Astrophysically Relevant Surfaces. Astrophys. J. 522, 305–312. doi:10.1086/307642

CrossRef Full Text | Google Scholar

Klots, C. E. (1976). Kinetic Energy Distributions from Unimolecular Decay: Predictions of the Langevin Model. J. Chem. Phys. 64, 4269–4275. doi:10.1063/1.432111

CrossRef Full Text | Google Scholar

Luca, A., Voulot, D., and Gerlich, D. (2002). “Low Temperature Reactions between Stored Ions and Condensable Gases: Formation of Protonated Methanol via Radiative Association,” in WDS 2002 Proceedings of Contributed Papers, Prague PART II (Praha, Czechia: MATFYZPRESS), 294–300.

Google Scholar

Luine, J. A., and Dunn, G. H. (1985). Ion-Molecule Reaction Probabilities Near 10 K. Astrophys. J. 299, L67–L70. doi:10.1086/184582

CrossRef Full Text | Google Scholar

Markwick, A. J. (2012). UMIST RATE12/astrochemistry.Net. Available at: http://udfa.ajmarkwick.net/.

Google Scholar

Marquette, J. B., Rowe, B. R., Dupeyrat, G., and Roueff, E. (1985). CRESU Study of the Reaction N⁺ + H₂ Yields NH⁺ + H between 8 and 70 K and Interstellar Chemistry Implications. Astron. Astrophys. 147, 115–120.

Google Scholar

McElroy, D., Walsh, C., Markwick, A. J., Cordiner, M. A., Smith, K., and Millar, T. J. (2013). The UMIST Database for Astrochemistry 2012. Astron. Astrophys. 550, A36. doi:10.1051/0004-6361/201220465

CrossRef Full Text | Google Scholar

McEwan, M. J., Anicich, V. G., Huntress, W. T., Kemperer, P. R., and Bowers, M. T. (1980). “An ICR Study of an Association Reaction at Low Pressure,” in Interstellar Molecules; Proceedings of the Symposium (Mont Tremblant, Quebec, Canada, Dordrecht: D. Reidel Publishing), 305–306. doi:10.1007/978-94-009-9097-5_72

CrossRef Full Text | Google Scholar

Minissale, M., Congiu, E., and Dulieu, F. (2016). Oxygen Diffusion and Reactivity at Low Temperature on Bare Amorphous Olivine-Type Silicate. J. Chem. Phys. 140 (7), 074705. doi:10.1063/1.4864657

CrossRef Full Text | Google Scholar

Minissale, M., Congiu, E., and Dulieu, F. (2016). Direct Measurement of Desorption and Diffusion Energies of O and N Atoms Physisorbed on Amorphous Surfaces. Astron. Astrophys. 585, A146. doi:10.1051/0004-6361/201526702

CrossRef Full Text | Google Scholar

Minissale, M., Congiu, E., Manicò, G., Pirronello, V., and Dulieu, F. (2013). CO₂ Formation on Interstellar Dust Grains: a Detailed Study of the Barrier of the CO + O Channel. Astron. Astrophys. 559, A49. doi:10.1051/0004-6361/201321453

CrossRef Full Text | Google Scholar

Mitchell, J. B. A., Angelova, G., Rebrion-Rowe, C., Novotny, O., Garrec, J. L. L., Bluhme, H., et al. (2005). Branching Ratios for the Dissociative Recombination of Hydrocarbon Ions. J. Phys. Conf. Ser. 4, 198–204. doi:10.1088/1742-6596/4/1/028

CrossRef Full Text | Google Scholar

Montroll, E. W., and Weiss, G. H. (1965). Random Walks on Lattices. II. J. Math. Phys. 6, 167–181. doi:10.1063/1.1704269

CrossRef Full Text | Google Scholar

Moseley, E. R., Draine, B. T., Tomida, K., and Stone, J. M. (2020). Turbulent Dissipation, CH⁺ Abundance, H₂ Line Luminosities, and Polarization in the Cold Neutral Medium. MNRAS 500, 3290–3308. doi:10.1093/mnras/staa3384

CrossRef Full Text | Google Scholar

Ocaña, A. J., Blázquez, S., Potapov, A., Ballesteros, B., Canosa, A., Antiñolo, M., et al. (2019). Gas-phase Reactivity of CH₃OH toward OH at Interstellar Temperatures (11.7-177.5 K): Experimental and Theoretical Study. Phys. Chem. Chem. Phys. 21, 6942–6957. doi:10.1039/c9cp00439d

PubMed Abstract | CrossRef Full Text | Google Scholar

Öjekull, J., Andersson, P. U., Någård, M. B., Pettersson, J. B. C., Derkatch, A. M., Neau, A., et al. (2004). Dissociative Recombination of NH₄⁺ and ND₄⁺ Ions: Storage Ring Experiments And ab Initio Molecular Dynamics. J. Chem. Phys. 120, 7391–7399. doi:10.1063/1.1669388

CrossRef Full Text | Google Scholar

Paulive, A., Shingledecker, C. N., and Herbst, E. (2020). The Role of Radiolysis in the Modelling of C₂H₄O₂ Isomers and Dimethyl Ether in Cold Dark Clouds. MNRAS 500, 3414–3424. doi:10.1093/mnras/staa3458

CrossRef Full Text | Google Scholar

Ruaud, M., Loison, J. C., Hickson, K. M., Gratier, P., Hersant, F., and Wakelam, V. (2015). Modelling Complex Organic Molecules in Dense Regions: Eley-Rideal and Complex Induced Reaction. MNRAS 447, 4004–4017. doi:10.1093/mnras/stu2709

CrossRef Full Text | Google Scholar

Ruaud, M., Wakelam, V., and Hersant, F. (2016). Gas and Grain Chemical Composition in Cold Cores as Predicted by the Nautilus Three-phase Model. Mon. Not. R. Astron. Soc. 459, 3756–3767. doi:10.1093/mnras/stw887

CrossRef Full Text | Google Scholar

Ryzhov, V., Klippenstein, S. J., and Dunbar, R. C. (1996). Radiative Association of NO⁺ with 3-Pentanone: Rate, Binding Energy, and Temperature Dependence. J. Am. Chem. Soc. 118, 5462–5468. doi:10.1021/ja953183b

CrossRef Full Text | Google Scholar

Schiff, H. I., and Bohme, D. K. (1979). An Ion-Molecule Scheme for the Synthesis of Hydrocarbon-Chain and Organonitrogen Molecules in Dense Interstellar Clouds. Astrophys. J. 232, 740–746. doi:10.1086/157334

CrossRef Full Text | Google Scholar

Shalabiea, O. M., Caselli, P., and Herbst, E. (1998). Grain Surface Chemistry: Modified Models. Astrophys. J. 502, 652–660. doi:10.1086/305942

CrossRef Full Text | Google Scholar

Shannon, R. J., Blitz, M. A., Goddard, A., and Heard, D. E. (2013). Accelerated Chemistry in the Reaction between the Hydroxyl Radical and Methanol at Interstellar Temperatures Facilitated by Tunnelling. Nat. Chem 5, 745–749. doi:10.1038/nchem.1692

PubMed Abstract | CrossRef Full Text | Google Scholar

Shingledecker, C. N., and Herbst, E. (2018). A General Method for the Inclusion of Radiation Chemistry in Astrochemical Models. Phys. Chem. Chem. Phys. 20, 5359–5367. doi:10.1039/C7CP05901A

PubMed Abstract | CrossRef Full Text | Google Scholar

Shingledecker, C. N., Incerti, S., Ivlev, A., Emfietzoglou, D., Kyriakou, I., Vasyunin, A., et al. (2020). Cosmic-Ray Tracks in Astrophysical Ices: Modeling with the Geant4-DNA Monte Carlo Toolkit. Astrophys. J. 904, 189. doi:10.3847/1538-4357/abbb30

CrossRef Full Text | Google Scholar

Shingledecker, C. N., Tennis, J., Gal, R. L., and Herbst, E. (2018). On Cosmic-Ray-driven Grain Chemistry in Cold Core Models. Astrophys. J. 861, 20. doi:10.3847/1538-4357/aac5ee

CrossRef Full Text | Google Scholar

Sivaramakrishnan, R., Michael, J. V., Wagner, A. F., Dawes, R., Jasper, A. W., Harding, L. B., et al. (2011). Roaming Radicals in the thermal Decomposition of Dimethyl Ether: Experiment and Theory. Combustion and Flame 158, 618–632. doi:10.1016/j.combustflame.2010.12.017

CrossRef Full Text | Google Scholar

Smith, D., and Adams, N. G. (1978). Molecular Synthesis in Interstellar Clouds - Radiative Association Reactions of CH₃⁺ Ions. Astrophys. J. 220, L87–L92. doi:10.1086/182642

CrossRef Full Text | Google Scholar

Smith, D., and Adams, N. G. (1981). Some Positive Ion Reactions with H₂: Interstellar Implications. Monthly Notices R. Astronomical Soc. 197, 377–384. doi:10.1093/mnras/197.2.377

CrossRef Full Text | Google Scholar

Smith, D. (1992). The Ion Chemistry of Interstellar Clouds. Chem. Rev. 92, 1473–1485. doi:10.1021/cr00015a001

CrossRef Full Text | Google Scholar

Smith, S. C., McEwan, M. J., Giles, K., Smith, D., and Adams, N. G. (1990). Unimolecular Decomposition of a Polyatomic Ion in a Variable-Temperature Selected-Ion-Flow-Drift Tube: Experiment and Theoretical Interpretation. Int. J. Mass Spectrom. Ion Process. 96, 77–96. doi:10.1016/0168-1176(90)80043-3

CrossRef Full Text | Google Scholar

Snyder, L. E., Buhl, D., Zuckerman, B., and Palmer, P. (1969). Microwave Detection of Interstellar Formaldehyde. Phys. Rev. Lett. 22, 679–681. doi:10.1103/PhysRevLett.22.679

CrossRef Full Text | Google Scholar

Solomon, P. M., and Klemperer, W. (1972). The Formation of Diatomic Molecules in Interstellar Clouds. Astrophys. J. 178, 389–422. doi:10.1086/151799

CrossRef Full Text | Google Scholar

Stantcheva, T., Shematovich, V. I., and Herbst, E. (2002). On the Master Equation Approach to Diffusive Grain-Surface Chemistry: The H, O, CO System. Astron. Astrophys. 391, 1069–1080. doi:10.1051/0004-6361:20020838

CrossRef Full Text | Google Scholar

Tennis, J., Loison, J.-C., and Herbst, E. (2021). Radiative Association between Neutral Radicals in the Interstellar Medium: CH₃ + CH₃O. Submitted Astrophys. J. [in press].

Google Scholar

Theulé, P. (2020). “Chemical Dynamics in Interstellar Ice, Laboratory Astrophysics: from Observations to Interpretation,” in IAU Symposium 350. Editors F. Salama, and H. Linnartz. doi:10.1017/S1743921319008342

CrossRef Full Text | Google Scholar

Theulé, P., Duvernay, F., Danger, G., Borget, F., Bossa, J. B., Vinogradoff, V., et al. (2013). Thermal Reactions in Interstellar Ice: A Step towards Molecular Complexity in the Interstellar Medium. Adv. Space Res. 52, 1567–1579. doi:10.1016/j.asr.2013.06.034

CrossRef Full Text | Google Scholar

Tielens, A. G. G. M. (2005). The Physics and Chemistry of the Interstellar Medium. Cambridge, UK: Cambridge University Press.

Google Scholar

Tielens, A. G. G. M., and Hagen, W. (1982). Model Calculations of the Molecular Composition of Interstellar Grain Mantles. Astron. Astrophys. 114, 245–260.

Google Scholar

Tomosada, A. E., Kim, S., Osamura, Y., Yang, S. W., Chang, A. H. H., and Kaiser, R. I. (2012). First Detection of the Silylgermylene (H3SiGeH) and D4-Silylgermylene (D3SiGeD) Molecules in Low Temperature Silane-Germane Ices. Chem. Phys. 409, 49–60. doi:10.1016/j.chemphys.2012.10.002

CrossRef Full Text | Google Scholar

Townes, C. H., and Schawlow, A. L. (1955). Microwave Spectroscopy. McGraw-Hill, New York: Kindle edition. Available at: https://store.doverpublications.com/0486162311.html.

Google Scholar

Vasyunin, A. I., Semenov, D. A., Wiebe, D. S., and Henning, T. (2009). A Unified Monte Carlo Treatment of Gas-Grain Chemistry for Large Reaction Networks. I. Testing Validity of Rate Equations in Molecular Clouds. Astrophys. J. 691, 1459–1469. doi:10.1088/0004-637X/691/2/1459

CrossRef Full Text | Google Scholar

Vuitton, V., Yelle, R. V., Lavvas, P., and Klippenstein, S. J. (2012). Rapid Association Reactions at Low Pressure: Impact on the Formation of Hydrocarbons on Titan. Astrophys. J. 744, 11. doi:10.1088/0004-637X/744/1/11

CrossRef Full Text | Google Scholar

Wakelam, V., Bron, E., Cazaux, S., Dulieu, F., Gry, C., Guillard, P., et al. (2017). H₂ Formation on Interstellar Dust Grains: The Viewpoints of Theory, Experiments, Models and Observations. Mol. Astrophysics 9, 1–36. doi:10.1016/j.molap.2017.11.001

CrossRef Full Text | Google Scholar

Wakelam, V., Dartois, E., Chabot, M., Spezzano, S., Navarro-Almaida, D., Loison, J.-C., et al. (2021). Efficiency of Non-thermal Desorptions in Cold-Core Conditions. Astron. Astrophys 652, A63. doi:10.1051/0004-6361/202039855

CrossRef Full Text | Google Scholar

Wakelam, V., Loison, J.-C., Herbst, E., Pavone, B., Bergeat, A., Béroff, K., et al. (2015). The 2014 Kida Network for Interstellar Chemistry. Astrophys. J. Suppl. Ser. 217, 20. doi:10.1088/0067-0049/217/2/20

CrossRef Full Text | Google Scholar

Watanabe, N., and Kouchi, A. (2002). Efficient Formation of Formaldehyde and Methanol by the Addition of Hydrogen Atoms to CO in H₂O-CO Ice at 10 K. Astrophys. J. 571, L173–L176. doi:10.1086/341412

CrossRef Full Text | Google Scholar

Watson, W. D., and Salpeter, E. E. (1972a). Molecule Formation on Interstellar Grains. Astrophys. J. 174, 321–340. doi:10.1086/151492

CrossRef Full Text | Google Scholar

Watson, W. D., and Salpeter, E. E. (1972b). On the Abundances of Interstellar Molecules. Astrophys. J. 175, 659–672. doi:10.1086/151587

CrossRef Full Text | Google Scholar

Willis, E. R., and Garrod, R. T. (2017). Kinetic Monte Carlo Simulations of the Grain-Surface Back-Diffusion Effect. Astrophys. J. 840, 61. doi:10.3847/1538-4357/aa6ea7

CrossRef Full Text | Google Scholar

Wilson, E. B., Decius, J. C., and Cross, P. C. (1980). Molecular Vibrations. The Theory of Infrared and Raman Vibrational Spectra. Mineola, NY, USA: Dover Publications.

Google Scholar

Woon, D. E. (2021). The Astrochymist. Available at: http://www.astrochymist.org/.

Google Scholar

Yuan, C., Cooke, I. R., and Yates, J. T. (2014). A New Source of CO₂ in the Universe: a Photoactivated Eley-Rideal Surface Reaction on Water Ices. Astrophys. J. 791, L21. doi:10.1088/2041-8205/791/2/L21

CrossRef Full Text | Google Scholar

Zajfman, D., Schwalm, D., and Wolf, A. (2003). Molecular Physics in Storage Rings: From Laboratory to Space. Hyperfine Interactions 146/147, 265–268. doi:10.1023/b:hype.0000004250.68609.53

CrossRef Full Text | Google Scholar

Zanchet, A., Godard, B., Bulut, N., Roncero, O., Halvick, P., and Cernicharo, J. (2013). H₂(v= 0,1) + C⁺(²P) ---> H + CH⁺ State-To-State Rate Constants for Chemical Pumping Models in Astrophysical Media. Astrophys. J. 80, 766. doi:10.1088/0004-637X/766/2/80

CrossRef Full Text | Google Scholar