- Faculty of Physics, University of Tabriz, Tabriz, Iran
By using 2.5-dimensional resistive MHD simulations, dynamics of the plasmoid instability in a Harris current sheet has been studied with taking into account two main controlling parameters: the plasma-β in the range (0 < β < 1) and the amplitude ratio of magnetic guide field to the reconnection plane field in three different cases with zero, uniform, and non-uniform guide field. Varying the plasma-β changes the plasma compressibility which affects significantly on the linear and nonlinear growth rates of the plasmoid instability. For each of three cases, some associated scaling relations between the instability growth rate, the plasma-β and the magnitude of guide field are obtained.
1 Introduction
Magnetic reconnection is a fundamental phenomenon in highly conductive magnetized plasmas such as space and astrophysical plasmas in which the magnetic energy is abruptly released and converted to the heating and kinetic energies as well as the acceleration of particles. Magnetic reconnection takes place in narrow regions where the frozen-in-flow constraint breaks down. As a result the field lines cut and reconnect to each other continuously and the large scale topology of magnetic field lines changes significantly (Birn and Priest, 2007; Yamada et al., 2010; Priest and Forbes, 2000; Gonzalez and Parker 2016).
The initial steady-state classical models of the magnetic reconnection process were discussed in MHD framework in two-dimensional by Sweet-Parker and Petschek models. In high Lundquist numbers, S = LvA/η (L is the system size,
Numerical simulation of the magnetic reconnection event plays a crucial role in the conception of plasmoid instability dynamics and what happens inside the current sheets. Hence, in the last decade, the study of numerical simulation of the plasmoid instability was interested (Huang and Bhattacharjee, 2013; Loureiro and Uzdensky, 2015). Some of these studies are MHD simulation in two (Yu et al., 2010; Murphy 2010; Bárta et al., 2008) and three dimensions (Ugai 2008; MacTaggart and Fletcher, 2019). These simulations have uncovered some new aspects of the non-linear evolution of magnetic reconnection and plasmoid instability. In addition, the plasmoid instability has also been observed and discussed in many kinetic simulations (Stanier et al., 2019; Daughton and Karimabadi, 2007) and also there is tentative observational evidence (Bemporad 2008) that plasmoid might play a key role in the dynamics of magnetic reconnection. Theoretically, plasmoid formation has been proposed as a mechanism of fast reconnection (Lapenta 2008; Daughton et al., 2006) and non-thermal particle acceleration in reconnection related events (Drake et al., 2006).
In MHD numerical simulations, some physical parameters play a major role in the dynamics of plasmoid instability and magnetic reconnection. Some publications have considered the effects of some main parameters on the plasmoid instability such as plasma viscosity (Comisso, et al., 2015; Comisso and Grasso, 2016), asymmetric magnetic field (Murphy et al., 2013), shear flow (Hosseinpour et al., 2018) and non-uniform plasma mass density in two sides of the current layer (Doss et al., 2015; Birn et al., 2008). Besides, magnetic and plasma pressure play important roles in MHD studies. The ratio of plasma pressure to the magnetic pressure is described by the plasma-β(≡ pplasma/pmag). This parameter in the upstream region is a key parameter in the reconnection dynamics and might vary from β > 1 in the photosphere at the base of the field line to β ≪ 1 in the mid-corona (Gary 2001).
In many of the researches on the plasmoid instability, the plasma-β effect has been ignored (Hosseinpour et al., 2018; Dong et al., 2018; Huang et al., 2017) and it is usually considered a constant and large. Hence, the β effect is not clear yet on the plasmoid dynamics. So, it is important to understand the physics of the plasmoid instability with various β values. The β effect not only shows itself in the linear phase of the instability but also in the nonlinear phase. The Lundquist number depends on the β and in the linear stage is proportional to β as S ∝ β−1/2.
Ni et al. (2012) and Baty (2014) with considering Harris current sheet configuration investigated the effect of plasma-β on the critical Lundquist number, Sc, for the onset of the plasmoid instability. In an initially uniform temperature configuration, Ni et al. (2012) concluded that the critical Lundquist number is strongly dependent on the plasma-β and claimed that the Sc varies between 104 for β = 0.2 and 2000 for β = 50. Also, Baty (2014) with changing plasma resistivity (η), investigated the effect of varying plasma-β (0.2–15) and the equilibrium structure (uniform temperature or uniform density) on the plasmoid instability in a Sweet-Parker like layer. They found that the critical Lundquist number depends on the β, and indicated that for higher β, the critical Lundquist number is smaller. Also, the simulation results of Ni et al. (2012) showed that the reconnection rate for larger β is higher than smaller β, and the current sheet becomes turbulent earlier in larger β. To reach this conclusion they usedβ = 0.2, 1, 5, 50. Recently Zenitani and Miyoshi (2020) investigated the properties of plasmoid instability for β = 0.2, 1, 5. They showed that the reconnection rate increases as β decreases.
Many physical systems observed in laboratory experiments, space and astrophysical plasmas can be modeled as a simple current sheet with a magnetic field reversal (Harris sheet). A current sheet in the solar corona is one of the few concrete examples of solar applications where force-free state is possible, which is not necessary the case in other applications. However, often additional component of the magnetic field need to be considered. In the Earth’s magnetopause, there is an out-of-plane magnetic field (referred to as guide field) of strength comparable to the lobe field on either side of the Harris sheet. The magnetic reconnection in the presence of a guide field is an important issue in magnetospheric physics. In astrophysical systems, such as jets from acceleration disk, the magnetic field is believed to be primarily aligned with the current and can be represented by Harris sheet with a very strong guide field much larger than the reconnection plane field. Additionally, in magnetic confinement fusion devices, reconnection develops in the presence of strong toroidal fields and the configuration can be represented by a Harris sheet in the poloidal plane with a strong guide field in the toroidal direction.
The presence of guide field has been shown to be important for particle acceleration issue (Zenitani and Hoshino, 2008; Hamilton et al., 2003; Li and Lin, 2012) and also is widely considered in kinetic simulations (Inoue et al., 2015; Fu et al., 2007; Huang et al., 2011), which have shown that the strength of the guide field controls the growth of secondary magnetic islands and can evidently alter not only the trajectory of the particles but also the structure of the electric and velocity fields in the vicinity of the reconnection region. These simulations showed that the reconnection rate decreases with the guide field. The dependence of Hall mediated magnetic reconnection dynamics on the guide field is also investigated (Yang et al., 2008; Huba 2005), and found that the reconnection rate and plasma energization are reduced by increasing the guide field strength. In the MHD scale, the guide field effect on the plasmoid instability is very different from the results of the kinetic simulations (Ni et al., 2013). However, in 3D MHD simulations it has been shown that the guide field makes the reconnected field lines, as well as the jet, inclined from the current sheet normal direction, and also the guide field acts as an obstacle to the jet formation (Huang and Bhattacharjee, 2016; Hashimoto et al., 2005).
In spite of many related simulation works, there are still some unambiguities regarding the detailed effects of the plasma-β and the guide field on the plasmoid instability. Therefore, in this work, we investigate the effect of plasma-β in the range (β ≤ 1) with and without a guide field on the dynamics of plasmoid instability. Three different cases are considered: A: with a zero guide field, B: with uniform guide field and C: with non-uniform guide field. It should be mentioned that the effect of plasma viscosity is ignored in our study by ignoring the respective term in MHD equations. The effect of plasma viscosity on the dynamics of plasmoid instability has already been discussed in detail by Comisso, et al., 2015, Comisso and Grasso, 2016. They have shown that plasma viscosity has the effect of decreasing the linear growth rate and the wavenumber of the instability. However, despite its damping effect, for very high Lundquist numbers the plasmoid instability turns out to be very rapid in the linear regime. The initial temperature is assumed to be uniform. Therefore, the initial plasma density and pressure are strongly dependent on the plasma-β. The paper is organized as follows. In Section 2, the basic MHD equations, numerical setup, and initial condition are described. In Section 3, numerical results are presented. A summary and a short discussion of the results are then given in Section 4.
2 Equations and Numerical Model
The compressible single-fluid resistive MHD equations are solved by using the OpenMHD code being developed by Zenitani (2016) to investigate the dynamics of the plasmoid instability in 2.5-dimensional cartesian coordinate system. The basic equations are
which are written in conservation-law form. Here, ρ, V, B, I, j, η are the plasma mass density, the flow velocity, the magnetic field, the unitary tensor, the electric current density and the magnetic diffusivity, respectively. The ptot = p + B2/2 is total pressure and ϵ = p/(Γ − 1) + ρv2/2 + B2/2 is total energy density. For the convenience of numerical calculations, all variables are normalized. For this purpose, the plasma mass density is normalized to the initial plasma mass density (ρ0), the magnetic field to the initial magnetic field (B0), the flow velocity to the Alfvén velocity (VA), the electric current density to L0B0/μ0 and resistivity to L0vA. Note that, L0 is the length scale of the system and all spatial variables are normalized to L0. We set the adiabatic index Γ = 5/3. All variables are function of space (x, y) and time (t) and the variation of variables in the z-direction is ignored, ∂/∂z = 0. Equations 1–5, are solved by a Godunov-type code. The code employs the HLLD scheme (Miyoshi and Kusano, 2005) to calculate numerical fluxes. The second-order Runge-Kutta method is used for time marching. Also, the hyperbolic divergence cleaning method (∇.B = 0) is employed for the solenoidal condition (Dedner et al., 2002). Moreover, the time step is based on convective and diffusive CFL condition. Our simulations are carried out in the x − y plane. The size of simulation box is set to be x = [ − 90, 90] and y = [ − 9, 9]. The number of grid points are Nx = 3,000 and Ny = 300 so that the grid sizes are Δx = 2Lx/Nx = 0.06, Δy = 2Ly/Ny = 0.06. We set open boundary condition at x = ±Lx direction, so that the reconnected field lines can leave boundaries freely. On the other hand, conducting boundary condition is considered for the bottom y = − Ly and top y = + Ly boundaries.
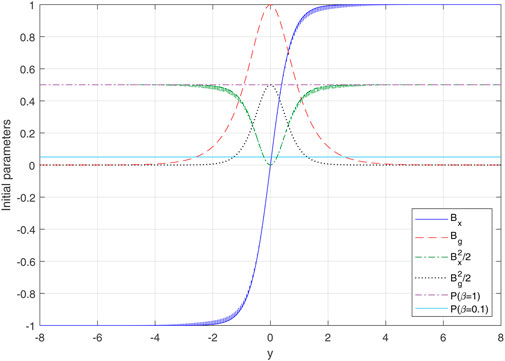
An initial Harris current sheet is used in the form (B = [Bx, 0, Bz]):
where B0 = 1.0 is initial asymptotic magnetic field strength and aB = 0.7 is the half width of the current sheet in the initial geometry. Bg is the guide field that is perpendicular to the reconnection plane. Initial plasma velocity is zero.
The initial static pressure, P, is obtained by solving the equilibrium equation and is given by:
Assuming the isothermal equation of state (P = 2ρT) and solving the above Equation 7, the initial plasma mass density is satisfied as follows:
The initial plasma pressure (Eq. 7) and plasma density (Eq. 8) depend on the plasma-
3 Simulation Results
In this section, we discuss three different cases: A: instability with a zero guide field (Bg = 0) where the effect of plasma-β in the range (0.1 ≤ β ≤ 1) is addressed. B: instability with a uniform guide field where Bg = 0.1, 0.3, 0.5B0 and β = 0.4, 1.0 is assumed. C: instability with the non-uniform guide field with β = 0.1, … , 1.0.
3.1 Instability With Zero Guide Field (Bg = 0)
In the first step, we consider the case without the presence of any guide field and discuss the growth of plasmoid instability with different values of plasma-β. The subsequent variation of main plasma parameters in the inflow region, such as (p, ρ, vA, S) with plasma-β is shown in Table 1. For all cases in Table 1, the Lundquist number is larger than the critical value (S > Sc), so the plasmoid instability is expected to be triggered in the current sheet.
We diagnose the magnetic reconnection rate during plasmoid instability with taking the average of the electric field component perpendicular to the reconnection plane, Ez, on the y = 0 line:
Where ψ is the reconnected flux function defined by B =
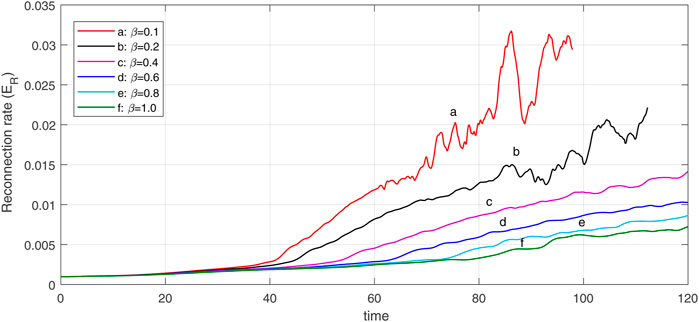
For smaller β cases (β = 0.1, 0.2) where the system transits faster into the non-linear phase, we find that the fast reconnection evolution becomes more drastic. To better understand the growth of plasmoid instability in the current layer, we consider a case that includes linear, transition, and non-linear phases, i.e. β = 0.2 (case b in Figure 1). Figure 2 shows the contour plots of the magnetic field lines at different phases according to plot b in Figure 1. From Figure 2 we can see that how the primary current sheet becomes unstable to plasmoid instability which is eventually filled with multiple X-points and O-points.
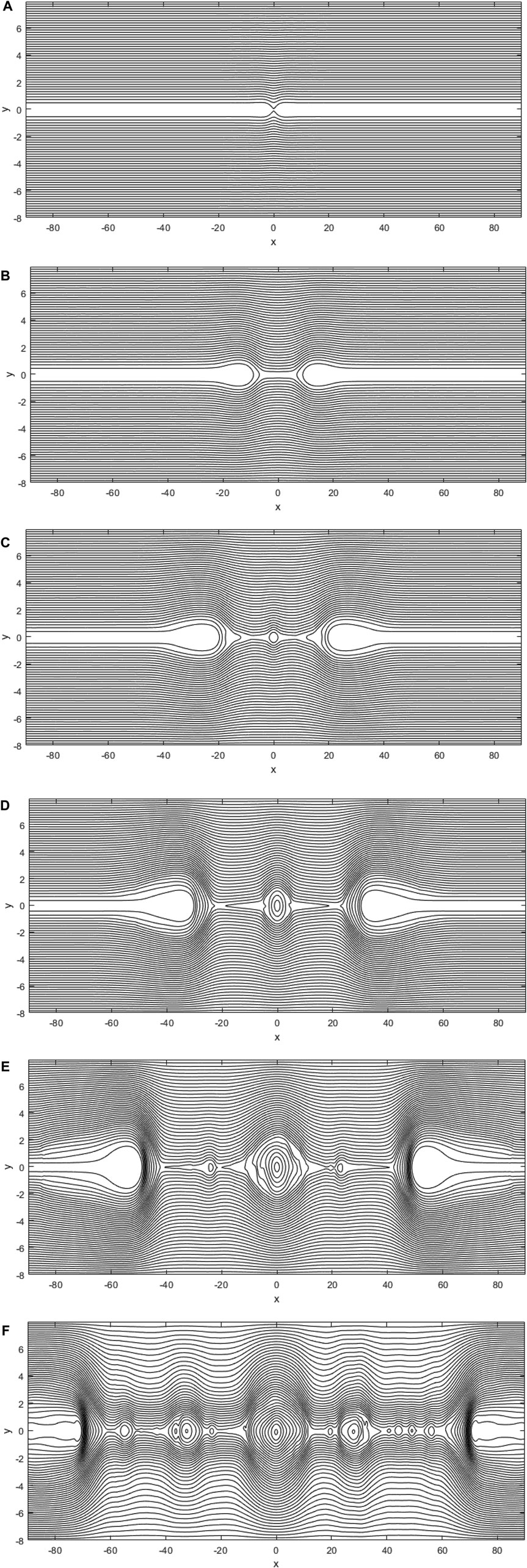
FIGURE 2. Magnetic field lines at different times of plasmoid instability for β = 0.2. (A): t = 5, (B): t = 30, (C): t = 50, (D): t = 65 and (E): t = 85, (F): t = 105.
Figures 2A,B are plotted in the linear phase. The initial X-point of Figure 2A is transformed into an elongated Sweet-Parker current sheet, while Figure 2C (at time t = 45) represents the transition state to the non-linear stage. New X-points are formed around the original O-point and in continue a small magnetic island, which its size is small compared to the width of current sheet (aB = 0.7) grows (Figure 2D). Figure 2E represents the field lines in the non-linear regime. Following the transition into the non-linear phase at t > 60 (for β = 0.2) the secondary magnetic islands are generated. As a result, they merge and form a larger magnetic island. As the merging of magnetic islands continues, a large size plasmoid, named “monster plasmoid”, can be produced whose size even exceeds the scale length of magnetic shear. Note that, inside plasmoid, high density and so high-pressure plasma is enclosed.
We now discuss the effect of different values of β on the dynamics of plasmoid instability by using contour plots of magnetic field lines. These contour plots are coordinate with the reconnection rate plots in Figure 1. Figure 3 shows the magnetic field lines for different values of β at the same time, t = 95. Figures 3A,B correspond to β = 0.1 and 0.2 show that the secondary magnetic islands form inside the current sheet and so the plasmoid instability developed at there. Since the β is low in these cases, the small plasma compressibility leads to increased reconnection rate, and thus the current sheet becomes unstable. The oscillations of reconnection rate decrease as β increases in the nonlinear phase. Each peak in the reconnection rate plot is related to the generation of new X-points where the dissipation of magnetic energy is significant. As the plasma-β increases the plasmoid instability growth rate decreases and the plasmoid generation turns out to be slower. This point can be seen from the size of the monster plasmoid in different panels of Figure 3. According to Figure 3, we see that in cases with smaller β, the magnetic field lines are piled up around the outflow regions. Therefore, the plasma outflow jets are ejected more rapidly due to the high pressure behind the plasma outflow jet, inside the islands.
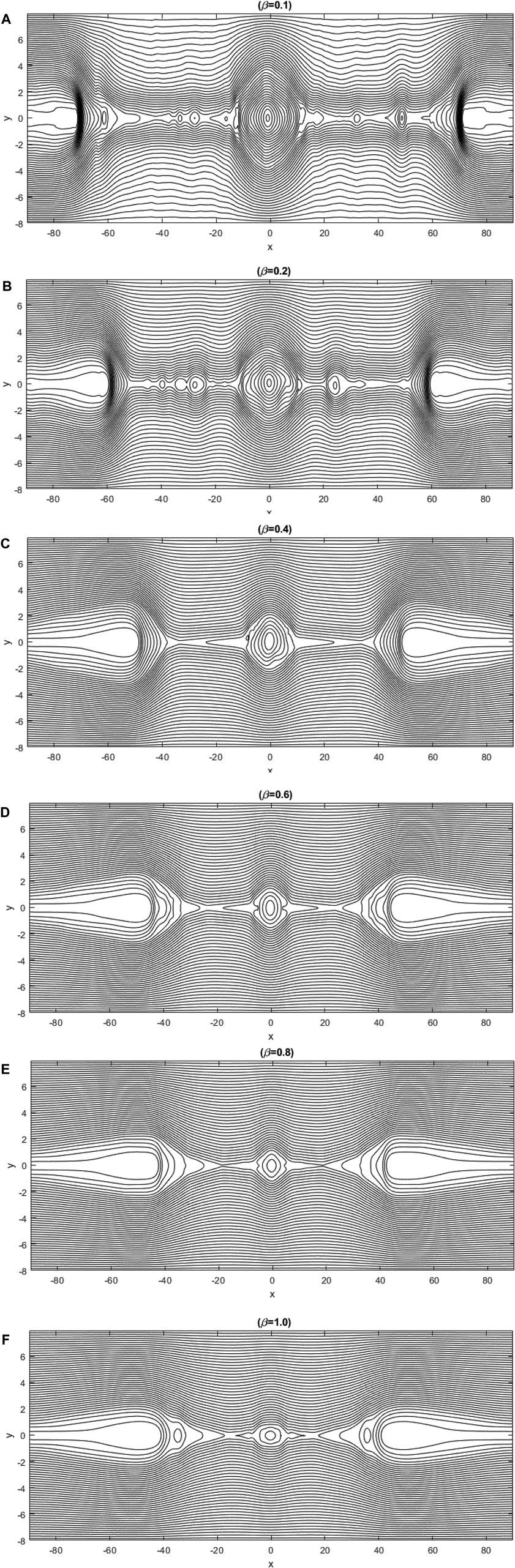
FIGURE 3. Magnetic field lines for different values of beta at t = 95 for (A): β = 0.1, (B): β = 0.2, (C): β = 0.4, (D): β = 0.6, (E): β = 0.8 and (F)β = 1.0.
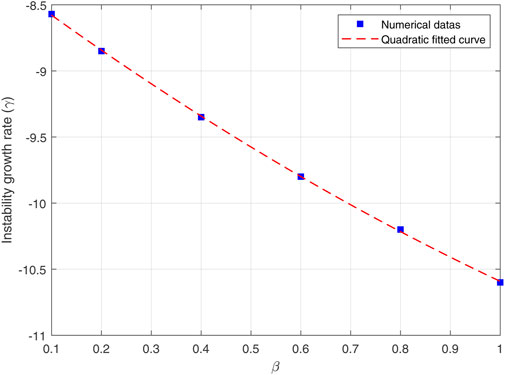
Figure 4 shows the variations of the logarithmic average of reconnection rate
where the coefficients are a = 0.51, b = − 2.74 and c = − 12.14. As a result, it can be seen that in plasmas with lower compressibility (a case with the higher β), the plasmoid instability growth rate also decreases following a reduction in the reconnection rate. Also, at the longer times (when the primary magnetic island grows), the growth rate of instability decreases faster.
3.2 Instability With Uniform Guide Field
In this section, we consider the presence of the uniform guide field and discuss the effect of this magnetic field on the dynamics of plasmoid instability. Different values of uniform guide field assumed in our study: Bz = Bg = 0.1, 0.3, 0.5B0. Due to the dependence of the initial plasma pressure to the guide field in our model (Eq. 7), plasma pressure decreases in the current sheet and upstream region with increasing the magnitude of the guide field. For a better understanding of the uniform guide field effect on the physical parameters, we consider β = 0.4, 1.0 in Table 2. In all of cases shown in Table 2, according to Eq. 7, and Eq. 8, increasing the magnitude of the guide field leads to increase in the Alfvén velocity and the Lundquist number. Therefore, it is expected that as the Lundquist number increases, the magnetic reconnection rate will increase. Figure 5 shows the magnetic reconnection rate for β = 0.4 with different values of the guide field. In a weak guide field (Bg = 0.1B0), the system behaves similar to the case of zero guide field (Bg = 0), but in the medium one the rate of magnetic reconnection increases, and for Bg = 0.5B0 the nonlinear stage appears faster, which means that the plasmoid instability developed and the secondary magnetic islands are formed in the current layer.
For all cases (β = 0.1, 1.0 and Bg = 0.1, 0.3, 0.5B0), the simulations are carried out. The results show that increasing the strength of the uniform guide field not only leads to the rise in the maximum reconnection rate, but also the linear phase of the system becomes shorter. Also, for all cases β > 0.4 and Bg = 0.5B0, although, the Lundquist number is greater than the critical value (S > Sc), the nonlinear phase was not observed, and secondary plasmoids do not form in the current layer, because in high β systems the plasma pressure is high at the center of the current sheet and the plasma behaves like an incompressible plasma which suppresses up to some extent the plasmoid instability.
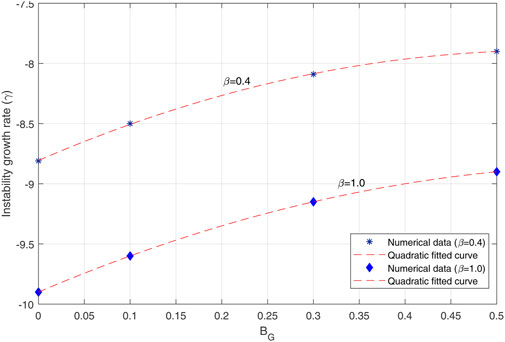
We now present a scaling for the growth rate of instability. Figure 6 shows the effect of the uniform guide field on the growth rate of instability for β = 0.4, 1.0 and Bg = 0, 0.1, 0.3, 0.5B0. Therefore, it can be seen that the presence of a guide field leads to an increase in the growth rate of instability for both β values. The blue stars and the blue diamonds represent the numerical values obtained from the simulations, and the red dashed lines are the quadratic fitted curve as a scaling of the instability growth rate as:
with a = − 3, b = − 0.55, c = − 7.9 for β = 0.4 and a = − 2.5, b = − 0.64, c = − 8.9 for β = 1.0.
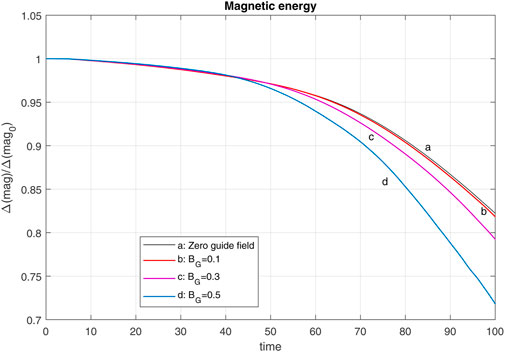
The variation of magnetic energy with uniform and zero guide fields are shown in Figure 7 which is normalized to the initial magnetic energy. As we know, the magnetic reconnection process is a mechanism to convert the stored magnetic energy to plasma kinetic and thermal energies. With an increased reconnection rate by applying the uniform guide field, the conversion of the magnetic energy becomes faster. This point is clear from Figure 7.
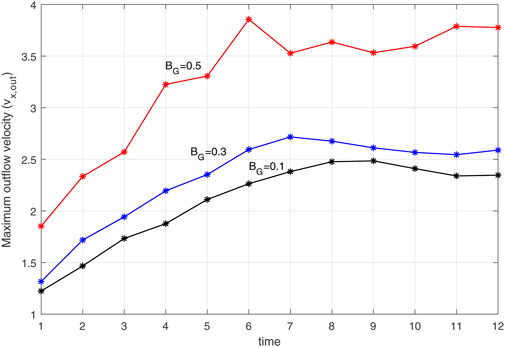
Figure 8 shows the time variation of the maximum outflow velocity at the X-points (Vx,out) in the presence of different values of the uniform guide field. In all three cases of the uniform guide field, the plasma outflow velocity from X-points increases until the system reaches the saturation state. After that, due to the increase of pressure in the outflow regions, the velocity slows down and becomes uniform. In general, as shown in Figure 8, the maximum outflow velocity increases with increasing guide field and around X-points is of the order of the Alfvén velocity.
Now, we are looking to find a scaling relation for variation of the maximum outflow velocity in different values of the guide field. Figure 9 shows the variation of the Vx,out with uniform Bg in our simulations. Plots are considered for two cases. The first case (red squares) is for the maximum outflow velocity between t1 = 65 and t2 = 75, while the second case (blue stars) is the maximum outflow velocity between t2 = 75 and t3 = 85. In both cases, the maximum outflow velocity increases as the uniform guide field increases. The dashed lines in Figure 9 represent the Vx,out scaling with the uniform Bg, which has been obtained from the quadratic fitted curve of the numerical values:
with a = 8.9, b = − 0.13, c = 2.15 for t1 < t < t2 curve and a = 8.7, b = − 0.13, c = 2.3 for t2 < t < t3 curve.
3.3 Instability With the Non-uniform Guide Field
Now, we discuss the effect of non-uniform guide field. Note that the general structure of three components of the initial equilibrium of the magnetic field is in the form
As we have described in Section 2, Eq. 7, we obtain the initial plasma pressure as:
Hence, for the case of non-uniform guide field the initial plasma pressure and so the plasma density are uniform everywhere.
The initial profiles of the plasma pressure (p), magnetic pressures
The reconnection rate plots are shows in the presence of the non-uniform guide field for different β in Figure 11. As seen, similar to the previous cases, the reconnection rate decreases by increasing the plasm-β. The presence of a non-uniform guide field makes much shorter the linear phase of the instability compared to previous cases (with zero and uniform guide field) for all β cases. Therefore, the instability rapidly enters the transition phase, and the initial plasmoid is generated and grows in the center of the current sheet. Unlike the previous cases, when a non-uniform guide field is added to the reconnection plane, the system cannot enter the nonlinear phase due to the increased magnetic pressure caused by the guide field in the center of the current layer, except β = 0.1 case, so secondary magnetic islands do not form in the current layer. Over time, the primary plasmoid grows, and when the width of the primary plasmoid is much larger than the width of the current layer, the system becomes saturated, and then the reconnection rates decrease.
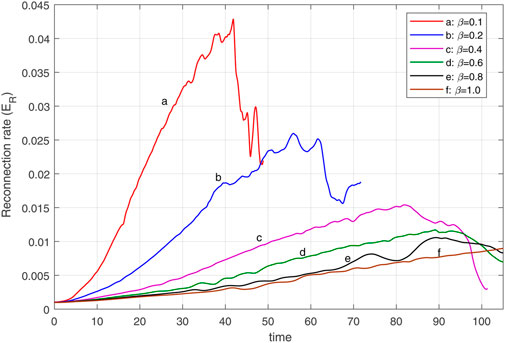
FIGURE 11. Time variation of magnetic reconnection for different values of β in presence of non-uniform guide field.
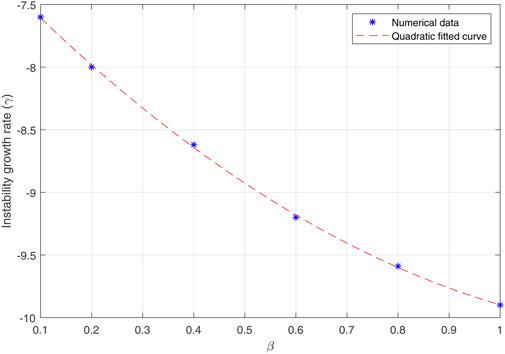
Figure 12 shows the linear growth rate of the plasmoid instability with β with a non-uniform guide field. As expected, the growth rate of the instability decreases as β increases. By comparing this case with the case A (without the guide field), we find that due to the presence of the non-uniform guide field, the decreasing slope of the linear instability growth rate is sharper. From the numerical values obtained in this simulation (blue stars) and quadratic fitted curve (red dashed line) in Figure 12, we can calculate the scaling of the linear growth rate as:
where the coefficients are a = 1.5, b = − 1.4 and c = − 10.14. The coefficient a in the quadratic equations expresses the slope of the parabolic graph, and its sign is related to its direction. According to the scaling equations for the instability growth rate in cases A and C, this coefficient increases with the presence of the guide field. Also, in case B, the presence of the medium guide field has led to an increase in this coefficient.
4 Summary and Conclusion
In this study, the plasma-β effect in the range of β(= 0.1, 0.2, 0.4, 0.6, 0.8, 1.0) is investigated on the dynamics of plasmoid instability as a fundamental parameter in the magnetic reconnection with and without guide field. We used 2.5-dimensional MHD simulations and considered a standard Harris current sheet profile to establish an initial equilibrium. We added a magnetic field component perpendicular to the reconnection plane (so-called “guide field”) to the standard Harris current sheet. Three different cases was considered: case A: instability with zero guide field, case B: instability with the uniform guide field (Bg = 0.1, 0.3, 0.5B0) and case C: instability with the non-uniform guide field
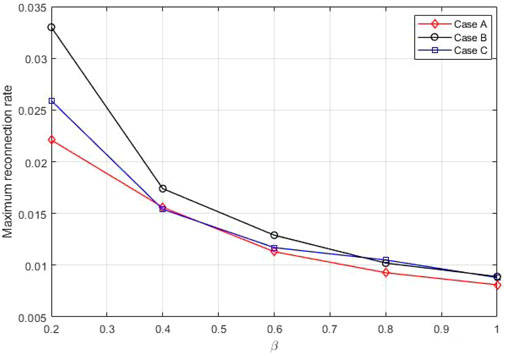
The simulation results can be listed as follows: 1. From case A, we found that the plasma-β leads to change in reconnection rate and growth rate of the plasmoid instability by affecting the plasma compressibility. Plasma compressibility decreases with increasing β, so the reconnection rate slows down, and the linear phase of the system becomes longer, which means a longer time is needed to achieve instability. For β > 0.2 cases, in which the Lundquist number is greater than the critical value (S > Sc), the nonlinear stage is not observed, and secondary magnetic islands do not form. Also, the growth rate of instability (Eq. 10) decreases with increasing β. 2. By adding the uniform guide field (Bg = 0.1, 0.3, 0.5B0) (case B), we saw that the weak guide field (0.1B0) does not much affect on the reconnection process, but for the larger guide fields (0.3B0 and 0.5B0) the reconnection rate increases and the system becomes unstable faster. In particular, for the β = 0.4 case, the medium guide filed (0.5B0) was investigated in detail. Comparing this case with the case of zero guide field showed that in the presence of the guide field the reconnection rate increases, and the system reaches the nonlinear phase, so the secondary magnetic islands are generated. For β > 0.4 cases, although the Lundquist number is larger than the critical value, but due to the significant flow incompressibility, the nonlinear stage is not observed at time scales on the order of previous cases. Moreover, according to Figure 8, by comparing the maximum outflow velocity (Vx,out), we found that Vx,out increases with increasing the uniform guide field, and we obtained the respective scalings. In the last case (case C), the non-uniform guide field was added. This guide field leads to a constant pressure and density everywhere. The magnetic pressure due to the guide field in the current sheet is an obstacle to the reconnection process. However, the linear stage for all β cases is very shorter than the cases of A and B, so the primary plasmoid in the center of the current sheet grows rapidly. In this state, the system cannot enter the non-linear phase and the secondary magnetic islands do not form. The reconnection rate decreases with increasing β in all cases. The presence of the uniform guide field has more impact on the reconnection rate than a non-uniform guide field. In cases B and C for β > 0.6, the reconnection rate shows almost equality, and for β < 0.4 cases the guide field has a more effect on the reconnection process (see Figure 13).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
HL: Doing the numerical simulations, visualizing the data and preliminary writing. MH: Analyzing the data and writing and revising some part of manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.768965/full#supplementary-material
References
Bárta, M., Vršnak, B., and Karlický, M. (2008). Dynamics of Plasmoids Formed by the Current Sheet Tearing. Astron. Astrophysics 477, 649–655. doi:10.1051/0004-6361:20078266
Baty, H. (2014). Effect of Plasma-β on the Onset of Plasmoid Instability in Sweet-Parker Current Sheets. J. Plasma Phys. 80, 655–665. doi:10.1017/s0022377814000208
Bemporad, A. (2008). Spectroscopic Detection of Turbulence in Post‐CME Current Sheets. Astrophysical J. 689, 572–584. doi:10.1086/592377
Bhattacharjee, A., Huang, Y.-M., Yang, H., and Rogers, B. (2009). Fast Reconnection in High-Lundquist-Number Plasmas Due to the Plasmoid Instability. Phys. Plasmas 16, 112102. doi:10.1063/1.3264103
Birn, J., and Priest, E. (2007). Reconnection of Magnetic Fields: Magnetohydrodynamic and Collisionless Theory and Observations. Cambridge, United Kingdom: Cambridge Univ. Press.
Birn, J., Borovsky, J. E., and Hesse, M. (2008). Properties of Asymmetric Magnetic Reconnection. Phys. Plasmas 15, 032101. doi:10.1063/1.2888491
Biskamp, D. (1986). Magnetic Reconnection via Current Sheets. Phys. Fluids 29, 1520–1531. doi:10.1063/1.865670
Comisso, L., and Grasso, D. (2016). Visco-Resistive Plasmoid Instability. Phys. Plasmas 23, 032111. doi:10.1063/1.4942940
Comisso, L., Grasso, D., and Waelbroeck, F. L. (2015). Extended Theory of the Taylor Problem in the Plasmoid-Unstable Regime. Phys. Plasmas 22, 042109. doi:10.1063/1.4918331
Comisso, L., Lingam, M., Huang, Y.-M., and Bhattacharjee, A. (2016). General Theory of the Plasmoid Instability. Phys. Plasmas 23, 100702. doi:10.1063/1.4964481
Comisso, L., Lingam, M., Huang, Y.-M., and Bhattacharjee, A. (2017). Plasmoid Instability in Forming Current Sheets. Astrophys. J. 850, 142. doi:10.3847/1538-4357/aa9789
Daughton, W., and Karimabadi, H. (2007). Collisionless Magnetic Reconnection in Large-Scale Electron-Positron Plasmas. Phys. Plasmas 14, 072303. doi:10.1063/1.2749494
Daughton, W., Scudder, J., and Karimabadi, H. (2006). Fully Kinetic Simulations of Undriven Magnetic Reconnection with Open Boundary Conditions. Phys. Plasmas 13, 072101. doi:10.1063/1.2218817
Dedner, A., Kemm, F., Kröner, D., Munz, C.-D., Schnitzer, T., and Wesenberg, M. (2002). Hyperbolic Divergence Cleaning for the MHD Equations. J. Comput. Phys. 175, 645–673. doi:10.1006/jcph.2001.6961
Dong, C., Wang, L., Huang, Y.-M., Comisso, L., and Bhattacharjee, A. (2018). Role of the Plasmoid Instability in Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 121, 165101. doi:10.1103/physrevlett.121.165101
Doss, C. E., Komar, C. M., Cassak, P. A., Wilder, F. D., Eriksson, S., and Drake, J. F. (2015). Asymmetric Magnetic Reconnection with a Flow Shear and Applications to the Magnetopause. J. Geophys. Res. Space Phys. 120, 7748–7763. doi:10.1002/2015ja021489
Drake, J. F., Swisdak, M., Schoeffler, K. M., Rogers, B. N., and Kobayashi, S. (2006). Formation of Secondary Islands during Magnetic Reconnection. Geophys. Res. Lett. 33, L13105. doi:10.1029/2006gl025957
Fu, X.-r., Guo, J., and Wang, S. (2007). Collisionless Magnetic Reconnection in the Presence of Initial Guide Field. Chin. Astron. Astrophysics 31, 117–127. doi:10.1016/j.chinastron.2007.03.002
Gary, G. A. (2001). Plasma Beta above a Solar Active Region: Rethinking the Paradigm. Solar Phys. 203, 71–86. doi:10.1023/a:1012722021820
Gonzalez, W., and Parker, E. (2016). Magnetic Reconnection Concepts and Applications. Cham, Switzerland: Springer.
Hamilton, B., McClements, K. G., Fletcher, L., and Thyagaraja, A. (2003). Field Guided Proton Acceleration at Reconnecting X-Points in Flares. Solar Phys. 214, 339–352. doi:10.1023/a:1024204928413
Hashimoto, C., TanDokoro, R., and Pujimoto, M. (2005). “Effects of Guide Field in Three-Dimensional Magnetic Reconnection,” in Frontiers in Magnetospheric Plasma Physics, COSPAR Colloq Ser. Editors M. Hoshino, Y. Omura, and L. J. Lanzerotti (New York: Elsevier), 16, 130–134. doi:10.1016/s0964-2749(05)80020-4
Hosseinpour, M., Chen, Y., and Zenitani, S. (2018). On the Effect of Parallel Shear Flow on the Plasmoid Instability. Phys. Plasmas 25, 102117. doi:10.1063/1.5061818
Huang, Y.-M., and Bhattacharjee, A. (2010). Scaling Laws of Resistive Magnetohydrodynamic Reconnection in the High-Lundquist-Number, Plasmoid-Unstable Regime. Phys. Plasmas 17, 062104. doi:10.1063/1.3420208
Huang, Y.-M., and Bhattacharjee, A. (2013). Plasmoid Instability in High-Lundquist-Number Magnetic Reconnection. Phys. Plasmas 20, 055702. doi:10.1063/1.4802941
Huang, Y.-M., and Bhattacharjee, A. (2016). Turbulent Magnetohydrodynamic Reconnection Mediated by the Plasmoid Instability. ApJ 818, 20. doi:10.3847/0004-637x/818/1/20
Huang, C., Lu, Q., Yang, Z., Wu, M., Dong, Q., and Wang, S. (2011). The Evolution of Electron Current Sheet and Formation of Secondary Islands in Guide Field Reconnection. Nonlin. Process. Geophys. 18, 727–733. doi:10.5194/npg-18-727-2011
Huang, Y.-M., Comisso, L., and Bhattacharjee, A. (2017). Plasmoid Instability in Evolving Current Sheets and Onset of Fast Reconnection. ApJ 849, 75. doi:10.3847/1538-4357/aa906d
Huba, J. D. (2005). Hall Magnetic Reconnection: Guide Field Dependence. Phys. Plasmas 12, 012322. doi:10.1063/1.1834592
Inoue, S., Ono, Y., Tanabe, H., Horiuchi, R., and Cheng, C. Z. (2015). Numerical Study of Energy Conversion Mechanism of Magnetic Reconnection in the Presence of High Guide Field. Nucl. Fusion 55, 083014. doi:10.1088/0029-5515/55/8/083014
Lapenta, G. (2008). Self-feeding Turbulent Magnetic Reconnection on Macroscopic Scales. Phys. Rev. Lett. 100, 235001. doi:10.1103/physrevlett.100.235001
Li, Y., and Lin, J. (2012). Acceleration of Electrons and Protons in Reconnecting Current Sheets Including Single or Multiple X-Points. Sol. Phys. 279, 91–113. doi:10.1007/s11207-012-9956-1
Loureiro, N. F., and Uzdensky, D. A. (2015). Magnetic Reconnection: from the Sweet-Parker Model to Stochastic Plasmoid Chains. Plasma Phys. Control Fusion 58, 014021. doi:10.1088/0741-3335/58/1/014021
MacTaggart, D., and Fletcher, L. (2019). The Plasmoid Instability in a Confined Solar Flare. Monthly Notices R. Astronomical Soc. Lett. 486, L96–L100. doi:10.1093/mnrasl/slz068
Miyoshi, T., and Kusano, K. (2005). A Multi-State HLL Approximate Riemann Solver for Ideal Magnetohydrodynamics. J. Comput. Phys. 208, 315–344. doi:10.1016/j.jcp.2005.02.017
Murphy, N. A., Young, A. K., Shen, C., Lin, J., and Ni, L. (2013). The Plasmoid Instability during Asymmetric Inflow Magnetic Reconnection. Phys. Plasmas 20, 061211. doi:10.1063/1.4811470
Murphy, N. A. (2010). Resistive Magnetohydrodynamic Simulations of X-Line Retreat during Magnetic Reconnection. Phys. Plasmas 17, 112310. doi:10.1063/1.3494570
Ni, L., Ziegler, U., Huang, Y.-M., Lin, J., and Mei, Z. (2012). Effects of Plasmaβon the Plasmoid Instability. Phys. Plasmas 19, 072902. doi:10.1063/1.4736993
Ni, L., Lin, J., and Murphy, N. A. (2013). Effects of the Non-Uniform Initial Environment and the Guide Field on the Plasmoid Instability. Phys. Plasmas 20, 061206. doi:10.1063/1.4811144
Priest, E., and Forbes, T. (2000). Magnetic Reconnection: MHD Theory and Applications. Cambridge, United Kingdom: Cambridge Univ. Press.
Stanier, A., Daughton, W., Le, A., Li, X., and Bird, R. (2019). Influence of 3d Plasmoid Dynamics on the Transition from Collisional to Kinetic Reconnection. Phys. Plasmas 26, 072121. doi:10.1063/1.5100737
Ugai, M. (2008). The Evolution of Fast Reconnection in a Three-Dimensional Current Sheet System. Phys. Plasmas 15, 082306. doi:10.1063/1.2969737
Uzdensky, D. A., Loureiro, N. F., and Schekochihin, A. A. (2010). Fast Magnetic Reconnection in the Plasmoid-Dominated Regime. Phys. Rev. Lett. 105, 235002. doi:10.1103/physrevlett.105.235002
Yamada, M., Kulsrud, R., and Ji, H. (2010). Magnetic Reconnection. Rev. Mod. Phys. 82, 603–664. doi:10.1103/revmodphys.82.603
Yang, H., Jin, S., and Liu, C. (2008). Hall MHD Reconnection with an Initial Guide Field By0. Adv. Space Res. 41, 1649–1657. doi:10.1016/j.asr.2007.09.035
Yu, H. S., Lyu, L. H., and Wu, S. T. (2010). On the Causes of Plasmoid Acceleration and Changes in Magnetic Flux in a Resistive Magnetohydrodynamic Plasma. ApJ 726, 79. doi:10.1088/0004-637x/726/2/79
Zenitani, S., and Hoshino, M. (2008). The Role of the Guide Field in Relativistic Pair Plasma Reconnection. ApJ 677, 530–544. doi:10.1086/528708
Zenitani, S., and Miyoshi, T. (2020). Plasmoid-Dominated Turbulent Reconnection in a Low-β Plasma. ApJ 894, L7. doi:10.3847/2041-8213/ab8b5d
Keywords: resistive plasmoid instability, MHD simulation, magnetic guide field, magnetic reconenction, space plasma
Citation: Lotfi H and Hosseinpour M (2021) Parametric Study of Resistive Plasmoid Instability. Front. Astron. Space Sci. 8:768965. doi: 10.3389/fspas.2021.768965
Received: 01 September 2021; Accepted: 21 September 2021;
Published: 11 October 2021.
Edited by:
Rony Keppens, KU Leuven, BelgiumReviewed by:
Zhixing Mei, Yunnan Observatories, National Astronomical Observatories, CAS, ChinaLuca Comisso, Columbia University, United States
Jordi De Jonghe, KU Leuven, Belgium
Copyright © 2021 Lotfi and Hosseinpour. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mahboub Hosseinpour, aG9zc2VpbnBvdXJAdGFicml6dS5hYy5pcg==
 Hossein Lotfi
Hossein Lotfi Mahboub Hosseinpour
Mahboub Hosseinpour