Denny M. Oliveira1,2*
Eftyhia Zesta2
Piyush M. Mehta3Richard J. Licata3Marcin D. Pilinski4W. Kent Tobiska5Hisashi Hayakawa6,7,8,9- 1Goddard Planetary Heliophysics Institute, University of Maryland, Baltimore County, Baltimore, MD, United States
- 2Geospace Physics Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, United States
- 3Department of Mechanical and Aerospace Engineering, West Virginia University, Morgantown, WV, United States
- 4Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO, United States
- 5Space Environment Technologies, Pacific Palisades, Los Angeles, CA, United States
- 6Institute for Space-Earth Environmental Research, Nagoya University, Nagoya, Japan
- 7Institute for Advanced Research, Nagoya University, Nagoya, Japan
- 8UK Solar System Data Centre, Space Physics and Operations Division, RAL Space, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, United Kingdom
- 9Nishina Center, Riken, Wako, Japan
Satellites, crewed spacecraft and stations in low-Earth orbit (LEO) are very sensitive to atmospheric drag. A satellite’s lifetime and orbital tracking become increasingly inaccurate or uncertain during magnetic storms. Given the planned increase of government and private satellite presence in LEO, the need for accurate density predictions for collision avoidance and lifetime optimization, particularly during extreme events, has become an urgent matter and requires comprehensive international collaboration. Additionally, long-term solar activity models and historical data suggest that solar activity will significantly increase in the following years and decades. In this article, we briefly summarize the main achievements in the research of thermosphere response to extreme magnetic storms occurring particularly after the launching of many satellites with state-of-the-art accelerometers from which high-accuracy density can be determined. We find that the performance of an empirical model with data assimilation is higher than its performance without data assimilation during all extreme storm phases. We discuss how forecasting models can be improved by looking into two directions: first, to the past, by adapting historical extreme storm datasets for density predictions, and second, to the future, by facilitating the assimilation of large-scale thermosphere data sets that will be collected in future events. Therefore, this topic is relevant to the scientific community, government agencies that operate satellites, and the private sector with assets operating in LEO.
Introduction
During magnetic storms, large amounts of magnetospheric energy enters the ionosphere-thermosphere system at high latitudes through field-aligned currents (Prölss, 2011; Emmert, 2015). Since ionospheric currents are intensified, the interaction of the moving plasma with the local neutral gas is enhanced through the collision between ions and neutral molecules, thereby further heating the neutral atmosphere. The atmosphere then expands upwards and satellites flying in higher regions experience increased atmospheric drag forces, which in turn intensify orbital drag effects. These effects ultimately decrease the satellite’s life time and introduce significant errors in orbital tracking which increase as the storm becomes more intense (Doornbos and Klinkrad, 2006; Zesta and Huang, 2016; Nwankwo et al., 2021).
The third satellite in the Sputnik series provided arguably the first observations of storm-induced orbital drag effects. Jacchia (1959) observed a strong decay of Sputnik 1958δ1 due to increased atmospheric drag forces. These pioneer observations led to the creation of many thermospheric empirical models throughout the decades, including the Jacchia (1970) model and subsequent series; the Mass Spectrometer Incoherent Scatter model series developed by Hedin (1987) and later improved by the Naval Research Laboratory to become the Mass Spectrometer Incoherent Scatter Extended model (Picone et al., 2002), and the Drag Temperature Model developed by Bruinsma (2015). In this work, we will discuss results provided by the High Accuracy Satellite Drag Model (HASDM; Storz et al., 2005), and the improved version of the Jacchia model series described by Bowman et al. (2008), henceforth JB2008.
The understanding of the thermosphere response to magnetic storms and the accurate capability of predicting subsequent satellite orbital drag effects is of paramount interest of, e.g., the U.S. Federal Government and the private sector (National Science and Technology Council, 2015a,b; Cakaj, 2021). The correct orbital tracking of low-Earth orbit (LEO) satellites particularly in a time window of 72 h into the storm is of great interest for taking actions such as pre-determined maneuvers as a means to avoid a satellite’s collision with debris in space or even with other satellites (Pardini and Anselmo, 2009; Wang, 2010; Lewis, 2019). Such actions may be characterized as an important tool for preventing the occurrence of the Kessler Syndrome. First introduced by Kessler and Cour-Palais (1978), the Kessler Syndrome suggests that by the dawn of the 22nd century LEO regions will pose high risks for satellite traffic due to the high probability of satellite collisions with significantly increased space debris levels. As we will discuss later, the need for accurate predictions of satellite orbital track during extreme magnetic storms is twofold: 1), the number of satellites in LEO has been and will be significantly increased; and 2), prediction models and historical data suggest solar activity will increase in the next years and decades.
In this paper, we will focus on four major LEO spacecraft missions that carried/carry high-precision accelerometers that can be used to obtain high-quality density data. These satellites are named CHAllenge Mini-satellite Payload (CHAMP; Reigber et al., 2002), Gravity Recovery And Climate Experiment (GRACE; Tapley et al., 2004), Gravity field and steady-state Ocean Circulation Explorer (GOCE; Drinkwater et al., 2003), and Swarm (Siemes et al., 2016). We will then pay particular attention to model performance during the only seven extreme magnetic storms observed by CHAMP and GRACE.
Data and Models
Data
CHAMP was launched in July 2000 at the initial altitude 456 km completing a full orbit around Earth in 90 min with orbit inclination 87.25°. CHAMP completed a longitudinal cycle in ∼130 days. The acceleration measurement precision by CHAMP was 3.0 ×10–8 m/s2 with 0.1 Hz cadence (Bruinsma et al., 2004). CHAMP re-entered in September 2010.
The GRACE mission was composed by two twin satellites, named GRACE-A and -B, that were launched in March 2002. GRACE-B followed GRACE-A within a controlled distance of ∼220 km. Therefore, densities derived by both spacecraft were generally very similar. We then use data from the first spacecraft, hereafter termed GRACE data. The initial altitudes of GRACE were around 500 km. The orbital period of GRACE was 95 min with orbit declination 89.5°. The longitudinal coverage by GRACE was usually completed within ∼160 days. The GRACE acceleration precision and cadence are 10 times higher in comparison to CHAMP (Flury et al., 2008). GRACE re-entered in March 2018.
GOCE was launched in March 2009 at the initial altitude 270 km and orbit inclination 96.5°. The GOCE accelerometer precision was as high as 1.0 × 10–11 m/s2, with measurements being performed within the bandwith 0.005–0.1 Hz (Bruinsma et al., 2014). GOCE re-entered in October 2013.
The Swarm mission is composed of three identical satellites that were launched after November 2013 at orbits within 480–538 km altitude with orbital inclination ∼88°. The Swarm acceleration precision is 1.0 × 10–11 m/s2 within a bandwith whose upper limit is 0.1 Hz (Siemes et al., 2016). As a simple choice, we use only data from Swarm A, hereafter Swarm. Swarm is the only mission analyzed in this study that is still in operation.
Models
The JB2008 empirical model computes thermospheric mass density using as inputs solar indices and the 3-hour time resolution ap index accounting for low geomagnetic activity. When geomagnetic activity intensifies (Dst < –75 nT), the model switches over to Dst as the proxy for geomagnetic activity (Bowman et al., 2008). The solar indices used by JB2008 map the energy input into the thermosphere provided by different solar irradiance sources, which in turn affect density variability in the most important thermospheric layers (Tobiska et al., 2008).
HASDM dynamically calibrates densities by assimilating the observed drag effects on a carefully selected set of low-perigee calibration satellites and it solves for the global thermospheric neutral density with 3-hour cadence by “correcting” the JB2008 density prediction. Typically, 75 calibration satellites are used to fit and correct the JB2008 density and the greater the number of calibration satellites, the higher the accuracy. Because HASDM is able to mitigate uncertainty in atmospheric effects, by resolving the differences between calibration satellites and the core JB2008 model at each epoch (time step), real-time nowcasting specification of the LEO drag environment has improved significantly (e.g., Storz et al., 2005; Bowman et al., 2008; Licata et al., 2021b; Calabia and Jin, 2021).
Forecasting is achieved with the JB2008 model, driven by forecasted solar and geomagnetic drivers, with uncertainties growing significantly a few hours post epoch. Marcos et al. (2010) demonstrated with detailed comparisons and validation that JB2008 is the most accurate empirical model. In JB 2008, the 1-sigma uncertainties at 400 km for a given epoch dropped from 15 to 8%. The use of JB2008 in HASDM, and the assimilation of calibration satellite data into the initial JB2008 density solutions, further dropped the comparable HASDM density uncertainties to less than 5% for current epoch, lower altitude, and quiet atmosphere.
Although HASDM is not available for direct use by the general scientific community, Space Environment Technologies (SET) has made global density outputs available to the public (Tobiska et al., 2021). The SET HASDM density data base, available from 2000 to 2019, covers altitudes in the range 175–825 km, with resolution of 15° (longitude), 10° (latitude), and 25 km (altitude) (Licata et al., 2021a; Tobiska et al., 2021).
Satellite Coverage in LEO During Magnetic Storms, Including Extreme Events
Figure 1A summarizes the altitudes plotted as a function of time of the four LEO satellites since the launching of CHAMP in May 2001 to December 2020. Although there has been significant coverage from ∼250 to ∼540 km altitude, this coverage is relatively sparse. As noted by Bruinsma et al. (2021), the most well-covered storm was a mild event that occurred in April 2010, with CHAMP and GOCE around 300 km altitude, and GRACE around 480 km altitude, all with very limited local solar time coverage.
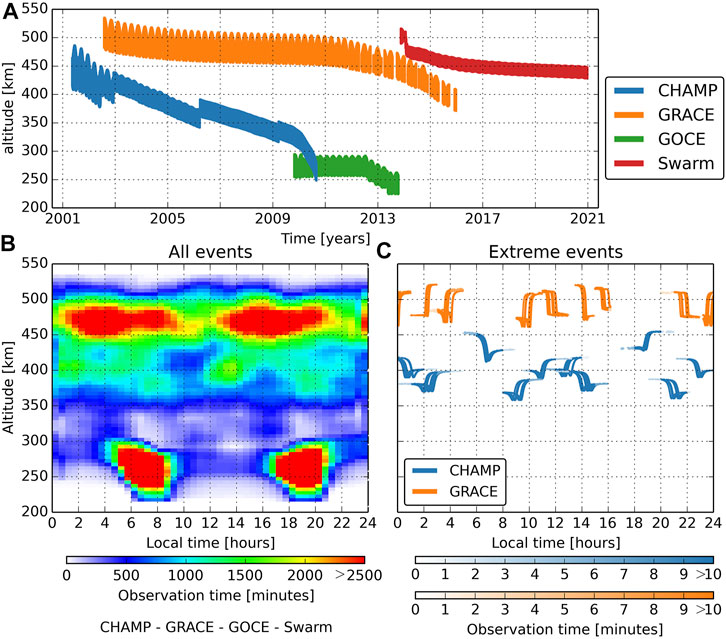
FIGURE 1. (A): CHAMP, GRACE, GOCE, and Swarm altitudes. Bottom row, (B): superposed epoch analysis of satellite observation times plotted as a function of local times and altitudes. The bin sizes are 5 km and 0.5 h. (C): the same as plotted in the left panel, but for the 7 extreme magnetic storms (minimum SYM-H ≤ –250 nT) observed by CHAMP and GRACE.
Figure 1B shows the observation time distributions as a function of altitude and local times for over 320 magnetic storms. The altitude data were collected within the 72-hour interval after the storm main phase onset as described by Oliveira et al. (2017). There is significant coverage above 400 km due to CHAMP, GRACE, and Swarm. Additionally, there is high coverage by GOCE between ∼180 km and ∼300 km concentrated around the dawn and dusk sectors. The coverage between ∼300 and 350 km is very low and comes from the late days of CHAMP’s observations. Many advancements in our understanding of the thermosphere response to magnetic storms in the past 2 decades come from these observations, including, e.g., thermosphere heating in polar cusp regions (Lühr et al., 2004), traveling atmospheric disturbance (TAD) propagation from high-to low-latitude regions (Fujiwara and Miyoshi, 2006; Bruinsma and Forbes, 2007), orbital drag effects induced by magnetic storms (Krauss et al., 2015; Oliveira and Zesta, 2019), high-latitude density enhancements due to magnetospheric compressions by solar wind pressure pulses (Connor et al., 2016; Shi et al., 2017), and thermosphere global time response to magnetic storms (Sutton et al., 2005, 2009; Oliveira et al., 2017).
Altitude coverages of all extreme events (minimum SYM-H ≤ –250 nT) ever observed by LEO spacecraft with high-accuracy accelerometers are shown in Figure 1C. The figure shows observation time plotted as a function of local time and altitude for the extreme storms observed by CHAMP (7 events) and GRACE (6 events). In comparison with all events, the LEO observational coverage during extreme magnetic storms is remarkably sparser and briefer, particularly due to the rarity of extreme events and the low number of concurring LEO missions operating during these events.
Comparing Model Performance During the Extreme Events Observed by Champ and Grace
The left column of Figure 2 shows thermosphere density response to the extreme storms whose coverages are shown in Figure 1C and dates shown in Table 1 of Zesta and Oliveira (2019). Density data are superposed in epoch time × MLAT bins with size 15 min × 3°. The zero epoch time is taken as the time of each respective storm main phase onset. The panels show log [ρ/ρ0], with ρ being the storm-time observed or modeled density and ρ0 being the background density estimated by JB2008 if there was no storm.
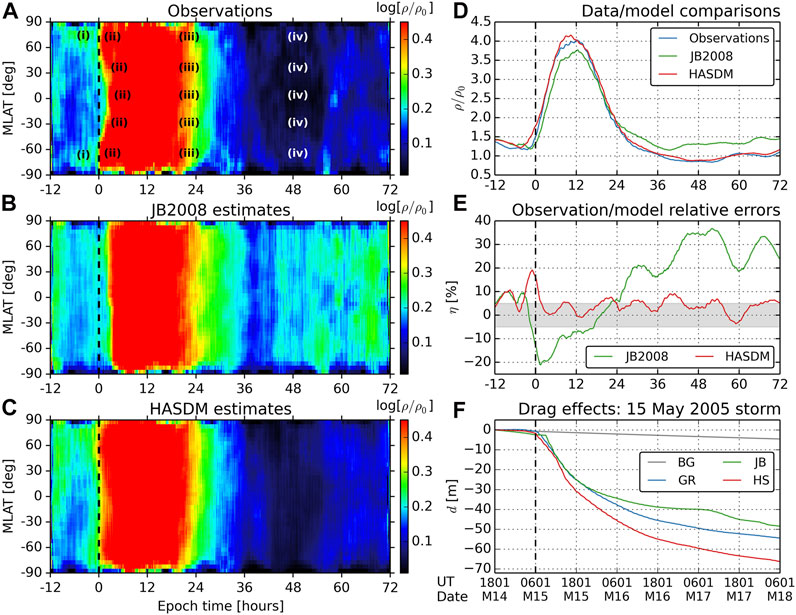
FIGURE 2. Left column: superposed epoch analysis results of thermospheric neutral mass density response using the methodology introduced by Oliveira et al. (2017) with observations (A), JB2008 estimates (B), and HASDM estimates (C). Right column: density averaged within –50° ≤ MLAT ≤ 50° in a 15-min cadence (D); density estimate errors with respect to observations computed as ηi = (ρi - ρobs)/ρobs, with i = (JB 2008, HASDM) (E); storm-time drag effects computed for GRACE’s orbit during the May 15, 2005 extreme storm using the framework provided by Oliveira and Zesta (2019) (F).
As described by Oliveira et al. (2017), ρ0 is obtained by the following steps: 1) JB2008 is used to compute the neutral density ρ1 during periods of low geomagnetic activity (|Dst| < 30 nT) to exclude effects of high magnetospheric compressions and intense magnetic storms; 2) a polynomial expansion (Arlinghaus, 1994) with degree 15 is fitted to the ratio ρ/ρ1 to obtain a calibration function f(t) (this degree order provided the best polynomial fitting for a few control events, including moderate and intense storms); and 3) with density computed by JB2008 with Dst = 0, i.e., ρ(Dst = 0), and f(t) interpolated for the whole dataset, the background density ρ0 is given by:
Results shown in Figure 2A were published by Zesta and Oliveira (2019), but here we removed effects caused by double storms, i.e., events in periods when another CME impacted Earth when the magnetosphere was highly driven. The data clearly show 1) high-latitude density enhancements due to the impacts of shocks in the driver leading edges; 2) TAD propagation effects from high to low latitudes after storm main phase onset within 1–2 orbits (∼2 h); 3) thermosphere cooling effects at all latitudes ∼22 h during storm time presumably due to Nitric Oxide (NO) cooling effects (Mlynczak et al., 2003; Knipp et al., 2017; Zesta and Oliveira, 2019) and 4) thermosphere overcooling during storm recovery meaning that density levels are now lower than density levels during pre-storm periods (Lei et al., 2012; Zhang et al., 2019). See Roman numbers in panel a for the corresponding effect described above on density data.
The comparison between JB2008 estimates (b) with observations (a) is quite remarkable. JB2008 does not capture effects caused by pre-storm shock compressions, nor does it capture TAD effects at storm main phase onset (white arrows in panel a). Additionally, JB2008 predicts thermosphere heating at low and high latitudes at the same time, which coincides with the time TADs take to reach equatorial latitudes as shown by observations. Although JB2008 predicts a major thermosphere cooling at ∼22 h, the model predicts a secondary cooling occurring ∼8 h later in comparison to observations, and the model does not predict thermosphere overcooling effects during the storm recovery phase. Quite the contrary, densities are slightly higher during recovery in comparison to pre-storm density levels.
HASDM results (c) are considerably improved in comparison to JB2008 results. Although HASDM does not clearly show high-latitude thermosphere heating due to pre-storm shock compressions, the model captures some patterns of TAD propagation, the extreme latitudinal cooling at t ∼ 22 h, and the thermosphere overcooling during storm recovery. Panel d shows mid- and low-latitude densities averaged within – 50° ≤ MLAT ≤ 50° every 15 min throughout the storms. Our results show that 1) JB2008 and HASDM densities agree moderately well with observations during pre-storm periods; 2) JB2008 underestimates and HASDM overestimates densities during storm main phase, and 3) HASDM estimates agree remarkably well with observations during storm recovery, reproducing cooling effects quite well, but JB2008 density levels always surpass observations during the recovery phase. Licata et al. (2021b) noted similar trends when comparing CHAMP and GRACE observations with HASDM and JB2008 results for the Halloween storms. Panel e shows the relative errors of the model estimates with respect to observations. The shaded grey area corresponds to the ±5% confidence interval suggested by the U.S. Space Force for optimizing orbit predictions (Lewis, 2019). Results show that HASDM errors stay most of the time within the confidence interval during all storm periods, but the model introduces high errors during times of pre-storm shock compressions. On the other hand, the standalone JB2008 performance is considerably worse during all storm periods. The model underestimates density during the main phase, but it considerably overestimates density during the recovery phase, reaching error levels as high as 35% during late recovery. As discussed in Oliveira and Zesta (2019) and Zesta and Oliveira (2019), JB2008 should be modified to accommodate effects induced by NO cooling for the improvement of density predictions particularly during extreme magnetic storms.
Finally, Figure 2F shows the comparison of observed and modeled drag effects on GRACE during the May 15, 2005 extreme magnetic storm. The drag effects are computed according to the framework developed by Oliveira and Zesta (2019). The nearly straight grey line corresponds to the drag effect caused by the background density ρ0 if there was no storm. Observations (blue curve) show that GRACE decayed by 55 m 72 h after storm onset. This is 11 times more severe in comparison to the orbital decay caused by the background density. As a result of the errors introduced by JB2008 and HASDM during different phases of the storm cycle (e), drag effects are underestimated by the former and overestimated by the latter.
Discussion and Conclusion
The Sputnik satellites opened the doors for human exploration in space (Launius, 2004). Jacchia (1959) used ephemeris data collected by Sputnik during an extreme magnetic storm in 1958 to link orbital drag effects with geomagnetic activity for the first time. Many empirical models were created and satellite missions were designed to study the dynamic thermosphere response to magnetic storms throughout the decades. However, orbital drag effects induced in LEO by extreme storms are yet relatively less understood partly due to the rarity of extreme storms during the space age. The International Geophysical Year (IGY) is marked by the adoption of the Dst index that became a standard trademark in assessing the intensity of magnetic storms. Interestingly, the largest yearly sunspot number ever recorded occurred in 1957 (e.g., Clette and Lefèvre, 2016), only a year before Sputnik launched and observed intense orbital drag effects (Jacchia, 1959). Although human exploration in space had just begun, the overall solar activity throughout the solar cycles (SCs) has been steadily decreasing since then. Since the IGY, relatively few extreme events (Dst ≤ – 250 nT) have occurred. Meng et al. (2019) reported on the occurrence of ∼ 40 extreme events, from which only 7 were observed by spacecraft with high-precision accelerometers for density derivations. The last extreme magnetic storm took place two SCs ago (SC23) on May 15, 2005.
Given the very low number of extreme magnetic storms amongst hundreds of events on record, a way to investigate more extreme events is to look in the past. Recently, many efforts have been undertaken to investigate magnetic activity represented by Dst-like indices reconstructed from archival materials generally drafted in the first half of the 20th century. Some of these events occurred in October/November 1903 (Hayakawa et al., 2020b), September 1909 (Hayakawa et al., 2019a; Love et al., 2019b), May 1921 (Love et al., 2019a), and March 1946 (Hayakawa et al., 2020a). These works showed that minimum Dst-like values of these storms went below –500 nT, which characterizes the event as a superstorm. Each reference provides the respective Dst-like index data for further investigations. For example, Oliveira et al. (2020) used the Dst-like data for the first 3 events mentioned above along with real Dst data for the March 1989 storm (Allen et al., 1989; Boteler, 2019) to show with JB2008 that, by comparison, long-lasting and less intense superstorms can induce more severe drag effects than short-lasting and more intense superstorms. Further investigations are needed here, as we have yet the unexplored events occurring in September 1859 (Tsurutani et al., 2003; Hayakawa et al., 2019b), February 1872 (Silverman, 2008; Hayakawa et al., 2018), and March 1946 (Hayakawa et al., 2020a).
Now looking to the future, a possibility to improve our understanding of extreme orbital drag is to foster international collaboration for the development of a central database of thermospheric density data. There has been increased interest of the private sector in the elaboration and construction of a very large constellation of satellites in LEO. For example, SpaceX launched in 2018 the first satellite prototypes for the Starlink project (Space Exploration Holdings, 2016). Starlink’s primary goal is to create a megaconstellation of over 12,000 LEO satellites bellow 600 km altitude with latitudinal distribution of 0.005–0.01 spacecraft per square meter for the formation of a worldwide internet network (McDowell, 2020). Another private company, OneWeb, intends so launch by the end of 2022 a 648-satellite constellation to provide worldwide internet service as well (Barnett, 2016). Using an evolutionary model with parameters provided by the respective operations application (Barnett, 2016; Space Exploration Holdings, 2016), Le May et al. (2018) showed that, within a 5-years operation time, the probability of occurring a catastrophic collision involving an OneWeb spacecraft is ∼5%, whereas the same for SpaceX is near 50%. However, the authors did not consider any effects introduced by solar activity, and, if they did, these figures would have certainly been higher. Therefore, the need of accurate models for orbital track prediction during magnetic storms, particularly during extreme events, is an important tool for preventing the occurrence of the Kessler Syndrome in space.
A future large-scale thermospheric density data base can be used in studies involving Machine Learning (ML) applications. ML studies have become very popular in the field of Earth and Space Sciences in the past decade (e.g., Keesee et al., 2020; Smith et al., 2020; Bortnik and Camporeale, 2021; Haines et al., 2021). For example, historical data sets (geomagnetic and solar indices, sunspot numbers) prior to 2000 can be used for training a model to predict storm drivers and the subsequent global thermospheric density and orbital drag of a LEO satellite in a given location (Licata et al., 2020; 2021c). This can be accomplished, e.g., by the use of ML linear regression for “training” the model to “learn” how to predict these effects (Rong and Bao-wen, 2018). Such technique is named by Bortnik and Camporeale (2021) as Time Series and Spatiotemporal Prediction, and is recognized by the authors as an important step for ML applications in Earth and Space Sciences. As shown in Figure 2, if HASDM provided remarkable results with the use of only 75 calibrated satellites, such results can be further improved by the assimilation of large-scale data provided by a few hundreds satellites in LEO, particularly for extreme events.
Finally, recent studies suggest that solar activity of SC25 will be approximately the same as the solar activity of SC24 (e.g., Javaraiah, 2017). However, McIntos et al. (2020) predict that SC25 will not only be stronger than SC24, but SC25 will rival the magnitude of the strongest SCs on record. Additionally, Javaraiah (2017) suggests that the transition between SC25 and SC26 will coincide with the end of the current Gleissberg cycle. The Gleisseberg cycle is characterized by the periodic occurrences of solar maxima every 77–88 years or so (Gleissberg, 1967; Feynman and Ruzmaikin, 2014). Therefore, all these predictions indicate that in the next years and decades the Sun will shift from its relatively quiet conditions to a much more active behavior. As a result, very accurate and precise thermospheric density models will play crucial roles in keeping and guaranteeing the safety of the ever increasing number of satellites in LEO by improved orbital tracking particularly during extreme magnetic storms.
Data Availability Statement
LEO satellite (ephemeris and density) data for CHAMP, GRACE, GOCE, and Swarm were obtained from the repository provided by the Delft University of Technology (http://thermosphere.tudelft. nl). Although not explicitly shown, geomagnetic index data represented by SYM-H (1-minute resolution), were downloaded from the World Data Center for Geomagnetism, Kyoto et al. (2015). The JB2008 model is publicly available at the Space Environment Technologies (SET) website (https://spacewx.com/ jb2008/). Dst and solar index data are also provided by SET with the source codes. The JB2008 and SET HASDM outputs can be obtained from the repository located at https://zenodo.org/record/ 4602380#.YRwSXC2cYkh.
Author Contributions
DO is the primary author of the article and performed the superposed epoch analyses and drag computations. EZ contributed with the overall discussions and helped the primary author set up the overall structure of the manuscript. PM and RL performed the computations of the JB2008 and SET HASDM densities for the extreme events. WT and MP provided support for the SET HASDM density computations. HH provided importance guidance with respect to historical data set discussions and interpretation of past and future solar activity discussions. All co-authors provided editorial comments thus contributing to the article and approved the submitted version.
Funding
This work was funded by the NASA Space Weather Science Applications Operations 2 Research program, under grant number 20-SWO2R20-2-0014.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors of this manuscript warmly thank Delft University of Technology for providing and making public the LEO satellite data used in this study. HH thanks World Data Center for the production, preservation and dissemination of the international sunspot number (WDC SILSO) and Data Analysis Center for Geomagnetism and Space Magnetism (WDC for Geomagnetism at Kyoto) for providing the international sunspot number and the Dst index.
References
Allen, J., Sauer, H., Frank, L., and Reiff, P. (1989). Effects of the March 1989 Solar Activity. Eos Trans. AGU 70, 1479–1488. doi:10.1029/89EO00409
Barnett, R. J. (2016). Tech. rep., Attachment to FCC Application SAT-LOI-20160428-00041. Washington, D.C. OneWeb Non-geostationary Satellite System: Technical Information to Supplement Schedule S.
Bortnik, J., and Camporeale, E. (2021). Ten Ways to Apply Machine Learning in Earth and Space Sciences. Eos 102. doi:10.1029/2021EO160257
Boteler, D. H. (2019). A 21st Century View of the March 1989 Magnetic Storm. Space Weather 17, 1427–1441. doi:10.1029/2019SW002278
Bowman, B. R., Tobiska, W. K., Marcos, F. A., Huang, C. Y., Lin, C. S., and Burke, W. J. (2008), A New Empirical Thermospheric Density Model JB2008 Using New Solar and Geomagnetic Indices. In AIAA/AAS Astrodynamics Specialist Conference. Honolulu, HI: American Institute of Aeronautics and Astronautics (AIAA) and American Astronautical Society (AAS), 1–19. AIAA 2008–6438. doi:10.2514/6.2008-6438
Bruinsma, S., Fedrizzi, M., Yue, J., and Siemes, C. (2021). Charting Satellite Courses in a Crowded Thermosphere. Eos Trans. AGU 102. doi:10.1029/2021eo153475
Bruinsma, S. L., Doornbos, E., and Bowman, B. R. (2014). Validation of GOCE Densities and Evaluation of Thermosphere Models. Adv. Space Res. 54, 576–585. doi:10.1016/j.asr.2014.04.008
Bruinsma, S. L., and Forbes, J. M. (2007). Global Observation of Traveling Atmospheric Disturbances (TADs) in the Thermosphere. Geophys. Res. Lett. 34. doi:10.1029/2007GL030243
Bruinsma, S., Tamagnan, D., and Biancale, R. (2004). Atmospheric Densities Derived from CHAMP/STAR Accelerometer Observations. Planet. Space Sci. 52, 297–312. doi:10.1016/j.pss.2003.11.004
Bruinsma, S. (2015). The DTM-2013 Thermosphere Model. J. Space Weather Space Clim. 5, A1. doi:10.1051/swsc/2015001
Cakaj, S. (2021). The Parameters Comparison of the "Starlink" LEO Satellites Constellation for Different Orbital Shells. Front. Comms. Net. 2, 7. doi:10.3389/frcmn.2021.643095
Calabia, A., and Jin, S. (2021). Thermospheric Mass Density Disturbances Due to Magnetospheric Forcing from 2014–2020 CASSIOPE Precise Orbits. J. Geophys. Res. Space Phys. 126, e2021JA029540. doi:10.1029/2021ja029540
Clette, F., and Lefèvre, L. (2016). The New Sunspot Number: Assembling All Corrections. Sol. Phys. 291, 2629–2651. doi:10.1007/s11207-016-1014-y
Connor, H. K., Zesta, E., Fedrizzi, M., Shi, Y., Raeder, J., Codrescu, M. V., et al. (2016). Modeling the Ionosphere-Thermosphere Response to a Geomagnetic Storm Using Physics-Based Magnetospheric Energy Input: OpenGGCM-CTIM Results. J. Space Weather Space Clim. 6, A25–A15. doi:10.1051/swsc/2016019
Doornbos, E., and Klinkrad, H. (2006). Modelling of Space Weather Effects on Satellite Drag. Adv. Space Res. 37, 1229–1239. doi:10.1016/j.asr.2005.04.097
Drinkwater, M. R., Floberghagen, R., Haagmans, R., Muzi, D., and Popescu, A. (2003). “GOCE: ESA's First Earth Explorer Core Mission,” in Earth Gravity Field from Space – from Sensors to Earth Sciences. Editors G. Beutler, M. R. Drinkwater, R. Rummel, and R. Von Steiger (Dordrecht, The Netherlands: Springer Netherlands), 17, 419–432. doi:10.1007/978-94-017-1333-7\\text{\\_}3610.1007/978-94-017-1333-7_36
Emmert, J. T. (2015). Thermospheric Mass Density: A Review. Adv. Space Res. 56, 773–824. doi:10.1016/j.asr.2015.05.038
Feynman, J., and Ruzmaikin, A. (2014). The Centennial Gleissberg Cycle and its Association with Extended Minima. J. Geophys. Res. Space Phys. 119, 6027–6041. doi:10.1002/2013ja019478
Flury, J., Bettadpur, S., and Tapley, B. D. (2008). Precise Accelerometry Onboard the GRACE Gravity Field Satellite mission. Adv. Space Res. 42, 1414–1423. doi:10.1016/j.asr.2008.05.004
Fujiwara, H., and Miyoshi, Y. (2006). Characteristics of the Large-Scale Traveling Atmospheric Disturbances during Geomagnetically Quiet and Disturbed Periods Simulated by a Whole Atmosphere General Circulation Model. Geophys. Res. Lett. 33. doi:10.1029/2006GL027103
Gleissberg, W. (1967). Secularly Smoothed Data on the Minima and Maxima of sunspot Frequency. Sol. Phys. 2, 231–233. doi:10.1007/BF00155925
Haines, C., Owens, M. J., Barnard, L., Lockwood, M., Ruffenach, A., Boykin, K., et al. (2021). Forecasting Occurrence and Intensity of Geomagnetic Activity with Pattern-Matching Approaches. Space Weather 19, e2020SW002624. doi:10.1029/2020sw002624
Hayakawa, H., Ebihara, Y., Cliver, E. W., Hattori, K., Toriumi, S., Love, J. J., et al. (2019a). The Extreme Space Weather Event in September 1909. Monthly Notices R. Astronomical Soc. 484, 4083–4099. doi:10.1093/mnras/sty3196
Hayakawa, H., Ebihara, Y., Pevtsov, A. A., Bhaskar, A., Karachik, N., and Oliveira, D. M. (2020a). Intensity and Time Series of Extreme Solar-Terrestrial Storm in 1946 March. Monthly Notices R. Astronomical Soc. 497, 5507–5517. doi:10.1093/mnras/staa1508
Hayakawa, H., Ebihara, Y., Willis, D. M., Hattori, K., Giunta, A. S., Wild, M. N., et al. (2018). The Great Space Weather Event during 1872 February Recorded in East Asia. ApJ 862, 15–10. doi:10.3847/1538-4357/aaca40
Hayakawa, H., Ebihara, Y., Willis, D. M., Toriumi, S., Iju, T., Hattori, K., et al. (2019b). Temporal and Spatial Evolutions of a Large Sunspot Group and Great Auroral Storms Around the Carrington Event in 1859. Space Weather 17, 1553–1569. doi:10.1029/2019SW002269
Hayakawa, H., Ribeiro, P., Vaquero, J. M., Gallego, M. C., Knipp, D. J., Mekhaldi, F., et al. (2020b). The Extreme Space Weather Event in 1903 October/November: An Outburst from the Quiet Sun. ApJ 897, L10. doi:10.3847/2041-8213/ab6a18
Hedin, A. E. (1987). MSIS-86 Thermospheric Model. J. Geophys. Res. 92, 4649–4662. doi:10.1029/JA092iA05p04649
Jacchia, L. G. (1959). Corpuscular Radiation and the Acceleration of Artificial Satellites. Nature 183, 1662–1663. doi:10.1038/1831662a0
Jacchia, L. G. (1970). New Static Models of the Thermosphere and Exosphere with Empirical Temperature Profiles. Spec. Rep. 313, 1–82. Cambridge, Massachusetts: Smithson, Astrophys. Obs.
Javaraiah, J. (2017). Will Solar Cycles 25 and 26 Be Weaker Than Cycle 24? Sol. Phys. 292. doi:10.1007/s11207-017-1197-x
Keesee, A. M., Pinto, V., Coughlan, M., Lennox, C., Mahmud, M. S., and Connor, H. K. (2020). Comparison of Deep Learning Techniques to Model Connections between Solar Wind and Ground Magnetic Perturbations. Front. Astron. Space Sci. 7, 72. doi:10.3389/fspas.2020.550874
Kessler, D. J., and Cour-Palais, B. G. (1978). Collision Frequency of Artificial Satellites: The Creation of a Debris belt. J. Geophys. Res. 83, 2637–2646. doi:10.1029/JA083iA06p02637
Knipp, D. J., Pette, D. V., Kilcommons, L. M., Isaacs, T. L., Cruz, A. A., Mlynczak, M. G., et al. (2017). Thermospheric Nitric Oxide Response to Shock‐led Storms. Space Weather 15, 325–342. doi:10.1002/2016SW001567
Krauss, S., Temmer, M., Veronig, A., Baur, O., and Lammer, H. (2015). Thermospheric and Geomagnetic Responses to Interplanetary Coronal Mass Ejections Observed by ACE and GRACE: Statistical Results. J. Geophys. Res. Space Phys. 120, 8848–8860. doi:10.1002/2015JA021702
Le May, S., Gehly, S., Carter, B. A., and Flegel, S. (2018). Space Debris Collision Probability Analysis for Proposed Global Broadband Constellations. Acta Astronautica 151, 445–455. doi:10.1016/j.actaastro.2018.06.036
Lei, J., Burns, A. G., Thayer, J. P., Wang, W., Mlynczak, M. G., Hunt, L. A., et al. (2012). Overcooling in the Upper Thermosphere during the Recovery Phase of the 2003 October Storms. J. Geophys. Res. 117, a–n. doi:10.1029/2011JA016994
Lewis, C. D. (2019). “The DARPA Space Environment Exploitation (SEE) Program,” in Friday AGU Chapman Conference Abstracts (Presented at the 2019 AGU Chapman Conference on Scientific Challenges Pertaining to Space Weather Forecasting Including Extremes (Pasadena, CA, 1. 11-15 February).
Licata, R. J., Mehta, P. M., Kent Tobiska, W., Bowman, B. R., and Pilinski, M. D. (2021a). CHAMP and GRACE-A Density Estimates with Associated HASDM and JB2008 Predictions. (Version v1) [Data Set]. Zenodo. doi:10.5281/zenodo.4602380
Licata, R. J., Mehta, P. M., Tobiska, W. K., Bowman, B. R., and Pilinski, M. D. (2021b). Qualitative and Quantitative Assessment of the Set Hasdm Database. Space Weather 19, e2021SW002798. doi:10.1029/2021SW002798
Licata, R. J., Mehta, P. M., Weimer, D. R., and Kent Tobiska, W. (2021c). Improved Neutral Density Predictions through Machine Learning Enabled Exospheric Temperature Model. Earth Space Sci. Open Archive. doi:10.1002/essoar.10507687.1
Licata, R. J., Tobiska, W. K., and Mehta, P. M. (2020). Benchmarking Forecasting Models for Space Weather Drivers. Space Weather 18, e2020SW002496. doi:10.1029/2020sw002496
Love, J. J., Hayakawa, H., and Cliver, E. W. (2019a). Intensity and Impact of the New York Railroad Superstorm of May 1921. Space Weather 17, 1281–1292. doi:10.1029/2019SW002250
Love, J. J., Hayakawa, H., and Cliver, E. W. (2019b). On the Intensity of the Magnetic Superstorm of September 1909. Space Weather 17, 37–45. doi:10.1029/2018sw002079
Lühr, H., Rother, M., Köhler, W., Ritter, P., and Grunwaldt, L. (2004). Thermospheric Up-Welling in the Cusp Region: Evidence from CHAMP Observations. Geophys. Res. Lett. 31, a–n. doi:10.1029/2003GL019314
Marcos, F., Lai, S., Huang, C., Lin, C., Retterer, J., Delay, S., et al. (2010). AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Toronto: Ontario Canada, 1–20. doi:10.2514/6.2010-7840Towards Next Level Satellite Drag Modeling.
McDowell, J. C. (2020). The Low Earth Orbit Satellite Population and Impacts of the SpaceX Starlink Constellation. ApJ 892, L36–L10. doi:10.3847/2041-8213/ab8016
McIntosh, S. W., Chapman, S., Leamon, R. J., Egeland, R., and Watkins, N. W. (2020). Overlapping Magnetic Activity Cycles and the Sunspot Number: Forecasting Sunspot Cycle 25 Amplitude. Sol. Phys. 295. doi:10.1007/s11207-020-01723-y
Meng, X., Tsurutani, B. T., and Mannucci, A. J. (2019). The Solar and Interplanetary Causes of Superstorms (Minimum Dst ≤ −250 nT) during the Space Age. J. Geophys. Res. Space Phys. 124, 3926–3948. doi:10.1029/2018JA026425
Mlynczak, M., Martin-Torres, F. J., Russell, J., Beaumont, K., Jacobson, S., Kozyra, J., et al. (2003). The Natural Thermostat of Nitric Oxide Emission at 5.3 μm in the Thermosphere Observed during the Solar Storms of April 2002. Geophys. Res. Lett. 30. doi:10.1029/2003GL017693
National Science and Technology Council (2015b). National Space Weather Action Plan. Tech. Rep. Washington, D.C: Executive Office of the President of the United States.
National Science and Technology Council (2015a). National Space Weather Strategy. Tech. Rep. Washington, D.C: Executive Office of the President of the United States.
World Data Center for Geomagnetism, Kyoto Nose, M., Iyemori, T., Sugiura, M., and Kamei, T. (2015). Geomagnetic AE index. [Data Set]. doi:10.17593/15031-54800
Nwankwo, V. U. J., Denig, W., Chakrabarti, S. K., Ajakaiye, M. P., Fatokun, J., Akanni, A. W., et al. (2021). Atmospheric Drag Effects on Modelled Low Earth Orbit (LEO) Satellites during the July 2000 Bastille Day Event in Contrast to an Interval of Geomagnetically Quiet Conditions. Ann. Geophys. 39, 397–412. doi:10.5194/angeo-39-397-2021
Oliveira, D. M., Zesta, E., Hayakawa, H., and Bhaskar, A. (2020). Estimating Satellite Orbital Drag during Historical Magnetic Superstorms. Space Weather 18, e2020SW002472. doi:10.1029/2020SW002472
Oliveira, D. M., and Zesta, E. (2019). Satellite Orbital Drag during Magnetic Storms. Space Weather 17, 1510–1533. doi:10.1029/2019SW002287
Oliveira, D. M., Zesta, E., Schuck, P. W., and Sutton, E. K. (2017). Thermosphere Global Time Response to Geomagnetic Storms Caused by Coronal Mass Ejections. J. Geophys. Res. Space Phys. 122 (10), 782. 762–10. doi:10.1002/2017ja024006
Pardini, C., and Anselmo, L. (2009). Assessment of the Consequences of the Fengyun-1C Breakup in Low Earth Orbit. Adv. Space Res. 44, 545–557. doi:10.1016/j.asr.2009.04.014
Picone, J. M., Hedin, A. E., Drob, D. P., and Aikin, A. C. (2002). NRLMSISE-00 Empirical Model of the Atmosphere: Statistical Comparisons and Scientific Issues. J. Geophys. Res. 107SIA 15–1–SIA 15–16. doi:10.1029/2002ja009430
Prölss, G. W. (2011). Density Perturbations in the Upper Atmosphere Caused by the Dissipation of Solar Wind Energy. Surv. Geophys. 32, 101–195. doi:10.1007/s10712-010-9104-0
Reigber, C., Lühr, H., and Schwintzer, P. (2002). CHAMP mission Status. Adv. Space Res. 30, 129–134. doi:10.1016/S0273-1177(02)00276-4
Rong, S., and Bao-wen, Z. (2018). The Research of Regression Model in Machine Learning Field. MATEC Web Conf. 176, 01033. doi:10.1051/matecconf/201817601033
Shi, Y., Zesta, E., Connor, H. K., Su, Y. J., Sutton, E. K., Huang, C. Y., et al. (2017). High‐Latitude Thermosphere Neutral Density Response to Solar Wind Dynamic Pressure Enhancement. J. Geophys. Res. Space Phys. 122 (11), 578. 559–11. doi:10.1002/2017JA023889
Siemes, C., de Teixeira da Encarnação, J., Doornbos, E., van den IJssel, J., Kraus, J., Pereštý, R., et al. (2016). Swarm Accelerometer Data Processing from Raw Accelerations to Thermospheric Neutral Densities. Earth Planet. Sp 68, 1–16. doi:10.1186/s40623-016-0474-5
Silverman, S. M. (2008). Low-latitude Auroras: The Great aurora of 4 February 1872. J. Atmos. Solar-Terrestrial Phys. 70, 1301–1308. doi:10.1016/j.jastp.2008.03.012
Smith, A. W., Rae, J., Forsyth, C., Oliveira, D. M., Freeman, P. M., and Jackson, D. (2020). Probabilistic Forecasts of Storm Sudden Commencements from Interplanetary Shocks Using Machine Learning. Space Weather 18, e2020SW002603. doi:10.1029/2020sw002603
Space Exploration Holdings (2016). “SpaceX Non-geostationary Satellite System,” in Tech. rep., Attachment to FCC Application SAT-LOA-20161115-00118 (Washington, D.C.
Storz, M. F., Bowman, B. R., Branson, M. J. I., Casali, S. J., and Tobiska, W. K. (2005). High Accuracy Satellite Drag Model (HASDM). Adv. Space Res. 36, 2497–2505. doi:10.1016/j.asr.2004.02.020
Sutton, E. K., Forbes, J. M., and Knipp, D. J. (2009). Rapid Response of the Thermosphere to Variations in Joule Heating. J. Geophys. Res. 114, a–n. doi:10.1029/2008JA013667
Sutton, E. K., Forbes, J. M., and Nerem, R. S. (2005). Global Thermospheric Neutral Density and Wind Response to the Severe 2003 Geomagnetic Storms from CHAMP Accelerometer Data. J. Geophys. Res. 110, 1–10. doi:10.1029/2004ja010985
Tapley, B. D., Bettadpur, S., Watkins, M., and Reigber, C. (2004). The Gravity Recovery and Climate experiment: Mission Overview and Early Results. Geophys. Res. Lett. 31, a–n. doi:10.1029/2004GL019920
Tobiska, W. K., Bouwer, S. D., and Bowman, B. R. (2008). The Development of New Solar Indices for Use in Thermospheric Density Modeling. J. Atmos. Solar-Terrestrial Phys. 70, 803–819. doi:10.1016/j.jastp.2007.11.001
Tobiska, W. K., Bowman, B. R., Bouwer, S. D., Cruz, A., Wahl, K., Pilinski, M. D., et al. (2021). The SET HASDM Density Database. Space Weather 19, e2020SW002682. doi:10.1029/2020SW002682
Tsurutani, B. T., Gonzalez, W. D., Lakhina, G. S., and Alex, S. (2003). The Extreme Magnetic Storm of 1-2 September 1859. J. Geophys. Res. 108. doi:10.1029/2002JA009504
Wang, T. (2010). Analysis of Debris from the Collision of the Cosmos 2251 and the Iridium 33 Satellites. Sci. Glob. Security 18, 87–118. doi:10.1080/08929882.2010.493078
Zesta, E., and Huang, C. Y. (2016). “Satellite Orbital Drag,” in Space Weather Fundamentals. Editor G. V. Khazanov (Boca Raton, FL: CRC Press), chap 18, 329–351. doi:10.1201/9781315368474-20
Zesta, E., and Oliveira, D. M. (2019). Thermospheric Heating and Cooling Times during Geomagnetic Storms, Including Extreme Events. Geophys. Res. Lett. 46 (12), 12739–12746. 739–12. doi:10.1029/2019GL085120
Keywords: magnetic storms, thermosphere neutral density, historical data assessment, machine learning, satellite orbital decay
Citation: Oliveira DM, Zesta E, Mehta PM, Licata RJ, Pilinski MD, Tobiska WK and Hayakawa H (2021) The Current State and Future Directions of Modeling Thermosphere Density Enhancements During Extreme Magnetic Storms. Front. Astron. Space Sci. 8:764144. doi: 10.3389/fspas.2021.764144
Received: 25 August 2021; Accepted: 08 October 2021;
Published: 29 October 2021.
Edited by:
Olga V. Khabarova, Institute of Terrestrial Magnetism Ionosphere and Radio Wave Propagation (RAS), RussiaReviewed by:
Andrés Calabia Aibar, Nanjing University of Science and Technology, ChinaDogacan Ozturk, University of Alaska System, United States
Copyright © 2021 Oliveira, Zesta, Mehta, Licata, Pilinski, Tobiska and Hayakawa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Denny M. Oliveira, ZGVubnkubS5kZW9saXZlaXJhQG5hc2EuZ292