Identification of DNA Bases and Their Cations in Astrochemical Environments: Computational Spectroscopy of Thymine as a Test Case

Zhao, Yage; Hochlaf, Majdi; Biczysko, Malgorzata

doi:10.3389/fspas.2021.757007

ORIGINAL RESEARCH article

Front. Astron. Space Sci., 14 October 2021

Sec. Astrochemistry

Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.757007

This article is part of the Research Topic Theoretical Characterization of Astrophysical Species View all 8 articles

Identification of DNA Bases and Their Cations in Astrochemical Environments: Computational Spectroscopy of Thymine as a Test Case

Yage Zhao¹

Majdi Hochlaf²

Malgorzata Biczysko¹*

¹Department of Physics, International Centre for Quantum and Molecular Structures, College of Sciences, Shanghai University, Shanghai, China
²Université Gustave Eiffel, COSYS/LISIS, 5 Bd Descartes, Champs sur Marne, France

Increased importance of vibrational fingerprints in the identification of molecular systems, can be highlighted by the upcoming interstellar medium (ISM) observations by the James Webb Space Telescope, or in a context of other astrochemical environments as meteorites or exoplanets, Mars robotic missions, such as instruments on board of Perseverance rover. These observations can be supported by combination of laboratory experiments and theoretical calculations, essential to verify and predict the spectral assignments. Astrochemical laboratory simulations have shown that complex organic molecules (COMs) can be formed from simple species by vacuum ultraviolet or X-ray irradiation expanding interest in searching for organic biological and prebiotic compounds. In this work an example of nucleobase, thymine, is selected as a test case for highlighting the utility of computational spectroscopic methods in astrochemical studies. We consider mid-infrared (MIR) and near-infrared (NIR) vibrational spectra of neutral (T) and cationic (T⁺) thymine ground states, and vibrationally-resolved photoelectron (PE) spectra in the far UV range from 8.7 to 9.4 eV. The theoretical framework is based on anharmonic calculations including overtones and combination bands. The same anharmonic wavenumbers are applied into the simulations of vibrationally-resolved photoelectron spectra based on Franck-Condon computations. The infrared and vibrationally-resolved photoelectron spectra are compared with the available experimental counterparts to verify their accuracy and provide assignment of the observed transitions. Finally, reliable predictions of spectra, going beyond currently available experimental data, either dealing with energy ranges, resolution or temperature, which can support astrochemistry studies are provided.

Introduction

Before the middle of the last century, it was widely believed that the environment in the cosmic space was not suitable to the formation and survival of molecules, and that most matter in space would exist as atoms or amorphous dust grains (Herzberg, 1988). With the development of new astronomical techniques, especially the advent of telescopes, detectors, and spectrometers operating in the radio, infrared (IR), and ultraviolet (UV)/visible ranges of the electromagnetic spectrum, it is currently proven that most of the matter in the circumstellar systems and interstellar environments exists in the molecular form (Allamandola et al., 1989; Sandford et al., 2020). Dense interstellar clouds are the regions where most of the chemical reactions involved occur. These are the environments where new planetary systems are formed, so, some of the chemical species produced in these environments are expected to be transported to small objects such as asteroids and comets. This implies that newly formed planetary systems likely possess an inventory of complex prebiotic organics, which can be delivered to and seed planets, as was the case for the primitive Earth (Sandford et al., 2020). Moreover, photochemistry with high-energy processing of the interstellar ice mantles, planetary atmospheres, or the planetary soil is a key mechanism for extraterrestrial synthesis of prebiotic molecules (Arumainayagam et al., 2021), but photochemistry can also lead to the molecules modification or destruction (Serrano-Andrés and Merchán, 2009).

Nowadays, it is thought that some starting prebiotic molecular materials may be widely distributed throughout the Universe (Sandford et al., 2020) and the search for the biosignatures is one of the main goals of current and future space missions involving the next generation of space telescopes (JWST, ARIEL, OST, HabEx, LUVOIR) (Lasne, 2021), spectrometers onboard of spacecrafts or rovers (Flasar et al., 2005; Vago et al., 2017; Vago et al., 2018; Williford et al., 2018) or the new class of high-resolution spectrometers operating in the UV region, (i.e., CHESS) (Hoadley et al., 2020) allowing observations beyond capacities of present-day facilities such as the Hubble Space Telescope (HST). In the case of essential molecules of life, it has been shown that carbonaceous meteorites contain a wide range of extraterrestrial nucleobases (Callahan et al., 2011), but uracil is still the only pyrimidine base formally reported in such meteorites (Stoks and Schwartz, 1979). It has been shown (Materese et al., 2017) that all desoxyribonucleic acid (DNA) and ribonucleic acid (RNA) nucleobases can be formed in icy astrophysical environments by UV irradiation of pyrimidine, but the relative abundance of these nucleobases greatly differs (Materese et al., 2013). Therefore, uracil and cytosine are more easily formed than thymine, which is consistent with the detection of uracil but not of thymine in meteorites. In 2019, (Oba et al., 2019) demonstrated that all DNA/RNA nucleobases, except guanine, can be also formed from a mixture of simple, abundant molecules (H₂O, CO, NH₃ and CH₃OH) exposed to UV photons at 10 K. So far, none of nucleobases have been detected in the interstellar medium (ISM), but other complex molecules exist in ISM, including two simplest nitrogen-bearing aromatic molecules: benzonitrile (c-C₆H₅CN) (McGuire et al., 2018) and 1-cyano-1,3-cyclopentadiene (c-C₅H₅CN) (McCarthy et al., 2021). Analysis of chemical composition and structure of any type of astrochemical “samples” (meteorites, comets, planetary atmosphere or soil, ISM) and search for prebiotic organic matter in extraterrestrial materials is a very challenging task (Callahan et al., 2011; Fornaro et al., 2020). The detection is usually performed employing spectroscopic measurements and their comparison with the data available from the laboratory experiments. However, the latter might be not available, or even difficult to obtain with the desired accuracy/resolution or in the conditions mimicking astrochemical environments of interest (Puzzarini and Barone, 2020b). Moreover, despite the large amount of information that can be obtained from experiments, uncertainties arise in the assignment of spectral peaks, even for small molecules (Puzzarini et al., 2014). In this respect quantum chemistry (QC) based simulations of spectra represents a very powerful tool to either 1) support laboratory experiments or 2) provide missing data not (yet) available from experiments (Biczysko et al., 2017; Puzzarini and Barone, 2020a). Indeed, computational spectroscopic techniques (Barone et al., 2021) may support either laboratory experiments or astrochemical observations in different wavelength/frequency ranges from the microwave (μw), infrared (IR), ultraviolet-visible (UV-VIS), up to the photoelectron (PE) spectra including soft X-rays, as schematically represented in Figure 1. Interestingly, the same quantum chemical computations can provide information in several spectral ranges, both absorption and emission, as well as with different resolutions. Finally, spectra computed for isolated molecules allow at the same time their own characterization in the absence of interactions, and may serve as the reference data for interpreting results obtained in more complex environments (Barone et al., 2015).

FIGURE 1

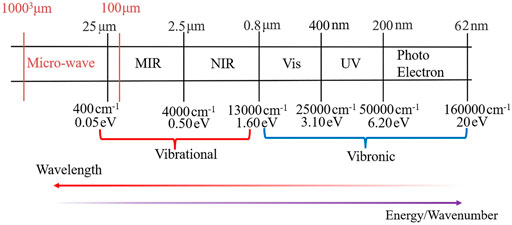
FIGURE 1. The wavelength and energy range corresponding to vibrational and vibronic spectra simulations.

In this work, we will illustrate the application of computational spectroscopy focusing on the thymine and its photoionization initiated by the absorption of a VUV photon, i.e., $t h y m i n e ({\tilde{X}}^{1} A ′) + hv \to t h y m i n e^{+} ({\tilde{X}}^{2} A ′′) + e^{-}$ photoionization transition. This study will include simulations of the vibrational infrared spectra for both thymine and its cation, in their ground electronic states, as well as the simulations of vibrationally-resolved photoelectron spectra. Thymine is a suitable example, for which several well resolved experimental (Choi et al., 2005) and highly accurate theoretical studies have been reported (Bravaya et al., 2010; Majdi et al., 2015). Generally speaking, DNA bases may have several low energy tautomers (Yarasi et al., 2007), but that is not the case of thymine, for which only one most stable diketo tautomer has been observed in the gas phase (Brown et al., 1989; Colarusso et al., 1997). Moreover, it has been shown that from the two possible (cis and trans) conformers due to the rotation of the methyl group (CH₃) the latter is a transition state (Majdi et al., 2015). So, we focus on the only stable cis conformer of thymine, for which a highly accurate structural parameters have been obtained by ab initio methodologies and semi-experimental approaches (Vogt et al., 2014). The infrared spectra of thymine in the mid-IR range have been also measured in both the gas phase (Colarusso et al., 1997) and by the low-temperature matrix isolation techniques (Nowak, 1989; Leś et al., 1992; Szczepaniak et al., 2000). Mass-analysed threshold ionization (MATI) spectrum of the thymine measured in a small energy range but with very high resolution (∼0.1 meV) was presented in 2005 by Choi et al. (Choi et al., 2005). The energy range was expanded in 2015 by Majdi et al. (Majdi et al., 2015) by slow photoelectron spectra (SPES) measurements, with experimental spectrum presenting a rich vibrational structure. These experimental results have been supported, or followed by theoretical studies of infrared spectra of thymine (Fornaro et al., 2014) and the Franck-Condon computations of theoretical photoelectron spectrum (Bravaya et al., 2010) from the thymine neutral ground state (T) to the thymine cationic state (T⁺). Despite these experimental and theoretical efforts still several spectral information are missing, that include accurate characterization of thymine cation MIR spectra, or the NIR spectra for both neutral and cationic species, as well as high resolution PE spectra in larger energy range or at higher temperatures. Computational methodologies illustrated in this work allow full characterization in the spectral range from the MIR (20 μm) up to the VUV (100 nm). However, we will focus on MIR-NIR and PE regions, firstly comparing the simulated infrared and vibrationally-resolved photoelectron spectra with the available experimental counterparts, and next providing prediction of not yet available spectra, which can support either laboratory or astrochemical studies. For the latter we consider astrochemical environments such as 1) atmospheres of exo-planets, with Titan Saturn’s moon as an example, 2) detection of molecular biosignatures by NIR spectroscopy, of particular relevance for two upcoming robotic missions to Mars, and 3) observation of photoelectron spectra in hot and cold ISM environments from HST and its successors.

Methods

Computational Details

The geometry optimizations, harmonic and anharmonic vibrational computations of neutral thymine and of its cation in their ground states (i.e. ${\tilde{X}}^{1} A ′$ and ${\tilde{X}}^{2} A^{″}$ , respectively) are performed as the starting points for the simulation of vibrational (infrared) and vibrationally-resolved (photoelectron) spectra by means of GAUSSIAN16 (Frisch et al., 2016). As required for the anharmonic computations the tight convergence criteria (maximum forces and displacements smaller than 1.5 × 10⁻⁵ Hartree/Bohr and 6.0 × 10⁻⁵ Å, respectively) are employed in all geometry optimizations. The equilibrium structures, harmonic force constants and first-order electric dipole moment derivatives have been computed by the double-hybrid density functional B2PLYP (Grimme, 2006; Biczysko et al., 2010), which has been demonstrated to provide accurate harmonic frequencies and has been recommended for spectroscopic studies of medium-sized biomolecules, such as the nucleobases (Fornaro et al., 2014; Fornaro et al., 2015; Fornaro et al., 2016). The atomic charge distribution analysis has been performed by means of natural bond orbital (NBO) (Foster and Weinhold, 1980; Reed and Weinhold, 1983) method.

The B2PLYP harmonic computations have been used together with the cubic and quartic semi-diagonal constants and the second and third order derivatives of dipole moment from B3LYP (Becke, 1993) computations to create anharmonic hybrid force fields employed in spectra simulations. Both B2PLYP and B3LYP computations are carried out in conjunction with the aug-cc-pVTZ (denoted hereafter as AVTZ) (Dunning and Thom, 1989; Kendall et al., 1992) basis set. The B2PLYP and B3LYP force fields are combined into the hybrid B2PLYP/AVTZ//B3LYP/AVTZ one by assuring the normal modes overlap between these two sets as implemented in GAUSSIAN16. Namely, the correspondence between two sets of normal modes (two different levels of theory, or the initial and the final states in electronic transition, vide infra) is defined using the linear transformation as proposed by Duschinsky (Duschinsky, 1937):

Q = J Q^{'} K

where Q and Q' represent the two sets of mass-weighted normal coordinates. The Duschinsky matrix J describes the projection of one normal coordinate basis vectors on those of the other. The displacement shift vector K corresponds to the displacements of the normal modes between the two structures. For a hybrid method involving harmonic and anharmonic data computed at different levels of theory the normal modes consistency was checked automatically. A cut-off of 90% for each coordinate was required to consider the two sets of normal modes as equivalent.

For anharmonic contributions, the second order vibrational perturbation theory (VPT2) (Nielsen, 1951; Mills, 1972) has been employed. In VPT2 computations the third and fourth order derivatives of the potential energy surface have been obtained by numerical differentiation (Barone, 2005; Bloino, 2015) of analytic second-order derivatives while the cubic electric dipole moment surfaces have been obtained through numerical differentiations of the dipole moment derivatives. As established in the literature (Amos et al., 1991; Martin et al., 1995; Barone, 2005; Vázquez and Stanton, 2007; Rosnik and Polik, 2014; Bloino, 2015; Franke et al., 2021; Mendolicchio et al., 2021), the VPT2 approaches accounting for the possible presence of anharmonic resonances is very effective in predicting infrared and Raman spectra of medium-sized molecules (Barone et al., 2014; Bloino, 2015; Bloino et al., 2015; Krasnoshchekov et al., 2015; Franke et al., 2021). In this work, we adopt the generalized VPT2 (GVPT2) model (Bloino and Barone, 2012; Bloino et al., 2015) where nearly-resonant contributions are removed from the perturbative treatment (leading to the deperturbed model, DVPT2) and treated in a second step variationally, using a set of default thresholds. Resonance definition and general recommendations on the applied computational procedures are described in detail in the tutorial review by Bloino et al. (Bloino et al., 2016).

The computation of vibrationally-resolved photoelectron spectra has been performed employing the sum-over-states Time-Independent (TI) (Barone et al., 2009; Barone, 2012) formulation, using the Adiabatic Hessian (AH) descriptions of the potential energy surfaces and the Franck-Condon (FC) (Condon, 1926; Franck and Dymond, 1926; Condon, 1928; Sharp and Rosenstock, 1964; Doktorov et al., 1977) approximation for the transition dipole moment, denoted as TI AH|FC (Bloino et al., 2016). This approach takes into account both the shift between the geometries and rotation of the normal modes upon the ionization through Duschinsky transformation. TI AH|FC spectra have been computed with the class-based prescreening method (Santoro et al., 2007a; Santoro et al., 2007b), including as well the temperature effects (Santoro et al., 2008). For the latter, all vibrational states with a Boltzmann population of at least 10% of that of the ground state zero vibrational level have been considered as the initial states for the vibronic transitions. The TI AH|FC computations have been done within the harmonic framework, but the initial and final levels harmonic wavenumbers have been replaced by their anharmonic counterparts from the B2PLYP/B3LYP GVPT2 computations, to partially recover anharmonicity in a cost-effective way. Finally the energy difference between the ${\tilde{X}}^{1} A ′$ and ${\tilde{X}}^{2} A ″$ states minima have been corrected based on the previously published results from (R)CCSD(T)-F12/cc-pVTZ-F12 computations including core-valence (CV) and scalar relativistic (SR) corrections (Majdi et al., 2015). Indeed, the corresponding adiabatic ionization energy of thymine agrees well with the best experimental determinations.

Results and Discussion

Equilibrium Structure and Vibrational Spectroscopy

Equilibrium geometrical parameters of neutral thymine and its cation calculated at the B2PLYP/AVTZ level are listed in Table 1, while the most significant structural and charge changes upon ionization are reported in Figure 2. Additional data, B3LYP/AVTZ structures and NBO atomic charges are reported in Supplementary Tables S1–S3, respectively (cf. the supplementary information). For neutral thymine accurate reference equilibrium structure has been obtained by two complementary techniques (Vogt et al., 2014), namely ab initio, r_e structural parameters from the composite approach based on the all-electron CCSD (T) (Raghavachari et al., 1989) geometry optimizations employing the cc-pwCVTZ basis set (Peterson and Dunning, 2002) and the semi-experimental (r_e^SE) (Pulay et al., 1978) method, based on the fit of equilibrium rotation constants (obtained from the experimental ones by extracting vibrational corrections), which agree with each other to within 0.002 Å and 0.2°, further confirming their high accuracy. B2PLYP/AVTZ and B3LYP/AVTZ structures compared with the r_e (ab initio) one exhibit mean absolute errors (MAE) of about 0.0025 Å with the largest discrepancies of about 0.008 Å and 0.01 Å, respectively. The latter are mainly due to the overestimation of C-N bond lengths. The accuracy is even better for the angles with MAE below 0.15° and largest discrepancies of ± 0.3°. Based on the good quality of both DFT structures for neutral thymine similar accuracy can be expected for the cation.

TABLE 1

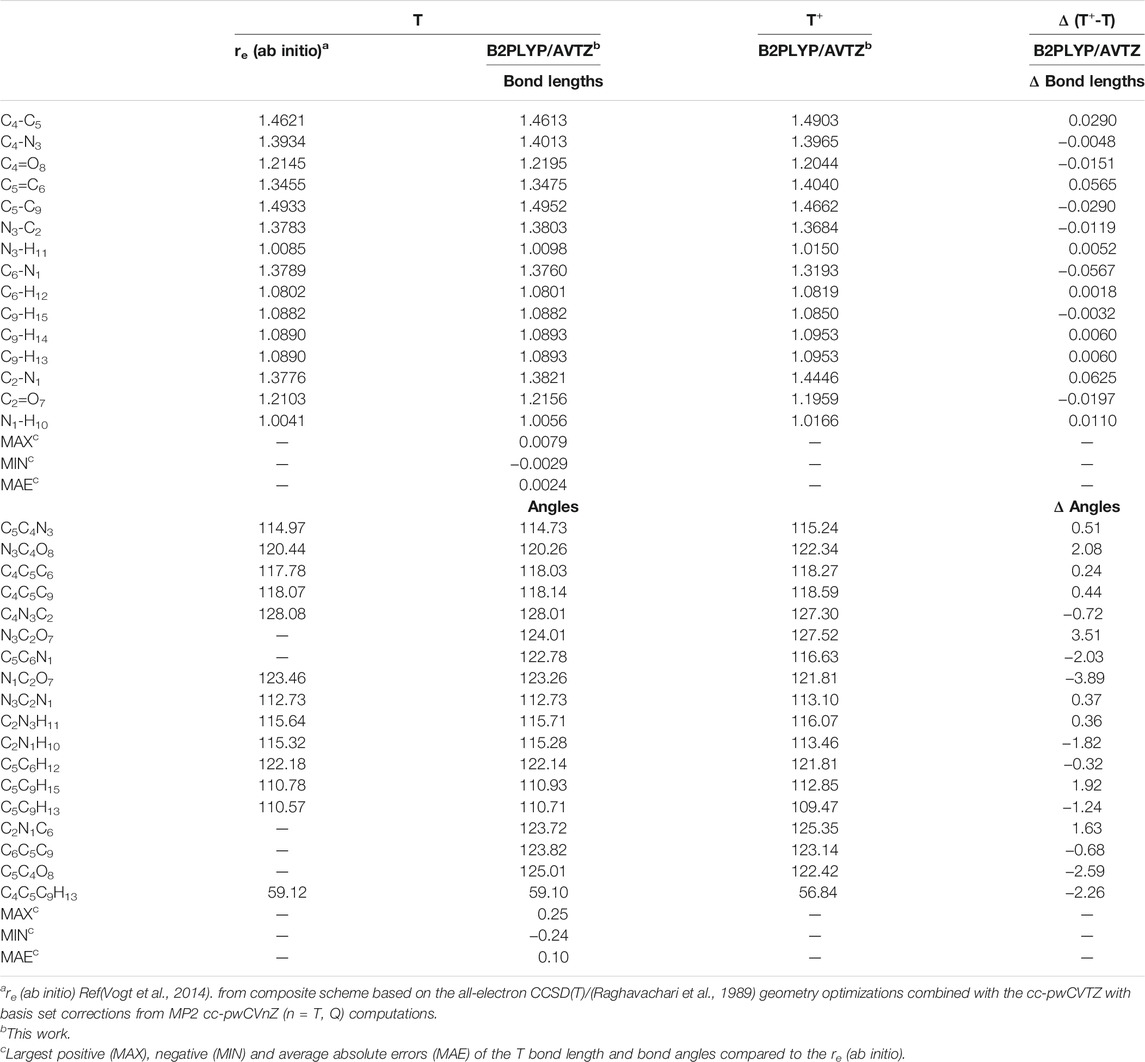
TABLE 1. Structural parameters of neutral Thymine and its cation (bond lengths in Å, angles in deg).

FIGURE 2

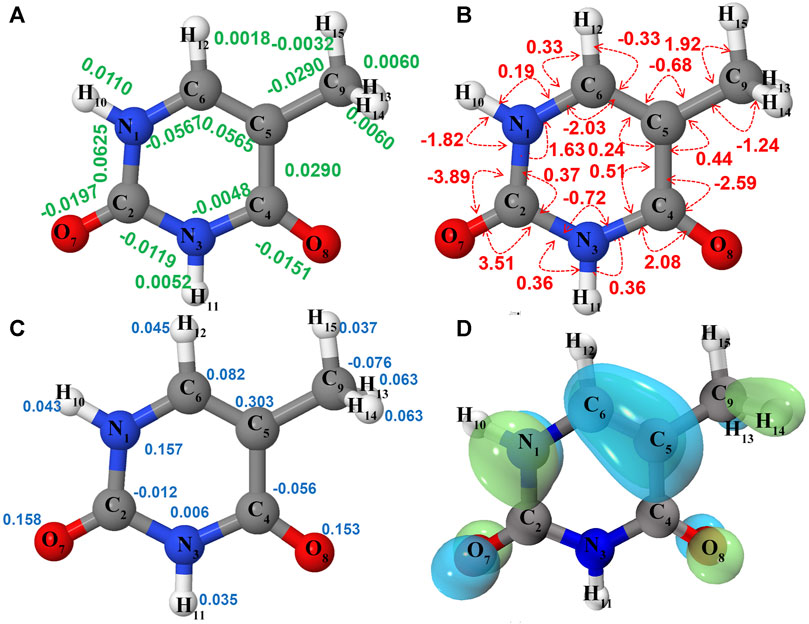
FIGURE 2. Structure and properties of neutral thymine ( ${\tilde{X}}^{1} A ′$ ) as computed at the B2PLYP/AVTZ level, along with the changes of specific parameters between cationic ( ${\tilde{X}}^{2} A^{″}$ ) and neutral ( ${\tilde{X}}^{1} A ′$ ) thymine. (A) bond length changes, green; (B) bond angle changes, red; (C) charge changes, blue; (D) HOMO orbital of thymine (neutral) ${\tilde{X}}^{1} A ′$ . (A) ∼ (D) numbering of the atoms constituting the thymine (neutral) molecule as used in the following tables.

Table 2 lists all fundamental anharmonic wavenumbers and IR intensities of T and T⁺ computed at the B2PLYP/AVTZ//B3LYP/AVTZ GVPT2 level, along with the most important overtones and combination bands. For neutral thymine, the assignment is based on the visual inspection of normal modes (Figure 3), and used as a basis to express T⁺ vibrations according to the Duschinsky rotation (Figure 4). Corresponding normal modes of T and T⁺ are listed in the same row, allowing a straight forward comparison of the changes in the wavenumbers and IR intensities upon ionization. The accuracy of simulated IR spectra of T $({\tilde{X}}^{1} A ′)$ in the 100 cm⁻¹ to 3900 cm⁻¹ range, can be assessed by comparison with experimental results recorded for gas phase T (Colarusso et al., 1997) and for T trapped in the low-temperature argon matrix (Szczepaniak et al., 2000). All these spectra are reported in Table 2, with the latter showing higher resolution allowing to identify and assign non-fundamental transitions. We note that the comparison between the gas phase and matrix results indicates that X-H (X = N, C) stretching frequencies of the latter are not affected by the matrix. The very good agreement with experiment is obtained not only for fundamental frequencies but also for all observed 52 transitions with MAE of ∼7.2 cm⁻¹, and the largest errors of 15 cm⁻¹ and 24 cm⁻¹, respectively. Importantly, agreement within about 5 cm⁻¹ is achieved for most characteristic vibrations such as both NH and CO stretchings, (modes 1/2 and 6/7, respectively). Accurate predictions of band positions are combined with reliable computed IR intensities [of 54 km/mol - 83 km/mol for ν(NH) and 244 km/mol - 480 km/mol for ν(CO)] which show a good qualitative agreement with experiment. The simulated harmonic and anharmonic spectra in the 1650 cm⁻¹ - 1850 cm⁻¹ range, characteristic for the carbonyl stretchings, are compared directly with the experiments in Figure 5. The experimental gas phase spectrum is dominated by two broad ν (CO) bands, but the one from Ar Matrix shows additionally several quite intense transitions. Obviously, the harmonic model not only systematically overestimates vibrational energies, but also is not able to simulate correctly the experimental spectral shape. At variance, the GVPT2 reproduces well the position and intensity of relative strong non-fundamental transitions resulting from the Fermi resonances (as discussed in the following). Thus, the same GVPT2 B2PLYP//B3LYP approach is expected to yield reliable predictions of cation IR spectra, in terms of both band positions and relative intensities.

TABLE 2

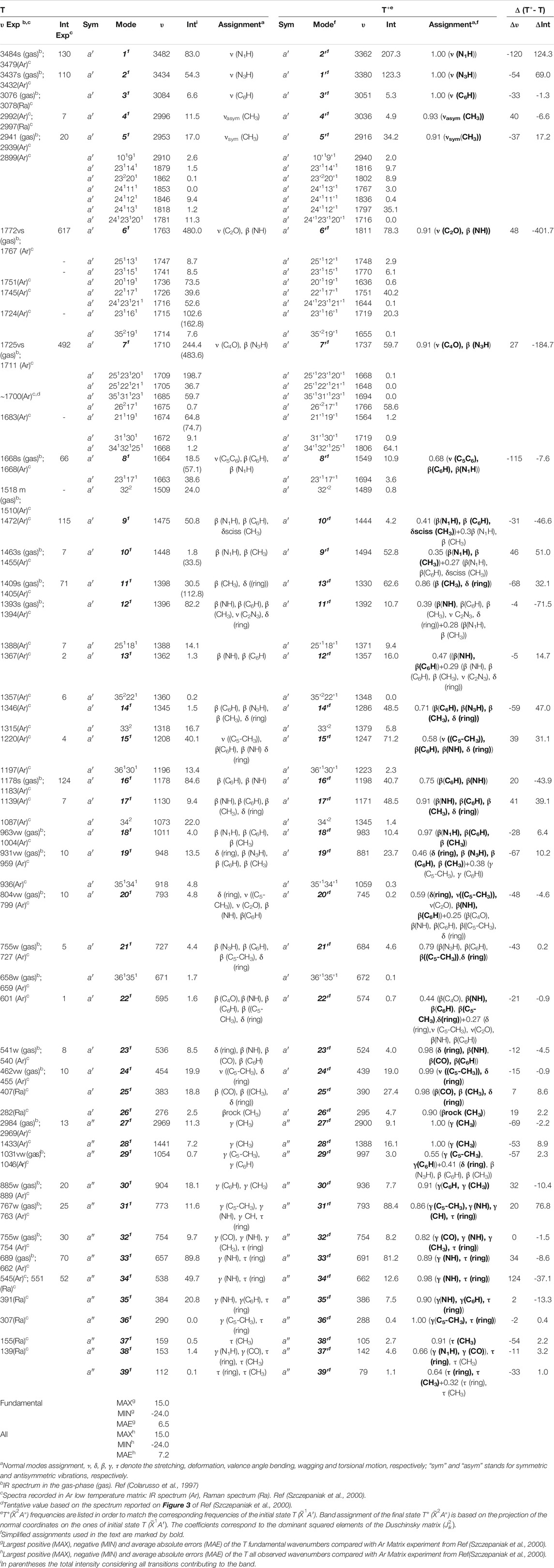
TABLE 2. Anharmonic wavenumbers ( $υ$ , cm⁻¹) and IR intensities (km/mol) computed at GVPT2//B2PLYP//B3LYP/AVTZ level for T (X ∼ ¹ A′) and T⁺(X ∼ ² A″) compared with experimental data.

FIGURE 3

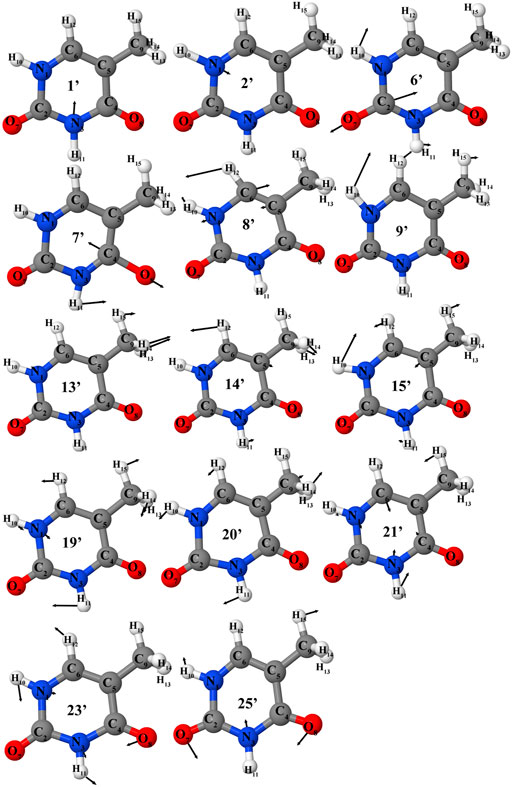
FIGURE 3. Selected vibrations of the thymine (in cation normal modes representation) corresponding to most intense transitions in IR or photoelectron spectra.

FIGURE 4

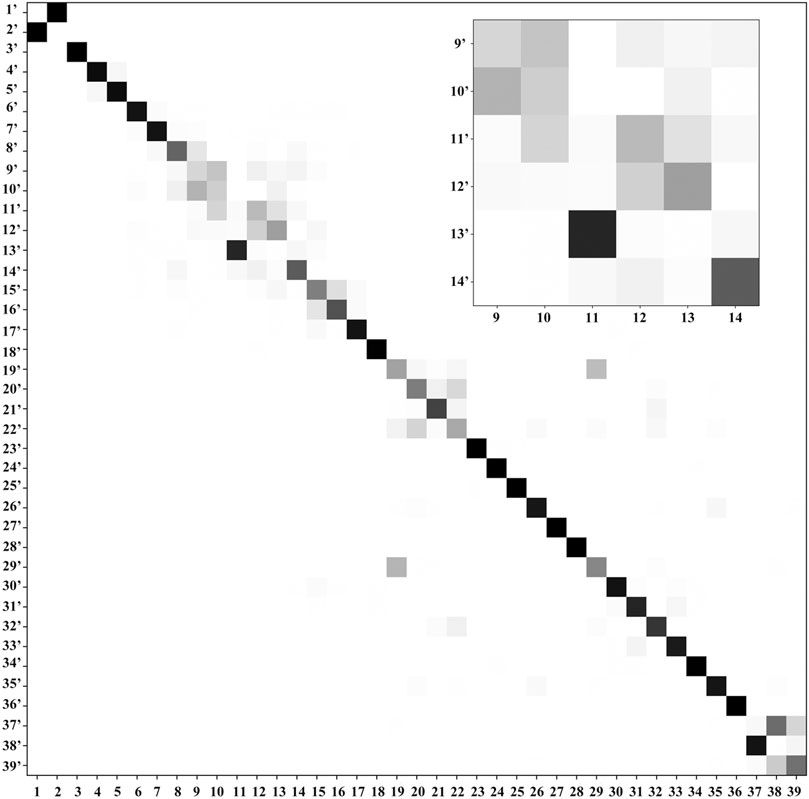
FIGURE 4. Duschinsky matrix: the normal coordinates of the final state T⁺ (columns) are expressed in the basis set of the normal coordinates of the initial state T (rows). A gray scale is used to represent the magnitude of each element of the J matrix, with a white square for a near-null value and a black square for 1 (equivalent normal modes). The part with largest mode coupling is shown in the inset.

FIGURE 5

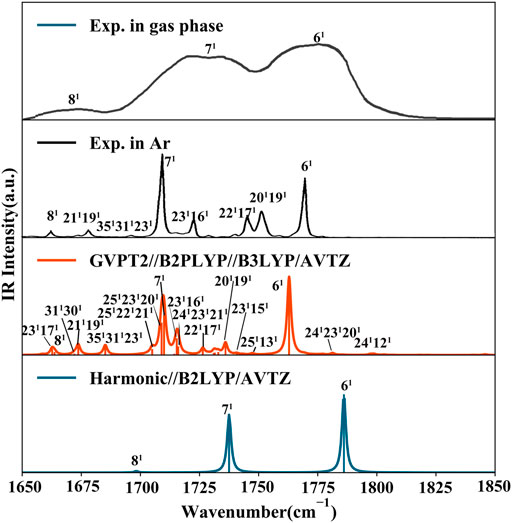
FIGURE 5. IR spectrum of thymine in the CO stretching range (1650 cm⁻¹ - 1850 cm⁻¹). Computed stick spectra were broadened by Lorentzian functions with half width at half-maximum (HWHM) of 1 cm⁻¹. Most significant contributions to intense bands are assigned as mⁿ where m is the normal mode and n is the number of quanta on this mode (1 fundamentals, 2 overtones). Experimental spectra of gas phase thymine (Colarusso et al., 1997) and of Ar low temperature matrix trapped thymine (Szczepaniak et al., 2000) are shown for comparison.

Ionization effects are correlated with the changes in electron density yielding structure modifications, which in turn tune the molecular vibrations and relative spectra. These changes are directly related to the active vibrational progression of photoelectron spectra, and reflected in the modification of infrared spectra patterns (band positions shifts and dipole moment/IR intensity variations). The most significant geometrical changes are related to the C₂-N₁-C₆-C₅ part of the ring, with the C₆-N₁ bond shorter by about 0.06 Å, the C₂-N₁ and C₆-C₅ longer by a similar amount, along with the C₅C₆N₁ bond angle decrease by 2.03° and C₂N₁C₆ bond angle increase by 1.63°. These structural modifications can be associated with the changes in the electron density upon removing an electron from a HOMO orbital mainly localized on C₂-N₁-C₆-C₅ part of the ring and both oxygen atoms (Figure 2D). Small changes in other structural parameters such as X-H (X = N, C) bond elongation by 0.0018 Å - 0.011 Å or C=O bonds shortening by 0.015 Å - 0.02 Å, introduce effects on relevant vibrations, with the wavenumbers redshifted between -30 cm⁻¹ to -120 cm⁻¹, or blue shifted by up to about 50 cm⁻¹, respectively (see Table 2). In addition to wavenumbers changes, IR spectra are influenced by the charge modifications and different polarity of relevant bonds (NBO charges are reported in the Supplementary Table S3). The negative charge decrease on oxygen atoms by over 0.15 e leads to smaller polarity of both C=O bonds, and in consequence lower IR intensity for these strong transitions in the case of T⁺. Moreover, ionization leads to some mode mixing which can be analyzed based on the projection of the normal coordinates between the two electronic states using the Duschinsky matrix J, which is graphically represented in Figure 4. Namely, the group of T⁺ modes related to the ring deformation, 9', 10', 11', 12' and 13' is described by contributions from 10, 9, 12, 13 and 11 T vibrations, as depicted in the inset of Figure 4. Non-negligible Duschinsky rotation is also observed for the modes 19', 22', 29' and 39'. Interestingly, most of the remaining modes are not affected by significant mode mixing. The ionization induced changes in the band position and IR intensities lead to very different spectrum patterns for T and T⁺, as presented in Figure 6. In general terms, the IR spectrum of T⁺ is characterized by several bands of similar intensities, while the spectrum of T is dominated by strong transitions corresponding to bands dominated by CO stretching (assigned as ν (CO), β (NH)). The latter, the T ( ${\tilde{X}}^{1} A ′$ ) 6 and 7 fundamentals, are over four times more intense than their T⁺ ( ${\tilde{X}}^{2} A ″$ ) counterparts 6' and 7' with intensity differences of -401.7 km/mol and -184.7 km/mol. It is interesting to analyze changes of the overall spectrum pattern in the 1650 cm⁻¹ - 1850 cm⁻¹ range, which are influenced not only by the ν (CO) fundamentals intensity and wavenmbers changes, but also by different resonances. Both Figure 6B and Table 2 show that the peak at 1662 cm⁻¹ - 1664 cm⁻¹ of T is composed by 8¹ [ν (C₅C₆), β (C₆H), β (N₁H)] fundamental and a very close-lying 23¹17¹ combination transition. Only the 8¹ fundamental band was assigned in the Ar matrix spectrum in Figure 5 and Table 2. The peak at 1672 cm⁻¹ - 1674 cm⁻¹ corresponds to two transitions, of which one is the combination 21¹19¹ [β (N₃H), β (C₆H), β (C₅-CH₃), δ (ring); δ (ring) β (N₃H), β (C₆H), β (CH₃)] and the other is the 31¹30¹ [γ (C₅-CH₃), γ (NH), γ (CH), τ (ring); (γ (C₆H), γ (CH₃)] involved in a Fermi resonance with the 8¹ fundamental. The intensity of the 21¹19¹ combination band is approximately 7 times larger than that of the 31¹30¹, so the experimental band can be tentatively assigned to 21¹19¹. The band at 1709 cm⁻¹ - 1710 cm⁻¹ is due to the 7¹ fundamental mode together with some combination transitions. The peak at 1715 cm⁻¹ - 1716 cm⁻¹ corresponds to two transitions, of which one is the combination 23¹16¹ and the other is the 24¹23¹21¹, the intensity of the 23¹16¹ combined band is about 2 times larger than that of the 24¹23¹21¹, allowing a simplified assignment of experimental band as 23¹16¹. Within the range of 1726 cm⁻¹ - 1747 cm⁻¹, there are several non-fundamental transitions, from which 22¹17¹ and 20¹19¹ [δ (ring), ν (C₅-CH₃), v (C₂O), β (NH), β (C₆H); δ (ring), β (N₃H), β(C₆H), β (CH₃)] are most intense. For the cationic species, within the range of ∼1720 cm⁻¹ - 1750 cm⁻¹, there are three peaks formed from 7'¹ fundamental and two transitions involved in resonances, which are 23'¹16'¹ and 22'¹17'¹. In the range 1797 cm⁻¹ - 1811 cm⁻¹, in addition to the 6'¹ fundamental there are peaks formed from transitions involved in resonances, which are 24'¹12'¹, 23'²20'¹, and 34'¹32'¹25'¹.

FIGURE 6

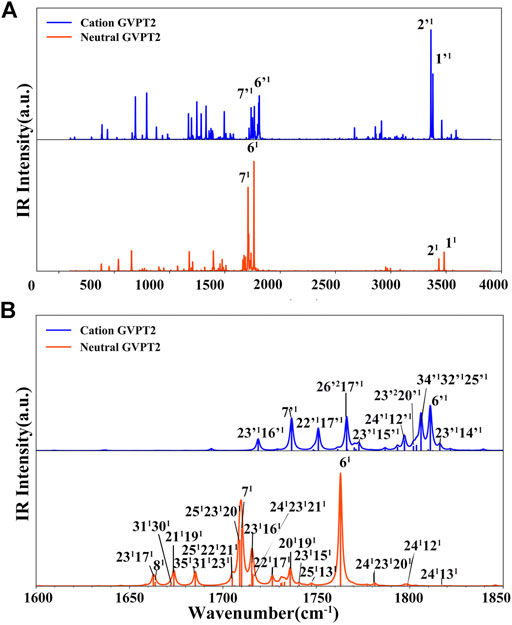
FIGURE 6. MIR spectra simulated at GVPT2//B2PLYP//B3LYP/AVTZ level. Spectra line-shapes were broadened by Lorentzian functions with HWHM of 1 cm⁻¹. (A) 100 cm⁻¹ - 4000 cm⁻¹ range (B) The 1600 cm⁻¹ -1850 cm⁻¹ range related to the modes 6, 7 and the non-fundamentals involved in the Fermi resonances. Most intense bands are assigned as mⁿ where m is normal mode and n number of quanta (1 fundamentals, 2 overtones).

In summary, neutral and cationic fundamental modes involved in Fermi resonances are 6/6' [ν (C₂O), β (NH)) and 7/7' (ν (C₄O), β (N₃H)]. Indeed, the T ( ${\tilde{X}}^{1} A ′$ ) fundamental mode 6 (at 1763 cm⁻¹) is involved in three Fermi resonances with combination transitions 25¹13¹ [β (CO), β (CH₃), δ (ring); β (NH), β (C₆H)), 23¹15¹ (δ (ring), β (NH), β (CO), β (C₆H); ν (C₅-CH₃), β (C₆H), β (NH), δ (ring)] and 20¹19¹ [δ (ring), ν (C₅-CH₃), ν (C₂O), β (NH), β (C₆H); δ (ring), β (N₃H), β (C₆H), β (CH₃)]. Besides, different combination bands participate to Fermi resonances with 6' mode of T⁺( ${\tilde{X}}^{2} A ″$ ), that is due to the wavenumber shift by +48 cm⁻¹ of the fundamental itself, but also due to the combination transitions shifts. For instance, the intensity of the neutral state combination band 20¹19¹ (at 1736 cm⁻¹) increases up to 73.5 km/mol, while its cationic counterpart, at 1636 cm⁻¹ is significantly redshifted. Therefore, it is no more involved in Fermi interactions, which may favor intensity trading. This results in a significant low intensity (of 0.6 km/mol) for this mode. At variance the 24'¹12'¹ [ν (C₅-CH₃), δ (ring); β (NH), β (C₆H)] combination band of cation, at 1797 cm⁻¹, gains intensity due to anharmonic interaction, while its neutral counterpart 24¹13¹, at 1818 cm⁻¹, is not involved in Fermi resonances. Moreover, the Fermi resonance combining 8¹ and 31¹30¹ of T ( ${\tilde{X}}^{1} A ′$ ) leads to the 9.1 km/mol intensity for the latter, much larger than the 0.9 km/mol for the same combination band for the cation. However, the combination transitions 22¹17¹ and 23¹16¹ and their cationic counterparts are both involved in Fermi resonances with 7¹/7'¹ fundamental, respectively.

Overall, we can conclude that the relatively small changes in the structure and electron density due to ionization lead to significant modifications of the vibrational properties, such as normal modes, wavenumbers, IR intensities and anharmonic resonances. Hence, the resulting IR spectra of T and T⁺ differ significantly.

Photoelectron Spectra

The $T^{+} {\tilde{X}}^{2} A^{′′} \leftarrow T {\tilde{X}}^{1} A ′$ spectrum simulated at the TI FC|AH level employing GVPT2 B2PLYP/B3LYP anharmonic wavenumbers for both initial and final states is reported in Table 3 and Figure 7 along with the available experimental results. The latter are the mass-analyzed threshold ionization (MATI) spectrum (Choi et al., 2005) and the slow photoelectron spectrum (SPES) of thymine (Majdi et al., 2015). The MATI spectrum is recorded with very high resolution (∼0.1 meV) but has been measured only in a limited energy range, within about 1800 cm⁻¹ from the 0–0 transition. An extended range allowing to analyze a rich vibrational structure is provided by the SPES technique, whereas the resolution is less (∼30 meV). These spectra were obtained with thymine seeded into a cooled molecular beam (with a temperature less than 60 K), thus in this section, we will consider the spectrum simulated at 60 K. However, as all significant transitions have been predicted to initiate from the neutral ground vibrational state |0>, the final assignment of the vibronic transitions refers to different vibrational levels of the cationic species. It can be observed that, although the most intense band in PE spectrum is related to the 0–0 transition, the spectrum shows also a set of vibrational progressions related to the active modes (Figure 3). Among them the most intense bands involve modes 8', 14', 21', 23' and 25', and are correlated with the structural changes upon ionization. For instance, mode 8' [ν (C₅C₆), β (C₆H), β (N₁H)] is associated with the C₅C₆ bond length increase by over 0.05 Å. The remaining most active vibrations are 14' assigned as [β (C₆H), β(N₃), β (CH₃), δ (ring)]; 19' as attributed to [δ (ring), β(N₃H), β (C₆H), β (CH₃)]; 21' assigned as [β (C₅-CH₃), δ (ring)]; 23' assigned as [δ (ring), β (NH), β (CO), β (C₆H)]; and 25' is attributed [β (CO), β (CH₃), δ (ring)]. Direct comparison of line-shapes reported in Figure 7 clearly indicates that the simulated most intense bands of TI FC|AH spectrum are in a good agreement with the SPES experiment (Majdi et al., 2015). This is confirming that a dominant direct process while photoionizing thymine is in action as suggested by Majdi et al. We note that previous attempts to assign the vibronic structure of the $T^{+} {\tilde{X}}^{2} A^{″} \leftarrow T {\tilde{X}}^{1} A ′$ photoionization transition, with FC spectra based on (scaled by 0.97) ωB97X-D harmonic computations (Bravaya et al., 2010), also showed a good agreement with the MATI experiment and have been characterized by the same intense bands as in the present work.

TABLE 3

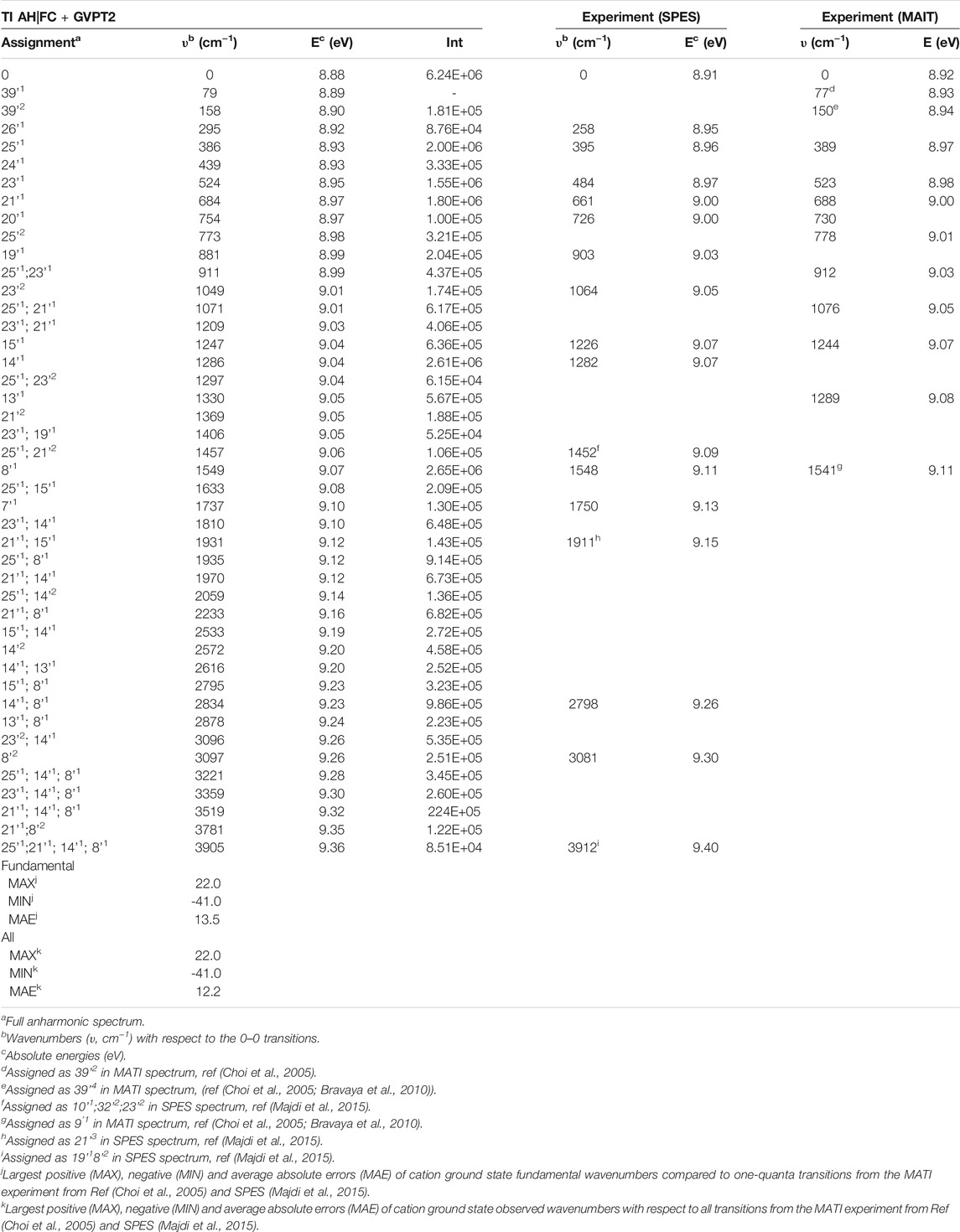
TABLE 3. TI AH|FC photoelectron spectra, selected transitions compared to the SPES and VUV-MATI experimental spectra.

FIGURE 7

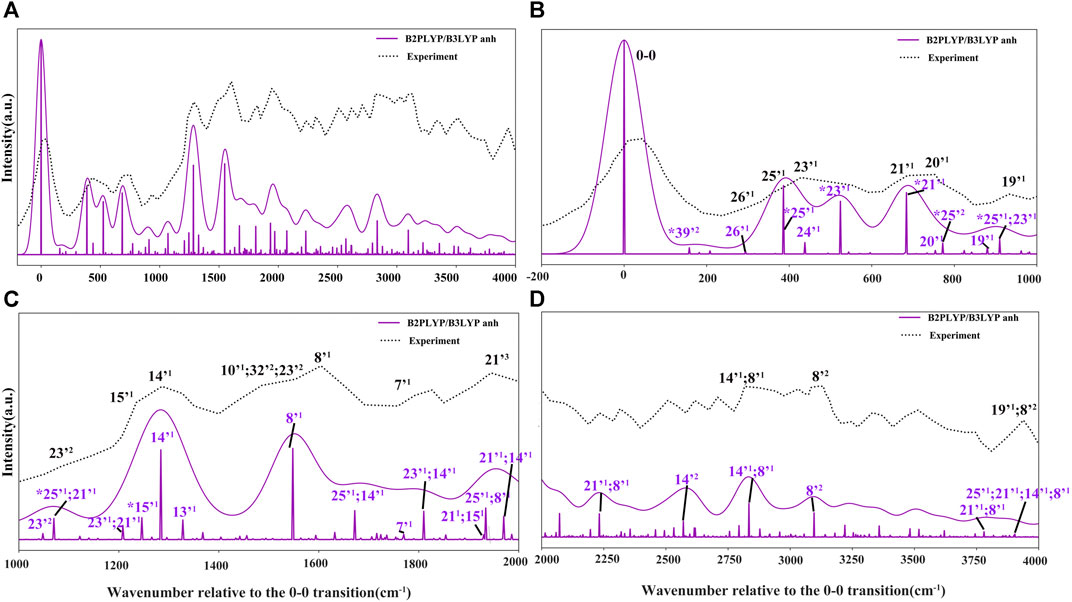
FIGURE 7. Photoelectron TI AH|FC spectrum (60 K) and SPES experimental spectrum (Majdi et al., 2015). The computed spectrum is represented as single transitions, with most intense ones assigned as mⁿ, which represents the final vibrational state with n quanta associated to mode m. The convoluted spectra line-shapes have been obtained by broadening with Gaussian function with HWHM of 50 cm⁻¹. Bands observed also in the VUV-MATI experimental spectrum (Choi et al., 2005; Bravaya et al., 2010) are marked by asterisk (*).

The more detailed comparison, including all experimentally observed transitions of both MATI and SPES spectra is reported in Table 3. In the energy range up to 1000 cm⁻¹ from 0–0, the calculated spectrum shows one-quanta transitions related to |26'¹>, |25'¹>, |23'¹>, |21'¹>, |20'¹>, |19'¹> modes, in agreement with the tentative assignments of experimental spectra proposed previously. Nevertheless, the two lowest transitions observed in the VUV-MATI experiment have been assigned as 2 and 4 quanta progressions of mode 39' > [τ (ring), γ (CH₃)] based on the harmonic computations at the B3LYP/6–311+G (d, p) level. At variance, based on anharmonic B2PLYP/B3LYP computations from this work, one and two quanta transitions of [γ (CH₃), τ (ring)], matches well the bands at 77 cm⁻¹ and 150 cm⁻¹ from VUV-MATI experiment. Consequently, we reassign these bands to the |39'¹> and |39'²> transitions, respectively. The intense |8'¹> transition simulated at 1549 cm⁻¹, shows a good agreement with the experimental band at 1541/1548 cm⁻¹ observed in both VUV-MATI and SPES experiments, which have been attributed to |9'¹> and |8'¹>, respectively, thus confirming the latter assignment. Moreover, for the broad band at about 1900 cm⁻¹, the calculated spectrum suggests assignment to the combination bands |25'¹; 8'¹>, |21'¹; 15'¹> instead of previously proposed three-quanta transition of mode 21 (|21'³>), which is over 100 cm⁻¹ blue-shifted and predicted much less intense. For remaining bands in the 0 cm⁻¹ - 2000 cm⁻¹ energy range observed in VUV-MATI and SPES spectra, TI FC|AH computations confirm previously proposed assignments to one and two quanta transitions. In the range of 2000 cm⁻¹ - 4000 cm⁻¹, the TI FC|AH simulations validate the assignment of SPES bands at 2798 cm⁻¹ and 3081 cm⁻¹ to the |14'¹; 8'¹>, |8'²> transitions, respectively. While, for the band at about 3900 cm⁻¹ a reassignment to four quanta combination |25'¹; 21'¹; 14’¹; 8'¹> mode is suggested, instead of the previously proposed three-quanta |19'¹; 8'²> one. Overall, the PE spectrum is dominated by the transitions related to the most active modes, with the 2 quanta transitions involving modes 39', 25', 23', 14' and 8' being also important for the assignment of the main peaks. Indeed, the very good agreement with the experimental SPES and VUV-MATI spectra is obtained not only for the fundamental wavenumbers but also includes all observed 22 transitions with MAE of ∼12.2 cm⁻¹.

Finally we would like to notice that the theoretical prediction of the 0–0 transition computed at B2PLYP/AVTZ level in conjunction with GVPT2 B2PLYP/B3LYP anharmonic zero-point-vibrational energies, of 70863 cm⁻¹ (8.79 eV) (Supplementary Table S4), shows an improvement over PBE0/AVDZ and B3LYP/AVTZ but is still differing by over 1000 cm⁻¹ from the experimental VUV-MATI 0–0 transition with the energy of 71920 cm⁻¹ (8.9178 ± 0.001 eV). Improved value is obtained by combining the same anharmonic zero-point-vibrational energies with the adiabatic electronic energy computed at the (R)CCSD(T)-F12(b) (+CV + SR) level (Majdi et al., 2015), leading to 0–0 transition energy of 72092cm⁻¹ (8.94 eV) in agreement within ∼165 cm⁻¹ (∼0.02 eV) with VUV-MATI experiment, highlighting the need for improved estimate of relative electronic energies.

Astrochemical Implications

Good accuracy of simulated vibrational and vibronic spectra, confirmed by comparison with available experimental results allows to provide predictions regarding the “missing” data, with particular relevance of computational support for the astrochemical observations.

In this respect the IR spectra of thymine cation is relevant for the studies of complex atmosphere of Titan, which is an ideal place for understanding the origins of life and chemical reactions due to its similarity to an early Earth environment. According to the data from the Cassini Composite Infrared Spectrometer (CIRS) (Flasar et al., 2005) and other observations (Samuelson et al., 1983; Coustenis et al., 1998; Niemann et al., 2010). Titan’s atmosphere is composed of nitrogen (95–98%), methane (1.8–5.0%), hydrogen (0.1–0.2%), and carbon monoxide (0.005%), with trace amounts of ethane, acetylene, propane, ethylene, hydrogen cyanide, cyanoacetylene, carbon dioxide, water vapor, along with significant amount of hydrocarbons (Cable et al., 2012). This rather dense atmosphere is characterized by a rich and complex organic chemistry (Way et al., 2002; Ali et al., 2013). For this reason, several studies involving the simulation of Titan’s atmosphere have been carried out. The complex organic mixtures that are formed in these simulation experiments (usually by the irradiation of N₂, CH₄, H₂, and CO) are known as “Tholins” (Cassidy et al., 2010). It was already shown that Tholins contain prebiotic molecules, particularly N-bearing cyclic compounds such as purines and pyrimidines. Cassini INMS measurements pointed out the presence of large molecules (>100 amu) in Titan’s atmosphere [see references (Puzzarini et al., 2017) and (Ali et al., 2013)]. Thus, the next step to be undertaken is the astronomical detection of key prebiotic molecules via the observation of their spectroscopic, infrared, or millimeter-wave features. Comparison with “Tholins” vibrational spectra (MIR) allows identifying which of these prebiotic molecules can be plausibly formed at such conditions, thus possibly present in Titan atmosphere.

In Figure 8 the simulated IR spectra of neutral thymine and of its cation in their electronic ground states are superposed to the experimental spectrum of “Tholins” (Gautier et al., 2012) matching well some of its characteristic bands. For instance, the fundamental transition of T⁺ at about 793 cm⁻¹ [γ (C₅-CH₃), γ (NH), γ (CH) and τ (ring)] matches well the broad band at 700 cm⁻¹ - 800 cm⁻¹, while the T β (C₆H), β (NH) fundamental at 1178 cm⁻¹ fits the shoulder at about 1150 cm⁻¹ - 1200 cm⁻¹. There are also several transitions of both T and T⁺, which can contribute to the most pronounced band at 1400 cm⁻¹ - 1700 cm⁻¹, such as T⁺ β (N₁H), β (CH₃) at about 1494 cm⁻¹ and T [β (N₁H), β (C₆H)] at about 1475 cm⁻¹ or [ν (C₅C₆), β (C₆H), β (N₁H)] at about 1664 cm⁻¹. Moreover, the ν (N₁H) of T⁺ at about 3362 cm⁻¹ corresponds well to the Tholins peak at about 3330 cm⁻¹. However, the intense band in the 2100 cm⁻¹ - 2400 cm⁻¹ range, cannot be associated with neither of T or T⁺. Moreover, the intense transitions of T and T⁺ at 1800 cm⁻¹ - 1850 cm⁻¹, are slightly blue-shifted with respect to the Tholins band, thus we can conclude that the IR spectra are roughly consistent with some peaks of the experimental “Tholins” spectrum. Consequently, both species can be potentially present in such complex mixture, but the final confirmation would require further analysis, which can be carried out with the aid of the simulated spectra reported presently.

FIGURE 8

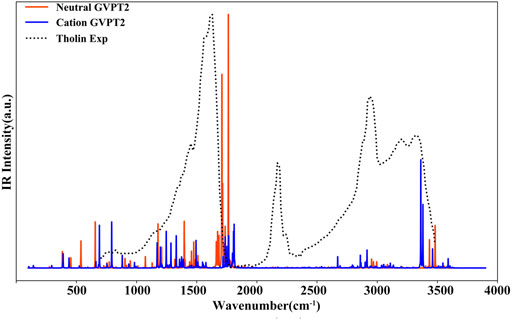
FIGURE 8. Comparison of the simulated IR spectrum of thymine with the experimental spectrum of Tholins (Gautier et al., 2012). GVPT2//B2PLYP//B3LYP/AVTZ stick spectra were broadened by Lorentzian functions with HWHM of 1 cm⁻¹.

Near-infrared spectroscopic studies are employed in order to assist interpretation of data collected by instruments such as SuperCam, ISEM (Infrared Spectrometer for ExoMars) or MicrOmega (Vago et al., 2017) from Mars 2020 (Williford et al., 2018) and ExoMars 2022 (ESZ-Roscosmos) (Vago et al., 2017) space missions. Such investigations target molecular spectroscopic features in NIR, which is less congested in comparison to MIR one. Nevertheless, it requires assignments of molecular vibrational modes in the NIR spectral region, which are very scarce in the literature (Fornaro et al., 2020). Indeed, the analysis of the astrochemical samples needs accurate reference for the assignment and identification of plausible molecules. In this respect, the NIR spectra of gas phase thymine have not been measured experimentally even for the neutral molecule, and is only available for the polycrystalline samples of nucleobases. Besides, the GVPT2//B2PLYP//B3LYP/AVTZ method has been already demonstrated to yield reliable predictions of NIR spectra (Bloino, 2015) but the simulation of thymine polycrystalline NIR spectra has shown to require contributions from monomeric, dimeric, and clustered thymine to reach agreement with experiment (Beć et al., 2019). Moreover, the assignment of NIR bands of gas phase isolated neutral thymine and its cation has not been studied in detail.

For T and T⁺, wavenumbers and intensities in the NIR range are listed in Table 4, while the spectrum line-shapes are shown in Figure 9, along with the assignment of observed transitions. In the whole NIR range of 4000 cm⁻¹ - 10500 cm⁻¹, two quanta transitions of NH and CH stretches are most intense. While, considering only the 8500 cm⁻¹ - 10500 cm⁻¹ range, three quanta transitions assigned to overtones bands for the excitation of the ν (CH), ν (C₅-CH₃) stretches are dominant. Remaining overtones and combination bands are related to (ν (NH) ν (CH), ν (C₅-CH₃)); (β (NH), β (CH), β (C₅-CH₃)); (γ (NH), γ (CH), γ (CO), γ (C₅-CH₃)); and δ (ring). As for the MIR range, the neutral and cation of thymine can be clearly distinguished by the NIR measurements.

TABLE 4

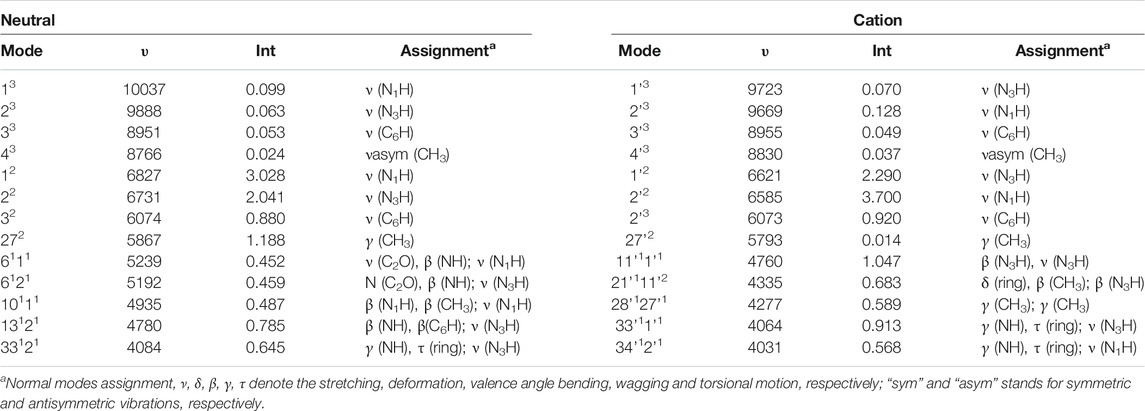
TABLE 4. NIR spectra computed at the GVPT2//B2PLYP//B3LYP/AVTZ level, wavenumbers (υ, cm⁻¹), IR intensities (km/mol) and assignment.

FIGURE 9

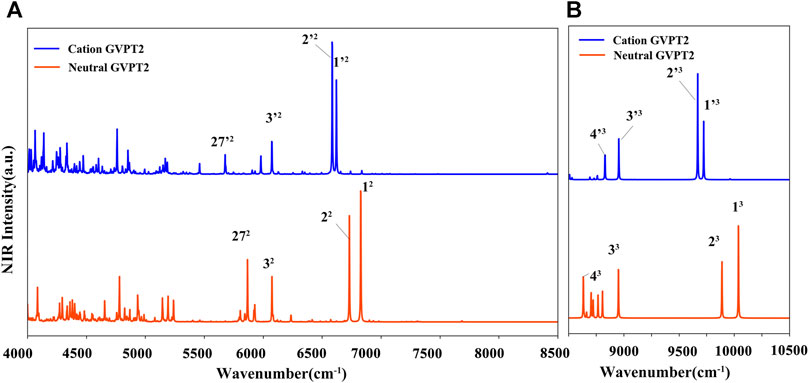
FIGURE 9. (A) (B) NIR spectra simulated at GVPT2//B2PLYP//B3LYP/AVTZ level. Spectra were broadened by Lorentzian functions with HWHM of 1 cm⁻¹. Most intense bands are assigned as mⁿ where n-number of quanta and m is the normal mode.

Finally we should note that photoionization occurs throughout the Universe, so that it is relevant for different astrochemical environments. Depending on the energy of the photon, it can be divided into ultraviolet photoelectron spectroscopy (UPS) and X-ray photoelectron spectroscopy (XPS), the former hitting the low energy of the electron, ejecting off the valence layer electrons, the latter hitting the high energy of the photon, ejecting off the inner layer electrons (Hollas, 2004). In this work we are focusing on the processes initiated by the absorption of a VUV photon leading to the ionization of a valence electron i.e., the $t h y m i n e ({\tilde{X}}^{1} A ′) + hv \to t h y m i n e^{+} ({\tilde{X}}^{2} A ″) + e^{-}$ photoionization transition. The available experimental studies have been mainly related to the low-temperature conditions and in more general terms the experimental description of radical cations is difficult. Instead, theoretical methods are ideal for this purpose allowing to predict spectra in a broad range of temperatures. As reported in Figure 10, the most intense transition of the $t h y m i n e ({\tilde{X}}^{1} A ′) + hv \to t h y m i n e^{+} ({\tilde{X}}^{2} A^{″}) + e^{-}$ vibrationally resolved electronic spectra at 0 K, 200 K, and 1000 K corresponds in all cases to the 0–0 band. Besides, the spectra at all temperatures show the same set of the most intense transitions mainly due to the |8'¹>, |14'¹> [β (C₆H), β (N₃H), β (CH₃), δ (ring)] bands. However, the overall spectral shape changes with temperature due to the increasing number of hot bands summing up to a significant contribution. This is especially the case for the spectra at 1000 K, where the previously discussed hot band involving the |6¹> - |0'> transitions become visible to the left of the band origin at ∼71245 cm⁻¹. The band is observable only at temperatures above 900–1000 K.

FIGURE 10

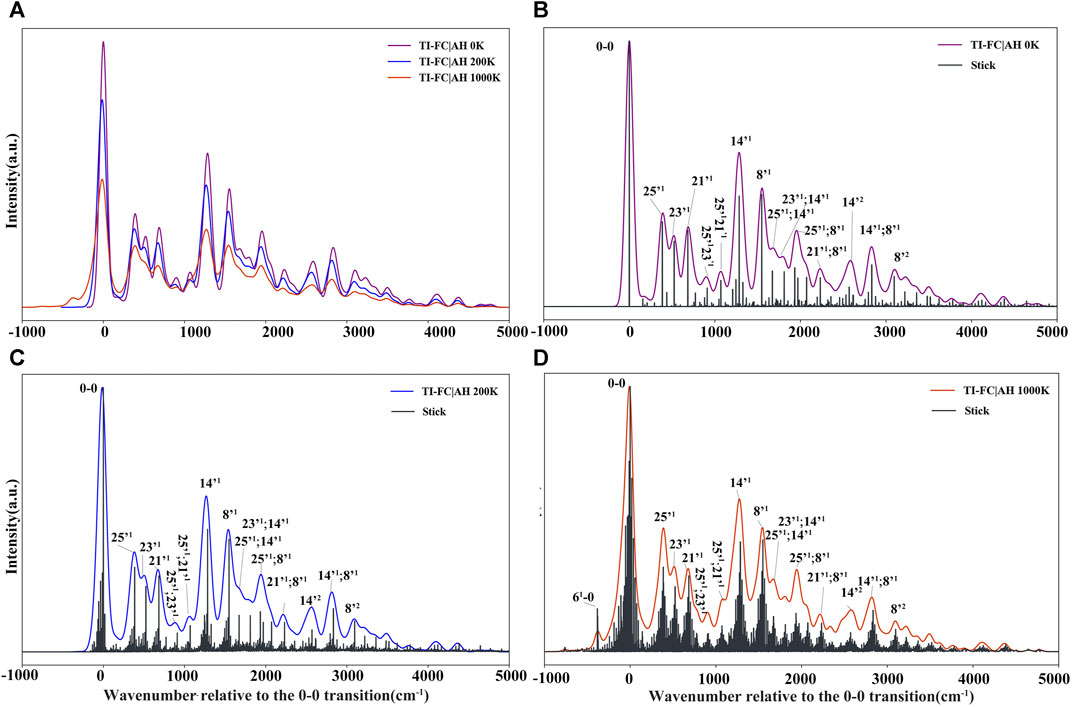
FIGURE 10. Vibrationally resolved electronic spectra: (A) comparison of spectra simulated at 0 K, 200 K, and 1000 K, spectra intensities have been normalized with respect to the most intense band; [(B–D)] convoluted and stick spectra simulated at 0 K, 200 K, and 1000 K, respectively. For all spectra, the line shapes have been convoluted with Gaussian distribution functions with HWHM of 50 cm⁻¹. The assignment for a selected vibronic transition (stick spectrum) is reported, where “mⁿ” and “m’ⁿ” represent the vibrational state with n quanta associated with modes m (initial/ground state) and m’ (final/ionic state), respectively.

Conclusion

The anharmonic GVPT2 hybrid B2PLYP//B3LYP/AVTZ computations for the thymine neutral state ${\tilde{X}}^{1} A ′$ and its ${\tilde{X}}^{2} A ″$ cation have been instrumental to obtain the very good qualitative and quantitative agreement with experiment for neutral thymine IR spectrum and the photoelectron ${\tilde{X}}^{2} A ″$ ← ${\tilde{X}}^{1} A ′$ spectra obtained within the TI AH|FC framework. The differences between the T and T⁺ IR spectra patterns, as well as the most intense transitions in the PE spectra have been correlated with the structural and charge density changes upon ionization. These modifications are sufficient to cause large changes in vibration properties (band position shifted) and dipole moment modifications (intensity variations). The former influence also the anharmonic resonances, so that mid-infrared spectrum in the 1650 cm⁻¹ - 1850 cm⁻¹ range shows more pronounced Fermi resonances for T ( ${\tilde{X}}^{1} A ′$ ) than for T⁺( ${\tilde{X}}^{2} A ″$ ). For the photoelectron spectrum of thymine in the 8.85–9.40 eV photon energy range, most of the previously proposed assignments have been confirmed, with the vibrational features related to one or multiple quanta transitions involving the vibrational modes 8', 13', 14', 15', 19', 20', 21', 23', 25', which correspond to ν (C₅C₆), ν (C₅C₉), ν (C₆N₁), ν(CH₃), β (N₁H), β (N₃H), β (CH), β (CO) and β (CH₃), δ (ring). These vibrational assignments are consistent with the largest bond lengths and bond angles changes after ionization. The final calculated vibrationally resolved electronic spectra obtained by GVPT2//B2PLYP//B3LYP/AVTZ method is in good agreement with the experimental VUV-MATI and SPES spectra.

The reliability of simulated spectra can be exploited to provide data for situations where the experimental observations have not been performed or are not feasible, with their potential applications supporting astrochemical studies. In this work, we have selected some possible cases, such as the analysis of infrared spectra of “Tholins”, the near-infrared spectra of samples from the Mars missions or the photoelectron spectra in cold and hot environments, from 0 to 1000 K. These examples have been selected due to the increasing role of the analysis of vibrational features in astrochemical studies, and can be extended toward more complex cases, as for instance the simulation of spectra of planet soil mixtures (Fornaro et al., 2014; Fornaro et al., 2020) or molecules absorbed on grains or ices (Barone et al., 2015).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

MB and MH designed the research; YZ performed the calculations; YZ and MB analyzed the data. YZ and MB prepared the original draft; MB and MH reviewed and edited final manuscript.

Funding

This work was enabled by the financial support from the National Natural Science Foundation of China (Grant No. 31870738). M.H. thanks the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of Centre National de la Recherche Scientifique (CNRS)/Institut National des Sciences de l’Univers (INSU) with Institut de Chimie (INC)/Institut de Physique (INP) co-funded by Commissariat à l’Energie Atomique (CEA) and Centre National d’Etudes Spatiales (CNES).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.757007/full#supplementary-material

References

Ali, A., Sittler, E. C., Chornay, D., Rowe, B. R., and Puzzarini, C. (2013). Cyclopropenyl Cation - the Simplest Huckel's Aromatic Molecule - and its Cyclic Methyl Derivatives in Titan's Upper Atmosphere. Planet. Space Sci. 87, 96–105. doi:10.1016/j.pss.2013.07.007