Links of the Plasmapause With Other Boundary Layers of the Magnetosphere: Ionospheric Convection, Radiation Belt Boundaries, Auroral Oval

The plasmapause marks the limit of the plasmasphere and is characterized by a sudden change in plasma density. This can influence the other regions of the magnetosphere, including due to different waves circulating inside and outside the plasmasphere. In the present work, we first compare the positions of the plasmapause measured by the NASA Van Allen Probes in 2015 with those of the Space Weather Integrated Forecasting Framework plasmasphere model (SPM). Using the Van Allen Probes and other satellite observations like PROBA-V, we investigate the links that can exist with the radiation belt boundaries. The inward motion of the outer radiation belt associated with sudden flux enhancements of energetic electrons can indeed be directly related to the plasmapause erosion during geomagnetic storms, suggesting possible links. Moreover, the position of the plasmapause projected in the ionosphere is compared with the ionospheric convection boundary. The equatorward motion of the plasmapause projected in the ionosphere is related to the equatorward edge motion of the auroral oval that goes to lower latitudes during storms due to the geomagnetic perturbation, like the low altitude plasmapause and the outer radiation belt. The links between these different regions are investigated during quiet periods, for which the plasmasphere is widely extended, as well as during geomagnetic storms for which plumes are generated, and then afterwards rotates with the plasmasphere. The magnetic local time dependence of these boundaries is especially studied on March 14, 2014 after a sudden northward turning of the interplanetary magnetic field (IMF) and for the geomagnetic storm of August 26, 2018, showing the importance of the magnetic field topology and of the convection electric field in the interactions between these different regions eventually leading to the coupling between magnetosphere and ionosphere.

Introduction

The plasmasphere is the extension of the ionosphere at low and mid-latitudes and is filled by low energy plasma (Lemaire and Gringauz, 1998; Darrouzet et al., 2009 for reviews). Plasmaspheric ion temperature is species dependent, with H⁺ and He⁺ typically in the range 0.1–1 eV and O⁺ warmer in the range 1–10 eV (Comfort et al., 1985; Comfort, 1996; Goldstein et al., 2019). The outer surface of the plasmasphere is often characterized by a “knee”, i.e., a sharp decrease of the plasma density: the plasmapause (Carpenter, 1963). Depending on the strength of the level of geomagnetic activity, usually parameterized or measured by the value of the Kp index (Bartels and Veldkamp, 1949), the equatorial position of the observed plasmapause can change from 7 Re to 2 Re, for low and high activity respectively (e.g., Pierrard et al., 2009 for a review). Analyses of ground-based whistler waves and in situ satellite observations of the cold plasma density show that the plasmapause forms closer to Earth when the geomagnetic activity level is enhanced (e.g., Pierrard and Cabrera, 2005). Above the plasmapause, the region of the plasmaspheric trough is characterized by much lower densities, generally below 10 cm⁻³.

The plasmapause boundary plays an important role in magnetospheric dynamics. In the present article, we study the links and possible coupled feedback mechanisms of the plasmapause with three other regions of the magnetosphere, i.e., the ionosphere, the radiation belts and the auroral oval. These regions and their interactions in the magnetosphere are described, for instance, in the review paper of Borovsky and Valdivia (2018) and in the book chapter of Fuselier et al. (2019).

Links between the inner edge of the outer radiation belt electrons and the innermost plasmapause location were first reported by Li et al. (2006) by using 12 years of 30-days averaged measurements of MeV electrons from both CRRES and SAMPEX satellites. The study was recently revisited in Khoo et al. (2018) with focus on storms. Links between the inner edge of the outer radiation belt and the plasmapause were also identified with previous observations from the LEO satellite SAC-C (Pierrard and Benck, 2012) and with CLUSTER (Darrouzet et al., 2013). Goldstein et al. (2016) quantified the outer belt and plasmapause position for the 5-day period of 15–20 January 2013 and found that for this event, electron fluxes earthward of belt’s peak are anti-correlated with cold plasma density. Here we will investigate such links using the Van Allen Probes and PROBA-V data, as well as some models.

We also study the links between the Magnetic Local Time (MLT) distribution of the plasmapause, the ionospheric convection boundary (using SuperDARN), the radiation belts for different energies from 10 keV to 8 MeV, and the auroral oval during two specific events: March 14, 2014 corresponding to a quiet period with a sudden Northward turning of the IMF, and August 26, 2018 corresponding to a geomagnetic storm. We start in Data and Models with the description of the satellite data and models used. In Long Term Variations of the Plasmapause: Comparison Between Observations and the Space Weather Integrated Forecasting Framework plasmasphere model Model, we compare the plasmapause observed by two satellites (Van Allen Probes and CRRES) with the plasmapause positions obtained from the dynamical SPM model (Pierrard and Lemaire, 2004). We show that long term plumes observed during long storm periods are reproduced by the model. Then, we discuss the long-term links of the plasmapause with the other regions of the magnetosphere, and especially with the radiation belts in Links Between the Plasmapause and the Radiation Belt Boundaries before analyzing specific cases. In Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During a Quiet Period: March 14, 2014, we analyze the quiet period of March 14, 2014 to determine the relations between the radial distance, the latitude, and the MLT distribution of the plasmapause, the ionospheric convection boundary, the radiation belt boundaries and the auroral oval. In Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During the Storm Event of August 26, 2018, we show the evolution of these links during the geomagnetic storm of August 26, 2018, and show the strong decrease in latitude of all these boundaries during the main phase of the storm in the framework of the global magnetospheric dynamics and its effects on the ionosphere-atmosphere. The links between the different boundaries and their MLT distribution are discussed in Discussion About the Links Between the Boundaries and Their the Magnetic Local Time Distribution and the results of the present work are summarized in the concluding section.

Data and Models

Satellite and Radar Data

Van Allen Probes

Data from the Van Allen Probes mission (Mauk et al., 2013) are used in this study. The NASA Van Allen Probes mission, formerly called RBSP (Radiation Belt Storm Probes A and B) was launched in 2012, enabling unprecedented studies of the electron radiation belt variability in response to solar activity. The two spacecraft of the Van Allen Probes mission flew on a low inclination (<20°) elliptical orbit ranging from 600 to 30,600 km. We will use three of the Van Allen Probes mission instruments, enabling us simultaneous observations of the radiation belts and the plasmapause. A review of recent radiation belt studies involving Van Allen Probes data is available in Ripoll J. F. et al. (2020).

The NASA Van Allen Probes have four magnetic spectrometers aboard each of the two spacecraft, one low-energy unit (20–240 keV), two medium-energy units (80–1,200 keV), and a high-energy unit (800–4,800 keV), which compose the MagEIS (Magnetic Electron Ion Spectrometer) instrument used to measure the radiation belt flux. MagEIS data are background corrected (Claudepierre et al., 2015). This instrument is part the Energetic Particle, Composition, and Thermal Plasma (ECT) suite (Spence et al., 2013), which combines the HOPE (Funsten et al., 2013), MagEIS (Blake et al., 2013), and REPT (Baker et al., 2012) instruments. We use the Level 2 ECT flux combined data (Boyd et al., 2019) which combine the data of these three instruments to bring a view of the radiation belt flux over the whole energy range. This study makes also use of data from the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) instrument suite (Kletzing et al., 2013) and the Electric Fields and Waves instrument (Wygant et al., 2013). Their measurement of electromagnetic waves allows the deduction of the cold plasma electron density and, then, the deduction of the plasmapause position.

PROBA-V/EPT Data

We use the Energetic Particle Telescope (EPT) on board the ESA PROBA-V satellite to provide radiation belt electron flux. PROBA-V operated simultaneously with the Van Allen Probes from 2013 to 2019, so that both data sets allow direct comparison of the electron radiation belt variability in response to solar activity. The EPT instrument has been developed to obtain the best discrimination between the particle species and determine uncontaminated particle spectra useful for space weather predictions (Cyamukungu et al., 2014). It was launched on May 7, 2013 to a polar orbit at an altitude of 820 km onboard the ESA satellite PROBA-V with an inclination of 98.73°, an orbital rotation period of 101.21 min and 10:30 AM as nominal local time at the descending node (Pierrard et al., 2014). The detector measures the particle fluxes for seven virtual channels for electrons, 11 channels for protons and 11 channels for helium ions.

Combined Release and Radiation Effects Satellite Data

We make use of some of the data from the Combined Release and Radiation Effects Satellite (CRRES) (e.g., Johnson and Kierein, 1992). The CRRES mission took place between August 1990 and October 1991. We use the Moldwin et al. (2002) CRRES database for nearly 1,000 orbits of the observed plasmapause positions sorted by the maximum geomagnetic index Kp during the previous 12 h. The plasmapause locations were identified as the innermost sharp density gradient of at least a factor of five within a radial distance of 0.5 L.

Super Dual Auroral Radar Network Observations

We use the SuperDARN (Super Dual Auroral Radar Network) network consisting of more than 30 low-power high frequency (HF) radars that observe the Earth’s upper atmosphere, beginning at mid-latitudes and extending into the polar regions (Ruohoniemi and Baker, 1998). SuperDARN serves to establish the ionospheric convection that, in part, defines the various boundaries we study.

Models

Plasmapause and Plasmasphere Model

Pierrard and Lemaire (2004) have developed a model for the formation of the plasmapause based on the influence of the convection electric field and the interchange instability mechanism. They showed that the plasmapause is formed in the post-midnight MLT sector (typically at MLT = 2h00) and is then propagated by co-rotation to other MLT sectors. This MLT dependence of the plasmapause was also confirmed by Bandic et al. (2016), Bandic et al. (2017) and Verbanac et al. (2018) with CRRES and THEMIS plasmapause observations. The plasmapause is related to Kp and Dst, as well as to other geomagnetic and solar wind indices (Verbanac et al., 2015).

The model has been improved to give not only the position of the plasmapause, but also the density and the temperature of the particles inside and outside the plasmasphere (Pierrard and Stegen, 2008). Later, it has been coupled to an ionosphere model (Pierrard and Voiculescu, 2011) in the framework of the SWIFF (Space Weather Integrated Forecasting Framework) project that allowed coupling of models for different regions of the magnetosphere (Lapenta et al., 2013). The SPM (SWIFF Plasmasphere model) provides daily nowcasts on the ESA SSA (Space Situational Awareness) website (https://swe.ssa.esa.int/space-radiation).

Auroral Oval Model

The OVATION (Oval Variation, Assessment, Tracking, Intensity, and Online Nowcasting) model is an empirical model of the intensity of the aurora (Newell et al., 2002, 2010; Machol et al., 2012). It gives a short-term forecast of the intensity of the auroral oval for both the Northern and the Southern hemispheres. It is based on the solar wind and IMF conditions as measured by the DSCOVR spacecraft. The OVATION model is used here to generate the intensity and location of the auroral oval in the Northern hemisphere for cases of quiet and disturbed periods.

Radiation Belt Model

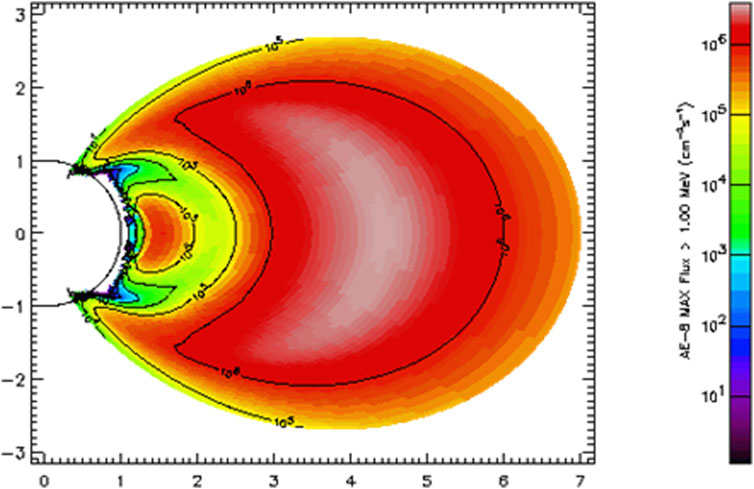
We make use of the empirical radiation belt model AE-8MAX (Vette, 1991; Fung, 1996) to illustrate the meridian view of the radiation belt during maximum solar activity. This model incorporates satellite measurements that date back into the 1960s from many orbital regimes, e.g., low Earth orbit LEO, (middle) MEO, (high) HEO and (geostationary) GEO.

Long Term Variations of the Plasmapause: Comparison Between Observations and the SWIFF plasmasphere model

Van Allen Probes Plasmapause Observations

The EMFISIS instrument on board of Van Allen Probes measures the upper hybrid resonance frequency allowing us to determine the plasma density (Kurth et al., 2015). When EMFISIS density is unavailable, the density is derived from spacecraft floating potential data, which has been calibrated against previous plasma densities determined from the upper hybrid resonance frequency (Thaller et al., 2015). Spacecraft floating potential is measured by the Electric Fields and Waves (EFW) instrument (Wygant et al., 2013). Here, the plasmapause locations (Lpp) are computed from the spacecraft floating potential measured by EFW onboard Probe B of the Van Allen Probes and are equal to the first minimum L-shell at which the density drops below the 100 cm⁻³ level within a 4-h temporal bin (Ripoll et al., 2020, 2021).

This method allows us to determine the plasmapause location (Lpp) from 1-3-2015 to 31-12-2015 represented in Figure 1 as a function of the logarithm of the minimum of Dst during the last 24 h (top panel). In the present study, we also determine the best linear relation for these data:

$\mathrm{Lpp}=-1.31\log 10\left|\min \mathrm{Ds}{\mathrm{t}}_{24h}\right|+6.35(1)$

with err (a) = 0.054 is the standard error on the regression coefficient, err (b) = 0.077 is the standard error on the constant and the Root Mean Square Error RMSE = 0.610. Even if the linear trend is obvious, the dispersion is quite high. Here we have kept all MLT to have enough data for the fit. During this period, Van Allen Probes apogee varied from 21 MLT to 11 MLT and the outbound crossing of the L = 3 field line varied from 17 MLT to 7 MLT, making the above law representative of more dusk and day side plasmapause.

FIGURE 1

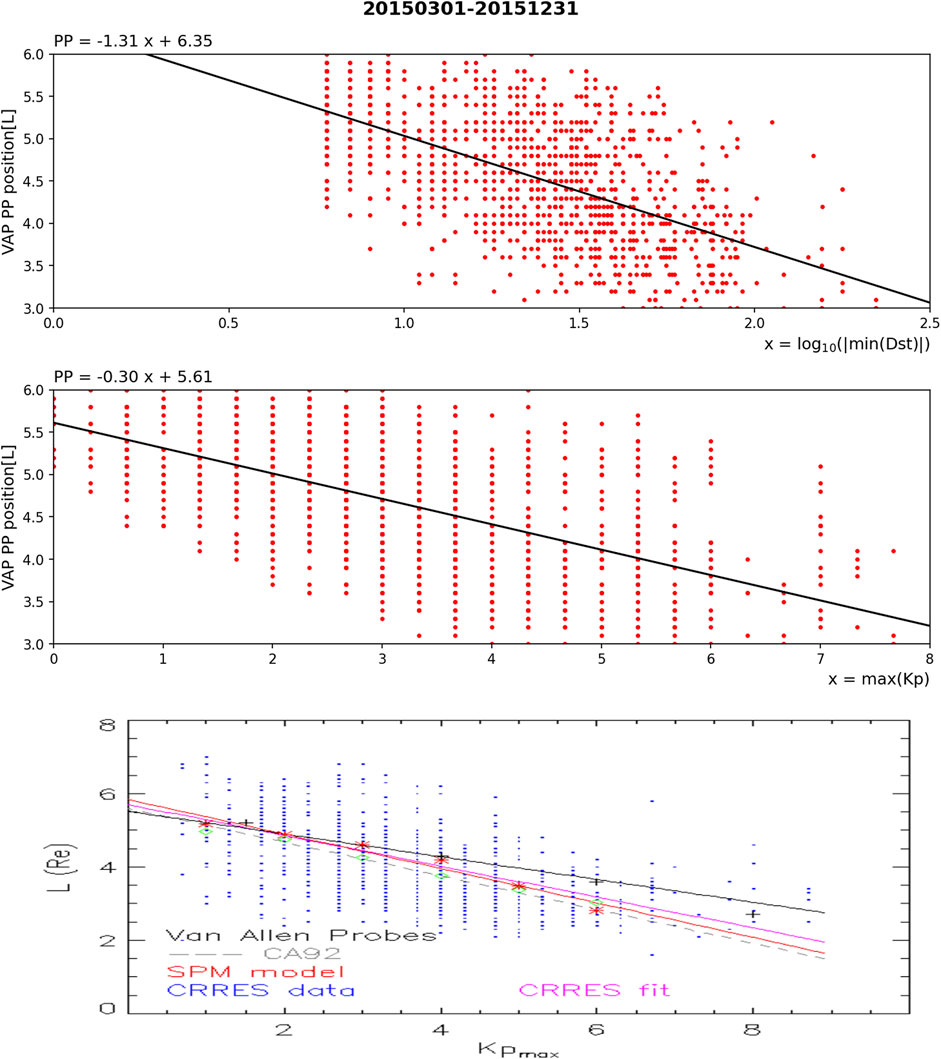
FIGURE 1. Upper panel: Plasmapause observed by Probe B of the Van Allen Probes from 1-3-2015 to 31-12-2015 as a function of the logarithm of the minimum value of Dst observed during the previous 24 h. The best linear relation is provided by the black line for which the expression is shown above the panel. Middle panel: Same plasmapause observed by Probe B of the Van Allen Probes from 1-3-2015 to 31-12-2015 as a function of max (Kp) during the previous 24 h. The best linear relation is provided by the black line for which the expression is shown above the panel. Bottom panel: (Blue dots) Plasmapause Lpp observed by CRRES as a function of Kp maximum during the previous 12 h (Green diamonds) Averaged values of CRRES Lpp as a function of Kp. (Pink line) Plasmapause linear relation found by Moldwin et al. (2002) in the 21-03 h MLT sector. (Gray dashed line) Plasmapause linear relation found by Carpenter and Anderson (1992) from ISEE data. (Black crosses) Mean plasmapause measured by Van Allen Probes from 2012 to 2019 for four Kp ranges in the night side. (Black line) Plasmapause linear relation found in top panel with Van Allen Probes data from March to end December 2015. (Red stars) Plasmapause positions found with the SPM model as a function of Kp. (Red line) Plasmapause linear relation found with the SPM model.

Similarly, we derive the expression of the plasmapause position for this same period as a function of Kp (middle panel) and find the best linear fit:

$\mathrm{Lpp}=-0.30\left|\max \mathrm{K}{\mathrm{p}}_{24h}\right|+5.61(2)$

with lower errors err(a) = 0.010, err(b) = 0.036 and RMSE = 0.601.

Comparison With CRRES Satellite

These new results can be compared with previous observations and fits. Moldwin et al. (2002) selected in the database of CRRES observations all orbits where a sharp density gradient indicated the presence of a well-defined plasmapause. The L-value of the observed plasmapause positions were ranked according to the maximum geomagnetic index Kp during the previous 12 h. The bottom panel of Figure 1 shows these plasmapause positions (blue dots) observed for all local time sectors as a function of the maximum value of Kp. The scatter of the observed values of Lpp is rather wide but there is a clear trend confirming that the plasmapause forms closer to the Earth when Kp is large. The green diamonds symbols in Figure 1 correspond to the mean value of the observed plasmapause positions for Kp_jmax between Kp_j − 0.4 and Kp_j + 0.4.

This trend is evidenced in all local time sectors, but the slope of this relationship is local time dependent (Moldwin et al., 2002). O’Brien and Moldwin (2003) determined linear fits of the average plasmapause locations as a function of Kp for four local time sectors for various time delays between 12 and 36 h. They found lower RMSE in the dawn and day sectors in comparison with dusk and night. Different studies have shown that it is around 2–3 h in MLT that the link between the plasmapause and geomagnetic indices is the clearest because it is the MLT sector where the plasmapause is formed due to a higher convection electric field (Pierrard and Cabrera, 2006; Reinisch et al., 2009). The linear relation found by Moldwin et al. (2002) in the MLT sector corresponding to 21-3 h is represented in magenta on Figure 1 (bottom) and is given by:

$\mathrm{Lpp}=-0.4204\mathrm{K}{\mathrm{p}}_{\max 12}+5.704(3)$

As a comparison, taking the Probe B of the Van Allen Probes mission in 09/2012–07/2019 in the night sector (21–3 h), we find that the mean plasmapause position (defined as the 100 #/cc level of the EFW density) is: Lpp = 2.7 for all events with Kp > 7, Lpp = 3.6 for Kp in ]5,7], Lpp = 4.3 for Kp in ]3,5], and Lpp = 5.2 for Kp < 3. These values are represented by the black crosses in Figure 1 (bottom panel), and the linear relation Eq. 2 that was found with the Van Allen Probes for 2015 is illustrated by the black line.

An empirical relationship between Lpp and Kp had also been deduced previously from ISEE one data for 0–15 LT (Carpenter and Anderson, 1992):

$\mathrm{Lpp}=-0.46\mathrm{K}{\mathrm{p}}_{\max 24}+5.6(4)$

where Kp_max24 is the maximum value during the preceding 24 h. This best fit linear relationship is shown by the gray dashed line in the bottom panel of Figure 1.

Other authors have derived empirical relations between the plasmapause equatorial distance (Lpp), and a variety of geomagnetic indices such as Kp, Dst or AE. O’Brien and Moldwin (2003) for instance used CRRES data for all MLT and found:

$\mathrm{Lpp}=-1.57\mathrm{Log}10\left|\mathrm{min Ds}{\mathrm{t}}_{24h}\right|+\mathrm{6.3.}(5)$

The large dispersion of the measurements from the linear fits (clearly visible in Figure 1) highlights that any plasmapause prediction based only on such linear relation could differ by up to 1 R_E from the actual locations depending on the events. A more sophisticated model is thus necessary for predictions, as the SPM model that takes into account the MLT dependence of the plasmapause and uses the historical variation of the Kp index during the 24 previous hours instead of its maximum value only.

Modeling the Plasmapause Position

The red stars in the bottom panel of Figure 1 show the theoretical plasmapause position M_j determined by our numerical SPM model (Pierrard and Lemaire, 2004) for a set of stationary values of the Kp index ranging from one to 6. They correspond to the average position of the plasmapause predicted by the theoretical model based on the mechanism of plasma interchange driven unstable by the enhancement of centrifugal effects and using McIlwain’s Kp-dependent electric field model E5D and his M2 equatorial magnetic field model to calculate the magnetospheric convection velocity (Pierrard and Stegen, 2008). The plasmapause position in the SPM model depends on the historical evolution of the geomagnetic index Kp during the previous days. The plasmapause is formed at MLT = 2 and is transmitted to other MLT sectors due to the plasma motion dominated almost entirely by corotation. It is thus necessary to have the Kp evolution during at least 24 h to determine the plasmapause in all MLT sectors. In Figure 1, stationary values of Kp during the previous 24 h are used to obtain the plasmapause position averaged on all MLT in the model.

We find with the model a best linear relation (red line on bottom panel of Figure 1) corresponding to

$\mathrm{Lpp}=-0.47\mathrm{Kp}+5.84(6)$

This relation based on averaged values can be used for long term comparisons, but the actual plasmapause positions given by the model are of course more precise since they take into account the historical evolution of Kp during the previous hours and the MLT sector of the plasmapause observation.

Discussion About the Long Term Plasmapause

The linear fits of the equatorial plasmapause positions versus Kp that are shown in the bottom panel of Figure 1 (Van Allen Probes black Eq. 2, CRRES magenta Eq. 3, ISEE1 gray Eq. 4, SPM model red Eq. 6) are rather similar for the satellite observations and the model. The slope for the Van Allen Probes data is lower than the others. This is probably due to the lower number of observations and to the fact that the computation is not restricted to the night side. In comparison, the four mean plasmapause positions (black crosses) given as a function of Kp established over the whole Van Allen Probes mission and restricted to the night side are closer to the other observations and models. The large scatter of the experimental data indicates that the actual plasmapause is a rather irregular and dynamic surface (cf. density plots for the case study in Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During a Quiet Period: March 14, 2014 and Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During the Storm Event of August 26, 2018). It indicates that simulations based on quasi-stationary E-field models with a 3-h time resolution may grasp the general trend but not the small dynamical features. Furthermore, the position of the plasmapause does not depend only on the value of Kp, but is also influenced by the history of the short time variations of the magnetospheric electric and magnetic fields (Pierrard et al., 2008). Moreover, as shown in the next section, the MLT sector can play an important role as the plasmapause can be very asymmetric, especially during geomagnetic storms and substorms, when plumes are created in the afternoon-dusk MLT sector.

Long Term Plumes

Large scale structures like plasmaspheric plumes are reproduced by the SPM numerical simulations as a result of enhancements of the overall convection velocities correlated with enhanced geomagnetic activity (Pierrard and Lemaire, 2004). The plumes rotate with the plasmasphere and are not only confined in the dusk sector, as in the ideal MHD simulation of Grebowsky (1970). Plume merging is one theoretical way of generating fine plasmaspheric structure from successive layers of wrapped residual plumes which merge with newer plumes, creating on the long term layers of filamentary density structure over multiple cycles (e.g., Goldstein et al., 2003; Sandel et al., 2003). In our dynamical model, plumes are convected around the Earth as indeed observed by the EUV/IMAGE experiment (Spasojevic et al., 2004; Pierrard and Cabrera, 2005, 2006; Darrouzet et al., 2006).

The SPM model can determine the plasmapause and the plasmaspheric density for any date. Only the knowledge of the Kp index for the 24 h before the date to be simulated is required to determine the position of the plasmapause at any MLT during stormy periods. This does not mean that plumes generated during storms do not have long term duration. Plumes can remain visible during several days, as we now discuss.

Figure 2 shows the results of the SPM density and plasmapause model for the period of May 1, 1994 to May 7, 1994 at different universal times (UT). For this period, Borovsky et al. (2014) reported observations of long duration plumes from the spacecraft 1989–046 at geosynchronous orbit. They observed dense plasmaspheric plasma advecting sunward toward the dayside magnetopause during more than 10 days. Such long-term plume is reproduced by the SPM model, as visible by the tails appearing in the afternoon MLT sector in the bottom of the left panels of Figure 2. The model shows that it is due to Kp remaining very high all along this 10-day period, always above Kp = 4 (cf. top panels of Figure 2) as soon as the first expansion on May 1, 1994 occurred.

FIGURE 2

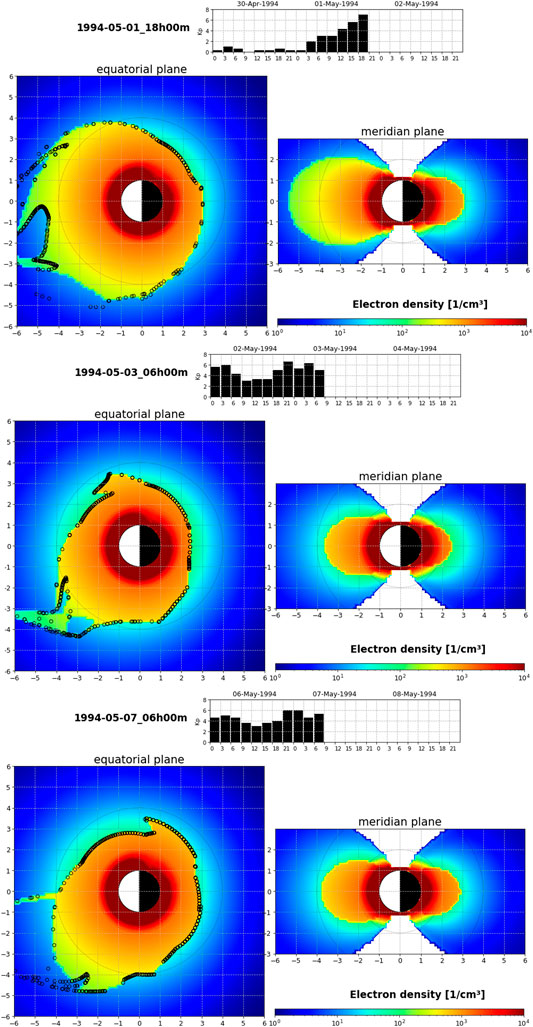
FIGURE 2. Plasmapause (black circles) and electron number density (color scale) in the plasmasphere obtained with the SPM model in the equatorial plane (left panels) and in the meridian plane (right panels) on May 1, 1994 18 h UT (top), May 3, 1994 6 h UT (middle), and May 7, 1994 6 h UT (bottom). These simulations are examples showing that plumes are reproduced in a continuous manner during the first weeks of May 1994 with the SPM model. Plume occurrence is due to the high values of the Bartels geomagnetic index Kp which is shown at the top of each panel.

Note that a longer period of historical evolution of Kp than 24 h is necessary in the most recent version of the model (Pierrard et al., 2021a) to take into account the refilling that takes around two or 3 days after the storm erosion (Gallagher et al., 2021) and the plasmaspheric wind appearing during prolonged quiet periods (Lemaire and Schunk, 1992).

Links Between the Plasmapause and the Radiation Belt Boundaries

The plasmapause is not the only boundary that is clearly correlated to the Dst index. Pierrard et al. (2020) obtained Dst-based relationships of the inner and the outer edges of the outer radiation belt for electrons of energy above 1 MeV. The position of the inner edge of the outer belt is very energy-dependent due to the dependence on electron lifetimes. This study also shows a correlation between the motion of the inner edge of outer belt and that of the innermost plasmapause location. This previous work indicates that it is useful to compare the plasmapause position with the position of the inner edge of the outer belt, as done in the next two sections with the observations of both the Van Allen Probes and the LEO PROBA-V satellite.

Van Allen Probes/MAGEIS and PROBA-V/EPT Observations of the Radiation Belts During 10 months in 2015

The top panel of Figure 3 represents the Van Allen Probes/MagEIS (Blake et al., 2013) electron fluxes (color scale) at 2.28 MeV as a function of the McIlwain (1966) parameter L in Earth radii from 1st March to December 31, 2015. The second panel of Figure 3 shows simultaneous observations of the Energetic Particle Telescope (EPT) instrument on board the PROBA-V satellite for E = 1–2.4 MeV for the active year 2015 that was especially studied with EPT in Pierrard and Lopez Rosson (2016). The inner and outer edges of the outer radiation belt are characterized by very sharp transitions, so that they are clearly visible by color changes from red to blue in Figure 3. The equatorial observations of MagEIS flux and the LEO observations of PROBA-V/EPT at higher latitude show similar electron flux variations, with fast increase during storms (easily identified by Dst inverted peaks given in the third panel of Figure 3) and slower decay afterwards. Differences in flux level and sensitivity to the pitch angle is discussed in Pierrard et al. (2020). The black line represents the plasmapause position that is discussed in the next section.

FIGURE 3

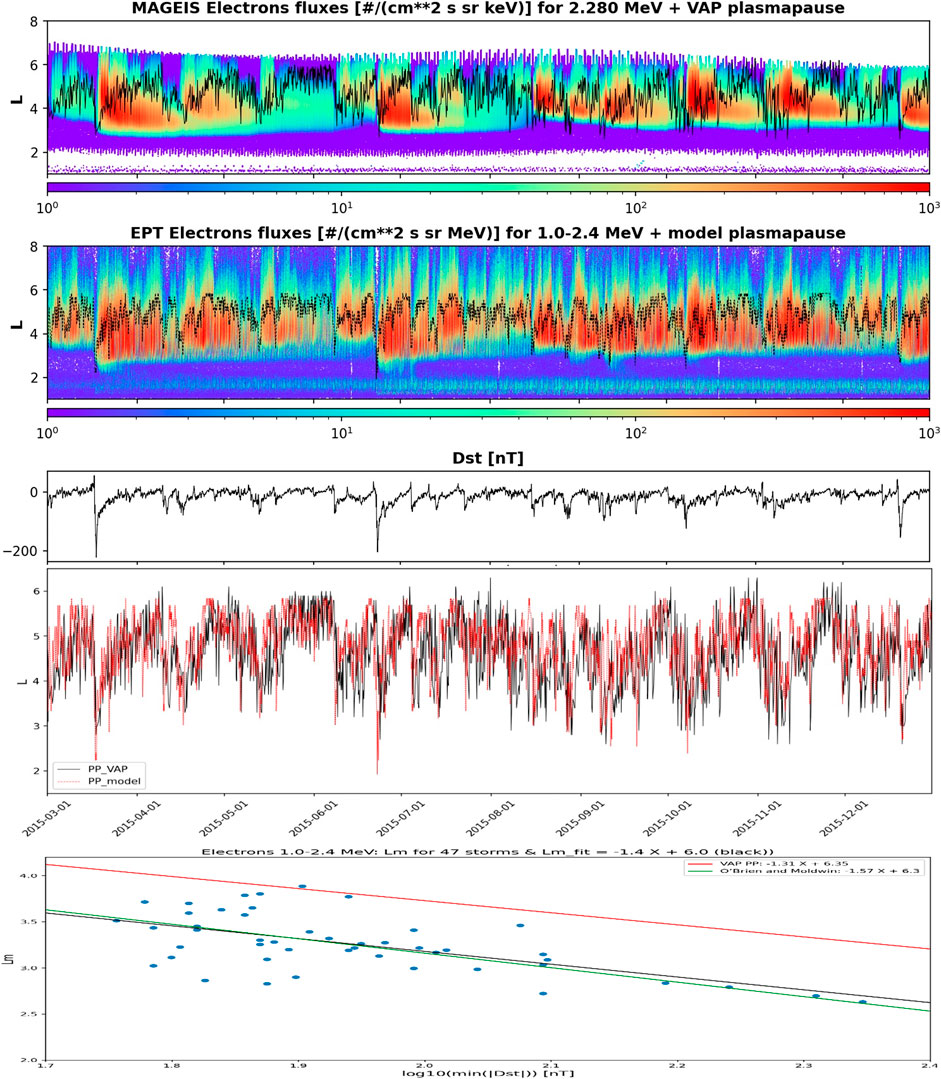
FIGURE 3. Upper panel: Electron flux measured by MagEIS on board the Van Allen Probes at 2.28 MeV from March 1, 2015 to December 31, 2015. The black line corresponds to the plasmapause computed from spacecraft charging measured by EFW on board the Van Allen Probes. Second panel: Electron flux measured by PROBA-V/EPT at 1–2.4 MeV from March 1, 2015 to December 31, 2015. The black line corresponds to the plasmapause obtained from the SPM model. Third panel: Observed Dst index from March 1, 2015 to December 31, 2015. Fourth panel: Comparison of the plasmapause observed by Van Allen Probes (black line) with the plasmapause obtained from the SPM model (red line) from March 1, 2015 to December 31, 2015. Bottom panel: Blue dots: lowest position Lm of the flux injected in the slot during the 47 biggest storms observed by PROBA-V/EPT Ch5 (1–2.4 MeV) from May 2013 to December 2019, as a function of log10|min Dst_24 h|. Black line: best linear fit function for Lm. Red line: Best fit of plasmapause position as a function of log10|min Dst_24 h| as observed by Van Allen Probes (Eq. 1). Green line: Best fit of plasmapause position as observed with CRRES (Eq. 5).

Links Between Plasmapause and Radiation Belts Observations

The solid black line on the top panel of Figure 3 corresponds to the plasmapause position measured by the Van Allen Probes as previously discussed. The dotted black line on the second panel corresponds to the plasmapause position estimated by the linear Equation 6 deduced from the SPM model. Both are superposed in the fourth panel of Figure 3. Spearman correlation gives a moderate coefficient of 0.36 and RMSE = 0.817. One can see that the linear relation deduced from the SPM plasmapause model based on the geomagnetic activity index Kp gives positions of the plasmapause close to the Van Allen Probes observations with quite similar time variations and a maximum L < 6.2. During the strongest events, the model gives lower plasmapause than what is observed, while on the contrary, some more moderate events show an observed plasmapause further than what predicted by the model. This can be due to the MLT sector anisotropy not taken into account in the comparison.

During moderate and big storms (e.g., in March 2015), the plasmapause (obtained by the model, as well as that observed by Van Allen Probes) is formed closer to the Earth and shows an inward motion similar to the inward motion of the inner edge of the outer belt, which appears only for the strongest events for the radiation belt. The plasmapause is clearly much more mobile than the inner edge of the outer belt.

Often in the top panel of Figure 3 (e.g., in April 2015), the plasmapause is located close to the outer edge of the outer belt for E = 2.28 MeV, especially during quiet periods longer than several days. During the main phase of storms (with Dst < 50 nT, e.g., mid-March 2015) and even for substorms (inverted Dst peak with 50 nT < minimum Dst < 30 nT), the plasmapause comes closer to the Earth.

The bottom panel of Figure 3 compares the plasmapause with the inner edge of the outer radiation belt for 1–2.4 MeV electrons during storms. The blue dots in the bottom panel show the lowest L-shell (Lm) value of flux penetration of electrons with E = 1–2.4 MeV (Ch 5) observed in the slot region by PROBA-V/EPT during the 47 strongest storms appearing from May 2013 to December 2019. The lower edges Lm of the outer radiation belt during storms are identified using the methodology explained in Pierrard et al. (2020) (see their Figures 8–10), i.e. by determining the lowest L-shell where the flux exceeds the threshold of 2. e2 electrons/(cm² s sr MeV) in the slot region. The Lm positions are here represented as a function of log10|min Dst_24 h|, like the plasmapause in Figure 1 (panel 1). The black line shows the best fit function for these Lm obtained to be

$\mathrm{Lm}=-1.4\mathrm{Log}10\left|\mathrm{min Ds}{\mathrm{t}}_{24h}\right|+6.0(7)$

with err(a) = 0.272, err(b) = 0.529 and RMSE = 0.25. The linear relation is very similar to Eq. 5 obtained for the plasmapause with CRRES observations and represented in green on the bottom panel of Figure 3. This shows a clear link between the radiation belt boundary for the 1–2 MeV energy range and the plasmapause position. Van Allen Probes plasmapause fit (Eq. 1) is also represented in green and shows a similar slope but a position typically 0.8 Re higher, may be due to the lower threshold of 100 cm⁻³ level used to define the plasmapause with Van Allen Probe data.

Independently of the nature of the acceleration, both inner boundary of ultra-relativistic peak flux and plasmapause are related during the storm main phase. A similar inward motion of the inner edge of the outer belt and the plasmapause is observed, but only for the biggest storms with Dst < 50 nT. In that case, the inward motion of the plasmapause during the storm gives a minimum position very close to that of the inner edge of the outer belt for 1 MeV electrons. During the recovery phase, the plasmapause goes gradually further away from the Earth due to ionospheric refilling that takes several days. Top panels of Figure 3 show no link between the plasmapause and the radiation belt boundary during these recovery times, since the inner edge of the outer belt remains close to the Earth during more extended periods from several days to weeks. Spearman correlation coefficients between the plasmapause and the flux of the radiation belts measured by PROBA-V/EPT do not show significant relation, except may be for 1–2.4 MeV (see Figure 14 in Pierrard et al., 2020).

In summary, we observe that the plasmapause corresponds with the inner edge of relativistic outer radiation belt electrons for E = 1–2.4 MeV during the storm main phase only, while it extends up to the outer edge of ultra-relativistic outer radiation belt electrons during prolonged quiet periods. We do not conclude in general that the depth of penetration of the outer radiation belt electrons into the inner magnetosphere is associated with the innermost plasmapause position as Li et al. (2006), a theory which has been revisited since then (Khoo et al., 2018). Here, in Figure 3, the only link we find is a coincident position of the plasmapause with the 1–2.4 MeV electron outer radiation belt during the storm main phase. No link is found during recovery periods, between the storm and the established quiet times, during which both edges evolve with their own dynamics, one driven by ionospheric refilling, the other by wave-particle interactions.

The inward motion of the outer radiation belt associated with sudden flux enhancements of energetic electrons (e.g., Turner et al., 2015) seems directly related to the plasmapause erosion during geomagnetic storms (e.g., October 2015 in Figure 3). The similar position of the plasmapause and the edges of the energetic outer belt suggests a link between these different populations. The plasmasphere can contribute to explain the impenetrable barrier discovered at L∼2.7 (Baker et al., 2014) through which ultra-relativistic energetic Van Allen belt electrons cannot migrate (Fennell et al., 2015). This barrier is seen during prolonged periods after enhancements at very high energy and could be generalized for lower energies at lower L down to the inner belt (Pierrard et al., 2020). The different waves that are generated inside and outside the plasmasphere and close to the plasmapause position are also able to contribute to the loss and acceleration of outer belt electrons, therefore changing its edges and spectrum (e.g., Reeves et al., 2016; Ripoll et al., 2016; Turner et al., 2019; Pierrard et al., 2020; 2021b). The two-belt radiation structure has been explained as arising from strong electron interactions with plasmaspheric hiss, existing from the inside of the plasmasphere up to the plasmapause boundary, with the inner edge of the outer radiation zone corresponding to the minimum plasmapause location just after the storm (Ripoll et al., 2017). Since during strong storms, the plasmasphere is eroded down to low L, local acceleration of MeV electrons by chorus waves can reach the new region outside of the plasmasphere that was previously located in the slot region and inner belt. On the other hand, during the early storm recovery, the quick recovery of the plasmasphere allows outer belt electrons to be situated in the plasmasphere where intense plasmaspheric hiss can scatter them (e.g., Ripoll et al., 2019).

Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During a Quiet Period: March 14, 2014

Radar and satellite observations for specific dates, as well as models, allow us also to analyze the MLT distribution of different boundaries, i.e., the position of the plasmapause, the limits of the outer belt and the limits of the auroral oval. We start in this section with a quiet period for which we have different observations (March 14, 2014) and we will analyze in the following section 6 the case of a geomagnetic storm (August 26, 2018).

Links Between the Plasmapause and the Ionospheric Convection Boundary

Plasmasphere Model

Figure 4 illustrates the electron density of the plasmasphere obtained with the SPM model on March 14, 2014 at 15h30 UT in the equatorial and meridian plane. The density is provided in geocentric solar magnetospheric (GSM) coordinates. Since Kp = 2 at 15h30 UT and Kp < 3 during the previous 24 h, the activity was low and the plasmasphere was quite extended with Lpp∼4.5 Re and almost circular in the equatorial plane. The meridian view shows clearly that the plasmapause is not only present in the equatorial plane, but also at all latitudes along the magnetic field lines, resulting in a high density gradient at low altitude, and thus also in the ionosphere. As shown on the right panel of Figure 5, a plasmapause between L = 4 and L = 5.2 in the equatorial plane corresponds to a latitude between 60° and 64° when projected in the ionosphere along the magnetic field line.

FIGURE 4

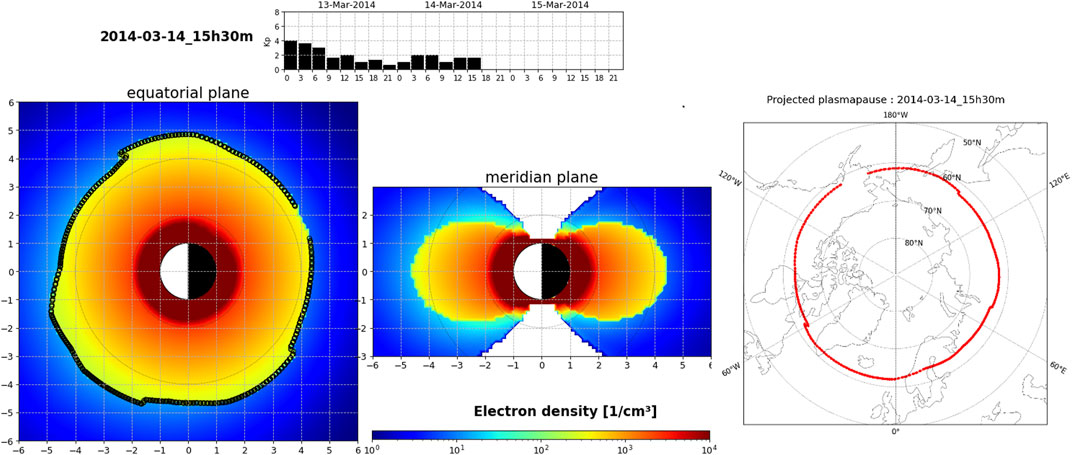
FIGURE 4. The electron density of the plasmasphere obtained with the SPM model on March 14, 2014 at 15 h 30 UT in the (left) equatorial and (middle) meridian plane. The right panel illustrates the footprint of the plasmapause projected at high latitude in the Northern ionosphere. The top panel shows the geomagnetic activity index Kp observed from 13 to March 15, 2014.

FIGURE 5

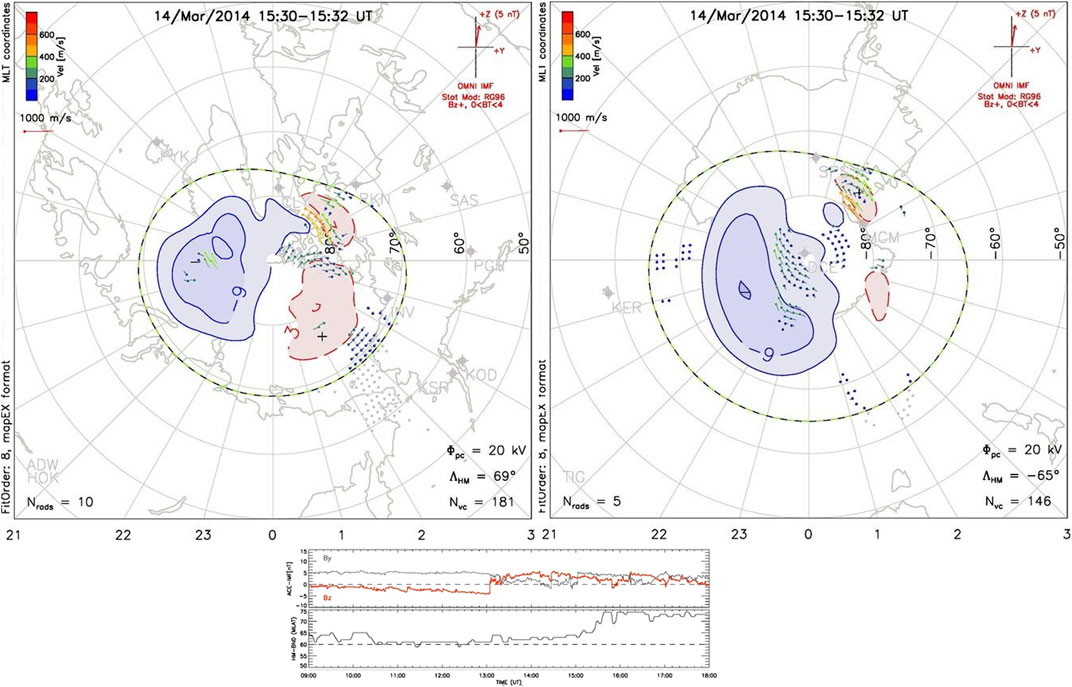
FIGURE 5. Top panels: ionospheric convection pattern measured by SuperDARN in the Northern hemisphere (left panel) and in the Southern hemisphere (right panel) on March 14, 2014 at 15 h 30 UT. The x-axis gives the MLT. The green lines represent the Heppner-Maynard Boundary (HMB). The blue-red shades show the ionospheric potential. Bottom panel: Time evolution from 9h00 to 18h00 UT of the HMB boundary on 14 March 2014 estimated by SuperDARN in degrees of geomagnetic latitude at 0h00 MLT.

Ionospheric Convection Observed by Super Dual Auroral Radar Network

The ionospheric convection pattern measured by the SuperDARN radars on March 14, 2014 at 15h30 UT is illustrated in Figure 5. The ionospheric convection boundary, Heppner Maynard Boundary (HMB), determined by SuperDARN (green line in Figure 5) can be used as a proxy for the geographic latitude of the auroral oval (Imber et al., 2013). The HMB delimits the latitudinal extent of the polar ionospheric convection and has also links with the plasmapause, as found by Matar (2021). The convection is less extended in the Northern hemisphere (NH left panel) than in the Southern hemisphere (SH right panel). The convection induced by the solar wind directly controls the different processes within the magnetosphere such as the aurora, the plasmasphere, and radiation belts response.

This is a period of contraction of the auroral zone following a northward turning of the IMF appearing around 13h00 UT, as illustrated in Figure 5 third panel. The bottom panel of Figure 5 shows a time series of the HMB from the NH from 9h00–18h00 UT on March 14, 2014. A sudden northward turning measured at the satellite just after 13h00 UT resulted in a steady rise of the HMB to higher latitudes, consistent with the contraction. The selected map (15h30 UT) from the NH looks like a good representation of this development with L_HMB = 69°, except in the noon sector where it is located at higher geographic latitude around 75° due to the compression of the magnetic field lines in the day side. The MLT is provided by the x axis, with 0h00 MLT (midnight) corresponding to the bottom of the top panels in Figure 5. The sequence in the SH is consistent with that in the NH and with some sign of residual plasma convection surviving at somewhat lower latitudes L_HMB = 65°. Note that the reconstructed convection pattern from SuperDARN is given by models in addition to the observations, leading to a HMB very different in the Northern and the Southern hemisphere, and a HMB located at higher latitudes in the noon MLT sector than at other MLT, due to strong compression of the terrestrial magnetic field associated to solar wind pressure. The HMB is found to be located at higher latitudes than the ionospheric footprint of the equatorial plasmapause obtained with the SPM model in both hemispheres, at all MLT but especially at noon. The accuracy of the SuperDARN convection pattern reconstruction is to large extent driven by the underlying model.

Radiation Belts

Flux Evolution Observed by PROBA-V/EPT

Figure 6 shows the electron fluxes measured by EPT on PROBA-V from 14 to March 20, 2014 during a quiet period. The SPM model gives a plasmapause position located around L = 5 that is located inside the outer radiation belt for the energies 500–600 keV and 1–2.4 MeV. For higher energies, the outer belt is less extended than at lower energies and the plasmapause around L = 5 lies beyond the outer edge of the outer belt, as also illustrated in Figure 7 with the 1.6 MeV channel. The plasmapause obtained by the model is very stable around L∼5 during this quiet period, which is confirmed by Van Allen Probes measurements of the local density (see bottom panel of Figure 7) showing a plasmapause oscillating between L = 4 (at the Dst minimum) and L = 6.

FIGURE 6

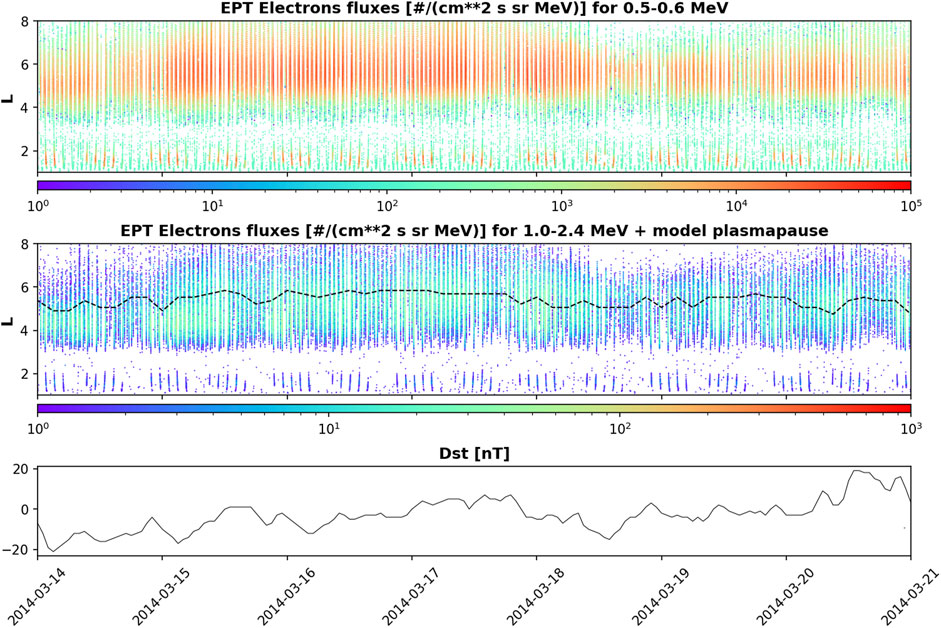
FIGURE 6. Upper panel: Electron flux measured by PROBA-V/EPT at 500–600 keV from 14 to March 20, 2014. Middle panel: Electron flux measured by PROBA-V/EPT at 1–2.4 MeV from 14 to March 20, 2014. The black dotted line in the middle panel corresponds to the plasmapause obtained from the SPM model. Bottom panel: Observed Dst index during the same period.

FIGURE 7

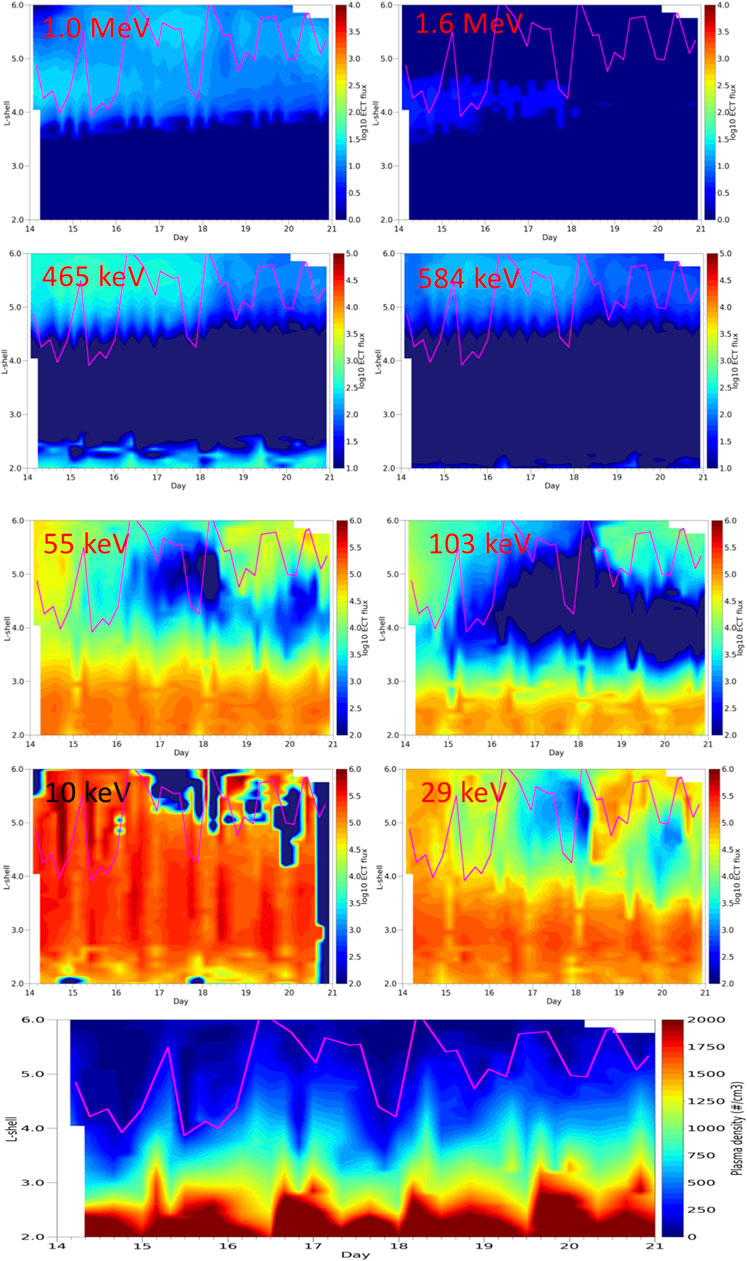
FIGURE 7. (Top four panels) Radiation belt flux versus time and L-shell for sub-relativistic and relativistic electrons for the quiet period of 14–20 March 2014 measured by the Van Allen Probes/ECT suite in the magnetic equatorial plane. (Next four panels) Low energy seed electrons (10–100 keV), which contribute to the electromagnetic environment and as source of aurora. The magenta line corresponds to the plasmapause position measured by EMFISIS on RBSP A. (Bottom panel) Density measured by RBSP A/EMFISIS during the same period.

Flux Evolution Observed by Van Allen Probes

Figure 7 shows Van Allen Probes/ECT Level 2 combined fluxes (Boyd et al., 2019). Fluxes are binned by temporal bins of 4 h corresponding to half an orbit, which allows to fill all (or almost) the L-shell of that bin (from perigee to apogee) with a flux value. Flux observations are then interpolated in the time direction to produce a smooth representation. This treatment produces a continuous view of the radiation belts (albeit time is frozen within a 4 h bin) for a wide range of energies, here, for a quiet magnetosphere (a similar treatment will be applied to disturbed time fluxes in the next section). At sub-relativistic and relativistic energy, the radiation belt is concentrated in the outer belt above L∼4. Fluxes are low compared with more active times (cf. Van Allen Probes/MAGEIS and PROBA-V/EPT Observations of the Radiation Belts During 10 months in 2015) and gradually decaying with time. The 1 MeV fluxes and above are closer to the inner belt than sub-relativistic electron fluxes, which is due to the fact that sub-relativistic electrons are more sensitive to whistler-mode hiss waves than higher energy electrons and thus are more scattered during extended quiet periods. This forms a remnant denser pocket of MeV electrons in the outer belt explained in Ripoll et al. (2019), which forms the top part of a structure called S-shape when plotted in the (L, E) plane (Reeves et al., 2016; Ripoll et al., 2016).

At lower energy, between 10 and 100 keV, fluxes are much higher and injections are more visible on 14–15 and on 18–20 March 2014, although the activity is very mild as shown by the Dst index in Figure 6. At these low energies, the inner belt reaches L∼4. At 10 keV, the slot fully disappears. These electrons are considered as potential source for in-situ VLF (very low frequency) whistler waves generation, ultimately able to produce local acceleration of hundreds of keV electrons to MeV energies (Tu et al., 2014; Jaynes et al., 2015).

For all these energies during this period of quiet geomagnetic activity, the plasmapause boundary measured by EMFISIS on RBSP A (magenta line) does not seem to correspond to any specific boundary of the electron fluxes. It varies between L = 4 and L = 6 during this time period and is much more irregular than the radiation belt boundaries.

Meridian View From AE8 Model

Van Allen Probes and PROBA-V observations do not give a meridian view due to their limited latitude coverage. That is why to illustrate the meridian view of the integral electron flux with E > 1 MeV in Figure 8, we use the empirical model AE-8MAX (Vette, 1991) to better see the radiation belts from the side view (see Loridan et al. (2019) for more latitudinal representations of the radiation belt dynamics). The slot region (yellow region) appears clearly between the inner belt and the outer belts (red regions). The boundaries depend on the geomagnetic activity, as shown in Figure 3, but also on the energy as shown in Figure 7. Typically, the slot in the AE8 model is located between L = 2 and L = 3 for E = 0.5–7 MeV with quite sharp boundaries. At lower energy, from 40 to 500 keV, the slot is a little bit higher between L = 2.5 and L = 3.5 with more gradual boundaries. This is consistent with the theoretical energy-dependent structure of the radiation belts (Lyons and Thorne, 1973; Reeves et al., 2016; Ripoll et al., 2016). The plasmasphere generally overlaps the radiation belts during low geomagnetic activity. Otherwise, there could not be interactions between plasmaspheric waves and the trapped electrons, and, thus, the observed energetic structure of the radiation belts would not exist.

FIGURE 8

FIGURE 8. Electron flux obtained with the empirical model AE-8MAX for 1 MeV.

High-Latitude Magnetic Local Time Maps

The top panels of Figure 9 illustrate the EPT observations of electron fluxes for E = 500–600 keV at 820 km from 14 to March 20, 2014 in the Northern hemisphere (left) and Southern hemisphere (right). At this altitude, the radiation belt population is constituted by low equatorial pitch angle particles, ready to be or soon scattered in the ionosphere. This is different from Figure 7 previously discussed, which showed equatorial electrons, which distribution is dominated by high pitch angle trapped particles. Detailed comparison between polar EPT and equatorial Van Allen Probe observations is made in Pierrard et al. (2020, 2021b).

FIGURE 9

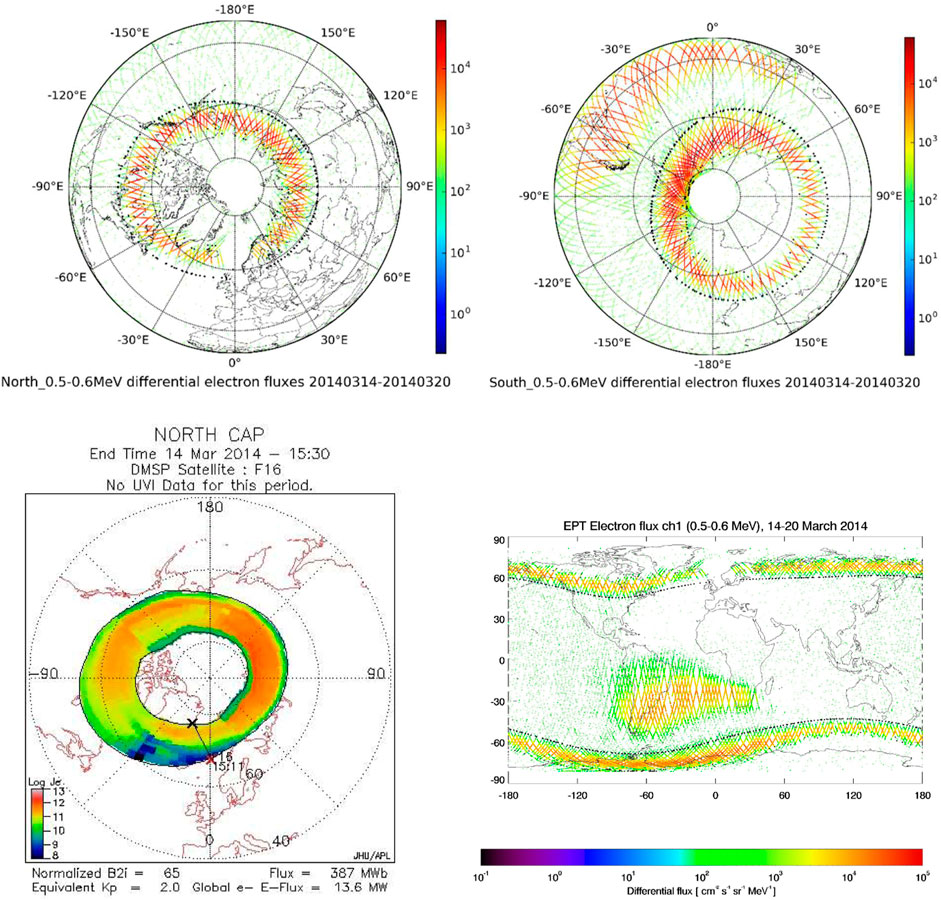
FIGURE 9. Top panels: EPT observations at 820 km of electron fluxes 500–600 keV from 14 to March 20, 2014 in the Northern hemisphere (left) and Southern hemisphere with the South Atlantic Anomaly SAA (right). The black circles with increasing radius correspond to constant latitudes of 80°, 60° and 30°. Bottom panels: (Left) The auroral oval as obtained with the OVATION model in the Northern hemisphere for March 14, 2014 at 15h30. The color scale indicates the energy flux producing the aurora. The dotted circles correspond to constant latitudes of 80°, 60° and 40°. (Right) The EPT observations of electron fluxes represented on a latitude/longitude map with the SAA at low latitudes and the outer belt at high latitudes. The black dots correspond to L = 3.5 (inner equatorward edge) and L = 8.5 (outer polar edge).

Figure 9 (top) allows visualization of the oval formed by the outer belt when penetrating at 820 km. The bottom right map in latitude-longitude shows that the outer belt corresponds to the high latitude band located above Scandinavia in the Northern hemisphere. The fluxes are always artificially low above Europe with EPT due to the pause in the measurements during the transmission of the data to the Belgian station of Redu.

One can see that in the Northern hemisphere, the radiation oval is located between L = 3.5 and 8.5 represented by the black dots in the bottom map. The South Atlantic Anomaly SAA is visible in the Southern hemisphere (top right) and in the latitude-longitude map (bottom). Due to the characteristics of the orbit of the PROBA-V satellite that has a period of 101 min (thus about 14 orbits around the Earth per day), it is necessary to accumulate the observations during several days to obtain good coverage on the maps. Here, the data are shown from 14 to March 20, 2014. This accumulation time is consistent with gradual mild loss occurring in both the slot and the outer belt at 500–600 keV (see, for instance, Figure 5 of Ripoll et al. (2019)). As such, Figure 9 represents the total loss accumulated during 6 days in the whole radiation belts region. Further integration (not attempted) would lead to the computation of the total radiation belt electron content (TRBEC) (e.g., Forsyth et al., 2016).

Auroral Oval

The bottom left panel of Figure 9 illustrates a map of the intensity and location of the auroral oval as obtained with the OVATION model in the Northern hemisphere for March 14, 2014 at 15h30. It shows the polar cap energy flux and combines discrete and diffuse electron precipitation, as well as proton precipitation producing the aurora. Boundaries of the auroral oval are clearly visible for direct comparison with the position of the outer belt shown in Figure 9 (top left panel). We find that the auroral oval is located at higher latitudes [from 70° to 80° at 0°–180° of longitude (right side) and from 60° to 70° at 180–360° of longitude (left side)] than the outer radiation belt oval [from 60° to 75° from 0° to 180° of longitude (right side) and from 50° to 60° from 180° to 360° of longitude (left side)] at this date. The auroral oval is at higher latitudes than Scandinavia for instance. The lower (equatorward) edge of the auroral oval corresponds to the outer (polar) edge of the outer belt, even if some overlap is partially observed. Both ovals have similar shape slightly elongated at lower latitudes for longitudes >180°, due to the configuration of the magnetic field. The auroral oval is located at higher latitude than the oval of the outer radiation belt for E = 500–600 keV measured from PROBA-V/EPT.

Thus, to summarize our findings up to now, the auroral oval is located at higher latitudes than the outer radiation belt, as expected since the plasma sheet is located at larger distances in the elongated tail than the inner magnetosphere regions. Globally, we observe that the inner (equatorial) edge of aurora as obtained by OVATION is close to the outer (polar) edge of the outer belt for E = 500–600 keV. Only for sufficiently long quiet periods, the plasmapause also lies beyond the polar edge of the outer belt, only for E > 1.6 MeV. For lower energies, the outer radiation belt is generally more extended than the plasmasphere. The plasmapause located far from the Earth during prolonged low activity periods is still generally below the equatorial edge of the auroral oval for most MLT. The energy of the particles is essential to explain the observed differences and some particular overlap of these regions, since the particle’s energy determines the particle drift velocity, therefore influences the MLT repartition, as well as the (trapped or not) position in the inner magnetosphere.

Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During the Storm Event of August 26, 2018

The August 26, 2018 storm is one of the three most powerful geomagnetic storms, which occurred since the launch of PROBA-V in 2013 (see Figure 1 in Pierrard et al. (2020) for a 7-years representation). For this storm, Kp exceeded 6 (see Figure 10) and Dst reached -174 nT, as illustrated in Figure 12.

FIGURE 10

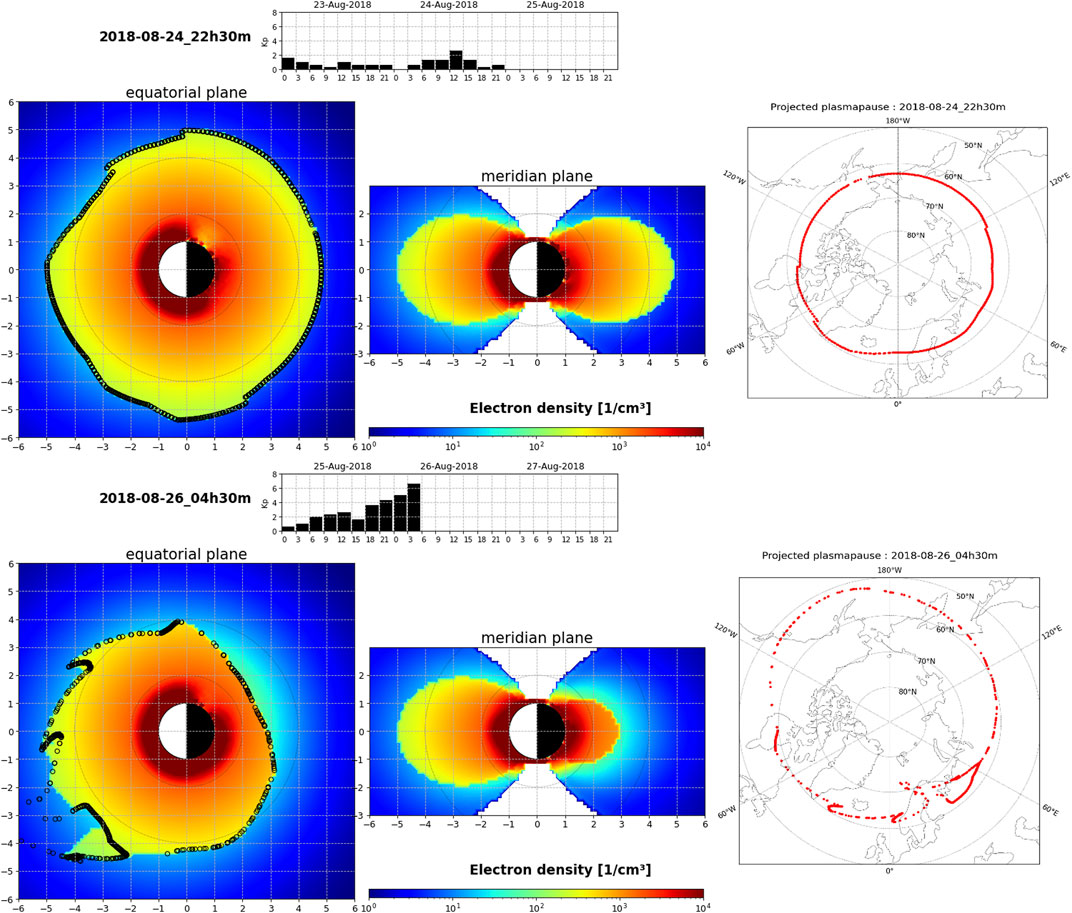
FIGURE 10. Plasmasphere electron density in cm⁻³ in (left) the equatorial plane and in (middle) the meridian plane, as well as the ionospheric footprint of the plasmapause at high latitude (right) obtained with the SPM model on (top panel) August 24, 2018 at 22h30, before the storm, and on (bottom panel) August 26, 2018 at 4h30 during the storm. The Kp index measured between 23 and August 26, 2018 4h30 is also shown in the top figure of each panel.

Links Between the Plasmapause and the Ionospheric Convection Boundary

Plasmasphere Model

Figure 10 illustrates how the position of the plasmapause varies with the geomagnetic activity before (top panels) and during (bottom panels) this storm. The plasmasphere electron density (in cm⁻³) is obtained in the equatorial (MLT distribution) and meridian planes with the SPM model on August 24, 2018 at 22h30, before the storm and on August 26, 2018 at 4h30 during the storm. The plasmapause develops structures like plumes and shoulders depending on the Kp variations (e.g., Pierrard and Lemaire, 2004; Bandic et al., 2020). A plume is clearly visible forming in the dusk sector on 26 August during the storm. The eroded and more anisotropic plasmasphere is also associated to an ionospheric projection of the plasmapause located at higher latitudes during the storm, as clearly visible on the right panels. Storm enhanced density observed in the ionosphere has been identified as ionospheric signature of plasmaspheric plumes (Foster et al., 2002). We will confirm in Flux Evolution Observed by Van Allen Probes that the plasmasphere observed by Van Allen Probes is highly dynamics for this period.

Ionospheric Convection Observed by Super Dual Auroral Radar Network

We quantify the intensity of convection before and during the storm case of August 26, 2018 in Figure 11 showing ionospheric convection patterns measured by the SuperDARN radars. The convection is much stronger after the storm (bottom panels) than before (top panels). The ionospheric convection boundary HMB determined by SuperDARN is shown by the green line on Figure 11.

FIGURE 11

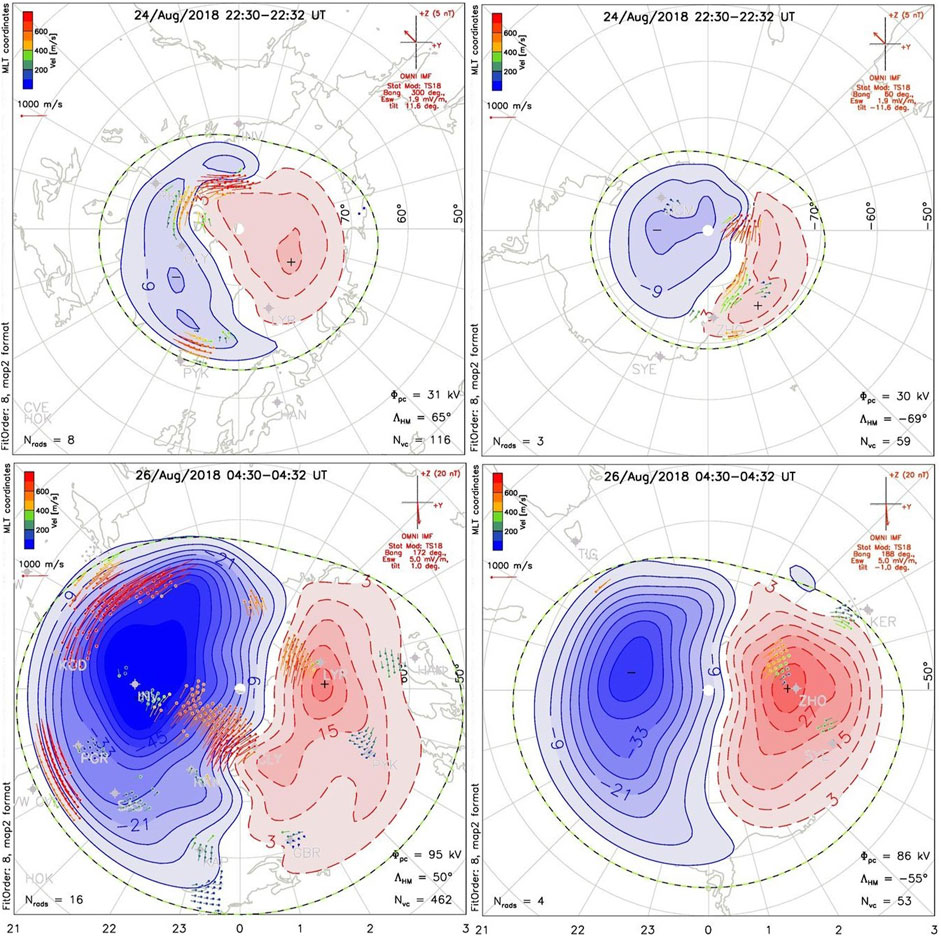
FIGURE 11. Ionospheric convection pattern measured by SuperDARN in the Northern hemisphere (left panels) and in the Southern hemisphere (right panels) on (top) August 24, 2018 at 22h30 before the storm and (bottom) during the storm of August 26, 2018 at 4h30. The green lines represent the ionospheric Heppner-Maynard Boundary (HMB). Arrows represent the measured ionospheric convection velocity (most seen on the Northern hemisphere during the storm). The blue-red shades show the ionospheric potential.

On August 24, 2018 at 22h30 before the storm, the plots are taken from an extended period of stable IMF and the pattern is fairly fixed in orientation through the 22–23 UT interval, giving high confidence. The pattern is characteristic of By-conditions. In the NH, we have L_HMB = 65°, in the SH, L_HMB = 69°. The amount of data in the SH is very limited (59 vectors), so we can only say that L_HMB ≤ 69° as the equatorward limit of the convection zone could extend equatorward of 69°.

On August 26, 2018 at 4h30 during the major storm, there are many vectors observed in the NH. They show that the convection zone is greatly expanded and L_HMB = 50°. Under such extreme conditions, SuperDARN may not be seeing the equatorward limit of convection. The problem is that the radar fields of view are limited to latitudes >50° due to the dynamic range of the instrument. So here L_HMB ≤ 50°. In the SH, there is evidence as well of a greatly expanded convection zone. Note the vectors that extend almost to the site of the Kerguelen radar (KER). With fewer radars operating at lower latitudes in the south, there is less scope for detecting the equatorward limit, and so here L_HMB ≤ 55°. Like the plasmapause, the HMB migrates to higher latitudes during storm, but with a different latitude and MLT distribution that depends significantly on the magnetic field model used to reconstruct the SuperDARN convection pattern.

Radiation Belts

Flux Evolution Observed by PROBA-V/EPT

Figure 12 shows the electron flux measured by PROBA-V/EPT at 500–600 keV (top), 1–2.4 MeV (second) and 2.4–8 MeV (third) from August 1, 2015 to September 20, 2018. The white regions correspond to periods when no observations are available. The black dashed lines (middle panels) shows the plasmapause position obtained with the SPM model. The inward motion of the plasmapause to lower L is clearly visible on August 26, 2018, and leads to a L ∼ 2.5 for E = 1–2.4 MeV similar to the lowest position of the inner edge of the outer belt during the storm. This position of the plasmapause close to the Earth is nevertheless lower than the lowest penetration of the inner edge of the outer belt for higher energy (around L∼3 for 2.4–8 MeV for instance). On the contrary, for 500–600 keV, the injection penetrates deeper, almost down to the inner belt, until a new slot forms 10 days later around L = 3. Note also the dropouts that appear during each substorm and penetrate down to L = 4 on August 26, 2018, due to magnetopause shadowing (e.g., Pierrard et al., 2020).

FIGURE 12

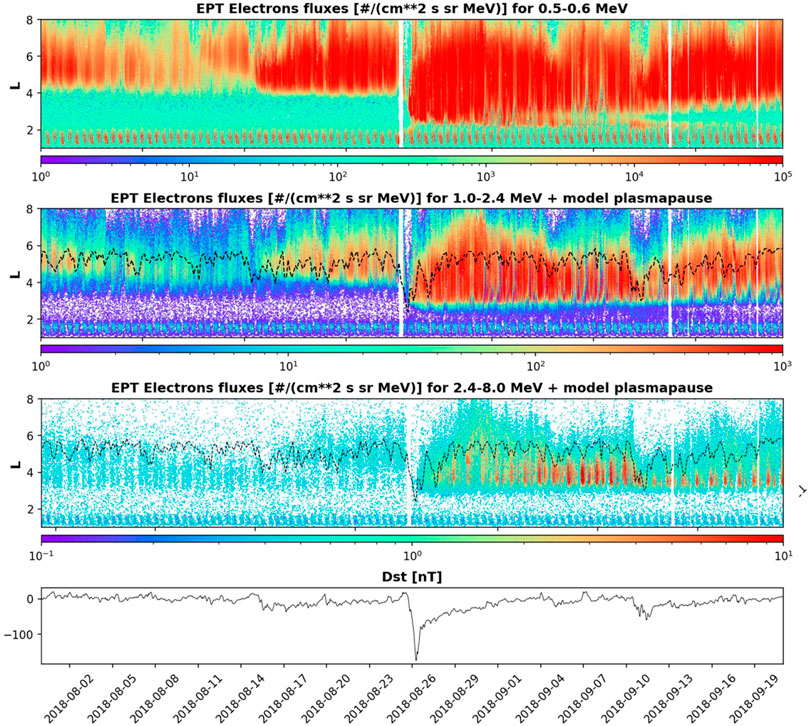
FIGURE 12. Electron flux measured by PROBA-V/EPT at 500–600 keV from 1 August to September 20, 2018. Second panel: Electron flux measured by PROBA-V/EPT at 1–2.4 MeV from 1 August to September 20, 2018. The black dotted line corresponds to the plasmapause obtained from the SPM model. Third panel: Same as second panel but for 2.4–8 MeV. Bottom panel: Observed Dst index.

Flux Evolution Observed by Van Allen Probes

This feature is confirmed in Figure 13 that shows the radiation belts prior and after the storm as observed by Van Allen Probes for different energies. The storm produced enhanced 1 MeV flux for 8 days, forming a hard-spectrum outer belt notably different from the quiet outer belt of the beginning of August 2018 (or the one shown previously in Figure 7). The 1 MeV belt reaches as low as L = 2.5 on 28 August. The injection of sub-relativistic electrons deep in the inner belt reaches almost 600 keV. This is quite rare. For comparison, the average energy of substorm injections is ∼250 keV (e.g., Turner et al., 2015). At low energy (30–100 keV), the injections are intense and repeated before and after the 26 August storm. The small substorm occurring on August 15, 2018 does not generate sub-relativistic injections but does inject low energy electrons. Below 30 keV, the inner belt and the outer belt start merging to form a unique active region surrounding the Earth. The waves creating the slot region separating the radiation belts are thus not effective at 10 keV and below.

FIGURE 13

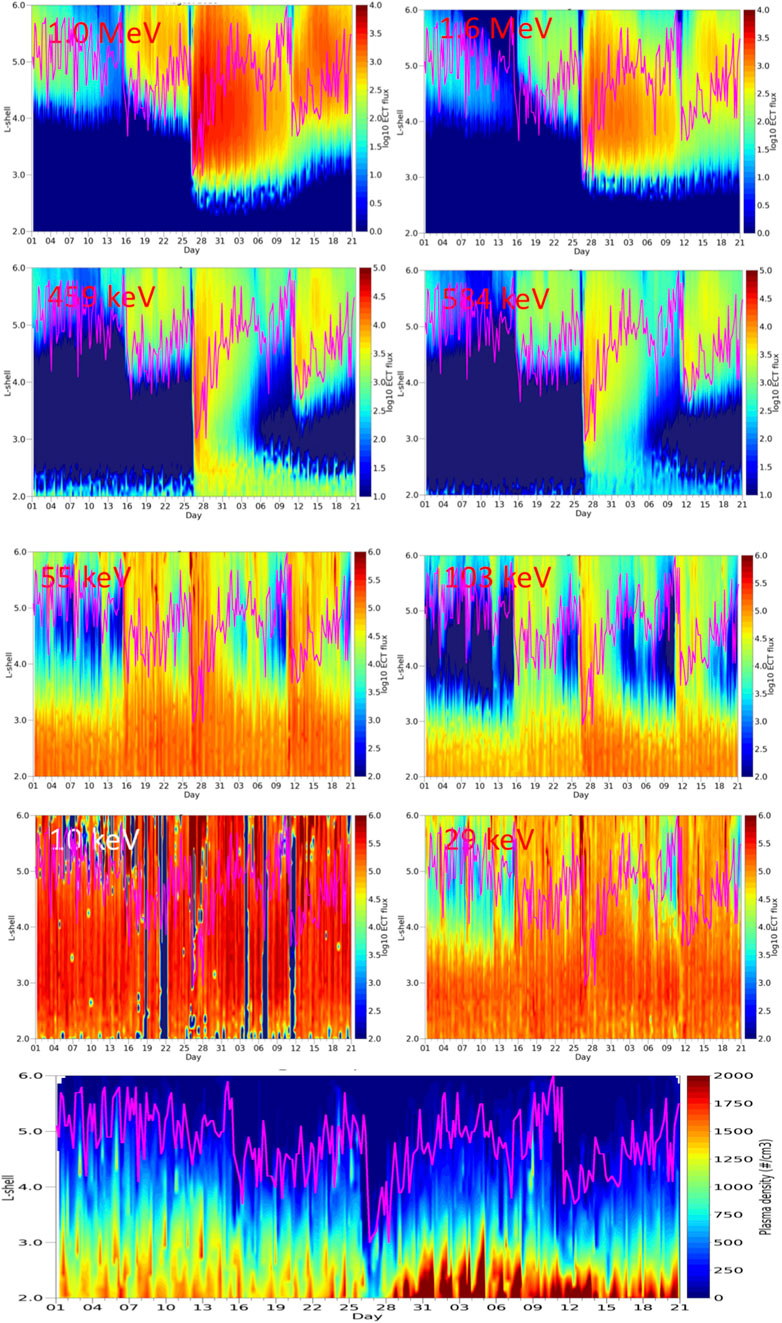
FIGURE 13. Level 2 ECT combined radiation belt spin-averaged flux plotted versus time and L-shell from 1 August to September 20, 2018 measured by the ECT suite of Van Allen Probes in the magnetic equatorial plane. The magenta line corresponds to the plasmapause position measured by EMFISIS on RBSP B. (Top 4) sub-relativistic and relativistic electrons. (Next 4) low energy seed electrons (10–100 keV). (Bottom panel) Plasma density of RBSP B/EMFISIS computed as explained in section Van Allen Probes Plasmapause Observations, from 1 August to September 21, 2018.

Last panel of Figure 13 shows the plasma density and the plasmapause extracted from it, also reported on the flux. There is a good coincidence of the plasmapause location with the 1.6 MeV channel during the couple of days of the storm recovery (26–28 August 2018), both reaching L = 3. Lower energy electrons penetrate deeper than the Lpp as shown in Figure 13. This confirms the claims made in section Links Between the Plasmapause and the Radiation Belt Boundaries. In August-September 2018, RBSP apogee is at ∼23–22 MLT and cross the L = 3 field line at 19–18 MLT so that the modeled minimum Lpp at 2.5 and the observed minimum plasmapause at L∼3 are consistent. The complex structure of the modeled density is confirmed by the filamentary structure of the observations with various detached regions of dense plasma and high variability in time as the probes scan a different region from one pass to another. After the early recovery period, both the outer radiation belt and the plasmasphere evolve at their own rates and no link exists anymore.

High-Latitude Magnetic Local Time Maps of the Outer Radiation Belt by PROBA-V/EPT

Figure 14 shows complementing polar maps of the 1–2.4 MeV electron differential flux measured by PROBA-V/EPT at 820 km of altitude in the Northern hemisphere (left panels) and in the Southern hemisphere (right panels). We show a new way to illustrate how radiation belts in the equatorial magnetosphere project and map at high latitudes. Before the storm, from 1 to August 24, 2018 (top panels), the outer radiation belt oval is thin. After the storm, (here accumulated from 25 August to September 20, 2018 on bottom panels), the outer radiation belt oval is more intense and extends at lower latitudes than before the storm, typically 10° lower, as also found for other storms (Pierrard and Lopez Rosson, 2016). It is interesting to note that losses in the slot are only slightly enhanced by the storm times. This is due to the high energy channel (>1 MeV) and the rarity of these particles in the deep slot region, although we note that these electrons reached L = 3 at the Dst peak of the storm (cf. Figure 12).

FIGURE 14

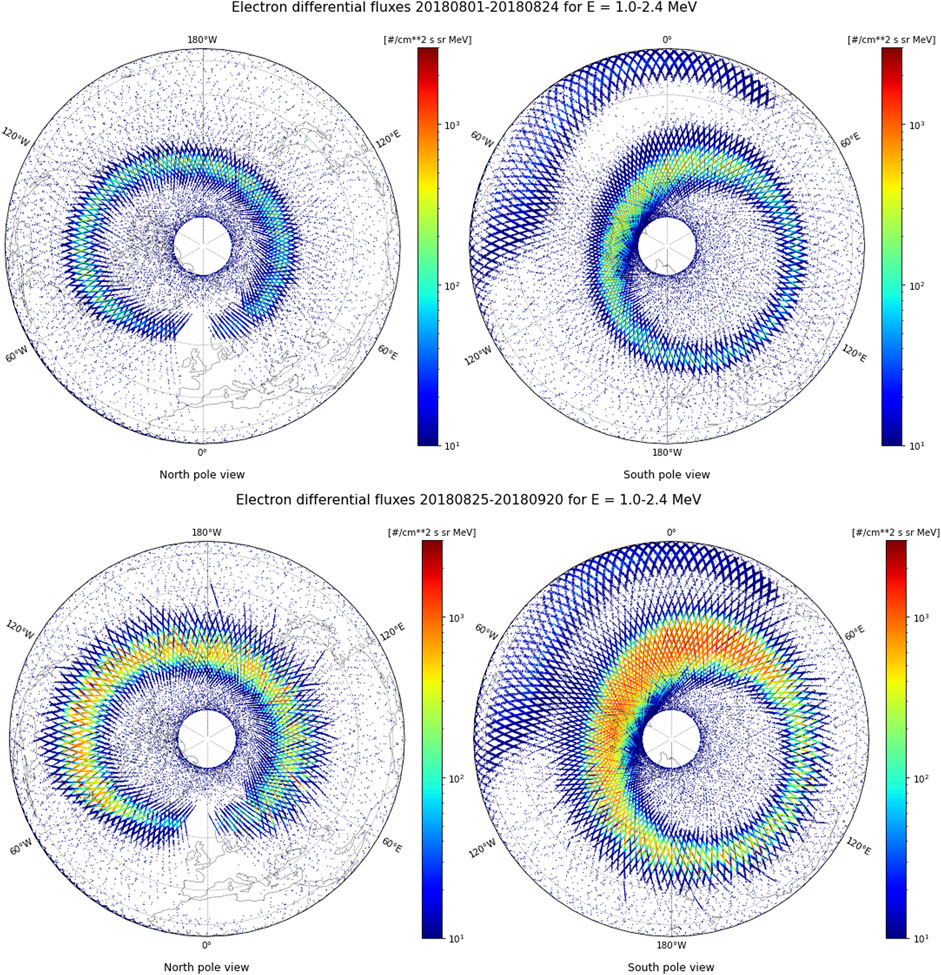
FIGURE 14. Maps of electron differential flux measured by PROBA-V/EPT in Channel 5 (1–2.4 MeV) at 820 km of altitude in the Northern hemisphere (left panels) and in the Southern hemisphere (right panels), before the storm from 1 to August 24, 2018 (top panels) and from 25 August to September 20, 2018 (bottom panels) during and after the storm. The thin black circles with increasing radius correspond to constant latitudes of 80°, 60°, 40° and 20°. Greenwich longitude of 0° corresponds to the bottom in the Northern hemisphere (left panels) and the top in the Southern hemisphere (right panels).

During the storm, the lowest boundary of the outer radiation belt oval for the high energy 1–2.4 MeV reaches 40° of latitude for longitudes between 60° and 120° West in the Northern hemisphere, and a latitude of 40° for longitudes between 60° and 180° East. The boundary is located at higher latitudes for other longitudes due to the configuration of the magnetic field.

Auroral Oval by the OVATION Model

Figure 15 illustrates the Northern hemisphere auroral oval as predicted by the OVATION model on 24-8-2018 at 22h25 UT (upper left) before the storm, and successively for three times following the storm. One can see that the auroral oval is very thin and faint before the storm, and becomes brighter and broader during the storm. The position of the oval and its intensity are very dependent on the MLT sector: the aurora is not visible at 12h00 MLT in the dayside, even during the storm, while the probability of auroral visibility oval is the most intense and wide in the nightside shown by the black background region. Already before the storm on 24-8-2018 at 22h25 and during the storm on 25-8-2018 at the same time, Sweden and Norway (easy to identify on Figure 15) are located under the auroral oval, as well as under the radiation belt oval as shown in Figure 14, showing that overlap between these regions are possible. On 26-8-2018 at 10h25 (bottom right), Sweden and Norway are located in the dayside so that the auroral oval does not cover these countries. As illustrated by Figures 14, 15 respectively, intensification and broadening of the auroral oval during storms are common characteristics with the outer radiation belt oval, but there are major differences concerning the position of the boundaries and the MLT distribution that are detailed in the next section, discussing also the plasmapause position and convection pattern during magnetic disturbances.

FIGURE 15

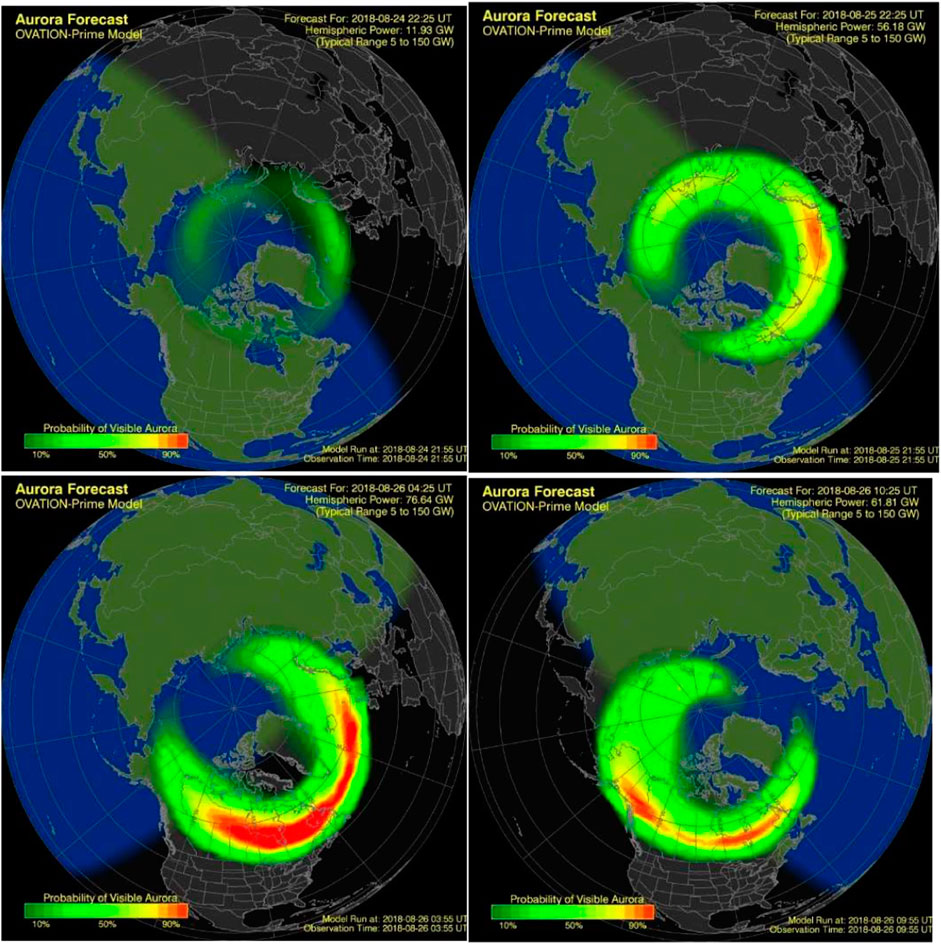
FIGURE 15. Northern hemisphere probability of aurora visibility as predicted by the OVATION model before the storm (upper left) on 24-8-2018 at 22h25, and then during the storm on (upper right) 25-8-2018 at 22h25, on (bottom left) 26-8-2018 at 4h25 and on (bottom right) 26-8-2018 at 10h25. Greenwich longitude of 0° is located in the right side of the panels.

Discussion About the Links Between the Boundaries and Their Magnetic Local Time Distribution

Links Between the Plasmapause and the Radiation Belt Boundaries

Empirical relations between the plasmapause and Dst have been found, as shown in Data and Models. Similar empirical relations exist also for the inner and outer edges of the radiation belts (for different energies) with the Dst index (Pierrard et al., 2020), indicating a possible link between these positions and the ring current responsible for the Dst decrease during storms. As shown in Long Term Variations of the Plasmapause: Comparison Between Observations and the Space Weather Integrated Forecasting Framework plasmasphere model Model, the plasmapause is located close to the inner edge of the energetic outer belt for E ∼ 1 MeV during the storm main phase and generally above the outer edge of the outer belt for E > 1.6 MeV after sufficiently prolonged quiet periods (Pierrard et al., 2020). The convection electric field that depends on the geomagnetic activity seems also implicated in the dynamics affecting these different regions.

Links between the plasmasphere and the radiation belts can be determinant for the global dynamics of the magnetosphere. The plasmapause boundary determines the electromagnetic waves that circulate in the plasma and may cause energization and loss of the particles. Outside the plasmasphere, whistler-mode chorus waves have been found to play an important role in the enhancement and precipitation of electrons (e.g., Thorne et al., 2013). Inside the plasmasphere, whistler-mode hiss waves can cause the slow decay of radiation belts electrons with loss time scales on the order of 5–10 days (e.g., Ripoll et al., 2019) and rarely contribute to local acceleration. In general, the plasmapause separates chorus waves outside the plasmasphere and hiss waves inside the plasmasphere (e.g., Thorne, 2010). Therefore, changes in plasmapause location can cause drastic change in the hardening or softening of the radiation belt flux. Poloidal ULF (ultra-low frequency) pulsations have also been investigated near the dayside plasmapause and these studies revealed that the wave field is confined in the Alfvén resonator at the outer edge of the plasmapause (Schäfer et al., 2007, 2008). O’Brien et al. (2003) found that electron acceleration at low L shells is closely associated with both ULF activity and MeV microbursts and thereby probably also with chorus activity. Electron flux enhancements across the outer radiation belt are, in general, related to both ULF and VLF/ELF activity. These authors suggest that electron flux peaks observed at L ∼ 4.5 are likely caused by VLF/ELF wave acceleration which appears to be excluded from the plasmasphere, while ULF activity probably produces the dominant electron acceleration at geosynchronous orbit and beyond. Intense local acceleration can occur outside of the plasmasphere from chorus waves (Thorne et al., 2013; Li et al., 2016), bringing very quickly sub-relativistic electrons (E < 500 keV) to ultra-relativistic energies (E > 2 MeV), using the terminology in Drozdov et al. (2015). While this is a classic scenario, with available chorus observations during the March 2015 storm for both a THEMIS spacecraft and Van Allen Probes (Li et al., 2016), there is still a debate on the respective importance of local acceleration and adiabatic transport (Ozeke et al., 2019).

Links Between the Plasmapause and Its Footprint in the Ionosphere

The plasmapause boundary has been shown to be related to mid-latitude ionospheric troughs (e.g., Lemaire, 2001). Such mid-latitude troughs, also called main ionospheric light ion troughs, are density depletions observed in the ionosphere in the F region above 150 km of altitude (e.g., Rycroft and Burnell, 1970). Because the low latitude boundary of the trough corresponds to the projection of the plasmapause into the ionosphere, the mid-latitude troughs have been proven to be a good indicator of the plasmapause location (Yizengaw and Moldwin, 2005; Anderson et al., 2008), including for recent events like the September 2017 storm (Obana et al., 2019). A new study compares the location of the mid-latitude trough and plasmapause boundary using Van Allen Probe observations (Weygand et al., 2021). Their results indicate that the mid-latitude trough observed within vertical total electron content maps represents an additional means of identifying the plasmapause boundary location.

Mid-latitude troughs have to be differentiated from high-latitude ionospheric troughs that are sometimes observed inside and poleward of the auroral oval. They are due to auroral precipitation processes (Collis and Haggstrom, 1988; Voiculescu et al., 2016).

Links Between the Radiation Belts and the Location of the Auroral Oval

We have found that the auroral oval is generally located at higher latitude than the oval of the outer radiation belt. This can be explained by the fact that auroras are due to particles coming from a ring located at larger distances in the equatorial plane than the radiation belts for electrons with E > 500 keV. This ring surrounds the Earth at geocentric distances from ∼7 Re to the magnetopause, near noon, and to∼10–13 Re near midnight, where it corresponds to the plasma sheet (Riazanteseva et al., 2018). Electric potential differences cause the precipitation of energetic particles from the plasma sheet along the elongated magnetic field lines located mainly in the night side, where the auroral oval is thus brighter (Pierrard et al., 2007). It is expected that the energetic ions originate from the ring current and can be scattered by the electromagnetic Ion Cyclotron (EMIC) waves through cyclotron resonance (Sigsbee et al., 2020 and references therein). The energetic electrons can also be precipitated by non-resonant interactions between the electrons and EMIC waves (e.g., Denton et al., 2019). Other studies show the link of proton auroral and plasmaspheric plumes through these same processes (Spasojevic et al., 2004). And several studies have shown that proton aurora spot sources are often located in the vicinity of the plasmapause (Yahnin et al., 2013; Zhou et al., 2019).

Riazanteseva et al. (2018) found that the high-latitude boundary of the outer radiation belt (>100 keV) can be located both inside the auroral oval or equatorward of the low-latitude boundary of the auroral precipitation zone. They also found that for slightly disturbed geomagnetic conditions, the polar boundary of the outer radiation belt is almost always located inside the auroral oval. This is important since the position of the trapping boundary for energetic electrons in the outer radiation belt contains information about the topology of the magnetic field lines of the Earth.

The scenario is different for diffuse aurora since they are caused by precipitations of electrons from 10–30 keV (e.g., Nishimura et al., 2020) and can occur where chorus waves are present. Chorus waves can also cause acceleration of hundreds of keV radiation belt electrons at a lower L-shell. Since chorus are mainly located outside the plasmasphere, this would lead to diffuse aurora being poleward of the plasmapause. Note also that some studies have shown that electron cyclotron harmonic (ECH) waves can also contribute to the formation of diffuse aurora (e.g. Zhang et al., 2015).

Magnetic Local Time Distribution of the Different Regions

The particles of the plasmasphere, of the auroral regions and of the radiation belts are all trapped in the magnetic field of the Earth, giving them a toroidal shape around the Earth in the meridian plane. When projected at low altitude, they correspond to different ovals, at very high latitude for the aurora and at mid-latitudes for the radiation belts and the plasmapause. Nevertheless, their shape is quite different due to their different energy that give them different motion.

The low energy particles (around 1 eV) of the plasmasphere are located in the same region of the inner magnetosphere as the inner and outer belt (500 keV–5 MeV) during quiet periods. The plasmasphere is almost in co-rotation with the Earth. In fact, the velocity of the ionosphere and the low altitude plasmasphere has sometimes a small lag (80–90% of corotation) (Burch et al., 2004; Lejosne and Mozer, 2016). The causes of sub-corotation variability have been explored by Galvan et al. (2010). The azimuthal drift is dominated by the electric force: v_drift= (ExB)/B². It takes thus approximately 24 h for the particles to make a complete rotation. The plasmapause and the plasmasphere density are thus highly dependent on MLT, with the development of some specific structures like plumes in the afternoon-dusk MLT sector.

The plasma sheet electrons with an energy from 100 eV to several keV causing the aurora are located in the nightside tail and are thus also very dependent on MLT. The auroral oval is clearly broader and brighter in the midnight sector, as shown in Figure 15. For the energetic particles of the radiation belts (E > 500 keV), the drift velocity is not dominated by the electric force anymore, but by the Lorentz force due to the gradient of B and the curvature of the magnetic field lines (Roederer, 1970). This force depends on the energy of the particles. A 1 MeV electron at L = 1.5 Re (respectively L = 6) takes approximately 45 (respectively 11) minutes to rotate around the Earth in the equatorial plane. The longitudinal dependence of the radiation belt is thus more determined by the configuration of the magnetic field than by the MLT. The MLT plays nevertheless a fundamental role in the radiation belts, because, for instance, magnetopause shadowing on the day side is responsible for particle dropouts during the main phase of the storms, highly affecting the outer edge of the outer belt (e.g., Pierrard et al., 2020) and wave-particle interactions determining the radiation belt structure are strongly MLT-dependent (cf. review of Ripoll et al. (2019)).

Since the energies of the particles filling the auroral regions, the radiation belts and the plasmasphere are very different, their drift velocity is also different and can explain some of the differences observed in MLT. The physical processes of plasmapause formation and auroral injections are related to the convection electric field that increases during the storm. The very energetic particles of the radiation belt are less affected by the electric field since their drift velocity is dominated by the effects of the magnetic (gradient and curvature) force during quiet times.

The MLT sector plays an important role for the distribution of the particles trapped in the terrestrial magnetic field. The plasmapause is formed in the post-midnight sector due to the plasma convection and is transmitted to the other MLT sectors by co-rotation (Pierrard and Lemaire, 2004). The formation of plumes in the afternoon-dusk sector and their rotation toward other MLT can influence the other regions. As shown by Imber et al. (2013), the ionospheric convection boundary, Heppner Maynard Boundary (HMB), measured by SuperDARN can be used as a proxy for the latitude of the auroral oval and is magnetically related to the plasmapause, in turn reflecting itself the topology of the system. Matar (2021) observed, by analyzing geomagnetic storms, that the plasmasphere density correlates with the open magnetic flux associated to reconnection, confirming the links we discussed in the present work between the plasmasphere and the aurora.

Global Motion During Storms

The different ovals (aurora, outer radiation belt at low altitude, footprint of the plasmapause projection in the ionosphere, and ionospheric convection pattern) have to be considered within a global view of the magnetosphere as they are all part of this dynamic system. The equatorward motion of the different regions of the magnetosphere during storms, i.e., the plasmapause, inner edge of the outer belt and inner edge of the auroral oval, implies some possible intersections of these different regions at particular times (as seen in Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During a Quiet Period: March 14, 2014 for quiet times and Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During the Storm Event of August 26, 2018 for storms), possibly linking them, all reflecting at their own scales a same magnetic topology of the system.

As shown in Auroral Oval by the OVATION Model, the auroral zone shifts poleward at times of low solar activity, while during periods of high solar activity, the auroral oval moves to lower latitudes (thus southward in the Northern hemisphere). This southward motion during storms and substorm is very similar to the motion of the plasmapause and of the outer radiation belt toward lower latitudes during the same disturbed periods, as shown in Links Between the Plasmapause, Ionospheric Convection Boundary, Radiation Belts and Auroral Oval During the Storm Event of August 26, 2018. The primary source mechanism of the polar aurora is nevertheless different since it is related to reconnection in the magnetotail that extends on the nightside (e.g., Kivelson and Russell, 1995). Reconnection of the geomagnetic field with the IMF mostly occurs when the IMF is directed southward and generates substorm injections. The plasmasphere and the outer belts are in turn also affected by such substorm injection events.

Conclusion

In the present work, we study and compare the positions (with respect to L-shell and magnetic local time) of the plasmapause, of the ionospheric convection, of the radiation belt boundaries and of the auroral oval, on the long term during a 10 months period of 2015 and also during two specific periods: one period of quiet geomagnetic activity in March 2014 and one period of disturbed geomagnetic activity associated with the geomagnetic storm of August 26, 2018. We combine different satellite observations (the NASA Van Allen Probes for the plasmapause and the radiation belts, and the ESA PROBA-V for the radiation belts at LEO), radar observations (SuperDARN for the ionospheric convection), and various models (the SPM plasmasphere model, OVATION for aurora, AE-8MAX for radiation belts). We show the dynamics of these regions in three dimensions, i.e., radially, in MLT, and as a function of the latitude. This is done by combining meridian, equatorial and polar maps. We show a similar equatorward motion of the plasmapause, the outer belt and the auroral oval during storms, suggesting a link due to the magnetic field topology and the convection electric field that increases during storms and substorms.

Maps in geographic coordinates allow direct comparison of the different boundaries in MLT sectors at the same UT times during quiet and active periods. We discuss links between the plasmapause and the projection of the plasmapause in the ionosphere. The plasmapause is located at similar distance as the outer edge of the outer belt, but only for E∼1.6 MeV and after sufficiently long quiet periods, and as the inner edge of the outer belt during the main phase of the storms, but only for E∼1 MeV. The radiation belt boundaries are strongly dependent on the energy of the particles. At lower energies, the plasmapause is located inside the outer radiation belt.

The equatorial edge of the auroral oval is often located close to the outer (polar) edge of the outer energetic belt, and to the plasmapause during quiet periods. There is often overlap between the plasmasphere region, the outer radiation belt and equatorward part of the auroral oval, especially in the nightside. During storms, the auroral oval position decreases in latitude, similarly to the plasmapause, the ionospheric trough, the ionospheric convection boundary and the inner edge of the outer belt. All these regions seem related by the magnetic field and the convection electric field.

The boundaries are dependent on the energy of the particles, especially for the outer radiation belt that include electrons from 100 keV to several MeV. The MLT dependence is also different for the plasmasphere, the auroral oval, and the radiation belts due to the relative contributions of convective and magnetic of the particles at different energies.

Recent research studies show the need of a more global view of the magnetosphere dynamics that takes into account the interactions between these different regions. The links between the plasmapause, the ionospheric convection, the boundaries of the radiation belts, and the auroral oval certainly need further investigations. In that perspective and to know further, links between compressions of the plasmapause, multi-keV electrons injections, and luminous phenomena reported in the ionosphere are discussed in Cully et al. of this special issue. Nevertheless, they remain difficult to explore due to the lack of simultaneous observations. Three dimensional dynamic models of different regions of the magnetosphere help providing some vision and understanding global and coupled dynamics between the magnetosphere and the ionosphere, with still the need to validate them from more observations.

Data Availability Statement

Publicly available datasets were analyzed in this study. The SPM model nowcast images are available on the ESA SSA (Space Situational Awareness) website (https://swe.ssa.esa.int/space-radiation). Ovation model, developed at the Johns Hopkins University, Applied Physics Lab by Patrick Newell and co-workers, and validated by NASA Polar satellite data, is available on NOAA, Colorado: https://www.swpc.noaa.gov/products/aurora-30-minute-forecast. EPT data are publicly available at the ESA website http://swe.ssa.esa.int/space-radiation. All RBSP-ECT data are publicly available at the Web site http://www.RBSP-ect.lanl.gov/. The EFW spacecraft potential is available from the University of Minnesota Van Allen Probes EFW site http://www.space.umn.edu/rbspefw-data/. EMFISIS data can be obtained from http://emfisis.physics.uiowa.edu. The authors acknowledge the use of on-line plotting tools hosted by the Virginia Tech SuperDARN group at their website (http://vt.superdarn.org/tiki-index.php?page=Conv+map+overview). The CRRES Plasmapause Data (Data set) have been put in repository by Moldwin, M., O'Brien, P., University of Michigan - Deep Blue: https://doi.org/10.7302/mwy1-v326.

Author Contributions

PV has written this article, has developed the SPM model, and contributed to the analysis of the data, including for EPT as co-I. EB contributed to improve the SPM model and to realize some plots. J-FR computed the plasmapause location from the EFW and EMFISIS density, and provided the ECT combined flux. J-FR contributed to the analysis of the data and to the writing of the article. ST provided the EFW electron density and GR checked the electron fluxes of Van Allen Probes. MM provided the CRRES plasmapause data set. MR provided and checked the SuperDARN data.

Funding

The SafeSpace project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 870437. The project Plasmasphere ionosphere Thermosphere Integrated Research Environment and Access services: a Network of Research Facilities PITHIA-NRF (https://www.pithia-nrf.eu/) has received funding from INFRAIA-02–2020, ID 101007599. Processing and analysis of the (HOPE, MagEIS, REPT, or ECT) data was supported by Energetic Particle, Composition, and Thermal Plasma (RBSP-ECT) investigation funded under NASA’s Prime contract no. NAS5-01072.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the editors for their invitation to contribute to this special issue about on Coupled Feedback Mechanisms in the Magnetosphere-Ionosphere System. The authors thank the EFW and EMFISIS teams of the Van Allen Probes mission for their support. Van Allen Probes wave data used in this work are available from the EFW and EMFISIS team websites (which one can link to http://rbspgway.jhuapl.edu). The authors thank the ECT team of the Van Allen Probes mission for their support. VP thanks the team of Center for Space Radiations for the validation of the EPT data. JFR thanks M. Cosmides for her contribution to the ECT combined flux figures. The authors thank the International Space Sciences Institute (ISSI) and the participants in a 2020 ISSI workshop for the project “Radiation belts physics”. The authors acknowledge the use of SuperDARN data. SuperDARN is a collection of radars funded by national scientific funding agencies of Australia, Canada, China, France, Italy, Japan,Norway, South Africa, United Kingdom and the United States.

References

Anderson, P. C., Johnston, W. R., and Goldstein, J. (2008). Observations of the Ionospheric Projection of the Plasmapause. Geophys. Res. Lett. 35, L15110. doi:10.1029/2008GL033978

CrossRef Full Text | Google Scholar

Baker, D. N., Jaynes, A. N., Hoxie, V. C., Thorne, R. M., Foster, J. C., Li, X., et al. (2014). An Impenetrable Barrier to Ultrarelativistic Electrons in the Van Allen Radiation Belts. Nature 515, 531–534. doi:10.1038/nature13956

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., Hoxie, V. C., Batiste, S., Bolton, M., Li, X., et al. (2012). The Relativistic Electron-Proton Telescope (REPT) Instrument on Board the Radiation Belt Storm Probes (RBSP) Spacecraft: Characterization of Earth's Radiation Belt High-Energy Particle Populations. Space Sci. Rev. 179, 337–381. doi:10.1007/s11214-012-9950-9

CrossRef Full Text | Google Scholar

Bandić, M., Verbanac, G., Moldwin, M. B., Pierrard, V., and Piredda, G. (2016). MLT Dependence in the Relationship between Plasmapause, Solar Wind, and Geomagnetic Activity Based on CRRES: 1990-1991. J. Geophys. Res. Space Phys. 121, 4397–4408. doi:10.1002/2015JA022278

CrossRef Full Text | Google Scholar

Bandić, M., Verbanac, G., Pierrard, V., and Cho, J. (2017). Evidence of MLT Propagation of the Plasmapause Inferred from THEMIS Data. J. Atmos. Solar-Terrestrial Phys. 161, 55–63. doi:10.1016/j.jastp.2017.05.005

CrossRef Full Text | Google Scholar

Bandić, M., Verbanac, G., and Pierrard, V. (2020). Relationship between Global Plasmapause Characteristics and Plasmapause Structures in the Frame of Interchange Instability Mechanism. J. Geophys. Res. Space Phys. 125, e2019JA026768. doi:10.1029/2019JA026768

CrossRef Full Text | Google Scholar

Bartels, J., and Veldkamp, J. (1949). International Data on Magnetic Disturbances, First Quarter, 1949. J. Geophys. Res. 54 (3), 295–299. doi:10.1029/JZ054i003p00295

CrossRef Full Text | Google Scholar

Blake, J. B., Carranza, P. A., Claudepierre, S. G., Clemmons, J. H., Crain, W. R., Dotan, Y., et al. (2013). The Magnetic Electron Ion Spectrometer (MagEIS) Instruments Aboard the Radiation Belt Storm Probes (RBSP) Spacecraft. Space Sci. Rev. 179, 383–421. doi:10.1007/s11214-013-9991-8

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Valdivia, J. A. (2018). The Earth's Magnetosphere: A Systems Science Overview and Assessment. Surv. Geophys. 39 (5), 817–859. doi:10.1007/s10712-018-9487-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, J. E., Welling, D. T., Thomsen, M. F., and Denton, M. H. (2014). Long-lived Plasmaspheric Drainage Plumes: Where Does the Plasma Come from. J. Geophys. Res. Space Phys. 119 (8), 6496–6520. doi:10.1002/2014JA020228

CrossRef Full Text | Google Scholar

Boyd, A. J., Reeves, G. D., Spence, H. E., Funsten, H. O., Larsen, B. A., Skoug, R. M., et al. (2019). RBSP‐ECT Combined Spin‐Averaged Electron Flux Data Product. J. Geophys. Res. Space Phys. 124, 9124–9136. doi:10.1029/2019JA026733

PubMed Abstract | CrossRef Full Text | Google Scholar

Burch, J. L., Goldstein, J., and Sandel, B. R. (2004). Cause of Plasmasphere Corotation Lag. Geophys. Res. Lett. 31 (L05802), 1–4. doi:10.1029/2003GL019164

CrossRef Full Text | Google Scholar

Carpenter, D. L., and Anderson, R. R. (1992). An ISEE/whistler Model of Equatorial Electron Density in the Magnetosphere. J. Geophys. Res. 97 (A2), 1097–1108. doi:10.1029/91ja01548

CrossRef Full Text | Google Scholar

Carpenter, D. L. (1963). Whistler Evidence of a 'knee' in the Magnetospheric Ionization Density Profile. J. Geophys. Res. 68, 1675–1682. doi:10.1029/jz068i006p01675

CrossRef Full Text | Google Scholar

Claudepierre, S. G., O'Brien, T. P., Blake, J. B., Fennell, J. F., Roeder, J. L., Clemmons, J. H., et al. (2015). A Background Correction Algorithm for Van Allen Probes MagEIS Electron Flux Measurements. J. Geophys. Res. Space Phys. 120, 5703–5727. doi:10.1002/2015JA021171

CrossRef Full Text | Google Scholar

Collis, P. N., and Häggström, I. (1988). Plasma Convection and Auroral Precipitation Processes Associated with the Main Ionospheric Trough at High Latitudes. J. Atmos. Terrestrial Phys. 50, 389–404. doi:10.1016/0021-9169(88)90024-4

CrossRef Full Text | Google Scholar

Comfort, R. H. (1996). Thermal Structure of the Plasmasphere. Adv. Space Res. 17, 175–184. doi:10.1016/0273-1177(95)00710-V

CrossRef Full Text | Google Scholar

Comfort, R. H., Waite, J. H., and Chappell, C. R. (1985). Thermal Ion Temperatures from the Retarding Ion Mass Spectrometer on DE 1. J. Geophys. Res. 90, 3475. doi:10.1029/JA090iA04p03475

CrossRef Full Text | Google Scholar

Cyamukungu, M., Benck, S., Borisov, S., Gregoire, G., Cabrera, J., Bonnet, J.-L., et al. (2014). The Energetic Particle Telescope (EPT) on Board Proba-V: Description of a New Science-Class Instrument for Particle Detection in Space. IEEE Trans. Nucl. Sci. 61 (6), 3667–3681. doi:10.1109/TNS.2014.2361955

CrossRef Full Text | Google Scholar

Darrouzet, F., De Keyser, J., Décréau, P. M. E., Gallagher, D. L., Pierrard, V., Lemaire, J. F., et al. (2006). Analysis of Plasmaspheric Plumes: CLUSTER and IMAGE Observations. Ann. Geophys. 24, 1737–1758. doi:10.5194/angeo-24-1737-2006

CrossRef Full Text | Google Scholar

F. Darrouzet, J. De Keyser, and V. Pierrard (Editors) (2009). The Earth’s Plasmasphere: Cluster and IMAGE – A Modern Perspective (Springer), 296.

Google Scholar

Darrouzet, F., Pierrard, V., Benck, S., Lointier, G., Cabrera, J., Borremans, K., et al. (2013). Links between the Plasmapause and the Radiation belt Boundaries as Observed by the Instruments CIS, RAPID, and WHISPER Onboard Cluster. J. Geophys. Res. Space Phys. 118, 4176–4188. doi:10.1002/jgra.50239

CrossRef Full Text | Google Scholar

Denton, R. E., Ofman, L., Shprits, Y. Y., Bortnik, J., Millan, R. M., Rodger, C. J., et al. (2019). Pitch Angle Scattering of Sub‐MeV Relativistic Electrons by Electromagnetic Ion Cyclotron Waves. J. Geophys. Res. Space Phys. 124, 5610–5626. doi:10.1029/2018JA026384

CrossRef Full Text | Google Scholar

Drozdov, A. Y., Shprits, Y. Y., Orlova, K. G., Kellerman, A. C., Subbotin, D. A., Baker, D. N., et al. (2015). Energetic, Relativistic, and Ultrarelativistic Electrons: Comparison of Long-Term VERB Code Simulations with Van Allen Probes Measurements. J. Geophys. Res. Space Phys. 120, 3574–3587. doi:10.1002/2014JA020637

CrossRef Full Text | Google Scholar

Fennell, J. F., Claudepierre, S. G., Blake, J. B., O'Brien, T. P., Clemmons, J. H., Baker, D. N., et al. (2015). Van Allen Probes Show that the Inner Radiation Zone Contains No MeV Electrons: ECT/MagEIS Data. Geophys. Res. Lett. 42, 1283–1289. doi:10.1002/2014GL062874

CrossRef Full Text | Google Scholar

Forsyth, C., Rae, I. J., Murphy, K. R., Freeman, M. P., Huang, C.-L., Spence, H. E., et al. (2016). What Effect Do Substorms Have on the Content of the Radiation Belts. J. Geophys. Res. Space Phys. 121, 6292–6306. doi:10.1002/2016JA022620

CrossRef Full Text | Google Scholar

Foster, J. C., Erickson, P. J., Coster, A. J., Goldstein, J., and Rich, F. J. (2002). Ionospheric Signatures of Plasmaspheric Tails. Geophys. Res. Lett. 29 (13), 1–4. doi:10.1029/2002GL015067

CrossRef Full Text | Google Scholar

Fung, S. F. (1996). “Recent Development in the NASA Trapped Radiation Models,” in Radiation Belts: Models and Standards, Geophys. Monogr. Ser., 97 (Washington, D. C: AGU), 79–91.

Google Scholar

Funsten, H. O., Skoug, R. M., Guthrie, A. A., MacDonald, E. A., Baldonado, J. R., Harper, R. W., et al. (2013). Helium, Oxygen, Proton, and Electron (HOPE) Mass Spectrometer for the Radiation Belt Storm Probes Mission. Space Sci. Rev. 179, 423–484. doi:10.1007/s11214-013-9968-7

CrossRef Full Text | Google Scholar

Fuselier, S., McPherron, D. B., Kletzing, C., and Pierrard, V. (2019). “Geomagnetism, Aeronomy and Space Weather: a Journey from the Earth’s Core to the Sun,” in IAGA Book. Editors M. Mandea, M. Korte, A. Yau, and E. Petrovsky (Cambridge University Press). doi:10.1017/9781108290135

CrossRef Full Text | Google Scholar

Gallagher, D. L., Comfort, R. H., Katus, R. M., Sandel, B. R., Fung, S. F., and Adrian, M. L. (2021). The Breathing Plasmasphere: Erosion and Refilling. J. Geophys. Res. Space Phys. 126, 4. doi:10.1029/2020ja028727

CrossRef Full Text | Google Scholar

Galvan, D. A., Moldwin, M. B., Sandel, B. R., and Crowley, G. (2010). On the Causes of Plasmaspheric Rotation Variability: IMAGE EUV Observations. J. Geophys. Res. 115 (A01214), 1–4. doi:10.1029/2009JA014321

CrossRef Full Text | Google Scholar

Goldstein, J., Baker, D. N., Blake, J. B., De Pascuale, S., Funsten, H. O., Jaynes, A. N., et al. (2016). The Relationship between the Plasmapause and Outer belt Electrons. J. Geophys. Res. Space Phys. 121, 8392–8416. doi:10.1002/2016JA023046

CrossRef Full Text | Google Scholar

Goldstein, J., Gallagher, D., Craven, P. D., Comfort, R. H., Genestreti, K. J., Mouikis, C., et al. (2019). Temperature Dependence of Plasmaspheric Ion Composition. J. Geophys. Res. Space Phys. 124, 6585–6595. doi:10.1029/2019ja026822

CrossRef Full Text | Google Scholar

Goldstein, J., Sandel, B. R., Hairston, M. R., and Reiff, P. H. (2003). Control of Plasmaspheric Dynamics by Both Convection and Sub-auroral Polarization Stream. Geophys. Res. Lett. 30 (24), 2243. doi:10.1029/2003GL018390

CrossRef Full Text | Google Scholar

Grebowsky, J. M. (1970). Model Study of Plasmapause Motion. J. Geophys. Res. 75, 4329–4333. doi:10.1029/JA075i022p04329

CrossRef Full Text | Google Scholar

Imber, S. M., Milan, S. E., and Lester, M. (2013). The Heppner-Maynard Boundary Measured by SuperDARN as a Proxy for the Latitude of the Auroral Oval. J. Geophys. Res. Space Phys. 118 (2), 685–697. doi:10.1029/2012ja018222

CrossRef Full Text | Google Scholar

Jaynes, A. N., Baker, D. N., Singer, H. J., Rodriguez, J. V., Loto'aniu, T. M., Ali, A. F., et al. (2015). Source and Seed Populations for Relativistic Electrons: Their Roles in Radiation belt Changes. J. Geophys. Res. Space Phys. 120, 7240–7254. doi:10.1002/2015ja021234

CrossRef Full Text | Google Scholar

Johnson, M. H., and Kierein, J. (1992). Combined Release and Radiation Effects Satellite (CRRES): Spacecraft and Mission. J. Spacecraft Rockets 29 (4), 556–563. doi:10.2514/3.55641

CrossRef Full Text | Google Scholar

Khoo, L. Y., Li, X., Zhao, H., Sarris, T. E., Xiang, Z., Zhang, K., et al. (2018). On the Initial Enhancement of Energetic Electrons and the Innermost Plasmapause Locations: Coronal Mass Ejection‐Driven Storm Periods. J. Geophys. Res. Space Phys. 123, 9252–9264. doi:10.1029/2018JA026074

CrossRef Full Text | Google Scholar

Kivelson, M., and Russell, C. T. (1995). Introduction to Space Physics. New York: Cambridge University Press.

Google Scholar

Kletzing, C. A., Kurth, W. S., Acuna, M., MacDowall, R. J., Torbert, R. B., Averkamp, T., et al. (2013). The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) on RBSP. Space Sci. Rev. 179 (1-4), 127–181. doi:10.1007/s11214-013-9993-6

CrossRef Full Text | Google Scholar

Kurth, W. S., De Pascuale, S., Faden, J. B., Kletzing, C. A., Hospodarsky, G. B., Thaller, S., et al. (2015). Electron Densities Inferred from Plasma Wave Spectra Obtained by the Waves Instrument on Van Allen Probes. J. Geophys. Res. Space Phys. 120 (2), 904–914. doi:10.1002/2014JA020857

PubMed Abstract | CrossRef Full Text | Google Scholar

Lapenta, G., Pierrard, V., Keppens, R., Markidis, S., Poedts, S., Šebek, O., et al. (2013). SWIFF: Space Weather Integrated Forecasting Framework. J. Space Weather Space Clim. 3 (1), A05–A17. doi:10.1051/swsc/2013027

CrossRef Full Text | Google Scholar

Lejosne, S., and Mozer, F. S. (2016). Van Allen Probe Measurements of the Electric Drift E × B/B 2 at Arecibo's L = 1.4 Field Line Coordinate. Geophys. Res. Lett. 43, 6768–6774. doi:10.1002/2016GL069875

CrossRef Full Text | Google Scholar

Lemaire, J. F. (2001). The Formation of the Light-Ion Trough and Peeling off the Plasmasphere. J. Atmos. Solar-Terrestrial Phys. 63, 1285–1291. doi:10.1016/s1364-6826(00)00232-7

CrossRef Full Text | Google Scholar

Lemaire, J., and Gringauz, K. I. (1998). The Earth’s Plasmasphere. Cambridge: Cambridge University Press.

Google Scholar

Lemaire, J., and Schunk, R. W. (1992). Plasmaspheric Wind. J. Atmos. Terr. Phys. 54 (3-4), 467–477. doi:10.1016/0021-9169(92)90026-H

CrossRef Full Text | Google Scholar

Li, W., Ma, Q., Thorne, R. M., Bortnik, J., Zhang, X. J., Li, J., et al. (2016). Radiation belt Electron Acceleration during the 17 March 2015 Geomagnetic Storm: Observations and Simulations. J. Geophys. Res. Space Phys. 121, 5520–5536. doi:10.1002/2016JA022400

CrossRef Full Text | Google Scholar

Li, X., Baker, D. N., O'Brien, T. P., Xie, L., and Zong, Q. G. (2006). Correlation between the Inner Edge of Outer Radiation belt Electrons and the Innermost Plasmapause Location. Geophys. Res. Lett. 33, L14107. doi:10.1029/2006GL026294

CrossRef Full Text | Google Scholar

Loridan, V., Ripoll, J. F., Tu, W., and Cunningham, G. S. (2019). On the Use of Different Magnetic Field Models for Simulating the Dynamics of the Outer Radiation belt Electrons during the October 1990 Storm. J. Geophys. Res. Space Phys. 124, 6453–6486. doi:10.1029/2018ja026392

CrossRef Full Text | Google Scholar

Lyons, L. R., and Thorne, R. M. (1973). Equilibrium Structure of Radiation belt Electrons. J. Geophys. Res. 78 (13), 2142–2149. doi:10.1029/JA078i013p02142

CrossRef Full Text | Google Scholar

Machol, J. L., Green, J. C., Redmon, R. J., Viereck, R. A., and Newell, P. T. (2012). Evaluation of OVATION Prime as a Forecast Model for Visible Aurorae. Space Weather 10, a–n. doi:10.1029/2011SW000746

CrossRef Full Text | Google Scholar

Matar, J. (2021). “Effect of Magnetic Reconnection over the Earth’s Space Environment,”. PhD thesis (Liège: University of Liège).

Google Scholar

Mauk, B. H., Fox, N. J., Kanekal, S. G., Kessel, R. L., Sibeck, D. G., and Ukhorskiy, A. (2013). Science Objectives and Rationale for the Radiation Belt Storm Probes mission. Space Sci. Rev. 179, 3–27. doi:10.1007/s11214-012-9908-y

CrossRef Full Text | Google Scholar

McIlwain, C. E. (1966). Magnetic Coordinates. Space Sci. Rev. 5, 585–598. doi:10.1007/BF00167327

CrossRef Full Text | Google Scholar

Moldwin, M. B., Downward, L., Rassoul, H. K., Amin, R., and Anderson, R. R. (2002). A New Model of the Location of the Plasmapause: CRRES Results. J. Geophys. Res. 107 (1339), 1–9. doi:10.1029/2001ja009211

CrossRef Full Text | Google Scholar

Newell, P. T., Sotirelis, T., Ruohoniemi, J. M., Carbary, J. F., Liou, K., Skura, J. P., et al. (2002). OVATION: Oval Variation, Assessment, Tracking, Intensity, and Online Nowcasting. Ann. Geophys. 20, 1039–1047. doi:10.5194/angeo-20-1039-2002

CrossRef Full Text | Google Scholar

Newell, P. T., Sotirelis, T., and Wing, S. (2010). Seasonal Variations in Diffuse, Monoenergetic, and Broadband aurora. J. Geophys. Res. 115, a–n. doi:10.1029/2009JA014805

CrossRef Full Text | Google Scholar

Nishimura, Y., Lessard, M. R., Katoh, Y., Miyoshi, Y., Grono, E., Partamies, N., et al. (2020). Diffuse and Pulsating Aurora. Space Sci. Rev. 216, 4. doi:10.1007/s11214-019-0629-3

CrossRef Full Text | Google Scholar

O'Brien, T. P., Lorentzen, K. R., Mann, I. R., Meredith, N. P., Blake, J. B., Fennell, J. F., et al. (2003). Energization of Relativistic Electrons in the Presence of ULF Power and MeV Microbursts: Evidence for Dual ULF and VLF Acceleration. J. Geophys. Res. 108 (A8), 1329. doi:10.1029/2002JA009784

CrossRef Full Text | Google Scholar

O'Brien, T. P., and Moldwin, M. B. (2003). Empirical Plasmapause Models from Magnetic Indices. Geophys. Res. Lett. 30, 1152. doi:10.1029/2002GL016007

CrossRef Full Text | Google Scholar

Obana, Y., Maruyama, N., Shinbori, A., Hashimoto, K. K., Fedrizzi, M., Nosé, M., et al. (2019). Response of the Ionosphere‐plasmasphere Coupling to the September 2017 Storm: What Erodes the Plasmasphere So Severely. Space Weather 17, 861–876. doi:10.1029/2019SW002168

CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Claudepierre, S. G., Henderson, M., Morley, S. K., Murphy, K. R., et al. (2019). The March 2015 Superstorm Revisited: Phase Space Density Profiles and Fast ULF Wave Diffusive Transport. J. Geophys. Res. Space Phys. 124, 1143–1156. doi:10.1029/2018JA026326

CrossRef Full Text | Google Scholar

Pierrard, V., and Benck, S. (2012). The Dynamics of the Terrestrial Radiation Belts and its Links to the Plasmasphere. AIP Conf. Proc. 1500, 216. doi:10.1063/1.4768769

CrossRef Full Text | Google Scholar

Pierrard, V., Botek, E., and Darrouzet, F. (2021a). Improving Predictions of the 3D Dynamic Model of the Plasmasphere. Front. Astron. Space Sci. 8, 681401. doi:10.3389/fspas.2021.681401

CrossRef Full Text | Google Scholar

Pierrard, V., Botek, E., Ripoll, J. F., and Cunningham, G. (2020). Electron Dropout Events and Flux Enhancements Associated with Geomagnetic Storms Observed by PROBA‐V/Energetic Particle Telescope from 2013 to 2019. J. Geophys. Res. Space Phys. 125, 12. doi:10.1029/2020JA028487

CrossRef Full Text | Google Scholar

Pierrard, V., and Cabrera, J. (2005). Comparisons between EUV/IMAGE Observations and Numerical Simulations of the Plasmapause Formation. Ann. Geophys. 23 (7), 2635–2646. doi:10.5194/angeo-23-2635-2005

CrossRef Full Text | Google Scholar

Pierrard, V., and Cabrera, J. (2006). Dynamical Simulations of Plasmapause Deformations. Space Sci. Rev. 122 (1-4), 119–126. doi:10.1007/s11214-006-5670-3

CrossRef Full Text | Google Scholar

Pierrard, V., Goldstein, J., André, N., Jordanova, V. K., Kotova, G. A., Lemaire, J. F., et al. (2009). Recent Progress in Physics-Based Models of the Plasmasphere. Space Sci. Rev. 145, 193–229. doi:10.1007/978-1-4419-1323-4_7

CrossRef Full Text | Google Scholar

Pierrard, V., Khazanov, G. V., Cabrera, J., and Lemaire, J. (2008). Influence of the Convection Electric Field Models on Predicted Plasmapause Positions during Magnetic Storms. J. Geophys. Res. 113, 1. doi:10.1029/2007JA012612

CrossRef Full Text | Google Scholar

Pierrard, V., Khazanov, G. V., and Lemaire, J. F. (2007). Current-voltage Relationship. J. Atmos. Solar-Terrestrial Phys. 69 (12), 2048–2057. doi:10.1016/j.jastp.2007.08.005

CrossRef Full Text | Google Scholar

Pierrard, V., and Lemaire, J. F. (2004). Development of Shoulders and Plumes in the Frame of the Interchange Instability Mechanism for Plasmapause Formation. Geophys. Res. Lett. 31 (5), a–n. doi:10.1029/2003GL018919

CrossRef Full Text | Google Scholar

Pierrard, V., Lopez Rosson, G., Borremans, K., Lemaire, J., Maes, J., Bonnewijn, S., et al. (2014). The Energetic Particle Telescope: First Results. Space Sci. Rev. 184, 87–106. doi:10.1007/s11214-014-0097-8

CrossRef Full Text | Google Scholar

Pierrard, V., and Lopez Rosson, G. (2016). The Effects of the Big Storm Events in the First Half of 2015 on the Radiation Belts Observed by EPT/PROBA-V. Ann. Geophys. 34, 75–84. doi:10.5194/angeo-34-75-2016

CrossRef Full Text | Google Scholar

Pierrard, V., Ripoll, J. F., Cunningham, G., Botek, E., Santolik, O., Thaller, S., et al. (2021b). Observations and Simulations of Dropout Events and Flux Decays in October 2013: Comparing MEO Equatorial with LEO Polar Orbit. J. Geophys. Res. Space Phys. 126, e2020JA028850. doi:10.1029/2020JA028850

CrossRef Full Text | Google Scholar

Pierrard, V., and Stegen, K. (2008). A Three-Dimensional Dynamic Kinetic Model of the Plasmasphere. J. Geophys. Res. 113, A10209. doi:10.1029/2008ja013060

CrossRef Full Text | Google Scholar

Pierrard, V., and Voiculescu, M. (2011). The 3D Model of the Plasmasphere Coupled to the Ionosphere. Geophys. Res. Lett. 38, a–n. doi:10.1029/2011GL047767

CrossRef Full Text | Google Scholar

Reeves, G. D., Friedel, R. H. W., Larsen, B. A., Skoug, R. M., Funsten, H. O., Claudepierre, S. G., et al. (2016). Energy‐dependent Dynamics of keV to MeV Electrons in the Inner Zone, Outer Zone, and Slot Regions. J. Geophys. Res. Space Phys. 121, 397–412. doi:10.1002/2015ja021569

CrossRef Full Text | Google Scholar

Reinisch, B. W., Moldwin, M. B., Denton, R. E., Gallagher, D. L., Matsui, H., Pierrard, V., et al. (2009). Augmented Empirical Models of Plasmaspheric Density and Electric Field Using IMAGE and CLUSTER Data. Space Sci. Rev. 145, 231–261. doi:10.1007/s11214-008-9481-6

CrossRef Full Text | Google Scholar

Riazanteseva, M. O., Antonova, E. E., Stepanova, M. V., Marjin, B. V., Rubinshtein, I. A., Barinova, V. O., et al. (2018). Relative Positions of the Polar Boundary of the Outer Electron Radiation belt and the Equatorial Boundary of the Auroral Oval. Ann. Geophys. 36, 1131–1140. doi:10.5194/angeo-36-1131-2018

CrossRef Full Text | Google Scholar

Ripoll, J.-F., Denton, M. H., Hartley, D. P., Reeves, G. D., Malaspina, D., Cunningham, G. S., et al. (2021). Scattering by Whistler-Mode Waves during a Quiet Period Perturbed by Substorm Activity. J. Atmos. Solar-Terrestrial Phys. 215, 105471. doi:10.1016/j.jastp.2020.105471

CrossRef Full Text | Google Scholar

Ripoll, J.-F., Denton, M., Loridan, V., Santolík, O., Malaspina, D., Hartley, D. P., et al. (2020b). How Whistler Mode Hiss Waves and the Plasmasphere Drive the Quiet Decay of Radiation Belts Electrons Following a Geomagnetic Storm. J. Phys. Conf. Ser. 1623, 012005. doi:10.1088/1742-6596/1623/1/012005

CrossRef Full Text | Google Scholar

Ripoll, J.-F., Loridan, V., Denton, M. H., Cunningham, G., Reeves, G., Santolík, O., et al. (2019). Observations and Fokker-Planck Simulations of the L-Shell, Energy, and Pitch Angle Structure of Earth’s Electron Radiation Belts during Quiet Times. J. Geophys. Res. Space Phys. 124, 1125–1142. doi:10.1029/2018ja026111

CrossRef Full Text | Google Scholar

Ripoll, J.-F., Reeves, G. D., Cunningham, G. S., Loridan, V., Denton, M., Santolík, O., et al. (2016). Reproducing the Observed Energy-dependent Structure of Earth's Electron Radiation Belts during Storm Recovery with an Event-specific Diffusion Model. Geophys. Res. Lett. 43, 5616–5625. doi:10.1002/2016GL068869

CrossRef Full Text | Google Scholar

Ripoll, J. F., Claudepierre, S. G., Ukhorskiy, A. Y., Colpitts, C., Li, X., Fennell, J. F., et al. (2020a). Particle Dynamics in the Earth's Radiation Belts: Review of Current Research and Open Questions. J. Geophys. Res. Space Phys. 125, e2019JA026735. doi:10.1029/2019JA026735

CrossRef Full Text | Google Scholar

Ripoll, J. F., Santolík, O., Reeves, G. D., Kurth, W. S., Denton, M. H., Loridan, V., et al. (2017). Effects of Whistler Mode Hiss Waves in March 2013. J. Geophys. Res. Space Phys. 122, 7433–7462. doi:10.1002/2017JA024139

CrossRef Full Text | Google Scholar

Roederer, J. G. (1970). “Dynamics of Geomagnetically Trapped Radiation,” in Physics and Chemistry in Space, Editors J. G. Roederer, and J. Zahringer (Berlin: Springer). doi:10.1007/978-3-642-49300-3

CrossRef Full Text | Google Scholar

Ruohoniemi, J. M., and Baker, K. B. (1998). Large-scale Imaging of High-Latitude Convection with Super Dual Auroral Radar Network HF Radar Observations. J. Geophys. Res. Space Phys. 103 (A9), 20797–20811. doi:10.1029/98JA01288

CrossRef Full Text | Google Scholar

Rycroft, M. J., and Burnell, S. J. (1970). Statistical Analysis of Movements of the Ionospheric Trough and the Plasmapause. J. Geophys. Res. 75, 5600–5604.

CrossRef Full Text | Google Scholar

Sandel, B. R., Goldstein, J., Gallagher, D. L., and Spasojevic, M. (2003). Extreme Ultraviolet Imager Observations of the Structure and Dynamics of the Plasmasphere. Space Sci. Rev. 109, 25–46. doi:10.1023/b:spac.0000007511.47727.5b

CrossRef Full Text | Google Scholar

Schäfer, S., Glassmeier, K. H., Eriksson, P. T. I., Mager, P. N., Pierrard, V., Fornaçon, K. H., et al. (2008). Spatio-temporal Structure of a Poloidal Alfvén Wave Detected by Cluster Adjacent to the Dayside Plasmapause. Ann. Geophys. 26, 1805–1817. doi:10.5194/angeo-26-1805-2008

CrossRef Full Text | Google Scholar

Schäfer, S., Glassmeier, K. H., Eriksson, P. T. I., Pierrard, V., Fornaçon, K. H., and Blomberg, L. G. (2007). Spatial and Temporal Characteristics of Poloidal Waves in the Terrestrial Plasmasphere: A CLUSTER Case Study. Ann. Geophys. 25, 1011–1024. doi:10.5194/angeo-25-1011-2007

CrossRef Full Text | Google Scholar

Sigsbee, K., Kletzing, C. A., Faden, J. B., Jaynes, A. N., Reeves, G. D., and Jahn, J. M. (2020). Simultaneous Observations of Electromagnetic Ion Cyclotron (EMIC) Waves and Pitch Angle Scattering during a Van Allen Probes Conjunction. J. Geophys. Res. Space Phys. 125 (4), e219JA0277424. doi:10.1029/2019ja027424

CrossRef Full Text | Google Scholar

Spasojević, M., Frey, H. U., Thomsen, M. F., Fuselier, S. A., Gary, S. P., Sandel, B. R., et al. (2004). The Link between a Detached Subauroral Proton Arc and a Plasmaspheric Plume. Geophys. Res. Lett. 31, L04803. doi:10.1029/2003GL018389

CrossRef Full Text | Google Scholar

Spence, H. E., Reeves, G. D., Baker, D. N., Blake, J. B., Bolton, M., Bourdarie, S., et al. (2013). Science Goals and Overview of the Radiation Belt Storm Probes (RBSP) Energetic Particle, Composition, and Thermal Plasma (ECT) Suite on NASA's Van Allen Probes Mission. Space Sci. Rev. 179, 311–336. doi:10.1007/s11214-013-0007-5

CrossRef Full Text | Google Scholar

Thaller, S. A., Wygant, J. R., Dai, L., Breneman, A. W., Kersten, K., Cattell, C. A., et al. (2015). Van Allen Probes Investigation of the Large‐scale Duskward Electric Field and its Role in Ring Current Formation and Plasmasphere Erosion in the 1 June 2013 Storm. J. Geophys. Res. Space Phys. 120, 4531–4543. doi:10.1002/2014ja020875

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid Local Acceleration of Relativistic Radiation-belt Electrons by Magnetospheric Chorus. Nature 504 (7480), 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt Dynamics: The Importance of Wave-Particle Interactions. Geophys. Res. Lett. 37, a–n. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Tu, W., Cunningham, G. S., Chen, Y., Morley, S. K., Reeves, G. D., Blake, J. B., et al. (2014). Event-specific Chorus Wave and Electron Seed Population Models in DREAM3D Using the Van Allen Probes. Geophys. Res. Lett. 41, 1359–1366. doi:10.1002/2013gl058819

CrossRef Full Text | Google Scholar

Turner, D. L., Claudepierre, S. G., Fennell, J. F., O'Brien, T. P., Blake, J. B., Lemon, C., et al. (2015). Energetic Electron Injections Deep into the Inner Magnetosphere Associated with Substorm Activity. Geophys. Res. Lett. 42, 2079–2087. doi:10.1002/2015gl063225

CrossRef Full Text | Google Scholar

Turner, D. L., Kilpua, E. K. J., Claudepierre, S. G., O'Brien, T. P., and Fennell, J. F. (2019). The Response of Earth's Electron Radiation Belts to Geomagnetic Storms: Statistics from the Van Allen Probes Era Including Effects from Different Storm Drivers. J. Geophys. Res. Space Phys. 124, 1013–1034. doi:10.1029/2018JA026066

CrossRef Full Text | Google Scholar

Verbanac, G., Bandić, M., Pierrard, V., and Cho, J. (2018). MLT Plasmapause Characteristics: Comparison between THEMIS Observations and Numerical Simulations. J. Geophys. Res. Space Phys. 123, 2000–2017. doi:10.1002/2017JA024573

CrossRef Full Text | Google Scholar

Verbanac, G., Pierrard, V., Bandić, M., Darrouzet, F., Rauch, J.-L., and Décréau, P. (2015). The Relationship between Plasmapause, Solar Wind and Geomagnetic Activity between 2007 and 2011. Ann. Geophys. 33, 1271–1283. doi:10.5194/angeo-33-1271-2015

CrossRef Full Text | Google Scholar

Vette, J. I. (1991). The AE-8 Trapped Electron Model Environment. Greenbelt: NSSDC/WDC-A-R&S, 91–24.

Google Scholar

Voiculescu, M., Nygren, T., Aikio, A., Vanhamaki, H., and Pierrard, V. (2016). Post Midnight Troughs at High Latitudes in Summer. J. Geophys. Res. Space Phys. 121, 12171–12185. doi:10.1002/2016ja023360

CrossRef Full Text | Google Scholar

Weygand, J. M., Zhelavskaya, I., and Shprits, Y. (2021). A Comparison of the Location of the Mid‐Latitude Trough and Plasmapause Boundary. J. Geophys. Res. Space Phys. 126, e2020JA028213. doi:10.1029/2020JA028213

CrossRef Full Text | Google Scholar

Wygant, J. R., Bonnell, J. W., Goetz, K., Ergun, R. E., Mozer, F. S., Bale, S. D., et al. (2013). The Electric Field and Waves Instruments on the Radiation Belt Storm Probes mission. Space Sci. Rev. 179 (1‐4), 183–220. doi:10.1007/978-1-4899-7433-4_6

CrossRef Full Text | Google Scholar

Yahnin, A. G., Yahnina, T. A., Frey, H., and Pierrard, V. (2013). Sub-oval Proton aurora Spots: Mapping Relatively to the Plasmapause. J. Atmos. Solar-Terrestrial Phys. 99, 61–66. doi:10.1016/j.jastp.2012.09.018

CrossRef Full Text | Google Scholar

Yizengaw, E., and Moldwin, M. B. (2005). The Altitude Extension of the Mid-latitude Trough and its Correlation with Plasmapause Position. Geophys. Res. Lett. 32, L09105. doi:10.1029/2005GL022854

CrossRef Full Text | Google Scholar

Zhang, X.-J., Angelopoulos, V., Ni, B., and Thorne, R. M. (2015). Predominance of ECH Wave Contribution to Diffuse aurora in Earth's Outer Magnetosphere. J. Geophys. Res. Space Phys. 120, 295–309. doi:10.1002/2014JA020455

CrossRef Full Text | Google Scholar

Zhou, S., Luan, X., Pierrard, V., and Han, D. (2019). Isolated Auroral Spots Observed by DMSP/SSUSI. J. Geophys. Res. Space Phys. 124 (11), 8416–8426. doi:10.1029/2019JA026853

CrossRef Full Text | Google Scholar