Interacting Shell Model Calculations for Neutrinoless Double Beta Decay of 82Se With Left-Right Weak Boson Exchange

In the present work, the λ mechanism (left-right weak boson exchange) and the light neutrino-exchange mechanism of neutrinoless double beta decay is studied. In particular, much attention is paid to the calculation of nuclear matrix elements for one of the neutrinoless double beta decaying isotopes ⁸²Se. The interacting shell model framework is used to calculate the nuclear matrix element. The widely used closure approximation is adopted. The higher-order effect of the pseudoscalar term of nucleon current is also included in some of the nuclear matrix elements that result in larger Gamow-Teller matrix elements for the λ mechanism. Bounds on Majorana neutrino mass and lepton number violating parameters are also derived using the calculated nuclear matrix elements.

1 Introduction

Neutrinoless double beta decay (0νββ) is a rare second-order weak nuclear process. In this process, neutrino comes as a virtual intermediate particle when two neutron pairs decay into two proton pairs inside some even-even nuclei. Thus, it violates the lepton number by two units. The 0νββ experiment is one of the possible ways to determine the effective neutrino mass (Schechter and Valle, 1982; Tomoda, 1991; Avignone et al., 2008; Rodejohann, 2011; Deppisch et al., 2012) and can help to solve many mysteries of neutrinos, such as whether neutrinos are their own anti-particle (Majorana neutrino) or not (Dirac neutrino) (Schechter and Valle, 1982; Rodejohann, 2011; Deppisch et al., 2012).

As lepton number conservation is not exact in most of the beyond the standard model (BSM) physics theories, many particle mechanisms of 0νββ have been proposed in different BSM theories such as light neutrino-exchange mechanism (Šimkovic et al., 1999; Rodin et al., 2006), heavy neutrino-exchange mechanism (Vergados et al., 2012), left-right symmetric mechanism (Mohapatra and Senjanović, 1980; Mohapatra and Vergados, 1981), and the supersymmetric particles exchange mechanism (Mohapatra, 1986; Vergados, 1987).

The decay rate for any particle mechanism of 0νββ is connected by nuclear matrix elements (NMEs) and absolute neutrino mass. These NMEs are calculated using theoretical nuclear many-body models (Engel and Menéndez, 2017). Popular nuclear models are quasiparticle random phase approximation (QRPA) (Vergados et al., 2012), the interacting shell-model (ISM) (Caurier et al., 2008; Horoi and Stoica, 2010; Sen’kov and Horoi, 2013; Brown et al., 2014; Iwata et al., 2016), the interacting boson model (IBM) (Barea and Iachello, 2009; Barea et al., 2012), the generator coordinate method (GCM) (Rodríguez and Martínez-Pinedo, 2010), the energy density functional (EDF) theory (Rodríguez and Martínez-Pinedo, 2010; Song et al., 2014), and the projected Hartree-Fock Bogolibov model (PHFB) (Rath et al., 2010). Other techniques includes, ab initio calculations for lower mass nuclei (A = 6–12) using variational Monte Carlo (VMC) method (Pastore et al., 2018; Cirigliano et al., 2019; Wang et al., 2019).

In the present work, we focus on the left-right weak boson (W_L-W_R) exchange λ mechanism along with the standard light neutrino-exchange mechanism (W_L − W_L exchange) of the 0νββ mediated by light neutrinos (Bhupal Dev et al., 2015; Horoi and Neacsu, 2016; Šimkovic et al., 2017). The λ mechanism has origin in the left-right symmetric mechanism with right-handed gauge boson at the TeV scale (Šimkovic et al., 2017). Thus, it will be interesting to study how the λ mechanism can compete with the standard light neutrino-exchange mechanism when both the mechanisms co-exist. Hence, in the present work, we are eager to study the λ and light neutrino-exchange mechanisms together.

In left-right symmetric model, there is another mass independent mechanism called η mechanism which occurs through W_L − W_R mixing. It will be interesting to study η mechanism along with λ mechanism of 0νββ. But, η mechanism is suppressed due to W_L − W_R mixing as compared to λ mechanism (Barry and Rodejohann, 2013). Hence, in the present work, we are interested to study the mass independent λ mechanism along with the mass dependent standard light neutrino-exchange mechanism. In future studies, we will extensively explore the η mechanism of 0νββ along with other mass independent and dependent mechanisms in left-right symmetric model.

One of the motivations of the present work is to include effects of some of the revisited formalism of Ref. (Štefánik et al., 2015) on light neutrino-exchange and λ mechanism of 0νββ. The revised formalism was exploited to include the effects of the pseudoscalar term of nucleon currents. Using the revised formalism of Ref. (Štefánik et al., 2015), the NMEs for λ, and light neutrino-exchange mechanisms of 0νββ are calculated using the QRPA model for several 0νββ decaying isotopes using closure approximation in Ref. (Šimkovic et al., 2017). Most of the NMEs relevant for λ and light neutrino-exchange mechanisms are also calculated using ISM in Ref. (Horoi and Neacsu, 2018) using the closure approximation for different 0νββ decaying isotopes (including ⁸²Se). In this case, some of the NMEs are calculated without including the higher-order terms (for example, pseudoscalar and weak magnetism terms) of the nucleon currents. Recently, using the revised formalism of Ref. (Štefánik et al., 2015), we have also calculated the NMEs for ⁴⁸Ca in Ref. (Sarkar et al., 2020a) using the non-closure approximation and found a significant change in some of the NMEs for including the pseudoscalar term. Thus, we have tried here to include the revised higher-order effect of the pseudoscalar term of nucleon current for the λ mechanism of 0νββ of ⁸²Se using ISM. The 0νββ of ⁸²Se is one of the experimental interests of CUPID (Dolinski et al., 2019; Pagnanini et al., 2019) and NEMO-3 (Arnold et al., 2020) experiments. Hence, it is important to study the nuclear structure aspects of 0νββ of ⁸²Se theoretically. In recent years, one of the most important studies on light neutrino-exchange 0νββ of ⁸²Se was performed in the ISM framework in Ref. (Sen’kov et al., 2014) using the non-closure approximation. Here we focus on the λ mechanism of 0νββ of ⁸²Se in the closure approximation using the revised nucleon current term.

This paper is organized as follows. In Section 2, the expression for decay rate and the theoretical formalism to calculate NMEs for the λ and light neutrino-exchange mechanisms of 0νββ are presented. The results and discussion are presented in Section 3. A summary of the work is given in Section 4.

2 Theoretical Framework

2.1 Decay Rate for λ Mechanism of 0νββ

If both light neutrino-exchange (W_L − W_L exchange) and λ mechanisms (W_L − W_R exchange) of 0νββ co-exist, one can write the decay rate for 0νββ as (Štefánik et al., 2015; Šimkovic et al., 2017)

${[T_{1/2}^{0\nu }]}^{-1}={\eta }_{\nu }^2{C}_{mm}+{\eta }_{\lambda }^2{C}_{\lambda \lambda }+{\eta }_{\nu }{\eta }_{\lambda }\text{cos}\psi C_{m\lambda },(1)$

where the coupling constant λ is defined as (Šimkovic et al., 2017)

$\lambda ={\left(M_{W_L}/M_{W_R}\right)}^2.(2)$

The $M_{W_L}$ and $M_{W_R}$ are masses of the Standard Model left-handed W_L and right-handed W_R gauge bosons, respectively. The η_ν of Eq. 1 is an effective lepton number violating parameters for W_L − W_L exchange, η_λ is an effective lepton number violating parameters for W_L − W_R exchange, and ψ denotes the CP violating phase. These parameters are given in Ref. (Šimkovic et al., 2017) as

$\begin{array}{ll}\hfill {\eta }_{\nu }& =\frac{m_{\beta \beta }}{m_e},{\eta }_{\lambda }=\lambda |\sum _{j=1}^3{m}_j{U}_{ej}{T}_{ej}^{*}|,\hfill \end{array}(3)$

$\begin{array}{ll}\hfill \psi & =\arg \left[\left(\sum _{j=1}^3{m}_j{U}_{ej}^2\right)\left(\sum _{j=1}^3{U}_{ej}{T}_{ej}^{*}\right)\right].\hfill \end{array}(4)$

Here, m_ββ is the effective Majorana neutrino mass defined by the neutrino mass eigenvalues m_j and the neutrino mixing matrix elements U_ej (Horoi and Stoica, 2010):

$\langle m_{\beta \beta }\rangle =|\sum _j{m}_j{U}_{ej}^2|.(5)$

The U, and T are the 3 × 3 block matrices in flavor space, which constitute a generalization of the Pontecorvo-Maki-Nakagawa-Sakata matrix, namely the 6 × 6 unitary neutrino mixing matrix (Štefánik et al., 2015; Šimkovic et al., 2017).

The amplitude of λ mechanism is given by (Bhupal Dev et al., 2015)

${\mathcal{A}}_{\lambda }=G_F^2\lambda \sum _i{U}_{ej}{T}_{ej}^{*}\frac{1}{q},(6)$

where λ is defined earlier, G_F is the Fermi constant for weak interaction, and q is the virtual Majorana neutrino momentum.

The coefficients C_I (I = mm, mλ and λλ) of Eq. 1 are linear combinations of products of nuclear matrix elements and phase-space factors (Šimkovic et al., 2017).

$\begin{array}{ll}\hfill C_{mm}& =g_A^4{M}_{\nu }^2{G}_{01},\hfill \end{array}(7)$

$\begin{array}{ll}\hfill C_{m\lambda }& =-g_A^4{M}_{\nu }(M_{2-}{G}_{03}-M_{1+}{G}_{04}),\hfill \end{array}(8)$

$\begin{array}{ll}\hfill C_{\lambda \lambda }& =g_A^4\left(M_{2-}^2{G}_{02}+\frac{1}{9}{M}_{1+}^2{G}_{011}-\frac{2}{9}{M}_{1+}{M}_{2-}{G}_{010}\right).\hfill \end{array}(9)$

Calculated values of phase-space factors G_0i (i = 1, 2, 3, 4, 10 and 11) for different 0νββ decaying nuclei are given in Ref. (Štefánik et al., 2015).

2.2 Nuclear Matrix Elements for λ Mechanism of 0νββ

Matrix elements required in the expression of C_I are (Šimkovic et al., 2017).

$\begin{array}{ll}\hfill M_{\nu }& =M_{GT}-\frac{M_F}{g_A^2}+M_T,\hfill \end{array}(10)$

$\begin{array}{ll}\hfill M_{\nu \omega }& =M_{\omega GT}-\frac{M_{\omega F}}{g_A^2}+M_{\omega T},\hfill \end{array}(11)$

$\begin{array}{ll}\hfill M_{1+}& =M_{qGT}+3\frac{M_{qF}}{g_A^2}-6M_{qT},\hfill \end{array}(12)$

$\begin{array}{ll}\hfill M_{2-}& =M_{\nu \omega }-\frac{1}{9}{M}_{1+}.\hfill \end{array}(13)$

The (M_GT,ωGT,qGT) (M_F,ωF,qF), and (M_T,ωT,qT) matrix elements of the scalar two-body transition operator ${\mathcal{O}}_{12}^{\alpha }$ of 0νββ can be expressed as (Brown et al., 2014)

$M_{\alpha }=\langle f|{\mathcal{O}}_{12}^{\alpha }|i\rangle (14)$

where, $\left|i\right.⟩$〉, and $\left|f\right.⟩$〉 are the initial and the final 0⁺ ground state (g.s) for 0νββ decay, respectively, and α = (GT, F, T, ν, ωGT, ωF, ωT, νω, qGT, qF, qT, 1 +, 2−), τ₋ is the isospin annihilation operator. The scalar two-particle transition operators ${\mathcal{O}}_{12}^{\alpha }$ of 0νββ containing spin and radial neutrino potential operators can be written as

$\begin{array}{cc}\hfill {\mathcal{O}}_{12}^{GT,\omega GT,qGT}& ={\tau }_{1-}{\tau }_{2-}({\sigma }_{\mathbf{1}}.{\sigma }_{\mathbf{2}})H_{GT,\omega GT,qGT}(r,E_k),\hfill \\ \hfill {\mathcal{O}}_{12}^{F,\omega F,qF}& ={\tau }_{1-}{\tau }_{2-}{H}_{F,\omega F,qF}(r,E_k),\hfill \\ \hfill {\mathcal{O}}_{12}^{T,\omega T,qT}& ={\tau }_{1-}{\tau }_{2-}{S}_{12}{H}_{T,\omega T,qT}(r,E_k),\hfill \end{array}(15)$

where, $S_{12}=3({\sigma }_{\mathbf{1}}.\widehat{\mathbf{r}})({\sigma }_{\mathbf{2}}.\widehat{\mathbf{r}})-({\sigma }_{\mathbf{1}}.{\sigma }_{\mathbf{2}})$, r = r₁ −r₂, and r = |r| is inter nucleon distance of the decaying nucleons. The E_k is the energy of the virtual intermediate state ($\left|k⟩\right.⟩$) of 0νββ. The intermediate state $|k⟩$ is achieved when one neutron from the initial state $|i⟩$ is converted into one proton. Subsequently, from the $|k⟩$ state, another neutron is converted into another proton to achieve the final state $|f⟩⟩$ of the 0νββ. For the present manuscript, $|i⟩⟩$ is the 0⁺ g.s. of ⁸²Se, $|f⟩⟩$ is the 0⁺ g.s. of ⁸²Kr, and $|k⟩$ are all the allowed spin-parity states of intermediate nucleus ⁸²Br.

There are two approximations for calculating the NME, one is non-closure approximation and another is the widely used closure approximation. In non-closure approximation, the radial neutrino potential H_α(r, E_k) has explicit dependence on energy of the intermediate state $|k⟩$〉. In non-closure approximation, the radial neutrino potential for λ mechanism of 0νββ are is given as integral over Majorana neutrino momentum q (Sen’kov and Horoi, 2013):

$H_{\alpha }(r,E_k)=\frac{2R}{\pi }{\int }_0^{\infty }\frac{f_{\alpha }(q,r)qdq}{q+E_k-(E_i+E_f)/2)\left.\right)}(16)$

where R is the radius of the parent nucleus, and the f_α(q, r) factor (Appendix B) contains the form factors that incorporates the effects of finite nucleon size (FNS), and higher-order currents (HOC) of nucleons (Šimkovic et al., 1999), which is given in Appendix B of the manuscript. The E_i and E_f   are the g.s. energy of the initial and final nucleus of the 0νββ decay, respectively. The non-closure approximation is computationally very challenging, because in this approximation, the NME has explicit dependence on the energy of large numbers of virtual intermediate state |k⟩ and calculating these states requires enormous computational power. Particularly, for higher mass region isotopes, some of the calculations are still beyond the reach of current generation’s high-performance computers. Fortunately, the most of the contributions on NME of 0νββ come from low lying energy states up to 10–12 MeV of the intermediate nucleus (Sen’kov and Horoi, 2013; Sarkar et al., 2020a). Thus, one can replace the effects of E_k with a suitable constant energy called closure energy $\langle E\rangle$ without affecting the value of NME too much, and this approximation is known as closure approximation. In this approximation, one assumes (Sen’kov and Horoi, 2013)

$(E_k-(E_i+E_f)/2)\to ⟨\langle E\rangle ⟩,(17)$

and the radial neutrino potential operator of Eq. 16 becomes

$H_{\alpha }(r)=\frac{2R}{\pi }{\int }_0^{\infty }\frac{f_{\alpha }(q,r)qdq}{q+⟨\langle E\rangle ⟩},(18)$

In closure approximation, the 0νββ decay operators defined in Eq. 15 become

$\begin{array}{ccc}\hfill O_{12}^{GT,\omega GT,qGT}& \hfill & ={\tau }_{1-}{\tau }_{2-}({\sigma }_{\mathbf{1}}.{\sigma }_{\mathbf{2}})H_{GT,\omega GT,qGT}(r),\hfill \\ \hfill O_{12}^{F,\omega F,qF}& \hfill & ={\tau }_{1-}{\tau }_{2-}{H}_{F,\omega F,qF}(r),\hfill \\ \hfill O_{12}^{T,\omega T,qT}& \hfill & ={\tau }_{1-}{\tau }_{2-}{S}_{12}{H}_{T,\omega T,qT}(r).\hfill \end{array}(19)$

The closure approximation is widely used in literature as it eliminates the complexity of calculating a large number of virtual intermediate states (Horoi and Stoica, 2010; Sen’kov and Horoi, 2013; Sarkar et al., 2020a). One can find suitable values of $⟨E⟩$ using the method described in Ref. (Sarkar et al., 2020a), such that using closure approximation, one can get NME near to the non-closure approximation.

In the calculation of the NME of 0νββ, it is also necessary to take into account the effects of short-range correlations (SRC). A standard method to include SRC is via a phenomenological Jastrow-like function (Vogel, 2012; Menéndez et al., 2009; Šimkovic et al., 2009). Including SRC effect in the Jastrow approach, one can write the NME of 0νββ defined in Eq. 14 as (Vogel, 2012)

$M_{\alpha }=\langle f|f_{Jastrow}(r)O_{12}^{\alpha }{f}_{Jastrow}(r)|i\rangle ,(20)$

where Jastrow-type SRC function is defined as

$f_{Jastrow}(r)=1-c{e}^{-a{r}^2}(1-b{r}^2).(21)$

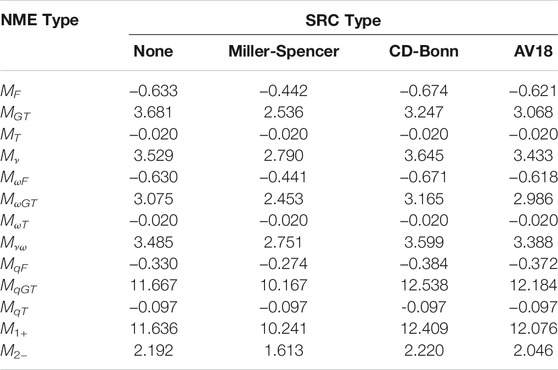
In literature, three different SRC prametrizationparameterization are used: Miller-Spencer, Charge-Dependent Bonn (CD-Bonn), and Argonne V18 (AV18) to parametrize a, b, and c (Horoi and Stoica, 2010). These parameters are chosen in such a way that the two-body wave function of two-body matrix elements (TBME) for 0νββ are still normalized. The parameters a, b, and c in different SRC parametrizations are given in Table 1.

TABLE 1

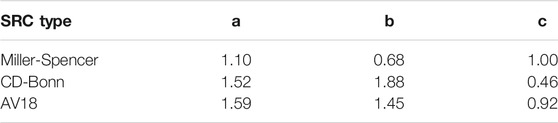
TABLE 1. Parameters for the short-range correlation (SRC) parametrization of Eq. 21. Values are taken from Ref. (Horoi and Stoica, 2010).

This approach of using a Jastrow-like function to include the effects of SRC is extensively used in Refs. (Menéndez et al., 2009; Horoi and Stoica, 2010; Neacsu et al., 2012).

2.3 The Closure Method of Nuclear Matrix Elements Calculation for 0νββ in ISM

The (M_GT,ωGT,qGT) (M_F,ωF,qF), and (M_T,ωT,qT) matrix elements of the scalar two-body transition operator $O_{12}^{\alpha }$ of 0νββ can be expressed as the sum over the product of the two-body transition density (TBTD) and anti-symmetric two-body matrix elements $(\langle k_1^{\prime },k_2^{\prime },JT|O_{12}^{\alpha }|k_1,k_2,J{T\rangle }_A)$ (Brown et al., 2014):

$\begin{array}{ccc}\hfill M_{\alpha }^{0\nu }& \hfill & =\langle f|O_{12}^{\alpha }|i\rangle \hfill \\ \hfill & \hfill & =\sum _{J,k_1^{\prime }\le k_2^{\prime },k_1\le k_2}\text{TBTD}(f,i,J)\times \langle k_1^{\prime },k_2^{\prime },JT|O_{12}^{\alpha }|k_1,k_2,J{T\rangle }_A,\hfill \end{array}(22)$

where, α = (F, GT, T, ωF, ωGT, ωT, qF, qGT, qT), J is the coupled spin of two decaying neutrons or two final created protons, τ₋ is the isospin annihilation operator, A denotes that the two-body matrix elements (TBME) (Appendix A) are obtained using anti-symmetric two-nucleon wavefunctions, and k₁ stands for the set of spherical quantum numbers (n₁; l₁; j₁) (similar definition for k₂, k₁′, k₂′). The |i⟩ is 0⁺ ground state (g.s.) of the parent nucleus, and |f⟩ is the 0⁺ g.s of the granddaughter nucleus.

The TBTD can be expressed as (Brown et al., 2014)

$\begin{array}{c}\hfill \mathbf{TBTD}(f,i,J)\\ \hfill & \hfill & =\langle f‖{[A^{+}(k_1^{\prime },k_2^{\prime },J)\otimes \tilde{A}(k_1,k_2,J)]}^{(0)}‖i\rangle ,\hfill \end{array}(23)$

where,

$A^{+}(k_1^{\prime },k_2^{\prime },J)=\frac{{[a^{+}(k_1^{\prime })\otimes a^{+}(k_2^{\prime })]}_M^J}{\sqrt{1+{\delta }_{k_1^{\prime }{k}_2^{\prime }}}},(24)$

and

$\tilde{A}(k_1,k_2,J)={(-1)}^{J-M}{A}^{+}(k_1,k_2,J,-M)(25)$

are the two particle creation and annihilation operator of rank J, respectively. Most of the available public shell model code does not provide the option to calculate TBTD directly. One of the ways is to calculate TBTD in terms of a large number of two nucleon transfer amplitudes (TNA), assuming 0νββ decay occurs through (n − 2) channel (Brown et al., 2014). In (n − 2) channel of 0νββ, the TNA are calculated with a large set of intermediate states |m⟩ of the (n − 2) nucleons system, where n is the number of nucleons for the parent nucleus. In this approach, the TBTD in terms of TNA is expressed as (Brown et al., 2014)

$\begin{array}{ccc}\hfill \text{TBTD}(f,i,J)& \hfill & \hfill \\ =\sum _m\text{TNA}(f,m,k_1^{\prime },k_2^{\prime },J_m)\text{TNA}(i,m,k_1,k_2,J_m),\hfill \end{array}(26)$

where, TNA are given by

$\text{TNA}(f,m,k_1^{\prime },k_2^{\prime },J_m)=\frac{\langle f‖A^{+}(k_1^{\prime },k_2^{\prime },J)‖m\rangle }{\sqrt{2J_0+1}}.(27)$

Here, J_m is the spin of the allowed states |m⟩ of intermediate nuclei. J₀ is spin of |i⟩ and |f⟩. J_m = J when J₀ = 0 (Brown et al., 2014).

3 Results and Discussion

We have used JUN45 effective shell model Hamiltonian (Honma et al., 2009) of fpg model space to calculate the relevant initial, intermediate, and final nuclear states for 0νββ of ⁸²Se. In the fpg model space, valence nucleons can occupy the orbitals 0f_5/2, 1p_3/2, 1p_1/2, and 0g_9/2. For the 0νββ decay of ⁸²Se through (n − 2) channel, the states of allowed spin-parity of ⁸⁰Se acts as intermediate states for TNA calculations. The nuclear shell model code KSHELL (Shimizu et al., 2019) was used in the calculation. For comparing some of the TNA values, NushellX@MSU (Brown and Rae, 2014) code was also used. In the present calculation, we have included the first 100 states of different allowed spin-parity of ⁸⁰Se in calculating the TNA. Earlier, it was found that considering around the first 50 states is enough to get the saturated value of NME, as the most dominating contributions come from the first few initial states (Brown et al., 2014; Sarkar et al., 2020b).

We have adopted the widely used closure approximation with the closure energy ⟨E⟩ = 0.5 MeV. Earlier studies of Refs. (Sarkar et al., 2020a; Sarkar et al., 2020b) suggested that ⟨E⟩ = 0.5 MeV is a suitable value that is close to optimal closure energy and, thus, gives NME near to the NME in the non-closure approximation. The non-closure method can give the exact value of NME, but the present study is beyond the scope of studying it. But, according to earlier results (Sarkar et al., 2020a; Sarkar et al., 2020b), with ⟨E⟩ = 0.5 MeV, one can get NME in the closure approximation close to the NME in non-closure approximation (within 1% difference).

Different types of NMEs for light neutrino-exchange and λ mechanism of 0νββ for ⁸²Se is shown in Table 2. Here, NMEs are calculated in different SRC parameterization schemes. All standard effects of FNS + HOC are taken care of in all calculations. It is found that the Gamow-Teller matrix elements dominate over Fermi and tensor type matrix elements. Also, it is found that the M_qGT type matrix element associated with the λ mechanism is relatively large as compared to standard light neutrino-exchange Gamow-Teller matrix element M_GT. This leads to the large value of total NME M₁₊ for λ mechanism as compared to total NME M_ν for light neutrino-exchange mechanism.

TABLE 2

TABLE 2. NMEs for 0νββ (light neutrino-exchange and λ mechanism) of ⁸²Se.

This increment of M_qGT type of NME, which is obtained through the new revised expression of the nucleon currents of Ref. (Šimkovic et al., 2017), is surprisingly high. It is coming through the new revised expression of the nucleon currents of Ref. (Šimkovic et al., 2017) which includes the higher-order term (pseudoscalar) of the nucleon currents. In our calculation, Eq. 39 is used to calculate M_qGT type NME using the revised formalism of nucleon currents of Refs. (Štefánik et al., 2015; Šimkovic et al., 2017).

An old equivalent expression of Eq. 39 is also found in Ref. (Horoi and Neacsu, 2018), which one can write using Eq. (A2c) and Eq. (A4b) of Ref. (Horoi and Neacsu, 2018) as

$f_{qGT}(q,r)=\frac{1}{{\left(1+\frac{q^2}{{\mathrm{\Lambda }}_A^2}\right)}^4}qr{j}_1(qr).(28)$

Using this old value of f_qGT (q, r), the M_qGT type NME will be significantly smaller, as reported earlier.

Here we include the higher-order current effect of pseudoscalar term in Eq. 39 as suggested in Ref. (Šimkovic et al., 2017) which is enhancing the M_qGT type NME as compared to standard M_GT type NME. A similar type of enhancement in M_qGT type NME was also found in our earlier study for ⁴⁸Ca (Sarkar et al., 2020a).

We have also decomposed the NME in terms of coupled spin-parity (J^π) of two decaying neutrons and two created protons in the decay. Decomposed NME gives us a picture of the role of individual spin-parity on NME. The contribution of NMEs through different J^π is shown in Figures 1–3 for different types of NME. Figure 1 examines the decomposition for M_F,GT,T type matrix elements associated with light neutrino-exchange mechanism, where Figures 2, 3 examine the NME as function of J^π for M_ωF,ωGT,ωT and M_qF,qGT,qT type NMEs, respectively, for λ and interference mechanism. All results are presented for AV18 SRC parameterization.

FIGURE 1

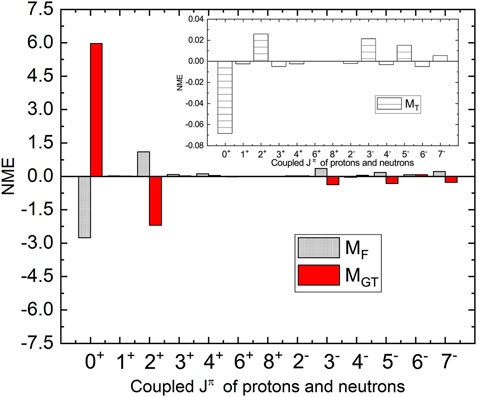
FIGURE 1. (Color online) Variation of M_F, M_GT, and M_T type NMEs with J^π of two initial neutron-neutron and final proton-proton pairs.

FIGURE 2

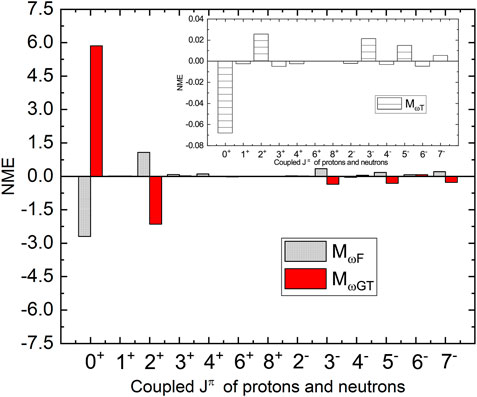
FIGURE 2. (Color online) Variation of M_ωF, M_ωGT, and M_ωT type NMEs with J^π of two initial neutron-neutron and final proton-proton pairs.

FIGURE 3

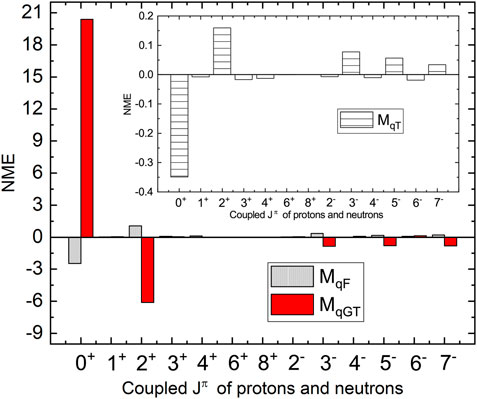
FIGURE 3. (Color online) Variation of M_qF, M_qGT, and M_qT type NMEs with J^π of two initial neutron-neutron and final proton-proton pairs.

For all types of NMEs, the most dominating contribution comes from 0⁺ states and 2⁺ states. The pairing effect is in play for dominating even-J^π contributions (Brown et al., 2014). The NME from 0⁺ and 2⁺ states has opposite signs and, thus, cancel the effects of each other. Other non-negligible contributions come through 4⁺, 3⁻, 5⁻, and 7⁻ states.

Now we will discuss how the calculated NMEs will help to determine the bounds on Majorana neutrino mass and various lepton number violating parameters, using the lower limit on the experimental half-life of the decay. The inverse of half-life for 0νββ is given in Eq. 1. It is found that the half-life is influenced by the term C_I (I = mm, mλ, λλ), lepton number violating term η_ν and η_λ, which are unknown, and CP-violating phase ψ. The C_I are defined in Eq 7 and (8), (9), which contains mainly phase space factors and relevant NMEs. To calculate C_I, we have used the improved values of phase space factors calculated in Ref. (Štefánik et al., 2015), and for the NMEs, we have used the results of Table 2 using ISM.

The results for C_I of light neutrino-exchange and λ mechanisms of 0νββ decay of ⁸²Se and ⁴⁸Ca are presented in Table 3. Here, the results for ⁴⁸Ca are taken from our earlier work using the closure approximation on the λ mechanism (Sarkar et al., 2020a). It is found that values of C_mm (light neutrino-exchange) and C_λλ (λ mechanism) are similar in values, which shows the dominance of each of these mechanisms on 0νββ half-life. The interference term (C_mλ) of both the mechanisms are relatively smaller, which shows the less importance of the interference mechanism.

TABLE 3

TABLE 3. Results for half-life and bounds on neutrino mass and lepton number violating parameters. The $T_{1/2}^{0\nu -exp}$ is taken from the experimental lower limit on half-life from Ref. (Arnold et al., 2005) for ⁸²Se and from Ref. (Arnold et al., 2016) for ⁴⁸Ca. All results are for AV18 type SRC parameterizaionparameterization. We have assumed CP conservation (ψ =0). The results are compared with QRPA calculations for λ mechanism of Ref. (Šimkovic et al., 2017).

We have also calculated the upper bound on unknown Majorana neutrino mass (m_ββ) and lepton number violating parameter: the right-handed current coupling strength η_λ, using the experimental constraint on $T_{1/2}^{0\nu -exp}$ of Ref. (Arnold et al., 2005) for ⁸²Se and of Ref. (Arnold et al., 2016) for ⁴⁸Ca. The upper limits on m_ββ and η_λ are also presented in Table 3 for ⁸²Se and ⁴⁸Ca when both light neutrino-exchange and λ mechanisms co-exist. With the experimental lower limit on $T_{1/2}^{0\nu -exp}$, the upper limits on Majorana neutrino mass (m_ββ) are found to be 1.83 and 17.92 eV, respectively, for ⁸²Se and ⁴⁸Ca. This difference of m_ββ value for ⁸²Se and ⁴⁸Ca is quite large and also found in earlier work (Šimkovic et al., 2017). With the recent progress and future prospects of new generation experiments, lower limits on $T_{1/2}^{0\nu -exp}$ will be gradually improved and thus, will improve the upper limit on m_ββ and also reduce the differences for different isotopes.

4 Summary

In summary, we have studied how the left-right weak boson exchange (λ) mechanism of 0νββ decay is competing with the standard light neutrino-exchange mechanism. Our interest of isotope was one of the prominent 0νββ decaying isotope ⁸²Se. Particularly, we have calculated the NMEs for 0νββ of ⁸²Se when both standard light neutrino-exchange and λ mechanisms co-exist. The revised formalism for nucleon currents to include the pseudoscalar term was taken care of. The nuclear shell model framework was used in the calculation, and the widely used closure approximation was adopted with suitable closure energy. Nuclear states of initial, final, and intermediate states are calculated for fpg model space with JUN45 effective shell model Hamiltonian using shell model code KSHELL. These nuclear states are used to calculate TNA, which comes in the expression of NME of 0νββ through (n − 2) decay channel. Using the calculated NMEs, we have also calculated the upper bounds on Majorana neutrino mass and lepton number violating parameters.

The results show that particularly M_qGT type matrix element of λ mechanism is significantly enhanced as compared to standard M_GT type NME for the inclusion of the higher-order effect of the pseudoscalar term in the nucleon current. A similar type of enhancement in M_qGT type NME was also found in our earlier study for ⁴⁸Ca (Sarkar et al., 2020a). The dominance of 0⁺ and 2⁺ states of neutron-neutron (proton-proton) pairs were also observed, just like earlier studies.

With the experimental lower limits on the half-life, we have used our calculated NMEs to set the upper bounds on Majorana neutrino mass (m_ββ). The upper limits of values of m_ββ are found to be 1.83 and 17.92 eV, respectively, for ⁸²Se and ⁴⁸Ca. With the new generation of experiments, the lower limit on half-life will be further improved, and thus we can expect a much more refined upper bound on m_ββ, which may be below 1 eV. Also, the difference for the value of m_ββ will be reduced.

The term C_I (I = mm, mλ, λλ), which contains the phase space factors and NMEs, was also evaluated. The C_mm for light neutrino exchange and C_λλ for λ mechanism were found to be similar in values, that were larger than the term C_mλ for the interference of both the mechanisms. This shows the dominance of light neutrino exchange and the λ mechanisms over the interference mechanism. The overall dominant effect of light neutrino-exchange mechanism is observed over λ mechanism and interference of both the mechanisms for very small values of lepton number violating η_λ parameter.

In the future, it will be interesting to see the competing effect of the λ mechanism on the light neutrino-exchange mechanism and also how their contribution on 0νββ half-life will be evaluated in the current and future generation experiments.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The idea of the article was originated by YI. He has also contributed to calculating the nuclear states, interpretation of results, and manuscript writing. SS is responsible for the calculation of the TNA and TBME part of the NME. He has also actively participated in preparing the manuscript. Overall, both the authors have contributed enough in to various stages of preparing the final manuscript.

Funding

YI is grateful for the funding support from JSPS KAKENHI Grant No.17K05440.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Numerical computation in this work was carried out at the Yukawa Institute Computer Facility. YI acknowledges the Tokyo Institute of Technology for allowing to use of the high-performance computing facility to perform nuclear states calculation using KSHELL. YI is also grateful to Prof. Noritaka Shimizu, CNS, the University of Tokyo, for providing the 2020 version of shell model code KSHELL.

References

Arnold, R., Augier, C., Baker, J., Barabash, A., Broudin, G., Brudanin, V., et al. (2005). First Results of the Search for Neutrinoless Double-Beta Decay with the NEMO 3 Detector. Phys. Rev. Lett. 95, 182302. doi:10.1103/PhysRevLett.95.182302

PubMed Abstract | CrossRef Full Text | Google Scholar

Arnold, R., Augier, C., Bakalyarov, A. M., and Baker, J. D. (2016). Measurement of the Double-Beta Decay Half-Life and Search for the Neutrinoless Double-Beta Decay of ⁴⁸Ca with the NEMO-3 Detector. Phys. Rev. D 93, 112008. doi:10.1103/PhysRevD.93.112008

CrossRef Full Text | Google Scholar

Arnold, R., Augier, C., Barabash, A. S., Basharina-Freshville, A., Blondel, S., Blot, S., et al. (2020). Search for the Double-Beta Decay of 82se to the Excited States of 82kr with Nemo-3. Nucl. Phys. A 996, 121701. doi:10.1016/j.nuclphysa.2020.121701

CrossRef Full Text | Google Scholar

Avignone, F. T., Elliott, S. R., and Engel, J. (2008). Double Beta Decay, Majorana Neutrinos, and Neutrino Mass. Rev. Mod. Phys. 80, 481–516. doi:10.1103/RevModPhys.80.481

CrossRef Full Text | Google Scholar

Barea, J., and Iachello, F. (2009). Neutrinoless Double-Βdecay in the Microscopic Interacting Boson Model. Phys. Rev. C 79, 044301. doi:10.1103/PhysRevC.79.044301

CrossRef Full Text | Google Scholar

Barea, J., Kotila, J., and Iachello, F. (2012). Limits on Neutrino Masses from Neutrinoless Double-β Decay. Phys. Rev. Lett. 109, 042501. doi:10.1103/PhysRevLett.109.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

Barry, J., and Rodejohann, W. (2013). Lepton Number and Flavour Violation in Tev-Scale Left-Right Symmetric Theories with Large Left-Right Mixing. J. High Energ. Phys. 2013, 1–45. doi:10.1007/jhep09(2013)153

CrossRef Full Text | Google Scholar

Bhupal Dev, P. S., Goswami, S., and Mitra, M. (2015). Tev-scale Left-Right Symmetry and Large Mixing Effects in Neutrinoless Double Beta Decay. Phys. Rev. D 91, 113004. doi:10.1103/PhysRevD.91.113004

CrossRef Full Text | Google Scholar

Brown, B. A., Horoi, M., and Sen’kov, R. A. (2014). Nuclear Structure Aspects of Neutrinoless Double-β Decay. Phys. Rev. Lett. 113, 262501. doi:10.1103/PhysRevLett.113.262501

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, B. A., and Rae, W. D. M. (2014). The Shell-Model Code NuShellX@MSU. Nucl. Data Sheets 120, 115–118. doi:10.1016/j.nds.2014.07.022

CrossRef Full Text | Google Scholar

Caurier, E., Menéndez, J., Nowacki, F., and Poves, A. (2008). Influence of Pairing on the Nuclear Matrix Elements of the Neutrinoless Betabeta Decays. Phys. Rev. Lett. 100, 052503. doi:10.1103/PhysRevLett.100.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

Cirigliano, V., Dekens, W., de Vries, J., Graesser, M. L., Mereghetti, E., Pastore, S., et al. (2019). Renormalized Approach to Neutrinoless Double-β Decay. Phys. Rev. C 100, 055504. doi:10.1103/physrevc.100.055504

CrossRef Full Text | Google Scholar

Deppisch, F. F., Hirsch, M., and Päs, H. (2012). Neutrinoless Double-Beta Decay and Physics beyond the Standard Model. J. Phys. G: Nucl. Part. Phys. 39, 124007. doi:10.1088/0954-3899/39/12/124007

CrossRef Full Text | Google Scholar

Dolinski, M. J., Poon, A. W. P., and Rodejohann, W. (2019). Neutrinoless Double-Beta Decay: Status and Prospects. Annu. Rev. Nucl. Part. Sci. 69, 219–251. doi:10.1146/annurev-nucl-101918-023407

CrossRef Full Text | Google Scholar

Engel, J., and Menéndez, J. (2017). Status and Future of Nuclear Matrix Elements for Neutrinoless Double-Beta Decay: a Review. Rep. Prog. Phys. 80, 046301. doi:10.1088/1361-6633/aa5bc5

PubMed Abstract | CrossRef Full Text | Google Scholar

Honma, M., Otsuka, T., Mizusaki, T., and Hjorth-Jensen, M. (2009). New Effective Interaction Forf5pg9-Shell Nuclei. Phys. Rev. C 80. doi:10.1103/physrevc.80.064323

CrossRef Full Text | Google Scholar

Horoi, M., and Neacsu, A. (2016). Analysis of Mechanisms that Could Contribute to Neutrinoless Double-Beta Decay. Phys. Rev. D 93, 113014. doi:10.1103/PhysRevD.93.113014

CrossRef Full Text | Google Scholar

Horoi, M., and Neacsu, A. (2018). Shell Model Study of Using an Effective Field Theory for Disentangling Several Contributions to Neutrinoless Double-β Decay. Phys. Rev. C 98, 035502. doi:10.1103/PhysRevC.98.035502

CrossRef Full Text | Google Scholar

Horoi, M., and Stoica, S. (2010). Shell Model Analysis of the Neutrinoless Double-β Decay of ⁴⁸Ca. Phys. Rev. C 81, 024321. doi:10.1103/PhysRevC.81.024321

CrossRef Full Text | Google Scholar

Iwata, Y., Shimizu, N., Otsuka, T., Utsuno, Y., Menéndez, J., Honma, M., et al. (2016). Large-Scale Shell-Model Analysis of the Neutrinoless ββ Decay of ⁴⁸Ca. Phys. Rev. Lett. 116, 112502. doi:10.1103/PhysRevLett.116.112502

PubMed Abstract | CrossRef Full Text | Google Scholar

Menéndez, J., Poves, A., Caurier, E., and Nowacki, F. (2009). Disassembling the Nuclear Matrix Elements of the Neutrinoless ββ Decay. Nucl. Phys. A 818, 139–151. doi:10.1016/j.nuclphysa.2008.12.005

CrossRef Full Text | Google Scholar

Mohapatra, R. N. (1986). New Contributions to Neutrinoless Double-Beta Decay in Supersymmetric Theories. Phys. Rev. D 34, 3457–3461. doi:10.1103/PhysRevD.34.3457

CrossRef Full Text | Google Scholar

Mohapatra, R. N., and Senjanović, G. (1980). Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 44, 912–915. doi:10.1103/PhysRevLett.44.912

CrossRef Full Text | Google Scholar

Mohapatra, R. N., and Vergados, J. D. (1981). New Contribution to Neutrinoless Double Beta Decay in Gauge Models. Phys. Rev. Lett. 47, 1713–1716. doi:10.1103/PhysRevLett.47.1713

CrossRef Full Text | Google Scholar

Neacsu, A., Stoica, S., and Horoi, M. (2012). Fast, Efficient Calculations of the Two-Body Matrix Elements of the Transition Operators for Neutrinoless Double-β Decay. Phys. Rev. C 86, 067304. doi:10.1103/physrevc.86.067304

CrossRef Full Text | Google Scholar

Pagnanini, L., Azzolini, O., Beeman, J., Bellini, F., Beretta, M., Biassoni, M., et al. (2019). “Results on Double Beta Decay of ⁸²se with CUPID-0 Phase I,” in AIP Conference Proceedings (AIP Publishing LLC), 020019. doi:10.1063/1.5130980

CrossRef Full Text | Google Scholar

Pastore, S., Carlson, J., Cirigliano, V., Dekens, W., Mereghetti, E., and Wiringa, R. B. (2018). Neutrinoless Double-β Decay Matrix Elements in Light Nuclei. Phys. Rev. C 97, 014606. doi:10.1103/PhysRevC.97.014606

PubMed Abstract | CrossRef Full Text | Google Scholar

Rath, P. K., Chandra, R., Chaturvedi, K., Raina, P. K., and Hirsch, J. G. (2010). Uncertainties in Nuclear Transition Matrix Elements for Neutrinoless ββ Decay within the Projected-Hartree-Fock-Bogoliubov Model. Phys. Rev. C 82, 064310. doi:10.1103/PhysRevC.82.064310

CrossRef Full Text | Google Scholar

Rodejohann, W. (2011). Neutrino-less Double Beta Decay and Particle Physics. Int. J. Mod. Phys. E 20, 1833–1930. doi:10.1142/s0218301311020186

CrossRef Full Text | Google Scholar

Rodin, V. A., Faessler, A., Šimkovic, F., and Vogel, P. (2006). Assessment of Uncertainties in QRPA 0ν ββ-decay Nuclear Matrix Elements. Nucl. Phys. A 766, 107–131. doi:10.1016/j.nuclphysa.2005.12.004

CrossRef Full Text | Google Scholar

Rodríguez, T. R., and Martínez-Pinedo, G. (2010). Energy Density Functional Study of Nuclear Matrix Elements for Neutrinoless ββ Decay. Phys. Rev. Lett. 105, 252503. doi:10.1103/physrevlett.105.252503

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, S., Iwata, Y., and Raina, P. K. (2020). Nuclear Matrix Elements for the λ Mechanism of 0ν ββ Decay of ⁴⁸Ca in the Nuclear Shell-Model: Closure versus Nonclosure Approach. Phys. Rev. C 102, 034317. doi:10.1103/PhysRevC.102.034317

CrossRef Full Text | Google Scholar

Sarkar, S., Kumar, P., Jha, K., and Raina, P. K. (2020). Sensitivity of Nuclear Matrix Elements of 0νββ of ⁴⁸Ca to Different Components of the Two-Nucleon Interaction. Phys. Rev. C 101, 014307. doi:10.1103/PhysRevC.101.014307

CrossRef Full Text | Google Scholar

Schechter, J., and Valle, J. W. F. (1982). Neutrinoless Double-Βdecay in SU(2)×U(1) Theories. Phys. Rev. D 25, 2951–2954. doi:10.1103/physrevd.25.2951

CrossRef Full Text | Google Scholar

Sen'kov, R. A., and Horoi, M. (2013). Neutrinoless Double-β Decay of ⁴⁸Ca in the Shell Model: Closure versus Nonclosure Approximation. Phys. Rev. C 88, 064312. doi:10.1103/PhysRevC.88.064312

CrossRef Full Text | Google Scholar

Sen’kov, R. A., Horoi, M., and Brown, B. A. (2014). Neutrinoless Double-β Decay of ⁸²Se in the Shell Model: Beyond the Closure Approximation. Phys. Rev. C 89, 054304. doi:10.1103/PhysRevC.89.054304

CrossRef Full Text | Google Scholar

Shimizu, N., Mizusaki, T., Utsuno, Y., and Tsunoda, Y. (2019). Thick-restart Block Lanczos Method for Large-Scale Shell-Model Calculations. Comp. Phys. Commun. 244, 372–384. doi:10.1016/j.cpc.2019.06.011

CrossRef Full Text | Google Scholar

Šimkovic, F., Faessler, A., Müther, H., Rodin, V., and Stauf, M. (2009). 0νββ-decay Nuclear Matrix Elements with Self-Consistent Short-Range Correlation. Phys. Rev. C 79, 055501. doi:10.1103/PhysRevC.79.055501

CrossRef Full Text | Google Scholar

Šimkovic, F., Pantis, G., Vergados, J. D., and Faessler, A. (1999). Additional Nucleon Current Contributions to Neutrinoless Double β Decay. Phys. Rev. C 60, 055502. doi:10.1103/PhysRevC.60.055502

CrossRef Full Text | Google Scholar

Šimkovic, F., Štefánik, D., and Dvornickỳ, R. (2017). The λ Mechanism of the 0νββ-Decay. Front. Phys. 5, 57. doi:10.3389/fphy.2017.00057

CrossRef Full Text | Google Scholar

Song, L. S., Yao, J. M., Ring, P., and Meng, J. (2014). Relativistic Description of Nuclear Matrix Elements in Neutrinoless Double-β Decay. Phys. Rev. C 90, 054309. doi:10.1103/PhysRevC.90.054309

CrossRef Full Text | Google Scholar

Štefánik, D., Dvornickỳ, R., Šimkovic, F., and Vogel, P. (2015). Reexamining the Light Neutrino Exchange Mechanism of the 0νββ Decay with Left-And Right-Handed Leptonic and Hadronic Currents. Phys. Rev. C 92, 055502. doi:10.1103/PhysRevC.92.055502

CrossRef Full Text | Google Scholar

Tomoda, T. (1991). Double Beta Decay. Rep. Prog. Phys. 54, 53–126. doi:10.1088/0034-4885/54/1/002

CrossRef Full Text | Google Scholar

Vergados, J. D., Ejiri, H., and Šimkovic, F. (2012). Theory of Neutrinoless Double-Beta Decay. Rep. Prog. Phys. 75, 106301. doi:10.1088/0034-4885/75/10/106301

PubMed Abstract | CrossRef Full Text | Google Scholar

Vergados, J. D. (1987). Neutrinoless Double β-decay without Majorana Neutrinos in Supersymmetric Theories. Phys. Lett. B 184, 55–62. doi:10.1016/0370-2693(87)90487-4

CrossRef Full Text | Google Scholar

Vogel, P. (2012). Nuclear Structure and Double Beta Decay. J. Phys. G: Nucl. Part. Phys. 39, 124002. doi:10.1088/0954-3899/39/12/124002

CrossRef Full Text | Google Scholar

Wang, X. B., Hayes, A. C., Carlson, J., Dong, G. X., Mereghetti, E., Pastore, S., et al. (2019). Comparison between Variational Monte Carlo and Shell Model Calculations of Neutrinoless Double Beta Decay Matrix Elements in Light Nuclei. Phys. Lett. B 798, 134974. doi:10.1016/j.physletb.2019.134974

CrossRef Full Text | Google Scholar

Appendix A

One can write anti-symmetric two-body matrix elements for transition operator $O_{12}^{\alpha }$ of 0νββ defined in Eq. 22 as

$\begin{array}{ccc}\hfill & \hfill & \langle n_1^{\prime }{l}_1^{\prime }{j}_1^{\prime },n_2^{\prime }{l}_2^{\prime }{j}_2^{\prime }:JT|{\tau }_{-1}{\tau }_{-2}{O}_{12}^{\alpha }|n_1{l}_1{j}_1,n_2{l}_2{j}_2:J{T\rangle }_A\hfill \\ \hfill & \hfill & =\frac{1}{\sqrt{(1+{\delta }_{j_1^{\prime }{j}_2^{\prime }})\left(\right.(1+{\delta }_{j_1{j}_2})}}\hfill \\ \hfill & \hfill & (\langle n_1^{\prime }{l}_1^{\prime }{j}_1^{\prime },n_2^{\prime }{l}_2^{\prime }{j}_2^{\prime }:JT|{\tau }_{-1}{\tau }_{-2}{O}_{12}^{\alpha }|n_1{l}_1{j}_1,n_2{l}_2{j}_2:JT\rangle \hfill \\ \hfill & \hfill & -{(-1)}^{j_1+j_2+J}\hfill \\ \hfill & \hfill & \times \langle n_1^{\prime }{l}_1^{\prime }{j}_1^{\prime },n_2^{\prime }{l}_2^{\prime }{j}_2^{\prime }:JT|{\tau }_{-1}{\tau }_{-2}{O}_{12}^{\alpha }|n_2{l}_2{j}_2,n_1{l}_1{j}_1:JT\rangle ),\hfill \end{array}(29)$

where,

$\begin{array}{ll}\hfill & \langle n_1^{\prime }{l}_1^{\prime }{j}_1^{\prime },n_2^{\prime }{l}_2^{\prime }{j}_2^{\prime }:J|O_{12}^{\alpha }|n_1{l}_1{j}_1,n_2{l}_2{j}_2:J\rangle \hfill \\ \hfill & =\sum _{S^{\prime },S}\sum _{{\lambda }^{\prime },\lambda }\left[\begin{array}{ccc}\hfill l_1^{\prime }\hfill & \hfill \frac{1}{2}\hfill & \hfill j_1^{\prime }\hfill \\ \hfill l_2^{\prime }\hfill & \hfill \frac{1}{2}\hfill & \hfill j_2^{\prime }\hfill \\ \hfill {\lambda }^{\prime }\hfill & \hfill S^{\prime }\hfill & \hfill J\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill l_1\hfill & \hfill \frac{1}{2}\hfill & \hfill j_1\hfill \\ \hfill l_2\hfill & \hfill \frac{1}{2}\hfill & \hfill j_2\hfill \\ \hfill \lambda \hfill & \hfill S\hfill & \hfill J\hfill \end{array}\right]\hfill \\ \hfill & \times \sum _{n^{\prime },l^{\prime },N^{\prime },L^{\prime }}\sum _{n,l,N,L}\sum _{\mathcal{J}}\frac{1}{\sqrt{2S+1}}\frac{1}{\sqrt{2\mathcal{J+}1}}U(L^{\prime },l^{\prime },J,S^{\prime }:{\lambda }^{\prime }\mathcal{J})\hfill \\ \hfill & \times U(L,l,J,S:\lambda \mathcal{J})\langle n^{\prime },l^{\prime },N^{\prime },L^{\prime }|n_1^{\prime },l_1^{\prime },n_2^{\prime },l_2^{\prime }{⟩}_{{\lambda }^{\prime }}\hfill \\ \hfill & \times {⟨n,l,N,L|n_1,l_1,n_2,l_2⟩}_{\lambda }\langle l^{\prime },S^{\prime }:\mathcal{J}‖S_{12}^{\alpha }‖l,S:\mathcal{J}\rangle \hfill \\ \hfill & \times \langle n^{\prime },l^{\prime }|H_{\alpha }(r)|n,l\rangle .\hfill \end{array}(30)$

One can write in terms of 9j symbol

$\begin{array}{ccc}\hfill & \hfill & \left[\begin{array}{ccc}\hfill l_1^{\prime }\hfill & \hfill \frac{1}{2}\hfill & \hfill j_1^{\prime }\hfill \\ \hfill l_2^{\prime }\hfill & \hfill \frac{1}{2}\hfill & \hfill j_2^{\prime }\hfill \\ \hfill {\lambda }^{\prime }\hfill & \hfill S^{\prime }\hfill & \hfill J\hfill \end{array}\right]\hfill \\ \hfill & \hfill & =\sqrt{(2j_1^{\prime }+1)(2j_2^{\prime }+1)(2{\lambda }^{\prime }+1)(2S^{\prime }+1)}\times \left\{\begin{array}{ccc}\hfill l_1^{\prime }\hfill & \hfill \frac{1}{2}\hfill & \hfill j_1^{\prime }\hfill \\ \hfill l_2^{\prime }\hfill & \hfill \frac{1}{2}\hfill & \hfill j_2^{\prime }\hfill \\ \hfill {\lambda }^{\prime }\hfill & \hfill S^{\prime }\hfill & \hfill J\hfill \end{array}\right\}.\hfill \end{array}(31)$

In terms of 6j symbol one can write

$\begin{array}{ccc}\hfill U(L^{\prime },l^{\prime },J,S^{\prime }:{\lambda }^{\prime }\mathcal{J})=& \hfill & {(-1)}^{L^{\prime }+l^{\prime }+S^{\prime }+J}\sqrt{2{\lambda }^{\prime }+1}\sqrt{2\mathcal{J}+1}\hfill \\ \hfill & \hfill & \left\{\begin{array}{ccc}\hfill L^{\prime }\hfill & \hfill l^{\prime }\hfill & \hfill {\lambda }^{\prime }\hfill \\ \hfill S^{\prime }\hfill & \hfill J\hfill & \hfill \mathcal{J}\hfill \end{array}\right\}.\hfill \end{array}(32)$

$\langle n^{\prime },l^{\prime },N^{\prime },L^{\prime }|n_1^{\prime },l_1^{\prime },n_2^{\prime },l_2^{\prime }{\rangle }_{{\lambda }^{\prime }}$ is the harmonic oscillator bracket used to convert the radial integral of neutrino potential from individual coordinate system of nucleons to relative and center of mass coordinate system of the nucleons.

Appendix B

The f_α(q, r) factor of Eq. 16 can be written in terms of radial dependence, spherical Bessel function j_p (qr) (p = 0, 1, 2 and 3), and FNS + HOC coupling form factors in closure approximation as (Šimkovic et al., 2017).

$\begin{array}{ccc}\hfill f_{GT}(q,r)& =\hfill & \frac{j_0(qr)}{g_A^2}\left(g_A^2(q^2)-\frac{g_A(q^2)g_P(q^2)}{m_N}\frac{q^2}{3}\right.\hfill \\ \hfill & \hfill & \left.+\frac{g_P^2(q^2)}{4m_N^2}\frac{q^4}{3}+\left(2\frac{g_M^2(q^2)}{4m_N^2}\frac{q^2}{3}\right)\right),\hfill \end{array}(33)$

$\begin{array}{ccc}\hfill f_F(q,r)& =\hfill & g_V^2(q^2)j_0(qr),\hfill \end{array}(34)$

$\begin{array}{ccc}\hfill f_T(q,r)& =\hfill & \frac{j_2(qr)}{g_A^2}\left(\frac{g_A(q^2)g_P(q^2)}{m_N}\frac{q^2}{3}-\frac{g_P^2(q^2)}{4m_N^2}\frac{q^4}{3}\right.\hfill \\ \hfill & \hfill & \left.+\frac{g_M^2(q^2)}{4m_N^2}\frac{q^2}{3}\right),\hfill \end{array}(35)$

$\begin{array}{ccc}\hfill f_{\omega GT}(q,r)& =\hfill & \frac{q}{(q+\langle E\rangle )}{f}_{GT}(q,r),\hfill \end{array}(36)$

$\begin{array}{ccc}\hfill f_{\omega F}(q,r)& =\hfill & \frac{q}{(q+\langle E\rangle )}{f}_F(q,r),\hfill \end{array}(37)$

$\begin{array}{ccc}\hfill f_{\omega T}(q,r)& =\hfill & \frac{q}{(q+\langle E\rangle )}{f}_T(q,r),\hfill \end{array}(38)$

$\begin{array}{ccc}\hfill f_{qGT}(q,r)& =\hfill & \left(\frac{g_A^2(q^2)}{g_A^2}q+3\frac{g_P^2(q^2)}{g_A^2}\frac{q^5}{4m_N^2}\right.\hfill \\ \hfill & \hfill & \left.+\frac{g_A(q^2)g_P(q^2)}{g_A^2}\frac{q^3}{m_N}\right)r{j}_1(q,r),\hfill \end{array}(39)$

$\begin{array}{ccc}\hfill f_{qF}(q,r)& =\hfill & r{g}_V^2(q^2)j_1(qr)q,\hfill \end{array}(40)$

$\begin{array}{ccc}\hfill f_{qT}(q,r)& =\hfill & \frac{r}{3}\left(\left(\frac{g_A^2(q^2)}{g_A^2}q-\frac{g_P(q^2)g_A(q^2)}{2g_A^2}\frac{q^3}{m_N}\right)j_1(qr)\right.\hfill \\ \hfill & \hfill & -\left.\left(9\frac{g_P^2(q^2)}{2g_A^2}\frac{q^5}{20m_N^2}\left[2j_1(qr)/3-j_3(qr)\right]\right)\right),\hfill \end{array}(41)$

where one can write in dipole approximation (Šimkovic et al., 1999).

$\begin{array}{ccc}\hfill g_V(q^2)& =\hfill & \frac{g_V}{{\left(1+\frac{q^2}{M_V^2}\right)}^2},\hfill \end{array}(42)$

$\begin{array}{ccc}\hfill g_A(q^2)& =\hfill & \frac{g_A}{{\left(1+\frac{q^2}{M_A^2}\right)}^2},\hfill \end{array}(43)$

$\begin{array}{ccc}\hfill g_M(q^2)& =\hfill & ({\mu }_p-{\mu }_n)g_V(q^2),\hfill \end{array}(44)$

$\begin{array}{ccc}\hfill g_P(q^2)& =\hfill & \frac{2m_p{g}_A(q^2)}{(q^2+m_{\pi }^2)}\left(1-\frac{m_{\pi }^2}{M_A^2}\right).\hfill \end{array}(45)$

μ_p − μ_n = 4.7, M_V = 850 MeV, M_A = 1,086 MeV m_p and m_π are the mass of protons and pions (Sen’kov and Horoi, 2013). In the present calculation, vector constant g_V = 1.0 and bare axial-vector constant g_A = 1.27 (Sarkar et al., 2020b) are used. Both the pseudo scalar and weak magnetism terms of the nucleon currents are included in f_{GT,T,ωGT,ωT} (q, r) factors whereas pseudo scalar term is included in f_qGT,qT (q, r) factors (Šimkovic et al., 2017).