Model Kinetic Equations for Multiply Ionized Gas Mixtures

Model kinetic equations are proposed for the description of ionized monoatomic gas mixture flows. The mixtures are assumed enough rarefied to be treated as ideal gases after multiple ionization steps. The model equations contain the equilibrium distribution functions for the components of the gas mixtures under consideration like it was done in BGK equations and their well-known generalizations. However, in this paper the new forms of the equilibrium distribution functions are used which correspond to the entropy maximum under the constraints of momentum, total energy, nuclei and electrons (both bound and free) conservation. It is shown that the derived model equations allow us to study the local equilibrium flows of the ionized gases and the transport processes of energy, nuclei and electrons in the non-equilibrium conditions.

1 Introduction

When studying gas flows near bodies moving in the upper atmosphere, it is necessary to take into account the dissociation and ionization processes. Therefore, many theoretical studies are devoted to consideration of the transport processes in gas flows with electronic degrees of freedom, ionization and recombination [see, for example, (Zhdanov, 2009; Capitelli et al., 2012; Bruno et al., 2007; Bruno et al., 2008; Istomin and Kustova, 2014; Zhdanov and Stepanenko, 2016a; Zhdanov and Stepanenko, 2016b; Istomin and Kustova, 2017; Istomin and Kustova, 2017)]. At present, a special attention is concentrated on the kinetic description problems of the ionized gas flows with multiple ion species [see, for example, the generalization (Simakov and Molvig, 2016) of the Braginskij ion fluid description of unmagnetized plasma (Braginskii, 1958) and Ref. (Arslanbekov and Kolobov, 2018)].

The present study is devoted to the kinetic description of monoatomic gas mixtures with multiple ion species. The mixtures are assumed enough rarefied to be treated as ideal gases and to be described in terms of single-particle distribution functions even after multiple ionization steps. Under these conditions one can use the generalized Boltzmann equations like it was done for the description of gas mixtures with excitation of molecular internal degrees of freedom and chemical reactions [see, for example, (Loureiro and Amorim, 2016; Ferziger and Kaper, 1972; Vallander et al., 1977; Giovangigli, 1999; Rydalevskaya, 2003; Nagnibeda and Kustova, 2009; Loureiro and Amorim, 2016)].

In derivation of any kinetic equations, the principal difficulties are connected with the complex structure of their integral collisions operators. Therefore, full collision operators were replaced with model collision operators, first in the kinetic equations derived by Bhatnagar, Gross and Krook (BGK) for simple monoatomic gases (Bhatnagar et al., 1954). Further, the BGK model was generalized for the gas mixtures with the internal degrees of freedom of molecules and with chemical reactions [see, for example, (Morse, 1964; Hanson and Morse, 1967; Groppi and Spiga, 2004)].

In the present paper, the generalization of the BGK model is proposed for the kinetic description of the multiply ionized monoatomic gases mixtures. In the model kinetic equations the new form of the local equilibrium distribution functions for the atoms, ions and free electrons is used. These model equations allow us to derive the reduced systems of the macroscopic conservation equations.

2 Generalization of BGK Model

Consider the flow of an ionized gas mixture which consists of the neutral atoms $A_{k0}$ of various chemical species $k=\mathrm{1,2},\dots ,k_{\text{*}}$, ions $A_{kc}$ with a charge $c=+1,+2,\dots ,+N\left(k\right)$ ($N\left(k\right)$ is the serial number of element $A_k$ in the periodic system) and free electrons $e^{-}$. Every particle $A_{kc}$ contains the nucleus $A_k^{\text{*}}$ and $\left(N\left(k\right)-c\right)$ electrons. All particles $A_{kc}$ and free electrons $e^{-}$ have translational energy $m_{kc}{\mathrm{u}}^2/2$ and $m_{e^{-}}{\mathrm{u}}^2/2$ ($m_{kc}$ and $m_{e^{-}}$ are their masses, u are the velocity vectors). Particles $A_{kc}$ ($c=\overline{0,N\left(k\right)-1}$) also have internal electronic energy ${\epsilon }_{kci}$ ($i=\overline{0,i_{kc}^{\text{*}}}$), subscript i characterizes a set of quantum numbers that specifies internal energy of particle $A_{kc}$.

If the translational energy of particles is described classically or quasi-classically and their internal energy is assumed quantum, then for the determination of the ionized gas mixtures states one can use the distribution functions $f_{kci}\left(\mathrm{r},\mathrm{u},t\right)$ and $f_{e^{-}}\left(\mathrm{r},\mathrm{u},t\right)$. The model kinetic equations which are analogous to the BGK equations can be presented in the form:

$D_{kci}{f}_{kci}=\frac{f_{kci}^{\left(0\right)}-f_{kci}}{\tau },i=\overline{0,i_{kc}^{\ast }},c=\overline{0,N\left(k\right)},k=\overline{1,k_{\ast }},(1)$

$D_{e^{-}}{f}_{e^{-}}=\frac{f_{e^{-}}^{\left(0\right)}-f_{e^{-}}}{\tau },(2)$

where $D_{kci}$ and $D_{e^{-}}$ are the traditional differential Boltzmann operators; $f_{kci}^{\left(0\right)}\left(\mathrm{r},\mathrm{u},t\right)$ and $f_{e^{-}}^{\left(0\right)}\left(\mathrm{r},\mathrm{u},t\right)$ are the local equilibrium distribution functions of corresponding particles, t is the relaxation time for the transition to the state of complete thermodynamic equilibrium (including chemical equilibrium of ionized and neutral species).

It should be noted that the normalization conditions for the functions $f_{kci}^{\left(0\right)}$ and $f_{e^{-}}^{\left(0\right)}$ coincide with the normalization conditions for the functions $f_{kci}$ and $f_{e^{-}}$.

In Ref. (Rydalevskaya, 2017), the equilibrium distribution functions $f_{kci}^{\left(0\right)}$ and $f_{e^{-}}^{\left(0\right)}$ were obtained, which correspond to the entropy maximum of the motionless spatially uniform ionized gas systems under the constraints of conservation of the total energy, the numbers of the nuclei $A_k^{\text{*}}$ ($k=\overline{1,k_{\text{*}}}$) and electrons (both bound and free) in these systems.

In the present study, to find local equilibrium functions $f_{kci}^{\left(0\right)}\left(\mathrm{r},\mathrm{u},t\right)$ and $f_{e^{-}}^{\left(0\right)}\left(\mathrm{r},\mathrm{u},t\right)$, we can use the famous Boltzmann formula (Boltzman, 1964) for the entropy density:

$\tilde{s}=k\ln W=k\ln \frac{\Delta \Gamma }{\Gamma },(3)$

where k is the Boltzmann constant; W, $\text{Γ}$ and $\text{ΔΓ}$ are respectively thermodynamic probability, the total number of the unit volume and the number of its microscopic states for the macroscopic state under consideration.

One can consider that $\text{Γ}$ is constant value in the gas flow under consideration. Therefore, for a mixture of ideal gases the entropy density can be written in the form

$\tilde{s}=k\ln \Delta \Gamma =k\ln \left({\displaystyle \prod _j\Delta {\Gamma }_j}\right),(4)$

where ${\text{ΔΓ}}_j$ is the number of microscopic states of $N_j$ identical particles. There particles are in the definite phase volume, and they are of identical chemical species and have an identical set of quantum numbers which correspond to their internal energy.

If one neglects the exchange effects and assumes

$1\ll N_j\ll s_j,j=\overline{1,j_{\ast }},$

then the expression Eq. 4 can be rewritten in the form [see (Rydalevskaya, 2003; Rydalevskaya, 2017)]

$\tilde{s}=k\ln \left({\displaystyle \prod _j{s}_j^{N_j}/N_j!}\right).(5)$

Using the Stirling formula, we obtain

$\tilde{s}=k{\displaystyle \sum _j\left(N_j\ln s_j-N_j\ln N_j+N_j\right)}.(6)$

To determine the local equilibrium values $N_j$ ($j=\overline{1,j_{\text{*}}}$) it is necessary to find the maximum of the entropy density Eq. 6 under the existing local constraints can be presented in the form

${\displaystyle \sum _j{N}_j{\psi }_j^{\left(\lambda \right)}}={\text{Ψ}}_{\lambda }\left(\mathrm{r},t\right),\lambda =\overline{0,\text{Λ}}.(7)$

Here ${\psi }_j^{\left(\lambda \right)}$ ($\lambda =\overline{0,\text{Λ}}$) are collision invariants of any collisions between the particles; ${\text{Ψ}}_{\lambda }\left(\mathrm{r},t\right)$ are sums of the collision invariants ${\psi }_j^{\left(\lambda \right)}$ in the unit volume under consideration. The notations ${\psi }_j^{\left(0\right)}$ and ${\text{Ψ}}_0\left(\mathrm{r},t\right)$ are used for the energy of an individual particle and for the whole unit volume energy.

The constraints which correspond to the momentum conservation can be presented in the form:

${\displaystyle \sum _j{N}_j{m}_j\mathrm{u}}=\mathit{\varrho }\left(\mathrm{r},t\right)\mathrm{v}\left(\mathrm{r},t\right).(8)$

In ionized monoatomic gas flow, in addition to the energy and momentum there are $k_{\text{*}}+1$ invariants on the type (Rydalevskaya, 2017):

$\begin{array}{l}{\psi }_{kci}^{\left(\lambda \right)}={\delta }_{\lambda k},k=\overline{1,k_{\ast }},c=\overline{0,N\left(k\right)},{\psi }_{e^{-}}^{\left(\lambda \right)}=0,\lambda =\overline{1,k_{\ast }};\\ {\psi }_{kci}^{\left(\lambda \right)}=N\left(k\right)-c,k=\overline{1,k_{\ast }},c=\overline{0,N\left(k\right)},{\psi }_{e^{-}}^{\left(\lambda \right)}=1,\lambda =k_{\ast }+1.\end{array}(9)$

Using the method of Lagrange multipliers, for the determination of entropy density Eq. 6 maximum under constraints Eq. 7, we obtain equilibrium values

$N_j^e=s_j\exp {\displaystyle \sum _{\lambda =0}^{\Lambda }{\gamma }_{\lambda }\left(\mathrm{r},t\right){\psi }_j^{\left(\lambda \right)}},j=\overline{1,j_{\ast }},(10)$

where $k{\gamma }_{\lambda }\left(\mathrm{r},t\right)$ are the Lagrange multipliers corresponding to the intensive parameters conjugate to the densities ${\text{Ψ}}_{\lambda }\left(\mathrm{r},t\right)$ ($\lambda =\overline{0,\text{Λ}}$) of the extensive parameters.

If the translational energy of particles is described quasi-classically and their internal energy is assumed quantum, then it is possible to turn from the numbers $N_j^{\left(e\right)}$ to the local equilibrium distribution functions of the atoms, ions, and free electrons:

$\begin{array}{l}{f}_{kci}^{\left(0\right)}\left(\mathrm{r},\mathrm{u},t\right)=s_{kci}\frac{m_{kc}^3}{h^3}\text{exp}\left({\gamma }_0\left(\frac{m_{kc}{u}^2}{2}+{\epsilon }_{kci}\right)+\overrightarrow{\gamma }\cdot m_{kc}\mathrm{u}+{\gamma }_k+{\gamma }_{e^{-}}\left(N\left(k\right)-c\right)\right),\\ i=\overline{0,i_{kc}^{\text{*}}},c=\overline{0,N\left(k\right)-1},k=\overline{1,k_{\text{*}}},\end{array}(11)$

$f_{kci}^{\left(0\right)}=\frac{m_{kc}^3}{h^3}\text{exp}\left({\gamma }_0\frac{m_{kc}{u}^2}{2}+\overrightarrow{\gamma }\cdot m_{kc}\mathrm{u}+{\gamma }_k\right),c=N\left(k\right),k=\overline{1,k_{\text{*}}},(12)$

$f_{e^{-}}^{\left(0\right)}=\frac{m_{e^{-}}^3}{h^3}\text{exp}\left({\gamma }_0\frac{m_{e^{-}}{u}^2}{2}+{\gamma }_{e^{-}}\right),(13)$

where h is Planck’s constant, $s_{kci}$ are statistical weights.

To determine unknown parameters $\overrightarrow{\gamma }$, ${\gamma }_0$, ${\gamma }_k$ ($k=\overline{1,k_{\ast }}$) and ${\gamma }_{e^{-}}$ in the expressions Eqs 11–13, it is necessary to use the normalization constraints under the existing conservation conditions.

The conservation of momentum can be written in the form

${\displaystyle \sum _{k,c,i}{\displaystyle \int m_{kc}\mathrm{u}{f}_{kci}^{\left(0\right)}d\mathrm{u}}+{\displaystyle \int m_{e^{-}}\mathrm{u}{f}_{e^{-}}^{\left(0\right)}d\mathrm{u}}}=\mathit{\varrho }\left(\mathrm{r},t\right)\mathrm{v}\left(\mathrm{r},t\right),(14)$

where $\mathit{\varrho }\left(\mathrm{r},t\right)$ and $\mathrm{v}\left(\mathrm{r},t\right)$ are the mass density and the velocity of the gas mixture.

Introducing the particles peculiar velocities $\mathrm{c}=\mathrm{u-v}\left(\mathrm{r},t\right)$ as well as the functions ${\tilde{f}}_{kci}\left(\mathrm{r},\mathrm{c},t\right)$ and ${\tilde{f}}_{e^{-}}\left(\mathrm{r},\mathrm{c},t\right)$, one can rewrite the model kinetic Eqs 1, 2 for an unmagnetized ideal plasma in the form:

$\begin{array}{l}\tilde{D}{\tilde{f}}_{kci}=\frac{d{\tilde{f}}_{kci}}{dt}+c\cdot \overrightarrow{\nabla }{\tilde{f}}_{kci}+\left(F_{kc}-\frac{dv}{dt}\right)\cdot {\overrightarrow{\nabla }}_c{\tilde{f}}_{kci}-\left({\overrightarrow{\nabla }}_c{\tilde{f}}_{kci}\right)c:\overrightarrow{\nabla }v=\frac{{\tilde{f}}_{kci}^{\left(0\right)}-{\tilde{f}}_{kci}}{\tau },\\ k=\overline{1,k_{\ast }},c=\overline{0,N\left(k\right)},i=\overline{0,i_{kc}^{\ast }},\end{array}(15)$

$\tilde{D}{\tilde{f}}_{e^{-}}=\frac{d{\tilde{f}}_{e^{-}}}{dt}+c\cdot \overrightarrow{\nabla }{\tilde{f}}_{e^{-}}+\left(F_{e^{-}}-\frac{dv}{dt}\right)\cdot {\overrightarrow{\nabla }}_c{\tilde{f}}_{e^{-}}-\left({\overrightarrow{\nabla }}_c{\tilde{f}}_{e^{-}}\right)c:\overrightarrow{\nabla }v=\frac{{\tilde{f}}_{e^{-}}^{\left(0\right)}-{\tilde{f}}_{e^{-}}}{\tau },(16)$

where $\frac{d\tilde{f}}{dt}=\frac{\partial \tilde{f}}{\partial t}+v\cdot \overrightarrow{\nabla }\tilde{f}$ and $\frac{d\mathrm{v}}{dt}=\frac{\partial \mathrm{v}}{\partial t}+\left(\mathrm{v}\cdot \overrightarrow{\nabla }\right)\mathrm{v}$; the operator ${\overrightarrow{\nabla }}_c$ supposes differentiation with respect to the peculiar velocity c; $m_{kc}{\mathrm{F}}_{kc}$ and $m_{e^{-}}{\mathrm{F}}_{e^{-}}$ are the external forces which do not depend on the particles velocities;

$\begin{array}{l}{\tilde{f}}_{kci}^{\left(0\right)}\left(\mathrm{r},\mathrm{c},t\right)=s_{kci}\frac{m_{kc}^3}{h^3}\text{exp}\left({\gamma }_0\left(\frac{m_{kc}{\mathrm{c}}^2}{2}+{\epsilon }_{kci}\right)+{\gamma }_k+{\gamma }_{e^{-}}\left(N\left(k\right)-c\right)\right),\\ c=\overline{0,N\left(k\right)},k=\overline{1,k_{\text{*}}},i=\overline{0,i_{kc}^{\text{*}}},\end{array}(17)$

${\tilde{f}}_{e^{-}}^{\left(0\right)}\left(\mathrm{r},\mathrm{c},t\right)=\frac{m_{e^{-}}^3}{h^3}\text{exp}\left({\gamma }_0\frac{m_{e^{-}}{\mathrm{c}}^2}{2}+{\gamma }_{e^{-}}\right).(18)$

For the determination of coefficients ${\gamma }_0$, ${\gamma }_k$ and ${\gamma }_{e^{-}}$ one can use the normalization conditions:

${\displaystyle \sum _{k,c,i}{\displaystyle \int \left(\frac{1}{2}{m}_{kc}{\mathrm{c}}^2+{\epsilon }_{kci}\right)}{\tilde{f}}_{kci}^{\left(0\right)}d\mathrm{c}}+{\displaystyle \int \frac{1}{2}{m}_{e^{-}}{\mathrm{c}}^2{\tilde{f}}_{e^{-}}^{\left(0\right)}d\mathrm{c}}=e\left(\mathrm{r},t\right),(19)$

${\displaystyle \sum _{c,i}{\displaystyle \int {\tilde{f}}_{kci}^{\left(0\right)}d\mathrm{c}}={\tilde{n}}_k\left(\mathrm{r},t\right)},k=\overline{1,k_{\text{*}}},(20)$

${\displaystyle \sum _{k,c,i}\left(N\left(k\right)-c\right){\displaystyle \int {\tilde{f}}_{kci}^{\left(0\right)}d\mathrm{c}}+{\displaystyle \int {\tilde{f}}_{e^{-}}^{\left(0\right)}d\mathrm{c}}}={\tilde{n}}_{e^{-}}\left(\mathrm{r},t\right).(21)$

Here $e\left(\mathrm{r},t\right)$, ${\tilde{n}}_k\left(\mathrm{r},t\right)$ ($k=\overline{1,k_{\text{*}}}$) and ${\tilde{n}}_{e^{-}}\left(\mathrm{r},t\right)$ are the values of the total energy of all particles (translational and internal), the total numbers of the nuclei $A_k^{\text{*}}$ ($k=\overline{1,k_{\text{*}}}$) and the electrons $e^{-}$ (both bound and free) in the unit volume. If the translational energy of the unit volume is defined as $\left(3/2\right)n^{\left(0\right)}{k}_{B}T$, where

$n^{\left(0\right)}={\displaystyle \sum _{k,c,i}{n}_{kci}^{\left(0\right)}+n_{e^{-}}^{\left(0\right)}}={\displaystyle \sum _{k,c,i}{\displaystyle \int {\tilde{f}}_{kci}^{\left(0\right)}d\mathrm{c}}+{\displaystyle \int {\tilde{f}}_{e^{-}}^{\left(0\right)}d\mathrm{c}}},(22)$

$k_B$ is the Boltzmann constant, T is the temperature of gas mixture, then relation (19) allows us to obtain the equality ${\gamma }_0=-1/\left(k_{B}T\right)$.

3 System of the Macroscopic Conservation Equations

The equations for the macroscopic parameters $\mathrm{v}\left(\mathrm{r},t\right)$, $e\left(\mathrm{r},t\right)$, ${\tilde{n}}_k\left(\mathrm{r},t\right)$ ($k=\overline{1,k_{\text{*}}}$) and ${\tilde{n}}_{e^{-}}\left(\mathrm{r},t\right)$ are derived from Eqs 15, 16.

The equation of momentum conservation is obtained as a sum of two relations. One of them follows from the kinetic Eq. 15, after multiplying them by $m_{kc}\mathrm{c}$, integrating over velocity c and summing over $i,c,k$. Other relation follows from Eq. 16 after multiplying it by $m_{e^{-}}\mathrm{c}$ and integrating over c. Thus, in that way, we obtain the equation:

$\mathit{\varrho }\frac{d\mathrm{v}}{dt}=\mathit{\varrho }\mathrm{F}-\overrightarrow{\nabla }\overleftrightarrow{P},(23)$

where

$\mathit{\varrho }\mathrm{F}={\displaystyle \sum }_{k,c,i}{m}_{kc}{\mathrm{F}}_{kc}{n}_{kci}^{\left(0\right)}+m_{e^{-}}{\mathrm{F}}_{e^{-}}{n}_{e^{-}}^{\left(0\right)},(24)$

$\overleftrightarrow{P}={\displaystyle \sum _{k,c,i}{\displaystyle \int {\tilde{f}}_{kci}{m}_{kc}\mathrm{cc}d\mathrm{c}}+{\displaystyle \int {\tilde{f}}_{e^{-}}{m}_{e^{-}}\mathrm{cc}d\mathrm{c}}}(25)$

is the stress tensor.

The equation of total energy conservation is derived similarly, combining two parts. One of them follows from Eq. 15, after multiplying them by $m_{kc}\left({\mathrm{c}}^2/2\right)+{\epsilon }_{kci}$, integrating over c and summing over $i,c,k$. Other relation follows from Eq. 16, after multiplying it by $m_{e^{-}}{\mathrm{c}}^2/2$ and integrating over c. Thus, in that way, we obtain equation:

$\frac{de}{dt}+e\overrightarrow{\nabla }\cdot \mathrm{v}+\overrightarrow{\nabla }\cdot \mathrm{q}+\overleftrightarrow{P}:\overrightarrow{\nabla }\mathrm{v}=0,(26)$

where

$\mathrm{q}={\displaystyle \sum _{k,c,i}{\displaystyle \int {\tilde{f}}_{kci}\left(\frac{m_{kc}{\mathrm{c}}^2}{2}+{\epsilon }_{kci}\right)}}\mathrm{c}d\mathrm{c}+{\displaystyle \int {\tilde{f}}_{e^{-}}\frac{m_{e^{-}}{\mathrm{c}}^2}{2}}\mathrm{c}d\mathrm{c}(27)$

is the transport energy flux.

The equations for the conservation of the nuclei $A_k^{\text{*}}$ numbers ${\tilde{n}}_k$ ($k=\overline{1,k_{\text{*}}}$) follow from the kinetic Eq. 15 after integrating them over the velocity c and summing over the subscripts i and c. Thus, in that way, we obtain equations:

$\frac{d{\tilde{n}}_k}{dt}+{\tilde{n}}_k\overrightarrow{\nabla }\cdot \mathrm{v}+\overrightarrow{\nabla }\cdot {\mathrm{q}}_k=0,k=\overline{1,k_{\text{*}}},(28)$

where

${\mathrm{q}}_k={\displaystyle \sum _{c,i}{\tilde{f}}_{kci}\mathrm{c}d\mathrm{c}},k=\overline{1,k_{\text{*}}},(29)$

are the transport fluxes of the nuclei $A_k^{\text{*}}$.

Derivation of the conservation equation for the total number of electrons ${\tilde{n}}_{e^{-}}$ (both bound and free) is also a two-step procedure. First, the kinetic Eq. 15 are integrated over the velocity c, summed over i, multiplied by $\left(N\left(k\right)-c\right)$ and summed over subscripts c and k. Other relation follows from Eq. 16 after integrating it over the velocity c. Then, two equations are summed. Thus, equation for the total number ${\tilde{n}}_{e^{-}}$ of the electrons (both bound and free) in the unit volume can be written in the form

$\frac{d{\tilde{n}}_{e^{-}}}{dt}+{\tilde{n}}_{e^{-}}\overrightarrow{\nabla }\cdot \mathrm{v}+\overrightarrow{\nabla }\cdot {\mathrm{q}}_{e^{-}}=0,(30)$

where

${\mathrm{q}}_{e^{-}}={\displaystyle \sum _{k,c,i}\left(N\left(k\right)-c\right){\displaystyle \int {\tilde{f}}_{kci}\mathrm{c}d\mathrm{c}}+{\displaystyle \int {\tilde{f}}_{e^{-}}\mathrm{c}d\mathrm{c}}}(31)$

is the transport flux of the electrons.

One may note that the continuity equation for density ϱ in the ionized gas mixtures is the consequence of Eqs 28, 30. Indeed, the equation

$\frac{d\mathit{\varrho }}{dt}+\mathit{\varrho }\overrightarrow{\nabla }\cdot \mathrm{v}=0(32)$

is obtained after the addition of the multiplied by the nuclei masses $m_k^{\text{*}}$Eq. 20 and multiplied by the electron mass $m_{e^{-}}$Eq. 30, since

$\mathit{\varrho }={\displaystyle \sum _{k=1}^{k_{\text{*}}}{m}_k^{\text{*}}{\tilde{n}}_k+m_{e^{-}}{\tilde{n}}_e},$

${\displaystyle \sum _{k=1}^{k_{\text{*}}}{m}_k^{\text{*}}\left(\overrightarrow{\nabla }\cdot {\mathrm{q}}_k\right)+m_{e^{-}}\left(\overrightarrow{\nabla }\cdot {\mathrm{q}}_{e^{-}}\right)}=\overrightarrow{\nabla }\cdot \left({\displaystyle \sum _{k=1}^{k_{\text{*}}}{m}_k{\mathrm{q}}_k+m_{e^{-}}{\mathrm{q}}_{e^{-}}}\right),$

and

${\displaystyle \sum _{k=1}^{k_{\text{*}}}{m}_k{\mathrm{q}}_k+m_{e^{-}}{\mathrm{q}}_{e^{-}}}={\displaystyle \sum _{k,c,i}{\displaystyle \int {\tilde{f}}_{kci}\left(m_k+\left(N\left(k\right)-c\right)m_{e^{-}}\right)}}\mathrm{c}d\mathrm{c}+{\displaystyle \int {\tilde{f}}_{e^{-}}{m}_{e^{-}}\mathrm{c}d\mathrm{c}=0}.(33)$

The macroscopic Eqs 23, 26, 28 and 30 do not differ from the corresponding conservation equations which can be obtained from the kinetic equations of the Boltzmann’s type. To close the system of Eqs 23, 26, 28 and 30, it is necessary to specify the stress tensor $\overleftrightarrow{P}$ and fluxes q, ${\mathrm{q}}_k$ ($k=\overline{1,k_{\text{*}}}$) and ${\mathrm{q}}_{e^{-}}$. The dependencies of these transport terms on the distribution functions ${\tilde{f}}_{kci}\left(\mathrm{r},\mathrm{c},t\right)$ and ${\tilde{f}}_{e^{-}}\left(\mathrm{r},\mathrm{c},t\right)$ are given by Eqs 25, 27, 29, 31.

4 Equilibrium and Non-equilibrium Solutions of the Model Kinetic Equations

The distribution functions Eq. 17 and Eq. 18 are the equilibrium solutions of Eqs 15, 16.

If parameters ${\gamma }_0=-1/\left(k_{B}T\right)$, $x_k=e^{{\gamma }_k}$ and $y=e^{{\gamma }_{e^{-}}}$ are determined from Eqs 19–21, then for the equilibrium concentrations of particles $A_{kc}$ and free electrons $e^{-}$ we obtain formulae (Rydalevskaya, 2017)

$n_{kc}=Z_{kc}\left(T\right)x_k{y}^{N\left(k\right)-c},k=\overline{1,k_{\ast }},c=\overline{0,N\left(k\right)},$

$n_{e^{-}}=Z_{e^{-}}\left(T\right)y.$

For the calculation of the equilibrium composition the gas mixture under consideration it is necessary to determine the partition functions $Z_{kc}\left(T\right)$ ($k=\overline{1,k_{\text{*}}}$, $c=\overline{0,N\left(k\right)}$) and $Z_{e^{-}}\left(T\right)$. For this, one can use a finite set of electronic levels ¹ or the partition functions which were calculated earlier [see (Giordano et al., 1994; D'Angola et al., 2008)].

The temperature dependencies of the equilibrium relative concentrations of the atoms, ions and free electrons in the monoatomic ionized nitrogen at atmospheric pressure are shown in (Rydalevskaya, 2017). In the present paper the such temperature dependencies one can show for the ionized mixture monoatomic oxygen (see Figure 1).

FIGURE 1

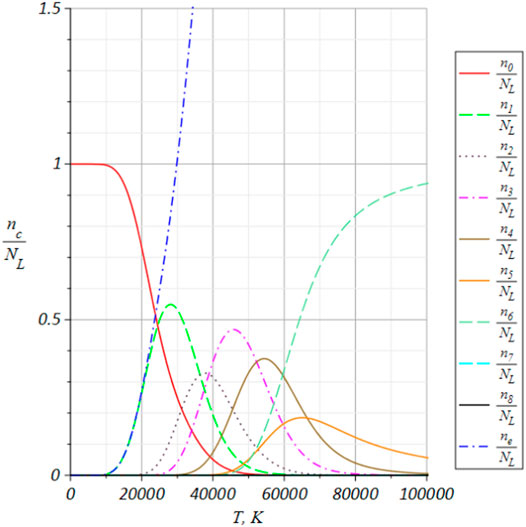
FIGURE 1. The temperature dependencies of the equilibrium relative concentrations of the atoms, ions and free electrons in the monoatomic ionized oxygen ($N_L$ is Loschmidt number).

In non-equilibrium conditions one can turn in model equations to the dimensionless form.

In the case when a mean time θ, characterizing the rate of the macroscopic parameters variation, is known, one can introduce the dimensionless parameter $\epsilon =\tau /\theta$.

If $\epsilon \ll 1$, the approximate solutions of Eq. 15 and Eq. 16 can be represented as the series in the small parameter ε:

${\widehat{f}}_{kci}\left(\mathrm{r},\mathrm{c},t\right)={\widehat{f}}_{kci}^{\left(0\right)}+{\displaystyle \sum _{n=1}^{\infty }{\epsilon }^n{\widehat{f}}_{kci}^{\left(n\right)}},i=\overline{0,i_k^{\text{*}}},c=\overline{0,N\left(k\right)},k=\overline{1,k_{\text{*}}},(34)$

${\widehat{f}}_{e^{-}}\left(\mathrm{r},\mathrm{c},t\right)={\widehat{f}}_{e^{-}}^{\left(0\right)}+{\displaystyle \sum _{n=1}^{\infty }{\epsilon }^n{\widehat{f}}_{e^{-}}^{\left(n\right)}}.(35)$

Under these conditions, for the solution of the model Eq. 15 and Eq. 16 one can use the Chapman–Enskog method (CEM), see, for example, (Chapman and Cowling, 1970; Ferziger and Kaper, 1972; Vallander et al., 1977; Giovangigli, 1999; Rydalevskaya, 2003; Nagnibeda and Kustova, 2009).

Substituting the expansions Eq. 26 and Eq. 27 in dimensionless model equations Eq. 7 and Eq. 8, equating the terms under the ε identical degrees and reverting to dimensionless variables, we can write

$f_{kci}^{\left(n\right)}\left(\mathrm{r},\mathrm{c},t\right)=-\tau {\tilde{D}}_{kci}^{\left(n\right)}\left(f_{kci}^{\left(0\right)},\dots ,f_{kci}^{\left(n-1\right)}\right),n\ge 1,(36)$

$f_{e^{-}}^{\left(n\right)}\left(\mathrm{r},\mathrm{c},t\right)=-\tau {\tilde{D}}_{e^{-}}^{\left(n\right)}\left(f_{e^{-}}^{\left(0\right)},\dots ,f_{e^{-}}^{\left(n-1\right)}\right),n\ge 1.(37)$

The operators $D_{kci}^{\left(n\right)}$ and $D_{e^{-}}^{\left(n\right)}$ are derived using traditional procedures of CEM (Groppi and Spiga, 2004; Ferziger and Kaper, 1972; Vallander et al., 1977; Giovangigli, 1999; Groppi and Spiga, 2004; Loureiro and Amorim, 2016).

The solutions of Eqs 15, 16 in the zero-order approximation of CEM coincide with the equilibrium distribution functions $f_{kci}^{\left(0\right)}\left(\mathrm{r},\mathrm{c},t\right)$ (17) and $f_{e^{-}}^{\left(0\right)}\left(\mathrm{r},\mathrm{c},t\right)$ (18). These functions must satisfy the normalization conditions Eqs. 19–21. Gas-dynamic parameters $\mathrm{v}\left(\mathrm{r},t\right)$, $e\left(\mathrm{r},t\right)$, ${\tilde{n}}_k\left(\mathrm{r},t\right)$ ($k=\overline{1,k_{\text{*}}}$) and ${\tilde{n}}_{e^{-}}\left(\mathrm{r},t\right)$ are determined from Eqs 23, 26, 28, 30. Under the equilibrium conditions, the transport terms Eqs. 25, 27, 2931 have the form:

$\overleftrightarrow{P}=p\Vert \begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\Vert ,\mathrm{q}=0,{\mathrm{q}}_k=0(k=\overline{1,k_{\text{*}}}),{\mathrm{q}}_{e^{-}}=0,(38)$

where $p=-n^{\left(0\right)}/{\gamma }_0=n^{\left(0\right)}{k}_{B}T$ is a pressure (the total number of the particles $n^{\left(0\right)}$ is given in Eq. 22).

As a result, for the description of the local equilibrium flows of ionized gas mixtures we have the set of conservation equations:

$\frac{d\mathrm{v}}{dt}=\mathrm{F}-\frac{1}{\mathit{\varrho }}\overrightarrow{\nabla }p,(39)$

$\frac{de}{dt}=-\left(e+p\right)\overrightarrow{\nabla }\cdot \mathrm{v},(40)$

$\frac{d{\tilde{n}}_k}{dt}=-{\tilde{n}}_k\overrightarrow{\nabla }\cdot \mathrm{v},k=\overline{1,k_{\text{*}}},(41)$

$\frac{d{\tilde{n}}_{e^{-}}}{dt}=-{\tilde{n}}_{e^{-}}\overrightarrow{\nabla }\cdot \mathrm{v}.(42)$

In the present situation, one can consider that Eqs 39–42 provide the closed description of the local equilibrium flows of multiply ionized monoatomic gases mixtures. One can note that the systems of these equations allow us to deduce the series of integral relations and to obtain the analytical formulae for the study of the ionization processes influence on adiabatic coefficient and a sound velocity (Romanova and Rydalevskaya, 2017; Romanova and Rydalevskaya, 2018).

After the transition to the following approximation of CEM, we can obtain the solution of the model kinetic Eq. 15 and Eq. 16 in first-order approximation. Under these conditions relations Eq. 36 and Eq. 37 have the form:

${\tilde{f}}_{kci}^{\left(1\right)}=-\tau {\tilde{D}}^{\left(1\right)}\left({\tilde{f}}_{kci}^{\left(0\right)}\right),i=\overline{0,i_{kc}^{\text{*}}},c=\overline{0,N\left(k\right)},k=\overline{1,k_{\text{*}}},(43)$

${\tilde{f}}_{e^{-}}^{\left(1\right)}=-\tau {\tilde{D}}^{\left(1\right)}\left({\tilde{f}}_{e^{-}}^{\left(0\right)}\right).(44)$

Relations Eq. 17 and Eq. 43 allow us to find the distribution functions for the atoms $A_{k0}$ and ions $A_{kc}$ ($k=\overline{1,k_{\text{*}}}$, $c=\overline{0,N\left(k\right)}$). Relations Eq. 18 and Eq. 44 allow us to find the distribution functions for free electrons $e^{-}$. After the substitution of these functions in Eqs 25, 27, 29, 31 we obtain the approximate expressions for the stress tensor $\overleftrightarrow{P}$ and the fluxes q, ${\mathrm{q}}_k$ ($k=\overline{1,k_{\text{*}}}$) and ${\mathrm{q}}_{e^{-}}$. One can see that the transport coefficients of the energy, nuclei and electrons are proportional to the relaxation time τ in this approximation and depend on the parameters $e\left(\mathrm{r},t\right)$, ${\tilde{n}}_k\left(\mathrm{r},t\right)$ ($k=\overline{1,k_{\text{*}}}$) and ${\tilde{n}}_{e^{-}}\left(\mathrm{r},t\right)$ which are determined from the solution of the Eqs 39–42.

5 Conclusions

In the paper the model kinetic equations for the study of the weakly non-equilibrium flows of multi-component plasma are proposed.

These equations are the generalization of BGK model where the equilibrium distribution functions of the atoms and ions depend on the number N of corresponding chemical element in the periodic system and electric charge of the particle [see (Rydalevskaya, 2017)].

It is shown that such model equations allow one to derive the systems of the conservation equations for the energy, momentum, the numbers of the nuclei of different species and the electrons (both bound and free).

It is shown that these systems provide the closed description for local equilibrium flows of the plasma with multiple ions species.

For the solution of the model kinetic equations under consideration the Chapman–Enskog method is proposed.

It should be noted that an application of the model kinetic Eq. 15, Eq. 16 with local equilibrium functions Eq. 17 and Eq. 18 can be very important when the ionization degree of gas medium and the probabilities of the electronic energy excitation, ionization and neutralization of microscopic particles are unknown.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

MR proposed a generalization of the BGK model. YV obtained the solution of the model kinetic equations. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank E. Kustova for useful advices.

Footnotes

¹WEBBOOK.NIST.GOV/CHEMISTRY

References

Arslanbekov, R., and Kolobov, V. (2018). Adaptive Kinetic-Fluid Models for Expanding Plasmas. J. Phys.: Conf. Ser. 1031, 012018. doi:10.1088/1742-6596/1031/1/012018

CrossRef Full Text | Google Scholar

Bhatnagar, P. L., Gross, E. P., and Krook, M. (1954). A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 94, 511–525. doi:10.1103/PhysRev.94.511

CrossRef Full Text | Google Scholar

Boltzman, L. (1964). Lectures on Gas Theory. Berkley: University of California Press.

Braginskii, S. I. (1958). Transport Phenomena in a Completely Ionized Two-Temperature Plasma. Journal of Experimental and Theoretical Physics 6, 358.

Google Scholar

Bruno, D., Capitelli, M., Catalfamo, C., and Laricchiuta, A. (2008). Cutoff Criteria of Electronic Partition Functions and Transport Properties of Atomic Hydrogen Thermal Plasmas. Physics of Plasmas 15, 112306. doi:10.1063/1.3012566

CrossRef Full Text | Google Scholar

Bruno, D., Capitelli, M., Catalfamo, C., and Laricchiuta, A. (2007). Transport of Internal Electronic Energy in Atomic Hydrogen Thermal Plasmas. Physics of Plasmas 14, 072308. doi:10.1063/1.2752518

CrossRef Full Text | Google Scholar

Capitelli, M., Colonna, G., and D’Angola, A. (2012). Fundamental Aspects of Plasma Chemical Physics. New York: Springer.

Chapman, S., and Cowling, T. (1970). The Mathematical Theory of Non-Uniform Gases. Cambridge: Cambridge Univ. Press.

D'Angola, A., Colonna, G., Gorse, C., and Capitelli, M. (2008). Thermodynamic and transport properties in equilibrium air plasmas in a wide pressure and temperature range. Eur. Phys. J. D. 46, 129–150. doi:10.1140/epjd/e2007-00305-4

CrossRef Full Text | Google Scholar

Ferziger, J. H., and Kaper, H. G. (1972). Mathematical Theory of Transport Processes in Gases. Amsterdam: North Holland Publ. Co.

Giordano, D., Capitelli, M., and Colonna, G. (1994). Tables of Internal Partition Functions and Thermodynamics Properties of High-Temperature Air Species from 50 K to 100000 K. Paris: European Space Agency (ESA).

Giovangigli, V. (1999). Multicomponent Flow Modeling. Boston: Birkhauser.

Groppi, M., and Spiga, G. (2004). A Bhatnagar-Gross-Krook-type approach for chemically reacting gas mixtures. Physics of Fluids 16, 4273–4284. doi:10.1063/1.1808651

CrossRef Full Text | Google Scholar

Hanson, F. B., and Morse, T. F. (1967). Kinetic Models for a Gas with Internal Structure. Phys. Fluids 10, 345–353. doi:10.1063/1.1762114

CrossRef Full Text | Google Scholar

Istomin, V. A., and Kustova, E. V. (2014). Effect of Electronic Excitation on High-Temperature Flows behind Strong Shock Waves. AIP Conference Proceedings 1628, 1221–1228. doi:10.1063/1.4902731

CrossRef Full Text | Google Scholar

Istomin, V. A., and Kustova, E. V. (2017). State-Specific Transport Properties of Partially Ionized Flows of Electronically Excited Atomic Gases. Chemical Physics 485-486, 125–139. doi:10.1016/j.chemphys.2017.01.012

CrossRef Full Text | Google Scholar

Istomin, V. A., and Kustova, E. V. (2017). Transport coefficients and heat fluxes in non-equilibrium high-temperature flows with electronic excitation. Physics of Plasmas 24, 022109. doi:10.1063/1.4975315

CrossRef Full Text | Google Scholar

Loureiro, J., and Amorim, J. (2016). Kinetics and Spectroscopy of Low Temperature Plasmas. Switzerland: Springer. doi:10.1007/978-3-319-09253-9

CrossRef Full Text

Morse, T. F. (1964). Kinetic Model for Gases with Internal Degrees of Freedom. Phys. Fluids 7, 159–169. doi:10.1063/1.1711128

CrossRef Full Text | Google Scholar

Nagnibeda, E. A., and Kustova, E. V. (2009). Non-Equilibrium Reacting Gas Flows. Berlin-Heidelberg: Springer-Verlag.

Romanova, M. S., and Rydalevskaya, M. A. (2017). Determination of equilibrium composition of thermally ionized monoatomic gas under different physical conditions. Tech. Phys. 62, 677–683. doi:10.1134/S1063784217050243

CrossRef Full Text | Google Scholar

Romanova, M. S., and Rydalevskaya, M. A. (2018). Motion integrals and sound velocity in local equilibrium flows of ionized monatomic gases. Mathematics. Mechanics. Astronomy 5, 310–320.

Google Scholar

Rydalevskaya, M. A. (2017). Simplified method for calculation of equilibrium plasma composition. Physica A: Statistical Mechanics and its Applications 476, 49–57. doi:10.1016/j.physa.2017.02.025

CrossRef Full Text | Google Scholar

Rydalevskaya, M. A. (2003). Statistical and Kinetic Models in Physical-Chemical Gas Dynamics. St. Petersburg: St. Petersburg Univ. Press.

Simakov, A. N., and Molvig, K. (2016). Hydrodynamic Description of an Unmagnetized Plasma with Multiple Ion Species. I. General Formulation. Phys. Plasmas 23, 032115. doi:10.1063/1.4943894

CrossRef Full Text | Google Scholar

Vallander, S. V., Nagnibeda, E. A., and Kustova, E. V. (1977). Some Quations of the Kinetic Theory of the Chemical Reacting Gas Mixtures. Leningrad: Leningrad Univ. Press.

Zhdanov, V. M (2009). Transport Phenomena in Multi-Component Plasma. Moscow: Fizmatlit Publ.

Zhdanov, V. M., and Stepanenko, A. A. (2016a). Kinetic Theory of Transport Processes in Partially Ionized Reactive Plasma, I: General Transport Equations. Physica A: Statistical Mechanics and its Applications 446, 35–53. doi:10.1016/j.physa.2015.11.012

CrossRef Full Text | Google Scholar

Zhdanov, V. M., and Stepanenko, A. A. (2016b). Kinetic Theory of Transport Processes in Partially Ionized Reactive Plasma, II: Electron Transport Properties. Physica A: Statistical Mechanics and its Applications 461, 310–324. doi:10.1016/j.physa.2016.05.058

CrossRef Full Text | Google Scholar