Past, Present, and Future of the Scaling Relations of Galaxies and Active Galactic Nuclei

We review the properties of the established Scaling Relations (SRs) of galaxies and active galactic nuclei (AGN), focusing on their origin and expected evolution back in time, providing a short history of the most important progresses obtained up to now and discussing the possible future studies. We also try to connect the observed SRs with the physical mechanisms behind them, examining to what extent current models reproduce the observational data. The emerging picture clarifies the complexity intrinsic to the galaxy formation and evolution process as well as the basic uncertainties still affecting our knowledge of the AGN phenomenon. At the same time, however, it suggests that the detailed analysis of the SRs can profitably contribute to our understanding of galaxies and AGN.

1 Introduction

With the term “Scaling Relations” (hereafter, SRs) astronomers indicate a series of correlations between the parameters describing the physical characteristics of galaxies. These can be radii, mean velocities of stars and gas, stellar population proxies as colors or mass-to-light ratios, density and total amount of gas and dust, black-hole masses, etc.

The study of SRs started when Edwin Hubble presented his famous tuning fork diagram for the morphological classification of galaxy types (Hubble, 1936). Very soon this beautiful scheme prompted the idea that the morphological sequence is driven by some physical parameters, such as mass, luminosity, color, angular momentum, and gas content, that progressively change along the sequence determining the observed types. Attempts to build a “physical” classification of galaxies characterized the following years [see e.g. (de Vaucouleurs, 1962; Brosche, 1973; Bender et al., 1992; Cappellari et al., 2011a; Kormendy and Bender, 2012a)].

The first questions arising from the morphological sequence concerned the different flattening observed among galaxies (Sandage et al., 1970). In this work the authors tried to answer why some galaxies have a flat disk while others do not and, in connection with this, why the spheroidal components of all galaxies contain only old stars, why S0’s and early-type spirals have lost their spiral arms and why up to 50% of galaxies are barred.

The basic idea was that the Hubble sequence is essentially an angular momentum sequence (Brosche, 1970; Sandage et al., 1970), where star formation (SF) occurs at increasing gas density. The spread of color within the morphological types was attributed to the different star formation rates (SFR) inside galaxies (Searle et al., 1973) and to the different stellar populations inside them (King, 1971).

Quite soon however, it was clear that the parameters describing the properties of galaxies can be considered a mathematical manifold (Brosche, 1973), because several correlations among them are in place. If we consider for example the galaxy luminosity (L), we observe that it correlates with: the effective radius (R_e; the radius enclosing half the total luminosity) (Fish, 1964), the central velocity dispersion of the stars (σ) (hereafter Faber-Jackson FJ relation (Faber and Jackson, 1976)), the effective surface brightness (I_e; the mean surface brightness inside R_e) (Kormendy, 1977; Binggeli et al., 1984), color (Sandage, 1972), and line-strength index (Mg₂) (Terlevich et al., 1981).

The great number of observed correlations promptly arose other fundamental questions. What are the most fundamental correlations? What parameters better describe their physics? How do the SRs evolve with time?

In an attempt to answer these questions Guzman et al. (1993) claimed that only three fundamental relations are necessary to describe all global SRs among the spheroidal systems, while Disney et al. (2008) found a striking correlation among five basic parameters that govern the galactic dynamics (R₅₀, R₉₀, M_HI, M_d, and L: respectively the 90%-light radius, the 50%-light radius, the H I mass, the dynamical mass, and the luminosity) and the color. The principal component analysis (PCA) further showed that the first eigenvector dominates the correlations among the parameters and can explain up to 83% of the variance in the data.

Unfortunately, the next investigations demonstrated that the SRs cannot be used as a basis for a theoretical understanding of galaxy formation and evolution. They can be used only “a posteriori” to verify the ability of theories in reproducing the observed correlations. Galaxies are complex and evolving systems requiring much complex statistical tools than simple PCA (Fraix-Burnet et al., 2019).

In other words the Hubble classification is only a qualitative scheme, influenced by subjective decisions and difficult to use for distant galaxies. The sequence rests only on the morphological parameters measured in the visual bands, while galaxies are complex systems that can be observed from X-rays to radio wavelengths. In addition a lot of information, such as chemical compositions, stellar populations, central black hole masses, kinematics of stars and gas, etc., can be obtained from the spectral analysis (Sandage, 2005).

Recently, new support to the study of the SRs was gained thanks to the data of the large sky surveys, such as the Sloan Digital Sky Survey (SDSS (Abazajian et al., 2003)), SAURON (Bacon et al., 2001), WINGS (Fasano et al., 2006), ATLAS3D (Cappellari et al., 2011b), CALIFA (Sánchez et al., 2012), SAMI (Croom et al., 2012), MaNGA (Bundy, 2015), etc. These surveys have provided data for thousands of galaxies permitting a more robust statistical analysis of the physical drivers behind their formation and evolution. Several SRs, such as the velocity-luminosity or Tully-Fisher relation (hereafter TF (Tully and Fisher, 1977; Courteau et al., 2007)), the Faber-Jackson (FJ) relation (Faber and Jackson, 1976), the I_e − R_e (hereafter Kormendy relation KR (Kormendy, 1977)), the fundamental plane of galaxies (hereafter FP (Djorgovski and Davis, 1987; Dressler et al., 1987; Bender et al., 1992; Bernardi et al., 2003; Cappellari et al., 2006; La Barbera et al., 2008), the bulge mass—black hole (BH) mass relation (Magorrian et al., 1998), the mass-radius (MR) relation (Chiosi et al., 2019) are now robust for the galaxies of the nearby Universe and have now well constrained the physical laws governing the assembly of stellar systems.

On the theoretical side, despite the recent progresses, galaxy formation models are still in difficulties with some basic properties of galaxies. For instance colors, radii (D’Onofrio et al., 2020), structural bimodalities [see e.g. (Dekel and Birnboim, 2006; McDonald et al., 2009)], angular momentum content (Fall and Romanowsky, 2013; Obreschkow and Glazebrook, 2014), variations of the stellar initial mass function (IMF), mass-to-light ratios (Dutton et al., 2011; Cappellari et al., 2012; Smith, 2014), central versus satellite distributions (Rodríguez-Puebla et al., 2015), and others cannot be satisfactorily matched by the models. Some fundamental dynamical tracers of galaxy structure (e.g. the circular velocity of galaxies and stellar-to-halo mass ratio) predicted by the models are still discrepant with observations.

Another remark to keep in mind is that the technical analysis of the SRs must be considered with due caution. The observed relations often depend on a number of factors, last but not least the structural parameter definitions (Courteau, 1996; Courteau, 1997), the environment that could influence the general distribution of galaxies (Mocz et al., 2012), the different fitting algorithms (Courteau et al., 2007; Avila-Reese et al., 2008; Hall et al., 2012) that provide different coefficients, redshift, and peculiar motions of the galaxies in the sample used (Willick et al., 1997; Fernández Lorenzo et al., 2011; Miller et al., 2011), projection effects and bandpass (Aaronson et al., 1986; D’Onofrio et al., 2008; Hall et al., 2012), the morphology of galaxies in the sample (Courteau et al., 2007; Tollerud et al., 2011), the stellar population content (Cappellari et al., 2006; Falcón-Barroso et al., 2011; Cappellari, 2013), the metallicity (Woo et al., 2008a), and the statistical properties of the dark matter (DM) halos [see e.g. Chiosi et al. (2019)].

In general we want to stress that SRs are today universally considered convenient tools to estimate quantities such as distances and masses in an efficient way (when the data sample is large), but most importantly, they permit a much deeper understanding of galaxy structure, formation, and evolution. For example Kassin et al. (2012), by examining the V_rot/σ ratio across redshift, found that galaxies accrete baryons at different rates during evolution. At the same time, Obreschkow and Glazebrook (2014) pointed out the link between the FP and FJ relations with the angular momentum (j), the stellar mass (M_s), and the bulge fraction (β) of spiral galaxies [see also Peebles (1969), Fall (1983)]. Lagos et al. (2017), using cosmological simulations, confirmed the correlation between galaxy mass and specific angular momentum, and the evolution of the M_s − j relation in passive and active galaxies, while Ferrarese et al. (2006a) showed that the correlation of the mass of the BHs and the bulge mass is a key element in favor of the coevolution of the AGN with their host galaxies. Desmond and Wechsler (2017) used the FP to predict the amount of DM in the central regions of elliptical galaxies, while Ouellette et al. (2017) found that the tilt of the FP correlates with the DM fraction of each galaxy and Chiosi et al. (2019) demonstrated that the DM halo growth function is able to shape the mass-radius relation. We will see many other examples of the utility of SRs in this review.

The utility of SRs has not been recognized only for galaxies. They are also very important to understand the central BHs in galaxies and the nature of the active galactic nuclei (AGN). The coevolution of the central black holes and galaxies has been known for more than 20 years [see e.g. (Kormendy and Richstone, 1995; Ferrarese and Merritt, 2000; Gebhardt et al., 2000; Graham et al., 2001; Ferrarese, 2002; Hring and Rix, 2004)]. Even the active nuclei have shown to obey several SRs that are useful to clarify their structure and evolution. We will therefore address in these pages several of these correlations involving the parameters that describe the properties of the central active nucleus in galaxies. This analysis will permit us to conclude that, even in this context, SRs are fundamental tools to infer the physical mechanisms at work in galaxies and AGN.

In conclusion we can say that SRs are fundamental for any theory of galaxy formation and evolution. The current view is that the diversity of galaxies appears to increase rapidly with the instrumental improvements so that a good understanding of their physics requires sophisticated numerical simulations that reproduce realistic objects. The physical processes that operate together during galaxy evolution are numerous and imply that the morphological Hubble sequence is only the first approach to the complex problem of galaxy classification (Fraix-Burnet et al., 2019). The SRs are the network of properties that the modern statistical tools and theoretical simulations must be able to explain and reproduce. How are their properties intertwined? How do they evolve over time? This is the challenge of future investigations.

In this work we will review some of the established SRs of galaxies and AGN, discussing our current understanding of their origin and evolution. The first six sections are dedicated to the SRs originating from the coupling of galaxies dynamics and stellar population properties. We start in Section 2 with the FJ relation, addressing next the TF (Section 3), the KR (Section 4), the MR relation (Sections 5, 6), and the FP (Section 7). We have analyzed the MR relation with more details because of its cosmological implication. We go on with the color-magnitude (CM) relation (Section 8), the relation between the star formation (and star formation history) with the mass and initial halo density in galaxies of different morphological types (Section 9), the mass-metallicity relation (Section 10). They all provide a useful insight of the stars and gas evolutionary properties. Then, we address the correlation among the DM halos and baryonic matter properties (Section 11) and the angular momentum–mass relationship (Section 12). Finally, we enter into the AGN domain, starting with a discussion of the correlations of the black-hole masses with the galaxy host properties (Section 13) and the most popular correlations observed among AGN (Sectiond 14, 15). Some conclusions are finally drawn in Section 16.

2 The Faber-Jackson Relation

The FJ relation is by far the most misunderstood correlation between galaxies parameters. Discovered by Faber and Jackson (1976), it is a correlation between the total luminosity of early-type galaxies (ETGs) L and the central velocity dispersion of their stars σ. The authors themselves did not attribute any physical significance to this relation, considering the observed trend a byproduct of the virial theorem, i.e. a translation of the correlation between mass and velocity dispersion, induced by the strong link between mass and luminosity.

The first fit on a sample of 25 ETGs gave L ∝ σ⁴, while further investigations provided values of the FJ parameters (slope and scatter) that depend on the magnitude range of the sample considered (Nigoche-Netro et al., 2010) (as in the case of the FP (D’Onofrio et al., 2008)). The slope varies from ∼ 2 to ∼ 5 and the scatter of the residuals ( ∼ 0.30) correlates with the effective radius R_e (in the sense that smaller than average objects have larger velocity dispersion) and with the mass-to-light ratio (D’Onofrio et al., 2020; Cappellari et al., 2013). The correlation however extends over 8 dex in luminosity, from Globular Clusters to Galaxy Clusters. A small curvature seems to exist at M_V ∼ − 21.5 mag, separating bright and faint objects. The bright galaxies have a slope of around 4–5, while the faint ones have it much closer to 2–3 (Choi et al., 2014; D’Onofrio and Chiosi, 2020).

The FJ is not one of the orthogonal projections of the FP relation $\sigma \propto I_e^a{R}_e^b$ (with a scatter of ∼ 0.09 in R_e). In the FJ relation the variable L includes both R_e and I_e. We can better say that it is a sort of 2D version of the FP¹. The deep analysis of Nigoche-Netro et al. (2011) concluded that the scatter of the FJ depends on the history of galaxies, i.e. on the number and nature of the transformations that have affected the galaxies along their life times (collapse, accretion, interaction, and merging). The investigations of ETGs from the ATLAS-3D survey have indeed shown that many of these galaxies possess high rotational velocities, while slow-rotating objects often present counter-rotating cores. There are multiple channels of formation, where secular processes, disk instability, mergers, and gas accretion are possible mechanisms. Star formation events are sometimes observed even in the brightest cluster galaxies (BCGs), today almost quenched, down to low redshifts [see e.g. (Liu et al., 2012; Oliva-Altamirano et al., 2015)].

Despite this complexity there is an ample consensus on the fact that ETGs are approximately virialized object from a dynamical point of view. Since luminosity is in general a quite good tracer of stellar mass, the deviation from the expected virial slope of 2 was explained with a smooth transition of the zero-point of the relation, essentially due to a variation of the mean mass-to-light ratio. This is the same explanation given for the observed tilt of the FP (see Section 7).

The existence of a physical correlation between luminosity and velocity dispersion of stars has never been considered a concrete possibility. Why should the global stars emission be aware of the mean stars velocity in a galaxy? This appears as an unphysical possibility. Recently, however, D’Onofrio et al. (2020) have opened the door to this remote possibility. The idea is that the total luminosity of galaxies is essentially the result of the stars assembly, of the SF history (SFH) and the stellar evolution. Luminosity is a nonmonotonic function of star’s evolution. In 1973 Brosche (1973) first suggested a failing of the simple SF law of Schmidt (Schmidt, 1959a), based only on the gas density ρ, favoring a scenario in which the SF is a function ∼ f(ρv^β), where v is the velocity of stars and β ∼ 3.6 for most of the galaxies. Stars born in large gas aggregates have a characteristic velocity that depends on the physical condition of the galaxy during the SF event (collapse, shock, and merging, etc.). For this reason the global SF might keep memory of the velocity of this gas. The SFH could therefore preserve such information, leading to a “physical” connection between L and σ.

The proof that such a physical link exists between luminosity and stellar velocity dispersion is encrypted in the appearance of some SRs. The way to demonstrate this is to write the FJ relation in this way:

$L=L_0^{\prime }{\sigma }^{\beta },(1)$

where $L_0^{\prime }$ and β are now fully variable parameters that depend on the complex channel of stars assembly inside galaxies (new SF, accretion and removal events, etc.), in other words on the complex SFH we mentioned above. The connection of this empirical law (that is valid for a single galaxy and should not be confused with the fit of the whole distribution of ETGs in the FJ relation in which L₀ and β are constant) with the virial theorem is the key to understand the observed distribution of galaxies in the SRs. The MR relation, the KR relation, and the FP relations are in fact perfectly reproduced when the parameters β and $L_0^{\prime }$ change. The data of the Illustris simulation (Vogelsberger et al., 2014) used by D’Onofrio et al. (2020) have shown that the values of β have an ample spectrum, going from large positive values, typical of star-forming objects, to large negative values, typical of passive and quenched objects (quite often the more massive old galaxies). The peak of the distribution is observed at β ∼ 3, i.e. exactly coincident with the slope of the fitted FJ relation (D’Onofrio et al., 2020).

In this new framework the slope of the classical FJ relation is mainly driven by the channel governing the star assembly inside galaxies. The bottom-up scenario of hierarchical merging gives the imprint on the slope of the FJ. Simulations indicate that this slope changes with time. The trend is from a slope equal to ∼ 5 at high redshift to ∼ 3 observed today. In other words there is a progressive convergence toward the value of 2 expected for the virial dynamical equilibrium. This is valid for all SRs involving mass, velocity, and luminosity.

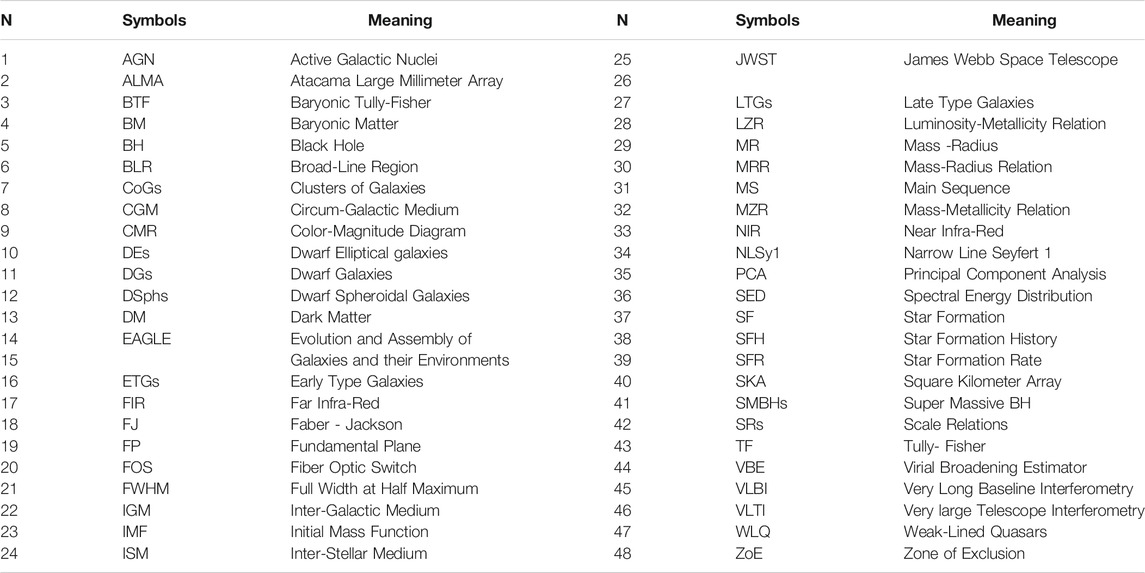
Figure 1 shows the FJ plane, the KR plane, and the MR plane. The gray dots mark the observational data extracted from the WINGS database (Fasano et al., 2006; Moretti et al., 2014). Three artificial galaxies simulated by Illustris are shown with different colors marking their evolution in these planes from z = 4 (blue dot) to z = 1 (green dot) and z = 0 (red dot). Note how the simulation is able to follow the FJ relation, keeping small the scatter of the relation despite the variations occurring in σ and L. This happens because the relation is driven by mass. The classical FJ is essentially a relation between mass and velocity dispersion. Since galaxies are always close to the dynamical equilibrium, the variation expected in luminosity and velocity dispersion, due to SF or merging events, are never bigger than the scatter of the relation ( ∼ 0.3 dex, which corresponds to a factor of 2). The DGs are the systems that are much distant to the virial equilibrium, probably for the strong feedback effects and SF activity still going on in many of them (Chiosi et al., 2019).

FIGURE 1

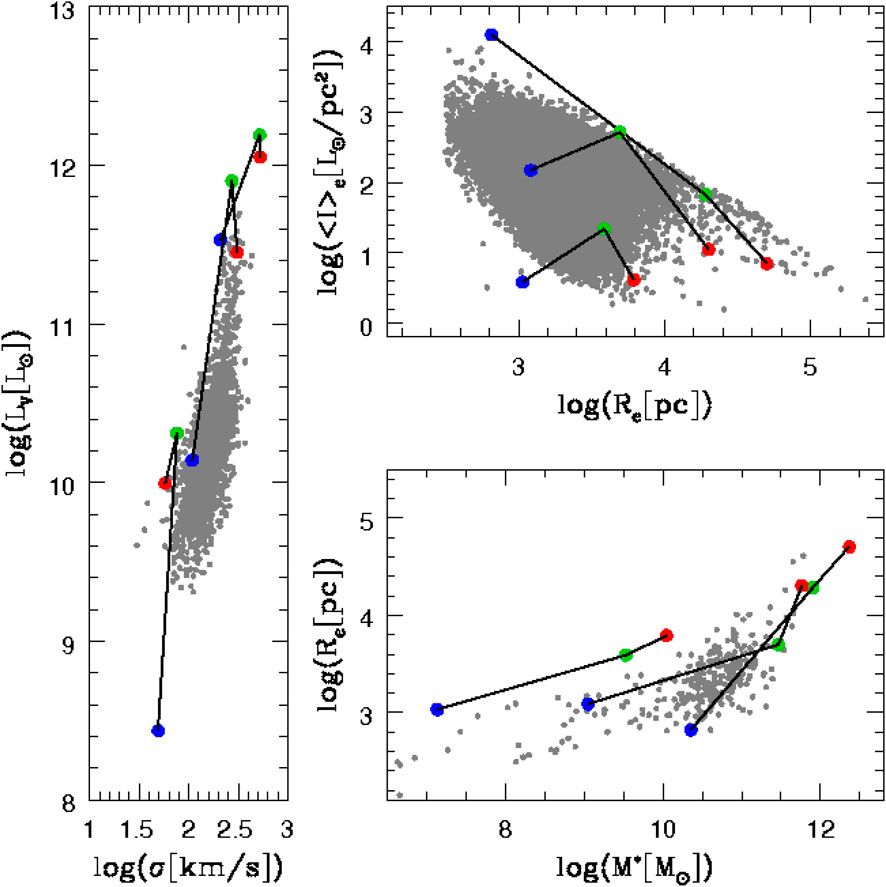
FIGURE 1. Left panel: the log(σ) −   log(L) FJ plane. The gray dots mark the observational data extracted from the WINGS database. The colored bigger points connected by lines are three objects extracted from the Illustris simulation respectively at redshift z = 4 (blue dot), z = 1 (green dot) and z = 0 (red dot). The lines show the evolution of these objects across the cosmic epochs. Right upper panel: the log(R_e) −   log(I_e) KR plane. The WINGS galaxies are in gray and the colored dots are the same objects of the left panel. Right lower panel: the log(M_s) −   log(R_e) MR plane. The symbols used are the same as before. The number of galaxies changes in each panel because masses and velocities are not available for the whole set of ETGs, in particular for the faint objects.

Note how the distribution at z = 0 in the KR and MR planes depends on the evolution of β. This parameter can be approximately estimated by looking at the direction of the lines connecting two redshift epochs (β is the slope of the log(σ) −  log(L) relation). Negative values of β in the FJ plane are those allowed only to quenched galaxies in passive evolution (where L decreases at nearly constant σ). As far as β becomes progressively negative the distributions in the KR and MR planes converge toward the slopes expected for virialized objects ( − 1 in the KR plane and 1 in the MR plane). In particular the tails observed in these two planes are that corresponding to the most massive and bright galaxies now in a quenched state of passive evolution [see Table 4 in D’Onofrio et al. (2020), for more details]. This means that the full virialization in a galaxy can be achieved only when SF and feedback effects are stopped.

The emerging picture from the hierarchical model of galaxy assembly is that the KR and MR relations, that is the linear relations (in log units) visible when the samples contain only massive and bright ETGs, are formed by the tails of massive and large objects appearing after z ∼ 1.5. This is the location of the objects that today are almost quenched and passive. Their SF is over, the systems have reached a full virial configuration.

3 The Tully-Fisher Relation

As we have seen for the FJ relation, the complex process of galaxy assembly has produced some regular SRs, which ultimately suggest a tight connection between the stellar component and the hosting DM halos. The Tully–Fisher relation (TF (Tully and Fisher, 1977)) is another example of a scaling law involving the luminosity of a galaxy [in this case of late-type galaxies (LTGs) spiral galaxies] and the rotation velocities V of stars. The dust-corrected TF relation has the form L ∝ V³ in the optical band, with a slope that steepens toward redder passbands (L ∝ V⁴ in the near-infrared (Verheijen, 1997; Tully et al., 1998)). The variation of the slope with the passband indicates that there is a trend in color and in the stellar M/L ratio with the galaxy mass. This change constrains galaxy formation and evolution models [see e.g. (Cole et al., 2000; Navarro and Steinmetz, 2000; van den Bosch et al., 2000)].

The TF is almost linear in log units for disk galaxies with well-ordered rotation, while objects with disturbed morphology and compact galaxies do not follow the main relation, exhibiting lower rotations at a given stellar mass (Kassin et al., 2007; Kassin et al., 2012). The velocity fields are affected by major merging events or tidal disruptions (Rampazzo et al., 2005; Kronberger et al., 2007; Covington et al., 2010; De Rossi et al., 2012), by accretion of external angular momentum (Brooks et al., 2009; Elmegreen and Burkert, 2010) and/or by disruptive feedback events (Mac Low and Ferrara, 1999; Lehnert et al., 2009). With spirals of the local Universe the TF relation is tight (Verheijen, 2001; Bekeraité et al., 2016; Ponomareva et al., 2017). Galaxies with rising rotation curves and those with declining rotation curve are differently distributed in the TF relation [e.g. (Persic et al., 1996)].

The TF was used to measure the distance of spiral galaxies [see e.g. (Giovanelli et al., 1997)] and to test cosmological models, arguing that its slope, zero-point, and tightness are set by the cosmological evolution of the galactic DM halos (Cole et al., 1994; Eisenstein and Loeb, 1996; Avila-Reese et al., 1998; Mo et al., 1998; Courteau and Rix, 1999; Navarro and Steinmetz, 2000). The properties of these halos were often derived from the rotation curves of galaxies. However, the ignorance of the values of the stellar M/L ratio (the gas contribution is typically well understood and relatively small (Verheijen, 1997; Swaters et al., 2000)) determines a degeneracy: many rotation curves can be equally well fitted by models in which the central part is dominated by stellar mass or by DM (van Albada et al., 1985; Swaters et al., 1999). To resolve the degeneracy, some independent constraints on M/L ratios are required.

The TF relation is considered a product of the virial theorem and the almost constant mass-to-light ratio of spiral galaxies. Its origin has been discussed by Silk [e.g. (Silk, 1997)], Mo et al. [e.g. (Mo et al., 1998)]. In their semi-analytical approach, Mo et al. (1998) reproduced the TF relation assuming a constant mass-to-light ratio and an empirical profile for disks and halos. Heavens and Jimenez (1999) used a similar approach, including an empirical star formation model, and successfully reproduced the TF relation in four pass-bands simultaneously. However, the exponential profile and the flat rotation curves of these galaxies were not constructed as the results of simulations, but assumed a priori. Steinmetz and Navarro (1999) provided the first numerical simulations within a cosmological context and explained the slope and scatter of the TF relation. They considered a volume much larger than the scale of galaxies, and some environmental effects (e.g., tidal field and infall/outflow of mass). Koda et al. (2000) also reproduced the slope and scatter of the TF relation. In their approach the slope originates from the difference of mass among galaxies, while the scatter from the difference in the initial spin.

A breakthrough was the discovery that the baryonic mass better correlates with rotational velocity than luminosity (McGaugh et al., 2000). The baryonic TF relation (BTF) is remarkably tight (Bell and de Jong, 2001; Verheijen, 2001; Pizagno et al., 2005; Kassin et al., 2006; Courteau et al., 2007; Masters et al., 2008; Reyes et al., 2011), but the exact slope still depends on the filters used (Courteau et al., 2007; Ponomareva et al., 2017; Schulz, 2017).

The parametrization of the BTF gives important constraint for models of disk galaxy formation (Mo et al., 1998; Somerville and Primack, 1999; Navarro and Steinmetz, 2000; Dutton et al., 2007). Using a semi-analytic model, Dutton (2012) predicted a minimum intrinsic scatter of ∼ 0.15 dex for the BTF while Di Cintio and Lelli (2016) had a scatter of 0.17, using semi-empirical models that were able to reproduce the mass discrepancy acceleration, i.e. the ratio of total-to-baryonic mass at a given radius that anticorrelates with the acceleration due to baryons (McGaugh, 2004). According to Bullock et al. (2001) most of the scatter comes from the mass–concentration relation of DM halos well constrained by cosmological simulations. The scatter of the BTF is therefore a key test for the ΛCDM model. The scatter is minimum when the velocity is measured in the flat part of the rotation curve well beyond the optical extent of the galaxies (Verheijen, 2001; Noordermeer and Verheijen, 2007), probably because such velocity is close to the virial velocity.

As remarked before, one possible application of the BTF is to constrain the properties of the DM halos. Übler et al. (2017) by investigating the stellar mass and BTF relations of massive star-forming disk galaxies at redshift z ∼ 2.3 and z ∼ 0.9 (using the data of the KMOS3D integral field spectroscopy survey), found that the contribution of DM to the dynamical mass increases toward lower redshift. Their comparison with the local relations reveals a negative evolution of the stellar and baryonic TF zero points from z = 0 to z ∼ 0.9, no evolution of the stellar TF from z ∼ 0.9 to z ∼ 2.3, and a positive evolution of the BTF from z ∼ 0.9 to z ∼ 2.3.

A useful progress came with the demonstration by Weiner et al. (2006) and Kassin et al. (2007) that, accounting for disordered motions (σ) and ordered rotation (V) in a new parameter $S_{0.5}=\sqrt{0.5V^2+{\sigma }^2}$, it is possible to get a tight S_0.5 − − M_s relation (Aquino-Ortíz et al., 2018). This relation is independent of the morphology of galaxies and is coincident with the FJ relation of ETGs, when σ dominates over V, and coincident with the TF when the opposite occurs. Numerical simulations seem to indicate that S_0.5 traces the potential well of the DM halos even in the case of merger events (Covington et al., 2010). The inclusion in the TF of galaxies with disordered velocity components (often due to major mergers) has been addressed by several people (Lemoine-Busserolle and Lamareille, 2010; Puech et al., 2010; Catinella et al., 2012; Vergani et al., 2012; Cortese et al., 2014; Wisnioski et al., 2015). The scatter of the relation seems mainly due to merger events as we have seen for the FJ relation.

Galaxy morphology is another possible source of scatter being a strong function of stellar mass and the less luminous systems quite often exhibit an irregular morphology [see e.g. (Roberts and Haynes, 1994; Bothwell et al., 2009; Mahajan et al., 2015)]. In general disturbed galaxies are increasingly more common at low masses in the early Universe (Mortlock et al., 2013). The kinematic surveys are often biased against galaxies with disturbed morphology, because their aim is to study the DM content (Bershady et al., 2010). Dwarfs galaxies (DGs) show rotational signatures in both their HI and stellar components (Swaters et al., 2002; McConnachie, 2012) and when irregular galaxies, compact galaxies, and close pairs are analyzed in their kinematics the presence of peculiar velocity fields and thick disks are found [see e.g. (Barton et al., 2001; Kannappan et al., 2002; Vaduvescu et al., 2005; Cortese et al., 2014; Kirby et al., 2014)] together with high star-forming dwarfs (van Zee et al., 1998; Cannon et al., 2004; Lelli et al., 2014). However, only few studies have placed large samples of these disordered systems on the TF.

In the future, it will be interesting to study the TF relation in the same perspective of the FJ, distinguishing the relation valid for a set of galaxies, which is a translation of the virial theorem (once the variations in the stellar population are taken into account), and the relation valid for single galaxies, where the luminosity and the rotational velocity are the result of the mass assembly history and of the stellar evolution. The work of D’Onofrio et al. (2020) has demonstrated that it is important to look at the variations of the positions of each galaxy in the different SRs if we want to understand the origin of the observed distributions.

4 The Kormendy Relation

The I_e − R_e relation of ETGs (often known as KR (Kormendy, 1977)) is a projection of the FP. In this case the variables are the effective radius and the mean surface brightness inside it. It is the most easily accessible correlation of galaxies parameters even at high redshift. First discovered by Kormendy in 1977, the linear relation visible in log units between these variables, soon showed an ample curvature toward faint and dwarf objects, suggesting the existence of two different populations of ETGs, the “ordinary” and the “bright,” following two different relations and therefore possibly originating from two different channels of evolution (Capaccioli et al., 1992). The “ordinary” family is bi-parametric ($L\propto I_e{R}_e^2$), its members are fainter than M_B ∼ − 19, and their radii are smaller than R_e ∼ 3 kpc. The “bright” family is mono-parametric (I_e depends only on R_e), it hosts only the brightest cluster galaxies (BCGs), and their members have radii exceeding R_e = 3 kpc. The bulges of spirals belong to the “ordinary” family.

The curved distribution visible in the I_e − R_e plane has been used (among other correlations) several times to argue for distinct formation mechanisms of dwarfs and giants ETGs (Capaccioli et al., 1993; Kormendy et al., 2009; Tolstoy et al., 2009; Kormendy and Bender, 2012a; Somerville and Davé, 2015; Kormendy, 2016). Many authors believe that there is a physical difference between elliptical and spheroidal galaxies. Elliptical and spheroidal galaxies exhibit different parameter correlations. Spheroidals are not low-luminosity ellipticals but rather the result of transformations induced in late-type galaxies by internal and environmental processes. Furthermore, there are possibly two distinct kinds of elliptical galaxies, whose properties differed during the last major mergers, wet or dry, according to whether cold gas dissipation and starbursts occurred or not.

The existence of two physically distinct families of ETGs has been at the center of an ample debate. Other researches did not use the effective half light radius parameter, advocated for a continuity among the ETG population (Caldwell, 1983a; Binggeli et al., 1984; Bothun et al., 1986; Caldwell and Bothun, 1987). Graham (2019) explored a range of alternative radii, showing that the transition at M_B ∼ − 19 mag is likely artificial and does not imply the existence of two different types of ETGs.

The shape of the light profiles of ETGs has been also used to claim a difference between dwarfs and ordinary ETGs: dwarfs have in general exponential light profiles (similar to the disks of LTGs), while ordinary ETGs have R^1/n Sérsic profiles (Sersic, 1968), with n ≥ 3. However, exponential light profiles are reproduced by the Sérsic law when n = 1. According to Graham (2019) the curved distribution of ETGs in the KR is likely associated with the continuous change of the Sérsic index n with the absolute magnitude (the M_B − n relation (Caon et al., 1993; D'Onofrio et al., 1994)). Along this view Graham and Guzmn (2003) argued that the only magnitude of importance in the I_e − R_e plane is at M_B = − 20.5 mag, where they see a division between ETGs with Sérsic profiles and core-Sérsic profiles. This magnitude corresponds to a mass of ∼ 2 × 10¹¹M_⊙.

There are indeed two linear scaling relations involving the structural parameters of ETGs: the M_B − μ₀ (i.e. total luminosity vs central surface brightness) and the M_B − n (total luminosity vs Sérsic index). These relations do not show evident signs of curvature. The first one is a restatement of the concentration classes introduced by Morgan (1958), later quantified by the concentration index C (Fraser, 1972; Binggeli et al., 1984; Kent, 1985; Ichikawa et al., 1986). The second is a consequence of the first, being the Sérsic parameter a measure of the radial concentration of galaxy light. Further examples of the M_B − n diagram can be found in the literature (Caon et al., 1993; Young and Currie, 1994; Graham et al., 1996a; Jerjen et al., 2000; Ferrarese et al., 2006b; Kormendy et al., 2009). The lack of curvature in these diagrams does not support the view of different formation mechanisms at work for ETGs. This debate is controversial: the original “nature” (Eggen et al., 1962) (monolithic collapse) versus “nurture” (formation through mergers) (Toomre and Toomre, 1972; Searle and Zinn, 1978; Schweizer, 1986) idea is still open.

Another interesting feature of the I_e − R_e diagram, well visible in Figure 2, is the presence of a zone of exclusion (ZoE). Note that there are no galaxies in the upper part of the diagram. The distribution of galaxies seems limited in the maximum surface brightness at each R_e. The slope of this line of avoidance is approximately − 1 in these units, i.e. very close to the slope of the fitted KR for the brightest galaxies ( ∼ − 1.5). First noted by Bender et al. (1992) in the k-space version of the FP, the ZoE was written as k₁ + k₂ ≤ 7.8.

FIGURE 2

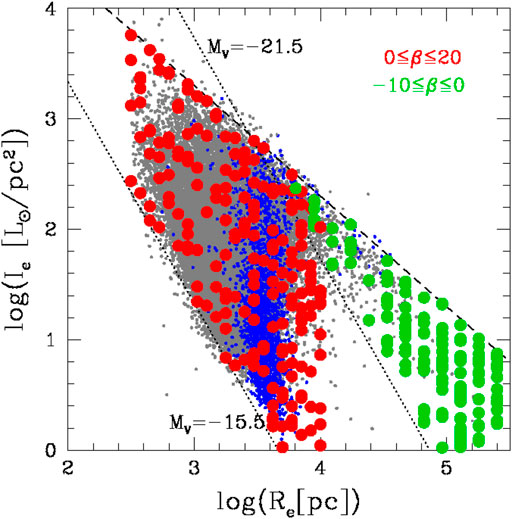
FIGURE 2. The KR plane. The gray dots mark the observational data of the WINGS survey. The red and green dots mark the values of I_e and R_e obtained starting from Eq. 1 [see D’Onofrio and Chiosi, 2020] using different values of β. The dashed line represents the ZoE. The dotted lines the locus of constant luminosity, respectively at M_V = − 21.5 and M_V = − 15.5.

Recently, D’Onofrio and Chiosi (2020) demonstrated that the FJ relation (with L₀ and β nearly constant) is incompatible with the distribution observed in the KR plane. On the contrary the use of the modified FJ relation expressed by Eq. 1 is perfectly compatible with the data (see Figure 2). This means that the parameters $L_0^{\prime }$ and β must be variable factors depending on the mass assembly history of galaxies. Note how the complex distribution of galaxies in the I_e − R_e plane is well reproduced by assuming different values of $L_0^{\prime }$ and β. The negative values in particular are able to explain the tail formed by bright and massive objects in a quenched state of evolution.

Under this perspective the appearance of the I_e − R_e plane is also connected to the mass assembly and stellar evolution history of galaxies. The tail of bright galaxies appears only at recent cosmic epochs, when some big objects start to quench their star formation and their luminosity begins to slowly decrease.

5 The Mass-Radius Relation: A Path Toward Virial Equilibrium

A considerable number of works have been dedicated in the past years to the MR relationship, i.e. the plot of the stellar mass of the galaxies M_s versus the effective radius R_e in log units [see e.g. (Bernardi et al., 2011; Graham et al., 2011; Shankar et al., 2013a; Graham, 2013; Bernardi et al., 2014; Agertz and Kravtsov, 2016; Kuchner et al., 2017; Huang et al., 2017; Somerville et al., 2018; Genel et al., 2018; Almeida, 2020; Terrazas et al., 2020)]. The increasing interest for the MR relation is due to the difficulty of explaining the observed distribution with the virial theorem and the various models of galaxy assembly predicted by the monolithic and hierarchical scenarios, in particular the curved shape, progressively steeper for the high masses, and the zone of exclusion (ZoE), that is, a region empty of any object on the side of the high masses (see Figure 1, lower right panel, and Figure 3). This nontrivial distribution is well apparent even when globular clusters (GCs) and clusters of galaxies (CGs) are added to the diagram (Chiosi et al., 2019).

FIGURE 3

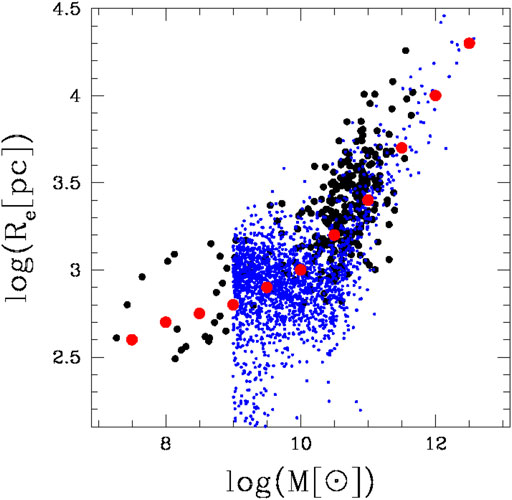
FIGURE 3. The MR plane. The black dots mark the observational data of the WINGS survey. The blue dots are the Illustris data of the TNG release shifted by a constant value in log(R_e) of − 0.45 (simulations still provide systematically larger radii). The red dots mark the values of R_e obtained from Eq. 2 (see the text).

Many papers have already emphasized that the distribution of galaxies in this plane depends on several factors, such as age (Valentinuzzi et al., 2010), mass-to-light ratio (Cappellari et al., 2015), color, Sérsic index, and velocity dispersion [see e.g. (D’Onofrio et al., 2020; Almeida, 2020)]. The distribution of the sizes has been approximated with a log-normal function (Shen et al., 2003), noting that it is clearly different for late- and early-type galaxies. The MR relation is roughly a single power law for the bright ETGs (M_s > 10¹⁰M_⊙), while for the LTGs and DGs the relation is significantly curved, with brighter galaxies showing a faster increase of R_e with M_s. For low-mass LTGs the trend is R_e ∝ M^0.14, while for the high-mass galaxies we have R_e ∝ M^0.39. The dispersion around the mean relation is high for low-mass galaxies ( ∼ 0.5) and smaller for big objects ( ∼ 0.3). For the ETGs the mean relation is R_e ∝ M^0.56, with a slope going progressively toward 1 for galaxies more massive than ∼ 10¹⁰M_⊙. Spirals do not seem to have objects along this linear tail (D’Onofrio et al., 2020).

According to Shen et al. (2003) the observed MR relation for LTGs can be attributed to the specific angular momentum (AM) of the stars, if it is similar to that of the halo and if the fraction of baryons that form stars is similar to that predicted by the standard feedback models. For ETGs, the observed MR relation is not consistent with the hypothesis that they are the remnants of major mergers, while it seems consistent with that of multiple mergers. One possibility is that the spheroids below a characteristic mass M_s ∼ 10¹⁰M_⊙ grow from disk instability and mergers, while galaxies above it from dry mergers. Gas dissipation, if present, contributes efficiently to shrink the size of the galaxies (Shankar et al., 2013a).

The pronounced curvature of the MR relation suggests again a dichotomy between “bright” and “ordinary” ETGs as in the case of the M_B − ⟨μ⟩_e diagram and the KR plane. A possible explanation invokes the role of supernova-driven winds blowing out the gas from the DGs (Mathews and Baker, 1971; Saito, 1979; Dekel and Silk, 1986). This feedback effect is one of the most efficient ways of puffing up galaxies sizes. However, these studies do not take into account the gravitational binding energy of the DM halo (Mac Low and Ferrara, 1999), so that other mechanisms should be sought to explain the discontinuity present in these relations. The discontinuity is not seen in fact in the luminosity-metallicity relation (Dekel and Silk, 1986; Mateo, 1998; Tremonti et al., 2004; Veilleux et al., 2005) and is only marginally visible in the L − σ relation.

More recently, D’Onofrio et al. (2020) found a unique explanation for the curved shape of the MR and KR relations in combination with the almost linear trend of the L − σ relation. They used the modified FJ relation L = L₀′σ^β introduced above that is able to reproduce the curved MR relation and I_e − R_e distribution once coupled with the virial equation. In this case one gets the relation:

$R_e={\left(\frac{1}{\frac{k_v}{G}{\left(\frac{2\pi ⟨I_e⟩}{L_0^{\prime }}\right)}^{2/\beta }}\right)}^{1/\left(4/\beta +1\right)}{M}^{1/\left(4/\beta +1\right)}.(2)$

and should accept the idea that the parameters $L_0^{\prime }$ and β are variable factors for each galaxy depending on the mass assembly history, with β that can assume both positive and negative values (see Figure 3). The advantage of this approach is that, in addition to the almost perfect reproduction of the observed SRs, it naturally predicts the existence of the ZoE as the locus of virialized and passively evolving quenched objects. Look at the red dots obtained by Eq. 2. The slope of the MR progressively changes from DGs to giants, converging toward the value of 1 for the bright and massive quenched objects in full virial equilibrium.

In this framework the key role of shaping the SRs is played by the merging and stripping events at play during galaxy encounters. These events may change either the luminosity or the radius of a galaxy (increasing or decreasing them). However, while luminosity rarely increases (decreases) by a factor of two ( ∼ 0.3 in log units), the radius may change considerably (up to a factor of 10). This explains why the L − σ relation does not change its linear shape and scatter (that is approximately ∼ 0.4). On the contrary in the SRs where the effective radius R_e is an explicit parameter, a strong curvature distinguishing DGs and giants is clearly present. Sánchez Almeida (Almeida, 2020) well showed that the MR relation changes its shape and scatter when different radii (probably much closer to the virial radius) are used instead of R_e.

When galaxies encounter result in significant stripping of stars and gas, the total luminosity of the galaxies and the velocity dispersion decrease. The same effect is induced by the quenching of SF and passive stellar evolution, producing values of β that can be negative. Notably this scenario is confirmed by numerical simulations (D’Onofrio and Chiosi, 2020). These also predict that the MR relation evolves with the cosmic epochs, since galaxies are much more dense and smaller in size at earlier epochs. The galaxy size-luminosity relation and the MR relation were then used to argue that the compact (R_e < 2 kpc) massive (M_s > 10¹¹M_⊙) spheroidal-shaped galaxies at high-redshifts (z ∼ 2 ± 1)—known as “red nuggets” (Damjanov et al., 2009)—evolved into the large massive ellipticals in the local (z = 1) Universe (Daddi et al., 2005; Kriek et al., 2006; Trujillo et al., 2006; van Dokkum et al., 2008). These massive galaxies (with stellar mass M_s > 3 × 10¹⁰M_⊙), evolving passively at redshifts z ≥ 1, have average sizes smaller by a factor of ∼ 3 with respect to local ETGs with similar stellar mass. Such small sizes are expected if dissipative collapses occur.

The small objects seen at high redshift are 2 ÷ 6 times more compact than local galaxies of similar stellar mass (van Dokkum et al., 2010a; Saracco et al., 2011), but observations have now established that many ETGs at high redshifts are not compact and that similar fractions of large and compact galaxies could coexist (Mancini et al., 2009; Valentinuzzi et al., 2010), with a variety of bulge-to-disk ratios (van der Wel et al., 2011).

From the analysis of the spectra of 62 ETGs at high redshifts Saracco et al. (2011) found that compact galaxies have most of their stars formed before z = 5, while larger objects at fixed stellar mass are generally younger. Graham et al. (2015) identified 24 “compact massive spheroids” as the bulge component of local lenticulars. These bulges have a similar distribution of size, mass, and Sérsic indices as the high-z compact massive galaxies, and comparable number densities (per unit volume) (de la Rosa et al., 2016). This similarity strongly suggests that the current evolutionary scenario does not explain the complete picture.

Another possibility is that the evolution of the red nuggets is driven by the growth of disks (Caldwell, 1983b; Morganti et al., 2006; Sancisi et al., 2008; Stewart et al., 2009; Pichon et al., 2011; Moffett et al., 2012; Stark et al., 2013; Graham et al., 2015; Kleiner et al., 2017). Gas accretion plays a key role for massive galaxies (Feldmann et al., 2016), while less massive objects accrete a small quantity of gas with time (Cowie et al., 1996; Graham et al., 2017).

The rapid stripping or ejection of baryonic matter (BM) might inflate galaxies to larger dimensions. The idea came from Biermann and Shapiro (1979), who linked the formation of S0s to that of disk galaxies. Recently, Ragone-Figueroa and Granato (2011) explained the existence of red-nuggets with this mechanism. The loss of BM could be triggered by quasars (QSO) and/or starburst-driven galactic winds or can be quiet for stars at the end of their evolution. In this scheme compact galaxies could transform into less massive and larger systems. Numerical models only approximately follow this scheme: the models show intense episodes of SF and significant galactic winds but, on average, the trend is toward larger masses and almost constant radii.

Guo et al. (2009) and van Dokkum et al. (2010a) investigated the possibility that the MR relation, at least for the most massive galaxies, is linked to a systematic variation of the Sérsic index n, parameterizing the surface density profiles with the redshift. According to van Dokkum et al. (2010a) the variation of the effective radius R_e (50% of the light) is:

$\frac{d\log (R_e)}{d\log (M)}\approx 3.56\log (n+3.09)-1.22(3)$

which is accurate to 0.01 dex for 1 ≤ n ≤ 6. This means that the radius might increase linearly with the mass if the projected density follows an exponential law, going as M^1.8 for the de Vaucouleurs profile with n = 4. A strong evolution in R_e is expected in all inside-out growth scenarios, unless the density profiles are close to exponential.

6 The MR Relation in Cosmological Context

A new explanation of the existence and curvature of the MR relation (thereinafter MRR) has been given recently by Chiosi et al. (2019) in the cosmological context of galaxy formation and evolution. They started from the empirical hint that a unique MRR seems to connect objects from Globular Clusters (GCs) to dwarf galaxies (DGs), early-type galaxies (ETGs) and Spiral Galaxies (LTGs), and finally Clusters of Galaxies (CoGs), the stellar masses M_s and radii R_e of which span about twelve and four orders of magnitude, respectively.

The data used by Chiosi et al. (2019) are those of Burstein et al. (1997) for GCs, galaxies in general, and CoGs, of Bernardi et al. (2010) for ETGs, and of WINGS for ETGs and CoGs. The situation is visible in Figure 4, where the pale-blue filled circles show the observational data with no distinction among the different sources. The sea-green filled circles are the Illustris models. Note that the minimum mass of the Illustris galaxies at z = 0 is 10⁹M_⊙, so the comparison with the observational data should be restricted to this mass limit. The figure shows the region of the MR plane populated by real objects of different mass, size, and morphological type. Let us quickly summarize the main features of the MR plane:

FIGURE 4

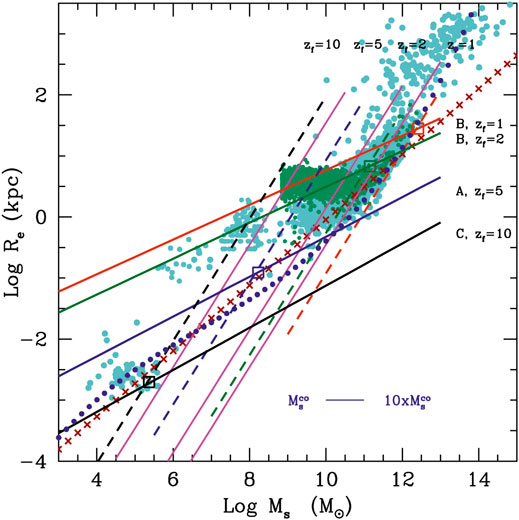
FIGURE 4. The Mass-Radius plane. Comparison between data and theory. Radii R_e and stellar masses M_s are in kpc and M_⊚, respectively. The pale-blue filled circles are the observational data, the sea-green filled circles the models of Illustris. The stellar masses of the observational data that refer to objects from GCs to CoGs span the range 10⁴–10¹⁴M_⊚ while the theoretical data that are designed to represent galaxies span the mass range 10⁸–10¹²M_⊚. The theoretical data overlap the observational ones for ETGs and partly also for DGs. The linear best fit of normal ETGs (M_T ≥ 10¹⁰ M_⊚) given by Eq. 4 is the dark-red thick crossed line that we prolonged down to the region of GCs and upward to that of CoGs. The four solid lines labeled A (z_f = 5, blue), B (z_f = 1, red and z_f = 2, dark green), and C (z_f = 10 black) are the analytical relationships of Eq. 19. They show the loci of galaxy models with different masses but constant initial density for different values of redshift of galaxy formation z_f. These lines are the best fit of the models by Chiosi and Carraro (2002), Merlin et al. (2012), and Chiosi et al. (2012). The magenta solid lines visualize the locus of virialized objects on the MR-plane for different values of the stellar velocity dispersion (50, 250, 500 km/s from left to right). The dashed black lines for different values of z_f are the MRRs expected for galaxies with total mass equal to 50 × M^CO(z), the cut-off mass of the Press-Schechter at varying z_f according to relation (20). The large empty squares mark the intersections between the lines of constant initial density and the MRRs for 50 × M^CO galaxies for equal values of the redshift. All the intersections lie very close to the relation of Eq. 4 shown by the dark-red crossed line. This is the linear interpretation of the observed MRR. Finally, the curved blue dotted line shows the expected MR relation for the baryonic component of DM halos whose mass distribution follows the cosmological HGF by Lukić et al. (2007). The curve has been extended to include the GCs and the CoGs. Note the changing slope of the MRR passing from CoGs to ETGS and GCs. Remarkably, the curved line first runs very close to the large empty squares, second to linear fit of the data (crossed line), and third accounts for the observed MRR passing from GCs to CoGs (about ten orders of magnitude difference in the stellar mass). Finally, the horizontal blue line gives the interval for M_s corresponding to initial masses M^CO(z) < M_T < 10 × M^CO(z) (the percentage amounts to ≃ 15%). It highlights that at each redshift the high-mass edge of the MRR has a natural width.

1) The family of GCs is well detached from that of normal/giant ETGs (with mass larger than about 10¹⁰ M_⊙). The region in between is populated by DGs and at the top of the distribution there are the CoGs with the largest radii and masses. The ETGs are the most numerous and the LTGs occupy more or less the same region, but are not visible in the bright tail. The relative number of objects per group is not indicative of the real number frequencies because severe selection effects are present. The best fit of the three samples of data yields linear relations with much similar slopes and zero points (they differ by 0.1 and 1.2, respectively). Therefore, one can consider them as fully equivalent and adopt the one derived from the sample of Bernardi et al. (2011) as the reference case for his richness

$\log R_e=(0.537\pm 0.001)\log M_s-(5.26\pm 0.01).(4)$

2) Extrapolating the relation for massive ETGs, Eqn. 4, downward to GCs and upward to CoGs, one notes that it provides a lower limit to GCs, passes through ωCen and M32, marks the lowest limit for the distribution of DGs, and finally reaches the region of CoGs.

3) There are no objects in the semi-plane for radii R_e smaller than the values fixed by relation (4), independently of mass, but for the “compact galaxies” [see Chiosi et al., 2012].

6.1 The MRR of Theoretical Models

The situation is more complicated for galaxy models. The monolithic hydrodynamic models by (Chiosi and Carraro, 2002), shortly indicated CC-A and CC-B and the early-hierarchical models by (Merlin et al., 2012), shortly indicated M-M] provide the following MRRs:

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.331\log M_s-3.644\text{\hspace{0.17em}CC}-\text{A}\hfill \end{array}(5)$

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.273\log M_s-1.994\text{\hspace{0.17em}CC}-\text{B}\hfill \end{array}(6)$

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.241\log M_s-1.750\text{\hspace{0.17em}M}-\text{M\hspace{0.17em}}\hfill \end{array}(7)$

We recall that the three groups of models (identical in the input physics) are calculated with different formation redshift z_f (hence initial density): CC-A have z_f ≃ 5, CC-B z_f ≃ 1, and M-M z_f ≃ 1 − 2. In the MR plane they lay on lines with similar slope but different zero points. This suggests that the slope is linked to the physical structure of the models while the zero-point is reminiscent of the initial density. Surprisingly, the slopes of the above relations are not identical to that of ETGs (Eq. 4), but close to that of DGs. Furthermore, along the sequence of each group, the duration of the star formation activity is long and in a burst-like mode of low intensity in low mass galaxies and short and intense (often a single burst of activity) in the high mass ones. Remarkably, only the most massive galaxies formed in redshift interval 5 ≥ z_f ≥ 2, in which star formation has ceased long ago, may fall into the region of ETGs.

The Illustris hierarchical models provide similar relationships, once they are split into two groups:

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.297\log M_s-2.513\mathrm{f}\mathrm{o}\mathrm{r}\log {\mathrm{M}}_{\text{s}}\le 10.5,\hfill \end{array}(8)$

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.519\log M_s-4.492\mathrm{f}\mathrm{o}\mathrm{r}\log {\mathrm{M}}_{\text{s}}\ge 10.5.\hfill \end{array}(9)$

The first relation holds for the vast majority of models and reminds that of normal DGs, while the second one holds for a small group of objects and is close to the case of ETGs. In the hierarchical scheme the models of the first group (in Eq. 8) are the seeds of those in the second group located along the MRR of Eq. 9.

Finally, there is the MRR proposed by Fan et al. (2010). This is derived in the following way. Independently of the monolithic or hierarchical scheme, the seeds of galaxies are perturbations of matter made of DM and BM. These collapse when the density contrast with respect to the surrounding medium reaches a suitable value. Assuming spherical symmetry and indicating with M_T and R_T the total mass and associated radius, and making the approximation M_T = M_D + M_B ≃ M_D and R_T ≃ R_D, the mass-radius relation for each individual galaxy is

$R_D^3=\left(\frac{3}{4\pi }\right)\frac{M_D}{\lambda {\rho }_u(z)}\to R_D\propto \frac{M_D^{1/3}}{1+z_f}(10)$

where ${\rho }_u(z_f)\propto {(1+z_f)}^3$ is the density of the Universe at the collapse redshift z_f, and λ the density contrast of the DM halo. This expression has a general validity, whereas λ depends on the cosmological model of the Universe, including the ΛCDM case. All details and demonstration of it can be found in Bryan and Norman [Bryan and Norman (1998), their Eq. 6]. The collapse increases the mean density of DM and BM so that, when a critical value of the BM density is reached, stars can form at the center of the system under suitable star formation rates. In the context of the ΛCDM cosmology, Fan et al. (2010) have adapted the general relation (10) to provide an equation connecting the halo mass M_D, the stellar mass M_s, the half light (mass) radius R_e, the shape of the BM S_S(n_S) related to the Sérsic profile index n_S, the velocity dispersion f_σ of the BM component with respect to that of DM, and finally the ratio m = M_D/M_s. The expression is

$R_e=0.9\left(\frac{S_S(n_S)}{0.34}\right)\left(\frac{25}{m}\right){\left(\frac{1.5}{f_{\sigma }}\right)}^2{\left(\frac{M_D}{10^{12}{M}_{⊚}}\right)}^{1/3}\frac{4}{(1+z_f)}.(11)$

where f_σ yields the three dimensional stellar velocity dispersion as a function of the DM velocity dispersion σ_s = f_σσ_D (here we adopt f_σ = 1). The typical value for S_S(n_S) is 0.34. For more details see Fan et al. (2010) and references therein.

The most important parameter of Eq. 11 is the ratio m = M_D/M_s. Using the Illustris data Chiosi et al. (2019) investigated how this ratio varies in the mass interval 8.5 < log  M_D < 13.5 (masses are in M_⊙) and from z = 0 to z = 4 (see Section 11). They find that the following relation is good for all practical purposes

$\log m=\log \frac{M_D}{M_s}=0.062\log M_D+0.429.(12)$

The slope of the Fan et al. (Fan et al., 2010) relation, which visualizes the position on the MR plane of systems born at the same redshift once their stars are formed, is 0.333. This is very similar to that of theoretical models, i.e. Eqs. 5–8.

The most intriguing question to answer is “Why is the observational MRR for ETGs so different from the theoretical one?”

6.2 The MRR From the DM Halo Growth Function n(M_D, z)

The observed distribution of astrophysical objects in the MR plane, going from GCs to galaxies of different mass and morphological type and eventually to CoGs, suggests that a unique relation could exist for all of them and that such a relation likely owes its origin to the cosmological growth of DM halos. The distribution of the DM halos and their number density as a function of redshift has been the subject of several studies which culminated with the large-scale numerical simulations of the Universe. We cite here one for all, the Millennium Simulation (Springel et al., 2005). In parallel the studies of the halo growth function, HGF, as the integral of the halo mass function, HMF, appeared in literature [see, for instance, Lukić et al. (2007), Angulo et al. (2012), Behroozi et al. (2013)]. The HGF gives the number density of halos of different mass per (Mpc/${h\left.\right)}^3$ emerging at each epoch by all creation/destruction events and consequently yields the halos that nowadays populate the MR plane and generate the observed galaxies. Chiosi et al. (2019) adopted the HGF of Lukić et al. (2007) who, using the ΛCDM cosmological model and the HMF of Warren et al. (2006), derived the number density of halos n(M_D, z) over ample intervals of halo masses and redshifts. Since the n(M_D, z) of Lukić et al. (2007) refers to a volume of 1 (Mpc/${\left.h\right)}^3$, before being compared with the observational data, it must be scaled by a suitable factor to match the volume sampled by observations. Anyway, the following characteristics of the HGF are worth being noted: 1) for each halo mass (or mass interval) the number density is small at high redshift, increases toward the present, and reaches a maximum at a certain redshift. The peak is either followed by a descent (for low mass halos) or a plateau (for high mass halos). In other words, first the creation of halos outnumbers the destruction, whereas the opposite occurs in general for low mass halos after a certain redshift. 2) At any epoch high mass halos are much less numerous than the low mass ones. This implies the existence of a cut-off mass at the high mass side. 3) The HGF also implies that halos of different mass have a given probability of existence at any redshift [see for more details Chiosi et al. (2012, 2019)].

Assuming a certain number density of halos N_s derived from the observational data, Chiosi et al. (2019) set up the equation n (M_D, z) = N_s whose solution yields the mass of the halos M_D(z) as a function of the redshift and vice-versa the redshift for each halo mass. In practice for any value N_s one gets a function M_D(z). To each value of M_D along this function, with the aid of Eqs. 11–12), one can associate a value of M_s and R_e. The MRR of luminous galaxies is the result.

Notably for the N_s corresponding to 10⁻² halos per (Mpc$/{\left.h\right)}^3$ (roughly the volume surveyed by the SDSS [see Chiosi et al., 2019, for details]), the curve R_e(M_s) falls at the edge of the observed distribution of ETGs in the MR plane. Higher N_s would shift the curve to larger halos, the opposite for lower N_s. One can therefore draw in the MR-plane the locus of the most massive M_D and associated M_s imposed by the halo HGF. The equation n (M_D, z) = N_s with N_s = 10⁻² or equivalently 10⁶ halos per 10⁸ Mpc³ rewritten to derive the halo mass M_D as a function of z is

$\log M_D=0.0031546z^3-0.006455z^2-0.183z+13.287.(13)$

Starting from this, Chiosi et al. (2019) associate M_s and R_e to each M_D for any value of the redshift. The best fit of the resulting MR relation, limited to the mass interval of normal ETGs, 9.5 ≤   log  M_s ≤ 12.5 (M_s in solar units), is

$\log R_e=0.048562{(\log M_s)}^3-1.4329{(\log M_s)}^2+14.544(\log M_s)-50.898.(14)$

Note that 1) the locus on the MR-plane predicted by N_s = 10⁻² halos per (Mpc$/{\left.h\right)}^3$ nearly coincides with the observational MRR; 2) the slope gradually changes from 0.5 to 1 going from low masses to high masses in agreement with the observational data [see van Dokkum et al. (2010b), and references therein]; 3) finally, Eq. 14 is ultimately linked to the top end of the halo masses (and their associated baryonic objects) that might exist at each redshift. Chiosi et al. (2019) named this locus the Cosmic Galaxy Shepherd.

The extrapolation of the Cosmic Galaxy Shepherd downward to GCs and upward to CoGs yields the relation

$\log R_e=0.007584{[\log (m\cdot M_s)]}^3-0.1874{[\log (m\cdot M_s)]}^2+1.908[\log (m\cdot M_s)]-9.027(15)$

where R_e and M_s are in the usual units and m is the ratio m = M_D/M_s, for which a mean value of m = 25 is adopted ². As already said this equation represents the cut-off mass of the HDF at different redshift, however translated into the R_e vs M_s. This gives a profound physical meaning to the line splitting the MR-plane in two regions, i.e. the region where galaxies are found, and that of avoidance, the so-called Zone of Exclusion (ZoE) found by Burstein et al. (1997).

Along the Cosmic Galaxy Shepherd, cut-off masses and redshift go in inverse order: low masses (and hence small radii) at high redshift and vice-versa. More precisely, halos and their luminous progeny that are born (collapse) at a certain redshift and are now located along the theoretical MRR of Eq. 11 associated to that redshift. Along each MRR only masses (both parent M_D and daughter M_s) smaller than the cut-off mass are in place, each of these with a different occurrence probability. Clearly the low mass halos are always more common than the high mass ones. We will argue that in the MR-plane, only the most massive GCs, DGs, and ETGs are expected to fall along the Cosmic Galaxy Shepherd. All other objects of lower mass, the DGs in particular, are expected to lie above this limit. This suggests that there are other physical processes concurring to shape the observed MRR. In other words, the question is “what really determines the position of each galaxy on the MR-plane?”

To answer the above question Chiosi et al. (2012, 2019) argue what follows. The gravitational collapse of a proto-cloud generating a luminous galaxy is surely accompanied by star formation, energy feed-back, gas cooling and heating, loss of mass and energy by winds, acquisition of mass and energy by mergers, etc. Therefore, the result of all these processes taking place together may largely differ from one case to another and also differ from the ideal case of a dissipation-less collapse. For this latter (Gott and Rees, 1975; Faber et al., 1984; Burstein et al., 1997) derived the relation

$R_D\propto M_D^{0.53}.(16)$

Inside this halo a galaxy with stellar mass M_s and a half-mass radius R_e is built up over the years. Chiosi et al. (2019) take the dissipation-less collapse as the reference case. Using the data of the Illustris models, they derive the following MRRs

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.541\log M_s-4.702+k_m\mathrm{f}\mathrm{o}\mathrm{r}\log M_s>10.5\hfill \end{array}(17)$

$\begin{array}{ccc}\hfill \log R_e& =\hfill & 0.102\log M_s-0.017+k_d\mathrm{f}\mathrm{o}\mathrm{r}\log M_s<10.5\hfill \end{array}(18)$

where the constants k_m and k_d can be determined by fixing the initial conditions of the collapsing proto-halo. The slope of Eq. 17 does not significantly differ from that of the dissipation-less collapse, Eq. 6 and that of the empirical MRR of ETGs, Eq. 4. Along each MRR of the theoretical manifold, the agreement between data and theoretical models seems to be possible only for the most massive galaxies. For smaller masses, the slope of the theoretical MRR, Eq. 18, is much flatter than the observational one (about a factor of two).

From the above considerations one could suggest that the Cosmic Galaxy Shepherd and Eq. 4 represent the locus in the MR-plane of galaxies formed by quasi dissipation-less collapses. In contrast, special conditions ought to hold for all other objects that deviate from this condition. The explanation is different for the monolithic and hierarchical scenarios:

a) In the monolithic view, in addition to star formation, galactic winds are the key ingredient to consider, in particular for low mass galaxies, because DGs show the largest deviation from the observed MRR, Eq. 4 or Eq. 16. The analysis of the problem made by Chiosi et al. (2019) shows that: (i) the stronger the galactic wind the larger is the final R_e. Galaxies depart from the locus represented by Eq. 4 and/or Eq. 16 at decreasing mass and increasing galactic wind, the low mass ones having the strongest effect; (ii) the efficiency of winds tends to decrease at increasing initial density. This means that the inflating effect of galactic winds in low mass galaxies of high initial density is low and the final radius of these galaxies will be close to the value predicted by Eq. 4 and/or Eq. 16. In conclusion the flatter slope of the theoretical MRR is likely produced by galactic winds.

b) In the hierarchical scenario the situation is more entangled because both mergers and galactic winds concur to inflate a galaxy. To clarify the issue Chiosi and Carraro (2002) discussed the merger between two disk galaxies calculated by Buonomo (2000). In this case an elliptical galaxy is generated with twice total mass of the component galaxies, but with stellar mass and effective radius smaller and higher, respectively, by ΔM_s/M_s ≃ − 0.9 and ΔR_e/R_e ≃ 0.5, with respect to the case of an elliptical of the same mass generated during a monolithic collapse. The reason for that is identified in the enhancement of galactic winds caused by the interaction. More gas is lost, less stars are formed, and the resulting body is in a state of weak gravitational energy.

When does the MRR develop in the course of time and evolutionary history of galaxies? In Figure 5 we show the R_e vs M_s distribution of the Illustris models at four cosmic epochs. At high redshifts, the distribution is clumpy and irregular. However, starting from z ∼ 1.5 and more clearly at z = 0, a tail-like feature develops on the side of large masses, say for masses ≳ 2 ⋅ 10¹¹ M_⊙. The best fit at redshift z = 0, using the relationship log  R_e = ϵ  log  M_s + η (masses and radii are in M_⊙ and kpc), yields the following values: for log  M_s > 11.3 ϵ = 0.651 and η = − 6.557, while for log  M_s < 11.3 ϵ = − 0.005 and η = 0.592. What are the causes of the cloud-like and tail-like distributions? Why a cloud dominates the low mass range? Why the tail is well visible only for the high masses at low redshifts? Which is the physical meaning of this distribution? To cast light on this Chiosi et al. (2019) examined the history of R_e and M_s for several individual galaxies. The main conclusion of their analysis is that mergers among objects of low and comparable mass can generate galaxies with larger masses and radii, but exceptions are possible in which either the mass or the radius or both decrease. In general the galaxies do not leave the cloud region. All this does not contradict the previous case of Buonomo (2000) because the monolithic counterparts to compare with are not available. The cloud region is instead roughly coincident with the distribution of DGs of different types (see the discussion by Chiosi and Carraro, 2002). At the same time mergers among galaxies with different masses and/or comparable masses can generate objects that shift outside the cloud producing the MR-sequence (actually they define it), the locus of which agrees with the observed distribution for ETGs [see e.g. Chiosi et al. (2019), and references therein]. The stellar content of massive ETGs suggests that star formation has ceased long ago so that strong energy feedbacks are absent and the systems are close to the virial equilibrium. This implies that important mergers do not longer occur. At variance DGs are still undergoing frequent mergers, active star formation episodes, and strong galactic winds. They cannot be therefore in this ideal condition of equilibrium and so they depart from the observed MRR. Nevertheless, there are some DGs that fall along the MRR of massive ETGs and therefore are likely in a similar dynamical and star-forming condition, e.g. ωCen and M32 [see Chiosi et al. (2019), for more details].

FIGURE 5

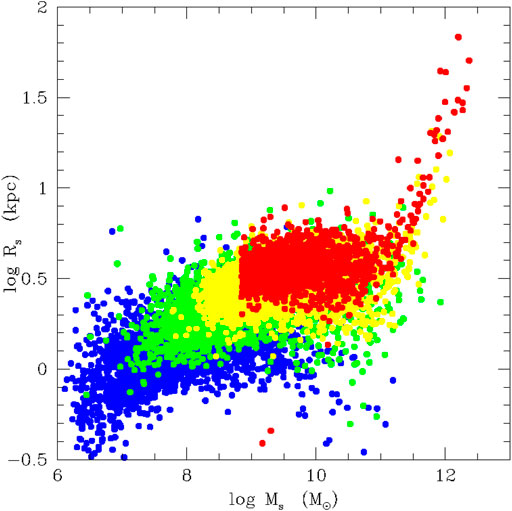
FIGURE 5. The stellar half-mass radius R_e plotted vs the total stellar mass M_s of galaxy models from the Illustris database at different values of the redshift, i.e. z = 4 (blue), z = 2 (green), z = 1 (yellow), and z = 0 (red).

On consideration of these premises, Chiosi et al. (2019) argued that the observed distribution of ETGs, inactive DGs and GCs, represents the locus of objects that have reached the ideal situation of mechanical equilibrium and pure passive evolution. They cannot go beyond this limit. Their MRR is therefore in the boundary between the permitted and forbidden regions of the MR-plane.

6.3 Genesis of the True MRR

Putting the many tessarae of the mosaic together, the conclusion is that the observational MRR is the intersection of the theoretical manifold of the MRRs (each curve being labeled by the collapse redshift from the past to the present) with the Cosmic Galaxy Shepherd, along which objects in mechanical equilibrium and passive evolutionary state are located. To prove this statement Chiosi et al. (2019) resorted to the method proposed long ago by Chiosi and Carraro [see Chiosi and Carraro (2002)], however updating it with recent theoretical and observational data. In the MR-plane of Figure 4 they draw two loci and a mass interval as a function of the initial density (redshift):

1) The first locus is the MRR traced by models of different mass but same initial density and formation redshift. Using all models to disposal (Chiosi and Carraro, 2002; Merlin and Chiosi, 2006; Merlin and Chiosi, 2007; Merlin et al., 2010; Chiosi et al., 2012; Merlin et al., 2012; Chiosi et al., 2019), this locus is described by the relation

$\log R_e=[-1.172-0.412(1+z_f)]+[0.244+0.0145(1+z_f)]\log M_s.(19)$

This expression is robust thanks to the regular behavior of the models and the density-mass-radius relationship of Eq. 16. Relation (19) is compatible with the MRRs predicted by Fan et al. (2010) and the models of Illustris by Vogelsberger et al. (2014). The cases shown in Figure 4 are: z_f ≃ 1, z_f ≃ 2, z ≃ 5 and z_f ≃ 10.

2) The second locus is the Cosmic Galaxy Shepherd. Among the various HGFs in literature (Lukić et al., 2007; Angulo et al., 2012; Behroozi et al., 2013), we adopt the HGF of Lukić et al. (2007) and make use of the analytical expression for the Cosmic Galaxy Shepherd extending across the whole MR-plane given by Eq. (15). However, to better illustrate this issue, we present here an analytical approach based on the classical halo mass distribution of Press and Schechter (1974) that is supposed to trace also the mass distribution of luminous galaxies (assuming one galaxy per halo). At each redshift, the HGF of Press and Schechter (1974) provides the relative number of galaxies per mass bin. The cut-off mass $M_D^{CO}$ of the Press and Schechter (1974) function yields the maximum limit for the galaxy masses at each redshift. In the Press and Schechter (Press and Schechter, 1974) formalism, the cut-off mass varies with redshift according to:

$M_D^{CO}=M_N\times {(1+z)}^{-\frac{6}{n+3}}(20)$

The exponent n represents the slope of the power spectrum perturbations and M_N is a suitable mass scale normalization. At any redshift, most galaxies have total masses smaller than $M_D^{CO}$, even if higher values cannot be excluded. It can be easily shown that the fractional mass in (or the fractional number of) galaxies with mass greater than $M_D^{CO}$ is a function of n. For n = −1.8, the percentage of galaxies in the interval $M_D^{CO}<M_D<10\times M_D^{CO}$ is about 15% while in the range $10\times M_D^{CO}<M_D<100\times M_D^{CO}$ is about 1%. Therefore, at any redshift galaxy masses up to say $50\times M_D^{CO}$ have a significant occurrence probability. Their radius is derived with the aid of the M_s vs M_D and R_e vs M_D relationships. For $M_D=\gamma M_D^{CO}$, γ = 50, and n = − 1.8, one gets:

$R_e=16.9\times 10^{-12}\times {\gamma }^{-0.79}\times {(1+z)}^{3.96}\times M_s,(21)$

where R_e and M_s are in kpc and M_⊚. These are shown in Figure 4 with the dotted lines labeled by the redshifts z ≃ 1, ≃ 2, ≃ 5 and ≃ 10. On the MR-plane, they give the rightmost extension of the lines of constant density and hence they identify the maximum galaxy mass. At decreasing redshift this boundary moves progressively toward higher masses. Similar results can be obtained by means of the HGFs of Lukić et al. (2007), Angulo et al. (2012), Behroozi et al. (2013), the first of which is the Cosmic Galaxy Shepherd.

3) Finally, the third locus gives the expected interval for M_s for objects with total mass M_T between $M_D^{CO}$ and $10\times M_D^{CO}$ as a function of redshift. Here the relation M_s (M_T) has been plugged into Eq. 20 for $M_T^{CO}$. The permitted intervals are visible in Figure 4 by the horizontal lines labeled $M_s^{CO}$. The interval for M_s going from 10¹⁰ M_⊙ to 10¹² M_⊙ is fully compatible with the redshift interval for the formation of the majority of stars in a galaxy, i.e. from 2 to 1. This is also the mass range over which at any epoch the probability for the occurrence of massive galaxies falls to a negligible value. In different words, the right-hand border of the MRR has a natural width.

In this context, the relationship for ETGs, see Eq. 4, extended to the whole mass range from GCs to CoGs should correspond to the intersection between the lines of constant initial density and the lines where $\gamma M_T=M_T^{CO}(z)$ for equal values of the redshift (at least for all values of redshift > 1). This is what we see in Figure 4, i.e. the straight line marked by the large empty squares. This line nearly coincides with the Cosmic Galaxy Shepherd derived from the HGF of Lukić et al. (2007) that is marked by the crossed dark-red line in Figure 4, i.e. Eq. 14 and/or (15). Finally, this line is also coincident with the locus traced by objects that underwent a dissipation-less collapse (or very close to it) and are nowadays in mechanical equilibrium and passive evolutionary state. This is mainly traced by GCs, few DGs (the large majority of DGs lie above it), ETGs, and a number of CoGs. This confirms the result by D’Onofrio et al. (2020): only passive galaxies (strongly decreasing today in their luminosity) trace the MRR with a slope varying from 0.5 to 1, the highest value being reached by galaxies that suffered the strongest luminosity decrease with the redshift, i.e. those that long ago ceased their stellar activity, i.e. the most massive ones. Spirals occupy approximately the same location of ETGs in the MR-plane, thus suggesting that their ongoing star formation is not affecting the overall situation of mechanical equilibrium. Furthermore, it is worth noting that the slope of MRR derived from the HGF is about 1 in the range of massive galaxies (say above 10¹² M_⊙), i.e. formally identical to the MRR derived from the virial theorem. This coincidence might suggest a dependence of the observed MRR slope from the virial condition. The true driver is instead the HGF, more precisely its fall off toward high values of the halos’ masses at any redshift. To conclude, all the objects along the MRR are in virial conditions and passive evolutionary state (all mechanical process and star formation activity are at rest).

7 The Fundamental Plane

In the local Universe ETGs are seen to lie along a plane, the so-called fundamental plane (FP (Djorgovski and Davis, 1987; Dressler et al., 1987)), connecting the surface brightness within the effective radius ⟨I_e⟩, the effective radius R_e, and the velocity dispersion of stars (central or within the effective radius σ_e). The intrinsic scatter around the FP is small ( ∼ 0.05 dex) (Bernardi et al., 2003; Saulder et al., 2013)) and the relation appears to extend across all ETGs, DGs, GCs, and CGs (Misgeld and Hilker, 2011; D'Onofrio et al., 2013a).

The FP is tilted with respect to the virial prediction. The origin of the tilt has been debated for several years. The first attempts to explain it invoked a progressive change of the mass-to-light (M/L) ratio of the stellar population with galaxy luminosity, but even systematic changes of the DM fraction and the structural and dynamical nonhomology of galaxies can be responsible for the observed tilt [see e.g. (Bender et al., 1992; Cappellari et al., 2006; Ciotti, 1991; Renzini and Ciotti, 1993; Jorgensen et al., 1996; D'Onofrio et al., 2013b)].

Recently, D’Onofrio et al. (2017) proposed another explanation for the tilt of the FP. In their work they demonstrated that the FP can originate from the combination of the virial theorem with the modified FJ relation given by Eq. 1. In this case the small scatter of the plane can be obtained if it exists a fine-tuning between the zero-points of the two relations. In other words it must exist a connection between the shape and structure of galaxies and their stellar population content [see also D’Onofrio et al. (2011)].

The FP evolves with redshift [see e.g. (Treu et al., 2005; Holden et al., 2010; Saglia et al., 2010; Fernández Lorenzo et al., 2011; van de Sande et al., 2014)]. Beifiori et al. (2017), using a sample of 19 massive red-sequence galaxies at 1.39 < z < 1.61 observed by the K-band Multi-object Spectrograph (KMOS) Cluster Survey, find that the ZP of the FP in the B-band evolves with redshift, from 0.44 (for Coma) to − 0.10 ± 0.09, − 0.19 ± 0.05, and − 0.29 ± 0.12 for clusters at z = 1.39, z = 1.46, and z = 1.61, respectively. Similar results are obtained by Prichard et al. (2017). The properties observed for the high redshift FP suggest an increase of the dynamical-to-stellar mass ratio by ∼ 0.2 dex from z = 2 to the present. Consequently these data seem to indicate that the fraction of DM contained within R_e, compared to that seen in likely descendants objects at low-redshift, was increased by a factor > 4 since z ∼ 2 (Mendel et al., 2020). The same work suggests the use of the dynamical-to-stellar mass ratio as a probe of the stellar IMF, finding that high-redshift data can constrain the IMF law.

While the debate is still open on whether the FP coefficients are constant up to z ∼ 1 [see (Holden et al., 2010; Saglia et al., 2010; S. di Serego Alighieri et al., 2005; Jorgensen and Chiboucas, 2013)], there is more consensus about the variation of these coefficients with the magnitude interval of the sampled population [see e.g. (D’Onofrio et al., 2008)] and on the variation of the zero-point with redshift as a result of an evolving M/L (Faber et al., 1987) caused by the younger stellar population at high-z (Dokkum and Franx, 1996; Bender et al., 1998; Kelson et al., 2000; Gebhardt et al., 2003; Wuyts et al., 2004; S. di Serego Alighieri et al., 2005; Holden et al., 2005; Jørgensen et al., 2006; van Dokkum and van der Marel, 2007; Holden et al., 2010; Toft et al., 2012; Bezanson et al., 2013) and by the structural evolution of galaxies with redshift (Saglia et al., 2010; Saglia et al., 2016). Other authors claim that there is not only a dependence of the zero point on redshift, but even the slopes of the structural relations are steeper for high redshift galaxies than for objects of the local Universe (Treu et al., 2005; Jørgensen et al., 2006; Fritz et al., 2009).

As discussed in the previous section, several papers have shown that a fraction of intermediate and high-redshift galaxies have smaller sizes (Trujillo et al., 2007; Houghton et al., 2012; Newman and Genzel, 2012; Beifiori et al., 2014; van der Wel et al., 2014; Chan et al., 2016) and higher stellar velocity dispersions (Cappellari et al., 2009; Javier Cenarro and Trujillo, 2009; van Dokkum et al., 2009; van de Sande et al., 2013; Belli et al., 2014) compared to their local counterparts of the same mass (Brammer et al., 2011; Muzzin et al., 2013; Patel et al., 2013). Part of this difference might be attributed to environmental effects and can be observed in the FP. The environment may have a role in accelerating the size evolution in clusters with respect to the field at z > 1.4 (Lani et al., 2013; Strazzullo et al., 2013; Delaye et al., 2014; Newman et al., 2014; Saracco et al., 2014), while in the local Universe there seem to be no significant differences between the mean galaxy sizes in different environments (Cappellari, 2013; Huertas-Company et al., 2013). The reason for that is not clear; is it because there is not enough time for evolution? In clusters central and satellite galaxies seem to lie on average above and below the FP, possibly for a higher and lower than average mass-to-light ratio (Joachimi et al., 2015).

Several studies (e.g. (Franx et al., 2008; Cimatti et al., 2012)) have also suggested that the size evolution with redshift is stronger for massive galaxies ( > 10¹¹M_⊙). This behavior is consistent with the idea that high-density environments play a major role in size evolution. Galaxies in denser environments probably evolve earlier as indicated by the observed color–density relation (e.g. (Chuter et al., 2011)). It is not clear yet if the environment itself influences the size evolution, since merging events alone do not seem to explain the observed size evolution of ETGs (e.g. (Damjanov et al., 2009; Nipoti et al., 2012)) or other growth mechanisms are at work, such as the adiabatic expansion due to mass-loss, that could indirectly lead to a correlation of size with environment (if it occurs at earlier epochs within the most massive dark matter halos). There is also the possibility of trends driven by faster quenching in high-density environments (e.g. (Cassata et al., 2013)). Whatever the reason of the size evolution, the underlying correlation is likely connected to the halo mass that is strongly related to the number of satellites (e.g. (Skibba and Sheth, 2009; Muldrew et al., 2012)). A full investigation of this problem requires a careful decoupling of large-scale clustering and small-scale halo occupation (e.g. (Hartley et al., 2013)).

The presumed universality of the FP makes it an appropriate tool for cosmology, e.g. for the Tolman test (Kjaergaard et al., 1993; Pahre et al., 1996; Moles et al., 1998), or to assess the evolution of M/L with z (Bender et al., 1992; Guzman et al., 1993; Dokkum and Franx, 1996; Kelson et al., 1997; Bender et al., 1998; Jorgensen et al., 1999; Ziegler et al., 1999; Kelson et al., 2000). The usefulness of the FP was recently demonstrated in the context of weak lensing magnification (Huff and Graves, 2014), and to map out the peculiar velocity field of galaxies (Springob et al., 2014). These are examples of the exploitation of the FP as cosmological probe. In such applications generally one measures the observed galaxy size and predicts it using the FP. The comparisons between predictions and observations are used to get the size changes due to lensing magnification, or the line-of-sight peculiar velocities that modify the redshift and the angular diameter distance used to obtain the physical sizes.

Again we should note that hierarchical numerical simulations, like Illustris, correctly predict a tilt of the FP and an evolution of its coefficients with redshift (Lu et al., 2020).

8 The Color–Magnitude Relation

The color–magnitude relation (CMR) is an important tool used to understand the physical properties of stellar systems. Its first original application started with the studies of star clusters (Hertzsprung, 1908; Russell, 1914), followed by the analysis of our Galaxy and the Local Group (Baade, 1944; Sandage, 1957; Blaauw and Greenstein, 1959) and by the analysis of the integrated light of galaxies in clusters, in particular in Virgo and Coma (Chester and Roberts, 1964; Chiosi, 1967; Visvanathan and Sandage, 1977; Sandage and Visvanathan, 1978). The modern CCD instrumentation has provided much richer CMRs [see e.g. (Bower et al., 1992; Kodama et al., 1998; Terlevich et al., 2001; Bell et al., 2004)] allowing the study of the past history of galaxy clusters themselves [see e.g. (Cariddi et al., 2018; Sciarratta et al., 2019)] up to distances of cosmological interest.

Since colors are independent of distance and are very similar for all cluster members, the CMRs have been considered good cosmological probes (Tully et al., 1982; Bower et al., 1992), in particular when we look at the fraction of blue and red galaxies and their morphological ratios, the so-called galaxy color bimodality (Baldry et al., 2004). Both seem to be different in clusters and in the field (Butcher and Oemler, 1978; Dressler, 1980).

In the CMR three main loci are of interest: the first is the red sequence (first noted by de Vaucouleurs (1961)), a linear band throughout a broad interval of luminosities mainly occupied by evolved ETGs. The others two are the blue cloud, in which gas-rich galaxies still form stars at high rates, and the green valley in between, where a complicated interplay between gas conversion and passive evolution is at work (Menci et al., 2005).

Thanks to the large-scale surveys, magnitudes, colors, morphological types, and redshifts for thousands of galaxies are now available. One example is the Galaxy Zoo, derived from the SDSS (Blanton et al., 2003; Lintott et al., 2008; Wong et al., 2012). These data have amply confirmed the existence and the evolution of the red sequence of galaxy clusters (Stott et al., 2009; Head et al., 2014). More recently, the faint end of the red sequence has been also investigated (Boselli and Gavazzi, 2014; Head et al., 2014; Roediger et al., 2017).

The theoretical analysis of the CMR is difficult because of the age–metallicity degeneracy: stars become red when age and metallicity increase [see e.g. (Tinsley, 1980; Silk and Mamon, 2012)]. Understanding the origin of the red sequence, its slope, and width has been the subject of several studies [see e.g. (Baum, 1959; Faber et al., 1977; Dressler, 1984; Bower et al., 1992; Burstein et al., 1995; Burstein et al., 1997; Gallazzi et al., 2006; Menci et al., 2008; Valentinuzzi et al., 2011)]. The general properties of the CMR have been investigated (Gladders et al., 1998; Tran et al., 2007; Mei et al., 2009), within the classical scenario of galaxy formation and evolution with supernova-driven winds (Larson, 1974; Arimoto and Yoshii, 1987; Tantalo et al., 1996; Kodama and Arimoto, 1997; Tantalo et al., 1998a; Chiosi et al., 1998), within semi-analytical models in the hierarchical scheme (White and Frenk, 1991; Kauffmann, 1996; Kauffmann and Charlot, 1998), and within N-body-Tree Smooth Particle Hydro-dynamics simulations [see e.g. Chiosi and Carraro, 2002].

The most accepted view is that the red sequence is more affected by metallicity than by age, even if the CMR has an age dispersion that increases at decreasing galaxy masses. Reproducing the slope requires a correct treatment of the chemical evolution (Kauffmann, 1996; Nelson et al., 2018). A crucial element is the knowledge of when and how the red sequence is formed. The downsizing phenomenon, discovered by spectroscopic analyses of nearby ETGs (Nelan et al., 2005; Thomas et al., 2005; Choi et al., 2014), implies that the red sequence was built over an extended period of time ( ∼ 5 Gyr), beginning with the most massive systems (Tanaka et al., 2005). Efforts to directly detect the formation of the red sequence have observed the color bimodality up to z ∼ 2 (Bell et al., 2004; Willmer et al., 2006; Cassata et al., 2008). The data of the legacy surveys GOODS, COSMOS, NEWFIRM, and UltraVISTA have also shown that massive quiescent galaxies (M_s ≥ 3 × 10¹⁰M_⊙) begin to appear as early as z = 4 (Fontana et al., 2009; Muzzin et al., 2013; Marchesini et al., 2014) and stop assembling by z = 1 − 2 (Ilbert et al., 2010; Brammer et al., 2011). Roediger et al. (2017) found that the red sequence flattens in all colors at the faint-magnitude end (starting between − 14 ≤ M_g ≤ − 13, around M_s ∼ 4 × 10⁷M_⊙), with a slope decreasing to ∼ 60% or less of its value at brighter magnitudes. This could indicate that the stellar populations of faint dwarfs share similar characteristics (e.g., constant mean age) over ∼ 3 mag in luminosity, suggesting that these galaxies were quenched coevally, likely via preprocessing in smaller hosts.

In recent times, large-scale numerical simulations of hierarchical galaxy formation in ΛCDM cosmogony, i.e. including DM and BM, appeared on the scene. In these simulations, much efforts have been made to include star formation, chemical enrichment, radiative cooling/heating, and feedback processes of different nature. With these simulations, the variation of the cosmic SF rate density (SFRD) with redshift (Madau and Dickinson, 2014; Katsianis et al., 2017) has been addressed and largely explained [see e.g. (Katsianis et al., 2017; Pillepich et al., 2018)]. Some of these take into account the photometric evolution of the stellar content of galaxies, permitting the analysis of the CMR, in particular for galaxies belonging to clusters. As shown by Sciarratta et al. (2019) these simulations nicely reproduce the red sequence, the green valley, and the blue cloud, the three main regions of the CMR.

The major drawback of these massive numerical simulations is their complexity, high cost in terms of time and effort, and lack of flexibility and prompt response to varying key input physics.

Since broadband optical colors are not good discriminants of stellar populations because of the age-metallicity degeneracy, attempts have been made to break the degeneracy by using stellar absorption line indexes (Worthey, 1994; Thomas and Maraston, 2003). Recent results suggest that metallicity, α-enhancement, and age vary along the mass or velocity dispersion sequence (Caldwell et al., 2003; Nelan et al., 2005; Thomas et al., 2005), and also vary as a function of environment (Thomas et al., 2005; Smith et al., 2006). The general impression, however, is that the age-metallicity degeneracy cannot be broken.

Finally, we want to remark a notable fact: as shown by Cariddi et al. (2018), galaxy clusters share with galaxies in clusters a red sequence that has a similar slope. The mean color of clusters correlates with their total absolute magnitude, in the sense that small and faint clusters are in general bluer than big and luminous clusters. This aspect of the CMR has never been addressed by dedicated studies up to now. It is interesting to note that, independently on the scale of the stellar systems, the behavior of the stellar population seems connected with the structural and dynamical properties of the system, a proof that gravity works in the same way at all scales. In general we can say that the global understanding of the CMR for clusters of galaxies is still in its infancy.

Great progresses are expected in this field with the new generation of ground and space telescopes, like ELT, JWST, etc., that will reach the faintest galaxies at high redshifts.

9 Star Formation in Galaxies

In a galaxy’s evolutionary history, SF is the starring actor. Thanks to it, gas is continuously turned into stars by a number of not yet fully understood processes, so that within the potential well of DM and BM a shining object is built that is populated by many generations of stars of different mass, age, and chemical composition. In the following we limit ourselves to mention only the most popular laws for the star formation rate that are customarily used in models of galaxy formation, leaving aside the much wider subject of the physical processes by which gas can be turned into stars. From an observational point of view, looking at the stellar populations in GCs, DGs, LTGs, and ETGs, the dominant history of SF changes a lot passing from one type to another: it is sharply peaked in one or a few initial episodes followed by quiescence in GCs, DSphs, and DEs, a series of bursts and quiescent periods in dwarf Irr, ever continuing in LTGs however showing a spatial and temporal grand design, and an initial dominant episode of high intensity and relatively long duration followed by minor activity or quiescence in ETGs. Can theoretical models reproduce and physically explain this variety of behaviors that apparently is related to the mass and morphological type? To answer the question one has to assume a general law of star formation and look for the physical situations in the history of star formation can change with the morphological type of the host galaxy.

9.1 Star Formation in ETGs: Mass and/or Initial Density?

In the case of ETGs the best tool highlighting the main driver of the SF and the SFH is the NB-TSPH hydrodynamic simulations, in which the rate of star formation is usually expressed by the Schmidt (Schmidt, 1959b) law

$\frac{d{\rho }_s}{dt}=-\frac{d{\rho }_g}{dt}=c^{\ast }\frac{{\rho }_g^k}{t_g}(22)$

where ρ_s is the current mass density of stars, ρ_g is the current mass density of gas, t_g is a characteristic time scale (typically the free-fall), k is a suitable exponent (typically k ≃ 1), and c^∗ is the so-called dimensionless efficiency of star formation (typically c^∗ = 0.01 ÷ 0.1).

Based on simple arguments, there are at least three prerequisites for gas (likely in the form of molecular clouds) to be eligible to star formation: the gas has to be in convergent motion, i.e. the velocity divergence must be negative; the gas must be gravitationally unstable, i.e. it must satisfy the Jeans condition t_sound ≥ t_ff (where t_sound is the time scale related to the local sound velocity); the gas must be cooling, i.e. it has to verify the relation t_cool ≪ t_ff. Normally, SPH codes treat star formation simply implementing the Schmidt law in the computational language and transforming part of the gaseous particles that satisfy the three conditions above in new, collisionless particles of different mass (“stars”). The characteristic time scale is chosen to be the maximum between t_cool and t_ff time-scales; however in most situations t_g = t_ff is also a good choice. Knowing ρ_g and ρ_s and integrating upon the current volume of the system one gets the current values of M_g and M_s. Nowadays there are numerous galaxy models whose stellar content has been calculated with the above prescription. However they differ in a number of important assumptions, chief among others the cosmological model of the Universe and the scenario in which galaxy formation and evolution is framed. In the following, for the sake of illustration we will summarize here the results of three paradigmatic cases, i.e. the pure monolithic scheme of Chiosi and Carraro (Chiosi and Carraro, 2002), the early hierarchical scheme of Merlin et al. (Merlin et al., 2010; Merlin et al., 2012), and the full hierarchical scheme, e.g. the Illustris case of Vogelsberger et al. [e.g. Vogelsberger et al., 2014, and references]. It is worth recalling here that care must be paid on the link between the Schmidt and Kennicutt-Schmidt SF laws and their implications for numerical simulations (Schaye and Dalla Vecchia, 2008).

The pure monolithic scheme. Chiosi and Carraro (2002) highlighted the role of over-density of the initial perturbation when exceeding the threshold value. Two groups of models were analyzed according to the initial over-density: 1) models with mean initial density ⟨ρ⟩≃ 200 × ρ_u(z) and collapse redshift z_f = 5 (shortly named A); 2) models with ⟨ρ⟩≃ 5 × ρ_u(z) and z_f ≃ 1 (named B). ρ_u(z) is the density of the Universe at redshift z ³. Perturbations with spherical symmetry, assigned mass, mean density exceeding the critical value (and hence suitable radius) are let collapse and form stars. A MonteCarlo procedure is adopted to fix the initial coordinates and velocities of the DM and BM particles. The key result of this study is that the star formation history (rate vs. time) is found to depend on the depth of the gravitational potential well of a galaxy. The following picture can be drawn. In the case of deep gravitational potentials (such as in massive and/or dense galaxies) once star formation has started energy is injected into the gas by supernova explosions, stellar wind, etc., but this is not enough to push the gas out of the potential well. The balance between cooling and heating is reached and the gas consumption by star formation goes to completion. Star formation cannot stop until the remaining gas is so little that any further energy injection will eventually heat it up to such high energies (temperatures) that the gravitational potential is overwhelmed. No more gas is left over and star formation is quenched. The star formation history resembles a strong unique burst of activity, a sort of monolithic star forming event, taking place over a certain amount of time, of the order of 1–2 Gyr. In contrast, in a galaxy of low mass and/or density and hence shallow gravitational potential, even a small star-forming activity will heat up the gas above the potential well. Some of it is soon lost in galactic wind, the remaining one becomes so hot that it will take long time to cool down and to form new stars. The cycle goes on many times in a sort of repeated bursting mode of star formation taking place during long periods of times if not forever. Out of all this we can derive what follows:

1) The duration, strength, and shape of the SFR as a function of time strongly depend on the galaxy mass and the initial density: (a) Galaxies of high initial density and total mass undergo a prominent initial episode of SF followed by quiescence. (b) The same happens to high mass galaxies of low initial density, whereas the low mass galaxies experience a series of burst-like episodes up to the present. The details of their SFH are very sensitive to the value of the initial density. The typical dependence of the SFR on time for models B is shown in the left panel of Figure 6, while the right panel shows the SFR of a low mass galaxy (M_T = 10⁹ M_⊙) for moderate variations of the initial density. Models A are not shown because their SFR is represented by a single initial spike.

2) The gas mass turned into stars (per unit total mass of the galaxy) is nearly constant. This means that the same engine is at work.

3) At increasing total mass of the galaxy the ratio between the left-over gas and the initial total BM decreases.

4) As a result of star formation, large amounts of gas are pushed out from the central regions to large distances. When this gas cool, part of it falls back toward the central object.

5) In general all galaxies eject part of their gas content into the inter-galactic medium, and the percentage of the ejected material increases at decreasing galaxy masses.

FIGURE 6

FIGURE 6. Left panel: The SFR as a function of time for the model galaxies of type B of Chiosi and Carraro (2002). Their initial conditions are rather simple and grouped according to the initial over-density: models of type A had mean initial density ⟨ρ⟩≃ 200 × ρ_u(z), whereas models of type B had ⟨ρ⟩≃ 5 × ρ_u(z) where ρ_u(z) is the density of the Universe at redshift z. The Hubble constant was H₀ = 65 km s⁻¹ Mpc⁻¹ and the redshift of the starting collapse z_f = 5. Only models B are shown here because they are particularly useful to highlight the effect of the mass at given initial over-density. From the bottom to the top, the SFRs refer to galaxies with M_T = M_DM + M_BM from 1 × 10⁸ M_⊙ to 5 × 10¹³ M_⊙. The initial baryonic and dark mass are M_BM = 0.1 M_h and M_DM = 0.9 M_h, respectively. Right panel: the SFR of low mass type B galaxies of the same mass, but different initial over-density. The mass is M_T = 10⁹ M_⊙. The initial over-density varies from low (LD) to intermediate (ID) to high values (HD). The figures are reproduced from Chiosi and Carraro (2002).

The early hierarchical scheme. Merlin et al. (2010, 2012) using initial conditions derived from large-scale cosmological simulations and abandoning the strict monolithic scheme, much improved the NB-TSPH galaxy models of Chiosi and Carraro (2002). They also adopted the ΛCDM cosmology instead of the classical CDM ⁴. Without entering into detail, they cut from large-scale simulations calculated with the free code COSMICS by Bertschinger (1995, 1998) a spherical portion containing proto-halos of DM and BM in cosmological proportions with the desired over-density, mass, and size (the reference proto-halo with the highest mass to consider). The same is made for halos with lower mass and smaller dimensions at fixed mean density. The procedure to obtain halos with the same mass but different initial mean density is more complicated and will not be reported here [see Merlin et al. (2010, 2012) for the details]. These proto-halos contain a number of distinct lumps of matter that will merger together later on. The cosmological simulation provides the initial positions and velocities of all the particles in the proto-halos. The expansion of the Universe is taken into account. The proto-halos are followed through their expansion (caused by the Hubble flow), down to their collapse and aggregation into single objects. The redshift of the collapse varies from model to model and, inside the same model, from the center to the periphery. In general the collapse occurs in the redshift interval 4 > z > 2, it starts in the central regions and gradually moves outward. The collapse is complete at redshift z ≃ 2. All models develop a stellar component. The more massive halos experience a single, intense burst of star formation (with rates ≥ 10³M_⊚/yr) at the early epochs. The intermediate mass halos (M_T ≃ 10¹¹M_⊙) have star formation histories that strongly depend on the initial over-density, i.e. with a single or a long lasting period of activity and strong fluctuations in the rate. The small mass halos (M_T ≃ 10⁹M_⊙) always have fragmented star formation histories: this is the so-called galactic breathing phenomenon. These models are classified as early hierarchical because they experience repeated episodes of mass accretion at very early epochs and then evolve in isolation ever since. They confirmed the correlation between the initial properties of proto-halos and the star formation history found by Chiosi and Carraro (2002). The models have morphologies, structures, and photometric properties similar to real galaxies [see Merlin et al. (2012),  for all other details].

The fully hierarchical scheme. This is the most difficult case to discuss because of mergers among galaxies of different mass, size, and age. If gas is present recurrent episodes of stronger star formation activity may occur. It is conceivable that seed galaxies prior to any encounter behave like the general scheme envisaged before and governed by the initial density and mass. Mergers among objects of similar mass would likely enhance the rate of star formation in a sort of burst of short duration and fold the two histories together. Mergers among objects of much different mass would simply generate a temporary perturbation on the star formation history of the most massive one, while less massive object simply loses its identity. In the hierarchical scenario, tracing the star formation history of single galaxies is a hard task. Anyway, the observational evidence provided by the stellar content of galaxies of different mass strongly supports the mass-density scheme we have described.

The general trends of the SFR described in this section agree with the picture envisaged long ago by Sandage (1986), examining the SFR in galaxies of different types [see also Tinsley (1980), Chiosi et al. (2014), Matteucci (2016)]. This scenario has been confirmed by studies of SF histories based on absorption line indices (Thomas et al., 2005), and by the recent study of Cassarà et al. (2016). A good agreement also exists with other independent numerical NB-TSPH models of galaxy formation and evolution by Kawata and Gibson (2003a, 2003b), Kobayashi (2005).

9.2 The Rate of Star Formation in Disk Galaxies

According to Matteucci (2016) the most common parameterization of the SFR in LTGs is the Kennicutt (Kennicutt and Jr., 1998a) generalization of the original Schmidt (Schmidt, 1959b) law, where the SFR is proportional to the gas density ρ. Kennicutt (Kennicutt and Jr., 1998a) suggested that the SFR can be written as:

$SFR(t)=\nu {\mathrm{\Sigma }}_g^{\kappa }(23)$

where Σ is the gas surface mass density, ν the efficiency of star formation (the SFR per unit mass of gas), and κ = 1.4 ± 0.15, as deduced by the data of the star-forming galaxies [see also Kennicutt (1998)]. Other parameters, such as gas temperature, viscosity, and magnetic field, are not considered.

Actually, the “Kennicutt law” was in use long before its discovery. In the mid-seventies Larson (1975, 1976) developed the first modern hydrodynamic models of formation and structure of elliptical and spiral galaxies, showing that a rate of star formation strongly declining during the latest stages of collapse was necessary to form a massive disk in spiral galaxies. However, once the gas has settled onto the equatorial plane and built up the disk, the rate of star formation should increase to a peak value and then decline again. The duration of this phase and the height of the peak were found to depend on the position on the disk. Larson envisaged several physical mechanisms that might strongly suppress star formation during the latest stage of collapse, e.g. velocity dispersion of the gas, tidal forces exerted on the remaining gas by the already formed spheroidal component, and dependence on the cloud-cloud collision frequency. The same processes were also invoked to control the second phase of star formation. Starting from this Talbot and Arnett (1975) correlated the process of star formation with the surface mass density of the gas in an already flattened disk, whose thickness is regulated by the balance between the gravitational attraction and the increase of the scale height by energy injection by short-lived stars (e.g. type II supernova explosions by massive stars). They proposed a star formation rate proportional to the surface mass density of gas. Chiosi (1980) folded the Larson (Larson, 1976) results into the Talbot and Arnett (Talbot and Arnett, 1975) mechanism and incorporated all this into a new model for the chemical evolution of galactic disks in the presence of infall. In this model the disk is described by a series of concentric rings (no mass exchange among them), whose surface mass distribution at the present time t_g is given by an exponential law of type Σ(r) = Σ_dexp( − r/R_d), where Σ_d and R_d are two scale parameters. The formation of the disk is supposed to occur by rapid infall of the gas left over by the formation of the halo and the central spheroidal component. The temporal and spatial dependence of the infall rate is given by

$\frac{d\mathrm{\Sigma }(r,t)}{dt}=A(r)exp(-t/\mathrm{\tau })(24)$

where A(r) is a suitable function to be determined. This is derived by integrating Eq. 24 with respect to time and by equating it to the present-day mass distribution. We obtain

$A(r)={\mathrm{\Sigma }}_{d}exp(-r/R_d){\mathrm{\tau }}^{-1}{[1-exp(-t_g/\mathrm{\tau })]}^{-1}(25)$

for r_B ≤ r ≤ r_D, where R_B ≃ 2 kpc and r_D ≃ 20 kpc are the typical radius of a bulge and of a disk of spiral galaxies, respectively. The scale parameters Σ_d and R_d are determined by knowing the rate and the surface mass at a certain position of the disk (e.g. the solar vicinity in our case). Thanks to the short time scale of the energy input from massive stars (a few million years), compared to the mass accretion time scale by infall (from hundred to thousand million years) the disk was supposed not to differ from an equilibrium state so that the Talbot and Arnett (Talbot and Arnett, 1975) formalism could be applied. Chiosi (1980) and Chiosi and Matteucci (1980) proposed and used the SFR:

$\frac{d{\mathrm{\Sigma }}_s(r,t)}{dt}=-\frac{d{\mathrm{\Sigma }}_g(r,t)}{dt}=\tilde{\nu }{\left[\frac{\mathrm{\Sigma }(r,t){\mathrm{\Sigma }}_g(r,t)}{\mathrm{\Sigma }(\tilde{r},t)}\right]}^{\kappa -1}{\mathrm{\Sigma }}_g(r,t)(26)$

where Σ_g (r, t) and Σ_s (r, t) are the surface mass densities of gas, stars at the position r or and time t, respectively. The quantities $\mathrm{\Sigma }(\tilde{r},t)$ and $\tilde{\nu }$ are the total surface mass density at a particular distance from the galaxy center, and an efficiency parameter. They play the role of a particular radial scale controlling star formation. In the Larson’s view they might be associated with the radial distance at which the central spheroidal component and the innermost regions of the disk exert their tidal effect on the residual external gas. The spatial and temporal dependence of the relation Eq. 26 in the infall model for the disk of the Milky Way and disk galaxies in general is such that at any time the SFR is strongly inhibited at distances $r>\tilde{r}$, while at any given r the SF starts small, increases to a peak value, and then declines again. This behavior of the SFR is typical of all infall models, where because of interplay between gas accretion and consumption, the SFR starts low, reaches a peak after a time approximately equal to τ, and then declines. Independently of the position, the net temporal dependence of the SFR is the time delayed exponentially declining law:

$SFR\propto \frac{t}{\mathrm{\tau }}\exp \left(-\frac{t}{\mathrm{\tau }}\right).(27)$

The Schmidt law is the link between gas accretion by infall and gas consumption by star formation. Thanks to the infall model by varying τ (time scale of the galaxy formation process) one can recover all types of star formation indicated by observational data going from GCs to LTGs and ETGs. The infall scheme and companion SFR have been widely used in many studies on the subject of galactic chemical evolution [e.g. Matteucci (2016), for a recent review and references]. The infall galaxy model is very flexible and can be adapted to a wide range of astrophysical problems. Suffice to recall that it has been used by Bressan et al. (1994) to model the spectro-photometric evolution of ETGs reduced to point mass objects, extended by Tantalo et al. (1998a) to the case of spherical systems made of BM and DM mimicking ETGs, adapted by Portinari and Chiosi (2000) to include radial flows of gas in disk galaxies, and recently used by Chiosi et al. (2017) to study the cosmic star formation rate and by Sciarratta et al. (2019) to investigate the color-magnitude diagram of galaxies in general.

9.3 The Mass–SFR Relation

The connection between the structure and dynamics of galaxies and their stellar population, which we have encountered addressing the FP problem, is also part of the SF problem of galaxies. Observations have in fact revealed that the SFR and the stellar mass (M_s) of active star-forming galaxies are tightly correlated ($SFR\propto M_s^{0.6}$). This trend is known as the galaxy “main sequence” (MS) (Brinchmann et al., 2004; Noeske et al., 2007; Salim et al., 2007; Elbaz et al., 2011; Salim et al., 2012; Whitaker et al., 2012; Rodighiero et al., 2014; Speagle et al., 2014; Schreiber et al., 2015). Adopting different samples the MS may be different, either in slope or in scatter, primarily for selection effects on the adopted SF indicator used (Popesso et al., 2019). One may select galaxies according to their mass and/or color, picking preferentially the blue cloud objects, or using the BzK color selection (Daddi et al., 2004; Daddi et al., 2007; Pannella et al., 2009) or the UVJ selection (Williams et al., 2009; Whitaker et al., 2012), or adopting a minimum threshold for the specific SFR (sSFR = SFR/M_s) (Karim et al., 2011).

The presence of a main sequence, with a scatter of 0.3 (in log units for active star-forming objects), indicates that these galaxies have an SFR that spans a factor of two. This can be explained by the self-regulating nature of the SF process, that is by the interplay between gas accretion, SF, and feedback (Schaye et al., 2010; Davé et al., 2011; Haas et al., 2013; Lilly et al., 2013; Rodríguez-Puebla et al., 2016; Tacchella et al., 2016).

The scatter however is much larger ( ∼ 0.6) if all types of galaxies are considered. We can see it in Figure 7. The red dots in the various panels represent the data of the WINGS database (Fritz et al., 2007; Fritz et al., 2011). The SFR in the last 20 Myrs, measured from the spectral energy distribution in more than 3,000 objects of all morphological types, is plotted versus the stellar mass. The artificial data coming from the Illustris simulations are also represented for different redshift epochs: z = 4 (blue dots), z = 1 (green dots), and z = 0 (black dots). Before drawing any conclusion, it is worth recalling that the model galaxies of the Illustris simulation were chosen to have stellar masses above 10⁹M_⊙ at z = 0. Therefore, the comparison between theory (black dots) and data (red dots) in Figure 7 is possible only for M_s ≥ 10⁹ M_⊙. We note that in the common region the simulations predict the correct slope and quite a similar scatter at z = 0. They also predict that the slope mildly changes with redshift and that the scatter increases going to the present epoch. This limit on M_s does not exist for the samples at higher redshifts.

FIGURE 7

FIGURE 7. The correlations between M_s, L_V, SFR, and σ. Mass and luminosity are in solar units, SFR in M_⊙/yr and σ in km s⁻¹. The red dots are the observational data of the WINGS survey for all morphological types (Fritz et al., 2007; Fritz et al., 2011). The blue dots are the prediction of the Illustris simulation for galaxies at z = 4. The green dots the prediction at z = 1 and the black dots the prediction at z = 0. Note the lack of objects with mass below 10⁹M_⊙ at z = 0.

The origin of the scatter and its amount might be different for dwarf and giant galaxies (Matthee and Schaye, 2019) and can be attributed to both short-time and long-time processes, such as the competing effects of inflows and outflows, the variation of the halo mass, the variation of the SFE, and the feedback effects from the active nuclei. Daddi et al. (2007), Elbaz et al. (2007), Noeske et al. (2007) claim that the correlation is present even at redshift ∼ 2, with a nearly constant slope and a dispersion similar to that observed for galaxies in the local Universe (Brinchmann et al., 2004).

The information that one can draw from the MS is still under debate (Kelson, 2014; Abramson et al., 2015). There are many open questions: does the main sequence imply that the SFH of galaxies of the same stellar mass is similar? Is the MS a median “attractor-solution” (Peng et al., 2010; Behroozi et al., 2013)? Is it an average sequence for a population at a certain age of the Universe (Gladders et al., 2013; Abramson et al., 2016)? Do galaxies of the same mass have different SFHs on longer time-scales? What effects are most significant at different mass and time-scales?

The slope and scatter of the MS might encode such crucial information. What makes the growth of galaxies different? Which are the important time-scales of SF? Which are the systematic and stochastic effects behind the scatter? Which is the role played by the environment and by the DM in the assembly accretion history?

The MS measured at higher redshifts shows a positive correlation evolving only a bit in slope and scatter [see e.g. Elbaz et al., 2007, Noeske et al., 2007, Whitaker et al., 2012]. This might support the idea that the link between structure and stellar population in galaxies is already in place at z ∼ 2.5 (Wuyts et al., 2011).

The SFR in a galaxy depends on a variety of factors, such as the rate at which the galaxy accretes mass from the IGM, the rate of shocking and cooling of gas onto the galaxy, the details of how the inter-stellar medium (ISM) converts gas into stars, the amount of galactic fountain and outflow, etc. This complex nonlinear physical mechanism is difficult to understand, in particular if one wants to discover what processes dominate, and if and how these change over time. The PCA reveals that neutral gas fraction f_gas, stellar mass M_s, and SFR form a nearly flat 2D surface (Lagos et al., 2016). The location of the plane varies with redshift, and galaxies can move along it when f_gas and SFR drop with redshift. Their position along the plane is correlated with gas metallicity. This is a sort of “fundamental plane of SF” whose curvature is determined by the dependence of the SFR on gas density and metallicity.

10 The Mass–Metallicity Relation

It has been known for a long time that the mean metallicity of galaxies correlates with the mass (and luminosity) (Faber, 1973; Lequeux et al., 1979; Skillman et al., 1989; Brodie and Huchra, 1991). By metallicity astronomers mean the abundance of heavy elements in the gas phase of the ISM. Such a relation is observed in either gas-rich or gas-poor galaxies and suggests a similar physical mechanism behind the origin of the phenomenon (Zaritsky et al., 1994). Recently, the data of the SDSS have permitted the analysis of the mass–metallicity (MZR) relation over a wide interval of masses and metallicities (Tremonti et al., 2004; Maiolino et al., 2008).

All studies confirm the trend of decreasing metallicity toward lower stellar masses, but the true form of the MZR is not yet well established. This depends on the strong systematic uncertainties affecting the measurement of the metallicity. There are a variety of methods to determine the metallicity (Kewley and Ellison, 2008). Some are based on the photoionization models for HII regions by reproducing some emission-line ratios, such as ([OII]λ3727 + [OIII]λλ4959, 5007)/Hβ (Kobulnicky and Kewley, 2004) and [NII]λ6583/[OII]λ3727 (Kewley and Dopita, 2002). Some others on the fits of the electronic temperature (T_e), using strong-line ratios for HII regions and galaxies, like ([OIII]λ5007/Hβ)/([NII]λ6583/Hα) and [NII]λ6583/Hα (Pettini and Pagel, 2004). However, there are some problems when using these strong-line metallicity calibrations. For example, the MZRs with different calibrations have different shapes and normalization (Kewley and Ellison, 2008). Furthermore, for high-z star-forming galaxies, these calibrations may not be valid, since their physical conditions in terms of gas density, ionization, N/O abundance, etc. might significantly be different from those in the local Universe (Ly et al., 2016).

Kewley and Ellison (2008) have shown that the method used to measure the oxygen abundance (log (O/H)), typically assumed to trace the ISM metallicity, affects the shape and normalization of the MZR. Differences up to 0.7 dex in the abundances at fixed stellar mass, using different emission-line methods, are measured. This difference is not constant with the stellar mass and can give significant differences in the shape of the MZR. Possible origins for these discrepancies are discussed in Stasińska et al. (2002), Kewley and Ellison (2008), López-Sánchez et al. (2012), Blanc et al. (2015), Bresolin et al. (2016).

The observations are commonly explained by gas outflows that are much stronger in dwarf galaxies than in giant elliptical galaxies. The massive galaxies are able to retain the gas much longer than low-mass objects. This permits an increase of metallicity, because the new generations of stars are formed in a metal-enriched environment. At the same time, low-mass objects lose their gas through galactic winds. Alternative explanations invoke a variable SF efficiency (SFE). This is larger in more massive systems, which formed most of their stars in a short time at high redshift, quickly enriching the ISM to solar or super-solar metallicities.

The MZR clearly depends on how gas accretion, SF, and outflows proceed with time and therefore it contains important information about these processes. Several examples of the MZR have been published adopting samples of massive star-forming galaxies at different redshifts (0 < z < 3.5) [see e.g. (Tremonti et al., 2004; Erb et al., 2006; Kewley and Ellison, 2008; Maiolino et al., 2008; Zahid et al., 2011; Henry et al., 2013; Maier et al., 2014; Steidel et al., 2014; Sanders et al., 2015)], while only few studies, mostly at z ∼ 0, have extended the MZR to low mass DGs (Lequeux et al., 1979; Lee et al., 2006; Vaduvescu et al., 2007; Zahid et al., 2012; Andrews and Martini, 2013). The luminosity–metallicity (LZR) relation has also been studied by several authors (Lequeux et al., 1979; Richer and McCall, 1995; Melbourne and Salzer, 2002; Salzer et al., 2005; Sweet et al., 2014).

Recently, the chemical evolution models of De Lucia et al. (2004), in a hierarchical context, have also explained the observed MZR and the Tully–Fisher relation. This was possible by including feedback processes into the cosmological simulations. The drawback is that the feedback includes some free parameters, such as the efficiency or the yield, that can be chosen to match the observations.

Another difficulty of the outflow scenario is that different amounts of DM can play a key role in stopping the outflow of gas (Dekel and Silk, 1986). The works of Lee et al. (2006) and Dalcanton (2007) have for example shown that the simple outflow of the gas does not reproduce correctly the yields observed in the ISM of DGs. The large variations in the effective yields and the dispersion in the relation are difficult to understand using only superwinds or outflows, in particular for the low metallicities observed at low masses and luminosities. It seems that neither the simple infall nor the outflow models are able to reproduce the low effective yields of low-mass galaxies.

In nearby galaxies, in the 10⁶ ÷ 10^9.5M_⊙ range, the MZR follows a shallow power-law ($Z\propto M_s^{\alpha }$) with slope α = 0.14±0.08. Approaching M_s ∼ 10^9.5M_⊙ the MZR steepens significantly, showing a slope of α = 0.37 ± 0.08 in the 10^9.5 ÷ 10^10.5M_⊚ range. Finally a flattening toward a constant metallicity is observed at higher stellar masses because the metallicity of the most massive galaxies saturates.

The evolution with redshift of the MZR (Maiolino et al., 2008; Yuan et al., 2013; Zahid et al., 2014) is a tool to trace the history of chemical enrichment in the different cosmic epochs. At high redshifts the MZR has a steeper slope. The MZR at z ∼ 3.5 seems to evolve much stronger than at lower redshifts (Maiolino et al., 2008). This is an epoch of strong SF activity and metal enrichment also for massive systems. The metallicity evolution of low-mass systems seems stronger with respect to that of high-mass systems, an effect that reminds the “downsizing” of galaxies in a chemical framework. Recent results concerning the evolution with redshift of the MZR up to z ≃ 2.7 are those by Wuyts et al. (2016). Using the Integral Field spectroscopy they obtained data in good agreement with the old long-slit spectra, except for the slope of the relation at z ∼ 2.3 in the low-mass regime, where they measured a steeper slope than in previous literature results.

The ISM of galaxies can be enriched by different effects: the accretion of gas from the inter-galactic medium (IGM), the injection and mixing of metals coming from the SF, the removal of these metals when they are locked into long-lived stars and stellar remnants, the ejection of these metals when galactic outflows are at work, the mixing of high and low metallicity gas in the circum-galactic medium (CGM), and the removal/reaccretion of this gas out of the halo or back in the galaxies (Lynden-Bell, 1975; Larson, 1976; Lacey and Fall 1985; Edmunds, 1990; Dalcanton, 2007; Oppenheimer et al., 2010; Lilly et al., 2013; Ma et al., 2016). All these processes play an important role in shaping the evolution of galaxies.

Not surprisingly, the links between the gas mass (M_g), the SFR, the stellar mass (M_s), and the metallicity Z are evident in a number of observed correlations. The most notable examples, in addition to the MZR, are: 1) the M_s − SFR correlation (dubbed the “Main Sequence,” MS (Brinchmann et al., 2004; Daddi et al., 2007; Noeske et al., 2007; Elbaz et al., 2011; Renzini and Peng, 2015); 2) the M_g − SFR correlation between (the so-called Schmidt-Kennicutt, SK, relation (Schmidt, 1959a; Kennicutt and Jr., 1998b; Bigiel et al., 2008; Leroy et al., 2009); that has already been discussed in the previous sections.

Before leaving the subject of the mass–metallicity relation in galaxies, we would like to briefly touch upon the companion, long debated subject of the age–metallicity relation for the stellar population. Age, metallicity, stellar mass are indeed the key parameters to play with to reconstruct the past history of formation and evolution of galaxies of any type. Unfortunately, the optical colors of old populations are affected by the age–metallicity degeneracy (Worthey, 1994; Worthey et al., 1994; Worthey et al., 1999): it implies that the spectro-photometric properties of an unresolved stellar population cannot be distinguished from those of another population three times older and with half the metal content (the so-called 3/2 degeneracy, i.e. in the space color(s)-age the axis is not each orthogonal). Many efforts have been made over the past 20 years to break the degeneracy. Worthey et al. (1994) analyzing some optical features of the spectrum built up the so-called Lick system of indices and found that if on one side the indices decrease the age degeneracy, on the other side the age degeneracy is still there. The Lick system has been improved (Trager et al., 2000a; Trager et al., 2000b; Vazdekis et al., 2010), other features have been added e.g. the CaII IR triplet of Cenarro et al. (2001a), Cenarro et al. (2001b), other high-resolution features have been introduced (Rodríguez-Merino et al., 2020). Spectral windows, in particular the mid-UV, seem to be more promising (Dorman et al., 2003; Yi, 2003; Kaviraj et al., 2007). The overall results indicate that the UV indeed helps to better constrain the age of unresolved systems (as would be expected since the MS turn-off is much more sensitive to age than the red giant branch), but the determination of chemical composition is still better determined by the more sensitive optical features. Li et al. (2007) to bypass the difficulty suggested the PCA method based on a large number of indices. The problem became even more complicated by recognizing that another parameter played an important role. i.e. the so-called α-enhancement measured by the ratio [α/Fe], where α is the abundance of elements such as C, O Mg, Ti, etc [see Tantalo et al. (1998b), Tantalo and Chiosi (2004a), Tantalo and Chiosi (2004b), Tantalo (2004), Tantalo et al. (2007), for a thorough discussion]. The enhancement factor adds another degree of freedom to the age–metallicity degeneracy that now becomes the age–metallicity–enhancement degeneracy. The new degeneracy has size comparable to the old one. The whole issue is still open [see Chiosi et al. (2014), for a recent review]. Despite the large uncertainties, the broad band color and line indices technique has been largely used to infer the age, metallicity, and degree of α-enhancement in galaxies of different morphological types. In relation to ETGs, the most massive objects of the galaxy population and the expectation from the classical hierarchical view of galaxy formation, Jimenez et al. (2007) analyzed the spectra of a larger number of ETGs from the SDSS to infer the ages, metallicities, and star formation histories and found clear evidence of “downsizing,” i.e. galaxies with large velocity dispersion and hence mass have older stellar populations. Most of the ETGs seem to complete their stellar content at redshift z > 2.5, to increase their metallicity on a rather short time scale, and to possess subsolar [α/Fe] ratios. This finding cannot be easily reconciled with the hierarchical scenario while it agrees with the early hierarchical models of Merlin et al. (2012). The issue is still open.

11 Relationships Between DM-Halo and BM-Guest Galaxy

11.1 The Stellar-To-Halo Mass Ratio

The previous sections have clearly demonstrated that the observed properties of galaxies are regulated by a complex series of physical effects tightly intertwined. Last, but not the least, is the ratio between the stellar mass in a galaxy and its dark matter component M_s/M_D (and its inverse M_D/M_s). The ratio M_s/M_D is a quantity that ultimately affects the half-luminosity radius R_e of the stellar component of a galaxy (see Section 6.1). The analysis of the Illustris data and the theoretical galaxy models of Chiosi and Carraro (2002), Merlin and Chiosi (2006), Merlin and Chiosi (2007), Merlin et al. (2010), Merlin et al. (2012), Chiosi et al. (2012) led Chiosi et al. (2019) to suggest that the ratio M_s/M_D depends on the total mass of the galaxy M_T ≃ M_D and the redshift z_f at which the bulk of SF occurs. This is shown by Figure 8 for the Illustris data. For low values of the redshift (say below 0.6), the ratio smoothly decreases with mass M_D (low mass galaxies are slightly more efficient in building their stellar content); the opposite occurs for higher redshifts, where M_s/M_D increases with M_D. Chiosi et al. (2019) give the following analytical expression for the ratio M_s/M_D as a function of M_D and z

$\log \frac{M_s}{M_D}=[0.218z-0.101]\log M_D+[0.169z-2.227](28)$

where the halo mass goes from 10⁴M_⊙ to 10¹⁴M_⊙ and the redshift from 0 to 4. The ratios M_s/M_D predicted by Eq. 28 are indicated by the small black dots of Figure 8.

FIGURE 8

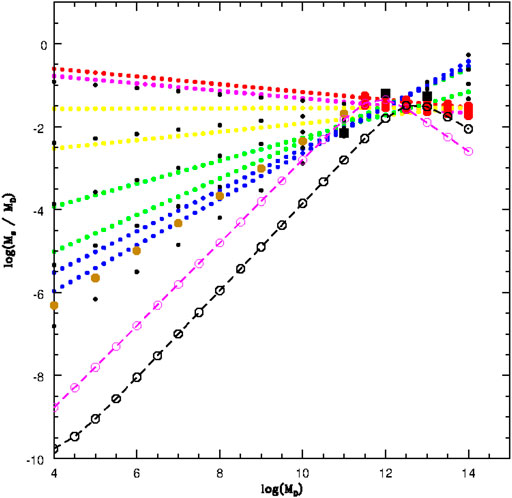
FIGURE 8. The relations between M_s/M_D and M_D at different redshifts for different theoretical models (all masses are in solar units). The colored dotted lines correspond to eight values of the redshift z = 0 and z = 0.2 (top, red), z = 0.6, z = 1.0 (intermediate, yellow), z = 1.6 and z = 2.2 (intermediate, green), z = 3 and z = 4 (bottom, blue). The black dots are the values resulting by Eq. 28 at varying log  M_D (from 4 to 14 in steps of 1) and redshift z (from 0 to 4 in steps of 1), respectively. The large red and golden circles are the combination of Eqs 29, 30. The open magenta (z = 0) and dark-olive (z = 3.95) open circles are the relations M_s/M_D vs M_D at different redshifts according to Girelli et al. (2020). Note that all relations agree at logM_D ≃ 12, while they badly disagree at lower values of M_D. Reproduced from Chiosi et al. (2019).

Other relationships for the inverse ratio m = M_D/M_s can be found in the literature [see, for instance, Shankar et al. (2006), Fan et al. (2010), Girelli et al. (2020)]. For M_D ≥ 10¹¹ M_⊚ Fan et al. (2010) propose the relation:

$m=\frac{M_D}{M_s}=25{\left(\frac{M_D}{10^{12}}\right)}^{0.1}{\left(\frac{1+z}{4}\right)}^{-0.25}(29)$

from which one derives the ratio M_s/M_D shown in Figure 8 by the red circles. In practice there is no dependence on redshift.

Notably, the curve of Fan et al. (2010) agrees with the one derived by Chiosi et al. (2019) using the Illustris models for the values of the redshift smaller than about 1.6 (the slope is nearly identical). Shankar et al. [Shankar et al. (2006), and references therein] presented a detailed analysis of the dependence of M_s on M_D. First, they claim that for M_D < 10¹¹ M_⊙ the relation should be

$m=\frac{M_D}{M_s}=C{M}_D^{-2/3}(30)$

with C a suitable proportionality constant to be determined. Assuming equality between the values of m derived with the two above relationships (at the transition mass M_D ≥ 10¹¹ M_⊚), the proportionality constant is log  C = 9.044. The ratios M_D/M_s resulting by Eq. 30 are shown in Figure 8 with the dark golden circles. Note that the relation of Shankar et al. (2006) agrees with that of the Illustris models for redshifts in the range from 2 to 4.

It is also worth noting that the linear extrapolation of the Fan et al. (Fan et al., 2010) relationship (red circles) in Figure 8 to lower masses and the linear extrapolation of the Shankar et al. (Shankar et al., 2006) curve (dark golden circles) to higher values of the mass encompass the predictions derived from the Illustris models for all the values of the redshift.

Shankar et al. (2006) derived a second analytical expression for the relation between M_s and M_D:

$M_s=2.3\times 10^{10}{M}_{⊚}\frac{{(M_D/3\times 10^{11}{M}_{⊚})}^{3.1}}{1+{(M_D/3\times 10^{11}{M}_{⊚})}^{2.2}}(31)$

for M_D ≥ 10¹¹M_⊙. In this relation there is not an explicit dependence on the redshift. The ratios M_s/M_D predicted by Eq. 31 are visible in Figure 8 with the black filled squares. Eq. 31 predicts ratios m(M_D, z) that are in agreement with those from Eq. 28 derived from the Illustris data, Eq. 29 from Fan et al. (2010), and Eq. 30 only in the region around log(M_D) ≃ 12 and z ≃ 0.

In a very recent study Girelli et al. (2020) have thoroughly investigated the stellar-to-halo mass ratio of galaxies (M_s/M_D) in the mass interval 10¹¹ < M_D < 10¹⁵ and redshifts from z = 0 to z = 4. They use a statistical approach to link the observed galaxy stellar mass function on the COSMOS field to the halo mass function from the ΛCDM-Dustgrain simulation and derive an empirical model to describe the variation of the stellar-to-halo mass ratio as a function of the redshift. Finally they provide analytical expressions for the function M_s(M_D, z). The relations M_s/M_D vs M_D as a function of the redshift obtained with the formalism of Girelli et al. (2020) are also shown in Figure 8 (the magenta and dark-olive-green open circles joined by dashed lines of the same color). See also for a similar analysis the study of Engler et al. (2020).

It is soon evident that while all studies agree on the M_s/M_D ratios for objects with halo mass in the interval 11.5 ≤ logM_D ≤ 12.5 nearly independently of the redshift, they badly disagree each other going to lower values of the halo mass. Furthermore, they also disagree with the theoretical results predicted by Illustris. The problem is open to future investigations.

11.2 Redshift Evolution of DM-Halos and Their BM-Guests

When galaxy formation started DM and BM were in cosmological proportions (i.e. M_D = ωM_B with ω ≃ 6). Then the SF gradually stored more and more BM into stars.

Here, exploiting again the Illustris library of model galaxies (Vogelsberger et al., 2014) we show the relationships between the stellar mass M_s (as a proxy of the BM component) and the dark mass M_D, and that between R_e and R_D for four different values of the redshift (z = 4, 2, 1, and 0). They are visible in the left and right panels of Figure 9, respectively. Masses (in M_⊚) and radii (kpc) are in log units and the color code indicates the redshift (z = 4, blue; z = 2, green; z = 1, yellow; z = 0, red).

FIGURE 9

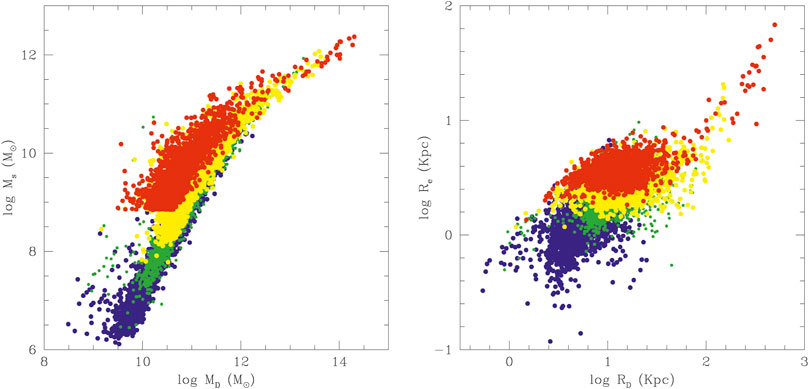
FIGURE 9. Left panel: The M_s − M_D relations at different redshifts (z = 4, blue; z = 2, green; z = 1, yellow; z = 0, red). Masses are in solar units. The solid lines are the best fits discussed in the text. Right panel: the same as in the left panel but for the R_e − R_D relations. Radii are in kpc.

It is clear that the efficiency of SF over the Hubble time, i.e. the transformation of gas in stars, is different in galaxies of different masses. Since M_B < M_D, M_s is always smaller than M_D. However, galaxies of different total mass can build stars at different efficiencies, and the ratio M_s/M_D is therefore expected to vary with M_D and redshift. In the left panel of Figure 9, we note that M_s increases with M_D, so that low mass galaxies build up less stars than the more massive ones. The slope of the relation however decreases as the redshift goes to zero. In more detail, for redshifts z ≳ 2 and masses M_D ≃ 10¹² M_⊚ the slope decreases at decreasing redshift so that more and more stars are present at given M_D. More precisely, for z ≲ 2 and M_D ≤ 10¹² M_⊙ the above trend holds, but above this limit the opposite occurs, at a given M_D less stellar mass is present than expected. In other words, massive galaxies are less efficient builders of their stellar content. We can approximate this relation between   log  M_s and   log  M_D with the linear dependence   log  M_s = α  log  M_D + β, where α and β may vary with the mass range and the redshift. From the linear fit we obtain: (z = 4, α = 1.55, β = − 8.19) (z = 2, α = 1.44, β = − 6.78) (z = 1, α = 1.16, β = − 3.37, for M_D < 12.0) (z = 1, α = 0.76, β = − 2.30, for M_D > 12.0) (z = 0, α = 0.93, β = − 0.43, for M_D < 11.5), and (z = 0, α = 0.79, β = − 1.22, for M_D > 11.5). The ratio M_s/M_D varies from 0.2 to 0.05 when the mass M_D increases from 10⁷ to 10¹² M_⊚ with mean value ≃ 0.10. The overall process of star formation is not highly efficient, large amounts of gas remain unused and likely expelled into the external medium through galactic winds partially enriched in metals. Similar results are given by Merlin et al. [Merlin et al. (2012), and references]. The efficiency of star formation is customarily measured by the ratio M_D/M_s as a function of M_D. This is simply given by:

$\frac{M_D}{M_s}=10^{-\beta }{M}_D^{1-\alpha }(32)$

that has already been discussed in Section 11.

Similarly we can derive the relations:   log  R_e = γ  log  R_D + η ($R_e=\eta R_D^{\gamma }$) that are shown in the right panel of Figure 9. From the linear fit we obtain: (z = 4, γ = 0.39, η = − 8.19) (z = 2, γ = 0.30, η = − 6.78) (z = 1, γ = 0.22, η = − 3.37, for M_D < 12.0) (z = 1, γ = 0.22, η = − 2.30, for M_D > 12.0) (z = 0, γ = 0.29, η = − 0.43, for M_D < 11.5), and (z = 0, γ = 0.29, η = − 1.22, for M_D > 11.0).

The radius R_D is larger than R_e by a factor of 3–10 as the galaxy mass increases from 10⁹ M_⊙ to 10¹³ M_⊙. The slope γ of the R_e-R_D relation (in log units) first decreases by about a factor of 2, from z = 4 to z = 1, and then increases again at z = 0. What is important is that while at high redshifts (our z = 4, z = 2, and z = 1 cases) the galaxy distribution on the R_e-R_D plane is a random cloud of points, at z = 0 a regular trend appears and R_e increases with R_D on the side of large values of R_D (largest masses). However, in the region of low radii and masses a cloud of points is still visible. The reason must be attributed to the effect of strong galactic winds and mergers among galaxies of similar mass in the hierarchical process that strongly perturb the mechanical equilibrium of these systems [see Chiosi et al. (2019)]. Finally, note that the ratios M_s/M_D ≃ 0.1 and R_e/R_D ≃ 0.1 − 0.3 confirm the predictions of Bertin et al. (1992), Saglia et al. (1992) based on analytical models for galaxies made of DM and BM.

12 The Angular Momentum—Mass Correlation

We now turn back our attention again to the correlations observed among galaxies. First we want to explore the correlation between angular momentum J and mass M, introduced by Fall (Fall and Athanassoula, 1983), that is one of the most fundamental SRs of galaxies. It is at least as important as the SRs between rotation velocity, velocity dispersion, characteristic size, and mass. The correlation between angular momentum and mass largely determines other basic properties of galaxies, such as the characteristic size (e.g. the half-mass radius R_h) of disk-dominated galaxies. The angular momentum is in fact linked to global dynamical processes and gravitational instability of galaxy discs to bar formation [see e.g. (Mo et al., 1998; Athanassoula, 2008; Agertz and Kravtsov, 2016; Sellwood, 2016; Okamura et al., 2018; Romeo and Mogotsi, 2018; Zoldan et al., 2018)].

Operationally, one defines the stellar-specific angular momentum j^∗ = J/M_s (the angular momentum per unit mass), the stellar mass M_s, and the bulge fraction ${\beta }^{\ast }=M_b^{\ast }/(M_d^{\ast }+M_b^{\ast })$, where M_d and M_b are the mass of the disk and the bulge respectively. In a plot of   log  j^∗ against log  M_s galaxies of different morphological types and bulge fraction β^∗ follow nearly parallel sequences. Over the mass range 8.9 ≤   log(M_s/M_⊚) ≤ 11.8 disks and bulges follow SRs of the form j^∗ ∝ M^α with α = 0.67 ± 0.07. The different sequences have a maximum offset in zero-point by a factor of 8 ± 2 (Fall and Romanowsky, 2018).

The specific angular momentum of halos scales approximately with the power 2/3 because of tidal torques (Peebles, 1969; Efstathiou and Jones, 1979). The shape of this law is in fact important to test galaxy formation models (a discrepancy is found only at the lowest masses), and constrain many fundamental parameters, such as, for example, the retained fraction of angular momentum. More recently, Posti et al. (2018) find that this relation is well described by a single, unbroken power-law over the entire mass range 7 ≤ logM_s/M_⊚ ≤ 11.5, with a slope of 0.55 ± 0.02 and an orthogonal intrinsic scatter of 0.17 ± 0.01 dex.

A similar result was obtained by Obreschkow and Glazebrook (2014), who discovered a strong correlation between the baryon mass M_b, j_b, and the bulge mass fraction β, fitted by $\beta =-(0.34\pm 0.03)\log \left(j_b\right.M_b^{-1}/{\left[10^{-7}kpc\mathrm{k}\mathrm{m}\mathrm{s}\right.}^{-1}{M}_{⊚}^{-1}\left.\left.\right]\right)-(0.04\pm 0.01)$ over a range of 0 ≤ β ≤ 0.3 and 10⁹M_⊚ < M_b < 10¹¹M_⊚. This M − j − β relation likely originates from the proportionality between jM⁻¹ and the surface density of disks.

Along the same vein Romeo and Mogotsi (2018) investigated the link between angular momentum and disc instability. They showed that the mass-weighted average of the Toomre parameter Q is a more reliable diagnostic of stability. Such a diagnostic parameter permits us to constrain the relation between stellar mass, stellar-specific angular momentum, and disc stability level. Romeo (2020) introduced a new set of galaxy SRs for the relative mass content of atomic gas, molecular gas, and stars, driven by disc instability and originating from the low galaxy-to-galaxy variance of the Toomre’s Q stability parameter.

The above picture seems to indicate that disks and spheroids are independent structures, formed by distinct physical processes: disks are likely formed by diffuse gas settling down on a flat surface within DM halos, while spheroids formed more violently by merging and collisions of cold gas clumps. In this scenario, disk-dominated galaxies are not affected by major mergers, while spheroid-dominated galaxies have properties substantially linked to stripping and merging. The interesting thing is that this relation offers a natural explanation of several classical SRs, such as the FP of spiral galaxies, the TF relation, and the MR relation. It can also be the basis for an objective classification scheme alternative to the Hubble sequence.

In CDM models, galaxies get their angular momentum in the initial phases of density perturbation growth, when the collapsing DM clouds are tidally torqued by neighboring overdensities (Hoyle, 1951; Peebles, 1969; Doroshkevich, 1970; White, 1984). The classical theory of disk galaxy formation (Fall and Efstathiou, 1980; Ryden and Gunn, 1987; Dalcanton et al., 1997; Mo et al., 1998) predicts that gas acquires nearly the same specific angular momentum of the host DM halo. This angular momentum sets the disk size, and largely determines the final morphology (Fall and Athanassoula, 1983; Fall and Romanowsky, 2013). The baryons increase their rotational support by falling into the potential wells of the DM halos conserving their angular momentum. To what extent the baryons preserve the angular momentum during this process is one of the key issues in our understanding of disk galaxy formation.

The angular momentum of the DM halos is often expressed with the dimensionless spin parameter $\lambda =j/\sqrt{2}{R}_{vir}{V}_{vir}$, where R_vir and V_vir are the virial radius and virial velocity of the halo, and j the specific angular momentum inside R_vir (Bullock et al., 2001). The spin parameter of DM within R_vir is found to have log-normal distribution with a median λ ∼ 0.04 and rms variance of σ ln λ ∼ 0.55 (Bullock et al., 2001; Vitvitska et al., 2002; Bett et al., 2010), while BM seems to have a spin higher than the halo’s average (Kimm et al., 2011; Pichon et al., 2011; Tillson et al., 2011; Codis et al., 2012; Danovich et al., 2012; Stewart et al., 2013; Übler et al., 2014; Danovich et al., 2015). In a set of zoom-in simulations Danovich et al. (2015) have shown that λ of the cold gas grows when crossing the virial radius (see also Pichon et al. (2011)).

From the side of numerical simulations we should highlight the long suffered problem of the “angular momentum catastrophe” (Navarro and White, 1994; Navarro and Steinmetz, 2000). The problem emerged from the comparison with observations of disk galaxies. While the observed disks have shown a specific angular momentum j lower by a factor of two, modeled disks appear to have radial scale-lengths smaller by a factor of 10, resembling bulges rather than disks (Navarro and Steinmetz, 2000). In the last years however, simulations seem to have solved the problem by inserting an efficient stellar feedback (Scannapieco et al., 2008; Zavala et al., 2008; Sales et al., 2010). For example, drop, and (Brook et al., 2011), but see also (Brook et al., 2012; Christensen et al., 2014; Übler et al., 2014) found that supernova feedback can selectively remove low angular momentum gas via outflows, leading to disk formation more in line with observations.

In a recent paper, Peng and Renzini (2020) argued that the stellar angular momentum of galaxies increased by a large factor over the last ∼ 10 Gyr (i.e. z ∼ 2), starting from an epoch when the majority of galaxies acquired their ordered rotation. The size of J follows directly from the SRs of spiral galaxies, i.e. from the connection:

$J\propto M^{\ast }{R}_e{V}_{rot}(33)$

between stellar mass, effective radius, and rotational velocity. This behavior could be driven by the baryonic gas vorticity of the circum-galactic filaments that might drive the galaxy evolution. In this framework, the gas in the filaments regulates the fluctuations in the specific SFR of galaxies, offering an explanation for the existence of the main sequence (Lilly et al., 2013).

For what concerns the angular momentum of galaxies at high redshift, we refer to the paper of Burkert et al. (2016). This work analyzes a sample of ∼ 360 massive star-forming galaxies at z ∼ 0.8 − 2.6. They found a J distribution broadly consistent with the theoretical prediction for the dark matter halos, in terms of either spin parameter ⟨λ⟩∼ 0.037 or its dispersion (σ_{log  λ} ∼ 0.2). These data support the hypothesis that on average, at high redshifts, the specific angular momentum of spirals is the same of dark matter halos (j_d = j_DM). Including the molecular gas, these authors measured a total BM to DM mass ratio of ∼ 5% for halos of ∼ 10¹²M_⊚, which corresponds to ∼ 31% of the available baryons. This means that high-z disks are strongly baryon dominated.

13 The Scaling Relations of Black-Holes and Galaxies

Today, the idea that the history of the massive black-holes (BHs) at the center of galaxies and that of galaxies themselves is strictly entwined is widely accepted, after the discovery that the BH mass correlates with various properties of the host galaxies (Ferrarese and Ford, 2005; Kormendy and Ho, 2013; Graham, 2016), such as bulge mass M_bulge (Kormendy and Richstone, 1995), total stellar mass M_s (Hring and Rix, 2004), velocity dispersion σ_⋆ (Ferrarese and Merritt, 2000; Gebhardt et al., 2000), light concentration (Graham et al., 2001), and halo circular velocity (Ferrarese, 2002). The ensuing paradigm of BH and host bulge/spheroid coevolution is today widely accepted and supported by these well-known correlations for quiescent and almost quiescent galaxies. Unfortunately, the physical nature of this connection is still obscure (Silk and Rees, 1998; Shapiro, 2005) despite intense observational efforts.

For galaxies whose nuclei are currently active, there are basic observational issues that remain open at the time of writing. The necessity to resort to type-1 AGN for studying the M_BH—σ_⋆ or M_BH and M_bulge⁵ relations outside of the local Universe raises two overarching questions. The first one is whether the M_BH—bulge relations are observationally consistent with the one obtained for quiescent galaxies at very low redshift. A related issue is about the selection effects specific to the M_BH—bulge relation for type-1 AGN with respect to the one of nonactive galaxies. The second question is whether there is a significant evolution of the M_BH—bulge relation with cosmic epoch.

Some general considerations are in order, before focusing on the analysis of the scaling relations and on the two main questions above. The most accurate black hole mass determinations are the ones that probe the truly central regions of a galaxy, where the gravity of the black hole is the dominant force. This occurs within a distance from the BH $r_{\text{h}}=G{M}_{\text{BH}}/{({\sigma }_{\star })}^2\approx 43M_{\text{BH,}8}{\sigma }_{\star ,100}^2$ pc, where M_BH is in units of 10⁸ solar masses, and the σ_⋆ of 100 km s⁻¹. The BH sphere of influence has been resolved in several nearby galaxies, presumably hosting the most massive BHs that were shining at z ≈ 2, where the most luminous quasars are observed (Lynden-Bell, 1969). In the local Universe, these galaxies mostly appear as spent or almost-spent active nuclei [e.g. (Lynden-Bell, 1969; King and Nealon, 2019)]. As long as a galaxy has a central black hole, there is no such a thing as a quiescent galaxy: some nuclear activity occurs, even if at extreme low level, and detected only in the nearest cases (i.e., Sagittarius A) and under particular circumstances. We consider here weakly active sources whose Eddington ratio is too low to enter into the domain of radiative efficient accretion mode (a typical example could be M87).

13.1 Massive Black Holes at the Center of Quiescent (or Weakly Active) Galaxies

The method employed for modeling stellar system in dynamical equilibrium is that of orbit superposition (Schwarzschild, 1979). The gravitational potential is defined as the sum of the central black hole (assumed a central point whose mass is to be determined) and of the stellar mass density derived from the stellar mass-to-light ratio. What is computed is the combination of orbits compatible with the spatially resolved stellar kinematics and photometric profiles. For the kinematically hot galaxies the early way to get the BH mass was based on the fit of the line-of-sight velocity dispersion of spherical galaxies assuming that the stellar distribution function is isotropic (Young et al., 1978). In more modern approaches, the fit is made over the entire line-of-sight velocity distribution (Rix et al., 1997; Gebhardt et al., 2007) for arbitrary galaxy models whose gravitational potential includes the effect of dark matter, and of triaxiality (Gebhardt and Thomas, 2009; van den Bosch et al., 2008). The most general and accurate possible models, with the highest resolution of spectroscopic observations, are reputed to be most accurate (Kormendy and Ho, 2013), provided that the BH sphere of influence is adequately resolved. A case in point is the estimate of the black hole mass in M87: early estimates yielded a mass ∼ 5 × 10⁹M_⊚ from spherical, isotropic models Young et al. (1978). More recent analyses based on stellar dynamics yielded M_BH in the range ≈ (6. − 6.5) ⋅ 10⁹ M_⊚ (Gebhardt and Thomas, 2009; Gebhardt et al., 2011). The stellar dynamics mass value has been spectacularly confirmed by the Event Horizon Telescopes observations that yielded M_BH ≈ 6.5 ± 0.2|stat ± 0.7|sys ⋅ 10⁹ M_⊙ from the inference of the angular size of the black hole gravitational radius (Akiyama et al., 2019).

One of the most promising developments in the last years has been the increasing number of dynamical mass estimates obtained with ALMA [e.g., (Barth et al., 2016; Boizelle et al., 2019), for mildly active and quiescent galaxies]. ALMA has the capability to resolve cold molecular gas kinematics on angular scales well below 1 arcsec. (Wootten and Thompson, 2009). This is becoming instrumental to high-precision measurements of black hole masses in the “intermediate” mass domain, a previously uncharted territory. For instance, sub-parsec resolution ALMA observations revealed a black hole with mass ∼ 5 ⋅ 10⁵ M_⊚ in the dwarf galaxy NGC404 (Davis et al., 2020).

Space-based long-slit spectra of optical emission lines yield a velocity cusp (Macchetto et al., 1997). A striking example is provided by the radial velocity curve of NGC4374 (Bower et al., 1998): the STIS spectra show a Keplerian swing beginning at ± 0.5 arcsec and culminating at ± 0.1 arcsec, with a radial velocity difference of δv_r ≈ 400 km s⁻¹, implying an M_BH $\approx (1.5_{-0.6}^{+1.1})\cdot 10^9$ M_⊚. The main concern is that gas motions could be affected by radiation forces, shocks, turbulence, and magnetic fields, and not only by gravitation. Relatively few galaxies have been found to have regular disk-like profile suggestive of a velocity field dominated by Keplerian motion in a dynamically cold disk (Kormendy and Ho, 2013). In addition, the Keplerian assumption is not consistent with gas flow toward low-accretion-rate SMBHs and at variance with observations of the Galactic Center (Jeter et al., 2019). For M87, both an early and a more recent analysis based on HST data suggest a black hole mass of ≈ (3 − 3.5) ⋅ 10⁹ M_⊚ (Harms et al., 1994; Macchetto et al., 1997; Walsh et al., 2013), and very close to the value obtained by modeling the jet boundary shape (Nokhrina et al., 2019), but always at variance with the values obtained from stellar dynamics (Section 13.1).

13.2 Relations M_BH vs M_bulge and σ_⋆ for Quiescent Galaxies

As mentioned earlier, the correlation between M_BH and host galaxy bulge properties—M_bulge and σ_⋆ or even bulge luminosity—is now an established fact since more than 20 years [see e.g. Kormendy and Richstone, 1995, Ferrarese and Merritt, 2000, Gebhardt et al., 2000]. Widely used forms of the relation between M_BH and σ_⋆ based on sources for which there is a dynamical M_BH determination are the ones of McConnell et al. (2011) and of Kormendy and Ho (2013) for early-type galaxies. Kormendy and Ho (2013) derived a power law:

$\log (M_{\text{BH}})\approx 8.491\pm 0.049+(4.384\pm 0.287)\log {\sigma }_{\star ,200},(34)$

where the mass is in solar units and σ_⋆ is units of 200 km s⁻¹. For both early type and spiral galaxies McConnell and Ma (2013) yield a significantly steeper slope ≳ 5, with a lower intercept for spiral galaxies, implying that M_BH in ETGs is about a factor 2 higher than in LTGs at a given σ_⋆ (McConnell and Ma, 2013). Equivalent relations (i.e., with similar scatter, around 0.30 dex) have been defined with the bulge mass, and infrared luminosity, usually suggesting a power-law relation between M_BH and M_bulge with an exponent ≈1 or larger (Kormendy and Ho, 2013; McConnell and Ma, 2013; Bennert et al., 2021).

There is still much ongoing research considering the linearity of the relation, its slope, and the origin of its dispersion. Theories that connect galaxy evolution and black hole growth predict the existence of a second parameter which may account for the dispersion in the M_BH—σ_⋆ correlation. Black hole—spheroid coevolution models would require that the BH mass scales with the gravitational binding energy of the spheroid host, ∼ M_bulge/r (Hopkins et al., 2007). The correlation can be easily turned into bivariate relations $M_{\text{BH}}\propto {M_{\text{BH}}}^{0.6}{\sigma }_{\star }^{1.2}$ and $\propto r_{\text{bulge}}^{0.6}{\sigma }_{\star }^{2.4}$ that imply correlations between M_BH and σ_⋆ and M_bulge consistent with the observed ones (Saglia et al., 2016). A correlation with the binding energy of the host galaxy (Aller and Richstone, 2007; Barway and Kembhavi, 2007) implies the presence of a second parameter that may compensate for the changes in the galaxy structural parameters occurring at fixed M_BH. Saglia et al. (2016) found significant bivariate correlations consistent with a connection between M_BH and binding energy and with bulge kinetic energy, although the scatter remains comparable to the one for the M_BH—σ_⋆ correlations obtained with the best dataset of M_BH dynamical mass measurements.

The log(M_BH) −   log(M_s,sph) relation reported by Kormendy and Richstone (1995), Franceschini et al. (1998), Magorrian et al. (1998), McLure and Dunlop (2002), Marconi and Hunt (2003), Hring and Rix (2004) is almost linear, but the inclusion of low-mass spheroids revealed departures from linearity. Laor (1998, 2001), Wandel (1999), and Ryan et al. (2007) obtained a much steeper power law with a slope of 1.53 ± 0.14. The mean M_BH/M_s,sph ratio is probably not a universal constant, as it drops from ∼ 0.5% in bright (M_V ∼ − 22) ellipticals to ∼ 0.05% in low-luminosity (M_V ∼ − 18) bulges. Salucci et al. (2000) claimed that the M_BH − M_s,sph relation is significantly steeper for spiral galaxies than for (massive) elliptical galaxies. Graham (2012) suggested that the relation between luminosity (L) and stellar velocity dispersion (σ) for low-luminous ETGs is inconsistent with the M_BH − L and M_BH − σ relations. They prefer a broken M_BH − M_s,sph power-law relation, with a near-linear slope at the high-masses and a near-quadratic slope at the low-masses. In a recent review article Graham (2016) analyzed the consequences of this steeper relation, which can be rich of implications for the theories of galaxy–BH coevolution. Scott et al. (2013), Graham and Scott (2013) offered an interpretation for the curvature of the M_BH − M_s,sph relation invoking the presence of core-Sérsic and Sérsic spheroids at the high- and low-mass ends of the distribution respectively.

The highest degree of correlation is obtained for ETGs and for bulges that follow a Sérsic—surface brightness profile. Galaxies obeying a Sérsic photometric profile down to the resolution limits of their surface brightness profiles are believed to be the product of wet mergers, i.e., merger of gas rich galaxies that provide material to sustain accretion on the central black hole and trigger a period of sustained nuclear activity. The ensuing feedback effects (both radiative and mechanical) on the host, due to the active nucleus and to the merger-induced star formation, make it possible to couple the growth of the central black hole to the host spheroid mass (Zubovas and King, 2012; King and Pounds, 2015): the feedback forces by the quasar expel so much gas to quench both star formation and stop black hole growth, ultimately accounting for the relation between M_BH and σ_⋆, and M_BH and M_bulge (Di Matteo et al., 2005; Robertson et al., 2006).

However, the most massive elliptical galaxies often exhibit surface brightness profiles that are flatter than the extrapolation of Sérsic-like profiles. Sources showing a deficit with respect to the Sérsic profile are contributing to the scatter in the M_BH—M_bulge relation (Kormendy and Bender, 2009). Core profiles are believed to be due to dissipationless mergers of galaxies that have central black holes. N-body simulations show that merging of two galaxies with a sharp cusp may result in a merger remnant with a shallower core (Milosavljević and Merritt, 2001; Kulkarni and Loeb, 2012; Bortolas et al., 2016). The formation of a core has been ultimately linked to a bound binary black hole system, which produces a depletion of the stellar component in the nucleus due to slingshot ejection of stars on nearly-radial orbits.

The size of the core and the starlight and mass deficits in the centers of core galaxies (i.e., the mass ejected by the binary) have been found to scale approximately with the mass of the central black hole (Graham, 2004; Kormendy and Ho, 2013), in agreement with theory that predicts a mass deficit (Merritt, 2006) to be 0.5 n M_BH, with n as the number of major merger events. The luminosity deficit correlation provides an independent way to estimate M_BH in core ellipticals. Core radius is most strongly correlated with the black hole mass and correlates better with total galaxy luminosity than it does with velocity dispersion (Rusli et al., 2013). In addition, core scouring changes the orbit distribution. Only radial orbits allow for close passage past the galaxy center and thus only those stars can reach the vicinity of the central binary black hole. Consequently, the orbital structure in the core after core scouring is predicted to be strongly biased in favor of tangential orbits, while the ejected stars contribute to enhanced radial motions outside the core (Quinlan and Hernquist, 1997; Milosavljević and Merritt, 2001). For example, the orbital structure of the S0 NGC524 shows tangential anisotropy right at the SMBH radius of influence, corresponding to the core region in the photometric profile (Krajnović et al., 2009). Similar results apply to the elliptical galaxy NGC1600 (Thomas et al., 2016), and agree well with predictions from numerical simulations where core profiles are the result of SMBH binaries impoverishing the central nuclear regions (Rantala et al., 2018).

Recent work emphasizes the presence of substructures in the M_BH—σ_⋆ relation (Sahu et al., 2020). Pseudo-bulges are associated with spiral galaxies, and studies of their photometric profiles reveal that they are disk-like with a different surface brightness profile than classical bulges (Kormendy and Kennicutt, 2004; Kormendy and Bender, 2012b). Pseudo-bulges are known to be offset in the M_BH—σ_⋆ relation in the sense of systematically lower M_BH (Saglia et al., 2016). In the case of pseudo-bulges, the growth of the central black hole may be decoupled from the growth of the host spheroid and not associated with galaxy merger, but instead with mechanisms of secular evolution not related to gravitational interaction with other galaxies; in observational terms, some studies (Kormendy and Ho, 2013) find weak M_BH correlations for pseudo-bulges, see, however, e.g., (Bennert et al., 2021).

The most massive BHs have been detected only in the more luminous galaxies ( − 22 ≤ M_B ≤ − 18) (Ferrarese and Ford, 2005) and it is not clear yet if fainter and less massive systems host massive BHs and whether they follow the extrapolations of the SRs defined by the brightest objects. Searches for BHs in less luminous galaxies of the Local Group have produced ambiguous results, as in the case of M33 (Gebhardt et al., 2001; Merritt et al., 2001), NGC205 (Valluri et al., 2004), and M32 (Verolme et al., 2002). Some galaxies exhibit a compact stellar nucleus (with half-light radius r_h ∼ 2 − 4 pc) in their center. This is ∼ 20 times brighter than a typical globular cluster (Kormendy and McClure, 1993; Butler and Martínez-Delgado, 2005). In the Virgo and Fornax Clusters ∼ 25% of dE galaxies contain such nuclei (Binggeli et al., 1985; Ferguson, 1989; Binggeli and Cameron, 1991), but the observations with the Hubble Space Telescope revealed that these structures are far more common: about 50–80% of the less luminous galaxies contain a distinct nuclear star cluster (Carollo et al., 1998; Matthews et al., 1999; Böker et al., 2002; Balcells et al., 2003; Graham and Guzmn, 2003; Lotz et al., 2004; Grant et al., 2005; Côté et al., 2006). Nuclear star clusters are not a replacement for black holes. On the contrary low mass galaxies (10⁹ − 10¹⁰ M_⊙) show a high incidence of nuclear star clusters coexisting with massive black holes (Greene et al., 2020). However, nuclear star clusters are rare in high mass galaxies (Graham and Spitler, 2009), suggesting that the growth of BH during activity may lead to the demise of the star cluster itself (Antonini et al., 2019).

The low mass end of the relation M_BH—σ_⋆ for quiescent galaxies is still poorly sampled and of uncertain interpretation (Graham and Scott, 2015). Tidal disruption events (TDEs) provide an independent method for M_BH estimation. First, TDEs are luminous flares predominantly detected in quiescent galaxies (very few events have been detected in AGN, as the luminosity of the AGN obliterates the brightness increase associated with the TDE). Flares are produced by the tidal debris that fall back toward the black hole and that form an accretion ring or a disk around an otherwise inactive black hole. Second, a TDE can take only with relatively low black hole masses, M_BH ≲ 10⁸ M_⊙ for a solar-mass star (Gezari, 2021) to avoid that the star crosses the black hole event horizon without being tidally disrupted. The central BH mass is recovered via synthetic multi-band optical light curves based on hydrodynamical simulations of polytropic tidally disrupted stars (Mockler et al., 2019). The method is not yielding yet a good agreement with other M_BH estimates, as it is not clear which parameter should be correlated with M_BH, in a model in which the TDE luminosity is powered by fall-back accretion (Gezari, 2021).

13.3 M_BH Measurements in Active Galactic Nuclei

Stellar dynamical determinations for AGN have been possible only for weakly or mildly active Seyfert 1 galaxies. Presently, only ≲ 100 dynamical M_BH measurements have been obtained by modeling stellar kinematics of quiescent and active nuclei [e.g. (Saglia et al., 2016; Kormendy and Ho, 2013)]. A case in point is the intermediate Seyfert 1 galaxy NGC3327 (Davies et al., 2006) which illustrates the complexity of the nuclear regions of a mildly active AGN, even if an application of the Schwarzschild method of orbit superposition allowed for a meaningful estimate of the stellar dynamic mass ∼ 10⁷ M_⊙. A Population B source (see §14.2 and Figure 12) radiating at modest Eddington ratio, NGC3227, shows a nuclear stellar distribution within a few parsecs of the central black hole affected by intense bursts of star formation occurring in its recent past. Similar considerations apply to the stellar dynamics results on MCG–6–30–15 (Raimundo et al., 2013). In general, stellar populations in the closeness of the active nucleus are not easy to model, also because of the uncertain distribution of obscuring dust, even in the least active nuclei, such as NGC4258. Nonetheless the stellar dynamical and maser masses agree very well for this source (Siopis et al., 2009). A dynamical mass estimate for Cen A also agrees with the estimate derived from cold molecular H₂ gas (Neumayer et al., 2007; Cappellari et al., 2009), suggesting that molecular gas could provide mass estimations as accurate as the ones based on stellar dynamics.

The most reliable method to probe distances within r_h from the black hole of galactic nuclei that are currently mildly active involves observation of H₂O masers (Miyoshi et al., 1995; Herrnstein et al., 2005; Greene et al., 2010). The H₂O emission profile shows a radial velocity “cusp” at distances where the velocity field is governed by the gravity of the black hole i.e., when r ≲ r_h. This method is not exempt by issues that could bias the results. A maser disk with Keplerian rotation could have a non-negligible disk mass comparable to the black hole mass (Huré et al., 2011), and the effects of disk self-gravity might lead to large systematic errors in the derivation of the black hole mass (Kuo et al., 2018). Disturbed morphology and kinematics are an ubiquitous feature of maser systems especially above Eddington ratio λ_Edd ≳ 0.1 (Kuo et al., 2020).

Outside of the local Universe (i.e., beyond 2.5 Mpc), VLBI observations of mega-maser systems can probe within the sphere of influence for BHs down to 10⁶ M_⊙ even at 100 Mpc (van den Bosch et al., 2016). Mega-masers are more frequently associated with active galaxies (Constantin, 2012), and they should be more common at high redshift (van den Bosch et al., 2016). The exploitation of mega-masers is however difficult, because the maser signal of high-redshift sources is lost in noise, and major surveys have until now failed to detect a mega-maser in the wide majority of galaxies. Mass determinations based on the resolved maser systems are completely independent of any other method, and best suited to cross-check the estimates obtained from stellar and gas dynamics. Several H₂O masers have been detected from the circumnuclear regions of quasars also at relatively high redshift (Broome et al., 2019; Stacey et al., 2020). The hope to go beyond modest distances rests with SKA—because of its unprecedented μJy sensitivity—and in future space based radio interferometry with μarcsec spatial resolution. Assuming Earth-space baselines of about 30,000 km, angular resolution of 2 μ-arcsec would be achievable at 8 GHz (Taylor et al., 2007). This angular scale corresponds to a projected linear size of ≈ 0.02 pc at z = 2, therefore allowing to probe within the BH sphere of influence even at the remote epochs of the “cosmic noon,” a key epoch of galaxies AGN when a population of most luminous quasars was shining bright and producing the maximum feedback on their host galaxies.

ALMA is today the most powerful tool to yield M_BH also for AGN [e.g. (Onishi et al., 2015)]. However, the CO J = 2-1 kinematics in a sample of nearby AGN reveals noncircular motions in the inner kiloparsec of all galaxies in the sample, although molecular gas and stellar kinematics show an overall agreement. The CO observations of nearby radio galaxies detect molecular disks, but also caution about the possibility of asymmetries and disruptions due to interactions with the radio jet (Ruffa et al., 2019).

Several studies have employed the capabilities of STIS on board HST to study the dynamics of line-emitting gas in proximity of the central black hole (Pastorini et al., 2007), or the sub-arcsec spatial resolution of imaging spectrometers or IFU units operating with adaptive optics (Hicks and Malkan, 2008). The concern is that radiation forces within the inner 100–1,000 pc of the central black hole may be affecting the dynamics of the line-emitting gas even more than in the case of cold gas dynamics, especially if the AGN is radiating at high Eddington ratio (Zamanov et al., 2002; Xu and Komossa, 2010; Marziani et al., 2016a; Berton et al., 2016; Schmidt et al., 2018).

Spectro-astrometry is another promising tool: the approach is based on the different photocenter positions of emission lines at different velocities (Gnerucci et al., 2011). Although a relatively modest spectral resolution ( ∼ 10 km s⁻¹) is sufficient, sub-arcsec spatial resolution is required, obviously the higher the better, achievable only from space or from ground using active optics (Abuter et al., 2021). This is the approach exploited by GRAVITY, an instrument of the Very Large Telescope Interferometer (VLTI) (Abuter et al., 2017). After first light in 2017, GRAVITY detected a spatial offset (with a resolution of 10 micro-arcseconds corresponding to approximately 0.03 parsecs) between the red and blue centers of the Paschen-α line of 3C273 (Sturm et al., 2018). This offset corresponds to a gradient in velocity and implies that the gas is orbiting the central supermassive BH. With the new capabilities of GRAVITY (Abuter et al., 2017) and with the wave-front corrections of an adaptive optics system, it will be possible to repeat this feat in many low-z type-1 (i.e., broad line) AGN (Bosco et al., 2021). The broad line region velocity field has been spatially resolved and modeled even in NGC3783 (Amorim et al., 2021) to provide an M_BH estimate, although this achievement will likely remain restricted to low-z Seyfert-1 nuclei for the time being.

If we exclude masers, for which BH masses can be inferred from rotation (Ferrarese and Ford, 2005) and spectro-astrometry, for the vast majority of Type-1 AGN the BH masses are derived from the (presumed) virial motions of the broad line region (BLR) gas clouds orbiting in the vicinity of the central compact object. If the motion in the emitting gas is in virial equilibrium, we can write the central black hole mass M_BH as:

$M_{\text{BH}}=\frac{r_{\text{BLR}}\delta v_{\text{K}}^2}{G}.(35)$

Here δv_K is the virial velocity module, r_BLR the radius of the BLR, G the gravitational constant. Eq. 35 can be useful if we can relate δv_K to the observed velocity dispersion, represented here either by the dispersion σ or by the FWHM of a suitable broad emission line:

$M_{\text{BH}}=f_{\text{S}}\frac{r_{\text{BLR}}{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}}^2}{G}(36)$

via the structure factor (a.k.a. form or virial factor) whose definition is given by:

$\delta v_{\text{K}}^2=f_{\text{S}}{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}}^2.(37)$

Mildly ionized gas dynamics i.e., gas motions within the broad line regions of type-1 AGN, is the basis of the estimate of the M_BH for large samples of quasars up to the highest z, following Eq. 36. In addition to a measure of the virial broadening provided by the emission line width, a measure of the line-emitting gas distance from the central black hole is needed. Under the assumption that the main source of line emission is provided by photoionization (Shuder, 1981), the distance is measured by the time lag of the emission lines with respect to continuum variations (Peterson, 1993): r_BLR ≈ cτ, where τ is the time delay. Recent observations measure τ as a function of wavelength across the line profile in an attempt to resolve the velocity field of the emitting region (Brotherton et al., 2020; Williams et al., 2021). The “reverberation mapping” technique has been described in several reviews that also include a critical discussion of the technique shortcomings (Horne et al., 2004; Marziani et al., 2006; Peterson, 2014). The r_BLR estimates have been carried out mainly for the HI Balmer line Hβ for ∼ 100 type-1 AGN, recently supplemented by the monitoring of the SDSS Reverberation Mapping Project that yielded data for 144 quasars (Li et al., 2017). The reverberation mapping determinations of r_BLR offer a sort of primary step over which a correlation between r_BLR and luminosity is built (Section 13.4), in turn instrumental to the determination of the M_BH in large samples of quasars (Section 13.5).

13.4 The Radius—Luminosity Relation

A correlation between the radius of the emitting regions and continuum luminosity is expected on the basis of the spectral similarity of quasars. Even if this is an oversimplification, we observe always the same lines, and their relative intensities change only within a limited range, also in response to continuum variation. The ionization parameter should remain roughly constant, implying that r ∝ L^a, with an exponent a at any rate close to 0.5 (Kaspi et al., 2000; Bentz et al., 2013). The scaling relation has been derived from spectroscopic monitoring of emission lines (mostly the HI Balmer line Hβ) that yield the time delay τ of the emission line response to continuum variations (Peterson, 1993; Peterson, 2017). A sufficient number of sources is available for a correlation analysis since the early 2000s (Kaspi et al., 2000). The consideration of various aspects (host galaxy subtraction and removal of the line narrow component believed to be emitted in a different region) and the increase of the number of monitored sources has led to a standard r − L relation with an exponent consistent with 0.5 within the uncertainties (Bentz et al., 2006; Bentz et al., 2009; Bentz et al., 2010; Bentz et al., 2013). However, the r − L relation suffers of significant scatter because it was derived neglecting the diversity of type-1 quasars organized by the quasar Main Sequence (MS, see below), and is biased in favor of sources radiating at a relatively low Eddington ratio. It is not difficult to account for this preferential selection: such sources are relatively low accretors and therefore more prone to variability associated with an unsteady accretion flow. Recent work (Du et al., 2016a; Du and Wang, 2019) has shown that sources that radiate at high L/L_Edd significantly deviate from the correlation of (Bentz et al., 2013): their radius is shorter than the one expected on the basis of their luminosity. Including high Eddington ratio sources in the correlation creates a cluster of data points that increases the scatter in the correlation. Figure 10 shows that the relation for sources radiating at the highest value of the Eddington ratio is significantly offset from the one of other spectral types along the quasar main sequence discussed in Section 14.2. Linear combination with the dimensionless accretion rate (i.e., the mass accretion rate normalized by the Eddington accretion rate) or Eddington ratio leads to a significant reduction of the scatter (Du and Wang, 2019; Martínez-Aldama et al., 2020).

FIGURE 10

FIGURE 10. The radius-luminosity relation, expressed as the relation between the time lag derived from reverberation mapping and the optical luminosity. Data are from Du and Wang (2019), and include, in addition to the sources of Bentz et al. (2013) also the xA sources monitored in dedicated campaigns (Du et al., 2016a; Du et al., 2018a). Sources are color coded according to the spectral types identified along the quasar main sequence: B1⁺⁺ (red), B1⁺ (orange), B1 (rose), B2 (gray), A1 (aquamarine), A2 (blue), A3 (magenta), A4 (purple), and roughly correspond to a sequence of increasing Eddington ratio. The gray line traces an unweighted least square fit for the full sample, the dotted magenta line refers to an unweighted lsq but for sources radiating at extreme Eddington ratios (A3 and A4) only.

13.5 Scaling Laws for Active Galactic Nuclei Black Hole Mass Estimates

The virial theorem can be conveniently rewritten as log  M_BH = α  log  L+β log FWHM + γ, where β = 2. The luminosity term comes from the use of the radius—luminosity relation, r − L^a. Several different scaling laws based on this expression have been defined for the width of different lines, and for different continuum and line luminosity as well. The most widely used has been perhaps the one formulated by Vestergaard and Peterson (2006) for Hβ and continuum luminosity at 5,100 Å.

The main underlying assumptions in the use of the virial theorem are that the broadening is due to Doppler effect because of the line-emitting gas, and that the velocity field is such that the emitting gas remains gravitationally bound to the black hole. Early UV and optical inter-line shift analysis provided evidence that not all the line-emitting gas is bound to the black hole (Gaskell, 1982; Tytler and Fan, 1992; Brotherton et al., 1994; Marziani et al., 1996; Leighly and Moore, 2004). The emerging scenario is that outflows are ubiquitous in AGN, they occur under a wide range of physical conditions, and are detected in almost every band of the electromagnetic spectrum and on a wide range of spatial scales, from few gravitational radii to tens of kpc (e.g., (Capetti et al., 1996; Colbert et al., 1998; Everett, 2007; Carniani et al., 2015; Cresci et al., 2015; Bischetti et al., 2017; Komossa et al., 2018).

For z > 4, M_BH estimates historically rely on the Civλ1549 high-ionization line, and the highest-z sources appear almost always high-accretors (Bañados et al., 2018; Nardini et al., 2019). The source of concern is that high-ionization lines such as Civλ1549 are subject to a considerable broadening and blueshifts associated with outflow motions already at low redshift (Coatman et al., 2016; Sulentic et al., 2017; Marinello et al., 2020a; Marinello et al., 2020b). Overestimates of the virial broadening by a factor as large as 5–10 (Netzer et al., 2007; Sulentic et al., 2007; Mejía-Restrepo et al., 2016; Mejía-Restrepo et al., 2018) for SMBHs at high z may pose a spurious challenge to concordance cosmology (Trakhtenbrot et al., 2015) and lead to erroneous inferences on the properties of the seed BHs believed to be fledgling precursors of massive BHs. The solution is either to carry out Hβ observations at high redshift (a feat that is becoming easier as more NIR spectrometers are being installed at the focus of large telescopes) or to use a surrogate line whose profile is also virially broadened. The Al iiiλ1860 and Ciii]λ1909 lines could be much robust estimator of the BH mass. These lines, in a blend at 1900 Å, can be easily observed with optical spectrometers up to redshift z ≈ 4. Similar considerations apply to the use of Mgiiλ2800 (Shen and Liu, 2012; Trakhtenbrot and Netzer, 2012) which however can be observed only up to z ≈ 2.5 without the use of NIR spectrometers. Another approach has been to apply corrections to the Civλ1549 line width (Coatman et al., 2017; Marziani et al., 2019), although such corrections, to be effective, require the knowledge of the quasar rest frame, which remains poorly known from rest-frame UV observations only. Shen and Liu (2012) propose scaling laws in which the virial assumption is released that is, with β ≠ 2. For Civλ1549, this means correcting for effect associated with the emission component due to an outflow, which overbroadens (and shifts) the line. The scaling law introduced by Park et al. (2013) follows this approach assuming γ = 0.5, that is, a FWHM dependence that is much weaker than the one of the virial law. The scaling law suggested by Park et al. (2013) applied to a high luminosity sample properly corrects for the overbroadening of the Civλ1549 line profiles of high Eddington ratio sources of a high-luminosity sample, but overcorrects the width in case of sources radiating at modest Eddington ratios, yielding a large deviation from the Hβ-derived M_BH values (Marziani et al., 2019).

13.5.1 The Virial Factor: Orientation and Radiation Effects

The application of Eq. 36 requires the knowledge of the f_S, a quantity of $\mathcal{O}\sim 1$ but that can be significantly different from source to source. The presence of a rotating accretion disk and a spin axis for the central black hole guarantees that axial, and not spherical symmetry, is satisfied for AGN (Antonucci, 1993; Urry and Padovani, 1995). Accordingly, unification schemes distinguish between sources that are observed with the line of sight oriented not very far from the disk axis, and sources that are seen almost edge-on, for which the observation of the BLR is precluded by obscuration (type-2 AGN). Leaving apart obscured sources, there is a considerable range of orientation angles (from 0 to 45–60) that are possible for type-1 AGN. The effect of orientation can be quantified by assuming that the line broadening is due to an isotropic component + a flattened component whose velocity field projection along the line of sight is ∝ 1/ sin θ (McLure and Jarvis, 2002; Collin et al., 2006; Decarli et al., 2011; Mejía-Restrepo et al., 2018). Even with this assumption, it is not known how to connect the viewing angle of the black hole + accretion disk system and the parameters measured on the optical and UV spectra. Only in a few special cases this feat has been possible. In such cases the viewing angle is constrained by data unrelated to the spectra, such as the radio morphology or the jet beaming (Wills and Browne, 1986; Decarli et al., 2011; Punsly et al., 2020). The dependence on orientation can be overcome by spectropolarimetric measurements: if the emission line light is scattered by an equatorial scatterer, then the width of the polarized line flux should be related to the velocity field as measured by an observer in the equatorial plane of the accretion disk, i.e., as if the viewing angle were θ = 90 from the disk axis, de facto removing the orientation effect. Spectropolarimetric measurements allowed for the estimate of the black hole mass in a few tens of type-1 AGN (Savić et al., 2018; Afanasiev et al., 2019; Savić et al., 2020; Capetti et al., 2021). The technique requires large-aperture telescopes even for nearby, bright AGN, whose polarization is notoriously low ( ≲1%; Sniegowska et al. 2021, in preparation).

A parameterization of the virial product dependent on the Balmer Hβ line has been suggested (Mejía-Restrepo et al., 2018) in the form f_BLR ∝ FWHM^−1.17 and exploited in several works (Martínez-Aldama et al., 2019; Bon et al., 2020). This relation is however especially risky in samples covering a wide range of luminosity, since it is not accounting for the increase in line width expected with increasing mass, if line broadening is predominantly virial (Section 15). In addition, orientation is not the only variable affecting f_S. Radiation forces act on gas motions and make the f_S dependent on Eddington ratio [e.g. (Netzer and Marziani, 2010; Khajenabi, 2015)]. The effect can be as large as a factor ≈ 2 and, perhaps more importantly, the efficiency of radiation forces is dependent on the gas column density, leading to the preferential expulsion of gas of lower column density (Netzer and Marziani, 2010). Recent attempts to derive the f_S from dynamical models still do not consider the role of radiation pressure on the gas motion (Pancoast et al., 2014a; Pancoast et al., 2014b; Pancoast et al., 2018; Williams et al., 2020). In addition, there are basic difficulties in modeling the BLR. One of the main issues is whether there are indeed gas clouds or whether the broad lines are emitted directly by a continuum-illuminated accretion disk (Collin-Souffrin et al., 1988; Dumont and Collin-Souffrin, 1990). If clouds are indeed present, the mechanism of confinement is unclear, although confinement by an external magnetic field is favored (Rees, 1987; Bottorff and Ferland, 2000; Chelouche and Netzer, 2001; Shadmehri, 2015; Esser et al., 2019). The quasar main sequence discussed in Section 14.2 provides a focus for these questions, but the physical processes of line-emitting gas dynamics have not yet been contextualized for different accretion modes (Section 14.3).

The virial factor f_S has been estimated by scaling the virial product r_BLRδv² to the M_BH—σ_⋆ for quiescent galaxies obtaining an average f_S ≈ 5.5 if the velocity dispersion of the broad emission line is used ( ≈ 2.3 from the FWHM). This approach provides a test of consistency for the reverberation mapping technique (Bennert et al., 2021) within a factor 2–3 uncertainty. In principle, the f_S uncertainties could be reduced, if a careful separation of different morphological types and of different accretion modes is carried out. For instance, the technique applied to NLSy1s yields f_S ≈ 1.1 (for FWHM (Woo et al., 2015)); Du and Wang (2019) show that sources accreting at high rates do not obey the Bentz et al. (Bentz et al., 2013) relation.

13.6 M_BH vs M_bulge and σ_⋆ for Active Galactic Nuclei and Its Consistency With Quiescent Galaxies at Low-z

There is a general consensus that most galaxies host massive BHs that went through phases of activity. This latter had a role in the BH growth and in the regulation of the SF activity of the host galaxy by means of wind/jet driven feedback mechanisms (Shankar et al., 2009a; Shankar et al., 2009b; Alexander and Hickox, 2012). The theoretical models show that an AGN and its host may coevolve (Silk and Rees, 1998; Granato et al., 2004), leading to characteristics (such as the M_s,sph/M_s ratio and/or the central stellar velocity dispersion σ) related to black hole mass (M_BH).

An early answer to the question “do galaxies hosting an AGN share the same M_BH − M_Bulge correlation of normal galaxies?” was affirmative: AGN have the same BH-bulge relation as ordinary (inactive) galaxies (Wandel, 2002). Fast forward 20 years, there is not yet an established view. A most recent work, based on state-of-the-art surface photometry, and spatially resolved kinematics to measure σ_⋆, find that correlations between M_BH and host galaxy properties hold for AGN within the limits of an intrinsic scatter 0.2–0.4 dex, and are consistent with the ones of quiescent galaxies (Bennert et al., 2021).

Recent works also point toward a complex scenario involving selection biases (Schulze and Wisotzki, 2011) and a better appreciation of the active galaxies diversity. We may represent the distribution of objects in the M_BH—M_bulge (or σ_⋆) diagram by the bivariate distribution function of bulge mass M_bulge and M_BH Ψ(M_BH,M_bulge). The Ψ distribution can be factorized as Ψ = γ(M_BH | M_bulge)ϕ(M_bulge) where ϕ(M_bulge) is the spheroid mass function and γ represents the M_BH—M_bulge correlation i.e., the probability of having the black hole mass M_BH for a given M_bulge. A correct evaluation of γ(M_BH | M_bulge) relies on: 1) the knowledge of ϕ(M_bulge), which is not a trivial task to achieve even in the local Universe, and needs a separate consideration of purely spheroidal (i.e., diskless) galaxies and galaxies with pseudo-bulges or with a bulge/disk system; 2) the absence of biases affecting γ(M_BH | M_bulge).

Both the determinations of M_BH and bulge parameters are challenging, when derived from conventional optical and NIR measurements. At present, black hole masses for type-1 AGN are more frequently derived through the so-called, single epoch virial broadening estimation i.e., through the measurement of the radial velocity broadening term that appears squared in Eq. 36 from single epoch spectra. In practice, it is the measurement of the FWHM or σ⁶ of broad emission lines [e.g. (McLure and Jarvis, 2002; Vestergaard and Peterson, 2006)]. To obtain M_BH, an estimate of the radius r_BLR is also needed, and a rather poorly defined scaling law of r_BLR vs luminosity is applied.

The bulge estimates in AGN samples are hampered by the luminous source associated with the active nucleus, which may well outshine the entire galaxy. The M_bulge has been frequently computed from the host galaxy luminosity (Peng et al., 2006a; Peng et al., 2006b; Treu et al., 2007; Schramm et al., 2008; McLeod and Bechtold, 2009; Bennert et al., 2010; Decarli et al., 2010; Targett et al., 2011). However, type-1 AGN remain offset from inactive galaxies in the M_BH—L_bulge relation: AGN have more luminous bulges at a given black hole mass (Nelson et al., 2004; Bennert et al., 2021). There are evidences that the M_BH − L_bulge relation defined by quiescent BH samples differs from that defined by the galaxies in the SDSS (Bernardi et al., 2007). Interestingly, the offset is larger for AGN of larger Eddington ratio (Barth et al., 2021). This suggests that the central regions of galaxies hosting an AGN have, in general, lower mass-to-light ratios than inactive galaxies, most likely for the presence of a young stellar population in the bulge of active systems (Kim and Ho, 2019).

The σ_⋆ has been measured either directly i.e., from the width of absorption lines associated with the stellar component of the host galaxies (Woo et al., 2006; Woo et al., 2008b; Shen et al., 2008) or by using the widths of narrow emission lines a proxy of the stellar velocity dispersion (Shields et al., 2003; Shields et al., 2006; Salviander et al., 2007). The latter approach is fraught from systematic effects. In the case of quasars and AGN radiating at moderate and high Eddington ratios, the [Oiii]λ5007 broadening is strongly affected by non-virial motions (Zamanov et al., 2002; Marziani et al., 2006; Mathur et al., 2011; Marziani and Sulentic, 2012; Cracco et al., 2016).

More reliable results for dynamical mass measurements of the host galaxy from spatially resolved images have been obtained with adaptive optics (Inskip et al., 2011). CO emission profiles have been used to estimate dynamical masses for individual objects since the early 2000s (Walter et al., 2003) even at fairly high redshift, and nowadays ALMA is rapidly adding to the available dynamical mass measurements for the host galaxy [e.g. (Tan et al., 2019; Molina et al., 2021)], considering that the velocity field of the molecular gas is often regular and consistent with rotation. State-of-the-art surface photometry of the AGN host galaxies in the NIR achieves decomposition in spheroid, disk, and bar component, as most of the host of nearby Seyfert galaxies are of morphological type Sa/SBa. As mentioned, a most recent work did not detect significant differences in the scaling with M_BH and σ_⋆ between active and nonactive galactic nuclei (Caglar et al., 2020; Bennert et al., 2021), and did not find difference between pseudo and classical bulges or barred and nonbarred galaxies in the M_BH—M_bulge relation (Bennert et al., 2021), although this result is still controversial (Kormendy et al., 2011; Ho and Kim, 2014). In addition, γ is still computed with the single epoch technique, without consideration of the diversity in accretion structure (and hence virial factor) that is expected in type-1 AGN samples. For type-1 active nuclei radiating at Eddington ratio above 0.01, the geometry and structure of the emitting region are affected by the accretion mode, which in turn affects the expression of the virial factor that is dependent on kinematics, geometry, and viewing angle (Collin et al., 2006; Park et al., 2012; Mejía-Restrepo et al., 2016; Mejía-Restrepo et al., 2018; Shankar et al., 2019). A study separately considering sources in different accretion modes and the statistical bias introduced by orientation effects is not available as yet.

Keeping the attention focused on γ, the radius of influence r_h is of the order of parsecs, and insufficient resolution may prevent reliable BH mass estimates or forces to target only the largest BHs (Gültekin et al., 2009; Gültekin et al., 2011), leading to a selection effect that yields an increase in the M_BH—σ relation for quiescent galaxies by a factor of a few (Shankar et al., 2016; Shankar et al., 2019). AGN will on average host more massive BHs than in the volume-limited case (Lauer et al., 2007), determining a Malmquist bias toward more massive BHs at a given spheroid mass, shifting γ upward and causing an offset in the zero-point of the M_BH—M_bulge relation. There are competing effects: the fraction of active galaxies among SMBHs varies considerably with mass (high-mass BHs are likely less active than low-mass BHs (Schulze and Wisotzki, 2011)). The strength of the bias depends on the limit in luminosity, the shape of the distribution function of spheroids, the scatter of the M_BH-M_bulge relation, and the Eddington ratios. If, as mentioned, the active fraction decreases as the BH mass increases, then for a given spheroid mass it will be more probable to find small-masses BHs in an AGN sample, causing a bias toward lower M_BH/M_bulge ratios, and a change in the slope of the relation.

The low-M_BH end of the correlation is especially problematic, as it is for quiescent galaxies. Narrow-line Seyfert 1s nuclei (NLSy1s, low-z type-1 AGN several of which are accreting at high rate (Marziani and Sulentic, 2014a)), often hosted in dwarf high surface brightness galaxies (Krongold et al., 2001) and in barred spirals (Crenshaw et al., 2003; Ohta et al., 2007), possess under-massive BHs (Mathur et al., 2001; Chao et al., 2008). NLSy1 nuclei often reside in disk-dominated galaxies with pseudo-bulges (Orban de Xivry et al., 2011; Mathur et al., 2012; Ermash and Komberg, 2013; Olguín-Iglesias et al., 2017; Järvelä et al., 2018; Doi et al., 2020). These types of bulges are more closely associated with the evolution of disks and may be typical of systems that did not experience a minor or major merger capable of leading to a real bulge development. Several studies found that disk-dominated galaxies deviate from the M_BH—M_bulge correlation, and, if considered as a distinct class, may not follow a M_BH—M_bulge correlation (Kormendy et al., 2011; Davis et al., 2018; Sahu et al., 2020). However, if one applies a correction for the disk component, and considers only the bulge, the AGN in the low black hole mass ranges M_BH ≲ 10⁸ M_⊙ might follow a relation consistent with the local M_BH—M_bulge correlation (Bennert et al., 2011; Sanghvi et al., 2014). At any rate, the relation between M_BH and σ_⋆ or M_bulge should be taken with special care in particular in the lower M_BH range. Relatively few objects are obscured type-1 AGN. Chandra observations are detecting a wealth of black holes in star-forming galaxies, in the range between 10⁶—10⁷ M_⊙, even at high z (Mezcua et al., 2016; Fornasini et al., 2018; Zou et al., 2020). They are low mass by supermassive black hole mass standards, and most likely still growing in an obscure phase. It is not known how they would be located in the M_BH—M_bulge plane. These elusive AGN are potential targets for JWST (Satyapal et al., 2021).

13.7 Over-Massive and Under-Massive Black Holes

At the time of its discovery, the luminous quasar HE0450-2,958 appeared as an oddity: a quasars without a host galaxy! (Magain et al., 2005). Understandably enough, the source attracted a lot of interest, and perhaps even a revival of the noncosmological interpretation of quasar redshifts (Arp et al., 1979; Sulentic and Arp, 1983; Sulentic and Arp, 1987). HE0450-2,958 appears hosted by a galaxy much fainter than that inferred from the correlation between BH mass and bulge luminosity (Kim et al., 2007). In the case of quiescent galaxies, compact dwarf galaxies whose BH has a mass reaching even 15% of the total galaxy mass (Reines et al., 2014; Seth et al., 2014; van Loon and Sansom, 2015) are observed. A possible explanation is that their outer parts may have been stripped by repeated encounters with other galaxies and produced an ultra-compact dwarf galaxy. The EAGLE cosmological and hydrodynamical simulations suggest that these kinds of objects are outliers resulting from the combination of stellar tidal stripping and the early formation epoch, which leaded to a rapid BH growth at high redshift, with the first mechanism being the most relevant for 2/3 of these sources (Barber et al., 2016). However, the disk/bulge decomposition is a delicate procedure. A careful reanalysis of the most striking cases, Mrk1216, NGC1277, NGC1271, and NGC1332, suggests that a proper reevaluation of the disk size with an ensuing increase in spheroid mass will bring these sources in better agreement with the M_BH—M_bulge relation (Savorgnan and Graham, 2016). The case of HE0450-2,958 has not been fully explained to date. Past works have considered intriguing lines of evidence suggesting high L/L_Edd and BAL outflow (Merritt et al., 2006; Lipari et al., 2007). However HE0450-2,958, which appears as a mini-BAL from a FOS spectrum, shows modest optical Feii emission, and a spectrum similar to the one of PG1211 + 143 (Merritt et al., 2006). According to the main sequence trends (see §14.2), the object should not be highly accreting (Marziani and Sulentic, 2014a; Du et al., 2016b). It is also unlikely that HE0450-2,958 is a recoiling black hole ejected by a companion galaxy at approximately 7 kpc of projected linear distance, on the ground of the strong narrow line emission of [Oiii]λλ4959,5007 (Merritt et al., 2006). HE0450-2,958 does not appear as an extraordinary powerful quasar. The upper limits on the host galaxy luminosity are not very constraining, so that this object could be well within the limits set by the scatter in the M_bulgevM_BH correlation (Kim et al., 2007).

However, recoiling black holes—provided that they are the active member of the binary, as suggested by numerical simulations (Nguyen and Bogdanović, 2016)—may systematically lower M_BH and ultimately increase the scatter of the observed BH–host galaxy bulge relation due to ejected BHs (Volonteri, 2007). Recoiling BHs have lower masses than their stationary counterparts, but the deficit in mass depends on kick speed and merger remnant properties (Blecha et al., 2011). The effect is of an overall downward shift in the normalization and an increase of the scatter in the M_BH—M_bulge relation: the offset between the stationary and the recoiling BH population can reach δ  log  g ≈ 0.4 dex, if the rotational velocity of the secondary BH is close to its escape velocity. The amplitude of the downward offset depends on the recoil velocity as well as on the accretion history of the stationary black hole, and can be lower, yielding a δ  log  ϕ ≈ 0.2 dex. This scenario is not as yet contextualized: a large fraction of type-1 AGN shows evidence that they do not host a sub-parsec binary black hole with a significant mass ratio between the secondary and the primary (say q ≳ 0.1). Conclusive evidences in favor of such binary systems are very rare at the time of writing.

13.8 Evolution of the M_BH—M_bulge Relation

Active galactic nuclei and quiescent bulge-dominant galaxies do not show strong evidence of evolution in the M_BH—M_bulge relation up to z ∼ 0.6 − 1 (Salviander et al., 2007; Schulze and Wisotzki, 2014; Li et al., 2021). At higher redshift, there is an increasing evidence of evolution, in the sense of high-z SMBHs that are overmassive at a given bulge mass than expected from the local scaling relation (McLure et al., 2006; Decarli et al., 2018). Between redshifts 1 and 2, Merloni et al. (2010) suggested a significant increase of the M_BH/M_Bulge ratio ( ∝ (1 + z)^0.68). Studies at even higher redshift used the velocity dispersion of the gas as a proxy of the stellar velocity dispersion and dynamical mass measurement from inclined disk models (Vayner et al., 2021). They suggest over-massive black holes (Targett et al., 2011) with respect to the local scaling law. The most recent results confirm that quasars host galaxies are under massive relative to M_BH, and detect a large difference, even by an order of magnitude, with systems at redshift in between 1.4 and 2.6 residing off the local scaling relation. Several quasar host galaxies have been resolved in their [C II] emission on a few kpc scale at redshift ≈6. Even in this case, the dynamical mass estimates for the host galaxies give masses more than an order of magnitude below the values expected from the local scaling relation (Decarli et al., 2018), in agreement with the results for galaxies at z ≈ 7 derived from cosmological hydrodynamical simulations (Marshall et al., 2020).

The evolution of the M_BH—M_bulge relation with the cosmic epochs can be interpreted in several ways: the most straightforward is that of a rapid growth of SMBHs at high redshift (Lupi et al., 2021). Also a variation of structural properties of AGN hosts remains possible (Shankar et al., 2013b; Zhu et al., 2021): elliptical galaxies are not really monolithic spheroids, but have undergone significant late-time dissipation-less assembly. There are intriguing caveats with the interpretation of a rapid black hole growth. First, very massive seed black holes need to be formed at z ≈ 20 to account for masses ∼ 10⁹ M_⊙ observed at redshift z ≳ 4 ((Volonteri, 2010; Trakhtenbrot, 2020), and references therein). Second, BH masses (unlike the masses of galaxies!) can only increase with cosmic epoch. If the merger-driven hierarchical scenario that implies the parallel growth of bulges and BHs is taken literally, the larger M_BH/M_Bulge ratio at high z means that mergers affect more bulge than BH masses (at cosmic epochs associated with z ≳ 1), an implication consistent with the anti-hierarchical growth and downsizing of the nuclear activity at low-z (Hirschmann et al., 2012). If pseudo-bulges follow the same M_BH scaling relations as that of classical bulges [e.g., Bennert et al., 2021], hierarchical growth might not be the only mechanism that drives the relation between M_BH—M_bulge: in spiral galaxies, secular evolution might lead to a parallel growth of bulge and central black hole. Clearly, this issue should be analyzed in connection to ongoing star formation properties of the pseudo-bulge hosts (Zhao et al., 2021). Host and black hole properties are different for different masses, and the relation between galaxy color and black hole mass is different for the red and blue sequence quiescent galaxies, suggesting different channels of black hole growth for the two sequences (Dullo et al., 2020).

In conclusion, AGN with “coreless” elliptical/bulge-dominated hosts may straightforwardly follow a relation similar to the one of normal galaxies. In other words, the M_BH—M_bulge relation may strictly hold for massive evolved systems, also if the nucleus is active, in a form that is as yet indistinguishable from the one of quiescent galaxies. It remains to be tested whether these sources could be mainly AGN accreting at relatively low rate and radiating at modest Eddington ratios (Population B, Section 14.2). Significant deviations may be associated with disk dominance, but a careful assessment of the relative disk and bulge contribution might bring the system with the over-massive BHs in agreement with the established relation (Caglar et al., 2020; Zhao et al., 2021). The local NLSy1s—all of which are Population A (Section 14.2), with a significant fraction of high accretors—are instead believed to be with black holes under massive with respect to their host masses. In this respect they are different from the high-z quasars with over-massive black holes. However, the observational properties of low-z AGN accreting at relatively high rate can still be regarded as typical of very high z quasars, when massive bulges were not yet formed, as originally suggested by Mathur (2000), Sulentic et al. (2000a). The analogy is based on the optical, UV, and X-ray AGN spectroscopic properties that are mainly governed by the Eddington ratio. In addition, modest masses of low-z quasars can grow by a factor ∼ 10 on time scales shorter than timescale of the cosmic evolution of quasar accretion rates, and therefore bring under massive BHs in line with the M_BH—M_bulge relation (Fraix-Burnet et al., 2017).

14 The Fundamental Plane of Active Galactic Nuclei and the Type-1 Active Galactic Nuclei Main Sequence

Some general considerations are in order when restricting the attention to the nuclei of galaxies. First, the central engine of nuclear activity is contained within a few parsec from its prime mover, the accreting massive black hole. Several scaling laws that are widely applied in the study of galaxies are not considered in the study of AGN: the Kormendy relation loses its meaning in the context of a system that is observed without spatial extension. Or, they might connect different physical bodies: when we speak about the r − L relation for AGN, r is the radius of the line-emitting region, and L is the luminosity of the AGN. The two parameters do not refer to cospatial entities. A similar consideration applies to the M_BH—r, or the M_BH—L, or the M_BH—metallicity relations.

The virial equation (Eq. 36) is yielding the same FWHM for the same r/M_BH; what matters is the radius in units of gravitational radii, a dimensionless quantity. A smaller mass can give the same line width of a larger mass provided that r scales with M_BH. This is why we need an estimate of the linear size r to recover a value of M_BH in physical units. This scale invariance is obviously not applicable to radiative phenomena: the flux reaching a distance r will decrease with the inverse of the square of r on a dimensional scale. The BLR radius r_BLR subtends such a small angle that has not been directly resolved if not in the last few year thanks to the GRAVITY instrument (Amorim et al., 2020; Amorim et al., 2021). The foundations of any AGN diagnostics therefore rest on the scale invariance of gravitational forces, and on electromagnetic phenomena instead of lacking such scale invariance. These considerations can be translated in mathematical terms to provide at least a self-similar framework that includes the fundamental plane of black holes, the modelization of jets (Heinz and Sunyaev, 2003) and the quasar main sequence (MS).

14.1 The Fundamental Plane of Black Hole Activity

The fundamental plane of black hole activity can be written as a correlation between black hole mass, X-ray, and radio luminosity. The correlation defines a plane in the space of parameters defined by the mass and the radio and X-ray luminosities. In its original formulation, the fundamental plane was written as (Merloni et al., 2003):

$log{L}_{\text{R}}=(0.60\pm 0.11)\log L_{\text{X}}+(0.78_{-0.09}^{+0.11})\log M_{BH}+7.33_{-4.07}^{+4.05}.(38)$

The scatter is large, implying that a fourth variable might be involved, for instance black hole spin (Ünal and Loeb, 2020). The salient point is however that the relation holds over a huge range of black hole masses, from a few times solar (i.e., from the domain of the so-called micro-quasars) to the largest black hole masses detected in the Universe ∼ 10¹⁰ M_⊚ [e.g. (Schindler et al., 2021; Valtonen et al., 2012)]. ⁷ It is remarkable that also stellar-mass black holes exhibit relativistic jets, as spectacularly demonstrated by the relatively recent discovery of superluminal motion in a Galactic black hole candidate by Mirabel and Rodríguez (1994). The self-similarity expressed in Eq. 38 allows for an invariant jet model and a simple relation between M_BH and radio power (Heinz and Sunyaev, 2003). The self-similarity notwithstanding, there is a nonlinear relation between BH mass and radio power, with P_ν ∝ ${M_{\text{BH}}}^{1.3-1.4}$, implying that the radio emission normalized to the bolometric luminosity should be much higher for AGN than for microquasars. In the framework of the model of Heinz and Sunyaev (2003), flat spectrum synchrotron jet emission is produced by an inefficient accretion mode. The fundamental plane of black hole activity refers to sources accreting at very low rate (dimensionless accretion rate $\dot{m}\lesssim$ 0.01), and radiating below a few hundredths of their Eddington luminosity (Gültekin et al., 2019). This means that the relation is best suited for sources such as micro-quasars (i.e., stellar-mass black hole candidates in the low state (Mirabel and Rodríguez, 1994)) and BL Lac objects, in which both radio and X-ray emissions are ultimately associated with the relativistic jet.⁸

14.2 The Quasar Main Sequence

The quasar main sequence is, in many ways, analogous to the FP for black holes in a different accretion mode sustained by higher $\dot{m}\sim 0.01-1$. The formulation is rather different, and follows a different discovery path based on the statistical analysis of sources that are predominantly radio-quiet. The quasar main sequence (MS) is defined from the first Eigenvector (E1) that was originally identified by a PCA of about 80 Palomar-Green (PG) quasars and associated with an anti-correlation between the strength of optical Feii emission measured from the prominence of the emission blend centered at λ 4,570 Å (Fe iiλ4570) with respect to Hβ (R_FeII = I (Fe iiλ4570)/I(Hβ)) and FWHM of Hβ (Boroson and Green, 1992). The E1 MS has withstood the test of time [Figure 11 (Sulentic et al., 2000b; Zamfir et al., 2010; Popović and Kovačević, 2011; Kruczek et al., 2011; Grupe and Nousek, 2015; Shen and Ho, 2014),], and the main optical trend shown in Figure 11 has been confirmed by samples of more than two order of magnitude larger in size than the original one (Shen and Ho, 2014). The importance of Feii stems from its extensive emission from UV to the IR that can dominate the thermal balance of the low-ionization BLR. The FWHM(Hβ) is associated with the velocity field in the low-ionization BLR, most likely predominantly virialized (Peterson and Wandel, 1999). These two parameters are related to the physical conditions and to the dynamics of the emitting regions, which are in turn influenced by the accretion mode of the central black hole, and its evolutionary stage.

FIGURE 11

FIGURE 11. The quasar main sequence as defined from the original paper by Boroson and Green (1992) based on 88 quasars (left) and the one based on the SDSS sample of 310 low-z quasars by Zamfir et al. (2010). The color shading from cyan to navy blue is proportional to the number density as a function of the Feii prominence parameter and of the FWHM of Hβ, and therefore to the source occupation in the parameter plane.

Trends associated with the MS have been extended to the radio (Sulentic et al., 2003; Shen and Ho, 2014; Zamfir et al., 2008; Ganci et al., 2019), FIR (Wang et al., 2006; Ganci et al., 2019), IR (Dultzin-Hacyan et al., 1999; Loli Martínez-Aldama et al., 2015; Panda et al., 2020), UV (Sulentic et al., 2000c; Reichard et al., 2003; Bachev et al., 2004; Sulentic et al., 2006; Śniegowska et al., 2020; Baskin and Laor, 2005; Richards et al., 2002; Richards et al., 2005) and X-ray domain (Wang et al., 1996; Grupe et al., 2001; Bensch et al., 2015), and to optical variability as well (Mao et al., 2009; Bon et al., 2018). Fraix-Burnet et al. (2017) provides a detailed list of the various parameters that have been measured in the various frequency domains. A summary description of the trends and a justification for the two quasar populations are also provided by several authors (Sulentic et al., 2008; Sulentic et al., 2011; Sulentic and Marziani, 2015). A nonlinear decay curve provides a quantitative description of the main sequence in the FWHM—R_FeII plane (Wildy et al., 2019).

TABLE 1

TABLE 1. Abbreviations and acronyms used in the text.

The distribution of the data in the plane R_FeII—FWHM(Hβ) makes it expedient to define spectral types [Figure 12 (Sulentic et al., 2002; Shen and Ho, 2014)]. This provides the considerable advantage that a composite spectrum within each bin could be representative of objects in similar physical conditions. In alternative, a prototype object can be defined for each spectral type and used to analyze systematic changes along the quasar MS. It is also expedient to distinguish between two populations: Population A made of sources with FWHM(Hβ) ≤ 4,000 km s⁻¹ and Population B (broader) with FWHM(Hβ) > 4,000 km s⁻¹. Extreme Population A are quasars with R_FeII ≳ 1 and extreme Pop. B with undetectable Feii emission and the broadest Balmer lines (extreme FWHM Hβ can reach ∼ 15, 000 − 20, 000 km s⁻¹ (Eracleous and Halpern, 2003; Strateva et al., 2003; Eracleous and Halpern, 2004)). Basically, Population B includes sources termed as “disk dominated,” where radiation forces exert a modest influence on the overall dynamics of the gas (Richards et al., 2002), while Population A is made of quasars radiating at relatively high Eddington ratio L/L_Edd ≳ 0.2, for which radiation forces are able to maintain a wind that leads to easily identified systematic wavelength displacements toward the blue with respect to the quasar rest frame in the high-ionization emission lines (Gaskell, 1982; Brotherton et al., 1994; Marziani et al., 1996; Richards et al., 2011; Coatman et al., 2016; Sulentic et al., 2017). The extreme of Population A identifies the class of “strong Feii emitters” (Lipari et al., 1993; Graham et al., 1996b). Feii emission overwhelming Hβ line emission (R_FeII ≳1) implies extreme Eddington ratio (L/L_Edd ∼ 1 (Marziani and Sulentic, 2014a)) and possibly super-Eddington accretion rate (Wang et al., 2014a; Sun and Shen, 2015; Du et al., 2016b; Du et al., 2016b; Panda et al., 2018; Panda et al., 2019).

FIGURE 12

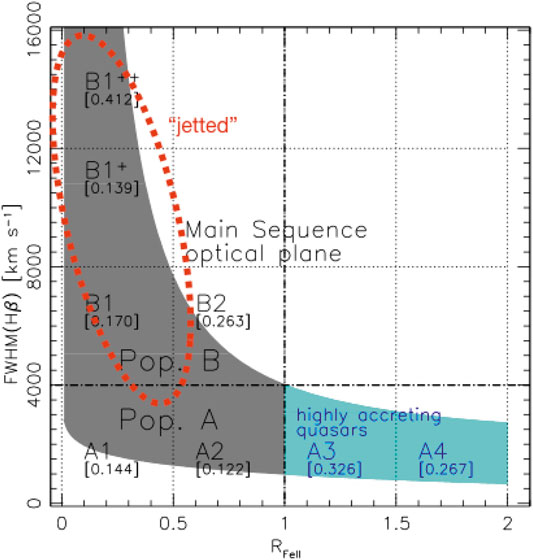
FIGURE 12. The optical plane of the quasar main sequence with the occupation accounted for by the combined effect of Eddington ratio and orientation, as claimed by Shen and Ho (2014). The two grids were computed for M_BH = 10⁸ M_⊚ and 10⁹ M_⊚ (gray), for several values of L/L_Edd and for viewing angle θ between 0 and 40°, following the toy model described in the text and in more detail in Ref. (Marziani et al., 2018). In the left panel, the labels identify the areas of Population A and B (respectively below and above the FWHM limit at 4,000 km s⁻¹), and of extreme Population A (R_FeII ≳ 1).

However, along the entire MS, the BLR gas emitting the low-ionization lines belongs to predominantly virialized systems (Peterson and Wandel, 1999). The main asymmetries in the low-ionization line profiles can be explained in the context of a dynamical system whose velocity field is predominantly Keplerian. The single peaked, symmetric, and unshifted profile typical of Population A has been traditionally explained as due to an extended disk (Dumont and Collin-Souffrin, 1990), and the same explanation apparently remains valid in the case of extreme Pop. A AGN that are characterized by extreme high-ionization blueshifts (Leighly and Moore, 2004; Sulentic et al., 2007; Richards et al., 2012; Marziani et al., 2016b; Bischetti et al., 2017; Sulentic et al., 2017). The high Civλ1549/Hβ intensity ratio of the blueshifted emission (Marziani et al., 2010) makes it possible that the Hβ profile remains almost symmetric and can be easily symmetrized by applying a small correction (Negrete et al., 2018). In general, the distinguishing feature of Pop. B sources, a redward asymmetric profile, can be explained by the sum of a disk contribution and emission from a larger distance (Bon et al., 2007; Bon et al., 2009). Reverberation mapping studies of lines from different ionic species have provided evidence of “ionization stratification” and velocity-resolved reverberation mapping of sources with asymmetric Hβ basically confirms the scenario of a Keplerian velocity field (Du et al., 2018b; Brotherton et al., 2020). The red-ward asymmetry has been interpreted as due to gravitational and transverse redshift (Bon et al., 2015; Punsly et al., 2020) or by gas clouds infalling toward the central black hole (Wang et al., 2017). At the extreme end of Pop. B sources, the profiles are often very broad and double peaked, accounted for by a bare Keplerian disk model with mild relativistic effects (Chen and Halpern, 1989; Strateva et al., 2003). So, all along the quasar MS the low-ionization lines (at variance with the high-ionization emission) appear to be predominantly associated with a bound, Keplerian dynamical system (Collin-Souffrin et al., 1988; Elvis, 2000).

Many studies still distinguish between the NLSy1s (FWHM Hβ ≲ 2000 km s⁻¹) and the rest of type-1 AGNs [e.g., Cracco et al., 2016], and consider NLSy1s an independent class. There is a general consensus that the limit at 2,000 km s⁻¹, albeit of historical importance, has no special meaning. The main reason behind extending the limit from 2,000 to 4,000 km s⁻¹ is that several properties of NLSy1s are consistent with the ones of “the rest of Population A” in the range 2,000 km s⁻¹ ≲ FWHM(Hβ) ≲ 4000 km s⁻¹. The change—in low redshift samples z ≲ 1—occurs around 4,000 km s⁻¹, not 2,000 km s⁻¹ (Cracco et al., 2016). On the converse Population A and B can be distinguished on the basis of the Balmer line profiles, and because of the amplitude of the systematic blueshift of the high-ionization lines with respect to the quasar rest frame. Composite Hβ profiles of spectral types along the MS are consistent with a Lorentzian for both NLSy1s and the rest of Population A. Other parameters (CIVλ1549 centroid, R_FeII) also span the same ranges in NLSy1s and the rest of Population A.

The governing accretion parameter accounting for the MS trends is most likely the Eddington ratio, which is related to the mass accretion rate by a monotonic albeit nonlinear relation (Mineshige et al., 2000; Sadowski, 2011; Sądowski et al., 2014). This explanation—originally suggested by Boroson & Green (Boroson and Green, 1992)—has also withstood the test of time (Marziani et al., 2001; Boroson, 2002; Ai et al., 2010; Zamfir et al., 2010; Xu et al., 2012; Shen and Ho, 2014; Sun and Shen, 2015; Panda et al., 2017; Panda et al., 2018), even if several key pieces needed to connect L/L_Edd to the observed parameters remain poorly understood to date. The evidence of a correlation between R_FeII and L/L_Edd is still made murky by the strong effect of orientation on the line broadening, affecting M_BH and L/L_Edd computations with both random and systematic errors (Marziani et al., 2019). Sun and Shen (2015) provided evidence of this based on the stellar velocity dispersion of the host spheroid (a proxy for M_BH) anticorrelation with R_FeII, implying that L/L_Edd increases with Feii. Recent approaches include a careful analysis of the role of metallicity and of density and ionization trends (Panda et al., 2018; Panda et al., 2019), and confirm L/L_Edd as the main physical parameter governing the MS “horizontal branch” along the R_FeII axis.

A toy scheme can explain in a qualitative way the occupation of the MS plane under the assumptions that Eddington ratio, mass, and an aspect angle θ (i.e., the angle between the line-of-sight and the accretion disk axis) are the parameters setting the location of quasar along the MS (Marziani et al., 2001; Marziani et al., 2018). If the BLR radius follows a scaling power-law with luminosity (r ∝ L^a, Kaspi et al. (2000), Bentz et al. (2013)), under the standard virial assumption, then

$\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}\propto f_{\text{S}}{(\theta )}^{-\frac{1}{2}}{\left(\frac{L}{M_{\text{BH}}}\right)}^{-\frac{a}{2}}{M}_{\text{BH}}^{\frac{1-a}{2}}\propto f_{\text{S}}^{-\frac{1}{2}}{L}^{\frac{1-a}{2}}{\left(\frac{L}{M_{\text{BH}}}\right)}^{-\frac{1}{2}}.(39)$

We can also write R_FeII as a function of (L/L_Edd) and θ, which needs to be established either empirically or theoretically. For illustrative purposes, we consider the “fundamental plane of accreting BHs” that relates L/L_Edd to R_FeII (Du et al., 2016b; Bon et al., 2020), ignoring other relevant factors, such as systematic differences in line shapes and in chemical composition along the MS (Panda et al., 2019; Śniegowska et al., 2020), and we assume that R_FeII depends on θ following a limb-darkening law (Marziani et al., 2001; Netzer, 2013).

As expected, the right panel of Figure 12 shows that θ predominantly affects FWHM Hβ and L/L_Edd predominantly (but not exclusively) affects R_FeII. Under the assumptions of the toy scheme the FWHM limit at 4,000 km s⁻¹ should include mainly sources with L/L_Edd ≳ 0.1 − 0.2. Sources at lower L/L_Edd are expected to be rare because they should be observed almost pole-on (for example, core-dominated radio-loud quasars whose viewing angle θ is relatively small (Marziani et al., 2001; Zamfir et al., 2008)), and the probability of observing a randomly oriented source at an angle θ between the symmetry axis and the line of sight is P(θ) ∝  sin θ. Even if such sources are expected to be rare, their number increases in flux-limited samples for a Malmquist bias, due to a continuum enhancement via relativistic beaming. We can say that separating Pop. A and B at 4,000 km s⁻¹ makes sense for low z samples and that, also by a fortunate occurrence, Pop. A includes mostly relatively high L/L_Edd sources.

The bolometric luminosity L can be estimated from optical or UV luminosities.⁹ The diagram L/L_Edd vs. bolometric luminosity (Figure 13) also provides a strong rationale for the existence of two populations: only above a threshold of L/L_Edd ≈ 0.1 large shifts are observed. Data points whose high-ionization lines are strongly blue shifted with respect to the rest frame are superimposed on the distribution of Figure 13, and are clearly seen for L/L_Edd ≳ 0.1 only. This corresponds to the population A and B of Sulentic et al. (2000a), of wind and disk-dominated quasars (Richards et al., 2002), and population 1 and 2 of Collin et al. (2006). The data of Figure 13 refer to sources with large blueshift in [Oiii]λλ4959,5007, but an equivalent behavior is observed also for the blueshift of Civλ1549. At the same time, Figure 13 (and Figure 15 as well) show the effect of a strong bias typically affecting quasar studies over a broad range of redshifts: at high z we detect only the high-luminosity sources that correspond to relatively high L/L_Edd.

FIGURE 13

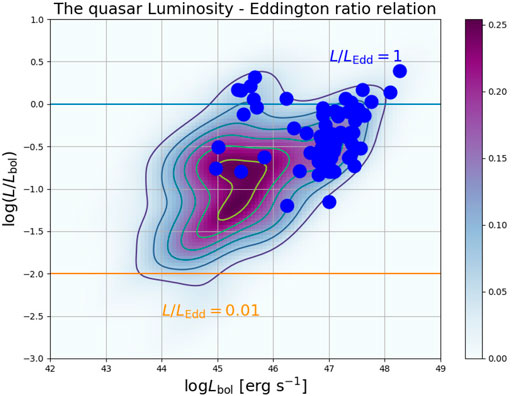
FIGURE 13. The relation between Eddington ratio L/L_Edd and bolometric luminosity for the sample described in Figure 11, second panel. Quasars occupy the range 0.01–1, but only above Eddington ratio ≈ 0.1 large shifts are observed, as shown by the distribution of the blue data points, which represent quasars with the largest [Oiii]λλ4959,5007 blueshift.

Figure 11 refers to low-z (z ≲ 1) samples. A complete mapping of the MS at high L is still missing (we consider high-luminosity quasars those with bolometric log  L ≳ 47 [erg/s]): the Hβ spectral range is therefore accessible only with IR spectrometers to observe the Hβ spectral regions of high-luminosity quasars that are very rare at z ≲ 1. A significant progress is expected in the next years, since IR spectral observations covering Hβ of high-z and high-L quasars are becoming widespread. A systematic increase in BH mass M_BH has a corresponding increase in FWHM. If a = 0.5, the FWHM grows with ${M_{\text{BH}}}^{0.25}$, i.e. a factor of 10 for   log  L, passing from 44 (relatively low luminosity) to 48 (very luminous quasars). The trend may not be detectable in low-z flux-limited samples, but becomes appreciable if quasars over a wide interval in L are considered. At high M_BH, the MS becomes displaced toward higher FWHM values; the displacement probably accounts for the wedge-shaped appearance of the MS when large samples of quasars are considered (Shen and Ho, 2014). If we consider a limiting Eddington ratio (L/L_Edd ∼ 0.1—0.2) as a physical criterion for the distinction between Pop. A and B, then the separation based on the FWHM becomes luminosity dependent. According to the toy scheme, the FWHM of Hβ (or of any other virialized line) should be $\propto \left(\right.L/L_{\text{Edd}}{\left.\right)}^{-\frac{1}{2}}\times L^{\frac{1-a}{2}}$. Figure 14 shows that the ∝ L^0.25 for the width of a low- and an intermediate ionization line. The maximum L/L_Edd should correspond to the minimum FWHM, expected to increase with luminosity as ∝ L^0.25. If the FWHM is plotted against the luminosity, a trend-line nicely envelops the lower FWHM end of the data point distribution (Marziani et al., 2009).

FIGURE 14

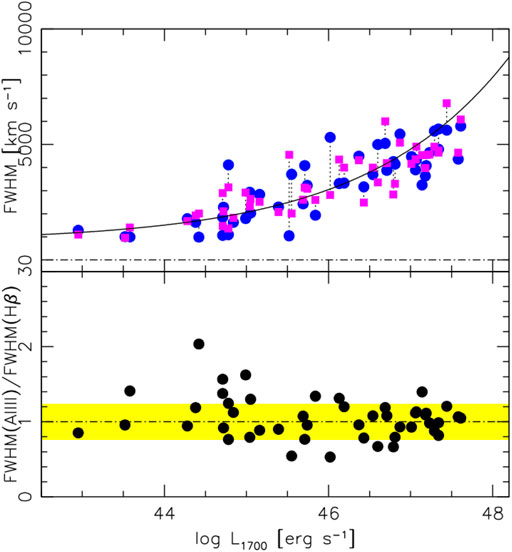
FIGURE 14. The relation between FWHM of Hβ (blue) and Al iiiλ1860 (magenta) and their FWHM ratio (bottom panel), and bolometric luminosity. The filled line represents the trend FWHM ∝ L^1/4, with arbitrary normalization. The yellow band defines the uncertainty range in the ratio FWHM Al iiiλ1860/FWHM Hβ.

14.3 The BH Mass—Luminosity Relation

Joining the fundamental plane and the main sequence trends for AGN, four main regimes can be isolated (c.f. (Giustini and Proga, 2019)) where the physics of the inner accretion and ejection is expected to change. Observationally, they range from low-luminosity AGN at extremely low accretion rates ($\dot{m}\lesssim 0.01$) and Population B quasars radiating at rates 0.01 ≲ L/L_Edd ≲ 0.1 − 0.2, to Population A sources with L/L_Edd ≳ 0.1 − 0.2, and extreme Population A sources radiating close or somewhat above the Eddington limit (L/L_Edd ≳ 1). There is a close formal analogy between the FP of accreting black hole and the MS. Eq. 38 can be rewritten as an implicit relation between L/L_Edd and M_BH. Similarly the MS is a sequence in the plane FWHM Hβ—R_FeII that can be translated into a relation between L/L_Edd ( ∝ R_FeII) and M_BH ( ∝ FWHM). The relations of the MS are, as in the case of the FP, self-similar over 9 orders of magnitude in M_BH (Zamanov and Marziani, 2002). Radiation-driven winds appear to dominate in the high-ionization line emission in Population A and especially extreme Pop. A, reflecting the importance of the balance between radiation and gravitation forces expressed by L/L_Edd in the accretion processes of AGN (Ferland et al., 2009; Marziani et al., 2010), whereas the black hole mass is the ultimate parameter governing the energetics (Sulentic et al., 2017).

The M_BH—luminosity relation can be constructed for large quasars samples once the M_BH has been computed (Figure 15). Figure 15 shows that the distribution of quasars in the plane M_BH—L is constrained within two well-defined diagonal lines, corresponding to the L/L_Edd ≈ 0.01 and L/L_Edd ≈ 1. The empty area at the top left corner is due to inefficient radiators accreting at very low rate (Narayan and Yi, 1995), which are most often not type-1 quasars and are difficult to detect; the bottom right area is associated with sources that should be super Eddington radiators. Such sources are not expected to exist; L/L_Edd ≈ a few could be a physical limit for highly super-Eddington accretion (Mineshige et al., 2000; Sądowski et al., 2014).

FIGURE 15

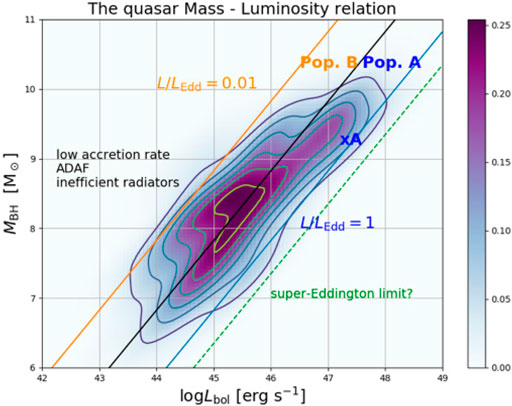
FIGURE 15. Mass-luminosity relation for a sample of ≈ 330 AGNs, made of 280 low-z quasars from Marziani et al. (2003) and high-luminosity 50 HE quasars of the sample described by Sulentic et al. (2004). The diagonal lines trace the lower ∼ 0.01⋅ L/L_Edd and ∼ 1.00⋅ L/L_Edd. The wide majority of AGN is included within these limits.

15 A Tully-Fisher Law for Quasars

Strong Feii emitters have attracted attention since long, but they have been linked to a particular accretion state only recently (Marziani and Sulentic, 2014a; Marziani and Sulentic, 2014b). The simple selection criterion R_FeII > 1.0 used for the identification of xA sources from optical data corresponds to an equally simple selection with UV criteria (Marziani and Sulentic, 2014a). In addition, the distinguishing features of the UV composite spectrum of Martínez-Aldama et al. (2018) reveal that the spectrum of xA sources can be recognized by a simple visual inspection.

Extreme Population A sources account for ∼ 10% of quasars in low-z, optically selected sample FeII in Pop. A. Lines have low equivalent width: some xAs are weak lined quasars [W(Civλ1549) ≤ 10 Å, WLQ (Diamond-Stanic et al., 2009)], whereas WLQs can be considered the extreme of Pop. A (Marziani et al., 2016b). The Ciii]λ1909 emission almost disappears. In the plane log  U −   log  n_H defined by CLOUDY simulations, UV line intensity ratio converges toward extreme values for density (high, n_H > 10¹² − 10¹³ cm³) (Negrete et al., 2012; Temple et al., 2020), ionization (low, ionization parameter U ∼ 10⁻³ − 10^−2.5). Extreme values of metallicity are also derived from the intensity ratios CIV/AlIII, CIV/HeII, AlIII/SiIII] (Negrete et al., 2012; Martínez-Aldama et al., 2018; Śniegowska et al., 2020), most likely above 10–20 times solar or with abundances anomalies that might selectively increase aluminum or silicon, or both.

XA quasars radiate at extreme L/L_Edd along the MS. The L/L_Edd dispersion has been found to be small (Marziani and Sulentic, 2014a). This result is consistent with the accretion disk theory that predicts low radiative efficiency at high accretion rate and that L/L_Edd converges toward a limiting value (Mineshige et al., 2000; Abramowicz et al., 1988; Sądowski et al., 2014). Another important fact is the self-similarity of the spectra selected by the R_FeII criterion: the low-ionization lines become broader with increasing luminosity according to Eq. 39, but the relative intensity ratios (and so the overall appearance of the spectrum) remain basically unchanged, although some redshift and luminosity effects are expected. Accretion disk theory predicts that at high accretion rate a geometrically thick, advection dominated disk should develop (Abramowicz et al., 1988; Sądowski et al., 2014). The innermost part of the disk is puffed up by radiation pressure, while the outermost one remains geometrically thin. The effect on the BLR structure can be addressed by two-dimensional reverberation mapping and by careful modeling of the coupling between dynamical and physical conditions (Li et al., 2013; Pancoast et al., 2014b; Li et al., 2018). However, this change from the standard thin disk provides two key elements for the BLR structure: the existence of a collimated cone-like region, where the high-ionization outflows might be produced, and the shadowing of the outer disk where low-ionization emission lines form (Wang et al., 2014b). The low-ionization emitting region may therefore remain shadowed from the intense radiation field that is associated with the continuum observed if the line of sight is not too far from the polar axis, and the velocity field stays unperturbed.

15.1 A Relation Between Luminosity and Velocity Dispersion for Quasars

Three conditions are satisfied for xA quasars: 1) constant Eddington ratio L/L_Edd, close to Eddington limit; 2) the assumption of virial motions of the low-ionization BLR, so that the black hole mass M_BH can be expressed by the virial relation (Eq. 36); 3) spectral invariance: for extreme Population A, the ionization parameter U can be written as $U=Q(H)/4\pi r_{\text{BLR}}^2{n}_{\text{H}}c\propto L/r_{\text{BLR}}^2{n}_{\text{H}}$ (Netzer, 2013), where Q(H) is the number of hydrogen-ionizing photons. U has to be approximately constant; otherwise, we would observe a significant change in the spectral appearance. The three constraints make it possible to derive a relation between line width (the FWHM of the Hβ broad component is expressed in units of 1,000 km s⁻¹) and luminosity:

$L(\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M})={\mathcal{L}}_{\text{0}}\cdot {(\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M})}_{1000}^4{\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{s}}^{-1}(40)$

where ${\mathcal{L}}_{\text{0}}$ depends on the square of L/L_Edd, the ionizing range of the spectral energy distribution, and a parameter directly derived from the UV spectra, the product density times ionization parameter that has been scaled to the typical value 10^9.6cm⁻³ (Padovani and Rafanelli, 1988; Matsuoka et al., 2008; Negrete et al., 2012). Until now, the FWHM of Hβ broad component and of Al iiiλ1860 have been adopted as VBEs (Dultzin et al., 2020; Czerny et al., 2020; Marziani et al., 2020). Equation (40) implies that a simple measurement of the FWHM of a low-ionization line yields a z − independent estimate of the accretion luminosity [Marziani and Sulentic, 2014a, c.f. (Teerikorpi, 2011)].

The virial luminosity equation is conceptually equivalent to the Tully-Fisher and the early formulation of the Faber Jackson laws for ETGs (Faber and Jackson, 1976; Tully and Fisher, 1977). Recent works proposed the “virial luminosity” could provide suitable distance indicators because several emission properties appear to be extreme and stable with luminosity scaling with black hole mass at a fixed ratio (Wang et al., 2013; Wang et al., 2014a; Franca et al., 2014). The virial equation has been applied to xA quasars only (L/L_Edd ∼ 1), although it in principle could be useful for all quasars with known L/L_Edd, provided a suitable emission line broadened by virial motions is used for the luminosity computation. At present, the virial equation can be considered for all xA quasars distributed over a wide range of luminosity and redshift, where conventional cosmological distance indicators are not available (Czerny et al., 2018; Czerny et al., 2020; Marziani et al., 2020).

16 Conclusion

In this work we have reviewed only a small part of the big efforts done up to now on the SRs of galaxies and AGN. We have not addressed for example the correlations that are observed in the X-ray and radio domain, as well as many correlations involving the line emissions visible in the spectra.

It should be now clear that SRs are used continuously in every research area. The aims are different, going from the estimation of masses and distances, or peculiar velocities, or simply to check the output of theories, or to extract from them some useful indications about the physical mechanisms shaping the structure and evolution of galaxies and AGN.

The clear message emerging from this vast panorama of connections between structural, dynamical, gas, and stellar population and halo parameters, is that galaxies are very complex objects formed through different channels, which include merging of subunits, inflows, shocks, collapses, etc., as some of the most influent processes at work. In addition, it is also clear that galaxies vary their properties across the cosmic time, changing their morphology and physical characteristics. The simple Hubble morphological classification is therefore only a first naive tentative of summarizing such complexity that today are leading astrophysicists to adopt new specific strategies to classify galaxies, describe their properties, and highlight the amount of diversity across the cosmic epochs, but always keeping in mind the necessity of looking at the most important parameters that are able to trace the evolution of galaxies.

This new way of working is now facing the need of sophisticated numerical simulations and new statistical tools able to tackle the big astronomical number of data, exploring different classification schemes and strategies and group galaxies according to their similar evolutionary paths.

The multivariate partitioning analyses appear to be one of the most appropriate techniques. The principal component analysis is one of these tools (Cabanac et al., 2002; Recio-Blanco et al., 2006), but it is not a clustering tool. Many new attempts have used multivariate clustering methods [see e.g. (Ellis et al., 2005; Chattopadhyay and Chattopadhyay, 2006; Chattopadhyay and Chattopadhyay, 2007; Chattopadhyay et al., 2009; Fraix-Burnet et al., 2009; Almeida et al., 2010; Fraix-Burnet et al., 2010)]. These sophisticated statistical tools are now used in different areas of astrophysics and are giving encouraging results, in particular for the problem of the identification of the galaxy ancestors and the processes more active in the transformation of galaxies (Fraix-Burnet et al., 2019).

In conclusion we can say that the world of SRs is big and complex. A lot of efforts are still necessary to organize such complexity, identify the key relationships having a real physical role for galaxies and AGN, and understand the profound implications behind their intrinsic nature. Possibly, the future high-z observations will add new information that will help the clarification of many long-standing open problems.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

MD want to thank Frontiers for the assistance in the production of the Research Topic.

Footnotes

¹By the way the FP was discovered by studying the residuals of the FJ relation.

²In Chiosi et al. (Chiosi et al., 2019) the same expression is written as $\log R_e=0.007584{(\log M_s)}^3-0.1874{(\log M_s)}^2+1.908(\log M_s)-9.027$, in which by mistake the term (log  M_s) does not contain the factor m.

³The cosmological parameters were H₀ = 65 km s⁻¹ Mpc⁻¹, Baryonic to Dark Matter ratio 1 to 9, i.e. for M_T = M_B + M_D, M_B = 0.1M_T, M_D = 0.9M_T.

⁴The cosmological background was the standard ΛCDM, with H₀ = 70.1 km/s/Mpc, flat geometry, Ω_Λ = 0.721, σ₈ = 0.817, and baryonic fraction ≃ 0.1656.

⁵It is yet unclear which of the two relation is the most fundamental, albeit the relation σ_⋆ with M_BH has been considered as the primary one in several past works. The two relations will be considered as interchangeable when the M_BH—bulge relation is mentioned in a generic context.

⁶Not to be confused with σ_⋆.

⁷As stressed by Sulentic et al. (Sulentic et al., 2004; Sulentic et al., 2006; Sulentic et al., 2007), M_BH much in excess of ∼ 10¹⁰ M_⊙ are unrealistic and probably the results of the use of a high-ionisation line affected by wind kinematics as a virial broadening estimator (VBE). This makes the primary black hole of OJ287 (Sillanpaa et al., 1988) as the most massive active black hole known to-date, with a mass of ≈ 1.8 ⋅ 10¹⁰ M_⊚, second to the black hole of Holm 15A, the central galaxy of galaxy cluster Abell 85, with ≈ 4 ⋅ 10¹⁰ M_⊚ (Mehrgan et al., 2019).

⁸There is as yet no consolidated way to compute bolometric corrections, and ideally the bolometric correction should be computed from the spectral energy distribution (SED) of each individual quasar (Shang et al., 2011), or at least for each spectral type along the quasar main sequence (Pennell et al., 2017). Bolometric corrections can be also computed from theoretical considerations on the emission properties of the accretion disk (Nemmen and Brotherton, 2010; Netzer, 2019). The simplest, and most widely used approach to compute the bolometric correction is to multiply the monochromatic luminosity by a constant scale factor that is obviously frequency-dependent and roughly 10 for λL_λ at 5,000 Å, and ≈ 2 − 3 for the UV wavelengths where the strongest lines are observed (Elvis et al., 1994; Woo and Urry, 2002; Richards et al., 2006).

⁹This might exclude NLSy1s that are believed to be genuinely jetted, such as the ones with γ-ray detections (Berton et al., 2019). Such sources are in a different accretion domain and might be more appropriately considered in the context of a scaling law with a L/L_Edd dependence (Foschini, 2014).

References

Aaronson, M., Bothun, G., Mould, J., Huchra, J., Schommer, R. A., and Cornell, M. E. (1986). A Distance Scale from the Infrared Magnitude/H I Velocity-Width Relations. V - Distance Moduli to 10 Galaxy Clusters, and Positive Detection of Bulk Supercluster Motion toward the Microwave Anisotropy. ApJ 302, 536. doi:10.1086/164014

CrossRef Full Text | Google Scholar

Abazajian, K., Adelman-McCarthy, J., Agüeros, M., Allam, S., Anderson, S. F., Annis, J., et al. (2003). The First Data Release of the Sloan Digital Sky Survey. Astronomical J. 126, 2081–2086. doi:10.1086/378165

CrossRef Full Text | Google Scholar

Abramowicz, M. A., Czerny, B., Lasota, J. P., and Szuszkiewicz, E. (1988). Slim Accretion Disks. ApJ 332, 646–658. doi:10.1086/166683

CrossRef Full Text | Google Scholar

Abramson, L. E., Gladders, M. D., Dressler, A., Oemler, A., Poggianti, B., and Vulcani, B. (2015). Matching the Evolution of the Stellar Mass Function Using Log-Normal Star Formation Histories. ApJ 801, L12. doi:10.1088/2041-8205/801/1/L12

CrossRef Full Text | Google Scholar

Abramson, L. E., Gladders, M. D., Dressler, A., Oemler, A., Poggianti, B., and Vulcani, B. (2016). Return to [Log-]Normalcy: Rethinking Quenching, the Star Formation Main Sequence, and Perhaps Much More. ApJ 832, 7. doi:10.3847/0004-637X/832/1/7

CrossRef Full Text | Google Scholar

Gravity Collaboration, Abuter, R., Abuter, R., Amorim, A., Bauböck, M., Berger, J. P., Bonnet, H., et al. (2021). Improved GRAVITY Astrometric Accuracy from Modeling Optical Aberrations. A&A 647, A59. doi:10.1051/0004-6361/202040208

CrossRef Full Text | Google Scholar

Gravity Collaboration, Abuter, R., Accardo, M., Amorim, A., Anugu, N., Ávila, G., Bonnet, H., et al. (2017). First Light for GRAVITY: Phase Referencing Optical Interferometry for the Very Large Telescope Interferometer. AAp 602, A94. doi:10.1051/0004-6361/201730838

CrossRef Full Text | Google Scholar

Afanasiev, V. L., Popović, L. Č., and Shapovalova, A. I. (2019). Spectropolarimetry of Seyfert 1 Galaxies with Equatorial Scattering: Black Hole Masses and Broad-Line Region Characteristics. MNRAS 482, 4985–4999. doi:10.1093/mnras/sty2995

CrossRef Full Text | Google Scholar

Agertz, O., and Kravtsov, A. V. (2016). The Impact of Stellar Feedback on the Structure, Size, and Morphology of Galaxies in Milky-Way-Sized Dark Matter Halos. ApJ 824, 79. doi:10.3847/0004-637X/824/2/79

CrossRef Full Text | Google Scholar

Ai, Y. L., Yuan, W., Zhou, H. Y., Wang, T. G., Dong, X.-B., Wang, J. G., et al. (2010). Dependence of the Optical/Ultraviolet Variability on the Emission-Line Properties and Eddington Ratio in Active Galactic Nuclei. ApJ 716, L31–L35. doi:10.1088/2041-8205/716/1/l31

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Asada, K., Azulay, R., Ball, D., et al. (2019). First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. ApJL 875, L1. doi:10.3847/2041-8213/ab0ec7

CrossRef Full Text | Google Scholar

Alexander, D. M., and Hickox, R. C. (2012). What Drives the Growth of Black Holes? New Astron. Rev. 56, 93–121. doi:10.1016/j.newar.2011.11.003

CrossRef Full Text | Google Scholar

Aller, M. C., and Richstone, D. O. (2007). Host Galaxy Bulge Predictors of Supermassive Black Hole Mass. ApJ 665, 120–156. doi:10.1086/519298

CrossRef Full Text | Google Scholar

Almeida, J. S., Aguerri, J. A. L., Muñoz-Tuñón, C., and de Vicente, A. (2010). Automatic Unsupervised Classification of All Sloan Digital Sky Survey Data Release 7 Galaxy Spectra. ApJ 714, 487–504. doi:10.1088/0004-637X/714/1/487

CrossRef Full Text | Google Scholar

Almeida, J. S. (2020). Analysis of the Galaxy Size versus Stellar Mass Relation. Mon. Not. R. Astron. Soc. 495, 78–89. doi:10.1093/mnras/staa1108

CrossRef Full Text | Google Scholar

GRAVITY Collaboration, Amorim, A., Amorim, A., Bauböck, M., Brandner, W., Clénet, Y., Davies, R., et al. (2020). The Spatially Resolved Broad Line Region of IRAS 09149−6206. A&A 643, A154. doi:10.1051/0004-6361/202039067

CrossRef Full Text | Google Scholar

GRAVITY Collaboration, Amorim, A., Bauböck, M., Brandner, W., Bolzer, M., Clénet, Y., Davies, R., et al. (2021). The central Parsec of NGC 3783: A Rotating Broad Emission Line Region, Asymmetric Hot Dust Structure, and Compact Coronal Line Region. arXiv:2102.00068.

Google Scholar

Andrews, B. H., and Martini, P. (2013). The Mass-Metallicity Relation with the Direct Method on Stacked Spectra of SDSS Galaxies. ApJ 765, 140. doi:10.1088/0004-637X/765/2/140

CrossRef Full Text | Google Scholar

Angulo, R. E., Springel, V., White, S. D. M., Jenkins, A., Baugh, C. M., and Frenk, C. S. (2012). Scaling Relations for Galaxy Clusters in the Millennium-XXL Simulation. Monthly Notices R. Astronomical Soc. 426, 2046–2062. doi:10.1111/j.1365-2966.2012.21830.x

CrossRef Full Text | Google Scholar

Antonini, F., Gieles, M., and Gualandris, A. (2019). Black Hole Growth through Hierarchical Black Hole Mergers in Dense star Clusters: Implications for Gravitational Wave Detections. MNRAS 486, 5008–5021. doi:10.1093/mnras/stz1149

CrossRef Full Text | Google Scholar

Antonucci, R. (1993). Unified Models for Active Galactic Nuclei and Quasars. Annu. Rev. Astron. Astrophys. 31, 473–521. doi:10.1146/annurev.aa.31.090193.002353

CrossRef Full Text | Google Scholar

Aquino-Ortíz, E., Valenzuela, O., Sánchez, S. F., Hernández-Toledo, H., Ávila-Reese, V., van de Ven, G., et al. (2018). Kinematic Scaling Relations of CALIFA Galaxies: A Dynamical Mass Proxy for Galaxies across the Hubble Sequence. Mon. Not. R. Astron. Soc. 479, 2133–2146. doi:10.1093/mnras/sty1522

CrossRef Full Text | Google Scholar

Arimoto, N., and Yoshii, Y. (1987). Chemical and Photometric Properties of a Galactic Wind Model for Elliptical Galaxies. Astron. Astrophysics 173, 23–38.

Google Scholar

Arp, H., Sulentic, J. W., and di Tullio, G. (1979). Quasars Aligned across NGC 3384. ApJ 229, 489–495. doi:10.1086/156980

CrossRef Full Text | Google Scholar

Athanassoula, E. (2008). Disc Instabilities and Semi-analytic Modelling of Galaxy Formation. MNRAS 390, L69–L72. doi:10.1111/j.1745-3933.2008.00541.x

CrossRef Full Text | Google Scholar

Avila‐Reese, V., Firmani, C., and Hernández, X. (1998). On the Formation and Evolution of Disk Galaxies: Cosmological Initial Conditions and the Gravitational Collapse. ApJ 505, 37–49. doi:10.1086/306136

CrossRef Full Text | Google Scholar

Avila-Reese, V., Zavala, J., Firmani, C., and Hernández-Toledo, H. M. (2008). On the Baryonic, Stellar, and Luminous Scaling Relations of Disk Galaxies. Astronomical J. 136, 1340–1360. doi:10.1088/0004-6256/136/3/1340

CrossRef Full Text | Google Scholar

Baade, W. (1944). The Resolution of Messier 32, NGC 205, and the Central Region of the Andromeda Nebula. ApJ 100, 137. doi:10.1086/144650

CrossRef Full Text | Google Scholar

Bachev, R., Marziani, P., Sulentic, J. W., Zamanov, R., Calvani, M., and Dultzin‐Hacyan, D. (2004). Average Ultraviolet Quasar Spectra in the Context of Eigenvector 1: A Baldwin Effect Governed by the Eddington Ratio? ApJ 617, 171–183. doi:10.1086/425210

CrossRef Full Text | Google Scholar

Bacon, R., Copin, Y., Monnet, G., Miller, B. W., Allington-Smith, J. R., Bureau, M., et al. (2001). The SAURON Project - I. The Panoramic Integral-Field Spectrograph. Mon. Not. R. Astron. Soc. 326, 23–35. doi:10.1046/j.1365-8711.2001.04612.x

CrossRef Full Text | Google Scholar

Balcells, M., Graham, A. W., Domínguez-Palmero, L., and Peletier, R. F. (2003). Galactic Bulges from [ITAL]Hubble Space Telescope[/ITAL] Near-Infrared Camera Multi-Object Spectrometer Observations: The Lack of [CLC][ITAL]r[/ITAL][/CLC][TSUP]1/4[/TSUP] Bulges. The Astrophysical J. Lett 582, L79–L82. doi:10.1086/367783

CrossRef Full Text | Google Scholar

Baldry, I. K., Glazebrook, K., Brinkmann, J., Ivezić, Ž., Lupton, R. H., Nichol, R. C., et al. (2004). Quantifying the Bimodal Color‐Magnitude Distribution of Galaxies. ApJ 600, 681–694. doi:10.1086/380092

CrossRef Full Text | Google Scholar

Bañados, E., Venemans, B. P., Mazzucchelli, C., Farina, E. P., Walter, F., Wang, F., et al. (2018). An 800-Million-Solar-Mass Black Hole in a Significantly Neutral Universe at a Redshift of 7.5. Nature 553, 473–476. doi:10.1038/nature25180

PubMed Abstract | CrossRef Full Text | Google Scholar

Barber, C., Schaye, J., Bower, R. G., Crain, R. A., Schaller, M., and Theuns, T. (2016). The Origin of Compact Galaxies with Anomalously High Black Hole Masses. Mon. Not. R. Astron. Soc. 460, 1147–1161. doi:10.1093/mnras/stw1018

CrossRef Full Text | Google Scholar

Barth, A. J., Son, S., Kim, M., and Ho, L. C. (2021). A Hubble Snapshot Survey of AGN Host Galaxies from the Swift-BAT Sample. Am. Astronomical Soc. Meet. Abstr. 53, 308–403.

Google Scholar

Barth, A. J., Boizelle, B. D., Darling, J., Baker, A. J., Buote, D. A., Ho, L. C., et al. (2016). Measurement of the Black Hole Mass in NGC 1332 from ALMA Observations at 0.044 Arcsecond Resolution. ApJ 822, L28. doi:10.3847/2041-8205/822/2/l28

CrossRef Full Text | Google Scholar

Barton, E. J., Geller, M. J., Bromley, B. C., van Zee, L., and Kenyon, S. J. (2001). The Tully-Fisher Relation as a Measure of Luminosity Evolution: A Low-Redshift Baseline for Evolving Galaxies. Astronomical J. 121, 625–648. doi:10.1086/318759

CrossRef Full Text | Google Scholar

Barway, S., and Kembhavi, A. (2007). A Supermassive Black Hole Fundamental Plane for Ellipticals. ApJ 662, L67–L70. doi:10.1086/519560

CrossRef Full Text | Google Scholar

Baskin, A., and Laor, A. (2005). What Controls the C Iv Line Profile in Active Galactic Nuclei? MNRAS 356, 1029–1044. doi:10.1111/j.1365-2966.2004.08525.x

CrossRef Full Text | Google Scholar

Baum, W. A. (1959). Population Inferences from Star Counts, Surface Brightness and Colors. Pasp 71, 106–117. doi:10.1086/127346

CrossRef Full Text | Google Scholar

Behroozi, P. S., Wechsler, R. H., Wu, H.-Y., Busha, M. T., Klypin, A. A., and Primack, J. R. (2013). Gravitationally Consistent Halo Catalogs and Merger Trees for Precision Cosmology. ApJ 763, 18. doi:10.1088/0004-637x/763/1/18

CrossRef Full Text | Google Scholar

Beifiori, A., Mendel, J. T., Chan, J. C. C., Saglia, R. P., Bender, R., Cappellari, M., et al. (2017). The KMOS Cluster Survey (KCS). I. The Fundamental Plane and the Formation Ages of Cluster Galaxies at Redshift 1.4. ApJ 846, 120. doi:10.3847/1538-4357/aa8368

CrossRef Full Text | Google Scholar

Beifiori, A., Thomas, D., Maraston, C., Steele, O., Masters, K. L., Pforr, J., et al. (2014). Redshift Evolution of the Dynamical Properties of Massive Galaxies from SDSS-III/BOSS. ApJ 789, 92. doi:10.1088/0004-637x/789/2/92

CrossRef Full Text | Google Scholar

Bekeraité, S., Walcher, C. J., Falcón-Barroso, J., Garcia Lorenzo, B., Lyubenova, M., Sánchez, S. F., et al. (2016). Space Density Distribution of Galaxies in the Absolute Magnitude - Rotation Velocity Plane: a Volume-Complete Tully-Fisher Relation from CALIFA Stellar Kinematics. A&A 593, A114. doi:10.1051/0004-6361/201527405

CrossRef Full Text | Google Scholar

Bell, E. F., and de Jong, R. S. (2001). Stellar Mass‐to‐Light Ratios and the Tully‐Fisher Relation. ApJ 550, 212–229. doi:10.1086/319728

CrossRef Full Text | Google Scholar

Bell, E. F., Wolf, C., Meisenheimer, K., Rix, H. W., Borch, A., Dye, S., et al. (2004). Nearly 5000 Distant Early‐Type Galaxies in COMBO‐17: A Red Sequence and its Evolution Sincez ∼ 1. ApJ 608, 752–767. doi:10.1086/420778

CrossRef Full Text | Google Scholar

Belli, S., Newman, A. B., and Ellis, R. S. (2014). Velocity Dispersions and Dynamical Masses for A Large Sample of Quiescent Galaxies Atz> 1: Improved Measures of the Growth in Mass and Size. ApJ 783, 117. doi:10.1088/0004-637X/783/2/117

CrossRef Full Text | Google Scholar

Bender, R., Burstein, D., and Faber, S. M. (1992). Dynamically Hot Galaxies. I - Structural Properties. ApJ 399, 462. doi:10.1086/171940

CrossRef Full Text | Google Scholar

Bender, R., Saglia, R. P., Ziegler, B., Belloni, P., Greggio, L., Hopp, U., et al. (1998). Exploring Cluster Elliptical Galaxies as Cosmological Standard Rods. ApJ 493, 529–535. doi:10.1086/305166

CrossRef Full Text | Google Scholar

Bennert, V. N., Treu, T., Ding, X., Stomberg, I., Birrer, S., Snyder, T., et al. (2021). A Local Baseline of the Black Hole Mass Scaling Relations for Active Galaxies. IV. Correlations between M_BH and Host Galaxy σ, Stellar Mass, and Luminosity. arXiv:2101.10355.

Google Scholar

Bennert, V. N., Auger, M. W., Treu, T., Woo, J.-H., and Malkan, M. A. (2011). The Relation Between Black Hole Mass and Host Spheroid Stellar Mass out Toz∼ 2. ApJ 742, 107. doi:10.1088/0004-637X/742/2/107

CrossRef Full Text | Google Scholar

Bennert, V. N., Treu, T., Woo, J.-H., Malkan, M. A., Le Bris, A., Auger, M. W., et al. (2010). Cosmic Evolution of Black Holes and Spheroids. IV. Thembh-Lsphrelation. ApJ 708, 1507–1527. doi:10.1088/0004-637x/708/2/1507

CrossRef Full Text | Google Scholar

Bensch, K., del Olmo, A., Sulentic, J., Perea, J., and Marziani, P. (2015). Measures of the Soft X-ray Excess as an Eigenvector 1 Parameter for Active Galactic Nuclei. J. Astrophysics Astron. 36, 467–474. doi:10.1007/s12036-015-9355-8

CrossRef Full Text | Google Scholar

Bentz, M. C., Denney, K. D., Grier, C. J., Barth, A. J., Peterson, B. M., Vestergaard, M., et al. (2013). The Low-Luminosity End of the Radius-Luminosity Relationship for Active Galactic Nuclei. ApJ 767, 149. doi:10.1088/0004-637X/767/2/149

CrossRef Full Text | Google Scholar

Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., and Vestergaard, M. (2009). The Radius-Luminosity Relationship for Active Galactic Nuclei: The Effect of Host-Galaxy Starlight on Luminosity Measurements. II. The Full Sample of Reverberation-Mapped AGNs. ApJ 697, 160–181. doi:10.1088/0004-637x/697/1/160

CrossRef Full Text | Google Scholar

Bentz, M. C., Peterson, B. M., Pogge, R. W., Vestergaard, M., and Onken, C. A. (2006). The Radius‐Luminosity Relationship for Active Galactic Nuclei: The Effect of Host‐Galaxy Starlight on Luminosity Measurements. ApJ 644, 133–142. doi:10.1086/503537

CrossRef Full Text | Google Scholar

Bentz, M. C., Walsh, J. L., Barth, A. J., Yoshii, Y., Woo, J.-H., Wang, X., et al. (2010). The Lick AGN Monitoring Project: Reverberation Mapping of Optical Hydrogen and Helium Recombination Lines. ApJ 716, 993–1011. doi:10.1088/0004-637x/716/2/993

CrossRef Full Text | Google Scholar

Bernardi, M., Shankar, F., Hyde, J. B., Mei, S., Marulli, F., and Sheth, R. K. (2010). Galaxy Luminosities, Stellar Masses, Sizes, Velocity Dispersions as a Function of Morphological Type. Mon. Not. R. Astron. Soc. 404, 2087–2122. doi:10.1111/j.1365-2966.2010.16425.x

CrossRef Full Text | Google Scholar

Bernardi, M., Meert, A., Vikram, V., Huertas-Company, M., Mei, S., Shankar, F., et al. (2014). Systematic Effects on the Size-Luminosity Relations of Early- and Late-type Galaxies: Dependence on Model Fitting and Morphology. Mon. Not. R. Astron. Soc. 443, 874–897. doi:10.1093/mnras/stu1106

CrossRef Full Text | Google Scholar

Bernardi, M., Roche, N., Shankar, F., and Sheth, R. K. (2011). Evidence of Major Dry Mergers at M* > 2 × 10¹¹ M_⊙ from Curvature in Early-type Galaxy Scaling Relations? Mon. Not. R. Astron. Soc. 412, L6–L10. doi:10.1111/j.1745-3933.2010.00982.x

CrossRef Full Text | Google Scholar

Bernardi, M., Sheth, R. K., Annis, J., Burles, S., Eisenstein, D. J., Finkbeiner, D. P., et al. (2003). Early-Type Galaxies in the Sloan Digital Sky Survey. III. The Fundamental Plane. Astronomical J. 125, 1866–1881. doi:10.1086/367794

CrossRef Full Text | Google Scholar

Bernardi, M., Sheth, R. K., Tundo, E., and Hyde, J. B. (2007). Selection Bias in theM‐σ andM‐LCorrelations and its Consequences. ApJ 660, 267–275. doi:10.1086/512719

CrossRef Full Text | Google Scholar

Bershady, M. A., Verheijen, M. A. W., Swaters, R. A., Andersen, D. R., Westfall, K. B., and Martinsson, T. (2010). The DiskMass Survey. I. Overview. ApJ 716, 198–233. doi:10.1088/0004-637X/716/1/198

CrossRef Full Text | Google Scholar

Bertin, G., Saglia, R. P., and Stiavelli, M. (1992). Elliptical Galaxies with Dark Matter. I - Self-Consistent Models. II - Optimal Luminous-Dark Matter Decomposition for a Sample of Bright Objects. ApJ 384, 423–447. doi:10.1086/170884

CrossRef Full Text | Google Scholar

Berton, M., Braito, V., Mathur, S., Foschini, L., Piconcelli, E., Chen, S., et al. (2019). Broadband X-ray Observations of Four Gamma-ray Narrow-Line Seyfert 1 Galaxies. A&A 632, A120. doi:10.1051/0004-6361/201935929

CrossRef Full Text | Google Scholar

Berton, M., Foschini, L., Ciroi, S., Cracco, V., La Mura, G., Di Mille, F., et al. (2016). [O III] Line Properties in Two Samples of Radio-Emitting Narrow-Line Seyfert 1 Galaxies. A&A 591, A88. doi:10.1051/0004-6361/201527056

CrossRef Full Text | Google Scholar

Bertschinger, E. (1995). COSMICS: Cosmological Initial Conditions and Microwave Anisotropy Codes. arXiv:astro-ph/9506070.

Google Scholar

Bertschinger, E. (1998). Simulations of Structure Formation in the Universe. Annu. Rev. Astron. Astrophys. 36, 599–654. doi:10.1146/annurev.astro.36.1.599

CrossRef Full Text | Google Scholar

Bett, P., Eke, V., Frenk, C. S., Jenkins, A., and Okamoto, T. (2010). The Angular Momentum of Cold Dark Matter Haloes with and without Baryons. Mon. Not. R. Astron. Soc. 404, 1137–1156. doi:10.1111/j.1365-2966.2010.16368.x

CrossRef Full Text | Google Scholar

Bezanson, R., van Dokkum, P. G., van de Sande, J., Franx, M., Leja, J., and Kriek, M. (2013). TIGHT CORRELATIONS BETWEEN MASSIVE GALAXY STRUCTURAL PROPERTIES AND DYNAMICS: THE MASS FUNDAMENTAL PLANE WAS IN PLACE BY z ∼ 2. ApJ 779, L21. doi:10.1088/2041-8205/779/2/L21

CrossRef Full Text | Google Scholar

Biermann, P., and Shapiro, S. L. (1979). Puffing up Flat Galaxies by Rapid Stripping and the Formation of S0 Galaxies. ApJ 230, L33. doi:10.1086/182956

CrossRef Full Text | Google Scholar

Bigiel, F., Leroy, A., Walter, F., Brinks, E., de Blok, W. J. G., Madore, B., et al. (2008). The Star Formation Law in Nearby Galaxies on Sub-kpc Scales. Astronomical J. 136, 2846–2871. doi:10.1088/0004-6256/136/6/2846

CrossRef Full Text | Google Scholar

Binggeli, B., and Cameron, L. M. (1991). Dwarf Galaxies in the Virgo Cluster. I. The Systematic Photometric Properties of Early-type Dwarfs. Astron. Astrophysics 252, 27.

Google Scholar

Binggeli, B., Sandage, A., and Tammann, G. A. (1985). Studies of the Virgo Cluster. II - A Catalog of 2096 Galaxies in the Virgo Cluster Area. V - Luminosity Functions of Virgo Cluster Galaxies. Astronomical J. 90, 1681–1758. doi:10.1086/113874

CrossRef Full Text | Google Scholar

Binggeli, B., Sandage, A., and Tarenghi, M. (1984). Studies of the Virgo Cluster. I - Photometry of 109 Galaxies Near the Cluster center to Serve as Standards. Astronomical J. 89, 64–82. doi:10.1086/113484

CrossRef Full Text | Google Scholar

Bischetti, M., Piconcelli, E., Vietri, G., Bongiorno, A., Fiore, F., Sani, E., et al. (2017). The WISSH Quasars Project. A&A 598, A122. doi:10.1051/0004-6361/201629301

CrossRef Full Text | Google Scholar

Blaauw, A. (1959). “Empirical Data on Age and Position in the Hertzsprung-Russell Diagram for O and B-type Stars,” in The Hertzsprung-Russell Diagram. Editor J. L. Greenstein, 10, 105–108. doi:10.1017/s0074180900177617

CrossRef Full Text | Google Scholar

Blanc, G. A., Kewley, L., Vogt, F. P. A., and Dopita, M. A. (2015). IZI: Inferring the Gas Phase Metallicity (Z) and Ionization Parameter (Q) of Ionized Nebulae Using Bayesian Statistics. Astrophysical J. 798, 99. doi:10.1088/0004-637X/798/2/99

CrossRef Full Text | Google Scholar

Blanton, M. R., Brinkmann, J., Csabai, I., Doi, M., Eisenstein, D., Fukugita, M., et al. (2003). Estimating Fixed-Frame Galaxy Magnitudes in the Sloan Digital Sky Survey. Astron. J. 125, 2348–2360. doi:10.1086/342935

CrossRef Full Text | Google Scholar

Blecha, L., Cox, T. J., Loeb, A., and Hernquist, L. (2011). Recoiling Black Holes in Merging Galaxies: Relationship to Active Galactic Nucleus Lifetimes, Starbursts and the MBH-σ* Relation. MNRAS 412, 2154–2182. doi:10.1111/j.1365-2966.2010.18042.x

CrossRef Full Text | Google Scholar

Boizelle, B. D., Barth, A. J., Walsh, J. L., Buote, D. A., Baker, A. J., Darling, J., et al. (2019). A Precision Measurement of the Mass of the Black Hole in NGC 3258 from High-Resolution ALMA Observations of its Circumnuclear Disk. ApJ 881, 10. doi:10.3847/1538-4357/ab2a0a

CrossRef Full Text | Google Scholar

Böker, T., Laine, S., van der Marel, R. P., Sarzi, M., Rix, H.-W., Ho, L. C., et al. (2002). A [ITAL]Hubble Space Telescope[/ITAL] Census of Nuclear Star Clusters in Late-type Spiral Galaxies. I. Observations and Image Analysis. Astronomical J. 123, 1389–1410. doi:10.1086/339025

CrossRef Full Text | Google Scholar

Bon, E., Popović, L. C., Gavrilović, N., and Dimitrijević, M. S. (2007). “The Hidden Disk Emission in the Single Peaked Sy1 Balmer Emission Lines,” in Spectral Line Shapes in Astrophysics. Editor M. S. Dimitrijevic (American Institute of Physics Conference Series), 938, 59–64. doi:10.1063/1.2800153

CrossRef Full Text | Google Scholar

Bon, E., Popović, L. C., Gavrilović, N., Mura, G. L., and Mediavilla, E. (2009). Contribution of a Disc Component to Single-Peaked Broad Lines of Active Galactic Nuclei. MNRAS 400, 924–936. doi:10.1111/j.1365-2966.2009.15511.x

CrossRef Full Text | Google Scholar

Bon, N., Bon, E., and Marziani, P. (2018). AGN Broad Line Region Variability in the Context of Eigenvector 1: Case of NGC 5548. Front. Astron. Space Sci. 5, 3. doi:10.3389/fspas.2018.00003

CrossRef Full Text | Google Scholar

Bon, N., Bon, E., Marziani, P., and Jovanović, P. (2015). Gravitational Redshift of Emission Lines in the AGN Spectra. Astrophys Space Sci. 360, 7. doi:10.1007/s10509-015-2555-5

CrossRef Full Text | Google Scholar

Bon, N., Marziani, P., Bon, E., Negrete, C. A., Dultzin, D., del Olmo, A., et al. (2020). Selection of Highly-Accreting Quasars. A&A 635, A151. doi:10.1051/0004-6361/201936773

CrossRef Full Text | Google Scholar

Boroson, T. A. (2002). Black Hole Mass and Eddington Ratio as Drivers for the Observable Properties of Radio‐loud and Radio‐quiet QSOs. ApJ 565, 78–85. doi:10.1086/324486

CrossRef Full Text | Google Scholar

Boroson, T. A., and Green, R. F. (1992). The Emission-Line Properties of Low-Redshift Quasi-Stellar Objects. ApJS 80, 109–135. doi:10.1086/191661

CrossRef Full Text | Google Scholar

Bortolas, E., Gualandris, A., Dotti, M., Spera, M., and Mapelli, M. (2016). Brownian Motion of Massive Black Hole Binaries and the Final Parsec Problem. Mon. Not. R. Astron. Soc. 461, 1023–1031. doi:10.1093/mnras/stw1372

CrossRef Full Text | Google Scholar

Bosco, F., Hennawi, J. F., Stern, J., and Ju, Pott. (2021). Spatially Resolving the Kinematics of the ≲ 100 μas Quasar Broad-Line Region Using Spectroastrometry II. The First Tentative Detection in a Luminous Quasar at Z = 2.3. arXiv:2106.15900.

Google Scholar

Boselli, A., and Gavazzi, G. (2014). On the Origin of the Faint-End of the Red Sequence in High-Density Environments. Astron. Astrophys Rev. 22, 74. doi:10.1007/s00159-014-0074-y

CrossRef Full Text | Google Scholar

Bothun, G. D., Mould, J. R., Caldwell, N., and MacGillivray, H. T. (1986). Comparative Photometric Parameters of dwarf Irregular and Elliptical Galaxies in the Virgo Cluster - Two Different Classes of dwarf Galaxies? Astronomical J. 92, 1007–1019. doi:10.1086/114231

CrossRef Full Text | Google Scholar

Bothwell, M. S., Kennicutt, R. C., and Lee, J. C. (2009). On the Interstellar Medium and star Formation Demographics of Galaxies in the Local Universe. Mon. Not. R. Astron. Soc. 400, 154–167. doi:10.1111/j.1365-2966.2009.15471.x

CrossRef Full Text | Google Scholar

Bottorff, M. C., and Ferland, G. J. (2000). Magnetic Confinement, Magnetohydrodynamic Waves and Smooth Line Profiles in Active Galactic Nuclei. Monthly Notices R. Astronomical Soc. 316, 103–106. doi:10.1046/j.1365-8711.2000.03465.x

CrossRef Full Text | Google Scholar

Bower, G. A., Green, R. F., Danks, A., Gull, T., Heap, S., Hutchings, J., et al. (1998). Kinematics of the Nuclear Ionized Gas in the Radio Galaxy M84 (NGC 4374). ApJL 492, L111–L114. doi:10.1086/311109

CrossRef Full Text | Google Scholar

Bower, R. G., Lucey, J. R., and Ellis, R. S. (1992). Precision Photometry of Early-type Galaxies in the Coma and Virgo Clusters: a Test of the Universality of the Colour-Magnitude Relation - I. The Data. Monthly Notices R. Astronomical Soc. 254, 589–600. doi:10.1093/mnras/254.4.589

CrossRef Full Text | Google Scholar

Brammer, G. B., Whitaker, K. E., van Dokkum, P. G., Marchesini, D., Franx, M., Kriek, M., et al. (2011). THE NUMBER DENSITY AND MASS DENSITY OF STAR-FORMING AND QUIESCENT GALAXIES AT 0.4 ⩽z⩽ 2.2. ApJ 739, 24. doi:10.1088/0004-637X/739/1/24

CrossRef Full Text | Google Scholar

Bresolin, F., Kudritzki, R.-P., Urbaneja, M. A., Gieren, W., Ho, I.-T., and Pietrzyński, G. (2016). Young Stars and Ionized Nebulae in M83: Comparing Chemical Abundances at High Metallicity. ApJ 830, 64. doi:10.3847/0004-637x/830/2/64

CrossRef Full Text | Google Scholar

Bressan, A., Chiosi, C., and Fagotto, F. (1994). Spectrophotometric Evolution of Elliptical Galaxies. 1: Ultraviolet Excess and Color-Magnitude-Redshift Relations. ApJS 94, 63. doi:10.1086/192073

CrossRef Full Text | Google Scholar

Brinchmann, J., Charlot, S., White, S. D. M., Tremonti, C., Kauffmann, G., Heckman, T., et al. (2004). The Physical Properties of star-forming Galaxies in the Low-Redshift Universe. Mon. Not. R. Astron. Soc. 351, 1151–1179. doi:10.1111/j.1365-2966.2004.07881.x

CrossRef Full Text | Google Scholar

Brodie, J. P., and Huchra, J. P. (1991). Extragalactic Globular Clusters. III - Metallicity Comparisons and Anomalies. ApJ 379, 157. doi:10.1086/170492

CrossRef Full Text | Google Scholar

Brook, C. B., Governato, F., Roškar, R., Stinson, G., Brooks, A. M., Wadsley, J., et al. (2011). Hierarchical Formation of Bulgeless Galaxies: Why Outflows Have Low Angular Momentum. Mon. Not. R. Astron. Soc. 415, 1051–1060. doi:10.1111/j.1365-2966.2011.18545.x

CrossRef Full Text | Google Scholar

Brook, C. B., Stinson, G., Gibson, B. K., Roškar, R., Wadsley, J., and Quinn, T. (2012). Hierarchical Formation of Bulgeless Galaxies - II. Redistribution of Angular Momentum via Galactic Fountains. Mon. Not. R. Astron. Soc. 419, 771–779. doi:10.1111/j.1365-2966.2011.19740.x

CrossRef Full Text | Google Scholar

Brooks, A. M., Governato, F., Quinn, T., Brook, C. B., and Wadsley, J. (2009). The Role of Cold Flows in the Assembly of Galaxy Disks. ApJ 694, 396–410. doi:10.1088/0004-637X/694/1/396

CrossRef Full Text | Google Scholar

Broome, M., Impellizerri, V., Ivison, R., and Messias, H. (2019). Hunting for High-Redshift Water Masers: Searching for Circumnuclear Megamasers Using the VLA. Am. Astronomical Soc. Meet. Abstr. 233, 454–513.

Google Scholar

Brosche, P. (1970). A Model for the Early Evolution of Galaxies. Astron. Astrophysics 6, 240–253.

Google Scholar

Brosche, P. (1973). The Manifold of Galaxies. Galaxies with Known Dynamical Parameters. Astron. Astrophysics 23, 259–268.

Google Scholar

Brotherton, M. S., Du, P., Xiao, M., Bao, D.-W., Zhao, B., McLane, J. N., et al. (2020). Monitoring AGNs with Hβ Asymmetry. II. Reverberation Mapping of Three Seyfert Galaxies Historically Displaying Hβ Profiles with Changing Asymmetry: Mrk 79, NGC 3227, and Mrk 841. ApJ 905, 77. doi:10.3847/1538-4357/abc2d2

CrossRef Full Text | Google Scholar

Brotherton, M. S., Wills, B. J., Steidel, C. C., and Sargent, W. L. W. (1994). Statistics of QSO Broad Emission-Line Profiles. 2: The C IV Wavelength 1549, C III) Wavelength 1909, and MG II Wavelength 2798 Lines. ApJ 423, 131–142. doi:10.1086/173794

CrossRef Full Text | Google Scholar

Bryan, G. L., and Norman, M. L. (1998). Statistical Properties of X‐Ray Clusters: Analytic and Numerical Comparisons. ApJ 495, 80–99. doi:10.1086/305262

CrossRef Full Text | Google Scholar

Bullock, J. S., Dekel, A., Kolatt, T. S., Primack, J. R., and Somerville, R. S. (2001). Strong Evolution in the Luminosity‐Velocity Relation Atz≳ 1? ApJ 550, 21–25. doi:10.1086/319738

CrossRef Full Text | Google Scholar

Bundy, K. (2015). MaNGA: Mapping Nearby Galaxies at Apache Point Observatory. Am. Astronomical Soc. Meet. Abstr. #225American Astronomical Soc. Meet. Abstr. 225, 143–229. doi:10.1017/s1743921315003476

CrossRef Full Text | Google Scholar

Buonomo, F. (2000). Formation and Evolution of Early-Type Galaxies in the Hierarchical Scheme with NB-TSPH Simulations. Ph.D. thesis, Padova, Italy: Astronomy Department, Padova University, Vicolo Osservatorio, 35122.

Google Scholar

Burkert, A., Schreiber, N. M. F., Genzel, R., Lang, P., Tacconi, L. J., Wisnioski, E., et al. (2016). THE ANGULAR MOMENTUM DISTRIBUTION AND BARYON CONTENT OF STAR-FORMING GALAXIES ATz∼ 1-3. ApJ 826, 214. doi:10.3847/0004-637X/826/2/214

CrossRef Full Text | Google Scholar

Burstein, D., Bender, R., Faber, S. M., and Nolthenius, R. (1995). Towards Understanding the Physical Properties of Stellar Systems. Astrophysical Lett. Commun. 31, 95.

Google Scholar

Burstein, D., Bender, R., Faber, S., and Nolthenius, R. (1997). Global Relationships Among the Physical Properties of Stellar Systems. Astronomical J. 114, 1365. doi:10.1086/118570

CrossRef Full Text | Google Scholar

Butcher, H., and Oemler, A. J. (1978). The Evolution of Galaxies in Clusters. II - the Galaxy Content of Nearby Clusters. ApJ 226, 559–565. doi:10.1086/156640

CrossRef Full Text | Google Scholar

Butler, D. J., and Martínez-Delgado, D. (2005). On the Stellar Populations in NGC 185 and NGC 205 and the Nuclear Star Cluster in NGC 205 fromHubble Space TelescopeObservations. Astron. J. 129, 2217–2231. doi:10.1086/429524

CrossRef Full Text | Google Scholar

Cabanac, R. A., de Lapparent, V., and Hickson, P. (2002). Classification and Redshift Estimation by Principal Component Analysis. A&A 389, 1090–1116. doi:10.1051/0004-6361:20020665

CrossRef Full Text | Google Scholar

Caglar, T., Burtscher, L., Brandl, B., Brinchmann, J., Davies, R. I., Hicks, E. K. S., et al. (2020). LLAMA: The MBH-Σ⋆ Relation of the Most Luminous Local AGNs. A&A 634, A114. doi:10.1051/0004-6361/201936321

CrossRef Full Text | Google Scholar

Caldwell, N., and Bothun, G. D. (1987). Dwarf Elliptical Galaxies in the Fornax Cluster. II - Their Structure and Stellar Populations. Astronomical J. 94, 1126. doi:10.1086/114550

CrossRef Full Text | Google Scholar

Caldwell, N., Rose, J. A., and Concannon, K. D. (2003). Star Formation Histories of Early-type Galaxies. I. Higher Order Balmer Lines as Age Indicators. Astron. J. 125, 2891–2926. doi:10.1086/375308

CrossRef Full Text | Google Scholar

Caldwell, N. (1983). Structure and Stellar Content of dwarf Elliptical Galaxies. Astronomical J. 88, 804–812. doi:10.1086/113367

CrossRef Full Text | Google Scholar

Caldwell, N. (1983). The Ages of the Disks of S0 Galaxies. ApJ 268, 90–101. doi:10.1086/160932

CrossRef Full Text | Google Scholar

Cannon, J. M., Dohm-Palmer, R. C., Skillman, E. D., Bomans, D. J., Cote, S., and Miller, B. W. (2004). “Extended Star Formation in the Dwarf Starburst/W-R Galaxy NGC 625,” in The Formation and Evolution of Massive Young Star Clusters. Editors H. J. G. L. M. Lamers, L. J. Smith, and A. Nota (California, United States: Astronomical Society of the Pacific Conference Series), 322, 207.

Google Scholar

Caon, N., Capaccioli, M., and D'Onofrio, M. (1993). On the Shape of the Light Profiles of Early-type Galaxies. Monthly Notices R. Astronomical Soc. 265, 1013–1021. doi:10.1093/mnras/265.4.1013

CrossRef Full Text | Google Scholar

Capaccioli, M., Caon, N., and D’Onofrio, M. (1993). “Structure, Dynamics and Chemical Evolution of Elliptical Galaxies,” in ESO Conference and Workshop Proceedings, Proceedings of an ESO/EIPC Workshop, Marciana Marina, Isola d'Elba, May 25-30, 1992. Editors W. W. John Danziger, J. Zeilinger, and Kurt Kjaer (Garching: European Southern Observatory (ESO)), 217.

Google Scholar

Capaccioli, M., Caon, N., and D'Onofrio, M. (1992). Families of Galaxies in the E-Re Plane. Monthly Notices R. Astronomical Soc. 259, 323–327. doi:10.1093/mnras/259.2.323

CrossRef Full Text | Google Scholar

Capetti, A., Axon, D. J., Macchetto, F., Sparks, W. B., and Boksenberg, A. (1996). Radio Outflows and the Origin of the Narrow-Line Region in Seyfert Galaxies. ApJ 469, 554. doi:10.1086/177804

CrossRef Full Text | Google Scholar

Capetti, A., Laor, A., Baldi, R. D., Robinson, A., and Marconi, A. (2021). Spectropolarimetry of Low Redshift Quasars: Origin of the Polarization and Implications for Black Hole Mass Estimates. MNRAS 502, 5086–5103. doi:10.1093/mnras/stab279

CrossRef Full Text | Google Scholar

Cappellari, M., Bacon, R., Bureau, M., Damen, M. C., Davies, R. L., de Zeeuw, P. T., et al. (2006). The SAURON Project--IV. The Mass-To-Light Ratio, the Virial Mass Estimator and the Fundamental Plane of Elliptical and Lenticular Galaxies. Monthly Notices R. Astronomical Soc. 366, 1126–1150. doi:10.1111/j.1365-2966.2005.09981.x

CrossRef Full Text | Google Scholar

Cappellari, M., di Serego Alighieri, S., Cimatti, A., Daddi, E., Renzini, A., Kurk, J. D., et al. (2009). DYNAMICAL MASSES OF EARLY-TYPE GALAXIES AT z ∼ 2: ARE THEY TRULY SUPERDENSE? ApJ 704, L34–L39. doi:10.1088/0004-637x/704/1/l34

CrossRef Full Text | Google Scholar

Cappellari, M. (2013). Effect of Environment on Galaxies' Mass-Size Distribution: Unveiling the Transition from Outside-In to Inside-Out Evolution. ApJ 778, L2. doi:10.1088/2041-8205/778/1/L2

CrossRef Full Text | Google Scholar

Cappellari, M., Emsellem, E., Krajnović, D., McDermid, R. M., Scott, N., Verdoes Kleijn, G. A., et al. (2011). The ATLAS3D Project - I. A Volume-Limited Sample of 260 Nearby Early-type Galaxies: Science Goals and Selection Criteria. Mon. Not. R. Astron. Soc. 413, 813–836. doi:10.1111/j.1365-2966.2010.18174.x

CrossRef Full Text | Google Scholar

Cappellari, M., Emsellem, E., Krajnović, D., McDermid, R. M., Serra, P., Alatalo, K., et al. (2011). The ATLAS3D Project - VII. A New Look at the Morphology of Nearby Galaxies: the Kinematic Morphology-Density Relation. Mon. Not. R. Astron. Soc. 416, 1680–1696. doi:10.1111/j.1365-2966.2011.18600.x

CrossRef Full Text | Google Scholar

Cappellari, M., McDermid, R. M., Alatalo, K., Blitz, L., Bois, M., Bournaud, F., et al. (2012). Systematic Variation of the Stellar Initial Mass Function in Early-type Galaxies. Nature 484, 485–488. doi:10.1038/nature10972

PubMed Abstract | CrossRef Full Text | Google Scholar

Cappellari, M., McDermid, R. M., Alatalo, K., Blitz, L., Bois, M., Bournaud, F., et al. (2013). The ATLAS3D Project - XX. Mass-Size and Mass-σ Distributions of Early-type Galaxies: Bulge Fraction Drives Kinematics, Mass-To-Light Ratio, Molecular Gas Fraction and Stellar Initial Mass Function. Mon. Not. R. Astron. Soc. 432, 1862–1893. doi:10.1093/mnras/stt644

CrossRef Full Text | Google Scholar

Cappellari, M. (2015). “Ynamical Mass Determinations and Scaling Relations of Early-type Galaxies,” in DGalaxy Masses as Constraints of Formation Models. Editors M. Cappellari, and S. Courteau, 20–30. doi:10.1017/s1743921315003324

CrossRef Full Text | Google Scholar

Cariddi, S., D’Onofrio, M., Fasano, G., Poggianti, B. M., Moretti, A., Gullieuszik, M., et al. (2018). Characterization of Omega-WINGS Galaxy Clusters. A&A 609, A133. doi:10.1051/0004-6361/201731605

CrossRef Full Text | Google Scholar

Carniani, S., Marconi, A., Maiolino, R., Balmaverde, B., Brusa, M., Cano-Díaz, M., et al. (2015). Ionised Outflows Inz∼ 2.4 Quasar Host Galaxies. A&A 580, A102. doi:10.1051/0004-6361/201526557

CrossRef Full Text | Google Scholar

Carollo, C. M., Stiavelli, M., and Mack, J. (1998). Spiral Galaxies with WFPC2. II. The Nuclear Properties of 40 Objects. Astronomical J. 116, 68–84. doi:10.1086/300407

CrossRef Full Text | Google Scholar

Cassarà, L. P., Maccagni, D., Garilli, B., Scodeggio, M., Thomas, R., Le Fèvre, O., et al. (2016). Effect of the star Formation Histories on the SFR − M* Relation at Z≥2. Astron. Astrophysics 593, A9. doi:10.1051/0004-6361/201526505)

CrossRef Full Text | Google Scholar

Cassata, P., Cimatti, A., Kurk, J., Rodighiero, G., Pozzetti, L., Bolzonella, M., et al. (2008). GMASS Ultradeep Spectroscopy of Galaxies at Z $\mathsf{\sim2}$. A&A 483, L39–L42. doi:10.1051/0004-6361:200809881

CrossRef Full Text | Google Scholar

Cassata, P., Giavalisco, M., Williams, C. C., Guo, Y., Lee, B., Renzini, A., et al. (2013). CONSTRAINING THE ASSEMBLY OF NORMAL AND COMPACT PASSIVELY EVOLVING GALAXIES FROM REDSHIFTz= 3 TO THE PRESENT WITH CANDELS. ApJ 775, 106. doi:10.1088/0004-637X/775/2/106

CrossRef Full Text | Google Scholar

Catinella, B., Kauffmann, G., Schiminovich, D., Lemonias, J., Scannapieco, C., Wang, J., et al. (2012). The GALEX Arecibo SDSS Survey - IV. Baryonic Mass-Velocity-Size Relations of Massive Galaxies. Mon. Not. R. Astron. Soc. 420, 1959–1976. doi:10.1111/j.1365-2966.2011.20012.x

CrossRef Full Text | Google Scholar

Cenarro, A. J., Cardiel, N., Gorgas, J., Peletier, R. F., Vazdekis, A., and Prada, F. (2001). Empirical Calibration of the Near-Infrared Ca II Triplet -- I. The Stellar Library and index Definition. Monthly Notices R. Astronomical Soc. 326, 959–980. doi:10.1046/j.1365-8711.2001.04688.x

CrossRef Full Text | Google Scholar

Cenarro, A. J., Gorgas, J., Cardiel, N., Pedraz, S., Peletier, R. F., and Vazdekis, A. (2001). Empirical Calibration of the Near-Infrared Ca II Triplet -- II. The Stellar Atmospheric Parameters. Monthly Notices R. Astronomical Soc. 326, 981–994. doi:10.1046/j.1365-8711.2001.04689.x

CrossRef Full Text | Google Scholar

Chan, J. C. C., Beifiori, A., Mendel, J. T., Saglia, R. P., Bender, R., Fossati, M., et al. (2016). Sizes, Colour Gradients and Resolved Stellar Mass Distributions for the Massive Cluster Galaxies in XMMUJ2235-2557 Atz= 1.39. Mon. Not. R. Astron. Soc. 458, 3181–3209. doi:10.1093/mnras/stw502

CrossRef Full Text | Google Scholar

Chao, L. H., Bian, W. H., and Huang, K. L. (2008). The Relation between the Black Hole Mass and the Bulge Mass for Low Redshift AGNs. Part I: Ground-Based Observations. Adv. Space Res. 42, 544–549. doi:10.1016/j.asr.2007.11.012

CrossRef Full Text | Google Scholar

Chattopadhyay, A. K., Chattopadhyay, T., Davoust, E., Mondal, S., and Sharina, M. (2009). Study of NGC 5128 Globular Clusters under Multivariate Statistical Paradigm. ApJ 705, 1533–1547. doi:10.1088/0004-637x/705/2/1533

CrossRef Full Text | Google Scholar

Chattopadhyay, T., and Chattopadhyay, A. K. (2007). Globular Clusters of the Local Group - Statistical Classification. A&A 472, 131–140. doi:10.1051/0004-6361:20066945

CrossRef Full Text | Google Scholar

Chattopadhyay, T., and Chattopadhyay, A. K. (2006). Objective Classification of Spiral Galaxies Having Extended Rotation Curves beyond the Optical Radius. Astron. J. 131, 2452–2468. doi:10.1086/503160

CrossRef Full Text | Google Scholar

Chelouche, D., and Netzer, H. (2001). Radiation Pressure Acceleration by X-Rays in Active Galactic Nuclei. Monthly Notices R. Astronomical Soc. 326, 916–926. doi:10.1046/j.1365-8711.2001.04586.x

CrossRef Full Text | Google Scholar

Chen, K., and Halpern, J. P. (1989). Structure of Line-Emitting Accretion Disks in Active Galactic Nuclei - ARP 102B. ApJ 344, 115. doi:10.1086/167782

CrossRef Full Text | Google Scholar

Chester, C., and Roberts, M. S. (1964). Properties of Galaxies: Color-Magnitude Diagram. Astronomical J. 69, 635. doi:10.1086/109339

CrossRef Full Text | Google Scholar

Chiosi, C., Bressan, A., Portinari, L., and Tantalo, R. (1998). A New Scenario of Galaxy Evolution under a Universal Initial Mass Function. Astron. Astrophysics 339, 355–381.

Google Scholar

Chiosi, C. (1980). Chemical Evolution of the Galactic Disk: the Inflow Problem. Astron. Astrophysics 83, 206–216.

Google Scholar

Chiosi, C., D’Onofrio, M., Merlin, E., Piovan, L., and Marziani, P. (2019). arXiv:1908.08808.The Parallelism between Galaxy Clusters and Early-type Galaxies: III. The Mass-Radius Relationship

Google Scholar

Chiosi, C., and Matteucci, F. (1980). Gradients of Chemical Composition in the Galactic Disk. Mem. Soc. Astron. It. 51, 107–115.

Google Scholar

Chiosi, C., Merlin, E., and Piovan, L. (2012). The Origin of the Mass-Radius Relation of Early-type Galaxies. arXiv:1206.2532.

Google Scholar

Chiosi, C. (1967). On the Colour Magnitude Diagram of Galaxies. Memorie della Società Astronomica Italiana 38, 3.

Google Scholar

Chiosi, C., and Carraro, G. (2002). Formation and Evolution of Elliptical Galaxies. Mon. Not. R. Astron. Soc. 335, 335–357. doi:10.1046/j.1365-8711.2002.05590.x

CrossRef Full Text | Google Scholar

Chiosi, C., Merlin, E., Piovan, L., and Tantalo, R. (2014). Monolithic View of Galaxy Formation and Evolution. Galaxies 2, 300–381. doi:10.3390/galaxies2030300

CrossRef Full Text | Google Scholar

Chiosi, C., Sciarratta, M., D’Onofrio, M., Chiosi, E., Brotto, F., Michele, R. D., et al. (2017). Cosmic Star Formation: A Simple Model of the SFRD(z). ApJ 851, 44. doi:10.3847/1538-4357/aa99d5

CrossRef Full Text | Google Scholar

Choi, J., Conroy, C., Moustakas, J., Graves, G. J., Holden, B. P., Brodwin, M., et al. (2014). THE ASSEMBLY HISTORIES OF QUIESCENT GALAXIES SINCEz= 0.7 FROM ABSORPTION LINE SPECTROSCOPY. ApJ 792, 95. doi:10.1088/0004-637x/792/2/95

CrossRef Full Text | Google Scholar

Christensen, C. R., Brooks, A. M., Fisher, D. B., Governato, F., McCleary, J., Quinn, T. R., et al. (2014). Simulating Disc Galaxy Bulges that Are Consistent with Observed Scaling Relations. Mon. Not. R. Astron. Soc. 440, L51–L55. doi:10.1093/mnrasl/slu020

CrossRef Full Text | Google Scholar

Chuter, R. W., Almaini, O., Hartley, W. G., McLure, R. J., Dunlop, J. S., Foucaud, S., et al. (2011). Galaxy Environments in the UKIDSS Ultra Deep Survey. MNRAS 413, 1678–1686. doi:10.1111/j.1365-2966.2011.18241.x

CrossRef Full Text | Google Scholar

Cimatti, A., Nipoti, C., and Cassata, P. (2012). Fast Evolving Size of Early-type Galaxies at Z > 2 and the Role of Dissipationless (Dry) Merging. MNRAS 422, L62–L66. doi:10.1111/j.1745-3933.2012.01237.x

CrossRef Full Text | Google Scholar

Ciotti, L. (1991). Stellar Systems Following the R1/m Luminosity Law. Astron. Astrophysics 249, 99–106.

Google Scholar

Coatman, L., Hewett, P. C., Banerji, M., and Richards, G. T. (2016). C Iv Emission-Line Properties and Systematic Trends in Quasar Black Hole Mass Estimates. Mon. Not. R. Astron. Soc. 461, 647–665. doi:10.1093/mnras/stw1360

CrossRef Full Text | Google Scholar

Coatman, L., Hewett, P. C., Banerji, M., Richards, G. T., Hennawi, J. F., and Prochaska, J. X. (2017). Correcting C IV-Based Virial Black Hole Masses. Mon. Not. R. Astron. Soc. 465, 2120–2142. doi:10.1093/mnras/stw2797

CrossRef Full Text | Google Scholar

Codis, S., Pichon, C., Devriendt, J., Slyz, A., Pogosyan, D., Dubois, Y., et al. (2012). Connecting the Cosmic Web to the Spin of Dark Haloes: Implications for Galaxy Formation. Monthly Notices R. Astronomical Soc. 427, 3320–3336. doi:10.1111/j.1365-2966.2012.21636.x

CrossRef Full Text | Google Scholar

Colbert, E. J. M., Baum, S. A., O'Dea, C. P., and Veilleux, S. (1998). Large‐Scale Outflows in Edge‐on Seyfert Galaxies. III. Kiloparsec‐Scale Soft X‐Ray Emission. ApJ 496, 786–796. doi:10.1086/305417

CrossRef Full Text | Google Scholar

Cole, S., Aragon-Salamanca, A., Frenk, C. S., Navarro, J. F., and Zepf, S. E. (1994). A Recipe for Galaxy Formation. Monthly Notices R. Astronomical Soc. 271, 781–806. doi:10.1093/mnras/271.4.781

CrossRef Full Text | Google Scholar

Cole, S., Lacey, C. G., Baugh, C. M., and Frenk, C. S. (2000). Hierarchical Galaxy Formation. Mon. Not. R. Astron. Soc. 319, 168–204. doi:10.1046/j.1365-8711.2000.03879.x

CrossRef Full Text | Google Scholar

Collin, S., Kawaguchi, T., Peterson, B. M., and Vestergaard, M. (2006). Systematic Effects in Measurement of Black Hole Masses by Emission-Line Reverberation of Active Galactic Nuclei: Eddington Ratio and Inclination. A&A 456, 75–90. doi:10.1051/0004-6361:20064878

CrossRef Full Text | Google Scholar

Collin-Souffrin, S., Dyson, J. E., McDowell, J. C., and Perry, J. J. (1988). The Environment of Active Galactic Nuclei - I. A Two-Component Broad Emission Line Model. MNRAS 232, 539–550. doi:10.1093/mnras/232.3.539

CrossRef Full Text | Google Scholar

Constantin, A. (2012). Linking the Supermassive Black Hole Growth with the Megamaser Emission. J. Phys. Conf. Ser.Journal Phys. Conf. Ser. 372, 012047. doi:10.1088/1742-6596/372/1/012047

CrossRef Full Text | Google Scholar

Cortese, L., Fogarty, L. M. R., Ho, I.-T., Bekki, K., Bland-Hawthorn, J., Colless, M., et al. (2014). The Sami Galaxy Survey: Toward a Unified Dynamical Scaling Relation for Galaxies of All Types. ApJ 795, L37. doi:10.1088/2041-8205/795/2/L37

CrossRef Full Text | Google Scholar

Côté, P., Piatek, S., Ferrarese, L., Jordán, A., Merritt, D., Peng, E. W., et al. (2006). The ACS Virgo Cluster Survey. VIII. The Nuclei of Early‐Type Galaxies. Astrophys J. Suppl. S 165, 57–94. doi:10.1086/504042

CrossRef Full Text | Google Scholar

Courteau, S. (1996). Deep R-Band Photometry for Northern Spiral Galaxies. ApJS 103, 363. doi:10.1086/192281

CrossRef Full Text | Google Scholar

Courteau, S., Dutton, A. A., van den Bosch, F. C., MacArthur, L. A., Dekel, A., McIntosh, D. H., et al. (2007). Scaling Relations of Spiral Galaxies. ApJ 671, 203–225. doi:10.1086/522193

CrossRef Full Text | Google Scholar

Courteau, S. (1997). Optical Rotation Curves and Linewidths for Tully-Fisher Applications. Astronomical J. 114, 2402. doi:10.1086/118656

CrossRef Full Text | Google Scholar

Courteau, S., and Rix, H. W. (1999). Maximal Disks and the Tully‐Fisher Relation. ApJ 513, 561–571. doi:10.1086/306872

CrossRef Full Text | Google Scholar

Covington, M. D., Kassin, S. A., Dutton, A. A., Weiner, B. J., Cox, T. J., Jonsson, P., et al. (2010). Evolution of the Stellar Mass Tully-Fisher Relation in Disk Galaxy Merger Simulations. ApJ 710, 279–288. doi:10.1088/0004-637x/710/1/279

CrossRef Full Text | Google Scholar

Cowie, L. L., Songaila, A., Hu, E. M., and Cohen, J. G. (1996). New Insight on Galaxy Formation and Evolution from Keck Spectroscopy of the Hawaii Deep Fields. Astronomical J. 112, 839. doi:10.1086/118058

CrossRef Full Text | Google Scholar

Cracco, V., Ciroi, S., Berton, M., Di Mille, F., Foschini, L., La Mura, G., et al. (2016). A Spectroscopic Analysis of a Sample of Narrow-Line Seyfert 1 Galaxies Selected from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 462, 1256–1280. doi:10.1093/mnras/stw1689

CrossRef Full Text | Google Scholar

Crenshaw, D. M., Kraemer, S. B., and Gabel, J. R. (2003). The Host Galaxies of Narrow-Line Seyfert 1 Galaxies: Evidence for Bar-Driven Fueling. Astron. J. 126, 1690–1698. doi:10.1086/377625

CrossRef Full Text | Google Scholar

Cresci, G., Marconi, A., Zibetti, S., Risaliti, G., Carniani, S., Mannucci, F., et al. (2015). The MAGNUM Survey: Positive Feedback in the Nuclear Region of NGC 5643 Suggested by MUSE. A&A 582, A63. doi:10.1051/0004-6361/201526581

CrossRef Full Text | Google Scholar

Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., Bryant, J. J., Fogarty, L., Richards, S., et al. (2012). The Sydney-AAO Multi-Object Integral Field Spectrograph. Mon. Not. R. Astron. Soc. 421, doi:10.1111/j.1365-2966.2011.20365.x

CrossRef Full Text | Google Scholar

Czerny, B., Beaton, R., Bejger, M., Cackett, E., Dall’Ora, M., Holanda, R. F. L., et al. (2018). Astronomical Distance Determination in the Space Age. Secondary Distance Indicators. Space Sci. Rev. 214, 32. doi:10.1007/s11214-018-0466-9

CrossRef Full Text | Google Scholar

Czerny, B., Martínez-Aldama, M. L., Wojtkowska, G., Zajaček, M., Marziani, P., Dultzin, D., et al. (2020). Dark Energy Constraints from Quasar Observations. arXiv:2011.12375.

Google Scholar

D'Onofrio, M., Bettoni, D., Bindoni, D., Cava, A., Fasano, G., Marziani, P., et al. (2013). The Fundamental Plane of Clusters of Galaxies. Astron. Nachr. 334, 373–376. doi:10.1002/asna.201211860

CrossRef Full Text | Google Scholar

D'Onofrio, M., Capaccioli, M., and Caon, N. (1994). On the shape of the light profiles of early-type galaxies - II. The $(D_\text n/A_\text e)-\langle\mu\rangle_\text e$ diagram. Mon. Not. R. Astron. Soc. 271, 523–529. doi:10.1093/mnras/271.3.523

CrossRef Full Text | Google Scholar

D'Onofrio, M., Fasano, G., Moretti, A., Marziani, P., Bindoni, D., Fritz, J., et al. (2013). The Hybrid Solution for the Fundamental Plane. Mon. Not. R. Astron. Soc. 435, 45–63. doi:10.1093/mnras/stt1278

CrossRef Full Text | Google Scholar

Daddi, E., Cimatti, A., Renzini, A., Fontana, A., Mignoli, M., Pozzetti, L., et al. (2004). A New Photometric Technique for the Joint Selection of Star‐forming and Passive Galaxies at 1.4 ≲z≲ 2.5. ApJ 617, 746–764. doi:10.1086/425569

CrossRef Full Text | Google Scholar

Daddi, E., Dickinson, M., Morrison, G., Chary, R., Cimatti, A., Elbaz, D., et al. (2007). Multiwavelength Study of Massive Galaxies Atz∼2. I. Star Formation and Galaxy Growth. ApJ 670, 156–172. doi:10.1086/521818

CrossRef Full Text | Google Scholar

Daddi, E., Renzini, A., Pirzkal, N., Cimatti, A., Malhotra, S., Stiavelli, M., et al. (2005). Passively Evolving Early‐Type Galaxies at 1.4 ≲z≲ 2.5 in the Hubble Ultra Deep Field. ApJ 626, 680–697. doi:10.1086/430104

CrossRef Full Text | Google Scholar

Dalcanton, J. J., Spergel, D. N., and Summers, F. J. (1997). The Formation of Disk Galaxies. ApJ 482, 659–676. doi:10.1086/304182

CrossRef Full Text | Google Scholar

Dalcanton, J. J. (2007). The Metallicity of Galaxy Disks: Infall versus Outflow. ApJ 658, 941–959. doi:10.1086/508913

CrossRef Full Text | Google Scholar

Damjanov, I., McCarthy, P. J., Abraham, R. G., Glazebrook, K., Yan, H., Mentuch, E., et al. (2009). RED NUGGETS ATz∼ 1.5: COMPACT PASSIVE GALAXIES AND THE FORMATION OF THE KORMENDY RELATION. ApJ 695, 101–115. doi:10.1088/0004-637X/695/1/101

CrossRef Full Text | Google Scholar

Danovich, M., Dekel, A., Hahn, O., Ceverino, D., and Primack, J. (2015). Four Phases of Angular-Momentum Buildup in High-Z Galaxies: from Cosmic-Web Streams through an Extended Ring to Disc and Bulge. Mon. Not. R. Astron. Soc. 449, 2087–2111. doi:10.1093/mnras/stv270

CrossRef Full Text | Google Scholar

Danovich, M., Dekel, A., Hahn, O., and Teyssier, R. (2012). Coplanar Streams, Pancakes and Angular-Momentum Exchange in High-Z Disc Galaxies. Mon. Not. R. Astron. Soc. 422, 1732–1749. doi:10.1111/j.1365-2966.2012.20751.x

CrossRef Full Text | Google Scholar

Davé, R., Oppenheimer, B. D., and Finlator, K. (2011). Galaxy Evolution in Cosmological Simulations with Outflows - I. Stellar Masses and star Formation Rates. Mon. Not. R. Astron. Soc. 415, 11–31. doi:10.1111/j.1365-2966.2011.18680.x

CrossRef Full Text | Google Scholar

Davies, R. I., Thomas, J., Genzel, R., Mueller Sanchez, F., Tacconi, L. J., Sternberg, A., et al. (2006). The Star‐forming Torus and Stellar Dynamical Black Hole Mass in the Seyfert 1 Nucleus of NGC 3227. ApJ 646, 754–773. doi:10.1086/504963

CrossRef Full Text | Google Scholar

Davis, B. L., Graham, A. W., and Cameron, E. (2018). Black Hole Mass Scaling Relations for Spiral Galaxies. II. M BH-M *,tot and M BH-M *,disk. ApJ 869, 113. doi:10.3847/1538-4357/aae820

CrossRef Full Text | Google Scholar

Davis, T. A., Nguyen, D. D., Seth, A. C., Greene, J. E., Nyland, K., Barth, A. J., et al. (2020). Revealing the Intermediate-Mass Black Hole at the Heart of the dwarf Galaxy NGC 404 with Sub-parsec Resolution ALMA Observations. MNRAS 496, 4061–4078. doi:10.1093/mnras/staa1567

CrossRef Full Text | Google Scholar

de la Rosa, I. G., La Barbera, F., Ferreras, I., Sánchez Almeida, J., Dalla Vecchia, C., Martínez-Valpuesta, I., et al. (2016). The Fate of High-Redshift Massive Compact Galaxies. Mon. Not. R. Astron. Soc. 457, 1916–1930. doi:10.1093/mnras/stw130

CrossRef Full Text | Google Scholar

De Lucia, G., Kauffmann, G., and White, S. D. M. (2004). Chemical Enrichment of the Intracluster and Intergalactic Medium in a Hierarchical Galaxy Formation Model. Mon. Not. R. Astron. Soc. 349, 1101–1116. doi:10.1111/j.1365-2966.2004.07584.x

CrossRef Full Text | Google Scholar

De Rossi, M. E., Tissera, P. B., and Pedrosa, S. E. (2012). Fingerprints of the Hierarchical Building-Up of the Structure on the Gas Kinematics of Galaxies. A&A 546, A52. doi:10.1051/0004-6361/201118409

CrossRef Full Text | Google Scholar

de Vaucouleurs, G. (1962). “Classification of Galaxies by Form, Luminosity and Color,” in IAU Symp. N. 15 (Texas: University of Texas Austin), 3–21.)

Google Scholar

de Vaucouleurs, G. (1961). Integrated Colors of Bright Galaxies in the U, B, V System. ApJS 5, 233. doi:10.1086/190056

CrossRef Full Text | Google Scholar

Decarli, R., Dotti, M., and Treves, A. (2011). Geometry and Inclination of the Broad-Line Region in Blazars. MNRAS 413, 39–46. doi:10.1111/j.1365-2966.2010.18102.x

CrossRef Full Text | Google Scholar

Decarli, R., Falomo, R., Treves, A., Kotilainen, J. K., Labita, M., and Scarpa, R. (2010). The Quasar Relation through Cosmic Time - I. Data Set and Black Hole Masses. MNRAS 402, 2441–2452. doi:10.1111/j.1365-2966.2009.16048.x

CrossRef Full Text | Google Scholar

Decarli, R., Walter, F., Venemans, B. P., Bañados, E., Bertoldi, F., Carilli, C., et al. (2018). An ALMA [C Ii] Survey of 27 Quasars Atz> 5.94. ApJ 854, 97. doi:10.3847/1538-4357/aaa5aa

CrossRef Full Text | Google Scholar

Dekel, A., and Birnboim, Y. (2006). Galaxy Bimodality Due to Cold Flows and Shock Heating. Monthly Notices R. Astronomical Soc. 368, 2–20. doi:10.1111/j.1365-2966.2006.10145.x

CrossRef Full Text | Google Scholar

Dekel, A., and Silk, J. (1986). The Origin of Dwarf Galaxies, Cold Dark Matter, and Biased Galaxy Formation. ApJ 303, 39. doi:10.1086/164050

CrossRef Full Text | Google Scholar

Delaye, L., Huertas-Company, M., Mei, S., Lidman, C., Licitra, R., Newman, A., et al. (2014). Larger Sizes of Massive Quiescent Early-type Galaxies in Clusters Than in the Field at 0.8. Mon. Not. R. Astron. Soc. 441, 203–223. doi:10.1093/mnras/stu496

CrossRef Full Text | Google Scholar

Desmond, H., and Wechsler, R. H. (2017). The Faber-Jackson Relation and Fundamental Plane from Halo Abundance Matching. Mon. Not. R. Astron. Soc. 465, 820–833. doi:10.1093/mnras/stw2804

CrossRef Full Text | Google Scholar

Di Cintio, A., and Lelli, F. (2016). The Mass Discrepancy Acceleration Relation in a ΛCDM Context. Mon. Not. R. Astron. Soc. Lett. 456, L127–L131. doi:10.1093/mnrasl/slv185

CrossRef Full Text | Google Scholar

Di Matteo, T., Springel, V., and Hernquist, L. (2005). Energy Input from Quasars Regulates the Growth and Activity of Black Holes and Their Host Galaxies. Nature 433, 604–607. doi:10.1038/nature03335

PubMed Abstract | CrossRef Full Text | Google Scholar

Diamond-Stanic, A. M., Fan, X., Brandt, W. N., Shemmer, O., Strauss, M. A., Anderson, S. F., et al. (2009). High-redshift SDSS Quasars with Weak Emission Lines. ApJ 699, 782–799. doi:10.1088/0004-637X/699/1/782

CrossRef Full Text | Google Scholar

Disney, M. J., Romano, J. D., Garcia–Appadoo, D. A., West, A. A., Dalcanton, J. J., and Cortese, L. (2008). Galaxies Appear Simpler Than Expected. Nature 455, 1082–1084. doi:10.1038/nature07366

PubMed Abstract | CrossRef Full Text | Google Scholar

Djorgovski, S., and Davis, M. (1987). Fundamental Properties of Elliptical Galaxies. ApJ 313, 59. doi:10.1086/164948

CrossRef Full Text | Google Scholar

Doi, A., Kino, M., Kawakatu, N., and Hada, K. (2020). The Radio-Loud Narrow-Line Seyfert 1 Galaxy 1H 0323+342 in a Galaxy Merger. MNRAS 496, 1757–1765. doi:10.1093/mnras/staa1525

CrossRef Full Text | Google Scholar

Dokkum, P. G. v., and Franx, M. (1996). The Fundamental Plane in CL 0024 at Z = 0.4: Implications for the Evolution of the Mass-To-Light Ratio. Monthly Notices R. Astronomical Soc. 281, 985–1000. doi:10.1093/mnras/281.3.985

CrossRef Full Text | Google Scholar

D’Onofrio, M., Cariddi, S., Chiosi, C., Chiosi, E., and Marziani, P. (2017). On the Origin of the Fundamental Plane and Faber-Jackson Relations: Implications for the Star Formation Problem. Astrophysical J. 838, 163. doi:10.3847/1538-4357/aa6540

CrossRef Full Text | Google Scholar

D’Onofrio, M., and Chiosi, C. (2020). A tomography of the log(⟨I⟩_e) −   log(R_e) plane. arXiv:2011.07315.

Google Scholar

D’Onofrio, M., Chiosi, C., Sciarratta, M., and Marziani, P. (2020). The Parallelism between Galaxy Clusters and Early-type Galaxies. II. Clues on the Origin of the Scaling Relations. Astron. Astrophysics 641, A94. doi:10.1051/0004-6361/202038221

CrossRef Full Text | Google Scholar

D’Onofrio, M., Valentinuzzi, T., Fasano, G., Moretti, A., Bettoni, D., Poggianti, B., et al. (2011). On the Connection between Shape and Stellar Population in Early-type Galaxies. Astrophysical J. Lett 727, L6. doi:10.1088/2041-8205/727/1/L6

CrossRef Full Text | Google Scholar

D’Onofrio, M., Fasano, G., Varela, J., Bettoni, D., Moles, M., Kjærgaard, P., et al. (2008). The Fundamental Plane of Early‐Type Galaxies in Nearby Clusters from the WINGS Database. Astrophysical J. 685, 875–896. doi:10.1086/591143

CrossRef Full Text | Google Scholar

Dorman, B., O’Connell, R. W., and Rood, R. T. (2003). Age and Abundance Discrimination in Old Stellar Populations Using Mid‐Ultraviolet Colors. ApJ 591, 878–890. doi:10.1086/375413

CrossRef Full Text | Google Scholar

Doroshkevich, A. G. (1970). Spatial Structure of Perturbations and Origin of Galactic Rotation in Fluctuation Theory. Astrophysics 6, 320–330. doi:10.1007/BF01001625

CrossRef Full Text | Google Scholar

Dressler, A. (1980). Galaxy Morphology in Rich Clusters - Implications for the Formation and Evolution of Galaxies. ApJ 236, 351–365. doi:10.1086/157753

CrossRef Full Text | Google Scholar

Dressler, A. (1984). Internal Kinematics of Galaxies in Clusters. I - Velocity Dispersions for Elliptical Galaxies in Coma and Virgo. ApJ 281, 512–524. doi:10.1086/162124

CrossRef Full Text | Google Scholar

Dressler, A., Lynden-Bell, D., Burstein, D., Davies, R. L., Faber, S. M., Terlevich, R., et al. (1987). Spectroscopy and Photometry of Elliptical Galaxies. I - A New Distance Estimator. ApJ 313, 42. doi:10.1086/164947

CrossRef Full Text | Google Scholar

Du, P., Brotherton, M. S., Wang, K., Huang, Z.-P., Hu, C., Kasper, D. H., et al. (2018). Monitoring AGNs with Hβ Asymmetry. I. First Results: Velocity-Resolved Reverberation Mapping. ApJ 869, 142. doi:10.3847/1538-4357/aaed2c

CrossRef Full Text | Google Scholar

Du, P., Lu, K.-X., Hu, C., Qiu, J., Li, Y.-R., Huang, Y.-K., et al. (2016). SUPERMASSIVE BLACK HOLES WITH HIGH ACCRETION RATES IN ACTIVE GALACTIC NUCLEI. VI. VELOCITY-RESOLVED REVERBERATION MAPPING OF THE HβLINE. ApJ 820, 27. doi:10.3847/0004-637X/820/1/27

CrossRef Full Text | Google Scholar

Du, P., Wang, J.-M., Hu, C., Ho, L. C., Li, Y.-R., and Bai, J.-M. (2016). The Fundamental Plane of the Broad-Line Region in Active Galactic Nuclei. ApJ 818, L14. doi:10.3847/2041-8205/818/1/L14

CrossRef Full Text | Google Scholar

Du, P., and Wang, J.-M. (2019). The Radius-Luminosity Relationship Depends on Optical Spectra in Active Galactic Nuclei. ApJ 886, 42. doi:10.3847/1538-4357/ab4908

CrossRef Full Text | Google Scholar

Du, P., Zhang, Z.-X., Wang, K., Huang, Y.-K., Zhang, Y., Lu, K.-X., et al. (2018). Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. IX. 10 New Observations of Reverberation Mapping and Shortened HβLags. ApJ 856, 6. doi:10.3847/1538-4357/aaae6b

CrossRef Full Text | Google Scholar

Dullo, B. T., Bouquin, A. Y. K., de Paz, A. G., Knapen, J. H., and Gorgas, J. (2020). The Black Hole Mass-Color Relations for Early- and Late-type Galaxies: Red and Blue Sequences. ApJ 898, 83. doi:10.3847/1538-4357/ab9dff

CrossRef Full Text | Google Scholar

Dultzin, D., Marziani, P., de Diego, J. A., Negrete, C. A., Del Olmo, A., Martínez-Aldama, M. L., et al. (2020). Extreme Quasars as Distance Indicators in Cosmology. Front. Astron. Space Sci. 6, 80. doi:10.3389/fspas.2019.00080

CrossRef Full Text | Google Scholar

Dultzin-Hacyan, D., Taniguchi, Y., and Uranga, L. (1999). “Where Is the Ca II Triplet Emitting Region in AGN? Gaskell CM,” in Structure and Kinematics of Quasar Broad Line Regions. Editors W. N. Brandt, M. Dietrich, D. Dultzin-Hacyan, and M. Eracleous (California, United States: Astronomical Society of the Pacific Conference Series), 175, 303.

Google Scholar

Dumont, A. M., and Collin-Souffrin, S. (1990). Line and Continuum Emission from the Outer Regions of Accretion Discs in Active Galactic Nuclei - Part IV - Line Emission. AAp 229, 313.

Google Scholar

Dutton, A. A., Conroy, C., van den Bosch, F. C., Simard, L., Mendel, J. T., Courteau, S., et al. (2011). Dark Halo Response and the Stellar Initial Mass Function in Early-type and Late-type Galaxies. Mon. Not. R. Astron. Soc. 416, 322–345. doi:10.1111/j.1365-2966.2011.19038.x

CrossRef Full Text | Google Scholar

Dutton, A. A. (2012). The Baryonic Tully-Fisher Relation and Galactic Outflows. Monthly Notices R. Astronomical Soc. 424, 3123–3128. doi:10.1111/j.1365-2966.2012.21469.x

CrossRef Full Text | Google Scholar

Dutton, A. A., van den Bosch, F. C., Dekel, A., and Courteau, S. (2007). A Revised Model for the Formation of Disk Galaxies: Low Spin and Dark Halo Expansion. ApJ 654, 27–52. doi:10.1086/509314

CrossRef Full Text | Google Scholar

Edmunds, M. G. (1990). General Constraints on the Effect of Gas Flows in the Chemical Evolution of Galaxies. Mon. Not. R. Astron. Soc. 246, 678.

Google Scholar

Efstathiou, G., and Jones, B. J. T. (1979). The Rotation of Galaxies: Numerical Investigations of the Tidal Torque Theory. MNRAS 186, 133–144. doi:10.1093/mnras/186.2.133

CrossRef Full Text | Google Scholar

Eggen, O. J., Lynden-Bell, D., and Sandage, A. R. (1962). Evidence from the Motions of Old Stars that the Galaxy Collapsed. ApJ 136, 748. doi:10.1086/147433

CrossRef Full Text | Google Scholar

Eisenstein, D. J., and Loeb, A. (1996). Can the Tully-Fisher Relation Be the Result of Initial Conditions? ApJ 459, 432. doi:10.1086/176905

CrossRef Full Text | Google Scholar

Elbaz, D., Dickinson, M., Hwang, H. S., Díaz-Santos, T., Magdis, G., Magnelli, B., et al. (2011). GOODS-herschel: an Infrared Main Sequence for star-forming Galaxies. Astron. Astrophysics 533, A119. doi:10.1051/0004-6361/201117239

CrossRef Full Text | Google Scholar

Elbaz, D., Daddi, E., Le Borgne, D., Dickinson, M., Alexander, D. M., Chary, R.-R., et al. (2007). The Reversal of the star Formation-Density Relation in the Distant Universe. A&A 468, 33–48. doi:10.1051/0004-6361:20077525

CrossRef Full Text | Google Scholar

Ellis, S. C., Driver, S. P., Allen, P. D., Liske, J., Bland-Hawthorn, J., and De Propris, R. (2005). The Millennium Galaxy Catalogue: on the Natural Subdivision of Galaxies. Mon. Not. R. Astron. Soc. 363, 1257–1271. doi:10.1111/j.1365-2966.2005.09521.x

CrossRef Full Text | Google Scholar

Elmegreen, B. G., and Burkert, A. (2010). Accretion-Driven Turbulence and the Transition to Global Instability in Young Galaxy Disks. ApJ 712, 294–302. doi:10.1088/0004-637X/712/1/294

CrossRef Full Text | Google Scholar

Elvis, M. (2000). A Structure for Quasars. ApJ 545, 63–76. doi:10.1086/317778

CrossRef Full Text | Google Scholar

Elvis, M., Wilkes, B. J., McDowell, J. C., Green, R. F., Bechtold, J., Willner, S. P., et al. (1994). Atlas of Quasar Energy Distributions. ApJS 95, 1–68. doi:10.1086/192093

CrossRef Full Text | Google Scholar

Engler, C., Pillepich, A., Joshi, G. D., Nelson, D., Pasquali, A., Grebel, E. K., et al. (2020). The Distinct Stellar-To-Halo Mass Relations of Satellite and Central Galaxies: Insights from the IllustrisTNG Simulations. arXiv:2002.11119.

Google Scholar

Eracleous, M., and Halpern, J. P. (2004). Accurate Redshifts and Classifications for 110 Radio‐Loud Active Galactic Nuclei. Astrophys J. Suppl. S 150, 181–186. doi:10.1086/37982310.1086/379823

CrossRef Full Text | Google Scholar

Eracleous, M., and Halpern, J. P. (2003). Completion of a Survey and Detailed Study of Double‐peaked Emission Lines in Radio‐loud Active Galactic Nuclei. ApJ 599, 886–908. doi:10.1086/379540

CrossRef Full Text | Google Scholar

Erb, D. K., Shapley, A. E., Pettini, M., Steidel, C. C., Reddy, N. A., and Adelberger, K. L. (2006). The Mass‐Metallicity Relation Atz≳2. ApJ 644, 813–828. doi:10.1086/503623

CrossRef Full Text | Google Scholar

Ermash, A. A., and Komberg, B. V. (2013). Morphology and Evolutionary Status of Narrow Line Seyfert (NLS) Active Galaxies. Astrophysics 56, 569–596. doi:10.1007/s10511-013-9309-2

CrossRef Full Text | Google Scholar

Esser, J., Pott, J.-U., Landt, H., and Vacca, W. D. (2019). Analyzing Temporal Variations of AGN Emission Line Profiles in the Context of (Dusty) Cloud Structure Formation in the Broad Line Region. A&A 621, A46. doi:10.1051/0004-6361/201834291

CrossRef Full Text | Google Scholar

Everett, J. E. (2007). Outflows from AGNs: a Brief Overview of Observations and Models. Astrophys Space Sci. 311, 269–273. doi:10.1007/s10509-007-9536-2

CrossRef Full Text | Google Scholar

Faber, S. M. (1984). “Galaxy Formation and Cosmology,” in Large-Scale Structure of the Universe. Editors G. Setti, and L. Van Hove, 187.

Google Scholar

Faber, S. M. (1977). “The Chemical Composition of Old Stellar Populations,” in Evolution of Galaxies and Stellar Populations. Editors B. M. Tinsley, and R. B. Larson (New Haven: Yale University Observatory), 157.

Google Scholar

Faber, S. M., Dressler, A., Davies, R. L., Burstein, D., Lynden-Bell, D., Terlevich, R., et al. (1987). “Global Scaling Relations for Elliptical Galaxies and Implications for Formation,” in Nearly Normal Galaxies. From the Planck Time to the Present. Editor S. M. Faber, 175–183. doi:10.1007/978-1-4612-4762-3_22

CrossRef Full Text | Google Scholar

Faber, S. M., and Jackson, R. E. (1976). Velocity Dispersions and Mass-To-Light Ratios for Elliptical Galaxies. ApJ 204, 668–683. doi:10.1086/154215

CrossRef Full Text | Google Scholar

Faber, S. M. (1973). Variations in Spectral-Energy Distributions and Absorption-Line Strengths Among Elliptical Galaxies. ApJ 179, 731–754. doi:10.1086/151912

CrossRef Full Text | Google Scholar

Falcón-Barroso, J., van de Ven, G., Peletier, R. F., Bureau, M., Jeong, H., Bacon, R., et al. (2011). The SAURON Project - XIX. Optical and Near-Infrared Scaling Relations of Nearby Elliptical, Lenticular and Sa Galaxies. Mon. Not. R. Astron. Soc. 417, 1787–1816. doi:10.1111/j.1365-2966.2011.19372.x

CrossRef Full Text | Google Scholar

Fall, S. M., and Efstathiou, G. (1980). Formation and Rotation of Disc Galaxies with Haloes. Monthly Notices R. Astronomical Soc. 193, 189–206. doi:10.1093/mnras/193.2.189

CrossRef Full Text | Google Scholar

Fall, S. M. (1983). “Galaxy Formation: Some Comparisons between Theory and Observation,” in Internal Kinematics and Dynamics of Galaxies. Editor E. Athanassoula, 100, 391–399. doi:10.1007/978-94-009-7075-5_108

CrossRef Full Text | Google Scholar

Fall, S. M., and Romanowsky, A. J. (2013). Angular Momentum and Galaxy Formation Revisited: Effects of Variable Mass-To-Light Ratios. ApJ 769, L26. doi:10.1088/2041-8205/769/2/L26

CrossRef Full Text | Google Scholar

Fall, S. M., and Romanowsky, A. J. (2018). Angular Momentum and Galaxy Formation Revisited: Scaling Relations for Disks and Bulges. ApJ 868, 133. doi:10.3847/1538-4357/aaeb27

CrossRef Full Text | Google Scholar

Fan, L., Lapi, A., Bressan, A., Bernardi, M., De Zotti, G., and Danese, L. (2010). Cosmic Evolution of Size and Velocity Dispersion for Early-type Galaxies. ApJ 718, 1460–1475. doi:10.1088/0004-637X/718/2/1460

CrossRef Full Text | Google Scholar

Fasano, G., Marmo, C., Varela, J., D'Onofrio, M., Poggianti, B. M., Moles, M., et al. (2006). WINGS: a WIde-Field Nearby Galaxy-Cluster Survey. A&A 445, 805–817. doi:10.1051/0004-6361:20053816

CrossRef Full Text | Google Scholar

Feldmann, R., Hopkins, P. F., Quataert, E., Faucher-Giguère, C.-A., and Kereš, D. (2016). The Formation of Massive, Quiescent Galaxies at Cosmic Noon. Mon. Not. R. Astron. Soc. Lett. 458, L14–L18. doi:10.1093/mnrasl/slw014

CrossRef Full Text | Google Scholar

Ferguson, H. C. (1989). Population Studies in Groups and Clusters of Galaxies. II - A Catalog of Galaxies in the central 3.5 Deg of the Fornax Cluster. Astronomical J. 98, 367. doi:10.1086/115152

CrossRef Full Text | Google Scholar

Ferland, G. J., Hu, C., Wang, J.-M., Baldwin, J. A., Porter, R. L., van Hoof, P. A. M., et al. (2009). Implications of Infalling Fe II-Emitting Clouds in Active Galactic Nuclei: Anisotropic Properties. ApJ 707, L82–L86. doi:10.1088/0004-637x/707/1/l82

CrossRef Full Text | Google Scholar

Fernández Lorenzo, M., Cepa, J., Bongiovanni, A., Pérez García, A. M., Ederoclite, A., Lara-López, M. A., et al. (2011). Evolution of the Fundamental Plane of 0.2. A&A 526, A72. doi:10.1051/0004-6361/201015368

CrossRef Full Text | Google Scholar

Ferrarese, L. (2002). Beyond the Bulge: A Fundamental Relation between Supermassive Black Holes and Dark Matter Halos. ApJ 578, 90–97. doi:10.1086/342308

CrossRef Full Text | Google Scholar

Ferrarese, L., Côté, P., Dalla Bontà, E., Peng, E. W., Merritt, D., Jordán, A., et al. (2006). A Fundamental Relation between Compact Stellar Nuclei, Supermassive Black Holes, and Their Host Galaxies. ApJ 644, L21–L24. doi:10.1086/505388

CrossRef Full Text | Google Scholar

Ferrarese, L., Côté, P., Jordán, A., Peng, E. W., Blakeslee, J. P., Piatek, S., et al. (2006). The ACS Virgo Cluster Survey. VI. Isophotal Analysis and the Structure of Early‐Type Galaxies. Astrophys J. Suppl. S 164, 334–434. doi:10.1086/501350

CrossRef Full Text | Google Scholar

Ferrarese, L., and Ford, H. (2005). Supermassive Black Holes in Galactic Nuclei: Past, Present and Future Research. Space Sci. Rev. 116, 523–624. doi:10.1007/s11214-005-3947-610.1007/s11214-005-3947-6

CrossRef Full Text | Google Scholar

Ferrarese, L., and Merritt, D. (2000). A Fundamental Relation between Supermassive Black Holes and Their Host Galaxies. Astrophysical J. Lett 539, L9–L12. doi:10.1086/312838

CrossRef Full Text | Google Scholar

Fish, R. A. (1964). A Mass-Potential Relationship in Elliptical Galaxies and Some Inferences Concerning the Formation and Evolution of Galaxies. ApJ 139, 284. doi:10.1086/147753

CrossRef Full Text | Google Scholar

Fontana, A., Santini, P., Grazian, A., Pentericci, L., Fiore, F., Castellano, M., et al. (2009). The Fraction of Quiescent Massive Galaxies in the Early Universe. A&A 501, 15–20. doi:10.1051/0004-6361/200911650

CrossRef Full Text | Google Scholar

Fornasini, F. M., Civano, F., Fabbiano, G., Elvis, M., Marchesi, S., Miyaji, T., et al. (2018). Low-luminosity AGN and X-Ray Binary Populations in COSMOS Star-forming Galaxies. ApJ 865, 43. doi:10.3847/1538-4357/aada4e

CrossRef Full Text | Google Scholar

Foschini, L. (2014). The Unification of Relativistic Jets. Int. J. Mod. Phys. Conf. Ser. 28, 1460188. doi:10.1142/S2010194514601884

CrossRef Full Text | Google Scholar

Fraix-Burnet, D. (2010). “Multivariate Evolutionary Analyses in Astrophysics,” in ADA 6 - Sixth Conference on Astronomical Data Analysis. Editors J. L. Starck, M. Saber Naceur, and R. Murtagh, 27.

Google Scholar

Fraix-Burnet, D., Davoust, E., and Charbonnel, C. (2009). The Environment of Formation as a Second Parameter for Globular Cluster Classification. Mon. Not. R. Astron. Soc. 398, 1706–1714. doi:10.1111/j.1365-2966.2009.15235.x

CrossRef Full Text | Google Scholar

Fraix-Burnet, D., D’Onofrio, M., and Marziani, P. (2019). Maximum Parsimony Analysis of the Effect of the Environment on the Evolution of Galaxies. A&A 630, A63. doi:10.1051/0004-6361/201935604

CrossRef Full Text | Google Scholar

Fraix-Burnet, D., Marziani, P., D'Onofrio, M., and Dultzin, D. (2017). The Phylogeny of Quasars and the Ontogeny of Their central Black Holes. Front. Astron. Space Sci. 4, 1. doi:10.3389/fspas.2017.00001

CrossRef Full Text | Google Scholar

Franca, F. L., Bianchi, S., Ponti, G., Branchini, E., and Matt, G. (2014). A New Cosmological Distance Measure Using Active Galactic Nucleus X-Ray Variability. ApJ 787, L12. doi:10.1088/2041-8205/787/1/L12

CrossRef Full Text | Google Scholar

Franceschini, A., Vercellone, S., and Fabian, A. C. (1998). Supermassive Black Holes in Early-type Galaxies: Relationship with Radio Emission and Constraints on the Black Hole Mass Function. Monthly Notices R. Astronomical Soc. 297, 817–824. doi:10.1046/j.1365-8711.1998.01534.x

CrossRef Full Text | Google Scholar

Franx, M., van Dokkum, P. G., Schreiber, N. M. F., Wuyts, S., Labbé, I., and Toft, S. (2008). Structure and Star Formation in Galaxies Out Toz= 3: Evidence for Surface Density Dependent Evolution and Upsizing. Astrophysical J. 688, 770–788. doi:10.1086/592431

CrossRef Full Text | Google Scholar

Fraser, C. W. (1972). Concentration Indices of Galaxies. The Observatory 92, 51–54.

Google Scholar

Fritz, A., Jørgensen, I., Schiavon, R. P., and Chiboucas, K. (2009). The Evolution of Cluster Early-type Galaxies over the Past 8 Gyr. Astron. Nachr. 330, 931–936. doi:10.1002/asna.200911266

CrossRef Full Text | Google Scholar

Fritz, J., Poggianti, B. M., Bettoni, D., Cava, A., Couch, W. J., D'Onofrio, M., et al. (2007). A Spectrophotometric Model Applied to Cluster Galaxies: the WINGS Dataset. A&A 470, 137–152. doi:10.1051/0004-6361:20077097

CrossRef Full Text | Google Scholar

Fritz, J., Poggianti, B. M., Cava, A., Valentinuzzi, T., Moretti, A., Bettoni, D., et al. (2011). WINGS-SPE II: A Catalog of Stellar Ages and star Formation Histories, Stellar Masses and Dust Extinction Values for Local Clusters Galaxies. A&A 526, A45. doi:10.1051/0004-6361/201015214

CrossRef Full Text | Google Scholar

Gallazzi, A., Charlot, S., Brinchmann, J., and White, S. D. M. (2006). Ages and Metallicities of Early-type Galaxies in the Sloan Digital Sky Survey: New Insight into the Physical Origin of the Colour-Magnitude and the Mg2-Σv Relations. Mon. Not. R. Astron. Soc. 370, 1106–1124. doi:10.1111/j.1365-2966.2006.10548.x

CrossRef Full Text | Google Scholar

Ganci, V., Marziani, P., D’Onofrio, M., del Olmo, A., Bon, E., Bon, N., et al. (2019). Radio Loudness along the Quasar Main Sequence. A&A 630, A110. doi:10.1051/0004-6361/201936270

CrossRef Full Text | Google Scholar

Gaskell, C. M. (1982). A Redshift Difference between High and Low Ionization Emission-Line Regions in QSOs - Evidence for Radial Motions. ApJ 263, 79–86. doi:10.1086/16048110.1086/160481

CrossRef Full Text | Google Scholar

Gebhardt, K., Adams, J., Richstone, D., Lauer, T. R., Faber, S. M., Gültekin, K., et al. (2011). The Black Hole Mass in M87 from Gemini/NIFS Adaptive Optics Observations. ApJ 729, 119. doi:10.1088/0004-637X/729/2/119

CrossRef Full Text | Google Scholar

Gebhardt, K., Bender, R., Bower, G., Dressler, A., Faber, S. M., Filippenko, A. V., et al. (2000). A Relationship between Nuclear Black Hole Mass and Galaxy Velocity Dispersion. Astrophysical J. Lett 539, L13–L16. doi:10.1086/312840

CrossRef Full Text | Google Scholar

Gebhardt, K., Faber, S. M., Koo, D. C., Im, M., Simard, L., Illingworth, G. D., et al. (2003). The DEEP Groth Strip Survey. IX. Evolution of the Fundamental Plane of Field Galaxies. ApJ 597, 239–262. doi:10.1086/378401

CrossRef Full Text | Google Scholar

Gebhardt, K., Lauer, T. R., Kormendy, J., Pinkney, J., Bower, G. A., Green, R., et al. (2001). M33: A Galaxy with No Supermassive Black Hole. Astronomical J. 122, 2469–2476. doi:10.1086/323481

CrossRef Full Text | Google Scholar

Gebhardt, K., Lauer, T. R., Pinkney, J., Bender, R., Richstone, D., Aller, M., et al. (2007). The Black Hole Mass and Extreme Orbital Structure in NGC 1399. ApJ 671, 1321–1328. doi:10.1086/522938

CrossRef Full Text | Google Scholar

Gebhardt, K., and Thomas, J. (2009). The Black Hole Mass, Stellar Mass-To-Light Ratio, and Dark Halo in M87. ApJ 700, 1690–1701. doi:10.1088/0004-637x/700/2/1690

CrossRef Full Text | Google Scholar

Genel, S., Nelson, D., Pillepich, A., Springel, V., Pakmor, R., Weinberger, R., et al. (2018). The Size Evolution of star-forming and Quenched Galaxies in the IllustrisTNG Simulation. Mon. Not. R. Astron. Soc. 474, 3976–3996. doi:10.1093/mnras/stx3078

CrossRef Full Text | Google Scholar

Gezari, S. (2021). Tidal Disruption Events. arXiv:2104.14580.

Google Scholar

Giovanelli, R., Haynes, M. P., da Costa, L. N., Freudling, W., Salzer, J. J., and Wegner, G. (1997). The Tully-Fisher Relation and [ITAL]H[/ITAL][TINF]0[/TINF]. Astrophysical J. Lett 477, L1–L4. doi:10.1086/310521

CrossRef Full Text | Google Scholar

Girelli, G., Pozzetti, L., Bolzonella, M., Giocoli, C., Marulli, F., and Baldi, M. (2020). The Stellar-To-Halo Mass Relation over the Past 12 Gyr. A&A 634, A135. doi:10.1051/0004-6361/201936329

CrossRef Full Text | Google Scholar

Giustini, M., and Proga, D. (2019). A Global View of the Inner Accretion and Ejection Flow Around Super Massive Black Holes. A&A 630, A94. doi:10.1051/0004-6361/201833810

CrossRef Full Text | Google Scholar

Gladders, M. D., Lopez‐Cruz, O., Yee, H. K. C., and Kodama, T. (1998). The Slope of the Cluster Elliptical Red Sequence: A Probe of Cluster Evolution. ApJ 501, 571–577. doi:10.1086/305858

CrossRef Full Text | Google Scholar

Gladders, M. D., Oemler, A., Dressler, A., Poggianti, B., Vulcani, B., and Abramson, L. (2013). The IMACS Cluster Building Survey. IV. The Log-normal Star Formation History of Galaxies. ApJ 770, 64. doi:10.1088/0004-637x/770/1/64

CrossRef Full Text | Google Scholar

Gnerucci, A., Marconi, A., Capetti, A., Axon, D. J., Robinson, A., and Neumayer, N. (2011). Spectroastrometry of Rotating Gas Disks for the Detection of Supermassive Black Holes in Galactic Nuclei. A&A 536, A86. doi:10.1051/0004-6361/201117388

CrossRef Full Text | Google Scholar

Gott, J. R., and Rees, M. J. (1975). A Theory of Galaxy Formation and Clustering. Astron. Astrophysics 45, 365–376.

Google Scholar

Graham, A., Lauer, T. R., Colless, M., and Postman, M. (1996). Brightest Cluster Galaxy Profile Shapes. ApJ 465, 534. doi:10.1086/177440

CrossRef Full Text | Google Scholar

Graham, A. W. (2012). BREAKING the LAW: THEMbh-MspheroidRELATIONS for CORE-Sérsic and SÉRSIC GALAXIES. ApJ 746, 113. doi:10.1088/0004-637X/746/1/113

CrossRef Full Text | Google Scholar

Graham, A. W. (2004). Core Depletion from Coalescing Supermassive Black Holes. ApJ 613, L33–L36. doi:10.1086/424928

CrossRef Full Text | Google Scholar

Graham, A. W., Dullo, B. T., and Savorgnan, G. A. D. (2015). Hiding in Plain Sight: An Abundance of Compact Massive Spheroids in the Local Universe. ApJ 804, 32. doi:10.1088/0004-637X/804/1/32

CrossRef Full Text | Google Scholar

Graham, A. W. (2013). Elliptical and Disk Galaxy Structure and Modern Scaling Laws, 6, 91–139. doi:10.1007/978-94-007-5609-0_2

CrossRef Full Text | Google Scholar

Graham, A. W., Erwin, P., Caon, N., and Trujillo, I. (2001). A Correlation between Galaxy Light Concentration and Supermassive Black Hole Mass. Astrophysical J. Lett 563, L11–L14. doi:10.1086/338500

CrossRef Full Text | Google Scholar

Graham, A. W. (2016). Galaxy Bulges and Their Massive Black Holes: A Review. A Rev. 418, 263–313. doi:10.1007/978-3-319-19378-6_11

CrossRef Full Text | Google Scholar

Graham, A. W., and Guzmn, R. (2003). HSTPhotometry of Dwarf Elliptical Galaxies in Coma, and an Explanation for the Alleged Structural Dichotomy between Dwarf and Bright Elliptical Galaxies. Astron. J. 125, 2936–2950. doi:10.1086/374992

CrossRef Full Text | Google Scholar

Graham, A. W. (2011). “How Non-linear Scaling Relations Unify Dwarf and Giant Elliptical Galaxies,” in EAS Publications Series. Editors M. Koleva, P. Prugniel, and I. Vauglin (Les Ulis Cedex, France: EAS Publications Series), 48, 231–236. doi:10.1051/eas/1148052

CrossRef Full Text | Google Scholar

Graham, A. W., Janz, J., Penny, S. J., Chilingarian, I. V., Ciambur, B. C., Forbes, D. A., et al. (2017). Implications for the Origin of Early-type Dwarf Galaxies: A Detailed Look at the Isolated Rotating Early-type Dwarf Galaxy LEDA 2108986 (CG 611), Ramifications for the Fundamental Plane's ${S}_{K}^{2}$ Kinematic Scaling, and the Spin-Ellipticity Diagram. ApJ 840, 68. doi:10.3847/1538-4357/aa6e56

CrossRef Full Text | Google Scholar

Graham, A. W. (2019). Re. I. Understanding Galaxy Sizes, Associated Luminosity Densities, and the Artificial Division of the Early-type Galaxy Population. Publ. Astron. Soc. Aust. 36, e035. doi:10.1017/pasa.2019.23

CrossRef Full Text | Google Scholar

Graham, A. W., and Scott, N. (2015). The (Black Hole)-Bulge Mass Scaling Relation at Low Masses. ApJ 798, 54. doi:10.1088/0004-637X/798/1/54

CrossRef Full Text | Google Scholar

Graham, A. W., and Scott, N. (2013). Thembh-lspheroidrelation at High and Low Masses, the Quadratic Growth of Black Holes, and Intermediate-Mass Black Hole Candidates. ApJ 764, 151. doi:10.1088/0004-637X/764/2/151

CrossRef Full Text | Google Scholar

Graham, A. W., and Spitler, L. R. (2009). Quantifying the Coexistence of Massive Black Holes and Dense Nuclear star Clusters. MNRAS 397, 2148–2162. doi:10.1111/j.1365-2966.2009.15118.x

CrossRef Full Text | Google Scholar

Graham, M. J., Clowes, R. G., and Campusano, L. E. (1996). A Quasar with Ultrastrong, Ultraviolet Fe II Emission. Monthly Notices R. Astronomical Soc. 279, 1349–1356. doi:10.1093/mnras/279.4.1349

CrossRef Full Text | Google Scholar

Granato, G. L., De Zotti, G., Silva, L., Bressan, A., and Danese, L. (2004). A Physical Model for the Coevolution of QSOs and Their Spheroidal Hosts. ApJ 600, 580–594. doi:10.1086/379875

CrossRef Full Text | Google Scholar

Grant, N. I., Kuipers, J. A., and Phillipps, S. (2005). Nucleated dwarf Elliptical Galaxies in the Virgo Cluster. Mon. Not. R. Astron. Soc. 363, 1019–1030. doi:10.1111/j.1365-2966.2005.09518.x

CrossRef Full Text | Google Scholar

Greene, J. E., Peng, C. Y., Kim, M., Kuo, C.-Y., Braatz, J. A., Impellizzeri, C. M. V., et al. (2010). Precise Black Hole Masses from Megamaser Disks: Black Hole-Bulge Relations at Low Mass. ApJ 721, 26–45. doi:10.1088/0004-637x/721/1/26

CrossRef Full Text | Google Scholar

Greene, J. E., Strader, J., and Ho, L. C. (2020). Intermediate-Mass Black Holes. Annu. Rev. Astron. Astrophys. 58, 257–312. doi:10.1146/annurev-astro-032620-021835

CrossRef Full Text | Google Scholar

Grupe, D., and Nousek, J. A. (2015). Is There a Connection between Broad Absorption Line Quasars and Narrow-Line Seyfert 1 Galaxies? AJ 149, 85. doi:10.1088/0004-6256/149/2/85

CrossRef Full Text | Google Scholar

Grupe, D., Thomas, H.-C., and Beuermann, K. (2001). X-ray Variability in a Complete Sample of Soft X-ray Selected AGN. A&A 367, 470–486. doi:10.1051/0004-6361:20000429

CrossRef Full Text | Google Scholar

Gültekin, K., King, A. L., Cackett, E. M., Nyland, K., Miller, J. M., Matteo, T. D., et al. (2019). The Fundamental Plane of Black Hole Accretion and its Use as a Black Hole-Mass Estimator. ApJ 871, 80. doi:10.3847/1538-4357/aaf6b9

CrossRef Full Text | Google Scholar

Gültekin, K., Richstone, D. O., Gebhardt, K., Lauer, T. R., Tremaine, S., Aller, M. C., et al. (2009). THEM-σ ANDM-LRELATIONS IN GALACTIC BULGES, AND DETERMINATIONS OF THEIR INTRINSIC SCATTER. ApJ 698, 198–221. doi:10.1088/0004-637x/698/1/198

CrossRef Full Text | Google Scholar

Gültekin, K., Tremaine, S., Loeb, A., and Richstone, D. O. (2011). OBSERVATIONAL SELECTION EFFECTS AND THEM-σ RELATION. ApJ 738, 17. doi:10.1088/0004-637X/738/1/17

CrossRef Full Text | Google Scholar

Guo, Y., McIntosh, D. H., Mo, H. J., Katz, N., Van Den Bosch, F. C., Weinberg, M., et al. (2009). Structural Properties of central Galaxies in Groups and Clusters. Mon. Not. R. Astron. Soc. 398, 1129–1149. doi:10.1111/j.1365-2966.2009.15223.x

CrossRef Full Text | Google Scholar

Guzman, R., Lucey, J. R., and Bower, R. G. (1993). The Fundamental Relations of Elliptical Galaxies. Monthly Notices R. Astronomical Soc. 265, 731–746. doi:10.1093/mnras/265.3.731

CrossRef Full Text | Google Scholar

Haas, M. R., Schaye, J., Booth, C. M., Dalla Vecchia, C., Springel, V., Theuns, T., et al. (2013). Physical Properties of Simulated Galaxy Populations at Z = 2 - I. Effect of Metal-Line Cooling and Feedback from star Formation and AGN. Mon. Not. R. Astron. Soc. 435, 2931–2954. doi:10.1093/mnras/stt1487

CrossRef Full Text | Google Scholar

Hall, M., Courteau, S., Dutton, A. A., McDonald, M., and Zhu, Y. (2012). An Investigation of Sloan Digital Sky Survey Imaging Data and Multiband Scaling Relations of Spiral Galaxies. Monthly Notices R. Astronomical Soc. 425, 2741–2765. doi:10.1111/j.1365-2966.2012.21290.x

CrossRef Full Text | Google Scholar

Harms, R. J., Ford, H. C., Tsvetanov, Z. I., Hartig, G. F., Dressel, L. L., Kriss, G. A., et al. (1994). HST FOS Spectroscopy of M87: Evidence for a Disk of Ionized Gas Around a Massive Black Hole. ApJ 435, L35. doi:10.1086/187588

CrossRef Full Text | Google Scholar

Hartley, W. G., Almaini, O., Mortlock, A., Conselice, C. J., Grützbauch, R., Simpson, C., et al. (2013). Studying the Emergence of the Red Sequence through Galaxy Clustering: Host Halo Masses at Z > 2. MNRAS 431, 3045–3059. doi:10.1093/mnras/stt383

CrossRef Full Text | Google Scholar

Head, J. T. C. G., Lucey, J. R., Hudson, M. J., and Smith, R. J. (2014). Dissecting the Red Sequence: the Bulge and Disc Colours of Early-type Galaxies in the Coma Cluster. Mon. Not. R. Astron. Soc. 440, 1690–1711. doi:10.1093/mnras/stu325

CrossRef Full Text | Google Scholar

Heavens, A. F., and Jimenez, R. (1999). The Role of star Formation in the Tully-Fisher Law. MNRAS 305, 770–774. doi:10.1046/j.1365-8711.1999.02448.x

CrossRef Full Text | Google Scholar

Heinz, S., and Sunyaev, R. A. (2003). The Non-linear Dependence of Flux on Black Hole Mass and Accretion Rate in Core-Dominated Jets. Monthly Notices R. Astronomical Soc. 343, L59–L64. doi:10.1046/j.1365-8711.2003.06918.x

CrossRef Full Text | Google Scholar

Henry, A., Scarlata, C., Domínguez, A., Malkan, M., Martin, C. L., Siana, B., et al. (2013). Low Masses and High Redshifts: The Evolution of the Mass-Metallicity Relation. ApJ 776, L27. doi:10.1088/2041-8205/776/2/L27

CrossRef Full Text | Google Scholar

Herrnstein, J. R., Moran, J. M., Greenhill, L. J., and Trotter, A. S. (2005). The Geometry of and Mass Accretion Rate through the Maser Accretion Disk in NGC 4258. ApJ 629, 719–738. doi:10.1086/431421

CrossRef Full Text | Google Scholar

Hertzsprung, E. (1908). Über die Sterne der Unterabteilungenc undac nach der Spektralklassifikation von Antonia C. Maury. Astr. Nachr.; 179, 373–380. doi:10.1002/asna.19081792402

CrossRef Full Text | Google Scholar

Hicks, E. K. S., and Malkan, M. A. (2008). Circumnuclear Gas in Seyfert 1 Galaxies: Morphology, Kinematics, and Direct Measurement of Black Hole Masses. Astrophys J. Suppl. S 174, 31–73. doi:10.1086/521650

CrossRef Full Text | Google Scholar

Hirschmann, M., Somerville, R. S., Naab, T., and Burkert, A. (2012). Origin of the Antihierarchical Growth of Black Holes. Monthly Notices R. Astronomical Soc. 426, 237–257. doi:10.1111/j.1365-2966.2012.21626.x

CrossRef Full Text | Google Scholar

Ho, L. C., and Kim, M. (2014). The Black Hole Mass Scale of Classical and Pseudo Bulges in Active Galaxies. ApJ 789, 17. doi:10.1088/0004-637x/789/1/17

CrossRef Full Text | Google Scholar

Holden, B. P., van der Wel, A., Franx, M., Illingworth, G. D., Blakeslee, J. P., van Dokkum, P., et al. (2005). The Fundamental Plane of Cluster Elliptical Galaxies at Z = 1.25. ApJ 620, L83–L86. doi:10.1086/428663

CrossRef Full Text | Google Scholar

Holden, B. P., van der Wel, A., Kelson, D. D., Franx, M., and Illingworth, G. D. (2010). M/LBAND COLOR EVOLUTION FOR A DEEP SAMPLE OFM⋆CLUSTER GALAXIES ATz∼ 1: THE FORMATION EPOCH AND THE TILT OF THE FUNDAMENTAL PLANE. ApJ 724, 714–729. doi:10.1088/0004-637X/724/1/714

CrossRef Full Text | Google Scholar

Hopkins, P. F., Hernquist, L., Cox, T. J., Robertson, B., and Krause, E. (2007). A Theoretical Interpretation of the Black Hole Fundamental Plane. ApJ 669, 45–66. doi:10.1086/521590

CrossRef Full Text | Google Scholar

Horne, K., Peterson, B. M., Collier, S. J., and Netzer, H. (2004). Observational Requirements for High‐Fidelity Reverberation Mapping. Publ. Astron. Soc. Pac. 116, 465–476. doi:10.1086/420755

CrossRef Full Text | Google Scholar

Houghton, R. C. W., Davies, R. L., Dalla Bontà, E., and Masters, R. (2012). Data and Two-Dimensional Scaling Relations for Galaxies in Abell 1689: a Hint of Size Evolution at Z∼ 0.2. Mon. Not. R. Astron. Soc. 423, 256–283. doi:10.1111/j.1365-2966.2012.20842.x

CrossRef Full Text | Google Scholar

Hoyle, F. (1951). The Origin of the Rotations of the Galaxies. Paris, France: Problems of Cosmical Aerodynamics, 195.

Google Scholar

Hring, N., and Rix, H.-W. (2004). On the Black Hole Mass-Bulge Mass Relation. ApJ 604, L89–L92. doi:10.1086/383567

CrossRef Full Text | Google Scholar

Huang, K.-H., Fall, S. M., Ferguson, H. C., van der Wel, A., Grogin, N., Koekemoer, A., et al. (2017). Relations between the Sizes of Galaxies and Their Dark Matter Halos at Redshifts 0. ApJ 838, 6. doi:10.3847/1538-4357/aa62a6

CrossRef Full Text | Google Scholar

Hubble, E. P. (1936). Realm of the Nebulae.

Google Scholar

Huertas-Company, M., Shankar, F., Mei, S., Bernardi, M., Aguerri, J. A. L., Meert, A., et al. (2013). No Evidence for a Dependence of the Mass-Size Relation of Early-type Galaxies on Environment in the Local Universe. ApJ 779, 29. doi:10.1088/0004-637X/779/1/29

CrossRef Full Text | Google Scholar

Huff, E. M., and Graves, G. J. (2014). Magnificent Magnification: Exploiting the Other Half of the Lensing Signal. Astrophysical J. Lett 780, L16. doi:10.1088/2041-8205/780/2/L16

CrossRef Full Text | Google Scholar

Huré, J.-M., Hersant, F., Surville, C., Nakai, N., and Jacq, T. (2011). AGN Disks and Black Holes on the Weighting Scales. A&A 530, A145. doi:10.1051/0004-6361/201015062

CrossRef Full Text | Google Scholar

Ichikawa, S.-I., Wakamatsu, K.-I., and Okamura, S. (1986). Surface Photometry of Dwarf Elliptical Galaxies in the Virgo Cluster. ApJS 60, 475. doi:10.1086/191094

CrossRef Full Text | Google Scholar

Ilbert, O., Salvato, M., Le Floc'h, E., Aussel, H., Capak, P., McCracken, H. J., et al. (2010). GALAXY STELLAR MASS ASSEMBLY BETWEEN 0.2. ApJ 709, 644–663. doi:10.1088/0004-637x/709/2/644

CrossRef Full Text | Google Scholar

Inskip, K. J., Jahnke, K., Rix, H.-W., and van de Ven, G. (2011). RESOLVING THE DYNAMICAL MASS OF Az∼ 1.3 QUASI-STELLAR OBJECT HOST GALAXY USING SINFONI AND LASER GUIDE STAR ASSISTED ADAPTIVE OPTICS. ApJ 739, 90. doi:10.1088/0004-637X/739/2/90

CrossRef Full Text | Google Scholar

Järvelä, E., Lähteenmäki, A., and Berton, M. (2018). Near-infrared Morphologies of the Host Galaxies of Narrow-Line Seyfert 1 Galaxies. A&A 619, A69. doi:10.1051/0004-6361/201832876

CrossRef Full Text | Google Scholar

Javier Cenarro, A., and Trujillo, I. (2009). MILD VELOCITY DISPERSION EVOLUTION OF SPHEROID-LIKE MASSIVE GALAXIES SINCE z ∼ 2. ApJ 696, L43–L47. doi:10.1088/0004-637X/696/1/L43

CrossRef Full Text | Google Scholar

Jerjen, H., Binggeli, B., and Freeman, K. C. (2000). Surface [ITAL]BR[/ITAL] Photometry of Newly Discovered Dwarf Elliptical Galaxies in the Nearby Sculptor and Centaurus A Groups. Astronomical J. 119, 593–608. doi:10.1086/301216

CrossRef Full Text | Google Scholar

Jeter, B., Broderick, A. E., and McNamara, B. R. (2019). Impact of Accretion Flow Dynamics on Gas-Dynamical Black Hole Mass Estimates. ApJ 882, 82. doi:10.3847/1538-4357/ab322110.3847/1538-4357/ab3221

CrossRef Full Text | Google Scholar

Jimenez, R., Bernardi, M., Haiman, Z., Panter, B., and Heavens, A. F. (2007). The Ages, Metallicities, and Star Formation Histories of Early‐Type Galaxies in the SDSS. ApJ 669, 947–951. doi:10.1086/521323

CrossRef Full Text | Google Scholar

Joachimi, B., Singh, S., and Mandelbaum, R. (2015). Detection of Spatial Correlations of Fundamental Plane Residuals, and Cosmological Implications. Mon. Not. R. Astron. Soc. 454, 478–488. doi:10.1093/mnras/stv1962

CrossRef Full Text | Google Scholar

Jorgensen, I., and Chiboucas, K. (2013). Stellar Populations and Evolution of Early-type Cluster Galaxies: Constraints from Optical Imaging and Spectroscopy of Z = 0.5-0.9 Galaxy Clusters. Astronomical J. 145, 77. doi:10.1088/0004-6256/145/3/77

CrossRef Full Text | Google Scholar

Jørgensen, I., Chiboucas, K., Flint, K., Bergmann, M., Barr, J., and Davies, R. (2006). The Fundamental Plane for Z = 0.8-0.9 Cluster Galaxies. ApJ 639, L9–L12. doi:10.1086/501348

CrossRef Full Text | Google Scholar

Jorgensen, I., Franx, M., Hjorth, J., and van Dokkum, P. G. (1999). The Evolution of Cluster E and S0 Galaxies Measured from the Fundamental Plane. Monthly Notices R. Astronomical Soc. 308, 833–853. doi:10.1046/j.1365-8711.1999.02761.x

CrossRef Full Text | Google Scholar

Jorgensen, I., Franx, M., and Kjaergaard, P. (1996). The Fundamental Plane for Cluster E and S0 Galaxies. Monthly Notices R. Astronomical Soc. 280, 167–185. doi:10.1093/mnras/280.1.167

CrossRef Full Text | Google Scholar

Kannappan, S. J., Fabricant, D. G., and Franx, M. (2002). Physical Sources of Scatter in the Tully-Fisher Relation. Astronomical J. 123, 2358–2386. doi:10.1086/33997210.1086/339972

CrossRef Full Text | Google Scholar

Karim, A., Schinnerer, E., Martínez-Sansigre, A., Sargent, M. T., van der Wel, A., Rix, H.-W., et al. (2011). The Star Formation History of Mass-Selected Galaxies in the COSMOS Field. ApJ 730, 61. doi:10.1088/0004-637x/730/2/61

CrossRef Full Text | Google Scholar

Kaspi, S., Smith, P. S., Netzer, H., Maoz, D., Jannuzi, B. T., and Giveon, U. (2000). Reverberation Measurements for 17 Quasars and the Size‐Mass‐Luminosity Relations in Active Galactic Nuclei. ApJ 533, 631–649. doi:10.1086/308704

CrossRef Full Text | Google Scholar

Kassin, S. A., de Jong, R. S., and Weiner, B. J. (2006). Dark and Baryonic Matter in Bright Spiral Galaxies. II. Radial Distributions for 34 Galaxies. ApJ 643, 804–824. doi:10.1086/502959

CrossRef Full Text | Google Scholar

Kassin, S. A., Weiner, B. J., Faber, S. M., Gardner, J. P., Willmer, C. N. A., Coil, A. L., et al. (2012). THE EPOCH OF DISK SETTLING:z∼ 1 TO NOW. ApJ 758, 106. doi:10.1088/0004-637X/758/2/106

CrossRef Full Text | Google Scholar

Kassin, S. A., Weiner, B. J., Faber, S. M., Koo, D. C., Lotz, J. M., Diemand, J., et al. (2007). The Stellar Mass Tully-Fisher Relation to Z = 1.2 from AEGIS. ApJ 660, L35–L38. doi:10.1086/517932

CrossRef Full Text | Google Scholar

Katsianis, A., Tescari, E., Blanc, G., and Sargent, M. (2017). The Evolution of the star Formation Rate Function and Cosmic star Formation Rate Density of Galaxies Atz∼ 1-4. Mon. Not. R. Astron. Soc. 464, 4977–4994. doi:10.1093/mnras/stw2680

CrossRef Full Text | Google Scholar

Kauffmann, G., and Charlot, S. (1998). The K-Band Luminosity Function at Z = 1: a Powerful Constraint on Galaxy Formation Theory. Mon. Not. R. Astron. Soc. 297, L23–l28. doi:10.1046/j.1365-8711.1998.01708.x

CrossRef Full Text | Google Scholar

Kauffmann, G. (1996). The Age of Elliptical Galaxies and Bulges in a Merger Model. Monthly Notices R. Astronomical Soc. 281, 487–492. doi:10.1093/mnras/281.2.487

CrossRef Full Text | Google Scholar

Kaviraj, S., Rey, S. C., Rich, R. M., Yoon, S. J., and Yi, S. K. (2007). Better Age Estimation Using Ultraviolet-Optical Colours: Breaking the Age-Metallicity Degeneracy. Monthly Notices R. Astronomical Soc. Lett. 381, L74–L78. doi:10.1111/j.1745-3933.2007.00370.x

CrossRef Full Text | Google Scholar

Kawata, D., and Gibson, B. K. (2003). GCD+: a New Chemodynamical Approach to Modelling Supernovae and Chemical Enrichment in Elliptical Galaxies. Monthly Notices R. Astronomical Soc. 340, 908–922. doi:10.1046/j.1365-8711.2003.06356.x

CrossRef Full Text | Google Scholar

Kawata, D., and Gibson, B. K. (2003). Multiwavelength Cosmological Simulations of Elliptical Galaxies. Monthly Notices R. Astronomical Soc. 346, 135–152. doi:10.1046/j.1365-2966.2003.07080.x

CrossRef Full Text | Google Scholar

Kelson, D. D. (2014). Decoding the Star-Forming Main Sequence or: How I Learned to Stop Worrying and Love the Central Limit Theorem. arXiv:1406.5191.

Google Scholar

Kelson, D. D., Illingworth, G. D., van Dokkum, P. G., and Franx, M. (2000). The Evolution of Early-type Galaxies in Distant Clusters. III. M/L_V Ratios in the z=0.33 Cluster CL 1358+62. Astrophysical J. 531, 184–199. doi:10.1086/308460

CrossRef Full Text | Google Scholar

Kelson, D. D., van Dokkum, P. G., Franx, M., Illingworth, G. D., and Fabricant, D. (1997). Evolution of Early-type Galaxies in Distant Clusters: The Fundamental Plane from [ITAL]Hubble Space Telescope[/ITAL] Imaging and Keck Spectroscopy. Astrophysical J. Lett 478, L13–L16. doi:10.1086/310545

CrossRef Full Text | Google Scholar

Kennicutt, R. C. (1998). Star Formation in Galaxies along the Hubble Sequence. Annu. Rev. Astron. Astrophys. 36, 189–231. doi:10.1146/annurev.astro.36.1.189

CrossRef Full Text | Google Scholar

Kennicutt, Jr., R. C. (1998). The Global Schmidt Law in Star‐forming Galaxies. ApJ 498, 541–552. doi:10.1086/305588

CrossRef Full Text | Google Scholar

Kennicutt, Jr., R. C. (1998). The Global Schmidt Law in Star‐forming Galaxies. ApJ 498, 541–552. doi:10.1086/305588

CrossRef Full Text | Google Scholar

Kent, S. M. (1985). CCD Surface Photometry of Field Galaxies. II - Bulge/disk Decompositions. ApJS 59, 115–159. doi:10.1086/191066

CrossRef Full Text | Google Scholar

Kewley, L. J., and Dopita, M. A. (2002). Using Strong Lines to Estimate Abundances in Extragalactic H II Regions and Starburst Galaxies. Astrophys J. Suppl. S 142, 35–52. doi:10.1086/341326

CrossRef Full Text | Google Scholar

Kewley, L. J., and Ellison, S. L. (2008). Metallicity Calibrations and the Mass‐Metallicity Relation for Star‐forming Galaxies. ApJ 681, 1183–1204. doi:10.1086/587500

CrossRef Full Text | Google Scholar

Khajenabi, F. (2015). On the Dynamics of Clouds in the Broad-Line Region of AGNs with an ADAF Atmosphere. MNRAS 446, 1848–1854. doi:10.1093/mnras/stu2193

CrossRef Full Text | Google Scholar

Kim, M., and Ho, L. C. (2019). Evidence for a Young Stellar Population in Nearby Type 1 Active Galaxies. ApJ 876, 35. doi:10.3847/1538-4357/ab11cf

CrossRef Full Text | Google Scholar

Kim, M., Ho, L. C., Peng, C. Y., and Im, M. (2007). The Host Galaxy of the Quasar HE 0450−2958. ApJ 658, 107–113. doi:10.1086/510846

CrossRef Full Text | Google Scholar

Kimm, T., Devriendt, J., Slyz, A., Pichon, C., Kassin, S. A., and Dubois, Y. (2011). The Angular Momentum of Baryons and Dark Matter Halos Revisited. arXiv:1106.0538.

Google Scholar

King, A., and Nealon, R. (2019). Supermassive Black Hole Demographics: Evading M − σ. MNRAS 487, 4827–4831. doi:10.1093/mnras/stz1569

CrossRef Full Text | Google Scholar

King, A., and Pounds, K. (2015). Powerful Outflows and Feedback from Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 53, 115–154. doi:10.1146/annurev-astro-082214-122316

CrossRef Full Text | Google Scholar

King, I. R. (1971). Stellar Populations in Galaxies. Pasp 83, 377. doi:10.1086/129146

CrossRef Full Text | Google Scholar

Kirby, E. N., Bullock, J. S., Boylan-Kolchin, M., Kaplinghat, M., and Cohen, J. G. (2014). The Dynamics of Isolated Local Group Galaxies. Mon. Not. R. Astron. Soc. 439, 1015–1027. doi:10.1093/mnras/stu025

CrossRef Full Text | Google Scholar

Kjaergaard, P., Jorgensen, I., and Moles, M. (1993). The Fundamental Plane and the Surface Brightness Test for the Expansion of the Universe. ApJ 418, 617. doi:10.1086/173421

CrossRef Full Text | Google Scholar

Kleiner, D., Pimbblet, K. A., Heath Jones, D., Koribalski, B. S., and Serra, P. (2017). Evidence for Hi Replenishment in Massive Galaxies through Gas Accretion from the Cosmic Web. Mon. Not. R. Astron. Soc. 466, stw3328–4710. doi:10.1093/mnras/stw3328

CrossRef Full Text | Google Scholar

Kobayashi, C. (2005). GRAPE-SPH Chemodynamical Simulation of Elliptical Galaxies -- II. Scaling Relations and the Fundamental Plane. Monthly Notices R. Astronomical Soc. 361, 1216–1226. doi:10.1111/j.1365-2966.2005.09248.x

CrossRef Full Text | Google Scholar

Kobulnicky, H. A., and Kewley, L. J. (2004). Metallicities of 0.3. ApJ 617, 240–261. doi:10.1086/425299

CrossRef Full Text | Google Scholar

Koda, J., Sofue, Y., and Wada, K. (2000). On the Origin of the Tully‐Fisher Relation. ApJ 532, 214–220. doi:10.1086/308579

CrossRef Full Text | Google Scholar

Kodama, T., Arimoto, N., Barger, A. J., and Arag’on-Salamanca, A. (1998). Evolution of the Colour-Magnitude Relation of Early-type Galaxies in Distant Clusters. Astron. Astrophysics 334, 99–109.

Google Scholar

Kodama, T., and Arimoto, N. (1997). Origin of the Colour-Magnitude Relation of Elliptical Galaxies. Astron. Astrophysics 320, 41–53.

CrossRef Full Text | Google Scholar

Komossa, S., Xu, D. W., and Wagner, A. Y. (2018). Extreme Gaseous Outflows in Radio-Loud Narrow-Line Seyfert 1 Galaxies. MNRAS 477, 5115–5126. doi:10.1093/mnras/sty901

CrossRef Full Text | Google Scholar

Kormendy, J., and Bender, R. (2012). A Revised Parallel-Sequence Morphological Classification of Galaxies: Structure and Formation of S0 and Spheroidal Galaxies. ApJS 198, 2. doi:10.1088/0067-0049/198/1/2

CrossRef Full Text | Google Scholar

Kormendy, J., and Bender, R. (2012). A Revised Parallel-Sequence Morphological Classification of Galaxies: Structure and Formation of S0 and Spheroidal Galaxies. ApJS 198, 2. doi:10.1088/0067-0049/198/1/2

CrossRef Full Text | Google Scholar

Kormendy, J., Bender, R., and Cornell, M. E. (2011). Supermassive Black Holes Do Not Correlate with Galaxy Disks or Pseudobulges. Nature 469, 374–376. doi:10.1038/nature0969410.1038/nature09694

PubMed Abstract | CrossRef Full Text | Google Scholar

Kormendy, J., and Bender, R. (2009). Correlations between Supermassive Black Holes, Velocity Dispersions, and Mass Deficits in Elliptical Galaxies with Cores. ApJ 691, L142–L146. doi:10.1088/0004-637X/691/2/L142

CrossRef Full Text | Google Scholar

Kormendy, J. (1977). Brightness Distributions in Compact and normal Galaxies. II - Structure Parameters of the Spheroidal Component. ApJ 218, 333–346. doi:10.1086/155687

CrossRef Full Text | Google Scholar

Kormendy, J. (2016). Elliptical Galaxies and Bulges of Disc Galaxies: Summary of Progress and Outstanding Issues, 418. Springer, Switzerland: Astrophysics and Space Science Library, 431–477. doi:10.1007/978-3-319-19378-6_16

CrossRef Full Text | Google Scholar

Kormendy, J., Fisher, D. B., Cornell, M. E., and Bender, R. (2009). Structure and Formation of Elliptical and Spheroidal Galaxies. ApJS 182, 216–309. doi:10.1088/0067-0049/182/1/216

CrossRef Full Text | Google Scholar

Kormendy, J., and Ho, L. C. (2013). Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. Annu. Rev. Astron. Astrophys. 51, 511–653. doi:10.1146/annurev-astro-082708-10181110.1146/annurev-astro-082708-101811

CrossRef Full Text | Google Scholar

Kormendy, J., and Kennicutt, R. C. (2004). Secular Evolution and the Formation of Pseudobulges in Disk Galaxies. Annu. Rev. Astron. Astrophys. 42, 603–683. doi:10.1146/annurev.astro.42.053102.134024

CrossRef Full Text | Google Scholar

Kormendy, J., and McClure, R. D. (1993). The Nucleus of M33. Astronomical J. 105, 1793. doi:10.1086/116555

CrossRef Full Text | Google Scholar

Kormendy, J., and Richstone, D. (1995). Inward Bound-The Search for Supermassive Black Holes in Galactic Nuclei. Annu. Rev. Astron. Astrophys. 33, 581–624. doi:10.1146/annurev.aa.33.090195.003053

CrossRef Full Text | Google Scholar

Krajnović, D., McDermid, R. M., Cappellari, M., and Davies, R. L. (2009). Determination of Masses of the central Black Holes in NGC 524 and 2549 Using Laser Guide star Adaptive Optics. MNRAS 399, 1839–1857. doi:10.1111/j.1365-2966.2009.15415.x

CrossRef Full Text | Google Scholar

Kriek, M., van Dokkum, P. G., Franx, M., Quadri, R., Gawiser, E., Herrera, D., et al. (2006). Spectroscopic Identification of Massive Galaxies at Z ∼ 2.3 with Strongly Suppressed Star Formation. ApJ 649, L71–L74. doi:10.1086/508371

CrossRef Full Text | Google Scholar

Kronberger, T., Kapferer, W., Schindler, S., and Ziegler, B. L. (2007). 2D Velocity fields of Simulated Interacting Disc Galaxies. A&A 473, 761–770. doi:10.1051/0004-6361:20077696

CrossRef Full Text | Google Scholar

Krongold, Y., Dultzin-Hacyan, D., and Marziani, P. (2001). Host Galaxies and Circumgalactic Environment of “Narrow Line” Seyfert 1 Nuclei. AJ 121, 702–709. doi:10.1086/318768

CrossRef Full Text | Google Scholar

Kruczek, N. E., Richards, G. T., Gallagher, S. C., Deo, R. P., Hall, P. B., Hewett, P. C., et al. (2011). C IV Emission and the Ultraviolet through X-Ray Spectral Energy Distribution of Radio-Quiet Quasars. Astronomical J. 142, 130. doi:10.1088/0004-6256/142/4/130

CrossRef Full Text | Google Scholar

Kuchner, U., Ziegler, B., Verdugo, M., Bamford, S., and Häußler, B. (2017). The Effects of the Cluster Environment on the Galaxy Mass-Size Relation in MACS J1206.2-0847. A&A 604, A54. doi:10.1051/0004-6361/201630252

CrossRef Full Text | Google Scholar

Kulkarni, G., and Loeb, A. (2012). Formation of Galactic Nuclei with Multiple Supermassive Black Holes at High Redshifts. MNRAS 422, 1306–1323. doi:10.1111/j.1365-2966.2012.20699.x

CrossRef Full Text | Google Scholar

Kuo, C. Y., Braatz, J. A., Impellizzeri, C. M. V., Gao, F., Pesce, D., Reid, M. J., et al. (2020). The Megamaser Cosmology Project − XII. VLBI Imaging of H2O Maser Emission in Three Active Galaxies and the Effect of AGN Winds on Disc Dynamics. MNRAS 498, 1609–1627. doi:10.1093/mnras/staa2260

CrossRef Full Text | Google Scholar

Kuo, C. Y., Reid, M. J., Braatz, J. A., Gao, F., Impellizzeri, C. M. V., and Chien, W. T. (2018). On Estimating the Mass of Keplerian Accretion Disks in H2O Maser Galaxies. ApJ 859, 172. doi:10.3847/1538-4357/aabff1

CrossRef Full Text | Google Scholar

La Barbera, F., Busarello, G., Merluzzi, P., de la Rosa, I. G., Coppola, G., and Haines, C. P. (2008). The SDSS‐UKIDSS Fundamental Plane of Early‐Type Galaxies. Astrophysical J. 689, 913–918. doi:10.1086/592769

CrossRef Full Text | Google Scholar

Lacey, C. G., and Fall, S. M. (1985). Chemical Evolution of the Galactic Disk with Radial Gas Flows. ApJ 290, 154–170. doi:10.1086/162970

CrossRef Full Text | Google Scholar

Lagos, C. d. P., Theuns, T., Schaye, J., Furlong, M., Bower, R. G., Schaller, M., et al. (2016). The Fundamental Plane of star Formation in Galaxies Revealed by the EAGLE Hydrodynamical Simulations. Mon. Not. R. Astron. Soc. 459, 2632–2650. doi:10.1093/mnras/stw717

CrossRef Full Text | Google Scholar

Lagos, C. d. P., Theuns, T., Stevens, A. R. H., Cortese, L., Padilla, N. D., Davis, T. A., et al. (2017). Angular Momentum Evolution of Galaxies in EAGLE. Mon. Not. R. Astron. Soc. 464, 3850–3870. doi:10.1093/mnras/stw2610

CrossRef Full Text | Google Scholar

Lani, C., Almaini, O., Hartley, W. G., Mortlock, A., Häußler, B., Chuter, R. W., et al. (2013). Evidence for a Correlation between the Sizes of Quiescent Galaxies and Local Environment to Z ∼ 2. Mon. Not. R. Astron. Soc. 435, 207–221. doi:10.1093/mnras/stt1275

CrossRef Full Text | Google Scholar

Laor, A. (1998). On Quasar Masses and Quasar Host Galaxies. Astrophysical J. Lett 505, L83–L86. doi:10.1086/311619

CrossRef Full Text | Google Scholar

Laor, A. (2001). On the Linearity of the Black Hole-Bulge Mass Relation in Active and in Nearby Galaxies. ApJ 553, 677–682. doi:10.1086/320989

CrossRef Full Text | Google Scholar

Larson, R. B. (1974). Effects of Supernovae on the Early Evolution of Galaxies. Monthly Notices R. Astronomical Soc. 169, 229–245. doi:10.1093/mnras/169.2.229

CrossRef Full Text | Google Scholar

Larson, R. B. (1976). Models for the Formation of Disc Galaxies. Monthly Notices R. Astronomical Soc. 176, 31–52. doi:10.1093/mnras/176.1.31

CrossRef Full Text | Google Scholar

Larson, R. B. (1975). Models for the Formation of Elliptical Galaxies. Monthly Notices R. Astronomical Soc. 173, 671–699. doi:10.1093/mnras/173.3.671

CrossRef Full Text | Google Scholar

Lauer, T. R., Tremaine, S., Richstone, D., and Faber, S. M. (2007). Selection Bias in Observing the Cosmological Evolution of theM‐σ andM‐LRelationships. ApJ 670, 249–260. doi:10.1086/522083

CrossRef Full Text | Google Scholar

Lee, H., Skillman, E. D., Cannon, J. M., Jackson, D. C., Gehrz, R. D., Polomski, E. F., et al. (2006). On Extending the Mass‐Metallicity Relation of Galaxies by 2.5 Decades in Stellar Mass. ApJ 647, 970–983. doi:10.1086/505573

CrossRef Full Text | Google Scholar

Lehnert, M. D., Nesvadba, N. P. H., Tiran, L. L., Matteo, P. D., van Driel, W., Douglas, L. S., et al. (2009). Physical Conditions in the Interstellar Medium of Intensely Star-forming Galaxies at Redshift∼2. ApJ 699, 1660–1678. doi:10.1088/0004-637X/699/2/1660

CrossRef Full Text | Google Scholar

Leighly, K. M., and Moore, J. R. (2004). Hubble Space TelescopeSTIS Ultraviolet Spectral Evidence of Outflow in Extreme Narrow‐Line Seyfert 1 Galaxies. I. Data and Analysis. ApJ 611, 107–124. doi:10.1086/422088

CrossRef Full Text | Google Scholar

Lelli, F., Verheijen, M., and Fraternali, F. (2014). The Triggering of Starbursts in Low-Mass Galaxies. Mon. Not. R. Astron. Soc. 445, 1694–1712. doi:10.1093/mnras/stu180410.1093/mnras/stu1804

CrossRef Full Text | Google Scholar

Lemoine-Busserolle, M., and Lamareille, F. (2010). 2D Kinematics and Physical Properties of 1.0 ≲z≲ 1.5 star-forming Galaxies. Mon. Not. R. Astron. Soc. 402, 2291–2307. doi:10.1111/j.1365-2966.2009.16082.x

CrossRef Full Text | Google Scholar

Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., and Torres-Peimbert, S. (1979). Reprint of 1979A&A.80\enleadertwodots 155L. Chemical Composition and Evolution of Irregular and Blue Compact Galaxies. Astron. Astrophysics 500, 145–156.

Google Scholar

Leroy, A. K., Bolatto, A., Bot, C., Engelbracht, C. W., Gordon, K., Israel, F. P., et al. (2009). The Structure of a Low-Metallicity Giant Molecular Cloud Complex. ApJ 702, 352–367. doi:10.1088/0004-637X/702/1/352

CrossRef Full Text | Google Scholar

Li, H., Mao, S., Cappellari, M., Ge, J., Long, R. J., Li, R., et al. (2018). SDSS-IV MaNGA: Global Stellar Population and Gradients for about 2000 Early-type and Spiral Galaxies on the Mass-Size Plane. MNRAS 476, 1765–1775. doi:10.1093/mnras/sty334

CrossRef Full Text | Google Scholar

Li, J. I.-H., Shen, Y., Ho, L. C., Brandt, W. N., Dalla Bontà, E., Alvarez, G. F., et al. (2021). The Sloan Digital Sky Survey Reverberation Mapping Project: The M BH-Host Relations at 0.2 ≲ Z ≲ 0.6 from Reverberation Mapping and Hubble Space Telescope Imaging. ApJ 906, 103. doi:10.3847/1538-4357/abc8e6

CrossRef Full Text | Google Scholar

Li, J., Shen, Y., Horne, K., Brandt, W. N., Greene, J. E., Grier, C. J., et al. (2017). The Sloan Digital Sky Survey Reverberation Mapping Project: Composite Lags Atz≤ 1. ApJ 846, 79. doi:10.3847/1538-4357/aa845d

CrossRef Full Text | Google Scholar

Li, Y.-R., Wang, J.-M., Ho, L. C., Du, P., and Bai, J.-M. (2013). A Bayesian Approach to Estimate the Size and Structure of the Broad-Line Region in Active Galactic Nuclei Using Reverberation Mapping Data. ApJ 779, 110. doi:10.1088/0004-637x/779/2/110

CrossRef Full Text | Google Scholar

Li, Z., Han, Z., and Zhang, F. (2007). Potential of Colors for Determining Age and Metallicity of Stellar Populations. A&A 464, 853–857. doi:10.1051/0004-6361:20066337

CrossRef Full Text | Google Scholar

Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., and Peng, Y. (2013). Gas Regulation of Galaxies: The Evolution of the Cosmic Specific Star Formation Rate, the Metallicity-Mass-Star-formation Rate Relation, and the Stellar Content of Halos. ApJ 772, 119. doi:10.1088/0004-637X/772/2/119

CrossRef Full Text | Google Scholar

Lintott, C. J., Schawinski, K., Slosar, A., Land, K., Bamford, S., Thomas, D., et al. (2008). Galaxy Zoo: Morphologies Derived from Visual Inspection of Galaxies from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 389, 1179–1189. doi:10.1111/j.1365-2966.2008.13689.x

CrossRef Full Text | Google Scholar

Lipari, S., Bergmann, M., Sanchez, S., Terlevich, R., Taniguchi, Y., Mediavilla, E., et al. (2007). Gemini GMOS IFU Spectroscopy of IRAS 04505-2958: A New Exploding BAL + IR + Fe II QSO. Boletin de la Asociacion Argentina de Astronomia La Plata Argentina 50, 259–262.

Google Scholar

Lipari, S., Terlevich, R., and Macchetto, F. (1993). Extreme Optical Fe II Emission in Luminous IRAS Active Galactic Nuclei. ApJ 406, 451–456. doi:10.1086/172456

CrossRef Full Text | Google Scholar

Liu, F. S., Mao, S., and Meng, X. M. (2012). Star Formation Activities in Early-type Brightest Cluster Galaxies. Mon. Not. R. Astron. Soc. 423, 422–436. doi:10.1111/j.1365-2966.2012.20886.x

CrossRef Full Text | Google Scholar

Loli Martínez-Aldama, M., Dultzin, D., Marziani, P., Sulentic, J. W., Bressan, A., Chen, Y., et al. (2015). O I and Ca II Observations in Intermediate Redshift Quasars. ApJS 217, 3. doi:10.1088/0067-0049/217/1/3

CrossRef Full Text | Google Scholar

López-Sánchez, Á. R., Dopita, M. A., Kewley, L. J., Zahid, H. J., Nicholls, D. C., and Scharwächter, J. (2012). Eliminating Error in the Chemical Abundance Scale for Extragalactic H Iiregions. Monthly Notices R. Astronomical Soc. 426, 2630–2651. doi:10.1111/j.1365-2966.2012.21145.x

CrossRef Full Text | Google Scholar

Lotz, J. M., Miller, B. W., and Ferguson, H. C. (2004). The Colors of Dwarf Elliptical Galaxy Globular Cluster Systems, Nuclei, and Stellar Halos. ApJ 613, 262–278. doi:10.1086/422871

CrossRef Full Text | Google Scholar

Lu, S., Xu, D., Wang, Y., Mao, S., Ge, J., Springel, V., et al. (2020). Redshift Evolution of the Fundamental Plane Relation in the IllustrisTNG Simulation. Mon. Not. R. Astron. Soc. 492, 5930–5939. doi:10.1093/mnras/staa173

CrossRef Full Text | Google Scholar

Lukić, Z., Heitmann, K., Habib, S., Bashinsky, S., and Ricker, P. M. (2007). The Halo Mass Function: High‐Redshift Evolution and Universality. ApJ 671, 1160–1181. doi:10.1086/523083

CrossRef Full Text | Google Scholar

Lupi, A., Haiman, Z., and Volonteri, M. (2021). Forming Massive Seed Black Holes in High-Redshift Quasar Host Progenitors. arXiv:2102.05051.

Google Scholar

Ly, C., Malkan, M. A., Rigby, J. R., and Nagao, T. (2016). THE METAL ABUNDANCES across COSMIC TIME (${ \mathcal M }{ \mathcal A }{ \mathcal C }{ \mathcal T }$) SURVEY. II. EVOLUTION of the MASS-METALLICITY RELATION over 8 BILLION YEARS, USING [O Iii] λ4363 Å BASED METALLICITIES. ApJ 828, 67. doi:10.3847/0004-637X/828/2/67

CrossRef Full Text | Google Scholar

Lynden-Bell, D. (1969). Galactic Nuclei as Collapsed Old Quasars. Nature 223, 690–694. doi:10.1038/223690a0

CrossRef Full Text | Google Scholar

Lynden-Bell, D. (1975). The Chemical Evolution of Galaxies. Vistas Astron. 19, 299–316. doi:10.1016/0083-6656(75)90005-7

CrossRef Full Text | Google Scholar

Ma, X., Hopkins, P. F., Faucher-Giguère, C.-A., Zolman, N., Muratov, A. L., Kereš, D., et al. (2016). The Origin and Evolution of the Galaxy Mass-Metallicity Relation. Mon. Not. R. Astron. Soc. 456, 2140–2156. doi:10.1093/mnras/stv2659

CrossRef Full Text | Google Scholar

Mac Low, M. M., and Ferrara, A. (1999). Starburst‐driven Mass Loss from Dwarf Galaxies: Efficiency and Metal Ejection. ApJ 513, 142–155. doi:10.1086/306832

CrossRef Full Text | Google Scholar

Macchetto, F., Marconi, A., Axon, D. J., Capetti, A., Sparks, W., and Crane, P. (1997). The Supermassive Black Hole of M87 and the Kinematics of its Associated Gaseous Disk. ApJ 489, 579–600. doi:10.1086/304823

CrossRef Full Text | Google Scholar

Madau, P., and Dickinson, M. (2014). Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 52, 415–486. doi:10.1146/annurev-astro-081811-125615

CrossRef Full Text | Google Scholar

Magain, P., Letawe, G., Courbin, F., Jablonka, P., Jahnke, K., Meylan, G., et al. (2005). Discovery of a Bright Quasar without a Massive Host Galaxy. Nature 437, 381–384. doi:10.1038/nature04013

PubMed Abstract | CrossRef Full Text | Google Scholar

Magorrian, J., Tremaine, S., Richstone, D., Bender, R., Bower, G., Dressler, A., et al. (1998). The Demography of Massive Dark Objects in Galaxy Centers. Astronomical J. 115, 2285–2305. doi:10.1086/300353

CrossRef Full Text | Google Scholar

Mahajan, S., Drinkwater, M. J., Driver, S., Kelvin, L. S., Hopkins, A. M., Baldry, I., et al. (2015). Galaxy and Mass Assembly (GAMA): the Unimodal Nature of the dwarf Galaxy Population. Mon. Not. R. Astron. Soc. 446, 2967–2984. doi:10.1093/mnras/stu2009

CrossRef Full Text | Google Scholar

Maier, C., Lilly, S. J., Ziegler, B. L., Contini, T., Pérez Montero, E., Peng, Y., et al. (2014). THE MASS-METALLICITY AND FUNDAMENTAL METALLICITY RELATIONS ATz> 2 USING VERY LARGE TELESCOPE AND SUBARU NEAR-INFRARED SPECTROSCOPY OF zCOSMOS GALAXIES. ApJ 792, 3. doi:10.1088/0004-637X/792/1/3

CrossRef Full Text | Google Scholar

Maiolino, R., Nagao, T., Grazian, A., Cocchia, F., Marconi, A., Mannucci, F., et al. (2008). Amaze. A&A 488, 463–479. doi:10.1051/0004-6361:200809678

CrossRef Full Text | Google Scholar

Mancini, C., Matute, I., Cimatti, A., Daddi, E., Dickinson, M., Rodighiero, G., et al. (2009). Searching for Massive Galaxies at Z ≥ 3.5 in GOODS-North. A&A 500, 705–723. doi:10.1051/0004-6361/200810630

CrossRef Full Text | Google Scholar

Mao, Y.-F., Wang, J., and Wei, J.-Y. (2009). Extending the Eigenvector 1 Space to the Optical Variability of Quasars. Res. Astron. Astrophys. 9, 529–537. doi:10.1088/1674-4527/9/5/004

CrossRef Full Text | Google Scholar

Marchesini, D., Muzzin, A., Stefanon, M., Franx, M., Brammer, G. G., Marsan, C. Z., et al. (2014). The Progenitors of Local Ultra-massive Galaxies across Cosmic Time: From Dusty Star-bursting to Quiescent Stellar Populations. ApJ 794, 65. doi:10.1088/0004-637X/794/1/65

CrossRef Full Text | Google Scholar

Marconi, A., and Hunt, L. K. (2003). The Relation between Black Hole Mass, Bulge Mass, and Near-Infrared Luminosity. ApJ 589, L21–L24. doi:10.1086/375804

CrossRef Full Text | Google Scholar

Marinello, M., Overzier, R. A., Röttgering, H. J. A., Kurk, J. D., De Breuck, C., Vernet, J., et al. (2020). VLT/SINFONI Study of Black Hole Growth in High-Redshift Radio-Loud Quasars from the CARLA Survey. MNRAS 492, 1991–2016. doi:10.1093/mnras/stz333310.1093/mnras/stz3333

CrossRef Full Text | Google Scholar

Marinello, M., Rodríguez-Ardila, A., Marziani, P., Sigut, A., and Pradhan, A. (2020). Panchromatic Properties of the Extreme Fe II Emitter PHL 1092. MNRAS 494, 4187–4202. doi:10.1093/mnras/staa934

CrossRef Full Text | Google Scholar

Marshall, M. A., Ni, Y., Di Matteo, T., Wyithe, J. S. B., Wilkins, S., Croft, R. A. C., et al. (2020). The Host Galaxies of Z = 7 Quasars: Predictions from the BLUETIDES Simulation. MNRAS 499, 3819–3836. doi:10.1093/mnras/staa2982

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Zajaček, M., Czerny, B., and Panda, S. (2020). Scatter Analysis along the Multidimensional Radius-Luminosity Relations for Reverberation-Mapped Mg II Sources. ApJ 903, 86. doi:10.3847/1538-4357/abb6f8

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Czerny, B., Kawka, D., Karas, V., Panda, S., Zajaček, M., et al. (2019). Can Reverberation-Measured Quasars Be Used for Cosmology? ApJ 883, 170. doi:10.3847/1538-4357/ab3728

CrossRef Full Text | Google Scholar

Martínez-Aldama, M. L., Del Olmo, A., Marziani, P., Sulentic, J. W., Negrete, C. A., Dultzin, D., et al. (2018). Highly Accreting Quasars at High Redshift. Front. Astron. Space Sci. 4, 65. doi:10.3389/fspas.2017.00065

CrossRef Full Text | Google Scholar

Marziani, P., del Olmo, A., D’ Onofrio, M., Dultzin, D., Negrete, C. A., Martiinez-Aldama, M. L., et al. (2018). Narrow-line Seyfert 1s: What Is Wrong in a Name? Padova, Italy: arXiv:1807.03003.

Google Scholar

Marziani, P., Dultzin, D., Del Olmo, A., D’Onofrio, M., de Diego, J. A., Stirpe, G. M., et al. (2020). The Quasar Main Sequence and its Potential for Cosmology. arXiv:2002.07219.

Google Scholar

Marziani, P., Dultzin-Hacyan, D., and Sulentic, J. W. (2006). “Accretion onto Supermassive Black Holes in Quasars: Learning from Optical/UV Observations,” in New Developments in Black Hole Research. Editor P. V. Kreitler (New York: Nova Press), 123.

Google Scholar

Marziani, P., del Olmo, A., Martínez-Carballo, M. A., Martínez-Aldama, M. L., Stirpe, G. M., Negrete, C. A., et al. (2019). Black Hole Mass Estimates in Quasars. A&A 627, A88. doi:10.1051/0004-6361/201935265

CrossRef Full Text | Google Scholar

Marziani, P., Martínez Carballo, M. A., Sulentic, J. W., Del Olmo, A., Stirpe, G. M., and Dultzin, D. (2016). The Most Powerful Quasar Outflows as Revealed by the Civ λ 1549 $\lambda1549$ Resonance Line. Astrophys Space Sci. 361, 29. doi:10.1007/s10509-015-2611-1

CrossRef Full Text | Google Scholar

Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., and Moles, M. (1996). Comparative Analysis of the High- and Low-Ionization Lines in the Broad-Line Region of Active Galactic Nuclei. ApJS 104, 37. doi:10.1086/192291

CrossRef Full Text | Google Scholar

Marziani, P., and Sulentic, J. W. (2012). Estimating Black Hole Masses in Quasars Using Broad Optical and UV Emission Lines. New Astron. Rev. 56, 49–63. doi:10.1016/j.newar.2011.09.001

CrossRef Full Text | Google Scholar

Marziani, P., and Sulentic, J. W. (2014). Highly Accreting Quasars: Sample Definition and Possible Cosmological Implications. MNRAS 442, 1211–1229. doi:10.1093/mnras/stu951

CrossRef Full Text | Google Scholar

Marziani, P., Sulentic, J. W., Negrete, C. A., Dultzin, D., Zamfir, S., and Bachev, R. (2010). Broad-line Region Physical Conditions along the Quasar Eigenvector 1 Sequence. MNRAS 409, 1033–1048. doi:10.1111/j.1365-2966.2010.17357.x

CrossRef Full Text | Google Scholar

Marziani, P., and Sulentic, J. W. (2014). Quasars and Their Emission Lines as Cosmological Probes. Adv. Space Res. 54, 1331–1340. doi:10.1016/j.asr.2013.10.00710.1016/j.asr.2013.10.007

CrossRef Full Text | Google Scholar

Marziani, P., Sulentic, J. W., Stirpe, G. M., Dultzin, D., Del Olmo, A., and Martínez-Carballo, M. A. (2016). Blue Outliers Among Intermediate Redshift Quasars. Astrophys Space Sci. 361, 3. doi:10.1007/s10509-015-2590-2

CrossRef Full Text | Google Scholar

Marziani, P., Sulentic, J. W., Stirpe, G. M., Zamfir, S., and Calvani, M. (2009). VLT/ISAAC Spectra of the Hβ Region in Intermediate-Redshift Quasars. A&A 495, 83–112. doi:10.1051/0004-6361:200810764

CrossRef Full Text | Google Scholar

Marziani, P., Sulentic, J. W., Zwitter, T., Dultzin‐Hacyan, D., and Calvani, M. (2001). Searching for the Physical Drivers of the Eigenvector 1 Correlation Space. ApJ 558, 553–560. doi:10.1086/322286

CrossRef Full Text | Google Scholar

Marziani, P., Zamanov, R. K., Sulentic, J. W., and Calvani, M. (2003). Searching for the Physical Drivers of Eigenvector 1: Influence of Black Hole Mass and Eddington Ratio. Monthly Notices R. Astronomical Soc. 345, 1133–1144. doi:10.1046/j.1365-2966.2003.07033.x

CrossRef Full Text | Google Scholar

Masters, K. L., Springob, C. M., and Huchra, J. P. (2008). 2Mtf. I. The Tully-fisher Relation in the Two Micron All Sky Surveyj,h, Andkbands. Astronomical J. 135, 1738–1748. doi:10.1088/0004-6256/135/5/1738

CrossRef Full Text | Google Scholar

Mateo, M. (1998). Dwarf Galaxies of the Local Group. Annu. Rev. Astron. Astrophys. 36, 435–506. doi:10.1146/annurev.astro.36.1.435

CrossRef Full Text | Google Scholar

Mathews, W. G., and Baker, J. C. (1971). Galactic Winds. ApJ 170, 241. doi:10.1086/151208

CrossRef Full Text | Google Scholar

Mathur, S., Fields, D., Peterson, B. M., and Grupe, D. (2012). Supermassive Black Holes, Pseudobulges, and the Narrow-Line Seyfert 1 Galaxies. ApJ 754, 146. doi:10.1088/0004-637X/754/2/146

CrossRef Full Text | Google Scholar

Mathur, S. (2011). “Host Galaxies of NLS1s,” in. Narrow-Line Seyfert 1 Galaxies and Their Place in the Universe. L. Foschini, M. Colpi, L. Gallo, D. Grupe, S. Komossa, K. Leighlyet al. 35. doi:10.22323/1.126.0035

CrossRef Full Text | Google Scholar

Mathur, S., Kuraszkiewicz, J., and Czerny, B. (2001). Evolution of Active Galaxies: Black-Hole Mass-Bulge Relations for Narrow Line Objects. New Astron. 6, 321–329. doi:10.1016/S1384-1076(01)00058-6

CrossRef Full Text | Google Scholar

Mathur, S. (2000). Narrow-line Seyfert 1 Galaxies and the Evolution of Galaxies and Active Galaxies. Monthly Notices R. Astronomical Soc. 314, L17–L20. doi:10.1046/j.1365-8711.2000.03530.x

CrossRef Full Text | Google Scholar

Matsuoka, Y., Kawara, K., and Oyabu, S. (2008). Low‐Ionization Emission Regions in Quasars: Gas Properties Probed with Broad Oiand CaiiLines. ApJ 673, 62–68. doi:10.1086/524193

CrossRef Full Text | Google Scholar

Matteucci, F. (2016). Introduction to Galactic Chemical Evolution. J. Phys. Conf. Ser. 703, 012004. doi:10.1088/1742-6596/703/1/012004

CrossRef Full Text | Google Scholar

Matthee, J., and Schaye, J. (2019). The Origin of Scatter in the star Formation Rate-Stellar Mass Relation. Mon. Not. R. Astron. Soc. 484, 915–932. doi:10.1093/mnras/stz030

CrossRef Full Text | Google Scholar

Matthews, L. D., Gallagher III, J. S., Krist, J. E., Watson, A. M., Burrows, C. J., Griffiths, R. E., et al. (1999). WFPC2 Observations of Compact Star Cluster Nuclei in Low-Luminosity Spiral Galaxies. Astronomical J. 118, 208–235. doi:10.1086/300909

CrossRef Full Text | Google Scholar

McConnachie, A. W. (2012). The Observed Properties of Dwarf Galaxies in and Around the Local Group. Astronomical J. 144, 4. doi:10.1088/0004-6256/144/1/4

CrossRef Full Text | Google Scholar

McConnell, N. J., Ma, C.-P., Gebhardt, K., Wright, S. A., Murphy, J. D., Lauer, T. R., et al. (2011). Two Ten-Billion-Solar-Mass Black Holes at the Centres of Giant Elliptical Galaxies. Nature 480, 215–218. doi:10.1038/nature10636

PubMed Abstract | CrossRef Full Text | Google Scholar

McConnell, N. J., and Ma, C.-P. (2013). Revisiting the Scaling Relations of Black Hole Masses and Host Galaxy Properties. ApJ 764, 184. doi:10.1088/0004-637x/764/2/184

CrossRef Full Text | Google Scholar

McDonald, M., Courteau, S., and Tully, R. B. (2009). Bulge-disc Decompositions and Structural Bimodality of Ursa Major Cluster Spiral Galaxies. Mon. Not. R. Astron. Soc. 393, 628–640. doi:10.1111/j.1365-2966.2008.14239.x

CrossRef Full Text | Google Scholar

McGaugh, S. S., Schombert, J. M., Bothun, G. D., and de Blok, W. J. G. (2000). The Baryonic Tully-Fisher Relation. Astrophysical J. Lett 533, L99–L102. doi:10.1086/312628

PubMed Abstract | CrossRef Full Text | Google Scholar

McGaugh, S. S. (2004). The Mass Discrepancy-Acceleration Relation: Disk Mass and the Dark Matter Distribution. ApJ 609, 652–666. doi:10.1086/421338

CrossRef Full Text | Google Scholar

McLeod, K. K., and Bechtold, J. (2009). HOST GALAXIES OFz= 4 QUASARS. ApJ 704, 415–438. doi:10.1088/0004-637X/704/1/415

CrossRef Full Text | Google Scholar

McLure, R. J., and Dunlop, J. S. (2002). On the Black Hole-Bulge Mass Relation in Active and Inactive Galaxies. Mon. Not. R. Astron. Soc. 331, 795–804. doi:10.1046/j.1365-8711.2002.05236.x

CrossRef Full Text | Google Scholar

McLure, R. J., and Jarvis, M. J. (2002). Measuring the Black Hole Masses of High-Redshift Quasars. MNRAS 337, 109–116. doi:10.1046/j.1365-8711.2002.05871.x

CrossRef Full Text | Google Scholar

McLure, R. J., Jarvis, M. J., Targett, T. A., Dunlop, J. S., and Best, P. N. (2006). On the Evolution of the Black Hole: Spheroid Mass Ratio. MNRAS 368, 1395–1403. doi:10.1111/j.1365-2966.2006.10228.x10.1111/j.1365-2966.2006.10228.x

CrossRef Full Text | Google Scholar

Mehrgan, K., Thomas, J., Saglia, R., Mazzalay, X., Erwin, P., Bender, R., et al. (2019). A 40 Billion Solar-Mass Black Hole in the Extreme Core of Holm 15A, the Central Galaxy of Abell 85. ApJ 887, 195. doi:10.3847/1538-4357/ab5856

CrossRef Full Text | Google Scholar

Mei, S., Holden, B. P., Blakeslee, J. P., Ford, H. C., Franx, M., Homeier, N. L., et al. (2009). Evolution of the Color-Magnitude Relation in Galaxy Clusters Atz∼ 1 from the Acs Intermediate Redshift Cluster Survey. ApJ 690, 42–68. doi:10.1088/0004-637X/690/1/42

CrossRef Full Text | Google Scholar

Mejía-Restrepo, J. E., Trakhtenbrot, B., Lira, P., Netzer, H., and Capellupo, D. M. (2016). Active Galactic Nuclei at z˜1.5: II. Black Hole Mass Estimation by Means of Broad Emission Lines. MNRAS 460. doi:10.1093/mnras/stw568

CrossRef Full Text | Google Scholar

Mejía-Restrepo, J. E., Lira, P., Netzer, H., Trakhtenbrot, B., and Capellupo, D. M. (2018). The Effect of Nuclear Gas Distribution on the Mass Determination of Supermassive Black Holes. Nat. Astron. 2, 63–68. doi:10.1038/s41550-017-0305-z

CrossRef Full Text | Google Scholar

Melbourne, J., and Salzer, J. J. (2002). Metal Abundances of KISS Galaxies. I. Coarse Metal Abundances and the Metallicity-Luminosity Relation. Astronomical J. 123, 2302–2311. doi:10.1086/339834

CrossRef Full Text | Google Scholar

Menci, N., Fontana, A., Giallongo, E., and Salimbeni, S. (2005). Bimodal Color Distribution in Hierarchical Galaxy Formation. ApJ 632, 49–57. doi:10.1086/432788

CrossRef Full Text | Google Scholar

Menci, N., Rosati, P., Gobat, R., Strazzullo, V., Rettura, A., Mei, S., et al. (2008). The Red Sequence of High‐Redshift Clusters: A Comparison with Cosmological Galaxy Formation Models. Astrophysical J. 685, 863–874. doi:10.1086/591016

CrossRef Full Text | Google Scholar

Mendel, J. T., Beifiori, A., Saglia, R. P., Bender, R., Brammer, G. B., Chan, J., et al. (2020). The Kinematics of Massive Quiescent Galaxies at 1.4. ApJ 899, 87. doi:10.3847/1538-4357/ab9ffc

CrossRef Full Text | Google Scholar

Merlin, E., Buonomo, U., Grassi, T., Piovan, L., and Chiosi, C. (2010). EvoL: the New Padova Tree-SPH Parallel Code for Cosmological Simulations. A&A 513, A36. doi:10.1051/0004-6361/200913514

CrossRef Full Text | Google Scholar

Merlin, E., and Chiosi, C. (2006). Formation and Evolution of Early-type Galaxies. A&A 457, 437–453. doi:10.1051/0004-6361:20054486

CrossRef Full Text | Google Scholar

Merlin, E., Chiosi, C., Piovan, L., Grassi, T., Buonomo, U., and Barbera, F. L. (2012). Formation and Evolution of Early-type Galaxies - III. Dependence of the star Formation History on the Total Mass and Initial Overdensity. Monthly Notices R. Astronomical Soc. 427, 1530–1554. doi:10.1111/j.1365-2966.2012.21965.x

CrossRef Full Text | Google Scholar

Merlin, E., and Chiosi, C. (2007). Simulating the Formation and Evolution of Galaxies: Multi-phase Description of the Interstellar Medium, star Formation, and Energy Feedback. A&A 473, 733–745. doi:10.1051/0004-6361:20077465

CrossRef Full Text | Google Scholar

Merloni, A., Bongiorno, A., Bolzonella, M., Brusa, M., Civano, F., Comastri, A., et al. (2010). On the Cosmic Evolution of the Scaling Relations between Black Holes and Their Host Galaxies: Broad-Line Active Galactic Nuclei in the zCOSMOS Survey. ApJ 708, 137–157. doi:10.1088/0004-637X/708/1/137

CrossRef Full Text | Google Scholar

Merloni, A., Heinz, S., and di Matteo, T. (2003). A Fundamental Plane of Black Hole Activity. Monthly Notices R. Astronomical Soc. 345, 1057–1076. doi:10.1046/j.1365-2966.2003.07017.x

CrossRef Full Text | Google Scholar

Merritt, D., Ferrarese, L., and Joseph, C. L. (2001). No Supermassive Black Hole in M33? Science 293, 1116–1118. doi:10.1126/science.1063896

PubMed Abstract | CrossRef Full Text | Google Scholar

Merritt, D. (2006). Mass Deficits, Stalling Radii, and the Merger Histories of Elliptical Galaxies. ApJ 648, 976–986. doi:10.1086/506139

CrossRef Full Text | Google Scholar

Merritt, D., Storchi-Bergmann, T., Robinson, A., Batcheldor, D., Axon, D., and Fernandes, R. C. (2006). The Nature of the HE0450-2958 System. Monthly Notices R. Astronomical Soc. 367, 1746–1750. doi:10.1111/j.1365-2966.2006.10093.x

CrossRef Full Text | Google Scholar

Mezcua, M., Civano, F., Fabbiano, G., Miyaji, T., and Marchesi, S. (2016). A Population of Intermediate-Mass Black Holes in Dwarf Starburst Galaxies up to Redshift = 1.5. ApJ 817, 20. doi:10.3847/0004-637X/817/1/20

CrossRef Full Text | Google Scholar

Miller, S. H., Bundy, K., Sullivan, M., Ellis, R. S., and Treu, T. (2011). THE ASSEMBLY HISTORY OF DISK GALAXIES. I. THE TULLY-FISHER RELATION TOz≃ 1.3 FROM DEEP EXPOSURES WITH DEIMOS. ApJ 741, 115. doi:10.1088/0004-637x/741/2/115

CrossRef Full Text | Google Scholar

Milosavljević, M., and Merritt, D. (2001). Formation of Galactic Nuclei. ApJ 563, 34–62. doi:10.1086/323830

CrossRef Full Text | Google Scholar

Mineshige, S., Kawaguchi, T., Takeuchi, M., and Hayashida, K. (2000). Slim-Disk Model for Soft X-Ray Excess and Variability of Narrow-Line Seyfert 1 Galaxies. Publ. Astron. Soc. Jpn. 52, 499–508. doi:10.1093/pasj/52.3.499

CrossRef Full Text | Google Scholar

Mirabel, I. F., and Rodríguez, L. F. (1994). A Superluminal Source in the Galaxy. Nature 371, 46–48. doi:10.1038/371046a0

CrossRef Full Text | Google Scholar

Misgeld, I., and Hilker, M. (2011). Families of Dynamically Hot Stellar Systems over 10 Orders of Magnitude in Mass. Mon. Not. R. Astron. Soc. 414, 3699–3710. doi:10.1111/j.1365-2966.2011.18669.x

CrossRef Full Text | Google Scholar

Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., Nakai, N., Diamond, P., et al. (1995). Evidence for a Black Hole from High Rotation Velocities in a Sub-parsec Region of NGC4258. Nature 373, 127–129. doi:10.1038/373127a0

CrossRef Full Text | Google Scholar

Mo, H. J., Mao, S., and White, S. D. M. (1998). The Formation of Galactic Discs. Monthly Notices R. Astronomical Soc. 295, 319–336. doi:10.1046/j.1365-8711.1998.01227.x

CrossRef Full Text | Google Scholar

Mockler, B., Guillochon, J., and Ramirez-Ruiz, E. (2019). Weighing Black Holes Using Tidal Disruption Events. ApJ 872, 151. doi:10.3847/1538-4357/ab010f

CrossRef Full Text | Google Scholar

Mocz, P., Green, A., Malacari, M., and Glazebrook, K. (2012). The Tully-Fisher Relation for 25 000 Sloan Digital Sky Survey Galaxies as a Function of Environment. Monthly Notices R. Astronomical Soc. 425, 296–310. doi:10.1111/j.1365-2966.2012.21458.x

CrossRef Full Text | Google Scholar

Moffett, A. J., Kannappan, S. J., Baker, A. J., and Laine, S. (2012). Extended Ultraviolet Disks and Ultraviolet-Bright Disks in Low-Mass E/S0 Galaxies. ApJ 745, 34. doi:10.1088/0004-637X/745/1/34

CrossRef Full Text | Google Scholar

Moles, M., Campos, A., Kjærgaard, P., Fasano, G., and Bettoni, D. (1998). On the Use of Scaling Relations for the Tolman Test. Astrophysical J. Lett 495, L31–L34. doi:10.1086/311208

CrossRef Full Text | Google Scholar

Molina, J., Wang, R., and Shangguan, J. (2021). Compact Molecular Gas Distribution in Quasar Host Galaxies. arXiv:2101.00764.

Google Scholar

Moretti, A., Poggianti, B. M., Fasano, G., Bettoni, D., D’Onofrio, M., Fritz, J., et al. (2014). WINGS Data Release: a Database of Galaxies in Nearby Clusters. A&A 564, A138. doi:10.1051/0004-6361/201323098

CrossRef Full Text | Google Scholar

Morgan, W. W. (1958). A Preliminary Classification of the Forms of Galaxies According to Their Stellar Population. Pasp 70, 364. doi:10.1086/127243

CrossRef Full Text | Google Scholar

Morganti, R., de Zeeuw, P. T., Oosterloo, T. A., McDermid, R. M., Krajnović, D., Cappellari, M., et al. (2006). Neutral Hydrogen in Nearby Elliptical and Lenticular Galaxies: the Continuing Formation of Early-type Galaxies. Mon. Not. R. Astron. Soc. 371, 157–169. doi:10.1111/j.1365-2966.2006.10681.x

CrossRef Full Text | Google Scholar

Mortlock, A., Conselice, C. J., Hartley, W. G., Ownsworth, J. R., Lani, C., Bluck, A. F. L., et al. (2013). The Redshift and Mass Dependence on the Formation of the Hubble Sequence at Z > 1 from CANDELS/UDS. Mon. Not. R. Astron. Soc. 433, 1185–1201. doi:10.1093/mnras/stt793

CrossRef Full Text | Google Scholar

Muldrew, S. I., Croton, D. J., Skibba, R. A., Pearce, F. R., Ann, H. B., Baldry, I. K., et al. (2012). Measures of Galaxy Environment - I. What Is 'environment'? MNRAS 419, 2670–2682. doi:10.1111/j.1365-2966.2011.19922.x

CrossRef Full Text | Google Scholar

Muzzin, A., Marchesini, D., Stefanon, M., Franx, M., McCracken, H. J., Milvang-Jensen, B., et al. (2013). THE EVOLUTION of the STELLAR MASS FUNCTIONS of STAR-FORMING and QUIESCENT GALAXIES TOz= 4 from the COSMOS/UltraVISTA SURVEY. ApJ 777, 18. doi:10.1088/0004-637X/777/1/18

CrossRef Full Text | Google Scholar

Narayan, R., and Yi, I. (1995). Advection-dominated Accretion: Underfed Black Holes and Neutron Stars. ApJ 452, 710. doi:10.1086/176343

CrossRef Full Text | Google Scholar

Nardini, E., Lusso, E., Risaliti, G., Bisogni, S., Civano, F., and Elvis, M. (2019). The Most Luminous Blue Quasars at 3.0 < Z < 3.3. I. A Tale of Two X-ray Populations. AAp 632, A109. doi:10.1051/0004-6361/201936911

CrossRef Full Text | Google Scholar

Navarro, J. F., and Steinmetz, M. (2000). Dark Halo and Disk Galaxy Scaling Laws in Hierarchical Universes. ApJ 538, 477–488. doi:10.1086/309175

CrossRef Full Text | Google Scholar

Navarro, J. F., and White, S. D. M. (1994). Simulations of Dissipative Galaxy Formation in Hierarchically Clustering Universes - II. Dynamics of the Baryonic Component in Galactic Haloes. Mon. Not. R. Astron. Soc. 267, 401–412. doi:10.1093/mnras/267.2.401

CrossRef Full Text | Google Scholar

Negrete, C. A., Dultzin, D., Marziani, P., Esparza, D., Sulentic, J. W., del Olmo, A., et al. (2018). Highly Accreting Quasars: The SDSS Low-Redshift Catalog. A&A 620, A118. doi:10.1051/0004-6361/201833285

CrossRef Full Text | Google Scholar

Negrete, C. A., Dultzin, D., Marziani, P., and Sulentic, J. W. (2012). Broad-line Region Physical Conditions in Extreme Population a Quasars: a Method to Estimate Central Black Hole Mass at High Redshift. ApJ 757, 62. doi:10.1088/0004-637x/757/1/62

CrossRef Full Text | Google Scholar

Nelan, J. E., Smith, R. J., Hudson, M. J., Wegner, G. A., Lucey, J. R., Moore, S. A. W., et al. (2005). NOAO Fundamental Plane Survey. II. Age and Metallicity along the Red Sequence from Line‐Strength Data. ApJ 632, 137–156. doi:10.1086/431962

CrossRef Full Text | Google Scholar

Nelson, C. H., Green, R. F., Bower, G., Gebhardt, K., and Weistrop, D. (2004). The Relationship between Black Hole Mass and Velocity Dispersion in Seyfert 1 Galaxies. ApJ 615, 652–661. doi:10.1086/424657

CrossRef Full Text | Google Scholar

Nelson, D., Pillepich, A., Springel, V., Weinberger, R., Hernquist, L., Pakmor, R., et al. (2018). First Results from the IllustrisTNG Simulations: the Galaxy Colour Bimodality. Mon. Not. R. Astron. Soc. 475, 624–647. doi:10.1093/mnras/stx3040

CrossRef Full Text | Google Scholar

Nemmen, R. S., and Brotherton, M. S. (2010). Quasar Bolometric Corrections: Theoretical Considerations. MNRAS 408, 1598–1605. doi:10.1111/j.1365-2966.2010.17224.x

CrossRef Full Text | Google Scholar

Netzer, H. (2019). Bolometric Correction Factors for Active Galactic Nuclei. MNRAS 488, 5185–5191. doi:10.1093/mnras/stz2016

CrossRef Full Text | Google Scholar

Netzer, H., Lira, P., Trakhtenbrot, B., Shemmer, O., and Cury, I. (2007). Black Hole Mass and Growth Rate at High Redshift. ApJ 671, 1256–1263. doi:10.1086/523035

CrossRef Full Text | Google Scholar

Netzer, H., and Marziani, P. (2010). The Effect of Radiation Pressure on Emission-Line Profiles and Black Hole Mass Determination in Active Galactic Nuclei. ApJ 724, 318–328. doi:10.1088/0004-637X/724/1/318

CrossRef Full Text | Google Scholar

Netzer, H. (2013). The Physics and Evolution of Active Galactic Nuclei. Cambridge University Press.

Google Scholar

Neumayer, N., Cappellari, M., Reunanen, J., Rix, H. W., van der Werf, P. P., de Zeeuw, P. T., et al. (2007). The Central Parsecs of Centaurus A: High‐excitation Gas, a Molecular Disk, and the Mass of the Black Hole. ApJ 671, 1329–1344. doi:10.1086/523039

CrossRef Full Text | Google Scholar

Newman, A. B., Ellis, R. S., Andreon, S., Treu, T., Raichoor, A., and Trinchieri, G. (2014). SPECTROSCOPIC CONFIRMATION OF THE RICHz= 1.80 GALAXY CLUSTER JKCS 041 USING THE WFC3 GRISM: ENVIRONMENTAL TRENDS IN THE AGES AND STRUCTURE OF QUIESCENT GALAXIES. ApJ 788, 51. doi:10.1088/0004-637x/788/1/51

CrossRef Full Text | Google Scholar

Newman, S., and Genzel, R. (2012). Compact, Dispersion-Dominated, Star-forming Galaxies at Z 2. Am. Astronomical Soc. Meet. Abstr. 219, 441–519.

Google Scholar

Nguyen, K., and Bogdanović, T. (2016). Emission Signatures from Sub-parsec Binary Supermassive Black Holes. I. Diagnostic Power of Broad Emission Lines. ApJ 828, 68. doi:10.3847/0004-637X/828/2/68

CrossRef Full Text | Google Scholar

Nigoche-Netro, A., Aguerri, J. A. L., Lagos, P., Ruelas-Mayorga, A., Sánchez, L. J., and Machado, A. (2010). The Faber-Jackson Relation for Early-type Galaxies: Dependence on the Magnitude Range. A&A 516, A96. doi:10.1051/0004-6361/200912719

CrossRef Full Text | Google Scholar

Nigoche-Netro, A., Aguerri, J. A. L., Lagos, P., Ruelas-Mayorga, A., Sánchez, L. J., Muñoz-Tuñón, C., et al. (2011). The Intrinsic Dispersion in the Faber-Jackson Relation for Early-type Galaxies as Function of the Mass and Redshift. A&A 534, A61. doi:10.1051/0004-6361/201016360

CrossRef Full Text | Google Scholar

Nipoti, C., Treu, T., Leauthaud, A., Bundy, K., Newman, A. B., and Auger, M. W. (2012). Size and Velocity-Dispersion Evolution of Early-type Galaxies in a Λ Cold Dark Matter Universe. MNRAS 422, 1714–1731. doi:10.1111/j.1365-2966.2012.20749.x

CrossRef Full Text | Google Scholar

Noeske, K. G., Weiner, B. J., Faber, S. M., Papovich, C., Koo, D. C., Somerville, R. S., et al. (2007). Star Formation in AEGIS Field Galaxies since Z = 1.1: The Dominance of Gradually Declining Star Formation, and the Main Sequence of Star-forming Galaxies. ApJ 660, L43–L46. doi:10.1086/517926

CrossRef Full Text | Google Scholar

Nokhrina, E. E., Gurvits, L. I., Beskin, V. S., Nakamura, M., Asada, K., and Hada, K. (2019). M87 Black Hole Mass and Spin Estimate through the Position of the Jet Boundary Shape Break. Mon. Not. R. Astron. Soc. 489, 1197–1205. doi:10.1093/mnras/stz2116

CrossRef Full Text | Google Scholar

Noordermeer, E., and Verheijen, M. A. W. (2007). The High-Mass End of the Tully-Fisher Relation. Monthly Notices R. Astronomical Soc. 381, 1463–1472. doi:10.1111/j.1365-2966.2007.12369.x

CrossRef Full Text | Google Scholar

Obreschkow, D., and Glazebrook, K. (2014). Fundamental Mass-Spin-Morphology Relation of Spiral Galaxies. ApJ 784, 26. doi:10.1088/0004-637x/784/1/26

CrossRef Full Text | Google Scholar

Ohta, K., Aoki, K., Kawaguchi, T., and Kiuchi, G. (2007). A Bar Fuels a Supermassive Black Hole?: Host Galaxies of Narrow‐Line Seyfert 1 Galaxies. Astrophys J. Suppl. S 169, 1–20. doi:10.1086/510204

CrossRef Full Text | Google Scholar

Okamura, T., Shimasaku, K., and Kawamata, R. (2018). Angular Momentum Evolution of Stellar Disks at High Redshifts. ApJ 854, 22. doi:10.3847/1538-4357/aaa423

CrossRef Full Text | Google Scholar

Olguín-Iglesias, A., Kotilainen, J. K., León Tavares, J., Chavushyan, V., and Añorve, C. (2017). Evidence of Bar-Driven Secular Evolution in the Gamma-ray Narrow-Line Seyfert 1 Galaxy FBQS J164442.5+261913. Mon. Not. R. Astron. Soc. 467, stx022–3722. doi:10.1093/mnras/stx022

CrossRef Full Text | Google Scholar

Oliva-Altamirano, P., Brough, S., Tran, K.-V., Couch, W. J., McDermid, R. M., Lidman, C., et al. (2015). The Accretion Histories of Brightest Cluster Galaxies from Their Stellar Population Gradients. Mon. Not. R. Astron. Soc. 449, 3347–3359. doi:10.1093/mnras/stv475

CrossRef Full Text | Google Scholar

Onishi, K., Iguchi, S., Sheth, K., and Kohno, K. (2015). A Measurement of the Black Hole Mass in NGC 1097 Using ALMA. ApJ 806, 39. doi:10.1088/0004-637X/806/1/39

CrossRef Full Text | Google Scholar

Oppenheimer, B. D., Davé, R., Kereš, D., Fardal, M., Katz, N., Kollmeier, J. A., et al. (2010). Feedback and Recycled Wind Accretion: Assembling the Z= 0 Galaxy Mass Function. Mon. Not. R. Astron. Soc. 406, 2325–2338. doi:10.1111/j.1365-2966.2010.16872.x

CrossRef Full Text | Google Scholar

Orban de Xivry, G., Davies, R., Schartmann, M., Komossa, S., Marconi, A., Hicks, E., et al. (2011). The Role of Secular Evolution in the Black Hole Growth of Narrow-Line Seyfert 1 Galaxies. MNRAS 417, 2721–2736. doi:10.1111/j.1365-2966.2011.19439.x

CrossRef Full Text | Google Scholar

Ouellette, N. N.-Q., Courteau, S., Holtzman, J. A., Dutton, A. A., Cappellari, M., Dalcanton, J. J., et al. (2017). The Spectroscopy and H-Band Imaging of Virgo Cluster Galaxies (SHIVir) Survey: Scaling Relations and the Stellar-To-Total Mass Relation. ApJ 843, 74. doi:10.3847/1538-4357/aa74b1

CrossRef Full Text | Google Scholar

Padovani, P., and Rafanelli, P. (1988). Mass-luminosity Relationships and Accretion Rates for Seyfert 1 Galaxies and Quasars. AAp 205, 53–70.

Google Scholar

Pahre, M. A., Djorgovski, S. G., and de Carvalho, R. R. (1996). A Tolman Surface Brightness Test for Universal Expansion and the Evolution of Elliptical Galaxies in Distant Clusters. Astrophysical J. Lett 456, L79. doi:10.1086/309872

CrossRef Full Text | Google Scholar

Pancoast, A., Barth, A. J., Horne, K., Treu, T., Brewer, B. J., Bennert, V. N., et al. (2018). Stability of the Broad-Line Region Geometry and Dynamics in Arp 151 over Seven Years. ApJ 856, 108. doi:10.3847/1538-4357/aab3c6

CrossRef Full Text | Google Scholar

Pancoast, A., Brewer, B. J., and Treu, T. (2014). Modelling Reverberation Mapping Data - I. Improved Geometric and Dynamical Models and Comparison with Cross-Correlation Results. MNRAS 445, 3055–3072. doi:10.1093/mnras/stu1809

CrossRef Full Text | Google Scholar

Pancoast, A., Brewer, B. J., Treu, T., Park, D., Barth, A. J., Bentz, M. C., et al. (2014). Modelling Reverberation Mapping Data - II. Dynamical Modelling of the Lick AGN Monitoring Project 2008 Data Set. MNRAS 445, 3073–3091. doi:10.1093/mnras/stu1419

CrossRef Full Text | Google Scholar

Panda, S., Martínez-Aldama, M. L., Marinello, M., Czerny, B., Marziani, P., and Dultzin, D. (2020). Optical Fe II and Near-Infrared Ca II Triplet Emission in Active Galaxies: (I) Photoionization Modelling. arXiv:2004.05201.

Google Scholar

Panda, S., Czerny, B., Adhikari, T. P., Hryniewicz, K., Wildy, C., Kuraszkiewicz, J., et al. (2018). Modeling of the Quasar Main Sequence in the Optical Plane. ApJ 866, 115. doi:10.3847/1538-4357/aae209

CrossRef Full Text | Google Scholar

Panda, S., Czerny, B., and Wildy, C. (2017). The Physical Driver of the Optical Eigenvector 1 in Quasar Main Sequence. Front. Astron. Space Sci. 4, 33. doi:10.3389/fspas.2017.00033

CrossRef Full Text | Google Scholar

Panda, S., Marziani, P., and Czerny, B. (2019). The Quasar Main Sequence Explained by the Combination of Eddington Ratio, Metallicity, and Orientation. ApJ 882, 79. doi:10.3847/1538-4357/ab3292

CrossRef Full Text | Google Scholar

Pannella, M., Carilli, C. L., Daddi, E., McCracken, H. J., Owen, F. N., Renzini, A., et al. (2009). STAR FORMATION AND DUST OBSCURATION AT z ≈ 2: GALAXIES AT THE DAWN OF DOWNSIZING. ApJ 698, L116–L120. doi:10.1088/0004-637X/698/2/L116

CrossRef Full Text | Google Scholar

Park, D., Kelly, B. C., Woo, J.-H., and Treu, T. (2012). RECALIBRATION OF THE VIRIAL FACTOR AND M BH -σ * RELATION FOR LOCAL ACTIVE GALAXIES. ApJS 203, 6. doi:10.1088/0067-0049/203/1/6

CrossRef Full Text | Google Scholar

Park, D., Woo, J.-H., Denney, K. D., and Shin, J. (2013). Calibrating C-IV-Based Black Hole Mass Estimators. ApJ 770, 87. doi:10.1088/0004-637X/770/2/87

CrossRef Full Text | Google Scholar

Pastorini, G., Marconi, A., Capetti, A., Axon, D. J., Alonso-Herrero, A., Atkinson, J., et al. (2007). Supermassive Black Holes in the Sbc Spiral Galaxies NGC 3310, NGC 4303 and NGC 4258. A&A 469, 405–423. doi:10.1051/0004-6361:20066784

CrossRef Full Text | Google Scholar

Patel, S., Van Dokkum, P. G., Franx, M., Quadri, R., Muzzin, A., Marchesini, D., et al. (2013). HST/WFC3 Confirmation of the Inside-Out Growth of Massive Galaxies at 0<z<2 and Identification of Their Star Forming Progenitors at 3. Am. Astronomical Soc. Meet. Abstr. 221, 129.

Google Scholar

Peebles, P. J. E. (1969). Origin of the Angular Momentum of Galaxies. ApJ 155, 393. doi:10.1086/149876

CrossRef Full Text | Google Scholar

Peng, C. Y., Impey, C. D., Ho, L. C., Barton, E. J., and Rix, H. W. (2006). Probing the Coevolution of Supermassive Black Holes and Quasar Host Galaxies. ApJ 640, 114–125. doi:10.1086/499930

CrossRef Full Text | Google Scholar

Peng, C. Y., Impey, C. D., Rix, H. W., Kochanek, C. S., Keeton, C. R., Falco, E. E., et al. (2006). Probing the Coevolution of Supermassive Black Holes and Galaxies Using Gravitationally Lensed Quasar Hosts. ApJ 649, 616–634. doi:10.1086/506266

CrossRef Full Text | Google Scholar

Peng, Y.-j., Lilly, S. J., Kovač, K., Bolzonella, M., Pozzetti, L., Renzini, A., et al. (2010). Mass and Environment as Drivers of Galaxy Evolution in SDSS and zCOSMOS and the Origin of the Schechter Function. ApJ 721, 193–221. doi:10.1088/0004-637X/721/1/193

CrossRef Full Text | Google Scholar

Peng, Y.-j., and Renzini, A. (2020). Disc Growth and Quenching. MNRAS 491, L51–L55. doi:10.1093/mnrasl/slz163

CrossRef Full Text | Google Scholar

Pennell, A., Runnoe, J. C., and Brotherton, M. S. (2017). Updating Quasar Bolometric Luminosity Corrections - III. [O III] Bolometric Corrections. MNRAS 468, 1433–1441. doi:10.1093/mnras/stx556

CrossRef Full Text | Google Scholar

Persic, M., Salucci, P., and Stel, F. (1996). The Universal Rotation Curve of Spiral Galaxies - I. The Dark Matter Connection. Mon. Not. R. Astron. Soc. 281, 27–47. doi:10.1093/mnras/278.1.27

CrossRef Full Text | Google Scholar

Peterson, B. M. (2014). Measuring the Masses of Supermassive Black Holes. Space Sci. Rev. 183, 253–275. doi:10.1007/s11214-013-9987-4

CrossRef Full Text | Google Scholar

Peterson, B. M. (1993). Reverberation Mapping of Active Galactic Nuclei. PASP 105, 247–268. doi:10.1086/133140

CrossRef Full Text | Google Scholar

Peterson, B. M. (2017). Space Telescope and Optical Reverberation Mapping Project: A Leap Forward in Reverberation Mapping. Proc. IAU 12, 215–218. doi:10.1017/S1743921316012680

CrossRef Full Text | Google Scholar

Peterson, B. M., and Wandel, A. (1999). Keplerian Motion of Broad-Line Region Gas as Evidence for Supermassive Black Holes in Active Galactic Nuclei. ApJL 521, L95–L98. doi:10.1086/312190

CrossRef Full Text | Google Scholar

Pettini, M., and Pagel, B. E. J. (2004). [O Iii]/[N Ii] as an Abundance Indicator at High Redshift. Mon. Not. R. Astron. Soc. 348, L59–L63. doi:10.1111/j.1365-2966.2004.07591.x

CrossRef Full Text | Google Scholar

Pichon, C., Pogosyan, D., Kimm, T., Slyz, A., Devriendt, J., and Dubois, Y. (2011). Rigging Dark Haloes: Why Is Hierarchical Galaxy Formation Consistent with the Inside-Out Build-Up of Thin Discs? Mon. Not. R. Astron. Soc. 418, 2493–2507. doi:10.1111/j.1365-2966.2011.19640.x

CrossRef Full Text | Google Scholar

Pillepich, A., Nelson, D., Hernquist, L., Springel, V., Pakmor, R., Torrey, P., et al. (2018). First Results from the IllustrisTNG Simulations: the Stellar Mass Content of Groups and Clusters of Galaxies. Mon. Not. R. Astron. Soc. 475, 648–675. doi:10.1093/mnras/stx3112

CrossRef Full Text | Google Scholar

Pizagno, J., Prada, F., Weinberg, D. H., Rix, H. W., Harbeck, D., Grebel, E. K., et al. (2005). Dark Matter and Stellar Mass in the Luminous Regions of Disk Galaxies. ApJ 633, 844–856. doi:10.1086/491614

CrossRef Full Text | Google Scholar

Ponomareva, A. A., Verheijen, M. A. W., Peletier, R. F., and Bosma, A. (2017). The Multiwavelength Tully-Fisher Relation with Spatially Resolved H I Kinematics. Mon. Not. R. Astron. Soc. 469, 2387–2400. doi:10.1093/mnras/stx1018

CrossRef Full Text | Google Scholar

Popesso, P., Concas, A., Morselli, L., Schreiber, C., Rodighiero, G., Cresci, G., et al. (2019). The Main Sequence of star-forming Galaxies - I. The Local Relation and its Bending. Mon. Not. R. Astron. Soc. 483, 3213–3226. doi:10.1093/mnras/sty3210

CrossRef Full Text | Google Scholar

Popović, L. Č., and Kovačević, J. (2011). Optical Emission-Line Properties of a Sample of the Broad-Line Active Galactic Nuclei: The Baldwin Effect and Eigenvector 1. ApJ 738, 68. doi:10.1088/0004-637X/738/1/68

CrossRef Full Text | Google Scholar

Portinari, L., and Chiosi, C. (2000). On Radial Gas Flows, the Galactic Bar and Chemical Evolution in the Galactic Disc. AAp 355, 929–948.

Google Scholar

Posti, L., Fraternali, F., Di Teodoro, E. M., and Pezzulli, G. (2018). The Angular Momentum-Mass Relation: a Fundamental Law from dwarf Irregulars to Massive Spirals. A&A 612, L6. doi:10.1051/0004-6361/201833091

CrossRef Full Text | Google Scholar

Press, W. H., and Schechter, P. (1974). Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. ApJ 187, 425–438. doi:10.1086/152650

CrossRef Full Text | Google Scholar

Prichard, L. J., Davies, R. L., Beifiori, A., Chan, J. C. C., Cappellari, M., Houghton, R. C. W., et al. (2017). The KMOS Cluster Survey (KCS). III. Fundamental Plane of Cluster Galaxies Atz≃ 1.80 in JKCS 041. ApJ 850, 203. doi:10.3847/1538-4357/aa96a6

CrossRef Full Text | Google Scholar

Puech, M., Hammer, F., Flores, H., Delgado-Serrano, R., Rodrigues, M., and Yang, Y. (2010). The Baryonic Content and Tully-Fisher Relation Atz∼ 0.6. A&A 510, A68. doi:10.1051/0004-6361/200912081

CrossRef Full Text | Google Scholar

Punsly, B., Marziani, P., Berton, M., and Kharb, P. (2020). The Extreme Red Excess in Blazar Ultraviolet Broad Emission Lines. ApJ 903, 44. doi:10.3847/1538-4357/abb950

CrossRef Full Text | Google Scholar

Quinlan, G. D., and Hernquist, L. (1997). The Dynamical Evolution of Massive Black Hole Binaries - II. Self-Consistent N-Body Integrations. New Astron. 2, 533–554. doi:10.1016/s1384-1076(97)00039-0

CrossRef Full Text | Google Scholar

Ragone-Figueroa, C., and Granato, G. L. (2011). Puffing up Early-type Galaxies by Baryonic Mass Loss: Numerical Experiments. Mon. Not. R. Astron. Soc. 414, 3690–3698. doi:10.1111/j.1365-2966.2011.18670.x

CrossRef Full Text | Google Scholar

Raimundo, S. I., Davies, R. I., Gandhi, P., Fabian, A. C., Canning, R. E. A., and Ivanov, V. D. (2013). The Black Hole and central Stellar Population of MCG-6-30-15. MNRAS 431, 2294–2306. doi:10.1093/mnras/stt327

CrossRef Full Text | Google Scholar

Rampazzo, R., Plana, H., Amram, P., Bagarotto, S., Boulesteix, J., and Rosado, M. (2005). Two-dimensional Warm Gas Kinematics in Interacting Galaxy Systems. Mon. Not. R. Astron. Soc. 356, 1177–1190. doi:10.1111/j.1365-2966.2004.08549.x

CrossRef Full Text | Google Scholar

Rantala, A., Johansson, P. H., Naab, T., Thomas, J., and Frigo, M. (2018). The Formation of Extremely Diffuse Galaxy Cores by Merging Supermassive Black Holes. ApJ 864, 113. doi:10.3847/1538-4357/aada47

CrossRef Full Text | Google Scholar

Recio-Blanco, A., Aparicio, A., Piotto, G., de Angeli, F., and Djorgovski, S. G. (2006). Multivariate Analysis of Globular Cluster Horizontal branch Morphology: Searching for the Second Parameter. A&A 452, 875–884. doi:10.1051/0004-6361:20053006

CrossRef Full Text | Google Scholar

Rees, M. J. (1987). Magnetic Confinement of Broad-Line Clouds in Active Galactic Nuclei. Monthly Notices R. Astronomical Soc. 228, 47P–50P. doi:10.1093/mnras/228.1.47P

CrossRef Full Text | Google Scholar

Reichard, T. A., Richards, G. T., Schneider, D. P., Hall, P. B., Tolea, A., Krolik, J. H., et al. (2003). A Catalog of Broad Absorption Line Quasars from the Sloan Digital Sky Survey Early Data Release. AJ 125, 1711–1728. doi:10.1086/368244

CrossRef Full Text | Google Scholar

Reines, A. E., Plotkin, R. M., Russell, T. D., Mezcua, M., Condon, J. J., Sivakoff, G. R., et al. (2014). A Candidate Massive Black Hole in the Low-Metallicity Dwarf Galaxy Pair Mrk 709. ApJ 787, L30. doi:10.1088/2041-8205/787/2/L30

CrossRef Full Text | Google Scholar

Renzini, A., and Ciotti, L. (1993). Transverse Dissections of the Fundamental Planes of Elliptical Galaxies and Clusters of Galaxies. ApJ 416, L49. doi:10.1086/187068

CrossRef Full Text | Google Scholar

Renzini, A., and Peng, Y.-j. (2015). An Objective Definition for the Main Sequence of Star-forming Galaxies. ApJ 801, L29. doi:10.1088/2041-8205/801/2/l29

CrossRef Full Text | Google Scholar

Reyes, R., Mandelbaum, R., Gunn, J. E., Pizagno, J., and Lackner, C. N. (2011). Calibrated Tully-Fisher Relations for Improved Estimates of Disc Rotation Velocities. Mon. Not. R. Astron. Soc. 417, 2347–2386. doi:10.1111/j.1365-2966.2011.19415.x

CrossRef Full Text | Google Scholar

Richards, G. T. (2012). “CIV Emission as a Probe of Accretion Disk Winds,” in AGN Winds in Charleston. Editors G. Chartas, F. Hamann, and K. M. Leighly (California, United States: Astronomical Society of the Pacific Conference Series), 460, 67.

Google Scholar

Richards, G. T., Croom, S. M., Anderson, S. F., Bland-Hawthorn, J., Boyle, B. J., De Propris, R., et al. (2005). The 2dF-SDSS LRG and QSO (2SLAQ) Survey: Thez. MNRAS 360, 839–852. doi:10.1111/j.1365-2966.2005.09096.x

CrossRef Full Text | Google Scholar

Richards, G. T., Kruczek, N. E., Gallagher, S. C., Hall, P. B., Hewett, P. C., Leighly, K. M., et al. (2011). Unification of Luminous Type 1 Quasars through C IV Emission. Astronomical J. 141, 167. doi:10.1088/0004-6256/141/5/167

CrossRef Full Text | Google Scholar

Richards, G. T., Lacy, M., Storrie‐Lombardi, L. J., Hall, P. B., Gallagher, S. C., Hines, D. C., et al. (2006). Spectral Energy Distributions and Multiwavelength Selection of Type 1 Quasars. Astrophys J. Suppl. S 166, 470–497. doi:10.1086/506525

CrossRef Full Text | Google Scholar

Richards, G. T., Vanden Berk, D. E., Reichard, T. A., Hall, P. B., Schneider, D. P., SubbaRao, M., et al. (2002). Broad Emission-Line Shifts in Quasars: An Orientation Measure for Radio-Quiet Quasars? AJ 124, 1–17. doi:10.1086/341167

CrossRef Full Text | Google Scholar

Richer, M. G., and McCall, M. L. (1995). Oxygen Abundances in Diffuse Ellipticals and the Metallicity-Luminosity Relations for Dwarf Galaxies. ApJ 445, 642. doi:10.1086/175727

CrossRef Full Text | Google Scholar

Rix, H. W., de Zeeuw, P. T., Cretton, N., van der Marel, R. P., and Carollo, C. M. (1997). Dynamical Modeling of Velocity Profiles: The Dark Halo Around the Elliptical Galaxy NGC 2434. ApJ 488, 702–719. doi:10.1086/304733

CrossRef Full Text | Google Scholar

Roberts, M. S., and Haynes, M. P. (1994). Physical Parameters along the Hubble Sequence. Annu. Rev. Astron. Astrophys. 32, 115–152. doi:10.1146/annurev.aa.32.090194.000555

CrossRef Full Text | Google Scholar

Robertson, B., Cox, T. J., Hernquist, L., Franx, M., Hopkins, P. F., Martini, P., et al. (2006). The Fundamental Scaling Relations of Elliptical Galaxies. ApJ 641, 21–40. doi:10.1086/500360

CrossRef Full Text | Google Scholar

Rodighiero, G., Renzini, A., Daddi, E., Baronchelli, I., Berta, S., Cresci, G., et al. (2014). A Multiwavelength Consensus on the Main Sequence of star-forming Galaxies at Z ∼ 2. Mon. Not. R. Astron. Soc. 443, 19–30. doi:10.1093/mnras/stu1110

CrossRef Full Text | Google Scholar

Rodríguez-Merino, L. H., Mayya, Y. D., Coelho, P. R. T., Bruzual, G., Charlot, S., Carrasco, E., et al. (2020). High-resolution Spectral Line Indices Useful for the Analysis of Stellar Populations. ApJ 889, L31. doi:10.3847/2041-8213/ab6d64

CrossRef Full Text | Google Scholar

Rodríguez-Puebla, A., Avila-Reese, V., Yang, X., Foucaud, S., Drory, N., and Jing, Y. P. (2015). The Stellar-To-Halo Mass Relation of Local Galaxies Segregates by Color. ApJ 799, 130. doi:10.1088/0004-637X/799/2/130

CrossRef Full Text | Google Scholar

Rodríguez-Puebla, A., Primack, J. R., Behroozi, P., and Faber, S. M. (2016). Is Main-Sequence Galaxy star Formation Controlled by Halo Mass Accretion? Mon. Not. R. Astron. Soc. 455, 2592–2606. doi:10.1093/mnras/stv2513

CrossRef Full Text | Google Scholar

Roediger, J. C., Ferrarese, L., Côté, P., MacArthur, L. A., Sánchez-Janssen, R., Blakeslee, J. P., et al. (2017). The Next Generation Virgo Cluster Survey (NGVS). XXIV. The Red Sequence to ∼106L_⊙ and Comparisons with Galaxy Formation Models. ApJ 836, 120. doi:10.3847/1538-4357/836/1/120

CrossRef Full Text | Google Scholar

Romeo, A. B. (2020). From Massive Spirals to dwarf Irregulars: a New Set of Tight Scaling Relations for Cold Gas and Stars Driven by Disc Gravitational Instability. MNRAS 491, 4843–4851. doi:10.1093/mnras/stz3367

CrossRef Full Text | Google Scholar

Romeo, A. B., and Mogotsi, K. M. (2018). Angular Momentum and Local Gravitational Instability in Galaxy Discs: Does Q Correlate with J or M ? MNRAS 480, L23–L27. doi:10.1093/mnrasl/sly119

CrossRef Full Text | Google Scholar

Ruffa, I., Davis, T. A., Prandoni, I., Laing, R. A., Paladino, R., Parma, P., et al. (2019). The AGN Fuelling/feedback Cycle in Nearby Radio Galaxies - II. Kinematics of the Molecular Gas. MNRAS 489, 3739–3757. doi:10.1093/mnras/stz2368

CrossRef Full Text | Google Scholar

Rusli, S. P., Erwin, P., Saglia, R. P., Thomas, J., Fabricius, M., Bender, R., et al. (2013). Depleted Galaxy Cores and Dynamical Black Hole Masses. AJ 146, 160. doi:10.1088/0004-6256/146/6/160

CrossRef Full Text | Google Scholar

Russell, H. N. (1914). Relations between the Spectra and Other Characteristics of the Stars. Popular Astron. 22, 275–294.

Google Scholar

Ryan, C. J., De Robertis, M. M., Virani, S., Laor, A., and Dawson, P. C. (2007). The Central Engines of Narrow‐Line Seyfert 1 Galaxies. ApJ 654, 799–813. doi:10.1086/509313

CrossRef Full Text | Google Scholar

Ryden, B. S., and Gunn, J. E. (1987). Galaxy Formation by Gravitational Collapse. ApJ 318, 15. doi:10.1086/165349

CrossRef Full Text | Google Scholar

Sadowski, A. (2011). Slim Accretion Disks Around Black Holes. arXiv:1108.0396.

Google Scholar

Saglia, R. P., Bertin, G., and Stiavelli, M. (1992). Elliptical Galaxies with Dark Matter. II. Optimal Luminous--Dark Matter Decomposition for a Sample of Bright Objects. ApJ 384, 433. doi:10.1086/170885

CrossRef Full Text | Google Scholar

Saglia, R. P., Opitsch, M., Erwin, P., Thomas, J., Beifiori, A., Fabricius, M., et al. (2016). The SINFONI Black Hole Survey: The Black Hole Fundamental Plane Revisited and the Paths of (Co)evolution of Supermassive Black Holes and Bulges. ApJ 818, 47. doi:10.3847/0004-637X/818/1/47

CrossRef Full Text | Google Scholar

Saglia, R. P., Sánchez-Blázquez, P., Bender, R., Simard, L., Desai, V., Aragón-Salamanca, A., et al. (2010). The Fundamental Plane of EDisCS Galaxies. A&A 524, A6. doi:10.1051/0004-6361/201014703

CrossRef Full Text | Google Scholar

Sahu, N., Graham, A. W., and Davis, B. L. (2020). Defining the (Black Hole)-Spheroid Connection with the Discovery of Morphology-dependent Substructure in the M BH-n sph and M BH-R e,sph Diagrams: New Tests for Advanced Theories and Realistic Simulations. ApJ 903, 97. doi:10.3847/1538-4357/abb675

CrossRef Full Text | Google Scholar

Saito, M. (1979). Note: On the Formation of Dwarf Spheroidal Galaxies, 31. Tokyo, Japan: Publications of the Astronomical Society of Japan, 193–198.

Google Scholar

Sales, L. V., Navarro, J. F., Schaye, J., Vecchia, C. D., Springel, V., and Booth, C. M. (2010). Feedback and the Structure of Simulated Galaxies at Redshift Z= 2. Mon. Not. R. Astron. Soc. 409, 1541–1556. doi:10.1111/j.1365-2966.2010.17391.x

CrossRef Full Text | Google Scholar

Salim, S., Fang, J. J., Rich, R. M., Faber, S. M., and Thilker, D. A. (2012). Galaxy-scale Star Formation on the Red Sequence: The Continued Growth of S0s and the Quiescence of Ellipticals. ApJ 755, 105. doi:10.1088/0004-637x/755/2/105

CrossRef Full Text | Google Scholar

Salim, S., Rich, R. M., Charlot, S., Brinchmann, J., Johnson, B. D., Schiminovich, D., et al. (2007). UV Star Formation Rates in the Local Universe. Astrophys J. Suppl. S 173, 267–292. doi:10.1086/519218

CrossRef Full Text | Google Scholar

Salucci, P., Ratnam, C., Monaco, P., and Danese, L. (2000). The Masses of Black Holes in the Nuclei of Spirals. Mon. Not. R. Astron. Soc. 317, 488–496. doi:10.1046/j.1365-8711.2000.03622.x

CrossRef Full Text | Google Scholar

Salviander, S., Shields, G. A., Gebhardt, K., and Bonning, E. W. (2007). The Black Hole Mass-Galaxy Bulge Relationship for QSOs in the Sloan Digital Sky Survey Data Release 3. ApJ 662, 131–144. doi:10.1086/513086

CrossRef Full Text | Google Scholar

Salzer, J. J., Lee, J. C., Melbourne, J., Hinz, J. L., Alonso‐Herrero, A., and Jangren, A. (2005). Metal Abundances of KISS Galaxies. IV. Galaxian Luminosity‐Metallicity Relations in the Optical and Near‐Infrared. ApJ 624, 661–679. doi:10.1086/429386

CrossRef Full Text | Google Scholar

Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., van de Ven, G., Vílchez, J. M., Wisotzki, L., et al. (2012). CALIFA, the Calar Alto Legacy Integral Field Area Survey. A&A 538, A8. doi:10.1051/0004-6361/201117353

CrossRef Full Text | Google Scholar

Sancisi, R., Fraternali, F., Oosterloo, T., and van der Hulst, T. (2008). Cold Gas Accretion in Galaxies. Astron. Astrophys Rev. 15, 189–223. doi:10.1007/s00159-008-0010-0

CrossRef Full Text | Google Scholar

Sandage, A. (1986). Star Formation Rates, Galaxy Morphology, and the Hubble Sequence. Astron. Astrophysics 161, 89–101.

Google Scholar

Sandage, A. (1972). Absolute Magnitudes of E and So Galaxies in the Virgo and Coma Clusters as a Function of U - B Color. ApJ 176, 21. doi:10.1086/151606

CrossRef Full Text | Google Scholar

Sandage, A., Freeman, K. C., and Stokes, N. R. (1970). The intrinsic flattening of e, so, and spiral galaxies as related to galaxy formation and evolution. ApJ 160, 831–844. doi:10.1086/150475

CrossRef Full Text | Google Scholar

Sandage, A. (1957). Observational Approach to Evolution. II. A Computed Luminosity Function for K0-K2 Stars from M_{v} = +5 to M_{v} = - 4.5. ApJ 125, 435. doi:10.1086/146319

CrossRef Full Text | Google Scholar

Sandage, A. (2005). The Classification of Galaxies: Early History and Ongoing Developments. Annu. Rev. Astron. Astrophys. 43, 581–624. doi:10.1146/annurev.astro.43.112904.104839

CrossRef Full Text | Google Scholar

Sandage, A., and Visvanathan, N. (1978). The Color-Absolute Magnitude Relation for E and S0 Galaxies. II - New Colors, Magnitudes, and Types for 405 Galaxies. ApJ 223, 707–729. doi:10.1086/156305

CrossRef Full Text | Google Scholar

Sanders, R. L., Shapley, A. E., Kriek, M., Reddy, N. A., Freeman, W. R., Coil, A. L., et al. (2015). THE MOSDEF SURVEY: MASS, METALLICITY, AND STAR-FORMATION RATE ATz∼ 2.3. ApJ 799, 138. doi:10.1088/0004-637X/799/2/138

CrossRef Full Text | Google Scholar

Sanghvi, J., Kotilainen, J. K., Falomo, R., Decarli, R., Karhunen, K., and Uslenghi, M. (2014). The Black Hole-Host Galaxy Relation for Very Low Mass Quasars. MNRAS 445, 1261–1268. doi:10.1093/mnras/stu1822

CrossRef Full Text | Google Scholar

Saracco, P., Casati, A., Gargiulo, A., Longhetti, M., Lonoce, I., Tamburri, S., et al. (2014). Scaling Relations of Cluster Elliptical Galaxies Atz∼ 1.3. A&A 567, A94. doi:10.1051/0004-6361/201423495

CrossRef Full Text | Google Scholar

Saracco, P., Longhetti, M., and Gargiulo, A. (2011). Constraining the star Formation and the Assembly Histories of normal and Compact Early-type Galaxies at 1. Mon. Not. R. Astron. Soc. 412, 2707–2716. doi:10.1111/j.1365-2966.2010.18098.x

CrossRef Full Text | Google Scholar

Satyapal, S., Kamal, L., Cann, J. M., Secrest, N. J., and Abel, N. P. (2021). The Diagnostic Potential of JWST in Characterizing Elusive AGNs. ApJ 906, 35. doi:10.3847/1538-4357/abbfaf10.3847/1538-4357/abbfaf

CrossRef Full Text | Google Scholar

Saulder, C., Mieske, S., Zeilinger, W. W., and Chilingarian, I. (2013). Calibrating the Fundamental Plane with SDSS DR8 Data. A&A 557, A21. doi:10.1051/0004-6361/201321466

CrossRef Full Text | Google Scholar

Savić, D., Goosmann, R., Popović, L. Č., Marin, F., and Afanasiev, V. L. (2018). AGN Black Hole Mass Estimates Using Polarization in Broad Emission Lines. A&A 614, A120. doi:10.1051/0004-6361/201732220

CrossRef Full Text | Google Scholar

Savić, Đ., Popović, L. Č., Shablovinskaya, E., and Afanasiev, V. L. (2020). Estimating Supermassive Black Hole Masses in Active Galactic Nuclei Using Polarization of Broad Mg Ii, H α, and H β Lines. MNRAS 497, 3047–3054. doi:10.1093/mnras/staa2039

CrossRef Full Text | Google Scholar

Savorgnan, G. A. D., and Graham, A. W. (2016). Explaining the Reportedly Overmassive Black Holes in Early-type Galaxies with Intermediate-Scale Discs. Mon. Not. R. Astron. Soc. 457, 320–327. doi:10.1093/mnras/stv2713

CrossRef Full Text | Google Scholar

Scannapieco, C., Tissera, P. B., White, S. D. M., and Springel, V. (2008). Effects of Supernova Feedback on the Formation of Galaxy Discs. Mon. Not. R. Astron. Soc. 389, 1137–1149. doi:10.1111/j.1365-2966.2008.13678.x

CrossRef Full Text | Google Scholar

Schaye, J., and Dalla Vecchia, C. (2008). On the Relation between the Schmidt and Kennicutt-Schmidt star Formation Laws and its Implications for Numerical Simulations. Mon. Not. R. Astron. Soc. 383, 1210–1222. doi:10.1111/j.1365-2966.2007.12639.x

CrossRef Full Text | Google Scholar

Schaye, J., Vecchia, C. D., Booth, C. M., Wiersma, R. P. C., Theuns, T., Haas, M. R., et al. (2010). The Physics Driving the Cosmic star Formation History. Mon. Not. R. Astron. Soc. 402, 1536–1560. doi:10.1111/j.1365-2966.2009.16029.x

CrossRef Full Text | Google Scholar

Schindler, J.-T., Fan, X., Novak, M., Venemans, B., Walter, F., Wang, F., et al. (2021). A Closer Look at Two of the Most Luminous Quasars in the Universe. ApJ 906, 12. doi:10.3847/1538-4357/abc554

CrossRef Full Text | Google Scholar

Schmidt, E. O., Oio, G. A., Ferreiro, D., Vega, L., and Weidmann, W. (2018). Asymmetric Emission of the [OIII]λ5007 Profile in Narrow-Line Seyfert 1 Galaxies. A&A 615, A13. doi:10.1051/0004-6361/201731557

CrossRef Full Text | Google Scholar

Schmidt, M. (1959). The Rate of Star Formation. ApJ 129, 243. doi:10.1086/146614

CrossRef Full Text | Google Scholar

Schmidt, M. (1959). The Rate of Star Formation. ApJ 129, 243. doi:10.1086/146614

CrossRef Full Text | Google Scholar

Schramm, M., Wisotzki, L., and Jahnke, K. (2008). Host Galaxies of Bright High Redshift Quasars: Luminosities and Colours. A&A 478, 311–319. doi:10.1051/0004-6361:20077319

CrossRef Full Text | Google Scholar

Schreiber, C., Pannella, M., Elbaz, D., Béthermin, M., Inami, H., Dickinson, M., et al. (2015). TheHerschelview of the Dominant Mode of Galaxy Growth Fromz= 4 to the Present Day. A&A 575, A74. doi:10.1051/0004-6361/201425017

CrossRef Full Text | Google Scholar

Schulz, E. (2017). Scaling Relations of Mass, Velocity, and Radius for Disk Galaxies. ApJ 836, 151. doi:10.3847/1538-4357/aa5b88

CrossRef Full Text | Google Scholar

Schulze, A., and Wisotzki, L. (2014). Accounting for Selection Effects in the BH-Bulge Relations: No Evidence for Cosmological Evolution. MNRAS 438, 3422–3433. doi:10.1093/mnras/stt245710.1093/mnras/stt2457

CrossRef Full Text | Google Scholar

Schulze, A., and Wisotzki, L. (2011). Selection Effects in the Black Hole-Bulge Relation and its Evolution. A&A 535, A87. doi:10.1051/0004-6361/201117564

CrossRef Full Text | Google Scholar

Schwarzschild, M. (1979). A Numerical Model for a Triaxial Stellar System in Dynamical Equilibrium. ApJ 232, 236–247. doi:10.1086/157282

CrossRef Full Text | Google Scholar

Schweizer, F. (1986). Colliding and Merging Galaxies. Science 231, 227–234. doi:10.1126/science.231.4735.227

PubMed Abstract | CrossRef Full Text | Google Scholar

Sciarratta, M., Chiosi, C., D’Onofrio, M., and Cariddi, S. (2019). Cosmological Interpretation of the Color-Magnitude Diagrams of Galaxy Clusters. ApJ 870, 70. doi:10.3847/1538-4357/aaf00d

CrossRef Full Text | Google Scholar

Scott, N., Graham, A. W., and Schombert, J. (2013). The Supermassive Black Hole Mass-Spheroid Stellar Mass Relation for Sérsic and Core-Sérsic Galaxies. ApJ 768, 76. doi:10.1088/0004-637X/768/1/76

CrossRef Full Text | Google Scholar

S. di Serego Alighieri, S., Vernet, J., Cimatti, A., Lanzoni, B., Cassata, P., Ciotti, L., et al. (2005). The Evolution of Early-type Galaxies at Z ∼ 1 from the K20 Survey. A&A 442, 125–136. doi:10.1051/0004-6361:20053168

CrossRef Full Text | Google Scholar

Searle, L., Sargent, W. L. W., and Bagnuolo, W. G. (1973). The History of Star Formation and the Colors of Late-type Galaxies. ApJ 179, 427–438. doi:10.1086/151882

CrossRef Full Text | Google Scholar

Searle, L., and Zinn, R. (1978). Compositions of Halo Clusters and the Formation of the Galactic Halo. ApJ 225, 357–379. doi:10.1086/156499

CrossRef Full Text | Google Scholar

Sellwood, J. A. (2016). Bar Instability in Disk-Halo Systems. ApJ 819, 92. doi:10.3847/0004-637x/819/2/92

CrossRef Full Text | Google Scholar

Sersic, J. L. (1968). Atlas de Galaxias Australes. Cordoba, Argentina: observatorio astronomico.

Google Scholar

Seth, A. C., van den Bosch, R., Mieske, S., Baumgardt, H., Brok, M. d., Strader, J., et al. (2014). A Supermassive Black Hole in an Ultra-compact dwarf Galaxy. Nature 513, 398–400. doi:10.1038/nature13762

PubMed Abstract | CrossRef Full Text | Google Scholar

Shadmehri, M. (2015). On the Orbital Motion of Cold Clouds in Broad-Line Regions. Mon. Not. R. Astron. Soc. 451, 3671–3678. doi:10.1093/mnras/stv1212

CrossRef Full Text | Google Scholar

Shang, Z., Brotherton, M. S., Wills, B. J., Wills, D., Cales, S. L., Dale, D. A., et al. (2011). The Next Generation Atlas of Quasar Spectral Energy Distributions from Radio to X-Rays. ApJS 196, 2. doi:10.1088/0067-0049/196/1/2

CrossRef Full Text | Google Scholar

Shankar, F., Bernardi, M., and Haiman, Z. (2009). THE EVOLUTION OF THEMBH-σ RELATION INFERRED FROM THE AGE DISTRIBUTION OF LOCAL EARLY-TYPE GALAXIES AND ACTIVE GALACTIC NUCLEI EVOLUTION. ApJ 694, 867–878. doi:10.1088/0004-637X/694/2/867

CrossRef Full Text | Google Scholar

Shankar, F., Bernardi, M., Richardson, K., Marsden, C., Sheth, R. K., Allevato, V., et al. (2019). Black Hole Scaling Relations of Active and Quiescent Galaxies: Addressing Selection Effects and Constraining Virial Factors. MNRAS 485, 1278–1292. doi:10.1093/mnras/stz376

CrossRef Full Text | Google Scholar

Shankar, F., Bernardi, M., Sheth, R. K., Ferrarese, L., Graham, A. W., Savorgnan, G., et al. (2016). Selection Bias in Dynamically Measured Supermassive Black Hole Samples: its Consequences and the Quest for the Most Fundamental Relation. Mon. Not. R. Astron. Soc. 460, 3119–3142. doi:10.1093/mnras/stw678

CrossRef Full Text | Google Scholar

Shankar, F., Lapi, A., Salucci, P., De Zotti, G., and Danese, L. (2006). New Relationships between Galaxy Properties and Host Halo Mass, and the Role of Feedbacks in Galaxy Formation. ApJ 643, 14–25. doi:10.1086/502794

CrossRef Full Text | Google Scholar

Shankar, F., Marulli, F., Bernardi, M., Mei, S., Meert, A., and Vikram, V. (2013). Size Evolution of Spheroids in a Hierarchical Universe. Mon. Not. R. Astron. Soc. 428, 109–128. doi:10.1093/mnras/sts001

CrossRef Full Text | Google Scholar

Shankar, F., Marulli, F., Bernardi, M., Mei, S., Meert, A., and Vikram, V. (2013). Size Evolution of Spheroids in a Hierarchical Universe. MNRAS 428, 109–128. doi:10.1093/mnras/sts00110.1093/mnras/sts001

CrossRef Full Text | Google Scholar

Shankar, F., Weinberg, D. H., and Miralda-Escudé, J. (2009). Self-Consistent Models of the AGN and Black Hole Populations: Duty Cycles, Accretion Rates, and the Mean Radiative Efficiency. ApJ 690, 20–41. doi:10.1088/0004-637x/690/1/20

CrossRef Full Text | Google Scholar

Shapiro, S. L. (2005). Spin, Accretion, and the Cosmological Growth of Supermassive Black Holes. ApJ 620, 59–68. doi:10.1086/427065

CrossRef Full Text | Google Scholar

Shen, S., Mo, H. J., White, S. D. M., Blanton, M. R., Kauffmann, G., Voges, W., et al. (2003). The Size Distribution of Galaxies in the Sloan Digital Sky Survey. Monthly Notices R. Astronomical Soc. 343, 978–994. doi:10.1046/j.1365-8711.2003.06740.x

CrossRef Full Text | Google Scholar

Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., and Schneider, D. P. (2008). Biases in Virial Black Hole Masses: An SDSS Perspective. ApJ 680, 169–190. doi:10.1086/587475

CrossRef Full Text | Google Scholar

Shen, Y., and Ho, L. C. (2014). The Diversity of Quasars Unified by Accretion and Orientation. Nature 513, 210–213. doi:10.1038/nature13712

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Y., and Liu, X. (2012). Comparing Single-Epoch Virial Black Hole Mass Estimators for Luminous Quasars. ApJ 753, 125. doi:10.1088/0004-637X/753/2/125

CrossRef Full Text | Google Scholar

Shields, G. A., Gebhardt, K., Salviander, S., Wills, B. J., Xie, B., Brotherton, M. S., et al. (2003). The Black Hole-Bulge Relationship in Quasars. ApJ 583, 124–133. doi:10.1086/345348

CrossRef Full Text | Google Scholar

Shields, G. A., Menezes, K. L., Massart, C. A., and Vanden Bout, P. (2006). The Black Hole-Bulge Relationship for QSOs at High Redshift. ApJ 641, 683–688. doi:10.1086/500542

CrossRef Full Text | Google Scholar

Shuder, J. M. (1981). Emission-line-continuum Correlations in Active Galactic Nuclei. ApJ 244, 12–18. doi:10.1086/158678

CrossRef Full Text | Google Scholar

Silk, J., and Rees, M. J. (1998). Quasars and Galaxy Formation. Astron. Astrophysics 331, L1–L4.

Google Scholar

Silk, J. (1997). Feedback, Disk Self‐Regulation, and Galaxy Formation. ApJ 481, 703–709. doi:10.1086/304073

CrossRef Full Text | Google Scholar

Silk, J., and Mamon, G. A. (2012). The Current Status of Galaxy Formation. Res. Astron. Astrophys. 12, 917–946. doi:10.1088/1674-4527/12/8/004

CrossRef Full Text | Google Scholar

Sillanpaa, A., Haarala, S., Valtonen, M. J., Sundelius, B., and Byrd, G. G. (1988). OJ 287 - Binary Pair of Supermassive Black Holes. ApJ 325, 628–634. doi:10.1086/166033

CrossRef Full Text | Google Scholar

Siopis, C., Gebhardt, K., Lauer, T. R., Kormendy, J., Pinkney, J., Richstone, D., et al. (2009). A Stellar Dynamical Measurement of the Black Hole Mass in the Maser Galaxy NGC 4258. ApJ 693, 946–969. doi:10.1088/0004-637X/693/1/946

CrossRef Full Text | Google Scholar

Skibba, R. A., and Sheth, R. K. (2009). A Halo Model of Galaxy Colours and Clustering in the Sloan Digital Sky Survey. MNRAS 392, 1080–1091. doi:10.1111/j.1365-2966.2008.14007.x

CrossRef Full Text | Google Scholar

Skillman, E. D., Kennicutt, R. C., and Hodge, P. W. (1989). Oxygen Abundances in Nearby Dwarf Irregular Galaxies. ApJ 347, 875. doi:10.1086/168178

CrossRef Full Text | Google Scholar

Smith, R. J., Hudson, M. J., Lucey, J. R., Nelan, J. E., and Wegner, G. A. (2006). The NOAO Fundamental Plane Survey - III. Variations in the Stellar Populations of Red-Sequence Galaxies from the Cluster Core to the Virial Radius. Monthly Notices R. Astronomical Soc. 369, 1419–1436. doi:10.1111/j.1365-2966.2006.10393.x

CrossRef Full Text | Google Scholar

Smith, R. J. (2014). Variations in the Initial Mass Function in Early-type Galaxies: a Critical Comparison between Dynamical and Spectroscopic Results. Mon. Not. R. Astron. Soc. 443, L69–L73. doi:10.1093/mnrasl/slu082

CrossRef Full Text | Google Scholar

Śniegowska, M., Kozowski, S., Czerny, B., Panda, S., and Hryniewicz, K. (2020). Quasar Main Sequence in the UV Plane. ApJ 900, 64. doi:10.3847/1538-4357/aba620

CrossRef Full Text | Google Scholar

Somerville, R. S., Behroozi, P., Pandya, V., Dekel, A., Faber, S. M., Fontana, A., et al. (2018). The Relationship between Galaxy and Dark Matter Halo Size from Z ∼ 3 to the Present. Mon. Not. R. Astron. Soc. 473, 2714–2736. doi:10.1093/mnras/stx2040

CrossRef Full Text | Google Scholar

Somerville, R. S., and Davé, R. (2015). Physical Models of Galaxy Formation in a Cosmological Framework. Annu. Rev. Astron. Astrophys. 53, 51–113. doi:10.1146/annurev-astro-082812-140951

CrossRef Full Text | Google Scholar

Somerville, R. S., and Primack, J. R. (1999). Semi-analytic Modelling of Galaxy Formation: the Local Universe. Mon. Not. R. Astron. Soc. 310, 1087–1110. doi:10.1046/j.1365-8711.1999.03032.x

CrossRef Full Text | Google Scholar

Speagle, J. S., Steinhardt, C. L., Capak, P. L., and Silverman, J. D. (2014). A HIGHLY CONSISTENT FRAMEWORK FOR THE EVOLUTION OF THE STAR-FORMING "MAIN SEQUENCE" FROM z ∼ 0-6. ApJS 214, 15. doi:10.1088/0067-0049/214/2/15

CrossRef Full Text | Google Scholar

Springel, V., White, S. D. M., Jenkins, A., Frenk, C. S., Yoshida, N., Gao, L., et al. (2005). Simulations of the Formation, Evolution and Clustering of Galaxies and Quasars. Nature 435, 629–636. doi:10.1038/nature03597

PubMed Abstract | CrossRef Full Text | Google Scholar

Springob, C. M., Magoulas, C., Colless, M., Mould, J., Erdoğdu, P., Jones, D. H., et al. (2014). The 6dF Galaxy Survey: peculiar Velocity Field and Cosmography. Mon. Not. R. Astron. Soc. 445, 2677–2697. doi:10.1093/mnras/stu1743

CrossRef Full Text | Google Scholar

Stacey, H. R., Lafontaine, A., and McKean, J. P. (2020). Smoke on the Water: CO and H2O in a Circumnuclear Disc Around a Quasar at Redshift 2.64. MNRAS 493, 5290–5300. doi:10.1093/mnras/staa494

CrossRef Full Text | Google Scholar

Stark, D. V., Kannappan, S. J., Wei, L. H., Baker, A. J., Leroy, A. K., Eckert, K. D., et al. (2013). The Fueling Diagram: Linking Galaxy Molecular-To-Atomic Gas Ratios to Interactions and Accretion. ApJ 769, 82. doi:10.1088/0004-637x/769/1/82

CrossRef Full Text | Google Scholar

Stasińska, G., Schaerer, D., and Leitherer, C. (2002). The Evolution of Emission Lines in HII Galaxies as a Probe of Interaction between Stellar and Interstellar Component. Astrophysics Space Sci. 281, 335–336. doi:10.1023/A:1019574425717

CrossRef Full Text | Google Scholar

Steidel, C. C., Rudie, G. C., Strom, A. L., Pettini, M., Reddy, N. A., Shapley, A. E., et al. (2014). STRONG NEBULAR LINE RATIOS IN the SPECTRA Ofz∼ 2-3 STAR FORMING GALAXIES: FIRST RESULTS from KBSS-MOSFIRE. ApJ 795, 165. doi:10.1088/0004-637X/795/2/165

CrossRef Full Text | Google Scholar

Steinmetz, M., and Navarro, J. F. (1999). The Cosmological Origin of the Tully‐Fisher Relation. ApJ 513, 555–560. doi:10.1086/306904

CrossRef Full Text | Google Scholar

Stewart, K. R., Brooks, A. M., Bullock, J. S., Maller, A. H., Diemand, J., Wadsley, J., et al. (2013). Angular Momentum Acquisition in Galaxy Halos. ApJ 769, 74. doi:10.1088/0004-637X/769/1/74

CrossRef Full Text | Google Scholar

Stewart, K. R., Bullock, J. S., Wechsler, R. H., and Maller, A. H. (2009). Gas-rich Mergers in LCDM: Disk Survivability and the Baryonic Assembly of Galaxies. ApJ 702, 307–317. doi:10.1088/0004-637X/702/1/307

CrossRef Full Text | Google Scholar

Stott, J. P., Pimbblet, K. A., Edge, A. C., Smith, G. P., and Wardlow, J. L. (2009). The Evolution of the Red Sequence Slope in Massive Galaxy Clusters. Mon. Not. R. Astron. Soc. 394, 2098–2108. doi:10.1111/j.1365-2966.2009.14477.x

CrossRef Full Text | Google Scholar

Strateva, I. V., Strauss, M. A., Hao, L., Schlegel, D. J., Hall, P. B., Gunn, J. E., et al. (2003). Double-peaked Low-Ionization Emission Lines in Active Galactic Nuclei. Astron. J. 126, 1720–1749. doi:10.1086/378367

CrossRef Full Text | Google Scholar

Strazzullo, V., Gobat, R., Daddi, E., Onodera, M., Carollo, M., Dickinson, M., et al. (2013). GALAXY EVOLUTION IN OVERDENSE ENVIRONMENTS AT HIGH REDSHIFT: PASSIVE EARLY-TYPE GALAXIES IN A CLUSTER ATz∼ 2. ApJ 772, 118. doi:10.1088/0004-637X/772/2/118

CrossRef Full Text | Google Scholar

Gravity Collaboration Sturm, E., Dexter, J., Pfuhl, O., Stock, M. R., Davies, R. I., Eckart, A., et al. (2018). Spatially Resolved Rotation of the Broad-Line Region of a Quasar at Sub-parsec Scale. Nature 563, 657–660. doi:10.1038/s41586-018-0731-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Sulentic, J., and Arp, H. C. (1983). Are Quasars Nearby/NGC4319 and MARKARIAN205. Sky& Tel 65, 322.

Google Scholar

Sulentic, J., Marziani, P., and Zamfir, S. (2011). The Case for Two Quasar Populations. Baltic Astron. 20, 427–434. doi:10.1515/astro-2017-0314

CrossRef Full Text | Google Scholar

Sulentic, J. W., Zamfir, S., Marziani, P., and Dultzin, D. (2008). Our Search for an H-R Diagram of Quasars. Revista Mexicana de Astronomia y Astrofisica Conf. Ser. 32, 51–58.

Google Scholar

Sulentic, J. W., and Arp, H. (1987). The Galaxy-Quasar Connection: NGC 4319 and Markarian 205. II. Spectroscopy. ApJ 319, 693. doi:10.1086/165490

CrossRef Full Text | Google Scholar

Sulentic, J. W., Bachev, R., Marziani, P., Negrete, C. A., and Dultzin, D. (2007). Civλ1549 as an Eigenvector 1 Parameter for Active Galactic Nuclei. ApJ 666, 757–777. doi:10.1086/519916

CrossRef Full Text | Google Scholar

Sulentic, J. W., del Olmo, A., Marziani, P., Martínez-Carballo, M. A., D’Onofrio, M., Dultzin, D., et al. (2017). What Does CIVλ1549 Tell Us about the Physical Driver of the Eigenvector Quasar Sequence? A&A 608, A122. doi:10.1051/0004-6361/201630309

CrossRef Full Text | Google Scholar

Sulentic, J. W., Marziani, P., and Dultzin-Hacyan, D. (2000). Phenomenology of Broad Emission Lines in Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 38, 521–571. doi:10.1146/annurev.astro.38.1.521

CrossRef Full Text | Google Scholar

Sulentic, J. W., and Marziani, P. (2015). Quasars in the 4D Eigenvector 1 Context: a Stroll Down Memory Lane. Front. Astron. Space Sci. 2, 6. doi:10.3389/fspas.2015.00006

CrossRef Full Text | Google Scholar

Sulentic, J. W., Marziani, P., Zamanov, R., Bachev, R., Calvani, M., and Dultzin-Hacyan, D. (2002). Average Quasar Spectra in the Context of Eigenvector 1. ApJL 566, L71–L75. doi:10.1086/339594

CrossRef Full Text | Google Scholar

Sulentic, J. W., Marziani, P., Zwitter, T., Dultzin-Hacyan, D., and Calvani, M. (2000). The Demise of the Classical Broad-Line Region in the Luminous Quasar PG 1416−129. ApJL 545, L15–L18. doi:10.1086/317330

CrossRef Full Text | Google Scholar

Sulentic, J. W., Repetto, P., Stirpe, G. M., Marziani, P., Dultzin-Hacyan, D., and Calvani, M. (2006). VLT/ISAAC Spectra of the Hβregion in Intermediate-Redshift Quasars. A&A 456, 929–939. doi:10.1051/0004-6361:20054153

CrossRef Full Text | Google Scholar

Sulentic, J. W., Stirpe, G. M., Marziani, P., Zamanov, R., Calvani, M., and Braito, V. (2004). VLT/ISAAC Spectra of the Hβregion in Intermediate Redshift Quasars. A&A 423, 121–132. doi:10.1051/0004-6361:20035912

CrossRef Full Text | Google Scholar

Sulentic, J. W., Zamfir, S., Marziani, P., Bachev, R., Calvani, M., and Dultzin-Hacyan, D. (2003). Radio-loud Active Galactic Nuclei in the Context of the Eigenvector 1 Parameter Space. ApJ 597, L17–L20. doi:10.1086/379754

CrossRef Full Text | Google Scholar

Sulentic, J. W., Zwitter, T., Marziani, P., and Dultzin-Hacyan, D. (2000). Eigenvector 1: An Optimal Correlation Space for Active Galactic Nuclei. ApJL 536, L5–L9. doi:10.1086/312717

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J., and Shen, Y. (2015). Dissecting the Quasar Main Sequence: Insight from Host Galaxy Properties. ApJ 804, L15. doi:10.1088/2041-8205/804/1/L15

CrossRef Full Text | Google Scholar

Swaters, R. (1999). “Dark Matter in Late-type Dwarf Galaxies,” in Galaxy Dynamics - A Rutgers Symposium. Editors D. R. Merritt, M. Valluri, and J. A. Sellwood (California, United States: Astronomical Society of the Pacific Conference Series), 182, 369.

Google Scholar

Swaters, R. A., Madore, B. F., and Trewhella, M. (2000). High-Resolution Rotation Curves of Low Surface Brightness Galaxies. Astrophysical J. Lett 531, L107–L110. doi:10.1086/312540

PubMed Abstract | CrossRef Full Text | Google Scholar

Swaters, R. A., van Albada, T. S., van der Hulst, J. M., and Sancisi, R. (2002). The Westerbork HI Survey of Spiral and Irregular Galaxies. A&A 390, 829–861. doi:10.1051/0004-6361:20011755

CrossRef Full Text | Google Scholar

Sweet, S. M., Drinkwater, M. J., Meurer, G., Bekki, K., Dopita, M. A., Kilborn, V., et al. (2014). Choirs H I Galaxy Groups: The Metallicity of Dwarf Galaxies. ApJ 782, 35. doi:10.1088/0004-637X/782/1/35

CrossRef Full Text | Google Scholar

Sądowski, A., Narayan, R., McKinney, J. C., and Tchekhovskoy, A. (2014). Numerical Simulations of Super-critical Black Hole Accretion Flows in General Relativity. MNRAS 439, 503–520. doi:10.1093/mnras/stt2479

CrossRef Full Text | Google Scholar

Tacchella, S., Dekel, A., Carollo, C. M., Ceverino, D., DeGraf, C., Lapiner, S., et al. (2016). The Confinement of star-forming Galaxies into a Main Sequence through Episodes of Gas Compaction, Depletion and Replenishment. Mon. Not. R. Astron. Soc. 457, 2790–2813. doi:10.1093/mnras/stw131

CrossRef Full Text | Google Scholar

Talbot, R. J. J., and Arnett, W. D. (1975). The Evolution of Galaxies. IV - Highly Flattened Disks. ApJ 197, 551–570. doi:10.1086/153543

CrossRef Full Text | Google Scholar

Tan, Q.-H., Gao, Y., Kohno, K., Xia, X.-Y., Omont, A., Hao, C.-N., et al. (2019). Resolving the Interstellar Medium in Ultraluminous Infrared QSO Hosts with ALMA. ApJ 887, 24. doi:10.3847/1538-4357/ab50be

CrossRef Full Text | Google Scholar

Tanaka, M., Kodama, T., Arimoto, N., Okamura, S., Umetsu, K., Shimasaku, K., et al. (2005). The Build-Up of the Colour-Magnitude Relation as a Function of Environment. Mon. Not. R. Astron. Soc. 362, 268–288. doi:10.1111/j.1365-2966.2005.09300.x

CrossRef Full Text | Google Scholar

Tantalo, R., Chiosi, C., and Bressan, A. (1998). Ages and Metallicities in Elliptical Galaxies from the H_beta, <Fe>, and Mg_2 Diagnostics. AAp 333, 419–432.

Google Scholar

Tantalo, R., Chiosi, C., Bressan, A., and Fagotto, F. (1996). Spectro-photometric Evolution of Elliptical Galaxies. II. Models with Infall. Astron. Astrophysics 311, 361–383.

Google Scholar

Tantalo, R., Chiosi, C., Bressan, A., Marigo, P., and Portinari, L. (1998). Spectro-photometric Evolution of Elliptical Galaxies. III. Infall Models with Gradients in Mass Density and star Formation. Astron. Astrophysics 335, 823–846.

Google Scholar

Tantalo, R. (2004). Measuring Age, Metallicity and Abundance Ratios from Absorption Line Indices. Mem. Soc. It. Fisica 75, 202. doi:10.1111/j.1365-2966.2004.08123.x

CrossRef Full Text | Google Scholar

Tantalo, R., and Chiosi, C. (2004). Measuring Age, Metallicity and Abundance Ratios from Absorption-Line Indices. MNRAS 353, 917–940. doi:10.1111/j.1365-2966.2004.08123.x

CrossRef Full Text | Google Scholar

Tantalo, R., Chiosi, C., and Piovan, L. (2007). New Response Functions for Absorption-Line Indices from High-Resolution Spectra. A&A 462, 481–494. doi:10.1051/0004-6361:20053774

CrossRef Full Text | Google Scholar

Tantalo, R., and Chiosi, C. (2004). Star Formation History in Early-type Galaxies - I. The Line Absorption Indices Diagnostics. MNRAS 353, 405–421. doi:10.1111/j.1365-2966.2004.08070.x

CrossRef Full Text | Google Scholar

Targett, T. A., Dunlop, J. S., McLure, R. J., Best, P. N., Cirasuolo, M., and Almaini, O. (2011). A Near-Infrared Morphological Comparison of High-Redshift Submillimetre and Radio Galaxies: Massive star-forming Discs versus Relaxed Spheroids. MNRAS 412, 295–317. doi:10.1111/j.1365-2966.2010.17905.x

CrossRef Full Text | Google Scholar

Taylor, A. R. (2007). “The Square Kilometre Array,” in A Giant Step: From Milli- to Micro-arcsecond Astrometry. Editors W. J. Jin, I. Platais, and M. A. C. Perryman, 3, 164–169. doi:10.1017/S1743921308018954

CrossRef Full Text | Google Scholar

Teerikorpi, P. (2011). On Öpik's Distance Evaluation Method in a Cosmological Context. A&A 531, A10. doi:10.1051/0004-6361/201116680

CrossRef Full Text | Google Scholar

Temple, M. J., Ferland, G. J., Rankine, A. L., Hewett, P. C., Badnell, N. R., Ballance, C. P., et al. (2020). Fe III Emission in Quasars: Evidence for a Dense Turbulent Medium. MNRAS 496, 2565–2576. doi:10.1093/mnras/staa1717

CrossRef Full Text | Google Scholar

Terlevich, A. I., Caldwell, N., and Bower, R. G. (2001). The Colour-Magnitude Relation for Galaxies in the Coma Cluster. Mon. Not. R. Astron. Soc. 326, 1547–1562. doi:10.1111/j.1365-2966.2001.04702.x

CrossRef Full Text | Google Scholar

Terlevich, R., Davies, R. L., Faber, S. M., and Burstein, D. (1981). The Metallicities, Velocity Dispersions and True Shapes of Elliptical Galaxies. Monthly Notices R. Astronomical Soc. 196, 381–395. doi:10.1093/mnras/196.2.381

CrossRef Full Text | Google Scholar

Terrazas, B. A., Bell, E. F., Pillepich, A., Nelson, D., Somerville, R. S., Genel, S., et al. (2020). The Relationship between Black Hole Mass and Galaxy Properties: Examining the Black Hole Feedback Model in IllustrisTNG. Mon. Not. R. Astron. Soc. 493, 1888–1906. doi:10.1093/mnras/staa374

CrossRef Full Text | Google Scholar

Thomas, D., Maraston, C., Bender, R., and de Oliveira, C. M. (2005). The Epochs of Early‐Type Galaxy Formation as a Function of Environment. ApJ 621, 673–694. doi:10.1086/426932

CrossRef Full Text | Google Scholar

Thomas, D., and Maraston, C. (2003). The Impact ofα/Fe Enhanced Stellar Evolutionary Tracks on the Ages of Elliptical Galaxies. A&A 401, 429–432. doi:10.1051/0004-6361:20030153

CrossRef Full Text | Google Scholar

Thomas, J., Ma, C.-P., McConnell, N. J., Greene, J. E., Blakeslee, J. P., and Janish, R. (2016). A 17-Billion-Solar-Mass Black Hole in a Group Galaxy with a Diffuse Core. Nature 532, 340–342. doi:10.1038/nature17197

PubMed Abstract | CrossRef Full Text | Google Scholar

Tillson, H., Miller, L., and Devriendt, J. (2011). The Environment and Redshift Dependence of Accretion on to Dark Matter Haloes and Subhaloes. Mon. Not. R. Astron. Soc. 417, 666–680. doi:10.1111/j.1365-2966.2011.19311.x

CrossRef Full Text | Google Scholar

Tinsley, B. M. (1980). Evolution of the Stars and Gas in Galaxies. Fundamentals Cosmic Phys. 5, 287–388.

Google Scholar

Toft, S., Gallazzi, A., Zirm, A., Wold, M., Zibetti, S., Grillo, C., et al. (2012). DEEP ABSORPTION LINE STUDIES OF QUIESCENT GALAXIES ATz∼ 2: THE DYNAMICAL-MASS-SIZE RELATION AND FIRST CONSTRAINTS ON THE FUNDAMENTAL PLANE. ApJ 754, 3. doi:10.1088/0004-637X/754/1/3

CrossRef Full Text | Google Scholar

Tollerud, E. J., Bullock, J. S., Graves, G. J., and Wolf, J. (2011). From Galaxy Clusters to Ultra-faint Dwarf Spheroidals: A Fundamental Curve Connecting Dispersion-Supported Galaxies to Their Dark Matter Halos. ApJ 726, 108. doi:10.1088/0004-637X/726/2/108

CrossRef Full Text | Google Scholar

Tolstoy, E., Hill, V., and Tosi, M. (2009). Star-formation Histories, Abundances, and Kinematics of Dwarf Galaxies in the Local Group. Annu. Rev. Astron. Astrophys. 47, 371–425. doi:10.1146/annurev-astro-082708-101650

CrossRef Full Text | Google Scholar

Toomre, A., and Toomre, J. (1972). Galactic Bridges and Tails. ApJ 178, 623–666. doi:10.1086/151823

CrossRef Full Text | Google Scholar

Trager, S. C., Faber, S. M., Worthey, G., and González, J. J. (2000). The Stellar Population Histories of Early-type Galaxies. II. Controlling Parameters of the Stellar Populations. AJ 120, 165–188. doi:10.1086/301442

CrossRef Full Text | Google Scholar

Trager, S. C., Faber, S. M., Worthey, G., and González, J. J. (2000). The Stellar Population Histories of Local Early-type Galaxies. I. Population Parameters. AJ 119, 1645–1676. doi:10.1086/301299

CrossRef Full Text | Google Scholar

Trakhtenbrot, B. (2020). What Do Observations Tell Us about the Highest-Redshift Supermassive Black Holes? arXiv:2002.00972.

Google Scholar

Trakhtenbrot, B., and Netzer, H. (2012). Black Hole Growth to Z = 2 - I. Improved Virial Methods for Measuring MBH and L/LEdd. Monthly Notices R. Astronomical Soc. 427, 3081–3102. doi:10.1111/j.1365-2966.2012.22056.x

CrossRef Full Text | Google Scholar

Trakhtenbrot, B., Urry, C. M., Civano, F., Rosario, D. J., Elvis, M., Schawinski, K., et al. (2015). An Over-massive Black Hole in a Typical star-forming Galaxy, 2 Billion Years after the Big Bang. Science 349, 168–171. doi:10.1126/science.aaa4506

PubMed Abstract | CrossRef Full Text | Google Scholar

Tran, K. V. H. (2007). “A Keck Spectroscopic Study of MS˜1054–03 (z=0.83): Forming the Red Sequence,” in Cosmic Frontiers. Editors N. Metcalfe, and T. Shanks (California, United States: Astronomical Society of the Pacific Conference Series), 379, 348.

Google Scholar

Tremonti, C. A., Heckman, T. M., Kauffmann, G., Brinchmann, J., Charlot, S., White, S. D. M., et al. (2004). The Origin of the Mass‐Metallicity Relation: Insights from 53,000 Star‐forming Galaxies in the Sloan Digital Sky Survey. ApJ 613, 898–913. doi:10.1086/423264

CrossRef Full Text | Google Scholar

Treu, T., Ellis, R. S., Liao, T. X., van Dokkum, P. G., Tozzi, P., Coil, A., et al. (2005). The Assembly History of Field Spheroidals: Evolution of Mass‐to‐Light Ratios and Signatures of Recent Star Formation. ApJ 633, 174–197. doi:10.1086/444585

CrossRef Full Text | Google Scholar

Treu, T., Woo, J. H., Malkan, M. A., and Blandford, R. D. (2007). Cosmic Evolution of Black Holes and Spheroids. II. Scaling Relations Atz = 0.36. ApJ 667, 117–130. doi:10.1086/520633

CrossRef Full Text | Google Scholar

Trujillo, I., Feulner, G., Goranova, Y., Hopp, U., Longhetti, M., Saracco, P., et al. (2006). Extremely Compact Massive Galaxies at Z 1.4. Monthly Notices R. Astronomical Soc. Lett. 373, L36–L40. doi:10.1111/j.1745-3933.2006.00238.x

CrossRef Full Text | Google Scholar

Trujillo, I., Förster Schreiber, N. M., Rudnick, G., Barden, M., Franx, M., Rix, H. W., et al. (2007). Size Evolution of Galaxies since Z∼3:Combining Sdss, Gems and Fires. Astrophysics Space Sci. Proc. 3, 481–486. doi:10.1007/978-1-4020-5573-7_83

CrossRef Full Text | Google Scholar

Tully, R. B., and Fisher, J. R. (1977). Reprint of 1977A&A.54\enleadertwodots 661T. A New Method of Determining Distance to Galaxies. Astron. Astrophysics 500, 105–117.

Google Scholar

Tully, R. B., Mould, J. R., and Aaronson, M. (1982). A Color-Magnitude Relation for Spiral Galaxies. ApJ 257, 527–537. doi:10.1086/160009

CrossRef Full Text | Google Scholar

Tully, R. B., Pierce, M. J., Huang, J.-S., Saunders, W., Verheijen, M. A. W., and Witchalls, P. L. (1998). Global Extinction in Spiral Galaxies. Astronomical J. 115, 2264–2272. doi:10.1086/300379

CrossRef Full Text | Google Scholar

Tytler, D., and Fan, X.-M. (1992). Systematic QSO Emission-Line Velocity Shifts and New Unbiased Redshifts. ApJS 79, 1–36. doi:10.1086/191642

CrossRef Full Text | Google Scholar

Übler, H., Förster Schreiber, N. M., Genzel, R., Wisnioski, E., Wuyts, S., Lang, P., et al. (2017). The Evolution of the Tully-Fisher Relation Betweenz∼ 2.3 Andz∼ 0.9 with KMOS^3D. ApJ 842, 121. doi:10.3847/1538-4357/aa7558

CrossRef Full Text | Google Scholar

Übler, H., Naab, T., Oser, L., Aumer, M., Sales, L. V., and White, S. D. M. (2014). Why Stellar Feedback Promotes Disc Formation in Simulated Galaxies. Mon. Not. R. Astron. Soc. 443, 2092–2111. doi:10.1093/mnras/stu1275

CrossRef Full Text | Google Scholar

Ünal, C., and Loeb, A. (2020). On Spin Dependence of the Fundamental Plane of Black Hole Activity. MNRAS 495, 278–284. doi:10.1093/mnras/staa1119

CrossRef Full Text | Google Scholar

Urry, C. M., and Padovani, P. (1995). Unified Schemes for Radio-Loud Active Galactic Nuclei. PASP 107, 803. doi:10.1086/133630

CrossRef Full Text | Google Scholar

Vaduvescu, O., McCall, M. L., and Richer, M. G. (2007). Chemical Properties of Star-Forming Dwarf Galaxies. Astron. J. 134, 604–616. doi:10.1086/518865

CrossRef Full Text | Google Scholar

Vaduvescu, O., McCall, M. L., Richer, M. G., and Fingerhut, R. L. (2005). Infrared Properties of Star-forming Dwarf Galaxies. I. Dwarf Irregular Galaxies in the Local Volume. Astron. J. 130, 1593–1626. doi:10.1086/444498

CrossRef Full Text | Google Scholar

Valentinuzzi, T., Fritz, J., Poggianti, B. M., Cava, A., Bettoni, D., Fasano, G., et al. (2010). Superdense Massive Galaxies in Wings Local Clusters. ApJ 712, 226–237. doi:10.1088/0004-637X/712/1/226

CrossRef Full Text | Google Scholar

Valentinuzzi, T., Poggianti, B. M., Fasano, G., D’Onofrio, M., Moretti, A., Ramella, M., et al. (2011). The Red-Sequence of 72 WINGS Local Galaxy Clusters. A&A 536, A34. doi:10.1051/0004-6361/201117522

CrossRef Full Text | Google Scholar

Valluri, M., Merritt, D., and Emsellem, E. (2004). Difficulties with Recovering the Masses of Supermassive Black Holes from Stellar Kinematical Data. ApJ 602, 66–92. doi:10.1086/380896

CrossRef Full Text | Google Scholar

Valtonen, M. J., Ciprini, S., and Lehto, H. J. (2012). On the Masses of OJ287 Black Holes. Monthly Notices R. Astronomical Soc. 427, 77–83. doi:10.1111/j.1365-2966.2012.21861.x

CrossRef Full Text | Google Scholar

van Albada, T. S., Bahcall, J. N., Begeman, K., and Sancisi, R. (1985). Distribution of Dark Matter in the Spiral Galaxy NGC 3198. ApJ 295, 305–313. doi:10.1086/163375

CrossRef Full Text | Google Scholar

van de Sande, J., Kriek, M., Franx, M., Bezanson, R., and van Dokkum, P. G. (2014). THE FUNDAMENTAL PLANE OF MASSIVE QUIESCENT GALAXIES OUT TO z ∼ 2. ApJ 793, L31. doi:10.1088/2041-8205/793/2/L31

CrossRef Full Text | Google Scholar

van de Sande, J., Kriek, M., Franx, M., van Dokkum, P. G., Bezanson, R., Bouwens, R. J., et al. (2013). STELLAR KINEMATICS OFz∼ 2 GALAXIES AND THE INSIDE-OUT GROWTH OF QUIESCENT GALAXIES,. ApJ 771, 85. doi:10.1088/0004-637x/771/2/85

CrossRef Full Text | Google Scholar

van den Bosch, F. C. (2000). “Constraints on Galaxy Formation from the Tully-Fisher Relation,” in Dynamics of Galaxies: From the Early Universe to the Present. Editors F. Combes, G. A. Mamon, and V. Charmandaris (California, United States: Astronomical Society of the Pacific Conference Series), 197, 179.

Google Scholar

van den Bosch, R. C. E., Greene, J. E., Braatz, J. A., Constantin, A., and Kuo, C.-Y. (2016). TOWARD PRECISION SUPERMASSIVE BLACK HOLE MASSES USING MEGAMASER DISKS. ApJ 819, 11. doi:10.3847/0004-637x/819/1/11

CrossRef Full Text | Google Scholar

van den Bosch, R. C. E., van de Ven, G., Verolme, E. K., Cappellari, M., and de Zeeuw, P. T. (2008). Triaxial Orbit Based Galaxy Models with an Application to the (Apparent) Decoupled Core Galaxy NGC 4365. Monthly Notices RAS 385, 647–666. doi:10.1111/j.1365-2966.2008.12874.x

CrossRef Full Text | Google Scholar

van der Wel, A., Franx, M., van Dokkum, P. G., Skelton, R. E., Momcheva, I. G., Whitaker, K. E., et al. (2014). 3D-HST+CANDELS: THE EVOLUTION OF THE GALAXY SIZE-MASS DISTRIBUTION SINCEz= 3. ApJ 788, 28. doi:10.1088/0004-637x/788/1/28

CrossRef Full Text | Google Scholar

van der Wel, A., Rix, H.-W., Wuyts, S., McGrath, E. J., Koekemoer, A. M., Bell, E. F., et al. (2011). THE MAJORITY OF COMPACT MASSIVE GALAXIES ATz∼ 2 ARE DISK DOMINATED. ApJ 730, 38. doi:10.1088/0004-637X/730/1/38

CrossRef Full Text | Google Scholar

van Dokkum, P. G., Franx, M., Kriek, M., Holden, B., Illingworth, G. D., Magee, D., et al. (2008). Confirmation of the Remarkable Compactness of Massive Quiescent Galaxies at Z ∼ 2.3: Early-type Galaxies Did Not Form in a Simple Monolithic Collapse. ApJ 677, L5–L8. doi:10.1086/587874

CrossRef Full Text | Google Scholar

van Dokkum, P. G., Kriek, M., and Franx, M. (2009). A High Stellar Velocity Dispersion for a Compact Massive Galaxy at Redshift Z = 2.186. Nature 460, 717–719. doi:10.1038/nature08220

PubMed Abstract | CrossRef Full Text | Google Scholar

van Dokkum, P. G., and van der Marel, R. P. (2007). The Star Formation Epoch of the Most Massive Early‐Type Galaxies. ApJ 655, 30–50. doi:10.1086/509633

CrossRef Full Text | Google Scholar

van Dokkum, P. G., Whitaker, K. E., Brammer, G., Franx, M., Kriek, M., Labbé, I., et al. (2010). THE GROWTH OF MASSIVE GALAXIES SINCEz= 2. ApJ 709, 1018–1041. doi:10.1088/0004-637X/709/2/1018

CrossRef Full Text | Google Scholar

van Dokkum, P. G., Whitaker, K. E., Brammer, G., Franx, M., Kriek, M., Labbé, I., et al. (2010). THE GROWTH OF MASSIVE GALAXIES SINCEz= 2. ApJ 709, 1018–1041. doi:10.1088/0004-637X/709/2/1018

CrossRef Full Text | Google Scholar

van Loon, J. T., and Sansom, A. E. (2015). An Evolutionary Missing Link? A Modest-Mass Early-type Galaxy Hosting an Oversized Nuclear Black Hole. Mon. Not. R. Astron. Soc. 453, 2342–2349. doi:10.1093/mnras/stv1787

CrossRef Full Text | Google Scholar

van Zee, L., Skillman, E. D., and Salzer, J. J. (1998). Neutral Gas Distributions and Kinematics of Five Blue Compact Dwarf Galaxies. Astronomical J. 116, 1186–1204. doi:10.1086/300510

CrossRef Full Text | Google Scholar

Vayner, A., Wright, S. A., Murray, N., Armus, L., Boehle, A., Cosens, M., et al. (2021). A Spatially-Resolved Survey of Distant Quasar Host Galaxies: II. Photoionization and Kinematics of the ISM. arXiv:2101.08291.

Google Scholar

Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., Cenarro, A. J., Beasley, M. A., Cardiel, N., et al. (2010). Evolutionary Stellar Population Synthesis with MILES - I. The Base Models and a New Line index System. MNRAS 404, 1639–1671. doi:10.1111/j.1365-2966.2010.16407.x

CrossRef Full Text | Google Scholar

Veilleux, S., Cecil, G., and Bland-Hawthorn, J. (2005). Galactic Winds. Annu. Rev. Astron. Astrophys. 43, 769–826. doi:10.1146/annurev.astro.43.072103.150610

CrossRef Full Text | Google Scholar

Vergani, D., Epinat, B., Contini, T., Tasca, L., Tresse, L., Amram, P., et al. (2012). MASSIV: Mass Assembly Survey with SINFONI in VVDS. A&A 546, A118. doi:10.1051/0004-6361/201118453

CrossRef Full Text | Google Scholar

Verheijen, M. A. W. (1997). “The Ursa Major Cluster of Galaxies: TF-Relations and Dark Matter,”. Ph.D. thesis (Netherlands: Univ. Groningen).

Google Scholar

Verheijen, M. A. W. (2001). The Ursa Major Cluster of Galaxies. V. HiRotation Curve Shapes and the Tully‐Fisher Relations. ApJ 563, 694–715. doi:10.1086/323887

CrossRef Full Text | Google Scholar

Verolme, E. K., Cappellari, M., Copin, Y., van der Marel, R. P., Bacon, R., Bureau, M., et al. (2002). A SAURON Study of M32: Measuring the Intrinsic Flattening and the central Black Hole Mass. Mon. Not. R. Astron. Soc. 335, 517–525. doi:10.1046/j.1365-8711.2002.05664.x

CrossRef Full Text | Google Scholar

Vestergaard, M., and Peterson, B. M. (2006). Determining Central Black Hole Masses in Distant Active Galaxies and Quasars. II. Improved Optical and UV Scaling Relationships. ApJ 641, 689–709. doi:10.1086/500572

CrossRef Full Text | Google Scholar

Visvanathan, N., and Sandage, A. (1977). The Color-Absolute Magnitude Relation for E and S0 Galaxies. I - Calibration and Tests for Universality Using Virgo and Eight Other Nearby Clusters. ApJ 216, 214–226. doi:10.1086/155464

CrossRef Full Text | Google Scholar

Vitvitska, M., Klypin, A. A., Kravtsov, A. V., Wechsler, R. H., Primack, J. R., and Bullock, J. S. (2002). The Origin of Angular Momentum in Dark Matter Halos. ApJ 581, 799–809. doi:10.1086/344361

CrossRef Full Text | Google Scholar

Vogelsberger, M., Genel, S., Springel, V., Torrey, P., Sijacki, D., Xu, D., et al. (2014). Properties of Galaxies Reproduced by a Hydrodynamic Simulation. Nature 509, 177–182. doi:10.1038/nature13316

PubMed Abstract | CrossRef Full Text | Google Scholar

Volonteri, M. (2010). Formation of Supermassive Black Holes. Astron. Astrophys Rev. 18, 279–315. doi:10.1007/s00159-010-0029-x

CrossRef Full Text | Google Scholar

Volonteri, M. (2007). Gravitational Recoil: Signatures on the Massive Black Hole Population. ApJ 663, L5–L8. doi:10.1086/519525

CrossRef Full Text | Google Scholar

Walsh, J. L., Barth, A. J., Ho, L. C., and Sarzi, M. (2013). The M87 Black Hole Mass from Gas-Dynamical Models of Space Telescope Imaging Spectrograph Observations. ApJ 770, 86. doi:10.1088/0004-637X/770/2/86

CrossRef Full Text | Google Scholar

Walter, F., Bertoldi, F., Carilli, C., Cox, P., Lo, K. Y., Neri, R., et al. (2003). Molecular Gas in the Host Galaxy of a Quasar at Redshift Z = 6.42. Nature 424, 406–408. doi:10.1038/nature01821

PubMed Abstract | CrossRef Full Text | Google Scholar

Wandel, A. (2002). Black Holes of Active and Quiescent Galaxies. I. The Black Hole-Bulge Relation Revisited. ApJ 565, 762–772. doi:10.1086/338134

CrossRef Full Text | Google Scholar

Wandel, A. (1999). The Black Hole-To-Bulge Mass Relation in Active Galactic Nuclei. Astrophysical J. Lett 519, L39–L42. doi:10.1086/312106

CrossRef Full Text | Google Scholar

Wang, J.-M., Du, P., Brotherton, M. S., Hu, C., Songsheng, Y.-Y., Li, Y.-R., et al. (2017). Tidally Disrupted Dusty Clumps as the Origin of Broad Emission Lines in Active Galactic Nuclei. Nat. Astron. 1, 775–783. doi:10.1038/s41550-017-0264-4

CrossRef Full Text | Google Scholar

Wang, J.-M., Du, P., Hu, C., Netzer, H., Bai, J.-M., Lu, K.-X., et al. (2014). Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. II. The Most Luminous Standard Candles in the Universe. ApJ 793, 108. doi:10.1088/0004-637x/793/2/108

CrossRef Full Text | Google Scholar

Wang, J.-M., Du, P., Valls-Gabaud, D., Hu, C., and Netzer, H. (2013). Super-Eddington Accreting Massive Black Holes as Long-Lived Cosmological Standards. Phys. Rev. Lett. 110, 081301. doi:10.1103/PhysRevLett.110.081301

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J.-M., Qiu, J., Du, P., and Ho, L. C. (2014). Self-shadowing Effects of Slim Accretion Disks in Active Galactic Nuclei: The Diverse Appearance of the Broad-Line Region. ApJ 797, 65. doi:10.1088/0004-637X/797/1/65

CrossRef Full Text | Google Scholar

Wang, J., Wei, J. Y., and He, X. T. (2006). A Sample ofIRASInfrared‐selected Seyfert 1.5 Galaxies: Infrared Color α(60, 25)‐dominated Eigenvector 1. ApJ 638, 106–119. doi:10.1086/498667

CrossRef Full Text | Google Scholar

Wang, T., Brinkmann, W., and Bergeron, J. (1996). X-ray Properties of Active Galactic Nuclei with Optical FeII Emission. A&Ap 309, 81–96.

Google Scholar

Warren, S., Lawrence, A., Almaini, O., Cirasuolo, M., Foucaud, S., Hambly, N., et al. (2006). Early Science Results from the UKIDSS ESO Public Survey. The Messenger 126, 7–10.

Google Scholar

Weiner, B. J., Willmer, C. N. A., Faber, S. M., Harker, J., Kassin, S. A., Phillips, A. C., et al. (2006). A Survey of Galaxy Kinematics Toz∼1 in the TKRS/GOODS‐N Field. II. Evolution in the Tully‐Fisher Relation. ApJ 653, 1049–1069. doi:10.1086/508922

CrossRef Full Text | Google Scholar

Whitaker, K. E., van Dokkum, P. G., Brammer, G., and Franx, M. (2012). The Star Formation Mass Sequence Out to Z = 2.5. ApJ 754, L29. doi:10.1088/2041-8205/754/2/L29

CrossRef Full Text | Google Scholar

White, S. D. M. (1984). Angular Momentum Growth in Protogalaxies. ApJ 286, 38–41. doi:10.1086/162573

CrossRef Full Text | Google Scholar

White, S. D. M., and Frenk, C. S. (1991). Galaxy Formation through Hierarchical Clustering. ApJ 379, 52. doi:10.1086/170483

CrossRef Full Text | Google Scholar

Wildy, C., Czerny, B., and Panda, S. (2019). Quasar Main Sequence: A Line or a Plane. A&A 632, A41. doi:10.1051/0004-6361/201935620

CrossRef Full Text | Google Scholar

Williams, P. R., Pancoast, A., Treu, T., Brewer, B. J., Peterson, B. M., Barth, A. J., et al. (2020). Space Telescope and Optical Reverberation Mapping Project. XII. Broad-Line Region Modeling of NGC 5548. ApJ 902, 74. doi:10.3847/1538-4357/abbad7

CrossRef Full Text | Google Scholar

Williams, P. R., Treu, T., Dahle, H., Valenti, S., Abramson, L., Barth, A. J., et al. (2021). The Black Hole Mass of the Z = 2.805 Multiply Imaged Quasar SDSS J2222+2745 from Velocity-Resolved Time Lags of the C IV Emission Line. ApJ 911, 64. doi:10.3847/1538-4357/abe943

CrossRef Full Text | Google Scholar

Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., and Labbé, I. (2009). Detection of Quiescent Galaxies in a Bicolor Sequence Fromz= 0-2. ApJ 691, 1879–1895. doi:10.1088/0004-637X/691/2/1879

CrossRef Full Text | Google Scholar

Willick, J. A., Courteau, S., Faber, S. M., Burstein, D., Dekel, A., and Strauss, M. A. (1997). Homogeneous Velocity‐Distance Data for Peculiar Velocity Analysis. III. The Mark III Catalog of Galaxy Peculiar Velocities. Astrophys J. Suppl. S 109, 333–366. doi:10.1086/312983

CrossRef Full Text | Google Scholar

Willmer, C. N. A., Faber, S. M., Koo, D. C., Weiner, B. J., Newman, J. A., Coil, A. L., et al. (2006). The Deep Evolutionary Exploratory Probe 2 Galaxy Redshift Survey: The Galaxy Luminosity Function Toz ∼ 1. ApJ 647, 853–873. doi:10.1086/505455

CrossRef Full Text | Google Scholar

Wills, B. J., and Browne, I. W. A. (1986). Relativistic Beaming and Quasar Emission Lines. ApJ 302, 56–63. doi:10.1086/163973

CrossRef Full Text | Google Scholar

Wisnioski, E., Förster Schreiber, N. M., Wuyts, S., Wuyts, E., Bandara, K., Wilman, D., et al. (2015). THE KMOS3DSURVEY: DESIGN, FIRST RESULTS, AND THE EVOLUTION OF GALAXY KINEMATICS FROM 0.7 ⩽z⩽ 2.7. ApJ 799, 209. doi:10.1088/0004-637X/799/2/209

CrossRef Full Text | Google Scholar

Wong, O. I., Schawinski, K., Kaviraj, S., Masters, K. L., Nichol, R. C., Lintott, C., et al. (2012). Galaxy Zoo: Building the Low-Mass End of the Red Sequence with Local post-starburst Galaxies. Mon. Not. R. Astron. Soc. 420, 1684–1692. doi:10.1111/j.1365-2966.2011.20159.x

CrossRef Full Text | Google Scholar

Woo, J.-H., Yoon, Y., Park, S., Park, D., and Kim, S. C. (2015). The Black Hole Mass-Stellar Velocity Dispersion Relation of Narrow-Line Seyfert 1 Galaxies. ApJ 801, 38. doi:10.1088/0004-637X/801/1/38

CrossRef Full Text | Google Scholar

Woo, J., Courteau, S., and Dekel, A. (2008). Scaling Relations and the Fundamental Line of the Local Group dwarf Galaxies. Mon. Not. R. Astron. Soc. 390, 1453–1469. doi:10.1111/j.1365-2966.2008.13770.x

CrossRef Full Text | Google Scholar

Woo, J. H., Treu, T., Malkan, M. A., and Blandford, R. D. (2008). Cosmic Evolution of Black Holes and Spheroids. III. TheMBH‐σ*Relation in the Last Six Billion Years. ApJ 681, 925–930. doi:10.1086/588804

CrossRef Full Text | Google Scholar

Woo, J. H., Treu, T., Malkan, M. A., and Blandford, R. D. (2006). Cosmic Evolution of Black Holes and Spheroids. I. TheMBH‐σ Relation Atz= 0.36. ApJ 645, 900–919. doi:10.1086/504586

CrossRef Full Text | Google Scholar

Woo, J. H., and Urry, C. M. (2002). Active Galactic Nucleus Black Hole Masses and Bolometric Luminosities. ApJ 579, 530–544. doi:10.1086/342878

CrossRef Full Text | Google Scholar

Wootten, A., and Thompson, A. R. (2009). The Atacama Large Millimeter/Submillimeter Array. Proc. IEEE 97, 1463–1471. doi:10.1109/jproc.2009.2020572

CrossRef Full Text | Google Scholar

Worthey, G. (1999). “The Age-Metallicity Degeneracy,” in Spectrophotometric Dating of Stars and Galaxies. Editors I. Hubeny, S. Heap, and R. Cornett (California, United States: Astronomical Society of the Pacific Conference Series), 192, 283.

Google Scholar

Worthey, G. (1994). Comprehensive Stellar Population Models and the Disentanglement of Age and Metallicity Effects. ApJS 95, 107. doi:10.1086/192096

CrossRef Full Text | Google Scholar

Worthey, G., Faber, S. M., Gonzalez, J. J., and Burstein, D. (1994). Old Stellar Populations. 5: Absorption Feature Indices for the Complete LICK/IDS Sample of Stars. ApJS 94, 687. doi:10.1086/192087

CrossRef Full Text | Google Scholar

Wuyts, E., Wisnioski, E., Fossati, M., Schreiber, N. M. F., Genzel, R., Davies, R., et al. (2016). THE EVOLUTION OF METALLICITY AND METALLICITY GRADIENTS FROMz= 2.7 TO 0.6 WITH KMOS3D. ApJ 827, 74. doi:10.3847/0004-637X/827/1/74

CrossRef Full Text | Google Scholar

Wuyts, S., Förster Schreiber, N. M., van der Wel, A., Magnelli, B., Guo, Y., Genzel, R., et al. (2011). GALAXY STRUCTURE AND MODE OF STAR FORMATION IN THE SFR-MASS PLANE FROMz∼ 2.5 TOz∼ 0.1. ApJ 742, 96. doi:10.1088/0004-637x/742/2/96

CrossRef Full Text | Google Scholar

Wuyts, S., van Dokkum, P. G., Kelson, D. D., Franx, M., and Illingworth, G. D. (2004). The Detailed Fundamental Plane of Two High‐Redshift Clusters: MS 2053−04 Atz = 0.58 and MS 1054−03 Atz = 0.83. ApJ 605, 677–688. doi:10.1086/381746

CrossRef Full Text | Google Scholar

Xu, D., and Komossa, S. (2010). New Insights into AGNs with Low-Mass Black Holes and High Accretion Rates: the Case of Narrow-Line Seyfert 1 Galaxies. Sci. China Phys. Mech. Astron. 53, 216–219. doi:10.1007/s11433-010-0060-y

CrossRef Full Text | Google Scholar

Xu, D., Komossa, S., Zhou, H., Lu, H., Li, C., Grupe, D., et al. (2012). Correlation Analysis of a Large Sample of Narrow-Line Seyfert 1 Galaxies: Linking Central Engine and Host Properties. Astronomical J. 143, 83. doi:10.1088/0004-6256/143/4/83

CrossRef Full Text | Google Scholar

Yi, S. K. (2003). Uncertainties of Synthetic Integrated Colors as Age Indicators. ApJ 582, 202–214. doi:10.1086/344640

CrossRef Full Text | Google Scholar

Young, C. K., and Currie, M. J. (1994). A New Extragalactic Distance Indicator Based on the Surface Brightness Profiles of dwarf Elliptical Galaxies. Monthly Notices R. Astronomical Soc. 268, L11–L15. doi:10.1093/mnras/268.1.L11

CrossRef Full Text | Google Scholar

Young, P. J., Westphal, J. A., Kristian, J., Wilson, C. P., and Landauer, F. P. (1978). Evidence for a Supermassive Object in the Nucleus of the Galaxy M87 from SIT and CCD Area Photometry. ApJ 221, 721–730. doi:10.1086/156076

CrossRef Full Text | Google Scholar

Yuan, T.-T., Kewley, L. J., and Richard, J. (2013). The Metallicity Evolution of Star-forming Galaxies from Redshift 0 to 3: Combining Magnitude-Limited Survey with Gravitational Lensing. ApJ 763, 9. doi:10.1088/0004-637x/763/1/9

CrossRef Full Text | Google Scholar

Zahid, H. J., Bresolin, F., Kewley, L. J., Coil, A. L., and Davé, R. (2012). The Metallicities of Low Stellar Mass Galaxies and the Scatter in the Mass-Metallicity Relation. ApJ 750, 120. doi:10.1088/0004-637X/750/2/120

CrossRef Full Text | Google Scholar

Zahid, H. J., Dima, G. I., Kudritzki, R.-P., Kewley, L. J., Geller, M. J., Hwang, H. S., et al. (2014). The Universal Relation of Galactic Chemical Evolution: The Origin of the Mass-Metallicity Relation. ApJ 791, 130. doi:10.1088/0004-637x/791/2/130

CrossRef Full Text | Google Scholar

Zahid, H. J., Kewley, L. J., and Bresolin, F. (2011). The Mass-Metallicity and Luminosity-Metallicity Relations From Deep2 Atz∼ 0.8. ApJ 730, 137. doi:10.1088/0004-637X/730/2/137

CrossRef Full Text | Google Scholar

Zamanov, R., and Marziani, P. (2002). Searching for the Physical Drivers of Eigenvector 1: From Quasars to Nanoquasars. ApJ 571, L77–L80. doi:10.1086/341367

CrossRef Full Text | Google Scholar

Zamanov, R., Marziani, P., Sulentic, J. W., Calvani, M., Dultzin-Hacyan, D., and Bachev, R. (2002). Kinematic Linkage between the Broad- and Narrow-Line-Emitting Gas in Active Galactic Nuclei. ApJL 576, L9–L13. doi:10.1086/342783

CrossRef Full Text | Google Scholar

Zamfir, S., Sulentic, J. W., Marziani, P., and Dultzin, D. (2010). Detailed Characterization of Hβ Emission Line Profile in Low-zSDSS Quasars. MNRAS 403, 1759–1786. doi:10.1111/j.1365-2966.2009.16236.x

CrossRef Full Text | Google Scholar

Zamfir, S., Sulentic, J. W., and Marziani, P. (2008). New Insights on the QSO Radio-Loud/radio-Quiet Dichotomy: SDSS Spectra in the Context of the 4D Eigenvector1 Parameter Space. Monthly Notices RAS 387, 856–870. doi:10.1111/j.1365-2966.2008.13290.x

CrossRef Full Text | Google Scholar

Zaritsky, D., Kennicutt, R. C. J., and Huchra, J. P. (1994). H II Regions and the Abundance Properties of Spiral Galaxies. ApJ 420, 87. doi:10.1086/173544

CrossRef Full Text | Google Scholar

Zavala, J., Okamoto, T., and Frenk, C. S. (2008). Bulges versus Discs: the Evolution of Angular Momentum in Cosmological Simulations of Galaxy Formation. Monthly Notices RAS 387, 364–370. doi:10.1111/j.1365-2966.2008.13243.x

CrossRef Full Text | Google Scholar

Zhao, Y., Ho, L. C., Shangguan, J., Kim, M., Zhao, D., and Gao, H. (2021). The Diverse Morphology, Stellar Population, and Black Hole Scaling Relations of the Host Galaxies of Nearby Quasars. arXiv:2102.09190.

Google Scholar

Zhu, P., Ho, L. C., and Gao, H. (2021). The Correlation between Black Hole Mass and Stellar Mass for Classical Bulges and the Cores of Ellipticals. ApJ 907, 6. doi:10.3847/1538-4357/abcaa1

CrossRef Full Text | Google Scholar

Ziegler, B. L., Saglia, R. P., Bender, R., Belloni, P., Greggio, L., and Seitz, S. (1999). Probing Early-type Galaxy Evolution with the Kormendy Relation. Astron. Astrophysics 346, 13–32.

Google Scholar

Zoldan, A., De Lucia, G., Xie, L., Fontanot, F., and Hirschmann, M. (2018). Structural and Dynamical Properties of Galaxies in a Hierarchical Universe: Sizes and Specific Angular Momenta. MNRAS 481, 1376–1400. doi:10.1093/mnras/sty2343

CrossRef Full Text | Google Scholar

Zou, F., Brandt, W. N., Vito, F., Chen, C.-T., Garmire, G. P., Stern, D., et al. (2020). X-ray Properties of Dust-Obscured Galaxies with Broad Optical/UV Emission Lines. MNRAS 499, 1823–1840. doi:10.1093/mnras/staa2930

CrossRef Full Text | Google Scholar

Zubovas, K., and King, A. (2012). Clearing Out a Galaxy. ApJ 745, L34. doi:10.1088/2041-8205/745/2/l34

CrossRef Full Text | Google Scholar