Spectral Asymmetry of Near-Concentric Traveling Ionospheric Disturbances Due to Doppler-Shifted Atmospheric Gravity Waves

Introduction

It is now generally well accepted that convective storms in the lower atmosphere generate upward traveling atmospheric gravity waves (AGWs) affecting all altitudes between the troposphere and the ionosphere. Therefore, there has been a growing interest in examining the details of atmosphere-ionosphere coupling via AGWs, such as whether the AGWs observed in the thermosphere/ionosphere are primary, secondary, or tertiary waves, what are their genesis mechanisms, and how far into the upper atmosphere can they propagate. These AGWs are an obvious pathway by which the ionosphere and thermosphere are coupled to the troposphere. Because their amplitudes grow exponentially with altitude, those AGWs with large amplitudes break near the mesopause. This causes the mesospheric jets to decelerate and drives the mesosphere away from radiative equilibrium (e.g., Fritts and Alexander, 2003). Wave-breaking excites small-scale, secondary gravity waves (e.g., Bacmeister and Schoeberl, 1989; Taylor and Hapgood, 1990; Walterscheid and Schubert, 1990; Taylor et al., 1995; Fritts et al., 1998; Franke and Robinson, 1999; Holton and Alexander, 1999; Liu et al., 1999; Nakamura et al., 1999; Satomura and Sato, 1999; Yamada et al., 2001; Fritts et al., 2002; Hecht, 2004; Li et al., 2005). These waves are easily ducted (Isler et al., 1997; Hecht et al., 2001; Pautet et al., 2005; Snively et al., 2007). It also results in the deposition of momentum into the background fluid (Yamada et al., 2001; Fritts et al., 2006), which creates momentum flux divergences (i.e. horizontal accelerations) in the direction of wave propagation. These divergences are highly intermittent and variable (Hecht et al., 1997; Yamada et al., 2001; Fritts et al., 2002; Vadas et al., 2003; Fritts et al., 2006). Such forces excite upward and downward propagating “secondary” gravity waves (Dickinson, 1969; Zhu and Holton, 1987; Fritts and Luo, 1992; Luo and Fritts, 1993; Medvedev and Gavrilov, 1995; Vadas and Fritts, 2001; Vadas and Fritts, 2002; Vadas et al., 2003; Vadas, 2013). Although most primary gravity waves from deep convection break or dissipate in the lower atmosphere, those primary gravity waves with intrinsic phase speeds c_IH > 100 m/s can propagate into the thermosphere and ionosphere (Vadas, 2007; Vadas and Crowley, 2010).

AGWs generated by thunderstorms have been observed in the mesosphere (Taylor and Hapgood, 1988; Yue et al., 2009; Vadas et al., 2012; Miller et al., 2015) and ionosphere (Vadas and Crowley, 2010; Nishioka et al., 2013; Azeem et al., 2015; Azeem et al., 2017; Lay et al., 2015). These severe storms act like point sources for the excitation of AGWs, which then propagate horizontally and vertically from their sources. In a windless isothermal background atmosphere, AGWs with shorter periods and slower phase speeds travel more obliquely relative to the zenith direction than the longer period and faster waves (Fritts and Alexander, 2003; Yue et al., 2013; Vadas and Azeem, 2021). As a result, these AGWs exhibit conically shaped phase progression as a function of altitude when propagating through a medium with small or zero background winds. When these features are viewed in the zenith, such as from a ground-based imager (Yue et al., 2009) or in nadir, such as a satellite (Azeem et al., 2015; Miller et al., 2015), they appear as circular rings traveling outward away from the center of the cone. The background neutral wind can distort the shape of the concentric AGWs via filtering effect causing them to appear as partial circular rings (Yue et al., 2009; Azeem et al., 2015).

With the proliferation of GNSS receivers worldwide, these convectively generated AGWs have been observed in Total Electron Content (TEC) data via their signatures in the ionosphere (e.g. Tsugawa et al., 2007; Nishioka et al., 2013; Azeem et al., 2015; Azeem et al., 2017). At ionospheric heights, AGWs manifest themselves as oscillations of the electron density in the ionosphere, resulting in a Traveling Ionospheric Disturbance (TID). TIDs are perturbations in the ionospheric electron densities that are caused by AGWs via ion-neutral collisions as the AGWs propagate in the thermosphere/ionosphere (Hooke, 1968; Bowman, 1990; Hocke and Schlegel, 1996). In recent years, TEC data from densely distributed GNSS receiver networks in the COntiguous United States (CONUS) have been used to create digital renderings of partially concentric TIDs caused by convectively generated AGWs (Nishioka et al., 2013; Azeem et al., 2015; Azeem and Barlage, 2017; Azeem et al., 2017; Vadas and Azeem, 2021). These TID images created by combining TEC data from distributed GNSS receivers provide details of the horizontal morphology of TIDs at all local times as well as their temporal evolution. The TEC-derived observations of TIDs can determine critical wave parameters of the underlying AGW packets, such as their horizontal phase speeds, horizontal wavelengths, and periods. Vadas and Azeem (2021) further showed that these TID images can be spectrally analyzed to provide insights into their propagation characteristics and elucidate potential sources of the underlying AGWs.

The impact of neutral wind filtering on TIDs has been addressed by various studies, e.g. Kalikhman, 1980; Waldock and Jones, 1986; Crowley et al., 1987; Vadas and Azeem, 2021. These studies show that when the phase velocity vectors of the TIDs are opposite to the direction of the background neutral wind they do not experience wind filtering which then leads to the azimuthal preferences in TID propagation. This wind filtering is particularly evident in TIDs associated with convective storms. Partially concentric TIDs, such as those presented by Nishioka et al. (2013), Azeem et al. (2015), and Vadas and Azeem (2021), are subjected to this wind filtering. The background neutral wind causes a segment of the ring structure to experience more dissipation at a lower altitude and resulting in the partially concentric structure of the TIDs. However, the impact of background neutral winds on the TID periods has not been adequately addressed in the literature. In this paper, we use GNSS receivers distributed throughout the CONUS to identify and “image” TIDs excited by a convective storm system on April 28, 2014. We analyze the 2D spatial maps of GPS TEC perturbations to calculate TID parameters, including horizontal wavelengths, phase speeds, and periods. We show that the TID spectrum is zonally asymmetric due to Doppler shifting by the background neutral wind. We compare the TEC data with the AGWs dispersion relationship (Vadas and Azeem, 2021) to illustrate consistency between the data and idealized point source theory. The paper is organized as follows: Materials and Methods Section describes the analysis of GPS TEC data for creating TID maps over CONUS, Results Section presents the results of the present study, and Discussion and Conclusion Section provides a discussion of these results in the context of AGWs theory.

Materials and Methods

We use GPS TEC data from ∼4,000 sites in the CONUS to image the TIDs on April 28, 2014. The detailed methodology of generating these TID maps can be found in Azeem et al. (2015) and Azeem and Barlage (2017). Since TEC is a line integrated quantity weighted by the maximum ionospheric density, these TIDs in GNSS data are assumed to be representative of the underlying gravity waves at the F2 peak altitude (between ∼250 and ∼300 km). Figure 1 shows electron density profiles computed using the International Reference Ionosphere (IRI) model (Bilitza et al., 2012) in the vicinity of the TIDs to determine the F2 peak height. IRI electron density profiles were computed for 34°N, 89.6°W on April 28, 2014. This location corresponds to the center of the TIDs seen in ground-based TEC data. The figure shows three profiles between 20 and 22 UT, which were closest in time to the observed TIDs. These IRI profiles represent the ionospheric vertical structure in the region where the TIDs on April 28, 2014 were observed. From the profiles in Figure 1, we see that the peak altitude of theF2 peak (or hmF2) is located near 300 km. We use this value of hmF2 in converting slant TEC to vertical TEC and for computing the intrinsic periods of the AGWs.

FIGURE 1

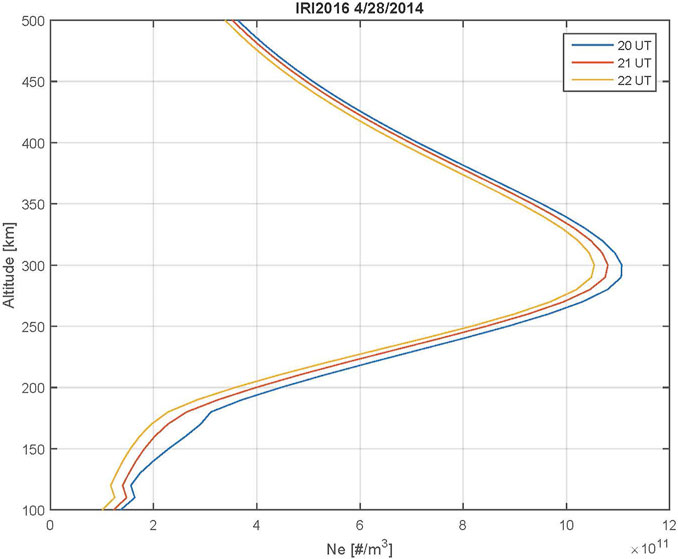
FIGURE 1. (a) IRI model electron density profiles at 33.9°N, 89.6°W on April 28, 2014 from 20 to 22 UT showing the height of the F2 peak.

Results

In this study, we present a case study of convectively generated AGWs and present their TID signatures in the GPS TEC data over the CONUS. We will show that these TIDs, associated with the convective storm, are spectrally asymmetric and that this behavior results from the Doppler shifting of the underlying AGWs due to the background neutral wind.

Convective Storm on April 28, 2014

On April 28, 2014, a series of supercell storms developed over Mississippi (MS) and Tennessee (TN), producing severe weather in the region and several tornadoes. Around the same time, the National Weather Service Storm Prediction Center reported severe storm activity in the South-Central U.S, including several tornados. Figure 2 shows the GOES satellite imagery of the convective storms over MS/TN at 19:15 UTC on April 28, 2014. This image shows anvil clouds generated by a deep convective system over MS/TN. Brightness temperatures above these overshooting tops were close to 200 K (see Figure 3), well below the climatological zonal-mean tropopause temperature of 210–215 K (Hoffmann et al., 2013), implying deep convection overshooting the tropopause in this region. The presence of convective cloud tops in GOES visible images and associated cold temperatures in the GOE IR data present strong evidence that a powerful convective storm was present over MS/TN in the afternoon sector (CST) on April 28, 2014.

FIGURE 2

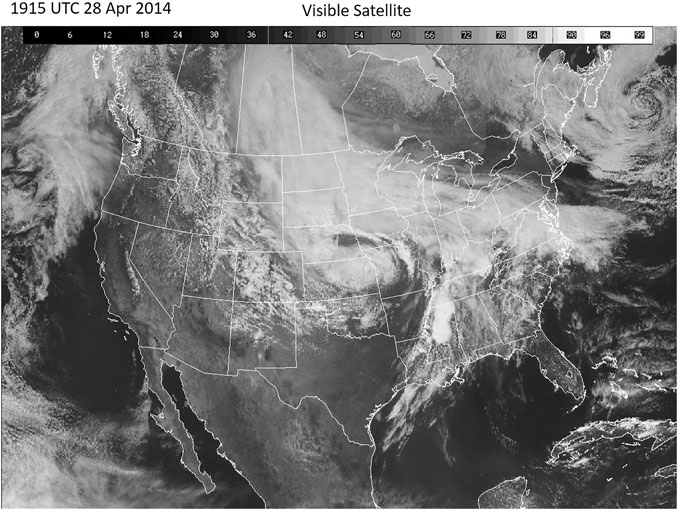
FIGURE 2. GOES image showing overshooting cloud tops near MS/TN at 19:15 UTC (13:15 CST) during the development of a convective system on April 28, 2014. [After https://www2.mmm.ucar.edu/imagearchive/].

FIGURE 3

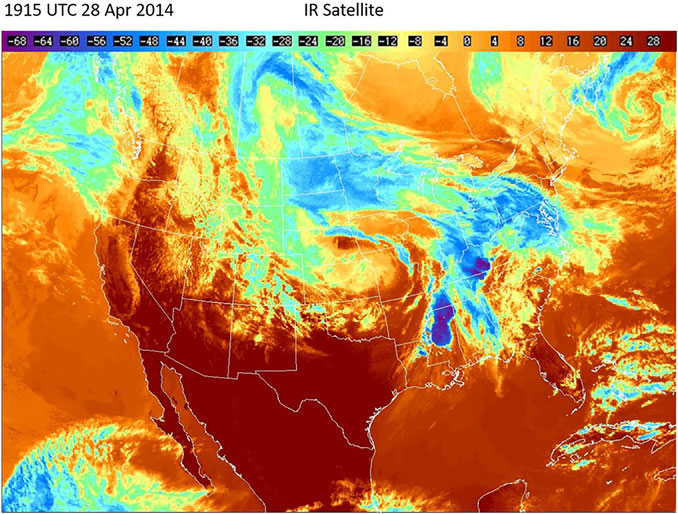
FIGURE 3. GOES satellite infrared (IR) observations showing convective storms over MS and TN on April 28, 2014 at 19:15 UTC. The temperature scale is in°C. [After https://www2.mmm.ucar.edu/imagearchive/].

Traveling Ionospheric Disturbances in GPS Total Electron Content Measurements

Figure 4 shows the GPS TEC maps on April 28, 2014 at 19:30, 20:00, 20:30, and 21:00 UT. Similar maps were generated, but not shown here, for the entire day at a cadence of 30 s. These maps have a resolution of 0.1 in latitude and longitude. Radially propagating concentric rings are seen extending 1,400 km from the center of the TIDs. This sequence of images reveals the concentric TIDs in the TEC data in the proximity of the storm center. The center of these centric TIDs is located at 33.9°N, 89.6°W. The wave-like perturbations have horizontal wavelengths between 100 and 200 km and propagate away from the center with horizontal phase speeds ranging from 200 to 300 m/s. An animation of these TIDs is included as Supplementary Video 1. The magnitudes of the TEC perturbations were between 0.1 and 0.2 TECU (1 TECU = 10¹⁶ electrons/m²).

FIGURE 4

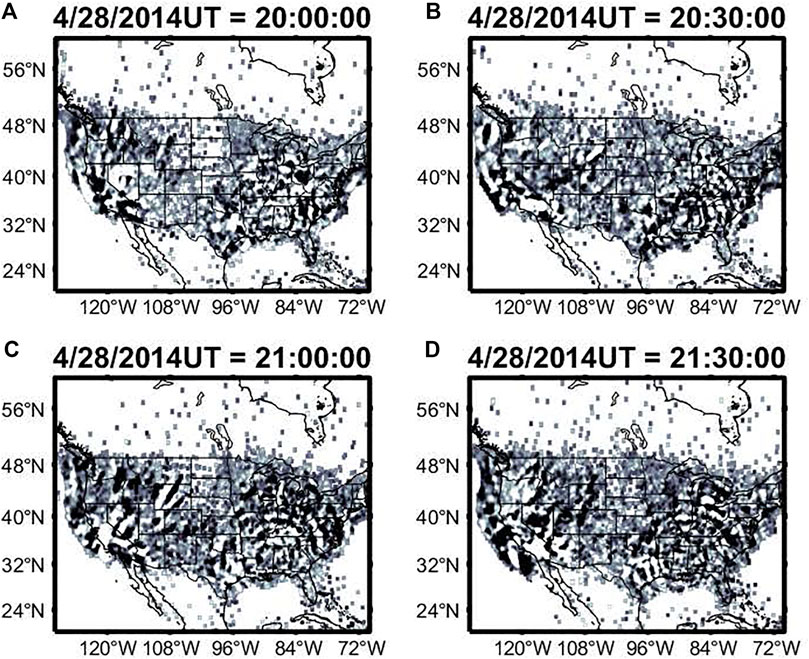
FIGURE 4. Maps of GPS-derived TEC perturbations showing concentric wavefronts on April 28, 2014 at (A) 20:00 UTC, (B) 20:00 UTC, (C) 20:30 UTC, and (D) 21:00 UTC emanating from the convective storm system centered over MS/TN.

Next, we examine the parameters of the concentric TIDs shown in Figure 4. Using wavelet analysis of the GPS TEC data we obtain their spectrograms and estimate the periodicities and horizontal wavelengths of the TID wave packet. This wavelet spectrogram method was previously used by Azeem et al. (2017) to estimate the periods and horizontal wavelengths of the TIDs in the GPS TEC data. Figure 5 shows the normalized wavelet power spectrum of the TIDs as a function of period and longitude at 33.9° N (the latitude of the center of concentric rings). The white and green lines in the figure show the calculated values of the observed periods (τ_r) in a windless isothermal background atmosphere and the intrinsic AGW periods (τ_Ιr), respectively, as defined in Vadas and Azeem (2021). We use the Horizontal Wind Model (HWM14) (Drob et al., 2015) to calculate the background neutral winds (U_H) at 300 km altitude (the F2 peak height from Figure 1). The HWM zonal and meridional winds near the center of the TIDs are shown in Figure 6 as a function of altitude and UT. The model shows an eastward peak in the wind at F-region altitudes between 0 and 3 UT and a westward jet between 11 and 15 UT. The HWM zonal wind near 21 UT is close to 30 m/s.

FIGURE 5

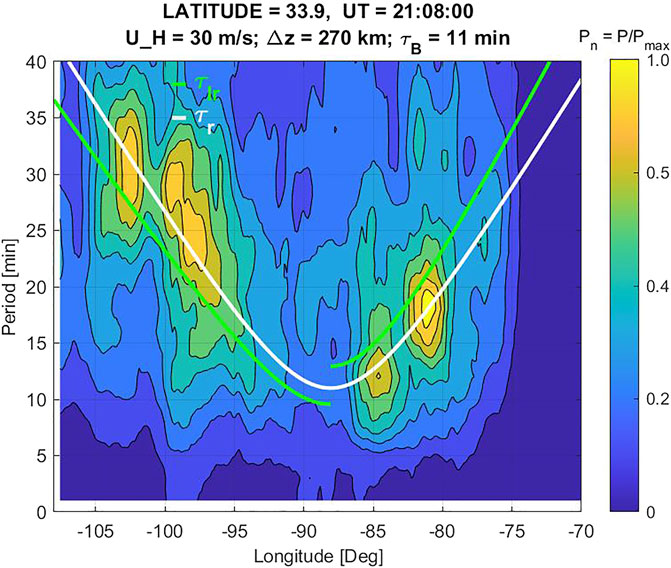
FIGURE 5. Wavelet spectrograms of the TIDs at 21:08:00 UT on April 28, 2014 at 33.9°N as a function of longitude. The contour lines represent the normalized wavelet power (P_n), which is defined here as the ratio of the wavelet power computed at each longitude and period grid point and the maximum wavelet power. The white and green lines show the observed and intrinsic (Doppler shifted) periods, respectively, for AGWs excited by a point source assuming U = 30 m/s, Δz = 270 km, and τ_B = 11 min.

FIGURE 6

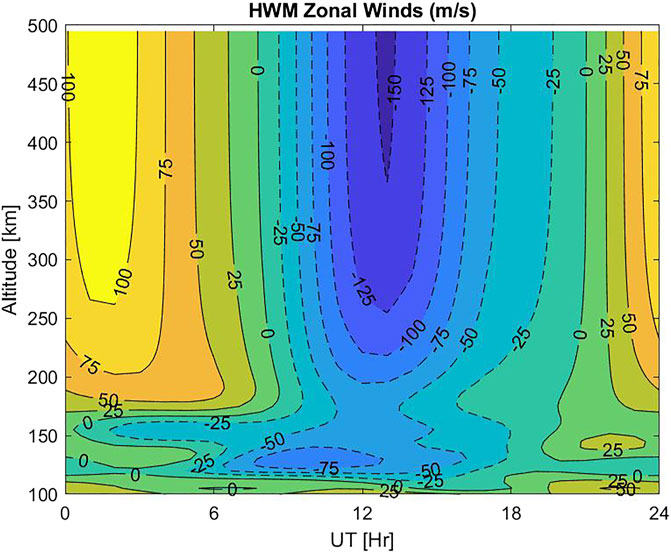
FIGURE 6. Altitude-latitude cross-section of the HWM zonal wind near the location of the center of the TIDs in Figure 4 on April 28, 2014.

We choose Δz = 270 km and τ_B = 11 min and use U_H = 30 m/s so that the white line agrees reasonably well with the peak of the spectrogram. Here, Δz is the altitude difference between the assumed AGW point source and the observation location, τ_B is the buoyancy period, and U_H is the component of the neutral wind along the AGW propagation direction. Since 33.9°N is the latitude of the estimated ring center, this spectrogram represents TIDs that propagate zonally outward from the center. The periods of the eastward and westward propagating concentric TIDs are seen to increase approximately linearly with longitude, with τ_r ∼ 10–35 min. The linear dependence of the TID periods in the spectrogram with the radial distance (R) from the center is consistent with the theoretical estimates of AGWs (τ_r) and illustrates the consistency between the data and idealized point source theory. The zonal asymmetry in the spectrogram is evident in the figure. This asymmetry, as we discuss below, is due to the background neutral wind, which leads to a Doppler shift. We consider idealized expressions of AGWs excited by a point source to gain insights into the Doppler shifting of the TIDs, which are discussed in the following section.

Discussion and Conclusion

The concentric TIDs shown in Figure 4 are likely induced by AGWs generated by a point source (Vadas and Azeem, 2021). The point source tends to excite rich spectra of AGWs with widely varying horizontal and vertical wavelengths (Vadas et al., 2003; Vadas et al., 2018). If the effects of winds and dissipation are negligible, concentric rings of AGWs are observed at the observation altitude (Yue et al., 2009; Vadas and Azeem, 2021). In a windless isothermal background atmosphere, the intrinsic period, τ_Ir, from the Boussinesq relation can be expressed as follows:

${\tau }_{Ir}={\tau }_B/cos\psi (1)$

where ψ is the angle between the wave vector and the local zenith and τ_B is the buoyancy period. For a zero wind case, the intrinsic wave period is the same as the observed period (τ_r). If we assume that the AGWs are excited by a point source at altitude z_source and the observation height is located at z_obs, then the angle of AGW propagation can be expressed in terms of the radius (R) of each circular wavefront by the following equation.

$\psi ={\tan }^{-1}\left(\frac{R}{\text{Δ}z}\right)(2)$

Here, $\text{Δ}z=z_{obs}-z_{source}$. Furthermore, the following relationship also holds for the angle of propagation of an AGW:

$\cos \psi =\frac{\Delta z}{\sqrt{R^2+\Delta z^2}}=\frac{{\tau }_B}{{\tau }_r}(3)$

From Eq. 3, we can express ${\tau }_{Ir}$ as:

${\tau }_r={\tau }_B{\left[{\left(\tan \psi \right)}^2+1\right]}^{1/2}(4)$

We note here that Eq. 4 assumes that the background winds are zero, and the atmosphere is isothermal (Yue et al., 2009). Therefore, for an AGW excited by a point source, τ_r increases linearly with R when R ≫ Δz. This is shown in Figure 5 by the white solid line. Now, in presence of the background neutral wind, ${\tau }_{Ir}$ is related to the observed period (${\tau }_r)$ by the following equation:

${\tau }_{Ir}={\tau }_r/\left(1-\frac{U_H}{c_H}\right)(5)$

where U_H is the component of the neutral wind along the AGW propagation direction and c_H is the horizontal phase speed. By tracking TID wavefronts in a sequence of TID images between 22:30:00 UT and 22:50:00 UT, we estimate the value of c_H. We find that the AGWs which created these TIDs have an average horizontal phase speed of c_H = 270 m/s. From Figure 6, we see that U_H is in the same direction as the eastward propagating AGWs while the westward propagating AGWs travel opposite to U_H. This difference in the relative motion between the AGWs and the background winds creates the spectral asymmetry seen in the TIDs. Vadas et al. (2009) simulated the effects of background winds on convectively generated AGWs and showed that the Doppler shifting of AGWs prevents propagation of a subset of frequencies to higher altitudes causing “distortion” (zonally asymmetry) in the concentric ring pattern of the AGWs. In Figure 5, the intrinsic period curve for the eastward propagating portion of the TIDs is Doppler shifted to longer periods while the TIDs propagating westward and against the zonal wind are Doppler shifted to shorter intrinsic periods.

Medium-scale TIDs with horizontal phase speeds of c_H ∼< 250–270 ms⁻¹ and periods τ_r < 1 h are believed to originate in the lower atmosphere (Georges, 1968; Waldock and Jones, 1986; Crowley et al., 1987; Ogawa et al., 1987). Although most primary AGWs from deep convection break or dissipate in the lower atmosphere, those primary AGWs with intrinsic phase speeds c_H > 100 m/s can propagate into the thermosphere (Vadas, 2007). In contrast, secondary AGWs have horizontal phase speeds ranging from ∼100–∼600 m/s (Vadas and Azeem, 2021). The intrinsic horizontal phase speeds of these secondary AGWs can be up to 98% of the sound speed (Vadas et al., 2019). Thus for secondary AGWs that reach ionospheric heights, their intrinsic horizontal phase speeds can be much greater than ∼300 m/s because the sound speed is much larger in the ionosphere-thermosphere region. In our case study, the horizontal phase velocity of the observed TIDs (∼270 m/s) is not fast enough to state with certainty whether the concentric wave pattern seen in the TEC data is due to the presence of primary or secondary AGWs. To ascertain the nature (primary, secondary, tertiary, etc.) of these AGWs requires reverse ray tracing, which is not performed in this study and is beyond the scope of this work. Nonetheless, the findings presented in this study apply to all TIDs associated with convective storms, regardless of whether the underlying AGWs are primary or secondary waves.

In this study, we examined the effects of neutral winds on the TID periods. We used TID images over the CONUS to compute a wavelet spectrum and elucidate its asymmetry as a function of the zonal distance from the center of the concentric wavefronts. The results show that if the relative motion of the AGWs and the background neutral wind is in the opposite direction, the intrinsic periods of the TIDs are Doppler shifted to shorter periods (intrinsic frequency will increase) and if both the AGWs and background winds are in the same direction, the Doppler shifting causes the observed periods to be longer (intrinsic frequency will decrease). Furthermore, our results show that the observed TID characteristics are consistent with the underlying AGWs being excited by point sources.

Data Availability Statement

The TID dataset for this study can be found on Zenodo [https://doi.org/10.5281/zenodo.4660548]. The GOES satellite data used in this study are publicly available from https://www2.mmm.ucar.edu/imagearchive/.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was partially supported by NSF grant AGS-1552310 to ASTRA.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the use of publicly available ground-based GPS TEC data from the Southern California Integrated GPS Network, International GPS Service for Geodynamics, UNAVCO, Hartebeesthoek Radio Astronomy Observatory, Natural Resources Canada, Geoscience Australia, the Brazilian Institute of Geography and Statistics, University of New Brunswick, National Oceanic and Atmospheric Administration, and National Aeronautics and Space Administration.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.690480/full#supplementary-material

Supplementary Video 1 | An animation of TIDs in the ground-based GPS TEC over CONUS between 19:00:00 UT and 23:00:00 UT on April 28, 2014 in the proximity of the storm center over MS/TN.

References

Azeem, I., and Barlage, M. (2017). Atmosphere-Ionosphere Coupling from Convectively Generated Gravity Waves. Adv. Space Res. 61, 1931–1941. doi:10.1016/j.asr.2017.09.029

CrossRef Full Text | Google Scholar

Azeem, I., Vadas, S. L., Crowley, G., and Makela, J. J. (2017). Traveling Ionospheric Disturbances over the United States Induced by Gravity Waves from the 2011 Tohoku Tsunami and Comparison with Gravity Wave Dissipative Theory. J. Geophys. Res. Space Phys. 122, 3430–3447. doi:10.1002/2016JA023659

CrossRef Full Text | Google Scholar

Azeem, I., Yue, J., Hoffmann, L., Miller, S. D., Straka, W. C., and Crowley, G. (2015). Multisensor Profiling of a Concentric Gravity Wave Event Propagating from the Troposphere to the Ionosphere. Geophys. Res. Lett. 42, 7874–7880. doi:10.1002/2015GL065903

CrossRef Full Text | Google Scholar

Bacmeister, J. T., and Schoeberl, M. R. (1989). Breakdown of Vertically Propagating Two-Dimensional Gravity Waves Forced by Orography. J. Atmos. Sci. 46, 2109–2134. doi:10.1175/1520-0469(1989)046<2109:bovptd>2.0.co;2

CrossRef Full Text | Google Scholar

Bilitza, D., Altadill, D., Zhang, Y., Mertens, C., Truhlik, V., Richards, P., et al. (2014). The International Reference Ionosphere 2012 - a Model of International Collaboration. J. Space Weather Space Clim. 4 (A07), A07–A12. doi:10.1051/swsc/2014004

CrossRef Full Text | Google Scholar

Bowman, G. G. (1990). A Review of Some Recent Work on Midlatitude Spread F Occurrence as Detected by Ionosondes. J. Geomagn. Geoelectr. 42, 109–138. doi:10.5636/jgg.42.109

CrossRef Full Text | Google Scholar

Crowley, G., Jones, T. B., and Dudeney, J. R. (1987). Comparison of Short Period TID Morphologies in Antarctica during Geomagnetically Quiet and Active Intervals. J. Atmos. Terrestrial Phys. 49, 1155–1162. doi:10.1016/0021-9169(87)90098-5

CrossRef Full Text | Google Scholar

Dickinson, R. E. (1969). Propagators of Atmospheric Motions 1. Excitation by point Impulses. Rev. Geophys. 7 (3), 483–514. doi:10.1029/RG007i003p00483

CrossRef Full Text | Google Scholar

Drob, D. P., Emmert, J. T., Meriwether, J. W., Makela, J. J., Doornbos, E., Conde, M., et al. (2015). An Update to the Horizontal Wind Model (HWM): The Quiet Time Thermosphere. Earth Space Sci. 2, 301–319. doi:10.1002/2014EA000089

CrossRef Full Text | Google Scholar

Franke, P. M., and Robinson, W. A. (1999). Nonlinear Behavior in the Propagation of Atmospheric Gravity Waves. J. Atmos. Sci. 56, 3010–3027. doi:10.1175/1520-0469(1999)056<3010:nbitpo>2.0.co;2

CrossRef Full Text | Google Scholar

Fritts, D. C., and Alexander, M. J. (2003). Gravity Wave Dynamics and Effects in the Middle Atmosphere. Rev. Geophys. 41, 1003. doi:10.1029/2001RG000106

CrossRef Full Text | Google Scholar

Fritts, D. C., Arendt, S., and Andreassen, Ø. (1998). Vorticity Dynamics in a Breaking Internal Gravity Wave. Part 2. Vortex Interactions and Transition to Turbulence. J. Fluid Mech. 367, 47–65. doi:10.1017/s0022112098001633

CrossRef Full Text | Google Scholar

Fritts, D. C., and Luo, Z. (1992). Gravity Wave Excitation by Geostrophic Adjustment of the Jet Stream. Part I: Two-Dimensional Forcing. J. Atmos. Sci. 49, 681–697. doi:10.1175/1520-0469(1992)049<0681:gwebga>2.0.co;2

CrossRef Full Text | Google Scholar

Fritts, D. C., Vadas, S. L., Wan, K., and Werne, J. A. (2006). Mean and Variable Forcing of the Middle Atmosphere by Gravity Waves. J. Atmos. Solar-Terrestrial Phys. 68, 247–265. doi:10.1016/j.jastp.2005.04.010

CrossRef Full Text | Google Scholar

Fritts, D. C., Vadas, S. L., and Yamada, Y. (2002). An Estimate of strong Local Body Forcing and Gravity Wave Radiation Based on OH Airglow and Meteor Radar Observations. Geophys. Res. Lett. 29 (10), 71–1. doi:10.1029/2001GL013753

CrossRef Full Text | Google Scholar

Georges, T. M. (1968). HF Doppler Studies of Traveling Ionospheric Disturbances. J. Atmos. Terrestrial Phys. 30, 735–746. doi:10.1016/s0021-9169(68)80029-7

CrossRef Full Text | Google Scholar

Hecht, J. H. (2004). Instability Layers and Airglow Imaging. Rev. Geophys. 42, RG1001. doi:10.1029/2003RG000131

CrossRef Full Text | Google Scholar

Hecht, J. H., Walterscheid, R. L., Fritts, D. C., Isler, J. R., Senft, D. C., Gardner, C. S., et al. (1997). Wave Breaking Signatures in OH Airglow and Sodium Densities and Temperatures: 1. Airglow Imaging, Na Lidar, and MF Radar Observations. J. Geophys. Res. 102 (D6), 6655–6668. doi:10.1029/96jd02619

CrossRef Full Text | Google Scholar

Hecht, J. H., Walterscheid, R. L., Hickey, M. P., and Franke, S. J. (2001). Climatology and Modeling of Quasi-Monochromatic Atmospheric Gravity Waves Observed over Urbana Illinois. J. Geophys. Res. 106, 5181–5195. doi:10.1029/2000jd900722

CrossRef Full Text | Google Scholar

Hocke, K., and Schlegel, K. (1996). A Review of Atmospheric Gravity Waves and Travelling Ionospheric Disturbances: 1982-1995. Ann. Geophys. 14, 917–940. doi:10.1007/s00585-996-0917-6

CrossRef Full Text | Google Scholar

Hoffmann, L., Xue, X., and Alexander, M. J. (2013). A Global View of Stratospheric Gravity Wave Hotspots Located With Atmospheric Infrared Sounder Observations. J. Geophys. Res. Atmos. 118, 416–434. doi:10.1029/2012JD018658

Holton, J. R., and Alexander, M. J. (1999). Gravity Waves in the Mesosphere Generated by Tropospheric Convention. Tellus B: Chem. Phys. Meteorology 51, 45–58. doi:10.3402/tellusb.v51i1.16259

CrossRef Full Text | Google Scholar

Hooke, W. H. (1968). Ionospheric Irregularities Produced by Internal Atmospheric Gravity Waves. J. Atmos. Terrestrial Phys. 30, 795–823. doi:10.1016/s0021-9169(68)80033-9

CrossRef Full Text | Google Scholar

Isler, J. R., Taylor, M. J., and Fritts, D. J. (1997). Observational Evidence of Wave Ducting and Evanescence in the Mesosphere. J. Geophys. Res. 102, 26301–26313. doi:10.1029/97jd01783

CrossRef Full Text | Google Scholar

Kalikhman, A. D. (1980). Medium-scale Travelling Ionospheric Disturbances and Thermospheric Winds in the F-Region. J. Atmos. Terrestrial Phys. 42, 697–703. doi:10.1016/0021-9169(80)90053-7

CrossRef Full Text | Google Scholar

Lay, E. H., Shao, X. M., Kendrick, A. K., and Carrano, C. S. (2015). Ionospheric Acoustic and Gravity Waves Associated with Midlatitude Thunderstorms. J. Geophys. Res. Space Phys. 120, 6010–6020. doi:10.1002/2015JA021334

CrossRef Full Text | Google Scholar

Li, F., Liu, A. Z., Swenson, G. R., Hecht, J. H., and Robinson, W. A. (2005). Observations of Gravity Wave Breakdown into Ripples Associated with Dynamical Instabilities. J. Geophys. Res. 110, D09S11. doi:10.1029/2004JD004849

CrossRef Full Text | Google Scholar

Liu, H.-L., Hays, P. B., and Roble, R. G. (1999). A Numerical Study of Gravity Wave Breaking and Impacts on Turbulence and Mean State. J. Atmos. Sci. 56 (13), 2152–2177. doi:10.1175/1520-0469(1999)056<2152:ansogw>2.0.co;2

CrossRef Full Text | Google Scholar

Luo, Z., and Fritts, D. C. (1993). Gravity-Wave Excitation by Geostrophic Adjustment of the Jet Stream. Part II: Three-Dimensional Forcing. J. Atmos. Sci. 50, 104–115. doi:10.1175/1520-0469(1993)050<0104:gwebga>2.0.co;2

CrossRef Full Text | Google Scholar

Medvedev, A. S., and Gavrilov, N. M. (1995). The Nonlinear Mechanism of Gravity Wave Generation by Meteorological Motions in the Atmosphere. J. Atmos. Terr. Phys. 57, 1221–1231.

Google Scholar

Miller, S. D., Straka, W. C., Yue, J., Smith, S. M., Alexander, M. J., Hoffmann, L., et al. (2015). Upper Atmospheric Gravity Wave Details Revealed in Nightglow Satellite Imagery. Proc. Natl. Acad. Sci. USA. 112 (49), E6728–E6735. doi:10.1073/pnas.1508084112

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, T., Higashikawa, A., Tsuda, T., and Matsushita, Y. (1999). Seasonal Variations of Gravity Wave Structures in OH Airglow with a CCD Imager at Shigaraki. Earth Planet. Sp. 51, 897–906. doi:10.1186/bf03353248

CrossRef Full Text | Google Scholar

Nishioka, M., Tsugawa, T., Kubota, M., and Ishii, M. (2013). Concentric Waves and Short-Period Oscillations Observed in the Ionosphere after the 2013 Moore EF5 Tornado. Geophys. Res. Lett. 40, 5581–5586. doi:10.1002/2013GL057963

CrossRef Full Text | Google Scholar

Ogawa, T., Igarashi, K., Aikyo, K., and Maeno, H. (1987). NNSS Satellite Observations of Medium-Scale Traveling Ionospheric Disturbances at Southern High-Latitudes. J. Geomagn. Geoelec. 39, 709–721. doi:10.5636/jgg.39.709

CrossRef Full Text | Google Scholar

Pautet, P.-D., Taylor, M. J., Liu, A. Z., and Swenson, G. R. (2005). Climatology of Short-Period Gravity Waves Observed over Northern Australia during the Darwin Area Wave Experiment (DAWEX) and Their Dominant Source Regions. J. Geophys. Res. 110, D03S90. doi:10.1029/2004JD004954

CrossRef Full Text | Google Scholar

Satomura, T., and Sato, K. (1999). Secondary Generation of Gravity Waves Associated with the Breaking of Mountain Waves. J. Atmos. Sci. 56, 3847–3858. doi:10.1175/1520-0469(1999)056<3847:sgogwa>2.0.co;2

CrossRef Full Text | Google Scholar

Snively, J. B., Pasko, V. P., Taylor, M. J., and Hocking, W. K. (2007). Doppler Ducting of Short-Period Gravity Waves by Midlatitude Tidal Wind Structure. J. Geophys. Res. 112. doi:10.1029/2006JA011895

CrossRef Full Text | Google Scholar

Taylor, M. J., and Hapgood, M. A. (1988). Identification of a Thunderstorm as a Source of Short Period Gravity Waves in the Upper Atmospheric Nightglow Emissions. Planet. Space Sci. 36, 975–985. doi:10.1016/0032-0633(88)90035-9

CrossRef Full Text | Google Scholar

Taylor, M. J., and Hapgood, M. A. (1990). On the Origin of Ripple-type Wave Structure in the OH Nightglow Emission. Planet. Space Sci. 38, 1421–1430. doi:10.1016/0032-0633(90)90117-9

CrossRef Full Text | Google Scholar

Taylor, M. J., Turnbull, D. N., and Lowe, R. P. (1995). Spectrometric and Imaging Measurements of a Spectacular Gravity Wave Event Observed during the ALOHA-93 Campaign. Geophys. Res. Lett. 22, 2849–2852. doi:10.1029/95gl02948

CrossRef Full Text | Google Scholar

Tsugawa, T., Otsuka, Y., Coster, A. J., and Saito, A. (2007). Medium-scale Traveling Ionospheric Disturbances Detected with Dense and Wide TEC Maps over North America. Geophys. Res. Lett. 34, L22101. doi:10.1029/2007GL031663

CrossRef Full Text | Google Scholar

Vadas, S. L., and Azeem, I. (2021). Concentric Secondary Gravity Waves in the Thermosphere and Ionosphere over the continental United States on March 25–26, 2015 from Deep Convection. J. Geophys. Res. Space Phys. 126, e2020JA028275. doi:10.1029/2020ja028275

CrossRef Full Text | Google Scholar

Vadas, S. L. (2013). Compressiblef-plane Solutions to Body Forces, Heatings, and Coolings, and Application to the Primary and Secondary Gravity Waves Generated by a Deep Convective Plume. J. Geophys. Res. Space Phys. 118, 2377–2397. doi:10.1002/jgra.50163

CrossRef Full Text | Google Scholar

Vadas, S. L., and Crowley, G. (2010). Sources of the Traveling Ionospheric Disturbances Observed by the Ionospheric TIDDBIT Sounder Near Wallops Island on 30 October 2007. J. Geophys. Res. 115, A07324. doi:10.1029/2009JA015053

CrossRef Full Text | Google Scholar

Vadas, S. L., Fritts, D. C., and Alexander, M. J. (2003). Mechanism for the Generation of Secondary Waves in Wave Breaking Regions. J. Atmos. Sci. 60, 194–214. doi:10.1029/2004JD00557410.1175/1520-0469(2003)060<0194:mftgos>2.0.co;2

CrossRef Full Text | Google Scholar

Vadas, S. L., and Fritts, D. C. (2001). Gravity Wave Radiation and Mean Responses to Local Body Forces in the Atmosphere. J. Atmos. Sci. 58, 2249–2279. doi:10.1175/1520-0469(2001)058<2249:gwramr>2.0.co;2

CrossRef Full Text | Google Scholar

Vadas, S. L., and Fritts, D. C. (2002). The Importance of Spatial Variability in the Generation of Secondary Gravity Waves from Local Body Forces. Geophys. Res. Lett. 29 (20), 45-1–45-4. doi:10.1029/2002GL015574

CrossRef Full Text | Google Scholar

Vadas, S. L. (2007). Horizontal and Vertical Propagation and Dissipation of Gravity Waves in the Thermosphere from Lower Atmospheric and Thermospheric Sources. J. Geophys. Res. 112. doi:10.1029/2006JA011845

CrossRef Full Text | Google Scholar

Vadas, S. L., Xu, S., Yue, J., Bossert, K., Becker, E., and Baumgarten, G. (2019). Characteristics of the Quiet‐Time Hot Spot Gravity Waves Observed by GOCE over the Southern Andes on 5 July 2010. J. Geophys. Res. Space Phys. 124, 7034–7061. doi:10.1029/2019JA026693

CrossRef Full Text | Google Scholar

Vadas, S. L., Yue, J., She, C. Y., Stamus, P. A., and Liu, A. Z. (2009). A Model Study of the Effects of Winds on Concentric Rings of Gravity Waves from a Convective Plume Near Fort Collins on 11 May 2004. J. Geophys. Res. 114, D06103. doi:10.1029/2008JD010753

CrossRef Full Text | Google Scholar

Vadas, S. L., Zhao, J., Chu, X., and Becker, E. (2018). The Excitation of Secondary Gravity Waves from Local Body Forces: Theory and Observation. J. Geophys. Res. Atmos. 123, 9296–9325. doi:10.1029/2017JD027970

CrossRef Full Text | Google Scholar

Vadas, S., Yue, J., and Nakamura, T. (2012). Mesospheric Concentric Gravity Waves Generated by Multiple Convective Storms over the North American Great Plain. J. Geophys. Res. 117. doi:10.1029/2011JD017025

CrossRef Full Text | Google Scholar

Waldock, J. A., and Jones, T. B. (1986). HF Doppler Observations of Medium-Scale Travelling Ionospheric Disturbances at Mid-latitudes. J. Atmos. Terrestrial Phys. 48, 245–260. doi:10.1016/0021-9169(86)90099-1

CrossRef Full Text | Google Scholar

Walterscheid, R. L., and Schubert, G. (1990). Nonlinear Evolution of an Upward Propagating Gravity Wave: Overturning, Convection, Transience and Turbulence. J. Atmos. Sci. 47 (1), 101–125. doi:10.1175/1520-0469(1990)047<0101:neoaup>2.0.co;2

CrossRef Full Text | Google Scholar

Yamada, Y., Fukunishi, H., Nakamura, T., and Tsuda, T. (2001). Breaking of Small-Scale Gravity Wave and Transition to Turbulence Observed in OH Airglow. Geophys. Res. Lett. 28, 2153–2156. doi:10.1029/2000gl011945

CrossRef Full Text | Google Scholar

Yue, J., Hoffmann, L., and Joan Alexander, M. (2013). Simultaneous Observations of Convective Gravity Waves from a Ground-Based Airglow Imager and the AIRS Satellite experiment. J. Geophys. Res. Atmos. 118, 3178–3191. doi:10.1002/jgrd.50341

CrossRef Full Text | Google Scholar

Yue, J., Vadas, S. L., She, C. Y., Nakamura, T., Reising, S. C., Liu, H. L., et al. (2009). Concentric Gravity Waves in the Mesosphere Generated by Deep Convective Plumes in the Lower Atmosphere Near Fort Collins, Colorado. J. Geophys. Res. 114, D06104. doi:10.1029/2008JD011244

CrossRef Full Text | Google Scholar

Zhu, X., and Holton, J. R. (1987). Mean fields Induced by Local Gravity-Wave Forcing in the Middle Atmosphere. J. Atmos. Sci. 44, 620–630. doi:10.1175/1520-0469(1987)044<0620:mfiblg>2.0.co;2

CrossRef Full Text | Google Scholar