- 1Department of Physics, Faculty of Science, Universiti Teknologi Malaysia, Johor Bahru, Malaysia
- 2National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
- 3Research Center for Nuclear Physics, Osaka University, Osaka, Japan
This is a brief review on ordinary muon capture (OMC) experiments at Research Center for Nuclear Physics (RCNP) Osaka University relevant for the study of double beta decays (DBDs) and astro anti-neutrinos (neutrino) nuclear responses. OMC usually leaves the nucleus in highly excited unbound state. OMC is a charge exchange reaction via the charged weak boson as given by (μ,vμ) reactions with μ and vμ being the muon and muon neutrino. Subjects discussed include 1) unique features of OMC for studying DBDs and astro anti-neutrino (neutrino) nuclear responses, 2) experiments of OMCs on 100Mo and natMo to study neutrino nuclear responses for DBDs and astro anti-neutrinos, 3) impact of the OMC results on neutrino nuclear responses for DBDs and astro anti-neutrinos. Remarks and perspectives on OMC experiments for neutrino nuclear responses are briefly described.
1 Introduction
Double beta decays (DBDs) and astro (solar and supernova) neutrinos and anti-neutrinos are of current interest. Neutrino-less DBDs are used to explore the fundamental neutrino properties such as the Majorana nature, the absolute mass scale, the mass hierarchy and the CP phases beyond the standard electroweak model. The zero-neutrino (0v) DBD rate is given by
The supernova nucleo-synthesis rates induced by neutrinos and anti-neutrinos are proportional to the respective nuclear responses
where
for each intermediate state (i) and in the respective isospin directions τ− for ν or τ+ for
Experimental studies for the neutrino nuclear responses are interesting to provide the nuclear parameters to be used for theoretical calculations. Charge exchange reactions (CERs) using light ions have been used to study the neutrino nuclear responses. In particular, high energy-resolution (3He, t) CERs have been used to study the neutrino nuclear responses for nuclei of DBD and astro neutrino interests in the broad energy and momentum regions. The responses studied by these light-ion CERs are the τ−-side ones, and the NMEs Mi− are derived from CERs. On the other hand, the τ+-side responses and the NMEs Mi+ are not well studied since the (t,3He) CERs to be used for studying the τ+-side responses require the radioactive t beam, and thus high precision measurements are difficult. Medium energy-resolution measurements are made by using (d,2He) reactions. Neutrino nuclear responses studied by these light-ion CERs are discussed in the recent review articles and references therein (Ejiri, 2000; Vergados et al., 2012; Frekers and Alanssari, 2018; Ejiri et al., 2019; Ejiri, 2020).
Recently ordinary muon capture reactions (OMC), where a negative muon in an atomic orbit is captured into the nucleus has been shown useful for studying the τ+-side responses, and the Mi+ NMEs at Research Center for Nuclear Physics (RCNP) Osaka University (Hashim, 2015; Hashim et al., 2018; Hashim and Ejiri, 2019). The present report is a brief mini-review on the OMC studies for the DBD and astro anti-neutrinos responses and related subjects on nuclear isotope productions at RCNP.
2 Unique Features of OMCs for Neutrino Nuclear Responses
In OMC some of the unique feature are as follows:
(1) OMC can be used to study the τ+-responses of proton (p)
(2) OMC transfers energy between 0–50 MeV and a momentum up to 100 MeV/c to the nucleus that are similar to those involved in neutrino-less DBD and supernova anti-neutrino.
(3) A negative muon is finally captured into the nucleus via the weak interaction. The capture probability in the medium and heavy nuclei is around 95% after a mean lifetime of about 100 ns in the atomic orbit. Low momentum (a few 10 MeV/c) beam muons at intensities of 103–104 muons/s are used for OMC studies.
(4) The OMC on AZX, where A and Z are the mass and the atomic numbers, excites the nucleus AZ−1X up to around 50 MeV, which decays by emitting a number (x) of mostly neutrons and gamma rays to the ground state of the residual nucleus A−xZ−1X. The number of neutrons reflects the excitation energy. Accordingly, the relative strength as a function of the excitation energy is evaluated by measuring the number (x) of the neutrons, i.e. the mass distribution A−x of the residual nuclei.
(5) Absolute OMC rate is obtained from the measured lifetime of the trapped muons, and thus the neutrino nuclear responses are derived from the OMC rate.
3 Neutrino Nuclear Responses for Mo Isotopes by OMC
The intense 400 MeV proton beam with an intensity around 1 μA from the RCNP cyclotron is used to produce pions. The momentum (
Recently OMCs were studied on natMo and 100Mo, which are interesting for DBD and astro neutrino studies (Ejiri et al., 2019). The OMC on A42Mo isotopes with the mass-number A = 92–100 produces A41Nb with the excitation energy
The OMC strength distribution as a function of the excitation energy E is derived from the mass-number (A−x) distribution (x distribution) through the particle cascade model (Hashim et al., 2018; Hashim & Ejiri, 2019; Hashim et al., 2020). The excited states in Nb isotopes decay by emitting mostly neutrons since the Coulomb barrier much suppresses proton emission. Thus, the neutron cascade emission model (NEM) (Hashim et al., 2017; Hashim et al., 2018) was developed to deduce the excitation energy in the initial isotope of ANb from the number 10(x) of the emitted neutrons, i.e., the mass-number A−x of the residual isotope A−xNb after the x neutron emission. The neutron energy spectrum for the first neutron consists of the pre-equilibrium (PEQ) and equilibrium (EQ) stages (Ejiri and de Voight, 1989). It is given as
where TEQ(E) and TPEQ(E) are the EQ and PEQ nuclear temperatures, respectively. TEQ(E) is given as a function of excitation energy E (Ejiri and de Voight, 1989). The ratio of TPEQ(E)/TEQ(E) = 3 for the medium excitation 10
The NEM analysis on the observed mass-number distribution of 100−xNb shows preferential excitation (muon giant resonance, μ-GR) at 10–14 MeV region and a broad bump at the higher excitation region of 25–40 MeV. The NEM analyses on other medium-heavy nuclei by (Ibrahim, 2018) using experimental data from (Measday et al., 2007b; Measday et al., 2007a) show similar features of the preferential excitation of the 10–15 MeV. This preferential excitation reflects the large branch of the one neutron (x = 1) emission. The NME analyses on the mass-number distributions for OMCs on light nuclei show a preferential excitation around 4–8 MeV region by (Muslim, 2018) using experimental data from (Evans, 1973; Measday et al., 2007c). This observation is consistent with the calculation in (Kortelainen and Suhonen, 2004).
The strength distribution is fitted by the sum of the μ-GR strengths of B1(μ,E1) and B2(μ,E2) given by
where EGi and Гi with i = 1,2 are the resonance energy and the width for the ith GR, and the constant Bi(μ) is given by σiГi/(2π) with σi being the total strength integrated over the excitation energy. The obtained GR energies are 12 MeV for the first GR and 32.5 MeV for the second GR, and the widths for both GRs are 8 MeV, as shown in Figure 1B. Here we note the GR2 is not entirely clear beyond the statistical error and maybe a broad bump. The μ-GR energy peaks at around 12 MeV, which is lower than the giant dipole resonance (GDR) energy of 14 MeV deduced from a photon-induced reaction (Ejiri et al., 2011). It also features a broader width of about 8 MeV compared to the 5 MeV width of the latter. This is, of course due to the additional multipole components of higher spin states excited by τ+, i. e.,: (n, p)-type, muon capture.
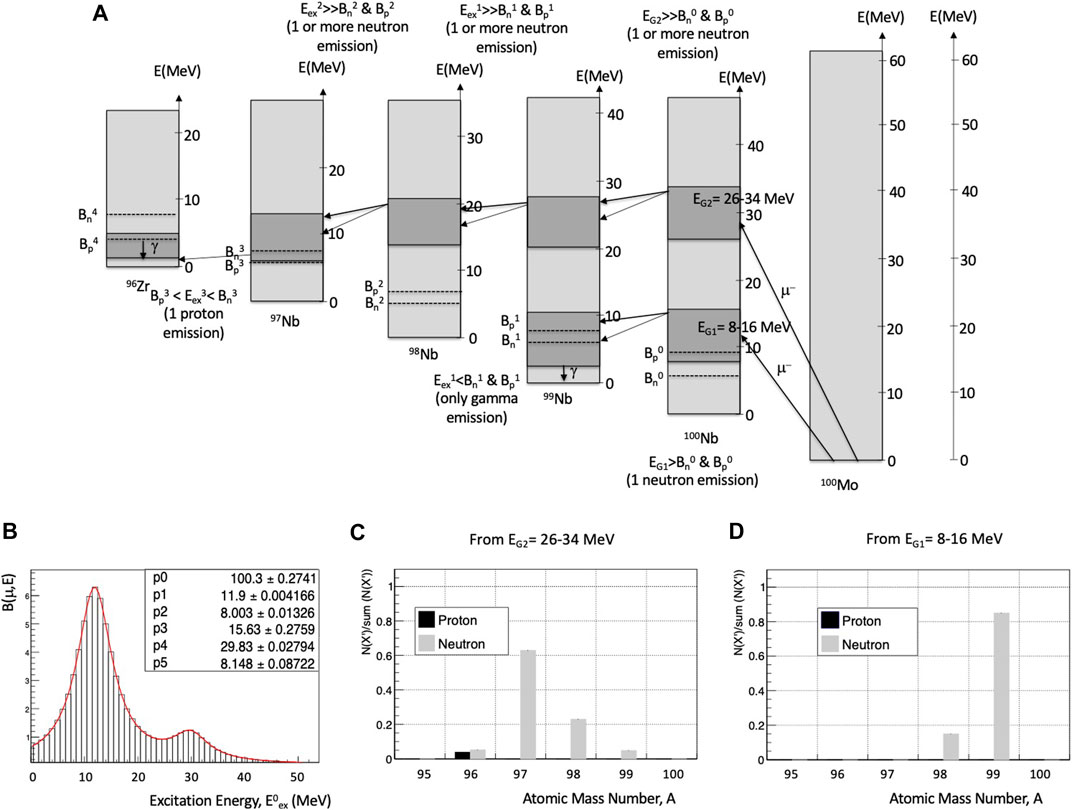
FIGURE 1. Proton neutron emission model (PNEM) (Hashim et al., 2020). (A) When OMC on 100Mo occurs, 100Nb is excited to some energy up to around 50 MeV, with Bn(Bp) = 5.68 MeV (9.46 MeV), 6.87 MeV (8.34 MeV), 5.99 MeV (7.87 MeV) and 8.07 MeV (7.46 MeV) for NbA with A = 100, 99, 98, and 97, respectively. (B) The excitation energy region of 8–16 MeV, which is strongly excited, decays by emitting mainly 1 neutron, and partly by 2 neutrons, depending on the neutron energy. (C) The excitation region of 26–34 MeV day by emitting 3–4 neutrons and also partly by emitting 3 neutrons and 1 proton. (D) The muon strength distribution, B(μ,E) for OMC on 100Mo from the excitation energy distribution in the daughter nucleus of Nb and Zr isotopes following the muon capture process. To reproduce the 100Mo experimental RI mass distribution, the EG1 and EG2 are observed at 12 MeV, and 30 MeV with an intensity ratio of EG1/EG2 = 1/6 (Hashim et al., 2018).
Recently a proton-neutron emission model (PNEM) has been developed by considering the probability of proton emission as well (Hashim et al., 2020). The proton energy spectrum is given by S(Ep) = m × exp(−n×Ep), where m and n are the density parameter constant with the value of 0.832 MeV and 0.163 MeV−1. Here, the proton is assumed to be emitted in the case of
Since then, various calculations have been made for understanding the formation of the GR populated by muon capture reactions in 98,
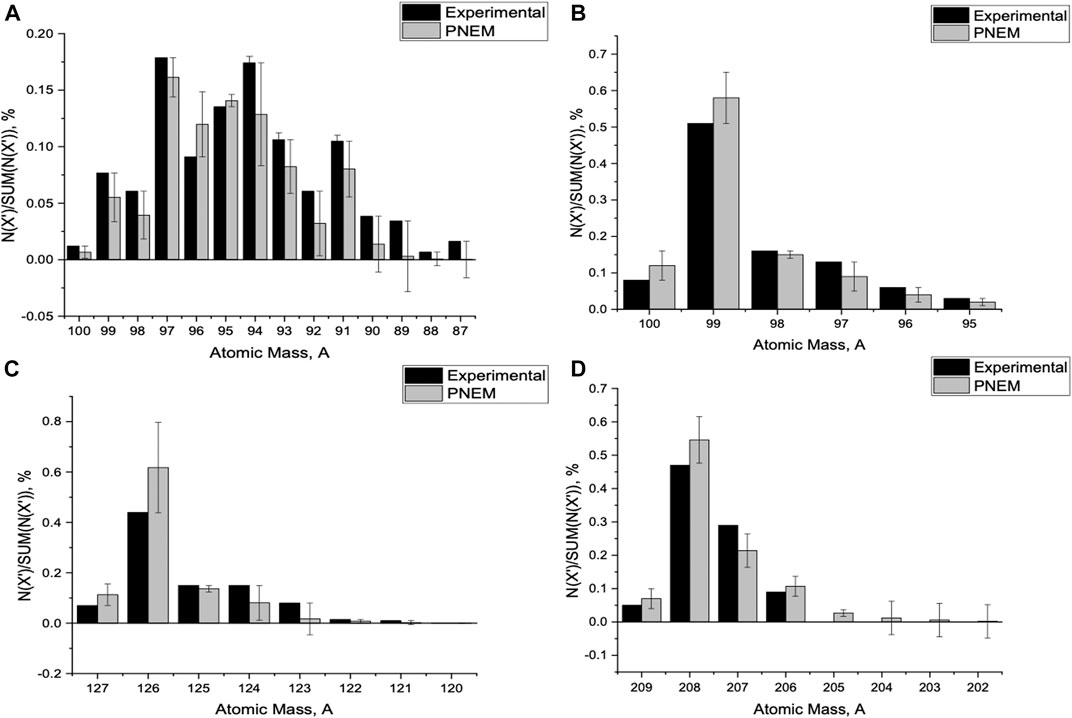
FIGURE 2. Radioactive isotope (RIs) mass-number distribution from the ratio of number of isotopes N (X′) where X being the atomic mass number of the daughter nucleus in experimental observations over the total isotopes
4 Implications for Double Beta Decays
The experimental OMC rate for 100Mo as a function of the excitation energy is compared with the theoretical calculation by using proton-neutron quasi-particle random-phase approximation (pn-QRPA) (Jokiniemi et al., 2019). The pn-QRPA well reproduces the GR at around 10–14 MeV with mainly low multipoles of Jπ = 0±,1± and 2±. The observed OMC rate is the same order of magnitude as the empirical value suggested by Primakoff (Suzuki et al., 1987) but is lower by a factor 5 than the pn-QRPA (Jokiniemi et al., 2019; Jokiniemi and Suhonen, 2019). This suggests a quenching coefficient for the axial-vector weak coupling of
It is interesting to note that the OMC results together with the (3He,t) CERs and
5 Remarks and Perspectives
The relative strength distribution of OMC on Mo isotopes show the μ-GR around
The extensive experimental programs on OMC for other nuclei of DBD and supernova anti-neutrino interests are under progress at RCNP and Paul Scherrer Institute (PSI), Switzerland, by the join group of Joint Institute for Nuclear Research (JINR), Dubna, RCNP, Osaka and Universiti Teknologi Malaysia (UTM) (Hashim and Ejiri, 2019). The pn-QRPA theoretical calculation is also in progress at Jyvaskyla (Jokiniemi et al., 2019).
Finally, it is remarked that muon capture isotope production (MuCIP) is used for producing efficiently nuclear isotopes with the atomic number Z−1, less by one than the atomic number Z of the target isotope. By using AZX target isotopes, isotopes of A−1Z−1X are preferentially produced, and several isotopes with A,A−2,A−3,A−4 are also produced (Ejiri et al., 2013; Zinatulina et al., 2019). There is potential for using them for basic and applied science. One RI used for medical checks is the 99Mo, which is well produced by OMC on 100Mo, as studied at RCNP (Ejiri et al., 2013). MuCIP is complementary to photon capture reactions where isotopes of A−1ZX are well produced (Ejiri et al., 2011; Szpunar et al., 2013). Note that ppb-level nuclei (impurities) are identified by measuring gamma rays from OMC, which are characteristic of the nuclei, as explained in (Ejiri et al., 2013).
Author Contributions
IH and HE are equally accounted for the content of the work.
Funding
This work was financially supported by the Universiti Teknologi Malaysia research grants (Q.J130000.3026.01M14 and R.J130000.7854.5F227) and the Ministry of Higher Education Malaysia Fundamental Research Grant Scheme (FRGS/1/2019/STG02/UTM/02/6).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to RCNP, UTM, and JINR colleagues for the collaboration and valuable discussions.
References
Ciccarelli, M., Minato, F., and Naito, T. (2020). Theoretical Study of Nb Isotope Productions by Muon Capture Reaction on Mo100. Phys. Rev. C 102, 034306. doi:10.1103/PhysRevC.102.034306
Ejiri, H., and de Voight, M. J. A. (1989). Gamma Ray and Electron Spectroscopy in Nuclear Physics, Oxford: Oxford University Press.
Ejiri, H., and Suhonen, J. (2015). “GT Neutrino-Nuclear Responses for Double Beta Decays and Astro Neutrinos. J. Phys. G: Nucl. Part. Phys., 42, 055201. doi:10.1088/0954-3899/42/5/055201
Ejiri, H., Shima, T., Miyamoto, S., Horikawa, K., Kitagawa, Y., Asano, Y., et al. (2011). Resonant Photonuclear Reactions for Isotope Transmutation. J. Phys. Soc. Jpn. 80, 094202. doi:10.1143/JPSJ.80.094202
Ejiri, H., H. Hashim, I., Hino, Y., Kuno, Y., Matsumoto, Y., Ninomiya, K., et al. (2013). Nuclear γ Rays from Stopped Muon Capture Reactions for Nuclear Isotope Detection. J. Phys. Soc. Jpn. 82, 044202. doi:10.7566/JPSJ.82.044202
Ejiri, H., Suhonen, J., and Zuber, K. (2019). Neutrino-nuclear Responses for Astro-Neutrinos, Single Beta Decays and Double Beta Decays. Phys. Rep. 797, 1–102. doi:10.1016/j.physrep.2018.12.001
Ejiri, H. (2000). Nuclear Spin Isospin Responses for Low-Energy Neutrinos. Phys. Rep. 338, 265–351. doi:10.1016/S0370-1573(00)00044-2
Ejiri, H. (2019a). Axial-vector Weak Coupling at Medium Momentum for Astro Neutrinos and Double Beta Decays. J. Phys. G: Nucl. Part. Phys. 46, 125202. doi:10.1088/1361-6471/ab4dcb
Ejiri, H. (2019b). Nuclear Matrix Elements for β and ββ Decays and Quenching of the Weak Coupling gA in QRPA. Front. Phys. 7, 30. doi:10.3389/fphy.2019.00030
Ejiri, H. (2020). Neutrino-mass Sensitivity and Nuclear Matrix Element for Neutrinoless Double Beta Decay. Universe 6, 225. doi:10.3390/universe6120225
Evans, H. J. (1973). Gamma-rays Following Muon Capture. Nucl. Phys. A 207, 379–400. doi:10.1016/0375-9474(73)90354-0
Frekers, D., and Alanssari, M. (2018). Charge-exchange Reactions and the Quest for Resolution. Eur. Phys. J. A. 54, 177. doi:10.1140/epja/i2018-12612-5
Hashim, I. H., and Ejiri, H. (2019). New Research Project with Muon Beams for Neutrino Nuclear Responses and Nuclear Isotopes Production. AAPPS Bull. 29, 21–26. doi:10.22661/AAPPSBL.2019.29.3.21
Hashim, I. H., Ejiri, H., Othman, F., Saroni, S. S., Amelia, W. N., Hamzah, S. A., et al. (2017). Statistical Neutron Emission Model for Neutrino Nuclear Response. EPJ Web Conf. 156, 00005. doi:10.1051/epjconf/201715600005
Hashim, I. H., Ejiri, H., Shima, T., Takahisa, K., Sato, A., Kuno, Y., et al. (2018). Muon Capture Reaction on Mo100 to Study the Nuclear Response for Double- β Decay and Neutrinos of Astrophysics Origin. Phys. Rev. C 97, 014617. doi:10.1103/PhysRevC.97.014617
Hashim, I. H., Ejiri, H., Othman, F., Ibrahim, F., Soberi, F., Ghani, N., et al. (2020). Nuclear Isotope Production by Ordinary Muon Capture Reaction. Nucl. Instr. Methods Phys. Res. Section A: Acc. Spectrometers, Detectors Associated Equipment 963, 163749. doi:10.1016/j.nima.2020.163749
Hashim, I. H. (2015). A Study of Weak Nuclear Response by Nuclear Muon capture. PhD Thesis. Osaka: Osaka University.
Hino, Y., Kuno, Y., Sato, A., Sakamoto, H., Matsumoto, Y., Tran, N. H., et al. (2014). “A Highly Intense Dc Muon Source, Music and Muon Clfv Search. Nucl. Phys. B - Proc. Supplements 253–255, 206–207. doi:10.1016/j.nuclphysbps.2014.09.051
Ibrahim, F. (2018). Excitation Energies of Compound Nucleus Following Ordinary Muon Capture on Medium Heavy Nuclei within Neutron Statistical Model. Thesis. Johor: Universiti Teknologi Malaysia
Jokiniemi, L., and Suhonen, J. (2019). Muon-capture Strength Functions in Intermediate Nuclei of 0νββ Decays. Phys. Rev. C 100, 014619. doi:10.1103/PhysRevC.100.014619
Jokiniemi, L., Suhonen, J., Ejiri, H., and Hashim, I. H. (2019). Pinning Down the Strength Function for Ordinary Muon Capture on 100Mo. Phys. Lett. B 794, 143–147. doi:10.1016/j.physletb.2019.05.037
Kortelainen, M., and Suhonen, J. (2004). Nuclear Muon Capture as a Powerful Probe of Double-Beta Decays in Light Nuclei. J. Phys. G: Nucl. Part. Phys. 30, 2003–2018. doi:10.1088/0954-3899/30/12/017
Measday, D. F., Stocki, T. J., Alarcon, R., Cole, P. L., Djalali, C., and Umeres, F. (2007a). Comparison of Muon Capture in Light and in Heavy Nuclei. AIP Conf. Proc. 947, 253–257. doi:10.1063/1.2813812
Measday, D. F., Stocki, T. J., and Tam, H. (2007b). Γrays from Muon Capture in I, Au, and Bi. Phys. Rev. C 75, 045501. doi:10.1103/PhysRevC.75.045501
Measday, D. F., Stocki, T. J., Moftah, B. A., and Tam, H. (2007c). γ Rays from Muon Capture inAl27and Natural Si. Phys. Rev. C 76, 035504. doi:10.1103/PhysRevC.76.035504
Measday, D. F. (2001). The Nuclear Physics of Muon Capture. Phys. Rep. 354, 243–409. doi:10.1016/S0370-1573(01)00012-6
Menéndez, J., Gazit, D., and Schwenk, A. (2011). Chiral Two-Body Currents in Nuclei: Gamow-Teller Transitions and Neutrinoless Double-Beta Decay. Phys. Rev. Lett. 107, 062501. doi:10.1103/PhysRevLett.107.062501
Muslim, N. F. H. (2018). Neutron Statistical Model for Muon Capture on Light Nuclei. Thesis. Johor: Universiti Teknologi Malaysia.
Šimkovic, F., Dvornický, R., and Vogel, P. (2020). Muon Capture Rates: Evaluation within the Quasiparticle Random Phase Approximation. Phys. Rev. C 102, 034301. doi:10.1103/PhysRevC.102.034301
Suhonen, J. (2017). Impact of the Quenching of gA on the Sensitivity of 0νββ Experiments. Phys. Rev. C 96, 055501. doi:10.1103/PhysRevC.96.055501
Suzuki, T., Measday, D. F., and Roalsvig, J. P. (1987). Total Nuclear Capture Rates for Negative Muons. Phys. Rev. C 35, 2212–2224. doi:10.1103/PhysRevC.35.2212
Szpunar, B., Rangacharyulu, C., Daté, S., and Ejiri, H. (2013). Estimate of Production of Medical Isotopes by Photo-Neutron Reaction at the Canadian Light Source. Nucl. Instr. Methods Phys. Res. Section A: Acc. Spectrometers, Detectors Associated Equipment 729, 41–50. doi:10.1016/j.nima.2013.06.106
Vergados, J. D., Ejiri, H., and Šimkovic, F. (2012). Theory of Neutrinoless Double-Beta Decay. Rep. Prog. Phys. 75, 106301. doi:10.1088/0034-4885/75/10/106301
Keywords: ordinary muon capture, muon charge exchange reaction, neutrino nuclear response, double beta decay, supernova neutrino, nuclear matrix element, neutrino mass
Citation: Hashim IH and Ejiri H (2021) Ordinary Muon Capture for Double Beta Decay and Anti-Neutrino Nuclear Responses. Front. Astron. Space Sci. 8:666383. doi: 10.3389/fspas.2021.666383
Received: 10 February 2021; Accepted: 05 May 2021;
Published: 28 May 2021.
Edited by:
Theocharis S. Kosmas, University of Ioannina, GreeceReviewed by:
Dieter Frekers, University Muenster, GermanyFrank Franz Deppisch, University College London, United Kingdom
Copyright © 2021 Hashim and Ejiri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izyan Hazwani Hashim, aXp5YW5AdXRtLm15
 Izyan Hazwani Hashim
Izyan Hazwani Hashim Hiroyasu Ejiri3
Hiroyasu Ejiri3