- SMART Laboratory, Scuola Normale Superiore, Pisa, Italy
Vibrational spectroscopy represents an active frontier for the identification and characterization of molecular species in the context of astrochemistry and astrobiology. As new missions will provide more data over broader ranges and at higher resolution, especially in the infrared region, which could be complemented with new spectrometers in the future, support from laboratory experiments and theory is crucial. In particular, computational spectroscopy is playing an increasing role in deepening our understanding of the origin and nature of the observed bands in extreme conditions characterizing the interstellar medium or some planetary atmospheres, not easily reproducible on Earth. In this connection, the best compromise between reliability, feasibility and ease of interpretation is still a matter of concern due to the interplay of several factors in determining the final spectral outcome, with larger molecular systems and non-covalent complexes further exacerbating the dichotomy between accuracy and computational cost. In this context, second-order vibrational perturbation theory (VPT2) together with density functional theory (DFT) has become particularly appealing. The well-known problem of the reliability of exchange-correlation functionals, coupled with the treatment of resonances in VPT2, represents a challenge for the determination of standardized or “black-box” protocols, despite successful examples in the literature. With the aim of getting a clear picture of the achievable accuracy and reliability of DFT-based VPT2 calculations, a multi-step study will be carried out here. Beyond the definition of the functional, the impact of the basis set and the influence of the resonance treatment in VPT2 will be analyzed. For a better understanding of the computational aspects and the results, a short summary of vibrational perturbation theory and the overall treatment of resonances for both energies and intensities will be given. The first part of the benchmark will focus on small molecules, for which very accurate experimental and theoretical data are available, to investigate electronic structure calculation methods. Beyond the reliability of energies, widely used for such systems, the issue of intensities will also be investigated in detail. The best performing electronic structure methods will then be used to treat larger molecular systems, with more complex topologies and resonance patterns.
1 Introduction
More than 200 molecules have been identified in the interstellar medium (ISM) during the last 50 years (McGuire, 2018), and a much larger number on comets or exoplanet atmospheres, thanks to their spectroscopic signatures. Among them, the so-called interstellar complex organic molecules (iCOMs), namely molecules containing more than five atoms with at least one carbon atom, are particularly significant because some of them are either biomolecular building blocks or their key precursors (Chyba and Sagan, 1992; Herbst and van Dishoeck, 2009; Hörst et al., 2012; Balucani, 2012; Saladino et al., 2012; Saladino et al., 2015).
While rotational spectroscopy plays a major role in characterizing molecules in the ISM (Puzzarini and Barone, 2020), this is not true on Earth and for exoplanet atmospheres, where the dominant regions are at shorter wavelengths. In this context, vibrational spectroscopies are often the methods of choice (Des Marais et al., 2002; Girish and Sony, 2008; Seager, 2014). Furthermore, chirality is one of the key features of life, at least as we know it. As a consequence, the study of prebiotic molecules cannot escape from this feature, and here chiroptical spectroscopies, (e.g., vibrational circular dichroism, VCD, and Raman optical activity, ROA) come into play. The intricacy of spectra and the difficulty of their interpretation due to the concomitant role of several factors has led to an increasing role of computational spectroscopy, which is able to match the extreme environments observable in space. Of course, a mandatory prerequisite to the use of computational approaches is their sufficient accuracy in order to prevent any risk of ambiguity in the interpretation. For the specific case of vibrational spectroscopies, this requirement necessarily includes the treatment of anharmonicity in nuclear motions, with the possible inclusion of the rotational sub-structure (Biczysko et al., 2018; Puzzarini et al., 2019). Beyond very sophisticated rovibronic models, still limited in practice to diatomic or triatomic systems in standard applications (Carter et al., 1990, 2000; Császár et al., 2012; Mitrushchenkov, 2012; Nauts and Lauvergnat, 2012; Yurchenko et al., 2016), variational methods in conjunction with electronic structure calculations at the coupled cluster (CC) or configuration interaction (CI) levels represent a gold standard (Biczysko et al., 2003; Mátyus et al., 2009; Papp et al., 2017; Erfort et al., 2020). Indeed, variational approaches can in principle be systematically improved to reach any target accuracy, by using higher-order force fields through an extensive sampling of the potential energy surface (PES). Besides the practical difficulties of attaining arbitrary precision, the convergence to the correct energy is generally slow, especially when the starting level is the harmonic approximation. In this case, an extensive description of the PES may be necessary, resulting in a high overall computational cost to obtain results in close agreement with the best experimental data.
As larger and more complex molecules gain greater astrochemical interest, for instance in connection with the issue of the exogenous origin of life, this cost can become prohibitive and less expensive alternatives are necessary. One possible strategy is to use a cheaper method to estimate a better starting point on which the variational correction is applied, like vibrational self-consistent field (VSCF). However, the efficiency of such an approach is strongly conditioned by the description of the nuclear vibrations (Bulik et al., 2017). Over the years, perturbative approaches, and in particular second-order vibrational perturbation theory (VPT2, Nielsen (1951)), have shown promising capabilities, offering significant improvements over the harmonic level at a more convenient cost than their variational counterparts (Puzzarini et al., 2019). From a computational perspective, the interest of these approaches is twofold. First, they require simpler descriptions of the PES, which can be achieved with a limited number of small displacements from the equilibrium along suitable coordinates. Second, few, analytic equations need to be derived and implemented to describe the vibrational energies and intensities, making their calculation very straightforward. As a result, VPT2 on top of electronic structures at a coupled-cluster level, in particular with single and double excitations, and a perturbative treatment of the triples (CCSD(T), Raghavachari et al. (1989)), has become a standard to get energy levels, notably in the mid-IR region. Several strategies have been proposed to lower the computer time required by the electronic structure calculations, which represent the bottleneck of accurate calculations for medium/large-size molecular systems, with hybrid schemes based on a separation of the harmonic problem and the anharmonic correction being particularly effective (Begue et al., 2005; Carbonniere et al., 2005; Puzzarini and Barone, 2008; Biczysko et al., 2018; Puzzarini et al., 2019). These approaches are rooted into the hypothesis that the largest source of errors in VPT2 results is related to the harmonic reference data, so that a good accuracy can be obtained by combining harmonic results produced by a very accurate electronic structure method, (e.g., CCSD(T)) with anharmonic contributions evaluated at a lower level, (e.g., DFT employing hybrid functionals) (Puzzarini et al., 2010; Barone et al., 2013a, 2015; Puzzarini et al., 2019). Of course, even harmonic contributions need to be computed by relatively cheap quantum mechanical methods, (e.g., DFT) for very large molecules, like polycyclic aromatic hydrocarbons or biomolecules (McGuire et al., 2021).
An important source of complications with DFT is the ever-growing range of exchange-correlation functionals, each with their own strengths and limitations. This has prompted an increasing activity of benchmarking in the literature to provide pointers for choosing the most suitable functionals for a given type of study (Goerigk et al., 2017; Mardirossian and Head-Gordon, 2017). Unfortunately, the quantities of interest have been predominantly structural parameters, energetics and thermodynamics, with vibrational spectroscopies limited to the harmonic level. Recently, the growing interest in VPT2 has led to more extensive studies with account for anharmonicity (Bloino et al., 2016; Barone et al., 2020; Mitra and Roy, 2020; Nejad et al., 2020). This paves the way to more robust computational protocols. However, two aspects remain insufficiently explored. First, intensities are still rarely considered, especially for Raman and chiral spectroscopies. As bioactivity in planetary atmospheres is being increasingly probed, the combination of multiple measurement techniques becomes appealing, which means having the capacity of predicting correctly multiple properties and their interaction, as it is the case in chiroptical spectroscopies. A further difficulty in assessing the quality of the DFT functionals and the effect of basis sets is that reference implementations in more sophisticated electronic structure calculation methods is often lacking, so direct comparison with experiment is the only viable path. On the other side, VPT2 can suffer from resonances, special conditions which lead to an incorrect account of the anharmonic effects. While several strategies have been proposed in the literature and automated schemes are being devised to overcome this issue (Martin et al., 1995; Kuhler et al., 1996; Barone, 2005; Bloino et al., 2012, 2015; Krasnoshchekov et al., 2014, 2020), the effect of these corrections on the final energies and intensities has still been scarcely investigated. With these considerations in mind, the study proposed here is divided in several steps, starting from small systems where VPT2 calculations are straightforward and accurate reference data are available. By increasing the size of the systems of interest and their structural complexity, more resonance patterns can appear, which can impact notably the results, independently of the quality of the underlying electronic structure calculation methods. The results of these studies will pave the way to the full simulation of vibrational spectra of larger systems.
The manuscript is organized as follows. First, key aspects of VPT2 for the calculation of energies and intensities, as well as the problem of resonances, are briefly recalled. Strategies to address the latter are presented and discussed. The computational protocol is then described, followed by an analysis of the quality of some representative functionals combined with a variety of basis sets. The impact of the VPT2 treatment is also assessed. Finally, larger molecular systems are used as case studies to investigate the overall quality of DFT and VPT2.
2 Theoretical Background
2.1 The VPT2 Framework
In this section, we highlight key aspects of VPT2, which can have important practical impacts on the results. This will also let us introduce the notation used in the manuscript. More details on the derivations of the equations can be found in References. (Nielsen, 1951; Plíva, 1990; Willets et al., 1990; Vázquez and Stanton, 2006; Bloino and Barone, 2012; Franke et al., 2021). For a similar reason, reference equations are recalled, but most of the concepts, especially regarding the problem of resonances, are introduced in a descriptive way, focusing on the physical concepts and implications.
First of all, it is noteworthy that a number of hypotheses are commonly made in the theoretical developments, namely that the Born-Oppenheimer approximation is valid for the separation of the electronic and nuclear wave functions, and the Eckart-Sayvetz conditions (Eckart, 1935) are met to separate translational and vibrational-rotational motions through specific position and orientation of the molecule, the Eckart frame. Among several alternatives, the most widely used starting point, chosen here as well, is the rovibrational Hamiltonian proposed by Watson and expressed in a basis of dimensionless normal coordinates
where h and c are respectively the Planck constant and the speed of light,
V and μ are respectively the potential energy operator and the effective inverse molecular inertia tensor, for which analytic definitions are generally not available. Both can be expanded as Taylor series of
with
In the present work, the systems under study are assumed to be in their rotational ground states, so the contributions of the rotational operator
with
The vibrational Hamiltonian of interest here, truncated at the zeroth-order of Eq. 3 and second-order of Eq. 4, is thus,
The U term is usually accounted for through its zeroth-order expansion,
where
Starting from the solution of the vibrational Schrödinger equation for the harmonic oscillator, labeled with the “(0)” superscript,
the vibrational wave function (ψ) and energy (ε) are expanded in perturbative series, and the Hamiltonian
A similar approach can be applied for the intensities, where the transition moments of each property of interest, labeled generically as
The perturbed wave functions,
2.2 Vibrational Energies
Let us consider first the case of vibrational energies. Following the resolution of the anharmonic vibrational Schrödinger equation at the VPT2 level, the vibrational energy of a state
with
In the present study, we are only interested in transition energies from the vibrational ground state, so,
The anharmonic correction is contained in the
Equation 10 corresponds to the VPT2 energy. From a quick analysis of Eqs 11, 12, singularity conditions, collectively known as Fermi resonances (FRs), can be identified, where the energy can tend toward infinite values. For simplicity, let us consider a single term,
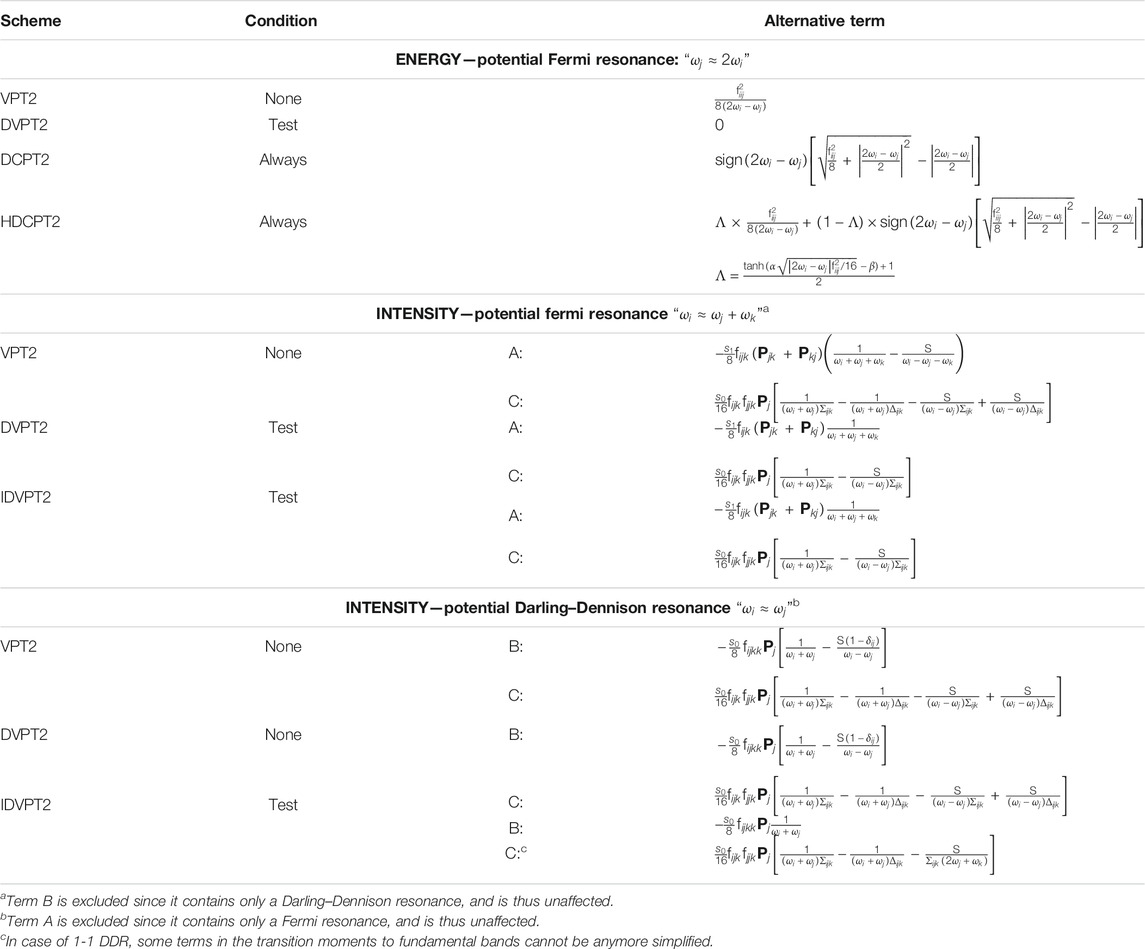
TABLE 1. Description of the treatment of Fermi resonant terms in the calculation of energy, and Fermi and Darling–Dennison resonance in intensities for some VPT2 schemes. The condition indicates in which cases the alternative term is used in place of the potentially resonant term (reported for the original VPT2 scheme since no transformation is done). See text for details.
In the deperturbed VPT2 (DVPT2) treatment, each potentially resonant term is screened, applying one or more criteria to establish if it is resonant and should be ignored, or not. The most common procedure involves two steps, first on the energetic proximity of the interacting states–here
1.
2.
As a result, the capacity of identifying correctly the resonances, and ultimately the quality of the DVPT2 results, will depend on the chosen thresholds,
Among these models, DVPT2 can lead to a truncated treatment since terms are selectively discarded. To recover them, a variational treatment is added, which reintroduces the terms as explicit couplings between the states with DVPT2 energies. In a simplified picture, a symmetric matrix is built, listing all fundamental
To conclude on the vibrational energies, some couplings are not accounted for at the VPT2 level. In standard calculations, they are the interaction between first overtones and two-quanta binary combinations–generally noted 2–2 –, and between fundamentals (noted 1–1). As originally documented by Darling and Dennison (Darling and Dennison, 1940), they can give important contributions to vibrational energies. These terms, collectively known as Darling–Dennison resonances (DDRs) or interactions, can be added during the variational step in GVPT2 (Krasnoshchekov et al., 2014; Rosnik and Polik, 2014). The polyads are then incremented by including these new couplings between states, and the corresponding matrices completed with the new contributions. The introduction of these corrections can further transform the final states from the original VPT2 states. Because of the cost involved in computing and integrating these terms, and the limitations in the quality of the variational correction, only significant contributions are normally included. This can be done, like FRs in DVPT2, through a two-step procedure, first by considering only close states, and then by looking at the magnitude of the coupling to be included in the variational matrix (Bloino et al., 2016).
As a final remark, Fermi resonances-like conditions can be present in Darling–Dennison interaction terms. Because they do not correspond to energies, (i.e. the eigenvalues of a well-defined Hamiltonian), the strategies proposed above cannot be directly applied. The transformation inspired by HDCPT2 is used here, as described in (Bloino et al., 2016). Formally, DD resonances cannot be used in conjunction with DCPT2, and by extension HDCPT2, because the effective Hamiltonian corresponding to the generated vibrational energies is unknown. Since the coupling terms to be added do not overlap with Fermi resonances–but can be coupled to them through common states involved in both–it is possible to build a variational matrix with the HDCPT2 energies and only the off-diagonal terms related to DDRs included. The corresponding model will be called GHDCPT2, by analogy with GVPT2 for DVPT2/VPT2. Possible schemes available to compute the vibrational energies within VPT2 are summarized in Table 2.
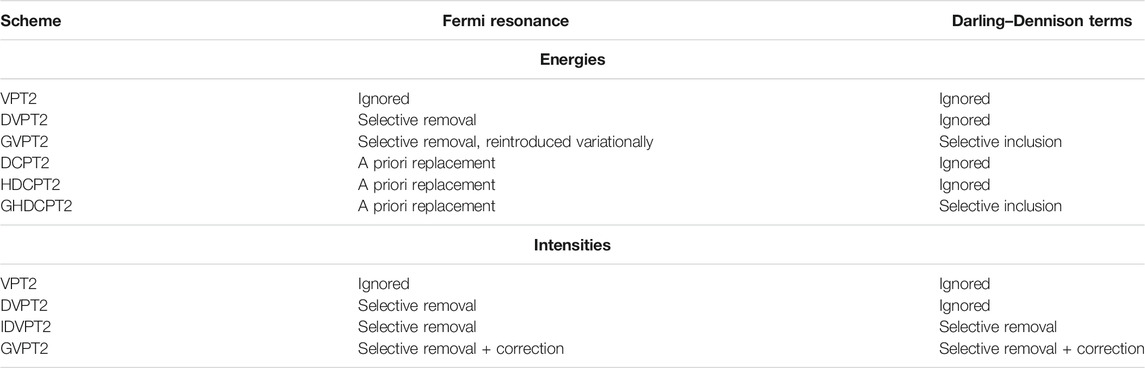
TABLE 2. Summary of the available VPT2 schemes to compute vibrational energies and intensities, and the strategies applied to deal with Fermi resonances and to include Darling–Dennison interaction terms. See text for details.
While relatively generic, the discussion deliberately omits the problem of true degeneracies present in linear-, symmetric- and spherical-top molecules. A proper treatment at the VPT2 level requires a special notation and an alternative derivation (Plíva, 1990; Piccardo et al., 2015), which has been explicitly carried out only for the energies of doubly degenerate representations. Because of these limitations and to avoid expanding too much this presentation, only asymmetric tops are considered in the following. The generalization of the VPT2 framework to any molecular symmetry through a unified framework is deferred to a forthcoming paper.
2.3 Transition Moments
Let us now consider the case of intensities, and the calculation of transition moments. Contrary to energies, multiple formulas are needed, depending on the type of transition, to fundamental, overtone or combination states, and the total number of quanta changing between the initial and final states (Willets et al., 1990; Vázquez and Stanton, 2006; Bloino and Barone, 2012; Bloino, 2015). Considering only transitions from the ground state, an interesting case is the transition moment associated to fundamental bands. The full equation can be found elsewhere (Bloino and Barone, 2012) and is reported in the Supplementary Material. Here, we consider only some characteristic terms.
In the above equations, S = 1 if the property is a function of the normal coordinates, like the electric dipole, (e.g., for IR) or the polarizability tensor (for Raman), and S = −1 if the property depend on their conjugate momenta, like the atomic axial tensor, (e.g., for VCD). The definition of
The first term (A) is similar to that found in the energy expression, with the potential presence of Fermi resonances. Strategies like those discussed in the previous section can in principle be employed. However, because the numerator
Cases B and C introduce a new form of resonances, between fundamentals. This can be related to the Darling–Dennison coupling in energy, which represent a correction to VPT2 shortcomings for the latter case, but can result in an incorrect account of the anharmonicity for intensities. A typical situation is the presence of one or more methyl groups, with the related C–H symmetric and antisymmetric stretching vibrations having very close energies. The treatment of DDRs is thus critical for intensity calculations, at least between fundamentals (1–1). Since Darling–Dennison couplings only appear in the variational treatment, they are absent in DVPT2, which makes it potentially unsuitable to deal with intensities without some improvement. To avoid confusion between the two formulations, the intensity-extended version, which performs exactly in the same way for the energies, will be labeled IDVPT2. Term C has the particularity of being sensitive to both Fermi and Darling–Dennison resonances. Robust strategies to identify DDRs in intensity calculations are still lacking in the literature, and may require the combination of multiple criteria. Indeed, the Darling–Dennison interaction terms being significantly different from the terms involved in the equation of transition moments, resonances between weakly coupled states could be ignored during the energy step. In practice, this problem usually arises for very close states. For this reason, a secondary test is added here on the magnitude of the DD term, by considering its magnitude weighted by the squared inverse of the energy difference between the potentially resonant states (
To summarize this section, GVPT2 represents here the most complete and accurate method, provided FRs and DDRs are correctly identified. However, the resulting states may depart significantly from the original basis of harmonic states, making band assignment more complex. This problem does not exist for DVPT2 and its variant IDVPT2, but the truncated treatment can limit the overall quality of the results. If only energies are of interest, for instance in thermodynamics and reaction kinetics, HDCPT2/GHDCPT2 can be appealing for the absence of selection criteria.
As a final remark, it should be noted that the schemes presented here cannot overcome inherent limitations of VPT2, which derive from both the limited Taylor expansion and low-order perturbative formulation. Large amplitude motions (LAMs) like torsions and some out-of-plane vibrations can be poorly described by quartic force fields especially when employing Cartesian-based normal modes, and require extensive samplings of the PES, coupled with ad hoc Hamiltonians. Since the aim of this work is to assess the quality achievable by the combination of VPT2 and DFT, only semi-rigid systems devoid of LAMs are considered in the following. Mitigation strategies are discussed in conclusion.
3 Computational Details
Very tight criteria were used for geometry optimization, which means that the convergence was reached when the maximum forces and displacements were smaller than
Anharmonic data were built by numerical differentiation of analytic second-derivatives of the potential energy and of first derivatives of the properties of interest, using a step of 0.01
The cost of generating the anharmonic force field can be prohibitive for some electronic structure calculation methods, starting with double-hybrid DFT functionals. Conversely, if the anharmonic correction is small compared to the harmonic reference, the need for accuracy becomes less critical. As a consequence, a reasonable mitigation technique would be to compute the harmonic terms in the vibrational Harmiltonian (Eq. 5) and in the Taylor expansion of the properties of interest at the highest possible level of theory, and the anharmonic terms with a more cost-effective alternative. Studies in the literature have already pointed out the ability of such hybrid schemes to producing very accurate results (Begue et al., 2005; Carbonniere et al., 2005; Puzzarini and Barone, 2008; Biczysko et al., 2018; Puzzarini et al., 2019). While very convenient, these models involve some technical challenges related to the necessity of combining two levels of calculation, with their respective equilibrium structures and normal coordinates. In the best conditions, the latter are the same, making the definition of the hybrid scheme simple, since a single basis of normal modes need to be considered. In practice, subtle or even larger differences appear, in particular for vibrations, which are more sensitive than geometrical parameters. Two approaches can be chosen, depending on the reference geometries and displacement vectors for the numerical differentiation. The first one is to use only the normal coordinates from the higher level, computing the force constants and first derivatives of properties with respect to the Cartesian coordinates at each displaced geometry at the lower level. Otherwise, the anharmonic force field and property surfaces are built using only reference data from the lower level. The second technique has the advantage of making any combination simple to test, harmonic data from one level are combined with pure anharmonic data from another one. The problem is that the two sets of normal coordinates must be very close, and the geometries very similar, especially to combine properties. The consistency between the two methods can be assessed by computing the Duschinsky transformation to pass from one set of normal coordinates to the other (see Bloino et al. (2016) for details). This problem does not exist with the first method. However, if the two levels are significantly different, some approximation is still present if the second numerical differentiation is only diagonal, which is typically the case with standard schemes involving only two displacements (
For the VPT2 schemes, the following parameters were used. For Fermi resonances (DVPT2/GVPT2), states distant by less than 200 cm−1 in energy, and with an associated value for Martin’s test greater than 1 cm−1 were flagged as resonant. For Darling–Dennison resonances (IDVPT2/GVPT2/GHDCPT2), the following criteria were used:
• 1–1: Frequency difference lower than 100 cm−1, minimum value of the coupling term: 10 cm−1, and weighted coupling greater than 1 cm−1.
• 2–2: Frequency difference lower than 100 cm−1, and minimum value of the coupling term: 10 cm−1.
For HDCPT2/GHDCPT2, the parameter for the
Optimization and harmonic frequency calculations were done with Gaussian 16 (Frisch et al., 2016) and anharmonic calculations with a development version of Gaussian (Frisch et al., 2020).
4 Results and Discussions
4.1 Phase I: Electronic Structure Calculation Methods
4.1.1 DFT Functionals
To identify the best performing functional, the group of representative small molecules sketched in Figure 1 (top panel, G1) was selected. They were chosen so that the Fermi resonances were minimal or even absent to prevent any ambiguity in their identification. In these conditions, as noted in the theoretical details, GVPT2 is expected to perform the best, and was used as reference. Building upon previous analyses (Bloino et al., 2016; Barone et al., 2020), a shortlist of well-performing hybrid–B3LYP, B3PW91 (Becke, 1993), APF (Austin et al., 2012)–and double-hybrid–B2PLYP (Grimme, 2006) and revDSD-PBEP86-D3(BJ) (Santra et al., 2019)–exchange-correlation functionals was built. The ensemble of functionals/basis sets combinations and their respective abbreviations can be found in Supplementary Table S1 of the Supplementary Material. Let us first consider the influence of the functional, adopting the calendar-based basis set jun-cc-pVTZ as reference (Papajak et al., 2011), since it has shown very good performance in previous studies (Barone et al., 2020). It should also be noted that a basis set of at least triple-ζ quality is needed to reach converged results with double hybrid functionals. The impact of the empirical dispersion using Grimme’s DFT-D3 scheme (Grimme et al., 2010) with Becke-Johnson damping (Grimme et al., 2011) (noted D3(BJ)) was also evaluated. APF has its own empirical-dispersion scheme, which could not be used here due to technical issues. The mean (MAE) and maximum (|MAX|) absolute errors for the fundamental energies at both harmonic (ω) and anharmonic (GVPT2, ν) levels are reported in Figure 2. A first observation is that the empirical dispersion on such small systems is negligible. In order to make the effects of the dispersion more apparent, the differences between the errors obtained for each functional with and without empirical dispersion are plotted in Supplementary Figures S1–S3 in Supplementary Material. In this particular case, D3(BJ) doesn’t show particular advantages for these small molecules and can slightly worsen the results, so it was not considered in the following. The influence of empirical dispersion on the prediction of vibrational spectra for larger-size molecules and complexes will be deferred to a separate work. For hybrid functionals, we observe a decrease by two thirds of the maximum error between the harmonic and anharmonic fundamental energies. The gain is lower for B3LYP, which is slightly closer to experiment at the harmonic level and less scattered (|MAX| = 150 cm−1). However, one should be careful in comparing harmonic computations with experimental data, since the latter refer actually to non-harmonic vibrations. Hence, an overestimation of the transition energies is expected. All functionals chosen here display similar trends at the anharmonic level, with an average error of about 13 cm−1 and a maximum error ranging from 49 to 76 cm−1. PW6B95 is performing slightly worse than the others, with the highest error, close to APF which, however, has an average unsigned error close to B3PW91 (13 vs 12 cm−1), the best at this level. Considering now the double-hybrid functionals, a first observation is that they are not significantly different at the harmonic level, having even a higher average error than B3LYP and B3PW91. Adding the anharmonic correction leads to significantly better results with an average error within 10 cm−1, and a maximum error below 20 cm−1 for revDSD-PBEP86-D3(BJ) (25 for B2PLYP). This confirms the very good performance of double hybrid functionals already noted in the literature (Biczysko et al., 2010) for vibrational energies.
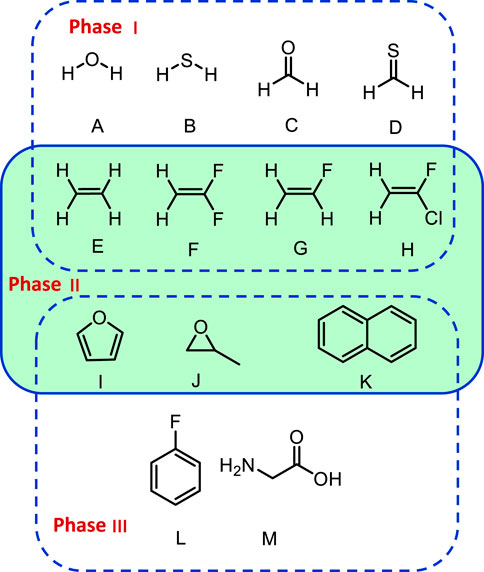
FIGURE 1. Structures of the molecules in this benchmark study. (A): Water, (B): H2S, (C): formaldehyde, (D): thioformaldehyde, (E): ethylene, (F): 1,1-difluoroethylene, (G): fluoroethylene, (H): 1-fluoro-1-chloro-ethylene, (I): furan, (J): methyloxirane, (K): naphthalene, (L): 1-fluorobenzene, (M): Glycine.
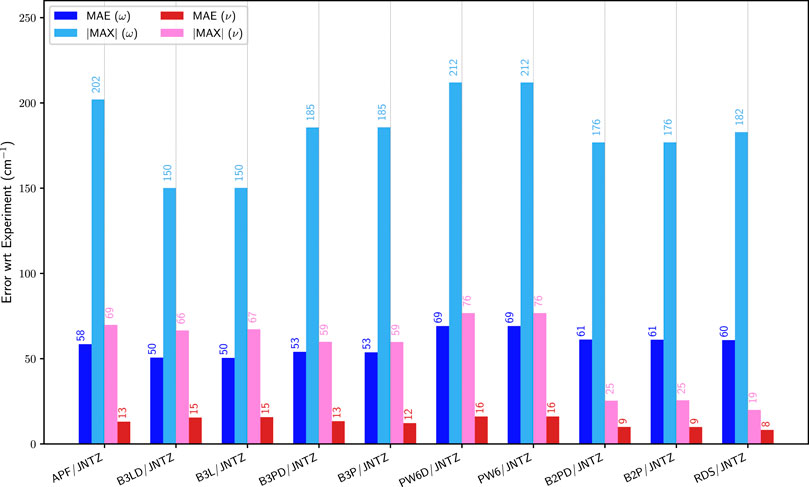
FIGURE 2. Comparison of the mean (MAE) and maximum absolute (|MAX|) errors for different functionals with the jun-cc-pVTZ (JNTZ) basis set over the first set of molecules (G1): APF: APF, B3L: B3LYP, B3P: B3PW91, PW6: PW6B95, B2P: B2PLYP, RDS: revDSD-PBEP86-D3(BJ). ω (blue) corresponds to the harmonic approximation, ν (pink/red) to GVPT2. The values are indicated on top of the bars. Reference experimental data taken from: water (Tennyson et al., 2001), H2S (Isoniemi et al., 1999), formaldehyde (Reisner et al., 1984), thioformaldehyde (Suzuki et al., 2007), ethylene (Nakanaga et al., 1979), 1,1-difluoroethylene (Krasnoshchekov et al., 2013), fluoroethylene (Tasinato et al., 2006), 1-fluoro-1-chloro-ethylene (Pietropolli Charmet et al., 2016).
4.1.2 Basis Sets
Let us now focus on the basis sets. Following the previous results, B3PW91 was chosen as model for the hybrid functionals, and revDSD-PBEP86-D3(BJ) for double hybrids. For B3PW91, three Pople-based basis sets were chosen, two double-ζ, 6–31+G(d) and SNSD, a basis set developed in our group with emphasis on the description of spectroscopic observables (SNSDT, 2021), and a large triple-ζ basis set, 6–311++G(3df,3pd). The SNSD basis set is obtained by adding to 6–31G(d,p) the diffuse functions of the aug-cc-pVDZ basis set and, for non-hydrogen atoms, a very tight s function. It is noteworthy that Cartesian, (e.g., 6d) functions were used in the original implementation and must be retained because, as is well known, this choice effectively increases also the space of s functions (details on the basis sets for the first 2 rows can be found in the Supplementary Material). Variations of the Dunning basis sets, of double-ζ (jul-cc-pVDZ) and triple-ζ (jun-cc-pVTZ and spaug-cc-pVTZ) quality were considered. Furthermore, the polarization consistent double- (pc-1) and triple-ζ (pc-2) basis sets proposed by Jensen (Jensen, 2001), as well as their augmented versions with diffuse functions, aug-pc-1 and aug-pc-2, were used. Some modifications were also applied to the latter two for this work. For aug-pc-1, the new version labeled naug-pc-1 had all d diffuse functions removed for all atoms present in the molecules of interest in this work. With the same aim of reducing the computational cost, all d and f diffuse functions were removed from the aug-pc-2 basis set, leading to the new naug-pc-2 set. For instance, in the case of 1-fluoro-1-chloroethylene, this reduces the number of basis functions from 114 to 94 (pc-1) and to 234 to 176 (pc-2). A decrease of about 31% (double-ζ) and 62% (triple-ζ) on the total computational cost needed to generate the anharmonic constants is observed on two octo-core processors machines (2.60 GHz). Provided that the overall accuracy is not very different, going from aug-pc to naug-pc basis sets represents an appealing strategy to tackle larger molecular systems. Finally, Ahlrichs and coworkers’ def2-TZVP basis set (Weigend and Ahlrichs, 2005) was also included. For revDSD-PBEP86-D3(BJ), only basis sets of at least triple-ζ quality were considered. In addition to spaug-cc-pVTZ, jun-cc-pVTZ and def2-TZVP already selected for B3PW91, Dunning’s aug-cc-pVTZ (Kendall et al., 1992) was used. Quadruple-ζ basis sets become quickly prohibitive when tackling larger molecular systems. For this reason, smaller and thus more affordable alternatives were explored, by combining s and p basis functions from cc-pVQZ with d and f basis functions from cc-pVTZ (Dunning, 1989). Recent investigations (Kruse et al., 2020) have shown that basis sets optimized for explicitly correlated methods do a very good job also in conventional computations. The main distinctive feature of these basis sets is to use an (n+1)ζ set for the sp space in conjunction with an nζ set for polarization functions. We have therefore tested also this family of basis sets. A version without diffuse functions was labeled M-cc-pV[T+Q]Z, and an extension with diffuse functions on all atoms except H was labeled M-aug-cc-pV[T+Q]Z. The errors on the first test suite with respect to the reference data are shown in Figure 3. Let us start with B3PW91. The harmonic results are relatively stable with all basis sets, with an average unsigned error ranging from 50 to 64 cm−1, for a maximum absolute error of 141–218 cm−1. With anharmonic contributions, a significant improvement in the mean unsigned error is observed for all basis sets, with values between 11 for SNSD and 16 cm−1. If we look at the maximum error, however, the results are more disparate, some performing well, others exhibiting very high errors. Overall, SNSD gives the best average energies, but def2-TZVP has a lower maximum deviation, of 54 cm−1. Basis sets of triple-ζ quality give very close results, with MAE of about 12–13 cm−1 and a maximum error of about 60 cm−1. The addition of diffuse functions tends to improve the results for double-ζ basis sets, as evidenced by comparison between pc-1 and aug-pc-1 results (|MAX| from 78 to 68 cm−1), as well as 6–31+G(d) with SNSD (|MAX| from 70 to 59 cm−1). Regarding the Pople basis sets, 6–31+G(d) seems to be clearly insufficient, in line with previous observations (Mitra and Roy, 2020). Since the main difference between 6–31+G(d) and SNSD basis sets is the presence in the latter of p functions on hydrogen and diffuse d functions on heavy atoms, our results confirm the importance of these contributions. For pc-1, the improvement on the maximum error with the addition of diffuse functions comes at the expense of a larger average error. It is noteworthy that the new naug-pc-1 basis set, despite being smaller than aug-pc-1, gives results substantially equal to the latter one. The maximum error of pc-1 and its related basis sets remains significantly higher than the others, which make them potentially ill-suited for spectroscopic applications. The improvement obtained with diffuse functions becomes less apparent at the triple-ζ level, with pc-2 vs aug-pc-2 being near equal in terms of performance. Here too, naug-pc-2 provides the same quality as aug-pc-2 for a significantly lower cost. The largest average error is found for jul-cc-pVDZ, with an average deviation of about 30% compared to the standard performance of the basis sets chosen here. The marginally higher maximum error hints at a more systematic issue, which could be investigated in the future on larger systems. The same procedure was applied to B3LYP for comparison purposes. The results can be found in the Supplementary Material (Supplementary Figure S6), with similar trends and conclusion.
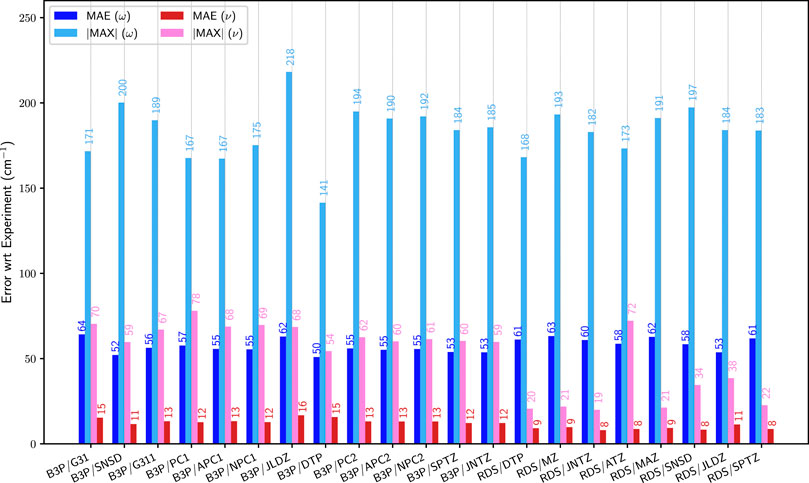
FIGURE 3. Comparison of the mean (MAE) and maximum absolute (|MAX|) errors at the B3PW91 (B3P) and revDSD-PBEP86-D3(BJ) (RDS) levels with different basis sets over the first set of molecules (G1). G31: 6–31+G(d), SNSD: SNSD, G311: 6–311++G (3df, 3pd), PC1: PC-1, APC1: aug-PC-1, NPC1a: naug-PC-1, JLDZ: jul-cc-pVDZ, DTP: def2-TZVP, PC2: PC-2, APC2: aug-PC-2, NPC2b: naug-PC-2, SPTZ: spaug-cc-pVTZ, JNTZ: jun-cc-pVTZ, ATZ: aug-cc-pVTZ, MZc: M-cc-pV[T+Q]Z, MAZd: M-aug-cc-pV[T+Q]Z. ω (blue) corresponds to the harmonic approximation, ν (pink/red) to GVPT2. The values are indicated on top of the bars. See Figure 2 for details on the reference data. (a): basis set built from aug-PC-1 Jensen (2001), by removing the d diffuse functions. (b): basis set built from aug-PC-2 Jensen (2001), by removing the d and f diffuse functions. (c): basis set built by combining s and p basis functions from cc-pVQZ, and d and f from cc-pVTZ. (d): basis set built by combining s and p basis functions from cc-pVQZ, and d and f from cc-pVTZ, augmented with d diffuse functions on all atoms except for H.
Switching to revDSD-PBEP86-D3(BJ), all chosen basis sets exhibit very close behaviors at the harmonic level, with mean unsigned errors between 58 and 63 cm−1, except for jul-cc-pVDZ, which performed slightly better here. At the GVPT2 level, these errors go down to 8–11 cm−1 with maximum errors typically situated between 18 and 21 cm−1, a third of what was found with B3PW91. The only exceptions are for the double-ζ basis sets, SNSD and jul-cc-pVDZ, with the largest error at 34 and 38 cm−1, respectively, and aug-cc-pVTZ, which has the highest maximum absolute error (|MAX| = 72 cm−1). This larger discrepancy is to be ascribed to the out-of-plane twisting motion of ethylene (mode 4, at about 1050 cm−1 at the harmonic level). The lower accuracy is not related to any variational correction, but to the anharmonic force field itself. The new basis set, M-aug-cc-pV[T+Q]Z does not suffer from this problem, with results indistinguishable from jun-cc-pVTZ and spaug-cc-pVTZ. To confirm these trends, a parallel study was done with B2PLYP as reference, showing relatively close behaviors (Supplementary Figure S6 in the Supplementary Material). To conclude this part, jun-cc-pVTZ provides very good results with double hybrid functionals for the systems of interest here, while for hybrid functionals, double-ζ basis sets augmented with diffuse functions are sufficient.
4.1.3 Hybrid Schemes
As mentioned above, the cost of double hybrid functionals with the associated basis sets can become prohibitive for large molecules, so that more cost-effective approaches are needed, possibly based on the use of hybrid schemes, which allow the computation of the anharmonic contributions at a lower level of theory. The performance of such models is illustrated in Figure 4, where the errors on the fundamental energies of the first group of molecules with respect to experiment are compared with the best data obtained with a single electronic structure calculation method. More explicitly, B3LYP/SNSD, B3PW91/SNSD and B3PW91/jul-cc-pVDZ for hybrid, and B2PLYP/jun-cc-pVTZ and revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ for double hybrid functionals were chosen. With revDSD-PBEP86-D3(BJ) as the harmonic reference, the improvement is apparent, with a mean unsigned error of 9 cm−1, on par with the full, more expensive double-hybrid calculations. revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ in conjunction with B3PW91/SNSD has also a maximum error almost on par with the full reference (23 vs. 20 cm−1), while the other combinations performs a bit worse, at 47 cm−1. This result is in contrast with what was observed with the pure hybrid functionals, where B3PW91/SNSD performed worse in terms of largest error. The most likely explanation is an error in the harmonic reference, well compensated by revDSD-PBEP86-D3(BJ) while the anharmonic force field is of very good quality. An excellent agreement is reached between the hybrid schemes and the full double hybrid anharmonic calculations, with the best performing combination being clearly revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD.
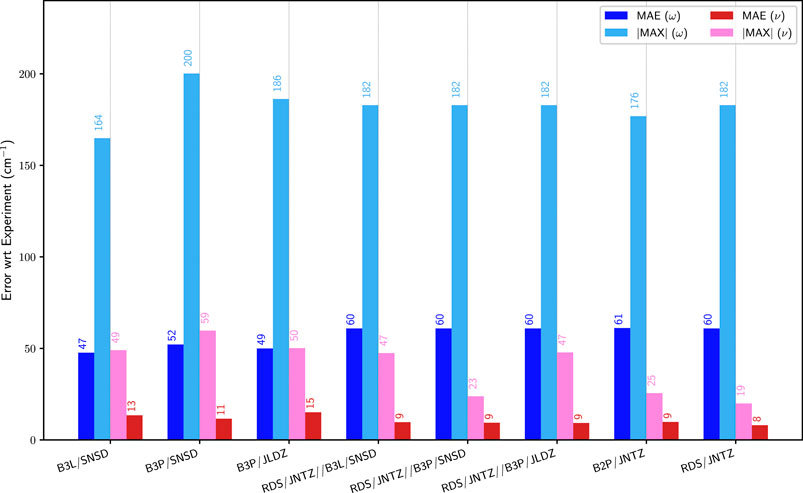
FIGURE 4. Comparison of the mean (MAE) and maximum absolute (|MAX|) errors of pure functionals and hybrid models over the first set of molecules (G1). ω (blue) corresponds to the harmonic approximation, ν (pink/red) to GVPT2. The values are indicated on top of the bars. The hybrid models are built by combining harmonic calculations with double hybrid functionals, with anharmonic force fields at a lower level, and noted “harmonic//anharmonic”. See Figures 2, 3 for details on the abbreviations and the reference data used.
4.2 Phase II: VPT2 Schemes
These preliminary tests have highlighted in some situations the sensitivity of the anharmonic correction. In the second phase of this study, the influence of the VPT2 schemes described in the theoretical details, first on the fundamental energies, and next on the intensities, will be analyzed. To be more representative of potential resonance patterns, larger molecular systems were chosen, starting from the derivatives of ethylene already included in G1 since they have simple resonance patterns. Another criterion for the selection of the molecules was the potential availability of reliable experimental data for the transition intensities in the literature. The final list is displayed in the middle panel (G2) of Figure 1. Based on their performance in the first part of this benchmark, three levels of theory were selected to proceed, B3PW91/SNSD, revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ and the hybrid scheme combining them, revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD. For the sake of readability, shortened labels will be used in the discussion, respectively B3PW91, REVDSD and HYBRID.
4.2.1 Ethylene and Halogenated Derivatives
Starting with the vibrational energies of ethylene (Table 3), the VPT2 fundamental energies are indeed fairly good for REVDSD and HYBRID, worsening with B3PW91. The largest error is to be ascribed to mode 9 (CH symmetric stretching), in resonance with the combination band 7 + 8. The energy gap between the resonant states with B3PW91 is half that of REVDSD and HYBRID (22.7 vs. 11.4 cm−1) while the coupling term, the cubic force constant involving the three modes, remains unchanged, which leads to a larger contribution to the anharmonic
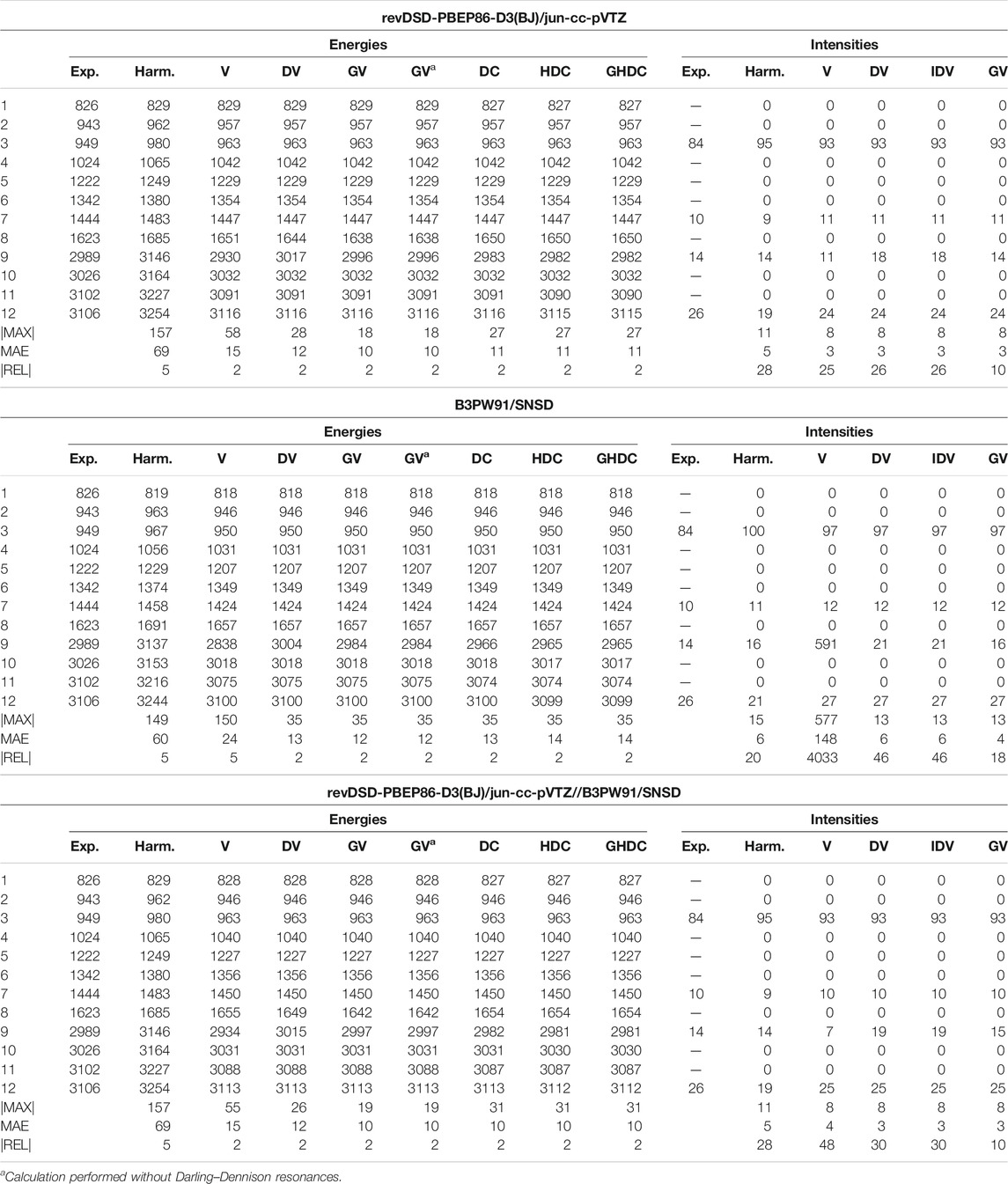
TABLE 3. Harmonic and anharmonic vibrational energies (in cm−1) and intensities (km/mol) of ethylene computed at the revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ, revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ and hybrid revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels of theory and with different VPT2 schemes, VPT2 (V), DVPT2 (DV), IDVPT2 (IDV), GVPT2 (GV), DCPT2 (DC), HDCPT2 (HDC), GHDCPT2 (GHDC). The maximum (MAX|) and mean (MAE) absolute errors, as well as the maximum relative error weighted by the reference value (|REL|, given in %) are reported with respect to experimental data from (Nakanaga et al., 1979).
Another interesting example is 1,1-difluoroethylene, whose results are collected in Table 4 (Supplementary Table S2 of the Supplementary Material for REVDSD). At the VPT2 level, this time, HYBRID gives a larger unsigned error compared to experiment than B3PW91, a behavior opposite to what was observed for ethylene. Upon investigation of the individual transition energies, similar patterns appear. The error is concentrated on one mode, 11, a CH symmetric stretching vibration. This mode is involved in a Fermi resonance with the 9 + 10 combination band. Between the two methods, HYBRID and B3PW91, the value of the cubic force constant between these modes is about the same, but the energy difference,
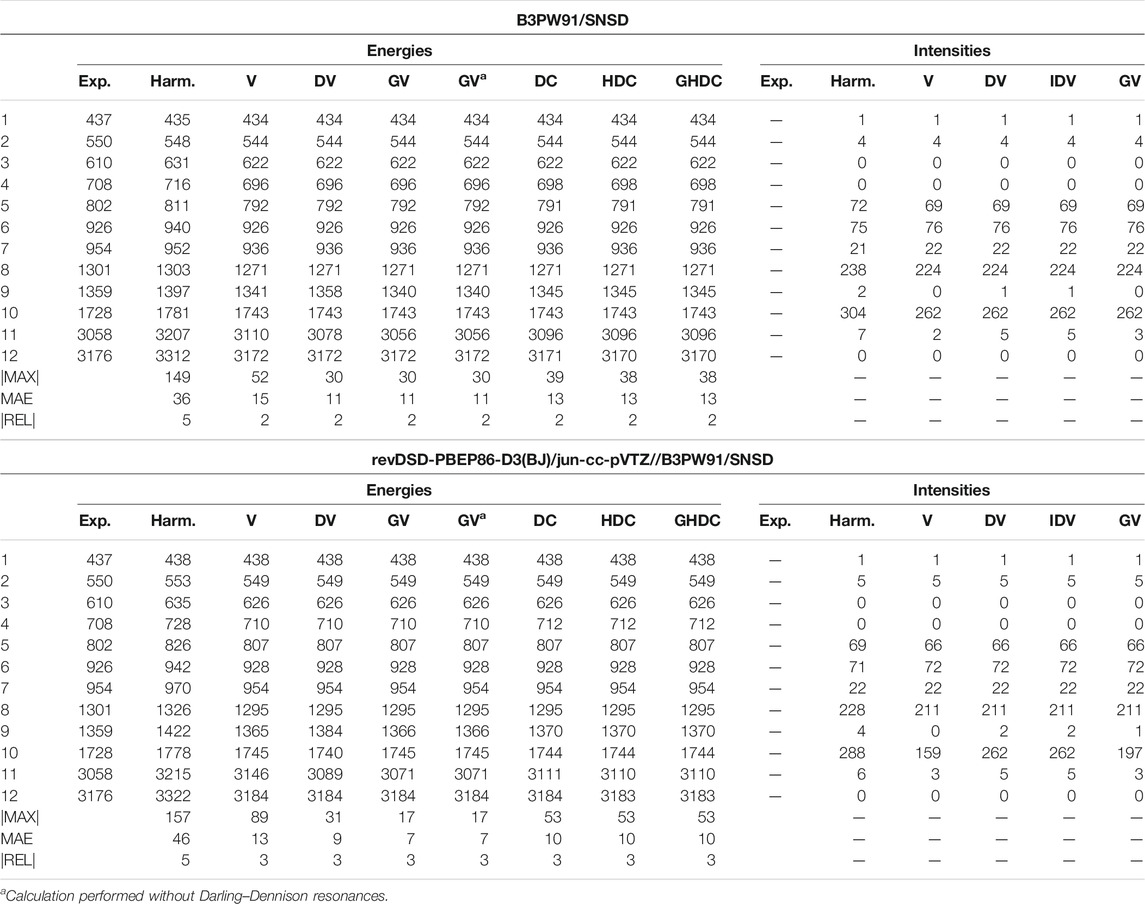
TABLE 4. Harmonic and anharmonic vibrational energies (in cm−1) and intensities (km/mol) of 1,1-difluoroethylene computed at the B3PW91/SNSD and hybrid revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels of theory and with different VPT2 schemes. The maximum (|MAX|) and mean (MAE) absolute errors, as well as the maximum relative error weighted by the reference value (|REL|, given in %) are reported with respect to experimental data from (Tasinato et al., 2006).
The fundamental energies of the last two ethylene derivatives, 1-fluoroethylene and 1-fluoro-1-chloroethylene, are listed in Supplementary Tables S3, S4 of the Supplementary Material, respectively. For the former molecule, a very good agreement is observed with all schemes, with patterns similar to ethylene and 1,1-difluoroethylene. An interesting aspect here is the influence of Darling–Dennison couplings between the fundamentals of modes 10 and 11, both related to CH stretchings. The impact can be assessed by comparing GVPT2 with GVPT2a, the latter having DDRs excluded, and GHDCPT2 with HDCPT2. For GVPT2, inclusion of these couplings increases the energy gap between the two states, lowering
4.2.2 Furan and Methyloxirane
For furan, shown in Table 5 (Supplementary Table S5 of the Supplementary Material for REVDSD), the predicted energies are very good at all levels, with the hybrid scheme improving over B3PW91 to lower the average error at 4 cm−1 with a maximum absolute error of 9 cm−1, compared to 5 and 11 cm−1, respectively. Because of the
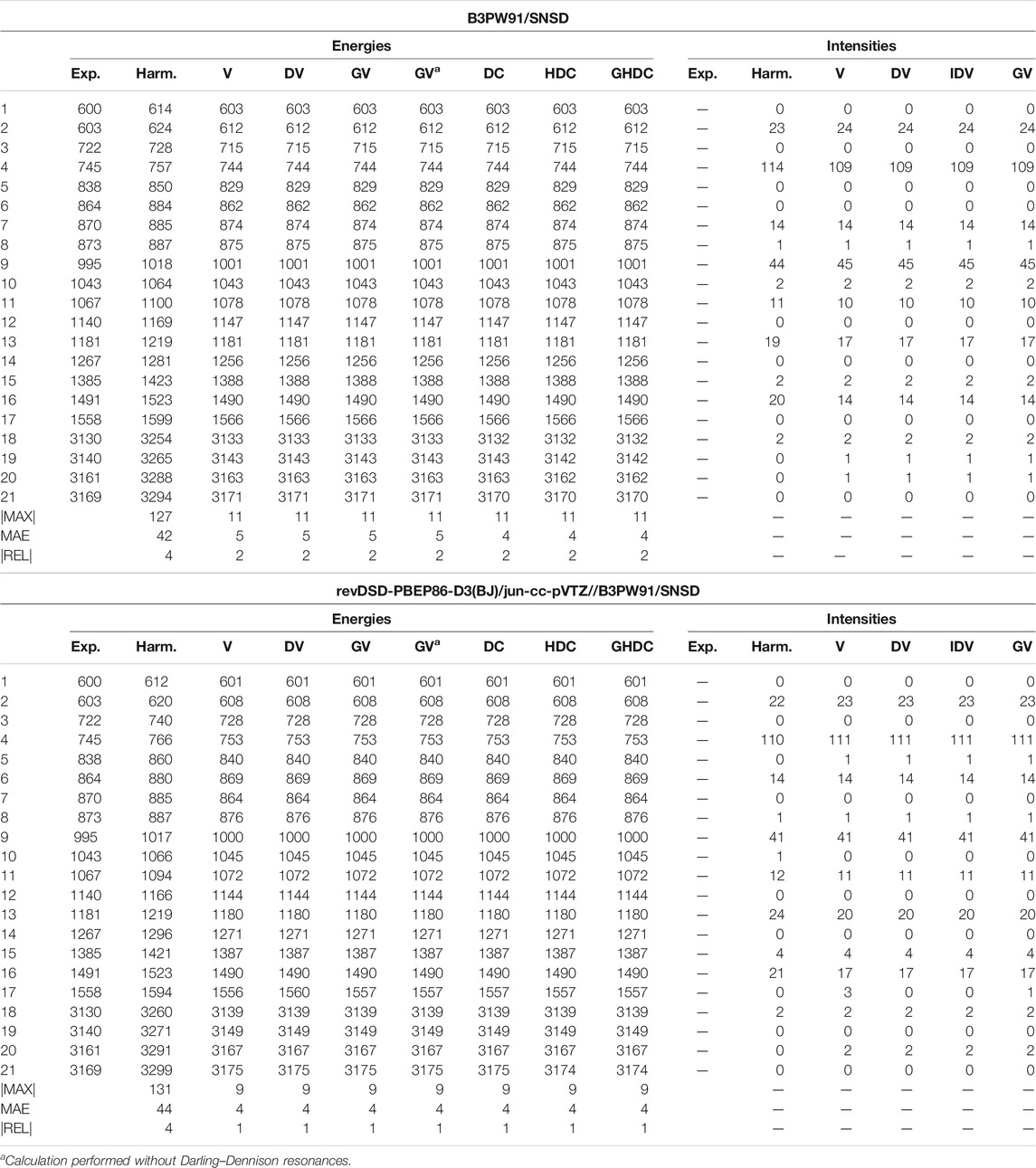
TABLE 5. Harmonic and anharmonic vibrational energies (in cm−1) and intensities (km/mol) of furan computed at the B3PW91/SNSD and hybrid revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels of theory and with different VPT2 schemes. The maximum (|MAX|) and mean (MAE) absolute errors, as well as the maximum relative error weighted by the reference value (|REL|, given in %) are reported with respect to experimental data from (Mellouki et al., 2001).
Methyloxirane has a comparable dimension, but
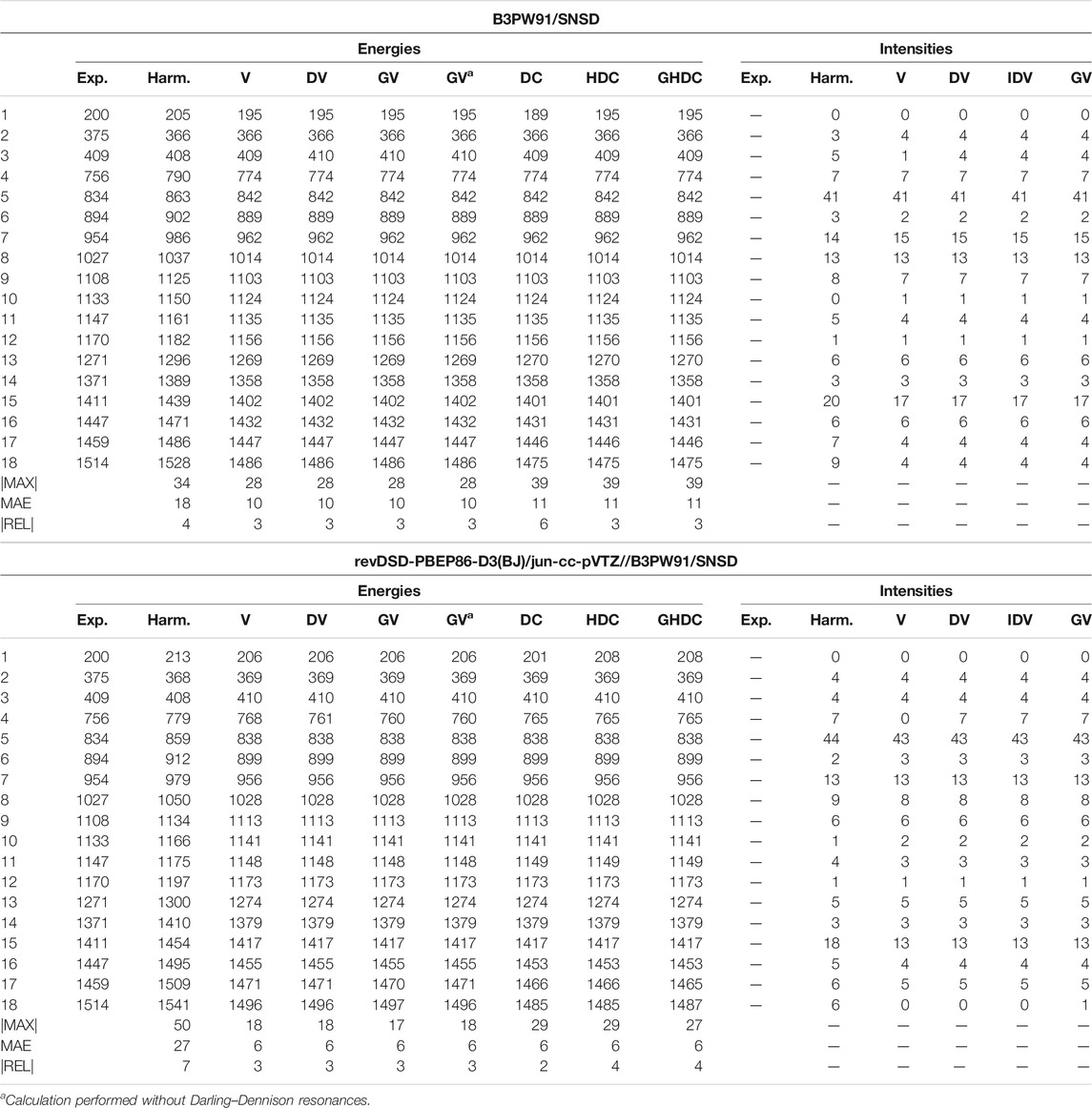
TABLE 6. Harmonic and anharmonic vibrational energies (in cm−1) and intensities (km/mol) for the first 18 modes (by increasing energy) of methyloxirane computed at the B3PW91/SNSD and hybrid revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels of theory and with different VPT2 schemes. The maximum (|MAX|) and mean (MAE) absolute errors, as well as the maximum relative error weighted by the reference value (|REL|, given in %) are reported with respect to experimental data from (Polavarapu et al., 1985; Sunahori et al., 2010; Merten et al., 2013).
4.2.3 Naphthalene
As the final example of the second phase, naphthalene is the standard prototype of polycyclic aromatic hydrocarbons (PAHs), which have been extensively studied in recent years (Bloino, 2015; Mackie et al., 2015, 2016). This is also a model system for various applications, thanks to its rigidity and high symmetry (Swofford et al., 1976; Dierksen and Grimme, 2004; Basire et al., 2008; Pirali et al., 2009, 2013). A practical consequence of the latter is the possibility to check straightforwardly potential numerical instability or noise in the generation of the anharmonic force field or property surface. The vibrational energies and IR intensities are reported in Table 7. Because of the larger size, a full anharmonic force field at the revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ level becomes very expensive, so only B3PW91 and the hybrid scheme were used here. Since some vibrations are both IR and Raman inactive, some experimental data are missing and were omitted in the evaluation of the maximum and average absolute errors. Because of the larger number of normal modes, critical conditions with very close resonant states are more likely to occur, albeit mitigated by the symmetry conditions in the present case. Like furan, a good agreement is generally observed, with a mean absolute error of 8–10 cm−1. The main exception is VPT2, which exhibit large errors, resulting in an average twice as large as DVPT2. For both B3PW91 and HYBRID, the largest deviation is related to mode 41 (CH stretching), involved in two Fermi resonances. One of them is with a combination band very close in energy, within 3 cm−1 (
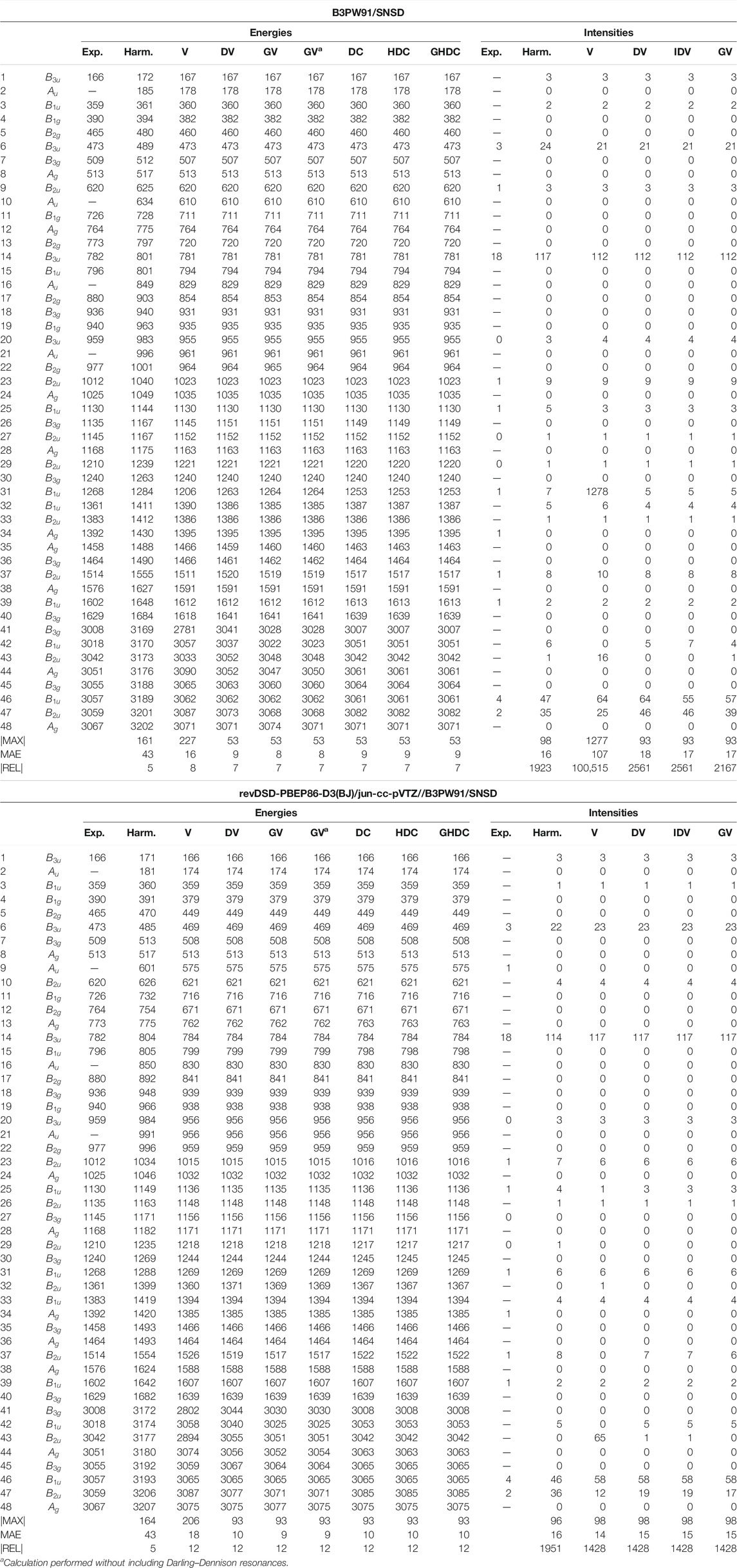
TABLE 7. Harmonic and anharmonic vibrational energies (in cm−1) and intensities (km/mol) of naphthalene computed at the B3PW91/SNSD and hybrid revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels of theory and with different VPT2 schemes. The maximum (|MAX|) and mean (MAE) absolute errors, as well as the maximum relative error weighted by the reference value (|REL|, given in %) are reported with respect to experimental data from (Cané et al., 2007).
4.3 Phase III: Spectral Band-Shapes
To conclude this study, we directly apply the most accurate GVPT2 level on top of the best-performing combination of electronic structure calculation methods to simulate full IR spectral band-shapes. The chosen molecules in this last step are furan, methyloxirane, and naphthalene, already extensively analyzed in the previous phase, as well as glycine (the four most stable conformers) and fluoro-benzene, depicted in Figure 1. Let us start with furan, shown in Figure 5. The earlier analysis showed a very good agreement with experimental data. The region above 2000 cm−1 has been magnified by a factor of 10 to emphasize the low-intensity vibrational structure due to overtones and combination bands, and thus absent at the harmonic level. In the fingerprint region (below 2000 cm−1), the performance of all methods with GVPT2 are confirmed in terms of band positions. The experimental spectrum shows a broader structure, with a splitting of the bands typical of a rotational sub-structure ignored here. The relative intensities of the peaks are qualitatively reproduced at all levels, with the heights of the peaks at about 750 cm−1 slightly overestimated by theory. The region above 2000 cm−1 exhibits a high density of peaks, dominated by the CH stretching zone above 3000 cm−1, well predicted by calculations in terms of position and shape. The experimental band shows a clear shoulder on the high-energy side, which can be related to the presence of two transitions of similar intensity,
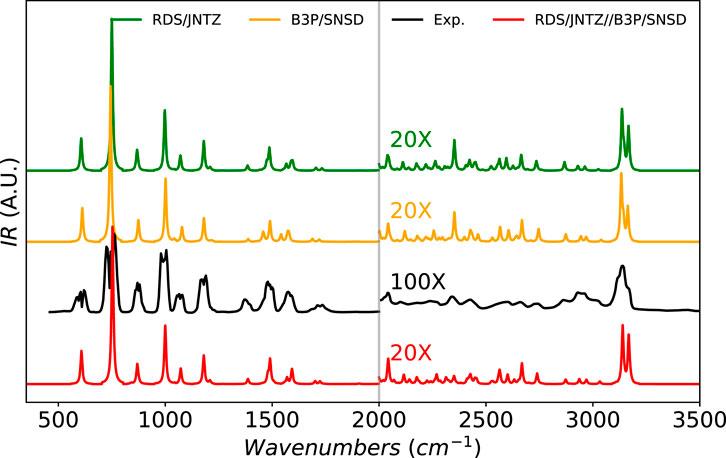
FIGURE 5. Infrared spectrum of furan at the B3PW91/SNSD (B3P/SNSD), revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ (RDS/JNTZ) and revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels using the GVPT2 scheme, compared to experiment taken from (Mellouki et al., 2001). Theoretical line-shapes were broadened by mean of Lorentzian distribution functions with half-widths at half-maximum of 4 cm−1. The region beyond 2000 cm−1 had been magnified to show the lower-intensity structure. To see more clearly the broader features of the experimental spectrum, a higher magnification was used compared to theory.
For methyloxirane as well, shown in Figure 6, the band-shape is well predicted by theory. Due to technical constraints related to the experimental setup, only the fingerprint region is available with a high level of confidence and used here as reference (Merten et al., 2013; Kreienborg et al., 2019). Some larger differences can be observed between the levels of theory, especially in the pattern around 1500 cm−1. B3PW91 with the SNSD basis set shows a series of small peaks of close intensities after the more intense peak at about 1415 cm−1
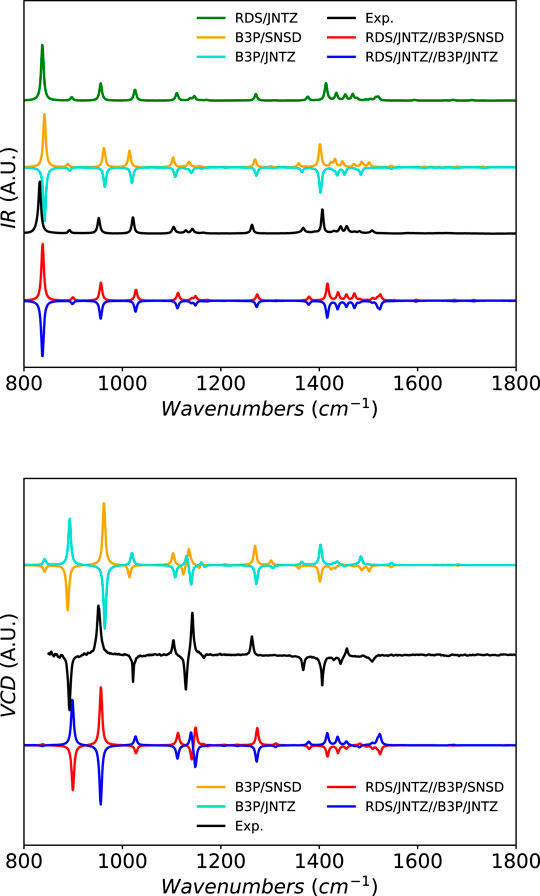
FIGURE 6. Infrared and vibrational circular dichroism spectra of methyloxirane at the B3PW91/SNSD (B3P/SNSD), B3PW91/jun-cc-pVTZ (B3P/JNTZ), revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ (RDS/JNTZ) and hybrid levels using the GVPT2 scheme, compared to experiment taken from (Merten et al., 2013). Theoretical line-shapes were broadened by mean of Lorentzian distribution functions with half-widths at half-maximum of 3 cm−1. The spectra generated with the anharmonic constants at the B3PW91/jun-cc-pVTZ were inverted (intensity multiplied by −1) to make the difference with B3PW91/SNSD more visible.
Beside its high astronomical interest, another appeal of naphthalene from a theoretical perspective comes from its high symmetry, which gives well-defined bands, with intense overtones and combination bands, especially in the 1500–2000 cm−1 region, as shown in Figure 7. It is thus easier to validate anharmonic models and highlight their improvement over the harmonic approximation, for which scaling factors are insufficient to reach even a qualitative agreement with experiment over the whole mid-IR range. Here, both B3PW91 and the hybrid scheme show very good agreement with the reference spectrum. The pattern of lower-intensity bands is well reproduced, and the band positions match very well their experimental counterparts, with only a minor underestimation of the peaks’ energy at about 1900 cm−1, confirming the low average error found on IR-active fundamental transitions during the second phase of this study. The small bump in the red-wing of the CH-stretching band is consistent with the low-intensity combination bands at about 3000 cm−1. It should be noted that a more thorough analysis of this region, supported by very accurate experimental data has been done in (Mackie et al., 2015). However, because of the density of peaks and the potential couplings between the CH stretching modes, such an extensive analysis would go beyond the purpose of the present study.
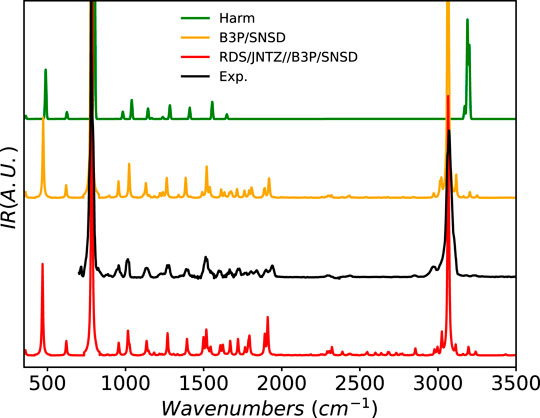
FIGURE 7. Infrared spectrum of naphthalene at the B3PW91/SNSD (B3P/SNSD), revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels using the GVPT2 scheme, compared to experiment taken from (Hudgins et al., 1994; NIST Mass Spec Data Center and Stein, 2015). The harmonic level was taken at the revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ level, which serves as basis for the hybrid model. Theoretical line-shapes were broadened by mean of Lorentzian distribution functions with half-widths at half-maximum of 4 cm−1.
As an example of halogenated system, the IR spectrum of fluorobenzene has been simulated and is compared to experiment in Figure 8. The main experimental features are well reproduced by all the computational models. However, B3PW91/SNSD provides a general blue-shift of the band positions, which are, instead, closely reproduced at the revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ level. The latter model also predicts very well the band-shape in the CH stretching region. This quality is preserved by the hybrid scheme, which further improves the band position and corrects the band at 1500 cm−1, split at the RDSD level. The low-intensity pattern of overtones and combination bands is also remarkably well described.
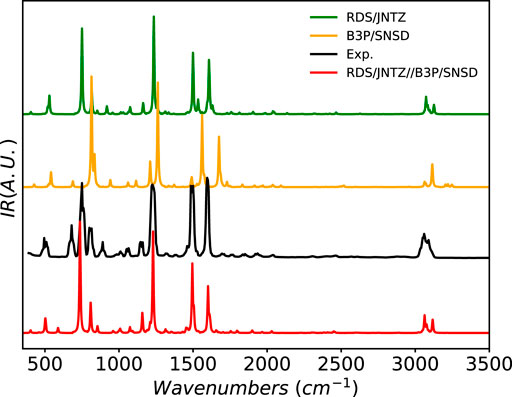
FIGURE 8. Infrared spectrum of fluorobenzene at the B3PW91/SNSD (B3P/SNSD), revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ (RDS/JNTZ) and revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ//B3PW91/SNSD levels using the GVPT2 scheme, compared to experiment taken from (NIST Mass Spec Data Center and Stein, 2015). Theoretical line-shapes were broadened by mean of Lorentzian distribution functions with half-widths at half-maximum of 4 cm−1.
To conclude this analysis of the quality of vibrational spectra computed at the GVPT2 level with DFT-based electronic structure calculation methods, we consider the IR spectrum of glycine, which has been extensively studied by some of us (Biczysko et al., 2012; Barone et al., 2013a, 2013b, 2013c). The molecule has several stable conformers (Shu et al., 2020) and the first two modes, related to torsions around the C-N and C-C bonds, are large amplitude motions (LAMs), which can be poorly described by quartic force fields in rectilinear coordinates. VPT2 is known to perform badly in these conditions, giving very inaccurate energies for these vibrations, as well as for any mode coupled with them. The standard treatment is to identify the LAMs and exclude them entirely from the anharmonic treatment. However, this was not a problem in the present case for two reasons. First, the two torsional modes are outside the available experimental range, and can be ignored. Second, their coupling with the rest of the system is relatively weak and can be kept, so the full force field was used in the computations. The final spectrum is compared to experiment in Supplementary Figure S13 of the Supplementary Material. In the present study, the four most stable conformers were considered. The main bands are well reproduced, both in terms of position and intensity. revDSD-PBEP86-D3(BJ) and the hybrid scheme reproduce more accurately the band positions compared to B3PW91, the latter being systematically blue-shifted with respect to experiment, especially for the bands beyond 1000 cm−1. Regarding the intensities, B3PW91 underestimate the intensities at about 800 cm−1, while the other methods overestimate them. The largest discrepancies are found in the 1000–1250 cm−1 zone, with revDSD-PBEP86-D3(BJ) and the hybrid model showing three peaks in place of the experimental doublet. Interestingly, the extra band at 1145 cm−1 is very intense for the hybrid scheme compared to revDSD-PBEP86-D3(BJ) or B3PW91. While this feature is related to the combination band
Conclusion
In this work, we have introduced different flavors of second-order vibrational perturbation theory, offering thus the possibility to easily choose the most convenient variant for any application in vibrational spectroscopy concerning both energies and intensities. Actually, to the best of our knowledge, this is the first completely general implementation of intensities in the framework of the double-perturbation theory. This general platform has been next employed to select the most effective combination of density functional and basis set for the study of molecular systems of medium-to-large dimensions. The main outcomes of our study can be summarized as follows:
1. Thanks to the availability of analytical second energy derivatives and first property derivatives, a very effective treatment of mechanical and electric/magnetic anharmonicities is possible in the framework of generalized second-order vibrational perturbation theory (GVPT2) for both hybrid and double-hybrid functionals.
2. Contrary to common claims, resonances can be effectively dealt for both energies and intensities in the framework of the GVPT2 model.
3. While the standard thresholds used for the recovery of resonances appear quite robust, some fine tuning of their value can (and should) be performed for specific cases especially for intensities.
4. The new GHDCPT2 variant provides a fully black-box tool for energies.
5. The most effective among the tested functionals are B3PW91 among the hybrid models and rev-DSD-PBEP86-D3(BJ) among the double-hybrid variants.
6. The quality of the results at the double-harmonic level is the most important factor for obtaining accurate frequencies and intensities. Here double-hybrid functionals are significantly more reliable than the hybrid ones, often approaching the accuracy of CCSD(T) computations with comparable basis sets.
7. Anharmonic contributions can be confidently computed by hybrid functionals in most cases.
8. Diffuse functions on non-hydrogen atoms always play a non-negligible role with at least single s, p, d sets being mandatory for intensities at all computational levels.
9. The smallest underlying basis set providing sufficiently converged results is of double-ζ quality for hybrid functionals and of triple-ζ quality for double-hybrid functionals.
10. Empirical dispersion corrections (D3BJ) play a marginal role. However, their inclusion is always suggested because the situation could be different for larger molecules and, in any case, they do not increase the computational cost, nor degrade the results in significant ways.
11. The suggested strategy for reliable yet effective computations of vibrational spectra includes harmonic frequencies obtained at the revDSD-PBEP86-D3(BJ)/jun-cc-pVTZ level together with anharmonic contributions evaluated at the B3PW91/SNSD level.
In summary, DFT/VPT2 represents a very reliable and cost/effective model for the analysis of vibrational spectra of medium- to large-size molecules. Even if further developments are needed especially for flexible systems due to the presence of large amplitude motions, which are poorly described by quartic force fields, the robust implementation of such a platform in a general computer code paves the route toward widespread application also by non-specialists in connection with both assignment and interpretation of experimental vibrational spectra of molecular systems of broad astrochemical interest.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Q.Y. and M.M. performed the computations and analyzed the results. J.B. supervised the work, analyzed the results and wrote part of the paper. V.B. devised the new basis sets introduced in this work, defined the general strategy and wrote part of the paper.
Funding
This work has been supported by the MIUR ‘PRIN 2017’ (Grant Number 2017A4XRCA) and by the Italian Space Agency (ASI; ‘Life in Space’ project, N. 2019-3-U.0).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The SMART@SNS Laboratory (http://smart.sns.it) is acknowledged for providing high-performance computing facilities.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.665232/full#supplementary-material
References
Austin, A., Petersson, G. A., Frisch, M. J., Dobek, F. J., Scalmani, G., and Throssell, K. (2012). A Density Functional with Spherical Atom Dispersion Terms. J. Chem. Theor. Comput. 8, 4989–5007. doi:10.1021/ct300778e
Balucani, N. (2012). Elementary Reactions of N Atoms with Hydrocarbons: First Steps towards the Formation of Prebiotic N-Containing Molecules in Planetary Atmospheres. Chem. Soc. Rev. 41, 5473–5483. doi:10.1039/c2cs35113g
Barone, V. (2005). Anharmonic Vibrational Properties by a Fully Automated Second-Order Perturbative Approach. J. Chem. Phys. 122, 014108. doi:10.1063/1.1824881
Barone, V., Biczysko, M., Bloino, J., Cimino, P., Penocchio, E., and Puzzarini, C. (2015). CC/DFT Route toward Accurate Structures and Spectroscopic Features for Observed and Elusive Conformers of Flexible Molecules: Pyruvic Acid as a Case Study. J. Chem. Theor. Comput. 11, 4342–4363. doi:10.1021/acs.jctc.5b00580
Barone, V., Biczysko, M., Bloino, J., and Puzzarini, C. (2013a). Accurate Structure, Thermodynamic and Spectroscopic Parameters from CC and CC/DFT Schemes: the Challenge of the Conformational Equilibrium in glycine. Phys. Chem. Chem. Phys. 15, 10094–10111. doi:10.1039/C3CP50439E
Barone, V., Biczysko, M., Bloino, J., and Puzzarini, C. (2013b). Characterization of the Elusive Conformers of glycine from State-Of-The-Art Structural, Thermodynamic, and Spectroscopic Computations: Theory Complements Experiment. J. Chem. Theor. Comput. 9, 1533–1547. doi:10.1021/ct3010672
Barone, V., Biczysko, M., Bloino, J., and Puzzarini, C. (2013c). Glycine Conformers: a Never-Ending Story? Phys. Chem. Chem. Phys. 15, 1358–1363. doi:10.1039/C2CP43884D
Barone, V., Ceselin, G., Fusè, M., and Tasinato, N. (2020). Accuracy Meets Interpretability for Computational Spectroscopy by Means of Hybrid and Double-Hybrid Functionals. Front. Chem. 8, 859. doi:10.3389/fchem.2020.584203
Basire, M., Parneix, P., and Calvo, F. (2008). Quantum Anharmonic Densities of States Using the Wang-Landau Method. J. Chem. Phys. 129, 081101. doi:10.1063/1.2965905
Becke, A. D. (1993). Density‐functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98, 5648–5652. doi:10.1063/1.464913
Begue, D., Carbonniere, P., and Pouchan, C. (2005). Calculations of Vibrational Energy Levels by Using a Hybrid Ab Initio and DFT Quartic Force Field: Application to Acetonitrile. J. Phys. Chem. A. 109, 4611–4616. doi:10.1021/jp0406114
Biczysko, M., Bloino, J., Carnimeo, I., Panek, P., and Barone, V. (2012). Fully Ab Initio IR Spectra for Complex Molecular Systems from Perturbative Vibrational Approaches: Glycine as a Test Case. J. Mol. Struct. 1009, 74–82. doi:10.1016/j.molstruc.2011.10.012
Biczysko, M., Bloino, J., and Puzzarini, C. (2018). Computational Challenges in Astrochemistry. Wires Comput. Mol. Sci. 8, e1349. doi:10.1002/wcms.1349
Biczysko, M., Panek, P., Scalmani, G., Bloino, J., and Barone, V. (2010). Harmonic and Anharmonic Vibrational Frequency Calculations with the Double-Hybrid B2PLYP Method: Analytic Second Derivatives and Benchmark Studies. J. Chem. Theor. Comput. 6, 2115–2125. doi:10.1021/ct100212p
Biczysko, M., Tarroni, R., and Carter, S. (2003). Variational Calculations of HBN Energy Levels in the X2Π and A2Σ+ States. J. Chem. Phys. 119, 4197–4203. doi:10.1063/1.1594174
Bloino, J. (2015). A VPT2 Route to Near-Infrared Spectroscopy: The Role of Mechanical and Electrical Anharmonicity. J. Phys. Chem. A. 119, 5269–5287. doi:10.1021/jp509985u
Bloino, J., Baiardi, A., and Biczysko, M. (2016). Aiming at an Accurate Prediction of Vibrational and Electronic Spectra for Medium‐to‐large Molecules: An Overview. Int. J. Quan. Chem. 116, 1543–1574. doi:10.1002/qua.25188
Bloino, J., and Barone, V. (2012). A Second-Order Perturbation Theory Route to Vibrational Averages and Transition Properties of Molecules: General Formulation and Application to Infrared and Vibrational Circular Dichroism Spectroscopies. J. Chem. Phys. 136, 124108. doi:10.1063/1.3695210
Bloino, J., Biczysko, M., and Barone, V. (2015). Anharmonic Effects on Vibrational Spectra Intensities: Infrared, Raman, Vibrational Circular Dichroism, and Raman Optical Activity. J. Phys. Chem. A. 119, 11862–11874. doi:10.1021/acs.jpca.5b10067
Bloino, J., Biczysko, M., and Barone, V. (2012). General Perturbative Approach for Spectroscopy, Thermodynamics, and Kinetics: Methodological Background and Benchmark Studies. J. Chem. Theor. Comput. 8, 1015–1036. doi:10.1021/ct200814m
Bulik, I. W., Frisch, M. J., and Vaccaro, P. H. (2017). Vibrational Self-Consistent Field Theory Using Optimized Curvilinear Coordinates. J. Chem. Phys. 147, 044110. doi:10.1063/1.4995440
Bunker, P. R., and Jensen, P. (1998). Molecular Symmetry and Spectroscopy. Ottawa, Canada: NRC Research Press.
Cané, E., Miani, A., and Trombetti, A. (2007). Anharmonic Force Fields of Naphthalene-H8 and Naphthalene-D8. J. Phys. Chem. A. 111, 8218–8222. doi:10.1021/jp071610p
Carbonniere, P., Lucca, T., Pouchan, C., Rega, N., and Barone, V. (2005). Vibrational Computations beyond the Harmonic Approximation: Performances of the B3LYP Density Functional for Semirigid Molecules. J. Comput. Chem. 26, 384–388. doi:10.1002/jcc.20170
Carter, S., Handy, N. C., Puzzarini, C., Tarroni, R., and Palmieri, P. (2000). A Variational Method for the Calculation of Spin-Rovibronic Energy Levels of Triatomic Molecules with Three Interacting Electronic States. Mol. Phys. 98, 1697–1712. doi:10.1080/00268970009483375
Carter, S., Handy, N. C., Rosmus, P., and Chambaud, G. (1990). A Variational Method for the Calculation of Spin-Rovibronic Levels of Renner-Teller Triatomic Molecules. Mol. Phys. 71, 605–622. doi:10.1080/00268979000102001
Chyba, C., and Sagan, C. (1992). Endogenous Production, Exogenous Delivery and Impact-Shock Synthesis of Organic Molecules: An Inventory for the Origins of Life. Nature 355, 125–132. doi:10.1038/355125a0
Császár, A. G. (2011). Anharmonic Molecular Force Fields. Wires Comput. Mol. Sci. 2, 273–289. doi:10.1002/wcms.75
Császár, A. G., Fábri, C., Szidarovszky, T., Mátyus, E., Furtenbacher, T., and Czakó, G. (2012). The Fourth Age of Quantum Chemistry: Molecules in Motion. Phys. Chem. Chem. Phys. 14, 1085–1106. doi:10.1039/C1CP21830A
Darling, B. T., and Dennison, D. M. (1940). The Water Vapor Molecule. Phys. Rev. 57, 128–139. doi:10.1103/PhysRev.57.128
Des Marais, D. J., Harwit, M. O., Jucks, K. W., Kasting, J. F., Lin, D. N. C., Lunine, J. I., et al. (2002). Remote Sensing of Planetary Properties and Biosignatures on Extrasolar Terrestrial Planets. Astrobiology 2, 153–181. doi:10.1089/15311070260192246
Dierksen, M., and Grimme, S. (2004). The Vibronic Structure of Electronic Absorption Spectra of Large Molecules: A Time-dependent Density Functional Study on the Influence of "Exact" Hartree−Fock Exchange. J. Phys. Chem. A. 108, 10225–10237. doi:10.1021/jp047289h
Dunning, T. H. (1989). Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153
Eckart, C. (1935). Some Studies Concerning Rotating Axes and Polyatomic Molecules. Phys. Rev. 47, 552–558. doi:10.1103/PhysRev.47.552
Erfort, S., Tschöpe, M., and Rauhut, G. (2020). Toward a Fully Automated Calculation of Rovibrational Infrared Intensities for Semi-rigid Polyatomic Molecules. J. Chem. Phys. 152, 244104–244114. doi:10.1063/5.0011832
Franke, P. R., Stanton, J. F., and Douberly, G. E. (2021). How to VPT2: Accurate and Intuitive Simulations of CH Stretching Infrared Spectra Using VPT2+K with Large Effective Hamiltonian Resonance Treatments. J. Phys. Chem. A. 125, 1301–1324. doi:10.1021/acs.jpca.0c09526
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 Revision A.03. Wallingford CT: Gaussian Inc.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2020). Gaussian Development Version, Revision J.13. Wallingford CT: Gaussian, Inc.
Fusè, M., Mazzeo, G., Longhi, G., Abbate, S., Masi, M., Evidente, A., et al. (2019). Unbiased Determination of Absolute Configurations by Vis-À-Vis Comparison of Experimental and Simulated Spectra: The Challenging Case of Diplopyrone. J. Phys. Chem. B. 123, 9230–9237. doi:10.1021/acs.jpcb.9b08375
Girish, T. E., Sony, K. S., Vaidyan, V. K., and Jayakumar, V. S. (2008). Vibrational Spectroscopy and Search for Extraterrestrial Life. AIP Conf. Proc. 1075, 196–199. doi:10.1063/1.3046211
Goerigk, L., Hansen, A., Bauer, C., Ehrlich, S., Najibi, A., and Grimme, S. (2017). A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 19, 32184–32215. doi:10.1039/c7cp04913g
Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344
Grimme, S., Ehrlich, S., and Goerigk, L. (2011). Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 32, 1456–1465. doi:10.1002/jcc.21759
Grimme, S. (2006). Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 124, 034108. doi:10.1063/1.2148954
Herbst, E., and van Dishoeck, E. F. (2009). Complex Organic Interstellar Molecules. Annu. Rev. Astron. Astrophys. 47, 427–480. doi:10.1146/annurev-astro-082708-101654
Hörst, S. M., Yelle, R. V., Buch, A., Carrasco, N., Cernogora, G., Dutuit, O., et al. (2012). Formation of Amino Acids and Nucleotide Bases in a Titan Atmosphere Simulation Experiment. Astrobiology 12, 809–817. doi:10.1089/ast.2011.0623
Hudgins, D. M., Sandford, S. A., and Allamandola, L. J. (1994). Infrared Spectroscopy of Polycyclic Aromatic Hydrocarbon Cations. 1. Matrix-Isolated Naphthalene and Perdeuterated Naphthalene. J. Phys. Chem. 98, 4243–4253. doi:10.1021/jp509985u
Isoniemi, E., Pettersson, M., Khriachtchev, L., Lundell, J., and Räsänen, M. (1999). Infrared Spectroscopy of H2S and SH in Rare-Gas Matrixes. J. Phys. Chem. A. 103, 679–685. doi:10.1021/jp9838893
Jensen, F. (2001). Polarization Consistent Basis Sets: Principles. J. Chem. Phys. 115, 9113–9125. doi:10.1063/1.1413524
Kendall, R. A., Dunning, T. H., and Harrison, R. J. (1992). Electron Affinities of the First‐row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 96, 6796–6806. doi:10.1063/1.462569
Krasnoshchekov, S. V., Craig, N. C., and Stepanov, N. F. (2013). Anharmonic Vibrational Analysis of the Gas-Phase Infrared Spectrum of 1,1-Difluoroethylene Using the Operator Van Vleck Canonical Perturbation Theory. J. Phys. Chem. A. 117, 3041–3056. doi:10.1021/jp311398z
Krasnoshchekov, S. V., Dobrolyubov, E. O., Syzgantseva, M. A., and Palvelev, R. V. (2020). Rigorous Vibrational Fermi Resonance Criterion Revealed: Two Different Approaches Yield the Same Result. Mol. Phys. 118, e1743887. doi:10.1080/00268976.2020.1743887
Krasnoshchekov, S. V., Isayeva, E. V., and Stepanov, N. F. (2014). Criteria for First- and Second-Order Vibrational Resonances and Correct Evaluation of the Darling-Dennison Resonance Coefficients Using the Canonical Van Vleck Perturbation Theory. J. Chem. Phys. 141, 234114. doi:10.1063/1.4903927
Kreienborg, N. M., Bloino, J., Osowski, T., Pollok, C. H., and Merten, C. (2019). The Vibrational CD Spectra of Propylene Oxide in Liquid Xenon: a Proof-Of-Principle CryoVCD Study that Challenges Theory. Phys. Chem. Chem. Phys. 21, 6582–6587. doi:10.1039/C9CP00537D
Kruse, H., Szabla, R., and Šponer, J. (2020). Surprisingly Broad Applicability of the Cc-pVnZ-F12 Basis Set for Ground and Excited States. J. Chem. Phys. 152, 214104. doi:10.1063/5.0006871
Kuhler, K. M., Truhlar, D. G., and Isaacson, A. D. (1996). General Method for Removing Resonance Singularities in Quantum Mechanical Perturbation Theory. J. Chem. Phys. 104, 4664–4671. doi:10.1063/1.471161
Mackie, C. J., Candian, A., Huang, X., Maltseva, E., Petrignani, A., Oomens, J., et al. (2015). The Anharmonic Quartic Force Field Infrared Spectra of Three Polycyclic Aromatic Hydrocarbons: Naphthalene, Anthracene, and Tetracene. J. Chem. Phys. 143, 224314. doi:10.1063/1.4936779
Mackie, C. J., Candian, A., Huang, X., Maltseva, E., Petrignani, A., Oomens, J., et al. (2016). The Anharmonic Quartic Force Field Infrared Spectra of Five Non-linear Polycyclic Aromatic Hydrocarbons: Benz[a]anthracene, Chrysene, Phenanthrene, Pyrene, and Triphenylene. J. Chem. Phys. 145, 084313. doi:10.1063/1.4961438
Mardirossian, N., and Head-Gordon, M. (2017). Thirty Years of Density Functional Theory in Computational Chemistry: an Overview and Extensive Assessment of 200 Density Functionals. Mol. Phys. 115, 2315–2372. doi:10.1080/00268976.2017.1333644
Martin, J. M. L., Lee, T. J., Taylor, P. R., and François, J. P. (1995). The Anharmonic Force Field of Ethylene, C2H4, by Means of Accurate Ab Initio Calculations. J. Chem. Phys. 103, 2589–2602. doi:10.1063/1.469681
Martin, J. M. L., and Taylor, P. R. (1997). Accurate Ab Initio Quartic Force Field for trans-HNNH and Treatment of Resonance Polyads. Spectrochimica Acta A: Mol. Biomol. Spectrosc. 53, 1039–1050. doi:10.1016/S1386-1425(96)01869-0
Mátyus, E., Czakó, G., and Császár, A. G. (2009). Toward Black-box-type Full- and Reduced-Dimensional Variational (Ro)vibrational Computations. J. Chem. Phys. 130, 134112. doi:10.1063/1.3076742
McGuire, B. A. (2018). 2018 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophysical J. Suppl. Ser. 239, 17. doi:10.3847/1538-4365/aae5d2
McGuire, B. A., Loomis, R. A., Burkhardt, A. M., Lee, K. L. K., Shingledecker, C. N., Charnley, S. B., et al. (2021). Detection of Two Interstellar Polycyclic Aromatic Hydrocarbons via Spectral Matched Filtering. Science 371, 1265–1269. doi:10.1126/science.abb7535
Mellouki, A., Liévin, J., and Herman, M. (2001). The Vibrational Spectrum of Pyrrole (C4H5N) and Furan (C4H4O) in the Gas Phase. Chem. Phys. 271, 239–266. doi:10.1016/S0301-0104(01)00447-5
Merten, C., Bloino, J., Barone, V., and Xu, Y. (2013). Anharmonicity Effects in the Vibrational CD Spectra of Propylene Oxide. J. Phys. Chem. Lett. 4, 3424–3428. doi:10.1021/jz401854y
Mitra, H., and Roy, T. K. (2020). Comprehensive Benchmark Results for the Accuracy of Basis Sets for Anharmonic Molecular Vibrations. J. Phys. Chem. A. 124, 9203–9221. doi:10.1021/acs.jpca.0c06634
Mitrushchenkov, A. O. (2012). A New General Renner-Teller (Including Ɛ ≳ 1) Spectroscopic Formalism for Triatomic Molecules. J. Chem. Phys. 136, 024108. doi:10.1063/1.3672162
Nakanaga, T., Kondo, S., and Saëki, S. (1979). Infrared Intensities and Coriolis Interactions in Ethylene. J. Chem. Phys. 70, 2471–2478. doi:10.1063/1.437709
Nauts, A., and Lauvergnat, D. (2012). Quantum Dynamics of Floppy Molecular Systems with Elvibrot and Tnum. AIP Conf. Proc. 1504, 948–952. doi:10.1063/1.4771853
Nejad, A., Meyer, E., and Suhm, M. A. (2020). Glycolic Acid as a Vibrational Anharmonicity Benchmark. J. Phys. Chem. Lett. 11, 5228–5233. doi:10.1021/acs.jpclett.0c01462
Nielsen, H. H. (1951). The Vibration-Rotation Energies of Molecules. Rev. Mod. Phys. 23, 90–136. doi:10.1103/RevModPhys.23.90
NIST Mass Spec Data Center, d., and Stein, S. E. (2015). NIST Chemistry WebBook, NIST Standard Reference Database Number 69 (Gaithersburg MD, 20899: National Institute of Standards and Technology), Available at: http://webbook.nist.gov (Accessed April 12, 2021).
Papajak, E., Zheng, J., Xu, X., Leverentz, H. R., and Truhlar, D. G. (2011). Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theor. Comput. 7, 3027–3034. doi:10.1021/ct200106a
Papousek, D., and Aliev, M. R. (1982). Molecular Vibrational-Rotational Spectra. New York): Elsevier.
Papp, D., Szidarovszky, T., and Császár, A. G. (2017). A General Variational Approach for Computing Rovibrational Resonances of Polyatomic Molecules. Application to the Weakly Bound H2He+ and H2·CO Systems. J. Chem. Phys. 147, 094106. doi:10.1063/1.5000680
Piccardo, M., Bloino, J., and Barone, V. (2015). Generalized Vibrational Perturbation Theory for Rotovibrational Energies of Linear, Symmetric and Asymmetric Tops: Theory, Approximations, and Automated Approaches to Deal with Medium‐to‐large Molecular Systems. Int. J. Quan. Chem. 115, 948–982. doi:10.1002/qua.24931
Pietropolli Charmet, A., Stoppa, P., Tasinato, N., Giorgianni, S., and Gambi, A. (2016). Study of the Vibrational Spectra and Absorption Cross Sections of 1-Chloro-1-Fluoroethene by a Joint Experimental and Ab Initio Approach. J. Phys. Chem. A. 120, 8369–8386. doi:10.1021/acs.jpca.6b07426
Pirali, O., Goubet, M., Huet, T. R., Georges, R., Soulard, P., Asselin, P., et al. (2013). The Far Infrared Spectrum of Naphthalene Characterized by High Resolution Synchrotron FTIR Spectroscopy and Anharmonic DFT Calculations. Phys. Chem. Chem. Phys. 15, 10141–10150. doi:10.1039/C3CP44305A
Pirali, O., Vervloet, M., Mulas, G., Malloci, G., and Joblin, C. (2009). High-resolution Infrared Absorption Spectroscopy of Thermally Excited Naphthalene. Measurements and Calculations of Anharmonic Parameters and Vibrational Interactions. Phys. Chem. Chem. Phys. 11, 3443–3454. doi:10.1039/B814037E
Plíva, J. (1990). Anharmonic Constants for Degenerate Modes of Symmetric Top Molecules. J. Mol. Spectrosc. 139, 278–285. doi:10.1016/0022-2852(90)90065-X
Polavarapu, P. L., Hess, B. A., and Schaad, L. J. (1985). Vibrational Spectra of Epoxypropane. J. Chem. Phys. 82, 1705–1710. doi:10.1063/1.448403
Puzzarini, C., and Barone, V. (2020). The Challenging Playground of Astrochemistry: an Integrated Rotational Spectroscopy—Quantum Chemistry Strategy. Phys. Chem. Chem. Phys. 22, 6507–6523. doi:10.1039/d0cp00561d
Puzzarini, C., and Barone, V. (2008). Toward Spectroscopic Accuracy for Organic Free Radicals: Molecular Structure, Vibrational Spectrum, and Magnetic Properties of F2NO. J. Chem. Phys. 129, 084306. doi:10.1063/1.2969820
Puzzarini, C., Biczysko, M., and Barone, V. (2010). Accurate Harmonic/anharmonic Vibrational Frequencies for Open-Shell Systems: Performances of the B3LYP/N07D Model for Semirigid Free Radicals Benchmarked by CCSD(T) Computations. J. Chem. Theor. Comput. 6, 828–838. doi:10.1021/ct900594h
Puzzarini, C., Bloino, J., Tasinato, N., and Barone, V. (2019). Accuracy and Interpretability: The Devil and the Holy Grail. New Routes across Old Boundaries in Computational Spectroscopy. Chem. Rev. 119, 8131–8191. doi:10.1021/acs.chemrev.9b00007
Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/S0009-2614(89)87395-6
Reisner, D. E., Field, R. W., Kinsey, J. L., and Dai, H. L. (1984). Stimulated Emission Spectroscopy: A Complete Set of Vibrational Constants for X̃1A1 Formaldehyde. J. Chem. Phys. 80, 5968–5978. doi:10.1063/1.446677
Rosnik, A. M., and Polik, W. F. (2014). VPT2+K Spectroscopic Constants and Matrix Elements of the Transformed Vibrational Hamiltonian of a Polyatomic Molecule with Resonances Using Van Vleck Perturbation Theory. Mol. Phys. 112, 261–300. doi:10.1080/00268976.2013.808386
Saladino, R., Botta, G., Pino, S., Costanzo, G., and Di Mauro, E. (2012). Genetics First or Metabolism First? The Formamide Clue. Chem. Soc. Rev. 41, 5526–5565. doi:10.1039/c2cs35066a
Saladino, R., Carota, E., Botta, G., Kapralov, M., Timoshenko, G. N., et al. (2015). Meteorite-catalyzed Syntheses of Nucleosides and of Other Prebiotic Compounds from Formamide under Proton Irradiation. Proc. Natl. Acad. Sci. USA 112, E2746–E2755. doi:10.1073/pnas.1422225112
Santra, G., Sylvetsky, N., and Martin, J. M. L. (2019). Minimally Empirical Double-Hybrid Functionals Trained against the GMTKN55 Database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A. 123, 5129–5143. doi:10.1021/acs.jpca.9b03157
Seager, S. (2014). The Future of Spectroscopic Life Detection on Exoplanets. Proc. Natl. Acad. Sci. 111, 12634–12640. doi:10.1073/pnas.1304213111
Shu, C., Jiang, Z., and Biczysko, M. (2020). Toward Accurate Prediction of Amino Acid Derivatives Structure and Energetics from DFT: glycine Conformers and Their Interconversions. J. Mol. Model. 26, 129. doi:10.1007/s00894-020-4342-7
SNSDT (2021). Double and Triple-ζ Basis Sets of SNS Family. Available at: https://smart.sns.it/?pag=download (Accessed April 12, 2021).
Sunahori, F. X., Su, Z., Kang, C., and Xu, Y. (2010). Infrared Diode Laser Spectroscopic Investigation of Four C-H Stretching Vibrational Modes of Propylene Oxide. Chem. Phys. Lett. 494, 14–20. doi:10.1016/j.cplett.2010.05.072
Suzuki, E., Yamazaki, M., and Shimizu, K. (2007). Infrared Spectra of Monomeric Thioformaldehyde in Ar, N2 and Xe Matrices. Vibrational Spectrosc. 43, 269–273. doi:10.1016/j.vibspec.2006.02.007
Swofford, R. L., Long, M. E., and Albrecht, A. C. (1976). C-H Vibrational States of Benzene, Naphthalene, and Anthracene in the Visible Region by Thermal Lensing Spectroscopy and the Local Mode Model. J. Chem. Phys. 65, 179–190. doi:10.1063/1.432815
Tasinato, N., Stoppa, P., Pietropolli Charmet, A., Giorgianni, S., and Gambi, A. (2006). High-Resolution Infrared Study of Vinyl Fluoride in the 750−1050 cm−1 Region: Rovibrational Analysis and Resonances Involving the ν8, ν10, and ν11 Fundamentals. J. Phys. Chem. A. 110, 13412–13418. doi:10.1021/jp064013w
Tennyson, J., Zobov, N. F., Williamson, R., Polyansky, O. L., and Bernath, P. F. (2001). Experimental Energy Levels of the Water Molecule. J. Phys. Chem. Reference Data 30, 735–831. doi:10.1063/1.1364517
Van Vleck, J. H. (1929). On σ-Type Doubling and Electron Spin in the Spectra of Diatomic Molecules. Phys. Rev. 33, 467–506. doi:10.1103/PhysRev.33.467
Vázquez, J., and Stanton, J. F. (2006). Simple(r) Algebraic Equation for Transition Moments of Fundamental Transitions in Vibrational Second-Order Perturbation Theory. Mol. Phys. 104, 377–388. doi:10.1080/00268970500290367
Watson, J. K. G. (1968). Simplification of the Molecular Vibration-Rotation Hamiltonian. Mol. Phys. 15, 479–490. doi:10.1080/00268976800101381
Weigend, F., and Ahlrichs, R. (2005). Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305. doi:10.1039/B508541A
Willets, A., Handy, N. C., Green, W. H., and Jayatilaka, D. (1990). Anharmonic Corrections to Vibrational Transition Intensities. J. Phys. Chem. 94, 5608–5616. doi:10.1021/j100377a038
Keywords: anharmonicity, second-order vibrational perturbation theory, density functional theory, basis sets, benchmark, infrared spectroscopy, Fermi resonances, Darling-Dennison resonances
Citation: Yang Q, Mendolicchio M, Barone V and Bloino J (2021) Accuracy and Reliability in the Simulation of Vibrational Spectra: A Comprehensive Benchmark of Energies and Intensities Issuing From Generalized Vibrational Perturbation Theory to Second Order (GVPT2). Front. Astron. Space Sci. 8:665232. doi: 10.3389/fspas.2021.665232
Received: 07 February 2021; Accepted: 29 April 2021;
Published: 31 May 2021.
Edited by:
Roberto Linguerri, Université Gustave Eiffel, FranceReviewed by:
Marcin Gronowski, Polish Academy of Sciences, PolandKenneth Ruud, UiT The Arctic University of Norway, Norway
Copyright © 2021 Yang, Mendolicchio, Barone and Bloino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julien Bloino, anVsaWVuLmJsb2lub0BzbnMuaXQ=
 Qin Yang
Qin Yang Marco Mendolicchio
Marco Mendolicchio Vincenzo Barone
Vincenzo Barone Julien Bloino
Julien Bloino