Comparison of Microscopic Interacting Boson Model and Quasiparticle Random Phase Approximation 0νββ Decay Nuclear Matrix Elements

The fundamental nature of the neutrino is presently a subject of great interest. A way to access the absolute mass scale and the fundamental nature of the neutrino is to utilize the atomic nuclei through their rare decays, the neutrinoless double beta (0νββ) decay in particular. The experimentally measurable observable is the half-life of the decay, which can be factorized to consist of phase space factor, axial vector coupling constant, nuclear matrix element, and function containing physics beyond the standard model. Thus reliable description of nuclear matrix element is of crucial importance in order to extract information governed by the function containing physics beyond the standard model, neutrino mass parameter in particular. Comparison of double beta decay nuclear matrix elements obtained using microscopic interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) has revealed close correspondence, even though the assumptions in these two models are rather different. The origin of this compatibility is not yet clear, and thorough investigation of decomposed matrix elements in terms of different contributions arising from induced currents and the finite nucleon size is expected to contribute to more accurate values for the double beta decay nuclear matrix elements. Such comparison is performed using detailed calculations on both models and obtained results are then discussed together with recent experimental results.

1. Introduction

The question of whether neutrinos are Majorana or Dirac particles and what is the neutrino mass parameter remains one of the most fundamental problems in physics today. Even though the neutrino oscillation experiments can investigate the neutrino mass differences and neutrino mixing amplitudes to high precision already, a complementary way is needed to access the absolute neutrino mass and the fundamental nature of the neutrino (see, e.g., de Salas et al., 2021). Observation of neutrinoless double beta decay (0νββ), hypothesized extremely rare second-order process of weak interaction, would verify the Majorana nature of the neutrino, constrain the absolute scale of the neutrino mass spectrum, and provide proof of lepton-number violation. It would have fundamental implications for neutrino physics, theories beyond the standard model, and cosmology. The 0νββ decay experiments aim to obtain the half-life of the process and information to be extracted from the experiments is subject to uncertainties arising from the uncertainties in the related nuclear matrix elements (NMEs). Hence, the reliable calculation of these NMEs is of utmost importance.

The inverse 0νββ decay half-life in a given isotope is conventionally expressed as

$\begin{array}{ll}{T}_{1/2}^{-1}={|f(m_i,U_{ei})|}^2{G}_{\nu }|{{M}}_{\nu }{|}^2,& (1)\end{array}$

with the phase space factor (PSF) G_ν and the nuclear matrix element (NME) ${{M}}_{\nu }$. In particular, the mass mechanism of 0νββ decay is sensitive to the neutrino mass parameter. In older calculations, PSFs were evaluated using approximate wave functions for electrons (Furry, 1939; Primakoff and Rosen, 1959; Molina and Pascual, 1977; Doi et al., 1981, 1985; Haxton and Stephenson, 1984; Tomoda, 1991; Suhonen and Civitarese, 1998) and in more recent calculations exact Dirac electron wave functions have been used (Kotila and Iachello, 2012, 2013; Stoica and Mirea, 2013; Kotila et al., 2014, 2015; Mirea et al., 2015; Graf et al., 2018; Deppisch et al., 2020). The 0νββ NMEs have been computed by a number of different models: the quasiparticle random-phase approximation (QRPA), in its proton-neutron version (Šimkovic et al., 2008, 2013; Fang et al., 2011, 2018; Faessler et al., 2012; Suhonen and Civitarese, 2012; Mustonen and Engel, 2013; Hyvärinen and Suhonen, 2015), the interacting shell model (ISM) (Caurier et al., 2005, 2007; Menéndez et al., 2009a,b; Horoi and Brown, 2013; Neacsu and Stoica, 2014; Neacsu and Horoi, 2015; Coraggio et al., 2020), the microscopic interacting boson model (IBM-2) (Barea and Iachello, 2009; Barea et al., 2013a,b, 2015a,b; Kotila et al., 2014, 2015; Graf et al., 2018; Deppisch et al., 2020), the energy density functional approach (EDF) along with density functional theory (Rodríguez and Martínez-Pinedo, 2010; Song et al., 2014, 2017; Yao et al., 2015), and the projected Hartree–Fock–Bogoliubov mean-field scheme (PHFB) (Rath et al., 2010, 2019) to name some most frequently used. In principle, the calculation of NME is straightforward but in practice the values predicted by different nuclear models differ by factors of up to three, causing a large uncertainty in the half-life for a given value of neutrino mass parameter (Rath et al., 2010). A way to avoid the model dependence and thus the uncertainties that are caused by model assumptions and approximation made in different models is to calculate the NMEs from first principles, which is currently the goal of several theoretical groups. However, applying modern ab initio methods to 0νββ decay is challenging and the 0νββ candidate nuclei are generally more complicated and heavier than those treated so far (Hergert et al., 2016; Pastore et al., 2018; Wang et al., 2019; Basili et al., 2020). Thus, traditional nuclear model calculations for 0νββ NMEs are still very much needed for the interpretation of the experimental results as well as for the planning of the future experiments. It is therefore important to try to understand the similarities and differences of different models. In this paper, the focus is on elaborate comparison between IBM-2 and QRPA nuclear matrix elements. For both of these models detailed calculations of individual NMEs that contribute to the full 0νββ NME are available.

The paper is organized as follows: The theoretical background is reviewed in section 2 and numerical results are summarized in section 3 for both light and heavy neutrino exchange. Differences and similarities of the two models are then discussed in section 4 along with possible explanations for the obtained results. Section 5 concludes the discussion with a summary and an outlook.

2. Theoretical Background

The theory of 0νββ decay was first formulated by Furry (1939) and further developed by Primakoff and Rosen (1959), Molina and Pascual (1977), Doi et al. (1981), Doi et al. (1983), Haxton and Stephenson (1984), and, more recently, by Tomoda (1991) and Šimkovic et al. (1999). All these formulations often differ by factors of 2, by the number of terms retained in the non-relativistic expansion of the current and by their contribution. Adopting the formulation of Šimkovic et al. (1999), which is the one used in most recent calculations, the transition operator for 0νββ in momentum space, $p=\left|\overrightarrow{q}\right|$, can be written as

$\begin{array}{ll}T(p)=H(p)f(m_i,U_{ei})& (2)\end{array}$

where for light neutrino exchange

$\begin{array}{ll}f\left(m_i,U_{ei}\right)=\frac{\langle m_{\nu }\rangle }{m_e},\langle m_v\rangle ={{\displaystyle \sum _{k=light}\left(U_{ek}\right)}}^2{m}_k,& (3)\end{array}$

while for heavy neutrino exchange

$\begin{array}{l}f(m_i,U_{ei})=m_p\langle m_{{\nu }_h}^{-1}\rangle ,\\ \langle m_{{\nu }_h}^{-1}\rangle ={\displaystyle \sum _{k=heavy}{\left(U_{e{k}_h}\right)}^2}\frac{1}{m_{k_h}}.& (4)\end{array}$

The (two-body) operator H(p) can be written as

$\begin{array}{ll}H(p)={\displaystyle \sum _{n,n^{\prime }}{\tau }_n^{†}}{\tau }_{n^{\prime }}^{†}[-h^F(p)+h^{GT}(p){\overrightarrow{\sigma }}_n·{\overrightarrow{\sigma }}_{n^{\prime }}-h^T(p)S_{n{n}^{\prime }}^p],& (5)\end{array}$

with the tensor operator defined as

$\begin{array}{ll}{S}_{n{n}^{\prime }}^p=3\left[\left({\overrightarrow{\sigma }}_n·\widehat{p}\right)\left({\overrightarrow{\sigma }}_{n^{\prime }}·\widehat{p}\right)\right]-{\overrightarrow{\sigma }}_n·{\overrightarrow{\sigma }}_{n^{\prime }}.& (6)\end{array}$

The Fermi (F), Gamow-Teller (GT), and tensor (T) contributions are further divided into $h_{VV}^F(p)$, $h_{AA}^{GT}(p)$, $h_{AP}^{GT}(p)$, $h_{PP}^{GT}(p)$, $h_{WW}^{GT}(p)$, $h_{AP}^T(p)$, $h_{PP}^T(p)$, and $h_{WW}^T(p)$ terms. The terms AP, PP, and WW are higher order corrections (HOC) arising from weak magnetism (W) and induced pseudoscalar terms (P) in the weak nucleon current. Finally, the terms h°(p) can be further factorized as

$\begin{array}{ll}h°\left(p\right)=v(p)\tilde{h}°(p)& (7)\end{array}$

where v(p) is called the neutrino potential and ${\tilde{h}}^{○}(p)$ are the form factors given in Table 1. The finite nucleon size (FNS) is taken into account by taking the coupling constants g_V and g_A as momentum dependent

$\begin{array}{l}{g}_V(p^2)=g_V\frac{1}{{\left(1+\frac{p^2}{M_V^2}\right)}^2},\\ g_A(p^2)=g_A\frac{1}{{\left(1+\frac{p^2}{M_A^2}\right)}^2}.& (8)\end{array}$

TABLE 1

Table 1. Double beta decay Fermi (${{M}}_F$), Gamow–Teller (${{M}}_{GT}$), and tensor (${{M}}_T$) NMEs appearing in Equation (12), with the associated reduced form factor product $\tilde{h}(q^2)$.

The value of M_V is well fixed by the electromagnetic form factor of the nucleon, $M_V^2=0.71$(GeV/c²)² (Dumbrajs et al., 1983) and g_V = 1 by the hypothesis of conserved vector current (CVC). The value of M_A is estimated to be M_A = 1.09(GeV/c²) (Schindler and Scherer, 2007) and free value of g_A = 1.269 (Yao et al., 2006).

The neutrino potential v(p) is written, in the closure approximation, for light neutrino exchange as

$\begin{array}{ll}v(p)=\frac{2}{\pi }\frac{1}{p\left(p+\tilde{A}\right)}.& (9)\end{array}$

In non-closure calculations, an average energy à is replaced with the actual intermediate state energies making the calculation more accurate but also much more complicated. For heavy neutrino exchange, the neutrino potential is given by

$\begin{array}{ll}v(p)=\frac{2}{\pi }\frac{1}{m_e{m}_p}.& (10)\end{array}$

Short-range correlations (SRC) are taken into account by multiplying the potential V(r) in coordinate space by a correlation function f(r) squared. The most commonly used correlation function is the Jastrow function

$\begin{array}{ll}{f}_J(r)=1-c{e}^{-a{r}^2}(1-b{r}^2)& (11)\end{array}$

with a = 1.1 fm⁻², b = 0.68 fm⁻² and c = 1 for the phenomenological Miller–Spencer parameterization (Miller and Spencer, 1976), and, in recent years, the Argonne/CD-Bonn parameterizations (Šimkovic et al., 2009) a = 1.59/1.52fm⁻², b = 1.45/1.88fm⁻² and c = 0.92/0.46. Since the formulation is in momentum space, SRC is taken into account by using the Fourier–Bessel transform of f_J(r).

From these ingredients, one can calculate the individual contributing NMEs listed also in Table 1. Furthermore, from these one can calculate the final NMEs for the standard mass mechanism, ${{M}}_{\nu }$ and heavy neutrino exchange ${{M}}_{{\nu }_h}$. To allow the analysis to be performed in section 3, it is convenient to introduce the quantities

$\begin{array}{l}{{M}}_{GT}={{M}}_{GT}^{AA}-\frac{g_P}{6g_A}{{M}}_{GT}^{\prime AP}+\frac{{(g_V+g_W)}^2}{6g_A^2}{{M}}_{GT}^{\prime WW}+\frac{g_P^2}{48g_A^2}{{M}}_{GT}^{″PP}\\ {{M}}_T=\frac{g_P}{6g_A}{{M}}_T^{\prime AP}+\frac{{(g_V+g_W)}^2}{12g_A^2}{{M}}_T^{\prime WW}-\frac{g_P^2}{48g_A^2}{{M}}_T^{″PP}& (12)\end{array}$

and write ${{M}}_{\nu }$ as

$\begin{array}{ll}{{M}}_{\nu }=g_A^2\left[-{\left(\frac{g_V}{g_A}\right)}^2{{M}}_F+{{M}}_{GT}-{{M}}_T\right],& (13)\end{array}$

and similarly for ${{M}}_{{\nu }_h}$.

The obtained NMEs, both individual and compound, are compared in two different models IBM-2 and QRPA. The method of evaluation 0νββ NMEs in IBM-2 is discussed in detail in Barea and Iachello (2009); Barea et al. (2015a). For QRPA calculations, see Suhonen and Civitarese (2012), Hyvärinen and Suhonen (2015) and references therein. For both models, versions with isospin restoration are used. In the case of 2νββ decay, if isospin is a good quantum number, the Fermi matrix elements should identically vanish. By a similar argument, the Fermi matrix elements in 0νββ are expected to be small, although not zero, the main difference between 2νββ and 0νββ being the neutrino potential, which for 2νββ is $v_{2\nu }(p)=\frac{\delta (p)}{p^2}$, being the Fourier–Bessel transform of the configuration space potential V(r) = 1. The method for isospin restoration is similar in spirit for both models but different in practice and is discussed further in section 4.1.

3. Results

The matrix elements of the operator H(p) have dimension fm⁻¹. In the following, NMEs are multiplied by nuclear radius in fm, $R=R_0{A}^{1/3}$, with R₀ = 1.2 fm in order to make them dimensionless, which is the way they are usually quoted.

3.1. Light Neutrino Exchange

The individual IBM-2 nuclear matrix elements were recently calculated in Deppisch et al. (2020) in order to study the potential interplay of non-standard short-range operators of 0νββ decay with standard light Majorana neutrino exchange. A selection of those NMEs is compared with QRPA nuclear matrix elements reported in Hyvärinen and Suhonen (2015). To avoid the differences arising from the use of different form factor charges, they are explicitly factored out for both models and NMEs are presented in the notation given in Deppisch et al. (2020). The individual QRPA nuclear matrix elements given in Tables 2, 4, for light and heavy neutrino exchange, respectively, are obtained from the values reported in Tables 2, 4 of Hyvärinen and Suhonen (2015) as follows: F and AA contributions are taken as they are; AP contributions are divided by $\mp (4*m_p^2/m_{\pi }^2)/6$, where − sign corresponds to ${{M}}_{GT}^{\prime AP}$ and + sign to ${{M}}_T^{\prime AP}$; WW contributions (in Hyvärinen and Suhonen (2015) these are called MM contributions): GT NMEs are divided by ${({\mu }_p-{\mu }_n)}^2/6$ and T NMEs by ${({\mu }_p-{\mu }_n)}^2/12$ with μ_p − μ_n = 3.7; finally PP contributions are divided by $\pm {(4*m_p^2/m_{\pi }^2)}^2/48$, where + sign corresponds to ${{M}}_{GT}^{″PP}$ and − sign to ${{M}}_T^{″PP}$. The thus obtained numerical values of individual ground state to ground state NMEs are given in Table 2 for ⁷⁶Ge, ⁸²Se, ⁹⁶Zr, ¹⁰⁰Mo, ¹¹⁰Pd, ¹¹⁶Cd, ¹²⁴Sn, ¹²⁸Te, ¹³⁰Te, and ¹³⁶Xe.

TABLE 2

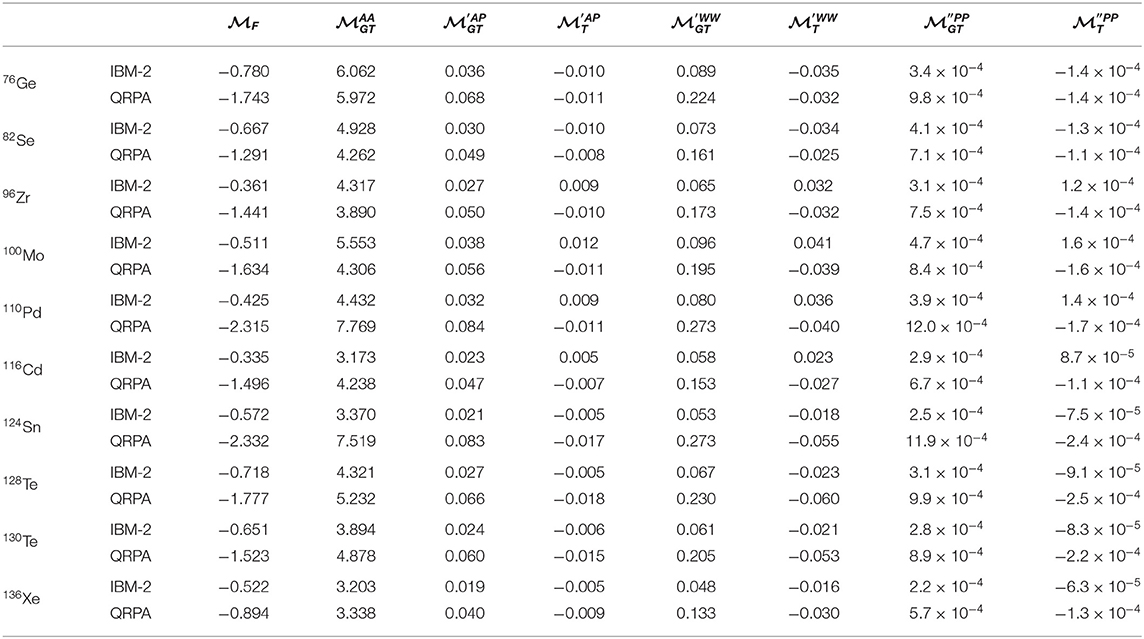
Table 2. Nuclear matrix elements (NMEs) for the standard light neutrino exchange 0νββ decay mechanism evaluated in the interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) as described in the text.

Since nuclei from A = 76 to A = 136 are covered, there are two classes of nuclei: those in which protons and neutrons occupy the same major shell (A = 76, 82, 124, 128, 130, 136) and those in which they occupy different major shells (A = 96, 100, 110, 116). Clearly notable difference between the two models is shown for the tensor matrix elements in these two classes. For QRPA, the sign of tensor NMEs is always negative. For IBM-2, it is negative if the protons and neutrons occupy the same major shell and positive when they occupy different major shells. This behavior can be traced to the fact that the neutrino potential V(r) is different for the tensor contribution than for Fermi and Gamow–Teller contributions. In the notation of Table 8 of Barea and Iachello (2009), V(r) = H(r) for Fermi and Gamow–Teller matrix elements and V(r) = −rH′(r) for tensor matrix elements.

Another considerable difference is the magnitude of ${{M}}_F$ matrix elements. They appear twice or more larger in QRPA than in IBM-2 for most of the studied nuclei, ¹³⁶Xe being a notable exception. On the other hand, the ${{M}}_{GT}^{AA}$, giving the biggest contribution to the full NME, have rather similar magnitudes in both models, exceptions being ¹¹⁰Pd and ¹²⁴Sn which are much larger in QRPA. The other contributions, AP, PP, and WW, are orders of magnitude smaller. ${{M}}_{GT}^{\prime AP}$, as well as, ${{M}}_{GT}^{″AP}$, have comparable magnitudes in both models, the exceptions again being ¹¹⁰Pd and ¹²⁴Sn, which are much larger in QRPA. ${{M}}_{GT}^{″WW}$, however, is twice or more larger in QRPA in all the studied nuclei. The contributions of tensor matrix elements are the smallest and their magnitudes are fairly similar in both models.

To analyze further the similarities and differences in these two models, it is useful to calculate the compound NMEs ${{M}}_{GT}$, and ${{M}}_T$ given in Equation (12) using the individual NMEs of Table 2. In the calculation, values g_V = 1.0 and g_W = 3.7 and quenched values for g_A = 1.0, $g_P=4g_A\frac{m_p^2}{m_{\pi }^2}(1-\frac{m_{\pi }^2}{m_A^2})=182$ are used in order to allow straightforward use of other values of g_A using Equation (13) for the full matrix element. ${{M}}_F$, ${{M}}_{GT}$, ${{M}}_T$, and full matrix element ${{M}}_{\nu }$ are listed in Table 3, along with their ratios in the two studied models. The ratio ${\chi }_F={{M}}_F/{{M}}_{GT}$ is also shown for each model.

TABLE 3

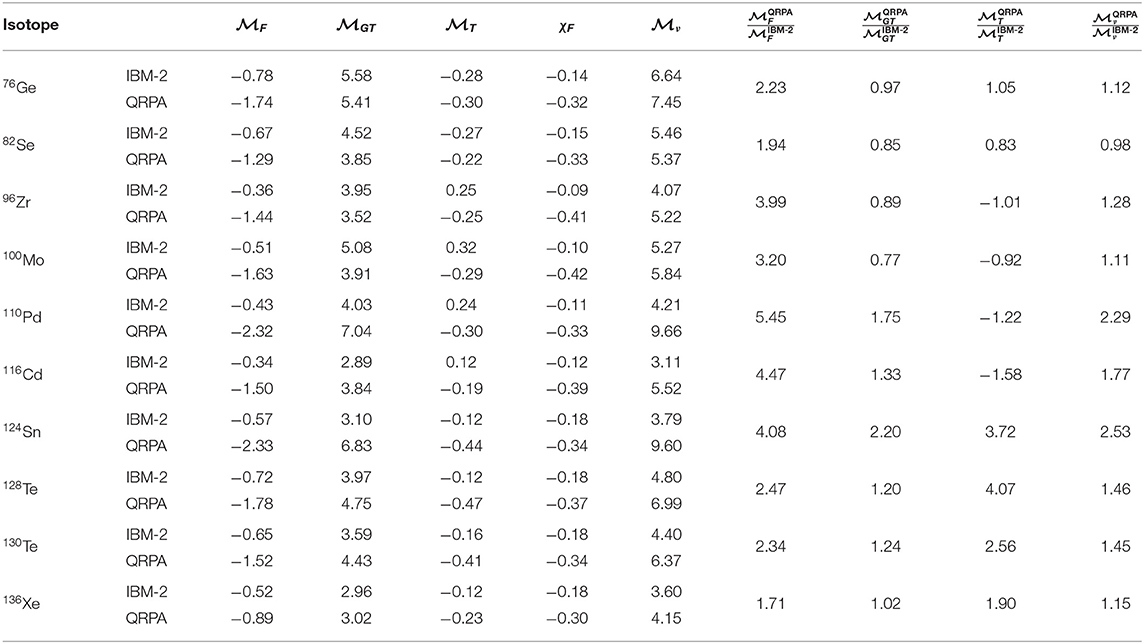
Table 3. Comparison between interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) light neutrino exchange Fermi (F), Gamow–Teller (GT), tensor (T), and full ${{M}}_{\nu }$ NMEs as defined in Equations (12) and (13) calculated using quenched value g_A = 1.0.

If we first look at the ratio ${\chi }_F={{M}}_F/{{M}}_{GT}$, we note that QRPA gives larger absolute value in all studied nuclei. For QRPA, this value varies between −0.30 and −0.42, largest absolute values being for ¹⁰⁰Mo and ⁹⁶Zr. For IBM-2 χ_F, values are between −0.09 and −0.18 and smallest absolute values are obtained for ¹⁰⁰Mo and ⁹⁶Zr. This shows that in addition to the absolute magnitude of ${{M}}_F$ being larger in QRPA than in IBM-2 also the relative magnitude of ${{M}}_F$ to ${{M}}_{GT}$ is larger in QRPA.

The ratios of compound NMEs ${{M}}_{GT}$ and ${{M}}_T$ in QRPA and IBM-2 are shown in the last two columns of Table 3. ${{M}}_{GT}$ gives the biggest contribution to the full matrix element defined in Equation (13). For ⁷⁶Ge and ¹³⁶Xe$,{{M}}_{GT}$ are in very close correspondence in QRPA and IBM-2. For ⁸²Se and ⁹⁶Zr, the difference is 15% or less, and for ¹⁰⁰Mo, ¹¹⁶Cd, ¹²⁸Te, and ¹³⁰Te, the difference is 33% or less. The largest differences are for ¹¹⁰Pd and ¹²⁴Sn, as was the case also for individual NMEs. For ${{M}}_T$, the situation is a bit different. Also for these nuclear matrix elements QRPA and IBM-2 give very similar results for ⁷⁶Ge and ⁸²Se. In ⁹⁶Zr, ¹⁰⁰Mo, ¹¹⁰Pd, and ¹¹⁶Cd, the magnitude is comparable but since these nuclei have protons and neutrons occupying different shells there is the sign difference. For ¹²⁴Sn, ¹²⁸Te, ¹³⁰Te, and ¹³⁶Xe, the difference is as large or larger than 90%. However, it is good to keep in mind that tensor contribution is an order of magnitude smaller than GT contribution.

The numerical values of full matrix element ${{M}}_{\nu }$ are discussed in sections 4.3 and 4.4.

3.2. Heavy Neutrino Exchange

The matrix elements for heavy neutrino exchange can be simply calculated by replacing the potential v(p) = 2π⁻¹[p(p + Ã)]⁻¹ of Equation (9) with the potential $v_h(p)=2{\pi }^{-1}{(m_e{m}_p)}^{-1}$ of Equation (10). Table 4 gives the corresponding individual nuclear matrix elements. The index h is added to distinguish these matrix elements from those with light neutrino exchange. As can be seen from Table 4, the situation is much more complicated than in the case of light neutrino exchange. In addition to Fermi matrix elements being larger in QRPA and tensor matrix elements having sign that varies depending whether neutrons and protons occupy the same shell in IBM-2 also the ${{M}}_{GT}^{AA}$ are much larger in QRPA and the sign of ${{M}}_{GT}^{\prime WW}$ is negative for all studied nuclei in IBM-2 and positive in QRPA. Furthermore, ${{M}}_{GT}^{\prime WW}$ is also much larger in magnitude in QRPA than in IBM-2.

TABLE 4

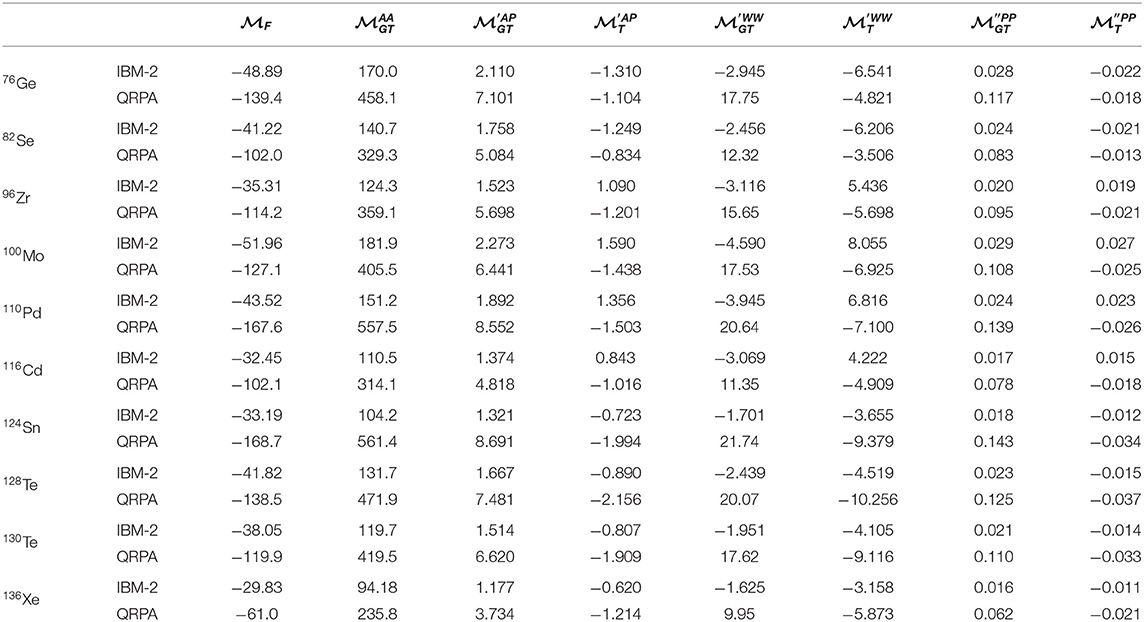
Table 4. Nuclear matrix elements (NMEs) for the heavy neutrino exchange 0νββ decay mechanism evaluated in the interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) as described in the text.

Table 5 presents the ${{M}}_F$, ${{M}}_{GT}$, ${{M}}_T$, and full matrix element ${{M}}_{{\nu }_h}$ along with their ratios in the two studied models in case of heavy neutrino exchange. Again, also the ratio ${\chi }_{{\nu }_h,F}={{M}}_{{\nu }_h,F}/{{M}}_{{\nu }_h,GT}$ is shown. Now we see that the absolute value of χ_{νh, F} is larger for IBM-2 in all studied nuclei on the contrary to light neutrino exchange. On the other hand, χ_{νh, F} ratios are rather close to each other: for QRPA, they vary from −0.30 to −0.39, and for IBM-2, they vary from −0.43 to −0.48. In addition to the Fermi matrix element being ~2 − 5 times larger in QRPA, the compound GT matrix elements are also ~3 − 7 larger in QRPA. As in the case of light neutrino exchange, the difference is largest for ¹¹⁰Pd and ¹²⁴Sn. If those two systems are disregarded, variation is much smaller, in average 2.8 and 3.6, for F and GT, respectively. The tensor matrix elements, however, behave similarly as in the case of light neutrino exchange and the ratios are comparable to those.

TABLE 5

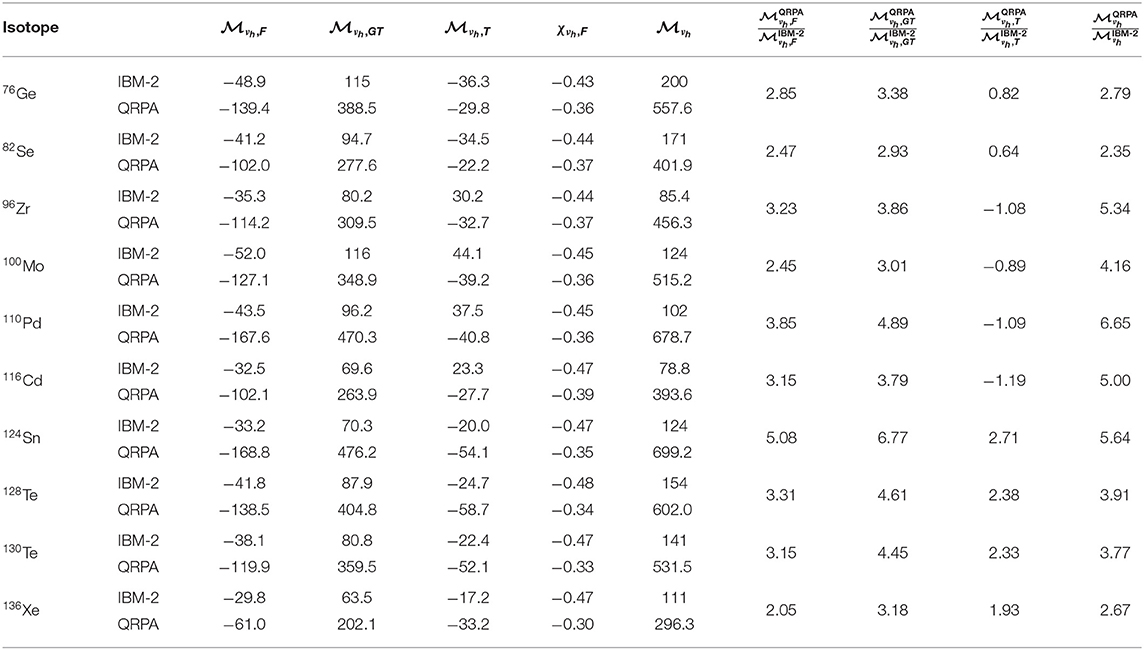
Table 5. Comparison between interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) heavy neutrino exchange Fermi (F), Gamow–Teller (GT), tensor (T), and full ${{M}}_{{\nu }_h}$ nuclear matrix elements (NMEs) as defined in Equations (12) and (13) and calculated using quenched value g_A = 1.0.

The numerical values of full matrix element ${{M}}_{{\nu }_h}$ are discussed in sections 4.3 and 4.4.

4. Discussion

There are several ingredients that go into the calculation of nuclear matrix elements. In the following, some of these are discussed in view of explaining similarities and differences obtained in the results of the two models studied, IBM-2 and QRPA. Various discussed assumptions are interrelated with each other.

4.1. Model Assumptions

4.1.1. Microscopic Interacting Boson Model

The IBM-2 is based on presentation of nucleon pairs as bosons with certain quantum numbers and features a truncation of the full shell-model space to a subspace. The procedure to obtaining wavefunctions is typically more phenomenological than in QRPA, and relies more on adjusting the model parameters to match available observables. However, there are no data on 0νββ matrix elements and the associated operators therefore must be derived from the shell model, at least approximately. The mapping is approximate since it involves only two- and four-nucleon states (which are mapped to one- and two-boson states) and a schematic surface-delta interaction (SDI) that is not fully consistent with the phenomenological boson interaction. In addition to three fundamental assumptions in IBM-2, those being a shell-model assumption, a mapping assumption, and a truncation assumption, all of which enter in a microscopic derivation of the parameters of the IBM-2 Hamiltonian, there are several assumptions specifically related to description of 0νββ decay, such as closure approximation, method of isospin restoration, and inclusion of short-range correlations.

• The shell model assumption and single particle energies

It is generally accepted that the shell model provides an appropriate microscopic framework for the description of the low-lying states of nuclei. The basic assumption is that nuclei contain a relatively inert doubly magic core and additional valence nucleons (or nucleon holes) restricted to a small number of valence shells. Interactions between the valence nucleons scatter them over the valence orbits, thereby dictating spectroscopic properties in the region of low excitation energies. In practice, this means that one major shell is active for neutrons and one for protons and corresponding single particle energies (SPEs) play considerable role. In Kotila and Barea (2016), the single-particle and single-hole energies and strengths of interaction were evaluated and discussed in connection to IBM-2. Furthermore, the occupancies of the single particle levels were calculated and compared to QRPA at BCS level and available experimental data in order to satisfy a two-fold goal: to assess the goodness of the single particle energies and check the reliability of the used wave functions. Both tests are particularly important in the case of nuclei involved in double beta decay, as they affect the evaluation of the NMEs and then their reliability (Engel, 2015).

In principle, the single particle energies can be considered as input parameters that can be fitted to reproduce the experimental occupancies. Instead of fitting, the single particle energies can also be calculated using, e.g., Woods–Saxon potential or extracted from experimental data on nuclei with a particle more or one particle less than a shell closure as is used in IBM-2. As part of the study reported in Kotila and Barea (2016), the single particle energies used in IBM-2 calculations were updated and in Deppisch et al. (2020), a notable increase for 0νββ NMEs was obtained particularly for ⁷⁶Ge, ⁸²Se and ⁹⁶Zr, and ¹⁰⁰Mo for which the SPEs changed the most. The obtained increase, ~20−40%, is mainly due GT contribution. One should note that in IBM-2 the number of the valence orbitals is dictated by magic numbers. The corresponding single particle energies enter the calculation through mapping procedure and the only parameter that is changed when SPEs change is the SDI strength parameter. Also, in the IBM-2 calculation the same single particle energies and SDI strength parameters for both initial and final states are used.

• The mapping and truncation assumption

Formally, any fermion problem can be transformed into an equivalent boson problem by carrying out a mapping from the original fermion space (the shell model space) onto space composed of many-boson states. Those states, which properly reflect the Pauli principle, define the so-called physical boson space. To avoid violating the suppressed effects of the Pauli principle, the boson operators that arise in such mappings will, in general, involve infinite expansions. Their use in practical applications requires that only low orders in the series expansion be maintained. Implicit in the IBM-2 is the assumption that the original fermion shell model Hamiltonian can be mapped to a good approximation onto a boson Hamiltonian which contains, at most, two-boson interactions.

In the current double beta decay calculations, the Otsuka–Arima–Iachello (OAI) mapping (Otsuka et al., 1978) is employed, where first the dominant, collective degrees of freedom in the fermion space are isolated and then only this collective subspace is mapped onto a boson space. In the zeroth-order OAl mapping, the series expansion for the boson Hamiltonian is truncated so that only one- and two-body terms are kept. One should note that for strongly deformed nuclei different mapping could be more suitable [e.g., the generalized Holstein–Primakoff (GHP) expansion, Marshalek, 1980]. Boson mapping procedures, in principle, map the entire fermion space onto a boson space. Practical application of any such procedure requires truncation to a small set of collective bosons: in IBM-2, this is two collective bosons (I = 0 and I = 2) for neutrons and likewise two collective bosons for protons.

In Barea and Iachello (2009), the role of approximations in the boson calculation was assessed by comparing generalized seniority (GS), IBM-2, and IBM-2 with next to leading order (NLO) calculation. It was observed that there was a systematic reduction of the matrix elements by about 20% when going from GS to IBM-2, while the effect of NLO terms was found to be very small. It was also found that the contribution of s bosons is dominant, the contribution of d bosons is sizable and of opposite sign, whereas NLO corrections are small and with random sign. It was concluded that NLO corrections appear to be small, they are henceforth neglected in the calculations of Deppisch et al. (2020).

• Isospin restoration

Isospin restoration was already briefly mentioned in section 2. The need for this improvement was obvious: the Fermi matrix elements ${{M}}_F^{(2\nu )}$ for 2νββ decay in IBM-2 did not vanish in cases where protons and neutrons occupy the same major shell. Similarly, the Fermi matrix elements ${{M}}_F^{(0\nu )}$ for 0νββ decay were large when protons and neutrons are in the same major shell, as can be seen from Table 7 of Barea et al. (2013a), where the quantity χ_F is reported. In IBM-2, the isospin is restored by modifying the mapped operator by imposing the condition that ${{M}}_F^{(2\nu )}=0$. This condition is simply implemented in the calculation by replacing the radial integrals of Appendix A of Barea and Iachello (2009) with ones given in Equations (9) and (10) in Barea et al. (2015a) that guarantee that the F matrix elements vanish for 2νββ as given in Barea et al. (2015a), and they also reduce the F matrix elements for 0νββ by subtraction of the monopole term in the expansion of the matrix element into multipoles. Even though the method of isospin restoration is similar in spirit in QRPA, it is different in practice. In IBM-2, the isospin restoration does not affect any model parameters in contrary to QRPA. When compared with the matrix elements without the isospin restoration in IBM-2 (Barea et al., 2013a), a considerable reduction of the F matrix elements to values comparable to those of the shell model (Caurier et al., 2007; Menéndez et al., 2009a), where isospin is a good quantum number by definition, and uniformly small (χ_F~ −0.15), are found. The overall reduction in full matrix element for light neutrino exchange ${{M}}^{(0\nu )}$ due isospin restoration is ~15%.

• Closure approximation

A standard way to consider a double beta decay process is to present it as a transitional process from an initial nucleus to an intermediate nucleus and then to a final nucleus, so that the corresponding nuclear matrix elements can be presented as a sum over the intermediate nuclear states. To calculate these matrix elements, one needs to calculate all the intermediate states, which could be a very challenging task. However, this can be avoided using closure approximation. The main idea behind the closure approximation is to replace the energies of the intermediate states with an average energy, and then the sum over the intermediate states can be found explicitly by using the completeness relation. In IBM-2, calculations closure approximation is assumed. In Barea et al. (2013a), the sensitivity to the closure energy (~10 MeV) is estimated to be 5%. This uncertainty in the value of the nuclear matrix elements is related to the ability to derive accurately enough the average energy associated with the closure approximation. Fortunately, the 0νββ nuclear matrix elements are not very sensitive to the value of closure energy since the typical, large value of momentum of the virtual neutrino is ~100 − 200 MeV, i.e., much larger than the typical nuclear excitations. In Yoshida and Iachello (2013), IBM-2 was employed without closure approximation in the description of 2νββ for A = 128, 130 systems. The results were found to be comparable with the ones using closure approximation, even though 2νββ is much more sensitive to the choice of closure energy. In 2νββ decay, the typical neutrino momentum is of the same order than nuclear excitations. Further IBM-2 calculations without closure approximations for 2νββ and 0νββ are in progress.

4.1.2. Quasiparticle Random Phase Approximation

The QRPA is a standard method for describing collective excitations in open-shell nuclei with stable mean-field solutions, either spherical or deformed. The advantage of the QRPA is the number of single-particle orbits that can be included in the calculation. In most QRPA calculations, all the orbitals within one, two, or even more oscillator shells of the Fermi surface are treated explicitly, with those further below assumed to be fully occupied and those further above completely empty. The cost for such large single-particle spaces in the QRPA is a restricted set of correlations. To compensate this, the effective nucleon–nucleon interaction used to generate the nuclear states needs to be modified. The original interaction is typically a realistic nucleon–nucleon potential adapted to the QRPA configuration space through many-body perturbation theory.

• Parameter fitting and isospin restoration

The interaction is usually modified independently in the particle-hole and pairing channels. The strengths of the pairing interaction are renormalized independently for protons, $g_p^{pair}$, and neutrons, $g_n^{pair}$, to reproduce the pairing gaps. The strengths of the interaction in the proton–neutron particle-hole channels are usually renormalized to properly reproduce the energies of the Gamow–Teller and spin-dipole giant resonances, altering both the 2νββ and 0νββ matrix elements somewhat. The particle–particle channel is used to cure the problem of isospin violation obtained in 2νββ decay. This is done by adjusting the renormalization constant $g_{pp}^{T=1}$ to make ${{M}}_F^{(2\nu )}$ vanish (Šimkovic et al., 2013). In order to restore the isospin symmetry, $g_{pp}^{T=1}$ should approximately equal to g^pair's (Rodin and Faessler, 2011). Then this adjusted value of $g_{pp}^{T=1}$ is used in further calculations for the 0νββ decay. The parameter $g_{pp}^{T=0}$ is usually independently fitted to reproduce the measured 2νββ-decay half-life and thus obtained value is then used in the calculation of the 0νββ NMEs. The fitted g_pp's depend naturally on the chosen nucleon–nucleon interaction. However, in Fang et al. (2018), it was found that even though the parameters that lead to same 2νββ NME are different for different interactions, they lead also basically to the same 0νββ NME.

When comparing the matrix elements without and with the restoration, the reduction is found to be smaller for QRPA (Hyvärinen and Suhonen, 2015) than for IBM-2. The effect on light neutrino exchange Fermi matrix elements is found to be very small or negligible and Gamow–Teller and tensor parts are found to be hardly affected in disagreement with QRPA calculations reported in Šimkovic et al. (2013). This deviation with different QRPA calculations is discussed further in section 4.4. For heavy neutrino exchange, the effect on F NMEs is less than 5% and very small or negligible for GT and T nuclear matrix elements. It should also be noted that for A = 110 and A = 124 systems, there are no 2νββ-decay data available, and in the QRPA calculation beta decay data were used for A = 110 and for A = 124 2νββ nuclear matrix element proposed in Šimkovic et al. (2013) was taken. These two nuclear systems are exactly the ones were nuclear matrix elements in Tables 2–5 for QRPA and IBM-2 differ the most. However, in Šimkovic et al. (2013), for these nuclei QRPA results are presented that are much closer to IBM-2 values.

• Size of the model space

Size of the model space and SPEs play considerable role in QRPA 0νββ calculations as was pointed out in Suhonen and Civitarese (2008). In QRPA calculations, the valence space usually spans more than just one harmonic oscillator shell. In Suhonen and Civitarese (2010), the effects of different orbital occupancies and model-space sizes on the magnitudes of 0νββ nuclear matrix elements were studied. It was found that the contributions coming from beyond the simple shell-model space are essential in obtaining a reliable value of the nuclear matrix element. Furthermore, inclusion of spin-orbit partners in the single particle basis is not only possible in QRPA but also found necessary in order to avoid underestimation of the 0νββ NMEs. Also, in QRPA rather different sets of single particle energies are employed for initial and final nucleus (Suhonen and Civitarese, 2010).

The size of the model space and SPEs affect also the fitting of g_pp parameters. Usually larger values of parameters g_pp are needed to obtain agreement for the 2νββ transition probabilities when smaller model space is considered and the 2νββ NMEs decrease with increasing particle–particle strength.

• Non-closure approach

In QRPA, the use of closure approximation is avoided when evaluating 0νββ NMEs. In this so-called non-closure approach, one needs to calculate the sum through all intermediate states explicitly, which is an obvious challenge due to the large number of intermediate states. As noted earlier, use of closure approximation in the description of 0νββ decay is much more justified than in the case of 2νββ decay. However, in QRPA 2νββ NMEs are needed to fit the g_pp parameters and thus the use of non-closure approximation is essential.

The QRPA calculations have also been used to estimate the difference between closure vs. non-closure and the validity of used closure energy. For example, results from Pantis and Vergados (1990) indicate a deviation of about up to 10% between closure and non-closure NMEs, but its magnitude and sign depend on the choice of g_pp. In Muto (1994), very small differences between closure and non-closure is reported, and in most cases the magnitude of the non-closure results is slightly smaller than the magnitude of the closure result.

4.2. Short Range Correlations

The short range correlation is important issue in the actual calculation of 0νββ NMEs. Early calculations use the Miller-Spencer SRC, which gives rather large reductions to the final results. More modern Argonne and CD-Bonn SRC behave much milder.

The short-range correlations affect heavy neutrino exchange, 0ν_hββ, decay differently than light neutrino exchange, 0νββ. This is because the neutrino potential for heavy neutrino exchange is a contact interaction in configuration space and thus strongly influenced by SRC. For light neutrino exchange, the effect is very small, especially when going from Argonne SRC to CD-Bonn SRC, which are the SRC parameterizations used in IBM-2 and QRPA calculations of interest here, respectively. For heavy neutrino exchange, however, the effect is considerable. In Hyvärinen and Suhonen (2015), effect of changing from Argonne to CD-Bonn SRC in case of heavy neutrino exchange in QRPA was studied and CD-Bonn NMEs were found to be roughly 1.5 larger than Argonne NMEs. Similar result is found also for IBM-2 (Barea et al., 2013a). Taking this into account, the difference between the results for heavy neutrino exchange obtained in IBM-2 and QRPA is reduced to factor ~1.9 for F nuclear matrix elements and ~2.5 for GT nuclear matrix elements and full matrix element.

4.3. Sign of the Tensor Matrix Element and Full 0νββ Nuclear Matrix Element

In recent papers (Graf et al., 2018; Deppisch et al., 2020), the mapping of the quark current products to nucleon matrix elements and finally to nuclear matrix elements was performed in detail. A different relative sign between GT and T matrix element was found than in previous papers available in literature. In case of light neutrino exchange, the tensor contribution is rather small, ~1%. However, for heavy neutrino exchange the sign affects the final 0ν_hββ NMEs considerably. In Figures 1, 2, total NMEs obtained with IBM-2 and QRPA using the same form factor charges, same overall sign for tensor matrix elements, and the convention that ${{M}}_{\nu }>0$, ${{M}}_{{\nu }_h}>0$, are plotted for light and heavy neutrino exchange, respectively. The numerical values are also given in Tables 3, 5. Total nuclear matrix element are found to be systematically larger in QRPA. However, for light neutrino exchange the correspondence is very good for A = 76, 82, 100, and 136 systems where the deviation is less or equal to 15%. For heavy neutrino exchange, the situation is more complicated and a factor up to 6.65 difference is found between the two models when ¹¹⁰Pd and ¹²⁴Sn are included. When ¹¹⁰Pd and ¹²⁴Sn are not included and different parameterization of short range correlation is taken into account, the factor reduces to ~2−3. However, even for the heavy neutrino exchange, the trend is found to be similar for IBM-2 and QRPA. The difference also seems to be rather regular and systematic.

FIGURE 1

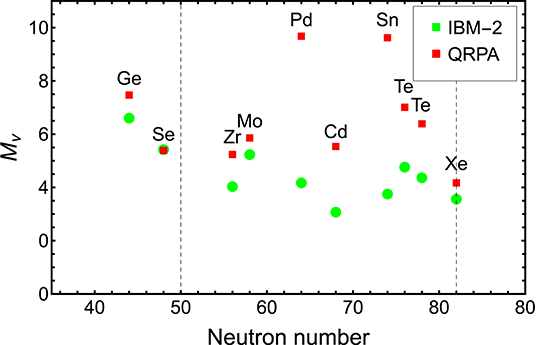
Figure 1. Total light neutrino exchange 0νββ nuclear matrix elements ${{M}}_{\nu }$ obtained with interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) using same form factor charges, same overall sign for tensor matrix elements, and the convention that ${{M}}_{\nu }>0$.

FIGURE 2

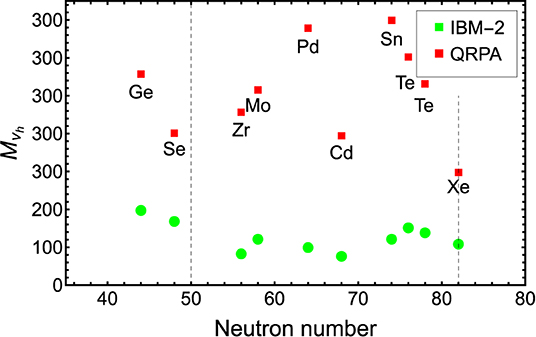
Figure 2. Total heavy neutrino exchange 0ν_hββ nuclear matrix elements ${{M}}_{{\nu }_h}$ obtained with interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) using same form factor charges, same overall sign for tensor matrix elements, and the convention that ${{M}}_{{\nu }_h}>$ 0.

The matrix elements ${{M}}_{\nu }$ attain their smallest values at the closed proton and neutron shells due to the form of the transition operator, which for β⁻β⁻ decay annihilates a neutron pair and creates a proton pair. These shell effects are very clear in Figure 1 and it even seems that both calculations suggest a kind of shell closure at A = 116 system, i.e., around N = 66. Shell effects are also responsible for the ratio of the matrix elements of two different isotopes of the same element. For example, a simple calculation using the pair operators of Equation (42) of Barea and Iachello (2009) gives ${{M}}_{\nu }\left({}^{128}\text{T}\text{e}\right)/{{M}}_{\nu }\left({}^{130}\text{T}\text{e}\right)=1.11$, which is nicely reproduced by both models.

4.4. Other QRPA Calculations

As already noted, there are also several other calculations available using QRPA in the description of double beta decay. In Šimkovic et al. (2013), a significant reduction in the Fermi matrix element was observed when comparing results without and with isospin restoration. On the other hand, the values of Fermi NMEs without isospin restoration were considerably higher than in the QRPA calculation analyzed here. As a consequence, after the isospin restoration the Fermi NMEs for light neutrino exchange of these two QRPA calculations (Šimkovic et al., 2013; Hyvärinen and Suhonen, 2015) are rather close to each other. Also the GT NMEs are generally in good agreement in these two calculations, exceptions being ¹¹⁰Pd and ¹²⁴Sn, where (Šimkovic et al., 2013) reports much smaller values that in fact are in good correspondence with IBM-2 results. In Šimkovic et al. (2013), the T NMEs are also found to be reduced slightly once isospin restoration is taken into account. Nonetheless, T nuclear matrix elements obtained in Šimkovic et al. (2013) are roughly twice as large compared to Hyvärinen and Suhonen (2015).

The nuclear matrix elements for heavy neutrino exchange with isospin restoration in QRPA were also calculated in Faessler et al. (2014) where only full matrix elements are given. The results of this calculation are somewhere between IBM-2 (Deppisch et al., 2020) and QRPA of Hyvärinen and Suhonen (2015). The results obtained with CD-Bonn parameterization of SRC are about 67% of those given in Hyvärinen and Suhonen (2015) obtained with the same SRC parameterization, exceptions being ¹¹⁰Pd and ¹²⁴Sn. Faessler et al. (2014) also gives results with Argonne parameterization of short range correlations and those are very similar to the ones obtained with IBM-2 (Deppisch et al., 2020) and calculated with same SRC parameterization.

Double beta decay nuclear matrix elements for ⁷⁶Ge, ⁸²Se, ¹³⁰Te, ¹³⁶Xe, and ¹⁵⁰Nd have also been calculated using deformed QRPA in Fang et al. (2018), where the results are presented for both CD-Bonn and Argonne parameterization of SRC. It is thus convenient to compare spherical and deformed QRPA calculations with CD-Bonn parameterization, where as the comparison with IBM-2 and deformed QRPA is made using Argonne parameterization. Compared to spherical QRPA calculations a reduction of ~30% was found for ⁷⁶Ge, ⁸²Se, and ¹³⁰Te, and about 60% for ¹³⁶Xe, which has a magic neutron number and different Fermi surfaces of initial non-paired and final paired neutrons.The reduction was concluded to be mainly due the presence of BCS overlap factor between the initial and ground states. This reduction leads to light neutrino exchange NMEs that are roughly half of those obtained with IBM-2 and spherical QRPA except for ¹³⁶Xe, where the reduction is larger. This holds also for heavy neutrino exchange between the QRPA calculations. The IBM-2 NMEs, however, are very close to those obtained with deformed QRPA when sign of the tensor matrix element is taken into account (exception again being ¹³⁶Xe).

4.5. Correlation of Light and Heavy Neutrino Exchange Matrix Elements

It has been suggested that measurement of 0νββ decay in different nuclei could be used to distinguish between the two mechanisms, light or heavy neutrino exchange. Unfortunately, the results in Tables 3, 5 are highly correlated as is evident from the fact that they are obtained one from the other just by replacing the potential v(p) with v_h(p). Therefore, this criterion cannot be used to distinguish between the two mechanisms (Lisi, 2011). The situation is further illustrated in Figure 3. For QRPA, the heavy neutrino nuclear matrix elements are roughly 80 times larger than light neutrino ones. For IBM-2, this factor is roughly 30.

FIGURE 3

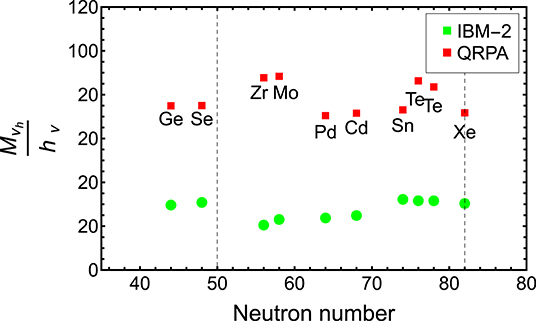
Figure 3. Ratio ${{M}}_{{\nu }_h}/{{M}}_{\nu }$ in interacting boson model (IBM-2) and quasiparticle random phase approximation (QRPA) using same form factor charges, same overall sign for tensor matrix elements, and the convention that ${{M}}_{\nu },{{M}}_{{\nu }_h}>$ 0.

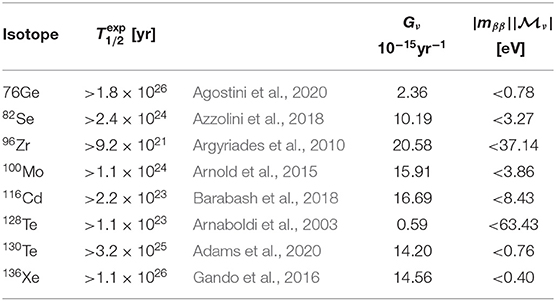
4.6. Experimental Half-Life Limits

Table 6 summarizes current bounds for $T_{1/2}^{\mathrm{\text{exp}}}$ at 90% CL from different experiments. For ⁷⁶Ge and ¹³⁶Xe, limit of 10²⁶yr has already been exceeded. Experimental half-life limits can be converted to limits on product of neutrino mass parameter |m_ββ| and nuclear matrix element as shown in the last column of Table 6. Once the nuclear matrix element is known accurately enough, these can be converted to limits on neutrino mass parameter |m_ββ|. As mentioned, the stringent limits are currently found for ⁷⁶Ge and ¹³⁶Xe. For these two systems the IBM-2 and QRPA give rather good correspondence as can be seen from Figure 1, deviation being ~15%. As a result, limits of |m_ββ| ~100 meV are deduced for both ⁷⁶Ge and ¹³⁶Xe.

TABLE 6

Table 6. Upper limits on $\left|m_{\beta \beta }\right|\left|{{M}}_{\nu }\right|$ from current experimental bounds $T_{1/2}^{\mathrm{\text{exp}}}$ at 90% CL and taking g_A = 1.0.

5. Summary

In this paper, a comparison between QRPA and IBM-2 calculations for 0νββ NMEs with isospin restoration in both models was presented in detailed level, i.e., looking at the individual NMEs that contribute to F, GT, and T matrix elements and finally to total 0νββ NME when multiplied with appropriate form factor charges. Possible explanations, including method of isospin restoration, short range correlations, single particle energies, and closure approximation, for obtained similarities and differences were then discussed. The agreement is found to be quite good in most cases for light neutrino exchange. However, there seems to be larger deviations for the A = 110, 124 systems. In these cases, there is no 2νββ data available that is used in the QRPA to fit parameter $g_{pp}^{T=1}$. For heavy neutrino exchange, the trend is found to be similar, but a factor of ~3 difference is obtained even when the effect of different short range correlation parameterization, which affects heavy neutrino exchange considerably, is taken into account. This suggest a need for a further investigation on heavy neutrino exchange 0νββ nuclear matrix elements. Once the origin of this systematic and rather regular difference is better understood, and perhaps solved, the connection between IBM-2 and QRPA could be used to combine the strengths of each model, in particular the large model space and non-closure of QRPA and capability to describe deformed nuclei of IBM-2.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was funded by the Academy of Finland, Grant Nos. 314733 and 320062.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adams, D. Q., Alduino, C., Alfonso, K., Avignone, III, F. T., Azzolini, O., Bari, G., et al. (2020). Improved limit on neutrinoless double-beta decay in ¹³⁰Te with CUORE. Phys. Rev. Lett. 124:122501. doi: 10.1103/PhysRevLett.124.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

Agostini, M., Araujo, G. R., Bakalyarov, A. M., Balata, M., Barabanov, I., Baudis, L., et al. (2020). Final results of GERDA on the search for neutrinoless double-β decay. Phys. Rev. Lett. 125:252502. doi: 10.1103/PhysRevLett.125.252502

PubMed Abstract | CrossRef Full Text | Google Scholar

Argyriades, J., Arnold, R., Augier, C., Baker, J., Barabash, A. S., Basharina-Freshville, A., et al. (2010). Measurement of the two neutrino double beta decay half-life of Zr-96 with the NEMO-3 detector. Nuclear Phys. A 847, 168–179. doi: 10.1016/j.nuclphysa.2010.07.009

CrossRef Full Text | Google Scholar

Arnaboldi, C., Brofferio, C., Bucci, C., Capelli, S., Cremonesi, O., Fiorini, E., et al. (2003). A Calorimetric search on double beta decay of Te-130. Phys. Lett. B 557, 167–175. doi: 10.1016/S0370-2693(03)00212-0

CrossRef Full Text | Google Scholar

Arnold, R., Augier, C., Baker, J. D., Barabash, A. S., Basharina-Freshville, A., Blondel, S., et al. (2015). Results of the search for neutrinoless double-β decay in ¹⁰⁰Mo with the NEMO-3 experiment. Phys. Rev. D 92:072011. doi: 10.1103/PhysRevD.92.072011

CrossRef Full Text | Google Scholar

Azzolini, O., Beeman, J.W., Bellini, F., and Barrera, M. T. (2018). First result on the neutrinoless double-β decay of ⁸²Se with CUPID-0. Phys. Rev. Lett. 120:232502. doi: 10.1103/PhysRevLett.120.232502

PubMed Abstract | CrossRef Full Text | Google Scholar

Barabash, A. S., Belli, P., Bernabei, R., Cappella, F., Caracciolo, V., Cerulli, R., et al. (2018). Final results of the Aurora experiment to study 2β decay of ¹¹⁶Cd with enriched ¹¹⁶CdWO₄ crystal scintillators. Phys. Rev. D 98:092007. doi: 10.1103/PhysRevD.98.092007

CrossRef Full Text | Google Scholar

Barea, J., and Iachello, F. (2009). Neutrinoless double-β decay in the microscopic interacting boson model. Phys. Rev. C 79:044301. doi: 10.1103/PhysRevC.79.044301

CrossRef Full Text | Google Scholar

Barea, J., Kotila, J., and Iachello, F. (2013a). Nuclear matrix elements for double-β decay. Phys. Rev. C 87:014315. doi: 10.1103/PhysRevC.87.014315

PubMed Abstract | CrossRef Full Text | Google Scholar

Barea, J., Kotila, J., and Iachello, F. (2013b). Neutrinoless double-positron decay and positron-emitting electron capture in the interacting boson model. Phys. Rev. C 87:057301. doi: 10.1103/PhysRevC.87.057301

CrossRef Full Text | Google Scholar

Barea, J., Kotila, J., and Iachello, F. (2015a). 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys. Rev. C 91:034304. doi: 10.1103/PhysRevC.91.034304

CrossRef Full Text | Google Scholar

Barea, J., Kotila, J., and Iachello, F. (2015b). Limits on sterile neutrino contributions to neutrinoless double beta decay. Phys. Rev. D 92:093001. doi: 10.1103/PhysRevD.92.093001

CrossRef Full Text | Google Scholar

Basili, R. A. M., Yao, J. M., Engel, J., Hergert, H., Lockner, M., Maris, P., et al. (2020). Benchmark neutrinoless double-β decay matrix elements in a light nucleus. Phys. Rev. C 102:014302. doi: 10.1103/PhysRevC.102.014302

CrossRef Full Text | Google Scholar

Caurier, E., Martínez-Pinedo, G., Nowacki, F., Poves, A., and Zuker, A. (2005). The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 77:427. doi: 10.1103/RevModPhys.77.427

CrossRef Full Text | Google Scholar

Caurier, E., Nowacki, F., and Poves, A. (2007). Beta beta decay and nuclear structure. Int. J. Mod. Phys. E 16, 552–560. doi: 10.1142/S0218301307005983

CrossRef Full Text | Google Scholar

Coraggio, L., Itaco, N., De Gregorio, G., Gargano, A., Mancino, R., and Pastore, S. (2020). Present status of nuclear shell-model calculations of 0νββ decay matrix elements. Universe 6:233. doi: 10.3390/universe6120233

CrossRef Full Text | Google Scholar

de Salas, P. F., Forero, D. V., Gariazzo, S., Martínez-Miravé, P., Mena, O., Ternes, C. A., et al. (2021). 2020 global reassessment of the neutrino oscillation picture. J. High Energ. Phys. 2021:71. doi: 10.1007/JHEP02(2021)071

CrossRef Full Text | Google Scholar

Deppisch, F. F., Graf, L., Iachello, F., and Kotila, J. (2020). Analysis of light neutrino exchange and short-range mechanisms in 0νββ decay. Phys. Rev. D 102:095016. doi: 10.1103/PhysRevD.102.095016

CrossRef Full Text | Google Scholar

Doi, M., Kotani, T., Nishiura, H., Okuda, K., and Takasugi, E. (1981). Neutrino mass, the right-handed interaction and the double beta decay. I: formalism. Prog. Theor. Phys. 66:1739. doi: 10.1143/PTP.66.1739

CrossRef Full Text | Google Scholar

Doi, M., Kotani, T., Nishiura, H., Okuda, K., and Takasugi, E. (1983). Double beta decay. Prog. Theor. Phys. 69:602. doi: 10.1143/PTP.69.602

CrossRef Full Text | Google Scholar

Doi, M., Kotani, T., and Takasugi, E. (1985). Double beta decay and Majorana neutrino. Prog. Theor. Phys. Suppl. 83, 1–175. doi: 10.1143/PTPS.83.1

CrossRef Full Text | Google Scholar

Dumbrajs, O., Koch, R., Pilkuhn, H., Oades, G. C., Behrens, H., de Swart, J. J., et al. (1983). Compilation of coupling constants and low-energy parameters. Nuclear Phys. B 216, 277–335. doi: 10.1016/0550-3213(83)90288-2

CrossRef Full Text | Google Scholar

Engel, J. (2015). Uncertainties in nuclear matrix elements for neutrinoless double-beta decay. J. Phys. G Nuclear Phys. 42:034017. doi: 10.1088/0954-3899/42/3/034017

CrossRef Full Text | Google Scholar

Faessler, A., González, M., Kovalenko, S., and Śimkovic, F. (2014). Arbitrary mass Majorana neutrinos in neutrinoless double beta decay. Phys. Rev. D 90:096010. doi: 10.1103/PhysRevD.90.096010

CrossRef Full Text | Google Scholar

Faessler, A., Rodin, V., and Šimkovic, F. (2012). Nuclear matrix elements for neutrinoless double-beta decay and double-electron capture. J. Phys. G Nuclear Phys. 39:124006. doi: 10.1088/0954-3899/39/12/124006

CrossRef Full Text | Google Scholar

Fang, D. L., Faessler, A., Rodin, V., and Šimkovic, F. (2011). Neutrinoless double-β decay of deformed nuclei within quasiparticle random-phase approximation with a realistic interaction. Phys. Rev. C 83:034320. doi: 10.1103/PhysRevC.83.034320

CrossRef Full Text | Google Scholar

Fang, D. L., Faessler, A., and Šimkovic, F. (2018). 0νββ-decay nuclear matrix element for light and heavy neutrino mass mechanisms from deformed quasiparticle random-phase approximation calculations for ⁷⁶Ge,⁸²Se,¹³⁰Te,¹³⁶Xe, and ¹⁵⁰Nd with isospin restoration. Phys. Rev. C 97:045503. doi: 10.1103/PhysRevC.97.045503

CrossRef Full Text | Google Scholar

Furry, W. H. (1939). On transition probabilities in double beta-disintegration. Phys. Rev. 56:1184. doi: 10.1103/PhysRev.56.1184

CrossRef Full Text | Google Scholar

Gando, A., Gando, Y., Hachiya, T., Hayashi, A., Hayashida, S., Ikeda, H., et al. (2016). Search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys. Rev. Lett. 117:082503. doi: 10.1103/PhysRevLett.117.082503

PubMed Abstract | CrossRef Full Text | Google Scholar

Graf, L., Deppisch, F. F., Iachello, F., and Kotila, J. (2018). Short-range neutrinoless double beta decay mechanisms. Phys. Rev. D 98:095023. doi: 10.1103/PhysRevD.98.095023

CrossRef Full Text | Google Scholar

Haxton, W. C., and Stephenson, G. J. (1984). Double beta decay Jr. Prog. Part Nuclear Phys. 12:409. doi: 10.1016/0146-6410(84)90006-1

CrossRef Full Text | Google Scholar

Hergert, H., Bogner, S. K., Morris, T. D., Schwenk, A., and Tsukiyama, K. (2016). The in-medium similarity renormalization group: a novel ab initio method for nuclei. Phys. Rep. 621:165. doi: 10.1016/j.physrep.2015.12.007

CrossRef Full Text | Google Scholar

Horoi, M., and Brown, B. A. (2013). Shell-model analysis of the ¹³⁶Xe double beta decay nuclear matrix elements. Phys. Rev. Lett. 110:222502. doi: 10.1103/PhysRevLett.110.222502

PubMed Abstract | CrossRef Full Text | Google Scholar

Hyvärinen, J., and Suhonen, J. (2015). Nuclear matrix elements for 0ββ decays with light or heavy Majorana-neutrino exchange. Phys. Rev. C 91:024613. doi: 10.1103/PhysRevC.91.024613

PubMed Abstract | CrossRef Full Text | Google Scholar

Kotila, J., and Barea, J. (2016). Occupation probabilities of single particle levels using the microscopic interacting boson model: application to some nuclei of interest in neutrinoless double-β decay. Phys. Rev. C 94:034320. doi: 10.1103/PhysRevC.94.034320

CrossRef Full Text | Google Scholar

Kotila, J., Barea, J., and Iachello, F. (2014). Neutrinoless double-electron capture. Phys. Rev. C 89:064319. doi: 10.1103/PhysRevC.89.064319

CrossRef Full Text | Google Scholar

Kotila, J., Barea, J., and Iachello, F. (2015). Phase-space factors and half-life predictions for Majoron-emitting β⁻β⁻ decay. Phys. Rev. C 91:064310. doi: 10.1103/PhysRevC.91.064310

CrossRef Full Text | Google Scholar

Kotila, J., and Iachello, F. (2012). Phase-space factors for double-β decay. Phys. Rev. C 85:034316. doi: 10.1103/PhysRevC.85.034316

CrossRef Full Text | Google Scholar

Kotila, J., and Iachello, F. (2013). Phase space factors for β⁺β⁺ decay and competing modes of double-β decay. Phys. Rev. C 87:024313. doi: 10.1103/PhysRevC.87.024313

CrossRef Full Text | Google Scholar

Lisi, E. (2011). On the discrimination of different mechanisms for 0ν2β decay. AIP Conf. Proc. 1417:74. doi: 10.1063/1.3671040

CrossRef Full Text | Google Scholar

Marshalek, E. G. (1980). How microscopic boson models work. Nuclear Phys. A. 347:253. doi: 10.1016/0375-9474(80)90528-X

CrossRef Full Text | Google Scholar

Menéndez, J., Poves, A., Caurier, E., and Nowacki, F. (2009a). Disassembling the nuclear matrix elements of the neutrinoless ββ beta decay. Nuclear Phys. A 818, 139–151. doi: 10.1016/j.nuclphysa.2008.12.005

CrossRef Full Text | Google Scholar

Menéndez, J., Poves, A., Caurier, E., and Nowacki, F. (2009b). Occupancies of individual orbits, and the nuclear matrix element of the ⁷⁶Ge neutrinoless ββ decay. Phys. Rev. C 80:048501. doi: 10.1103/PhysRevC.80.048501

CrossRef Full Text | Google Scholar

Miller, G. A., and Spencer, J. E. (1976). A survey of pion charge-exchange reactions with nuclei. Annu. Phys. (1976) 100:562. doi: 10.1016/0003-4916(76)90073-7

CrossRef Full Text | Google Scholar

Mirea, M., Pahomi, T., and Stoica, S. (2015). Values of the phase space factors involved in double beta decay. Roman Rep. Phys. 67, 872–889. doi: 10.1063/1.4934913

CrossRef Full Text | Google Scholar

Molina, A., and Pascual, P. (1977). Double beta decay. Il Nuovo Cimento A 41:756. doi: 10.1007/BF02730270

CrossRef Full Text | Google Scholar

Mustonen, M. T., and Engel, J. (2013). Large-scale calculations of the double-β decay of ⁷⁶Ge, ¹²⁸Te, ¹³⁶Xe, and ¹⁵⁰Nd in the deformed self-consistent skyrme quasiparticle random phase approximation. Phys. Rev. C 87:064302. doi: 10.1103/PhysRevC.87.064302

CrossRef Full Text | Google Scholar

Muto, K. (1994). Neutrinoless double beta decay beyond closure approximation. Nuclear Phys. A 577, 415c–420c. doi: 10.1016/0375-9474(94)90890-7

CrossRef Full Text | Google Scholar

Neacsu, A., and Horoi, M. (2015). Shell model studies of the ¹³⁰Te neutrinoless double-β decay. Phys. Rev. C 91:024309. doi: 10.1103/PhysRevC.91.024309

CrossRef Full Text | Google Scholar

Neacsu, A., and Stoica, S. (2014). Shell model calculations for neutrinoless double beta decay through the exchange of heavy neutrinos. Roman Rep. Phys. 66, 376–381.

Google Scholar

Otsuka, T., Arima, A., and Iachello, F. (1978). Nuclear shell model and interacting bosons. Nuclear Phys. A 309, 1–33. doi: 10.1016/0375-9474(78)90532-8

CrossRef Full Text | Google Scholar

Pantis, G., and Vergados, J. D. (1990). Neutrinoless double beta decay matrix elements beyond closure approximation. Phys. Lett. B 242:1. doi: 10.1016/0370-2693(90)91584-X

CrossRef Full Text | Google Scholar

Pastore, S., Carlson, J., Cirigliano, V., Dekens, W., Mereghetti, E., and Wiringa, R. B. (2018). Neutrinoless double-β decay matrix elements in light nuclei. Phys. Rev. C 97:014606. doi: 10.1103/PhysRevC.97.014606

CrossRef Full Text | Google Scholar

Primakoff, H., and Rosen, S. P. (1959). Double beta decay. Rep. Prog. Phys. 22:121. doi: 10.1088/0034-4885/22/1/305

CrossRef Full Text | Google Scholar

Rath, P. K., Chandra, R., Chaturvedi, K., and Raina, P. K. (2019). Nuclear transition matrix elements for double-β decay within PHFB model. Front. Phys. 7:64. doi: 10.3389/fphy.2019.00064

CrossRef Full Text | Google Scholar

Rath, P. K., Chandra, R., Chaturvedi, K., Raina, P. K., and Hirsch, J. G. (2010). Uncertainties in nuclear transition matrix elements for neutrinoless ββ decay within the projected-Hartree-Fock-Bogoliubov model. Phys. Rev. C 82:064310. doi: 10.1103/PhysRevC.82.064310

CrossRef Full Text | Google Scholar

Rodin, V., and Faessler, A. (2011). Origin of a sensitive dependence of calculated ββ -decay amplitudes on the particle-particle residual interaction. Phys. Rev. C 84:014322. doi: 10.1103/PhysRevC.84.014322

CrossRef Full Text | Google Scholar

Rodríguez, T. R., and Martínez-Pinedo, G. (2010). Energy density functional study of nuclear matrix elements for neutrinoless ββ decay. Phys. Rev. Lett. 105:252503. doi: 10.1103/PhysRevLett.105.252503

PubMed Abstract | CrossRef Full Text | Google Scholar

Schindler, M. R., and Scherer, S. (2007). Nucleon form factors of the isovector axial-vector current. Eur. Phys. J. A 32:429. doi: 10.1140/epja/i2006-10403-3

CrossRef Full Text | Google Scholar

Šimkovic, F., Faessler, A., Müther, H., Rodin, V., and Stauf, M. (2009). 0νββ-decay nuclear matrix elements with self-consistent short-range correlations. Phys. Rev. C 79:055501. doi: 10.1103/PhysRevC.79.055501

CrossRef Full Text | Google Scholar

Šimkovic, F., Faessler, A., Rodin, V., Vogel, P., and Engel, J. (2008). Anatomy of nuclear matrix elements for neutrinoless double-beta decay. Phys. Rev. C 77:045503. doi: 10.1103/PhysRevC.77.045503

CrossRef Full Text | Google Scholar

Šimkovic, F., Pantis, G., Vergados, J. D., and Faessler, A. (1999). Additional nucleon current contributions to neutrinoless double β decay. Phys. Rev. C 60:055502. doi: 10.1103/PhysRevC.60.055502

CrossRef Full Text | Google Scholar

Šimkovic, F., Rodin, V., Faessler, A., and Vogel, P. (2013). 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys. Rev. C 87:045501. doi: 10.1103/PhysRevC.87.045501

CrossRef Full Text | Google Scholar

Song, L. S., Yao, J. M., Ring, P., and Meng, J. (2014). Relativistic description of nuclear matrix elements in neutrinoless double-β decay. Phys. Rev. C 90:054309. doi: 10.1103/PhysRevC.90.054309

CrossRef Full Text | Google Scholar

Song, L. S., Yao, J. M., Ring, P., and Meng, J. (2017). Nuclear matrix element of neutrinoless double-β decay: relativity and short-range correlations. Phys. Rev. C 95:024305. doi: 10.1103/PhysRevC.95.024305

CrossRef Full Text | Google Scholar

Stoica, S., and Mirea, M. (2013). New calculations for phase space factors involved in double-β decay. Phys. Rev. C 88:037303. doi: 10.1103/PhysRevC.88.037303

CrossRef Full Text | Google Scholar

Suhonen, J., and Civitarese, O. (1998). Weak-interaction and nuclear-structure aspects of double beta decay. Phys. Rep. 300, 123–214. doi: 10.1016/S0370-1573(97)00087-2

CrossRef Full Text | Google Scholar

Suhonen, J., and Civitarese, O. (2008). Nuclear matrix elements for double beta decay in the QRPA approach: a critical review. Phys. Lett. B 668:277. doi: 10.1088/1742-6596/173/1/012012

CrossRef Full Text | Google Scholar

Suhonen, J., and Civitarese, O. (2010). Effects of orbital occupancies and spin-orbit partners on 0νββ-decay rates. Nuclear Phys A 847, 207–232. doi: 10.1016/j.nuclphysa.2010.08.003

CrossRef Full Text | Google Scholar

Suhonen, J., and Civitarese, O. (2012). Double-beta-decay nuclear matrix elements in the QRPA framework. J. Phys. G Nuclear Phys. 39:085105. doi: 10.1088/0954-3899/39/8/085105

CrossRef Full Text | Google Scholar

Tomoda, T. (1991). Double beta decay. Rep. Prog. Phys. 54:53. doi: 10.1088/0034-4885/54/1/002

CrossRef Full Text | Google Scholar

Wang, X., Hayes, A., Carlson, J., Dong, G., Mereghetti, E., Pastore, S., and Wiringa, R. B. (2019). Comparison between variational Monte Carlo and shell model calculations of neutrinoless double beta decay matrix elements in light nuclei. Phys. Lett. B 798:134974. doi: 10.1016/j.physletb.2019.134974

CrossRef Full Text | Google Scholar

Yao, J. M., Song, L. S., Hagino, K., Ring, P., and Meng, J. (2015). Systematic study of nuclear matrix elements in neutrinoless double-β decay with a beyond-mean-field covariant density functional theory. Phys. Rev. C 91:024316. doi: 10.1103/PhysRevC.91.024316

CrossRef Full Text | Google Scholar

Yao, W-M., Amsler, C., Asner, D., Barnett, R. M., Beringer, J., Burchat, P. R., et al. (2006). Review of particle physics. J. Phys. G Nuclear Phys. (2006) 33:1. doi: 10.1088/0954-3899/33/1/001

CrossRef Full Text | Google Scholar

Yoshida, N., and Iachello, F. (2013). Two-neutrino double-β decay in the interacting boson-Fermion model. Prog. Theor. Exp. Phys. 2013:043D01. doi: 10.1093/ptep/ptt007

CrossRef Full Text | Google Scholar