Acceleration of Charged Particles in Astrophysical Plasmas

The origin of high-energy particles in the Universe is one of the key issues of high-energy solar physics, space science, astrophysics, and particle astrophysics. Charged particles in astrophysical plasmas can be accelerated to very high energies by electric fields. Based on the characteristics of interactions between charged particles and electric fields carried by the background plasma, the mechanisms of charged particle acceleration can be divided into several groups: resonant interactions between plasma waves and particles, acceleration by electric fields parallel to magnetic fields, and acceleration caused by drift of the guiding center of particle gyro-motion around magnetic fields in magnetic field in-homogeneity-related curvature and gradient, etc. According to macroscopic energy conversion mechanisms leading to acceleration of particles, several theories of particle acceleration have been developed: stochastic particle acceleration by turbulent electromagnetic fields, diffusive shock acceleration of particles, and particle acceleration during magnetic re-connections. These theories have their own assumptions and characteristics and find applications in different astrophysical contexts. With advances in high-energy astrophysical observations and in combination with analyses of characteristics of high-energy particle acceleration and radiation, we can better understand the underlying physical processes in dramatically evolving astrophysical environments.

1 Introduction

The origin of high-energy astrophysics can be traced back to the early 20th century when cosmic rays, high energy particles that can ionize gases in the atmosphere, were discovered by Victor Francis Hess (1936 Nobel Laureate in Physics)¹. Later with the birth and advances of radio astronomy, X-ray astronomy, γ-ray astronomy, as an important branch of astrophysics, high-energy astrophysics has been playing an increasingly important role in astrophysics research. High-energy particles are the main emitter of varieties of high-energy astrophysical sources. Given the high energy of these particles, they can emit efficiently in all electromagnetic wave bands ranging from radio to gamma rays (Blumenthal and Gould, 1970; Kelner et al., 2006). High-energy astrophysical sources therefore can be readily detected and constitute an important kind of astrophysical objects ubiquitous in the Universe.

With the development of space astronomy, people started to realize that plasma disturbances in solar flares, Earth’s magnetosphere, and interplanetary space can also produce a large amount of high-energy particles. The acceleration of energetic particles then becomes a key issue in high-energy space science, high-energy solar physics, high-energy astrophysics, and particle astrophysics. The radiative characteristics of high-energy astrophysical sources depend on properties of high-energy particles they produced. High-energy particles from the Sun or outer space can also be detected directly by satellites in space. Cosmic rays with energies exceeding ∼10¹³ eV can be detected indirectly via observation of the cascading shower they produce in the atmosphere. Observation and analysis of properties of high-energy particles in high-energy astrophysics sources play an essential role in exploring the underlying physical processes.

It is generally accepted that most of the observed high-energy particles originate from acceleration of charged particles in the background plasma ubiquitous in the Universe. These high-energy charged particles may collide with nuclei in the background producing energetic secondaries. They can also produce energetic neutrals via charge exchange process². Since Lorentz force of a magnetic field does not change the energy of charged particles, acceleration of charged particles needs to be realized through an electric field. In most astrophysical environment, conductivity of the background plasma is high and the corresponding electric field parallel to magnetic field is too weak to accelerate particles to observed high energies. Considering the fact that particle acceleration always occurs in intense energy dissipation processes of magnetized plasmas, motion of the background plasma with respect to magnetic field can produce inductive electric fields, and some electromagnetic fluctuations can effectively suppress the conductivity giving rise to electric field parallel to the magnetic field. In a strong magnetic field with very low density of charged particles, a strong electric field parallel to the magnetic field may also exist due to lack of current carriers to drive evolution of the magnetic field. All in all, under appropriate physical conditions, electric fields generated in a free energy dissipation process can effectively accelerate charged particles.

Since the discovery of cosmic rays at the beginning of last century, several mechanisms have been proposed for quantitative modelling of acceleration processes. Generally speaking, intense release of free energy of a magnetized plasma will produce a variety of plasma disturbances. Stochastic interaction of charged particles with electric field fluctuations on average will lead to an increase in the particle energy, which constitutes the base of the theory of stochastic particle acceleration. Some of the electric field fluctuations may be described as waves that can exchange energy with charged particles via resonant interactions. The energy distribution of charged particles accelerated by electric field fluctuations depends on statistical properties of these electric fields. The theory of stochastic particle acceleration is developed to address this dependence. The stochastic particle acceleration process is generic to all free energy dissipation in magnetized plasmas. However as a second order Fermi acceleration process (Fermi, 1949), which corresponds to diffusion in the momentum space, the corresponding acceleration efficiency may not be very high.

Over the past few decades, the so-called diffusive shock theory of particle acceleration has been introduced and studied extensively. Based on theories of magneto-hydrodynamics (MHD) and transport of charged particles in a magnetized plasma, the diffusive shock acceleration theory shows that particles can be accelerated in shock dissipation process via repeated crossing of the shock front. In particular, if the particle distribution is isotropic in the co-moving frame of the background plasma, it can be shown that the energy distribution of accelerated particles follows a power law with the spectral index determined by the compression ratio of the shock. Since the theory naturally links the energy distribution of accelerated particles to macroscopic properties of the fluid with rather general assumptions, this theoretical result is considered generic to energy dissipation via collionless shocks. In fact, it can be shown that as far as the particle distribution is isotropic, the energy of particles can only be changed by compressible modes of a fluid for the first order processes, which correspond to convection in the momentum space. Moreover high-energy astrophysical observations are generally consistent with this theory. This theory was developed independently by several teams in the 1970s (Blandford and Ostriker, 1978; Bell, 1978a, Bell, 1978b; Axford, 1981) and has drawn widespread attentions in high-energy astrophysics community (Drury, 1983).

When there is a large-scale magnetic field, charged particles in the background plasma can be accelerated by parallel electric fields associated with the reconnection current sheet and by inductive electric fields via coupling with curvature and/or gradient of the magnetic field. Compression of a large scale magnetic field can also lead to betatron acceleration (Bogachev and Somov, 2005), the underlining process for betratron accelerators that, as the magnetic gradient draft acceleration, leads to an increase of the perpendicular momentum of accelerated particles. Detailed processes of particle acceleration depends on the structure of the large scale magnetic field, which may lead to a variety of energy distribution of accelerated particles. However, given the importance of magnetic field in the process of particle acceleration, particle acceleration during magnetic reconnection is considered generic to magnetic energy dissipation process.

It should be noted that not all processes pertaining to energy gain of charged particles in the background plasma are considered as particle acceleration process. If an energization process is not selective resulting in comparable energy gain of all charged particles in the background plasma, it is considered as a plasma heating process. The corresponding distribution function of charged particles can be approximated as a Gaussian in velocity (Maxwellian in energy). The theory of particle acceleration mainly studies momentum distribution and transport of particles with their energy much higher than the mean energy of the background particles. The selective acceleration of some low-energy charged particles in the background plasma to high energies so that these particles may participate in the acceleration processes at larger scales is called the injection problem. The above-mentioned resonant wave-particle interaction, resonant interaction of waves and charged dust, and some particular configuration of the magnetic field can cause charged particles in the background plasma to be selectively accelerated to high energies (Ellison et al., 1997; Meyer et al., 1997). Neutral atoms moving with a high speed relative to the background plasma will appear as high-energy charged particles when being ionized, which can also be an effective mechanism for injection under appropriate astrophysical conditions. In high-energy solar physics and space science, where the energy spectrum can be measured from the thermal background to very high energies, injection of particles into the acceleration process is an important issue.

When charged particles with increasing energy decouple from background particles, they can interact with electromagnetic fields on larger scales due to their relatively long mean free paths. An important aspect of high-energy astrophysics research is to analyze acceleration and radiation mechanisms of these energetic particles via interactions with the background plasma. The stochastic particle acceleration mechanism originally proposed by Fermi (i.e., charged particles are accelerated gradually to higher energies via stochastic interactions with electromagnetic field fluctuations carried by the background plasma) is still the starting point of most macroscopic theories of particle acceleration (Fermi, 1949; Parker, 1958; Toptygin, 1980; Petrosian and Liu, 2004). Current researches in this area focus on using the associated radiation mechanisms to infer distribution function of energetic particles from observations, then in combination with the relevant energy release processes (such as magnetic reconnection, shocks, MHD instabilities, etc.), analyzing the related particle acceleration and transport, plasma heating, and magnetic field amplification processes.

This review is organized as the following: General Characteristics of HIGH-ENERGY Particle Acceleration in a Fluid discusses microscopic interactions leading to changes in particle energy; Specific Acceleration Mechanisms summarize particle acceleration in specific astrophysical conditions; Conclusions are drawn in Conclusion.

2 General Characteristics of HIGH-ENERGY Particle Acceleration in a Fluid

In what follows, we take the energetic particles to sufficiently rare that they do not affect the background thermal plasma or electromagnetic field, so the electric and magnetic fields are determined by the ambient thermal plasma. This test-particle limit is usually a good approximation for the energetic particles emphasized in this review. In reality, there are situations (notably supernova blast waves) where the effects of cosmic rays on the background plasma and magnetic field must be considered (Lucek and Bell, 2000; Blasi, 2004; Bell et al., 2013).

2.1 Energy Change and Instantaneous Acceleration Rate

Let us begin with some general comments regarding charged particle acceleration in astrophysical plasmas. Since particle-particle collisions are extremely rare in the plasmas which we are considering, and neglecting the gravitational force, motion of a particle with charge q velocity w and moment p is determined by the electric and magnetic fields E and B. We have

$\dot{\mathrm{p}}\mathrm{=}\frac{\text{d}\mathbf{p}}{\text{dt}}\mathrm{=}q\left(\mathbf{E}\mathrm{+}\frac{\mathbf{w}\times \mathbf{B}}{c}\right)(1)$

where c is the speed of light and the upper dot indicates a derivative with respective to time t. Then, the rate change of the energy T of a charged particle in such a plasma is via the electric field $\mathbf{E}\left(\mathbf{r},t\right)$ and may be written as

$\dot{T}=\frac{\text{dT}}{\text{dt}}=\mathbf{w}\cdot \dot{\mathrm{p}}=q\mathbf{w}\cdot \mathbf{E}\left(\mathbf{r},t\right)(2)$

The electric field may be ambient or associated with scattering by turbulent fluctuations. Clearly, in order to evaluate the energy change, we must know the particle trajectory in the electromagnetic field. This leads to the general requirements that acceleration and spatial transport be intimately coupled and both $\mathbf{E}\left(\mathbf{r},t\right)$ and $\mathbf{B}\left(\mathbf{r},t\right)$ must be considered together.

It turns out that the spatial scales of the plasma and magnetic-field variations which are most important in determining cosmic-ray motions are those comparable to or larger than the particle gyro-radii, which are much larger than the thermal particle gyro-radii. Therefore, the relevant plasma scales are such that the MHD approximation is valid and the ambient electric field in a nonrelativistic plasma may be determined from the fluid velocity $\mathbf{U}\ll \mathbf{c}$ and magnetic field by the relation

$\mathbf{E}=-\frac{\mathbf{U}\times \mathbf{B}}{c}+\frac{\mathbf{j}}{\sigma }(3)$

where $\mathbf{j}=\left(c\nabla \times \mathbf{B}-\partial \mathbf{E}/\partial t\right)/4\pi$ is the electric current density, σ is the ordinary conductivity, and $\mathbf{j}/\sigma$ is the electric field in the fluid frame. Note that in the relativistic theory, both $\mathbf{j}$ and σ vary with the frame. For nonrelativistic fluids with $U\ll c$, we can ignore their frame dependence. The corresponding corrections are on the order of $U/c$. The $\partial \mathbf{E}/\partial t$ term can also be ignored in nonrelativistic plasmas since it is much smaller than $c\nabla \times \mathbf{B}$ and is on the order of ${\left(U/c\right)}^2$.

In this case, the rate of energy gain of the particle is given by

$\frac{\text{dT}}{\text{dt}}=-q\mathbf{w}\cdot \left(\frac{\mathbf{U}\times \mathbf{B}}{c}-\frac{\mathbf{j}}{\sigma }\right)(4)$

which, upon using a basic vector identity to rearrange the terms, can be rewritten as

$\frac{\text{dT}}{\text{dt}}=q\left(\mathbf{U}\cdot \frac{\mathbf{w}\times \mathbf{B}}{c}+\mathbf{w}\cdot \frac{\mathbf{j}}{\sigma }\right)(5)$

Then the instantaneous energy change rate of a particle can be written as

$\frac{\text{dT}}{\text{Tdt}}=q\left(\mathbf{U}\cdot \frac{\mathbf{w}\times \mathbf{B}}{cT}+\mathbf{w}\cdot \frac{\mathbf{j}}{\sigma T}\right)(6)$

where the first term on the right-hand side gives the acceleration rate by the inductive electric field: $U_{\perp }\left(\gamma +1\right)\text{cos}\varphi {\text{sin}}^2\theta /\gamma r_g$, where $\gamma ={\left(1-w^2/c^2\right)}^{-1/2}$, $r_g=pc\text{sin}\theta /qB$, θ, and ϕ are the Lorentz factor, gyro-radius, pitch angle, and gyro-phase angle of the particle, respectively, $U_{\perp }$ represents the component of $\mathbf{U}$ in perpendicular to $\mathbf{B}$, and the second term on the right-hand side corresponds to acceleration by resistive electric fields.

Note that $T=\left(\gamma -1\right)m{c}^2=\gamma pw/\left(\gamma +1\right)$, where m is the mass of the particle, $\dot{T}/T=\dot{p}\left(\gamma +1\right)/p\gamma =\left(\gamma +1\right)\gamma \dot{w}/w$, and the acceleration rates are proportional to the charge to mass ratio $q/m$. The change rate of the amplitude of momentum $\dot{p}$ by the inductive electric field only depends on the direction of the velocity and rigidity of the particle $R=p/q$ explicitly. The instantaneous rate of acceleration by the inductive electric field reaches the maximum value of

${\tau }_{acc.int}^{-1}={\left(\frac{\text{dT}}{\text{Tdt}}\right)}_{max}=\frac{U_{\perp }\left(\gamma +1\right)qB}{\gamma pc}=\frac{U_{\perp }\left(\gamma +1\right)}{\gamma r_g}={\nu }_g\frac{2\pi U_{\perp }\left(\gamma +1\right)}{\gamma w}<{\nu }_g(7)$

for $\text{sin}\theta =1$ and $\text{cos}\varphi =1$, where ${\nu }_g=w/2\pi r_g$ is the gyro-frequency, and the gyro-phase averaged acceleration rate is negligible if the changes of $\mathbf{U}$ and $\mathbf{B}$ on the scale of $r_g$ are negligible. Variations of $\mathbf{U}$ and/or $\mathbf{B}$ on the scale of $r_g$ therefore play an essential role in the acceleration of particles by the inductive electric field (Zhang and Lee, 2013).

In the presence of electric fields parallel to the magnetic field or electromagnetic fields varying on the same scales of the particle gyro-motion, the acceleration process will depend on the charge and/or mass of the particles, and therefore become selectively. These processes are essential at low energies when the particle velocity is comparable to the flow velocity and the particle distribution may not be isotropic. The details of these accelerations are complicated, depending on properties of the plasma waves and parallel electric fields. The former usually leads to stochastic particle acceleration, a second order process, while the latter leads to direct acceleration, a first order process.

If the variation scale of $\mathbf{B}$ is much larger than the particle gyro-radius, one may use the guiding center approximation to describe the motion of charged particles in an in-homogeneous $\mathbf{B}$. Besides moving along magnetic fields with a speed of $w_{\parallel }$, the guiding center of particle gyro-motion also drifts across magnetic field lines with a velocity (Northrop, 1963):

$\begin{array}{l}{\mathbf{v}}_D\simeq {\mathbf{U}}_{\perp }+\frac{2\mu c{w}_{\parallel }^2}{q\gamma w_{\perp }^2}\left[\mathbf{b}\times \left(\mathbf{b}\cdot \nabla \right)\mathbf{b}\right]+\frac{\mu c}{q\gamma B}\left[\mathbf{b}\times \left(\nabla B\right)\right]\\ ={\mathbf{U}}_{\perp }+\frac{r_g{w}_{\parallel }^2}{w_{\perp }}\left[\mathbf{b}\times \left(\mathbf{b}\cdot \nabla \right)\mathbf{b}\right]+\frac{r_g{w}_{\perp }}{2B}\left[\mathbf{b}\times \left(\nabla B\right)\right]\end{array}(8)$

where ${\mathbf{U}}_{\perp }=c\mathbf{E}\times \mathbf{B}/B^2$, $p_{\perp }=\gamma m{w}_{\perp }$, $\mathbf{b}=\mathbf{B}/B$ is the unit vector along B, $\mu =p_{\perp }^2/2mB$ is the magnetic moment of the particle motion, and we have ignored resistive electric field and terms on higher orders of $U/w$. Note that the magnetic moment μ is approximately conserved for slowly varying B.

It can be shown that drift of the guiding center in magnetic field gradients (3rd term on the right-hand side of Eq. 8) and curvatures (2nd term on the right-hand side of Eq. 8) will lead to changes of energies associated with motions in perpendicular and parallel to B, respectively (Zhou et al., 2015):

$\frac{\text{d}{\left(\gamma w_{\perp }\right)}^2}{2\text{d}t}=\frac{\mu \partial B}{m\partial t}+\frac{\mu w_{\parallel }}{m}\mathbf{b}\cdot \nabla B+\frac{{\left(\gamma w_{\perp }\right)}^2}{2B}{\mathbf{U}}_{\perp }\cdot \nabla B(9)$

$\frac{\text{d}{\left(\gamma w_{\parallel }\right)}^2}{2\text{d}t}=-\frac{\mu w_{\parallel }}{m}\mathbf{b}\cdot \nabla B+{\left(\gamma w_{\parallel }\right)}^2{\mathbf{U}}_{\perp }\cdot \left[\left(\mathbf{b}\cdot \nabla \right)\mathbf{b}\right](10)$

where the last terms on the right-hand side of Eqs 9, 10 can lead to changes in the particle speed and may be rewritten as $\left(\gamma q/m\right)\mathbf{E}\cdot {\mathbf{v}}_{Dg\perp }$ and $\left(\gamma q/m\right)\mathbf{E}\cdot {\mathbf{v}}_{Dc\perp }$, respectively, where ${\mathbf{v}}_{Dg\perp }=\left(r_g{w}_{\perp }/2B\right)[\mathbf{b}\times \left(\nabla B\right)]$ and ${\mathbf{v}}_{Dv\perp }=\left(r_g{w}_{\parallel }^2/w_{\perp }\right)[\mathbf{b}\times \left(\mathbf{b}\cdot \nabla \right)\mathbf{b}]$. Since the betatron and the Fermi mechanism can lead to the increase of the perpendicular and the parallel momentum of charged particles, respectively, Eqs 9, 10 are associated with the betatron and Fermi processes, respectively (Bogachev and Somov, 2005). It is interesting to note that since the drift velocity associated with magnetic curvature and gradient is inversely proportional to the charge to mass ratio, the acceleration caused by drift in magnetic gradient and curvature only depends on the particle velocity and does not depend on the charge and mass! Since $r_g$ depends on the sign of the charge q, particles with opposite charges drift in opposite directions leading to identical speed change. (The corresponding current can lead to magnetic energy conversion and/or dissipation via coupling with the inductive electric field.) One would expect identical speed distribution for all particle species if the acceleration is dominated by drift in magnetic gradient and/or curvature. Compared with the acceleration rate given by Eq. 6, the acceleration rate caused by drift in magnetic gradient and curvature is lower by a factor of $L/r_g$, where L represents the curvature radius of $\mathbf{B}$ or the variation scale of B, due to average over gyro-motion of the particle:

${\tau }_{acc.drf}^{-1}\simeq \frac{U}{L}(11)$

In principle, in combination with particle trajectory, Eqs. 5 or 9 and 10 can be used to study acceleration of individual particles (Turkmani et al., 2006; Zhou et al., 2015). However, the results heavily depend on the structure of $\mathbf{B}$ and $\mathbf{E}$ covering many orders of magnitude in spatial scales. Direct comparison of such simulations with observations is challenging given the complexity of the structure of $\mathbf{B}$ and $\mathbf{E}$ in actual astrophysical situations. To have statistically converging results, such test particle simulations can also be computationally extensive. Moreover, such studies are only valid when the density of accelerated particles are too low to affect the evolution of $\mathbf{E}$ and $\mathbf{B}$, which may not be true for acceleration of particles near the shock front (Bell et al., 2013).

The problem can be simplified dramatically for test particles in MHD. Jones (1990) first pointed out that the microscopic energy exchange between charge particles and electromagnetic fields discussed above can be expressed in terms of compression of the fluid $\nabla \cdot \mathbf{U}$:

$\frac{\text{dT}}{\text{dt}}\simeq q\mathbf{E}\cdot {\mathbf{v}}_D+\frac{q^{2}B}{2\pi \gamma mc}{\displaystyle \underset{C}{\oint }\mathbf{E}\cdot \text{d}\mathbf{l}}(12)$

$\simeq -\frac{\gamma m{w}_{\perp }^2}{2}\nabla \cdot {\mathbf{U}}_{\perp }-\frac{\gamma m{w}_{\parallel }^2}{B}\left(\mathbf{U}\times \mathbf{B}\right)\cdot \left(\mathbf{b}\times \left(\mathbf{b}\cdot \nabla \right)\mathbf{b}\right)+\frac{\gamma m{w}_{\perp }^2}{2B}\left(\mathbf{U}\times \mathbf{B}\right)\cdot \left(\nabla \times \mathbf{b}\right)(13)$

For isotropic particle distributions, the last two terms cancel if averaged over the direction of motion. The mean energy gain is then proportional to the divergence of $\mathbf{U}$. Since we only consider the inductive electric field, the parallel component of $\mathbf{U}$ does not show up in Eq. 13. In ideal MHD, compression along magnetic field needs to be associated with collisions. We also note that isotropy of the particle distribution is assumed here in the laboratory frame instead of the fluid frame as we will assume in the following.

Using Eqs 1, 3 for $\dot{\mathrm{p}}$ and $\mathbf{E}$ above, respectively, Eq. 5 may be written as

$\frac{\text{dT}}{\text{dt}}=\mathbf{U}\cdot \dot{\mathrm{p}}+q\left(\mathbf{w}-\mathbf{U}\right)\cdot \frac{\mathbf{j}}{\sigma }(14)$

Again by simply rearranging terms this may then be rewritten as

$\frac{\text{d}}{\text{dt}}\left(T-\mathbf{U}\cdot \mathbf{p}\right)=-\mathbf{p}\cdot \frac{\text{d}\mathbf{U}}{\text{dt}}+q\left(\mathbf{w}-\mathbf{U}\right)\cdot \frac{\mathbf{j}}{\sigma }(15)$

Noting that $T\prime \simeq T-\mathbf{U}\cdot \mathbf{p}+\gamma m{U}^2/2$ is the particle kinetic energy in the fluid frame, and writing $\mathbf{p}\prime$, the momentum in the fluid frame as $\mathbf{p}\prime \simeq \mathbf{p}-\gamma m\mathbf{U}$, Eq. 4 may be written as

$\begin{array}{l}\frac{{\text{dT}}^{\prime }}{\text{dt}}=-\frac{\text{d}\mathbf{U}}{\text{dt}}\cdot \mathbf{p}\prime +q\left(\mathbf{w}-\mathbf{U}\right)\cdot \frac{\mathbf{j}}{\sigma }\\ =-\left(\frac{\partial \mathbf{U}}{\partial \mathbf{t}}+\mathbf{w}\cdot \nabla \mathbf{U}\right)\cdot \mathbf{p}\prime +q\mathbf{w}\prime \cdot \frac{\mathbf{j}}{\sigma }\end{array}(16)$

where the particle velocity in the fluid frame $\mathbf{w}\text{′}=\mathbf{w}-\mathbf{U}$ and we have ignored the relativistic effects. Using $\text{dT′}=\text{w′dp′}$,

$w\prime \frac{\text{dp}\prime }{\text{dt}}=-\left(\frac{\partial \mathbf{U}}{\partial \mathbf{t}}+\mathbf{w}\cdot \nabla \mathbf{U}\right)\cdot \mathbf{p}\prime +q\mathbf{w}\prime \cdot \frac{\mathbf{j}}{\sigma }(17)$

where we have used the notation that for an arbitrary vector $\mathbf{V}$, $\text{d}\mathbf{V}/\text{d}t=\partial \mathbf{V}/\partial t+\left(\mathbf{w}\cdot \nabla \right)\mathbf{V}$. Eq. 17 is quite general, depending only on the MHD approximation for the ambient electric field E given above.

One may also obtain Eq. 17 by considering the Lorentz force in the fluid frame (Zhang and Lee, 2013):

$\frac{\text{d}\mathbf{p}\prime }{\text{dt}}=-\gamma m\frac{\text{d}\mathbf{U}}{\text{dt}}+q\left(\frac{\mathbf{j}}{\sigma }+\frac{\mathbf{w}\prime \times \mathbf{B}}{c}\right)(18)$

where the first term on the right hand side corresponds to acceleration of the fluid. Then from $\text{dT′}=\mathbf{w}\text{′}\cdot \text{d}\mathbf{p}\text{′}$ and $\mathbf{p}\text{′}=\gamma m\mathbf{w}\text{′}$, one obtains Eq. 17 by projecting Eq. 18 in the direction of $\mathbf{w}\text{′}$.

For energetic particles, $\mathbf{w}\gg \mathbf{U}$. For most astrophysical plasmas, $\sigma \sim \infty$. Eqs. 1,3 show that the magnetic force on the particle that changes the direction of motion is much stronger than the electric force that changes the particle energy, magnetic irregularities can scatter particles efficiently (Zhang and Lee, 2013). The angular distribution of energetic particles should be nearly isotropic, which is confirmed by observations. If the particle angular distribution is isotropic in the fluid frame, (so that the averages over pitch angle: $\langle \mathbf{w}\text{′}\cdot \mathbf{j}/\sigma \rangle =0$, $\langle {w\prime }_i{p\text{′}}_j\rangle ={\delta }_{ij}w\text{′}p\text{′}/3$, and $\langle \mathbf{U}\cdot \mathbf{p}\text{′}\rangle =0$), then one may average Eq. 17 over angle at a given momentum $p\text{'}$ to obtain

$\langle \frac{\text{dp}\prime }{\text{dt}}\rangle =-\frac{p\prime }{3}\nabla \cdot \mathbf{U}(19)$

This is precisely the rate of energy change appearing in the Parker equation (Parker, 1965) and corresponds to the adiabatic thermodynamic process. The averaged acceleration rate is then determined by the compression rate and does not depend on the particle charge and mass as far as the particle distribution is isotropic. Although for an isotropic particle distribution, Eq. 18 shows that the momentum change rate averaged over angle $\langle \mathbf{p}\prime \rangle$ is always 0, the averaged change rate of the amplitude of momentum $\langle \dot{p}\prime \rangle$ is proportional to $\nabla \cdot \mathbf{U}$, which is intimately related to non-vanishing gyro-motion averaged energy change rate of a particle for variations of $\mathbf{B}$ and $\mathbf{U}$ over the gyro-period (Zhang and Lee, 2013). Eq. 18 shows that the energy change is associated with the acceleration of the fluid and does not depend on the details of the microscopic interactions. Eq. 19 therefore is a direct consequence of the fluid theory and can be used to describe plasma heating as well.

Eq. 19 for energy change clearly also applies at discontinuities in the flow and/or magnetic field, such as shocks or current sheets, if scattering is sufficient to keep the anisotropies small. In what follows, we will suppress the angular brackets in Eq. 19. Also, in most applications, $w\gg U$ and we may neglect the distinction between $p\prime$ and p. It follows from Eq. 19 that one must have anisotropies to obtain efficient acceleration of energetic particles when $\nabla \cdot \mathbf{U}=0$, such as in in-compressible ideal MHD flows.

In most cases, the anisotropies will, like the electric field, be proportional to the flow speed or its derivatives. Hence in these cases, the acceleration rate will be of the second order in the flow velocity $\mathbf{U}$. This also follows for resonant acceleration by hydro-magnetic waves (Petrosian and Liu, 2004). For energetic particles with $w\gg U$, the second-order terms are generally much smaller than the first-order term in $\nabla \cdot \mathbf{U}$, and the acceleration is consequently slower than that given by Eq. 19.

However, the amount of energy gain via the adiabatic process is limited by the extent of compression of the background plasma (Schatzman, 1963; Drury, 1983). The acceleration also does not depend on the charge and mass of accelerated particles. Without consideration of other physical processes, the compression process alone clearly cannot account for the observed high energies of cosmic ray particles and spectral variations among different particle species. As we will see below, the acceleration rate will be further reduced from

${\tau }_{acc.MHD}^{-1}=\nabla \cdot \mathbf{U}(20)$

when considering other processes.

2.2 Transport Equations of Cosmic Rays and Energetics

As mentioned above, the acceleration process is intimately related to the spatial transport of particles. A robust and widely applicable transport theory, applicable to particles with $w\gg U$, has been developed. It may be viewed as an expansion in powers of the ratio $U/w$. The theory utilizes the fact that the plasmas in space are turbulent, with broadband fluctuations over scales including the particle gyro-radii. Magnetic field fluctuations (either in terms of curvature or gradient) on scales near the particle gyro-radii in the ambient magnetic field will lead to fluctuations of the particle pitch angle, which can lead to chaotic trajectories and very efficient scattering (Figure 1) (Buechner and Zelenyi, 1989; Xie and Liu, 2020). The particle motions are described statistically, and the magnetic fluctuations “scatter” the particles in angle, making them nearly isotropic relative to the local plasma coordinate frame (on scale larger than the gyro-radius of the particle), and resulting in diffusive transport. As pointed out in the previous section, this near-isotropy is observed in the cosmic-rays.

FIGURE 1

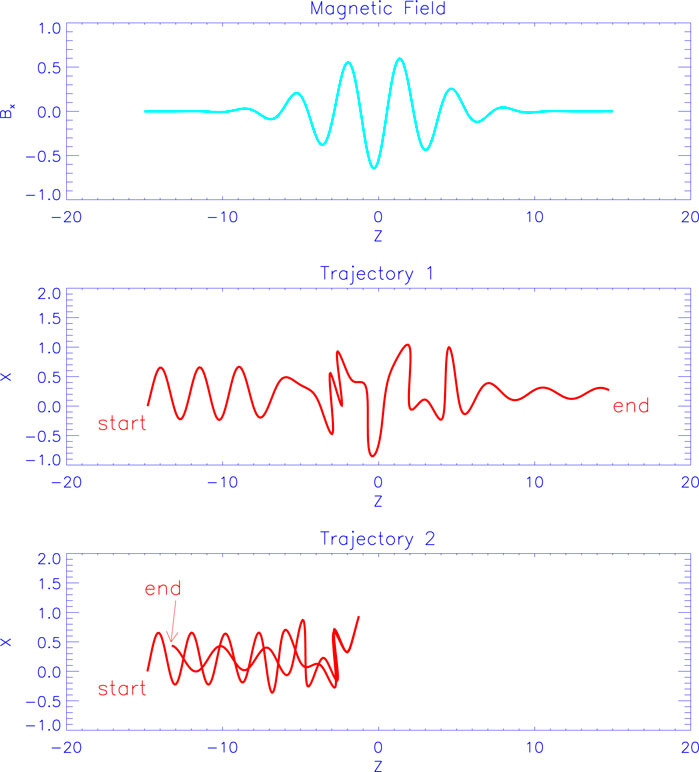
FIGURE 1. Computed orbits of two particles in a specified magnetic field that is axisymmetric along the z axis. The two particles are started with nearly the same initial velocity and position, but behave quite differently. This sensitivity to initial conditions results in chaotic or random trajectories (Buechner and Zelenyi, 1989; Xie and Liu, 2020).

The resulting spatial diffusion coefficient can be obtained in terms of the statistical properties of the turbulent magnetic field by using a variety of approximations: quasi-linear theory (Ptuskin, 1988; Bykov and Toptygin, 1993) and integration of particle orbits in a synthesized magnetic field are the most often used. The trajectories become effectively randomized and are made isotropic in the local frame (Figure 1). Under a wide range of conditions this drives them to near-isotropy in the fluid frame (or, more generally, the frame of the scatter) with a time scale τ, which usually depends on the charge to mass ratio of particles. Unfortunately, a general theory for lower-energy particles whose speeds are comparable to U or smaller is not yet available³ and observations of narrow band radio bursts from solar flares suggest that these lower-energy particles can be highly an-isotropic (Kliem et al., 2000).

We work in terms of the energetic-particle distribution function $f\left(\mathbf{r},p,t\right)$. If we neglect U entirely (zeroth order in $U/w$) and consider time scales much larger than τ, the resulting particle motion may be approximated as diffusive, and the phase space distribution satisfies

$\frac{\text{df}}{\text{dt}}=\frac{\text{d}}{{\text{dx}}_{\text{i}}}\left[{\kappa }_{ij}\frac{\text{df}}{{\text{dx}}_{\text{j}}}\right]+Q(21)$

where ${\kappa }_{ij}$ is the diffusion tensor, determined by the spectrum of the magnetic fluctuations, and Q represents any source. The flow velocity of the background fluid does not appear, and because $\mathbf{E}=0$ in this limit, advection or energy change do not appear. This equation gives a crude, but sometimes acceptable description of the behavior of very high energy particles (with correspondingly fast diffusion) occasionally emitted by the Sun. However, it is too simple for most purposes.

Proceeding to the next order in $U/w$ we obtain a much more useful equation, the Parker transport equation Parker (1965), which may be written in the following form:

$\begin{array}{l}\frac{\partial f}{\partial t}=\frac{\partial }{\partial x_i}\left[{\kappa }_{ij}\frac{\partial f}{\partial x_j}\right]\left(\text{diffusion}\right)\\ -U_i\frac{\partial f}{\partial x_i}\left(\text{convection}\right)\\ -V_{di}\frac{\partial f}{\partial x_i}\left(\text{guiding}\mathrm{–}\text{center drift}\right)\\ +\frac{1}{3}\frac{\partial U_i}{\partial x_i}\left[\frac{p\partial f}{\partial p}\right]\left(\text{energy}\text{change}\right)\\ +Q\left(x_i,t,p\right)\left(\text{source}\right)\end{array}(22)$

$=\frac{\partial }{\partial x_i}\left[{\kappa }_{ij}\frac{\partial f}{\partial x_j}-U_{i}f\right]-\frac{\partial }{\partial p_i}\left[p_{i}f\right]-V_{di}\frac{\partial f}{\partial x_i}+Q\left(x_i,t,p\right)(23)$

$=\frac{\partial }{\partial x_i}[{\kappa }_{ij}\frac{\partial f}{\partial x_j}+\frac{U_i}{3}\frac{p\partial f}{\partial p}]-U_i\frac{\partial }{\partial x_i}\left[f+\frac{1}{3}\frac{p\partial f}{\partial p}\right]-V_{di}\frac{\partial f}{\partial x_i}+Q\left(x_i,t,p\right)(24)$

$=\frac{\partial }{\partial x_i}[{\kappa }_{ij}\frac{\partial f}{\partial x_j}+\frac{U_i}{3}\frac{p\partial f}{\partial p}]-\frac{1}{p^2}\frac{\partial }{\partial p}\left(p^2\frac{p}{3}{U}_i\frac{\partial }{\partial x_i}f\right)-V_{di}\frac{\partial f}{\partial x_i}+Q\left(x_i,t,p\right)(25)$

where we have used Eq. 19 for $\dot{p}$. Here the diffusion tensor ${\kappa }_{ij}$ may be written in terms of the magnetic field, the parallel diffusion coefficient, ${\kappa }_{\parallel }$, and the perpendicular diffusion coefficient, ${\kappa }_{\perp }$ as:

${\kappa }_{ij}={\kappa }_{\perp }{\delta }_{ij}+\left({\kappa }_{\parallel }-{\kappa }_{\perp }\right)\frac{B_i{B}_j}{B^2}(26)$

The associated streaming flux (in the observer’s frame) of the particles may be written as:

$F_i=-{\kappa }_{ij}\frac{\partial f}{\partial x_j}-\frac{U_i}{3}\frac{p\partial f}{\partial p}(27)$

where the second term on the right hand side is due to the Doppler effect. The associated anisotropy is given by:

${\delta }_i=\frac{3F_i}{wf}(28)$

The drift velocity of the guiding center ${\mathbf{V}}_d$ is given by Isenberg and Jokipii (1979):

${\mathbf{V}}_d=\frac{pwc}{3q}\nabla \times \left(\frac{\mathbf{B}}{B^2}\right)(29)$

In this equation we have the spatial diffusion contained in the zeroth order Eq. 21, with new terms containing the advection and acceleration/deceleration caused by the fluid flow. Note that the electric field does not appear explicitly in Eq. 22. However, as shown above on the energy change, it is nonetheless contained in the terms involving the flow velocity $\mathbf{U}$. Eq. 22 was first written down by Parker (1965). It is the basis of most current work on cosmic-ray transport and is often called the Parker equation. The equation is a good approximation for energetic particles ($U/w\ll 1$) if there is enough scattering by magnetic irregularities so that τ is much shorter than the macroscopic time scales and the distribution is nearly isotropic. It applies at shocks (which appear as discontinuities in $\mathbf{U}$ ) and at thin current sheets. In this limit, if the divergence of the flow velocity $\mathbf{U}$ is zero, there is no energy change to first order in $U/w$.

Upon carrying out the expansion to second order in $U/w$, we obtain new effects involving the viscosity of the cosmic rays and the acceleration of the flow (Earl et al., 1988; Webb, 1989; Williams et al., 1993). These give additional terms representing acceleration of cosmic rays caused by the fluid velocity shear, other gradients in velocity, and fluid acceleration. The viscosity can give acceleration in divergence free flows, which are absent in the first-order equation. For ${\kappa }_{\parallel }={\kappa }_{\perp }=\kappa =\tau w^2/3$, we have:

$\begin{array}{c}\frac{\partial f}{dt}=\frac{\partial }{\partial x_i}\left[\frac{w^2\tau }{3}\frac{\partial f}{\partial x_i}\right]-U_i\frac{\partial f}{\partial x_i}+\frac{p}{3}\frac{\partial U_i}{\partial x_i}\frac{\partial f}{\partial p}+\frac{\text{Γ}}{3p^2}\frac{\partial }{\partial p}\left[\tau p^4\frac{\partial f}{\partial p}\right]-\frac{1}{3p^2}\frac{\partial \left(\tau p^3\right)}{\partial p}{A}_i\frac{\partial f}{\partial x_i}-\frac{p}{3}\frac{\partial \left(\tau A_i\right)}{\partial x_i}\frac{\partial f}{\partial p}-\frac{2\tau p}{3}{A}_i\frac{{\partial }^{2}f}{\partial x_i\partial p},\end{array}(30)$

$\begin{array}{c}=-\frac{\partial }{\partial x_i}\left[U_{i}f-\kappa \frac{\partial f}{\partial x_i}+\kappa \frac{p{A}_i}{w^2}\frac{\partial f}{\partial p}\right]-\frac{1}{p^2}\frac{\partial }{\partial p}{p}^2\left[\dot{p}f-\kappa \frac{p^2\text{Γ}}{w^2}\frac{\partial f}{\partial p}+\kappa \frac{p{A}_i}{w^2}\frac{\partial f}{\partial x_i}\right],\end{array}(31)$

$\begin{array}{c}=-\frac{\partial }{\partial x_i}\left[\kappa \frac{p{A}_i}{w^2}\frac{\partial f}{\partial p}-\kappa \frac{\partial f}{\partial x_i}-\frac{U_i}{3}\frac{p\partial f}{\partial p}\right]-\frac{1}{p^2}\frac{\partial }{\partial p}{p}^2\left[\frac{p}{3}{U}_i\frac{\partial }{\partial x_i}f-\kappa \frac{p^2\text{Γ}}{w^2}\frac{\partial f}{\partial p}+\kappa \frac{p{A}_i}{w^2}\frac{\partial f}{\partial x_i}\right]\end{array}(32)$

where the source and guiding-center drift terms have been ignored and the coefficient of viscous momentum transfer $\text{Γ}$ and the fluid acceleration vector $A_i$ are defined by

$\text{Γ}=\frac{1}{10}{\left[\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right]}^2-\frac{2}{15}\frac{\partial U_i}{\partial x_i}\frac{\partial U_j}{\partial x_j}(33)$

$A_i=\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}(34)$

In Eq. 30, the first term on the right-hand side describes diffusion, the second: convection, the third: adiabatic energy change and the last four terms describe energy changes due to velocity shear and fluid acceleration. The order of magnitude of the new terms are of the second order of $U/w$ for the reasons discussed above. Also, the temporal and spatial scales of the variation of $\mathbf{U}$ must be larger than the scattering time τ or the associated scattering mean free path $\lambda =\tau w$, respectively, for the validity of the diffusion approximation (Earl et al., 1988). In Eq. 32, one may also incorporate gradual momentum change due to radiative loss or acceleration by resistive electric fields into the convection term in the momentum space. Stochastic particle acceleration due to resonant wave-particle interaction may be incorporated as a diffusion term in the momentum space (Petrosian and Liu, 2004). With Eq. 30, one can readily distinguish the first and the second order Fermi acceleration. The first order Fermi acceleration is defined as a convection term in the momentum space while the second order Fermi acceleration contributes to the diffusion term in the momentum space.

Using Eq. 33, Earl et al. (1988) (ELM) derived the average rate of momentum change:

$\frac{\langle \text{Δ}p\rangle }{\text{Δ}t}=\frac{\text{Γ}}{p^2}\frac{\text{d}}{\text{dp}}\left[p^4\frac{\kappa }{w^2}\right](35)$

and the average rate of momentum dispersion:

$\frac{\langle \text{Δ}{p}^2\rangle }{\text{Δ}t}=2D_{pp}=2\text{Γ}{p}^2\frac{\kappa }{w^2}(36)$

Note that this momentum or energy change is caused by the fluctuating electric fields associated with the moving magnetic scattering centers, and results in both deceleration and acceleration. The associated viscosity introduced by high-energy particle acceleration is given by:

$\nu =-\frac{4\pi }{15}{\displaystyle \int w\tau p^4}\frac{\partial f}{\partial p}\text{d}p(37)$

where the integration is for p satisfying $w\tau \ll L$, the variation scale of $\mathbf{U}$.

This mechanism is distinguished from previous discussions in which the energy change was associated with compression. The transport equation of EJM has been solved using stochastic integration for an idealized, divergence-free flow similar to that in 2-dimensional reconnection with the flow vector in the x-z plane given by the expression

$\mathbf{U}\left(\mathbf{x},\mathbf{y}\right)=U_0\left[\text{tanh}\left(\frac{x}{L}\right){\mathbf{e}}_x-\frac{y}{L}{\text{sech}}^2\left(\frac{x}{L}\right){\mathbf{e}}_z\right](38)$

It is readily shown that the values of $\langle \text{Δ}p\rangle /\text{Δ}t$ and $\langle \text{Δ}{p}^2\rangle /\text{Δ}t$ given above in Eqs. 35, 36 are non-zero and acceleration occurs because of the shear (Ohira, 2013). In this case, the acceleration rate is slow on the order of

${\tau }_{acc.vis}^{-1}=\frac{U^2\kappa }{w^2{L}^2}\sim {\left(\frac{U}{w}\right)}^2{\left(\frac{\lambda }{L}\right)}^2{\tau }^{-1}=\left(\frac{\lambda }{L}\right)\left(\frac{U}{w}\right)\left(\frac{U}{L}\right)<\frac{U}{L}={\tau }_{acc.dft}^{-1}(39)$

Although the derivation of Eq. 30 assumes that $\lambda \ll L$ for the diffusion approximation to valid, the particle acceleration by shearing flow is most efficient when λ is comparable to L, reminiscence of resonant interactions. In fact, even in the case where $\lambda \gg L$, viscous dissipation still exists. Acceleration of cosmic rays is expected if there are repeated crossings of a shearing flow layer. The corresponding acceleration rate should be on the order of $\left(U^2/w^2\right){\tau }^{-1}$. The viscosity induced by cosmic ray acceleration is a feedback of cosmic rays on the shearing flow of the background plasma. Similarly, the acceleration of the flow may be treated as a pressure term of cosmic rays.

Finally, the acceleration of particles is directly related to dissipation of energy stored in the magnetic field and/or damping of the flow velocity (Melia et al., 2001). From MHD equations, we have

$\begin{array}{c}\frac{\partial }{\partial t}\left(\frac{B^2+E^2}{8\pi }\right)=-\frac{c}{4\pi }\nabla \cdot \left(\mathbf{E}\times \mathbf{B}\right)-\mathbf{j}\cdot \mathbf{E}\\ =-\frac{c}{4\pi }\nabla \cdot \left(\mathbf{E}\times \mathbf{B}\right)-\frac{j^2}{\sigma }+\frac{1}{c}\mathbf{j}\cdot \left(\mathbf{U}\times \mathbf{B}\right),\end{array}(40)$

$\begin{array}{c}\frac{\partial }{\partial t}\left(\frac{1}{2}\rho U^2\right)=-\nabla \cdot \left(\frac{1}{2}\rho U^2\mathbf{U}\right)-\mathbf{U}\cdot \nabla P\\ -\frac{1}{c}\mathbf{j}\cdot \left(\mathbf{U}\times \mathbf{B}\right)+2\mathbf{U}\nabla \cdot \left(\mathbf{S}\nu \right)+\xi \mathbf{U}\cdot \nabla \left(\nabla \cdot \mathbf{U}\right)\end{array}(41)$

where ρ and P are the mass density and pressure of the background plasma, respectively, the second and the last two terms on the right-hand side of Eqs 40, 41 are associated with dissipation via resistive and inductive electric fields, respectively,

$S_{ij}=\frac{1}{2}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}-\frac{2}{3}{\delta }_{ij}\nabla \cdot \mathbf{U}\right)$

and the coefficient of viscous momentum transfer $\text{Γ}=2S_{ij}{S}_{ji}/5=2{\mathbf{S}}^2/5$. ξ is the second viscosity or the volume viscosity, which is related to anisotropy of the pressure p.

Both the acceleration via drift in magnetic gradient and/curvature (Eqs. 9, 10) and the acceleration due to compression (Eq. 19) are associated with kinetic energy dissipation via the inductive electric field. The Fermi mechnism and shock drift acceleration are associated with the inductive electric field as well (Fermi, 1949; Jokipii, 1982). In the MHD, the dissipation of magnetic energy via the inductive electric field also leads to acceleration of the flow and vice versa via the third terms on the right-hand side of Eqs. 40, 41. The particle acceleration by the shear and by deceleration of the flow is associated with scattering of particles by the background plasma leading to viscosity and cosmic ray pressure which can cause damping of the shear and a force acting to decelerate the background flow, respectively. These accelerations are caused by inductive electric fields at small scales directly, reminiscence of acceleration by compression.

Resistive dissipation in MHD usually leads to heating of the background plasma:

$\frac{\partial \left(\rho \mathit{ϵ}\right)}{\partial t}=-\nabla \cdot \left(\mathbf{U}\rho \mathit{ϵ}\right)-\nabla \cdot \mathbf{q}-P\nabla \cdot \mathbf{U}+\frac{{\mathbf{j}}^2}{\sigma }+2\nu {\mathbf{S}}^2+\xi {\left(\nabla \cdot \mathbf{U}\right)}^2(42)$

where $\rho \mathit{ϵ}$ is the internal energy density of the background plasma and $\mathbf{q}$ is the heating flux. At the presence of high-energy particles, some of the magnetic energy dissipated via resistive electric fields can go into particle acceleration directly via the $\dot{p}$ term in Eq. 32.

Therefore in the context of MHD, the acceleration of high-energy particles can be classified into two kinds: direct acceleration by resistive electric fields, which can be very efficient and only operates in particular astrophysical environments where the resistivity may be high, and acceleration by inductive electric fields via effective scattering with the background plasma, which appears to be ubiquitous and is relatively less efficient than acceleration by resistive electric fields. Statistical properties of the latter can be described with the diffusion coefficient κ, which also determines the spatial transport of high-energy particles. The issue of high-energy particle acceleration in MHD then can be fully addressed with κ and the source term Q, which describes the particle acceleration at relatively low energies and therefore smaller scales where MHD may not be appropriate to describe the characteristics of particle energizing electric fields.

3 Specific Acceleration Mechanisms

The basic transport equation discussed above has been used in a variety of contexts to discuss the acceleration of energetic particles. The most successful and widely applicable is that of standard diffusive shock acceleration, which results from the application of the first-order Eqs. 22 to a planar shock wave. As we will see, this has the singular property of producing a power law momentum spectrum which is extremely insensitive to model parameters and is close to that observed.

3.1 Diffusive Shock Acceleration

Consider a steady, plane shock propagating in a uniform medium. Define the x-direction as the direction of propagation and let particles be introduced uniformly and steadily at the shock with a rate of A at an injection momentum $p_0$. Work in the shock-normal coordinate system, with the shock at the fixed position $x=x_{\text{sh}}$. The shock compression ratio r is defined as the ratio of upstream to downstream flow speed $U_1/U_2>1$. It depends on the Mach number and the adiabatic indexes of the upstream and downstream flows (Zhang and Liu, 2019). It is readily found that the steady solution to the Parker equation in this case is given by (Drury, 1983)

$f\left(x,p\right)=\frac{3A}{4\pi \left(r-1\right)p_0^3{U}_2}{\left(\frac{p}{p_0}\right)}^{-3r/\left(r-1\right)}H\left(p-p_0\right)f\left(x\right)(43)$

where

$f\left(x\right)=\text{exp}\left({\displaystyle {\int }_{x_{\text{sh}}}^x\frac{U\left(x^{\prime }\right)}{{\kappa }_{xx}\left(p,x^{\prime }\right)}\text{d}{x}^{\prime }}\right)\text{ for}x<x_{\text{sh}}\text{ and}$

$f\left(x\right)=1\text{ for}x>x_{\text{sh}}$

where H is the Heaviside step function. Note that in the limit of a strong non-relativistic shock, $r\to 4$, the momentum dependence of the distribution function becomes $f\left(p\right)\propto p^{-4}$, which corresponds to an energy spectrum $\text{d}n/\text{d}T\propto T^{-2}$ for relativistic particles and $\text{d}n/\text{d}T\propto T^{-3/2}$ for non-relativistic particles which is not far from the distribution of energetic electrons inferred from radio observation of supernova remnants (Reynolds et al., 2012), the distributions of Galactic cosmic rays (Strong et al., 2007), and solar energetic particles (Mewaldt et al., 2007). This energy dependence is independent of shock speed, diffusion coefficients and other parameters. Since shocks in astrophysics tend to be strong, this is in effect the desired “universal” spectrum.

One should note that since the diffusion coefficient κ usually depends on the momentum, the particle distribution in the upstream of the shock is usually not a power law. The distribution function integrated in the upstream is given by

$F\left(p\right)={\displaystyle {\int }_{x_{\text{sh}}}^{-\infty }f\left(x,p\right)\text{d}x}=\frac{3A\kappa \left(p\right)}{4\pi \left(r-1\right)p_0^3{U}_2{U}_1}{\left(\frac{p}{p_0}\right)}^{-3r/\left(r-1\right)}H\left(p-p_0\right)$

where we have assumed that κ is independent of x in the upstream. Therefore in the shock precursor, one may have a distribution harder than that in the downstream of the shock. If one has an escape boundary in the upstream, the particle distribution will be softer (Zhang and Liu, 2020).

Solving the time-dependent version of Eq. 22 with particles injected at a low momentum $p_0$ turned on at a specific time reveals that the spectrum is indeed the universal power law given in Eqs. 43, but with a high-momentum cutoff, $p_c$ which increases at a rate $\text{d}\text{ln}\left(p_c\right)/\text{d}t\approx 4U_1^2/{\kappa }_{xx}$ for ${\kappa }_{xx}$ increasing rapidly with the increase of p (Forman and Drury, 1983). For a weak dependence of the ${\kappa }_{xx}$ on p, one will have a distribution gradually softening toward high energies and approaching the steady-state one with the increase of time (Zhang et al., 2017). The rate of particle acceleration by shocks ((Lagage and Cesarsky, 1983)) is therefore on the order of

${\tau }_{acc.shk}^{-1}\sim \frac{U^2}{\kappa }\sim {\left(\frac{U}{w}\right)}^2{\tau }^{-1}={\left(\frac{L}{\lambda }\right)}^2{\tau }_{acc.vis}^{-1}(44)$

which is higher than the rate caused by shearing by a factor of ${\left(L/\lambda \right)}^2$. From this we may see that quasi-perpendicular shocks will in general accelerate particles faster than will quasi-parallel shocks. For quasi-perpendicular shocks ${\kappa }_{xx}={\kappa }_{\perp }$ which is generally significantly smaller than ${\kappa }_{\parallel }$, which is the relevant diffusion coefficient for quasi-parallel shocks.

Although the Parker equation and the discussion leading to Eq. 22 apply for arbitrary direction of the local average magnetic field with appropriate diffusion tensor, the acceleration at a shock is physically quite different for quasi-parallel shocks (upstream plasma flow velocity nearly parallel to the magnetic field) than for perpendicular shocks, where the upstream flow is nearly perpendicular to the magnetic field (Jokipii, 1982; Drury, 1983; Jokipii, 1987). For quasi-parallel shocks the particle acceleration is best thought of as resulting from particles being scattered by upstream and downstream scattering centers which in the shock frame are converging and accelerating the particles which cross the shock more than once. Statistically, some particles will cross the shock many times and others not so many. This process can be shown to produce the power-law spectrum (Drury, 1983).

The acceleration process is physically quite different for quasi-perpendicular shocks. In this case the average magnetic field magnitude jumps suddenly at the shock by the shock ratio r, which causes a gradient drift along the shock face in the direction of the electric field $\mathbf{E}=-\left(\mathbf{U}\times \mathbf{B}\right)/\mathbf{c}$. As long as the scattering rate is sufficient to maintain near-isotropy, this acceleration can be much faster than the rate for a parallel shock (Jokipii, 1987). This mechanism is illustrated in Figure 2.

FIGURE 2

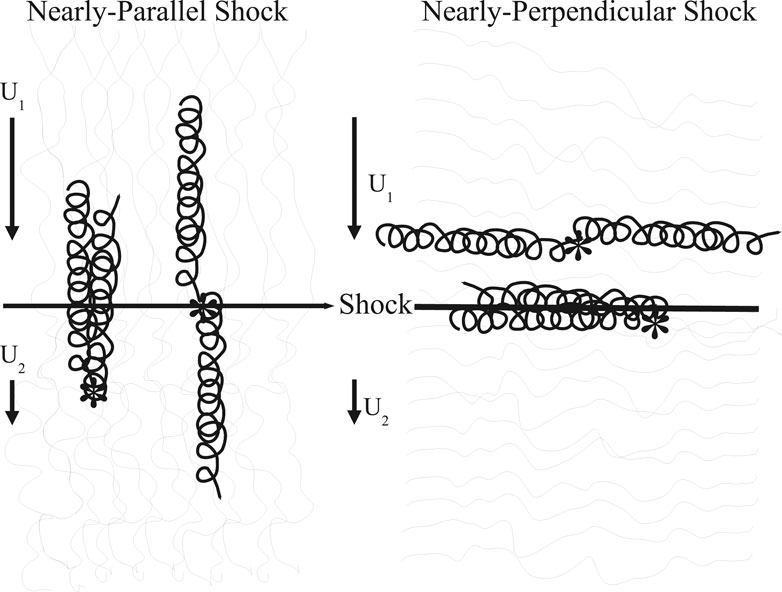
FIGURE 2. Cartoon illustrating the difference in the acceleration of charged particles at parallel (left) and perpendicular (right) shocks. In the former, the particles can move back and forth across the shock moving along the magnetic field, whereas in the latter, the particles cannot move as easily normal to the shock front and the energy gain at the shock comes in large part from drift. The electric field is perpendicular to the magnetic field and the flow velocity.

A discontinuous change in the flow speed, such as at a shock, is not necessary for this acceleration to occur. As demonstrated by Giacalone et al. (2002), when a finite-scale compression (with characteristic scale $L_c$) propagating in the x direction at a speed $U_x$ encounters a charged particle which has a diffusion coefficient ${\kappa }_{xx}$, then if the parameters are such that the dimensionless quantity $U_x{L}_c/{\kappa }_{xx}\ll 1$ the solution is the same as that for a shock.

Because large-scale astrophysical fluids are generally turbulent, with large-amplitude fluctuations in fluid parameters, the theory of diffusive shock acceleration has been applied to shocks propagating through a turbulent medium. This gives one possible explanation of the Voyager 1 observations as it crossed the termination shock (Figure 3). Recently Arthur and le Roux (2013) have considered a similar model with similar results.

FIGURE 3

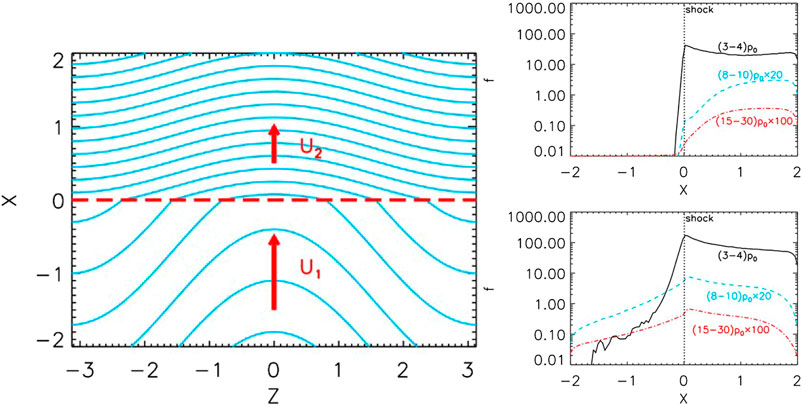
FIGURE 3. Left: Shock (red dashed line) and magnetic field (blue lines) geometry for an upstream average magnetic field perpendicular to the shock normal. U1 and U2 give the upstream and downstream flow velocities, respectively. Right: Profiles of density of the accelerated particles, for low (black lines), medium (blue dashed lines), and high (red dot-dashed lines) energy ranges at different locations z = 0.0 (top) and π (bottom), respectively (Guo et al., 2010).

The Parker transport equation has acceleration of particles occurring only if the term $\nabla \cdot \mathbf{U}$ is non-zero. As shown above, this occurs at shocks. Another possibility is that there are fluctuations in the fluid density caused by compressional oscillations. This possibility has been considered by many authors (Ptuskin, 1988; Jokipii et al., 2003) and most recently by Jokipii and Lee (2010). In analogy with the term ‘diffusive shock acceleration’ used for shocks, Jokipii et al. (2003) termed this acceleration ‘diffusive compression acceleration’.

Consider the case that the diffusive skin depth $L_d=\kappa /U\widetilde{>}{L}_c$, the compression length scale, but where the flow varies smoothly. Note that the scattering mean free path λ does not appear explicitly in this inequality. So it is possible to have λ small compared with $L_c$ (so that the diffusion approximation applies) but where $L_d$ is of the order of $L_c$ or larger. We find that such non-shock compression may be efficient accelerators, even if there are associated expansions. The corresponding acceleration rate is the same as the diffusive shock acceleration given by Eq. 44.

The physical basis of the acceleration is the interplay between 1) the energy change caused by the compression or expansion of the fluid and 2) the diffusion into or away from the region of compression or expansion. Rapid diffusion leads to the particle being able to diffuse away from a region of compression or expansion before the compensating expansion or compression can occur. Hence, statistically, some few particles will be fortunate enough to gain energy in several compression regions. In this process, for large κ, the accelerations dominate the particle energy change, even in those cases where the compression and expansions are equally present in the fluid flow. This is because, statistically, some particles can reach very high energies, but they cannot be decelerated to energies lower than zero.

Note also that this acceleration can take place for any orientation of the magnetic field. Gradient and curvature drifts can in general significantly affect the particle trajectories as they are accelerated. To illustrate this process, consider the simple, periodic one-dimensional velocity profile $U_x\left(x\right)=U_0\left(1+a\text{ sin}\left(kx\right)\right)$ and ${\kappa }_{xx}$ independent of x or p. We have not been able to solve this analytically for general parameters, but it is simple to solve numerically, and the solutions depend only on the dimensionless parameters $\chi =[U_0/{\kappa }_{xx}]x$, $\tau =[U_0^2/{\kappa }_{xx}]t$ and $\eta =[{\kappa }_{xx}/U_0]k$ and the amplitude a. The solutions are clearly periodic in χ with a period $2\pi /\eta$. For a constant value of κ, the acceleration timescale is given by $\kappa /U_0^2$. The momentum distribution in the steady-state is then proportional to $p^{-3}$, which is confirmed by statistical integration of Parker equation for test particles.

Using the quasi-linear approximation to the Parker Eq. 22, for small-amplitude compression, Jokipii and Lee (2010) find an equation which is diffusive in the momentum space. For no spatial variations except for the fluctuating density, they find

$\frac{\partial f}{\partial t}=\frac{1}{p^2}\frac{\partial }{\partial p}\left[p^2{D}_{pp}\frac{\partial f}{\partial p}\right](45)$

where $D_{pp}$ is the diffusion coefficient in the momentum space caused by compression. They also concluded that the non-diffusive equation for compression acceleration found by Fisk and Gloeckler (2008) does not conserve number of particles.

3.2 Stochastic Acceleration

Acceleration by fluctuating electric and magnetic fields, such as those found in a turbulent medium has been discussed ever since the seminal paper by Fermi (1949), who considered acceleration by randomly moving magnetic clouds. This has been subsequently generalized to apply to turbulent fluctuations (Bykov and Toptygin, 1993), and is also often termed the second-order Fermi acceleration. This form of acceleration, contained as the diffusion in momentum term in Eq. 30, has an extensive history. It is quite often the mechanism of choice for possible diffuse re-acceleration of cosmic rays in the interstellar medium and in solar flares (Petrosian and Liu, 2004). Nonetheless, it has at least one considerable disadvantage. Being of the second order in the wave or fluid flow velocity, this term, which is generally much slower than shock acceleration at high energies, may simply be added to the right side of Eq. 22 and is often invoked where shocks are believed not to be present or the diffusion coefficient in the shock upstream is too large to accelerate particles efficiently.

This acceleration can arise in two physically distinct processes. One can consider the effect of randomly moving waves which scatter the particle resonantly (Tverskoǐ, 1968) or one can consider larger-scale turbulent fluid motions where the energy change results from the stochastic shear or compression as discussed in the previous section (Ptuskin, 1988; Jokipii and Lee, 2010; Ohira, 2013). The former does not produce a power law spectrum with the desired value in a robust way since both acceleration time and scattering time, which is inversely proportional to the diffusive escape time, is inversely proportional to the wave intensity. The shape of the spectrum depends sensitively on the transport parameters in the acceleration region. Hence it is probably not the source of most of the observed cosmic-ray spectra which are almost-always power laws. Nonetheless, it may produce power-law with variable indexes and remains popular in some applications. The latter can lead to a power law distribution since both the acceleration and diffusive escape times are inversely proportional to the scattering time (see discussion below).

For scattering by Alfvén waves propagating both along the magnetic field and opposite to the field with a speed $V_a$, $D_{pp}$ may be written in terms of the scattering time τ

$D_{pp}=p^2\frac{V_a^2}{w^2}{\tau }^{-1}(46)$

The corresponding acceleration rate is given by

${\tau }_{acc.sa}^{-1}=\frac{D_{pp}}{p^2}=\frac{V_a^2}{w^2}{\tau }^{-1}=\frac{V_a^2}{U^2}{\tau }_{acc.shk}^{-1}(47)$

which is lower than the acceleration rate by shocks by a factor of $U^2/V_a^2$. For viscous acceleration in a shearing flow where $\mathbf{U}={\mathbf{U}}_{\mathbf{x}}\left(\mathbf{y}\right){\widehat{e}}_{\mathbf{x}}$ we write

$D_{pp}=2p^2{\left(\frac{\partial U_x}{\partial y}\right)}^2\tau (48)$

Here, τ must be significantly less than $L/w$ for the diffusion approximation to be valid. Even for the case where the Alfvén speed and fluid speed are comparable, the viscous acceleration rate is lower than that by stochastic acceleration by a factor of $L^2/{\lambda }^2$. Therefore acceleration caused by shearing flow is usually less efficient than stochastic acceleration, which is less efficient than shock acceleration.

Because of the term $V_a^2/w^2$, stochastic acceleration is quite slow for energetic particles, where $V_a\ll w$. The maximum acceleration rate can be estimated by setting $\tau =2\pi /{\omega }_g$, where ${\omega }_g$ is the gyro-period in the ambient magnetic field. Doing this just beyond the termination shock yields a reasonable upper bound on the time to accelerate singly charged Oxygen ions to 200 MeV/nucleon yields a time of 200 years. Observations of the charge state of ACR oxygen place an upper limit of about 1 year on the acceleration time. It is possible that the magnetic field becomes larger in the outer helio-sheath, ameliorating this difficulty if the statistical acceleration occurs there.

Stochastic particle acceleration focuses on addressing the gradual and statistical energy gain of charged particles via interactions with a spectrum of turbulent electromagnetic fields. It is essentially a second order Fermi acceleration process, where the acceleration of a population of high energy particles is described with a diffusive term in the momentum space Webb (1989). For the case where the turbulence is homogeneous and isotropic with the spectrum given by $W\left(k\right)$, some unified theory has been developed to include the mechanisms discussed above (Bykov and Toptygin, 1993). The turbulent velocity $\delta U\left(k\right)$ on a scale of $\sim 1/k$ is then given by ${\left[{\displaystyle {\int }_0^{k}W\left(k^{\prime }\right)\text{d}{k}^{\prime }}\right]}^{1/2}$. The two point correlation function of the velocity is given by:

$\langle U_i\left({\mathbf{r}}_{\mathbf{1}},t_1\right)U_j\left({\mathbf{r}}_{\mathbf{2}},t_2\right)\rangle ={\left(2\pi \right)}^{-4}{\displaystyle \int K_{ij}\left(\mathbf{k},\omega \right)\text{exp}[i\left(\mathbf{k}\left({\mathbf{r}}_{\mathbf{1}}-{\mathbf{r}}_{\mathbf{2}}\right)-\omega \left(t_1-t_2\right)\right){\text{d}}^3\mathbf{k}\text{d}\omega }(49)$

where

$K_{ij}\left(\mathbf{k},\omega \right)=T\left(k,\omega \right)\left({\delta }_{ij}-k_i{k}_j/k^2\right)+S\left(k,\omega \right)k_i{k}_j/k^2(50)$

T and S correspond to the transverse (sharing) and the longitudinal (compressible) component, respectively. Then we have the ensemble averaged turbulence energy density per unit mass:

$\langle U_i\left(\mathbf{r},t\right)U_i\left(\mathbf{r},t\right)\rangle /2={\displaystyle {\int }_0^{\infty }W\left(k\right)dk}(51)$

$=2{\left(2\pi \right)}^{-3}{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }\left[2T\left(k,\omega \right)+S\left(k,\omega \right)\right]k^2\text{d}k\text{d}\omega }}(52)$

and

$W\left(k\right)={\left(4{\pi }^3\right)}^{-1}{\displaystyle {\int }_0^{\infty }\left[2T\left(k,\omega \right)+S\left(k,\omega \right)\right]k^2\text{d}\omega }(53)$

As long as the velocity change of the background plasma over a particle scattering mean-free-path λ is much smaller than the particle speed w, the particle distribution in the comoving frame of the fluid is approximately isotropic with an anisotropy on the order of $\delta U\left({\lambda }^{-1}\right)/w$ (Earl et al., 1988) and the diffusive approximation is valid. The spatial diffusion coefficient $\kappa =w^2\tau /3$ can be also enhanced by the turbulent flow (Bykov and Toptygin, 1993):

$\chi =\kappa +\frac{1}{3{\left(2\pi \right)}^4}{\displaystyle \int {\text{d}}^3\mathbf{k}\text{d}\omega \left[\frac{2T\left(k,\omega \right)+S\left(k,\omega \right)}{I\omega +k^2\chi }-\frac{2k^2\chi S\left(k,\omega \right)}{{\left(I\omega +k^2\chi \right)}^2}\right]}(54)$

where $I^2=-1$ is used to represent imaginary number. The diffusion coefficient in the momentum space is then given by:

$D_{pp}=\frac{p^2\chi }{9{\left(2\pi \right)}^4}{\displaystyle \int {\text{d}}^3\mathbf{k}\text{d}\omega \frac{k^{4}S\left(k,\omega \right)}{{\omega }^2+k^4{\chi }^2}}(55)$

For acceleration by acoustic wave with a wave speed of $c_s$, $\omega =\pm c_{s}k$, $S(k,\omega )=S\left(k\right)\left[(\delta (\omega +c_{s}k)+\delta (\omega -c_{s}k)\right]$ (Ptuskin, 1988; Jokipii et al., 2003; Jokipii and Lee, 2010):

$D_{pp}=\frac{2p^2\chi }{9{\left(2\pi \right)}^4}{\displaystyle \int {\text{d}}^3\mathbf{k}\frac{k^{2}S\left(k\right)}{c_s^2+k^2{\chi }^2}}(56)$

If the waves have a length of L so that $S\left(k\right)={\left(2\pi \right)}^4\langle U^2\rangle \delta \left(k-L^{-1}\right)/8\pi k^2$, then we have

$D_{pp}=\frac{p^2\chi \langle U^2\rangle }{9\left[c_s^2{L}^2+{\chi }^2\right]}(57)$

Diffusion of particles in a shear flow can also introduce particle diffusion in the momentum space (Earl et al., 1988; Ohira, 2013):

$D_{pp}=\frac{p^2\kappa }{30w^2}\langle 3{\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)}^2-4{\left(\frac{\partial U_i}{\partial x_i}\right)}^2\rangle (58)$

$=\frac{p^2\kappa }{30{\left(2\pi \right)}^4{w}^2}{\displaystyle \int {\text{d}}^3\mathbf{k}\text{d}\omega \left(6k_i{k}_j{K}_{ij}+6k_i{k}_i{K}_{jj}-4k_i{k}_j{K}_{ij}\right)}(59)$

$=\frac{2p^2\kappa }{15{\left(2\pi \right)}^4{w}^2}{\displaystyle \int {\text{d}}^3\mathbf{k}\text{d}\omega k^2\left[2S\left(k,\omega \right)+3T\left(k,\omega \right)\right]}$

The last integration diverges as $k\to \infty$ for typical turbulence spectra. For the diffusion approximation to be valid, $\delta U\left({\lambda }^{-1}\right)$ needs to be much less than w. For a power-law turbulence spectrum with an index of α, i.e., $T\propto S\propto k^{-\alpha }$. $\delta U\left({\lambda }^{-1}\right)\propto {\lambda }^{\left(\alpha -3\right)/2}$, one can multiply the integral by a factor of ${[1+kU\left(k\right)\lambda /w]}^{\beta }$ with $\beta >2$ to make the integration converge:

$D_{pp}=\frac{2p^2\kappa }{15{\left(2\pi \right)}^4{w}^2}{\displaystyle \int {\text{d}}^3\mathbf{k}\text{d}\omega \frac{k^2\left[2S\left(k,\omega \right)+3T\left(k,\omega \right)\right]}{{\left[1+kU\left(k\right)\lambda /w\right]}^3}}(60)$

where we have assumed $\beta =3$. This theory has been applied to particle acceleration in the downstream of shocks of supernova remnants (Fan et al., 2010).

Although stochastic acceleration of high energy particles is slower than that by shocks by a factor of $U^2/V_a^2$, at low energies, stochastic acceleration can be very efficient for fast phase speeds of kinetic plasma waves (Petrosian and Liu, 2004), which may address the injection problem of diffusive shock acceleration. Moreover, shock acceleration is less efficient since low energy particles may not see the shock structure for their short scattering mean free path $\lambda \sim r_g$, and the diffusion approximation may not be valid as mentioned above. Since different particle species interact with different kinds of waves at small kinetic scales, the acceleration at low energies are usually selective for the resonance condition. Since ultimately energetic particles origin from low-energy charged particles in the background plasma, the acceleration at low energies then determines the overall acceleration efficiency of different particle species, which is essential to constrain the acceleration mechanism via observations.

Observations of cosmic rays abundance show that heavier elements and those in refractories are strongly enhanced. Figure 4 shows the corresponding results (Meyer et al., 1997). This can be attributed to the small charge to mass ratio of these elements and/or corresponding dust (Ellison et al., 1997) so that they may resonantly interact with larger scale waves than those with higher charge to mass ratio. For a given magnetic field, the gyro-radius is inversely proportional to the change to mass ratio and waves at larger scales usually carry more energies.

FIGURE 4

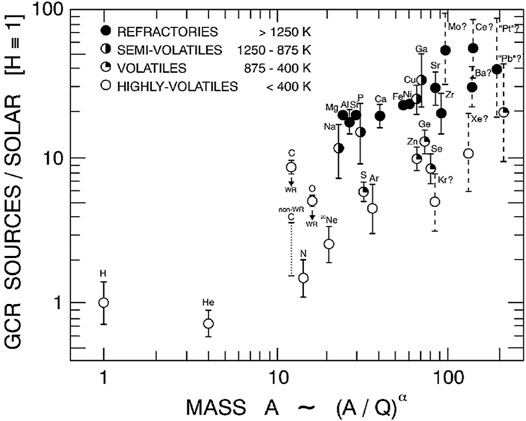
FIGURE 4. Dependence of the cosmic ray abundance enhancement on the atomic number A (Meyer et al., 1997).

The best example to illustrate resonance wave-particle interactions is perhaps the prominent enhancement of MeV ³He abundance relative to ⁴He in small impulsive solar energetic particle events (SEPs) (Liu et al., 2006). Figure 5 shows the relative abundance of energetic helium isotopes for some SEPs (Ho et al., 2005). It can be seen that the fluence of 3He is distributed in a relative narrow range, which the fluence of 4He can spead out over 4 order of magnitude. The enhancement of ³He is most prominent for small events with a lower ⁴He fluence.

FIGURE 5

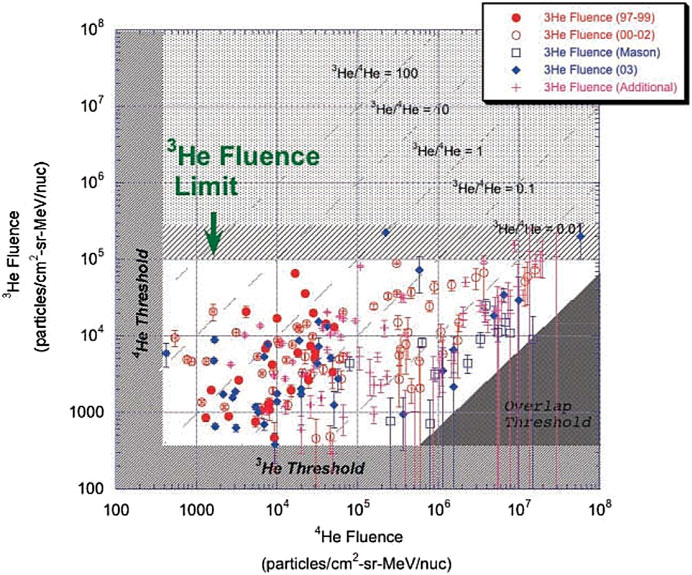
FIGURE 5. Relative abundance of Helium isotopes accelerated in solar flares (Ho et al., 2005; Petrosian et al., 2009).

Liu et al. (2006) attributed this phenomenon to resonant interaction of ³He with proton cyclotron waves. Figure 6 shows dispersion relations with different Alfvén speed for waves propagating along the magnetic field lines and the corresponding resonance conditions for ³He and ⁴He. It can be seen different helium isotopes interact with different modes of waves and this interaction also depends on the particle energy.

FIGURE 6

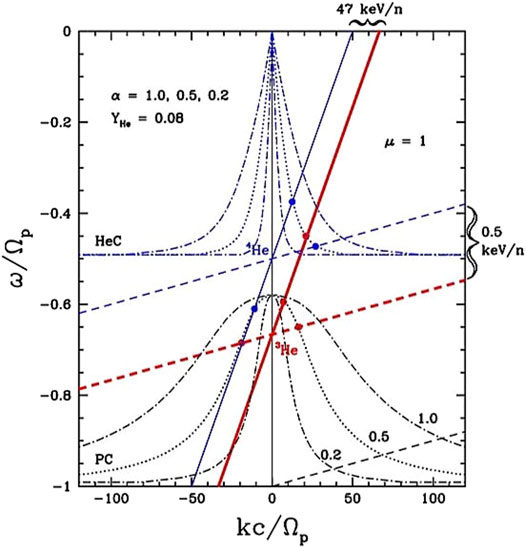
FIGURE 6. Resonant interactions of Helium 3 and 4 with plasma waves in different background plasmas indicated with α, the ratio of the electron plasma frequency to gyro-frequency (Liu et al., 2006). The straight lines stand for resonance conditions for helium isotopes with different energies. The proton gyro-frequency is given by ${\text{Ω}}_p$.

If one approximates the spatial diffusion as an escape term from the acceleration region, the theory of stochastic particle acceleration can be simplified as a diffusion equation in the momentum space with both source and escape terms (Petrosian and Liu, 2004). This model has been applied to observation of SEPs with prominent ³He enhancement. Figure 7 shows such an example. It can be seen that due to selective acceleration of ³He, all ³He in the background are accelerated to the MeV energy range. For ⁴He ions, as a major component of the background plasma, they affect the dispersion relations (Figure 6) and cause strong damping of waves in resonance with the background ⁴He. As a result, only a small fraction of ⁴He is accelerated to MeV, explaining the observed enhancement of high energy ³He. This also can also explain the fluence distribution of ³He and ⁴He (Petrosian et al., 2009).

FIGURE 7

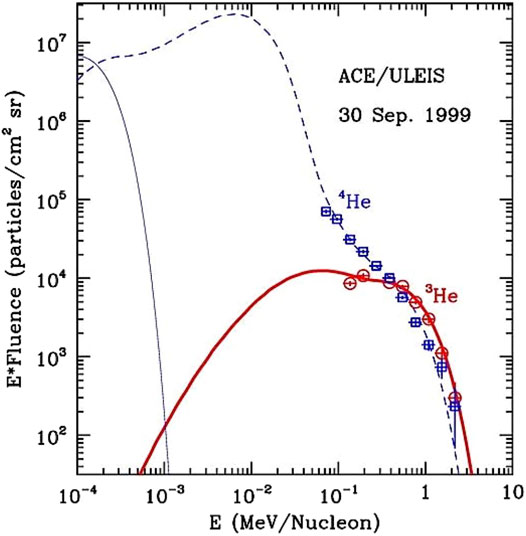
FIGURE 7. Selective acceleration of ³He in impulsive solar flares (Liu et al., 2006).

4 Conclusion

The acceleration of charged particles from low energies in the background to high energies covers a broad energy range. The associated spatial and temporal scales are also wide. These multi-scale couplings make the study of particle acceleration a very challenging task. To have quantitative modeling, dramatically simplifications are necessary.

If one concerns very high-energy particles with a very low number density, the test particle and fluid approaches can be taken. Then the leading order acceleration is associated with compression. In the context of acceleration by diffusive shocks, a simple power-law distribution can be obtained for the lack of scales in this model. In the case of strong non-relativistic shocks in supernova remnants (SNRs), one may consider the feedback of the cosmic ray acceleration to the shock structure (Bell et al., 2013). Multi-wavelength observations of a sample of SNRs appears to favor such a model (Zeng et al., 2019; Zhang and Liu, 2019).

Stochastic particle acceleration is generic to magnetic energy dissipation processes. Although it is not as efficient as diffusive shocks, it may dominate the acceleration of low energy particles (Petrosian and Liu, 2004). In cases where the shock acceleration is suppressed due to lack of scattering in the upstream, the stochastic acceleration may dominate in the shock downstream (Fan et al., 2010). The most prominent feature of this mechanism is selective acceleration of background particles with different change to mass ratio. It can not only explain the abundance enhancement of heavy elements in cosmic rays, but also account for enhancement of MeV ³He relative to ⁴He by up to 4 orders of magnitude in some impulsive SEPs. Such kind of resonant interactions have been realized in plasma devices (Zhang et al., 2017). Since both the acceleration and scatter rates of particles by waves are proportional to the wave intensity, the resulting particle distribution is very sensitive to the wave intensity, which can lead to a broad range of spectral index and may explain the impulsive nature of high energy burst.

Study of particle acceleration in magnetic reconnection and in general astrophysical context rely heavily on numerical simulations due to complexity of the related electromagnetic field configuration (Kowal et al., 2011, 2012; Guo et al., 2014; Dahlin et al., 2015; Zhou et al., 2015; Beresnyak and Li, 2016; Comisso and Sironi, 2018). On the other hand, power-law distribution may result from an emergence phenomenon due to the lack of characteristic scales in the system (Mewaldt et al., 2007).

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was partially supported by the National Key R&D Program of China (Grant No. 2018YFA0404203), NSFC grants (Nos. U1738122, U1931204, and 11761131007), and by the International Partnership Program of the Chinese Academy of Sciences (Grant No. 114332KYSB20170008). SL thanks the support of a startup grant at Southwest Jiaotong University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This study benefited from discussions within the International Space Science Institute (ISSI) team on “Origins of 3He-Rich Solar Energetic Particles.”

Footnotes

¹Although supernovae as high-energy astrophysical phenomena had been observed before, due to lack of observations of high-energy radiation at that time, it is not considered as the birth of high-energy astrophysics here.

²Although decay or annihilation of some heavy particles beyond the standard model of elementary particles may also produce energetic particles, conclusive evidence for these processes has not been discovered yet.

³See the section on stochastic particle acceleration below.

References

Arthur, A. D., and le Roux, J. A. (2013). Particle Acceleration at the Heliospheric Termination Shock with a Stochastic Shock Obliquity Approach. ApJ 772, L26. doi:10.1088/2041-8205/772/2/L26

CrossRef Full Text | Google Scholar

Axford, W. I. (1981). The Acceleration of Cosmic Rays by Shock Waves. Ann. NY Acad. Sci. 375, 297–313. doi:10.1111/j.1749-6632.1981.tb33702.x

CrossRef Full Text | Google Scholar

Bell, A. R., Schure, K. M., Reville, B., and Giacinti, G. (2013). Cosmic-ray Acceleration and Escape from Supernova Remnants. Monthly Notices R. Astronomical Soc. 431, 415–429. doi:10.1093/mnras/stt179

CrossRef Full Text | Google Scholar

Bell, A. R. (1978a). The Acceleration of Cosmic Rays in Shock Fronts - I. Monthly Notices R. Astronomical Soc. 182, 147–156. doi:10.1093/mnras/182.2.147

CrossRef Full Text | Google Scholar

Bell, A. R. (1978b). The Acceleration of Cosmic Rays in Shock Fronts - II. Monthly Notices R. Astronomical Soc. 182, 443–455. doi:10.1093/mnras/182.3.443

CrossRef Full Text | Google Scholar

Beresnyak, A., and Li, H. (2016). First-order Particle Acceleration in Magnetically Driven Flows. ApJ 819, 90. doi:10.3847/0004-637X/819/2/90

CrossRef Full Text | Google Scholar

Blandford, R. D., and Ostriker, J. P. (1978). Particle Acceleration by Astrophysical Shocks. ApJ 221, L29–L32. doi:10.1086/182658

CrossRef Full Text | Google Scholar

Blasi, P. (2004). Nonlinear Shock Acceleration in the Presence of Seed Particles. Astroparticle Phys. 21, 45–57. doi:10.1016/j.astropartphys.2003.10.008

CrossRef Full Text | Google Scholar

Blumenthal, G. R., and Gould, R. J. (1970). Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 42, 237–270. doi:10.1103/RevModPhys.42.237

CrossRef Full Text | Google Scholar

Bogachev, S. A., and Somov, B. V. (2005). Comparison of the Fermi and Betatron Acceleration Efficiencies in Collapsing Magnetic Traps. Astron. Lett. 31, 537–545. doi:10.1134/1.2007030

CrossRef Full Text | Google Scholar

Büchner, J., and Zelenyi, L. M. (1989). Regular and Chaotic Charged Particle Motion in Magnetotaillike Field Reversals: 1. Basic Theory of Trapped Motion. J. Geophys. Res. 94, 11821–11842. doi:10.1029/JA094iA09p11821

CrossRef Full Text | Google Scholar

Bykov, A. M., and Toptygin, I. N. (1993). Particle Kinetics in Highly Turbulent Plasmas (Renormalization and Self-Consistent Field Methods). Phys.-Usp. 36, 1020–1052. doi:10.1070/PU1993v036n11ABEH002179

CrossRef Full Text | Google Scholar

Comisso, L., and Sironi, L. (2018). Particle Acceleration in Relativistic Plasma Turbulence. Phys. Rev. Lett. 121, 255101. doi:10.1103/PhysRevLett.121.255101

PubMed Abstract | CrossRef Full Text | Google Scholar

Dahlin, J. T., Drake, J. F., and Swisdak, M. (2015). Electron Acceleration in Three-Dimensional Magnetic Reconnection with a Guide Field. Phys. Plasmas 22, 100704. doi:10.1063/1.4933212

CrossRef Full Text | Google Scholar

Drury, L. O. C. (1983). An Introduction to the Theory of Diffusive Shock Acceleration of Energetic Particles in Tenuous Plasmas. Rep. Prog. Phys. 46, 973–1027. doi:10.1088/0034-4885/46/8/002

CrossRef Full Text | Google Scholar

Earl, J. A., Jokipii, J. R., and Morfill, G. (1988). Cosmic-Ray Viscosity. ApJ 331, L91. doi:10.1086/185242

CrossRef Full Text | Google Scholar

Ellison, D. C., Drury, L. O. C., and Meyer, J. P. (1997). Galactic Cosmic Rays from Supernova Remnants. II. Shock Acceleration of Gas and Dust. ApJ 487, 197–217. doi:10.1086/304580

CrossRef Full Text | Google Scholar

Fan, Z. H., Liu, S. M., Yuan, Q., and Fletcher, L. (2010). Lepton Models for TeV Emission from SNR RX J1713.7-3946. A&A 517, L4. doi:10.1051/0004-6361/201015169

CrossRef Full Text | Google Scholar

Fermi, E. (1949). On the Origin of the Cosmic Radiation. Phys. Rev. 75, 1169–1174. doi:10.1103/PhysRev.75.1169

CrossRef Full Text | Google Scholar

Fisk, L. A., and Gloeckler, G. (2008). Acceleration of Suprathermal Tails in the Solar Wind. Astrophysical J. 686, 1466–1473. doi:10.1086/591543

CrossRef Full Text | Google Scholar

Forman, M. A., and Drury, L. O. (1983). “Time-Dependent Shock Acceleration: Approximations and Exact Solutions,” in Proceedings of the 18th International Cosmic Ray Conference, Bangalore, India, August 22–September 3, 267.

Google Scholar

Giacalone, J., Jokipii, J. R., and Kóta, J. (2002). Particle Acceleration in Solar Wind Compression Regions. ApJ 573, 845–850. doi:10.1086/340660

CrossRef Full Text | Google Scholar

Guo, F., Jokipii, J. R., and Kota, J. (2010). Particle Acceleration by Collisionless Shocks Containing Large-Scale Magnetic-Field Variations. ApJ 725, 128–133. doi:10.1088/0004-637X/725/1/128

CrossRef Full Text | Google Scholar

Guo, F., Li, H., Daughton, W., and Liu, Y.-H. (2014). Formation of Hard Power Laws in the Energetic Particle Spectra Resulting from Relativistic Magnetic Reconnection. Phys. Rev. Lett. 113, 155005. doi:10.1103/PhysRevLett.113.155005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, G. C., Roelof, E. C., and Mason, G. M. (2005). The Upper Limit on 3 He Fluence in Solar Energetic Particle Events. ApJ 621, L141–L144. doi:10.1086/429251

CrossRef Full Text | Google Scholar

Isenberg, P. A., and Jokipii, J. R. (1979). Gradient and Curvature Drifts in Magnetic fields with Arbitrary Spatial Variation. ApJ 234, 746–752. doi:10.1086/157551

CrossRef Full Text | Google Scholar

Jokipii, J. R., Giacalone, J., and Kota, J. (2003). “Diffusive Compression Acceleration of Charged Particles,” in Proceedings of the 28th International Cosmic Ray Conference, Tsukuba, Japan, July 31–August 7, 3685.

Google Scholar

Jokipii, J. R., and Lee, M. A. (2010). Compression Acceleration In Astrophysical Plasmas And The Production Off (V) ∝V-5 spectra In The Heliosphere. ApJ 713, 475–483. doi:10.1088/0004-637X/713/1/475

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1982). Particle Drift, Diffusion, and Acceleration at Shocks. ApJ 255, 716–720. doi:10.1086/159870

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1987). Rate of Energy Gain and Maximum Energy in Diffusive Shock Acceleration. ApJ 313, 842. doi:10.1086/165022

CrossRef Full Text | Google Scholar

Jones, F. C. (1990). The Generalized Diffusion-Convection Equation. ApJ 361, 162. doi:10.1086/169179

CrossRef Full Text | Google Scholar

Kelner, S. R., Aharonian, F. A., and Bugayov, V. V. (2006). Energy Spectra of Gamma Rays, Electrons, and Neutrinos Produced at Proton-Proton Interactions in the Very High Energy Regime. Phys. Rev. D 74, 034018. doi:10.1103/PhysRevD.74.034018

CrossRef Full Text | Google Scholar

Kliem, B., Karlický, M., and Benz, A. O. (2000). Solar Flare Radio Pulsations as a Signature of Dynamic Magnetic Reconnection. Astron. Astrophys. 360, 715–728.

Google Scholar

Kowal, G., de Gouveia Dal Pino, E. M., and Lazarian, A. (2011). Magnetohydrodynamic Simulations of Reconnection and Particle Acceleration: Three-Dimensional Effects. ApJ 735, 102. doi:10.1088/0004-637X/735/2/102

CrossRef Full Text | Google Scholar

Kowal, G., de Gouveia Dal Pino, E. M., and Lazarian, A. (2012). Particle Acceleration in Turbulence and Weakly Stochastic Reconnection. Phys. Rev. Lett. 108, 241102. doi:10.1103/PhysRevLett.108.241102

PubMed Abstract | CrossRef Full Text | Google Scholar

Lagage, P. O., and Cesarsky, C. J. (1983). The Maximum Energy of Cosmic Rays Accelerated by Supernova Shocks. Astron. Astrophys. 125, 249–257.

Google Scholar

Liu, S., Petrosian, V., and Mason, G. M. (2006). Stochastic Acceleration of3He and4He in Solar Flares by Parallel‐propagating Plasma Waves: General Results. ApJ 636, 462–474. doi:10.1086/497883

CrossRef Full Text | Google Scholar

Lucek, S. G., and Bell, A. R. (2000). Non-linear Amplification of a Magnetic Field Driven by Cosmic ray Streaming. Monthly Notices R. Astronomical Soc. 314, 65–74. doi:10.1046/j.1365-8711.2000.03363.x

CrossRef Full Text | Google Scholar

Melia, F., Liu, S., and Coker, R. (2001). A Magnetic Dynamo Origin for the Submillimeter Excess in Sagittarius A*. ApJ 553, 146–157. doi:10.1086/320644

CrossRef Full Text | Google Scholar

Mewaldt, R. A., Cohen, C. M. S., Mason, G. M., Haggerty, D. K., and Desai, M. I. (2007). Long-Term Fluences of Solar Energetic Particles from H to Fe. Space Sci. Rev. 130, 323–328. doi:10.1007/s11214-007-9200-8

CrossRef Full Text | Google Scholar

Meyer, J. P., Drury, L. O. C., and Ellison, D. C. (1997). Galactic Cosmic Rays from Supernova Remnants. I. A Cosmic‐Ray Composition Controlled by Volatility and Mass‐to‐Charge Ratio. ApJ 487, 182–196. doi:10.1086/304599

CrossRef Full Text | Google Scholar

Northrop, T. G. (1963). Adiabatic Charged-Particle Motion. Rev. Geophys. 1, 283–304. doi:10.1029/RG001i003p00283

CrossRef Full Text | Google Scholar

Ohira, Y. (2013). Turbulent Shear Acceleration. ApJ 767, L16. doi:10.1088/2041-8205/767/1/L16

CrossRef Full Text | Google Scholar

Parker, E. N. (1965). “A Brief Outline of the Development of Cosmic ray Modulation Theory,” in Proceedings of the 9th International Cosmic Ray Conference, London, United Kingdom, 26.

Google Scholar

Parker, E. N. (1958). Origin and Dynamics of Cosmic Rays. Phys. Rev. 109, 1328–1344. doi:10.1103/PhysRev.109.1328

CrossRef Full Text | Google Scholar

Petrosian, V., Jiang, Y. W., Liu, S., Ho, G. C., and Mason, G. M. (2009). Relative Distributions of Fluences Of ³He And ⁴He In Solar Energetic Particles. ApJ 701, 1–7. doi:10.1088/0004-637X/701/1/1

CrossRef Full Text | Google Scholar

Petrosian, V., and Liu, S. (2004). Stochastic Acceleration of Electrons and Protons. I. Acceleration by Parallel‐Propagating Waves. ApJ 610, 550–571. doi:10.1086/421486

CrossRef Full Text | Google Scholar

Ptuskin, V. S. (1988). Cosmic-Ray Acceleration by Long-Wave Turbulence. Soviet Astron. Lett. 14, 255.

Google Scholar

Reynolds, S. P., Gaensler, B. M., and Bocchino, F. (2012). Magnetic Fields in Supernova Remnants and Pulsar-Wind Nebulae. Space Sci. Rev. 166, 231–261. doi:10.1007/s11214-011-9775-y

CrossRef Full Text | Google Scholar

Schatzman, E. (1963). On the Acceleration of Particles in Shock Fronts. Ann. d’Astrophysique 26, 234.

Google Scholar

Strong, A. W., Moskalenko, I. V., and Ptuskin, V. S. (2007). Cosmic-Ray Propagation and Interactions in the Galaxy. Annu. Rev. Nucl. Part. Sci. 57, 285–327. doi:10.1146/annurev.nucl.57.090506.123011

CrossRef Full Text | Google Scholar

Toptyghin, I. N. (1980). Acceleration of Particles by Shocks in a Cosmic Plasma. Space Sci. Rev. 26, 157–213. doi:10.1007/BF00167370

CrossRef Full Text | Google Scholar

Turkmani, R., Cargill, P. J., Galsgaard, K., Vlahos, L., and Isliker, H. (2006). Particle Acceleration in Stochastic Current Sheets in Stressed Coronal Active Regions. A&A 449, 749–757. doi:10.1051/0004-6361:20053548

CrossRef Full Text | Google Scholar

Tverskoǐ, B. A. (1968). Theory of Turbulent Acceleration of Charged Particles in a Plasma. Soviet J. Exp. Theor. Phys. 26, 821.

Google Scholar

Webb, G. M. (1989). The Diffusion Approximation and Transport Theory for Cosmic Rays in Relativistic Flows. ApJ 340, 1112. doi:10.1086/167462

CrossRef Full Text | Google Scholar

Williams, L. L., Schwadron, N., Jokipii, J. R., and Gombosi, T. I. (1993). A Unified Transport Equation for Both Cosmic Rays and Thermal Particles. ApJ 405, L79. doi:10.1086/186770

CrossRef Full Text | Google Scholar

Xie, Y., and Liu, S. (2020). From Period to Quasiperiod to Chaos: A Continuous Spectrum of Orbits of Charged Particles Trapped in a Dipole Magnetic Field. Chaos 30, 123108. doi:10.1063/5.0028644

PubMed Abstract | CrossRef Full Text | Google Scholar

Yi-ran, Z., and Si-ming, L. (2020). The Origin of Cosmic Rays from Supernova Remnants. Chin. Astron. Astrophysics 44, 1–31. doi:10.1016/j.chinastron.2020.04.001

CrossRef Full Text | Google Scholar

Zeng, H., Xin, Y., and Liu, S. (2019). Evolution of High-Energy Particle Distribution in Supernova Remnants. ApJ 874, 50. doi:10.3847/1538-4357/aaf392

CrossRef Full Text | Google Scholar

Zhang, M., and Lee, M. A. (2013). Stochastic Acceleration of Energetic Particles in the Heliosphere. Space Sci. Rev. 176, 133–146. doi:10.1007/s11214-011-9754-3

CrossRef Full Text | Google Scholar

Zhang, Y., and Liu, S. (2019). Global Constraints on Diffusive Particle Acceleration by strong Non-relativistic Shocks. Mon. Not. R. Astron. Soc. 482, 5268–5274. doi:10.1093/mnras/sty3136

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, S., and Yuan, Q. (2017). Anomalous Distributions of Primary Cosmic Rays as Evidence for Time-dependent Particle Acceleration in Supernova Remnants. ApJ 844, L3. doi:10.3847/2041-8213/aa7de1

CrossRef Full Text | Google Scholar

Zhou, X., Büchner, a. J., Bárta, M., Gan, W., and Liu, S. (2015). Electron Acceleration by Cascading Reconnection in the Solar Corona. I. Magnetic Gradient and Curvature Drift Effects. ApJ 815, 6. doi:10.1088/0004-637X/815/1/6

CrossRef Full Text | Google Scholar